Abstract
Intermodal networks offer much flexibility in transport planning, and have the potential to efficiently consolidate goods, even if these goods have distinct pickup locations and destinations. Typically, there is an abundant amount of feasible routes and consolidation opportunities, which makes it challenging to quickly identify good solutions. We propose a planning algorithm for dynamic pickup- and delivery problems in intermodal networks, where freight is consolidated by means of reloads to reduce both costs and emissions. Based on an enumerative arc-expansion procedure, a large number of intermodal routes is generated for each order, of which we store the k best. We subsequently evaluate consolidation opportunities for the k best routes by applying a decision tree structure, taking into account reload operations, timetables, and synchronization of departure windows. Compared to direct road transport, numerical experiments on various virtual problem instances show an average cost saving of 34 %, and an average reduction in \(CO_2\) emissions of 30 %. Furthermore, we test our algorithm on a real-life case of a leading logistics service provider based in the Netherlands, which yields significant benefits as well, both in terms of costs and environmental impact.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Intermodal transport is becoming an increasingly important alternative to road transport. Developments in real-time information provisioning, planning systems, governmental regulation, and more consideration to external costs (e.g., emissions, congestion, noise hindrance), make intermodal transport both increasingly relevant and competitive. In a typical intermodal setting, a load is placed in a container (or another transportation unit, such as a trailer), picked up by a truck at the customer, then transported via one or more railroad/waterway connections that are linked by transfer hubs, and finally distributed by truck towards its destination location. The transfer hubs allow for transshipments of containers from one modality to the other, but also facilitate the unloading and reloading of goods on the level of the individual container, i.e., splitting or merging loads if this yields consolidation benefits Crainic and Kim (2006). Although intermodal networks are traditionally associated with transporting full containers, transfer hubs that allow for reload operations could be regarded as a step towards the Physical Internet Montreuil (2011). Reload operations help to create a dynamic transport network, via which we can transport small volumes by allocating them to the large load capacities of existing transport flows.
From an environmental perspective, the potential benefits of increasing the share of intermodal transport is twofold. First, the additional flexibility offered by such networks allows for more efficient transport, thus requiring less transport movements. Second, barges and trains have distinct advantages over trucks in terms of emissions. A shift from road transport to other transport modes could significantly reduce emissions and other external costs Janic (2007). However, for fractional container loads, it is challenging to integrate these modes with road transport while maintaining high container fill rates. To be a financially viable alternative for direct road transport, the detour- and transshipment costs of intermodal transport should be compensated by a reduction in transport costs Konings (1996), Trip and Bontekoning (2002). For networks with reloads, consolidating orders in a container results in lower transport costs and allows to divide the transshipment costs per container over multiple loads, but it introduces reload costs as well.
In this paper, we consider the case in which the logistics coordination in an intermodal setting is in the hands of a 4PL service provider, i.e., a logistics service provider that matches orders to the transport services of external carriers. The 4PL matches incoming orders—specified by a volume, a pickup location, a delivery location, and a corresponding time window—to contracted carriers. In an intermodal setting, the 4PL can construct routes between a pickup location and a delivery location by combining various route segments (arcs) that connect transfer hubs, each arc being operated by a separate vehicle. We distinguish between two sorts of arcs. Main arcs are fixed connections between two hubs, and are operated by a specific type of modality (in this paper either barge, train, or truck). These modalities may operate according to a timetable. Free arcs are connections between any two points in the network, and are operated by trucks that can be commissioned at any desired time. The key distinction between both types is that there exist regular transport flows on main arcs, while transport on free arcs must be rented for the individual order.
Although intermodal networks have the potential to significantly improve transport efficiency, attention for consolidation in networks with reloads remains limited. In this paper, we aim to contribute to this knowledge domain, more specifically the operational planning of consolidated routes in a dynamic environment. We present a scheduling algorithm that is able to efficiently identify and plan consolidated routes for networks with reloads, and might serve as a decision support system for 4PL planners. The 4PL can take into account multiple criteria to evaluate routes, e.g., costs, \(CO_2\) emissions, and duration. As the transport market is characterized by strong competition and low profit margins, cost minimization remains the leading objective for most 4PLs. However, the resulting efficiency gains in itself significantly contribute to a reduction in \(CO_2\) emissions; we measure this reduction in our numerical experiments. We illustrate our algorithm using a case study at a leading 4PL based in the Netherlands, which is active in the European transport market. In this paper, we apply our algorithm on intermodal networks in which containers are placed on and lifted from the transport modes at transfer hubs. For the sake of completeness, we note that many transport modes are designed to carry wheeled cargo. In common forms of waterway transport (RoRo) and railroad transport (RoLa), lifting operations are not required. As the associated transshipment costs are lower and transshipment times are shorter, intermodal transport becomes a more attractive alternative in this case. We therefore see applications of our consolidation algorithm in this context as well.
The remainder of the paper is structured as follows. We provide a literature review in Sect. 2, assessing studies on several topics that are relevant to our work. In Sect. 3, we outline our problem setting, followed by a description of the consolidation algorithm in Sect. 4. We conduct experiments on several networks, measuring the performance of our algorithm—both with respect to costs and emissions—under a variety of circumstances (Sect. 5). We finish with our conclusions in Sect. 6.
2 Literature review
In this study, we assess the consolidation of goods in an intermodal transport setting. Intermodal transport is formally defined as the transport of goods via at least two arcs that are operated by distinct transport means, with transshipments taking place at transfer hubs Crainic and Kim (2006), Dewitt and Clinger (2000). Examples of such hubs are rail yards, harbors, and inland terminals Bektaş and Crainic (2008). A common feature in intermodal transport is the use of fixed timetables, particularly in railroad- and waterway transport Macharis and Bontekoning (2004). Despite the increasing number of applications of intermodal networks, serious knowledge deficits exist in the research fields of multi-modality, network design, and operational planning Veenstra and Zuidwijk (2010).
Macharis and Bontekoning (2004), Caris et al. (2008), and SteadieSeifi et al. (2014) provide overviews of intermodal transport research, and all indicate that only few studies have been performed on operational planning. Additional insights can be obtained from the conceptually related ride-sharing problem. Some problems in this field also consider the fixed schedules of public transport and transfers between different transport means. An overview on the dynamic ride-sharing problem can be found in Agatz et al. (2012).
Before assessing the studies that relate to our problem, we refer to a number of studies that provide building blocks to construct routes in an intermodal setting. In a full truckload setting, Boardman et al. (1997) use a k-shortest path algorithm to perform intermodal planning, evaluating multiple routes before selecting the route that best fits the established criteria. By coupling a vector of path length estimates to each vertex and using these estimates as a criterion on whether to evaluate a route, the authors keep computational time limited. Ziliaskopoulos and Wardell (2000) explicitly take into account timetables and transfer times, making use of Bellmans optimality principle while recursively updating time windows for every route segment. Horn (2004) provides an arc-expansion approach for the problem with timetables. He starts by generating routes consisting of only a single arc, and gradually increases the number of arcs in a route while simultaneously establishing upper bounds. He states that this procedure generally leads to an optimal schedule quickly; good routes tend to contain only few arcs, as this keeps detour distance and transshipment costs limited. Mes and Iacob (2016) use a comparable arc-extension approach, generating a large number of routes, and storing the k best routes as suitable planning options. To incorporate departure times based on timetables in an operational planning problem, two main approaches exist. The first is to create a time-expanded graph, where each arc is characterized by a time component Köhler et al. (2002), e.g., every arc corresponds to a unique departure time. A more compact representation is the time-dependent graph Delling and Wagner (2009), Ding et al. (2008). Such a graph is defined only in space. Time-dependent arc characteristics are taken into account by applying a mapping function, e.g., feasible departure times are determined as a function of the arc, timetable, and departure window.
We classify our problem as a dynamic pickup and delivery problem with reloads and timetables. Amongst others, Chang (2008) and Masson et al. (2013), Oertel (2000) address the static variant of this problem. Due to the complexity of the problem, heuristics are used to solve it, mainly utilizing local search principles. Literature on the dynamic variant of the problem is scarce. Bock (2010) describes a local search algorithm for the dynamic variant, focusing on real-time applications. Although providing a rich model, different modes operating on fixed routes and their corresponding timetables are not addressed. Ferrucci and Bock (2015) provide a tabu search heuristic that builds upon the framework provided by Bock (2010). Another heuristic solution for the dynamic problem is described by Goel (2010). The proposed solution evaluates routing and shipment decisions on a time-expanded network that includes multiple modalities and timetables. However, the consolidation role of transfer hubs is explicitly left out of his research scope.
Our contribution to the intermodal planning literature is twofold. First, we present an algorithm to schedule the transport of LTL freight via intermodal networks, thereby contributing to the limited amount of dynamic planning studies in this field. In particular, we deviate from existing studies by explicitly focusing on constructing consolidated routes, rather than the more improvement-based heuristics typically encountered in literature. In addition, we believe that our problem description as a time-dependent intermodal network with reloads and timetables contributes to the formal definition of this problem class. Second, we present an efficient method to identify and plan consolidation opportunities in a delimited solution space, for which various parameters can be fixed to control the maximum computational effort.
3 Problem definition
We study a dynamic planning problem with reloads and timetables. Orders are tentatively planned once they become known. Our choice to consider dynamic planning rather than static optimization (over a rolling horizon) is motivated by two arguments encountered in practice. First, the time between pickup and delivery in an intermodal setting spans several days, and volumes with the same order-destination pairs are low. When modalities with low travel speed or low departure frequencies are considered, a delay of the actual planning moment might result in exclusion of routes with longer duration. This would eliminate certain opportunities for consolidation. Second, we design our algorithm to be used as a decision support tool for planners at a 4PL, allowing to directly reply to customers requests while retaining flexibility to consolidate with future orders. For these reasons, we directly plan orders when the shipper poses a request, while retaining the opportunity to alter the plan at a later stage.
Our representation of the intermodal network is as follows. Let \({\mathcal {G}}=\{{\mathcal {V}},{\mathcal {A}}\}\) be a directed graph with \({\mathcal {V}}\) the set of vertices and \({\mathcal {A}}\) the set of arcs. \({\mathcal {V}}^H \subset {\mathcal {V}}\) represents the set of transfer hubs in the network. The remaining vertices signify the subset of order origins, \({\mathcal {V}}^O \subset {\mathcal {V}} \setminus {\mathcal {V}}^H\), and the subset of order destinations, \({\mathcal {V}}^D \subset {\mathcal {V}} \setminus {\mathcal {V}}^H.\) The set of arcs can be divided into a set of free arcs \({\mathcal {A}}^F \subset {\mathcal {A}}\) and a set of main arcs \({\mathcal {A}}^M={\mathcal {A}}\setminus {\mathcal {A}}^F\). Every vertex pair in the graph is connected by a free arc, and operated by vehicles without time schedules. Free arcs can therefore be used to link origins and destinations either directly to each other or to transfer hubs, but may also facilitate transport between hubs. The main arcs connect fixed vertex pairs of the subset \({\mathcal {V}}^H\), and possibly operate on a timetable. A single hub pair can be connected by multiple arcs, representing the availability of various modalities or carriers.
Each arc \(a\in {\mathcal {A}}\) is described by the tuple \((v_a, v_a^{\prime }, \tau _a^{tr})\), where \(v_a \in {\mathcal {V}}\) is the starting vertex of the arc, \(v_{a}^{\prime } \in {\mathcal {V}}\) is the end vertex of the arc, and \(\tau _a^{tr} \in {\mathbb {R}}^+\) is the deterministic transport time (based on the transport means operating the arc). An arc connects exactly one vertex pair, meaning that containers using this arc are not reloaded or transshipped at intermediate hubs. Every arc has a corresponding volume-dependent transport cost function \(C_a^{tr}:f \mapsto {\mathbb {R}}^+\), with f being the order volume. We define a transshipment as moving a container from one mode to another. We use \(c_v^{tm}\) to denote the costs of placing a container on a mode at hub v at the start of the arc, and \(c_{v^\prime }^{tm}\) to denote the costs of lifting the container off the mode at the end of the arc. We split the transshipment costs in two components to ease the cost allocation to individual orders, since a reload may take place between lifting and placing the container. We define a reload as unloading orders from one container and subsequently loading them into another container; the corresponding reload costs at hub \(v^\prime\) are given by \(c_{v^\prime }^{rl}\). Finally, \(\tau _v^{tm}\) denotes the transshipment times at the hubs \(v \in {\mathcal {V}}^H\).
Let \(i\in {\mathbb {N}}\) and \(j \in {\mathbb {N}}\) be order indicators, with order i representing an order that just became known, and order j an open order (i.e., an order that has not yet arrived at its destination). Each order i can be described by a tuple \((v_i^O, v_i^D, t_i^{min}, t_i^{max}, f_i)\). Here, \(v_{i}^{O} \in {\mathcal {V}}^O\) is the origin vertex and \(v_i^D \in {\mathcal {V}}^D\) the destination vertex. The order has an earliest pickup time \(t_i^{min}\); from this time onwards the order can be retrieved from the origin \(v_i^O\). Furthermore, it has a strict deadline \(t_i^{max}\); the order must arrive at its destination \(v_i^D\) at or before this time. Finally, we define the set of feasible order sizes—expressed in terms of fractional container capacity—as \(\mathcal {F}=\{\frac{1}{y},\frac{2}{y},\ldots ,1\}\), with integer \(y\ge 1\). The size of order i is \(f_i \in \mathcal {F}\).
We make a number of key assumptions in the definition of our problem. First, we assume that consolidation is only possible on the main arcs. Free arcs generally correspond to first-mile and last-mile transport; typically a 4PL will outsource the task of constructing detailed tours to the carrier. Our second assumption is that carriers utilize a concave and monotonically increasing cost function with respect to volume, reflecting economies of scale. This assumption is in line with general practice, and retains a large degree of flexibility. Third, we assume that all travel times and transshipment times are deterministic. Transshipment times are independent of whether reloads take place; in practice the time required for a reload is often minor compared to the full transshipment time. In case of disturbances, the algorithm could be rerun with updated departure windows to alter routes during execution, yet this aspect is beyond our research scope. A fourth assumption is that reload costs are independent of the volume moved; a fixed fee is charged for every reload operation. Also, we assume that reload costs are independent of the time the orders are held at the transfer hub, i.e., no holding costs are charged. Fifth, as we consider hard time windows, we assume that for every order a time-feasible route exists. Sixth, we ignore capacity constraints on the main arcs. We do this because we adopt the perspective of an individual 4PL; the volumes handled by such actors typically only marginally contribute to the total container capacity on trains and barges. However, we note that this assumption can be relaxed in our problem, by simply removing the departure of a completely filled mode from the timetable.
4 Consolidation algorithm
In this section, we describe the consolidation algorithm. First, we briefly describe our solution method in Sect. 4.1. Subsequently, we outline the three key steps of the algorithm: planning k individual routes for an incoming order (Sect. 4.2), constructing a decision tree with all consolidation actions (Sect. 4.3), and finally evaluating and implementing consolidation actions (Sect. 4.4).
4.1 Solution method
We briefly explain the general idea behind the consolidation algorithm. The algorithm is triggered by every new order arrival. First, a large preset number of unconsolidated routes is generated for the new order, of which the k best routes are stored. To generate the initial routes, we use an arc expansion approach comparable to Horn (2004) and Mes and Iacob (2016). The key benefits of this method are that it is efficient, takes into account the cost structure of routes (small numbers of arcs generally yield the cheapest routes), and its computational effort can be controlled. To incorporate timetables in our model, we use a time-dependent graph, with the departure time being the only varying component. A time-dependent graph provides a compact representation of the network, but is somewhat more difficult to evaluate than a time-expanded graph. Especially when modes depart with high frequency, time-dependent graphs have computational benefits compared to time-expanded graphs; a physical route needs to be evaluated at most once. Furthermore, time-dependent graphs provide high flexibility in adjusting departure times of existing schedules.
After obtaining the k best routes, we construct an evaluation set for every main arc in each of these routes that include all consolidation opportunities on the arc. Let an open order be any order that has not yet arrived at its destination. A consolidation opportunity exists if a route corresponding to an open order (or set of orders) has (1) the same main arc incorporated in its route as the route of the current order, (2) a mutually feasible departure time on the arc (with the departure time lying in the future), and (3) sufficient capacity in the container to add the new order. To assess the consolidation opportunities on the various main arcs in conjunction, we construct a decision tree to compute the achievable savings and check whether the consolidation action yields a time-feasible schedule for all orders involved. Note that the opportunity refers to consolidation on a single arc, whereas the action refers to a unique combination of opportunities. Consolidation divides the fixed transshipment costs per container over the consolidated orders and typically reduces transport costs, but also introduces reload costs. The savings should compensate any higher costs for selecting routes that are non-optimal when considering the individual orders.
After consolidating, we fix the routes of orders that are consolidated on at least one arc of their respective routes, and update the departure schedules and container fill rates. We fix the routes because (1) if not, replanning routes may undo existing consolidation actions, therefore potentially requiring to re-solve the static problem at every order arrival, (2) it significantly reduces our solution space, and (3) it requires to change the selection of modes at most once, which is preferable in most practical settings. Although we geographically fix routes after consolidation, further consolidation and the adjustment of departure windows remains possible on these routes. The main structure of the algorithm is shown in the flowchart in Fig. 1. Throughout this section, we use pseudo-code to describe the algorithm. We use a running example to illustrate its working.
4.2 Generating k routes for an incoming order
For each incoming order i, we start by generating routes using a k-shortest path procedure similar to Mes and Iacob (2016), based on iteratively expanding the number of main arcs in a route. Free legs are added to ensure the route connects the order origin to its destination. As good routes generally contain only a few main legs, we expect to identify these routes and their costs early in the process. Storing alternative routes with higher initial costs than the best individual route provides more consolidation opportunities; their excess costs should be compensated by the consolidation savings. Therefore we introduce a factor \(\beta >1\). To set a dynamic threshold, we multiply \(\beta\) with the cost of the cheapest route found so far; we do not store a route if its costs exceed the threshold. Hence, we should set \(\beta\) such that we can reasonably expect a route to contribute to improving solutions (e.g., \(\beta =1.2\) implies no route is allowed to be over 20 % more expensive than the best route). Also for partially constructed routes, we can use \(\beta\) to check whether we can discard them, thereby considerably speeding up the procedure. In Theorem 1 (Appendix 1), we provide a theoretical upper bound on \(\beta\) that guarantees that the optimal solution can be found within the routes having costs lower than the threshold resulting from \(\beta\). Finally, we also discard routes that are not time-feasible.
After generating a large number of routes, we store the k least expensive routes for the individual order, not yet taking into account consolidation opportunities. The order is tentatively scheduled to follow the least expensive route. Timetables may result in slack in the schedule; departure policies—setting a tentative departure time—determine where in the schedule this slack will be allocated. The chosen departure policy impacts the consolidation opportunities on the route, given that we continue to seek for consolidation opportunities while the route is being executed Powell (1987).
To formally describe the properties of a route, we introduce some mathematical notation. Let \(R_i\) denote the set of all k stored routes for order i. A route \(r_{i,n}\in R_i\), with \(n\in \{1,\dots ,k\}\) consists of an ordered set of arcs—both main arcs and free arcs—connecting \(v_{i}^O\) to \(v_{i}^D\). We define an indicator \(z\in \{1,2,\dots ,|r_{i,n}|\}\) to specify the arc sequence of a route. We refer to the \(z^{th}\) arc incorporated in \(r_{i,n}\) as \(a_{i,n,z}\in r_{i,n}\); a route is formally defined by the ordered set \(r_{i,n}=\bigcup _{z=1}^{|r_{i,n}|} a_{i,n,z}\). Each arc \(a_{i,n,z} \in r_{i,n}\) has an associated departure window \([t_{i,n,z}^{ed}, t_{i,n,z}^{ld}]\); departing at any point in time within this window ensures that the destination can be reached before the delivery deadline. Let \({\mathcal {T}}_{i,n,z}\) be the set of feasible departure times on arc \(a_{i,n,z}\). We define a function \(T_a\) that maps the departure window to a set of feasible departure times, i.e., \(T_{a}:(t_{i,n,z}^{ed}, t_{i,n,z}^{ld})\mapsto {\mathcal {T}}_{i,n,z}\). If no timetable exists for the arc (e.g., a free arc), every departure time within the window is feasible, otherwise \({\mathcal {T}}_{i,n,z}\) contains a finite number of departure times. Finally, we introduce a number of counters used in our algorithm: M is the number of main arcs in a route, \(M^{max}\) the maximum number of main arcs that we allow in a route, \(\#Routes_M\) an indicator for the number of routes generated, and \(\#Routes_M^{max}\) the maximum number of routes that we generate containing M main arcs. We describe the route-generating procedure in Algorithm 1. For more details on the procedure, we refer to Mes and Iacob (2016). In Algorithm 2, we calculate the departure windows for all arcs; the same algorithm is also used to update the departure windows after consolidation. In the latter case, we can input a mutually feasible departure window \([\hat{t}_{i,n,z}^{ed},\hat{t}_{i,n,z}^{ld}]\) of two orders to synchronize their departure windows.


Example 1 Route structure for incoming orders
Consider the network as described in Fig. 2, where order 1 has a load size \(f_1=0.3\), pickup location 1, and delivery location \(1^\prime\). Suppose \(k=4\). We denote each route \(r_{1,n} \in R_i\) as an ordered set of arcs; every free arc is referred to as 0. In this example, suppose that route \(r_{1,2}\) is the least expensive solution, such that this route is set as the initial solution.
Order 1 has an earliest pickup time of 11.40 and a latest delivery time of 20.00 on the same day. Assume that vehicles traverse main arc 1 with an hourly departure, that traversing this arc takes two hours, and that the reload time is always half an hour. In Fig. 3, the corresponding time schedule for the route is provided, given a latest departure policy. In this figure, window 1 indicates the time interval in which departure on main arc 1 yields a feasible schedule.
4.3 Construction of a decision tree
After generating and storing k routes for the new order i, we look for consolidation opportunities to reduce the system-wide costs (Table 1). Let \(j \in {\mathbb {N}}\) refer to an open order, i.e., an order that has not reached its destination yet. Let \({\mathcal {J}}\) be the set of all open orders, excluding the current order i. For an open order j, we use the route index \(m \in \{1,\dots ,k\}\). Consolidation opportunities are arcs found in both \(r_{i,n} \in R_i\) and \(r_{j,m} \in R_j, \forall j \in {\mathcal {J}}\), for which (1) a mutually feasible departure time exists and (2) container capacity is sufficient to consolidate the orders. We note that order j may already have been consolidated with other orders at a preceding decision moment.
To retain flexibility and account for possible future consolidation opportunities, we assign orders to a container to be transported via the main arc, rather than to a transport means departing at a fixed time. Let \(q,q^\prime \in {\mathbb {N}}, q\ne q^\prime\) be container indices. We define a consolidation opportunity \(\Omega _{q,a}\) as the set of order- and route indices representing the orders (and their corresponding routes) currently assigned to container q on arc a. We may always decide not to consolidate on an arc; we define the corresponding opportunity as \(\Omega _{q,a}=\{(0,0)\}\). The remaining feasible consolidation opportunities with order j on arc a in route m are denoted by \(\Omega _{q,a} \ni (j,m)\). We also keep track of the orders that are consolidated with order i on arc a in route n during the consolidation process; we describe the corresponding set as \(\hat{\Omega }_{q^\prime ,a}\). Before consolidating on route n, we have \(\hat{\Omega }_{q^\prime ,a}=\{(i,n)\}\). After a consolidation action x takes place—described in more detail later on—we update the set of consolidated orders and obtain \(\hat{\Omega }_{q,a}^x=\hat{\Omega }_{q^\prime ,a}\cup \Omega _{q,a}\); subsequently we update \(\hat{\Omega }_{q^\prime ,a}\) and \(\Omega _{q,a}\) as well. Note that we move goods from container \(q^\prime\) to q, requiring a reload.
After we confirm that consolidating order sets \(\hat{\Omega }_{q^\prime ,a}\) and \(\Omega _{q,a_{i,n,z}}\) is feasible, we can store \(\Omega _{q,a_{i,n,z}}\) in the evaluation set \({\mathcal {S}}_{i,n,z}\). As the opportunity to not consolidate always exists, it is guaranteed that \(|{\mathcal {S}}_{i,n,z}|\ge 1\). To keep the evaluation set as small as possible, we can use the upper bound on attainable savings as described in Theorem 2. A set \(\Omega _{q,a} \ni (j,m)\) is not included in \({\mathcal {S}}_{i,n,z}\) if this bound is negative. When route \(r_{i,n}\) contains multiple main arcs, we might consolidate with distinct order sets on the various main arcs. We define our action space for route \(r_{i,n}\) as \({\mathcal {X}}_{i,n}=\prod _{z=1}^{|r_{i,n}|} {\mathcal {S}}_{i,n,z}\).
A consolidation action \(x \in {\mathcal {X}}_{i,n}\) represents a unique combination of consolidation opportunities, i.e., \(x=\bigcup _{z=1}^{|r_{i,n}|}\Omega _{q,a_{i,n,z}}\). We assess all actions to (1) compute their corresponding savings (reload costs can only be computed when assessing consolidation on all main arcs simultaneously) and (2) check whether actions are time-feasible (as consolidation actions alter the departure windows of the entire schedule). To this end, we construct a decision tree for every \(r_{i,n} \in R_i\), with every path representing an action. As we show in Theorem 3, the number of actions may increase exponentially with the number of main arcs in the route. In a practical setting, routes rarely contain more than two main arcs, keeping the decision tree at a well-manageable size. We assess consolidation opportunities per main arc with one order set \(\Omega _{q,a}\) at a time; simultaneously evaluating all possible combinations of orders may result in an unfeasibly large decision tree. Instead, after selecting the best action from the tree, we update the order sets and departure windows, and use them as input to construct an new decision tree. We repeat this procedure until no more feasible cost-saving actions can be found. In Algorithm 3, we outline the procedure to create evaluation sets and decision trees.
The costs of a route \(r_{i,n} \in R_{i}\) of order i—taking into account possible consolidation actions—consist of three components, (1) the transport costs \(C^{tr}(i,n)\), (2) the transshipment costs \(C^{tm}(i,n)\), and (3) the reload costs \(C^{rl}(i,n)\). We give detailed descriptions of these functions in Appendix 2; for a general understanding of the algorithm we only need the aggregate cost function \(C(i,n)= C^{tr}(i,n)+C^{tm}(i,n)+C^{rl}(i,n)\). In our experiments, we also demonstrate a multi-objective cost function, in which we monetize emissions, delays, and hub risk (representing, e.g., missed connections and damage during handling). This extension shows how planners may embed non-financial objectives into the cost function.
The savings S(x) for an action \(x \in {\mathcal {X}}_{i,n}\) are given by the difference between the total costs before and after consolidation. Savings are composed by (1) the reduction in transport cost, plus (2) the reduction in transshipment costs, minus (3) the additional reload costs, minus (4) the cost differences between the best routes and the evaluated routes of the orders involved. Again, we provide the formal definition of the savings S(x) in Appendix 2.

Example 1 [Continued] Construction of a decision tree
Cycling through all k routes for order 1, assume we now arrived at route \(r_{1,3}\), with trajectory 0-1-2-0. Suppose three open orders (2,3 and 4) have main arcs in common with this route, that are feasible in departure time and capacity, and therefore included in the evaluation set. Orders 2 and 3 were already consolidated in an earlier stage, hence only one route remains for both of these orders. Order 4 still has four available routes, Fig. 4 shows the current schedule, Table 2 shows all available routes for the orders.
In Table 3, the timetable corresponding to the relevant main arcs is presented, giving the departure times with the routes that are eligible for leaving at each departure time between parentheses. The transshipment times at the transfer hubs are 30 min.
When constructing the evaluation set, we see that consolidation at main arc 1 is feasible for three routes of order 4, corresponding to two nodes in the decision tree. On main arc 2, consolidation is possible with \(r_{2,1}\), \(r_{3,1}\), and \(r_{4,3}\). Observe that since orders 2 and 3 utilize the same container on main arc 2, this consolidation opportunity needs to be assessed only once. Finally, on both arcs we can also choose not to consolidate, leaving the original time window intact. With five opportunities on main arc 1 and three on main arc 2 (including not consolidating), we have fifteen combinations to assess. However, not all of them are feasible. It is not possible to combine different routes for order 4 in the same schedule, while it is not possible either to consolidate both on main arc 1 with \(r_{2,1}\) and on main arc 2 with \(r_{4,3}\) due to time constraints. As shown in Algorithm 3, such infeasible combinations are identified and discarded. The decision tree in Fig. 5 shows all combinations. By calculating the savings corresponding to each path, the decision maker can determine the consolidation opportunity with the largest feasible saving.
4.4 Verifying actions and updating the solution
In the previous sections, we showed how to generate routes and how to construct the corresponding decision trees. The next step is to identify the consolidation actions that yield the largest savings. We evaluate the consolidation actions for every \(r_{i,n} \in R_i\). The procedure to evaluate these actions consists of (1) generating a decision tree corresponding to \(r_{i,n}\), (2) selecting the feasible action that yields the largest savings, (3) updating the schedules. Attempting to fill up the remaining container capacity, we recursively execute these three steps until no cost-saving actions can be identified, and store the obtained savings \(S_{i,n}\). After performing this evaluation for all \(r_{i,n} \in R_i\), we select the solution (e.g., the set of actions for a certain route) that yields the largest savings, thereby also taking into account the cost differences between routes. In Algorithm 4, we describe the evaluation procedure.
After identifying and fixing the best set of actions \(x_{i,n}^*\), we must update our schedules accordingly. As we may consolidate with distinct order sets on the various main arcs in a route, this could also affect the departure schedules of orders that we do not consolidate with. As an example, suppose that we consolidate orders i and j on a given main arc. Further suppose that on a subsequent main leg in its route, order j was already consolidated with order \(j^\prime\). Then the departure time of order \(j^\prime\) may be affected by consolidating order i, even though orders i and \(j^\prime\) are not consolidated. We therefore distinguish between consolidated and interrelated orders. The latter refers to every order for which departure times may need to be adjusted due to a consolidation action. Formally, we denote the set of orders interrelated to order j according to Eq. (1), where we combine all existing sets of consolidated orders corresponding to the current action. To ensure that our planning is updated consistently after a consolidation action, we must update the schedules for all order-route pairs \((j^\prime ,m^\prime ) \in \tilde{\Omega }_j\). We outline this procedure in Algorithm 5.
Example 1 [Continued] Updating the departure windows after consolidation
Based on the decision tree as constructed in the preceding section, we decide to consolidate \(r_{1,3}\) on main arc 1 with \(r_{4,4}\) and on main arc 2 with \(\{r_{2,1},r_{3,1}\}\). In this example, we describe how the departure windows are updated for consolidation, and how updating affects the rest of the schedule. We again assume that departures are tentatively scheduled as late as possible; however, earlier departure times can be selected to facilitate consolidation. From Fig. 6, the mutually feasible departure times on both arcs can be observed.
It can be seen that 13.00, 14.00 and 15.00 are feasible departure times for both order 1 and 4. However, when selecting 15.00, consolidation at main arc 2 would no longer be possible. Hence, 13.00 and 14.00 are the only feasible departure times for this particular combination. The departure window is therefore narrowed, causing scheduled slack after the second main arc. The schedule after consolidation for order 1 is shown in Fig. 7.


5 Numerical experiments
In this section, we describe the experiments to test the performance of our algorithm. In Sect. 5.1, we identify three key design choices of our algorithm, and describe alternative solution methods as a benchmark to test the impact of these choices. Section 5.2 describes our experimental settings and instances, consisting of both virtual networks and a real-life case of a Dutch 4PL. In Sect. 5.3 we provide the numerical results of our simulation study, providing insights in the cost performance, impact on \(CO_2\) emissions, and computational times.
5.1 Solution methods for benchmarks
Three key design choices for our algorithm are that (a) our search space for consolidation opportunities is limited to k routes per order, (b) routes are geographically fixed after consolidating, and (c) orders are planned dynamically. Although these choices greatly reduce the computational effort, they may also prematurely eliminate fruitful consolidation opportunities. In Table 4, we propose a number of alternative solution methods (denoted by \(\pi\)) as benchmarks to evaluate the impact of these design choices.
To assess the impact of (a), we use various settings for k to evaluate the marginal contributions of storing an extra route (\(\pi ^{k=k^\prime }\)). The rationale is that as routes become more expensive, they have lower potential for savings, hence their marginal contribution to the solution quality will decrease. To quantify the impact, we compute multiple comparison metrics, using the basic solution methods \(\pi ^{dir}\) and \(\pi ^{int}\). Here, \(\pi ^{dir}\) always directly transports orders from origin to destination by road transport, and \(\pi ^{int}\) uses the cheapest (possibly intermodal) route for each individual order.
To test the effect of design choice (b), we use a solution method where we completely replan all orders that are not yet shipped. We do this by replanning all open orders at each new order arrival, thereby essentially solving the static problem at every arrival. The orders are planned one-by-one according to a given sequence. We consider two forms of sequences, (1) sorted based on the latest delivery time (\(\pi ^{tim}\)), and (2) random planning sequence \(\pi ^{rnd}\). The first sequence form gives priority to urgent orders, granting them more opportunities to be consolidated. With the random sequence benchmark, we test multiple random sequences, and select the cheapest solution. Evaluating all possible sequences would solve the static variant of our problem to optimality, but this is computationally unmanageable for larger instances.
Finally, we define our benchmark for design choice (c). The optimal solution can only be achieved by having perfect foresight for all orders to come (i.e., the static problem rather than the dynamic problem), and solve the associated scheduling problem to optimality with \(\pi ^{opt}\). We define ‘optimality’ here within the constraint that a finite number of routes is available. The acquired solution is always at least as good as solving the dynamic problem to optimality (the same is not true without perfect foresight). Due to the high computational effort, this solution method can only be applied to instances containing a small number of orders.
5.2 Experimental settings
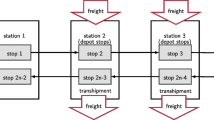
We perform simulation experiments on four virtual networks, each one representing generalizations of common consolidation scenarios. In Fig. 8, panel a) shows a cluster with pickup locations, a cluster with delivery locations, transfer hubs in the center of both clusters, and a single main arc connecting these two hubs (STR). Panel b) shows a split network, consisting of a single origin cluster and two distant destination clusters (SPL). Panel c) shows a triangular network (TRI), where making a detour could yield additional consolidation opportunities. Finally, panel d) shows a scaled-down version of a semi-random network (RND). The pickup points and distributions are uniformly generated within a distance of \(\frac{1000\,km}{\# hubs}\) from the nearest hub, based on the notion that hubs tend to be positioned within areas of high demand and vice versa. Orders generated have a preset minimum distance of 250 km between origin and destination, and always move to the right. The random networks vary in the number of hubs and the number of main arcs—denoted as RND(# hubs/# main arcs)—namely RND(15/30), RND(20/40), and RND(20/100). For all virtual networks, we consider variants where all main legs are either trucks, electric trains, diesel trains, or barges. Furthermore, we perform experiments on the 4PL case. We study their operations on the Rhine-Alpine corridor, which connects a variety of economic regions in the Netherlands, Germany, Austria, Switzerland and Italy. The 4PL ships orders (with an average volume of 0.33 container) from several locations in the Netherlands to a variety of locations within this corridor. To facilitate this transport, the 4PL utilizes a network operated by various contracted carriers. This dedicated network consists of 37 hubs, which are connected by 110 waterway and railroad arcs. We use the real timetables and travel times for these arcs.
The mode characteristics used in our experiments are shown in Table 5. We obtain container volume data and the \(CO_2\) emission per modality (calculated by 2020 engine standards) from Boer et al. (2011). Emissions are computed on a well-to-wheel basis, including both exhaust emission and upstream emission (i.e., electricity production and refinement). We consider containerized average density goods; for these goods container volume is more restrictive than weight. Extrapolating the figures for twenty-feet containers to forty-feet containers Boer et al. (2011), we set a full container load equal to 21 ton.
For trucks, we take into account the load factor when computing \(CO_2\) emissions. Emissions strongly depends on whether the truck drives in an urban area, non-urban area, or on a motorway; we take the average emissions over the road shares corresponding to a truck trailer. The obtained bounds on \(CO_2\) emission are 589 g/km (empty truck) and 897 g/km (full truck); Boer et al. (2011) assume that between these bounds emission increases linearly with the transported weight. For trains and barges, we use the average container weight to compute \(CO_2\) emissions, as container consolidation by the 4PL only marginally affects the total weights of these modes.
Our standard cost functions (shown in Table 5) are based on the case of the Dutch 4PL; costs are normalized for confidentiality reasons. For our experiments on virtual networks, all modes have a fixed rate per container. For the real-life case, the barges and trains on the main arcs use the same fixed rate, but the trucks on the free arcs have a capped linear cost function of the form \(\min (1,0.31+0.78\cdot f)\). Travel speeds per mode are also obtained from the Dutch 4PL, averaging over often-used train- and barge connections. Finally, we set the costs for a single transshipment operation (container lift or placement) at 22 (hence 44 for a full transshipment) and for a reload (per order, including both unloading and loading) at 35.
To demonstrate how our algorithm could handle multiple criteria, we test an extension in which we monetize various additional objectives. We add the following costs to the original objective function: 40 per ton \(CO_2\) emission (based on 2020 standards, see Maibach et al. 2008), 0.10 per hour of additional transport time (compared to direct transport), and 20 per order transfer to represent hub risk.
For the virtual networks, orders are randomly generated, with their origin, destination and volume—selected from the range [0.04–1.00]—being drawn from uniform distributions. The times between order arrivals follow a Poisson distribution with a mean of 3 h. We make use of common random numbers, thus excluding the influence of stochastic fluctuation when comparing performances. Orders can be picked up directly after becoming known; the latest delivery time is 5 days ahead. Modes operating on the main arcs depart every 6 h. For our case study, we use an order set of the Dutch 4PL, consisting of 1006 orders transported over a quartile in 2013. Their actual locations, order volumes, pickup- and delivery times are used. The operating modes are subject to the real timetables and travel speeds. The case study shows to some extent how our algorithm performs under non-uniform distributions. Future research may further explore the impact of such distributions.
We conclude this section with the key simulation settings. Unless specified otherwise, we use 6 replications with instances of 650 orders—setting both the warm-up and cool-down periods to 25—to achieve a relative cost error of at most 5 % for the 95 % confidence intervals. Based on preliminary tests, we use \(k=2\) for the straight and split networks, \(k=3\) for the triangular network, \(k=31\) for the random networks, and \(k=40\) for the 4PL network. Furthermore, we set \(\beta =2\), meaning that we store routes being up to twice as expensive as the cheapest route found. Settings for \(\beta >2\) did not show any performance improvement. Some other values \(1<\beta < 2\) yielded comparable results, while requiring less computational effort. However, as \(\beta =2\) already yields reasonable computational times for our simulation study, we did not attempt to fine-tune this setting. Finally, preliminary tests indicated that a latest departure policy clearly and consistently outperformed an earliest departure policy due to offering more flexibility and consolidation opportunities. We stress that we assume deterministic travel times in our experiments; in practical applications we might add some safety margin to account for disturbances. In our experiments, every order therefore leaves its route vertices as late as the corresponding departure windows allow. The algorithm was coded in Plant Simulation 11, and ran on a computer with 8GB RAM and a 2.90GHz Intel Core i7 processor.
5.3 Numerical results
We divide the presentation of our numerical experiments in two parts: (i) the performance of the algorithm under various network settings and (ii) the performance of our algorithm compared to several alternative solution methods. We start by presenting the performance for a variety of networks. First, we describe the results for the experiments on the virtual networks, using the standard settings. In Table 6, we provide key insights on the performance of the algorithm. We assess the reduction in costs and \(CO_2\) emissions, as well as the increase in container fill rate, compared to the benchmarks \(\pi ^{dir}\), \(\pi ^{int}\), and \(\pi ^{k=1}\). The first two policies (which do not consider consolidation) are clearly outperformed. Compared to road transport, electric train networks yield the greatest reduction in \(CO_2\) emissions, as the \(CO_2\) emission of electric trains is significantly lower than the emission associated with trucks. Similarly, the low costs of barges translate in the greatest reduction in terms of costs. Diesel train networks perform worst in terms of emission. For the semi-random networks, direct road transport even outperforms diesel train transport. For the first three network configurations, comparison to \(\pi ^{k=1}\) indicates that storing \(k>1\) routes has virtually no effect. Due to the small diversity in routes for these networks, the algorithm is generally able to use the best routes of orders when consolidating, such that storing more than one route has a negligible impact. However, for the random networks we see that the added flexibility of storing more routes can yield 3–17 % reduction in \(CO_2\) emissions, 3–12 % cost savings, and a 14–50 % improvement in fill rates. Furthermore, we show the results for the multi-objective extension in Table 6 as well; the tests are performed on the semi-random truck networks. We see that while average savings decrease, intermodal transport is still financially attractive. The impact on emissions and fill rates is negligible. Hence, the solutions appear to be fairly robust when taking into account non-financial objectives of the planner. We conclude our analysis with some notes on how typical solutions look like. The use of two or more main arcs within one route is exceptional. Compared to direct transport, the average increase in travel time is 22 %. Of the consolidated solutions, the average drayage distance comprises 32 % of the route. The average volume of consolidated orders is 0.41 container load; orders with a volume over 0.60 are notably more difficult to consolidate.
Next, we discuss the results of our experiment with the real-life 4PL case. Orders transported from the Netherlands to Germany do not favor the use of the intermodal network; for distances below 200km intermodal transport is not beneficial. For distances over 500km we see the most use of the intermodal network. Therefore, without considering consolidation, only 21 % of orders is transported via the intermodal network. When considering only the best routes, the 215 intermodal routes use 28 distinct main arcs. Consequently, when we only consider the best routes (\(k=1\)), only few consolidation opportunities exist. As indicated by the results in Table 6, increasing planning flexibility by storing multiple routes notably increases the performance, illustrating the added value of our algorithm. Compared to \(\pi ^{k=1}\), costs are reduced with 6 %, \(CO_2\) emissions drops by 20 %, and container fill rates are increased by 28 %.
We continue with the results regarding our evaluation of the design choices, comparing to the benchmark methods. First, we assess the impact of storing k routes. Figure 9 shows the outcomes for applying \(k=\{1,2,\dots ,40\}\) on three semi-random truck networks; 15 hubs with 30 main arcs, 20 hubs with 40 main arcs, and 20 hubs with 100 main arcs. The same procedure is applied to the real-life network. The added value of storing more alternative routes is significant, yielding savings up to 12 % compared to \(\pi ^{k=1}\). Note that the saving potential for the 4PL case are lower due to the larger amount of short-distance orders. Marginal savings decrease with increasing settings of k; the lower quality of the stored routes decrease the savings potential. As illustrated in Fig. 9, the marginal savings decrease, such that at a certain point storing additional routes no longer significantly impacts the solution quality. This implies that we can fix k at some level, such that higher values for k would not yield additional benefits. Furthermore, we note that a higher setting for k does not guarantee a higher saving. This may seem counter-intuitive at first. However, a higher k results in a higher probability to identify and fix opportunities with minor savings, thus reducing consolidation opportunities at a later point in time.
We proceed with the benchmark results of fixing routes after consolidating. Our instances are the 20/40 semi-random networks for truck, train, and barge. To keep the experiment computationally manageable, we use the relatively small setting of \(k=5\); recall that the benchmarks policies re-solve the static problem at every order arrival. Whereas our algorithm takes less than 1s to plan in an order, \(\pi ^{rnd}\) takes close to 10 s per order. Also, it is not scalable to larger instances, making this benchmark method unfit as an online solution method. The policy \(\pi ^{tim}\) outperforms our algorithm 0.4 % on average. In Fig. 10, we show the performance gap between our algorithm and \(\pi ^{rnd}\). Testing up to 50 random sequences, we see that the performance gap remains below 3 %, seemingly converging to a stable performance gap.
The last design choice that we test is that of planning orders dynamically, comparing performance to \(\pi ^{opt}\). As the benchmark policy is computationally intensive, we require a small and simplistic instance for this experiment. We run 1,000 instances on a straight truck network, each consisting of 7 orders. Solving these toy-sized instances takes 15 s per instance, compared to a fraction of a second for the k-path algorithm. We emphasize that \(\pi ^{opt}\) yields a strong upper bound due to perfect foresight, as the dynamic planning problem does not entail future information. In Fig. 11, we show the average deviation. In 38 % of the instances, we obtain the optimal solution with our algorithm; the average deviation in terms of costs is 4.7 %.
6 Conclusions
A shift from road transport to barge- and train transport has the potential to significantly reduce the environmental impact of transport. However, the required transshipments introduce a financial barrier for this shift. For intermodal transport to compete with road transport of LTL goods, it is essential that freight is consolidated as much as possible. We therefore proposed an algorithm to dynamically plan routes in intermodal networks with transshipments and reloads. Timetables of the modes are captured in a time-dependent graph. We used an intuitive arc-expansion approach to efficiently construct intermodal routes. The best k routes for every order are stored, yielding a controlled solution space to search for consolidation opportunities. To facilitate consolidation, we created flexibility in both space and time, by (i) storing multiple geographically distinct routes for every order, and (ii) using departure windows rather than fixed departure times. The algorithm is designed as a decision support tool for human planners at 4PLs, allowing to plan orders using multiple modes and to provide a direct reply to their customers.
To make the algorithm suitable for online planning, we introduced three key design choices to restrict the search space. We experimentally tested the impact of these design choices by introducing alternative solution methods as benchmarks. First, we assessed the effect of storing only k routes. We showed that due to decreasing marginal savings, a relatively small number of stored routes already captures the savings potential. Second, we assessed the impact of fixing routes once they contain consolidated orders. We compared our algorithm to a policy in which we solve the static problem at every order arrival. The cost reduction compared to our algorithm remained below 3 %. These results give a feeling for the improvements that could be achieved by, e.g., extending our algorithm with local search techniques. Finally, we tested the impact of considering dynamic planning rather than static planning, e.g., the effect of directly planning incoming orders rather than periodically re-optimizing the schedule. For this purpose, we solved small instances to optimality, yielding an average performance gap of 4.7 %. As we assumed perfect foresight for this benchmark, this provides an upper bound for our results.
For multiple networks, we showed the potential of our solution method to significantly and consistently reduce costs and \(CO_2\) emissions, while improving container fill rates. First, we performed numerical experiments on a variety of virtual networks. Compared to direct road transport, on average we save 34 % in costs, reduce \(CO_2\) emissions by 30 %, and improve the container fill rate by 57 %. Compared to the case in which we consolidate on the best routes only, the additional flexibility yields 5 % cost savings, 9 % \(CO_2\) reduction, and a 21 % increase in fill rate. Furthermore, we performed a numerical experiment on a real-life 4PL network. For orders transported from the Netherlands to Austria and Italy, consolidated planning notably improved performance. Compared to consolidation on the best route only (i.e., \(k=1\)), our solution method saves 6 % in costs, 20 % in \(CO_2\) emissions, and 28 % in container fill rate. The results indicate that the flexibility introduced by our solution method has the potential to significantly reduce both costs and \(CO_2\) emissions, thus being a promising planning tool for 4PLs active in intermodal transport.
We conclude with some managerial insights, which may aid in service network design and the pursue of horizontal collaboration in intermodal transport. The numerical results show that consolidated trips typically contain only one main arc, with drayage operations on average comprising \(1/3\hbox {rd}\) of the total travel distance. Detours of over 20 % are common, implying that intermodal networks not necessarily need to offer perfect connections between origin and destination to facilitate consolidated trips. The orders that are most viable for consolidated trips require no more than 40 % container volume, and have an origin-destination distance of at least 250km. Barge transport is the most cost-efficient mode, whereas electric trains are most beneficial in terms of emission reduction. In the present work, we focused on applications in which lifting operations are required. A sizable proportion of transport takes place with rolling cargo, allowing for transshipments on vessels and trains against minimal transshipment costs and -times. This lower barrier renders intermodal transsport a more attractive alternative to road transport, making it an interesting environment to explore in future research.
References
Agatz N, Erera A, Savelsbergh M, Wang X (2012) Optimization for dynamic ride-sharing: a review. Eur J Oper Res 223(2):295–303
Bektaş T, Crainic TG (2008) A brief overview of intermodal transportation. In: Taylor G (ed) Logistics engineering handbook, vol 28. Taylor and Francis Group, Boca Raton, pp 1–16
Boardman BS, Malstrom EM, Butler DP, Cole MH (1997) Computer assisted routing of intermodal shipments. Comput Ind Eng 33(1):311–314
Bock S (2010) Real-time control of freight forwarder transportation networks by integrating multimodal transport chains. Eur J Oper Res 200(3):733–746
Boer E, Otten MBJ, Essen H (2011) STREAM International freight: comparison of various transport modes on a EU scale with the STREAM database. CE Delft
Caris A, Macharis C, Janssens GK (2008) Planning problems in intermodal freight transport: accomplishments and prospects. Transp Plan Technol 31(3):277–302
Chang TS (2008) Best routes selection in international intermodal networks. Comput Oper Res 35(9):2877–2891
Crainic TG, Kim KH (2006) Intermodal transportation. Transportation 14:467–537
Delling D, Wagner D (2009) Time-dependent route planning. In: Robust and Online Large-Scale Optimization, pp. 207–230. Springer, Berlin
Dewitt W, Clinger J (2000) Intermodal freight transportation. Transportation in the New Millennium
Ding B, Yu JX, Qin L (2008) Finding time-dependent shortest paths over large graphs. In: Proceedings of the 11th international conference on extending database technology: Advances in database technology, pp 205–216. ACM
Ferrucci F, Bock S (2015) A general approach for controlling vehicle en-route diversions in dynamic vehicle routing problems. Transp Res Part B Methodol 77:76–87
Goel A (2010) The value of in-transit visibility for supply chains with multiple modes of transport. Int J Logist Res Appl 13(6):475–492
Horn ME (2004) Procedures for planning multi-leg journeys with fixed-route and demand-responsive passenger transport services. Transp Res Part C Emerg Technol 12(1):33–55
Janic M (2007) Modelling the full costs of an intermodal and road freight transport network. Transp Res Part D Transp Environ 12(1):33–44
Köhler E, Langkau K, Skutella M (2002) Time-expanded graphs for flow-dependent transit times. In: AlgorithmsESA 2002, pp. 599–611. Springer
Konings J (1996) Integrated centres for the transshipment, storage, collection and distribution of goods: A survey of the possibilities for a high-quality intermodal transport concept. Transp Policy 3(1):3–11
Macharis C, Bontekoning YM (2004) Opportunities for or in intermodal freight transport research: a review. Eur J Oper Res 153(2):400–416
Maibach M, Schreyer C, Sutter D, Van Essen H, Boon B, Smokers R, Schroten A, Doll C, Pawlowska B, Bak M (2008) Handbook on estimation of external costs in the transport sector. CE Delft, Delft
Masson R, Lehuédé F, Péton O (2013) An adaptive large neighborhood search for the pickup and delivery problem with transfers. Transp Sci 47(3):344–355
Mes MR, Iacob ME (2016) Synchromodal transport planning at a logistics service provider. In: Logistics and Supply Chain Innovation, pp. 23–36. Springer
Montreuil B (2011) Toward a physical internet: meeting the global logistics sustainability grand challenge. Logist Res 3(2–3):71–87
Oertel P (2000) Routing with reloads. Ph.D. thesis, Universität zu Köln
Powell WB (1987) An operational planning model for the dynamic vehicle allocation problem with uncertain demands. Transp Res Part B Methodol 21(3):217–232
SteadieSeifi M, Dellaert NP, Nuijten WP, Van Woensel T, Raoufi R (2014) Multimodal freight transportation planning: a literature review. Eur J Oper Res 233(1):1–15
Trip JJ, Bontekoning Y (2002) Integration of small freight flows in the intermodal transport system. J Transp Geogr 10(3):221–229
Veenstra A, Zuidwijk R (2010) The future of seaport hinterland networks. Liber Amicorum Jo van Nunen, Dinalog and RSM-Erasmus University of Rotterdam, Rotterdam
Ziliaskopoulos A, Wardell W (2000) An intermodal optimum path algorithm for multimodal networks with dynamic arc travel times and switching delays. Eur J Oper Res 125(3):486–502
Acknowledgments
We thank the Dutch LSP for providing us with network data and order characteristics. This research is partially funded by Dinalog, the Dutch Institute for Advanced Logistics.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Runtime and upper bound analysis
We provide three theorems and their corresponding proofs. Theorem 1 gives an upper bound on the savings for a given route; this result can be used to set \(\beta\) such that optimal solutions are guaranteed to be in the search space. Theorem 2 provides an upper bound on the savings achievable by consolidating with a given order, which allows to exclude certain orders from the decision tree up front. Finally, Theorem 3 gives the computational complexity of evaluating the decision tree (Algorithm 4).
Theorem 1
Let \(C_a^{tr}\) be a concave monotonically increasing cost function of the fill rate \(f \in (0,1]\) on arc a. There exists a finite threshold factor \(\beta \in {\mathbb {R}}_{\ge 1}\), which guarantees that \(r_{i,n}\) will never yield an improving solution if \(\beta \cdot C(r_{i,n^\prime }^*)<C(\mathcal {R}_{i,n^\prime })\).
Proof
Suppose that \(\sum \limits _{{(i^\prime ,n^\prime )} \in \hat{\Omega }_{q^\prime ,a}}f_{i^\prime }<1\). From the inequality posed in Equation (2), we see that \(\exists \hat{\Omega }_{q,a}^x=\hat{\Omega }_{q^\prime ,a}\cup \Omega _{q,a}\) such that
Hence, maximum savings on transport costs are obtained by consolidating to \(f=1\). Let \(f^{min}=\min (\mathcal {F})\) be the smallest possible order size. Recall that with every action \(x \in {\mathcal {X}}_{i,n}\), we consolidate with at most one order set per arc. It follows that before Algorithm 4 terminates, we can consolidate with up to \(\frac{1}{f^{min}}\) orders per arc. By means of deduction, the following inequality holds
As every \(f\in \mathcal {F}\) is a multiplier of \(f^{min}\), the maximum savings are \(\frac{1}{f^{min}}\cdot C_a^{tr}\left( f^{min}\right) -C_a^{tr}\left( \frac{1}{f^{min}} \cdot f^{min}\right)\), achieved by consolidating with \(\frac{1}{f^{min}}\) orders of size \(f^{min}\).
Next, we show that for any consolidation action x and any \(a \in {\mathcal {A}}^M\), the savings on transshipment costs are \(c_v^{tm}+c_{v^\prime }^{tm}\):
It readily follows that we maximize savings on transshipment costs by consolidating with as many orders as possible, i.e., we again only consolidate with orders of size \(f^{min}\), thereby saving \(\left(\frac{1}{f^{min}}-1\right)\cdot \left(c_v^{tm}+c_{v^\prime }^{tm}\right)\).
Theorem 1 states that an upper bound on savings is found by consolidation on all main arcs in a route. Let \(M^{max} \leftarrow {\mathbb {N}}\) be the maximum number of main arcs we allow in a route, and let \(a^* \in {\mathcal {A}}^M\) be the arc that yields the highest upper bound on savings, obtained by solving
We denote the corresponding savings (representing the upper bound on savings for any route) as
Let \(C(r_{i,n^\prime })-C(r_{i,n}^*)\) be the cost difference between the best route found so far and the current route. Based on the maximum attainable savings \(\bar{S}^*\), it follows \(\exists \beta \in {\mathbb {R}}_{\ge 1}\) that satisfies
Hence, if \(\beta C(r_{i,n^\prime }^*)<C(r_{i,n})\), then \(r_{i,n}\) cannot contribute to improving solutions. \(\square\)
Theorem 2
For all \(a \in {\mathcal {A}}\), let \(C_a^{tr}\) be a concave, monotonically increasing cost function of the fill rate \(f \in (0,1]\). Let i be an order which we seek to consolidate with \(j\in {\mathcal {J}}\). Let x be the action were we consolidate on all \(a \in r_{i,n} \cap r_{j,m}\). The upper bound on savings by consolidating on the routes \(r_{i,n}\) and \(r_{j,m}\) is given by
Proof
We first show that maximum savings in transshipment costs are attained when consolidating on all mutual arcs \(a \in r_{i,n} \cap r_{j,m^\prime }\). Depending on possible previous consolidations of order j, for all mutual arcs we have a set of consolidated orders \(\Omega _{q,a}\), with \((j,m) \in \Omega _{q,a}\). To define the set of orders currently consolidated with order i on arc a, we have \(\hat{\Omega }_{q^\prime ,a}\). Finally, we denote the set of orders after consolidating orders i and j as \(\hat{\Omega }_{q,a}^x=\hat{\Omega }_{q^\prime ,a}\cup \Omega _{q,a}\). Clearly, \(|\hat{\Omega }_{q^\prime ,a}|\le |\hat{\Omega }_{q,a}^x|\). Given that \(c_{v}^{tm}\ge 0, \forall v \in {\mathcal {V}}^H\), the following inequality holds \(\forall a \in r_{i,n} \cap r_{j,m}\), such that overall transshipment costs are minimized by consolidating on all mutual arcs:
We show that the lowest transport costs are also achieved by consolidating on all mutual arcs. To show this, we make use of the fact that the function \(C_a^{tr}(f),\forall a \in {\mathcal {A}}\) is concave and monotonically increasing. Given these properties, the following inequality is satisfied when substituting the fill rates of all orders involved (before and after consolidation) into Eq. (3):
We showed that both transport costs and transshipment costs are minimized by consolidating on all \(a \in r_{i,n} \cap r_{j,m}\). By substituting the corresponding action into Eq. (6), we would get an upper bound that deducts the cost differences \(C(r_{j,m})-C(r_{j,m^\prime }^*)\) and \(C(r_{i,n})-C(r_{i,n^\prime }^*)\) from the maximum savings. However, the latter term cannot be fully allocated to \(\bar{S}_{j,m}\). Let \(w_{j^\prime ,m^\prime } \in [0,1], \forall (j^\prime ,m^\prime ) \in x\) be an allocation weight, subject to \(\sum _{(j^\prime ,m^\prime ) \in x} w_{j^\prime ,m^\prime }\le 1\). We show that this allocation constraint is necessary to guarantee that \(S(x)\le \sum _{(j^\prime ,m^\prime ) \in x} \bar{S}_{j^\prime ,m^\prime }\) for any action x. For the sake of our proof by contradiction, suppose that \(\sum _{(j^\prime ,m^\prime ) \in x} w_{j^\prime ,m^\prime }>1\), and that \(\Omega _{q,a} \cap \Omega _{q^\prime ,a^\prime }=\emptyset , \forall a,a^\prime \in r_{i,n},a\ne a^\prime\) (i.e., we consolidate with a unique order set on every main arc in \(r_{i,n}\)). The following inequality then holds—implying that the sum of upper bounds on savings are lower than the actual savings obtained by solving Eq. (6)—which is a contradiction.
We have established that \(\sum _{(j^\prime ,m^\prime ) \in x} w_{j^\prime ,m^\prime }\le 1\) must hold to establish a feasible upper bound. In theory, we could freely allocate the weights \(w_{j^\prime ,m^\prime }\), as long as this property is satisfied. However, to guarantee that the sum of \(w_{j^\prime ,m^\prime }\) for independently established upper bounds never exceeds 1, we set \(w_{j,m}=\frac{1}{|\Omega _{q,a}|\cdot |r_{i,n}\cap {\mathcal {A}}^M|}\). From this definition, it follows that for any x, \(S(x)\le \sum _{(j^{\prime },m^{\prime }) \in x} \bar{S}_{j^{\prime },m^{\prime }}\) holds.
Finally, we relax the assumption that reload costs are 0. If we have \(C^{rl}(r_{i,n})\ge 0\), it is no longer guaranteed that maximum savings are attained by consolidating on all mutual main arcs. However, we know that for any x with \((j,m) \in x\), at least two reloads are required, such that the minimum reload costs are given by \({{\mathrm{arg\,min}}}_{a \in r_{i,n}\cap r_{j,m}} 2 \cdot C^{rl}(a)\). Hence, when including reload costs, we obtain the upper bound. With this proof, we establish an upper bound on the maximum savings that can be attained by consolidating orders i and j using routes \(r_{i,n} \in R_i\) and \(r_{j,m} \in R_j\). \(\square\)
Theorem 3
Let \(R_{i}\) be the route set corresponding to order i which we seek to consolidate, \({\mathcal {J}}\) be the set of open orders, k be the number of routes stored per order, and \(f^{min}\in (0,1]\) be the smallest possible load size. Take \(r_{i,n}\in R_i\) such that \(|r_{i,n}|\ge |r_{i,n^\prime }|, \forall r_{i,n^\prime } \in R_i\). Algorithm 4 has a worst-case complexity of \({\mathcal {O}}\left(k\cdot \frac{1}{f^{min}}\cdot (|{\mathcal {J}}|\cdot k)^{|r_{i,n}|}\right)\).
Proof
Recall that the set of actions is defined as \({\mathcal {X}}_{i,n}=\prod _{z=1}^{|r_{i,n}|} {\mathcal {S}}_{i,n,z}\), with \({\mathcal {S}}_{i,n,z}\) being the evaluation set for arc \(a_{i,n,z}\). Clearly an order cannot be allocated to more than one container on an arc, such that for every order-route combination per arc, there exists at most one \(\Omega _{q,a} \ni (j,m)\). As we have an open order set of size \(|{\mathcal {J}}|\) and up to k routes per order, it follows that there are at most \(|{\mathcal {J}}|\cdot k \ge {\mathcal {S}}_{i,n,z}\) opportunities per arc \(a_{i,n,z} \in r_{i,n}\) to consolidate order i with some order \(j \in {\mathcal {J}}\). As route \(r_{i,n}\) contains \(|r_{i,n}|\) arcs, a decision tree contains up to \((|{\mathcal {J}}|\cdot k)^{|r_{i,n}|}\) actions. For every decision tree, we consolidate with at most one order set per arc, hence we must evaluate up to \(\frac{1}{f^{min}}\) decision trees per route \(r_{i,n^\prime }\in R_i\). The same procedure is repeated for all \(r_{i,n^\prime } \in R_i\), hence computational effort increases linearly with the number of routes \(|R_i|=k\). Hence, the worst-case complexity for Algorithm 4 is given by \({\mathcal {O}}\left(k\cdot \frac{1}{f^{min}}\cdot (|{\mathcal {J}}|\cdot k)^{|r_{i,n}|}\right)\). \(\square\)
Appendix 2: Cost functions and savings
In this appendix, we provide detailed cost functions for a route \(r_{i,n}\), adopting a generic notation that handles both consolidated and unconsolidated orders. The transport costs are given by
Transshipment costs are shared by all orders in the same container. From a system point of view, transshipment costs can be arbitrarily allocated to orders transported in the same container. We therefore equally distribute them over all orders in a container:
To ease the notation of the reload costs, we first provide the cost formula per \(a_{i,n,z} \in r_{i,n},z<|r_{i,n}|\):
The total reload costs for order i are given by
Finally, we define S(x) as the savings of an action \(x \in {\mathcal {X}}_{i,n}\). To account for the cost differences between routes for the same order, let \(r_{i,n^\prime }^* \in R_i, r_{j,m^\prime }^* \in R_j,\) be such that \(C(r_{i,n^\prime }^*)\le C(r_{i,n}), \forall r_{i,n} \in R_i\) and \(C(r_{j,m^\prime }^*)\le C(r_{j,m}), \forall r_{j,m} \in R_j\). The savings for an action \(x \in {\mathcal {X}}_{i,n}\) are defined as
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van Heeswijk, W.J.A., Mes, M.R.K., Schutten, J.M.J. et al. Freight consolidation in intermodal networks with reloads. Flex Serv Manuf J 30, 452–485 (2018). https://doi.org/10.1007/s10696-016-9259-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10696-016-9259-1