Integrating Micro-Depot Freight Transport in Existing Public Transport Services

Abstract

As conventional last-mile transport contributes to traffic congestion and pollution, urban areas need new approaches to transporting freight. One promising idea is integrating freight deliveries with existing public transport infrastructures like light rail. However, this concept creates the challenge of offering a high service quality for passengers and freight. In this work, we consider a setting where freight originates from and is transhipped at several public transit stops that serve as micro-depots with a limited storage capacity. Furthermore, the system relies on shared vehicles, where a dedicated share of the capacity can be used to fasten freight containers or as a standing area for passengers. For this setting, we propose an optimisation model that integrates the tactical scheduling of transport services and the allocation of freight containers to those services. To solve realistically sized instances, we propose an adaptive large neighbourhood search heuristic. We use this heuristic to evaluate the system’s sensitivity to the capacity of micro-depots and vehicles.

1 Introduction

Given close quarters and a high population density in urban areas, sustainably moving humans and freight on the "last mile" is challenging [1]. Both public transport and freight transport require space within cities’ infrastructure and meet similar expectations: Passengers expect short travel times and frequent departures, while freight customers expect quick and punctual deliveries. At the same time, citizens expect the municipality to limit air and noise pollution and traffic for a better quality of life.

Integrating freight transport into public transport may offer chances to improve both services: The option to exploit capacity overhangs profitably can justify financial investments in public transport while limiting the adverse ecological effects of freight transport. Capacity overhangs occur in on-demand [2] and in fixed transportation services [3]. Here, we consider the challenge of integrating passengers and freight on a fixed infrastructure, such as light rail, thereby further justifying the investment while exploiting the opportunity of short travel times compared to crowded streets [4]. We allow for a partially shared vehicle capacity, e.g., a dedicated area in each shared vehicle can either carry securely attached freight containers or serve as standing space for passengers. Although this concept currently faces legal restrictions in many European countries, it features in the pilot project LogIKtram in Karlsruhe, Germany [5].

Integrating passengers and freight must not disadvantage passengers to ensure the system’s acceptance and keep public transport attractive [6]. The success of such systems depends on strategic decisions, such as the inclusion of public transport lines, vehicle capacity, and the capacity and positioning of depot stations [7, 8], as well as on operational decisions, such as how much freight to accept and which parcels to transport on which vehicle [9].

To support planning for such an integrated system and to evaluate its sensitivity to strategic decisions, we extend a model first presented in [10]. That contribution proposed a lexicographical model to create demand-oriented schedules and to assign freight containers to shared services given a single depot. The optimisation model prioritises passenger service by minimising the passengers’ waiting time first and minimising the number of rejections and the delivery delay of cargo requests second. The extended model presented here lets freight originate and end at multiple micro-depots with a limited capacity. To solve realistically sized instances, we propose an adaptive large neighbourhood search (ALNS) heuristic as inspired by [11].

We evaluate the heuristic’s solution performance and the system’s sensitivity to the vehicle and micro-depot capacities by planning and processing a simulated day of operations. To that end, we generate artificial passenger and freight demand for various combinations of demand scenarios and network designs. Thus, the contribution of this paper is threefold:

• We formulate an extended problem allowing for the flexible pick-up and delivery of freight in a fixed public transport infrastructure.

• We extend ALNS operators for an ALNS-based approach to creating demand-oriented schedules and assign freight to transport services.

• We evaluate the system’s sensitivity to strategic capacity decisions.

In the next section, we briefly review the state of integrated passenger and freight transport research before presenting an overview of related contributions featuring ALNS. Subsequently, in Sect. 3, we describe the problem setting in further detail. In Sect. 4, we introduce the hierarchical optimisation model. Section 5 describes the proposed ALNS, specifically expounding on destroy and repair operators. We analyse the solution performance of the ALNS compared to simple scheduling rules and the mathematically optimal solution in Sect. 6. Section 7 analyses the resulting system’s sensitivity to alternative combinations of the depot and vehicle capacity given by earlier strategic decisions. Finally, Sect. 8 summarises our findings and provides an agenda for further research in the domain.

2 State of the Art

Cooperative transport of freight and passengers becomes possible when the public transport system is not always fully utilised. Cavallaro and Nocera [7] provide a broad, concept-centric literature review focused on the idea. Hörsting and Cleophas [10] survey existing optimisation models considering the shared transportation of passengers and freight in an urban area on a fixed infrastructure. However, to provide a path to success for such integrated systems, decision-makers must find operational modes that ensure both passenger and freight service quality. In that regard, the research presented here is further motivated by a call-to-action stated in [12]: “model the impacts of [...] the projects [...] to estimate impacts on congestion, operations, and environmental outcomes”.

As shown in [13], significant distance savings can result when public transport systems deliver freight to micro-depots, from where they can reach their final destination. The idea of these micro-depots motivates the extended model presented here, in which, at a variety of stops, both passengers and freight can leave and enter the vehicles.

As we propose, on the one hand, a prescriptive approach to schedule vehicles and allocate freight and, on the other hand, evaluate the outcomes for various scenarios, our research is related to several further contributions. For example, [14] evaluate scheduling decisions for cargo vehicles in a freight rail system based on a discrete event-based simulation. Taking a much broader view of the matter, [15] evaluate a range of urban logistics schemes in an agent-based simulation to estimate implications for sustainability and the schemes’ attractiveness for stakeholders.

In the remainder of this section, we focus on two aspects that drive the model and the solution approach proposed in this paper: Firstly, we briefly summarise existing research on multi-depot transportation and relate it to the idea of micro-depots on a fixed infrastructure. Secondly, we provide some background for the adaptive large neighbourhood search algorithm we rely on to solve the scheduling problem.

2.1 Micro-Depot Transportation

Fragmented freight flows and inefficient delivery operations are two challenges in last-mile transportation that increase the need for consolidation [15]. At the same time, ecologically friendly transportation modes like cargo bikes and electronic trucks often offer a lower capacity and a shorter range than conventional trucks. This conundrum has sparked increasing interest in urban consolidation centres or micro-depots. Katsela et al. [16] evaluate the advantages and disadvantages of micro-hubs by analysing and comparing case studies. Planning a micro-depot network involves optimisation problems on various levels.

In recent research, [17] propose a method to locate distribution hubs in a metro network, while [18] consider location planning problems for multiple depots when cargo bikes take over the last part of freight transport. Furthermore, [19] review existing hub location problems and propose ideas to improve modelling. Delle Donne et al. [8] envision a system where freight enters and leaves the public transport system via a set of drop-in and drop-out stations. In that setting, the authors evaluate strategic decisions on which public transport lines to recruit for freight transport and where to locate drop-in and drop-out stations.

In vehicle routing, multiple depots are a prominent concept [20,21,22,23]. Multi-depot solutions also combine well with new logistics schemes like crowd shipping or mobile depots [24,25,26].

In passenger transport, approaches to scheduling focus on depots that describe the starting and ending point of the trip for each vehicle. For example, [27] consider a multi-depot vehicle scheduling problem where buses are assigned to given timetabled trips, whereas [28] focus on an integrated multi-depot vehicle and crew scheduling problem.

In this work, we consider a micro-depot network for shared passenger and freight transport. In that, we consider location and capacity decisions as given from strategic planning but evaluate their implications for integration success. Given the idea of fixed infrastructure and line plans, scheduling services and allocating freight to services overtakes routing.

2.2 Adaptive Large Neighbourhood Search (ALNS)

The adaptive large neighbourhood search (ALNS) is a meta-heuristic first proposed by [29] to solve a pickup and delivery problem with time windows. It extends the idea of large neighbourhood search (LNS) by allowing for a variety of destroy and repair operations as opposed to a single pair of one destroy and one repair operator. In each iteration, these destroy and repair operators are selected randomly according to weights that are updated based on different search strategies. For instance, operators leading to an improvement in the objective value are more likely to be selected in future iterations. The advantage of ALNS over LNS is the extended search space, which reduces the risk of getting stuck in local optima. Most ALNS algorithms include operators that aim for diversification and intensification. Diversification means the operator randomly searches a large part of the neighbourhood to find new solutions. Intensification implies that the operator searches purposefully to improve the quality of the current solution. For more information, we refer the reader to the definitions by [30].

Today, ALNS is applied to various large-scale routing and scheduling problems. For instance, for variants of the pickup and delivery problems [29, 31, 32], two-echelon vehicle routing problems [34, 33], or workforce routing and scheduling problems [35,36,37]. Windras Mara et al. [38] present a detailed survey of the recent development on ALNS.

Barrena et al. [39] introduce an ALNS heuristic to solve a rail rapid transit problem with dynamic passenger demand, minimising the passenger waiting time. They improve the results of a branch-and-bound algorithm in [40] by 26%. Similarly, [11] propose an ALNS to find a demand-oriented timetable, minimising the passenger congestion at stops. Their model includes limited vehicle capacities and multiple lines. Yuan et al. [41] use ALNS to design an urban network combining a fixed-line transport system and a demand-responsive transport system.

For this work, we are interested in applying ALNS to demand-oriented service scheduling problems. To that end, we adapt the heuristic of [11] to integrate the freight transport in Sect. 5.

3 Problem Setting

In the following, we explain the problem framework and underlying assumptions. We extend the model of [10] by considering multiple micro-depots to be located at selected stops and feature a limited storage capacity. Furthermore, we focus on the operational mode featuring shared vehicles, assuming a limited share of the vehicle capacity can be used to secure freight.

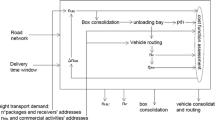
The setting features an existing public transit infrastructure with a fixed set of stops and connecting legs, e.g., a single line in a light-rail network. Each station consists of two stops with opposite directions. Furthermore, we assume that the stops of each station are close to each other, i.e., it is possible to walk from the first to the second stop of the same station in, at most, a few minutes. Such a network configuration is common in many European cities that are the inspiration for this work. The vehicles operate on a circular, bi-directional single route, i.e., they start at a joint start stop and turn around when arriving at the boundary station (see Fig. 1).

Fig. 1

Assumed network topology: a circular, bi-directional single route

The expected passenger demand takes the form of quantity flows driven by the arrival and alighting rates per time period and stop. First, we consider the number of passengers arriving per stop and period. When a vehicle arrives at a stop, a fixed ratio of passengers alights. Since the network is bi-directional and each stop serves a dedicated direction, every passenger waiting at a stop wants to board the arriving vehicle.

Several stops are pre-defined micro-depots, where freight can be loaded and unloaded. We consider freight as containers carrying parcels with the same requirements, i.e., time and place of release, due time, and destination. Every container should be transported to its destination stop within a soft due time. Additionally, a hard due time per container sets the time of the latest acceptable arrival at the destination. We allow for the rejection of container requests to guarantee feasibility. Note that we assume that the service provider decides on the acceptance of containers before the start of the period so that freight customers can still find alternative means of transport. The micro-depots can only store a limited number of containers between release and pick-up. Containers do not require storage capacity after drop-off at their destination stop, as we assume they are picked up instantly or immediately forwarded to their final destination.

The vehicle capacity is also limited. Specifically, we assume that parts of the standing area for passengers are modified so that parcel containers can be attached there, i.e., we assume that passengers and cargo share a selected vehicle space. Again, the transport of passengers is prioritised. First, passengers alight and board the vehicle. If there is enough space left, the parcel containers are secured in the remainder of the shared area.

This work focuses on satisfying the demand for the passenger and freight service while integrating freight into the public transit system. For this reason, we consider an irregular time schedule with variable dwell times. Each service in the time schedule is defined by an individual vehicle’s arrival and departure time per stop over the course of the considered horizon. All processes, like boarding and alighting passenger and loading and unloading containers, must be executed during the dwell time. Additionally, there must be a sufficient dwell time between the departure of two subsequent vehicles from the same stop, and no two vehicles must occupy the same platform simultaneously.

In practice, the planners usually determine the lines and the timetable before considering the vehicle routes and crew schedules [42]. Here, we disregard the challenges of rolling stock. Thus, we set an upper bound for the maximal number of services offered within the planning horizon instead of defining a specific fleet size. Nevertheless, given a time schedule, we can deduce the maximal number of simultaneously operating vehicles and, thus, the minimum required fleet size to operate the line. We aim to determine an irregular, demand-oriented time schedule and assign containers to operating services following the problem formulation detailed in the next section.

4 Mathematical Formulation

The problem considered here entails defining a time schedule $\mathcal {T}$ as a set of individual services. Since we consider demand-oriented scheduling, we allow for aperiodic services, i.e., vehicles may arrive and depart irregularly. We formally define a schedule in Sect. 4.1. For a given schedule, we compute the passenger flows and the resulting passenger service quality as described in Sect. 4.2.

Additionally, the problem entails assigning cargo containers to vehicles as formalised in Sect. 4.3, while minimising cargo delay and rejection. In Sect. 4.4, we link both sub-problems through a global lexicographical objective function defined, where we minimise the passenger congestion first and afterward the delay and rejection rate of cargo requests. Tables 1, 2, and 3 list the notation for sets, variables, and parameters introduced in the following.

Table 1 List of index sets

Table 2 List of variables

Table 3 List of parameters

4.1 Time Schedule Formulation

We consider a discrete planning horizon, given as a set of time periods $\mathcal{P}$. Furthermore, we define a time schedule $\mathcal {T}$ as a set of individual services, where each service ${t\in \mathcal {T} }$ must pass all stops in the bi-directional network, represented by the set $\mathcal {S}$. The number of services in $\mathcal {T}$ is limited by the parameter $V\in \mathbb {N}$. Each service $t\in \mathcal {T}$ consists of a departure time ${d_{s,\,t} \in \mathcal{P} }$, an arrival time ${a_{s,\,t} \ge 0}$, and a dwell time $h_{s,\,t} \ge 0$ per stop ${s \in \mathcal {S}}$. The parameter $\mu _{s_1,\,s_2}>0$ gives the time-independent travel time between two stops $s_1$ and ${s_2 \in \mathcal {S}}$. A given parameter $\beta ^{\text {min}}\ge 0$ defines a minimal dwell time. Analogously, a maximal dwell time $\beta ^{\text {max}}\ge 0$ per service ensures a limited overall travel time. In a feasible solution, two vehicles cannot dwell at the same stop at the same time. A minimal headway $H\ge 0$ spaces the departure of two consecutive services from the same stop.

Formally, a feasible time schedule $\mathcal {T}$ solves the following decision model:

$$\begin{aligned}&a_{s,\,t} = d_{s\mathop{-}1,\,t} + \mu _{s\mathop{-}1,\,s},&\forall s \in \mathcal {S}\setminus \{0\}, t \in \mathcal {T} , \end{aligned}$$

(1)

$$\begin{aligned}&h_{s,\,t} = d_{s,\,t} - a_{s,\,t},&\forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(2)

$$\begin{aligned}&h_{s,\,t} \ge \beta ^{\text {min}},&\forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(3)

$$\begin{aligned}&h_{s,\,t} \le \beta ^{\text {max}},&\forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(4)

$$\begin{aligned}&a_{s,\,t} \ge d_{s,\,t\mathop{-}1},&\forall s \in \mathcal {S}, t \in \mathcal {T} \setminus \{0\}, \end{aligned}$$

(5)

$$\begin{aligned}&d_{s,\,t} \ge d_{s,\,t\mathop{-}1} + H,&\forall s \in \mathcal {S}, t \in \mathcal {T} \setminus \{0\}, \end{aligned}$$

(6)

$$\begin{aligned}&|\mathcal {T} |\le V,&\end{aligned}$$

(7)

$$\begin{aligned}&d_{s,\,t} \in \mathcal{P} , h_{s,\,t}, a_{s,\,t} \ge 0,&{\forall s \in \mathcal {S}, t \in \mathcal {T} .} \end{aligned}$$

(8)

Through constraints (1), each service’s arrival time at the next stop results from adding up the departure time of the current stop and the travel time between both stops. Per stop, each service also provides a dwell time for the vehicle defined as in constraints (2). The minimal and maximal dwell are modelled in constraints (3) and (4). Constraints (5) set the order of the services, as a service’s arrival cannot take place before the previous service’s departure from the respective stop. Furthermore, constraints (6) ensure the headway between two consecutive departures from the same stop. Finally, constraint (7) limits the number of maximal services.

4.2 First Sub-Problem: Determine the Passenger Flow

We consider minimising freight transport’s interference with passenger transport quality as a crucial success factor for their integration. To quantify the passenger service quality, we measure the average passenger waiting time, overall stops, and times resulting from the passenger flow that a specific schedule produces.

We let a mixed-integer program describe the passenger flow for a given time schedule $\mathcal {T}$. The parameter $N_{s,p} \in \mathbb {N}$ represents the new arriving passengers at stop $s \in \mathcal {S}$ and period $p \in \mathcal{P}$. Note that the number of passengers and containers at each stop only decreases at a service’s departure. For this reason, we are particularly interested in the departure times, defined as set ${\mathcal{P} ^{\text {dep}}_s \subset \mathcal{P} }$ for each stop $s \in \mathcal {S}$. Analogously, the set $\mathcal {T} _{s,p}^{\text {dep}} \subset \mathcal {T}$ includes the services that depart from stop $s \in \mathcal {S}$ at period p.

Additionally, the parameter $\tau ^s_p>0$ describes the duration between period $p \in \mathcal{P} ^{\text {dep}}_s$ to the next larger period in $\mathcal{P} ^{\text {dep}}_s$ for each stop $s \in \mathcal {S}$. The parameters $\beta ^{\text {board}} \ge 0$ and $\beta ^{\text {alight}} \ge 0$ give the required boarding and alighting time per passenger. Based on the schedule $\mathcal {T}$, the value of $\bar{h}_{s,t}$ represents the dwell time of service $t \in \mathcal {T}$ at stop $s\in \mathcal {S}$. The parameter $C^{pas }$ is the vehicle capacity that can be used by passengers. The parameter $\lambda ^{\text {alight}}_{s,t} \in [0,1]$ represents the ratio of passengers alighting at stop $s\in \mathcal {S}$ from service $t\in \mathcal {T}$, where the boundary values indicate that none ($\lambda ^{\text {alight}}_{s,t} = 0$) or all ($\lambda ^{\text {alight}}_{s,t} = 1$) of the passengers alight.

The integer variable $w_{s,\,p\mathop{+}\tau ^s_p}$ describes the number of passengers waiting during the time interval [p, $p + \tau ^s_p]$ for period $p \in \mathcal{P} ^{\text {dep}}_s \cup \{0\}$ at stop $s\in \mathcal {S}$. Analogously, the integer variable $w^{\text {cum}}_{s,\,p\mathop{+}\tau ^s_p}$ represents the number of passengers accumulated over the time window $[p, p + \tau ^s_p]$ for period p at stop s. The accumulation is important to record the waiting times per passenger. The integer variable $n_{s,t}$ represents the number of passengers travelling via service $t\in \mathcal {T}$ when departing from stop $s\in \mathcal {S}$. Finally, the integer variables $b_{s,t}$ and $e_{s,t}$ are the number of boarding and alighting passengers at stop s and for service t, respectively.

The overall sub-problem is defined as

$$\begin{aligned} \min \,&A(\mathcal {T} ) := \sum _{s\, \in\, \mathcal {S}} \sum _{p\, \in\, \mathcal{P} ^{\text {dep}}_s \cup \{0\} } \frac{w^{\text {cum}}_{s,\,p\mathop{+}\tau ^s_{p}}}{|\mathcal {S} |\cdot |\mathcal{P} |}, \end{aligned}$$

(9)

$$\begin{aligned}\text {s.t. } w_{s,\,p\mathop{+}\tau ^s_{p}} = w_{s,p} - \sum _{t\, \in\, \mathcal {T} ^{\text {dep}}_{p \mathop{+} \tau ^s_{p},\, s}} b_{s,\,t} + \sum _{\tau \mathop{=} 0}^{\tau ^s_{p}-1} N_{s,\,p \mathop{+} \tau }, \qquad \forall p \in \mathcal{P} _s^{\text {dep}} \cup \{0\}, s \in \mathcal {S}, \end{aligned}$$

(10)

$$\begin{aligned}w^{\text {cum}}_{s,\,p\mathop{+}\tau ^s_{p}} = \tau ^s_{p} \cdot w_{s,\,p} - \sum _{t \in \mathcal {T} ^{\text {dep}}_{p \mathop{+} \tau ^s_{p},\, s}} b_{s,\,t} + \sum _{\tau \mathop{=} 0}^{\tau ^s_{p}\mathop{-}1} (\tau ^s_{p} - \tau ) \cdot N_{s,\,p \mathop{+}\tau }, \qquad \forall p \in \mathcal{P} _s^{\text {dep}} \cup \{0\}, s \in \mathcal {S}, \end{aligned}$$

(11)

$$\begin{aligned} n_{s,\,t} = n_{s\mathop{-}1,\,t} + b_{s,\,t} - e_{s,\,t}, \qquad \forall s \in \mathcal {S}\setminus \{0\}, t \in \mathcal {T} , \end{aligned}$$

(12)

$$\begin{aligned} n_{0,\,t} = b_{0,\,t},\qquad \forall t \in \mathcal {T} , \end{aligned}$$

(13)

$$\begin{aligned} e_{s,\,t} \le \lambda ^{\text {alight}}_{s,\,t} \cdot n_{s\mathop{-}1,\,t}, \qquad \forall s \in \mathcal {S}\setminus \{0\}, t \in \mathcal {T} , \end{aligned}$$

(14)

$$\begin{aligned} e_{s,\,t} \ge \lambda ^{\text {alight}}_{s,\,t} \cdot n_{s\mathop{-}1,\,t} - 1,\qquad \forall s \in \mathcal {S}\setminus \{0\}, t \in \mathcal {T} , \end{aligned}$$

(15)

$$\begin{aligned} n_{s,\,t} \le C^{\text{pas}}, \qquad \forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(16)

$$\begin{aligned} \beta ^{\text {board}} \cdot b_{s,\,t} + \beta ^{\text {alight}} \cdot e_{s,\,t} \le \bar{h}_{s,\,t}, \qquad \forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(17)

$$\begin{aligned} w_{s,\,p}, w^{\text {cum}}_{s,\,p} \in \mathbb {N} \qquad \forall p \in \mathcal{P} _s^{\text {dep}} \cup \{0\}, s \in \mathcal {S}, \end{aligned}$$

(18)

$$\begin{aligned} n_{s,\,t}, b_{s,\,t}, e_{s,\,t} \in \mathbb {N} \qquad \forall s \in \mathcal {S}, t \in \mathcal {T} . \end{aligned}$$

(19)

The objective function (9) minimises the average passenger waiting time. Constraints (10) and (11) determine the absolute and accumulated number of waiting passengers. The number of passengers travelling on a service is represented by constraints (12). Constraints (13) set the number of initially boarding passengers to the number of initially waiting passengers. Constraints (14) and (15) consider the number of passengers who alight a service at a particular stop. Constraints (16) limit the number of onboard passengers to the available vehicle capacity. Constraints (17) model the required service times for passenger transportation and limit it to the overall dwell time per stop and service.

4.3 Second Sub-Problem: Allocate Containers in a Given Schedule

Given a schedule that maximises passenger service quality, we want to reward freight allocations that produce an acceptable freight service quality. Here, we measure freight service quality via delays and rejection penalties.

We introduce several index sets to model the transport of parcel containers, represented by the set $\mathcal {R}$. The set $\mathcal {T} _r$ contains all services suitable for transporting container $r \in \mathcal {R}$, i.e., ensuring that the service’s departure does not occur before the container is released and loaded. The set $\mathcal {T} ^{\text {dep}}_{s,\, \mathop{\le} \,p}$ includes all services that depart stop $s \in \mathcal {S}$ at period $p \in \mathcal{P}$ and earlier. The set $\mathcal {R} _s$ includes all containers for which stop $s \in \mathcal {S}$ is included in the delivery path. The set $\mathcal {R} ^{\text {start}}_s \subset \mathcal {R}$ ($\mathcal {R} ^{\text {end}}_s \subset \mathcal {R}$) includes all containers with start (destination) $s \in \mathcal {S}$. The set $\mathcal {R} ^{\text {start}}_{s,\, \mathop{\ge}\, p}$ includes the containers released at period $p\in \mathcal{P}$ and later. The set $\mathcal{P} ^{\text {start}}_s$ includes all periods at which stop $s\in \mathcal {S}$ releases a container.

The binary decision variable $y_{r,\,t}$ models whether container $r\in \mathcal {R}$ is assigned to service $t\in \mathcal {T}$ (${y_{r,\,t} = 1}$) or not (${y_{r,t}=0}$). Furthermore, the binary variable $z_r$ decides whether a container $r\in \mathcal {R}$ is accepted (${z_r=1}$) or rejected (${z_r=0}$).

Fig. 2

Illustration for the concept of shared vehicle capacity

The parameters $\beta ^{\text {load}}\ge 0$ and $\beta ^{\text {unld}}\ge 0$ represent the required time for loading and unloading a container. Furthermore, the value of $\bar{h}_{s,\,t}$ denotes the dwell time of service $t\in \mathcal {T}$ at stop $s\in \mathcal {S}$. The value $T_{r,t}$ presents the delay of containers $r\in \mathcal {R}$ if transported via service $t\in \mathcal {T}$. Furthermore, the delay of a container must not exceed the parameter $T^{\text {max}} \ge 0$. Each rejected container is penalised with a parameter $P \ge 0$.

As stated before, the parameter $C^{\text{pas}} > 0$ is the total vehicle capacity that can be used by passengers. However, the vehicle’s standing area can alternatively hold parcel containers; its size is represented by the parameter $C^{\text {fre}} \ge 0$. Thus, $C^{\text {fre}} \le C^{\text{pas}}$ always holds. The parameter $Q_r > 0$ gives the space required to transport a single container $r\in \mathcal {R}$ in relation to the space required by one passenger. Figure 2 illustrates the relation of the parameters $C^{\text{pas}}$, $C^{\text {fre}}$ and $Q_r$, for $r \in \mathcal {R}$. The number of passengers $\bar{n}_{s,\,t}$ travelling on service $t\in \mathcal {T}$ by departure from stop $s\in \mathcal {S}$ results from solving the first sub-problem (cf. Sect. 4.2). Additionally, the parameter $C^{s} \ge 0$ describes the freight storage capacity of the depot stop $s\in \mathcal {S}$.

Thus, allocating containers to vehicles in a given schedule entails solving the following second sub-problem:

$$\begin{aligned} \min \,&B(\mathcal {T} ) := \sum _{r\, \in\, \mathcal {R} } \left( \sum _{t\, \in\, \mathcal {T} } \frac{ T_{r,\,t} \cdot y_{r,\,t} }{ |\mathcal {R} |} + P \cdot (1 - z_r) \right) \end{aligned}$$

(20)

$$\begin{aligned} \text {s.t.}&\sum _{t\, \in\, \mathcal {T} _r} y_{r,\,t} = z_r,&\forall r \in \mathcal {R} , \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{t\, \in\, \mathcal {T} \setminus \mathcal {T} _r} y_{r,\,t} = 0,&\forall r \in \mathcal {R} , \end{aligned}$$

(22)

$$\begin{aligned}&\sum _{r \,\in\, \mathcal {R} _s} Q_r \cdot y_{r,\,t} \le C^{\mathrm{pas }} - \bar{n}_{s,\,t},&\forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(23)

$$\begin{aligned}&\sum _{r\, \in\, \mathcal {R} _s} Q_r \cdot y_{r,\,t} \le C^{\text {fre}},&\forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(24)

$$\begin{aligned}&\sum _{r\, \in\, \mathcal {R} ^{\text {start}}_{s, \mathop{\ge} p}} \left( z_r - \sum _{t \,\in\, \mathcal {T} ^{\text {dep}}_{s,\mathop{\le} p}} y_{r,\,t} \right) \le C^{s},&\forall p \in \mathcal{P} _s^{\text {start}}, s \in \mathcal {S}, \end{aligned}$$

(25)

$$\begin{aligned}&\sum _{r\, \in\, \mathcal {R} ^{\text {start}}_s} \beta ^{\text {load}} \cdot y_{r,\,t} + \sum _{r\, \in\, \mathcal {R} ^{\text {end}}_s} \beta ^{\text {unld}} \cdot y_{r,\,t} \le \bar{h}_{s,\,t},&\forall s \in \mathcal {S}, t \in \mathcal {T} , \end{aligned}$$

(26)

$$\begin{aligned}&T_{r,\,t} \le T^{\text {max}} \cdot y_{r,\,t},&\forall r \in \mathcal {R} , t \in \mathcal {T} , \end{aligned}$$

(27)

$$\begin{aligned}&y_{r,\,t}, z_{r} \in \{0,1\},&\forall r \in \mathcal {R} , t\in \mathcal {T} . \end{aligned}$$

(28)

Objective function (20) minimises the average cargo delay and the total rejection penalty. Constraints (21) ensure the delivery of each container via exactly one suitable service. Conversely, a service must not be selected if its departure at a stop is set before the containers are released (cf. constraints (22)). Constraints (23) guarantee the restriction to the left-over capacity after the passengers boarded. Simultaneously, constraints (24) limit the used space to the dedicated cargo capacity of the vehicle. Constraints (25) model a limited stop capacity to store accepted containers in micro-depots between their release and pick-up by the assigned service. Rejected containers do not require storage. Constraints (26) model the required service times for cargo transportation. Constraints (27) enforce a maximal delay per container.

4.4 Global Objective Function

We rely on a lexicographical objective as previously implemented in [10] to optimise passenger and freight service quality. We prioritise passenger transport, such that the primary objective is to reduce the average waiting time $A(\mathcal {T} )$ accumulated over all periods and stops (cf. Sect. 4.2). The secondary objective minimises the penalty $B(\mathcal {T} ,y,z)$ for average container delivery delay or container rejection (cf. Sect. 4.3). Thus, the global objective function is

$$\begin{aligned} {\text {lex} \min }_{\mathcal {T} ,\,y,\,z}&\left\{ A(\mathcal {T} ), B(\mathcal {T} ,y,z) \right\} , \end{aligned}$$

(29)

where $\mathcal {T}$ is a feasible time schedule according to Sect. 4.1, and the assignment variable $y\in \{0,1\}^{\mathcal {R} \times \mathcal {T} }$ and the acceptance variable $z \in \{0,1\}^{\mathcal {R} }$ satisfy the restrictions stated in Sect. 4.3.

5 Adaptive Large Neighbourhood Search (ALNS)

Hörsting and Cleophas [10] show that solving a simpler version of the problem considered here to optimality is computationally expensive. As we aim to support planning and analysis for instances of realistic size in terms of the number of vehicles, stops, and periods, we propose to solve the problem via an ALNS heuristic. In that, we adapt the solution approach of [11] by integrating cargo transport. To that end, we propose iteratively optimising the cargo allocation and extending the ALNS by adding an operator that accounts for cargo service quality.

Figure 3 illustrates the ALNS procedure for the integrated cargo and passenger scheduling problem. The heuristic starts by constructing an initial time schedule (see Sect. 5.1), which it considers as the current schedule. Subsequently, it applies firstly a destroy operator (Sect. 5.2) and secondly a repair operator (Sect. 5.3). It selects operators based on probabilities given by the current weights. Applying the operators results in a new candidate schedule. The heuristic evaluates the passenger service quality for this candidate solution by solving the passenger flow problem. After a given number of warm-up iterations and if the candidate solution produces a passenger service quality that is at least equal to that in the current solution, the heuristic computes the optimal cargo assignment, i.e., solving the sub-problem introduced in Sect. 4.3. If the overall objective value improves, the candidate solution becomes the new best solution. Finally, the heuristic updates the operator weights and decides whether the candidate solution becomes the new current solution based on an acceptance criterion. This procedure repeats until a maximum number of iterations, a maximum number of iterations without improvement, or a maximal running time is exceeded. In the following, we discuss each step in more detail.

Fig. 3

Adaptive large neighbourhood search for the integrated cargo and passenger scheduling problem

5.1 Initialisation

The ALNS algorithm creates an initial schedule before searching for improvements via destroy and repair operations. Specifically, the initialisation constructs a time schedule with regularly spaced departures and fixed dwell times at each stop. Figure 4 illustrates an exemplary initial schedule.

Fig. 4

Initial time schedule

First, the initialisation fixes the latest feasible service for an initial constant dwell time h and stops $|\mathcal {S} |$. This service departs from the last stop at the last possible period, i.e., $|\mathcal{P} |- 1$. Thus, the last possible arrival at the starting stop depends on the dwell time h and travel time $\mu _{s\mathop{-}1,\, s}$ between stops $s-1$ and s;

$$\begin{aligned} A(h) := |\mathcal{P} |- 1 - |\mathcal {S} |\cdot h - \sum _{s\, \in\, \mathcal {S} \setminus \{0\}} \mu _{s\mathop{-}1,\, s}. \end{aligned}$$

(30)

If A(h) is smaller than zero, the initial dwell time h is too large to ensure a feasible schedule. In that case, the initialisation iteratively decrements the dwell time and computes the new resulting A(h).

As the initial schedule features a constant headway, the initialisation defines this headway between two departures from the same stop for V services as

$$\begin{aligned} H(h,V) := \frac{A(h)}{V-1}. \end{aligned}$$

(31)

If $\lfloor {H(h,V)}\rfloor$ is smaller than the given minimal headway time or the dwell time per stop, the initialisation procedure iteratively updates $V \rightarrow V - 1$ until a feasible time schedule with a sufficient headway H(h, V) results.

Subsequently, the initialisation constructs the schedule by fixing the last service and adding the remaining services with headway H(h, V). This procedure rounds up the departure times to ensure they are feasible, i.e., included in the set $\mathcal{P}$. Accordingly, service $t \in \{1, \dots , V\}$ ends at

$$\begin{aligned} D(h,V,t) := \lceil {|\mathcal{P} |-1-H(h,V)\cdot (V-t)}\rceil . \end{aligned}$$

(32)

The remaining departures at previous stops are added according to the given dwell time h and the travel time between two stops.

5.2 Destroy Operators

The heuristic proposed here features three destroy operators as illustrated in Fig. 5. The operator random deletion and shift supports diversification, while the operators passenger-driven deletion and freight-driven deletion drive intensification. Figure 5 illustrates how the destroy operators’ steps change a given schedule.

Fig. 5

Destroy operators

5.2.1 Random Deletion and Shift

This operator features of two consecutive steps to create space for new services, a random deletion followed by a shift of the remaining service. The first step (see Fig. 5b) randomly selects a period between the first period and the last departure from the first stop. It removes the next service leaving the first stop after the selected time period from the schedule. The second step (see Fig. 5c) aims to distribute the gained space across the whole time window. To achieve this, it shifts an either all preceding or subsequent services in a random direction (left or right). The intensity of the shift is also randomly chosen to fall between zero and the size of the gap gained through the first step. If the direction of the shift is left (right), it shifts the service released after (before) the previously deleted service and all earlier (subsequently) released services. Due to the limited time window, shifting the first or last service may create an infeasible schedule. Therefore, the operator only shifts the boundary services as far as possible while maintaining feasibility. Then, it iteratively shifts the next services following the same approach. The second step is omitted if no shift creates a feasible schedule.

5.2.2 Passenger-Driven Deletion

This operator aims to improve passenger service quality by deleting low-quality services. To that end, it either deletes a service with insufficient dwell times for all passenger processes (see Fig. 5d) or, if that does not exist, deletes the service expected to carry the lowest accumulated number of passengers. To support the insertion of a new service by the following repair operator (see Sect. 5.3), the destroy operator stores and optionally adapts the pattern of dwell times of the deleted service. As illustrated in Fig. 6, it adapts the dwell times by increasing it for all stops with insufficient for the boarding and alighting process.

5.2.3 Freight-Driven Deletion

This operator deletes services of poor freight service quality. First, if the current solution includes rejected containers, the operator randomly selects one of those and deletes the service that departs after its arrival. Secondly, if the current solution includes delayed containers, it deletes the service departing after the release of the most severely delayed container. If the current solution plans for all containers to be delivered punctually, the operator returns the current solution without changes. Again, it saves the dwell times for each stop of the deleted service. If the increment of the dwell time at a particular stop allows for loading or unloading an additional freight container, it adapts the pattern accordingly (see Fig. 6).

Fig. 6

Passenger and freight-driven deletion: adapt the dwell times for the new service

Consequentially, for a feasible current schedule, the destroy operators guarantee a feasible output schedule. Repair operators use the resulting gaps between services to introduce new services.

5.3 Repair Operators

Following the destroy operator, the heuristic randomly selects and applies one of two possible repair operators based on the given weights. Figure 7 illustrates how each repair operator adjusts the schedule. Each repair operator inserts a new service according to certain criteria. The new services follow either the default or an adapted dwell time pattern, depending on the previously applied destroy operator.

Fig. 7

Repair operators

5.3.1 Greedy Time-Driven

The first repair operator (see Fig. 7b) selects the largest gap between the departure time of one service and the arrival of the next one in the given time schedule. Considering A(s, t) as the arrival time and D(s, t) as the departure time of service t at stop s, it computes this gap as

$$\begin{aligned} \max _{s\, \in\, \mathcal {S},\,t\, \in\, \mathcal {T} } I(s,t) = {\left\{ \begin{array}{ll} A(s,t), &{} \text {if }t\text { is the first service,}\\ |\mathcal{P} |- 1 - D(s,t), &{} \text {if }t\text { is the last service,}\\ A(s,t+1) - D(s,t), &{} \text {else}.\\ \end{array}\right. } \end{aligned}$$

(33)

The operator inserts a new service at the centre of the gap if this still allows for the required minimal headway. Then, it selects the now largest gap and repeats the insertion until either reaching the maximal number of services or violating the headway requirement.

5.3.2 Greedy Passenger-Driven

The second repair operator (see Fig. 7c) selects a gap for service insertion based on the expected effect on passenger service quality. To that end, the operator first identifies all time points $p\in \mathcal{P}$ where a service could be feasibly inserted. For each p, the operator ignores capacity and time limitations and computes the savings from picking up passengers who are currently waiting via the new service released at period p at the depot, $t^{\text {new}}$:

$$\begin{aligned} S(p) := \sum _{s\, \in\, \mathcal {S}} w_{s,\,D(s,\, t^{\text {new}})\mathop{-}1} \cdot \left( D(s, t^{\text {new}}) - D(s, t^{\text {new}}+1) \right) , \end{aligned}$$

(34)

Then, the operator selects the time to insert the service to maximise the potential savings:

$$\begin{aligned} S(p^*) := \max _{p\, \in\, \mathcal{P} } S(p) \end{aligned}$$

(35)

This operator also repeats insertions until reaching the maximum number of services or violating the headway requirements. Note that the operator computes the number of waiting passengers after each insertion by re-solving the passenger flow problem.

5.4 Search Strategy and Updating Weights

In the proposed ALNS, a simple scheme continuously updates the weights assigned to the two randomly applied repair operators. First, the initialisation assigns a uniform weight $\rho _i$ to each repair operator i. Then, the probability of selecting the repair operator i is defined as

$$\begin{aligned} \theta _i = \frac{\rho _i}{\sum _{\rho _k \in \Omega ^+} \rho _k}, \end{aligned}$$

(36)

where $\Omega ^+$ is the set of all repair operators. Thus, the larger the weight $\rho _i$, the higher the probability of selecting operator i. The weights of destroy operators are computed analogously with a set $\Omega ^-$ including all destroy operators.

Whenever a new candidate solution results from applying the destroy and repair operators, we define the new weights of the operator that contributed to creating that candidate solution as

$$\begin{aligned} \Psi := {\left\{ \begin{array}{ll} \omega _1, \text { if the new solution is new global best,}\\ \omega _2, \text { if the new solution is better than the current solution,}\\ \omega _3, \text { if the new solution satisfies the acceptance criterion,}\\ \omega _4, \text { otherwise.}\\ \end{array}\right. } \end{aligned}$$

(37)

Since the algorithm favours operators resulting in an improvement, we assume the order $\omega _1 \ge \omega _2 \ge \omega _3 \ge \omega _4$.

Furthermore, an acceptance criterion decides whether the current solution should reflect the newly found candidate solution. Thereby, the acceptance criterion sets the searching strategy through the neighbourhood. The hill climbing (HC) criterion accepts only solutions that are as good as or better than the current best, i.e., a candidate solution x is accepted if

$$\begin{aligned} f(x) \le f(x^*), \end{aligned}$$

(38)

where $x^*$ is the best solution observed so far and f is the objective function.

Following the recommendation by [43], we also implement a linear record-to-record travel (RRT). The RRT criterion accepts a new solution if the relative difference to the global best is less than a continuously updated threshold. First, we define an initial threshold $T^{\text {start}}$ and a smaller end threshold value $T^{\text {end}}$. A candidate solution x is accepted if

$$\begin{aligned} f(x) - f(x^*)\le T. \end{aligned}$$

(39)

At the end of each iteration, we linearly update the threshold value by

$$\begin{aligned} T \leftarrow \max \{T - \frac{T^{\text {start}}-T^{\text {end}}}{I^{\text {max}}}, T^{\text {end}}\}, \end{aligned}$$

(40)

where $I^{\text {max}}$ is the maximal number of iterations.

Finally, the algorithm updates the weight as

$$\begin{aligned} \rho _a = \lambda \rho _a + ( 1 - \lambda ) \Psi , \end{aligned}$$

(41)

where the decay parameter $\lambda \in [0,1]$ controls the sensitivity to changes. If $\lambda$ is close to one, the weighting distribution only changes slowly, whereas a value close to zero highly rewards those operators that lead to improvement or acceptance in past iterations.

6 Performance Analysis

Before evaluating the sensitivity of the resulting system on instances of realistic size, we validate the performance of the ALNS versus the outcome from solving the problem to optimality. To this end, we implement the mixed-integer program given in Sect. 4 in Gurobi (v9.0.1) and limit the runtime to 9 h for both objectives. We implement the ALNS from Sect. 5 in Python 3 based on the open-source package alns (v4.1.0). The hill climbing (HC) and record-to-record-travel (RRT) acceptance criterion rely on a starting threshold of $25\%$ and an ending threshold of $1\%$ of the initial first objective value. The algorithm starts with at most 100 warm-up iterations for both criteria, followed by at most 1900 regular iterations. Additionally, the heuristic stops after 500 iterations without an objective value improvement or after a maximal running time of 1 h. All computations are run on an INTEL Sandy Bridge processor with 2.6 GHz.

As performance indicators, we consider the global runtime and the runtime per objective function. Additionally, we consider the average relative gap to the best value found and the average relative optimality gap, defined as

$$\begin{aligned} \frac{\text {solution value} - \text {best value}}{\text {solution value}}\quad \text {and}\quad \frac{\text {lower bound} - \text {solution value}}{\text {solution value}}. \end{aligned}$$

(42)

The source code underlying these results is publicly available at [44]. Furthermore, all instances and results presented in the following are publicly available under the same link.

For the performance analysis, we evaluate five problem settings with 60, 70, 80, 90, and 100 periods. We choose small instances to solve the problem to optimality within an acceptable runtime. We create 10 stochastic instances for each setting by randomly drawing the number of released containers per stop from a uniform probability distribution. Additionally, we consider ten instances of an exemplary large-scale scenario with 2880 periods. The scenario, termed uniform freight flow, all-depots, is introduced in more detail in Sect. 7. Due to their size, these instances are not solvable to optimality; therefore, we exclude a comparison to the solver.

Table 4 shows the average runtime and solution quality for the varying number of periods. Noticeably, the solver runtime rises exponentially with increasing periods. The solver cannot solve the problem to optimality within the given time limitations of 9 h per objective for more than 100 periods.

Table 4 Average runtime and solution quality for a varying number of periods. The column time (sec.) includes the average optimisation time. Additionally, we consider the average time, the average relative gap to the best value found (best), and the average relative optimality gap to the best lower bound found (opt) for both objective functions individually

The overall results in terms of the objective values and runtime of attempting to solve the problem to optimality are similar to those of solving the predecessor model introduced in [10] under the equivalent computational settings. That contribution compared large-scale instances with 180 periods and small-scale instances with 60 periods. For the small-scale instances, the solver found an optimal solution for the majority of instances; only instances with a high number of parcel containers could not be solved to optimality in the second objective. None of the large-scale instances could be solved to optimality, remaining with optimality gaps between 65 and 99% for the first objective function. Hence, extending the model to allow for multiple micro-depots with limited and stop-dependent storage capacities seems to have no significant effect on the problem’s computational cost. Both models show that the scale of the planning horizon is the primary driver of runtime and solving the problem for realistic horizons calls for efficient solution approaches like the ALNS presented in this paper.

To evaluate the heuristics’ performance, we first consider the results for instances with at most 100 periods. In these instances, both ALNS variants still find a close-to-best solution with a gap of 2 to $5\%$ to the best solution found by the solver in the first objective. The runtimes are at most 14 min for HC and at most 2 min for RRT. The difference in runtime mostly stems from HC solving the MIP for the second objective function more frequently. As described in Sect. 5, it only pursues the second objective if the first objective of the candidate solution is at least as good as the current solution. Additionally, HC often includes more iterations because of the improvement stop criterion.

Different results emerge regarding the solution quality for the second objective value. Here, the ALNS cannot achieve the same performance as the solver. However, the average gap to the best solution reduces from 11 to $5\%$ for more periods. This suggests that the heuristic is still valid for finding acceptable solutions for larger-scaled instances.

For the instances featuring 1880 periods, the average runtime is 47 min for HC and 24 min for RRT. HC finds better solutions in the first objective function ($3\%$ gap to RRT). RRT is more successful in the second objective but probably also the least restrictive because of the higher first objective value.

Fig. 8

Objective value across iterations for an exemplary instance

Table 5 Average count of operator usage for an exemplary set of instances

Figure 8 illustrates the progress of solution development when applying the ALNS based on HC or RTT to the large-scale instance. As visible in Fig. 8a, HC achieves the most improvement during the very first iterations. After the first hundred iterations, the first objective plateaus and only slowly improves. At the same time, the second objective incrementally decreases over time, interrupted by a temporary increment because of an improved first objective. Figure 8b shows that, for RRT, the first objective value oscillates between the current best and given threshold. As the threshold shrinks, the amplitude also shrinks. Overall, HC achieves the most improvement in the earlier iterations, whereas RRT might require even more iterations to achieve the same level. Running HC only for a low number of iterations, followed by a more intense search through RRT, might be an acceptable compromise for a low runtime and a good global solution quality.

Table 5 indicates the average number of times that each destroy and repair operator from Sect. 5 was applied in the large scenario. It also lists the average number of times the candidate solution was the new best solution, better than the current solution, accepted according to the chosen criterion, or rejected.

For HC, the candidate solution is either the new best, the same as the current solution (accepted), or worse than the current solution (rejected). Random deletion and shift is the most successful destroy operator, followed by the passenger-driven deletion. Nevertheless, HC regularly applies freight-driven deletion, and this accounts for approximately $13\%$ of the iterations where the best solution is found. The passenger-driven insertion significantly outperforms the temporal-driven insertion. RRT stops after fewer iterations than HC. Here, the passenger-driven deletion induces more improvements than the random deletion and shift. A possible reason might be that the overall algorithm design includes more randomisation than HC and therefore, requires more operators for intensification.

Having thus validated and benchmarked the ALNS variants, we use HC to create schedules and allocate freight for larger instances that cannot be solved to optimality in an acceptable time. Based on the results, we analyse the system’s sensitivity to capacity settings given different depot, freight-flow, and demand settings in the next section.

7 Sensitivity Analysis

When implementing a system for shared passenger and freight transport, the available capacities for freight transport, storage, and transhipment are important factors. While strategic fleet planning determines the vehicles’ capacity, the strategic choice and design of micro-depots determine the capacity for storage and transhipment. To support such considerations, we showcase a sensitivity analysis that considers two depot-location settings and three freight-flow settings. Section 7.1 describes the experimental setting including the design of problem settings and instances. Subsequently, Sect. 7.2 presents the results for the computational experiments.

7.1 Instance and Scenario Design

In general, we consider a bi-directional network of ten equidistant stations, i.e., each service must pass twenty stops in total when going back and forth. The travel time between any two stops is 1 min. We limit the analysis to equidistant stations, as we also test for certain network characteristics.

Each experiment covers 1 day of operations. We discretise this time horizon into 2280 periods, such that each time period equals 30 s. Within the time horizon, given travel times, at most 100 services can circulate through the network.

To describe the temporal curve of the daily passenger demand, we extract the popular times for exemplary stations in the light rail network of Hamburg, Germany from [45]. According to a field study by [46], a single passenger needs 0.87 s on average to board or alight a vehicle. To account for simultaneous passenger processes in a vehicle with nine doors, we set the boarding and alighting parameters $\beta ^{board }$ and $\beta ^{alight }$ to $0.87 / 9 = 0.09$ s. In addition, we set a minimum dwell time $\beta ^min$ of 30 s to guarantee sufficient time for boarding and alighting processes. Furthermore, we expect a loading time of 20 s and an unloading time of 15 s per container. We assume that service times increase linearly with the number of passengers and containers. Each vehicle fits 500 passengers. The cargo releases are uniformly distributed between 7 am and 4 pm. The soft deadline is 1 h after release and the maximal delay is set to 1 h. The shared capacity for cargo ranges between 1 and 5 cargo containers for sensitivity analysis.

7.1.1 Freight Flow

To consider structural effects from differences in freight demand, we consider three freight-flow settings governing the probability of containers originating from certain arrival stops and ending at certain destination stops.

Uniform Freight Flow

The first scenario considers uniformly distributed freight demand, i.e., each container may originate at or be destined for each stop with the same probability. We do not consider this a realistic setting but use it as a benchmark for the two alternative settings described in the following.

Central Freight In-flow

The second setting implements the idea that goods are transhipped from long-distance transport in the suburbs for further transport to destinations in the city centre. Thus, most containers originate in the outer areas of the network and have destinations in the centre (cf. Fig. 9a).

Directed Freight Flow

The third scenario implements the idea that goods must be transported from an appropriate transhipment area in the city to an industrial area outside of the city. Hence, the majority of containers originate on one side of the network and must be transported to the other side (cf. Fig. 9b).

Fig. 9

Probability distributions for the freight-flow-settings

7.1.2 Depot Locations

Depending on the network layout, not all stops might be suitable for transhipping freight through micro-depots. As a strategic decision, the designers of a shared passenger and freight system must choose appropriate locations for depots. These choices result in alternative depot-location settings.

We assume that freight demand can arise at any stop, but that containers are always transported to the micro-depot closest to the original source and destination. These are the stops we term origin and destination stops here. To render different settings comparable, we adapt the deadline and release time of each container by adding up the travel time from the selected depot stops to the underlying source or destination.

For the sensitivity analysis, we consider two depot-location settings.

All-Depots

In this setting, all stops are available as micro-depots. Thus, all stops in the public transit networks offer sufficient capacity to store at least a small number of freight containers (cf. Fig. 10a). For the sensitivity analysis, the stop capacity ranges from one to five containers. To guarantee only minimal disturbance for the passenger service, we limit the maximal dwell time at each stop. All freight processes must be executable within a maximal dwell time of 1 min, i.e. two periods.

Edge-Depots

The second setting assumes that the network does not allow for transhipment at intermediate stops. Instead, only stops that are situated at the outer edges of the network are depots (cf. Fig. 10b). To compensate for the lower depot density, we assume that the edge depots offer more capacity and consider stop capacities of two, four, six, eight, and ten containers in the sensitivity analysis. Since vehicles must also change directions at the related stations, additional dwell time results. We set the maximal dwell time in this design to 10 min, i.e., 20 periods.

Fig. 10

Scenarios depending on the location and design of depots

To summarise, we consider three freight-flow settings, two depot-location settings, and twenty-five demand variants in the sensitivity analysis, creating 150 variations of the problem. As the freight demand is randomly drawn from a probability distribution, a single instance has only limited significance for the overall view of the problem. At the same time, we can only solve a limited number of instances, given a large number of problem variations. To balance efficiency and reliability, we randomly generate 10 instances for each of the 150 variations. Hence, we solve 1500 problem instances in total. All instances and result files are publicly available at [44].

7.2 Computational Results

We use the ALNS with hill climbing (HC) to solve the randomly generated instances generated from the parameter settings in the previous sub-section. As result indicators, we consider the passenger waiting time, the cargo acceptance rate, and the cargo delay. As expected, the passenger waiting time is stable across scenarios (results not shown). Because of the lexicographical objective, solutions with lower passenger waiting times are always prioritised. This results in only a $2\%$ gap between the best and worst passenger waiting time found. Thus, the ALNS ensures a stable level of passenger service quality. From the maximal 100 services, all instances include at most five simultaneous services in peak times. Thus, the minimum fleet size to operate the computed time schedules is five vehicles.

Fig. 11

Average number of accepted cargo containers for different scenarios

Figure 11 shows the average number of accepted cargo containers for varying vehicle and stop capacities. Following intuitive expectations, the all-depots setting is advantageous. The larger number of depots makes up for the more restrictive dwell times, letting this design outperform the turning-depot-design by 0.91 (for central freight flow and high capacity values) to $25.52\%$ (for directed freight flow with minimal capacity values). To analyse under what settings the edge-depot setting enables good results, we further consider the structural characteristics.

First, we evaluate the results for the all-depot setting. When freight demand follows a uniform pattern, the average load per vehicle can be reduced to a minimum, and less vehicle and stop capacity is required. Figure 11a shows that the stop capacity threshold for accepting all freight is two and that this is independent of the vehicle capacity. If stops include only capacity for one container, the acceptance rate is still greater than $94\%$. Thus, the all-depot setting allows for an almost ideal acceptance rate given a uniform freight flow.

The central freight in-flow setting causes a lower acceptance rate (cf. Fig. 11c). As, in this setting, most freight originates at the outer stops, the required storage capacity at those stops increases. If a stop can only store a single container, the acceptance rate ranges between 73 and $80\%$, i.e., 11 to $18\%$ less than for a uniform freight flow. The acceptance rate growth logarithmically with increasing stop-capacity. Containers with closely spaced release times will probably be picked up by the same service, leading to overlaps in storage time. The probability of overlapping storage times decreases with increasing capacity. The vehicle capacity also gains more relevance in the central freight in-flow setting. The acceptance rate rises by 4 to $18\%$ when vehicles can carry an additional container. Given a uniform freight flow, certain containers are already delivered before new containers are picked up. This is much less likely under central freight in-flow.

For the directed freight-flow setting, freight originates at yet fewer depot stops. Additionally, the origin and destination stops do not overlap, i.e., all containers of the service must be picked up before any container reaches its destination. For this reason, the vehicle capacity becomes more crucial (see Fig. 11e). If there is only space for one cargo container in each vehicle, the acceptance rate ranges between 0 and $60\%$.

Next, we discuss the results for the edge-depots setting. As freight always originates from the nearest stop featuring a micro-depot, the origin distribution resulting from the uniform flow and the central freight-in-flow settings is the same given edge-depots. The results of the two depot-location settings are most similar for the central freight in-flow. From a practical perspective, a better use case for the edge-depot setting is the directed freight-flow setting. However, sufficient vehicle and stop capacity are crucial factors for the system’s success (cf. Fig. 11b).

Figure 12 visualises the average delay of accepted containers in the various scenarios. Since we only evaluate the delay of accepted containers, a higher capacity does not automatically result in a lower delay. Overall, we observe low delay rates from 0 to 2 min. Especially with a high stop capacity and a low vehicle capacity, a high number of containers is accepted, but the average delay increases up to almost 19 min (cf. Figs. 11a, 12c, and e).

Fig. 12

Average delay of accepted freight

7.3 Managerial Implications

To highlight the managerial implications, we compare our findings to the computational study in [10]. In particular, this predecessor model differed from the one considered here in that it assumed both unlimited stop capacity and that all freight originates from a single depot.

In general, the findings of [10] emphasise the importance of optimisation techniques to satisfy passenger and freight demand simultaneously. In that setting, a shared capacity between passengers and freight appeared more suitable for urgent containers with a tight deadline than a system with vehicles dedicated to either passenger or freight transportation. Furthermore, [10] highlight the impact of the freight loading and unloading processes. In that study, the dwell time represents the bottleneck in the considered system and the vehicle capacity plays only a minor role.

Beyond demonstrating that the ALNS is an appropriate alternative to solving the problem to optimality, our results indicate that the storage capacity of micro-depots is an essential factor for the system’s success when allowing for pick-ups beyond a central depot. Additionally, the dwell time still has a high impact on the system’s service quality. Especially for the edge-depot network design, a sufficient maximal dwell time is crucial to enable acceptable acceptance rates. However, for a high micro-depot capacity but a low vehicle capacity, the solutions can accept most of the containers but lack punctuality. Thus, we conclude that the shared capacity mode is only suited for urgent parcel containers when both stops and vehicles offer sufficient freight capacity.

8 Conclusion

In this work, we considered the problem of scheduling services and allocating cargo in a shared passenger and freight transit system featuring multiple micro-depots with limited storage capacity. To prioritise the passenger service, we considered a lexicographic objective function, where the first of the two objectives is to increase the average passenger waiting time across stops. The second objective function reduces the average freight delay. Furthermore, we presented an adaptive large neighbourhood search (ALNS) to find good solutions for large-scale problem instances. As acceptance criteria, we implemented and compared hill climbing and record-to-record travel.

The performance analysis results indicated that the ALNS is appropriate for solving realistic-sized problems. The hill climbing approach achieved the best improvement in early iterations, while the record-to-record travel required more iterations to adapt.

Sharing resources, e.g., vehicle capacity, is one of the main advantages of such a system and one of its main challenges. We considered the effect of freight flow settings and depot locations in a sensitivity analysis for varying vehicle and stop capacities. Due to the lexicographic objective function, we found that the average waiting time was stable for various settings. The result showed that dense freight demand flows require sufficient depot and vehicle capacity.

Lower storage capacities can suffice if every stop is a micro-depot. However, this requires sufficient space at each stop to handle the transhipment process and to store containers. Additionally, the design might come with higher initial costs because of the reconstruction work to enable transhipping at depot stops. At the same time, the realism of an edge-depot setting under a central freight flow is questionable. Apart from the adaptation of release and deadline times, the distance between the depot station and desired demand locations might be too large to ensure a valid satisfactory transportation service.

Our results when evaluating freight delay illustrate that a high stop capacity is insufficient to reach a high service degree if the cargo delay is also an important factor. A high storage capacity at the stops may ensure a high acceptance rate for freight, but vehicle capacity is an important factor in reducing delays.

The model presented here only considers a single line. Extending the model to a network of intersecting lines, where freight can change lines at transhipment depots, is an interesting concept for future work. Further extensions could also include the problem of rolling stock, i.e., assigning the vehicles in the fleet to services instead of setting an approximated upper boundary for the number of services. In the computational study, we evaluated a network with closely situated stops for each station. In future work, a transit system with sparsely distributed stops is also worth analysing. Additionally, this work did not consider further transport from the micro-depots over the "last meter". Future work could also anticipate the capacity request acceptance over time to avoid late denials. At the moment, the ALNS algorithm solves the freight assignment problem with a commercial solver. The evaluation of different algorithms to find a feasible assignment and further accelerate the heuristic might also be a promising approach.