Micro-Prudential Regulation and Loan Monitoring

Abstract

We evaluate the value of loan monitoring systems for a bank controlled by a micro-prudential regulator. We investigate dynamic systems (an information channel that generates information flow about quality) and static systems (where the lender receives a single signal about loan quality). We find that dynamic systems carry a regulatory charge that dominates the benefit of the systems and are therefore unprofitable, whereas static systems have positive value. Specifically, lenders can profitably dismantle their dynamic systems and instead turn to static monitoring systems. The model reveals, therefore, a potential weakness of micro-prudential regulation.

1 Introduction

This paper evaluates the value of loan monitoring systems for a regulated bank in a micro-prudential regulation framework. Many argue that the micro-prudential approach to financial regulation is inadequate. See, for instance, Kahou and Lehar (2017), who argue that the regulator’s focus on institutions can expose the banking system to systemic vulnerability. Our paper points out a direct negative effect of micro-prudential regulation: it discourages loan monitoring. Loan monitoring is essential in establishing a good lender-borrower relationship. Our paper argues that financial regulation threatens this relationship. Thus, even if the regulator aims to strengthen individual financial institutions, the effects on loan monitoring can be harmful as it jeopardizes the benefits arising from the closeness between borrowers and lenders (Boot 2000).

Our paper analyzes the use of monitoring systems. We define dynamic systems as an information channel that reveals information about loan quality in real-time, whereas static systems produce an information signal that instantly reveals information about loan quality. The systems work differently: Static monitoring means that the bank makes the risk management decision about the loan while purchasing information about the loan quality. Loan monitoring therefore leads to a resolution of risk with immediate effect. Dynamic monitoring means that the bank monitors the loan until the bank determines the optimal loan management policy. In the latter case, the bank accumulates risk while monitoring the loans; thus, it is likely to take more risk penalized by the regulator. Hence, we find that a micro-prudential regulator indirectly encourages the bank to dismantle its dynamic monitoring systems to reduce regulatory charges.

In a micro-prudential framework for regulation, the regulator imposes a charge on the bank calibrated to the bank’s loan portfolio’s amount of risk. Our model’s fundamental assumption, which is consistent with current practice, is that the charge is metered to the loans’ risk so that the charge for safer loans is less than for riskier ones. A higher charge incentivizes the bank to offload some of its risky loans, consistent with observed behavior. With static monitoring, the bank instantly takes into account the information revealed by the system. In contrast, the information arrives as an information flow with dynamic systems, separating information gathering from risk management decisions. The bank therefore anticipates new information before making risk management decisions. The risk accumulates until the bank has sufficient information to manage risk, leading to higher regulatory charges. The fact that dynamic monitoring leads to higher risk does not, in itself, explain our findings. One would think that the higher regulatory charge makes dynamic systems less profitable than static systems rather than downright unprofitable. The paper’s point is to demonstrate loss-making: even if the bank can acquire better dynamic systems free of cost, it would never choose to do so — in fact, it would choose to dismantle its existing ones.

The lack of investment in dynamic monitoring is an obvious concern. As noted by Boot (2000), the literature on banking assumes that banks develop a relationship with their borrowers. Thus, the efficiency and stability of the banking sector require that information about borrowers is available. The Basel Committee states “that a significant cause of bank failures is poor credit quality and credit risk assessment. Failure to identify and recognize deterioration in credit quality in a timely manner can aggravate and prolong the problem. Thus, inadequate credit risk assessment policies and procedures, which may lead to inadequate and untimely recognition and measurement of loan losses, undermine the usefulness of capital requirements and hamper proper assessment and control of a bank’s credit risk exposure.”¹ A compelling argument in this context is that the bank should be able to invest in loan monitoring systems to both strengthen its ability to handle regulatory pressure as well as to boost the value of its loan portfolio. The static analysis of our model supports this view. The dynamic analysis produces the exact opposite conclusion: regulation encourages banks to dismantle their monitoring systems because the private value of monitoring is negative. There may be other benefits of monitoring. For instance, the bank may learn new features about the loan market through loan monitoring to design and offer new credit products to the market. However, the fundamental problem remains that the bank is better off gathering such information through static monitoring systems rather than dynamic ones.

We strip down the model to its simplest form. It consists of a regulated lender with fixed lending opportunities but may have different monitoring systems with varying quality. The regulator imposes a charge on the bank that depends on the loan’s riskiness: higher risk leads to a higher charge. Static monitoring produces a single signal. A credit scoring system is an example of a static monitoring system. The process is thus binary: it produces a positive or negative signal with no time delay. Dynamic monitoring is an ongoing activity (an information channel) that detects and records new information in real-time. An example is relationship banking, surveyed in Boot (2000). Relationship banking describes a situation where the bank builds a relationship with the borrower to offer advice and, in turn, collects information about the borrower. A related system, described in Mester et al. (2001), involves monitoring the borrower’s current account activity to assess the quality of the borrower’s loans continuously. A costly dynamic monitoring process has a starting point and a stopping point, which requires the bank to hold monitored loans until the monitoring stops. The fact that the monitoring activity itself is riskier in the dynamic setting than in the static setting is thus intuitive.

Nevertheless, it is still an open question why the extra profit from using improved monitoring technology is overwhelmed by the additional cost of regulation. The answer to this question depends on the way bank regulation works. The regulator controls bank risk by loading costs on the bank for holding risky loans. The bank therefore only monitors loans above a certain quality threshold with dynamic monitoring. The improved monitoring technology will, therefore, extend into new loans that are already relatively safe. Hence, the total monitoring cost increases without the bank taking new risks in the loan market. The bank therefore will find it profitable to dismantle its monitoring technology to comply with the regulation. This effect will not happen with static systems, as improvements in monitoring technology lead to monitoring new risky loans. With the monitoring signal available, the bank can immediately manage the loan by offloading it if the risk turns out to be too high.

We measure monitoring quality along two dimensions, which are similar for both the static and the dynamic systems. First, otherwise equivalent monitoring systems with smaller monitoring costs are better than those with higher monitoring costs. Second, otherwise equivalent monitoring systems revealing more information are better than those that reveal less information. Also, to measure the usefulness of such improvements, we use two dimensions, a social one and a private one. First, the use of loan monitoring systems has implications for the riskiness of the bank. Bank risk has a social cost. Hence, a system that lowers bank risk is socially desirable. Second, the use of loan monitoring systems has implications for the profitability of the bank; thus, there is a private value of loan monitoring systems, and the system that increases bank value is privately desirable. The first dimension is neutralized with adaptive bank regulation since the regulator controls the bank’s risk within tight limits. Adaptive bank regulation therefore keeps the social value of monitoring systems constant (the regulator does not allow social slack). The value of the investments in loan monitoring is determined exclusively by the private benefit to the bank’s shareholders. With dynamic systems, the bank’s shareholders are always worse off with a better monitoring system, and with static systems, the bank’s shareholders are better off with a cheaper monitoring system and a more informative system under certain conditions. With dynamic systems, the regulator loads regulatory costs on the bank as long as the bank holds the loan, whether it is under monitoring or not. There is no regulatory cost associated with the monitoring activity itself for static systems.

Our model adds to many useful applications of continuous-time optimal stopping modeling techniques to economics and finance problems. Among related works, Daley and Green (2012) formulates a model in which an informed seller decides the optimal timing of the sale of a good to an uninformed buyer who gradually learns about the good’s quality. In the finance literature, El Caroui et al. (2005) applies the technique to portfolio management involving option based portfolio insurance, Dai et al. (2007) to mortgagors’ prepayment decisions, and (Thijssen 2008) to mergers and acquisitions.

Concerning existing works on loan monitoring, the interpretations of our results require some care. Some existing works view monitoring as an intervention exercise, see for instance Holmstrom and Tirole (1997), Parlour and Plantin (2008), Pennacchi (1988), and Loranth and Morrison (2009) and Chemla and Hennessy (2014). In contrast, our model sees monitoring as a pure information-gathering exercise, separating intervention from information gathering. The value of the option to intervene is, moreover, derived endogenously. However, we should note that the information gathered by the bank cannot lead to gains when dealing with investors (when selling loans), as it is essentially made public. Monitoring often appears as a feature in the agency literature. See for instance Barbos (2019) for a recent example. We note that in this literature, monitoring is used primarily as a synonym for the term verification. Finally, our paper is related to Boot (2000) who surveys relationship banking. Boot (2000) analyzes the benefits of information gathering for the bank through building a close relationship with its borrowers, whereas our paper discusses how regulation is a threat to bank monitoring. An empirical study of relevance to our model is Kara et al. (2015), which finds that securitized loans deteriorate in quality more rapidly than loans held by the original lender. This finding is consistent with the notion that banks sell low-quality loans, which also arises in our model.

The paper proceeds as follows. In Section 2, we present a model of dynamic monitoring systems. In Section 3, we carry out an equilibrium analysis of this model and a static benchmark model. Section 4 concludes.

2 Model

This section describes a model of dynamic loan monitoring under micro-prudential regulation. We set the model within a risk-neutral framework with a constant risk-free interest rate of r. The first part of the model describes the monitoring process for individual loans, and the second part describes the regulation of the lender’s loan portfolio. We assume throughout that the bank faces the same lending opportunities regardless of the monitoring technology but will adapt the risk management policy of its loan portfolio to the available monitoring technology and the requirements imposed by the regulator.

2.1 Monitoring individual loans

The lender operates in a loan market where it decides how to manage its loans to control risk. The management boils down to deciding which loans to keep in-house on its books and which loans to sell to others. The bank grants all loans based on an initial assessment of loan quality. The loan contracts are identical and consist of a promise to pay a perpetual coupon c. Each loan is either safe or risky. If the loan is safe, it has an intrinsic value of $\frac {c}{r}$, which is the discounted value of the loan’s coupon flow. If the loan is risky, it has an intrinsic value of $\frac {c}{r} - k$ where the first term is the discounted value of the loan’s coupon flow and the second term is the present value of the lender’s losses. Throughout the model, we assume that an observable credit event triggering the losses k does not happen within the time-span of loan monitoring, so that the lender’s monitoring systems produce all new information about the loan quality.²

Let π denote the probability that the loan is safe and 1 − π the probability that the loan is risky. The initial assessment at time 0 is π₀, and the bank offers the borrower a value V_S(π₀), which is the opportunity cost of the loan. The opportunity cost is the value of the loan if it is sold immediately to the market. The value $V_{S} = \frac {c}{r} - (1-\pi _{0})k - g$, which consists of the expected value of the cash flows of the loan, $\frac {c}{r} - (1-\pi _{0})k$, minus a signalling cost g that is incurred to convey the loan quality π₀ to the investors in the market.

The monitoring system allows the bank to observe a signal process {x_t}, t ≥ 0, which gives the bank an option to hold the loan in-house if it values the loan higher than its opportunity cost. In line with existing models of loan monitoring such as Holmstrom and Tirole (1997) and Parlour and Plantin (2008), we assume the bank can observe this signal at a continuous cost of m. The signal process follows a Brownian motion dx_t = 𝜃μdt + σdB_t where 𝜃 = 1 if the loan is safe and 𝜃 = 0 if the loan is risky. The drift and diffusion parameters μ and σ are strictly positive, and B_t is a standard Brownian motion. The bank observes the realization path of x_t, which generates a posterior belief process π_t. The posterior probability process is $\pi _{t} = \mathbb {P} (\theta = 1 | {\mathcal {F}}_{t}^{x} )$. This process solves the following stochastic differential equation whose derivation is given in Appendix 1:

$$ d\pi_{t} = \frac{\mu}{\sigma} \pi_{t} (1-\pi_{t}) d\tilde{B}_{t}, \pi_{0} = \pi, \tilde{B}_{t} = \frac{1}{\sigma} \left( x_{t} - \mu {{\int}_{0}^{t}} \pi_{s} ds \right), $$

(1)

where $\tilde {B}_{t}$ is a standard Brownian motion. Any claim under monitoring will depend on the posterior process (1). If the loan is not under monitoring, the claim value is constant and depends only on the prior beliefs π₀. Figure 1 illustrates the optimal monitoring process, which is derived below.

Fig. 1

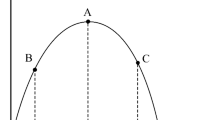
Loan monitoring with dynamic monitoring systems: The probability of loan quality is π. The bank uses the system to observe the posterior beliefs π in real time. When the loans are of sufficiently high quality and reaches the upper barrier point π^∗, the monitoring stops and the loan is held in-house. When the loans are of sufficiently low quality and reaches a lower barrier point π^∗∗, the monitoring stops and the loan is sold

We impose a regulatory cost for retaining risky loans. Following Parlour and Plantin (2008) and Wu and Zhao (2016), the cost is given by the parameter κ. The cost to the bank of holding a loan of quality π is calibrated to the loan quality π so that it equals r(1 − π)κ. We assume that the regulator can restrict lending only by calibrating the regulatory cost κ. We assume further that the regulatory cost is always small compared to the losses associated with bad loans, or κ < k. The regulator accesses the bank’s internal monitoring technology, observing individual loans’ quality π. Thus, the parameter k determines the market’s assessment of loan risk, and the parameter κ determines the regulator’s loan risk assessment.³ If the loan is placed in-house with no further monitoring, the prior belief about the loan quality determines the regulatory charge if no monitoring ever took place, or the most recent posterior belief about loan quality if monitoring did take place. We can see right away that if the signaling cost g is zero, then no loans would ever be held in-house, and if the regulatory cost κ is zero, then no loans would ever be sold. In either case, no monitoring would ever take place. Monitoring is optimal only if the bank wants to keep some loans in-house and sell some loans.

The monitoring decision is an optimal stopping problem, where the bank monitors loans until an optimal stopping time t^∗. At the stopping time, t^∗, the bank decides to hold the loan in-house or sell the loan. The event that π_t for the first time goes through the barrier π^∗ from below signifies that the bank decides to hold the loan in-house with no further monitoring. The event that π_t for the first time goes through the barrier π^∗∗ from above signifies that the bank decides to sell the loan with no further monitoring. If π₀∉(π^∗∗,π^∗), then t^∗ = 0 and the loan is held in-house or sold immediately. The loan value at the barrier π^∗ is V_I(π^∗). The value of the loan at the barrier π^∗∗ is V_S(π^∗∗). The values V_I and V_S take simple forms: $V_{I}(\pi ^{*}) = \frac {c}{r} - k(1 - \pi ^{*}) - \kappa (1-\pi ^{*})$, which consists of the discounted value of the risk free cash flow c minus the expected discounted losses and minus the discounted regulatory charge for holding risky loans. As mentioned above, the sale value $V_{S} (\pi ^{**})= \frac {c}{r} - k(1-\pi ^{**}) - g$, which consists of the risk free cash flow minus the expected discounted losses and minus a signaling cost g. The signaling cost g conveys the information π to the investors buying the loan. The value of a loan that is being monitored, denoted V_M(π_t), is expressed as follows (the derivation is shown in Appendix A): For $\pi _{t} \in \left [\pi ^{**}, \pi ^{*}\right ]$,

$$ V_{M}(\pi_{t}) = \mathbb{E} \left\{ {\int}_{0}^{t^{*}} e^{-ru} (c-m - r\kappa (1-\pi)) du + e^{-rt^{*}} \max\left\{V_{S}(\pi_{\tau}), V_{I}(\pi_{\tau})\right\} \right\} . $$

(2)

We describe the dynamic monitoring system by its cost m and its efficiency as measured by the signal-to-noise ratio of $\frac {\mu }{\sigma }$. We define an optimal monitoring policy as follows.

Definition 1

Bank’s optimal stopping rule is a pair (π^∗,π^∗∗) that satisfies the following conditions:

• The value function V_M satisfies (A.5) for all π_t ∈ [π^∗∗,π^∗], and $V_{M}(\pi _{t}) \geq \max \limits \{V_{I}(\pi _{t}),V_{S}(\pi _{t})\}$;

• The trigger point π^∗ satisfies V_M(π^∗) = V_I(π^∗) and $\frac {d}{d\pi } V_{M}(\pi ^{*}) = \frac {d}{d\pi } V_{I}(\pi ^{*})$;

• The trigger point π^∗∗ satisfies V_M(π^∗∗) = V_S(π^∗∗) and $\frac {d}{d\pi } V_{M}(\pi ^{**}) = \frac {d}{d\pi } V_{S}(\pi ^{**})$.

Condition (a) repeats the rational valuation condition plus the condition that the value of a monitored loan V_M given by (2) must be higher than both V_I and V_S in the monitoring region as otherwise, monitoring cannot be optimal. Conditions (b) and (c) are value matching and standard smooth pasting conditions. With this definition, we obtain the following proposition.

Proposition 1

For m, σ/μ and κ given, the optimal thresholds π^∗ and π^∗∗ have the following properties:

• π^∗ is strictly decreasing and π^∗∗ is strictly increasing with m;

• π^∗ is strictly decreasing and π^∗∗ is strictly increasing with σ/μ;

• π^∗ andπ^∗∗ are both strictly increasing with κ.

(Proof) See Appendix B.

The monitoring region is the interval between the lower bound π^∗∗ and the upper bound π^∗. Proposition 1 outlines how the monitoring region is affected by changes to the monitoring technology and regulation. If the cost of monitoring increases, the monitoring region narrows. The narrowing consists of a reduction of the upper bound and an increase of the lower bound. The narrowing occurs because the bank will optimally abandon the monitoring activity on some loans near the bounds due to the higher cost. The monitoring will also narrow with a reduction of the signal-to-noise ratio. Such a reduction represents a decrease in the informativeness of the monitoring activity. The bank will consequently abandon the monitoring activity on some loans near the upper and lower bounds. Finally, there is an upward shift in the monitoring region when there is an increase in regulation cost. As the cost of holding loans under monitoring or placed in-house increases, the bank becomes more reluctant to engage in both, and the monitoring region shifts upwards with the increase in the regulatory cost. We illustrate the monitoring equilibrium in Fig. 2. In the area where the loan quality is below the lower monitoring barrier π^∗∗, the loan will be sold immediately as the value of keeping the loan in-house is too small. In the region where the loan quality is higher than the upper monitoring barrier π^∗, the loan will be placed in-house with no further monitoring. In between the two boundaries, the bank monitors the loan. Depending on the information signal, the bank will ultimately hold the loan in-house if the information signal pushes the loan quality up to the upper barrier and sold if the information signal drives the loan quality down to the lower boundary.

Fig. 2

Loan value as a function of loan quality π: Loans that are of quality below the lower monitoring barrier π^∗∗ are sold and valued at the sale value V_S. Loans that are of quality above the upper monitoring barrier π^∗ are held in-house at the holding value V_I. The loans that in between are monitored and valued at the monitoring value V_M. The figure shows in blue the higher of the three values

What happens for limiting values of the parameters? We expect that κ will be calibrated to the desired outcome of regulation, which we discuss in more detail below. However, the cost of monitoring and the noise-to-signal ratio are exogenous, and it may be interesting to discuss what happens when the cost of monitoring and the noise-to-signal ratio become high. The monitoring region vanishes for some finite cost of monitoring, as the benefit of monitoring only has a finite value. Thus, there must exist a limiting cost that prevents all monitoring altogether. As for the noise-to-signal ratio, we know that a higher noise-to-signal ratio leads to a narrower monitoring region (Proposition 1 (b)), and therefore also a lower monitoring gain. Thus, there is a finite noise-to-signal ratio at some point that makes monitoring too costly (whatever the monitoring cost m). Limiting equilibria could only exist, therefore, if m = 0 and $\sigma /\mu \rightarrow \infty$. However, as $\sigma /\mu \rightarrow \infty$, the value function will not be properly defined (see Appendix A and the derivation of the value function V_M). Thus, the equilibrium degenerates in the limit because the equilibrium conditions as set out in Definition 1 cannot be satisfied.

2.2 Regulation of loan portfolios

Loans arrive and exit (through prepayment) randomly. We need to assume withdrawal to avoid the bank growing its portfolio indefinitely. The intensity of arriving loans is uniform across all loan qualities on the interval [0,1], and the intensity of exiting loans is also fixed and uniform on the interval [0,1]. The outflow of loans depends on the number of loans the bank holds. Therefore, the bank will grow its holding of a given quality loan until the outflow equals the inflow. We arrive, therefore, at a steady-state where the bank’s loan portfolio is stationary in the sense that the distribution of loans the bank holds of various riskiness is constant, and in particular, uniformly distributed between the lower monitoring barrier π^∗∗ and the upper barrier 1. The bank sells arriving loans of quality below π^∗∗ immediately.

The regulator chooses an adaptive policy of regulation where the regulator calibrates the charge κ to keep the bank risk below a certain threshold. In steady-state, the bank holds a loan portfolio with uniform distribution of quality between the lower barrier π^∗∗ and the upper barrier 1. The bank will monitor loans that are between the lower barrier π^∗∗ and the upper monitoring barrier π^∗. Also, note that the steady-state assumption has no bearing on each loan’s risk management, as outlined in Proposition 1, since the withdrawal of loans happens randomly. Hence, the bank’s incentive to monitor each loan within the barriers π^∗∗ and π^∗ remain the same. The regulator’s choice of κ may influence the lower barrier point π^∗∗. If there is an increase in the lower monitoring barrier, the bank will respond by selling a chunk of loans so that all loans under monitoring have quality above the new barrier. The uniformity assumption thus remains in place. However, if there is a lowering in the monitoring barrier, the bank will temporarily wish to hold more incoming loans of quality lower than the old barrier point when there is no existing portfolio to generate an offsetting outflow. Therefore, the bank will adjust its portfolio until it finds a new steady state.

In steady-state, each loan of quality π leads to expected losses k(1 − π). A uniform distribution of loans between π^∗∗ and 1 means that we can define the expected loan losses by φ(κ):

$$ \varphi(\kappa) = {\int}_{\pi^{**}(\kappa)}^{1} k(1-\pi)d\pi . $$

(3)

The regulator imposes an optimal regulatory cost κ^∗ such that the risk measure in (3) takes a maximum tolerance value $\varphi (\kappa ^{*}) = \bar {\varphi }$. The monitoring region will shift upwards as the regulator increases the regulatory cost κ (Proposition 1). The regulator therefore reduces the bank’s loan losses by increasing the regulatory cost of κ. Hence, the regulator chooses the optimal regulation κ^∗ such that the expected loan losses do not exceed a certain threshold of $\bar {\varphi }$.

3 Equilibrium analysis

This section asks whether an improvement in the monitoring systems increases the loan portfolio’s average value. First, we analyze the dynamic framework set out in the preceding section. We provide the necessary formal proofs in the appendix. However, the conclusions are ultimately clear cut and show that an improvement hurts the loan portfolio’s average value and can make the bank lose out to its competitors. Second, we analyze the static monitoring systems, and we find the opposite result.

3.1 Equilibrium under dynamic monitoring systems

A loan of quality π has a market value of V_S(π). The bank can enhance this value by holding the loan in-house at the value V_I(π) or monitoring the loan at the value V_M(π). The intermediation surplus of a given loan is the maximum of these three values minus the market value, that is,

$$ V(\pi) = \max \{V_{S}(\pi), V_{M}(\pi), V_{I}(\pi)\} - V_{S}(\pi) . $$

(4)

We notice that the intermediation surplus in (4) measures the excess value of a loan over and above its sale value V_S, thus loans that are sold immediately will not contribute to the value of the bank. The bank operates in a steady-state equilibrium where the distribution of loan quality is constant. If we assume it is uniform across the interval [0,1], the expected value of intermediation of a loan is a function of κ, m and σ/μ:

$$ \mathbb{E} V(\pi_{0}; \kappa, m, \sigma / \mu) = {{\int}_{0}^{1}} V(\pi_{0}; \kappa, m, \sigma / \mu) d\pi_{0} = {\int}_{\pi^{**}(\kappa)}^{1} V(\pi_{0} ; \kappa , m , \sigma / \mu ) d\pi_{0} . $$

(5)

The expected intermediation surplus in (5) and the risk measure in (3) depend on the assumption that the uniformity of the distribution of loan quality in steady state is not affected by regulation. A change in regulation could lead to both (3) and (5) becoming functions not only of the lower monitoring barrier π^∗∗(κ) but also of distributional changes to the loan portfolio. However, the following proposition demonstrates that regulation implies no distributional changes to the loan portfolio so that the loan quality distribution remains uniform.

Proposition 2

Regulatory cost κ has no impact on the steady state distribution of loan quality.

(Proof) See Appendix B.

Hence, we can define the following value function for the intermediation surplus for the bank, as a function of regulation, the monitoring cost, and the noise-to-signal ratio:

$$ W(m, \sigma / \mu) := \mathbb{E} V(\pi_{0}; \kappa^{*}(m, \sigma / \mu), m, \sigma / \mu). $$

(6)

We analyze the impact on the intermediation surplus in (6) from making improvements in the monitoring technology, particularly the effects of a reduction in the cost of monitoring, m, and an increase in the signal-to-noise ratio μ/σ.

Proposition 3

The monitoring cost m has the following effects on the bank’s surplus W(m,σ/μ), the upper threshold π^∗ and the regulatory cost of risk capital κ^∗ imposed by the regulator:

• W(m,σ/μ) is strictly increasing in m;

• π^∗ is strictly decreasing in m;

• κ^∗ is strictly decreasing in m.

(Proof) See Appendix B.

Lowering the monitoring cost reduces the bank’s intermediation surplus, and it becomes more reluctant to place a loan in-house by monitoring the loan longer. The main reason for the first effect is that lowering the monitoring cost leads to a higher regulatory cost of risk capital κ^∗, as pointed out in Proposition 3 (c). The bank is, therefore, penalized by the regulator for making investments to lower the monitoring. The second effect is a consequence of the fact that lowering the monitoring cost leads to more monitoring activity. Even though the two effects are offsetting, it will always be the case that the increase in the regulatory charge dominates the effect of lowering the monitoring cost. Hence, the bank is always worse off with cheaper monitoring. Next, we present the following result concerning the effects of signal quality σ/μ.

Proposition 4

The signal quality σ/μ has the following effects on the bank’s surplus W(m,σ/μ), the upper threshold π^∗ and the regulatory cost of risk capital κ^∗ imposed by the regulator:

• W(m,σ/μ) is strictly increasing in σ/μ;

• π^∗ is strictly decreasing in σ/μ;

• κ^∗ is strictly decreasing in σ/μ.

(Proof) See Appendix B.

A higher signal-to-noise ratio means that the bank incurs a higher regulatory cost of risk capital κ^∗, which will lower the intermediation surplus. The bank will also, in this case, monitor loans with a broader range of quality. The implications for financial regulation are straightforward. The bank is always better off without than with a dynamic monitoring system. Therefore, as long as regulatory costs are binding, the bank has an incentive to dismantle its dynamic monitoring systems and instead reject many loans deemed of marginal value at the outset. The cost of monitoring these loans and picking the good ones is higher than the regulatory charge attached. This finding does not imply that regulation could not be adapted to mitigate the problem. The standard approach to micro-prudential bank regulation is to allocate weights to the bank’s various risk categories and to arrive at a risk-weighted aggregate risk capital requirement. In principle, it does not matter whether the risk arises from lending activities or non-lending activities. Our results, however, suggest the regulator should apply a pecking order approach to regulation. First, the regulator should control the bank’s non-lending activities to keep bank risk within acceptable limits. Thus, the bank is encouraged to seek a competitive advantage in lending through investment in monitoring systems. Second, the model highlights a regulatory trade-off between controlling bank risk and encouraging banks to gain a competitive advantage from investments in superior monitoring technology. We could investigate this issue further, but it requires rigorous treatment in a model that endogenizes lending and non-lending bank activities, which goes beyond this paper’s scope.

3.2 Equilibrium under static monitoring systems

To provide a benchmark for the analysis, we analyze a version of the model where the bank uses a static monitoring system. The fact that the system produces a single information signal means that we are, in effect, analyzing the dynamic model’s snapshot rather than the full dynamic version. Hence, if the loan portfolio has a uniformly distributed steady-state distribution of loan quality in the dynamic model, we assume the static snapshot also has a similar uniformly distributed distribution of loan quality.

To simplify, we adapt the notation from the dynamic framework as far as we can. A lender intermediates loans that have uniformly distributed quality with π₀ ∈ [0,1], and a loan that kept in-house is worth $\frac {c}{r} - (1-\pi _{0})(k + \kappa )$, and the proceeds from selling a loan is $\frac {c}{r} - (1-\pi _{0})k - g$.⁴ The bank can pay a monitoring cost M that reveals a signal whether the loan is of high or low quality.⁵ Conditional on the event that the loan is safe, the probability of a positive signal is Φ > 0.5, and conditional on the event that the loan is risky, the probability of a negative signal is Φ.⁶ The conditional probabilities are:

$$ \begin{array}{@{}rcl@{}} \mathbb{P}(\text{High Quality}|\text{Positive Signal}) & =& \frac{\pi_{0} {\Phi}}{{\Phi}_{P}} , {\Phi}_{P} = \pi_{0} {\Phi} + (1-\pi_{0})(1-{\Phi}) , \\ \mathbb{P}(\text{Low Quality}|\text{Negative Signal}) & =& \frac{(1-\pi_{0}){\Phi}}{{\Phi}_{N}} , {\Phi}_{N} = (1-\pi_{0}){\Phi} + \pi_{0} (1-{\Phi}) . \end{array} $$

The unconditional probability of observing a positive or negative signal is Φ_P and Φ_N, respectively.

The question is whether the bank can increase the loans’ average value by improving the static monitoring systems, either by reducing the monitoring cost M or increasing the precision Φ. Given π₀, the bank can choose one of three actions: (i) the bank holds the loan without monitoring its quality; (ii) the bank sells the loan without monitoring its quality; and (iii) the bank monitors the loan and keeps the loan if the signal is positive and sells the loan if the signal is negative.⁷ For a given π₀, the value of the loan is the maximum of the three options:

$$ \max \left( \frac{c}{r} - (1-\pi_{0})(k + \kappa), \frac{c}{r} - (1-\pi_{0})k - g, \frac{c}{r} - M - ({\Phi}_{P} - \pi_{0}{\Phi})(k+\kappa) - ((1-\pi_{0}){\Phi} k + {\Phi}_{N} g) \right) . $$

(7)

We work out the third term in (7), the value of a monitored loan, in Appendix A. The following two probabilities $\hat {\pi }^{**}$ and $\hat {\pi }^{*}$ define the solution to the maximization program above: $\hat {\pi }^{*} = \frac {\Phi (\kappa - g) - M}{\Phi \kappa -(2{\Phi } -1)g}$ and $\hat {\pi }^{**} = \frac {M + (1-{\Phi })(\kappa - g)}{(1-{\Phi })\kappa + (2{\Phi } - 1)g}$.⁸ The option to hold the loan in-house is optimal for $\pi _{0} \geq \hat {\pi }^{*}$, the option to sell the loan is optimal for $\pi _{0} < \hat {\pi }^{**}$, and the option to monitor the loan is optimal for $1 \geq \hat {\pi }^{*} \geq \hat {\pi }^{**} \geq 0$.⁹ These probabilities are derived in the appendix, as well as the conditions which ensures that $1 \geq \hat {\pi }^{*} \geq \hat {\pi }^{**} \geq 0$.

The regulator sets out to use the regulatory cost of κ to control bank risk, similarly to the dynamic case. For given π, the intermediation surplus is defined as the added value of the loan as compared to its sale value in the open market:

$$ \begin{array}{@{}rcl@{}} \hat{V}(\pi_{0};\kappa,M,{\Phi}) &=& \max \left( \frac{c}{r} - (1-\pi)(k + \kappa), \frac{c}{r} - (1-\pi)k - g, \right. \\ && \left. \frac{c}{r} - M - ({\Phi}_{P} - \pi{\Phi})(k+\kappa) - ((1-\pi){\Phi} k + {\Phi}_{N} g) \right) - \left( \frac{c}{r} - (1-\pi)k - g \right) . \end{array} $$

(8)

The expected intermediation surplus is $\mathbb {E} \hat {V}(\pi _{0};\kappa , M, {\Phi })$, which is the expectation of (8) across loan qualities (we assume, as we did for dynamic systems, that there is uniform distribution of π₀ on the interval [0,1]):

$$ \mathbb{E} \hat{V}(\pi_{0} ; \kappa, M, {\Phi}) = {{\int}_{0}^{1}} \hat{V}(\pi_{0}; \kappa, M, {\Phi}) d\pi_{0} = {\int}_{\hat{\pi}^{**}(\kappa)}^{1} \hat{V}(\pi_{0};\kappa,M,{\Phi}) d\pi_{0} . $$

(9)

As for the dynamic version of the model, the integration in (9) can be taken over the loans that the bank decides to hold outright or monitor (that is, the loans of quality $\hat {\pi }^{**}$ or higher). Loan risk feeds into the bank from two sources. First, the loans held in-house without monitoring, that is, the loans for which $\pi _{0} \geq \hat {\pi }^{*}$, contribute to loan risk because they are generally not safe for sure. There is a probability of 1 − π₀ that they are risky. Second, the bank holds loans that are monitored and produce a positive signal in-house, that is, the loans within the region $\hat {\pi }^{*} \geq \pi _{0} > \hat {\pi }^{**}$. Even if the bank observes a positive monitoring signal, the loan may be risky because the information revealed through monitoring is not perfect. The risk measure is, therefore,

$$ \hat{\varphi}(\kappa) = {\int}_{\hat{\pi}^{**}}^{\hat{\pi}^{*}} \left( {\Phi}_{P} - \pi_{0}{\Phi} \right) k f(\pi_{0}) d\pi_{0} + {\int}_{\hat{\pi}^{*}}^{1} (1-\pi_{0}) k f(\pi_{0}) d\pi_{0} . $$

(10)

The measure $\hat {\varphi }$ in (10) is the static equivalent of the dynamic risk measure φ in (3). We notice that the measure in (3) involves only the lower barrier point for the monitoring region π^∗∗, whereas the measure in (10) involves both the lower and the upper barrier points $\hat {\pi }^{**}$ and $\hat {\pi }^{*}$.

We first investigate what happens to the bank risk when we increase κ. The bank is encouraged to sell loans, and the bank is discouraged from holding loans in-house without monitoring, hence both $\hat {\pi }^{**}$ and $\hat {\pi }^{*}$ increase.¹⁰ Therefore, an increase in κ leads to a reduction in $\hat {\varphi }$, which is what we would expect. Therefore, a reduction in κ leads to the bank selling fewer loans and holding more loans in-house without monitoring. Hence, a reduction of κ will always increase the intermediation surplus. We can evaluate the effect of changing the loan monitoring technology by evaluating the effect on the risk measure $\hat {\varphi }$. We find the following result.

Proposition 5

The risk measure $\hat {\varphi }$ is increasing with the monitoring cost M, and for sufficiently large Φ, decreasing with the informativeness of monitoring, Φ.

(Proof) See Appendix B.

Any reduction in the monitoring cost increases the loan portfolio’s average value and, therefore, leads to higher private profits and lower cost of regulation, a win-win. Similarly, if the monitoring system’s informativeness is already sufficiently high, a further increase has the same effect.

3.3 Comparison of dynamic and static systems

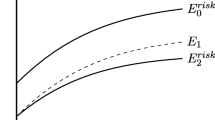
Why do we find that the two monitoring systems give such opposite answers? We can illustrate the intermediation surplus with dynamic systems; see Fig. 3. We see here the effects of increasing the monitoring cost. Since the regulator adjusts the regulation cost to keep risk-taking constant, the equilibrium always produces a fixed lower monitoring trigger point π^∗∗. Hence, the increase in the monitoring cost justifies a lowering of the regulatory cost. A lowering of the monitoring cost has an asymmetric impact on the loans near the boundary points. For loans that are just sold or are close to being sold, there is little impact. There is a negative impact on loans that are just placed in-house or are close to being placed in-house. These loans have less worth to the bank if the regulatory charge for holding them increases. The bank therefore benefits from the rise in the monitoring cost.

Fig. 3

Intermediation Surplus: The figure shows the effects on the intermediation surplus from an increase in the monitoring cost from m₀ to m₁. The increase justifies a reduction in the regulatory charge, which means that the in-house value V_I increases for all loan quality levels, and the upper monitoring region reduces from π^∗(m₀) to π^∗(m₁). The lower monitoring barrier remains constant to maintain a constant aggregate bank risk. Thus, the bank’s intermediation surplus increases as a consequence of increasing the monitoring cost and reducing the monitoring activity

With static systems, an increase in the monitoring cost will reduce the monitoring region at both ends, so the bank monitors fewer risky loans and fewer safe loans. Consequently, increasing the monitoring cost will increase the banks’ risk, leading to lower loan value. We expect, therefore, that given a choice between a static monitoring system (at least one with a sufficient level of informativeness) and none, the bank will choose to adopt a static monitoring system. The restrictions on informativeness is given in Appendix A, under the heading ‘Derivation of the Probabilities $\hat {\pi }^{*}$ and $\hat {\pi }^{**}$’, and it states that $\frac {M}{g} \leq \left (1 - \frac {g}{\kappa } \right ) \left (2 {\Phi } - 1 \right )$. That is, the monitoring cost M must be sufficiently small relative to the informativeness Φ in order that a static monitoring system is profitable. Thus, if a static system is profitable, bank regulation leads to a substitution effect where banks abandon their dynamic monitoring systems and instead adopt static monitoring systems. If the static system is not profitable, then the regulated bank prefers no monitoring of its loans by any kind of system.

A second relevant question is a comparison of the welfare effects in the two systems. Welfare is not directly observable in our model. If the relevant welfare effects arise due to the bank’s risk, the bank takes the same amount of risk regardless of how effective the monitoring systems are because the adaptive regulator controls the bank’s risk with that objective in mind. The borrowers are equally well off as the monitoring system’s choice will not affect the borrowing opportunities. So, we measure all remaining welfare effects by the monitoring surplus of the bank. Therefore, the analysis above shows that acquiring effective monitoring systems is encouraged by welfare concerns if the systems are static but discouraged if they are dynamic.

4 Conclusions

A vital aim of a micro-prudential regulatory framework is to ensure the stability of financial institutions. Our analysis demonstrates that loan monitoring can jeopardize this job through harmful incentive effects. We contrast the use of static monitoring systems (which produce a single information signal) with dynamic ones (which produce an information flow) and find that banks are encouraged to invest in static systems but are discouraged from investing in dynamic ones (see Berger et al. 2005). The reason is that dynamic systems increase the number of risky loans under observation, leading to higher regulatory risk charges. The higher regulatory cost penalizes the bank for using its dynamic monitoring systems.

This finding raises obvious questions concerning bank regulation and whether we can achieve stability in the financial system by regulating individual financial institutions. Moreover, regulation may impact lending in a harmful way. A switch from dynamic to static systems is not a problem as long as static monitoring systems are a perfect substitute for dynamic systems. However, there is a danger that the two types of systems are not perfect substitutes for some borrowers. For instance, for small or young companies with a lack of credit history, loan screening may be relatively ineffective as there is limited past data to go on. A dynamic system will produce a flow that picks up new information as it arrives and may thus be a better choice for this type of borrowers.

Appendices

Appendix A: Derivations

Posterior Process Eq. 1

With Brownian uncertainty, the increments x_t − x₀ are normal with mean 𝜃μt and variance σ²t, with density function

$$ f(x; \theta) = \frac{1}{\sigma\sqrt{2\pi t}} \exp \left( - \frac{1}{2} \left( \frac{x - \theta \mu t}{\sigma \sqrt{t}} \right)^{2} \right). $$

(A.1)

Normalize x₀ = 0, so conditional on observing x_t, the likelihood of 𝜃 = 1 is π_t which according to Bayes Law is

$$ \pi_{t} = \frac{f(x_{t};1)\pi_{0}}{f(x_{t};1)\pi_{0} + f(x_{t};0)(1-\pi_{0})}. $$

(A.2)

Using the formula for the density function in Eq. A.1, we can write Eq. A.2 as

$$ \pi_{t} = \frac{\frac{\pi_{0}}{1-\pi_{0}} \exp \left( \frac{1}{2} \left( \frac{x_{t}}{\sigma \sqrt{t}} \right)^{2} - \frac{1}{2} \left( \frac{x_{t} - \mu t}{\sigma \sqrt{t}} \right)^{2} \right)}{1 + \frac{\pi_{0}}{1-\pi_{0}} \exp \left( \frac{1}{2} \left( \frac{x_{t}}{\sigma \sqrt{t}} \right)^{2} - \frac{1}{2} \left( \frac{x_{t} - \mu t}{\sigma \sqrt{t}} \right)^{2} \right)} = \frac{\frac{\pi_{0}}{1-\pi_{0}}\phi_{t}}{1 + \frac{\pi_{0}}{1-\pi_{0}}\phi_{t}} , $$

(A.3)

where we define ϕ as the likelihood function ϕ_t = f(x_t; 1)/f(x_t; 0). Using Ito’s lemma and the definition of ϕ_t, we work out

$$ \begin{array}{@{}rcl@{}} d\phi_{t} &=& \frac{\mu}{\sigma^{2}} \phi_{t} dx_{t} , \\ d\pi_{t} &=& \frac{\mu}{\sigma^{2}} \pi_{t} (1-\pi_{t}) dx_{t} - \frac{\mu^{2}}{\sigma^{2}} {\pi_{t}^{2}} (1-\pi_{t}) dt . \end{array} $$

(A.4)

Using the change of probability measure $d\tilde {B}_{t} = \frac {1}{\sigma }dx_{t} - \frac {\mu }{\sigma }\pi _{t} dt$, the process in Eq. A.4 becomes a martingale, $d\pi _{t} = \frac {\mu }{\sigma } \pi _{t} (1-\pi _{t}) d\tilde {B}_{t}$. $\Box$

Derivation of V _M(π)

We analyze the optimal stopping problem in π_t rather than x_t. The infinitesimal generator for {π_t; t ≥ 0} is $\mathbb {L} = \frac {\mu ^{2}}{2\sigma ^{2}} \pi ^{2} (1-\pi )^{2} \frac {\partial ^{2}}{\partial \pi ^{2}} - r\mathbb {I}$, which applies to any value function V that depends on π_t. The first term arises from the diffusion term in dπ_t, and the second term (where $\mathbb {I}$ is the identity operator) arises from the fact that any claim must earn a return of r. Since for π_t > 0 there is also the possibility of a credit event, the claim V_M satisfies

$$ \mathbb{L} V_{M}(\pi_{t}) + (c - m - r\kappa (1-\pi)) = 0 . $$

(A.5)

The first term in Eq. A.5 is the “capital gains” net of the required rate of return associated with the arrival of new information, and the second term (c − m − rκ(1 − π)) is the net cash flow from holding a loan under monitoring, consisting of the coupon flow minus the monitoring cost and minus the regulatory charge levied on risky loans. In a rational market, the sum of the two is zero. The general solution to Eq. A.5 is

$$ V_{M}(\pi) = Af_{1}(\pi) + B f_{2}(\pi) + \frac{c}{r} - \frac{m}{r} - \kappa (1-\pi) , $$

(A.6)

where the functions f_i(π), i = 1, 2, in Eq. A.6 are given by

$$ f_{i}(\pi) = \pi^{\frac{1}{2}(1 + (-1)^{i} \xi)} (1-\pi)^{\frac{1}{2}(1 + (-1)^{i+1})}, i = 1,2 , $$

(A.7)

and A and B are arbitrary constants to be determined by the smooth pasting conditions. The parameter ξ in Eq. A.7 is given by ξ = (1 + 8r(σ/μ)²)^0.5 > 1.

Derivation of Eq. 7

The two first expressions in the maximum-operator are straightforward, so we concentrate on the third term, which is the value of a loan that has been subject to monitoring. We find,

$$ \begin{array}{@{}rcl@{}} \text{Value of a monitored loan} & =& -M + \mathbb{P}(\text{Positive Signal}) \mathbb{E} (\text{Value} | \text{Positive Signal}) \\ & &+ \mathbb{P}(\text{Negative Signal}) \mathbb{E}(\text{Value} | \text{Negative Signal}) \\ & =& - M + \frac{c}{r} - ({\Phi}_{P} - \pi_{0} {\Phi})(k + \kappa) - {\Phi}_{N} g - (1-\pi_{0}){\Phi} k , \end{array} $$

and Eq. 7 follows.

Derivation of the Probabilities $\hat {\pi }^{*}$ and $\hat {\pi }^{**}$:

The probability $\hat {\pi }^{*}$ is defined as the probability π for which $\frac {c}{r} - (1-\pi )(k + \kappa ) = \frac {c}{r} - M - (\pi {\Phi } + (1-\pi )(1-{\Phi }) - \pi {\Phi })(k + \kappa ) - ((1-\pi ){\Phi } k + ((1-\pi ){\Phi } + \pi (1-{\Phi }))g)$. Eliminating and rearranging terms, we find the solution $\pi = \hat {\pi }^{*}$

$$ \hat{\pi}^{*} = \frac{\Phi(\kappa - g) - M}{\Phi \kappa - (2{\Phi} - 1)g} . $$

(A.8)

It is necessary that Φ(κ − g) > M in order that the probability in Eq. A.8 is well defined. Similarly, the probability $\hat {\pi }^{**}$ is defined as the probability π for which $\frac {c}{r} - (1-\pi )k - g = \frac {c}{r} - M - (\pi {\Phi } + (1-\pi )(1-{\Phi }) - \pi {\Phi })(k + \kappa ) - ((1-\pi ){\Phi } k + ((1-\pi ){\Phi } + \pi (1-{\Phi }))g)$. Eliminating and rearranging terms, we find the solution $\pi = \hat {\pi }^{**}$

$$ \hat{\pi}^{**} = \frac{M + (1-{\Phi})(\kappa - g)}{(1-{\Phi})\kappa + (2{\Phi} - 1)g} . $$

(A.9)

We find that $1 \geq \hat {\pi }^{*}$ provided that Φκ − (2Φ − 1)g ≥Φ(κ − g) − M, or (1 −Φ)g ≥−M which is always true. Using Eq. A.9 find that $\hat {\pi }^{**} > 0$ provided that M + (1 −Φ)(κ − g) ≥ 0 which is true. We then need to check that $\hat {\pi }^{*} \geq \hat {\pi }^{**}$, which is true for

$$ \frac{\Phi(\kappa - g) - M}{\Phi \kappa - (2{\Phi} - 1)g} \geq \frac{M + (1-{\Phi})(\kappa - g)}{(1-{\Phi})\kappa + (2{\Phi} - 1)g} , $$

which is true for $\frac {M}{g} \leq \left (1 - \frac {g}{\kappa } \right ) (2{\Phi } - 1)$. Since the right hand side is always less than 1, it is necessary that the monitoring cost is smaller than the sales cost g.

Appendix B: Proofs

Proof Proof of Proposition 1:

First we obtain Lemma 1: □

Lemma 1

The points π^∗ and π^∗∗ satisfying conditions (b) and (c) in Definition 1 are the solutions to the following system:

$$ \mathbb{M}_{1}^{-1} \left( \begin{array}{c} k \\ k - \kappa \end{array} \right) = \mathbb{M}_{2}^{-1} \left( \begin{array}{c} - k (1 - \pi^{*}) + \frac{m}{r} \\ - k(1-\pi^{**}) + \kappa (1 - \pi^{**}) - g + \frac{m}{r} \end{array} \right). $$

(B.1)

where

$$ \mathbb{M}_{1} = \left( \begin{array}{cc} f_{1}(\pi^{*}) g_{1}(\pi^{*}) & f_{2}(\pi^{*}) g_{2}(\pi^{*}) \\ f_{1}(\pi^{**}) g_{1}(\pi^{**}) & f_{2}(\pi^{**})g_{2}(\pi^{**}) \end{array} \right) , \mathbb{M}_{2} = \left( \begin{array}{cc} f_{1}(\pi^{*}) & f_{2}(\pi^{*}) \\ f_{1}(\pi^{**}) & f_{2}(\pi^{**}) \end{array} \right), $$

$$ f_{i}(\pi) = \pi^{\frac{1}{2}(1 + (-1)^{i} \xi)} (1-\pi)^{\frac{1}{2}(1 + (-1)^{i+1}\xi)}, i = 1,2 , $$

$$ g_{i}(\pi) := \frac{1}{2} (1 + (-1)^{i} \xi) \pi^{-1} - \frac{1}{2} (1 + (-1)^{i+1} \xi) (1-\pi)^{-1} , \quad i = 1,2 . $$

A necessary and sufficient condition for condition (a) in Definition 1 to hold is that V_M as given in Lemma 4 is strictly convex over the region [π^∗∗,π^∗].

Proof Proof of Lemma 1

We derive the system of equations directly from the value matching and smooth pasting conditions (b) and (c) in Definition 1. The condition that

$$ V_{M}(\pi) \geq \max \left\{ \frac{c}{r} - (k + \kappa)(1-\pi), \frac{c}{r} - k(1-\pi) - g \right\} $$

ensures that the value function of the optimal stopping problem is indeed V_M(π) for all π ∈ [π^∗∗,π^∗]. We can verify that $\frac {df_{i}}{d\pi } = f_{i} g_{i}$, i = 1, 2. Hence, we can write the smooth pasting conditions as

$$ \mathbb{M}_{1} \left( \begin{array}{c} A \\ B \end{array} \right) = \left( \begin{array}{c} k \\ k - \kappa \end{array} \right) $$

(B.2)

and the value matching conditions as

$$ \mathbb{M}_{2} \left( \begin{array}{c} A \\ B \end{array} \right) = \left( \begin{array}{c} -k(1-\pi^{*}) + \frac{m}{r} \\ -k(1-\pi^{**}) + \kappa (1-\pi^{**}) - g + \frac{m}{r} \end{array} \right) $$

(B.3)

Combining Eq. B.2 and Eq. B.3, we find Eq. B.1. The functions $\pi ^{\frac {1}{2}(1-\xi )}(1-\pi )^{\frac {1}{2}(1+\xi )}$ and $\pi ^{\frac {1}{2}(1+\xi )}(1-\pi )^{\frac {1}{2}(1-\xi )}$ are both strictly convex because ξ > 1 (see Appendix A, Derivation of V_M), so it is possible to find coefficients A and B such that the function is strictly convex over the monitoring region, and strict convexity of V_M is clearly sufficient for V_M to strictly dominate both V_I and V_S since the latter two functions are both linear. It is also necessary because if V_M is not convex over the whole range, it will be non-convex in the neighborhood of π^∗ or π^∗∗, and in this case, the value of V_M will dip below V_S − g if it is non-convex near π^∗∗ or below V_I if it is non-convex near π^∗. □

Using Lemma 1, we proceed with the rest of the proof of Proposition 1. We can write

$$ \begin{array}{@{}rcl@{}} V_{M} &=& Af_{1} + Bf_{2} + \frac{c-m}{r} - \kappa (1-\pi) \end{array} $$

(B.4)

$$ \begin{array}{@{}rcl@{}} {V^{\prime}}_{M} &=& Af_{1}g_{1} + Bf_{2} g_{2} + \kappa\\ &=& Af_{1} \frac{1}{2}(1-\xi) \pi^{-1} - Af_{1} \frac{1}{2} (1+\xi) (1-\pi)^{-1} + B f_{1} \frac{1}{2} (1+\xi) \pi^{-1} - B f_{2} \frac{1}{2} (1-\xi) (1-\pi)^{-1} + \kappa\\&=& Af_{1} \frac{1}{2} (\pi^{-1} - (1-\pi)^{-1}) + B f_{2} \frac{1}{2} (\pi^{-1} - (1-\pi)^{-1}) - Af_{1} \frac{\xi}{2} (\pi^{-1} + (1-\pi)^{-1}) \\ & & + B f_{2} \frac{\xi}{2} (\pi^{-1} + (1-\pi)^{-1}) + \kappa\\ &=& (Af_{1} + Bf_{2}) \frac{1-2\pi}{2\pi(1-\pi)} - (Af_{1} - Bf_{2})\frac{\xi}{2\pi(1-\pi)} + \kappa , \end{array} $$

(B.5)

$$ \begin{array}{@{}rcl@{}} {V^{\prime\prime}}_{M} &=& Af_{1}({g_{1}^{2}} + {g^{\prime}}_{1}) + Bf_{2} ({g_{2}^{2}} + {g^{\prime}}_{2})\\ &=& (Af_{1} + Bf_{2}) \frac{\xi^{2} -1}{4 \pi^{2} (1-\pi)^{2}}. \end{array} $$

(B.6)

$$ \begin{array}{@{}rcl@{}} {g_{1}^{2}} + {g^{\prime}}_{1} &=& \left( \frac{1}{2} (1-\xi)\pi^{-1} - \frac{1}{2} (1+\xi)(1-\pi)^{-1} \right)^{2} - \frac{1-\xi}{2} \pi^{-2} - \frac{1+\xi}{2} (1-\pi)^{-2} \\ & =& \frac{1}{4} (1 - 2\xi + \xi^{2})\pi^{-2} - \frac{1}{2} (1 - \xi^{2}) \pi^{-1}(1-\pi)^{-1} + \frac{1}{4} (1 + 2\xi + \xi^{2}) (1-\pi)^{-2}\\ & & - \frac{1}{2}(1-\xi) \pi^{-2} - \frac{1}{2} (1+\xi) (1-\pi)^{-2}\\ & = & -\frac{1}{4} (\pi^{-2} + 2 \pi^{-1}(1-\pi)^{-1} + (1-\pi)^{-2}) + \frac{\xi^{2}}{4} (\pi^{-2} + 2\pi^{-1}(1-\pi)^{-1} + (1-\pi)^{-2})\\ & = & \frac{\xi^{2} - 1}{4} \left( \frac{1}{\pi(1-\pi)} \right)^{2}. \end{array} $$

The latter equality of the final equations follows since we find the following expressions for ${g_{i}^{2}} + {g^{\prime }}_{i}$: A similar calculation yields the same expression for ${g_{2}^{2}} + {g^{\prime }}_{2}$. The smooth pasting problem states that at π^∗∗, $V_{M} = \frac {c}{r} - k(1-\pi ^{**}) - g$ and ${V^{\prime }}_{M} = k$, and that at π^∗, $V_{M} = \frac {c}{r} - (k+\kappa )(1-\pi )$ and ${V^{\prime }}_{M} = (k + \kappa )$. We prove (a) and (b) using the second derivative.

Claim: π ^∗∗ is strictly increasing and π ^∗ strictly decreasing in m

Suppose m₁ > m₀ and $\pi ^{**}_{1} \leq \pi ^{**}_{0}$. We use Eq. B.4. Since V_M is always increasing, $A_{1} f_{1} + B_{1} f_{2} = \frac {m_{1}}{r} - k(1-\pi ) - g$ is greater than $A_{0} f_{1} + B_{0}f_{2} = \frac {m_{0}}{r} - k(1-\pi ) - g$ at $\pi ^{**}_{0}$. Therefore, ${V^{\prime \prime }}_{M}$ is greater for m₁ than for m₀, so if $\pi ^{**}_{1} \leq \pi ^{**}_{0}$ there cannot be smooth pasting on $(\pi ^{**}_{0},1]$, contradicting the assumption that $\pi ^{**}_{1} \leq \pi ^{**}_{0}$.

Similarly, suppose $\pi ^{*}_{1} \geq \pi ^{*}_{0}$. Again, since V_M is always increasing, $A_{1} f_{1} + B_{1} f_{2} = \frac {m_{1}}{r} - (k+\kappa )(1-\pi )$ is greater than $A_{0} f_{1} + B_{0} f_{2} = \frac {m_{0}}{r} - (k+\kappa )(1-\pi )$ at $\pi ^{*}_{0}$. Therefore, ${V^{\prime \prime }}_{M}$ is greater for m₁ than for m₀ so if $\pi ^{*}_{1} \geq \pi ^{*}_{0}$ there cannot be smooth pasting on $[0,\pi ^{*}_{0})$, contradicting the assumption that $\pi ^{*}_{1} \geq \pi ^{*}_{0}$.

Claim: π ^∗∗ is strictly increasing and π ^∗ strictly decreasing in σ/μ

The way the noise-to-signal ratio affects the problem is through the parameter ξ. Suppose ξ₁ > ξ₀ and $\pi ^{**}_{1} \leq \pi ^{**}_{0}$. We know that $V_{M} = \frac {c}{r} - k(1-\pi ) - g$ at π^∗∗ but since ξ₁ > ξ₀ the function grows faster (second derivative greater and first derivative always positive) for ξ₁ than for ξ₀, so A₁f₁ + B₁f₂ ≥ A₀f₁ + B₀f₂ at $\pi ^{**}_{0}$. This implies that there is no smooth pasting on $(\pi ^{**}_{0},1]$, contradicting the assumption that $\pi ^{**}_{1} \leq \pi ^{**}_{0}$.

Similarly, suppose $\pi ^{*}_{1} \geq \pi ^{*}_{0}$. We know that $V_{M} = \frac {c}{r} - (k+\kappa )(1-\pi )$ at π^∗ but since ξ₁ > ξ₀ the function grows faster for ξ₁ than for ξ₀, so A₁f₁ + B₁f₂ ≥ A₀f₁ + B₀f₂ at $\pi ^{*}_{0}$. This implies that there is no smooth pasting on $[0,\pi ^{*}_{0}]$, contradicting the assumption that $\pi ^{*}_{1} \geq \pi ^{*}_{0}$.

Claim: π ^∗∗ and π ^∗ are strictly increasing in κ

Suppose κ₁ > κ₀. V_M(π|κ₁) and V_I(π|κ₁) have lower cash flows than the corresponding V_M(π|κ₀) and V_I(π|κ₀), hence it must be the case that V_M(π|κ₁) < V_M(π|κ₀) so it is impossible that the two value functions V_M(π|κ₁) and V_M(π|κ₀) cross each other. Since both functions smooth-pastes into V_S(π) (which is independent of κ) it must be the case that $\pi _{1}^{**} > \pi _{0}^{**}$.

We now turn to π^∗. We use Eqs. B.5 and B.6. We know that ${V^{\prime }}_{M} = k$ at π^∗∗ and ${V^{\prime }}_{M} = k+ \kappa$ at π^∗, and we know that ${V^{\prime \prime }}_{M} \geq 0$ (convex) as otherwise it would not be optimal. Suppose π^∗ is decreasing in κ, then the function V_M must be more convex for increasing κ because the first derivative increases more (from k to k + κ) over a shorter distance (from π^∗∗ to π^∗). Hence, Af₁ + Bf₂ must be increasing in κ. But, since the value matching condition at π^∗ is independent of κ, and given by $A f_{1} + B f_{2} = -k(1-\pi ^{*}) + \frac {m}{r}$, the left hand side is increasing in κ and π^∗ must therefore also be increasing in κ.

Proof Proof of Proposition 2

This proposition shows why the truncation effect at the barrier point π^∗ which separates the loans that are not monitored (i.e., above π^∗) from the loans are monitored (i.e., below π^∗), does not change the uniform distribution of loans even though the barrier point may change.

The quality of the loans that are monitored will vary over time, but all monitoring activity is truncated at the barrier point π^∗. Thus, we may expect that the loans could accumulate from below at the barrier point π^∗. To address this point, we look in more detail at the steady state distribution of loan quality.

Suppose there is a fixed uniform inflow of loans, 1 − π^∗ flow into the region above the monitoring region, π^∗− π^∗∗ flow into the monitoring region, and π^∗∗ flow into the region below the monitoring region. We divide the unit interval into n smaller intervals ${\Delta }_{n}^{\pi }$, i = 0,…,n such that ${\sum }_{\pi } {\Delta }_{n}^{\pi } = 1$ and for given π, ${\Delta }^{\pi } = \frac {\mu }{\sigma } \pi (1-\pi ) \sqrt {\Delta t}$, where Δt are the time steps, to make sure that the Binomial process has the same volatility as (1). We will let $n \rightarrow \infty$ and ${\Delta } t \rightarrow 0$ to study the convergence to the continuous time model in the text.

Above the monitoring region, for each node π there is an inflow Δ^π and an outflow d(π)η, where d(π) is the number of loans of quality π and η is the outflow rate. In steady state, therefore, $d(\pi ) = \frac {{\Delta }^{\pi }}{\eta }$. As ${\Delta } t \rightarrow 0$, the number of loans converges to a uniform density.

In the monitoring region things are different. Let us label π₀ := π^∗, $\pi _{1} := \pi ^{*} - {\Delta }^{\pi _{1}}$, $\pi _{2} := \pi ^{*} - {\Delta }^{\pi _{1}} - {\Delta }^{\pi _{2}}$, and so on, until we have exhausted all nodes between π^∗∗ and π^∗. At node π₀, the inflow of new loans is ${\Delta }^{\pi _{0}} + \frac {1}{2} d(\pi _{1})(1-\eta )$ (the latter term is the non-exiting loans from the node below migrating up) and the outflow is d(π₀)η, hence $d(\pi _{0}) = \frac {{\Delta }^{\pi _{0}}}{\eta } + \frac {1}{2} d(\pi _{1})\frac {1-\eta }{\eta }$, which is higher than the number of loans at the nodes in the non-monitoring region above. Using a similar argument, at node π₁ the inflow of new loans is ${\Delta }^{\pi _{1}} + \frac {1}{2} d(\pi _{2})(1-\eta )$ (the latter term is the inflow of non-exiting loans from the node below migrating up), and the outflow is d(π₁)η + d(π₁)(1 − η) (non-exiting loans at this node that migrates up or down one node). This implies that $d(\pi _{1}) = \frac {{\Delta }^{\pi _{1}}}{\eta } + \left (\frac {1}{2} d(\pi _{2}) - d(\pi _{1}) \right ) \frac {1-\eta }{\eta }$, which is lower than for the nodes in the non-monitoring region above. At the next node, and any node π_i, i ≥ 2, we use a similar argument to find $d(\pi _{i}) = \frac {{\Delta }^{\pi _{i}}}{\eta } + \left (\frac {1}{2} d(\pi _{i+1}) + \frac {1}{2} d(\pi _{i-1}) - d(\pi _{i}) \right ) \frac {1-\eta }{\eta }$. This number eventually converges to the number of loans at the nodes in the non-monitoring region above. Thus, the truncation effect will create a “bump” in the distribution at π^∗ which leads to a below-average number below π^∗, which then is gradually evened out as we go further down the nodes.

The average density at nodes π₀ and π₁ is $\frac {1}{2} \left (\frac {{\Delta }^{\pi _{0}}}{\eta } + \frac {{\Delta }^{\pi _{1}}}{\eta } \right ) + \frac {1}{4} \left (d(\pi _{2}) - d(\pi _{1}) \right ) \frac {1-\eta }{\eta }$. The Δ terms are of order $\sqrt {\Delta t}$ because they represent the volatility terms, whereas the functions d(π) are of order Δt. Hence, the difference between the average number of loans at the neighboring nodes and the current node will vanish at a quicker rate than the Δ terms. Moreover, the difference between d(π₂) and d(π₁) will also vanish at a quicker rate. Therefore, the second term in the expression for the number of loans at each node will vanish in the limit (it will vanish in expectation for the first two nodes, but this will not affect the limiting density). Hence, in the limit we obtain a uniform distribution of loan quality independent of regulation. □

Proof Proof of Proposition 3

We first show that $\frac {\partial ^{2} V_{M}}{\partial \pi ^{2}} (\pi ; \kappa (m, \sigma / \mu ), m, \sigma / \mu )$ is strictly decreasing in m, for all σ/μ fixed. Suppose 0 < m₀ < m₁. Since $\bar {\psi } = \frac {k}{2}(1-\pi ^{**})^{2}$ is fixed by assumption, π^∗∗ is fixed for both m₀ and m₁. By letting A₀ and B₀ associated with m₀ and A₁ and B₁ with m₁ for every σ/μ fixed, the optimality conditions outlined in Eq. B.1 imply:

$$ \begin{array}{@{}rcl@{}} A_{0} f_{1}(\pi^{**}) + B_{0} f_{2}(\pi^{**}) & =& \frac{m_{0}}{r} - k(1-\pi^{**}) - g,\\ A_{1} f_{1}(\pi^{**}) + B_{1} f_{2}(\pi^{**}) & =& \frac{m_{1}}{r} - k(1-\pi^{**}) - g, \end{array} $$

which implies that $(A_{0} - A_{1})f_{1}(\pi ^{**}) + (B_{0} - B_{1})f_{2}(\pi ^{**}) = \frac {m_{0} - m_{1}}{r}$. Eq. B.1 also implies:

$$ \begin{array}{@{}rcl@{}} A_{0} f_{1}(\pi^{**}) g_{1}(\pi^{**}) + B_{0} f_{2}(\pi^{**}) g_{2}(\pi^{**}) & =& k,\\ A_{1} f_{1}(\pi^{**}) g_{1}(\pi^{**}) + B_{1} f_{2}(\pi^{**}) g_{2}(\pi^{**}) & =& k, \end{array} $$

which implies that (A₀ − A₁)f₁(π^∗∗)g₁(π^∗∗) + (B₀ − B₁)f₂(π^∗∗)g₂(π^∗∗) = 0. Combining both we can find expressions for (A₀ − A₁) and (B₀ − B₁):

$$ \begin{array}{@{}rcl@{}} (A_{0} - A_{1}) & =& \frac{m_{0}-m_{1}}{r} \frac{1}{1 + g_{2}(\pi^{**})} \frac{1}{f_{2}(\pi^{**})},\\ (B_{0} - B_{1}) & =& \frac{m_{0}-m_{1}}{r} \frac{g_{2}(\pi^{**})}{1 + g_{2}(\pi^{**})} \frac{1}{f_{1}(\pi^{**})}. \end{array} $$

Since f_i, i = 1, 2, and g₂ are strictly positive, we find that sign(A₀ − A₁) = sign(B₀ − B₁) = sign(m₀ − m₁), which implies that for m₁ > m₀, A₁ > A₀ and B₁ > B₀. Since f_i, i = 1, 2, are strictly convex, we have for every σ/μ fixed,

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{2} V_{M}}{\partial \pi^{2}}(\pi; \kappa^{*}_{0}, m_{0}, \sigma / \mu) & =& A_{0} \frac{\partial^{2} f_{1}}{\partial \pi^{2}}(\pi) + B_{0} \frac{\partial^{2} f_{2}}{\partial \pi^{2}}(\pi) \\ & <& A_{1} \frac{\partial^{2} f_{1}}{\partial \pi^{2}}(\pi) + B_{1} \frac{\partial^{2} f_{2}}{\partial \pi^{2}}(\pi) \\ & =& \frac{\partial^{2} V_{M}}{\partial \pi^{2}}(\pi; \kappa^{*}_{1}, m_{1}, \sigma / \mu). \end{array} $$

(B.7)

By Lemma 1, Eq. B.7 implies that for every σ/μ fixed, $V(\pi _{0} ; \kappa ^{*}_{0}, m_{0}, \sigma / \mu ) < V(\pi _{0} ; \kappa ^{*}_{1}, m_{1}, \sigma / \mu )$ for all π₀. By integrating over π₀, this implies W(m₀,σ/μ) < W(m₁,σ/μ) for all σ/μ fixed. This completes the proof of part (a). Also, by Lemma 1, (b) and (c) directly follow from Eq. B.7. □

Proof Proof of Proposition 4:

First we obtain Lemma 2: □

Lemma 2

For every (m₀,σ₀/μ₀) and (m₁,σ₁/μ₁), if

$$ \frac{d^{2}}{d \pi^{2}}V_{M}(\pi; \kappa^{*}_{0}, m_{0}, \sigma_{0}/\mu_{0}) > \frac{d^{2}}{d \pi^{2}} V_{M} (\pi; \kappa^{*}_{1}, m_{1}, \sigma_{1}/\mu_{1}), \forall \pi \in [\pi^{**}, \min(\pi^{*}_{0}, \pi^{*}_{1})], $$

(B.8)

then the following statements hold:

• (a) $V(\pi ; \kappa ^{*}_{0}, m_{0}, \sigma _{0} / \mu _{0}) \ge V(\pi ; \kappa ^{*}_{1}, m_{1}, \sigma _{1} / \mu _{1})$ for all π, with > for π > π^∗∗;

• (b) $\pi ^{*}_{0} < \pi ^{*}_{1}$;

• (c) $\kappa ^{*}_{0} < \kappa ^{*}_{1}$.

Proof Proof of Lemma 2

Before we proceed, associate A_i, B_i, and ξ_i with the pair (m_i,σ_i/μ_i), i = 0, 1, and recall the expressions for V_M and ${V^{\prime }}_{M}$ in Eqs. B.4 and B.5. □

Claim (b)

By condition Eq. B.8, the functions ${V^{\prime }}_{M}$ and V_M will grow faster for (m₀,σ₀/μ₀) than for (m₁,σ₁/μ₁). At the point $\min \limits (\pi _{0}^{*}, \pi _{1}^{*})$ therefore, both

$$ V_{M}(\pi; \kappa_{0}^{*}, m_{0}, \sigma_{0}/\mu_{0}) > V_{M}(\pi; \kappa_{1}^{*},m_{1},\sigma_{1}/\mu_{1}) $$

and

$$ {V^{\prime}}_{M}(\pi; \kappa_{0}^{*}, m_{0}, \sigma_{0}/\mu_{0}) > {V^{\prime}}_{M}(\pi; \kappa_{1}^{*},m_{1},\sigma_{1}/\mu_{1}). $$

Suppose $\pi _{1}^{*} \leq \pi _{0}^{*}$. Then there must be smooth pasting for $V_{M}(\pi ; \kappa _{1}^{*},m_{1},\sigma _{1}/\mu _{1})$. Then there cannot be smooth pasting for $V_{M}(\pi ; \kappa _{0}^{*}, m_{0}, \sigma _{0}/\mu _{0})$ since either $\kappa _{0}^{*} < \kappa _{1}^{*}$ so that the first derivative of $V_{M}(\pi ; \kappa _{0}^{*}, m_{0}, \sigma _{0}/\mu _{0})$ has already grown too large for smooth pasting to happen, or else $\kappa _{0}^{*} \geq \kappa _{1}^{*}$ in which case the function $V_{M}(\pi ; \kappa _{0}^{*}, m_{0}, \sigma _{0}/\mu _{0})$ itself has grown too large for value matching. This is a contradiction; thus, $\pi _{1}^{*} > \pi _{0}^{*}$.

Claim (c)

We know from (b) that $\min \limits (\pi _{1}^{*}, \pi _{0}^{*}) = \pi _{0}^{*}$, and by definition of $\pi _{0}^{*}$, $V_{M}(\pi ; \kappa _{0}^{*}, m_{0}, \sigma _{0}/\mu _{0})$ smooth pastes at this point. Assume $\kappa _{0}^{*} \geq \kappa _{1}^{*}$. Then $V_{M}(\pi ; \kappa _{1}^{*}, m_{1}, \sigma _{1}/\mu _{1})$ will never smooth paste on $[\pi _{0}^{*},1]$ since at $\pi _{0}^{*}$ it must be the case that $V_{M}(\pi ; \kappa _{1}^{*}, m_{1}, \sigma _{1}/\mu _{1}) < V_{I}(\pi ; \kappa _{1}^{*}, m_{1}, \sigma _{1}/\mu _{1})$. This is a contradiction, so $\kappa _{1}^{*} > \kappa _{0}^{*}$.

Claim (a)

It is straightforward from Eq. B.8 that $V_{M}(\pi ; \kappa _{0}^{*}, m_{0}, \sigma _{0}/\mu _{0}) > V_{M}(\pi ; \kappa _{1}^{*}, m_{1}, \sigma _{1}/\mu _{1})$ on $[\pi ^{**}, \pi _{0}^{*}]$, and also from (c) that $V_{I}(\pi ; \kappa _{0}^{*}, m_{0}, \sigma _{0}/\mu _{0}) > V_{I}(\pi ; \kappa _{1}^{*}, m_{1}, \sigma _{1}/\mu _{1})$ on $[\pi _{1}^{*}, 1]$. For the interval $[\pi _{0}^{*}, \pi _{1}^{*}]$, $V_{I}(\pi ; \kappa _{0}^{*},m_{0},\sigma _{0}/\mu _{0})$ is linear and has a greater starting point at $\pi _{0}^{*}$ and a greater end point in $\pi _{1}^{*}$ than the function $V_{M}(\pi ; \kappa _{1}^{*},m_{1},\sigma _{1}/\mu _{1})$ which is concave. Therefore, it must be the case that $V_{I}(\pi ; \kappa _{0}^{*},m_{0},\sigma _{0}/\mu _{0}) > V_{M}(\pi ; \kappa _{1}^{*},m_{1},\sigma _{1}/\mu _{1})$ on this interval also. The result follows immediately.

We continue the proof of Proposition 3. We show that an increase in σ/μ leads to a decrease in the convexity of the function V_M(π). First, since σ/μ enters the equilibrium conditions only through the parameter ξ, and since an increase in σ/μ leads to an increase in ξ, we will consider a change in the equilibrium conditions from ξ to ξ + Δ (where obviously Δ > 0). Corresponding to the case above, therefore, we find the following.

$$ \begin{array}{@{}rcl@{}} A_{0} f_{1}(\pi^{**}; \xi) + B_{0} f_{2}(\pi^{**}; \xi) &=& \frac{m}{r} - k(1-\pi^{**}) - g, \end{array} $$

(B.9)

$$ \begin{array}{@{}rcl@{}} A_{1} f_{1}(\pi^{**}; \xi+{\Delta}) + B_{1}f_{2}(\pi^{**}; \xi + {\Delta}) &=& \frac{m}{r} - k(1-\pi^{**}) - g, \end{array} $$

(B.10)

and

$$ \begin{array}{@{}rcl@{}} A_{0} f_{1}(\pi^{**}; \xi)g_{1}(\pi^{**}; \xi) + B_{0}f_{2}(\pi^{**}; \xi)g_{2}(\pi^{**}; \xi) &=& k, \end{array} $$

(B.11)

$$ \begin{array}{@{}rcl@{}} A_{1} f_{1}(\pi^{**}; \xi+{\Delta})g_{1}(\pi^{**}; \xi+{\Delta}) + B_{1}f_{2}(\pi^{**}; \xi+{\Delta})g_{2}(\pi^{**}; \xi+{\Delta}) &=& k. \end{array} $$

(B.12)

We can use the fact that $f_{1}(\pi ^{**}; \xi +{\Delta }) = f_{1}(\pi ^{**}; \xi )\pi ^{**-\frac {\Delta }{2}}(1-\pi ^{**})^{\frac {\Delta }{2}}$ and $f_{2}(\pi ^{**}; \xi +{\Delta })=f_{2}(\pi ^{**}; \xi )\pi ^{**\frac {\Delta }{2}}(1-\pi ^{**})^{-\frac {\Delta }{2}}$, and also that $g_{1}(\pi ^{**}; \xi +{\Delta }) = g_{1}(\pi ^{**}; \xi ) - \frac {\Delta }{2\pi ^{**}(1-\pi ^{**})}$ and $g_{2}(\pi ^{**}; \xi +{\Delta })= g_{2}(\pi ^{**}; \xi ) + \frac {\Delta }{2\pi ^{**}(1-\pi ^{**})}$. Rewriting Eq. B.10 and Eq. B.12 we find the following.

$$ A_{1} f_{1}(\pi^{**}; \xi) \left( \frac{1-\pi^{**}}{\pi^{**}}\right)^{\frac{\Delta}{2}} + B_{1} f_{2}(\pi^{**}; \xi) \left( \frac{\pi^{**}}{1 - \pi^{**}}\right)^{\frac{\Delta}{2}} = \frac{m}{r} - k (1-\pi^{**}) - g, $$

(B.13)

and

$$ \begin{array}{@{}rcl@{}} A_{1} f_{1}(\pi^{**}; \xi) \left( \frac{1 - \pi^{**}}{\pi^{**}}\right)^{\frac{\Delta}{2}} && \left[g_{1}(\pi^{**}; \xi) - \frac{\Delta}{2\pi^{**}(1-\pi^{**})}\right] \\ & +& B_{1} f_{2} (\pi^{**}; \xi) \left( \frac{\pi^{**}}{1 - \pi^{**}}\right)^{\frac{\Delta}{2}} \left[g_{2}(\pi^{**}; {\Delta}) + \frac{\Delta}{2\pi^{**}(1-\pi^{**})}\right] = k. \end{array} $$

(B.14)

Taking the difference between Eqs. B.9 and B.13 and eliminating terms, we find

$$ \left[A_{0} - A_{1} \left( \frac{1 - \pi^{**}}{\pi^{**}}\right)^{\frac{\Delta}{2}} \right] \left( \frac{1 - \pi^{**}}{\pi^{**}}\right)^{\xi} + \left[B_{0} - B_{1} \left( \frac{\pi^{**}}{1 - \pi^{**}}\right)^{\frac{\Delta}{2}}\right] = 0. $$

(B.15)

Taking the difference between Eqs. B.11 and B.14 and eliminating terms and using additionally Eq. B.15, we find

$$ \left( \frac{1-\pi^{**}}{\pi^{**}}\right)^{\xi} \left[ A_{0} \xi - A_{1} (\xi - {\Delta}) \left( \frac{1 - \pi^{**}}{\pi^{**}}\right)^{\frac{\Delta}{2}} \right] = B_{0} \xi - B_{1} (\xi - {\Delta}) \left( \frac{\pi^{**}}{1 - \pi^{**}}\right)^{\frac{\Delta}{2}}. $$

(B.16)

Clearly, for Δ = 0 the term inside the bracket on the left hand side of Eq. B.16 becomes A₀ξ − A₁ξ and the right hand side B₀ξ − B₁ξ, so we need that A₁ = A₀ and B₁ = B₀. We expand, therefore, the effects on both sides for small changes dΔ around the point Δ = 0. Taking the point A₁ξ as the starting point we find the expansion $\xi dA_{1} - A_{1} \left (1 - \frac {\xi }{2} \ln \frac {1-\pi ^{**}}{\pi ^{**}} \right ) d{\Delta } = 0$. Rearranging we find that $\frac {dA_{1}}{d{\Delta }} = \frac {A_{1}}{\xi } \left (1 - \frac {\xi }{2} \ln \frac {1-\pi ^{**}}{\pi ^{**}} \right )$. Taking the point B₁ξ as the starting point we find the expansion $\xi dB_{1} - B_{1} \left (1 - \frac {\xi }{2} \ln \frac {\pi ^{**}}{1-\pi ^{**}} \right ) d{\Delta } = 0$. Rearranging again we find that $\frac {dB_{1}}{d{\Delta }} = \frac {B_{1}}{\xi } \left (1 - \frac {\xi }{2} \ln \frac {\pi ^{**}}{1-\pi ^{**}} \right )$.

Next, we need to look at the effect that a change in $\frac {\sigma }{\mu }$, or equivalently, ξ, has on the functions f₁ and f₂. We use the same idea as above to study the impact that the change in ξ has on the convexity of the value function V_M. Namely, by showing $\frac {\partial ^{3} V_{M}}{\partial \xi \partial \pi ^{2}} (\pi ; \xi ) > 0$, we prove V_M(π; ξ₀) < V_M(π; ξ₁) for all $\pi \in (\pi ^{**}, \min \limits \{\pi ^{*}_{0}, \pi ^{*}_{1}\}]$ when ξ₀ < ξ₁. Note that we are slightly abusing notation to simplify the expression – V_M(π; ξ) is more precisely V_M(π; κ^∗(m,h^− 1(ξ)),m,h^− 1(ξ)), where h^− 1(ξ) is the inverse function of $h(\sigma / \mu ) = \sqrt {1 + 8r\frac {\sigma ^{2}}{\mu ^{2}}}$.

A change in the parameter ξ will lead to a change of the second derivative $\frac {\partial ^{2} V_{M}}{\partial \pi ^{2}}(\pi ; \xi )$,

$$ \frac{\partial^{3} V_{M}}{\partial \xi \partial \pi^{2}}(\pi; \xi) = \frac{\partial A}{\partial \xi}(\xi) \frac{\partial^{2} f_{1}}{\partial \pi^{2}}(\pi; \xi) + \frac{\partial B}{\partial \xi}(\xi) \frac{\partial^{2} f_{2}}{\partial \pi^{2}}(\pi; \xi) + A \frac{\partial^{3} f_{1}}{\partial \xi \partial \pi^{2}}(\pi; \xi) + B \frac{\partial^{3} f_{2}}{\partial \xi \partial \pi^{2}}(\pi; \xi). $$

(B.17)

We know from the above that

$$ \begin{array}{@{}rcl@{}} \frac{\partial A}{\partial \xi}(\xi) &=& \frac{d A}{d {\Delta}} = \frac{A_{1}}{\xi} \left( 1 - \frac{\xi}{2} \ln \frac{1-\pi^{**}}{\pi^{**}} \right), \end{array} $$

(B.18)

$$ \begin{array}{@{}rcl@{}} \frac{\partial B}{\partial \xi}(\xi) &=& \frac{d B}{d {\Delta}} = \frac{B_{1}}{\xi} \left( 1 - \frac{\xi}{2} \ln \frac{\pi^{**}}{1-\pi^{**}} \right). \end{array} $$

(B.19)

We now need to work on the last two terms. By straightforward differentiation we find

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{3} f_{1}}{\partial \xi \partial \pi^{2}}(\pi; \xi) &=& \frac{f_{1}(\pi; \xi)}{2} \ln \frac{1-\pi}{\pi} \left( \frac{\xi^{2} - 1}{4}\right) \left[ \frac{1}{\pi(1-\pi)} \right]^{2} + \frac{f_{1}(\pi; \xi)}{2} \xi \left[ \frac{1}{\pi(1-\pi)} \right]^{2}, \end{array} $$

(B.20)

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{3} f_{2}}{\partial \xi \partial \pi^{2}}(\pi; \xi) &=& \frac{f_{2}(\pi; \xi)}{2} \ln \frac{\pi}{1-\pi} \left( \frac{\xi^{2} - 1}{4}\right) \left[ \frac{1}{\pi(1-\pi)} \right]^{2} + \frac{f_{2}(\pi; \xi)}{2} \xi \left[ \frac{1}{\pi(1-\pi)} \right]^{2}. \end{array} $$

(B.21)

Using Eqs. B.18, B.19, B.20 and B.21, some mechanical calculations yield the following expression for Eq. B.17

$$ \frac{\partial^{3} V_{M}}{\partial \xi \partial \pi^{2}}(\pi; \xi) = \left[ A f_{1}(\pi; \xi) + B f_{2}(\pi; \xi) \right] \frac{3 \xi^{2} - 1}{4\xi} \left[ \frac{1}{\pi(1-\pi)} \right]^{2} > 0. $$

An increase in $\frac {\sigma }{\mu }$ leads to an increase in ξ, so the result follows immediately by applying Lemma 2.

Proof Proof of Proposition 5

We analyse the effect on the risk measure $\hat {\psi }$ from a reduction in M or an increase in Φ. We at M first. Calculating directly the derivative $\frac {\partial \hat {\psi }}{\partial M}$ we find

$$ \frac{\partial \hat{\psi}}{\partial M} = k ((1-{\Phi})g + M) \left( \frac{\Phi}{({\Phi} \kappa - (2{\Phi} -1)g)^{2}} + \frac{1-{\Phi}}{((1-\phi)\kappa + (2{\Phi} -1)g)^{2}} \right) > 0 $$

Hence, if we reduce the monitoring cost M the regulator will always reduce the regulatory cost κ. Next, we consider the derivative $\frac {\partial \hat {\psi }}{\partial {\Phi }}$. We find,

$$ \frac{\partial \hat{\psi}}{\partial {\Phi}} = k \left( -(1-{\Phi}) (1-\hat{\pi}^{**}) \frac{\partial \hat{\pi}^{**}}{\partial {\Phi}} - {\Phi} (1-\hat{\pi}^{*}) \frac{\partial \hat{\pi}^{*}}{\partial {\Phi}} - {\int}_{\hat{\pi}^{**}}^{\hat{\pi}^{*}} (1-\pi_{0}) d\pi_{0}\right) $$

We find that $\frac {\partial \hat {\pi }^{*}}{\partial {\Phi }} > 0 > \frac {\partial \hat {\pi }^{**}}{\partial {\Phi }}$ since an increase in the precision Φ makes the monitoring region more attractive. This fact implies that for sufficiently large Φ, the expression in the large bracket on the right-hand side is negative because the weight on the positive term vanishes. For sufficiently large Φ, a further increase in precision will reduce the risk measure and the regulatory cost κ. □