Abstract
Multicellular organisms coordinate growth and differentiation from single cell starting points with developmental programs. While the evolutionary origins of these programs are unknown, it is likely that they are closely tied to the evolution of regulated—not stochastic—phenotypic expression. To determine how such regulation might arise, we consider experimental populations of Pseudomonas fluorescens which evolved stochastic switching in the lab. This switching is directly coupled with environmental oscillations generated by the bacteria themselves. This unique example of niche construction provides reliable information that organisms may incorporate into regulation of phenotypes. We use mathematical models to investigate the success of two forms of regulation that rely on sensing either external or internal information. We find that both strategies can outcompete stochastic strategies for certain combinations of parameters. In particular, external sensing mechanisms are very effective over a large range of parameter space—including parameters that correspond to poor sensing of the extracellular signal and gradual responses. We show with evolutionary simulations that this robustness makes them more likely to evolve from initially stochastically switching populations rather than internal sensing mechanisms which require more tuning of parameters. These results demonstrate that, within this oscillating system, if regulatory mechanisms can evolve to incorporate environmental information then their selective advantage is sufficient for them to fix in the population.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Many multicellular organisms grow and develop from a stage in which they are only a single cell (Buss 1987; Grosberg and Strathmann 1998; Wolpert 1990). As cells reproduce they differentiate to produce a multicellular form composed of different cellular phenotypes often organized into specialized tissues. This process usually relies on genetically encoded developmental programs that coordinate cell reproduction and differentiation (Davidson 2001). Regulation of cell differentiation decisions reduces randomness that might impair the cohesion or function of the multicellular form (Balázsi et al. 2011). Thus, in this way, developmental programs play a pivotal role in ensuring the integrity and success of multicellularity. Despite this, their evolutionary origins are unknown (Minelli and Fusco 2010; Rainey and Kerr 2010; Schlichting 2003).
A hallmark of developmental programs is that phenotypic expression is linked to some signal (either internal or external to a cell) and expression can be adjusted and reliably predicted (Moczek et al. 2011; West-Eberhard 2003). If phenotypic expression cannot be adjusted then it will have limited use in the evolution of new multicellular forms; and if it cannot be reliably predicted then the process can be described as stochastic. Stochastic phenotypic expression, in and of itself, may not be disadvantageous. Indeed, it is a common strategy among organisms to survive harsh and changing environments via bet hedging (Balaban et al. 2004; Bull 1987; Donaldson-Matasci et al. 2008; Levins 1962; Ratcliff et al. 2015; Slatkin 1974). However, in a multicellular context stochastic changes in phenotype can be disadvantageous both to the cell and the organism (Balázsi et al. 2011). Put in this context, the evolutionary origins of developmental programs is intimately connected with the evolution of regulated—as opposed to stochastic—phenotypic expression.
Conditions that select for regulating phenotypic expression presupposes a need for at least two different phenotypes. To do this, models typically make use of two environmental states that preferentially select for one phenotype over the other: one environmental state selects for one phenotype and the other environmental state selects for the other phenotype (Acar et al. 2008; Balaban et al. 2004; Libby and Rainey 2011; Moran 1992; Thattai and van Oudenaarden 2004). If the environment fluctuates between these two states then there can be selection for genotypes with the capacity to switch between phenotypes. Depending on the nature of the environmental fluctuations, different switching strategies may be favored (Acar et al. 2008; Gaal et al. 2010; Lachmann and Jablonka 1996; Libby and Rainey 2011; Liberman et al. 2011; Salathé et al. 2009). Previous theoretical studies have investigated scenarios in which there might be some signal that indicates an environmental switch (Kussell and Leibler 2005; Levins 1963). Organisms that evolve to respond to this signal may outcompete those that switch stochastically, i.e. without regard to the signal (Kussell and Leibler 2005; Thattai and van Oudenaarden 2004). The relative benefit of switching according to a signal versus stochastic switching has been linked to many factors including the reliability (information content) of the signal, the cost of maintaining a regulated switch, the delay in switching between phenotypes, and the cost of being the wrong phenotype in an environment (Arnoldini et al. 2012; Donaldson-Matasci et al. 2010; Friedman et al. 2014; Geisel 2011; Kussell and Leibler 2005; Moran 1992; Thattai and van Oudenaarden 2004).
In these theoretical models, the signal that is linked to environmental fluctuations is external to the system and is typically abiotic. While there are important abiotic environmental fluctuations, e.g. the diurnal cycle, considering only such cases limits the possibility for evolving regulation. Organisms, as a result of their own growth and reproduction, modify environments and produce many reliable signals that indicate a changing environment (Laland et al. 1999; Moczek et al. 2011; Odling-Smee et al. 2013). For example, the consumption of resources and generation of waste products are reliable indicators of increasing population size and depleting environmental quality. Such ecological signals are abundant, reliable, and involve compounds familiar to the organism. As a consequence, these signals could be harnessed to help organisms decide when the environment has changed and it is time to disperse or generate spores (Fujita and Losick 2005; Garti-Levi et al. 2013; McDougald et al. 2011). If we assume an external restorative process that rejuvenates environments then responding to these signals could help organisms complete a life cycle. This added assumption may not be strictly necessary because some organisms induce intrinsic environmental oscillations.
One example of intrinsically induced environmental fluctuations are experimental populations of the bacterium Pseudomonas fluorescens (Rainey and Travisano 1998; Rainey and Kerr 2010). When grown in a laboratory microcosm, P. fluorescens establishes a cycle of environmental states and phenotypes. Initially, in liquid medium, smooth type cells (S) reproduce rapidly. Occasionally, they give rise to a mutant type, the wrinkly phenotype, that produces a costly extracellular glue. As a result of the population expansion, the liquid media becomes deplete of oxygen and the only available oxygen is at the surface of the microcosm. The wrinkly (W) types are able to colonize the air–liquid interface by constructing a mat. The mat niche expands and denies access to the S types in the liquid media underneath. As the W types reproduce they also yield mutants who do not produce the glue, effectively S phenotypes. Eventually the mat collapses under its own weight, condemning the W types to the bottom and mixing oxygen back into the media. The new S mutants escape into an environment similar to the original state (in practice, experimental regimes often place these new S types into fresh media completing the cycle). Since the P. fluorescens experimental system features an organism that switches between two states, one being strictly unicellular (S types) and one forming a physically connected group (W types), it has been used as a model to study the evolutionary origins of multicellularity. The wrinkly stage represents a multicellular body while the smooth stage is similar to a reproductive germ line as it has the capacity to eventually give rise to another multicellular group (Rainey and Kerr 2010).
The intrinsically induced environmental oscillations can also be viewed as a niche-constructing trait (Odling-Smee et al. 2003). When the smooth cell population is most abundant, consumption of oxygen results in a type of negative niche construction because the depleted resources shift the balance of fitness and allow wrinkly types to increase in frequency. Similarly, as wrinkly phenotypes construct a mat they initially benefit from its presence but ultimately pave the way for oxygen to be restored into the environment, which in turn, allows smooth cells to increase in frequency. Each organism conditions the environment for the other phenotype. As in other niche construction models, this permits coexistence of the two phenotypes (Odling-Smee et al. 2013). Furthermore, the combined effects of wrinkly and smooth niche construction can actually be adaptive. The resulting environmental oscillations select for genotypes that can readily switch between smooth and wrinkly types. Invading organisms must be able to adapt to these challenging, fluctuating conditions in order to be successful.
Initially in the P. fluorescens experimental system, phenotypes switch via mutations (Rainey and Travisano 1998; Rainey and Rainey 2003). However, repeated experimental evolution in this system has found the evolution of phenotypes that switch more rapidly via epigenetic mechanisms (Beaumont et al. 2009; Gallie et al. 2015; Hammerschmidt et al. 2014). Mathematical models show that because of the coupling between environmental oscillations and organismal populations, there is a single optimal stochastic switching frequency that is mostly independent of population size, the number of competing genotypes, the switching strategies of competitors, and the relative differences in growth rates of different types (Libby and Rainey 2013). Evolutionary models show that populations that evolve this optimal stochastic switching frequency create a niche of frequently oscillating environments which cannot be invaded by other switching or non-switching types (Libby and Rainey 2013). Although successful, this optimal stochastic switching strategy may not be the end point of the system’s evolution. Since the environmental fluctuations are driven by the organisms themselves, there are ecological signals that act as informative cues to predict environmental change such as population density, oxygen availability, and resource abundance. Strategies that use this information to regulate switching may be able to invade and replace stochastic switching strategies. This, however, assumes that the organisms can detect this information and use it appropriately. It is likely that the first instantiations of such regulation are noisy and rely on receptors poorly tuned to measuring information or translating it into action. It is unknown how tuned phenotypic regulatory mechanisms must be in order to be successful.
In this paper, we consider the P. fluorescens system and the potential for evolution of regulatory control of phenotype switching. We use mathematical models to compete switching strategies that use either the extracellular cue of population density or internal cues of cell history. We find that while both of these strategies might be able to outcompete the optimal stochastic switching strategy, there are significant differences in the amount of evolutionary tuning required to be successful. We also find that switching strategies under regulatory control have single optimal strategies within parameter space, suggesting that the fitness landscape of this system is single-peaked and cycles between strategies are unlikely. Ultimately, these results highlight the ecological and evolutionary opportunity in the P. fluorescens system for evolution of regulated phenotypic expression and thereby primitive developmental programs.
Materials and methods
To model competitions between modes of regulating phenotypic expression, we use differential equations that describe the population growth of SW genotypes in terms of their S and W phenotypes. This differential equation approach ignores random cell-level decisions in order to capture mean population-level behavior. Equations that represent different SW genotypes are independent except for a population density term, D, which corresponds to the total number of all organisms divided by the carrying capacity N, i.e. \(D= \frac{S+W}{N}\). This density term is used to enforce a carrying capacity, via the term \((1-D)\), common to logistic growth equations. We use Eq. 1 to compute the population growth of the SW genotype that switches without regard to informative signals (\(S_s\) and \(W_s\) for “stochastic”) in environmental state \(E_S\). Since these equations apply to growth in the \(E_S\) environmental state, there is a growth deficiency for W types described by the factor \(c_w\) where \(c_w<1\). The model assumes, for simplicity, that the switch rate \(p_s\) between S and W phenotypes is the same in both directions, i.e. the switch rates are symmetric.
Alternatively, the SW genotype that switches based on an external signal of population density (D) is modeled with Eq. 2. Here, \(S_e\) and \(W_e\) are the smooth and wrinkly phenotypes which reproduce at the same rate as those of the stochastic genotype. The key difference between Eqs. 2 and 1 is that the rate of switching is not constant. Instead, the SW genotype that relies on external signals switches according to a Hill function of the form \(p_e \frac{D^n}{D^n+\theta ^n}\). This functional form permits the frequency of switching to increase with increasing population density and reach a maximum value of \(p_e\). The Hill function has two other parameters: the Hill coefficient n and a threshold coefficient \(\theta \). The Hill coefficient n varies between 1 and 8 and determines the sharpness of the response such that higher n produce sharper responses. We call \(\theta \), which ranges from \(10^{-1}\) to 10, the threshold parameter because it largely determines when the switching rate increases—higher values of \(\theta \) correspond to delayed responses.
Finally, there is the mechanism of switching that relies on internal signals, whereby SW organisms switch phenotypes after a set number of reproductive events (called z). We model this by splitting both smooth and wrinkly phenotypes into subpopulations based on how many divisions they have undergone. So, for example, if phenotypes switch after three divisions (\(z=3\)) then there are three populations of S phenotype (\(S_{i1}\), \(S_{i2}\), and \(S_{i3}\)) and three populations of W phenotype (\(W_{i1}\), \(W_{i2}\), and \(W_{i3}\)). All S and W phenotypes reproduce at the same rate as in the stochastic SW genotype. Equation 3 shows the dynamics of the S and W subpopulations. When \(S_{i1}\) reproduces it yields an \(S_{i2}\) and an \(S_{i1}\) cell because one daughter cell continues the countdown to switching while the other starts at the beginning of the countdown. A similar case is true for \(W_{i1}\), \(S_{i2}\), and \(W_{i2}\). When either \(S_{i3}\) or \(W_{i3}\) reproduce they give rise to an \(S_{i1}\) and a \(W_{i1}\) cell because one daughter switches and the other keeps the same phenotype but with a fresh counter.
Each competition between switching strategies begins with a population of two genotypes, with one member of each, in the S phenotypic state growing in the \(E_S\) environmental state. The populations reproduce until they reach the carrying capacity, N (when \(D=1\)), and the environment switches states to \(E_W\). Since it is advantageous to have a larger investment in the phenotype that grows preferentially in \(E_W\), the genotype with the most W at the end of growth in \(E_S\) will have the advantage and “win” the competition. We could consider completing the full cycle with growth in \(E_W\) and transfer to \(E_S\) but as long as the switching rates are the same this would not affect which strategy wins. This follows from the fact that the strategy that won after growth in the first environment would have a numerical advantage to begin growth in the second environment. In this system, there is no frequency dependence of growth which means that a strategy cannot do better if it made up less of the population (Libby and Rainey 2013). For simplicity, we also assume that the W phenotype does not reproduce in \(E_S\) and thereby acts more like a spore. Previously, it was shown that the actual growth rate of the non-favored type does not alter the results as long as it is much slower than the favored type (Libby and Rainey 2013).
The evolutionary simulations used to generate Fig. 6 adopt an agent-based modeling approach with time discretized according to the generation time of S and W phenotypes. Each simulation begins with a single genotype that stochastically switches with probability \(p_s=10^{-4}\). Each time an organism reproduces there is the possibility of two types of mutations. First there is a probability of \(10^{-3}\) the organism mutates so that it switches according to the same mechanism but with different parameters. Alternatively, there is a probability of \(10^{-4}\) that the organism mutates and produces a genotype that switches according to a different mechanism. If the second type of mutation occurs then parameters are sampled from the following ranges: \([ 10^{-4},1 ]\) for \(p_s\) of stochastic switching strategies; \([ 10^{-4},1 ]\) for \(p_e\), \([ 10^{-3},10 ]\) for \(\theta \), and [1, 8] for n of external sensing strategies; and [1, 25] for z of internal sensing strategies. Non-favored types (W in \(E_S\) and S in \(E_W\)) grow at a quarter of the rate of favored types. When the population reaches the carrying capacity (\(N=10^7\)), ten organisms of the phenotype favored in the next environmental state are selected to seed growth in the next environment. This process is repeated for 1000 oscillations of \(E_S\) to \(E_W\) to \(E_S\).
Results
We model experimental populations of Pseudomonas fluorescens by extending a previously published model (Libby and Rainey 2013) in which environmental fluctuations are generated by populations of bacteria. The environment alternates between two states, \(E_{S}\) and \(E_{W}\). Switches between states occur when the total population of cells reaches a fixed number, N, the carrying capacity. In addition to the two environmental states, the bacteria also switch between two phenotypic states, S and W. We refer to the bacteria as “SW organisms” due to their capacity to generate both phenotypes from a single genotype. The S and W phenotypes differ in their reproductive performance in environmental states. S phenotypes grow faster than W phenotypes in environmental state \(E_S\) while the inverse is true in \(E_W\). To be competitive in this environment, SW organisms must balance growth (investment in the type favored in the current environment) with diversification (investment in the type favored in the next environment).
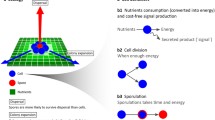
The mechanism of phenotype switching is the topic of investigation in this paper so it will differ depending on whether it is independent of an apparent signal (called “stochastic”), uses extracellular signals, or relies on intracellular signals (see Fig. 1). For the stochastic mechanism, we assume that switching between W and S phenotypes is random and occurs with a fixed rate or probability, \(p_s\), depending on whether the model is a set of continuous differential equations or a discrete time agent-based simulation (see “Materials and methods” section). To make communication easier, we will use “probability” preferentially over “rate” but it should be noted that the two are proportional. For the mechanism that uses extracellular signals (called “external sensing”), the probability of switching is modulated by a signal. Although in the actual experimental system there may be many extracellular signals available, we use population density (ratio of total population to the carrying capacity) which might be sensed directly or indirectly via a proxy like resource limitation. We assume that the probability of switching is modified by this information such that with increasing population density, the switch probability increases. Thus, we use a sigmoidal curve (the Hill curve) with three parameters to reflect this decision (for justification of sigmoid responses, see Perkins and Swain 2009). We could have considered a functional form with the inverse relationship, i.e. decreasing switch probability with increasing population density, but this would not be adaptive as it would lead to an over investment in the slow-growing phenotype early on when the populations should be focusing on growth rather than diversification. Finally, for the mechanism that relies on intracellular signals (called “internal sensing”), we use a record of a cell’s history so that cells switch after a certain number of reproductive events—a parameter of the model. This mechanism is similar to an internal oscillator (Thattai and van Oudenaarden 2004) and represents a type of memory which may occur via the internal accumulation of some molecule. This contrasts with the mechanism using extracellular signals because the cell has no information about the state of its extracellular environment. With appropriate tuning of its oscillator it may be able to synchronize with environmental fluctuations.
Schematic displaying the model framework. When organisms use a stochastic strategy, they switch between phenotypes at a constant probability \(p_s\) (blue curve on top right) that is independent of time or population density (“pop”). In contrast, cells that switch according to a mechanism that incorporates external signals, modulate the switch probability \(p_e\) according to population density—which can be sensed as the depletion of resources. As the population density increases, the switch probability increases in a sigmoidal fashion. Finally, there is a mechanistic model that uses internal signals from the organism’s reproductive history—which can be detected via the internal accumulation of some molecule. After a set number of divisions (z), the organism switches phenotypes and so the switch probability \(p_i\) equals 1. (Color figure online)
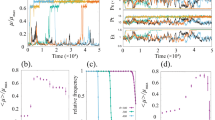
From previous analysis of the stochastic switching strategy (Libby and Rainey 2013), we know that there exists a single optimal probability of switching (\(p_s \approx 10^{-1}\)) that can invade all other strategies and avoid being invaded itself. To see if the mechanism that uses extracellular information can evolve within the context of an environment taken over by the optimal stochastic switching strategy, we compete the two strategies over a range of parameter values of the external sensing strategy (see “Materials and methods” section). Initially, we hold the Hill coefficient fixed at \(n=2\) and vary the threshold parameter (\(\theta \)) and the maximal switching probability (\(p_e\)). We find that there is an area of parameter space in which the external sensing mechanism beats the optimal stochastic strategy (see Fig. 2a). In general the parameter combinations that offer the largest magnitude of victory, i.e. the most W types to seed the \(E_W\) environment, have high values of \(p_e\) and \(\theta \) values between 0.1 and 1. This corresponds to a strategy that switches frequently just as the environment is about to change states. This reduces the cost of investing in the non-favored type (W in \(E_S\)) too early when its growth deficiency will hinder the growth rate of the population. It also ensures mass production of W types when they are most needed. If we compute the average switch probability over the course of population growth for external sensing strategies (Fig. 2b), we find that the parameter space where the external sensing strategy wins includes average switching probabilities both higher and lower than the optimal stochastic switching probability. Since both \(\theta \) and \(p_e\) can vary by a factor of ten and still beat the optimal stochastic switching strategy, the external sensing strategy does not require fine tuning (narrow area of parameter space) to be successful.
Competition between external sensing and stochastic strategies. a External sensing strategies are competed against the optimal stochastic strategy. The contour plot shows the proportion of W of the external sensing genotype for different combinations of the probability of switching and the value of \(\theta \). The carrying capacity is \(N=10^7\) and the Hill coefficient (n) is fixed at 2. The black line indicates the boundary between strategies that beat the optimal stochastic and those that lose. b Contour plot of the average switch probability (\(\log _{10}\)) over population growth for combinations of \(\theta \) and \(p_e\) for external sensing strategies (\(N=10^7\) and \(n=2\)). By increasing switch probability with increasing population size, the external sensing strategy can outcompete the optimal stochastic strategy over a larger range of average switch rates. c The best external sensing strategy parameters are shown as a function of the Hill coefficient. The probability of switching \(p_e\) (blue) and \(\theta \) (red) are relatively constant. The green points show the proportion of W types of the external sensing strategy compared to the optimal stochastic strategy. d The contour regions for strategies that beat the optimal stochastic strategy are shown for different Hill coefficients (n values). The \(n=1\) (blue) boundary encompasses the largest range of parameters \(p_e\) and \(\theta \). In contrast, the \(n=8\) strategy has the smallest region and requires a finer tuning of parameters. (Color figure online)
Another result of Fig. 2a is that there is a single optimal external sensing strategy in terms of its degree of winning over the stochastic strategy, i.e. the most W types to seed the \(E_W\) environment. This single optimal external sensing strategy adopts the maximum probability of switching in our parameter space (\(p_{e}\) = \(10^{-.1}\)) and a threshold coefficient \(\theta = .4\). This means that the population increases its switch probability to half maximal when the density is 40 % of the carrying capacity. This single optimal strategy is robust to changes in the Hill coefficient n (Fig. 2c) and enables the external sensing strategy to compose over 90 % of the W types at the end of growth in \(E_S\). In fact, as the Hill coefficient decreases there is a larger area of parameter space in which the external sensing strategy wins (see Fig. 2d). This means that a sharp response with a higher value of the Hill coefficient requires more tuning of parameters than a more gradual response represented by lower Hill coefficients (\(n=1\)).
While there are a range of parameters for which the external sensing strategy beats the optimal stochastic switching strategy, it is possible that there are other stochastic switching strategies that may fare better. To test this, we compete external sensing strategies against a range of stochastic switching strategies with probabilities of switching (\(p_s\)) between \(10^{-5}\) and \(10^{-.1}\) (data not shown). We find that if an external sensing strategy beats the optimal stochastic strategy then it beats all other stochastic switching strategies.
Once an external sensing strategy outcompetes a stochastic strategy and takes over the population, there could be a different set of external sensing strategies that perform better against other external sensing strategies. Stochastic strategies have a constant probability of switching and so over time there is a fixed proportion of the population that switches—this appears as a linear relationship in the differential equations (see “Materials and methods” section). In contrast, external sensing strategies alter the probability of switching with respect to population density, increasing it towards the end of growth in an environmental state. It could be that the dynamics of these competitions lead to different combinations of parameters being more successful. We test these possibilities in Fig. 3a by competing external sensing strategies against one another. The results show that the same parameter combinations that were effective against stochastic strategies also perform well against other external sensing strategies. Indeed, there is a single optimal external sensing strategy for the parameter combinations that we evaluated and this strategy is the same as the best performer against the optimal stochastic strategy. Though there is a single optimal external sensing strategy, it does not outcompete all other external sensing strategies by a large magnitude. There is a range of \(p_e\) and \(\theta \) values for which the optimal external sensing strategy makes up 50–60 % of the population. This indicates that there is not a sharp fitness peak but rather a plateau of effective sensing strategies.
Competition among external sensing strategies. a External sensing strategies are competed against other external sensing strategies over a range of \(p_{e}\) and \(\theta \) values (\(N=10^7\) and \(n=2\)). The contour plot shows the fraction of other strategies that a particular combination of \(p_{e}\) and \(\theta \) beat (1 being all other strategies and 0 being none). There is a single unbeatable strategy shown by the white dot which is the same strategy that performed best in terms of magnitude of victory against the optimal stochastic strategy. b The best external sensing strategy is competed against all other external sensing strategies. The contour plot shows the proportion of W-types from the optimal sensing genotype at the end of growth in \(E_S\). Although there is a single optimal sensing strategy there is a wide parameter space in which it makes up less than 60 % of the population, indicating that a range of other strategies perform similarly, i.e. the fitness landscape is not sharply peaked
Now we shift from considering the external sensing mechanism of switching to one that relies on internal information, switching every zth division. This internal sensing mechanism has only one parameter, z, which allows us to compete it against a range of stochastic switching strategies (see Fig. 4a). We find that when \(N=10^7\), there is a single optimal internal sensing strategy that beats all stochastic switching strategies. However, any other internal sensing strategy loses against some collection of stochastic switching strategies. This optimal z value for switching varies between 3 and 5 depending on the carrying capacity (see Fig. 4b). For a large range of carrying capacities, \(10^5\le N \le 10^9\), \(z=4\) is unbeatable. At \(N=10^4\) and \(N=10^{10}\), \(z=4\) is beaten by some stochastic strategies because it results in switching too slowly or too quickly, respectively—this explains why \(z=3\) and \(z=5\) supplant \(z=4\) at those values of N. When internal sensing strategies are competed against other internal sensing strategies, the optimal z value against stochastic switching strategies is again unbeatable (see Fig. 4c). In addition, the magnitude of this victory quickly increases as z moves away from the optimal so that \(z=4\) makes up more than 80 % of the W population compared to \(z=7\) when grown in \(E_S\).
Internal sensing strategies versus stochastic strategies and other internal sensing strategies. a A contour plot shows the proportion of W types for internal sensing strategies at the end of growth in \(E_S\) (\(N=10^7\)) when in competition with stochastic switching strategies. At \(z=4\) the internal sensing strategy is unbeaten for all stochastic switching strategies tested. The black line indicates the boundary where internal sensing strategies perform the same as stochastic strategies. b The optimal z value is shown as a function of the carrying capacity when the environment switches. For a wide range of carrying capacities there is a single optimal strategy that switches every fourth generation. c A contour plot shows the proportion of W types produced after growth in \(E_S\) of the optimal internal sensing strategy \(z=4\) at \(N=10^7\) when competed against other internal sensing strategies. The same z value is unbeatable against stochastic and other internal sensing strategies. As z moves away from the optimal, the proportion of W types rapidly increases in favor of the optimal z
The narrow range of parameter space for which internal sensing strategies outcompete stochastic strategies indicates that internal sensing strategies may not perform well against external sensing strategies. We test this hypothesis by competing a range of external sensing strategies (\(p_e\) and \(\theta \) are varied) against internal sensing strategies for z between 1 and 20 (see Fig. 5). The results show that the same parameter combinations with which external sensing strategies beat stochastic strategies are also unbeatable against internal sensing strategies, i.e. high \(p_e\) and \(\theta <1\).
Internal sensing versus external sensing strategies. The proportion of internal sensing strategies beaten (\(1 = \hbox {all}\)) is shown as a function of two parameters for external sensing strategies, \(p_e\) and \(\theta \) (\(N=10^7\) with a Hill coefficient of 2). The parameter combinations that allow external sensing strategies to beat stochastic strategies are also successful against internal sensing strategies (top left high \(p_e\) and \(\theta <1\)). Above the black line, external sensing strategies beat all internal sensing strategies
Thus far, we have considered scenarios in which competing strategies start at equal numbers. In reality, strategies that arise via mutation and fix must be able to invade when rare. Moreover, they must be able to survive the selective pressures of the niche constructed by the resident genotypes, namely oscillating environments at a certain frequency. To see how mechanisms with regulatory control fare in such a scenario we use evolutionary simulations (see “Materials and methods” section). Initially each simulation begins with a uniform population that switches stochastically with \(p_s=10^{-4}\). With each reproductive event there is a chance of generating a mutant with different parameter values but employing the same mechanism of switching. There is also a smaller probability of producing a mutant that switches according to a different mechanism. We run these simulations through 1000 environmental cycles of growth in \(E_S\) and growth in \(E_W\). As the environment changes, ten members of the population are chosen randomly to survive passage to the next environmental state. Types that are not favored in the current environment reproduce at 25 % the rate of favored phenotypes.
With this setup, we find that over time all simulations become dominated by external sensing strategies (Fig. 6a). Internal sensing strategies appear during growth in environments but because they require fine tuning of parameters they are unable to successfully invade and survive the transition to the next environment. Ultimately, by the 1000th environmental oscillation, all simulations have the majority genotypes using external sensing mechanisms to regulate switching. The parameter values of these genotypes are not the same but vary within the ranges found to be successful in previous competitions (see Fig. 6b). The \(p_e\) values are all high, above \(10^{-1}\), and the \(\theta \) values are all much less than 1. The Hill coefficients (n) show more variation but this is likely due to the fact that they are less significant in terms of the performance of the external sensing strategy.
Evolutionary simulations. a The proportion of the population selected for transfer to the next environmental state of the three mechanisms of switching (stochastic, external sensing, and internal sensing) is shown over the course of environmental oscillations for 100 evolutionary simulation runs. All simulations begin with stochastic switching strategies (red) but over time external switching strategies (blue) invade and replace them. Internal sensing strategies (green) are present during growth in environmental states but are rarely at high enough frequency to be selected for passage to the next environmental state. b The parameter values for the majority genotype of the population at the end of each simulation is shown. All simulations ended with an external sensing strategy as the majority genotype. The \(p_e\) values (blue) are all above \(10^{-1}\) and the \(\theta \) values are all less than 1. The n values tend to be above 1 although this could be due to the sampling interval for n values which was between 1 and 8
Discussion
Multicellular organisms rely on developmental programs that regulate expression of different phenotypes to coordinate growth and reproduction. Yet, the evolutionary origins of these programs are unknown. We consider a hallmark feature of developmental programs to be the linking of phenotypic expression to a signal. To determine if this type of regulation can displace stochastic switching strategies we consider experimental populations of Pseudomonas fluorescens which evolved stochastic switching in the lab (Beaumont et al. 2009). Using mathematical models we compare the performance of two types of phenotypic regulation, using external or internal cues, against stochastic strategies in an oscillating environment constructed by the organisms themselves. We find that both strategies can beat the stochastic strategy for certain combinations of parameters. The difference between them is that the external sensing strategy requires far less refinement of parameters and is therefore more likely to evolve. We demonstrate this increased likelihood with evolutionary simulations in which populations that initially rely on stochastic switching are soon taken over by external sensing strategies. These results show that the selective benefit of regulated phenotypic expression and its robustness to mechanistic parameter choices (in external sensing strategies) is sufficient to permit the evolutionary origin of primitive developmental programs.
One reason for the success of the external sensing strategy is the quality of information contained in the environmental cue. In our model, the population density is a perfect indicator of when the environment switches. Thus, a strategy that is able to use this information, even imperfectly, will have an advantage against strategies that do not use this information, e.g. internal sensing and stochastic strategies. This explains why external sensing requires little tuning in order to be successful against other strategies. It is likely that this would be less true if the environmental cue were not a perfect indicator. Indeed, in the extreme case in which there is no available reliable signal, stochastic switching strategies are expected to prevail (Balaban et al. 2004; Thattai and van Oudenaarden 2004). In such environments, stochastic switching allows organisms to bet hedge without the need to maintain potentially complex regulatory control.
Internal sensing strategies, in contrast, do not enjoy the benefit of either stochastic switching or external sensing mechanisms. They do not make use of an information source which is well-correlated with environmental change and they require careful tuning to perform well. This may be responsible for their rarity in extant biological systems. Organisms that use similar strategies, e.g. volvocine algae (Kirk 1998), often have other features such as physically connected cells. This spatial structure can be built reliably by internal sensing strategies and without any additional information. It may be that in assembling physical structures, these programs have advantages over other regulatory mechanisms. In the system considered here, however, without spatial structure and where responding to environmental change is instrumental to survival, external sensing strategies perform best.
For both internal and external sensing mechanisms, we considered only one type of regulation with specific subtleties in implementation that might affect performance. For example, the internal sensing strategy always generates one daughter cell with an initialized setting for the internal clock, z divisions away from switching. This is but one implementation of such a mechanism as it could also be valid that the internal clock is set randomly somewhere between 0 and z or set to the same stage as the parent cell. Another implementation choice was for switching to occur during reproductive events. This was done under the assumption that DNA replication is a source of genetic mutations, but it could be the case that cells switch continuously. In this case, one effective strategy would be for all cells to switch to the type favored in the next environmental state just as the environment changes. We would still expect external sensing to be successful with such an implementation but it could change the range of winning parameters. In addition to changes in implementation of these switching mechanisms, there are other types of mechanisms that regulate phenotypic expression which might be likely to evolve. For instance, switching could be mediated by quorum sensing molecules or the density of different phenotypes in a local environment (assuming some form of spatial structure). Such mechanisms would allow subpopulations of cells to coordinate their behavior and may be effective in competition against other mechanisms. While consideration of a range of these mechanisms lies outside the scope of this paper, it would be interesting to understand the conditions under which each regulatory mechanism may evolve.
Even though our model and simulations show from a selective point of view how primitive developmental programs might evolve, we do not address the molecular details. It is unknown by what means a mutation may bring a stochastic response under regulatory control (Moczek et al. 2011). Certainly, it would depend on the genetic architecture and background of the genotype. If there existed a way of sensing a proxy for population density (say nutrient concentration) and the genotype could already produce two phenotypes, then there is potential for linking these two systems. Although we cannot say how this comes about, our results show that even early, imperfect systems that link information sensing to phenotypic expression have the potential to outcompete purely stochastic strategies. To run the evolutionary simulations we needed some estimate of the frequency of mutations that change the type of regulatory control. We assumed that these mutations occur a factor of 10 less often than mutations that tune the regulation without changing its mode of operation. It could be that these mutations are rarer, but even so, given enough time and evolutionary opportunity the simulations show that they would be able to outcompete stochastic strategies.
In this paper, we considered the evolution of regulated phenotype expression which requires a system that expresses at least two phenotypes. We chose a particular experimental system, Pseudomonas fluorescens, in which two phenotypes must be produced in order to complete a life cycle. This is not the only system with selection favoring expression of two phenotypes. Indeed, there are many other types of arrangements in which an organism might benefit from producing two phenotypes without necessarily progressing through a life cycle. Filamentous cyanobacteria, for instance, produce heterocysts along with vegetative cells in order to fix nitrogen and survive oxic conditions (Zhang et al. 2006). Although our modeling does not consider the gamut of such systems, our differential equation models may be adapted to fit a subset of these cases. For example, if heterocysts do not reproduce but rather help vegetative types grow faster then we could transform Eq. 1 into Eq. 4 with the modifications shown in brackets and the \(S_s\) terms representing vegetative cells and the \(W_s\) terms representing heterocysts.
Interestingly, if the [0] term is changed to an [S s ] in Eq. 4 then the equations would describe a mutualism between different species in which it costs each organism reproductive potential to produce a benefit for the other. This could be used to understand how mutualistic interactions could be regulated. Thus, while the experimental system we consider is a limited case, our framework is plastic enough to analyze other types of interactions.
A caveat to our model system is that it only considers two phenotypes. In other systems or organisms, such as animals, multicellular developmental programs must regulate expression of hundreds of phenotypes. Based on our results, it would be advantageous for organisms to find and use reliable sources of information. Since environments may not provide enough information sources on their own, one solution that is commonly used by multicellular organisms is to produce the information sources themselves (Davidson 2001; Donohue 2005; West-Eberhard 2003). As the multicellular organism grows and develops from a single cell, it synthesizes and transmits molecules that may be harnessed by cells for spatial and temporal information. The developmental program, therefore, encodes both construction of a niche and appropriate phenotypic expression at times and places in the niche. These more complex forms of regulation require larger coordination among cells and are rare if non-existent in unicellular organisms. It could be that their evolution may be intimately tied to the evolution of multicellularity, itself.
References
Acar M, Mettetal JT, van Oudenaarden A (2008) Stochastic switching as a survival strategy in fluctuating environments. Nat Genet 40:471–475
Arnoldini M, Mostowy R, Bonhoeffer S, Ackermann M (2012) Evolution of stress response in the face of unreliable environmental signals. PLoS Comput Biol 8(8):e1002627. doi:10.1371/journal.pcbi.1002627
Balázsi G, van Oudenaarden A, Collins JJ (2011) Cellular decision-making and biological noise: from microbes to mammals. Cell 144(6):910–925
Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S (2004) Bacterial persistence as a phenotypic switch. Science 305:1622–1625
Beaumont HJE, Gallie J, Kost C, Ferguson GC, Rainey PB (2009) Experimental evolution of bet hedging. Nature 462:90–93
Bull JJ (1987) Evolution of phenotypic variance. Evolution 41:303–315
Buss LW (1987) The evolution of individuality. Princeton University Press, Princeton
Davidson EH (2001) Genomic regulatory systems. Academic Press, New York
Donaldson-Matasci MC, Lachmann M, Bergstrom CT (2008) Phenotypic diversity as an adaptation to environmental uncertainty. Evol Ecol Res 10:493–515
Donaldson-Matasci MC, Bergstrom C, Lachmann M (2010) The fitness value of information. Oikos 119:1–31
Donohue K (2005) Niche construction through phenological plasticity: life history dynamics and ecological consequences. New Phytol 166(1):83–92
Friedman G, McCarthy S, Rachinskii D (2014) Hysteresis can grant fitness in stochastically varying environment. PLoS One 9(7):e103241
Fujita M, Losick R (2005) Evidence that entry into sporulation in Bacillus subtilis is governed by a gradual increase in the level and activity of the master regulator Spo0A. Genes Dev 19(18):2236–2244
Gaal B, Pitchford JW, Wood A (2010) Exact results for the evolution of stochastic switching in variable asymmetric environments. Genetics 109:113431
Gallie J, Libby E, Bertels F, Remigi P, Jendresen CB, Ferguson GC et al (2015) Bistability in a metabolic network underpins the de novo evolution of colony switching in pseudomonas fluorescens. PLoS Biol 13(3):e1002109
Garti-Levi S, Eswara A, Smith Y, Fujita M, Ben-Yehuda S (2013) Novel modulators controlling entry into sporulation in Bacillus subtilis. J Bacteriol 195(7):1475–1483
Geisel N (2011) Constitutive versus responsive gene expression strategies for growth in changing environments. PLoS One 6(11):e27033
Grosberg RK, Strathmann RR (1998) One cell, two cell, red cell, blue cell: the persistence of a unicellular stage in multicellular life histories. Trends Ecol Evol 13(3):112–116
Hammerschmidt K, Rose CJ, Kerr B, Rainey PB (2014) Life cycles, fitness decoupling and the evolution of multicellularity. Nature 515(7525):75–79
Kirk DL (1998) Volvox: molecular-genetic origins of multicellularity and cellular differentiation. Developmental and cell biology series. Cambridge University Press, Cambridge
Kussell E, Leibler S (2005) Phenotypic diversity, population growth, and information in fluctuating environments. Science 309:2075–2078
Lachmann M, Jablonka E (1996) The inheritance of phenotypes: an adaptation to fluctuating environments. J Theor Biol 181(1):1–9
Laland KN, Odling-Smee FJ, Feldman MW (1999) Evolutionary consequences of niche construction and their implications for ecology. PNAS 96(18):10242–10247
Levins R (1962) Theory of fitness in a heterogeneous environment. I. The fitness set and the adaptive function. Am Nat 96:361–373
Levins R (1963) Theory of fitness in a heterogeneous environment. II. Developmental flexibility and niche selection. Am Nat 97:75–90
Libby E, Rainey PB (2011) Exclusion rules, bottlenecks and the evolution of stochastic phenotype switching. Proc Biol Sci 278(1724):3574–3583
Libby E, Rainey PB (2013) Eco-evolutionary feedback and the tuning of proto-developmental life cycles. PLoS One 8(12):e82274
Liberman U, Van Cleve J, Feldman MW (2011) On the evolution of mutation in changing environments: recombination and phenotypic switching. Genetics 187(3):837–851
McDougald D, Rice SA, Barraud N, Steinberg PD, Kjelleberg S (2011) Should we stay or should we go: mechanisms and ecological consequences for biofilm dispersal. Nat Rev Microbiol 10(1):39–50
Minelli A, Fusco G (2010) Developmental plasticity and the evolution of animal complex life cycles. Philos Trans R Soc Lond B Biol Sci 365:631–640
Moczek AP, Sultan S, Foster S, Ledón-Rettig C, Dworkin I, Nijhout HF, Abouheif E, Pfennig DW (2011) The role of developmental plasticity in evolutionary innovation. Proc Biol Sci 278(1719):2705–2713
Moran NA (1992) The evolutionary maintenance of alternative phenotypes. Am Nat 139(5):971–989
Odling-Smee FJ, Erwin D, Palkovacs E, Feldman MW, Laland KN (2013) Niche construction theory: a practical guide for ecologists. Q Rev Biol 88:3–28
Odling-Smee FJ, Laland KN, Feldman MW (2003) Niche construction. The neglected process in evolution. Monographs in Population Biology 37. Princeton University Press, Princeton
Perkins TJ, Swain PS (2009) Strategies for cellular decision-making. Mol Syst Biol 5:326
Rainey PB, Travisano M (1998) Adaptive radiation in a heterogeneous environment. Nature 394:69–72
Rainey PB, Rainey K (2003) Evolution of cooperation and conflict in experimental bacterial populations. Nature 425(4):72–74
Rainey PB, Kerr B (2010) Cheats as first propagules: a new hypothesis for the evolution of individuality during the transition from single cells to multicellularity. BioEssays 32:872–880
Ratcliff WC, Hawthorne P, Libby E (2015) Courting disaster: how diversification rate affects fitness under risk. Evolution 69(1):126–135
Salathé M, Van Cleve J, Feldman MW (2009) Evolution of stochastic switching rates in asymmetric fitness landscapes. Genetics 182:1159–1164
Schlichting CD (2003) Origins of differentiation via phenotypic plasticity. Evol Dev 5(1):98–105
Slatkin M (1974) Hedging one’s evolutionary bets. Nature 250:704–705
Thattai M, van Oudenaarden A (2004) Stochastic gene expression in fluctuating environments. Genetics 167:523–530
West-Eberhard MJ (2003) Developmental plasticity and evolution. Oxford University Press, Oxford
Wolpert L (1990) The evolution of development. Biol J Linn Soc 39(2):109–124
Zhang CC, Laurent S, Sakr S, Peng L, Bédu S (2006) Heterocyst differentiation and pattern formation in cyanobacteria: a chorus of signals. Mol Microbiol 59(2):367–375
Acknowledgments
Funding for EW is provided by the Santa Fe Institute REU Program which is supported by the National Science Foundation under Grant Number ACI-1358567. The authors thank Paul Rainey and anonymous reviewers whose feedback greatly improved this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wolinsky, E., Libby, E. Evolution of regulated phenotypic expression during a transition to multicellularity. Evol Ecol 30, 235–250 (2016). https://doi.org/10.1007/s10682-015-9814-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10682-015-9814-3