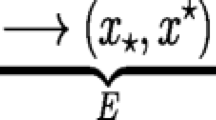Abstract
Changes in the seasonal timing of life history events are documented effects of climate change. We used a general model to study how dispersal and competitive interactions affect eco-evolutionary responses to changes in the temporal distribution of resources over the season. Specifically, we modeled adaptation of the timing of reproduction and population dynamic responses in two competing populations that disperse between two habitats characterized by an early and late resource peak. We investigated three scenarios of environmental change: (1) food peaks advance in both habitats, (2) in the late habitat only and (3) in the early habitat only. At low dispersal rates the evolutionarily stable timing of reproduction closely matched the local resource peak and the environmental change typically caused population decline. Larger dispersal rates rendered less intuitive eco-evolutionary population responses. First, dispersal caused mismatch between evolutionarily stable timing of reproduction and local resource peaks and as a result, reproductive output for subpopulations could increase as well as decrease when resource availability underwent temporal shifts. Second, population responses were contingent on competition between populations. This could accelerate population declines and cause extinctions or even reverse population trends from negative to positive compared to the low dispersal case. When dispersal rate was large and the early resource peak was advanced available niche space was reduced. Hence, even when a population survived the environmental change and obtained positive equilibrium population density, subsequent adaptation of competing populations could drive it to extinction due to convergent evolution and competitive exclusion. These results shed new light on the role of competition and dispersal for the evolution of timing of life history events and provide guidelines for understanding short and long-term population response to climate change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The importance of the timing of seasonal activities in relation to abiotic conditions and ecological interactions, e.g. in relation to food resources, has been empirically demonstrated in several taxa (Thomas et al. 2001; Visser and Both 2005; Inouye 2008). Several bird species with seemingly similar niches do, for example, respond differently to temporal change in their resources (Visser et al. 1998; Cresswell and McCleery 2003; Charmantier et al. 2008; Both et al. 2009; Bauer et al. 2010). It has also been shown that advancements in the temporal distribution of resources can lead to mistimed reproduction with subsequent negative fitness consequences (Both et al. 2006).
A rapidly growing body of theory (reviewed in Johansson et al. 2015b) is devoted to the task of better understanding and interpreting patterns of phenological change.
Recent theoretical studies have, for example, explored the role of territory competition (Johansson and Jonzén 2012a, b; Day and Kokko 2015), stochastic environmental variation (Lof et al. 2012) and intraspecific competition (Reed et al. 2015) for phenological adaptations to climate change. These studies highlight the complex causalities between environmental change, local population dynamics, ecological interactions and trait evolution (see also Ferriere et al. 2004; Johansson 2008; Kokko 2011). The abiotic and biotic properties of the environment and their spatial distribution also affect species distributions. The complexity thus becomes even more prominent when the spatial structure of the environment is considered (Urban et al. 2012).
The spatial dimension has with a few exceptions (see e.g. Revilla et al. 2015) received little attention in the development of phenology theory. Ignoring the role of space in phenological studies is potentially crucial, since it is well known that climate change influences both the geographic distribution of species as well as the timing of seasonal events (e.g. Parmesan 2006) and these two types of changes may influence each other. As an example, based on process-based vegetation models, Chuine (2010) argued that phenology is one of the most important traits that defines a species niche and shapes its spatial distribution. Geographic variation in phenological responses to temperature changes has also been documented (e.g. Visser et al. 2003; Both et al. 2004; Both and te Marvelde 2007).
Here we build on our increased knowledge about how timing of life history events evolve in dynamic eco-evolutionary models (e.g. Johansson and Jonzén 2012a, b; Reed et al. 2015) to develop theory for how populations respond on ecological and evolutionary time scales to phenological change in spatially structured communities. We used adaptive dynamics theory (Geritz et al. 1998) and a general two-patch model for geographically distributed competitive populations, inspired by Kisdi (2002) and Brown and Pavlovic (1992), to study phenological adaptation on an evolutionary time scale as well as more short-term population dynamic responses to temporal shifts in resource availability. Compared to the network theory approach to study effects of phenological change in metacommunities used by Revilla et al. (2015) in which only the presence/absence of species is considered, we explicitly studied the changes in equilibrium population densities. The model used here is less mechanistic than process-based models of phenological change (reviewed by Chuine 2010) and therefore less species-specific, more transparent and easier to link to previous general theory on metacommunity dynamics (e.g. Kisdi 2002; Pontarp et al. 2012). Critically, in contrast to these previous studies, we here explored the long-term evolutionary consequences of shifting phenologies in spatially distributed communities.
Specifically, we here studied how the eco-evolutionary response in the timing of reproduction to environmental change is affected by extrinsic factors such as the type (symmetric or asymmetric changes between patches) and strength (magnitude) of the temporal shift in resource phenology. We also investigated the effects and intrinsic properties of the model organism such as dispersal rate and niche width. Our results allowed us to extend the current theory for the link between the evolutionary stable baseline and adaptation in the timing of life history traits and population dynamics during phenological resource shifts.
Model and methods
Inspired by Kisdi (2002) we assume that individuals of two asexual and therefore reproductively isolated populations or species (i = 1, 2) occupy two habitats (j = A, B) connected by passive dispersal [see also Brown and Pavlovic (1992) for a similar modelling approach]. We also assume a non-fluctuating environment and contrary to Kisdi (2002) we use a fixed, non-evolving dispersal rate. We define populations as a group of individuals having a similar ‘habitat-specialization’ trait referred to by Kisdi (2002). The different populations are otherwise equivalent and compete with equal efficiency for common resources.
The model is formulated such that the timing of life history traits (e.g. reproduction) corresponds well with the ‘habitat-specialization’ trait in Kisdi (2002). In this particular case we thus define populations according to their timing of reproduction. Reproductive success (fitness) is determined by the temporal mapping between reproduction and the occurrence of some relevant resource (e.g. leaf bud burst or insect density). As an example one could imagine a northern and a southern habitat in a temperate region where the peak of, for example, insect density occurs at different times of the year. Also, due to a trade-off in reproductive success between the habitats, populations that match its reproduction to the resource in the southern habitat have lower fitness in the northern habitat and vice versa (Fig. 1).
A three dimensional illustration of the model. Density-independent potential reproductive output in two spatially distinct habitats A (black line) and B (gray line) modelled as Gaussian functions. The Gaussian functions can also be interpreted as the amount of resources available in each habitat at different time of the year. Population 1 reproduces early (e.g. early spring) and is optimally adapted to habitat A resulting in an abundant subpopulation in A (1,A) and a less abundant subpopulation of dispersers in B (1,B). Population 2 reproduces late (e.g. late in spring) and is optimally adapted to habitat B resulting in an abundant subpopulation in B (2,B) and a less abundant subpopulation of dispersers in A (2,A)
Below we present the model in detail, the adaptive dynamics approach (Geritz et al. 1998) that underpin our analysis, and a description of the environmental change scenarios for which we studied the eco-evolutionary responses.
Reproduction, offspring survival and recruitment
We assume that the resource level within each habitat is distributed around some date in the season according to a Gaussian function with a resource peak at time d, and that reproductive output (λ) is a function of how well the timing of reproduction (x, time away from the peak) matches the resource. Expected reproductive output a given year for an individual of population i in habitat j is then given as:
where a + c and c represent maximal and minimal reproductive output (number of young produced), respectively. The parameter d j represents the optimal time for reproduction in habitat j, henceforth referred to as the resource peak. The more the trait value x (timing of reproduction) deviates from the optimal timing, the poorer the reproductive output. The width parameter σ describes how the reproductive output of a given population declines as its timing of reproduction deviates from the optimal one (in this case according to a Gaussian function). The parameter σ determines, in other words, the trade-off between fitness in different habitats—the decrease in reproductive output due to increased deviation from the resource peak. Note also that σ can be viewed as either the width of the temporal distribution of resources or as niche width of the population. We will refer to it as niche width, ultimately affecting the trade-off in fitness between patches.
We let N j (x) denote the density of individuals with trait x in habitat j. We assume that the proportion surviving young is dependent on the density of all individuals competing for the same resources in the habitat regardless of their trait value, according to
where β (here set to 1) determines maximum survival and b controls the strength of density dependence. N i,j denotes the density of individuals of population i in habitat j and the vector N = [N 1,A N 1,B N 2,A N 2,B]. Finally, the per capita recruitment rate of population i to the subpopulation in habitat j, is modelled as the product of reproductive output and offspring survival i.e.
Population dynamics
Population growth rates are assumed to depend on reproduction and juvenile survival (Eqs. 1–3) and are expressed as follows:
where t represents time (year). Furthermore, the parameter s represents annual survival rate of adult individuals, including the new recruits, regardless of population and habitat and the parameter m is the density-independent passive dispersal rate between the two habitats. Throughout our analyses the default setting of the parameters is: β = 1, a = 1000, d A = 0, d B = 1, σ = 0.6, c = 1, m = 0.25, s = 0.2. We let m and σ vary between 0.01–0.4 and 0.3–0.8, respectively, to investigate the influence of the degree of interconnectivity between the habitats and niche width. The equilibrium population densities were calculated by iterating Eqs. 4 until N reached a stable distribution, denoted as N*.
Evolutionary analysis
We assume that the timing of reproduction, x, is under selection with the potential to evolve as a response to environmental change. The point of departure for our investigations is a system with a set of resident traits and we ask whether this set can be invaded by a mutant strategy through adaptive evolution. In order to do so, we calculate the invasion fitness (per capita growth rate) of a mutant alternative strategy x′ attempting to invade a community with resident strategies x = [x 1, x 2]. Following the adaptive dynamics framework (Geritz et al. 1998) the resident populations are assumed to be at equilibrium between invasion attempts, and we study only the growth of a rare mutant population that does not influence the competitive environment. In this model, this means that the reproductive output depends on the resident population densities (N*) only. We let the habitat-specific densities of a mutant population with trait x’ be denoted by n A and n B. Following from Eqs. 4 the growth rate of the mutant population then corresponds to:
To emphasize that the resident equilibrium populations depend on the trait distribution however, we write them as \({\mathbf{N}}^{\varvec{*}} \left( {\mathbf{x}} \right)\) in Eqs. 5, but note that they are assumed to be independent of time (t) during the invasion process. By letting \({\mathbf{n}} = [n_{\text{A}} ,n_{\text{B}} ]\) be the vector of mutant population densities the dynamics of the mutant can thereby be written in matrix form as:
where \({\mathbf{M}}\left( {x^{'} ,{\mathbf{N}}^{\varvec{*}} \left( {\mathbf{x}} \right)} \right)\) is the time-independent matrix:
Following Kisdi (2002) (see also Metz et al. 1992; Geritz et al. 1998; Caswell 2001) the invasion fitness then corresponds to the dominant eigenvalue of \({\mathbf{M}}\left( {x^{'} ,{\mathbf{N}}^{\varvec{*}} \left( {\mathbf{x}} \right)} \right).\) If the dominant eigenvalue is >1 it means that the initially rare mutant strategy attempting to invade has positive population growth rate and thus can invade, else it cannot. By relabeling the (time-independent) entries of M and for brevity omitting their arguments according to
we then calculate the dominant eigenvalue as:
Following McGill and Brown (2007) we define the evolutionary stable strategy (ESS) for the timing of reproduction (x*) as a trait distribution that cannot be invaded by any other strategy and can be approached by a series of small mutational steps (convergence stability Eshel et al. 1997). The ESS distribution can be thought of as adaptive peaks that are likely to be reached by gradual evolution. The dominant eigenvalue (growth rate of the mutant) is used to calculate the selection gradient for the resident strategies. Candidate ESS trait distributions are found when the selection gradient is equal to zero. The model contains ESSs consisting of either one or two species (cf. Kisdi 2002). For the single species case, and for a population with trait x the selection gradient is:
The single species ESS \(x^{*}\) is found where H(x) = 0 provided it fulfils the condition for (local) invasion resistance:
and the condition for convergence stability:
An alternative outcome to ESS is an evolutionary branching point which occurs when the condition in Eq. 9 is reversed and Eq. 10 holds (Geritz et al. 1998). For the two species cases we found ESS trait distributions by numerically solving the system of equations \(H\left( {x_{i} } \right) = 0\) for i = 1, 2 and by checking whether these point were resistant to invasions and convergent stable using generalisations of Eqs. 9 and 10 to multiple traits (Leimar 2009; Ravigné et al. 2009).
Evolutionary and ecological equilibrium
The settings of the model parameters determine the evolutionary stable trait distribution as well as the equilibrium population densities. In essence both evolutionary and ecological equilibrium can be understood through factors such as differences among habitats and dispersal propensity and niche width of the model organisms. In this section we provide an argumentative explanation of such effects (see also illustration in Fig. 1).
Due to passive dispersal, some well adapted individuals of population 1, specializing on habitat A, are also found in habitat B (and vice versa). Individuals of population 1 in habitat B have low reproductive output, and hence subpopulation 1,B is largely maintained by dispersal from habitat A (and vice versa for population 2) (Holt 1996). The equilibrium population density and the location of the ESS(s) are influenced by the distance between the resource peaks (|d A − d B|), the width of the resource distribution (σ) and dispersal rate (m). If the distance between peaks is small or if the niche width is large, a generalist ESS is expected. Long distance between peaks and narrow niche width, on the other hand, lead to a specialist ESS (Brown and Pavlovic 1992; Kisdi 2001, 2002). Secondly, dispersal affects population dynamics by connecting patches and determines to which extent a population encounters different environments and, hence, whether a specialist or generalist strategy is favored (Brown and Pavlovic 1992; Kisdi 2002). Figure 2 illustrates how dispersal rate (m) and niche width (σ) affect the equilibrium density(Fig. 2c, d) as well as the ESS solution(Fig. 2a, b). When dispersal rate increases or when niche width increases, the difference between two ESS strategies decreases to a point where there is only a single generalist population at ESS, halfway between the two resource peaks (Fig. 2).
Evolutionary stable strategy (ESS) distribution (a, b) and equilibrium population density for the four subpopulations (1,A; 1,B; 2,A and 2,B) (c, d) for different dispersal rates (m) and niche widths (σ). Dotted lines show the resource peak position in trait space. Default parameter values, if nothing else is stated: ∆d = 1, σ = 0.6, m = 0.25. For visibility the black lines in panels c and d are shifted vertically
Scenarios of environmental change and eco-evolutionary analysis
We investigate the responses in population density and the adaptive changes in trait values assuming three different scenarios of temporal shifts in resource availability in the form of (instantaneous) shifts of the resource distributions along the time axis (Fig. 3, top). In scenario 1 the resource peaks in both habitats undergo shifts of equal magnitude towards earlier dates. In scenario 2 only the resource peak in the late (“northern”) habitat (B) advances and in scenario 3, only the resource peak in the early (“southern”) habitat (habitat A) advances. For each of these scenarios, short-term ecological and long-term evolutionary responses were analysed. We assume that the populations are in ecological and evolutionary equilibrium prior to environmental change. As measures of short-term ecological change we use changes in equilibrium population density for the four subpopulations (1,A; 1,B; 2,A and 2,B) without allowing for any concomitant adaptive changes in the timing of reproduction. Our measure of long-term evolutionary responses were changes in the ESS values.
Change in equilibrium population density as a function of environmental change (∆d i) for the four subpopulations (1,A; 1,B; 2,A and 2,B), calculated as % of population density at equilibrium before change. Two different dispersal rates (m) 0.1 (a, b, c) and 0.4 (d, e, f) for different change scenarios. Where the scenarios are defined as: Scenario 1 Resource distribution is switched to earlier dates in both habitats. Scenario 2 Resource distribution in B (northern hab.) is switched towards A (south). Scenario 3 Resource distribution in A is switched away from B. Default parameter values, if nothing else is stated: ∆d = 1, σ = 0.5, m = 0.25
Results
Short-term ecological change
A symmetric change in resource phenology, according to scenario 1, caused a reduction in reproductive output (Eq. 1) in all subpopulations, except for the subpopulation of population 1 in suboptimal habitat B (1,B) (Table 1; cf. Fig. 1). When dispersal is low there was a direct correspondence between the changes in reproductive output and the resulting population trends: all subpopulations decreased except subpopulation 1,B that increased (Fig. 3a). This was caused by a increased mismatch between the timing of reproduction and the resource peak in all subpopulations except 1,B. When dispersal rate was high the well adapted subpopulation 1,A also increased (Fig. 3d), although reproductive output in this subpopulation has decreased. This was partly due to individuals from the increasing subpopulation 1,B dispersing into habitat A. It is also due to decreased competition from subpopulation 2,A which decreased in abundance.
In scenario 2, only the optimal timing of reproduction in one patch (B, “the late one”) advanced. As a consequence, the similarity in the timing of the resources peaks between patches increased. Reproductive output increased in the subpopulation of population 1 in suboptimal habitat B (subpopulation 1,B) and decreased in the well adapted subpopulation 2,B (Table 1; cf. Fig. 1). This was reflected in an increase of subpopulation 1,B and a decrease in subpopulation 2,B (Fig. 3b). Due to changes in rates of immigration from these two subpopulations, the well adapted subpopulation 1,A increased and the maladapted subpopulation 2,A decreased. The changes in subpopulations 1,A and 2,A were reinforced by competitive release for population 1 and increased competition with population 2 (changed survival, Table 1). There was no qualitative difference when dispersal increased, but with high enough dispersal the negative population trends became stronger (Fig. 3e).
Finally, in scenario 3 where the optimal timing for reproduction in patch A (“the early one”) was advanced, reproductive output decreased for both subpopulations 1,A and 2,A (Table 1; cf. Fig. 1). This was reflected in a decrease in these two subpopulations when dispersal was low (Fig. 3c). When subpopulation 1,A decreased subpopulation 1,B also decreased since they are interconnected. As a result, 2,B is increased because of competitive release. In the case with high dispersal rate, we saw that subpopulation 2,A increased (Fig. 3f). This was due to individuals from subpopulation 2,B dispersing into patch A, which in turn decreased population 1 in both patches even further and reinforced the competitive release in population 2.
In Table 1 we summarize the different effects of environmental changes on population densities. In all cases there was a primary effect on reproductive output in both populations in the changed habitat, regardless of whether they belonged to the well adapted or the less adapted subpopulation. However, there was also a secondary effect on the survival of young as population densities changed. This sometimes counteracted the effect of changed reproductive output. An additional result was that the probability of extinction increased with increased dispersal rate (Fig. 3d–f). This was due to higher immigration into unsuitable habitats and higher competition from immigrating individuals in the relatively poor habitat.
The results presented were largely robust over the full range of the niche width parameter (not shown). When niche width was very low (σ < 0.3), the positive effect on population 1 in the suboptimal habitat B (1,B) was restricted when both habitats underwent change (scenario 1). As a result, all subpopulations decreased in size in that scenario, irrespective of dispersal rate. Also, with a wide niche width (σ > 0.6) in combination with high dispersal rate, the differences in response between subpopulations of the same population disappeared. The reason is that the ESS consisted of generalist populations with similar reproductive output in the different habitats.
Long-term adaptive responses
In scenario 1, the optimal timing of reproduction was changing the same amount and in the same direction in both habitats. There will be no imbalances in the subpopulation structure and the populations timing of reproduction will adapt to the new environment (given that the change does not lead to extinction) (Fig. 4a, d). In scenario 2, when the habitats were made more similar by shifting the “late” habitat B towards habitat A, the difference in optimal trait value decreased to a point where the ESS converged to a single generalist population (Fig. 4b, e). This change was accompanied by an increased total population density due to the decreased trade-off in reproductive output between habitats. Increased dispersal rate (making the environment more fine-grained from the point of view of the individual) may also result in a single population ESS (Fig. 2). However, in that case the total population density decreased because individuals dispersed more into unsuitable habitats while the trade-off in reproduction remains unchanged. The adaptive response to scenario 3 was the reverse of the adaptive response to scenario 2 and results in larger distance between the strategies in combination with stronger specialization to the respective habitats (Fig. 4c, f). The well adapted subpopulations (1,A and 2,B in Fig. 1) maintained their population densities but the subpopulation of dispersers became more maladapted and, consequently, the total population density decreased (Fig. 3d, h). Finally, note that although the change was restricted to one of the habitats in scenario 2 and 3, the evolutionary response occured in both habitats since the populations are interconnected.
Evolutionary stable strategy (ESS) distribution (a, b, c) and equilibrium population density (N *) (d, e, f)) as a function of environmental change for the four subpopulations (1,A; 1,B; 2,A and 2,B) for different environmental change scenarios. The different scenarios are defined as in Fig. 3. For visibility the black lines in panels d, e and f are shifted vertically
Discussion
Understanding the consequences of climate change on interacting populations in a biogeographic context is a fundamental challenge for modern conservation biology (Urban et al. 2012). Using a two-patch model (Brown and Pavlovic 1992; Holt 1996; Kisdi 2002) we have investigated the consequences of climate-driven changes in the timing of resource availability for consumer populations. By reinterpreting the evolving trait in those classical models as timing of reproduction, our study links previous theory on evolutionary stable niche positions to the problem of understanding adaptation in the timing of life history events (Fig. 2). One interesting outcome of this interpretation is that the evolutionary stable timing of reproduction typically deviates from local resource maxima (Fig. 2). In other words, in a heterogenous environment it is typically adaptive to be generalists rather than specialized to the conditions in one particular habitat (e.g. Brown and Pavlovic 1992; Ronce and Kirkpatrick 2001; Kisdi 2002; Mizera and Meszena 2003; Parvinen and Egas 2004). Alongside with prior-residency advantages in competition for mating opportunities (Fagerstrom and Wiklund 1982) or territories (Kokko 1999), asymmetric fitness landscapes (Lof et al. 2012) and life history trade-offs (Visser et al. 2012) this provides an additional mechanistic explanation to why evolutionarily stable consumer reproduction may not exhibit perfect temporal match with resource maxima.
Population dynamic responses to environmental change
Our investigation of the consequences of directional changes in the resource availability along the trait axis represents an addition to previous general theory that considered static (Brown and Pavlovic 1992) or fluctuating but stationary (Kisdi 2002) environments. Particularly, such directional changes are relevant for understanding different scenarios of climate change. Our analysis shows that dispersal, competitive interactions and spatially resource heterogeneity can have fundamental influences on eco-evolutionary responses to shifts in the temporal distribution of available resources. To see this clearly, one can contrast our results with a scenario in which dispersal is absent and where adaptation of timing of reproduction depends on local resource availability only (cf. the baseline model for phenological mismatch in Johansson et al. 2015a). In such a scenario, the ESS is to perfectly match timing of reproduction with the resource peak. From this starting point a temporal shift in resource availability will reduce reproductive output and consequently lead to reduced population density (or extinction). This scenario has an intuitive appeal, it is how many ecologists think about phenology. Furthermore, it, underlies concerns that phenological shifts can lead to ‘disrupted synchrony’ and ‘disconnected interactions’ with negative consequences for populations of different species (Stenseth and Mysterud 2002; Miller-Rushing et al. 2010).
The ESS timing of reproduction we find when dispersal is low is similar to that of the scenario presented above: the majority of individuals in the population matches its reproduction to the resource phenology peak in one habitat (Fig. 1). Therefore a resource shift reduces reproductive output for the majority of the individuals. However, there are also small subpopulations of dispersers that benefit from the shifts and increase in abundance (for all scenarios of change; Fig. 3a–c). Thus even a low dispersal seems to be sufficient to violate the expectation from the scenario without dispersal discussed above that shifts affect consumer population densities negatively. When dispersal was large, the ESS timing of reproduction deviated significantly from the local resource maxima (Fig. 2a). With this adaptive mismatch as the starting point, resource shifts increased the deviation from the reproductive maximum in some subpopulations and decreased it in others. Therefore, it is a much more open question exactly which subpopulations that will benefit or lose out in a metacommunity, compared to the model described above, where there are only losers. In addition to these “primary effects” of changed reproductive output on population growth we also identified “secondary effects” owing to changes in the competitive pressure among populations in different habitats. Such secondary effects may accelerate population declines and cause extinctions (cf. population 2 in Fig. 3a, b, d, e), and when dispersal was high even reverse a population trend from negative to positive (cf. subpopulation 1,A in Fig. 3a, d) compared to the cases with no or low dispersal.
Adaptive responses to environmental change
When resources shifted symmetrically (scenario 1), the ESS solution followed the environmental change and the population densities at eco-evolutionary equilibrium did not deviate from the initial condition (Fig. 4a, d). In contrast, asymmetric shifts of resources across patches lead to interesting, counter-intuitive effects. When resources were shifted to become increasingly similar (scenario 2), both populations evolved to be less specialized (Fig. 4b). Depending on dispersal rate and niche width the ESS ultimately converged to a monomorphic solution implying a reduction in the available niche space. Even though the population may retain a positive equilibrium population density after the shift (Fig. 3b), it may thus nevertheless be doomed to extinction on an evolutionary time scale when the competing population evolves to adopt a generalist strategy (Fig. 4b) (cf. secondary evolutionary extinctions in Johansson and Dieckmann 2009).
The results provide information about equilibrium population densities and evolutionary stable trait distributions. We do, however, also acknowledge that the eco-evolutionary dynamics that lead to such equilibrium end points may play an interesting role in the response to environmental change. As an example, we interpret our results on evolutionary time scale with the prerequisite that both populations have the evolutionary potential to match the speed of the environmental change. It is, however, possible that, for whatever reason (e.g. low population density, few beneficial mutations or stochastic events), one of the populations goes extinct at the onset of the environmental change. This can change the fitness landscape due to competition in such a way that the extant species can start evolving towards a generalist strategy, even though the final ESS is dimorphic. The generalist strategy in such cases corresponds to a convergent stable minima (Eq. 9 is reversed but Eq. 10 holds), a branching point, in the fitness landscape. The dimorphic ESS may eventually be restored through evolutionary branching of the single remaining species and subsequent divergent evolution (Geritz et al. 1998).
Future directions and conclusions
Our results show that when taking spatial structure into account, competitive interactions and dispersal, we can expect much more variation in the long- and short-term responses to shifted resource phenology than when considering the temporal matching between resource availability and timing of reproduction alone. Although we are using a general model and have minimized the number of assumptions, we hope that our results can provide researchers with new hypotheses to understand and explain variability of population responses in specific systems. Interestingly, populations of passerine birds throughout Europe occupy habitats with distinctly different resource phenology in line with our model assumptions. For example, several species breed either in oak habitats, where caterpillars exist in great abundance during a short time period during spring or in coniferous habitats with lower and later caterpillar abundance peaks (Visser et al. 2006; Blondel 2007; Veen et al. 2010). The resource phenology in coniferous habitats seems relatively constant while the resource peak in oak habitats is correlated with spring temperature (Visser et al. 2006; Burger et al. 2012), which is in line with one of our assumed scenarios of change (scenario 3, Fig. 2). The similarities between our model assumptions and data suggest that our result can provide qualitative predictions for natural systems that undergo climate change.
We conclude that ecological interactions, spatial structure, dispersal among habitats and niche evolution are essential factors that need to be considered when population responses to temporal shifts in resources are interpreted and predicted. For future theoretical studies this investigation provides entry points for more detailed studies on specific aspects that may influence population responses. It may, for example, be of interesting to consider other types of environmental change such as gradual or stochastic changes of the resource distribution. Other possibilities for extensions include phenotypic plasticity in the timing of reproduction, sexual reproduction, density dependent dispersal or to study asymmetries in the resource abundances among habitats (e.g. Veen et al. 2010). Already with this simple model, using a minimum of assumptions, we obtained a surprising richness in eco-evolutionary responses to resource shifts. We demonstrate that dispersal and competition for resources can cause adaptive mismatch between resource peaks and timing of reproduction. The possibility of such mismatches in turn makes the consequences of shifted resource phenologies harder to predict and more case dependent. Population responses are furthermore contingent on density dependent effects that can reinforce or counteract the primary resource match/mismatch effects. We also show that the presence of a population with a certain phenological strategy at the onset of environmental change does not necessarily predict its presence after evolutionary adjustments in the community. We find these results intriguing and we hope that they will provide guidance when phenological shifts in complex natural systems are interpreted.
References
Bauer Z, Trnka M, Bauerova J, Mozny M, Stepanek P, Bartosova L, Zalud Z (2010) Changing climate and the phenological response of great tit and collared flycatcher populations in floodplain forest ecosystems in Central Europe. Int J Biometeorol 54:99–111
Blondel J (2007) Coping with habitat heterogeneity: the story of Mediterranean blue tits. J Ornithol 148:3–15
Both C, te Marvelde L (2007) Climate change and timing of avian breeding and migration throughout Europe. Clim Res 35:93–105
Both C, Artemyev AV, Blaauw B, Cowie RJ, Dekhuijzen AJ, Eeva T, Enemar A, Gustafsson L, Ivankina EV, Jarvinen A, Metcalfe NB, Nyholm NEI, Potti J, Ravussin PA, Sanz JJ, Silverin B, Slater FM, Sokolov LV, Torok J, Winkel W, Wright J, Zang H, Visser ME (2004) Large-scale geographical variation confirms that climate change causes birds to lay earlier. Proc R Soc Lond B 271:1657–1662
Both C, Bouwhuis S, Lessells CM, Visser ME (2006) Climate change and population declines in a long-distance migratory bird. Nature 441:81–83
Both C, van Asch M, Bijlsma RG, van den Burg AB, Visser ME (2009) Climate change and unequal phenological changes across four trophic levels: constraints or adaptations? J Anim Ecol 78:73–83
Brown JS, Pavlovic NB (1992) Evolution in heterogeneous environments—effects of migration on habitat specialization. Evol Ecol 6:360–382
Burger C, Belskii E, Eeva T, Laaksonen T, Magi M, Mand R, Qvarnstrom A, Slagsvold T, Veen T, Visser ME, Wiebe KL, Wiley C, Wright J, Both C (2012) Climate change, breeding date and nestling diet: how temperature differentially affects seasonal changes in pied flycatcher diet depending on habitat variation. J Anim Ecol 81:926–936
Caswell H (2001) Matrix population models: construction, analysis, and interpretation. Sinauer Associates, Sunderland
Charmantier A, McCleery RH, Cole LR, Perrins C, Kruuk LEB, Sheldon BC (2008) Adaptive phenotypic plasticity in response to climate change in a wild bird population. Science 320:800–803
Chuine I (2010) Why does phenology drive species distribution? Philos Trans R Soc B 365:3149–3160
Cresswell W, McCleery R (2003) How great tits maintain synchronization of their hatch date with food supply in response to long-term variability in temperature. J Anim Ecol 72:356–366
Day E, Kokko H (2015) Relaxed selection when you least expect it: why declining bird populations might fail to respond to phenological mismatches. Oikos 124:62–68
Eshel I, Motro U, Sansone E (1997) Continuous stability and evolutionary convergence. J Theor Biol 185:333–343
Fagerstrom T, Wiklund C (1982) Why do males emerge before females? Protandry as a mating strategy in male and female butterflies. Oecologia 52:164–166
Ferriere R, Dieckmann U, Couvet D (2004) Evolutionary conservation biology. Cambridge University Press, Cambridge
Geritz SAH, Kisdi E, Meszena G, Metz JAJ (1998) Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol Ecol 12:35–57
Holt RD (1996) Adaptive evolution in source-sink environments: direct and indirect effects of density-dependence on niche evolution. Oikos 75:182–192
Inouye DW (2008) Effects of climate change on phenology, frost damage, and floral abundance of montane wildflowers. Ecology 89:353–362
Johansson J (2008) Evolutionary responses to environmental changes: how does competition affect adaptation? Evolution 62:421–435
Johansson J, Dieckmann U (2009) Evolutionary responses of communities to extinctions. Evol Ecol Res 11:561–588
Johansson J, Jonzén N (2012a) Effects of territory competition and climate change on timing of arrival to breeding grounds: a game-theory approach. Am Nat 179:463–474
Johansson J, Jonzén N (2012b) Game theory sheds new light on ecological responses to current climate change when phenology is historically mismatched. Ecol Lett 15:881–888
Johansson J, Kristensen NP, Nilsson J-Å, Jonzén N (2015a) The eco-evolutionary consequences of interspecific phenological asynchrony—a theoretical perspective. Oikos 124:102–112
Johansson J, Nilsson J-Å, Jonzén N (2015b) Phenological change and ecological interactions: an introduction. Oikos 124:1–3
Kisdi E (2001) Long-term adaptive diversity in Levene-type models. Evol Ecol Res 3:721–727
Kisdi E (2002) Dispersal: risk spreading versus local adaptation. Am Nat 159:579–596
Kokko H (1999) Competition for early arrival in migratory birds. J Anim Ecol 68:940–950
Kokko H (2011) Directions in modelling partial migration: how adaptation can cause a population decline and why the rules of territory acquisition matter. Oikos 120:1826–1837
Leimar O (2009) Multidimensional convergence stability. Evol Ecol Res 11:191–208
Lof ME, Reed TE, McNamara JM, Visser ME (2012) Timing in a fluctuating environment: environmental variability and asymmetric fitness curves can lead to adaptively mismatched avian reproduction. Proc Biol Sci 279:3161–3169
McGill BJ, Brown JS (2007) Evolutionary game theory and adaptive dynamics of continuous traits. Annu Rev Ecol Evol Syst 38:403–435
Metz JAJ, Nisbet RM, Geritz SAH (1992) How should we define fitness for general ecological scenarios. Trends Ecol Evol 7:198–202
Miller-Rushing AJ, Hoye TT, Inouye DW, Post E (2010) The effects of phenological mismatches on demography. Philos Trans R Soc B 365:3177–3186
Mizera F, Meszena G (2003) Spatial niche packing, character displacement and adaptive speciation along an environmental gradient. Evol Ecol Res 5:363–382
Parmesan C (2006) Ecological and evolutionary responses to recent climate change. Annu Rev Ecol Evol Syst 37:637–669
Parvinen K, Egas M (2004) Dispersal and the evolution of specialisation in a two-habitat type metapopulation. Theor Popul Biol 66:233–248
Pontarp M, Ripa J, Lundberg P (2012) On the origin of phylogenetic structure in competitive metacommunities. Evol Ecol Res 14:269–284
Ravigné V, Dieckmann U, Olivieri I (2009) Live where you thrive: joint evolution of habitat choice and local adaptation facilitates specialization and promotes diversity. Am Nat 174:E141–E169
Reed TE, Gienapp P, Visser ME (2015) Density dependence and microevolution interactively determine effects of phenology mismatch on population dynamics. Oikos 124:81–91
Revilla TS, Encinas‐Viso F, Loreau M (2015) Robustness of mutualistic networks under phenological change and habitat destruction. Oikos 124:22–32
Ronce O, Kirkpatrick M (2001) When sources become sinks: migrational meltdown in heterogeneous habitats. Evolution 55:1520–1531
Stenseth NC, Mysterud A (2002) Climate, changing phenology, and other life history and traits: nonlinearity and match-mismatch to the environment. PNAS 99:13379–13381
Thomas DW, Blondel J, Perret P, Lambrechts MM, Speakman JR (2001) Energetic and fitness costs of mismatching resource supply and demand in seasonally breeding birds. Science 291:2598–2600
Urban MC, De Meester L, Vellend M, Stoks R, Vanoverbeke J (2012) A crucial step toward realism: responses to climate change from an evolving metacommunity perspective. Evol Appl 5:154–167
Veen T, Sheldon BC, Weissing FJ, Visser ME, Qvarnstrom A, Saetre G-P (2010) Temporal differences in food abundance promote coexistence between two congeneric passerines. Oecologia 162:873–884
Visser ME, Both C (2005) Shifts in phenology due to global climate change: the need for a yardstick. Proc R Soc Lond B 272:2561–2569
Visser ME, van Noordwijk AJ, Tinbergen JM, Lessells CM (1998) Warmer springs lead to mistimed reproduction in great tits (Parus major). Proc R Soc Lond B 265:1867–1870
Visser ME, Adriaensen F, van Balen JH, Blondel J, Dhondt AA, van Dongen S, du Feu C, Ivankina EV, Kerimov AB, de Laet J, Matthysen E, McCleery R, Orell M, Thomson DL (2003) Variable responses to large-scale climate change in European Parus populations. Proc R Soc Lond B 270:367–372
Visser ME, Holleman LJM, Gienapp P (2006) Shifts in caterpillar biomass phenology due to climate change and its impact on the breeding biology of an insectivorous bird. Oecologia 147:164–172
Visser ME, te Marvelde L, Lof ME (2012) Adaptive phenological mismatches of birds and their food in a warming world. J Ornithol 153:75–84
Acknowledgments
This study is part of the research environment BECC (Biodiversity and Ecosystem Services in a Changing Climate). It was financially supported by grants from the Swedish Research Council (to PL, NJ and MP) and the Swedish research council FORMAS (to NJ). We also thank two anonymous reviewers for useful and important comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pontarp, M., Johansson, J., Jonzén, N. et al. Adaptation of timing of life history traits and population dynamic responses to climate change in spatially structured populations. Evol Ecol 29, 565–579 (2015). https://doi.org/10.1007/s10682-015-9759-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10682-015-9759-6