Demand forecasting of green metal materials using non-equidistant grey prediction with robust nonlinear interval regression analysis

Abstract

The main advantages of magnesium alloys are that they are lightweight, easy to recycle, and have high vibration absorption. These unique characteristics make magnesium alloys important green metal materials for manufacturing, especially for the automotive and 3C products industries. The developing trends of these related industries can be recognized by forecasting the demand for magnesium alloys. This study develops grey prediction power models to forecast the demand for such a promising green metal material. Grey prediction is an appropriate technique because available data regarding the demand for magnesium alloys are not in line with any statistical assumptions. In particular, because outliers might cause a deterioration of forecasting performance, a robust nonlinear interval regression analysis with neural networks is applied to detect outliers by estimating data intervals. Then, a power model is applied to the newly generated non-equidistant data sequence without outliers. Residual modification is further considered here to improve the forecasting performance of the power model. The forecasting abilities of the proposed grey residual modification models are verified using actual magnesium alloy demand data. The experimental results for ex-post testing show that the mean absolute percentage errors of the proposed models that can work on non-equidistant data were minimal among all considered models.

1 Introduction

Magnesium is a lightweight engineering material, and magnesium alloys are regarded as a twenty-first century green metal material. Compared with other metal materials, magnesium alloys have a few advantages: they are lightweight, have high impact resistance, high corrosion resistance, and are easy to recycle. These advantages are the reason why magnesium alloys have been widely used for the development and manufacture of various products, including the components of automobiles, aircraft, bicycles, sports equipment, and the metal cases of computer, consumer electronic, and computer (3C) products (Hong, 2016; Lu, 2014). In 2016, as a result of major demand from the automotive industry, 32% of the worldwide magnesium was consumed in the die casting of magnesium alloys (Lee et al., 2017). Next, as the main determinant of fuel consumption is vehicle weight, lightweight components are essential for the automotive and aerospace industries. As national authorities make efforts to significantly mitigate the effects of CO₂ emissions and promote waste recycling, using magnesium materials in the manufacture of products, such as vehicles and 3C products, can have a very positive influence on environmental protection and energy conservation. Therefore, magnesium alloy demand forecasting can help these industries understand developing trends to quickly recognize market configurations and set up investment strategies.

In contrast to artificial intelligence techniques and time series models, grey system theory has been applied to many real-world problems (Gao et al., 2021; Rajesh, 2020). Grey prediction has drawn attention because of the need to use limited samples to characterize an unknown system without complying to any statistical assumptions (Liu & Lin, 2010). This characteristic motivated us to apply a power model of a first-order grey model with one variable (GM(1,1)), abbreviated to GM(1,1)-P, to predict the demand trends for magnesium alloys. Indeed, the GM(1,1)-P model has been widely applied to real-world problems. The literature on the applications of GM(1,1)-P is briefly described in Table 1.

Table 1 Summary of the literature on the applications of GM(1,1)-P

In light of the applicability of the GM(1,1)-P model to real-world problems, it is interesting to apply the GM(1,1)-P and its variants to forecast the magnesium alloy demand. Two issues are particularly addressed in this paper. First, GM(1,1)-P often works well on annual or equidistant data; however, there is always the possibility that outliers might worsen the performance of the prediction model (Huang et al., 1998). To avoid outliers adversely affecting forecasting performance, robust interval regression analysis can be used to detect outliers by gauging the intervals consisting of upper and lower bounds (Hladík & Černý, 2014; Wang et al., 2015). Thus, it is interesting to develop the GM(1,1)-P that can work on a newly generated non-equidistant data sequence after removing those outliers to better forecast magnesium alloy demand.

Next, it has been demonstrated that residual modification is available to promote forecasting accuracy of an original prediction model (Liu et al., 2017). Therefore, it is reasonable to incorporate the mechanism of residual modification into GM(1,1)-P. Based on these features, this study aims to develop GM(1,1)-P and its residual version that works on non-equidistant data sequences, generated using robust nonlinear interval models to remove outliers.

To deal with the first aforementioned issue, we use two neural networks (NNs) to build a nonlinear interval model that is robust against outliers. This approach is adopted here because several studies have demonstrated the effectiveness of using two NNs on the construction of nonlinear interval models. The related literature is summarized in Table 2. As for the second issue with respect to residual modification, the functional-link net (FLN) is considered because Hu (2017) and Hu et al. (2019) indicate the effectiveness of the FLN on the combination of a grey prediction model with its residual version. The main advantage of FLNs is relieving the restrictions arising from commonly used sign estimation methods, such as Markov-chain estimation (Hsu, 2003) and genetic programming (Lee & Tong, 2011).

Table 2 Summary of the literature on the use of NNs to build nonlinear interval models

The remainder of this paper is organized as follows. The robust nonlinear interval regression analysis using NNs and grey prediction are introduced in Sects. 2 and 3, respectively. The proposed GM(1,1)-P along with its residual model that work on non-equidistant sequences are presented in Sect. 3. For forecasting magnesium alloy demand, we investigate the forecasting accuracy of the different grey prediction models in Sect. 4. Finally, the conclusions are presented in Sect. 5.

2 Robust nonlinear interval regression analysis using NNs

Imprecise observations can be represented by estimated data intervals (Xie et al., 2014; Zeng et al., 2014). Nonetheless, an unsatisfactory interval can be obtained when a data sequence contain outliers. In Sect. 2.1, Eqs. (1), (2), (3), (4), (5), and (6) describe nonlinear interval regression analysis using NNs, and Eqs. (7), (8), (9), (10), and (11) in Sect. 2.2 describe the development of the robust nonlinear interval models against outliers.

2.1 Nonlinear interval regression analysis

In practice, a nonlinear interval model can be determined using two NNs, denoted by NN_u and NN_l, from a given original data sequence x = (x₁, x₂,…, x_m). As a result, (t₁, x₁), (t₂, x₂),…, and (t_m, x_m) comprise a data set for the two NNs (NN_u and NN_l) where (t_p, x_p) denotes the p-th input–output pattern at time t_p. Also, let $g_{u} (t_{p} )$ and $g_{l} (t_{p} )$ be the upper and lower limits obtained from NN_u and NN_l, respectively, such that the difference between $g_{u} (t_{p}^{{}} )$ and $g_{l} (t_{p}^{{}} )$ denotes the width of the gauged interval. A nonlinear optimization problem is formulated as.

$${\rm{Minimize}}\;\left( {{g_u}(t_1^{}) - {g_l}(t_1^{})} \right) + \left( {{g_u}(t_2^{}) - {g_l}(t_2^{})} \right) + ... + \left( {{g_u}({t_m}) - {g_l}({t_m})} \right)$$

(1)

subject to

$$g_{u} (t_{p}^{{}} ) \le {\text{xp}} \le g_{l} (t_{p} ), \, p \, = \, 1, \, 2,..., \, m$$

(2)

To approximately satisfy the constraint condition, Ishibuchi and Tanaka (1992) proposed an NN-based approach in which two MLPs are used to set up the nonlinear interval model, and each MLP has a single output, a single input, and one hidden layer with five hidden units. Note that what the NN this study addresses is MLP. With a weighting parameter $\omega_{p}$, a cost function E_u is formulated to discover the upper limit:

$$E_{u} = \sum\limits_{p = 1}^{m} {\frac{1}{2}\omega_{p}^{{}} (x_{p}^{{}} - g_{u} {(}t_{p}^{{}} {))}^{{2}} }$$

(3)

in which

$$\omega_{p}^{{}} = \left\{ {_{{\omega ,{\text{ if }}x_{p}^{{}} \le g_{u} {(}t_{p}^{{}} {)}}}^{{1,{\text{ if }}x_{p}^{{}} > g_{u} {(}t_{p}^{{}} {)}}} } \right.$$

(4)

where ω ∈ (0, 1). To determine the lower limit, cost function E_l is formulated as

$$E_{l} = \sum\limits_{p = 1}^{m} {\frac{1}{2}\omega_{p}^{{}} (x_{p}^{{}} - g_{l} {(}t_{p}^{{}} {))}^{{2}} }$$

(5)

in which

$$\omega_{p}^{{}} = \left\{ {_{{\omega ,{\text{ if }}x_{p}^{{}} \ge g_{l} {(}t_{p}^{{}} {)}}}^{{1,{\text{ if }}x_{p}^{{}} < g_{l} {(}t_{p}^{{}} {)}}} } \right.$$

(6)

2.2 Robust nonlinear interval models

A robust nonlinear interval model can be built on the basis of the aforementioned NN-based approach, where the quality index, $\psi_{p}$, with respect to (t_p, $x_{p}^{(0)}$) at time t_p beyond the estimated interval should be considered to help the MLP training resist outliers. The quality index is given as follows:

$$\psi_{p} = \left\{ {_{{\psi ,{\text{ if }}r_{p}^{{}} > c}}^{{1,{\text{ if }}r_{p}^{{}} \le c}} } \right.$$

(7)

where c is a cutoff point, and $\psi$ is a very small positive real value. During the model construction, r_p > c means that (t_p, x_p) falls in the rejection region. To determine the upper limit against outliers, the absolute residual, r_p, with respect to (t_p, x_p) is defined as follows (Chen & Jain, 1994; Huang et al., 1998):

$${r_p} = \left\{ {\begin{array}{*{20}{l}}{{x_p} - {g_u}\left( {{t_p}} \right),}\\{0,}\end{array}} \right.\begin{array}{*{20}{l}}{{x_p} \ge {g_u}\left( {{t_p}} \right)}\\{{x_p} < {g_u}\left( {{t_p}} \right)}\end{array}$$

(8)

In this approach, data in the rejection region impose little effect on the construction of NN_u.

To determine c, we renumber the data by sorting r_p in descending order, such that (t_p, $x_{p}^{(0)}$) is renumbered as one as it has min{r₁, r₂,…, r_m}. $r_{{(1 - q_{u} )m}}$ is assigned to c, where q_u (0 ≤ q_u ≤ 1) indicates the tolerable limit on the rate of outliers beyond the true interval. With $\psi_{p}$, cost function E_u is defined as (Hu, 2009, 2014)

$$E_{u} = \sum\limits_{p = 1}^{m} {\frac{1}{2}\omega_{p}^{{}} \psi_{p} (x_{p}^{{}} - g_{u} {(}t_{p}^{{}} {))}^{{2}} }$$

(9)

To determine the lower limit, r_p is defined as

$${r_p} = \left\{ {\begin{array}{*{20}{l}}{{g_l}\left( {{t_p}} \right) - {x_p},}\\{0,}\end{array}\begin{array}{*{20}{l}}{{x_p} \le {g_l}\left( {{t_p}} \right)}\\{{x_p} > {g_l}\left( {{t_p}} \right)}\end{array}} \right.$$

(10)

In a similar manner, with q_l being the tolerable limit on the rate of outliers beneath the true interval, c is given by $r_{{(1 - q_{l} )m}}$ as well. With $\psi_{p}$, cost function E_l is defined as

$$E_{l} = \sum\limits_{p = 1}^{m} {\frac{1}{2}\omega_{p}^{{}} \psi_{p} (x_{p}^{{}} - g_{l} {(}t_{p}^{{}} {))}^{{2}} }$$

(11)

The data in the rejection region also impose little effect on the construction of NN_l.

By defining the fitness function as E_u (E_l), the connection weights of NN_u (NN_l) can be determined using the toolbox in MATLAB to implement a real-valued genetic algorithm (GA). The estimated data intervals can be obtained from the best chromosome whose fitness value is a minimum among the straight generations. As a result, any data outside the data intervals can be treated as outliers. The details of applying MLPs to robust nonlinear interval regression analysis using GAs are omitted here for simplicity, but the reader is referred to Hu (2014) for further information.

3 Grey prediction

3.1 Equidistant grey prediction

GM(1,1)-P and its residual model, both of which use equidistant data sequences are described here prior to the introduction of the grey prediction models that use non-equidistant data sequences. Section 3.1 including Eqs. (12)-(20) introduces the traditional GM(1,1)-P first. Then, the residual modification model, NGM(1,1)-P, consisting of GM(1,1)-P and its residual version, is described in Sect. 3.2 including Eqs. (21)-(25).

3.1.1 GM(1,1)-P model

Given an equidistant data sequence ${\mathbf{x}}_{{}}^{(0)}$ = ($x_{1}^{(0)}$,$x_{2}^{(0)}$,…,$x_{n}^{(0)}$) composed of n data samples, a new sequence ${\mathbf{x}}_{{}}^{(1)}$ = ($x_{1}^{(1)}$,$x_{2}^{(1)}$,…,$x_{n}^{(1)}$) is generated from ${\mathbf{x}}_{{}}^{(0)}$ by a one-order accumulated generating operation (1-AGO) as (Liu & Lin, 2010)

$$x_{k}^{(1)} = \sum\limits_{j = 1}^{k} {x_{j}^{(0)} } ,k = \, 1, \, 2, \ldots ,n$$

(12)

Since ${\mathbf{x}}_{{}}^{(1)}$ monotonically increases, the following first-order Bernoulli equation can be used as the mathematical form of the GM(1,1)-P as

$$\frac{{dx^{(1)} (t)}}{dt} + ax^{(1)} \left( t \right) = \, b\left( {x_{{}}^{(1)} } \right)^{r}$$

(13)

where a denotes the developing coefficient, b represents the control variable, and r represents the power exponent.

The time response function with respect to Eq. (13) is (Chen, 2008; Chen et al., 2008)

$$\hat{x}_{k}^{(1)} = \left[ {\left( {\left( {x_{1}^{(0)} } \right)^{1 - \beta } - \frac{b}{a}} \right)e^{{ - a\left( {k - 1} \right)\left( {1 - \beta } \right)}} + \frac{b}{a}} \right]^{{1/\left( {1 - \beta } \right)}} ,\;k = 1,2,\; \ldots \;,n$$

(14)

where r ≠ 1. Then, a and b can be estimated by a linear regression model consisting of n–1 grey difference equations with the following form:

$$x_{k}^{(0)} + az_{k}^{\left( 1 \right)} = \, b\left( {z_{k}^{\left( 1 \right)} } \right)^{r}$$

(15)

where the background value $z_{k}^{(1)}$ is given by

$$z_{k}^{(1)} = \alpha x_{k}^{(1)} + \left( {1 - \alpha } \right)x_{k}^{(1)}$$

(16)

in which 0 ≤ $\alpha$ ≤ 1. The interpolation coefficient $\alpha$ is usually set to 0.5 for convenience, although such a setting may not be optimal.

In turn, with the ordinary least squares (OLS) method, a and b can be derived as

$$\left[ {a,b} \right]^{T} = \, \left( {{{B}}^{T} {{B}}} \right)^{ - 1} {{B}}^{T} {\mathbf{y}}$$

(17)

in which

$${\mathbf{B}} = \left[ {\begin{array}{*{20}c} { - z_{2}^{(1)} } & {(z_{2}^{(1)} )^{r} } \\ { - z_{3}^{(1)} } & {(z_{3}^{(1)} )^{r} } \\ \vdots & \vdots \\ { - z_{n}^{(1)} } & {(z_{n}^{(1)} )^{r} } \\ \end{array} } \right],\;{\mathbf{y}} = \left[ {\begin{array}{*{20}c} {x_{2}^{(0)} } \\ {x_{3}^{(0)} } \\ \vdots \\ {x_{n}^{(0)} } \\ \end{array} } \right]$$

(18)

Finally, the predicted value of $x_{k}^{(0)}$ can be obtained by the inverse 1-AGO (1-IAGO):

$$\hat{x}_{k}^{(0)} = \hat{x}_{k}^{(1)} - \hat{x}_{k - 1}^{(1)} ,k = \, 2, \, 3, \ldots ,n$$

(19)

To optimally construct GM(1,1)-P, we apply the well-known optimization modeling software, Linear Interactive and General Optimizer (LINGO), to solve the optimization problem by minimizing the mean absolute percentage error (MAPE) as

$$Minimize\,\,MAPE = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left| {\frac{{\hat{x}_{k}^{(0)} - x_{k}^{(0)} }}{{x_{k}^{(0)} }}} \right|}$$

(20)

subject to r ≠ 1, $\hat{x}_{1}^{(1)}$ = $x_{1}^{(1)}$, Eq. (3), and Eqs. (5), (6), (7) and (8).

That is, MAPE is the sum of the APE of x_k (k = 1, 2,…, n) divided by the sample size. The computational steps of setting up the optimized GM(1,1)-P model are as follows.

Step 1 Generate accumulated generating sequence from the equidistant data sequence.

Step 2 Construct GM(1,1)-P with LINGO to obtain the optimal parameters, including the developing coefficient (a), control variable (b), interpolation coefficient ($\alpha$), and power exponent (r).

Step 3 Obtain the predicted sequence with 1-IAGO.

It should be noted that GM(1,1)-P, also called the nonlinear grey Bernoulli model, is identical to GM(1,1) when r = 0. In particular, the power exponent makes GM(1,1)-P much more useful than GM(1,1) (Dang et al., 2016; Lu et al., 2016).

3.1.2 Residual modification of GM(1,1)-P model

After constructing the GM(1,1)-P model, a sequence of absolute residual values, ${{\varvec{\upvarepsilon}}}_{{}}^{(0)}$ = ($\varepsilon_{2}^{(0)}$, $\varepsilon_{3}^{(0)}$,…, $\varepsilon_{n}^{(0)}$), is generated where

$$\varepsilon_{k}^{(0)} = \left| {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right|,k = \, 2, \, 3, \ldots ,n$$

(21)

A residual model is established with respect to ${{\varvec{\upvarepsilon}}}_{{}}^{(0)}$ as GM(1,1)-P using ${\mathbf{x}}_{{}}^{(0)}$ such that the corresponding time response function is

$$\hat{\varepsilon }_{k}^{(1)} = \left[ {\left( {\left( {\varepsilon_{2}^{(0)} } \right)^{1 - r} - \frac{{b_{\varepsilon } }}{{a_{\varepsilon } }}} \right)e^{{ - a_{\varepsilon } (1 - r)(t_{k} - t_{1} )}} + \frac{{b_{\varepsilon } }}{{a{}_{\varepsilon }}}} \right]^{{\frac{1}{1 - r}}} ,k = \, 3, \, 4, \ldots ,n$$

(22)

In common with GM(1,1)-P, a_ε and b_ε can be derived by the OLS method. A new predicted value can be obtained by modifying the predicted value produced by GM(1,1)-P as

$$\hat{x}_{k}^{(0)} = \hat{x}_{k}^{(0)} + s_{k} \hat{\varepsilon }_{k}^{(0)} ,k = \, 2, \, 3, \ldots ,n$$

(23)

The resultant prediction model consisting of GM(1,1)-P and its residual version is called RGM(1,1)-P.

Traditionally, s_k is 1 or − 1 (Liu & Lin, 2010). Even so, to optimally determine s_k, since it has been indicated that an FLN without hidden layers is effective for building a residual modification model (Hu et al., 2019), we set up an FLN to better integrate GM(1,1)-P and its residual version. Let t_k denote the time k with respect to $\hat{x}_{k}^{(0)}$. The input pattern for the FLN is an enhanced pattern, v_k = (t_k, sin(πt_k), cos(πt_k), sin(2πt_k), cos(2πt_k)). Let w = (w₁, w₂, w₃, w₄, w₅) be a vector of connection weights. Then, the actual output of v_k can be obtained as:

$$y_{k} = {\text{ tanh}}({{w}}^{t} {{v}}_{k} + \theta )$$

(24)

where θ is the bias and ˗1 ≤ y_k ≤ 1. As a result, a new predicted value generated from the proposed model can be computed as follows:

$$\hat{x}_{k}^{(0)} = \hat{x}_{k}^{(0)} + \eta y_{k} \hat{\varepsilon }_{k}^{(0)} ,k = \, 2, \, 3, \ldots ,n$$

(25)

in which $\eta$ > 0 and s_k = $\eta$ y_k. Thus, the new value of $\hat{x}_{k}^{(0)}$ ranges from $\hat{x}_{k}^{(0)} - \eta y_{k} \hat{\varepsilon }_{k}^{(0)}$ to $\hat{x}_{k}^{(0)} + \eta \hat{\varepsilon }_{k}^{(0)}$.

To set up the RGM(1,1)-P, we use the toolbox in MATLAB to develop a real-valued GA, using MAPE as the fitness function, by which the connection weights of the FLN can be optimally determined. The relevant parameters can be obtained from the best chromosome whose fitness value is a minimum among all the straight generations. As a result, the computational steps to construct the RGM(1,1)-P are briefly summarized as follows.

Step 1 Build the optimized GM(1,1)-P using the equidistant data sequence with LINGO.

Step 2 In common with the construction of the optimized GM(1,1)-P model, use the equidistant residual sequence to establish the optimized residual GM(1,1)-P model with LINGO.

Step 3 Obtain the predicted sequence using an FLN to optimally combine the predicted values obtained from the optimized GM(1,1)-P and its optimized residual model. The optimized FLN is derived with the GA toolbox in MATLAB.

3.2 Non-equidistant grey prediction

After removing outliers with the robust nonlinear interval model, the original equidistant data sequence becomes non-equidistant (Li et al., 2012). We use NGM(1,1)-P to denote a GM(1,1)-P model that can work on non-equidistant data. In our design, we first construct NGM(1,1)-P and then the residual NGM(1,1)-P. Therefore, NGM(1,1)-P is first introduced in Sect. 4.1 including Eqs. (26), Eq. (27) and Eq. (28). Generation of the proposed residual combination model, called RNGM(1,1)-P, consisting of NGM(1,1)-P and its residual version, is then described in Sect. 4.2 including Eqs. (29), (30), (31), and (32).

3.2.1 NGM(1,1)-P model

A non-equidistant sequence, (x⁽⁰⁾(t₁), x⁽⁰⁾(t₂),…, x⁽⁰⁾(t_n)) (n ≤ m), is obtained by removing outliers from the original sequence, where x⁽⁰⁾(t_i) denotes the actual value at time t_i (i ≤ n). Let $\Delta {t_i} = {t_i} - {t_i}_{ - 1}$, where i = 2, 3,…, n. Of course, $\Delta t_{i}$ is not a constant. Let ${\mathbf{x}}_{{}}^{(0)}$ = ($x_{1}^{(0)}$,$x_{2}^{(0)}$,…,$x_{n}^{(0)}$) = (x⁽⁰⁾(t₁), x⁽⁰⁾(t₂),…, x⁽⁰⁾(t_n)). There are four main differences between GM(1,1)-P and NGM(1,1)-P.

First, GM(1,1)-P and NGM(1,1)-P are set up by equidistant and non-equidistant sequences, respectively. Next, instead of 1-AGO, ${\mathbf{x}}_{{}}^{(1)}$ = (x⁽¹⁾(t₁), x⁽¹⁾(t₂),…, x⁽¹⁾(t_n)) = ($x_{1}^{(1)}$,$x_{2}^{(1)}$,…,$x_{n}^{(1)}$) for NGM(1,1)-P can be generated by the following AGO as (Dang et al., 2016; Liu et al., 2017)

$$x_{k}^{(1)} = x_{1}^{(0)} + \sum\limits_{j = 2}^{k} {x_{j}^{(0)} } \Delta t_{j} ,k = \, 2, \, 3, \ldots ,n$$

(26)

Then, the time response function obtained by solving the following whitening equation is

$$\hat{x}_{k}^{(1)} = [((x_{1}^{(0)} )^{1 - r} - \frac{b}{a})e^{{ - a(1 - r)(t_{k} - t_{1} )}} + \frac{b}{a}]^{{\frac{1}{1 - r}}}$$

(27)

where r ≠ 1 and k = 2, 3,…, n. Finally, with the following IAGO, the predicted value for NGM(1,1)-P with respect to $x_{k}^{(0)}$ is given by

$$\hat{x}_{k}^{(0)} = \frac{{\hat{x}_{k}^{(1)} - \hat{x}_{k - 1}^{(1)} }}{{\Delta t_{k} }}$$

(28)

Being analogous with the construction of GM(1,1)-P, the computational steps of setting up the optimized NGM(1,1)-P model are as follows.

Step 1 Remove outliers from the equidistant data sequence using the robust nonlinear interval model to detect outliers.

Step 2 Generate the accumulated generating sequence from the non-equidistant data sequence.

Step 3 Construct NGM(1,1)-P with LINGO to obtain the optimal parameters, including the developing coefficient, control variable, and interpolation coefficient.

Step 4 Obtain the predicted sequence with IAGO.

3.2.2 Residual modification of NGM(1,1)-P model

We set up the residual model of NGM(1,1)-P using the absolute residual value, $\varepsilon_{k}^{(0)}$, which is defined as

$$\varepsilon_{k}^{(0)} = \left| {x_{k}^{(0)} - \hat{x}_{k}^{(0)} } \right|,k = \, 2, \, 3, \ldots ,n$$

(29)

The prediction model consisting of NGM(1,1)-P and its residual version is called RNGM(1,1)-P. There are four main differences between RGM(1,1)-P and RNGM(1,1)-P as well. First, RGM(1,1)-P and RNGM(1,1)-P are set up using equidistant and non-equidistant residual sequences, respectively. Next, RNGM(1,1)-P follows the specific AGO where

$$\varepsilon_{k}^{(1)} = \varepsilon_{1}^{(0)} + \sum\limits_{j = 2}^{k} {\varepsilon_{j}^{(0)} } \Delta t_{j} ,k = \, 2, \, 3, \ldots ,n$$

(30)

Then, the corresponding time response function is

$$\hat{\varepsilon }_{k}^{(1)} = \left[ {\left( {\left( {\varepsilon_{2}^{(0)} } \right)^{1 - r} - \frac{{b_{\varepsilon } }}{{a_{\varepsilon } }}} \right)e^{{ - a_{\varepsilon } (1 - r)(t_{k} - t_{1} )}} + \frac{{b_{\varepsilon } }}{{a{}_{\varepsilon }}}} \right]^{{\frac{1}{1 - r}}} ,k = \, 3, \, 4, \ldots ,n$$

(31)

where r ≠ 1. In common with NGM(1,1)-P, a_ε and b_ε can be derived by the OLS method. Lastly, with the specific IAGO, the predicted value for RNGM(1,1)-P can be generated by

$$\hat{\varepsilon }_{k}^{(0)} = \frac{{\hat{\varepsilon }_{k}^{(1)} - \hat{\varepsilon }_{k - 1}^{(1)} }}{{\Delta k_{i} }}$$

(32)

Figure 1 depicts a flowchart of the construction the proposed RNGM(1,1)-P model. The computational steps to set up the RNGM(1,1)-P are briefly summarized as follows.

Fig. 1

Flowchart for constructing the RNGM (1,1)-P model

Step 1 Build the optimized NGM(1,1)-P using the non-equidistant data sequence with LINGO.

Step 2 In common with the construction of an optimized NGM(1,1)-P model, use the non-equidistant residual sequence to establish the optimized residual NGM(1,1)-P model with LINGO.

Step 3 Obtain the predicted sequence with an FLN to optimally combine the predicted values obtained from the optimized NGM(1,1)-P and its optimized residual model. The GA toolbox in MATLAB is applied to optimize the connection weights of the FLN.

4 Experiments

Experiments were conducted for magnesium alloy demand forecasting to make comparisons between the different grey prediction models using the equidistant sequences and those using the non-equidistant sequences. The former include the optimized GM(1,1) and optimized GM(1,1)-P, and the latter includes the proposed NGM(1,1), NGM(1,1)-P, and RNGM(1,1)-P. It is reasonable to include GM(1,1) with equidistant sequences and NGM(1,1) with non-equidistant sequences because GM(1,1) is the most commonly used grey prediction model (Liu et al., 2017). Several distinctive prediction models, the adaptive NGM(1,1) (ANGM(1,1)) (Chang et al., 2014) and FLNGM(1,1) (Hu (2017)), were included as well. It should be noted that, when a grey prediction model is developed on the basis of GM(1,1), “GM(1,1)” can be incorporated into the corresponding acronym by convention. The considered prediction models include:

• (1) NGM(1,1): A non-equidistant version of GM(1,1);

• (2) GM(1,1)-P: A power model of the GM(1,1);

• (3) NGM(1,1)-P: A non-equidistant version of GM(1,1)-P;

• (4) RGM(1,1)-P: A power model that integrates GM(1,1)-P with residual modification;

• (5) RNGM(1,1)-P: A power model that integrates NGM(1,1)-P with residual modification;

• (6) ANGM(1,1): Adaptive NGM(1,1) proposed by Chang et al. (2014) has shown its superiority over some prediction models for non-equidistant data sequences on some real cases including synthetic control charts and color filter manufacturing.

• (7) FLNGM(1,1): FLNGM(1,1) was originally developed for equidistant data, which uses an FLN to optimally integrate the optimized GM(1,1) and its residual model. For simplicity, the details of FLNGM(1,1) are omitted here, but the study of Hu (2017) can be consulted for more information.

• (8) NFLNGM(1,1): NFLNGM(1,1) denotes a non-equidistant FLNGM(1,1);

• (9) NN: The NN we use is a multi-layer perceptron (MLP) that has a single output, a single input, and one hidden layer with five hidden units.

As for parameter specifications involving the construction of the proposed model, when using the GA to set up the MLPs introduced in Sect. 2.2, we assigned values of 1000, 50, 0.8, and 0.01 to the total generations, population size, crossover, and mutation probabilities, respectively. In addition, ω in Eq. (4) and $\psi$ in Eq. (7) are equal to 0.2 and 10^–5, respectively. To construct the proposed model, $\eta$ in Eq. (25) was specified as 20. Although several factors could affect the performance of the GA, there are no optimal values that can be assigned to its parameter specifications (Osyczka, 2003).

4.1 Case I: Magnesium die castings demand of China

China has consumed most of the magnesium in the world since 1999, and it has provided at least 80% of all magnesium materials used worldwide since 2008. With a demand of 70% from the automotive industry and 20% from the 3C products industry, about 35% of the magnesium has been consumed in die casting production with magnesium alloys (Lee et al., 2017). Magnesium die casting demand forecasting can thus reflect magnesium alloy demand and can indicate the developing trends of the automotive and 3C products industries in China.

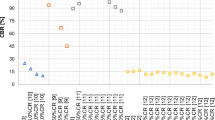
We used the historical data of the demand for magnesium die casting that was reported and analyzed by Hsu (2012), Hong (2015a, 2015b), and Lee et al. (2017). Data from 2002 to 2012 were used for model fitting, and data from 2013 and 2014 were used for ex-post testing. The upper and lower limits are shown in Fig. 2 after performing the robust nonlinear interval regression analysis with q_u = q_l = 0.1. There are two outliers outside of the identified data intervals. The optimized NGM(1,1), NFLNGM(1,1), AGM(1,1), optimized NGM(1,1)-P, and RNGM(1,1)-P were constructed using the non-equidistant sequence by removing data in 2007 and 2009. The forecasting results are described in Table 3. Table 4 shows the forecasting accuracy obtained by the NN, GM(1,1), FLNGM(1,1), GM(1,1)-P, and RGM(1,1)-P that worked on the equidistant data sequence.

Fig. 2

Outlier detection of training data for Case I

Table 3 MAPEs of different grey prediction models working on non-equidistant data for Case I (unit: 1000 tons)

Table 4 MAPEs of different prediction models working on equidistant data for Case I (unit: 1000 tons)

Table 5 summarizes forecasting accuracy for model fitting and ex-post testing. In terms of MAPE, we can see that the proposed RNGM(1,1)-P outperformed all the other models considered for model fitting and ex-post testing. In addition to MAPE, Table 5 also includes two commonly used measures mean absolute deviation (MAD) and root mean square error (RMSE) defined as (Xiao et al., 2021):

$$MAD = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left| {\hat{x}_{k}^{(0)} - x_{k}^{(0)} } \right|}$$

(33)

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{k = 1}^{n} {{(}\hat{x}_{k}^{(0)} - x_{k}^{(0)} {)}^{{2}} } }$$

(34)

Table 5 Forecasting accuracy for model fitting and ex-post testing for Case I

In terms of MAD and RMSE, we can see that the RNGM(1,1)-P outperformed most of the other considered prediction models for ex-post testing, despite that the RNGM(1,1)-P was slightly inferior to RGM(1,1)-P for ex-post testing.

4.2 Case II: Magnesium alloy ingot and powder demand of Taiwan

In Taiwan, all magnesium materials are imported from abroad. Magnesium alloy ingots and scrap are the main materials imported for the magnesium alloy industry. Most of the magnesium alloys are used to manufacture the cases of 3C products, such as smart phones, tablet computers, and notebooks, by die casting and thixomolding. Taiwan is the global leader in the die casting of magnesium alloys for 3C products (Hong, 2016). To maintain this competitive advantage, magnesium alloy forecasting can be important in enabling 3C product manufacturers to recognize developing trends in related markets. Accordingly, the imported quantity of magnesium alloy ingots and scrap can be used to indirectly reflect the trends of the magnesium alloy demand of Taiwan.

We used the historical data of the import quantity of magnesium alloy ingots and scrap that was reported and analyzed by Lu (2014) and Hong (2016). Data from 2002 to 2012 were used for model fitting, and data from 2013 and 2015 were used for ex-post testing. In Fig. 3, Two circles indicate outliers outside of the data intervals that were identified after performing the robust nonlinear interval regression analysis with q_u = q_l = 0.1. The optimized NGM(1,1), NFLNGM(1,1), AGM(1,1), optimized NGM(1,1)-P, and RNGM(1,1)-P were constructed using the non-equidistant sequence by removing data in 2004 and 2010. Table 6 shows the prediction results. The prediction results obtained by NN, GM(1,1), FLNGM(1,1), GM(1,1)-P, and RGM(1,1)-P that worked on the original equidistant sequence are described in Table 7.

Fig. 3

Outlier detection of training data for Case II

Table 6 MAPEs of different grey prediction models working on non-equidistant data for Case II (unit: tons)

Table 7 MAPEs of different prediction models working on equidistant data for Case II (unit: tons)

In terms of MAPE, Table 7 indicates that, among the prediction models considered here, the proposed RNGM(1,1)-P model demonstrated its superiority in the ex-post testing, despite that the RNGM(1,1)-P was slightly inferior to FLNGM(1,1) and NFLNGM(1,1) for model fitting. Indeed, one should place more emphasis on the results with respect to generalization (Luo et al, 2013). Table 8 summarizes forecasting accuracy for model fitting and ex-post testing. In addition to MAPE, we can see that the RNGM(1,1)-P outperformed most of the other considered prediction models in terms of MAD and RMSE for ex-post testing. The RNGM(1,1)-P outperformed all the other models by RMSE, but it was slightly inferior to NFLNGM(1,1) and ANGM(1,1) by MAD.

Table 8 Forecasting accuracy for model fitting and ex-post testing for Case II

4.3 Statistical analysis

To demonstrate the superiority of the proposed RNGM(1,1)-P, statistical analysis was conducted by using the Wilcoxon signed-rank test. The forecasting accuracy of the RNGM(1,1)-P was compared with that each of the other prediction models considered for ex-post testing. Let the statistic $R^{ - }$ denote the sum of ranks for the last four and three years of Cases I and II, respectively, in which the accuracy of the proposed RNGM(1,1)-P was inferior to that of one prediction model. For instance, compared to NGM(1,1), $R^{ - }$ was equal to the sum of ranks for the seven years in which the accuracy of the RNGM(1,1)-P was inferior to that of the NGM(1,1). As $R^{ - }$ = 4 which was less than the critical value of 6 at a significance level of 0.1 with respect to a right-tailed test, the RNGM(1,1)-P was significantly superior to the NGM(1,1). It was found that $R^{ - }$ = 7 which was slightly greater than the critical value at a significance level of 0.1 when comparing with the NFLNGM(1,1), the RNGM(1,1)-P seems to be superior to the NFLNGM(1,1) as well. As a result, the RNGM(1,1)-P significantly outperformed most of the considered prediction models except for the GM(1,1)-P and NN. Even so, the RNGM(1,1)-P performed better than the GM(1,1)-P and NN from the viewpoint of the MAPE for ex-post testing.

5 Discussion

The prediction accuracy of the proposed RNGM(1,1)-P was examined using real magnesium alloy demand data from China and Taiwan. The experimental results for ex-post testing show that the MAPEs of the proposed model were minimal among all considered models. Statistical analysis further indicated that the RNGM(1,1)-P significantly outperformed the most of the considered prediction models as well. In terms of MAPEs, since the RNGM(1,1)-P outperformed the RGM(1,1)-P that can only deal with the original equidistant sequence, this indicated that the forecasting performance of the RGM(1,1)-P can be improved by removing outliers from data sequences. Altogether, the above results demonstrated the high applicability of the proposed RNGM(1,1)-P in the forecast of magnesium alloy demand.

As mentioned above, MAPE is the primary measure to examine forecasting accuracy of the considered prediction models here. From Tables 5 and 8, we can see that the RNGM(1,1)-P outperformed the other considered models in terms of MAPE for ex-post testing. However, it cannot beat the other considered models in terms of MAD and RMSE. The reason is that all considered grey prediction models were constructed by minimizing MAPE rather than MAD and RMSE. Even so, with MAD and RMSE, the proposed RNGM(1,1)-P is comparable to the other considered models. It should be noted that, for magnesium material demand forecasting, Hu (2020) applied grey relational analysis to access the relative importance of each sample for GM(1,1), and a residual modification without constructing residual models was then provided. Indeed, the contributions of this study are quite different from those of Hu (2020).

6 Conclusions

Many countries have established high standards for lowering CO₂ emissions and energy consumption for automobiles, and constructing lightweight products has become an effective way to achieve these standards. Undoubtedly, magnesium alloys are important metal materials for the automotive industry, as well as for 3C products, aircraft, and medical appliances. As manufacturers need to invest in research and development in the use of magnesium alloys, the development of well-performed demand forecasting models is important and can help manufacturers understand the developing trends of related markets.

The main contribution of this study is to develop the grey residual modification model, namely RNGM(1,1)-P, to forecast the demand of magnesium alloy demand. To remove outliers that might give rise to a deterioration of forecasting accuracy, the robust nonlinear interval models were particularly employed to generate non-equidistant data sequences. It turns out that the proposed RNGM(1,1)-P can work on the resultant non-equidistant data sequences, and it is not necessary for the available data to comply with any statistical assumption.

The findings of this study also highlight several directions for our future work. First, this study did not consider exogenous variables such as the price of magnesium and business indicators in the context of the demand for magnesium alloy. As multivariate models may yield better predictions than single-variable models (Hu, 2020; Ma et al., 2019; Wu et al., 2019), we will investigate the applicability of several models, such as the multivariable models of Moonchai and Chutsagulprom (2020), the cumulative sum operator in grey prediction using integral transformations of Wei et al. (2020), and the background value optimization nonlinear model of Wu et al. (2020), to forecast the demand for magnesium alloy. Next, since there are shortcomings of MAPE outlined by Vandeput (2021), we will investigate how to incorporate the other measures such as MAD and RMSE into the construction of the proposed models to improve forecasting accuracy.