Buckling analysis of functionally graded plates subjected to combined in-plane loads

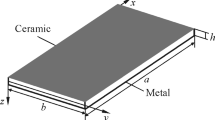
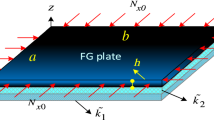
Abstract

The displacement field components of functionally graded plates (FGPs) couple the equilibrium equations due to the bending-extension interaction. There is no general study of FGPs buckling loads subjected to the combination of all in-plane loads in the literature. This study develops an analytical approach to finding the buckling coefficients of FGPs under combined biaxial and shear loads. The generalized integral transform technique (GITT) is simultaneously applied to the coupled buckling equations for the first time. Then, the partial differential equations are transformed into a set of linear equations, leading to the corresponding eigenvalue problem, which may be coded in Python’s programming language. The uniaxial (pure) buckling coefficients are initially obtained considering the power law and the rule of mixture approximations (including the Voigt, Modified, or Reuss models). Then, some interaction curves are developed for the biaxially and multi-axially loaded plates. The interaction curves are normalized versus the uniaxial buckling coefficient for fully clamped plates, so they only depend on the plate aspect ratio. Accordingly, a step-by-step procedure is presented for all loading states, including compression–compression–shear (CCS), compression–tension–shear (CTS or TCS), and tension–tension–shear loads (TTS).

Appendices

Appendix A

If the in-plane loads are not applied in the neutral plane in an FGP, the in-plane and out-of-plane boundary conditions are coupled due to bending-extension interaction. Thus, four types of boundary conditions may be called clamped edges:

$$\begin{aligned}{} & {} C1:\, \, \, \, u=0,\, \, \, \, \, \, \, \, v=0,\, \, \, \, \, \, \, \, \, w=0,\, \, \, \, \, \, \frac{\partial w}{\partial x}=0, \end{aligned}$$

(29a)

$$\begin{aligned}{} & {} C2:\, \, \, \, N_{x}=0,\, \, \, \, \, \, \, \, v=0,\, \, \, \, \, \, \, \, \, w=0,\, \, \, \, \, \, \frac{\partial w}{\partial x}=0, \end{aligned}$$

(29b)

$$\begin{aligned}{} & {} C3:\, \, \, \, u=0,\, \, \, \, \, \, \, N_{xy}=0,\, \, \, \, \, \, \, \, \, w=0,\, \, \, \, \, \, \frac{\partial w}{\partial x}=0, \end{aligned}$$

(29c)

$$\begin{aligned}{} & {} C4:\, \, \, \, N_{x}=0,\, \, \, \, \, \, \, \, N_{xy}=0,\, \, \, \, \, \, \, \, \, w=0,\, \, \, \, \, \, \frac{\partial w}{\partial x}=0. \end{aligned}$$

(29d)

The C2 boundary conditions are considered in this study, as shown in Eqs. (16a–h).

Appendix B

Equations (30a–f) show the transformed terms of Eqs. (15a–c).

$$\begin{aligned}{} & {} \int _0^1 \int _0^1 {\left\{ {\begin{array}{l} \frac{\partial ^{2}u}{\partial \xi ^{2}} \\ \frac{\partial ^{2}u}{\partial \eta ^{2}} \\ \end{array}} \right\} {X_{1,m}\left( \xi \right) Y}_{1,n}\left( \eta \right) \textrm{d}\xi \textrm{d}\eta =-\left\{ {\begin{array}{l} \alpha _{1,m}^{2} \\ \beta _{1,n}^{2} \\ \end{array}} \right\} u_{mn}}, \end{aligned}$$

(30a)

$$\begin{aligned}{} & {} \int _0^1 \int _0^1 \left\{ {\begin{array}{l} {\begin{array}{l} \frac{\partial ^{2}v}{\partial \xi \partial \eta } \\ \frac{\partial ^{3}w}{{\partial \xi }^{3}}, \\ \end{array}} \\ \frac{\partial ^{3}w}{\partial \xi {\partial \eta }^{2}} \\ \end{array}} \right\} {X_{1,m}\left( \xi \right) Y}_{1,n}\left( \eta \right) \textrm{d}\xi \textrm{d}\eta \nonumber \\{} & {} \quad =\mathop {\sum }\limits _{r=1}^\infty \mathop {\sum }\limits _{s=1}^\infty \left\{ {\begin{array}{l} {\begin{array}{l} {\bar{v}}_{rs}H_{12,mr}L_{12,ns} \\ w_{rs}\left( \alpha _{1,m}^{2}H_{13,mr}+\alpha _{3,r}^{2}\delta _{13,mr} \right) \, K_{13,ns} \\ \end{array}} \\ w_{rs}\beta _{1,n}^{2}H_{13,mr}K_{13,ns} \\ \end{array}} \right\} , \end{aligned}$$

(30b)

$$\begin{aligned}{} & {} \int _0^1 \int _0^1 {\left\{ {\begin{array}{l} \frac{\partial ^{2}v}{\partial \xi ^{2}} \\ \frac{\partial ^{2}v}{\partial \eta ^{2}} \\ \end{array}} \right\} {X_{2,m}\left( \xi \right) Y}_{2,n}\left( \eta \right) \textrm{d}\xi \textrm{d}\eta =-\left\{ {\begin{array}{l} \alpha _{2,m}^{2} \\ \beta _{2,n}^{2} \\ \end{array}} \right\} {\bar{v}}_{mn}}, \end{aligned}$$

(30c)

$$\begin{aligned}{} & {} \int _0^1 \int _0^1 {\left\{ {\begin{array}{l} {\begin{array}{*{20}c} \frac{\partial ^{2}u}{\partial \xi \partial \eta }\\ \frac{\partial ^{3}w}{{\partial \xi }^{2}\partial \eta }\\ \end{array} } \\ \frac{\partial ^{3}w}{{\partial \eta }^{3}} \\ \end{array}} \right\} {X_{2,m}\left( \xi \right) Y}_{2,n}\left( \eta \right) \textrm{d}\xi \textrm{d}\eta } \nonumber \\{} & {} \quad =\mathop {\sum }\limits _{r=1}^\infty \mathop {\sum }\limits _{s=1}^\infty \left\{ {\begin{array}{l} {\begin{array}{*{20}c} u_{rs}H_{21,mr}L_{21,ns}\\ w_{rs}\alpha _{2,m}^{2}G_{23,mr}L_{23,ns}\\ \end{array} } \\ w_{rs}\left( \beta _{2,n}^{2}L_{23,ns}+\beta _{3,s}^{2}\delta _{23,ns} \right) G_{23,mr} \\ \end{array}} \right\} , \end{aligned}$$

(30d)

$$\begin{aligned}{} & {} \int _0^1 \int _0^1 {\left\{ {\begin{array}{l} \frac{\partial ^{4}w}{{\partial \xi }^{4}} \\ \frac{\partial ^{4}w}{{\partial \eta }^{4}} \\ \end{array}} \right\} X_{3,m}\left( \xi \right) Y_{3,n}\left( \eta \right) \textrm{d}\xi \textrm{d}\eta } =\left\{ {\begin{array}{l} \alpha _{3,m}^{4} \\ \beta _{3,n}^{4} \\ \end{array}} \right\} w_{mn}, \end{aligned}$$

(30e)

$$\begin{aligned}{} & {} \int _0^1 \int _0^1 {\left\{ {\begin{array}{l} {\begin{array}{l} {\begin{array}{l} \frac{\partial ^{3}u}{{\partial \xi }^{3}} \\ \frac{\partial ^{3}u}{\partial \xi {\partial \eta }^{2}} \\ \frac{\partial ^{3}v}{{\partial \xi }^{2}\partial \eta } \\ \frac{\partial ^{3}v}{{\partial \eta }^{3}} \\ \end{array}} \\ \frac{\partial ^{4}w}{{\partial \xi }^{2}{\partial \eta }^{2}} \\ \frac{\partial ^{2}w}{{\partial \xi }^{2}} \\ \frac{\partial ^{2}w}{\partial \xi \partial \eta } \\ \end{array}} \\ \frac{\partial ^{2}w}{{\partial \eta }^{2}} \\ \end{array}} \right\} X_{3,m}\left( \xi \right) Y_{3,n}\left( \eta \right) \textrm{d}\xi \textrm{d}\eta } \nonumber \\{} & {} \quad =\sum \limits _{r=1}^\infty \sum \limits _{s=1}^\infty \left\{ {\begin{array}{l} {\begin{array}{l} -u_{rs}\left( J_{31,mr}-\alpha _{3,m}^{2}\delta _{31,mr} \right) K_{31,ns} \\ -u_{rs}H_{31,mr}P_{31,ns} \\ -{\bar{v}}_{rs}I_{32,mr}L_{32,ns} \\ -{\bar{v}}_{rs}\left( Q_{32,ns}-\beta _{3,n}^{2}\delta _{32,ns} \right) G_{32,mr} \\ \end{array}} \\ w_{rs}I_{33,mr}P_{33,ns} \\ w_{rs}I_{33,mr}K_{33,ns} \\ w_{rs}H_{33,mr}L_{33,ns} \\ w_{rs}G_{33,mr}P_{33,ns} \\ \end{array}} \right\} , \end{aligned}$$

(30f)

where $\alpha _{i,m}$ and $\beta _{j,n}$; $ij=1,2,3$ are defined in Eqs. (22a–d) and

$$\begin{aligned} G_{23,mr}= & {} \int _0^1 {X_{3,r}\left( \xi \right) X_{2,m}\left( \xi \right) \textrm{d}\xi =} 2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] \frac{m\pi \alpha _{3,r}^{2}}{m^{4}\pi ^{4}-\alpha _{3,r}^{4}}, \end{aligned}$$

(31a)

$$\begin{aligned} G_{32,mr}= & {} \int _0^1 {X_{2,r}\left( \xi \right) X_{3,m}\left( \xi \right) \textrm{d}\xi =} 2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] \frac{r\pi \alpha _{3,m}^{2}}{r^{4}\pi ^{4}-\alpha _{3,m}^{4}}, \end{aligned}$$

(31b)

$$\begin{aligned} G_{33,mr}= & {} \int _0^1 {X_{3,r}\left( \xi \right) X_{3,m}\left( \xi \right) \textrm{d}\xi =} \left\{ {\begin{array}{l} 1\, \,;\, \, m=r \\ 0\, \, \,;\, \, m\ne r \\ \end{array}} \right. , \end{aligned}$$

(31c)

$$\begin{aligned} H_{12,mr}= & {} \int _0^1 {X_{2,r}\left( \xi \right) X_{1,m}^{'}\left( \xi \right) \textrm{d}\xi =} \left\{ {\begin{array}{l} -m\pi \, \,;\, \, m=r \\ 0\, \, \, \, \, \, \, \, \,;\, \, m\ne r \\ \end{array}} \right. , \end{aligned}$$

(32a)

$$\begin{aligned} H_{21,mr}= & {} \int _0^1 {X_{1,r}\left( \xi \right) X_{2,m}^{'}\left( \xi \right) \textrm{d}\xi =} \left\{ {\begin{array}{l} m\pi \, \, \, \, \,;\, \, m=r \\ 0\, \, \, \, \, \, \, \, \,;\, \, m\ne r \\ \end{array}} \right. , \end{aligned}$$

(32b)

$$\begin{aligned} H_{13,mr}= & {} \int _0^1 {X_{3,r}\left( \xi \right) X_{1,m}^{'}\left( \xi \right) \textrm{d}\xi =-2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] \frac{m^{2}\pi ^{2}\alpha _{3,r}^{2}}{m^{4}\pi ^{4}-\alpha _{3,r}^{4}}}, \end{aligned}$$

(32c)

$$\begin{aligned} H_{31,mr}= & {} \int _0^1 {X_{1,r}\left( \xi \right) X_{3,m}^{'}\left( \xi \right) \textrm{d}\xi =2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] \frac{r^{2}\pi ^{2}\alpha _{3,m}^{2}}{r^{4}\pi ^{4}-\alpha _{3,m}^{4}}}, \end{aligned}$$

(32d)

$$\begin{aligned} H_{33,mr}= & {} \int _0^1 {X_{3,r}\left( \xi \right) X_{3,m}^{'}\left( \xi \right) \textrm{d}\xi =\left\{ {\begin{array}{l} 0\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,;\, m=r \\ \left[ 1-\left( -1 \right) ^{m+r} \right] \frac{4\alpha _{3,r}^{2}\alpha _{3,m}^{2}}{\alpha _{3,r}^{4}-\alpha _{3,m}^{4}}\, \,;\, m\ne r \\ \end{array}} \right. \, \, } \end{aligned}$$

(32e)

$$\begin{aligned} I_{32,mr}= & {} \int _0^1 {X_{2,r}\left( \xi \right) X_{3,m}^{''}\left( \xi \right) \textrm{d}\xi =} -2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] \frac{r^{3}\pi ^{3}\alpha _{3,m}^{2}}{r^{4}\pi ^{4}-\alpha _{3,m}^{4}}, \end{aligned}$$

(33a)

$$\begin{aligned} I_{33,mr}= & {} \int _0^1 {X_{3,r}\left( \xi \right) X_{3,m}^{''}\left( \xi \right) \textrm{d}\xi =} \left\{ {\begin{array}{l} c_\textrm{m}\alpha _{3,m}\left[ 2-c_\textrm{m}\alpha _{3,m} \right] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,;m=r \\ \frac{4\alpha _{3,m}^{2}\alpha _{3,r}^{2}}{\alpha _{3,m}^{4}-\alpha _{3,r}^{4}}\left[ c_\textrm{m}\alpha _{3,m}-c_{r}\alpha _{3,r} \right] \left[ 1+\left( -1 \right) ^{m+r} \right] \, \,;m\ne r \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(33b)

$$\begin{aligned} J_{31,mr}= & {} \int _0^1 {X_{1,r}\left( \xi \right) X_{3,m}^{'''}\left( \xi \right) \textrm{d}\xi =} -2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] \frac{\alpha _{3,m}^{6}}{r^{4}\pi ^{4}-\alpha _{3,m}^{4}}, \end{aligned}$$

(34)

$$\begin{aligned} K_{13,ns}= & {} \int _0^1 {Y_{3,s}\left( \eta \right) Y_{1,n}\left( \eta \right) \textrm{d}\eta =} 2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] \frac{n\pi \beta _{3,s}^{2}}{n^{4}\pi ^{4}-\beta _{3,s}^{4}}, \end{aligned}$$

(35a)

$$\begin{aligned} K_{31,ns}= & {} \int _0^1 {Y_{1,s}\left( \eta \right) Y_{3,n}\left( \eta \right) \textrm{d}\eta =} 2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] \frac{s\pi \beta _{3,n}^{2}}{s^{4}\pi ^{4}-\beta _{3,n}^{4}}, \end{aligned}$$

(35b)

$$\begin{aligned} K_{33,ns}= & {} \int _0^1 {Y_{3,s}\left( \eta \right) Y_{3,n}\left( \eta \right) \textrm{d}\eta =} \left\{ {\begin{array}{l} 1\, \,;\, \, n=s \\ 0\, \, \,;\, n\ne s \\ \end{array}} \right. , \end{aligned}$$

(35c)

$$\begin{aligned} L_{12,ns}= & {} \int _0^1 {Y_{2,s}\left( \eta \right) Y_{1,n}^{'}\left( \eta \right) \textrm{d}\eta =} \left\{ {\begin{array}{l} n\pi \, \, \,;\, \, n=s \\ 0\, \, \, \, \, \,;\, \, n\ne s \\ \end{array}} \right. , \end{aligned}$$

(36a)

$$\begin{aligned} L_{21,ns}= & {} \int _0^1 {Y_{1,s}\left( \eta \right) Y_{2,n}^{'}\left( \eta \right) \textrm{d}\eta =} \left\{ {\begin{array}{l} -n\pi \, \,;\, \, n=s \\ 0\, \, \, \, \, \, \, \, \,;\, \, n\ne s \\ \end{array}} \right. , \end{aligned}$$

(36b)

$$\begin{aligned} L_{23,ns}= & {} \int _0^1 {Y_{3,s}\left( \eta \right) Y_{2,n}^{'}\left( \eta \right) \textrm{d}\eta =-2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] \frac{n^{2}\pi ^{2}\beta _{3,s}^{2}}{n^{4}\pi ^{4}-\beta _{3,s}^{4}}}, \end{aligned}$$

(36c)

$$\begin{aligned} L_{32,ns}= & {} \int _0^1 {Y_{2,s}\left( \eta \right) Y_{3,n}^{'}\left( \eta \right) \textrm{d}\eta =2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] \frac{s^{2}\pi ^{2}\beta _{3,n}^{2}}{s^{4}\pi ^{4}-\beta _{3,n}^{4}}}, \end{aligned}$$

(36d)

$$\begin{aligned} L_{33,ns}= & {} \int _0^1 {Y_{3,s}\left( \eta \right) Y_{3,n}^{'}\left( \eta \right) \textrm{d}\eta =\, \left\{ {\begin{array}{l} 0\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,;\, n=s \\ \left[ 1-\left( -1 \right) ^{n+s} \right] \frac{4\beta _{3,s}^{2}\beta _{3,n}^{2}}{\beta _{3,s}^{4}-\beta _{3,n}^{4}}\, \, \, \, \, \,;\, n\ne s \\ \end{array}} \right. \, \, \, \, \, \, }, \end{aligned}$$

(36e)

$$\begin{aligned} P_{31,ns}= & {} \int _0^1 {Y_{1,S}\left( \eta \right) Y_{3,n}^{''}\left( \eta \right) \textrm{d}\eta =} -2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] \frac{s^{3}\pi ^{3}\beta _{3,n}^{2}}{s^{4}\pi ^{4}-\beta _{3,n}^{4}}, \end{aligned}$$

(37a)

$$\begin{aligned} P_{33,ns}= & {} \int _0^1 {Y_{3,s}\left( \eta \right) Y_{3,n}^{''}\left( \eta \right) \textrm{d}\eta =} \left\{ {\begin{array}{l} c_{n}\beta _{3,n}\left[ 2-c_{n}\beta _{3,n} \right] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \,;n=s, \\ \frac{4\beta _{3,n}^{2}\beta _{3,s}^{2}}{\beta _{3,n}^{4}-\beta _{3,s}^{4}}\left[ c_{n}\beta _{3,n}-c_{s}\beta _{3,s} \right] \left[ 1+\left( -1 \right) ^{n+s} \right] \, \, \,;n\ne s \\ \end{array}} \right. , \end{aligned}$$

(37b)

$$\begin{aligned} Q_{32,ns}= & {} \int _0^1 {Y_{1,s}\left( \eta \right) Y_{3,n}^{'''}\left( \eta \right) \textrm{d}\eta =} -2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] \frac{\beta _{3,n}^{6}}{s^{4}\pi ^{4}-\beta _{3,n}^{4}}, \end{aligned}$$

(38)

$$\begin{aligned} \delta _{13,mr}= & {} \delta _{31,mr}=2\sqrt{2} \left[ 1+\left( -1 \right) ^{m+r} \right] , \end{aligned}$$

(39a)

$$\begin{aligned} \delta _{23,ns}= & {} \delta _{32,ns}=2\sqrt{2} \left[ 1+\left( -1 \right) ^{n+s} \right] , \end{aligned}$$

(39b)

Appendix C

In Table 13, pure shear buckling coefficients are shown for FPGs with $\phi =1,\, 4$, $p=1,\, 2,\, 5$, $\lambda =50,\, 100,\, 125$, and $\nu =0.1,\, \, 0.2,\, \, 0.3$. The results show that the buckling coefficient has no sensitivity to the plate’s thickness ratio $\left( \lambda \right)$ and Poisson’s ratio $\left( \nu \right)$ to at least the fourth significant digits.

Table 13 Pure shear buckling coefficient of FGPs (Voigt model) with various parameters