1 Introduction

General nonlinear theories of rods can be found in [1–7]. Two models of a nonlinear hyperelastic rod with a rigid cross-section admitting bending, tangential shear deformation and torsion are considered in this note. The kinematics and strain energies of both models are identical but the treatment of angular momentum in the two models is different. One model considers a constrained theory of a Cosserat rod. In this model the kinematics are determined by the balances of linear and director momentum as well as the kinematic constraints. The kinetic quantities are determined by hyperelastic constitutive equations and constraint responses that ensure the kinematic constraints are satisfied. Also, the balance of angular momentum is satisfied by restricting a second order tensor to be symmetric in a similar manner to the symmetry of the Cauchy stress in the three-dimensional theory. The second model is the special Cosserat theory of rods developed in ([2], Ch. XIII) and is denoted as the Antman model. In the Antman model the kinematics are determined by satisfying the balances of linear and angular momentum and constitutive equations are specified directly for the force and mechanical moment applied to the rod.

It was shown in [8] that if the restriction due to the balance of angular momentum is satisfied in the constrained Cosserat model, then the kinematics can be determined by the balances of linear and angular momentum, as in the Antman model. This note poses and answers the question:

Are the solutions of these two models identical for the same strain energy?

2 A Constrained Cosserat Rod with a Rigid Cross-Section

This section summarizes relevant results in [8]. Greek indices take the range \((\alpha =1,2)\), Latin indices take the range \((1,2,3)\) and the usual summation convention is used for repeated indices. The notation in this note is the same as in [7, 8] where details can be found.

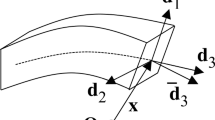
In its current configuration at time \(t\), the position of a material point \({\mathbf{x}}\) on the rod’s centroidal curve and the director vectors \({\mathbf{d}}_{i}\) are expressed in the forms

$$ \begin{aligned} &{\mathbf{x}}= {\mathbf{x}}(S,t) \,, &&{\mathbf{d}}_{i} = {\mathbf{d}}_{i}(S,t) \,, &&{\mathbf{d}}_{3} = {\mathbf{d}}_{3}(S,t) = \frac{{\partial }{\mathbf{x}}}{{\partial }S} \,, \\ &d^{1/2} = {\mathbf{d}}_{1} \times {\mathbf{d}}_{2} \cdot {\mathbf{d}}_{3} > 0 \,, \\ &{\mathbf{d}}^{1} = d^{-1/2} {\mathbf{d}}_{2} \times {\mathbf{d}}_{3} \,, &&{\mathbf{d}}^{2} = d^{-1/2} {\mathbf{d}}_{3} \times {\mathbf{d}}_{1} \,, &&{\mathbf{d}}^{3} = d^{-1/2} {\mathbf{d}}_{1} \times {\mathbf{d}}_{2} \,, \end{aligned} $$
(1)

where \({\mathbf{d}}_{\alpha}\) describe the orientation of the rod’s cross-section, \({\mathbf{d}}_{3}\) is tangent to the centroidal curve and \({\mathbf{d}}^{i}\) are the reciprocal vectors (see Fig. 1). Without loss in generality, the values \({\mathbf{D}}_{i}\), \({\mathbf{D}}^{i}\) of \({\mathbf{d}}_{i}\), \({\mathbf{d}}^{i}\) in a zero-stress reference configuration can be specified as a rotating orthonormal triad

$$ \begin{aligned} &{\mathbf{D}}_{i}(S) = {\mathbf{D}}^{i}(S) \,, \quad {\mathbf{D}}_{i} \cdot {\mathbf{D}}_{j} = \delta _{ij} \,, \quad {\mathbf{D}}_{1} \times {\mathbf{D}}_{2} \cdot {\mathbf{D}}_{3} = 1 \,, \end{aligned} $$
(2)

where \(\delta _{ij}\) is the Kronecker delta. This specification ensures that \(S\) is the arclength coordinate of the rod’s centroidal curve in its reference configuration.

Fig. 1
figure 1

Sketch of the rigid cross-section of a rod showing the Cosserat director \({\mathbf{d}}_{3}\), which is tangent to the centroidal curve, and the director \(\tilde{{\mathbf{d}}}_{3}\) of the Antman model, which is normal to the cross-section

Full size image

From [8] it is recalled that the balance of linear momentum and the two balances of director momentum depend on the force \({\mathbf{t}}^{3}\), the intrinsic director couples \({\mathbf{t}}^{\alpha}\) and the director couples \({\mathbf{m}}^{\alpha}\). Moreover, the balance of angular moment depends on the mechanical moment \({\mathbf{m}}\) defined by

$$ \begin{aligned} &{\mathbf{m}}= {\mathbf{d}}_{\alpha }\times {\mathbf{m}}^{\alpha }\,. \end{aligned} $$
(3)

As, in the three-dimensional theory, these balance laws are used to write the balance of angular moment as a restriction that requires the second order tensor \({\mathbf{T}}\) to be symmetric

$$ \begin{aligned} &\lambda {\mathbf{T}}= {\mathbf{d}}_{i} \otimes {\mathbf{t}}^{i} + \frac{{\partial }{\mathbf{d}}_{\alpha}}{{\partial }S} \otimes { \mathbf{m}}^{\alpha }= \lambda {\mathbf{T}}^{T} \,, \end{aligned} $$
(4)

where \({\mathbf{a}}\otimes {\mathbf{b}}\) is the tensor product of two vectors \({\mathbf{a}}\), \({\mathbf{b}}\) and \(\lambda \) is the stretch of the rod’s centroidal curve. In the general theory, a strain energy \(\Sigma \) per unit mass is proposed and hyperelastic constitutive equations are developed for \({\mathbf{T}}\), \({\mathbf{m}}^{\alpha}\), which satisfy the restriction (4), Then, \({\mathbf{t}}^{i}\) are determined by

$$ \begin{aligned} &{\mathbf{t}}^{i} = \Big(\lambda {\mathbf{T}}- \frac{{\partial }{\mathbf{d}}_{\alpha}}{{\partial }S} \otimes { \mathbf{m}}^{\alpha }\Big) {\mathbf{d}}^{i} \,. \end{aligned} $$
(5)

For a rigid cross-section the directors \({\mathbf{d}}_{\alpha}\) satisfy the kinematic constraints

$$ \begin{aligned} &{\mathbf{d}}_{\alpha }\cdot {\mathbf{d}}_{\beta }= \delta _{\alpha \beta} \,, \end{aligned} $$
(6)

where \(\delta _{ij}\) is the Kronecker delta. From [8], the current tangential stretch \(\lambda \) of the rod’s centroidal curve, the shear strains \(\gamma _{\alpha}\), the bending strains \(\beta _{\alpha}\) and the torsional strain \(\beta _{3}\) are defined by

$$ \begin{aligned} &\lambda = |{\mathbf{d}}_{3}| \,, \quad \gamma _{\alpha }= { \mathbf{d}}_{\alpha }\cdot {\mathbf{d}}_{3} \,, \quad \beta _{\alpha }= {\mathbf{d}}^{3} \cdot \frac{{\partial }{\mathbf{d}}_{\alpha}}{{\partial }S} - {\mathbf{D}}^{3} \cdot \frac{{\partial }{\mathbf{D}}_{\alpha}}{{\partial }S} \,, \\ &\beta _{3} = \frac{1}{2} \Bigl({\mathbf{d}}^{2} \cdot \frac{{\partial }{\mathbf{d}}_{1}}{{\partial }S} - {\mathbf{d}}^{1} \cdot \frac{{\partial }{\mathbf{d}}_{2}}{{\partial }S}\Bigr) - \frac{1}{2} \Bigl({ \mathbf{D}}^{2} \cdot \frac{{\partial }{\mathbf{D}}_{1}}{{\partial }S} - {\mathbf{D}}^{1} \cdot \frac{{\partial }{\mathbf{D}}_{2}}{{\partial }S}\Bigr) \,. \end{aligned} $$
(7)

For the constrained theory, part of \({\mathbf{T}}\) is determined by a constraint response that does no work and ensures that the constraints (6) are satisfied. The remainder of \({\mathbf{T}}\), and \({\mathbf{m}}^{\alpha}\) are determined by hyperelastic constitutive equations based on the strain energy function

$$ \begin{aligned} &\Sigma = \Sigma ( \lambda , \gamma _{\alpha}, \beta _{i}) \,, \end{aligned} $$
(8)

with these constitutive equations satisfying the restriction (4). Specifically, it was shown in [8] that the force \({\mathbf{t}}^{3}\) and mechanical moment \({\mathbf{m}}\) are determined by the constitutive equations

$$ \begin{aligned} &{\mathbf{t}}^{3} = m \frac{{\partial }\Sigma}{{\partial }\gamma _{\sigma}} {\mathbf{d}}_{ \sigma }+ m \lambda ^{-1} \frac{{\partial }\Sigma}{{\partial }\lambda} {\mathbf{d}}_{3} - \Big( \frac{{\partial }{\mathbf{d}}_{1}}{{\partial }S} \cdot {\mathbf{d}}^{3} \Big) \Big(\frac{1}{2} m \frac{{\partial }\Sigma}{{\partial }\beta _{3}} {\mathbf{d}}^{2} + m \frac{{\partial }\Sigma}{{\partial }\beta _{1}} {\mathbf{d}}^{3} \Big) \\ &\quad \quad - \Big(\frac{{\partial }{\mathbf{d}}_{2}}{{\partial }S} \cdot {\mathbf{d}}^{3} \Big) \Big(- \frac{1}{2} m \frac{{\partial }\Sigma}{{\partial }\beta _{3}} {\mathbf{d}}^{1} + m \frac{{\partial }\Sigma}{{\partial }\beta _{2}} {\mathbf{d}}^{3} \Big) \,, \\ &{\mathbf{m}}= m \frac{{\partial }\Sigma}{{\partial }\beta _{2}} \, ({ \mathbf{d}}_{2} \times {\mathbf{d}}^{3}) + m \frac{{\partial }\Sigma}{{\partial }\beta _{1}} ({\mathbf{d}}_{1} \times {\mathbf{d}}^{3}) + \frac{1}{2} m \frac{{\partial }\Sigma}{{\partial }\beta _{3}} ({\mathbf{d}}_{1} \times {\mathbf{d}}^{2} - {\mathbf{d}}_{2} \times {\mathbf{d}}^{1}) \,, \end{aligned} $$
(9)

where \(m(S)\) is the mass per unit arclength \(dS\). Since \({\mathbf{d}}_{\alpha}\) define the plane of the rod’s cross-section and \({\mathbf{d}}^{3}\) is normal to this cross-section, it follows that the terms in \({\mathbf{m}}\) associated with \({\partial }\Sigma /{\partial }\beta _{\alpha}\) are pure bending terms. Whereas the term associated with \({\partial }\Sigma /{\partial }\beta _{3}\) controls torsion about the cross-section’s normal and includes bending components.

3 Antman’s Special Cosserat Rod

Using the notational connections

$$ \begin{aligned} &{\mathbf{{r}}}= {\mathbf{x}}\,, \quad \frac{{\partial }{\mathbf{{r}}}}{{\partial }S} = {\mathbf{d}}_{3} \,, \quad {\mathbf{n}}= {\mathbf{t}}^{3} \,, \end{aligned} $$
(10)

the Antman model [2] introduces an orthonormal triad \(\tilde{{\mathbf{d}}}_{i}\) defined by (see Fig. 1)

$$ \begin{aligned} &\tilde{{\mathbf{d}}}_{\alpha }= {\mathbf{d}}_{\alpha }\,, \quad \tilde{{\mathbf{d}}}_{3} = {\mathbf{d}}_{1} \times {\mathbf{d}}_{2} \,. \end{aligned} $$
(11)

Also, the vectors \({\mathbf{u}}\) and \({\mathbf{v}}\) are defined by the equations

$$ \begin{aligned} &\frac{{\partial }\tilde{{\mathbf{d}}}_{k}}{{\partial }S} = { \mathbf{u}}\times \tilde{{\mathbf{d}}}_{k} \,, \quad u_{k} = { \mathbf{u}}\cdot \tilde{{\mathbf{d}}}_{k} \,, \quad {\mathbf{v}}= { \mathbf{d}}_{3} \,, \quad v_{k} = {\mathbf{d}}_{3} \cdot \tilde{{\mathbf{d}}}_{k} \,. \end{aligned} $$
(12)

Then, with the help of these definitions it can be shown that

$$ \begin{aligned} &{\mathbf{d}}_{3} = v_{\alpha }{\mathbf{d}}_{\alpha }+ v_{3} \tilde{{\mathbf{d}}}_{3} \,, \quad \tilde{{\mathbf{d}}}_{3} = - \frac{v_{\alpha}}{v_{3}} {\mathbf{d}}_{\alpha }+ \frac{1}{v_{3}} { \mathbf{d}}_{3} \,, \\ & d^{1/2} = {\mathbf{d}}_{1} \times {\mathbf{d}}_{2} \cdot { \mathbf{d}}_{3} = v_{3} > 0 \,, \\ &{\mathbf{u}}= \Big( u_{1} - \frac{u_{3}v_{1}}{v_{3}} \Big) { \mathbf{d}}_{1} + \Big(u_{2} - \frac{u_{3}v_{2}}{v_{3}} \Big) { \mathbf{d}}_{2} + \frac{u_{3}}{v_{3}} {\mathbf{d}}_{3} \,, \\ &\frac{{\partial }{\mathbf{d}}_{1}}{{\partial }S} = \frac{u_{2}v_{1}}{v_{3}} {\mathbf{d}}_{1}+ \Big(u_{3} + \frac{u_{2} v_{2}}{v_{3}} \Big) {\mathbf{d}}_{2} - \frac{u_{2}}{v_{3}} {\mathbf{d}}_{3} \,, \\ &\frac{{\partial }{\mathbf{d}}_{2}}{{\partial }S} =- \Big(u_{3} + \frac{u_{1} v_{1}}{v_{3}} \Big) {\mathbf{d}}_{1} - \frac{u_{1}v_{2}}{v_{3}} {\mathbf{d}}_{2} + \frac{u_{1}}{v_{3}} { \mathbf{d}}_{3} \,. \end{aligned} $$
(13)

This Antman model limits attention to a rod which is straight in its zero-stress reference configuration with \({\mathbf{D}}_{i}\) being constant vectors. For this case, (7) and (13) can be used to deduce that

$$ \begin{aligned} &\lambda = \sqrt{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}} \,, &&\gamma _{ \alpha }= v_{\alpha }\,, \\ &\beta _{1} = - \frac{u_{2}}{v_{3}} \,, \quad \beta _{2} = \frac{u_{1}}{v_{3}} \,, &&\beta _{3} = u_{3} + \frac{1}{2} \Big( \frac{u_{1} v_{1}+u_{2} v_{2}}{v_{3}} \Big) \,. \end{aligned} $$
(14)

Then, from [2] [Ch, XIII, (7.16)] the constitutive equations for the force \(\tilde{{\mathbf{t}}}^{3}\) and the mechanical moment \(\tilde{{\mathbf{m}}}\) can be expressed in the forms

$$ \begin{aligned} & \Sigma = \tilde{\Sigma}(u_{i}, v_{i}) = \Sigma (\lambda , \gamma _{ \alpha}, \beta _{i}) \,, \\ &\tilde{{\mathbf{t}}}^{3} = m \frac{{\partial }\tilde{\Sigma}}{{\partial }v_{i}} \tilde{{\mathbf{d}}}_{i} = \Big(m \frac{{\partial }\tilde{\Sigma}}{{\partial }v_{\alpha}} - \frac{v_{\alpha}}{v_{3}} m \frac{{\partial }\tilde{\Sigma}}{{\partial }v_{3}} \Big) {\mathbf{d}}_{ \alpha }+ \frac{m}{v_{3}} \frac{{\partial }\tilde{\Sigma}}{{\partial }v_{3}} {\mathbf{d}}_{3} \,, \\ &\tilde{{\mathbf{m}}} =m \frac{{\partial }\tilde{\Sigma}}{{\partial }u_{i}} \tilde{{\mathbf{d}}}_{i} = \Big(m \frac{{\partial }\tilde{\Sigma}}{{\partial }u_{\alpha}} - \frac{v_{\alpha}}{v_{3}} m \frac{{\partial }\tilde{\Sigma}}{{\partial }u_{3}} \Big) {\mathbf{d}}_{ \alpha }+ \frac{m}{v_{3}} \frac{{\partial }\tilde{\Sigma}}{{\partial }u_{3}} {\mathbf{d}}_{3} \,, \end{aligned} $$
(15)

where a superposed \(\tilde{(\,\,)}\) is used to distinguish the values \((\tilde{{\mathbf{t}}}^{3}, \tilde{{\mathbf{m}}})\) of the functional forms for the Antman model from those (9) for \(({\mathbf{t}}^{3}, {\mathbf{m}})\) in the constrained Cosserat model. These strain energy functions will be identical when \((\lambda , \gamma _{\alpha}, \beta _{i})\) are specified by (14).

4 Do the Two Models Yield the Same Solutions?

In [8] is was shown that the constrained Cosserat model and the Antman model yield the same balances of linear and angular momentum. Consequently, these two models will yield the same solutions if the constitutive equations (9) for \({\mathbf{t}}^{3}\), \({\mathbf{m}}\) are identical to (15) for \(\tilde{{\mathbf{t}}}^{3}\), \(\tilde{{\mathbf{m}}}\) for all strain energy functions \(\Sigma \).

From the above summary it is clear that constrained Cosserat approach requires constitutive equations for \({\mathbf{T}}\) and \({\mathbf{m}}^{\alpha}\) with constraint responses to ensure that the constraints (6) are satisfied. Moreover, the constitutive equations must satisfy the restriction (4) that \({\mathbf{T}}\) be a symmetric tensor in order for the balance of angular momentum to be automatically satisfied. This procedure yields the constitutive equations (9) for \({\mathbf{t}}^{3}\), \({\mathbf{m}}\). Also, the kinematics \({\mathbf{x}}\), \({\mathbf{d}}_{\alpha}\) are determined by the balance of linear momentum and the non-trivial balances of director momentum. In contrast, the Antman model proposes constitutive equations (15) directly for \(\tilde{{\mathbf{t}}}^{3}\), \(\tilde{{\mathbf{m}}}\) and uses the balances of linear and angular momentum to determine the kinematics \({\mathbf{x}}\), \({\mathbf{d}}_{\alpha}\).

From comparison of (9) and (15) it is not obvious that these expressions are identical. However, by using (13), (14) and the chain rule of differentiation

$$ \begin{aligned} &\frac{{\partial }\tilde{\Sigma}}{{\partial }u_{j}} = \frac{ {\partial }\Sigma}{{\partial }\lambda} \frac{{\partial }\lambda}{{\partial }u_{j}} + \frac{ {\partial }\Sigma}{{\partial }\gamma _{\alpha}} \frac{{\partial }\gamma _{\alpha}}{{\partial }u_{j}} + \frac{ {\partial }\Sigma}{{\partial }\beta _{i}} \frac{{\partial }\beta _{i}}{{\partial }u_{j}} \,, \\ &\frac{{\partial }\tilde{\Sigma}}{{\partial }v_{j}} = \frac{ {\partial }\Sigma}{{\partial }\lambda} \frac{{\partial }\lambda}{{\partial }v_{j}} + \frac{ {\partial }\Sigma}{{\partial }\gamma _{\alpha}} \frac{{\partial }\gamma _{\alpha}}{{\partial }v_{j}} + \frac{ {\partial }\Sigma}{{\partial }\beta _{i}} \frac{{\partial }\beta _{i}}{{\partial }v_{j}} \,, \end{aligned} $$
(16)

it can be shown that (9) and (15) are identical. This result begs the question: Why? The answer is that proper analysis of a strain energy function that is uninfluenced by superposed rigid body motions will yield elastic constitutive equations that automatically satisfy the reduced form of the balance of angular momentum. This means that the restriction (4) is automatically satisfied so the reduced form of the balance of angular momentum can replace the results of the nontrivial components of the balances of director momentum, which causes the solutions of the constrained Cosserat model and the Antman model to be identical for the same strain energy function.

Furthermore, it is noted that the constrained Cosserat model, based on the general kinematics (7), can be used for a rod that is curved and twisted in its zero-stress reference configuration.