Homogenization of Perforated Elastic Structures

Abstract

The paper is dedicated to the asymptotic behavior of $\varepsilon$-periodically perforated elastic (3-dimensional, plate-like or beam-like) structures as $\varepsilon \to 0$. In case of plate-like or beam-like structures the asymptotic reduction of dimension from $3D$ to $2D$ or $1D$ respectively takes place. An example of the structure under consideration can be obtained by a periodic repetition of an elementary “flattened” ball or cylinder for plate-like or beam-like structures in such a way that the contact surface between two neighboring balls/cylinders has a non-zero measure. Since the domain occupied by the structure might have a non-Lipschitz boundary, the classical homogenization approach based on the extension cannot be used. Therefore, for obtaining Korn’s inequalities, which are used for the derivation of a priori estimates, we use the approach based on interpolation. In case of plate-like and beam-like structures the proof of Korn’s inequalities is based on the displacement decomposition for a plate or a beam, respectively. In order to pass to the limit as $\varepsilon \to 0$ we use the periodic unfolding method.

1 Introduction

This paper deals with the linearized elasticity problem posed in different periodic domains. These domains are obtained by reproducing a representative cell of size $\varepsilon$ in such a way that one can get beam-like, plate-like or $N$-dimensional structures. It is assumed that a part of their exterior boundary denoted by $\varGamma _{\varepsilon }$ is fixed.

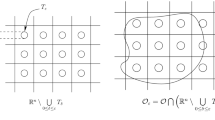
The $\varepsilon$-cells are made of elastic materials. The reference cell is denoted by ${\mathbf{C}}$ (Fig. 1). We assume that $\mathbf{C}$ has a Lipschitz boundary and that the interior of the closure of the union of two contiguous cells is connected. Under these assumptions, the whole periodic structure might have a non-Lipschitz boundary. Throughout this article, the cell ${\mathbf{C}}$ is included in the unit parallelotope of ${\mathbb{R}}^{N}$ (resp. ${\mathbb{R}}^{3}$), and one can replace this parallelotope by any bounded domain having the paving property with respect to a discrete group of rank $N$ (resp. 3).

Fig. 1

Periodicity cells

Our aim is to investigate the asymptotic behavior of these elastic periodic structures as $\varepsilon$ tends to 0. Since these structures might be non-Lipschitz, one of the main difficulties is to obtain a priori estimates. The classical extension approach (see [25]) and Korn’s inequalities for Lipschitz domains (see [9, 10]) cannot be used. Thus, in order to derive a priori estimates we use interpolations as suggested in [14, Sect. 5.5]. This makes it possible to prove Korn’s inequalities with constants independent of $\varepsilon$. Note that in case of beam-like and plate-like domains the derivation of Korn’s inequalities is also based on the decomposition of beam or plate displacements. These decompositions have been introduced in [2, 18].

To derive the limit problems, we use the periodic unfolding method introduced in [11]. This method has been applied to a vast number of problems such as problems in perforated domains [5, 6, 13, 16], transmission problems [17], contact problems [20, 22], problems including a thin layer [21], problems in domains with “rough boundary” [1, 3, 4], to name but a few. In our work, in contrast to earlier works for plate-like or beam-like structures [14, 19, 21, 22, 24], we simultaneously proceed to the homogenization and reduction of dimension. The periodic unfolding method used in this paper includes the following steps:

• introducing and applying appropriate unfolding operators, depending on the problem,

• obtaining a priori estimates for the displacements, then uniform estimates for the unfolded displacements, which, in turn, are used to pass to a weak limit in appropriate spaces over a fixed domain,

• establishing an unfolded limit problem from which a homogenized problem is derived.

As a general reference for the homogenization of elasticity problems in $3D$ periodically perforated domains with Lipschitz boundary we refer to [25]. In case of a plate-like domain we mention [14, Chapter V] where the interaction of homogenization and domain reduction, involving two small parameters such as plate thickness $\delta$ and periodicity $\varepsilon$, in its large dimensions was investigated. For similar results in case of a beam-like domain we refer to [19]. The novelty of this paper is the extension of the results to non-Lipschitz perforated domains.

The paper is organized as follows. Sections 2, 3 and 4 deal with periodically perforated $3D$, plate-like and beam-like domains, respectively. We begin every of these sections by introducing the notation and describing the specific type of a periodic domain. Then, for every type of a periodic domain, we introduce the unfolding operator, we derive weak limits of the fields, we specify the limit problem for characterize the limit fields. Moreover, at the end of every section, there is a conclusion in which we provide an approximation of the solution to the elasticity problem.

The proofs of Korn’s inequalities for different types of domains, namely $N$-dimensional, plate-like and beam-like, are given in Appendix A. The proofs of all lemmas and propositions are given in Appendix B.

Throughout this paper we use Einstein’s summation convention. Moreover, in all the estimates the constants do not depend on  $\varepsilon$ .

2 $N$-Dimensional Periodic Domain

This section deals with the asymptotic behavior of the solution to the linearized elasticity problem for $\varepsilon$-periodically perforated $N$-dimensional structures as $\varepsilon \to 0$. At first, we explain the notation, introduce the structure and state the elasticity problem. Then, we introduce the unfolding operator and its properties. And finally, we derive the unfolded limit problem and the homogenized problem.

2.1 Notation and Geometric Setting

Let $\varOmega \subset {\mathbb{R}}^{N}$, $N\in {\mathbb{N}}\setminus \{0,1\}$, be a bounded domain with a Lipschitz boundary and $\varGamma$ be a subset of $\partial \varOmega$ with non-zero measure. We assume that there exists an open set $\varOmega ^{\prime }$ with a Lipschitz boundary such that $\varOmega \subset \varOmega ^{\prime }$ and $\varOmega ^{\prime }\cap \partial \varOmega = \varGamma$.

We will use the following notations through this section:

• $Y\doteq (-1/2,1/2)^{N}$ is the unit cube,

• ${\mathbf{C}}\subset Y$ is a domain with Lipschitz boundary such that the $\hbox{interior}\big (\overline{\mathbf{C}}\cup (\overline{\mathbf{C}}+{\mathbf{e}}_{i}) \big )$, $i=\overline{1,N}$, is connected,

• $\varXi _{\varepsilon }\doteq \big \{\xi \in {\mathbb{Z}}^{N}\;|\; \varepsilon (\xi +Y)\cap \varOmega \neq \emptyset \big \}$,

• $\varXi '_{\varepsilon }\doteq \big \{\xi \in {\mathbb{Z}}^{N}\;|\; \varepsilon (\xi +Y)\cap \varOmega '\neq \emptyset \big \}$,

• $\varXi _{\varepsilon ,i}\doteq \big \{\xi \in \varXi _{\varepsilon }\;|\;\xi +{ \mathbf{e}}_{i}\in \varXi _{\varepsilon }\big \}$, $i=\overline{1,N}$,

• $\varOmega ^{*}_{\varepsilon }\doteq \hbox{interior}\Big ( \bigcup _{\xi \in \varXi _{\varepsilon }}\varepsilon (\xi + \overline{\mathbf{C}})\Big )$,

• $\varOmega ^{ext}_{\varepsilon }\doteq \hbox{interior}\Big ( \bigcup _{\xi \in \varXi _{\varepsilon }}\varepsilon (\xi +\overline{Y}) \Big )$,

• $\varOmega ^{\prime\,*}_{\varepsilon }\doteq \hbox{interior}\Big ( \bigcup _{\xi \in \varXi '_{\varepsilon }}\varepsilon (\xi + \overline{\mathbf{C}})\Big )$,

• $\varOmega _{1}\doteq \big \{x\in {\mathbb{R}}^{N}\;|\; \hbox{dist}(x, \varOmega )<1\big \}$,

• $M_{s}^{N}$ is the space of $N\times N$ symmetric matrices,

• for a.e. $x\in {\mathbb{R}}^{N}$ one has

  $$ x=\varepsilon \left (\left [\frac{x}{\varepsilon }\right ]+\left \{ \frac{x}{\varepsilon }\right \} \right ),\qquad \hbox{where }\; \left [ \frac{x}{\varepsilon }\right ]\in {\mathbb{Z}}^{N},\;\; \left \{ \frac{x}{\varepsilon }\right \} \in Y. $$

Note that ${\bigcup _{i=1}^{N} } \varXi _{ \varepsilon ,i}\subset \varXi _{\varepsilon }$ and that the domains $\varOmega ^{*}_{\varepsilon }$, $\varOmega^{\prime\,*}_{\varepsilon }$ are connected.

We are interested in the elastic behavior of a structure occupying the domain $\varOmega ^{*}_{\varepsilon }$ which is fixed on a part of its boundary $\varGamma _{\varepsilon }=\varGamma \cap \varOmega _{\varepsilon }^{*}$. The space of all admissible displacements is

$$ {\mathbf{V}}_{\varepsilon }=\big\{ u \in H^{1}(\varOmega ^{*}_{\varepsilon })^{N} \;\; |\; \; \exists u^{\prime }\in H^{1}(\varOmega ^{\prime\,*}_{\varepsilon })^{N} \; \mbox{such that} \; u^{\prime }_{|\varOmega ^{*}_{\varepsilon }}=u \; \hbox{and}\; u^{\prime }=0\;\hbox{in } \varOmega^{\prime\,*}_{\varepsilon } \setminus \overline{\varOmega ^{*}_{\varepsilon }}\big\} . $$

This means that the displacements belonging to ${\mathbf{V}}_{\varepsilon }$ “vanish” on the part $\varGamma _{\varepsilon }$ of $\partial \varOmega ^{*}_{\varepsilon }$.

Remark 1

Note that the domain $\varOmega ^{*}_{\varepsilon }$ might be non-Lipschitz (see Fig. 2). In this case, one cannot extend the displacements to the holes of this domain as it is proposed in [25].

Fig. 2

Domains $\varOmega ,\;\varOmega ',\;\varOmega _{\varepsilon }^{*},\;\varOmega^{\prime\,*}_{ \varepsilon }$ and sets $\varXi _{\varepsilon }$, $\varXi '_{\varepsilon}$

2.2 Statement of the Elasticity Problem

For a displacement $u\in H^{1}(\varOmega ^{*}_{\varepsilon })^{N}$, we denote by $e$ the linearized strain tensor (or symmetric gradient)

$$ e(u)\doteq \frac{1}{2} \Big(\nabla u+ (\nabla u)^{T}\Big), \quad e_{ij}(u) \doteq \frac{1}{2} \Big(\frac{\partial u_{i}}{\partial x_{j}}+ \frac{\partial u_{j}}{\partial x_{i}}\Big). $$

(2.1)

Let $a_{ijkl}\in L^{\infty }({\mathbf{C}}), i,j,k,l=\overline{1,N}$ be the components of the elasticity tensor. These functions satisfy the usual symmetry and positivity conditions:

• $a_{ijkl}(X)=a_{jikl}(X)=a_{klij}(X) \hbox{ for a.e. } X\in {\mathbf{C}}$;

• for any $\tau \in M_{s}^{N}$, there exists $c_{0}>0$ such that

  $$ a_{ijkl}(X)\tau _{ij}\tau _{kl}\geq c_{0} \tau _{ij}\tau _{ij} \quad \hbox{for a.e. } X\in {\mathbf{C}}. $$

  (2.2)

The constitutive law for the material occupying the domain $\varOmega ^{*}_{\varepsilon }$ is given by the relation between the linearized strain tensor and the stress tensor

$$ \sigma _{ij}^{\varepsilon }(u)\doteq a_{ijkl}^{\varepsilon }e_{kl}(u), \quad \forall \, u\in {\mathbf{V}}_{\varepsilon }, $$

(2.3)

where the coefficients $a_{ijkl}^{\varepsilon }$ are given by

$$ a_{ijkl}^{\varepsilon }(x)=a_{ijkl} \Big( \Big\{ \frac{x}{\varepsilon } \Big\} \Big) \quad \hbox{for a.e. } x\in \varOmega ^{*}_{\varepsilon }. $$

Let $f$ be in ${L^{2}(\varOmega _{1})}^{N}$, one defines the applied forces $f_{\varepsilon }$ by

$$ f_{\varepsilon } =f|_{\varOmega ^{*}_{\varepsilon }}. $$

(2.4)

The unknown displacement $u_{\varepsilon }:\varOmega ^{*}_{\varepsilon }\to \mathbb{R}^{N}$ is the solution to the linearized elasticity system in the strong formulation

$$ \textstyle\begin{cases} \nabla \cdot \sigma ^{\varepsilon }(u_{\varepsilon })=-f_{\varepsilon } &\mbox{in} \quad \varOmega ^{*}_{\varepsilon },\\ u_{\varepsilon }=0 &\mbox{on}\quad \varGamma _{\varepsilon },\\ \sigma ^{\varepsilon }(u_{\varepsilon })\cdot \nu _{\varepsilon }=0&\mbox{on} \quad \partial \varOmega ^{*}_{\varepsilon }\setminus \varGamma _{\varepsilon }, \end{cases} $$

(2.5)

where $\nu _{\varepsilon }$ is the outward normal vector to $\partial \varOmega ^{*}_{\varepsilon }$.

The variational formulation of (2.5) is given by

$$ \left \{ \begin{aligned} &\text{Find }u_{\varepsilon }\in {\mathbf{V}}_{\varepsilon }\text{ such that}, \\ &\int _{\varOmega ^{*}_{\varepsilon }}\sigma ^{\varepsilon }(u_{ \varepsilon }):e(v)\,dx=\int _{\varOmega ^{*}_{\varepsilon }}f_{ \varepsilon }\cdot v\,dx, \qquad \forall v\in {\mathbf{V}}_{\varepsilon }. \end{aligned} \right . $$

(2.6)

2.3 The Unfolding Operator

As mentioned above, for the derivation of the limit problem we use the periodic unfolding method. This method requires the introduction of an unfolding operator depending on the geometry of the problem. One of the main properties of this operator is that it replaces the integrals over the periodically oscillating domain $\varOmega ^{*}_{\varepsilon }$ by integrals over the “almost fixed” domain $\varOmega ^{ext}_{\varepsilon }\times {\mathbf{C}}$ which includes the whole domain $\varOmega$ and the periodicity cell ${\mathbf{C}}$. Moreover, it allows us to decompose any function into a main part without micro-oscillations and a remainder which takes the micro-oscillations into account. Below, in a similar way as for domains with holes (see [14]), we introduce a specific unfolding operator and give its properties.

Definition 1

For every measurable function $\phi \,:\, \varOmega ^{*}_{\varepsilon }\to \mathbb{R}$, the unfolding operator ${\mathcal{T}}_{\varepsilon }^{*}\,:\, \varOmega ^{ext}_{\varepsilon }\times {\mathbf{C}}\to \mathbb{R}$ is defined as follows:

$$ {\mathcal{T}}_{\varepsilon }^{*}(\phi )(x, X)= \phi \Big(\varepsilon \Big[\frac{x}{\varepsilon }\Big]+\varepsilon X\Big)\quad \hbox{for a.e. }(x,X)\in \varOmega ^{ext}_{\varepsilon }\times {\mathbf{C}}. $$

Below are some properties of ${\mathcal{T}}_{\varepsilon }^{*}$, which are similar to those of the unfolding operators introduced in [14]. That is due to the fact that

$$ \varLambda ^{ext}_{\varepsilon }\doteq \varOmega ^{ext}_{\varepsilon }\setminus \overline{\varOmega }\quad \hbox{satisfies}\quad \lim _{ \varepsilon \to 0}|\varLambda ^{ext}_{\varepsilon }|=0. $$

Proposition 1

For every $\phi \in L^{1}(\varOmega ^{*}_{\varepsilon })$

$$ \begin{aligned} &\int _{ \varOmega ^{*}_{\varepsilon }}\phi (x)\, dx= \int _{\varOmega ^{ {ext}}_{\varepsilon }\times {\mathbf{C}}}{\mathcal{T}}_{\varepsilon }^{*}(\phi )(x,X)\,dxdX, \\ & \|{\mathcal{T}}_{\varepsilon }^{*}(\phi )\|_{L^{1}(\varOmega ^{{ext}}_{\varepsilon }\times {\mathbf{C}})}=\|\phi \|_{L^{1}(\varOmega ^{*}_{ \varepsilon })}. \end{aligned} $$

(2.7)

For every $\phi \in L^{2}(\varOmega ^{*}_{\varepsilon })$

$$ \|{\mathcal{T}}_{\varepsilon }^{*}(\phi )\|_{L^{2}(\varOmega ^{{ext}}_{\varepsilon }\times {\mathbf{C}})}=\|\phi \|_{L^{2}(\varOmega ^{*}_{ \varepsilon })}. $$

(2.8)

For every $\phi \in H^{1}(\varOmega ^{*}_{\varepsilon })$

$$ {\mathcal{T}}_{\varepsilon }^{*}(\nabla \phi )(x,X)= \frac{1}{\varepsilon } \nabla _{X}{\mathcal{T}}_{\varepsilon }^{*}( \phi )(x,X)\quad \textit{for a.e. }(x,X)\in \varOmega ^{{ext}}_{\varepsilon }\times {\mathbf{C}}. $$

(2.9)

For more properties see [14].

2.4 Weak Limits of the Fields and the Limit Problem

Set

$$ {({\mathbb{R}}^{N})}^{*}_{\varepsilon }\doteq \hbox{interior}\Big( \bigcup _{\xi \in \mathbb{Z}^{N}}\varepsilon (\xi +\overline{\mathbf{C}}) \Big). $$

Denote by $H^{1}_{N,per}({\mathbf{C}})$ the subspace of the periodic functions belonging to $H^{1}_{loc}({({\mathbb{R}}^{N})}^{*}_{\varepsilon })$

$$ H^{1}_{N,per}({\mathbf{C}})\doteq \Big\{ \psi \in H^{1}_{loc}({({ \mathbb{R}}^{N})}^{*}_{\varepsilon })\;|\;\psi (\cdot +\xi )=\psi ( \cdot )\;\; \hbox{a.e. in }{({\mathbb{R}}^{N})}^{*}_{\varepsilon },\; \forall \,\xi \in \mathbb{Z}^{N}\Big\} , $$

by $H^{1}_{N,per,0}({\mathbf{C}})$ the subspace of the functions in $H^{1}_{N,per}({\mathbf{C}})$ with zero mean

$$ H^{1}_{N,per,0}({\mathbf{C}})\doteq \Big\{ \psi \in H^{1}_{N,per}({\mathbf{C}}) \;|\; \int _{{\mathbf{C}}} \psi (X)\, dX=0\Big\} , $$

and by $H^{1}_{\varGamma }(\varOmega )$ the space of the functions in $H^{1}(\varOmega )$ that vanish on $\varGamma$¹

$$ H^{1}_{\varGamma }(\varOmega )\doteq \big\{ \phi \in H^{1}(\varOmega )\;|\; \phi =0 \quad \hbox{on}\; \varGamma \big\} . $$

The proof of the following lemma is given in Appendix B.1.

Lemma 1

The solution $u_{\varepsilon }$of problem (2.5) satisfies

$$ \|u_{\varepsilon }\|_{H^{1}(\varOmega ^{*}_{\varepsilon })}\leq C\|f\|_{L^{2}( \varOmega _{1})}. $$

(2.10)

The proof of the proposition below is also postponed to Appendix B.1.

Proposition 2

(The unfolded limit problem)

Let $u_{\varepsilon }$be the solution of problem (2.5). There exist $u \in H^{1}_{\varGamma }(\varOmega )^{N}$and $\widehat{u}\in L^{2}(\varOmega ; H^{1}_{N,per,0}({\mathbf{C}}))^{N}$such that

$$ \begin{aligned} {\mathcal{T}}_{\varepsilon }^{*} (u_{\varepsilon })&\to u \quad \textit{strongly in}\quad L^{2}(\varOmega ; H^{1}({\mathbf{C}}))^{N}, \\ {\mathcal{T}}_{\varepsilon }^{*}(\nabla u_{\varepsilon })& \rightharpoonup \nabla u+\nabla _{X}\widehat{u}\quad \textit{ weakly in}\quad L^{2}(\varOmega \times {\mathbf{C}})^{N\times N}, \\ {\mathcal{T}}_{\varepsilon }^{*}\big(e(u_{\varepsilon })\big)&\to e(u)+e_{X}( \widehat{u})\quad \textit{strongly in}\quad L^{2}(\varOmega \times {\mathbf{C}})^{N \times N}, \end{aligned} $$

(2.11)

and the pair $(u, \widehat{u})$is the unique solution to the following unfolded problem:

$$ \left \{ \begin{aligned} &\int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}\big(e_{kl}(u)+e_{X,kl}( \widehat{u})\big) \big(e_{ij}(v)+e_{X,ij}(\widehat{v})\big)\,dx\,dX=|{ \mathbf{C}}|\int _{\varOmega }\,f\cdot v\,dx, \\ &\forall \, v\in H^{1}_{\varGamma }(\varOmega )^{N},\;\;\forall \,\widehat{v} \in L^{2}(\varOmega ;H^{1}_{N,per,0}({\mathbf{C}}))^{N}, \end{aligned} \right . $$

(2.12)

where for all $\widehat{v}\in H^{1}({\mathbf{C}})^{N}$

$$ e_{X,kl}(\widehat{v})=\frac{1}{2} \Big( \frac{\partial \widehat{v}_{k}}{\partial X_{l}} + \frac{\partial \widehat{v}_{l}}{\partial X_{k}} \Big),\quad k,l= \overline{1,N}. $$

2.5 Homogenization

In this section, we give the expressions of the microscopic field $\widehat{u}$ in terms of the macroscopic displacement $u$. First, taking $v=0$ as a test function in (2.12), we obtain

$$ \int _{{\mathbf{C}}}\,a_{ijkl}\big(e_{kl}( u )+e_{X,kl}(\widehat{u} )\big) e_{X,ij}( \widehat{v})\,dx\,dX =0,\quad \forall \,\widehat{v}\in H^{1}_{per,0}({ \mathbf{C}})^{N},\quad \hbox{a.e. in }\varOmega . $$

This shows that the displacement $\widehat{u}$ can be written in terms of the elements of the tensor $e(u)$.

Denote by ${\mathbf{M}}^{np}$ the $N\times N$ symmetric matrix with following coefficients

$$ {\mathbf{M}}^{np}_{kl}=\frac{1}{2}\big(\delta _{kn}\delta _{lp}+\delta _{kp} \delta _{ln}\big),\quad n,p,k,l\in \overline{1,N}, $$

where $\delta _{ij}$ is the Kronecker symbol.

Since the tensor $e(u)$ has $N^{2}$ components, we introduce the $N^{2}$ correctors

$$ \widehat{\chi }_{np}\in H_{per,0}^{1}({\mathbf{C}})^{N},\quad n,p= \overline{1,N}, $$

which are solutions to the following cell problems

$$ \int _{{\mathbf{C}}} a_{ijkl}\big(e_{X,kl}(\widehat{\chi }_{np})+{\mathbf{M}}^{np}_{kl} \big)e_{X,ij}(\widehat{v})\,dX=0,\quad \forall \,\widehat{v}\in H_{per,0}^{1}({ \mathbf{C}})^{N}. $$

(2.13)

Observe that $\widehat{\chi }_{np}=\widehat{\chi }_{pn}$$n,p=\overline{1,N}$. As a consequence, the function $\widehat{u}$ can be written in the form

$$ \widehat{u} (x,X)=\sum _{n,p=1}^{N} e_{np}( u )(x)\widehat{\chi }_{np}(X) \quad \hbox{for a.e. }(x,X)\in \varOmega \times {\mathbf{C}}. $$

(2.14)

Theorem 1

(The homogenized limit problem)

The limit displacement $u\in H^{1}_{\varGamma }(\varOmega )^{N}$is the unique solution of the following homogenized problem:

$$ \int _{\varOmega }\,a_{ijnp}^{hom}\, e_{np}( u )e_{ij}(v)\,dx=\int _{ \varOmega }\,f\cdot v\,dx, \quad \forall \,v\in H^{1}_{\varGamma }(\varOmega )^{N}, $$

(2.15)

where²

$$ a_{ijnp}^{hom}=\frac{1}{|\mathbf{C}|}\int _{\mathbf{C}}\,a_{ijkl}\,\big({\mathbf{M}}^{np}_{kl}+e_{X,kl}( \widehat{\chi }_{np})\big)\,dX. $$

(2.16)

Proof

Taking $\widehat{v}= 0$ as a test function in (2.12) and using (2.14) provides

$$ \int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}\big(e_{kl}( u )+e_{np}( u )e_{X,kl}( \widehat{\chi }_{np})\big) e_{ij}(v)\,dx\,dX =|{\mathbf{C}}|\int _{\varOmega } \,f\cdot v\,dx, \quad \forall \,v\in H^{1}_{\varGamma }(\varOmega )^{N}. $$

After straightforward computations, we have

$$ \int _{\varOmega }\,\Big(\int _{\mathbf{C}}\,a_{ijkl}\big({\mathbf{M}}^{np}_{kl}+e_{X,kl}( \widehat{\chi }_{np})\big)\,dX\Big) e_{np}(u)\,e_{ij}(v)\,dx =|{\mathbf{C}}| \int _{\varOmega }\,f\cdot v\,dx,\quad \forall \,v\in H^{1}_{\varGamma }( \varOmega )^{N}, $$

and the assertion of the theorem follows.

Now, we prove that the operator in problem (2.15) is elliptic. Using formulas (2.16) of the homogenized coefficients and (2.13), we obtain

$$ a_{npn'p'}^{hom}\tau _{np}\tau _{n'p'}=\frac{1}{|\mathbf{C}|}\int _{\mathbf{C}}a_{ijkl} \big(e_{X,kl}(\varPsi )+M_{kl}\big) \big(e_{X,ij}(\varPsi )+M_{ij}\big)\,dX, \quad \tau \in M_{s}^{N\times N}, $$

where

$$ M_{kl}=\tau _{np}{\mathbf{M}}^{np}_{kl},\qquad \varPsi =\tau _{np} \widehat{\chi }_{np}. $$

Then, in view of (2.2) and following the proof of [14, Lemma 11.19], we have

$$ \begin{aligned} a_{npn'p'}^{hom}\tau _{np}\tau _{n'p'}\ge \frac{c_{0}}{|\mathbf{C}|}\int _{ \mathbf{C}}\Big(e_{X,ij}(\varPsi )+M_{ij}\Big) \Big(e_{X,ij}(\varPsi )+M_{ij} \Big)\,dX\ge c_{0}\tau _{np}\tau _{np}. \end{aligned} $$

Thus, the operator in problem (2.15) is elliptic and by virtue of the Lax-Milgram theorem this problem admits a unique solution. □

2.6 Conclusion

We summarize the result of this section: for $\varepsilon$-periodic porous materials with a known structure, for e.g. structures made of beams whose thicknesses are of order $\varepsilon$, or dense packages of small compressed balls, the solution to the linearized elasticity problem (2.5)-(2.6) in a heterogeneous $3D$ domain is approximated by

$$ u_{\varepsilon }(x) \approx u(x)+\varepsilon \sum _{n,p=1}^{N} e_{np}( u )(x)\widehat{\chi }_{np}\Big(\Big\{ \frac{x}{\varepsilon }\Big\} \Big) \quad \hbox{for } x\in \varOmega ^{*}_{\varepsilon }, $$

(2.17)

where $u$ is the solution of the homogenized problem (2.16) and where the correctors $\widehat{\chi }_{np}$ are given by (2.13). In (2.17), the sum represents the warpings of the cells.

3 Periodic Plate

This section is devoted to the study of the asymptotic behavior of the solution to the linearized elasticity problem for a $\varepsilon$-periodic plate-like structure as $\varepsilon \to 0$. Note that this structure is 3-dimensional and only periodic in two directions. In the third direction it is “thin”, that is, its thickness is of the same order $\varepsilon$ as the period of the other two dimensions. The section is organized in a similar way as the previous one. It can be considered as an extension of the results obtained for the homogenization of a periodic plate (see [8], [14, Chap. 11], [22], [23], [26, Sect. 3.2] and also [24] for a shell).

3.1 Notation and Geometric Setting

We consider a bounded domain $\omega$ in ${\mathbb{R}}^{2}$ with Lipschitz boundary. As in Sect. 2, we introduce $\gamma$, a subset of $\partial \omega$ with a non-zero measure. We assume that there exists a bounded domain $\omega '$ with Lipschitz boundary such that

$$ \omega \subset \omega '\quad \hbox{and}\quad \omega '\cap \partial \omega =\gamma . $$

In this section we use the following notations:

• $Y'\doteq (-1/2,1/2)^{2}$, $Y\doteq Y'\times (-1/2,1/2)=(-1/2,1/2)^{3}$,

• ${\mathbf{C}}\subset Y$ is a domain with Lipschitz boundary such that the $\hbox{interior}\big (\overline{\mathbf{C}}\cup (\overline{\mathbf{C}}+{\mathbf{e}}_{\alpha })\big )$, $\alpha =\overline{1,2}$, is connected,

• $\varXi _{\varepsilon }\doteq \big \{\xi \in {\mathbb{Z}}^{2}\; |\; ( \varepsilon \xi +\varepsilon Y')\cap \omega \neq \emptyset \big \}$,

• $\varOmega _{\varepsilon }^{*}=\hbox{interior}\Big (\bigcup _{\xi \in \varXi _{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{\mathbf{C}})\Big )$,

• $\varXi ^{\prime }_{\varepsilon }\doteq \big \{\xi \in {\mathbb{Z}}^{2}\;| \;(\varepsilon \xi +\varepsilon Y')\cap \omega ^{\prime }\neq \emptyset \big \}$,

• $\varOmega ^{\prime *}_{\varepsilon }\doteq \hbox{interior}\Big (\bigcup _{ \xi \in \varXi ^{\prime }_{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{\mathbf{C}})\Big )$,

• $\omega ^{{ext}}_{\varepsilon }=\hbox{interior}\Big (\bigcup _{ \xi \in \varXi _{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{Y'}) \Big )$,

• $\omega _{1}=\big \{ x\in {\mathbb{R}}^{2}\;|\;\hbox{dist}(x,\omega )< 1 \big \}$, ${\omega }\subset \omega _{1}$,

• $\omega ^{int}_{3\varepsilon }=\big \{x\in \omega \;|\;\hbox{dist}(x, \partial \omega )>3\varepsilon \big \}$,

• $\omega ^{'\,int}_{3\varepsilon }=\big \{x\in \omega \;|\; \hbox{dist}(x, \partial \omega ')>3\varepsilon \big \}$,

• $\varXi ^{int}_{\varepsilon }\doteq \big \{\xi \in {\mathbb{Z}}^{2}\;|\; ( \varepsilon \xi +\varepsilon Y')\subset \omega ^{int}_{3\varepsilon } \big \}$,

• $\varOmega ^{int}_{\varepsilon }=\hbox{interior}\Big (\bigcup _{\xi \in \varXi ^{int}_{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{\mathbf{C}})\Big )$,

• $\varXi ^{\prime \,int}_{\varepsilon }\doteq \big \{\xi \in \varXi _{\varepsilon }\;|\;(\varepsilon \xi +\varepsilon Y')\cap \omega ^{'\,int}_{3 \varepsilon }\neq \emptyset \big \}$,

• $\varOmega ^{\prime \, int}_{\varepsilon }\doteq \hbox{interior}\Big ( \bigcup _{\xi \in \varXi ^{\prime \, int}_{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{\mathbf{C}})\Big )$,

• $\varXi _{\varepsilon ,\alpha }\doteq \big \{\xi \in \varXi _{\varepsilon }\; \; |\;\; \xi +{\mathbf{e}}_{\alpha }\in \varXi _{\varepsilon }\big \}$, $\alpha =\overline{1,2}$.

Note that the domain $\varOmega _{\varepsilon }^{*}$ is a connected open set, and if $\varepsilon$ is small enough, we have $\varOmega _{\varepsilon }^{*}\subset \omega _{1}\times (-\varepsilon /2, \varepsilon /2)$.

The space of all admissible displacements is denoted by ${\mathbf{V}}_{\varepsilon }$:

$$ {\mathbf{V}}_{\varepsilon }\doteq \Big\{ v\in H^{1}(\varOmega _{\varepsilon }^{*})^{3} \;\big|\; \exists v^{\prime }\in H^{1}(\varOmega ^{\prime *}_{\varepsilon })^{3}, \;\; v= v^{\prime }_{|\varOmega _{\varepsilon }^{*}}, \;\; v^{\prime }=0 \text{ in } \varOmega ^{\prime *}_{\varepsilon }\,\setminus \, \overline{\varOmega ^{*}_{\varepsilon }}\Big\} . $$

3.2 Statement of the Elasticity Problem

We are interested in the elastic behavior of a structure occupying the domain $\varOmega _{\varepsilon }^{*}$ and fixed on the part $\varGamma _{\varepsilon }$ of its boundary, $\varGamma _{\varepsilon }\doteq (\gamma \times (-\varepsilon /2, \varepsilon /2)) \cap \varOmega ^{*}_{\varepsilon }$.

Let $f$ be in ${L^{2}(\omega _{1})}^{3}$. We define the applied forces $f_{\varepsilon }$ as follows

$$ f_{\varepsilon ,\alpha }=\varepsilon ^{2} f_{\alpha }, \quad f_{ \varepsilon ,3} =\varepsilon ^{3} f_{3}, \quad \alpha =1,2,\quad \hbox{a.e. in } \; {\varOmega _{\varepsilon }^{*}}. $$

(3.1)

Again, the unknown displacement $u_{\varepsilon }:\varOmega _{\varepsilon }^{*}\to \mathbb{R}^{3}$ is the solution to the linearized elasticity system

$$ \textstyle\begin{cases} \nabla \cdot \sigma ^{\varepsilon }(u_{\varepsilon })=-f_{\varepsilon } & \mbox{in} \quad \varOmega _{\varepsilon }^{*}, \\ u_{\varepsilon }=0 & \mbox{on} \quad \varGamma _{\varepsilon }\cap \overline{\varOmega _{\varepsilon }^{*}}, \\ \sigma ^{\varepsilon }(u_{\varepsilon }) \cdot \nu _{\varepsilon }= 0 & \mbox{on} \quad \partial \varOmega _{\varepsilon }^{*}\setminus \varGamma _{\varepsilon }, \end{cases} $$

(3.2)

in the strong formulation, where $\nu _{\varepsilon }$ is the outward normal vector to $\partial \varOmega _{\varepsilon }^{*}$.

The variational formulation of problem (3.2) is given by

$$ \left \{ \begin{aligned} &\hbox{Find $u_{\varepsilon }\in {\mathbf{V}}_{\varepsilon }$ such that} \\ &\int _{\varOmega _{\varepsilon }^{*}} \sigma ^{\varepsilon }(u_{ \varepsilon }):e(v)\,dx =\int _{\varOmega _{\varepsilon }^{*}}f_{ \varepsilon } \cdot v\,dx, \quad \forall \,v\in {\mathbf{V}}_{\varepsilon }. \end{aligned} \right . $$

(3.3)

3.3 The Unfolding-Rescaling Operator

Below, we introduce the unfolding operator for a plate-like structure and state its properties. Note that, since this structure is periodic only in two directions and it is “thin” in the third one, the unfolding operator is a “rescaling” operator in the third direction. As a consequence, the asymptotic reduction from $3D$ plate-like structure to $2D$ takes place. The reduction of dimension is done by the standard scaling to a fixed thickness (see the pioneer papers [7, 15]).

Definition 2

For every measurable function $u:\; \varOmega _{\varepsilon }^{*} \to \mathbb{R}^{3}$ the unfolding operator ${\mathcal{T}}^{*}_{\varepsilon }$ is defined as follows:

$$ {\mathcal{T}}^{*}_{\varepsilon }(u)(x^{\prime }, X)= u\Big(\varepsilon \Big[\frac{x^{\prime }}{\varepsilon }\Big]+\varepsilon X^{\prime }, \varepsilon X_{3}\Big) \quad \hbox{for a.e. } (x^{\prime },X) \in \omega ^{ext}_{\varepsilon }\times {\mathbf{C}}, $$

where $x^{\prime }=(x_{1},x_{2}),\, X=(X^{\prime }, X_{3})=(X_{1},X_{2},X_{3})$.

Below we recall some properties of ${\mathcal{T}}^{*}_{\varepsilon }$ (for further results see [14]).

Proposition 3

For every $u \in L^{1}(\varOmega _{\varepsilon }^{*})$

$$ \begin{aligned} &\int _{\omega ^{{ext}}_{\varepsilon }\times {\mathbf{C}}}{ \mathcal{T}}^{*}_{\varepsilon }(u)(x^{\prime },X)\, dx^{\prime }dX= \frac{1}{\varepsilon } \int _{\varOmega _{\varepsilon }^{*}}u(x)\,dx, \\ &\|{\mathcal{T}}^{*}_{\varepsilon }(u)\|_{L^{1}(\omega ^{ext}_{\varepsilon }\times {\mathbf{C}})}=\frac{1}{\varepsilon }\|u\|_{L^{1}( \varOmega _{\varepsilon }^{*})}. \end{aligned} $$

(3.4)

For every $u \in H^{1}(\varOmega _{\varepsilon }^{*})$

$$ {\mathcal{T}}^{*}_{\varepsilon }(\nabla u)(x^{\prime },X)= \frac{1}{\varepsilon } \nabla _{X}{\mathcal{T}}^{*}_{\varepsilon }(u)(x^{\prime },X)\quad \textit{for a.e. }(x^{\prime },X)\in \omega ^{{ext}}_{\varepsilon }\times {\mathbf{C}}. $$

(3.5)

3.4 Weak Limits of the Fields and the Limit Problem

Denote by $H^{1}_{\gamma }(\omega )$ the space of functions in $H^{1}(\omega )$ that vanish on $\gamma$,

$$ H^{1}_{\gamma }(\omega ) \doteq \Big\{ u\in H^{1}(\omega )\;|\; u=0\; \hbox{on}\; \gamma \Big\} , $$

and by $H^{2}_{\gamma }(\omega )$ the space of functions in $H^{2}(\omega )$ that vanish on $\gamma$ and their first derivatives vanish on $\gamma$ as well

$$ H^{2}_{\gamma }(\omega ) \doteq \Big\{ u\in H^{2}(\omega )\;|\; u=0\; \hbox{and}\; \nabla u=0 \;\hbox{on}\; \gamma \Big\} . $$

Since we are dealing with a plate-domain, we use the decomposition of the displacements of a plate (see [18] and Sect. A.2 of Appendix A). Any displacement $u \in {\mathbf{V}}_{\varepsilon }$ can be decomposed as

$$ \begin{aligned} u(x)=&{\mathbf{U}}^{e}(x)+\overline{u}(x)={\mathcal{U}}(x')+{\mathcal{R}}(x') \land x_{3}{\mathbf{e}}_{3}+\overline{u}(x) \\ =&\begin{pmatrix} {\mathcal{U}}_{1}(x^{\prime })+x_{3}{\mathcal{R}}_{2}(x^{\prime }) \\ {\mathcal{U}}_{2}(x^{\prime })-x_{3}{\mathcal{R}}_{1}(x^{\prime }) \\ {\mathcal{U}}_{3}(x^{\prime }) \end{pmatrix} + \overline{u}(x),\quad \hbox{for a.e. }\; x=(x^{\prime },x)=(x_{1},x_{2},x_{3}) \in \varOmega ^{\prime \, int}_{\varepsilon }, \end{aligned} $$

(3.6)

where ${\mathcal{U}}$ stands for the displacement of the mid-surface of the plate restricted to $\varOmega ^{*}_{\varepsilon }\cap \{x_{3}=0\}$, ${\mathcal{R}}(x')\land x_{3}{\mathbf{e}}_{3}$ represents the small rotation of a “fiber” from $x'\in \varOmega ^{*}_{\varepsilon }\cap \{x_{3}=0\}$ and $\overline{u}$ is the warping of the “fibers”.

Here, ${\mathcal{U}}\in H^{1}_{\gamma }(\omega ^{'\,int}_{3\varepsilon })^{3}$, ${\mathcal{R}}\in H^{1}_{\gamma }(\omega ^{'\,int}_{3\varepsilon })^{2}$ and $\overline{u}\in H^{1}\big (\omega ^{'\,int}_{3\varepsilon }\times (- \varepsilon /2,\varepsilon /2)\big )^{3}$.³

In the next step, we compute the strain tensor of the displacement $u$, using the decomposition (3.6)

$$ \begin{aligned} e(u)&=e({\mathbf{U}}^{e})+e(\overline{u})\\ &= \begin{pmatrix} \frac{\partial {\mathcal{U}}_{1}}{\partial x_{1}}+x_{3} \frac{\partial {\mathcal{R}}_{2}}{\partial x_{1}} &\frac{1}{2}\Big( \frac{\partial {\mathcal{U}}_{1}}{\partial x_{2}}+ \frac{\partial {\mathcal{U}}_{2}}{\partial x_{1}}\Big) +\frac{x_{3}}{2} \Big(-\frac{\partial {\mathcal{R}}_{1}}{\partial x_{1}} + \frac{\partial {\mathcal{R}}_{2}}{\partial x_{2}}\Big) &\frac{1}{2}\Big({ \mathcal{R}}_{2}+\frac{\partial {\mathcal{U}}_{3}}{\partial x_{1}}\Big) \\ *&\frac{\partial {\mathcal{U}}_{2}}{\partial x_{2}} -x_{3} \frac{\partial {\mathcal{R}}_{1}}{\partial x_{2}} &\frac{1}{2}\Big(-{\mathcal{R}}_{1}+ \frac{\partial {\mathcal{U}}_{3}}{\partial x_{2}}\Big) \\ *&*&0 \end{pmatrix} + \\ &+ \begin{pmatrix} \frac{\partial \overline{u}_{1}}{\partial x_{1}}&\frac{1}{2} \Big( \frac{\partial \overline{u}_{1}}{\partial x_{2}} + \frac{\partial \overline{u}_{2}}{\partial x_{1}} \Big)&\frac{1}{2} \Big(\frac{\partial \overline{u}_{1}}{\partial x_{3}} + \frac{\partial \overline{u}_{3}}{\partial x_{1}} \Big) \\ *&\frac{\partial \overline{u}_{2}}{\partial x_{2}}&\frac{1}{2}\Big( \frac{\partial \overline{u}_{2}}{\partial x_{3}} + \frac{\partial \overline{u}_{3}}{\partial x_{2}} \Big) \\ *&*&\frac{\partial \overline{u}_{3}}{\partial x_{3}} \end{pmatrix} . \end{aligned} $$

(3.7)

Further, we extend ${\mathcal{U}}$, ℛ by 0 to $\omega '\setminus \overline{\omega ^{'int}_{3\varepsilon }}$ and the field $\overline{u}$ by 0 to $\varOmega ^{\prime }_{\varepsilon }\setminus \overline{\varOmega ^{\prime \, int}_{\varepsilon }}$.

The following lemma is proved in Appendix B.2.

Lemma 2

The solution $u_{\varepsilon }$of the problem (3.2) satisfies

$$ \|e(u_{\varepsilon })\|_{L^{2}(\varOmega _{\varepsilon }^{*})} \le C \varepsilon ^{5/2}\big(\|f\|_{L^{2}(\omega _{1})}+\|g\|_{L^{2}( \omega _{1})}\big). $$

(3.8)

The proof of the following lemma is postponed to Appendix B.2.

Lemma 3

Let $\{u_{\varepsilon }\}_{\varepsilon }$be a sequence of displacements belonging to ${\mathbf{V}}_{\varepsilon }$, decomposed as in (3.6) and satisfying

$$ \|e(u_{\varepsilon })\|_{L^{2}(\varOmega _{\varepsilon }^{*})} \leq C \varepsilon ^{5/2}. $$

Then, for a subsequence of $\{\varepsilon \}$, still denoted by $\{\varepsilon \}$,

• (i) there exist ${\mathcal{U}}_{\alpha }\in H^{1}(\omega '),\;\;\alpha =1,2,\; {\mathcal{U}}_{3} \in H^{2}(\omega ')$such that

  $$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}{\mathcal{U}}_{\varepsilon ,\alpha }{\mathbf{1}}_{ \omega ^{' int}_{3\varepsilon }} \to {\mathcal{U}}_{\alpha }\quad \textit{strongly in}\quad L^{2}(\omega '), \\ &\frac{1}{\varepsilon }{\mathcal{U}}_{\varepsilon ,3}{\mathbf{1}}_{ \omega ^{' int}_{3\varepsilon }} \to {\mathcal{U}}_{3} \quad \textit{strongly in }\quad L^{2}(\omega '), \\ &\frac{1}{\varepsilon ^{2}}\nabla {\mathcal{U}}_{\varepsilon , \alpha }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }}\rightharpoonup \nabla {\mathcal{U}}_{\alpha }\quad \textit{weakly in}\quad L^{2}(\omega ')^{2}, \\ &\frac{1}{\varepsilon }\nabla {\mathcal{U}}_{\varepsilon ,3}{\mathbf{1}}_{ \omega ^{' int}_{3\varepsilon }}\rightharpoonup \nabla {\mathcal{U}}_{3} \quad \textit{weakly in}\quad L^{2}(\omega ')^{2}, \end{aligned} $$

  (3.9)

• (ii) there exists ${\mathcal{R}}\in {H^{1}(\omega ')}^{2}$such that

  $$ \begin{aligned} &\frac{1}{\varepsilon }{\mathcal{R}}_{\varepsilon ,\alpha } {\mathbf{1}}_{ \omega ^{' int}_{3\varepsilon }} \to {\mathcal{R}}_{\alpha }\quad \textit{strongly in } \quad L^{2}(\omega '), \\ &\frac{1}{\varepsilon }{\nabla \mathcal{R}}_{\varepsilon ,\alpha }{\mathbf{1}}_{ \omega ^{' int}_{3\varepsilon }} \rightharpoonup \nabla {\mathcal{R}}_{\alpha }\quad \textit{weakly in } \quad {L^{2}(\omega ')}^{2}, \end{aligned} $$

  (3.10)

  and

  $$ {\mathcal{R}}_{1}=- \frac{\partial {\mathcal{U}}_{3}}{\partial x_{2}},\quad { \mathcal{R}}_{2}=\frac{\partial {\mathcal{U}}_{3}}{\partial x_{1}} \quad \textit{a.e. in}\;\; \omega ', $$

  (3.11)

  furthermore, the fields ${\mathcal{U}}_{\alpha }$, ℛ, ${\mathcal{U}}_{3}$and $\nabla {\mathcal{U}}_{3}$vanish in $\omega ^{\prime }\setminus \overline{\omega }$,

• (iii) there exists $\overline{u}\in L^{2}(\omega ';H^{1}_{2,per}({\mathbf{C}}))^{3}$such that

  $$ \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(\overline{u}_{\varepsilon }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} ) \rightharpoonup \overline{u}\quad \textit{weakly in } L^{2}(\omega ' ; H^{1}({ \mathbf{C}}))^{3}. $$

  (3.12)

Since the fields ${\mathcal{U}}_{\alpha }$, ℛ, ${\mathcal{U}}_{3}$ and the gradient ${\mathcal{U}}_{3}$ vanish in $\omega '\setminus \overline{\omega }$, we obtain

$$ {\mathcal{U}}_{\alpha }\in H^{1}_{\gamma }(\omega ),\quad {\mathcal{U}}_{3} \in H^{2}_{\gamma }(\omega ),\quad {\mathcal{R}}\in H^{1}_{\gamma }( \omega )^{2}. $$

Lemma below is proven in Appendix B.2.

Lemma 4

For a subsequence, still denoted $\{\varepsilon \}$, we have

$$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}({\mathcal{U}}_{ \varepsilon ,\alpha }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} )\to { \mathcal{U}}_{\alpha }\quad \textit{strongly in} \quad L^{2}(\omega ' \times {\mathbf{C}}), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}({\mathcal{U}}_{ \varepsilon ,3}{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} )\to { \mathcal{U}}_{3}\quad \textit{strongly in } \quad L^{2}(\omega '\times { \mathbf{C}}), \\ &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,\alpha }}{\partial x_{\beta }}{ \mathbf{1}}_{\omega ^{' int}_{3\varepsilon }}\Big)\rightharpoonup \frac{\partial {\mathcal{U}}_{\alpha }}{\partial x_{\beta }} \quad \textit{weakly in } \quad L^{2}(\omega '\times {\mathbf{C}}), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{\beta }}{ \mathbf{1}}_{\omega ^{' int}_{3\varepsilon }}\Big)\to \frac{\partial {\mathcal{U}}_{3}}{\partial x_{\beta }},\quad \textit{strongly in } \quad L^{2}(\omega '\times {\mathbf{C}}), \end{aligned} \quad \alpha ,\beta =1,2, $$

(3.13)

and

$$ \begin{aligned} &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}({\mathcal{R}}_{ \varepsilon ,\alpha }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} )\to { \mathcal{R}}_{\alpha },\quad \textit{strongly in } \quad L^{2}(\omega ' \times {\mathbf{C}}), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}\Big(\nabla { \mathcal{R}}_{\varepsilon ,\alpha }{\mathbf{1}}_{\omega ^{' int}_{3 \varepsilon }}\Big)\rightharpoonup \nabla {\mathcal{R}}_{\alpha }, \quad \textit{weakly in }\quad {L^{2}(\omega '\times {\mathbf{C}})}, \end{aligned} \quad \alpha =1,2. $$

(3.14)

For any $u\in H^{1}(\omega )^{2}$, $v\in H^{2}(\omega )$ we denote

$$ E^{M}(u)\doteq \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}}&\frac{1}{2}\Big( \frac{\partial u_{1}}{\partial x_{2}}+ \frac{\partial u_{2}}{\partial x_{1}}\Big)&0 \\ \frac{1}{2}\Big(\frac{\partial u_{1}}{\partial x_{2}}+ \frac{\partial u_{2}}{\partial x_{1}}\Big) &\frac{\partial u_{2}}{\partial x_{2}}&0 \\ 0&0&0 \end{pmatrix} , \quad E^{B}(v)\doteq \begin{pmatrix} \frac{\partial ^{2} v}{\partial x_{1}^{2}}&\frac{\partial ^{2} v}{\partial x_{1} \partial x_{2}}&0 \\ \frac{\partial ^{2} v}{\partial x_{1} \partial x_{2}} &\frac{\partial ^{2} v}{\partial x_{2}^{2}}&0 \\ 0&0&0 \end{pmatrix} . $$

Define

$$ {\mathcal{M}}_{3}\doteq \frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}x_{3}\,dx,\qquad I_{3} \doteq \frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}x^{2}_{3}\, dx. $$

The following proposition provides the first main result of this section. Its proof is given in Appendix B.2.

Proposition 4

(The unfolded limit problem)

Let $u_{\varepsilon }$be the solution to (3.2). Then the following convergences hold:

$$ \begin{aligned} \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,1}) &\to {\mathcal{U}}_{1}-X_{3}\frac{\partial {\mathcal{U}}_{3}}{\partial x_{1}} \quad \textit{strongly in } \quad L^{2}(\omega \times {\mathbf{C}}), \\ \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,2}) &\to {\mathcal{U}}_{2}-X_{3}\frac{\partial {\mathcal{U}}_{3}}{\partial x_{2}} \quad \textit{strongly in } \quad L^{2}(\omega \times {\mathbf{C}}), \\ \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,3}) & \to {\mathcal{U}}_{3} \quad \textit{strongly in } \quad L^{2}(\omega \times { \mathbf{C}}). \end{aligned} $$

(3.15)

Moreover

$$ \begin{aligned} \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*} (e(u_{\varepsilon }){\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }})& \rightharpoonup E^{M}({\mathcal{U}}_{m})-X_{3}E^{B}({\mathcal{U}}_{3})+e_{X}( \widehat{u}) \quad \textit{weakly in } L^{2}(\omega \times {\mathbf{C}})^{3 \times 3}, \\ \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }_{ij}(u_{\varepsilon }){\mathbf{1}}_{\omega ^{' int}_{3 \varepsilon }}) &\rightharpoonup a_{ijkl}\Big(E^{M}_{kl}({\mathcal{U}}_{m})-X_{3} E^{B}_{kl}({\mathcal{U}}_{3}) +e_{X,kl}(\widehat{u})\Big) \quad \textit{weakly in } \; L^{2}(\omega \times {\mathbf{C}}), \end{aligned} $$

(3.16)

where ${\mathcal{U}}_{m}\doteq ({\mathcal{U}}_{1}, {\mathcal{U}}_{2})\in {H_{\gamma }^{1}( \omega )}^{2},\,{\mathcal{U}}_{3}\in H_{\gamma }^{2}(\omega ),\,\widehat{u} \in L^{2}(\omega ; H_{2,per,0}^{1}({\mathbf{C}}))^{3}$are the solution to the following unfolded problem:

$$ \left \{ \begin{aligned} &\int _{\omega \times {\mathbf{C}}} a_{ijkl}\Big(E^{M}_{kl}({\mathcal{U}}_{m})-X_{3}E^{B}_{kl}({ \mathcal{U}}_{3})+e_{X,kl}(\widehat{u})\Big) \Big(E^{M}_{ij}({\mathcal{V}}_{m})-X_{3} E^{B}_{ij}({\mathcal{V}}_{3})+e_{X,ij}(\widehat{v})\Big)\, dx^{\prime }dX \\ &=|{\mathbf{C}}|\Big(\int _{\omega }f_{\alpha }{\mathcal{V}}_{\alpha }\,dx^{\prime }+{\mathcal{M}}_{3} \int _{\omega }\Big(f_{\alpha }\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}+g_{\alpha }{ \mathcal{V}}_{\alpha }\Big)\,dx^{\prime }+I_{3} \int _{\omega }g_{\alpha }\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}\,dx^{\prime }\Big), \\ &\qquad \forall \; {\mathcal{V}}_{m}=({\mathcal{V}}_{1}, { \mathcal{V}}_{2}) \in H_{\gamma }^{1}(\omega )^{2},\quad {\mathcal{V}}_{3} \in H^{2}_{\gamma }(\omega ),\quad \widehat{v}\in L^{2}(\omega ; H_{2,per,0}^{1}({ \mathbf{C}}))^{3}. \end{aligned} \right . $$

(3.17)

3.5 Homogenization

In this section, we give the expressions of the microscopic displacement $\widehat{u}$ in terms of the membrane displacements ${\mathcal{U}}_{m}$ and the bending ${\mathcal{U}}_{3}$.

Taking ${\mathcal{V}}=0$ as a test function in (3.17), we obtain

$$ \int _{{\mathbf{C}}} a_{ijkl}(E^{M}_{kl}({\mathcal{U}}_{m})-X_{3}E^{B}_{kl}({ \mathcal{U}}_{3}) +e_{X,kl}(\widehat{u})) e_{X,ij}(\widehat{v})\, dX=0, \quad \forall \,\widehat{v}\in H_{2,per,0}^{1}({\mathbf{C}})^{3}. $$

This shows that the microscopic displacement $\widehat{u}$ can be written in terms of the tensors $E^{M},\,E^{B}$.

Define

$$ {\mathbf{M}}^{11}= \begin{pmatrix} 1&0&0 \\ 0&0&0 \\ 0&0&0 \end{pmatrix} ,\quad {\mathbf{M}}^{12}= \begin{pmatrix} 0&1&0 \\ 1&0&0 \\ 0&0&0 \end{pmatrix} ,\quad {\mathbf{M}}^{22}= \begin{pmatrix} 0&0&0 \\ 0&1&0 \\ 0&0&0 \end{pmatrix} . $$

Since the tensors $E^{M}({\mathcal{U}}_{1},{\mathcal{U}}_{2}),\,E^{B}({\mathcal{U}}_{3})$ have 6 components

$$ \begin{aligned} &E^{M}({\mathcal{U}}_{1},{\mathcal{U}}_{2})= \frac{\partial {\mathcal{U}}_{1}}{\partial x_{1}}{\mathbf{M}}^{11}+\Big( \frac{\partial {\mathcal{U}}_{1}}{\partial x_{2}}+ \frac{\partial {\mathcal{U}}_{2}}{\partial x_{1}}\Big){\mathbf{M}}^{12}+ \frac{\partial {\mathcal{U}}_{2}}{\partial x_{2}}{\mathbf{M}}^{22}, \\ & E^{B}({ \mathcal{U}}_{3})=\frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{1}^{2}}{ \mathbf{M}}^{11}+ \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{1} \partial x_{2}}{\mathbf{M}}^{12}+ \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{2}^{2}}{\mathbf{M}}^{22}, \end{aligned} $$

we introduce 6 correctors

$$ \chi _{\alpha \beta }^{M},\,\chi _{\alpha \beta }^{B}\in {H_{2,per,0}^{1}({ \mathbf{C}})}^{3},\quad (\alpha ,\,\beta )\in {(1,1),\,(1,2),\,(2,2)}, $$

which are the unique solutions to the following cell problems

$$ \begin{aligned} &\int _{{\mathbf{C}}} a_{ijkl}\left (e_{X,kl}(\chi _{\alpha \beta }^{M})+{ \mathbf{M}}^{\alpha \beta }_{kl}\right )e_{X,ij}(\widehat{v})\,dX=0, \\ &\int _{{\mathbf{C}}} a_{ijkl}\left ( e_{X,kl}(\chi _{\alpha \beta }^{B})-X_{3}{ \mathbf{M}}^{\alpha \beta }_{kl}\right )e_{X,ij}(\widehat{v})\,dX =0, \end{aligned} \quad \alpha ,\beta =1,2, $$

(3.18)

for all $\widehat{v}\in L^{2}(\omega ; H_{2,per,0}^{1}({\mathbf{C}}))^{3}$.

As a consequence, the function $\widehat{u}$ from (3.16) is given in terms of ${\mathcal{U}}$ as follows

$$ \widehat{u}(x^{\prime },X)=\sum _{\alpha ,\beta =1}^{2} \Big[ e_{ \alpha \beta }({\mathcal{U}}_{m}(x^{\prime })) \chi _{\alpha \beta }^{M}(X) + \frac{\partial ^{2}{\mathcal{U}}_{3}(x^{\prime })}{\partial x_{\alpha }\partial x_{\beta }} \chi _{\alpha \beta }^{B}(X) \Big] \qquad \hbox{for a.e. }(x^{\prime },X) \in \omega \times {\mathbf{C}}. $$

(3.19)

This substitution allows us to separate the scales and formulate the second main result:

Theorem 2

(The homogenized limit problem)

The limit field

$$ {\mathcal{U}}=\big({\mathcal{U}}_{m},{\mathcal{U}}_{3}\big)\in H_{\gamma }^{1}(\omega )^{2} \times H^{2}_{\gamma }(\omega ) $$

is the unique solution to the homogenized problem

$$ \left \{ \begin{aligned} &\int _{\omega }\Big(a^{hom}_{\alpha \beta \alpha '\beta '}e_{\alpha \beta }({\mathcal{U}}_{m} )e_{\alpha '\beta '}({\mathcal{V}}_{m} ) +b^{hom}_{ \alpha \beta \alpha '\beta '} \frac{\partial ^{2}{\mathcal{U}}_{3} }{\partial x_{\alpha }\partial x_{\beta }}e_{ \alpha '\beta '}({\mathcal{V}}_{m} ) \\ &\;\; +b^{hom}_{\alpha \beta \alpha '\beta '}e_{\alpha \beta }({\mathcal{U}}_{m} ) \frac{\partial ^{2}{\mathcal{V}}_{3} }{\partial x_{\alpha '}\partial x_{\beta '}} +c^{hom}_{\alpha \beta \alpha '\beta '} \frac{\partial ^{2}{\mathcal{U}}_{3} }{\partial x_{\alpha }\partial x_{\beta }} \frac{\partial ^{2}{\mathcal{V}}_{3} }{\partial x_{\alpha '}\partial x_{\beta '}} \Big)\,dx^{\prime }\\ =&\int _{\omega }f_{\alpha }{\mathcal{V}}_{\alpha }\,dx^{\prime }+{\mathcal{M}}_{3} \int _{\omega }\Big(f_{\alpha }\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }} +g_{\alpha }{ \mathcal{V}}_{\alpha }\Big)\,dx^{\prime }+I_{3}\int _{\omega }g_{\alpha }\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }} \,dx^{\prime }, \\ &\qquad \forall \; ({\mathcal{V}}_{m}, {\mathcal{V}}_{3} )\in H_{\gamma }^{1}(\omega )^{2}\times H^{2}_{\gamma }(\omega ), \end{aligned} \right . $$

(3.20)

where

$$ \begin{aligned} &a^{hom}_{\alpha \beta \alpha '\beta '}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}} a_{ijkl}\Big(e_{X,kl}\big(\chi _{\alpha \beta }^{M}\big) +{\mathbf{M}}^{ \alpha \beta }_{kl}\Big)\Big(e_{X,ij}\big(\chi _{\alpha ' \beta '}^{M} \big)+{\mathbf{M}}^{\alpha '\beta '}_{ij}\Big)\,dX, \\ &b^{hom}_{\alpha \beta \alpha '\beta '}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}} a_{ijkl}\Big(e_{X,kl}\big(\chi _{\alpha \beta }^{B}\big) -X_{3}{\mathbf{M}}^{ \alpha \beta }_{kl}\Big)\Big(e_{X,ij}\big(\chi _{\alpha ' \beta '}^{M} \big)+{\mathbf{M}}^{\alpha '\beta '}_{ij}\Big)\,dX, \\ &c^{hom}_{\alpha \beta \alpha '\beta '}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}} a_{ijkl}\Big(e_{X,kl}\big(\chi _{\alpha \beta }^{B}\big) -X_{3}{\mathbf{M}}^{ \alpha \beta }_{kl}\Big)\Big(e_{X,ij}\big(\chi _{\alpha ' \beta '}^{B} \big)-X_{3}{\mathbf{M}}^{\alpha '\beta '}_{ij}\Big)\,dX. \end{aligned} $$

(3.21)

Proof

Take $\widehat{v}=0$ as a test function in (3.17). Replacing $\widehat{u}$ by its representation (3.19), yields

$$ \begin{aligned} &\int _{\omega \times {\mathbf{C}}} a_{ijkl}\Big( e_{\alpha \beta }({\mathcal{U}}_{m} )\Big( e_{X,kl}\big(\chi _{\alpha \beta }^{M}\big)+{\mathbf{M}}^{\alpha \beta }_{kl}\Big) + \frac{\partial ^{2}{\mathcal{U}}_{3} }{\partial x_{\alpha }\partial x_{\beta }} \Big(e_{X,kl}\big(\chi _{\alpha \beta }^{B}\big)-X_{3}{\mathbf{M}}^{ \alpha \beta }_{kl} \Big)\Big) \\ &\times {\mathbf{M}}^{\alpha '\beta '}_{ij}\Big(e_{\alpha '\beta '}({ \mathcal{V}}_{m} )-X_{3} \frac{\partial ^{2}{\mathcal{V}}_{3} }{\partial x_{\alpha '}\partial x_{\beta '}} \Big)\,dx^{\prime }dX \\ &=|{\mathbf{C}}|\int _{\omega }f_{\alpha }{\mathcal{V}}_{\alpha }\,dx^{\prime }+ \int _{\mathbf{C}}X_{3}\,dX \int _{\omega }\Big[f_{\alpha }\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }} +g_{\alpha }{ \mathcal{V}}_{\alpha }\Big]\,dx^{\prime }+\int _{\mathbf{C}}X_{3}^{2}\,dX \int _{\omega }g_{\alpha }\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }} \,dx^{\prime }. \end{aligned} $$

Taking into account the variational problems (3.18) satisfied by the correctors, the problem (3.20) with the homogenized coefficients given by (3.21) is obtained by a simple computation.

Now, we prove the ellipticity of the operator in Problem (3.20). Using the formulas (3.21) for the homogenized coefficients, we obtain

$$ \begin{aligned} &a^{hom}_{\alpha \beta \alpha '\beta '}\tau ^{m}_{\alpha \beta }\tau ^{m}_{ \alpha '\beta '} +b^{hom}_{\alpha \beta \alpha '\beta '}\tau ^{b}_{ \alpha \beta }\tau ^{m}_{\alpha '\beta '} +b^{hom}_{\alpha \beta \alpha '\beta '}\tau ^{m}_{\alpha \beta }\tau ^{b}_{\alpha '\beta '} +c^{hom}_{ \alpha \beta \alpha '\beta '}\tau ^{b}_{\alpha \beta }\tau ^{b}_{ \alpha '\beta '} \\ =&\int _{\mathbf{C}}a_{ijkl} \Big(e_{X,kl}\big(\varPsi \big) +M_{kl}\Big) \Big(e_{X,ij}\big(\varPsi \big)+M_{ij}\Big)\,dX,\qquad \tau ^{m}_{ \alpha \beta },\; \tau ^{b}_{\alpha \beta }\in M_{s}^{2\times 2}, \end{aligned} $$

where

$$ M=\big(\tau ^{m}_{\alpha \beta }-X_{3}\tau ^{b}_{\alpha \beta }\big){ \mathbf{M}}^{\alpha \beta },\qquad \varPsi =\tau ^{m}_{\alpha \beta }\chi _{ \alpha \beta }^{M}+\tau ^{b}_{\alpha \beta }\chi _{\alpha \beta }^{B}. $$

Then, in view of (2.2) and following the proof of [14, Lemma 11.19], we obtain

$$ \begin{aligned} &a^{hom}_{\alpha \beta \alpha '\beta '}\tau ^{m}_{\alpha \beta }\tau ^{m}_{ \alpha '\beta '} +b^{hom}_{\alpha \beta \alpha '\beta '}\tau ^{b}_{ \alpha \beta }\tau ^{m}_{\alpha '\beta '} +b^{hom}_{\alpha \beta \alpha '\beta '}\tau ^{m}_{\alpha \beta }\tau ^{b}_{\alpha '\beta '} +c^{hom}_{ \alpha \beta \alpha '\beta '}\tau ^{b}_{\alpha \beta }\tau ^{b}_{ \alpha '\beta '} \\ \geq &c_{0}\int _{\mathbf{C}} \Big(e_{X,ij}\big(\varPsi \big)+M_{ij}\Big) \Big(e_{X,ij}\big(\varPsi \big)+M_{ij}\Big)\,dX\geq C\big(\tau ^{m}_{ \alpha \beta }\tau ^{m}_{\alpha \beta } +\tau ^{b}_{\alpha \beta } \tau ^{b}_{\alpha \beta }\big). \end{aligned} $$

Thus, the operator of problem (3.20) is elliptic and this problem has a unique solution. □

3.6 Conclusion

We summarize the results of this section. The solution to the linearized elasticity problem (3.2) (in the strong form), or (3.3) (in the weak/variational form) is approximated by

$$\begin{aligned} u_{\varepsilon }(x)& \approx \varepsilon ^{2} \begin{pmatrix} \displaystyle \varepsilon ^{2}{\mathcal{U}}_{1}(x^{\prime })- \varepsilon x_{3} \frac{\partial {\mathcal{U}}_{3}(x^{\prime })}{\partial x_{1} } \\ \displaystyle \varepsilon ^{2}{\mathcal{U}}_{2}(x^{\prime })- \varepsilon x_{3} \frac{\partial {\mathcal{U}}_{3}(x^{\prime })}{\partial x_{2} } \\ \displaystyle \varepsilon {\mathcal{U}}_{3}(x^{\prime }) \end{pmatrix}\\ &\quad{}+\varepsilon ^{3}\sum _{\alpha ,\beta =1}^{2} \Big[ e_{\alpha \beta }({ \mathcal{U}}_{m}(x^{\prime })) \chi _{\alpha \beta }^{M}\Big(\Big\{ \frac{x^{\prime }}{\varepsilon }\Big\} ,\frac{x_{3}}{\varepsilon }\Big) + \frac{\partial ^{2}{\mathcal{U}}_{3}(x^{\prime })}{\partial x_{\alpha }\partial x_{\beta }} \chi _{\alpha \beta }^{B}\Big(\Big\{ \frac{x^{\prime }}{\varepsilon } \Big\} ,\frac{x_{3}}{\varepsilon }\Big) \Big], \end{aligned}$$

where ${\mathcal{U}}$ is the solution of the homogenized $2D$-problem with constant effective coefficients (3.21) and $\chi _{\alpha \beta }^{M},\,\chi _{\alpha \beta }^{B}\in {H_{2,per}^{1}({ \mathbf{C}})}^{3}$ with $\alpha ,\,\beta =1,2$ are 6 $3D$ displacement correctors, the solutions of auxiliary problems (3.18) on the periodicity cell (see Fig. 3).

Fig. 3

Perturbations for periodic corrector-problems $\chi _{\alpha \beta }^{M}(X)$ and $\chi _{\alpha \beta }^{B}(X)$ in the example of a plate with fibre structure (a textile)

As usual for a plate, we first recognize a Kirchhoff-Love displacement plus here a second term which represents the warpings of the cells.

4 Periodic Beam

In this section, we study the asymptotic behavior of the solution to the linearized elasticity problem for $\varepsilon$-periodic beam-like structure as $\varepsilon \to 0$. This structure is 3-dimensional and periodic in one dimension. In two other directions the structure is “thin”, that is, its size in each of these directions, is of order $\varepsilon$. The section is organized in a similar way as the previous ones. It can be considered as an extension of the results of [19] to beam-like structures with a boundary that does not have to be a Lipschitz boundary.

4.1 Notation and Geometric Setting

Let ${\mathbf{C}}\in {\mathbb{R}}^{3}$ be a bounded domain with Lipschitz boundary and let $L$ be a fixed positive constant. In this section, we also assume that the interior of $\overline{\mathbf{C}}\cup (\overline{\mathbf{C}}+{\mathbf{e}}_{3})$ is connected and ${\mathbf{C}}\cap ({\mathbf{C}}+{\mathbf{e}}_{3})=\emptyset$. The beam-like structure is introduced in the following way:

$$ \varOmega ^{*}_{\varepsilon }=\hbox{interior}\Big(\bigcup _{i=0}^{N-1} \varepsilon \big( i{\mathbf{e}}_{3}+\overline{\mathbf{C}}\big)\Big),\qquad \varepsilon =\frac{L}{N}. $$

We choose as centerline of the structure the segment whose direction is ${\mathbf{e}}_{3}$ and place the origin at the center of mass of the first cell (thus the centers of mass of the other cells are also on this segment). The orthonormal basis $({\mathbf{e}}_{1},\,{\mathbf{e}}_{2}, {\mathbf{e}}_{3})$ is chosen in such a way that $\int _{\mathbf{C}}\,x_{1}x_{2}\,dx=0$, and we set

$$ I_{\alpha }=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}x^{2}_{\alpha }\, dx. $$

Concerning the directions ${\mathbf{e}}_{1}$ and ${\mathbf{e}}_{2}$, it is important to note that they do not necessary correspond to the principal axes of inertia.

The space of all admissible displacements is denoted by ${\mathbf{V}}_{\varepsilon }$

$$ {\mathbf{V}}_{\varepsilon }=\big\{ u \in H^{1}(\varOmega ^{*}_{\varepsilon })^{3} \; | \; u=0 \; \mbox{on} \; \varGamma _{\varepsilon }\big\} ,\quad \hbox{where} \quad \varGamma _{\varepsilon }\doteq (\varepsilon \overline{\mathbf{C}}- \varepsilon {\mathbf{e}}_{3})\cap \varepsilon \overline{\mathbf{C}}. $$

4.2 Statement of the Elasticity Problem

As before, we are interested in the elastic behavior of a structure occupying the domain $\varOmega ^{*}_{\varepsilon }$ and fixed on the part $\varGamma_{\varepsilon }$ of its boundary.

Let $f$ and $g$ be in $L^{2}(0,L)^{3}$, we define the applied forces $f_{\varepsilon }\in L^{2}(\varOmega ^{*}_{\varepsilon })^{3}$ by

$$ \begin{aligned} f_{\varepsilon ,1}(x)&=\varepsilon ^{2} f_{1}(x_{1})+x_{2} g_{3}(x_{1}), \\ f_{\varepsilon ,2}(x)&=\varepsilon ^{2} f_{2}(x_{1}) -x_{1} g_{3}(x_{1}), \\ f_{\varepsilon ,3} (x)&=\varepsilon f_{3}(x_{1}) -x_{1}g_{1}(x_{1})-x_{2}g_{2}(x_{1}), \end{aligned} \qquad \hbox{for a.e. } x\in \varOmega ^{*}_{\varepsilon }. $$

(4.1)

The unknown displacement $u_{\varepsilon }:\varOmega ^{*}_{\varepsilon }\to \mathbb{R}^{3}$ is the solution to the linearized elasticity system

$$ \textstyle\begin{cases} \nabla \cdot \sigma ^{\varepsilon }(u_{\varepsilon })=-f_{\varepsilon } & \mbox{in} \quad \varOmega ^{*}_{\varepsilon }, \\ u_{\varepsilon }=0 & \mbox{on} \quad \varGamma _{\varepsilon }\cap \overline{\varOmega ^{*}_{\varepsilon }}, \\ \sigma ^{\varepsilon }(u_{\varepsilon }) \cdot \nu _{\varepsilon }= 0 & \mbox{on} \quad \partial \varOmega ^{*}_{\varepsilon }\setminus \varGamma _{\varepsilon }, \end{cases} $$

(4.2)

where $\nu _{\varepsilon }$ is the outward normal vector to $\partial \varOmega ^{*}_{\varepsilon }$.

The variational formulation of problem (4.2) is given by

$$ \left \{ \begin{aligned} &\hbox{Find $u_{\varepsilon }\in {\mathbf{V}}_{\varepsilon }$ such that}, \\ &\int _{\varOmega ^{*}_{\varepsilon }} \sigma ^{\varepsilon }(u_{ \varepsilon }):e(v)\,dx =\int _{\varOmega ^{*}_{\varepsilon }}f_{ \varepsilon } \cdot v\,dx, \quad \forall \, v\in {\mathbf{V}}_{ \varepsilon }. \end{aligned} \right . $$

(4.3)

4.3 The Unfolding-Rescaling Operator

Below, we introduce the unfolding operator for a beam-like structure and provide its properties. Note that since this structure is only periodic in one direction and is “thin” in the other two directions, the unfolding operator is a “rescaling” operator in two direction. As a consequence, the asymptotic reduction from $3D$ beam-like structure to $1D$ takes place.

Definition 3

For every measurable function $\phi :\,\varOmega ^{*}_{\varepsilon }\to \mathbb{R}^{3}$, the unfolding-rescaling operator ${\mathcal{T}}_{\varepsilon }^{*}$ is defined as follows:

$$ {\mathcal{T}}_{\varepsilon }^{*}(\phi )(x_{3}, X)= \phi \Big(\varepsilon X_{1}, \varepsilon X_{2}, \varepsilon \Big[\frac{x_{3}}{\varepsilon }\Big]+ \varepsilon X_{3}\Big) \quad \hbox{for a.e. } (x_{3},X) \in (0,L) \times {\mathbf{C}}. $$

Proposition 5

(Properties of the operator ${\mathcal{T}}_{\varepsilon }^{*}$)

• (a) For every $\phi \in L^{2}(\varOmega ^{*}_{\varepsilon })$

  $$ \begin{aligned} &\int _{(0,L) \times {\mathbf{C}}}{\mathcal{T}}_{\varepsilon }^{*}( \phi )(x_{3},X) \,dx_{3} dX =\frac{1}{\varepsilon ^{2}} \int _{\varOmega ^{*}_{ \varepsilon }} \phi (x)\,dx, \\ &\|{\mathcal{T}}^{*}_{\varepsilon }( \phi )\|_{L^{2}((0,L)\times {\mathbf{C}})} =\frac{1}{\varepsilon } \|\phi \|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned} $$

  (4.4)

• (b) For every $\phi \in H^{1}(\varOmega ^{*}_{\varepsilon })$

  $$ {\mathcal{T}}^{*}_{\varepsilon }(\nabla \phi )(x_{3},X)= \frac{1}{\varepsilon } \nabla _{X}{\mathcal{T}}^{*}_{\varepsilon }( \phi )(x_{3},X)\quad \textit{for a.e. }(x_{3},X)\in (0,L)\times {\mathbf{C}}. $$

  (4.5)

4.4 Weak Limits of the Fields and the Limit Problem

Denote

$$ H^{1}_{\varGamma }(0,L) \doteq \Big\{ u\in H^{1}(0,L)\;|\; u(0)=0\Big\} , \quad H^{2}_{\varGamma }(0,L) \doteq \Big\{ u\in H^{2}(0,L)\;|\; u(0)=u'(0)=0 \Big\} . $$

As in [18], we decompose the displacement field $u \in {\mathbf{V}}_{\varepsilon }$ in the following way:

$$\begin{aligned} &u(x)={\mathbf{U}}^{e}(x)+\overline{u}(x)={\mathcal{U}}(x_{3})+{ \mathcal{R}}(x_{3}) \wedge (x_{1} {\mathbf{e}}_{1}+x_{2} {\mathbf{e}}_{2})+ \overline{u}(x), \\ &\quad \hbox{for a.e. }\; x=(x_{1},x_{2},x_{3})\in \varOmega ^{*}_{\varepsilon }, \end{aligned}$$

(4.6)

where ${\mathcal{U}}, {\mathcal{R}}\in H^{1}_{\varGamma }(0,L)^{3}$. The displacement $\overline{u}$ belongs to ${\mathbf{V}}_{\varepsilon }$.

The field ${\mathcal{U}}$ stands for the displacement of the centerline of the structure. The term ${\mathcal{R}}(x_{3}) \wedge (x_{1} {\mathbf{e}}_{1}+x_{2} {\mathbf{e}}_{2})$ represents the small rotation of the cross-section at the point $x_{3}$ of the centerline, whereas the last term $\overline{u}(\cdot ,x_{3})$ is the warping of the cross-section at the point $x_{3}$ of the centerline.

The strain tensor of the displacement $u$ is

$$ \begin{aligned} e(u)&=e({\mathbf{U}}^{e})+e(\overline{u}) \\ &= \begin{pmatrix} 0&0&\frac{1}{2}\Big(\frac{d{\mathcal{U}}_{1}}{d x_{3}}-{\mathcal{R}}_{2}-x_{2} \frac{d{\mathcal{R}}_{3}}{d x_{3}}\Big) \\ *&0&\frac{1}{2}\Big(\frac{d{\mathcal{U}}_{2}}{d x_{3}}+{\mathcal{R}}_{1}+x_{1} \frac{d{\mathcal{R}}_{3}}{d x_{3}}\Big) \\ *&*&\frac{d{\mathcal{U}}_{3}}{d x_{3}}+x_{2}\frac{d{\mathcal{R}}_{1}}{d x_{3}}-x_{1} \frac{d{\mathcal{R}}_{2}}{d x_{3}} \end{pmatrix} + \begin{pmatrix} \frac{\partial \overline{u}_{1}}{\partial x_{1}}&\frac{1}{2} \Big( \frac{\partial \overline{u}_{1}}{\partial x_{2}} + \frac{\partial \overline{u}_{2}}{\partial x_{1}} \Big)&\frac{1}{2} \Big(\frac{\partial \overline{u}_{1}}{\partial x_{3}} + \frac{\partial \overline{u}_{3}}{\partial x_{1}} \Big) \\ *&\frac{\partial \overline{u}_{2}}{\partial x_{2}}&\frac{1}{2}\Big( \frac{\partial \overline{u}_{2}}{\partial x_{3}} + \frac{\partial \overline{u}_{3}}{\partial x_{2}} \Big) \\ *&*&\frac{\partial \overline{u}_{3}}{\partial x_{3}} \end{pmatrix} . \end{aligned} $$

(4.7)

In order to simplify the expression of the strain tensor $e({\mathbf{U}}^{e})$, we define a new triplet $({\underline{u}},\,{\mathbb{U}},\,\varTheta )$ (see also [19]) by

$$\begin{aligned} &{\mathbb{U}}(x_{3})=\int _{0}^{x_{3}}\,{\mathcal{R}}(t)\wedge {\mathbf{e}}_{3} \,dt,\qquad {\underline{u}}(x_{3})={\mathcal{U}}(x_{3})-{ \mathbb{U}}(x_{3}),\qquad \varTheta (x_{3})={\mathcal{R}}_{3}(x_{3})\\ &\quad \text{ for a.e. }x_{3}\in (0,L). \end{aligned}$$

Then, we have

$$ \left \{ \begin{aligned} &\frac{d{\mathcal{R}}_{1}}{dx_{3}}=- \frac{d^{2}{\mathbb{U}}_{2}}{dx_{3}^{2}},\quad \frac{d{\mathcal{R}}_{2}}{dx_{3}}= \frac{d^{2}{\mathbb{U}}_{1}}{dx_{3}^{2}}, \\ &\frac{d{\mathcal{U}}_{1}}{dx_{3}}-{\mathcal{R}}_{2}= \frac{d({\mathcal{U}}_{1}-{\mathbb{U}}_{1})}{dx_{3}}= \frac{d{\underline{u}}_{1}}{dx_{3}},\quad \frac{d{\mathcal{U}}_{2}}{dx_{3}}+{\mathcal{R}}_{1}= \frac{d({\mathcal{U}}_{2}-{\mathbb{U}}_{2})}{dx_{3}}= \frac{d{\underline{u}}_{2}}{dx_{3}}, \\ &{\mathbb{U}}_{3}\equiv 0. \end{aligned} \right . $$

From now on, we have a new decomposition of the field ${\mathbf{U}}^{e}(x)$

$$ \begin{aligned} {\mathbf{U}}^{e}(x)&={\underline{u}}(x_{3})+{\mathbb{U}}(x_{3})+ \begin{pmatrix} -\frac{d{\mathbb{U}}_{2}}{dx_{3}}(x_{3}) \\ \frac{d{\mathbb{U}}_{1}}{dx_{3}}(x_{3}) \\ \varTheta (x_{3}) \end{pmatrix} \wedge (x_{1} {\mathbf{e}}_{1}+x_{2} {\mathbf{e}}_{2}) \\ &= \begin{pmatrix} {\mathbb{U}}_{1}(x_{3})+{\underline{u}}_{1}(x_{3})-x_{2}\varTheta (x_{3}) \\ {\mathbb{U}}_{2}(x_{3})+{\underline{u}}_{2}(x_{3})+x_{1}\varTheta (x_{3}) \\ {\underline{u}}_{3}(x_{3})-x_{1}\frac{d{\mathbb{U}}_{1}}{dx_{3}}(x_{3})-x_{2} \frac{d{\mathbb{U}}_{2}}{dx_{3}}(x_{3}) \end{pmatrix} \quad \hbox{for a.e. }\;\; x \in \varOmega ^{*}, \end{aligned} $$

(4.8)

and the strain tensor of the displacement ${\mathbf{U}}^{e}$ is

$$ e({\mathbf{U}}^{e})= \begin{pmatrix} 0&0&\frac{1}{2}\Big(\frac{d{\underline{u}}_{1}}{d x_{3}}-x_{2} \frac{d\varTheta _{\varepsilon }}{dx_{3}}\Big) \\ *&0&\frac{1}{2}\Big(\frac{d{\underline{u}}_{2}}{dx_{3}}+x_{1} \frac{d\varTheta }{dx_{3}}\Big) \\ *&*&\frac{d{\underline{u}}_{3}}{dx_{3}}-x_{1} \frac{d^{2}{\mathbb{U}}_{1}}{dx_{3}^{2}}-x_{2} \frac{d^{2}{\mathbb{U}}_{2}}{d x_{3}^{2}} \end{pmatrix} . $$

(4.9)

Note that the boundary conditions for the terms of this new decomposition are

$$ {\underline{u}}(0)={\mathbb{U}}(0)=\frac{d{\mathbb{U}}}{dx_{3}}(0)= \varTheta (0)=0. $$

Also note that, since ${\mathcal{R}}_{\alpha }\in H^{1}_{\varGamma }(0,L)$, we have ${\mathbb{U}}_{\alpha }\in H^{2}_{\varGamma }(0,L)$.

The estimates for the functions from the decomposition of $u_{\varepsilon }$ can be obtained using Lemma 6 and Lemmas 15, 16 from Appendix A. They are given in the following lemma:

Lemma 5

For every displacement $u\in {\mathbf{V}}_{\varepsilon }$one has ($\alpha =1, \,2$)

$$ \begin{aligned} &\|{\underline{u}}\|_{H^{1}(0,L)}\leq \frac{C}{\varepsilon }\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}, \\ &\|{\mathbb{U}}_{\alpha }\|_{H^{2}(0,L)}+\|\varTheta \|_{H^{1}(0,L)} \leq \frac{C}{\varepsilon ^{2}}\|e(u)\|_{L^{2}(\varOmega ^{*}_{ \varepsilon })}, \end{aligned} $$

(4.10)

and

$$ \|u_{3}\|_{L^{2}(\varOmega ^{*})}+\varepsilon \big(\|u_{\alpha }\|_{L^{2}( \varOmega ^{*})}+\|\nabla u\|_{L^{2}(\varOmega ^{*})}\big)+\|\nabla \overline{u}\|_{L^{2}(\varOmega ^{*})}+\frac{1}{\varepsilon }\| \overline{u}\|_{L^{2}(\varOmega ^{*})}\leq C\|e(u)\|_{L^{2}(\varOmega ^{*}_{ \varepsilon })}. $$

(4.11)

The proofs of the following two lemmas are given in Appendix B.3.

Lemma 6

The solution $u_{\varepsilon }$to problem (4.2) satisfies the following estimate:

$$ \|e(u_{\varepsilon })\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} \le C \varepsilon ^{2}\big(\|f\|_{L^{2}(0,L)}+\|g\|_{L^{2}(0,L)}\big). $$

(4.12)

Lemma 7

For a subsequence of $\{\varepsilon \}$, still denoted $\{\varepsilon \}$,

• (i) there exists ${\mathbb{U}}\in H^{2}_{\varGamma }(0,L)^{2}$such that the following convergences hold:

  $$\begin{aligned} &{\mathbb{U}}_{\varepsilon }\rightharpoonup {\mathbb{U}}\quad \textit{weakly in } \quad H^{2}(0,L)^{2}, \end{aligned}$$

  (4.13)
  $$\begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}({\mathbb{U}}_{\varepsilon })\to {{ \mathbb{U}}}\quad \textit{strongly in } \quad L^{2}((0,L); H^{2}(0,1))^{2}, \end{aligned}$$

  (4.14)
  $$\begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\mathbb{U}}_{\varepsilon }}{dx_{3}}\Big)\to \frac{d{\mathbb{U}}}{dx_{3}}\quad \textit{strongly in } \quad L^{2}((0,L) ; H^{1}(0,1))^{2}, \end{aligned}$$

  (4.15)
  $$\begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d^{2}{\mathbb{U}}_{\varepsilon }}{dx_{3}^{2}}\Big) \rightharpoonup \frac{d^{2}{\mathbb{U}}}{dx_{3}^{2}}\quad \textit{weakly in } \quad L^{2}((0,L)\times (0,1))^{2}; \end{aligned}$$

  (4.16)

• (ii) there exists $\varTheta \in H^{1}_{\varGamma }(0,L)$such that the following convergences hold:

  $$\begin{aligned} &\varTheta _{\varepsilon }\rightharpoonup \varTheta \quad \textit{weakly in } \quad H^{1}(0,L), \end{aligned}$$

  (4.17)
  $$\begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}(\varTheta _{\varepsilon })\to {\varTheta }\quad \textit{strongly in } \quad L^{2}((0,L) ; H^{1}(0,1)), \end{aligned}$$

  (4.18)
  $$\begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}\Big(\frac{d\varTheta _{\varepsilon }}{dx_{3}} \Big)\rightharpoonup \frac{d\varTheta }{dx_{3}}\quad \textit{weakly in } \quad L^{2}((0,L)\times (0,1)); \end{aligned}$$

  (4.19)

• (iii) there exist ${\underline{u}}\in H^{1}_{\varGamma }(0,L)^{3}$, $\widehat{{\underline{u}}}_{\alpha }\in L^{2}((0,L),H^{1}_{1,per}(0,1)) \,(\alpha =1,2)$such that

  $$\begin{aligned} &\frac{1}{\varepsilon }{\underline{u}}_{\varepsilon }\rightharpoonup { \underline{u}}\quad \textit{weakly in } \quad H^{1}(0,L)^{3}, \end{aligned}$$

  (4.20)
  $$\begin{aligned} &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}({\underline{u}}_{\varepsilon })\to {\underline{u}}\quad \textit{strongly in } \quad L^{2}((0,L) ; H^{1}(0,1))^{3}, \end{aligned}$$

  (4.21)
  $$\begin{aligned} &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\underline{u}}_{\varepsilon ,\alpha }}{dx_{3}}\Big) \rightharpoonup \frac{d{\underline{u}}_{\alpha }}{dx_{3}}+ \frac{\partial \widehat{{\underline{u}}}_{\alpha }}{\partial X_{3}} \quad \textit{weakly in } \quad L^{2}((0,L)\times (0,1)),\quad \alpha =1,2, \end{aligned}$$

  (4.22)
  $$\begin{aligned} &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\underline{u}}_{\varepsilon ,3}}{dx_{3}}\Big) \rightharpoonup \frac{d{\underline{u}}_{3}}{dx_{3}}\quad \textit{weakly in } \quad L^{2}((0,L)\times (0,1)), \end{aligned}$$

  (4.23)

• (iv) there exists $\overline{u}\in L^{2}((0,L);H^{1}_{1,per}({\mathbf{C}}))^{3}$such that

  $$ \begin{aligned} &\frac{1}{\varepsilon ^{2}} {\mathcal{T}}_{\varepsilon }^{*}(\overline{u}_{\varepsilon })\rightharpoonup \overline{u} \quad \textit{weakly in } L^{2}((0,L);H^{1}({ \mathbf{C}}))^{3}, \\ &\frac{1}{\varepsilon } {\mathcal{T}}_{\varepsilon }^{*}(\nabla \overline{u}_{\varepsilon })\rightharpoonup \nabla _{X} \overline{u} \quad \textit{weakly in } L^{2}((0,L)\times {\mathbf{C}})^{3\times 3}, \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(e(\overline{u}_{\varepsilon }))\rightharpoonup e_{X}(\overline{u}) \quad \textit{weakly in } L^{2}((0,L) \times {\mathbf{C}})^{3\times 3}. \end{aligned} $$

  (4.24)

Let us introduce the following vector space:

$$ {\mathbf{V}}_{M}\doteq \Big\{ ({\underline{u}}, {\mathbb{U}},\varTheta )\in H^{1}(0,L)^{3} \times H^{2}(0,L)^{2}\times H^{1}(0,L)\; |\; {\underline{u}}(0)={ \mathbb{U}}(0)=\frac{d{\mathbb{U}}}{dx_{3}}(0)=\varTheta (0)=0\Big\} . $$

For every $({\underline{u}},\,{\mathbb{U}},\,\varTheta )\in {\mathbf{V}}_{M}$, we define the symmetric tensor $E$ by

$$ E({\underline{u}},\,{\mathbb{U}},\,\varTheta )= \begin{pmatrix} 0&0&\frac{1}{2}\Big(\frac{d{\underline{u}}_{1}}{d x_{3}}-X_{2} \frac{d\varTheta }{dx_{3}}\Big) \\ *&0&\frac{1}{2}\Big(\frac{d{\underline{u}}_{2}}{dx_{3}}+X_{1} \frac{d\varTheta }{dx_{3}}\Big) \\ *&*&\frac{d{\underline{u}}_{3}}{dx_{3}}-X_{1} \frac{d^{2}{\mathbb{U}}_{1}}{dx_{3}^{2}}-X_{2} \frac{d^{2}{\mathbb{U}}_{2}}{dx_{3}^{2}} \end{pmatrix} . $$

The following proposition provides the first main result of this section. Its proof is given in Appendix B.3.

Proposition 6

(The unfolded limit problem)

Let $u_{\varepsilon }$be the solution to (4.2). There exist functions $({\underline{u}},\,{\mathbb{U}},\,\varTheta )\in {\mathbf{V}}_{M}$and $\widehat{u}\in L^{2}((0,L) ; H^{1}_{1,per,0}C))^{3}$such that the following convergences hold:

$$ \begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,\alpha })\rightharpoonup { \mathbb{U}}_{\alpha }\quad \textit{weakly in }\quad L^{2}((0,L) ; H^{1}({ \mathbf{C}})), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,1}-{ \mathbb{U}}_{\varepsilon ,1})\rightharpoonup {\underline{u}}_{1}-X_{2} \varTheta \quad \textit{weakly in }\quad L^{2}((0,L) ; H^{1}({\mathbf{C}})), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,2}-{ \mathbb{U}}_{\varepsilon ,2})\rightharpoonup {\underline{u}}_{1}+X_{1} \varTheta \quad \textit{weakly in }\quad L^{2}((0,L) ; H^{1}({\mathbf{C}})), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(u_{\varepsilon ,3}) \rightharpoonup {{\underline{u}}}_{3} -X_{1} \frac{d{\mathbb{U}}_{1}}{dx_{3}}-X_{2} \frac{d{\mathbb{U}}_{2}}{d x_{3}}\quad \textit{weakly in } \quad L^{2}((0,L) ; H^{1}({\mathbf{C}})), \end{aligned} $$

(4.25)

and

$$ \begin{aligned} &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*} (e(u_{\varepsilon })) \rightharpoonup E({\underline{u}},\,{\mathbb{U}},\,\varTheta )+e_{X}( \widehat{u}) \quad \textit{weakly in } L^{2}((0,L)\times {\mathbf{C}})^{3 \times 3}, \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }_{ij}(u_{\varepsilon })) \rightharpoonup a_{ijkl}\Big(E_{kl}({\underline{u}}, \,{\mathbb{U}},\,\varTheta ) +e_{X,kl}(\widehat{u})\Big) \quad \textit{weakly in } \; L^{2}((0,L)\times {\mathbf{C}}), \end{aligned} $$

(4.26)

where the functions ${\underline{u}},\,{\mathbb{U}},\,\varTheta ,\,\widehat{u}$are the solutions to the following unfolded problem:

$$ \left \{ \begin{aligned} &\int _{(0,L)\times {\mathbf{C}}} a_{ijkl}(E_{kl}({\underline{u}},\,{ \mathbb{U}},\,\varTheta ) +e_{X,kl}(\widehat{u}))(E_{ij}({ \underline{v}},{\mathbb{V}},{\mathbf{T}}) +e_{X,ij}(\widehat{v}))\,dx_{3} dX \\ =&|\boldsymbol{C}|\Big[\int _{(0,L)}\,f_{\alpha }{\mathbb{V}}_{\alpha }\,dx_{3} +I_{\alpha }\int _{(0,L)}\,\Big(g_{\alpha }\frac{d{\mathbb{V}}_{\alpha }}{dx_{3}}-g_{3}{\mathbf{T}}\Big)\,dx_{3}+\int _{(0,L)} \,f_{3} {\underline{v}}_{3}\,dx_{3}\Big], \\ & \hskip35 mm \forall \; ({\underline{v}},\,{\mathbb{V}},\,{\mathbf{T}}) \in {\mathbf{V}}_{M},\quad \forall \, \widehat{v}\in L^{2}((0,L);H_{1,per,0}^{1}({ \mathbf{C}}))^{3}. \end{aligned} \right . $$

(4.27)

4.5 Homogenization

In this section, we derive the representation of the microscopic displacement $\widehat{u}$ in terms of the macroscopic fields ${\underline{u}}$, ${\mathbb{U}}$ and $\varTheta$.

Taking $({\underline{v}},\,{\mathbb{V}},\,{\mathbf{T}})=0$ as a test function in (4.27), we obtain

$$ \int _{(0,L)\times {\mathbf{C}}} a_{ijkl}\big(E_{kl}({\underline{u}},{ \mathbb{U}},\varTheta ) +e_{X,kl}(\widehat{u})\big)e_{X,ij}(\widehat{v})) \,dx_{3} dX =0,\quad \forall \,\widehat{v}\in {H^{1}_{1,per,0}({\mathbf{C}})}^{3}. $$

This shows that the microscopic displacement $\widehat{u}$ can be written in terms of the tensor $E$.

Define

$$ {\mathbf{M}}^{13}=\frac{1}{2} \begin{pmatrix} 0&0&1 \\ 0&0&0 \\ 1&0&0 \end{pmatrix} ,\quad {\mathbf{M}}^{23}=\frac{1}{2} \begin{pmatrix} 0&0&0 \\ 0&0&1 \\ 0&1&0 \end{pmatrix} ,\quad {\mathbf{M}}^{33}= \begin{pmatrix} 0&0&0 \\ 0&0&0 \\ 0&0&1 \end{pmatrix} . $$

The tensors $E({\underline{u}},\,{\mathbb{U}},\,\varTheta )$ have 6 components

$$ E({\underline{u}},\,{\mathbb{U}},\,\varTheta )=\sum _{m=1}^{3}\, \frac{d{\underline{u}}_{m}}{d x_{3}}{\mathbf{M}}^{m 3}-\sum _{\alpha =1}^{2} \,X_{\alpha }\frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}}{\mathbf{M}}^{33}+ \Big(X_{1}{\mathbf{M}}^{23}-X_{2}{\mathbf{M}}^{13}\Big)\frac{d\varTheta }{dx_{3}}, $$

and we introduce 6 correctors

$$ \chi _{m}^{\underline{u}},\,\chi _{\alpha }^{\mathbb{U}},\,\chi ^{\varTheta }\in H^{1}_{1,per,0}({\mathbf{C}})^{3}, \quad \alpha =1,2,\quad m=1,2,3, $$

which are the unique solutions to the following cell problems

$$ \begin{aligned} &\int _{\mathbf{C}} a_{ijkl}\big(e_{X,kl}\big(\chi _{m}^{{\underline{u}}} \big)+{\mathbf{M}}^{m3}_{kl}\big)e_{X,ij}(\widehat{v})\,dX=0,\quad m=1,2,3, \\ &\int _{\mathbf{C}} a_{ijkl}\left ( e_{X,kl}\big(\chi _{\alpha }^{ \mathbb{U}}\big)-X_{\alpha }{\mathbf{M}}^{33}_{kl}\right )e_{X,ij}( \widehat{v})\,dX=0,\quad \alpha =1,2, \\ &\int _{\mathbf{C}} a_{ijkl}\left ( e_{X,kl}\big(\chi ^{\varTheta }\big)+X_{1}{ \mathbf{M}}^{23}_{kl}-X_{2}{\mathbf{M}}^{13}_{kl}\right )e_{X,ij}(\widehat{v})\,dX=0 \end{aligned} $$

(4.28)

for all $\widehat{v}\in H_{1,per,0}^{1}({\mathbf{C}})^{3}$.

Thus, the function $\widehat{u}$ can be represented in terms of ${\underline{u}},\,{\mathbb{U}},\,\varTheta$ in the following way

$$ \widehat{u}=\sum _{m=1}^{3}\,\frac{d{\underline{u}}_{m}}{d x_{3}} \chi _{m}^{\underline{u}}-\sum _{\alpha =1}^{2}\,X_{\alpha }\frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}}\chi _{\alpha }^{ \mathbb{U}}+\frac{d\varTheta }{dx_{3}}\chi ^{\varTheta }\quad \hbox{a.e. in } (0,L) \times {\mathbf{C}}. $$

(4.29)

Theorem 3

(The homogenized limit problem)

The limit field $({\underline{u}},\,{\mathbb{U}},\,\varTheta )\in {\mathbf{V}}_{M}$is the unique solution to the homogenized problem ($\alpha ,\alpha '\in \{1,2\}$, $m\in \{1,2,3\}$)

$$ \left \{ \begin{aligned} &\int _{0}^{L}\,\Big\{ a^{hom}_{\alpha \alpha '} \frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}} \frac{d^{2}{\mathbb{V}}_{\alpha '}}{dx_{3}^{2}} +b^{hom}_{mm'} \frac{d{\underline{u}}_{m}}{d x_{3}} \frac{d{\underline{v}}_{m'}}{d x_{3}} \\ &+c^{hom} \frac{d\varTheta }{dx_{3}}\frac{d{\mathbf{T}}}{dx_{3}} -ab^{hom}_{\alpha m} \left (\frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}} \frac{d{\underline{v}}_{m}}{d x_{3}}+ \frac{d{\underline{u}}_{m}}{d x_{3}} \frac{d^{2}{\mathbb{V}}_{\alpha }}{dx_{3}^{2}}\right ) \\ &-ac^{hom}_{\alpha }\left (\frac{d\varTheta }{dx_{3}} \frac{d^{2}{\mathbb{V}}_{\alpha }}{dx_{3}^{2}}+ \frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}}\frac{d{\mathbf{T}}}{dx_{3}} \right ) +bc^{hom}_{m}\left (\frac{d{\underline{u}}_{m}}{d x_{3}} \frac{d{\mathbf{T}}}{dx_{3}}+\frac{d\varTheta }{dx_{3}} \frac{d{\underline{v}}_{m}}{d x_{3}}\right )\Big\} \,dx_{3} \\ &= \int _{0}^{L}\,f_{\alpha }{\mathbb{V}}_{\alpha }\,dx_{3}+ I_{\alpha }\int _{0}^{L}\,\Big(g_{\alpha }\frac{d{\mathbb{V}}_{\alpha }}{dx_{3}}-g_{3}{ \mathbf{T}}\Big)\,dx_{3} +\int _{0}^{L}\,f_{3}{\underline{v}}_{3}\,dx_{3}, \qquad \forall \; ({\underline{v}},{\mathbb{V}}, {\mathbf{T}}) \in {\mathbf{V}}_{M}, \end{aligned} \right . $$

(4.30)

where

$$ \begin{aligned} &a^{hom}_{\alpha \alpha '}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}\,a_{ijkl} \left ({\mathbf{M}}^{33}_{kl}+e_{X,kl}\big(\chi _{\alpha }^{\mathbb{U}} \big)\right )\left ({\mathbf{M}}^{33}_{ij}+e_{X,ij}\big(\chi _{\alpha '}^{ \mathbb{U}}\big)\right )X_{\alpha }X_{\alpha '}\,dX, \\ &b^{hom}_{mm'}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}\, a_{ijkl}\left ({ \mathbf{M}}^{m 3}_{kl}+e_{X,kl}\big(\chi _{m}^{\underline{u}}\big)\right ) \left ({\mathbf{M}}^{m' 3}_{ij}+e_{X,ij}\big(\chi _{m'}^{\underline{u}} \big)\right )\,dX, \\ &c^{hom}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}\,a_{ijkl}\left (X_{1}{\mathbf{M}}^{23}_{kl}-X_{2}{ \mathbf{M}}^{13}_{kl} +e_{X,kl}\big(\chi ^{\varTheta }\big)\right )\left (X_{1}{ \mathbf{M}}^{23}_{ij}-X_{2}{\mathbf{M}}^{13}_{ij} +e_{X,kl}\big(\chi ^{\varTheta }\big)\right )\,dX, \\ &ab^{hom}_{\alpha m}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}\, a_{ijkl} \left ({\mathbf{M}}^{33}_{kl}+e_{X,kl}\big(\chi _{\alpha }^{\mathbb{U}} \big)\right )\left ({\mathbf{M}}^{m 3}_{ij}+e_{X,ij}\big(\chi _{m}^{ \underline{u}}\big)\right )X_{\alpha }\,dX, \\ &ac^{hom}_{\alpha }=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}\, a_{ijkl}\left ({ \mathbf{M}}^{33}_{kl}+e_{X,kl}\big(\chi _{\alpha }^{\mathbb{U}}\big)\right ) \left (X_{1}{\mathbf{M}}^{23}_{ij}-X_{2}{\mathbf{M}}^{13}_{ij} +e_{X,ij}\big( \chi ^{\varTheta }\big)\right )X_{\alpha }\,dX, \\ &bc^{hom}_{m}=\frac{1}{|{\mathbf{C}}|}\int _{\mathbf{C}}\,a_{ijkl}\left ({\mathbf{M}}^{m 3}_{kl}+e_{X,kl}\big(\chi _{m}^{\underline{u}}\big)\right )\left (X_{1}{ \mathbf{M}}^{23}_{ij}-X_{2}{\mathbf{M}}^{13}_{ij}+e_{X,ij}\big(\chi ^{\varTheta }\big)\right )\,dX. \end{aligned} $$

(4.31)

Proof

We take ${\widehat{v}}=0$ in (4.27). Replacing $\widehat{u}$ by its expression (4.29), for every $({\underline{v}},\,{\mathbb{V}},\,{\mathbf{T}})\in {\mathbf{V}}_{M}$ yields

$$ \begin{aligned} &\int _{(0,L)\times {\mathbf{C}}} a_{ijkl}\Big( \frac{d{\underline{u}}_{m}}{d x_{3}}\Big({\mathbf{M}}^{m 3}_{kl}+e_{X,kl} \big(\chi _{m}^{\underline{u}}\big)\Big)-X_{\alpha }\frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}}\Big({\mathbf{M}}^{33}_{kl}+e_{X,kl} \big(\chi _{\alpha }^{\mathbb{U}}\big)\Big)\\ &+\frac{d\varTheta }{dx_{3}} \Big(X_{1}{\mathbf{M}}^{23}_{kl}-X_{2}{\mathbf{M}}^{13}_{kl} +e_{X,kl}\big( \chi ^{\varTheta }\big)\Big)\Big) \\ &\times \Big(\frac{d{\underline{v}}_{m}}{d x_{3}}{\mathbf{M}}^{m 3}_{ij}-X_{\alpha }\frac{d^{2}{\mathbb{V}}_{\alpha }}{dx_{3}^{2}}{\mathbf{M}}^{33}_{ij}+ \Big(X_{1}{\mathbf{M}}^{23}_{ij}-X_{2}{\mathbf{M}}^{13}_{ij}\Big) \frac{d{\mathbf{T}}}{dx_{3}}\Big)\,dx_{3} dX \\ &=|\boldsymbol{C}|\Big[\int _{(0,L)}\,f_{\alpha }{\mathbb{V}}_{\alpha }\,dx_{3} +I_{\alpha }\int _{(0,L)}\,\Big[g_{\alpha }\frac{d{\mathbb{V}}_{\alpha }}{dx_{3}}-g_{3}{\mathbf{T}}\Big]\,dx_{3} + \int _{(0,L)}\,f_{3} {\underline{v}}_{3}\,dx_{3}\Big]. \end{aligned} $$

Taking into account the variational problems (4.28) satisfied by the correctors, the problem (4.30) with the homogenized coefficients given by (4.31) is obtained by a simple computation.

Now, we show that the operator on the left-hand side problem (4.30) is uniformly elliptic. Using formulas (4.31) of the homogenized coefficients, we obtain

$$ \begin{aligned} &a^{hom}_{\alpha \alpha '}\tau ^{\mathbb{U}}_{\alpha }\tau ^{ \mathbb{U}}_{\alpha '} +b^{hom}_{mm'}\tau ^{\underline{u}}_{m}\tau ^{ \underline{u}}_{m'} +c^{hom}\tau ^{\varTheta }\tau ^{\varTheta }+2ab^{hom}_{ \alpha m}\tau ^{\mathbb{U}}_{\alpha }\tau ^{\underline{u}}_{m} +2ac^{hom}_{ \alpha }\tau ^{\mathbb{U}}_{\alpha }\tau ^{\varTheta }+2bc^{hom}_{m}\tau ^{ \underline{u}}_{m}\tau ^{\varTheta }\\ &=\int _{\mathbf{C}}a_{ijkl}\Big(e_{X,kl}\big(\varPsi \big) +M_{kl}\Big) \Big(e_{X,ij}\big(\varPsi \big)+M_{ij}\Big)\,dX, \end{aligned} $$

where

$$\begin{aligned} M =&\Big(\tau ^{\underline{u}}_{1}-X_{2}\tau ^{\varTheta }\Big){\mathbf{M}}^{13} + \Big(\tau ^{\underline{u}}_{2}+X_{1}\tau ^{\varTheta }\Big){\mathbf{M}}^{23} + \Big(\tau ^{\mathbb{U}}_{1}+\tau ^{\mathbb{U}}_{2}+\tau ^{ \underline{u}}_{3}\Big){\mathbf{M}}^{33},\\ \varPsi =&\chi _{\alpha }^{\mathbb{U}}\tau ^{\mathbb{U}}_{\alpha }+\chi _{m}^{ \underline{u}}\tau ^{\underline{u}}_{m}+\chi ^{\varTheta }\tau ^{\varTheta }, \qquad \tau ^{\mathbb{U}}_{\alpha },\;\; \tau ^{\underline{u}}_{m},\; \; \tau ^{\varTheta }\in {\mathbb{R}},\quad \alpha =1,2,\,m=1,2,3. \end{aligned}$$

Then, in view of (2.2) and following the proof of [14, Lemma 11.19], we obtain

$$ \begin{aligned} &a^{hom}_{\alpha \alpha '}\tau ^{\mathbb{U}}_{\alpha }\tau ^{ \mathbb{U}}_{\alpha '} +b^{hom}_{mm'}\tau ^{\underline{u}}_{m}\tau ^{ \underline{u}}_{m'} +c^{hom}\tau ^{\varTheta }\tau ^{\varTheta }+2ab^{hom}_{ \alpha m}\tau ^{\mathbb{U}}_{\alpha }\tau ^{\underline{u}}_{m} +2ac^{hom}_{ \alpha }\tau ^{\mathbb{U}}_{\alpha }\tau ^{\varTheta }+2bc^{hom}_{m}\tau ^{ \underline{u}}_{m}\tau ^{\varTheta }\geq \\ \geq &\int _{\mathbf{C}} c_{0}\Big(e_{X,kl}\big(\varPsi \big)+M_{kl}\Big) \Big(e_{X,ij}\big(\varPsi \big)+M_{ij}\Big)\,dX\geq C\big(\tau ^{ \mathbb{U}}_{\alpha }+\tau ^{\underline{u}}_{m}+\tau ^{\varTheta }\big)^{2}. \end{aligned} $$

 □

4.6 Conclusion

For $\varepsilon$-periodic porous materials, the solution of problem (4.2) (in the strong form), or (4.3) (in the weak/variational form) is approximated by (for $x\in \varOmega ^{*}_{\varepsilon }$)

$$ \begin{aligned} u_{\varepsilon }(x)\approx & \begin{pmatrix} \displaystyle {\mathbb{U}}_{1}(x_{3})+\varepsilon {\underline{u}}_{1}(x_{3})-x_{2} \varTheta (x_{3}) \\ \displaystyle {\mathbb{U}}_{2}(x_{3})+\varepsilon {\underline{u}}_{2}(x_{3})+x_{1} \varTheta (x_{3}) \\ \displaystyle \varepsilon {\underline{u}}_{3}(x_{3})-x_{1} \frac{d{\mathbb{U}}_{1}}{dx_{3}}(x_{3})-x_{2} \frac{d{\mathbb{U}}_{2}}{dx_{3}}(x_{3}) \end{pmatrix} +\sum _{m=1}^{3}\,\varepsilon ^{2} \frac{d{\underline{u}}_{m}}{d x_{3}}(x_{3})\chi _{m}^{\underline{u}} \Big(\frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon },\Big\{ \frac{x_{3} }{\varepsilon }\Big\} \Big) \\ &-\sum _{\alpha =1}^{2}\,\varepsilon x_{\alpha }\frac{d^{2}{\mathbb{U}}_{\alpha }}{dx_{3}^{2}}(x_{3})\chi _{\alpha }^{ \mathbb{U}}\Big(\frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon }, \Big\{ \frac{x_{3}}{\varepsilon }\Big\} \Big)+\varepsilon ^{2} \frac{d\varTheta }{dx_{3}}(x_{3})\chi ^{\varTheta }\Big(\frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon },\Big\{ \frac{x_{3}}{\varepsilon }\Big\} \Big), \end{aligned} $$

(4.32)

where $({\underline{u}},\,{\mathbb{U}},\,\varTheta )\in {\mathbf{V}}_{M}$ is the solution to the homogenized $1D$ problem (4.30) and $\chi _{m}^{\underline{u}},\,\chi _{\alpha }^{\mathbb{U}},\,\chi ^{\varTheta }\in H^{1}_{1,per,0}({\mathbf{C}})^{3}$, $\alpha =1,2,\,m=1,2,3$, are the solutions to corresponding auxiliary cell problems (4.28) (see Fig. 4).

Fig. 4

Illustration of the two-scale approach for one pure bending experiment: compute the corrector $\chi _{\alpha }^{\mathbb{U}}(X)$ on the periodicity cell, compute $1D$ bending deflection ${\mathbb{U}}(x_{3})$ and put them into the approximating formula for the local stresses

The first term in the previous formula is a Bernoulli-Navier displacement completed by the displacements $\varepsilon \underline{u}$, and the term $\varepsilon \underline{u}_{3}$ stands for the stretching-compression of the structure. The remaining terms represents the warpings of the cells.

Appendices

Appendix A: Korn’s Inequalities

For every open bounded set ${\mathcal{O}}$ in ${\mathbb{R}}^{N}$ and $\delta >0$, denote ${\mathcal{O}}^{int}_{\delta }=\big \{x\in {\mathcal{O}}\;|\; \hbox{dist}(x,\partial {\mathcal{O}})>\delta \big \}$. The following lemma is used to pass from convergences in ${\mathcal{O}}^{int}_{\delta }$ to convergences in the whole domain $\mathcal{O}$.

Lemma 8

Let ${\mathcal{O}}$be an open bounded set in ${\mathbb{R}}^{N}$, and let $\{\phi _{\varepsilon }\}_{\varepsilon }$be a sequence of functions belonging to $H^{1}({\mathcal{O}}^{int}_{\kappa \varepsilon })$ ($\kappa$is a fixed strictly positive constant) satisfying

$$ \|\phi _{\varepsilon }\|_{H^{1}({\mathcal{O}}^{int}_{\kappa \varepsilon })} \leq C, $$

(A.1)

where $C$does not depend on $\varepsilon$. We extend $\phi _{\varepsilon }$by 0 to ${\mathbb{R}}^{N}\setminus \overline{{\mathcal{O}}^{int}_{\kappa \varepsilon }}$ (extension with the same name).

Then, there exists a subsequence of $\{\varepsilon \}$, still denoted by $\{\varepsilon \}$, and $\phi \in H^{1}({\mathcal{O}})$such that

$$ \begin{aligned} &\phi _{\varepsilon }\rightharpoonup \phi \quad \textit{weakly in } L^{2}({ \mathcal{O}}), \\ &\nabla \phi _{\varepsilon }{\mathbf{1}}_{{\mathcal{O}}^{int}_{\kappa \varepsilon }}\rightharpoonup \nabla \phi \quad \textit{weakly in } {L^{2}({ \mathcal{O}})}^{N}. \end{aligned} $$

Proof

It follows from (A.1) that there exist $\phi \in L^{2}({\mathcal{O}})$ and $\varPhi \in L^{2}({\mathcal{O}})^{N}$ such that (up to a subsequence still denoted by $\{\varepsilon \}$)

$$ \begin{aligned} &\phi _{\varepsilon }\rightharpoonup \phi \quad \hbox{weakly in } L^{2}({ \mathcal{O}}), \\ &\nabla \phi _{\varepsilon }{\mathbf{1}}_{{\mathcal{O}}^{int}_{\kappa \varepsilon }}\rightharpoonup \varPhi \quad \hbox{weakly in } L^{2}({ \mathcal{O}})^{N}. \end{aligned} $$

Now, we show that $\nabla \phi =\varPhi$, so $\phi$ belongs to $H^{1}({\mathcal{O}})$.

Let ${\mathcal{O}}'$ be an open subset of ${\mathcal{O}}$ such that ${\mathcal{O}}'$ is strictly included in ${\mathcal{O}}$. If $\varepsilon$ is small enough, one has ${\mathcal{O}}'\subset {\mathcal{O}}^{int}_{\kappa \varepsilon }$. For all $\psi \in {\mathcal{D}}({\mathcal{O}}')^{N}$, using the convergences given above we obtain on the one hand

$$ \int _{{\mathcal{O}}'}\,\nabla \phi _{\varepsilon }\cdot \psi \,dx =-\int _{{ \mathcal{O}}'}\,\phi _{\varepsilon }\,\hbox{div}(\psi )\,dx\to -\int _{{\mathcal{O}}'} \,\phi \, \hbox{div}(\psi )\,dx =\int _{{\mathcal{O}}'}\,\nabla \phi \cdot \psi \,dx, $$

and on the other hand

$$ \int _{{\mathcal{O}}'}\,\nabla \phi _{\varepsilon }\cdot \psi \,dx \to \int _{{ \mathcal{O}}'}\,\varPhi \cdot \psi \,dx. $$

Hence $\varPhi =\nabla \phi$ in every open set ${\mathcal{O}}'$ strictly included in ${\mathcal{O}}$. Thus $\varPhi =\nabla \phi$ a.e. in ${\mathcal{O}}$. So, we have $\phi \in H^{1}({\mathcal{O}})$. □

1.1 A.1 Korn’s Inequality on $N$-Dimensional Domains

See Sect. 2.1 for the principal notations. We also denote (see Fig. 5)

$$ \varXi _{\varepsilon }^{int}\doteq \big\{ \xi \in {\mathbb{Z}}^{N}\;|\; \varepsilon (\xi +Y)\subset \varOmega ^{int}_{2\varepsilon \sqrt{N}} \big\} . $$

First, we recall the following results proved in [14, Lemmas 5.21, 5.23 and 5.34]:

Fig. 5

Sets $\varOmega ,\,\varOmega _{2\varepsilon \sqrt{N}}^{int}, \varXi _{\varepsilon }$ and $\varXi _{\varepsilon }^{int}$

Proposition 7

Let $\varOmega$be a bounded domain in ${\mathbb{R}}^{N}$with Lipschitz boundary. There exists $\delta _{0}>0$such that for all $\delta \in (0,\delta _{0}]$the sets $\varOmega _{\delta }^{int}$are uniformly Lipschitz.

Proposition 8

Suppose $p\in [1,+\infty )$. Let $\ell$be a function defined on $\varXi _{\varepsilon }$. There exists a constant $C$which only depends on $p$and $\partial \varOmega$such that

$$ \sum _{\xi \in \varXi _{\varepsilon }}|\ell (\xi )|^{p}\leq C\Big( \sum _{ \xi \in \varXi ^{int}_{\varepsilon }}|\ell (\xi )|^{p}+ \sum _{i=1}^{N} \sum _{\xi \in \varXi _{\varepsilon ,i}} |\ell (\xi +{\mathbf{e}}_{i})-\ell ( \xi )|^{p}\Big). $$

Proposition 9

(Poincaré-Wirtinger inequality for $\varOmega ^{int}_{\delta }$)

Let $\varOmega$be a bounded domain in ${\mathbb{R}}^{N}$with Lipschitz boundary. Then, there exists $\delta _{0}>0$such that the domains $\varOmega _{\delta }^{int}$for $\delta \in (0,\delta _{0}]$are uniformly Lipschitz. These domains satisfy a uniform Poincaré-Wirtinger inequality for every $p\in [1,+\infty )$, i.e., there exists a constant $C$independent of $\delta$ ($C$depends only on $p$and $\partial \varOmega$) such that

$$ \|\varphi -{\mathcal{M}}_{\varOmega _{\delta }^{int}}(\varphi )\|_{L^{p}( \varOmega _{\delta }^{int})}\leq C\|\nabla \varphi \|_{L^{p}(\varOmega _{ \delta }^{int})},\quad \forall \varphi \in W^{1,p}(\varOmega _{\delta }^{int}), $$

(A.2)

where ${\mathcal{M}}_{\varOmega _{\delta }^{int}}(\varphi )$is the mean value of the function $\varphi$in the domain $\varOmega _{\delta }^{int}$.

Below, in every cell we compare a displacement to a rigid displacement. Then, in a second step, we compare the rigid displacements obtained in two neighboring cells. After that, we build a global displacement in order to obtain a Korn’s type inequality.

Let ${\mathbf{C}}_{i}=\hbox{interior}(\overline{\mathbf{C}}\cup {\overline{C}+{\mathbf{e}}_{i}})$ and $\varPhi$ be a displacement in ${W^{1,p}({\mathbf{C}}_{i})}^{N}$, $p\in (1,+\infty )$ and $i\in \{1,\ldots ,N\}$. Applying Korn’s inequality in ${\mathbf{C}}$ and ${\mathbf{C}}+{\mathbf{e}}_{i}$ yields two rigid displacements ${\mathbf{R}}_{i,0}$, ${\mathbf{R}}_{i,1}$, given by

$$ \begin{aligned} &{\mathbf{R}}_{i,0}(x)={\mathbf{a}}_{i,0}+{\mathbf{B}}_{i,0}\, x, \\ &{\mathbf{R}}_{i,1}(x)={\mathbf{a}}_{i,1}+{\mathbf{B}}_{i,1}\,(x-{\mathbf{e}}_{i}), \end{aligned} \qquad {\mathbf{a}}_{i,0},\;{\mathbf{a}}_{i,1} \in {\mathbb{R}}^{N},\quad x \in {\mathbb{R}}^{N}, $$

where ${\mathbf{B}}_{i,0}$, ${\mathbf{B}}_{i,1}$ are antisymmetric $N\times N$ matrices. We have

$$ \begin{aligned} &\|\varPhi -{\mathbf{R}}_{i,0}\|_{W^{1,p}( {\mathbf{C}})}\leq C\|e(\varPhi )\|_{L^{p}( {\mathbf{C}})}, \\ &\|\varPhi -{\mathbf{R}}_{i,1}\|_{W^{1,p}({\mathbf{C}}+{\mathbf{e}}_{i})}\leq C\|e( \varPhi )\|_{L^{p}({\mathbf{C}}+{\mathbf{e}}_{i})}, \end{aligned} $$

(A.3)

where the constant depends only on ${\mathbf{C}}$.

Lemma 9

The following estimates hold:

$$ \begin{aligned} &|{\mathbf{B}}_{i,1}-{\mathbf{B}}_{i,0}|\leq C \|e(\varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}, \\ &|{\mathbf{a}}_{i,1}-{\mathbf{a}}_{i,0}- {\mathbf{B}}_{i,1}\,{\mathbf{e}}_{i}|\leq C\|e( \varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}, \end{aligned} \qquad i=1,\ldots , N, $$

(A.4)

where the constant $C$depends only on ${\mathbf{C}}$.

Proof

Since the domain ${\mathbf{C}}_{i}$ is connected and has a Lipschitz boundary, it satisfies Korn’s inequality. Hence, there exists a rigid displacement ${\mathbf{R}}_{i}$,

$$ {\mathbf{R}}_{i}(x)={\mathbf{a}}_{i}+{\mathbf{B}}_{i}\,(x-{{\mathbf{e}}_{i}/2}),\quad { \mathbf{a}}_{i}\in {\mathbb{R}}^{N}, \quad x \in \mathbb{R}^{N}, $$

where ${\mathbf{B}}_{i}$ is an antisymmetric $N\times N$ matrix. The rigid displacement ${\mathbf{R}}_{i}$ satisfies

$$ \|\varPhi -{\mathbf{R}}_{i}\|_{W^{1,p}( {\mathbf{C}}_{i})}\leq C\|e(\varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}, $$

(A.5)

where the constant $C$ depends on ${\mathbf{C}}_{i}$. Hence, by (A.3) and (A.5)

$$ \|\nabla ({\mathbf{R}}_{i}-{\mathbf{R}}_{i,0})\|_{L^{p}( {\mathbf{C}})}+ \|\nabla ({\mathbf{R}}_{i}-{\mathbf{R}}_{i,1})\|_{L^{p}({\mathbf{C}}+{\mathbf{e}}_{i})}\leq C\|e( \varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}. $$

(A.6)

Taking into account the inequality (A.6), we obtain

$$ \begin{aligned} &|{\mathbf{B}}_{i}-{\mathbf{B}}_{i,0}| \leq C\|\nabla ({\mathbf{R}}_{i}-{\mathbf{R}}_{i,0}) \|_{L^{p}( {\mathbf{C}})}\leq C\|e(\varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}, \\ &|{\mathbf{B}}_{i}-{\mathbf{B}}_{i,1}| \leq C\|\nabla ({\mathbf{R}}_{i}-{\mathbf{R}}_{i,1}) \|_{L^{p}({\mathbf{C}}+{\mathbf{e}}_{i})}\leq C\|e(\varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}. \end{aligned} $$

(A.7)

Subtracting yields (A.4)₁.

Now we prove (A.4)₂. First observe that

$$ \Big\| {\mathbf{a}}_{i}-{\mathbf{a}}_{i,0}-\frac{1}{2} {\mathbf{B}}_{i}\,{\mathbf{e}}_{i} \Big\| _{L^{p}({\mathbf{C}})}\leq \Big\| {\mathbf{a}}_{i}+{\mathbf{B}}_{i}\,(x-\frac{1 }{2} {\mathbf{e}}_{i})-\big({\mathbf{a}}_{i,0}+{\mathbf{B}}_{i,0}x\big)\Big\| _{L^{p}({ \mathbf{C}})}+\big\| {\mathbf{B}}_{i}x-{\mathbf{B}}_{i,0}x\big\| _{L^{p}({\mathbf{C}})}. $$

(A.8)

Besides, we have

$$ \begin{aligned} &\Big\| {\mathbf{a}}_{i}+{\mathbf{B}}_{i}\,(x-\frac{1}{2}{\mathbf{e}}_{i})-\big({\mathbf{a}}_{i,0}+{ \mathbf{B}}_{i,0}x\big)\Big\| _{L^{p}({\mathbf{C}})}\\ &\quad= \big\| {\mathbf{R}}_{i}-{\mathbf{R}}_{i,0} \big\| _{L^{p}({\mathbf{C}})}\le \big\| \varPhi -{\mathbf{R}}_{i}\big\| _{L^{p}({ \mathbf{C}})}+\big\| \varPhi -{\mathbf{R}}_{i,0} \big\| _{L^{p}({\mathbf{C}})} \leq C\|e(\varPhi )\|_{L^{p}({\mathbf{C}}_{i})}. \end{aligned} $$

The previous estimate together with (A.8) and (A.7) gives

$$ \Big|{\mathbf{a}}_{i}-{\mathbf{a}}_{i,0}-\frac{1}{2}{\mathbf{B}}_{i}\,{\mathbf{e}}_{i} \Big|\leq C\|e(\varPhi )\|_{L^{p}( {\mathbf{C}}_{i})}. $$

Similarly, we obtain

$$ \Big|{\mathbf{a}}_{i}-{\mathbf{a}}_{i,1}+\frac{1}{2}{\mathbf{B}}_{i}\,{\mathbf{e}}_{i} \Big|\leq C\|e(\varPhi )\|_{L^{p}({\mathbf{C}}_{i})}. $$

Hence (A.4)₂ holds. Thus Lemma 9 is proved. □

Now, let $u$ be a displacement in ${W^{1,p}(\varOmega _{\varepsilon }^{*})}^{N}$. By Korn’s inequality in $\varepsilon (\xi + {\mathbf{C}})$ there exist rigid displacements ${\mathbf{R}}_{\varepsilon \xi }$ ($\xi \in \varXi _{\varepsilon }$),

$$ {\mathbf{R}}_{\varepsilon \xi }(x)={\mathbf{a}}(\varepsilon \xi )+{\mathbf{B}}( \varepsilon \xi )\,(x-\varepsilon \xi ),\quad x\in {\mathbb{R}}^{N}, $$

such that (using (A.3) and after $\varepsilon$-scaling)

$$ \begin{aligned} &\|\nabla (u-{\mathbf{R}}_{\varepsilon \xi })\|_{L^{p}(\varepsilon (\xi + { \mathbf{C}}))}\leq C\|e(u)\|_{L^{p}(\varepsilon (\xi + {\mathbf{C}}))}, \\ & \|u-{\mathbf{R}}_{\varepsilon \xi }\|_{L^{p}(\varepsilon (\xi + {\mathbf{C}}))} \leq C\varepsilon \|e(u)\|_{L^{p}(\varepsilon (\xi + {\mathbf{C}}))}. \end{aligned} $$

(A.9)

As above we obtain the following estimates for every $\xi \in \varXi _{\varepsilon ,i}$:

$$ \begin{aligned} &|{\mathbf{B}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{i})-{\mathbf{B}}( \varepsilon \xi )|\le C\varepsilon ^{-N/p}\|e(u)\|_{L^{p}( \varepsilon {\mathbf{C}}^{\xi }_{i})}, \\ &|{\mathbf{a}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{i})-{\mathbf{a}}( \varepsilon \xi )-\varepsilon {\mathbf{B}}(\varepsilon \xi +\varepsilon { \mathbf{e}}_{i}){\mathbf{e}}_{i}|\le C\varepsilon ^{1-N/p}\|e(u)\|_{L^{p}( \varepsilon {\mathbf{C}}^{\xi }_{i})}, \end{aligned} $$

where ${\mathbf{C}}_{i}^{\xi }=\hbox{interior} \big ((\overline{\mathbf{C}}+\xi )\cup ({ \mathbf{e}}_{i}+\xi +\overline{\mathbf{C}})\big )$.

An immediate consequence of Lemma 9, we have

Lemma 10

The following estimates hold:

$$ \begin{aligned} &\sum _{i=1}^{N}\sum _{\xi \in \varXi _{\varepsilon ,i}} |{\mathbf{B}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{i})-{\mathbf{B}}( \varepsilon \xi )|^{p}\varepsilon ^{N}\leq C\|e(u)\|^{p}_{L^{p}( \varOmega _{\varepsilon }^{*})}, \\ &\sum _{i=1}^{N}\sum _{\xi \in \varXi _{\varepsilon ,i}} |{\mathbf{a}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{i})-{\mathbf{a}}( \varepsilon \xi )-\varepsilon {\mathbf{B}}(\varepsilon \xi +\varepsilon { \mathbf{e}}_{i})\,{\mathbf{e}}_{i}|^{p}\varepsilon ^{N} \leq C\varepsilon ^{p}\|e(u)\|^{p}_{L^{p}(\varOmega _{\varepsilon }^{*})}, \end{aligned} $$

(A.10)

where the constant $C$depends only on ${\mathbf{C}}$.

Let $\xi$ be in $\varXi _{\varepsilon }$. If all the vertices of the parallelotope $\varepsilon (\xi +\overline{Y})$ belong to $\varXi _{\varepsilon }$, we extend the field ${\mathbf{a}}$ (or ${\mathbf{B}}$, resp.) to this parallelotope as the $Q_{1}$ interpolate of its values at the vertices of the parallelotope.

We obtain a field, still denoted ${\mathbf{a}}$ (or ${\mathbf{B}}$, resp.), defined at least in $\varOmega ^{int}_{2\varepsilon \sqrt{N}}$. This field belongs to $W^{1,\infty }(\varOmega ^{int}_{2\varepsilon \sqrt{N}})^{N}$ (resp. $W^{1,\infty }(\varOmega ^{int}_{2\varepsilon \sqrt{N}})^{N\times N}$).

Lemma 11

For every displacement $u\in W^{1,p}(\varOmega _{\varepsilon }^{*})^{N}$the following estimates hold

$$ \begin{aligned} &\|\nabla {\mathbf{B}}\|_{L^{p}(\varOmega ^{int}_{2\varepsilon \sqrt{N}})} \leq \frac{C}{\varepsilon }\|e(u)\|_{L^{p}(\varOmega _{\varepsilon }^{*})}, \\ &\big\| \nabla {\mathbf{a}}- {\mathbf{B}}\big\| _{L^{p}(\varOmega ^{int}_{2 \varepsilon \sqrt{N}})}\leq C\|e(u)\|_{L^{p}(\varOmega _{\varepsilon }^{*})}, \\ &\big\| e({\mathbf{a}})\big\| _{L^{p}(\varOmega ^{int}_{2\varepsilon \sqrt{N}})} \leq C\|e(u)\|_{L^{p}(\varOmega _{\varepsilon }^{*})}, \end{aligned} $$

(A.11)

where the constants do not depend on $\varepsilon$.

Proof

A straightforward calculation and the estimates in Lemma 10 yield (A.11)_1,2. Then (A.11)₂ gives (A.11)₃ (recall that ${\mathbf{B}}$ is an antisymmetric $N\times N$ matrix). Thus Lemma 11 is proved. □

We assume that there exists a domain $\varOmega '$ with a Lipschitz boundary such that $\varOmega \subset \varOmega '$ and $\varOmega '\cap \partial \varOmega =\varGamma$.

Denote

$$ \begin{aligned} W^{1,p}_{\varGamma } (\varOmega _{\varepsilon }^{*})\doteq \left \{ \psi \in W^{1,p}( \varOmega _{\varepsilon }^{*})\;\big|\; \exists \psi ^{\prime } \in W^{1,p}( \varOmega ^{\prime *}_{\varepsilon }), \; \psi =\psi ^{\prime }_{| \varOmega _{\varepsilon }^{*}}, \; \psi ^{\prime }=0 \text{ in } \varOmega ^{ \prime *}_{\varepsilon }\setminus \overline{\varOmega _{\varepsilon }^{*}} \right \} , \end{aligned} $$

where

$$ \varOmega ^{\prime *}_{\varepsilon }\doteq \hbox{interior}\Big(\bigcup _{ \xi \in \varXi ^{\prime }_{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{\mathbf{C}})\Big),\quad \varXi ^{\prime }_{\varepsilon }\doteq \big\{ \xi \in {\mathbb{Z}}^{3}\;\; |\;\; (\varepsilon \xi +\varepsilon Y) \cap \varOmega ^{\prime }\neq \emptyset \big\} . $$

Theorem 4

(Korn’s inequality)

For every displacement $u\in W^{1,p}(\varOmega _{\varepsilon }^{*})^{N}$, $p\in (1,+\infty )$, there exists a rigid displacement ${\mathbf{R}}$such that

$$ \|u-{\mathbf{R}}\|_{W^{1,p}(\varOmega _{\varepsilon }^{*})}\leq C\|e(u)\|_{L^{p}( \varOmega ^{*}_{\varepsilon })}. $$

(A.12)

Furthermore, if $u\in W^{1,p}_{\varGamma }(\varOmega _{\varepsilon }^{*})^{N}$then

$$ \|u\|_{W^{1,p}(\varOmega _{\varepsilon }^{*})}\leq C\|e(u)\|_{L^{p}( \varOmega ^{*}_{\varepsilon })}, $$

(A.13)

where the constants $C$in (A.12), (A.13) do not depend on $\varepsilon$.

Proof

Since the boundary of $\varOmega ^{int}_{2\varepsilon \sqrt{N}}$ is uniformly Lipschitz, Korn’s inequality and (A.11)₃ give a rigid displacement $\overline{{\mathbf{R}}}$ such that

$$ \big\| {\mathbf{a}}-\overline{{\mathbf{R}}}\big\| _{W^{1,p}(\varOmega ^{int}_{2 \varepsilon \sqrt{N}})}\leq C\big\| e({\mathbf{a}})\big\| _{L^{p}(\varOmega ^{int}_{2 \varepsilon \sqrt{N}})}\leq C\|e(u)\|_{L^{p}(\varOmega _{\varepsilon }^{*})}. $$

Then (A.11)₂ and the previous estimate lead to

$$ \big\| {\mathbf{B}}-\nabla \overline{{\mathbf{R}}}\big\| _{L^{p}(\varOmega ^{int}_{2 \varepsilon \sqrt{N}})}\leq C\|e(u)\|_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

Denote ${\mathcal{B}}=\nabla \overline{{\mathbf{R}}}$. Hence

$$ \sum _{\xi \in \varXi ^{int}_{\varepsilon }}|{\mathbf{B}}(\varepsilon \xi )-{ \mathcal{B}}|^{p}\varepsilon ^{N}\leq C\|e(u)\|^{p}_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

The estimate (A.10)₁ in Lemma 10 together with the previous estimate and Lemma 8 yield

$$ \sum _{\xi \in \varXi _{\varepsilon }}|{\mathbf{B}}(\varepsilon \xi )-{\mathcal{B}}|^{p} \varepsilon ^{N}\leq C\|e(u)\|^{p}_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

(A.14)

Now, from Proposition 9 and (A.11)₃, there exits $a\in {\mathbb{R}}$ such that

$$ \|{\mathbf{a}}-a\|_{L^{p}(\varOmega ^{int}_{2\varepsilon \sqrt{N}})}\leq C\|e(u) \|_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

Hence

$$ \sum _{\xi \in \varXi ^{int}_{\varepsilon }}|{\mathbf{a}}(\varepsilon \xi )-a|^{p} \varepsilon ^{N}\leq C\|e(u)\|^{p}_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

The estimates (A.14), (A.10)₂ together with the previous estimate and Lemma 8 yield

$$ \sum _{\xi \in \varXi _{\varepsilon }}|{\mathbf{a}}(\varepsilon \xi )-a|^{p} \varepsilon ^{N}\leq C\|e(u)\|^{p}_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

(A.15)

Let ${\mathbf{R}}=a+{\mathcal{B}}x$. Then estimates (A.9) and (A.14), (A.15) lead to (A.12).

If $u$ belongs to $W^{1,p}_{\varGamma }(\varOmega _{\varepsilon }^{*})^{N}$, applying the previous result (A.12) with $u'$ in place of $u$, and $\varOmega '$ in place of $\varOmega$, gives a rigid displacement ${\mathbf{R}}'$ such that

$$ \|u'-{\mathbf{R}}'\|_{W^{1,p}(\varOmega ^{\prime *}_{\varepsilon })}\leq C\|e(u) \|_{L^{p}(\varOmega ^{*}_{\varepsilon })}. $$

Let ${\mathcal{O}}$ be an open set such that ${\mathcal{O}}$ strictly included in $\big (\varOmega '\setminus \overline{\varOmega }\big )$. For $\varepsilon$ small enough, the function $u'$ vanishes in ${\mathcal{O}}\cap \varOmega ^{\prime *}_{\varepsilon }$.

Hence

$$ \|{\mathbf{R}}'\|_{W^{1,p}({\mathcal{O}}\cap \varOmega ^{\prime *}_{\varepsilon })} \leq C\|e(u)\|_{L^{p}(\varOmega ^{*}_{\varepsilon })} $$

which yields an estimate, independent of $\varepsilon$, for the components of ${\mathbf{R}}'$. Thus the estimate (A.13) follows. □

1.2 A.2 Korn’s Inequality on a Plate-Like Domain

In this subsection, the proofs of the lemmas are similar to the proofs of those in the previous subsection.

The notations are those of Sect. 3.1. We recall that ${\mathbf{C}}$ is a domain with Lipschitz boundary included in $Y=(-1/2,1/2)^{3}$ and such that the sets ${\mathbf{C}}_{\alpha }=\hbox{interior}\big (\overline{\mathbf{C}}\cup ( \overline{\mathbf{C}}+{\mathbf{e}}_{\alpha })\big )$, $\alpha =1,2$, are connected.

Let $u$ be in $H^{1}(\varOmega ^{*}_{\varepsilon })^{3}$. For every $\xi \in \varXi _{\varepsilon }$ there exists a rigid displacement ${\mathbf{R}}_{\varepsilon \xi }$,

$$ {\mathbf{R}}_{\varepsilon \xi }(x)=\boldsymbol{\mathcal{U}}(\varepsilon \xi )+ \boldsymbol{\mathcal{R}}(\varepsilon \xi )\land (x-\varepsilon \xi ),\quad x \in {\mathbb{R}}^{3}, $$

such that

$$ \begin{aligned} \|\nabla (u-{\mathbf{R}}_{\varepsilon \xi })\|_{L^{2}(\varepsilon (\xi +{ \mathbf{C}}))}\leq C\|e(u)\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))},\quad \|u-{ \mathbf{R}}_{\varepsilon \xi }\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))}\leq C \varepsilon \|e(u)\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))}. \end{aligned} $$

(A.16)

Remark 2

By construction, the fields $\boldsymbol{\mathcal{U}},\,\boldsymbol{\mathcal{R}}$ are piecewise linear in each cell.

In the same way as in Lemma 10 we get the following lemma:

Lemma 12

The following estimates hold:

$$ \begin{aligned} &\sum _{\alpha =1}^{2}\sum _{\xi \in \varXi _{\varepsilon ,\alpha }}| \boldsymbol{\mathcal{R}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{\alpha })- \boldsymbol{\mathcal{R}}(\varepsilon \xi )|^{2}\varepsilon ^{3}\leq C\|e(u)\|^{2}_{L^{2}( \varOmega ^{*}_{\varepsilon })}, \quad \alpha =1,2, \\ &\sum _{\alpha =1}^{2}\sum _{\xi \in \varXi _{\varepsilon ,\alpha }}| \boldsymbol{\mathcal{U}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{\alpha })- \boldsymbol{\mathcal{U}}(\varepsilon \xi )-\varepsilon \boldsymbol{\mathcal{R}}( \varepsilon \xi +\varepsilon {\mathbf{e}}_{\alpha })\land {\mathbf{e}}_{\alpha }|^{2} \varepsilon ^{3}\leq C\varepsilon ^{2}\|e(u)\|^{2}_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned} $$

(A.17)

The constant $C$depends only on ${\mathbf{C}}$.

As in the previous subsection, using $Q_{1}$ interpolation we extend the fields $\boldsymbol{\mathcal{U}}$ and $\boldsymbol{\mathcal{R}}$ to the whole domain $\omega ^{int}_{3\varepsilon }$ and obtain two fields ${\mathcal{U}}\in W^{1,\infty }(\omega ^{int}_{3\varepsilon })^{3}$ and ${\mathcal{R}}\in W^{1,\infty }(\omega ^{int}_{3\varepsilon })^{2}$ satisfying

$$ {\mathcal{U}}(\varepsilon \xi )=\boldsymbol{\mathcal{U}}(\varepsilon \xi ), \quad {\mathcal{R}}(\varepsilon \xi )=\boldsymbol{\mathcal{R}}(\varepsilon \xi ), \quad \forall \,\xi \in \varXi _{\varepsilon }\cap \omega ^{int}_{3 \varepsilon }. $$

Below, we use the plate decomposition from [18]. We define the displacement ${\mathbf{U}}^{e}$ as

$$ {\mathbf{U}}^{e}(x)={\mathcal{U}}(x')+{\mathcal{R}}(x')\land x_{3}{\mathbf{e}}_{3}, \quad \forall \,x \in \varOmega ^{int}_{\varepsilon },\quad x'=(x_{1},x_{2}). $$

Lemma 13

For every displacement $u\in H^{1}(\varOmega _{\varepsilon }^{*})^{3}$we have

$$ \begin{aligned} &\|\nabla {\mathcal{R}}\|_{L^{2}(\omega ^{int}_{3\varepsilon })} \leq \frac{C}{\varepsilon ^{3/2}}\|e(u)\|_{L^{2}(\varOmega _{\varepsilon }^{*})}, \\ &\Big\| \frac{\partial {\mathcal{U}}}{\partial x_{\alpha }}- { \mathcal{R}}\land {\mathbf{e}}_{\alpha }\Big\| _{L^{2}(\omega ^{int}_{3 \varepsilon })} \leq \frac{C}{\varepsilon ^{1/2}}\|e(u)\|_{L^{2}( \varOmega _{\varepsilon }^{*})}, \quad \alpha =1,2. \end{aligned} $$

(A.18)

The constant $C$depends only on ${\mathbf{C}}$.

Proof

The estimates (A.18) are the consequences of (A.17) and the fact that the fields ${\mathcal{U}}$ and ℛ are piecewise linear in every cell. □

Theorem 5

For every displacement $u\in H^{1}(\varOmega ^{*}_{\varepsilon })^{3}$, there exists a rigid displacement ${\mathbf{R}}$such that

$$ \|u_{\alpha }-{\mathbf{R}}_{\alpha }\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\leq C \|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })},\quad \|u_{3}-{\mathbf{R}}_{3} \|_{L^{2}(\varOmega ^{*}_{\varepsilon })}+\|\nabla (u -{\mathbf{R}})\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}\leq \frac{C}{\varepsilon }\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}. $$

The constant $C$does not depend on $\varepsilon$.

Proof

From Proposition 9, there exits $(b_{1}, b_{2})\in {\mathbb{R}}^{2}$ such that

$$ \|{\mathcal{R}}_{\alpha }-b_{\alpha }\|_{L^{2}(\omega ^{int}_{3 \varepsilon })} \leq \frac{C}{\varepsilon ^{3/2}}\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}. $$

(A.19)

Then, the previous estimate, (A.17)₁ and Proposition 8 yield

$$ \sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{R}}_{\alpha }(\varepsilon \xi )-b_{\alpha }|^{2}\varepsilon ^{3} \leq \frac{C}{\varepsilon ^{3}}\|e(u) \|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

Furthermore, (A.18)₂ and (A.19) lead to

$$ \Big\| \frac{\partial {\mathcal{U}}_{3} }{\partial x_{1}} +b_{2}\Big\| _{L^{2}( \omega ^{int}_{3\varepsilon })}+\Big\| \frac{\partial {\mathcal{U}}_{3} }{\partial x_{2}} - b_{1}\Big\| _{L^{2}(\omega ^{int}_{3 \varepsilon })}\leq \frac{C}{\varepsilon ^{1/2}}\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}, \quad \alpha =1,2. $$

Proceeding as above, there exists $a_{3}\in {\mathbb{R}}$ such that

$$ \sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{U}}_{3}(\varepsilon \xi )-a_{3}+b_{2} \varepsilon \xi _{1}- b_{1}\varepsilon \xi _{2}|^{2}\varepsilon ^{3} \leq \frac{C}{\varepsilon ^{3}}\varepsilon \|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

From (A.18)₂ we also obtain

$$ \Big\| \frac{\partial {\mathcal{U}}_{1} }{\partial x_{1}}\Big\| _{L^{2}( \omega ^{int}_{3\varepsilon })}+\Big\| \frac{\partial {\mathcal{U}}_{2} }{\partial x_{2}}\Big\| _{L^{2}(\omega ^{int}_{3\varepsilon })}+ \Big\| \frac{\partial {\mathcal{U}}_{1} }{\partial x_{2}}+\frac{\partial { \mathcal{U}}_{2} }{\partial x_{1}}\Big\| _{L^{2}(\omega ^{int}_{3 \varepsilon })} \leq \frac{C}{\varepsilon ^{1/2}}\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}. $$

Since the boundary of $\omega ^{int}_{3\varepsilon }$ is uniformly Lipschitz, Korn’s inequality for $2D$ gives a rigid displacement $r(x_{1},x_{2})=(a_{1}-b_{3} x_{2}){\mathbf{e}}_{1}+(a_{2}+b_{3} x_{1}){ \mathbf{e}}_{2}$ such that

$$ \|{\mathcal{U}}_{1}-r_{1}\|_{H^{1}(\omega ^{int}_{3\varepsilon })}+ \|{\mathcal{U}}_{2}-r_{2}\|_{H^{1}(\omega ^{int}_{3\varepsilon })} \leq \frac{C}{\varepsilon ^{1/2}}\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

These estimates and (A.18)₂ imply that

$$ \|{\mathcal{R}}_{3}-b_{3}\|_{L^{2}(\omega ^{int}_{3\varepsilon })} \leq \frac{C}{\varepsilon ^{1/2}}\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

Then, as above, we obtain

$$\begin{aligned} &\sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{R}}_{3}(\varepsilon \xi )-b_{3}|^{2} \varepsilon ^{3} +\sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{U}}_{1}( \varepsilon \xi )-a_{1}+b_{3}\varepsilon \xi _{2}|^{2}\varepsilon ^{3}+ \sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{U}}_{2}(\varepsilon \xi )-a_{2}-b_{3} \varepsilon \xi _{1}|^{2}\varepsilon ^{3} \\ &\quad\leq \frac{C}{\varepsilon } \|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned}$$

By choosing ${\mathbf{R}}(x)=a+b\land x$ and using (A.16) we complete the proof of the theorem. □

Let $\gamma$ be a subset of $\partial \omega$ with a non-zero measure. Assume that there exists a domain $\omega '$ with Lipschitz boundary such that

$$ \omega \subset \omega '\quad \hbox{and}\quad \omega '\cap \partial \omega =\gamma . $$

Denote

$$ {\mathbf{V}}_{\varepsilon }\doteq \Big\{ v\in H^{1}(\varOmega ^{*}_{\varepsilon })^{3} \;\big|\; \exists v' \in H^{1}(\varOmega ^{\prime *}_{\varepsilon })^{3}, \;\; v=v'_{|\varOmega ^{*}_{\varepsilon }}, \;\; v'=0 \text{ in } \varOmega ^{ \prime *}_{\varepsilon }\,\setminus \, \overline{\varOmega ^{*}_{\varepsilon }}\Big\} , $$

where

$$ \varOmega ^{\prime *}_{\varepsilon }\doteq \hbox{interior}\Big(\bigcup _{ \xi \in \varXi ^{\prime }_{\varepsilon }}(\varepsilon \xi +\varepsilon \overline{\mathbf{C}})\Big), \quad \varXi ^{\prime }_{\varepsilon }\doteq \big\{ \xi \in {\mathbb{Z}}^{2}\;\; |\;\; (\varepsilon \xi + \varepsilon Y')\cap \omega ^{\prime }\neq \emptyset \big\} . $$

Theorem 6

For every displacement $u$in ${\mathbf{V}}_{\varepsilon }$the following estimates hold

$$ \|u_{1}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}+\|u_{2}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} \leq C\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \quad \|u_{3}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}+\|\nabla u\|_{L^{2}( \varOmega ^{*}_{\varepsilon })} \leq \frac{C}{\varepsilon }\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}. $$

(A.20)

The constant $C$does not depend on $\varepsilon$.

Proof

Since $u$ belongs to ${\mathbf{V}}_{\varepsilon }$, there exists $u'\in H^{1}(\varOmega ^{\prime *}_{\varepsilon })^{3}$ such that $u=u'_{|\varOmega ^{*}_{\varepsilon }}$, $u'=0$ in $\varOmega ^{\prime *}_{\varepsilon }\,\setminus \, \overline{\varOmega ^{*}_{\varepsilon }}$. Then, applying Theorem 5 with $u'$ in place of $u$, and $\varOmega '$ in place of $\varOmega$, gives a rigid displacement ${\mathbf{R}}'$ such that

$$ \begin{aligned} &\|u'_{\alpha }-{\mathbf{R}}'_{\alpha }\|_{L^{2}(\varOmega ^{\prime *}_{\varepsilon })}\leq C \|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \\ & \|u'_{3}-{\mathbf{R}}'_{3}\|_{L^{2}(\varOmega ^{\prime *}_{\varepsilon })}+ \|\nabla (u' -{\mathbf{R}}')\|_{L^{2}(\varOmega ^{\prime *}_{\varepsilon })} \leq \frac{C}{\varepsilon }\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned} $$

(A.21)

Let ${\mathcal{O}}$ be an open set such that ${\mathcal{O}}$ is strictly included in $\big (\omega '\setminus \overline{\omega }\big )$. For $\varepsilon$ small enough, the function $u'$ vanishes in ${\mathcal{O}}\times (-\varepsilon /2,\varepsilon /2)\cap \varOmega ^{\prime *}_{\varepsilon }$. Then the terms of its decomposition ${\mathcal{U}}'$ and ${\mathcal{R}}'$ also vanish in ${\mathcal{O}}$. Hence, one can choose ${\mathbf{R}}'=0$ without changing the estimates (A.21). So, (A.20) follows. □

As a consequence of the two previous theorems, we obtain the following result

Corollary 1

For every displacement $u$in ${\mathbf{V}}_{\varepsilon }$the following estimates hold:

$$ \begin{aligned} &\|{\mathcal{U}}_{1}\|_{H^{1}(\omega ^{int}_{3\varepsilon })}+\|{ \mathcal{U}}_{2}\|_{H^{1}(\omega ^{int}_{3\varepsilon })}+\|{ \mathcal{R}}_{3} \|_{H^{1}(\omega ^{int}_{3\varepsilon })}\leq \frac{C }{\varepsilon ^{1/2}}\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \\ &\|{\mathcal{U}}_{3}\|_{H^{1}(\omega ^{int}_{3\varepsilon })}+\| { \mathcal{R}}_{1} \|_{H^{1}(\omega ^{int}_{3\varepsilon })}+\| { \mathcal{R}}_{2} \|_{H^{1}(\omega ^{int}_{3\varepsilon })}\leq \frac{C }{\varepsilon ^{3/2}}\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \\ &\|\overline{u_{1}}\|_{L^{2}(\varOmega ^{int}_{\varepsilon })}+| \overline{u_{2}}\|_{L^{2}(\varOmega ^{int}_{\varepsilon })}\leq C \varepsilon \|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })},\\ &|\overline{u_{3}}\|_{L^{2}(\varOmega ^{int}_{\varepsilon })}+\|\nabla \overline{u}\|_{L^{2}(\varOmega ^{int}_{\varepsilon })}\leq C\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}, \end{aligned} $$

(A.22)

and

$$ \begin{aligned} &\sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{R}}_{1}(\varepsilon \xi )|^{2}\varepsilon ^{2}+\sum _{\xi \in \varXi _{\varepsilon }}|{ \mathcal{R}}_{2}(\varepsilon \xi )|^{2}\varepsilon ^{2}+\sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{U}}_{3}(\varepsilon \xi )|^{2} \varepsilon ^{2} \leq \frac{C}{\varepsilon ^{3}}\|e(u)\|^{2}_{L^{2}( \varOmega ^{*}_{\varepsilon })}, \\ &\sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{R}}_{3}(\varepsilon \xi )|^{2}\varepsilon ^{2} +\sum _{\xi \in \varXi _{\varepsilon }}|{ \mathcal{U}}_{1}(\varepsilon \xi )|^{2}\varepsilon ^{2}+\sum _{\xi \in \varXi _{\varepsilon }}|{\mathcal{U}}_{2}(\varepsilon \xi )|^{2} \varepsilon ^{2}\leq \frac{C}{\varepsilon }\|e(u)\|^{2}_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned} $$

(A.23)

The constants $C$do not depend on $\varepsilon$.

1.3 A.3 Korn’s Inequality on a Beam-Like Domain

In this subsection, the notations are those of Sect. 4.1.

For every displacement $u\in H^{1}(\varOmega ^{*}_{\varepsilon })^{3}$, Korn’s inequality applied on the domain $\varepsilon (\xi +{\mathbf{C}}), \,\xi \in \varXi _{\varepsilon }$, gives a rigid displacement ${\mathbf{R}}_{\varepsilon \xi }$,

$$ {\mathbf{R}}_{\varepsilon \xi }(x)=\boldsymbol{\mathcal{U}}(\varepsilon \xi )+ \boldsymbol{\mathcal{R}}(\varepsilon \xi )\land (x-\varepsilon \xi ),\quad x \in {\mathbb{R}}^{3}, $$

such that

$$ \|\nabla (u-{\mathbf{R}}_{\varepsilon \xi })\|_{L^{2}(\varepsilon (\xi +{ \mathbf{C}}))} \leq C\|e(u)\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))},\quad \|u-{ \mathbf{R}}_{\varepsilon \xi }\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))} \leq C \varepsilon \|e(u)\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))}. $$

(A.24)

Remark 3

By construction, the fields $\boldsymbol{\mathcal{U}}$ and $\boldsymbol{\mathcal{R}}$ are piecewise constant.

In the same way as in Lemmas 10-12 we get

Lemma 14

The following estimates hold:

$$ \begin{aligned} &\sum _{\xi \in \varXi _{\varepsilon }}|\boldsymbol{\mathcal{R}}(\varepsilon \xi + \varepsilon {\mathbf{e}}_{3})-\boldsymbol{\mathcal{R}}(\varepsilon \xi )|^{2} \varepsilon ^{3}\leq C\|e(u)\|^{2}_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \\ &\sum _{\xi \in \varXi _{\varepsilon }}|\boldsymbol{\mathcal{U}}(\varepsilon \xi + \varepsilon {\mathbf{e}}_{3})-\boldsymbol{\mathcal{U}}(\varepsilon \xi )- \varepsilon \boldsymbol{\mathcal{R}}(\varepsilon \xi +\varepsilon {\mathbf{e}}_{3}) \land {\mathbf{e}}_{3}|^{2}\varepsilon ^{3}\leq C\varepsilon ^{2}\|e(u)\|^{2}_{L^{2}( \varOmega ^{*}_{\varepsilon })}. \end{aligned} $$

(A.25)

The constant $C$depends only on ${\mathbf{C}}$.

Define

$$ \boldsymbol{\mathcal{R}}(N\varepsilon )=\boldsymbol{\mathcal{R}}((N-1)\varepsilon ), \quad \boldsymbol{\mathcal{U}}(N\varepsilon )=\boldsymbol{\mathcal{U}}((N-1) \varepsilon )+\varepsilon \boldsymbol{\mathcal{R}}(N\varepsilon )\land {\mathbf{e}}_{3}. $$

Now, using $Q_{1}$ interpolation, we extend the fields $\boldsymbol{\mathcal{U}}$ and $\boldsymbol{\mathcal{R}}$ to fields ${\mathcal{U}}$, ℛ belonging to $W^{1,\infty }(0,L)^{3}$ and such that

$$ {\mathcal{U}}(\varepsilon \xi )=\boldsymbol{\mathcal{U}}(\varepsilon \xi ), \qquad {\mathcal{R}}(\varepsilon \xi )=\boldsymbol{\mathcal{R}}(\varepsilon \xi ), \quad \forall \, \xi \in \{0,\ldots ,N\}. $$

Let us introduce the displacement ${\mathbf{U}}^{e}$ as follows:

$$ {\mathbf{U}}^{e}(x)={\mathcal{U}}(x_{3})+{\mathcal{R}}(x_{3})\land (x_{1}{ \mathbf{e}}_{1}+ x_{2}{\mathbf{e}}_{2}),\quad \forall \, x\in \varOmega ^{*}_{\varepsilon }. $$

Lemma 15

For every displacement $u\in H^{1}(\varOmega ^{*}_{\varepsilon })^{3}$the following estimates hold:

$$ \begin{aligned} &\Big\| \frac{d{\mathcal{R}}}{dx_{3}}\Big\| _{L^{2}(0,L)}\leq \frac{C}{\varepsilon ^{2}}\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \\ &\Big\| \frac{d{\mathcal{U}}}{dx_{3}}-{\mathcal{R}}\land {\mathbf{e}}_{3} \Big\| _{L^{2}(0,L)}\leq \frac{C}{\varepsilon }\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \\ &\big\| e({\mathbf{U}}^{e})\big\| _{L^{2}(\varOmega _{\varepsilon }^{*})}\leq C\|e(u) \|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned} $$

(A.26)

Moreover,

$$ \|\nabla \big(u-{\mathbf{U}}^{e}\big)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} \leq C\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })},\qquad \|u-{\mathbf{U}}^{e} \|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\leq C\varepsilon \|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}. $$

(A.27)

The constant $C$in (A.26), (A.27) depends only on $\mathbf{C}$.

Proof

The estimates (A.25) yield (A.26)_1,2. A straightforward calculation and (A.26)_1,2 lead to (A.26)₃. Then, taking into account (A.24), we obtain (A.27). □

Denote

$$ {\mathbf{H}}(0,L)\doteq \big\{ \phi \in H^{1}(0,L)\;|\; \phi (0)=0\big\} . $$

Lemma 16

For every displacement $u\in {\mathbf{V}}_{\varepsilon }$the following estimates hold:

$$ \|{\mathcal{U}}_{3}\|_{H^{1}(0,L)}+\varepsilon \big( \|{\mathcal{U}}_{1} \|_{H^{1}(0,L)}+\|{\mathcal{U}}_{2}\|_{H^{1}(0,L)}+ \| {\mathcal{R}} \|_{L^{2}(0,L)}\big)\leq \frac{C}{\varepsilon }\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} $$

(A.28)

and

$$ \|u_{3}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}+\varepsilon \big(\|u_{1} \|_{L^{2}(\varOmega ^{*}_{\varepsilon })}+\|u_{2}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}+\|\nabla u\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\big) \leq C\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

(A.29)

The constant $C$in (A.28), (A.29) does not depend on $\varepsilon$.

Proof

We extend $u$ by 0 to the cell $\varepsilon \big (-{\mathbf{e}}_{3}+{\mathbf{C}})$. Then, proceeding as in Lemma 9 we obtain

$$ |{\mathcal{R}}(0)|^{2}\varepsilon ^{3}\leq C\|e(u)\|^{2}_{L^{2}( \varOmega ^{*}_{\varepsilon })},\qquad |{\mathcal{U}}(0)|\varepsilon ^{3} \leq C\varepsilon ^{2}\|e(u)\|^{2}_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

Without losing the estimates (A.26), we set ${\mathcal{U}}(0)={\mathcal{R}}(0)=0$. Estimates (A.28) are the immediate consequences of (A.26)_1,2 and the Poincaré inequality. Finally (A.24) and (A.28) lead to (A.29). □

As a consequence of the previous lemma and (A.24), we have the following decomposition of a displacement $u \in {\mathbf{V}}_{\varepsilon }$:

$$ u={\mathbf{U}}^{e}+\overline{u}, $$

where the displacement ${\mathbf{U}}^{e}$ is given by

$$ {\mathbf{U}}^{e}(x)={\mathcal{U}}(x_{3})+{\mathcal{R}}(x_{3})\land (x_{1}{ \mathbf{e}}_{1}+ x_{2}{\mathbf{e}}_{2}),\quad \forall \, x\in \varOmega ^{*}_{\varepsilon },\quad {\mathcal{U}},\; {\mathcal{R}}\in {\mathbf{H}}(0,L)^{3} $$

and where the displacement $\overline{u}\in {\mathbf{V}}_{\varepsilon }$ satisfies the estimates (see [18])

$$ \|\overline{u}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\leq C\varepsilon \|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })},\quad \|\nabla \overline{u}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\leq C\|e(u)\|_{L^{2}( \varOmega ^{*}_{\varepsilon })}. $$

(A.30)

The constant $C$ in (A.30) does not depend on $\varepsilon$.

Appendix B: Proofs of the Results of Sects. 2, 3 and 4

2.1 B.1 Results of Sects. 2

Proof of Lemma 1

From (A.13) in Theorem 4, we have

$$ \|u_{\varepsilon }\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\le C \|e(u_{\varepsilon })\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. $$

Then, using the Cauchy-Schwarz inequality, we obtain

$$ \Big| \int _{\varOmega ^{*}_{\varepsilon }} f_{\varepsilon } \cdot u_{ \varepsilon }\, dx \Big| \le \|f\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} \|u_{\varepsilon }\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}\le C \|f\|_{L^{2}( \varOmega _{1})}\|e(u_{\varepsilon })\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, $$

and thus (2.10) follows from (2.2). □

Proof of Proposition 2

There exists a subsequence of $\{\varepsilon \}$, still denoted $\{\varepsilon \}$, and exist $u \in H^{1}_{\varGamma }(\varOmega )^{N}$ and $\widehat{u}\in L^{2}(\varOmega ; H^{1}_{N,per,0}({\mathbf{C}}))^{N}$ such that (see [14, Theorem 4.43])

$$ \begin{aligned} {\mathcal{T}}_{\varepsilon }^{*} (u_{\varepsilon })&\to u\quad \text{strongly in}\quad L^{2}(\varOmega ; H^{1}( {\mathbf{C}}))^{N}, \\ {\mathcal{T}}_{\varepsilon }^{*}(\nabla u_{\varepsilon })& \rightharpoonup \nabla u+\nabla _{X}\widehat{u} \quad \text{weakly in} \quad L^{2}(\varOmega \times {\mathbf{C}})^{N\times N}. \end{aligned} $$

(B.1)

In order to obtain the limit problem (2.12), we use the same approach as in [13, Theorem 4.3]. Let us introduce the following fields

$$ v\in H^{1}(\varOmega _{1})^{N}\;\;\hbox{such that}\; v=0\;\; \hbox{in }\; \varOmega _{1}\cap \big(\varOmega '\setminus \overline{\varOmega }\big),\quad \varphi \in {\mathcal{D}}(\varOmega ),\;\; \psi \in H^{1}_{N,per,0}({\mathbf{C}})^{N}, $$

and take $v_{\varepsilon }(x)=v(x)+\varepsilon \psi _{\varepsilon }(x)\varphi (x)$ as a test function in (2.6), where $\psi _{\varepsilon }(x)=\psi \Big (\frac{x}{\varepsilon } \Big )$. Note that

$$ \begin{aligned} e_{ij}(v_{\varepsilon })(x) &=e_{ij}(v)(x)+\varepsilon e_{ij}(\psi _{\varepsilon }\varphi )(x) \\ &=e_{ij}(v)(x) +e_{X,ij}(\psi )\Big(\frac{x}{\varepsilon }\Big) \varphi (x) +\frac{\varepsilon }{2}\Big(\psi _{j}\Big( \frac{x}{\varepsilon }\Big)\frac{\partial \varphi }{\partial x_{i}}(x) +\psi _{i}\Big(\frac{x}{\varepsilon }\Big) \frac{\partial \varphi }{\partial x_{j}}(x)\Big) \\ &=e_{ij}(v)(x) +e_{X,ij}(\psi )(X)\varphi (x) +\frac{\varepsilon }{2} \Big(\psi _{j}(X)\frac{\partial \varphi }{\partial x_{i}}(x) +\psi _{i}(X) \frac{\partial \varphi }{\partial x_{j}}(x)\Big),\\ &\quad x \in \varOmega ^{*}_{\varepsilon },\; i,j=\overline{1,N}. \end{aligned} $$

Then, applying ${\mathcal{T}}_{\varepsilon }^{*}$ to $v_{\varepsilon }$, gives

$$ \begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon })\to v\quad \hbox{strongly in} \quad L^{2}(\varOmega \times {\mathbf{C}})^{N}, \\ &{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon }))\to e(v)+e_{X}(\psi ) \varphi \quad \hbox{strongly in} \quad L^{2}(\varOmega \times {\mathbf{C}})^{N \times N}. \end{aligned} $$

Unfolding the left-hand side of (2.6), using $\|e(v_{\varepsilon })\|_{L^{2}(\varLambda ^{ext}_{\varepsilon })}=\|e(v)\|_{L^{2}( \varLambda ^{ext}_{\varepsilon })} \to 0$ and passing to the limit, we obtain

$$ \begin{aligned} \int _{\varOmega ^{*}_{\varepsilon }} \sigma ^{\varepsilon }(u_{ \varepsilon }): e(v_{\varepsilon })\,dx &=\int _{\varOmega ^{ext}_{\varepsilon }\times {\mathbf{C}}}{\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }(u_{\varepsilon })):{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon }))\,dx\,dX \\ &=\int _{\varOmega \times {\mathbf{C}}}{\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }(u_{\varepsilon })):{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon }))\,dx\,dX+\int _{\varLambda ^{{ext}}} \sigma ^{\varepsilon }(u_{\varepsilon }): e(v_{\varepsilon })\,dx \\ &\to \int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}(e_{kl}(u)+e_{X,kl}( \widehat{u})) (e_{ij}(v)+e_{X,ij}(\psi )\varphi )\,dx\,dX. \end{aligned} $$

Taking into account (2.4) and using $\|v_{\varepsilon }\|_{L^{2}(\varLambda ^{ext}_{\varepsilon })}=\|v\|_{L^{2}( \varLambda ^{ext}_{\varepsilon })}\to 0$, we have

$$ \begin{aligned} \int _{\varOmega ^{*}_{\varepsilon }} f\cdot v_{\varepsilon }\,dx &=\int _{ \varOmega ^{ext}_{\varepsilon }\times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f) \cdot {\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon })\,dxdX \\ &=\int _{\varOmega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f)\cdot {\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon })\,dxdX+\int _{\varLambda ^{ext}} f\cdot v_{\varepsilon }\,dx \\ &\to \int _{\varOmega \times {\mathbf{C}}}\,f(x)\cdot v(x)\,dx\,dX =|{\mathbf{C}}| \int _{\varOmega }\,f(x)\cdot v(x)\,dx. \end{aligned} $$

Hence, the convergences given above lead to

$$ \int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}(e_{kl}(u)+e_{X,kl}( \widehat{u})) (e_{ij}(v)+e_{X,ij}(\psi )\varphi )\,dx\,dX=|{\mathbf{C}}| \int _{\varOmega }\,f\cdot v\,dx. $$

Finally, since the functions $v\in H^{1}(\varOmega _{1})^{N}$ satisfying $v=0\;\; \hbox{in }\; \varOmega _{1}\cap \big (\varOmega '\setminus \overline{\varOmega }\big )$ are dense in $H^{1}_{\varGamma }(\varOmega )$ and since the tensor product ${\mathcal{D}}(\varOmega ) \otimes H^{1}_{N,per,0}({\mathbf{C}})$ is dense in $L^{2}(\varOmega ; H^{1}_{N,per,0}({\mathbf{C}}))$, we obtain (2.12).

The solution to the variational problem (2.12) is unique. Indeed, if there are two solutions $(u_{1},\widehat{u}_{1})$ and $(u_{2},\widehat{u}_{2})$ to this problem, denote $U=u_{1}-u_{2}$ and $\widehat{U}=\widehat{u}_{1}-\widehat{u}_{2}$. Taking into account the respective equalities from (2.12) and choosing the test functions $U,\; \widehat{U}$, we obtain

$$ \int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}\big(e_{kl}(U)+e_{X,kl}( \widehat{U})\big) \big(e_{ij}(U)+e_{X,ij}(\widehat{U}\big)\,dx\,dX=0. $$

The property (2.2) of the elasticity tensor $\{a_{ijkl}\}$ yields

$$ c_{0}\|e(U)+e(\widehat{U})\|^{2}_{L^{2}(\varOmega \times {\mathbf{C}})}\le \int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}\big(e_{kl}(U)+e_{X,kl}( \widehat{U})\big) \big(e_{ij}(U)+e_{X,ij}(\widehat{U})\big)\,dx\,dX=0. $$

So $e(\widehat{U})=-e(U)$ and thus the field $\widehat{U}$ is an affine function with respect to $X$. Since $\widehat{U}$ is periodic with respect to $X$ and belongs to $L^{2}(\varOmega ; H^{1}_{N,per,0}({\mathbf{C}}))^{N}$, it is equal to 0 (because its mean value on the cell is equal to 0). Hence, $e(U)=0$ and due to the boundary conditions we obtain $U=0$. Finally, the whole sequences in (B.1) converge to respective limits.

Now, we prove the strong convergences (2.11)_2,3. By Proposition 1, (2.6) and (2.12) we have

$$ \begin{aligned} &\int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}\big(e_{kl}(u)+e_{X,kl}( \widehat{u}))\big(e_{kl}(u)+e_{X,kl}(\widehat{u}))\,dx\,dX \\ &\leq \liminf _{\varepsilon \to 0}\,\int _{\varOmega \times {\mathbf{C}}}\, { \mathcal{T}}_{\varepsilon }^{*}(a^{\varepsilon }_{ijkl})\,{\mathcal{T}}_{\varepsilon }^{*}(e_{kl}(u_{\varepsilon })){\mathcal{T}}_{\varepsilon }^{*}(e_{ij}(u_{\varepsilon }))\,dx\,dX+\liminf _{\varepsilon \to 0}\int _{\varLambda ^{ {ext}}} \sigma ^{\varepsilon }(u_{\varepsilon }): e(v_{\varepsilon })\,dx \\ &\leq \liminf _{\varepsilon \to 0}\int _{\varOmega ^{*}_{\varepsilon }}\, \sigma (u_{\varepsilon }) : e (u_{\varepsilon })\,dx\leq \limsup _{ \varepsilon \to 0}\int _{\varOmega ^{*}_{\varepsilon }}\, \sigma (u_{\varepsilon }) : e (u_{\varepsilon })\,dx =\limsup _{\varepsilon \to 0} \int _{\varOmega ^{*}_{\varepsilon }}\,f\cdot u_{\varepsilon }\,dx \\ &=|{\mathbf{C}}|\int _{\varOmega \times {\mathbf{C}}}\,f\cdot u\,dx =\int _{\varOmega \times {\mathbf{C}}}\,a_{ijkl}\big(e_{kl}(u)+e_{X,kl}(\widehat{u}))\big(e_{kl}(u)+e_{X,kl}( \widehat{u}))\,dx\,dX. \end{aligned} $$

Thus, the strong convergence (2.11)₃ holds. □

2.2 B.2 Results of Sects. 3

Proof of Lemma 2

Taking into account the decomposition of the displacements introduced in Sect. A.2 of Appendix A, the Cauchy–Schwarz inequality and the estimates (A.16) and (A.23) of Corollary 1, we have

$$\begin{aligned} \Big|\int _{\varOmega _{\varepsilon }^{*}}f_{\varepsilon }\cdot u_{ \varepsilon }\,dx\Big| &=\Big|\sum _{\xi \in \varXi _{\varepsilon }}\int _{ \varepsilon (\xi +{\mathbf{C}})}f_{\varepsilon }\cdot u_{\varepsilon }\,dx \Big| \\ &\leq \sum _{\xi \in \varXi _{\varepsilon }}\Big|\int _{\varepsilon ( \xi +{\mathbf{C}})}f_{\varepsilon }\cdot (u_{\varepsilon }-{\mathbf{R}}_{ \varepsilon \xi })\,dx\Big|+\sum _{\xi \in \varXi _{\varepsilon }}\Big| \int _{\varepsilon (\xi +{\mathbf{C}})}f_{\varepsilon }\cdot {\mathbf{R}}_{ \varepsilon \xi }\,dx\Big|. \end{aligned}$$

(B.2)

Each term on the right-hand side of (B.2) can be estimated as follows:

$$\begin{aligned} &\sum _{\xi \in \varXi _{\varepsilon }}\Big|\int _{\varepsilon (\xi +{\mathbf{C}})}f_{ \varepsilon }\cdot (u_{\varepsilon }-{\mathbf{R}}_{\varepsilon \xi })\,dx \Big| \\ &\quad\le \sum _{\xi \in \varXi _{\varepsilon }}\int _{\varepsilon (\xi +{ \mathbf{C}})}\Big|f_{\varepsilon }\cdot (u_{\varepsilon }-{\mathbf{R}}_{ \varepsilon \xi })\Big|\,dx\le \sum _{\xi \in \varXi _{\varepsilon }}\|f_{ \varepsilon }\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))}\|u_{\varepsilon }-{ \mathbf{R}}_{\varepsilon \xi }\|_{L^{2}(\varepsilon (\xi +{\mathbf{C}}))} \\ &\quad\le \sqrt{\sum _{\xi \in \varXi _{\varepsilon }}\|f_{\varepsilon }\|^{2}_{L^{2}( \varepsilon (\xi +{\mathbf{C}}))}}\sqrt{\sum _{\xi \in \varXi _{\varepsilon }} \|u_{\varepsilon }-{\mathbf{R}}_{\varepsilon \xi }\|^{2}_{L^{2}( \varepsilon (\xi +{\mathbf{C}}))}}\le C\varepsilon ^{7/2} \|f\|_{L^{2}( \omega _{1})}\|e(u_{\varepsilon })\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}. \end{aligned}$$

Hence

$$ \begin{aligned} \sum _{\xi \in \varXi _{\varepsilon }}\Big|\int _{\varepsilon (\xi +{\mathbf{C}})} & f_{\varepsilon }\cdot {\mathbf{R}}_{\varepsilon \xi }\,dx\Big| = \sum _{ \xi \in \varXi _{\varepsilon }}\Big|\int _{\varepsilon (\xi +{\mathbf{C}})}f_{ \varepsilon }\cdot (\boldsymbol{\mathcal{U}}(\varepsilon \xi )+ \boldsymbol{\mathcal{R}}(\varepsilon \xi )\wedge (x-\varepsilon \xi ))\,dx \Big| \\ &\leq \varepsilon ^{3} C\sum _{\xi \in \varXi _{\varepsilon }}\int _{ \varepsilon (\xi +Y')}|\boldsymbol{\mathcal{U}}_{1}(\varepsilon \xi )f_{1}(x')| \,dx'+\varepsilon ^{3}C\sum _{\xi \in \varXi _{\varepsilon }}\int _{ \varepsilon (\xi +Y')}|\boldsymbol{\mathcal{U}}_{2}(\varepsilon \xi )f_{2}(x')| \,dx' \\ &+\varepsilon ^{4}C\sum _{\xi \in \varXi _{\varepsilon }}\int _{ \varepsilon (\xi +Y')}|\boldsymbol{\mathcal{U}}_{3}(\varepsilon \xi )f_{3}(x')| \,dx'\\ &+\varepsilon ^{4}C\sum _{\xi \in \varXi _{\varepsilon }}\int _{ \varepsilon (\xi +Y')}\big|\boldsymbol{\mathcal{R}}_{1}(\varepsilon \xi ) \big|\Big(\varepsilon \big|f_{3}(x')|+\big|f_{2}(x')\big|\Big)\,dx' \\ &+\varepsilon ^{4}C\sum _{\xi \in \varXi _{\varepsilon }}\int _{ \varepsilon (\xi +Y')}\big|\boldsymbol{\mathcal{R}}_{2}(\varepsilon \xi ) \big|\Big(\big|f_{1}(x')\big|+\varepsilon \big|f_{3}(x')\big|\Big)\,dx'\\ &+\varepsilon ^{4}C\sum _{\xi \in \varXi _{\varepsilon }}\int _{\varepsilon ( \xi +Y')}\big|\boldsymbol{\mathcal{R}}_{3}(\varepsilon \xi )\big|\Big(\big|f_{2}(x') \big|+\big|f_{1}(x')\big|\Big)\,dx' \\ &\le \varepsilon ^{3}C\|f_{1}\|_{L^{2}(\omega _{1})}\sqrt{\sum _{\xi \in \varXi _{\varepsilon }}|\boldsymbol{\mathcal{U}}_{1}(\varepsilon \xi )|^{2} \varepsilon ^{2}}+\varepsilon ^{3}C\|f_{2}\|_{L^{2}(\omega _{1})} \sqrt{\sum _{\xi \in \varXi _{\varepsilon }}|\boldsymbol{\mathcal{U}}_{2}( \varepsilon \xi )|^{2}\varepsilon ^{2}} \\ &+\varepsilon ^{4}C\|f_{3}\|_{L^{2}(\omega _{1})}\sqrt{\sum _{\xi \in \varXi _{\varepsilon }}|\boldsymbol{\mathcal{U}}_{3}(\varepsilon \xi )|^{2} \varepsilon ^{2}}+C \varepsilon ^{4}\sqrt{\sum _{\xi \in \varXi _{\varepsilon }}|\boldsymbol{\mathcal{R}}(\varepsilon \xi )|^{2}\varepsilon ^{2}} \|f\|_{L^{2}(\omega _{1})} \\ &\le C\varepsilon ^{5/2}\|f\|_{L^{2}(\omega _{1})}\|e(u_{\varepsilon }) \|_{L^{2}(\varOmega _{\varepsilon }^{*})}. \end{aligned} $$

And finally, from the previous two estimates

$$ \Big|\int _{\varOmega _{\varepsilon }^{*}}f_{\varepsilon }\cdot u_{ \varepsilon }\,dx\Big|\leq C\varepsilon ^{5/2}\|f\|_{L^{2}(\omega _{1})} \|e(u_{\varepsilon })\|_{L^{2}(\varOmega _{\varepsilon }^{*})}. $$

Using this estimate, we obtain (3.8). □

Proof of Lemma 3

In order to prove (i)-(ii), we note that from the estimates (3.8) and $\text{(A.22)}_{1}$ in Corollary 1 and Lemma 8, it follows that there exist functions ${\mathcal{U}}\in H^{1}(\omega ')^{3}$ and ${\mathcal{R}}\in H^{1}(\omega ')^{2}$ such that the following convergences hold

$$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}{\mathcal{U}}_{\varepsilon ,\alpha } \rightharpoonup {\mathcal{U}}_{\alpha }\quad \hbox{weakly in}\quad L^{2}( \omega '),\quad &&\frac{1}{\varepsilon ^{2}}\nabla {\mathcal{U}}_{ \varepsilon ,\alpha }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} \rightharpoonup \nabla {\mathcal{U}}_{\alpha }\quad \hbox{weakly in} \quad L^{2}(\omega ')^{2}, \\ &\frac{1}{\varepsilon }{\mathcal{U}}_{\varepsilon ,3} \rightharpoonup {\mathcal{U}}_{3}\quad \hbox{weakly in }\quad L^{2}( \omega '),\quad && \frac{1}{\varepsilon }\nabla {\mathcal{U}}_{ \varepsilon ,3}{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} \rightharpoonup \nabla {\mathcal{U}}_{3}\quad \hbox{weakly in}\quad L^{2}( \omega ')^{2}, \\ &\frac{1}{\varepsilon }{\mathcal{R}}_{\varepsilon ,\alpha } \rightharpoonup {\mathcal{R}}_{\alpha }\quad \hbox{weakly in } \quad L^{2}( \omega '),\quad &&\frac{1}{\varepsilon }{\nabla \mathcal{R}}_{\varepsilon , \alpha }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }} \rightharpoonup \nabla {\mathcal{R}}_{\alpha }\quad \hbox{weakly in } \quad {L^{2}(\omega ')}^{2}. \end{aligned} $$

Now we prove that the fields ${\mathcal{U}}_{\alpha }$, ℛ, ${\mathcal{U}}_{3}$ and $\nabla {\mathcal{U}}_{3}$ vanish in $\omega ^{\prime }\setminus \overline{\omega }$.

Let ${\mathcal{O}}$ be an open subset such that ${\mathcal{O}}$ is strictly included in $\omega '\setminus \overline{\omega }$. Since $u_{\varepsilon }$ vanishes in $\varOmega ^{\prime *}_{\varepsilon }\setminus \overline{\varOmega _{\varepsilon }^{*}}$, then the fields ${\mathcal{U}}_{\varepsilon }$, ${\mathcal{R}}_{\varepsilon }$ vanish in $\omega ^{\prime }_{\varepsilon }\setminus \overline{\omega ^{\prime int}_{3\varepsilon }}$. If $\varepsilon$ is small enough then ${\mathcal{O}}\subset \omega ^{\prime }_{\varepsilon }\setminus \overline{\omega ^{\prime int}_{3\varepsilon }}$. Thus, by construction, the fields ${\mathcal{U}}_{\varepsilon ,\alpha }$, ${\mathcal{R}}_{\varepsilon }$, ${\mathcal{U}}_{\varepsilon ,3}$ and $\nabla {\mathcal{U}}_{\varepsilon ,3}$ vanish in ${\mathcal{O}}$. As a consequence, their weak limits also vanish in ${\mathcal{O}}$. Since this holds for every open set $\mathcal{O}$ strictly included in $\omega '\setminus \overline{\omega }$, this is also satisfied in the full set $\omega '\setminus \overline{\omega }$. Estimate $\text{(A.18)}_{2}$ in Lemma 13 leads to

$$ \begin{aligned} &\frac{1}{\varepsilon }\left ( \frac{\partial {\mathcal{U}}_{3,\varepsilon }}{\partial x_{2}}+{ \mathcal{R}}_{1,\varepsilon }\right ){\mathbf{1}}_{\omega ^{' int}_{3 \varepsilon }}\to 0\quad \hbox{strongly in }L^{2}(\omega '), \\ &\frac{1}{\varepsilon }\left ( \frac{\partial {\mathcal{U}}_{3,\varepsilon }}{\partial x_{1}}-{ \mathcal{R}}_{2,\varepsilon }\right ){\mathbf{1}}_{\omega ^{' int}_{3 \varepsilon }}\to 0\quad \hbox{strongly in }L^{2}(\omega '). \end{aligned} $$

From convergences (3.9)₄ and (3.10)₁ we also have

$$ \begin{aligned} &\frac{1}{\varepsilon }\left ( \frac{\partial {\mathcal{U}}_{3,\varepsilon }}{\partial x_{2}}+{ \mathcal{R}}_{1,\varepsilon }\right ){\mathbf{1}}_{\omega ^{' int}_{3 \varepsilon }}\rightharpoonup \frac{\partial {\mathcal{U}}_{3}}{\partial x_{2}}+{\mathcal{R}}_{1} \quad \hbox{weakly in }L^{2}(\omega '), \\ &\frac{1}{\varepsilon }\left ( \frac{\partial {\mathcal{U}}_{3,\varepsilon }}{\partial x_{1}}-{ \mathcal{R}}_{2,\varepsilon }\right ){\mathbf{1}}_{\omega ^{' int}_{3 \varepsilon }}\rightharpoonup \frac{\partial {\mathcal{U}}_{3}}{\partial x_{1}}-{\mathcal{R}}_{2} \quad \hbox{weakly in }L^{2}(\omega ') \end{aligned} $$

and then we get the equalities (3.11). Thus, we have ${\mathcal{U}}_{3}\in H^{2}(\omega ')$.

(iii) From estimates $\text{(A.22)}_{3,4}$ in Corollary 1, we obtain

$$ \begin{aligned} &\|{\mathcal{T}}_{\varepsilon }^{*}(\overline{u}_{\varepsilon })\|_{L^{2}( \omega '\times {\mathbf{C}})} \leq \frac{1}{\sqrt{\varepsilon }}\| \overline{u}_{\varepsilon }\|_{L^{2}(\varOmega ^{int}_{\varepsilon })}\le C \varepsilon ^{1/2}\|e(u_{\varepsilon })\|_{L^{2}(\varOmega _{\varepsilon }^{*})} \le C \varepsilon ^{3}, \\ &\|\nabla _{X}{\mathcal{T}}_{\varepsilon }^{*}(\overline{u}_{\varepsilon }{ \mathbf{1}}_{\varOmega ^{\prime }_{\varepsilon }})\|_{L^{2}(\omega ' \times { \mathbf{C}})} =\varepsilon \|{\mathcal{T}}_{\varepsilon }^{*}(\nabla \overline{u}_{\varepsilon }{\mathbf{1}}_{\varOmega ^{\prime *}_{\varepsilon }})\|_{L^{2}( \omega '\times {\mathbf{C}})} \\ &\quad\leq \varepsilon ^{1/2} \|\nabla \overline{u}_{\varepsilon }\|_{L^{2}(\varOmega ^{\prime \, int}_{ \varepsilon })}\le C\varepsilon ^{1/2}\|e(u_{\varepsilon })\|_{L^{2}( \varOmega _{\varepsilon }^{*})} \le C\varepsilon ^{3}. \end{aligned} $$

Thus, for a subsequence, still denoted by $\{\varepsilon \}$, there exists $\overline{u}\in L^{2}(\omega ^{\prime };H^{1}_{2,per}({\mathbf{C}}))$ such that the convergences $\text{(3.12)}_{1,2}$ hold. □

Proof of Lemma 4

Applying [12, Proposition 2.9] and the equality (3.11) we have the convergences (3.13)_1,2, (3.14)₁ and there exist functions $\widehat{\mathcal{{R}}}_{\alpha },\;\widehat{\mathcal{{U}}}_{\alpha },\; \widehat{\mathcal{{U}}}_{3} \in L^{2}(\omega ';H^{1}_{2,per,0}({\mathbf{C}})), \,( \alpha =1,2)$ such that

$$ \begin{aligned} \frac{1}{\varepsilon } {\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{\partial {\mathcal{R}}_{\varepsilon ,\alpha }}{\partial x_{\beta }}{ \mathbf{1}}_{\omega ^{' int}_{3\varepsilon }}\Big)&\rightharpoonup - \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{\alpha }\partial x_{\beta }}+ \frac{\partial \widehat{\mathcal{R}}_{\alpha }}{\partial X_{\beta }} \quad \hbox{weakly in } \quad L^{2}(\omega '\times {\mathbf{C}}), \\ \frac{1}{\varepsilon ^{2}} {\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,\alpha }}{\partial x_{\beta }}{ \mathbf{1}}_{\omega ^{' int}_{3\varepsilon }}\Big)&\rightharpoonup \frac{\partial {\mathcal{U}}_{\alpha }}{\partial x_{\beta }}+ \frac{\partial \widehat{\mathcal{U}}_{\alpha }}{\partial X_{\beta }} \quad \hbox{weakly in } \quad L^{2}(\omega '\times {\mathbf{C}}), \\ \frac{1}{\varepsilon } {\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{\beta }}{\mathbf{1}}_{ \omega ^{' int}_{3\varepsilon }}\Big)&\rightharpoonup \frac{\partial {\mathcal{U}}_{3}}{\partial x_{\beta }}+ \frac{\partial \widehat{\mathcal{U}}_{3}}{\partial X_{\beta }} \quad \alpha , \beta =\overline{1,2} \quad \hbox{weakly in } \quad L^{2}(\omega ' \times {\mathbf{C}}). \end{aligned} $$

(B.3)

From Remark 2, the functions ${\mathcal{R}}_{\varepsilon ,\alpha },\,{\mathcal{U}}_{\varepsilon ,\alpha },\; { \mathcal{U}}_{\varepsilon ,3}$ are piecewise linear with respect to the variables $X_{\beta }\,(\beta =\overline{1,2})$. Thus, the functions $\widehat{\mathcal{R}}_{\alpha },\,\widehat{\mathcal{U}}_{\alpha },\, \widehat{\mathcal{U}}_{3}$ are also piecewise linear. As they are periodic, these fields are independent of $X_{\beta }$, $\beta \in \{1,2\}$. Hence

$$ \frac{\partial \widehat{{\mathcal{R}}}_{\alpha }}{\partial X_{\beta }}= \frac{\partial \widehat{{\mathcal{U}}}_{\alpha }}{\partial X_{\beta }}= \frac{\partial \widehat{{\mathcal{U}}}_{3}}{\partial X_{\beta }}=0, $$

and the convergences $\text{(3.13)}_{3}$, $\text{(3.14)}_{2}$ hold. □

Proof of Proposition 4

From $\text{(3.13)}_{1,2}$, $\text{(3.14)}_{1}$ and $\text{(3.12)}_{2}$, we obtain the convergences (3.15).

From estimate $\text{(A.18)}_{2}$ and (3.8) we have

$$ \left \| \Big( \frac{\partial {\mathcal{U}}_{\varepsilon }}{\partial x_{\alpha }}-{ \mathcal{R}}_{\varepsilon }\wedge {\mathbf{e}}_{\alpha }\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\right \| _{L^{2}(\omega )}\leq C\varepsilon ^{2}. $$

Then there exists ${\mathcal{X}}\in {L^{2}(\omega )}^{2}$ such that

$$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{1}}-{ \mathcal{R}}_{\varepsilon ,2}\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\rightharpoonup {\mathcal{X}}_{1} \quad \hbox{weakly in } \quad L^{2}(\omega ), \\ &\frac{1}{\varepsilon ^{2}}\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{2}}+{ \mathcal{R}}_{\varepsilon ,1}\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\rightharpoonup {\mathcal{X}}_{2} \quad \hbox{weakly in } \quad L^{2}(\omega ). \end{aligned} $$

(B.4)

Due to $\text{(3.14)}_{2}$, (B.4) and [14, Lemma 11.11], there exists a function $\widehat{\mathcal{{Z}}}\in L^{2}(\omega ;H^{1}_{2,per}({\mathbf{C}}))$ such that, up to subsequence,

$$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}\Big(\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{1}}-{ \mathcal{R}}_{\varepsilon ,2}\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\Big)\rightharpoonup {\mathcal{X}}_{1}+ \frac{\partial \widehat{\mathcal{Z}}}{\partial X_{1}}-\widehat{\mathcal{R}}_{2} \quad \hbox{weakly in } \quad L^{2}(\omega \times {\mathbf{C}}), \\ &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}\Big(\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{2}}+{ \mathcal{R}}_{\varepsilon ,1}\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\Big)\rightharpoonup {\mathcal{X}}_{2}+ \frac{\partial \widehat{\mathcal{Z}}}{\partial X_{2}}+\widehat{\mathcal{R}}_{1} \quad \hbox{weakly in }\quad L^{2}(\omega \times {\mathbf{C}}), \end{aligned} $$

where the field $\widehat{{\mathcal{R}}}_{\alpha }$ is introduced in Lemma 4 (see (B.3)). Since $\widehat{\mathcal{{R}}}$ is independent of $X_{1}$ and $X_{2}$ and mean value of $\widehat{\mathcal{{R}}}$ on a cell equal to zero, we have

$$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}\Big(\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{1}}-{ \mathcal{R}}_{\varepsilon ,2}\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\Big)\rightharpoonup {\mathcal{X}}_{1}+ \frac{\partial \widehat{\mathcal{Z}}}{\partial X_{1}}\quad \hbox{weakly in } \quad L^{2}(\omega \times {\mathbf{C}}), \\ &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}\Big(\Big( \frac{\partial {\mathcal{U}}_{\varepsilon ,3}}{\partial x_{2}}+{ \mathcal{R}}_{\varepsilon ,1}\Big){\mathbf{1}}_{\omega ^{int}_{3 \varepsilon }}\Big)\rightharpoonup {\mathcal{X}}_{2}+ \frac{\partial \widehat{\mathcal{Z}}}{\partial X_{2}}\quad \hbox{weakly in } \quad L^{2}(\omega \times {\mathbf{C}}). \end{aligned} $$

(B.5)

In order to prove $\text{(3.16)}_{1}$, note that from (3.7) and convergences (3.13), (3.14), we have

$$ \begin{aligned} &\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}\big(e(u_{\varepsilon }{\mathbf{1}}_{\omega ^{' int}_{3\varepsilon }})\big) \rightharpoonup \begin{pmatrix} \frac{\partial {\mathcal{U}}_{1}}{\partial x_{1}} -X_{3} \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{1}^{2}} &\frac{1}{2} \Big(\frac{\partial {\mathcal{U}}_{1}}{\partial x_{2}} + \frac{\partial {\mathcal{U}}_{2}}{\partial x_{1}}\Big) -X_{3} \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{1}\partial x_{2}} &\frac{1}{2} \left ({\mathcal{X}}_{1}+\frac{\partial {\widehat{\mathcal{Z}}}}{\partial X_{1}} \right ) \\ *&\frac{\partial {\mathcal{U}}_{2}}{\partial x_{2}} -X_{3} \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{2}^{2}} &\frac{1}{2} \left ({\mathcal{X}}_{2}+\frac{\partial {\widehat{\mathcal{Z}}}}{\partial X_{2}} \right ) \\ *&*&0 \end{pmatrix} +e_{X}(\overline{u}) \\ &= \begin{pmatrix} \frac{\partial {\mathcal{U}}_{1}}{\partial x_{1}} &\frac{1}{2}\Big( \frac{\partial {\mathcal{U}}_{1}}{\partial x_{2}} + \frac{\partial {\mathcal{U}}_{2}}{\partial x_{1}}\Big)&0 \\ *&\frac{\partial {\mathcal{U}}_{2}}{\partial x_{2}}&0 \\ *&*&0 \end{pmatrix} - X_{3} \begin{pmatrix} \frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{1}^{2}} &\frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{1}\partial x_{2}} &0 \\ *&\frac{\partial ^{2}{\mathcal{U}}_{3}}{\partial x_{2}^{2}} &0 \\ *&*&0 \end{pmatrix} +\frac{1}{2} \begin{pmatrix} 0&0&{\mathcal{X}}_{1}+\frac{\partial {\widehat{\mathcal{Z}}}}{\partial X_{1}} \\ *&0&{\mathcal{X}}_{2}+\frac{\partial {\widehat{\mathcal{Z}}}}{\partial X_{2}} \\ *&*&0 \end{pmatrix} +e_{X}(\overline{u}). \end{aligned} $$

Denote

$$ \widehat{u}(x,X)\doteq \begin{pmatrix} \overline{u}_{1}(x,X)+X_{3}{\mathcal{X}}_{1}(x) \\ \overline{u}_{2}(x,X)+X_{3}{\mathcal{X}}_{2}(x) \\ \overline{u}_{3}(x,X)+{\widehat{\mathcal{Z}}}(x,X) \end{pmatrix} +C, $$

where $C$ is determined in order to get $\int _{\mathbf{C}}\,\widehat{u}(\cdot ,X)\,dX=0$ a.e. in $\omega$. And thus $\text{(3.16)}_{1}$ follows. Then, taking into account the definition (2.3), we have $\text{(3.16)}_{2}$.

To obtain the limit problem (3.17), let us define the following fields

$$ {\mathcal{V}}_{\alpha }\in H^{1}_{\gamma }(\omega ), \; \alpha =1,2, \quad {\mathcal{V}}_{3} \in H^{2}_{\gamma }(\omega ), \quad \varphi \in {\mathcal{D}}(\omega ), \quad \psi \in H^{1}_{2,per}({\mathbf{C}})^{3}, $$

and take the test function in (3.3) as

$$ v_{\varepsilon }(x)=\varepsilon ^{2} \begin{pmatrix} {\mathcal{V}}_{1}(x^{\prime })-\frac{x_{3}}{\varepsilon } \frac{\partial {\mathcal{V}}_{3}}{\partial x_{1}}(x^{\prime }) \\ {\mathcal{V}}_{2}(x^{\prime })-\frac{x_{3}}{\varepsilon } \frac{\partial {\mathcal{V}}_{3}}{\partial x_{2}}(x^{\prime }) \\ \frac{1}{\varepsilon }{\mathcal{V}}_{3}(x^{\prime }) \end{pmatrix} + \varepsilon ^{3} \begin{pmatrix} \varphi (x^{\prime })\psi _{\varepsilon ,1}(x) \\ \varphi (x^{\prime })\psi _{\varepsilon ,2}(x) \\ \varphi (x^{\prime })\psi _{\varepsilon ,3}(x) \end{pmatrix} , $$

where $\psi _{\varepsilon }(x)=\psi \Big (\frac{x}{\varepsilon } \Big )$. Then

$$ \begin{aligned} e(v_{\varepsilon })&=\varepsilon ^{2} \begin{pmatrix} \frac{\partial {\mathcal{V}}_{1}}{\partial x_{1}} &\frac{1}{2}\Big( \frac{\partial {\mathcal{V}}_{1}}{\partial x_{2}}+ \frac{\partial {\mathcal{V}}_{2}}{\partial x_{1}}\Big)&0 \\ \frac{1}{2}\Big(\frac{\partial {\mathcal{V}}_{1}}{\partial x_{2}}+ \frac{\partial {\mathcal{V}}_{2}}{\partial x_{1}}\Big)&\frac{\partial {\mathcal{V}}_{2}}{\partial x_{2}}&0 \\ 0&0&0 \end{pmatrix} - \varepsilon x_{3} \begin{pmatrix} \frac{\partial ^{2}{\mathcal{V}}_{3}}{\partial x_{1}^{2}} &\frac{\partial ^{2}{\mathcal{V}}_{3}}{\partial x_{1} \partial x_{2}}&0 \\ \frac{\partial ^{2}{\mathcal{V}}_{3}}{\partial x_{1} \partial x_{2}}&\frac{\partial ^{2}{\mathcal{V}}_{3}}{\partial x_{2}^{2}}&0 \\ 0&0&0 \end{pmatrix} \\ &+\varepsilon ^{3} \begin{pmatrix} \frac{\partial \varphi }{\partial x_{1}}\psi _{1} &\frac{1}{2}\Big( \frac{\partial \varphi }{\partial x_{2}}\psi _{1}+ \frac{\partial \varphi }{\partial x_{1}}\psi _{2}\Big) &\frac{1}{2} \Big(\frac{\partial \varphi }{\partial x_{3}}\psi _{1}+ \frac{\partial \varphi }{\partial x_{1}}\psi _{3}\Big) \\ \frac{1}{2}\Big(\frac{\partial \varphi }{\partial x_{2}}\psi _{1}+ \frac{\partial \varphi }{\partial x_{1}}\psi _{2}\Big) &\frac{\partial \varphi }{\partial x_{2}} \psi _{2} &\frac{1}{2}\Big(\frac{\partial \varphi }{\partial x_{2}} \psi _{3}+\frac{\partial \varphi }{\partial x_{3}}\psi _{2}\Big) \\ \frac{1}{2}\Big(\frac{\partial \varphi }{\partial x_{3}}\psi _{1}+ \frac{\partial \varphi }{\partial x_{1}}\psi _{3}\Big)&\frac{1}{2} \Big(\frac{\partial \varphi }{\partial x_{2}}\psi _{3}+ \frac{\partial \varphi }{\partial x_{3}}\psi _{2}\Big)&\frac{\partial \varphi }{\partial x_{3}} \psi _{3} \\ \end{pmatrix}\\ &+\varepsilon ^{2}\varphi \begin{pmatrix} \frac{\partial \psi _{1}}{\partial X_{1}} &\frac{1}{2}\Big( \frac{\partial \psi _{1}}{\partial X_{2}}+ \frac{\partial \psi _{2}}{\partial X_{1}}\Big) &\frac{1}{2}\Big( \frac{\partial \psi _{1}}{\partial X_{3}}+ \frac{\partial \psi _{3}}{\partial X_{1}}\Big) \\ \frac{1}{2}\Big(\frac{\partial \psi _{1}}{\partial X_{2}}+ \frac{\partial \psi _{2}}{\partial X_{1}}\Big)&\frac{\partial \psi _{2}}{\partial X_{2}} &\Big(\frac{\partial \psi _{3}}{\partial X_{2}}+ \frac{\partial \psi _{\varepsilon ,2}}{\partial X_{3}}\Big) \\ \frac{1}{2}\Big(\frac{\partial \psi _{1}}{\partial X_{3}}+ \frac{\partial \psi _{3}}{\partial X_{1}}\Big)&\Big( \frac{\partial \psi _{3}}{\partial X_{2}}+ \frac{\partial \psi _{\varepsilon ,2}}{\partial X_{3}}\Big)&\frac{\partial \psi _{3}}{\partial X_{3}} \end{pmatrix} . \end{aligned} $$

(B.6)

Applying the unfolding operator ${\mathcal{T}}_{\varepsilon }^{*}$ to the stress tensor $e(v_{\varepsilon })$, given by (B.6), and passing to the limit as $\varepsilon \to 0$, we obtain

$$ \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon })) \to E^{M}({\mathcal{V}}_{m})-X_{3}E^{B}({\mathcal{V}}_{3})+e_{X}( \psi )\varphi \quad \hbox{strongly in } L^{2}(\omega \times {\mathbf{C}})^{9}, $$

(B.7)

where ${\mathcal{V}}_{m}=({\mathcal{V}}_{1},{\mathcal{V}}_{2})$.

Unfolding the left-hand side of (3.3) and taking into account that by virtue of (3.8), (B.6) and Cauchy-Schwarz inequality

$$\begin{aligned} &\int _{\varOmega _{\varepsilon }^{*}\setminus \varOmega ^{'int}_{\varepsilon }} \sigma ^{\varepsilon }(u_{\varepsilon }):e(v_{\varepsilon })\,dx \\ &\quad\le \| \sigma ^{\varepsilon }(u_{\varepsilon })\|_{L^{2}(\varOmega ^{\prime *}_{\varepsilon })}\|e(v_{\varepsilon })\|_{L^{2}(\varOmega _{\varepsilon }^{*} \setminus \varOmega ^{'int}_{\varepsilon })}=O\Big(\varepsilon ^{5/2}\Big)O \Big(\varepsilon ^{7/2}\Big)=o\Big(\varepsilon ^{5}\Big), \end{aligned}$$

we have

$$ \begin{aligned} &\int _{\varOmega _{\varepsilon }^{*}} \sigma ^{\varepsilon }(u_{ \varepsilon }):e(v_{\varepsilon })\,dx \\ &=\varepsilon \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }(u_{\varepsilon }{\mathbf{1}}_{\omega ^{'int}_{3\varepsilon }}):{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon }))\, dx^{\prime }dX +\int _{\varOmega _{\varepsilon }^{*}\setminus \varOmega ^{'int}_{\varepsilon }} \sigma ^{\varepsilon }(u_{\varepsilon }):e(v_{\varepsilon })\,dx \\ &=\varepsilon ^{5}\int _{\omega \times {\mathbf{C}}} \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }(u_{\varepsilon }{\mathbf{1}}_{\omega ^{'int}_{3\varepsilon }}): \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon })) \, dx^{\prime }dX+o(\varepsilon ^{5}). \end{aligned} $$

Unfold the right hand side of (3.3)

$$ \begin{aligned} \int _{\varOmega _{\varepsilon }^{*}}f_{\varepsilon }v_{\varepsilon }\, dx &= \varepsilon \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{\varepsilon }){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon })\, dx^{\prime }dX \\ &=\varepsilon \sum _{\alpha =1}^{2} \int _{\omega \times {\mathbf{C}}} { \mathcal{T}}_{\varepsilon }^{*}(f_{\varepsilon ,\alpha }){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon ,\alpha })\, dx^{\prime }dX + \varepsilon \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{ \varepsilon ,3}){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon ,3})\, dx^{\prime }dX. \end{aligned} $$

(B.8)

Taking into account the form of the applied forces (3.1), the first term on the right-hand side of (B.8) can be rewritten as follows

$$ \begin{aligned} \varepsilon \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{ \varepsilon ,\alpha }){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon , \alpha })\, dxdX &=\varepsilon ^{5} \int _{\omega \times {\mathbf{C}}} { \mathcal{T}}_{\varepsilon }^{*}(f_{\alpha }) \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon ,\alpha })\, dx^{\prime }dX \\ &+\varepsilon ^{5} \int _{\omega \times {\mathbf{C}}} X_{3} {\mathcal{T}}_{\varepsilon }^{*}(g_{\alpha })\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon , \alpha })\,dx^{\prime }dX,\quad \alpha =1,2, \end{aligned} $$

and, thus, as $\varepsilon \to 0$ we obtain

$$ \begin{aligned} & \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{\alpha }) \frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon , \alpha })\, dx^{\prime }dX +\int _{\omega \times {\mathbf{C}}} X_{3} {\mathcal{T}}_{\varepsilon }^{*}(g_{\alpha })\frac{1}{\varepsilon ^{2}}{\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon , \alpha })\,dx^{\prime }dX \\ &\to \int _{\omega \times {\mathbf{C}}}f_{\alpha }(x^{\prime }) \Big({ \mathcal{V}}_{\alpha }(x^{\prime })+X_{3} \frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}(x^{\prime }) \Big)\, dx^{\prime }dX\\ &+\int _{\omega \times {\mathbf{C}}}X_{3}g_{\alpha }(x^{\prime }) \Big({\mathcal{V}}_{\alpha }(x^{\prime })+X_{3} \frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}(x^{\prime }) \Big)\, dx^{\prime }dX \\ &=|{\mathbf{C}}|\int _{\omega }f_{\alpha }(x^{\prime }){\mathcal{V}}_{\alpha }(x^{\prime })\,dx^{\prime }+\int _{\mathbf{C}}X_{3}\,dX\int _{\omega }f_{\alpha }(x^{\prime }) \frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}(x^{\prime })\,dx^{\prime }\\ &+\int _{\mathbf{C}}X_{3}\,dX \int _{\omega }g_{\alpha }(x^{\prime }){ \mathcal{V}}_{\alpha }(x^{\prime })\,dx^{\prime }+\int _{\mathbf{C}}X_{3}^{2}\,dX \int _{\omega }g_{\alpha }(x^{\prime }) \frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}(x^{\prime })\,dx^{\prime }, \quad \alpha =1,2. \end{aligned} $$

Using (3.1) the second term on the right-hand side of (B.8) can be rewritten as follows

$$ \begin{aligned} \varepsilon \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{ \varepsilon ,3}){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon ,3})\, dx^{\prime }dX &=\varepsilon ^{5} \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{3}) \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(v_{ \varepsilon ,3})\,dx^{\prime }dX, \end{aligned} $$

and, thus, as $\varepsilon \to 0$

$$ \begin{aligned} \int _{\omega \times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(f_{3}) \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon ,3})\,dx^{\prime }dX \to \int _{\omega \times {\mathbf{C}}}f_{3}(x^{\prime }) { \mathcal{V}}_{3}(x^{\prime })\, dx^{\prime }dX =|{\mathbf{C}}|\int _{\omega }f_{3}(x^{\prime }){\mathcal{V}}_{3}(x^{\prime })\,dx^{\prime }. \end{aligned} $$

Hence, taking into account $\text{(3.16)}$, (B.7) and the convergences obtained above, we can pass to the limit as $\varepsilon \to 0$

$$ \begin{aligned} &\int _{\omega \times {\mathbf{C}}} a_{ijkl}(E^{M}_{kl}({\mathcal{U}}_{m})-X_{3}E^{B}_{kl}({ \mathcal{U}}_{3}) +e_{X,kl}(\widehat{u}))(E^{M}_{ij}({\mathcal{V}}_{m})-X_{3} E^{B}_{ij}({\mathcal{V}}_{3}) +\varphi e_{X,ij}(\psi ))\, dx^{\prime }dX \\ &=|{\mathbf{C}}|\int _{\omega }f_{\alpha }(x^{\prime }){\mathcal{V}}_{\alpha }(x^{\prime })\,dx^{\prime }+\int _{\mathbf{C}}X_{3}\,dX \int _{\omega }[f_{\alpha }(x^{\prime })\frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}(x^{\prime })\,dx^{\prime }+g_{\alpha }(x^{\prime }){\mathcal{V}}_{\alpha }(x^{\prime })]\,dx^{\prime }\\ &+\int _{\mathbf{C}}X_{3}^{2}\,dX \int _{\omega }g_{\alpha }(x^{\prime }) \frac{\partial {\mathcal{V}}_{3}}{\partial x_{\alpha }}(x^{\prime })\,dx^{\prime }. \end{aligned} $$

Finally, since the tensor product ${\mathcal{D}}(\omega ) \otimes H^{1}_{2,per}({\mathbf{C}})$ is dense in $L^{2}(\omega ; H^{1}_{2,per}({\mathbf{C}}))$, we obtain the limit problem (3.17). □

2.3 B.3 Results of Sects. 4

Proof of Lemma 6

Taking into account the estimates in Lemma 16, we have

$$ \begin{aligned} &\Big|\int _{\varOmega ^{*}_{\varepsilon }}\,f_{\varepsilon }\cdot u_{ \varepsilon }\,dx\Big|\\ &=\Big|\int _{\varOmega ^{*}_{\varepsilon }}\Big( \big(\varepsilon ^{2} f_{1}(x_{3})+x_{2} g_{3}(x_{3})\big)\big({\mathcal{U}}_{ \varepsilon ,1}(x_{3})-x_{2}{\mathcal{R}}_{\varepsilon ,3}(x_{3})+ \overline{u}_{\varepsilon ,1}(x)\big) \\ &+\big(\varepsilon ^{2} f_{2}(x_{3})-x_{1} g_{3}(x_{3})\big)\big({ \mathcal{U}}_{\varepsilon ,2}(x_{3})+x_{1}{\mathcal{R}}_{\varepsilon ,3}(x_{3})+ \overline{u}_{\varepsilon ,2}(x)\big) \\ &+\big(\varepsilon f_{3}(x_{3})-x_{1} g_{1}(x_{3})-x_{2} g_{2}(x_{3}) \big)\big({\mathcal{U}}_{\varepsilon ,3}(x_{3})+x_{2}{\mathcal{R}}_{ \varepsilon ,1}(x_{3})-x_{1}{\mathcal{R}}_{\varepsilon ,2}(x_{3})+ \overline{u}_{\varepsilon ,3}(x)\big)\Big)\,dx\Big| \\ &\le \varepsilon ^{2}\Big|\int _{\varOmega ^{*}_{\varepsilon }}f_{1}(x_{3}){ \mathcal{U}}_{\varepsilon ,1}(x_{3})\,dx\Big| +\varepsilon ^{2}\Big|\int _{ \varOmega ^{*}_{\varepsilon }}f_{1}(x_{3})\overline{u}_{\varepsilon ,1}(x) \,dx\Big| +\Big|\int _{\varOmega ^{*}_{\varepsilon }}x_{2}^{2} g_{3}(x_{3}){ \mathcal{R}}_{\varepsilon ,3}(x_{3})\,dx\Big| \\ &+\varepsilon ^{2}\Big|\int _{\varOmega ^{*}_{\varepsilon }}f_{2}(x_{3}){ \mathcal{U}}_{\varepsilon ,2}(x_{3})\,dx\Big| +\varepsilon ^{2}\Big|\int _{ \varOmega ^{*}_{\varepsilon }}f_{2}(x_{3})\overline{u}_{\varepsilon ,2}(x) \,dx\Big| +\Big|\int _{\varOmega ^{*}_{\varepsilon }}x_{1}^{2} g_{3}(x_{3}){ \mathcal{R}}_{\varepsilon ,3}(x_{3})\,dx\Big| \\ &+\varepsilon \Big|\int _{\varOmega ^{*}_{\varepsilon }}f_{3}(x_{3}){ \mathcal{U}}_{\varepsilon ,3}(x_{3})\,dx\Big| +\varepsilon \Big|\int _{ \varOmega ^{*}_{\varepsilon }}f_{3}(x_{3})\overline{u}_{\varepsilon ,3}(x) \,dx\Big| +\Big|\int _{\varOmega ^{*}_{\varepsilon }}x_{2}^{2} g_{2}(x_{3}){ \mathcal{R}}_{\varepsilon ,1}(x_{3})\,dx\Big| \\ &+\Big|\int _{\varOmega ^{*}_{\varepsilon }}x_{1}^{2} g_{1}(x_{3}){\mathcal{R}}_{ \varepsilon ,2}(x_{3})\,dx\Big| \\ &\le C\varepsilon ^{4}\|f_{1}\|_{L^{2}(0,L)}\|{\mathcal{U}}_{\varepsilon ,1} \|_{L^{2}(0,L)} + C\varepsilon ^{3}\|f_{1}\|_{L^{2}(0,L)}\| \overline{u}_{\varepsilon ,1}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} +C \varepsilon ^{4}\|g_{3}\|_{L^{2}(0,L)}\|{\mathcal{R}}_{\varepsilon ,3}\|_{L^{2}(0,L)} \\ &+C\varepsilon ^{4}\|f_{2}\|_{L^{2}(0,L)}\|{\mathcal{U}}_{\varepsilon ,2} \|_{L^{2}(0,L)} +C\varepsilon ^{3}\|f_{2}\|_{L^{2}(0,L)}\| \overline{u}_{\varepsilon ,2}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} +C \varepsilon ^{4}\|g_{3}\|_{L^{2}(0,L)}\|{\mathcal{R}}_{\varepsilon ,3}\|_{L^{2}(0,L)} \\ &+C\varepsilon ^{3}\|f_{3}\|_{L^{2}(0,L)}\|{\mathcal{U}}_{\varepsilon ,3} \|_{L^{2}(0,L)} +C\varepsilon ^{2}\|f_{3}\|_{L^{2}(0,L)}\| \overline{u}_{\varepsilon ,3}\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} +C \varepsilon ^{4}\|g_{2}\|_{L^{2}(0,L)}\|{\mathcal{R}}_{\varepsilon ,1}\|_{L^{2}(0,L)} \\ &+C\varepsilon ^{4}\|g_{1}\|_{L^{2}(0,L)}\|{\mathcal{R}}_{\varepsilon ,2} \|_{L^{2}(0,L)} \le C\varepsilon ^{2}\Big(\|f\|_{L^{2}(0,L)} +\|g\|_{L^{2}(0,L)} \Big)\|e(u)\|_{L^{2}(\varOmega ^{*}_{\varepsilon })}, \end{aligned} $$

and thus (4.12) follows. □

Proof of Lemma 7

(i)-(iii) From (4.10)_1,3 in Lemma 5, [12, Theorem 3.6] and [14, Corollary 1.37] it follows that there exist functions ${\mathbb{U}}\in H^{2}_{\varGamma }(0,L),\,\varTheta \in H^{1}_{\varGamma }(0,L), \,{\underline{u}}\in H^{1}_{\varGamma }(0,L)^{3}$ such that the convergences (4.13), $\text{(4.14)}_{1,2}$, (4.17), $\text{(4.18)}_{1}$, (4.20) and $\text{(4.21)}_{1}$ hold.

The functions ${\mathcal{R}}_{\varepsilon }$, ${\underline{u}}_{\varepsilon ,3}$ are piecewise linear with respect to the variable $x_{3}$, hence

$$ {\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\mathcal{R}}_{\varepsilon }}{dx_{3}}\Big)\rightharpoonup \frac{d{\mathcal{R}}}{dx_{3}}\quad \hbox{weakly in } \quad L^{2}((0,L) \times (0,1)). $$

As a consequence, we obtain

$$\begin{aligned} &{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d^{2}{\mathbb{U}}_{\varepsilon }}{dx_{3}^{2}}\Big)={\mathcal{T}}_{\varepsilon }^{*}\Big(\frac{d{\mathcal{R}}_{\varepsilon }}{dx_{3}} \wedge {\mathbf{e}}_{3}\Big)\rightharpoonup \frac{d{\mathcal{R}}}{dx_{3}} \wedge {\mathbf{e}}_{3}=\frac{d^{2}{\mathbb{U}}}{dx_{3}^{2}}\quad \hbox{weakly in } \quad L^{2}((0,L)\times (0,1))^{3}, \\ &{\mathcal{T}}_{\varepsilon }^{*}\Big(\frac{d\varTheta _{\varepsilon }}{dx_{3}} \Big)={\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\mathcal{R}}_{\varepsilon }}{dx_{3}}\cdot {\mathbf{e}}_{3}\Big) \rightharpoonup \frac{d\varTheta }{dx_{3}}\quad \hbox{weakly in } \quad L^{2}((0,L) \times (0,1)), \\ &\frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\underline{u}}_{\varepsilon ,3}}{dx_{3}}\Big) \rightharpoonup \frac{d{\underline{u}}_{3}}{dx_{3}}\quad \hbox{weakly in } \quad L^{2}((0,L)\times (0,1)). \end{aligned}$$

From the estimates (4.12) and (4.10), there exists $\widehat{{\underline{u}}}_{\alpha }\in L^{2}((0,L),H^{1}_{1,per}(0,1))$ ($\alpha \in \{1,2\}$) such that

$$ {\mathcal{T}}_{\varepsilon }^{*}\Big( \frac{d{\underline{u}}_{\varepsilon ,\alpha }}{dx_{3}}\Big) \rightharpoonup \frac{d{\underline{u}}_{\alpha }}{dx_{3}}+ \frac{\partial \widehat{{\underline{u}}}_{\alpha }}{\partial X_{3}} \quad \hbox{weakly in } \quad L^{2}((0,L)\times (0,1)). $$

(iv) From (4.11), $\text{(4.4)}_{2}$ and (4.5), it follows that

$$ \begin{aligned} \|{\mathcal{T}}_{\varepsilon }^{*}(\overline{u}_{\varepsilon })\|_{L^{2}((0,L) \times {\mathbf{C}})} &=\frac{1}{\varepsilon }\|\overline{u}_{\varepsilon }\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} \le C\varepsilon ^{2}, \\ \|\nabla _{X}{\mathcal{T}}_{\varepsilon }^{*}(\overline{u}_{\varepsilon })\|_{L^{2}((0,L) \times {\mathbf{C}})} &=\varepsilon \|{\mathcal{T}}_{\varepsilon }^{*}(\nabla \overline{u}_{\varepsilon })\|_{L^{2}((0,L)\times {\mathbf{C}})} = \|\nabla \overline{u}_{\varepsilon }\|_{L^{2}(\varOmega ^{*}_{\varepsilon })} \le C \varepsilon ^{2} \end{aligned} $$

and, thus, for a subsequence, still denoted by $\{\varepsilon \}$, there exists $\overline{u}\in L^{2}((0,L);H^{1}({\mathbf{C}}))$ such that the convergence $\text{(4.24)}_{1}$ holds. The periodicity of $\overline{u}$, that is $\overline{u} \in L^{2}((0,L),H^{1}_{1,per}({\mathbf{C}}))$, can be proved in a similar way as in [13, Theorem 2.1]. From $\text{(4.24)}_{1}$ and $\text{(4.4)}_{2}$ we have $\text{(4.24)}_{2}$ and $\text{(4.24)}_{3}$. □

Proof of Proposition 6

From $\text{(4.14)}_{1,2}$, $\text{(4.18)}_{1}$, $\text{(4.21)}_{1}$ and $\text{(4.24)}_{1}$, we obtain the convergences (4.25).

By virtue of (4.9), $\text{(4.14)}_{3}$, $\text{(4.18)}_{2}$ and $\text{(4.21)}_{2,3}$ we have

$$ \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(e({\mathbf{U}}^{e}_{\varepsilon }))\rightharpoonup \frac{1}{2} \begin{pmatrix} 0&0&\frac{d{\underline{u}}_{1}}{d x_{3}}- X_{2} \frac{d\varTheta }{dx_{3}} \\ *&0&\frac{d{\underline{u}}_{2}}{dx_{3}}+X_{1}\frac{d\varTheta }{dx_{3}} \\ *&*&2\frac{d{\underline{u}}_{3}}{dx_{3}}-2X_{1} \frac{d^{2}{\mathbb{U}}_{1}}{dx_{3}^{2}}-2X_{2} \frac{d^{2}{\mathbb{U}}_{2}}{d x_{3}^{2}} \end{pmatrix} +\frac{1}{2} \begin{pmatrix} 0&0&\frac{\partial \widehat{{\underline{u}}}_{1}}{\partial X_{3}} \\ *&0&\frac{\partial \widehat{{\underline{u}}}_{2}}{\partial X_{3}} \\ *&*&0 \end{pmatrix} . $$

Denote

$$ \widehat{u}(x,X)\doteq \begin{pmatrix} \overline{u}_{1}(x,X)+\widehat{{\underline{u}}}_{1}(x_{3},X_{3}) \\ \overline{u}_{2}(x,X)+\widehat{{\underline{u}}}_{2}(x_{3},X_{3}) \\ \overline{u}_{3}(x,X) \end{pmatrix} +C, $$

where $C$ is determined in order to get $\int _{\mathbf{C}}\,\widehat{u}(\cdot ,X)\,dX=0$ a.e. in $(0,L)$. And thus $\text{(4.26)}_{1}$ follows. Then, taking into account the definition (2.3), we get $\text{(4.26)}_{2}$.

To obtain the limit problem (4.27), let us introduce the following fields

$$ ({\underline{v}},\,{\mathbb{V}},\,{\mathbf{T}})\in {\mathbf{V}}_{M} $$

and take the test function in (4.3) as

$$ v_{\varepsilon }(x)=\varepsilon \begin{pmatrix} \frac{1}{\varepsilon }{\mathbb{V}}_{1}(x_{3})+{\underline{v}}_{1}(x_{3})- \frac{x_{2}}{\varepsilon }{\mathbf{T}}(x_{3}) \\ \frac{1}{\varepsilon }{\mathbb{V}}_{2}(x_{3})+{\underline{v}}_{2}(x_{3})+ \frac{x_{1}}{\varepsilon }{\mathbf{T}}(x_{3}) \\ {\underline{v}}_{3}(x_{3})-\frac{x_{1}}{\varepsilon } \frac{d{\mathbb{V}}_{1}}{dx_{3}}(x_{3})-\frac{x_{2}}{\varepsilon } \frac{d{\mathbb{V}}_{2}}{dx_{3}}(x_{3}) \end{pmatrix} + \varepsilon ^{2}\varphi (x_{3}) \begin{pmatrix} \psi _{\varepsilon ,1}(x) \\ \psi _{\varepsilon ,2}(x) \\ \psi _{\varepsilon ,3}(x) \end{pmatrix} , $$

where $\psi _{\varepsilon }(x)=\psi \Big (\frac{x}{\varepsilon } \Big )$, $\psi \in {H^{1}_{1,per}({\mathbf{C}})}^{3}$. Then

$$ \begin{aligned} e(v_{\varepsilon })&=\frac{\varepsilon }{2} \begin{pmatrix} 0&0&\frac{d{\underline{v}}_{1}}{dx_{3}}(x_{3})- \frac{x_{2}}{\varepsilon }\frac{d{\mathbf{T}}}{dx_{3}} \\ *&0&\frac{d{\underline{v}}_{2}}{dx_{3}}(x_{3})+ \frac{x_{1}}{\varepsilon }\frac{d{\mathbf{T}}}{dx_{3}} \\ *&*&2\frac{d{\underline{v}}_{3}}{dx_{3}}-2\frac{x_{1}}{\varepsilon } \frac{d^{2} {\mathbb{V}}_{1}}{d x_{3}^{2}}-2 \frac{x_{2}}{\varepsilon }\frac{d^{2} {\mathbb{V}}_{2}}{d x_{3}^{2}} \end{pmatrix} +\frac{\varepsilon ^{2}}{2} \begin{pmatrix} 0&0&\frac{\partial \varphi }{\partial x_{3}}\psi _{1} \\ *&0&\frac{\partial \varphi }{\partial x_{3}}\psi _{2} \\ *&*&2\frac{\partial \varphi }{\partial x_{3}}\psi _{3} \\ \end{pmatrix}\\ &+\varepsilon \varphi \begin{pmatrix} \frac{\partial \psi _{1}}{\partial X_{1}} &\frac{1}{2}\Big( \frac{\partial \psi _{1}}{\partial X_{2}}+ \frac{\partial \psi _{2}}{\partial X_{1}}\Big) &\frac{1}{2}\Big( \frac{\partial \psi _{1}}{\partial X_{3}}+ \frac{\partial \psi _{3}}{\partial X_{1}}\Big) \\ *&\frac{\partial \psi _{2}}{\partial X_{2}} &\frac{1}{2}\Big( \frac{\partial \psi _{3}}{\partial X_{2}}+ \frac{\partial \psi _{2}}{\partial X_{3}}\Big) \\ *&*&\frac{\partial \psi _{3}}{\partial X_{3}} \end{pmatrix} . \end{aligned} $$

(B.9)

Applying the unfolding operator ${\mathcal{T}}_{\varepsilon }^{*}$ to the stress tensor $e(v_{\varepsilon })$ (B.9) and passing to the limit as $\varepsilon \to 0$, we obtain

$$ \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*} (e(v_{\varepsilon })) \to E({\underline{v}},{\mathbb{V}},{\mathbf{T}})+e_{X}(\psi )\varphi \quad \hbox{strongly in } L^{2}((0,L)\times {\mathbf{C}})^{3\times 3}. $$

(B.10)

Unfolding the left-hand side of (4.3) gives

$$ \begin{aligned} \int _{\varOmega ^{*}_{\varepsilon }} \sigma ^{\varepsilon }(u_{\varepsilon }):e(v_{\varepsilon })\,dx &=\varepsilon \int _{(0,L)\times {\mathbf{C}}} {\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }(u_{\varepsilon })):{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon }))\,dx_{3}\,dX\\ &=\varepsilon ^{3} \int _{(0,L)\times {\mathbf{C}}} \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(\sigma ^{\varepsilon }(u_{\varepsilon })): \frac{1}{\varepsilon }{\mathcal{T}}_{\varepsilon }^{*}(e(v_{\varepsilon }))\,dx_{3} \,dX. \end{aligned} $$

Unfolding the right-hand side of (4.3) and applying (4.1) leads

$$ \begin{aligned} &\int _{\varOmega ^{*}_{\varepsilon }}f_{\varepsilon }v_{\varepsilon }\,dx =\varepsilon \int _{(0,L)\times {\mathbf{C}}}\,{\mathcal{T}}_{\varepsilon }^{*}(f_{\varepsilon }){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon })\,dx_{3} dX = \varepsilon \sum _{i=1}^{3}\int _{(0,L)\times {\mathbf{C}}}\,{\mathcal{T}}_{\varepsilon }^{*}(f_{i}){\mathcal{T}}_{\varepsilon }^{*}(v_{\varepsilon ,i}) \,dx_{3}dX \\ &=\varepsilon ^{3}\int _{(0,L)\times {\mathbf{C}}}\,\Big[f_{1}{\mathbb{V}}_{1}+f_{2}{ \mathbb{V}}_{2} +f_{3}{\underline{v}}_{3}-X_{2}^{2}g_{3}{\mathbf{T}}-X_{1}^{2}g_{3}{ \mathbf{T}}+X_{1}^{2}g_{1}\frac{d{\mathbb{V}}_{1}}{dx_{3}}+X_{2}^{2}g_{2} \frac{d{\mathbb{V}}_{2}}{dx_{3}}\Big]\,dx_{3}dX. \end{aligned} $$

Hence, taking into account $\text{(4.26)}$, (B.10) and the convergences obtained above, we can pass to the limit as $\varepsilon \to 0$

$$ \begin{aligned} &\int _{(0,L)\times {\mathbf{C}}} a_{ijkl}(E_{kl}({\underline{u}},{ \mathbb{U}},\varTheta ) +e_{X,kl}(\widehat{u}))(E_{ij}({\underline{v}},{ \mathbb{V}},{\mathbf{T}}) +\varphi e_{X,ij}(\psi ))\,dx_{3} dX \\ &=\sum _{\alpha =1}^{2}\Big\{ |{\mathbf{C}}|\int _{(0,L)}\,f_{\alpha }{ \mathbb{V}}_{\alpha }\,dx_{3} +I_{\alpha }\int _{(0,L)}\,\Big[g_{\alpha }\frac{d{\mathbb{V}}_{\alpha }}{dx_{3}}-g_{3}{\mathbf{T}}\Big]\,dx_{3}\Big\} +|{ \mathbf{C}}|\int _{(0,L)}\,f_{3} {\underline{v}}_{3}\,dx_{3}. \end{aligned} $$

Finally, since the tensor product ${\mathcal{D}}(0,L) \otimes H^{1}_{1,per}({\mathbf{C}})$ is dense in $L^{2}((0,L); H^{1}_{1,per}({\mathbf{C}}))$, we obtain the limit problem (4.27). □