1 Introduction

Plane vertical surfaces at a temperature different to their surroundings are prevalent in our everyday environment. Examples include an area of a wall in a room that is heated by solar radiation and the façade of a glazed atrium cooled by outdoor air. Heat transfer from the surface results in a warming or cooling of the fluid adjacent to it and, consequently, a local buoyancy force which drives vertical motion under gravity leading to the development of a convective boundary layer. This boundary layer, referred to as a vertically distributed plume [3, 5, 15] or wall plume, can also form following a supply of buoyant fluid from a vertical source. An example is the plume that forms due to the ablation of a vertical ice wall submerged in a polar ocean (Kerr and McConnochie [10]). A brief review of experimental and numerical studies undertaken on vertically distributed plumes is given in Tsuji and Nagano [24] and Abedin et al. [1], respectively. Theoretical modelling of vertically distributed plumes is discussed in Cooper and Hunt [5], George and Capp [7], and Wells and Worster [27].

The Grashof number, Gr, relates driving buoyancy forces to momentum diffusivity and in a rising wall plume Gr increases with height. At a sufficiently large height, typically for \(Gr \gtrsim 10^9\) [25], the plume becomes fully turbulent. In this turbulent regime, a horizontal section through the flow can be separated into three distinct regions, each with different dynamics: a laminar near-wall conductive region; an intermediate viscous turbulent layer; and an outer inertial turbulent layer [27]. In their measurements, Vliet and Liu [26] show that the inner layers account for less than \(0.25 \%\) of the local volume flux. As a consequence, approaches that have focussed solely on modelling the outer layer (e.g. Caudwell et al. [3], Cooper and Hunt [5]) have proven successful in capturing the bulk flow physics in vertically distributed plumes. At sufficiently large scales, for example, the plume adjacent to a tall building façade heated by the sun, Wells and Worster [27] predict that buoyancy forces are also dominant in the inner layers of the flow and, thereby, exhibit identical scalings to the outer layer.

The literature on vertically distributed plumes is mainly centred on those which develop adjacent to isothermal surfaces. These studies primarily focus on identifying the vertical variation of the convective heat flux, H, from the vertical surface (the plume source). Knowledge of this flux is useful, for instance, to predict the lifespan of a submerged ice feature, for which the melting rate is controlled by the heat supplied to the ice–water interface [27]. The dimensionless heat flux is represented by the Nusselt number

$$\begin{aligned} Nu = \dfrac{Hz}{\rho _{\mathrm{a}} c_{\mathrm{h}} D \Delta T} \end{aligned}$$
(1)

[12], where \(\rho _{\mathrm{a}}\) is the ambient fluid density, \(c_{\mathrm{h}}\) the specific heat capacity of the ambient fluid, D the relevant thermal diffusivity, \(\Delta T\) the temperature difference between the surface and the ambient, and z the vertical coordinate with origin at the base of the plume source. Experimental studies, including those of Cheesewright [4], Tsuji and Nagano [23] and Tsuji and Nagano [24], conclude that in the turbulent region of the plume flow

$$\begin{aligned} Nu \propto Ra^{1/3}, \quad {\text{where}} \quad Ra = Gr \cdot Pr = \dfrac{g' z^3}{D \nu } \end{aligned}$$
(2)

is the Rayleigh number, \(\nu \) the kinematic viscosity, \(Pr = \nu / D \) the Prandtl number and \(g' = g (\rho _{\mathrm{a}} - \rho )/{\rho _{\mathrm{a}} }\) (where g is the gravitational acceleration) the buoyancy based on the density difference between the ambient and the plume fluids. The scaling (2) has also been proposed based on dimensional and asymptotic arguments by George and Capp [7] and Hölling and Herwig [8]. Expressions (1) and (2) suggest that the heat flux H from the source is independent of height. The constant value of the coefficient \({\mathcal{C}}\) relating the convective heat flux to the plume buoyancy flux B:

$$\begin{aligned} B = {\mathcal{C}} H, \quad {\mathcal{C}} = \dfrac{ g e}{\rho _{\mathrm{a}} c_{\mathrm{h}}} \end{aligned}$$
(3)

[13], where e is the thermal expansion coefficient, indicates that the turbulent region of the plume adjacent to an isothermal surface can be considered to have identical dynamics to that of a source with a uniform buoyancy flux. This equivalence leads to universal scalings for the time-averaged quantities of interest in the distributed plume. The scalings with height for the time-averaged width b, vertical velocity w and buoyancy \(g'\) in the turbulent region [5, 27] are

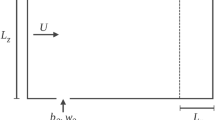
$$\begin{aligned} b \propto z, \quad w \propto z^{1/3} \quad {\text{and}} \quad g' \propto z^{-1/3}. \end{aligned}$$
(4)

While a focus of the literature on the vertically distributed plume has been to gain insight into the plume, the secondary flow in the ambient that the plume induces has been overlooked. Our primary aim is to model the flow induced by the turbulent wall plume, which is perpendicular to a horizontal boundary, that develops adjacent to a vertical plane that supplies a constant flux of buoyancy per unit area. Figure 1a (left) shows a schematic of the situation considered. Such an induced flow can have practical implications, for example, to the comfort of occupants in a room where the flow of air induced naturally toward a warm or a cool wall may prove beneficial by leading odours, stale air or humidity away from occupants.

The paper is laid out as follows. First, in Sect. 2 the general method we adopt to model the plume induced flow is introduced. The vertically distributed plume boundary condition is then formulated in Sect. 2.1. Following this, in Sect. 3 an analytical solution for the induced flow is derived. In Sect. 4 the solution is analysed—we examine the general features of the flow, including the streamline pattern, the flow speeds induced and the effect that the plume source strength has on the induced flow. The solution is then considered in the context of an application in the built environment. Conclusions are drawn in Sect. 5.

Fig. 1
figure 1

(left) Schematic of a uniform vertical planar source (red) adjacent to a horizontal boundary for a\(a = 0\) and b\(a > 0\). The rising convective plume draws a bulk secondary inflow (in the direction indicated by the curved arrows) from an otherwise quiescent ambient. (right) The corresponding domain, boundary conditions and coordinates for the boundary value problem formulated to model the plume induced flow

Full size image

2 Model development

It is not possible to identify a suitable characteristic length scale in order to enable a similarity scaling for the flow induced by a vertically distributed plume emanating from a uniform input of buoyancy as in Fig. 1a for which the offset is zero. The only existing scale, \(\beta ^2/g^3\), has little physical significance and is too small to be considered for any problems in practice. As a result, from a modelling perspective, we opt to reframe the problem in terms of a more general geometry, namely that corresponding to a distributed plume which is offset vertically by a distance a from the horizontal boundary (illustrated in the schematic in Fig. 1b (left)). Our original problem now represents the limiting case when the characteristic length scale \(a \rightarrow 0\).

We draw inspiration from Taylor [22] to formulate a boundary value problem describing the flow induced by the vertically distributed plume. Specifically, the induced flow is modelled as a two-dimensional potential flow, e.g. Kotsovinos [11], Lippisch [14]. The flow is assumed to be inviscid, an assumption that is readily justified based on the order of magnitude arguments by Schneider [20]. Schneider [20] reasons that the local Reynolds number of the induced flow is comparable with that of the plume. This is a consequence of the lower induced flow speeds measured relative to the plume flow being compensated for by the markedly larger characteristic region over which the induced flow occurs. In terms of the stream function \(\chi \), the inviscid potential flow model for the plume induced flow is governed by the Laplace equation

$$\begin{aligned} \nabla ^2 \chi = 0. \end{aligned}$$
(5)

From the reference frame of the ambient, the plume acts as a sink owing to the continuous entrainment of ambient fluid and, as such, is modelled here as a vertical distribution of line sinks. The local strength of the sinks is governed by the local entrainment velocity which is determined based on solutions for the plume from Cooper and Hunt [5].

With reference to Fig. 1b, we introduce a global plane polar coordinate system (\(r, \theta \)), originating at the base of the offset plume, and a second system, (\(r_{a}, {\theta }_{a}\)), originating at a distance a below the horizontal boundary—the latter to account for the offset. This dual coordinate system was used by Hunt and Ingham [9] when modelling the flow induced by industrial exhaust hoods. The local coordinate system (x, z) relates to the distributed plume (Sect. 2.1) which originates at the offset \(z = a\) on the vertical axis (as indicated by the dot in Fig. 1b).

Measurements of a saline plume adjacent to a sintered vertical plate in a fresh water environment by Cooper and Hunt [5] showed that the distributed plume is straight-sided and slender. Based on these results, we approximate the plume width as infinitesimal and apply the plume boundary condition, \(\chi = {\chi }_{\mathrm{p}}\), along the vertical axis for \(z \ge a\). A constant value for \(\chi \) is enforced along the horizontal axis to represent the horizontal boundary and along the vertical boundary for \(0 \le z \le a\).

Referring to the diagram in Fig. 1b (right), the governing boundary value problem for the induced flow can be represented mathematically by the Laplace equation (5) subject to the boundary conditions

$$\begin{aligned} \chi= \,\,& {} {\chi _{\mathrm{p}}} \quad {\text{on}} \quad \theta = \pi \quad {\text{and}} \quad \theta _{a} = 0 \quad {\text{for}} \quad r > 0, \quad r_a \ge 2a, \end{aligned}$$
(6)
$$\begin{aligned} \chi=\,\, & {} 0 \quad {\text{when}} \quad \theta = 0 \quad {\text{and}} \quad \theta _{a} = 0, \end{aligned}$$
(7)
$$\begin{aligned} \chi= \,\,& {} 0 \quad {\text{when}} \quad r = r_{a} \quad {\text{and}} \quad \theta = \theta _a. \end{aligned}$$
(8)

Boundary conditions (7) and (8) account for the vertical offset and horizontal boundary, respectively. In the limiting case of a zero offset, the two coordinate origins coincide, \(r = r_{a}\) and \(\theta = \pi - \theta _{a}\). Working in terms of the coordinates (r, \(\theta \)), illustrated in Fig. 1a (right), the boundary value problem simplifies to solving the Laplace equation subject to the following reduced form of the boundary conditions

$$\begin{aligned} \chi= \,\,& {} {\chi _{\mathrm{p}}} \quad {\text{on}} \quad \theta = \pi , \end{aligned}$$
(9)
$$\begin{aligned} \chi= \,\,& {} 0 \quad {\text{on}} \quad \theta = \pi /2. \end{aligned}$$
(10)

2.1 Plume boundary condition

To model the flow induced by a vertically distributed plume we require the form of the boundary condition \(\chi = {\chi }_{\mathrm{p}}\) that describes the influence of plume entrainment on the surrounding environment. For this, we adopt the model of the plume formulated by Cooper and Hunt [5] as outlined below — their formulation is based on the classic integral technique popularised by Morton, Taylor and Turner [17]. Such a model assumes that the laminar portion of the plume above the base of the source is negligibly small, and further, that viscous forces in the relatively thin sublayers of the turbulent flow adjacent to the source have a negligible effect on entrainment. The entrainment hypothesis, \(u_{\mathrm{e}} =\alpha w\), introduced in Taylor [21] is used to close the governing equations. This hypothesis links the local entrainment velocity, \(u_{\mathrm{e}}\), to a characteristic local plume velocity, w, using the entrainment coefficient \(\alpha \).

By tracking the position of a front in a freshwater filled ‘filling box’ (cf. Baines and Turner [2]) formed by supplying saline solution through a sintered vertical plate, Cooper and Hunt [5] estimated that the (top-hat) entrainment coefficient takes a value of \(\alpha = 0.02\). Using an identical measurement technique McConnochie and Kerr [15] estimate a value of \(\alpha = 0.014\) – 0.017, which is in close agreement with Cooper and Hunt [5], for the plume formed following the dissolution of a vertical ice wall in a saline water tank. The value of \(\alpha = 0.02\) from Cooper and Hunt [5] is used herein.

The plume source considered supplies a buoyancy flux per unit area of \(\beta = \textit{const.}\). Assuming top-hat profiles for vertical velocity and buoyancy, Cooper and Hunt [5] derive the following system of ordinary differential equations to describe a vertically distributed plume in a uniform environment:

$$\begin{aligned} \dfrac{dQ}{dz} = \alpha \dfrac{M}{Q}, \quad \dfrac{dM}{dz} =\dfrac{QB}{M}, \quad \dfrac{dB}{dz} = \beta . \end{aligned}$$
(11a -- c)

Expressed in terms of the integral fluxes of volume (\(Q = b w\)), momentum (\(M = b w^2\)) and buoyancy (\(B = b w g'\)), with b denoting the local plume width and \(g'\) the local buoyancy, (11a – c) represent equations describing the vertical variation of fluxes (per unit length) of volume, momentum and buoyancy, respectively.

Solving (11a – c) subject to \(Q = M = B = 0\) at \(z = 0\), Cooper and Hunt [5] develop the similarity solutions

$$\begin{aligned} Q= \,\,& {} \dfrac{3}{4} \left( \dfrac{4}{5}\right) ^{1/3} {\alpha }^{2/3} \beta ^{1/3}z^{4/3}, \end{aligned}$$
(12)
$$\begin{aligned} M= \,\,& {} \dfrac{3}{4} \left( \dfrac{4}{5}\right) ^{2/3} {\alpha }^{1/3} \beta ^{2/3}z^{5/3}, \end{aligned}$$
(13)
$$\begin{aligned} B= \,\,& {} \beta z. \end{aligned}$$
(14)

Using the solution for Q given in (12), a quantity identical to the two-dimensional stream function \(\chi \), we take the plume boundary condition (6) to be

$$\begin{aligned} \chi _{\mathrm{p}} = \dfrac{3}{4} \left( \dfrac{4}{5}\right) ^{1/3} {\alpha }^{2/3} \beta ^{1/3} z^{4/3}. \end{aligned}$$
(15)

3 Solution for the induced flow

Applying the method of separation of variables [19], a broad family of solutions to the Laplace equation (5) is identified which takes the form

$$\begin{aligned} \chi (r,\theta ) = (k_0 {\text{ln}} r + l_0)(m_0 \theta + n_0) + \sum _{\lambda = 1}^{\infty } ( k_{\lambda } r^\lambda + l_{\lambda } r^{-\lambda } ) ( m_{\lambda } {\text{cos}}(\lambda \theta ) + n_{\lambda } {\text{sin}}(\lambda \theta ) ), \end{aligned}$$
(16)

for constant coefficients \(k_{\lambda }\), \(l_{\lambda }\), \(m_{\lambda }\) and \(n_{\lambda }\), where \(\lambda \) takes positive integer values to ensure that \(\chi \) is single-valued. Owing to the linearity of the Laplace equation, we linearly superpose a second family of solutions to (5) in order to account for the plume offset, giving

$$\begin{aligned} \chi (r, \theta , r_{a}, \theta _{a}) =\,\,&(k_0 {\text{ln}} r + l_0)(m_0 \theta + n_0) + \sum _{\lambda = 1}^{\infty } ( k_{\lambda } r^\lambda + l_{\lambda } r^{-\lambda } ) ( m_{\lambda } {\text{cos}}(\lambda \theta ) + n_{\lambda } {\text{sin}}(\lambda \theta ) ) \nonumber \\&\pm \, (k_0 {\text{ln}} r_{a} + l_0)(m_0 \theta _{a} + n_0) \pm \sum _{\lambda = 1}^{\infty } ( k_{\lambda } r_{a}^\lambda + l_{\lambda } r_{a}^{-\lambda } ) ( m_{\lambda } {\text{cos}}(\lambda \theta _{a}) + n_{\lambda } {\text{sin}}(\lambda \theta _{a}) ). \end{aligned}$$
(17)

To satisfy (6)–(8), we match the boundary conditions to (17). To model the streamline representing the horizontal boundary (8) we take the difference between the superposed solutions in (17). To represent the streamline along the vertical offset we set \(k_0 = n_0 = m_{\lambda } = 0\), reducing (17) to

$$\begin{aligned} \chi = l_0 m_0 (\theta - \theta _{a}) + n_{\lambda } \left( ( k_{\lambda } r^\lambda + l_{\lambda } r^{-\lambda } ) {\text{sin}} \left( {\lambda } \theta \right) - ( k_{\lambda } r_{a}^\lambda + l_{\lambda } r_{a}^{-\lambda } ) {\text{sin}} ( \lambda \theta _{a} ) \right) . \end{aligned}$$
(18)

As a partially-confined problem, the exponent \(\lambda \) in (18) need not be restricted to integer values to maintain single-valuedness. To match the exponent of z in expression (15) with that of the global induced flow coordinates r and \(r_a\), we assign \(\lambda = 4/3\) in (18). The resulting expression is then matched to the plume boundary condition (15) along the vertical axis above the offset at \(\theta = \pi \), \(\theta _a = 0\) on setting \(l_{\lambda = 4/3} = l_0 m_0 = 0\) and assigning \(n_{\lambda = 4/3}k_{\lambda = 4/3} = {3}/{4} \cdot ({4}/{5})^{1/3} {\alpha }^{2/3} \beta ^{1/3}/{\text{sin}}(4\pi /3)\).

3.1 Non-dimensional variables

Introducing the offset a, we have a characteristic scale with which we scale all lengths to give

$$\begin{aligned} \bar{x} = \dfrac{x}{a}, \quad \bar{z} = \dfrac{z}{a}, \quad \bar{r} = \dfrac{r}{a}. \end{aligned}$$
(19a–c)

Given \(\beta \) characterises the strength of the source, the following scalings are obtained for the stream function, volume flux, velocity and time:

$$\begin{aligned} \bar{\chi } = \dfrac{\chi }{a^{4/3}\beta ^{1/3}}, \quad q = \dfrac{Q}{a^{4/3} \beta ^{1/3}}, \quad \bar{u} = \dfrac{u}{(a\beta )^{1/3}}, \quad \bar{t} = \dfrac{t}{a^{2/3}\beta ^{-1/3}}, \end{aligned}$$
(20a–d)

respectively.

3.2 Solution for non-zero offset (\(a > 0\))

The dimensionless solution for the flow induced by a vertically offset distributed plume (Fig. 1b) is

$$\begin{aligned} \bar{\chi } = \dfrac{3^{1/2}}{2} \left( \dfrac{4}{5} \right) ^{1/3} {\alpha }^{2/3} \left( {\bar{r}_{a}}^{4/3} {\text{sin}} \left( {\dfrac{4 \theta _{a}}{3} } \right) - \bar{r}^{4/3} {\text{sin}} {\left( {\dfrac{4 \theta }{3} } \right)} \right) . \end{aligned}$$
(21)

From (21), the corresponding dimensionless plane polar velocity components are

$$\begin{aligned} \bar{u}_{\theta }= & {} \dfrac{\partial \bar{\chi }}{\partial \bar{r}} = \dfrac{3^{1/2}}{2} \left( \dfrac{4}{5} \right) ^{1/3} {\alpha }^{2/3} \left( \dfrac{4({ \bar{r} - 2 {\text{cos}}\theta })}{3} {\bar{r}_{a}}^{-2/3}{\text{sin}}\left( \dfrac{4 \theta _{a}}{3} \right) \right. \nonumber \\&\left. + \dfrac{{8 {\text{sin}}\theta }}{3(4 - 4\bar{r} {\text{cos}} \theta + \bar{r}^2)} {\bar{r}_{a}}^{4/3}{\text{cos}}\left( \dfrac{4 \theta _{a}}{3} \right) - \dfrac{4}{3} \bar{r}^{1/3} {\text{sin}} {\left( \dfrac{4 \theta }{3} \right)} \right) \end{aligned}$$
(22)

and

$$\begin{aligned} \bar{u}_r= & {} - \dfrac{1}{\bar{r}} \dfrac{\partial \bar{\chi }}{\partial \theta } = - \dfrac{3^{1/2}}{2} \left( \dfrac{4}{5} \right) ^{1/3} {\alpha }^{2/3} \left( \dfrac{{8 \text{sin}\theta }}{3} {\bar{r}_{a}}^{-2/3}{\text{sin}}\left( \dfrac{4 \theta _{a}}{3} \right) \right. \nonumber \\&\left. - \dfrac{{4 (\bar{r} - 2 {\text{cos}}\theta ) }}{3(4 - 4\bar{r} {\text{cos}} \theta + \bar{r}^2)} {\bar{r}_{a}}^{4/3}{\text{cos}}\left( \dfrac{4 \theta _{a}}{3} \right) - \dfrac{4}{3} \bar{r}^{1/3} {\text{cos}}{\left( \dfrac{4 \theta }{3} \right)} \right) . \end{aligned}$$
(23)

To evaluate the derivatives in (22) and (23) in a dual coordinate system we expressed the coordinates \(\bar{r}_{a}\) and \(\theta _{a}\) in terms of \(\bar{r}\) and \(\theta \). The speed of the induced flow corresponds to the square root of the sum of the squares of the velocity components, given by

$$\begin{aligned} \bar{U}(\bar{r}, \theta ) = ({{\bar{u}_r}^2 + {\bar{u}_{\theta }}^2})^{1/2}. \end{aligned}$$
(24)

3.3 Solution for zero offset (\(a = 0\))

In the case when the offset \(a = 0\), the origin of the coordinate system (r, \(\theta \)) and the image system (\(r_{a}\), \(\theta _{a}\)) coincide (Fig. 1b), and thus \(r = r_{a}\) and \(\theta = \pi - \theta _{a}\). Working in terms of the dimensional coordinates (r, \(\theta \)) (Fig. 1a), (21) reduces to

$$\begin{aligned} \chi = \dfrac{3}{4} \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}} ({4 (\theta _{\mathrm{p}} - \pi /2) /3})}} \beta ^{1/3} r^{4/3} {\text{sin}} \left( {\dfrac{4}{3} \left( \theta - \dfrac{\pi }{2} \right) } \right) \quad {\text{for}} \quad \pi /2 \le \theta \le \theta _{\mathrm{p}}, \end{aligned}$$
(25)

where \(\theta _{\mathrm{p}} = \pi \) represents the line along which the plume boundary condition is applied. The solution cannot be expressed in terms of the dimensionless stream function \(\bar{\chi }\) (defined in Sect. 3.1) as now \(a = 0\). The velocity components can be derived from (25) as

$$\begin{aligned} u_r = - \dfrac{1}{r} \dfrac{\partial \chi }{\partial \theta } = - \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}}({4 (\theta _{\mathrm{p}} - \pi /2) /3})}} \beta ^{1/3} r^{1/3} {\text{cos}} \left( {\dfrac{4 }{3} \left( \theta - \dfrac{\pi }{2} \right) } \right) \end{aligned}$$
(26)

and

$$\begin{aligned} u_{\theta } = \dfrac{\partial \chi }{\partial r} = \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}} ({4 (\theta _{\mathrm{p}} - \pi /2) /3} )}} \beta ^{1/3} r^{1/3} {\text{sin}} \left( {\dfrac{4}{3} \left( \theta - \dfrac{\pi }{2} \right) } \right) . \end{aligned}$$
(27)

The induced flow speed is therefore

$$\begin{aligned} U(r) = ({{u_r}^2 + {u_{\theta }}^2})^{1/2} = \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}} ({4 (\theta _{\mathrm{p}} - \pi /2)/3})}} \beta ^{1/3} r^{1/3}. \end{aligned}$$
(28)

Although in the above we have taken the plume width to be zero, one may account for the plume width by a straightforward modification of our solution in (25) for instances when the width is of a considerable scale. Based on (12) and (13), the plume width grows linearly as

$$\begin{aligned} b = \dfrac{Q^2}{M} = \dfrac{3 \alpha }{4}z, \end{aligned}$$
(29)

which can be modelled by applying the solution (25) on \(\theta = \theta _{\mathrm{p}}\) where

$$\begin{aligned} \theta _{\mathrm{p}} = {\pi } - {\text{tan}}^{-1}\left( \dfrac{3 \alpha }{4} \right) . \end{aligned}$$
(30)

4 Analysis of solution

4.1 Non-zero offset (\(a > 0\))

Fig. 2
figure 2

a Streamlines, \(\bar{\chi } = \textit{const.}\), and contours of constant speed, \(\bar{U} = \textit{const.}\) (dashed lines), for the flow induced in the region \(0 \le (x/a, z/a) \le 10\) by a vertically distributed plume with \(a > 0\). Values of the stream function and speed are overlain. The arrows indicate the direction of flow and the dot corresponds to the base of the plume source. b Zoom in of streamline pattern and speeds near the base of the plume source located at \(z/a = 1\)

Full size image

Dimensionless streamlines, \(\bar{\chi } = \textit{const.}\), and contours of constant dimensionless speed, \(\bar{U} = \textit{const.}\), are plotted in Fig. 2 for the induced flow of an offset vertically distributed plume. The dimensionless offset is \(z/a = 1\). The streamline pattern and speed contours are independent of the offset distance a and the plume source strength \(\beta \) (cf. (21) and (24) with scalings from (19) and (20)). Immediately evident from the streamline pattern is the upward inclination of the induced flow as it approaches the source. The inclination to the horizontal is approximately \(\pi /3\) radians (\(\equiv 60^{\circ }\)) at the source. The contours of constant speed in Fig. 2a show an asymmetry which is more readily visible in the zoomed in picture close to the offset in Fig. 2b. Reasoning for this asymmetry is given in Sect. 4.2 after we consider the symmetric case achieved for \(a = 0\). The speeds in the induced flow increase with distance from the coordinate origin. Whilst this trend is readily explained physically (see below), it points to the limit of applicability of the model for large x and z. This is discussed further in Sect. 4.4. The increasing induced flow speeds and inclined flow pattern occur due to the increasing entrainment velocity \({u_{\mathrm{e}}}\) with height. The increasing entrainment velocity is evident on differentiating the local plume volume flux (12) with respect to z, expressed in dimensionless terms as

$$\begin{aligned} \dfrac{dq}{d\bar{z}} = {{\bar{u}}_{\mathrm{e}}} = \dfrac{\alpha }{(a\beta )^{1/3}} \dfrac{M}{Q} = \left( \dfrac{4}{5}\right) ^{1/3} {\alpha }^{2/3} {\bar{z}}^{1/3}. \end{aligned}$$
(31)

Buoyancy, continuously input over the entire surface of the source, does work and thereby increases the local momentum flux of the plume M, as expressed in (13). The momentum flux \(M \propto z^{5/3}\) increases vertically at a faster rate than the corresponding volume flux \(Q \propto z^{4/3}\). Given the plume’s entrainment velocity \({\bar{u}}_{\mathrm{e}}\) is proportional to the local ratio \(M/(\beta ^{1/3} Q)\), see (31), \({\bar{u}}_{\mathrm{e}}\) also increases with height as \({\bar{u}}_{\mathrm{e}} \propto {\bar{z}}^{1/3}\). This indicates a stronger plume entrainment demand at greater heights, which leads to the increasing induced flow speeds with distance from the coordinate origin as illustrated in Fig. 2.

4.2 Zero offset (\(a = 0\)) and application to flow induced by a heated wall in a room

Fig. 3
figure 3

a Streamlines, \(\chi = \textit{const.}\) (solid lines) \({{\text{m}}^{{2}}} {{\text{s}}^{{-1}}}\), and contours of constant speed, \(U = \textit{const.}\) (dashed lines) \({{\text{ms}}^{{-1}}}\), in the induced flow of a vertically distributed plume with zero offset with source strength \(1\ \text{kWm}^{-2}\). Values of the stream function and air speeds are overlain. The perimeter of the plume (dotted line) predicted by (30) has been superposed. The arrows indicate the direction of the induced flow. b Contours of constant speed for the difference between the speeds induced in a and the (lower) speeds induced based on assuming a horizontal flow in the environment, where the velocity at a given height is equivalent to the entrained velocity at that height at the vertical axis

Full size image

Thus far the focus has been on identifying the general flow features in the induced flow of a plume with an offset \(a > 0\). In the following, we focus on an application in the built environment for the case when the offset is zero (\(a = 0\)).

Consider the wall of a large room that is heated by solar radiation. Heat transfer from the wall to the adjacent air leads to an upward flowing vertically distributed thermal plume and an associated induced airflow in the environment. With this example in mind, we now estimate a representative source heat flux. The solar constant, denoting the average incident extraterrestrial solar radiation has been measured as \(1.36\ \text{kWm}^{-2}\) [16]. This solar energy is considerably weakened due to absorption, scattering and reflection by the Earth’s atmosphere. In addition, solar rays are typically at some inclination to the vertical surface of the wall. For these reasons, we take a lower estimate for the (steady) plume source heat flux (assuming a clear sky day) of \(1\ \text{kWm}^{-2}\) [18, p. 60]. This is equivalent to a source buoyancy flux per unit area of \({\beta } = 0.0281\ {{\text{m}^{{2}}{\text{s}}^{{-3}}}}\) based on expression (3). Figure 3a is a (dimensional) plot of the streamline pattern for the induced flow adjacent to the solar heated wall of a room predicted from (25) with \({\beta } = 0.0281\ {{\text{m}^{{2}}{\text{s}}^{{-3}}}}\) and \(\theta _{\mathrm{p}}\) given in (30). In contrast to an offset plume case, here ambient fluid is entrained for all heights \(z > 0\). Contours of constant speed from (28) are overlain in Fig. 3a. Not unsurprisingly the contours of speed appear, at first sight, similar to those in Fig. 2. However, here they are symmetric, forming concentric quarter circles about the base of the plume source.

Having analysed the induced flow for the plume with zero offset above, we now provide a physical explanation for the asymmetry predicted in the contours of constant speed for the plume with an offset in Fig. 2. Consider a streamline (\(\chi =\)const.) close to the horizontal boundary (\(\chi = 0\)) for \(x>> 1\). The volume flow rate in the streamtube bounded by \(\chi = 0\) and \(\chi = \textit{const.}\) is identical to that entrained into the plume between its base and a height, say \(z_c\), above the base. Consequently, the streamline \(\chi =\)const. intersects the plume at height \(z = z_c\) for \(a = 0\). Beginning with the reference case \(a = 0\) for which the profiles of constant speed are concentric circles centred at (0, 0), as dimension a is increased the streamline \(\chi = \textit{const.}\) intersects the plume at a height \(z = a + z_c\). Thus, as the streamline pattern distorts from the reference case with increasing dimension a, the speed contours in turn respond, breaking the symmetry.

In the interests of developing a simplified model, it may have been tempting at the very outset to consider modelling the induced flow as a purely horizontal flow, in other words without reference to the Laplace equation and without satisfying the irrotationality condition. From volume conservation, (31), this would indicate a speed of

$$\begin{aligned} U_{\mathrm{s}} = \left( \dfrac{4}{5}\right) ^{1/3} {\alpha }^{2/3} \beta ^{1/3} {{r}}^{1/3} \left( {\text{sin}}\left( \theta - \dfrac{\pi }{2} \right) \right) ^{1/3} \end{aligned}$$
(32)

for the induced flow of the plume with zero offset (where the subscript \((\cdot )_{\mathrm{s}}\) denotes ‘simplified’). Expression (32) represents a constant speed along horizontal layers in the induced flow. In Fig. 3b we have plotted contours of constant difference between the speeds from our solution in expression (28) illustrated in Fig. 3a and that based on the simplified calculation in (32). From Fig. 3b it is evident that (32) underpredicts the induced flow speeds. The difference is largest at lower heights and, rather counter-intuitively, away from the source. This highlights the role of the irrotationality condition.

Figure 4a presents the variation of speed with height in the induced flow at different horizontal distances from the source. The plot indicates that speeds increase with distance from the source and that the profiles become increasingly uniform away from the source. The variation in the speeds implies that a heated surface can influence the flow in a region a considerable distance from that surface. Although the induced flow speeds are small in this application, smaller than what is typically considered to be a draughtFootnote 1, the induced flow can in principle transport fluid over significant distances. For example, at the approximate head height of an occupant (\(\approx 1.5 {\hbox{m}}\)), air located at a horizontal distance of 6m from the wall will reach the wall in approximately 3 min. This estimation is based on calculating the average speed along the trajectory of a fluid parcel following the streamline \(\chi = 0.05\ {\text{m}}^2 {\text{s}}^{-1}\) in Fig. 3a. Given that 3 min is short relative to the time spent by an occupant in an office during a typical working day, the induced flow could lead to the spread of airborne contaminants (e.g. a virus such as the common cold) from occupant to occupant. Alternatively, these findings indicate that a wall could be actively heated or cooled to improve the air quality in a large internal space, e.g. by drawing heat, humidity and stale air in an office environment, or aerosols discharged from an industrial process, to the perimeter of the room.

4.2.1 Effect of source strength

If one considers a vertical surface which is actively heated, rather than passively by solar radiation, we can assess the effect of source strength. Figure 4b illustrates the role of the source heat flux per unit area on the speeds induced at the approximate head height (\(z = 1.5\ {\hbox{m}}\)) of an occupant. The source strength imposed is increased in unit increments of \(H = 1\ {\text{kWm}}^{-2}\) from \(H = 1\ {\text{kWm}}^{-2}\) to \(H = 5\ {\text{kWm}}^{-2}\). A greater source strength drives larger induced flow speeds (28). The factor increase in speed at a given location is small in comparison to that of the respective source strength increase as \(U\ \sim \ \beta ^{1/3}\), and from the decreased spacing between adjacent curves, the incremental increase in the induced flow speed diminishes with increasing source strength.

Fig. 4
figure 4

Plume induced flow speeds along a vertical cross-sections at \(x = \{1.5, \ 3, \ 6, \ 12 \}\)m and b the horizontal section at \(z = 1.5m\) for source strengths H, 2H, 3H, 4H and 5H with \(H = 1\ {{\text{kWm}^{{-2}}}}\). The arrows indicate the direction of increasing distance x in a and source strength H in b

Full size image

4.3 Accelerating and decelerating flow regions

The contours of constant speed in Figs. 2 and 3a provide additional insights into the flow features of the induced flow. Note that while the streamlines are concave, the contours of constant speed have a convex form. This implies that the acceleration of fluid parcels in the induced flow changes sign. Though one might have initially anticipated the induced flow to gradually accelerate towards the plume, as we establish below, parcels accelerate following an initial period of deceleration along their trajectories. From volume conservation, this would suggest that the spacing between adjacent streamlines increases and then decreases as the flow approaches the source. This is clearly evident on close inspection of the streamline portraits (Figs. 2 (left), 3a).

To establish the aforementioned behaviour, we re-analysed the flows in a Lagrangian framework wherein individual fluid parcels of the induced flow were followed. We reframe expressions (22) and (23) corresponding to induced flow velocity components of the plume with an offset \(a > 0\), as

$$\begin{aligned} \dfrac{d {\theta _{\mathrm{pc}}}}{d \bar{t}}= \,\,& {} \dfrac{\bar{u}_{\theta _{\mathrm{pc}}}}{\bar{r}_{\mathrm{pc}}} = \dfrac{3^{1/2}}{2} \left( \dfrac{4}{5} \right) ^{1/3} {\alpha }^{2/3} \left( \dfrac{4({ \bar{r}_{\mathrm{pc}} - 2 {\text{cos}}\theta _{\mathrm{pc}}})}{3{\bar{r}_{\mathrm{pc}}}} {\bar{r}_{a_{\mathrm{pc}}}}^{-2/3}\text{sin}\left( \dfrac{4 \theta _{a_{\mathrm{pc}}}}{3} \right) \right. \nonumber \\&\left. + \dfrac{{8 {\text{sin}}\theta _{\mathrm{pc}} }}{3{\bar{r}_{\mathrm{pc}}}(4 - 4\bar{r}_{\mathrm{pc}} {\text{cos}} \theta _{\mathrm{pc}} + {\bar{r}_{\mathrm{pc}}}^2)} {\bar{r}_{a_{\mathrm{pc}}}}^{4/3}\text{cos}\left( \dfrac{4 \theta _{a_{\mathrm{pc}}}}{3} \right) - \dfrac{4}{3} {{\bar{r}}_{\mathrm{pc}}}^{-2/3} \text{sin}{\left( \dfrac{4 \theta _{\mathrm{pc}}}{3} \right)} \right) \end{aligned}$$
(33)

and

$$\begin{aligned} \dfrac{d \bar{r}_{\mathrm{pc}}}{d \bar{t}}= \,\,& {} \bar{u}_{r_{\mathrm{pc}}} = - \dfrac{3^{1/2}}{2} \left( \dfrac{4}{5} \right) ^{1/3} {\alpha }^{2/3} \left( \dfrac{{8 \text{sin}\theta _{\mathrm{pc}}}}{3} {{\bar{r}}_{a_{\mathrm{pc}}}}^{-2/3}{\text{sin}}\left( \dfrac{4 \theta _{a_{\mathrm{pc}}}}{3} \right) \right. \nonumber \\&\left. - \dfrac{{4 (\bar{r}_{\mathrm{pc}} - 2 {\text{cos}}\theta _{\mathrm{pc}} ) }}{3(4 - 4\bar{r}_{\mathrm{pc}} \text{cos} \theta _{\mathrm{pc}} + {\bar{r}_{\mathrm{pc}}}^2)} {\bar{r}_{a_{\mathrm{pc}}}}^{4/3}\text{cos}\left( \dfrac{4 {\theta _{a}}_{\mathrm{pc}}}{3} \right) - \dfrac{4}{3} {\bar{r}_{\mathrm{pc}}}^{1/3} \text{cos}{\left( \dfrac{4 \theta _{\mathrm{pc}}}{3} \right)} \right) , \end{aligned}$$
(34)

respectively (with the subscript \((\cdot )_{\mathrm{pc}}\) reading ‘parcel’). Expressions (33) – (34) enable the coordinates (\(\bar{r}_{\mathrm{pc}}\), \(\theta _{\mathrm{pc}}\)) of a parcel in the induced flow to be determined at each instant in time from a given initial position (\({\bar{r}}_{\mathrm{i}}\), \(\theta _{\mathrm{i}}\)). Similarly, the corresponding expressions (26) and (27) for the plume with zero offset, lead to

$$\begin{aligned} \dfrac{d r_{\mathrm{pc}}}{d t} = u_{r_{\mathrm{pc}}} = -\left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}}({4 (\theta _{\mathrm{p}} -\pi /2)/3})}} \beta ^{1/3} {r_{\mathrm{pc}}}^{1/3} {\text{cos}} \left( {\dfrac{4}{3} \left( \theta _{\mathrm{pc}} - \dfrac{\pi }{2} \right) } \right) \end{aligned}$$
(35)

and

$$\begin{aligned} \dfrac{d {\theta _{\mathrm{pc}}}}{d t} = \dfrac{u_{\theta _{\mathrm{pc}}}}{r_{\mathrm{pc}}} = \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}} ({4 (\theta _{\mathrm{p}} - \pi /2) /3} )}} \beta ^{1/3} {r_{\mathrm{pc}}}^{-2/3} \text{sin} \left( {\dfrac{4}{3} \left( \theta _{\mathrm{pc}} - \dfrac{\pi }{2} \right) } \right) , \end{aligned}$$
(36)

respectively, enabling the coordinates (\(r_{\mathrm{pc}}\), \(\theta _{\mathrm{pc}}\)) of a parcel in the induced flow to be determined at each instant in time from an initial location (\(r_{\mathrm{i}}\), \(\theta _{\mathrm{i}}\)). By definition, the trajectory of a parcel will correspond to a streamline for the steady flows considered. Figure 5 (left) presents the trajectories of (a) five parcels A, B, C, D and E for the plume with \(a > 0\) and (b) four parcels F, G, H and I for the plume with \(a = 0\), all parcels initially located along \(\theta = 3\pi /4\). The trajectories are determined on numerically solving the respective coupled non-linear ordinary differential equations (33), (34) and (35), (36) using a Runge–Kutta scheme.

Fig. 5
figure 5

The trajectories (left) of fluid parcels a A, B, C, D and E and b F, G, H and I released along \(\theta = 3\pi /4\) in the induced flows. These trajectories correspond to the streamlines \(\bar{\chi } = 0.05, 0.15\), 0.45, 0.75 and 1.05 and \(\chi = 0.05\), 0.15, 0.25 and \(0.35\ {\text{m}}^2 {\text{s}}^{-1}\) in Figs. 2a and 3, respectively. Arrowheads indicate the direction of motion. The corresponding speed (right) of each fluid parcel as it moves along each of the trajectories, with s denoting the distance along a trajectory from the initial position \(s = 0\)

Full size image

The speed of each fluid parcel was predicted on inputting the coordinates from solving (33), (34) and (35), (36) into expressions (24) and (28), respectively. The distance s along a given parcel trajectory is given by

$$\begin{aligned} s = \int ^{\theta _{\mathrm{pc}}}_{\theta _{\mathrm{i}}} \left( {{r_{\mathrm{pc}}}^2 + \left( {\dfrac{d r_{\mathrm{pc}}}{d{\theta }}}\right) ^2}\right) ^{1/2} \ d\theta . \end{aligned}$$
(37)

Figure 5a (right) represents the corresponding speed \(\bar{U}\) of the parcels in Fig. 5a (left) along their trajectories. The equivalent dimensional plot is illustrated in Fig. 5b for \(a = 0\). Evidently, there is a turning point, a local minima, in each profile. Moreover, following each profile in turn a parcel experiences a reduced acceleration and deceleration with height. On comparison of Fig. 5a and b (right), the profiles of speed are asymmetric for the plume with a non-zero offset. The asymmetry becomes increasingly pronounced for streamlines at lower heights. Furthermore, the steep positive gradient of the speed contours evident in this region indicates that there is a strong acceleration in the vicinity of the offset.

Fig. 6
figure 6

Locus separating the induced flow into regions of decelerating and accelerating flow for a\(a > 0\) and b\(a = 0\). The locus is \(\theta _{\mathrm{min}} = 7\pi /8\) for \(a = 0\)

Full size image

Our attention now turns to identifying the precise location in the environment at which the transition from deceleration to acceleration occurs. The position at which the acceleration of a fluid parcel changes sign is where the speed is a local minimum (Fig. 5 (right)), or equivalently, where the separation between adjacent streamlines in Figs. 2a and 3a is largest. For the offset plume, this location has been identified on numerically evaluating the speeds along each streamline and identifying a locus of minima. The position of the locus is depicted in Fig. 6a, where it has been superposed onto the streamline portrait of the plume induced flow from Fig. 2. Figure 6 indicates that the high velocity flow further from the source initially (small s) slows before increasing in speed closer to the source. For the zero offset case, we use the fact that induced flow speeds are solely a function of the radial coordinate (cf. (28)) in order to formulate an expression locating the locus. First, we focus on a single streamline, by equating the stream function in (25) to a constant value \(\mu \), giving

$$\begin{aligned} \dfrac{3}{4} \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}} ({4 (\theta _{\mathrm{p}} - \pi /2) /3})}} \beta ^{1/3} r^{4/3} {\text{sin}} \left( {\dfrac{4}{3}}\left( \theta - \dfrac{\pi }{2} \right) \right) = \mu . \end{aligned}$$
(38)

Given the speed is solely a function of the radial coordinate r, and increases with r, we seek the location along each streamline where the radial coordinate is minimised. A global locus can be identified once this location is determined for all streamlines \(0 \le \mu \le \chi _{\mathrm{p}}\). To identify the location at which the radial coordinate is minimised along a given streamline, we rearrange expression (38) for r to give

$$\begin{aligned} r = \left( {\dfrac{3}{4 \mu } \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}} ({4 (\theta _{\mathrm{p}} - \pi /2) /3})}} \beta ^{1/3} {\text{sin}} \left( {\dfrac{4}{3}} \left( \theta - \dfrac{\pi }{2} \right) \right) } \right) ^{-3/4}. \end{aligned}$$
(39)

Differentiating (39) with respect to \(\theta \) and equating to zero results in

$$\begin{aligned} \dfrac{dr}{d\theta }= & {} - \left( \left( \dfrac{1}{\mu } \left( {\dfrac{3}{4}}\right) ^{10/3} \left( \dfrac{4}{5} \right) ^{1/3} \dfrac{{\alpha }^{2/3}}{{{\text{sin}}( {4 (\theta _{\mathrm{p}} - \pi /2) /3})}} \beta ^{1/3} \right) ^{3/7} \right. \nonumber \\&{\left. {\text{sin}} \left( {\dfrac{4}{3} \left( \theta - \dfrac{\pi }{2} \right) } \right) \right)} ^{-7/4} \text{cos} \left( {\dfrac{4}{3} \left( \theta - \dfrac{\pi }{2} \right) }\right) = 0. \end{aligned}$$
(40)

Solving expression (40) for \(\theta \), we derive the periodic solution

$$\begin{aligned} \theta = \dfrac{7\pi }{8} + \dfrac{3\pi }{4}n \ \ {\text{for}} \ \ n \in {\mathbb{Z}}, \end{aligned}$$
(41)

from which we select the first root (\(n = 0\)) to give

$$\begin{aligned} \theta = \theta _{\mathrm{min}} = \dfrac{7 \pi }{8}. \end{aligned}$$
(42)

This result indicates that fluid moving along a given streamline in the induced flow of a vertically distributed plume with zero offset (\(a = 0\)) will undergo a transition from deceleration to acceleration once it encounters the locus at \(\theta = 7\pi /8\) radians (\(\equiv 157.5^{\circ }\)). The position of this locus is depicted in Fig. 6b, where it has been superposed onto the streamline portrait of the plume induced flow from Fig. 3a. The locus for the non-zero offset plume has a shallow inclination close to the offset of \(\theta = 22\pi /30\) radians (\(\equiv 132^{\circ }\)). The inclination increases with height to \(\theta = 7 \pi /8\) radians (\(\equiv 157.5^{\circ }\)) in the vertical limit and matches that of the plume with zero offset in (b).

4.4 Limit on applicability of model

Figures 2 and 3a illustrate that the model predicts speeds in the induced flow that increase with distance from the plume source. In the vertical limit as \(z \rightarrow \infty \), the speeds tend to infinity in response to the infinite plume entrainment velocity (31). This naturally leads to the question of the practical limit on the induced flow solutions derived, particularly as sources do not extend over an infinite extent in practice.

To address this question it is useful to consider the more realistic case of a source with a finite height \({\mathcal{L}}\). In the solution domain as \(z \rightarrow \infty \), the relative source height is infinitesimal (\(({\mathcal{L}}+ a)/z \rightarrow 0\)) and the far-field induced flow approximates to that above a horizontal line source and thereby induces a flow with a finite speed [22]. Owing to the elliptic nature of the governing equation (5), the far-field plume entrainment behaviour (above the finite height source) only governs the induced flow field at large radial distances from the base of the plume source; the near-field region at smaller radial distances \(r < {\mathcal{L}}\) remains unaffected. For these reasons we anticipate that our induced flow solutions can be used to describe the near-field induced flow region, for radial distances that are less than the vertical dimension of the source.

5 Conclusions

Analytical solutions have been developed for the flow induced by a rising turbulent plume adjacent to a vertical wall source supplying a constant flux of buoyancy. Two cases are considered: a plume from an elevated source that is offset vertically a distance \(a > 0\) from a horizontal boundary, and a source with zero offset \(a = 0\). Crucially, the induced flow solution for \(a > 0\) enables a similarity scaling, which is not afforded for the case \(a = 0\). This scaling enables a universal solution to be formulated that can be straightforwardly utilised to describe a range of problems in practice.

The analytical solutions derived, for both \(a > 0\) and \(a = 0\), indicate that the induced flow follows an increasingly upwardly inclined path towards the plume. Speeds in the induced flow increase with horizontal distance from the source. These flow features occur as a result of the increasing plume entrainment demand with height. On further inspection of the induced flow solutions, we find that fluid parcels do not purely accelerate towards the source but, in fact, encounter a period of deceleration, followed by acceleration closer to the source. For the plume with zero offset, this is predicted to occur once fluid parcels cross the locus at \(\theta = 7 \pi /8\) radians (\(\equiv 157.5^{\circ }\)). The locus is located at a greater horizontal distance from the source for the plume with non-zero offset. Further, the plume offset creates a strong asymmetry in the profiles of constant speed adjacent to the offset, resulting in a strong acceleration of the flow in this region.

The solutions developed are applied in the context of the built environment to describe the plume induced flow adjacent to the wall of a room heated by the sun. We find that the influence of the wall, somewhat counter-intuitively, increases with increasing distance from the wall.