1 Introduction

Turbulent plumes in crossflow are a common phenomenon in various environmental fluid mechanics applications, such as pollutant dispersion in rivers and atmospheric dispersion of gases and particulate matter, either natural or man-made [1, 2]. These plumes result from the release of a buoyant fluid into a crossflow, which induces complex interactions between the plume and the surrounding fluid, bending the plume over and sweeping it downstream. Understanding the behavior and characteristics of turbulent plumes in crossflow is crucial for predicting and mitigating the environmental impact of fluid release events, from cooling tower vapour plumes [3] to volcanic eruption columns [4].

Forced turbulent plumes have been a topic of interest for several decades owing to their prevalent nature. The typical setup is that of a circular source of buoyancy and momentum, which in a uniform environment generates an axisymmetric flow which expands radially due to entrainment as it rises [5,6,7,8]. The addition of a crossflow acts to break the axisymmetry and cause the plume to bend over, and has been studied extensively both numerically and experimentally [9,10,11,12]. The complexity of the phenomena and the variability of environmental conditions make it challenging to develop accurate and reliable predictive models; Muppidi and Mahesh [13], in their study of forced jets in crossflow, remark on the difficulties involved in RANS and eddy viscosity models for this type of flow, particularly in the near-field around the source, owing to the steep velocity gradients in this region, which is far from a state of turbulent equilibrium. Indeed, the studies of Yuan et al. [14] and Muppidi and Mahesh [15] observed the sensitivity of the near-field flow to the boundaries imposed on the source.

In this paper, a comprehensive analysis of a forced turbulent plume in uniform crossflow is presented, as outlined by Middleton [16], using data from Direct Numerical Simulation (DNS). DNS is a powerful tool that resolves the Navier–Stokes equations up to the smallest energetic scales in the flow, the Kolmogorov scale, making it ideal for exploring the dynamics of turbulent fluctuations in the absence of any turbulence modelling. Remarkably few studies exist that use DNS to explore turbulent plumes in crossflows, presumably as the computational requirements have been hitherto prohibitive. Jordan et al. [17] used DNS to study an infinitely lazy plume in cross-flow, i.e. a plume for which the injection velocity is zero. The DNS study of Wang et al [18] investigated instead a jet in crossflow, i.e. no buoyancy. Most numerical studies use Large-Eddy Simulation (LES) or Reynolds-averaged Navier Stokes (RANS) models. Cintolesi et al [19] performed a detailed analysis of first- and second-order statistics of the forced plume in crossflow using LES, repeating the experiment of Fan [20], identifying three regions of the plume evolution: a momentum phase where the initial plume momentum flux dominates; a buoyancy phase where the initial plume buoyancy flux dominates; and the entrainment phase, where the crossflow momentum bends over the plume and the well-known counter-rotating vortex pair forms [21].

This study builds upon the work of Jordan et al [17], analysing a forced plume with a source-to-crossflow velocity ratio of unity. The paper is organised as follows. The flow studied is outlined, and the governing equations are stated alongside all simplifying assumptions. The numerical parameters of the DNS are then given. A phenomenological analysis of the flow is then presented with reference to the vortical structures and mean temperature, velocity and pressure fields. The plume trajectory is then assessed via the central streamline, centres of mass of velocity and temperature, and positions of the maxima of velocity and temperature, and the resulting paths are compared. Finally, the eddy viscosity and diffusivity are analysed, and characteristic integral values are calculated that hold for the entire fully developed regime of the plume, leading to a constant characteristic turbulent Prandtl number.

2 Numerical modeling

2.1 Problem setup

The subject of the present study is that of a turbulent buoyant plume with source buoyancy \(b_0\) exiting from a circular source of radius \(r_0\) with initial velocity \(w_0\) in the vertical z-direction, that is subject to a uniform crossflow U in the streamwise x-direction. The only symmetry in this flow is a reflective symmetry along the plume centre in the x-z plane, removing the cylindrical symmetry of the plume in the absence of crossflow. The plume develops spatially as it is swept along with the crossflow, bending over and expanding as it rises. The problem setup is identical to that used in Jordan et al. [17], except for the non-zero source velocity \(w_0\) implemented in this study.

For sufficiently small buoyancy differences and a low Mach number release, the governing equations can be reduced to the Navier–Stokes equations in the Boussinesq approximation

$$\begin{aligned} \frac{\partial u_j}{\partial x_j}&=0, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j}&= -\frac{\partial p}{\partial x_i} + \nu \frac{\partial ^2 u_i}{\partial x_j \partial x_j} + b \delta _{i3}, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial b}{\partial t} + u_j \frac{\partial b}{\partial x_j}&= \kappa \frac{\partial ^2 b}{\partial x_j \partial x_j}, \end{aligned}$$
(3)

where \((x_1,x_2,x_3)=(x,y,z)\) are respectively the streamwise, spanwise and vertical Cartesian spatial co-ordinates, \((u_1, u_2, u_3) = (u,v,w)\) is the fluid velocity field and \(b=g(\rho _0 - \rho )/\rho _0\) is the buoyancy field, both evolving over time t, with density \(\rho\), a constant reference density \(\rho _0\) and gravitational acceleration g. \(\delta _{ij}\) is the Kronecker delta, equal to 1 only when \(i=j\) and zero otherwise. In the Boussinesq approximation, buoyancy is proportional to temperature via the coefficient of thermal expansion, \(b=\alpha g (T-T_0)\) for reference temperature \(T_0\) and coefficient of thermal expansion \(\alpha\), and therefore b can be freely referred to as both temperature and buoyancy throughout. The kinematic pressure perturbation is given by \(p=\tilde{p}/\rho _0 + gz\) for the standard pressure \(\tilde{p}\). Kinematic viscosity and thermal diffusivity are given respectively by \(\nu\) and \(\kappa\).

Using the velocities \(w_0\) and U, the source buoyancy \(b_0\), and the viscous and thermal velocity parameters \(\nu\) and \(\kappa\), four dimensionless quantities can be defined [17]:

$$\begin{aligned} R_0 = \frac{w_0}{U}, \quad \mathrm{{Ri}}_0 = \frac{b_0 r_0}{w_0^2}, \quad \mathrm{{Re}}_0 = \frac{2r_0 w_0}{\nu }, \quad \mathrm{{Pr}}=\frac{\nu }{\kappa }, \end{aligned}$$
(4)

where \(R_0\) is the source-to-crossflow ratio of velocities, \(\mathrm{{Ri}}_0\) the source Richardson number, \(\mathrm{{Re}}_0\) the source Reynolds number and \(\mathrm{{Pr}}\) the Prandtl number. The case studied here is parameterised by \(R_0=1\), \(\mathrm{{Ri}}_0=1\), \(\mathrm{{Re}}_0=1000\) and \(\mathrm{{Pr}}=1\).

2.2 Direct numerical simulation

Fig. 1
figure 1

A schematic of the DNS domain in the central (x, z) plane

Full size image

The dataset analysed in this work has been obtained by means of a DNS approach employing the code SPARKLE, utilised and validated in previous studies of plumes [8, 22, 23], which spatially makes use of a fourth-order symmetry-preserving central difference scheme, and integrates temporally via a third-order Adams–Bashforth scheme.

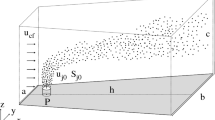
The domain is laid out as per the schematic of Fig. 1. The domain dimensions are \((L_x \times L_y \times L_z)= (28 r_0 \times 24 r_0 \times 24 r_0)\), and the simulation grid is made up of \((N_x \times N_y \times N_z )= (1344 \times 768 \times 768)\) points, leading to \(\Delta x/r_0 = 0.021\) and \(\Delta y/r_0 = \Delta z/r_0 = 0.031\). These are of the same order as the smallest Kolmogorov length scale \(\eta = (\nu ^3/\varepsilon )^{1/4}=0.02r_0\) in the fully developed region of the flow, calculated a posteriori using the maximum dissipation rate \(\varepsilon\) in this region, indicating that the grid resolution is sufficient to capture the dynamics at the dissipative scales.

The boundary conditions are periodic in the streamwise x and spanwise y directions, and free-slip on \(z=0\) and \(z=L_z\), with the exception of a constant top-hat velocity function \(\textbf{w}_0 = (0,0,w_0)\) imposed on the plume source centred at \((x,y)=(0,0)\) with radius \(r_0\), positioned at a distance of \(5r_0\) from the start of the computational domain in the x-direction. It is noted that the top-hat profile will not represent the velocity distribution at the source of a real plume, which will not be uniform and will likely feature turbulence. Smith and Mungal [24] and Moussa et al. [25] state that the flow dynamics are sensitive to the plume exit boundary, however the experiments of Savory et al [26] demonstrate that the the source-to-crossflow velocity ratio is the main parameter influencing the flow in the far field. Neumann boundary conditions are imposed on the buoyancy at \(z=0\) and \(z=L_z\), again with the exception of the plume source, which has a uniform top-hat buoyancy \(b_0\). In order to introduce the required fluctuations to break down the potential core of the plume rapidly, the source velocity and buoyancy are perturbed using Gaussian white noise with an amplitude of 0.1% of the source velocity and buoyancy respectively. This white noise is applied uniformly on the source only, with no vertical extension. The magnitude is chosen to perturb the source fluid enough to facilitate the transition to turbulence.

In order to enforce the uniform inflow in the x-direction that serves as the crossflow source with the periodic boundary conditions, a nudging region of length \(L_n=4r_0\) is introduced in the last section of the domain. In this region, denoting the distance downstream from the start of the nudging region as \(x^*\), the velocity and buoyancy is gradually reduced to that of the ambient field via \(\textbf{u}^* = (1-x^*/L_n)\textbf{u} + (x^*/L_n)\textbf{u}_0\), where \(\textbf{u}\) is the DNS-calculated velocity field and \(\textbf{u}_0 = (U,0,0)\) is the ambient crossflow velocity field. This reduces the field from \(\textbf{u}^*=\textbf{u}\) at the start of the nudging region \(4r_0\) upstream from the end of the domain to \(\textbf{u}^*=\textbf{u}_0\) at \(x=L_x\). The same treatment is performed on the temperature to reduce it to a null field at the inflow. It is evident that therefore any dynamics in this region do not represent the physical flow; these have been omitted from the analysis of the results. The choice of spanwise domain length \(L_y\) guarantees that the dynamics of the plume are not affected by the periodic boundary conditions in this direction. At its widest point downstream, on the nudging region boundary, the 1% threshold of the average temperature field was found to occupy a width of approximately \(25\%\) of \(L_y\) and \(37.5\%\) of \(L_z\), and therefore the plume spans less than \(9\%\) of the total domain area at its widest region; this is small enough so as to ensure that boundary effects were negligible. Studies performed by Rooney [27] indeed indicate that for a row of adjacent plumes, a plume spanning approximately 25% of the domain is not affected in a significant manner by the entrainment of the neighbouring plumes.

The initial condition is a neutral environment with a uniform flow, i.e. \(\textbf{u}(\textbf{x}, t=0) = (U,0,0)\) and \(b(\textbf{x}, t=0) = 0\). This led to an initial transient period, which is defined as ending when the buoyancy field first reaches the downstream nudging region, and has been discarded in the analysis.

3 Results

The results are analysed using the instantaneous fields produced by the DNS, and the three-dimensional fields of Reynolds averaged first- and second-order statistics are calculated in post-production by averaging across the approximately 1200 such fields each produced at time intervals of \(5r_0/U\). This is chosen such that a number of inertial flow timescales \(r_0/U\) have passed between subsequent snapshots, allowing the system to evolve sufficiently between each snapshot to avoid correlation. These averages are indicated by an overbar. It is noted that the the crossing time, defined as the time taken for a fluid particle originating at the plume source to cross the domain, is approximately equal to \(20r_0/U\). Over the duration of the simulation, it is found that 240 of these timescales have passed. This is suitably large enough to capture the complete flow dynamics a significant number of times. Owing to the absence of spatially homogeneous directions in this problem, the statistical averages are temporal only, and a small amount of noise is present in the higher order observables. The overall behaviour of the flow is discussed in this section by analysing the vortical structures and the mean buoyancy, velocity and pressure fields.

3.1 Vortical structures

Figure 2 (left) shows a snapshot of the instantaneous enstrophy field \(\omega ^2\), where \(\varvec{\omega } = \varvec{\nabla } \times \textbf{u}\) is the local vorticity, via isocontours at the 1% threshold of the maximum mean enstrophy \(\overline{\omega ^2}\). The tube-like Intense Vorticity Structures (IVSs) shown demonstrate the tell-tale signs of turbulent flow almost immediately out of the plume source, and the plume expansion as it is swept downstream by the crossflow. As the plume is deflected by the crossflow, these IVSs first appear as annular rings across the top of the plume, which will cause fluctuations in the temperature field. In the fully developed region further downstream, the IVSs take on less regular structure, however they follow counter-rotating helical paths, most visible in the right arm of the snapshot of Fig. 2 (left), indicating a larger vortical structure present in the flow. It is evident from the 0.2% isosurface of mean enstrophy demonstrated in Fig. 2 (right), chosen to best visualise the field throughout the domain, that there exist twin vortical structures traversing the x-direction and separating in the y-direction as the plume is swept downstream by the crossflow.

Fig. 2
figure 2

3D snapshots of the instantaneous enstrophy isocontour \(\omega ^2\) at the 1% threshold of the maximum in the mean field (left) and mean enstrophy isocontour \(\overline{\omega ^2}\) at the 0.2% threshold (right) demonstrating the IVSs and twin vortical structure respectively

Full size image

3.2 Reynolds-averaged flow features

Assuming statistically steady state, when applying Reynolds averaging to the governing Eqs. (1)–(3), they read as follows

$$\begin{aligned} \frac{\partial \bar{u}_j}{\partial x_j}&= 0 \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial }{\partial x_j} \bigg (\bar{u}_j \bar{u}_i + \overline{u'_j u'_i} \bigg )&= \frac{\partial \bar{p}}{\partial x_i} + \nu \frac{\partial ^2 \bar{u}_i}{\partial x_j \partial x_j} + \bar{b}\delta _{i3} \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial }{\partial x_j}\bigg (\bar{u}_j \bar{b} + \overline{u'_j b'}\bigg )&= \kappa \frac{\partial ^2 \bar{b}}{\partial x_j \partial x_j} \end{aligned}$$
(7)

where the classical Reynolds decompositions of the velocity, \(\textbf{u}' = \textbf{u}-\bar{\textbf{u}}\), pressure \(p' = p - \bar{p}\) and buoyancy \(b' = b-\bar{b}\) have been used. Here and in the remainder of the paper the prime denotes the fluctuating components. The buoyancy (or temperature) field is often used to identify the fluid within the plume, for example Fig. 3 shows the mean buoyancy field at \(y/r_0=0\), divided by the maximum value at each x, \(\bar{b}_{\textrm{max}}(x)\). This quantity tries to map the 3D evolution of the plume to a 2D plane; the source possesses a normalised magnitude of 1 and the fluid around this region maintains this value, which decreases for larger \(x/r_0\). The edge of the plume is represented in the same figure as the \(1\%\) threshold of the global maximum value, as one expects the buoyancy field to tend to zero as it approaches the ambient fluid. The picture derived from Fig. 3 tells us that the plume initially rises vertically, due to the source fluxes, and is somewhat diffused downstream on the leading edge interacting with the crossflow, but hardly shifts in the streamwise direction on the downstream edge, thus narrowing the plume. It then proceeds to remain approximately constant in width in the non-spanwise directions until roughly \(x/r_0=5\), before beginning to expand.

Fig. 3
figure 3

Mean buoyancy field at \(y/r_0=0\) divided by the maximum value at each x, \(\bar{b}/\bar{b}_{\textrm{max}}\). The plume source is centred at \(x/r_0=0\) where \(r_0\) is the source radius. The black line represents the 1% threshold of the maximum value of the mean buoyancy, bounding the plume radius

Full size image

Cintolesi et al. [19] identified three phases of the plume dynamics. The momentum phase is the phase in which the initial momentum flux at the source mainly drives the plume; the buoyancy phase where the buoyancy force dominates the plume dynamics; and the entrainment phase, where the crossflow bends the plume horizontally and the counter-rotating vortex pair forms. These phases are not necessarily distinct; if the initial momentum is that much stronger than the buoyancy force, then the momentum phase and buoyancy phase can overlap, and there does not exist a pure buoyancy phase.

Fig. 4
figure 4

Average buoyancy \(\bar{b}/b_0\) over (y, z) plane at four slices along the streamwise direction: a the source centre \(x/r_0=0\), b the downstream source edge \(x/r_0=1\), c in the near-field downstream at \(x/r_0=5\) and d far downstream \(x/r_0=15\). The outline represents the 1% threshold of the maximum buoyancy in each plane

Full size image

The vertical length scale at which momentum and buoyancy fluxes dominate the upward acceleration of the plume are given by, respectively (Fischer et al. [21]),

$$\begin{aligned} z_M = r_0 \sqrt{\pi }\frac{w_0}{U}, \quad \quad z_B = \frac{\pi }{2}\frac{r_0}{\mathrm{{Fr}}^2}\bigg (\frac{w_0}{U}\bigg )^3, \end{aligned}$$
(8)

where \(\mathrm{{Fr}}=Ri_0^{-1/2}\) is the source Froude number. Here, \(z_M=1.77\) and \(z_B=1.57\); \(z_B < z_M\) and therefore a pure buoyancy driven phase does not exist, as the influence of the source momentum flux extends past \(z_B\); that is to say that the momentum forces dominate the vertical acceleration of the plume throughout the initial ascent. The transition to the entrainment region defined by Fischer et al. [21] occurs at

$$\begin{aligned} z^* \ge z_M \bigg (\frac{z_M}{z_B}\bigg )^{\frac{1}{3}}. \end{aligned}$$
(9)

In this instance, \(z^*/r_0=1.84\). This is where the crossflow dominates over the initial momentum, and one can see in the instantaneous flow field of Fig. 2 that this is indeed approximately where the annular tube-like structures signalling the transition to turbulence begin to form.

Cross-sections of temperature in the y–z plane are shown in Fig. 4 for a number of positions along the flow. At \(x/r_0= 0\), directly above the centre of the plume, rolling structures form along the upper edge, which develop into the rolling tendrils seen at \(x/r_0=1\) and in the mean enstrophy surface in the right plot of Fig. 2. Further downstream at \(x/r_0=5\) these begin to coalesce into a pair of uniform central core structures reflected about the central plane of symmetry, becoming more localised by \(x/r_0=15\), demonstrating once more the twin buoyant vortical core structure which continues downstream.

Figure 5 shows the average velocity fields by means of isocontours and streamlines in the central x–z plane and in the y–z plane at \(x=15\). Close to the source, a convergence of streamlines can be observed of the within-plume and incoming-flow streamlines. This is due to a combination of the incoming crossflow, and the twin counter-rotating vortical feature of the plume demonstrated in the y–z plane, which injects fluid into the plume from below along the central x–z plane and forces it upward until the crossflow dominates and bounds the plume.

While the convergence of the streamlines in the x–z plane seems to imply an increase in velocity flux, and therefore a large acceleration which is not observed, it is noted that a particle emanating from the plume source would trace one of the counter-rotating vortex pairs. Statistically, these would average out to a zero \(\bar{v}\) spanwise velocity in the central plane, however this does not imply a zero \(\partial \bar{v}/\partial y\). At infinitesimal distances either side of the central plane, these quantities are clearly non-zero due to the counter-rotating vortex pair, and the fully 3D streamlines in the mean flow will follow the trajectories of the vortices, rather than converging as seen in the 2D plane; that is to say, any streamline contraction observed in the x–z plane corresponds to an expansion in the y–z plane.

Fig. 5
figure 5

Average velocity fields in the central (x, z) plane (left) and (y, z) plane at \(x/r_0=15\) (right). Isocontours denote x-velocity magnitudes, with white representing \(\bar{u}/U=1\), the ambient crossflow velocity. Streamlines are calculated in each plane. It is noted once more that the full computational domain is not shown

Full size image

It can also be seen in the x–z central plane that there is in fact a slight back flow into the downstream edge of the plume immediately adjacent to the downstream plume source boundary at \(x/r_0 = 1\). This is due to the velocity boundary function possessing a singularity on this edge, where the top-hat plume inflow condition and free-slip boundary meet, causing a high back-pressure differential and accelerating the fluid immediately backward and into the plume. The influence of the crossflow is negligible in this region; the plume source effectively blocks the ambient flow, owing to the effect of the circular plume source possessing zero streamwise or spanwise velocity, becoming phenomenologically analogous in this plane to the two dimensional cylinder in a potential flow.

The pressure field is visualised by the contours of Fig. 6, which are taken in the x–z centre plane and the y–z plane at \(x/r_0=15\), overlaid with the planar velocity vectors and 1% temperature threshold to indicate the plume boundary. The x–z centre plane demonstrates the aforementioned high back-pressure gradient along the downstream edge leading to the back flow in this region. It further shows a region of high positive pressure along the upper edge of the plume, which acts in x to accelerate the plume downstream. There is also a slight pressure gradient beneath the centre of the plume, where the double vortex structure injects fluid into the plume from below.

Fig. 6
figure 6

Average pressure over (x, z) centre plane (left) and (y, z) plane at \(x/r_0=15\), overlaid with planar velocity vectors and contours of 1% temperature threshold in each plane to indicate plume boundary

Full size image

The plume cross section at \(x/r_0=15\) demonstrates a high positive vertical pressure gradient immediately atop the plume, which opposes the vertical acceleration due to temperature as previously observed by Jordan et al [17]. This also acts to prevent the ejection of fluid along the x–z centreline by the twin vortices, leading to the thin film seen in the temperature contours of Fig. 4 connecting the twin vortices across the top, leading to the kidney-like structure of the plume cross section in the turbulent region.

3.3 Plume trajectory

The plume trajectory centreline is an important concept for integral models of plumes in crossflow, and it typically thought of as the central streamline of the plume [29], denoted here as \(z_U\). This streamline can be determined by following a fluid particle from the centre of the plume source. However, as has been demonstrated in Figs. 4 and 5, the central plane does not capture the much more prominent effect of the twin vortical structures, which in this flow sit some distance below the maxima in the central plane. Alternative plume trajectories based on centre of mass of temperature \(\bar{b}\) and velocity \(V=\sqrt{\bar{u}^2+\bar{w}^2}\) are also used, calculated by

$$\begin{aligned}{} & {} z_c(x) = \frac{\iint _\Omega z \overline{b} \; \textrm{d}y \; \textrm{d}z}{\iint _\Omega \overline{b} \;\textrm{d}y \;\textrm{d}z}, \nonumber \\{} & {} z_V(x) = \frac{\iint _\Omega z V \; \textrm{d}y \; \textrm{d}z}{\iint _\Omega V \;\textrm{d}y \;\textrm{d}z}, \end{aligned}$$
(10)

where the integration is performed over plume area \(\Omega\) in the y–z plane, defined on the 1% maximum temperature threshold. These trajectories are plotted in Fig. 7, along with the z-positions of the maximum values of \(\bar{b}\) and V at each x, and overlaid with the temperature field integrated across the spanwise direction \(\langle \bar{b}\rangle _{y}\).

Fig. 7
figure 7

Plume trajectories based on the central streamline \(z_U\), the centres of mass of \(\bar{b}\) and \(V=\sqrt{\bar{u}^2 + \bar{w}^2}\), maximum of \(\bar{b}\) and maximum of V, overlaid with isocontours of the y-integrated temperature field \(\langle \bar{b}\rangle _{y}\). The maxima of \(\bar{b}\) and V have been omitted for \(x/r_0<2\) due to noise

Full size image

The central streamline follows the very top of the plume, consistent with the streamline plot shown in Fig. 5. This is a markedly different behavior than for the infinitely lazy plume (\(w_0=0\)) case studied in Jordan et al. [17]; in their study, it was impossible to define a central streamline starting from the plume source, owing to the imposed zero-velocity at the outlet, which is why a central streamline was constructed from starting some distance above the source. In that case, the central streamline remained much more in the middle of the plume. The higher central streamline in the presence of non-zero source momentum flux is noted in the experiments of Su and Mungal [30] and also observed by Muppidi and Mahesh [13] for the turbulent jet in crossflow; the severe asymmetry in the radius of plume fluid above and below the central streamline in the fully developed region is due to the upstream fluid at the leading edge of the source being stripped away by the crossflow, while the central momentum dominated region less influenced by the crossflow in the near field continues its upward trajectory less affected. In the infinitely lazy case of Jordan et al. [17] with zero source momentum flux, this phenomenon does not occur.

The centre of mass trajectories both evolve similarly along the domain, with the centre of mass of V only marginally higher than that of \(\bar{b}\). These quantities are, by definition, more representative of the entire plume than the plume centreline. The maxima of \(\bar{b}\), which follows roughly the centres of the vortical structures as shown by Fig. 4, sits only marginally below the centres of mass, suggesting that the largest contributions to the centre of mass of \(\bar{b}\) come from the accumulation of temperature within these structures. The maximum of V within the plume also follows the maximum of \(\bar{b}\) very closely, as it does with the centre of mass. This suggests the central streamline represents the path followed by top of the plume, whilst the other definitions are more representative of the plume as a whole.

4 Eddy viscosity and diffusivity

4.1 Eddy viscosity

Closure of the Reynolds-averaged Navier–Stokes Eq. (6) is obtained by modelling the Reynolds stress tensor, \(-\overline{u_i' u_j'}\). The most common modelling approaches are based on the eddy viscosity assumption,

$$\begin{aligned} -\overline{u'_i u'_j}=2\nu _T S_{ij} - \frac{2}{3}k \delta _{ij}, \end{aligned}$$
(11)

where \(\nu _T\) is an eddy viscosity, \(k=\overline{u_i' u_i'}/2\) is the turbulence kinetic energy and \(S_{ij} = (\partial \overline{u}_i / \partial x_j + \partial \overline{u}_j / \partial x_i)/2\) is the mean strain rate tensor. Each component of the tensorial relation (11) would give different behaviour for the eddy viscosity, especially in strongly inhomogeneous and anisotropic flows like the present case. In order to study a single behaviour of eddy viscosity that is representative of the flow evolution, both sides of (11) are contracted with the strain rate tensor,

$$\begin{aligned} \underbrace{-\overline{u'_i u'_j} S_{ij}}_{\Pi } = 2 \nu _T S_{ij}S_{ij}. \end{aligned}$$
(12)

Such an approach is instructive from a physical point of view as the left hand side of the above equation can be easily recognised as the turbulence shear production \(\Pi\), which is typically positive in instances of turbulence. In fact, when a Reynolds decomposition of the flow is performed, the energetics of the flow can be studied by analysing the two contributions to the kinetic energy associated with the mean field and with the fluctuating fields, respectively. In this decomposition, the dissipative nature of turbulent flows can be recognized in the draining of the kinetic energy of the mean field due to interactions of the mean shear with turbulent fluctuations, which are finally dissipated by viscosity into heat. Generally we expect positivity of the shear production to hold also in buoyancy driven flows even if in these cases an extra production term due to density differences also appears. Reynolds-averaged turbulence closures are classically based on these arguments, as demonstrated by the Boussinesq hypothesis (11). However, while in most problems the volume integral of the turbulent production term should be positive for statistically stationary flows, as it should be balanced by dissipation, locally it could be of either sign [31]. Indeed, in the remainder of the paper we will use the relation (12) to study the behaviour of an effective eddy viscosity that, from an energetic point of view, guarantees the same local turbulence production of the actual flow. As such we anticipate that this quantity could also be negative in the positions where \(\Pi\) is negative.

Fig. 8
figure 8

Turbulence production (left half) mirrored with strain rate tensor contraction (right half) in the y–z plane at \(x/r_0=15.\)

Full size image

Figure 8 shows slices of turbulence production \(\Pi\) and of \(S_{ij}S_{ij}\) reflected side by side in the y–z plane. It is immediately evident that \(\nu _T\) cannot be positive throughout the entire flow, as there exist sinks of turbulence kinetic energy along the plume trajectory in the negative values of \(\Pi\), typically along the lower boundary of the plume, indicated in red. Furthermore, any potential model would have to modulate \(\nu _T\); there are regions of negligible turbulence production that correspond to areas in which the norm of the strain rate tensor is of similar order of magnitude to its maximal values in each plane.

A characteristic eddy viscosity can be constructed instead based on the average value of \(\nu _T\), which is not assumed to be constant throughout the plume, but instead dependent on the distance from the plume source. Approximating the plume as fully bent over such that the angle made with the horizontal is small, the resultant characteristic integral turbulent viscosity is given by

$$\begin{aligned} \nu _{Tm}=\bigg (\iint _{\Omega } \Pi \; \textrm{d}y \; \textrm{d}z \bigg ) \bigg (\iint _{\Omega } 2 S_{ij}S_{ij} \; \textrm{d}y \; \textrm{d}z \bigg )^{-1}, \end{aligned}$$
(13)

where \(\Omega\) is the plume area, defined by the 1% threshold of the maximum buoyancy at each x, as outlined in Fig. 4. The appropriate length and velocity scales \(r_m\) and U for the flow are the characteristic radius of the plume and the crossflow velocity respectively, such that \(r_m=(Q/U)^{1/2}\), where

$$\begin{aligned} Q=\frac{1}{\pi }\iint _\Omega \bar{u} \; \textrm{d}y \;\textrm{d}z \end{aligned}$$
(14)

is the integral volume flux, again assuming a fully bent over solution. The characteristic plume radius can be shown to increase linearly with x. Figure 10 demonstrates that for this flow there is an initial transitional region immediately out of the plume source, then in the fully developed regime \(x/r_0 > 5\), \(\nu _{Tm}/r_m U\) is approximately constant with x. These DNS data provide a benchmark with which to compare such a characteristic integral turbulent viscosity from numerical models, and the constant nature of this eddy viscosity implies a global self-similarity, whereby turbulent flow structures at different locations in the plume are geometrically similar, but differ only in size and intensity, as found experimentally for turbulent round buoyant jets in crossflow by Papaspyros et al. [32].

4.2 Eddy diffusivity

Using the identity \(\partial (\bar{u}_i \bar{b})/\partial x_i = \bar{u}_i (\partial \bar{b}/\partial x_i) + \bar{b} (\partial \bar{u}_i/\partial x_i)\) and the statement of incompressibility (1) in the Reynolds averaged buoyancy Eq. (7) one finds that

$$\begin{aligned} \frac{\partial (\bar{u}_i\bar{b})}{\partial x_i} = \frac{\partial }{\partial x_i} \bigg (\kappa \frac{\partial \bar{b}}{\partial x_i} - \overline{u'_i b'}\bigg ) \end{aligned}$$
(15)

where \(\kappa \partial \bar{b}/\partial x_i\) can be interpreted as a diffusive buoyancy flux and \(-\overline{u'_i b'}\) the buoyancy flux due to turbulent eddies, playing an analogous role to the Reynolds stress term in the momentum balance equation. The high Péclet number \(\mathrm{{Pe}}_0\) condition of this flow, where \(\mathrm{{Pe}}_0=\mathrm{{Re}}_0 \mathrm{{Pr}}= 2 r_0 w_0 / \kappa\), ensures the \(\kappa \partial \bar{b}/\partial x_i\) term is negligible and thus does not contribute to the temperature flux. However, a common assumption used in models of eddy diffusion to close the system (15), for example in gradient diffusion models, is that these two terms are proportional, such that

$$\begin{aligned} -\overline{u_i'b'}=\kappa _T \frac{\partial \bar{b}}{\partial x_i}, \end{aligned}$$
(16)

where \(\kappa _T\) is the turbulent diffusivity, \(\kappa _T=\nu _T/Pr_T\) for turbulent Prandtl number \(\mathrm{{Pr}}_T\). One of the limitations of the gradient diffusion model is that it is not necessarily the case that the temperature flux vector \(-\overline{u_i'b'}\) is parallel to the direction of the gradient. One can indeed obtain interesting insight on what happens in the present flow by inspecting the left hand plot of Fig. 9 which shows the cosine of the angle between these two quantities, \(\cos {(\theta )}=(-\overline{\textbf{u}'b'}\cdot \varvec{\nabla }\bar{b})/\left| \overline{\textbf{u}'b'} \right| \left| \varvec{\nabla }\bar{b} \right|\). In the top part of the plume, the cosine of the angle between the directions of the turbulent transport and the gradient of the mean buoyancy is substantially equal to 1, confirming that in this region of the flow the modeling hypothesis based on the Boussinesq assumption (16) holds. A different scenario is depicted from the inspection of the bottom of the figure; in the boundary regions the cosine changes sign altogether, clearly indicating counter gradient behavior of the turbulent transport. In the intermediate regions, the value of the cosine is neither close to 1 nor to \(-1\), suggesting that an anisotropic model should be invoked in this part of the flow. In order to obtain quantitative information on \(\kappa _T\), the anisotropy can be absorbed by contracting both sides of Eq. (16) with the buoyancy gradients \(\partial \bar{b}/\partial x_i\), following a similar approach to the eddy viscosity. Unfortunately, even with this procedure, a direct calculation of \(\kappa _T\) from (16) is not completely well defined, as the contraction of \(\partial \bar{b}/\partial x_i\) with itself tends rapidly to zero at the plume boundary, and at points within the plume as well, as seen in the right plot of Fig. 9. In any case, the inspection of the plot would confirm the need for a large quantitative variation of the eddy diffusivity in the (y, z) plane to obtain a point-wise correspondence between the turbulent flux of buoyancy and the modeled one.

On the other hand, a characteristic eddy diffusivity \(\kappa _{Tm}\) for a given distance from the plume source can be constructed by means of the same arguments as (13) and it is defined as

$$\begin{aligned} \kappa _{Tm}= & {} -\bigg ( \iint _{\Omega } \overline{u_k'b'} \frac{\partial \bar{b}}{\partial x_k} \; \textrm{d}y \; \textrm{d}z \bigg ) \nonumber \\{} & {} \qquad \bigg (\iint _{\Omega } \frac{\partial \bar{b}}{\partial x_l}\frac{\partial \bar{b}}{\partial x_l} \; \textrm{d}y\; \textrm{d}z \bigg )^{-1}. \end{aligned}$$
(17)

Figure 10 demonstrates its x-behaviour alongside \(\nu _{Tm}\). It is observed that the local maxima for both quantities around \(x/r_0=6\) are too small compared to the statistical noise to be given a physical meaning and hence we can assume that \(\kappa _{Tm}\) is also roughly constant in the fully developed region of the flow. This implies that the mixing of temperature within the plume is consistent for any cross section in the fully developed flow. The temperature will also disperse similarly throughout the plume, simplifying the prediction of heat transfer dynamics in the modelling of this type of flow. However, it is important to stress that a constancy assumption of the eddy diffusivity does not account for the spatial variations in the flow fields within the plume, as already discussed for Fig. 9, and instead \(\kappa _{Tm}\) should be regarded as a bulk property of the plume. Instead, the presence of the large peak on the downstream edge of the plume at approximately \(x/r_0=2\) suggests a more complex mechanism for the mixing of temperature in the early development.

Fig. 9
figure 9

Left: Cosine of the angle between \(-\overline{\textbf{u}'b'}\) and \(\varvec{\nabla }\bar{b}\) at \(x/r_0=15\) inside the plume—red = parallel, blue = anti-parallel. Right: \(-\overline{u'_i b'}\frac{\partial \bar{b}}{\partial x_i}\) (left half) mirrored with \(\frac{\partial \bar{b}}{\partial x_i}\frac{\partial \bar{b}}{\partial x_i}\) (right half) for the same cross section

Full size image
Fig. 10
figure 10

Plot of \(\kappa _{Tm}/r_m U\) and \(\nu _{Tm}/r_m U\) (left) and \(\mathrm{{Pr}}_{Tm}\) (right) as functions of \(x/r_0\)

Full size image

A characteristic integral turbulent Prandtl number can further be defined via \(\mathrm{{Pr}}_{Tm}=\nu _{Tm}/\kappa _{Tm}\), which returns an approximately constant value of \(\mathrm{{Pr}}_{Tm}=0.45\) from \(x/r_0=5\), as shown in Fig. 10. This definition of \(\mathrm{{Pr}}_{Tm}\) is consistent with that of Craske et al. [33], who analytically demonstrate the the turbulent Prandtl number in a pure plume with Gaussian velocity profile is a constant, equal to 3/5. The fact that the characteristic Prandtl number is constant throughout the fully developed region of the flow indicates that the turbulent mixing of momentum and heat is strongly coupled, and occurring in a consistent manner throughout the plume, despite variations in the plume geometry such as its trajectory and width as it is swept downstream. This observation is significant, as it suggests the plume is behaving in a consistent and predictable way throughout the flow despite geometrical changes, which could have important implications for the modelling of such flows in the far field. Furthermore, it lends credence to the assumption used in many key theoretical models of turbulent plumes, that the plume is behaving in a self-similar manner, implying that the forced plume in crossflow under these conditions could be described by a set of governing equations that are independent of specific flow geometry, simplifying the modelling of such flows. Further work is required to establish whether altering the flow conditions, such as raising or lowering the source-to-crossflow velocity ratio \(R_0\) or implementing a less idealised inlet boundary condition, impact these findings.

5 Conclusion

In this study, a detailed phenomenological assessment of a forced buoyant turbulent plume in crossflow has been conducted via the analysis of a very large DNS dataset. The instantaneous and Reynolds-averaged flow field structures have been reported, along with various measures of the plume trajectories, with particular mention given to the discrepancy between this forced plume and the infinitely lazy plume of previous studies. In order to inform future modelling efforts, the large amount of available data have been utilised to evaluate the pointwise behaviour of eddy viscosity and diffusivity. We have demonstrated that a detailed model for Reynolds stresses and buoyancy turbulent flux is far from trivial, with instances of negative turbulent production and countergradient turbulent transport for buoyancy that challenge classical RANS models based on the Boussinesq approximation. Successively, we have constructed a characteristic eddy viscosity and diffusivity, based on an integral approach, which gives x-dependent functions of these quantities. For this particular flow parameterisation these are shown to be approximately constant in the fully developed plume. The resultant constant value of the turbulent Prandtl number indicates the self-similarity of the flow fields, and further suggests the mechanisms involved in the mixing of momentum and temperature are one and the same. Additional DNS studies are required to investigate the impact of varying parameters such as the source-to-crossflow velocity ratio or the inlet boundary condition on these findings, to give further modelling insight.