Geometry and spatial reasoning are a critical mental foundation for learning other topics in mathematics (Clements et al., 2018). Figures play a predominant role. Lemonidis (1997) analyzed the characteristics of geometrical figures and described the way in which students use the figures in order to learn basic mathematical concepts (e.g., area). A figure is a representation of a geometrical situation easier to understand compared to a representation with linguistic elements only. From understanding the data in a given figure to using it for reasoning, proving, and solving problems, there is a path (Daher & Jaber, 2010). The geometrical figure is used for constructing either the arguments or the proof. In Japan, constructing arguments as part of reasoning is introduced at an early age, and later on, in Grades 7–9, students are also introduced to the significance and methodology of a formally structured geometric proof (Fujita & Jones, 2014).

Although geometry is an important part of the mathematics curriculum (Clements et al., 2018), students do not show strong conceptual knowledge and sometimes consider it to be a different domain. A known characteristic of geometry is “its dual nature as simultaneously a theoretical domain and perhaps the most reality-linked part of mathematics” (Fujita et al., 2010, p. 3). As a consequence, when examining the properties of geometrical objects, students generate various conjectures based on experimental verification. Kaur (2015) argues that many of the difficulties that students face in geometry occur during the transition from primary to secondary education. Despite the fact that many changes regarding students’ knowledge, abilities, and performance (Commission for Educational Reform, 2005) occur in the transition from lower to upper secondary school, research has paid limited attention.

Teaching methods, students’ performance, and misconceptions, as well as the use of different representations in relation to spatial abilities, are a few of the geometrical understanding perspectives which are usually investigated. In order to manage students’ misconceptions, researchers suggest technology (e.g., Chivai et al., 2022; Laborde et al., 2006; Sinclair et al., 2017) or alternative teaching methods (Abdeen et al., 2022). There are studies examining students’ learning achievements in geometry in relation to their motivation, beliefs, and attitudes (e.g., Pambudi, 2022). Additionally, other studies relate geometrical figure apprehension to geometrical proof (Miyazaki et al., 2022) or present different models which include the role of visualization (e.g., Dundar et al., 2012). There are approaches focusing explicitly on figures and visualization and have therefore established the theoretical frameworks for the learning of geometry (e.g., Duval, 1988; Fischbein, 1993; Houdement & Kuzniak, 2003; van Hiele, 1986).

The present study examines lower and upper secondary school students’ cognitive understanding of the geometrical figure based on Duval’s approach (Duval, 1995, 1998). Duval’s starting point is the use of a geometrical figure as a helpful tool to solve a geometrical problem. According to his theory, students’ performance is analyzed according to the various types of geometrical figure apprehension: the perceptual, the operative, the sequential, and the discursive type. We consider that such a large-scale quantitative study on students’ performance would be useful to interpret students’ understanding of geometrical figures. Having in mind the difficulties observed in the transition from one educational level to another, such as changes in students’ attitudes regarding school subjects, self-confidence, beliefs, competence, and performance (Mullins & Irvin, 2000), with this study, we aim to identify similarities, differences, and problems that may occur in the transition from lower to upper secondary education.

We believe that there is a need to investigate students’ cognitive processes and the type of apprehension they use during the resolution of geometrical tasks and examine whether these lead to a proper way of “looking” at a geometrical figure. There are many factors that can inhibit these visual operations, which can be studied experimentally. Thus, the present study constitutes an attempt to identify the factors relating to the apprehension of geometrical figures. The following research questions were posed:

  1. 1.

    Can the cognitive structure of geometrical figure apprehension, as proposed by Duval, be confirmed empirically?

  2. 2.

    What are the interrelations between the different types of geometrical figure apprehension?

  3. 3.

    How do lower and upper secondary school students perform in geometrical figure apprehension tasks?

1 Theoretical framework

Geometrical research in the 1970s concentrated on the relationship between spatial abilities and mathematical learning and problem solving (Owens & Outhred, 2006). During the next decades, visual representations as well as the process of visualization gained an important role in geometry learning (Zakelj & Klancar, 2022). Several theoretical models about geometry learning look at geometrical figures and their use, but the figure itself is not the main target of their inquiry. Only a few approaches study figures explicitly (e.g., Duval, 1988; Fischbein, 1993; van Hiele, 1986). Van Hiele (1986) developed a model referring to levels of geometric thinking (visualization, analysis, abstraction, deduction, and rigor) which led to a hierarchical teaching of geometry. The emphasis was not on the cognitive processes but rather on the cognitive characteristics of each age and the respective teaching content. This specific model has led to the belief that students who have difficulties understanding geometrical concepts are being taught at a higher Van Hiele’s level (geometrical thinking level) than the one they are ready for. Students use geometrical figures according to their cognitive abilities: for example, in the first level, the figure is recognized as an image, while in the second level, mathematical properties are recognized through the figure.

Fischbein (1993) introduced the theory of figural concepts and Samara and Clements (2009) proposed a six-level theory about the composition and decomposition of geometrical figures, according to which children begin forming a conceptual understanding of geometric figures in the early childhood years (Clements et al., 2018). Fischbein (1993) attempted to interpret geometrical figures as mental entities with both conceptual and figural properties. He observed that while a geometrical figure can be described as having intrinsically conceptual properties, it is not solely a concept, but it is an image too. He argues that all geometrical figures represent mental constructs which possess both conceptual and figural properties, and that geometrical reasoning is characterized by the interaction between the figural and the conceptual aspects.

Parzysz (1988) has described the distinction between drawings and figures. In the first case, there is a presentation of a picture, while in the second case, the object is represented by the drawings as a tool that students must manage in order to make productive use of a diagram in formulating a geometric argument. He noted that students’ activity in geometry involves “knowing” and “seeing” as a mix of observational deduction (Mithalal & Balacheff, 2019). As Karpuz and Atasoy (2019) claim because geometric figures cannot be considered independent of concepts, students need to establish accurate relationships between a geometric figure and its properties which are used for mathematical proof. Duval (2005) explains that there are two modalities of visualization which guide the exploration and the interpretation of a figure: the iconic and the non-iconic. In the first case, one recognizes an object because its shape is similar to an already known object. In the second case, the figure is a representation of a geometrical object.

1.1 Duval’s cognitive approach: types of geometrical figure apprehension

Duval (1988) analyzed the different possible ways of seeing a geometrical figure. He suggested that in order to analyze the heuristic role of geometrical figures, a figure must be seen through cognitive apprehension. He distinguished four apprehensions of a geometrical figure: the perceptual, the sequential, the operative, and the discursive. Each type of apprehension has its specific laws of organization and processing of the visual stimulus array (Panaoura & Gagatsis, 2008).

According to Duval, the perceptual apprehension of a figure is an organization of elements, which, depending on the number of its dimensions, can be points, lines, areas, or planes. Points and lines are respectively characterized by their discrete or continuous character, while areas are characterized by their form (Duval, 1988). People recognize something (a shape, a representation of an object, etc.) in a plane or in depth at first glance. Figural organization laws and pictorial cues determine what the perceived figure shows (Duval, 1994). The perception of the figure results from an unconscious integration, and thus, the perceived figure can differ from the retinal image. The retinal image can change, while the perceived properties of the figure (shape, size, brightness, etc.) remain the same. This is called perceptual constancy. People are also able to name what they recognize and to discriminate and recognize several subfigures in the perceived figure.

Sequential apprehension happens when a construction of a figure or its description is needed. The different figural units that emerge by the construction of the figure occur following a specific order. The organization of the elementary figural units does not depend on pictorial cues and laws but on technical constraints and mathematical properties. These technical constraints depend on the tools that are used for the construction of figures, which can be a ruler and compass or available primitives in geometrical software.

Duval states that operative apprehension becomes a starting point in order to investigate other configurations that can be obtained by visual operations. A related difficulty is due to the fact that for a given figure, various figural modifications are possible, as well as many operations to bring them out (Duval, 1995). Also, the ability to divide the geometric figure into parts is one of the outward signs of operative apprehension (Duval, 1999).

Discursive apprehension of a figure corresponds to the explicitness of other mathematical properties of the figure besides those that are indicated from the stated hypothesis (which make certain properties explicit and presented in the figure). Sometimes, the properties that are seen in a geometric figure are not the same for everyone (Duval, 1995). What the figure can represent depends on the deductive dependence between statements. For this reason, it is possible to have a gap between what the figure shows and what it represents (Duval, 1995). Duval claims that the transition from the geometry of drawing to the geometry of figures requires a double transition from iconic to non-iconic visualization and from instrumental deconstruction to dimensional deconstruction.

The students’ apprehension of a mathematical concept is not independent of the corresponding teaching methodology. The present study has been conducted in a centralized educational context where the teaching methodology is based on suggestions proposed through the textbooks which are commonly used. The textbook analysis which is presented in the following section was necessary in order to construct an instrument which could take into consideration the expected students’ geometric figure apprehension.

1.2 Textbook analysis

For the present study, we relied on Michael’s (2013) textbook analysis to decide which types of Duval’s geometric figure apprehension could be included. The educational system in Cyprus is centralized in the sense that the curriculum, the textbooks, and the teaching materials are all common and produced by the Ministry of Education (Maths Curriculum, 2010). It is widely acknowledged that school textbooks reflect the aims of the curriculum (Pepin & Haggarty, 2002), so if someone needs to understand the teaching methodology of a mathematical concept, he/she can study the structure which is presented in a textbook. The analysis focused on the last grade of lower secondary and the first two grades of upper secondary school textbooks. Michael (2013) analyzed the content of mathematics textbooks regarding geometry and placed each example, exercise, or task in one of the four categories according to the type of apprehension that was required for its solution. Michael–Chrysanthou found that most of the exercises for Grades 9, 10, and 11 require the activation of perceptual apprehension and that the number of exercises demanding perceptual apprehension decreases from lower to upper secondary school. On the other hand, the number of exercises involving discursive and operative apprehension increases from lower to upper secondary school. The analysis of the presented examples in the textbooks gave different results. The majority of examples in the mathematics textbooks of all three grades involved perceptual apprehension, while only a small percentage of examples required operative apprehension. As for discursive apprehension, a small number of examples mobilizing this type of apprehension appear in Grade 9 only. Usually, the examples presented for the understanding of a concept and the exercises are analogous. In this specific case, the number of exercises requiring operative and discursive apprehension increased from lower to upper secondary grades, while the number of presented examples decreased. According to the geometry content examined, perceptual apprehension was the dominant type of apprehension required in both the exercises and the examples, as it intervened in the solution of most of the textbook tasks.

It is noteworthy that in all three grades examined (Grades 9, 10, and 11), the perceptual, operative, and discursive apprehension types were mainly involved in the different figures presented. For this reason, we excluded the examination of sequential apprehension from the specific study. It was almost absent from the secondary education curriculum in Cyprus, and we therefore assumed that students would not be able to solve tasks demanding sequential apprehension. The results of the specific analysis together with Duval’s theoretical framework were the base for the model presented and examined in this study.

1.3 Hypothesized model of students’ geometrical figure apprehension

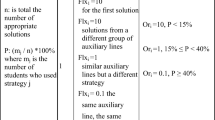
The two-level hierarchy model examined the three different grades about the role of perceptual, operative, and discursive figure apprehension types, as defined in Duval’s theoretical perspective. The model involved three first-order factors: perceptual (PE), operative (OP), and discursive (DI) geometrical figure apprehension which were regressed on a second-order factor that stands for geometrical figure apprehension. The model was examined based on the hypothesis that interrelations exist among the three first-order factors (Fig. 1), rather than a second-order model. The instrument given to the students consisted of two perceptual apprehension tasks (PE1, PE2), four operational apprehension (OP1, OP2, OP3, OP4) tasks, and four tasks involving discursive apprehension (DI1, DI2, DI3, DI4). The theoretical model examined had to be consistent with the expected cognitive processes. The qualitative analysis of students’ answers led us to discriminate between two ways of solving OP2 (OP2op and OP2al), and therefore, the examined model was constructed accordingly. The specific task (OP2) enabled students to work on it in two different ways. The first was based on the functional understanding of the figure (denoted as OP2op); it concerns the transformation of the original figure, and therefore, it naturally belongs to the operative apprehension category. However, many students chose the algorithmic way of solving the task, used the formula of finding the area of the trapezoid, and solved the equation (OP2al). We assume that students who choose this solution either do not “see” the functional transformation of the shape of the trapezoid into a rectangle or follow the implicit teaching contract, according to which they need to use a formula to solve a problem. Two indicative examples of the different types of solutions for task OP2 are presented below (Figs. 2 and 3).

Fig. 1
figure 1

The hypothesized model of interrelations of the three first-order factors

Full size image
Fig. 2
figure 2

An example of a solution based on the operational procedure (OP2op)

Full size image
Fig. 3
figure 3

An example of a solution based on the formula (Op2al)

Full size image

2 Methodology

2.1 Participants

The study examines secondary school students’ geometrical figure apprehension, with a special interest in the changes that occur during students’ transition from lower to upper secondary school. Lower secondary school courses are mandatory for all students. However, starting from Grade 10, students can choose their major courses with respect to their future plans. Mathematics can be chosen as a major course for students who intend to study engineering, economics, and natural sciences.

The study was conducted with 881 students from 17 urban and 4 rural secondary schools in Cyprus. The sample consisted of 312 Grade 9 (15 years old, 170 girls), 304 Grade 10 (16 years old, 170 girls), and 265 Grade 11 (17 years old, 163 girls) students. The sample was not representative of the respective population, as the schools were chosen based on the researchers’ network as well as the positive disposition of the school community to take part in a study without compensation.

2.2 Description of the instrument

We requested permission from the Ministry of Education in order to conduct the study. Participants’ parents gave their consent, and teachers agreed to administer the instrument according to the researchers’ instructions. The tasks included in the instrument were chosen after the researchers’ careful examination of the curriculum and after completing the content analysis of the mathematics textbooks presented previously. Our aim was to use tasks relevant to perceptual, operative, and discursive apprehension. We used tasks from our previous studies and modified them in order to fit the educational level of the participants (Deliyianni et al., 2010; Elia et al., 2009). The final paper and pencil instrument was administered by the mathematics teachers at each school. The teachers did not intervene during the solution of the tasks, and the duration was 80 min.

The instrument consisted of ten tasks examining perceptual (first group of tasks), operative (second group), and discursive (third group) apprehension. We present one task for each of the three modes of apprehension in order to explain how we score students’ responses (see all the tasks in the supplementary materials). The first group consisted of two tasks examining students’ perceptual apprehension (PE) that is students’ ability to discriminate, recognize, and name several subfigures in a complex figure. In task 1 (PE1), students were asked to identify the type of subfigures in the given figures. In task 2 (PE2), students were asked to identify and then name each square they recognize in the given figure (Fig. 4). For PE2, students identifying and naming correctly all squares (the seven squares HUST, UIKS, SKLM, TSMN, FXRS, SRPO, and HILN) were given a score of 1. Students identifying any number of false squares and giving a wrong total number were given a score of 0.

Fig. 4
figure 4

Task examining students’ perceptual apprehension (PE2)

Full size image

The second group of tasks consisted of four tasks that were expected to examine students’ operative apprehension of the geometrical figure. These tasks tested students’ ability to modify a geometrical figure, because figure reconfiguration was needed for their solution. In task 1 (OP1, see supplementary material), students were asked to compare the area of figures A and B. A reconfiguration of figure B, and the realization that by cutting its left part and moving it to the right, a rectangle similar to figure A is formed, led to the expected solution. Two different types of responses were identified, indicating different types of apprehension: when a student used the strategy of counting to find the answer, perceptual apprehension was activated, whereas when a student added some new lines to the figure, the operative approach was activated, since this strategy involved figure modification.

In task 2 (OP2), students were asked to find the length of the missing side of the rectangle, using the idea that the area of the rectangle is equal to the area of the trapezium (Fig. 5). Based on students’ solutions, we made assumptions about their way of thinking. Students were expected to reconfigure the trapezium pieces into a rectangle and solve the task by visualization only, using operative apprehension (OP2op) and without the need for formulas or calculations. However, there were students who recognized the trapezium as a whole figure, and they solved the task using the formula of the area of the trapezium. In this case, we assumed that the solution revealed a discursive perspective (OP2al), mainly related to an algebraic approach.

Fig. 5
figure 5

Task 2 (OP2) examining students’ operative apprehension

Full size image

In task 3 (OP3), students were asked to compare the perimeter of two figures (see supplementary material). In this task, it was anticipated that students would reconfigure the pieces by dividing and moving them in order to get two identical figures and then check the equivalence of their perimeters. Additionally, there could be students who solved the task by “flipping” the small curves mentally.

Task 4 (OP4) of this group includes a rectangle, divided into different subfigures (triangles and rectangles) (see supplementary material). In figure ABCD, the diagonal AC divides the rectangle into two equal right-angled triangles (ADC and ABC). Each of these triangles includes two other right-angled triangles, resulting from the division of the two white rectangles shown in figure ABCD respectively. From the triangles ADC and ABC, equal parts are subtracted, and thus, rectangle 1 and rectangle 2 have equal areas. For this solution, operative apprehension was necessary in order to discriminate the different reconfigurations and recognize the relations between these subfigures.

Next, four tasks examined discursive apprehension. In task DI1, students were asked to evaluate a statement related to the length of a segment (NH) and explain their choice (see supplementary material). Students’ answers were considered correct when a correct proof that NH = MH was given. In task DI2, students were given information about subfigures that were included in a whole figure and had to prove that three sides (AC, LF, and FG) were equal. Thus, students were expected to make an inference, based on the properties of the geometrical figures.

In task DI3, students were expected to make an inference using Thales’ theorem and prove the statement by explaining that the segment that joins two midpoints is parallel to the opposite segment and equal to its half. In this task, the mathematically correct answers involved proofs using this theorem with each of the three parallelograms (Fig. 6).

Fig. 6
figure 6

Task 3 (DI3) examining students’ discursive apprehension

Full size image

Task DI4 assesses students’ ability to construct a figure based on data (Fig. 7). Students’ success in this task is determined by whether the arc they construct is equal to the one given. Although it is a construction task, students are also asked to describe the way they constructed the geometrical figure, to ensure that they followed a mathematically correct procedure and that they did not draw a random arc. Thus, the use of discursive apprehension is necessary for the successful description of the construction procedure, as students need to base their answers on a theoretical system of reference and give mathematical properties through language.

Fig. 7
figure 7

Task 4 (DI4) examining students’ discursive apprehension

Full size image

The initial content validity of the instrument was assessed by two mathematics supervisors working at the Ministry of Education (holding a PhD) and three mathematics teachers (who were teaching in Grades 9, 10, and 11 the previous year). The mathematics teachers confirmed that the wording of the tasks was clear and that the time participants would have to complete the instrument was adequate. The two supervisors confirmed that the tasks assessed the different types of apprehension we were investigating. The reliability of the research instrument can be considered to be satisfactory, as the calculation of Cronbach a, after conducting the study, gave a value higher than 0.75 (Cronbach’s a = 0.803, p < 0.05) (Cronbach, 1990).

There are two methodological limitations of the study. First, even though the sample was large, it was not representative of the respective student population at this age (almost 18,000 students), as schools and students were not selected randomly. However, we are talking about a small country, with a centralized educational system, and the results are interpreted in a specific context. The participation of schools which indicated a positive disposition toward the aim of the study enables us to assume that students probably completed the instrument by putting in the necessary effort. As for the second limitation, our analysis was based on participants’ written responses only, while cognitive interviews could have revealed the involvement of specific cognitive processes. Based on this limitation, a follow-up study could be conducted, characterized by a qualitative perspective.

3 Results

In this section, we present the results of the statistical analyses addressing the research questions of the study. First, we present the cognitive structure and the respective interrelations between the different types of the geometrical figure apprehension model examined. Then, we discuss students’ performance in geometrical figure apprehension tasks by focusing on the differences in students’ geometrical figure apprehension in lower and upper secondary school.

3.1 Cognitive structure and the respective interrelations between the different types of geometrical figure apprehension

The examination of the structure of geometrical figure apprehension was conducted by using the confirmatory factor analysis, through the use of structural equation modeling. The tenability of the models for the sample in total and the different grades were determined by using the accepted measures of goodness of fit: χ2/df < 2, CFI > 0.90, and RMSEA < 0.06 (Kline, 1998). Three models were tested in order to ensure that the theoretical model fits the data better than other models: the first-order factor structure of geometrical figure apprehension was first investigated in order to confirm that all the variables do load on only one first-order factor associated with all the tasks. This model tests the assumption that a single source of variance is sufficient to account for performance on all tasks addressed to the participants of the research. The fit of this model was poor [χ2(34) = 7.156, CFI = 0.852, RMSEA = 0.32].

Then, the theoretical model about the structure of geometrical figure apprehension was examined for the total sample and the three grades independently (Fig. 8). A chi-squared difference test indicated a significant improvement in fit between the first (with all the variables loaded on one factor) and the second model (Δχ2(7) = 21.401, p < 0.05) due to the second-order factor. The first first-order factor included the two perceptual apprehension tasks in which students were asked to recognize and name geometrical figures that were included in a geometrical figure (PE1 and PE2). The second first-order factor consisted of tasks (OP1, OP2op, OP3, and OP4) that examined students’ operative apprehension of a geometrical figure. The third group of tasks examined students’ discursive apprehension (OP2al, DI1, DI2, DI3, and DI4). These three first-order factors corresponded to perceptual, operative, and discursive apprehension respectively and were regressed on the second-order factor standing for geometrical figure apprehension. The fit of the model was acceptable in all cases [Grade 9: χ2(27) = 52.741, CFI = 0.972, RMSEA = 0.25; Grade 10: χ2(27) = 49.221, CFI = 0.984, RMSEA = 0.27; Grade 11: χ2(27) = 51.506, CFI = 0.956, RMSEA = 0.31]. The instrument seems to distinguish between three types of geometrical figure apprehension.

Fig. 8
figure 8

The structural model of geometrical figure apprehension

Full size image

In the last model (Fig. 9), the majority of the loadings of the observed variables on the first-order factors are higher for the upper secondary school students, especially for Grade 11. It is also noteworthy that some loadings of the first-order factors on the second-order factor are higher in the group of the upper school students (Grades 10 and 11) suggesting that the specific structural organization potency increases across the two educational levels (the loadings of OP on geometrical figure apprehension are lower than 0.800, and the loadings of DI on GFA are lower than 0.900 only in the case of Grade 9). More importantly, the loadings are higher in Grade 10 than in Grade 11 indicating that the model fits better at this age.

Fig. 9
figure 9

Interrelations among the three first-order factors for the total sample and the three grades

Full size image

In a third model, we examined the interrelations among the three first-order factors (Fig. 10). As it was expected, the fit of the model was acceptable [Grade 9: χ2(30) = 51.201, CFI = 0.973, RMSEA = 0.27; Grade 10: χ2(30) = 48.153, CFI = 0.982, RMSEA = 0.26; Grade 11: χ2(30) = 55.127, CFI = 0.964, RMSEA = 0.35]. Two extremely high and statistically significant interrelations were found: (a) between perceptual and operative apprehension and (b) between perceptual and discursive apprehension. This phenomenon could have two possible explanations: the instrument’s tasks involved different types of apprehension at the same time (it is rejected due to the lack of good fit in the case of a one-factor model) or students with high operative apprehension are students who also show high perceptual apprehension (while the relation with discursive apprehension is not so strong). It seems that perceptual apprehension has a predominant role among the other two types of geometric apprehension. The interrelations between operative and discursive apprehension were not so strong, indicating that there are students who have high performance in operative tasks and lower performance in discursive tasks, and vice versa.

Fig.10
figure 10

Mean scores of the three groups in the three types of apprehension

Full size image

3.2 Lower and upper secondary school students’ performance in geometrical figure apprehension tasks

The interrelations between the types of apprehension in the different grades indicated that there were differences which could be further examined through the use of descriptive analysis. In order to be able to further analyze the different types of understanding among the three grades, we calculate the mean performance and the standard deviations of the three main apprehension types which were confirmed previously (Table 1).

Table 1 Mean performance and the standard deviations of the three types of apprehension by grades
Full size table

An analysis of variance (ANOVA), using Scheffe’s test, revealed that in the case of perceptual apprehension (F2,879 = 17.888, p < 0.05) and operative apprehension (F2,879 = 18.497, p < 0.05), there were statistically significant differences between the participants’ scores in Grade 9 and the two other grades. In the case of the mean scores in discursive apprehension (F2,779 = 14.625, p < 0.05), there were statistically significant differences between all grades. As it is obvious in Fig. 10, there is an increase from the lower to the upper secondary grades, especially in perceptual and operative apprehension, which seems to stabilize in upper secondary education. The scores in the discursive apprehension tasks have a continuing increase, despite the means being low.

Because the discursive apprehension scores are the lowest across the three grades, we suggest that discursive apprehension requires a higher-order cognitive process. By using cluster analysis, we divided participants into three groups based on their performance in the discursive apprehension tasks. In the low-performance category, there were 245 participants; in the medium-performance category, there were 439 participants; and in the high-performance category, there were 197 participants. The mean performance of students with low, medium, and high discursive apprehension in perceptual and operative apprehension is presented in Fig. 11. The differences were statistically significant between all the groups in the case of perceptual apprehension (F2,779 = 54.443, p < 0.05) and the operative apprehension (F2,779 = 56.663, p < 0.05). Students with high scores in discursive apprehension have high scores in both perceptual and operative apprehension. In contrast, students with low or medium discursive apprehension scores have lower scores in perceptual than in operative apprehension. This confirms the previous finding that there are students with high scores in operative and low scores in perceptual tasks.

Fig. 11
figure 11

Mean scores of the three groups of all participants in perceptual and operative apprehension. PE = perceptual apprehension, OP = operative apprehension, DI = discursive apprehension

Full size image

We pursued a similar analysis in order to investigate differences by grade. In lower secondary education (Grade 9), the differences concerning perceptual apprehension were statistically significant between all three groups (F2,311 = 20.271, p < 0.05). Similarly, in upper secondary education (Grade 10), the differences were statistically significant between all the groups (F2,303 = 9.107, p < 0.05). As far as operative apprehension is concerned, statistically significant differences were found between the group with low scores in discursive apprehension and the two other groups (with medium and high scores) (F2,311 = 16.495, p < 0.05). Finally, in Grade 11, the differences were statistically significant between all the groups (F2,264 = 20.983, p < 0.05), both in perceptual and operative apprehension (F2,264 = 20.923, p < 0.05). The scores between the groups with low and medium performance were similar (Fig. 12).

Fig. 12
figure 12

Mean performance scores in perceptual and operative apprehension of the three age groups (Grades 9, 10, and 11). PE = perceptual apprehension, OP = operative apprehension, DI = discursive apprehension

Full size image

Results indicated that, in all cases, students with high scores in discursive apprehension are students with high scores in perceptual and operative apprehension and that those types of apprehensions are at the same level. However, students with medium or low discursive apprehension have higher performance in operative than in perceptual apprehension.

4 Discussion

Geometry is related to various spatial skills, and geometrical problems are usually accompanied by figures which have to be understood and used (Gridos et al., 2021). Duval’s cognitive model theorizes processes experienced during figure apprehension which he named figure apprehension processes. The present study constitutes an effort to confirm students’ geometrical figure apprehension dimensionality via the use of an instrument that assesses three different types of apprehension: the perceptual, the operative, and the discursive type. This instrument can be used in the future for relating geometrical figure apprehension to other cognitive processes. We used the instrument to investigate the possible differences in geometrical figure apprehension of students transitioning from lower to upper secondary school. The confirmed structure of the instrument is independent of age, although there are differences in the loadings of the variables and tasks that highlight its value as a research tool. However, it seems to be more stable in Grade 10 (with higher loadings). The low means of correct responses in the different types of apprehension tasks confirmed the recent results of Karpuz and Atasoy (2019) that the perceptual, discursive, and operative types of students’ apprehension can be further improved. In fact, this seems to continue after secondary education, as Ramatlapana and Berger (2018) revealed the difficulties of prospective mathematics teachers in connecting visualization and reasoning, because of their weak perceptual and discursive apprehension. The present study indicated interrelations between the different types of geometrical figure apprehensions, without examining any relations of causality which could lead to specific teaching interventions. This could be the main purpose of a follow-up study which will further enrich the respective theoretical framework.

Three out of the four types of geometrical figure apprehension examined through this instrument seemed to corroborate a hierarchical level (Fig. 13). Based on Duval’s theory, in order for any drawing to act as a geometrical figure, it must provoke perceptual apprehension and at least one of the other types of apprehension. However, on its own, perceptual apprehension is not a predictor of the other types of apprehension. Students with high scores in discursive apprehension have at the same time similar and high scores in perceptual and operative apprehension. On the contrary, students with low scores in discursive apprehension have lower scores in perceptual tasks than in operative tasks. This finding underlines the predominant role of discursive tasks in order to ensure the success of the other types of geometric apprehension and probably the didactic emphasis which has to be given to the specific type of apprehension. It seems to contrast with the teaching practice of emphasizing the use of perceptual apprehension examples and tasks, with respect to Michael’s (2013) textbook analysis.

Fig. 13
figure 13

The hierarchical levels of geometrical figure apprehension

Full size image

At the perceptual apprehension level, according to Duval’s theory, information about the geometric elements of a figure can be obtained at first glance, and this first impression is what leads to either a correct or a wrong solution. This level is assumed to be a prerequisite for operative apprehension tasks which ask for either a decomposition of a given geometric figure or the concentration on some parts of a figure independently of position or direction. Discursive apprehension presupposes the presence of perceptual apprehension. In the tasks of the perceptual and operational factors, there is evidently the common element of perceptual apprehension. However, this is not sufficient for solving the three tasks of the operational apprehension level. Additionally, in the first task of the trapezium (OP1), additional mental or design movement of one triangle is required so that the figure is transformed into its equivalent rectangle. In the second task (OP2), it additionally requires the mental rotation or the redesign of the curves of the second figure so that it becomes apparent that there is equality of perimeters. Finally, in the third figure (OP3), a mereological approach is required, namely, the removal of equivalent shapes from other equivalent shapes in order to obtain the desired result.

Students’ scores in the different types of geometrical apprehension tasks allow for an interpretation relative to Houdement and Kuzniak’s (2003) theoretical framework by defining the types of geometry in which students’ work is situated. Our results indicate that three levels of geometrical skills can be determined as described in Table 2. There is a relation between the different clusters of students and school grades (9, 10, and 11). We expect many students to be fluent in recognizing and naming figures and in decomposing a given figure (mereological apprehension), while few of them will properly relate their theoretical geometrical knowledge and reach a formal proof, under the control of the discursive figure apprehension. We expect that students with high scores in geometric apprehension tasks are mostly Grade 11 students. In the second cluster, we expect students with the lowest scores in perceptual recognition. They are not restrained to what the eye captures at the first glance of a figure, and the system of reference does not always seem to be necessary. Thus, it seems that students with low perceptual figure apprehension will show moderate ability in solving geometrical problems. We expect that Grades 9 and 10 students belong to this second group. Finally, in the third group, we expect students with a weak perceptual figure apprehension. A prerequisite for a drawing to function as a figure is perceptual apprehension, and the students with low scores will show low ability in solving geometrical problems and low perception, visualization, and discursive processes. As Kuzniak and Rauscher (2011) claim, students’ work is mostly produced using arguments based on perception. Overall, the transition from lower to upper secondary education seems to be related to a progression from Natural Geometry GI toward Natural Axiomatic Geometry GII.

Table 2 Geometrical apprehension scores and types of geometrical work
Full size table

5 Conclusion

The present study is exploratory; we plan to replicate the findings after conducting cognitive interviews so as to investigate the cognitive load of the different processes used. Secondary education curricula need to include activities that develop students’ figure apprehension processes in order to help them understand and construct geometrical proofs. Geometrical tasks addressing different types of apprehension need to be included on purpose taking into consideration students’ difficulties with each type of geometric apprehension during different secondary school ages. The instrument which was conducted in the present study can be used in other studies in order to confirm the structure of the geometric figure apprehension at the specific ages, identify causal relations, and then intervene didactically by accepting those different forms of apprehension with the aim to improve the related students’ geometrical performance. The possible hierarchical structure of figure apprehension reveals the necessity to study further the curriculum in order to examine the degree of identification. A future study can focus on other characteristics of students, teachers, and schools such as gender, learning or cognitive style, teaching style, and type of school.