Abstract
Mathematical modelling competencies have become a prominent construct in research on the teaching and learning of mathematical modelling and its applications in recent decades; however, current research is diverse, proposing different theoretical frameworks and a variety of research designs for the measurement and fostering of modelling competencies. The study described in this paper was a systematic literature review of the literature on modelling competencies published over the past two decades. Based on a full-text analysis of 75 peer-reviewed studies indexed in renowned databases and published in English, the study revealed the dominance of an analytical, bottom-up approach for conceptualizing modelling competencies and distinguishing a variety of sub-competencies. Furthermore, the analysis showed the great richness of methods for measuring modelling competencies, although a focus on (non-standardized) tests prevailed. Concerning design and offering for fostering modelling competencies, the majority of the papers reported training strategies for modelling courses. Overall, the current literature review pointed out the necessity for further theoretical work on conceptualizing mathematical modelling competencies while highlighting the richness of developed empirical approaches and their implementation at various educational levels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Modelling and applications are essential components of mathematics, and applying mathematical knowledge in the real world is a core competence of mathematical literacy; thus, fostering students’ competence in solving real-world problems is a widely accepted goal of mathematics education, and mathematical modelling is included in many curricula across the world. Despite this consensus on the relevance of mathematical modelling competencies, various influential approaches exist that define modelling competencies differently. In psychological discourse, competencies are mainly defined as cognitive abilities for solving specific problems, complemented by affective components, such as the volitional and social readiness to use the problem solutions (Weinert, 2001). In the mathematics educational discourse, Niss and Højgaard (2011, 2019) emphasized cognitive abilities as the core of mathematical competencies within their extensive framework, an updated version of which has recently been published; therefore, the question of how to conceptualize competence as an overall construct, with competency and competencies as associated derivations, remains open.
The discussion on the teaching and learning of mathematical modelling, which began in the 1980s, has emphasized the practical application of mathematical modelling skills; for example, the prologue of the proceedings of the first conference on the teaching and learning of mathematical modelling and applications (hereafter ICTMA) stated: “To become proficient in modelling, you must fully experience it – it is no good just watching somebody else do it, or repeat what somebody else has done – you must experience it yourself” (Burghes, 1984, p. xiii). This strong connection to proficiency may be one reason for the early development of the discourse on modelling competencies compared to other domains, such as teacher education.
Despite this broad consensus on the importance of modelling competencies and the relevance of the modelling cycle in specifying the expected modelling steps and phases, no worldwide accepted research evidence exists on the effects of short- and long-term mathematical modelling examples and courses in school and higher education on the development of modelling competencies. One reason for this research gap may be the diversity of instruments for measuring modelling competencies and the lack of agreed-upon standards for investigating the effects of fostering mathematical modelling competencies at various educational levels, which depends on reliable and valid measurement instruments. Finally, only a few approaches have addressed or further developed the construct of mathematical modelling competencies and/or its descriptions and components. Precise conceptualizations of mathematical modelling competence as a construct are needed to underpin reliable and valid measurement instruments and implementation studies to foster mathematical modelling competencies effectively.
With this systematic literature review, the results of which are presented in this paper, we aimed to analyze current state-of-the-art research regarding the development of modelling competencies and their conceptualization, measurement, and fostering. This analysis hopefully will contribute to a better understanding of the previously mentioned research gaps and may encourage further research.
1 Theoretical frameworks as the basis for the research questions and analysis
To date, only one comprehensive literature review on modelling competencies—a classical literature search on modelling competencies by Kaiser and Brand (2015)—has been conducted, constituting an important starting point for the current discourse on mathematical modelling. Contrasting with the present systematic literature review using reputable databases, this classical literature review was based on the proceedings of the biennial ICTMA series. A study by the International Commission on Mathematics Instruction (ICMI) on modelling and applications (the 14th ICMI Study), conducted at the International Congress of Mathematical Education’s (ICME’s) international quadrennial congresses, reviewed related books published by special groups, together with special issues of mathematics educational journals and other journal papers. Based on this literature survey, the development of the discourse on modelling competencies since the start of the international conference series in 1983 was reconstructed by Kaiser and Brand (2015).
The review indicated that the early discourse addressed the constructs of modelling skills or modelling abilities, including metacognitive skills. The first widespread use of the modelling competence construct emerged with the 14th ICMI Study on Applications and Modelling, a separate part of which was devoted to modelling competencies (Blum et al., 2007). More or less simultaneously, the discussion on modelling competence, and its conceptualization and measurement, started at ICTMA12 (Haines et al., 2007) and continued at ICTMA14 (Kaiser et al., 2011), with both proceedings containing sections on modelling competencies.
In their literature review, Kaiser and Brand (2015) distinguished four central perspectives on mathematical modelling competencies with different emphases and foci. These four perspectives were characterized as follows:
-
Introduction of modelling competencies and an overall comprehensive concept of competencies by the Danish KOM project (Niss & Højgaard, 2011, 2019)
-
Measurement of modelling skills and the development of measurement instruments by a British-Australian group (Haines et al., 1993; Houston & Neill, 2003)
-
Development of a comprehensive concept of modelling competencies based on sub-competencies and their evaluation by a German modelling group (Kaiser, 2007; Maaß, 2006)
-
Integration of metacognition into modelling competencies by an Australian modelling group (Galbraith et al., 2007; Stillman, 2011; Stillman et al., 2010).
These perspectives shaping the discourse on modelling competencies followed two distinct approaches to understanding and defining mathematical modelling competence: a holistic understanding and an analytic description of modelling competencies, referred to as top-down and bottom-up approaches by Niss and Blum (2020).
In the following, we describe these two diametrically opposite approaches and identify intermediate approaches.
1.1 A holistic approach to mathematical modelling competence—the top-down approach
The Danish KOM project first clarified the concept of modelling competence, which was embedded by Niss and Højgaard (2011) into an overall concept of mathematical competence consisting of eight mathematical competencies. The modelling competency was defined as one of the eight competencies, which were seen as aspects of a holistic description of mathematical competency, in the sense of Shavelson (2010). The modelling competency was defined by Niss and Højgaard (2011) as follows:
This competency involves, on the one hand, being able to analyze the foundations and properties of existing models and being able to assess their range and validity. Belonging to this is the ability to ‘de-mathematise’ (traits of) existing mathematical models; i.e. being able to decode and interpret model elements and results in terms of the real area or situation which they are supposed to model. On the other hand, competency involves being able to perform active modelling in given contexts; i.e. mathematising and applying it to situations beyond mathematics itself. (p. 58)
In their revised version of the definition of mathematical competence, Niss and Højgaard (2019) explicitly excluded affective aspects such as volition and focused on cognitive components. Referring to the mastery of the modelling competency, Blomhøj and Højgaard Jensen (2007) developed three dimensions for evaluation:
-
Degree of coverage, referring to the part of the modelling process the students work with and the level of their reflection
-
Technical level, describing the kind of mathematics students use
-
Radius of action, denoting the domain of situations in which students perform modeling activities.
Niss and Blum’s (2020) description of these approaches called this definition the “top-down” definition, referring explicitly to the expression “modelling competency” as singular, denoting a “distinct, recognizable and more or less well-defined entity” (p. 80).
Concerning the fostering of modelling competencies, Blomhøj and Jensen (2003) distinguished holistic and atomistic approaches. The holistic approach depends on a full-scale modelling process, with the students working through all phases of the modelling process. In the atomistic approach, students concentrate on selected phases of the modelling process, especially the processes of mathematizing and analyzing models mathematically, because these phases are seen as especially demanding. However, the authors issued a strong plea for a balance between these two approaches, since neither of them alone was seen as adequate.
1.2 An analytic approach to modelling competencies and sub-competencies—the bottom-up approach
The analytic definition of competence refers to the seminal work of Weinert (2001), which described it as “the cognitive abilities and skills available to individuals or learnable through them to solve specific problems, as well as the associated motivational, volitional and social readiness and abilities to use problem solutions successfully and responsibly in variable situations” (Weinert, 2001, p. 27f). Based on this definition, modelling competencies were distinguished from modelling abilities: “Modelling competencies include, in contrast to modelling abilities, not only the ability but also the willingness to work out problems, with mathematical aspects taken from reality, through mathematical modelling” (Kaiser, 2007, p. 110). Similarly, Maaß (2006) described modelling competencies as the ability and willingness to work out problems with mathematical means, including knowledge as the inevitable basis for competencies. The emphasis on knowledge as part of competence is in line with the discussion on competencies in the professional development of teachers; the most recent approach within this discussion on competence as a continuum aims to connect dispositions, including knowledge and beliefs, with situation-specific skills and classroom performance (Blömeke et al., 2015). Due to the fact that no standard methods exist for mathematical modelling as a means to find solutions to real-world problems, many cognitive and affective barriers must be overcome. This situation makes metacognitive skills and knowledge needed to monitor modelling activities highly relevant to the development of non-standard approaches. The construct of metacognition has been introduced into the broad discussion about the teaching and learning of mathematical modelling and plays an increasing role within the current modelling discourse, which was called for by Stillman and Galbraith in 1998 and further developed by, among others, Stillman (2011) and Vorhölter (2018).
Departing from the developments described above, a distinction has been developed between global modelling competencies and the sub-competencies of mathematical modelling within the mathematical modelling discourse (Kaiser, 2007; Maaß, 2006). Global modelling competencies are defined as the abilities necessary to perform and reflect on the whole modelling process, to at least partially solve a real-world problem through a model developed by oneself, to reflect on the modelling process using meta-knowledge, and to develop insight into the connections between mathematics and reality and into the subjectivity of mathematical modelling. Furthermore, social competencies, such as the ability to work in groups and communicate about and via mathematics, are part of global competencies.
The sub-competencies of mathematical modelling relate to the modelling cycle, of which different descriptions exist, including the different competencies essential for performing individual steps of the modelling cycle. Based on early work by Blum and Kaiser (1997) and subsequent extensive empirical studies, the following sub-competencies of modelling competence were distinguished by Kaiser (2007, p. 111) and similarly by Maaß (2006):
-
Competencies to understand real-world problems and to develop a real-world model
-
Competencies to create a mathematical model out of a real-world model
-
Competencies to solve mathematical problems within a mathematical model
-
Competencies to interpret the mathematical results in a real-world model or a real-world situation
-
Competencies to challenge the developed solution and carry out the modelling process again, if necessary
Due to the strong reference to sub-competencies as part of the construct competence, this approach is called the analytic approach or, according to Niss and Blum (2020), the “bottom-up approach” (p. 80). Stillman et al. (2015) noted in their summarized description of this perspective the comprehensive character of this approach, referring to the early development of assessment instruments with multiple-choice items mapped to indicators of each sub-competence (e.g., Haines et al., 1993), which was adopted by further studies. Additionally, different levels of modelling competence were distinguished based, for example, on various test instruments (Maaß, 2006; Kaiser, 2007) and metacognitive frameworks (Stillman, 2011).
1.3 Further approaches to mathematical modelling competence
Further approaches concerning the construct of mathematical modelling competence can be distinguished, which this section briefly summarizes.
In their survey paper for the ICMI study on mathematical modelling and applications, Niss et al. (2007) proposed an enrichment of the top-down method, which integrated the main characteristics of the top-down approach with elements of the bottom-up approach. Referring to the holistic approach to competency, they defined mathematical modelling competency as follows:
[The] ability to identify relevant questions, variables, relations or assumptions in a given real world situation, to translate these into mathematics and to interpret and validate the solution of the resulting mathematical problem in relation to the given situation, as well as the ability to analyze or compare given models by investigating the assumptions being made, checking properties and scope of a given model etc. in short: modelling competency in our sense denotes the ability to perform the processes that are involved in the construction and investigation of mathematical models. (p. 12–13)
Furthermore, social competencies and mathematical competencies were included in this approach, which had (at least initially) some similarities to the bottom-up approach; however, with the inclusion of a critical analysis of modelling activities, this approach can be seen as resembling the top-down approach. In our systematic literature review, we call this approach a top-down enriched approach.
Other approaches have also been developed in the past, and hierarchical level-oriented approaches in particular have received some attention; for example, Henning and Keune (2007) focused on the cognitive demands of modelling competencies and distinguished them as follows: level one recognition and understanding of modelling, level two independent modelling, and level three meta-reflection on modelling. Furthermore, design-based model-eliciting activity principles, which had been developed as assessment tools for modelling competencies, were proposed as competence framework (Lesh et al., 2000). Another framework taken up within the discourse was the framework for the successful implementation of mathematical modelling (Stillman et al., 2007).
Summarizing the description of the theoretical approaches to mathematical modelling competencies, we can state that only a few established theoretical frameworks currently exist, which are difficult to discriminate between, as they refer to each other and the ongoing discourse. Overall, although modelling competencies are clearly conceptualized, as evidenced by the inclusion of current approaches in the ongoing discussion, we could not identify a rich variety of conceptualizations on which to build our literature review.
1.4 Research questions
Building upon the above-mentioned theoretical frameworks for conceptualizing modelling competencies and ways to measure and foster them, our study systematically reviewed the existing literature in the field of modelling competencies. In order to reveal how cumulative progress has been made in research over the past few decades, we endeavored to answer the following research questions and analyze them over time (i.e., the last three decades):
1.4.1 Study characteristics and research methodologies
-
How are the studies on modelling competencies distributed, and how can they be characterized by the country of origin of the authors, appearance over time, type of paper (theoretical or empirical; conference proceedings papers or journal papers), use of research methods, educational level involved, previous modelling experience before implementing the study, and type of modelling task used?
1.4.2 Characteristics of the studies concerning the conceptualization, measurement, and fostering of modelling competencies
-
How have researchers conceptualized modelling competencies? Are the theoretical perspectives identified and described in the theoretical frameworks also reflected in the various empirical studies? Are modelling competencies conceptualized as a holistic construct, or are they further differentiated as analytic constructs using various sub-competencies?
-
Which instruments for measuring modelling competencies have researchers used to study (preservice) teachers’ or school students’ modelling competencies? Specifically, what types of instruments and data collection methods were used, which groups were targeted, and what were the sample sizes?
-
Which interventions for fostering and measuring modelling competencies have researchers used to support (preservice) teachers’ or school students’ modelling competencies?
In the following section, we describe the methods used for this literature review before we present the results. The paper closes with an outlook on further perspectives on the work based on this systematic literature review and on the contributions of the papers in this special issue of Educational Studies in Mathematics on modelling competencies.
2 Methodology of the systematic literature review
2.1 Search strategies and manuscript selection procedure
To uncover the current state of the research conceptualizing mathematical modelling competencies and their measurement and fostering, we conducted a systematic literature review. This approach involves “a review of a clearly formulated question that uses systematic and explicit methods to identify, select, and critically appraise relevant research, and to collect and analyze data from the studies that are included in the review” (Moher et al., 2009, p. 1).
The current review followed the most recent Preferred Reporting Items for Systematic Reviews and Meta-Analysis (PRISMA) guidelines (Page et al., 2021). The final literature search was carried out on March 17, 2021 in the following databases: (1) Web of Science (WoS) Core Collection, (2) Scopus, (3) PsycINFO, (4) ERIC, (5) Teacher Reference Center, (6) IEEEXplore Digital Library, (7) SpringerLink, (8) Taylor & Francis Online Journals, (9) zbMATH Open, (10) JSTOR, (11) MathSciNet, and (12) Education Source. These databases have high-quality indexing standards and a high international reputation. Furthermore, they contain many studies in the field of educational sciences, particularly in mathematics education research. In order to capture the relevant studies in the field of mathematics education research, search strings with Boolean operators and asterisks were used in the systematic review, as shown in Table 1.
The current survey focused on studies conducted in the field of mathematics education, published in English, which closely related to the conceptualization, measurement, or fostering of mathematical modelling competencies. Our search embraced studies conducted at all levels of mathematics education and did not restrict the publication year of the studies. Overall, to specify eligible manuscripts for the review, we used five inclusion and five exclusion criteria as presented in Table 2; since not all exclusion criteria were exact opposites of the inclusion criteria, we separated exclusion and inclusion criteria. All the authors of this study were responsible for determining the eligibility of the papers for inclusion.
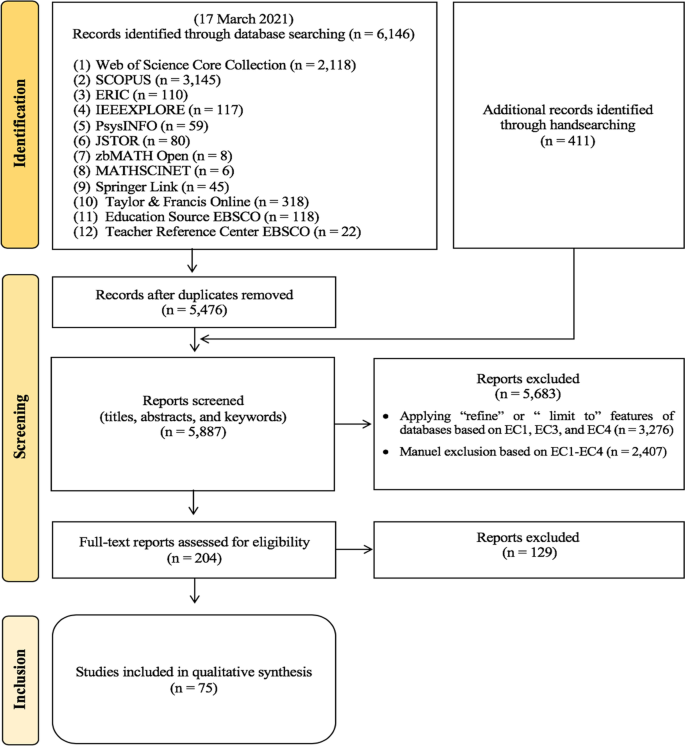
In addition to the electronic database search, on the basis of the first four criteria (IC1-IC4 and EC1-EC4), we conducted a hand-search for key conference proceedings that are important for mathematical modelling research, although they were not indexed in the electronic databases (amongst others as they were not registered by their publishers). We therefore screened the ICTMA proceedings from 1984 to 2009 and the recently published ICTMA19 proceedings. There was no need to manually screen the remaining ICTMA proceedings since they were already indexed in databases covered by IC5. Hand-searching is an accepted way of identifying the most recent studies that have not yet been included in or indexed by academic databases (Hopewell et al., 2007).The manuscript selection process was conducted in three main stages: (1) identification, (2) screening, and (3) inclusion (Page et al., 2021). In the identification stage, search strings from Table 1 were used, and a literature search of the 12 listed databases yielded 6,146 records. Endnote served as bibliographic software for managing references and removing duplicate records. After discarding 670 duplicate records, we moved to the initial screening of 5,476 records. Additionally, we found 411 potentially eligible records through hand-searching and screened all 5,887 reports based on their titles, abstracts, and keywords. First, we used the “refine” or “limit to” features of the electronic databases to exclude 3,276 papers by selecting the document type as journal article, book chapter, or conference proceedings; the language as English (all databases); and subject areas as education/educational research and educational scientific disciplines (WoS), education (Taylor & Francis Online Journals, SpringerLink, and JSTOR), social sciences (Scopus), and mathematics (WoS and Scopus). We then manually screened the remaining 2,611 reports’ titles, abstracts, and keywords on the basis of our ICs and ECs and found 204 potentially relevant studies through independent examination by the authors. At the end of the screening stage, we examined the full-text versions of these 204 studies based on our eligibility criteria, as mentioned in Table 2. Ultimately, we included 75 studies in the systematic review with the full agreement of all the authors. Figure 1 illustrates the flow chart for the entire manuscript selection process.
2.2 Data analysis
Our analysis included 75 papers, which are described in Tables 9, 10, 11, and 12 in the Appendix and displayed in the electronic supplementary material. The analysis of the current review mainly consisted of a screening and a coding procedure. First, the eligible studies were screened three times by the authors and examined in-depth. A coding scheme was then developed, and the codes were structured around our research questions according to four overarching categories:
-
Study characteristics and research methodologies (research question 1)
-
Theoretical frameworks for modelling competencies (research question 2)
-
Measuring mathematical modelling competencies (research question 3)
-
Fostering mathematical modelling competencies (research question 4)
Table 3 exemplifies our coding concerning the theoretical conceptualization of the reviewed papers.
The analysis was carried out according to the qualitative content analysis method (Miles & Huberman, 1994), focusing on the topics the reviewed studies addressed. We analyzed the studies that concerned our research interests, systematized according to the four main categories. First, concerning research question 1, we categorized the general characteristics of the reviewed studies and the research methodologies they had used based on ten sub-categories (e.g., publication year, document type, geographic distribution, research methods, sample/participants, participants’ level of education, sample size, participants’ previous experience in modelling, task types and modelling activities, and data collection methods). Second, with a special focus on research question 2, we analyzed the theoretical frameworks for modelling competencies that motivated the studies. Regarding research questions 3 and 4, we identified the measurement and fostering strategies developed, used, or suggested in the reviewed studies.
The main parts of the coding manual can be found in the Appendix, displayed in the electronic supplementary material (Tables 9, 10, 11, and 12) with a sample coding in Table 12. Our initial coding was conducted by the first author, and multiple strategies were then used to check the coding reliability using Miles and Huberman’s (1994, p.64) formula: “reliability = number of agreements / (total number of agreements + disagreements).” First, we applied a code-recode strategy, which involved recoding all the studies after an interval of four weeks, and the consistency rate between the two distinct coding sessions was computed as 0.97. Second, to test coding reliability, 20% of the reviewed papers were randomly selected and cross-checked for coherence by a coder other than the authors, who had previous experience in mathematical modelling research area and qualitative data analysis. The intercoder reliability was found to be 0.93. Third, the first two authors separately coded the theoretical frameworks of all the included studies because these frameworks for modelling competencies were more complex to code than the other categories due to more interpretative elements. After double coding all the data concerning the theoretical frameworks underpinning the studies, the intercoder reliability rate was 0.91. After applying these strategies, all coders discussed the coding schedule, with a particular focus on the discrepancies between different codes, to achieve full consensus. All the computed reliability rates illustrated that the coding system was sufficiently reliable (Creswell, 2013).
3 Results of the systematic literature review on mathematical modelling competencies
3.1 Study characteristics and research methodologies of the papers (research question 1)
3.1.1 Types of documents and publication years
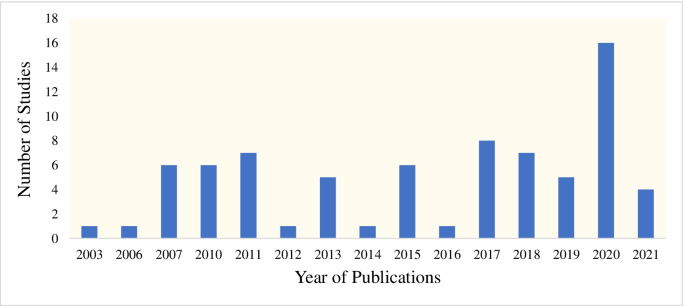
The 75 papers included in our study consisted of 67 empirical studies, 4 theoretical studies, 3 survey or overview studies, and 1 document analysis study with the following distribution of papers: 31 journal articles, 42 conference proceedings, and 2 book chapters. Eligible papers were published in 21 different scientific journals, including 10 mathematics education journals, 5 educational journals, and 4 interdisciplinary scientific journals focusing on science, technology, engineering, and mathematics (STEM) education. The reviewed articles published in mathematics education journals constituted only 7% of all the reviewed studies. Concerning conference proceedings, the majority of the eligible papers came from ICTMA proceedings (n = 31), with only a few studies from other mathematics education conferences (mainly ICME, Psychology in Mathematics Education [PME], and Congress of the European Society for Research in Mathematics Education [CERME]). Concerning publication years, the reviewed studies appeared between 2003 and 2021, and an increase was observed in studies on modelling competencies in 2020 (see Fig. 2). The visualization in Fig. 2 does not show steady progress over time, especially regarding the impact of the biennial ICTMA conferences and their subsequently published proceedings. We called papers stemming from the books from the ICTMA conference series as conference proceedings, although the books have not been named like that in the past decade due to their selectivity and rigorous peer-review process carried out.
3.1.2 Geographic distribution
The results concerning geographic distribution revealed the contributions of researchers from different countries to research on mathematical modelling competencies. An analysis conducted separately based on all authors’ affiliations and first authors’ affiliations found few important differences; thus, only the results based on all authors’ country affiliations are tabulated. When reviewing the studies, geographical origins were critical, as the classification criteria reflected the research culture of the countries to a certain extent; for example, the competence construct is especially prominent in Europe, whereas in other parts of the world, other constructs, such as proficiency, are more common. We therefore found as expected that most authors came from Europe, followed by Asia, Africa, and America, and only one came from Australia. In particular, the authors came from 18 different countries, with Germany being the most prominent. Table 4 indicates the distribution of the authors by country and continent.
3.1.3 Research designs and data collection methods
The analysis revealed that roughly one-third of the reviewed studies (32%, n = 24) used quantitative research methods (e.g., experimental, quasi-experimental, comparative, correlational research, survey, and relational survey models), followed by qualitative research methods (e.g., case study and grounded theory; 27%, n = 20) and design-based research methods (5%, n = 4). Only one study used both qualitative and quantitative research methods, and another study relied on document analysis. A few theoretical studies (5%, n = 4) and overview/survey studies (4%, n = 3) were counted among the remainder. For 18 eligible studies (24%), it was not possible to identify the research method used.
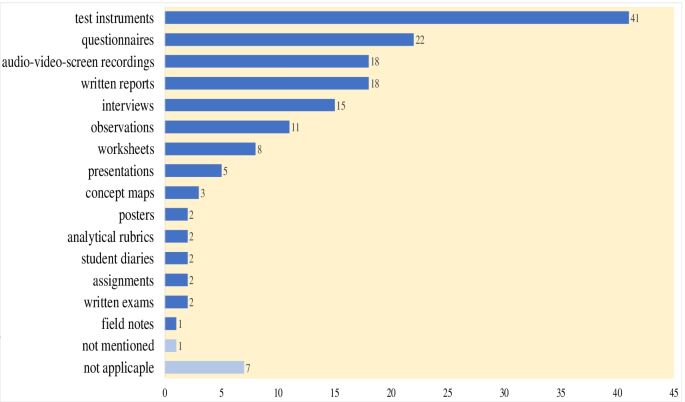
Various data collection methods were used in the reviewed studies, with (non-standardized) test instruments being the most frequently used method (see Fig. 3). The majority of the studies (44 of 75 studies, 59%) used more than one data collection method, whereas 23 studies (31%) used only one method. Seven papers reporting theoretical and overview/survey studies were not applicable to this category. We took into account that data collection might not be restricted to the evaluation of modelling competencies, but could include in addition other constructs, such as beliefs or attitudes.
3.1.4 Focus samples, sample sizes, and study participants’ levels of education
In this review study, we analyzed the sample characteristics of the reviewed studies. When we categorized the participants of the studies, we took into consideration the authors’ reports concerning the educational level of the participants. There is no clear international distinction between elementary and lower secondary education with elementary education covering year 1 to 4 or 1 to 6, which has to be taken into account.
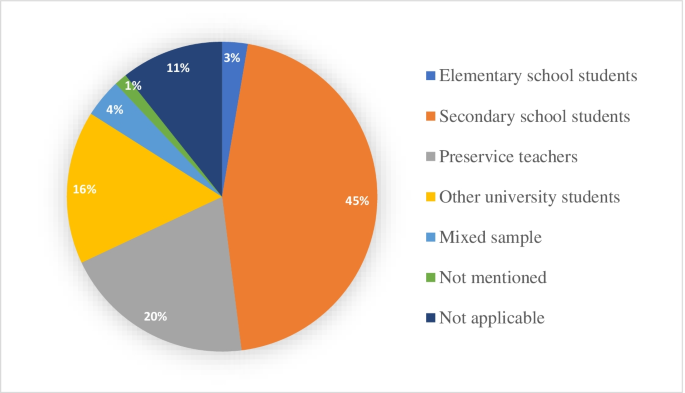
The analysis showed that the majority of the reviewed studies (45%, n = 34) recruited secondary school students (grades 6–12), and 20% (n = 15) used samples of preservice (mathematics) teachers. Moreover, 12 studies (16%) focused on university students, including engineering students (n = 8), mathematics and natural science students (n = 1), and students from an interdisciplinary program (n = 1), an introductory and interdisciplinary study program in science (n = 1), and STEM education (n = 1). Additionally, three studies (4%) used mixed samples of students, preservice teachers, and experienced teachers as their participants. Only two studies (3%) dealt with elementary school students (one group focusing on first graders and the other on fifth graders). One study did not mention the sample. The remaining eight studies (11%) were not applicable to this category, as they did not report on an empirical study or were of a theoretical nature. Figure 4 illustrates the distribution of the reviewed studies’ participants.
Table 5 shows the analysis of the sample sizes of the studies. The majority of the studies (32%, n = 24) recruited 0-50 participants, and overall, 51% (n = 38) had less than 200 participants. Additionally, 14 studies (19%) conducted research with 201-500 participants, and 3 large-scale studies (4%) had more than 1,000 participants. We also analyzed the sample sizes of the studies based on the participants’ levels of education, and we used two categories (school/university students and preservice teachers). The results for these two categories did not differ substantially from each other; the most striking difference seemed to be in the range of 201-500 participants who were school students. The table illustrates the difficulties in higher education in collecting data from larger samples.
3.1.5 Participants’ previous modelling experience and modelling task types
Since participants’ previous modelling experience was mentioned as an important factor for success by several studies, we analyzed this information given in the papers. Our results showed that in 25% (n = 19) of the studies, participants had very limited or no experience in modelling (i.e., they had participated in only one or two modelling activities by the time of the study). Furthermore, two studies reported that their participants had previous modelling experience (e.g., experience gained by attending modelling courses and seminars) before the research interventions. One study mentioned that the participants were heterogeneous in terms of their experience in modelling. Besides these results, we found that the majority of the reviewed studies (65%, n = 45) did not provide any information regarding participants’ previous experience in modelling.
In our review, we also evaluated how modelling activities were carried out during the research interventions and which types of tasks were used by the studies. The results revealed that modelling activities were predominantly performed in group work (37%, n = 28), 5 studies (7%) reported that they guided participants in individual/independent modelling activities, and the other 6 studies (8%) stated that they used both individual and group work. However, numerous reviewed studies (39%, n = 29) did not state how they performed modelling activities.
The types of modelling tasks used in the studies were not clearly described in the majority of the reviewed studies (59%, n = 44). We did not use a predefined classification, but used the classification given by the authors as in many papers no detailed information about the task was provided. This did not allow to use a predefined classification scheme, although we admit the advantages of predefined classifications. In this sense, we found that 11 studies (15%) applied more than 1 task type in the research; however, 18 reviewed studies (24%) employed a single type of modelling task. The results on type of tasks used by the reviewed studies are displayed in Table 6.
Connected to the low information to the task type is the missing information about the context of the modelling examples (e.g., closeness to students’ world, workplace, citizenship, etc.) in many papers, which did not allow us to analyze this important category.
3.2 Results concerning the theoretical frameworks for modelling competencies (research question 2)
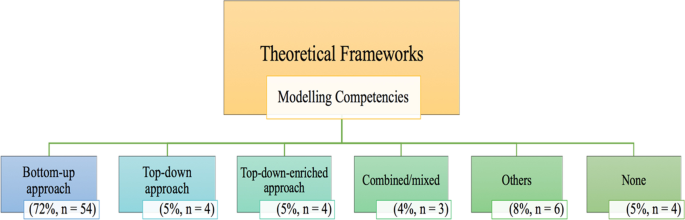
In our review, we classified the theoretical frameworks of the studies for mathematical modelling competencies into six categories. The main approaches used were as described in the theoretical part of this paper, and the results are displayed in Fig. 5. The most prevalent theoretical framework was the bottom-up approach; other different theoretical frameworks comprised model-eliciting activities and principles as assessment tools for modelling competencies (Lesh et al., 2000), level-oriented descriptions of modelling competencies (Henning & Keune, 2007), or the framework for success in modelling (Stillman et al., 2007). Overall, the results indicated a scarcity of theoretical frameworks underpinning studies that investigated modelling competencies.
3.3 Results concerning the measurement of modelling competencies (research question 3)
Our results revealed that a number of methods were used to measure modelling competencies. The most prevalent approaches used (mainly non-standardized) test instruments (55%, n = 41), written reports, and audio/video and screen recordings (24%, n = 18). The least-used methods were multidimensional item response theory (IRT) approaches (n = 1) and field notes (n = 1). Table 7 illustrates the methods described by the researchers for measuring modelling competencies.
The reviewed studies applied 16 different approaches to measure mathematical modelling competencies: 33% (n = 25) of the studies used one method, 27% (n = 20) applied two methods, 17% (n = 13) used three methods, 7% (n = 5) followed four methods, 4% (n = 3) applied 5 methods, and 1 study used 6 different measurement methods for modelling competencies. For one of the reviewed studies, the modelling competency measurement method was not specified.
3.4 Results concerning the fostering of modelling competencies (research question 4)
The analysis revealed that the majority of the reviewed studies (79%, n = 59) contributed to the discourse on fostering modelling competencies by designing, developing, testing, or discussing various activities, including recommendations for the improvement of these activities. The remaining 16 studies (21%) did not mention results about fostering modelling competencies. The activities suggested in the reviewed studies for fostering modelling competencies could be divided into eight groups (see Table 8).
In detail, about half of the studies (48%, n = 36) designed and/or used training strategies (e.g., modelling courses/seminars, teaching units, professional development programs, and modelling projects) to foster students’ modelling competencies. Most researchers conducted studies as part of ongoing teaching activities (in schools or universities) or modelling-oriented projects, or they designed specific teaching units aimed at fostering students’ modelling competencies. Concerning modelling tasks, roughly one-third of the studies (31%, n = 23) found that the development of modelling tasks supported students’ modelling competencies. About 9% (n = 7) of the reviewed studies reported that psychological factors (e.g., motivation, self-efficacy, attitudes, and beliefs) can affect students’ modelling competencies. The analysis revealed that studies found positive correlations between students’ modelling competencies and their levels of self-efficacy and motivation as well as their attitudes and beliefs towards modelling. Moreover, 6 eligible studies (8%) reported that metacognitive factors influenced the modelling competencies of the study participants. A few studies (5%, n = 4) focused on the effects of digital technologies/tools on modelling competencies. The results indicated that using digital devices, such as programmable calculators, special mathematical software (e.g., MATLAB), and dynamic geometry software (e.g., GeoGebra), fostered students’ modelling competencies. Three other eligible studies (4%) discussed the efficiency of the holistic and atomistic approaches to supporting modelling competencies, which we report in detail due to their relevance to the theoretical discourse: The empirical results of these studies illustrated that both approaches foster students’ modelling competencies, although both approaches have weaknesses and strengths. Kaiser and Brand (2015) found in their comparison of both approaches that the holistic approach had larger effects in interpreting and validating, the atomistic approach had larger effects on working mathematically, and there were mixed results on mathematizing and simplifying. Furthermore, the holistic approach seemed to be more effective than the atomistic approach for students who have relatively weak performance in mathematics (Brand, 2014). To summarize, from a developmental perspective, Blomhøj and Jensen (2003) highlighted the importance of a balance between holistic and atomistic approach to foster students’ modelling competencies.
Seven eligible studies (9%) provided other fostering strategies to develop students’ modelling competencies, as reported in Table 7.
Overall, the results of the literature review confirmed the richness of the implementation strategies for modelling competencies and emphasized the focus of the current discourse on implementing (or at least suggesting) teaching strategies.
4 Discussion and limitations of the study and further prospects
This review study systematically investigated the current state of research on mathematical modelling competencies through analyzing 75 included papers. Our major focus concerned basic study characteristics, the conceptualization of modelling competencies, and theoretical frameworks and strategies for measuring and fostering modelling competencies.
4.1 Discussion of the results and limitations of the study
Concerning our first research question, our results indicated that the number of reported studies on modelling competencies relatively reached a satisfactory level, with a substantial increase in 2020, but there is still a need for further studies on this topic. Moreover, the vast majority of the reviewed studies were empirical studies, with only a few theoretical or survey studies, and Kaiser and Brand’s (2015) literature review on modelling competencies, which differed in nature from this one, remains the only other one to date. Conference proceedings, especially ICTMA proceedings, constituted an important proportion of the reviewed studies, followed by journal articles. Notably, the articles published in mathematics education journals accounted for only 7% of the reviewed papers. These results indicate that specialized international mathematics education conferences have a major impact on modelling competence research. Moreover, many articles in high-ranking journals have been written by psychologists rather than mathematics educators, confirming the well-known impression of the low visibility of research on mathematical modelling competencies in mathematics education.
Most authors from reviewed studies came from Europe, particularly Germany; several authors stemmed from Africa and Asia; a very limited number of authors came from North and South America; and only one from Australia. On the one hand, we need to consider the cultural contexts of studies that investigate modelling competencies, and from this point of view, there are plenty of opportunities for future intercultural research on modelling competencies. On the other hand, these results might be influenced by the fact that the competence discussion has been strongly guided by European, especially German, scholars, and that in other discourses, other terminology (e.g., performance, proficiency, skill, and ability) may be used. Further studies should focus on how modelling competencies are conceptualized and identified and consider the terms used for modelling competencies, thus enabling studies to identify the differences or similarities between different approaches to modelling competencies across different countries or cultures. Our review study illustrates that the ICTMA conferences have an influence on the distribution of the papers in terms of country affiliations of the authors. For example, ICTMA18 conducted in Cape Town (South Africa) had a great influence on the number of reviewed papers from South Africa; however, there is no similar effect for South American papers following the ICTMA16 conference held in Blumenau (Brazil), probably reflecting other theoretical perspectives such as socio-cultural approaches, in which modelling competencies play a less pronounced role (Kaiser & Sriraman, 2006). Furthermore, institutional restrictions may play an important role concerning the differences in country distribution of these studies.
Our results revealed that approximately one-third of the reviewed studies relied on quantitative research methods, followed by qualitative and design-based research methods. No researcher had named their study approach as mixed-methods research, but only one author reported that both quantitative and qualitative research methods were used. Overall, it is promising that the reviewed studies used a wide variety of data collection methods and more than half of them applied more than one data collection approach, which supports the development of a reliable database (Cevikbas & Kaiser, 2021). Moreover, a significant number of the studies focused on secondary school students as participants, followed by preservice teachers and university students from engineering, STEM, and interdisciplinary study programs. However, only two studies recruited elementary school students as participants. In line with these results, the majority of the studies were conducted in secondary education, followed by higher education, but no studies investigated early childhood education or adult education. These results showed that research is needed on modelling competencies in these areas (i.e., early childhood education, elementary education, and adult education).
Notably, interpreting study results regarding students’ modelling competencies crucially depends on knowing the participants’ previous modelling experience, but the majority of the studies provided no information about their participants’ experience in modelling. Additionally, a quarter of the studies reported that their participants had either extremely limited or no experience in modelling, and only two studies stated that their participants had substantial previous experience in mathematical modelling. These results imply that teachers and teacher educators should put great effort into developing students’ modelling experience during their school and university education. Overall, it seems advisable to share information concerning the study participants’ previous experience in modelling to enable readers to make accurate inferences from the study results and compare the results of different studies.
Furthermore, our results indicated that many reviewed studies did not mention which type of task they had used. The analysis of the remaining studies showed that various types of modelling tasks had been implemented. As the core of modelling activities are the modelling tasks or problems, it is crucial to know for the modelling discourse, which modelling tasks are used in studies and what their characteristics are. Using diverse types of modelling tasks can allow researchers to investigate the strengths and weaknesses of these tasks for teaching and learning mathematical modelling and for the promotion of students’ modelling competencies. Using different types of tasks can provide rich opportunities in the learning and teaching of modelling. Further studies should investigate which types of tasks are most effective for developing students’ modelling competencies and should make recommendations for teachers or teacher educators.
Concerning the theoretical frameworks, the results indicated that the predominant framework used by the studies was the bottom-up approach and only a few studies adopted top-down or top-down enriched approaches or other frameworks. Therefore, there is a great need to investigate modelling competencies using a variety of theoretical frameworks and to extend existing frameworks by using innovative approaches. The lack of diversity within the frameworks used directly relates to the conceptualization of modelling competencies; therefore, more theoretical research focusing on the conceptualization of modelling competencies is needed.
The strategies of the reviewed studies for measuring modelling competencies were aligned with their research methods; hence, the results showed that modelling competencies tended to be measured using (mainly non-standardized) test instruments and questionnaires. It is promising that the reviewed studies used various approaches to measure modelling competencies; however, we could not identify any study investigating which method or strategy was most effective for measuring the modelling competencies of students (e.g., focusing on the strengths and weaknesses of different measurement approaches and comparing the capabilities of these approaches to measure students’ modelling competencies). Future studies should focus on producing new tools or strategies to extend existing approaches to measuring students’ modelling competencies by, for example, using digital technologies to measure students’ modelling competencies according to these technologies’ pedagogical potential.
Although the studies reported that students’ or preservice teachers’ mathematical modelling competencies were still far from reaching an expert level, their modelling competencies could be fostered by the various strategies mentioned above (see Results 3.4). In this vein, the reviewed studies contributed to the discourse on fostering modelling competencies by designing, developing, testing, or recommending specific modelling activities. To foster students’ modelling competencies, most of the reviewed studies used instructional strategies that focused on practice in modelling and gaining experience through modelling tasks.
Moreover, several studies found that motivation, self-efficacy, beliefs, and attitudes regarding modelling, and metacognitive competencies, could affect students’ modelling competencies. A few of the studies recommended maintaining a balance between holistic and analytic approaches in the teaching and learning of modelling. Furthermore, few studies have analyzed the use of digital technologies/tools to promote students’ modelling competencies. Accordingly, using mathematical software (e.g., MATLAB and GeoGebra) for modelling has been identified as an effective strategy for fostering modelling competencies, but only a limited number of studies have focused on how and what types of technologies could be used to improve students’ modelling competencies.
In summary, we emphasize that the main foci of this systematic review (i.e., the conceptualization of modelling competencies and the related theoretical frameworks for measuring and fostering modelling competencies) are closely interrelated. Fostering and measuring strategies for modelling competency depend on its conceptualization. To this end, theoretical and empirical studies could contribute strongly to both the epistemology of modelling and its application and are greatly needed.
The results of our systematic literature review are limited by several restrictions. The first significant limitation relates to the restrictions of the databases: The exclusion of papers published in books and journals not included in WoS, Scopus, and the other high-ranking databases led to the exclusion of local/national journals that may have had the potential to provide interesting research studies. Furthermore, the exclusion of papers not written in English excluded many potentially interesting papers, especially those from the Spanish/Portuguese-speaking countries. Further research should try to overcome this limitation by including native speakers from this language area.
Other restrictions related to the automated selection process (i.e., the so-called jingle-jangle fallacy; Gonzalez et al., 2021). In our systematic literature review, we used the terms modelling and competence; however, we identified studies that used modelling competence differently, particularly regarding the use of modelling competencies in psychometric or educational modelling (large-scale studies) or in economics or engineering. Manual screening could help overcome this problem; however, we could not prevent the omission of papers that examined modelling competencies but used different terms, such as modelling performance or modelling proficiency. We therefore might have missed an important number of studies that employed other terminology. This is a systemic problem of our approach. Further studies should use a broader theoretical framework to identify and examine these other types of studies.
4.2 Contributions of this special issue to the discourse on modelling competencies
With this present special issue, which the current systematic literature review introduces, we aim to present advances in the research on mathematical modelling competencies. A broad body of past research has investigated modelling processes and students’ barriers to solving modelling problems. Descriptive analyses of students’ solution processes have identified the importance of specific sub-processes and related sub-competencies, such as comprehension, structuring, simplifying, mathematizing, interpretation of mathematical results, and validation of mathematical results and mathematical models for mathematical modelling. However, only a limited amount of research has investigated the effects of short- and long-term interventions on the implementation of mathematical modelling in schools and higher education institutes using rigorous methodological standards. These observations are consistent with the systematic review presented in the previous section, which identified only a limited number of studies contributing to these research aims. In line with these considerations, we argue that much more research effort should be devoted to evaluating measurement instruments and approaches to fostering mathematical modelling in schools and universities (Schukajlow et al., 2018). The papers in this special issue contribute to closing these significant gaps by addressing (1) the measurement and (2) the fostering of modelling competencies as well as (3) comparing groups of participants with different expertise or participants from different cultures.
The first group of papers presented assessment instruments for measuring modelling competencies. Based on their conceptualization of modelling competencies, Brady and Jung developed an assessment instrument for analyzing classroom modelling cultures. Their quantitative analysis of the modelling activities of secondary school students demonstrated differences between classroom cultures and revealed shifts in cultures within a classroom, and their qualitative analysis of students’ discourse during presentations of their solutions in classrooms offered an explanation for the phenomenon identified by the quantitative analysis. Brady and Jung interpreted these results as indicative of the validity of the measurement instrument. The new contribution of this study laid in pointing out the importance of using this new assessment instrument to analyze classroom modelling cultures in future studies.
Noticing competencies during mathematical modelling is considered important for research on modelling and on teachers’ situation-specific competencies. Alwast and Vorhölter answered the call to be more specific in the assessment of teachers’ competencies and focused on situation-specific modelling competencies in their study. Alwast and Vorhölter developed staged videos and used these videos as prompts for the assessment of preservice teachers’ noticing competencies in mathematical modelling. They performed a series of studies that aimed to collect evidence of the validity of the new instrument. This instrument could be used in the future to analyze the development of preservice teachers’ noticing skills and to examine the relationship between teachers’ noticing and their decisions and interventions in classrooms.
Students’ creativity, as a research field with a long tradition, has rarely been analyzed in relation to mathematical modelling competencies in the past. Lu and Kaiser identified the importance of creativity for the assessment of modelling competencies and evaluated students’ creative solutions to modelling problems by analyzing three central dimensions of mathematical creativity: usefulness, fluency, and originality. Their analysis of upper secondary school students’ responses indicated a close association between fluency and originality, which has important theoretical implications for the assessment of modelling competencies and the relationship between factors that contribute to mathematical creativity.
The second group of papers examined various approaches to fostering modelling sub-competencies. Geiger, Galbraith, and Niss developed a task design and implementation framework for mathematical modelling tasks aimed at supporting the instructional modelling competence of in-service teachers. The core of this approach was researcher-teacher collaboration over a long period. The results of this study have theoretical implications for implementation research by connecting the task design and task implementation streams of research in a joint model. Furthermore, this research extended the concept of pedagogical competence from numeracy to mathematical modelling competence.
Reading comprehension is an essential part of modelling processes, and improving reading comprehension can help to foster modelling competencies. Krawitz, Chang, Yang, and Schukajlow analyzed the effects of reading comprehension prompts on competence to construct a real-world model of the situation and interest of secondary school students in Germany and Taiwan. Reading comprehension prompts did not affect modelling, but they did affect interest. In-depth analysis of students’ responses indicated a positive relationship between reading comprehension and modelling. Krawitz et al. suggested that the high-quality responses to reading prompts are essential for modelling and should be given more attention in research and practice.
Teaching methods and their impact on the modelling competencies and attitudes of engineering students were the focus of the contribution by Durandt, Blum, and Lindl. The researchers analyzed the effects of independence-oriented and teacher-guided teaching styles in South Africa. The group of students taught according to the independence-oriented teaching style had the strongest competency growth and reported more positive attitudes after the treatment. Students’ independent work supported by adaptive teacher interventions and by a metacognitive scaffold, which encourage individual solutions, is a promising approach that should be analyzed in future studies and evaluated in teaching practice for mathematical modelling competencies.
Greefrath, Siller, Klock, and Wess investigated the effects of two teaching interventions on preservice secondary teachers’ pedagogical content knowledge for teaching mathematical modelling. Preservice teachers in one group designed modelling tasks for use with students, and those in another group were trained to support mathematical modelling processes. Both groups improved some facets of pedagogical content knowledge compared to a third group that received no modelling intervention. As one practical implication of the study, Greefrath et al. underlined the importance of practical sessions for improving preservice teachers’ pedagogical content knowledge of modelling.
The third group of papers included two contributions to comparative studies and a commentary. Preservice teachers’ professional modelling competencies are essential for the teaching of modelling. Yang, Schwarz, and Leung compared this construct in Germany, Mainland China, and Hong Kong. The results indicated that preservice teachers in Germany had higher levels of mathematical content knowledge and mathematical pedagogical knowledge of modelling. Yang et al. suggested that possible reasons for these results might lie in the history of mathematical modelling in mathematics curricula, teacher education, and the teaching cultures in these three regions. Future research should pay more attention to international comparative studies regarding modelling competencies.
Cai, LaRochelle, Hwang, and Kaiser compared expert and novice (preservice) secondary teachers’ competencies in noticing students’ thinking about modelling. The expert teachers noticed the students’ needed to make assumptions to complete the task more often than the novice teachers did. The researchers identified many important characteristics of the differences between experts and novices. Future research should analyze the development of preservice teachers’ and experts teachers’ competencies for noticing students’ thinking about modelling and identify what components of noticing affect the teaching of mathematical modelling competencies.
Finally, Frejd and Vos analyzed the contributions of the papers in this special issue and reflected on further developments in a commentary paper.
Summarizing the contributions of the systematic literature survey and the papers in this special issue, we recognize––despite certain limitations––many insights offered by the special issue that can enhance the current discourse on mathematical modelling competencies. The papers point to a great need for further theoretical work on the conceptualization of modelling competencies, although most papers have adopted a clear theoretical framework in their study. The low number of theoretical papers in this area strongly confirms the need for approaches that have the potential to further develop the current theoretical frameworks, especially taking socio-cultural and socio-critical aspects into account (Maass et al., 2019). Furthermore, the development of more standardized test instruments should be encouraged, and an exchange of these instruments within the modelling community (similar to the tests developed by Haines et al., 1993) is desirable. In addition, the inclusion of qualitatively oriented, in-depth studies within quantitative studies, leading to mixed-methods designs, seems to be highly desirable. Concerning teachers’ professional competencies, it seems essential to use more recent approaches to competence development, such as developing situation-specific noticing skills of preservice teachers, which should be included in further studies. Scaling-up of established learning environments within implementations under controlled conditions (e.g., by laboratory studies) seems to be highly necessary in order to strengthen the link to psychological research in this area. Despite the high methodological standards in the studies examined in the systematic literature survey and in this special issue, more studies with rigorous methodological standards that rely on the theory of modelling competencies seem to be necessary. One theoretical prediction is that knowledge about modelling and the modelling cycle is a prerequisite for developing modelling competencies. In earlier research, students’ knowledge (e.g., their procedural and conceptual knowledge of modelling as addressed by Achmetli et al., 2019) was analyzed as a decisive factor. Future research should assess the various facets of teachers’ modelling competence in relation to its overall construct and students’ modelling competence to contribute to the validation of theories of modelling competencies.
Change history
25 February 2022
The original version of this paper was updated to add the missing compact agreement Open Access funding note.
References
Asterisk denotes inclusion in the database.
Achmetli, K., Schukajlow, S., & Rakoczy, K. (2019). Multiple solutions to solve real-world problems and students’ procedural and conceptual knowledge. International Journal of Science and Mathematics Education, 17, 1605–1625.
*Alpers, B. (2017). The mathematical modelling competencies required for solving engineering statics assignments. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 189–199). Springer.
*Anhalt, C. O., Cortez, R., & Bennett, A. B. (2018). The emergence of mathematical modelling competencies: An investigation of prospective secondary mathematics teachers. Mathematical Thinking and Learning, 20(3), 202–221.
*Aydin-Güç, F., & Baki, A. (2019). Evaluation of the learning environment designed to develop student mathematics teachers’ mathematical modelling competencies. Teaching Mathematics and its Applications, 38(4), 191–215.
*Bali, M., Julie, C., & Mbekwa, M. (2020). Occurrences of mathematical modelling competencies in the nationally set examination for mathematical literacy in South Africa. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 361–370). Springer.
*Beckschulte, C. (2020). Mathematical modelling with a solution plan: An intervention study about the development of grade 9 students’ modelling competencies. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 129–138). Springer.
*Biccard, P., & Wessels, D. (2017). Six principles to assess modelling abilities of students working in groups. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 589–599). Springer.
*Biccard, P., & Wessels, D. C. (2011). Documenting the development of modelling competencies of grade 7 mathematics students. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14) (pp. 375–383). Springer.
*Blomhøj, M. (2020).Characterising modelling competency in students’ projects: Experiences from a natural science bachelor program. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making, (pp. 395–405). Springer.
*Blomhøj, M., & Højgaard Jensen, T. (2007). What’s all the fuss about competencies? Experiences with using a competence perspective on mathematics education to develop the teaching of mathematical modelling. In W. Blum, P. L. Galbraith, H. W. Henn, & M. Niss (Eds.), Modelling and Applications in Mathematics Education. The 14th ICMI study (pp. 45–56). Springer.
*Blomhøj, M., & Jensen, T. H. (2003). Developing mathematical modelling competence: Conceptual clarification and educational planning. Teaching Mathematics and its Applications, 22(3), 123–139.
*Blomhøj, M., & Kjeldsen, T. H. (2010). Mathematical modelling as goal in mathematics education-developing of modelling competency through project work. In B. Sriraman, L. Haapasalo, B. D. Søndergaard, G. Palsdottir, S. Goodchild, & C. Bergsten (Eds.), The first sourcebook on Nordic research in mathematics education (pp. 555–568). Information Age Publishing.
Blömeke, S., Gustaffsson, J. E., & Shavelson, R. (2015). Beyond dichotomies: Viewing competence as a continuum. Zeitschrift für Psychologie, 223(1), 3–13.
*Blum, W. (2011). Can modelling be taught and learnt? Some answers from empirical research. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14) (pp. 15–30). Springer.
Blum, W., Galbraith, P. L., Henn, H. W., & Niss, M. (Eds.). (2007). Modelling and applications in mathematics education, the 14th ICMI Study. Springer.
Blum, W., & Kaiser, G., (1997). Vergleichende empirische Untersuchungen zu mathematischen Anwendungsfähigkeiten von deutschen und englischen Lernenden. Unpublished application to German Research Association (DFG).
*Brand, S. (2014). Effects of a holistic versus an atomistic modelling approach on students' mathematical modelling competencies. In P. Liljedahl, C. Nicol, S. Oesterle, & D. Allan (Eds.), Proceedings of the Joint Meeting of PME 38 and PME-NA 36 (Vol. 2, pp. 185–192). PME.
Burghes, D. N. (1984). Prologue. In J. S. Berry, D. N. Burghes, I. D. Huntley, D. J. G. James, & O. Moscardini (Eds.), Teaching and applying mathematical modelling (pp. xi–xvi). Horwood.
Cevikbas, M., & Kaiser, G. (2021). A systematic review on task design in dynamic and interactive mathematics learning environments (DIMLEs). Mathematics, 9(4), 399. https://doi.org/10.3390/math9040399
*Cosmes Aragón, S. E., & Montoya Delgadillo, E. (2021). Understanding links between mathematics and engineering through mathematical modelling—The case of training civil engineers in a course of structural analysis. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 527–538). Springer.
Creswell, J. W. (2013). Qualitative inquiry and research design; choosing among five approaches. Sage.
*Czocher, J. A., Kandasamy, S. S., & Roan, E. (2021). Design and validation of two measures: Competence and self-efficacy in mathematical modelling. In A. I. Sacristán, J. C. Cortés-Zavala, & P. M. Ruiz-Arias (Eds.), Mathematics Education Across Cultures: Proceedings of the 42nd Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 2308–2316). PME-NA. https://doi.org/10.51272/pmena.42.2020
*de Villiers, L., & Wessels, D. (2020). Concurrent development of engineering technician and mathematical modelling competencies. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 209–219). Springer.
*Djepaxhija, B., Vos, P., & Fuglestad, A. B. (2017). Assessing mathematizing competences through multiple-choice tasks: Using students’ response processes to investigate task validity. In G. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 601–611). Springer.
*Durandt, R., Blum, W., & Lindl, A. (2021). How does the teaching design influence engineering students’ learning of mathematical modelling? Acase study in a South African context. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 539–550). Springer.
*Durandt, R., & Lautenbach, G. (2020). Strategic support to students’ competency development in the mathematical modelling process: A qualitative study. Perspectives in Education, 38(1), 211–223.
*Durandt, R., & Lautenbach, G. V. (2020). Pre-service teachers’ sense-making of mathematical modelling through a design-based research strategy. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 431–441). Springer.
*Engel, J., & Kuntze, S. (2011). From data to functions: Connecting modelling competencies and statistical literacy. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14) (pp. 397–406). Springer.
*Fakhrunisa, F., & Hasanah, A. (2020). Students’ algebraic thinking: A study of mathematical modelling competencies. Journal of Physics: Conference Series, 1521(3), 032077.
*Frejd, P. (2013). Modes of modelling assessment—A literature review. Educational Studies in Mathematics, 84(3), 413–438.
*Frejd, P., & Ärlebäck, J. B. (2011). First results from a study investigating Swedish upper secondary students’ mathematical modelling competencies. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14) (pp. 407–416). Springer.
Galbraith, P. L., Stillman, G., Brown, J., & Edwards, I. (2007). Facilitating middle secondary modelling competencies. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 130–140). Horwood.
*Gallegos, R. R., & Rivera, S. Q. (2015). Developing modelling competencies through the use of technology. In G. A. Stillman, W. Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 443–452). Springer.
Gonzalez, O., MacKinnon, D. P., & Muniz, F. B. (2021). Extrinsic convergent validity evidence to prevent jingle and jangle fallacies. Multivariate Behavioral Research, 56(1), 3–19.
*Govender, R. (2020). Mathematical modelling: A‘growing tree’ for creative and flexible thinking in pre-service mathematics teachers. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 443–453). Springer.
*Greefrath, G. (2020). Mathematical modelling competence. Selected current research developments. Avances de Investigación en Educación Matemática, 17, 38–51.
*Greefrath, G., Hertleif, C., & Siller, H. S. (2018). Mathematical modelling with digital tools—A quantitative study on mathematising with dynamic geometry software. ZDM – Mathematics Education, 50(1), 233–244.
*Große, C. S. (2015). Fostering modelling competencies: Benefits of worked examples, problems to be solved, and fading procedures. European Journal of Science and Mathematics Education, 3(4), 364–375.
*Grünewald, S. (2013). The development of modelling competencies by year 9 students: Effects of a modelling project. In G. A. Stillman, G. Kaiser, W. Blum, & J. P. Brown (Eds.), Teaching Mathematical Modelling: Connecting to Research and Practice (pp. 185–194). Springer.
*Hagena, M. (2015). Improving mathematical modelling by fostering measurement sense: An intervention study with pre-service mathematics teachers. In G. A. Stillman, W. Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 185–194). Springer.
*Hagena, M., Leiss, D., & Schwippert, K. (2017). Using reading strategy training to foster students’ mathematical modelling competencies: Results of a quasi-experimental control trial. Eurasia Journal of Mathematics, Science and Technology Education, 13(7b), 4057–4085.
Haines, C., Galbraith, P., Blum, W., & Khan, S. (2007). Mathematical modelling (ICTMA 12): Education, engineering and economics. Horwood.
Haines, C., Izard, J., & Le Masurier, D. (1993). Modelling intensions realized: Assessing the full range of developed skills. In T. Breiteig, I. Huntley, & G. Kaiser-Messmer (Eds.), Teaching and Learning Mathematics in Context (pp. 200–211). Ellis Horwood.
*Hankeln, C. (2020).Validating with the use of dynamic geometry software. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 277–286). Springer.
*Hankeln, C., Adamek, C., & Greefrath, G. (2019). Assessing sub-competencies of mathematical modelling—Development of a new test instrument. In G. A. Stillman, & J. P. Brown (Eds.), Lines of Inquiry in Mathematical Modelling Research in Education, ICME-13 Monographs (pp. 143–160). Springer.
*Henning, H., & Keune, M. (2007). Levels of modelling competencies. In W. Blum, P. L. Galbraith, H. W. Henn, & M, Niss (Eds.), Modelling and Applications in Mathematics Education, the 14th ICMI Study (pp. 225–232). Springer.
*Hidayat, R., Zamri, S. N. A. S., & Zulnaidi, H. (2018). Does mastery of goal components mediate the relationship between metacognition and mathematical modelling competency? Educational Sciences: Theory & Practice, 18(3), 579–604.
*Hidayat, R., Zamri, S. N. A., Zulnaidi, H., & Yuanita, P. (2020). Meta-cognitive behaviour and mathematical modelling competency: Mediating effect of performance goals. Heliyon, 6(4), e03800.
*Hidayat, R., Zulnaidi, H., & Syed Zamri, S. N. A. (2018). Roles of metacognition and achievement goals in mathematical modelling competency: A structural equation modelling analysis. PloS One, 13(11), e0206211.
*Højgaard, T. (2010). Communication: The essential difference between mathematical modelling and problem solving. In R. Lesh, P. L. Galbraith, C. R. Haines, & A. Hurford (Eds.), Modelling Students’ Mathematical Modelling Competences. Springer.
Hopewell S, Clarke M, Lefebvre C, & Scherer R. (2007). Handsearching versus electronic searching to identify reports of randomized trials. Cochrane Database of Systematic Reviews, 2, MR000001. https://doi.org/10.1002/14651858.MR000001.pub2
Houston, K., & Neil, N. (2003). Assessing modelling skills. In S. Lamon, W. Parker, & K. Houston (Eds.), Mathematical Modelling: A Way of Life (pp. 165–178). Horwood.
*Huang, C. H. (2011). Assessing the modelling competencies of engineering students. World Transactions on Engineering and Technology Education, 9(3), 172–177.
*Huang, C. H. (2012). Investigating engineering students’ mathematical modelling competency from a modelling perspective. World Transactions on Engineering and Technology Education, 10(2), 99–104.
*Ikeda, T. (2015). Applying PISA ideas to classroom teaching of mathematical modelling. In K. Stacey, & R. Turner (Eds.), Assessing Mathematical Literacy: The PISA Experience (pp. 221–238). Springer.
*Jensen, T. H. (2007). Assessing mathematical modelling competency. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 141–148). Horwood.
*Julie, C. (2020). Modelling competencies of school learners in the beginning and final year of secondary school mathematics. International Journal of Mathematical Education in Science and Technology, 51(8), 1181–1195.
*Kaiser, G. (2007). Modelling and modelling competencies in school. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 110–119). Horwood.
Kaiser, G. (2017). The teaching and learning of mathematical modelling. In J. Cai (Ed.), Compendium for Research in Mathematics Education (pp. 267–291). National Council of Teachers of Mathematics.
Kaiser, G., Blum, W., Borromeo Ferri, R., & Stillman, G. (2011). Trends in teaching and learning of mathematical modelling, (ICTMA 14). Springer.
*Kaiser, G., & Brand, S. (2015). Modelling competencies: Past development and further perspectives. In G. A. Stillman, W. Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 129–149). Springer.
*Kaiser, G., & Maaß, K. (2007). Modelling in lower secondary mathematics classroom—Problems and opportunities. In W. Blum, P. L. Galbraith, H. W. Henn, & M, Niss (Eds.), Modelling and Applications in Mathematics Education, the 14th ICMI Study (pp. 99–108). Springer.
Kaiser, G., & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. ZDM – Mathematics Education, 38(3), 302–310.
*Keisar, E., & Peled, I. (2018). Investigating new curricular goals: What develops when first graders solve modelling tasks? Research in Mathematics Education, 20(2), 127–145.
*Kreckler, J. (2017). Implementing modelling into classrooms: Results of an empirical research study. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical Modelling and Applications. Crossing and Researching Boundaries in Mathematics Education (pp. 277–287). Springer.
*Krüger, A., Vorhölter, K., & Kaiser, G. (2020). Metacognitive strategies in group work in mathematical modelling activities–The students’ perspective. In G. A. Stillman, G. Kaiser, & C. E. Lampen (Eds.), Mathematical Modelling Education and Sense-making (pp. 311–321). Springer.
*Leiss, D., Schukajlow, S., Blum, W., Messner, R., & Pekrun, R. (2010). The role of the situation model in mathematical modelling—Task analyses, student competencies, and teacher interventions. Journal für Mathematik-Didaktik, 31(1), 119–141.
*Leong, K. E., & Tan, J. Y. (2020). Exploring secondary students’ modelling competencies. The Mathematics Enthusiast, 17(1), 85–107.
Lesh, R., Hoover, M., Hole, B., Kelly, A., & Post, T. (2000). Principles for developing thought revealing activities for students and teachers. In A. Kelly & R. A. Lesh (Eds.), Handbook of Research Design in Mathematics and Science Education (pp. 591–645). Lawrence Erlbaum.
*Ludwig, M., & Reit, X. R. (2013). A cross-sectional study about modelling competency in secondary school. In G. A. Stillman, G. Kaiser, W. Blum, & J. P. Brown (Eds.), Teaching Mathematical Modelling: Connecting to Research and Practice (pp. 327–337). Springer.
*Ludwig, M., & Xu, B. (2010). A comparative study of modelling competencies among Chinese and German students. Journal für Mathematik-Didaktik, 31(1), 77–97.
*Maaß, K. (2006). What are modelling competencies? ZDM – Mathematics Education, 38(2), 113–142.
*Maaß, K. (2007).Modelling in class: What do we want the students to learn. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (pp. 63–78). Horwood.
Maass, K., Doorman, L. M., Jonker, V. H., & Wijers, M. M. (2019). Promoting active citizenship in mathematics teaching. ZDM - International Journal on Mathematics Education, 51(6), 991–1003. https://doi.org/10.1007/s11858-019-01048-6
Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis (2nd ed.). Sage.
*Mischo, C., & Maaß, K. (2013). The effect of teacher beliefs on student competence in mathematical modelling - An intervention study. Journal of Education and Training Studies, 1(1), 19–38.
Moher, D., Liberati, A., Tetzlaff, J., Altman, D. G., & the PRISMA Group. (2009). Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med, 6(7), e1000097. https://doi.org/10.1371/journal.pmed.1000097
Niss, M., & Blum, W. (2020). The learning and teaching of mathematical modelling. Routledge.
Niss, M., Blum, W, & Galbraith, P. (2007). Introduction. In W. Blum, P. L. Galbraith, H. W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education. The 14th ICMI study (pp. 3–32). Springer.
Niss, M., & Højgaard, T. (2011). Competencies and mathematical learning—Ideas and inspiration for the development of mathematics teaching and learning in Denmark. Roskilde University Press. English translation of Danish original (2002).
Niss, M., & Højgaard, T. (2019). Mathematical competencies revisited. Educational Studies in Mathematics, 102, 9–28. https://doi.org/10.1007/s10649-019-09903-9
Page, M. J., Moher, D., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., ... & McKenzie, J. E. (2021). PRISMA 2020 explanation and elaboration: Updated guidance and exemplars for reporting systematic reviews. BJM. https://doi.org/10.1136/bmj.n71
*Rensaa, R. J. (2011). A task based two-dimensional view of mathematical competency used to analyse a modelling task. International Journal of Innovation in Science and Mathematics Education, 19(2), 37–50.
*Schukajlow, S., Kaiser, G., & Stillman, G. (2018). Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. ZDM – Mathematics Education, 50, 5–18.
*Schukajlow, S., Kolter, J., & Blum, W. (2015). Scaffolding mathematical modelling with a solution plan. ZDM – Mathematics Education, 47(7), 1241–1254.
*Sekerak, J. (2010). Competences of mathematical modelling of high school students. Mathematics Teaching, 220, 8–12.
*Shahbari, J. A., & Tabach, M. (2020). Features of modelling processes that elicit mathematical models represented at different semiotic registers. Educational Studies in Mathematics, 105(2), 115–135.
Shavelson, R. (2010). On the measurement of competency. Empirical Research in Vocational Education and Training, 2(1), 41–63.
Stillman, G. (2011). Applying metacognitive knowledge and strategies in applications and modelling tasks at secondary school. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling, (ICTMA 14) (pp. 165–180). Springer.
Stillman, G. A., Blum, W., & Biembengut, M.S., (2015). Cultural, social, cognitive and research influences on mathematical modelling education. In G. A. Stillman, W., Blum, & M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice (pp. 1–32). Springer.
Stillman, G., Brown, J. P., Edwards, I., & Galbraith, P. (2007). A framework for success in implementing mathematical modelling in the secondary classroom. In J. Watson, & K. Beswick (Eds.), Mathematics: Essential Research, Essential Practice. Proceedings of the 30th Annual conference of the Mathematics Education Research Group of Australasia (pp. 688–707). Mathematics Education Research Group of Australasia.
Stillman, G. A., Brown, J. P., & Galbraith, P. (2010). Identifying challenges within phases of mathematical modeling activities in year 9. In R. Lesh, P. Galbraith, C. R. Haines, & A. Hurford (Eds.), Modeling Students’ Mathematical Modeling Competencies (pp. 385–398). Springer.
Stillman, G., & Galbraith, P. (1998). Applying mathematics with real world connections: metacognitive characteristics of secondary students. Educational Studies in Mathematics, 36(2), 157–194.
*Tong, D. H., Loc, N. P., Uyen, B. P., & Giang, L. T. (2019). Developing the competency of mathematical modelling: A case study of teaching the cosine and sine theorems. International Journal of Learning, Teaching and Educational Research, 18(11), 18–37.
*Vorhölter, K. (2017). Measuring metacognitive modelling competencies. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical modelling and applications. Crossing and Researching Boundaries in Mathematics Education (pp. 175–185). Springer.
Vorhölter, K. (2018). Conceptualization and measuring of metacognitive modelling competencies: Empirical verification of theoretical assumption. ZDM – Mathematics Education, 50(1–2), 343–354.
*Vorhölter, K., Krüger, A., & Wendt, L. (2017, February). Metacognitive modelling competencies in small groups. In T. Dooley, & G. Gueudet (Eds.), Proceedings of the tenth congress of the European Society for research in mathematics education (CERME10, February 1-5, 2017). DCU Institute of Education and ERME.
*Wang, Y. (2021). Investigation of the mathematics modelling competency of mathematics undergraduate student teachers. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 239–247). Springer.
Weinert, F. E. (2001). Concept of competence: A conceptual clarification. In D. S. Rychen & L. H. Salganik (Eds.), Defining and Selecting Key Competencies (pp. 45–65). Hogrefe & Huber.
*Wess, R., Klock, H., Siller, H. S., & Greefrath, G. (2021). Measuring professional competence for the teaching of mathematical modelling. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical Modelling Education in East and West (pp. 249–260). Springer.
*Wijaya, A. (2017). Exploring students’ modelling competences: A case of a GeoGebra-based modelling task. In AIP Conference Proceedings, 1848, 040008. AIP Publishing LLC.
*Winter, M., & Venkat, H. (2013). Pre-service teacher learning for mathematical modelling. In G. A. Stillman, G. Kaiser, W. Blum, & J. P. Brown (Eds.), Teaching mathematical modelling: Connecting to research and practice (pp. 395–404). Springer.
*Yilmaz, S., & Dede, A. T. (2016). Mathematization competencies of pre-service elementary mathematics teachers in the mathematical modelling process. International Journal of Education in Mathematics, Science and Technology, 4(4), 284–298.
*Zöttl, L., Ufer, S., & Reiss, K. (2010). Modelling with heuristic worked examples in the KOMMA learning environment. Journal für Mathematik-Didaktik, 31(1), 143–165.
*Zöttl, L., Ufer, S., & Reiss, K. (2011). Assessing modelling competencies using a multidimensional IRT-approach. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modelling, (ICTMA 14) (pp. 427–437). Springer.
*Zubi, I. A., Peled, I., & Yarden, M. (2019). Children with mathematical difficulties cope with modelling tasks: What develops? International Journal of Mathematical Education in Science and Technology, 50(4), 506–526.
Zubi, I. A., Peled, I., & Yarden, M. (2019). Modelling tasks and students with mathematical difficulties. In G. A. Stillman & J. P. Brown (Eds.), Lines of Inquiry in Mathematical Modelling Research in Education, ICME-13 Monographs (pp. 213–231). Springer.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cevikbas, M., Kaiser, G. & Schukajlow, S. A systematic literature review of the current discussion on mathematical modelling competencies: state-of-the-art developments in conceptualizing, measuring, and fostering. Educ Stud Math 109, 205–236 (2022). https://doi.org/10.1007/s10649-021-10104-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-021-10104-6