Abstract
Constructing multiplicative reasoning is critical for students’ learning of mathematics, particularly throughout the middle grades and beyond. Tzur, Xin, Si, Kenney, and Guebert [American Educational Research Association, ERIC No. ED510991, (2010)] conclude that an assimilatory composite unit is a conceptual spring to multiplicative reasoning. This study examines patterns in the percentages of students who construct multiplicative reasoning across the middle grades based on their fluency in operating with composite units. Multinomial logistic regression models indicate that students’ rate of constructing an assimilatory composite unit but not multiplicative reasoning in sixth and seventh grades is significantly greater than that in eighth and ninth grades. Furthermore, the proportion of students who have constructed multiplicative reasoning in sixth and seventh grades is significantly less than the proportion of those who have constructed multiplicative reasoning in eighth and ninth grades. One implication of this is the quantitative verification of Tzur, Xin, Si, Kenney, and Guebert’s (2010) conceptual spring. That is, students who construct assimilatory composite units early in the middle grades are likely to construct multiplicative reasoning; students who do not construct assimilatory composite units early in the middle grades likely do not construct multiplicative reasoning in the middle grades.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multiplication is a topic of elementary mathematics instruction, but multiplicative reasoning is a form of mathematical thinking that is a cognitive precursor to many forms of advanced mathematics (Clark & Kamii, 1996). Multiplicative reasoning is pervasive in the middle-grade curriculum (e.g., Common Core State Standards Initiative [CCSSI], 2010) and supports students’ development of advanced concepts such as fractional reasoning (Hackenberg, 2007, 2013) and algebraic reasoning (Hackenberg, 2013; Hackenberg & Lee, 2015). Despite its prevalence and importance, many students cannot reason multiplicatively by the middle grades (Kosko, 2019; Kosko & Singh, 2018; Ulrich & Wilkins, 2017; Wilkins, Woodward, & Norton, 2020). This makes many of the demands of a middle-grade curriculum difficult, if not impossible. Understanding key developmental hurdles to children’s multiplicative reasoning could make it possible to better support this development.
There are multiple perspectives through which students’ multiplicative reasoning could be studied and understood. For instance, Vergnaud’s (1988) pioneering work on children’s multiplicative reasoning defines multiplicative structures as a conceptual field made up of “a set of situations, the mastering of which requires mastery of several concepts of different natures” (p. 141). In this view, children’s multiplicative reasoning develops through a comprehensive investigation of simple and multiple proportion problems within many contexts involving multiplication and division. In addition, Davydov and Elkonin propose to view the development of multiplicative reasoning through a measurement perspective in which children understand multiplication “as the use of an intermediate unit to find the number of units in a quantity” (Dougherty & Simon, 2014, p. 206). In this view, children’s development of multiplicative reasoning does not derive from their counting, but instead from the manipulation of a derived measurement unit. A third viewpoint, which we use to ground our study, is that of Steffe (1992), who defines multiplicative reasoning as mental actions that support the distribution of one composite unit (i.e., a unit of units) over another composite unit. Steffe’s (1992) definition further asserts that students construct multiplicative reasoning by making modifications to their additive numerical reasoning schemes, which initially derive from their early counting schemes.
Building from Steffe’s view of multiplicative reasoning, Tzur et al. (2010) qualitatively demonstrated that an assimilatory composite unit instigates the construction of multiplicative reasoning; however, this result has not been quantitatively tested. The purpose of the current research is to determine the existence of and nature of the relationships between students’ construction of multiplicative reasoning in the middle grades and their fluency operating with composite units, thereby testing the qualitative result that an assimilatory composite unit launches the construction of multiplicative reasoning.
2 Literature review
A main distinction between additive and multiplicative reasoning is a “hidden assumption” (Carrier, 2014, p. 87) that must be understood to reason multiplicatively about a situation. Additive reasoning involves operating on units of one. For example, adding a group of three apples to a group of four apples is additive and thus requires reasoning only about units of one—apples. Multiplicative reasoning requires interpreting a problem involving units of one and also units of units (i.e., composite units). To determine how many apples are in three bags of four apples each, for instance, is multiplicative because it requires students to reason about units of one (apples) and about composite units (bags of apples). The composite units are the hidden assumption.
The hidden assumption can be understood through Piaget’s (1941/1965) work. He pointed out that reasoning multiplicatively requires the coordination of two units. Steffe (1992) similarly indicated that for a situation to be multiplicative “it is always necessary at least to coordinate two composite units in such a way that one of the composite units is distributed over the elements of another composite unit” (p. 264). In this context, a composite unit is a unit that is formed as the result of mentally uniting a group of singleton units into a larger unit (e.g., apples into bags; Ulrich, 2015). The distribution of the elements of one composite unit over another is accomplished mentally when students can conceive of filling each of the three bags with a group of four apples.
In addition to difficulty identifying the hidden assumption, students may also conflate additive and multiplicative reasoning (Degrande, Verschaffel, & Van Dooren, 2018, 2019, 2020; van Dooren, de Bock, & Verschaffel, 2010). Degrande et al. (2018, 2019) determined that students’ conflations may result from preferring additive reasoning over multiplicative, or vice versa. Alternatively, some students made decisions about reasoning additively or multiplicatively based on irrelevant criteria, such as whether or not the result had an integer value. Degrande et al. (2019) conducted an additional analysis of the additive and multiplicative preferences of students who demonstrated both additive and multiplicative skill (i.e., accuracy) and discrimination (i.e., determining whether tasks required additive or multiplicative reasoning). This allowed the researchers to ascertain that a preference for additive reasoning was a significant predictor of erroneously applying additive reasoning to multiplicative tasks, despite demonstrating multiplicative skill and discrimination. Similarly, a preference for multiplicative reasoning was a significant predictor of erroneously applying multiplicative reasoning to additive tasks, despite demonstrating additive skill and discrimination. This research contributes important results to an understanding of students’ applications of additive and multiplicative reasoning; however, multiplicative skill is distinct from multiplicative reasoning. Thus, research must continue to examine whether students who demonstrate a preference for additive reasoning in multiplicative situations have constructed the cognitive structures that Steffe (1992) described as necessary to support multiplicative reasoning, namely, the distribution of one composite unit over another.
Clark and Kamii (1996) examined the thinking of elementary students and found that 45% of second graders demonstrated some level of multiplicative reasoning. However, by fifth grade, only 49% of students demonstrated consistent and successful multiplicative reasoning. This illustrates students’ transition from additive to multiplicative reasoning as a slow climb and highlights that a majority of students does not reason multiplicatively by the conclusion of the elementary grades.
Clark and Kamii’s (1996) percentages are similar to Kosko’s (2019) and Kosko and Singh’s (2018). In two related studies, 54.3% of third-grade students were premultiplicative (Kosko & Singh, 2018), where premultiplicative implies the student is yet to construct composite units in activity, thereby precluding them from reasoning multiplicatively as Steffe (1992) describes. However, only 15.7% of fourth-grade students and 6.8% of fifth-grade students were premultiplicative. Conversely, 62.5% of fifth-grade students reasoned multiplicatively at the most sophisticated stage (Kosko, 2019). This result is more optimistic than Clark and Kamii’s (1996), but illuminating the complementary result that 37.5% of fifth-grade students are not reasoning multiplicatively (Kosko, 2019) with a level of sophistication that will support their conceptions of fractions and algebraic concepts is troubling.
The most sophisticated stage of multiplicative reasoning aligns with Steffe’s (1992, 1994) arithmetic stage, which implies students’ preparedness to construct concepts of quotative and partitive division (Steffe, 1994), fractions as “numbers in their own right” (Hackenberg, 2007, p. 27), and to write and reverse multiplicative algebraic equations (Hackenberg & Lee, 2015). The theoretical implications of reasoning multiplicatively for middle-grade mathematics bring Clark and Kamii’s (1996), Kosko’s (2019), and Kosko and Singh’s (2018) results into focus by theoretically rationalizing some of the mathematical difficulties that many middle-grade students encounter.
Tzur et al. (2010) offer insight into the difficulty students have in constructing multiplicative reasoning. Their research presented the results of a constructivist teaching experiment (see Steffe & Ulrich, 2013) involving 12 fourth- or fifth-grade students with learning disabilities who did not reason multiplicatively. The students also had not constructed assimilatory composite units, meaning they could not mentally operate on composite units of apples within bags, for instance. This aligns with Steffe’s (1992) definition of multiplicative reasoning, making it an unsurprising result. However, Tzur et al. (2010) found that when students constructed an assimilatory composite unit, it served as a “conceptual spring” (p. 9) that preceded the construction of multiplicative reasoning.
Characterizing assimilatory composite units as conceptual springs that precede and even instigate students’ construction of multiplicative reasoning (Tzur et al., 2010) provides a theoretical basis for the present research study. This study seeks to quantitatively examine Tzur et al.’s result by determining the rates at which students with different levels of fluency operating on composite units construct multiplicative reasoning in the middle grades. This question will be analyzed within the number sequences framework (Steffe, 2010; Ulrich, 2016b) which distinguishes between students who (1) do not construct composite units, (2) construct composite units in activity, (3) assimilate with composite units and do not reason multiplicatively, and (4) assimilate with composite units and reason multiplicatively.
3 Theoretical framework
The number sequences (Steffe, 2010) form a stage theory that describe students’ interpretations of and operations on number. They are based, in part, on students’ units coordination and construction (Ulrich, 2015; Ulrich, 2016a). Within this frame of reference, students’ construction of multiplicative reasoning can be attributed to modifications made to their number sequences (Steffe, 1992), which is to say that multiplicative reasoning is “rooted in and indicative of” the number sequences (Tzur et al., 2013, p. 95). Accordingly, the number sequences will be used as a framework for understanding students’ construction of multiplicative reasoning in this study. The number sequences (Steffe, 2010; Ulrich, 2016b) are a neo-Piagetian hierarchy of stages through which students construct an increasingly complex understanding of number. Each distinct stage is based on the student’s ability to construct and operate on units with increasing complexity (Ulrich, 2015, 2016a).
The original number sequence trajectory, as defined through work with elementary-grade children, included the initial number sequence (INS), tacitly nested number sequence (TNS), explicitly nested number sequence (ENS), and generalized number sequence (GNS; Steffe, 2010). In related work with middle-grade students, Ulrich (2016b) defined the advanced tacitly nested number sequence (aTNS), which falls between the tacitly and explicitly nested number sequences. Ulrich’s amendment to the number sequence hierarchy will be considered as a step toward the construction of multiplicative reasoning in the present research.
Figure 1 shows the trajectory of number sequences from least (INS) to most (GNS) sophisticated. The number sequences are shown in an Euler diagram, with the more sophisticated number sequences subsuming the less, because students who have constructed a GNS, for instance, have also constructed each of the less sophisticated number sequences. A GNS student can operate in a manner that is consistent with an ENS, or any less sophisticated number sequence. Therefore, to speak of a GNS student or a student who has constructed a GNS implies that the student has also constructed an INS, TNS, aTNS, and ENS. The mental constructions that define the number sequences and facilitate multiplicative reasoning are also shown in Fig. 1 to summarize relevant criteria for attributing multiplicative reasoning based on number sequence attribution.
INS, TNS, and aTNS students can only reason additively, whereas ENS and GNS students can reason additively and multiplicatively. Students’ construction of multiplicative reasoning is consistent with having constructed an ENS (Tzur et al., 2013; Ulrich, 2016a). Therefore, to understand the numbers of students who have constructed multiplicative reasoning, and who have yet to construct multiplicative reasoning, the remainder of this section focuses on explicating the INS, TNS, aTNS, and ENS as they relate to multiplicative reasoning.
3.1 Initial number sequence
Students’ construction of an INS is marked behaviorally by counting on (Steffe, 2010). This means that if told that two collections of counters had seven and four counters, respectively, an INS student could find the total number of counters by saying “seven; eight, nine, ten, eleven.” For an INS student, the number word “seven” stands in for the counting sequence from one through seven, making it unnecessary for them to count the first collection. Counting on is supported by the mental construction of one level of units in activity and is “initial” because it is the first stage of numerical reasoning (Steffe, 2010).
Although INS students are numerical, “the mathematical reality [of INS students] was premultiplicative” (Steffe, 1992, p. 304). This conclusion was drawn from longitudinal research in which INS students attempted to solve multiplicative tasks. An INS student, Zachary, was told there were four rows of three blocks under a cover, and some more rows of three blocks were added, totaling seven rows of three blocks. When asked how many rows were added, Zachary formed a goal of using his number concept for seven and counting three, seven times. He used finger patterns for three to count by threes. However, he lost track of how many times he had counted by three and stopped when he reached 24, rather than 21. Moreover, Zachary missed the point of the task, which was to find a number of rows. In a second attempt, Zachary attended to the rows, but finally conceded that “I can’t do that one [task]” (Steffe, 1992, p. 265). Without a TNS, Steffe (1992) concludes that Zachary, and other INS students, remains premultiplicative.
3.2 Tacitly nested number sequence
Students can construct a TNS once they can construct composite units in activity (Steffe, 2010). This implies that the student interprets a number, such as seven, as seven individual units of one but in mental activity can imagine chunking the seven units into one composite unit (Fig. 2). Because the composite unit is constructed in mental activity, it is not anticipated prior to activity, nor is it available for reflection following activity (Ulrich, 2015). It is the lack of anticipation and reflection that makes the students’ conception of composite units “tacit” in nature.
A visual representation of seven as units of one (left) and as a composite unit (right). Adapted from Ulrich (2015)
The construction of a composite unit in activity is powerful because it allows TNS students to make sense of questions like how many blocks are in four rows of three, without counting by ones (Steffe, 1992). This situation is not multiplicative to TNS students.
Steffe (1992) describes a TNS student, Maya, who solved this task by filling each unit of the composite units of four with a unit of three in mental activity. However, while the mental activity of filling one composite unit with the elements of a second composite unit is multiplicative in nature, Maya’s activity does not constitute multiplicative reasoning because it is only implicitly multiplicative (Steffe, 1992). As long as composite units must be constructed in activity, multiplicative reasoning cannot be explicit.
3.3 Explicitly nested number sequence Footnote 1
ENS students assimilate with composite units which means that they can immediately interpret a number, such as seven, as a composite unit containing seven individual units of one. Assimilating with composite units makes the students’ conception of a composite unit anticipatory and material for reflection and, in turn, allows the students’ conception to be “explicit.” With this explicit understanding of a composite unit, ENS students can, in mental activity, construct a unit of units of units—21 as three groups of seven, for example (Fig. 3), although the third level of units is not anticipated prior to activity and decays following activity (Ulrich, 2016a). Furthermore, ENS students have constructed a disembedding operation and an iterable unit of one (Steffe, 2010). A disembedding operation allows ENS students to think about mentally removing units from the composite unit without destroying either quantity (Ulrich, 2016a). This facilitates comparison of the two units. An iterable unit of one implies the ability to mentally repeat a unit of one and conceive of it as identical to other units of one (Olive, 2001). In combination, disembedding and iterating units of one facilitate multiplicative reasoning (Ulrich, 2016a) because they support ENS students in reasoning that a composite unit of seven, for instance, is seven times the size of one. Assimilating with composite units, disembedding, and iterating units of one make an ENS the onset of multiplicative reasoning (Tzur et al., 2013; Ulrich, 2016a).
These operations support the multiplicative reasoning of ENS students, like Johanna (Steffe, 1992). Johanna was shown four rows of three blocks and told there were some more rows of three blocks hidden beneath a screen, for a total of seven rows. When asked how many rows were hidden, she almost immediately responded that there were three. Johanna could operate on the rows as if they were units of one while mentally maintaining the three blocks within the rows (composite units), which constitutes multiplicative reasoning (Steffe, 1992).
3.4 Advanced tacitly nested number sequence
aTNS students assimilate with composite units (Ulrich, 2016b), which is more sophisticated than TNS students (Ulrich, 2016a), and the qualifier “advanced” in aTNS is literal in its meaning (Ulrich, 2016b); aTNS students have a more advanced concept of composite units than do TNS students. For aTNS students, a number like seven can be assimilated as a unit containing seven units. Then, in mental activity, aTNS students can conceive of a unit of units of units—21 as three groups of seven, for example (Fig. 4). Although the three-level unit structure is not anticipated prior to activity and decays following activity, the composite unit is available for reflection (Ulrich, 2016a). This is in comparison to TNS students, for whom the composite unit is unavailable for reflection following mental activity (Ulrich, 2015).
aTNS students’ reasoning about number, however, is less sophisticated than ENS students’. Whereas both groups assimilate with composite units, aTNS students neither disembed nor iterate units of one (Ulrich, 2016b). ENS students can conceive of a number, such as seven, as seven iterations of identical units of one, and can mentally disembed and compare units to the composite unit (see Fig. 3); aTNS students cannot. Rather, aTNS students conceive of seven as a counting sequence from one to seven, or ten to sixteen, for example. Furthermore, to mentally remove a unit from the composite would destroy the mental records of the composite unit for aTNS students. For these reasons, the cognitive structures of aTNS students do not support multiplicative reasoning.
4 Purpose and research questions
Students construct multiplicative reasoning when they make accommodations to their number sequences (Steffe, 1992). Research has also directly linked number sequences to constructing multiplicative reasoning. Wilkins et al. (2020) found that students who construct an INS by the beginning of second grade are 1.79 and 2.80 times more likely to construct multiplicative reasoning by the beginning of fourth and fifth grades, respectively, compared to students who have not constructed at least an INS in second grade. Similarly, students who construct a TNS by the beginning of second grade are 2.03 and 4.57 times more likely to construct multiplicative reasoning by the beginning of fourth and fifth grades, respectively, compared to students who had not constructed at least an INS. These results quantify the relationship between students’ number sequences and their construction of multiplicative reasoning. Furthermore, Tzur et al. (2010) stated that “when teaching does promote construction of … numbers as the conceptual prerequisite—substantial progress into multiplication and division can be nurtured” (p. 10, emphasis in original). Therefore, students must construct sufficiently sophisticated concepts of number, including assimilatory composite units, before the spring that engenders multiplicative reasoning is released.
The purpose of this study is to examine students’ construction of multiplicative reasoning, as understood through the number sequences. This study asks: Do the proportions of students who have constructed multiplicative reasoning compared to the proportions who have not constructed multiplicative reasoning differ across the middle grades? Analyzing this question through the number sequence framework supports a focus on students’ fluency with composite units: INS students do not construct composite units, TNS students construct composite units in activity, aTNS students assimilate with composite units but do not reason multiplicatively, and ENS students assimilate with composite units and reason multiplicatively. Thus, we will analyze the relative proportions of these different groups of students between grade levels to investigate Tzur et al.’s (2010) conclusion that assimilating with composite units, as indicated by a student’s construction of an aTNS in this study, is a conceptual spring to multiplicative reasoning, as indicated by a student’s construction of an ENS in this study. This will be accomplished by comparing the proportions of students at each grade level who have not constructed assimilatory composite units (i.e., INS and TNS students) to multiplicative reasoning (i.e., an ENS) and the proportions of students at each grade level who have constructed assimilatory composite units but not multiplicative reasoning (i.e., aTNS students) to multiplicative reasoning (i.e., an ENS). A significant difference in these proportions would indicate the significant role of assimilatory composite units in the development of multiplicative reasoning.
5 Methods
5.1 Participants
This study was conducted in the rural southeastern USA and involved 326 students in grades 6 through 9. Participants in grades six through eight attended a single middle school, and students in grade 9 attended a single high school. All students who attended the participating middle school would advance to the participating high school upon entrance to ninth grade, and no other middle schools advanced to the participating high school. Therefore, the participants represent a trajectory within a school district. The town in which the school district is located has approximately 7000 residents and is located in Appalachia. At the schools included in the study, 49.1% of students are identified as economically disadvantaged, and 92.0% are White.
All students in grades six through nine who were present at school and enrolled in a mathematics class during data collection were invited to participate. Of the students in the school, 74.6% of sixth-grade students (100 out of 134), 79.3% of seventh-grade students (92 out of 116), 63.2% of eighth-grade students (74 out of 117), and 56.6% of ninth-grade students (60 out of 106) participated. Among all grades, 5.7% of students did not participate because they did not give assent, and 25.4% were not surveyed due to scheduling conflicts or absences. Overall, 68.9% of students (326 out of 473) participated in the study.
Of the 326 students who participated in the study, all sixth-grade students were in a general Math 6 course. Seventh-grade students were split between a Pre-Algebra course and a general Math 7 course. Eighth-grade students were split between an Algebra 1 course and a Pre-Algebra course, and ninth-grade students were split among an Algebra 1-part 2 course, a Geometry course, and an Algebra 2 course. In total, students from 18 classes participated: four sections of Math 6, three sections of Math 7, four sections of Pre-Algebra, one section of Algebra 1, two sections of Algebra 1 Part 2, two sections of Geometry, and two sections of Algebra 2.
The school district in which data were collected did not have a prescribed curriculum; rather, the teachers independently developed lessons based on the state standards (Virginia Department of Education, 2016). These standards prescribe that multiplicative reasoning be explicitly addressed in Math 6 and Math 7. In Math 6, students learn to represent, notate, find equivalencies, and compare ratios, fractions, mixed numbers, decimals, and percents. They also multiply and divide fractions, mixed numbers, decimals, and integers. In Math 7, students investigate powers of 10, and solve problems using rational numbers and proportions. None of the additional course standards for the classes in which participants were enrolled had an explicit focus on multiplicative reasoning, or operations on whole numbers, integers, or rational numbers. Although the autonomy given to teachers within this school district makes it difficult to parse out the role of curriculum in students’ construction of multiplicative reasoning in this study, this brief description is offered to provide context to the participants’ mathematical experiences.
5.2 Measures
5.2.1 Number sequences
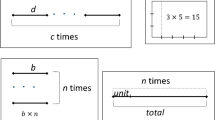
To ascertain students’ number sequence, we used a survey instrument designed to elicit students’ ways of operating that are characteristic of each number sequence (Ulrich & Wilkins, 2017). The instrument includes 25 questions, and students were given approximately 1 h to complete the survey. Face and content validity were established by aligning survey items with existing theory and by consulting an expert in mathematics education. Further validity evidence was provided by comparing student classifications based on the survey with the classifications based on clinical interviews. Interrater reliability, as indicated by a weighted Kappa statistic, for the overall student classifications based on the instrument was documented to be 0.95 (Ulrich & Wilkins, 2017). Figure 5 shows selected items from the survey. The cupcake task was accessible to most students regardless of their number sequence and elicited varied solution strategies based on their number sequences. On this item, the cupcakes represent units of one and the boxes of cupcakes represent units of three, therefore allowing the researchers to interpret the students’ written work in terms of their operations on composite units.
Selected items from the survey instrument (Ulrich & Wilkins, 2017)
The bars tasks (Fig. 5) also elicited different solutions for students who had constructed different number sequences. The five tasks are ordered here by increasing difficulty, although they are not arranged in succession on the survey. In each of these tasks, the small rectangle represents a composite unit. Ulrich and Wilkins (2017) found a statistically significant, and strong, positive association between the tasks and the number sequences such that INS students did not solve any of the bar tasks, TNS students typically only solved B1, aTNS students typically solved B1-B3, and ENS students typically solved all of the tasks. This result is theoretically supported by the students’ increasingly sophisticated operations with composite units.
This survey instrument was selected because scores from the survey assign a stage classification to students. Stage classifications are related to the student’s number sequence and are hierarchical. The classifications are as follows: (1) pre-numerical or INS, which includes students whose responses overwhelmingly indicated that they had constructed at most an INS; (2) TNS, which includes students whose responses overwhelmingly indicated that they had constructed at most a TNS; (3) aTNS, which includes students whose responses overwhelmingly indicated that they had constructed at most an aTNS; and (4) ENS or GNS, which includes students whose responses overwhelmingly indicated that they had constructed at least an ENS.
The stage classifications acknowledge the limitations of assessing students’ number sequences using a paper survey because it is possible that an ENS student, for example, may solve problems in a manner that is consistent with any of the less sophisticated number sequences. Thus, the stage classifications are understood to represent the “lower bound” (Ulrich & Wilkins, 2017, p. 7) of students’ number sequence attributions.
The surveys were scored independently by two researchers. The researchers calibrated their scoring by individually scoring 10% of the surveys using the scoring guide and rubric (Ulrich & Wilkins, 2015). Then, the researchers reconciled scoring inconsistencies on individual questions. After reconciling scores, each researcher independently scored the remaining surveys. The resulting stage classifications were compared, and the researchers reconciled inconsistencies in stage classification.
To assess the level of agreement, or interrater reliability, for the stage classifications, we computed the weighted kappa statistic, Κ, (Cohen, 1968). The weighted kappa statistic is appropriate due to the ordinal nature of the stage classifications and because there are more than two levels (Cohen, 1968). By using weighted kappa, mismatched stage classifications between researchers are weighted proportionately based on the level of disagreement. The weighted kappa statistic ranges between 0 and 1, where 1 represents perfect agreement. The weighted kappa statistic for grades six (K = 0.92), seven (K = 0.87), eight (K = 0.88), and nine (K = 0.94), represent “almost perfect” agreement (Landis & Koch, 1977, p. 165). The overall weighted kappa score (K = 0.91) also represents “almost perfect” agreement (Landis & Koch, 1977, p. 165). These kappa statistics are consistent with those presented by Ulrich and Wilkins (2017).
5.2.2 Grade level
To measure students’ developmental levels, we used their grade level. We created four dummy-coded variables to indicate student grade level (grade 6, grade 7, grade 8, and grade 9).
5.3 Data analysis
To address our research question, we estimated a multinomial logistic regression model that regressed the existence of multiplicative reasoning on grade level. The model was used to analyze patterns in the proportions of students’ construction of multiplicative reasoning in the middle grades, as measured by an ENS stage classification. Tzur et al.’s (2010) conceptual spring suggests that students who assimilate with composite units may construct multiplicative reasoning at different rates than students who do not. Accordingly, a multinomial logistic regression model facilitated a comparison of the proportions of students who have constructed multiplicative reasoning to the proportions who have constructed each of the preceding stages at each grade level.
In this model, Y is the dependent variable which represents the student’s construction of multiplicative reasoning and includes the four stage classifications: INS, which indicates no operations on composite units; TNS, which indicates construction of composite units in activity; aTNS, which indicates assimilatory composite units but not multiplicative reasoning; and ENS, which indicates assimilatory composite units and multiplicative reasoning. ENS was the reference category because it is used as a proxy for measuring student’s multiplicative reasoning. X1i, X2i, and X3i are the independent variables, representing a student’s enrollment in sixth, seventh, or eighth grade, respectively. Each of these was dummy coded, and ninth grade was the reference category. b1, b2, and b3 quantify the change in the logit of Y associated with a student belonging to the identified grade level. Finally, b0 is the model’s intercept. Statistical significance of the coefficients was determined using a Wald chi-square statistic. After estimating the model, each regression coefficient was exponentiated to produce the odds ratios of constructing multiplicative reasoning in each grade relative to each of the preceding stage classifications. Then, relative risks were calculated to better facilitate interpretations; odds ratios often lead to less straightforward interpretations. According to Olivier, May, and Bell (2017), relative risks of 1.22, 1.86, and 3.00 represent benchmarks for small, medium, and large effect sizes, respectively. We offer these benchmarks as a guide, but caution readers when interpreting relative effect sizes absolutely without context or reference (Bakker et al., 2019). In our study, we view relative risk, in terms of an effect size, as a “measure of clarity” with regard to the meaningfulness of differences between groups (Simpson, 2020, p. 129).
The aim of this analysis was to determine the existence of and nature of the relationship between students’ construction of multiplicative reasoning in the middle grades and their operations on composite units. Are the proportions of students who reason multiplicatively similar to the proportions of students who do not construct composite units, construct composite units in activity, and assimilate with composite units? Which of these groups, all of whom are constrained to additive reasoning, are most likely to construct multiplicative reasoning, and is this construction more likely to happen at certain points in time across the middle grades? By answering these questions, we are able to explicitly link differences in proportions by number sequence to the conceptual spring, and in particular, answering these questions will investigate the role of assimilatory composite units in children’s construction of multiplicative reasoning.
6 Results
6.1 Descriptive statistics
Students who are constrained to reasoning additively, measured by not yet having constructed an ENS, make up 60.1% (196 out of 326) of the middle-grade students surveyed (Table 1). The largest group of students who are still constrained to additive reasoning are aTNS students. They make up 46.6% (152 out of 326) of the sample, and 77.6% (152 out of 196) of the additive reasoners.
The percentage of students who assimilate with composite units but do not reason multiplicatively (i.e., aTNS students) is comparable in grades six and seven, and in grades eight and nine, and drops approximately 20% from seventh grade to eighth grade (Fig. 6). In a complementary pattern, the percentage of students who assimilate with composite units and reason multiplicatively (i.e., ENS students) is similar in grades six and seven, and in grades eight and nine, but from grades 7 to 8 the number of students who have constructed at least an ENS increases by approximately 23%. No such patterns emerged for students who do not assimilate with composite units (i.e., INS and TNS students), indicating that the numbers of students who had constructed only an INS or a TNS were relatively consistent across the middle grades.
The percentage of students who have constructed an advanced tacitly nested number sequence (aTNS) decreases from grade 7 to 8, while the percentage of students who have constructed at least an explicitly nested number sequence (ENS) increases. There are no similar changes in the percentages of students who have constructed an initial number sequence (INS) or a tacitly nested number sequence (TNS)
6.2 Relationship between students’ construction of multiplicative reasoning and grade level
Multinomial logistic regression models were estimated, in which students’ construction of multiplicative reasoning was regressed on their grade level. The results from the model utilizing the ENS stage classification as the reference group are presented in Table 2.Footnote 2 Incorporating students’ grade level as a predictor into this model significantly improved model fit compared to the null model (likelihood ratio test: χ2(9) = 20.545, p = 0.015).
Interpreting the regression coefficients based on their statistical significance, or lack thereof, leads to the conclusion that the proportion of students constructing an INS relative to an ENS is not significantly less in grades 6 through 8 compared to grade 9 (grade 6: b11 = 0.950, ns; grade 7: b12 = 0.223, ns; grade 8: b13 = − 0.089, ns). The rate of students constructing a TNS relative to an ENS is also not significantly less in grades 6 through 8 compared to grade 9 (grade 6: b21= 0.370, ns; grade 7: b22 = 0.182, ns; grade 8: b23 = − 1.229, ns). Thus, the proportion of students who have constructed multiplicative reasoning compared to the proportions of those who do not construct composite units (i.e., INS students) and of those who construct composite units in activity (i.e., TNS students) does not increase in higher grades. This suggests that INS and TNS students have the same likelihood of constructing multiplicative reasoning when they exit the middle grades as they did when they entered the middle grades.
In contrast, the proportions of students constructing an aTNS relative to an ENS were significantly greater in several grade-level comparisons, as indicated by statistically significant regression coefficients (Table 2). The proportion of sixth-grade students who assimilate with composite units and are constrained to additive reasoning (aTNS) relative to reasoning multiplicatively (ENS) is larger than the proportion in ninth-grade (b31 = 0.978, p < 0.01); this is also the case for seventh-grade students compared to ninth-grade students (b32 = 0.887, p< 0.05). Thus, sixth- and seventh-grade students are more likely to construct an aTNS than ninth-grade students. Similarly, the proportions of sixth- and seventh-grade students who assimilate with composite units and are constrained to additive reasoning relative to multiplicative reasoning are statistically significantly greater than the proportion of eighth-grade students (grade 6: b31 = 1.077, SE = 0.340, p = 0.002, OR = 0.341; grade 7: b32 = 0.986, SE = 0.340, p = 0.004, OR = 0.373). Although the proportions of students who have constructed an aTNS relative to an ENS were greater in sixth and seventh grades compared to eighth and ninth grades, the proportions of students were not significantly different in sixth compared to seventh grade (b31 = 0.091, SE = 0.325, p = 0.780), nor in eighth compared to ninth grade (b33 = 0.099, ns). Sixth- and seventh-grade aTNS students construct multiplicative reasoning at a greater rate than eighth- and ninth-grade aTNS students.
Relative risks were calculated to facilitate the interpretation of the effect sizes of the larger proportions of aTNS students to ENS students in sixth and seven grades compared to eighth and ninth grades. Sixth-grade students were approximately 1.54 times more likely to have constructed an aTNS in comparison to both eighth- and ninth-grade students. Seventh-grade students were approximately 1.57 times more likely to have constructed an aTNS than eighth- and ninth-grade students. In combination, sixth- and seventh-grade students are more likely to have constructed assimilatory composite units and be constrained to additive reasoning than eighth- and ninth-grade students. These effect sizes indicate that the larger proportion of students in sixth and seventh grades who assimilate with composite units and are constrained to additive reasoning compared to those in eighth and ninth grades represents a meaningful difference.
Examining the trends in the construction of multiplicative reasoning shows that eighth-grade students are 1.91 times more likely to have constructed multiplicative reasoning than sixth-grade students and 1.69 times more likely to have constructed multiplicative reasoning than seventh-grade students. We also find that ninth-grade students are 1.72 times and 1.52 times more likely to have constructed multiplicative reasoning than are sixth- and seventh-grade students, respectively. These effect sizes suggest that the larger proportion of students in eighth and ninth grades who construct multiplicative reasoning compared to students in the sixth and seventh grades represents a meaningful difference.
7 Discussion
Clark and Kamii (1996) concluded that the number of students who reason multiplicatively changes slowly across the elementary grades. This was based on the result that 45% of second-grade children were reasoning multiplicatively in some capacity, but only 49% of fifth-grade students progressed to a level of consistent multiplicative reasoning. The present study found that in the middle grades, however, these changes are quite swift. As opposed to a 4% increase in multiplicative reasoning across the elementary grades, this study shows an approximate 23% increase in the percentage of students who reasoned multiplicatively in seventh grade compared to eighth and a complementary 20% decrease in the percentage of students who assimilated with composite units but were constrained to additive reasoning in seventh grade compared to eighth. The log odds associated with these changes were both statistically significant. Thus, the swift construction of multiplicative reasoning is unique to the middle grades.
Additionally, unique to the middle grades is the stagnant growth of INS and TNS students. The proportion of students who had constructed an INS relative to an ENS, and a TNS relative to an ENS, was not significantly different in grades 6 through 8 compared to grade 9. This is presented in comparison to Wilkins et al.’s (2020) finding that students who have constructed an INS or a TNS in second grade are significantly more likely to construct multiplicative reasoning by fourth or fifth grade than are students who have not constructed an INS or TNS in second grade. This points to the time-sensitive nature of students’ development of number.
7.1 Theoretical implications
The data suggest that aTNS students are the only group of students for whom the swift construction of multiplicative reasoning occurred. Figure 6 visually represents this swift construction, as well as the relative stagnancy in the percentages of students who have constructed an INS and a TNS across the middle grades. The rate of INS or TNS students to ENS students is no different in any grade-level comparison; however, the rate of aTNS students to ENS students is lower in eighth and ninth grades compared to that in sixth and seventh grades. This suggests that an assimilatory composite unit hastens the construction of multiplicative reasoning in the middle grades. This provides a quantitative verification of Tzur et al.’s (2010) “conceptual spring” (p. 9) and suggests that the spring’s release is time sensitive.
Tzur et al.’s (2010) research included fourth- and fifth-grade students with learning disabilities in a constructivist teaching experiment. The results of studying elementary students with learning disabilities were not a priori assumed to apply to the participants in this study, the majority of whom did not have documented learning disabilities and all of whom were in the middle grades. Regardless, the construction of assimilatory composite units proved just as important for students in the present study because the proportion of students with an assimilatory composite unit who were constrained to additive reasoning increased between seventh and eighth grades, whereas the proportion of students without an assimilatory composite unit did not change significantly at any point during the middle grades. Therefore, the higher proportion is attributed to the students’ construction of an assimilatory composite unit. In addition to verifying the importance of an assimilatory composite unit to poise students to construct multiplicative reasoning, the results of this study suggest that an assimilatory composite unit becomes particularly critical in seventh grade.
Norton and Wilkins (2013) have documented a parallel conceptual spring in middle-grade students’ construction of fractional thinkingFootnote 3 and the splitting operation. Splitting refers to a student’s simultaneous application of iterating and partitioning (Steffe & Olive, 2010). A typical splitting task shows an arbitrary line segment and says, “The stick shown is five times as long as your stick. Draw your stick.” Students must posit a hypothetical stick that has a one-to-five relationship with the given stick to solve the task. Splitting is critical in students’ conceptions of fractions (Steffe & Olive, 2010) because it fosters thinking of the shorter stick as one-fifth of the longer stick, in the preceding example. Norton and Wilkins (2013) found that the odds of students who have constructed fractional thinking by the end of sixth grade constructing splitting by the end of seventh grade are 13.33 times the odds of a student who has not constructed fractional thinking by the end of sixth grade constructing splitting by the end of seventh grade. Thus, fractional thinking is the parallel “spring” that catalyzes the construction of splitting for students between sixth and seventh grades.
Norton and Wilkins (2013) also found that the odds of students who have constructed fractional thinking by the end of sixth grade constructing splitting by the end of seventh grade were 9.30 times the odds of a student who had not constructed fractional thinking by the end of sixth grade constructing even fractional thinking by the end of seventh grade. This result parallels the stagnancy observed in the percentages of INS and TNS students in the present study because INS and TNS students have constructed neither fractional thinking nor splitting. The present study demonstrates that the percentages of INS and TNS students did not change significantly between grades six and seven, which implies that the percentages of students who have constructed fractional thinking in sixth and seventh grades also did not change significantly. The present study’s results also extend those of Norton and Wilkins because in this study, the percentages of INS and TNS students did not change significantly across the entirety of the middle grades. Norton and Wilkins’ conceptual spring to the construction of splitting is engaged by constructing fractional thinking by the end of sixth grade. The present study adds that if the spring is not engaged by the end of sixth grade, it is unlikely to be engaged in the middle grades at all.
Another extension of this result is the significant decrease in the percentages of aTNS students between grades seven and eight; this deviates from the pattern of change observed among INS and TNS students, and from the result observed by Norton and Wilkins (2013). aTNS students have not constructed fractional thinking. Thus, Norton and Wilkins’ result would predict that the likelihood of an aTNS student constructing fractional thinking or splitting by the end of seventh grade is lower than their peers who have constructed fractional thinking in sixth grade. This result is upheld in the present study because the rate of aTNS to ENS students in sixth grade compared to seventh grade was not significantly different. However, this study found that sixth- and seventh-grade students are 1.54 and 1.57 times more likely, respectively, to have constructed an aTNS than eighth-grade students. Given the preparedness of ENS students to construct fractional thinking and a splitting operation (Steffe & Olive, 2010), these grade-level effect sizes indicate that students who have not constructed fractional thinking and splitting in seventh grade (i.e., aTNS students) may construct fractional thinking and splitting in eighth grade. Longitudinal research should build on Norton and Wilkins’ (2013) result by examining students’ construction of fractional thinking and splitting across the middle grades, because the present study suggests that the rate at which students without fractional thinking and splitting construct these operations may increase in eighth grade if they assimilate with composite units.
A limitation of this study is that it cannot conjecture a rationale for the significant change in the numbers of students who constructed multiplicative reasoning between seventh and eighth grades. Nor can this study conjecture a rationale for the non-significant changes in the numbers of students who had constructed multiplicative reasoning between sixth and seventh grades and between eighth and ninth grades. Because this study was cross-sectional, conclusions are drawn between students. A more striking case could be made by examining the within-student changes afforded by longitudinal data. This is a topic for future consideration. Furthermore, as this study outlined the trajectory of children’s construction of number as it relates to multiplicative reasoning, the unit of analysis was the child; our focus was to document a student-level phenomenon. As our study was situated within one school district, it was limited in its investigation of contextual factors associated with community and culture; thus, we caution broader generalizations. Also, our study did not involve enough classrooms differing by course curriculum to investigate the role of curriculum and instruction on students’ developmental trajectories. Future research should consider classroom- and school-level factors, in particular, curricular and cultural factors that may impede or advance the timing with which children construct multiplicative reasoning.
7.2 Instructional implications
Early middle-grade instruction should foster students’ construction of assimilatory composite units, as this study shows that such a construction instigates multiplicative reasoning. Tzur et al. (2013) found that an instructional activity using snap cubes supports this construction by shifting students’ focus from units of one to composite units (see also Wilkins & Ulrich, 2017). In this activity, students are asked to “go and bring me five towers of three cubes each,” for example. In response, students snap together five groups of three cubes and then determine the total number of cubes. Wilkins and Ulrich (2017) similarly showed how manipulatives can be used to support students’ construction of assimilatory composite units on problems such as the cupcake task (Fig. 5). Creating the towers or boxes of cupcakes and determining the number of cubes physically simulates the nature of mentally constructing composite units and may also support anticipation of composite units, thereby supporting multiplicative reasoning.
Other instructional activities that support assimilatory composite units are a series of apps created by the Learning Transformation Research Group (LTRG; CandyFactory, CandyDepot, and CandyBot). In the CandyDepot app, for instance, students group candy bars into bundles and place bundles into boxes, with the goal of loading a delivery truck with the correct amount of candy in the fewest possible number of boxes, bundles, and bars. The bundling actions inherent in this app mimic the mental actions of students’ units coordination, thereby supporting assimilation with composite units (LTRG, 2013). The physical replication of uniting units of one into composite units and repeating these units allows students to reflect on composite units constructed in activity, subsequently supporting assimilatory composite units. This study finds that such instructional strategies are critical in sixth and seventh grades to support multiplicative reasoning.
These activities engender students’ construction of more sophisticated whole number operations as a means of supporting multiplicative reasoning. However, typical middle-grade curriculum in the USA focuses on fraction concepts (CCSSI, 2010). Boyce and Norton (2016) concluded that “fractions may be a fertile context for students to continue developing units coordination” (p. 23), including assimilatory composite units. Thus, in instances where middle-grade curriculum limits instruction of whole number concepts, fractional instruction may provide a more curriculum-appropriate setting to engender students’ construction of assimilatory composite units, thereby supporting the release of the conceptual spring to multiplicative reasoning. Future research may also consider the effects of different curricula on students’ construction of assimilatory composite units and multiplicative reasoning.
8 Conclusion
The overarching purpose of this research study was to examine students’ construction of multiplicative reasoning in the middle grades, as understood through the number sequences framework (Steffe, 2010; Ulrich, 2016b). In response to this purpose, this study finds that aTNS students construct multiplicative reasoning at a different rate than INS and TNS students do. Moreover, aTNS students are uniquely poised to construct multiplicative reasoning due to their construction of an assimilatory composite unit. Theoretically, this result provides a quantitative validation of Tzur et al.’s (2010) conceptual spring and additionally highlights the importance of focusing early middle-grade instruction on supporting students’ construction of assimilatory composite units.
Availability of data and materials
Not applicable.
Notes
Recall that the number sequence trajectory is TNS ➔ aTNS ➔ ENS (Fig. 1; Ulrich, 2016b; cf. Steffe, 2010). In this section, however, the ENS is discussed prior to the aTNS because aTNS students demonstrate reasoning that is characteristic of both TNS and ENS students. By discussing the aTNS after the TNS and ENS, it can be situated between the two number sequences.
The model was also estimated with grades 6, 7, and 8 as the reference group to support interpretations of relevant grade-level comparisons. All of these models are statistically equivalent, therefore, for brevity and to eliminate the redundancy of a repeated model, these additional comparison results are presented in the text, as appropriate.
To say that students have constructed fractional thinking is synonymous with saying they have constructed the partitive unit fraction scheme, which supports their thinking about a whole being n-times the size of a unit fraction, 1/n (Steffe & Olive, 2010).
References
Bakker, A., Cai, J., English, L., Kaiser, G., Mesa, V., & Van Dooren, W. (2019). Beyond small, medium, or large: Points of consideration when interpreting effect sizes. Educational Studies in Mathematics, 102(1), 1–8.
Boyce, S., & Norton, A. (2016). Co-construction of fraction schemes and units coordinating structures. The Journal of Mathematical Behavior, 41, 10–25.
Carrier, J. (2014). Student strategies suggesting emergence of mental structures supporting logical and abstract thinking: Multiplicative reasoning. School Science and Mathematics, 114(2), 87–96.
Clark, F. B., & Kamii, C. (1996). Identification of multiplicative thinking in children in grades 1-5. Journal for Research in Mathematics Education, 27(1), 41–51.
Cohen, J. (1968). Weighted kappa: Nominal scale agreement with provision for scaled disagreement or partial credit. Psychological Bulletin, 70, 213–220.
Common Core State Standards Initiative. (2010). Common Core State Standards for Mathematics. http://www.corestandards.org/wp-content/uploads/Math_Standards.pdf. Accessed 27 Oct 2020.
Degrande, T., Verschaffel, L., & Van Dooren, W. (2018). Beyond additive and multiplicative reasoning abilities: How preference enters the picture. European Journal of Psychology of Education, 33(4), 559–576.
Degrande, T., Verschaffel, L., & Van Dooren, W. (2019). To add or to multiply? An investigation of the role of preference in children’s solutions of word problems. Learning and Instruction, 61, 60–71.
Degrande, T., Verschaffel, L., & Van Dooren, W. (2020). To add or to multiply in open problems? Unraveling children’s relational preference using a mixed-method approach. Educational Studies in Mathematics, 104, 405–430.
Dougherty, B., & Simon, M. (2014). Elkonin and Davydov curriculum in mathematics education. In S. Lerman (Ed.), Encyclopedia of Mathematics Education (pp. 204–207). New York, NY: Springer.
Hackenberg, A. J. (2007). Units coordination and the construction of improper fractions: A revision of the splitting hypothesis. The Journal of Mathematical Behavior, 26, 27–47.
Hackenberg, A. J. (2013). The fractional knowledge and algebraic reasoning of students with the first multiplicative concept. The Journal of Mathematical Behavior, 32, 538–563.
Hackenberg, A. J., & Lee, M. Y. (2015). Relationships between students’ fractional knowledge and equation writing. Journal for Research in Mathematics Education, 46(2), 196–243.
Kosko, K. W. (2019). A multiplicative reasoning assessment for fourth and fifth grade students. Students in Educational Evaluation, 60, 32–42.
Kosko, K. W., & Singh, R. (2018). Elementary children’s multiplicative reasoning: Initial validation of a written assessment. The Mathematics Educator, 27(1), 3–32.
Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33, 159–174.
Learning Transformation Research Group. (2013). Getting started with the CandyDepot educational game. https://ltrg.centers.vt.edu/projects/games/docs/CandyDepotHandbook.pdf. Accessed 27 Oct 2020.
Norton, A., & Wilkins, J. L. M. (2013). Supporting students’ constructions of the splitting operation. Cognition and Instruction, 31(1), 2–28.
Olivier, J., May, W. L., & Bell, M. L. (2017). Relative effect sizes for measures of risk. Communications in Statistics – Theory and Methods, 46(14), 6774–6781.
Piaget, J. (1965). The child’s conception of number (C. Gattegno & F. M. Hodgson, Trans.). New York, NY: Routledge. (Original work published in 1941)
Simpson, A. (2020). On the misinterpretation of effect size. Educational Studies in Mathematics, 103, 125–133.
Steffe, L. P. (1992). Schemes of action and operation involving composite units. Learning and Individual Differences, 4(3), 259–309.
Steffe, L. P. (1994). Children’s multiplying schemes. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 3–40). Albany, NY: State University of New York Press.
Steffe, L. P. (2010). Operations that produce numerical counting schemes. In L. P. Steffe & J. Olive (Eds.), Children’s fractional knowledge (pp. 27–47). New York, NY: Springer.
Steffe, L. P., & Olive, J. (2010). Children’s fractional knowledge. New York, NY: Springer.
Steffe, L. P., & Ulrich, C. (2013). Constructivist teaching experiment. In S. Lerman (Ed.), Encyclopedia of mathematics education: SpringerReference (pp. 102–107). Berlin, Germany: Springer-Verlag.
Tzur, R., Johnson, H. L., McClintock, E., Kenney, R. H., Xin, Y. P., Si, L., … Jin, X. (2013). Distinguishing schemes and tasks in children’s development of multiplicative reasoning. PNA, 7(3), 85–101.
Tzur, R., Xin, Y. P., Si, L., Kenney, R., & Guebert, A. (2010). Students with learning disability in math are left behind in multiplicative reasoning? Number as abstract composite unit is a likely “culprit”. Paper presented at the American Educational Research Association, Denver, CO. (ERIC Document Reproduction Service No. ED510991).
Ulrich, C. (2015). Stages in constructing and coordinating units additively and multiplicatively (part 1). For the Learning of Mathematics, 35(3), 2–7.
Ulrich, C. (2016a). Stages in constructing and coordinating units additively and multiplicatively (part 2). For the Learning of Mathematics, 36(1), 34–39.
Ulrich, C. (2016b). The tacitly nested number sequence in sixth grade: The case of Adam. The Journal of Mathematical Behavior, 43, 1–19.
Ulrich, C., & Wilkins, J. L. M. (2015). A written instrument for assessing children’s number sequences. Blacksburg, VA: Virginia Tech.
Ulrich, C., & Wilkins, J. L. M. (2017). Using written work to investigate stages in sixth-grade students’ construction and coordination of units. International Journal of STEM Education, 4(23), 1–20.
Van Dooren, W., De Bock, D., & Verschaffel, L. (2010). From addition to multiplication … and back. The development of students’ additive and multiplicative reasoning skills. Cognition and Instruction, 28, 360–381.
Vergnaud, G. (1988). Multiplicative structures. In J. Hiebert & M. Behr (Eds.), Number concepts and operations in the middle grades (pp. 141–161). Hillsdale, NJ: Erlbaum and Reston, VA: NCTM.
Virginia Department of Education. (2016, September). Mathematics standards of learning for Virginia public schools. https://www.doe.virginia.gov/testing/sol/standards_docs/mathematics/2016/stds/k-12-math-sol.pdf. Accessed 27 Oct 2020.
Wilkins, J. L. M., & Ulrich, C. (2017). The role of skip counting in children’s reasoning. Virginia Mathematics Teacher, 43(2), 8–14.
Wilkins, J. L. M., Woodward, D., & Norton, A. (2020). Children’s number sequences as predictors of later mathematical development. Mathematics Education Research Journal. Advance online publication. https://doi.org/10.1007/s13394-020-00317-y
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
Dr. Zwanch was responsible for data collection and writing. Drs. Zwanch and Wilkins were responsible for data analysis. Dr. Wilkins was responsible for interpretation of the data analysis and writing.
Corresponding author
Ethics declarations
IRB approval was obtained prior to beginning work on this research, and all participants gave their assent to participate.
Conflict of interest
The authors declare that they have no conflict of interest.
Code availability
Not applicable.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zwanch, K., Wilkins, J.L.M. Releasing the conceptual spring to construct multiplicative reasoning. Educ Stud Math 106, 151–170 (2021). https://doi.org/10.1007/s10649-020-09999-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-020-09999-4