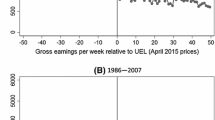Abstract
Social security contributions (SSCs) are typically formally split between employers and employees as payroll taxes, levied on earnings at a constant tax rate that applies only up to a ceiling, above which the marginal tax rate falls to a reduced rate, often 0. Such contribution ceilings create a concave kink point in the budget set of workers and hence should generate a dip in the distribution of earnings around the ceiling through labour supply responses (the reverse of bunching expected at convex kink points) but such a dip is not observed empirically. This paper sets out a new approach to infer the incidence of SSCs that exploits the absence of this dip and the fact that (mechanically) the distributions of labour cost (earnings inclusive of all payroll taxes), gross earnings (net of employer payroll taxes) and net earnings (net of both employer and employee payroll taxes) cannot all be smooth around a kink. The other papers in this special issue apply the method to data for Germany, France, the Netherlands and the UK and all find that distribution of gross earnings is smooth around kinks (implying that the distributions of labour costs and net-of-tax earnings are not) even though the concept of gross earnings is irrelevant in the standard static model of labour supply and demand that dominates the public economics literature. This suggests that other features of the labour market, such as wage bargaining based on the gross earnings concept, are relevant for determining the incidence of SSCs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
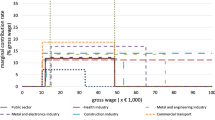
Social security contributions (SSCs) are a common feature of many advanced economies. They are typically shared formally between employers and employees as payroll taxes, levied on earnings at a constant tax rate that applies only up to a ceiling, above which the marginal tax rate falls to a reduced rate, often 0. In 2015, for example, US federal payroll taxes were levied at a rate of 12.4% on earnings up to $118,500 per year, but 0% above.
In the standard static model of individual and firm behaviour that dominates the public economics literature, the economic incidence of these taxes depends on the relative responsiveness of labour supply and demand, not on who the tax is formally levied (Fullerton and Metcalf 2002). In principle, as we expect labour demand to be substantially more elastic than labour supply (Hamermesh 1993), the incidence of these taxes should be borne primarily by workers. However, empirical work that uses changes in payroll taxes to investigate their incidence of has found mixed results (e.g. Hamermesh 1979; Neubig 1981; Holmlund 1983; Poterba et al. 1986; Gruber 1997; Lang 2003; Liang et al. 2004) while Saez et al. (2012) provided compelling evidence against the invariance of incidence proposition; that, excepting constraints imposed by minimum wages, the nominal splitting of payroll taxes between employees and employers should not matter for their economic incidence. Exploiting a cohort-based reform in Greece that applied different rates of SSCs to perfectly substitutable workers, Saez et al. (2012) showed that neither employers nor employees shift the burden of their SSC, implying that the economic incidence of SSCs coincides with their statutory incidence.
We contribute to this literature by proposing a new approach to investigate the incidence of payroll taxes that exploits variation induced by contribution ceilings. This is based on the observation that when the marginal rate of SSCs falls at a ceiling, the distributions of gross earnings, net earnings and labour cost cannot all be continuous. Which of the distributions is discontinuous at the ceiling can, under certain conditions, provide information on the economic incidence of SSCs. The other papers in this volume apply our approach to administrative (or quasi-administrative) data for Germany, France, the Netherlands and the UK, and provide empirical evidence at odds with the standard model.
This paper proceeds as follows. We first describe our basic conceptual approach (Sect. 2) and its empirical implementation (Sect. 3). We then summarise the results from each country (Sect. 4), before concluding with a discussion of how these findings might be rationalised.
2 Contribution ceilings and Incidence
The standard static model used in the public economics literature to assess the incidence of, and behavioural responses to, taxes, posits that agents decide how many hours of labour to supply by equating the marginal utility of after-tax (i.e. disposable) income with the marginal disutility of work. In other words, individuals value the utility obtained from consumption, but not the effort required to obtain it. Gross income, the measure of earnings on which income tax or employee SSCs are levied and that is typically posted in job ads, is irrelevant. Similarly, firms aim to maximise profits given a production technology, and so care about minimising the cost of inputs used in production. As a result, they care about labour cost, not what is paid to employees after income taxes and SSCs. As a consequence, with no barriers to market clearing, all that should matter for the incidence of taxes on earnings in this model is the relative elasticities of labour supply and labour demand (Fullerton and Metcalf 2002).
2.1 Dip in the Earnings Distribution at the Ceiling
Another key prediction of this standard model is that a fall in the tax rate at a threshold (a downwards kink) should induce nearby individuals to increase their earnings, creating a dip in the density distribution of before or after tax earnings around the threshold: the analogue of bunching expected at an upwards kink. Figure 1 illustrates this prediction. Panel A shows that an individual with convex preferences who locates at \(y^1\) under a linear tax schedule can attain a higher level of utility (\(U_2>U_1\)) from locating at \(y^2>y^1\) in a world where the marginal tax rate applied to earnings falls from \(\tau _1 > 0\) to \(\tau _2 = 0\) at \(y^*\). Panel B shows—with the assumption that preferences for leisure are smoothly distributed—that this creates a dip in the density of the tax base around the threshold \(y^*\), with some of the individuals who would locate nearby under a linear SSC schedule moving above the threshold in response to the lower marginal tax rate.
Downwards kinks and behavioural responses. a Indifference curve and budget set. b Density distribution. Note: Panel A shows indifference curves \(U_1\) and \(U_2\) for an individual who chooses to locate at \(y^1\) under a linear SSC schedule (with slope \(1-t\)) and at \(y^2>y^1\) when SSCs are capped at the ceiling \(y^*\) (with slope 1). Panel B shows we should therefore expect to see a dip in the distribution of gross earnings around the ceiling as—with a smooth distribution of preferences for leisure—some individuals will increase their earnings in response the to lower marginal tax rate above the threshold
Saez (2010) showed that the extent of this dip (bunching) at downwards (upwards) kinks is proportional to the elasticity of earnings locally. While some bunching at upwards kink points created by income tax or SSC schedules has been documented in the US (Saez 2010), Denmark (Chetty et al. 2011) and Sweden (Bastani and Selin 2014), few papers have looked at downwards kinks.Footnote 1 In this special issue, we find no evidence of such a dip or gap at large downwards kinks in the Netherlands, France, Germany or the United Kingdom. This suggests that taxable earnings are inelastic, at least for those located near the threshold.
2.2 Discontinuities in Labour Costs, Gross Earnings, Net Earnings Densities at the Ceiling
The absence of a dip or gap at a contribution ceiling allows us to investigate the incidence of SSCs in these countries exploiting another feature of such kinks, namely that they imply that at most one of the density distributions of gross earnings, net earnings, and labour cost can be continuous at the threshold. To see this, let us denote by z labour costs (inclusive of all payroll taxes), y gross earnings (net of the employer payroll tax but not the employee payroll tax), and c net earnings (net of both employer and employee payroll taxes). The gross earnings concept y is economically irrelevant because employers should care only about z while workers should care only about c. However, the gross earnings concept y typically defines posted wages (in wage negotiations and contracts) and is also used to assess payroll taxes. Let us denote by \(y^*\) the gross earnings ceiling where the SSC stop. Let use denote by \(t_R\) the employer payroll tax rate and by \(t_E\) the employee payroll tax rate. Both \(t_R\) and \(t_E\) apply up to gross earnings level \(y^*\). Hence, z, y, and c are linked by the following equations:
We can use this relationship to link the distribution of labour cost and net earnings to that of gross earnings. Let us denote the cumulative distribution functions for labour cost z, gross earnings y, and net earnings c by F(z), G(y), and H(c) and the corresponding density distributions by f(z), g(y), and h(c). From Eq. (1), it follows:
This expression implies that if \(t_R>0\), at least one of the densities g(y) or f(z) must exhibit a discontinuity at the cap \(y^*\). For example, if f(z) is continuous at \(z^*=y^* \cdot (1+t_R)\), then it must be that \(g(y^*)_- = (1+t_R) \cdot g(y^*)_+ = f(z^*)\), where the subscripts − and \(+\) denote limits on the left and right respectively. Given the identity in Eq. (2), it then must be that the density of gross earnings g drops by a factor equal to \(1+t_R\) at the cap \(y^*\). Alternatively, if g(y) is continuous at \(y^*\), then \((1+t_R) \cdot f(z^*)_- = f(z^*)_+ = g(y^*)\) and so f(z) must be discontinuous at \(z^*\). Similarly, if \(t_E>0\), then g(.) and h(.) cannot be both continuous at the cap. If the gross earnings density is continuous, then the density of net earnings is not (and conversely). This implies that at most one of gross earnings, net earnings, and labour cost can be continuous at a contribution ceiling.Footnote 2
Given that individuals and firms have preferences defined over net earnings and labour costs respectively, we might expect the distributions of each to be continuous around the threshold under certain conditions. For example, if labour supply is perfectly inelastic, labour demand perfectly elastic (e.g., because workers around a kink are perfect substitutes in production), we would expect the full burden of any SSCs to fall on employees and for the distribution of labour costs to be smooth around the threshold (and therefore to see a negative discontinuity in the distribution of both gross and net earnings at the threshold). Conversely, if labour supply is perfectly elastic, labour demand inelastic and preferences are smoothly distributed, we would expect the full burden of any SSCs to fall on employers and for the distribution of net earnings to be smooth (and therefore to see a positive discontinuity in the distribution of both gross earnings and labour cost).
However, as gross earnings are economically irrelevant in the standard model, there is little reason to expect gross earnings to be continuous at the contribution ceiling: it reflects neither the preferences nor marginal productivity of individuals, and is therefore irrelevant for the decisions of both firms and individuals. Hence, a smooth gross earnings density at \(y^*\) should only happen by chance in the standard model, if the statutory and economic incidence just happen to coincide.
In the next section, we outline an empirical approach to test for a discontinuous shift in the density of gross earnings at a contribution ceiling.
3 Empirical Approach
The presence of a gap in the distribution of gross earnings at a ceiling, arising from behavioural responses to the different tax rates above and below, may serve to obscure the mechanical discontinuity described above. As neither a dip nor gap is observable, the papers in this special issue apply a straightforward test for a step-change in the distribution of gross earnings to infer the incidence of SSCs. This involves fitting a flexible polynomial to the distribution of gross earnings y, regressing a \(n^{th}\) order polynomial of bins of y on the density at the midpoint of these bins, along with an indicator variable that take the value 1 if the bin is above the SSC ceiling and 0 otherwise. Our primary test for whether there is a step-change in the distribution of gross earnings is whether the coefficient on this indicator, normalised by the density at the SSC ceiling, is statistically different from 0. A negative coefficient indicates a downwards shift in the density of gross earnings, which may be consistent with the full incidence of SSCs on workers, whereas a positive coefficient may be consistent with full incidence of SSCs on employers.
As a secondary test, we apply the estimator of McCrary (2008), developed to check the validity of the ‘no manipulation’ assumption underlying regression discontinuity design (RDD) studies.Footnote 3 This extends the local linear density estimator of Cheng et al. (1997), and is implemented as a Wald test of the null-hypothesis that the density of a running variable is discontinuous at a point. However, this test is not entirely suitable for our purposes because it tests for a discontinuity in the density exactly at the threshold, comparing only an epsilon above and epsilon below. Such a discontinuity is necessary for the mechanical step-change in density that we are interested in, but it is not sufficient: the density must also continue to be different further above from the threshold. As a result, we place greater weight on results from the polynomial approach.
In order to apply this empirical approach, we require large datasets that contain detailed information on the earnings of individuals, otherwise classical measurement error may lead us to make type I or II errors. We also require an accurate measure of the base that SSCs are levied on, so that we can correctly identify the earnings of individuals relative to the contribution ceiling; typically gross employment earnings, as SSCs are usually not levied on self-employment or savings income. The papers in this volume—which we now summarise—use administrative (or quasi-administrative) data that fulfils both these criteria.
4 The Incidence of Payroll Taxes in 4 EU Economies
In this section, we briefly summarise the findings of the country papers, before concluding with a discussion of some possible interpretations, focusing on models of bargaining where gross rather than net earnings, or labour costs, are important. All four papers focus on evaluating whether the gross earnings density g(y) is discontinuous at thresholds where the payroll tax rates drop. In contradiction with the standard model, all four papers find no discontinuity in gross earnings densities at these thresholds.
Bozio et al. (2017) exploit employer-employee data from France for the period 1976–2010. They estimate discontinuities in gross earnings densities at three distinct thresholds each year for both executive and non-executive workers (as the legislation is different for both types of workers) and show that the fraction of estimated discontinuities that are significantly different from 0 at the 5% statistical level is close to 5%. Taking advantage of a large number of kinks, they also exploit variations over time, across thresholds, and across group of workers (executives vs non-executives) in the size of the kinks in both the employer and employee SSC schedule to assess the incidence of both types of contributions separately. They finally investigate whether the estimated discontinuities in the gross earnings distribution vary across time periods, the size of the corresponding kink, or the location of the kink in the earnings distribution (median wage earners versus top wage earners). None of those factors significantly affect the discontinuities, which remain inexistent in all cases.
Kai-Uwe and Neumann (2017) provide a comprehensive analysis of the earnings cap for health insurance that existed in Germany over the period 1975–2010. They find that neither employers nor employees shift a substantial part of their SSC burden. These results are consistent over the whole time period and in robustness checks corroborating previous findings. A small trend towards a slight increase in the SSC burden falling on employees is found, but its small magnitude and the statistical uncertainty attached to it lead the authors to the conclusion that their results are consistent with economic incidence coinciding with statutory incidence.
Adam et al. (2017) investigate the incidence of National Insurance contributions (NICs) in the UK, exploiting the ceiling that applied to employee and employer contributions between 1975 and 1985, and to employee contributions only between 1986 and 2007. Using data from the New Earnings Survey Panel Dataset, a mandatory survey of British employers’ payroll records, they show there is no dip at the ceiling in either period and that the full economic incidence of NICs on one side of the market can be rejected. As with other papers in this volume, they fail to reject that the distribution of gross earnings is smooth around the threshold, consistent with economic mirroring statutory incidence.
Finally, Bosch and Micevska-Scharf (2017) use a very rich Dutch administrative dataset for the period 2006–2012. Their data contain information on both the labour cost of firms and the gross earnings of employees. This means that they can directly test for discontinuities in the distribution of both, whereas other countries are restricted to examining only gross earnings. Doing so, they find that the distribution of gross pay is smooth but that there is a positive discontinuity in the distribution of labour cost, confirming that the economic burden of employer SSCs seems to fall on employers, and that the absence of discontinuities in the gross earnings distribution is not simply due to measurement error.
5 Conclusion and Possible Explanations
The papers in this special issue provide evidence from hundreds of contribution caps in four large European countries that seems inconsistent with the standard static model of labour supply and demand that dominates the public economics literature. There is no dip or gap in the distribution of gross earnings around downwards kinks (suggesting that earnings are completely inelastic with respect to the rate of SSCs), and we cannot reject the hypothesis that gross earnings are smooth and continuous around the threshold (suggesting that statutory and economic incidence coincide). In particular, the second of these findings is hard to reconcile with the standard model, as statutory and economic incidence should only coincide if the relative elasticities of labour supply and demand happen to be the same as the relative rates of employer and employee SSCs. As the latter differ across both countries and time, it would be an extremely unlikely coincidence that the relative elasticities of labour supply and demand just happen to vary in a similar manner.
However the standard model makes strong Walrasian assumptions: supply and demand are considered separately, and market clearing is assumed at any time. Furthermore, some important features of the labour market are neglected, such as matching frictions, productive complementarities between firms and workers, firm-specific human and physical capital investments, and wage bargaining. The search and matching literature has studied intensively those mechanisms and showed how they generate job-specific surpluses or rents. This is, for example, because moving from one firm to another takes time, and it implies a loss of firm-specific human capital and of worker-firm complementarities. Those rents on the labour market can be split in a variety of ways, possibly leading to a full range of possible different wages compatible with a given level of supply and demand. Acknowledging the existence of rents therefore offers a natural way to rationalise the combined finding of an economic incidence close to the statutory one and of limited behavioural responses.
Standard bargaining models such as Nash, Kalai or proportional bargaining do not however provide rent-sharing mechanisms directly consistent with our findings. In the simplest rendition of those models, as in the standard static model described above, the statutory incidence of SSCs should not matter. However, those models usually rely on an exogenous parameter to measure workers’ or firms’ bargaining power are they remain poorly equipped to understand the various determinants affecting the way rents generated in the labour market are shared. Conventions or norms regarding bargaining and the salience of the various earnings concepts during the negotiations are likely to play a role. Institutions such as unions, or pay fairness norms and reference points may also matter. We now review how those possible determinants of wage setting in a bargaining framework can provide possible explanations for our findings.
A key convention likely to play a role is that bargaining is typically based on gross earnings rather than labour costs or net earnings. Even if firms and workers ultimately care only about labour costs and net earnings respectively, it may be costly to calculate these from gross earnings. Knowing in advance the amount of SSCs they will have to pay indeed requires economic actors to know and apply without mistake the computation rules for those contributions. In the countries we study here, the opportunity cost of doing so can be high: see, for example, the complex rules described by Bozio et al. (2017) for France. If the cost to acquire this information is higher than the expected gain during the bargaining process, firms and workers may decide to negotiate on gross earnings without converting those earnings in a metric that directly matters to them. The cost to acquire the relevant information is not the only possible reason why the statutory incidence can matter. Even in countries where SSCs are relatively straightforward to compute (such as the UK), the norm to bargain on posted wages still makes the other earnings concepts less salient and possibly harder to use during the negotiations. Individual negotiation norms may for example imply that some types of arguments weigh more than others during the negotiations. If a consideration is not customary and never used by economic actors, it could be awkward and counter-productive to use it. For example, it might be hard for a worker whose earnings have reached a concave kink in the SSCs schedule to argue during a face-to-face annual negotiation that pay raises in terms of posted wages have become less costly to her employer, so that she can get a higher raise.
As argued by Saez et al. (2012), pay fairness norms may also play a role. For example, an employer engaged in pay negotiations who proposed an across-the-board rise defined in terms of labour cost (to reflect increased aggregate productivity) would in effect be offering a proportionally lower increase to workers paid below an SSC ceiling than to those above, which could adversely impact morale and productivity inside the firm. This is because the standard reference variable used for wage comparisons between workers is posted wages defined as gross earnings. Again, the fact that other earnings concepts are less salient to workers renders harder and less intuitive earnings comparisons based on those concepts. Note that pay fairness norms are compatible with the idea that workers bear the cost of SSCs at the firm level. Instead of discriminating between workers because of their individual SSCs rate, firms simply pass on all their employees the extra cost induced by having a larger share of workers typically paying large amounts of SSCs.
The mechanisms discussed so far—individual negotiations norms and pay fairness norms—apply when wages are directly determined at the individual level, with possible account of interactions between workers. Individual negotiations are more likely to arise for high-wage earners and senior white-collar workers. As many of the thresholds and caps in the SSC schedule are often located high up in the earnings distribution, the results presented in this issue apply primarily to such workers. For those whose earnings tend to be set by collective bargaining, additional norms regarding collective negotiations can also play a role. In the countries we study, firm-level or industry-level negotiated pay scales (when they exist) are expressed in terms of gross earnings. This suggests that SSCs may not be systematically considered during the negotiations. A closer look to collective agreements provides further evidence. In France for example, gross earnings scales are posted in each industry (branch) for four distinct occupation groups (clerks, blue collars, technicians, and managers). For each of these groups, the industry collective agreement specifies a series of minimum gross earnings to be paid according to seniority and the exact qualification.Footnote 4 A quick examination of those complex and detailed scales suggests they are not systematically affected by the different rates of SSCs that apply.
Pay fairness and bargaining norms might then explain why the economic incidence of SSCs seems equal to their statutory incidence in a partial equilibrium model. However, as explained by Saez et al. (2012), it is harder to argue that those results are still valid under a general equilibrium approach, and that they can be sustained in the long-run. Indeed, firms that intentionally or even accidentally hire workers that are less costly due to lower amounts of employer SSCs should make more profits and eventually be more likely to survive. Even if firms are not trying at all to optimise labour costs, competition on the good market may eventually benefit to those whose worker composition happens to both fit skill requirements and limit labour costs.
Another possible explanation could be that in a labour market which generates a lot of rents, a split of SSCs according to the statutory incidence would only prevent a handful of firm-worker matches to be formed. When a match between a worker and a firm generates a positive surplus, there are usually a large range of possible posted earnings that guarantee the worker and the firm to get more than there outside option in the bargaining problem. The split of SSCs according to the statutory incidence would drive posted earnings outside this range only in a very few cases. In those cases only, earnings could be readjusted or employment effects could be visible, but such behaviours may be too rare and remain too limited to be detectable at a more macro level.
Finally, in an uncertain economic environment, the success of firms may only depend moderately on labour costs, so that small differences across firms in those costs due to the statutory incidence of SSCs may barely affect survival rates. Together, those arguments suggest that even in the long run, competitive market forces may not be sufficient to steer the economic incidence of SSCs away from their statutory incidence for the vast majority of employment spells.
Notes
For clarity, the discussion here focuses on the case of ceilings where contributions are capped above the threshold. However, similar expressions can be deprived for ceilings where the rate of SSCs falls to a non-zero reduced rate.
RDDs rely on the assumption that the conditional expectation of an outcome variable is continuous in the ‘running’ or assignment variable, which may be violated if individuals are able to manipulate the running variable; for example, by exerting control on the duration of an unemployment spell in order to avoid (or obtain) assignment into a training programme that is only open to individuals who have been unemployed for a certain period of time.
Note that seniority rules may not need to be collectively bargaining (they may also consist in more or less implicit norms) to induce wage dynamics that are largely independent from SSCs and induce rigidities preventing the fast adjustment of earnings around SSCs ceilings each calendar year.
References
Adam, S., Roantree, B., & Phillips, D. (2017). The incidence of social security contributions in the UK: Evidence from discontinuities at contribution ceilings. De Economist. doi:10.1007/s10645-017-9295-6.
Bastani, S., & Selin, H. (2014). Bunching and non-bunching at kink points of the Swedish tax schedule. Journal of Public Economics, 109, 36–49.
Bosch, N., & Micevska-Scharf, M. (2017). Who bears the burden of social security contributions in the Netherlands? Evidence from Dutch administrative data. De Economist. doi:10.1007/s10645-017-9296-5.
Bozio, A., Breda, T., & Grenet, J. (2017). Incidence and behavioural response to social security contributions: An Analysis of Kink Points in France. De Economist. doi:10.1007/s10645-017-9297-4.
Cheng, M.Y., Fan, J., & Marron, J.S. (1997). On automatic boundary corrections, Annals of Statistics, 8 25 (4), 1691–1708.
Chetty, R., Friedman, J. N., Olsen, T., & Pistaferri, L. (2011). Adjustment costs, firm responses, and micro vs. macro labor supply elasticities: Evidence from Danish tax records. The Quarterly Journal of Economics, 126(2), 749–804.
Fullerton, D., & Metcalf, G. E. (2002). Tax incidence. In A. Auerbach & M. Feldstein (Eds.), Handbook of public economics (Vol. 4, pp. 1787–1872). Amsterdam: Elsevier.
Gruber, J. (1997). The incidence of payroll taxation: Evidence from Chile. Journal of Labor Economics, 15(3), 72–101.
Hamermesh, D. S. (1979). New estimates of the incidence of the payroll tax. Southern Economic Journal, 45(4), 1208–1219.
Hamermesh, D. S. (1993). Labor demand. Pinceton: Pinceton University Press.
Holmlund, B. (1983). Payroll taxes and wage inflation: The Swedish experience. The Scandinavian Journal of Economics, 85(1), 1–15.
Lang, K. (2003). The effect of the payroll tax on earnings: A test of competing models of wage determination. National Bureau of Economic Research working paper w9537.
Liang, X., Kubik, J., & Engelhardt, G. (2004). The incidence of the social security payroll tax: Evidence from the 1977 amendments to the social security act. Technical report.
Liebman, J. B., Luttmer, E. F. P., & Seif, D. G. (2009). Labor supply responses to marginal Social Security benefits: Evidence from discontinuities. Journal of Public Economics, 93(1112), 1208–1223.
McCrary, J. (2008). Manipulation of the running variable in the regression discontinuity design: A density test. Journal of Econometrics, 142(2), 698–714. The regression discontinuity design: Theory and applications.
Neubig, Thomas S. (1981). The social security payroll tax effect on wage growth. Proceedings of the Annual Conference on Taxation of the National Tax Association JSTOR, 1981, 196–201.
Kai-Uwe, M., & Neumann, M (2017). Who bears the burden of social security contributions in Germany? Evidence from 35 years of administrative data. De Economist. doi:10.1007/s10645-017-9298-3.
Poterba, J. M., Rotemberg, J. J., & Summers, L. H. (1986). A tax-based test for nominal rigidities. The American Economic Review, 76(4), 659–675.
Saez, Emmanuel. (2010). Do taxpayers bunch at kink points? American Economic Journal: Economic Policy, 2(3), 180–212.
Saez, Emmanuel, Matsaganis, Manos, & Tsakloglou, Panos. (2012). Earnings determination and taxes: Evidence from a cohort-based payroll tax reform in Greece. The Quarterly Journal of Economics, 127(1), 493–533.
Author information
Authors and Affiliations
Corresponding author
Additional information
We thank Casper van Ewijk, Stuart Adam, Nicole Bosch, Antoine Bozio, David Card, Raj Chetty, Julien Grenet, Peter Haan, Luke Haywood, Michael Neumann and David Phillips, for helpful comments and discussions. The authors gratefully acknowledge funding from the European Research Council (reference ERC-2010-AdG-269440-WSCWTBDS), the ESRC Centre for the Microeconomic Analysis of Public Policy based at the Institute for Fiscal Studies (ES/M010147/1), ESRC Research Grant ES/K006185/1, NSF Grant SES-0134946, the Foundation Gould and the French national agency for research (ANR).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Alvaredo, F., Breda, T., Roantree, B. et al. Contribution Ceilings and the Incidence of Payroll Taxes. De Economist 165, 129–140 (2017). https://doi.org/10.1007/s10645-017-9294-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10645-017-9294-7