Explaining the Stylized Facts of Foreign Exchange Markets with a Simple Agent-based Version of Paul de Grauwe’s Chaotic Exchange Rate Model

Abstract

We propose a simple agent-based version of Paul de Grauwe’s chaotic exchange rate model. In particular, we assume that each speculator follows his own technical and fundamental trading rule. Moreover, a speculator’s choice between these two trading philosophies depends on his individual assessment of current market circumstances. Our agent-based model setup is able to explain a number of important stylized facts of foreign exchange markets, including bubbles and crashes, excess volatility, fat-tailed return distributions, serially uncorrelated returns and volatility clustering. A stability and bifurcation analysis of its deterministic skeleton provides us with useful insights that foster our understanding of exchange rate dynamics.

1 Introduction

According to the triennial survey of the Bank for International Settlements (2019), the foreign exchange market is the largest financial market in the world. Moreover, its trading volume largely reflects speculative orders. Questionnaire studies, summarized by Menkhoff and Taylor (2007), reveal that speculators rely on technical and fundamental trading rules when determining their orders. Technical trading rules derive trading signals from past price movements. Due to their extrapolative nature, technical trading rules typically trigger buy (sell) signals when they detect positive (negative) exchange rate trends. Fundamental analysis presumes that the exchange rate will return towards its fundamental value, suggesting to buy (sell) undervalued (overvalued) currencies. Foreign exchange market models by, for instance, Frankel and Froot (1986), Kirman (1991), Westerhoff (2003a), de Grauwe and Grimaldi (2005, 2006a), Manzan and Westerhoff (2007), Beine et al. (2009), de Grauwe and Kaltwasser (2012), Federici and Gandolfo (2012), de Grauwe and Markiewicz (2013), Goldbaum and Zwinkels (2014), Gori and Ricchiuti (2018) and Gardini et al. (2022), are based on such observations. The overarching message of the latter contributions is that the interplay between speculators relying on technical and fundamental trading rules accounts for a substantial part of the dynamics of exchange rates.¹

In this paper, we revisit the seminal exchange rate model proposed by de Grauwe and Dewachter (1992, 1993) and de Grauwe et al. (1993). For ease of exposition, we refer to their work hereafter as “Paul de Grauwe’s chaotic exchange rate model”. Let us recall the main assumptions on which this model rests.² First of all, the exchange rate is driven by the expectations of two types of speculators, namely chartists and fundamentalists. Chartists base their expectations on past movements of the exchange rate, using extrapolative forecasting rules. In contrast, fundamentalists predict that the exchange rate will converge towards its fundamental value. Moreover, speculators’ perceptions of the fundamental value of the exchange rate are normally distributed around its true fundamental value. Finally, the market impact of chartists and fundamentalists depends on market circumstances. In particular, the market impact of fundamental analysis increases with mispricing in the foreign exchange market.

We can outline the main mechanism that causes endogenous exchange rate dynamics in Paul de Grauwe’s chaotic exchange rate model as follows. Chartists’ extrapolative expectations are destabilizing. Since chartists dominate the foreign exchange market near its fundamental value, their behavior tends to drive the exchange rate away from its fundamental value. Fundamentalists have stabilizing regressive expectations. These expectations become increasingly relevant for the determination of the exchange rate as its mispricing worsens, pushing back the exchange rate towards its fundamental value. Since this development automatically leads to a revival of technical analysis in the foreign exchange market, the exchange rate remains in constant motion. Interactions between chartists and fundamentalists may even lead to chaotic exchange rate dynamics. In this case, the exchange rate oscillates almost erratically around its fundamental value, an outcome that triggers, at least in a stylized way, bubbles and crashes and excess volatility.

The goal of our paper is to show that Paul de Grauwe’s chaotic exchange rate model is more powerful than previously appreciated. In fact, we demonstrate that a simple agent-based version of Paul de Grauwe’s chaotic exchange rate model is able to replicate a number of important stylized facts of foreign exchange markets. Within our agent-based model setup, each speculator places orders based on his own technical and fundamental trading rule. We model this aspect by assuming that speculators’ technical and fundamental trading rules contain two elements—a common deterministic element and an agent-specific random element. Moreover, a speculator’s choice between technical and fundamental analysis is probabilistic and depends on his individual assessment of current market circumstances. To be precise, the probability that a speculator opts for fundamental analysis increases with the distance between the exchange rate and what he regards as its true fundamental value. Clearly, each speculator has his own view about the true fundamental value of the exchange rate. Finally, speculators also manage their speculative investment position. Overall, there are three agent-specific sources of randomness in our agent-based model setup, related to speculators’ probabilistic rule-selection behavior, their perception of the exchange rate’s fundamental value and their actual trading rules. Simulations reveal that our agent-based model setup is able to produce bubbles and crashes, excess volatility, fat-tailed return distributions, serially uncorrelated returns and volatility clustering.

A stability and bifurcation analysis of the deterministic skeleton of our agent-based model setup helps us to understand why this is the case. As it turns out, the exchange rate of the deterministic skeleton of our agent-based model setup is due to a three-dimensional nonlinear map, which, in turn, possesses a unique steady state at which the exchange rate is equal to its fundamental value. The local stability of this steady state depends, amongst other things, on how aggressively speculators rely on their trading rules. Simulations furthermore reveal that the map’s nonlinearities may produce chaotic exchange rate dynamics, similar to those observed in Paul de Grauwe’s chaotic exchange rate model. Essentially, we observe that the exchange rate runs away from (towards) its fundamental value when chartists (fundamentalists) dominate the foreign exchange market.

Activating the three agent-specific random elements of our agent-based model setup, simulated exchange rates start to mimic the behavior of actual exchange rates much more closely. The key functioning of our agent-based model remains as just described. Due to speculators’ probabilistic rule-selection behavior, their perception of the exchange rate’s fundamental value and their reliance on trading rules that contain random elements, however, the path of the exchange rate now resembles a random walk. Nevertheless, distinct bubbles may emerge when the majority of speculators opt for technical analysis. During these periods, we typically witness volatility outbreaks, occasionally associated with extreme changes in the exchange rate. The latter require that speculators receive similar trading signals. When fundamentalists regain control over the foreign exchange market, bubbles disappear and the volatility of the exchange rate decreases. As in the deterministic skeleton of our agent-based model setup, speculators eventually return to technical analysis. Investigating the trading activity of individual speculators reveals that their inventory management behavior has a stabilizing impact on the dynamics of the foreign exchange market.

Against this backdrop, we are tempted to draw the following general conclusions. While the modeling of realistic exchange rate dynamics apparently requires the acknowledgement of some kind of stochastic influence factors, the main forces accountable for the dynamics of the exchange rate are deeply rooted in the nonlinear interplay between chartists and fundamentalists. In this sense, we argue that it is important to develop stylized chartist-fundamentalist models that offer new perspectives on the emergence of endogenous exchange rate dynamics. Of course, it is also necessary to check whether stochastic versions of these models have the power to explain the dynamics of the exchange rate in greater detail.

We continue as follows. In Sect. 2, we present a number of stylized facts of foreign exchange markets. In Sect. 3, we propose a simple agent-based version of Paul de Grauwe’s chaotic exchange rate model. In Sect. 4, we study the behavior of this model’s deterministic skeleton. In Sect. 5, we demonstrate that our agent-based model setup is able to mimic the behavior of actual exchange rates. Section 6 concludes our paper. “Appendix A” contains a number of robustness checks.

2 Stylized Facts of Foreign Exchange Markets

In this section, we recall five important stylized facts of foreign exchange markets. As we will see, actual exchange rates give rise to (1) bubbles and crashes, (2) excess volatility, (3) fat-tailed return distributions, (4) serially uncorrelated returns and (5) volatility clustering. Our attention focuses on the behavior of three major exchange rates, namely the US dollar versus the euro, the US dollar versus the British pound and the Japanese yen versus the US dollar, downloaded from the FRED database of the Federal Reserve Bank of St. Louis. All three time series run from January 1999 to September 2022 and comprise 5959 daily observations. For more background on the statistical properties of actual exchange rates and tools to quantify them, we refer the reader to de Vries (1994), Guillaume et al. (1997), de Grauwe and Grimaldi (2006b) and Westerhoff (2009).

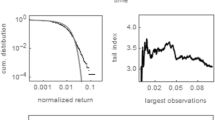
Figure 1 illustrates the behavior of the USD/EUR exchange rate. The black line in the first panel of Fig. 1 presents the evolution of the USD/EUR exchange rate in the time domain; the gray line marks its mean. The boom-bust behavior of the USD/EUR exchange rate is truly remarkable. Between 1999 and 2003, for instance, the USD/EUR exchange rate decreased by around 30 percent. Over the next five years, the USD/EUR exchange rate not only recovered from this sharp decline, but also increased by nearly 100 percent. The second panel of Fig. 1 reports the corresponding returns, defined as changes in log exchange rates in percent. The average absolute return of the USD/EUR exchange rate is about 0.44 percent, i.e. the USD/EUR exchange rate changed by 0.44 percent per trading day over this period. The largest and smallest returns for this time series are equal to 4.62 percent and − 3.00 percent, respectively. Most economists regard such exchange rate fluctuations as excessive. The black dots in the third panel of Fig. 1 visualize the log probability density function of normalized returns of the USD/EUR exchange rate; the gray line depicts what we would expect to see from standard normally distributed returns. Obviously, the returns of the USD/EUR exchange rate are not normally distributed. In particular, their distribution displays fat tails. The fourth panel of Fig. 1 shows autocorrelation functions of raw returns (gray line) and absolute returns (black line) for the first 100 lags. Almost all autocorrelation coefficients of raw returns are within their 95 percent confidence intervals (thin gray lines), reflecting the random-walk-like nature of the USD/EUR exchange rate path. In contrast, the autocorrelation coefficients of absolute returns are significant for more than 100 lags, a clear sign of volatility clustering. Of course, the fact that periods of low volatility alternate with periods of high volatility is already visible from the second panel of Fig. 1.

Fig. 1

The USD/EUR exchange rate. The first panel shows the evolution of the USD/EUR exchange rate from January 1999 to September 2022, containing 5959 daily observations. The second panel shows the corresponding return dynamics. The third panel shows the log probability density function of normalized returns. The fourth panel shows autocorrelation functions of raw returns (gray line) and absolute returns (black line)

Figures 2 and 3 show the same statistical properties for the USD/GBP and the JPY/USD exchange rate, respectively. Note that these time series display bubbles and crashes, excess volatility, fat-tailed return distributions, serially uncorrelated returns and volatility clustering, too. Besides the visual evidence witnessed so far, we report in Table 1 estimates of key summary statistics for our exchange rate data. The first block of Table 1 contains the smallest return, the largest return and the first four moments of the distribution of the returns. The second and third blocks of Table 1 present selected autocorrelation coefficients for raw returns and absolute returns, respectively. In Sect. 5, we explore the extent to which our simple agent-based version of Paul de Grauwe’s chaotic exchange rate model is able to replicate these statistical properties.

Fig. 2

The USD/GBP exchange rate. The first panel shows the evolution of the USD/EUR exchange rate from January 1999 to September 2022, containing 5959 daily observations. The second panel shows the corresponding return dynamics. The third panel shows the log probability density function of normalized returns. The fourth panel shows autocorrelation functions of raw returns (gray line) and absolute returns (black line)

Fig. 3

The JPY/USD exchange rate. The first panel shows the evolution of the USD/EUR exchange rate from January 1999 to September 2022, containing 5959 daily observations. The second panel shows the corresponding return dynamics. The third panel shows the log probability density function of normalized returns. The fourth panel shows autocorrelation functions of raw returns (gray line) and absolute returns (black line)

Table 1 Descriptive statistics for actual exchange rate data

3 A Simple Agent-based Exchange Rate Model

In this section, we propose a simple agent-based model of the foreign exchange market that is consistent with the key assumptions of Paul de Grauwe’s chaotic exchange rate model. However, we deviate from that model as follows. First, our starting point for modeling the foreign exchange market is that a market maker adjusts the exchange rate with respect to speculators’ excess demand.³ Second, our agent-based model contains a discrete number of heterogeneous speculators. Third, each speculator places orders based on his own technical and fundamental trading rule. Fourth, a speculator’s choice between these two trading philosophies depends on his individual assessment of current market circumstances. Fifth, each speculator has his own view about the true fundamental value of the exchange rate. Sixth, in order to prevent speculators’ buying and selling activity from causing unreasonably large speculative investment positions in the foreign exchange market, we also consider their inventory management behavior. As we will see in Sect. 4, however, the dynamics of the deterministic skeleton of our stochastic agent-based model setup is very close to the original dynamics.

Let us turn to the details of our agent-based model setup. As already mentioned, we consider two types of market participants—a market maker and $N$ heterogeneous speculators. The market maker mediates speculators’ orders out of equilibrium and adjusts the exchange rate in response to their excess demand. We denote the order placed by speculator $i$ in period $t$ by ${D}_{t}^{i}$. Then, the market maker quotes the log exchange rate for period $t+1$ as

$${S}_{t+1}={S}_{t}+m\sum_{i=1}^{N}{D}_{t}^{i},$$

(1)

where parameter $m>0$ indicates how strongly the market maker changes the exchange rate with respect to speculators’ order imbalances. Obviously, the market maker increases the exchange rate when speculators’ buying orders exceed their selling orders, and vice versa.

Although the log fundamental value $F$ of the exchange rate is constant, speculators have heterogeneous views about it. Within Paul de Grauwe’s chaotic exchange rate model, these views are normally distributed around the true fundamental value of the exchange rate. We formalize speculator $i$’s perception of the log fundamental value in period $t$ as

$${\widehat{F}}_{t}^{i}=F+{\sigma }^{F}{\varepsilon }_{t}^{i},$$

(2)

where ${\varepsilon }_{t}^{i}\sim N\left(\mathrm{0,1}\right)$. Parameter ${\sigma }^{F}>0$ regulates the dimension of speculators’ perception errors. However, speculators display no systematic prediction error.

In a given period, speculator $i$ uses either a technical or a fundamental trading rule. The probability that speculator $i$ will pick the technical trading rule is equal to

$${\pi }_{t}^{C,i}=\frac{1}{1+{s}_{0}+{{s}_{1}({\widehat{F}}_{t}^{i}-{S}_{t})}^{2}},$$

(3)

where ${s}_{0}$ and ${s}_{1}$ are positive switching parameters. Naturally, the probability that speculator $i$ will opt for fundamental analysis is then

$${\pi }_{t}^{F,i}=1-{\pi }_{t}^{C,i}.$$

(4)

Let us discuss the rationale behind (3) and (4). If the exchange rate is near its fundamental value, speculator $i$ chooses the technical trading rule with a relatively high probability, hoping to benefit from exchange rate trends. As mispricing of the foreign exchange market increases, however, speculator $i$ is more and more convinced that a fundamental market correction is about to set in. In such an environment, speculator $i$ selects the fundamental trading rule with a relatively high probability.⁴ Parameters ${s}_{0}$ and ${s}_{1}$ influence the bell-shaped function of ${\pi }_{t}^{C,i}$ as follows. Parameter ${s}_{0}$ marks the maximum probability with which speculator $i$ will rely on technical analysis. For ${s}_{0}=0.05$ and ${\widehat{F}}_{t}^{i}={S}_{t}$, for instance, we obtain ${\pi }_{t}^{i,C}\approx 0.95$. In contrast, larger values of parameter ${s}_{1}$ make it more likely that speculator $i$ will switch to fundamental analysis as the misalignment in the foreign exchange market increases.

The actual order placed by speculator $i$ in period $t$ depends on two components—a speculative component and an inventory control component. Let ${D}_{t}^{C,i}$ and ${D}_{t}^{F,i}$ stand for speculator $i$’s speculative order component, as suggested by his technical and fundamental trading rule, and ${I}_{t}^{i}$ for his inventory control operations. We formalize speculator $i$’s order placement in period $t$ as follows

$${D}_{t}^{i}=\left\{\begin{array}{c}{D}_{t}^{C,i}+{I}_{t}^{i}\; with \; prob\; {\pi }_{t}^{C,i}\\ {D}_{t}^{F,i}+{I}_{t}^{i} \; with \; prob\; {\pi }_{t}^{F,i}\end{array}\right..$$

(5)

Two aspects deserve attention here. First, speculators’ probabilistic rule-selection behavior adds a random element to the dynamics of the exchange rate. Second, probabilities ${\pi }_{t}^{C,i}$ and ${\pi }_{t}^{F,i}$ depend on the perceived fundamental value ${\widehat{F}}_{t}^{i}$, which, in turn, is subject to normally distributed random shocks.

Speculators’ fundamental trading rules presume that the exchange rate will return to its fundamental value. Hence, we formulate speculator $i$’s fundamental exchange rate forecast for period $t+1$ in period $t$ as

$${E}_{t}^{F,i}\left({S}_{t+1}\right)={S}_{t}+{f}^{\prime}\left({\widehat{F}}_{t}^{i}-{S}_{t}\right).$$

(6)

Parameter $0<f{\prime}<1$ denotes speculators’ expected mean reversion speed. Since the fundamental trading rule suggests submitting buying (selling) orders when the fundamental forecasting rule indicates that the exchange rate increases (decreases), we express the speculative order component triggered by speculator $i$’s fundamental trading rule as

$${D}_{t}^{F,i}={f}^{{\prime}{\prime}}\left({E}_{t}^{F,i}\left({S}_{t+1}\right)-{S}_{t}\right)=f\left({\widehat{F}}_{t}^{i}-{S}_{t}\right)=f\left(F-{S}_{t}\right)+f{\sigma }^{F}{\varepsilon }_{t}^{i},$$

(7)

where ${f}^{{\prime}{\prime}}>0$ and $f={f}^{\prime}{f}^{{\prime}{\prime}}>0$. Due to speculator $i$’s perception of the exchange rate’s fundamental value, his fundamental trading rule entails a random element.

Technical trading rules rely on past movements of the exchange rate as an indicator of market sentiment, which are extrapolated into the future. Although de Grauwe et al. (1993) discuss several technical trading rules, their main attention focuses on a rule that bets on an increase (decrease) in the exchange rate when a short-term moving average of the exchange rate crosses a long-term moving average of the exchange rate from below (above). Following their lead, we formalize the exchange rate’s short-term moving average by ${SMA}_{t}=({S}_{t}-{S}_{t-1})$ and the exchange rate’s long-term moving average by ${LMA}_{t}=0.5({S}_{t}-{S}_{t-2})$. According to Murphy’s (1999) survey on technical analysis in financial markets, there is a myriad of different technical forecasting rules. To capture at least part of the variety of the technical predictors applied in foreign exchange markets, we add a random element to speculator $i$’s technical forecasting rule. Together, this results in

$${E}_{t}^{C,i}\left({S}_{t+1}\right)={S}_{t}+{c}^{\prime}\left({SMA}_{t}-{LMA}_{t}\right)+{{{\sigma }^{C}}^{{\prime}}{\delta }_{t}^{i}},$$

(8)

where ${\delta }_{t}^{i}\sim N\left(\mathrm{0,1}\right)$.⁵ The relevance of the deterministic and random element of speculator $i$’s technical forecasting rule hinges on parameters $c^{\prime}>0$ and ${\sigma }^{C{\prime}}>0$, respectively. Since speculator $i$’s technical trading rule suggests submitting buying (selling) orders when the exchange rate is expected to increase (decrease), we arrive at

$${D}_{t}^{C,i}={c}^{{\prime}{\prime}}\left({E}_{t}^{C,i}\left({S}_{t+1}\right)-{S}_{t}\right)=c\left(\left({S}_{t}-{S}_{t-1}\right)-0.5\left({S}_{t}-{S}_{t-2}\right)\right)+{\sigma }^{C}{\delta }_{t}^{i},$$

(9)

where ${c}^{{\prime}{\prime}}>0$, $c={c}^{\prime}{c}^{{\prime}{\prime}}>0$ and ${\sigma }^{C}={{\sigma }^{C}}^{\prime}{c}^{{\prime}{\prime}}>0$. Obviously, chartists’ trading behavior contains a random element, too.

Over time, speculators’ fundamental and technical trading behavior may lead to the build-up of larger speculative investment positions in the foreign exchange market. In fact, speculator $i$’s position in the foreign exchange market evolves as

$${P}_{t}^{i}={P}_{t-1}^{i}+{D}_{t}^{i}.$$

(10)

Due to the strong variability of the exchange rate, such positions may entail a substantial level of risk, which is why speculators may seek to limit their speculative investment positions. We formalize speculators’ inventory management behavior as follows. Let ${\overline{P} }^{i}$ stand for speculator $i$’s desired (long-run) speculative investment position in the foreign exchange market. To manage his inventory, speculator $i$ engages in inventory control orders

$${I}_{t}^{i}=d\left({\overline{P} }^{i}-{P}_{t-1}^{i}\right),$$

(11)

where parameter $0<d<1$ marks the strength of speculator $i$’s inventory management. For instance, speculator $i$ submits inventory control buying orders in addition to his speculative buying or selling orders if his current speculative investment position in the foreign exchange market falls short of his desired position. While speculators are obviously risk-averse, our agent-based model setup implies that the market maker is risk-neutral. Since the market maker absorbs speculators’ excess demand, his position is the opposite of speculators’ aggregate speculative investment positions, say

$${M}_{t}=-\sum_{i=1}^{N}{P}_{t}^{i}.$$

(12)

As we will see in Sect. 5, one consequence of speculators’ inventory management is that the market maker’s position remains bounded, too. For this reason, we abstain from modeling the market maker’s inventory management. Instead, we assume that the market maker is risk-neutral, which makes his exchange rate quotation economically consistent.⁶

Before we continue, we note that our simple agent-based version of Paul de Grauwe’s chaotic exchange rate model has—besides the exchange rate’s log fundamental value $F$, the total number of speculators $N$ and speculators’ desired inventory positions ${\overline{P} }^{i}$—eight additional parameters that need to be set to simulate its dynamics. These are $m>0$, $c>0$, $0<d<1$, $f>0$, ${s}_{0}>0$, ${s}_{1}>0,$ ${\sigma }^{F}>0$ and ${\sigma }^{C}>0$. Moreover, the model features three agent-specific sources of randomness, associated with speculators’ perception of the true fundamental value, their probabilistic switching between technical and fundamental analysis and their actual trading rules.

4 Properties of the Deterministic Skeleton

To facilitate the understanding of the functioning of our simple agent-based model setup, we first explore the behavior of its deterministic skeleton. Setting ${\sigma }^{C}={\sigma }^{F}=0$ implies that (1) speculators correctly perceive the exchange rate’s true fundamental value, i.e.

$${\widehat{F}}_{t}^{i}=F$$

(13)

and that (2) speculators’ technical and fundamental trading rules lose their agent-specific stochastic elements. For analytical tractability, we furthermore do not keep track of the behavior of individual speculators, an aspect that also precludes modeling their inventory management behavior. Hence, a speculator’s technical and fundamental trading rules reduce to

$${D}_{t}^{C}=c\left(\left({S}_{t}-{S}_{t-1}\right)-0.5\left({S}_{t}-{S}_{t-2}\right)\right),$$

(14)

and

$${D}_{t}^{F}=f\left(F-{S}_{t}\right),$$

(15)

respectively. Assuming that there is a continuum of speculators with mass $N$, we can express the market shares of speculators relying on technical and fundamental analysis as

$${W}_{t}^{C}=\frac{1}{1+{s}_{0}+{s}_{1}{\left({S}_{t}-F\right)}^{2}}$$

(16)

and

$${W}_{t}^{F}=1-{W}_{t}^{C},$$

(17)

respectively. Consequently, the equation that describes the market maker’s exchange rate adjustment simplifies to

$${S}_{t+1}={S}_{t}+mN\left({W}_{t}^{C}{D}_{t}^{C}+{W}_{t}^{F}{D}_{t}^{F}\right),$$

(18)

which completes the description of the model setup.

Combining (13)–(18) yields the deterministic skeleton of our agent-based model setup. Using the auxiliary variables ${X}_{t+1}={S}_{t}$ and ${Y}_{t+1}={X}_{t}$, we obtain the three-dimensional nonlinear deterministic map

$$M := \left\{\begin{array}{l}{S}_{t+1}={S}_{t}+mN\left(\frac{c\left(\left({S}_{t}-{X}_{t}\right)-0.5\left({S}_{t}-{Y}_{t}\right)\right)-f\left(F-{S}_{t}\right)}{1+{s}_{0}+{s}_{1}{\left({S}_{t}-F\right)}^{2}}+f\left(F-{S}_{t}\right)\right)\\ {X}_{t+1}={S}_{t} \\ {Y}_{t+1}={X}_{t} \end{array},\right.$$

(19)

which determines the behavior of the exchange rate. Parameters $m$, $N$, $c$, $f$, ${s}_{0}$ and ${s}_{1}$ are positive; parameter $F$ is unrestricted.

In the following, we explore map $M$. Straightforward computations reveal that map $M$ possesses the unique (fundamental) steady state

$$FSS=\left(\overline{S }, \overline{X }, \overline{Y }\right)=\left(F,F,F\right).$$

(20)

Accordingly, the exchange rate corresponds to its fundamental value when the dynamics is at rest. The Jacobian matrix of map $M$ at the steady state $FSS$ reads

$$J\left(FSS\right)=\left[\begin{array}{ccc}1+\frac{mNc-2{s}_{0}fmN}{2(1+{s}_{0})}& -\frac{mNc}{1+{s}_{0}}& \frac{mNc}{2(1+{s}_{0})}\\ 1& 0& 0\\ 0& 1& 0\end{array}\right].$$

(21)

From (21), we obtain the characteristic polynomial

$${P\left(\lambda \right)=\lambda }^{3}+{a}_{1} {\lambda }^{2}+{a}_{2}\lambda +{a}_{3},$$

(22)

where ${a}_{1}=-1-\frac{mNc-2{s}_{0}fmN}{2(1+{s}_{0})}$, ${a}_{2}=\frac{mNc}{1+{s}_{0}}$ and ${a}_{3}=-\frac{mNc}{2(1+{s}_{0})}$. Using the stability and bifurcation results by Lines et al. (2020) and Gardini et al. (2021), we can conclude that the steady state $FSS$ of map $M$ loses its local stability if one of the following three stability conditions becomes broken: (i) $1+{a}_{1}+{a}_{2}+{a}_{3}>0$; (ii) $1-{a}_{1}+{a}_{2}-{a}_{3}>0$; and (iii)$1-{a}_{2}+{a}_{1}{a}_{3}-{{a}_{3}}^{2}>0$. Moreover, a separate violation of stability condition (i), (ii) or (iii), while the other two stability conditions hold, is associated with the emergence of a fold, a flip and a Neimark-Sacker bifurcation, respectively. Stability condition (i) is always satisfied, as can easily be checked. Stability condition (ii) results in

$$f<\frac{2\left(1+{s}_{o}+mNc\right)}{{s}_{0}mN}.$$

(23)

If this inequality becomes violated, the steady state $FSS$ of map $M$ loses its local stability via a flip bifurcation, giving rise to zigzag exchange rate dynamics. In contrast, stability condition (3) requires that

$$c<\frac{2{\left(1+{s}_{0}\right)}^{2}}{mN\left(1+{s}_{0}\left(1+fmN\right)\right)}.$$

(24)

If this inequality becomes violated, the steady state $FSS$ of map $M$ loses its local stability via a (supercritical) Neimark-Sacker bifurcation, giving rise to quasi-periodic exchange rate dynamics. Hence, the exchange rate becomes unstable when speculators rely too heavily on their technical or fundamental trading signal.⁷ Stability conditions (i)–(iii) determine when a steady state of a three-dimensional map loses its local stability. To derive necessary and sufficient conditions for such a steady state to be locally stable, it is relevant to check a fourth stability condition, namely (iv) ${|a}_{3}|<1$. Since the latter condition is automatically met when (24) holds, (23) and (24) constitute necessary and sufficient conditions for the steady state $FSS$ to be locally stable.

The following proposition summarizes our analytical results.

Proposition 1

The (fundamental) steady state $FSS=\left(\overline{S }, \overline{X }, \overline{Y }\right)=\left(F,F,F\right)$ of map $M$ is locally stable if and only if inequalities $f<\frac{2\left(1+{s}_{o}+mNc\right)}{{s}_{0}mN}$ and $c<\frac{2{\left(1+{s}_{0}\right)}^{2}}{mN\left(1+{s}_{0}\left(1+fmN\right)\right)}$ jointly hold. A separate violation of the first inequality results in a flip bifurcation and the onset of zigzag dynamics. A separate violation of the second inequality is associated with a (supercritical) Neimark-Sacker bifurcation and the birth of quasi-periodic dynamics.

Let us illustrate the dynamics of the deterministic skeleton of our agent-based model setup. The flip bifurcation scenario, while theoretically possible, requires extreme values for parameter $f$. Setting ${s}_{o}=0.1$, for instance, implies that parameter $f$ has to be at least 20 times larger than parameter $c$. We therefore focus on the (supercritical) Neimark–Sacker bifurcation scenario. Figure 4 displays bifurcation diagrams for parameter $c$, assuming that $F=0$, $m=1$, $N=1$, $f=0.3$, ${s}_{0}=0.05$ and ${s}_{1}=\mathrm{2500}$. The first panel of Fig. 4 is based on initial conditions ${S}_{0}=0.01$, ${X}_{0}=0$ and ${Y}_{0}=0$, while the second panel of Fig. 4 is based on ${S}_{0}=-0.01$, ${X}_{0}=0$ and ${Y}_{0}=0$. The third panel of Fig. 4 combines the outcomes of both bifurcation diagrams. We increase parameter $c$ from 0 to 10 in 250 discrete steps, omitting for each value of parameter $c$ a transient period of 5000 observations. As is visible from the bifurcation diagrams, the log exchange rate converges towards its log fundamental value for $0<c\lesssim 2.07$. In line with Proposition 1, a (supercritical) Neimark-Sacker bifurcation occurs at $c\approx 2.07$, associated with the emergence of endogenous quasi-periodic exchange rate dynamics. As parameter $c$ increases further, additional bifurcations arise and the exchange rate becomes more volatile. The deterministic skeleton of our agent-based model setup may also give rise to coexisting attractors, e.g. for $4<c<6$. Overall, Fig. 4 underlines the destabilizing nature of technical trading.

Fig. 4

Parameter $c$. The first two panels depict bifurcation diagrams in which the log exchange rate is portrayed as a function of parameter $c$ for two different sets of initial conditions, given by ${S}_{0}=0.01$, ${X}_{0}=0$, ${Y}_{0}=0$ and ${S}_{0}=-0.01$, ${X}_{0}=0$, ${Y}_{0}=0$, respectively. The third panel displays both bifurcation diagrams. Remaining parameters: $F=0$, $m=1$, $N=1,$ $f=0.3$, ${s}_{0}=0.05$ and ${s}_{1}=2500$

Figure 5 presents the dynamics of the deterministic skeleton of our agent-based model setup for $F=0$, $m=1$, $N=1$, $c=10$, $f=0.3$, ${s}_{0}=0.05$ and ${s}_{1}=\mathrm{2,500}$. Note that this parameter setting corresponds to the uttermost right scenarios depicted in Fig. 4 in which $c=10$. The first two panels of Fig. 5 show the development of the log exchange rate and the corresponding weights of chartists in the time domain. These two panels are useful to understand what is going on in the foreign exchange market. Note that the majority of speculators opt for the technical trading rule when the log exchange rate is near its log fundamental value. Since the trading behavior of chartists is destabilizing, their orders push the log exchange rate away from its log fundamental value. However, when the log exchange rate is far away from the log fundamental value, speculators favor the fundamental trading rule. The orders placed by fundamentalists have a stabilizing effect on the dynamics of the foreign exchange market and drive the log exchange rate closer towards its log fundamental value. As the log exchange rate returns to its log fundamental value, chartists regain control over the foreign exchange market and the above pattern repeats itself, albeit in an intricate manner. Indeed, the dynamics of the exchange rate is chaotic. We can conclude this from the fact that a strange attractor appears when we plot the log exchange rate in period $t+1$ against the log exchange rate in period $t$. See the third panel of Fig. 5.⁸

Fig. 5

Deterministic dynamics. The first two panels present the log exchange rate and the weight of chartists in the time domain. The third panel shows the log exchange rate in period $t+1$ versus the log exchange rate in period $t$. Parameter setting: $F=0$, $m=1$, $N=1$, $c=10$, $f=0.3$ and $s=2500$

5 Matching the Stylized Facts of Foreign Exchange Markets

In the previous section, we have seen that the deterministic skeleton of our agent-based model setup may generate endogenous exchange rate dynamics. From a qualitative perspective, this dynamics demonstrates that Paul de Grauwe’s chaotic exchange rate model is able to explain the boom-bust behavior of foreign exchange markets. Moreover, the simulated exchange rate evolves quite erratically and, since the fundamental value of the exchange rate is constant, we may regard its fluctuations as excessive. The goal of this section is to show that our agent-based model setup, as specified in Sect. 3, has the potential to mimic the behavior of actual exchange rates in greater detail.

Figures 6, 7, 8 and 9 show three representative simulation runs of our agent-based model setup. The simulation runs contain 6000 observations, reflecting a time span of 24 years with 250 trading days per year, comparable to the actual exchange rate data depicted in Figs. 1, 2 and 3. The underlying parameter setting is given by $F=0$, $N=100$, ${\overline{P} }^{i}=0$ for all $i$, $m=1$, $c=0.002$, $d=0.005$, $f=0.00001$, ${s}_{0}=0.05$, ${s}_{1}=2600$, ${\sigma }^{F}=0.01$ and ${\sigma }^{C}=0.0013$.

Fig. 6

Simulation run #1. The first panel shows the evolution of simulated exchange rates (black line) and their fundamental values (gray line) for 6000 observations. The second panel shows the corresponding return dynamics. The third panel shows the log probability density function of normalized returns. The fourth panel shows autocorrelation functions of raw returns (gray line) and absolute returns (black line)

Fig. 7

Simulation run #2. The first panel shows the evolution of simulated exchange rates (black line) and their fundamental values (gray line) for 6000 observations. The second panel shows the corresponding return dynamics. The third panel shows the log probability density function of normalized returns. The fourth panel shows autocorrelation functions of raw returns (gray line) and absolute returns (black line)

Fig. 8

Simulation run #3. The first panel shows the evolution of simulated exchange rates (black line) and their fundamental values (gray line) for 6000 observations. The second panel shows the corresponding return dynamics. The third panel shows the log probability density function of normalized returns. The fourth panel shows autocorrelation functions of raw returns (gray line) and absolute returns (black line)

Fig. 9

Excerpt of simulation run #1. The panels show the evolution of the exchange rate, the corresponding returns, speculators’ average weight of selecting the technical trading rule and their total speculative investment position, respectively

A few comments are in order:

• Simulations indicate that parameter $F$ merely controls the level around which exchange rate fluctuations occur. For ease of exposition, we assume that the log fundamental value is equal to $F=0$.

• It is clear from our analysis in Sect. 4 that parameter $m$ is a scaling parameter, which is why we set $m=1$.

• We also assume that speculators prefer a net position of zero in the foreign exchange market. Hence, we fix ${\overline{P} }^{i}=0$ for all speculators.

• Moreover, $d=0.005$ reflects a half-life of speculators’ inventory position of about 138 trading periods, roughly equivalent to 6 months.

• Since questionnaire evidence by Menkhoff and Taylor (2007) reveals that a small fraction of speculators always rely on fundamental analysis, we decided to set ${s}_{0}=0.05$.

• To reduce the computational burden of our simulations, we focus on $N=100$ speculators, representing, for instance, large institutional players in the foreign exchange market. Keeping track of all the quantities captured by building blocks (1)–(11) requires simulating 1001 model equations for $N=100$ speculators. Doubling the number of speculators would increase the number of model equations to 2001 equations, and so on. However, “Appendix A” contains a number of robustness checks that suggest that our agent-based model setup may also yield reasonable exchange rate dynamics when the number of speculators increases to $N=1000$ and $N=2500$.⁹

• We identified the remaining five model parameters, i.e. $c$, $f$, ${s}_{1}$, ${\sigma }^{F}$ and ${\sigma }^{C}$, via a cumbersome trial and error process with the aim of matching the behavior of actual exchange rates.

• Initial conditions for the log exchange rate and speculators’ positions are equal to zero, i.e. identical to their steady-state values. Exchange rate fluctuations are set in motion via the random elements of our agent-based model setup.

Let us start with Fig. 6. Its first panel shows that the exchange rate (black line) circles in a complex fashion around its fundamental value (gray line). Note that the exchange rate’s boom-bust behavior may span several years, although such behavior can also be rather short-lived. The second panel of Fig. 6 reports the corresponding return dynamics. Since the fundamental value is constant, changes in the exchange rate are excessive. The third panel of Fig. 6 reveals that the distribution of the returns possesses fat tails. Indeed, extreme exchange rate movements occur more frequently than warranted by a comparable normal distribution. The gray line in the fourth panel of Fig. 6 depicts the autocorrelation coefficients of raw returns. Since the autocorrelation coefficients of raw returns are not significant, the evolution of the exchange rate resembles a random walk. The black line in the fourth panel portrays the autocorrelation function of absolute returns. Obviously, there is significant evidence of volatility clustering.

The simulated exchange rate depicted in Fig. 6 oscillates within a rather static band that is centered around its constant fundamental value. We conduct two further experiments to address this issue. In Fig. 7, we model the evolution of the log fundamental value of the exchange rate in the form of a random walk, i.e.

$${F}_{t}={F}_{t-1}+{\sigma }^{\eta }{\eta }_{t},$$

(25)

with ${\eta }_{t}\sim N(\mathrm{0,1})$. In our simulations, we set ${\sigma }^{\eta }=0.0015$. Clearly, the term ${\sigma }^{\eta }{\eta }_{t}$ reflects a random fundamental (news) shock. The path of the fundamental value of the exchange rate is shown by the gray line in the first panel of Fig. 7. Moreover, we assume that the market maker takes into account the fundamental (news) shock when adjusting the log exchange rate, resulting in

$${S}_{t+1}={S}_{t}+m\sum_{i=1}^{N}{D}_{t}^{i}+{\sigma }^{\eta }{\eta }_{t}.$$

(26)

Since the standard deviation of simulated changes in the log exchange rate, equal to 0.00622, is about four times higher than ${\sigma }^{\eta }$, the simulated exchange rate is still excessively volatile. In Fig. 8, the log fundamental value of the exchange rate follows an AR(1) process, represented by

$${F}_{t}={\alpha F}_{t-1}+{\sigma }^{\eta }{\eta }_{t},$$

(27)

with ${\eta }_{t}\sim N(\mathrm{0,1})$. Again, the market maker takes into account the change in the log fundamental value when adjusting the log exchange rate, yielding

$${S}_{t+1}={S}_{t}+m\sum_{i=1}^{N}{D}_{t}^{i}+({\alpha -1)F}_{t-1}+{\sigma }^{\eta }{\eta }_{t}.$$

(28)

For ${\sigma }^{\eta }=0.0015$ and $\alpha =0.999$, the standard deviation of simulated changes in the log exchange rate, equal to 0.00620, is again about four times higher than ${\sigma }^{\eta }$. Note that both experiments lend the simulated exchange rate a less static appearance, without interfering with its ability to mimic the statistical properties of actual exchange rates.

In fact, Figs. 6, 7 and 8 highlight that our calibrated agent-based model setup is capable of producing bubbles and crashes, excess volatility, fat-tailed returns distribution, serially uncorrelated returns and volatility clustering. Table 2 supports this finding. Estimates of the summary statistics for actual exchange rate data, reported in Table 1, and simulated exchange rate data, reported in Table 2, are quite similar. Extreme returns may be larger than 3 percent. The level of the volatility of simulated and actual exchange rates is comparable. Estimates of the mean and skewness indicate that the distribution of returns is symmetric. In addition, there is clear evidence of excess kurtosis. While returns are serially uncorrelated, autocorrelation coefficients of absolute returns indicate significant volatility clustering. However, the autocorrelation coefficients for absolute returns seem to us to be slightly too high at shorter lags and slightly too low at larger lags.

Table 2 Descriptive statistics for simulated exchange rate data

Having established that the behavior of simulated exchange rate data closely resembles the behavior of actual exchange rate data, let us now turn to the question why this is the case. Figures 9 and 10 shed light on the internal functioning of our agent-based model setup, focusing on an excerpt of simulation run #1 that extends from period 4000 to period 5000 (see Fig. 6 for the whole simulation run). Since we calibrated our agent-based model setup to daily data, 1000 observations reflect a time span of four years. The four panels of Fig. 9 depict the evolution of the exchange rate, the corresponding returns, speculators’ average probability of selecting the technical trading rule and their aggregate speculative investment position in the foreign exchange market, respectively. The four panels of Fig. 10 show the probabilities of selecting the technical trading rule, the speculative investment positions, the speculative orders and the inventory control operations of three speculators, marked purple, pink and cyan, respectively.

Fig. 10

Behavior of three individual speculators. The panels show the probability of selecting the technical trading rule, the speculative orders, the speculative investment position and the inventory control operations of three individual speculators, marked purple, pink and cyan, respectively. The dynamics corresponds to the simulations depicted in Fig. 9

According to the first panel of Fig. 9, the exchange rate is below its fundamental value between periods 4000 and 4200. As a result, the clear majority of speculators decide in favor of fundamental analysis and, not surprisingly, their trading behavior pushes the exchange rate slowly upwards, reducing mispricing in the foreign exchange market. Around period 4300, the market impact of chartists starts to increase. Speculators are now convinced that the current exchange rate trend will persist for a while, which is why they seek to exploit it. Their behavior sparks a self-fulfilling prophecy. Chartists’ extrapolative trading behavior drives the exchange rate higher and higher, and a bubble process materializes. Since the exchange rate is a relative price, we may refer to this as a “positive bubble”. Note that chartists’ trading behavior also increases the volatility of the exchange rate. As can be seen, the volatility outburst contains a number of more pronounced changes in the exchange rate. Extreme changes in the exchange rate occur when sufficiently many chartists receive similar trading signals. Their orders then result in greater excess demand, prompting the market maker to adjust the exchange rate more significantly.

Overall, the exchange rate evolves quite erratically during this bubble episode. For instance, there are brief periods when fundamental analysis is the dominant trading strategy, pulling the exchange rate temporarily back towards its fundamental value. In addition, technical analysis may also initiate downward movements of the exchange rate. Ultimately, the collapse of the bubble originates from both technical and fundamental trading.¹⁰ Around period 4500, chartists’ trading behavior creates a negative bubble, pushing the exchange rate far below its fundamental value. Consequently, the majority of speculators start to return towards fundamental analysis, resulting in rather calm exchange rate movements between periods 4500 and 4700. As fundamental orders eventually reduce mispricing of the exchange rate, a new market phase occurs. Many speculators now opt for technical analysis, thereby initiating the next bubble process, associated with another volatility outburst and extreme changes in the exchange rate. Once again, the exchange rate behaves quite erratically during the bubble process. This has to do with the fact that speculators’ rule-selection behavior is probabilistic, and that their perception of the exchange rate’s fundamental value and their trading rules are subject to random influence factors.¹¹

The bottom panel of Fig. 9 presents speculators’ aggregate investment position in the foreign exchange market. As can be seen, speculators’ aggregate investment position in the foreign exchange market evolves proportionally to the exchange rate, as quoted by the market maker. Moreover, the position of the market maker in the foreign exchange market is the mirror image of those of speculators, as is also clear from (12). This suggests that as long as the path of the exchange rate remains bounded—which is always the case in our simulations—the positions of the market maker in the foreign exchange market as well as those of speculators remain bounded, too. Naturally, this relationship works in both directions. Speculators’ inventory control keeps the market maker’s position in check and limits mispricing in the foreign exchange market.

Our agent-based model setup allows us to keep track of the behavior of individual speculators. According to the third panel of Fig. 10, the three speculators that we track here have a negative speculative investment position in the foreign exchange market between periods 4000 and 4200. Consequently, their inventory management operations result in buy orders, as witnessed by the fourth panel of Fig. 10. Furthermore, all three speculators select the fundamental trading rule with a relatively high probability. Since the exchange rate is below its fundamental value, speculators opting for the fundamental trading rule tend to place speculative buy orders, which further reduces their speculative investment position in the foreign exchange market. Together, the fundamentally motivated speculative orders and the inventory control transactions reduce mispricing of the exchange rate.

A regime change occurs between period 4300 and 4500. All three speculators now pick their technical trading rules with a relatively high probability. Although orders stemming from technical trading rules have a larger random element (see the second panel of Fig. 10), the three speculators tend to place buy orders. This drives up the exchange rate and their speculative investment position in the foreign exchange market. In the long run, however, speculators’ investment positions in the foreign exchange market circle around their desired target levels, i.e. around zero in our simulations. Similarly, the exchange rate oscillates around its fundamental value in the long run. Once again, we note that the exchange rate’s random-walk-like evolution originates from agent-specific aspects of speculators’ trading behavior, as visible from the quantities plotted in Fig. 10.

6 Concluding Remarks

De Grauwe and Dewachter (1992, 1993) and de Grauwe et al. (1993) proposed one of the first behavioral exchange rate models featuring nonlinear deterministic interactions between chartists and fundamentalists. Their ingenious work tremendously fostered our understanding of the behavior of foreign exchange markets. Simply speaking, there are two dominant regimes in their model. In the first regime, chartists reign the foreign exchange market. This is the case when the exchange rate is near its fundamental value. Since chartists’ behavior is destabilizing, the exchange rate disconnects from its fundamental value. In the second regime, fundamentalists govern the foreign exchange market. This is the case when the exchange rate is far from its fundamental value. Since fundamentalists’ behavior is stabilizing, the exchange rate eventually returns to its fundamental value. Via an everlasting competition between these two regimes, i.e. between chartists and fundamentalists, their model may produce chaotic exchange rate dynamics.

In this paper, we sought to show that the explanatory power of Paul de Grauwe’s chaotic exchange rate model is richer than previously appreciated. In particular, we proposed a simple agent-based version of Paul de Grauwe’s chaotic exchange rate model that is capable of explaining a whole battery of stylized facts of foreign exchange markets. Most importantly, we assumed that each speculator places orders based on his own technical and fundamental trading rule. Moreover, a speculator’s choice between these two trading philosophies is probabilistic and depends on his individual assessment of current market circumstances. The latter aspect follows from the assumption that each speculator has his own view about the true fundamental value of the exchange rate. Speculators also monitor their speculative investment position in the foreign exchange market and adjust their order placement such that their speculative investment positions remain bounded. Based on our calibrated agent-based model setup, we documented that simulated exchange rates gave rise to bubbles and crashes, were excessively volatile, repeatedly displayed extreme movements, were hardly predictable and were subject to lasting volatility outbursts.

On a more general level, we dare to argue that speculators’ switching between destabilizing technical trading rules and stabilizing fundamental trading rules is the main driver of the dynamics of the exchange rate. While the modeling of realistic exchange rate dynamics apparently requires the consideration of some kind of stochastic influence factors, the main force accountable for the dynamics of the exchange rate seems to us to be deeply rooted in the nonlinear interplay between chartists and fundamentalists. Using analytical and numerical tools from the research field of nonlinear dynamical systems to investigate chartist-fundamentalist models lends us the opportunity to better understand the endogenous component of the dynamics of the exchange rate.

Since we kept our agent-based version of Paul de Grauwe’s chaotic exchange rate model relatively simple, we conclude our paper by pointing out five avenues for future research. First, while speculators have different views about the exchange rate’s fundamental value, their views are free from systematic perception errors. It may be interesting to add some kind of persistent optimism and pessimism in this respect. For instance, speculators may believe in a higher (lower) fundamental value when the exchange rate increases (decreases). Second, we have not yet considered social interactions between speculators, although there is evidence of herding behavior in foreign exchange markets. It may be worth placing speculators on a network and letting their switches between technical and fundamental trading rules also depend on their neighbors’ behavior. Third, the parameters that characterize the behavior of all speculators are identical. We could allow for more heterogeneity among speculators by relaxing this assumption, i.e. by drawing these parameters from certain distributions. Fourth, we added a random variable to the expectation rule of chartists to capture part of the variety of existing technical expectation rules. While this keeps the deterministic skeleton of our agent-based model setup analytically tractable, it adds an exogenous component to our approach. We may reduce the relevance of this exogenous component by considering more than one technical expectation rule. A speculator’s technical trading rules may even evolve over time. Fifth, we calibrated our agent-based model setup such that it mimics a number of important statistical properties of exchange rates. Future work may seek to estimate our agent-based model setup, i.e. by applying tools such as the method of simulated moments. In this respect, it would be desirable to account also for characteristics that capture the trading behavior of individual speculators, e.g. their order placement and inventory management behavior.

To sum up, we hope that our paper serves others as a playground to shed further light on the true potential of Paul de Grauwe’s chaotic exchange rate model. In general, we believe that empirically based chartist-fundamentalist models offer reasonable descriptions of what is going on in foreign exchange markets. Needless to say, much more can and needs to be done to understand the captivating behavior of exchange rates.

Appendix A

In this appendix, we present a number of robustness checks. In particular, we are interested in how changes in the number of speculators affect the performance of our agent-based model setup. Table

Table 3 Descriptive statistics for the first robustness check

3 reports summary statistics for our three model versions, assuming that there are $N=1000$ speculators. Simulations are based on the same parameter setting, except that parameters $m$, ${\sigma }^{F}$ and ${\sigma }^{C}$ are rescaled by $m=m/10$, ${\sigma }^{F}={\sigma }^{C}/\sqrt{10}$ and ${\sigma }^{F}={\sigma }^{C}/\sqrt{10}$ (the number of speculators increased by a factor of 10). Table

Table 4 Descriptive statistics for the second robustness check

4 reports the same for $N=2500$ speculators. Now parameters $m$, ${\sigma }^{F}$ and ${\sigma }^{C}$ are rescaled by $m=m/25$, ${\sigma }^{F}={\sigma }^{F}/\sqrt{25}$, and ${\sigma }^{C}={\sigma }^{C}/\sqrt{25}$ (the number of speculators increased by a factor of 25). Note that the summary statistics presented in Table 3 and 4 are in line with those presented in Table 2, obtained for $N=100$ speculators. Overall, we may thus conclude that our agent-based model setup may also yield reasonable exchange rate dynamics when the number of speculators is set to $N=1000$ and $N=2500$.