1 Introduction

Concerted international efforts are needed to control climate change caused by greenhouse gas (GHG) emissions, whilst meeting the challenge to achieve these objectives cost effectively. Technological developments play an important role in combating the associated efficiency issues and unequal distribution of innovation in green technology. The dilemma facing the world today, is how to reduce fossil fuel associated (GHG) emissions, accepting that their demand will continue to exist in the coming decades to maintain economic growth, employment and sustainability. In the energy sector, many solutions have been proposed to completely replace fossil fuels for electricity generation, such as massive deployment of renewable energy generation and increased energy efficiency. There are many restrictions, however, to achieve this result in the medium term, ranging from technological limitations in the massive deployment of energy efficiency and renewable energies, to the political economy of countries unlikely to reduce their oil and carboniferous production as long as demand exists.

Carbon capture and storage (CCS) offers an alternative to mitigate \(CO_{2}\) emissions from fossil fuel power plants whilst considering that both current and future energy needs and subsequent operation of these plants will continue in the coming years. CCS could mitigate up to 90% of fossil fuel associated carbon dioxide emissions in electricity generation and industrial processes. Additionally, the use of CCS with renewable biomass is one of the few carbon reduction technologies that can be used in a “carbon-negative” mode. If biomass from fuel-wood crops were used, carbon could be absorbed and simultaneously generate electricity. CCS, therefore, is a viable alternative to solve the dilemma of reducing emissions while satisfying the growing energy needs of the world.

One salient way to improve cost efficiency in GHG abatement is to transfer existing technologies from the developed to developing world. Recognizing the potential benefits brought about by technology transfer, the Conference of the Parties (COP) in 2002 and 2003, called for unified efforts by developed countries to transfer technology to developing countries. More recently, the COP initiated a technology mechanism for the promotion and spread of climate-friendly technologies and investing in new technologies that will lower emissions and support jobs and growth. Hence, the technology investment and collaboration road map will play an important part in the long-term strategy to reduce global emissions. The importance of developing such CCS technology was reiterated in recent days by the Prime Minister of Australia Morrison (2021), describing technology as a “game-changer” and critical in decarbonizing the Australian and global economy, whilst being “ crucial in protecting and creating the jobs of today and positioning Australia for the jobs of the future”.

Large scale mathematical modelling related to climate change has often included technology transfer as an instrument in policy analysis, Weyant et al. (1996). More specifically within the broader trans-boundary pollution control debate, game theory models provide a useful tool in articulating when and why emissions reduction negotiations between stakeholders can either fall through or be successful. However, the success of such agreements are somewhat limited by the unilateral incentive for each party to deviate from the terms of the agreement.

Trans-boundary industrial pollution is defined as the pollution that originates in one country but is able to cause damage in another country’s environment by crossing borders through pathways such as land, sea or air. Trans-boundary pollution control models specifically examine how a government can both effectively deal with external pollution within a country and between countries using technology. If emission-output ratios are fixed, then the option is to stimulate investment in clean technology to lower the emission output ratio. Such a framework allows the analysis of elements of the environmental debate between optimists who favor growth in order to have resources to invest in clean technology, and pessimists who favor bringing down production and pollution by-products. The answer, of course, depends on the elasticity of the emission-output ratio against the stock of clean technology. A simple and general formulation to begin with is that pollution is a by-product of production, which can be modelled by means of an emission-output ratio. Dasgupta (1982) considered an intertemporal welfare index, which takes into account both the benefits of production and damage caused by the stock of pollutants. Maximization of this welfare index, subject to the accumulation dynamics of the pollutants, yields a path of emission charges which internalizes the pollution externality. As a result, the energy economy is highly exposed to these processes.

Game theory is the formal, mathematical methodology for analyzing decision making processes in an interactive environment. Foundations of modern game theory were laid by Von Neumann–Morgenstern (1944). Since then many researchers have applied game theory to study trans-boundary industrial pollution, with more recent studies incorporating the assumption that countries are primarily motivated to maximize their net benefits from pollution control, as measured by its impact on the environment and economy. Kaitala et al. (1992a, b) applied a cooperative and non-cooperative game to analyze the benefits of bilateral cooperation between Finland and the Soviet Union, subject to abatement cost. Under the fairly general utility and damage cost function, Kaitala et al. (1992a, b) re-visited the same trans-boundary pollution problem and concluded that efficient cooperation may entail financial transfers from Finland to the Soviet Union, because it is cheaper to abate sulfur there. Since then many researchers, Yeung (2007), Yeung and Petrosyan (2008), Long (1992), Van der Plong and de Zeeue (1992), Dockner and Long (1993), Martin et al. (1993), Zagonari (1998), Li (2013), Huang et al. (2016), Greening et al. (2000), Sorrell and Dimitropoulos (2008), Jørgensen and Zaccour (2001), Benchekroun and Chaudhuri (2014), Li and Mao (2019), El Ouardighi et al. (2020), Yeung et al. (2019), Perera (2020, 2021), Yi et al. (2020) have applied the game theory paradigm to study trans-boundary industrial pollution problems. Within such models, it is the government of each country that decides the pollution control strategy implemented due to the fact that pollution can be controlled via the amount of pollutants emitted by each country’s production processes. However, within many of these environmental policy models, technology is incorporated as an exogenous variable, with limited attention given to the role of endogenous technology, other technological breakthroughs, potential government subsidies or collaborative innovations integrated within low carbon technologies. In recent years, researchers have also developed models to discuss the importance of lowering carbon emissions and its potential impact on society by examining economic growth, international trade, and associated health benefits. Researchers such as Khan et al. (2020) have examined the development of such carbon lowering emission policies and their potential benefits to the environment and ecological sustainability to economies under logistics operations. However, there remains a need for exploiting the role of technology, its dynamics, and limitations on the reduction of international pollution levels within the wider carbon emissions debate, by incorporating technology as an endogenous variable when implementing new policies. In doing so, this provides a more realistic and suitable measure of the effect and role of technology within a broader trans-boundary carbon pollution problem.

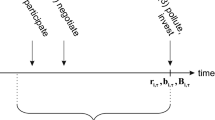
In this analysis, we propose a trans-boundary emission control model under an international emissions trading permit market, when the sum of pollution flow emitted by two countries is limited by the number of issued permits. In each country, the pollution industry is competitive and government subsidies serve to enhance the innovation process in pollution abatement technology and analyze optimal strategies under a Stochastic linear quadratic differential game (SDG) paradigm. Adopting such cleaner technologies within a carbon trading market framework that considers trans-boundary pollution emissions will encourage firm’s to undertake research and development (R&D) measures to develop cleaner technologies and promote international carbon permit trading rather than simply reducing production output. In this study, we draw upon Yeung (2007) by considering a trans-boundary industrial pollution with emission permit trading, when the dynamics of each country’s endogenous technology is governed by a stochastic differential equation (SDE). We assume that the output of each county’s domestic consumption good production is proportional to the level of pollution emissions, with pollutant remittance from production processes adding to existing pollution, common to both countries (stock externality). As a result, consumers derive positive utility from consuming goods and costs from current pollution stocks, consequently requiring countries to take measures to decrease pollution levels. However, the level of pollution can be controlled through the production process or undertaking necessary R&D measures to improve the efficiency of CCS and technology.

Therefore, the aim of this paper is to analyze how investments, emission strategies and net revenues of both countries influence the introduction of a cooperative implementation mechanism in a dynamic context. The choice to incorporate technology as an endogenous variable within our model presents numerous policy implications, whilst making the following contributions to existing game theory/energy economic literature:

  1. 1.

    Governments can determine the appropriate level of subsidy required for the development of pollution lowering technologies and advance collaborative measures to meet global emissions reduction targets.

  2. 2.

    Policymakers should continue encouraging industry to utilize carbon capture and storage technologies, whilst emphasizing that efforts to coordinate emissions control should be pursued jointly because of its mutual benefit to government and industry.

  3. 3.

    Governments should promote firm’s R&D measures to improve pollution lowering technology.

As a result of our stochastic game theory analysis, we also contribute to the existing literature:

  1. 1.

    A strategic interaction between endogenous stochastic carbon capture utilization and storage technology within a trans-boundary industrial pollution problem with random interference factors and emissions permits. These random interference factors capture uncertain external environment factors and the internal limitations of the decision maker.

  2. 2.

    Via the optimal control theory, we obtain a closed-loop (Markov perfect) Nash equilibrium to obtain the optimal emission paths when each country’s discounted stream of net revenue is maximized.

  3. 3.

    By articulating the Nash non-cooperative and cooperative games, we define the two equilibria via a feedback control strategy. We show that under the feedback strategies, the inefficiency of the non-cooperative equilibrium over the cooperative equilibrium is increased.

  4. 4.

    We prove the stability of the cooperation via a pareto optional solution.

  5. 5.

    Additionally, a government subsidy incentive is proposed to examine the collaboration required to integrate low carbon technologies and consequently increase each country’s net revenue. As a result, the variance improvement degree of the cooperative game equilibria dominate the non-copperative equilibra.

In Sect. 2, the proposed model is outlined. In Sect. 3, by implementing a non-cooperative game, we examine the feedback non-cooperative Nash equilibria, optimal emission path and limit of expectation and variance. In Sect. 4 by implementing a cooperative game, we examine the feedback cooperative Nash equilibria and limit of expectation and variance under shared technology. In Sect. 5, we simulate the results discussed in Sect. 4. Section 6 concludes the study. Appendix 1 and 2 contain proofs.

2 Model

2.1 Definition of Model Parameters

For the completeness of this analysis see Table 1 for the description of the model parameters.

Table 1 Description of model parameters
Full size table

2.2 Basic Model

Time is measured continuously and extends from 0 to \(+\infty \). The state of the system at time t is denoted by \(K(t)\in \mathbb {R}\), \(P(t)\in \mathbb {R}.\) We indexed two neighboring countries such that \(h=i,j\). Each country produces one domestic consumption good \(Q_{h}(t)\) with a set of fixed endowment factors using a heterogeneous time-variant carbon capture utilization and storage technology K(t). Consumers are homogeneous within each country and heterogeneous across countries. Production of consumption goods \(Q_{h}(t)\) subject to K(t) results in an amount of emissions, \(E_{h}(t)\). Assuming that the output of each county’s domestic consumption good production is proportional to the level of pollutant emissions, we define the emission-consumption trade-off function according to Yeung (2007), Li (2014), Perera (2020) as:

$$\begin{aligned} Q_{h}(t)=K(t)\left( E_{h}(t)\right) , \end{aligned}$$
(1)

where the dynamics of each country’s carbon capture utilization and storage technology K(t) is governed by the differential equation (DE):

$$ {\begin{array}{*{20}l} {dK(t) = \left[ {\vartheta _{i} (t)E_{i} (t) + \vartheta _{j} (t)E_{j} (t) - \xi K(t)} \right]dt + \rho (K)d_{k} W(t)} \\ {K(0) = K_{0} > 0} \\ \end{array} } $$
(2)

where \(\xi \in \left( 0,1\right] \) is the attenuation coefficient of technology and \(\vartheta _{h}(t)>0\) denotes the effect of each country’s homogeneous technology towards \(E_{h}(t)\). \(W_{k}(t)\) is a standard Brownian motion and \(\rho (K)\) denotes a random interference factor on technology used by country’s i and j at time t. The total payoff for producing consumption good \(Q_{h}(t)\) in country h less than any flow damages is defined as

$$\begin{aligned} \pi _{h}\left( K(t)\right) =\vartheta _{h}(t)E_{h}(t)+\left( \gamma _{h}+\lambda _{h}\right) K(t), \end{aligned}$$
(3)

where \(\gamma _{h}\in \left( 0,1\right] \) is the innovation influence coefficient of technology and \(\lambda _{h}\in \left( 0,1\right] \) is the government subsidy coefficient for improvements on carbon capture utilization and storage technologies under collaborative innovation, see Perera (2020).

Remark 1

Subsidies play an important role in the renewable energy (RE) industry. In an effort to reach the ambitious targets of the EUs Strategic Energy Technology Plan (SET–Plan), EU member states have implemented support mechanisms of various forms (e.g., price mechanisms, such as a carbon tax or permit trading schemes) intended to encourage and accelerate the adoption of RE technologies.

Production of \(Q_{h}(t)\) results in a level of net surplus (consumer surplus plus profit), less than any flow damages. We define production revenue of region h

$$\begin{aligned} \Pi _{h}\left( K(t)\right) =\vartheta _{h}(t)E_{h}(t)+\left( \gamma _{h}+\lambda _{h}\right) K(t)-\frac{1}{2}\beta ^{h}E_{h}^{2}(t), \end{aligned}$$
(4)

where \(0<\beta ^{h}\le 1\) is the cost coefficient parameter associated with each country’s \(E_{h}(t)\in \left[ 0,\,\vartheta _{h}\right] .\)

Let \(E_{h}(0)>0\) be the initial emission permit of country h, which was allocated by grandfather principle, \(\varUpsilon _{h}(t)\) be the quantity of emission permits bought or sold at time t for a price \(\delta (t)\), which is determined by the permit market equilibrium conditions. Then the quantity of emission permits bought or sold by country h (where \(h=i,j\) ) is

$$\begin{aligned} \varUpsilon _{h}(t)=E_{h}(t)-E_{h}(0), \end{aligned}$$
(5)

for further details see Yeung (2007), Li (2014). The level of purchased or sold emission permits in each country is reflected as an upper bound for the environmental standards. On the other hand, it can be interpreted as a pollution tax (extra cost or revenue). It is now widely agreed among economists and regulatory authorities that tradable emission permits can be a cost-effective strategy for controlling environmental pollutants.

Remark 2

Under an emission trading program the regulatory authority issues a certain number of emission permits for each country, who subsequently can only legally emit the level of emissions accounted for by the number of emission permits it holds. Each country can then buy and sell these emission permits with one another creating a market for emission permit tradings. Each country can also reallocate these emission permits among different emission sources within itself.

Then country \(h's\) industrial net revenue with emission permits trading at time t can be express as:

$$\begin{aligned} \Pi _{h}\left( K(t)\right)&=\vartheta _{h}(t)E_{h}(t)+\left( \gamma _{h}+\lambda _{h}\right) K(t) -\frac{1}{2}\beta ^{h}E_{h}^{2}(t)-\delta (t)\left( E_{h}(t)-E_{h}(0)\right) \nonumber \\&=\left( \vartheta _{h}-\delta (t)\right) E_{h}(t)-\frac{1}{2}\beta ^{h} E_{h}^{2}(t)+\delta (t)E_{h}(0)+\left( \gamma _{h}+\lambda _{h}\right) K(t). \end{aligned}$$
(6)

The amount of pollutants emitted for both countries at time t \(\left\{ P(t)\right\} _{t\ge 0}\) and is driven by the following diffusion process

$$ dP(t) = \left( {\vartheta _{i} (t)E_{i} (t) + \vartheta _{j} (t)E_{j} (t) - mP(t)} \right)dt + \sigma (P)dW_{p} (t),\quad P(0) = P_{0} , $$
(7)

where \(0<m<1\) denotes the environment self-clearing capacity, \(W_{p}(t)\) is a standard Brownian motion and \(\sigma \left( P(t)\right) \) a random interference factor on the pollution stock by country i and j at time t . We define the emission pollution damage agonized by country h at time t \(C_{h}(t)\) such that

$$\begin{aligned} C_{h}(t)=\left( 1+\theta _{h}\right) P(t), \end{aligned}$$
(8)

where \(\theta _{h}>0\) denotes a relative loading factor capturing the damage parameter for each country. Furthermore, each country’s regulatory authority can be interpreted as the relative loading factor when setting pollution taxes or demand compensations. These differences could be due to differences in environmental damages from the flow of emissions and the stock of pollution or abatement costs, (List et al., 2001). Then the problem of country h is as follows:

$$\begin{aligned} J_{h}\left( P(t),K(t)\right)&=\underset{E_{h}(t)\ge 0}{\max }\int _{0}^{+\infty }\exp \left( -r_{h}t\right) \left[ \left( \vartheta _{h}(t)-\delta (t)\right) E_{h}(t)-\frac{1}{2}\beta ^{h}E_{h}^{2}(t)\right. \nonumber \\&\left. \quad +\delta (t)E_{h}(0)+\left( \gamma _{h}+\lambda _{h}\right) K(t)-\left( 1+\theta _{h}\right) P(t)\right] dt.\nonumber \\ s.t&{\left\{ \begin{array}{ll} dP(t)=\left( \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-mP(t)\right) dt+\sigma (P)dW_{p}(t)\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P(0)=P_{0},\,\,\,\,\,\,\,\,\,P(t)\ge 0, \end{array}\right. }\nonumber \\ s.t&\left\{ \begin{array}{l} dK(t)=\left( \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-\xi K(t)\right) dt+\sigma (K)dW_{k}(t)\\ K(0)=K_{0}>0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{array}\right. \end{aligned}$$
(9)

where \(r_{h}\) is each country’s risk-free rates and \(J_{h}\left( P(t),K(t)\right) \) is the net revenue of country h.

3 Solution to a Non-cooperative Game

In game theory, a non-cooperative game is one in which players make decisions independently and any cooperation must be self-enforcing. Hence, regions \(h'\text {s}\) and optimization problem can be written as follows:  

$$\begin{aligned} J_{i}\left( P(t),K(t)\right)&=\underset{E_{i}(t)\ge 0}{\max }\int _{0}^{+\infty }\exp \left( -r_{i}t\right) \left[ \left( \vartheta _{i}(t)-\delta (t)\right) E_{i}(t)-\frac{1}{2}\beta ^{i}E_{i}^{2}(t)\right. \nonumber \\&\left. \quad +\delta (t)E_{i}(0)+\left( \gamma _{i}+\lambda _{i}\right) K(t)-\left( 1+\theta _{i}\right) P(t)\right] dt. \end{aligned}$$
(10)
$$\begin{aligned} s.t&\left\{ \begin{array}{l} dP(t)=\left( \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-mP(t)\right) dt+\sigma (P(t))dW_{p}(t)\\ P(0)=P_{0},\,\,\,\,\,\,\,\,\,P(t)\ge 0, \end{array}\right. \nonumber \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad s.t\left\{ \begin{array}{l} dK(t)=\left[ \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-\xi K(t)\right] dt+\rho (K)d_{k}W(t)\\ K(0)=K_{0}>0. \end{array}\right. \nonumber \\ J_{j}\left( P(t),K(t)\right)&=\underset{E_{j}(t)\ge 0}{\max }\int _{0}^{+\infty }\exp \left( -r_{j}t\right) \left[ \left( \vartheta _{j}(t)-\delta (t)\right) E_{j}(t)-\frac{1}{2}\beta ^{j}E_{j}^{2}(t)\right. \nonumber \\&\left. +\delta (t)E_{j}(0)+\left( \gamma _{j}+\lambda _{j}\right) K(t)-\left( 1+\theta _{j}\right) P(t)\right] dt.\\ \quad s.t&\left\{ \begin{array}{l} dP(t)=\left( \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-mP(t)\right) dt+\sigma (P(t))dW(t)\\ P(0)=P_{0},\,\,\,\,\,\,\,\,\,P(t)\ge 0, \end{array}\right. \nonumber \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,s.t\left\{ \begin{array}{l} dK(t)=\left[ \vartheta _{i}(t)+\vartheta _{j}(t)E_{j}(t)-\xi K(t)\right] dt+\rho (K)d_{k}W(t)\\ K(0)=K_{0}>0. \end{array}\right. \nonumber \end{aligned}$$
(11)

The models illustrated by Eqs. (10) and (11) are the optimal control problems with pure state variable constraints. The control variable of the model is the emission level \(E_{h}(t)\) and the state variables are the pollution stock level P(t) and technology K(t). Our objective is to find the optimal path of \(E_{h}(t)\) such that \(J_{h}\left( E_{h}(t)\right) \) is maximized \(h=i,j.\)

We define the value functions in regions i and j as \(V_{i}(P,K)\) and \(V_{j}(P,K),\) respectively. Then the HJB equations for the maximization problem faced at time t are:

$$\begin{aligned}r_{i}V_{i}\left( P,K\right)&=\underset{E_{i}(t)}{\max }\left\{ \left[ \left( \vartheta _{i}(t)-\delta (t)\right) E_{i}(t)-\frac{1}{2}\beta ^{i}E_{i}^{2}(t)+\delta (t)E_{i}(0)+\left( \gamma _{i}+\lambda _{i}\right) K(t)\right. \right. \nonumber \\&\left. \quad -\left( 1+\theta _{i}\right) P(t)\right] dt+\left[ \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-mP(t)\right] \frac{\partial V_{i}(P,K)}{\partial P}\nonumber \\& \quad +\frac{1}{2}\sigma ^{2}(P(t))\frac{\partial ^{2}V_{i}(P,K)}{\partial P^{2}}+\left[ \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-\xi K(t)\right] \frac{\partial V_{i}(P,K)}{\partial K}\nonumber \\& \quad +\frac{1}{2}\rho ^{2}\left( K(t)\right) \frac{\partial ^{2}V_{i}\left( P,K\right) }{\partial K^{2}}\left. \quad +2\sigma \left( (P(t)\right) \rho \left( K(t)\right) \frac{\partial V_{i}^{2}(P,K)}{\partial K\partial P}\right\} , \end{aligned}$$
(12)
$$\begin{aligned}r_{j}V_{j}\left( P,K\right) &=\underset{E_{j}(t)}{\max }\left\{ \left[ \left( \vartheta _{j}(t)-\delta (t)\right) E_{j}(t)-\frac{1}{2}\beta ^{j}E_{j}^{2}(t)+\delta (t)E_{j}(0)+\left( \gamma _{j}+\lambda _{j}\right) K(t)\right. \right. \nonumber \\& \quad -\left. \left( 1+\theta _{j}\right) P(t)\right] dt+\left[ \vartheta _{j}E_{j}(t)+\vartheta _{i}E_{i}(t)-mP(t)\right] \frac{\partial V_{j}(P,K)}{\partial P}\nonumber \\& \quad +\frac{1}{2}\sigma ^{2}(P(t))\frac{\partial ^{2}V_{j}(P,K)}{\partial P^{2}}+\left[ \vartheta _{j}(t)E_{j}(t)+\vartheta _{i}(t)E_{i}(t)-\xi K(t)\right] \frac{\partial V_{j}(P,K)}{\partial K}\nonumber \\& \quad +\frac{1}{2}\rho ^{2}\left( K(t)\right) \frac{\partial ^{2}V_{j}\left( P,K\right) }{\partial K^{2}}+\left. 2\sigma \left( (P(t)\right) \rho \left( K(t)\right) \frac{\partial V_{j}^{2}(P,K)}{\partial K\partial P}\right\} . \end{aligned}$$
(13)

Next we propose a specific discussion on deriving a continuously differentiable solution to HJB Eqs. (10) and (11).

Theorem 1

Assume that continuously differentiable solutions to HJB Eqs. (10) and (11) are obtained by

$$\begin{aligned} V_{i}(P,K)&=\gamma _{1i}P^{2}+\gamma _{2i}P+\gamma _{3i}K^{2}+\gamma _{4i}K+\gamma _{5i}PK+\gamma _{6i},\\ V_{j}(P,K)&=\gamma _{1j}P^{2}+\gamma _{2j}P+\gamma _{3j}K^{2}+\gamma _{4j}K+\gamma _{5j}PK+\gamma _{6j}, \end{aligned}$$

when both countries participate in a non-cooperative game. The optimal Nash equilibrium emission strategies \(\left( E_{iN}^{*},E_{jN}^{*}\right) \) are expressed as:

$$\begin{aligned} E_{iN}^{*}\left( P,K\right) =\frac{\vartheta _{i}}{\beta ^{i}}\left[ \left( \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) \right) +\left( 2\gamma _{1i}+\gamma _{5i}\right) P+\left( \gamma _{5i}+2\gamma _{3i}\right) K\right] ,\\ E_{jN}^{*}\left( P,K\right) =\frac{\vartheta _{j}}{\beta ^{j}}\left[ \left( \gamma _{2j}+\gamma _{4j}+\left( 1-\frac{\delta }{\vartheta _{j}}\right) \right) +\left( 2\gamma _{1j}+\gamma _{5j}\right) P+\left( \gamma _{5j}+2\gamma _{3j}\right) K\right] , \end{aligned}$$

and the market clearing non-cooperative Nash equilibrium price for an emission permit is:

$$\begin{aligned} \delta _{N}^{*}\left( P,K\right)&=\frac{1}{\left( \beta ^{j}-\beta ^{i}\right) }\left[ \beta ^{j}\vartheta _{i}\left( \gamma _{2i}+\gamma _{4i}+1\right) -\beta ^{i}\vartheta _{j}\left( \gamma _{2j}+\gamma _{4j}+1\right) \right. \\& \quad +\left( \beta ^{j}\vartheta _{i}\left( 2\gamma _{1i}+\gamma _{5i}\right) -\beta ^{i}\vartheta _{j}\left( 2\gamma _{1j}+\gamma _{5j}\right) \right) P\\& \quad +\left. \left( \beta ^{j}\vartheta _{i}\left( \gamma _{5i}+2\gamma _{3i}\right) -\beta ^{i}\vartheta _{j}\left( \gamma _{5j}+2\gamma _{3j}\right) \right) K\right] . \end{aligned}$$

Proof

Via the first-order condition to Eqs. (12) and (13), we identify the optimal emission levels \((E_{i}^{*},E_{j}^{*})\) as:

$$\begin{aligned} {\left\{ \begin{array}{ll} E_{i}^{*}(t)&= {} \frac{\vartheta _{i}(t)}{\beta ^{i}}\left( \left( 1-\frac{\delta (t)}{\vartheta _{i}(t)}\right) +\frac{\partial V_{i}(P,K)}{\partial P}+\frac{\partial V_{i}(P,K)}{\partial K}\right) ,\\ E_{j}^{*}(t)&= {} \frac{\vartheta _{j}(t)}{\beta ^{j}}\left( \left( 1-\frac{\delta (t)}{\vartheta _{j}(t)}\right) +\frac{\partial V_{j}(P,K)}{\partial P}+\frac{\partial V_{j}(P,K)}{\partial K}\right) . \end{array}\right. } \end{aligned}$$

Substituting these \(\left( E_{i}^{*}(t),E_{j}^{*}(t)\right) \)values and assuming Eqs. (14) and (15) are solutions to Eqs. (12) and (13), respectively

$$\begin{aligned} V_{iN}(P,K)&=\gamma _{1i}P^{2}+\gamma _{2i}P+\gamma _{3i}K^{2}+\gamma _{4i}K+\gamma _{5i}KP+\gamma _{6i}, \end{aligned}$$
(14)
$$\begin{aligned} V_{jN}(P,K)&=\gamma _{1j}P^{2}+\gamma _{2j}P+\gamma _{3j}K^{2}+\gamma _{4j}K+\gamma _{5j}KP+\gamma _{6j}, \end{aligned}$$
(15)

we obtain

$$\begin{aligned} r_{i}\left( \gamma _{1i}P^{2}+\gamma _{2i}P+\gamma _{3i}K^{2}+\gamma _{4i}K+\gamma _{5i}KP+\gamma _{6i}\right)&=\left( \vartheta _{i}-\delta \right) E_{i}-\frac{1}{2}\beta ^{i}E_{i}^{2}\nonumber \\& \quad +\delta E_{i}(0)+\left( \gamma _{i}+\lambda _{i}\right) K-\left( 1+\theta _{i}\right) P\nonumber \\& \quad +\left[ \vartheta _{i}E_{i}+\vartheta _{j}E_{j}-mP\right] \left[ 2\gamma _{1i}P+\gamma _{2i}+\gamma _{5i}K\right] \nonumber \\& \quad +\left[ \vartheta _{i}E_{i}+\vartheta _{j}E_{j}-\xi K\right] \left[ 2\gamma _{3i}K+\gamma _{4i}+\gamma _{5i}P\right] \nonumber \\& \quad +\gamma _{1i}\sigma ^{2}(P), \end{aligned}$$
(16)
$$\begin{aligned} r_{j}\left( \gamma _{1j}P^{2}+\gamma _{2j}P+\gamma _{3j}K^{2}+\gamma _{4j}K+\gamma _{5j}KP+\gamma _{6j}\right)&=\left( \vartheta _{j}-\delta \right) E_{j}-\frac{1}{2}\beta ^{j}E_{j}^{2}\nonumber \\& \quad +\delta E_{j}(0)+\left( \gamma _{j}+\lambda _{j}\right) K-\left( 1+\theta _{j}\right) P\nonumber \\& \quad +\left[ \vartheta _{j}E_{j}+\vartheta _{i}E_{i}-mP\right] \left[ 2\gamma _{1j}P+\gamma _{2j}+\gamma _{5j}K\right] \nonumber \\& \quad +\left[ \vartheta _{j}E_{j}(t)+\vartheta _{i}E_{i}-\xi K\right] \left[ \gamma _{3j}K+\gamma _{4j}+\gamma _{5j}P\right] \nonumber \\& \quad +\gamma _{1j}\sigma ^{2}(P), \end{aligned}$$
(17)

we obtain

$$\begin{aligned} E_{iN}^{*}\left( P,K\right)&=\frac{\vartheta _{i}}{\beta ^{i}}\left[ \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) +\left( 2\gamma _{1i}+\gamma _{5i}\right) P+\left( \gamma _{5i}+2\gamma _{3i}\right) K\right] , \end{aligned}$$
(18)
$$\begin{aligned} E_{jN}^{*}\left( P,K\right)&=\frac{\vartheta _{j}}{\beta ^{j}}\left[ \gamma _{2j}+\gamma _{_{4j}}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) +\left( 2\gamma _{1j}+\gamma _{5j}\right) P+\left( \gamma _{5j}+2\gamma _{3j}\right) K\right] , \end{aligned}$$
(19)

where \(\gamma _{1i},\,\gamma _{2i},\gamma _{3i},\,\gamma _{4i},\gamma _{5i},\,\gamma _{6i}\,\gamma _{1j},\,\gamma _{2j},\gamma _{3j},\,\gamma _{4j},\,\gamma _{5j}\) and \(\gamma _{6j}\) are undetermined parameters and given in Appendix 1.

Finally, by setting \(E_{iN}^{*}(t)=E_{jN}^{*}(t)\) and simplifying, we obtain \(\delta \). This completes the proof.□

Lemma 1

Both countries value functions are inversely proportional to the pollutant stock, and carbon lowering technology, that is \(\frac{\partial V_{hN}}{\partial P}<0,\,\,\frac{\partial V_{hN}}{\partial K}<0,\,\,h=i,j\) and proportional to the initial emission permit.

Proof

From Eqs. (14) and (15), we have

$$\begin{aligned} \frac{\partial V_{iN}(P,K)}{\partial P}&=2\gamma _{1i}P+\gamma _{2i}+\gamma _{5i}K<0,\,\frac{\partial V_{iN}(P,K)}{\partial K}=2\gamma _{3i}K+\gamma _{4i}+\gamma _{5i}P<0,\\ \mathrm {and}\,\,&\frac{\partial V_{iN}(P,K)}{\partial E_{i}(0)}=\delta (t)>0,\\ \frac{\partial V_{jN}(P,K)}{\partial P}&=2\gamma _{1j}P+\gamma _{2j}+\gamma _{5j}K<0,\,\frac{\partial V_{jN}(P,K)}{\partial K}=2\gamma _{3j}K+\gamma _{4j}+\gamma _{5j}P<0,\\ \mathrm {and}\,\,&\frac{\partial V_{iN}(P,K)}{\partial E_{j}(0)}=\delta (t)>0, \end{aligned}$$

due to \(\gamma _{1i},\gamma _{1j},\gamma _{2i},\gamma _{2j},\gamma _{3i},\gamma _{3j},\gamma _{4i},\gamma _{4j},\gamma _{5i},\gamma _{5j}.\)□

Proposition 1

When \(\frac{\vartheta _{i}}{\beta ^{i}}\left( \vartheta _{i}-\delta \right) >\delta E_{i}(0)\), country i will purchase emissions permits and \(\frac{\vartheta _{i}}{\beta ^{i}}\left( \vartheta _{i}-\delta \right) <\delta E_{i}(0)\) will sell emission permits. Similarly, country j \(\frac{\vartheta _{j}}{\beta ^{j}}\left( \vartheta _{j}-\delta \right) >\delta E_{j}(0)\) will purchase emissions permits and \(\frac{\vartheta _{j}}{\beta ^{j}}\left( \vartheta _{j}-\delta \right) <\delta E_{j}(0)\) will sell emission permits.

Proof

Inserting the optimal values given by Eqs. (18) and (19) into Eq. (6), and simplifying, we obtain the results.

Proposition 2

Optimal emission purchasing prices \(\delta \), that maximizes country \(h's\) industrial net revenue at time t is given for country h : 

$$\begin{aligned} \delta&=\vartheta _{i}-\beta ^{i}E_{i}(0),\\ \delta&=\vartheta _{j}-\beta ^{j}E_{j}(0). \end{aligned}$$

Proof

Using the above Proposition, setting \(\frac{\partial \Pi _{iN}\left( E_{i}^{*}(t)\right) }{\partial \delta }=0\) and \(\frac{\partial \Pi _{jN}\left( E_{j}^{*}(t)\right) }{\partial \delta }=0\), we obtain the results.□

Remark 3

Furthermore, country \(h's\) industrial net revenue functions with emission permits are convex functions such that \(\frac{\partial ^{2}\Pi _{iN}\left( E_{i}^{*}(t)\right) }{\partial \delta ^{2}}=\frac{1}{\beta ^{i}}>0\), and \(\frac{\partial ^{2}\Pi _{jN}\left( E_{i}^{*}(t)\right) }{\partial \delta ^{2}}=\frac{1}{\beta ^{j}}>0\). Lemma 1 and Proposition 1 shows that the initial allocation of emission permits affect the revenue of the country. If country h obtains larger number of initial emission permits then its revenue increases monotonically with increasing permit prices.

On the other hand, if country h obtains a small number of initial emission permits then its revenue decreases monotonically with increasing permit prices. Both country’s react for the worst-case scenario by adopting an emission strategy \(E_{iN}^{*}\) and \(E_{jN}^{*}\) given under Theorem 1.

Now, let country i be the leader. Then the equilibrium strategy of the leader satisfies the following HJB equation subject to Eq. (9) as:

$$\begin{aligned} r_{i}\left( \gamma _{1i}P^{2}+\gamma _{2i}P+\gamma _{3i}K^{2}+\gamma _{4i}K+\gamma _{5i}PK+\gamma _{6i}\right)&=\left( \vartheta _{i}-\delta \right) E_{i}-\frac{1}{2}\beta ^{i}E_{i}^{2}\nonumber \\& \quad\,\, +\delta E_{i}(0)+\left( \gamma _{i}+\lambda _{i}\right) K-\left( 1+\theta _{i}\right) P\nonumber \\& \quad \,\,+\left[ \vartheta _{i}E_{i}+\vartheta _{j}E_{j}-mP\right] \left[ 2\gamma _{1i}P+\gamma _{2i}+\gamma _{5i}K\right] \nonumber \\& \quad\,\, +\left[ \vartheta _{i}E_{i}+\vartheta _{j}E_{j}-\xi K\right] \left[ 2\gamma _{3i}K+\gamma _{4i}+\gamma _{5i}P\right] \nonumber \\& \,\,\quad +\gamma _{3i}\rho ^{2}(K)+\gamma _{1i}\sigma ^{2}(P)+2\sigma (P)\rho (K)\gamma _{5i}. \end{aligned}$$
(20)

The maximization of the right-hand side of Eq. (20) yields the same result as the maximization of the right-hand side of Eq. (16). This coincide occurs because the reaction functions (18) and (19) are independent of the control variable of the other player (country). Obviously, this result doesn’t depend on the symmetry assumption.

Lemma 2

In our continuous-time differential game paradigm the Stackelberg equilibrium will not coincide with the non-cooperative Nash equilibrium. This occurs as the reaction functions (18) and (19) are dependent of the control variable of the other player. Since in this setting both equilibrium coincide, the first mover advantage will disappear.

Theorem 2

The limit of expectation \(\mathbb {E}\left( P_{C}^{*}(t)\right) \) and variance \(\mathbb {E}\left( P_{C}^{*}(t)\right) \) in a non-cooperative game feedback equilibrium satisfy

$$\begin{aligned}\mathbb {E}\left[ P_{N}^{*}(t):t\ge 0\right] &=\frac{\left( B_{1}+B_{2}\right) }{\chi _{N}}+\exp \left( -\chi _{N}t\right) \left( P_{0}-\frac{\left( B_{1}+B_{2}\right) }{\chi _{N}}\right) ,\,\,\,\,\underset{t\rightarrow \infty }{\lim }\mathbb {E}\left( P_{N}^{*}(t)\right) =\frac{\left( B_{1}+\hat{B}_{2}\right) }{\chi _{N}},\\\mathbb {D}\left[ P_{N}^{*}(t):t\ge 0\right] &=\frac{\sigma ^{2}(P)}{2\chi _{N}^{2}}\left[ \left( B_{1}+B_{2}\right) -2\left( B_{1}+B_{2}-\chi _{N}P_{0}\right) \exp \left( -\chi _{N}t\right) \right. ,\\&\left. \quad +2\left( B_{1}+B_{2}-2\chi _{N}P_{0}\right) \exp \left( -2\chi _{N}t\right) \right] \\\underset{t\rightarrow \infty }{\lim }\mathbb {D}\left( P_{N}^{*}(t)\right) &=\frac{\sigma ^{2}\left( B_{1}+\hat{B}_{2}\right) }{2\chi _{N}^{2}}. \end{aligned}$$

Furthermore, \(\left\{ P_{N}^{*}(t):t\ge 0\right\} \) has a stationary distribution of \(N_{N}\left( \frac{\left( B_{1}+\hat{B}_{2}\right) }{\chi _{N}},\frac{\sigma ^{2}\left( B_{1}+\hat{B}_{2}\right) }{2\chi _{N}^{2}}\right) \) and the expected value and variance of the worst-case pollution levels are decreasing in \(\delta \).

Proof

At optimality the dynamics of the worst-case pollution process \(P_{N}^{*}\) can be given by the following (SDE):

$$\begin{aligned} dP_{N}^{*}&=\left[ \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) \right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{2j}+\gamma _{4j}+\left( 1-\frac{\delta }{\vartheta _{j}}\right) \right) \right. \\& \quad +\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{5i}+2\gamma _{3i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{5j}+2\gamma _{3j}\right) \right) K_{N}^{*}\\& \quad -\left. \left( m-\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\gamma _{1i}+\gamma _{5i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\gamma _{1j}+\gamma _{5j}\right) \right) \right) P_{N}^{*}\right] dt\\& \quad +\sigma (P)dW(t). \end{aligned}$$

Then the expected value \(\mathbb {E}\left\{ P_{N}^{*}(t):\,t\,\ge 0\right\} \) of the above SDE can be defined as:

$$\begin{aligned} \mathbb {E}\left( dP_{N}^{*}\right)&=\left[ \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) \right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{2j}+\gamma _{4j}+\left( 1-\frac{\delta }{\vartheta _{j}}\right) \right) \right. \nonumber \\& \quad +\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{5i}+2\gamma _{3i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{5j}+2\gamma _{3j}\right) \right) \mathbb {E}\left( K_{N}^{*}\right) \nonumber \\& \quad -\left. \left( m-\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\gamma _{1i}+\gamma _{5i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\gamma _{1j}+\gamma _{5j}\right) \right) \right) \mathbb {E}\left( P_{N}^{*}\right) \right] dt\nonumber \\& \quad +\sigma (P)dW(t). \end{aligned}$$
(21)

The limit of expectations on technology \(\mathbb {E}\left[ K_{N}^{*}(t):t\ge 0\right] \) using Eq. (2), we obtain

$$\begin{aligned} \mathbb {E}\left[ dK_{N}^{*}(t)\right]&=\left[ \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) \right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{2j}+\gamma _{4j}+\left( 1-\frac{\delta }{\vartheta _{j}}\right) \right) \right. \\& \quad +\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{5i}+2\gamma _{3i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{5j}+2\gamma _{3j}\right) -\xi \right) \mathbb {E}\left[ K_{N}^{*}\right] \\&\left. \quad +\left( \left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\gamma _{1i}+\gamma _{5i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\gamma _{1j}+\gamma _{5j}\right) \right) \right) \mathbb {E}\left[ P_{N}^{*}\right] \right] . \end{aligned}$$

Since, \(\gamma _{5i}<0\),\(\gamma _{3i}<0\) and \(K(0)=K_{0}\), \(\mathbb {E}\left\{ K_{N}^{*}(t):\,t\,\ge 0\right\} \) will imply that

$$\begin{aligned} \mathbb {E}\left[ K_{N}^{*}(t)\right] =\frac{A_{1}}{\varphi _{N}}+\exp \left( -\varphi _{N}t\right) \left( K_{0}-\frac{A_{1}}{\varphi _{N}}-\frac{A_{2}}{\varphi _{N}}\mathbb {E}\left( P_{N}^{*}\right) \right) , \end{aligned}$$

and \(\underset{t\rightarrow \infty }{\lim }\mathbb {E}\left( K_{N}^{*}(t)\right) =\frac{A_{1}}{\varphi _{N}},\) where

$$\begin{aligned} A_{1}&=\frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) \right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{2j}+\gamma _{4j}+\left( 1-\frac{\delta }{\vartheta _{j}}\right) \right) ,\\ A_{2}&=\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\gamma _{1i}+\gamma _{5i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\gamma _{1j}+\gamma _{5j}\right) \right) .\\ \varphi _{N}&=-\left( \xi -\frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{5i}+2\gamma _{3i}\right) -\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{5j}+2\gamma _{3j}\right) \right) . \end{aligned}$$

We rewrite Eq. (21) as a non-homogeneous linear differential equation:

$$\begin{aligned} \left\{ \begin{array}{ll} d\mathbb {E}(P_{N}^{*}(t))=\left[ \left( B_{1}+B_{2}\right) \mathbb {E}\left( P_{N}^{*}\right) -\chi _{N}\mathbb {E}\left( P_{N}^{*}\right) \right] dt\,\,\\ P_{N}(0)=P_{N}(0),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{array}\,\right. \end{aligned}$$
(22)

where

$$\begin{aligned} B_{1}&=\frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{2i}+\gamma _{4i}+\left( 1-\frac{\delta }{\vartheta _{i}}\right) \right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{2j}+\gamma _{4j}+\left( 1-\frac{\delta }{\vartheta _{j}}\right) \right) ,\\ B_{2}&=\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{5i}+2\gamma _{3i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{5j}+2\gamma _{3j}\right) \right) \left( \frac{A_{1}}{\varphi _{N}}+\exp \left( -\varphi _{N}t\right) \left( K_{0}-\frac{A_{1}}{\xi _{N}}\right) \right) ,\\ \chi _{N}&=\left( m-\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\gamma _{1i}+\gamma _{5i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\gamma _{1j}+\gamma _{5j}\right) \right) -\exp \left( -\varphi _{N}t\right) \frac{A_{2}}{\varphi _{N}}\right) . \end{aligned}$$

Applying Itø’s formula to Eq. (21), we derive the expectation value \(\mathbb {E}\left( P_{N}^{*}\right) ^{2}\)

$$\begin{aligned} \left\{ \begin{array}{cc} d(P_{N}^{*}(t))^{2}=\left[ \left( 2\left( B_{1}+B_{2}\right) +\sigma ^{2}(P)\right) P_{N}^{*}-2\chi _{N}\mathbb {E}\left( P_{N}^{*}\right) ^{2}\right] dt+2P_{N}^{*}\sigma (P)dW(t)\\ \left( P_{N}(0)\right) ^{2}=\left( P_{N}(0)\right) ^{2}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{array}\right. \end{aligned}$$

Therefore \(\mathbb {E}\left( P_{N}^{*}\right) \) and \(\mathbb {E}\left( P_{N}^{*}\right) ^{2}\)satisfy the following set of non-homogeneous linear differential equations:

$$\begin{aligned}&\left\{ \begin{array}{cc} d\mathbb {E}(P_{N}^{*}(t))=\left[ \left( B_{1}+B_{2}\right) \mathbb {E}\left( P_{N}^{*}\right) -\chi _{N}\mathbb {E}\left( P_{N}^{*}\right) \right] dt\\ P_{N}(0)=P_{N}(0),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &{} \,\,\,\,\,\,\,\,\,\,\, \end{array}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\right. \\&\left\{ \begin{array}{cc} d\mathbb {E}(P_{N}^{*}(t))^{2}=\left[ \left( 2\left( B_{1}+B_{2}\right) +\sigma ^{2}(P)\right) \mathbb {E}\left( P_{N}^{*}\right) -2\chi _{N}\mathbb {E}\left( P_{N}^{*}\right) ^{2}\right] dt\\ \left( P_{N}(0)\right) ^{2}=\left( P_{N}(0)\right) ^{2}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{array}\right. \end{aligned}$$

Solving the above non-homogeneous liner differential equations leads to

$$\begin{aligned} \mathbb {E}\left[ P_{N}^{*}(t):t\ge 0\right] =\frac{\left( B_{1}+B_{2}\right) }{\chi _{N}}+\exp \left( -\chi _{N}t\right) \left( P_{0}-\frac{\left( B_{1}+B_{2}\right) }{\chi _{N}}\right) , \end{aligned}$$

and \(\underset{t\rightarrow \infty }{\lim }\mathbb {E}\left( P_{N}^{*}(t)\right) =\frac{\left( B_{1}+\hat{B}_{2}\right) }{\chi _{N}},\)where

$$\begin{aligned} \hat{B}_{2}=\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \gamma _{5i}+2\gamma _{3i}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \gamma _{5j}+2\gamma _{3j}\right) \right) \left( \frac{A_{1}}{\varphi _{N}}\right) . \end{aligned}$$

Finally we obtain the variance as

$$\begin{aligned} \mathbb {D}\left[ P_{N}^{*}(t):t\ge 0\right]&=\frac{\sigma ^{2}(P)}{2\chi _{N}^{2}}\left[ \left( B_{1}+B_{2}\right) -2\left( B_{1}+B_{2}-\chi _{N}P_{0}\right) \exp \left( -\chi _{N}t\right) \right. \\&\left. \quad +2\left( B_{1}+B_{2}-2\chi _{N}P_{0}\right) \exp \left( -2\chi _{N}t\right) \right] , \end{aligned}$$

and \(\underset{t\rightarrow \infty }{\lim }\mathbb {D}\left( P_{N}^{*}(t)\right) =\frac{\sigma ^{2}(P)\left( B_{1}+\hat{B}_{2}\right) }{2\chi _{N}^{2}}.\)□

4 Solution to a Cooperative Game

In this section we claim that at any time both countries satisfy individual rationality and group rationality in-order to implement a cooperate pollution control strategy. Cooperation will cease if any country deviates at any time within the game horizon. Let us assume that the discount rate for both countries are the same \(r=r_{i}=r_{j}\). To secure group optimality, the participating countries would seek to maximize their joint expected payoff by solving the following stochastic control problem.

$$\begin{aligned} J \, \left( P,K\right) &=\underset{E_{i}(t)\ge 0,E_{j}(t)\ge 0}{\max }\int _{0}^{+\infty }\exp \left( -rt\right) \left\{ \left[ \left( \vartheta _{i}(t)-\delta (t)\right) E_{i}(t)+\left( \vartheta _{j}(t)-\delta (t)\right) E_{j}(t)\right. \right. \nonumber \\& \quad -\frac{1}{2}\left( \beta ^{i}E_{i}^{2}(t)+\beta ^{j}E_{j}^{2}(t)\right) +\delta (t)\left( E_{i}(0)+E_{j}(0)\right) +\left( \gamma _{i}+\gamma _{j}+\lambda _{i}+\lambda _{j}\right) K(t)\nonumber \\&\left. \quad -\left( 1+(\theta _{i}+\theta _{j})\right) P(t)\right] dt\nonumber \\& \quad +\left[ \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-mP(t)\right] \frac{\partial V_{C}(P,K)}{\partial P}+\frac{1}{2}\sigma ^{2}(P(t))\frac{\partial ^{2}V_{C}(P,K)}{\partial P^{2}}\nonumber \\& \quad +\left[ \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-\xi K(t)\right] \frac{\partial V_{C}(P,K)}{\partial K}\nonumber \\& \quad +\rho ^{2}(K(t))\frac{\partial ^{2}V_{C}(P,K)}{\partial K^{2}}+\left. 4\sigma (P(t))\rho (K(t))\frac{\partial ^{2}V_{C}\left( P,K\right) }{\partial P\partial K}\right\} ,\\ \nonumber \\ s.t&\left\{ \begin{array}{l} dP(t)=\left( \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-mP(t)\right) dt+\sigma (P(t))dW(t)\\ P(0)=P_{0},\,\,\,\,\,\,\,\,\,P(t)\ge 0, \end{array}\right. \nonumber \\&s.t\left\{ \begin{array}{l} dK(t)=\left[ \vartheta _{i}(t)E_{i}(t)+\vartheta _{j}(t)E_{j}(t)-\xi K(t)\right] dt+\rho (K(t))dW_{k}(t)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\ K(0)=K_{0}>0. \end{array}\right. \nonumber \end{aligned}$$
(23)

Theorem 3

Assume that a continuously differentiable solution to HJB Eq. (23) is obtained by

$$\begin{aligned} V_{C}(P,K)&=\phi _{1}P^{2}+\phi _{2}P+\phi _{3}K^{2}+\phi _{4}K+\phi _{5}PK+\phi _{6}. \end{aligned}$$
(24)

If both countries participate in a cooperative game, the optimal Nash equilibrium emission strategies \(\left( E_{iCN}^{*}(t),E_{jCN}^{*}(t)\right) \) are expressed as:

$$\begin{aligned} E_{iCN}^{*}\left( P,K\right)&=\frac{\vartheta _{i}}{\beta ^{i}}\left[ \left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2}+\phi _{4}\right) +\left( 2\phi _{1}+\phi _{5}\right) P+\left( 2\phi _{3}+\phi _{5}\right) K\right] ,\\ E_{jCN}^{*}\left( P,K\right)&=\frac{\vartheta _{j}}{\beta ^{j}}\left[ \left( \left( 1-\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) +\left( 2\phi _{1}+\phi _{5}\right) P+\left( 2\phi _{3}+\phi _{5}\right) K\right] , \end{aligned}$$

and the market clearing cooperative Nash equilibrium price for emission permit is:

$$\begin{aligned} \delta _{CN}^{*}\left( P,K\right)&=\frac{1}{\left( \beta ^{i}\vartheta _{j}-\beta ^{i}\vartheta _{i}\right) }\left[ \left( \beta ^{j}\vartheta _{i}-\beta ^{i}\vartheta _{j}\right) \phi _{4}+\left( \beta ^{j}\vartheta _{i}-\beta ^{i}\vartheta _{j}\right) \phi _{2}\right. \\& \quad +\left( \beta ^{j}\vartheta _{i}^{2}-\beta ^{i}\vartheta _{j}^{2}\right) \\& \quad +\left( \left( \beta ^{j}\vartheta _{i}-\beta ^{i}\vartheta _{j}\right) \phi _{5}+\left( 2\beta ^{j}\vartheta _{i}-2\beta ^{i}\vartheta _{j}\right) \phi _{1}\right) P\\& \quad +\left. \left( \left( \beta ^{j}\vartheta _{i}-\beta ^{i}\vartheta _{j}\right) \phi _{5}+\left( 2\beta ^{j}\vartheta _{i}-2\beta ^{i}\vartheta _{j}\right) \phi _{3}\right) K\right] . \end{aligned}$$

Proof

Via the first-order conditions, we identify the optimal emission levels \((E_{i}^{*}(t),E_{j}^{*}(t))\) associated with Eq. (23) as:

$$\begin{aligned} {\left\{ \begin{array}{ll} E_{i}^{*}(t)&= {} \frac{\vartheta _{i}}{\beta ^{i}}\left( \left( \vartheta _{i}(t)-\delta (t)\right) +\frac{\partial V_{i}(P,K)}{\partial P}+\vartheta _{i}\frac{\partial V_{i}(P,K)}{\partial K}\right) ,\\ E_{j}^{*}(t)&= {} \frac{\vartheta _{j}}{\beta ^{j}}\left( \left( \vartheta _{j}(t)-\delta (t)\right) +\frac{\partial V_{j}(P,K)}{\partial P}+\vartheta _{j}\frac{\partial V_{j}(P,K)}{\partial K}\right) . \end{array}\right. } \end{aligned}$$

Inserting optimal values back into Eq. (23) and assuming Eq. (24) is a solution to Eq. (23), we obtain

$$\begin{aligned}&r\left( \phi _{1}P^{2}+\phi _{2}P+\phi _{3}K^{2}+\phi _{4}K+\phi _{5}PK+\phi _{6}\right) \nonumber \\&\quad = \left[ \left( \vartheta _{i}-\delta \right) E_{i}+\left( \vartheta _{j}-\delta \right) E_{j}-\frac{1}{2}\left( \beta ^{i}E_{i}^{2}+\beta ^{j}E_{j}^{2}\right) \right. \nonumber \\&\quad +\delta \left( E_{i}(0)+E_{j}(0)\right) +\left( \gamma _{i}+\gamma _{j}+\lambda _{i}+\lambda _{j}\right) K\nonumber \\&\quad \left. -\left( 1+\theta _{i}+\theta _{j}\right) P\right] +\left[ \vartheta _{i}E_{i}+\vartheta _{j}E_{j}-mP\right] \nonumber \\&\quad \times \left[ \left( 2\phi _{1}P+\phi _{2}+\phi _{5}K\right) \right] \nonumber \\&\quad +\phi _{1}\sigma ^{2}(P)+\left[ \vartheta _{i}E_{i}+\vartheta _{j}(t)E_{j}-\xi K\right] \nonumber \\&\quad \times \left( 2\phi _{3}K+\phi _{4}+\phi _{5}P\right) \nonumber \\&\quad +2\rho ^{2}(K)\phi _{3}+4\sigma (P)\rho (K)\phi _{5}. \end{aligned}$$
(25)

Via the first order conditions of Eq. (25), we also obtain

$$\begin{aligned} E_{iCN}^{*}\left( P,K\right)&=\frac{\vartheta _{i}}{\beta ^{i}}\left[ \left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2}+\phi _{4}\right) +\left( 2\phi _{1}+\phi _{5}\right) P+\left( 2\phi _{3}+\phi _{5}\right) K\right] . \end{aligned}$$
(26)
$$\begin{aligned} E_{jCN}^{*}\left( P,K\right)&=\frac{\vartheta _{j}}{\beta ^{j}}\left[ \left( \left( 1-\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) +\left( 2\phi _{1}+\phi _{5}\right) P+\left( 2\phi _{3}+\phi _{5}\right) K\right] . \end{aligned}$$
(27)

where \(\phi _{1},\phi _{2},\phi _{3},\phi _{4},\,\phi _{5}\) and \(\phi _{6}\) are undetermined parameters and given in Appendix 2.

Finally, by setting \(E_{CN}^{*}(t)=E_{CN}^{*}(t)\) and simplifying we obtain \(\delta \). This completes the proof.□

Lemma 3

The difference between both country’s optimal emission under a cooperative game strategy is equal to the difference between each country’s utility parameter such that

$$\begin{aligned} E_{iCN}^{*}-E_{jCN}^{*}=\frac{\vartheta _{i}}{\beta ^{i}}\left( 1-\frac{\delta }{\vartheta _{i}}\right) -\frac{\vartheta _{j}}{\beta ^{j}}\left( 1-\frac{\delta }{\vartheta _{j}}\right) . \end{aligned}$$

Theorem 4

The limit of expectation \(\mathbb {E}\left( P_{C}^{*}(t)\right) \) and variance \(\mathbb {D}\left( P_{C}^{*}(t)\right) \), in a cooperative game feedback equilibrium satisfies

$$\begin{aligned}\mathbb {E}\left[ P_{C}^{*}(t):t\ge 0\right] &=\frac{\left( \tilde{B}_{1}+\tilde{B}_{2}\right) }{\chi _{C}}+\exp \left( -\chi _{C}t\right) \left( P_{0}-\frac{\left( \tilde{B}_{1}+\tilde{B}_{2}\right) }{\chi _{C}}\right) ,\,\,\,\,\underset{t\rightarrow \infty }{\lim }\mathbb {E}\left( P_{C}^{*}(t)\right) =\frac{\left( \tilde{B}_{1}+\bar{B}_{2}\right) }{\chi _{C}},\\\mathbb {D}\left[ P_{C}^{*}(t):t\ge 0\right] &=\frac{\sigma ^{2}(P)}{2\chi _{C}^{2}}\left[ \left( \tilde{B}_{1}+\tilde{B}_{2}\right) -2\left( \tilde{B}_{1}+\tilde{B}_{2}-\chi _{C}P_{0}\right) \exp \left( -\chi _{C}t\right) \right. ,\\&\left. \quad +2\left( \tilde{B}_{1}+\tilde{B}_{2}-2\chi _{C}P_{0}\right) \exp \left( -2\chi _{C}t\right) \right] ,\\\underset{t\rightarrow \infty }{\lim }\mathbb {D}\left( P_{C}^{*}(t)\right) &=\frac{\sigma ^{2}\left( \tilde{B}_{1}+\bar{B}_{2}\right) }{2\chi _{C}^{2}}, \end{aligned}$$

where

$$\begin{aligned}&\tilde{A}_{1}=\frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2} +\phi _{4}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \left( 1-\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) ,\\&\tilde{A}_{2}=\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( 2\phi _{1}+\phi _{5}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}} \left( 2\phi _{1}+\phi _{5}\right) \right) ,\\&\varphi _{C}=-\left( \xi -\frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( 2\phi _{3}+\phi _{5}\right) -\frac{\vartheta _{j}^{2}}{\beta ^{j}} \left( 2\phi _{3}+\phi {}_{5}\right) \right) ,\\&\tilde{B}_{1}=\frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2}+\phi _{4} \right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \left( 1 -\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) ,\\&\tilde{B}_{2}=\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( \phi _{5}+2\phi _{3}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}} \left( \phi _{5}+2\phi _{3}\right) \right) \left( \frac{\tilde{A}_{1}}{\varphi _{C}}+\exp \left( -\varphi _{c}t\right) \left( K_{0} -\frac{\tilde{A}_{1}}{\varphi _{C}}\right) \right) ,\\&\chi _{C}=\left( m-\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2} +\phi _{4}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \left( 1-\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) \right) -\exp \left( -\varphi _{C}t\right) \frac{\tilde{A}_{2}}{\varphi _{C}} \right) .\\&\bar{B}_{2}=\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}} \left( \phi _{5}+2\phi _{3}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}} \left( \phi _{5}+2\phi _{3}\right) \right) \left( \frac{\tilde{A}_{1}}{\varphi _{C}}\right) . \end{aligned}$$

Furthermore, \(\left\{ P_{N}^{*}(t):t\ge 0\right\} \) has a stationary distribution of \(N_{C}\left( \frac{\left( \tilde{B}_{1}+\bar{B}_{2}\right) }{\chi _{C}},\frac{\sigma ^{2}\left( \tilde{B}_{1}+\bar{B}_{2}\right) }{2\chi _{C}^{2}}\right) \) and the expected value and variance of the worst-case pollution levels are decreasing in \(\delta \).

Proof

Applying the analysis of Theorem 2 to Eq. (25), and using the optimal values given in Eqs. (26) and (27) this can be shown.□

Lemma 4

The variance improvement degree of the cooperative game is different to the results of the non-cooperative game.

4.1 Individually Rational and Time-Consistent Imputation and Payment Distribution Mechanism

The dynamic stability of solutions to any cooperative differential game involved the property that, as the game proceeds along an optimal trajectory, players are guided by the same optimality principle at each instant of time, and hence do not possess incentives to deviate from the previously adopted optimal behavior throughout the game. Hence, the optimality condition is an agreement required to allocate each country’s cooperative payoffs and individual rationality must be maintained during the game’s horizon \(\left[ \left. t_{0},\infty \right) \right. \), along with the cooperative trajectory. Furthermore, there can be many Pareto optimal solutions with different payoffs for each player. That is why the Pareto optimal solution (PO-solution) is also a cooperative solution, because choosing such a solution requires coordinated player’ behavior and contains the property of group rationality. Pollution dynamics under a cooperative arrangement is defined as:

$$\begin{aligned} dP_{C}^{*}&=\left[ \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2}+\phi _{4}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \left( 1-\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) \right. \nonumber \\& \quad +\left( \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\phi _{3}+\phi _{5}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\phi _{3}+\phi _{5}\right) \right) K_{C}^{*}\nonumber \\& \quad -\left. \left( m-\frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\phi _{1}+\phi _{5}\right) -\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\phi _{1}+\phi _{5}\right) \right) P_{C}^{*}\right] dt\nonumber \\& \quad +\sigma (P)dW(t), \end{aligned}$$
(28)

and Eq. (28) can be rewritten as:

$$\begin{aligned} dP_{C}^{*}=\delta _{1C}\left[ \delta _{2C}+\delta _{3C}K_{C}^{*}-P_{C}^{*}\right] dt+\sigma dW(t), \end{aligned}$$
(29)

where

$$\begin{aligned} \delta _{1C} & =-\left[ m-\frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\phi _{1}+\phi _{5}\right) -\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\phi _{1}+\phi _{5}\right) \right] ,\\ \delta _{2C} & =\frac{1}{\delta _{1C}}\left[ \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( \left( 1-\frac{\delta }{\vartheta _{i}}\right) +\phi _{2}+\phi _{4}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( \left( 1-\frac{\delta }{\vartheta _{j}}\right) +\phi _{2}+\phi _{4}\right) \right] ,\\ \delta _{3C} &=\frac{1}{\delta _{1C}}\left[ \frac{\vartheta _{i}^{2}}{\beta ^{i}}\left( 2\phi _{3}+\phi _{5}\right) +\frac{\vartheta _{j}^{2}}{\beta ^{j}}\left( 2\phi _{3}+\phi _{5}\right) \right] . \end{aligned}$$

Let \(X_{t}^{*}\) denote the set of realized values of \(\left( P^{*}(t),K^{*}(t)\right) \) at time t generated by Eq.(28), such that \(\left( P^{*}(t),K^{*}(t)\right) \in X_{t}^{*}\). Then for a given \(\tau \in \left[ \left. t_{0},\infty \right) \right. \)we define a vector \(v_{h}\left( P_{t}^{*}\right) =\left\{ v_{i}\left( P_{t}^{*},K_{t}^{*}\right) ,v_{j}\left( P_{t}^{*},K_{t}^{*}\right) \right\} \) as the solution imputation (the payoff under cooperation), over the period \(\left[ \left. \tau ,\infty \right) \right. \) to country h. Individual rationality along the cooperative trajectory requires

$$\begin{aligned} v_{h}^{\tau }\left( \tau ,P_{\tau }^{*},K_{\tau }^{*}\right) \ge V_{h}^{\tau }\left( \tau ,P_{\tau }^{*},K_{\tau }^{*}\right) \,\,,\text {for}\,\,\,\,h\in \left( i,j\right) , \end{aligned}$$
(30)

where \(V_{h}^{\tau }\left( \tau ,P_{\tau }^{*},K_{\tau }^{*}\right) \) denote the payoff to country h under non-cooperation over the period. Let \(G(s)=\left[ G_{i}(s),G_{j}(s)\right] \) denote the instantaneous payoff of the cooperative game at time \(s\in \left[ \left. t_{0},\infty \right) \right. \) for the cooperative game \(\pi _{C}\left( P_{t_{0}}^{*},K_{t_{0}}^{*}\right) \).

Proposition 3

An instantaneous payment at time \(\tau \in \left[ \left. t_{0},\infty \right) \right. \) will be

$$\begin{aligned} G^{l}(\tau )=r\delta ^{l}\left( P_{\tau }^{*},K_{\tau }^{*}\right) -\delta _{\left( p_{\tau }^{*},k_{\tau }^{*}\right) }^{l}\left( \left( p_{\tau }^{*},k_{\tau }^{*}\right) \in X_{\tau }^{*}\right) \left( P_{\tau }^{*}\left\{ p(t)^{*}\right\} _{t\ge t_{0}}+K_{\tau }^{*}\left\{ k(t)^{*}\right\} _{t\ge t_{0}}\right) , \end{aligned}$$
(31)

for \(\left( p_{\tau }^{*},k_{\tau }^{*}\right) \in X_{\tau }^{*}\), and \(l\in \left\{ i,j\right\} \) yields a sub-game consistent solution to the cooperative game \(\pi _{C}\left( x_{t_{0}}^{*}\right) .\)

Proof

Along the cooperative trajectory \(\left\{ P(t)^{*},K(t)^{*}\right\} _{t\ge t_{0}}\), we define

$$\begin{aligned} \mu ^{h}\left( \tau \,;\tau ,P_{\tau }^{*},K_{\tau }^{*}\right)&=v_{h}\left( P_{\tau }^{*},K_{\tau }^{*}\right) =\int _{\tau }^{\infty }G^{l}(s)\exp \left( -r\left( s-\tau \right) \right) ds\\ \mu ^{h}\left( \tau \,;t,P_{\tau }^{*},K_{\tau }^{*}\right)&=\int _{t}^{\infty }G^{l}(s)\exp \left( -r\left( s-\tau \right) \right) ds, \end{aligned}$$

for \(t\ge \tau .\) Claiming that the optimal trajectory will remain optimal even if the solution policy is extended to a delayed commencing time, we obtain

$$\begin{aligned} \mu ^{h}\left( \tau \,;t,P_{\tau }^{*},K_{\tau }^{*}\right)&=\exp \left( -r\left( t-\tau \right) \right) \int _{t}^{\infty }G^{l}(s)\exp \left( -r\left( s-t\right) \right) ds\nonumber \\&=\exp \left( -r\left( t-\tau \right) \right) \mu _{h}\left( t;t,P_{\tau }^{*},K_{\tau }^{*}\right) . \end{aligned}$$
(32)

Hence, Eq. (31) guarantees time consistency of the solution imputations. Since, \(\mu ^{n}\left( t,t,x_{t}^{*}\right) \) is continuously differentiable in t and \(\left( P_{t}^{*},K_{t}^{*}\right) \), we obtain

$$\begin{aligned} \mu ^{n}\left( \tau \,;t,P_{\tau }^{*},K_{\tau }^{*}\right) \nonumber \\&=\int _{\tau }^{\,\tau +\Delta t}G^{l}(s)\exp \left( -r\left( s-\tau \right) \right) ds\nonumber \\& \quad +\exp \left( -r\left( \Delta t\right) \right) G^{l}\left( \tau +\Delta t\,;\tau +\Delta t,P_{\tau }^{*}+\Delta P_{\tau }^{*},K_{\tau }^{*}+\Delta K_{\tau }^{*}\right) , \end{aligned}$$
(33)

for \(\tau \in \left[ t_{0},T\right] ,l\in \left( i,j\right) \), where \(\Delta P_{\tau }^{*}=P_{\tau }^{*}\Delta t+o\left( \Delta t\right) \), \(\Delta K_{\tau }^{*}=K_{\tau }^{*}\Delta t+o\left( \Delta t\right) ,\) and as \(\Delta t\rightarrow 0\), \(\frac{o\left( \Delta t\right) }{\Delta t}\rightarrow 0\).

From Eq. (32), we have \(\Delta P_{\tau }^{*}=P_{\tau +\Delta t}^{*}\), \(\Delta K_{\tau }^{*}=K_{\tau }^{*}\Delta t+o\left( \Delta t\right) \). Hence, we have

$$\begin{aligned} \mu ^{n}\left( \tau \,;\tau +\Delta t,P_{\tau +\Delta t}^{*},K_{\tau +\Delta t}^{*}\right)&=\exp \left( -r\Delta t\right) v_{h}\left( P_{\tau +\Delta t}^{*},K_{\tau +\Delta t}^{*}\right) \nonumber \\&=\exp \left( -r\Delta t\right) \mu ^{n}\left( \tau \,+\Delta t;\tau +\Delta t,P_{\tau +\Delta t}^{*},K_{\tau +\Delta t}^{*}\right) . \end{aligned}$$
(34)

Therefore Eq. (32) can be expressed as:

$$\begin{aligned} \mu ^{n}\left( \tau \,;\tau ,P_{\tau }^{*},K_{\tau }^{*}\right)&=\int _{\tau }^{\,\tau +\Delta t}G^{l}(s)\exp \left( -r(s-\tau )\right) ds\nonumber \\& \quad +\mu ^{h}\left( \tau \,;\tau +\Delta t,P_{\tau +\Delta t}^{*},K_{\tau +\Delta t}^{*}\right) , \end{aligned}$$
(35)

and Eq. (34) implies that

$$\begin{aligned} \int _{\tau }^{\,\tau +\Delta t}G^{l}(s)\exp \left( -r(s-\tau )\right) ds=\mu ^{h}\left( \tau \,;\tau ,P_{\tau }^{*},K_{\tau }^{*}\right) -\mu ^{h}\left( \tau \,;\tau +\Delta t,P_{\tau +\Delta t}^{*},K_{\tau +\Delta t}^{*}\right) . \end{aligned}$$
(36)

When \(\Delta t\rightarrow 0\), Eq. (35) can be expressed as

$$\begin{aligned} G^{l}(\tau )\Delta t&=-\left[ \mu ^{h}\left( \tau \,;t,P_{t}^{*},K_{t}^{*}\right) \mid _{t=\tau }\right] \Delta t\nonumber \\& \quad -\left[ \mu ^{h}\left( \tau \,;t,P_{t}^{*},K_{t}^{*}\right) \mid _{t=\tau }\right] \left( P_{\tau }^{*}\Delta t+K_{\tau }^{*}\Delta t\right) -2o\Delta t. \end{aligned}$$
(37)

Dividing Eq. (35) throughout by \(\Delta t\), with \(\Delta t\rightarrow 0\), we have

$$\begin{aligned} G^{l}(\tau )=-\left[ \mu ^{h}\left( \tau \,;t,P_{t}^{*},K_{t}^{*}\right) \mid _{t=\tau }\right] -\left[ \mu ^{h}\left( \tau \,;t,P_{t}^{*},K_{t}^{*}\right) \mid _{t=\tau }\right] \left( P_{\tau }^{*}+K_{\tau }^{*}\right) . \end{aligned}$$
(38)

Applying Eq. (31), we obtain \(\mu ^{h}\left( \tau \,;\,t,P_{t}^{*},K_{t}^{*}\right) =\exp \left( -r(t-\tau )\right) v_{h}\left( P_{\tau }^{*},K_{\tau }^{*}\right) ,\) and \(\mu ^{h}\left( \tau \,;\,t,P_{t}^{*},K_{t}^{*}\right) =v_{h}\left( P_{\tau }^{*},K_{\tau }^{*}\right) \). Then Eq. (37) can be converted to Eq. (30).□

Proposition 4

The specific payment imputation in the game \(\pi _{C}\left( P_{0},K_{0}\right) ,\) at time \(\left( t=0\right) \), can be given by

$$\begin{aligned} NV_{i}\left( P,K\right)&=\frac{1}{2}\left[ \phi _{1}P^{2}+\phi _{2}P+\phi _{3}K^{2}+\phi _{4}K+\phi _{5}PK+\phi _{6}\right. \\& \quad +\gamma _{1i}P^{2}+\gamma _{2i}P+\gamma _{3i}K^{2}+\gamma _{4i}K+\gamma _{5i}PK+\gamma _{6i}\\& \quad -\left. \gamma _{1j}P^{2}+\gamma _{2j}P+\gamma _{3j}K^{2}+\gamma _{4j}K+\gamma _{5j}PK+\gamma _{6j}\right] , \end{aligned}$$

and

$$\begin{aligned} NV_{j}\left( P,K\right)&=\frac{1}{2}\left[ \phi _{1}P^{2}+\phi _{2}P+\phi _{3}K^{2}+\phi _{4}K+\phi _{5}PK+\phi _{6}\right. \\& \quad +\gamma _{1j}P^{2}+\gamma _{2j}P+\gamma _{3j}K^{2}+\gamma _{4j}K+\gamma _{5j}PK+\gamma _{6j}\\& \quad -\left. \gamma _{1i}P^{2}+\gamma _{2i}P+\gamma _{3i}K^{2}+\gamma _{4i}K+\gamma _{5i}PK+\gamma _{6i}\right] . \end{aligned}$$

Proof

To consider the time consistent solution under specific principles, we apply (Yeung and Petrosyan 2008; Yeung 2007) principle of equality to build a payment distribution mechanism under which both country’s expected gain from cooperation is shared proportionally to the each country’s relative size of expected non-cooperative payoffs. Then the payment imputation in the game \(\pi _{C}\left( P_{0},K_{0}\right) \) at time \(\left( t=0\right) \) and at time \(\tau \in \left[ \left. t_{0},\infty \right) \right. \) is given as

$$\begin{aligned}&v_{h}\left( P_{0},K_{0}\right) =V_{hN}\left( P_{0},K_{0}\right) +\frac{1}{2}\left[ V_{C}\left( P_{0},K_{0}\right) -V_{iN}\left( P_{0},K_{0}\right) -V_{jN}\left( P_{0},K_{0}\right) \right] .\\&v_{h}\left( P_{\tau }^{*},K_{\tau }^{*}\right) =V_{hN}\left( P_{\tau }^{*},K_{\tau }^{*}\right) +\frac{1}{2}\left[ V_{C}\left( P_{\tau }^{*},K_{\tau }^{*}\right) -V_{iN}\left( P_{\tau }^{*},K_{\tau }^{*}\right) -V_{jN}\left( P_{\tau }^{*},K_{\tau }^{*}\right) \right] . \end{aligned}$$

Applying Proposition 3, we obtain an instantaneous payoff of the cooperative game at time \(\tau \in \left[ \left. t_{0},\infty \right) \right. \)

$$\begin{aligned} G^{l}\left( \tau \right)&=\frac{1}{2}\left[ rV_{iN}\left( P_{\tau }^{*},K_{\tau }^{*}\right) -V_{iN\left( P_{\tau }^{*},K_{\tau }^{*}\right) }\left( P_{\tau }^{*},K_{\tau }^{*}\right) \left( P_{\tau }^{*}+K_{\tau }^{*}\right) \right] \\& \quad +\frac{1}{2}\left[ rV_{C}\left( P_{\tau }^{*},K_{\tau }^{*}\right) -V_{C\left( P_{\tau }^{*},K_{\tau }^{*}\right) }\left( P_{\tau }^{*},K_{\tau }^{*}\right) \left( P_{\tau }^{*}+K_{\tau }^{*}\right) \right] \\& \quad -\frac{1}{2}\left[ rV_{jN}\left( P_{\tau }^{*},K_{\tau }^{*}\right) -V_{jN\left( P_{\tau }^{*},K_{\tau }^{*}\right) }\left( P_{\tau }^{*},K_{\tau }^{*}\right) \left( P_{\tau }^{*}+K_{\tau }^{*}\right) \right] . \end{aligned}$$

This completes the proof.□

5 Numerical results

5.1 Calibration of the model

In this section, we compare our approach and the optimal strategy discussed in Sects. 3 and 4 under the game-theoretic paradigm to analyze the quantitative implications of our model under CCS technology in the context of trans-boundary industrial pollution. Therefore, the dilemma we face is whether the development of such technologies will truly alleviate the consequences of failing to reach a global international agreement over GHG emissions. For example, Australia’s climate change strategies focus on the role of low emission technologies to underpin the nation’s long -term emissions reduction. There is increasing support in the current literature for the view that innovative technology, such as CCS technology could play a central role in resolving the climate change predicament. Barrett Barrett (2009) argues that to stabilize carbon concentration at levels capable of preventing an increase in global temperature by 2 °C will require a technological revolution. Similarly, Galiana and Green (2009) also suggest that reducing carbon emissions will require an energy-technology revolution and subsequently induce a “global technology race”.

We used the following parameter values throughout our analysis for the baseline scenario and utilized Math-Lab to simulate the trans boundary industrial pollution between two asymmetric nations in an infinite time horizon. The numerical simulations are provided to characterize the behavior and establish the stability of the cooperation by using Pareto optimal solution while assuming that the industrial firm in one country \(j\,,\left( \vartheta _{j}\right) \) has more cost/energy efficient carbon capturing and storage technology than the other, \(\vartheta _{j}>\vartheta _{i}\), (generally speaking pollution abatement effort efficiency is higher in developed nations). We show that in a closed-loop (Markov perfect) Nash equilibrium, setting the Stackelberg equilibrium will not coincide with the Nash equilibrium effectively gaining the first mover advantage in a cooperative game paradigm. This can be interpreted as the outcome of international negotiations, provided that such negotiations and technological collaborative strategies between countries are important and its findings are summarized below as propositions. Furthermore, the role of technological advances and cooperation in the trans-boundary industrial pollution control debate plays an important role in

  1. 1.

    determining the optimal level of government subsidy on CCS and technology,

  2. 2.

    determining the optimal innovation influence coefficient of cCCS and technology,

  3. 3.

    determining the cost coefficient parameters associated with technology improvements.

These concerns are important and will dictate current and future pollution abatement debates. Having obtained the optimal solution under the cooperative game, we prove the stability of the game by using Parreto Optimal solution under Table 2 parameters.

Table 2 Model parameter values
Full size table

Proposition 5

In this closed-loop (Markov perfect) Nash equilibrium, setting the Stackelberg equilibrium will coincide with the Nash equilibrium effectively eliminating the first mover advantage in a cooperative game paradigm. This can be interpreted as the outcome of international negotiations, provided that such negotiations are selected and the importance of technological collaborative strategies for each country is emphasized. Figures 1 and 2 clearly justify that technological developments and collaboration would facilitate both economic gain (via the revenue) and pollution abatement.

Fig. 1
figure 1

Value function with respect to P

Full size image
Fig. 2
figure 2

Value function with respect to K

Full size image

By solving this system, under the assumption that both value functions (12) and (13) are identical, we can find the equilibrium strategies, if, we assume that region j, could be the leader of this game and examine the game equilibrium strategy. However, under this strategy, we obtain the same equilibrium strategy as the Nash equilibrium. Therefore, the coincidence between the two equilibria concepts in the stochastic differential game does not depend on the asymmetry assumption. This occurs because the reaction functions given by Theorem 1 are dependent on the control variable of the other player. This shows that for a class of dynamic differential games with a state-dependent closed-loop (Markov perfect) the Nash equilibrium coincide with the Stackelberg equilibrium.

Proposition 6

For the non-cooperative case, if \(\gamma _{5h}<-\frac{2\gamma _{1h}}{\varphi _{Nh}}\), \(h=i,j,\) then \(E_{hN}^{*}\left( P,K\right) \) is decreasing in P. For the cooperative case, if \(\gamma _{5h}<-\frac{2\phi _{h}}{\varphi _{Ch}}\), \(h=i,j,\)then \(E_{hC}^{*}\left( P,K\right) \) is decreasing in P due to the direct outcome of Theorems 1 and 3. This yields both negative and positive results. The negative result is that the fully cooperative outcome, which yields a Pareto-optimal time path for pollution controls, is not attainable without binding agreements, and that there always exists an incentive for one country to deviate from the agreement; i.e., the cooperative outcome is Pareto-efficient but not a sustainable equilibrium. The positive result is that if \(\varphi _{Ch}\) is small enough and a self-enforcing equilibrium exists, then it indeed approximates the Pareto-efficient welfare level. We also capture the monotone property with respect to m, but do not capture such a monotone property with respect to \(\xi \), highlighting a diminished return on technology. See Figs. 3, 4, 5, 6, 7, 8, 9 and 10.

Fig. 3
figure 3

Optimal emission level \(E_{iN}^*\) for non-cooperation with different values of m

Full size image
Fig. 4
figure 4

Optimal emission level \(E_{jN}^*\) for non-cooperation with different values of m

Full size image
Fig. 5
figure 5

Optimal emission level \(E_{iN}^*\) for cooperation with different values of m

Full size image
Fig. 6
figure 6

Optimal emission level \(E_{jN}^*\) for cooperation with different values of m

Full size image
Fig. 7
figure 7

Optimal emission level \(E_{iN}^*\) for non-cooperation with different values of \(\xi \)

Full size image
Fig. 8
figure 8

Optimal emission level \(E_{jN}^*\) for non-cooperation with different values of \(\xi \)

Full size image
Fig. 9
figure 9

Optimal emission level \(E_{iN}^*\) for cooperation with different values of \(\xi \)

Full size image
Fig. 10
figure 10

Optimal emission level \(E_{jN}^*\) for cooperation with different values of \(\xi \)

Full size image

Proposition 7

The outcome of the game depends on the parameters of the game and there exists a unique pair of strategies such that the net revenue under the cooperative game dominates the non-cooperative game subject to \(m,\xi ,\theta ,\,\sigma ,\,\beta ^{i}\)and \(\lambda ^{i}\), improving the welfare level of each country. Therefore, the failure of coordination/engagement over emissions of trans-boundary pollutants may prevent the international community from reaping any benefit from the creation and adoption of a cleaner technology and may even result in exacerbating the tragedy of the commons. An increase in the net revenue has two components, the direct effect of which is a decrease in emissions subject to \(m,\,\theta \) and \(\xi \), whilst indirectly motivating each player to commit to improving their carbon capture utilization and storage technologies, emphasizing that the implementation of such measures control should be pursued jointly. Consequently, a Pareto-efficient equilibrium steady-state pollution stock can be supported as a subgame perfect equilibrium. See Figs. 11, 12, 13, 14 and 15.

Fig. 11
figure 11

Values function with respect to m

Full size image
Fig. 12
figure 12

Optimal emission level with different values of m

Full size image
Fig. 13
figure 13

Values function with respect to \(\sigma \)

Full size image
Fig. 14
figure 14

Optimal emission level with different values of \(\sigma \)

Full size image
Fig. 15
figure 15

Values function with respect to \(\theta _i\)

Full size image

Remark 4

Via the Stochastic Linear Quadratic differential game paradigm mechanism reduces total net emissions, in terms of cooperation and noncooperation due to technological advantages, thereby improving the atmospheric environment. In the case of noncooperative games, the carbon emissions used for production will not change, and the improvement of the environment will be achieved through the increase of investment in foreign carbon reduction projects in one country. In the cooperative game scenario, the amount of carbon emission used for production is also reduced. Thus, carbon stocks are reduced more quickly. For example this could be applicable to EU region and Asia Pacific regions (Fig. 16).

Fig. 16
figure 16

Optimal emission level with different values of \(\theta _i\)

Full size image

6 Concluding Remarks

In this study we examine the strategic interaction between endogenous stochastic carbon capture utilization and storage technology and a trans-boundary industrial pollution problem to ensure mutual benefit for the players. We formulate this problem via a SDG to obtain a closed-loop (Markov perfect) Nash equilibrium. We then articulate the non-cooperative and cooperative Nash optimal emission paths with random interference factors (due to technology) such that each country’s discounted stream of net revenues is maximized. We then articulate and define the non-cooperative and cooperative attainable games and equilibria. This shows that for a class of dynamic differential games with state-dependent closed-loop (Markov perfect), the Nash equilibrium coincide with the Stackelberg equilibrium. We show that each country’s optimal emission paths are inversely proportional to the cost coefficient parameters of each country. Ultimately, our incorporation of endogenous stochastic technology within this model, provides a more robust model within the broader trans-boundary industrial pollution literature.

The proposed quantitative framework could potentially assist national policy-makers to determine the appropriate level of subsidy required for the development of pollution lowering technologies, whilst advancing collaborative measures to meet global emission reduction targets. The main policy recommendation is that the efforts of discovering and reducing carbon emissions and improving storage technologies should be viewed as a valid substitute for the need to succeed in the multilateral coordination of global emissions reduction. Hence, the effort of creating such technologies should be pursued jointly.