Introduction

Cellulose is one of the most common and well-known polymer materials, bio-based, and with unique properties. In recent decades, especially crystalline nanocellulose (cellulose nanocrystals (CNCs) and nanofibrils) have resulted in emergence of a plethora of new cellulose materials applications. For recent reviews, see e.g. Habibi et al. (2010), Mali and Sherje (2022), Calle-Gil et al. (2022), Mu et al. (2019), Hamad (2015), Li et al. (2022), George and Sabapathi (2015) and Seabra et al. (2018). The excellent mechanical properties, low toxicity, and good biocompatibility (Mali and Sherje 2022) promote cellulose use: the number of studies devoted to cellulose-based materials has grown exponentially since the beginning of the twenty first century.

A key target in cellulose material development is obtaining control of the interactions between the cellulose nanoparticles and their distribution in solution. A common means is directed modification of the surfaces by chemical functionalization via the hydroxyl groups of crystalline cellulose surfaces. Besides chemical functionalization, also solution conditions, such as variations in the salt concentration or pH, are used for fine-tuning the interactions. This is because cellulose nanoparticle surfaces often contain charged groups due to the presence of the impurities (Li et al. 2021). Functionalization can result in charged groups but also the method of producing the nanoparticles often includes acid hydrolysis (Mariano et al. 2014). In consequence, the interactions between cellulose nanoparticles, and thus also the properties of cellulose-based materials, are sensitive to ionic strength and pH.

Interestingly, ionic strength can also affect the properties of aqueous solutions of native, non-functionalized cellulose nanoparticles obtained without acid hydrolysis (Sim et al. 2015; Saarikoski et al. 2012; Rahmini et al. 2020; Arola et al. 2022). For example, Sim et al. (2015) demonstrated that NaCl (in the concentration range between \(\sim 10\) mM and \(\sim 3\) M) affects the drying process of unmodified cellulose hydrogel. Saarikoski et al. (2012) noticed that unmodified cellulose nanofibril (CNF) hydrogels have significant flocculation in the presence of NaCl (at concentrations above 10 mM). Rahmini et al. (2020) pointed out that gel strength has a positive relationship with ion concentration. In the recent review of the rheological properties of cellulose materials, Li et al. (2021) suggested that this behavior results from the presence of impurities in the raw cellulose pulp that contains charged salt-sensitive groups.

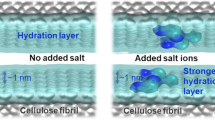
However, several examples where the effect of salt on cellulose materials does not relate to screening of electrostatic interactions have been reported recently. For example, Gurtovenko et al. showed in atomistic simulations that a monovalent salt increases interaction between native unmodified CNC and lipid bilayer (Gurtovenko and Karttunen 2021). In our previous work (Arola et al. 2022), we demonstrated the significant effect that salt has on the rheological properties of native cellulose nanofiber hydrogels, in particular, storage and loss moduli. Even a very small concentration of a monovalent salt (\(\sim 1\) mM) in the solution leads to significant changes in the hydrogel, specifically the transitions of the system from a gel state to a stronger, more stiff gel state (Arola et al. 2022). The observed changes cannot be explained solely by the screening of electrostatic repulsion between the cellulose impurities in the system. The findings point to effects associated with the interaction between the ions and the hydroxyl groups at the cellulose surface as the cause of increased interaction between the fibers. This interaction leads to changes in the hydration shell at the cellulose surface (Arola et al. 2022). Simplifying, the adsorbed ions enhance the hydration layer of the fibril and increase its extent from the surface. Additional contributions to the interactions could rise from the adsorption of ions onto the surface of cellulose, leading to surface charging: if present, surface charging can induce long-range interaction between the cellulose nanoparticles.

It is clear that both hydration changes and surface charging can significantly change the interactions between cellulose nanoparticles and that this directly modifies the properties of cellulose materials. However, the role of these effects in controlling the properties of cellulose materials has not, to our knowledge, been studied in detail. Especially, the difficulties associated with differentiating the findings from the effects rising from possible electrostatic repulsion between impurities in the cellulose structure have made addressing the topic challenging.

Atomistic molecular dynamics (MD) simulations allow studying the salt-induced changes in cellulose materials so that the challenges posed by the presence of impurities in samples are circumvented. The approach allows extracting both the mechanism of salt-induced changes in cellulose-based materials and the effects of salt both on hydration and charge accumulation level. Indeed, MD simulations of the interfacial regions between cellulose material (both in native and functionalized forms) and the salt solution have been carried out in many studies (Lukasheva and Tolmachev 2016; Lukasheva et al. 2019; Tolmachev and Lukasheva 2014; Valencia et al. 2020; Miyamoto et al. 2015; Malaspina and Faraudo 2019; Uetani et al. 2022; Tolmachev et al. 2021), including NaCl solution (Bellesia and Gnanakaran 2013). However, none of these studies has focused on the molecular level origins of the salt sensitivity of cellulose materials. Most related, Belessia et al. have shown that Na\(^+\) ions can affect the interfacial structure and conformation of surface molecules (Bellesia and Gnanakaran 2013). This could point toward favorable interaction between the ions and the cellulose surface, giving rise to either one of the effects discussed above.

Here, we target isolating the effects of the salt on the native cellulose material, i.e. the role of charge accumulation vs. changes in hydration in cellulose materials salt sensitivity. We examine in detail the effect of NaCl on the structure of interfacial regions between cellulose surfaces and water solution targeting elucidating the molecular mechanisms of NaCl salt influence on the cellulose material properties.

Methods

Force field and simulation parameters

For the investigation of the NaCl distribution and hydration layer structure in the interfacial regions between cellulose surfaces and water solution, classical unbiased MD simulations were performed. Umbrella sampling was used to study the interaction between the cellulose surface and the ions and to assess the differences in active groups on the cellulose surface in terms of ion adsorption preference. Detailed simulation protocols for both the unbiased and the umbrella sampling simulations are presented in Supplementary Information (SI). The presented protocols also include assessment of relaxation (SI Fig. S1).

The simulations were performed by GROMACS\(-\)2016.6 and GROMACS\(-\)2019.3 software (Abraham et al. 2015). The CHARMM36 force field (Best et al. 2012; Huang and MacKerell 2013) was used to describe the interactions between the components of the system. For water simulation, the TIP3P water model (MacKerell et al. 1998) compatible with this force field was used. Long-range electrostatics employed the smooth Particle-Mesh Ewald (PME) algorithm (Essmann et al. 1995; Abraham and Gready 2011) with cubic interpolation and 0.12 nm grid spacing for the fast Fourier transform (FFT). The short-range electrostatics and van der Waals cutoff was 1.2 nm. The van der Waals potential was smoothly switched to zero between 1.0 nm and the cut-off distance. For temperature control, the stochastic velocity rescale thermostat (Bussi et al. 2007) with a 300 K reference temperature was used. Pressure was controlled by the semi-isotropic Parrinello–Rahman barostat (Parrinello and Rahman 1981), with 1 bar reference pressure and 4.5e\(-\)5 bar\(^{-1}\) compressibility perpendicular to the cellulose surface. Time constants for temperature and pressure control were 0.2 ps and 2.0 ps, respectively. The simulation time step was 2 fs.

Model and simulation setup

Table 1 Summary of simulation system details. For each surface pair, the examined NaCl concentrations, number of salt ions, number of water molecules, and the simulation box dimensions are specified
Full size table
Fig. 1
figure 1

From top to bottom: The chemical structure of a glucose chain with oxygen and hydrogen sites labeled; The six surface facets of the examined model CNC labeled according to their crystalline planes; visualizations of the simulated systems in which the opposite facets of the model CNC are constructed as continuous surfaces such that they form infinite planes across the simulation box xy-plane. Simulation box dimensions are shown. In the visualization, oxygen atoms are in red, carbon in cyan, and hydrogen in gray

Full size image

The simulation system consisted of a model CNC set into the simulation box such that a slab corresponding to the opposing crystal facets surrounded by the aqueous solution of NaCl as ions forms. Three different simulation systems, such that all six CNC facets were formed as infinite surfaces, were examined, see Fig. 1. The main regions of interest were the interfacial regions formed by the different surfaces of CNC and the surrounding solution. The sizes of the simulation boxes are shown in Fig. 1 and collected in Table 1. Native CNCs and fibrils exceed in dimensions of the simulation box; this and the periodicity allow generalizing the conclusions of the simulations to both CNC and CNF systems. Notably, cellulose nanoparticles vary in morphology and their surfaces can correspond to different crystallographic planes (Moon et al. 2011). The surface structure, density of functional groups at the surface, and the availability of the groups on the surface determine the interaction of cellulose nanoparticles with their environment.

For modelling purposes, we chose for the study the most pronounced surfaces of cellulose nanoparticles that correspond to {110}, {\(\bar{1}\bar{1}\)0}, {\(\bar{1}\)10}, {1\(\bar{1}\)0}, {100} and {\(\bar{1}\)00} crystalline planes, Fig. 1. In constructing the CNC models, 36 glucose chains of 12 glucose rings were employed for the {110}/{\(\bar{1}\bar{1}\)0} and {\(\bar{1}\)10}/{1\(\bar{1}\)0} systems while 10 glucose ring chains were used for the {100}/{\(\bar{1}\)00} system. The initial assembly configurations were constructed using the cellulose builder (Gomes and Skaf 2012). The glucose chains were set into a cellulose I\(\beta\) structure (Nishiyama et al. 2002; Kubicki et al. 2018). All 36 glucose chains are constructed periodically such that the ends of the chains are connected by covalent bonds across the periodic boundary of the simulation box, resulting in infinite chains across the box. The simulation boxes were monoclinic with the parameters of I\(\beta\) cellulose crystal unit cell with the angle between the axes equal to 96.5 degrees.

The CNC models were solvated by Gromacs tools. NaCl as ions were introduced into the system by random replacement of water molecules by the ions. Two concentrations of salt were examined: 0.1 M and 1.0 M aqueous NaCl solutions. In our previous study (Arola et al. 2022), the rheology experiments indicated significant changes in hydrogel properties already at very low salt concentrations (\(\approx 1\) mM). Here, even the smaller, 0.1 M NaCl concentration is significantly above this. This NaCl concentration was used here because the number of ions in the simulation system remains very small even with this concentration (see Table 1). For improved statistics and a more pronounced salt effect, we also considered the 1.0 M NaCl concentration. Figure 1 presents snapshots of the initial simulation systems. The details of the initial and final simulated systems in terms of box dimensions, number of water molecules, and number of ions in the system are summarized in Table 1.

The setups for the localized binding energy calculation using umbrella sampling (Torrie and Valleau 1977) were similar to the unbiased simulations: the same simulation box sizes, temperature and pressure coupling parameters, and interaction parameters were used. However, in the umbrella sampling simulations, the boxes contained only two ions: one probe ion to map the interactions, and the corresponding free counterion located in the water bulk for neutralizing the total charge of the system. The ion interactions with the cellulose surface were mapped using the probe ions via assessing the potential of mean force (PMF) (Kirkwood 1935; Roux 1995). In assessing the binding energy and the free energy landscape visible for the ions, the motion of the Na\(^+\) or Cl\(^-\) ion used as a probe was restricted to z-direction for each identified binding site on the surface. The examined binding pairs were Na\(^+\)-O2, Na\(^+\)-O3, Na\(^+\)-O6, Cl\(^-\)-HO2, Cl\(^-\)-HO3, and Cl\(^-\)-HO6, see Fig. 1 for site labels. In total, 21 umbrella sampling windows corresponding to ion-binding site separations between 0.2 nm and 2.0 nm at 0.1 nm intervals, and additionally 0.25 nm and 0.35 nm separations were sampled. The sampling configurations were generated by using a pull rate of 4 nm/ns and a harmonic force constraint \(k = 1000\) kJ\(\cdot\)mol\(^{-1}\) \(\cdot\)nm\(^{-2}\). The umbrella force constant was set as 2000 kJ\(\cdot\)mol\(^{-1}\) \(\cdot\)nm\(^{-2}\) and the sampling windows were 5 ns in duration, with the same pressure and temperature control setup as described above. The weighted histogram analysis method (WHAM) (Kumar et al. 1992) was used to extract the PMFs. Error estimates were based on bootstrapping over 200 histograms.

Results

Structure of the interfacial cellulose/water regions

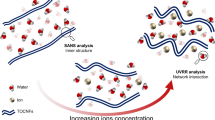
To understand the molecular details of the structure of interfacial regions between cellulose and salt solution, we analyzed the distribution of Na\(^+\) and Cl\(^-\) ions and water near the cellulose surfaces. The data is presented in Fig. 2 and shows that the water distribution has two well-defined peaks close to the cellulose surface. The peaks are separated from each other by a distance of 0.2–0.3 nm, which corresponds to the size of one water molecule. These peaks indicate water ordering caused by the presence of the cellulose surface. Immobilization and ordering of water molecules on the CNC surface have been shown before both by experimental and simulations studies (Lindh et al. 2017; Malm et al. 2010; Yurtsever et al. 2022; Heiner et al. 1998; Matthews et al. 2006; Biermann et al. 2001; Maurer et al. 2013; Mudedla et al. 2021).

Fig. 2
figure 2

Normalized water and ion number density calculated along the z-axis near the cellulose surfaces. Since water density data for each concentration is similar, the water density corresponding to the 0.1 M NaCl concentration is used to represent the water density for all examined NaCl concentrations. The z-axial center of mass for the surface layer glucose chains in each cellulose facet corresponds to the zero distance. Both water and ion particle densities are normalized such that bulk solution density is 1.0. The axis at left corresponds to water and the 1.0 M concentration of ions. The axis at right corresponds to the 0.1 M concentration of ions. Unnormalized data are presented in the SI as Fig. S2

Full size image
Fig. 3
figure 3

Qualitative visualizations of Na\(^+\) and Cl\(^-\) preferential locations (from left to right) on the {1\(\bar{1}\)0}, {100}, and {110} surface. Data for 1.0 M NaCl concentration is presented. The blue (Na\(^+\)) and orange (Cl\(^-\)) shaded regions show the highest ion density regions on each surface. The red, green, and purple spheres indicate the O2, O3, and O6 oxygen atoms at the surfaces, see Fig. 1. Visualizations use a density isosurface cut-off based on Fig. 2 data. A cut-off value of 0.0012 Å\(^3\) is used. For all graphs, a slab corresponding to z-axial distance of less than 1.0 nm from the cellulose surface O6 atoms was used for the analysis

Full size image

Notably, the data of Fig. 2 does not show any significant effect of salt on the water density distribution: The systems with different concentrations of salt have very similar density distributions. However, the ions influence water orientation, discussed further in Sect. 3.1. The different CNC surfaces affect water distribution differently. The most hydrophobic surface ({100}) has the highest first peak of water density. This counterintuitive fact is well-known and has been observed for various cellulose structures. Maurer et al. (2013) state that this behavior rises due to the high regularity and flat structure of the hydrophobic surface, which increases the density of the first water slab close to the \(\{\)100\(\}\) and \(\{\) \(\bar{1}\)00\(\}\) surfaces.

The distribution of ions has two pronounced peaks close to the cellulose surfaces in the ordered water layers. This can be understood by considering the hydration layers of the ions and the interface: disrupting the favorable solvation is costly in terms of solvation energy, which leads to the depletion of ions very close to the interface. Similar observations for ions at liquid-liquid interfaces exist: depending on the ion species, the ions can either experience depletion or enrichment at the interface, see e.g. Refs. Holmberg et al. (2014) and Petersen and Saykally (2006). Also, the ion distribution near the water-air interface depends on the hydration shell structure of the ions (Jungwirth and Tobias 2006; Luo et al. 2006; Jungwirth and Tobias 2001).

The two ion condensation peaks in Fig. 2 can indicate that ions adsorb to multiple preferable locations. Additionally, the Na\(^+\) and Cl\(^-\) peaks are mutually exclusive. This results from the ions preferring different locations in the interfacial region depending on their charge. Additional insight can be obtained by the molecular structure of the glucose chains composing the cellulose surfaces: Glucose monomers (Fig. 1) contain three hydroxyl groups, which have different accessibility and location on each surface. These hydroxyl groups can act as ion-binding sites.

The localization of ions on the cellulose surfaces is shown by the ion density maps calculated for the interfacial regions, see Fig. 3 for the distribution of the ions and their variation along the surface (at 1.0 M NaCl concentration). The Na\(^+\) ions adsorb visibly differently to the different surfaces: For the {1\(\bar{1}\)0} and {100} surfaces, the areas occupied by Na\(^+\) ions are isolated. In contrast, the hydroxyl groups on the {110} surface have shorter separation distance (0.48 nm) than those of {1\(\bar{1}\)0} and {100} surfaces (0.62 nm and 0.54 nm, respectively). This facilitates the exchange of ions between different hydroxyl groups and results in the movement of the adsorbed ions along the direction perpendicular to the cellulose chains. This shows as the connected ion residence regions in Fig. 3. The density distributions show clearly that Na\(^+\) and Cl\(^-\) ions have different occupation positions. While Na\(^+\) ions adsorb mainly to the most exposed primary hydroxyl groups (O6 atoms), Cl\(^-\) ions bind most readily to the secondary hydroxyl groups (HO2 and HO3 atoms). These groups are located deeper in the surface. The difference in binding site exposure to ion binding explains the difference in the position of peaks in the density profiles for Cl\(^-\) and Na\(^+\) ions in Fig. 2. Notably, Cl\(^-\) ions are deeper in the cellulose interfacial layer because they bind to the less exposed secondary hydroxyl groups. The difference in the binding sites for different ions is also shown by the analysis of the distribution of ions around hydroxyl groups (see SI Fig. S3, and SI Table S1).

Analysis reveals the presence of two types of adsorbed ions, namely the ions that form direct contact with the hydroxyl groups and the ions that interact with the hydroxyl groups via a water molecule bridging (see SI Fig. S3). SI Table S1 in the SI collects the number of ions adsorbed to the different hydroxyl groups at 1.0 M NaCl concentration. The ratio of the hydroxyl groups occupied by ions changes depending on the surface: for hydrophilic surfaces ({1\(\bar{1}\)0} and {110}), more than half of the hydroxyl groups are occupied by ions; for the hydrophobic surface ({100}), only a third of the hydroxyl groups are occupied. This corresponds to the surface density of ions on the cellulose surfaces (Fig. 3).

Notably, Fig. 2 shows that the {\(\bar{1}\)00} and {100} surfaces attract significantly more ions than the other surfaces. However, the distribution presented in Fig. 3 indicates that there are no clearly preferential binding sites on this surface. In this case, instead of active groups on the surface, the ordering of the water close to the hydrophobic surfaces discussed above determines the distribution of ions. The resulting relatively even distribution of the ions is also visible in the visualization data of Fig. 3. The {100} surface shows significantly less shading indicating elevated ion density in comparison to the other two examples where the ions are more localized. As already discussed in relation to interfacial ion depletion, the ordered hydration shell of the \(\{\)100\(\}\) and \(\{\) \(\bar{1}\)00\(\}\) surfaces can decrease ion binding at these surfaces in comparison to the other surfaces.

Fig. 4
figure 4

The potential of mean force as the function of the z-axial distance from selected binding sites on {110}, {100}, and {1\(\bar{1}\)0} CNC surfaces. The data is from umbrella sampling simulations

Full size image

According to basic thermodynamics, the local number density of ions \(\rho _{\text{ion}}\) at equilibrium is connected to the free energy via the Boltzmann distribution:

$$\begin{aligned} G_{\text{ion}}(r)=-k_{\text{B}} T \ln \rho _{\text{ion}}(r). \end{aligned}$$
(1)

Here \(G_{\text{ion}}(r)\) represents the ion free energy at position r, \(k_{\text{B}}\) is the Boltzmann constant, T the temperature, and \(\rho _{\text{ion}}(r)\) is the time-averaged localized ion density. A direct consequence is that the distributions presented in Fig. 3 relate with the corresponding ion free energy with the highest number densities rising at positions corresponding to the lowest free energy. Consequently, the largest binding free energy can be expected for the most populated regions. In the MD simulations, the statistical sampling approaches ergodicity but due to the finite time duration of the simulations, the density peak proportions provide guidelines to free energy landscape, not absolute features. For an improved understanding of the molecular details of the interaction of ions with the cellulose surface and the reason for the discussed ion distribution, as well as to assess how strongly the ions are bound by hydroxyl groups, i.e. binding energy estimation, we performed umbrella sampling simulations to obtain a potential of mean force estimate for the distance dependency of the interaction between the ions and the hydroxyl groups.

The calculated PMFs provide a more quantitative view of the free energy landscape visible to the ions near the cellulose surfaces and allow differentiating the roles of different hydroxyl groups in the interaction with the ions. Figure 4 summarizes the obtained PMF data. The PMFs are calculated for Na\(^+\) and Cl\(^-\) ions along a distance measured perpendicular to the cellulose surface for the binding sites identified in Fig. 3. Data for {110}, {100}, and {1\(\bar{1}\)0} CNC surfaces is presented. SI Fig. S4 shows molecular visualizations of the ions at locations corresponding to the main minima on PMF. Notably, the PMFs have been calculated with the positions of the interacting atoms of the binding sites and the xy-plane position of the probe ion fixed to avoid the ion switching binding to a neighbor hydroxyl group during the umbrella sampling. This allows concluding on the role of different hydroxyl groups, but the approach limits the conformational freedom of the hydroxyl groups. This leads to a slight underestimation of the free energy of interaction. The effect is most pronounced for primary hydroxyl groups, as shown by the mismatch of the data between the primary hydroxyl group and Cl\(^-\) ions interactions in Fig. 4 and SI Table S1, one data set rising from the biased and the other from the unbiased MD simulations.

An estimate for the ion binding free energy at each binding site can be obtained from the depth of the deepest PMF curve minimum with the PMF zero level specified by the ion PMF value in the bulk water (at large distances). The data shows that the ions bind at shallow free energy minima at cellulose surfaces. For all examined sites, the estimated free energy difference for the ion at binding minimum vs. bulk water solvation environment is comparable to the thermal energy. This means that, the partitioning of ions remains weak but that there are preferential locations that correlate with elevated ion occupation likelihood at the surfaces.

The PMF curves of Fig. 4 reveal two preferable positions for ions close to hydroxyl groups. The first, a local minimum, is at the \(0.23-0.26\) nm distance range and corresponds to direct contact between hydroxyl groups and ions. Indeed, this value is in line with the distance between Na\(^+\) ion and the hydroxyl group in cellobiose NaI hydrate crystal (Peralta-Inga et al. 2002). The second, characteristically a significantly lower free energy state is located at the \(0.42-0.53\) nm distance range. It corresponds to solvent-separated contact of the ion and the hydroxyl groups. For all situations, the direct contact is energetically disfavored in comparison to the solvent-separated pairing (the PMF associated with this position minima are at a higher level than the bulk solvation PMF level).

The data shows that for the {1\(\bar{1}\)0} surface, Na\(^+\) ions interact energetically favorably only through water molecules. In the unbiased simulations, a small fraction of ions could be observed also within 0.32 nm cut-off, see, SI Table S1. This points toward the fixing of the hydroxyl groups causing the short-distance ion binding to appear artificially low. However, preference for the Cl\(^-\) ions to interact with the most exposed HO3 and HO6 groups both by direct contact (\(0.23-0.26\) nm) and through water molecule (\(0.42-0.53\) nm) can be observed. This is also clearly visible in the direct, unbiased simulations (see SI Table S1).

A similar situation rises for the {100} surface with the Na\(^+\) ions interacting with the surface only through water molecules with the HO6 and HO3 groups. Both umbrella sampling (Fig. 4 and unbiased MD simulation, see SI Table S1, show this consistently. This surface attracts fewer ions than the others due to its hydrophobicity and the surface hydroxyl groups forming intracellulose hydrogen bonds. This hydrogen bonding prevents interaction with the environment. Ions can form direct contact with hydroxyl groups only with the Cl\(^-\)–HO3 pair. Here, it is worth noting that the water ordering near the hydrophobic surface influences ion distribution, as already discussed.

The \(\{110\}\) surface attracts Na\(^+\) ions strongly. The data points to that even direct contact with the Na\(^+\) ions is possible for the primary hydroxyl groups. In contrast, Cl\(^-\) ions interact with this surface much less. Despite this, in Fig. 2, the Cl\(^-\) resides closer to the cellulose surface than Na\(^+\). This is because the ions interact with the secondary hydroxyl groups hydrogens. The hydroxyl groups have thus more conformational freedom to adjust their orientation and one ion can form contact with two hydroxyl groups. This increases the binding energy. A visualization of such ion binding at this position for an adsorbed Cl\(^-\) ion is shown in SI Fig. S4. On the other hand, the Na\(^+\) ions prefer O6 atoms more than the O2 and O3 sites because the O2 and O3 atoms are closer to the glucose ring. Furthermore, the distance between the binding sites is longer than the distance between the HO2 and HO3 locations. Thus, a Na\(^+\) ion binds to only a single site instead of residing between the sites in contact with two groups. Instead, Na\(^+\) adsorbs only to the most exposed, primary hydroxyl group that also has the most conformational freedom so that the ion can form energetically favorable contacts.

A summary of the binding distances, corresponding to PMF calculations local minimum positions, and the corresponding free energy values, i.e. the binding free energies, are collected in Table 2.

Table 2 Summary of potential of mean force local minima (PMF) corresponding to ion binding for different surfaces and sites
Full size table

Electrostatic potential

Ions adsorbed on the native cellulose could lead to non-zero surface charge leading to electrostatic interactions between CNFs. Figure 5 presents the electrostatic potential profiles perpendicular to the cellulose surface. The potential profiles have been calculated by double integration of the charge distribution corresponding to the density distribution in the simulations shown in Fig. 2. Since the CNC model is electrically neutral, the potential was calculated from the density distributions of water atoms and ions. Periodicity was accounted for by the linear correction proposed by Gurtovenko and Vattulainen (2009).

Fig. 5
figure 5

Electrostatic potential provided by water and ions close to cellulose surfaces. Potential in bulk solution is settled as zero. Linear correction is done based on periodical boundary conditions proposed by Gurtovenko and Vattulainen (2009)

Full size image

A comparison of the 1.0 M and 0.1 M NaCl concentrations electrostatic potentials reveals that increasing the salt concentration does not give a significant rise in the potential despite the density distributions of the ions being very different for different concentrations (Fig. 2). This is because the main contribution to the electrostatic potential comes from the water ordering in the hydration layer close to the cellulose surface. The effect of ions remains small due to the relatively low ion concentration on the surface but also because both negative and positive ions adsorb on the surface, resulting in effective neutralization of the surface total charge. This can also be deduced from the data collected in SI Table S1. The potentials show a stronger effect on the surface in the cases with more ordered water in the surface hydration layer. However, the extent does not reach beyond one nanometer from the surface even in these cases.

Overall, the analysis of electrostatic potential dependencies of the surfaces and the accumulated charge distributions due to the adsorbed ions show that even though native cellulose can adsorb some amount of ions from the solution, this cannot induce significant electrostatic interaction between the CNFs.

Hydration shells

As rheology characterization clearly identified even a significantly lower NaCl concentration than in these simulations inducing a transition from gel to a stiff gel (Arola et al. 2022), the lack of charge build-up here signifies that the response likely rises from changes in the structure of the hydration shell of the CNFs. Indeed, the ion distributions and calculated free energy profiles for binding and binding preferences all point toward the hydration shell of the cellulose surface having a crucial role.

Fig. 6
figure 6

Illustration of the changes of hydration shell depending on the distance between ion and hydroxyl groups for 110 surface. Na\(^+\) and Cl\(^-\) ions are represented by blue and orange balls, and binding sites O6 and HO2 are presented by purple and red balls. The red and blue powder-like dots are water oxygen and hydrogen

Full size image

To allow analyzing this, Fig. 6 presents the radial density maps of water calculated at different probe ion and hydroxyl group atom z-axial separations (O6 and HO2 atoms to Na\(^+\) and Cl\(^-\) ions separations, respectively). Data is presented for the {110} surface. Based on Figs. 4 and SI Fig. S4, on the {110} surface, both Na\(^+\) and Cl\(^-\) bind clearly and have both a direct contact and shared water binding configuration for the examined sites. The data at each separation has been calculated keeping the ion fixed by the umbrella sampling protocol for the corresponding window. The data thus corresponds to a mean number density over 5 ns simulation time period. Simulation protocols are detailed in the SI.

A highly ordered first hydration shell and a less ordered second hydration shell can be clearly seen in the data irrespective of reference atom-ion separation distance. As expected, the first hydration shell thus is more strongly bound, has higher organization, and also slower exchange kinetics with bulk water molecules. More interestingly, ion adsorption changes the orientation of the water molecules in the hydration shell at the surface. This is clearly visible in the data of Fig. 6: water molecules at the binding site are oriented opposite to those in the hydration shell of the adsorbing ion. This means that upon ion adsorption, reorganization of the water shell takes place, contributing to entropy change in binding, but also the PMF curves.

Considering the examined ions and their binding site chemistry, ion binding is expected to occur as solvent separated (Bruce et al. 2020; Jungwirth and Tobias 2002). However, also direct contact with hydroxyl group can exist, especially under incomplete hydration or at high local ion concentrations (Hou et al. 2017).

At ion-reference atom separation of 0.5 nm the secondary hydration shells of the binding reference atom and the ion overlap for both Na\(^+\) and Cl\(^-\) ion. For Na\(^+\) ions the data shows a clear change in hydration shell ordering because of this. In practice, the ion carries with it a layer of significantly ordered water close to the surface which imposes enhanced order to the water locally at the binding site. This binding of the ion to O6 via water bridging also corresponds to the first PMF minima for Na\(^+\) on {110} surface in Fig. 4. The second, lower energy PMF minimum corresponds to complete overlap of the ion and binding site hydration shells. As a result, the Na\(^+\) ion expands and strengthens the hydration shell of the primary hydroxyl group when binding to O6 atoms. Molecular configurations for the ions at different sites are visualized as SI Fig. S4.

On the other hand, the secondary hydroxyl groups of cellulose (O2-HO2, O3-HO3) have weaker hydration shells than the primary hydroxyl group (O6-HO6) (Glasser et al. 2012). Indeed, the simulation data shows the hydration shell for HO2 appears clearly only when Cl\(^-\) is relatively distanced from the surface. The Cl\(^-\) ion, at separations corresponding to the binding distances, disrupts the hydration shell without similar synergestic effect as with the Na\(^+\) ion. However, the presence of the Cl\(^-\) ion pushes the ordered water further from the surface, creating a protrusion on the surface.

In conclusion, the water orientation and layering analyses reveal that the adsorption of ions to the secondary hydroxyl group significantly changes both the structure and the surface protrusion of ordered water in the vicinity of the hydroxyl group. Additionally, the hydrophilicity of the surface increases. A direct consequence is that ions with larger hydration shells should cause a more pronounced effect on the rheological properties of cellulose materials. Furthermore, the response should be more sensitive to anions since the anion hydration shell is likely to have more significant changes. Naturally, for large and soft ions, this deduction becomes less evident. Regardless, for monovalent salts, these basic deductions are consistent with the responses reported based on rheology characterization in our previous work (Arola et al. 2022). In Ref. Arola et al. (2022), we indeed showed that the effect of salt on the rheological response of CNF gel depends on the type of salt. For example, NaI salt where I\(^+\) has a larger hydrated solvation shell than Cl\(^-\) (Bauer and Patel 2010), the transition of the gel state occurs at a lower salt concentration than with NaCl. Other monovalent salts examined in the work follow. However, it is important to note that the Na\(_2\)SO\(_4\) salt makes an exception to the observed trend, and cannot be considered in terms of these simple considerations. Na\(_2\)SO\(_4\) had a smaller effect than the respective monovalent salts despite the divalent, large size anion (Arola et al. 2022). The deviation can be explained by considering the complex structure of sulfate anion, multiple ionization states, and the high hydration enthalpy which all can be expected to influence surface interactions.

Conclusions

We used atomistic MD simulations to examine the interactions of monovalent ions, in particular NaCl, with cellulose surfaces. Ion adsorption to surface structure-dependent, specific binding sites is energetically favorable at all examined different CNC model surfaces. However, the energy gain due to the adsorption of the ion remains below or comparable to \(k_{\text{B}}\)T in most examined cases. Resulting ion adsorption remains weak but finite. Preferential binding of the ions is at most examined locations solvent separated but the monovalent ion at the surface can also form direct contact with the hydroxyl groups, especially in confined binding locations.

Solvent-separated binding involves the binding site and the ion sharing their hydration shells which can have both a constructive and destructive effect on the water ordering. Regardless, total water ordering increases in the vicinity of an ion bound to the surface. Additionally, the ordered water extends further to the solution from the CNC model surfaces. Throughout, the response is dependent on the surface facet chemical structure and hydration shell structure. These are mainly determined by the distribution and orientation of hydroxyl groups on the surfaces: in terms of ion binding, Na\(^+\) ions prefer the more exposed primary hydroxyl groups but the Cl\(^-\) ions locate mainly near the secondary hydroxyl groups. This is because they are able to form contacts with several binding sites on the cellulose surface, making such binding energetically favorable. Such differences in ion binding configurations rise from both ion size and hydration shell structure, see e.g. Eneh et al. (2022)

An analysis of the density profiles and the distribution of the adsorbed ions showed that although some of the ions reside at the cellulose surfaces, the total surface charge resulting from the adsorbed ions remains practically zero. This points toward long-range electrostatic interactions between CNFs through the charge created by adsorbed ions being unlikely to rise. However, the adsorbed ions significantly change the water ordering in the interfacial region around the adsorbed ions. Additionally, the water ordering protrudes to a larger separation distance from the surface, mediated by the ion. Furthermore, any adsorbed ions make the cellulose surface more hydrophilic and have more exposed regions with ordered water. This connects with the high salt sensitivity of CNF hydrogel rheological characteristics (Arola et al. 2022). Furthermore, the observations set local hydration and ordering of the hydration layers as a key factor to cellulose materials response. The ion-induced enhancement of the cellulose hydration layer leads to a strengthening of the interaction between cellulose fibers. In consequence, this changes the rheological properties of the cellulose hydrogel, driving for crowding of the gels (Arola et al. 2022). Additionally, the molecular mechanism of the salt sensitivity here aids in explaining the salt species dependency of the viscosity response shown previously (Arola et al. 2022). Namely, the adsorbed ions with more exposed and ordered hydration shells can be expected to give rise to a more pronounced effect. Together, the presented conclusions on hydration shell importance in the salt response of cellulose materials set both water and the added salt species as means to fine-tune the material’s properties.