General relativistic effects acting on the orbits of Galileo satellites

Abstract

The first pair of satellites belonging to the European Global Navigation Satellite System (GNSS)—Galileo—has been accidentally launched into highly eccentric, instead of circular, orbits. The final height of these two satellites varies between 17,180 and 26,020 km, making these satellites very suitable for the verification of the effects emerging from general relativity. We employ the post-Newtonian parameterization (PPN) for describing the perturbations acting on Keplerian orbit parameters of artificial Earth satellites caused by the Schwarzschild, Lense–Thirring, and de Sitter general relativity effects. The values emerging from PPN numerical simulations are compared with the approximations based on the Gaussian perturbations for the temporal variations of the Keplerian elements of Galileo satellites in nominal, near-circular orbits, as well as in the highly elliptical orbits. We discuss what kinds of perturbations are detectable using the current accuracy of precise orbit determination of artificial Earth satellites, including the expected secular and periodic variations, as well as the constant offsets of Keplerian parameters. We found that not only secular but also periodic variations of orbit parameters caused by general relativity effects exceed the value of 1 cm within 24 h; thus, they should be fully detectable using the current GNSS precise orbit determination methods. Many of the 1-PPN effects are detectable using the Galileo satellite system, but the Lense–Thirring effect is not.

Introduction

General relativity (GR) predicts a number of effects that could not be explained by the classical Newtonian theory of gravity. These include, e.g., deflection of light, Shapiro time delay of light, gravitational waves, time dilation, and effects explaining the peculiar motion of celestial bodies (Einstein et al. 1938; Will 2014). The relativistic effects acting on Earth-orbiting satellites can be considered as perturbations of the Keplerian motion. The masses of artificial satellites are negligible with respect to the mass of the central body, the velocities of artificial Earth satellites are much smaller than the speed of light ($v^2/c^2<6.8\cdot 10^{-10}$), the size of the Earth and the satellite heights are much larger than the Earth’s Schwarzschild radius; all of which allow for a simplification of the GR effects in the post-Newtonian approximation (PPN). The orbital perturbations are sought to be small deviations from the motion predicted by the classical celestial mechanics (Beutler 2004). The perturbations include secular effects, such as drifts of Keplerian elements describing the orientation of the orbit in the pre-defined reference frame; periodic variations of the Keplerian elements with the typical period of once per satellite revolution of its $n{\mathrm{th}}$ harmonics; and small constant offsets of the Keplerian elements, such as a reduction of the satellite semi-major axis. So far, only the secular GR orbit perturbations were vastly discussed, whereas the remaining effects, i.e., periodic variations and constant offsets of Keplerian parameters, are not discussed in the literature in detail.

The very first test of the GR effects on orbits was conducted by Albert Einstein, who considered Mercury as the test body moving in a gravitational field of the Sun, explaining the observed secular drift of the Mercury’s periapsis (Einstein 1915). The anomaly in Mercury’s orbit discovered by Le Verrier in 1859 could better be explained by GR than some other theories, including the existence of a new planet Vulcan near the Sun. Much later, the secular drifts of Keplerian orbital parameters explained by GR were detected in pulsar (Kopeikin and Potapov 1994; Will 2018), Lunar (Williams et al. 1996, 2004), Martian (Konopliv et al. 2011), and Mercury’s (Imperi and Iess 2017) orbits. Artificial Earth satellites, such as LAser GEOdynamic Satellites (LAGEOS-1 and -2) (Ciufolini et al. 1998; Ciufolini and Pavlis 2004; Iorio 2003; Lucchesi 2003; Lucchesi and Peron 2010), LAser RElativistic Satellite (LARES-1) (Ciufolini et al. 2016; Roh et al. 2016; Paolozzi and Ciufolini 2013), and Gravity Probe B (Everitt et al. 2011; Will 2011; Everitt et al. 2015) were employed for testing secular behavior of Keplerian parameters. Testing of GR effects acting on artificial satellite orbits is possible using the current high-accuracy observational techniques that allow for mm-accuracy satellite tracking, such as Satellite Laser Ranging (SLR, Pearlman et al. 2019) and L-band Global Navigation Satellite Systems (GNSS, Teunissen and Montenbruck 2017). In 2021, a new satellite mission—LARES-2—is going to be launched with the primary goal of the verification of GR effects together with LAGEOS-1/2 and LARES-1 observed by SLR stations (Paolozzi et al. 2019; Ciufolini et al. 2017c, b). The secular motion of LARES-2 orbital parameters will be compared and combined with those of LAGEOS-1 to verify GR effects with unprecedented accuracy.

Ashby (2003) discussed GR effects on GNSS signal propagation, frequency shift, reference frames, satellite clocks, and time systems. Kouba (2004, 2019) discussed the GNSS clock effects for satellites including Galileo E14 and E18 (Delva et al. 2018; Herrmann et al. 2018). However, the impact on satellite orbits, particularly how the shape and size of satellite orbits vary due to GR, has not been discussed as yet.

The first pair of Fully Operational Capability (FOC) European GNSS—Galileo, E14 and E18, was accidentally launched into highly eccentric orbits on August 22, 2014 (Sośnica et al. 2018; Hadas et al. 2019). Instead of reaching the circular orbit at the altitude of 23,225 km above the Earth’s surface with an inclination of $56^\circ$ and a revolution period of 14$^h$05$^m$, the satellites ended at heights between 17,180 and 26,020 km with an inclination of $50^\circ$ and a revolution period of 12$^h$56$^m$. Despite that the usefulness of these satellites for navigation is limited, these can be used for the verification of the effects emerging from general relativity due to the variable distance from the Earth, high-quality onboard hydrogen masers, and rubidium atomic clocks (Delva et al. 2018; Herrmann et al. 2018), as well as two independent techniques for orbit determination: GNSS and SLR.

The goal of this paper is to describe the effects emerging from general relativity acting on Galileo orbits and to compare how well the first-order PPN perturbations approximate the orbital perturbations derived from numerical solutions. We discuss the perturbations of Keplerian elements and changes in the satellite angular momentum, velocity, mean motion, and orbital heights. We also derive the mean offsets of the semi-major axis and the value of the change of the revolution period due to the main three effects emerging from GR—the Schwarzschild, Lense–Thirring, and de Sitter effects. We concentrate on practical aspects of GR effects acting on GNSS satellites focusing on those effects that are important for the precise orbit determination of 1-day orbital arcs considering the current accuracy of GNSS-derived orbits at several mm-level.

General relativistic effects acting on artificial Earth satellites

From the practical point of view, the main effects emerging from GR in the geocentric reference frame acting on Earth-orbiting satellites can be approximated by three constituents—the Schwarzschild effect, Lense–Thirring or frame-dragging effect, and de Sitter or geodetic precession effect (Huang et al. 1990). Only these three GR effects are recommended for precise orbit determination for Earth satellites in the Conventions of the International Earth Rotation and Reference Systems Service (IERS, Petit and Luzum 2010).

The relativistic corrections to the accelerations of Earth satellites of negligible masses in a PPN system written in a local inertial geocentric coordinate system that is kinematically nonrotating read as (Brumberg and Kopeikin 1989):

$$\begin{aligned} \begin{aligned} \varDelta \ddot{\mathbf {r}}&= \frac{G M}{c^{2} r^{3}}\left\{ \left[ 2(\beta +\gamma ) \frac{G M}{r}-\gamma \dot{\mathbf {r}} \cdot \dot{\mathbf {r}}\right] \mathbf {r}+2(1+\gamma )(\mathbf {r} \cdot \dot{\mathbf {r}}) \dot{\mathbf {r}}\right\} \\&\quad +(1+\gamma ) \frac{G M}{c^{2} r^{3}}\left[ \frac{3}{r^{2}}(\mathbf {r} \times \dot{\mathbf {r}})(\mathbf {r} \cdot \mathbf {J})+(\dot{\mathbf {r}} \times \mathbf {J})\right] \\&\quad +\left\{ (1+2 \gamma )\left[ \dot{\mathbf {R_{S}}} \times \left( \frac{-G M_{S} \mathbf {R}_{\mathbf {S}}}{c^{2} R_{S}^{3}}\right) \right] \times \dot{\mathbf {r}}\right\} , \end{aligned} \end{aligned}$$

(1)

where GM is the standard Earth gravitation product; $GM_S$ is the standard Sun gravitation product; $\beta , \gamma$ are PPN parameters equal to 1 in GR; c is the speed of light; $\mathbf {r}$, $\dot{\mathbf {r}}$ are the position and velocity of a satellite with respect to the geocenter; $\mathbf {R_{S}}$, $\dot{\mathbf {R_{S}}}$ are the position and velocity of the Earth with respect to the Sun; $\mathbf {J}$ is Earth’s angular momentum per unit mass.

The first line describes the so-called Schwarzschild term (Schwarzschild 1916, 2003), the second is the frame-dragging gravitomagnetic Lense–Thirring effect (Lense and Thirring 1918), whereas the third corresponds to the de Sitter effect (De Sitter 1917). Other relativistic effects are related to, e.g., other celestial bodies, which can be approximated as small corrections to the non-relativistic tidal forces, Thomas precession, or Earth’s oblateness quadruple term; however, they are currently not considered in the precise GNSS orbit solutions, due to their very small magnitudes (Huang et al. 1990; Brumberg and Kopeikin 1989; Soffel 2000; Damour et al. 1991).

Early attempts to write the equations of a satellite in the geocentric coordinates were based on using the Einstein–Infeld–Hoffman equations of motion written in the barycentric coordinates of the solar system with the origin taken at the geocenter. These equations have quite a number of relativistic terms which stem from the fact that the geocentric coordinates built in this way, are not locally inertial. Brumberg and Kopeikin (1989) showed how to eliminate all these relatively large ‘non-inertial’ relativistic effects from the geocentric equations of Earth’s satellites.

The GR effects in the form as in Eq. (1) are valid for geocentric reference frames and Earth-orbiting satellites. For lunar laser ranging, the geocentric coordinates are physically relevant as they allow excluding spurious relativistic effects from the orbital motion of the Moon which are pretty large numerically but not observable in practice because they are produced by nonvanishing Christoffel symbols in the barycentric coordinates (Kopeikin and Xie 2010). For the interplanetary ranging, it is more convenient to use the barycentric coordinates, whereas for very long baseline interferometry, the geocentric coordinate system must be used along with the barycentric coordinates (Soffel et al. 2017). Ries et al. (1988) compared the determined Earth satellite orbits in the geocentric and barycentric reference frames and confirmed their equivalence provided that the proper transformation of the time, scale (signal propagation), and motion between frames are considered.

Keplerian orbits and perturbations

The geometry of the satellite orbit at a particular epoch can be described by two Keplerian osculating elements: the semi-major axis a and eccentricity e. Another three Keplerian elements describe the orientation of the orbital planes in 3D space: the argument of perigee $\omega$, the right ascension of ascending node $\varOmega$, and the inclination i, whereas the mean anomaly $\nu$ describes the instantaneous position of a satellite. When any perturbing force acts on a satellite, Keplerian parameters are subject to changes caused by forces acting in the radial R, along-track S, and cross-track W orbital directions (or $\mathbf {e_R}$, $\mathbf {e_S}$, $\mathbf {e_W}$ directions). The first-order perturbations of Keplerian parameters can be derived on the basis of the Gaussian or Lagrangian perturbation equations, however, the latter assumes that the forces must be conservative.

Fig. 1

Accelerations acting on Galileo on the eccentric orbit due to the Schwarzschild effect in $m \, s^{-2}$. The magnitude of the effect depending on satellites position is denoted using the color bar, whereas the directions of the accelerations are denoted by arrows. Note that the Schwarzschild effect causes an outward radial acceleration

Fig. 2

Accelerations acting on Galileo on the eccentric orbit due to the de Sitter effect in $m \, s^{-2}$. The magnitude of the effect depending on satellites position is denoted using the color bar, whereas the directions of the accelerations projected onto the orbital plane are denoted by arrows

Fig. 3

Accelerations acting on Galileo on the eccentric orbit due to the Lense–Thirring effect in $m \, s^{-2}$. The magnitude of the effect depending on satellites position is denoted using the color bar, whereas the directions of the accelerations projected onto the orbital plane are denoted by arrows

The Schwarzschild accelerations on Galileo E14 range between $123.3 \cdot 10^{-12}$ and $388.3 \cdot 10^{-12}$ m$\cdot$s$^{-2}$, see Fig. 1. The de Sitter accelerations are between $-5.6 \cdot 10^{-12}$ and $-25.3 \cdot 10^{-12}$ m$\cdot$s$^{-2}$, whereas Lense–Thirring are between $0.7 \cdot 10^{-12}$ and $4.6 \cdot 10^{-12}$ m$\cdot$s$^{-2}$. Hence, for Galileo satellites, the Schwarzschild and de Sitter accelerations introduce stronger perturbations than the Lense–Thirring effect by two and one order of magnitude, respectively. In the radial direction, Schwarzschild and Lense–Thirring introduce outward accelerations from the perspective of the geocenter, thus in the opposite direction as the Newtonian accelerations, whereas the de Sitter accelerations are pointed toward the geocenter. The sign of the accelerations in the radial direction can be opposite for satellites with different inclination angles and a different orientation with respect to the Sun. However, all GNSS satellites have inclinations below $67^\circ$ and thus, the directions of the accelerations from Figs. 1, 2, and 3 are valid for all GNSS satellites. A special case of other satellites with higher inclinations angles is discussed in the last section.

For a circular orbit, the Schwarzschild effect introduces only the acceleration in the radial direction $\mathbf {e_R}$, whereas $\mathbf {e_S}$ and $\mathbf {e_W}$ are equal to zero. For a noncircular orbit, accelerations acting on the along-track $\mathbf {e_S}$ and the radial $\mathbf {e_R}$ components occur, whereas the cross-track component $\mathbf {e_W}=0$ (Roh et al. 2016). Such an acceleration makes the Schwarzschild effect change the size a and shape e of the orbit as well as the in-plane orientation $\omega$, whereas it cannot change the cross-track components, such as the ascending node $\varOmega$ and inclination i.

De Sitter and Lense–Thirring change all Keplerian parameters, as the accelerations act in all orbital directions. Lense–Thirring depends on the orientation of the Earth’s angular momentum vector $\mathbf {J}$, whereas de Sitter depends on the geocentric position and velocity of the Sun $\mathbf {R_{S}}$, $\dot{\mathbf {R_{S}}}$ with respect to the position and velocity of a satellite and can be explained as a change induced in a vector by parallel transport. Figure 2 shows that the accelerations caused by the de Sitter effect are almost constant, pointing toward the central body when projected onto the orbital plane. However, from the color bar, it is clear that the accelerations vary by a factor of three during one revolution. The Lense–Thirring effect depends not only on the relative orientation between $\mathbf {J}$ and the satellite state vector but also on the distance between the satellite and the geocenter, see Fig. 3.

Fig. 4

Accelerations acting on Galileo E14 satellite due to a the Schwarzschild, b de Sitter, and c Lense–Thirring effects decomposed into the radial, along-track, and cross-track components in $m \, s^{-2}$

De Sitter and Lense–Thirring introduce none or very small along-track accelerations, depending on the orbital eccentricity. The cross-track component dominates for the De Sitter and Lense–Thirring effects for satellites with high inclination angles, thus including all GNSS satellites in medium orbits. In contrast, for satellites orbiting in the equatorial plane, such as geostationary satellites, the accelerations in the radial component dominate. Hence, for Galileo in eccentric orbits, no cross-track Schwarzschild accelerations and negligible along-track accelerations due to the de Sitter and Lense–Thirring effects are expected. On the contrary, the radial accelerations dominate due to the Schwarzschild effect, and the cross-track accelerations dominate due to de Sitter and Lense–Thirring with the maximum absolute value in the perigee, see Fig. 4.

Methods of analysis

The goal of this study is to provide a comprehensive study on the impact of GR effects on Earth-orbiting satellites. We selected Galileo satellites because their positions can be determined with the highest, several millimeter accuracy, to date (Bury et al. 2020). Galileo satellites are equipped with two independent techniques for precise orbit determination: laser retroreflectors for SLR and L-band transmitters of GNSS signals that are tracked by hundreds of globally distributed GNSS stations (Zajdel et al. 2019; Bury et al. 2019). Detection of sub-daily anomalies in Earth rotation of several $\upmu as$ (microseconds of an arc) corresponding to a few millimeters has been confirmed when using Galileo satellites and a number of more than 100 tracking stations (Zajdel et al. 2021). Moreover, the stability of the determination of the length-of-day excess is 14 times more stable in time when based on Galileo than when based on the GPS constellation, because of the deep resonance 2:1 between GPS satellite revolution periods and Earth rotation (Zajdel et al. 2020). Therefore, we search for millimeter-sized relativistic effects that can be detected using the current accuracy of Galileo orbit determination (Katsigianni et al. 2019; Bury et al. 2021).

We conduct numerical simulations of the Galileo satellite orbits assuming no GR effects by excluding one or all out of the Schwarzschild, Lense–Thirring, and de Sitter effects and a simulation of the Galileo orbits assuming all GR effects. The orbit integration is conducted for satellite positions and velocities with a step of 0.5 s in 24 h intervals. For each epoch, we derive the osculating Keplerian orbit parameters and some derivative orbit characteristics, such as velocity, areal velocity, mean motion, angular momentum, revolution period, and satellite height. The simulated values of Keplerian parameters and orbit characteristics are then compared to the expected effects derived from the first-order Gaussian orbit perturbations.

The first-order Gaussian orbit perturbations for the periodic and secular perturbations can be found in the literature. The constant offset of the semi-major axis has been derived in this study and confirmed by simulated values.

Fig. 5

Satellites from the GPS (blue), GLONASS (red), and Galileo (green) constellations as a function of the inclination angle and the height difference between perigee and apogee

The first-order Gaussian perturbation equations describing the changes of the six Keplerian parameters due to the accelerations in the radial R, along-track S, and cross-track W directions read as (Kopeikin and Potapov 1994; Beutler 2004):

$$\begin{aligned} \begin{aligned} \dot{a}&=\sqrt{\frac{p}{G M}} \frac{2 a}{1-e^{2}}\left[ e \sin \nu \cdot R+\frac{p}{r} \cdot S\right] \\ \dot{e}&=\sqrt{\frac{p}{G M}}[\sin \nu \cdot R+(\cos \nu +\cos E) \cdot S] \\ \dot{i}&=\frac{r \cos u}{n a^{2} \sqrt{1-e^{2}}} \cdot W \\ \dot{\varOmega }&=\frac{r \sin u}{n a^{2} \sqrt{1-e^{2}} \sin i} \cdot W \\ \dot{\omega }&=\frac{1}{e} \sqrt{\frac{p}{G M}}\left[ -\cos \nu \cdot R+\left( 1+\frac{r}{p}\right) \sin \nu \cdot S\right] -\dot{\varOmega } \cos i \\ \dot{M}_{0}&=\frac{1-e^{2}}{n a e}\left[ \left( \cos \nu -2 e \frac{r}{p}\right) \cdot R-\left( 1+\frac{r}{p}\right) \sin \nu \cdot S\right] -\frac{3 n}{2 a}\left( t-t_{0}\right) \dot{a}, \end{aligned} \end{aligned}$$

(2)

where p denotes the semi-latus rectum $p=a(1-e^2)$, n is the mean motion, $M_0$ denotes the initial mean anomaly, E is the eccentric anomaly, $\nu$ is the true anomaly. Here, we concentrate on the five Keplerian parameters, as the geometrical interpretations of the $M_0$ changes are derivatives with respect to other Keplerian parameters and have a secondary meaning. Instead of $M_0$ changes, we discuss the difference in the satellite mean motion, velocity, and the revolution period.

Fig. 6

Satellites from the GPS (blue), GLONASS (red), and Galileo (green) constellations as a function of the argument of latitude and the range between perigee and apogee

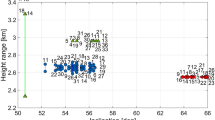
Figures 5 and 6 show satellites from three GNSS constellations: GPS, GLONASS, and Galileo, as a function of the inclination angle, the argument of latitude, and the height difference between perigee and apogee. The Galileo satellites in nominal orbits have the most circular orbits out of all constellations, whereas the eccentric orbits have the most considerable differences between the heights in the perigee and apogee. Therefore, Galileo in eccentric orbits and nominal orbits represent good proxies of extreme cases of existing high and low-eccentric satellites with different inclination angles. In this paper, we search for the GR effects in satellite orbits that can potentially be detected using real observations.

Table 1 Initial values of osculating orbital elements used in numerical simulations

Table 1 provides the initial orbit parameters used in the simulations. The values of a, e, i are taken from real orbit solutions, whereas $\omega$ and $\nu _0=u_0$ are assumed to be zero to better capture the initial position phase of satellites, whereas $\varOmega$ assumes nonzero values to avoid similarities in the estimation of some osculating Keplerian parameters. The initial orbit parameters are corrected for the mean offsets emerging from GR effects by the values derived in this paper. All numerical constants describing the standard gravitational parameters of the Earth, the Sun, Earth’s angular momentum, the position of the Sun, astronomical unit, obliquity of the Earth’s axis with respect to the ecliptic, and the eccentricity of the Earth’s orbit are taken from the IERS Conversions 2010 (Petit and Luzum 2010).

Schwarzschild effect

Semi-major axis changes due to Schwarzschild term

The first-order Gaussian perturbations can be used for deriving periodic perturbations and secular variations of the Keplerian elements. However, the constant offsets which are the integration constants cannot be derived based on Gaussian perturbation equations. Therefore, we will begin with the classical celestial mechanics equations for deriving the offsets of Keplerian parameters.

Considering Kepler’s law $GM=a^3n^2$, where n is the mean motion, and assuming that GM is constant whereas n and a are subject to change due to perturbing accelerations, the effect of the relative change of semi-major axis a and mean motion n equals:

$$\begin{aligned} \frac{\varDelta n}{n} = -\frac{3}{2} \frac{\varDelta a}{a}. \end{aligned}$$

(3)

From the first-order orbit perturbations, any acceleration acting on a satellite in the radial direction $R_0$ changes the mean motion n by (Beutler 2004):

$$\begin{aligned} \varDelta n = \frac{2}{na} R_0. \end{aligned}$$

(4)

Considering Eqs. (4) and (3), we may conclude that any radial acceleration $R_0$ changes the semi-major axis by:

$$\begin{aligned} \varDelta a = -\frac{4}{3} \frac{a^3}{GM} R_0 \end{aligned}$$

(5)

which will be useful not only for the Schwarzschild effect but also for studying the impact of the Lense–Thirring and de Sitter effects on satellite orbits.

The Schwarzschild acceleration acting on a satellite in a circular orbit introduces a constant radial acceleration:

$$\begin{aligned} R_{Sch}=\mathbf {e}_{R} \cdot \varDelta \ddot{\mathbf {r}}_{\mathrm {Sch}}=3 \frac{(G M)^{2}}{c^{2} a^{3}}. \end{aligned}$$

(6)

Substituting $R_0$ in Eq. (5) by the Schwarzschild term $R_{Sch}$ from Eq. 6, one obtains the final equation of the change of the osculating semi-major axis for circular orbits due to the Schwarzschild term:

$$\begin{aligned} \varDelta a_{Sch} = -4 \frac{GM}{c^2} = - 17.74 \, mm . \end{aligned}$$

(7)

The change of the semi-major axis is thus independent of the satellite height for all circular orbits. Interestingly, the change of the semi-major axis due to the Schwarzschild effect is exactly twice larger than the Schwarzschild radius defining the event horizon for the Earth of a Schwarzschild black hole (Schwarzschild 1916).

Here, we assume that the GM value is the same in the classical theory of gravity as well as in GR. The constant offset would be different if we allow the gravitational constant G to change, as considered by Hugentobler (2008), who assumed that the mean motion n is unchanged, whereas the GM and a differ between Newtonian and post-Newtonian motion of Earth satellites. However, this assumption does not hold as we expect changes of the mean motion due to GR.

Fig. 7

Semi-major axis change of E14 (total effect) due to the Schwarzschild acceleration as a function of a time and b the satellite height for E14 in an elliptical orbit and c for E08 in a circular orbit. The initial point coincides with the orbit’s perigee

For noncircular orbits, the change of the semi-major axis consists of two parts—a constant offset and periodic variations:

$$\begin{aligned} \varDelta a_{Sch}^{Tot}= \varDelta a_{Sch} + \varDelta a _{Sch}. \end{aligned}$$

(8)

The periodical component can be derived on the basis of Gaussian first-order perturbations on the basis of radial and along-track accelerations and can be expressed as a function of the argument of latitude u:

$$\begin{aligned} \varDelta a _{Sch}= -14 \frac{ GM e }{c^2 (1-e^2)^2} \cos u , \end{aligned}$$

(9)

or, to a higher-order:

$$\begin{aligned} \varDelta a _{Sch}= \frac{ GM }{c^2 (1-e^2)^2} [(-14-6e^2)e \cos u -5e^2\cos 2u], \end{aligned}$$

(10)

which agrees with the formula derived by Kopeikin et al. (2011) for extragalactic pulsars, when neglecting the contribution of the second celestial object. The sum of the constant offset and periodical variations describes the evolution of osculating, that is short-term, semi-major axis variations. It is worth noting that the Schwarzschild acceleration changes as $r^{-3}$ with the height (when assuming $r=a$), whereas the Newton’s acceleration changes as $r^{-2}$, hence both effects can be easily separated for elliptical orbits. In contrast, for circular orbits, the Schwarzschild effect can be explained by a slight modification of the GM value. For elliptical orbits, the change as $r^{-3}$ with the height is only an approximation because Schwarzschild introduced the along-track accelerations and cannot be considered as a central force.

Figure 7 shows the change of the semi-major axis of E14 as a function of time derived from the numerical simulations and the first-order perturbations based on Eqs. (8) and 10. The discrepancies between the simulated and approximated values are caused by $O(c^{-4})$ limitation and neglecting the higher-order perturbations of Keplerian elements, assuming that all other elements are constant. In numerical simulations, we allow all Keplerian elements to change simultaneously. The discrepancies disappear for circular orbits, because then, only the constant offset of the semi-major axis of $- 17.74 \, mm$ occurs with no periodic variations dependent on e.

For Galileo E14 (and for E18, which is not shown here because the results are the same), the total change of a from the simulation is $-29.02$ mm in perigee and $-8.65$ mm in apogee, which gives the difference more than 20 mm, thus, fully detectable using current techniques of GNSS precise orbit determination (Bury et al. 2020). Please note that the orbit becomes smaller with the largest magnitude in the perigee and the smallest in the apogee due to the Schwarzschild term. For high-eccentric Earth satellites with a large value of e, such as the Laser Ranging Equipment (LRE) with $e=0.73$, the offset of a could even be positive in the apogee.

Eccentricity changes due to Schwarzschild term

Fig. 8

Eccentricity changes due to the Schwarzschild acceleration as a function of time for a E14 and b E08. The initial point coincides with the orbit’s perigee

The eccentricity changes due to the Schwarzschild term described by Gaussian first-order perturbations. After integrating Eq. (2) over t-dependent values with $u=n(t-t_0)=n \varDelta t$ where $t_0$ is the reference epoch, the final equation for the eccentricity changes includes only periodical variations and reads as follows:

$$\begin{aligned} \varDelta e_{Sch}= -3\frac{GM}{c^2 a (1-e^2)}\cos u \end{aligned}$$

(11)

and when also considering higher-order $e^2$ and $e^4$ contributions (Kopeikin and Potapov 1994):

$$\begin{aligned} \varDelta e_{Sch}= -\frac{GM}{c^2 a e (1-e^2)}[(3+7e^2)e\cos u+\frac{5}{2}e^2 \cos 2u]. \end{aligned}$$

(12)

Figure 8 shows that the first-order approximations from Eq. (12) describe the majority of orbital eccentricity changes, however, for elliptical orbits of E14, the approximations are overestimated in apogee, whereas for the circular orbit of E08, a small shift in phase occurs with a proper value of the overall amplitude. The periodical changes of the orbital eccentricity are similar, even though the initial value of the E14 eccentricity was $e=0.1612$ and for E08 $e=0.0001$. The eccentricity changes in the perigee and apogee have opposite signs for both the eccentric and circular orbits.

For Galileo satellites in eccentric orbits, the change of the semi-major axis is negative in the perigee and the apogee, with the maximum change in the perigee. However, the size of the orbit is always reduced. The change of eccentricity is negative in the perigee, which implies a more circular orbit as the perigee goes higher, and positive in the apogee, which implies a more eccentric orbit, as the apogee also goes higher from the geocenter perspective. The Schwarzschild term changes the shape and the size of the orbit instantaneously in opposite directions. When using the chosen parameterization and the nonrotating geocentric frame, the Schwarzschild effect translates the circular orbits and elliptical orbits into irregular curves, as shown in Fig. 9.

Fig. 9

Comparison between E14 orbit without and with the Schwarzschild accelerations with the exaggeration of the total displacement effect in the geocentric reference frame

Revolution period and velocity

The revolution period T of an Earth-orbiting satellite can be described as:

$$\begin{aligned} T= \frac{2 \pi }{n}, \end{aligned}$$

(13)

where n denotes the mean motion. Estimating the mean motion for each epoch, one obtains the ‘osculating’ mean motion and the ‘osculating’ revolution period, whereas, from the first-order perturbations based on Eq. (4), one obtains the constant change of n:

$$\begin{aligned} n_{Sch}=\left( \frac{GM}{a^3} \right) ^{1/2} \left( 1+\frac{6 GM}{c^2a} \right) \end{aligned}$$

(14)

and when considering higher-order $e^2$ and $e^4$ contributions:

$$\begin{aligned} n_{Sch}=\left( \frac{GM}{a^3} \right) ^{1/2} \left( 1+\frac{GM}{2c^2a(1-e^2)^2}[12-21e^2-6e^4] \right) . \end{aligned}$$

(15)

The mean motion change translates into a change of $\varDelta T=-44.552$ $\upmu s$ of the revolution period with a change in a range between $-72.449$ and $-21.569$ $\upmu s$ for Galileo E14, see Fig. 10. This means that the revolution period under the Schwarzschild acceleration is shorter than under the Keplerian motion with the maximum change in the perigee and the minimum change in the apogee.

Fig. 10

Impact of the Schwarzschild term on the a revolution period, b areal velocity, and c linear velocity of E14. The velocities are neither corrected by the change of the mean anomaly nor by the secular drift of perigee. Blue lines correspond to the numerical simulations, whereas red lines correspond to approximations based on Eqs. (15) and (17)

According to the second Kepler’s law, the angular momentum and the areal velocity A are constant over time in the solution of the two-body problem. The areal velocity can be defined as

$$\begin{aligned} A= \frac{1}{2} |\mathbf {h}| = \frac{1}{2} | \mathbf {r} \times \dot{\mathbf {r}}|, \end{aligned}$$

(16)

where $\mathbf {h}$ is the angular momentum of a satellite.

The length of the angular momentum vector, as well as the areal velocity vary in time. When considering the mean term, we obtain:

$$\begin{aligned} |\mathbf {h}_{Sch}|=\left[ GM a (1-e^2) \right] ^{1/2}\left[ 1-\frac{GM}{2c^2a} + \frac{4GM}{c^2a(1-e^2)} \right] . \end{aligned}$$

(17)

Figure 10 shows a comparison between the ‘osculating’ areal velocity derived from numerical simulations and the mean change based on Eq. (17). During the satellite revolution, the position and velocity vectors change their lengths, as well as the mutual orientation; however, the temporal variations of the product $| \mathbf {r} \times \dot{\mathbf {r}}|$ are regular. For circular orbits, A is changed by a constant offset described by Eq. 17, but the angular momentum and energy are conserved. For elliptical orbits, the second Kepler’s law does not hold, and the temporal A variations are similar to those of the temporal a variations.

The Schwarzschild effect acts as a $r^{-3}$ term for circular orbits, which is a modification to the Newtonian $r^{-2}$ central force. Kepler’s second law is equivalent to the conservation of angular momentum, and angular momentum is conserved in central forces. Thus, for circular orbits, Kepler’s second law is hold. For noncircular orbits, the Schwarzschild effect has the radial and along-track components (see Fig. 1), thus cannot be considered a central force. The angular momentum shows periodic variations and the Kepler’s second law does not hold when considering short-term variations for noncircular orbits. No secular term is included in the angular momentum changes, thus, over long periods, the angular momentum and energy are conserved, however, they vary for elliptical orbits over short periods.

The temporal changes of the length of the velocity vector also depend on the variable orientation of the perigee which results in a complicated non-periodic curve from Fig. 10c for the nonrotating reference systems as in the case of this study.

Perigee changes due to Schwarzschild term

The argument of perigee $\omega$ is the only angular Keplerian element describing the orientation of the orbit that changes due to the Schwarzschild term. To observe the secular drift of $\omega$ properly, an elliptical orbit is needed because for circular orbits $\omega$ is undefined.

The approximated value of the secular drift of perigee was derived by Einstein and equaled to:

$$\begin{aligned} \varDelta \omega _{Sch}=\frac{3GM}{c^2a(1-e^2)}n \varDelta t . \end{aligned}$$

(18)

The component $n \varDelta t = 2 \pi \frac{\varDelta t}{T}$ contains the multiple of the full angle $2 \pi$ in the radian measure. Kopeikin (2020) derived equations for the 1PN and 2PN precession of the orbital pericenter

$$\begin{aligned} \varDelta \omega _{Sch}=\frac{3GM}{c^2a(1-e^2)} n \varDelta t \left[ 1+\frac{3GM}{4c^2a(1-e^2)}-\frac{GM}{4c^2a} \right] . \end{aligned}$$

(19)

The equation gives a difference of $8.2 \cdot 10^{-11}$ with respect to the Einstein’s equation. Figure 11 compares the secular drift of perigee derived from the Einstein’s term, first-order approximation, and the calculated osculating argument of perigee from the numerical simulation. The osculating argument of perigee is subject to periodic variations because of the temporal variations of the semi-major axis, eccentricity, and the revolution period, which introduce small changes of these quantities in the same epochs when the orientation of the lines of apsides changes.

Fig. 11

Impact of the Schwarzschild term on the perigee of Galileo a E14 and b E08 from the numerical simulation (corrected by a change of the mean anomaly), first and second-order approximations, and the Einstein’s term

Interestingly, the secular rate of perigee assumes similar values for the elliptical orbit of E14 and the circular orbit of E08, see Fig. 11. For E14, the rate is 0.6327 and 0.5825 mas over one revolution period for E14 and E08, respectively, which corresponds to a change of 1.2034 and 1.0471 mas after 24 h (please note that the revolution periods for E14 and E08 are different). The perigee change of E14 due to the Schwarzschild effect over one day is 163.2 mm, which is fully detectable when using the Galileo orbit determination techniques with the accuracy at several millimeter level. However, for near-circular orbits, the argument of perigee is hardly detectable, which leads to substantial formal errors of the determined parameter. For Galileo E14, the mean formal error of perigee determination is 0.2232 mas from 1-day solutions, whereas for E08, the perigee error is 95.4684 mas (Bury et al. 2020). Thus, the formal error of E14 perigee is almost 500 more accurate than the formal error of E08 perigee. For Galileo E14, the mean formal error of perigee determination after 1 day is over 5 times smaller than the expected drift due to the Schwarzschild effect. Thus, perigee observations for eccentric Galileo can be used for the verification of GR effects. For deriving GR effects based on short arcs, the periodical variations of the perigee should also be considered, because the amplitudes have a similar order of magnitude to the observed rate.

For E14, the perigee derived from numerical simulation is also about 500 times more accurate than that for E08 due to the ambiguities in the perigee realization in near-circular orbits, which causes differences in Fig. 11 between the theoretical and simulated values for E08. Therefore, the perigee observations of eccentric orbits are much more suited for the verification of the Schwarzschild effect than near-circular orbits.

Iorio (2020) derived a secular drift of the perigee up to the second-order with periodical terms. A modified version of Iorio (2020)’s equation 23, which is multiplied by missing coefficient $n^{-3}$, reads as:

$$\begin{aligned} \begin{aligned} \varDelta \omega _{Sch}&=\frac{(GM)^2 [5(23+20e^2-4e^4)]}{2n^2c^4a^2(1-e^2)^3}\\&\quad +\frac{(GM)^2 6e[(34+26e^2)\cos u + 15e \cos (2u)] }{2n^2c^4a^2(1-e^2)^3} + O(c^{-4}). \end{aligned} \end{aligned}$$

(20)

A comparison between a modified version of Iorio’s equation and Einstein’s term for E14 is shown in Fig. 11a. For the near-circular orbit of E08, the equation does not describe well the simulated perturbations. The periodic variations can only be slightly better described when based on Iorio (2020) than the static Einstein’s term. The equation proposed by Iorio (2020) cannot be used for elliptical orbits, because it causes issues with the proper description of the secular drift, which is different than that from Eq. (19).

We can also derive, based on Gaussian equations, a more concise version of the first-order perturbations that includes the periodical perturbations:

$$\begin{aligned} \varDelta \omega _{Sch}=\frac{3GM}{c^2a(1-e^2)} \left( n \varDelta t+ \sin 2u \right) . \end{aligned}$$

(21)

The first-order perturbations are shown in Fig. 11b and compared to the perigee drift of Galileo E08 in a circular orbit. The periodic variations are well captured; however, a small shift in the rate occurs due to the uncertainties in the determination of the perigee for near-circular orbits. Nevertheless, the simple first-order perturbation equation describes well the short-term perturbations of the perigee.

De Sitter

Geodetic precession, known as the de Sitter effect or de Sitter-Fokker effect (De Sitter 1916, 1917; Ciufolini 1986b), depends on the relative position and velocity of the satellite–Earth–Sun geometry. This effect causes cross-track accelerations because the Sun does not lay in the satellite orbital plane and the maximum elevation angle of the Sun above the orbital plane $\beta _{ele}$ varies in the range $|i-\varepsilon |<\beta _{ele}<|i+\varepsilon |$ where $\varepsilon$ denotes the obliquity of Earth’s equatorial plane with respect to the ecliptic. De Sitter effect causes a precession of a local inertial, parallelly transported frame with respect to the celestial (inertial) reference frame (Ciufolini 1986a; Schäfer 2004). The precession vector $\varvec{\omega }_{dS}$ points to the southern ecliptic pole and equals

$$\begin{aligned} \varvec{\omega }_{dS}=\dot{\mathbf {R_{S}}} \times \frac{-3G M_{S} \mathbf {R_{S}}}{2c^{2} R_{S}^{3}}. \end{aligned}$$

(22)

Neglecting the variable distance between the Earth and the Sun, the de Sitter precession is equal to $\omega _{dS} = 53$ $\upmu$as/day for all objects, independently of the orbital radius in the vicinity of the Earth. Figure 2 shows that the de Sitter effect mainly causes radial and cross-track accelerations, whereas the along-track component is zero for circular orbits and very small for elliptical orbits.

The de Sitter acceleration acting on a satellite in circular orbit introduces a constant radial acceleration:

$$\begin{aligned} R_{dS}=-\frac{3G M_{S}}{{c^{2} R_{S}}} n_S \sqrt{1-e_S^2} \cos \beta _{ele}, \end{aligned}$$

(23)

where $n_S$ is the mean motion of the Sun and $e_S$ is the eccentricity of the Earth’s orbit.

Semi-major axis, eccentricity, and the revolution period

Substituting $R_0$ in Eq. (4) by the de Sitter term $R_{dS}$ from Eq. (23) and introducing the result to Eq. (3), one obtains the final equation of the change of the osculating semi-major axis for circular orbits due to the de Sitter term:

$$\begin{aligned} \varDelta a_{dS} = +4 \frac{GM_S}{c^2} \frac{a}{R_{S}} \frac{n_S}{n} \sqrt{1-e_S^2} \cos \beta _{ele}. \end{aligned}$$

(24)

or, when getting rid of the mean motion n:

$$\begin{aligned} \varDelta a_{dS} = +4 \frac{GM_S}{\sqrt{GM}c^2} \frac{a^{\frac{5}{2}}}{R_{S}} n_S \sqrt{1-e_S^2} \cos \beta _{ele}. \end{aligned}$$

(25)

Fig. 12

Impact of the de Sitter effect on the a semi-major axis, b eccentricity, c orbital height, and d revolution period of Galileo E14 from the numerical simulations (blue line) and first-order Gaussian perturbations (red line). The first-order perturbations for a are based on Eq. (24)

For Galileo in eccentric orbits, the theoretical value of the constant shift of the semi-major axis equals $\varDelta a_{dS} = + 0.459$ mm. The equation contains the mean motion term; hence, the total change of the semi-major axis depends on the initial value of a as $a^{5/2}$. For geostationary orbits with $i=0$ and $\beta _{ele}=0$, $\varDelta a_{dS} = + 4.160$ mm, whereas for the same conditions and low-Earth orbits $\varDelta a_{dS} = + 0.012$ mm. Please note that de Sitter causes a positive change of the semi-major axis for most of the Earth satellites (for which $\beta _{ele}<90^{\circ }$), thus, opposite to the Schwarzschild effect, which causes the negative change, independently of the orbital height.

The periodic variation of the semi-major axis can be expressed as:

$$\begin{aligned} \varDelta a _{dS} = -6 \frac{e}{\sqrt{1-e^2}} \frac{GM_S}{c^2R_S} n_S \sqrt{1-e_S^2} \cos \beta _{ele} \sin u. \end{aligned}$$

(26)

However, the amplitude of $\varDelta a _{dS}$ is of the order of $10^{-15}$ m, thus, fully negligible.

De Sitter changes the mean motion and the associated revolution period by:

$$\begin{aligned} n_{dS}=\left( \frac{GM}{a^3} \right) ^{1/2} \left( 1-\frac{6G M_{S}}{{a c^{2} R_{S}}} \frac{n_S}{n} \sqrt{1-e_S^2} \cos \beta _{ele}\right) . \end{aligned}$$

(27)

Figure 12 shows how the de Sitter effect changes the semi-major axis, eccentricity, orbital height, and revolution period of Galileo E14. Despite that the distance between the Earth and the satellite varies, the change of the semi-major axis and the associated revolution period remain constant for the eccentric satellites. The osculating revolution period changes by $\varDelta T = +1.144$ $\upmu$s, making the total revolution of an Earth satellite longer, and depends on the initial semi-major axis. For E08 in a circular orbit, the revolution period changes by $\varDelta T = +0.797$ $\upmu$s, whereas $\varDelta a_{dS} = +0.3098$ mm, which is smaller than the value for E14 because of the larger inclination angle and thus the smaller value of $\cos \beta _{ele}$.

Considering the first-order Gaussian perturbations and the acceleration due to de Sitter effect, we can derive an analytical formula describing the periodic variations of the eccentricity:

$$\begin{aligned} \varDelta e_{dS}=\frac{3}{4}\frac{GM_S}{c^2 R_S}\frac{n_S}{n}\sqrt{1-e_S^2}\sqrt{1-e^2}\sin \beta _{ele}(\cos u -1). \end{aligned}$$

(28)

The orbit becomes more circular in the apogee, whereas the orbit keeps its initial shape in the perigee due to the geodetic precession. Hence, the orbit is not an ellipse anymore, instead, it becomes ‘pear-shaped.’ The effect of the shape variation is opposite to that observed in the case of the Schwarzschild effect, for which the effect of more circular orbits was observed in perigee. However, the magnitude of de Sitter is smaller by one order of magnitude than the Schwarzschild effect.

Taking two effects into account: the constant change of a and the periodical variation of e, we obtain variations of the satellite height from $+0.0406$ mm in apogee to $+0.1887$ mm in perigee for E14. Therefore, de Sitter changes the satellite heights between perigee and apogee and satellite angular momentum without any prominent periodic variations of the osculating revolution period (see Fig. 12).

Inclination, perigee, and ascending node

The cross-track acceleration caused by the de Sitter effect can be described as:

$$\begin{aligned} W_{dS}=3 \frac{G M_{S}}{c^{2} R} n_{S} \sqrt{1-e_{S}^{2}} a n \sin \beta _{ele} \sin u. \end{aligned}$$

(29)

The value of the $\beta _{ele}$ depends on the relative position between the satellite ascending node $\varOmega$ and the geocentric ascending node of the Sun $\varOmega _S$:

$$\begin{aligned} \cos \beta _{ele}=\cos \varepsilon \cos i+\sin \varepsilon \sin i \cos ( \varOmega - \varOmega _S). \end{aligned}$$

(30)

Considering the de Sitter accelerations in the cross-track direction and the first-order Gaussian perturbations, we may derive simplified perturbations of the angular Keplerian elements $\varDelta \varOmega _{dS}$, $\varDelta i_{dS}$, and $\varDelta \omega _{dS}$:

$$\begin{aligned} \varDelta \varOmega _{dS}= & {} \frac{3}{2 }\frac{GM_S}{ c^2 R_S}\frac{n_S}{n}\sqrt{\frac{1-e_S^2}{1-e^2}}\left( n\varDelta t-\frac{1}{2}\sin 2u \right) \frac{\sin (\beta _{ele})}{\sin i} \end{aligned}$$

(31)

$$\begin{aligned} \varDelta i_{dS}= & {} -\frac{3}{2}\frac{GM_S }{ c^2 R_S}\frac{n_S}{n}\sqrt{\frac{1-e_S^2}{1-e^2}}\left( n\varDelta t \sin (\beta _{ele}-i)-\frac{1}{2}\sin 2u \right) \nonumber \\&\quad \cdot \sin (\beta _{ele}) \end{aligned}$$

(32)

$$\begin{aligned} \varDelta \omega _{dS}= & {} \frac{3}{4}\frac{GM_S}{e c^2 R_S}\frac{n_S}{n}\sqrt{1-e_S^2}\sqrt{1-e^2}\sin (\beta _{ele}-i)\sin u \nonumber \\&\quad - \varDelta \varOmega _{dS} \cos i. \end{aligned}$$

(33)

These equations are valid for a nonrotating reference frame under the assumption that $u=\nu$ following the approach described by Hugentobler (2008).

For a proper recovery of the phase of periodic perturbations, one has to consider the nodal longitude of the Sun $\varOmega _S$ with respect to the satellite position $\varOmega$, whereas the secular components depend on the elapsed time from the initial epoch $\varDelta t$.

The value of $\beta _{ele}$ slowly changes over time as it depends on the difference between $\varOmega$ and $\varOmega _S$ and the orientation of the satellite orbital plane w.r.t. the ecliptic $|i\pm \varepsilon |$. The value of $\varOmega$ changes mostly due to the Earth’s oblateness described by the normalized spherical harmonic of the Earth’s gravity potential $C_{20}$ (Beutler 2004):

$$\begin{aligned} \bar{\dot{ \varOmega }} [^\circ /day]= \frac{10.0^\circ \cos i}{(\frac{a}{a_e})^{\frac{7}{2}}(1-e^2)^2}, \end{aligned}$$

(34)

where ${a_e}$ is the Earth’s radius. For Galileo in circular orbits, the full revolution of $\varOmega$ lasts 37 years, whereas for Galileo in eccentric orbits, it takes 26 years for $\varOmega$ to come back to its initial position. The full revolution of extreme values of $\beta _{ele}$, i.e., from $|i-\varepsilon |$ thought $|i+\varepsilon |$ to $|i-\varepsilon |$ lasts 26 years for Galileo in eccentric orbits. Therefore, the secular drift of the ascending node over shorter periods differs by the coefficient $\frac{\sin (\beta _{ele})}{\sin i}$. The relative orientation between the ecliptic plane and the satellite orbital plane changes along with the drift of the node.

Fig. 13

Impact of the de Sitter effect on the a inclination, b right ascension of ascending node, and c argument of perigee (in-plane component only) of Galileo E14

The perturbations for all angular Keplerian elements have two components—periodic variations with the major twice-per-revolution signal and a secular drift, which is close to the value of the precession imposed on the local inertial frame with respect to the celestial reference frame for $\varOmega _{dS}$ and equals 52.53 $\upmu$as/day for circular polar orbits over long periods. For noncircular orbits, the effect is rescaled by $(1-e^2)^{-0.5}$ for $\varDelta i_{dS}$ and $\varDelta \varOmega _{dS}$, whereas one of the constituents of $\varDelta \omega _{dS}$ is also rescaled by $e^{-1}(1-e^2)^{0.5}$.

The mean secular drift of $\varOmega _{dS}$ which equals 52.53 $\upmu$as/day, or 19.185 mas/y, corresponds to a drift of 7.2 mm/day at the Galileo heights after 1 day. Therefore, the effect should be detectable using GNSS satellites provided that it can be separated from other effects that cause the secular drift of the ascending node, such as the zonal harmonics of the Earth’s gravity field of the even degree. The detection of the effect is only slightly easier when based on Galileo satellites in eccentric orbits than the nominal Galileo satellites because the inclination angle is lower and $(1-e^2)^{-0.5}=1.013$ for E14 and E18.

For $\beta _{ele}=i$, the secular drift of the inclination angle disappears. Otherwise, the secular term of $\varDelta i_{dS}$ remains smaller than the $\varOmega _{dS}$ drift. Iorio (2019) also noticed that the geodetic precession might introduce a secular drift of the inclination angle with the maximum value when $\varOmega - \varOmega _S=90^{\circ }$. However, only for polar orbits $\varOmega - \varOmega _S$ may remain relatively unchanged because of no secular nodal drift caused by $C_{20}$. Otherwise, keeping the constant value of $\varOmega - \varOmega _S$ over very long periods would not be possible.

In Fig. 13, the variations of $\varDelta \omega _{dS}$ contain only an in-plane component in the nonrotating frame. However, the first-order perturbations do not describe well periodic variations of $\varDelta \omega _{dS}$ observed in the simulations, mostly because of the variable value of the eccentricity and velocity during one revolution period which make the estimates of osculating $\omega$ absorb these variations.

Huang et al. (1990) conducted a test of the geodetic precession using LAGEOS-1 satellites in the form of numerical orbit integration. They concluded that ‘The result of the comparison test verified that the geodesic precession causes an average of 17.6 mas/y precession in the node of the LAGEOS orbit and only periodic effects on the inclination and the argument of perigee.’ We found that the inclination may also have some low-amplitude periodic (with periods shorter of the nodal revolution) $\beta _{ele}$-dependent drifts, whereas the secular drift of the perigee should always be present for nonpolar orbits. The inclination angle of LAGEOS-1 is $109.9^\circ$, that is close to the polar orbits, which may explain why Huang et al. (1990) did not detect any secular drift in the perigee in their numerical tests. Moreover, the elevation of the Sun above the orbital plane could be close to zero, which can explain no drift observed of the inclination angle in the study by Huang et al. (1990).

Fig. 14

Impact of the de Sitter effect on the a inclination and b right ascension of ascending node of a geostationary orbit with $i=0.2^{\circ }$

The best satellite orbit for verifying the geodetic precession is the orbit with $i = 0^{\circ }$, i.e., the geostationary orbit, because it maximizes the secular drift of $\varDelta \varOmega _{dS}$. Assuming that $\beta _{ele} = \varepsilon$, i.e., $\beta _{ele}$ is maximum and changes very slowly and $i=0.2^\circ$ to avoid ambiguities in the determination of the node position, then $\sin (\beta _{ele})/{\sin i} = 114$, which means that the drift of the ascending node is 114 larger than in the case of the polar orbit and $\beta _{ele}$ perpendicular to the equatorial plane (see Fig. 14). For geostationary orbits with $a=42,164$ km and $i=0.2^\circ$, the nodal drift after 1 day would exceed one meter equalling 1,236 mm, which is far above the current accuracy of the orbit determination and can be determined with a high certainty after several days, despite that the accuracy of geostationary GNSS satellites is lower than that of GNSS in medium orbits (Sośnica et al. 2020). Some of the GNSS analysis centers neglect the Lense–Thirring and de Sitter effects, which may have a severe impact on the quality of orbits of geostationary GNSS, such as BeiDou satellites.

Interestingly, the precession of the ascending node can be much larger than the geodetic precession of the frame due to the ease of nodal changes for satellites at low inclination angles, i.e., small periodic accelerations in the cross-track direction impose relatively large changes of the node because of the $\sin i$ in the denominator of the first-order Gaussian perturbation equations (Eq. 2). Considering such Sun–Earth-satellite configuration, the nodal drift is greater than the value of 19.2 mas/y $\times \cos 23.5^{\circ }$ = 17.6 mas/y, which is commonly considered in the literature as independent of the satellite inclination (Ciufolini et al. 2017a).

The primary goal of the Gravity Probe B mission was the confirmation of the de Sitter effect. Gravity Probe B had an inclination angle of $i=90.007^\circ$, which minimized the secular rate of the node that equaled on average 53 $\upmu$as/day (when neglecting the $\beta _{ele}$ temporal variability). The mean secular nodal drift of Gravity Probe B corresponds to 1.8 mm/day for the semi-major axis of 7,027 km. We found that this configuration minimized the rates of the ascending node, which are in fact periodic variations of very long periods.

Lense–Thirring

The Lense–Thirring effect (Lense and Thirring 1918) causes the spacetime frame dragging of all near-Earth objects due to the rotating Earth (Lucchesi et al. 2015; Ciufolini et al. 2017a). The accelerations in the along-track component due to the Lense–Thirring effect are near zero for eccentric orbits and zero for circular orbits (see Fig. 4). The radial accelerations are near-constant, whereas cross-track accelerations vary during one revolution period with the maximum negative acceleration close to the perigee and a positive acceleration in the apogee. The accelerations also depend on the orientation of Earth’s angular momentum vector $\mathbf {J}$ with respect to the angular momentum vector $\mathbf {h}$.

The Lense–Thirring effect causes constant offsets, periodic variations, and secular changes of Keplerian orbit parameters.

Fig. 15

Impact of the Lense–Thirring on a the semi-major axis, b eccentricity, and c the revolution period of E14

Semi-major axis, eccentricity, and the revolution period

The radial acceleration due to the Lense–Thirring effect can be approximated as:

$$\begin{aligned} R_{LT}=2 \frac{G M}{c^{2} a^{2}} n J \cos i. \end{aligned}$$

(35)

Considering the constant change of the semi-major axis due to any radial acceleration, one obtains:

$$\begin{aligned} \varDelta a_{LT}= -\frac{8}{3} \frac{J}{c^2} \sqrt{\frac{GM}{a}} \cos i. \end{aligned}$$

(36)

For E14 and E08, the $\varDelta a_{LT}=-0.0703$ and $\varDelta a_{LT}=-0.0581$ mm, respectively, whereas the periodic component equals:

$$\begin{aligned} \varDelta a _{LT}= 4 \frac{e}{\sqrt{1-e^2}} \frac{Jn}{c^2} \cos i \sin u \end{aligned}$$

(37)

and has the amplitude below $10^{-12}$ m for E14 and even smaller for E08, thus is fully negligible. The change of the semi-major axis depends on the inclination of the orbit and semi-major axis as of $\sqrt{a^{-1}}$. Please note that for inclination angles $i>90^{\circ }$, e.g., for LAGEOS-1 with $i=109.9^{\circ }$, the offset of the semi-major axis is positive as opposed to the majority of all artificial Earth satellites.

The periodical change of the eccentricity equals:

$$\begin{aligned} \varDelta e_{LT}= -2 \sqrt{1-e^2} \frac{Jn}{c^2} \cos i (\cos u -1). \end{aligned}$$

(38)

The maximum difference between the positive and negative change of e is $3.86 \times 10^{-12}$, which is equal to 0.108 mm in apogee after multiplying by the value of the semi-major axis of E14. Thus, the changes of the a and e induced by Lense–Thirring are hardly detectable. The analytical formula for the $\varDelta e_{LT}$ variations does not fully explain all effects as detected by the numerical simulation of E14 orbit due to neglecting of higher-order terms (see Fig. 15).

The mean motion due to the Lense–Thirring effect changes as:

$$\begin{aligned} n_{LT}=\left( \frac{GM}{a^3} \right) ^{1/2} \left( 1+4 \frac{G M}{c^{2} a^{3}} J \cos i \right) . \end{aligned}$$

(39)

Lense–Thirring changes the revolution period of E14 and E08 by $-1.8 \times 10^{-7}$ and $-1.5\times 10^{-7}$ s, respectively (see Fig. 15). No periodic variations of the osculating revolution period can be found, because of the marginal periodic variations of the semi-major axis. The changes of the semi-major axis and eccentricity depend on $\cos i$, thus are equal to zero for polar orbits and are maximal for equatorial orbits.

Inclination, perigee, and ascending node

The cross-track acceleration caused by the Lense–Thirring effect can be described as:

$$\begin{aligned} W_{LS}=4 \frac{G M}{c^{2} a^{2}} n J \sin i \sin u. \end{aligned}$$

(40)

Fig. 16

Impact of the Lense–Thirring on the a inclination, b ascending node, and c perigee (in-plane component only) of E14

The secular drift of the right ascension of ascending node, inclination, and argument of perigee can be described as:

$$\begin{aligned} \varDelta \varOmega _{LT}= & {} 2 \frac{GMJ}{c^2a^3(1-e^2)^{\frac{3}{2}}n}\left( n\varDelta t - \frac{1}{2}\sin 2 u\right) \end{aligned}$$

(41)

$$\begin{aligned} \varDelta i_{LT}= & {} \frac{GMJ \sin i}{c^2a^3(1-e^2)^{\frac{3}{2}}n}\left( - \frac{1}{2}\sin 2 u\right) \end{aligned}$$

(42)

$$\begin{aligned} \varDelta \omega _{LT}= & {} -2 \frac{GMJ \cos i}{c^2a^3(1-e^2)^{\frac{1}{2}}n}\left( n\varDelta t - \frac{3}{2}\sin 2 u\right) \end{aligned}$$

(43)

The secular drift of $\varOmega _{LT}$ for E14 is 7.3585 $\upmu$as/day, of $\omega _{LT}$ is $-4.7152$ $\upmu$as/day, and of $i_{LT}$ is zero. Thus, Lense–Thirring changes the ascending node of Galileo E14 by about 1 mm per day, the perigee by 3 mm per day, and the in-plane component of the perigee associated with the mean anomaly by 0.6 mm per day. Iorio (2008) suggested that the inclination angle should also have a secular drift due to the Lense–Thirring effect of $-0.6$ mas/y in the case of LARES orbit due to coupling between the Lense–Thirring effect and the atmospheric drag. However, no secular rate of inclination is expected due to the Lense–Thirring effect itself, as shown in this study.

The secular rate of $\varOmega _{LT}$ is independent from the inclination angle i, despite that the accelerations in W depend on the inclination. Oppositely, the secular rate of $\omega _{LT}$ can be prograde or retrograde depending on the inclination angle and vanishes for polar orbits.

Figure 16 shows the simulated and approximated variations of the inclination angle, ascending node, and perigee of Galileo E14. Again, the osculating perigee is not well described by the first-order approximations due to the variable velocity during the satellite revolution. For the inclination angle and ascending node, the approximated equations describe well the perturbations obtained from simulations. Lense–Thirring introduces zero acceleration in cross-track W for $u=0$ and $u=180^\circ$, thus, when the satellite crosses the equatorial plane. Lense–Thirring introduces maximum accelerations with opposite signs for $u=90$ and $u=270^\circ$. Such an acceleration causes a drag of the whole orbital plane reflected by the secular drift of $\varDelta \varOmega _{LT}$. We do not observe any secular drift of the orbital inclination $\varDelta i$, because for $u=0$ and $u=180^\circ$ the cross-track accelerations are nullified. If only any cross-track acceleration existed for $u=0$ and $u=180^\circ$, we would have observed a secular drift of the inclination angle as in the case of the de Sitter effect.

Summary and conclusions

In this study, we conducted simulations of orbit perturbations due to the main effects emerging from GR—Schwarzschild, Lense–Thirring, and de Sitter effects. The simulation results were compared with the first-order perturbations for 24 h intervals, that is, the interval typically used for deriving precise GNSS orbits by the International GNSS Service, because very long arcs of GNSS orbits, exceeding 1 week, are typically affected by systematic errors of solar radiation pressure modeling (Teunissen and Montenbruck 2017; Bury et al. 2019). We compared the effects acting on Galileo satellites in nominal orbits, which are very good proxies of circular orbits, and the orbits of Galileo satellites accidentally launched into highly eccentric orbits. The separation of the GR effects from other orbit perturbations can be better done in the case of the eccentric orbits thanks to variable heights of the satellites and different dependencies between GR effects as a function of satellite height. Such a separation is indispensable when observing variations of Keplerian elements without secular rates due to GR effects, such as the semi-major axis. We derive the analytical formulas of temporal variations of Keplerian parameters based on the first-order Gaussian perturbations and compare how well they agree with the observed perturbations from numerical simulations. We concentrate especially on eccentric orbits, for which the first-order perturbations may be invalid due to the assumption in the Gaussian perturbations that one parameter changes at one time.

Table 2 Changes of the Keplerian elements and revolution period due to GR effects within 24 h based on numerical orbit simulations for selected GNSS and SLR satellites. The secular rates of $\omega '$ contain only the in-plane component in a nonrotating frame

So far, only the secular rates of Keplerian elements were used to verify the GR effects using artificial Earth satellites (Will 2014). For the first time to our knowledge with artificial satellites, this study shows that the periodical variations of Keplerian elements can also be used for the verification of the GR effects, as their magnitudes substantially exceed the current accuracy of precise orbit determination of GNSS satellites, even within 24 h-satellite arcs.

Table 2 summarizes the GR effects on Keplerian orbital parameters and the revolution period for Galileo in a circular orbit, E08, Galileo in an eccentric orbit, E14, GPS G18 in a slightly eccentric orbit $e=0.01812$, BeiDou-2 geostationary satellite C01, LAGEOS-1, and the future LARES-2. To demonstrate an extreme case for LAGEOS-1 with $i=109.9^\circ$, we assume that $\beta _{ele}=i+\epsilon -180^\circ =-46.6^\circ$, because the elevation of the Sun above the orbital plane exceeds $90^\circ$, which is also true for LARES-2 with $i=70.2^\circ$.

Schwarzschild: conclusions

The Schwarzschild effect introduces a constant and periodic change of a and T, periodic variations of e, and a secular motion of $\omega$, all of which exceed the level of 1 mm. The secular rate of $\omega =1.3$ mas/day corresponds even to 167 mm/day at GPS heights. However, GPS satellites are in the 2:1 resonance with Earth rotation, whereas geostationary satellites are in an even stronger 1:1 resonance, which causes instabilities of Keplerian parameters and a substantial vulnerability to small variations of accelerations, e.g., of the solar radiation pressure. Galileo satellites have a much weaker resonance of 17:10 for nominal orbits and 37:20 for eccentric orbits, making them suitable platforms for detecting secular and periodic variations of Keplerian parameters. The Schwarzschild effect does not affect the ascending node and the inclination angle. The Schwarzschild acceleration approximately changes as $r^{-3}$ with the height (when assuming $r=a$), whereas the Newton’s acceleration changes as $r^{-2}$, hence both effects can easily be separated for elliptical orbits, whereas for circular orbits, the Schwarzschild effect can be explained by a slight modification of the GM value. For circular orbits, the Schwarzschild term can be considered as a central force, whereas for elliptical orbits, the along-track component occurs. Thus, for elliptical orbits, the angular momentum shows periodic variations, but the angular momentum is conserved over long periods.

For Galileo E14 in eccentric orbits, the total change of a due to the Schwarzschild effect is $-29.02$ mm in perigee and $-8.65$ mm in apogee. This gives a difference of more than 20 mm, thus, fully detectable using current techniques of GNSS precise orbit determination. Thus, the observations of periodical changes of the semi-major axis of Galileo satellites in eccentric orbits can be used as a new method for verifying GR effects.

For Galileo eccentric satellites, the change of the semi-major axis is negative in the perigee and apogee, with the maximum change in perigee. The change of eccentricity is negative in perigee, which implies a more circular orbit as the perigee goes higher, and positive in the apogee, which implies a more eccentric orbit, as the apogee also goes higher. The Schwarzschild term changes the shape and the size of the orbit instantaneously in opposite directions. Using the chosen parameterization and nonrotating geocentric reference frame, the Schwarzschild effect translates the elliptical orbits into irregular orbits.

De Sitter: conclusions

We found that the geodetic precession strongly depends on the orientation of the ecliptic with respect to the orbital plane. This orientation slowly varies due to the precession of the orbital plane, mostly caused by the Earth’s oblateness. For an extreme case and the maximum value of the elevation of the ecliptic associated with very low inclination angles, large variations of the ascending node are expected due to the de Sitter effect. The inclination angle also may show some nonzero rates for the satellite orbital plane inclined with respect to the ecliptic. One has to keep in mind that the large rates of the ascending node and the inclination angle are in fact periodical variations of very long periods and not the actual secular rates of these Keplerian parameters. For Galileo in circular orbits, this long period equals 37 years, whereas for Galileo in eccentric orbits—26 years. The rate of the node on GEO orbit due to geodetic precession can exceed 1 m over 1 day for an extreme case of the Sun elevation above the orbital plane. The offset of the semi-major axis due to the geodetic precession may have a positive or a negative sign depending on the $\beta _{ele}$ that is the inclination of the orbital plane with respect to the ecliptic. For GEO satellites, the geodetic precession causes the largest change in the semi-major axis of more than 4 mm and a change of the revolution period of more than 12 $\upmu$s.

Lense–Thirring: conclusions

The frame dragging—the Lense–Thirring effect—causes a very small secular effect on the ascending node, which depends on a and is independent from i. The perigee has a small secular rate, whereas the inclination and eccentricity have very small periodic variations. The change of the semi-major axis and the revolution period have opposite signs for LAGEOS-1 than for other satellites due to the highest inclination angle. All effects are far below the mm-level for the heights of GNSS satellites; Therefore, the Lense–Thirring effect cannot be detected using GNSS satellites, as opposed to the de Sitter and Schwarzschild effects that should be detectable using SLR and GNSS observations characterized by the accuracy of a few millimeters.

Nevertheless, the future steps will include the search of empirical evidence of the perturbations of Keplerian parameters to confirm the effects described in this paper.