Rethinking the Roughness Height: An Improved Description of Temperature Profiles over Short Vegetation

Abstract

In this study, we present an extension to the Monin–Obukov similarity theory (MOST) for the roughness sublayer (RSL) over short vegetation. We test our theory using temperature measurements from fiber optic cables in an array-shaped set-up. This provides a high vertical measurement resolution that enables us to measure the sharp temperature gradients near the surface. It is well-known that MOST is invalid in the RSL as the flow is distorted by roughness elements. However, to derive the surface temperature, it is common practice to extrapolate the logarithmic profiles down to the surface through the RSL. Instead of logarithmic behaviour defined by MOST near the surface, our observations show near-linear temperature profiles. This log-to-linear transition is described over an aerodynamically smooth surface by the Van Driest equation in classical turbulence literature. Here we propose that the Van Driest equation can also be used to describe this transition over a rough surface, by replacing the viscous length scale with a surface length scale $L_s$ that represents the size of the smallest eddies near the grass structures. We show that $L_s$ scales with the geometry of the vegetation and that the model shows the potential to be scaled up to tall canopies. The adapted Van Driest model outperforms the roughness length concept in describing the temperature profiles near the surface and predicting the surface temperature.

1 Introduction

1.1 Diagnosis of the Problem

Accurate estimations of the surface temperature and momentum profiles are crucial to determine the exchange of energy and moisture between the surface and the atmosphere (Physick and Garratt 1995; Holtslag et al. 2013). Yet, getting a good estimate of the temperature profile over the widespread and frequently studied grass surface remains challenging (e.g. Beljaars and Holtslag 1991; Duynkerke 1992; Sun 1999; Best and Hopwood 2001). Here, we present a (semi-) analytical model to describe vertical temperature profiles just centimetres above the grass. The framework is inspired by the well-known Van Driest equations (Van Driest 1956) for flow in smooth channels and is now applied to a rough grass surface. We test our model using high-resolution temperature observations from fiber optic cables.

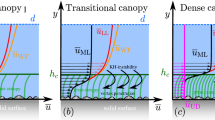
Traditionally, the temperature profiles in the atmospheric surface layer (ASL), the lowest 10% of the atmospheric boundary layer (Fig. 1a), are represented by the Monin–Obukov Similarity Theory (MOST) (Monin and Obukov 1954; Foken 2006). This theory relates the vertical gradients of transported quantities to stability and surface fluxes via the law of the wall: large turbulent eddies are broken down into smaller eddies closer to the surface (von Kármán 1930). This results in the characteristic logarithmic behaviour of the wind and temperature profiles.

Fig. 1

Visualisation of the analogy between the Monin–Obukov model and the Van Driest model. Panel a shows the Monin–Obukov model for near-surface temperatures highlighting the difference in RSL temperature ($\theta$) between the model (blue line) and observations (black dots). Panel b shows the different layers used in the Van Driest model for flow over a smooth surface. The green eddy and round inset show the scale difference between the viscous length scale ($\nu /u_*$) and a surface length scale, $L_s$. Here h represents the grass height, $z_{0h}$ the roughness height for heat, and d the displacement height

From turbulent channel flow, we know that over a flat surface, the logarithmic profiles naturally transition to linear profiles in the viscous sublayer. As turbulent mixing lengths decrease (i.e. the turbulent eddies become smaller), viscous transport takes over (Prandtl 1905). From the surface upwards, we can therefore recognize a viscous sublayer, a buffer layer and a log layer (Fig. 1b). Their heights are well-defined in terms of dimensionless distance to the wall (Kundu et al. 2016).

For a natural, vegetated surface, such a normalization becomes complex. Since grass is three-dimensional, consisting of individual vertical blades, the viscous sublayer follows the shape of the leaves and is orders of magnitudes smaller than the grass height (Fig. 1a). Such a surface is considered aerodynamically rough. Here, the air has to flow around individual roughness obstacles and this disturbs the profiles from their logarithmic shape. This part of the atmospheric sublayer is called the roughness sublayer (RSL): the layer in which the flow is influenced by the spatial variation of the rough surface (Raupach et al. 1980). The RSL stretches from the surface up to 2–5 times the height of the roughness elements. As the flow is influenced by the individual roughness elements, the MOST equations are only valid above the RSL.

Special RSL modifications to the MOST theory have been introduced (e.g. Harman and Finnigan 2007, 2008; De Ridder 2010) and tested for tall canopies (Ryder et al. 2016; Chen et al. 2016; Bonan et al. 2018). However, for short vegetation such as grass, it is still common practice to extrapolate the logarithmic profiles to the surface [or the displacement height d (Thom 1971)] through the RSL (Viterbo and Beljaars 1995; Mitchell 2005; Clark et al. 2010; Meier et al. 2022; Zhang et al. 2022).

If the surface height would be defined at z = 0, mathematically speaking the surface temperature and wind speed are undefined, as the logarithm goes to minus infinity. To overcome this, the roughness heights for heat and momentum have been introduced. In the case of momentum, the roughness height $z_{0m}$ is defined as the height where wind speed decreases to its surface value (i.e., zero). It is assumed that a similar concept can be applied to heat. So, the roughness height for heat $z_{0h}$ is the height where the temperature equals the surface temperature.

To estimate $z_{0h}$, often a fixed ratio of 0.1 relative to $z_{0m}$ is assumed (Garratt and Hicks 1973; Garratt and Francey 1978; Brutsaert 1982a; Beljaars and Holtslag 1991), since the underlying physical mechanisms responsible for these transports differ. Heat exchange at the surface occurs by less effective molecular diffusion, while momentum is exchanged through (form) drag caused by pressure effects.

However, even for the same site, it was shown that the ratio $z_{0h}/z_{0m}$ can vary up to 6 orders of magnitude (Duynkerke 1992). The consequences of this uncertainty are significant due to the logarithmic shape of the profiles. This is illustrated in Fig. 2. For a given surface temperature (derived from radiation measurements), an uncertain $z_{0h}/z_{0m}$ ratio results in a wide spread of predicted temperatures higher up in the temperature profile (Fig. 2a). Conversely, when for example the 1.5 m temperature is measured in situ, the predicted surface temperature for a slightly different $z_{0h}$ can show a large divergence due to the large gradients near the surface (Fig. 2b).

Fig. 2

Sketch highlighting the consequences of the extrapolation of the logarithmic profile down to the surface and the uncertainty in $z_{0h}$. The black dots show observed temperatures, and the blue lines possible MOST profiles for a range of $z_{0h}$ values. To match observations above the RSL and the surface temperature non-physical $z_{0h}$ values may be needed. Panel a shows how a relatively small difference in $z_{0h}/z_{0m}$ can propagate as a large difference in temperature above the RSL ($[\theta _{r1}, \theta _{r2}, \theta _{r3} ]$). Panel b shows the reverse problem, how for a known reference temperature, a small difference in $z_{0h}$ results in a large difference in surface temperatures ($[\theta _{s1}, \theta _{s2}, \theta _{s3} ]$)

The robustness of the ratio between $z_{0h}/z_{0m}$ has been the subject of many earlier studies (e.g. Brutsaert 1982b; Andreas 1987; Beljaars and Holtslag 1991; Blyth and Dolman 1995; Zilitinkevich 1995; Verhoef et al. 1997a; Massman 1999; Blümel 1999; Sun 1999; Chaney et al. 2016; Rigden et al. 2018). Partly, its uncertainty lies in the fact that it cannot be measured directly, but must be derived from the measurements of other quantities. In particular, the surface temperature (Garratt et al. 1993; Su et al. 2001) proves challenging.

It is common practice to use the radiative temperature as the surface temperature in MOST. That signal is a composite of the skin temperature of different surface types within the view of the pyrgeometer (e.g. bare soil, dry grass, living grass). To derive $z_{0h}$ and apply MOST correctly, we need to know the effective surface temperature, i.e. the temperature of the air that it is in contact with the roughness elements (vegetation, soil, etc.) Garratt et al. (1993). A recent study by Hicks and Eash (2021) highlights how these temperatures derived from infrared radiation can differ from the effective surface temperature by up to 2K during the day.

However, we argue that another important source of uncertainty stems from the incorrectness of the underlying physical model. Extrapolating the logarithmic profile down to the surface implies a decrease in the eddy size to zero towards the surface. A vanishing length scale leads to an infinite gradient, which is a nonphysical asymptotic limit.

In this paper, we therefore propose a more physics-based approach to describe near-surface temperatures, thereby enhancing the robustness of heat transfer parameters near the surface.

1.2 Alternative Approach: Surface Length Scale for Short Canopies

As explained, extrapolation of the logarithmic profile is still common practice for short canopies. This leads to nonphysical profiles in the RSL, which limits the generality of the $z_{0h}$ concept. Eventually, this affects the modelling of the full ASL temperature profile. We therefore aim to provide a more physical description of the temperature profile over short vegetation. Such a description should have a gradient of finite magnitude near the surface and asymptotically merge into the traditional log layer higher up in the atmosphere. With finite gradient, we imply e.g. a linear, quadratic or exponential temperature profile, rather than logarithmic.

Van Driest (1956) describes such an asymptotic transition from the log layer into the viscous layer for smooth channel flow. The Van Driest equation is based on first principles, closely follows laboratory measurements (Monin and Yaglom 1973) and was later also confirmed by direct numerical simulations (e.g. Donda et al. 2014). For our new formulation, we adapt the existing Van Driest equation by replacing the viscous length scale with a characteristic surface length scale. However, we would like to emphasize here, that although we choose a Van Driest-inspired model description, alternative formulations are also possible.

The empirical RSL models available for tall canopies include a similar surface length scale. This length scale represents the size of the dominant turbulent eddies that scale with the canopy height (Raupach et al. 1996). Also for short canopies, we expect that the surface length scale scales with the canopy geometry. Just like tall canopies, the grass surface is rough and partly permeable, which results in shear instabilities and vortex shedding at the top. We hypothesize that the minimal eddy size at the surface is finite and determined by the distance between the clustered groups of grass leaves (Fig. 1a). The actual eddy size near the top of the grass is therefore larger than anticipated through a proportional relationship with z as assumed when extrapolating the log-law. Moreover, it is orders of magnitude larger than the viscous length scale.

Due to the lack of a method for high-resolution temperature measurements, it has not been possible to observe the actual shape of the temperature profiles near the surface over short vegetation until recently. We apply Distributed Temperature Sensing (DTS) for temperature sampling at a high spatial and temporal resolution. DTS is a technique that uses fiber-optic cables as temperature sensing elements (Selker et al. 2006; Tyler et al. 2009). This enables measurements of the small-scale and rapidly changing gradients and individual turbulent eddies. By installing the cable in different configurations such as coils (Sigmund et al. 2017; Zeller et al. 2021), or arrays (Thomas et al. 2012), sharp temperature gradients near the surface can be measured. Here, we apply a harp-shaped DTS set-up to measure the temperature profile over and within the grass with 2 cm resolution.

In Sect. 2, we describe the field measurements and introduce the adapted Van Driest model. In Sect. 3, the adapted Van Driest model will be compared to the observations and the roughness length concept. Additionally, we will illustrate the model’s equivalence to established tall-canopy models. Finally, Sect. 4 summarizes conclusions and provides an outlook on further applications of the new model concept.

2 Methods

2.1 High Resolution Temperature Profiles, Experimental Set-Up

The supporting measurement campaign took place at the Veenkampen meteorological site in the Netherlands (51.98$^\circ$ N, 5.62$^\circ$ E), between 1 to 24 May 2022. This site has been operated and maintained by Wageningen University & Research since 2011. Here we installed DTS cables to measure temperature profiles at two vertical resolutions: a 9-m mast with 25-cm resolution, and a 64 cm high harp-shaped configuration with 2-cm resolution (Fig. 3).

DTS uses the backscatter of a laser signal to infer local temperature at different cable sections with a sampling resolution of 25 cm and 10 s (Thomas et al. 2012). A thin, white, 1.6 mm fiber optic cable and an Ultima-M system were used. The data calibration was done using the DTS Calibration Python package (des Tombe et al. 2020). Two well-mixed calibration baths were kept in the maintenance hut: one at ambient temperature ($\sim$ 19 $^\circ$C) and one heated ($\sim$ 35 $^\circ$C). The baths were placed at the start and end of the cable to allow for a double-ended configuration.

For the mast, two vertical DTS cables were extended along a support structure. The temperatures recorded by the two cables deviate by 1–2 K from each other near the surface and the top of the mast. This is most likely due to the influence of the support structure on the airflow. We therefore only considered the cable closest to the harp in our analyses and excluded the upper and lower 30 cm.

The harp consisted of horizontal layers of cable that were 2 cm apart. This resulted in a vertical measurement resolution of 2 cm, with 30 temperature observations per measurement height, from 2 cm above the surface up to 64 cm. The cables were glued to a fiberglass mesh every meter, to maintain alignment and keep sagging to within 1 cm. The harp was split into 4 measurement sections, each $\sim$ 2 m long (Fig. 3). Along these sections, different mowing regimes were applied. Measurements were averaged horizontally along sections to reduce sensitivity to spatial variation.

The grass height along the DTS harp was recorded (and maintained) every 3 days. Four mowing regimes were applied: at fixed heights of 3 cm, 10 cm, and 20 cm, and a variable section where grass grew naturally from 3 cm to over 20 cm. Grass heights including variation within a plot, are provided in Appendix A, Fig. 12. In our analyses, we focused on the 10 cm grass plot, unless stated otherwise, in agreement with the dominant grass height in the surrounding fields.

Fig. 3

DTS field set-up at the Veenkampen measurement site showing the harp and mast. The DTS cables are sketched in white for visualization purposes. The grass heights are written in their respective plots. The relative widths of the plots are (from front to back): 2.09 m, 2.06 m, 1.85 m, 1.70 m. The maintenance hut is visible in the back

The Veenkampen automated weather station provides 10-min averages of several meteorological variables, of which we used the radiation, eddy covariance and sonic-anemometer measurements (wind direction and wind speed at 2 m). We verified the DTS measurement using the shielded and ventilated 1.5 m and shielded 0.1 m temperature measurements (Sect. 3.1). Additionally, we used the longwave radiative measurements of the pyrgeometer to derive the surface skin temperature.

The soil at the Veenkampen site consists of a clay layer down to 1 m depth, on top of peat. The groundwater level during the experiment varied between $-$0.8 m and $-$0.6 m. The site was sown with ryegrass in 2011, and the grass height is kept at approximately 10 cm. Neighbouring fields are not maintained and here grass and reeds up to 1.5 m can be found (Schulte et al. 2021). The 17-ha field is surrounded by ditches, where the water level was close to the surface during the experiment. The field is located in a flat area, with a 50 m moraine at a 4 km distance.

During the measurement period, the weather conditions were relatively constant with mostly warm and sunny days without precipitation. The only precipitation occurred during a heavy thunderstorm with measured wind gusts of up to 30 m $\hbox {s}^{-1}$ at 10 m. The storm ripped the harp on 19 May 2022 at 1230 UTC. We repaired the harp on 21 May 2022. Observations from 19 May 2022 till 21 May 2022 were therefore not included in the analyses.

When the wind direction was perpendicular to the harp, the airflow was deflected due to the fiberglass mesh. This resulted in temperature profiles that were not representative of the undisturbed surroundings. We therefore excluded observations from wind directions $45^\circ$–$135^\circ$ relative to the harp. This was the case 43% of the time. After 10-min averaging and filtering, 1350 timestamps were retained for analysis.

2.2 Adapted Van Driest Model

Our new formulation is an adapted version of the Van Driest model for momentum transport in smooth channel flow (Van Driest 1956). Van Driest (1956) introduced a model for the buffer layer where the eddy diffusivity (or rather turbulent velocity fluctuations) gradually decreases to zero in the viscous layer, instead of a hard boundary between the viscous and logarithmic layer. Therefore the eddy diffusivity model can be used in the entire surface layer through the introduction of a damping function A. A expresses the damping effect of the wall on the eddy diffusivity with $A = 1 - \exp (-\beta z)$, where $\beta$ $\approx$ 1/26 is an empirical constant for smooth walls. Donda et al. (2014) adapted the Van Driest formulation to correct for stability effects that dominate with increasing distance to the wall. They describe the turbulence near a smooth wall using the following equation:

$$\begin{aligned} u_* = \left[ \frac{(A \kappa z)^2 \frac{\partial {u} }{\partial z}}{u_* \left( \varPhi _m \left( \frac{z}{L_{ob}}\right) \right) ^2} + (\nu /u_*) \right] \frac{\partial {u} }{\partial z}. \end{aligned}$$

(1)

Here, u is the wind speed, $u_*$ the friction velocity, $\kappa$ the Von Kármán constant of 0.4. Function $\varPhi _m$ is the similarity function for momentum and depends on the stability of the atmosphere via the Obukov length $L_{Ob}$. We used the formulations by Dyer (1974).

We hypothesized that for a rough grass surface, the logarithmic layer does not continue into a viscous layer, but instead continues into a layer where the eddy size is determined by the geometry of the vegetation. The individual roughness elements, i.e. individual grass leaves and clustered groups (i.e. tussocks), prescribe the minimum eddy size close to the surface. Note that, also with a well-maintained grass height, significant structural variation exists, that will promote mixing at the top of the grass (Fig. 12).

We hence replaced the original viscous length scale $\nu / u_*$ in the Van Driest equation with a surface length scale $L_s$. $L_s$ represents the smallest eddies just over and within the grass (Fig. 1a). Additionally, we applied the similarity assumptions and replaced momentum with heat. This gives an adapted Van Driest formulation:

$$\begin{aligned} \theta _* = \left[ \frac{(A \kappa z)^2 \frac{\partial {\theta } }{\partial z}}{\theta _* \left( \varPhi _h\left( \frac{z}{L_{ob}}\right) \right) ^2} + L_s \right] \frac{\partial {\theta } }{\partial z} , \end{aligned}$$

(2)

where $\theta$ is the potential temperature and $\theta _*$ is the turbulent temperature scale. The function $\varPhi _h$ is the similarity function for heat:

$$\begin{aligned} \begin{matrix} \varPhi _h = \left( 1 - 16 \frac{z}{L}\right) ^{-1/2} for \frac{z}{L} \le 0 \\ \varPhi _h = \left( 1 + 5 \frac{z}{L}\right) for \frac{z}{L} \ge 0 \end{matrix}. \end{aligned}$$

(3)

The distinctive feature of the adapted Van Driest equation compared to MOST is the introduction of a finite gradient, i.e. linear temperature profile, within the roughness sublayer. Note the limits of this formulation: close to the surface (small z) the linear velocity profile in the roughness sublayer is obtained, whereas for larger z MOST is recovered. Above the RSL, the formulation asymptotically approaches MOST and the gradients are identical to the traditional MOST framework. The temperature itself is not per se the same, as different boundary conditions may result in a different offset.

Our new RSL description was compared to the MOST formulation. The MOST equation for the temperature gradient with height is:

$$\begin{aligned} \frac{\partial {\theta } }{\partial z} \frac{\kappa z}{ \theta _*} = \varPhi _h\left( \frac{z}{L_{Ob}}\right) . \end{aligned}$$

(4)

In its integrated form from the surface to height z, Eq. 4 becomes:

$$\begin{aligned} \theta (z) - \theta _s = \frac{\theta _*}{\kappa } \left[ \ln {\left( \frac{z}{z_{0h}}\right) } - \Psi _h \left( \frac{z}{L_{Ob}}\right) + \Psi _h \left( \frac{z_{0h}}{L_{Ob}}\right) \right] , \end{aligned}$$

(5)

with $\theta _s$ as the surface temperature, and $\Psi _H$ the integrated form of the similarity functions.

To compare the MOST and adapted Van Driest model to each other and the observations, we needed a non-dimensional form of the equations. In the classical MOST framework, potential temperature is normalized using the turbulent heat flux scale $\theta _*$ and height using the Obukov length $L_{Ob}$ in the form of $z/L_{Ob}$. In the Van Driest model a different length scale is introduced, the viscous length scale $\nu /u_*$ (c.q. $L_s$ in our adaptation).

To apply the normalization, we needed a first guess of $L_s$. By applying Eq. 2 in the limit for $z\rightarrow 0$ we derived:

$$\begin{aligned}{} & {} \lim _{z\rightarrow 0} \theta _* = \left[ 0 + L_s \right] \lim _{z\rightarrow 0} \frac{\partial {\theta } }{\partial z}, \end{aligned}$$

(6)

$$\begin{aligned}{} & {} L_s = \frac{\theta _*}{\frac{\partial \theta }{\partial z}_{z\rightarrow 0}} . \end{aligned}$$

(7)

Note here the analogy with the vorticity thickness used for tall canopies, which will be elaborated in Sect. 3.5.

Normalizing MOST by $\theta _*$ and $L_s$ gives:

$$\begin{aligned} \frac{{\partial \hat{\theta }} }{\partial \hat{z}} \frac{\kappa \hat{z}}{ 1} = \varPhi _h\left( \frac{\hat{z}}{\hat{L}}\right) , \end{aligned}$$

(8)

in which $\hat{\theta } = (\theta - \theta _{s} ) / \theta _*$, $\hat{z} = z / L_s$ where $z = Z - d$, and $\hat{L} = L_{ob}/L_s$. Z is the height above the substrate (i.e. soil). d is the displacement height, assumed to be $\frac{2}{3}h$ (Shaw and Pereira 1982), with h the grass height. $\theta _{s}$ was here taken as the temperature at the top of the grass.

The adapted Van Driest model after normalization becomes:

$$\begin{aligned} 1 = \left[ \frac{(A \kappa \hat{z})^2 \frac{{\partial \hat{\theta }} }{\partial \hat{z}}}{\varPhi _h \left( \frac{\hat{z}}{\hat{L}}\right) ^2} + 1 \right] \frac{{\partial \hat{\theta }} }{\partial \hat{z}} . \end{aligned}$$

(9)

Note that in the limit for $z\rightarrow 0$, $\frac{{\partial \hat{\theta }} }{\partial \hat{z}}$ in the adapted Van Driest model goes to 1, whereas in MOST it goes to infinity. Derivations of the normalized equations can be found in Appendix B.

3 Results and Discussion

In this section, we first analyze the near-surface temperature profiles provided by the DTS measurements. Then, the adapted Van Driest model and roughness length model are compared to the DTS observations. Finally, we show how our model relates to the existing literature, as our adapted Van Driest approach closely resembles existing RSL models for tall canopies.

3.1 Near-Surface Temperature Observations

To assess the accuracy of the DTS measurements, the DTS temperatures were compared to the reference measurements at the Veenkampen site. Results are shown in Fig. 4 for a selection of days. A nearly constant bias of approximately +1 K was observed for the temperature at the DTS mast at 1.5 m, relative to the shielded and ventilated sensor, persisting during both day and night. The consistent sign of the bias suggests that the calibration, rather than radiation, was likely responsible for this effect. A similar bias of 1 K was observed for DTS observations at 10 cm height during the night, while the bias is near zero during the day.

We suspected that the daytime DTS temperature at 10 cm is also biased, yet remained undetected because tall grass obstructed the sensor. Had the sensor not been overgrown by the grass, it would probably have recorded a lower temperature during the day, subsequently revealing the +1 K bias of the DTS measurements. Given the uncertainty in the reference temperature, we did not apply a correction but assumed a 1 K measurement uncertainty.

It is common practice to use the radiative temperature as the surface temperature in MOST. The green dotted line in Fig.  4 shows the surface temperature derived from radiative measurements. This represents the skin temperature and not the air temperature. This difference can be 1–2 K at night, but up to 10 K during the day (compare the pyrgeometer to the 10 cm observations). Note that, MOST assumes knowledge of the near-surface air temperature and not skin temperature (Hicks and Eash 2021). If one wants to use these radiative measurements in combination with MOST or the adapted Van Driest model, the skin temperature first needs to be translated to air temperature.

Fig. 4

Temperature measurements with the DTS compared to the reference measurements at the Veenkampen measurement site during three radiatively different days and nights

3.2 Finite Gradient Near the Surface?

For decreasing z the MOST model prescribes a temperature gradient approaching infinity at the surface (Eq. 4). In Sect. 1, we argued our belief that this is a nonphysical boundary condition. Additionally, we hypothesized that instead, the surface gradient is finite. Using the high-resolution temperature profiles measured with DTS we can evaluate this hypothesis. Figure 5 shows two examples of observed temperature profiles for stable (panel a) and unstable (panel b) conditions. Below 0.4 m (panel a) and 0.2 m (panel b), the observations no longer follow a logarithmic profile (shown as the blue line).

Fig. 5

Examples of observed temperature profiles for a a stable case (12 May 2022 0330 UTC $L_{Ob}$ = 3) and b an unstable case (18 May 2022 0900 UTC $L_{Ob}$ = -12)

Next, we hypothesized that this profile in the RSL can be more accurately described with a linear approximation, inspired by the Van Driest equation. Figure 6 zooms in on the lower part of the temperature profiles and here the profile predicted by the adapted Van Driest model is added (at 1.4 m and 0.2 m for respectively Fig. 6a, b). Above the RSL both models converge to the same gradient. In the RSL, the logarithmic profile transitions into a linear profile at the top of the grass. The absolute height at which the profile becomes linear depends on the stability (Eq. 2).

Fig. 6

Examples of predicted temperature profiles using MOST (blue) and adapted Van Driest (red) with optimal $L_s$ = 0.08 m (Fig. 9a), for stable (a) and unstable (b) cases. The explanation of the observation symbols is given in Fig. 5. Above the roughness sublayer, both models converge to the same gradient. The exact height for which this happens depends on $L_{Ob}$

Figure 6 also highlights the difference in predicted surface temperatures using MOST and the adapted Van Driest model (i.e. $-$ 1.5 K for the stable, and 3.4 K for the unstable case). We derived the surface temperature from the locally observed 1.5 m temperature (DTS mast measurement) using Eqs. 8 and 9. Values for $\theta _*$ and $L_{Ob}$ were calculated from the sonic-anemometer observations. According to MOST (Eq. 5), the surface temperature was defined at $d + z_{0\,h}$ = 0.067 m (blue star in Fig. 6). We used a displacement height of 2/3th of the grass height and took $z_{0h}$ = 0.1 $\times$ $z_{0m} = 0.001$ m. In the adapted Van Driest equation we took the surface temperature at the top of the grass (at 0.1 m) since we assumed that the linear profile approximation only applies above the vegetation layer. We point out that the lower boundary condition of the adapted Van Driest equation is still an open question. We suspect it is linked to the density at the top of the vegetation, as e.g. eddies may penetrate deeper into a very open canopy than a closed one. Note that this uncertainty is orders of magnitude smaller compared to the uncertainty in choosing a value for $z_{0h}$.

In Fig. 7 we compared the predicted surface temperatures by MOST and the adapted Van Driest model to the observed temperature (DTS harp) at the top of the vegetation, at 0.10 m for the full measurement period. The adapted Van Driest equation outperformed the traditional MOST approach with a mean absolute error (MAE) of 0.6 K compared to 2.1 K, respectively. The strongest improvement was seen around noon, when the air is well-mixed, and MOST overestimates the gradient at the surface.

The performance of the adapted Van Driest model compared to MOST depended on the height (i.e. 0.1 m) that is used to determine the "true" surface temperature. Choosing a reference height within the vegetation (e.g. at $d + z_{0h}$ = 0.067 m), resulted in a higher MAE (0.82 K) for the adapted Van Driest model. Yet it still outperformed MOST (MAE = 2.0 K) since the behaviour above (and within!) the vegetation is better captured by a linear than a logarithmic profile description (see e.g. Fig. 6).

Fig. 7

Plot of predicted surface temperature over the 10 cm plot, a the potential temperature at 10 cm, b the mean absolute error between predicted and observed (DTS harp) temperature. The grey shaded bar shows the measurement uncertainty of the DTS harp (± 1 K)

3.3 Predicting Temperature Profiles

To assess the model’s performance in predicting temperature profiles in the RSL, we compared it against 1350 observed temperature profiles under various atmospheric stabilities. Six composites were created by averaging multiple cases to reduce the effect of outliers. Classes of composites were defined based on the Obukov length. Each class contained the same number of profiles (225) (Fig. 8).

Fig. 8

Profiles of normalized temperature versus height for stability classes (defined as $L_{Ob}$ ranges), for the adapted Van Driest (a) and MOST based on different $z_{0h}$ (b–d) predictions. Dots represent DTS observations at 2 and 30 cm resolution for the lower 0.64 m and between 0.41–8.7 m respectively (as described in Sect. 2.1). Length scale $L_s$ was set to its optimal value of 0.08 m (Fig. 9a). The full (unstable atmospheric conditions) and dashed (stable atmospheric conditions) lines show the median modelled values per class, and shaded areas show the predicted spread between the maximum and minimum $L_{Ob}$ per class

Here we used a “bottom-up” approach to predict the normalized temperature profiles. From a known surface temperature and corresponding height, we predicted the temperature profiles up to 8.5 m. This means that we prescribed the surface temperature at $d + z_{0\,h}$ for MOST and at the top of the grass (i.e. 10 cm) for the adapted Van Driest model.

To obtain temperature profiles using the MOST approach, an estimation of $z_{0h}$ was required. Generally, realistic values of $z_{0h}$ are in the order of 0.1$z_{0m}$ (Garratt and Hicks 1973; Garratt and Francey 1978; Brutsaert 1982a; Beljaars and Holtslag 1991). We found an average $z_{0m}$ of 0.01 m for the Veenkampen site, by applying the MOST equations for momentum to a year of wind measurements at 2 m and 10 m. Values show a seasonal dependence varying between 0.006 m (November) and 0.04 m (July). This is in correspondence with typical values for short grass reported in the literature (Wieringa 1993).

Figure 8b gives the profile description using the literature value of 0.1 $\times$ $z_{0m}$. The MOST model clearly failed to describe the temperature profiles using this value of $z_{0h}$. The incorrect estimate of the surface temperature height offsets the temperature profiles by $\hat{\theta }$ $\sim$ 5 – 15, which for e.g. $\theta _*$ = 0.1 K translates into $\sim$ 0.5 – 1.5 K. Taking a larger $z_{0h}$ of 0.01 m (i.e. $z_{0\,h} = z_{0\,m}$), improved the fit but still resulted in an offset of 0.5–1 K (Fig. 8c).

The optimal $z_{0h}$ value that minimized MAE for the surface temperature prediction based on the locally observed 1.5 m temperature was approximately 0.1 m (Fig. 9d). However, this implies that $z_{0h}$ equals 10 $\times$ $z_{0m}$ implying heat transport to be more efficient than momentum transport, which is physically unrealistic. Using $z_{0h}$ = 0.1 m in the model gave a good match for values of $\hat{z}$ above $\sim$ 2, i.e 0.2 m, roughly the RSL height (Fig. 8c). For lower values of $\hat{z}$, in the RSL, the observed temperature profiles deviated from the profile predicted by MOST and were linear instead of logarithmic. Since the lower boundary of MOST is $d + z_{0h}$ (17 cm in this case, $\hat{z}$ = 1.7), there is no description for the temperature profiles below this height.

For the adapted Van Driest model, we similarly derived the optimal value for $L_s$ by optimizing MAE. This gave $L_s$ = 0.08 m for the 10 cm grass and $L_s$ = 0.16 m for the 20 cm grass (Fig. 9a). $L_s$ thus seems to scale with the canopy height as $\sim 0.8h$. The sensitivity of the MAE to the exact value of $L_s$ was much lower than the sensitivity to $z_{0h}$ (Fig. 9b), showing that the adapted Van Driest approach is a more robust alternative to $z_{0h}$.

Fig. 9

Mean absolute error of the surface temperature (at 10 and 20 cm respectively) prediction against possible length scales $L_s$ (panel a) and a range of $z_{0h}$ values (panel b) over the 10 cm and 20 cm grass. The grey band in panel b indicates the physically realistic range of $z_{0h}$ values. The optimal values that minimize MAE for the surface temperature fall outside of this range

The adapted Van Driest model correctly captured the transition to a near-linear temperature profile in the RSL ($\hat{z}<$3), closely following the observations (Fig. 8a). For large $\hat{z}$ ($\hat{z}>$ 5) it predicted similar temperature profiles as compared to the optimised MOST model. Parameter $\beta$ (Eq. 2, $A = 1 - \exp (-\beta z)$) was empirically determined by minimizing the MAE. For smooth flow, an empirical value of 1/26 is found in the literature (Van Driest 1956). Here, the flow is aerodynamically rough and we found an optimized value of about 1/5.

The values predicted by the adapted Van Driest model deviated by up to 1.5 ($\sim$ 0.15 K for $\theta _*$ = 0.1 K) from the observations, which can partly be attributed to the measurement uncertainty of the DTS set-up (± 1 K). In cases of extreme stability ($L_{Ob}$ = [0, 10]), the largest deviations occurred. These can be explained by the difficulty of obtaining representative temperature measurements under very low wind conditions. Due to the lack of wind, conduction and radiation dominated over convection in the energy exchange between the cable and the air (Sigmund et al. 2017). The temperature of the cable was therefore not representative of the temperature of the air. Additionally, another explanation may lie in the stability correction itself, which is insufficient to correctly capture the typical challenges that come with extremely stable conditions (e.g. intermittent turbulence (Holtslag et al. 2013), submesoscale circulations (Mahrt 2009) and radiative divergence (Edwards 2009)). Deviations of the models from the observations during unstable conditions, can partly be attributed to the warming of the cable due to solar radiation (Fig. 4), but may also lie in the empirical nature of the Dyer stability corrections (Högström 1996). Moreover, during very unstable (free convection) conditions, $\theta _*$ is not a proper scaling parameter. Using $\theta _*$ for scaling is based on the assumption that $\overline{w'\theta '}$ and $u_*$ are linked, which is only the case for shear driven turbulence.

3.4 Determining Surface Length scale $L_s$

The surface length scale $L_s$ can be approximated through optimization against observations, as described in Sect. 3.3. We hypothesized that $L_s$ is associated with the smallest eddies just in and above the vegetation. This implies that it is independent of the flow characteristics, but mostly depends on the dimensions of the vegetation. So, ideally, $L_s$ should be a measurable quantity related to the vegetation height.

By studying the limit behaviour of the adapted Van Driest model (Eq. 6), we found that $L_s$ equals the ratio of $\theta _*$ over $(\partial \theta /\partial z)_{z=h}$. Using the high-resolution DTS observations, this ratio could be measured. Therefore we explored whether $\theta _*/(\partial \theta /\partial z)_{z=h}$ increased with vegetation height. The distribution of $\theta _* / (\partial \theta /\partial z)_{z=h}$ for two grass heights is shown in Fig. 10. Panels a and c depict the 20 cm grass section of the harp, and panels b and d show the 10 cm section, for dominant wind directions west and east respectively. For wind from the east, airflows over the 3 cm grass, and for the west over the undisturbed plot.

The variation between the two plots was larger than the variation associated with the wind direction. From this, we inferred that $\theta _* / (\partial \theta /\partial z)_{z=h}$ can be reasonably approximated as a fixed length scale equal to $\sim 0.2-0.4h$. Accounting for the standard deviation, the typical range is similar to $L_s/h$ derived for momentum fluxes in tall canopies, i.e. $\sim 0.3--0.6h$ (De Ridder 2010).

Despite being 2–4 times smaller than the optimal values for $L_s$ of 0.8h we found before (Fig. 9a), a length scale 2–4 times smaller only slightly increases the MAE by 0.05 – 0.12 K. Hence, $\theta _* / (\partial \theta /\partial z)_{z=h}$ is a reasonable estimate of $L_s$. The difference between the expected and optimal $L_s$ might be, because $L_s$ depends on the density of the grass (i.e. the distance between the tussocks) rather than its height (Fig. 1a). Note that, similar canopy concepts have been introduced for sparse canopies such as bushes (Raupach 1992; Jacobs and Verhoef 1997; Verhoef et al. 1997b). Further research into the grass structure is needed to support this claim. For now, we introduce as a rule of thumb that $L_s$ $\sim 0.5h$.

Fig. 10

Histogram of $\theta _* / (\partial \theta /\partial z)_{z=h}$ (an estimate of $L_s$) over the 20 cm and 10 cm plot for different wind directions for length scales in the 5th to 95th percentile range

3.5 Relation to Tall Canopies

The failure of similarity laws above tall canopies has long been recognized (e.g. Högström et al. 1989; LeMone et al. 2019). Often the standard boundary-layer flux-gradient relationships are adjusted for the RSL over tall canopies via the introduction of a correction term $\phi (z/\delta )$, e.g. Cellier and Brunet (1992), Verhoef et al. (1997b), Graefe (2004), Harman and Finnigan (2007), Harman and Finnigan (2008), De Ridder (2010). The correction terms introduce a length scale $\delta$ that relates to the canopy height, similar to our adapted Van Driest approach. However, the smallest canopies that were studied, were at least an order of magnitude taller than grass (Brunet 2020).

Raupach et al. (1996) hypothesized that tall canopy flows are more similar to a plane mixing layer than a boundary layer. A plane mixing layer is formed at the boundary of two atmospheric layers with different wind speeds, in contrast to a boundary layer at a fixed surface. Such a plane mixing layer occurs at the top of a canopy, where the logarithmic profile above the canopy continues into a more or less exponential profile in the canopy. The mixing layer depth is quantified by the vorticity thickness:

$$\begin{aligned} \delta = U(h)/\left( \frac{\partial U}{\partial z}\right) _{max}, \end{aligned}$$

(10)

where h is canopy height, U is mean velocity and $(\partial U/\partial z)_{max}$ is the maximum of the vertical wind velocity gradient and often (but not always) found at the top of the canopy. The dominant turbulent eddies are about the size of the mixing layer depth. This is because in large canopies, the eddies scale with the canopy height, instead of the individual plant elements (i.e., leaves, twigs, branches, etc.). It is reasonable to assume that the flow over short vegetation also behaves as a plane mixing layer. Preliminary DNS studies by our group indeed pointed towards the occurrence of vortex shedding and shear instabilities over (flexible) grass (Sauerbier 2024). By studying the behaviour of the adapted Van Driest equation near the surface (Eq. 7), we found that the formulation of the new length scale $L_{s}$ closely resembles that of the vorticity thickness used for tall canopies.

Here we compared a relatively simple RSL correction (De Ridder 2010) and a complex (Harman and Finnigan 2008) correction to our adapted van Driest model. By scaling the tall canopy models with their respective length scales, we could compare them to the adapted Van Driest model, and we show how they describe similar behaviour near the surface. De Ridder (2010) uses the RSL height as a scaling length scale, while Harman and Finnigan (2008) uses $\delta$. The normalization procedure is detailed in Appendix B. Figure 11 shows that overall behaviour is very similar (though the second derivatives differ near the surface). This implies that –in a scaled sense– the boundary layer flow does not behave very differently when the height of the roughness elements changes between grass and e.g. forests. Just like the inertial sublayer scaling (log-law) is rather universal, the buffer layer (RSL) could be as well. Why should grass essentially behave differently from e.g. mais etc.?

Fig. 11

Normalized Monin–Obukov (blue), Van Driest (red), De Ridder (2010) (green) and Harman and Finnigan (2007), Harman and Finnigan (2008) (grey) model for the temperature gradient with height (a) and numerically integrated temperature profile (b). Note the difference between MOST and the other models for small values of $\hat{z}$

For completeness, we note that explicit (physical) matching of the log-layer to the RSL has also been proposed over snow by Brutsaert (1975) and Andreas (1987). Snow is often rough, but typically smoother than grass. They hypothesized that heat exchange near the surface happens through diffusion while the eddies are temporarily trapped by the roughness elements (Grass 1971). The diffusion by one eddy has to be integrated over time to find the average RSL temperature profile. This integration introduced a new length scale that is the ratio of $T_b - T_s$ over the surface gradient (where $T_b$ is the bulk temperature, above the RSL). Their models described separate formulations for the RSL and log layer (that cross at a $z_{0h}$-dependent height), instead of describing a smooth transition like we do here.

4 Conclusion and Outlook

In this study, we introduced a new approach to predict temperature profiles for the roughness surface layer over short vegetation (grassland). It is well-known that MOST does not hold in the RSL, yet the logarithmic behaviour is conventionally extrapolated down to the surface.

Based on high-resolution temperature observations, we showed that MOST failed to accurately describe the temperature profiles in the lowest 1–2 m. Instead of logarithmic behaviour near the surface, we observed near-linear temperature profiles. Inspired by the Van Driest equation that describes the log–linear transition from turbulent to viscous flow over a smooth surface, we developed a similar model for flow over a rough vegetation surface. We therefore adapted the Van Driest model, by replacing the viscous length scale with a surface length scale $L_s$. We showed that over a rough surface, the geometry of the vegetation determines the size of the smallest eddies near the surface. The adapted Van Driest model outperformed the roughness length concept in describing the temperature profiles near the surface and predicting the surface temperature.

The adapted Van Driest equation described a similar shape as the De Ridder (2010) and Harman and Finnigan (2007, 2008) model for tall canopies. This showed the potential for upscaling. Moreover, we found that the surface length scale can be linked to the height of the vegetation. Future research is needed to prove the general applicability of the adapted Van Driest equation over different types of surface cover.

Appendices

Additional Figures

See Fig. 12.

Fig. 12

Grass height as measured over time, with uncertainty bars giving the standard deviation for the growing grass based on 8 measurements. There is no standard deviation measured for the 3 cm and 10 cm plots, as the grass was kept at a constant height

Derivation Normalized Models

In the next section, we study the behaviour of the Monin–Obukov Similarity Theory, the Van Driest model, and a simple and complex RSL correction for tall canopies. We derived the appropriate length scales to normalize the models by studying the limit behaviour near the surface. Next, the limits of the normalized models and their derivatives were studied. This shows how the adapted Van Driest model and the RSL corrections have the same limit of 1 near the surface but differ in their second derivative.

1.1 Normalized Monin–Obukov Equation

For the normalization, we used the following normalized variables:

$$\begin{aligned} \hat{\theta } = \frac{\theta }{\theta _*}, \hat{z} = \frac{z}{L_s}, \hat{L} = \frac{L_{ob}}{L_s}. \end{aligned}$$

(11)

This gives:

$$\begin{aligned} \frac{\partial {\hat{\theta }} }{\partial \hat{z}} \frac{\kappa \hat{z}}{ 1} = \varPhi _h\left( \frac{\hat{z}}{\hat{L}}\right) . \end{aligned}$$

(12)

1.2 Normalized Van Driest Equation

The Van Driest equation is given by Donda et al. (2014) as:

$$\begin{aligned} u_*^2 = \left[ \frac{(A \kappa z)^2 \frac{\partial {u} }{\partial z}}{\varPhi _n\left( \frac{z}{L_{ob}}\right) ^2} + \nu \right] \frac{\partial {u} }{\partial z}. \end{aligned}$$

(13)

Rewriting gives:

$$\begin{aligned} u_* = \left[ \frac{(A \kappa z)^2 \frac{\partial {u} }{\partial z}}{u_* \varPhi _m\left( \frac{z}{L_{ob}}\right) ^2} + (\nu /u_*) \right] \frac{\partial {u} }{\partial z}. \end{aligned}$$

(14)

Taking the limit at the surface gives the scaling parameters $u_*$ and $\nu /u_*$.

$$\begin{aligned}{} & {} \lim _{z\rightarrow 0} u_* = \left[ 0 + (\nu /u_*) \right] {\lim _{z\rightarrow 0} \frac{\partial {u} }{\partial z}}, \end{aligned}$$

(15)

$$\begin{aligned}{} & {} {\lim _{z\rightarrow 0} \frac{\partial {u} }{\partial z}} = \frac{u_*}{(\nu /u_*)}. \end{aligned}$$

(16)

For a rough surface, we replaced the viscous length scale $u_*/\nu$ with $L_s$. This gives:

$$\begin{aligned} u_* = \left[ \frac{(A \kappa z)^2 \frac{\partial {u} }{\partial z}}{u_* \varPhi _h\left( \frac{z}{L_{ob}}\right) ^2} + L_s \right] \frac{\partial {u} }{\partial z}. \end{aligned}$$

(17)

Replacing momentum by heat:

$$\begin{aligned} \theta _* = \left[ \frac{(A \kappa z)^2 \frac{\partial {\theta } }{\partial z}}{\theta _* \varPhi _h\left( \frac{z}{L_{ob}}\right) ^2} + L_s \right] \frac{\partial {\theta } }{\partial z}. \end{aligned}$$

(18)

Replacing $\theta$ and z for their normalized values:

$$\begin{aligned} 1 = \left[ \frac{(A \kappa \hat{z})^2 \frac{\partial {\hat{\theta }} }{\partial \hat{z}}}{\varPhi _h^2 \left( \frac{\hat{z}}{\hat{L}}\right) } + 1 \right] \frac{\partial {\hat{\theta }} }{\partial \hat{z}}. \end{aligned}$$

(19)

This can be solved with the quadratic formula, which has only one physical solution:

$$\begin{aligned} \frac{\partial \hat{\theta }}{\partial \hat{z}}= \frac{-1 + \sqrt{1+ 4 \left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) ^2}}{2 \left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) ^2}. \end{aligned}$$

(20)

The normalized gradient is always positive; in stable situations, both the gradient and $\theta _*$ are positive, while in unstable situations, a negative $\theta _*$ corresponds to a negative gradient, which then results in a positive normalized gradient.

To derive the limit at the surface, we applied a Taylor-expansion, relying on the binomial series: $(1+x)^{1/2} = 1 + \frac{1}{2} x - \frac{1}{8}x^2 + \frac{1}{16} x^3 -\cdots$

$$\begin{aligned} \frac{\partial \hat{\theta }}{\partial \hat{z}} = \frac{-1 + 1+ 2 \left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) ^2 - \left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) ^4}{2 \left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) ^2} = 1 - \frac{1}{2}\left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) ^2. \end{aligned}$$

(21)

Using the standard $\varPhi _H$-relation (see Sect. 2), the limit of $z \rightarrow 0$, for $\frac{\partial \hat{\theta }}{\partial \hat{z}}$ goes to 1.

The second derivative becomes:

$$\begin{aligned} \frac{\partial ^2 \hat{\theta }}{\partial \hat{z}^2}= - \left( \frac{A\kappa \hat{z}}{\varPhi _H\left( \frac{\hat{z}}{\hat{L}}\right) ^2}\right) . \end{aligned}$$

(22)

So, the limit of the curvature for $z \rightarrow 0$ thus goes to 0.

1.3 Normalized De Ridder Equation

De Ridder (2010) presents a simple bulk transfer model to account for RSL effects over tall canopies. The model for neutral conditions is given by:

$$\begin{aligned} \frac{\partial {\theta } }{\partial z} = \frac{\theta _*}{\kappa z} \left( 1 - e^{\mu z / z_*} \right) . \end{aligned}$$

(23)

We can recognize a correction term $\left( 1 - e^{\mu z / z_*} \right)$. We translated this into a length-scale type expression, that scales height with $z_*$ as a new length scale, similar to our $L_s$ approach. Here $z_*$ represents the height of the roughness sublayer and $\mu \approx 0.95$ is an empirical constant. We merged these into $\gamma = \mu / z_*$.

Using Taylors’ expansion this gives:

$$\begin{aligned} \frac{\partial {\theta } }{\partial z} = \frac{\theta _* \gamma z - \frac{\theta _* \gamma ^2 z ^2}{2} + \frac{\theta _*\gamma ^3 z^3}{6} +\cdots }{\kappa z} = \frac{\theta _* \gamma - \frac{\theta _* \gamma ^2 z }{2} + \frac{\theta _*\gamma ^3 z^2}{6} +\cdots }{\kappa }. \end{aligned}$$

(24)

Taking the limit at the surface gives the scaling parameters:

$$\begin{aligned} \lim _{z\rightarrow 0} \frac{\partial {\theta } }{\partial z} = \frac{\theta _* \gamma }{\kappa }. \end{aligned}$$

(25)

This gives a length scale $L_{R} = \kappa / \gamma = \kappa z_*/ \mu$.

The non-dimension equation then becomes:

$$\begin{aligned} \frac{\theta _*}{L_{R}} \frac{\partial \hat{\theta }}{\partial \hat{z}} = \frac{\theta _*}{\kappa \hat{z} L_{R}} \left( 1 - e^{-L_{R} \hat{z} L_{R} } \right) = \frac{1}{\kappa z} \left( 1 - e^{-\hat{z}} \right) . \end{aligned}$$

(26)

To derive the limit, we applied Taylors’ expansion:

$$\begin{aligned} \frac{\partial {\hat{\theta }} }{\partial \hat{z}} = \frac{\kappa \hat{z} - \frac{\kappa ^2 \hat{z}^2}{2} + \frac{\kappa ^3 \hat{z}^3}{6} +\cdots }{\kappa z} = 1 - \frac{\kappa z}{2} + \frac{\kappa ^2z^2}{6} +\cdots . \end{aligned}$$

(27)

The limit of $z \rightarrow 0$ is at 1.

The second derivative becomes:

$$\begin{aligned} \frac{\partial {^2\hat{\theta }} }{\partial \hat{z}^2} = \frac{\kappa }{2} + \frac{\kappa ^2z}{3} +\cdots . \end{aligned}$$

(28)

The limit of the curvature for $z \rightarrow 0$ thus goes to $\frac{1}{2}\kappa$.

1.4 Normalized Harman and Finnigan Equation

The model dominating the field of canopy-layer turbulence is the Harman and Finnigan model (Harman and Finnigan 2007, 2008). Harman and Finnigan provide a continuous model for RSL correction $\phi (z/L_s)$ with an exponential shape that asymptotically approaches 1 at 2–3 times the roughness sublayer height. This model has been implemented in the Community Land Model, and showed a substantially improved prediction of the surface exchange over several surface types, among which is grassland (Oleson et al. 2010; Bonan et al. 2018). An important feature of the Harman and Finnigan model is that they introduce the virtual displacement height ($d_v$), which scales with $u^2_*$, and lowers the displacement height compared to the origin.

In a very simplified form, this model can be written as:

$$\begin{aligned} \frac{\partial {\theta } }{\partial z} = \frac{ \theta _*}{\kappa (z + d_{v})} \varPhi _h\left( \frac{z}{L_{ob}}\right) . \end{aligned}$$

(29)

Taking the limit at the surface gives the scaling parameters:

$$\begin{aligned} \lim _{z\rightarrow 0} \frac{\partial {\theta } }{\partial z} = \frac{ \theta _*}{\kappa d_{v}}. \end{aligned}$$

(30)

This gives us the length scale $\kappa d_v = L_{HF}$, and temperature scale $\theta _*$.

If we normalize this equation using a length scale $L_{HF}$, the equation (for neutral conditions) becomes:

$$\begin{aligned} \frac{\theta _*}{L_{HF}} \frac{\partial \hat{\theta }}{\partial \hat{z}} = \frac{ \theta _*}{\kappa (\hat{z} L_{HF} + d_{v})}, \end{aligned}$$

(31)

$$\begin{aligned} \frac{\theta _*}{L_{HF}} \frac{\partial \hat{\theta }}{\partial \hat{z}} = \frac{ \theta _*}{\kappa d_v + \kappa \hat{z} L_{HF}}, \end{aligned}$$

(32)

$$\begin{aligned} \frac{\partial \hat{\theta }}{\partial \hat{z}} = \frac{L_{HF}}{\kappa d_v + \kappa \hat{z} L_{HF}}. \end{aligned}$$

(33)

Using $L_{HF} = \kappa d_v$, this gives:

$$\begin{aligned} \frac{\partial \hat{\theta }}{\partial \hat{z}} = \frac{1}{1 + \kappa \hat{z} }. \end{aligned}$$

(34)

So, the limit of $z \rightarrow 0$ is at 1.

The second derivative becomes:

$$\begin{aligned} \frac{\partial ^2\hat{\theta }}{\partial \hat{z}^2} = \frac{-\kappa }{(1 + \kappa \hat{z})^2 }. \end{aligned}$$

(35)

The limit of the curvature for $z \rightarrow 0$ thus goes to $-\kappa$.