1 Introduction

The thermal properties of soil play an important role in many physical processes in the upper soil layers as well as in engineering applications. Soil temperature is exploited in the design of low enthalpy heating pumps (Buzăianu et al. 2015) and also affects nutrient and water uptake by plants, influencing crop development (Kaspar and Bland 1992). In addition, surface temperature affects the exchange of sensible and latent heat between the surface of the Earth and its atmosphere (Kiehl and Trenberth 1997; Jacobs et al. 2008) and is required in local-scale hydrometeorological models (Heusinkveld et al. 2004) as well as in global scale general circulation models (Sellers et al. 1996; Dai et al. 2003).

The temperature distribution in the soil is determined by the heat transfer occurring through conduction and through intra-porous convection (Nassar and Horton 1992a; Passerat de Silans et al. 1996). A long line of research has been to ignore the convective processes and focus on heat conduction that is mainly governed by the thermal diffusivity of soil. The diffusivity depends on the physical and chemical properties of the soil, such as its composition, density and porosity as well as its water content (Farouki 1981; Chen 2008). The thermal diffusivity can be measured in the laboratory using soil samples and various techniques such as the dual-probe heat-pulse and the hot plate methods (Pratt 1969; Bristow et al. 1994). However, these laboratory measurements do not take into account the strong influence that the time-dependent soil moisture in the field exerts on the diffusivity (Wang et al. 2005; Lu et al. 2007). Consequently, there are various indirect methods to estimate thermal diffusivity from on-site observations of either the heat flux or the temperature at various depths (Horton et al. 1983; Peng et al. 2015).

Most of the indirect estimates of soil diffusivity from temperature measurements are based on analytical solutions of the one-dimensional heat conduction equation in a semi-infinite medium under the assumption that the soil diffusivity is independent of time and depth. The equation is solved using either the Laplace transform to obtain the transient response of soil temperature to changes in the surface temperature (Carslaw and Jaeger 1959; Asrar and Kanemasu 1982), or the harmonic method which involves fitting the observed temperature variability with harmonic functions (Van Wijk and de Vries 1963; Nerpin and Chudnovskii 1967). Based on these solutions, there were several methods developed to estimate the soil diffusivity such as the amplitude and the phase algorithms that are based on a single harmonic, the arctangent, and the logarithmic algorithms that are based on two harmonics as well as the harmonic method that is based on many harmonics and were tested in various sites and conditions (Horton et al. 1983; Verhoef et al. 1996).

However, evaporation of soil moisture at the surface and infiltration are expected to play a significant role in the transfer of heat in the soil. For example, one of the models commonly used for estimating global land surface turbulent fluxes (SiB2) tends to overestimate sensible heat flux and to underestimate latent heat flux (Zhang et al. 1996; Schelde et al. 1997). Since the model takes into account only heat transfer by conduction, one point of improvement could be the inclusion of convective processes. When taking moisture into account, the dynamics of heat transfer and moisture advection are coupled as higher temperatures lower the water viscosity and increase the infiltration rate (Constantz 1982; Constantz et al. 1994), while liquid water and vapour flowing through the porous medium transfer heat affecting the temperature (Pilotti et al. 2002). The heat and moisture transport processes are complex and depend on many factors such as the osmotic and matric potential, water evaporation that can take place more than 10 cm below the soil surface (Piri et al. 2021), water vapour adsorption that is important in Mediterranean ecosystems (Kosmas et al. 2001), and soil ventilation that can cause diurnal oscillations in the surface–atmosphere gas exchanges (Roland et al. 2013).

Philip and deVries (1957) modelled the heat transfer and water movement dynamics with two coupled nonlinear partial differential equations including temperature-dependent moisture and heat diffusivities, and the theory was later extended by Nassar and Horton (1992a) to include solute concentration effects. Numerical solutions of the coupled dynamics led to insights into the intricate processes involved and their effects such as the diurnal variation exhibited by the infiltration at the soil surface due to the daily temperature variations (Jaynes 1990; Nassar and Horton 1992b). Based on this observation, Shao et al. (1998) ignored the gas phase and developed a simplified version of the dynamics that consists of a thermal conduction–convection equation and allows for analytical solutions in the case in which both the water flux and the surface temperature vary sinusoidally in time, while Wang et al. (2012) obtained the solution for any surface temperature variations. Gao et al. (2003) used the Laplace transform and the harmonic method to solve the conduction–convection equation in the case of constant water flux. Based on this solution, they developed the conduction–convection algorithm to obtain the soil diffusivity and the water flux density from soil temperature measurements. This algorithm was tested against the methods based on the conducting solution, using temperature measurements (Gao et al. 2008; Wang et al. 2010; Tong et al. 2017) as well as using temperature and heat flux measurements (An et al. 2016) and was also implemented to improve the calculation of the surface heat flux (Gao 2005).

Most of these comparison studies reported different values for thermal diffusivity and water flux density in different layers even though the conduction as well as the conduction–convection solutions on which the algorithms are based assume homogeneous properties for the soil. Similar results were also reported by Holmes et al. (2008), who found that the conduction solution performs well in deep soil layers, but results in large errors when applied to layers near the surface. Such variations with depth are expected due to the dependence of soil diffusivity on moisture and its variable depth penetration. To address the non-homogeneous properties of soil, Lettau (1954) used the harmonic method to solve the conduction equation with a depth-dependent soil diffusivity. He assumed a Taylor expansion for the depth-dependent Fourier coefficients as well as the soil diffusivity and provided a method to calculate the first few terms of these coefficients based on temperature measurements and their gradients at various depths. It is, therefore, an approximate method that was also shown to require smoothing of temperature before calculation of its gradient in order to avoid negative results for the diffusivity (Nassar and Horton 1990). Exact solutions were obtained by Novak (1986) and Massman (1993) in cases in which the soil diffusivity has a specific dependence on depth (linear, exponential, and power law). These solutions have had limited use in field experiments, probably due to the fact that they require a number of constants which have to be inferred from the general properties of the soil. Gao et al. (2008) assumed a constant gradient of thermal diffusivity and showed that the solution to the conduction–convection equation is similar to the one obtained previously by Gao et al. (2003). However, this solution is approximate as the linear dependence of soil diffusivity is assumed small and is not fully taken into account when solving the equation. In addition, only the sum of the gradient of soil diffusivity and the water flux density can be calculated using the conduction–convection method and thus the two effects cannot be fully separated.

The goal of this work is to obtain a solution to the conduction–convection equation for non-homogeneous soil that is both exact and easy to use with field measurements of temperature for the modelling of temperature variability and the estimation of the soil properties. The basic assumption is that the soil properties are piecewise-constant within layers. That is, we assume that the soil is separated into layers over which the thermal diffusivity has different values and then calculate analytically the spatio-temporal distribution of soil temperature. Based on this solution, we develop a method to calculate the values of soil diffusivity and water flux density using temperature measurements at various depths. The proposed method is then applied to field data from the meteorological station of the University of Ioannina, Greece, and is compared to three of the most commonly used algorithms: the amplitude, the phase, and the conduction–convection algorithm.

This paper is organized as follows: The conduction–convection equation for the transfer of heat is presented in Sect. 2 along with a review of the previously obtained solutions on which the amplitude, the phase, and the conduction–convection algorithms are based. In Sect. 3, we present the novel analytical solution to the equation based on the piecewise-constant assumption and also develop the method to calculate the water flux density and the depth dependent thermal diffusivity based on temperature measurements. The method is applied in Sect. 4 to field data and the obtained results regarding the soil properties as well as the comparison of its predictions with the measured temperature variability are discussed. In addition, the performance of the method in capturing the spatio-temporal variability of the temperature is compared to the three algorithms. Finally, we end with our brief conclusions in Sect. 5.

2 Equations for the Transfer of Heat in the Soil

We consider the one-dimensional heat transfer model of Gao et al. (2003). In this model, soil is considered as horizontally homogeneous and isotropic and heat is transferred vertically via conduction and convection of soil water through the porous medium. While convection also occurs through water vapour, the gas-phase flows in this model are neglected, as the goal is to obtain a simplified version of the dynamics that allows for analytic solution and can be easily implemented. The time rate of change of soil temperature T(z, t) is given by:

$$\begin{aligned} \frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left( k\frac{\partial T}{\partial z}+WT\right) . \end{aligned}$$
(1)

The first term on the right-hand side of (1) is the heat flux convergence due to conduction and k is the thermal diffusivity of soil. The second term is the heat flux convergence due to convection and \(W=(c_w/c_s)w\theta \) is the water flux density, where \(c_w\) and \(c_s\) are the heat capacities of water and soil, respectively, w is the liquid infiltration rate (positive downward), and \(\theta \) is the water content in the soil. The conduction–convection equation is solved under the following boundary conditions. The first is that soil is considered as a semi-infinite layer with negligible temperature variation at large depth, therefore:

$$\begin{aligned} \lim _{z\rightarrow \infty }T=T_\infty , \end{aligned}$$
(2)

where \(T_\infty \) is the constant mean temperature at large depth. The second is that temperature at the surface \(T(z=0,t)\) is a known function from temperature measurements and is typically decomposed into a Fourier series or transform:

$$\begin{aligned} T(z=0,t)=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^\infty \hat{T}_0(\omega )e^{i\omega t}\,{\textrm{d}}\omega =\frac{1}{\sqrt{8\pi }}\int _0^\infty \left[ \hat{T}_0(\omega )+\hat{T}_0^*(\omega )\right] e^{i\omega t}\,{\textrm{d}}\omega . \end{aligned}$$
(3)

The integral is restricted to positive values for the frequency by taking advantage of the fact that for a real temperature field \(\hat{T}_j(z,-\omega )=\hat{T}_j^*(z,\omega )\) and \(\hat{T}_0(0)=T_\infty \) as the mean temperature at the surface is assumed to be the same as in large depths due to heat conservation.

Due to linearity of (1), and assuming that the soil diffusivity and the water flux are independent of time, we can apply the same Fourier transform on the temperature at every depth and plug it in (1) to obtain the second-order ordinary differential equation for the Fourier amplitude at each depth \(\hat{T}(z,\omega )\):

$$\begin{aligned} \frac{{\textrm{d}}}{{\textrm{d}}z}\left( k\frac{{\textrm{d}}\hat{T}}{{\textrm{d}}z}\right) +W\frac{{\textrm{d}}\hat{T}}{{\textrm{d}}z}-i\omega \hat{T}=0. \end{aligned}$$
(4)

The solution to (4) along with the corresponding boundary conditions:

$$\begin{aligned} \lim _{z\rightarrow \infty }\hat{T}=0, \end{aligned}$$
(5)

and

$$\begin{aligned} \hat{T}(z=0,\omega )=\hat{T}_0, \end{aligned}$$
(6)

gives the temperature variability at each depth.

2.1 Existing Methods for the Determination of Thermal Diffusivity and Water Flux Density

Most of the methods that are used to indirectly calculate the soil thermal diffusivity are based on the solution of Van Wijk and de Vries (1963) who ignored heat transfer by convection (\(W=0\)) and assumed that diffusivity is constant with depth. In this case, (4) is simplified to:

$$\begin{aligned} k\frac{{\textrm{d}}^2\hat{T}}{{\textrm{d}}z^2}-i\omega \hat{T}=0, \end{aligned}$$
(7)

and has the solution:

$$\begin{aligned} \hat{T}=\hat{T}_0e^{-(1+i)z/d}. \end{aligned}$$
(8)

According to this solution, the amplitude of temperature variation relative to the variation at the surface is exponentially decreasing with depth as:

$$\begin{aligned} a(z)=\ln \left| \frac{\hat{T_0}}{\hat{T}}\right| =\frac{z}{d}, \end{aligned}$$
(9)

where \(d=\sqrt{2k/\omega }\) is the corresponding damping depth. In addition, the phase difference between temperature variation at the surface and temperature variation at some depth increases linearly with depth at a rate 1/d:

$$\begin{aligned} \phi (z)=\arg \left( \frac{\hat{T}_0}{\hat{T}}\right) =\frac{z}{d}. \end{aligned}$$
(10)

Based on (8) and temperature measurements at various depths, the thermal diffusivity can be calculated using several methods (algorithms), two of which are used more frequently (Horton et al. 1983). The first method is to obtain the Fourier amplitude of measured temperature \(\hat{T}_m(z,\omega )\) at various depths and plot the phase difference:

$$\begin{aligned} \phi _m(z)=\arg \left( \frac{\hat{T}_0}{\hat{T}_m}\right) , \end{aligned}$$
(11)

with depth. Assuming it is close to linear and equating the slope \(s_\phi \) to 1/d from (10) yields the thermal diffusivity:

$$\begin{aligned} k_\phi =\frac{\omega }{2 s_\phi ^2}. \end{aligned}$$
(12)

This is referred to as the phase algorithm. The second method is to plot the logarithm of the measured amplitude ratio:

$$\begin{aligned} a_m(z)=\ln \left| \frac{\hat{T}_0}{\hat{T}_m}\right| , \end{aligned}$$
(13)

with depth. Again, assuming it is close to linear and equating the slope \(s_a\) to 1/d from (9) yields the soil thermal diffusivity:

$$\begin{aligned} k_a=\frac{\omega }{2s_a^2}. \end{aligned}$$
(14)

This is referred to as the amplitude algorithm. Note that if temperature variability is indeed captured by (8), then \(s_\phi =s_a\) and the two algorithms give the same result. These two algorithms have also been directly applied to the temperature time series rather than the amplitudes in the Fourier transform. In this case, the amplitudes \(|\hat{T}_m(z)|\) are calculated as the maximum values of temperature variation (regardless of the frequency) and the phase difference is calculated from the difference between the times at which the maximum temperature is attained at two different depths (Horton et al. 1983).

Gao et al. (2003) introduced a method that also takes into account convection (\(W\ne 0\)). Assuming again that thermal diffusivity is constant with depth reduces (4) to:

$$\begin{aligned} k\frac{{\textrm{d}}^2\hat{T}}{{\textrm{d}}z^2}+W\frac{{\textrm{d}}\hat{T}}{{\textrm{d}}z}-i\omega \hat{T}=0. \end{aligned}$$
(15)

Gao et al. (2003) showed that the solution to (15) is given by:

$$\begin{aligned} \hat{T}=\hat{T}_0e^{-(W+\sqrt{W^2+4i\omega k})z/2k}. \end{aligned}$$
(16)

Therefore, the amplitude of temperature variation again decreases exponentially,

$$\begin{aligned} a(z)=\frac{z}{D_a}, \end{aligned}$$

with a damping depth:

$$\begin{aligned} D_a=\frac{\omega d\sqrt{2}}{W\sqrt{2}+\sqrt{W^2+\sqrt{W^4+4\omega ^4d^4}}}, \end{aligned}$$
(17)

and the phase difference increases linearly:

$$\begin{aligned} \phi (z)=\frac{z}{D_\phi } \end{aligned}$$
(18)

with an inverse slope:

$$\begin{aligned} D_\phi =\frac{\sqrt{W^2+\sqrt{W^4+4\omega ^4d^4}}}{\sqrt{2}\omega }, \end{aligned}$$
(19)

that differs from the damping scale in this case. The method to determine W and k is to calculate the measured slopes \(s_\phi \) and \(s_a\) of \(\phi _m(z)\) and \(a_m(z)\), respectively, to plug \(D_a=1/s_a\) and \(D_\phi =1/s_\phi \) into (17) and (19) and solve for k and W to obtain:

$$\begin{aligned} k_{cc}= & {} \frac{\omega s_a}{s_\phi (s_a^2+s_\phi ^2)}, \end{aligned}$$
(20)
$$\begin{aligned} W_{cc}= & {} \frac{\omega (s_a^2-s_\phi ^2)}{s_\phi (s_a^2+s_\phi ^2)}. \end{aligned}$$
(21)

This is referred to as the conduction–convection method. All three algorithms assume that thermal diffusivity is constant with depth. However, calculation of this quantity in different layers in the soil typically yields different results, with a complicated dependence of k on depth (Gao et al. 2008; Wang et al. 2010; Tong et al. 2017; An et al. 2016). To take into account the dependence of thermal diffusivity on depth, Gao et al. (2008) rewrote (4) as:

$$\begin{aligned} k(z)\frac{{\textrm{d}}^2T}{{\textrm{d}}z^2}+\left( \frac{{\textrm{d}}k}{{\textrm{d}}z}+W\right) \hat{T}-i\omega \hat{T}=0, \end{aligned}$$
(22)

and assumed a constant gradient of diffusivity that was incorporated in a new constant, \(\tilde{W}=W+(dk/dz)\). They then solved (22) without taking into account the linear dependence of k in the first term. The inherent assumption is that the gradient of k is small so that the thermal diffusivity can be taken as almost constant. Under this Wentzel–Kramers–Brillouin approximation that the diffusivity is slowly varying (Bender and Orszag 1999), the solution is again given by (16) with merely a different interpretation for W. However, the large differences between values of thermal diffusivity at different depths obtained by the application of this method (Gao et al. 2008) showed that it can only be considered as approximate. In the next section, we develop a method that takes into account the dependence of thermal diffusivity on depth without any assumptions on the magnitude of its variation.

3 The Non-homogeneous Conduction–Convection Method

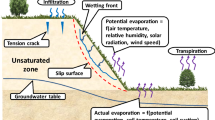
In order to obtain an analytic solution of (4) with depth dependent soil diffusivity that is exact but easy to implement with regards to field measurements, we assume that soil properties are piece-constant within soil layers. Since the solution will be employed to field data, the width of the different layers is imposed by the depths of the temperature sensors. That is, since any theoretical model is tested against the field data and the temperature sensors are placed at specific depths, the zeroth-order assumption without further information is that soil properties are constant in the layer between two consecutive sensors. So, if we have measurements at n depths \(z_j\) with \(j=1,2,\cdots ,n\), as shown in Fig. 1, we assume that k has constant but different values \(k_j\) in each of the layers \(z\in [z_{j-1},z_j]\), with \(z_0=0\) corresponding to the surface. The Fourier amplitude of temperature \(\hat{T}_j(z,t)\) within each of these layers evolves according to (15). Therefore, we have similar solutions as in (8):

$$\begin{aligned} \hat{T}_j=A_j^+e^{m_j^+z}+A_j^-e^{m_j^-z}, \end{aligned}$$
(23)

where:

$$\begin{aligned} m_j^\pm =-\frac{W}{2k_j}\pm \frac{\sqrt{W^2+4i\omega k_j}}{2k_j}. \end{aligned}$$

The solutions are then connected at the boundaries of the layers according to the conditions that the temperature is continuous across the interface of each layer:

$$\begin{aligned} \hat{T}_j(z_j,\omega )=\hat{T}_{j+1}(z_j,\omega ), \end{aligned}$$
(24)

and that the heat flux is continuous as well:

$$\begin{aligned} k_j\left( \frac{{\textrm{d}}\hat{T}_j}{{\textrm{d}}z}\right) _{z_j}+W\hat{T}_j(z_j,t)= k_{j+1}\left( \frac{{\textrm{d}}\hat{T}_{j+1}}{{\textrm{d}}z}\right) _{z_j}+W\hat{T}_{j+1}(z_j,t). \end{aligned}$$
(25)

In addition, we have the boundary condition at the surface (e.g. Eq. 5) obeyed by \(\hat{T}_1(z,t)\) and the condition at large depth (e.g. Eq. 6) obeyed by \(\hat{T}_n(z,t)\). Applying these boundary conditions yields the coefficients \(A_j^\pm \):

$$\begin{aligned} A_j^\pm =\frac{b_j^\pm \hat{T}_0}{b_1^++b_1^-}, \end{aligned}$$
(26)

where

$$\begin{aligned} b_j^\pm= & {} \pm \frac{k_jm_j^\mp -k_{j+1}m_{j+1}^+}{k_j(m_j^--m_j^+)}b_{j+1}^+e^{(m_{j+1}^+-m_j^\pm )z_j}\end{aligned}$$
(27)
$$\begin{aligned}{} & {} \pm \frac{+k_jm_j^\mp -k_{j+1}m_{j+1}^-}{k_j(m_j^--m_j^+)}b_{j+1}^-e^{(m_{j+1}^--m_j^\pm )z_j}, \end{aligned}$$
(28)

for \(j\le n-2\),

$$\begin{aligned} b_{n-1}^\pm =\pm \frac{k_{n-1}m_{n-1}^\mp -k_nm_n^-}{k_{n-1}(m_{n-1}^--m_{n-1}^+)}e^{(m_n^--m_{n-1}^\pm )z_{n-1}}, \end{aligned}$$
(29)

and

$$\begin{aligned} b_n^+=0,\;\;b_n^-=1. \end{aligned}$$
(30)

Note that contrary to the solutions (8) and (16), the temperature variation (23) does not in general produce amplitude decay and phase difference functions that increase linearly with depth, with the only exception of the last layer for which temperature is given by:

$$\begin{aligned} \hat{T}_n=\frac{\hat{T}_0}{b_1^++b_1^-}e^{-m_n^-z}. \end{aligned}$$
(31)
Fig. 1
figure 1

Separation of the soil into layers by the depths \(z_j\) of the temperature sensors and set-up of the solution of the conduction–convection equation with piecewise-constant soil diffusivity

Full size image

Based on this solution, the soil diffusivity for each layer and the water flux density can be calculated from the temperature measurements at the depths \(z_j\) using the following method. For the deepest layer for which temperature is given by (31), the amplitude decay a(z) and the phase difference \(\phi (z)\) functions are linearly increasing with depth and the conduction–convection method can be applied using the slope of the measured amplitude decay \(a_m(z)\) and phase difference \(\phi _m(z)\) between the depths \(z_{n-1}\) and \(z_n\) to calculate \(k_n\) and W. We then form the \(n-1\) multivariate functions:

$$\begin{aligned} f_j^a(k_1, \cdots ,k_{n-1},W)=\ln \left| \frac{\hat{T}_m(z_{j+1},\omega )}{\hat{T}_m(z_j,\omega )}\right| -\ln \left| \frac{\hat{T}_j(z_{j+1},\omega )}{\hat{T}_j(z_j,\omega )}\right| . \end{aligned}$$
(32)

The first term is the decay of the measured amplitude of temperature variation within the j-th layer, while the second is the corresponding decay predicted by (23). For a perfect fit between the observations and the analytical solution, these functions should be zero. The zeros of the functions are surfaces in the n-dimensional space defined by the variables \(k_1, k_2, \cdots k_{n-1}, W\) and the values of the diffusivities and the flux density are the single point of intersection among all of these surfaces. Therefore, a root-finding method could be used to calculate these values. This method is thus similar to the amplitude algorithm in the case of constant diffusivity. Similarly, we can form the \(n-1\) functions:

$$\begin{aligned} f_j^\phi (k_1,\cdots ,k_{n-1},W)=\arg \left( \frac{\hat{T}_m(z_{j+1},\omega )}{\hat{T}_m(z_j,\omega )}\right) -\arg \left( \frac{\hat{T}_j(z_{j+1},\omega )}{\hat{T}_j(z_j,\omega )}\right) , \end{aligned}$$
(33)

where the first term is the measured phase difference between the temperature variation at the boundaries of the j-th layer and the second is the corresponding phase difference predicted by (23). Again, a root finding method could be used to find the zeros of these functions that would correspond to the values of the diffusivities and the flux density yielding a perfect fit between the observations and the analytical solution. This is similar to the phase algorithm in the case of constant diffusivity. In case the measurements do not agree exactly with the theoretical model, the values of \(k_1, k_2, \cdots k_{n-1}, W\) producing the smallest error can be calculated by minimizing the sum of the absolute value of these functions \(f_j^a\) and \(f_j^\phi \) for all n layers.

4 Application of the Method to Field Data

4.1 Experimental Site and Temperature Measurements

To apply the method and compare it with the existing algorithms, we use soil temperature data from the meteorological station located within the University campus in the city of Ioannina, north-western Greece (\(39.62^{\circ }\)N, \(20.84^{\circ }\)E). The climate in the region is classified as Csa according to Köppen–Geiger (Rubel and Kottek 2010). The average mean temperature is \(2.5\,^{\circ }\)C in January and \(23.8\,^{\circ }\)C in August and precipitation ranges from 21 mm in August to 187 mm in November. The city is located in a plateau at 485 m above sea level and the measurement site is flat with soil consisting mainly of sand and clay and covered with common grass.

The station is equipped with thermocouples measuring soil temperature at depths \(z_1=10\) cm, \(z_2=30\) cm, and \(z_3=60\) cm as well as very near the surface (\(z_0=0.02\) cm) with a \(0.1\;^{\circ }\)C accuracy. The temperature is recorded and averaged over 30-min intervals and the overall time series covers a seven-year period. The missing values account for only a small fraction of less than 1% of the total values and are typically a few isolated 30-min intervals. Therefore, the missing values are approximately calculated via linear interpolation using neighbouring known values to form a complete time series of temperature at these depths.

The times series for temperature at various depths is shown in Fig. 2. We observe that temperature variability is dominated by the annual cycle at all depths. In addition, the variability at larger frequencies (such as the diurnal frequency) is greatly reduced with depth as expected by all of the theoretical models in Sects. 2 and 3.

Fig. 2
figure 2

Time series of temperature at the surface (a) and at depths \(z_1=10\) cm (b), \(z_2=30\) cm (c), and \(z_3=60\) cm (d). The temperature mean which is approximately the same at all depths has been subtracted

Full size image

A discrete Fourier transform performed on the time series of temperature confirms these results, as we observe in the periodograms shown in Fig. 3 that the dominant frequency at all depths is the annual frequency accounting for about half the temperature variance. We also have secondary peaks at the diurnal frequency and its higher order harmonics that account for 2% of the variance. In order to calculate the thermal diffusivity and the water flux density, we first chose to analyse the Fourier amplitudes for the dominant annual frequency using the full time series and then chose to calculate the thermal diffusivity and the water flux density on the diurnal time scale using two limited parts of the time series over a few days each. Such a choice is suggested by the dependence of k and W on time. As discussed in the introduction, both the diffusivity and the water flux density are significantly influenced by soil water and its infiltration and are expected to change on daily to monthly time scales (Jaynes 1990). The annual variability of heat transfer is expected to be influenced by the average value for these two parameters over one year that can be approximated as constant. But for the diurnal variability, they can only be considered as constant over the course of a few days in which water infiltration and soil moisture have not changed significantly. As a result, we chose two representative parts of the time series that are shown in Fig. 4, one over the dry period of August (Fig. 4a) and the other one (Fig. 4b) over a period with episodes of precipitation that is also shown in the Fig. 4b. These two cases are thus representative of heat transfer in dry and wet soil. The Fourier amplitudes of temperature at the surface for these two time series that is shown in Fig. 4c, d reveal that the diurnal frequency is dominant (accounting for roughly half the temperature variance) and is followed by its first (12-h) harmonic.

Fig. 3
figure 3

Periodograms of temperature at the surface (a) and at depths \(z_1=10\) cm (b), \(z_2=30\) cm (c), and \(z_3=60\) cm (d)

Full size image
Fig. 4
figure 4

a, b Time series of temperature at the surface for a dry (a) and a wet (b) period. In b, the precipitation over 30-min intervals (red bars) is also shown. c, d Periodograms of the two time series of temperature shown in (a) and (b)

Full size image

4.2 Calculation of the Water Flux Density and the Depth-Dependent Thermal Diffusivity

We first calculate the logarithm of the amplitude ratio \(a_m(z)\) and the phase difference \(\phi _m(z)\) given by (11) and (13) with \(\hat{T}_m\) being the measured Fourier amplitude at the annual frequency using the full time series. The functions that are plotted in Fig. 5 are monotonically increasing. While the phase difference function appears close to linear, the amplitude ratio function is not as it exhibits a rapid initial increase close to the surface followed by a gradual increase at larger depths. Therefore, the existing three algorithms analysed in Sect. 2 that assume a linear increase can only be approximately applied in this case. However, we can apply the novel algorithm developed in the previous section that takes into account such depth variations. Due to the measurements at three depths, we separate the soil into three layers with the soil thermal diffusivity being a piecewise constant function over these layers. For the last layer, we applied the conduction–convection method to find from (20) and (21) the values of W and \(k_3\). We then formed the four functions (32)–(33) and applied Broyden’s method (Broyden 1965) to find the roots of these functions. However, the method did not give positive results, as the theoretical model did not exactly match the observations. We therefore applied an interior point algorithm (Byrd et al. 2000) to find the minimum of the absolute value of the six functions \(f_j^a\) and \(f_j^\phi \) under the conditions that \(k_j\) is positive. The global minimum was found for the values shown in Table 1.

Table 1 Values for the soil thermal diffusivity in the soil layers, as well as the water flux density obtained by the non-homogeneous conduction–convection method
Full size table

Regarding the thermal diffusivity, we observe for all layers values that are representative of clay soil (Garratt 1992) and we also observe that diffusivity increases in the second layer and decreases in the third. Controlled laboratory experiments with soil samples (Farouki 1981) as well as indirect estimation from on-site temperature measurements (Gao et al. 2008) have shown that such dependence of diffusivity on depth is not uncommon. In addition, the value for the water flux density reveals that convection accounts for 10% of the heat transfer in the soil. The logarithm of the amplitude ratio and the phase difference resulting from these values and the solution (23) in each of the layers are also shown in Fig. 5 (solid line), where we observe a very good agreement between the theoretical predictions and the measured values.

Fig. 5
figure 5

a Logarithm of the ratio of the amplitude of measured annual temperature variation \(a_m(z)=\ln |\hat{T}_0/\hat{T}_m|\) as a function of depth (circles). b Phase difference \(\phi _m(z)\) between the measured annual temperature variation at the surface and the temperature variation at depth z as a function of depth (circles). Also shown in both panels are the corresponding functions obtained by the non-homogeneous conduction–convection method (solid lines) and a linear fit (dashed line) used to calculate the soil diffusivity and the water flux density via the three existing algorithms

Full size image

Similarly, we applied the same method on the two limited parts of the time series representing dry and wet soil. The amplitude ratio \(a_m(z)\) and the phase difference \(\phi _m(z)\) functions with \(\hat{T}_m\) being the measured Fourier amplitude at the diurnal frequency are shown in Fig. 6. Since the amplitude of the diurnal variation decays rapidly with depth, daily temperature variability at depth \(z_3\) is smaller than the sensor sensitivity. We have therefore plotted the functions using only the depths \(z_1\) and \(z_2\). As in the annual temperature variation, the functions in both cases are monotonically increasing but are not linear. The non-homogeneous algorithm was applied for the two first layers. Since Broyden’s method did not give positive results for the roots of the functions \(f_j^a\) and \(f_j^\phi \), we again applied the interior point algorithm to find the minimum of the absolute value of the four functions \(f_j^a\) and \(f_j^\phi \). The global minimum was found for the values shown in the final two columns in Table 1 for the dry and the wet cases, respectively. We observe the same depth dependence as in the case of annual temperature variation, with values of thermal diffusivity being slightly lower compared to the values obtained from the annual variation of temperature. The differences in the diffusivities between the dry and the wet case are more significant in the surface layer (around 20% difference between the two cases), but the most significant difference between the dry and the wet case is the shut-down of convection in the former case. The logarithm of the amplitude ratio and the phase difference resulting from these values and (23) in each of the layers are also shown in Fig. 6 (solid line), where we again observe a very good agreement between the theoretical predictions and the measured values.

Fig. 6
figure 6

a, b Logarithm of the ratio of the amplitude of measured diurnal temperature variation \(a_m(z)=\ln |\hat{T}_0/\hat{T}_m|\) as a function of depth (circles) for the dry (a) and the wet (b) cases. b Phase difference \(\phi _m(z)\) between the measured diurnal temperature variation at the surface and the temperature variation at depth z as a function of depth (circles) for the dry (c) and the wet (d) cases. Also shown in all panels are the corresponding functions obtained by the non-homogeneous conduction–convection method (solid lines) and a linear fit (dashed line) used to calculate the thermal diffusivity and the water flux density via the three existing algorithms

Full size image

4.3 Comparison of the Non-homogeneous Conduction–Convection Method to Existing Algorithms

To compare these values with the results of the other three algorithms, we first apply the amplitude, the phase, and the conduction–convection algorithms to the field data for the annual variation of temperature and the daily variation in the dry and the wet cases. Since all three algorithms assume a linear increase of the logarithm of the amplitude ratio and the phase difference, we approximately fit \(a_m(z)\) and \(\phi _m(z)\) with linear functions as shown in Figs. 5 and 6. The slopes of the lines are \(s_a=0.437\) and \(s_\phi =0.423\) for the annual variation and \(s_a^d=9.1\), \(s_\phi ^d=9\), \(s_a^w=10.2\), and \(s_\phi ^w=9\) for the dry and wet cases, respectively. The phase and the amplitude algorithms expressed by (12) and (14) and the conduction–convection method expressed by (20) and (21) yield the values of thermal diffusivity and water flux density shown in Table 1. A rough comparison of the depth-dependent thermal diffusivity obtained above and these values obtained by the three algorithms can be made by calculating an average value for the depth-dependent k using the depth weighted average:

$$\begin{aligned} k_{av}=\frac{1}{z_N}\sum _{j=1}^N(z_{j}-z_{j-1})k_j. \end{aligned}$$
(34)

The main difference observed is not in the averaged soil diffusivity, which is slightly larger than the estimates of the three algorithms, but in the water flux density which differs by almost an order of magnitude. Since none of the four algorithms can exactly capture the measured temperature variation, their performance can be measured by calculating the relative root-mean-square error for the amplitude and phase of temperature variation at the measured depths:

$$\begin{aligned} a_{\textrm{RMSE}}= & {} \sqrt{\sum _{j=1}^N\left( |\hat{T}(z_j,\omega )|-|\hat{T}_m(z_j,\omega )|\right) ^2}\bigg / \sqrt{\sum _{j=1}^N|\hat{T}_m(z_j,\omega )|^2},\end{aligned}$$
(35)
$$\begin{aligned} \phi _{\textrm{RMSE}}= & {} \sqrt{\sum _{j=1}^N\left[ \arg \left( \hat{T}(z_j,\omega )\right) -\arg \left( \hat{T}_m(z_j,\omega )\right) \right] ^2}\bigg / \sqrt{\sum _{j=1}^N\arg \left( \hat{T}_m(z_j,\omega )\right) ^2},\qquad \end{aligned}$$
(36)

where \(\hat{T}\) is given by (8), (16), and (23) for the four algorithms. The relative errors are shown in Table 2. For the annual variability of temperature, we observe in general small errors for all algorithms with small differences between the first three methods, while the non-homogeneous method reduces the errors by half an order of magnitude. The main advantage of the novel method appears in the daily variability of temperature, where the three algorithms produce large errors due to the highly nonlinear increase of the amplitude decay and the phase difference functions, whereas the error with the non-homogeneous conduction–convection algorithm is reduced by more than an order of magnitude. It is thus much more accurate in this case.

Table 2 Relative root-mean-square error for the amplitude and phase of temperature variation for the four algorithms in the cases of temperature annual variation and in the dry and wet cases of temperature daily variation
Full size table

5 Conclusion

In this work, the transfer of heat in soil via conduction and convection of soil water through the porous medium was studied. Under the assumption that the temperature at the surface is known and that the soil diffusivity as well as the water flux density are independent of time, the resulting conduction–convection equation was solved using a harmonic decomposition of temperature. In contrast to previous studies, the soil is assumed to be non-homogeneous with the thermal diffusivity being piecewise-constant. In order to apply the theoretical model to field observations, the layers over which the soil properties are constant are assumed to be determined by the depths of consecutive temperature sensors.

A method to obtain the values of water flux density and thermal diffusivity within the different layers was developed and is based on finding the values that nullify or minimize the error between the predicted and the observed temperature variability at the depths of each layer’s boundary. The method was then applied to field data from the meteorological station in Ioannina, Greece, and was compared to three existing algorithms (amplitude, phase, and conduction–convection) that are based on a homogeneous assumption for the soil. The annual variability of soil temperature that was available at three depths over a seven-year period in time and accounts for roughly half the temperature variance was analysed, as well as the daily variability over two short time periods that represent a dry and a wet condition for the soil. The thermal diffusivity was found to increase in the layer below the surface and decrease for larger depths, while convection was found to account for 10% of the heat flux. Compared to the existing algorithms, the root mean-square-error calculated as the difference between the predicted and the measured temperature variability was found to be significantly decreased by between half and more than one order of magnitude. Since the proposed method takes into account the non-homogeneous properties of soil in a systematic manner, while it is easy to implement and apply to field data, we believe that it is a promising new tool for modelling the spatio-temporal variability of soil temperatures. Application to field data from other locations and with different soil properties and extensive comparison to the commonly used algorithms will be followed in future work.