Effective Roughness and Displaced Mean Flow over Complex Terrain

Abstract

Via analysis of velocity and stress fields from Reynolds-Averaged Navier–Stokes simulations over diverse complex terrains spanning several continents, in neutral conditions we find displaced areal-mean logarithmic wind speed profiles. The corresponding effective roughness length ($z_\text {0,eff}$), friction velocity ($u _{*\text {,eff}}$), and displacement height ($d_\text {eff}$) characterise the drag exerted by the terrain. Simulations and spectral analyses reveal that the terrain statistics—and consequently $d_\text {eff}$, $u _{*\text {,eff}}$ and $z_\text {0,eff}$—can change significantly with flow direction, including flow in opposite directions. Previous studies over scaled or simulated fractal surfaces reported $z_\text {0,eff}$ to depend on the standard deviation of terrain elevation ($\sigma _h$), but over real terrains we find $z_\text {0,eff}$ varies with standard deviation of terrain slopes ($\sigma _{\Delta h/\Delta x}$). Terrain spectra show the dominant scales contributing to $\sigma _{\Delta h/\Delta x}$ vary from $\sim$1–10 km, with power-law behaviour over smaller scales corresponding to fractal terrain used in earlier works. The dependence of $z_\text {0,eff}$ on $\sigma _{\Delta h/\Delta x}$ is consistent with fractal terrain having $\sigma _{\Delta h/\Delta x} \propto \sigma _h$, as well as classic theory for individual hills. We obtain relationships for $z_\text {0,eff}$, $d_\text {eff}$, and $u _{*\text {,eff}}$ in terms of $\sigma _{\Delta h/\Delta x}$, finding that $d_\text {eff}$ acts as a characteristic length scale within $z_\text {0,eff}$. Considering flow in opposite directions, use of upslope statistics did not improve $z_\text {0,eff}$ predictions; sheltering effects likely require more sophisticated treatment. Our findings impact practical applications and research, including micrometeorological flow, computational fluid dynamics, atmospheric model coupling, and mesoscale and climate modelling. We discuss limitations of the $z_\text {0,eff}$ formulations developed herein, and provide recommendations for practical use.

1 Introduction, Background, and Theory

1.1 Motivation and Outline

In general we are interested in understanding flow in the atmospheric boundary layer (ABL) over hilly terrain, and simulation of such. This includes use of computational fluid dynamics (CFD); because CFD is used both in research and various applications, we have some focus on Reynolds-averaged Navier–Stokes (RANS) solvers, which give mean flow solutions while also modelling turbulence. We also wish to better understand some simpler (one-dimensional) aspects, such as vertical profiles of stress and mean wind speed; typical measurements capture these, and they are also present in parametrisations of larger-scale models such as mesoscale, weather, and even climate models. For various applications one wishes to use mesoscale-model output, but needs to know the degree to which the model does or does not treat variations in terrain elevation; we wish to advance quantification of the unresolved (subgrid) terrain-induced drag, for a given model resolution and terrain. Further, for driving RANS (or large-eddy) simulations over complex terrain—whether via mesoscale output or prescription of inflow conditions—we wish to account for the terrain-induced drag experienced by the flow in a given simulation, as well as minimise adjustment of simulated inflow into the most finely resolved computational domains. Yet another motivation arises when considering applications where a large-scale roughness is required in flow parametrisation; for example, use of the geostrophic drag law in wind energy applications requires a geostrophic-scale roughness length.

More directly, we wish to test the effective roughness concept over actual terrain (elevation maps) spanning a range of complexities from locations around the world. Further, we aim to find not only the degree to which complex terrain increases drag on the flow (via a roughness length), but how the effect of the terrain may systematically vary with height depending on statistical terrain characteristics; this also includes checking where and whether a surface-layer (logarithmic) type of wind profile exists above the surface.

1.1.1 Outline

First we introduce the concept of effective roughness and review previous work on the topic; this ranges from analytical estimates, based on flow physics for single-scale hills, to empirical expressions for multiscale terrain. Section 2 looks into spectra and statistics of terrain elevation, with particular attention given to terrain-slope statistics. Section 3 presents analysis of mean flow from computational fluid dynamics simulations, including determination of quantities describing flow over complex terrain (effective friction velocity, diplacement height, and roughness) for five different cases. Section 4 compares predictions using previous formulations with effective roughnesses diagnosed from the flow simulations; it further presents new forms for effective roughness and analysis of their predictions. Section 5 distills the utility of the new forms developed herein, and failure of previous forms over multiscale terrain; it also discusses combination of slope-associated roughness with background (aerodynamic) roughness, limitations of our investigation, and recommendations for application of the new forms. We then summarise the main points of this work, and share our outlook on its continuation and future research.

1.2 Effective Roughness Concept and Theory

The concept of an effective roughness is not new, particularly if one generalises to include roughness over obstacle arrays, forests, and urban canopies—let alone over complex terrain. Fiedler and Panofsky (1972) first described it as “that roughness length which homogeneous terrain would have in order to produce the correct space-average downward flux of momentum near the ground, with a given wind near the ground.” In the current paper we further develop this concept without the constraint of being near the ground, further including the terrain-induced displacement of mean flow analogous to that due to forests, as shown the sections below.

To deal with the mean effect of hills, Smith and Carson (1977) suggested an effective roughness relation,

$$\begin{aligned} z_\text {0h} = 0.2\frac{\left( \overline{\Delta h}\right) ^2}{L_c} , \end{aligned}$$

(1)

for use in single-layer calculations over “variable” (non-uniform) terrain at resolutions coarser than 10 km; $\overline{\Delta h}$ was the average height range in a given area, and $L_c$ was the average distance between peaks or ridges. For the relatively flat terrain of the Netherlands Wieringa (1986) used (1), but set $\overline{\Delta h}$ to be the maximum elevation difference within 5$\times$5 km squares, picking $L_c$=5 km, to obtain an ‘elevation variability roughness length’.

Noting a number of observational studies over hilly terrain and numerical simulations over hills, Wood and Mason (1993) noted that areally averaged flow follows the generic law of the wall; they thus defined effective roughness via the displaced logarithmic profile:

$$\begin{aligned} \overline{U}(z) = \frac{u_{*0,\text {eff}}}{\kappa } \ln \left( \frac{z-d}{z_\text {0,eff}}\right) , \end{aligned}$$

(2)

where $\overline{U}$ is the areally averaged wind speed profile, and $u_{*0,\text {eff}}^2$ is the areally averaged surface force (per area and normalised by density).¹ They proposed expressions for the pressure force due to turbulent flow over hills, employing such to derive an approximate relation for the effective roughness. Adding the pressure-force and surface-stress contributions to total momentum transfer, Wood and Mason (1993) gave:

$$\begin{aligned} \ln \left( \frac{Z_m}{z_\text {0,eff}}\right) \simeq \left[ \frac{C_a}{\kappa ^2} + \frac{1}{\ln ^2(Z_m/z_0)} \right] ^{-1/2}, \end{aligned}$$

(3)

for hills of height h and streamwise scale $\lambda _x$; $C_a$ was a constant proportional to the product of bulk slope ($h/\lambda _x$) and ratio of frontal hill area to domain size (“packing fraction”), with $Z_m$ being a pressure scale height.² The effective roughness in (3) is non-monotonic in hill slope and packing fraction, though for each it has an increasing behaviour for moderate values (after first dropping at small values); it converges to $z_0$ for flat terrain. Though Finnigan (2002) called the Wood and Mason (1993) formulation (3) an “ad hoc derivation,” he admitted that it performs reasonably well for slopes less than $\sim$0.3; Hignett and Hopwood (1994) found a crude version of it to estimate $z_\text {0,eff}$ within a factor of $\sim$3 for sites over moderately hilly terrain.³ Finnigan (2002) further wrote that the terrain-perturbed region of mean flow extends up to $z\sim L$ (where L is the horizontal lengthscale of the hills)—and that unlike canopies, flow patterns around hills are not commonly affected by their neighbours. However, here we note that (3) does not account for collections of hills of different slopes and sizes, as found in most complex terrain—i.e. over terrain with a broad-band spectrum of elevations; perhaps more importantly, it does not deal with the interacting effects of shears and stresses induced by neighbouring hills, which may become significant where there are steep slopes.

Addressing the multiscale aspect of terrain, Beljaars et al. (2004) built upon the Wood and Mason (1993) formulation, and additionally upon Wood et al. (2001) for stress induced by sinusoidal hills, to derive height-dependent stress due to orography having a broad-band spectrum. However, because their work was aimed at parametrisation of unresolved terrain-induced stress in mesoscale and regional models (having resolutions on the order of $\sim$10 km or coarser), Beljaars et al. (2004) prescribed a fixed form for terrain spectra, and did not include an effective roughness.

Towards characterization of flow over complex multiscale surfaces, particularly at smaller scales, large-eddy simulation (LES) has been used to find the effective roughness over surfaces having elevation spectra that follow a power law; examples are Wan and Porte-Agel (2011) and Anderson and Meneveau (2011). The latter works, along with the review of Flack and Schultz (2010) for engineering flows based on wind-tunnel observations, gave some evidence for a connection between the standard deviation of surface elevation ($\sigma _h$) and the effective roughness; this is elucidated more in the next subsection. Recently Finnigan et al. (2020) summarised progress in simulating flow over complex topography, stating that future parametrisations for drag due to unresolved terrain “would use the statistics of the topography to inform the statistics of the space-time structure of the airflow”; this is precisely what the current work has aimed to do, as previously seen in presentation of preliminary results (Kelly et al. 2019a). Here we investigate the connection between areal statistics of terrain elevation and the flow above, particularly considering complex terrain having broad-band elevation spectra.

1.3 Previous Attempts to Find Effective Roughness over Multiscale Terrain

Several studies have worked towards finding an effective roughness to account for the (pressure) drag induced by surface height variations occuring at horizontal scales smaller than some threshold; the latter can correspond to a flow model resolution, to allow parametrisation of roughness due to unresolved terrain. One commonality they share is the assumption of $\sigma _h$ as the characteristic length scale for $z_\text {0,eff}$; this was first proposed by Stone and Dugundji (1965) for broad geophysical application.

Flack and Schultz (2010) considered numerous engineering forms for frictional drag due to rough surfaces, and subsequently derived an empirical relationship for roughness over irregular (random) surfaces. Their roughness estimate depended primarily on the standard deviation of surface elevation variations ($\sigma _h$), as well as incorporating the skewness $Sk_h$; it is expressible as:

$$\begin{aligned} z_\text {0,eff} = c_\text {fs}\sigma _h(1+Sk_h)^{1.37} , \end{aligned}$$

(4)

where they reported a proportionality constant equivalent to $c_\text {fs}=0.148$.

Through large-eddy simulations over a series of synthesised multiscale topographies, Wan and Porte-Agel (2011) investigated the postulate that the effective roughness length scales with the standard deviation of unresolved surface heights, $\sigma _{h,\text {sgs}}$. To account for the lower limit of roughness in the case of zero subgrid height variations, they suggested a form expressible as:

$$\begin{aligned} z_\text {0,eff}^2 = z_0^2 + C \sigma _h^2 . \end{aligned}$$

(5)

Examining flows over synthesised terrain whose spectra had roughly the same spectral form (following a power-law with exponent $\beta \simeq -2$), they found (5) to hold, but with the coefficient C increasing with $z_0$.

Anderson and Meneveau (2011) also used LES to examine the response of flow over flat rough surfaces whose roughness-element heights were synthesised to possess power-law spectra (i.e. fractal terrain), considering different surfaces over a range of spectral exponents $\beta$. Over statistically homogeneous surfaces they found the hydrodynamic roughness length (effective $z_0$ within the log-law) to follow $z_{0,\Delta }=\alpha \sigma _{h,\Delta }$, where the $\Delta$ corresponds to the filter scale of the LES and $\alpha$ is a coefficient depending on the power-law exponent ($\beta$) of the terrain spectrum. To account for flows over intrinsically rough surfaces⁴ with (background) roughness $z_0$, for “numerical convenience” they suggested an effective roughness of the form:

$$\begin{aligned} z_\text {0,eff}^2 = z_{0}^2+[\alpha (\beta )\sigma _{h|\Delta }]^2 . \end{aligned}$$

(6)

This expression appears to rectify the problem of C not being constant in the form (5) of Wan and Porte-Agel (2011). However, Anderson and Meneveau (2011) did not include a background $z_0$ in their analysis; this is because they state consideration of cases (LES) only where $\alpha \sigma _{h|\Delta }\gg z_0$. But they did find $\alpha$ to be monotonic in $\beta$, and showed $\alpha$ was invariant to LES resolution and filter scale ($\Delta$) for the fractal surfaces and flows simulated. From Fig. 8 of Anderson and Meneveau (2011), which plots $\alpha$ diagnosed over different surfaces with spectral exponents in the range $-3\lesssim \beta \lesssim -1.4$, the dependence of $\alpha$ on $\beta$ can be inferred as:

$$\begin{aligned} \alpha (\beta )\simeq 46e^{5.1\beta } . \end{aligned}$$

(7)

We note their assumption $\alpha \sigma _{h|\Delta }\gg z_0$ means that for surfaces with more negative spectral exponents (steeper roll-off of the spectrum), such as their flattest case having $\beta =-3$, then $\sigma _h/z_0$ needs to be at least $\sim 10^6$.

Another form for effective roughness was developed by Kelly (2016), but through a different means, stemming from simplified treatment of flow over roughness changes. To account for flow perturbations induced by roughness changes within a quasi-linearised spectral model, Astrup and Larsen (1999) described friction velocity perturbations in Fourier space using a characteristic length scale of $(z_0\ell _s^2)^{1/3}$, where $\ell _s$ is the reciprocal of streamwise wavenumber. Adapting this form for an efffective roughness to be used in estimation of uncertainty in shear-based vertical extrapolation of mean winds, Kelly (2016) suggested $z_\text {0,eff} = [z_0(\sigma _h+z_0)^2]^{1/3}$, taking the characteristic length scale as $\sigma _h$.

We note that the form of Astrup and Larsen (1999) can be seen to follow from Jensen et al. (1984), who described the depth of the turbulence-dominated inner layer of (unseparated) flow over rough hills, where the characteristic hill size (outer scale) $L_h$ is used instead of $\ell _s$. Recalling also that both the Jensen et al. (1984) and Astrup and Larsen (1999) forms describe equilibrium-layer depths, it is sensible to adapt such for a statistical or mean description of multiscale terrain effects. Over complex terrain the characteristic length scale due to terrain elevation variations has been presumed to be $\sigma _h$ in the studies named thus far; this was also done for the Kelly (2016) form, which can be written more generally as:

$$\begin{aligned} z_\text {0,eff} = \left[ z_0\left( c_m\sigma _h+z_0\right) ^2\right] ^{1/3} = z_0\left[ 1+c_m \sigma _h/z_0\right] ^{2/3}, \end{aligned}$$

(8)

with the coefficient $c_m$ requiring empirical determination. Looking at the forms (5), (6), and (8) from Wan and Porte-Agel (2011), Anderson and Meneveau (2011), and Kelly (2016), respectively, we see that they can be generalised to the $\sigma _h$-dependent form

$$\begin{aligned} z_\text {0,eff} = z_0 \left[ 1 + \left( c\frac{\sigma _h}{z_0}\right) ^b\right] ^{1/a}, \end{aligned}$$

(9)

the coefficient c can depend on the shape of terrain spectrum, as in Anderson and Meneveau (2011).

2 Terrain Analysis

Here we start by considering the statistical character of complex terrain, in terms of surface elevation variations. We examine a number of sites, each possessing different geological and geometric character (created via various physical mechanisms over different time scales). These sites include: a hilly area in north-east China with modest slopes, a Portuguese area of sharp orography with steep slopes, a South African area with a range of hills, and two Norwegian areas dominated by mountains and valleys. Again, one aim is to develop robust, universal statistical descriptions of non-uniform terrain and the (mean) flow above it, so we have chosen sites with different spectral and statistical character, as will be seen in the next subsections; however, the number of sites is limited by computational resources needed for the corresponding flow simulations.

The elevation maps have resolutions which range from $\sim \,$20–100 m, according to the spacing of contours/points in their digital formats (however, as we will see below, the actual resolution of the maps can be significantly cruder). The resolution of the terrain data analyzed herein is sampled at a constant 56 m in the streamwise direction parallel to the terrain. To calculate terrain statistics we use linear transects across the domains, which span roughly 40 km.

2.1 Spectra of Terrain Elevation and Slopes

Towards statistical characterization of terrain variations in a general sense, we first examine their spectra. One-dimensional power spectra of the terrain elevation h, defined as $S_{hh}(k_1)\equiv \mathcal{F}[h(x)]$, where $\mathcal{F}$ denotes the Fourier transform and $k_1$ is the wavenumber corresponding to a given x direction (later corresponding also to the mean flow direction), were calculated via fast Fourier transform. This was done in 12 different directions (every $30^{\circ }$), along 21 transects in each direction over a lateral span of 4 km (i.e., every 200 m). An average over the 21 lateral spectra was also taken to provide a single ‘mean’ spectrum in each direction; these are shown in the upper plots of Fig. 1 for the least complex (old hills in north-east China, at left) and most complex (Portuguese mountains, at right) areas considered in this study. Due to symmetry, only six unique spectra are shown in each plot, along with the omnidirectional spectrum (average of the six directional spectra). To mitigate the aliasing effect, which is caused by sampling with a constant spacing $\Delta x$ that is less than the resolution in the outer part of the domain⁵ we have applied a fourth-order low-pass Butterworth filter with cutoff wavenumber of $k_\text {cut}=0.5k_\text {Nyquist}$ (i.e., $2\pi /k_\text {cut}=4\Delta x$) to the spectra displayed.

Fig. 1

Spectra of terrain elevation variations (top) and terrain slopes (bottom); 12 directions considered (6 colour lines), with black the mean over all directions. Beljaars et al. (2004) form shown in cyan; minimum/maximum spectral slopes in sub-mesoscale range ($k_1>k_\text {peak}$) shown by dotted lines. Left: north-east China site; right: Aveiro (Portugal)

Note the lowest wavenumber portion of the terrain elevation spectra represents variations at horizontal scales approaching the domain size; thus the spectra and the total variance $\sigma ^2_h$ can be influenced by the choice of domain size. The latter is particularly evident in Fig. 1 due to the highest spectral magnitudes being found at the lowest wavenumbers, which is not uncommon for complex terrain. However, the spectra of terrain slope are generally not affected by the domain size⁶; these are shown in the bottom of Fig. 1 below $S_{hh}(k_1)$. Subsequently the domain size has less impact on statistics of dh/dx than on statistics of h. This is seen by noting that the power spectrum of terrain slope is simply the product of wavenumber squared and the terrain spectrum, i.e.,

$$\begin{aligned} {\mathcal {F}}[dh/dx]= k_1^2S_{hh}(k_1), \end{aligned}$$

(10)

for a given x-direction.

We can see that a power law is generally observable from scales of several hundred metres up to several kilometres; this is shown by the terrain-slope power spectra $k^2 S_{hh}(k)$ plots as well as the terrain spectra in Fig. 1. The plots of $S_{hh}$ further show that a different behaviour occurs at wavenumbers smaller than (scales larger than) the peak of $k^2 S_{hh}(k)$; such a peak ($k_\text {peak}$) implies a characteristic length scale $2\pi /k_\text {peak}$ for the terrain along a given direction. The peak in $k^2S_{hh}(k)$ corresponds to the change in power-law exponent (spectral slope) of $S_{hh}(k)$ noted by Beljaars et al. (2004); they parametrised a change in spectral exponent to occur at $k=0.003\,$m$^{-1}$, i.e. at a horizontal scale of roughly 2 km. We find that the peak of the one-dimensional terrain-slope spectrum varies around this value from one site and direction to another, generally in the range $\sim$1–10 km. The Beljaars et al. (2004) prescription for terrain spectra is shown by the cyan line in Fig. 1 for the omnidirectional mean. Its quite practical parametrisation is anchored to the observed value of $S_{hh}$ near $k=0.00035\,$m$^{-1}$, resulting in spectra which basically follow observed omnidirectional spectra within a factor of $\sim 3$. However, looking at the terrain-slope spectra one sees that the shape of $k^2S_{hh}(k)$—including the peak wavenumber—varies sufficiently from one place or even direction to another; the robust Beljaars et al. (2004) form can (counterintuitively) overpredict slope variance for complex sites and underpredict it for simpler ones by a factor of $\sim 3$, due to its anchor point being at a relatively low wavenumber and its prescription of a low-k spectral exponent of $-1.9$ differing from observations.

The description of smaller-scale terrain features by single power-law spectra is not new. Numerous works simply assume this for the entire landscape in a given area; i.e., for fractal terrain the surface elevation spectrum is taken to follow the simple form:

$$\begin{aligned} S_{hh}(k) \propto k^{\beta } . \end{aligned}$$

(11)

Following Mandelbrot (1989), for fractal terrain its fractal dimension can be described by $D=E+(3+\beta )/2=(7+\beta )/2$, where $E=2$ is the Euclidean (actual spatial) dimension. At any rate, like various studies in previous decades (Anderson and Meneveau 2011) and our earlier work considering various sites around the world for the Global Wind Atlas (Badger et al. 2015), here we find a power law with $\beta$ ranging between approximately $-4.3$ and $-1.2$; for the most complex (Aveiro) area the mean $\beta$ over all directions was equal to the Beljaars et al. (2004) prescription of $\beta =-2.8$ for $k>0.003\,$m$^{-1}$, with less complex areas having smaller (more negative) $\beta$. We note this range of $\beta$ only corresponds to scales smaller than the spectral peak of the slope spectrum (i.e., at $k>k_\text {peak})$. For larger scales ($k<k_\text {peak}$) one sees either a different power law, or yet more complicated behaviour, as notable from the terrain-slope spectra shown in Fig. 1. In other words, terrain is not mono-fractal in nature—or at least not having the same fractal dimension across all scales.⁷

2.1.1 Terrain Slopes and Finite Differencing

In Fig. 1 we showed spectra that had an anti-aliasing filter applied to treat the effects of sampling a domain having non-constant horizontal spacing. In practice we can also mitigate the aliasing issue by calculating the spectra of $\partial h/\partial x$ using $\mathcal{F}(\Delta h/\Delta x)$, where $\Delta x$ is optimally the map resolution (grid spacing). A first-order finite difference in physical space corresponds to combination of low-pass filter $\text {sinc}^2(k_1 \Delta x/2)$ and multiplying by $k^2$ in wavenumber space, i.e., $\mathcal{F}(\Delta h/\Delta x)=\mathcal{F}(\partial h/\partial x) \text {sinc}^2(k_1 \Delta x/2)$.

For the least complex terrain we studied (north-east China case in left-hand plots of Fig. 1), without the anti-aliasing filter a spurious upturn at high $k_1$ occurs not only in $\mathcal{F}(\partial h/\partial x)$, but even in $\mathcal{F}(h)$ (not shown); such noise is more easily seen in terrain-slope spectra, because the factor of $k^2$ amplifies such.⁸ Due to this $k^2$ amplification, map processing artifacts may be substantial enough to also cause an upturn in the spectrum of finite-differenced slope, $S_{\Delta h/\Delta x}$ at the finest scales; this is the case for the north-east China region when considering the entire map, due to the subsampling which occurs for the parts of the map at distances increasing beyond $\sim 8\,$km from the domain center.⁹ This is seen in Fig. 2, which displays $S_{\Delta h/\Delta x}$ for the same cases shown in Fig. 1, but without an anti-aliasing filter applied. The top plots in Fig. 2 present finite-differenced terrain slope spectra, with the upper-left plot (north-east China region) exhibiting a high-wavenumber upturn.

Fig. 2

Spectra of finite-differenced slopes for Chinese (left) and Portuguese (right) cases corresponding to Fig. 1, without anti-aliasing filters. Top: spectra in log-log coordinates to show power-law shapes and Beljaars et al. (2004) form (cyan). Bottom: spectra from fine-resolution central subdomain, plotted in variance-preserving coordinates

The spectra of finite-differenced slopes from Aveiro (upper-right) do not suffer from the high-wavenumber upturn; unlike all other regions considered, its finest-resolution area was larger (the central 17$\times 17\,$km), so that sampling issues only occurred over a small part near the outer-most domain edges.

To further demonstrate terrain-slope spectra via finite-differencing, the bottom plots of Fig. 2 display $S_{\Delta h/\Delta x}$ calculated over the finest resolution central 1/3 of the maps ($r<12\,$km), where there is less undersampling. These plots in Fig. 2 are also made in variance-preserving coordinates, specifically $k_1 S_{\Delta h/\Delta x}(k_1)$ versus $\ln k_1$, meaning they directly show the terrain scales which contribute to $\sigma _{\Delta h/\Delta x}$. For hilly terrain we find the majority of variance in slopes is contributed by variations at horizontal scales ranging from $\sim 0.5\,$km to 3 km, as seen by the peaks in the bottom plots of Fig. 2 for the least and most complex cases analyzed in this work.

Employment of anti-aliasing filters or $\Delta h/\Delta x$ to damp the high-wavenumber noise is defensible from a physical standpoint, as the geological processes which create the terrain on average cause an observed decay in $S_{hh}(k)$ with wavenumber, particularly at the smallest scales $\left( k\gtrsim 0.1\,\text {m}^{-1}\right)$; erosion processes, such as those driven by the wind, help to wear down sharp edges which would otherwise give contributions to the spectrum at these scales (e.g. Brown and Scholz 1985; Sulebak 1999). The use of low-order finite difference is justifiable, as long as the map resolution is fine enough relative to the variance-containing part of the spectrum; this is evident from Figs. 1, 2.

For robustness and universal applicability, hereafter we primarily consider statistics of $\Delta h/\Delta x$ for our analyses, because the anti-aliasing filter needed could depend on both the range of resolutions for a given terrain map and any processing that may have been done on the map. Further, calculation of such statistics are more accessible to readers, and advanced filter techniques are not the focus of this work. As we will see in later sections, the high-wavenumber noise, discussed above, does not prevent relation of terrain-slope statistics to large-scale effective roughness—rather, it facilitates the latter.

If a spectral exponent can be estimated for $k>k_\text {peak}$, this can be used to extend the spectrum and avoid the effects of processing-induced noise, provided that care is taken to ensure that the exponent is not affected by the filtering caused by finite-differencing; this is pertinent considering the left-hand plot in Fig. 2, for example. For the purposes of this work—notably considering effective roughness as seen from hundreds of metres (or more) from the surface—the smallest-scale effects due to the highest wavenumber slope variations act more locally and do not contribute substantially to the mean flow at such heights.¹⁰

2.1.2 Terrain Asymmetry: Upslopes

In the above presentation of one-dimensional terrain spectra, for the 12 directions considered, only 6 unique spectra were found for each area, as shown in the figures above; this is because the Fourier spectra of elevation are invariant to coordinate reversal. But the geological processes that form terrain, including wind-driven erosion (for example), are not expected to be symmetric: for a one-dimensional transect across the terrain, the upslopes and their statistics differ when viewed from opposite directions.

Indeed one can calculate upslope spectra, e.g., by setting the negative slopes to zero. Doing so, we obtained different spectra in all 12 directions for each terrain map (not shown); the upslope spectra have the same peaks as the slope spectra shown in Fig. 2, but with more variation of spectral shapes. Across all sites and directions we find the standard deviation of upslope in a given direction can be as much as 8/5 times larger than in the opposite direction, with the ratio of mean up/downslopes reaching 4/3. Collecting all cases together we note both these ratios are centered around 1 (with the mean slope ratio following from neglect of domain-mean slope, see Sect. 3.1.2). Considering the slope asymmetry found, and that the upslope portion of hills tend to dictate more of the form drag, upslope terrain statistics may be of use in predicting effective roughness and other complex terrain effects; this is discussed in the following sections.

2.2 Terrain Statistics and Universal Statistical Features

One exploitable aspect, which can find use in predictive applications such as ours and potentially be described in a universal way, is the statistics of terrain slopes; most notably, this includes the probability distribution function (PDF) of slopes and subsequently low-order moments. In particular one sees a pattern emerge upon comparing the PDFs of slopes, in contrast with terrain elevation distributions. To show this, the probability density function of $\Delta h/\Delta x$ is displayed in Fig. 3 for the Portuguese and Chinese areas analysed, for all 12 directions and across 21 different transects over 4 km (separated by 200 m) for each direction; i.e., each line corresponds to a histogram over 21 transects, covering an area of 4 km$\times$34 km. Only positive slopes are shown, because the twelve directions span 360$^{\circ }$; for a given direction $\Delta h/\Delta x<0$ simply appears as $\Delta h/\Delta x>0$ from the opposite direction.

Fig. 3

Probability density function of terrain upslopes from central 1/3 of domain, for least complex (Chinese) and most complex (Portuguese/Aveiro) cases; transects shown for every $30^{\circ }$

One can see a collapse of $P(\Delta h/\Delta x)$ for the most common slopes; we note that the shape of the PDF in this range depends on the power-law exponent $\beta$ defined in the high-wavenumber (sub-mesoscale) range. The magnitude of what is common (e.g., the slope where the cumulative density function exceeds 0.3) depends on the complexity of the area, with more complex sites having larger slopes occuring more frequently. Again, as with Figs. 1 and 2, only the least and most complex sites are shown; the other three sites have plots which fall between these two, depending on the complexity.

With regards to the PDFs of terrain slopes shown in Fig. 3 and asymmetry of opposing directions, we note that the mean upslope varied from 1/40 to 1/8, while the standard deviation of upslope ($\sigma _{\Delta h_+/\Delta x}$) ranged from roughly 0.035 to 0.21.

3 Analysis of Mean Simulated Flow over Complex Terrain

3.1 Flow Simulations

Simulations were made for 36 directions, i.e. every $10^\circ$, for each site; however, due to the terrain and flow statistics not changing significantly over such a small angular increment, we analyse the flow in every third 10$^{\circ }$ sector, as done for the spectra in Sect. 2.1.

Though we present results for five cases, several more had been considered, including the Columbia Gorge region in the north-west contiguous United States and a Pakistani site in the outer Himalayas; however, achieving convergence in all directions for these simulations required excessive resources, so these sites were not included.¹¹

3.1.1 Flow Model and Mesh

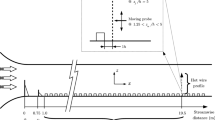
The RANS solver Ellipsys3D (Sørensen 1995) was used to simulate mean flow in 36 directions over each of the various areas considered here, calculating steady-state solutions (as opposed to unsteady solutions from so-called ‘URANS’). Ellipsys3D is a parallelised multi-block finite-volume code, employing the two-equation k-$\epsilon$ turbulence model and the SIMPLE pressure-solving algorithm (Patankar and Spalding 1972)¹². The circular computational surface mesh, suitable for calculation of any wind direction, was created with the hyperbolic generator HypGrid2d (Sørensen 1998). The three-dimensional hexagonal volume mesh is grown away from the surface (thus vertical faces can be treated) using the HypGrid3d mesh generator, with nearly orthogonal cells having negligible skewness. The surface boundary is treated via shear stress prescribed with a high-Reynolds number assumption, consistent with both k-$\epsilon$ closure and surface-layer theory (Cavar et al. 2016).

The simulations were conducted with neither buoyancy nor Coriolis force, and were consequently Reynolds-number independent (Chew et al. 2018; van der Laan et al. 2020). So the solutions do not depend on the geostrophic wind or $U_\text {in}(z)$ or $u_{*\text {in}}$, and only one simulation is needed per direction per map.

3.1.2 Model Boundary Conditions

Bottom conditions: The bottom boundary has a uniform roughness $z_0=9\,$cm, essentially equal to the roughness $z_\text {0,in}$ characterising the logarithmic inflow wind profile. The height of the bottom surface is dictated by an elevation map for each site/area considered. For manageable calculations the RANS mesh resolution is 20 m only in the innermost $4\times 4\,$km of the domain, and gradually stretches outward, reaching 25–40 m within a $7\times 7\,$km extent around domain center. Beyond that, the map is gradually smoothed, and the computational grid spacing likewise increases, with both approaching a resolution of 80–100 m for $r\gtrsim 10\,$km from the center and progressing to $\sim 200\,$m for $r\sim 20\,$km. The elevation is smoothed to a uniform height towards the outermost part of the circular domain bottom. The flat outer zone is designed to both ensure the incoming log-law profile from inlet on the upwind side, and that the flow can settle to a steady-state near the outflow boundary on the downwind side with proper convergence (flow variable residuals less than $10^{-6}$).

Top boundary conditions: The top boundary is located at a constant height of about 15 km above the mean surface and has a constant wind velocity boundary condition imposed. It is sufficiently high to ensure (a) no damping of any variable is necessary, and (b) no artificial speed-up effects arise due to height differences between the inner domain’s hilly surface and the uniformly flat surface in the horizontal outer zone. A constant-velocity condition was also chosen at the top boundary to enhance the numerical stability of the computations, ensuring that only the streamwise velocity component has a constant non-zero value at domain top. Thus we are considering RANS in neutral conditions without a capping inversion, where the domain height $z_\text {top}$ is much greater than the dominant terrain scale ($z_\text {top}\gg \sigma _h\gg z_0$) such that there are no ‘top-down’ effects.

Fig. 4

Depiction of flow domain with terrain, inflow direction, outflow region (shaded), and coordinate system; analysis domain denoted by black circle. Case shown corresponds to Norwegian ‘NO52’ area

Inlet/outlet conditions: The RANS simulations have an inlet condition described by a logarithmic wind profile, covering the incoming part of the cylindrical surface of the grid domain (which has a uniform flat surface). A zero-gradient boundary condition was applied to define the outflow part of the cylindrical domain boundary on the downwind side; the outflow zone width is approximately 45$^{\circ }$, which gives optimal trade-off between the outlet zone needed for the finite-volume RANS solver, and ability to obtain numerically stable convergence. An example flow domain is shown in Fig. 4.

3.1.3 Consideration of Flow-Field Analysis Domain

Here we have avoided the effect of transition from flat inflow far-field to hilly surface (and more broadly the momentum flux footprint aspect), by conservatively limiting the calculation of flow statistics to the downwind two-thirds of each ($\sim$40 km long) simulated domain; even for the least complex terrain cases, such a buffer (wider than $12\,$km) eliminated the impact of such artifacts on finding the effective roughnesses and (displaced) friction velocities. Also, the peaks of the terrain slope spectra correspond to scales much smaller than the domain extent, so the terrain was statistically well-sampled; the loss at the lowest wavenumbers due to taking flow statistics from the downwind 2/3 of each domain, did not affect the terrain statistics ($<1\%$ loss in standard deviations of slopes). Further, when taken over the lateral extent considered (or just the 4 km width corresponding to the flow variables output for each direction simulated), the terrain statistics in the downwind 2/3 of the domains differ negligibly from the statistics over the entire (unsmoothed portion of the) domain: i.e., despite the progressive smoothing of the outermost parts approaching the domain edges, the terrain statistics were essentially homogeneous.

3.2 Statistical Displacement by Complex Terrain

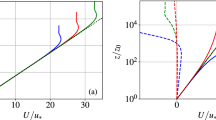
Wieringa (1993) discussed the general notion of a transition sublayer over heterogeneous terrain, whose depth was also known as the blending height ($z_b$); above this height, horizontal homogeneity of the mean flow is approached. Similarly over forests, a logarithmic profile and effective roughness length can be found for the areal-mean flow above a displacement height d; this was derived for flow over forest canopies (Thom 1971; Finnigan 2002; Sogachev and Kelly 2016) and has become a common approach there. In order for the concept of an effective roughness to be valid, the displaced logarithmic form (2) should apply to the mean wind speed profile; an effective displacement height $d_\text {eff}$ can be defined as the height above which a log-law describes the temporal and areal mean speed following the surface, depending on the character (statistics) of the terrain.¹³ Towards describing the flow, it is useful to consider how the kinematic streamwise momentum flux (negative shear stress) $\overline{uw}$ or local friction velocity $u_*\equiv (\overline{-uw})^{1/2}$ behaves, particularly the vertical profile of its horizontal-area mean in terrain-following coordinates. Similar to behaviour in the ideal surface layer over a uniform rough surface, the height of maximum $\langle u_*\rangle _{xy}$ defines $d_\text {eff}$; above this virtual displaced surface, $\langle u_*\rangle _{xy}$ decreases with z, as in a flat homogeneous ABL. This is shown in Fig. 5, which presents vertical profiles of the terrain-following areal (and implicitly temporal) mean $\langle u_*\rangle _{xy}$ from the RANS simulations for all directions at the sites considered.

Fig. 5

Profiles of plane-mean friction velocity for all (12) directions at each site, in (roughly) terrain-following coordinates

Figure 5 illustrates that for different directions in a given area, the character of the terrain affects the height of maximum $\langle u_*\rangle _{xy}$ (i.e. $d_\text {eff}$), as well as the magnitude of $\langle u_*\rangle _{xy}$ and shape of its vertical profile. Larger variations in both of these are seen for increasingly complex terrain; this is elucidated further below.

3.3 Diagnosing Effective Friction Velocity and Roughness Length

To find the roughness length representative of the terrain’s effect on the flow in a given direction over a given area, there are a number of methods one could consider, when invoking the logarithmic profile (2). In addition to considering the flow above $d_\text {eff}$, these generally depend on how one finds an effective friction velocity ($u_{*,\text {eff}}$).

Starting with the blending-height ($z_b$) concept, Wieringa (1986) and Mason (1988) proposed finding $u_{*,\text {eff}}$ at $z=z_b$. This was used by Bou-Zeid et al. (2004) to find $z_{0,\text {eff}}$ over a heterogeneous flat surface possessing different $z_0$. However, picking $u_*$ at just one height can incur significant uncertainty, due to vertical variations in $\langle u_*\rangle _{xy}$. A more robust method is to fit the (displaced) log law to the profile of terrain-following areal mean wind speed above the estimated $d_\text {eff}$. This is what we do here; it gives both $u_{*,\text {eff}}$ and $z_\text {0,eff}$, with less sensitivity to diagnosed (or estimated) $d_\text {eff}$ than selecting $\langle u_*\rangle _{xy}$ from a single height, as shown below. Further, it is sensible given the area-mean friction velocity profiles observed: $\partial \langle u_*\rangle _{xy}/\partial z$ is zero in the neighbourhood of $d_\text {eff}$, just like a displaced ‘surface layer,’ with $\langle u_*\rangle _{xy}$ beginning to decrease further above as typical in ABL flow over flat terrain.

For the results and analysis presented here, we calculate vertical profiles of $\langle U\rangle _{xy}$ and $\langle u_*\rangle _{xy}$ in terrain-following coordinates, for each wind direction. In order to examine and mitigate the effects of adjustment of the inflow, we first consider areal means for calculating flow statistics using both the downwind two-thirds of the domain (i.e., excluding the first $\sim$10 km of the flow) in addition to flow statistics calculated over the entire horizontal domain.

Examining the plane-mean profiles of friction velocity and wind speed, we indeed find a logarithmic profile for $\langle U\rangle _{xy}$ above the height of maximum $\langle u_*\rangle _{xy}$, following (2); again we take this maximum to be the effective displacement height, $d_\text {eff}$. Examples of this logarithmic fit and the corresponding planar-mean profiles of $u_*$ are shown in Fig. 6.

Fig. 6

Terrain-following areal-averaged profiles of wind speed U(z) and friction velocity $u_*(z)$ for two cases, to illustrate diagnosis of effective roughness and displacement height. Blue lines denote full-domain values; red lines denote ‘downwind’ 2/3 of domain values. Bars (on U) and points (on $u_*$) correspond to d, and dashed lines correspond to log-law fits above d for the full and 2/3-domain profiles

Instead of showing dozens of profiles and fits, in Fig. 6 we present the two most extreme and different cases: one site and direction where the terrain is quite complex, such that the downwind-2/3 and full-domain $u _{*\text {,eff}}$ differ the most; and a site where the terrain variations are mildest but with a flatter $\langle u_*\rangle _{xy}$ profile, which gives largest variation in $d_\text {eff}$. The maximum $\langle u_*\rangle _{xy}$ and the height of its occurence ($d_\text {eff}$) are both higher in the downwind subdomain, due to the full-domain flow still retaining some residual artifacts of the more uniform inflow. One can see that even in these most deviant cases (compared to other flow directions at all sites), the logarithmic profile fits the data well. Also slightly notable is that near the top of the domain there can be a deviation from the terrain-induced mean log law, where the background upwind roughness over smoothed simulated inflow surface is still felt. To mitigate this effect, when fitting (2) above $d_\text {eff}$, the top height of the $\langle U\rangle _{xy}$ profile being fit was taken to be the maximum of half the domain height and $3d_\text {eff}$; thus one can see the dotted/dashed lines (fit log-law) in Fig. 6 falling slightly below the mean profiles at the very top of the left-hand plot. Further, to check this fitting, the dimensionless sensitivity of fitted $z_\text {0,eff}$ to the upper cutoff height $z_\text {cut}$ was calculated: $d\ln z_\text {0,eff}/d\ln z_\text {cut}$ was found to be on average less than 0.5%, and did not exceed 1%.

4 Results

4.1 Prediction of Effective Displacement Height

One might expect simple relations based on $\sigma _h$—perhaps like previously postulated dependences for $z_\text {0,eff}$ (such as Eqs. 5–9)—to suffice for predicting $d_\text {eff}$. But $\sigma _h$ depends on the domain size, as shown earlier considering the terrain spectra (Fig. 1): larger domains include yet more contributions from smaller wavenumbers (larger scales). Further, $\sigma _h$ does not account for the steepness of slopes and contains no information about different steepness occurring in opposite directions. Thus low-order statistics of terrain slope—such as the standard deviation ($\sigma$) of ${\partial h/\partial x}$, its finite-difference approximation $\Delta h/\Delta x$, or the upslope finite-difference $\Delta h_+/\Delta x\equiv (\Delta h/\Delta x)|_{\Delta h>0}$—are expected to be more appropriate for predicting $d_\text {eff}$ and ultimately $z_\text {0,eff}$. Figure 7 demonstrates this, showing simple predictions for $d_\text {eff}$ assuming it is proportional to $\sigma _h$, $\sigma _{\Delta h/\Delta x}$, or $\sigma _{\Delta h_+/\Delta x}$, respectively. In the figure the estimates for $d_\text {eff}$ are plotted against diagnosed $d_\text {eff}$, where the latter is again simply the height of maximum stress (thus maximum $u_*$) as shown earlier in Fig. 5; the respective proportionality constants relating $\sigma _h$, $\sigma _{\Delta h/\Delta x}$, and $\sigma _{\Delta h_+/\Delta x}$ to $d_\text {eff}$ are shown above each plot.

Fig. 7

Estimates for effective displacement height $d_\text {eff}$, versus $d_\text {eff}$ diagnosed as the height of maximum $u_*$. Each point corresponds to one direction (of 12); colours correspond to site (cyan: north-east China, orange: S. Africa, green: Norway 56, brown: Norway 52, magenta: Portugal). Blue lines indicate ‘perfect’ (1:1) prediction

The effective diplacement height is somewhat difficult to predict accurately from terrain statistics, though a monotonic and roughly linear relationship is observed in Fig. 7. The figure demonstrates that $\sigma _h$ might only predict a lower-bound for $d_\text {eff}$ (but it may contain some useful information for simpler sites). However, taking $d_\text {eff}$ to be simply proportional to $\sigma _{\Delta h/\Delta x}$ or $\sigma _{\Delta h_+/\Delta x}$, as:

$$\begin{aligned} d_\text {eff} \approx \; r_{d_+} \sqrt{\left\langle \left( \frac{\Delta h_+}{\Delta x}\right) ^2\right\rangle _{xy}} \; \approx \; r_d \sqrt{\left\langle \left( \frac{\Delta h}{\Delta x}\right) ^2\right\rangle _{xy}} , \end{aligned}$$

(12)

provides modestly good approximation (with an r.m.s. error of $\sim$40%). While one can see that $\sigma _{\Delta h/\Delta x}$ and $\sigma _{\Delta h_+/\Delta x}$ are much better than $\sigma _h$ for predicting $d_\text {eff}$, they also require prescription of a length scale ($r_{d_+}$ or $r_d$). For the estimations shown in Fig. 7, these were found to be $r_{d_+}=1\,$km and $r_d=1.65\,$km; these values give distributions of $d_\text {pred}/d_\text {eff}$ with maxima at 1, as does the coefficient in $d_\text {eff}\approx 1.6\sigma _h$; the latter approximiation provides a much cruder estimate. The figure also shows that the upslope statistic $\sigma _{\Delta h_+/\Delta x}$ provides little improvement over $\sigma _{\Delta h/\Delta x}$. This is likely because calculating the variance of upslopes does not consider the shadowing effect that bigger hills have on the smaller ones immediately downwind. It also hints at the difficulty of defining a unique upslope version of terrain-slope variance; e.g., including shadowing effects would itself introduce an extra length scale, and we leave such to future work.

We also note that the slope statistics thus far have been calculated using first-order finite differences, and thus differ from (are smaller than) $\sigma _{\partial h/\partial x}$ due to the filtering effect at the finest scales. This can be seen considering the previous section on terrain spectra, as in Figs. 1 and 2. We also calculated $\sigma _{\partial h/\partial x}$, by integrating the spectra $\mathcal{F}(dh/dx)=k_x^2\mathcal{F}(h)$ over wavenumber and averaging across all y for each wind direction. But use of the exact slope statistic $\sigma _{\partial h/\partial x}$ leads to predictions of $d_\text {eff}$ significantly poorer than those using $\sigma _{\Delta h/\Delta x}$ or $\sigma _{\Delta h_+/\Delta x}$.

Fig. 8

Estimates for effective displacement height versus diagnosed height of maximum $u_*$. Blue/large dots: $1000\sigma _{\Delta h/\Delta x}$; yellow/small dots: $670\sigma _{\partial h/\partial x}$ (blue is same as in Fig.7b). Each point corresponds to one direction (of 12), at one site. Blue line indicates perfect (1:1) prediction

Figure 8 compares predictions using areal $\sigma _{\Delta h/\Delta x}$ and $\sigma _{\partial h/\partial x}$, respectively, showing the latter to be less accurate. We postulate that the decreased utility of the exact terrain slope $\partial h/\partial x$, i.e., the increased error and reduced correlation with $d_\text {eff}$, is due to the smallest-scale fluctuations contributing a relatively larger amount of variance (in part due to sampling issues as discussed earlier in Sect. 2.1), while contributing relatively little to the aggregate drag. The smallest features are the most likely to be sheltered by larger hills upwind, and the pressure-blocking effect of larger hills contributes more to the drag. Further, since the maps used for the simulations had 20-m horizontal resolution, the 56 m-resolution output data (which we use to calculate statistics) is not likely to be affected by any processing on the original maps.

Given that expressions simply based on slope statistics such as these also require a length scale (such as $r_{d_+}$ or $r_d$ in Eq. 12), dimensionally one might expect that a form such as $\sigma _h\sigma _{\Delta h/\Delta x}$ would improve results; in fact, combinations involving $\sigma _h$ were found to degrade estimates of $d_\text {eff}$. We also note that fits using combinations of $\sigma _h$ and $\sigma _{\Delta h/\Delta x}$ (including additive and multiplicative forms, including exponents on each $\sigma$) did not give $d_\text {eff}$ estimates appreciably better than those given in (12). Linear (arithmetic, additive) combinations of $\langle \Delta h/\Delta x\rangle _{xy}^{e_\mu }$ and $\sigma _{\Delta h/\Delta x}^{e_\sigma }$, where $e_\mu$ and $e_\sigma$ are exponents of order 1 from fits to data, gave only slightly better results than the simple forms in (12).

However, it is not necessary to have a very accurate $d_\text {eff}$ in order to obtain $z_\text {0,eff}$. That is, fitting planar-mean wind profiles above $d_\text {eff}$ to the logarithmic form (2) does not significantly affect $z_\text {0,eff}$; more on this is shown in the following subsections. We also note that using upslope standard deviations, whether $\sigma _{\Delta h_+/\Delta x}^{e_{\sigma +}}$ by itself or in combination with $\langle \Delta h/\Delta x\rangle _{xy}^{e_\mu }$, did not improve results; again using a simple form in terms of $\sigma _{\Delta h_+/\Delta x}$ gave slightly worse results than using $\sigma _{\Delta h/\Delta x}$, as shown in Fig. 7.

4.2 Prediction of Effective Friction Velocity

Associated with the displaced areal-mean logarithmic flow is an effective friction velocity, $u_{*\text {,eff}}$; this is diagnosed via log-law fits to the areal-mean wind profile above $d_\text {eff}$, as detailed further in the next section. As with the effective displacement $d_\text {eff}$, the friction velocity $u _{*\text {,eff}}$ can be predicted using a simple form based on the standard deviation of terrain slope or upslope. The most robust form is found to be a simple linear relationship between $u _{*\text {,eff}}/u_{*\text {in}}$ and the standard deviation of slope; for terrain slope and upslope, we find:

$$\begin{aligned} u _{*\text {,eff}}= & {} u_{*\text {in}}(1+2.7\sigma _{\Delta h/\Delta x}), \end{aligned}$$

(13)

$$\begin{aligned} u _{*\text {,eff}}= & {} u_{*\text {in}}(1+5\sigma _{\Delta h_+/\Delta x}) . \end{aligned}$$

(14)

These give predictions with an r.m.s. error of 8–9%; expression (13), based on $\sigma _{\Delta h/\Delta x}$, performs slightly better. More complicated empirical relations may be fit, but do not offer much improvement over the above; further, they tend to lack physical justification. However, crudely including the effect of the cross-sectional area through the mean absolute lateral slope $\mu _{|\Delta h/\Delta y|}$ is possible via:

$$\begin{aligned} u _{*\text {,eff}} = u_{*\text {in}}[1+4\sigma _{\Delta h/\Delta x} (1-c_{s\mu }\mu _{|\Delta h/\Delta y|})] , \end{aligned}$$

(15)

and is seen to give a small amount of improvement for $c_{s\mu }$ between 4 and 5; e.g., for $c_{s\mu }=4.5$ the r.m.s. error is reduced to 6%.¹⁴ This is shown in Fig. 9, along with predictions using (13) and (14).

Fig. 9

Predicted effective friction velocity $u _{*\text {,eff}}$, versus $u _{*\text {,eff}}$ diagnosed from $\langle U\rangle _{xy}(z)$ above the effective displacement height $d_\text {eff}$. Blue dots are (13) based on $\sigma _{\Delta h/\Delta x}$; yellow crosses are (14) based on $\sigma _{\Delta h_+/\Delta x}$; green open squares are (15) based on $\sigma _{\Delta h/\Delta x}$ with $\mu _{|\Delta h/\Delta y|}$. Blue lines indicate perfect (1:1) prediction

We also note that a pair of relations like (13)–(14), but which add to $u_{*\text {in}}$ instead of scaling by it, perform slightly better. That is, the form:

$$\begin{aligned} u _{*\text {,eff}}=u_{*\text {in}}+a_{u*}\sigma _{\Delta h/\Delta x}, \end{aligned}$$

(16)

and its counterpart $u _{*\text {,eff}}=u_{*\text {in}}+a_{u_\text {*up}}\sigma _{\Delta h_+/\Delta x}$ reduce the r.m.s. error to 6–7%, if choosing $a_{u*}=1.7\,$m s$^{-1}$ and $a_{u_\text {*up}}=2.8\,$m s$^{-1}$. Extending them by incorporating $(1-c_{s\mu }\mu _{|\Delta h/\Delta y|})$ as in (15), but with $c_{s\mu }=3$, reduces the error to 5–6%. Nevertheless, it is not clear what the velocity scales $a_{u*}$ and $a_{u_\text {*up}}$ are comprised of or represent, and the improvement they appear to offer is small compared to the error itself. We view (13)–(14) as defensible, with more work needed to understand or endorse additive forms like (16) which use a characteristic velocity scale that is independent of $u_{*\text {in}}$, though such independence is logical considering the terrain-affected integral length scales of the turbulent flow.

4.3 Prediction of Effective Roughness

4.3.1 Performance of Earlier Theories

For context and comparison, we first examine the behavior of the parametrisations which precede this work and have been discussed in the previous sections. Using the simulated flow data and corresponding terrain statistics discussed in Sects. 2–3, we calculated $z_\text {0,eff}$ via the form (4) of Flack and Schultz (2010), (6) of Anderson and Meneveau (2011), and (8) of Kelly (2016). For the Anderson and Meneveau (2011) form we have already obtained the high-wavenumber spectral exponent $\beta$ from fits to the terrain spectra in every direction at every site; then (7) gives $\alpha (\beta )$ for use in (6). Figure 10 shows $z_\text {0,eff}$ predicted by these earlier formulations, versus the effective roughness diagnosed from the simulated flows.

Fig. 10

Prediction of previous theories (i.e., based on $\sigma _h$), versus diagnosed $z_\text {0,eff}$. Left: Flack and Schultz (2010); middle: Anderson and Meneveau (2011); right: Kelly (2016) in blue, with updated form (9) using $a=b=2$ and $c=0.01$ in yellow

The figure shows that none of the extant forms capture the effective roughness, giving predictions which do not generally follow $z_\text {0,eff}$. The Flack and Schultz (2010) parametrisation overpredicts $z_\text {0,eff}$ by one order of magnitude, though it does show a slight correlation (upward trend) for $z_\text {0,eff}$ beyond 1 m. Similarly, the Kelly (2016) form overpredicts $z_\text {0,eff}$, but not as severely, though it does not increase as much with $z_\text {0,eff}$. The Anderson and Meneveau (2011) form, on the other hand, underpredicts $z_\text {0,eff}$ by roughly an order of magnitude, and is not correlated with $z_\text {0,eff}$. In the right-hand plot of Fig. 10 one can also see that the general form (9) can be made to give predictions within one order of magnitude of diagnosed $z_\text {0,eff}$ by using $a=b=2$ and $c=0.01$, but it does not really follow $z_\text {0,eff}$.

4.3.2 New Forms for Effective Roughness Based on Terrain Slope Statistics

Considering all of the data analyzed from the five areas, using only the standard deviation of terrain slope $\sigma _{\Delta h/\Delta x}$, an optimal fit in logarithmic $z_\text {0,eff}$ space was found when using the form:

$$\begin{aligned} z_\text {0,eff} = z_\text {0,in}+r_s\sigma _{\Delta h/\Delta x}^{\gamma } , \end{aligned}$$

(17)

considering r.m.s. upslope $\sigma _{\Delta h_+/\Delta x}$, the analogous relationship:

$$\begin{aligned} z_\text {0,eff} = z_\text {0,in}+r_{s_+}\sigma _{\Delta h_+/\Delta x}^{\gamma _+}, \end{aligned}$$

(18)

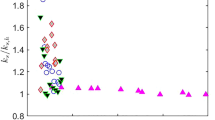
emerged. Whether using $\sigma _{\Delta h/\Delta x}$ or $\sigma _{\Delta h_+/\Delta x}$, i.e., for both (17) and (18) above, the best fits were found when the exponent value was between 2.5 and 3. For $\gamma =\gamma _{+}=2.5$, characteristic length scales $r_s\simeq 125\,$m and $r_{s_+}\simeq 500\,$m were found; but for $\gamma =\gamma _+=3$, the corresponding scales were found to be $r_s\simeq 325\,$m and $r_{s_+}\simeq 1450\,$m. The standard deviation of $\ln (z_\text {0eff,pred}/z_\text {0eff,obs})$ was essentially equal for both sets of exponents and coefficients mentioned above, but we note that a better fit across all $z_\text {0,eff}$ was exhibited for $\gamma =\gamma _+=3$. The left-hand plot of Fig. 11 shows estimates of the effective roughness length employing (17) and (18), with the optimal exponent $\gamma =\gamma _+=3$.

Fig. 11

Left: $z_\text {0,eff}$ predicted using only terrain statistics, via (17)–(18); right: predictions using terrain statistics along with diagnosed $d_\text {eff}$, via (19)–(20). Both have $\gamma =\gamma _{+}=3$. Circles are results using terrain slopes, triangles using terrain-upslopes

Given the character of the problem, one may expect the length scale in simple formulations such as (17) or (18) to have physical meaning; we note $r_s$ is on the order of the diagnosed terrain-induced displacement over all sites and directions, $\langle d_\text {eff}\rangle \simeq 150\,$m. Further noting that earlier in (12) we found $d_\text {eff}\propto \sigma _{\Delta h/\Delta x}$, we anticipate $z_\text {0,eff}$ to then be proportional to either $d_\text {eff\,}\sigma ^{\gamma -1}_{\Delta h/\Delta x}$ or alternately $d_\text {eff\,}\sigma ^{\gamma _{+}-1}_{\Delta h_+/\Delta x}$. Indeed fitting diagnosed $z_\text {0,eff}$ and using $d_\text {eff}$ as the characteristic length scale (instead of $r_s$ or $r_{s_+}$), we find the best results are offered by:

$$\begin{aligned} z_\text {0,eff} = z_\text {0,in} + c_d \, d_\text {eff} (\sigma _{\Delta h/\Delta x})^{\gamma -1} \, \simeq \, z_\text {0,in} + \frac{1}{3}d_\text {eff} \sigma _{\Delta h/\Delta x}^2, \end{aligned}$$

(19)

and:

$$\begin{aligned} z_\text {0,eff} = z_\text {0,in} + c_{d_+}d_\text {eff}(\sigma _{\Delta h_+/\Delta x})^{\gamma _+-1} \,\simeq \, z_\text {0,in} +d_\text {eff} \sigma _{\Delta h_+/\Delta x}^2 . \end{aligned}$$

(20)

As with (17)–(18), again optimal $\gamma =\gamma _+$ is found to be in the range 2.5–3, with the best fit over all scales ocurring for $\gamma =\gamma _+=3$; here $c_d\simeq 1/3$ and $c_{d+}\simeq 1$. The results of using (19) and (20) are shown in the right-hand plot of Fig. 11. Comparing these results to those from (17)–(18) in the left-hand plot of the figure, one can note the improvement when incorporating the $d_\text {eff}$ found from the simulations. For $z_\text {0,eff}$ predictions which include $d_\text {eff}$, the standard deviation of $\ln (z_\text {0eff,pred}/z_\text {0eff,obs})$ is reduced by roughly $40\%$. Whether including $d_\text {eff}$ or not, the $z_\text {0,eff}$ parametrisations based on simple terrain slope, i.e. (17) and (19), give better results than (18) and (20) based on terrain upslope.

Earlier we found that incorporation of lateral terrain-slope statistics, i.e. $\mu _{|\Delta h/\Delta y|}$ in (15), offered some improvement to predictions of $u _{*\text {,eff}}$ based on streamwise terrain-slope variance. This was attempted in part because $\Delta h/\Delta y$ is the only information that we have about the terrain silhouette (cross-sectional area), which is expected to be a scaling factor for the terrain-induced drag (e.g. Brown and Wood 2003). Doing so for (19), analogous to (15), we obtain the form:

$$\begin{aligned} \begin{aligned} z_\text {0,eff}&= z_\text {0,in} + c_{d,y} d_\text {eff} (\sigma _{\Delta h/\Delta x})^{\gamma -1} (1-c_{\mu y}\mu _{|\Delta h/\Delta y|}) \\&\quad \simeq z_\text {0,in} + 0.5d_\text {eff\,} \sigma _{\Delta h/\Delta x}^2 (1-4.7\mu _{|\Delta h/\Delta y|}), \end{aligned} \end{aligned}$$

(21)

where optimal results are found with $c_{d,y}=0.5$ and $c_{\mu y}=4.7$. Using expression (21) gives a further decrease of 10–15% in the standard deviation of $\ln (z_\text {0eff,pred}/z_\text {0eff,obs})$, compared to (19); this is conveyed by Fig. 12.

Fig. 12

Red plusses are $z_\text {0,eff}$ predicted using terrain statistics including $\langle |\Delta h/\Delta y|\rangle$ and diagnosed $d_\text {eff}$, via (21). Blue circles are (19) without $\langle |\Delta h/\Delta y|\rangle$, as in Fig. 11

A similar form in terms of $\sigma _{\Delta h_+/\Delta x}$ was also found (but with $c_{d,y}=1.4$ instead of 0.5), and also decreased the error by about 10% compared to (20); however, it still does not give an improvement compared to (19), let alone (21).

Recalling that the Wood and Mason (1993) approximation (3) for $z_\text {0,eff}$ due to a collection of single-scale hills incorporated both the slope as well as the area fraction (density) of hills in an area, we can adapt (3) to be generically expressed in terms of terrain-slope statistics for complex terrain with broad-band spectra. Their form (3) has $C_a\propto (h\lambda _y/A_d)(h/\lambda _x)$ where h is hill height, $\{\lambda _x,\lambda _y\}$ are the characteristic hill scales in the streamwise and crosswind directions, and $A_d$ is the domain size; this becomes $\sim (|dh/dy|)(dh/dx)$ in terms of the terrain statistics analyzed here. Using $\sigma _{\Delta h/\Delta x}$ for the streamwise slope dependence and $|\Delta h/\Delta y|$ for the cross-sectional area per domain ($h\lambda _y/A_d$ in Wood and Mason 1993), we have:

$$\begin{aligned} \ln \left( \frac{Z_p}{z_\text {0,eff}}\right) \simeq \left[ c_\sigma \sigma _{\Delta h/\Delta x}\, \langle |\Delta h/\Delta y|\rangle + \frac{1}{\ln ^2(Z_p/z_0)} \right] ^{-1/2}, \end{aligned}$$

(22)

where the pressure scale-height is $Z_p$, and the constant $c_\sigma$ is of order 1. By fitting to the diagnosed $z_\text {0,eff}$ we find the scale $Z_p\simeq 100\,$m and $c_\sigma \simeq 4$, but this still gives predictions with 40% larger error than (17); the analagous version of (22) using upslopes gives yet worse predictions. However, taking the scale height in (22) to be proportional to the diagnosed effective displacement height, optimal results using (22) arise for $Z_p\simeq 0.06d_\text {eff}$, with the same r.m.s. log-error as (19); we note that expression (21), which also uses $\langle |\Delta h/\Delta y|\rangle$, gives better results. Alternate forms were also examined for the terrain-drag portion of (22), but did not give reasonable predictions (e.g. using other combinations involving $\langle |\Delta h/\Delta x|\rangle$ and/or means and standard deviations of $\Delta h/\Delta x$, instead of the product $\sigma _{\Delta h/\Delta x}\langle |\Delta h/\Delta y|\rangle$).

Recognizing the physical basis for the summation of roughness- and terrain-induced stresses which gave rise to (3), if the latter is applied with the terrain-induced contributions shown in (17)–(21), we have the generalised expression:

$$\begin{aligned} \ln \left( \frac{a_d d_\text {eff}}{z_\text {0,eff}}\right) \simeq \left\{ \left[ \ln \left( \frac{a_d d_\text {eff}}{z_\text {0,terrain}}\right) \right] ^{-2} + \left[ \ln \left( \frac{a_d d_\text {eff}}{z_\text {0,in}}\right) \right] ^{-2} \right\} ^{-1/2} , \end{aligned}$$

(23)

where $z_\text {0,terrain}$ is equivalent to the right-most terms in each of (17)–(21); i.e., $z_\text {0,terrain}\equiv (z_\text {0,eff}- z_\text {0,in})$ for linear combinations of roughness. Here in (23) we have written $Z_p=a_d d_\text {eff}$ with $a_d$ a constant; this is preferable to attempting to find some $\langle Z_p\rangle$ applicable over all terrain, which is physically difficult to defend, as the pressure scale-height should depend on the terrain statistics. It is analogous to use of $c_d d_\text {eff}$ in (19) giving substantially better results than the implied all-terrain scale $r_s$ in (17).

For the form $z_\text {0,terrain}=\frac{1}{3} d_\text {eff}\sigma ^2_{\Delta h/\Delta x}$ of (19), fitting (23) to diagnosed $z_\text {0,eff}$ we find $a_d\simeq 0.04$; the mean of implied pressure scale-heights is then $0.04\langle d_\text {eff}\rangle \simeq 6\,$m, varying from about 2–17 m over the range of terrains considered here.¹⁵ The resultant $z_\text {0,eff}$ are shown in Fig. 13, along with those predicted by (19) alone.

Fig. 13

Left: predictions of summed-stress form (23), using the terrain-driven part of (19), $z_\text {0,terrain}\propto d_\text {eff}\sigma ^2_{\Delta h/\Delta x}$ (black triangles); blue circles are (19) as in Fig. 11. Right:  error metric of predictions, $\ln (z_\text {0,eff}|_\text {pred}/z_\text {0,eff}|_\text {obs})$, corresponding to triangles in left-hand figure; colours correspond to different terrains as in Fig. 7

From the left-hand plot in the figure one can see that the two expressions are essentially identical over complex terrain with $z_\text {0,eff}\gtrsim 1\,$m; over simpler terrain, the form (23) gives yet better predictions. The right-hand plot in Fig. 13 also shows that using (23) with $z_\text {0,terrain}$ from (19) gives predictions of $z_\text {0,eff}$ that do not appear to favor complex or simpler terrain.

Similar to using (23) with $z_\text {0,terrain}$ from (19), if using the $z_\text {0,terrain}$ part of (20) in (23), one obtains analogous results, with slightly better predictions by (23) at the smallest $z_\text {0,eff}$ compared to (20); however, this is still not an improvement over (19) or using its $z_\text {0,terrain}$ in (23). Further, use of $z_\text {0,terrain}$ from (21) in (23) gives slightly improved predictions over (21) alone, though negligibly compared to the r.m.s. log error of 0.25 found for (21).

Although the summed-stress form (23) gives better results for smaller $z_\text {0,eff}$ when employing $z_\text {0,terrain}=\frac{1}{3}d_\text {eff}\sigma ^2_{\Delta h/\Delta x}$ from (19) with $a_d=0.04$, there is no clear basis for this value of $a_d$. Considering the coefficient $C_a$ of (3) is proportional to the ratio of hill cross-sectional area to domain area (Wood and Mason 1993), one might might suppose $a_d\propto dh_+/dx$; but taking $a_d\propto \Delta h_+/\Delta x$ considerably degraded predictions when used in (23).

Earlier we obtained estimates for $d_\text {eff}$ such as (12), which could also be used with (19) or (20), but doing so does not improve predictions over the simple estimates given by (17)–(18). Further, one could also simply invert the log law, using $u _{*\text {,eff}}$ based on terrain statistics; using (13) and assuming $d_\text {eff}\ll L_z$, as $z\rightarrow L_z$ one obtains:

$$\begin{aligned} z_\text {0,eff} \approx z_\text {0,in}^{1/(1+2.4\sigma _{\Delta h/\Delta x})} L_z^{1-1/(1+2.4\sigma _{\Delta h/\Delta x})} . \end{aligned}$$

(24)

However, this relation, as well as its analogue using $\Delta h_+/\Delta x$ from (14), result in log-prediction errors 2–3 times larger than using (17)–(20); because of this, and since it depends on the domain depth $L_z$, use of (24) is not recommended.

5 Discussion

Above we found from RANS simulations over large areas ($>40\times 40\,$km) of complex terrain that the horizontally (areally) averaged flow exhibits a displaced logarithmic wind speed profile, with an effective roughness and displacement height diagnosed from the output of $\mathcal {O}(100)$ simulations. Effective roughness formulations based on terrain elevation variance (e.g. Flack and Schultz 2010; Anderson and Meneveau 2011; Kelly 2016) have difficulty predicting $z_\text {0,eff}$ within one order of magnitude, over the range of terrain complexities found in nature. This is due primarily to form-drag being connected to the slopes of hills, while $\sigma _h$ is not directly related to slope statistics—unless the terrain elevation (and slope) spectra exhibit a simple power-law dependence. As shown in Sect. 2.1, actual terrain slope spectra exhibit a more complex behavior, with a peak occuring at scales between 1 km and 10 km.

For example, the Anderson and Meneveau (2011) expression (6) underpredicts $z_\text {0,eff}$ by at least an order of magnitude for $z_\text {0,eff}$ greater than about 0.5 m, increasingly so for more complex terrain. This is presumably due to its design originally being for smaller-scale roughness, where a fractal-like surface was (reasonably) assumed to induce the drag. Fractal terrain, i.e. those whose surface-slope spectra have simple power-law behavior, permit direct connection between $\sigma _h$ and $\sigma _{\Delta h/\Delta x}$; this kind of idealised terrain allows $\sigma _h$-based forms for effective roughness. The Flack and Schultz (2010) formulation (4) exhibits the opposite behavior to Anderson and Meneveau (2011), predicting within an order of magnitude for most cases with $z_\text {0,eff}>\sim 5\,$m but giving worse results for less complex sites. Incorporation of the skewness of h in Flack and Schultz’s model provides a slight correlation in predictions (rising with increasing $z_\text {0,eff}$); we find $Sk_h$ exhibits modest correlation with $z_\text {0,eff}$ only for more complex cases having $z_\text {0,eff}>1$, while it offers no predictive value for less complex terrain.

5.1 Combining Surface Roughness with Roughness Induced by Terrain Slopes

The addition of stresses caused by complex terrain at different distances upwind is still somewhat of an open research question, due in part to the difficulty of defining or calculating a momentum-flux footprint. One can expect the extent of upwind terrain that contributes significantly to $z_\text {0,eff}$ over a given area to depend on $d_\text {eff}$ and the terrain-slope statistics themselves, though analysis of such is beyond the scope of the current article. At any rate, for practical use, the excess stress caused by hills (pressure drag) must be combined along with the roughness-induced stress for a given area—or expressed as an effective roughness length which is somehow added to the background $z_0$.

5.1.1 Summation of Stresses

A number of works have summed stresses due to heterogeneous surfaces, to obtain an effective roughness. This has included contributions from different roughnesses (i.e. patches) on a flat surface (e.g. Wieringa 1986), or summing contributions due to a collection of identical hills (e.g. Wood and Mason 1993). These provide $z_\text {0,eff}$ formulae which all have the same mathematical character as (3) and (22)–(23), i.e. quadratic in $1/\ln (Z_p/z_{0,i})$ where $Z_p$ is a pressure-drag scale height and $z_{0,i}$ represent the different roughness contributions. The form (23) indeed offers good predictions of $z_\text {0,eff}$, when using (17)–(21) for the terrain-induced part of roughness; e.g. $z_\text {0,terrain}=d_\text {eff}\sigma ^2_{\Delta h/\Delta x}/3$ from (19), as shown earlier in Fig. 13. However, such combination via summation of stresses, as in (23), requires knowledge of the effective pressure scale-height $a_d d_\text {eff}$; one might question how ‘universal’ the value of $a_d$ is, as its physical basis is not clear. We note that different values of $a_d$ were found, depending on whether we used $z_\text {0,terrain}(\sigma _{\Delta h/\Delta x})$ from (19), $z_\text {0,terrain}(\sigma _{\Delta h_+/\Delta x})$ from (20), or alternately the $z_\text {0,terrain}(\sigma _{\Delta h/\Delta x},\mu _{|\Delta h/\Delta y|})$ from (21) for the terrain-drag contribution to (23). Mason (1988) reported this vertical scale to be $\sim L_c/200$ for summing drag quadratically as in (23), where $L_c$ is the characteristic horizontal scale of variations; here taking $L_c$ to be the peak scale from terrain-slope spectra, this and $a_d=0.04$ would imply $L_c\sim 8d_\text {eff}$, though we find $d_\text {eff}$ to be roughly 1/25th to 1/15th of the peak spectral scale; this difference is reasonable, considering the PDF and spectra of slopes are quite broad (with significant contributions spanning several orders of magnitude of slope and wavenumber, respectively). Although $a_d$ is of similar magnitude as $\langle |\Delta h/\Delta y|\rangle$, and the constant $C_a$ in Wood and Mason’s formulation suggests use of such (it is proportional to sillhouette $h\lambda _y$ per area for uniform hills), incorporating first- or second-order statistics of $\Delta h/\Delta y$ within the pressure-scale height (via $a_d$) caused degradation of predictions.¹⁶

5.1.2 Simpler Combinations

The best results for $z_\text {0,eff}$ were obtained using the stress-based form (23) to add contributions from background roughness and terrain drag, as shown in the previous section. However, we also find robust results using simple addition: the inflow roughness $z_\text {0,in}$, which corresponds to the profile over flat terrain upwind and the surface roughness, is simply added to the terrain-induced drag contribution as in (17)–(20). Such summation gives the same results as stress-based addition, except for some lower-complexity cases where it underestimates $z_\text {0,eff}$, as shown in Fig. 11. We again note that (19)–(20) offered better predictions compared to (17)–(18); i.e., $d_\text {eff}$ appears to be the characteristic length scale which acts as a coefficient multiplying the terrain slope variance and carries additional information about $z_\text {0,eff}$, while use of a constant length scale resulted in $\ln z_\text {0,eff}$ error that was at least 1/3 larger.

Alternatively, formulations like (5) of Wan and Porte-Agel (2011) and (6) of Anderson and Meneveau (2011) follow a quadratic form, summing the squares of roughness contributions; adapting these for use with terrain-slope variance, they can be generally expressed with the form $z^2_\text {0,eff}=z^2_\text {0,in}+z^2_\text {0,sl}$, where $z_\text {0,sl}$ is the terrain slope-induced component. Employing this form to combine $z_\text {0,in}$ with the respective $z_\text {0,sl}$ parts of (17)–(21), we get results nearly equal to the linear combinations (17)–(21) for more complex terrain, $z_\text {0,eff}\gtrsim 1\,$m. Unsurprisingly, however, over less complex terrain this quadratic combination causes yet more substantial underpredictions; this follows by noting that:

$$\begin{aligned} \sqrt{z^2_\text {0,in}+z^2_\text {0,sl} }= (z_\text {0,in}+z_\text {0,sl})\sqrt{1-\frac{2z_\text {0,in}z_\text {0,sl}}{(z_\text {0,in}+z_\text {0,sl})^2}} . \end{aligned}$$

(25)

5.2 Limitations and Interpretation

For clarity in assessing the slope-induced contributions to $z_\text {0,eff}$, we used only a uniform background (surface) roughness in all simulations, $z_\text {0,in}=9\,$cm. Previous studies (see Sect. 1) indicate that other (uniform) values of $z_\text {0,in}$ would combine with terrain slope-induced roughnesses in the same way as found here; however, for smaller $z_\text {0,in}$, our results and analysis imply that simple addition of $z_\text {0,in}$ to $z_\text {0,sl}$ would be equal to the stress-based combination over a wider range of $z_\text {0,eff}$ than shown here, i.e. down to lower $z_\text {0,eff}$. For areas where $z_\text {0,in}$ is appreciably larger than the 9 cm considered here, the stress-based summation of $z_0$ would give relatively better results, but such large roughnesses generally occur only in forested or built-up areas, which tend to be inhomogeneous. We do not consider inhomogeneous surface roughnesses, as this is beyond the work of the present study.

The high-resolution part of the domains in the simulations had limited extent, with the amount of high-wavenumber terrain-slope variance decreasing with distance beyond 7 km from the center (due to progressive smoothing, see Sect. 3); this could be interpreted as a weak violation of homogeneity of terrain statistics. However, the limited extent of the high-resolution area had negligible effect, for multiple reasons: first, the relative contribution of smallest-scale terrain-slope variance ($2\pi /k<\sim 300\,$m) was much smaller than that from larger scales; secondly, the use of the downwind two-thirds of the domain for analysis reduced this effect; third, the output data analyzed had a resolution of 56 m, corresponding to a region about 8–10 km from domain center. Reduction of the analysis domain to the downwind 2/3 portion for each wind direction was intentionally done, to reduce the aforementioned issue: conducting tests where we analysed subdomains progressively further downwind and with decreasing areas, we found that the displacement heights first increased and then converged, with $u _{*\text {,eff}}$ and $z_\text {0,eff}$ following suit.

The results here correspond to terrain-induced momentum transfer under neutral atmospheric stratification, such that hundreds of metres above the terrain a logarithmic profile is recovered—with an effective roughness that we can predict based on the terrain statistics. In that regard, the simulations and analysis have been capturing ‘bottom-up’ effects, ignoring anything from above; we remind that the RANS simulations have no capping temperature inversion, but rather a tall domain much larger than the diagnosed terrain-displacement heights. Consequently for shallower ABLs observed to have depths approaching or less than the terrain-induced mean displacement ($z_i\lesssim 3d$) occurring under neutral conditions, obviously the theory presented here would break down. Stability effects are also neglected, but the effective roughness results and expressions here can be taken as a representative average: most places have nearly neutral conditions in the mean, i.e. the long-term distribution of inverse Obukhov length has a significant peak and is centered around zero (Kelly and Gryning 2010).

5.2.1 Beyond $\sigma _{\Delta h/\Delta x}$: Consideration of Other Terrain Statistics

We have shown that the variance of streamwise terrain slope is the key quantity for characterizing the effective roughness of areal-mean wind profiles displaced by complex terrain. In particular, $\sigma _{\Delta h/\Delta x}$ was found to be the optimal predictive terrain statistic, in contrast with $\sigma _{\partial h/\partial x}$. Statistics of $\partial h/\partial x$ (calculated in Fourier space) were not as well-correlated with $z_\text {0,eff}$ and offered less predictive power; we attribute this to high-wavenumber noise, as well as the more local impact of the smaller scales filtered out by $\Delta h/\Delta x$. For example, analogous relations to (17)–(21), but using $\sigma _{\partial h/\partial x}$ instead of $\sigma _{\Delta h/\Delta x}$ (with different fitted constants), gave 2–4 times larger error in predicted $\ln (z_\text {0,eff})$.

Streamwise upslope statistics were also considered, since the flow experiences different slopes, and presumably different terrain drag, in opposite directions; we thus expect statistics of $h_+$, notably $\sigma _{\Delta h_+/\Delta x}$, to facilitate better prediction of effective roughness. Indeed $u _{*\text {,eff}}$, $d_\text {eff}$, and $z_\text {0,eff}$ were all found to differ in opposing directions. The effective roughness differs by a factor as large as 5, while the rectified geometric mean¹⁷ of $z_{\text {0,eff}|\varphi +180^{\circ }}/z_{\text {0,eff}|\varphi }$, over all directions $\varphi$ and sites considered, is a roughly 1.6; i.e., on average $z_\text {0,eff}$ in a given direction is different from $z_\text {0,eff}$ in the opposite direction by a factor of about $1.6^{\pm 1}$. Complementing this, the difference in $d_\text {eff}$ seen from opposite directions was on average about 40% of $d_\text {eff}$ from either direction, with the largest difference having $d_\text {eff}$ being three times larger in one direction than its opposite. However, $\sigma _{\Delta h_+/\Delta x}$ did not give better predictions of $z_\text {0,eff}$ (or $d_\text {eff}$) compared to $\sigma _{\Delta h/\Delta x}$. The inability of $\sigma _{\Delta h_+/\Delta x}$ to predict this asymmetry appears to be due to the simple definition of $h_+$, along with the complexity of the flow: when considering upslopes, $h_+$ does not account for the sheltering effect of larger hills on smaller hills. In other words, the form drag due to a hill can also depend on the flow both upwind and downwind; a hill in the wake of a significantly taller (but not necessarily steeper) mountain will tend to provide relatively less drag than if it were not sheltered. Introducing a spatially-varying weighting, to incorporate sheltering in the definition of $h_+$, could in principle help to exploit observed slope asymmetry; but doing so may depend on the terrain shape itself, quickly becomes complicated, and is beyond the scope of current work.

Statistics of the lateral slope were also considered here, because form drag for single hills has been shown to relate to frontal area (e.g. Wood and Mason 1993) and thus $\Delta h/\Delta y$. The use of $\langle |\Delta h/\Delta y|\rangle _{xy}$ as in (21) indeed added small improvements to predictions of $z_\text {0,eff}$, shown earlier in Fig. 12; in contrast, $\sigma _{\Delta h/\Delta y}$ is not seen to carry information about $z_\text {0,eff}$. However, the improvements which can be offered by using a representative frontal area or $\Delta h/\Delta y$ are also limited by the sheltering aspect.

5.2.2 Turbulence Model Considerations

As noted by Wood and Mason (1993) and later summarised by Wood et al. (2001), the amount of form drag captured will tend to depend on the turbulence closure, with eddy-viscosity closures giving larger drag and $z_\text {0,eff}$ compared to second-order closure. But, as Ayotte et al. (1994) pointed out, the mean flow over hills will only be weakly affected by the turbulence parametrisation. A weakness of commonly-used two-equation RANS closures, such as the k-$\epsilon$ one used here, is the lack of accounting for the pressure-strain terms (see e.g. Pope 2000) which become significant due to hills. The results of the current work are expected to hold for RANS using typical (eddy-viscosity) closures. Use of more advanced turbulence modelling which includes e.g. pressure-transport or pressure-related anisotropy for RANS (e.g. Reece and Rodi 1975; Speziale et al. 1991; Wallin and Johansson 2000), or alternately using LES, will reduce the total form drag; the latter would subsequently require reduction of the leading coefficient in each of (17)–(21), consistent with the reduction in Wood and Mason (1993) of their shear factor. The equations given in the current work may thus slightly overpredict $z_\text {0,eff}$ if compared with LES or RANS with higher-order closure. However, for common stand-alone application or for RANS driven by mesoscale modelling, this will not be an issue: the forms given here correspond to the displaced effective roughness reproduced by RANS with eddy-viscosity closure.

5.3 Application and Recommendations

Because the terrain-slope variance is easier to calculate than the corresponding upslope statistic, and because the latter was not found to improve predictions, we recommend use of (17), (19), or (21) to find $z_\text {0,eff}$ in applications. Though it is not as accurate as (19) or (21), the form (17), using $\gamma =\gamma _+=3$, serves as a practical estimate of effective roughness in applications where one cannot observe or diagnose $d_\text {eff}$ a priori. But given the results shown in Sect. 4.3.2, for applications where $d_\text {eff}$ can be diagnosed following the method given in Sect. 3.3 (such as those involving RANS), we recommend the simple and robust form (19). In such applications, if the map and model resolution is finer than $\sim$1 km and the lateral slopes can be readily calculated, one may obtain further improvement by using (21).

6 Summary and Outlook

For brevity, we summarise what we have found and reported, via bullet points below.

• Complex terrain causes a displaced areal-mean logarithmic profile, with effective displacement height $d_\text {eff}$, friction velocity $u _{*\text {,eff}}$, and roughness length $z_\text {0,eff}$.

  • Terrains have different $\{u _{*\text {,eff}},d_\text {eff},z_\text {0,eff}\}$ in opposite directions.

• Previous works cast $z_\text {0,eff}$ in terms of $\sigma _h$, but

  • $\sigma _h$ does not correlate with $z_\text {0,eff}$ unless terrain is mono-fractal.

  • Previous methods mis-predict $z_\text {0,eff}$ by one order of magnitude.

• We can predict $\{u _{*\text {,eff}},d_\text {eff},z_\text {0,eff}\}$ using variance of streamwise terrain slopes.

  • $\sigma _{\Delta h/\Delta x}$ using first-order finite differences gives robust results. $\qquad \cdot$ Incorporating $d_\text {eff}$ from flow field improves results, where $d_\text {eff}$ is diagnosed from terrain-following plane-mean profiles $u_*(z)$. $\qquad \cdot$ Further improvement found by also using lateral terrain slope.

  • Using up-slope $\sigma _{\Delta h_+/\Delta x}$ does not improve over $\sigma _{\Delta h/\Delta x}$; $\qquad \cdot$ this upslope statistic does not account for hill sheltering.

We note that the arguments of Beljaars et al. (2004) for choosing to parametrise terrain-induced stress (instead of $z_\text {0,eff}$) can still be considered, if one is looking to parametrise unresolved terrain drag in mesoscale and climate models having (effective) resolutions of several kilometres or greater. Consistent with this, and because we have seen that terrain slope spectra can differ significantly from the Beljaars et al. (2004) form (see Fig. 1), ongoing work includes extension of (17)–(21) to further account for limited mesoscale resolutions. One can argue that simple analytical adjustment of our $z_\text {0,eff}$ for a given model resolution is possible, if one knows $\sigma _{\Delta h/\Delta x}$ along with the high-wavenumber spectral exponent $\beta$ and peak of the terrain-slope spectrum for a given terrain (map); however, this needs to be further explored and verified.

Our findings and statistical relations for terrain-induced effective roughness have multiple applications involving microscale flow models, not limited to RANS. This includes choice of $z_\text {0,eff}$ for inflow profiles to microscale flow models, to reduce the amount and spatial extent of adjustment of the incoming flow as it approaches finely-resolved terrain. Another usage involves the geostrophic drag law (GDL) in applications such as wind energy; use of $z_\text {0,eff}$ in the GDL allows observations from an area of one terrain complexity to be used for predictions in another area following the European Wind Atlas method (Troen and Petersen 1989), whether using e.g. linearised flow models or RANS solvers. The forms given here also facilitate better coupling of mesoscale with RANS models: output from the former, which typically do not resolve the drag below scales of several or even tens of kilometres (e.g. for WRF having an effective resolution of 6–8 times its horizontal grid spacing, Pielke 2013), may not resolve the peak part of the terrain-slope spectrum, while typical RANS application resolves the terrain drag as found in this work. Mesoscale model wind speed (and possibly velocity) output could be scaled using the ratio of low-pass filtered terrain slope variance to said variance resolved by a microscale model, per direction; study and validation of such is an ongoing task.

Brown and Wood (2003) found for stable conditions that using an effective roughness length, independent of stability, gave reasonable results within one-dimensional models predicting total surface drag. Future work can include use of RANS solvers in stable conditions (see van der Laan et al. 2017, 2020) to check the validity of such, and potentially extend our $z_\text {0,eff}$ forms for these conditions. Further, RANS with length-scale limited k-$\epsilon$ turbulence closure (Apsley and Castro 1997) or capping inversion can be used to investigate the development of displaced mean profiles where the ABL depth is limited and stable stratification spreads downward (Kelly et al. 2019b), though we note that RANS solvers generally cannot address hill- or inversion-induced waves. Large-eddy simulation can more effectively facilitate such investigation, though it is currently expensive in terms of computational resources.

Other ongoing and future work involves continued investigation into discoveries made in this study, but beyond the scope of the current article. This includes: a relation observed between the profile of terrain-following areal mean eddy viscosity and shape of the probability density function of terrain slopes, which can be used to inform or improve e.g. single-column models or PBL schemes; relations between terrain-slope PDF shape and the high-wavenumber power-law exponent $\beta$; and relating spatial spectra of mean (Reynolds-averaged) velocity and shear stress to terrain spectra at heights approaching (or exceeding) $d_\text {eff}$. Growth of $d_\text {eff}$ over complex terrain, downwind of simpler terrain, is also ripe for investigation; this goes along with further testing of the results here in larger finely-resolved domains, as well as investigation over terrain having different aerodynamic roughnesses.