1 Introduction

Land cover in nature often contains heterogeneous variations in surface properties; this is including (but not limited to) albedo, roughness, and soil moisture. The aggregated effects of these properties interact with the atmosphere above and influence the structure of local and areal mean vertical temperature, wind, and scalar profiles. This interaction has wide-ranging implications for such applications as wind energy, air quality, structural engineering, and many others. As such, the accurate numerical modelling of these interactions is crucial for predicting atmospheric impacts on these applications. Of further complication is the distribution and length scale of the surface variations, which is often of finer scales than the resolution of operational numerical weather prediction models (Bou-Zeid et al. 2020). As such, it is not surprising that efforts to parameterize the aggregated effects of regional surface heterogeneity have been ongoing for several decades.

In the case of changes in surface roughness, flow encountering a rough (smooth) surface from a smooth (rough) one slows down (speeds up) at and just upstream of the roughness change. The turbulent response from the resulting convergence (divergence) is distributed in the vertical direction and downstream of the roughness change. The aforementioned turbulent response is confined within an internal boundary layer (IBL) (Garratt 1990; Kaimal and Finnigan 1994). The IBL response to roughness changes has been investigated for several decades. Elliott (1958) developed an early theory for determining the height of the IBL downstream of a single roughness change. Since Elliott (1958), numerous similar analytical models have been developed for IBL development following a step change in roughness (for example, Panofsky and Townsend 1964; Chamorro and Porté-Agel 2009; Ghaisas 2020). Bradley (1968) documented the atmospheric response to spikes placed on an airport tarmac. Claussen (1987) used a streamfunction-vorticity model to study the upstream effects of the IBL and modelled the stress response to the roughness change. In an extension of the work by Jackson and Hunt (1975), Belcher et al. (1990) introduced a triple-layer analytical model to describe the atmospheric response to arbitrary changes in surface roughness. Differently from the hill case described in Jackson and Hunt (1975), the roughness did not generate a sufficiently strong pressure gradient to make the three levels interactive, so that two layers were already sufficient to describe the flow perturbation at leading order. Using wind tunnel experiments, Segalini and Chericoni (2021) investigated the growth of the internal boundary layer over long wind farms, with budget analyses showing the importance of the advection of kinetic energy transported by vertical velocity.

Many recent studies have examined the development of internal boundary layers using large eddy simulation (LES). Bou-Zeid et al. (2004) used LES to examine flows over strips of roughness changes in neutral conditions and extended this work to arbitrary roughness changes in Bou-Zeid et al. (2007). Bergot et al. (2015) performed LES experiments to study the impact of airport buildings on fog development at Charles de Gaulle airport. Tomas et al. (2016) studied the effect of stable stratification on rural to urban roughness transitions to investigate pollutant dispersion. Allaerts and Meyers (2018) used LES to examine IBL development over wind farms. Segalini (2017) developed a model based upon the linearized Navier–Stokes equations that simulates flows interacting with wind farms in complex terrain, which was validated against LES data. Momen et al. (2021) found distinctive mean and turbulence structures within the IBL formed at the coastal roughness transition in LES of a hurricane making landfall. In another LES study, Janzon (2022) developed a model aggregating the IBL effects over a wide range of heterogeneity length scales given a diurnal cycle and including rotational effects due to the Coriolis force.

Despite of the plethora of data available, several open questions remain (see Janzon 2022, for a review) especially concerning the impact of land-cover heterogeneity on the boundary layer. The estimate of the effect of a surface roughness texture in the boundary layer above is an open issue: even by knowing the surface roughness statistically, the IBL development depends on the actual roughness geometry and surface wind conditions in terms of mean flow and turbulent momentum transfer. These are in turn affected by the model resolution at the lower layers (both horizontal and vertical resolutions are important) and might affect the simulation results. When a finite-volume code is used, the surface stress imposed at the bottom of the cell closest to the ground replaces the effect of the boundary condition, but this requires a reliable model to connect the shear stress with the roughness (Stoll and Porté-Agel 2006).

Given the computational expense of running full-physics numerical simulations (together with their modeling assumptions), analytical models remain an attractive option for studying these effects. A reliable analytical model can be used with relative ease to examine the continuous effects of a large sweep of background atmospheric conditions and land-cover distributions.

In this study, a new analytical theory is presented that examines the atmospheric response to arbitrary changes in surface roughness, revisiting the theory proposed by Belcher et al. (1990): the latter theory was developed for two-dimensional roughness distributions. The new theory is here validated against experimental data and LES results. Surface stress and velocity distribution in the boundary layer are estimated for several roughness patches providing physical insight into the IBL development and how that is affected by the roughness. The paper is structured as follows. Section 1 describes the theory in terms of the equations, base flow and perturbation in response to the roughness heterogeneity. The model is first validated in Sect. 3 against two experimental datasets (Bradley 1968; Li et al. 2021). An additional validation is provided by the numerical simulations described in Sect. 4 while the comparison between theory and numerical results is reported in Sect. 5. Concluding remarks are reported in Sect. 6.

2 Theory

The equations for the flow above heterogeneous roughness are written by means of the incompressible approximation in Cartesian coordinates. The x direction is considered oriented along the surface wind direction, z orthogonal to the surface and y orthogonal to the xz plane.

The steady-state Boussinesq equations used to investigate the roughness problem are:

$$\begin{aligned}&\displaystyle \frac{\partial U}{\partial x}+\frac{\partial V}{\partial y} +\frac{\partial W}{\partial z} =\nabla _h\cdot \textbf{U}+\frac{\partial W}{\partial z}=0\,, \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \left( \textbf{U}\cdot \nabla _h\right) \textbf{U}+W\frac{\partial \textbf{U}}{\partial z} +f\textbf{e}_z\times \textbf{U}=-\nabla _h\varPi -\frac{\partial \overline{\textbf{u}'w'}}{\partial z}\,, \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \left( \textbf{U}\cdot \nabla _h\right) W+W\frac{\partial W}{\partial z} =-\frac{\partial \varPi }{\partial z}\,. \end{aligned}$$
(3)

The horizontal velocity vector \(\textbf{U}=\left( U,\,V\right) \) is separated from the vertical velocity component W. The horizontal gradient operator is here indicated as \(\nabla _h\). The Coriolis parameter is indicated as f. The term \(\varPi \) includes the normal Reynolds stresses (assumed to be isotropic) and the pressure normalised by the background density, \(\rho _0\). The use of Boussinesq equations assumes a constant background density value that appears suitable for the analysis close to the surface. The neglect of buoyancy effects in the vertical momentum equation implies weak stratification effects on the flow dynamics, although the stratification might change the turbulence properties by affecting the eddy viscosity or the mixing length.

Similarly to Belcher et al. (1990), the horizontal Reynolds stresses \(\overline{\textbf{u}'w'}\) are modeled by means of the mixing-length approximation:

$$\begin{aligned} -\overline{\textbf{u}'w'}=l_m^2\left| \frac{\partial \textbf{U}}{\partial z}\right| \frac{\partial \textbf{U}}{\partial z} \qquad \textrm{with}\qquad l_m =\frac{\kappa z}{\phi _m\left( z/L_{o}\right) }\,, \end{aligned}$$
(4)

where \(\kappa \approx 0.4\) indicates the von Kármán constant, \(L_{o}\) the Obukhov length scale and \(\phi _m\) the flux function for the momentum transfer (Högström 1990). The mixing length, \(l_m\), is used here as an empirical parameter that grows linearly in the logarithmic region, namely the region most affected by the roughness perturbation. No displacement height (Jackson 1981) is considered in the present analysis. Above of the logarithmic region, it is expected that the mixing length should saturate following a Escudier (1966) model, although this is not implemented in the present work. In the present formulation, density stratification is introduced only by means of the mixing length via the flux function, \(\phi _m\).

By considering a slight velocity deviation, \(\textbf{u}\), from a base state, \(\textbf{U}_0\) (with known shear stress, \(\left| \overline{\textbf{u}'w'}_0\right| =u_*^2\)) in the constant stress layer above the roughness, the total shear stress can be written as:

$$\begin{aligned} -\overline{\textbf{u}'w'}\approx u_*^2\textbf{e}_x+u_*l_m \left( \frac{\partial \textbf{u}}{\partial z} +\frac{\partial \textbf{e}_x\cdot \textbf{u}}{\partial z}\,\textbf{e}_x\right) =u_*^2\textbf{e}_x+\underbrace{u_*l_m\left( 2\frac{\partial {u}}{\partial z}, \,\frac{\partial {v}}{\partial z} \right) }_{-\overline{\textbf{u}'w'}_{\textrm{pert}}}\,, \end{aligned}$$
(5)

where \(\textbf{e}_x=\left( 1,\,0,\,0\right) \) indicates the surface velocity direction vector, while it is assumed that the velocity deviation does not affect the mixing length, \(l_m\). Equation (5) is obtained by considering a Maclaurin expansion of the square root operator considering only terms proportional to the velocity perturbation. The last term of (5) is the perturbation shear stress and it is denoted as \(-\overline{\textbf{u}'w'}_{\textrm{pert}}\) in the following to highlight its corrective meaning. Equation (5) is approximated to the first-order term, while the inclusion of higher order terms will introduce nonlinear corrections: this is acceptable away from the region most affected by the roughness where the full nonlinear expression (4) must be used instead.

At the bottom surface the roughness boundary condition is imposed as:

$$\begin{aligned} \textbf{U}\left( z\rightarrow 0\right) =\frac{\widetilde{u_*}}{\kappa }\ln \left( \frac{z}{z_1}\right) \textbf{e}_x\,, \end{aligned}$$
(6)

where \(\widetilde{u_*}\) is the local friction velocity associated to the flow development over the roughness \(z_1\). \(\widetilde{u_*}\) is expected to be modified with respect to the undisturbed one, \(u_*\). The friction velocity is computed as:

$$\begin{aligned} \widetilde{u_*}=\left( \overline{u'w'}^2+\overline{v'w'}^2\right) ^{1/4} =l_m\left| \frac{\partial \textbf{U}}{\partial z}\right| \qquad \textrm{as}\qquad z\rightarrow 0\,. \end{aligned}$$
(7)

2.1 Base Flow Determination

When the roughness is homogeneous at the surface, the nonlinear column model:

$$\begin{aligned}&\displaystyle W_0=0\,, \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle f\textbf{e}_z\times \textbf{U}_0=-\nabla _h\varPi _0+\frac{\partial }{\partial z} \left[ l_m^2\left| \frac{\partial \textbf{U}_0}{\partial z}\right| \frac{\partial \textbf{U}_0}{\partial z}\right] \,, \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \frac{\partial \varPi _0}{\partial z}=0\,, \end{aligned}$$
(10)

is obtained. Capital quantities with a 0 subscript are used here to indicate basic unperturbed quantities associated to the homogeneous roughness, \(z_0\). By coupling Eqs. (8–10) with the surface and free-stream boundary conditions they can be integrated to obtain the undisturbed velocity profile over a homogeneous roughness. If a constant eddy-viscosity model was instead adopted, the Ekman spiral would have been obtained (Vallis 2017).

The assessment of the base flow is done by integrating (8–9) from the ground to the top of the boundary layer. As no thermal wind is considered here (the present analysis considers a barotropic atmosphere only), the velocity distribution approaches a constant geostrophic wind given by the geopotential gradient, i.e.:

$$\begin{aligned} \textbf{U}_0(z\rightarrow \infty )=f\,\textbf{e}_z \times \nabla _h\varPi _0=\left( U_G,\,V_G\right) \,. \end{aligned}$$
(11)

Near the ground (at \(z=z_0\)) the no-slip condition is imposed as \(\textbf{U}_0\left( z_0\right) =\textbf{0}\). The inclusion of baroclinic effects will change the RANS balance, affecting the turbulence properties as discussed by Momen et al. (2018).

From a practical point of view, the velocity at a given reference height is usually known as a two-dimensional vector while the friction velocity is not known and it is a result of the integration of a nonlinear problem (or of direct measurements of the shear stress). The integration of the velocity equations is here done by means of a tentative friction velocity value; the obtained velocity field is then normalized at the reference height obtaining a new value for the friction velocity from the surface stress and the estimation is started again until convergence. Figure 1 shows an example of the U and V velocity profiles for different roughness heights in neutral conditions and for different stability classes. Since the steady-state mixing-length model is numerically stiff, a spectral approach with Chebyshev polynomials (Peyret 2002) was used to solve the nonlinear flow equations with a Newton–Raphson method.

Fig. 1
figure 1

Zonal (solid line) and meridional (dashed line) velocity profiles for \(f=10^{-4}~1/\textrm{s}\) and velocity at \(z_{\textrm{ref}}=100~\textrm{m}\) equal to \((U_{\textrm{ref}}, \,V_{\textrm{ref}})=(10~\textrm{m}/\textrm{s},\,0)\). a \(z_0=0.001~\textrm{m}\) (green line), \(z_0=0.01~\textrm{m}\) (red line) and \(z_0=0.1~\textrm{m}\) (blue line) with \(L_o\rightarrow \infty \). b \(L_o\rightarrow \infty \) (green line), \(L_o=-100~\textrm{m}\) (red line) and \(L_o=100~\textrm{m}\) (blue line) with \(z_0=0.1~\textrm{m}\). The dotted line indicates the logarithmic law. The reference height can be quickly identified as the zero crossing of the V profile

Full size image

When looking at Fig. 1, it is clear that very close to the roughness (say for \(z<100z_0\)) the velocity profile is independent of stratification, while in the neutral case it follows the logarithmic law until the edge of the boundary layer. According to Monin–Obukhov similarity theory (Högström 1990; Kaimal and Finnigan 1994), the windwise mean flow profile in the constant stress layer is given by:

$$\begin{aligned} U_0=\frac{u_*}{\kappa }\left[ \ln \left( \frac{\delta }{z_0}\right) +\ln \eta -\varPsi \left( \frac{\delta }{L_o}\eta \right) +\varPsi \left( \frac{z_0}{L_o}\right) \right] \qquad ,\qquad V_0=0\,, \end{aligned}$$
(12)

where \(\eta =z/\delta \) is a dimensionless coordinate where z is scaled by the length scale \(\delta \gg z_0\). Away from the surface, the first term is dominating: the stratification terms (expressed by the \(\varPsi \) function, Kaimal and Finnigan 1994) play a role only for extremely high stratification (or when \(z/L_o=O(1)\)). They are very important to establish the base flow profile but their role is marginal for the perturbative terms at leading order.

The V component is smaller than U and does not show a logarithmic law. The growth of the V component takes place apparently when U deviates from the logarithmic behaviour: close to the surface this is not surprising since the shear stress is constant while the integrated ageostrophic wind grows linearly with the distance from the ground. This implies that in the constant-stress layer, the V component remains small and therefore negligible compared to the U component. This does not imply that Coriolis effects are negligible everywhere: the base velocity profile is in fact determined by solving (9) as a boundary value problem. However, near the surface the base flow is oriented as the surface wind, although the reader is reminded that Fig. 1 is in logarithmic scaling.

Finally, from now on all the velocity components, shear stress and scaled pressure are normalized with the unperturbed \(u_*\) or \(u_*^2\), in order to ease the notation: this is motivated by the connection between friction velocity and wall shear stress (\(\tau _w=\rho _0u_*^2\) by definition), a quantity of paramount importance in the surface layer.

2.2 The Roughness Layer

Very close to the roughness, Eq. (2) is dominated by the turbulent stress term as the advective term has magnitude 1/L (with L indicating a characteristic horizontal length scale for the moment left undefined but assumed to be sufficiently large when compared to \(z_0\)) while the turbulent term has magnitude \(1/z_0\). As long as the horizontal variations have a scale \(L\gg z_0\), the turbulent term dominates. The mixing length (4) is approximated by \(l_m=\kappa z\) as the stratification correction is negligible very close to the surface (in stable stratification the momentum flux function is proportional to the height normalised by the Monin–Obukhov length scale \(L_o\), here assumed to be very large). The velocity field remains aligned with the x direction since the rotation effect is negligible at such small scales. Consequently, the total shear stress is given by \(-\overline{\textbf{u}'w'}=\left( 1+\tau \right) ^2\textbf{e}_x\) with \(\left( 1+\tau \right) ^2\) indicating the corrective shear stress factor due to the roughness. By using the closure model (4), the total velocity derivative is found as:

$$\begin{aligned} \frac{\partial \textbf{U}}{\partial z}=\frac{1+\tau }{\kappa z}\textbf{e}_x\,, \end{aligned}$$
(13)

that can be integrated in the windwise direction to:

$$\begin{aligned} U(x,y,z)=\frac{1+\tau }{\kappa }\ln \left( \frac{z}{z_1}\right) =\underbrace{\frac{1}{\kappa }\ln \left( \frac{z}{z_0}\right) }_{U_0}+u(x,y,z)\,, \end{aligned}$$
(14)

with the velocity perturbation:

$$\begin{aligned} u(x,y,z)=-\frac{1}{\kappa }\ln \left( \frac{z_1}{z_0}\right) +\frac{\tau }{\kappa }\left[ \ln \left( \frac{z}{z_0}\right) -\ln \left( \frac{z_1}{z_0}\right) \right] \,, \end{aligned}$$
(15)

that satisfies already the no-slip boundary condition at \(z=z_1\). The friction velocity associated to this layer is not anymore \(u_*\) but rather \(\widetilde{u_*}=u_*(1+\tau )\) pointing out to a direct effect of the roughness to the turbulent activity. The term \(\kappa ^{-1}\ln \left( z_1/z_0\right) \) indicates the magnitude of the velocity perturbation in the roughness layer: this does not have to be very small since the roughness-layer analysis is not linearised and remains valid as long as the turbulent stress dominates and remains constant in the vertical direction.

By introducing the two-dimensional Fourier transform and its inverse:

$$\begin{aligned} \widehat{u}={\mathcal {F}}(u)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } u(x,y)e^{-i\left( k_xx+k_yy\right) }\textrm{d}x\textrm{d}y \quad ,\quad u={\mathcal {F}}^{-1}(\widehat{u})\,, \end{aligned}$$
(16)

the horizontal Fourier transform of (15) is:

$$\begin{aligned} \widehat{u}(k_x,k_y,z)=-\frac{1}{\kappa }{\mathcal {F}} \left[ \left( 1+\tau \right) \ln \left( \frac{z_1}{z_0}\right) \right] +\frac{\widehat{\tau }}{\kappa }\ln \left( \frac{z}{z_0}\right) \,. \end{aligned}$$
(17)

At this point the roughness analysis has revealed that the velocity change goes logarithmically with the height, similarly to several of the simplified models proposed in the literature (Elliott 1958; Panofsky and Townsend 1964; Chamorro and Porté-Agel 2009). However, the function \(\tau \) is still undefined and must be determined by considering the balances above the roughness layer where mean flow advection enters the analysis, as discussed in the followings.

2.3 Perturbation Structure Far from the Roughness

As clear from the analysis of the previous section, very close to the roughness a nonlinear analysis provided the velocity perturbation due to the roughness expressed by (15) in physical coordinates, or by (17) after the Fourier transform. Away from the roughness, one expects that the velocity perturbation should be smaller than the base flow: in light of this, the following decompositions are introduced:

$$\begin{aligned} \textbf{V}&=\left( \textbf{U},\,W\right) =\left( \textbf{U}_0,\,0\right) +\omega _u\left( \textbf{u},\,w\right) \,, \end{aligned}$$
(18)
$$\begin{aligned} \varPi&=\varPi _0\left( x,y,\eta \right) +\omega _pp\,, \end{aligned}$$
(19)

where \(\omega _u\,, \,\omega _p\ll 1\) indicate the dimensionless weights of the perturbation with respect to the base state. These are dependent on the distance from the roughness and are obtained as a result of the analysis. The steady perturbation equations are obtained from (1–3) subtracted by the parallel-state equations and linearised leading to:

$$\begin{aligned}&\displaystyle \nabla _h\cdot \textbf{u}+\frac{\partial w}{\partial z}=0\,, \end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle \left( \textbf{U}_0\cdot \nabla _h\right) \textbf{u}+w\frac{\partial \textbf{U}_0}{\partial z}+ \frac{f}{u_*} \textbf{e}_z\times \textbf{u} =-\frac{\omega _p}{\omega _u}\nabla _hp-\frac{\partial }{\partial z} \left( \overline{\textbf{u}'w'}_{\textrm{pert}}\right) \,, \end{aligned}$$
(21)
$$\begin{aligned}&\displaystyle \left( \textbf{U}_0\cdot \nabla _h\right) w=-\frac{\omega _p}{\omega _u} \frac{\partial p}{\partial z}\,. \end{aligned}$$
(22)

In order to perform a scale analysis, the linearised Eqs. (20–22) are first Fourier transformed. The vertical coordinate is scaled as \(\eta =z/\delta \) where \(\delta \) is an arbitrary length scale. A characteristic horizontal length scale should be now introduced to do a scale analysis: this however appears quite arbitrary for a generic roughness distribution. Similarly to the two-dimensional formulation of Belcher et al. (1990), the equations are normalised by the wave-vector norm \(\left| \textbf{k}\right| =(k_x^2+k_y^2)^{1/2}\) as the inverse of a characteristic length scale (so that the characteristic horizontal length scale is \(L=1/\left| \textbf{k}\right| \) and proportional to the wavelength of the considered Fourier wave). The wavenumbers normalised by \(\left| \textbf{k}\right| \) are denoted as \(\overline{k}_x=k_x/\left| \textbf{k}\right| \) and \(\overline{k}_y=k_y/\left| \textbf{k}\right| \) and are expected to be O(1). In order to balance the continuity equation at all layers, the vertical velocity is scaled by \(\delta \left| \textbf{k}\right| \) so that \(\widehat{w}=\delta \left| \textbf{k}\right| \widetilde{w}\).

The dimensionless perturbation equations become:

$$\begin{aligned}&\displaystyle i\overline{k}_x\widehat{u}+i\overline{k}_y\widehat{v} +\frac{\partial \widetilde{w}}{\partial \eta }=0\,, \end{aligned}$$
(23)
$$\begin{aligned}&\displaystyle \left( i\overline{k}_xU_0+i\overline{k}_yV_0\right) \widehat{u} +\widetilde{w}\frac{\partial U_0}{\partial \eta } -\frac{f}{u_*\left| \textbf{k}\right| }\widehat{v} =-i\overline{k}_x\frac{\omega _p}{\omega _u}\widehat{p} +\frac{1}{\delta \left| \textbf{k}\right| }\frac{\partial }{\partial \eta } \left( 2\frac{l_m}{\delta }\frac{\partial \widehat{u}}{\partial \eta }\right) \,, \end{aligned}$$
(24)
$$\begin{aligned}&\displaystyle \left( i\overline{k}_xU_0+i\overline{k}_yV_0\right) \widehat{v}+\widetilde{w} \frac{\partial V_0}{\partial \eta }+ \frac{f}{u_*\left| \textbf{k}\right| } \widehat{u}=-i\overline{k}_y\frac{\omega _p}{\omega _u}\widehat{p} +\frac{1}{\delta \left| \textbf{k}\right| }\frac{\partial }{\partial \eta } \left( \frac{l_m}{\delta }\frac{\partial \widehat{v}}{\partial \eta }\right) \,, \end{aligned}$$
(25)
$$\begin{aligned}&\displaystyle \left( i\overline{k}_xU_0+i\overline{k}_yV_0\right) \widetilde{w} =-\frac{\omega _p}{\omega _u}\frac{1}{\left( \delta \left| \textbf{k}\right| \right) ^2} \frac{\partial \widehat{p}}{\partial \eta }\,, \end{aligned}$$
(26)

where the shear-stress perturbations have been replaced by the forms assumed in the constant stress layer, by assuming that these are significant in the logarithmic region of the base velocity profile.

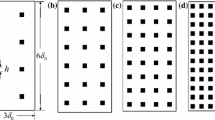
Similarly to Jackson and Hunt (1975) and Segalini et al. (2015), three layers are used in the present theory, each characterised by different vertical length scales, \(\delta _1=z_0\), \(\delta _2\) and \(\delta _3\) for the roughness, main and outer layer, respectively. The outer layer thickness verifies \(\delta _3\left| \textbf{k}\right| =1\) to match the horizontal and vertical scales in the outermost layer. A schematic representation of the layers structure is shown in Fig. 2.

Fig. 2
figure 2

Schematic representation of the triple-deck decomposition used in this work. The thickness of the roughness layer and main layer is exaggerated for the sake of clarity

Full size image

As a consequence of (12), the velocity field in both the main and outer layer is dominated by \(U_0\approx \kappa ^{-1}\ln \left( \delta /z_0\right) \). When considering the main layer, \(z_0\ll \delta _2\) suggesting to introduce \(\epsilon =z_0/\delta _2\ll 1\) as the small parameter of the problem describing the main-layer thickness compared to the inner layer. In the main layer the turbulent transport and advection terms dominate the horizontal momentum balance leading to:

$$\begin{aligned} {\frac{1}{\kappa }\ln \left( \frac{\delta _2}{z_0}\right) =\frac{1}{\delta _2 \left| \textbf{k}\right| }\longrightarrow \ln \left( \frac{1}{\epsilon }\right) =\frac{\epsilon \,\kappa }{z_0\left| \textbf{k}\right| } \,.} \end{aligned}$$
(27)

The distinguished limit (27) provides a quantification of the \(\epsilon \) parameter in relation to another small parameter of the problem, namely \(z_0\left| \textbf{k}\right| \), the latter representing the scale ratio between the roughness and outer layer size. Figure 3 shows the behaviour of the \(\epsilon \) parameter for several values of \(z_0\left| \textbf{k}\right| \) (interpreted as the ratio between the roughness height and the characteristic horizontal length scale): for \(z_0\left| \textbf{k}\right| <0.01\), \(\epsilon \) is quite small and provides one order of magnitude of scale separation between the main and outer layer. For larger \(z_0\left| \textbf{k}\right| \) (i.e. for short wavelengths comparable with \(z_0\)), the scale separation is not sufficient to establish a good asymptotic matching and the theory is expected to have increasing discrepancies.

Fig. 3
figure 3

(a) Value of the small parameter \(\epsilon \) and (b) ratio between main and outer layer thickness \(\delta _2/\delta _3=z_0\left| \textbf{k}\right| /\epsilon \) as function of \(z_0\left| \textbf{k}\right| \)

Full size image

As a consequence of (12) and of the relationship (27), the velocity field can be rewritten in the main layer as:

$$\begin{aligned} {\textbf{U}_0=\frac{1}{\kappa }\ln \left( \frac{1}{\epsilon }\right) \textbf{e}_x +\textbf{U}_{1}\qquad \textrm{with}\qquad \textbf{U}_{1}=\textbf{U}_0 -\frac{1}{\kappa }\ln \left( \frac{1}{\epsilon }\right) \,,} \end{aligned}$$
(28)

where:

$$\begin{aligned} \textbf{U}_{1}\rightarrow \frac{1}{\kappa }\ln \eta _2\,\textbf{e}_x\qquad \textrm{as} \qquad \eta _2=\frac{z}{\delta _2}\rightarrow 0\,. \end{aligned}$$
(29)

The outer layer is more subtle since the main wind magnitude is given by:

$$\begin{aligned} {\textbf{U}_0=\frac{1}{\kappa }\ln \left( \frac{\delta _3}{z_0}\right) \textbf{e}_x+\textbf{U}_1=\frac{1}{\kappa }\ln \left( \frac{1}{\epsilon }\right) \textbf{e}_x+\frac{1}{\kappa }\ln \left[ \ln \left( \frac{1}{\epsilon }\right) \right] \textbf{e}_x+O(1)\,.} \end{aligned}$$
(30)

Now the first term is 2 up to 5 times bigger than the second, implying that the two share the same order of magnitude for realistic values of \(z_0\left| \textbf{k}\right| \). Therefore, while a mismatch exists between the two dominant mean-flow velocities in the main and outer layer, their discrepancy is not sufficiently scale separated. This aspect will become of importance when assessing the pressure correction order of magnitude.

Finally, by considering a Coriolis parameter \(f=10^{-4}~\textrm{s}^{-1}\), a roughness height \(z_0=0.1~\textrm{m}\), a typical horizontal length of \(1/\left| \textbf{k}\right| =1000~\textrm{m}\) and a friction velocity value of \(u_*=0.2~\textrm{m}/\textrm{s}\), one obtains that the small parameter \(\approx 2\cdot 10^{-4}\) while the Rossby number is \(u_*\left| \textbf{k}\right| /f\approx 2\) and therefore quite large. This suggests that, as long as the inhomogeneity scale is within 0-10 km, Coriolis effects can be excluded from the leading perturbation analysis (they will appear at higher-order analyses though). It is important to underline that the base velocity profile is anyhow determined from Eq. (11) that accounts for the Coriolis force: that means that at leading order the Coriolis force enters the analysis only by means of the advection operated by the mean velocity profile, and only at higher order it will influence the perturbation field as a force.

2.4 Outer Layer

The outer layer is characterized by a stretching factor \(\delta _3\left| \textbf{k}\right| =1\) and a large value of the undisturbed characteristic normalised velocity \(\kappa ^{-1}\ln \left( \delta _3/z_0\right) \). The stretched variable will be indicated as \(\eta _3=z/\delta _3\) in the outer layer. Since the stretching factor is unitary, \(\widehat{w}=\widetilde{w}\) in the outer layer only.

As a result of matching the pressure order of magnitude with the advective terms, \(\omega _p=\omega _{u,3}\ln \left( \delta _3/ z_0\right) \approx O\left( \omega _{u,3}\ln \left( 1/\epsilon \right) \right) \). The order of magnitude of the velocity perturbation, \(\omega _{u,3}\), depends on the roughness perturbation and how that influences the outer layer and remains for now unknown.

The matching at the vertical velocity at the interface between the outer (where \(\delta _3\left| \textbf{k}\right| =1\)) and main layer (where \(\delta _2\left| \textbf{k} \right| =\kappa /\ln (1/ \epsilon )\)) implies that:

$$\begin{aligned} \delta _2\left| \textbf{k}\right| \omega _{u,2} \widehat{w}_{2} (\eta _2\rightarrow \infty )=\omega _{u,3}\widehat{w}_3(\eta _3\rightarrow 0)\,. \end{aligned}$$
(31)

The above condition implies that the order of magnitude of the velocity perturbation in the main layer \(\omega _{u,2}=\omega _{u,3}/(\delta _2\left| \textbf{k}\right| )\gg \omega _{u,3}\). Due to this difference, the main flow horizontal velocity must vanish as \(\eta _2\rightarrow \infty \). The pressure perturbation is found to be:

$$\begin{aligned} {\omega _{p}=\omega _{u,2}\frac{\ln \left( \delta _3/z_0\right) }{\ln \left( \delta _2/z_0\right) }\approx \omega _{u,2}\,,} \end{aligned}$$
(32)

and will not change in the main and roughness layers. The pressure perturbation is therefore comparable to the velocity perturbation in the main layer. However, as the advective term is multiplied by the base velocity, the pressure contribution will be present at the second-order approximation, which is beyond the analysis performed here. Therefore, the analysis of the outer layer is not continued here. The interested reader can find further details in Segalini et al. (2015).

2.5 Main Layer

From the order of magnitude analysis of the previous section, the perturbation equations for the main layer can be written at leading order as:

$$\begin{aligned}&i\overline{k}_x\widehat{u}_0+i\overline{k}_y\widehat{v}_0 +\frac{\partial \widetilde{w}_0}{\partial \eta _2}=0\,, \end{aligned}$$
(33)
$$\begin{aligned}&i\overline{k}_x\widehat{u}_0=\frac{\partial }{\partial \eta _2} \left( 2\kappa \eta _2\frac{\partial \widehat{u}_0}{\partial \eta _2}\right) \,, \end{aligned}$$
(34)
$$\begin{aligned}&i\overline{k}_x\widehat{v}_0=\frac{\partial }{\partial \eta _2} \left( \kappa \eta _2\frac{\partial \widehat{v}_0}{\partial \eta _2}\right) \,, \end{aligned}$$
(35)
$$\begin{aligned}&\frac{\partial \widehat{p}_0}{\partial \eta _2}=0\,. \end{aligned}$$
(36)

Equations (34–35) approximate still the mixing length to its neutral value \(l_m\approx \kappa z\), implying no stratification effects in the main layer. This is not true even at leading order but, since \(L_o\gg z_0\), it is expected that the effect of stratification on the mixing length is weak and relevant only at higher orders.

By introducing the coordinate transformation \(\zeta =\left( 2i\overline{k}_x\eta _2/\kappa \right) ^{1/2}\), the momentum equation (34) reduces to a modified Bessel equation (Abramowitz and Stegun 1984) with solution \(\widehat{u}_{0}=\widehat{c}\,K_0\left( \zeta \right) \) (where \(K_0(\zeta )\) indicates a modified Bessel function of the second kind). Since \(u_{0}\rightarrow 0\) as \(\eta _2\rightarrow \infty \), the approach is consistent with the absence of a high-order velocity perturbation in the outer layer (that is of higher order). On the other hand, as \(\eta _2\rightarrow 0\), the perturbation approaches:

$$\begin{aligned} \widehat{u}_{0}\rightarrow -\widehat{c}\left[ \gamma +\ln \left( \frac{\zeta }{2}\right) \right] =-\frac{\widehat{c}}{2}\left[ 2\gamma +\frac{i\pi }{2}\textrm{sgn}(\overline{k}_x) +\ln \left( \frac{\left| \overline{k}_x\right| }{2\kappa }\right) +\ln \eta _2\right] \,, \end{aligned}$$
(37)

where \(\gamma =0.57721...\) is the Euler-Mascheroni constant (Abramowitz and Stegun 1984). The last expression is logarithmically singular as \(\eta _2\rightarrow 0\), preventing to impose the no-slip boundary condition at the surface and requiring an additional layer below the main one (i.e. the roughness layer).

The case with \(\overline{k}_x=0\) is singular and requires the direct solution of (34) as \(\widehat{u} =-\widehat{c}\ln \eta _2/2+\widehat{A}\). However, since \(\widehat{u}\rightarrow 0\) as \(\eta _2\rightarrow \infty \), the only possible solution is to have \(\widehat{u}=0\) for \(\overline{k}_x=0\).

The vertical velocity distribution at leading order can be obtained from the continuity equation as:

$$\begin{aligned} \widetilde{w}_0= - \widehat{c}\int _0^\zeta \xi K_0\left( \xi \right) \textrm{d} \xi =\widehat{c}\left[ \zeta K_1\left( \zeta \right) -1\right] \,. \end{aligned}$$
(38)

The function \(\widehat{c}\) and the order of magnitude \(\omega _{u,2}\) are still unknown and can be determined from the matching of the roughness layer that exists to remove the logarithmic singularity of (37) as \(\eta _2\rightarrow 0\).

At this point it is time to match (37) with (17). The matching of the logarithmic term \(\ln \eta _2\) provides the relationship:

$$\begin{aligned} {\frac{\widehat{\tau }}{\kappa }=-\frac{\widehat{c}}{2}\,,} \end{aligned}$$
(39)

corresponding to the matching of the perturbation shear stress between the two layers. The matching of the constant term is however complicated by the presence of logarithm terms since:

$$\begin{aligned} \widehat{\tau }\left[ \ln \left( \frac{1}{\epsilon }\right) -2\gamma -\frac{i\pi }{2}\textrm{sgn}(\overline{k}_x) -\ln \left( \frac{\left| \overline{k}_x\right| }{2\kappa }\right) \right] ={\mathcal {F}}\left[ \ln \left( \frac{z_1}{z_0}\right) \right] +{\mathcal {F}} \left[ \tau \ln \left( \frac{z_1}{z_0}\right) \right] \,. \end{aligned}$$
(40)

An asymptotic sequence for \(\widehat{\tau }\) could be proposed where the leading term would be:

$$\begin{aligned} \widehat{\tau }=\frac{1}{\ln (1/\epsilon )}{\mathcal {F}} \left[ \ln \left( \frac{z_1}{z_0}\right) \right] +O \left[ \frac{1}{\ln ^2(1/\epsilon )}\right] \,, \end{aligned}$$
(41)

still creating a mismatch between the sides of Eq. (41). The analysis of the next order will not help since the singularity will be still given by \(\widehat{u_1}=\widehat{d}_1K_0(\zeta )+\widehat{d}_0\) so that a mismatch will always be present. The block matching principle of Crighton and Leppington (1973) is thereby introduced so that all terms involving the same power of \(\epsilon \) are treated as of same order. This implies that:

$$\begin{aligned} {\widehat{\tau }=\frac{{\mathcal {F}}\left[ \ln \left( {z_1}/{z_0}\right) \right] +{\mathcal {F}}\left[ \tau \ln \left( {z_1}/{z_0}\right) \right] }{\ln \left( 1/\epsilon \right) -2\gamma -{i\pi }\,\textrm{sgn} (\overline{k}_x)/2-\ln \left( {\left| \overline{k}_x\right| }/{2\kappa }\right) }\,.} \end{aligned}$$
(42)

Expression (42) guarantees that both the logarithmic slope and the intercept are consistent between the main and roughness layer, so that the latter can be seen as a continuation of the former. The velocity correction in the main layer is only the first correction and subsequent corrections should be estimated as Eq. (42) is only an approximated expression the matches the shear stress and the velocity between the two layers. Equation (41) is a consistent leading-order approximation of the surface shear stress that, however, does not verify the continuity of the velocity between the two layers. However, it is a simple expression of the stress that can be rapidly computed and it is exploited in the present work as a simplified approximation.

2.6 Practical Implementation

The proposed theory has been developed in Python using standard NumPy routines. Since the solution is analytical, the computational cost is extremely low and even simulations with horizontal grid of \(512\times 512\) points took less than 2 seconds to complete. Given a roughness distribution, this is first Fourier transformed. The code calculates then the \(\epsilon \) values according to (27) and then the shear-stress corrections according to (42) or (41) for its simplified form. The constant \(\widehat{c}\) is afterward computed from (39) and (42) enabling the assessment of the main-layer velocity field by means of the modified Bessel function.

The zero wavenumber is singular in the main layer as that cannot be matched with the upper layer. Therefore, this issue has been circumvented by considering that the spatial average of \(\ln \left( z_1/z_0\right) \) was equal to 0, therefore providing the definition of \(z_0\). This implies that the perturbation field generated at the wavenumber zero is zero and that the spatial average of the perturbation velocity field is zero as well.

The only parameters needed in the model are in principle the roughness distribution and the shear stress assuming that the mixing length is known. Alternatively, since the mixing length is important only up to the main layer, where a linear mixing length behaviour is still expected, the undisturbed base velocity profile over constant roughness (or the averaged one) could be provided, bypassing the need of an accurate mixing length knowledge.

3 Model Validation

Two cases have been used to validate the model, both coming from experimental setups with sharp roughness transitions. The first validation case is the smooth-to-rough transition from Bradley (1968). The initial roughness height \(z_0=z_1(x<0)=0.02~\textrm{mm}\) is followed by a roughness increase with \(z_1(x>0)=2.5~\textrm{mm}\), i.e. a change in roughness height of two orders of magnitude, or \(M=\ln \left[ z_1(x>0)/z_0\right] =4.83\). Model calculations have been performed with a two dimensional simulation with \(N_x=4096\) points and a domain of 420 m (so that the grid spacing was \(\varDelta x\approx 0.1\) m). The smooth-to-rough transition was located at \(x=0\) while the artificial rough-to-smooth transition was located at \(x=\)210 m. The first transition was smoothed with a cosine blending function with length scale \(\varDelta x\), while the second transition was smoothed with length scale \(10\varDelta x\). The reason for this second artificial transition was to remove the shear stress perturbation created by the sudden roughness jump at the end/beginning of the numerical domain, where the Fourier transform imposes a periodic boundary condition. Nevertheless, the domain was sufficiently long to limit the influence of this second artificial transition on the region near the smooth-to-rough transition where experimental data is available.

Figure 4 shows a contour plot of the wind velocity field calculated in the main layer only. The emergence of an IBL after the smooth-to-rough transition is quite evident as the flow velocity decreases at constant height. Interestingly, a weak upwind effect is also noticeable before the transition associated to a velocity increase instead.

Fig. 4
figure 4

Wind velocity contours in a smooth-to-rough transition. Only the main layer is here shown. The vertical red lines indicate the stations \(x=2.32\) m and \(x=6.42\) m where the velocity profiles reported in Fig. 6 are collected

Full size image

The first quantitative test comes from the surface stress. Here both (42) and (41) are used to assess the surface stress since the former is more complete while the latter is more straightforward. The data points have been taken from the figures reported in the publication of Belcher et al. (1990). The agreement between the theory and the experimental values is reasonably good, providing a fast assessment of the shear stress with the simplest correction. The full correction provides a sharper transition upwind of the step and a decay of the shear stress downwind of that although a bit biased towards higher shear stress. The model is able to predict also the sharp shear stress variation near the roughness transition.

Fig. 5
figure 5

Surface shear stress distribution after a smooth-to-rough transition. The model refers to Eq. (42) while the simple model is Eq. (41)

Full size image

Additional insight comes from the analysis of the velocity profiles shown in Fig. 6. Two distances from the roughness step are used (and indicated in Fig. 4) assessing the effect of the IBL growth on the measured velocity profile. The velocity profiles from the main-layer analysis are shown for comparison. It is evident that the main-layer velocity profile agrees well with the measurement data both near and away from the wall, as it was intended with Eq. (42).

Fig. 6
figure 6

Velocity profiles after the smooth-to-rough transition of Bradley (1968). a \(x=2.32\) m and b \(x=6.42\) m

Full size image

The second test case is provided by the rough-to-smooth transition experimental data from Li et al. (2021). The analysis has here focused on their case Re07ks160 characterised by the longest wall stress measurement (in terms of boundary-layer thickness). The numerical domain was 150 m long with 32768 points. The rough-to-smooth transition was located at \(x=0\) and a smooth-to-rough step at \(x=100\) m. According to Li et al. (2021), the von Kármán constant used in the experiment was \(\kappa =0.384\) and the model was therefore run with the same value. Similarly to the data presented by Li et al. (2021), the spatial coordinates are normalised by the boundary-layer thickness \(\delta _0=0.11\) m. The shear stress estimated from the present theory and from oil-film interferometry (in the smooth part only) are shown in Fig. 7: a reasonably good agreement is visible although the full theory shows a higher discrepancy compared to the simplified theory. This discrepancy might be also influenced by the uncertainty in the assessment of the shear stress over the rough surface, obtained in the experimental dataset by fitting the outer part of the velocity profile according to Townsend hypothesis (Li et al. 2021).

Fig. 7
figure 7

Surface shear stress distribution after a rough-to-smooth transition

Full size image

The horizontal velocity component is shown in Fig. 8. The qualitative response of the boundary layer is quite similar between the experiment and the theory, although it appears a bit more sudden in the experimental results. The boundary-layer growth after \(x/\delta _0\approx 50\) is clearly visible in the experimental results but absent in the theory: this is not surprising since the theory assumes a parallel undisturbed boundary layer and it focuses just on the response of the flow to the roughness change.

Fig. 8
figure 8

U velocity field (normalized by the velocity at \(x=-0.1\) m and \(z/\delta _0=0.091\)) for the experimental dataset (a) and as estimated from the present theory by using the main layer only (b)

Full size image

4 Numerical Details

The large eddy simulation (LES) code used for the verification dataset in this study is version 5.4.3 of the Mesoscale-Nonhydrostatic (Meso-NH) model developed by the Laboratoire d’Aerologie and the Centre National de Recherches Meteorologiques (CNRM) (Lac et al. 2018). Meso-NH is a nonhydrostatic anelastic numerical modelling package with filtered prognostic equations for heat, humidity, and momentum. Contained within the Meso-NH package are a number of subgrid schemes that allow for the parameterization of turbulence, radiative transfer, surface processes, cloud microphysics, condensation, and moist convection. The turbulence parameterization scheme (Cuxart et al. 2000) is a scale-dependent isotropic scheme that contains a subgrid three-dimensional turbulence model; as such, Meso-NH is capable of simulating processes at the large eddy scales. The surface parameterization used in the verification set is the ISBA land surface scheme within version 8.1 of the Surface Externalisee (SURFEX), which is an externalized package that contains physical parameterizations for calculating the energy exchange between the surface and atmosphere (Le Moigne et al. 2009). Using Meso-NH coupled with SURFEX allows users to run simulations with real or idealized physiographic maps of surface cover.

The LES simulations used in this study (which is similar to a setup described in Janzon 2022) contained a 300x300x125 grid point domain with \(\varDelta x=\varDelta y=\,\)20 m grid spacing in the horizontal and vertical levels starting at 0.5 m above the surface and stretching 6.5% until reaching 20 m at the model top. Momentum is advected using the centered 4th-order scheme (CEN4TH) (Lunet et al. 2017), while scalar variables–including temperature, moisture, and turbulent kinetic energy–are advected using the piecewise parabolic method (PPM) (Lin and Rood 1996). Time-splitting is handled using the Runge-Kutta centered 4th-order temporal scheme (RKC4) (Lunet et al. 2017) and the model is discretized on a staggered Arakawa C-grid. Microphysics is not activated and the atmosphere is dry.

The surface cover is defined as a chessboard pattern of alternating homogeneous patches with constant land cover type. The surface roughness patches were defined within the surface model using the ECOCLIMAP II cover types 11 (Boreal Evergreen Needleleaf Forest) for a relatively rough surface and 123 (Bare soil with sparse polar vegetation) for a relatively smooth one (Faroux et al. 2013). Two different heterogeneity length scales are considered: one where each roughness patch in the chessboard had size 300 m and another one where each patch had a length of 3000 m, to better analyse the equilibrium boundary layer established after the roughness transition (Garratt 1990). The initial condition contains a neutral temperature profile with 10 by 10 grid point \(\pm 0.5\) K perturbations up to an elevation of 398 meters for exciting turbulent eddies (see Muñoz-Esparza et al. 2014) and an Ekman spiral wind profile with a geostrophic wind of 8 m/s. In order to maintain numerical stability, the LES was run with 0.5 s time steps. Differing from Janzon (2022), the simulations were run with the radiative transfer scheme turned off, with all downward radiative fluxes set to zero and the model was allowed to run until obtaining a near-neutral stability condition. The simulations were integrated for a total of 13.9 hours; after 11.5 hours of simulation, the Obukhov length asymptotically reached 700 m and the gridded model output was saved at half-hour intervals for the last 2 hours of integration and these were then time-averaged. At this time in the simulations, the 3D gridded instantenous wind and stress components were obtained for the analysis described below.

The 300 m roughness patch LES simulation was filtered by averaging the unique patterns in the chessboard to obtain a single four-patch pattern, providing a consistent phase average (in light of the domain periodicity). For the 3000 m patch however, only one such unique pattern was available and this was used in the analysis.

5 Comparison with 3D Simulations

The analysis of the available LES data was initiated by the identification of the roughness value for each patch. Both the 300 m and 3000 m heterogeneity length scale domains were characterized by the alternation of \(z_0\approx 0.004\) m to \(z_0\approx 0.1\) m with a sharp transition between the two. In the 300 m case, the transition is milder due to the used grid resolution. The surface wind is not blowing aligned with the roughness orientation but it has a small angle of about \(20^\circ \) inclination. The roughness height was here determined by fitting a logarithmic law to the total velocity \(\left( U^2+V^2\right) ^{1/2}\) below \(z=\)3 m to avoid being influenced by the growth of internal boundary layers starting at the roughness transitions. While this fit provided also an estimate of the friction velocity, this has been determined instead from the available shear stress as:

$$\begin{aligned} u_*=\left( \overline{u'w'}^2+\overline{v'w'}^2\right) ^{1/4}\,. \end{aligned}$$
(43)

The latter shear stress differed from the fitted one of approximately 25% and it was preferred in light of its enhanced physical content. The spatially-averaged friction velocity for the 300 m and 3000 m patch were 0.43 and 0.39 m/s, respectively, with a slightly higher surface friction for the shorter roughness.

The friction velocity distribution is shown in Figs. 9 and 10 for the chessboard pattern with 300 m and 3000 m, respectively, for both the LES and theory (namely Eq. (42)). Both cases agree qualitatively well, especially in the regions with low \(z_0\) but also in the friction enhancement downstream of the roughness transitions. The friction appears a bit overestimated by the model in the regions of high \(z_0\), although this is visible only in the 300 m case, while the 3000 m case does not provide clear evidence due to the presence of residuals turbulent spatial structures in the velocity field.

Fig. 9
figure 9

Distribution of the local friction velocity estimated from the LES with chessboard spacing 300 m (left) and according to the present model (right)

Full size image
Fig. 10
figure 10

Distribution of the local friction velocity estimated from the LES with chessboard spacing 3000 m (left) and according to the present model (right)

Full size image

The velocity profiles in the zonal and meridional components are shown in Figs. 11 and 12 for both the available chessboard configurations. In order to limit the effect of local turbulent eddies (absent in the present theoretical model as it would be in Reynolds-averaged Navier-Stokes simulations), the profiles have been averaged in two categories depending on the roughness height. The velocity profiles calculated from the proposed model are obtained from the integration of the parallel-flow equations (described in Sect. 2.1), plus a spatially-varying perturbation due to the roughness inhomogeneity. However, the obtained velocity profile did not match the spatially-averaged profile from the LES, making the comparison of the spatial development meaningless. This discrepancy might be due to an incorrect mixing-length distribution (in the model it was assumed to be equal to \(l_m=\kappa z\)). Rather than trying to fit the LES-averaged flow by changing the mixing-length value, the mean velocity from the LES was directly used as an averaged value, while the perturbation from the roughness distribution was estimated according to the proposed model. While this unfortunately points out to a deficiency of the model and to the limits of the mixing-length methodology, this is still practically relevant as the theoretical model can be used combined with a velocity profile measured in the interested area by means of a meteorological mast, providing a velocity profile unaffected by the systematic bias of the analysis. Figures 11 and 12 demonstrate that the theory provides a good quantification of the effect of surface roughness on the velocity profile for both components (the reader is reminded that the theory at leading order is unaffected by the Coriolis force and therefore the perturbation is just projected into the different directions according to the surface wind orientation). The short chessboard pattern has a small deviation between the high and low roughness regions mostly concentrated within the first 10 m from the surface. The theory predicts a similar qualitative behaviour with a better agreement for the high surface roughness region than for the low one. The analysis of the 3000 m patch shows instead that the roughness pattern (statistically the same of the 300 m one) creates an effect that is much deeper in the boundary layer (up to approximately 40 m) with larger variations between the low and high roughness regions, a trend visible in both the LES and theoretical model.

Fig. 11
figure 11

Zonal (pluses and solid lines) and meridional (crosses and dashed lines) velocity profiles averaged over the high \(z_0\) regions (red) and low \(z_0\) regions (blue) for the pattern with chessboard spacing 300 m. The symbols are from LES data while the lines are averages of the main layer from the proposed theory

Full size image
Fig. 12
figure 12

Zonal (pluses and solid lines) and meridional (crosses and dashed lines) velocity profiles averaged over the high \(z_0\) regions (red) and low \(z_0\) regions (blue) for the pattern with chessboard spacing 3000 m. The symbols are from LES data while the lines are averages of the main layer from the proposed theory

Full size image

6 Conclusions

The present work describes a theoretical framework to calculate the effects of surface roughness heterogeneity in the boundary layer above. The theory is composed mainly by two layers: one very near the surface roughness where the shear stress is constant in the vertical and the flow is dominated by the surface boundary condition, and another one where turbulent diffusion balances mean flow advection. The latter layer (called the main layer) enables the determination of the shear stress applied to the layer underneath (called the roughness sublayer). The region above the main layer (called the outer layer) is characterised by the balance between advection and pressure gradient and determines the pressure gradient that will influence the main layer at higher orders: the description of higher-order corrections has not been performed in the present work since the leading correction is the one that usually provides the largest contribution and insight. The proposed theoretical model is a revisitation of the work of Belcher et al. (1990) on heterogeneous roughness, with a consistent grouping of asymptotic terms at leading order.

Three validation cases have been used: two featuring two-dimensional roughness transitions from experimental campaigns and one with a three-dimensional chessboard pattern from large-eddy simulations. The first quantity to be scrutinized was the surface stress estimated from the theory that overall agreed qualitatively and quantitatively with the validation data. The simplest model, composed by the leading-order expression of the shear stress, performed better, pointing out to a deficiency of the full model that requires higher-order corrections or the numerical solution of the main-layer problem. This is due to the matching approach that considers all powers of \(\ln (1/\epsilon )\) of the same order of magnitude (similarly to Crighton and Leppington 1973). The possibility to extend to higher-order the present analysis should be explored. Velocity profiles indicated also reasonable agreement between experimental and theoretical predictions showing that it is possible to just use the main-layer analysis. The velocity contours from the experiments of Li et al. (2021) showed as well a good agreement in the flow response to the rough-to-smooth transition, although these were a bit steeper in the experimental data when compared to the model.

The final validation case was provided by three-dimensional LES over chessboard roughness patterns with two heterogeneity length scales: 300 m and 3000 m. The theory performed reasonably well, although less satisfactorily than what the experimental data suggested, probably associated to the roughness model implemented in the LES being different from the pure boundary condition used in the proposed theory. This was evident, for instance, in the necessity to analyse the LES data as if they were experimental results to find a posteriori the roughness distribution from the near surface data points (Perry et al. 1969; Arnqvist et al. 2015). Furthermore, even with a homogeneous roughness distribution the mixing-length model used was not able to provide a velocity profile close enough to the LES, jeopardizing the comparison between the theory and the numerical data. In order to cope with this problem, the perturbation velocity profiles obtained with the theory were added to the numerical spatially-averaged velocity profile to focus only on the roughness change effect: when this was done, the agreement between the two was reasonably good, suggesting that the proposed model may be used as a standalone tool (if the real mixing-length distribution is sufficiently linear) or combined with experimental data from a single mast to provide the base flow to be used. The velocity profiles averaged over low- and high-roughness height regions pointed to a different penetration of the surface boundary condition into the surface layer (deeper for longer roughness patches), a behavior well detected by the proposed theoretical model.