Large-Eddy Simulations of the Steady Wintertime Antarctic Boundary Layer

Abstract

Observations of two typical contrasting weakly stable and very stable boundary layers from the winter at Dome C station, Antarctica, are used as a benchmark for two centimetre-scale-resolution large-eddy simulations. By taking the Antarctic winter, the effects of the diurnal cycle are eliminated, enabling the study of the long-lived steady stable boundary layer. With its homogeneous, flat snow surface, and extreme stabilities, the location is a natural laboratory for studies on the long-lived stable boundary layer. The two simulations differ only in the imposed geostrophic wind speed, which is identified as the main deciding factor for the resulting regime. In general, a good correspondence is found between the observed and simulated profiles of mean wind speed and temperature. Discrepancies in the temperature profiles are likely due to the exclusion of radiative transfer in the current simulations. The extreme stabilities result in a considerable contrast between the stable boundary layer at the Dome C site and that found at typical mid-latitudes. The boundary-layer height is found to range from approximately $50\,\mathrm {m}$ to just $5\,\mathrm {m}$ in the most extreme case. Remarkably, heating of the boundary layer by subsidence may result in thermal equilibrium of the boundary layer in which the associated heating is balanced by the turbulent cooling towards the surface. Using centimetre-scale resolutions, accurate large-eddy simulations of the extreme stabilities encountered in Antarctica appear to be possible. However, future simulations should aim to include radiative transfer and sub-surface heat transport to increase the degree of realism of these types of simulations.

Introduction

Two high-resolution large-eddy simulations (LES) are performed of a typical weakly stable boundary layer (WSBL) and a very stable boundary layer (VSBL) as observed at the Dome C station on the Antarctic Plateau in wintertime during a continuous 41-$\mathrm {h}$ period in 2015. We assess whether a state-of-the-art LES model is capable of modelling the extreme stability encountered in Antarctica, and investigate both similarities and differences with respect to the common stable boundary layer (SBL) encountered at mid-latitudes. We show that the wintertime Antarctic SBL is an attractive alternative case for idealized theoretical modelling studies aiming to simulate the steady, homogeneous SBL under well-controlled conditions.

Most LES investigations of the SBL rarely attempt a direct comparison with observations, with recent exceptions including the comparisons of LES results with observations of the SBL over the Arctic Ocean (Mirocha and Kosović 2010) and with observations made during intermittently turbulent conditions in the CASES-99 campaign (Zhou and Chow 2014). Another notable exception is the ongoing fourth Global Energy and Water Exchange (GEWEX) Atmospheric Boundary Layer Study (GABLS) based on the Antarctic summertime SBL (Bazile et al. 2014). Such direct comparisons are typically hindered by the fact that most high-resolution LES models are strongly idealized compared with the realistic environmental complexity. In reality, non-stationarity and heterogeneity in the advection forcing, for example, are required to be extensively prescribed in both time and space, such as in the GABLS3 study (Bosveld et al. 2014), making the translation into an idealized LES investigation non-trivial. Additionally, the diurnal cycle itself imposes a challenge on LES models, as day and night intrinsically differ in their characteristic length scales, and thus have largely different resolution requirements. Furthermore, the diurnal cycle prevents the study of long-lived stable boundary-layer behaviour.

Interestingly, alternative simulation cases may be found on the Antarctic continent. First, the diurnal cycle and its associated convective boundary layer are removed by selecting wintertime observations (polar night), which effectively removes the varying resolution requirement between the SBL and convective boundary layer, enabling the comparison of a steady-state flow with a LES model subject to constant forcing. In particular, regional warming by subsidence allows a truly steady state to emerge in contrast to the mid-latitude SBL where only quasi-steady states are found (see Sect. 4.3). Second, an especially interesting location is the flat Dome C site in the interior of the Antarctic Plateau with an ‘undisturbed’ fetch of several hundreds of kilometres in all directions. The location is characterized by long periods of cloud-free sky and low total water content (Ricaud et al. 2015). The local snow surface is quite homogeneous and very smooth, often leading to small effective roughness lengths $z_0\ll 0.01\,\mathrm {m}$ (Vignon et al. 2017a). Furthermore, this location experiences a full range of stabilities ranging from unstable (in summer) to extremely stable during winter with vertical temperature gradients $>2.5\,\mathrm {K\,m^{-1}}$ (Genthon et al. 2013).

In recent years, the focus of SBL research has indeed been extended to the Antarctic. Apart from its own relevance in a changing global climate and the difficulty of accurately predicting the Antarctic weather (King and Connolley 1997; King et al. 2001; Smith and Polvani 2017), the extreme stabilities encountered make it an attractive region for in-depth SBL research (see, e.g., Connolley 1996; Hudson and Brandt 2005; Pietroni et al. 2014; Vignon et al. 2017b).

From the modelling perspective, LES models have become an indispensable simulation tool to study the atmospheric boundary layer, and have been applied with moderate success to the WSBL with large geostrophic wind speeds (Derbyshire 1999; Beare et al. 2006). However, (very) strong stratifications, such as those found in Antarctica, arguably still pose a challenge for the LES technique. Under such conditions, the combination of a decrease in turbulent length scale and relatively coarse mesh sizes may make the results overly reliant on the particular choice of subfilter-scale (SFS) model (Beare et al. 2006; Basu and Porté-Agel 2006) or even lead to flow laminarization (see, e.g., Jiménez and Cuxart 2005).

It is expected that these issues can be partly tackled by increasing the resolution of the numerical grid, apart from using or developing new SFS schemes (see Huang and Bou-Zeid 2013; Matheou and Chung 2014). In recent work, Sullivan et al. (2016) extended the original GABLS1 case (Beare et al. 2006) using a finest mesh resolution of $0.39\,\mathrm {m}$ in combination with surface cooling rates of $1\,\mathrm {K\,h^{-1}}$ to increase overall stratification. Although they did not yet reach full convergence, for example, in the height of the low-level jet, these high-resolution cases enabled Sullivan et al. (2016) to identify and analyze coherent structures that lead to characteristic temperature ramps similar to those encountered in outdoor observations (see, e.g., Balsley et al. 2003). These studies, however, still used the (relatively high) original geostrophic wind speed of $8\,\mathrm {m\,s^{-1}}$ of GABLS1, so that the SBL remained in a weakly stable state. In contrast, Zhou and Chow (2011) used larger cooling rates resulting in a temperature contrast of approximately $25\,\mathrm {K}$ over $150\,\mathrm {m}$ albeit at a higher geostrophic wind speed of $10\,\mathrm {m\,s^{-1}}$. The aforementioned GABLS4 intercomparison study aims to simulate the VSBL by a combination of high cooling rates and relatively low geostrophic wind speeds of $1.5\,\mathrm {K\,h^{-1}}$ and 5–$6\,\mathrm {m\,s^{-1}}$, respectively (Bazile et al. 2014).

Here, apart from simulating the observed WSBL, we simulate the VSBL using a geostrophic wind speed of just $3.5\,\mathrm {m\,s^{-1}}$ in combination with a total inversion (vertical temperature difference) of $25\,\mathrm {K}$. In particular, for the selected VSBL, it appears that the boundary-layer height is well below $40\,\mathrm {m}$ and, thus, the dominant features of the boundary layer are entirely encompassed by the 45-m meteorological tower of Dome C, enabling the use of a fine-scale resolution (< 1 m). The ability of our model to simulate the extreme stability encountered in the VSBL is discussed, and discrepancies between simulations and observations identified.

In Sect. 2, after a short description of the Dome C site and the measurements, the observed case is described and placed within the framework of the regime transitions. The computational model, the physical model derived from observations, and the numerical set-up are presented in Sect. 3. The results are presented and analyzed in Sect. 4, followed by an outlook in Sect. 5, with summary and conclusions given in Sect. 6.

Observational Results

In-Situ Observations

The boundary-layer observations used are obtained at the French–Italian polar station Concordia at Dome C, Antarctica ($75^\circ 06'\mathrm {S},\,123^\circ 20'\mathrm {E}$, $3233\,\mathrm {m}$ above sea level), which is located within a homogeneous snow desert at a distance of approximately $1000\,\mathrm {km}$ from the coast. The local topography is flat with a slope $< 0.1\%$ (Genthon et al. 2016), which prevents the local generation of katabatic flows (Aristidi et al. 2005). Furthermore, Vignon et al. (2017a) have shown that the surface is characterized by a typical roughness length $z_0\ll 0.01\,\mathrm {m}$ for both momentum and heat, although the roughness lengths have a clear dependence on wind direction due to the preferential orientation of sastrugi (small snow ridges).

Wind speed and temperature have been measured at six vertical levels on a 45-$\mathrm {m}$ tower situated approximately $1\,\mathrm {km}$ west of the main buildings since 2009. Measurements are performed by aerovanes for wind speed, and thermohygrometers for temperature and humidity. The instruments are positioned to face the dominant south-west wind direction (Genthon et al. 2010, 2013). An additional mast of 2.5-$\mathrm {m}$ height has been in operation since 2013 to provide more detailed measurements in the lowest few metres above the surface. Note that, due to the harsh conditions in the Antarctic winter, it is impossible to obtain reliable sonic-anemometer measurements of the turbulence. A detailed description of the measurement site, measurements and instrumentation can be found in Genthon et al. (2010, 2013) and Vignon et al. (2017a).

Mechanical Cycle and Regime Transition

The observed ‘steady-state’ WSBL and VSBL are modelled with the LES approach. However, first we discuss why, in the absence of a diurnal cycle, a transition between those states may be due to changing external conditions. As those mechanical cycles are the rule rather than the exception in the Antarctic winter, an in-depth analysis of the climatology is presented, and a canonical case of such a cycle is presented. The ‘steady states’ of this cycle are simulated with the LES technique. Though interesting, the transition itself is not simulated, as it primarily results from changes in the external forcing (see Baas et al. 2019). Here we focus on the boundary layer itself in its steady state.

During the Antarctic winter months (June to August), the boundary layer at the Dome C station is almost continuously stratified and can reach its most stable conditions. Due to the absence of convective activity, the boundary layer may reach moments of ‘steady state’ in which the wind speed and temperature profiles do not significantly change over periods sometimes exceeding a few days. Vignon et al. (2017b) noted that such a steady state can be disturbed by two different processes. The first involves sudden warming events related to a warm and/or moist cloudy airmass advected from the coastal regions into the interior of the Antarctic continent (see, e.g., Genthon et al. 2010; Vignon et al. 2017b). This process may lead to significant warming of the air near the surface by several $10\,\mathrm {K}$ within several hours (see, e.g., Argentini et al. 2001; Gallée and Gorodetskaya 2010) and can effectively ‘reset’ the stratification as a whole. Second, regime transitions under clear-sky conditions may be caused by strongly changing boundary-layer flow due to a varying horizontal pressure gradient (Vignon et al. 2017b; Baas et al. 2019). It is this case from which two representative boundary-layer regimes will be considered in more detail.

From the climatology of the site, Baas et al. (2019) identified transitions during the extended Antarctic winters (April to September) of 2011 to 2016 in which the near-surface temperature inversion increased or decreased by more than $15\,\mathrm {K}$, with the near-surface temperature inversion defined as the temperature difference between approximately a height of $10\,\mathrm {m}$ and the surface. They applied a threshold on the incoming longwave radiative flux ($LW_{down}<100\,\mathrm {W\,m^{-2}}$) to eliminate transitions due to overcast conditions and sudden warming events, yielding a total of 138 transitions due to changes in the mechanical forcing of the boundary-layer flow.

We focus on one of these mechanical transitions starting at 2030 LT (local time $=$ UTC $+\,8\,\mathrm {h}$) on 21 July, and ending at 1330 LT on 23 July 2015. Figure 1 shows the temporal evolution of the observed wind speed and air temperature during the selected period. For all measurement heights, the wind speeds decrease during an initial 24-$\mathrm {h}$ period. Between $t\approx 24\,\mathrm {h}$ and $t\approx 27\,\mathrm {h}$, the wind-speed measurements are absent at all levels. Although the aerovanes have a ‘start-up’ threshold of $1\,\mathrm {m\,s^{-1}}$ and an accuracy of $0.3\,\mathrm {m\,s^{-1}}$ (Vignon et al. 2017a), this indicates that flow of any significance is absent in this 3-$\mathrm {h}$ time interval. After $t\approx 27\,\mathrm {h}$, the observed wind speeds at all measurement heights increase.

The observed tendency of the wind speeds is consistent with a decrease and subsequent increase of the near-surface pressure gradient with quiescent periods during which the pressure gradient is nearly absent. During these ‘mechanical cycles’ at the Dome C site, it is expected that the boundary layer adapts to the variation in the near-surface pressure gradient. Indeed, Baas et al. (2019) show, using a single-column model, that during these events the decrease (increase) of local wind speed, for example at $10\,\mathrm {m}$, is correlated with changes in the geostrophic wind speed (a proxy of the pressure gradient). Furthermore, although subject to a diurnal cycle, observations from Cabauw in the Netherlands, show that the strength of the turbulent mixing and the thermal inversion are dependent on this pressure gradient, which acts as an external forcing of the boundary layer as a whole (van der Linden et al. 2017).

During the decrease in wind speed, high-level temperatures increase by more than $10\,\mathrm {K}$, but at lower levels, this increase occurs later: around $t=17\,\mathrm {h}$ the 2.9-$\mathrm {m}$ temperature increases by $9\,\mathrm {K}$ over the course of approximately $4\,\mathrm {h}$ (cf. Fig. 1b). Just prior to the time when all wind speeds are below the measurement threshold, the two lowest levels also experience an increase in temperature. In contrast, the surface cools a total of $8.8\,\mathrm {K}$. The increase in the strength of the inversion is, therefore, caused by two effects: a cooling at the surface, and a larger warming at, for example, the 10-$\mathrm {m}$ level. Note that such behaviour differs from typical mid-latitude climatologies where the nocturnal inversion primarily develops from below due to surface cooling (van der Linden et al. 2017).

When the wind speeds increase after $t>27\,\mathrm {h}$, the general tendencies in temperature are reversed: the surface temperature increases, and the air temperatures decrease. In addition, the timing of the decrease is reversed, with the lowest levels decreasing first and the highest level the latest. No discernible decrease is observed for the 41.5-$\mathrm {m}$ level within the plotted time frame.

Fig. 1

Temporal evolution of the, a wind speed, and b temperature measured at the tower and surface during the selected 41-$\mathrm {h}$ period starting 2030 LT on 21 July 2015

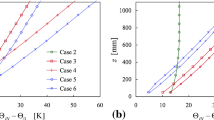
The temporal relationship between the local wind speed and thermal gradient for the selected period is shown in Fig. 2 (phase space-diagram). To demonstrate the representativity of our specific case, the temperature–wind speed relation is embedded in the overall climatology obtained from the Antarctic winter months of 2011–2015. Figure 2 shows that the selected mechanical cycle produces a regime transition between the WSBL and VSBL, and vice versa, and indicates a non-monotonic relation between wind speed and thermal gradient. Vignon et al. (2017a) first identified this dependence, highlighting the appearance of a ‘back-folding’, and stating it resembles a reversed ‘S’ shape. Indeed, the trajectory of the selected period shows this non-monotonicity. Interestingly, van de Wiel et al. (2017) show, using a conceptual model, that the equilibrium value of the thermal inversion strength can be predicted as a function of the wind speed at a crossing level where the wind speed is relatively constant with time and thereby serves as a proxy for the external geostrophic wind speed. This crossing-level height at the Dome C station was identified to be at approximately $10\,\mathrm {m}$ above the surface in summer (Vignon et al. 2017a; van de Wiel et al. 2017).

The trajectory starts (in red) at a high local wind speed ($\approx 10\,\mathrm {m\,s^{-1}}$) and a relatively low thermal inversion strength ($\approx 5\,\mathrm {K}$), before the 9-m wind speed starts decreasing. At approximately $6\,\mathrm {m\,s^{-1}}$, the thermal inversion strength rapidly increases after which it levels off. This corresponds to the time frame 10–$20\,\mathrm {h}$ in Fig. 1b during which the temperatures at $10\,\mathrm {m}$ and the surface change by approximately $+12\,\mathrm {K}$ and $-4\,\mathrm {K}$, respectively. In addition, whereas the overall tendency of all wind speeds is a decrease prior to $t=24\,\mathrm {h}$, during this time frame, a small local increase of the wind speed at $9\,\mathrm {m}$ is observed, which causes the trajectory to incline ‘backwards’ and exhibit the reversed ‘S’ shape. After the sharp increase, the inversion strength levels off while the wind speed is still decreasing. The slight increase of thermal inversion strengths for $U(9\,\mathrm {m})<2\,\mathrm {m\,s^{-1}}$ is caused by a continuing decrease of the surface temperature.

The characteristic (sharp) increase in the 10-$\mathrm {m}$ temperature in this wind-speed interval can be understood as follows: at the boundary-layer top, a continuous competition is present between turbulence acting to elevate (or at least maintain) the height of the thermal inversion, and subsidence pushing it down. For a small decrease of the large-scale pressure gradient, turbulent mixing weakens and the inversion sinks below the 10-$\mathrm {m}$ level. As a result, the air temperature at this height increases until a new balance is reached. As a second-order effect, Baas et al. (2019) show, using their single-column model, that at the same time stress divergence at this height is inhibited, i.e., the effective drag exerted by the surface is reduced, resulting in a local acceleration of the flow.

For $t>27\,\mathrm {h}$, the wind speed increases and the trajectory (in blue) reverses. The overall shape of the blue trajectory is similar to the shape of the red trajectory, i.e., when the wind speed reaches a threshold value, the thermal inversion strength rapidly decreases. By a similar argument, turbulent mixing now strengthens, resulting in an increase in the height of the thermal inversion and effective cooling at $10\,\mathrm {m}$.

It is observed that, for both low and high wind speeds, viz., $U(9\,\mathrm {m})<3.5\,\mathrm {m\,s^{-1}}$ and $U(9\,\mathrm {m})>6\,\mathrm {m\,s^{-1}}$, the two trajectories appear to overlap, suggesting that, in this example, well-defined, robust ‘steady states’ exist that represent the final state of a mechanical cycle. Therefore, our modelling efforts are directed towards the simulation of the ‘end points’. For intermediate wind speeds, the trajectories do not completely overlap. While the observed asymmetry in this region may be a systematic feature of these mechanical cycles (Baas et al. 2019, see their Fig. 4a), no conclusive cause or explanation has been identified to date. Detailed simulations under a wide range of conditions, for example, the rate of change of geostrophic wind speed or the strength of subsidence, are expected to help clarify these issues in future.

Fig. 2

Scatter plot of the thermal-inversion strength between the height of $10\,\mathrm {m}$ and the surface versus the wind speed at $9\,\mathrm {m}$ as found in the winter climatology of the Dome C station. The trajectories belonging to our selected cycle (cf. Fig. 1) are depicted by the red and blue lines. Each step along the trajectory corresponds to 30 min. The green (purple) circles and diamonds indicate the reference points that are studied in detail through numerical simulations. Circles indicate the WSBL and VSBL from the initial phase of the large-scale wind-speed decrease, and diamonds indicate those taken from the phase of the large-scale wind-speed increase

Contrast Between Weakly Stable and Very Stable Conditions

Figure 3 shows the representative vertical profiles of wind speed and relative temperature of the WSBL at $t=5.5\,\mathrm {h}$ and $t=31.5\,\mathrm {h}$, and the VSBL at $t=21.5\,\mathrm {h}$ and $t=41\,\mathrm {h}$, with the relative temperature defined as the air temperature minus the surface temperature. These times roughly correspond to those points at which the trajectories of both transitions start (finish) overlapping, and mark the region of rapid regime shift (see the circles and diamonds in Fig. 2). Interestingly, the wind-speed and temperature profiles from both the increasing and decreasing large-scale wind-speed phases are remarkably similar in both shape and magnitude (see Fig. 3).

Fig. 3

Profiles of measured, a wind speed, and b air temperature minus the surface temperature corresponding to the reference points in Fig. 2. The very stable and weakly stable regimes are coloured in purple and green, respectively. Circles indicate the WSBL and VSBL from the initial phase of large-scale wind-speed decrease, and diamonds indicate those taken from the phase of large-scale wind-speed increase

The profiles of wind speed indicate a large difference in scale between the VSBL and WBSL at the Dome C station. For the WSBL, the wind speed consistently increases with height, and reaches approximately $14\,\mathrm {m\,s^{-1}}$ at $z\approx 41\,\mathrm {m}$—it is possible a local wind-speed maximum is present above the observation tower. During summer, low-level jets typically form in the Antarctic SBL between 15 m and $60\,\mathrm {m}$ (Gallée et al. 2015) due to the diurnal cycle, but it is unclear if a similar mechanism is present during the long-lived wintertime SBL. As the observation tower is not sufficiently high to capture the entire boundary layer, it is unknown at which height this maximum is present. In addition, it is unknown if the wind speed at the top of the boundary layer converges to a fixed value, and if so, to which value. In contrast, the height of the observation tower appears to be sufficient to capture the main features of the VSBL, such as the jet-like structure with a local maximum at $z\approx 9\,\mathrm {m}$. At greater heights ($\ge 18\,\mathrm {m}$), the variation in wind speed with height is relatively small and measured wind speeds are $\approx 3.5\,\mathrm {m\,s^{-1}}$.

The vertical profiles of the relative temperature also indicate a large contrast between the WSBL and VSBL measured during the transition. In the weakly stable regime, the temperature profile is mostly linear with height apart from very close to the surface ($z<1\,\mathrm {m}$) where it attains a more convex shape; the change in temperature over the height of the tower is about $18\,\mathrm {K}$. In contrast, the temperature profile in the very stable regime is exponential in shape in which the largest change in temperature occurs in a thin layer close to the surface, i.e., a change of $22\,\mathrm {K}$ within $10\,\mathrm {m}$. Moving from $10\,\mathrm {m}$ to the top of the tower, the remaining increase of temperature is 3 K. This marked difference in the shape of the temperature profile with a more ‘convex–concave–convex’ profile for the weakly stable regime and exponential (convex) profile for the very stable regime has been reported by van Ulden and Holtslag (1985) for Cabauw, and Vignon et al. (2017a) for the Dome C station, respectively. Note that, in the selected weakly stable regime, the maximum measurement height is probably not sufficient to observe the full ‘convex–concave–convex’ structure. A convex (exponential) temperature profile is indicative of the SBL dominated by radiative transport (Brunt 1934; Cerni and Parish 1984), whereas concave profiles indicate non-linear diffusion by turbulent mixing of heat is dominant (Garratt and Brost 1981; André and Mahrt 1982; Estournel and Guedalia 1985; Derbyshire 1990).

Numerical Simulations

Formulation and Model Description

The set of equations describing the evolution of the LES model are the filtered equation for conservation of mass, the filtered Navier–Stokes equations under the Boussinesq approximation for the filtered velocity vector $\widetilde{u_i}$, and the filtered equation for energy written in terms of the filtered potential temperature ${\widetilde{\theta }}$

$$\begin{aligned} \frac{\partial {\widetilde{u}}_j}{\partial x_j}&=0, \end{aligned}$$

(1a)

$$\begin{aligned} \frac{\partial {\widetilde{u}}_i}{\partial t}+\frac{\partial {\widetilde{u}}_j{\widetilde{u}}_i}{\partial x_j}&=-\frac{\partial {\widetilde{\pi }}}{\partial x_i}-\frac{\partial \tau _{ij}}{\partial x_j}+\frac{g}{\theta _0}\left( {\widetilde{\theta }}-\theta _0\right) \delta _{i3}+f_C\epsilon _{ij3}\left( {\widetilde{u}}_j-G\delta _{j1}\right) , \end{aligned}$$

(1b)

$$\begin{aligned} \frac{\partial {\widetilde{\theta }}}{\partial t}+\frac{\partial {\widetilde{u}}_j{\widetilde{\theta }}}{\partial x_j}&=-\frac{\partial R_{\theta ,j}}{\partial x_j}-w_s(x_3)\frac{\partial \langle {\widetilde{\theta }}\rangle }{\partial x_3}, \end{aligned}$$

(1c)

where the tensors $\tau _{ij}$ and $R_{\theta ,j}$ represent the SFS fluxes of momentum and temperature, ${\widetilde{\pi }}$ is the modified pressure, and $w_s(x_3)$ the vertical profile of the subsidence velocity, with $x_3$ representing the vertical coordinate. The angled brackets indicate domain averaging in the horizontal directions. Furthermore, the Coriolis parameter is denoted by $f_C$ and the geostrophic wind speed by G. The velocity boundary conditions are no-slip (${\widetilde{u}}={\widetilde{v}}=0$) and no-penetration ${\widetilde{w}}=0$ at the bottom, and stress-free $\partial {\widetilde{u}}/\partial z= \partial {\widetilde{v}}/\partial z=0$ and no-penetration ${\widetilde{w}}=0$ at the top. A fixed temperature is prescribed both at the bottom and top (Dirichlet condition). In the lateral directions, periodic boundary conditions are employed for both the velocity and temperature. For simplicity, the tilde indicating the filtering is dropped in the remainder of the text.

The SFS flux tensors, which are the result of spatial filtering of the conservation equations for momentum and temperature, account for the unresolved momentum and temperature fluxes. As both tensors contain the filtered product of the unfiltered quantities, a closure relation (or parametrization) is required to relate the SFS fluxes to the resolved quantities. The numerous closures reported in the literature vary greatly in formulation and complexity (see, e.g., Deardorff 1980; Sullivan et al. 1994; Bou-Zeid et al. 2005; Basu and Porté-Agel 2006; Zhou and Chow 2011; Chung and Matheou 2014; Abkar and Moin 2017). Here, we use a simple Smagorinsky–Lilly-type eddy-viscosity model (Lilly 1962; Smagorinksy 1963), which includes stratification effects by retaining the buoyancy flux in the SFS turbulent-kinetic-energy equation (Lilly 1962; Mason 1989) assuming local equilibrium, and thereby neglecting the tendency, advection and turbulent transport terms. In this model, which is adopted due to its ease of implementation and low computational costs, the eddy viscosity is given by

$$\begin{aligned} K_m = \lambda ^2 S \left( 1-\frac{\frac{g}{\theta _0}\frac{\partial \theta }{\partial z}}{{Pr}_t S^2}\right) ^\frac{1}{2}, \end{aligned}$$

(2)

where $\lambda$ is a mixing length, $S=\left( 2S_{ij}S_{ij}\right) ^\frac{1}{2}$ is the magnitude of the strain tensor, g is the acceleration due to gravity, $\theta _0$ is a reference temperature, and ${Pr}_t$ is the turbulent Prandtl number. For the mixing length, we use the wall-correction formulation of Mason and Thomson (1992) to match the local wall scale $\kappa (z+z_{0,m})$ and the subfilter length scale $\varDelta \equiv (\varDelta x\varDelta y\varDelta z)^{1/3}$ according to

$$\begin{aligned} \frac{1}{\lambda ^n}=\frac{1}{\left( c_s\varDelta \right) ^n}+\frac{1}{\left( \kappa (z+z_{0,m})\right) ^n}, \end{aligned}$$

(3)

where $c_s$ is the Smagorinksy constant and $n=2$.

Apart from the von Kármán constant $\kappa$, the adoption of this scheme requires specification of two parameters: the turbulent Prandtl number ${Pr}_t$ and the Smagorinsky constant $c_s$. Field observations suggest that ${Pr}_t \gtrsim 1$ for stable stratification (Ohya 2001; Zilitinkevich et al. 2007, 2008), whereas the Smagorinksy constant $c_s$ is smaller than (or at least equal to) its isotropic turbulence value (Kleissl et al. 2003; Bou-Zeid et al. 2010). Also, too high a value of the Smagorinsky constant may lead to excessive mixing compared with empirical data (de Roode et al. 2017). Therefore, these parameters are set to ${Pr}_t=1$ and $c_s=0.12$, where the latter is based on the expected range of stability (from our observations). Additionally, de Roode et al. (2017) show that the use of anisotropic grids may lead to excessive diffusion for very stable stratification. Furthermore, to limit over-reliance on the particular choice of SFS scheme and possible excessive diffusion, we employ isotropic grids of very high resolution ($\varDelta =0.08$, 0.125 and $0.7\,\mathrm {m}$).

At the bottom boundary, rough-wall boundary conditions are used to calculate the surface fluxes using Monin–Obukhov similarity theory (MOST). In stable conditions, the similarity functions of Högström (1988) are used.

Heating of the air due to subsidence is implemented by the last term in the filtered equation for conservation of energy in which the largest gradients are expected (see Eq. 1c). Subsidence of momentum is not included in the current LES cases. For simplicity, and to limit computational expense, the local vertical gradient ($x_3$ being the vertical coordinate) of the (filtered) potential temperature is replaced by the vertical gradient of its horizontally-averaged value indicated by $\langle .\rangle$. In future work, the impact of these simplifications will be assessed in more detail. In addition, the term is calculated within the model using a first-order upwind scheme. A short note on the implementation of subsidence can be found in Appendix 1.

We use the open-source code MicroHH (http://microhh.org), which is a combined finite-difference LES/direct numerical simulation code supporting two-dimensional parallelization using the message passing interface standard. For the advection of momentum and scalars, a second-order finite-difference scheme is used. Integration in time is performed with a low-storage third-order Runge–Kutta algorithm, and pressure is evaluated each timestep by solving a Poisson equation. A damping layer is applied at the top of the domain to prevent the reflection of gravity waves downwards. A full description of the MicroHH code can be found in van Heerwaarden et al. (2017).

Physical Model

The simulations are based on the two selected steady-state cases (see Fig. 3) for which a steady-state physical model of both the WSBL and VSBL is constructed. A background large-scale temperature difference (inversion strength) $\varDelta \theta$ is imposed in the vertical direction, meaning the temperature above the SBL is at maximum $\varDelta \theta$ higher than the surface temperature. At the surface, the typical roughness lengths for momentum $z_{0,m}$ and heat $z_{0,h}$ are given below. A linear profile for the subsidence velocity is set to zero at the surface and to $w_s$ at $100\,\mathrm {m}$. The boundary layer is subjected to a large-scale pressure forcing given as the product of the Coriolis parameter $f_C$ and the geostrophic wind speed G. The latter is preset to a fixed value to obtain either a steady WSBL or steady VSBL (see below).

The values of $\varDelta \theta$ and G are estimated from the tower observations. Because of the unavailability of detailed high-quality observations extending above the tower height $z>41.5\,\mathrm {m}$, uncertainties in the estimated parameter values are introduced. The maximum inversion strength is taken as $\varDelta \theta =25\,\mathrm {K}$, which is approximately the temperature between the surface and top of the tower in the very stable state (see Fig. 3b). Note that, due to the large inversion and limited height, the correction factor between absolute and potential temperature is neglected in our idealization. The geostrophic wind speed is estimated to be $G=12\,\mathrm {m\,s^{-1}}$ in the WSBL and $G=3.5\,\mathrm {m\,s^{-1}}$ in the VSBL. The former value is somewhat lower than the maximum wind speed observed in the weakly stable regime which is possibly influenced by the presence of a nocturnal jet. The value of the subsidence velocity as inferred from the ERA-Interim model reanalysis for the selected period is set to $w_s=-\,0.004\,\mathrm {m\,s^{-1}}$ at $z=100\,\mathrm {m}$, and subsequently linearly interpolated to zero at the surface for simplicity. The simulations of Baas et al. (2019) show that this value is representative of the transition of the WSBL to the VSBL under a decreasing geostrophic wind speed (see their Fig. 12c). Furthermore, they show that the average large-scale horizontal advection of temperature is small ($<10^{-4}\,\mathrm {K\,s^{-1}}$) and decreases (approximately) linearly to zero towards the surface (see their Fig. A1), and is, therefore, not included in the current model.

Determining the values of the roughness lengths for momentum and heat is complicated by the large variability of the roughness length found at the Dome C site. Vignon et al. (2017a, see their Fig. 3) show that the aerodynamic roughness length can vary over two orders of magnitude depending on the wind direction and surface temperature, which is partly due to the preferential alignment of sastrugi, i.e., small snow ridges. As during our selected case, the near-surface wind direction is from the south and surface temperatures are $-70\,^\circ \mathrm {C}$ to $-60\,^\circ \mathrm {C}$, a value for the aerodynamic roughness length of $z_{0,m}=0.001\,\mathrm {m}$ is adopted. Based on Vignon et al. (2017a), the roughness length for heat is set to $z_{0,h}=z_{0,m}/10$.

An overview of the model parameters and other physical parameters set in the model is given in Table 1.

Table 1 Overview of model and physical parameters

Numerical Set-Up

As the focus is on simulating the typical Antarctic WSBL and VSBL, the simulation must be designed to reach a steady state in phase space (cf. the green and purple circles in Fig. 2). Unless stated otherwise, we follow a procedure similar to the GABLS1 study (see, e.g., Beare et al. 2006; Sullivan et al. 2016). The simulation is initialized with constant temperature $\theta _0$ throughout the domain and at the surface, and with the x-component of the velocity equal to the geostrophic wind speed (${\mathbf {u}}=\left\{ G,0,0\right\}$) at all levels. Random perturbations are added to the velocity components below the height of the damping layer $z_{bf}$ to trigger turbulence (see Table 2). From the start of the simulation, the surface temperature is reduced at a cooling rate ${CR}=\{-1;-4\}\,\mathrm {K\,h^{-1}}$ for the weakly stable and very stable simulation, respectively, until the surface has been cooled by $\varDelta \theta$ (here $25\,\mathrm {K})$, after which cooling ceases (see the sketch in Fig. 4). Imposing the required stratification from the onset prevents the initial generation of turbulence by damping fluctuations at the resolved scale. These particular cooling rates are taken as a balance between sustaining the initial development of turbulence and limiting the computational expense. After cooling, the simulation is continued for a number of physical hours to enable the flow to reach a steady state, viz., profiles and fluxes do not vary significantly in time at the end of the simulation. Subsidence heating is switched on from the beginning.

Fig. 4

Sketch of the initial simulation procedure. The blue curve indicates the steady state of the 10-$\mathrm {m}$ to surface inversion strength as a function of the geostrophic wind speed. The orange arrows show the evolution to steady state (black diamonds) from neutral initial conditions by cooling the surface by $25\,\mathrm {K}$ and simulating an additional period

Simulations for the WSBL and VSBL are performed on different domain sizes as the resolution requirements for the VSBL make it too computationally expensive to match the domains. In addition to the highest resolution VSBL simulation, an additional simulation (VSBLc) is performed at slightly coarser resolution to test the convergence of first- and second-order statistics. All runs use an isotropic grid spacing to minimize excessive diffusion in the very stable limit (see Sect. 3.1). An overview of the simulations is presented in Table 2.

Table 2 List of the simulations cases, their geostrophic wind speed G, number of cells $N_i$, isotropic grid spacing $\varDelta$, cooling time $t_c$, total run time $t_r$, start of damping layer $z_{bf}$, surface friction velocity $u_*$, surface kinematic temperature flux $Q_*$, surface Obukhov length L, and the height of the boundary layer h

Numerical Results

The steady-state profiles of wind speed and relative temperature are first presented and compared to the observations in Sect. 4.1, Sect. 4.2 presents the turbulent fluxes, Sect. 4.3 discusses the effect of subsidence heating and its implication for a steady-state flow simulated by the LES approach, and Sect. 4.4 finally gives a brief sensitivity analysis for the very stable simulation.

General Characteristics

The results of the WSBL and VSBL simulations are averaged over the horizontal plane and over the final hour of simulation to calculate bulk quantities and vertical profiles. The simulations reach an approximate quasi-steady equilibrium during this hour, since the relevant quantities do not change significantly. An exception is the presence of an inertial oscillation in the velocity profile with a time scale $T_i\approx 12.6\,\mathrm {h}$. The time-averaged surface friction velocity $u_*$, surface kinematic temperature flux $Q_*$, surface Obukhov length L, and diagnosed boundary-layer height h are listed in Table 2. Here, we diagnose the boundary-layer height using the method used by Kosović and Curry (2000) and Beare et al. (2006). First, the height at which the total horizontal stress reaches $5\%$ of its surface value is calculated, and is subsequently linearly extrapolated to the height at which the stress vanishes assuming a linear stress profile.

Figure 5 shows the profiles of wind speed, relative wind direction, and relative temperature for the WSBL (top row) and VSBL (bottom row) simulations compared with the observed values (red) of our selected cases. The observed wind directions are shifted to match the simulated values at $z=1.23$ and $z=18.11\,\mathrm {m}$ for the WSBL and VSBL cases, respectively (see below).

Fig. 5

Simulated vertical profiles (black) and observed values (red bullets) of, a, d wind speed, b, e relative wind direction, and c, f air temperature minus the surface temperature for the WSBL (top row) and VSBL (bottom row) cases. The simulated profiles are averaged over the final hour of the simulation. The horizontal scale for wind speed and the vertical scales for all variables are not equal for the WSBL and VSBL cases

In general, good agreement between the simulated and observed wind speeds is found for the WSBL case. With the exception of the highest observation level, discrepancies between the simulation and observations are less than $0.9\,\mathrm {m\,s^{-1}}$. The estimate of the geostrophic wind speed for this case appears to be realistic. As noted in Sect. 2.3, the observed wind speed in the WSBL case at $41.2\,\mathrm {m}$ is possibly influenced by the presence of a local wind-speed maximum. Correspondingly, the simulation exhibits a jet with maximum $13.1\,\mathrm {m\,s^{-1}}$ (about $9\%$ of G) at $z\approx 43\,\mathrm {m}$.

In the WSBL case, the observation tower does not capture the full extent of the boundary layer and its associated wind turning. For this reason, the observed and simulated values of the wind direction are matched at the lowest observation height. A relatively good correspondence is found for the relative wind direction for the WSBL case, where the turning of the wind with respect to height is accurately represented by the simulation with the exception of the highest observation level, which appears to deviate from the lower observations. No explanation for this observed value is found. However, a partial blocking of the aerovanes due to riming or deposition of ice cannot be excluded. The total wind turning at the surface is approximated by local linear extrapolation (over five points) of the simulated values and is approximately $45^\circ$.

As the boundary-layer depths in the simulations and observations are similar, the relative temperature profiles are comparable, but a number of differences remain. The observed temperatures increase more rapidly with height below $25\,\mathrm {m}$ than the simulated temperatures, but more slowly above 25 m. Except near the surface, the observed temperature profile appears to be more linearly shaped and has only a weakly pronounced inflection point. This is in contrast to the simulated temperature profile, which exhibits two pronounced inflection points at approximately $5\hbox { m}$ and $35\,\mathrm {m}$, resulting in a strongly ‘convex–concave–convex’ profile. At the second inflection point, the averaged temperature gradient in the simulation attains a local maximum of $\partial _z \langle \theta \rangle =0.85\,\mathrm {K\,m^{-1}}$, which is twice as large as the observed gradient $\partial _z T_\mathrm {obs}\approx 0.4\,\mathrm {K\,m^{-1}}$. Mirocha and Kosović (2010) show that a relatively small increase in the subsidence rate leads to an increased magnitude of the potential temperature gradient throughout the bulk of the boundary layer in addition to a lower boundary-layer height.

For the VSBL case, the agreement between the simulated and observed wind speed is remarkably good, with the difference $< 0.5\,\mathrm {m\,s^{-1}}$ (see Fig. 5d), and the estimate of the geostrophic wind speed appears to be accurate. The hour-averaged simulation result indicates the occurrence of a weak low-level jet at $z\approx 5.3\,\mathrm {m}$ with peak wind speed $3.8\,\mathrm {m\,s^{-1}}$ ($10\%$ of G). It should be noted that the full simulation of the VSBL case at steady state covered one inertial period ($12.6\,\mathrm {h}$) during which the strength of the jet ranges from 3.7 to $4\,\mathrm {m\,s^{-1}}$. The inertial oscillation has a minor impact on the velocity profile below the jet ($z\le 4\,\mathrm {m}$) resulting in variations of $0.1\,\mathrm {m\,s^{-1}}$ (not shown).

The wind directions are compared to the observed value at $18\,\mathrm {m}$ as this point is situated above the bulk of the boundary layer. Close to the surface, the observed and simulated wind directions deviate by 10–$15^\circ$, but, particularly under low wind speeds, the observed wind direction is not fully reliable. Local linear interpolation towards the surface results in a total wind turning of $52^\circ$ in the simulation, which is slightly larger than in the WSBL case.

The simulated temperature profile in the VSBL case has the same overall shape as in the WSBL case (cf. Fig. 5c, f), but with the change in temperature distributed over a smaller total height. In the lowest $5\,\mathrm {m}$, the horizontally-averaged temperature gradient varies between $\partial _z \langle \theta \rangle \approx 1.4\,\mathrm {K\,m^{-1}}$ at the lowest inflection point ($z\approx 0.4\,\mathrm {m}$) and $\partial _z \langle \theta \rangle \approx 7.8\,\mathrm {K\,m^{-1}}$ at the second inflection point situated at $3.6\,\mathrm {m}$. Here, the gradient from the surface to the first grid point above the surface is excluded as MOST is applied from the surface to this level. At the same time, the observed bulk gradient between $z = 0.7$ and $2.9\,\mathrm {m}$ is equal to $\varDelta T_\mathrm {obs}/\varDelta z\approx 5\,\mathrm {K\,m^{-1}}$. Although the boundary layer is under-sampled in the very stable case, since not enough measurement levels are present on the tower, the shape of the observed temperature profile is expected to be exponential (see Sect. 2.3). Both Estournel and Guedalia (1985) and Edwards (2009) show that the inclusion of radiative fluxes in a one-dimensional model indeed results in a more exponentially-shaped temperature profile for low geostrophic wind speeds, and so it is expected that the inclusion of radiative transfer in future simulations will improve the agreement with the observed temperature profile.

The simulated profiles suggest that the boundary-layer heights are approximately $40\,\mathrm {m}$ and $5\,\mathrm {m}$ for the weakly stable and very stable cases, respectively, where the height of the jet is used as a proxy. An accurate prediction from the observations is impossible. Whereas in the WSBL case, the tower is not high enough to capture the full boundary layer, the region $z=4$–$10\,\mathrm {m}$ is under-sampled in the VSBL case. Nevertheless, the simulations and observations seem to be in agreement on the order of magnitude of the boundary-layer height. Note that, following Nieuwstadt (1984) and Banta et al. (2006), the profiles can be scaled using diagnosed values at the surface or jet maximum height. Such scaling of our simulated boundary layer results in a rather similar structure between the WSBL and VSBL cases (not shown), qualitatively resembling the non-dimensional profiles of Nieuwstadt (1984). In summary, although a number of estimates and assumptions have been made, and radiative processes have been omitted, the simulations successfully mimic the selected weakly stable and very stable regimes found during the Antarctic winter.

Turbulent Fluxes

Figures 6 and 7 show the total and resolved fluxes of momentum $F(u_i)$ ($i=x,y$) and temperature $F(\theta )$ for the WSBL and VSBL cases, respectively. Note that, for clarity, a different notation is adopted here for the vertical fluxes as compared with the tensor notation in Eq. 1 (e.g., $F(u_i)$ instead of $\tau _{i3}$). In the WSBL case, the total cross-isobaric momentum flux at the surface is equal to the isobaric flux, whereas in the VSBL case, the surface cross-isobaric momentum flux is found to exceed the isobaric flux by approximately $30\%$. Here, isobaric and cross-isobaric are defined as being parallel and perpendicular, respectively, to the direction of the geostrophic velocity aligned along the x-coordinate. The increasing ratio of the cross-isobaric to the isobaric momentum flux for increasing stratification was also reported by Sullivan et al. (2016).

Inspection of the momentum-flux profiles reveals that, at the diagnosed boundary-layer height (see Table 2), the isobaric momentum flux is reduced to $<1\%$ of its surface value. The corresponding reduction for the cross-isobaric momentum fluxes is found to be $\approx 5\%$. In both simulations, the relative contribution of the SFS fluxes to the total fluxes increases near the top of the boundary layer, and accounts for roughly half of the flux at the top of the SBL. In the lower half of the SBL, more than $80\%$ of the momentum fluxes are resolved for both cases with the exception of the first gridpoint above the surface where MOST is applied.

The total temperature fluxes have a tendency towards a constant value with height close to the surface (see Figs. 6b and 7b), whereas more curvature is present in the SBL further from the surface, which contradicts the results for the typical SBL at mid-latitudes (see, e.g., Nieuwstadt 1984; Galmarini et al. 1998; Beare et al. 2006; Svensson et al. 2011), where quasi-steadiness implies a linearly decreasing temperature flux. This discrepancy with the traditional shape can be explained by the role of subsidence heating in our simulations, which is discussed further in Sect. 4.3. The kinematic temperature fluxes at the surface correspond to surface heat fluxes of $H_0=-24.7\,\mathrm {W\,m^{-2}}$ in the WSBL case and $H_0=-3.1\,\mathrm {W\,m^{-2}}$ in the VSBL case. Although the gradient Richardson number ${Ri}_g$ exceeds 0.25 at $z>2.5\,\mathrm {m}$ for the VSBL case, the local shear is sufficient to maintain continuous mixing throughout the bulk of the boundary layer. As for the flux of momentum at the top of the SBL, the SFS scheme accounts for roughly half of the total flux. The explanation for this reduction in the amount of resolved fluxes may be twofold. First, somewhat unsurprisingly, the mesh size is no longer sufficient to resolve the same proportion of the flux-carrying eddies as the characteristic length of the large eddies is reduced by the increased amount of stratification with respect to the shear, viz., an increase in the gradient Richardson number. As a consequence, more flux has to be accounted for by the SFS scheme. Note also that the SFS fluxes may be partly overestimated, since the eddy diffusivities $K_{m,h}$ may be too large at the top of the SBL, which is an artefact of the Smagorinksy–Lilly-type closure as it depends on the local strain (see Eq. 2). Therefore, there may be excessive SFS mixing in weak turbulent flow with large shear (Germano et al. 1991), but a quantification of these effects is beyond the scope of our study due to the computational requirement of higher resolutions or a change of the SFS scheme. Nevertheless, Sect. 4.4 gives a brief sensitivity analysis for the VSBL case.

Fig. 6

Vertical profiles of the vertical fluxes of, a the isobaric (solid) and cross-isobaric (dashed-dotted) momentum, and b temperature for the WSBL simulation. Total and resolved fluxes are coloured in black and orange, respectively. The simulations are averaged over the final hour of the simulation

Fig. 7

As in Fig. 6, but for the VSBL simulation. The scales differ with respect to the WSBL simulation

Steady Versus Quasi-Steady?

Figure 8 presents the hourly- and domain-averaged vertical profile of the rate of change of the potential temperature ${\dot{\theta }}$ due to subsidence heating and divergence of the kinematic temperature flux for the VSBL simulation, illustrating that the heating by subsidence has a maximum of approximately $1.14\times 10^{-3}\,\mathrm {K\,s^{-1}}$ around the inflection point of the temperature profile. The heating rate decreases to zero towards the surface and above the boundary layer. This decrease is caused by a decrease in the subsidence velocity towards the surface and a decrease in the temperature gradient above the SBL, respectively. Interestingly, the cooling induced by the divergence of the total heat flux almost balances the subsidence heating (cf. the black line in Fig. 8). Some residual heating and cooling $<10^{-4}\,\mathrm {K\,s^{-1}}$ is observed in the boundary layer. Possible causes include numerical inaccuracies, i.e., discretization errors, in evaluating the divergence of the temperature flux, and the averaging procedure. Here, the results were averaged over 1 h with statistics output every two simulation seconds. It is expected that, for simulations at higher resolutions, this residual decreases and the total rate-of-changes reach zero. Note that similar results were obtained for the WSBL case (not shown).

Fig. 8

Vertical profile of the rate-of-change of the potential temperature for the VSBL simulation. Note that only the lower half of the computational domain is shown. The simulations are averaged over the final hour of the simulation

The turbulent temperature flux and the heating by subsidence are both internally coupled to the gradient of the temperature field as they depend on and modify the temperature. However, as the heating by subsidence is a slower process, one may suppose that the temperature flux adapts to the subsidence heating. As a result, the shape of the time- and domain-averaged temperature flux profile is such that, at each height, subsidence heating is balanced (see Fig. 8), which leads to a horizontally-averaged state of thermal equilibrium in which the averaged temperature does not change in time. A general, but simple, condition for this steady state is given by integrating the evolution equation for the horizontally-averaged temperature $\left<\theta \right>$

$$\begin{aligned} \frac{\partial \left<\theta \right>}{\partial t}= 0 =-\frac{\partial \left<F_z(\theta )\right>}{\partial z} - w_s(z)\frac{\partial \left<\theta \right>}{\partial z} \end{aligned}$$

(4)

in which the horizontal transport terms are neglected due to horizontal homogeneity. Additionally, the change of temperature due to the divergence of the subsidence velocity $w_s$ is also neglected (see Appendix 1). Setting the rate of change equal to zero and integrating in the vertical direction gives the condition

$$\begin{aligned} -\left<F_s(\theta ; s)\right>\Big |_{s=0}^{s=z} - \int _{0}^{z} w_s(s)\frac{\partial \left<\theta \right>}{\partial s}\,\mathrm {d}s= {constant}, \end{aligned}$$

(5)

where a dummy variable s is used to represent height. The value of this constant is zero as both contributions on the left-hand side vanish at the surface. Indeed, this is consistent with the simulated temperature flux that tends towards a constant value with respect to height near the surface for both the WSBL and VSBL simulations (see Figs. 6b and 7b) since, near to the surface, the integral contribution of subsidence heating is close to zero. Furthermore, this condition implies that the integrated amount of subsidence heating is equal to the surface flux of temperature, thereby setting an integral constraint.

The steady state at the Dome C site is different from the quasi-steady conditions sometimes encountered at mid-latitudes (Nieuwstadt 1984). In the absence of subsidence, the SBL continues to cool as a whole, whereas the shape of the vertical temperature profile remains largely unchanged in time (Derbyshire 1990; van de Wiel et al. 2012). The condition for the quasi-steady state is found by neglecting subsidence and differentiating with respect to z in Eq. 4, and changing the order of differentiation

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial \left<\theta \right>}{\partial z}\right) =0. \end{aligned}$$

(6)

As discussed in Derbyshire (1990), true quasi-steadiness is not possible in the realistic atmospheric SBL. For a quasi-steady, continuously cooling SBL with zero heat flux at the SBL top, the temperature contrast between the bulk and the top would become unlimited (and so would the local Richardson number). In the absence of any gradient-smoothing processes, e.g., radiation or molecular diffusion, this would result in a singularity at the top of the SBL. As such, even quasi-steadiness is not achievable in the mid-latitudes, which makes the present case an attractive alternative for idealized studies of the atmospheric SBL. Indeed, such quasi-steady behaviour has been approached in LES studies of the SBL without subsidence (see, e.g., Beare et al. 2006; Zhou and Chow 2011; Sullivan et al. 2016). A disadvantage, however, is that a continuous surface cooling or surface heat flux has to be prescribed to more-or-less approach this quasi-steady state.

The results indicate that the inclusion of a source term of energy by subsidence opens the possibility of attaining a true thermal steady state for LES investigations of the SBL apart from possible inertial oscillations. It is important to note that a similar conclusion was reached by Mirocha and Kosović (2010), who show that the inclusion of subsidence results in a “nearly steady behaviour” of the SBL in their LES case, which applied a cubic subsidence profile and the calculation of the heating rate per grid cell using the local thermal gradient. Interestingly, observations in the Arctic clear-sky SBL by Mirocha et al. (2005) provide compelling evidence that a significant part of the negative turbulent heat flux at the surface is balanced by warm air entrained into SBL by subsiding motions. Similarly, the importance of subsidence on the near-surface Antarctic heat budget was also found in model studies of regional climate and the general circulation (van de Berg et al. 2007; Vignon et al. 2018).

Sensitivity to Resolution

A Smagorinksy–Lilly closure with stability correction is used despite its limitations and dependence on model parameters, such as the Smagorinksy constant and grid size. However, Matheou (2016) shows that the Smagorinksy–Lilly-type closure can accurately simulate the moderately stable boundary layer and give results comparable to the reference stretched-vortex SFS model (Chung and Matheou 2014; Matheou and Chung 2014), but an a priori choice of the optimal model parameters and resolution is challenging.

A first and relevant test for consistency of the LES approach is to investigate the grid convergence by investigating whether first- and second-order statistics reach a constant value for a change in resolution. Figure 9 shows the simulation results for the wind-speed profile and kinematic temperature flux for the VSBL and VSBLc simulations at 0.08-$\mathrm {m}$ and 0.125-$\mathrm {m}$ resolution, respectively. While the simulated wind-speed profiles are similar with differences $<0.03\,\mathrm {m\,s^{-1}}$, the highest resolution simulation has a slightly lower jet height than the case with a coarser resolution, with the difference in jet height approximately $0.25\,\mathrm {m}$. Additionally, a steeper increase of the temperature is found for the VSBL simulation, than for the VSBLc simulation, with the maximum difference reaching about $1.5\,\mathrm {K}$ at a height of $4.7\,\mathrm {m}$ (not shown).

Some differences are also found in the second-order statistics, such as the kinematic temperature flux (see Fig. 9b). For the highest resolution of $0.08\,\mathrm {m}$, the total and resolved fluxes are both negligibly small above the diagnosed boundary-layer height, although the SFS contribution reaches approximately $50\%$ near the top of the boundary layer. Physically speaking, at the top of the SBL, the vertical temperature gradient (hence local gradient Richardson number ${Ri}_g$) can become very large (cf. Fig. 5c, f), so that the integral length scale may locally become smaller than the grid size. As expected, the SFS contribution is enlarged in the case of a coarser grid. Here, the resolved temperature flux becomes zero at $4.5\,\mathrm {m}$, whereas the SFS fluxes only become negligibly small around $z=7\,\mathrm {m}$. First, this indicates that, in the region $z=4.5$ to $5.5\,\mathrm {m}$ ($\approx h$ in the highest resolution run), the dominant turbulent length scale is reduced below the grid spacing of $0.125\,\mathrm {m}$ due to the increased stratification. Second, it suggests that, in the coarse-grid case, the region $z=5.5$–$7\,\mathrm {m}$ is influenced by excessive diffusion of the SFS scheme. The increase in boundary-layer height for lower resolutions is consistent with Beare et al. (2006) and Sullivan et al. (2016).

In contrast, the relative difference in the surface kinematic temperature flux is only $2.5\%$, with the corresponding differences for the surface momentum fluxes of $4.5\%$, which shows that, for a small change of resolution, the eventual surface fluxes are robust. Although the relative difference is small, it is not known how this difference changes under a further increase (or decrease) of resolution. Due to a combination of long integration times and the required number of grid points, an investigation of possible grid convergence for a doubling of the resolution to $0.04\,\mathrm {m}$, for example, is beyond the current scope of research. However, also taking into account that both the total and the resolved flux become negligible at the same height for the 0.08-$\mathrm {m}$ simulation, it is expected that a further increase in resolution would not significantly change the diagnosed boundary-layer height or surface fluxes, but merely increase the contribution of the resolved fluxes to the total fluxes.

Fig. 9

Vertical profiles of the a wind speed and b vertical flux of temperature for the VSBL simulation [0.08-$\mathrm {m}$ resolution; solid line] and VSBLc simulation [0.125-$\mathrm {m}$ resolution; dash-dotted line]. Total and resolved fluxes are coloured in black and orange, respectively

Outlook

The results indicate that the inclusion of heating by subsidence enables the simulation of the steady-state WSBL and VSBL with the LES strategy. As the Dome C site is subject to a persistent continental-scale subsidence related to the divergence of katabatic flow (James 1989), this same process is likely to contribute to the observed quasi-steady behaviour at the Dome C site, which is in contrast to mid-latitude boundary layers, such as at Cabauw. Additionally, whereas the SBL height usually ranges from $100\,\mathrm {m}$ to $300\,\mathrm {m}$ at Cabauw (Baas et al. 2009), the SBL height at the Dome C site is typically $< 50\,\mathrm {m}$ even in the weakly stable regime (Pietroni et al. 2014). These features make the wintertime Antarctic boundary layer an ideal test case for research models aiming to study the long-lived SBL at (relatively) high resolution. However, a number of challenges remain both from an observational and a modelling perspective.

In Sect. 4.1, a comparison of mean variables, such as the wind speed and temperature, with the observations is made. Unfortunately, during the observational period used, the harsh, cold conditions prevented accurate measurements of turbulent fluxes by standard sonic thermo-anemometers (Vignon et al. 2017a), preventing a one-to-one comparison of turbulent fluxes. Note, however, that sonic anemometers have been operated before in similarly harsh conditions (e.g., King and Anderson 1994). As an alternative to sonic anemometry, scintillometry could be used to infer turbulent fluxes over the Dome C station. For example, Hartogensis et al. (2002) show the potential of measuring turbulent fluxes in the SBL using displaced-beam small-aperture scintillometry during the CASES-99 campaign to obtain statistically-accurate fluxes for short averaging times $<1$ min (cf. their Fig. 5) and close to the surface, which is not possible using traditional eddy-covariance techniques. Scintillometry has previously been applied in wintertime conditions in Scandinavia (de Bruin et al. 2002) and on sea-ice (Andreas 2012).

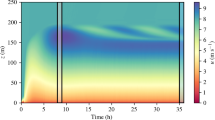
Apart from observing turbulent surface fluxes, information on the turbulent state of the atmosphere may also be obtained using remote-sensing techniques, such as sodar techniques. Recently, Petenko et al. (2019) demonstrate the use of high-resolution sodar at the Dome C station in similar conditions to ours to confirm the occurrence of both very shallow continuous turbulent layers of depth $<10\,\mathrm {m}$ and less shallow layers extending up to $60\,\mathrm {m}$. An example of the sodar backscatter signals obtained during the winter of 2012 is given in Fig. 10, indicating boundary-layer heights of approximately $40\,\mathrm {m}$ and 2–$5\,\mathrm {m}$ in the top and bottom panels, respectively, which qualitatively resemble the two selected cases used here, confirming that the SBL can be extremely shallow at the Dome C site as compared with the SBL at mid-latitudes. Although an in-depth comparison is beyond the scope here, it would be of interest to compare turbulent parameters inferred from the backscatter signal, such as the structure-function parameter for temperature $C_T^2$, with those diagnosed from the LES results, which may provide a more direct comparison in the future between simulations and the observed SBL with respect to turbulent intensity.

Fig. 10

Sodar echograms during, a 27 August 2012 starting at 1900 LT, and b 31 August 2012 starting at 1900 LT. Adapted from Petenko et al. (2019)

Apart from (measuring) turbulent mixing, it is expected that radiative processes are equally important for the accurate representation of the near-surface temperature profiles. The radiative-flux divergence is, however, often not measured as a default during field campaigns (see Steeneveld et al. 2010; Gentine et al. 2018, and references therein). Likewise, radiation is generally neglected in the LES modelling of the SBL partly due to its complexity and partly due to its computational expense. In contrast, Edwards et al. (2014) show that a simplified radiation scheme in predefined cases may give improved accuracy in temperature.

In relation to this, our LES model uses a prescribed surface temperature and, as such, the feedback of heat conduction through the snow/ice surface is neglected. While the effect on the simulated steady-state SBL by the LES model subject to constant forcing is assumed to be small, temporal changes and the natural variability of the surface temperature cannot be neglected in a dynamic SBL forced by changing large-scale conditions. During the transition, approximately $25\%$ of the change in the inversion strength is caused by a decrease in surface temperature (see Fig. 1). The evolution of the SBL can be influenced by the partitioning of the components of the surface energy budget, which are all strongly interdependent (Steeneveld et al. 2006; King et al. 2006). Therefore, for a future realistic LES approach that captures the observed transition between the WSBL and VSBL cases, such LES models should ideally include both interactive radiation and realistic snow/ice schemes.

Summary and Conclusions

Representative WSBL and VSBL cases observed at the Dome C station have been analyzed and used to set up two realistic LES cases. These two typical boundary layers are taken from a continuous 41-$\mathrm {h}$ period in the Antarctic winter of 2015.

Although the Antarctic wintertime boundary layer is undisturbed by the diurnal cycle, transitions within the boundary layer occur at longer time scales. During the selected period, it is observed that all wind speeds measured along the tower decrease, become negligibly small and increase again simultaneously, which is caused by a vanishing and reemerging large-scale pressure gradient. As a result, the boundary layer undergoes transition steadily from the weakly stable to the very stable regime, and back again. Remarkably, the boundary-layer structure appears to map back onto itself after completion of a mechanical cycle in both the weakly stable and very stable limit (cf. Baas et al. 2019).

The two simulation cases are based on these steady-state-limit cases, differing only in the imposed geostrophic wind speed. Heating by subsidence is included as it critically affects the budget of temperature at the Dome C site. The surface is progressively cooled by $25\,\mathrm {K}$ after which the simulation is continued to reach steady state.

Generally, a good correspondence between the simulated wind-speed profiles and the observed wind speeds is found for both cases. The simulations exhibit a minor jet with a magnitude of approximately 10% of the geostrophic wind speed. The total wind veering in the simulations amounts to 40–$50^\circ$, which is in reasonable agreement with the observations. The simulated temperature profiles show a ‘convex–concave–convex’ shape, whereas this appears not to be the case in the observations, with the difference likely due to the lack of radiative transfer in our model, and the assumption of the subsidence profile and magnitude.

The turbulent fluxes highlight the contrast between both the weakly stable and very stable regime, and the extreme SBL at the Dome C site as compared with the mid-latitudes. In the weakly stable regime, the boundary layer extends up to $47\,\mathrm {m}$. In contrast, in both the simulation and observations, only a continuous turbulent layer of approximately $5.5\,\mathrm {m}$ is found for the very stable case. Turbulent fluxes in this regime are one order of magnitude smaller than in the weakly stable regime, and this shallow and weak turbulent layer places a strain on the LES model, requiring high resolution near the surface. While a brief sensitivity analysis shows that surface fluxes appear to be robust, ranging from 0.125-$\mathrm {m}$ to 0.08-$\mathrm {m}$ resolution for the VSBL simulation, complete grid convergence at the top of the boundary layer does not occur due to the presence of the strong inversion.

Heating by subsidence is found to significantly affect the simulated boundary layer, with results suggesting that its inclusion leads to a steady boundary layer whose heating is balanced by turbulent cooling at all heights. The resulting temperature-flux profile contrasts to the usual linear flux profile produced in models without a heat source. A new condition for this thermal steady state is proposed, stating that the integral contribution of subsidence minus the heat flux is constant with height. At the same time, it remains unknown a priori how these two are internally distributed in the boundary layer. As such, the results corroborate the conclusion of Mirocha and Kosović (2010), viz., that the subsidence velocity is an important scaling parameter of the SBL, and further theoretical and simulation work is needed to fully understand the interplay between subsidence, radiation and turbulent heat transfer.

The accurate simulation of both the WSBL and VSBL observed at the Dome C station, appears to be possible given the submetre-scale resolutions of LES models ( $\sim 0.1\,\mathrm {m}$). However, it is expected that further improvements can be obtained with the inclusion of radiative transfer, especially for the very stable case. In addition, an interactive snow/ice scheme would make the study of long-term dynamic effects possible. Due to the uncertainty of the real subsidence, further insight may be gained from varying its magnitude and profile. Apart from these, it would be worthwhile to revisit these cases using a suite of different LES models with differing SFS formulations to test the robustness of the current findings. Finally, a critical test for any LES model would be to simulate the full transition from weakly stable to very stable and back again as observed at the Dome C station.

Appendix 1: Calculating the Subsidence Heating

The heating rate by large-scale subsidence $Q_s$ of the air is usually calculated according to

$$\begin{aligned} Q_s = -w_s(x_3)\frac{\partial \theta }{\partial x_3}, \end{aligned}$$

(7)

where this source term is subsequently added to the filtered equation for the potential temperature. The subsidence velocity itself $w_s(x_3)$ is not superimposed on the resolved field of the vertical velocity component. Superimposing this term on the vertical velocity component formally results in a second source (sink) term in the equation for the filtered potential temperature

$$\begin{aligned} Q_{s,2} = -\theta \frac{\partial w_s}{\partial x_3}, \end{aligned}$$

(8)

which represents a change of internal energy due to convergence (divergence) of the flow. However, this second term is commonly not included in the incompressible Navier–Stokes flow with subsidence while, in the current simulations for example, this term can be of the same order of magnitude. One questions the validity of such an approach.

The presence of a vertical gradient in the subsidence velocity, such as $\partial _{x_3} w_s$, implies an additional large-scale horizontal divergence

$$\begin{aligned} \frac{\partial {\mathbf {u}}_{H,s}}{\partial {\mathbf {x}}_H} = -\frac{\partial w_s}{\partial x_3}, \end{aligned}$$

(9)

where ${\mathbf {u}}_{H,s}=\{u_s,v_s\}$ is the additional horizontal velocity vector resulting from subsidence. In computational domains with periodic lateral boundary conditions, this large-scale divergence cannot exist and is, therefore, commonly discarded.

However, in turn, this divergence implies the existence of (yet) another term in the budget equation for the filtered temperature

$$\begin{aligned} D = -\theta \frac{\partial {\mathbf {u}}_{H,s}}{\partial {\mathbf {x}}_H}. \end{aligned}$$

(10)

A straightforward substitution shows that this horizontal transport of temperature (energy) at the resolved scale acts to counteract the neglected source term $Q_{s,2}$. Reversing the argument then indicates that discarding the (additional) horizontal divergence is only valid if the term $Q_{s,2}$ is also discarded at the same time.