Consistent Boundary-Condition Treatment for Computation of the Atmospheric Boundary Layer Using the Explicit Algebraic Reynolds-Stress Model

Abstract

Standard turbulence models for the atmospheric boundary layer (ABL) typically use boundary conditions based on the Monin–Obukhov similarity theory (MOST). This can lead to inconsistency between the boundary condition and the closure model. Here, we propose a new boundary-condition treatment of the stratified ABL, derived for the so-called explicit algebraic Reynolds-stress model. The boundary conditions correspond to the relations for vanishing buoyancy effects that are valid close to the ground. The solution for the stratified surface layer is in agreement with the surface scaling physics and MOST functions. This was validated in a simulation of an idealized diurnal cycle of the ABL based on the second Global Energy and Water cycle Experiment (GEWEX) Atmospheric Boundary Layer Study (GABLS2) case.

1 Introduction

In the atmospheric boundary layer (ABL) viscous effects are negligible due to ubiquitous rough surfaces and high Reynolds numbers and a rough-wall model is needed (Raupach et al. 1991). The model relates the surface flux to the aerodynamic roughness length giving the well-known logarithmic law of the wall that is strictly valid only for the neutrally-stratified ABL and vanishing pressure gradient.

For numerical computations the first grid point is commonly placed inside the logarithmic layer. Close to the surface buoyancy effects are usually negligible and turbulence is predominantly produced by shear effects. This makes the logarithmic law for a neutrally-stratified environment applicable, thus relating the surface flux to the mean wind speed in a simple form. Above this lower part of the logarithmic layer, turbulence can be strongly affected by buoyancy forces, and in this case corrections to the logarithmic law are introduced through the non-dimensional functions proposed in the well-known Monin–Obukhov similarity theory (MOST) (Monin and Obukhov 1954). These functions are empirically determined from atmospheric measurements, as in Businger et al. (1971) and Högström (1988), and generalize the logarithmic law for stratified flows. There have been numerous atmospheric experiments, see Foken (2006) for a review, proposing different functions relating the surface fluxes to the mean wind speed and potential temperature profiles.

Turbulence models, used for computations in the ABL, are categorized according to their complexity regarding the methods used to solve the closure problem (Mellor and Yamada 1974). Regardless of the complexity, all turbulence models require boundary conditions that influence the solution in the surface layer. Models with detailed physical descriptions, such as Reynolds-stress transport models, can be corrupted by poor boundary-condition treatment. On the other hand, proper boundary conditions cannot make up for poor turbulence modelling. Implementing empirical relations in the boundary condition (e.g. MOST functions) for improving the model solution in the stratified surface layer is not straightforward. In numerous models of the ABL, e.g. Freedman and Jacobson (2003) and Alinot and Masson (2005), the near-surface behaviour in the model was adjusted in order to give behaviour according to MOST. However, ABL models are often not fully consistent with MOST (van der Laan et al. 2017) leading to deviations between the model solution and profiles obtained by using MOST. This raises a question as to whether the use of MOST in boundary conditions is the right approach for ABL turbulence models that cannot reproduce the MOST behaviour. In Richards and Hoxey (1993) and Richards and Norris (2011) boundary conditions for the neutrally-stratified ABL were presented that should produce the logarithmic law but results showed anomalous behaviour near the surface, illustrating that the boundary conditions are not fully consistent with the turbulence parametrization used for the ABL. The authors explain that these deviations are due to the discretization of the shear production term in the equation for turbulent kinetic energy.

In the present study we aim to develop a new and consistent treatment for the boundary conditions. By consistency we mean that the boundary conditions are consistent with the parametrized relations used in the ABL model and that the boundary conditions together with the ABL model produce the correct stable and grid-independent near-surface solution. The requirement of our approach is that the grid resolution is fine enough to resolve the near-surface layer where buoyancy effects can be neglected. The boundary-condition treatment that we propose does not involve MOST or other empirically-derived relations.

The boundary-condition treatment is developed for the recently proposed explicit algebraic Reynolds-stress (EARS) model. The model has been developed in Lazeroms et al. (2013) and applied in the simulation of the stratified ABL and an ABL involving a diurnal cycle (Lazeroms et al. 2015, 2016). The EARS model is based on algebraic relations that follow from the Reynolds-averaged Navier–Stokes (RANS) equations, ensuring that the model is less dependent on empirical functions and ad hoc corrections than many other ABL turbulence models. We validate the consistency of the boundary-condition treatment and investigate if the EARS model with these boundary conditions is consistent with MOST without a priori involving MOST in the model and boundary-condition development. The complexity of the model requires careful formulations for consistency in the surface layer. The resulting boundary-condition treatment can be implemented in a similar way to simpler ABL turbulence models, for example, models that use the transport equation for the turbulent kinetic energy (TKE).

The following section gives a short model description, while a more detailed derivation of the EARS model is given in the Appendices. Section 3 covers the derivation of the boundary conditions that are responsible for the model’s behaviour near the surface. In Sect. 4 the set-up of the numerical simulation is explained. Finally, in Sect. 5 results are presented in both qualitative and quantitative ways and also a new scaling length is introduced that we refer to as the physical Obukhov length. A summary and discussion are given in Sect. 6.

2 Description of the Turbulence Model

This section gives a description of a single-column model (SCM) version of the recently derived EARS model for the ABL. The description is based on Lazeroms et al. (2016), where the EARS model is derived from the full Reynolds-stress model. Further details about the model derivation are given in Appendices 1 and 2. The so-called, weak-equilibrium assumption is applied that makes the model explicit and somewhat similar to the Mellor and Yamada level-3 model. However, there are significant differences between these two models that are explained in Lazeroms et al. (2016).

The SCM approach is commonly used to model a vertical column of the ABL where statistical variations in the horizontal directions are neglected. The solution is considered to be spatially averaged in the horizontal directions. In the current form, where the flow is considered to be incompressible and molecular diffusion is neglected, the main quantities are the mean horizontal wind velocity $\mathbf {V} = (U,V)$ and the mean potential temperature $\varTheta$. The main equations are

$$\begin{aligned} \frac{\text {D}{U}}{\text {D}t}&= -\frac{\partial \,\overline{u'w'}}{\partial z} - f(V_g-V), \end{aligned}$$

(1a)

$$\begin{aligned} \frac{\text {D}{V}}{\text {D}t}&= -\frac{\partial \,\overline{v'w'}}{\partial z} + f(U_g-U), \end{aligned}$$

(1b)

$$\begin{aligned} \frac{\text {D} \varTheta }{\text {D}t}&= - \frac{\partial \,\overline{w'\theta '}}{\partial z}, \end{aligned}$$

(1c)

where $\text {D}/\text {D}t \equiv \partial /\partial t + \mathbf {V} \cdot \nabla$ is the material derivative in the direction of the mean flow, $\mathbf {V}_g=(U_g,V_g)$ is the geostrophic velocity, $f\!=\!2\,\varOmega \sin \phi$ is the Coriolis parameter depending on the rotation rate $\varOmega$ of the Earth and $\phi$ is the latitude. The quantities $\overline{u'w'}$ and $\overline{v'w'}$ are the vertical components of the turbulent momentum flux and $\overline{w'\theta '}$ is the vertical component of the turbulent heat flux.

All turbulent fluxes are expressed in terms of correlations of the velocity fluctuations $(u',v',w')$ and temperature fluctuation $\theta '$, which are parametrized in terms of the mean wind speed and mean potential temperature. The EARS model is an advanced turbulence model that predicts the full Reynolds-stress tensor and heat-flux vector thereby, e.g. being able to account for anisotropy and horizontal fluxes. More information about the horizontal turbulent fluxes and model details can be found in Appendix 1. Using the SCM approach the vertical fluxes appearing in (1) are more important than the horizontal fluxes, and are expressed as

$$\begin{aligned} \overline{u'w'}&= -\nu _t \frac{\partial U}{\partial z}, \end{aligned}$$

(2a)

$$\begin{aligned} \overline{v'w'}&= -\nu _t \frac{\partial V}{\partial z}, \end{aligned}$$

(2b)

$$\begin{aligned} \overline{w'\theta '}&= -\kappa _t \frac{\partial \varTheta }{\partial z}+\varPhi , \end{aligned}$$

(2c)

where $\nu _t$ and $\kappa _t$ are the eddy viscosity and eddy diffusivity (the latter is also known as the eddy thermal diffusivity), respectively, and $\varPhi$ is an additional term. These terms can be expressed as

$$\begin{aligned} \nu _t&= \frac{K^2}{\epsilon } f_\text {m}, \end{aligned}$$

(3a)

$$\begin{aligned} \kappa _t&= \frac{K^2}{\epsilon } f_\text {h}, \end{aligned}$$

(3b)

$$\begin{aligned} \varPhi&= \frac{g}{T_0}\frac{K K_\theta }{\epsilon } f_{\varPhi }, \end{aligned}$$

(3c)

where $K = (\overline{u'u'}+\overline{v'v'}+\overline{w'w'})/2$ is the TKE, $K_\theta = \overline{\theta '\theta '}/2$ is half the potential temperature variance, $\epsilon$ is the dissipation rate of TKE, $T_0$ is the reference temperature, g is the acceleration due to gravity and $f_\text {m}, f_\text {h}, f_{\varPhi }$ are the core functions of the model.

Instead of relying on empirical model constants as in many eddy-viscosity and eddy-diffusivity models derived using the Boussinesq approximation (Boussinesq 1897) or K-theory closure, the EARS model has non-constant core functions following directly from the model derivation. These are derived from the algebraic approximations of the transport equations for the normalized Reynolds-stress tensor and normalized turbulent heat-flux vector. Core functions contain model parameters that have been calibrated for various generic flow cases and not only atmospheric flows (Wallin and Johansson 2000; Wikström et al. 2000; Lazeroms et al. 2013, 2016), which makes the EARS model more general and applicable to different stratified and non-stratified turbulent flows. Full details on core functions are found in Lazeroms et al. (2015, 2016) and in Appendix 1.

In order to close the expressions in (3) the $K-\epsilon$ model together with a prognostic equation for $K_\theta$ are used, leading to three additional transport equations

$$\begin{aligned} \frac{\text {D} K}{\text {D} t} =&\underbrace{-\overline{u'w'}\frac{\partial U}{\partial z} -\overline{v'w'}\frac{\partial V}{\partial z}}_{\mathcal {P}} -{\epsilon } + \underbrace{\frac{g}{T_0} \overline{w'\theta '}}_{{\mathcal {G}}}+\underbrace{\frac{\partial }{\partial z} \left( \frac{\nu _t}{\sigma _K}\frac{\partial K}{\partial z} \right) }_{\mathcal {D}_K}, \end{aligned}$$

(4a)

$$\begin{aligned} \frac{\text {D} \epsilon }{\text {D} t} =&\,{C_{\epsilon 1} \frac{\epsilon }{K}{\mathcal {P}}}-{C_{\epsilon 2} \frac{\epsilon }{K} \epsilon }+ {C_{\epsilon 3} \frac{\epsilon }{K}{\mathcal {G}}}+\underbrace{\frac{\partial }{\partial z} \left( \frac{\nu _t}{\sigma _\epsilon }\frac{\partial \,\epsilon }{\partial z} \right) }_{\mathcal {D}_\epsilon } , \end{aligned}$$

(4b)

$$\begin{aligned} \frac{\text {D} K_\theta }{\text {D} t} =&\underbrace{-\overline{w'\theta '}\frac{\partial \varTheta }{\partial z}}_ {{\mathcal {P}}_{\theta }}-\underbrace{\frac{K_\theta }{rK}\epsilon }_{\epsilon _{\theta }}+\underbrace{\frac{\partial }{\partial z} \left( \frac{\nu _t}{\sigma _{K_{\theta }}}\frac{\partial K_{\theta }}{\partial z} \right) }_{\mathcal {D}_{K_\theta }} , \end{aligned}$$

(4c)

where $K/\epsilon$ represents the time scale for turbulence and r is the ratio between the two time scales $K_\theta /\epsilon _{\theta }$ and $K/\epsilon$. The terms ${\mathcal {P}}$ and ${\mathcal {G}}$ represent the production of TKE due to shear and buoyancy effects (source terms), $\epsilon$ is a sink term, $\mathcal {D}_{K,\epsilon ,K_\theta }$ is diffusion (transport terms) and ${\mathcal {P}}_{\theta }$ production of $K_\theta$ due to buoyancy and atmospheric stratification. In the EARS model the source terms ${\mathcal {P}}$ and ${\mathcal {G}}$ are given in closed form, which implies that these terms are exactly represented without further modelling, and in contrast with simpler turbulence models. The model parameters follow from earlier studies: $C_{\epsilon 1}=1.44$, $C_{\epsilon 2}=1.92$, $C_{\epsilon 3}=-0.8$, $\sigma _K=\sigma _{K_{\theta }}=1.0$, $\sigma _{\epsilon }=1.3$ and $r=0.55$.

Many other turbulence models use the eddy-viscosity/eddy-diffusivity (EVD) hypothesis together with empirical functions in order to determine the turbulence length scale, as in Blackadar (1962). A group of more advanced EVD models such as the Mellor–Yamada 2.5-level model (Mellor and Yamada 1982) can be derived from simplifying the RANS equation. Besides a transport equation for TKE this model uses a prognostic equation for the length scale that contains an empirical correction term. Another EVD approach based on two-equation modelling, used in ABL modelling for wind-energy applications, is to use the $K-\epsilon$ model. The model behaviour is controlled by tuning the coefficients and modelling them as empirical functions of Richardson number and a length scale limiter (Koblitz et al. 2015; Rodrigo et al. 2017). Such models are to a large extent empirical and typically use integral relations. They are derived and calibrated for statistically quasi-steady situations, and are unable to capture the effects of local turbulence in more general cases, for example during the morning and evening transition periods with residual turbulence and turbulence in a growing layer. Compared to these models, the EARS model is not based on the EVD hypothesis and has less dependence on empirical functions.

3 Boundary-Condition Treatment

Close to the surface, the turbulent length scale is smaller than the Ozmidov scale (Zonta and Soldati 2018). Therefore, neutral conditions used for setting the boundary-condition treatment are locally neutral in the sense that the buoyancy effects vanish close to the surface, also in the stratified ABL. It is common practice to use the roughness length for boundary-condition treatment in the ABL. The surface influence on the flow is modelled by the roughness lengths $z_0$ and $z_{0_h}$ for vertical profiles of the wind speed and potential temperature (Wyngaard 2010; Foken and Nappo 2008), i.e.

$$\begin{aligned} \frac{{\mathbb {V}}(z)}{u_*} = \frac{1}{\varkappa } \ln {\frac{z}{z_0}}, \end{aligned}$$

(5)

for the mean wind speed, where $u_*$ is the friction velocity, ${\mathbb {V}}=\sqrt{U^2+V^2}$ and $\varkappa = 0.4$ is the von Kármán constant according to Högström (1996), and

$$\begin{aligned} \frac{\varTheta (z)-\varTheta (z_{0_h})}{\theta _*} = \frac{Pr_t}{\varkappa }\ln {\frac{z}{z_{0_h}}} , \end{aligned}$$

(6)

for the mean potential temperature profile, where $\theta _*$ is the characteristic temperature scale, $\varTheta (z_{0_h})$ is the potential temperature at height $z_{0_h}$ and $Pr_t$ is the turbulent Prandtl number defined as the ratio between the eddy viscosity and eddy diffusivity, $\nu _t$ and $\kappa _t$ respectively.

The boundary conditions are prescribed at $z_0$, and in order to have a consistent model both boundary conditions and modelled solution must satisfy the proper logarithmic law at the points closest to the ground. Having consistent boundary conditions, however, is not straightforward due to the strong non-linear coupling between the solution, boundary conditions, surface fluxes and model $K - \epsilon - K_{\theta }$ equations. Aside from the solution being consistent with the logarithmic law it also should be grid independent and the formulation must be numerically stable in all parameter regimes.

The boundary conditions influence the model solution in the surface layer, and a consistent treatment is crucial for obtaining an accurate solution. The boundary conditions are imposed at the boundary height $z_0$ as

$$\begin{aligned} U(z_0)&= V(z_0) = 0, \end{aligned}$$

(7)

$$\begin{aligned} \qquad \qquad \varTheta (z_0) =&\,\, \varTheta _{\mathrm {S}}(t) +\frac{Pr_t \, \theta _*}{\varkappa }\ln \frac{z_0}{z_{0_h}}, \end{aligned}$$

(8)

where $z_0$ is defined as the location where the artificially extended logarithmic profile for wind speed reaches zero. Similarly, $\varTheta _S$ is the temperature at $z_{0_h}$, representing the surface temperature. The temperature offset between $z=z_{0_h}$ and $z_0$ is given by the last term in (8), following the logarithmic law for $\varTheta (z)$. In the present study a time-dependent function $\varTheta _{\mathrm {S}}$ represents the surface forcing of the ABL.

From the transport equations for TKE and $K_{\theta }$, (4a) and (4c), and assuming that the ABL is in quasi-stationary state so that the time and advective derivatives as well as the diffusion terms can be neglected, and by using the logarithmic law for neutrally-stratified boundary layer, ${\mathcal {P}} = \epsilon$ and $\mathcal {P_{\theta }} = \epsilon _\theta$, we can derive the following boundary conditions

$$\begin{aligned} K(z_0)&= \frac{{u_*}\!^2}{\sqrt{{f_\text {m}^{}}}}, \end{aligned}$$

(9)

$$\begin{aligned} K_{\theta }(z_0)&= \frac{r Pr_t}{\sqrt{f_\text {m}^{}}}{\theta _*}\!^2. \end{aligned}$$

(10)

The core function $f_\text {m}$ in the EARS model acts as a generalization of the coefficient $C_\mu$ used in standard eddy-viscosity models (Richards and Hoxey 1993; Richards and Norris 2011). Usually, $Pr_t$ is given as an explicit constant but in the EARS model it is expressed as a part of the solution using $Pr_t = f_\text {m}/f_\text {h}$. For neutral stratification it can be shown that the EARS model predicts $f_\mathrm{m} = 0.087$ and $Pr_t = 0.75$. Therefore, these constants are used for setting the boundary conditions in order to have a consistent solution in the interior and at the boundaries.

In the following, details of the numerical implementation of the boundary conditions are given for a cell-centred scheme in a finite volume context. Surface-flux related quantities $u_*$ and $\theta _*$ are estimated at the height of the first cell centre $z_1$ respectively from the logarithmic law for ${\mathbb {V}}(z)$ (Eq. 5) and the surface-heat-flux scaling relation as

$$\begin{aligned} u_*&= \frac{\varkappa }{\ln {z_1}/{z_{0}}}{\mathbb {V}}(z_1), \end{aligned}$$

(11)

$$\begin{aligned} \theta _*&= -\frac{\overline{w'\theta '}_s}{u_*}, \end{aligned}$$

(12)

where $\overline{w'\theta '}_s$ is the kinematic heat flux obtained by using (2c). Finally, the boundary condition for $\epsilon$ is derived from the balance relation between the dissipation and production terms in the logarithmic layer

$$\begin{aligned} \epsilon = {\mathcal {P}} = {u_*}\!^2 \frac{\text {d}{\mathbb {V}}}{\text {d}z}, \end{aligned}$$

(13)

where the last step is an approximation of the production term that is valid only in the surface layer. Together with the differential form of (5), expanded in finite differences at the height $z_1$, and (11) it gives

$$\begin{aligned} \epsilon (z_0) = \frac{{u_*}\!^3}{\varkappa (z_1-z_0)} \ln {\frac{z_1}{z_0}}. \end{aligned}$$

(14)

Equation 14 is an approximation of the standard logarithmic law and using L’Hôpital’s rule it can be shown that, in the limiting case $z_1 \rightarrow z_0$, it becomes $\epsilon =u_*^3/\varkappa z_0$. This ensures a balance between the production term and dissipation at the height where the boundary conditions are set. The boundary conditions in (7)–(10) and (14), combined with surface fluxes through $u_*$ and $\theta _*$ from (11) and (12), are not sufficient to ensure that the solution has the correct physical behaviour near the surface and gives ${\mathcal {P}} = \epsilon$. Therefore, the transport equations (4) need to be modified for the first cell centre to correct the solution in that region. We use

$$\begin{aligned} \frac{\text {D}K}{\text {D}t}&= b({\mathcal {P}}_{log}-\epsilon )+(1-b)\left( {\mathcal {P}}-\epsilon + {\mathcal {G}} + \mathcal {D}_K\right) , \end{aligned}$$

(15a)

$$\begin{aligned} \frac{\text {D}\epsilon }{\text {D}t}&= b({\epsilon }_{log}-\epsilon )p+(1-b)\left( \frac{\epsilon }{K} \left( C_{\epsilon 1}{\mathcal {P}}-C_{\epsilon 2}\epsilon +C_{\epsilon 3}{\mathcal {G}}\right) + \mathcal {D}_\epsilon \right) , \end{aligned}$$

(15b)

$$\begin{aligned} \frac{\text {D}K_{\theta }}{\text {D}t}&= b({\mathcal {P}}_{\theta }-\epsilon _{\theta })+(1-b)\left( {\mathcal {P}}_{\theta } -\epsilon _{\theta } + \mathcal {D}_{K_\theta }\right) , \end{aligned}$$

(15c)

where $b = 1$ in the first cell centre and $b = 0$ everywhere else. This approach eliminates the diffusion terms in (15a) and (15c) for the first cell, making the solution in the first cell centre consistent with the prescribed boundary conditions in (9) and (10). The source term that is responsible for the total production of TKE in the first cell centre is

$$\begin{aligned} {\mathcal {P}}_{log} = \epsilon _{log} = \frac{{u_*}\!^3}{\varkappa z_1} = \frac{{u_*}\!^4}{\varkappa {f_\text {m}}^{\frac{1}{4}}K^{\frac{1}{2}}z_1}, \end{aligned}$$

(16)

where the last step is added using relation (9) for improved numerical stability. The first term in (15b) is introduced to relax the value of dissipation rate in the first cell towards

$$\begin{aligned} \epsilon _{log} = \frac{{u_*}\!^3}{\varkappa z_1} = \frac{{f_\text {m}}^\frac{3}{4}K^{\frac{3}{2}}}{\varkappa z_1}, \end{aligned}$$

(17)

where the value $p = 0.5/\varDelta t$ ensures that in the first cell $\epsilon = \epsilon _{log}$ is valid at every timestep. Introducing the parameters b and p in the transport equations is a way of predefining the solution for turbulent properties in the first cell according to the logarithmic law. The current method is very similar to that in Sørensen (1995) for non-stratified flows where ${\mathcal {P}}$ and $\epsilon$ are predefined according to the logarithmic-law relation ${\mathcal {P}}=\epsilon$ and diffusion terms are neglected. Equations 16 and 17 share the same form, because they have to be consistent with the predefined boundary conditions ${\mathcal {P}} = \epsilon$ near the surface (when ${\mathcal {G}}\rightarrow 0$), although numerically they are expected to behave differently. For numerical stability reasons it is convenient to express these equations as a function of K, with the source term inversely proportional to TKE and the sink term directly proportional to TKE. This implies that for larger values of K the system tends to limit the growth of TKE, which leads to improved stability of the simulations. Although this is a somewhat hand-waving argument, a full numerical stability treatment is beyond the scope of the present study. The scheme of the proposed boundary-condition treatment, following the description, is illustrated in Fig. 1.

Fig. 1

Scheme of the boundary-condition treatment applied on a stretched grid. The height of $z_0$ is exaggerated in order to visualize the scheme

4 Case Description

The boundary-condition treatment is tested in the idealized version of the second Global Energy and Water cycle Experiment (GEWEX) Atmospheric Boundary Layer Study (GABLS2) case, which is based on the recent intercomparison study (Svensson et al. 2011). Compared to the original GABLS2 case, for the sake of simplicity we have adapted the approach used in Rodrigo et al. (2017) and neglected the small subsidence that linearly increases with height, as well as humidity since its effect on the mean wind speed and potential temperature is not significant due to the very dry environment. Simulating the transition between the stable and unstable stratifications is an ideal case to test the consistency and stability of the new boundary-condition treatment.

The diurnal cycle is considered for three levels of grid refinement, with the size of the first grid cell $\varDelta = (0.5, \, 1, \, 1.75)\;\text {m}$ and a total of $N= (60, \, 40, \, 22)$ grid points between the ground and the height of $65\;\text {m}$. The grids are log-linearly distributed (stretched) with finer resolution near the surface and coarser higher up in the atmosphere. The geostrophic velocity is considered to be constant during the whole simulation and is taken to be $U_g\!=3\;{\text {m s}}^{-1}$ in the x-direction and $V_g\!=9\;\text {m s}^{-1}$ in the y-direction. The diurnal cycle is driven by the change in surface temperature $\varTheta _{\mathrm {S}}$, which forces the ABL to be stably or unstably stratified. Figure 2 shows the variation of the surface temperature during the simulation at the roughness length for the temperature $z_{0_h}\!=0.1z_0$. The model domain is bounded between the roughness length $z_0\!=0.03\;\text {m}$ and $H\!=4000\;\text {m}$. Initial profiles of K, $\epsilon$ and $K_\theta$ correspond to an ABL with low turbulence levels. For other initial profiles and parameters we refer to Svensson et al. (2011). Furthermore, the first three hours of the simulation are regarded as the spin-up period of the model and are not considered. The timestep in all simulations is $\varDelta t = 60$ s.

Since the aim is to test the new treatment of the boundary conditions and not model performance we will not make a comparison with observations and the large-eddy simulations (LES) of GABLS2. Instead, we compare results to theoretical predictions, which are known to be valid in the surface layer. Since MOST functions are not explicitly used in the boundary condition for estimating the surface fluxes, the consistency with these is investigated as well.

Fig. 2

Forcing function that is used in the lower boundary condition for $\varTheta _S$ as a function of time, see Svensson et al. (2011). Results from the time intervals coloured with red and blue are used for the analysis during the unstable and stable part of the day respectively

5 Results

5.1 General Behaviour of Surface Fluxes and Mean Profiles

Fig. 3

Time evolution of (a) characteristic temperature and b friction velocity for the grid resolution $\varDelta = 0.5\;\text {m}$ () , $1\;\text {m}$ (- - -), and $1.75\;\text {m}$ ( )

Figure 3 shows the time evolution of $u_*$ and $\theta _*$. Although $u_*$ is explicitly dependent on the height of the first cell centre ($z_1\approx \varDelta /2$), the solution is basically grid independent due to the use of proper boundary conditions and their consistency with the turbulence model. When a coarser grid is used $\theta _*$ slightly deviates during the transition periods of the day. The deviations occur in periods when $u_*$ is low and $|\,\theta _*|$ is high; however, they converge to a unique solution as the grid is refined. The deviations are probably related to the strong imbalance between the turbulence momentum and heat flux.

Fig. 4

Vertical profiles of (a), b horizontal wind speed and c scaled horizontal wind speed. Results at 0200 LT stable (blue) and 1400 LT unstable (red) ABL correspond to the periods marked in Fig. 2. Legend as in Fig. 3, with the addition of green points at the height of first cell centre $z_1$ for different grid resolutions and (- - -) representing a $1/\varkappa$ slope for the neutrally-stratified ABL

Figures 4 and 5 show ${\mathbb {V}}(z)$ and $\varTheta (z)$ at 1400 LT and 0200 LT in the near-surface region from the periods marked in red and blue in Fig. 2 when the ABL is unstably and stably stratified, respectively. The results are shown starting from the height $z_0$ where the boundary conditions are set. The results for different grid resolutions coincide well, showing that the profiles for ${\mathbb {V}}$ and $\varTheta$ are grid independent. Figure 4c shows that the slope of the non-dimensional wind-speed profile ${\mathbb {V}}/u_*$ in the first several grid points is $1/ \varkappa$, in accordance with the logarithmic law for neutrally-stratified conditions given by (5). Similarly in Fig. 5c, the slope of the non-dimensional potential temperature profile $\bigr (\varTheta (z)-\varTheta (z_0)\bigr )/ \theta _*$ in the lowest cell centres is in good agreement with the logarithmic law given by (6).

In Richards and Norris (2011) a good agreement is obtained with the logarithmic law but with a slight deviation in the lowest grid points, considered to be a result of an inconsistency in the discretization of the production term. Results in the first few cell centres obtained with the present boundary-condition treatment, presented in Fig. 4c, are closer to the values predicted by (5) than those presented in Richards and Norris (2011). To show the influence of boundary conditions on the model solution at the lowest grid points, our results are plotted from the height $z_0$ at which at the boundary conditions are set. In Richards and Norris (2011) the results are not shown at the height where the boundary conditions are set, therefore it is unclear if their boundary-condition treatment leads to the correct asymptotic near-surface behaviour.

Fig. 5

Vertical profiles of (a), b potential temperature and c scaled difference between the potential temperature and surface temperature. Results at 0200 LT stable (blue) and 1400 LT unstable (red) ABL correspond to the periods marked in Fig. 2. Legend as in Fig. 4, with a difference that ( ) represents the $Pr_{t}/\varkappa$ slope for the neutrally-stratified ABL

Figures 4c and 5c indicate that the buoyancy effects are negligible close to the wall and that turbulence in this region is driven mainly by the wind shear. Further away from the surface, in the region where the buoyancy effects strongly influence the TKE, ${\mathbb {V}}$ and $\varTheta$ deviate from the slope that is characteristic for the shear-driven logarithmic layer. The character of the deviation depends on the type of stratification in the ABL. In Fig. 5c the results in the first cell centre at the coarsest resolution for both the stable and unstable ABL deviate slightly from the neutral-stratification results since the production of TKE due to buoyancy at the height of $z_1$ is not fully negligible.

Results for ${\mathbb {V}}(z)$ and $\varTheta (z)$ for a stable atmosphere have also been reported in Lazeroms et al. (2016) using the EARS model but with other boundary conditions using a fixed value of $Pr_t$, which is not consistent with the neutral limit of the EARS model, and $\theta _*$ was obtained from (6) at the height of the first cell centre. This procedure resulted in an inconsistency between the surface momentum and heat flux causing the $\varTheta (z)$ profile to deviate from the logarithmic law, and also (12) was not valid in the surface layer. The present formulation allows $Pr_t = \nu _t / \kappa _t$ to change dynamically, while using (12) for $\theta _*$ overcomes the previous inconsistency and produces much better results in the region near the surface.

Fig. 6

Time evolution of the wind direction interpolated at the height $z\!=\!1\,\text {m}$ ($0^{\circ }$ mean that the mean flow is directed towards north and $-90^{\circ }$ towards east). Legend is the same as in Fig. 3

Results for wind direction for different grids interpolated to the same height are shown in Fig. 6. When the solution is interpolated to the height $z\!=\!1\,\text {m}$, which is lower than the height of the first cell in the case of the coarsest grid, the model results are still consistent with the results from the two finer grids. Also at other heights (not shown) the wind direction is independent of the grid resolution.

In the context of turbulence model behaviour, it is relevant to investigate the total vertical momentum flux in the direction of the horizontal mean flow ${\overline{u^{\prime } w^{\prime }}}^{T}$, i.e.

$$\begin{aligned} \overline{u^{\prime } w^{\prime }}^{T} = \overline{u^{\prime } w^{\prime }} \frac{U}{\sqrt{U^2 + V^2}}+ \overline{v^{\prime } w^{\prime }} \frac{V}{\sqrt{U^2 + V^2}}. \end{aligned}$$

(18)

Figure 7 shows that the scaled total vertical turbulent momentum-flux profile tends to $-1$ when approaching the surface, which is consistent with the surface-layer scaling $\overline{u^{\prime } w^{\prime }}^{T}\!/{u_*}\!^2=-1$. The deviations for different grid resolutions for the unstable surface layer are related to the deviation of $u_*$ (Fig. 3) during the convective part of the day. Since the turbulent fluxes are scaled with ${u_*}^2$ this error is emphasized. Figure 7 illustrates that the turbulence modelling is consistent with the boundary-condition treatment and the way $u_*$ is computed using the roughness-length model.

Aside from the quantities presented above, the EARS model also predicts turbulence properties such as anisotropy and horizontal fluxes for the SCM solution. For instance, Fig. 8 shows not only that the EARS model predicts anisotropy but also that it predicts suppressed and increased vertical mixing, respectively, for the stably- and unstably-stratified ABL. The boundary-condition treatment controls the solution of the EARS model at the points closest to the ground making $\overline{u^{\prime } u^{\prime }}, \, \overline{v^{\prime } v^{\prime }}$ and $\overline{w^{\prime } w^{\prime }}$ profiles consistent and grid independent (not shown). An important difference as compared to EVD models is that these simpler models predict horizontal and vertical correlations $\overline{u^{\prime } u^{\prime }} = \overline{v^{\prime } v^{\prime }} = \overline{w^{\prime } w^{\prime }} = (2/3) K$.

Additionally, the EARS model with the improved boundary-condition treatment was tested for the GABLS2 case using the offshore values of roughness length $z_0=10^{-4}$ m. The results show the same grid-independent behaviour as the results for the original GABLS2 test case reported in this section.

Fig. 7

Vertical profiles of $\overline{u^{\prime } w^{\prime }}^{T}$ for a 0200 LT stable, and b 1400 LT unstable ABL. Time instances correspond to the periods marked in Fig. 2. Legends as in Fig. 3

Fig. 8

Vertical profiles of non-dimensional $\overline{u^{\prime } u^{\prime }}, \, \overline{v^{\prime } v^{\prime }}$ and $\overline{w^{\prime } w^{\prime }}$ for a 0200 LT stable and b 1400 LT unstable ABL. Time instances correspond to the periods marked in Fig. 2

5.2 Monin–Obukhov Similarity Theory

The accuracy of the EARS model with the previously proposed boundary-condition treatment is tested by comparing the results with experimentally obtained MOST profiles (Businger et al. 1971; Högström 1988). MOST postulates the existence of dimensionless universal functions, $\phi _\text {M}$ and $\phi _\text {H}$, for the ${\mathbb {V}}(z)$ and $\varTheta (z)$, i.e.

$$\begin{aligned} \frac{\partial {\mathbb {V}}}{\partial z}&= \frac{u_*}{\varkappa z} \phi _\text {M}\left( \frac{z}{L}\right) , \end{aligned}$$

(19a)

$$\begin{aligned} \frac{\partial \varTheta }{\partial z}&= \frac{\theta _*}{\varkappa z} \phi _\text {H}\left( \frac{z}{L}\right) . \end{aligned}$$

(19b)

Usually, it is assumed that the universal functions depend on only one dimensionless group¹$\xi = z/L$, where L is the Obukhov length defined as

$$\begin{aligned} L = - \frac{u_*^3T_0}{\varkappa g\overline{w^{\prime }\theta ^{\prime }}_s} = \frac{u_*^2T_0}{\varkappa g\theta _*}, \end{aligned}$$

(20)

where the latter form is obtained by using (12). MOST has been validated by numerous atmospheric experiments, and the functions $\phi _\text {M}$ and $\phi _\text {H}$ have been determined from atmospheric measurements (Foken 2006) and more recently from high-resolution LES of the ABL (Maronga 2014; Maronga and Reuder 2017). Most commonly referred shapes of the universal functions are given in Businger et al. (1971), which were obtained from the Kansas experiment, and in Högström (1988).

Fig. 9

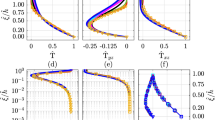
Scaled profiles showing stability function for a horizontal wind speed, and b potential temperature plotted against the stability parameter, obtained by scaling the height with the physical Obukhov length $L_{\varDelta }$ (blue) and classical Obukhov length L (yellow); Experimental data: (- - -) from Businger et al. (1971) and ( ) from Högström (1988)

Results of the simulation with the finest grid resolution, corresponding to the marked periods in Fig. 2, are cast in form of dimensionless functions $\phi _\text {M}$ and $\phi _\text {H}$ using (19). The dimensionless group $\xi$ was obtained by scaling the height at which the results were taken by the Obukhov length. In the present analysis, two different formulations for the Obukhov length are used: the classical formulation for defining L from (20) in terms of near-surface local conditions, and the presently introduced physical Obukhov length$L_{\varDelta }$ defined as the height where the buoyancy term ${\mathcal {G}}(z)$ in (4a) equals the shear production. Appendix 3 contains a detailed explanation of $L_{\varDelta }$. It should be pointed out that the calculation of $L_\varDelta$ would require an analysis of the boundary layer in the vertical direction. The classical Obukhov length, on the other hand, is completely expressed in terms of surface fluxes.

Figure 9 shows that the model results in the surface layer agree with the scaling predictions of MOST. That is to say, when ${\mathbb {V}}$ and $\varTheta$ are scaled appropriately, as in (19), the results collapse and form functional dependences. Thus, the results in Fig. 9 indicate a realistic physical treatment of the turbulence in the EARS model. The results for the stably-stratified surface layer ($\xi >0$) agree well with the experimental data. The results scaled with L follow Businger’s data, while the results scaled with $L_{\varDelta }$ are closer to Högström’s data. Results for the unstably-stratified surface layer ($\xi <0$) deviate substantially from the experimental data for both $\phi _\text {M}$ and $\phi _\text {H}$, but the prediction is slightly improved for $\phi _\text {H}$. In Mellor and Yamada (1982) a similar underestimation of $\phi _\text {M}$ was obtained with the level-2.5 closure model.

In the simulated ideal diurnal cycle the boundary layer undergoes transition from stable to unstable conditions and vice versa, and does not remain neutrally stratified. Consequently, part of the results corresponding to the neutral region ($z/L \!=\! 0$) is missing from Fig. 9. In order to obtain results in the near-neutral limit, data are taken near the surface where $z/L \rightarrow 0$. This requires caution because MOST is not valid on the scale of the roughness length $z_0$, see discussion in Basu and Lacser (2017). The results are obtained without any tuning of model coefficients with the given experimental data, in contrast to Mellor (1973) where the model coefficients were tuned to match the data. Furthermore, the present model does not rely on MOST functions for calculating $u_*$ and $\theta _*$, meaning that MOST is not predefined in the EARS model. This is not so in Chang et al. (2018), where MOST was used as a wall function for estimating $u_*$ and $\theta _*$ and then for comparing the profiles of ${\mathbb {V}}(z)$ and $\varTheta (z)$ predicted by MOST to the model result. Hence, their model results cannot be considered to be independent of the imposed MOST functions.

6 Discussion and Conclusions

New boundary conditions for the recently developed EARS model are proposed. The boundary conditions require that the grid is fine enough for the model to capture the region near the surface where buoyancy effects can be neglected. The surface fluxes are estimated according to the logarithmic law valid for neutral stratification. In order to ensure that the neutral logarithmic law is valid at the height of the first cell centre the conditions $z_1 < 0.05 L$ and $z_1 < 0.17 L$ for the finest and coarsest resolution respectively were imposed in the simulation. Our approach is different from that commonly used where surface fluxes are estimated from the empirical Monin–Obukhov functions. The proposed boundary conditions lead to results that agree well with the standard logarithmic law very near the surface. The general approach in this new boundary-condition treatment could also be applied to simpler eddy-viscosity/eddy-diffusivity models, and should be expected to give improvements also there.

Simulations of an idealized diurnal cycle were carried out with different grid resolutions. Results of the vertical profiles for the stable and unstable surface layer indicate that the EARS model with these new boundary conditions predicts the stratified logarithmic law for the mean horizontal wind-speed and mean potential-temperature profiles without using empirical functions. It is shown that the boundary conditions are consistent with turbulence modelling in the EARS model and MOST functions for the stable ABL, and gives a grid-independent solution, with accurate prediction of the surface fluxes, despite the explicit dependence on the height of the first cell centre. Results for the wind direction also give a grid-independent solution even when interpolation is done to a height below the height of the first cell. We emphasize that the present boundary treatment is basically driven by the behaviour of the modelling in the interior and no inconsistency was observed with MOST in Figs. 4 and 5 for stable and unstable conditions. Moreover, in the transition phases between stable and unstable conditions, when the assumptions of MOST are not strictly valid, the boundary conditions are consistent with the interior modelling. This is not explicitly shown but indicated by the grid independence shown in Figs. 3 and 6. Another limitation is that the MOST formulation is not applicable in cases with strong lateral inhomogeneity when there are rapid variations in atmospheric conditions or surface topography. Such conditions should not cause major inconsistencies with the present boundary formulation, although not tested yet.

When expressed in dimensionless MOST form the model results collapsed on to a single curve, forming a clear functional dependence and indicating that the physics is well described by the turbulence model. The comparison with experimentally observed MOST profiles shows good agreement for the stably-stratified surface layer, but there are discrepancies in the unstably-stratified surface layer.

Appendices

Appendix 1: Details for the Generalized EARS Model

The basis for the generalized EARS model is the standard differential Reynolds-stress model. The model is derived from Reynolds averaging of the Navier–Stokes equations and a generalized coordinate-free formulation of a differential Reynolds-stress model with buoyancy effects, and has the following form

$$\begin{aligned} \frac{\text {D}\overline{u_i' u_j'}}{\text {D}t} - \mathcal {D}_{ij}&= {\mathcal {P}}_{ij}+{\mathcal {G}}_{ij}+\varPi _{ij}-\epsilon _{ij}, \end{aligned}$$

(21a)

$$\begin{aligned} \frac{\text {D}\overline{u_i' \theta '}}{\text {D}t} - \mathcal {D}_{\theta i}&= {\mathcal {P}}_{\theta i}+{\mathcal {G}}_{\theta i}+\varPi _{\theta i}-\epsilon _{\theta i}, \end{aligned}$$

(21b)

where terms correspond to (from left to right) advection, diffusion, shear and buoyancy production, pressure redistribution and dissipation. The shear and buoyancy production terms are explicit and follow directly from the derivation of the differential Reynolds-stress model, and so need no modelling

$$\begin{aligned} {\mathcal {P}}_{ij} =&-\overline{u_i' u_k'}\,\frac{\partial U_j}{\partial x_k}-\overline{u_j' u_k'}\, \frac{\partial U_i}{\partial x_k}, \end{aligned}$$

(22a)

$$\begin{aligned} {\mathcal {P}}_{\theta i} =&-\overline{u_i' u_j'}\,\frac{\partial \varTheta }{\partial x_j}-\overline{u_j' \theta '}\, \frac{\partial U_i}{\partial x_j}, \end{aligned}$$

(22b)

$$\begin{aligned} {\mathcal {G}}_{ij} =&-\frac{g_i \overline{u_j'\theta '}+g_j \overline{u_i'\theta '}}{T_0}, \end{aligned}$$

(22c)

$$\begin{aligned} {\mathcal {G}}_{\theta i} =&-\frac{2 K_\theta g_i}{T_0}. \end{aligned}$$

(22d)

The dissipation rate tensor is assumed to be isotropic, hence

$$\begin{aligned} \epsilon _{ij} = \frac{2}{3} \epsilon \, \delta _{ij}, \end{aligned}$$

(23)

where $\delta _{ij}$ is the Kronecker delta. The pressure redistribution terms contain new correlations and therefore require further modelling. The model for $\varPi _{ij}$ follows from Rotta (1951) and Launder et al. (1975) and where the buoyancy contribution is added from Launder (1975) so that

$$\begin{aligned} \varPi _{ij}&= -c_1 \epsilon \left( \frac{\overline{u_i' u_j'}}{K}-\frac{2}{3}\delta _{ij}\right) -\frac{c_2+8}{11}\left( {\mathcal {P}}_{ij}-\frac{1}{3}{\mathcal {P}}_{kk}\delta _{ij}\right) \nonumber \\&\quad -\frac{30c_2-2}{55}K\left( \frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right) \nonumber \\&-\frac{8c_2-2}{11}\left( -\overline{u_i' u_k'}\,\frac{\partial U_k}{\partial x_j}-\overline{u_j' u_k'}\, \frac{\partial U_k}{\partial x_i}-\frac{1}{3}{\mathcal {P}}_{kk}\delta _{ij}\right) -c_3\left( {\mathcal {G}}_{ij}-\frac{1}{3}{\mathcal {G}}_{kk}\delta _{ij}\right) . \end{aligned}$$

(24)

The other pressure redistribution term $\varPi _{\theta i}$ is modelled according to Launder (1975) and Wikström et al. (2000) as

$$\begin{aligned} \varPi _{\theta i}-\epsilon _{\theta i}&= -\left( c_{\theta 1}+c_{\theta 5}\frac{K}{\epsilon K_\theta } \overline{u_k'\theta '}\frac{\partial \varTheta }{\partial x_k}\right) \frac{\epsilon }{K}\overline{u_i'\theta '}+c_{\theta 2}\overline{u_j'\theta '}\frac{\partial U_i}{\partial x_j} \nonumber \\&+ c_{\theta 3}\overline{u_j'\theta '}\frac{\partial U_j}{\partial x_i} +c_{\theta 4}\overline{u_i'u_j'}\frac{\partial \varTheta }{\partial x_j}+c_{\theta g}\frac{K_\theta g_i}{T_0}, \end{aligned}$$

(25)

where $c_1,\,c_2,\,c_3,\,c_{\theta 1},\,c_{\theta 2},\,c_{\theta 3},\,c_{\theta 4},\,c_{\theta 5}$ and $c_{\theta g}$ are the model constants that are not defined. The differential Reynolds-stress model can be expressed in terms of dimensionless quantities (Mellor and Yamada 1974), Reynolds-stress anisotropy and normalized heat flux that are respectively given as

$$\begin{aligned} a_{ij}&= \frac{\overline{u_i'u_j'}}{K}-\frac{2}{3}\delta _{ij}, \end{aligned}$$

(26a)

$$\begin{aligned} \xi _{i}&= \frac{\overline{u_i'\theta '}}{\sqrt{K K_{\theta }}}. \end{aligned}$$

(26b)

The prognostic Eqs. 21a and 21b are then rewritten as

$$\begin{aligned} \frac{\mathrm {D}a_{ij}}{\mathrm {D}t} -&\frac{1}{K} \left( \mathcal {D}_{ij}-\frac{\overline{u_i'u_j'}}{K}\mathcal {D}_K\right) \nonumber \\&=\frac{1}{K} \left( {\mathcal {P}}_{ij}+{\mathcal {G}}_{ij}+\varPi _{ij}-\epsilon _{ij}- \frac{\overline{u_i'u_j'}}{K}({\mathcal {P}}-\epsilon +{\mathcal {G}})\right) , \end{aligned}$$

(27a)

$$\begin{aligned} \frac{\mathrm {D}\xi _i}{\mathrm {D}t} -&\frac{1}{\sqrt{K K_\theta }} \left( \mathcal {D}_{\theta i}-\frac{\overline{u_i'\theta '}}{2}\left( \frac{\mathcal {D}_K}{K}+\frac{\mathcal {D}_{K_\theta }}{K_\theta }\right) \right) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \nonumber \\&=\frac{1}{\sqrt{K K_\theta }}\left( {\mathcal {P}}_{\theta i}+{\mathcal {G}}_{\theta i}+\varPi _{\theta i}-\epsilon _{\theta i} -\frac{\overline{u_i'\theta '}}{2}\left( \frac{{\mathcal {P}}-\epsilon +{\mathcal {G}}}{K}+\frac{{\mathcal {P}}_\theta -\epsilon _\theta }{K_\theta }\right) \right) , \end{aligned}$$

(27b)

where all the terms are still generalized and in coordinate-free form so that ${\mathcal {P}}$ and ${\mathcal {G}}$ are respectively half the trace of ${\mathcal {P}}_{ik}$ and ${\mathcal {G}}_{ik}$ and ${\mathcal {P}}_{\theta } = -\overline{u_j'\theta '} \partial \varTheta /\partial x_j$.

The main idea of algebraic models is to solve for turbulent fluxes using algebraic equations instead of solving the prognostic equations. In order to simplify (27) Rodi (1972, 1976) introduced the weak-equilibrium assumption that states that both advection and diffusion of $a_{ij}$ and $\xi _i$ can be neglected. This assumption is more general than neglecting advection and diffusion of the turbulent fluxes in (21). After applying the weak-equilibrium assumption the left-hand side of Eq. 27 is neglected, viz.

$$\begin{aligned}&\displaystyle \frac{\overline{u_i'u_j'}}{K}({\mathcal {P}}-\epsilon +{\mathcal {G}}) = {\mathcal {P}}_{ij}+{\mathcal {G}}_{ij}+\varPi _{ij}-\epsilon _{ij}, \end{aligned}$$

(28a)

$$\begin{aligned}&\displaystyle \frac{\overline{u_i'\theta '}}{2}\left( \frac{{\mathcal {P}} -\epsilon +{\mathcal {G}}}{K}+\frac{{\mathcal {P}}_\theta -\epsilon _\theta }{K_\theta }\right) = {\mathcal {P}}_{\theta i}+{\mathcal {G}}_{\theta i}+\varPi _{\theta i}-\epsilon _{\theta i}. \end{aligned}$$

(28b)

The transport equations for TKE, $\epsilon$ and $K_\theta$ in their general form (similar to Eqs. 4, only generalized), together with (28), form a closure problem similar to Mellor–Yamada level 3 that is discussed in Lazeroms et al. (2016). The following relations

$$\begin{aligned} S_{ij} =&\frac{\tau }{2} \left( \frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i} \right) , \end{aligned}$$

(29a)

$$\begin{aligned} \varTheta _i =&\tau \sqrt{\frac{K}{K_\theta }} \frac{\partial \varTheta }{\partial x_i}, \end{aligned}$$

(29b)

$$\begin{aligned} \varOmega _{ij} =&\frac{\tau }{2} \left( \frac{\partial U_i}{\partial x_j}-\frac{\partial U_j}{\partial x_i} \right) , \end{aligned}$$

(29c)

$$\begin{aligned} \varGamma _i =&\tau \sqrt{\frac{K_\theta }{K}} \frac{g_i}{T_0}, \end{aligned}$$

(29d)

where $\tau =K/\epsilon$ is the turbulence time scale, together with (26), transform (28) into non-dimensional form

$$\begin{aligned} N a_{ij}&= -\frac{8}{15} S_{ij} + C_1 \left( a_{ik}S_{kj}+S_{ik}a_{kj}-\frac{2}{3}a_{km}S_{km}\delta _{ij}\right) \nonumber \\&+ C_2(a_{ik}\varOmega _{kj}-\varOmega _{ik}a_{kj}) - C_3 \left( \varGamma _i \xi _j + \xi _i \varGamma _j - \frac{2}{3}\varGamma _k \xi _k \delta _{ij}\right) , \end{aligned}$$

(30a)

$$\begin{aligned} N_\theta \xi _i&= - (c_S S_{ij}+c_\varOmega \varOmega _{ij})\xi _j -c_\varTheta \left( a_{ij}+\frac{2}{3}\delta _{ij}\right) \varTheta _j - c_\varGamma \varGamma _i. \end{aligned}$$

(30b)

The constants are related to those previously introduced, as follows

$$\begin{aligned} C_1&= \frac{9c_2-5}{11},&\! \! \! \! \! \! \quad C_2&= \frac{7c_2+1}{11},&\quad C_3&= 1-c_3, \nonumber \\ c_S&= 1-c_{\theta 2}-c_{\theta 3},&\quad c_\varOmega&= 1-c_{\theta 2}+c_{\theta 3}, \! \! \! \! \! \! \quad&c_\varTheta&= 1-c_{\theta 4}, \quad \; \; \, c_\varGamma = 2 - c_{\theta g}. \end{aligned}$$

(31)

In Wallin and Johansson (2000) it was argued that the constant $c_2=5/9$; such a choice leads to $C_1=0$, implying that the second term on the right-hand side in Eq. 30a vanishes and significantly simplifies the complexity of the EARS model derivation. However, the two parts of Eq. 30 are still implicit in $a_{ij}$ and $\xi _i$ and mutually coupled trough the buoyancy term. Additionally, they are also non-linear as they contain two non-constant factors

$$\begin{aligned} N =&c_1 -1 + \frac{{\mathcal {P}}+{\mathcal {G}}}{\epsilon } \nonumber \\ =&\, c_1 - 1 - a_{km}S_{km} - \varGamma _k \xi _k, \end{aligned}$$

(32a)

$$\begin{aligned} N_\theta =&c_{\theta 1} +\frac{1}{2} \left( \frac{{\mathcal {P}} +{\mathcal {G}}}{\epsilon } - 1 - \frac{1}{r} \right) + \left( \frac{1}{2}-c_{\theta 5}\right) \frac{{\mathcal {P}}_\theta }{r \epsilon _\theta } \nonumber \\ =&\, c_{\theta 1} + \frac{1}{2}\left( N-c_1-\frac{1}{r}\right) + \left( c_{\theta 5}-\frac{1}{2}\right) \xi _j \varTheta _j. \end{aligned}$$

(32b)

This problem of non-linearity was carefully addressed in Lazeroms et al. (2015) and an approximative solution for N and $N_\theta$ was found using the shear- and buoyancy-dominated limits of the flow. A summary explaining the approximative solution for N and $N_\theta$ is given in Appendix 2. Therefore, we assume that N and $N_\theta$ are known and that the non-linearity has been dealt with. As in the method used in Pope (1975), however with an extended solution for buoyant flows, $a_{ij}$ and $\xi _i$ are written as linear expansions of basis tensors and vectors

$$\begin{aligned} \mathbf {a} = \sum _{k=1}^{M} \beta _k \mathbf {T}^{\;(k)}, \end{aligned}$$

(33a)

$$\begin{aligned} \varvec{\xi } = \sum _{k=1}^{M'} \lambda _k \mathbf {V}^{\;(k)}. \end{aligned}$$

(33b)

It has been found that in the case of a two-dimensional mean flow there exists a set of 10 basis tensors $\mathbf {T}^{\;(k)}$

$$\begin{aligned} {T_{ij}}^{(1)}&= {S_{ij}}, \quad {T_{ij}}^{(2)} = {S_{ik}S_{kj}}-\frac{1}{3}I\!I_S\,{\delta _{ij}}, \quad {T_{ij}}^{(3)} = {\varOmega _{ik}\varOmega _{kj}}-\frac{1}{3}I\!I_\varOmega \,{\delta _{ij}}, \nonumber \\ {T_{ij}}^{(4)}&= {S_{ik}\varOmega _{kj}}-{\varOmega _{ik}S_{kj}}, \quad {T_{ij}}^{(\theta 1)} = \varGamma _i\varTheta _j + \varTheta _i\varGamma _j - \frac{2}{3}\gamma ^{(\theta )}\,\delta _{ij}, \nonumber \\ {T_{ij}}^{(\theta 2)}&= \varGamma _i\varTheta _k S_{kj} + S_{ik}\varTheta _k\varGamma _j - \frac{2}{3}\gamma _S^{(\theta )}\,\delta _{ij}, \nonumber \\ {T_{ij}}^{(\theta 3)}&= \varGamma _i\varTheta _k \varOmega _{kj} - \varOmega _{ik}\varTheta _k\varGamma _j - \frac{2}{3}\gamma _\varOmega ^{(\theta )}\,\delta _{ij}, \nonumber \\ {T_{ij}}^{(\theta 4)}&= \varGamma _i\varTheta _k S_{kl}\varOmega _{lj} - \varOmega _{ik}S_{kl}\varTheta _l\varGamma _j - \frac{2}{3}\gamma _{S\varOmega }^{(\theta )}\,\delta _{ij}, \nonumber \\ {T_{ij}}^{(g1)}&= \varGamma _i\varGamma _j-\frac{1}{3}\varGamma ^{\,2}\delta _{ij}, \quad {T_{ij}}^{(g2)} = \varGamma _i\varGamma _k\varOmega _{kj}-\varOmega _{ik}\varGamma _k \varGamma _j, \end{aligned}$$

(34)

and eight basis vectors $\mathbf {V}^{(k)}$

$$\begin{aligned} {V_{i}}^{(\theta 1)}&= \varTheta _i, \quad {V_{i}}^{(\theta 2)} = S_{ij}\varTheta _j, \quad {V_{i}}^{(\theta 3)} = \varOmega _{ij}\varTheta _j, \quad {V_{i}}^{(\theta 4)} = S_{ik}\varOmega _{kj}\varTheta _j, \nonumber \\ {V_{i}}^{(g 1)}&= \varGamma _i, \quad {V_{i}}^{(g 2)} = S_{ij}\varGamma _j, \quad {V_{i}}^{(g 3)} = \varOmega _{ij}\varGamma _j, \quad {V_{i}}^{(g 4)} = S_{ik}\varOmega _{kj}\varGamma _j. \end{aligned}$$

(35)

These $\mathbf {T}^{(k)}$ and $\mathbf {V}^{(k)}$ span the solution space of (30) and any other tensorial combination of $S_{ij}$, $\varOmega _{ij}$, $\varTheta _i$ and $\varGamma _i$ can be reduced to $\mathbf {T}^{(k)}$ and $\mathbf {V}^{(k)}$ groups using the Cayley-Hamilton theorem. Substituting $a_{ij}$ and $\xi _i$ with tensorial and vector groups forms an $18\times 18$ linear system for the coefficients $\beta _k$ and $\lambda _k$. The solution for this system was found in Lazeroms et al. (2013) for the special case of horizontal two-dimensional mean flow with coplanar gradients of mean velocity, mean temperature and gravitational acceleration and $c_S=c_\varOmega =0$. The extended model (different from Lazeroms et al. (2013)) is

$$\begin{aligned} \beta _{1}= & {} -\frac{8}{15}\frac{N}{D_u}, \quad \beta _{2} = 0, \quad \beta _{3} = -\frac{8}{15} \frac{C_2 C_3 Q_6}{D_u Q_2}, \quad \beta _4 = -\frac{8}{15}\frac{C_2}{D_u}, \nonumber \\ \beta _{\theta 1}= & {} \frac{2}{15} \frac{c_\varTheta C_3 Q_3 Q_4}{D_u Q_1 Q_2}, \quad \beta _{\theta 2} = -\frac{16}{15} \frac{c_\varTheta C_3}{D_u Q_1} \left( N_\theta {\tilde{D}}_u-c_\varTheta C_3 N \gamma ^{(\theta )} \right) , \nonumber \\ \beta _{\theta 3}= & {} \frac{4}{15} \frac{c_\varTheta C_2 C_3 N_\theta Q_4}{D_u Q_1 Q_2}, \quad \beta _{\theta 4} = -\frac{32}{15} \frac{c_\varTheta C_2 C_3}{D_u Q_1} \left( N N_\theta +Q_3 \right) , \nonumber \\ \beta _{g 1}= & {} \frac{8}{15} \frac{C_3 Q_3 Q_5}{D_u Q_1 Q_2}, \quad \beta _{g 2} = \frac{8}{15} \frac{C_2 C_3 N_\theta Q_5}{D_u Q_1 Q_2}, \nonumber \\ \lambda _{\theta 1}= & {} -\frac{2}{15} \frac{c_\varTheta Q_4}{D_u Q_1 Q_2} \left( N_\theta D_u - c_\varTheta C_3 N \gamma ^{(\theta )}\right) , \quad \lambda _{\theta 2} = \frac{16}{15} \frac{c_\varTheta Q_3}{Q_1}, \nonumber \\ \lambda _{\theta 3}= & {} \frac{4}{15} \frac{{c_\varTheta }^2 C_2 C_3 Q_4 \gamma ^{(\theta )}}{D_u Q_1 Q_2}, \quad \lambda _{\theta 4} = \frac{32}{15} \frac{c_\varTheta C_2 N_\theta }{Q_1}, \nonumber \\ \lambda _{g 1}= & {} -\frac{4}{15} \frac{Q_5}{D_u Q_1 Q_2} \left( N_\theta D_u - c_\varTheta C_3 N \gamma ^{(\theta )}\right) , \quad \lambda _{g 2} = 0, \nonumber \\ \lambda _{g 3}= & {} \frac{8}{15} \frac{c_\varTheta C_2 C_3 Q_5 \gamma ^{(\theta )}}{D_u Q_1 Q_2}, \quad \lambda _{g 4} = 0, \end{aligned}$$

(36)

where

$$\begin{aligned} D_u= & {} N^2 -2\,{C_2}^2 I\!I_\varOmega \ge 0, \quad {\tilde{D}}_u = N^2 +2\,{C_2}^2 I\!I_\varOmega , \nonumber \\ Q_1= & {} 2\, {Q_3}^2 - 4\, {C_2}^2 I\!I_\varOmega {N_\theta }^2 \ge 0, \nonumber \\ Q_2= & {} 6N D_u {N_\theta }^2 - 2\,c_\varTheta C_3 \gamma ^{(\theta )}N_\theta (6N^2+D_u)+8\,{c_\varTheta }^2{C_3}^2 N{\gamma ^{(\theta )}}^2, \nonumber \\ Q_3= & {} N N_\theta -c_\varTheta C_3 \gamma ^{(\theta )}, \nonumber \\ Q_4= & {} \, Q_2(15D_u + 8\,C_2I\!I_\varOmega )+2\,c_\varTheta C_3 \gamma ^{(\theta )}N_\theta D_u (15 D_u + 16\,C_2I\!I_\varOmega ) \nonumber \\&-\, 6D_u N {N_\theta }^2 (5D_u + 8\,C_2 I\!I_\varOmega ) - 60\,c_\varGamma C_3 D_u \varGamma ^2 (N Q_3 + {C_2}^2I\!I_\varOmega N_\theta ), \nonumber \\ Q_5= & {} \, 15 c_\varGamma {c_\varTheta }^2 {C_3}^2 N D_u {\gamma ^{(\theta )}}^2 -30 c_\varGamma c_\varTheta C_3 \gamma ^{(\theta )} N_\theta D_u (2N^2-{C_2}^2 I\!I_\varOmega ) \nonumber \\&+\, 45 c_\varGamma N {N_\theta }^2 {D_u}^2 \nonumber \\&+\, 2\,{c_\varTheta }^2C_3 N \varTheta ^2\left( 3 N N_\theta \left( 5D_u+8C_2I\!I_\varOmega \right) -c_\varTheta C_3 \gamma ^{(\theta )} \left( 15 D_u+16C_2 I\!I_\varOmega \right) \right) , \nonumber \\ Q_6= & {} -16\, C_3 N {c_\varTheta }^2 {\gamma ^{(\theta )}}^2 + 6\, c_\varTheta N_\theta {\gamma ^{(\theta )}}\left( 5 \,C_2 D_u + 2{\tilde{D}}_u\right) +45c_\varGamma C_2 N_\theta \varGamma ^2 D_u, \end{aligned}$$

(37)

and the invariants are

$$\begin{aligned} I\!I_\varOmega&= \varOmega _{km}\varOmega _{mk},&\quad \!\! \varTheta ^2&= \varTheta _k\varTheta _k,&\quad \!\! \gamma ^{(\theta )}&= \varGamma _k\varTheta _k,&\quad \!\! \gamma _\varOmega ^{(\theta )}&= \varGamma _k\varTheta _m\varOmega _{mk}, \nonumber \\ I\!I_S&= S_{km}S_{mk},&\quad \!\! \varGamma ^2&= \varGamma _k\varGamma _k,&\quad \!\! \gamma _S^{(\theta )}&= \varGamma _k\varTheta _m S_{mk},&\quad \!\! \gamma _{S\varOmega }^{(\theta )}&= \varGamma _k\varTheta _m S_{mj}\varOmega _{jk}. \end{aligned}$$

(38)

The extended model is somewhat simplified as compared to Lazeroms et al. (2013, 2015, 2016), and is consistent with the EARS model given in Wallin and Johansson (2000) for the case of vanishing stratification and the passive scalar model in Wikström et al. (2000). The remaining constants in the EARS model are $c_1 = 1.8,\, c_3 = 0.3,\, c_{\theta 1}= 4.51,\, c_{\theta 2} = 1,\, c_{\theta 3} = 0,\, c_{\theta 4} = 0,\, c_{\theta 5} = 0.5,\, c_{\theta g} = 0.75$. Singularities in the model are very unlikely, but possible because $Q_2$ cannot be proven to be positive in all conditions. This is not the case for $D_u$ and $Q_1$, which are always positive. Potential singularities can be treated numerically using the substitution

$$\begin{aligned} \frac{1}{Q_2} \rightarrow \frac{Q_2}{\max ({Q_2}^2,\epsilon )}, \end{aligned}$$

(39)

where $\epsilon$ is a small number, e.g. $\epsilon =0.001$ so that the sign is retained. All denominators in $\beta _k$ and $\lambda _k$ expressions must be limited by $\epsilon$, e.g. 

$$\begin{aligned} \frac{1}{D_u} \rightarrow \frac{1}{\max (D_u,\epsilon )}, \quad \frac{1}{Q_2} \rightarrow \frac{Q_2}{\max (D_uQ_1{Q_2}^2,\epsilon )}. \end{aligned}$$

(40)

At this point, the turbulent momentum flux $\overline{u_i'u_j'}$ and heat flux $\overline{u_i'\theta '}$ are expressed using (26) and (33). The basic tensors and vectors have to be formed in terms of (29). Considering only the terms with $\beta _1$ and $\lambda _{\theta 1}$ corresponds to the simple EDV model, and including the additional terms leads to the full EARS model solution containing the complete $\overline{u_i'u_j'}$ tensor and $\overline{u_i'\theta '}$ vector. In the turbulent parametrization of the ABL, the most commonly parametrized turbulent fluxes are the vertical fluxes. In their most compact form, the vertical fluxes in the EARS model can be written in the following form

$$\begin{aligned} \overline{u'w'} =&-f_\mathrm{m} \frac{K^2}{\epsilon }\frac{\partial U}{\partial z}, \end{aligned}$$

(41a)

$$\begin{aligned} \overline{v'w'} =&-f_\mathrm{m}\frac{K^2}{\epsilon }\frac{\partial V}{\partial z}, \end{aligned}$$

(41b)

$$\begin{aligned} \overline{w'\theta '} =&-f_\mathrm{h}\frac{K^2}{\epsilon }\frac{\partial \varTheta }{\partial z}+ f_\varPhi \frac{K K_\theta }{\epsilon }\frac{g}{T_0}, \end{aligned}$$

(41c)

where the core functions are

$$\begin{aligned} f_\text {m} =&-\frac{1}{2}\left( \beta _1+\left( \beta _{\theta 2}-\beta _{\theta 3}\right) \gamma ^{(\theta )}-\beta _{g2}\varGamma ^2\right) , \end{aligned}$$

(42a)

$$\begin{aligned} f_\text {h} =&-\left( \lambda _{\theta 1}-\frac{1}{2}I\!I_\varOmega \lambda _{\theta 4}\right) , \end{aligned}$$

(42b)

$$\begin{aligned} f_\varPhi =&-\lambda _{g1}. \end{aligned}$$

(42c)

In addition, in a similar way, the EARS model also predicts the individual normal stresses $\overline{u'u'}$ etc. (not shown here) and horizontal fluxes

$$\begin{aligned} \overline{u'\theta '} =&\; \frac{1}{2}\left( \lambda _{\theta 2}+\lambda _{\theta 3}\right) \frac{K^3}{\epsilon ^2}\frac{\partial U}{\partial z}\frac{\partial \varTheta }{\partial z}-\lambda _{g3}\frac{K^2K_\theta }{\epsilon ^2}\frac{g}{2T_0}\frac{\partial U}{\partial z}, \end{aligned}$$

(43a)

$$\begin{aligned} \overline{v'\theta '} =&\; \frac{1}{2}\left( \lambda _{\theta 2}+\lambda _{\theta 3}\right) \frac{K^3}{\epsilon ^2}\frac{\partial V}{\partial z}\frac{\partial \varTheta }{\partial z}-\lambda _{g3}\frac{K^2K_\theta }{\epsilon ^2}\frac{g}{2T_0}\frac{\partial V}{\partial z}, \end{aligned}$$

(43b)

which hence are non-zero also for the SCM solution.

Appendix 2: Approximative Solution for N and $N_\theta$

Treating Eqs. 30 as a linear set of equations involves computing N and $N_\theta$ in advance. An analytical solution for (32) does not exist and numerically solving such a coupled system of polynomial equations is not trivial due to the existence of multiple solutions. Therefore an approximative explicit solution is used. Substituting $a_{ij}$ and $\xi _i$ in (32a) gives

$$\begin{aligned} N =&\; c_1 - 1 + \overbrace{I\!I_\varOmega \left( \beta _1+\gamma ^{(\theta )}(\beta _{\theta 2}-\beta _{\theta 3})- \varGamma ^2 \beta _{g 2} \right) }^{{\mathcal {P}}/\epsilon } \nonumber \\&\underbrace{- \left( \gamma ^{(\theta )} \left( \lambda _{\theta 1} -\frac{1}{2}I\!I_\varOmega \lambda _{\theta 4} \right) + \varGamma ^2 \lambda _{g1} \right) }_{{\mathcal {G}}/\epsilon }, \end{aligned}$$

(44)

and for the choice of model constant $c_{\theta 5} = 0.5$, the last term in (32b) is zero and $N_\theta$ becomes a function of N. The approximative solution for N in the case of parallel shear flow depends on atmospheric stability

$$\begin{aligned} N = {\left\{ \begin{array}{ll} N^{(0)}, &{} \gamma ^{(\theta )} \ge 0 \quad \text {(unstable/neutral)} \\ N^{(1)}, &{} \gamma ^{(\theta )} < 0 \quad \text {(stable)}. \end{array}\right. } \end{aligned}$$

(45)

It is shown in Lazeroms et al. (2015) that for unstable/neutral stratification $N^{(0)}$ is sufficiently accurate but for stable stratification a one-step iteration $N^{(1)}$ is required. The zeroth approximation used for unstable/neutral and stable stratification is, respectively, given by

$$\begin{aligned} N^{(0)}&= N^{(S)}+N^{(B)}-c_1+1, \end{aligned}$$

(46)

$$\begin{aligned} {\widetilde{N}}^{(0)}&= {\widetilde{N}}^{(S)}+N^{(B)}-c_1+1. \end{aligned}$$

(47)

$N^{(S)}$ and ${\widetilde{N}}^{(S)}$ are the shear-dominant limits for unstable/neutral and stable stratification respectively ($\gamma ^{(\theta )} \rightarrow 0$) and $N^{(B)}$ is the buoyancy-dominant limit ($I\!I_{\varOmega } \rightarrow 0$) of Eq. 44. In the mentioned limits (44) together with (32b) forms a third-order polynomial equation that has analytical solutions

$$\begin{aligned} N^{(S)} =&\; \frac{4}{9} \left( \frac{c^\prime _1}{3} + f_M(P_1, P_2) \right) , \end{aligned}$$

(48a)

$$\begin{aligned} {\widetilde{N}}^{(S)} =&\; \frac{4}{9} \left( \frac{c^\prime _1}{3} + f_M({\widetilde{P}}_1, {\widetilde{P}}_2) \right) , \end{aligned}$$

(48b)

$$\begin{aligned} N^{(B)} =&\frac{c^\prime _{\theta 1}}{3} + f_M(P_{b 1}, P_{b_2}), \end{aligned}$$

(48c)

where $c^\prime _1 = 9/4 (c_1-1)$, $c^\prime _{\theta 1} = 2c_1-2c_{\theta 1}+1/r-1$ and

$$\begin{aligned} f_M(R_1,R_2) = {\left\{ \begin{array}{ll} f_V(R_1+\sqrt{R_2})+f_V(R_1-\sqrt{R_2}), &{} R_2 \ge 0, \\ 2({R_1}^2-R_2)^{1/6}\cos \left( \frac{1}{3} \arccos \left( \frac{R_1}{\sqrt{{R_1}^2-R_2}}\right) \right) , &{} R_2 < 0, \end{array}\right. } \end{aligned}$$

(49)

and in order to chose the real negative root of $(R_1\pm R_2)^{1/3}$ when the argument is negative Wallin and Johansson (2000) suggested

$$\begin{aligned} f_V(R) = \text {sign}(R)|R|^{1/3}. \end{aligned}$$

(50)

The roots in Eqs. 48 are

$$\begin{aligned}&P_1 = c'_1 \left( \frac{1}{27}{c'_1}^2 + \frac{9}{20}I\!I_{S} - \frac{2}{3}I\!I_{\varOmega }\right) , \nonumber \\&P_2 = {P_1}^2 - \left( \frac{1}{9}{c'_1}^2 + \frac{9}{10}I\!I_{S} + \frac{2}{3}I\!I_{\varOmega }\right) ^3, \nonumber \\&{\widetilde{P}}_1 = c'_1 \left( \frac{1}{27}{c'_1}^2 + \frac{9}{20}I\!I_{S} A_S - \frac{2}{3} \left( I\!I_{\varOmega } - \frac{\widetilde{Q}}{2 {C_2}^2} \right) \right) , \nonumber \\&{\widetilde{P}}_2 = {\;\!{\widetilde{P}}_{1}}^2 - \left( \frac{1}{9}{c'_1}^2 + \frac{9}{10}I\!I_{S} A_S + \frac{2}{3} \left( I\!I_{\varOmega } - \frac{\widetilde{Q}}{2 {C_2}^2} \right) \right) ^3, \nonumber \\&P_{b1} = c'_{\theta 1} \left( \frac{1}{27}{c'_{\theta 1}}^2 + \frac{1}{3} \alpha _\theta \left( c_1 - 1\right) + \frac{2}{9} c_\varTheta \left( 2 C_3 + 1\right) \gamma ^{(\theta )} + \frac{1}{3} c_\varGamma \varGamma ^2\right) \nonumber \\&\qquad \;\;\,- \frac{4}{3} c_\varTheta C_3 \left( c_1 - 1\right) \gamma ^{(\theta )}, \nonumber \\&P_{b2} = {P_{b1}}^2 - \left( \frac{1}{9}{c'_{\theta 1}}^2 + \frac{2}{3} \alpha _\theta \left( c_1 - 1\right) + \frac{4}{9} c_\varTheta \left( 2 C_3 + 1\right) \gamma ^{(\theta )} + \frac{2}{3} c_\varGamma \varGamma ^2 \right) ^3\!\!, \qquad \end{aligned}$$

(51)

where $\alpha _\theta = c_{\theta 1}-(c_1+1/r)/2$,

$$\begin{aligned}&A_S = 1 + \frac{1}{6} \frac{c_\varTheta C_3}{c_1 N_\theta ^*} \left( 15 C_2 - 8\right) \gamma ^{(\theta )} + \frac{15}{4} \frac{c_\varGamma C_2 C_3}{c_1 N_\theta ^*}\varGamma ^2, \nonumber \\&{\tilde{Q}} = - \frac{1}{3} \frac{c_\varTheta C_3}{c_1 N_\theta ^*} \left( 7 {c_1}^2 + 2 {C_2}^2 I\!I_{S}\right) \gamma ^{(\theta )} + \frac{4}{3} \left( c_\varTheta C_3 \frac{\gamma ^{(\theta )}}{N_\theta ^*}\right) ^2, \end{aligned}$$

(52)

and $N_\theta ^* = c_1/2+\alpha _\theta$.

As mentioned, for stable stratification a one-step iteration of ${\widetilde{N}}^{(0)}$ is used to improve the accuracy of the approximative solution. The iteration is based on computing (44)

$$\begin{aligned} N^{(1)} =&\; c_1-1+I\!I_\varOmega \left( {\beta _1}'+\gamma ^{(\theta )}({\beta _{\theta 2}}'-{\beta _{\theta 3}}')- \varGamma ^2 {\beta _{g 2}}' \right) \nonumber \\&- \left( \gamma ^{(\theta )} \left( {\lambda _{\theta 1}}' -\frac{1}{2}I\!I_\varOmega {\lambda _{\theta 4}}' \right) + \varGamma ^2 {\lambda _{g1}}' \right) , \end{aligned}$$

(53)

where ${\widetilde{N}}^{(0)}$ replaces N for all $\beta '$ and $\lambda '$ in (36).

Fig. 10

Profile of $|\,{\mathcal {G}}\,|$ scaled by $u^3_*/\varkappa z$ at a 0200 LT for the stable, and b 1400 LT unstable ABL. Time instances correspond to the periods marked in Fig. 2. Black dot indicates $z = L_{\varDelta }$ where the dimensionless quantity $|\,{\mathcal {G}}\,|\varkappa z/u^3_*=1$

Appendix 3: Definition of the Physical Obukhov Length

The physical Obukhov length $L_{\varDelta }$ is a new scaling length for the surface layer. The classical Obukhov length (20) is derived from non-dimensionalizing Eq. 4a in the surface layer with ${\mathcal {P}}$ (Stull 1988). The dimensionless buoyancy production term ${\mathcal {G}}/{\mathcal {P}}$ has the following form

$$\begin{aligned} \frac{{\mathcal {G}}}{{\mathcal {P}}}&= \frac{g}{T_0}\frac{\overline{w^\prime \theta ^\prime }_s}{-\overline{u^{\prime }w^{\prime }}^T {{d}{{V}}}/{{d}z}} \approx \frac{g}{T_0}\frac{\varkappa z \theta _*}{u_*^2} = z/L. \end{aligned}$$

(54)

Close to the surface ${{\mathcal {G}}}/{{\mathcal {P}}} < 1$ implies that $z < L$, however higher up in the atmosphere the buoyancy production term becomes comparable with the shear production term leading to ${{\mathcal {G}}}/{{\mathcal {P}}} \ge 1$ where in that case $z \ge L$ must be fulfilled. Therefore, the physical meaning of the Obukhov length is the height above which the buoyancy production term is comparable to the shear production term.

In order to obtain $L_\varDelta$, the absolute value of ${\mathcal {G}}$ is scaled by ${\mathcal {P}}$ relevant for the surface layer $u^3_*/\varkappa z$. This length scale represents the height at which the buoyancy effects on turbulence become comparable to the shear effects, which is consistent with the physical meaning of the Obukhov length (54). Figure 10 shows vertical profiles of the dimensionless quantity $|\,{\mathcal {G}}\,|\varkappa z/u^3_*=f(z)$, for unstably- and stably-stratified surface layer, where the height at which $|\,{\mathcal {G}}(z = L_\varDelta )\,|\varkappa z/u^3_*=1$ is defined as $L_\varDelta$. This way of defining the Obukhov length is convenient for the EARS model because ${\mathcal {G}}$ is given in a closed form (Lazeroms et al. 2013), unlike most eddy-visocsity/eddy-diffusivity models.