On the Discrepancy in Simultaneous Observations of the Structure Parameter of Temperature Using Scintillometers and Unmanned Aircraft

Abstract

We elaborate on the preliminary results presented in Beyrich et al. (in Boundary-Layer Meteorol 144:83–112, 2012), who compared the structure parameter of temperature (${C_{T}^2}_{}$) obtained with the unmanned meteorological mini aerial vehicle ($\text{ M }^{2}\text{ AV }$) versus ${C_{T}^2}_{}$ obtained with two large-aperture scintillometers (LASs) for a limited dataset from one single experiment (LITFASS-2009). They found that ${C_{T}^2}_{}$ obtained from the $\text{ M }^{2}\text{ AV }$ data is significantly larger than that obtained from the LAS data. We investigate if similar differences can be found for the flights on the other six days during LITFASS-2009 and LITFASS-2010, and whether these differences can be reduced or explained through a more elaborate processing of both the LAS data and the $\text{ M }^{2}\text{ AV }$ data. This processing includes different corrections and measures to reduce the differences between the spatial and temporal averaging of the datasets. We conclude that the differences reported in Beyrich et al. can be found for other days as well. For the LAS-derived values the additional processing steps that have the largest effect are the saturation correction and the humidity correction. For the $\text{ M }^{2}\text{ AV }$-derived values the most important step is the application of the scintillometer path-weighting function. Using the true air speed of the $\text{ M }^{2}\text{ AV }$ to convert from a temporal to a spatial structure function rather than the ground speed (as in Beyrich et al.) does not change the mean discrepancy, but it does affect ${C_{T}^2}_{}$ values for individual flights. To investigate whether ${C_{T}^2}_{}$ derived from the $\text{ M }^{2}\text{ AV }$ data depends on the fact that the underlying temperature dataset combines spatial and temporal sampling, we used large-eddy simulation data to analyze ${C_{T}^2}_{}$ from virtual flights with different mean ground speeds. This analysis shows that ${C_{T}^2}_{}$ does only slightly depends on the true air speed when averaged over many flights.

1 Introduction

During the past twenty years, large-aperture scintillometers (LASs) have proven to be reliable instruments for providing area-averaged surface fluxes over natural landscapes (among others Green et al. 2001; Meijninger et al. 2002b, 2006). These measurements are important for the validation of numerical models and satellite-based retrieval algorithms (for an extensive literature review, see Beyrich et al. (2012), hereafter denoted as B12).

A scintillometer does not measure the area-averaged surface fluxes directly, and obtaining fluxes from scintillation measurements involves several steps (Moene et al. 2004). From the scintillation measurements the path-averaged structure parameter of the refractive index of air (${C_{n}^2}_{\mathrm {}}$) is determined. Large-aperture scintillometers operate at optical wavelengths for which ${C_{n}^2}_{\mathrm {}}$  is basically determined by temperature fluctuations. Hence ${C_{n}^2}_{\mathrm {}}$ is subsequently used to derive the path-averaged structure parameter of temperature (${C_{T}^2}_{}$, e.g. Hill et al. 1992; Ward et al. 2013). Finally, the sensible heat flux can be derived from ${C_{T}^2}_{}$ by applying Monin–Obukhov similarity theory (MOST, Monin and Obukhov 1954; Wyngaard 1973; among others).

Until now, the validation of LAS measurements over heterogeneous surfaces has been performed by comparing the scintillometer-based fluxes with fluxes from aggregated eddy-covariance (EC) data (Meijninger et al. 2002a, b, 2006) or from airborne measurements (Beyrich et al. 2006; Moene et al. 2006). However a direct validation of the path-averaged structure parameters against independent measurements is still missing. Such a direct validation is needed, because the relation between structure parameters and fluxes is non-linear. For measurements above heterogeneous terrain, this non-linear relation results in a consistent overestimation of the flux obtained from a LAS compared to an aggregated flux using a number of EC systems (Meijninger 2003; Meijninger et al. 2006).

Beyrich et al. (2005) were among the first to validate ${C_{T}^2}_{}$ from the scintillometer with independent measurements; however, they compared path-averaged LAS-based ${C_{T}^2}_{}$ with EC point measurements. Maronga et al. (2013) validate ${C_{T}^2}_{}$ of the LAS with data obtained from a large-eddy simulation (LES) and aircraft data obtained during the RECAB campaign near Cabauw in the Netherlands. That study extends beyond Beyrich et al. (2005) and considers a path-averaged ${C_{T}^2}_{}$, but it is limited to two case studies over relatively homogeneous terrain. Furthermore, the lowest flight level of the aircraft was located at about twice the height of the scintillometer path.

The aim of the LITFASS-2009 and LITFASS-2010 experiments was to validate ${C_{T}^2}_{}$ from the LAS with independent measurements over a moderately heterogeneous surface (B12, Kroonenberg et al. 2012, hereafter denoted as vdK12). To that end, ${C_{T}^2}_{}$ was derived from data of the unmanned meteorological mini aerial vehicle ($\text{ M }^{2}\text{ AV }$, Spiess et al. 2007) that flew along the path of a LAS over a distance of several kilometres.

B12 show a first comparison for one flight day (13 July 2009). The 30-min and path-averaged ${C_{T}^2}_{}$ derived from the LAS was compared to the ${C_{T}^2}_{}$ determined from the $\text{ M }^{2}\text{ AV }$ data obtained within the particular 30-min interval. B12 observed that the decrease with time of ${C_{T}^2}_{}$ in the afternoon is consistent between $\text{ M }^{2}\text{ AV }$ and LAS (Fig. 5 in B12), but the values of ${C_{T}^2}_{}$ from the $\text{ M }^{2}\text{ AV }$  are systematically larger than those from the LAS (Fig. 6 in B12). For this preliminary validation, the data of both systems were processed using a standard procedure, which is not optimal for such a comparison. The question arises whether the processing could explain (part of) the observed differences. For instance, the temporal averaging differs: 30 min for the LAS compared to about 2 min for the $\text{ M }^{2}\text{ AV }$. Moreover, despite the fact that the $\text{ M }^{2}\text{ AV }$ flew along the scintillometer path, the spatial averaging differs: the path-averaged ${C_{T}^2}_{}$ from the LAS has a bell-shaped weighting function (Wang et al. 1978), whereas the flight-track ${C_{T}^2}_{}$ from the $\text{ M }^{2}\text{ AV }$ was obtained from the leg as a whole.

During LITFASS-2009 the meteorological conditions were unfavourable for making measurements over a complete undisturbed diurnal cycle with the $\text{ M }^{2}\text{ AV }$. Therefore a second small flight campaign was performed on 11 and 12 July 2010 (vdK12). So far, the $\text{ M }^{2}\text{ AV }$ data of LITFASS-2010 have only been compared with EC data. Both systems show good agreement in the morning and in the afternoon, but ${C_{T}^2}_{}$ from the $\text{ M }^{2}\text{ AV }$ is larger than that from the EC method around noon (Fig. 4 in vdK12), which might be caused by a difference in the footprint of both observations.

The present study attempts to improve on the studies of B12 and vdK12 by answering the following research questions:

• 1. Are the differences between LAS and $\text{ M }^{2}\text{ AV }$ (initially diagnosed for 13 July 2009) also found for the other days during LITFASS-2009 and LITFASS-2010 (results discussed in Sect. 4.1)?

• 2. Can the differences be reduced or explained by a more elaborate processing of either or both the LAS data and the $\text{ M }^{2}\text{ AV }$  data (results in Sects. 4.2 and 4.3, respectively)?

Such a more elaborate processing includes:

• a. the normalization of measured ${C_{T}^2}_{}$ values to a reference height for both systems taking into account stability,

• b. the consideration of possible saturation effects on the LAS data (also called saturation correction),

• c. the proper treatment of the effect of humidity fluctuations on ${C_{n}^2}_{\mathrm {}}$ in deriving ${C_{T}^2}_{}$ from the LAS data (also called humidity correction),

• d. the reduction of the LAS averaging time to the flight leg duration,

• e. the use the true air speed $u_{\mathrm {air}}$ of the $\text{ M }^{2}\text{ AV }$ rather than the ground speed $u_{\mathrm {gr}}$ to convert from a temporal structure function to a spatial structure function,

• f. the use of alternative mathematical methods to determine the structure parameters from $\text{ M }^{2}\text{ AV }$ data,

• g. the proper weighting of the $\text{ M }^{2}\text{ AV }$ data by taking into account the scintillometer’s path-weighting function.

A side-effect of applying such an elaborate data processing is that for each step of the data processing different options can be compared. This brings us to the third research question,

• 3. What is the influence on ${C_{T}^2}_{}$ of applying the various options in the data processing for the two measurement systems (results in Sect. 4.4)?

Finally, one reason for the deviation of the $\text{ M }^{2}\text{ AV }$ results from the ${C_{T}^2}_{}$ derived from sonic and LAS data may be related to the determination of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ from a temperature dataset that results from a combination of spatial and temporal sampling. The relative importance of the displacement of the observations in space and time is related to the speed of the aircraft. It might be possible that the simultaneous sampling in time and space creates an additional contribution to ${C_{T}^2}_{}$ as compared to when ${C_{T}^2}_{}$ is determined in the classical way where the data are considered to result from spatial sampling only.

Therefore, our last research question is:

• 4. What is the influence on ${C_{T}^2}_{}$ of the mean ground speed of the aircraft (results in Sect. 4.5)?

This question is answered through an additional analysis of the sensitivity of ${C_{T}^2}_{}$ to the mean ground speed, using virtual flights through a spatio-temporal temperature field resulting from LES. The use of LES allows us to vary the ground speed while still sampling exactly the same turbulent field. In addition, tower observations (zero translation speed) will be simulated with the same dataset.

Fig. 1

Overview of the instrumental set-up of LITFASS-2009 and LITFASS-2010 experiments as used herein. In the lower part of the figure the path-weighting function W(x) of the LAS is shown

2 Data and Methods

The LITFASS-2009 and LITFASS-2010 experiments (where LITFASS stands for LIndenberg-To-Falkenberg Aircraft Scintillometer Study) were performed in the area around the Meteorological Observatory Lindenberg - Richard-Aßmann-Observatory (MO Lindenberg) of the German Meteorological Service (Deutscher Wetterdienst, DWD). The surface in the so-called LITFASS area (Beyrich et al. 2002) is moderately heterogeneous with a mixture of farmland, forest, small lakes and small villages (see Fig. 1 in B12 for a map of the different land-use types during LITFASS-2009; a schematic representation is provided later in the text, see Fig. 4). The vegetation of the farmland mainly consists of maize, sunflowers, colza, barley and triticale, and typical horizontal dimensions of the crop fields vary between 300 and 1000 m. Figure 1 shows a schematic overview of the instrumental set-up during the two experiments along the LAS path. The weather conditions during the two experiments differed. During LITFASS-2009 (29 June–24 July 2009) cloudless conditions never lasted longer than a few hours, with rain occurring on more than 50 % of the days. The wind speed at 10 m frequently exceeded 6 $~\mathrm {m~s}^{-1}$, preventing safe operation of the $\text{ M }^{2}\text{ AV }$ (B12). During LITFASS-2010 (11 and 12 July 2010) the sky was mostly cloud-free, and during daytime the wind speed at 10 m was between 2 and 5 $~\mathrm {m~s}^{-1}$  (vdK12).

In the sections below we present the methodology used to determine ${C_{T}^2}_{}$ from data of the three measurement systems. In Sect. 2.6, we give the details of the LES sensitivity analysis on the impact of the mean ground speed on ${C_{T}^2}_{}$.

2.1 ${C_{T}^2}_{}$ from LAS

During the two experiments two scintillometers were operated at effective heights ($z_{\mathrm {eff}}$) of 43 and 63 m over a path of $\approx$4800 m between the 99-m tower at GM Falkenberg (see Fig. 1, where GM stands for “Grenzschichtmessfeld”, German translation for boundary-layer field site) and a 26-m tower at MO-Lindenberg. Note that the lower path is almost parallel to the slanted surface, while the height above ground decreases from Falkenberg to Lindenberg for the upper path. The scintillometer signal was sampled in several ways (see Table 1).

Table 1 The scintillometers operating during the two experiments, where $z_{\mathrm {eff}}$ is the effective height of the scintillometer above the surface (Beyrich et al. 2012)

During LITFASS-2009, the data from two LAS systems (built at Wageningen University, the Netherlands, Meijninger et al. 2000) were sampled and stored at a frequency of 500 Hz on a Campbell CR9000 datalogger. The WURLAS98005 is in long-term operation at DWD, and its internal data logger routinely stores data as well (G2 datalogger with a storage interval of 10 min). Furthermore, it was combined with a microwave scintillometer (MWS) built by the University of Bern (MWUB, logged on the CR9000). For a more detailed description of the set-up of the scintillometers we refer to B12, and for a comparison of data obtained from the two dataloggers to Braam et al. (2012b) and van Kesteren et al. (2015).

During LITFASS-2010, the WURLAS98005 was routinely operated with the G2 datalogger. Moreover, at $z_{\mathrm {eff}} =$ 63 m a BLS900 (Scintec AG 2006, Scintec, Germany) was operated and stored data with a sampling interval of 10 min (replacing the WURLAS98006 used in 2009). Data from the systems were processed with an averaging time of 10 min. In addition, for LITFASS-2009 the WURLAS98005 and WURLAS98006 data were processed over the exact time window of the flight legs as well (see item d of the elaborate processing list in Sect. 1). This was not possible for LITFASS-2010, because for that second experiment no raw data of the LAS were available.

2.1.1 From the Scintillometer Signal to ${C_{n}^2}_{\mathrm {}}$

The first step when analyzing LAS data is to obtain the path-averaged ${C_{n}^2}_{\mathrm {}}$ from the variance of the logarithmic signal intensity ($\sigma _{\ln (I)}^2$). For the G2-logger (Meijninger et al. 2000) and the BLS900 (Scintec AG 2006) this step was already applied internally, hence, it had to be applied for the raw data logged on the CR9000 only. For the 500-Hz data, the following relation was used,

$$\begin{aligned} {C_{n}^2}_{\mathrm {}} = \frac{\sigma _{\ln (I)}^2}{4 b(D,L)} \end{aligned}$$

(1)

in which the constant b was obtained from the scintillometer equation (compare Eq. 1 in B12), depending on the aperture size D and the path length L. For both WURLAS instruments $b \approx 20.60 \times 10^{12}$. The CR9000 datalogger at Falkenberg used to record the signal from WURLAS98006 did not have a stable calibration, and so a correction for each day was applied (Braam et al. 2012b).

2.1.2 Saturation Correction

One issue related to scintillometry is the limitation of the theory to a weak scattering regime. In the case of stronger scattering ${C_{n}^2}_{\mathrm {}}$ is no longer linearly proportional to $\sigma _{\ln (I)}^2$: the signal becomes saturated. While it is better to prevent saturation (by reducing the path length or increasing the observation level), one can also correct the ${C_{n}^2}_{\mathrm {}}$ signal. Based on an extensive comparison of different saturation correction methods, Kleissl et al. (2010) recommended the Clifford correction method (Clifford et al. 1974). For both the WURLAS and BLS instruments, the saturation correction factor $m={C_{n}^2}_{\mathrm {cor}}/{C_{n}^2}_{\mathrm {uncor}}$ was calculated for nine values of ${C_{n}^2}_{\mathrm {uncor}}$.¹ Based on these values a linear interpolation method was used to obtain ${C_{n}^2}_{\mathrm {cor}}$ for each time interval. In order to be consistent between the WURLAS and the BLS, we decided to apply this saturation correction also to the BLS900 data, instead of using the correction that is implemented in the Scintec software (Scintec AG 2006).

2.1.3 From ${C_{n}^2}_{\mathrm {}}$ to ${C_{T}^2}_{}$: Corrections for Humidity Contribution

The structure parameter of the refractive index of air is related to ${C_{T}^2}_{}$, $C_{q}^2$ and $C_{Tq}$ via (Hill 1989; Lüdi et al. 2005; Ward et al. 2013),

$$\begin{aligned} {C_{n}^2}_{\mathrm {}} =\frac{A_{T}^2}{\overline{T} ^2}{C_{T}^2}_{} +\frac{A_{T} A_q}{\overline{T} \overline{q}}C_{Tq}+\frac{A_q^2}{\overline{q} ^2}C_{q}^2 \end{aligned}$$

(2)

in which $A_{T}$ and $A_q$ are the partial derivatives of the refractive index of air with respect to temperature (T) and humidity (q), respectively, and the overbar indicates averaging. For the WURLAS98005-MWUB system, which measured ${C_{n}^2}_{\mathrm {}}$ at two wavelengths, ${C_{T}^2}_{}$ was explicitly solved. In the literature, two methods to obtain ${C_{T}^2}_{}$ from a two-wavelength scintillometer system are described, using either

• 1. the covariance between the signal of the two instruments ($cov_{\ln (I\mathrm {LAS}),\ln (I\mathrm {MWS})}$, see Lüdi et al. 2005; Ward et al. 2013), or

• 2. the correlation coefficient between T and q ($R_{Tq}$, see Hill 1989).

For the systems that measured ${C_{n}^2}_{\mathrm {}}$ at an optical wavelength only, the humidity contribution to ${C_{n}^2}_{\mathrm {}}$ (the second and third terms in Eq. 2) had to be estimated from other meteorological measurements. This reduces Eq. 2 to,

$$\begin{aligned} {C_{n}^2}_{\mathrm {}} =\frac{A_{T}^2}{\overline{T} ^2}{C_{T}^2}_{} \, c_{q\mathrm {con}} \end{aligned}$$

(3)

in which $c_{q\mathrm {con}}$ is a correction for the humidity contribution that can be estimated in three different ways (see Moene 2003, hereafter denoted as M03), from $A_q, A_{T}, \overline{q}, \overline{T}$ and:

• 3. $R_{Tq}$ and the standard deviation of temperature and humidity ($\sigma _{T}$ and $\sigma _{q}$) using Eq. 8 of M03,

• 4. $R_{Tq}$ and the Bowen ratio ($\beta$, the ratio of the sensible to the latent heat flux) using Eq. 11 of M03, or

• 5. $\beta$ using Eq. 12 of M03, which is comparable to Eq. 10 of Wesely (1976).

M03 has shown that the relative error for the last three methods is $<$1 % if $|\beta |>1$. For $|\beta |<1$, the deviation of the three methods is larger: using method 3 gives errors of $<$3 %, whereas method 5 gives errors of 5–40 % (his Fig. 8). Because his analysis was based on EC data, he did not include the methods of the two-wavelength scintillometers in his analysis (methods 1 and 2). In Sect. 4.2.2 we discuss the effect of the various options for the humidity correction for the present dataset.

2.2 ${C_{T}^2}_{}$ from the $\text{ M }^{2}\text{ AV }$

The $\text{ M }^{2}\text{ AV }$ is an unmanned aircraft built by the Institute of Aerospace Systems of the Technische Universität Braunschweig (TU-BS, Spiess et al. 2007; Martin et al. 2011, vdK12). The wind direction and wind speed are obtained using a 5-hole probe, an inertial navigation unit and a GPS receiver. The true air speed of the $\text{ M }^{2}\text{ AV }$ is derived from the 5-hole probe data directly. Air temperature is measured with a Vaisala HMP 50 (response frequency of 1 Hz) and a custom-made thermocouple (response frequency 10 Hz). More details on the applied thermocouple thermometer can be found in Martin et al. (2011). The final temperature data are a combination of the data from both instruments using complementary filtering with a cut-off frequency of 0.02 Hz (vdK12). All data were stored at a 100-Hz sampling rate by the onboard computer.

During the two experiments different flight patterns were flown (B12, vdK12). In this study, we only analyze the ‘line profile’ and ‘scintillometer profile’ data (both called leg in vdK12) where the aircraft flew at different levels below 110 m along the scintillometer path either parallel to the surface or parallel to the LAS beam. These patterns were flown on seven days: five days in 2009 (7, 12, 13, 17 and 21 July), and two days in 2010 (11, 12 July). Both patterns covered only the southern part of the scintillometer path (3.3 km $\approx 70$ %), because no permission could be obtained to fly above the village of Lindenberg. The mean ground speed was about 24 $~\mathrm {m~s}^{-1}$, and consequently a leg took between 2 and 3 min. In Fig. 1 a schematic example of the line profile is given.

Related to the data of the $\text{ M }^{2}\text{ AV }$ two remarks have to be made. First, following the experiments it appeared that the temperature of the Vaisala HMP 50 (slow thermometer) showed a dependency on solar exposure (personal communication: Sabrina Martin, TU-BS, 2010). Second, on some flights during the LITFASS-2009 experiment the height above the surface was not well determined. For these flights the average height was estimated as the level pre-set when programming the flight mission. This is a reasonable estimate as proven for those flights where the altimeter worked properly.

2.2.1 Different Methods to Calculate ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$

The first method to calculate ${C_{T}^2}_{}$ from the aircraft data employs the traditional approach using the structure function ($D_{TT}=\overline{\left[ T_i-T_{i-\varDelta i}\right] ^2}$, in which i is the temperature measurement at a certain location or time and $\varDelta i$ is the separation in either time or space). Here we largely follow the methods described in vdK12. The 100-Hz temperature data obtained with the $\text{ M }^{2}\text{ AV }$ are considered as a time series, from which the temporal structure function is calculated over a range of separations. Then the conversion of the temporal to the spatial structure function is done by applying Taylor’s hypothesis using the speed of the aircraft. In B12 and vdK12 the leg-mean ground speed, $u_{\mathrm {gr}}$, was used for this. Here we investigate the effect on ${C_{T}^2}_{}$ when using the leg-mean true air speed, $u_{\mathrm {air}}$ (see issue e). It is more logical to use the latter because what is relevant in the determination of the structure parameter is the speed relative to the airmass. Furthermore, use of the true air speed makes the transition between a moving platform ($\text{ M }^{2}\text{ AV }$) and a stationary platform (sonic anemometer) consistent. Note that the issue studied here is different from that discussed in Martin and Bange (2014) who considered turbulence-related in-leg variations in the ground speed and their effect on sampling errors in the vertical fluxes. Here we only consider the effect of the leg-mean wind on the difference between ground speed and true air speed, and the related difference in the interpretation of the spatial separation of samples.

In the end ${C_{T}^2}_{}$ is calculated as the mean of $D_{TT}$ times the separation to the power $-2/3$ over a range of spatial separations within the inertial subrange (${C_{T}^2}_{} =\overline{D_{TT}\varDelta i^{-2/3}}^{\mathrm {IS}}$). In the present dataset, the inertial subrange exists for separations between 2.5 and 25 m (vdK12). Firstly, we calculated $D_{TT}$ and ${C_{T}^2}_{}$ over the leg as a whole, as was done in B12 and vdK12. Secondly, following vdK12 we calculated $D_{TT}$ over a moving window to obtain the spatial series for applying the LAS path-weighting function. The length of the window was about 300 m.

The second method used to calculate ${C_{T}^2}_{}$ is via the Fourier spectrum using the routines as described in Hartogensis et al. (2002). Within this routine, the inertial subrange is automatically determined. Here again the 100-Hz data were analyzed as a time series and the true air speed was used in the conversion from temporal to spatial data.

The third method to calculate ${C_{T}^2}_{}$ uses the wavelet spectrum as described in Maronga et al. (2013). The wavelet spectrum was calculated for each point in the time series; the wavelet function used was the Morlet wavelet with a non-dimensional frequency of 6. Again, the spatial separation is determined from the temporal separation using the true air speed. In this we deviate from Maronga et al. (2013) where the time series was converted to a spatial series based on the geo-location of the samples. Subsequently, ${C_{T}^2}_{}$ was derived from Eq. 14 in Maronga et al. (2013) and was spatially-averaged over a running window of 300 m around each measurement point and stored for every 2 m along the flight leg. Spectral averaging was applied over a range of scales from 2.5 to 25 m.

2.2.2 Applying the Path-Weighting Function

In order to obtain spatial averaging similar to that of the scintillometers, we also applied the LAS-path weighting function (W(x), Wang et al. 1978) to the spatial series obtained with the $\text{ M }^{2}\text{ AV }$. This procedure consists of three steps:

• 1. the spatial series of ${C_{T}^2}_{}$ as derived from the $\text{ M }^{2}\text{ AV }$ data (using the structure function, see Sect. 2.2.1) is projected on to the scintillometer path. This gives ${C_{T}^2}_{} (x)$, with x in m. Note that the spacing of the $\text{ M }^{2}\text{ AV }$ data along the scintillometer path varies slightly between the different flights due to slight variations in the ground speed of the $\text{ M }^{2}\text{ AV }$ and slight variations in the angle between the flight path and the scintillometer path;

• 2. W(x) is determined for each location x along the scintillometer path where a $\text{ M }^{2}\text{ AV }$ data point has been projected;

• 3. the mean ${C_{T}^2}_{}$ along the path, including the path-weighting function of the LAS (${C_{T}^2}_{}$[W(x)LAS]) is calculated as

  $$\begin{aligned} {C_{T}^2}_{W(x)\mathrm {LAS}} = \sum _i {C_{T}^2}_{} (x_i)W(x_i)\frac{\varDelta x_i}{L}~, \end{aligned}$$

  (4)

where $\varDelta x_i$ is the spatial separation of the ${C_{T}^2}_{} (x_i)$ data points along the scintillometer path.

2.3 ${C_{T}^2}_{}$ from Sonic Measurements at the Tower

In order to have an independent validation, ${C_{T}^2}_{}$ was also determined from two sonic anemometer/thermometer instruments (USA-1, METEK GmbH, Germany) located at heights of 50 and 90 m on the 99-m tower of GM-Falkenberg. We calculated ${C_{T}^2}_{}$ from the temporal structure function of temperature over the same time window as the LAS (10 min), following the procedure described in Braam et al. (2014). Because the ${C_{T}^2}_{}$ from the USA-1 instrument only serves as an extra independent validation, we do not repeat details of the method to calculate ${C_{T}^2}_{}$ here.²

2.4 Normalizing ${C_{T}^2}_{}$ to One Reference Level

The mean structure parameter decreases with height in the atmospheric surface layer (Wyngaard et al. (1971)). The scintillometers, $\text{ M }^{2}\text{ AV }$ and the sonics measured ${C_{T}^2}_{}$ at different levels ($z_\mathrm {m}$), which makes it difficult to compare ${C_{T}^2}_{}$ between the instruments. Therefore, we normalized all ${C_{T}^2}_{}$ data to a common reference level of 50 m (${C_{T}^2}_{50\mathrm {m}}$). For this we used Monin–Obukhov similarity theory (MOST) scaling. The normalization of the structure parameter at the observation level (${C_{T}^2}_{z_\mathrm {m}}$) to 50 m is, for unstable conditions (subscript un), given by,

$$\begin{aligned} {C_{T}^2}_{\mathrm {un50m}} = {C_{T}^2}_{z_\mathrm {m}} \frac{z_\mathrm {m}^{2/3}\left( 1-c_{2\mathrm {un}}z_\mathrm {m}/L_{ob}\right) ^{2/3}}{50^{2/3}\left( 1-c_{2\mathrm {un}}50/L_{ob}\right) ^{2/3}}, \end{aligned}$$

(5a)

and for stable conditions (subscript st) by,

$$\begin{aligned} {C_{T}^2}_{\mathrm {st50m}} = {C_{T}^2}_{z_\mathrm {m}} \frac{z_\mathrm {m}^{2/3}\left( 1+c_{2\mathrm {st}}\left( z_\mathrm {m}/L_{ob}\right) ^{2/3}\right) }{50^{2/3}\left( 1+c_{2\mathrm {st}}\left( 50/L_{ob}\right) ^{2/3}\right) } \end{aligned}$$

(5b)

in which $L_{ob}$ is the Obukhov length ($L_{ob} = {{\overline{T_v} u_{*}}^2}/({\kappa g {T_{v*}}})$ where $\overline{T}_{v}$ is the mean virtual temperature, $u_{*}$ is the friction velocity, $\kappa = 0.4$ is the von Kármán constant, $g = 9.81~~\mathrm {m~s}^{-2}$ is the acceleration due to gravity, and ${T_{v*}}$ is the virtual temperature scale); $c_2$ is the second regression coefficient used in the most common expression of MOST. In this study, we used the regression coefficients of Andreas (1988): $c_{2\mathrm {un}}=6.1$ and $c_{2\mathrm {st}}=2.2$. The Obukhov length needed in the normalization was obtained from the fluxes measured with the EC system at 50 m (see the first item in the list of Sect. 2.5).

2.5 Other Data

For the humidity correction and the height normalization additional data are needed:

• $R_{Tq}, \sigma _{T}, \sigma _{q}, \beta$ and L were derived from data obtained with the USA-1 instrument together with a LI7500 infrared hygrometer (LiCor Inc., U.S.) at heights of 50 and 90 m. They were calculated over a 10-min window with the EC-Pack flux-software package (version 2.5.23) developed by Wageningen University (van Dijk et al. 2004) (Braam et al. 2014 ³). The influence of unreliable data points and data gaps in the time series is minimized to reduce possible errors if applying the humidity corrections. Therefore, for each variable we excluded in the times series of 10-min means both spikes (following the method of Vickers and Mahrt 1997) and data points with a relative uncertainty $>$ 0.3. Afterwards, all gaps in the 10-min time series were filled using linear interpolation and the dataset was smoothed using a running average of two data points. Moreover, the third humidity correction was not applied if $\beta ~\approx \left( \frac{A_q}{\overline{q}}\right) \left( \frac{\overline{T}}{A_{T}}\right) \frac{c_p}{L_v}\approx -0.03$, because then ${C_{T}^2}_{}$ becomes numerically ill-defined.⁴

• pressure, measured at 1 m (PTB220, Vaisala Oy, Finland). The pressure at heights of 50 and 90 m was estimated by assuming a linear decrease of 12.5 Pa m$^{-1}$,

• precipitation, measured with a weighing precipitation gauge (Pluvio, Ott GmbH, Germany).

2.6 Sensitivity Analysis of Mean Ground Speed on ${C_{T}^2}_{}$ in LES

For the sensitivity study we used data from high-resolution simulations using the LES model PALM (PArallelized LES Model, Raasch and Schröter 2001) with a grid spacing of $\varDelta _x=\varDelta _y=$ 3.3125 m, $\varDelta _z=$ 2 m and a domain with a size of 5.3 km $\times$ 5.3 km. We used input and boundary conditions from a real case representing 30 May 2003 during the LITFASS-2003 experiment (case LIT2E), which has been studied extensively before (Sühring and Raasch 2013; Maronga and Raasch 2013; Maronga et al. 2014). This case represents a situation with clear-sky and low wind-speed conditions over the same area where LITFASS-2009 and LITFASS-2010 took place. We used a case from 2003 because a day with such favourable weather conditions did not occur during LITFASS-2009, and for LITFASS-2010 the surface fluxes for the different fields, needed as input to the LES, were not available. To clarify the analysis, we used spatially homogeneous surface fluxes, based on the area average of fluxes from various fields. The diurnal cycle was simulated from 0500 UTC onward. Within the large-eddy simulation 15 min of raw temperature data at 50-m height were saved ($\varDelta _{t}=0.1$ s, 9000 data points, 1245 to 1300 UTC). During the analysis period the wind speed at 50-m height was 1.7 $~\mathrm {m~s}^{-1}$ from a direction of 80 degrees. We have analyzed 158 parallel lines (legs) aligned in the north–south direction, equally spaced in the east–west direction with a spacing of 10 grid points. The length of the legs in the north–south direction is 900 points ($\approx 3$ km, which is comparable to the length of the flight path of the $\text{ M }^{2}\text{ AV }$ during both campaigns).

From the temperature datasets we created space-time series representing data from several virtual aircrafts (VA) flying in the north–south direction with different ground speeds ($u_\mathrm {gr,VA}\approx 4.7, 5.5, 6.6, 8.3, 11.0, 16.6, 33.1$, infinite (Inf) $~\mathrm {m~s}^{-1}$) through the temperature field. The spatial separation (3.3 m = 1 data point) within these temperature series (900 data points in total) is equal for each flight, but the temporal separation within the dataset varies (from 0.7 s for $u_\mathrm {gr,VA}=$ 4.73$~\mathrm {m~s}^{-1}$ to 0.1 s for $u_\mathrm {gr,VA}\approx 33.1$ $~\mathrm {m~s}^{-1}$). Along each of the 158 north–south lines, 300 virtual aircraft flights were simulated for different starting times, which gives a total of 47400 virtual aircraft flights. A simulation of a virtual aircraft that flies at a lower speed covers a longer period than a virtual aircraft that flies at a higher speed. Because we wanted to sample the same turbulent field, the separation in time ($\varDelta _{t_\mathrm {VA}}$) between the individual flights was chosen such that the 300 flights were evenly distributed in time over the 15 min. Consequently, $\varDelta _{t_\mathrm {VA}}$ is 0.5, 0.8, 1.1, 1.4, 1.7, 2.0 s, respectively.

Moreover, we used a temporal temperature series corresponding to the data of a virtual sonic (VS) installed at 300 different locations along the path ($y, \varDelta _{y_\mathrm {VS}}=9.94$ m) at every north–south line (in total 47400 virtual sonics). These series cover the same time window of 15 min as the virtual aircraft flights, i.e., 9000 data points. The temperature series for calculating ${C_{T}^2}_{\mathrm {VS}}$ is longer than the series for calculating ${C_{T}^2}_{\mathrm {VA}}$ (900 points) with respect to the number of data points. However, in the context of turbulent scales 15 min corresponds to roughly 1500 m of spatial data (taking into account a mean wind speed of 1.7 $~\mathrm {m~s}^{-1}$), which is smaller than the 3 km used in the case of the virtual aircraft.

The conversion of the structure function obtained from the time series (in the case of the virtual sonics) or space-time series (in the case of the virtual aircraft) into the spatial structure function was done following Bosveld (1999) using Eq. 5 of Braam et al. (2012a). The first step in this conversion consists of the application of Taylor’s hypothesis to account for advection of the turbulent field by the mean wind (in the case of the virtual sonic) or the true air speed (in the case of the virtual aircraft). This step is identical to what is done in the analysis of the $\text{ M }^{2}\text{ AV }$ and sonic data (see Sects. 2.2 and 2.3). The second step consists of a correction for the variation in the advection due to turbulence, identical to what is used for the sonic data (see Sect. 2.3). This correction is only significant for the virtual sonic and the slow virtual aircraft. To determine the correction factor for the virtual sonic, we used the variance of the wind vector ($\sigma _u^2 = \sigma _v^2 =$1.8 $~\mathrm {m~s}^{-1}$ and $\sigma _w^2 = 0.7$ $~\mathrm {m~s}^{-1}$) as well as the mean wind speed (1.7 $~\mathrm {m~s}^{-1}$) at a height of 50 m. The correction factor for the structure function derived from the virtual aircraft data is again based on the variance of the wind vector, but now in combination with the true air speed of the virtual aircraft. Consequently, the correction factor is (1 / 1.23) for the virtual sonic and it varies from (1 / 1.02) ($u_\mathrm {air,VA}\approx 5.3$) up to (1 / 1.00) ($u_\mathrm {air,VA}\approx 33.5$) for the virtual aircraft. From these spatial structure functions, we calculated ${C_{T}^2}_{\mathrm {VS}}$ and ${C_{T}^2}_{\mathrm {VA}}$ at a separation distance ($\varDelta$) of 10 m.

In the end, we calculated for each flight speed the mean value of ${C_{T}^2}_{\mathrm {VA}}$ from the 47,400 virtual flights, and the mean ${C_{T}^2}_{\mathrm {VS}}$ from the 47,400 virtual sonics. Moreover, in order to investigate if the dependence of this mean ${C_{T}^2}_{}$ on the speed of the aircraft is not a statistical artefact, we calculated the uncertainty in the mean ${C_{T}^2}_{}$ as $\varDelta _{{C_{T}^2}_{}}=2\sigma ({C_{T}^2}_{})/\sqrt{n_{\mathrm {indep}}}$, in which $n_{\mathrm {indep}}$ is the number of independent samples. For $n_{\mathrm {indep}}$ we took a rough estimate assuming that the turbulent structures at 50-m height above the surface have a size of the order of 50 m, and a time scale of $\approx$30 s (assuming a wind speed of 1.7 $~\mathrm {m~s}^{-1}$). With a domain size of 5300 m in the east–west direction, a length of the flight legs of 3000 m in the north–south direction and duration of the experiment of 900 s, $n_{\mathrm {indep}}$ is estimated to be $\tfrac{5300}{50} \tfrac{900}{30}\approx 3180$ for the virtual aircraft and $\tfrac{5300}{50} \tfrac{3000}{50}\approx 6360$ for the virtual sonics.

3 Research Strategy

This study consists of four parts, in which we use linear least square regressions forced through the origin abbreviated as LLSRO. With LLSRO we evaluate the slope (a), the coefficient of determination ($r^2$) and the coefficient of variation of the root-mean-square deviation (abbreviated as CV). The coefficient of determination is a measure of the strength of the correlation, and CV indicates how much each point deviates from the 1:1-line on average. For the comparison of the results from the LAS data and the sonic data, and for the evaluation of the different data processing methods of the LAS data, we analyze the data obtained on the flight days between 0500 UTC and 1800 UTC (local summer time is UTC + 2 h). Furthermore, we mainly focus on ${C_{T}^2}_{50\mathrm {m}}$, i.e. ${C_{T}^2}_{}$ normalized to 50-m height (see Sect. 4.1.1). To simplify notation, we remove the subscript 50 m hereafter. For example, ${C_{T}^2}_{\mathrm {LAS43m}}$ refers to the 50-m normalized structure parameter obtained from the LAS with $z_{\mathrm {eff}} = 43$ m.

Table 2 Overview of the options used for the elaborate data processing in this study

In part 1 (Sect. 4.1) we answer our first research question and compare ${C_{T}^2}_{}$ obtained with the LAS and $\text{ M }^{2}\text{ AV }$ for all the days. For this, we calculate ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ as follows (see also Table 2): ${C_{T}^2}_{\mathrm {LAS}}$ is not corrected for saturation, it is corrected for humidity using Eq. 12 of M03, and it is averaged over 10 min. ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ is calculated directly over the entire leg, using the method as proposed by vdK12.

In part 2 (Sects. 4.2, 4.3) we focus on the third research question: the impact on ${C_{T}^2}_{}$ of applying different options from the elaborate data processing list (see Sect. 1). The ${C_{T}^2}_{}$ obtained with the different options as suggested above are therefore compared to each other. In this part we evaluate the LAS (part 2a) and $\text{ M }^{2}\text{ AV }$ (part 2b) separately.

The weather conditions differed between LITFASS-2009 and LITFASS-2010, which may have an effect on the corrections. Therefore, we analyze the two experiments separately. During LITFASS-2009 conditions were moister than for LITFASS-2010; the noontime Bowen ratio (determined with the EC system data at 50 m and averaged between 1000 and 1500 UTC) is 0.8 for LITFASS-2009 and 3.2 for LITFASS-2010.

In part 3 (Sect. 4.4) we investigate whether the elaborate data processing done in the analysis can reduce and explain the deviations between LAS and $\text{ M }^{2}\text{ AV }$ as found in B12 (research question 2). Finally, in part 4 (Sect. 4.5) we focus on answering our last research question based on the additional sensitivity analysis using LES data.

4 Results and Discussion

4.1 Part 1: Comparison of ${C_{T}^2}_{}$ for All Flight Days

The bottom panel of Fig. 2 shows the daytime evolution of ${C_{T}^2}_{}$ obtained with the various instruments during the days where the $\text{ M }^{2}\text{ AV }$ flew the line profile or the scintillometer profile at $z < 110$ m.

Fig. 2

The daytime evolution of ${C_{T}^2}_{\mathrm {LAS43m}}$ (solid black line), ${C_{T}^2}_{\mathrm {LAS63m}}$ (dashed black line), ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ (blue circles), ${C_{T}^2}_{\mathrm {sonic50m}}$ (solid green line), and ${C_{T}^2}_{\mathrm {sonic90m}}$ (dashed green line) during the flight days of the LITFASS-2009 and LITFASS-2010 experiments. All data shown are normalized to 50 m, see Sect. 3 and Table 2 for the applied methods and corrections to obtain ${C_{T}^2}_{}$. The top panel shows the normalized differences ($ND_{\mathrm {M}^2\mathrm {AV,LAS}}$, see Eq. 6) between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ and ${C_{T}^2}_{}$ obtained with the other instruments for each leg (black times $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$ and green triangle $ND_{\mathrm {M}^2\mathrm {AV,sonic}}$) and their daily averaged value (black lines $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$, and green lines $ND_{\mathrm {M}^2\mathrm {AV,sonic}}$)

4.1.1 Validation of the Height Normalization (Item a)

We first evaluate the method to normalize ${C_{T}^2}_{}$ to 50 m, by comparing ${C_{T}^2}_{}$ derived from the LAS data and sonic data at the different observation levels. It can be seen that for both systems the normalized ${C_{T}^2}_{}$ obtained at the two levels are comparable. LLSRO between the normalized ${C_{T}^2}_{}$ obtained at the upper level and lower level gives $a=$ 1.01 and $r^2=$ 0.91 for the two LAS systems, and $a=1.10$ and $r^2=0.69$ for the two sonics. The closer correspondence between ${C_{T}^2}_{}$ at both levels for the LAS as compared to the results of both sonics is probably due to the fact that vertical separation of the two LAS systems is less than that of the sonics and the LAS instruments are centred around 50 m. The largest deviation is found during the evening transition. Separation of the data by stability shows that for unstable conditions ($z/L<0$) $a=0.99$ and $r^2=0.97$ for the LASs, and $a=1.07$ and $r^2=0.75$ for the sonics. For stable conditions ($z/L>0$) $a=1.39$ and $r^2=0.69$ for the LASs, and $a=1.74$ and $r^2=0.58$ for the sonics. These deviations for stable conditions illustrate the limited applicability of MOST at several tens of metres above the ground (see also Braam et al. 2012a). Because most of the flight data were obtained during unstable conditions, we conclude that the method to normalize ${C_{T}^2}_{}$ to 50 m can be applied in the comparison of the ${C_{T}^2}_{}$ derived from the $\text{ M }^{2}\text{ AV }$ data and LAS data.

4.1.2 Comparison of ${C_{T}^2}_{}$ Obtained with LAS, $\text{ M }^{2}\text{ AV }$ and Sonic

Comparing ${C_{T}^2}_{}$ obtained from the three instruments, we observe that ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ is generally higher than ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {sonic}}$. This is also visible in the top panel of Fig. 2, which shows the normalized difference (abbreviated as ND) between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ and ${C_{T}^2}_{}$ of either other instrument (subscript ’other’, either LAS or sonic) defined as,

$$\begin{aligned} ND_{\mathrm {M}^2\mathrm {AV,other}} = \frac{{C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}} -{C_{T}^2}_{\mathrm {other} \overline{z}}}{{C_{T}^2}_{\mathrm {other} \overline{z}}} \end{aligned}$$

(6)

in which, $\hbox {C}_{T\mathrm{other}~\overline{z}}^{2}$ is the average ${C_{T}^2}_{}$ of the normalized values from the two measurement levels.

In general ND values are between zero and two (indicating an overestimation of ${C_{T}^2}_{}$ by the $\text{ M }^{2}\text{ AV }$ data), as also observed in B12 and vdK12. Most of the time $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$ is larger than $ND_{\mathrm {M}^2\mathrm {AV,sonic}}$, especially during LITFASS-2010; for these data ${C_{T}^2}_{\mathrm {LAS}}$ is typically smaller than ${C_{T}^2}_{\mathrm {sonic}}$. From LLSRO between ${C_{T}^2}_{\mathrm {sonic\overline{z}}}$ and ${C_{T}^2}_{\mathrm {LAS\overline{z}}}$, we observe an overestimation of 18 % with $r^2 = 0.49$. The underestimation of the LAS can be explained by the notion that the saturation correction is not applied (this will be discussed in more depth in the next section). Another possible reason for the deviation may be the difference in the footprints of the two instruments. The relatively small value for $r^2$ is attributed to the fact that LAS-derived ${C_{T}^2}_{}$ exhibits a smoother temporal variation than sonic-derived values (Figure 2), caused by the path-averaging of the LAS (Hartogensis et al. 2002).

Despite the general tendency that $ND > 0$ (which implies ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}} >{C_{T}^2}_{\mathrm {other}}$), there are also a few flight legs for which $ND < 0$ (${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}} <{C_{T}^2}_{\mathrm {other}}$). Figure 2 suggests that these situations only occur in the early morning or late afternoon. These exceptions indicate that there may be a physical reason for the overestimation of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ when compared to ${C_{T}^2}_{}$ of the other methods. Therefore, we searched for a relation between ND and different meteorological variables, such as mean wind speed, mean cross wind, wind direction, $R_{Tq}, z/L, \beta$. However, scatter plots between ND and these variables did not give any clear indication of a relation between any of those variables and ND (figures not shown, usually $r^2<0.05$).

In addition, we investigated the dependence of $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$ on the flight level and flight direction (more or less north–south or south–north). However, no clear relationship was found between $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$ and either flight level or flight direction (figures not shown) The flight direction was considered because one possible reason for the overestimation of ${C_{T}^2}_{}$ from the $\text{ M }^{2}\text{ AV }$ could be errors in the temperature measurements due to solar heating of the temperature sensor. In this context it should be noted that the dependency on solar heating of the Vaisala HMP 50 cannot be the reason, because this temperature is only used for the low-frequency range ($<$0.02 Hz), whereas ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ is calculated over a range of scales between 2.5 and 25 m (corresponding to 9.6 and 0.96 Hz, assuming a true air speed of 24 $~\mathrm {m~s}^{-1}$). It cannot can be excluded that the thermocouple showed a dependency on solar heating too, although this is not very likely (see Wildmann et al. 2013).

Finally, additional temperature fluctuations due to intermittent cloudy situations along the flight leg could potentially be a reason for the large values of ND. However, this reason can be discarded, because an overestimation by $\text{ M }^{2}\text{ AV }$ is also observed during LITFASS-2010 that was characterized by cloud-free conditions.

To conclude, we cannot explain the differences in ${C_{T}^2}_{}$ between the instruments by a clear relation to atmospheric conditions or flight parameters. Therefore we investigate whether a more elaborate data processing can reduce and explain the differences.

4.2 Part 2a: Evaluation of the Determination of ${C_{T}^2}_{}$ from LAS Measurements

4.2.1 Saturation Correction (Item b)

The applied saturation correction only depends on the measured ${C_{T}^2}_{}$. The correction factor m is largest if ${C_{T}^2}_{}$ is large. Because ${C_{T}^2}_{}$ decreases with height, the correction has a larger influence on ${C_{T}^2}_{}$ at 43-m than at 63-m data. On average the values of ${C_{T}^2}_{}$ obtained during LITFASS-2009 and LITFASS-2010 are comparable, so the effect of the correction is comparable between the two experiments as well; during LITFASS-2009, m is on average 1.16 for ${C_{T}^2}_{\mathrm {LAS43m}}$, and 1.11 for ${C_{T}^2}_{\mathrm {LAS63m}}$, and during LITFASS-2010, m is 1.17 for ${C_{T}^2}_{\mathrm {LAS43m}}$, and 1.11 for ${C_{T}^2}_{\mathrm {LAS63m}}$.

The saturation correction of ${C_{T}^2}_{\mathrm {LAS}}$ improves the comparison of ${C_{T}^2}_{}$ obtained from the LAS and the sonic. LLSRO between ${C_{T}^2}_{\mathrm {LAS\overline{z}}}$ and ${C_{T}^2}_{\mathrm {sonic\overline{z}}}$ now gives a slope of 1.01 (before it was 1.18), taking both experiments together.

4.2.2 From ${C_{n}^2}_{\mathrm {}}$ to ${C_{T}^2}_{}$—Correction for Humidity Contribution (Item c)

The results regarding the effect on ${C_{T}^2}_{}$ of the various correction methods for the humidity contribution to ${C_{n}^2}_{\mathrm {}}$ are given in Table 3. We choose to focus on the level of 43 m for two reasons. First, methods 1 and 2 could be validated at 43 m only, because a MWS was not available at 63 m. Second, for the last three methods the corrections are identical, because we had to use the data obtained with the sonic at 50 m for the corrections at both levels.

Table 3 Comparison (through LLSRO, $y=ax$) of ${C_{T}^2}_{\mathrm {LAS}}$ corrected for humidity (dependent variable y) relative to uncorrected for humidity (independent variable x) for the WURLAS98006 ($z_{\mathrm {eff}} =43$ m), together with the coefficient of determination ($r^2$) and the coefficient of variation of the root-mean-square deviation (CV)

The table shows that the correction for the humidity contribution to ${C_{n}^2}_{\mathrm {}}$ is larger for LITFASS-2009 (within 10 %) than for LITFASS-2010 (within 3 %), as expected, because the LITFASS-2009 experiment was characterized by more humid conditions. During LITFASS-2009 the noontime Bowen ratio is in the range for which M03 found the highest relative error between methods 3 and 5 ($|\beta |<1$). Note that M03 compared ${C_{T}^2}_{}$ obtained from the three correction methods with the real value based on EC data, whereas we compare it with the uncorrected value from the LAS. As a consequence, the a value we find does reflect the error as given in Fig. 8 of M03. During LITFASS-2009, the deviations between the methods are large. The correction is largest for method 5, and smallest for method 2. The two methods using the LAS-MWS combination (method 1 and 2) give a similar correction. The two methods of M03 based on $R_{Tq}$ are also in this range (method 3 and 4), indicating that the humidity correction should be $\approx$5 % during LITFASS-2009.

During LITFASS-2010, the deviation between the three methods is much smaller, and is to be expected, because under dry conditions ($\beta = 3.15$) the influence of humidity is negligible and the error in the three methods is similar (M03).

We conclude that ${C_{T}^2}_{}$ is underestimated by about 4–5 % for the LITFASS-2009 data using the traditional Bowen ratio method (method 5) as used in the first validation in B12 and in Fig. 2. In Part 3 we will therefore use method 3, because it shows similar results as the methods obtained via the LAS-MWS and it has the smallest error according to M03.

4.2.3 Synchronizing Averaging Times (Item d)

In order to investigate the effect of using a different time window for the LAS data than for the $\text{ M }^{2}\text{ AV }$ data, we determine ${C_{T}^2}_{\mathrm {LAS}}$ exactly over the time intervals of the flights of the $\text{ M }^{2}\text{ AV }$ during LITFASS-2009 from the 500-Hz data available. LLSRO between the ${C_{T}^2}_{\mathrm {LAS\overline{z}}}$ based on the 10-min interval (dependent variable y) compared to ${C_{T}^2}_{\mathrm {LAS\overline{z}}}$ based on the flight interval (independent variable x) gives a slope of 0.97, $r^2=$ 0.83 and $CV=$ 0.21. These results indicate that ${C_{T}^2}_{\mathrm {LAS}}$ changes when averaging at shorter intervals. However, the comparison does not show a clear bias, implying that flight intervals of the $\text{ M }^{2}\text{ AV }$ are not systematically related to intervals with large ${C_{T}^2}_{}$.

4.3 Part 2b: Evaluation of the Determination of ${C_{T}^2}_{}$ from the $\text{ M }^{2}\text{ AV }$ Data

4.3.1 Flight Speed Used to Convert from Temporal to Spatial Structure Function (Item e)

The effect of the choice of either $u_{\mathrm {air}}$ or $u_{\mathrm {gr}}$ for the conversion of temporal to spatial structure function obtained from the $\text{ M }^{2}\text{ AV }$ data was evaluated using ${C_{T}^2}_{}$ derived from the structure function determined over the entire leg, without weighting (${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$). For the dataset under consideration the mean absolute difference in ${C_{T}^2}_{}$ between both methods is 7 % with deviations up to 28 % for specific combinations of wind speed and wind direction. However, as all legs were flown both in the north–south direction and in the south–north direction, the mean bias in ${C_{T}^2}_{}$ is smaller: 4 %, with ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ based on $u_{\mathrm {gr}}$ being larger than ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ based on $u_{\mathrm {air}}$. This difference is roughly consistent with the difference between the all-leg averages of ground speed and true air speed (23.0 $~\mathrm {m~s}^{-1}$ versus 24.1). We conclude that the use of $u_{\mathrm {gr}}$, rather than $u_{\mathrm {air}}$, in B12 has contributed to the observed mean positive bias in ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ relative ${C_{T}^2}_{}$ from the other instruments, although the mean difference between the two approaches is small

The fact that all legs have been flown in two opposite directions (at the same height, close in time) offers the opportunity to investigate whether the use of $u_{\mathrm {air}}$ improves the correspondence between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ from both legs. One would expect the difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ derived from the tail-wind leg and the head-wind leg to be larger when ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ is derived with $u_{\mathrm {gr}}$ than with $u_{\mathrm {air}}$ (as the former does not take into account the motion of the airmass relative to the aircraft). However, the statistical error in ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ derived from individual legs is such that the differences due to the use of either $u_{\mathrm {air}}$ or $u_{\mathrm {gr}}$ are indiscernible ($r^2$ between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ from the head-wind legs and tail-wind legs is only 0.66 and 0.67 for $u_{\mathrm {gr}}$ and $u_{\mathrm {air}}$, respectively).

4.3.2 Different Methods to Calculate ${C_{T}^2}_{}$ (Item f)

Because ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ deviates from the ${C_{T}^2}_{}$ obtained with both other systems, we extensively checked the methodology and its implementation to calculate ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$. Table 4 shows the comparison of the three methods (see Sect. 4.3.2) to calculate ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$, noting that the methods using $D_{TT}$ and the Fourier spectrum give similar results. Both methods are mathematically equivalent if a spectrum with an infinite inertial subrange can be assumed. Apart from the possible invalidity of this assumption differences may occur due to the fact that the $D_{TT}$-based method averaged over a predefined inertial subrange (scales between 5 and 25 m), whereas the Fourier-based method takes all points within the spectrum that pass the check for the $-$5/3 slope. However, the effects of both issues appear to be minimal for the present data.

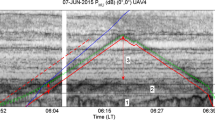
The wavelet method gives lower values, which better corresponds to ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {sonic}}$. Figure 3 shows that in particular the positive excursions from the mean are lower for the wavelet method than for the $D_{TT}$-based method. Further analysis of the wavelet results shows that a reduction of the scale of spatial averaging (now 300 m) leads to larger positive deviations from the mean. However, negative excursions also increase, leading to a leg-mean value of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ that is nearly insensitive to the scale of spatial averaging. To investigate if our particular choice of the wavelet function (Morlet-6) is the reason for the discrepancy between wavelet-derived and structure-function-derived ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ we also tested other wavelet functions. It turns out that the exact level of the inertial subrange (and hence the value of ${C_{T}^2}_{}$) varies with the choice of the wavelet function (e.g. the Paul wavelet with order 4 gives a slope of 0.61).

Because the structure-function method and the Fourier-spectrum method show comparable results, we conclude that the method to obtain ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$, as well as its implementation, cannot explain the higher values of ${C_{T}^2}_{}$ derived from $\text{ M }^{2}\text{ AV }$ data when compared to those from the other instruments. Therefore, in the following paragraphs we determine ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ using the structure-function method as we need a method that provides a spatially explicit ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$.

Table 4 Comparison (through LLSRO, $y=ax$) of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ calculated using a Fourier spectrum or wavelet spectrum (dependent variable y) relative to ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ calculated using the structure function over the entire leg (independent variable x), together with the coefficient of determination ($r^2$) and the coefficient of variation of the root-mean-square deviation (CV)

Fig. 3

The variation of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ along the scintillometer path during one leg (flown on July 11 2010), for the structure function method (black lines) and for the wavelet method (grey lines). Together with the averaged values along the leg: constant-weighted (dotted horizontal line, $W(x)=c$), applying the path-weighting function (solid horizontal line, W(x) from LAS), and calculated over the leg as a whole via the structure function (dashed line)

Table 5 Comparison (through LLSRO, $y = ax$) of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ (dependent variable) calculated from the spatial series along the path evenly weighted ($W(x)=c$) or applying the path-weighting function (W(x) from LAS) relative to ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ calculated over the leg as a whole (independent variable x), together with the coefficient of determination ($r^2$) and the coefficient of variation of the root-mean-square deviation (CV)

4.3.3 Applying the LAS Path-Weighting Function (Item g)

Here, we evaluate the effect of applying the LAS path-weighting function on the leg-mean structure parameter derived from $\text{ M }^{2}\text{ AV }$ data. The determination of a mean ${C_{T}^2}_{}$ weighted with the LAS path-weighting function (${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)LAS }}}$) entails two steps. First a local estimate of ${C_{T}^2}_{}$ is needed. As described in Sect. 2.2.1, this local estimate at each location along the leg is obtained by determining ${C_{T}^2}_{}$ from the 300 m of data surrounding that point (i.e. with a moving window). Subsequently, the weighting function is applied to each local estimate.

As a result, differences between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ derived from an entire leg (${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$, as discussed in the previous section) and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ determined from the local ${C_{T}^2}_{}$ combined with the weighting function can be due to (a combination of) two effects: a difference between global and local ${C_{T}^2}_{}$, and the shape of the weighting function. Therefore, we first compare the ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ obtained over the entire leg (${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$) with ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ obtained as the average of local values of ${C_{T}^2}_{}$ (i.e. with constant weighting, ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$, first line in Table 5). In both cases ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ is determined with the same method (via $D_{TT}$) and uses exactly the same data. Therefore we expect the same values from both methods. However, for both LITFASS-2009 and LITFASS-2010 we observe that ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$ is larger than ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$. There are three possible reasons for this deviation:

• 1. calculating $D_{TT}$ from a smaller dataset ($\approx$300 m instead of $\approx$3000 m, in case of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$) leads to a larger random error in the individual local estimates, relative to ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$;

• 2. calculating $D_{TT}$ from a smaller dataset implies that at the edges of each sub sample (300 m) the temperature observations are taken into account only once (via $T_i$ or $T_{i-\varDelta i}$): the importance of this edge effect increases with increasing separation $\varDelta i$;

• 3. applying the moving window implies that in the averaged ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$ temperature fluctuations ($[T_i-T_{i-\varDelta i}]$) in the centre of the entire leg are more frequently considered than those at the borders. Consequently, turbulence at the borders of the leg has less influence on ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$.

Although the first reason affects the local ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$, it is not expected that the mean over the entire leg will be affected consistently. The second and third arguments can only lead to a consistent difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$ if parts of the leg that are more frequently sampled in each flight consistently show higher or lower temperature fluctuations. Hence, the second and third arguments can only play a role when variations in ${C_{T}^2}_{}$ along the path are tied to heterogeneity of the land surface. Note that the deviation due to the second reason vanishes if one first obtains a dataset of the temperature deviations ($T'=[T_i-T_{i-\varDelta i}]$) and then determines $D_{TT}$ using a moving window over this new series. However, we choose to be consistent with vdK12, and determine $D_{TT}$ using a moving window over the original temperature series.

Fig. 4

Schematic land-use map for the area surrounding the scintillometer path. The three fields dominating the signal of the scintillometer are indicated as far as fields overlapped between 2009 and 2010. The underlying map shows the land use in 2009 (where the fill patterns ($\backslash \backslash$, $//$, and =) correspond to the patterns used in the 3 land use types shown in green). For 2009 land use of the fields was: barley (1), triticale (2), and maize (3). For 2010 the land use of the fields was colza (1), maize (2) and barley (3). Adapted from Beyrich et al. (2012)

Applying the path-weighting function of the LAS (${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x) LAS}}}$, second line in Table 5) gives higher values of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ for LITFASS-2009 and lower values for LITFASS-2010. This indicates that surface heterogeneity can play a role, as the contribution of ${C_{T}^2}_{}$ in the centre of the path is enhanced by the path-weighting function (see Fig. 4). During LITFASS-2009, the vegetation at the border of the path near Falkenberg was maize that was actively transpiring, whereas in the centre of the path triticale (in the south) and barley (in the north) were grown, both being senescent. Above barley and triticale the daily averaged ${C_{T}^2}_{}$ was larger than above maize (see B12), which results in a net increase in ${C_{T}^2}_{}$ when applying the LAS path-weighting function W(x) in the spatial averaging.

In contrast, during LITFASS-2010, the field at the southern border near Falkenberg was planted with barley. The vegetation at the two centre fields was maize (in the south) and colza (in the north). Because LITFASS-2010 took place in July as well, we can assume that barley and colza were both dry and senescent, while the maize was actively transpiring. Consequently, ${C_{T}^2}_{}$ decreases when applying the LAS path-weighting function.

Now we return to the difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$. If this difference is due to surface heterogeneity in combination with an undersampling of the edges of the path, one would expect that the ratio ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$ ${\big /}$ ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x) LAS}}}$ ${\big /}$ ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ would change in the same direction between the two campaigns. This is, however, not the case. Hence, the difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x) =c}}}$ is probably not related to the undersampling of the edges of the path (option 3 in the list above), leaving the second option as the possible reason for the difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x) =c}}}$ (still related to surface heterogeneity).

In order to investigate if ${C_{T}^2}_{}$ calculated from $D_{TT}$ based on a moving window can be used to study the effect of surface heterogeneity on ${C_{T}^2}_{}$ (as done in vdK12), we compare the spatial series of ${C_{T}^2}_{}$ using this method with the wavelet method (Fig. 3). We already observed that the averaged values of the wavelet method were lower, so we focus now on the spatial pattern of both methods. Figure 3 shows that the spatial pattern of the two methods is similar. This means that, while for both methods the average value differs, they can both be used to indicate the relative effect of surface heterogeneities on ${C_{T}^2}_{}$ along a leg, which was the main goal of vdK12. In order to remove time variations, vdK12 normalized the spatial series of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ with ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ over the entire leg. Note that for the latter ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$ should have been used, because of the differences between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\,EL}}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV\, W(x)=c }}}$.

Another issue is the question as to whether the path-weighting function should be applied before or after the height normalization. The differences between these two options turn out to be less than 1 %. Applying the height normalization first requires spatial information of the flight level, which is not available for a number of legs where the height above the surface was not well measured. Therefore, we applied the path-weighting function first in our analysis. Note that even for legs that would be flown at a constant height above the surface both methods would give slightly different values due to the non-linearity of the height normalization.

4.4 Part 3: Effect of the Elaborate Data Processing

Here we investigate if the differences between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ and ${C_{T}^2}_{\mathrm {LAS}}$ can be reduced or explained by applying the more elaborate data processing. The effect on ${C_{T}^2}_{}$ is shown in Fig. 5.

Fig. 5

The daytime evolution of ${C_{T}^2}_{\mathrm {LAS43m}}$ (solid black line), ${C_{T}^2}_{\mathrm {LAS63m}}$ (dashed black line), ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ (blue circles), ${C_{T}^2}_{\mathrm {sonic50m}}$ (solid green line), and ${C_{T}^2}_{\mathrm {sonic90m}}$ (dashed green line) during the flight days of LITFASS-2009 and LITFASS-2010 experiments after applying the more elaborate data processing (see Sect. 3 and Table 2 for the applied methods and corrections to obtain ${C_{T}^2}_{}$). The black symbols represents ${C_{T}^2}_{\mathrm {LAS}}$ during the flight legs (times is ${C_{T}^2}_{\mathrm {LAS43m}}$ and open circle is ${C_{T}^2}_{\mathrm {LAS63m}}$). The top panel shows the normalized difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ and the other instruments for each leg (black times $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$ and green triangle $ND_{\mathrm {M}^2\mathrm {AV,sonic}}$, in which $ND_{\mathrm {M}^2\mathrm {AV,other}} = \left( {C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}} -{C_{T}^2}_{\mathrm {other} \overline{z}} \right) /{C_{T}^2}_{\mathrm {other} \overline{z}}$) and the daily averaged value (black lines $ND_{\mathrm {M}^2\mathrm {AV,LAS}}$ and green lines $ND_{\mathrm {M}^2\mathrm {AV,sonic}}$)

Here we determine ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ as follows: ${C_{T}^2}_{\mathrm {LAS}}$ is corrected for saturation, it is corrected for humidity using Eq. 8 of M03, and it is either averaged over 10 min (LITFASS-2010) or averaged over the time window during the flight legs (LITFASS-2009). ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ is calculated via $D_{TT}$ (item f), using $u_{\mathrm {air}}$ to convert from a temporal to a spatial structure function (e), and applying the path-weighting function (item g). As already expected from the results of the analysis of Sect. 4.2 and Sect. 4.3 the normalized difference between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ and ${C_{T}^2}_\mathrm{other}$ decreases, but is still substantial in most cases.

Applying the two corrections for the LAS improves the correlation between the sonic and LAS. Now, LLSRO between ${C_{T}^2}_{\mathrm {LAS\overline{z}}}$ and ${C_{T}^2}_{\mathrm {sonic\overline{z}}}$ has a slope of 1.01 with $r^2 = 0.47$, taking data from both experiments together. The slope of 1.01 indicates that ${C_{T}^2}_{}$ does not show systematic deviations for these datasets, although the footprints of the two instruments differ (footprint for a point observation versus footprint for a line observation). It is therefore unlikely that the reason for the observed differences between LAS and $\text{ M }^{2}\text{ AV }$ is the fact that the $\text{ M }^{2}\text{ AV }$ legs covered only the southern 70 % of the LAS path and missed the village of Lindenberg.

With respect to the effect of exact synchronization of the estimates from LAS and $\text{ M }^{2}\text{ AV }$ (for LITFASS-2009 only), we refer to our conclusion in Sect. 4.2.3: the time intervals of the $\text{ M }^{2}\text{ AV }$ are not systematically related to the time intervals with large values of ${C_{T}^2}_{\mathrm {LAS}}$ and hence cannot explain the differences between the two instruments.

Fig. 6

Mean ${C_{T}^2}_{\mathrm {VS}}$ and ${C_{T}^2}_{\mathrm {VA}}$ derived from LES for different true air speeds of virtual flights along the LAS path, the red line indicates the ground speed of the $\text{ M }^{2}\text{ AV }$ for comparison. Top the upper segment of the bar charts of the bottom plot, where the error bar indicates the 95 % confidence interval. The right axis shows the normalized differences between virtual aircraft (VA) and the virtual sonic (VS) ($ND_{\mathrm {VA,VS}}=\tfrac{{C_{T}^2}_{\mathrm {VA}} -{C_{T}^2}_{\mathrm {VS}} }{{C_{T}^2}_{\mathrm {VS}} }$). Bottom The full range of ${C_{T}^2}_{}$ where the dashed lines indicate the extent of the ${C_{T}^2}_{}$ axis of the top graph

4.5 Part 4: Analysis of the Effect of Flight Speed on ${C_{T}^2}_{}$ in LES

Here we analyze the influence of the mean ground speed (and resulting true air speed) on the determination of ${C_{T}^2}_{}$ using the additional sensitivity analysis based on LES data. The bottom plot of Fig. 6 shows the mean of the 47400 ${C_{T}^2}_{\mathrm {VS}}$ and ${C_{T}^2}_{\mathrm {VA}}$ for the different true air speeds. At first sight it seems that the ${C_{T}^2}_{}$ is relatively independent of the true air speed. However, when zooming in to the top segment of the bar charts (see top plot of Fig. 6) a small dependence on the true air speed is found. An increase in the true air speed results in a decrease of ${C_{T}^2}_{}$. The normalized difference between virtual aircraft and virtual sonic ($ND=\tfrac{{C_{T}^2}_{\mathrm {VA}} -{C_{T}^2}_{\mathrm {VS}} }{{C_{T}^2}_{\mathrm {VS}} }$) is smaller than $-0.05$ for all true air speeds. This is much smaller than the differences observed in the data ($ND_{\mathrm {M}^2\mathrm {AV,sonic}}$, Fig. 5), which are $>$1 during noon on many days. The small difference in the LES is not a statistical artefact, however, as the error bar (indicating the 95 % confidence interval) is smaller than the differences in ${C_{T}^2}_{}$ with different true air speeds. Moreover, the small decrease of ${C_{T}^2}_{}$ between the virtual aircraft and the virtual sonic is in a direction opposite to the discrepancy found during LITFASS-2009 and LITFASS-2010. The non-monotonous differences between the virtual sonic and the two slowest virtual aircraft is statistically insignificant.

5 Conclusions and Outlook

We have presented an elaborate comparison of the structure parameter of temperature, ${C_{T}^2}_{}$, from two LAS systems, the $\text{ M }^{2}\text{ AV }$, and two sonic anemometers during the LITFASS-2009 and LITFASS-2010 experiments. It is an extension of the preliminary results presented in Beyrich et al. (2012), who found that the ${C_{T}^2}_{}$ obtained with $\text{ M }^{2}\text{ AV }$ is higher than ${C_{T}^2}_{}$ from the LAS for one flight day when data from the LAS and $\text{ M }^{2}\text{ AV }$ were processed using standard procedures.

We conclude that for the other measurement days during LITFASS-2009 and LITFASS-2010 similar differences can be found. ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ overestimates both ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {sonic}}$. A more elaborate data analysis improved the agreement between ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {sonic}}$, but did not substantially improve the agreement of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ with either ${C_{T}^2}_{\mathrm {LAS}}$ or ${C_{T}^2}_{\mathrm {sonic}}$.

Furthermore, from the more elaborate data analysis we determine that

• it is important to apply the saturation correction for the LAS at 43 and 63 m along the 5-km scintillometer path between Falkenberg and Lindenberg,

• during the LITFASS-experiments the correction for humidity should be performed based on the correlation between T and q and the standard deviation of T and q (method 3). The use of the Bowen ratio method underestimates the true ${C_{T}^2}_{}$ during LITFASS-2009, which agrees with the study of M03,

• calculating ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ with structure functions or the Fourier spectrum gives similar results, whereas the wavelet method gives lower ${C_{T}^2}_{}$, which might be related to the choice of the wavelet function,

• using the leg-mean true air speed rather than the mean ground speed in converting the temporal data of the $\text{ M }^{2}\text{ AV }$ to spatial data can have a significant impact on the ${C_{T}^2}_{}$ derived for individual legs (up to 20 %); however, the mean bias associated with the use of the ground speed is smaller (4 % for our data), provided that head-wind legs and tail-wind legs are equally present in the dataset.

• ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ obtained from the structure function determined over the leg as a whole slightly differs from the leg-averaged value obtained from a spatial series of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ determined over sections of the leg and using a moving window,

• the spatial pattern of ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ along the leg is consistent between the structure function method and the wavelet method,

• whether or not the LAS weighting function is applied to the $\text{ M }^{2}\text{ AV }$ data has a significant impact on the leg-mean ${C_{T}^2}_{}$ due to heterogeneity of the surface fluxes.

A sensitivity study regarding the effect of the mean ground speed (and related true air speed) on ${C_{T}^2}_{}$ was performed using data from a LES. We found that ${C_{T}^2}_{}$ depends slightly on the true air speed of an aircraft, but that the variation is smaller than 5 % when comparing ${C_{T}^2}_{}$ as obtained from a virtual sonic and from a aircraft with an infinite speed. We found that the structure parameter decreases for increasing flight speed. As the dependency is both small and in a direction opposite to the observed discrepancies in ${C_{T}^2}_{}$, we conclude that the simultaneous variation in time and space within the dataset of the $\text{ M }^{2}\text{ AV }$ data cannot be the reason for the discrepancy between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ and ${C_{T}^2}_{\mathrm {sonic}}$.

Finally, we have to conclude that the deviations between ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ on the one hand, and ${C_{T}^2}_{\mathrm {LAS}}$ and ${C_{T}^2}_{\mathrm {sonic}}$ on the other hand, cannot be explained so far. Therefore, we recommend further experimental studies. A useful modification of the measurement strategy for any new experiment is to use multiple unmanned aircraft flying synchronously along the scintillometer path, in order to obtain statistical information on ${C_{T}^2}_{\mathrm {M}^2{\mathrm {AV}}}$ as well. An additional point of attention in the determination of structure parameters from aircraft data is the in-leg variation of the true air speed as it will influence the relative presence of updrafts and downdrafts in the total time series (e.g. the increased head wind associated with a downdraft will slow down the aircraft). This calls for an analysis similar to that performed by Martin and Bange (2014) for fluxes.