1 Introduction

In this work, we are going to examine surface coupled multiphysics problems that are inspired by fluid-structure interaction (FSI) problems [24]. We couple the heat equation with the wave equation through an interface, where the typical FSI coupling conditions or Dirichlet-Neumann type act. Despite its simplicity, each of the subproblems exhibits different temporal dynamics which is also found in FSI. The solution of the heat equation, as a parabolic problem, manifests smoothing properties. Thus, it can be characterized as a problem with slow temporal dynamics. The wave equation, on the other hand, is an example of a hyperbolic equation with highly oscillatory properties.

FSI problems are characterized by two specific difficulties: the coupling of an equation of parabolic type with one of hyperbolic type gives rise to regularity problems at the interface. Further, the added mass effect [6] is present for problems coupling materials of a similar density which calls for strongly coupled discretization and solution schemes. This is the monolithic approach for modeling FSI, in contrast to partitioned approaches, where each of the subproblems is treated and solved as a separate system. The monolithic approach allows for a more rigorous mathematical setting and the use of large time-steps. The partitioned approach allows using fully optimized separate techniques for both of the subproblems. Most realizations for FSI, such as the technique described here, have to be regarded as a blend of both philosophies: while the formulation and discretization are monolithic, ideas of partitioned approaches are borrowed for solving the algebraic problems.

Since FSI problems feature distinct time scales in the two subproblems the use of multirate time-stepping schemes with adapted step sizes for fluid and solid is obvious. For parabolic problems, the concept of multirate time-stepping was discussed in [4, 9, 17]. In the hyperbolic setting, it was considered in [3, 7, 8, 23]. In the context of fluid-structure interactions, such subcycling methods are used in aeroelasticity [22]. There, explicit time integration schemes are used for the flow problem and implicit schemes for the solid problem [10]. In the low Reynolds number regime, common in hemodynamics, the situation is different. Here, implicit and strongly coupled schemes are required by the added mass effect. Hence, large time steps can be applied for the flow problem, but smaller time-steps might be required within the solid. A study on benchmark problems in fluid dynamics (Schäfer, Turek ’96 [26]) and FSI presented in [18] shows that FSI problems demand a much smaller step size. However, the problem configuration and the resulting nonstationary dynamics are very similar to oscillating solutions with nearly the same period [25].

We will derive a monolithic variational formulation for FSI like problems that can handle different time-step sizes in the two subproblems. Implicit coupling of two problems with different step sizes will give rise to very large systems where multiple states must be solved at once. In Sect. 3 we will study different approaches for an efficient solution of these coupled systems, a simple partitioned relaxation scheme and a shooting like approach.

Next, in Sect. 4 we present a posteriori error estimators based on the dual weighted residual method [2] for automatically identifying optimal step sizes for the two subproblems. Numerical studies on the efficiency of the time adaptation procedure are presented in Sect. 5.

2 Presentation of the model problem

Let us consider the time interval \(I=[0, T]\) and two rectangular domains

$$\begin{aligned} \varOmega ^f :=(0,4) \times (0,1), \quad \varOmega ^s :=(0,4)\times (0, -1) \end{aligned}$$

The interface is defined as \(\varGamma :=\overline{\varOmega }^f \cap \overline{\varOmega }^s=(0,4)\times \{0\}\) and the remaining boundaries are shown in Fig. 1. Since our example might be treated as a simplified case of an FSI problem, in the text we will use the corresponding nomenclature. We will refer to the domain \(\varOmega ^f\) as the fluid domain and the problem defined there as the fluid problem. Similarly, we will use solid domain and solid problem phrases. In this sense, the superscript “f” will always refer to entities connected to the fluid problem and “s” denotes the solid problem.

Fig. 1
figure 1

View of the domain \(\varOmega =(0,4)\times (-1,1)\) split into fluid \(\varOmega ^f\) and solid \(\varOmega ^s\) along the common interface \(\varGamma \). On the outer boundary, homogenous Dirichlet values are given on \(\varGamma _D^f\) and \(\varGamma _D^s\), whereas Neumann conditions are set on \(\varGamma _N^f\) and \(\varGamma _N^s\)

Full size image

In the domain \(\varOmega ^f\) we pose the heat equation

$$\begin{aligned} \partial _t v^f - \nu \varDelta v^f + \beta \cdot \nabla v^f = g^f \quad \text { in }I\times \varOmega ^f, \end{aligned}$$
(2.1)

and in the domain \(\varOmega ^s\) we set the wave equation

$$\begin{aligned} \partial _t v^s - \lambda \varDelta u^s - \delta \varDelta v^s = g^s, \quad \partial _t u^s = v^s \quad \text { in } I \times \varOmega ^s, \end{aligned}$$
(2.2)

written as a first order system. By \(v^f\) and \(v^s\) we denote the velocities of fluid and solid and by \(u^s\) the solid’s displacement. \(\nu >0\) is heat diffusion parameter, \(\sqrt{\lambda }\) is the wave propagation speed and \(\delta \ge ~0\) a damping parameter. By \(\beta \in \mathbb {R}^2\) we introduce a transport direction. The two problems are coupled on the interface \(\varGamma \) by the transmission conditions

$$\begin{aligned} v^f=v^s,\quad \lambda \partial _{\mathbf {n}_s}u^s+\nu \partial _{\mathbf {n}_f}v^f=0 \quad \text { on }I\times \varGamma \end{aligned}$$
(2.3)

which are similar to the kinematic and dynamic coupling conditions from fluid-structure interactions, compare [24, Sec. 3.1]. We use symbols \(\mathbf {n}_f\) and \(\mathbf {n}_s\) to distinguish between normal vectors for different space domains. On the interface it holds \(\mathbf {n}_f=-\mathbf {n}_s\). To mimic the similarity to fluid-structure interaction formulations in Arbitrary Eulerian Lagrangian (ALE) coordinates, see [12], we harmonically extend the solid deformation \(u^s\) to the fluid domain where we call it \(u^f\)

$$\begin{aligned} -\varDelta u^f = 0\text { in }I\times \varOmega ^f,\quad u^f=u^s \quad \text { on }I\times \varGamma . \end{aligned}$$
(2.4)

Usually, this artificial deformation defines the ALE domain map used to transfer the fluid problem to ALE coordinates, see [24, Sec. 5.3.5]. In the fluid domain, the left and right boundaries model free inflow and outflow, whereas the upper boundary models a no-slip condition. In the solid domain, the left and right boundary model a fixed solid, whereas the solid is free to move on the lower boundary, resulting in

$$\begin{aligned} \begin{aligned} u^f=v^f=0&\quad \text { on }I\times \varGamma _{D}^f,\quad&\partial _{\mathbf {n}_f}v^f=\partial _{\mathbf {n}_f}u^f&=0\quad \text { on }I\times \varGamma _N^f\\ u^s=v^s=0&\quad \text { on }I\times \varGamma _{D}^s,\quad&\lambda \partial _{\mathbf {n}_s}u^f +\delta \partial _{\mathbf {n}_s}v^s&=0\quad \text { on }I\times \varGamma _N^s.\\ \end{aligned} \end{aligned}$$
(2.5)

At time \(t=0\), all initial values are zero, i.e. \(u^f(0)=u^s(0)=v^f(0)=v^s(0)=0\). The exact values of the parameters read as

$$\begin{aligned} \nu = 0.001,\quad \beta = \left( \begin{matrix} 2 \\ 0 \end{matrix}\right) ,\quad \lambda = 1000,\quad \delta = 0.1, \end{aligned}$$

and they are chosen similar to the configuration of the fluid-structure interaction benchmark problems by Hron and Turek [18], to resemble a similar coupling structure. However, we consider a softer “solid”. The external forces are set to be products of functions of space and time \({g^f(\mathbf {x},t):=h^f(\mathbf {x})f(t)}\) and \({g^s(\mathbf {x},t):=h^s(\mathbf {x})f(t)}\) where \(h^f(\mathbf {x})\), \(h^s(\mathbf {x})\) are space components and f(t) is a time component which models a periodic pulse

$$\begin{aligned} f(t) = {\left\{ \begin{array}{ll} 1&{} z\le t\le z+0.1\\ 0&{} z+0.1< t\le z+1, \end{array}\right. }\quad \forall z\in \mathbb {Z}.\\ \end{aligned}$$

We will consider two different configurations of the right hand side. In Configuration 2.1, the right hand side is concentrated in \(\varOmega ^f\) where the space component consists of an exponential function centered around \(\left( \frac{1}{2}, \frac{1}{2} \right) \). For Configuration 2.2 we take a space component concentrated in \(\varOmega ^s\) with an exponential function centered around \(\left( \frac{1}{2}, -\frac{1}{2} \right) \).

Configuration 2.1

$$\begin{aligned} h^f(\mathbf {x}):=&\quad e^{-\left( (x_1 - \frac{1}{2})^2 + (x_2 - \frac{1}{2})^2\right) }, \quad h^s(\mathbf {x}):=0, \quad \end{aligned}$$

Configuration 2.2

$$\begin{aligned} h^f(\mathbf {x}):=&\quad 0,\quad h^s(\mathbf {x}):=e^{-\left( (x_1 - \frac{1}{2})^2 + (x_2 + \frac{1}{2})^2\right) }. \end{aligned}$$

2.1 Continuous variational formulation

By \(H^1(\varOmega )\) we denote the space of \(L^2\)-functions with the first weak derivative in \(L^2(\varOmega )\). To incorporate the Dirichlet boundary conditions on parts of the boundary into trial and test spaces we further define

$$\begin{aligned} H^1_0(\varOmega ; \varUpsilon ) = \left\{ v \in H^1(\varOmega )|\; v_{|\varUpsilon } = 0 \right\} , \end{aligned}$$

where \(H^{-1}(\varOmega )=H^1_0(\varOmega ;\varUpsilon )^*\) is the dual space. To incorporate the Dirichlet data in the fluid domain we introduce \(V^f:=H^1_0(\varOmega ^f;\varGamma _D^f)\) and, in the case of the solid domain, \(V^s:=H^1_0(\varOmega ^s;\varGamma _D^s)\). In the space-time domain \(I\times \varOmega \) we define the family of Hilbert spaces

$$\begin{aligned} X(V) = \left\{ v \in L^2(I, V) |\; \partial _t v \in L^2(I, V^*) \right\} . \end{aligned}$$

For the fluid problem it will hold \((v^f,u^f)\in X^f:=\big (X(V^f)\big )^2\) and for the solid \((v^s,u^s)\in X^s:=\big (X(V^s)\big )^2\).

For any given domain G, which can take the place of the entire domain \(\varOmega \), the fluid domain \(\varOmega ^f\) or the solid domain \(\varOmega ^s\) we denote by \((u,v)_G:=\int _G u\cdot v\,\text {d}x\) the usual \(L^2\)-inner product. Given an element of the dual space \(f\in H^{-1}(G)\), we denote by \(\langle f,\phi \rangle _{H^{-1}(G)\times H^1(\varOmega )}=f(\phi )\) the duality pairing. For \(f\in H^{-\frac{1}{2}}(\varGamma )\) we denote by

$$\begin{aligned} \langle f,\phi \rangle _\varGamma :=\langle f,\phi \rangle _{H^{-\frac{1}{2}}(\varGamma )\times H^{\frac{1}{2}}(\varGamma )}=f(\phi ) \end{aligned}$$

the duality pairing on the interface. Finally, we introduce the abbreviations \((\cdot ,\cdot )_f:=(\cdot ,\cdot )_{\varOmega _f}\) and \(\langle \cdot ,\cdot \rangle _f :=\langle \cdot ,\cdot \rangle _{H^{-1}(\varOmega ^f)\times H^1(\varOmega ^f)}\) as well as the corresponding notation within the solid domain \(\varOmega ^s\).

We acquire the continuous variational formulation by multiplication of (2.1) and (2.4). Afterwards, we integrate in space and time using (2.5). The trial function is given by \(\mathbf {U} = (\mathbf {U}^f, \mathbf {U}^s) \in X :=X^f \times X^s\), which is further split to \(\mathbf {U}^f = (v^f, u^f)\) and \(\mathbf {U}^s = (v^s, u^s)\). Similarly, we set the test function as \(\varvec{\varPhi } = (\varvec{\varPhi }^f, \varvec{\varPhi }^s)\) and split it to \(\varvec{\varPhi }^f = (\varphi ^f, \psi ^f)\) and \(\varvec{\varPhi }^s = (\varphi ^s, \psi ^s)\). Given that, we define the space-time variational forms

$$\begin{aligned} B^f(\mathbf {U})(\varvec{\varPhi }^f) :=&\int _I \langle \partial _t v^f, \varphi ^f \rangle _f \mathop {}\!\mathrm {d}t + \int _I a^f(\mathbf {U})(\varvec{\varPhi }^f) \mathop {}\!\mathrm {d}t + (v^f(0), \varphi ^f(0))_f, \end{aligned}$$
(2.6a)
$$\begin{aligned} B^s(\mathbf {U})(\varvec{\varPhi }^s) :=&\int _I \langle \partial _t v^s, \varphi ^s \rangle _s \mathop {}\!\mathrm {d}t + \int _I \langle \partial _t u^s, \psi ^s \rangle _s \mathop {}\!\mathrm {d}t + \int _I a^s(\mathbf {U})(\varvec{\varPhi }^s) \mathop {}\!\mathrm {d}t \nonumber \\&\qquad + (v^s(0), \varphi ^s(0))_s + (u^s(0), \psi ^s(0))_s, \\ F^f(\varvec{\varPhi }^f) :=&\int _I ( g^f, \varphi ^f )_f \mathop {}\!\mathrm {d}t, \nonumber \\ F^s(\varvec{\varPhi }^s) :=&\int _I ( g^s, \varphi ^s )_s \mathop {}\!\mathrm {d}t \nonumber \end{aligned}$$
(2.6b)

with

$$\begin{aligned} a^f(\mathbf {U})(\varvec{\varPhi }^f) :=&\, (\nu \nabla v^f, \nabla \varphi ^f)_f + (\beta \cdot \nabla v^f, \varphi ^f)_f + (\nabla u^f, \nabla \psi ^f )_f \nonumber \\&- \langle \partial _{\mathbf {n}_f} u^f, \psi ^f \rangle _{\varGamma } + \frac{\gamma }{h}\langle u^f-u^s, \psi ^f \rangle _{\varGamma }\nonumber \\&- \langle \nu \partial _{\mathbf {n}_f} v^f, \varphi ^f \rangle _{\varGamma } + \frac{\gamma }{h} \langle \nu (v^f-v^s), \varphi ^f \rangle _{\varGamma }, \end{aligned}$$
(2.7a)
$$\begin{aligned} a^s(\mathbf {U}) (\varvec{\varPhi }^s) :=&\, (\lambda \nabla u^s, \nabla \varphi ^s)_s + (\delta \nabla v^s, \nabla \varphi ^s)_s - (v^s, \psi ^s )_s \nonumber \\&+ \langle \nu \partial _{\mathbf {n}_f} v^f, \varphi ^s \rangle _{\varGamma } - \langle \delta \partial _{\mathbf {n}_s} v^s, \varphi ^s \rangle _{\varGamma }. \end{aligned}$$
(2.7b)

All the Laplacian terms were integrated by parts and the dynamic coupling condition was added. The kinematic coupling condition was incorporated into the fluid problem, while the dynamic condition became a part of the solid problem. The Dirichlet boundary conditions over the interface \(\varGamma \) were formulated in a weak sense using Nitsche’s method [21]. The parameter \(\gamma \) can be seen as a penalization parameter enforcing \(u^f=u^s\) and \(v^f=v^s\) weakly. The parameter \(\gamma >0\) should be large enough to counter-balance different constants, like the one from the inverse estimate. We set \(\gamma = 10\), while h is the mesh size. Too small values for \(\gamma \) might cause a discrepancy from the Dirichlet condition, too large values worsen the conditioning of the resulting system. We refer to [5] for the analysis of a full fluid-structure interaction system with Nitsche coupling on the interface.

The compact version of the variational problem presents itself as:

Problem 2.1

Find \(\mathbf {U} \in X\) such that

$$\begin{aligned}&B^f(\mathbf {U})(\varvec{\varPhi }^f) = F^f(\varvec{\varPhi }^f) \\&B^s(\mathbf {U})(\varvec{\varPhi }^s) = F^s(\varvec{\varPhi }^s) \end{aligned}$$

for all \(\varvec{\varPhi }^f \in X^f \) and \(\varvec{\varPhi }^s \in X^s\).

This coupled heat-wave system carries some similarities to fluid-structure interactions [24] in terms of the parabolic / hyperbolic type of the equations and also in the set of interface coupling conditions of Dirichlet / Neuman type. It can be considered as a further simplification of a linear fluid-structure interaction system coupling the Stokes equations with the Navier-Lame equations, which has been extensively studied [1, 13, 14]. Here, the existence and regularity of the solution is shown, compare [16] for an overview of the results. Zhang and Zuazua [29] analyze the long time behavior of the coupled scalar heat and wave system, similar to our set of equations. However, as further simplification, our model problem contains a strong damping term within the heat equation. Given a sufficiently smooth domain, e.g. \(C^2\)-parametrizable or convex polygonal boundary, right hand side \(g^f,g^s\) in \(L^2\) and initial values \(u^s\in H^1(\varOmega ^s)\) and \(v^s\in L^2(\varOmega ^s)\), \(v^f\in L^2(\varOmega ^s)\), \(v^f \in L^2(\varOmega ^f)\), the solution has at least the regularity \(v^f\in L^2(I,H^1(\varOmega ^f))\) and \(u^s\in W^{1,\infty }(I,H^1(\varOmega ^s))\).

2.2 Semi-discrete Petrov–Galerkin formulation

One of the main challenges emerging from the discretization of Problem 2.1 is the construction of a satisfactory time interval partitioning. Our main objectives include:

  1. 1.

    Allowing for different time-step sizes (possibly non-uniform) in both subproblems

    We introduce two distinct subdivisions \(I^f\) and \(I^s\) of the interface \(I=[0,T]\)

    $$\begin{aligned} 0=t_0^f<t_1^f<\dots< t_{N^f}^f=T,\quad 0=t_0^s<t_1^s<\dots < t_{N^s}^s=T. \end{aligned}$$

    with \(N^f,N^s\in \mathbb {N}\). We will refer to these meshes as micro time meshes and we will denote them by \(I^f\) and \(I^s\), respectively. Their step sizes \(k_n^f:=t_n^f-t_{n-1}^f\) and \(k_n^s:=t_n^s-t_{n-1}^s\) can be non-uniform and fluid- and solid-steps do not have to match.

  2. 2.

    Handling coupling conditions

    Based on the micro partitionings \(I^f\) and \(I^s\) we introduce the coarse time mesh of the interval \(I=[0, T]\) that consists of all discrete points in time which are shared by both of the subproblems, i.e.

    $$\begin{aligned} 0 = t_0< t_1< ... < t_N = T, \end{aligned}$$

    with \(N\le \min \{N^f,N^s\}\). For each \(n=0\dots ,N\) there exist two indices \(i\in \{0,\dots ,N^f\}\) and \(j\in \{0,\dots N^s\}\) such that \(t_n=t_i^f=t_j^s\). We will refer to this mesh as the macro time mesh and denote it by \(I_N\).

In practice, this mesh structure is generated in a top-down design: we start with a shared macro mesh \(I^f=I^s=I_N\) and generate finer meshes by successive refinement of the single steps. After each refinement cycle we identify common nodes \(t_i^f=t_j^s\) to generate the new macro mesh. We define the grid sizes as:

$$\begin{aligned} k^f :=\max _{n = 1,\ldots ,N^f} k_n^f,\quad k^s :=\max _{n = 1,\ldots ,N^s} k_n^s,\quad k:=\max \{k^f, k^s \}. \end{aligned}$$

Figure 2 visualizes this construction.

Fig. 2
figure 2

Visualization of the temporal mesh: macro mesh with steps \(t_{n-1}, t_n\) and \(t_{n+1}\) and subdivision into two distinct partitionings for fluid and solid, \(t_i^f\) and \(t_j^s\), respectively

Full size image

As trial spaces, we choose functions that are continuous in time on the complete interval \(I=[0,T]\) and piecewise linear on the subdivisions. In space, they take values in the corresponding Sobolev spaces \(V^f\) and \(V^s\) which have been introduced above:

$$\begin{aligned} X^{f, 1}_k&={} \big \{ v \in C(\bar{I}, L^2(\varOmega ^{f}))|\; v|_{(t_{n-1}^f,t_{n}^f]} \in \mathcal{P}_1(V^{f}) \text { for all } n=1,\dots ,N^f\big \},\\ X^{s, 1}_k&={} \big \{ v \in C(\bar{I}, L^2(\varOmega ^{s}))|\; v|_{(t_{n-1}^s,t_{n}^s]} \in \mathcal{P}_1(V^{s}) \text { for all } n=1,\dots ,N^s\big \}. \end{aligned}$$

We set \(X^f_k :=\big (X^{f, 1}_k\big )^2\) and \(X^s_k :=\big (X^{s, 1}_k\big )^2\). The test spaces \(Y_k^f\) and \(Y_k^s\) are defined likewise, however, these functions are not necessarily continuous on \(I=[0,T]\) and they are piecewise constant on each of the micro steps

$$\begin{aligned} Y^{f, 0}_k =&\big \{ v \in L^2(\bar{I}, L^2(\varOmega ^{f}))|\; v|_{(t_{n-1}^f,t_n^f]} \in \mathcal{P}_0(V^{f}) \text { for all } n=1,\dots ,N^f\big \},\\ Y^{s, 0}_k =&\big \{ v \in L^2(\bar{I}, L^2(\varOmega ^{s}))|\; v|_{(t_{n-1}^s,t_{n}^s]} \in \mathcal{P}_0(V^{s}) \text { for all } n=1,\dots ,N^s\big \}. \end{aligned}$$

with \(Y^f_k :=\big (Y^{f, 0}_k\big )^2\) and \(Y^s_k :=\big (Y^{s, 0}_k\big )^2\). By \(\mathcal {P}_r(H)\) we denote the space of piecewise polynomials with degree r and values in H.

With that at hand, we can pose a semi-discrete variational problem:

Problem 2.2

Find \(\mathbf {U}_k \in X_k:=X_k^f\times X_k^s\) such that:

$$\begin{aligned} B^f(\mathbf {U}_k)(\varvec{\varPhi }^f_k)&= F^f(\varvec{\varPhi }_k^f)\\ B^s(\mathbf {U}_k)(\varvec{\varPhi }^s_k)&= F^s(\varvec{\varPhi }^s_k) \end{aligned}$$

for all \(\varvec{\varPhi }^f_k \in Y_{k}^f\) and \(\varvec{\varPhi }^s_k \in Y_{k}^s\).

Since the operators \(B^f\) and \(B^s\) are linear, the resulting scheme is equivalent to the Crank-Nicolson scheme up to the numerical quadrature of the right hand sides \(F^f\) and \(F^s\), see also [15, 28]. Operator \(B^f\) depends on the solid solution \((v^s_k,u^s_k)\) and, vice versa the solid operator \(B^s\) depends on the fluid solution \(v^f_k\), see (2.6a), (2.7a) and (2.6b), (2.7b). Hence, we have to integrate discrete (so, piecewise linear or piecewise constant) functions from the one micro mesh on the other. To be precise, on the macro step \(I_n=(t_{n-1},t_n]\) it will be necessary to evaluate integrals which couple functions on both discrete and non-matching meshes, like

$$\begin{aligned} \int _{t_{n-1}}^{t_n} \langle \nu \partial _{\mathbf {n}_f} v^f,\varphi ^s\rangle _\varGamma . \end{aligned}$$
(2.8)

This will ask for a costly interpolation of the fluid velocity \(v^f\) to the solid mesh on each macro step, compare Fig. 2. To simplify this coupling, we will transfer discrete functions by means of a simple interpolation into the space of linear functions on the macro mesh, i.e. for \(v\in X_k^f\) or \(v\in X_k^s\) we define

$$\begin{aligned} t\in (t_{n-1},t_n]\qquad I_k v(t) :=\frac{t_n-t}{k_n} v(t_{n-1}) +\frac{t-t_{n-1}}{k_n} v(t_n) \end{aligned}$$
(2.9)

which can be easily evaluated on both submeshes. Hereby, (2.8) is approximated by

$$\begin{aligned} \int _{t_{n-1}}^{t_n} \langle \nu \partial _{\mathbf {n}_f} v^f,\varphi ^s\rangle _\varGamma \approx \int _{t_{n-1}}^{t_n} \langle \nu \partial _{\mathbf {n}_f} I_k v^f,\varphi ^s\rangle _\varGamma . \end{aligned}$$
(2.10)

3 Decoupling methods

Even though Problem 2.2 is discretized in time, it is still coupled across the interface. That makes solving the subproblems independently impossible. To deal with this obstacle, we chose to use an iterative approach on each of the subintervals \(I_n\) and introduce decoupling strategies. Throughout this section, we only consider the semi-discrete problem. Hence, for better readability, we will skip the index “k”. For a fixed time interval \(I_n\) the i-th iteration of a decoupling method consists of the following steps:

  1. 1.

    Using the solution of the solid subproblem from the previous iteration \(\mathbf {U}^{s,(i - 1)}\), we set the boundary conditions on the interface at the time \(t_n\), solve the fluid problem and get the solution \(\mathbf {U}^{f,(i)}\).

  2. 2.

    Similarly, we use the solution \(\mathbf {U}^{f,(i)}\) for setting the boundary conditions of the solid problem and obtain an intermediate solution \(\widetilde{\mathbf{U}}^{s,(i)}\).

  3. 3.

    We apply a decoupling function to the intermediate solution \(\widetilde{\mathbf {U}}^{s,(i)}\) and acquire \(\mathbf {U}^{s,(i)}\).

This procedure is visualized by

$$\begin{aligned} \mathbf {U}^{s,(i - 1)} \xrightarrow [\text {subproblem}]{\text {fluid}} \mathbf {U}^{f,(i)} \xrightarrow [\text {subproblem}]{\text {solid}} \widetilde{\mathbf {U}}^{s,(i)} \xrightarrow [\text {function}]{\text {decoupling}} \mathbf {U}^{s,(i)}. \end{aligned}$$

The main challenge emerges from the transition between \(\widetilde{\mathbf {U}}^{s,(i)}\) and \(\mathbf {U}^{s,(i)}\). In the next subsections, we will present two techniques. The first one is the relaxation method described in Sect. 3.1. The second one, in Sect. 3.2, is the shooting method. We clarify how the intermediate solution \(\widetilde{\mathbf {U}}^{s,(i)}\) is obtained from \(\mathbf {U}^{s,(i - 1)}\) by the definition of Problem 3.1.

Problem 3.1

For a given \(\mathbf {U}^{s,(i - 1)} \in X^s_k\), find \(\mathbf {U}^{f,(i)} \in X^f_k\) and \(\widetilde{\mathbf {U}}^{s,(i)} \in X^s_k\) such that:

$$\begin{aligned} B^f_n&\left( \begin{array}{l} \mathbf {U}^{f,(i)} \\ \mathbf {U}^{s,(i - 1)} \end{array}\right) (\varvec{\varPhi }^f) = F^f_n(\varvec{\varPhi }^f) \\ B^s_n&\left( \begin{array}{l} \mathbf {U}^{f,(i)} \\ \widetilde{\mathbf {U}}^{s,(i)} \end{array}\right) (\varvec{\varPhi }^s) = F^s_n(\varvec{\varPhi }^s) \end{aligned}$$

for all \(\varvec{\varPhi }^f \in Y_{k}^f\) and \(\varvec{\varPhi }^s \in Y_{k}^s\). By \(B^f_n\) and \(B^s_n\) we denote restrictions of forms \(B^f\) and \(B^s\) to \(I_n\). Forms \(F^f_n\) and \(F^s_n\) are defined accordingly.

3.1 Relaxation method

The first of the presented methods consists of a simple interpolation operator being an example of a fixed point method. It contains the iterated solution of each of the two subproblems, taking the interface values from the last iteration of the other problem. For reasons of stability, such explicit partitioned iteration usually requires the introduction of a damping parameter. Here, we only consider fixed damping parameters.

Definition 3.1

(Relaxation Function) Let \(\mathbf {U}^{s,(i -1)} \in X^s_k\) and \(\widetilde{\mathbf {U}}^{s,(i)} \in X^s_k\) be the solid solution of Problem 3.1. Then for \(\tau \in [0, 1]\) the relaxation function \(R: X^s_k \rightarrow X^s_k\) is defined as:

$$\begin{aligned} R(\mathbf {U}^{s,(i -1)}):=\tau \widetilde{\mathbf {U}}^{s,(i)} + (1 - \tau )\mathbf {U}^{s,(i -1)} \end{aligned}$$

Assuming that we already know the value \(\mathbf {U}^s(t_{n -1})\), we pose

$$\begin{aligned} \mathbf {U}^{s,(0)}(t_n):=\mathbf {U}^s(t_{n - 1}),\qquad \mathbf {U}^{s,(i)}(t_n):=R(\mathbf {U}^{s,(i-1)})(t_n)\text { for }i=1,2,\dots . \end{aligned}$$

The stopping criterion is based on checking how far the computed solution is from the fixed point. We evaluate the \(L^{\infty }\) norm on the interface degrees of freedom. If for a given tolerance \(tol>0\) we have \(\Vert \widetilde{\mathbf {U}}^{s,(i + 1)}(t_n) - \mathbf {U}^{s,(i)}(t_n)\Vert _{L^\infty (\varGamma )}<tol\), we stop the iteration and accept the last approximation.

3.2 Shooting method

Here we present another iterative method where we define a root-finding problem on the interface. We use the Newton method with a matrix-free GMRES method for approximation of the inverse of the Jacobian.

Definition 3.2

(Shooting Function) Let \(\mathbf {U}^{s,(i -1)} \in X^s_k\) and \(\widetilde{\mathbf {U}}^{s,(i)} \in X^s_k\) be the solid solution of Problem 3.1. Then the shooting function \(S: X^s_k \rightarrow (L^2(\varGamma ))^2\) is defined as:

$$\begin{aligned} S(\mathbf {U}^{s,(i -1)}):=\left( \mathbf {U}^{s,(i - 1)}(t_n) - \widetilde{\mathbf {U}}^{s,(i)}(t_n) \right) \Big |_{\varGamma } \end{aligned}$$
(3.1)

We aim to find the root of function (3.1). To do so, we employ the Netwon method

$$\begin{aligned} S'(\mathbf {U}^{s,(i - 1)})\mathbf {d}^{(i)} = -S(\mathbf {U}^{s,(i - 1)}). \end{aligned}$$

In each iteration of the Newton method, the greatest difficulty causes computing and inverting the Jacobian \(S'(\mathbf {U}^{s,(i - 1)})\). Instead of approximating all entries of the Jacobian matrix, we consider an approximation of the matrix-vector product only. Since the Jacobian matrix-vector product can be interpreted as a directional derivative, one can assume

$$\begin{aligned} S'(\mathbf {U}^{s,(i - 1)})\mathbf {d}^{(i)} \approx \frac{S(\mathbf {U}^{s,(i - 1)} + \varepsilon \mathbf {d}^{(i)} ) - S(\mathbf {U}^{s,(i - 1)} )}{\varepsilon }. \end{aligned}$$
(3.2)

In principle, the vector \(\mathbf {d}^{(i)}\) is not known. Thus, the formula above can not be used for solving the system directly. However, it is possible to use this technique with iterative solvers which only require the computation of matrix-vector products. Because we did not want to assume much structure of the operator (3.2), we chose the matrix-free GMRES method. Such matrix-free Newton-Krylov methods are frequently used if the Jacobian is not available or too costly for evaluation [19]. Once \(\mathbf {d}^{(i)}\) is computed, we set

$$\begin{aligned} \mathbf {U}^{s,(0)}(t_n)\big |_{\varGamma }: = \mathbf {U}^s(t_{n - 1})\big |_{\varGamma },\qquad \mathbf {U}^{s,(i)}(t_n)\big |_{\varGamma }:=\mathbf {U}^{s,(i - 1)}(t_n)\big |_{\varGamma } + \mathbf {d}^{(i)}\text { for }i=1,2,\dots \end{aligned}$$

Here, we stop iterating when the \(L^{\infty }\) norm of \(S(\mathbf {U}^{s,(i)})\) is sufficiently small and then we accept the last available approximation.

We note that the method presented here is similar to the one presented in [11], where the authors also introduced a root-finding problem on the interface and solved it with a quasi-Newton method. The main difference lies in the approximation of the inverse of the Jacobian. Instead of using a matrix-free linear solver, there the Jacobian is approximated by solving a least-squares problem.

3.3 Numerical comparison of the performance

Fig. 3
figure 3

Performance of decoupling methods for Configuration 2.1 in one macro time-step in the case of \(N^f = N^s = N\) (top), \(N^f = 10N\) and \(N^s = N\) (left), \(N^f = N\) and \(N^s = 10N\) (right)

Full size image
Fig. 4
figure 4

Performance of decoupling methods for Configuration 2.2 in one macro time-step in the case of \(N^f = N^s = N\) (top), \(N^f = 10N\) and \(N^s = N\) (left), \(N^f = N\) and \(N^s = 10N\) (right)

Full size image

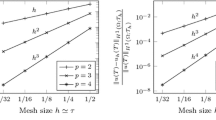
In Figs. 3 and 4 we present the comparison of the performance of both methods based on the number of micro time-steps. We assumed that both micro and macro time-steps have uniform sizes. We performed the simulations in the case of no micro time-stepping (\(N^f = N^s = N\)), micro time-stepping in the fluid subdomain (\(N^f = 10N\), \(N^s = N\)) and the solid subdomain (\(N^f = N\), \(N^s = 10N\)). Figure 3 shows results for the right hand side according to Configuration 2.1. Figure 4 corresponds to Configuration 2.2. We investigated one macro time-step \(I_2 = [0.02, 0.04]\). We set the relaxation parameter to \(\tau = 0.7\). Both methods are very robust concerning the number of micro time-steps. The relaxation method, as expected, has a linear convergence rate. In both cases, despite the nested GMRES method, the performance of the shooting method is much better. For Configuration 2.1, the relaxation method needs 13 iterations to converge. The shooting method needs only 2 iterations of the Newton method (which is the reason why each of the graphs in Fig. 3 displays only two evaluations of the error) and overall requires 6 evaluations of the decoupling function. In the case of Configuration 2.2, both methods need more iterations to reach the same level of accuracy. The number of iterations of the relaxation method increases to 20 while the shooting method needs 3 iterations of the Newton method and 11 evaluations of the decoupling function.

Fig. 5
figure 5

Number of evaluations of the decoupling functions for Configuration 2.1 needed for convergence on the time interval \(I = [0, 1]\) for \(N = 50\) in the case of \(N^f = N^s = N\) (top), \(N^f = 10N\) and \(N^s = N\) (left), \(N^f = N\) and \(N^s = 10N\) (right)

Full size image
Fig. 6
figure 6

Number of evaluations of the decoupling functions for Configuration 2.2 needed for convergence on the time interval \(I = [0, 1]\) for \(N = 50\) in the case of \(N^f = N^s = N\) (top), \(N^f = 10N\) and \(N^s = N\) (left), \(N^f = N\) and \(N^s = 10N\) (right)

Full size image

In Figs. 5 and 6 we show the number of evaluations of the decoupling function needed to reach the stopping criteria throughout the complete time interval \(I = [0, 1]\) for \(N = 50\). Similarly, we performed the simulations in the case of no micro time-stepping, micro time-stepping in the fluid and the solid subdomain. We considered both Configuration 2.1 and 2.2. In the case of Configuration 2.1, the number of evaluations of the decoupling function using the relaxation method varied between 14 and 15. For the shooting function, this value was mostly equal to 6 with a few exceptions when only 5 evaluations were needed. For Configuration 2.2, the relaxation method needed between 18 and 21 iterations while for the shooting method it was almost always equal to 11. For each configuration, graphs corresponding to no micro time-stepping and micro time-stepping in the fluid subdomain are the same, while introducing micro time-stepping in the solid subdomain resulted in slight variations. For both decoupling methods, the independence of the performance from the number of micro time-steps extends to the whole time interval \(I=[0,1]\).

4 Goal oriented estimation

In Section 1 we formulated the semi-discrete problem enabling usage of different time-step sizes in fluid and solid subdomains, whereas in Section 2 we presented methods designed to efficiently solve such problems. However, so far the choice of the step sizes was purely arbitrary. In this section, we are going to present an easily localized error estimator, which can be used as a criterion for the adaptive choice of the time-step size.

For the construction of the error estimator, we used the dual weighted residual (DWR) method [2]. Given a differentiable goal functional \(J: X \rightarrow \mathbb {R}\), our aim is finding a way to approximate \(J(\mathbf {U}) - J(\mathbf {U}_k)\), where \(\mathbf {U}\) is the exact solution (Problem 2.1) and \(\mathbf {U}_k\) is the semi-discrete solution (Problem 2.2). The goal functional is split into two parts \(J^f: X^f \rightarrow \mathbb {R}\) and \(J^s:X^s \rightarrow \mathbb {R}\) which refer to the fluid and solid subdomains, respectively

$$\begin{aligned} J(\mathbf {U}): = J^f(\mathbf {U}^f) + J^s(\mathbf {U}^s). \end{aligned}$$

The DWR method is based on the following constrained optimization problem

$$\begin{aligned} J(\mathbf {U}) = \min !\quad \text { such that }\quad B(\mathbf {U})(\varvec{\varPhi }) = F(\varvec{\varPhi }) \text { for all }\varvec{\varPhi } \in X, \end{aligned}$$

where

$$\begin{aligned} B(\mathbf {U})(\varvec{\varPhi })&:=B^f(\mathbf {U})(\varvec{\varPhi }^f) + B^s(\mathbf {U})(\varvec{\varPhi }^s), \\ F(\varvec{\varPhi })&:=F^f(\varvec{\varPhi }^f) + F^s(\varvec{\varPhi }^s). \end{aligned}$$

Solving this problem corresponds to finding stationary points of a Lagrangian \(\mathcal {L}\)

$$\begin{aligned} \mathcal {L}(\mathbf {U}, \mathbf {Z}): = J(\mathbf {U}) + F(\mathbf {Z}) - B(\mathbf {U})(\mathbf {Z}). \end{aligned}$$

Because form B describes a linear problem, finding stationary points of \(\mathcal {L}\) is equivalent to solving the following problem:

Problem 4.1

For a given \(\mathbf {U} \in X\) being the solution of Problem 2.1, find \(\mathbf {Z} \in X\) such that:

$$\begin{aligned} B(\varvec{\varPsi }, \mathbf {Z}) = J'_{\mathbf {U}}(\varvec{\varPsi }) \end{aligned}$$

for all \(\varvec{\varPsi } \in X\).

The solution \(\mathbf {Z}\) is called an adjoint solution. By \(J'_{\mathbf {U}}(\varvec{\varPsi })\) we denote the Gateaux derivative of \(J(\cdot )\) at \(\mathbf {U}\) in direction of the test function \(\varvec{\varPsi }\).

4.1 Adjoint problem

4.1.1 Continuous variational formulation

As the first step in decoupling the Problem 4.1, we would like to split the form B into forms corresponding to fluid and solid subproblems. However, we can not fully reuse the forms (2.7a) and (2.7b) because of the interface terms—the forms have to be sorted regarding test functions. The adjoint solution is written as \(\mathbf {Z}=(\mathbf {Z}^f,\mathbf {Z}^s)\), each split to \(\mathbf {Z}^f=(z^f,y^f) \in X^f\) and \(\mathbf {Z}^s=(z^s,y^s) \in X^s\). Likewise, for the test function, we set \(\varvec{\varPsi }=(\varvec{\varPsi }^f,\varvec{\varPsi }^s)\) with \(\varvec{\varPsi }^f=(\eta ^f, \xi ^f) \in X^f\) and \(\varvec{\varPsi }^s=(\eta ^s, \xi ^s) \in X^s\). Then we introduce the adjoint forms, sorted by the test functions

$$\begin{aligned} B(\varvec{\varPsi })(\mathbf {Z}):=\widetilde{B}^f(\varvec{\varPsi }^f)(\mathbf {Z}) + \widetilde{B}^s(\varvec{\varPsi }^s)(\mathbf {Z}), \end{aligned}$$

we have

$$\begin{aligned} \widetilde{B}^f(\varvec{\varPsi }^f)(\mathbf {Z}) :=&- \int _I \langle \partial _t z^f,\eta ^f\rangle _f \mathop {}\!\mathrm {d}t + \int _I \widetilde{a}^f(\varvec{\varPsi }^f)(\mathbf {Z}) \mathop {}\!\mathrm {d}t + (\eta ^f(T), z^f(T))_f, \\ \widetilde{B}^s(\varvec{\varPsi }^s)(\mathbf {Z}) :=&- \int _I \langle \partial _t z^s ,\eta ^s\rangle _s \mathop {}\!\mathrm {d}t - \int _I \langle \partial _t y^s,\xi ^s \rangle _s \mathop {}\!\mathrm {d}t + \int _I \widetilde{a}^s(\varvec{\varPsi }^s)(\mathbf {Z}) \mathop {}\!\mathrm {d}t\\&\qquad + (\eta ^s(T), z^s(T))_s + (\xi ^s(T), y^s(T))_s \end{aligned}$$

and

$$\begin{aligned} \widetilde{a}^f(\varvec{\varPsi }^f)(\mathbf {Z}) :=&\, (\nu \nabla \eta ^f, \nabla z^f)_f + (\beta \cdot \nabla \eta ^f, z^f)_f + (\nabla \xi ^f, \nabla y^f)_f \\&- \langle \partial _{\mathbf {n}_f} \xi ^f, y^f \rangle _{\varGamma } + \frac{\gamma }{h} \langle \xi ^f, y^f \rangle _{\varGamma } - \langle \nu \partial _{\mathbf {n}_f} \eta ^f, z^f \rangle _{\varGamma } \\&+ \frac{\gamma }{h}\langle \nu \eta ^f, z^f \rangle _{\varGamma } + \langle \nu \partial _{\mathbf {n}_f} \eta ^f, z^s \rangle _{\varGamma }, \\ \widetilde{a}^s (\varvec{\varPsi }^s)(\mathbf {Z}) :=&\, (\lambda \nabla \xi ^s, \nabla z^s)_s + (\delta \nabla \eta ^s, \nabla z^s)_s - (\eta ^s, y^s)_s \\&- \frac{\gamma }{h} \langle \xi ^s, y^f \rangle _{\varGamma } - \frac{\gamma }{h} \langle \nu \eta ^s, z^f \rangle _{\varGamma } - \langle \delta \partial _{\mathbf {n}_s} \eta ^s, z^s \rangle _{\varGamma }. \end{aligned}$$

We have applied integration by parts in time which reveals that the adjoint problem runs backward in time. That leads to the formulation of a continuous adjoint variational problem:

Problem 4.2

For a given \(\mathbf {U} \in X\) being the solution of Problem 2.1, find \(\mathbf {Z} \in X\) such that:

$$\begin{aligned} \begin{aligned} \widetilde{B}^f(\varvec{\varPsi }^f)(\mathbf {Z})&= (J^f)'_{\mathbf {U}}(\varvec{\varPsi }^f) \\ \widetilde{B}^s(\varvec{\varPsi }^s)(\mathbf {Z})&= (J^s)'_{\mathbf {U}}(\varvec{\varPsi }^s) \end{aligned} \end{aligned}$$

for all \(\varvec{\varPsi }^f \in X^f \) and \(\varvec{\varPsi }^s \in X^s \).

4.1.2 Semi-discrete Petrov–Galerkin formulation

The semi-discrete formulation for the adjoint problem is similar to the one of the primal problem. The main difference lies in the fact that this time trial functions are piecewise constant in time \(\mathbf {Z}_k \in Y_k :=Y_k^f \times Y_k^s\), while test functions are piecewise linear in time \(\varvec{\varPsi }^f_k \in X^f_k\), \(\varvec{\varPsi }^s_k \in X^s_k\). With that at our disposal, we can formulate a semi-discrete adjoint variational problem:

Problem 4.3

For a given \(\mathbf {U} \in X\) being the solution of Problem 2.1, find \(\mathbf {Z}_k \in Y_k\) such that:

$$\begin{aligned} \begin{aligned} \widetilde{B}^f(\varvec{\varPsi }^f_k)(\mathbf {Z}_{k})&= (J^f)'_{\mathbf {U}}(\varvec{\varPsi }^f_k), \\ \widetilde{B}^s(\varvec{\varPsi }^s_k)(\mathbf {Z}_k)&= (J^s)'_{\mathbf {U}}(\varvec{\varPsi }^s_k) \end{aligned} \end{aligned}$$

for all \(\varvec{\varPsi }^f_k \in X^f_k\) and \(\varvec{\varPsi }^s_k \in X^s_k\).

After formulating the problem in a semi-discrete manner, the decoupling methods from Sect. 3 can be applied.

4.2 A posteriori error estimate

We define the primal residual, split into parts corresponding to the fluid and solid subproblems

$$\begin{aligned} \rho (\mathbf {U})(\varvec{\varPhi }) :=\rho ^f(\mathbf {U})(\varvec{\varPhi }^f) + \rho ^s(\mathbf {U})(\varvec{\varPhi }^s), \end{aligned}$$

where

$$\begin{aligned} \rho ^{f}(\mathbf {U})(\varvec{\varPhi }^{f})&:=F^{f}(\varvec{\varPhi }^{f}) - B^{f}(\mathbf {U})(\varvec{\varPhi }^{f}), \\ \rho ^{s}(\mathbf {U})(\varvec{\varPhi }^{s})&:=F^{s}(\varvec{\varPhi }^{s}) - B^{s}(\mathbf {U})(\varvec{\varPhi }^{s}). \end{aligned}$$

Similarly, we establish the adjoint residual resulting from the adjoint problem

$$\begin{aligned} \rho ^*(\mathbf {Z})(\varvec{\varPsi }):=\rho ^{f,*}(\mathbf {Z})(\varvec{\varPsi }^f) + \rho ^{s,*}(\mathbf {Z})(\varvec{\varPsi }^s) \end{aligned}$$

with

$$\begin{aligned} \rho ^{f,*}(\mathbf {Z})(\varvec{\varPsi }^{f})&:=(J^{f})'_{\mathbf {U}}(\varvec{\varPsi }^{f}) - \widetilde{B}^{f}(\varvec{\varPsi }^{f})(\mathbf {Z}), \\ \rho ^{s,*}(\mathbf {Z})(\varvec{\varPsi }^{s})&:=(J^{s})'_{\mathbf {U}}(\varvec{\varPsi }^{s}) - \widetilde{B}^{s}(\varvec{\varPsi }^{s})(\mathbf {Z}) \end{aligned}$$

Becker and Rannacher [2] introduced the a posteriori error representation:

$$\begin{aligned} J(\mathbf {U}) - J(\mathbf {U}_k)= & {} \frac{1}{2} \min _{\varvec{\varPhi }_k \in Y_{ k}}\rho (\mathbf {U}_k)(\mathbf {Z} - \varvec{\varPsi }_k) + \frac{1}{2}\min _{\varvec{\varPsi }_k \in X_k}\rho ^*(\mathbf {Z}_k)(\mathbf {U} - \varvec{\varPhi }_k)\nonumber \\&+ \mathcal {O}(|\mathbf {U} - \mathbf {U}_k|^3, |\mathbf {Z} - \mathbf {Z}_k|^3) \end{aligned}$$
(4.3)

This identity can be used to derive an a posteriori error estimate. Two steps of approximation are required: first, the third order remainder is neglected and second, the approximation errors \(\mathbf {Z}-\varvec{\varPsi }_k\) and \(\mathbf {U}-\varvec{\varPhi }_k\), the weights, are replaced by interpolation errors \(\mathbf {Z}-i_k\mathbf {Z}\) and \(\mathbf {U}-i_k \mathbf {U}\). These errors are then replaced by discrete reconstructions, since the exact solutions \(\mathbf {U}, \mathbf {Z}\in X\) are not available. See [20, 27] for a discussion of different reconstruction schemes. Due to these approximation steps, this estimator is not precise and it does not result in rigorous bounds. The estimator consists of a primal and adjoint component. Each of them is split again into a fluid and a solid counterpart

$$\begin{aligned} \sigma _k :=\theta ^{f} + \theta ^{s} + \vartheta ^{f} + \vartheta ^{s}. \end{aligned}$$
(4.4)

The primal estimators are derived from the primal residuals using \(\mathbf {U}_k\) and \(\mathbf {Z}_k\) being the solutions to Problems 2.2 and 4.3, respectively

$$\begin{aligned} \theta ^{f} :=\frac{1}{2} \rho ^f(\mathbf {U}_k)(\mathbf {Z}^{f,(1)}_k - \mathbf {Z}^f_k),\quad \theta ^{s} :=\frac{1}{2} \rho ^s(\mathbf {U}_k)(\mathbf {Z}^{s,(1)}_k - \mathbf {Z}^s_k). \end{aligned}$$

The adjoint reconstructions \(\mathbf {Z}^{f,(1)}_k\) and \(\mathbf {Z}^{s,(1)}_k\) approximating the exact solution are constructed from \(\mathbf {Z}_k\) using linear extrapolation (see Fig. 7, right)

$$\begin{aligned} \mathbf {Z}_{k}^{(1)}(t)\big |_{I_{n}} :=&\frac{t - \bar{t}_{n + 1}}{\bar{t}_{n - 1} - \bar{t}_{n + 1}}\mathbf {Z}_{k}(t_{n - 1}) + \frac{t - \bar{t}_{n - 1}}{\bar{t}_{n + 1} - \bar{t}_{n - 1}}\mathbf {Z}_{k}(t_{n + 1}) \end{aligned}$$

with the interval midpoints \(\bar{t}_{n} :=\frac{t_{n} + t_{n - 1}}{2}\). To simplify the notation, we defined the reconstruction on the macro time-mesh level. However, we use this idea in the same spirit on each of the micro meshes \(I_n^f\) and \(I_n^s\). The adjoint estimators are based on the adjoint residuals

$$\begin{aligned} \vartheta ^{f} :=\frac{1}{2}\rho ^{f,*}(\mathbf {Z}_k)(\mathbf {U}^{f,(2)}_k - \mathbf {U}^f_k), \qquad \vartheta ^{s} :=\frac{1}{2}\rho ^{s,*}(\mathbf {Z}_k)(\mathbf {U}^{s,(2)}_k - \mathbf {U}^s_k). \end{aligned}$$

The primal reconstructions \(\mathbf {U}^{f,(2)}_k\) and \(\mathbf {U}^{s,(2)}_k\) are extracted from \(\mathbf {U}_k\) using quadratic reconstruction (see Fig. 7, left). We perform the reconstruction on the micro time-mesh level on local patches consisting of two neighboring micro time-steps. In general, the patch structure does not have to coincide with the micro and macro time-mesh structure—two micro time-steps being in the same local patch do not have to be in the same macro time-step. Additionally, we demand two micro time-steps from the same local patch to have the same length.

Fig. 7
figure 7

Reconstruction of the primal solution \(\mathbf {U}_{k}^{(2)}\) (left) and the adjoint solution \(\mathbf {Z}_{k}^{(1)}\) (right)

Full size image

We compute the effectivity of the error estimate using

$$\begin{aligned} \text {eff}_k :=\frac{\sigma _k}{J(\mathbf {U}_{\text {exact}}) - J(\mathbf {U}_k)} , \end{aligned}$$

where \(J(\mathbf {U}_{\text {exact}})\) can be approximated by extrapolation in time.

4.3 Adaptivity

The residuals (4.4) can be easily localized by restricting them to a specific subinterval, e.g., the primal fluid-residuals \(\theta ^f\), restricted to \(I_n^f:=[t_{n-1}^f,t_n^f)\) is denoted as \(\theta ^f_{n}\), see Sect. 2.2 and Fig. 2. All further residuals \(\theta ^s,\vartheta ^f\) and \(\vartheta ^s\) are restricted in the same fashion. We then can compute an average for each of the components

$$\begin{aligned} \bar{\sigma }_{k}:=\frac{1}{2N^f} \sum _{n = 1}^{N^f} \left( |\theta ^{f}_{n}| + |\vartheta ^{f}_{n}| \right) + \frac{1}{2N^s} \sum _{n = 1}^{N^s} \left( | \theta ^{s}_{n}| + |\vartheta ^{s}_{n}|\right) . \end{aligned}$$
(4.5)

This way we can obtain satisfactory refining criteria as

$$\begin{aligned} \begin{aligned} \left( \left| \theta ^{f}_{n} \right| \ge \bar{\sigma }_k \text { or } \left| \vartheta ^{f}_{n} \right| \ge \bar{\sigma }_k \right)&\Longrightarrow \text { refine } I^f_{n}=[t_{n-1}^f,t_n^f), \\ \left( \left| \theta ^{s}_{n} \right| \ge \bar{\sigma }_k \text { or } \left| \vartheta ^{s}_{n} \right| \ge \bar{\sigma }_k \right)&\Longrightarrow \text { refine } I^s_{n}=[t_{n-1}^s,t_n^s). \end{aligned} \end{aligned}$$
(4.6)

Taking into account the time interval partitioning structure, we arrive with the following algorithm:

  1. 1.

    Mark subintervals using the refining criteria (4.6).

  2. 2.

    Adjust the local patch structure—in case only one subinterval from a specific patch is marked, mark the other one as well (see Fig. 8).

  3. 3.

    Perform time refining.

  4. 4.

    Adjust the macro time-step structure—in case within one macro time-step there exist a fluid and a solid micro time-step that coincide, split the macro time-step into two macro time-steps at this point (see Fig. 9).

Fig. 8
figure 8

An example of preserving the local patch structure during the marking procedure: if the time-step is refined, the other time-step belonging to the same patch will also be refined

Full size image
Fig. 9
figure 9

An example of a splitting mechanism of macro time-steps. On the left, we show the mesh before refinement: middle (in black) the macro nodes, top (in blue) the fluid nodes and bottom (in red) the solid nodes with subcycling. In the center sketch, we refine the first macro interval once within the fluid domain. Since one node is shared between fluid and solid, we refine the macro mesh to resolve subcycling. This final configuration is shown on the right

Full size image

5 Numerical results

5.1 Fluid subdomain functional

For the first example, we chose to test the derived error estimator on a goal functional concentrated in the fluid subproblem

$$\begin{aligned} J^f(\mathbf {U}):=\int _{0}^T \nu \Vert \nabla v^f\Vert ^2_f\mathop {}\!\mathrm {d}t, \quad J^s(\mathbf {U}) :=0. \end{aligned}$$

The functional is integrated only over the right half of the fluid subdomain, that is \(\widetilde{\varOmega }^f = (2, 4) \times (0, 1)\). For this example, we also took the right hand side concentrated in the fluid subdomain, presented in Configuration 2.1. As the time interval, we choose \(I = [0, 1]\). Then we have

$$\begin{aligned} (J^f)'_{\mathbf {U}}(\varvec{\varPsi }^f) = \int _{0}^T 2\nu \left( \nabla v^f, \nabla \eta ^f\right) _f \mathop {}\!\mathrm {d}t. \end{aligned}$$

Since the functional is nonlinear, we use a 2-point Gaussian quadrature for integration in time. In Table 1 we show the results of the a posteriori error estimator on a sequence of uniform time-meshes. Here, we considered the case without any micro time-stepping, that is the time-step sizes in both fluid and solid subdomains are uniformly equal. That gives a total number of time-steps in the fluid domain equal to \(N^f = N\) and \(N^s = N\) in the solid domain. Table 1 consists of partial residuals \(\theta ^f_k,\theta ^s_k,\vartheta ^f_k\) and \(\vartheta ^s_k\), overall estimate \(\sigma _k\), extrapolated errors \(\widetilde{J}-J(\mathbf {U}_k)\) and effectivities \(\text {eff}_k\). The values of the goal functional on the three finest meshes were used for extrapolation in time. As a result, we got the reference value \(\widetilde{J} = 6.029469 \times 10^{-5}\). Except for the coarsest mesh, the estimator is very accurate and the effectivities are almost 1. On finer meshes, values of \(\theta ^f_k\) and \(\vartheta ^f_k\) are very close to each other which is due to the linearity of the coupled problem [2]. A similar phenomenon happens for \(\theta ^s_k\) and \(\vartheta ^s_k\). The residuals are concentrated in the fluid subdomain, which suggests the usage of smaller time-step sizes in this space domain.

Table 1 Residuals and effectivities for fluid subdomain functional in case of uniform time-stepping in case \(N^f=N^s= N\)
Full size table
Table 2 Residuals and effectivities for fluid subdomain functional in case of uniform time-stepping in case \(N^f = 2N\) and \(N^s = N\)
Full size table
Table 3 Residuals and effectivities for fluid subdomain functional in case of adaptive time-stepping
Full size table

Table 2 collects the results for another sequence of uniform time-meshes. In this case, each of the macro time-steps in the fluid domain is split into two micro time-steps of the same size. That results in \(N^f = 2N\) time-steps in the fluid domain and \(N^s = N\) in the solid domain. The performance is still highly satisfactory. The residuals remain mostly concentrated in the fluid subdomain. Additionally, after comparing Tables 1 and 2, one can see that corresponding values of \(\theta ^f_k\) and \(\vartheta ^f_k\) are the same (value for \(N = 800\) in Table 1 and \(N = 400\) in Table 2, etc.). Overall, introducing micro time-stepping improves performance and reduces extrapolated error \(\widetilde{J} - J(\mathbf {U}_k)\) more efficiently.

In Table 3 we present findings in the case of adaptive time mesh refinement. We chose an initial configuration of uniform time-stepping without micro time-stepping for \(N = 50\) and applied a sequence of adaptive refinements. On every level of refinement, the total number of time-steps is \(N^f + N^s\). One can see that since the error is concentrated in the fluid domain, only time-steps corresponding to this space domain were refined. Again, effectivity gives very good results. The extrapolated error \(\widetilde{J} - J(\mathbf {U}_k)\) is even more efficiently reduced.

5.2 Solid subdomain functional

For the sake of symmetry, for the second example, we chose a functional concentrated on the solid subdomain

$$\begin{aligned} J^f(\mathbf {U}) = 0, \quad J^s(\mathbf {U}) = \int _{0}^T \lambda \Vert \nabla u^s\Vert ^2_s \mathop {}\!\mathrm {d}t. \end{aligned}$$

Also here the functional is integrated only over the right half of the solid subdomain \(\widetilde{\varOmega }^s = (2, 4) \times (-1, 0)\). This time we set the right hand side according to Configuration 2.2. Again, \(\bar{I} = [0, 1]\). The derivative reads as

$$\begin{aligned} (J^s)'_{\mathbf {U}}(\varvec{\varPsi }^s) = \int _{0}^T 2\lambda \left( \nabla u^s, \nabla \xi ^s\right) _s \mathop {}\!\mathrm {d}t. \end{aligned}$$

A third test case with functional evaluations in both domains gave comparable results without additional information, such that we refrain from adding it to this manuscript. Similarly, Table 4 gathers results for a sequence of uniform meshes without any micro time-stepping (\(N^f = N^s = N\)). The last three solutions are used for extrapolation in time which gives \(\widetilde{J} = 3.458826 \times 10^{-4}\). Also for this example, the effectivity is very satisfactory. On the finest discretization, the effectivity slightly declines. This might come from the limited accuracy of the reference value. Once more, on finer meshes, fluid residuals \(\theta ^f_k, \vartheta ^f_k\) and solid residuals \(\theta ^s_k, \vartheta ^s_k\) have similar values. This time, the residuals are concentrated in the solid subdomain and, in this case, the discrepancy is a bit bigger.

Table 4 Residuals and effectivities for solid subdomain functional in case of uniform time-stepping in case \(N^f = N^s = N\)
Full size table

In Table 5 we display outcomes for a sequence of uniform meshes where each of the macro time-steps in the solid subdomain is split into two micro time-steps. That gives \(N + 2N\) time-steps. Introducing micro time-stepping does not have a negative impact on the effectivity and significantly saves computational effort. Corresponding values of \(\theta ^s_k\) and \(\vartheta ^s_k\) in Tables 4 and 5 are almost the same. Residuals remain mostly concentrated in the solid subdomain.

Table 5 Residuals and effectivities for solid subdomain functional in case of uniform time-stepping in case \(N^f = N\) and \(N^s = 2N\)
Full size table
Table 6 Residuals and effectivities for solid subdomain functional in case of adaptive time-stepping
Full size table

Following the fluid example, in Table 6 we show calculation results in the case of adaptive time-mesh refinement. Here as well we took the uniform time-stepping without micro time-stepping for \(N = 50\) as the initial configuration and the total number of time-steps is \(N^f + N^s\). Except for the last entry, only the time-steps corresponding to the solid domain were refined. On the finest mesh, the effectivity deteriorates. However, adaptive time-stepping is still the most effective in reducing the extrapolated error \(\widetilde{J} - J(\mathbf {U}_k)\).

Finally, we show in Fig. 10 a sequence of adaptive meshes that result from this adaptive refinement strategy. In the top row, we show the initial mesh with 50 macro steps and no further splitting in fluid and solid. For a better presentation, we only show a small subset of the temporal interval [0.1, 0.4]. In the middle plot, we show the mesh after 2 steps of adaptive refinement and in the bottom line after 4 steps of adaptive refinement. Each plot shows the macro mesh, the fluid mesh (above) and the solid mesh (below). As expected, this example leads to a sub-cycling within the solid domain. For a finer approximation, the fluid problem also requires some local refinement. Whenever possible we avoid excessive subcycling by refining the macro mesh as described in Sect. 4.3.

Fig. 10
figure 10

Adaptive meshes for the solid functional. Top: uniform initial mesh; middle: 2 steps of adaptive refinement; bottom: 4 steps. Each plot shows the macro mesh (middle), the fluid mesh (top, in blue) and the solid mesh (bottom, in red)

Full size image

6 Conclusion

In this paper, we have developed a multirate scheme and a temporal error estimate for a coupled problem that is inspired by fluid-structure interactions. The two subproblems, the heat equation and the wave equation feature different temporal dynamics. In this example, balanced approximation properties and stability demands ask for different step sizes.

We introduced a monolithic variational Galerkin formulation for the coupled problem and then used a partitioned framework for solving the algebraic systems. Having different time-step sizes for each of the subproblems couples multiple states in each time-step. That would require an enormous computational effort. To solve this, we discussed two different decoupling methods: first, a simple relaxation scheme that alternates between fluid and solid problem. In the second one, similar to the shooting method, we defined a root-finding problem on the interface and used matrix-free Newton-Krylov method for quickly approximating the zero. Both of the methods were able to successfully decouple our specific example and showed good robustness concerning different subcycling of the multirate scheme in fluid- or solid-domain. However, the convergence of the shooting method was faster and it required fewer evaluations of the variational formulation.

As the next step, we introduced a goal-oriented error estimate based on the dual weighted residual method to estimate errors with regard to functional evaluations. The monolithic space-time Galerkin formulation allowed to split the residual errors into contributions from the fluid and solid problems. Finally, we established the localization of the error estimator. That let us derive an adaptive refinement scheme for choosing optimal distinct time-meshes for each problem. Several numerical results for two different goal functionals showed very good effectivity of the error estimate.

In future work, it remains to extend the methodology to nonlinear problems, in particular, to fully coupled fluid-structure interactions.