The effect of uncertain geometries on advection–diffusion of scalar quantities

Abstract

The two dimensional advection–diffusion equation in a stochastically varying geometry is considered. The varying domain is transformed into a fixed one and the numerical solution is computed using a high-order finite difference formulation on summation-by-parts form with weakly imposed boundary conditions. Statistics of the solution are computed non-intrusively using quadrature rules given by the probability density function of the random variable. As a quality control, we prove that the continuous problem is strongly well-posed, that the semi-discrete problem is strongly stable and verify the accuracy of the scheme. The technique is applied to a heat transfer problem in incompressible flow. Statistical properties such as confidence intervals and variance of the solution in terms of two functionals are computed and discussed. We show that there is a decreasing sensitivity to geometric uncertainty as we gradually lower the frequency and amplitude of the randomness. The results are less sensitive to variations in the correlation length of the geometry.

1 Introduction

When solving partial differential equations, uncertain geometry of the computational domain may arise for many reasons. Examples include irregular materials, inaccurate Computer-Aided Design (CAD) software, imprecise manufacturing machines and non-perfect mesh generators. We study the effects of this uncertainty and impose the boundary condition at stochastically varying positions in space. Related techniques are boundary perturbation [26], Lagrangian approach [1] and isoparametric mapping [5]. Other techniques dealing with geometric uncertainty include polynomial chaos with remeshing of geometry [8, 9] as well as chaos collocation methods with fictious domains [3, 17].

We transform the stochastically varying domain into a fixed one. This procedure has previously been used in Xiu et al. [25] for elliptic problems. Numerical techniques can be employed if the analytical transformation of the geometry is unavailable [4]. In this article it is extended to the analysis of the time-dependent advection–diffusion equation. The continuous problem is analyzed using the energy method, and strong well-posedness is proved [14, 15].

We discretize using high-order finite difference methods on summation-by-parts form with weakly imposed boundary conditions, and prove strong stability [23, 24]. The statistics of the solution such as the mean, variance and confidence intervals are computed non-intrusively using quadrature rules for the given stochastic distributions [10, 12]. As an application, we analyze the heat transfer at rough surfaces in incompressible flow [2, 18, 22].

The paper will proceed as follows: in Sect. 2 we define the continuous problem in two space dimensions, transform it to the unit square using curvilinear coordinates and derive energy estimates that lead to well-posedness. We formulate a finite difference scheme for the continuous problem and prove stability in Sect. 3. In Sect. 4, we consider a heat transfer problem in incompressible flow. Finally, in Sect. 5 we draw conclusions.

2 The continuous problem

Consider the advection–diffusion problem on the stochastically varying domain $\Omega (\mathbf {\theta })$

$$\begin{aligned} \begin{array}{rlllll} u_t + \bar{u} u_x + \bar{v} u_y &{}= (\epsilon u_x)_x + (\epsilon u_y)_y + F(x,y,t), &{}(x,y) &{}\in &{} \Omega (\mathbf {\theta }), &{}\quad t \ge 0 \\ H u(x,y, t, \mathbf {\theta }) &{}= g(x,y,t), &{}(x,y) &{}\in &{} \partial \Omega (\mathbf {\theta }), &{}\quad t \ge 0 \\ u(x,y, 0, \mathbf {\theta }) &{}= f(x,y), &{}(x,y) &{}\in &{} \Omega (\mathbf {\theta }),&{} \quad t = 0.\qquad \end{array} \end{aligned}$$

(2.1)

In (2.1), $\bar{u}$ and $\bar{v}$ are the known mean velocities in the x- and y-directions satisfying the divergence relation $\bar{u}_x + \bar{v}_y = 0$ stemming from an incompressible Navier–Stokes solution. Furthermore, $\epsilon = \epsilon (x,y,t)$ is a positive diffusion coefficient, $u = u(x, \, y, \, t, \, \mathbf {\theta })$ represents the solution to the problem and $\mathbf {\theta } = (\theta _1, \, \theta _2,\dots )$ is a vector of random variables describing the geometry of the domain. F, g and f are data to the problem. The goal of this study is to investigate the effects of placing the boundary condition $Hu = g$ at the stochastically varying boundary $\partial \Omega (\mathbf {\theta })$.

2.1 The transformation

We transform the stochastically varying domain $\Omega$ into the unit square by the transformation,

$$\begin{aligned} x= & {} x(\xi , \, \eta , \, \mathbf {\theta }), \quad \xi = \xi (x, \, y, \, \mathbf {\theta }) \\ y= & {} y(\xi , \, \eta , \, \mathbf {\theta }), \quad \eta = \eta (x, \, y, \, \mathbf {\theta }), \end{aligned}$$

where $0 \le \xi ,\,\eta \le 1$. The Jacobian matrix of the transformation is given by,

$$\begin{aligned}{}[J] = \begin{bmatrix} x_{\xi }&y_{\xi } \\ x_{\eta }&y_{\eta } \end{bmatrix}. \end{aligned}$$

By applying the chain rule to (2.1) and multiplying by $J = x_{\xi } y_{\eta } - x_{\eta } y_{\xi } > 0$, we obtain

$$\begin{aligned}&J u_t + J (\bar{u} \xi _x + \bar{v} \xi _y) u_{\xi } + J (\bar{u} \eta _x + \bar{v} \eta _y) u_{\eta } + JF \nonumber \\&\qquad \ = J ( (\epsilon u_x)_{\xi } \xi _x +\,(\epsilon u_y)_{\xi } \xi _y) + J ( (\epsilon u_x)_{\eta } \eta _x + (\epsilon u_y)_{\eta } \eta _y). \end{aligned}$$

(2.2)

The final formulation of the transformed problem is

$$\begin{aligned} \begin{array}{rllll} J u_t + (\tilde{a} u)_{\xi } + (\tilde{b} u)_{\eta } &{}= \tilde{f}_{\xi } + \tilde{g}_{\eta } + J F(\xi , \eta ,t), &{} (\xi , \eta ) &{}\in \Phi , &{}\quad t \ge 0 \\ \quad \quad \tilde{H} u(\xi , \eta , t, \mathbf {\theta }) &{}= g(\xi , \eta , t),&{} (\xi , \eta )&{}\in \partial \Phi , &{}\quad t \ge 0 \\ u(\xi , \eta , 0, \mathbf {\theta }) &{}= f(\xi , \eta ), &{}(\xi , \eta ) &{}\in \Phi , &{}\quad t = 0, \end{array} \end{aligned}$$

(2.3)

where

$$\begin{aligned} \tilde{a}= & {} J [(\bar{u}, \bar{v}) \cdot \nabla \xi ] \tilde{f} = J [\epsilon ( \nabla u \cdot \nabla \xi )] \nonumber \\ \tilde{b}= & {} J [(\bar{u}, \bar{v}) \cdot \nabla \eta ] \tilde{g} = J [\epsilon ( \nabla u \cdot \nabla \eta )] \end{aligned}$$

(2.4)

and $\Phi = [0, \, 1] \times [0, \, 1]$. A more complete derivation of the transformed problem is included in “Appendix A”. In (2.4), we have used the notation $\nabla = (\frac{\partial }{\partial x}, \frac{\partial }{\partial y})^\mathrm{T}$. The transformed fixed domain including normal vectors are given in Fig. 1. Note that the wave speeds $\tilde{a}$ and $\tilde{b}$ depend on the stochastic variables $\mathbf {\theta }$.

Fig. 1

The transformed domain including normal vectors for the east, west, north and south boundaries ($n_E, n_W, n_N$ and $n_S$)

2.2 The energy method

We multiply the transformed problem (2.3) with u, integrate over the domain $\Phi$ (ignoring the forcing function F), and apply the Green–Gauss theorem. This yields

$$\begin{aligned} \frac{d}{dt}\left\| u(\xi , \eta ,t)\right\| _{J}^2 + 2 DI = - \oint _{\partial \Phi } u^2 \bar{A} \, - 2 u \bar{F} \, ds, \end{aligned}$$

(2.5)

where $\bar{A} = (\tilde{a}, \tilde{b}) \cdot n$, $\bar{F} = (\tilde{f}, \tilde{g}) \cdot n$ and n is the outward pointing normal vector from $\partial \Phi$, see Fig. 1. In (2.5), $\left\| u \right\| _{J}^2 = \int _{\Phi } u^2 J \, d \xi \, d \eta = \int _{\Omega } u^2 \, d x \, d y$ is the $L_2$-norm, while

$$\begin{aligned} DI= & {} \int _{\Phi } \begin{bmatrix} u_{\xi } \\ u_{\eta } \end{bmatrix}^\mathrm{T} \begin{bmatrix} \tilde{D}_{11}&\tilde{D}_{12} \\ \tilde{D}_{21}&\tilde{D}_{22} \end{bmatrix} \begin{bmatrix} u_{\xi } \\ u_{\eta } \end{bmatrix} \, d \xi \, d \eta = \int _{\Omega } \epsilon J |\nabla u|^2 \, d x \, d y \ge 0 \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} \tilde{D}_{11} &{}= \epsilon J( \xi _x^2 + \xi _y^2), &{}\quad \tilde{D}_{12} = \epsilon J( \eta _x \xi _x + \eta _y \xi _y) \\ \tilde{D}_{21} &{}= \tilde{D}_{12}, &{}\quad \tilde{D}_{22} = \epsilon J( \eta _x^2 + \eta _y^2). \end{array} \end{aligned}$$

The right-hand side (RHS) of (2.5) can be expanded as

$$\begin{aligned} \frac{d}{dt}\left\| u(\xi , \eta ,t)\right\| _{J}^2 + 2DI = - \int _0^1 \tilde{a} u^2 - 2 u \tilde{f} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta - \int _0^1 \tilde{b} u^2 - 2 u \tilde{g} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi \nonumber \\ \end{aligned}$$

(2.6)

where for example the fluxes at the boundaries $\xi = 1$ and $\eta = 1$ are

$$\begin{aligned} \tilde{f}= & {} (f,g) \cdot J \nabla \xi = \epsilon (u_x J \xi _x + u_y J \xi _y) = \epsilon \frac{\partial u}{ \partial n} J \left| \nabla \xi \right| \\ \tilde{g}= & {} (f,g) \cdot J \nabla \eta = \epsilon (u_x J \eta _x + u_y J \eta _y) = \epsilon \frac{\partial u}{ \partial n} J \left| \nabla \eta \right| , \end{aligned}$$

respectively. Further, we note that $\tilde{f}$ and $\tilde{g}$ can also be written in terms of $u_{\xi }$ and $u_{\eta }$ as

$$\begin{aligned} \tilde{f}= & {} \tilde{D}_{11} u_{\xi } + \tilde{D}_{12} u_{\eta }, \quad \tilde{g} = \tilde{D}_{21} u_{\xi } + \tilde{D}_{22} u_{\eta } \end{aligned}$$

The formulation (2.6) in matrix form can be written

$$\begin{aligned} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI= & {} - \int _0^1 \begin{bmatrix} u \\ \tilde{f} \end{bmatrix}^\mathrm{T} \begin{bmatrix} \tilde{a}&-1 \\ -1&0 \end{bmatrix} \begin{bmatrix} u \\ \tilde{f} \end{bmatrix} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta \nonumber \\&- \int _0^1 \begin{bmatrix} u \\ \tilde{g} \end{bmatrix}^\mathrm{T} \begin{bmatrix} \tilde{b}&-1 \\ -1&0 \end{bmatrix} \begin{bmatrix} u \\ \tilde{g} \end{bmatrix} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi . \end{aligned}$$

(2.7)

The matrices in (2.7) are symmetric, and hence they can be diagonalized as

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI &{}= &{}\displaystyle - \int _0^1 \begin{bmatrix} u - \frac{\tilde{f}}{\tilde{a}} \\ \tilde{f} \end{bmatrix}^\mathrm{T} \begin{bmatrix} \tilde{a} &{} 0 \\ 0 &{} -\frac{1}{\tilde{a}} \end{bmatrix} \begin{bmatrix} u - \frac{\tilde{f}}{\tilde{a}} \\ \tilde{f} \end{bmatrix} \bigg |_{\xi = 0}^{\xi = 1}\, d \eta \\ &{}&{}- \displaystyle \int _0^1 \begin{bmatrix} u - \frac{\tilde{g}}{\tilde{a}} \\ \tilde{g} \end{bmatrix}^\mathrm{T} \begin{bmatrix} \tilde{b} &{} 0 \\ 0 &{} -\frac{1}{\tilde{b}} \end{bmatrix} \begin{bmatrix} u - \frac{\tilde{g}}{\tilde{a}} \\ \tilde{g} \end{bmatrix} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi , \end{array} \end{aligned}$$

(2.8)

for $\tilde{a}, \tilde{b} \ne 0$. By imposing the boundary conditions

$$\begin{aligned} H_E^- u = g_E \quad H_W^- u = g_W \quad H_N^- u = g_N \quad H_S^- u = g_S \end{aligned}$$

(2.9)

where

$$\begin{aligned} \begin{array}{rclrcl} H_E^- &{} = &{} {\left\{ \begin{array}{ll} 1 - \frac{1}{\tilde{a}} \left( \tilde{D}_{11} \frac{\partial }{\partial \xi } + \tilde{D}_{12} \frac{\partial }{\partial \eta } \right) &{} \hbox {if}\;\tilde{a}\big |^{\xi = 1}< 0 \\ \tilde{D}_{11} \frac{\partial }{\partial \xi } + \tilde{D}_{12} \frac{\partial }{\partial \eta } &{} \hbox {if}\;\tilde{a}\big |^{\xi = 1}> 0 \end{array}\right. } \\ H_W^- &{} = &{} {\left\{ \begin{array}{ll} 1 - \frac{1}{\tilde{a}} \left( \tilde{D}_{11} \frac{\partial }{\partial \xi } + \tilde{D}_{12} \frac{\partial }{\partial \eta } \right) &{} \hbox {if}\;\tilde{a}\big |_{\xi = 0}> 0 \\ \tilde{D}_{11} \frac{\partial }{\partial \xi } + \tilde{D}_{12} \frac{\partial }{\partial \eta } &{} \hbox {if}\; \tilde{a}\big |_{\xi = 0}< 0 \end{array}\right. } \\ H_N^- &{} = &{} {\left\{ \begin{array}{ll} 1 - \frac{1}{\tilde{b}} \left( \tilde{D}_{21} \frac{\partial }{\partial \xi } + \tilde{D}_{22} \frac{\partial }{\partial \eta } \right) &{} \hbox {if}\;\tilde{b}\big |^{\eta = 1}< 0 \\ \tilde{D}_{21} \frac{\partial }{\partial \xi } + \tilde{D}_{22} \frac{\partial }{\partial \eta } &{} \hbox {if}\;\tilde{b}\big |^{\eta = 1}> 0 \\ \end{array}\right. } \\ H_S^- &{} = &{} {\left\{ \begin{array}{ll} 1 - \frac{1}{\tilde{b}} \left( \tilde{D}_{21} \frac{\partial }{\partial \xi } + \tilde{D}_{22} \frac{\partial }{\partial \eta } \right) &{} \hbox {if}\;\tilde{b}\big |_{\eta = 0} > 0 \\ \tilde{D}_{21} \frac{\partial }{\partial \xi } + \tilde{D}_{22} \frac{\partial }{\partial \eta } &{} \hbox {if}\;\tilde{b} \big |_{\eta = 0}< 0, \end{array}\right. } \end{array} \end{aligned}$$

(2.10)

the (RHS) of (2.8) is bounded by data and hence gives an energy estimate.

2.3 Weak imposition of boundary conditions

As a preparation for the numerical approximation, we now impose the boundary conditions weakly using penalty terms. This gives

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI =&{} &{} - \displaystyle \int _0^1 \tilde{a} u^2 - 2 u \tilde{f} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta - \int _0^1 \tilde{b} u^2 - 2 u \tilde{g} \bigg |_{\eta = 0}^{\eta = 1}\, d \xi \\ &{}&{} \displaystyle +\,2 \int _{0}^{1} u \Sigma _E (W_E^- - g_E) \bigg |^{\xi = 1} \!\!\!\!\!\!\!\! + u \Sigma _W (W_W^- - g_W) \bigg |_{\xi = 0} \!\!\!\!\! d\eta \\ &{}&{} \displaystyle +\,2 \int _{0}^{1} u \Sigma _N (W_N^- - g_N) \bigg |^{\eta = 1} \!\!\!\!\!\!\!\! + u \Sigma _S (W_S^- - g_S) \bigg |_{\eta = 0} \!\!\!\!\! d\xi . \end{array} \end{aligned}$$

(2.11)

To illustrate the procedure, we assume $\tilde{a} \big |_{\xi = 0}^{\xi = 1} > 0$ and $\tilde{b}\big |_{\eta = 0}^{\eta = 1} > 0$ and impose the boundary conditions using the operators in (2.10), which yields

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI &{}= &{} -\displaystyle \int _0^1 \tilde{a} u^2 - 2 u \tilde{f} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta - \int _0^1 \tilde{b} u^2 - 2 u \tilde{g} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi \\ &{}&{}\displaystyle +\,2 \int _{0}^{1} u \Sigma _E ( \tilde{f} - g_E) \bigg |^{\xi = 1} + u \Sigma _W (u - \frac{\tilde{f}}{\tilde{a}} - g_W) \bigg |_{\xi = 0} \, d\eta \\ &{}&{}\displaystyle +\,2 \int _{0}^{1} u \Sigma _N (\tilde{g} - g_N) \bigg |^{\eta = 1} + u \Sigma _S (u - \frac{\tilde{g}}{\tilde{b}} - g_S) \bigg |_{\eta = 0}\, d\xi . \end{array} \end{aligned}$$

(2.12)

The indefinite terms in (2.12) are canceled by letting

$$\begin{aligned} \Sigma _{E} = -1, \quad \Sigma _W = -\tilde{a} \quad \Sigma _{N} = -1, \quad \Sigma _S = -\tilde{b}. \end{aligned}$$

(2.13)

By using (2.13) in (2.12) we obtain

$$\begin{aligned} \begin{array}{rllll} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI = &{}\displaystyle - \int _0^1 \tilde{a}\left( u - \frac{g_E}{\tilde{a}}\right) ^2 - \frac{g_E^2}{\tilde{a}} \bigg |^{\xi = 1} \, d \eta \\ &{}\displaystyle - \int _0^1 \tilde{a}(u - g_W)^2 - g_W^2 \tilde{a} \bigg |_{\xi = 0} \, d \eta \\ &{}\displaystyle - \int _0^1 \tilde{b}\left( u - \frac{g_N}{\tilde{b}}\right) ^2 - \frac{g_N^2}{\tilde{b}}\bigg |^{\eta = 1} \, d \xi \\ &{}\displaystyle - \int _0^1 \tilde{b}(u - g_S)^2 - g_S^2 \tilde{b} \bigg |_{\eta = 0} \, d \xi , \end{array} \end{aligned}$$

(2.14)

which lead directly to an energy estimate.

For general $\tilde{a}$ and $\tilde{b}$, the choices

$$\begin{aligned} \begin{array}{rclrcl} \Sigma _E &{} = &{} {\left\{ \begin{array}{ll} -\tilde{a} &{} \hbox {if}\;\tilde{a}< 0 \\ -1 &{} \hbox {if}\;\tilde{a}> 0 \end{array}\right. } &{} \Sigma _W &{} = &{} {\left\{ \begin{array}{ll} -\tilde{a} &{} \hbox {if}\;\tilde{a}> 0 \\ -1 &{} \hbox {if}\;\tilde{a}< 0 \end{array}\right. } \\ \Sigma _N &{} = &{} {\left\{ \begin{array}{ll} -\tilde{b} &{} \hbox {if}\;\tilde{b}< 0 \\ -1 &{} \hbox {if}\;\tilde{b}> 0 \end{array}\right. } &{} \Sigma _S &{} = &{} {\left\{ \begin{array}{ll} -\tilde{b} &{} \hbox {if}\;\tilde{b} > 0 \\ -1 &{} \hbox {if}\;\tilde{b} < 0 \end{array}\right. } \end{array} \end{aligned}$$

(2.15)

bounds the (RHS) of (2.11), in a similar way. The special cases with $\tilde{a},\tilde{b} = 0$ are treated in a similar way, see “Appendix B”.

We can now prove

Proposition 2.1

The problem (2.3) with the boundary conditions (2.9) and the penalty coefficients in (2.15) is strongly well-posed.

Proof

Consider the specific case in (2.14). For other values of $\tilde{a}$ and $\tilde{b}$, the same general procedure is used. Time integration (from 0 to T) of (2.14) results in

$$\begin{aligned} \displaystyle \left\| u(T) \right\| _{J}^2 + 2 \int _0^{T} \!\!\! DI \, dt= & {} \left\| f \right\| _{J}^2 \nonumber \\&- \displaystyle \int _0^{T} \int _0^1 \tilde{a}\left( u - \frac{g_E}{\tilde{a}}\right) ^2 - \frac{g_E^2}{\tilde{a}} \bigg |^{\xi = 1} d \eta \, dt \nonumber \\&- \displaystyle \int _0^{T} \int _0^1\tilde{a}(u - g_W)^2 - g_W^2 \tilde{a} \bigg |_{\xi = 0} d \eta \, dt \nonumber \\&- \displaystyle \int _0^{T} \int _0^1 \tilde{b}\left( u - \frac{g_N}{\tilde{b}}\right) ^2 - \frac{g_N^2}{\tilde{b}}\bigg |^{\eta = 1} d \xi \, dt \nonumber \\&- \displaystyle \int _0^{T} \int _0^1 \tilde{b}(u - g_S)^2 - g_S^2 \tilde{b} \bigg |_{\eta = 0} \!\!\!\!\!\! d \xi \, dt. \end{aligned}$$

(2.16)

In (2.16), the boundary terms with zero data all give a non-positive contribution, and hence the solution is bounded by data. The bound leads directly to uniqueness, and existence is guaranteed by the fact that we use the correct (i.e., minimal) number of boundary conditions.

3 The semi-discrete formulation

In this section we consider the numerical approximation of (2.3) formulated by using Summation-By-Parts (SBP) operators with Simultaneous Approximation Terms (SAT), the so called SBP-SAT technique [24]. First, we rewrite our variable coefficient continuous problem (2.3) using the splitting technique described in [13], to obtain,

$$\begin{aligned} J u_t + \frac{1}{2}[(\tilde{a} u)_{\xi } + \tilde{a} u_{\xi } + \tilde{a}_{\xi } u + (\tilde{b} u)_{\eta } + \tilde{b} u_{\eta } + \tilde{b}_{\eta } u] = \tilde{f}_{\xi } + \tilde{g}_{\eta }. \end{aligned}$$

(3.1)

In (3.1), we note that the lower order terms vanish, since $\tilde{a}_{\xi } + \tilde{b}_{\eta } = 0$. The corresponding semi-discrete version of (3.1) including penalty terms for the boundary conditions is

$$\begin{aligned}&\tilde{J} U_t + \frac{1}{2}[ D_{\xi } \tilde{A} U + \tilde{A} D_{\xi } U + D_{\eta } \tilde{B} U + \tilde{B} D_{\eta } U]\nonumber \\&\qquad \,\, - D_{\xi } \tilde{F}_{\xi } - D_{\eta } \tilde{G}_{\eta } = (P_{\xi }^{-1} E_{NN} \otimes I_{\eta }) \varvec{\varSigma }_E (\mathbf{{H}_E^-} U - g) \nonumber \\&\qquad \,\, +\, (P_{\xi }^{-1} E_{0N} \otimes I_{\eta })\varvec{\varSigma }_W (\mathbf{{H}_W^-} U - g) \nonumber \\&\qquad \,\,+\,(I_{\xi } \otimes P_{\eta }^{-1} E_{MM})\varvec{\varSigma }_N (\mathbf{{H}_N^-} U - g) \nonumber \\&\qquad \,\, +\, (I_{\xi } \otimes P_{\eta }^{-1} E_{0M})\varvec{\varSigma }_S (\mathbf{{H}_S^-} U - g) \nonumber \\&U(0) = f. \end{aligned}$$

(3.2)

where

$$\begin{aligned} \begin{array}{rclrcl} D_{\xi } &{} = &{} (P_{\xi }^{-1} Q_{\xi } \otimes I_{\eta }) &{} D_{\eta } &{} = &{} (I_{\xi } \otimes P_{\eta }^{-1} Q_{\eta }) \\ \tilde{F} &{} = &{} \tilde{\mathbf{D}}_{\mathbf{11}} D_{\xi } U + {\tilde{\mathbf{D}}_\mathbf{12}} D_{\eta } U &{} \tilde{G} &{} = &{} {\tilde{\mathbf{D}}_\mathbf{21}} D_{\xi } U + {\tilde{\mathbf{D}}_\mathbf{22}} D_{\eta } U \\ {\tilde{\mathbf{D}}_\mathbf{11}} &{} = &{} \tilde{\epsilon } \tilde{J} ( \tilde{\xi }_x^2 + \tilde{\xi }_y^2), &{} {\tilde{\mathbf{D}}_\mathbf{12}} &{} = &{} \tilde{\epsilon } \tilde{J} ( \tilde{\eta }_x \tilde{\xi }_x + \tilde{\eta }_y \tilde{\xi }_y) \\ {\tilde{D}_\mathbf{21}} &{} = &{} {\tilde{\mathbf{D}}_\mathbf{12}}, &{} {\tilde{\mathbf{D}}_\mathbf{22}} &{} = &{} \tilde{\epsilon } \tilde{ J}( \tilde{\eta }_x^2 + \tilde{\eta }_y^2). \end{array} \end{aligned}$$

(3.3)

In (3.2) and (3.3), $P_{\xi , \eta }^{-1} Q_{\xi , \eta }$ are the finite difference operators, $P_{\xi , \eta }$ are diagonal positive definite matrices, and $Q_{\xi , \eta }$ are almost skew-symmetric matrices satisfying $Q_{\xi , \eta } + Q_{\xi , \eta }^\mathrm{T} = B = diag[-1,0,\dots ,0,1]$.

U is a vector containing the numerical solution $U_{i,j}$ which approximates $u(\xi _i, \eta _j)$ ordered as

$$\begin{aligned} U = \begin{bmatrix} U_0 \\ U_1 \\ \vdots \\ U_N \\ \end{bmatrix}, \quad U_{i} = \begin{bmatrix} U_{i,0} \\ U_{i,1} \\ \vdots \\ U_{i,M} \\ \end{bmatrix}. \end{aligned}$$

The indices $i = 0,1,\dots ,N$ and $j = 0,1,\dots ,M$ correspond to the grid points in $\xi$- and $\eta$-direction.

To ease the notation we denote $(P_{\xi }^{-1} Q_{\xi }\otimes I_{\eta })U = U_{\xi }$ and $(I_{\xi } \otimes P_{\eta }^{-1} Q_{\eta })U = U_{\eta }$ as the discrete derivatives with respect to $\xi$ and $\eta$. $E_{0N}$ and $E_{0M}$ are zero matrices with the exception of the first element which is equal to one, and the corresponding sizes of the matrices are $(N+1) \times (N+1)$ and $(M+1) \times (M+1)$. Similarly, $E_{NN}$ and $E_{MM}$ are zero matrices with the exception of the last element which is equal to one, and the corresponding sizes of the matrices are $(N+1) \times (N+1)$ and $(M+1) \times (M+1)$. The notations $I_{\xi }$, $I_{\eta }$ and $I_{\xi \eta }$ correspond to the identity matrices of sizes $(N+1) \times (N+1)$, $(M+1) \times (M+1)$ and $(M+1)(N+1) \times (M+1)(N+1)$, respectively. $\tilde{A}$, $\tilde{B}$, $\tilde{F}$, $\tilde{G}$, $\tilde{\xi }_x$, $\tilde{\xi }_y$, $\tilde{\eta }_x$, $\tilde{\eta }_y$, $\tilde{\epsilon }$ and $\tilde{J}$ are diagonal matrices approximating $\tilde{a}$, $\tilde{b}$, $\tilde{f}$, $\tilde{g}$, $\xi _x$, $\xi _y$, $\eta _x$, $\eta _y$, $\epsilon$ and J pointwise.

The discrete boundary operators $\mathbf {H}_E^-$, $\mathbf {H}_W^-$, $\mathbf {H}_N^-$ and $\mathbf {H}_S^-$ are defined as

$$\begin{aligned} \begin{array}{rclrcl} \mathbf{H_E^-} &{} = &{} {\left\{ \begin{array}{ll} I_{\xi \eta } - \tilde{A}^{-1} \left( {\tilde{\mathbf{D}}_{11}} D_{\xi } + {\tilde{\mathbf{D}}_{12}} D_{\eta } \right) &{} \hbox {if}\;\tilde{A}\big |^{\xi = 1}< 0 \\ {\tilde{\mathbf{D}}_{11}} D_{\xi } + {\tilde{\mathbf{D}}_{12}} D_{\eta } &{} \hbox {if}\;\tilde{A}\big |^{\xi = 1}> 0 \end{array}\right. } \\ \mathbf{H_W^-} &{} = &{} {\left\{ \begin{array}{ll} I_{\xi \eta } - \tilde{A}^{-1} \left( {\tilde{\mathbf{D}}_{11}} D_{\xi } + {\tilde{\mathbf{D}}_{12}} D_{\eta } \right) &{} \hbox {if}\;\tilde{A}\big |_{\xi = 0}> 0 \\ {\tilde{\mathbf{D}}_{11}} D_{\xi } + {\tilde{\mathbf{D}}_{12}} D_{\eta } &{} \hbox {if}\;\tilde{A}\big |_{\xi = 0}< 0 \end{array}\right. } \\ \mathbf{H_N^-} &{} = &{} {\left\{ \begin{array}{ll} I_{\xi \eta } - \tilde{B}^{-1} \left( {\tilde{\mathbf{D}}_{21}} D_{\xi } + {\tilde{\mathbf{D}}_{22}} D_{\eta } \right) &{} \hbox {if}\;\tilde{B}\big |^{\eta = 1}< 0 \\ {\tilde{\mathbf{D}}_{21}} D_{\xi } + {\tilde{\mathbf{D}}_{22}} D_{\eta } &{} \hbox {if}\;\tilde{B}\big |^{\eta = 1}> 0 \end{array}\right. } \\ \mathbf{H_S^-} &{} = &{} {\left\{ \begin{array}{ll} I_{\xi \eta } - \tilde{B}^{-1} \left( {\tilde{\mathbf{D}}_{21}} D_{\xi } + {\tilde{\mathbf{D}}_{22}} D_{\eta } \right) &{} \hbox {if}\;\tilde{B}\big |_{\eta = 0} > 0 \\ {\tilde{\mathbf{D}}_{21}} D_{\xi } + {\tilde{\mathbf{D}}_{22}} D_{\eta } &{} \hbox {if}\;\tilde{B}\big |_{\eta = 0} < 0 \end{array}\right. } \end{array} \end{aligned}$$

which corresponds to the continuous counterparts in (2.10). Finally, The penalty matrices $\varvec{\varSigma }_E, \varvec{\varSigma }_W, \varvec{\varSigma }_N$ and $\varvec{\varSigma }_S$ will be chosen such that the numerical scheme (3.2) becomes stable. For more details on the SBP-SAT techniques, see [24].

3.1 Stability

To prove stability (we only consider the west boundary, as the treatment of the other boundaries is similar), we multiply (3.2) with $U^\mathrm{T} (P_{\xi } \otimes P_{\eta })$ from the left, add the transpose of the outcome and define the discrete norm $\left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 = U^\mathrm{T} \tilde{J} (P_{\xi } \otimes P_{\eta }) U$ to obtain

$$\begin{aligned}&\frac{d}{dt} \left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 + \frac{1}{2}[ U^\mathrm{T}(Q_{\xi } + Q_{\xi }^\mathrm{T}\otimes P_{\eta })\tilde{A} U + U^\mathrm{T} \tilde{A} (Q_{\xi } + Q_{\xi }^\mathrm{T} \otimes P_{\eta }) U] \nonumber \\&\qquad \qquad \qquad \qquad \quad +\frac{1}{2}[ U^\mathrm{T} (P_{\xi } \otimes Q_{\eta } + Q_{\eta }^\mathrm{T}) \tilde{B} U + U^\mathrm{T} \tilde{B} (P_{\xi } \otimes Q_{\eta } + Q_{\eta }^\mathrm{T}) U] \nonumber \\&\qquad \qquad \qquad \qquad \quad - U ( Q_{\xi }\otimes P_{\eta }) \tilde{F} - \tilde{F}^\mathrm{T} (Q_{\xi }^\mathrm{T} \otimes P_{\eta }) T \nonumber \\&\qquad \qquad \qquad \qquad \quad - U (P_{\xi } \otimes Q_{\eta }) \tilde{G} - \tilde{G} (P_{\xi } \otimes Q_{\eta }^\mathrm{T} ) U \nonumber \\&\qquad \qquad \qquad \qquad \quad = U^\mathrm{T} (E_{0N} \otimes P_{\eta }) \varvec{\varSigma }_W (\mathbf{{H}_W^-} U - g) \nonumber \\&\qquad \qquad \qquad \qquad \quad + (\mathbf{{H}_W^-} U - g)^\mathrm{T} \varvec{\varSigma }_W^\mathrm{T} (E_{0N} \otimes P_{\eta }) U \end{aligned}$$

(3.4)

By observing that $\mathbf{{H}_W^-} U = U - \tilde{A}^{-1} \tilde{F}$, $Q_{\xi }+Q_{\xi }^\mathrm{T} = E_{NN} - E_{0N}$, $Q_{\eta }+Q_{\eta }^\mathrm{T} = E_{MM} - E_{0M}$, and ignoring the contribution from the other boundaries (the terms including $E_{NN}, E_{MM}$ and $E_{0M}$) we can rewrite (3.4) as

$$\begin{aligned} \frac{d}{dt} \left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 + 2 \overline{DI}= & {} U^\mathrm{T} \tilde{A} (E_{0N} \otimes P_{\eta }) U \nonumber \\- & {} U^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{F} - \tilde{F}^\mathrm{T} (E_{0N} \otimes P_{\eta }) U \nonumber \\+ & {} U^\mathrm{T} (E_{0N} \otimes P_{\eta }) \varvec{\varSigma }_W (U - \tilde{A}^{-1}\tilde{F} - g) \nonumber \\+ & {} (U - \tilde{A}^{-1} \tilde{F} - g)^\mathrm{T} \varvec{\varSigma }_W^\mathrm{T} (E_{0N} \otimes P_{\eta }) U \end{aligned}$$

(3.5)

where

$$\begin{aligned} \begin{array}{rcl} \overline{DI} &{} = &{} \begin{bmatrix} U_{\xi } \\ U_{\eta } \end{bmatrix}^\mathrm{T} (I_2 \otimes P_{\xi } \otimes P_{\eta }) \begin{bmatrix} {\tilde{\mathbf{D}}_{11}} &{} {\tilde{\mathbf{D}}_{12}} \\ {\tilde{\mathbf{D}}_{21}} &{} {\tilde{\mathbf{D}}_{22}} \end{bmatrix} \begin{bmatrix} U_{\xi } \\ U_{\eta } \end{bmatrix} \ge 0. \end{array} \end{aligned}$$

The remaining derivations leading to the discrete energy estimate

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt} \left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 + 2 \overline{DI} = &{} - &{} ((U - g)^\mathrm{T} \tilde{A} (E_{0N} \otimes P_{\eta }) (U - g) \\ &{} - &{} g^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{A} g) \end{array} \end{aligned}$$

(3.6)

is included in “Appendix C”.

We can now prove

Proposition 3.1

The numerical approximation (3.2) using the penalty coefficients

$$\begin{aligned} \begin{array}{rclrcl} \varvec{\varSigma }_E &{} = &{} {\left\{ \begin{array}{ll} -\tilde{A} &{} \hbox {if}\;\tilde{a}< 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{a}> 0 \end{array}\right. } &{} \varvec{\varSigma }_W &{} = &{} {\left\{ \begin{array}{ll} -\tilde{A} &{} \hbox {if}\;\tilde{a}> 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{a}< 0 \end{array}\right. } \\ \varvec{\varSigma }_N &{} = &{} {\left\{ \begin{array}{ll} -\tilde{B} &{} \hbox {if}\;\tilde{b}< 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{b}> 0 \end{array}\right. } &{} \varvec{\varSigma }_S &{} = &{} {\left\{ \begin{array}{ll} -\tilde{B} &{} \hbox {if}\;\tilde{b} > 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{b} < 0 \end{array}\right. } \end{array} \end{aligned}$$

(3.7)

is strongly stable.

Proof

For ease of presentation we prove the special case when $\tilde{a}, \tilde{b} > 0$. By integrating (3.6) in time, considering also the remaining boundaries and using the penalty parameters in (3.7) we find

$$\begin{aligned} \begin{array}{rcl} \left\| U(T) \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 &{} + &{} 2 \displaystyle \int _{0}^\mathrm{T} \overline{DI} \, dt = \left\| f \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 \\ &{} - &{} \displaystyle \int _{0}^\mathrm{T} (U - \tilde{A}^{-1} g)^\mathrm{T} \tilde{A} (E_{NN} \otimes P_{\eta }) (U - \tilde{A}^{-1} g) \\ &{} - &{} \displaystyle g^\mathrm{T} (E_{NN} \otimes P_{\eta }) \tilde{A}^{-1} g \, d t \\ &{} - &{} \displaystyle \int _{0}^\mathrm{T} (U - g)^\mathrm{T} \tilde{A} (E_{0N} \otimes P_{\eta }) (U - g) \\ &{} - &{} \displaystyle g^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{A} g \, d t \\ &{} - &{}\displaystyle \int _{0}^\mathrm{T} (U - \tilde{B}^{-1} g)^\mathrm{T} \tilde{B} ( P_{\xi } \otimes E_{MM}) (U - \tilde{B}^{-1} g) \\ &{} - &{} \displaystyle g^\mathrm{T} (P_{\xi } \otimes E_{MM}) \tilde{B}^{-1} g \, dt \\ &{} - &{}\displaystyle \int _{0}^\mathrm{T} (U - g)^\mathrm{T} \tilde{B} ( P_{\xi } \otimes E_{0M}) (U - g) \\ &{} - &{} \displaystyle g^\mathrm{T} (P_{\xi } \otimes E_{0M}) \tilde{B} g \, d t. \end{array} \end{aligned}$$

(3.8)

As in the continuous energy estimate (2.14), the RHS of (3.8) consists of boundary data and negative semi-definite dissipative boundary terms which result in a strongly stable numerical approximation.

Remark 3.1

Note the similarity between the discrete energy estimate (3.8) and its continuous counterpart (2.16).

Remark 3.2

The possibility of applying the SBP-SAT technique to the coupled PDEs resulting from the use of polynomial chaos in combination with a stochastic Galerkin projection is shown in Pettersson et al. [19, 20].

4 Numerical results

We start with a quality control by using the method of manufactured solution [16, 21] to verify the accuracy and stability of the scheme.

4.1 Rate of convergence for the deterministic case

We use $\bar{u} = \sin (x) \cos (y)$, $\bar{v} = -\cos (x)\sin (y)$, $\epsilon = 0.01$ in order to satisfy the incompressibility condition. The rate of convergence is verified by computing the order of accuracy p defined as

$$\begin{aligned} p = \log _2 \left( \frac{\left\| u_a - u_h \right\| _P}{\left\| u_a - u_{h/2} \right\| _P} \right) . \end{aligned}$$

(4.1)

In (4.1), $u_h$ is the numerical solution, using the grid spacing h, and the manufactured solution is

$$\begin{aligned} u_a = \sin ( 2 \pi (x - t)) + \sin (2\pi (y - t)). \end{aligned}$$

The order of accuracy computed for different number of grid points and SBP-operators, is shown in Table 1. As time-integrator, the classical 4th-order Runge–Kutta method with 5000 grid points was used. The results shown in Table 1 confirm that the scheme is accurate for the 2nd-, 3rd-, 4th- and 5th-order SBP-SAT schemes [23].

Table 1 The order of accuracy for the 2nd-, 3rd-, 4th- and 5th-order SBP-SAT schemes for different number of grid points in space

4.2 Heat transfer at rough surfaces

Equipped with a provably stable scheme, we will now investigate the stochastic properties of a heat distribution problem in incompressible flow. The problem in two dimensions is of the form

$$\begin{aligned} T_t + \bar{u} T_x + \bar{v} T_y = (\epsilon T_x)_x + (\epsilon T_y)_y, \end{aligned}$$

(4.2)

where we specify the following boundary conditions

$$\begin{aligned} \begin{array}{rrcl} \text {North: } &{} T + \epsilon \frac{\partial T}{\partial n} &{} = &{} T_{\infty } \\ \text {South: } &{} \frac{\partial T}{\partial n} &{} = &{} 0 \\ \text {East: } &{} \frac{\partial T}{\partial n} &{} = &{} 0 \\ \text {West: } &{} \bar{u} T - \epsilon \frac{\partial T}{\partial n} &{} = &{} \bar{u} \sqrt{\epsilon } (1 - e^{-\alpha y}) \\ \end{array} \end{aligned}$$

(4.3)

In (4.2), T is the temperature, $(\bar{u}, \bar{v})$ the given velocity field, $\epsilon$ the viscosity. The boundary conditions in (4.3) are a well-posed subset of the general ones derived previously.

To simulate a boundary layer the quantities $\bar{u}, \bar{v}$ and $\epsilon$ are chosen as

$$\begin{aligned} (\bar{u}, \bar{v}) = \left( 1 - e^{-\alpha y}, 0\right) , \qquad \epsilon = 0.01, \qquad \alpha = 1/\sqrt{\epsilon }. \end{aligned}$$

(4.4)

where $T_{\infty } = \sqrt{\epsilon }$ and $\frac{\partial T}{\partial n} = n \cdot \nabla T$. The velocity field is generated on the unit square (Fig. 2), then injected on the corresponding grid points on the varying domain. The simplified velocity field in (4.4) satisfies the divergence relation $\bar{u}_x + \bar{v}_y = 0$ and has a boundary layer.

4.3 Statistical results

In the calculations below, the 4th-order Runge–Kutta method is used together with 3rd-order SBP-operators on a grid with 50 and 100 grid points in the x- and y-direction and 9000 grid points in time, in order to minimize the time discretization error.

We start by enforcing the following stochastic variation on the south boundary of the geometry, (see Fig. 3)

$$\begin{aligned} \begin{array}{rclrcl} y_S(x, \theta _1, \theta _2)= & {} 0.05 \theta _1 \sin (2 \pi x \theta _2 ) \end{array} \end{aligned}$$

where $\theta _1 \sim N(-1,1)$ and $\theta _2 \sim U(2,10)$ are stochastic variables controlling the amplitude and frequency of the periodic variation respectively. In order to study the influence of different correlation lengths, we use

$$\begin{aligned} \begin{array}{rcl} y_{S_{long}}(x, \theta _1) &{} = &{} 0.05 \theta _1 \sin (2 \pi x) \\ y_{S_{short}}(x, \theta _1) &{} = &{} 0.05 \theta _1 \sin (2 \pi x) + 0.005 \sin (16 \pi x ), \end{array} \end{aligned}$$

where we let $y_{S_{short}}$ and $y_{S_{long}}$ represent short and long correlation lengths respectively.

Fig. 2

An illustration of the mean velocity profile for $(\bar{u}, \bar{v})$ as a function of y

Fig. 3

A schematic of the computational domain with definitions of $y_S$, $\theta _1$ and $\theta _2$

As typical measures of the results, we compute statistics of the integral of the solution and squared solution over the domain, that is

$$\begin{aligned} \iint _{\Omega } u(x,y,t, \theta _1, \theta _2) \, dx \, dy, \quad \text {and} \quad \iint _{\Omega } u^2(x,y,t, \theta _1, \theta _2) \, dx \, dy. \end{aligned}$$

To compute the integrals in the stochastic analysis, we have used 20 grid points in both the $\theta _1$- and $\theta _2$-direction. For high-dimensional problems adaptive sparse grid techniques or multilevel Monte Carlo methods can be used to improve the efficiency of calculations like these, see for example [6, 11]. However, in this particular case, with only two stochastic dimensions, straightforward quadrature is efficient enough.

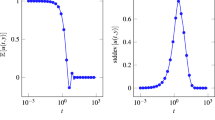
Figures 4 and 5 show the variance with respect to $\theta _2$ of the integral of the solution and squared solution respectively, as a function of time for different realizations of $\theta _1$ with $y_S$ as south boundary. Figures 4 and 5 both illustrate the fact that the variance increase with increasing amplitude, as could be expected.

Figures 6 and 7 depict the variance with respect to $\theta _1$ of the integral of the solution and squared solution respectively, as a function of time for fixed values of $\theta _2$ using $y_S$ as south boundary. As can be seen, an increased frequency leads to an increased variance. Hence high-frequency random variation in the geometry affects the solution more than low-frequency random variation.

Fig. 4

The variance of the linear functional $\iint _{\Omega } u(x, y, t, \theta ) \, dx \, dy$ with respect to $\theta _2$ (frequency) for different realizations of $\theta _1$ (amplitude)

Fig. 5

The variance of the non-linear functional $\iint _{\Omega } u^2(x, y, t, \theta ) \, dx \, dy$ with respect to $\theta _2$ (frequency) for different realizations of $\theta _1$ (amplitude)

Fig. 6

The variance of the linear functional $\iint _{\Omega } u(x, y, t, \theta ) \, dx \, dy$ with respect to $\theta _1$ (amplitude) for different realizations of $\theta _2$ (frequency)

Fig. 7

The variance of the non-linear functional $\iint _{\Omega } u^2(x, y, t, \theta ) \, dx \, dy$ with respect to $\theta _1$ (amplitude) for different realizations of $\theta _2$ (frequency)

Fig. 8

The variance of the linear functional $\iint _{\Omega } u(x, y, t, \theta ) \, dx \, dy$ with respect to $\theta _1$ (amplitude) for different correlation lengths

Fig. 9

The variance of the non-linear functional $\iint _{\Omega } u^2(x, y, t, \theta ) \, dx \, dy$ with respect to $\theta _1$ (amplitude) for different correlation lengths

Figures 8 and 9 illustrate the effects of correlation length on the variance. The variance as a function of time is shown for two different correlation lengths (one short $y_{S_{short}}$ and one long $y_{S_{long}}$). The figures show no significant difference between the two cases, and we conclude that the correlation length has a minor impact on the variance of the solution.

5 Conclusions and future work

We have studied how the solution to the advection–diffusion equation is affected by imposing boundary data on a stochastically varying geometry. The problem was transformed to the unit square resulting in a formulation with stochastically varying wave speeds. Strong well-posedness and strong stability were proven.

As an application, the two-dimensional heat transfer problem in incompressible flow with a given velocity field was studied. One of the boundaries was assumed to be stochastically varying. The geometry of the boundary was prescribed to have a periodic behaviour with stochastic variations in both amplitude and frequency.

The variances were computed for different fixed realizations of $\theta _1$ (when varying $\theta _2$) and $\theta _2$ (when varying $\theta _1$) controlling the amplitude and frequency respectively. A tentative conclusion is that an increased frequency of the randomness in the geometry leads to an increased variance in the solution. Also, as expected, the variance of the solution grows as the amplitude of the randomness in the geometry increases. Finally, computational results suggests that the correlation length of the geometry has no significant impact on the variance of the solution.

In the next paper we will extend the analysis using polynomial chaos combined with stochastic Galerkin projection to incompletely parabolic systems, including calculations using the Navier–Stokes equations.

Appendices

Appendix A: Transformation

Using the product rule (2.2) becomes

$$\begin{aligned}&J u_t + [J (\bar{u} \xi _x + \bar{v} \xi _y) u]_{\xi } + [J (\bar{u} \eta _x + \bar{v} \eta _y) u]_{\eta } + J F \nonumber \\&\qquad \,\, - [J \bar{u}_{\xi } \xi _x + J \bar{u}_{\eta } \eta _x + J \bar{v}_{\xi } \xi _y + J \bar{v}_{\eta } \eta _y]u \nonumber \\&\qquad \,\, - [\bar{u}( (J \xi _x)_{\xi } + (J \eta _x)_{\eta }) + \bar{v}( (J \xi _y)_{\xi } + (J \eta _y)_{\eta })]u \nonumber \\&\qquad \,\, = [J ( (\epsilon u_x) \xi _x + (\epsilon u_y) \xi _y)]_{\xi } + [J ( (\epsilon u_x) \eta _x + (\epsilon u_y) \eta _y)]_{\eta }\nonumber \\&\qquad \,\, - [(J \xi _x)_{\xi } + (J \eta _x)_{\eta }] \epsilon u_x - [(J \xi _y)_{\xi } + (J \eta _y)_{\eta }] \epsilon u_y. \end{aligned}$$

(A.1)

We use the Geometric Conservation Law (GCL) ($(J \xi _x)_{\xi } + (J \eta _x)_{\eta } = 0$ and $(J \xi _y)_{\xi } + (J \eta _y)_{\eta } = 0$, see [7] for more details) and note that $\bar{u}_x = J \bar{u}_{\xi } \xi _x + J \bar{u}_{\eta } \eta _x$ and $\bar{v}_y = J \bar{v}_{\xi } \xi _y + J \bar{v}_{\eta } \eta _y$ in (A.1), resulting in

$$\begin{aligned}&J u_t + [J (\bar{u} \xi _x + \bar{v} \xi _y) u]_{\xi } + [J (\bar{u} \eta _x + \bar{v} \eta _y) u]_{\eta } + JF \nonumber \\&\qquad \,\, = [J ( (\epsilon u_x) \xi _x + (\epsilon u_y) \xi _y)]_{\xi } + [J ( (\epsilon u_x) \eta _x + (\epsilon u_y) \eta _y)]_{\eta } \nonumber \\&\qquad \,\, + [\bar{u}_x + \bar{v}_y]u. \end{aligned}$$

(A.2)

Finally, the divergence relation $\bar{u}_x + \bar{v}_y = 0$ is utilized to (A.2).

Appendix B: Boundary conditions for the case $\tilde{a} = \tilde{b} = 0$

By considering (2.7) with $\tilde{a} = \tilde{b} = 0$ we obtain

$$\begin{aligned} \begin{array}{rclcl} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI = &{} - &{} \displaystyle \int _0^1 \begin{bmatrix} u \\ \tilde{f} \end{bmatrix}^\mathrm{T} \begin{bmatrix} 0 &{} -1 \\ -1 &{} 0 \end{bmatrix} \begin{bmatrix} u \\ \tilde{f} \end{bmatrix} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta \\ &{} - &{} \displaystyle \int _0^1 \begin{bmatrix} u \\ \tilde{g} \end{bmatrix}^\mathrm{T} \begin{bmatrix} 0 &{} -1\\ -1 &{} 0 \end{bmatrix} \begin{bmatrix} u \\ \tilde{g} \end{bmatrix} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi . \end{array} \end{aligned}$$

(B.1)

Due to symmetry, the matrices in (B.1) can be diagonalized as

$$\begin{aligned} \begin{array}{rclcl} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI = &{} - &{} \int _0^1 \begin{bmatrix} u - \tilde{f} \\ u + \tilde{f} \end{bmatrix}^\mathrm{T} \begin{bmatrix} \frac{1}{2} &{} 0 \\ 0 &{} -\frac{1}{2} \end{bmatrix} \begin{bmatrix} u - \tilde{f} \\ u + \tilde{f} \end{bmatrix} \bigg |_{\xi = 0}^{\xi = 1}\, d \eta \\ &{} - &{} \int _0^1 \begin{bmatrix} u - \tilde{g} \\ u + \tilde{g} \end{bmatrix}^\mathrm{T} \begin{bmatrix} \frac{1}{2} &{} 0 \\ 0 &{} -\frac{1}{2} \end{bmatrix} \begin{bmatrix} u - \tilde{g} \\ u + \tilde{g} \end{bmatrix} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi . \end{array} \end{aligned}$$

(B.2)

To bound the RHS of (B.2) we impose the following boundary conditions

$$\begin{aligned} W_E^- = H_E^- u = g_E \quad W_W^- = H_W^- u = g_W \quad W_N^- = H_N^- u = g_N \quad W_S^- = H_S^- u = g_S \end{aligned}$$

(B.3)

where

$$\begin{aligned} \begin{array}{rcl} H_E^- &{} = &{} 1 + \left( \tilde{D}_{11} \frac{\partial }{\partial \xi } + \tilde{D}_{12} \frac{\partial }{\partial \eta } \right) \\ H_W^- &{} = &{} 1 - \left( \tilde{D}_{11} \frac{\partial }{\partial \xi } + \tilde{D}_{12} \frac{\partial }{\partial \eta } \right) \\ H_N^- &{} = &{} 1 + \left( \tilde{D}_{21} \frac{\partial }{\partial \xi } + \tilde{D}_{22} \frac{\partial }{\partial \eta } \right) \\ H_S^- &{} = &{} 1 - \left( \tilde{D}_{21} \frac{\partial }{\partial \xi } + \tilde{D}_{22} \frac{\partial }{\partial \eta } \right) . \end{array} \end{aligned}$$

(B.4)

By imposing (B.4) in (B.1) weakly gives

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI &{} = &{} \displaystyle \int _0^1 2 u \tilde{f} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta + \int _0^1 2 u \tilde{g} \bigg |_{\eta = 0}^{\eta = 1}\, d \xi \\ &{}+&{}\displaystyle 2 \int _{0}^{1} u \Sigma _E (W_E^- - g_E) \bigg |^{\xi = 1}\, d\eta \\ &{}+ &{}\displaystyle 2 \int _{0}^{1} u \Sigma _W (W_W^- - g_W) \bigg |_{\xi = 0} \, d\eta \\ &{}+ &{}\displaystyle 2 \int _{0}^{1} u \Sigma _N (W_N^- - g_N) \bigg |^{\eta = 1} \, d\xi \\ &{}+ &{}\displaystyle 2 \int _{0}^{1} u \Sigma _S (W_S^- - g_S) \bigg |_{\eta = 0} \, d\xi . \end{array} \end{aligned}$$

We expand the boundary terms $W_{E,W,N,S}^-$ to obtain

$$\begin{aligned} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI= & {} \displaystyle \int _0^1 2 u \tilde{f} \bigg |_{\xi = 0}^{\xi = 1} \, d \eta + \int _0^1 2 u \tilde{g} \bigg |_{\eta = 0}^{\eta = 1} \, d \xi \nonumber \\+ & {} \displaystyle 2 \int _{0}^{1} u \Sigma _E ( u + \tilde{f} - g_E) \bigg |^{\xi = 1} \, d\eta \nonumber \\+ & {} \displaystyle 2 \int _{0}^{1} u \Sigma _W (u - \tilde{f} - g_W) \bigg |_{\xi = 0} \, d\eta \nonumber \\+ & {} \displaystyle 2 \int _{0}^{1} u \Sigma _N (u + \tilde{g} - g_N) \bigg |^{\eta = 1} \, d\xi \nonumber \\+ & {} \displaystyle 2 \int _{0}^{1} u \Sigma _S (u - \tilde{g} - g_S) \bigg |_{\eta = 0}\, d\xi . \end{aligned}$$

(B.5)

In an attempt to cancel the indefinite terms in (B.5) we choose

$$\begin{aligned} \Sigma _E = -1 \quad \Sigma _W = -1 \quad \Sigma _N = -1 \quad \Sigma _S = -1 \end{aligned}$$

(B.6)

The choices (B.6) in (B.5) gives

$$\begin{aligned} \frac{d}{dt}\left\| u \right\| _{J}^2 + 2 DI =- & {} \displaystyle \int _0^1 2 \left( u - \frac{g_E}{2}\right) ^2 - \frac{g_E^2}{2} \bigg |^{\xi = 1} \, d \eta \nonumber \\- & {} \displaystyle \int _0^1 2 \left( u + \frac{g_W}{2}\right) ^2 - \frac{g_W^2}{2} \bigg |_{\xi = 0} \, d \eta \nonumber \\- & {} \displaystyle \int _0^1 2 \left( u - \frac{g_N}{2}\right) ^2 - \frac{g_N^2}{2} \bigg |^{\eta = 1} \, d \xi \nonumber \\- & {} \displaystyle \int _0^1 2 \left( u + \frac{g_S}{2}\right) ^2 - \frac{g_S^2}{2} \bigg |_{\eta = 0} \, d \xi . \end{aligned}$$

(B.7)

From (B.7), we note as in (2.14) that the solution is bounded by data.

Proposition B.1

The problem (2.3) with the boundary conditions (B.3) and the penalty coefficients in (B.6) is strongly well-posed.

Proof

Time integration (from 0 to T) of (B.7) results in

$$\begin{aligned} \begin{array}{rclcl} \left\| u(T) \right\| _{J}^2 + 2 \int _0^\mathrm{T} DI \, dt &{} - &{} \displaystyle \int _0^\mathrm{T} \int _0^1 2 \left( u - \frac{g_E}{2}\right) ^2 - \frac{g_E^2}{2} \bigg |^{\xi = 1} \, d \eta \, dt \\ &{} - &{} \displaystyle \int _0^\mathrm{T} \int _0^1 2 \left( u + \frac{g_W}{2}\right) ^2 - \frac{g_W^2}{2} \bigg |_{\xi = 0} \, d \eta \, dt \\ &{} - &{} \displaystyle \int _0^\mathrm{T} \int _0^1 2 \left( u - \frac{g_N}{2}\right) ^2 - \frac{g_N^2}{2} \bigg |^{\eta = 1} \, d \xi \, dt \\ &{} - &{} \displaystyle \int _0^\mathrm{T} \int _0^1 2 \left( u + \frac{g_S}{2}\right) ^2 - \frac{g_S^2}{2} \bigg |_{\eta = 0} \, d \xi \, dt. \end{array} \end{aligned}$$

Similarly to Proposition 2.1, the solution is bounded by data.

Appendix C: Stability

The matrix $I_2$ is the identity matrix of size $2 \times 2$. Note that $\overline{DI}$ is positive semi-definite and mimics its continuous counterpart in (2.5).

By rewriting (3.5) we find

$$\begin{aligned} \frac{d}{dt} \left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 + 2 \overline{DI}= & {} U^\mathrm{T} (\tilde{A} + \varvec{\varSigma }_W + \varvec{\varSigma }_W^\mathrm{T}) (E_{0N} \otimes P_{\eta }) U \nonumber \\- & {} \tilde{F}^\mathrm{T} (I_{\xi \eta } + \varvec{\varSigma }_W \tilde{A}^{-1})^\mathrm{T}(E_{0N} \otimes P_{\eta }) U \nonumber \\- & {} U^\mathrm{T} (E_{0N} \otimes P_{\eta }) (I_{\xi \eta } + \varvec{\varSigma }_W \tilde{A}^{-1}) \tilde{F} \nonumber \\+ & {} U^\mathrm{T} (E_{0N} \otimes P_{\eta }) (I_{\xi \eta } + 2 \varvec{\varSigma }_W) (\tilde{A}_{\xi } + \tilde{B}_{\eta }) U \nonumber \\- & {} U^\mathrm{T} (E_{0N} \otimes P_{\eta }) \varvec{\varSigma }_W g\nonumber \\- & {} g^\mathrm{T} \varvec{\varSigma }_W^\mathrm{T} (E_{0N} \otimes P_{\eta }) U. \end{aligned}$$

(C.1)

As in the continuous case, see (2.15), we cancel the indefinite terms, by the choice

$$\begin{aligned} \varvec{\varSigma }_W = - \tilde{A}. \end{aligned}$$

(C.2)

The use of (C.2) in equation (C.1) results in

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt} \left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 + 2 \overline{DI} &{} = &{} U^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{A} g + g^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{A} U \\ &{} -&{} U^\mathrm{T} \tilde{A} (E_{0N} \otimes P_{\eta }) U. \end{array} \end{aligned}$$

(C.3)

By adding and subtracting $g^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{A} g$ in (C.3) one obtains

$$\begin{aligned} \begin{array}{rcl} \frac{d}{dt} \left\| U \right\| _{J(P_{\xi } \otimes P_{\eta })}^2 + 2 \overline{DI} = &{} - &{} ((U - g)^\mathrm{T} \tilde{A} (E_{0N} \otimes P_{\eta }) (U - g) \\ &{} - &{} g^\mathrm{T} (E_{0N} \otimes P_{\eta }) \tilde{A} g) \end{array} \end{aligned}$$

(C.4)

and hence, the RHS of (3.6) is bounded by data with the initial assumption (as in the continuous case) that $\tilde{A} > 0$. Note the resemblance between (C.4) and the related continuous estimate in (2.14) considering only the west boundary.

When considering all the boundaries, the following choices

$$\begin{aligned} \begin{array}{rclrcl} \varvec{\varSigma }_E &{} = &{} {\left\{ \begin{array}{ll} -\tilde{A} &{} \hbox {if}\;\tilde{a}< 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{a}> 0 \end{array}\right. } &{} \varvec{\varSigma }_W &{} = &{} {\left\{ \begin{array}{ll} -\tilde{A} &{} \hbox {if}\;\tilde{a}> 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{a}< 0 \end{array}\right. } \\ \varvec{\varSigma }_N &{} = &{} {\left\{ \begin{array}{ll} -\tilde{B} &{} \hbox {if}\;\tilde{b}< 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{b}> 0 \end{array}\right. } &{} \varvec{\varSigma }_S &{} = &{} {\left\{ \begin{array}{ll} -\tilde{B} &{} \hbox {if}\;\tilde{b} > 0 \\ -I_{\xi \eta } &{} \hbox {if}\;\tilde{b} < 0 \end{array}\right. } \end{array} \end{aligned}$$

give us a discrete energy estimate.