Introduction

Invasion of nonindigenous species is considered one of the most urgent problems affecting native ecosystems with 87% of imperiled species threatened by invasive species (Mack et al. 2000; McClure et al. 2018). Additionally, nonindigenous species threaten agricultural systems requiring considerable policy activity to mitigate invasive species concerns (Miller et al. 2018; Miller 2020). Existing theory indicates that the distribution and spread of invasive species is the result of complex ecological processes that include the frequency and size of introduction (propagule pressure), species-specific traits that provide a fitness advantage (high reproductive capacity and dispersal), and biotic and abiotic characteristics of the recipient ecosystem that limit or facilitate invasion (Simberloff 2009; Lustig et al. 2017). However risk assessments of establishment and spread typically lack explicit consideration of these interacting factors (Catford et al. 2011; Gallien et al. 2015) and broad scale predictions of invasive species distributions are typically based on static approaches linking species occurrence to biotic and abiotic factors (Guisan and Zimmermann 2000; Lustig et al. 2017). Mechanistic models that account for short-term population dynamics (i.e. transient dynamics) can improve prediction because they incorporate differing demographic processes that link the environmental conditions of a spatial location explicitly with the invasion process (Buhnerkempe et al. 2011; Miller 2017). Yet short-term population dynamics are rarely accounted for in spatial models of invasive species spread (Lustig et al. 2017).

When populations are not at equilibrium (e.g., the age structure is not the stable age structure and population growth deviates from the equilibrium population growth rate, λ), they are expected to exhibit transient dynamics (Caswell and Werner 1978; Hodgson and Townley 2004; Tremblay et al. 2015). Transient dynamics can cause populations either to grow or shrink at a much faster rate than would be expected under equilibrium conditions (Stott et al. 2011; McDonald et al. 2017). When a small group of conspecific individuals is introduced to a new location (a “propagule”), it is not likely to be a stable population, and transient dynamics can lead to either rapid growth and establishment of a population or local extinction (Iles et al. 2016). Further these transient dynamics can differ from dynamics simulated using approaches that assume asymptotic population growth (Bieber and Ruf 2005; Tabak et al. 2018).

Invasive wild pigs (Sus scrofa), also known as feral hogs, feral swine, or wild boar, are recognized as one of the most widespread and destructive invasive species in the world (Barrios-Garcia and Ballari 2012). Wild pigs are native to Eurasia and Northern Africa, but have been widely introduced for centuries, often deliberately, and now occupy every continent except Antarctica (Mayer and Brisbin 1991; Lewis et al. 2017). Once introduced spread rates have been estimated to range from 2.75 to 12.6 km per year (Singer 1981; Snow et al. 2017). In North America it is an extremely destructive invasive species that is of concern for human and animal health (Miller et al. 2017), causes significant economic damage (Engeman et al. 2004; Anderson et al. 2016), negatively impacts imperiled species (McClure et al. 2018), and is commonly introduced into new locations (Tabak et al. 2017; Hernandez et al. 2018). These concerns have generated significant Federal policy to mitigate these impacts with the US Department of Agriculture establishing the Animal Plant Health Inspection Service (APHIS) National Feral Swine Damage Management Program in 2013 aimed at reducing the spread of wild pigs in the United States (USDA, 2015; Miller et al., 2018).

Nevertheless, the distribution of wild pigs in Canada and the United States has increased dramatically in recent years (Michel et al. 2017; Snow et al. 2017), and research suggests that a major mechanism of their spread is translocation of individuals to augment populations for recreational hunting (Tabak et al. 2017). Wild pigs evolved as pulsed resource consumers of mast crops; they have larger litter sizes and reproduce more often under favorable forage conditions, and have reduced fecundity under poor forage conditions (Ostfeld and Keesing 2000). This variability in fecundity makes wild pigs especially susceptible to transient population dynamics (Bieber and Ruf 2005; Miller 2017; Tabak et al. 2018). Despite their ancestral dependence on mast crops, wild pigs have evolved to be dietary generalists, as agricultural crops can replace mast in their diets (Schley and Roper 2003; Rosell et al. 2012) and they currently thrive in ecosystems that lack mast producing species (Caley 1997; Choquenot and Ruscoe 2003). Nevertheless, their reproductive biology retains this variability of fecundity, which can cause populations to rapidly grow and establish following introduction in new environments, leading to the further expansion of this species. Despite significant efforts to forecast the spread of wild pigs (Snow et al. 2017), estimate the probability of occurrence (McClure et al. 2015), and predict the potential density of wild pig populations (Lewis et al. 2017) there are no available spatial predictions of population growth and establishment risk if wild pigs were released into a given spatial location.

Our objective was to predict the stochastic population growth rate and establishment probability of wild pigs (accounting for transient dynamics) following introduction into any location in North America. We then compared predicted stochastic population growth rate with observed geographic rates of spread to determine if increased population growth was associated with increased spread (e.g. invasion). According to foundational work of Fisher (1937), Skellam (1951) and later van den Bosch et al. (1992) the rate of spatial spread is expected to be proportional to the square root of the intrinsic population growth rate. However more recent empirical studies have compared rates of spatial spread in more than one type of habitat finding that environmentally dependent spread rates are common (Williamson and Harrison 2002; With 2002). Additionally, the spatial arrangement of habitat has been empirically demonstrated to drive spread rates in some systems (Bailey et al. 2000). To investigate the relationship between stochastic population growth rate and observed geographic rates of spread we used geospatial data on the distribution of mast producing tree species (a primary forage resource of wild pigs) and agricultural crops that can replace mast in their diets (Choquenot 1998; Choquenot and Ruscoe 2003) to predict population dynamics using transient population simulations. We simulated populations under different propagule sizes and for different amounts of time following introduction. By varying the initial population size and simulation time, we were able to identify areas in North America with high probability for establishment if wild pigs are introduced. Our findings can be used to inform proactive surveillance and removal efforts to reduce the potential establishment and spread of wild pigs.

Methods

Predicting stochastic population growth and establishment

We used transient population dynamics models to simulate population trajectories for invasive wild pig populations under different types of environments that they could potentially experience in North America. Using the approach of Tabak et al. (2018) the demographic distribution in each subsequent year (\({n}_{t+1}\)) was estimated as,

$$n_{{t + 1}} = \left\| {{\text{\^A}}_{t} \hat{n}_{t} } \right\|_{1} n_{t} A_{t}$$

where \({A}_{t}\) is the population projection matrix for year \(t\), that is specific to the environmental conditions (i.e. forage) experienced in that year. The projection matrix is standardized using \(\hat{A}_{t} = A_{t} /\lambda _{{\max }}\) where \({\lambda }_{max}\) is the dominant eigenvector of \({A}_{t}\). The standardized demographic distribution, \({\hat n}_{t}\), is the proportion of individuals in each age class at the current time step. Thus \(\left\| {\hat{A}_{t} \hat{n}_{t} } \right\|_{1}\)is the 1-norm of the product of \(\hat{A}_{t} \hat{n}_{t}\) and is equal to the reactivity of the population (Neubert and Caswell 1997; Townley et al. 2007; Stott et al. 2011).

Following Tabak et al. (2018) for each simulated environment initial population sizes of 5, 10, and 20 were used as the number of females introduced in the first year of simulations. These initial population sizes were selected for two reasons. First these sizes represent a range of initial population sizes that could be introduced accidentally (i.e. escape from a farm) or intentionally to establish a population (i.e. transported via a truck or livestock trailer). Second, Tabak et al. (2018) found that wild pig populations could be established with as few as five individuals after accounting for transient dynamics. The individuals in each initial population were randomly assigned to age classes (juvenile, sub-adult, and adult) using Latin hypercube sampling (Xu et al. 2005) and in subsequent generations a sex ratio of 1:1 was assumed in litters.

We estimated stochastic population growth rate (\({\lambda }_{s}\)) and probability of establishment for wild pig populations in these environments and in environments with agricultural subsidy using the methods and the R scripts of Tabak et al. (2018). Using the methods of Tabak et al. (2018), Bierzychudek (1982), and Zúñiga-Vega et al. (2007) \({\lambda }_{s}\) was calculated as \({\lambda }_{s}={e}^{r}\). Where \(r\) is the intrinsic rate of population growth calculated as the slope of the regression between the logarithm of simulated population size and time. A simulated population was considered established if \({\lambda }_{s}\) > 1 and the population size at the end of simulation was ≥ 60. Tabak et al. (2018) found that \({\lambda }_{s}\) stabilized at 60 individuals across a range of environments. Simulations were run for 1, 5, or 10 years representing a range of times post-introduction that a population might be identified and management to control the population might start.

Survival and fecundity rates for different mast qualities (poor, intermediate, and good) provided in Tabak et al. (2018) and Bieber and Ruf (2005) were used (see Supplemental Table S1). These vital rates are currently the only available estimates that demonstrate variation by age and forage condition for wild pigs. They have been used to estimate the influence of forage quality on asymptotic population growth (Bieber and Ruf 2005) as well as the influence of forage quality on transient population growth and population establishment (Tabak et al. 2018).

Environmental conditions and making geographic predictions of stochastic population growth and establishment

Following Tabak et al. (2018) we simulate three broad types of environmental conditions to which wild pigs might be introduced in North America: (1) an environment with one mast tree species (poor forage quality), (2) an environment with a mast community (intermediate quality), and (3) an environment with agricultural subsidy (good quality). We conducted simulations in these three environments under nine different introduction scenarios using initial population sizes of 5, 10, or 20 as the number of females introduced at the beginning of the simulations. Data are scarcely available for the quality of mast from trees over time. However available empirical data and theory indicates that increasing the number of masting species in a community will increase both the frequency of years with mast as well as the intensity (i.e. number of trees producing mast) of the mast in good years (Koenig et al. 1994; Touzot et al. 2020) (see supplemental Figure S4). In the literature we found historic data from one common mast species, Fagus sylvatica, over 114 years (Hilton and Packham 2003) and from a community of five mast tree species, Quercus spp., over 12 years (Koenig et al. 1994). Unfortunately, data are unavailable for mast records from areas with 2–4 mast species and from areas with > 5 mast species. Therefore, we assumed that five mast species represented the maximum population growth potential resulting from their consumption of mast crops. For areas with 2–4 mast species, we estimated \({\lambda }_{s}\) and establishment probability using loess regression, where the predictor variable was the number of mast species (1 or 5) and the response variable was \({\lambda }_{s}\) or establishment probability. To calculate the \({\lambda }_{s}\) in areas with both mast and agriculture, we estimated \({\lambda }_{s}\) as the mean between the growth rate estimated as a result of mast and the growth rate estimated as a result of agricultural subsidy. To calculate establishment probability in such situations, we took the sum of probability of establishment that was estimated as a result of mast species and that resulting from agricultural subsidy.

There are clearly limitations in our estimation of growth rate and of establishment probability as we extrapolated to areas with numbers of mast trees for which we do not know the frequency of mast and we are unaware of how wild pig growth potential changes in the presence of both agriculture and mast trees. We also only considered the effects of forage on population growth, but other factors might affect growth rate (e.g., climate could have strong effects on survival) or dispersal from adjacent populations might serve as demographic rescue. However, we are interested in the general trends of population growth and establishment across the continent more than precisely estimating these rates.

To apply these growth rates and establishment probabilities to geographic locations, we used a geospatial layer depicting the number of mast species in each 1 km2 and the presence of crops that can replace mast in wild pigs’ diets using the USDA’s CropScape data (NASS, 2019). A detailed description of how the mast species data was generated is provided in the supplemental information. CropScape data are only available for USA, and we wanted to extend our model results to all of North America, so we also used the consensus land-cover layer for North America (Tuanmu and Jetz 2014) and compared this with the results in USA that were produced using the detailed CropScape data (Fig S3). Since the maps created using these two datasets were similar for the USA, we assume that it is reasonable to use the consensus land-cover and apply our results to all of North America. We have provided these mast layers as well as all other data layers used in the supplemental.

Determining rates of spread

We estimated the geographic rate of spread of wild pigs in the contiguous United States using data from the National Feral Swine Mapping System (Corn and Jordan 2017). These data describing the known distribution of wild pigs were compiled at irregular intervals from 1982 to 2008 and annually since 2008. They are the best available data describing the known distribution of wild pigs over the past 36 years and have been used to forecast the spread of wild pigs (Snow et al. 2017), estimate the probability of occurrence (McClure et al. 2015), determine wild pig agricultural damage risk (Miller et al. 2017), predict federal policy to control wild pigs (Miller et al. 2018), and determine the risk wild pigs pose to imperiled species (McClure et al. 2018). Polygons representing the known geographic extent of established wild pig populations (defined as populations present for two or more years with evidence of reproduction) are reported to the National Feral Swine Mapping System nationally by wildlife professionals in state wildlife resource agencies and the United States Department of Agriculture. The resulting distribution data is curated for accuracy with national data available annually.

Polygons representing the observed distribution for 1982, 1988, 2004, 2008, 2013, 2017, and 2021 were aggregated to watershed boundary data as described in McClure et al. (2015) to discretize consistent, comparable, and ecologically relevant sampling units. We selected the sub-watershed unit (hydrologic unit code 12; HUC12) as our primary sampling unit for several reasons. First theory indicates that rates of spread are primarily driven by population growth rate and dispersal (van den Bosch et al. 1992). Our interest here is to investigate associations among population growth rate and spread rate. To account for potential dispersal, HUC12 watersheds were selected because they encompass potential dispersal processes. Natural wild pig dispersal distance in North America has been reported to range from 0.5 to 2.4 km (Casas-Díaz et al. 2013) and empirical data suggests low dispersal rates (Stubbe et al. 1989; Truvé and Lemel 2003; Truvé 2004). The median distance from the centroid to the furthest edge of HUC12 watersheds with wild pigs occurring at any time point is 9.6 km and shortest distance was 3.2 km. Because HUC12 watersheds are larger than the expected dispersal distance we assume that they account for potential dispersal occurring. Second watersheds are frequently used as an ecologically relevant sampling unit for large scale studies (Odum and Barrett 1971; Montgomery et al. 1995; McClure et al. 2018) have been used to model the occurrence of wild pigs and other species (Collins and Glenn 1990; Peterson et al. 2003; McClure et al. 2015, 2018), and are expected to represent a discrete set of biotic and abiotic factors (McClure et al. 2015).

We chose to use watershed rates of spread rather than a linear measure of spread distance for several reasons. First, there is uncertainty in the polygons describing the known range of wild pigs in each year and converting these data to watershed level presence / absence smooths over potential uncertainties but also obscures the linear spread distance. Second, watershed rate of spread allows for the measure of range contraction (negative rates) while a linear measure of spread does not provide a useful measure of contraction. Lastly, wild pigs are frequently moved long distances and released by humans (Tabak et al. 2017). This means that an initial introduction into a new region will have a very large linear measure while subsequent spread will have shorter linear distances and is expected to be driven by local environmental conditions that drive population growth rates.

The annual watershed rate of spread among HUC12 watersheds was then calculated for three coarser watershed scales – sub-region (HUC4), basin (HUC6), sub-basin (HUC8). This was done because the spatial scale used for analysis can influence inference (Farnsworth et al. 2006). We calculated the annual rate (watershed/year) of spread (\(\theta\)) for each watershed\(j\) in each period \(t\) as,

$${\theta }_{j,t}=\frac{{\eta }_{i,t+1}-{\eta }_{i,t}}{T}$$

where \({\eta }_{i,t}\) is the count of HUC12 watersheds occupied by wild pigs in the coarser watershed \(j\) in year \(t\), and \(T\) is the number of years between \(t\) and \(t+1\). We also calculated the mean annual rate of spread from 1982 to 2013, the final year in this range was the beginning of a National Feral Swine Damage Management Program to control wild pigs, and from 2013 to 2017 which represents the period after the National Program began.

Associations among stochastic population growth rate and annual rate of spread

To determine if the predicted stochastic population growth rate (\({\lambda }_{s}\)) was associated with the annual rate of spread (\(\theta\)) in watersheds we regressed the annual rate of spread, \(\theta\), on the mean watershed stochastic population growth rate, \({\lambda }_{s}\). To investigated potential non-linear relationship we included a quadratic term (\({\lambda }_{s}^{2}\)) for watershed stochastic population growth rate. Estimates of \({\lambda }_{s}\) included three different initial populations sizes over three establishment time periods resulting in nine estimates of \({\lambda }_{s}\) per watershed. To account for these differences in initial population size and establishment period lengths we included establishment time (1, 5, or 10 years) and the propagule size (5, 10, or 20 individuals) as fix effect terms in the regression models. We used ordinary least-squares assuming a Gaussian error structure. We used adjusted R2 as a measure of goodness of fit of each model (Kutner et al. 2005). We used the percent of model deviance explained by each predictor as a measure of strength of association.

Results

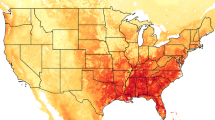
Our spatial estimates of \({\lambda }_{s}\) that used the detailed cropscape data for the US were similar to estimates using the cultivated layer that is available for all of North America (Fig. 1). Since these estimates were similar and using the cultivated data allows our results to have broader interpretation, we focus on the continental scale. With a small initial population size (propagule size = 5), mean \({\lambda }_{s}\) was < 1, regardless of the number of years that populations persisted following introduction (Fig. 1 and Table S7). As we increased propagule size and the number of years of simulation, \({\lambda }_{s}\) increased so that with a propagule size of 20 and ten years of simulation, \({\lambda }_{s}\) was > 1 for the majority of North America (mean = 1.16). We found the highest growth rates in the upper Midwestern United States, regions along the Mississippi river, and the southern prairie region of Canada.

Fig. 1
figure 1

Estimated stochastic population growth rates (\({\lambda }_{s}\)) for wild pigs in North America by years after introduction (x axis) and initial population size (y axis)

Full size image

The mean establishment probability was very low (< 0.03) when the initial population size was 5 female wild pigs (Fig. 2 and Table S8). When propagule size was increased to 20 and simulations ran for 5 to 10 years mean establishment probability increased to 0.497. Establishment probabilities were high in the same locations we found the highest growth rates (Figs. 1 and 2). Establishment probabilities approached 1 for many locations in the upper Midwestern United States and regions along the Mississippi river.

Fig. 2
figure 2

Estimated probability of establishment for wild pigs in North America by years after introduction (x axis) and initial population size (y axis)

Full size image

Annual spread rate

The annual spread rate (\(\theta\)) was proportionally consistent across the three watershed scales, however it demonstrated strong spatial heterogeneity (Fig. 3, see supplemental Figure S1 and Tables S2-S4 for all watershed scales). Mean annual rates of spread changed among time periods (Fig. 4) with the greatest rates of spread (watershed/year) occurring from 2008 to 2013 across all watershed scales (\({\theta }_{HUC4}\)=5.80, \({\theta }_{HUC6}\)=3.67, \({\theta }_{HUC8}\)=0.85; see supplemental for all spread rates including linear rates of spread). Annual rates of spread demonstrated spatial heterogeneity and were not constantly greatest along the northern extent of wild pig distribution. During the earliest periods from 1982 to 2004 spread rates were positive across the majority of the wild pig distribution. From 2004 to 2013 watersheds along the Red River, Rio Grande River, and Ohio River consistently had the highest spread rates. Annual spread rates declined 82% after the establishment of the National Feral Swine control program in 2013 with 65.2–69.0% of watersheds having spread rates ≤ 0 (Table S2). The highest rates of spread after 2013 were confined to watersheds in the southeastern portion of the United States.

Fig. 3
figure 3

Annual watershed level spread rate (watersheds/year) for wild pigs from 1982 to 2021 for HUC6 level watershed (see supplemental for other watershed scales). Red indicates positive rates of spread and blue indicates negative rates of spread (i.e. contractions in the number of occupied watersheds). Light gray indicates rates of spread that were zero and dark gray indicates areas with no wild pigs present

Full size image
Fig. 4
figure 4

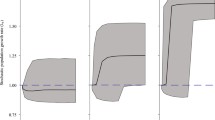
Mean annual rates (watersheds/year) with confidence intervals for spread (Panel a), gain (Panel b) and loss (Panel c) rates for wild pigs from 1982 to 2021. Spread rates (Panel a) were positive from 1982 until 2013 after which they slowed and demonstrated higher loss rates. A national wild pig control program was initiated in 2013 with the objective of reducing the range of wild pigs in the United States

Full size image

Association of spread rate and stochastic population growth rate

We found significant relationships between the annual rate of spread and stochastic population growth rates. Stochastic population growth rate explained a large amount of variation (79.3–92.1%) in annual rate of watershed spread of wild pigs across all time periods (Table 1). The linear term for the mean stochastic population growth rate explained the largest amount of deviation (Table 1 and S6) while the non-linear term for mean stochastic population growth rate was a significant term in most models but explained on average 4.01% (0.05 − 9.19%) of total deviance (Table 1). Propagule size and length of time for establishment were not significant in any models (Figure S3) and accounted for little to no deviance (Table S6). For all periods prior to the National Feral Swine control program, except for 1982 to 1988, population growth rates were a significant positive predictor of the annual rate of spread for all watershed scales (Fig. 5). Models including all periods explained a large amount of variation in rate of spread with adjusted R2 values ranging from 0.784 to 0.917 (Table 1 and Table S7). There was a difference among models that included all periods prior to (1982–2013) and after (2013–2021) the establishment of the National Feral Swine control program. Models including all periods from 1982 to 2013 had adjusted R2 values ranging from 0.887 to 0.913 while models including all periods from 2013 to 2021 had adjusted R2 values ranging from 0.46 to 3.26. For the period after the establishment of the Feral Swine control program (2013 to 2021), population growth rates were either not a significant predictor or had a negative association with annual watershed rate of spread.

Table 1 Performance of regression models and percent of total deviance in watershed spread rates explained by stochastic population growth rate terms (\({\lambda }_{s}\) and \({\lambda }_{s}^{2}\))
Full size table
Fig. 5
figure 5

Regression coefficients with 95% confidence intervals for linear models regressing wild pig spread rate on stochastic population growth rate. Spread rate was increasingly positively associated with stochastic population growth rate in all time periods except the period from 2013 to 2021. A national wild pig control program was initiated beginning in 2013 with the goal of reducing the range of wild pigs in the United States

Full size image

Discussion

Explicitly accounting for initial population size and age structure allowed us to account for transient dynamics and demographic stochasticity that influence predictions of population growth and probability of establishment. Our geospatial projections of stochastic population growth rate and establishment probability (Figs. 1 and 2) highlight areas at increased risk of successful establishment of wild pig populations if introduced. The strong correlation between our estimates of stochastic population growth (\({\lambda }_{s}\)) and the annual watershed rate of spread (\(\theta\)) supports the validity of our population growth estimates. In other systems, transient population growth rate has been identified as important in predicting establishment success and long term viability of invading species (Iles et al. 2016). The relationship we found between population growth and watershed rate of spread corresponds to existing theory suggesting the rate of spatial spread is expected to be proportional to the intrinsic population growth rate (van den Bosch et al. 1992). However positive associations between population growth rate and spatial spread varied across time and watershed indicating that spread rates are potentially influenced by environmental or other more local factors such as the spatial arrangement of habitat (Bailey et al. 2000; Williamson and Harrison 2002; With 2002). Beyond aligning with established ecological theory our results can be used to target areas for surveillance that have higher potential for wild pig establishment and rapid population growth allowing for early identification of wild pigs and facilitating efforts to minimize population expansion once new wild pig populations are identified.

Applying mechanistic models to geospatial projections

While mechanistic models are often used for distribution and niche modeling for invasive species (Kearney and Porter 2009; Peterson et al. 2015), population dynamic processes across spatial scales are more commonly evaluated using statistical models to correlate population processes with spatial covariates (but see Chandler et al., 2018; Quintana-Ascencio et al., 2018). Correlative spatial models are convenient, especially in systems with less biological data, because they do not require an understanding of the mechanistic links between an organism and its environment. However, mechanistic processes tend to limit the expansion of species distributions, so it can be useful to build models that evaluate mechanistic processes across large spatial extents when the goal is to predict the growth and establishment potential of a species. Furthermore, for populations that experience transient dynamics, mechanistic models may be more applicable than correlative statistical models. When a population is introduced into a new environment, it will usually exhibit transient dynamics (Iles et al. 2016) and wild pigs are especially prone to transient dynamics due to their evolution as pulsed resource consumers (Bieber and Ruf 2005; Tabak et al. 2018).

Comparison to other studies

Our estimates of stochastic population growth and establishment probability correspond well to the reported establishment of wild pigs throughout the United States and the prairie provinces of central Canada (Lewis et al. 2017, 2019; Michel et al. 2017). However, our estimates of establishment probability differ in several ways from the predicted spread of wild pigs in the United States (Snow et al. 2017). We found high establishment probability throughout the upper Mississippi and Ohio River drainages while previous studies predicted lower probability of spread in these areas. The historical spread of wild pigs in the United States demonstrated by Snow et al. (2017) implicitly includes factors such as human translocation of wild pigs which previous studies have found to be important in the spread of wild pigs (Tabak et al. 2017). The differences between Snow et al. (2017) and our results may stem from differences in the frequency of introduction, that is likely driven by anthropogenic factors. This indicates that while the probability of establishment is generally high in some regions of the United States, the historical frequency of introduction has likely been low. The distribution of our predicted probability of establishment and stochastic population growth rates generally correspond well with the predicted equilibrium population density of wild pigs by Lewis et al. (2017).

Additionally Tabak et al. (2018), which is the basis for the approach used in this study, found that fewer individuals are required to establish a population of wild pigs when compared with other studies (Howells and Edwards-Jones 1997; Leaper et al. 1999). These previous studies use more traditional population modeling approaches that have an underlaying assumption of asymptotic growth and population at the stable-stage distribution. While these studies accounted for stochasticity either in demographics or environment, they do not explicitly account for the interaction of age structure and vital rates that can result in transient effects that either amplify or attenuate population growth (Caswell and Werner 1978; Townley et al. 2007). Explicitly modeling transient dynamics provides important insights into the effects of altering age structure and the corresponding changes in population size (Stott et al. 2011). Studies have demonstrated that greater than 50% of population dynamics can result from transient effects (Ellis and Crone 2013; McDonald et al. 2016) and empirical studies have documented the interaction of demographics and initial population size on growth rates (Komers and Curman 2000). Further predictions of population trajectories that account for transient dynamics can be very different than methods using asymptotic growth approaches for wild pigs (Bieber and Ruf 2005; Tabak et al. 2018). Interestingly a retrospective analysis of exotic ungulate introductions found that introductions with as few as six individuals were successful which is similar to the propagule size of ten that Tabak et al. (2018) found to be a threshold for wild pigs and is similar to our results (Forsyth and Duncan 2001).

The differences among the predictions of wild pig spread (Snow et al. 2017), population density (Lewis et al. 2017), and probability of establishment (McClure et al. 2015) are not mutually exclusive. The differences among these results is largely due to each study focusing on a different component of the invasion process - introduction, establishment, population growth, and spread (Reise et al. 2006). These differences highlight the need to develop integrated mechanistic approaches that explicitly include factors that drive introduction pressure (e.g. Snow et al. (2017) and Tabak et al. (2017)) probability of establishment and population growth (e.g. our study), and factors regulating long-term population growth and equilibrium population size (e.g. Lewis et al., 2017). Accounting for the invasion process in a spatially explicit context would allow for greatly improved predictions of establishment risk and consequences once established.

Management implications

Establishment probability was very low when initial population size was small and when populations had fewer years to become established (Fig. 3), because populations in these simulations were unlikely to meet one of the criteria for establishment: a population size of 60 individuals in the final simulation year. This indicates that there may be the opportunity to prevent population establishment if actions are undertaken quickly upon discovery of new introductions. With larger initial populations and more time following introduction, the potential for population establishment increased dramatically, indicating that it is best to prevent introductions of large numbers of individuals and to begin interventions early. Reducing the frequency and size (number of animals) of releases of wild pigs can reduce establishment probability, but these goals may be difficult to implement, as movement and release of wild pigs is common and has been documented on multiple continents (Hampton et al. 2004; Tabak et al. 2017; Hernandez et al. 2018). This is often complicated by limitations of current tools available for detecting newly released pigs. Tools such as pig detection dogs (Keiter et al. 2016) and passive monitoring using camera traps (Tabak et al. 2019) are difficult to deploy over large geographic extents for long periods of time. Our results can be used to refine where monitoring using these tools is conducted, improving the chances of early detection of pigs. When considering management to prevent population establishment, it is important to note that our methods only account for a single introduction event so likely represent a conservative estimate of establishment probability. Wild pigs are often repeatedly introduced to the same location (Mayer and Brisbin 1991), which can increase establishment probability through demographic rescue of the founder population (Hufbauer et al. 2015).

Extensions

Our method of estimating stochastic population growth and establishment success has some important limitations that offer opportunities to extend our approach. Complete data on the frequency and intensity of mast and how these change with the size and community structure of mast species is limited. To address this data limitation, we extrapolated using available data, however there is uncertainty in our approach for making this extrapolation. The collection of data describing mast frequency and intensity over large geographies in North America would have significant value for population dynamic modeling of many species that consume seasonal mast and fruit. Additionally, we used data linking how mast frequency and intensity affect vital rates of wild pigs from Europe (Briedermann 1967; Bieber and Ruf 2005); data describing this relationship in other continents are needed to better extrapolate globally. In our predictions the primary driver of wild pig vital rates was assumed to be access to mast. However, previous studies have indicated that precipitation and temperature can influence survival of younger age classes impacting transient population dynamics of wild pigs (Miller 2017). Currently most studies reporting survival, litter size, and frequency of litters and how these factors correlate with environmental conditions are from wild pig populations in Europe. Studies collecting these vital rates for wild pig populations in North American would be of great value. We also do not account for inter and intra species interactions that may also be limiting for founder populations. For example Lewis et al. (2017) found that predator species richness was negatively associated with wild pig population density. Accounting for these interactions within a dynamical modeling framework that accounts for transient dynamics would be an exciting extension of our work. Lastly, our matrix model approach does not account for non-linearity in population growth (e.g., density dependence) that we assume maybe influencing the vital rates from Bieber and Ruf (2005), although, Lewis et al. (2019) found that many wild pig populations in the United States may be at or near equilibrium. Despite these limitations, predicted population growth and the spread rate of wild pigs in areas where they have been introduced were highly correlated. The positive correlation indicates that despite the data uncertainties, our projections are reasonable estimates of population growth and establishment potential for wild pigs.

Conclusion

Risk assessments of establishment and spread of invasive species can be improved by using mechanistic models that consider the frequency and size of introduction along with the biotic and abiotic characteristics of the recipient ecosystem, while accounting for short-term population dynamics can improve prediction. Accounting for short-term population dynamics in spatial models of invasive species spread will become increasingly important as variation in climatic conditions increases. For many invasive species, including wild pigs, increasing temperature is expected to increase invasion success and expand regions with the potential for invasion (Vetter et al. 2015). Spatial models that account for short-term population dynamics can allow for uncertainties resulting from increased climate variation to be explicitly considered, improving predictions. An important extension of our work is to integrate, using mechanistic approaches that account for short-term population dynamics, ecological and anthropocentric processes that determine introduction, establishment, and spread of invasive species.