1 Introduction

Multistory reinforced concrete (RC) buildings with masonry infill walls (MIWs) are a common construction practice especially in highly populated cities (El-Kholy et al. 2018a). The multistory RC buildings resist the lateral load through a structural system of frames and/or shear walls (SWs). Investigating the contribution of MIWs to the lateral stiffness of multistory RC buildings, and the interaction between the MIWs and the surrounding RC frames elements go back to the early 1950s. Studying the structural behavior of multistory RC frames buildings is more crucial for those that were not seismically designed (old buildings in the developing countries; El-Kholy et al. 2018b). Nonetheless, analyzing the multistory RC frames (or SWs) buildings with MIWs through nonlinear finite element analysis (FEA) is challenging because of the inevitable large number of degrees of freedom, the nonlinear deformation of the RC members, the nonlinear deformation of the RC joints, the brittle behavior of MIWs, and the interaction between the RC and MIWs.

1.1 Micromodeling of multistory RC buildings with MIWs

Micromodeling of the RC frames, SWs, and MIWs using solid brick finite elements for the concrete and the masonry, truss elements for the rebar, and interface elements for the mortar between the masonry and the concrete provides rigorous 3D simulation (Yekrangnia and Asteris 2020; Asteris et al. 2013; Cavaleri et al. 2020; Li et al. 2019, 2016; El-Kashif et al. 2019; Mohyeddin et al. 2013; Koutromanos et al. 2011; Sharma et al. 2009). Also, earlier pioneer studies presented a 2D micromodeling of the MIWs and a simulation for the separation between the MIW and the surrounding RC frame using plane finite elements (Asteris 2003; Shing and Mehrabi 2002; Mehrabi and Shing 1997). However, it is needless to mention that the micromodeling of a complete multistory RC frames (or SWs) building with MIWs is an unattainable goal because of the infinite number of degrees of freedom.

1.2 Macromodeling of multistory RC buildings with MIWs

Macromodeling provides a good trade-off between the computation cost and the accuracy of the results. Therefore, macromodeling is the possible gateway for the challenging of analyzing a complete multistory RC frames (or SWs) building with MIWs. This challenging is the scope of this paper. To achieve this objective, a) inclusive experimental investigations, and b) reliable nonlinear macromodels for the three main structural elements; 1) frames, 2) MIWs, and 3) SWs; of the multistory RC buildings are involuntary. Regarding a) the experimental investigations, there are many studies for the structural behavior of the RC frames with or without MIWs (Vecchio and Emara 1992; Angel et al. 1994; Mehrabi et al. 1996; Negro et al. 1996; Carvalho et al. 1999; Duong et al. 2007; Sharma et al. 2013; Cavaleri and Trapani 2014; Basha and Kaushik 2016; Shan et al. 2016; Dautaj et al. 2018; Dautaj and Kabashi 2018; Pallarés et al. 2021; Demirel et al. 2023), and the RC SWs (Chen and Qian 2002; Thomsen and Wallace 2004; Dazio et al. 2009; Alarcon et al. 2014; Kolozvari et al. 2015; Takahashi et al. 2013; Park et al. 2015; Sanada et al. 2018; Wang and Wang 2021) under lateral loading. The references introduced in this paper were only indicative and not exhaustive. Also, regarding (b) the macromodeling, there existed numerous studies that developed different reliable macromodels for simulating the (1) bare frames, (2) MIWs frames, and (3) SWs in either two-dimensional (2D) or three-dimensional (3D) analysis under lateral loads. Indicative studies are briefly presented in the following three subsections.

1.2.1 Macromodeling of bare frames

First, the macromodeling of bare frames (in the majority of the reviewed studies) was accomplished using the concentrated plasticity (CP) approach in a form of plastic hinge (PH) through lumping the plasticity at the critical sections. Alternatively, the distributed plasticity (DP) approach was employed in few studies. Also, a truss unit (assemblage of truss members; Salinas et al. 2022) approach was recently used to model the RC frames. Regarding the CP approach, there are different forms of the PHs to represent the flexural, shear, and torsional deformations in the RC members. Moreover, the shear failure and the bond failure in the frame joints could be represented by joint PHs. The characteristics of the flexural PH play a major role in determining the response of RC buildings (Sunil and Kamatchi 2022; Inel and Ozmen 2006). López-López et al. (2016) investigated the influence of different flexural PH models on the response of typical simple five-story and eight-story buildings using SAP2000 in 2D. For the studies investigating the CP versus DP approaches using different software, Zendaoui et al. (2016), Carvalho et al. (2013), Noh et al. (2017), and Li et al. (2019) utilized the SeismoStruct, SAP2000 versus SeismoStruct, OpenSees, and SAP2000 versus OpenSees, respectively, to analyze a four-story frame in 2D, an existing five-story building in 3D, a portal frame in 2D, and a four-bay two-story frame in 2D using different alternatives of macromodels. It was concluded that the DP approach provides more accurate results compared with CP. Also, Carvalho et al. (2013) and Li et al. (2019) concluded that using the CP approach in SAP2000 is more convenient, and it provides reliable results with low computation cost and less convergence difficulties. Based on the conclusions of the reviewed studies, the CP approach (PH models) and SAP2000 were utilized in this paper. Many researchers made significant trials to simplify the modeling of flexural PH zone by representing it with a constant length \({l}_{p}\) namely the flexural PH length (Park and Paulay 1975; Priestley et al. 1996). Several formulas for estimating \({l}_{p}\) will be reviewed in Sect. 3.1.1 and Table 1. The common practice is to utilize one \({l}_{p}\) formula for all the PHs in the studied frame/building unlike the proposed iterative model (FHCM; Sect. 3.1.2) that assigns a proper formula for each PH based on its axial load ratio. The PH length might be magnified for the sections exhibiting flexural deformation accompanied with significant shear deformation (Elmenshawi et al. 2012). If the shear deformation is prevailing, the shear PH becomes mandatory. The shear failure of RC frames was experimentally investigated (Vecchio and Emara 1992; Simokaichi 1994; Elwood and Moehle 2003; Duong et al. 2007), and different shear models were introduced (Watanabe and Lee 1998; Elwood 2004; Elwood and Moehle 2005). For modeling the shear failure of RC joints, many macromodels such as Pan et al. (2017), Sharma et al. (2011a), Yu (2006), Ziyaeifara and Noguchib (2000), and Ghobarah and Biddah (1999) were presented.

1.2.2 Macromodeling of masonry infill walls (MIWs)

Second, the macromodeling of MIWs had been explored in-depth since 1950s (Thomas 1953; Polyakov 1960; Smith 1962), and it is still an open issue (Elgamel et al. 2023; Adnan et al. 2022; Roosta and Liu 2022; Mazza and Donnici 2022; Srechai et al. 2022; Pradhan et al. 2022) owing to the brittle behavior of MIWs that exhibit distinct directional properties (Syrmakezis and Asteris 2003) besides the interaction between the MIW and the bounding RC frame. For more studies, an inclusive literature review was presented by Dias-Oliveira et al. (2022) for the experimental work and the numerical models of the MIWs frames. The single equivalent strut macromodel is convenient to track the global behavior of MIWs frames unlike the multi-strut models that sophisticatedly capture the local effects in the bounding frame. Crisafulli et al. (2000), Asteris et al. (2011), Chrysostomou and Asteris (2012), Li et al. (2019), and Pallarés et al. (2021) established extensive comparison between the different macromodels utilizing single-strut, double-strut, and multi-strut for modeling MIWs frames. The backbone curve (material nonlinearity) of the equivalent strut model might be idealized to trilinear, quadlinear, or pentalinear force–displacement envelope (Mbewe and Zijl 2011; Mucedero et al. 2020). The simplicity of the one-strut model motivated its use in many studies (Saneinejad and Hobbs 1995; Madan et al. 1997; Cavaleri et al. 2005; Cavaleri and Di Trapani 2014; Perrone et al. 2017; Al-Balhawi and Zhang 2017; Liberatore et al. 2018; Van et al. 2022). Therefore, the one-strut model with trilinear backbone curve was utilized in this paper for simplicity. Seeking the representation of all potential failure modes of MIWs frames, Adnan et al. 2022, Roosta and Liu 2022 and Srechai et al. 2022 presented novel multi-strut-spring macromodels. Moreover, Yekrangnia and Asteris (2020) presented a novel multi-strut macromodel for representing the openings in MIWs frames. Also, Salinas et al. (2022) modeled the MIWs as an assemblage of nonlinear truss elements.

1.2.3 Macromodeling of shear walls (SWs)

Third, macromodeling of RC SWs is very challenging due to their inherently complicated characteristics. Wu et al. (2017), Kolozvari et al. 2018b, 2019a), Pozo et al. (2020), and Clark et al. (2021) presented inclusive assessment of different macromodels such as the multiple-vertical-line-element with and without shear-flexural interaction model, the equivalent truss model, the 2D shear panel element, and the fiber-based element. Despite Rojas et al. (2016, 2019) and Kolozvari et al. (2019b) categorized the multilayer membrane and shell elements as a first level of the micromodeling for RC SWs, these elements were considered as macromodels by Clark et al. (2021) and Chen and Qian (2002). The computational cost of these elements is relatively low compared with the full finite element analysis (complete micromodeling) using 3D solid brick elements for the concrete and truss elements for the rebar. This paper utilized the multilayer shell element in which the SW is discretized through its thickness into fully bonded concrete and reinforcement layers and a good trade-off between the computation cost and the accuracy of the results could be achieved (Kolozvari et al. 2022).

1.2.4 Macromodeling of complete multistory buildings in 3D

Utilizing the macromodels of the RC frames (Sect. 1.2.1), the MIWs (Sect. 1.2.2), and the SWs (Sect. 1.2.3) together to model a complete existing multistory building is the most important goal for this paper.

1.2.4.1 Bare frames buildings

Carvalho et al. (2013) utilized SAP2000 versus SeismoStruct to analyze an existing five-story building located in Turkey (Bal et al. 2008). The building was asymmetric along the y-axis. It consisted of seven bays in x-direction and three bays in y-direction (19.2 × 9.1 m). Carvalho et al. (2013) concluded that utilizing flexural PHs in SAP2000 is the most convenient and reliable approach with minimized convergence problems. Also in 2013, Sharma et al. presented an innovative 3D experimental study for a four-story building, and employed the Kent and Park (1971) model, Watanabe and Lee (1998) model, Park and Paulay (1975) model, Sharma et al. (2011a) model for numerically addressing the deformation of the flexural PHs, shear PHs, torsional PHs, and joint shear PHs, respectively, that were defined in three alternative 3D macromodels using SAP2000 software in order to capture the global behavior of the small building under pushover analysis. The small building comprised only one bay in each direction, just like one room (5 × 5 m), with four main edge beams and one secondary internal beam in x-direction. The beam-column connections were non-seismically detailed. Sharma et al. (2013) concluded that the joints PHs were obligatory for non-seismically detailed connections to accurately capture the global lateral response of the building. Similar 3D experimental and numerical study was presented by Sharma et al. (2011b) for a three-story building comprising two bays in each direction (1.5 m equal spans for all bays). This ideal building comprised nine columns and twelve main beams with constant cross-section of 150 × 200 mm. Sharma et al. (2011b) concluded that not only the flexural deformation in both beams and columns but also the shear deformation in the joints were important to address the nonlinear lateral response of the building. It is worth mentioning that utilizing different PHs (flexure, shear, torsion, and joint) together into one 3D analysis (Sharma et al. 2011b, 2013) was a pioneer step towards the analysis of a complete multistory building even if the studied building was ideal with limited number of stories and bays.

1.2.4.2 MIWs frames buildings

Perrone et al. (2017), Al Hanoun et al. (2019), and Pallarés et al. (2021) preferred using the SAP2000 to analyze MIWs frames buildings. Perrone et al. (2017) performed 2D parametric analysis for an ideal equal four-bay MIWs frames with story range from two to ten. The MIWs frames were designed for only gravity loads. Seeking simplicity for such a parametric analysis, Perrone et al. (2017) utilized the single strut model for representing the MIWs. The results showed that the seismic behavior of the gravity loads designed frames was highly affected by the existence of the MIWs. Al Hanoun et al. (2019) provided 3D analysis for a four-story MIWs frames building with two unequal bays in each direction. This building was tested in a full-scale experiment by Negro et al. in 1994. Al Hanoun et al. (2019) provided an advanced model for the MIW that was represented by four elastic beam elements pinned to the joints of the RC frame elements and linked with a nonlinear axial link element in order to represent the in-plane and out-of-plane behavior of the MIWs. Pallarés et al. (2021) provided 3D analysis for a real six-story MIWs frames building located in Spain. The building was approximately rectangular with aspect ratio of 3.1, and no symmetry existed in either x or y-direction. It was a good practice for analyzing a real building. The MIW was represented using the single strut model. The results showed that the MIWs magnified the lateral stiffness of the building and changed the mechanism of resisting the lateral loads. Lemonis et al. (2019) presented an attempt for developing a macromodel that estimates the global stiffness of multistory frames using an assembly of equivalent springs representing each infill panel.

1.2.4.3 SWs buildings (either bare or with MIWs)

To the best of our knowledge, no studies are available for the contribution of the MIWs to the stiffness of seismically designed SWs buildings. The majority of the studies investigating the SW nonlinear lateral behavior were conducted for a single shear wall (Sect. 1.2.3) not for a complete building (either bare or with MIWs). This could be attributed to three reasons; (1) the SWs buildings are often well seismically designed, 2) the MIWs are considered as nonstructural elements in these buildings, and (3) the computation cost of modeling the SW itself is high.

2 Need for research

Based on the previous review, there is still room for research in the issues of macromodeling (1) the bare frames, (2) the MIWs frames, and (3) the SWs despite the three issues were the focus of numerous rigorous studies since more than a half-century. Moreover, the wide-variety and the enormous number of the available nonlinear macromodels with no definitive practical procedure for each issue caused confusion for the designers who opted to perform linear analysis and consider the MIWs as nonstructural elements. Furthermore, the studies that used the macromodels for the three issues together to simulate a complete real multistory building (the top challenging and the main target of this paper) were rare and they did not conform all the reality conditions. In this paper, "real" implies that the studied building should be not a typical ideal case with limited number of stories, limited number of spans, equal spans, constant column/beam cross-section, or uniform distribution of the vertical elements (columns, SWs, and MIWs). In other words, the layout of the real building is governed by the architectural needs.

In this paper, a simple integrated nonlinear macromodeling strategy for simulating RC frames buildings and SWs buildings (with/without MIWs) is presented to provide confidence enough to use in every day engineering practice of modeling real large-scale multistory buildings. The presented strategy integrates a newly proposed flexural PH consistent model (FHCM), a shear PH model, a torsion PH model, a joint PH model, a multilinear plastic link model for the MIWs, a nonlinear multilayer shell element for the SWs together to analyze complete real multistory buildings in 3D using SAP2000 (CSI 2020). Moreover, the presented FHCM includes a newly proposed iterative technique for estimating the PH length \({l}_{p}\) using four \({l}_{p}\) formulas where the proper formula for each section is selected based on the axial load ratio. This means that different \({l}_{p}\) formulas can be used for the different PHs in the same frame unlike the reviewed studies. After validation of the presented strategy through comparison with the results of eleven experimental tests, the macromodeling strategy was applied to 3D analysis of real ten-story MIWs RC frames and SWs buildings to investigate the power of the presented strategy and the structural behavior of these buildings.

3 Nonlinear macromodeling strategy

Figure 1 presents the nonlinear analysis strategy that was conducted in this work using SAP2000 software (CSI 2020). The nonlinearities of the frame members, the MIWs and the SWs were simulated using the CP approach (flexural, shear, torsion, and joint PHs), a multilinear plastic link, and a nonlinear multilayer shell element, respectively. The model FHCM was implemented into the strategy in order to provide a consistent modeling for the flexural PH in different RC frames by defining its modeling type (Table 2 and Fig. 2a), position (Fig. 2b, c), and length (\({l}_{p}\)) using a proposed technique (Fig. 3). For the slabs in the 3D models, elastic behavior was assumed, and the slab joints were constrained using a diaphragm in the slab plane.

Table 1 Plastic hinge length \({l}_{p}\) formulas
Full size table
Fig. 1
figure 1

Nonlinear macromodeling strategy

Full size image
Table 2 Flexural plastic hinge modeling alternatives
Full size table
Fig. 2
figure 2

Fibers and positions of flexural PHs in FHCM

Full size image
Fig. 3
figure 3

Proposed technique for estimating \({l}_{P}\)

Full size image

3.1 RC frames modeling

In this work, the frame elements were modeled using a bar element with two nodes. Each column within a story (and similarly each span of a beam) was modeled using one element to simply define the PH position relative to the element length. Auto divided elements were used for the beams connected with slabs, and for the main beams supporting other secondary beams in the 3D models. The confined concrete stress–strain curve was defined according to Mander et al. (1988) based on the volumetric ratio of the transverse reinforcement (\({\rho }_{w}\)). Four PH models (flexural, shear, torsion, and beam–column joint) were used to capture the behavior of different nonlinearities. In addition, a consistent procedure for modeling the flexural PH was introduced in Sect. 3.1.2.

3.1.1 Flexural PH

The flexural PHs were inserted at the maximum moment positions. Many researchers made significant trials to simplify the modeling of flexural PH zone by representing it with a constant length \({l}_{p}\) namely the flexural PH length (Park and Paulay 1975; Priestley et al. 1996). The ultimate deformation capacity of a PH depends on the ultimate curvature and the \({l}_{p}\). The rotation and displacement are determined by integrating the curvature and strain, respectively, over \({l}_{p}\). Table 1 introduces 11 empirical formulas used for estimating \({l}_{p}\) as a function in several parameters representing the cross-section geometry, the reinforcement, and the concrete strength. The five important parameters used in the majority of \({l}_{p}\) formulas were the shear length Z (moment to shear ratio), the cross-section height h, longitudinal bar diameter \({d}_{b}\), the yield stress of longitudinal reinforcement \({f}_{y}^{l}\), and the concrete compressive strength \({f}_{c}^{\prime}\). Baker (1956) and Bae and Bayrak (2008) prompted that \({l}_{p}\) is proportional to the ratio of the initial axial load \({P}_{1}\) to the axial load capacity \({P}_{o}\). The last formula listed in the Table 1 was presented by Elmenshawi et al. (2012) to account for the inelastic shear deformation. Elmenshawi et al. (2012) presented a normalized shear spread parameter \(k=(1-{q}_{s}/{2q}_{u})\) in which \({q}_{s}\) and \({q}_{u}\) are the transverse shear strength and the actual shear stress at the ultimate lateral load, respectively. The transverse shear strength \(q_{s}\) is equal to \({\rho }_{w}{f}_{y}^{s}\) in which \({\rho }_{w}\) and \({f}_{y}^{s}\) are the volumetric ratio and the yield stress of the transverse reinforcement, respectively. For \(k\le 0\) (pure flexural failure mode), the shear deformation had no significant effect on the element response. For \(0<k\le 0.5\) (flexural failure mode with significant shear deformation), Elmenshawi et al. (2012) increased \({l}_{p}\) by a shear contribution length \({l}_{s}=kd\) to account for the expected significant shear deformation. For \(k>0.5\), the section showed a brittle shear failure mode, and an explicit shear PH should be defined according to Sect. 3.1.3.

Four modeling alternatives for the flexural PH were presented in Table 2. They were categorized into two types according to the definition of the cross-section (discretized or not). The first type (explicit curve) directly defines the M-θ curve, whereas the second type (fibers) discretizes the cross-section into fibers to accurately track the nonlinear behavior of RC frames (Van et al. 2022; Salihovic and Ademovic 2017; Belejo and Bhatt 2012). The two types could be defined either by the user or automatically using SAP2000. The \({l}_{p}\) must be defined for the fibers type.

3.1.2 Proposed flexural PH consistent model (FHCM)

The FHCM identifies the PH modeling type, prescribes the positions of PHs, and introduces an iterative technique for estimating \({l}_{p}\) of RC frames members. The fibers auto-hinge PH type (Table 2) was used because of its high accuracy and simplicity compared with the explicit curve and the user fibers, respectively. The PH section was discretized into fibers with a maximum size of 30 mm along the flexural axis and 24 mm perpendicular to the flexural axis (Fig. 2a). The end length offset was set to automatic form connectivity (CSI 2020) for all members (Fig. 2b, c), and therefore the PHs positions were defined relative to the clear length ends. For the purpose of simplifying \({l}_{p}\) estimation using the iterative technique (Fig. 3), the PHs positions were set at the clear length ends of all the frame elements. Afterwards and using the estimated \({l}_{p}\) in the target nonlinear analysis, the positions of only the upper PHs of each column in the first story were moved a \({l}_{p}\)/2 distance from the bottom face of the beam (Fig. 2b). Furthermore, the bottom PH of the column pushing the masonry wall in the MIW frame models was moved to the middle of the column clear height if its slenderness ratio λ > 9 (Fig. 2c) based on the observations of the authors on the failure of the frames tested by Dautaj et al. (2018). Similar criterion was presented by Alwashali et al. (2018) for the weak frames.

Seeking the reliability of the empirical \({l}_{p}\) formulas (Table 1), different RC frames were analyzed eleven times using one formula in each analysis. Seven important findings were achieved based on comparing the results of the analyses with previous experiments. First, it was observed that \({l}_{p}^{A}\) < \({l}_{p}^{B}\) < \({l}_{p}^{C}\) < \({l}_{p}^{D}\) for all investigated frames unlike the remaining formulas which did not show a specific sequence for different frames. Second, the \({l}_{p}^{A}\) and \({l}_{p}^{B}\) formulas provided results closer to the experimental results for the frames with low initial axial load ratio (\({P}_{1}/{P}_{o}\)), whereas the results of \({l}_{p}^{C}\) and \({l}_{p}^{D}\) formulas fitted better the frames with relatively higher \({P}_{1}/{P}_{o}\). Third, choosing a proper formula (\({l}_{p}^{A}\), \({l}_{p}^{B}\), \({l}_{p}^{C}\), or \({l}_{p}^{D}\)) for each PH in the same frame was a good tool to achieve better results than the common practice that assigns one formula for all PHs. Fourth, the ductility of RC frame and consequently \({l}_{p}\) were proportional to the longitudinal reinforcements (\({A}_{S}\)) and \({P}_{1}\) (Bae and Bayrak 2008). Fifth, the axial load ratio \(r\) at ultimate lateral load (\(r={P}_{u}\)/\({P}_{o}\); Fig. 3) was proposed as a FHCM indicator to determine the proper formula (\({l}_{p}^{A}\), \({l}_{p}^{B}\), \({l}_{p}^{C}\) or \({l}_{p}^{D}\)) for each PH based on \({P}_{u}\) and \({P}_{o}\) of the member comprising the considered PH. Sixth, simply setting \({l}_{p}\) equal to 0.5 h for the PHs in typical stories (as suggested by Paulay and Priestley 1992) did not cause a significant difference in the results. Seventh, considering the shear deformation through increasing \({l}_{p}\) by a shear contribution length \({l}_{s}\) (Elmenshawi et al. 2012; Table 1), improved the agreement between the numerical and experimental results.

The introduced iterative \({l}_{p}\) technique (Fig. 3) is simple and employed the aforementioned seven findings. The \({l}_{p}\) value is preliminarily assumed 10% of the clear element length for each PH in the first story and 0.5 h for each PH in the typical stories. A pushover analysis is then conducted at the start of the first/new iteration. Subsequently, for each PH, the axial force (\({P}_{u}\)), the bending moment (\({M}_{u}\)), and the shear force (\({V}_{u}\)) are determined at the ultimate lateral load. Consequently, the current axial force ratio (\(r={P}_{u}/{P}_{0}\)) is calculated for the considered PH if it was in the first story. And then, \({l}_{p}\) is updated to \({l}_{p}^{A}\), \({l}_{p}^{B}\), \({l}_{p}^{C}\) or \({l}_{p}^{D}\) in case that r < 1%, \({1}\% \le r < 6\%\), \({6}\% \le r < 10\%\), or \(r \ge {1}0\%\), respectively, yet \({l}_{p}\) is set to 0.5 h if the PH was in a typical story. The normalized shear spread parameter k is estimated for the considered PH, and the shear contribution \({l}_{s}\) is added to the latest \({l}_{p}\) if \(0 < k \le 0.5\). After updating \({l}_{p}\) for all PHs, the errors in \({l}_{p}\) are calculated and compared with a 0.05 tolerance. The iteration is invoked again to improve \({l}_{p}\) values if the tolerance was not achieved.

3.1.3 Shear PH

In general, estimating the shear behavior of element is more complex. Watanabe and Lee (1998) presented an incremental analytical approach to predict the shear force–deformation response. Their approach was based on the truss mechanism. The stirrup strain is increased with small increments and the corresponding shear force is estimated at each step. In this paper, the approach of Watanabe and Lee (1998) was coded to find the shear–displacement relationship for the shear PHs that were defined at the sections whose \(k > 0.5\) (Fig. 3). More details about the incremental approach could be found in Sayed (2023).

3.1.4 Torsional PH

In this work, bilinear torsion–rotation behavior was adopted similar to Sharma et al. (2013). The cracking torsion, the ultimate torsion resistance, and the cracked torsion stiffness are estimated as functions in the section geometry, concrete strength, and transverse reinforcement properties to determine the torsion–rotation relationship (Park and Paulay 1975). Detailed description for the PH characteristics could be found in Sayed (2023). In this paper, torsional PHs were assigned for the columns and beams of only the 3D models.

3.1.5 Beam–column joint PH

The beam–column connection might suffer severe damages especially if it was a non-seismically detailed. In this paper, the seismically detailed connection was modeled as a rigid joint (Hashemi 2007). Contrariwise, the non–seismically detailed connection was modeled using a beam–column joint PH (Sharma et al. 2011a) to simply model the nonlinearity in the joint and track its real response. Sharma et al. (2011a and 2013) modeled the poorly detailed beam–column connection using flexural PHs at the connected beams, and shear PHs at the connected columns. The flexural and shear PHs characteristics were estimated based on the joint shear deformation. Each beam element is divided at the face of each connected column. Likewise, the column element is divided at the face of each connected beam. Thus, three joint elements with three PHs (two shear PHs for the columns and one flexural PH for the beam) exist for one exterior connection between two stories in 2D modeling. Similarly, two shear PHs and four flexural PHs exist for one interior joint connected with beams in each direction (x and y) in 3D modeling. For these joint elements, the concrete elasticity modulus (Ec) was reduced by 50% to account for the cracks in the connection (Sharma et al. 2013).

3.2 Masonry infill walls (MIWs) modeling

In this paper, the MIW was modeled as a single equivalent strut. There are several empirical approaches to estimate the strength, modulus of elasticity, and equivalent width of the strut based on the characteristics of the MIW. Cavaleri and Di Trapani (2014) used the mechanical properties of the masonry block and prism (Fig. 4a, b, respectively), and the geometry of the masonry panel to model the equivalent strut of the masonry panel (Fig. 4c) using a multilinear plastic link (Fig. 4d) through determining the force–displacement backbone curve (Fig. 4e) for the considered MIW frame. Cavaleri and Di Trapani (2014) model was adopted and the modeling procedure is briefly presented as follows. First, the ultimate lateral load of the bare frame (fub) is determined based on the moment capacity (\({M}_{uc}\)) of the column cross-section at the initial vertical load \({P}_{1}\) (Cavaleri and Di Trapani 2014). Second, the mechanical properties of the masonry infill prism are experimentally determined (Ei, fi, v12, G12, and fvo which refer to the Young's modulus in direction i, strength in direction i, Poisson’s ratio, shear modulus, and mean shear strength of the masonry prism). Third, based on these mechanic properties and the aspect ratio of the panel, the Young's modules (Ed) and the Poisson’s ratio (vd) along the diagonal direction for the masonry panel are determined (Cavaleri et al. 2014 and Jones 1999). Fourth, the equivalent strut width (w; Fig. 4c) is determined according to Papia et al. (2003) as a function in the panel geometry, frame geometry, beam area, column area, Ec, Ed and vd. Fifth, the characteristics of the backbone force–displacement curve are defined by determining the peak, yield and failure forces (S2, S1, and S3, respectively), and their corresponding displacements (∆2, ∆1, and ∆3, respectively). These characteristics values are determined as functions in fub, w, fvo, and the geometry of masonry panel (Cavaleri et al. 2005 and Cavaleri and Di Trapani 2014).

Fig. 4
figure 4

MIW modeling (Cavaleri and Di Trapani 2014)

Full size image

3.3 Shear wall (SW) modeling

The shear wall was modeled using a multilayer shell element. Two layers (one plat and one membrane) were used to model the concrete core, and another two membrane layers were used to model the two side longitudinal reinforcements. The thickness of the concrete membrane layer was equal to the SW thickness, whereas the thickness of each reinforcement membrane layer was evaluated by distributing the total reinforcement area of each side on the SW length. The stiffness of the concrete plate layer was reduced by 75% (the thickness was reduced by 37%, CSI 2011). The effect of transverse bars is taken into the confinement model of concrete (Mander et al. 1988). In order to achieve good agreement between the numerical and experimental results, the SW should show flexural failure mode but sufficient shear strength.

4 Verification plan for the modeling strategy

The presented nonlinear modeling strategy (Sect. 3, and Figs. 1–4) was applied to analyze eleven experimental specimens under pushover load using SAP2000 (CSI 2020). Figure 5 shows the IDs and the corresponding experimental references for the presented eleven models. Ten models represented the RC frames (six bare and four with MIWs) with stories range 1–4 in either a 2D or 3D analysis, whereas the eleventh model validated the SW modeling.

Fig. 5
figure 5

Eleven verification models

Full size image

4.1 RC frames (bare and with MIWs)

4.1.1 Geometry, loading, concrete and steel reinforcement data

For the ten simulated frames, Table 3 presents the layout, loads, concrete properties, steel properties and reinforcement details (Mehrabi et al. 1996, Dautaj et al. 2018, Duong et al. 2007, and Sharma et al. 2013). All the ten frames were subjected to pushover analysis except the F-B-2S model that was subjected to two loading phases (loading and unloading). The horizontal arrows in Table 3 show the levels and the direction of the lateral loading. It is noticeable that the two-story model F-B-2S was loaded at only the top story level unlike the four-story model F-B-4S3D which was loaded at each level. The applied lateral loads for F-B-4S3D model formed inverted triangle load pattern. The unconfined concrete strains; \({\varepsilon }_{c}\) and \({\varepsilon }_{u}\) in Table 3; were corresponding to the compressive strength and zero stress (spalling), respectively (Fig. 6a). The stress–strain relations for the concrete (unconfined and confined), general steel reinforcement, and longitudinal steel reinforcement of F-B-4S3D model were defined in Figs. 6a, 6b, and 6c, respectively. The Young’s modulus \({E}_{s}\) of the steel reinforcements in all models was set to 200 GPa expect for F-B-2S model in which \({E}_{s}\) was set to 198, 192, and 210 GPa for the longitudinal bars, ties, and stirrups, respectively (Duong et al. 2007). The hardening onset strain (\({\varepsilon }_{sh}\)) was equal to the yield strain (\({\varepsilon }_{y}\)) for the steel reinforcements in all the 2D models except for F-B-2S model (Duong et al. 2007) in which \({\varepsilon }_{sh}\) was equal to 1.71%, 2.28% and 2.83%, respectively, for the longitudinal bars, ties, and stirrups (Fig. 6b).

Table 3 Layout, material properties, and reinforcement details for the simulated RC frames
Full size table
Fig. 6
figure 6

Stress–strain relationships

Full size image

4.1.2 MIWs data

For the four MIW frame models (F-M-1S-01–04; Fig. 5), two masonry block types were used. The hollow concrete masonry blocks were used for the first model (Mehrabi et al. 1996), whereas the hollow clay masonry blocks were used for the other three models (Dautaj et al. 2018). Table 4 summarized the five steps introduced in Sect. 3.2 for determining the characteristics of the backbone curve (w, S1, S2, S3, ∆1, ∆2, and ∆3; Fig. 4) of each MIW frame model. Empirical values were assumed for fvo because they were not available in the experiment references. The values of the strength parameters α, β and ζ (Cavaleri and Di Trapani 2014) were assumed 0.5, 0.15 and 0.02, respectively according to Cavaleri and Di Trapani (2015).

Table 4 Multilinear plastic link characteristics for the MIW frames according to Cavaleri & Di Trapani (2014)
Full size table

4.1.3 PHs data

For the ten frames, the flexural PHs were defined according to the presented FHCM (Sect. 3.1.2). The \({l}_{p}\) lengths estimated using the proposed technique (Fig. 3) will be discussed in Sect. 5. The \({l}_{p}\) technique showed that \(k>0.5\) for only the two beams of F-B-2S model, and consequently two shear PHs (Sect. 3.1.3) were added for each beam at \(d/2\) distance from the column face. Torsional PHs (Sect. 3.1.4) were used in only the F-B-4S3D model for all the columns and for the beams that were perpendicular to the loading direction. Beam–column joint PHs (Sect. 3.1.5) were used in only the F-B-4S3D model for all the joints to represent the non-seismically detailed connections. Detailed calculations for the characteristics of all the flexural, shear, torsional, and joint PHs for the ten frames could be found in Sayed (2023).

4.2 Shear wall (SW)

The eleventh model SW-B-1S (Fig. 5) simulated a SW (Fig. 7) that was tested by Chen and Qian (2002) under a vertical load (44% from the capacity) and a monotonic lateral loading till failure. The SW dimensions were 1000 mm length × 1900 mm height × 100 mm thickness. The concrete properties \({f}_{c}^{\prime}\), Ec, ɛc and ɛu were equal to 20.2 MPa, 21.1 GPa, 0.19% and 0.38%, respectively. The steel reinforcement details for the considered SW were shown in Fig. 7. The yield stress for Ф4, Ф6 and Ф10 was 631.7, 451.7 and 395 MPa, respectively. The SW was modeled according to Sect. 3.3, and it was analyzed under a pushover load. The shell element size was taken 100 × 237.5 mm (horizontal × vertical). The thickness of the concrete membrane layer was set to 100 mm, whereas the thickness of the concrete plate layer was set to 63 mm. The thickness of the both longitudinal steel reinforcement layers was set to 1.18 mm and 0.19 mm for the two end strips and the middle strip, respectively (Fig. 7). The confinement of concrete was defined according to Mander et al. (1988).

Fig. 7
figure 7

Details of SW-B-1S model (Chen and Qian 2002) (cross-section and steel reinforcements)

Full size image

5 Results of the verification plan (macromodels versus experiments)

For each flexural PH, Table 5 shows the application of the proposed lp technique (Fig. 3) to determine the lp value and the failure mode for each flexural PH in three sample models F-B-1S-01, F-B-1S-04, and F-B-2S. The highlighted cells show the chosen \({l}_{p}\) (\({l}_{p}^{A}\), \({l}_{p}^{B}\), \({l}_{p}^{C}\) or \({l}_{p}^{D}\)) for each PH. It is evident that different formulas were used in the same frame. For example, \({l}_{p}^{C}\) and \({l}_{p}^{D}\) were used for F-B-1S-01, whereas \({l}_{p}^{A}\), \({l}_{p}^{C}\) and \({l}_{p}^{D}\) were used for F-B-1S-04. Also, it is noticeable that smaller \({l}_{p}\) was used for the PHs of the left column that was under smaller compressive stress (smaller \(r\) or negative) unlike the right column whose PHs showed lager \({l}_{p}\). For the models F-B-1S-02, F-B-1S-03 and F-B-1S-04, the failure mode of all the PHs was flexural (F; \(k<0\)). For model F-B-1S-01, flexural failure mode with significant shear deformation (\(\overline{\mathrm{F}}\)) was monitored because \(0<k<0.5\). Shear failure mode (S) was recorded for the beams of F-B-2S model because their transverse reinforcement was very weak compared with a large actual shear stress (\(k>0.5\)). For F-B-4S3D model, all the four \({l}_{p}\) formulas (\({l}_{p}^{A}\), \({l}_{p}^{B}\), \({l}_{p}^{C}\) and \({l}_{p}^{D}\)) were used.

Table 5 Proposed flexural plastic hinge length \({{\varvec{l}}}_{{\varvec{p}}}\) for sample models
Full size table

The studied eight one-story models (four bare and four MIW frames; Fig. 5) were analyzed eleven times using the eleven \({l}_{p}\) formulas introduced in Table 1, respectively. Following the common practice, each \({l}_{p}\) formula was used for all the flexural PHs in the same frame in a separate run. These trials led to drive the \({l}_{p}\) technique presented in Sect. 3.1.2 and Fig. 3. The results of the eleven trials (representing the common practice) and the response of the proposed \({l}_{p}\) technique compared with the reference experiment were shown in Fig. 8 for sample two bare models (F-B-1S-01 and F-B-1S-02) and two MIW models (F-M-1S-01 and F-M-1S-02). It was observed that the initial stiffness of the frame decreases as \({l}_{p}\) increases. Figure 8 revealed that the result of the proposed \({l}_{p}\) technique matched the experimental result better than any of those achieved using the common practice. The average error in ultimate lateral load of the four bare models and the four MIW models ranged from 11.3% to 21.1% and from 3.5% to 11.1%, respectively, for the eleven formulas. Contrariwise, the proposed \({l}_{p}\) technique resulted in an average error of 9.2% and 3.6% for the four bare models and the four MIW models, respectively.

Fig. 8
figure 8

Lateral response for sample bare and masonry infill models using the investigated eleven \(lp\) formulas versus the proposed \(lp\) technique

Full size image

Figure 9 shows the numerical results of the eleven macromodels (refer to Fig. 5) compared with the experimental references. Good agreement was noticeable between the presented numerical and experimental results. The good agreement for Figs. 9a-9f demonstrates the power of the macromodeling in analyzing the RC frames and MIWs RC frames with low computation cost. For example, Mohyeddin et al. (2013) achieved similar numerical results for F-B-1S-01 model (Fig. 9a) using a micromodel comprising solid and interface elements in full nonlinear finite element analysis with high computation cost. The agreement between the numerical result and the reference experiment for model F-M-1S-02 (Fig. 9b) was attributed to locating the bottom flexural PH of the left column at the middle of its clear height (λ > 9; Sect. 3.1.2 and Fig. 2c). For the other three MIW models (F-M-1S-01, F-M-1S-03 and F-M-1S-04) with columns of λ = 6–8, the bottom PH of the left column was typically located at the base. Better consistency between the experimental and the nonlinear analysis results for the MIW models (Fig.9a–d) could be achieved if the mean shear strength (fv0) of masonry prisms were experimentally available. The consistency between the numerical and experimental results of model F-B-2S (Fig. 9e) was attributed to the use of the shear PHs (Sect. 3.1.3) based on the \(k\) values (Table 5). The error in the ultimate lateral load would increase from 9.3% to 71.8% if the shear PHs were ignored. Also, using the torsional PHs and the beam–column joint PHs in the model F-B-4S3D improved the agreement between the numerical and experimental results in Fig. 9f. If the torsional PHs were ignored, the error in the ultimate lateral load would increase from 6.8 to 42.5%. Furthermore, ignoring the beam–column PHs would increase the error from 6.8 to 216.4%.

Fig. 9
figure 9

Lateral response of the eleven verification models (nonlinear analysis versus experiment)

Full size image

For the SW, the consistency between the numerical and experimental results in Fig. 9g confirmed that the nonlinear multilayer shell element is a good tool to model the SW. Eighty nonlinear multilayer shell elements were sufficient to accurately capture the capacity lateral load of a shear wall with 1.9 m2 area. Figures 8 and 9 validated the presented nonlinear analysis strategy (Sect. 3) for modeling the frames (either bare or with MIWs) and for modeling the SWs. This strategy will be employed for the analysis of RC ten-story buildings presented in the next section.

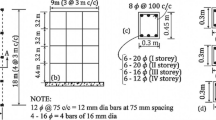
6 Simulations of ten-story frames/SWs buildings (bare and with MIWs)

A ten-story residential building with two alternative structural systems (frames and shear walls) and with/without MIWs was analyzed under pushover analysis in the X and Y directions through eight simulations (Fig. 10). The building was located in Cairo with area of 22.9 m × 24.2 m, and story height of 3.1 m. The studied frames building and the shear walls building were presented in Fig. 11a and b, respectively. The MIWs were located based on the architectural needs, and were drawn with yellow color in Figs. 11a and b. The MIWs were constituted from hollow clay masonry blocks. The experimental data of the masonry prisms for model F-M-1S-02 (Table 4) was used for the current eight simulations. The MIWs with openings were neglected and were not shown on the plans. The frames old building (Fig. 11a) was designed under vertical loads only. The SWs building (Fig. 11b) was designed under vertical and lateral loads. All designs were carried out according to ECL (2017) and ECCS (2020). The concrete characteristic strength (\({f}_{cu}\) for 150 mm standard cube) of the slabs and the beams was 25 MPa, whereas \({f}_{cu}\) for the columns and the SWs was 30 MPa. The yield stress for all longitudinal steel reinforcement bars and the SWs transverse steel reinforcement was 350 MPa. The yield stress for the transverse steel reinforcement in both the columns and beams was 240 MPa. The flooring, walls, and live loads were set to 1.5, 3.0 and 2.0 kN/m2, respectively. The sections details for the columns, beams, and SWs were shown in Fig. 11c. Based on the presented nonlinear modeling strategy (Sect. 3), the 3D model for the MIWs frames building was depicted in Fig. 11d. The slab modeling was performed by considering a rigid diaphragm at every story levels. The staircases were disregarded in the presented model since their contribution to the stiffness was insignificant (Furtado et al. 2019), yet their loads were definitely considered in the model.

Fig. 10
figure 10

Eight Simulations of ten-story building (frames and SWs structural systems)

Full size image
Fig. 11
figure 11

The studied ten-story building (bare and with MIWs) with frames and SWs structural systems

Full size image

Flexural, shear, and torsional PHs were set for all the columns and beams. No beam–column joint PH was used because the joints in the considered building were seismically detailed. For the same flexural PH, the lp values in X and Y directions were different based on the section depth and the loading direction. For each story of model F-B-X, the number of flexural PHs was 86 and 150 for the columns and beams, respectively. For each story of model SW-B-X, the number of flexural PHs was 56 and 48 for the columns and beams, respectively. The shear contribution length (\({l}_{s}\)) existed for a significant number of PHs in the model F-B-X compared with SW-B-X because of the SWs that resisted the lateral load and relaxed the shear stresses in the columns. The seven SWs in each story of the building shown in Fig. 11b were modeled using 160 nonlinear multilayer shell elements (approximately square shape of 750 mm length). The MIWs were modeled using 18 and 15 multilinear plastic links (in each story) for the buildings shown in Fig. 11a and b respectively. The characteristics data of all the PHs, the SWs nonlinear elements, and the masonry plastic links could be found in Sayed (2023).

7 Results of the ten-story buildings simulations

Figures 12 and 13 shows the shear capacity curves and the story shear, respectively, of the ten-story buildings (frames and SWs) obtained from the eight pushover analyses introduced in Fig. 10. Compared with the corresponding bare models, the increment in the ultimate lateral load for the models F-M-X, F-M-Y, SW-M-X, and SW-M-Y were 24%, 83%, 20%, and 50%, respectively, whereas the increment in the stiffness for these models were 76%, 206%, 62%, and 130%, respectively. Besides, eight important outcomes could be drawn from Figs. 12 and 13 as follows. First, the contribution of MIWs to the lateral capacity in Y-direction (Figs. 12b, d, 13b, and d) was higher than in X-direction (Figs. 12a, c, 13a, and c). This was attributed to the higher number of MIWs in Y-direction (17–20 walls; Fig. 11a) compared with X-direction (9 walls; Fig. 11b). Second, the ultimate lateral load and the story shear of F-M-X (Figs. 12a and 13a) and F-M-Y (Figs. 12b and 13b) was approximately equal to SW-B-X (Figs. 12c and 13c) and SW-B-Y (Figs. 12d and 13d), respectively. In other words, the capacity of the frames structural system with MIWs was approximately equivalent to the SWs structural system without MIWs. Third, the contributions of the edge and inner MIWs were approximately equal for the studied building. Fourth, the MIWs contribution to the ultimate lateral load for the studied building was smaller than that gained in the verification models (Sect. 5 and Figs. 9a–d) because of the existence of the MIWs in limited bays in the considered ten-story building based on the architectural requirements, and because of the weak columns (low compressive strength and low reinforcement ratio) in the verification models F-M-1S-02–04. Fifth, monitoring the critical stresses (damage) of the column x, column y, SWx, and SWy (refer to Figs. 11a, b, and 12) showed that the damage of the vertical RC elements could be described in the following sequence; (1) local tensile concrete failure at the edge of the concrete core (red square; Fig. 12), (2) tensile yield of the corner steel rebar (red circle; Fig. 12), (3) compressive yield of the opposite corner steel rebar (brown circle; Fig. 12), and (4) local compressive concrete failure at the edge of the concrete core (brown square; Fig. 12) similar to the discussion presented by El-Kholy et al. (2022). Sixth, the compressive yield of the corner steel rebar (on the compression edge) might precede the tensile yield of the steel rebar (on the opposite edge) for the columns located in the compression zone such as column x (Figs. 11a and 12a) because of the higher initial vertical load. Seventh, the ultimate lateral load at the initiation of either the concrete crack or the rebar yield was higher for the MIWs model compared with the corresponding bare model. Finally, the higher gab between the red and brown concrete markers in Fig. 12a and b compared with Fig. 12c and d, respectively, demonstrated the higher ductility of the frames structural system over the SWs structural system. Figures 14, 15, 16, and 17 illustrate the lateral load–stress histories for the concrete and the steel rebar at the tension and compression edges for the column x, column y, SWx, and SWy, respectively. The histories were plotted for both the bare and MIWs models in each figure. These histories confirmed the previous eight outcomes drawn from Figs. 12 and 13.

Fig. 12
figure 12

Lateral response of the ten-story buildings (frames and SWs structural systems)

Full size image
Fig. 13
figure 13

Story shear at peak lateral response for the ten-story buildings

Full size image
Fig. 14
figure 14

History of stresses in column x (F-B-X and F-M-X models)

Full size image
Fig. 15
figure 15

History of stresses in column y (F-B-Y and F-M-Y models)

Full size image
Fig. 16
figure 16

History of stresses in SWx (SW-B-X and SW-M-X models)

Full size image
Fig. 17
figure 17

History of stresses in SWy (SW-B-Y and SW-M-Y models)

Full size image

Figure 18 illustrates the stress history for a sample masonry panel (M10) in the frames building (Fig. 11a) at different levels. Figure 18 showed that M10 reached the yield stress (S1; Fig. 4e) in the ninth story. However, it reached the peak stress (S2; Fig. 4e) and the failure stress (S3; Fig. 4e) in the first story as expected. Figure 19 illustrates the stress history for three sample masonry panels M10, M3, and M12 at the first story of both the frames building (Fig. 11a) and the SWs building (Fig. 11b). Comparing the yield displacements of these sample panels with the displacements of the local damage observed for the columns and the SWs (Figs. 12b and d) demonstrated that the yield onset of the MIWs was simultaneous with the recorded local damage on the edges of the columns and shear walls. Figure 19 confirmed that the SWs relaxed the stress in the MIWs in which some panels did not reach the complete failure (for example M12 in the SW building). On the contrary, the majority of the MIWs in the frames buildings reached the peak stress and the failure stress close to the ultimate deformation of the building. It is noticeable that the panel M10 showed the highest peak stress and the highest initial stiffness among the presented samples unlike M12. This was interpreted in view of the panel geometry and the rigidity of the columns of the surrounding RC frame; the inclination angle of the panel diagonal was larger and the columns surrounding the panel were more rigid for M10 compared with M12 (Figs. 11a and 4c). Based on the MIWs model (Cavaleri and Di Trapani 2014) that was adopted in this paper, the peak stress of the equivalent strut was proportional to the inclination angle of the panel diagonal and to the ultimate load of the bare frame, whereas the initial stiffness was inversely proportional to the diagonal of the masonry panel.

Fig. 18
figure 18

Stress history of the masonry panel M10 in the model F-M-Y at different stories

Full size image
Fig. 19
figure 19

Stress history of the masonry panels M3, M12 and M10 at the 1st story of both the F-M-Y and SW-M-Y buildings

Full size image

Finally, the Figs. 12–19 and the low computation cost used for such large-scale 3D simulations (Fig. 11) demonstrated the effectiveness of the presented nonlinear macromodeling strategy and the power of the utilized nonlinear analysis software in tracking the nonlinear behavior of the multistory RC buildings (frames or SWs) with masonry infill walls.

8 Conclusions

This work was motivated to provide a practical nonlinear macromodeling of the multistory RC buildings with masonry infill walls under lateral load. Two structural systems for resisting the lateral loads were investigated in this work; frames and shear walls. A simple nonlinear macromodeling strategy was presented by integrating a newly proposed consistent model for the flexural plastic hinge, a shear plastic hinge model, a torsional plastic hinge model, a beam–column joint plastic hinge model, a shear wall model using a nonlinear multilayer shell element, and a masonry infill model using a multilinear plastic link. This collection of six macromodels in one model was challenging and increased the reliability of the presented strategy to model different and real RC buildings. The presented strategy was validated through ten RC frame models and a SW model under pushover analysis. Finally, the presented strategy was employed in challenging pushover three-dimensional simulations of ten-story buildings with masonry infill walls. The layout of the simulated buildings was not ideal or typical but real based on the architectural needs. The following conclusions could be drawn.

  1. 1.

    The presented nonlinear macromodeling strategy was effective and accurate enough to numerically achieve the experimental ultimate lateral load with average error of 9.2%, 3.6%, and 0.4% for investigated six bare frames, four masonry infill frames, and a shear wall. Although the flexural macromodel predominated the structural behavior of all frames, excluding the shear model, the torsional model, or the joint model from modeling special frames (sensitive to a certain deformation) increased the numerical error in the ultimate lateral load to 71.8%, 42.5%, or 216.4%, respectively.

  2. 2.

    The proposed consistent flexural hinge model recommended using fibers hinges with approximately 24 mm length for each fiber. Also, it was recommended to set the hinges at the ends of the clear length of each frame element except the first story columns whose upper hinges were preferably moved half the hinge length from the bottom face of beams. Moreover, it was recommended for the columns with slenderness ratio greater than nine to set the bottom hinge of the column pushing the masonry panel at the middle of its clear height.

  3. 3.

    The proposed consistent flexural hinge model recommended estimating the plastic hinge length of each hinge in a certain frame using an iterative technique in which a distinct formula is assigned for each hinge based on its axial load ratio. For a certain hinge, the larger load ratio the more expected length by using an alternative formula. Therefore, various formulas for estimating the plastic hinge length might be utilized in the same frame unlike the common practice. Furthermore, different formulas might be used for estimating the updated length of the same hinge during the iterations until the process converged to a prescribed tolerance. Using the common practice by assigning one formula for estimating the lengths for all the flexural plastic hinges in the whole frame increased the average numerical error in the lateral capacity from 9.2% and 3.6% to a range of 11.3–21.1% (eleven formulas were investigated) and a range of 3.5–11.1% for the bare frames and the masonry infilled frames, respectively.

  4. 4.

    For the studied ten-story buildings, the frames buildings showed higher ductility than the shear walls buildings. For both types, the masonry walls increased the lateral load capacity and the stiffness, respectively, with an average of 44.3% and 118.6% although the masonry walls existed not in all bays according to the architectural requirements. The increment was proportional to the number of the masonry walls in each direction. Also, the frames building with masonry infill walls was approximately equivalent to the shear walls building without masonry infill walls in terms of the ultimate lateral load.

  5. 5.

    For the columns and the shear walls in the studied ten-story buildings, the monitored local damage initiation was tension cracks on the edge of the concrete core followed by a tensile yield of the close rebar, and then a compressive yield of the rebar followed by a concrete crushing was recorded on the opposite edge. For the columns located in the compression zone of the building, the compressive yield of the edge rebar might precede the tensile yield of the opposite rebar.

  6. 6.

    For the masonry infill walls in the studied ten-story buildings, their yield onset was simultaneous with the recorded local damage on the edges of the columns and the shear walls. The majority of the masonry panels in the first story of the frames building reached the failure close to the ultimate deformation of the building unlike the shear walls building in which the stresses were relaxed in their masonry walls. The masonry infill panel with smaller diagonal length, a larger inclination angle of its diagonal, and more rigid surrounding RC columns was stiffer and reached the failure earlier than other panels. A larger thickness for such critical masonry panels is recommended.

  7. 7.

    The presented macromodeling strategy and the utilized software were reliable enough to conduct a three-dimensional pushover analysis for a large-scale real ten-story RC building with masonry infill walls in a low computation cost.