Simulation of the E-Defense 2015 test on a 10-storey building using macro-models

Abstract

The capabilities of certain standard macro numerical models were evaluated by simulating a shaking table experiment that was performed on a full-scale ten-storey fixed-base building with a frame and dual structural system in two perpendicular directions (denoted as the frame and wall directions) at the largest shaking table in the E-Defense centre in Japan. The lumped plasticity model for columns and beams, the multiple-vertical-line-element model for walls and the scissors model for beam-column joints were evaluated. The results indicated that the experiment was simulated reasonably well. The most significant discrepancy was observed between the maximum drifts along the wall direction in the strongest cycle of the strongest test (calculated drift of 1.9% versus measured drift of 1.5%). In other cycles and tests, these differences were smaller. The calculated and measured maximum accelerations along the wall direction in the strongest test were 13.8 m/s² and 13.5 m/s², respectively. The discrepancy between the analysis and experiment results was smaller along the frame direction. The maximum calculated and measured drifts were 2.9% and 3.1%, respectively. The maximum calculated and measured accelerations were 15.8 m/s² and 19.0 m/s², respectively. In general, the standard input parameters were used in the evaluated models. However, some parameters required modifications, particularly when modelling weakly reinforced beam-column joints with substandard reinforcement that were considerably damaged. Their yielding rotation and near-collapse strength were, on average, reduced to 55% and 30% of the standard value, respectively. One of the most important parameters influencing the response was the effective width of the slabs, which was increased to the total span length for the highly loaded beams. The ratios of the strength, stiffness and amount of dissipated energy in the joints, beams and columns also significantly influenced the response. The adequate ratio of the dissipated energy was obtained by reducing the standard unloading stiffness in the beams and columns. The initial stiffness considerably influenced the response, particularly under weaker excitations. This stiffness was reduced threefold to account for various factors that typically reduce its value, which, among others, includes the influence of preceding tests on the same building with sliding foundations, as well as the assembly, transportation and handling of the specimen.

1 Introduction

The seismic response of most structures subjected to strong earthquakes is expected to be nonlinear. However, the majority of seismic analyses are mainly based on elastic procedures, which can be less reliable even for seemingly simple and regular structures. The rapid development of information technology has provided the potential for improving seismic analyses with more reliable nonlinear methods. The modern codes also reflect the increasing awareness of the need for more reliable seismic design and assessment. For example, in the second generation of the Eurocode 8 standard (CEN/TC 250/SC 8 2021), the nonlinear pushover-based method becomes one of the reference methods for designing new structures and assessing existing structures from a seismic perspective.

Reliable and simple numerical models are needed to successfully introduce nonlinear analysis methods in building design. Nonlinear seismic analysis performed using sophisticated finite element models requires significant computational time. Furthermore, there is a lack of input data for these models to reliably simulate the different phenomena of complex seismic response of reinforced concrete (RC) structures. The processing and analysis of the results is also quite time-consuming.

Considering the input data, computational time and results processing, various macro-models may be used to perform more efficient nonlinear seismic analysis. Generally, the macromodels for RC beams and columns can be divided into two categories: lumped and distributed plasticity models. In lumped plasticity models, the nonlinear response is modelled using concentrated springs, whereas, in distributed plasticity models, the nonlinear response is spread over a certain element length.

The standard Giberson’s model (Giberson 1967) is a typical lumped plasticity model that has been used for decades. The nonlinear response is described using different hysteretic rules, depending on the response type. Takeda hysteresis rules are typically used to simulate flexural response (Takeda et al. 1970), but several other solutions are also available. For example, the first law defining the response of nonlinear springs was formulated by Clough et al. (1965), Saiidi (1982) proposed the Q-hysteresis model, etc. Several attempts have been made to develop a model for hysteretic behaviour under shear, such as those proposed by Celebi and Penzien (1973) and Ozcebe and Saatcioglu (1989).

Soleimani (1979) introduced the first model that accounted for the spread of inelastic deformations in the member. Nowadays, several such models that account for axial-flexural interaction are available. For example, the OpenSees (Mazzoni et al. 2006) program platform includes the ‘Displacement-based beam-column element’, which follows the standard finite element procedure (Zienkiewicz and Taylor 2000); the ‘Force-based beam-column element’, which was initially formulated by Spacone et al. (1996); and the ‘Beam with hinges element’ (Scott and Fenves 2006). Different distributed plasticity models that account for axial-flexural-shear interaction have also been proposed. An overview and analysis of these models can be found in Ceresa et al. (2007).

The seismic response of RC beam-column joints can be addressed implicitly by modifying the response of beams and columns (Otani 1974; Anderson and Townsend 1977; Hoffmann et al. 1992; Kunnath et al. 1995) or by using explicit models. One of the first explicit models (strut and truss model) for such joints was proposed by Park and Paulay (1975). Subsequently, various researchers have proposed relatively simple zero-length element models (El Metwally and Chen 1988; Alath and Kunnath 1995; Deng et al. 2000). Alath and Kunnath (1995) extended this model by adding rigid connections between elements representing joints, beams and columns. This model is referred to as the ‘scissor model’ in the literature. Different hysteretic rules associated with the scissor model were proposed (e.g. Kim et al. 2009). Later, several more sophisticated joint models were developed (e.g. Shiohara 2001; Lowes and Altoontash 2003).

Several types of macro numerical models can be used for nonlinear analysis of the seismic response of RC walls. An excellent state-of-the-art systematic overview of such modelling approaches, titled ‘Nonlinear modelling of reinforced concrete structural walls’, was recently presented in a special issue of the Bulletin of Earthquake Engineering (Fischinger et al. 2019). Kolozvari et al. (2018) also published an extensive review of macro-models for RC walls and their capabilities. The OpenSees programme includes an extended version of the stress–strain-based multiple-vertical-line-element model (MVLEM) (Kolozvari et al. 2019) that was initially proposed by Kabayesawa et al. (1984). It can be used to consider the shear-axial-flexural interaction in the nonlinear range. Another force–displacement version of the MVLEM that can consider this interaction was developed at the University of Ljubljana (Isakovic and Fischinger 2019). It was included in the local version of the OpenSees programme. The Nonlinear Truss Model—initially formulated by Panagioutou et al. (2012) and later assessed by Alvarez et al. (2019)—has also been frequently applied to the nonlinear analysis of RC walls. Recently, this model was extended by Areta et al. (2019) and Hoult et al. (2023).

Some models mentioned above have been used for decades and are relatively well-evaluated. However, most of these evaluations have been based on different scaled experiments, where the degree of scaling may qualitatively influence the response.

To date, only a handful of full-scale tests—particularly shake-table tests of RC buildings—have been conducted as they are expensive and require highly capable testing equipment. Some of these rare tests were performed at the University of California San Diego (Panagiotou et al. 2011; Chen et al. 2016), but most have been performed using the largest shake table in the world at the E-Defense centre in Japan (Nakashima et al. 2018).

Recently, several unique and extraordinary tests on full-scale ten-storey buildings were performed at this centre (Kajiwara et al. 2017; Sato et al. 2017; Tosauchi et al. 2017; Kajiwara 2021). Both seismically isolated and traditional fixed-base buildings were studied. These experiments provided the unique opportunity to test various standard numerical models under more realistic conditions, considering specific issues such as the effective width of slabs during strong earthquakes, the reduction of the initial stiffness of structural elements and the entire building, the influence of substandard RC joints on the response, particularly the ratios of strength, stiffness and amount of dissipated energy in joints compared to those in beams and columns. These tests also provided the rare opportunity to evaluate numerical models for walls other than cantilevered walls, as the tested buildings included walls that were partly fixed at the top.

A research team from the University of Ljubljana (UL) analysed the response of a fixed-base structure. The lateral resisting system consisted of RC frames in one direction and a dual structural system comprising RC frames and walls in the other direction. The specimen was heavily equipped, providing adequate information about the response. This presented a unique opportunity to evaluate the numerical models that are typically employed at UL for the nonlinear seismic analysis and assessment of RC structures. The standard Giberson’s lumped plasticity macro model (Giberson 1967) with modified Takeda hysteresis rules (Takeda et al. 1970) was employed for beams and columns. The walls were modelled using UL’s version of MVLEM (Fischinger et al. 2004; Isaković and Fischinger 2019). The initial model of the analysed building did not include a numerical model for the joints. This was subsequently added to the building model as the relatively weak joints were considerably damaged under the strongest excitation, which significantly influenced the response. The model proposed by Alath and Kunnath (1995) was used, considering the modified response envelopes proposed by Kim et al. (2009). A 3D model of the building was generated, and the 3D dynamic response analysis was performed based on the experimental loading protocols. Some of the other modelling options mentioned in the previous paragraphs are addressed in other papers included in a special issue of the Bulletin of Earthquake Engineering—‘International Joint Research on the Ten-story RC Full-scale Buildings Tested at E-Defense Shaking Table’ (2023), which is devoted to different aspects of the analysis of the building evaluated in this study.

The rest of this paper proceeds as follows. The main properties of the full-scale fixed-base tested structure relevant to the analysis are summarised in Sect. 2. Further details about the building and its response during the shake table tests can be found in the above-mentioned special issue’s introductory paper (Kang et al. 2023). Section 3 provides a detailed description of the models used for the columns, beams, beam-column joints and walls and their properties. The numerical model of the building is evaluated at a global and local level, and an overview of the damage patterns corresponding to different excitation levels is provided in Sect. 4. Generally, the standard, recommended values were used for most of the input parameters in the numerical models. However, some values were modified to achieve better simulation. These modifications are presented in Sect. 5, which also analyses the most important parameters influencing the response of the tested building.

2 A short overview of the building features considered in the analysis

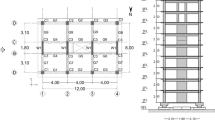
This section summarises those features of the tested 10-storey building (see Fig. 1) which were most important for the numerical analysis presented in this paper. Only the conventional fixed-base structure is addressed.

Fig. 1

a Plan view and b side view (wall direction) of the tested building

In the longitudinal direction (referred to as the ‘frame direction’ in this paper; see Fig. 1a), the lateral load-resisting system consisted of RC frames. The width and height of the RC beams’ cross-section ranged from 230–400 mm to 370–550 mm, respectively. The width and height of the RC columns’ cross-section ranged from 450–550 mm to 230–550 mm, respectively. In the transverse direction (referred to as the ‘wall direction’ in this paper; see Fig. 1a), a dual structural system was provided, which consisted of RC walls linked to the RC columns by RC beams. Walls were provided up to the top of the 7th floor. Their length and thickness were 2.25 m and 0.23 m, respectively. On the 7th floor, the thickness of the walls was reduced to 0.15 m.

The width and length of the typical floor in the building were 9.50 m and 13.50 m, respectively. Each floor consisted of a two-way 0.12 m thick solid RC slab. The storey height gradually decreased from 2.8 m on the bottom storey to 2.5 m on the top three storeys (for more details, see Fig. 1b). The total height of the building, including the foundations, was 27.45 m.

The measured concrete compressive strength varied from 40 (on the top floor) to 70 MPa (on the bottom floor). Steel grade SD345 with an average measured yield strength of 390 MPa was used for longitudinal reinforcement in beams and columns. The diameter of the reinforcing bars varied between 19 and 22 mm (more details can be found in Kajiwara et al. 2017). The amount of longitudinal reinforcement (μ) was in the range of μ = 0.91% and 2.51% for columns and μ = 0.62% and 1.74% for beams.

The boundary regions of the walls were reinforced by six or eight longitudinal bars, the diameters of which varied from 16 to 19 mm, with the same steel quality as in beams and columns. The amount of reinforcement in the boundary regions was in the range of μ = 1.17–2.19%. The walls’ webs were reinforced by meshes consisting of bars with a diameter of 10 mm or 13 mm at a distance of 200–250 mm (μ = 0.33% and 0.44%). The average measured yielding stress of the walls’ longitudinal bars was 360 MPa (steel grade SD295A). The same steel grade was used for the slabs’ reinforcement, consisting of bars with a diameter of 10 mm at a distance of 200–250 mm (μ = 0.26–0.33%).

For most hoops and ties, steel grade SD295A was used (on average, the measured yielding stress was 360 MPa). The exception was the lateral reinforcement of columns on the 1st–4th floors and some beams on the 2nd–6th floors, which were made of steel grade KSS785 (on average, the measured yielding stress was 930 MPa). The diameters of the hoops and ties ranged from 10 to 13 mm, and the amount of lateral reinforcement ranged from 0.29 to 0.68% in columns and 0.22–1.37% in beams.

In the lower part of the building, the lateral reinforcement in beam-to-column joints was reduced to approximately half of that provided in the columns. In the upper part of the building, the lateral reinforcement in columns and joints was the same.

The total mass of the tested building was 1026 t. The masses of individual storeys, as reported in Kajiwara et al. (2017), were considered in the numerical analysis (see Fig. 2).

Fig. 2

The 3D numerical model of the building. a Structural elements and masses, and b the scheme of the gravity load

The specimen was excited three-axially (along the vertical and horizontal axes) using the accelerations registered during Kobe’s 1995 earthquake (henceforth referred to as JMA-Kobe). The intensity of the input signal was gradually increased (10%, 25%, 50%, 100%). For the last test, it was decreased to 60% JMA-Kobe to test the aftershock response.

The response was essentially elastic up to the 50% JMA-Kobe test. A more detailed description of the observed response can be found in Tosauchi et al. (2017). During the 100% JMA-Kobe test, significant damage was observed in beam-to-column joints and beams in the lower part of the building, particularly on the 4th floor. The bottom parts of the walls and corner columns near the foundations were also noticeably damaged.

When all tests were completed, the fundamental period of vibration was increased from the initial 0.85 s to 2.62 s and from 0.59 to 1.19 s in the frame and wall direction, respectively.

3 Model description

One of the purposes of the presented study was to analyse the ability of the robust macro-numerical models to simulate the 3D response of the tested building. A series of consecutive 3D nonlinear dynamic analyses with a gradually increased excitation intensity was performed (these values have been reported in the previous section) using the 3D numerical model presented in Fig. 2. To do this, the local version of the OpenSees programme platform available from UL with the support of the locally developed preprocessor ToolBox (Dolsek 2010; Janevski 2022) was used.

Giberson's nonlinear beam-column lumped plasticity model (Giberson 1967) was used to model the columns and the beams. It is described in Sect. 3.1. The inelastic behaviour of the beam-column joints was simulated using the scissors model proposed by Alath and Kunnath (1995), as described in Sect. 3.2. Walls were modelled using a force–displacement UL version of the three-dimensional MVLEM (Fischinger et al. 2004; Isaković and Fischinger 2019), presented in Sect. 3.3.

The floor diaphragms were assumed to be rigid in their planes. Each floor’s mass and mass moments of inertia were lumped at the corresponding centre of gravity. The gravity load was modelled by the tributary concentrated forces applied at each floor at the top of the columns and the walls (see Fig. 2b). Based on experiences obtained during the simulations of other shaking table experiments (e.g. Fischinger et al. 2017; Gams et al. 2022), 2% viscous damping was taken into account. The considered value of viscous damping agrees well with the values reported in other studies (e.g. Ile and Reynouard 2003; Gilles and McClure G 2012, Karaton et al. 2021).

Rayleigh damping model was used, considering the structure’s mass and initial stiffness of elements used to model walls and nonlinear springs used to describe the nonlinear response of beams, columns and hinges (please see the description in the following sections). Considering the findings and opinions from the literature (Ibarra and Krawinkler 2005; Chopra and McKenna, 2016), the stiffness proportional damping was defined based on the initial stiffness of these elements. The stiffness proportional damping was not considered in very rigid elements between hinges of beams and columns and rigid elements between walls and beams to minimise the spurious damping forces.

3.1 The model for beams and columns

Each beam and column was modelled by one Giberson’s element consisting of two nonlinear rotational springs located at the element nodes, connected by an infinitely rigid elastic part (see Fig. 3a). Beams in axis B and C were attached to rigid elements between the walls and transverse beams in axis 1–4. For the beams, the nonlinear uniaxial bending response was considered. For the columns, the nonlinear biaxial bending was simulated; however, the response in two directions was uncoupled. The shear and torsional responses were modelled to remain elastic.

Fig. 3

Nonlinear responses of columns and beams: a the numerical model, b the quadri-linear moment–chord rotation response envelope, c the typical cyclic response of beams, and d the typical cyclic response of columns

The response of the nonlinear springs was defined using the modified Takeda hysteresis rules (Takeda et al. 1970). The original Takeda model was extended using a model for the post-peak response (see Fig. 3b). The overall response was defined by the quadri-linear moment-rotation envelope, with characteristic points representing the following limit states: cracking of the concrete (CR), yielding of the reinforcement (Y), maximum strength (M) and near collapse (NC).

The moment-rotation envelope of plastic hinges was defined based on the moment–curvature analysis of their cross-section. Moment–curvature analysis was performed considering the geometry of the cross-section, longitudinal reinforcement, unconfined cover, confined core concrete and the axial force corresponding to the gravity load. The beams’ cross-section included the effective part of the slab. Initially, the effective width of the slab was defined according to standard Eurocode 2 (EC2—CEN 2004). Later, it was modified as explained in Sect. 5.1.

The measured compression strength of the concrete was considerable (see the previous section); thus, the properties of the confined concrete were estimated based on the model proposed by Razvi and Saatcioglu (1999). Using OpenSees (Mazzoni et al. 2006), all concrete fibres were modelled using Concrete01 uniaxial material. The reinforcement fibres were modelled using Steel02 uniaxial material proposed by Menegotto and Pinto (1973). The parameters defining the transition from elastic to plastic branch were determined according to the authors’ recommendations.

To account for the reduction in the initial stiffness of the beams and columns (see the discussion in Sect. 5.3), the cracking rotation θ_cr:

$$\theta_{cr} = \frac{{M_{cr} L_{v} }}{3EI}$$

(1)

was tripled. Here, M_cr is the cracking moment, EI is the flexural stiffness, and L_v is the distance from the element node to the location of the zero-moment. The yield chord rotation $\theta_{y}$ was calculated according to Eurocode 8–2 (CEN 2005a), considering the elastic-perfectly plastic idealisation of the moment–curvature envelope as:

$$\theta_{Y} = \frac{{\phi_{y} L_{v} }}{3}$$

(2)

where ϕ_y is the yielding curvature.

The chord rotation at near-collapse limit state $\theta_{NC}$ was estimated according to Eurocode 8–3 (CEN 2005b) as:

$$\theta_{NC} = 0.016\left( {0.3^{\nu } } \right)\left[ {\frac{{max\left( {0.01;\omega ^{\prime}} \right)}}{{max\left( {0.01;\omega } \right)}}f_{c} } \right]^{0.225} \left( {\frac{{L_{v} }}{h}} \right)^{0.35} 25^{{\left( {\alpha \rho_{sx} \frac{{f_{yw} }}{{f_{c} }}} \right)}} \left( {1.25^{{100\rho_{d} }} } \right)$$

(3)

where $\nu$ is normalised axial load, $\omega$ and $\omega ^{\prime}$ represent the mechanical reinforcement ratio of the tension (including the web reinforcement) and compression reinforcement, respectively, $h$ is the depth of cross-section, $\alpha$ is the confinement effectiveness factor, ${\uprho }_{{{\text{sx}}}}$ is the ratio of transverse steel parallel to the direction of loading, and $f_{c}$ and $f_{yw}$ are the concrete compressive strength and the stirrups’ yield strength in MPa, respectively. $\rho_{d}$ is the ratio of diagonal reinforcement. The near-collapse moment M_NC was defined as 80% of the maximum flexural strength M_M.

The chord rotation $\theta_{M} {\text{corresponding to the maximum strength was defined as}}$:

$$\theta_{M} = \frac{{\theta_{NC} }}{{0.2r_{CM} + 0.8}}$$

(4)

where $r_{CM}$ is the ratio between the collapse rotation and the rotation at the maximum moment. The ratio $r_{CM}$ was defined according to Anžlin (2017) as:

$$r_{CM} = min\left[ {0.19\omega_{\alpha } \left( \% \right) + 1.80; - 0.22\omega_{\alpha } \left( \% \right) + 6.86;4} \right]; \omega_{\alpha } \le 22 \%$$

(5)

where $\omega_{\alpha }$ is the volumetric mechanical ratio of the lateral reinforcement.

The typical cyclic responses of the beams and columns are illustrated in Fig. 3c and d. The unloading response was defined using the coefficient β (see Fig. 3a). Its typical value is β = 0.5. In this study, it was increased to β = 0.8 since a better agreement with the experiment was obtained in this scenario (see the discussion in Sect. 5.4). The yield chord rotations θ_y, near-collapse chord rotations $\theta_{NC}$, the yield moment M_Y and maximum flexural strength M_M considered in the study are summarised in Tables 1 and 2 for columns and beams, respectively.

Table 1 Absolute corner values of M−θ envelope in columns (envelopes were symmetric)

Table 2 Corner values of M−θ envelope in beams. The positive and negative values correspond to tension deformations at the bottom and the top edge of the cross-section, respectively

3.2 The model for the beam-column joints

The scissors model proposed by Alath and Kunnath (1995) was used to model beam-column joints (see Fig. 4). It consists of a zero-length rotational spring element (see Fig. 4a), which is used to simulate the shear response of the joint core and rigid links to adjacent beams and columns. To account for a biaxial response, each joint was modelled by two rotational springs. Their response was uncoupled.

Fig. 4

Nonlinear response of beam-column joints: a the numerical model, and b typical cyclic response of the rotational spring

The response of the joint core was described using the modified joint shear strength model proposed by Kim et al. (2009). It was simulated using the quadri-linear moment-rotation envelope, defined by four corner points corresponding to the CR, Y, M, and NC states (see Fig. 4b and Sect. 3.1, where the notation used is explained).

Since some joints were relatively weakly reinforced, the model proposed by Kim et al. (2009) needed some modifications. To account for the reduced initial stiffness (see the discussion in Sect. 5.3), the cracking rotation θ_cr was tripled (in the same manner as in the columns and the beams). Instead of the originally proposed value for the yielding rotation (θ_Y), the value observed during the experiment was taken into account. The strength at NC limit state M_NC was defined as 25% of the maximum strength M_M. The maximum moments M_M and the corresponding rotations θ_M of the moment-rotation envelopes for different joints are summarised in Table 3. Other corner points were computed as: M_CR = 0.44 M_M, θ_cr = 0.06 θ_M, M_Y = 0.98 M_M, θ_Y = 0.002, M_NC = 0.25 M_M, θ_NC = 2.02 θ_M.

Table 3 Corner values of the moment-rotation envelopes of beam-column joints

Using Opensees, the response of beam-column joints was simulated using the uniaxial material Pinching4 model proposed by Lowes and Altoontash (2003), considering the properties defined based on data listed in Table 3. The hysteresis rules were defined by the following parameters: $rDispP=rDispN=0.5$, $rForceP=rForceN=0.1$, $uForceP=uForceN=-0.15$.

3.3 The model of walls

The nonlinear behaviour of the walls was simulated using a 3D force–displacement-based version of the MVLEM developed at UL (Fischinger et al. 2004; Isaković and Fischinger 2019; see Fig. 5a). The element consists of an arbitrary number of rigidly connected vertical springs. The nonlinear response of each spring is described by the force–displacement hysteretic relationship, presented in Fig. 5. Shear and torsional behaviour are represented by horizontal and torsional springs located at the centroid of the cross-section (in the horizontal plane) and the centre of the rotation of the corresponding element (in the vertical plane), respectively (see Fig. 5a). The shear and torsional responses were modelled as elastic.

Fig. 5

a 3-D force–displacement MVLEM, and b the mesh of elements, element segments corresponding to vertical springs, and the typical force–displacement response of vertical springs

Walls were modelled using several MVLEMs of different lengths. Shorter elements were used to model the walls’ potential plastic hinges, and the remaining parts of the walls were modelled by longer elements. Each element included 24–28 vertical springs (with tributary areas, presented in Fig. 5b), which were used to model its axial-flexural response. The number of vertical springs depended on the number of longitudinal bars in the wall. Each spring corresponded to one segment with one reinforcing bar each (see Fig. 5b).

The vertical springs were modelled using uniaxial material VertSpringType1 (see Fig. 5). The tension response was defined by a three-linear force–displacement relationship, characterised by the CR, Y and NC states (see Fig. 5a and Table 4). The compressive forces and displacements corresponding to the mean compression strength of concrete were used to define the compression response. The typical values of the element parameters, $\mathrm{\alpha }=1.0$, $\upbeta =1.5$, $\upgamma =1.05$, and $\updelta =0.5$, describing the hysteretic response of vertical springs (see Fig. 5a), were taken into account.

Table 4 Properties of the springs in boundary and the inner part of shortest MVLEM used

The main properties of typical vertical springs in the boundary regions and the internal part of the shortest MVLEM used are presented in Table 4. In longer elements, the characteristic displacements (see Fig. 5a) were increased in proportion to the length of the element. The cracking, yielding, and ultimate forces were the same in all segments with the same amount of reinforcement, since these values were independent of element length.

4 Evaluation of the numerical model

The results of the simulations were evaluated in terms of the global and the local response parameters in sections Sect. 4.1 and 4.2, respectively. In Sect. 4.3, analytically defined damage patterns are analysed and compared with the experimental observations.

4.1 The global response parameters

4.1.1 The wall direction

The global response parameters in the wall direction were simulated quite well for all considered seismic excitation levels, including the simulation of the aftershock response. This is illustrated in Fig. 6, where the hysteretic responses at different storeys, corresponding to 50% (essentially elastic response), 100% (nonlinear response) and 60% (aftershock response) JMA-Kobe, are presented. The analytical and measured storey acceleration–displacement relationships are presented.

Fig. 6

Acceleration–displacement responses for a 50% JMA-Kobe, b 100% JMA-Kobe, and c 60% JMA-Kobe

The results of the analyses and experiments correspond reasonably well for all excitation levels. The model successfully captured the degradation of the stiffness as well as the acceleration and displacement demand.

Somewhat larger differences between the analysis and experiment can be observed only in the strongest negative cycles of 100% and 60% JMA-Kobe excitation. In these two cycles, the measured displacements in the upper storeys were approximately 30% smaller than the estimated values. It is assumed that this difference can be related to the abrupt stiffness change at the top of the 7th storey, where the walls were terminated. The parameters that influenced the upper storeys’ responses are discussed later, in Sect. 5.1.

The displacement and acceleration response histories confirmed a reasonably good agreement between the analysis and the experiment. Examples are presented in Figs. 7 and 8. The displacements and accelerations at the top of the 7th storey (the location at which the walls were terminated) and at the top of the building are presented.

Fig. 7

Displacement response history at the top of the 7th storey and at the top of the building

Fig. 8

Acceleration response histories at the top of the 7th storey and at the top of the building

The maximum storey drifts and displacements were also simulated reasonably well. The envelopes are presented in Fig. 9. The most significant discrepancies between the analysis and experiment can be observed for the 100% and 60% JMA-Kobe excitations, particularly in the strongest cycle in the negative direction. In this cycle, the maximum measured values were, on average, 27% and 24% smaller than the estimated values. In the positive direction, the differences were smaller (20% and 11% for 100% and 60% JMA-Kobe, respectively).

Fig. 9

Maximum storey drift profiles for a 50% JMA-Kobe, b 100% JMA-Kobe, and c 60% JMA-Kobe

The overturning moment distribution along the building was captured quite well. This is illustrated in Fig. 10, where the maximum overturning moments corresponding to 100% and 60% JMA-Kobe are presented.

Fig. 10

Overturning moment distribution for a 100% JMA-Kobe, and b 60% JMA-Kobe

4.1.2 The frame direction

The model was also effective in the frame direction. The stiffness of the structure was captured reasonably well for all seismic excitation and storey levels. This is illustrated in Fig. 11, where the measured and calculated acceleration–displacement responses are compared.

Fig. 11

Acceleration–displacement response: a 50% JMA-Kobe, b 100% JMA-Kobe, c 60% JMA-Kobe

The displacements and acceleration response histories confirmed the reasonably good efficiency of the model at different storeys; some examples are presented in Figs. 12 and 13. In Fig. 12, the displacement response histories at the top of the 4th storey (where the most significant damage was observed) and at the top of the building are presented for 100% and 60% JMA-Kobe. In Fig. 13, the acceleration response quantities at the same locations are presented.

Fig. 12

Displacement response history at the top of the 4th story and at the top of the building

Fig. 13

Acceleration response histories at the top of the 4th story and at the top of the building

The measured values of maximum displacement and storey drift were larger than the estimated values. The agreement between the analysis and the experiment was better in this case than that in the wall direction (see Fig. 14). At 100% JMA-Kobe excitation, the maximum difference between the analysis and experiment was 15%. The simulation of the overturning moment distribution (see Fig. 15) was somewhat less accurate than that obtained in the wall direction (particularly in the negative excitation direction).

Fig. 14

Maximum storey drift profiles at a 50% JMA-Kobe, b 100% JMA-Kobe, and c 60% JMA-Kobe

Fig. 15

Overturning moment distribution at a 100% JMA-Kobe, and b 60% JMA-Kobe

4.2 The local response parameters

4.2.1 The response of the walls

The accuracy of the MVLEM in predicting the local response quantities of the walls was evaluated by comparing the experimental and analytical values of curvatures at the plastic hinges of the walls. The vertical displacements measured by the Linear Variable Differential Transformers (LVDT) installed at both sides of the bottom part of the walls (see Fig. 16) were divided by the length of the LVDTs to define the deformations. The curvatures were estimated based on these deformations. These were then compared with the curvatures obtained using the numerical analysis, which were calculated in a similar manner. The sum of displacements in the outermost springs of the bottom four MVLEMs was divided by their total length (approximately the same as that of the LVDTs) to obtain the deformations. These deformations were then used to calculate the curvatures.

Fig. 16

LVDTs that were used to measure the vertical deformations at the base of the walls

The measured and calculated vertical deformations and corresponding curvatures matched quite well. This is illustrated in Fig. 17, where the curvature response histories of outer wall W11 (see Fig. 16) corresponding to the 100% and 60% JMA-Kobe excitation levels are presented. The agreement between the experiment and analysis was also good for the inner wall at all excitation levels.

Fig. 17

The curvature response histories at the plastic hinges of the outer wall

4.2.2 The response of the columns and beams

It was not possible to perform a quantitative comparison of the experiment and analysis in terms of local response quantities for columns and beams directly. Giberson’s model provides data about chord rotations of beams and columns; however, there was not enough measured data to estimate these quantities. Thus, the accuracy of the model on the local (element) level was evaluated indirectly by comparing the damage patterns observed in the experiment and analysis. This analysis is presented in Sect. 4.3.

4.2.3 The response of the joints

The modified model of the joints, as described in Sect. 3.2, simulated the local response of all instrumented joints (joints at the intersection of axis A and 2 in the 1st–4th storeys and 6th storey; see Fig. 1) with reasonable accuracy. The calculated and measured shear strain response histories are compared in Fig. 18 for the joints on the 4th and 6th storeys. A somewhat larger discrepancy between the analysis and experiment can be observed only in the joint on the 4th storey at the 100% JMA-Kobe excitation level. In other cases, the agreement between the experiment and analysis is better.

Fig. 18

The shear deformation response history in joints A2 on the 4th and the 6th storeys

4.3 Damage evaluation

The gradual increase of damage observed during the analysis at 50% and 100% JMA-Kobe is illustrated for the wall and frame directions in Figs. 19a and b, respectively. The damage pattern corresponding to 60% JMA-Kobe is qualitatively the same as that of 100% JMA-Kobe excitation. In the case of the green and yellow elements (see Fig. 19), the cracking and yielding limit states, respectively, were exceeded. The elements shown in red exhibited considerable damage, approaching the near-collapse limit state. Failure was observed in the black elements. The most damaged beams, columns and beam-column joints are encircled, and the corresponding ratio of the maximum chord rotation demand versus the chord rotation capacity (corresponding to the NC limit state) is shown. The most damaged parts of the walls are also marked, and the curvature demand versus curvature capacity ratio in the most critical cross-section is documented.

Fig. 19

Damage evaluation in the a wall direction, and b frame direction

The yielding of the most critical elements was observed at 50% JMA-Kobe in both the wall and the frame directions. In the wall direction, yielding was observed at the bottom of the walls and in the beams in the six lower storeys.

When the seismic intensity was increased to 100% JMA-Kobe, damage to the walls was spread over the entire first storey. It was greater compared with the previous run but was still moderate. The maximum curvature demand did not exceed 40% of the curvature capacity at the critical cross-section. Yielding of the walls was also observed in upper storeys, particularly at the top of the wall.

At 100% JMA-Kobe, the yielding of the beams spread to the upper storeys. The damage was moderate in the majority of the beams. Chord rotation demand did not exceed 65% of the total capacity. The columns were not considerably damaged. The maximum chord rotation demand was observed at the foundation level and did not exceed 20% of the capacity. Damage to the joints was minor.

In general, the damage in the frame direction was more significant and qualitatively different from that observed in the wall direction. The most severely damaged elements were the joints, particularly in the 4th and 3rd storeys. The joints in the 4th story were noticeably damaged even during the 50% JMA-Kobe excitation, where the chord rotation demand was as great as 78% of the total capacity. In other joints, the damage was considerably smaller. The beams and columns were moderately damaged. The chord rotation demand did not exceed 14% and 38% of the capacity in the columns and beams, respectively.

During 100% JMA-Kobe excitation, the joints in the 3rd and 4th storeys failed. Damage to the beams was increased. In some beams in the 3rd and 4th storeys, the chord rotation demand increased to almost 80% of the total capacity. Other beams were moderately damaged (the chord rotation demand did not exceed 50% of the capacity). All columns were moderately damaged. The greatest chord rotation demand at the foundation level did not exceed 34% of the capacity.

The estimated damage patterns matched the experimental observations reasonably well. The analysis successfully detected the critical elements in both directions. According to Tosauchi et al. (2017), in the frame direction, the most damaged elements were joints and beams in the 4th storey. The spalling of concrete was observed in the corner columns. In the wall direction, the walls were the most severely damaged on the first storey and spalling of the concrete was observed. Damage to the beams at the top of this storey was also reported.

5 Important parameters influencing the response

5.1 The effective width of the slab

The effective width (EW) of the slab had a major influence on the response since it directly affected the strength and stiffness of the beams. In general, the EW of the slab depends on many parameters, including the level of the drift demand (the excitation intensity). According to different experiments reported in the literature (e.g., Kabeyasawa et al. 2017; Isaković et al. 2020), the effective width increases proportionally with the drift demand and can be as large as the total span length. A similar observation was also reported by Pantazopoulou and French (2001).

In this study, the effective width of the slabs was initially defined based on recommendations of Eurocode 2 (CEN 2004). The typical values were 1.30 m and 1.20 m in the wall and frame directions, respectively. However, the analysis revealed that in some parts of the building, the EW of the slabs was underestimated, particularly at 100% JMA-Kobe excitation. In these parts of the building, the EW of the slabs was increased to the total span length, as described below.

In the wall direction, the underestimated slabs’ EW primarily influenced the response of the top three storeys. When EW was defined according to EC2, the top part of the building was too weak to realistically limit the rotations of the upper parts of the walls, which were terminated at the top of the 7th storey. Consequently, the estimated shape of the drift profile was different from that observed in the experiment (see Fig. 20a), particularly for the top three storeys. When the EW of the slabs on the upper storeys (slabs at the top of the 7th–10th storeys) was increased to the total span length (assuming that the beams are more engaged in the upper storeys since the walls were terminated), the estimated shape of the drift profile improved, particularly for the upper stories (see Fig. 20b).

Fig. 20

Storey drift profiles at 100% JMA-Kobe for a wall direction; EW—EC2, b wall direction; EW—total span, c frame direction; EW—EC2, and d frame direction; EW—total span,

In the frame direction, the EW of the slab was increased on the 3rd and the 4th storeys, where the largest storey drifts were observed. In this way, the shape of the drift profile (see Figs. 20c and d, which correspond to EW according to EC2 and half-span EW, respectively) was somewhat improved and better matched the shape of the drift profile observed during the experiment.

The EW of the slab had an important influence on the strength of the beams. When it was underestimated, the damage pattern of the structure was, in some cases, unrealistic. Due to the underestimated strength, the beams sustained damage instead of the beam-column joints. In general, in the frame direction, the ratio of the joints’ strength and the strength of the adjacent beams had a significant influence on the response (see the discussion in the following subsection).

5.2 The influence of the beam-column joints on the response

The initial numerical model of the building did not include the model for the joints. This did not considerably influence the response until the 100% JMA-Kobe excitation, where the more noticeable discrepancies between the experiment and analysis were observed (see Fig. 21a). These discrepancies were expected since more severe damage to the joints was observed in that run. The model for the joints particularly influenced the shape of the drift profile.

Fig. 21

The storey drifts defined a without the model for the beam-column joints, b with a modified model for the beam-column joints, and c with the original model for the beam-column joints, as proposed by Kim et al. (2009)

When the model for the joints was included, the analysis agreed with the experiment better. For example, the shape of the drift profile was considerably improved (see Fig. 21b). However, the original model for the joints, proposed by Kim et al. (2009), was somewhat changed. According to the experimental observations, the yielding rotation was reduced to 0.02 rad, and the NC strength was decreased to 25% of the maximum value. These modifications were needed because the joints were relatively poorly reinforced.

As mentioned previously, the ratio of the joints’ strength and the strength of the adjacent beams had an important influence on the response. When the original model for the joints was used, the yielding occurred in some beams instead of the joints. Consequently, an unrealistic damage pattern was obtained, and the response was different than that observed in the experiments. For example, the storey drifts in the lower storeys were underestimated (see Fig. 21c).

5.3 Initial stiffness

In the analysis, only the tests for the fixed-base building were simulated. These were preceded by tests of the same building on sliding foundations. Since this building was cracked (Tosauchi et al. 2017) during the testing, the initial stiffness of the fixed-base building was reduced compared to the theoretical stiffness corresponding to the gross cross-section of the structural elements. Additionally, the initial stiffness was also decreased due to the transportation, handling and assembly of the specimen.

Based on the experiences when simulating other shaking table experiments (e.g. Fischinger et al. 2002; Fischinger et al. 2017; Gams et al. 2022) and considering that the axial force levels in columns and walls were low (considering the gravity load, it was less than 5% of the medium compression strength of concrete), the initial theoretical stiffness of all structural elements was reduced threefold. This primarily affected the response at lower levels of seismic excitation. Examples of these are provided in Fig. 22, where the base shear–top displacement response, top displacement response history and the storey-drift envelope in the frame direction at 25% JMA-Kobe in the case of the theoretical and reduced initial stiffness are presented. When the initial theoretical stiffness of structural elements was taken into account, the overall stiffness of the building was too large. Consequently, the displacements and storey drifts were underestimated.

Fig. 22

The response at 25% JMA-Kobe in the frame direction; a the base shear–top displacement response; b top displacement response history, and c drift envelope

5.4 The unloading stiffness of beams and columns

In Giberson’s model, where the Takeda hysteresis rules are used to describe the response, the unloading response is defined using the parameter β, which is used to define the unloading stiffness based on the initial stiffness. The typical value of β is 0.5.

When the standard value of β was used in the analysed building, the energy dissipation in some beams and columns was overestimated. Consequently, the maximum displacements and storey drifts (particularly in the frame direction) were underestimated (compare the green and red lines in Fig. 23). When β was increased to 0.8, the energy dissipation in the beams and columns was reduced. The maximum displacements and storey drifts then matched the experimental values better (compare the blue and red lines in Fig. 23). The unloading stiffness in the beams and columns was less important in the wall direction since the walls predominately governed the response.

Fig. 23

The influence of the unloading stiffness of the beams and columns to the: a maximum story displacements, and b maximum storey drifts in the frame direction

6 Conclusions

Tests on the ten-storey RC fixed-base building performed at the E-Defense shaking table were used to evaluate the capabilities of some common numerical macro-models of RC beams, columns, beam-column joints and walls. The analytical results matched the experimental results reasonably well for all seismic excitation levels corresponding to predominantly elastic, nonlinear and aftershock responses. The evaluated models exhibited reasonably good accuracy at both the global and local response levels. The acceleration–displacement response, the overall stiffness of the structure, drift profiles, overturning moment profiles and displacement and acceleration response histories agreed with the measured values within the accuracy of the measurements along both the frame and wall directions of the building.

Local response quantities, such as the curvature response histories at the base of the walls and the shear deformation response histories of the joints, were also captured reasonably well. The good agreement between the analysis and experiment was predominantly achieved by using the standard input parameters for the models. However, some parameters were modified because of certain specific structural solutions or non-standard structural details in the tested building.

The effective width (EW) of the slab was found to be one of the most important parameters influencing the response. Initially, it was defined according to the standard EC2. Subsequently, for some slabs, the EW was increased to the total span length to better simulate certain response parameters, such as the shape of the drift profiles (particularly under strong seismic excitations). Along the wall direction, the EW of the slabs of the three uppermost storeys was increased, starting from the slab at the top of the seventh floor, where the RC walls terminated, to the top of the building. Consequently, the top floors were strong enough to limit the rotation of the walls more realistically. Along the frame direction, the slabs’ EW was increased for the third and fourth storeys, which is where the largest storey drifts were observed. These modifications improved the agreement between the analysis and experiment (for example, the storey drift profiles). These observations are in good agreement with some findings reported in the recent literature (e.g., Pantazopoulou and French 2001; Kabeyasawa et al. 2017; Isaković et al. 2020) that state that the EW of slabs could be considerably higher than that defined in different codes, particularly when the drift demand is significant. In general, the EW of slabs subjected to strong seismic excitations (larger drifts) should be revised, considering that the EW can be as large as the span width.

Relatively weak joints were noticeably damaged under the strongest seismic excitations. The considerable damage to the joints was confirmed by the analysis using a somewhat modified model for joints compared to the original one presented in the literature (see Sect. 3.2). In the modified model, the yielding deformations and near-collapse strength were reduced. These changes were needed because some joints were relatively poorly reinforced. Revising the original numerical model for lightly reinforced beam-column joints is recommendable based on these observations.

Overall, the response and damage patterns did not depend solely on the ratios of the stiffness and strength between the joints, beams and columns, but were also strongly influenced by the ratio of the dissipated energy within these elements. As the damage primarily occurred in the weak joints, the plastic deformations and dissipated energy in the beams and columns were somewhat reduced compared to those in the standard models. These reductions were considered in the numerical model by reducing the unloading stiffness of the beams and columns. Without this modification, the energy dissipation in the beams and columns was too large compared to that in the joints.

Based on these observations, the standard numerical models for beams and columns in structures with weak joints with substandard details are reasonable to revise. In such structures, the plastic deformations and energy dissipation in beams and columns are appropriate to reduce. In Giberson’s model with Takeda hysteretic rules, this reduction can be achieved by increasing the unloading stiffness parameter β. In the analysed building, this parameter was increased from the standard β = 0.5 to β = 0.8. Further studies considering different ratios for the beams’, columns’ and joints’ strength, stiffness and energy dissipation capabilities are needed to generalise the value of β = 0.8.