Adjacent interacting masonry structures: shake table test blind prediction discrete element method simulation

Abstract

This study presents the numerical simulation of a shake table experimental earthquake campaign of a building aggregate composed of two adjacent unreinforced rubble stone masonry buildings. The experimental testing was performed with the purpose of studying the interaction between a single-storey and a two-storey building connected with a dry joint consisting of a smooth mortared surface. Before performing the experimental testing, various research teams were sent the construction details to participate in a blind prediction competition using different prediction strategies. The approach reported herein to simulate the shake table tests is the discrete element method (DEM) with rigid elements and damage and deformation lumped in inter-block joints that represent the mortar interfaces governed by a non-linear Mohr–Coulomb constitutive laws. The material properties implemented in the model after calibrating using piers shear tests was observed unrealistically stiff. Hence, it was reduced based on the outcome of pushover and eigenvalue analyses. A sequence of earthquakes with incremental acceleration was input to the real and numerical models. Numerical overestimation of damage and displacement was observed probably due to underestimating the damping ratio. Unexpected sliding of the single-storey building occurred at early stages of the simulation. However, the overall behaviour in terms of base shear force, building displacement and damage progression was well captured in the DEM model. The in-plane flexural and rocking mechanism in the two-storey building was correctly simulated. Damage at the interface between the two buildings with separation and pounding was also reasonably well predicted.

1 Introduction

Interaction causing damage between nearby buildings has been observed (Stone et al. 1987; Kasai et al. 1992; Cole et al. 2010a, 2012; Dizhur et al. 2011) after multiple earthquakes, typically ranging from 6 to 15% of reported buildings. This common observation called pounding is an undesirable phenomenon that should be prevented or mitigated and has not being widely studied or simulated in unreinforced masonry (URM) buildings (Kasai et al. 1992; Cole et al. 2010b; Abdel Raheem 2014; Chesi et al. 2018; Maniatakis et al. 2018; Miari et al. 2019). Post-earthquake observations outlined that non-alignment of storey levels led to pounding, and in most cases was the taller building that collapsed, while when no collapse was observed the lower rise building withstood higher damage at the highest point of collision (Abdel Raheem 2014). Buildings of dissimilar natural frequencies built side by side tended to vibrate out-of-phase causing pounding (Stone et al. 1987; Maniatakis et al. 2018). However, the most critical construction aspect triggering pounding was insufficient seismic gap mostly observed in tightly spaced buildings. In many historical city centres it is typical to observe how, as part of the city layout development, adjacent buildings usually shared structural walls that supported floors and roofs. The façade of the newly added building besides an existing one was usually not connected with other than a dry joint. Observations after the 2016 Central Italy earthquakes (Sorrentino et al. 2018) led to the conclusion that the dry joint between adjacent buildings were damaged during the first seconds of the earthquake causing pounding between buildings. Miari et al. (2019) observed that pounding collision between buildings might generate high impact forces and short duration acceleration pulses which is not considered in current engineering design. Examples of mitigation measures developed to prevent pounding are insertion of bracing or shear walls, inclusion of seismic gap, use of impact absorbing materials between the buildings as rubber shock absorbers, polystyrene and polymers. Another option is connecting the adjacent buildings to make them vibrate in phase, sometimes using viscoelastic or friction dampers (Abdel Raheem 2014; Kumar and Karuna 2015; Charleson and Southcombe 2017; Miari et al. 2019).

Several studies have identified the damage observed after earthquakes of URM buildings for different building typologies. The level of damage (DL) is generally divided into 5 categories associated with the extent of the damaged structural elements (No damage DL0; Slight damage DL1: < 33%; Moderate-substantial damage DL2-3, between 33 and 66%; Very heavy damage or collapse DL4-5 > 33%) (Del Gaudio et al. 2019; D’Amato et al. 2020). Such studies showed that the seismic vulnerability of a URM building is strongly related to the quality of the masonry, the type of diaphragm and the presence of connections between structural elements (Sisti et al. 2018; Rosti et al. 2020). Clear evidence about strengthening and mitigation policies effectivity in URM buildings was reported after the 2016–2017 Central Italy earthquake sequence, where very few strengthened or buildings built after 1982 became unstable or were damaged after the earthquakes (Sisti et al. 2018). Contrary to the popular belief, heavy roofs did not affect the behaviour of buildings when global strengthening strategies were implemented in the underlying walls.

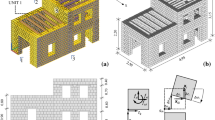
In order to investigate the unknowns of pounding between URM buildings, two structurally simple double-leaf stone URM half-scale buildings with timber floors at different heights (Tomić et al. 2020, Tomic et al. 2022a) were built in a shake table and experimentally tested by the Seismology and Earthquake Engineering Research Infrastructure Alliance for Europe (SERA), within the program of Adjacent Interacting Masonry Structures (AIMS) subjecting the buildings to earthquakes incrementally increasing its intensity. The shake table experimental campaign was performed at the Civil Engineering National Laboratory (LNEC) in Lisbon, Portugal, and a competition was organised to blindly model the experiment by different research groups invited by the SERA-AIMS program and to expand on the modelling approaches to simulate URM. A summary of all the predictions conducted and a comparison with the experimental results are included in Tomic et al. (2022b). The reported study addresses the discrete element method (DEM) approach using the software 3DEC (Itasca 2013), which was used to develop the model seen Fig. 1c. It is acknowledged that a sliding error in Unit 1 was observed but not corrected because of computation time constrains to deliver the results and expiration date of the software license. In addition, an error in the algorithm input the same accelerogram to both X and Y directions at every simulated sequence. Such errors did not prevent observing reasonably good agreement when comparing the experimental and simulated results, and they reflect the complexity of working with DEM.

Fig. 1

Unit 1 (Right) and Unit 2 (Left) of the built model and numerical model

2 Description of the experimental specimen

The test specimen is an aggregate formed by two buildings constructed in the laboratory consisted of two units. Unit 1 (see Fig. 1b) is a U-shaped one-storey building with plan dimensions 2.5 m × 2.45 m, 2.2 m of height and 0.30 m wall thickness, with total mass of 7,434 kg. Unit 2 (see Fig. 1b) is a two-storey building with a floor and a roof, plan dimensions 2.5 m × 2.5 m, total height of 3.15 m and 0.35 m and 0.25 m of wall thickness of the first and second floors respectively, with total mass of 16,272 kg. 1.5 tonnes of additional evenly distributed mass were added at the floors. The buildings share one common wall connected to Unit 2 with mortared joints and to the façades of Unit 1 with a dry joint with no physical gap nor interlocking between the units. To ensure that there is no interlocking between the units, Unit 2 was constructed first and when finished, the 30 cm wide strip of the interacting surface between units was smoothed with a layer of mortar. When dried, the construction of Unit 1 was resumed as seen in Fig. 1a. Wall leaves within the thickness of the walls had no interlocking and spandrels under the openings have the thickness decreased to 0.15 m. The material for the construction of the stone masonry walls was chosen to be similar to the one used in Guerrini et al. (2017) and Senaldi et al. (2018a) (see Table 3).

3 Description of the simulated discrete element model

Four main modelling techniques are available to simulate the response of masonry structures when subjected to earthquake motion (Calderini et al. 2010; Giamundo et al. 2014; D’Altri et al. 2019). First, block-based models where each brick of the structure is modelled with independent rigid or deformable blocks, and the interaction between blocks can be simulated with several possible formulations. It has been demonstrated that the DEM, within the block-based models represent one of the most accurate strategies to analyse the mechanical response of complex masonry structures when subjected to earthquake motion. However, high computational demand restricts the widespread use of this modelling technique. Secondly, models with masonry simulated as a deformable continuum governed by a particular material constitutive law (e.g. FEM), representing the most widely used approach to simulate complex URM structures. Algorithms that combined FEM and DEM have been developed to better simulate the behaviour of specific case studies (AlShawa et al. 2017). Thirdly, macroelement models where parts of the structure, that are generally piers and spandrels, are idealised as a single element with constitutive laws representing the mechanical behaviour of the complete element (e.g. EFM). Because of its simplicity of use, it is the strategy that most practitioners use. However, careful must be taken to interpret the result as currently the major challenges of the approach are the connection between perpendicular walls and interaction between in-plane and out-of-plane actions and damage. Lastly, geometry-based models where the masonry elements are simulated as rigid body blocks, which generally based on limit analysis the model is solved to investigate the state of equilibrium or collapse. Even though it is a simple strategy, the results can be greatly useful serving as a ballpark solution of the problem or to validate the solution of more complex strategies.

DEM was first presented by Cundall (1971) and later extended using a 3D version (Cundall and Hart 1985) originally conceived for jointed rock simulations. One of the principal strengths of using DEM is the ability to simulate large relative displacements between elements. Complete separation between elements that were previously in contact may happen and new contacts can be formed, allowing the modelling of the dynamic collapse behaviour of complex structures. Explicit time-stepping algorithms are commonly used for DEM where the equations of motion are integrated using a central-difference scheme (Itasca 2013; Šmilauer et al. 2015). The same algorithm is often used for quasistatic and dynamic simulations, overdamping the kinetic energy of the system in the quasistatic case by applying viscous damping forces to each element. In order to achieve numerical stability of DEM simulations, the required timestep Δ_t is calculated in relation to the mass of the smallest block (m_min) and the maximum contact stiffness of the model (j_kmax) as Δ_t = 0.2 $\sqrt {m_{min} /k_{max} }$ (Dimitri et al. 2011; Itasca 2013; Pulatsu et al. 2020).

The geometry of the building was modelled using the software Rhinoceros® (McNeel and Associates, 2014), which allows a script to be run that contains an algorithm capable of exporting a text file of the building geometry compatible with the DEM software 3DEC (Itasca 2013). The software 3DEC utilises rigid or deformable blocks with flat surfaces as discrete elements. The rubble stone masonry walls of the two buildings needed to be adapted to the geometrical limitations of 3DEC elements and were simulated with 8,871 discrete rigid blocks modelled using a random pattern that was repeated in alternative courses to simplify the geometry (see Fig. 2). The rigid option to simulate blocks was chosen because the deformation and failure of masonry structures built with competent stone are mostly determined by the inter-block displacements at the joints (Lemos 1997; DeJong and Vibert 2012; Çaktı et al. 2020). Additionally, deformable blocks involve the discretisation of every element using a finite element mesh which for dynamic analysis lead to substantially longer computation time. In order to account for elastic deformation, the modulus of elasticity of mortar and stone were used to calculate normal joint stiffness values which effectively lumps all elastic deformation into the joints of the model (expanded in Sect. 3.1).

Fig. 2

Unit 2 masonry bond pattern configuration

Every wall was modelled with two layers instead of three, as opposed to the real model, to allow for any possible leaves disintegration while reducing the number of elements for computation practicality. Floor slabs, beams and lintels were geometrically modelled identical to the real model using rigid blocks. However, the floor slabs were connected to the beams through an interface connection with the properties specified in joint number 5 from Table 1 obtained from laboratory and on-site tests from the literature (Giongo et al. 2013; NZSEE 2017; Gubana and Melotto 2018). It was considered the discretisation of the beams into smaller blocks to simulate the elastic nature of the wood beams, but it was decided to keep the single element beams because it is easier to control the shear stiffness of the composite diaphragm (beams and floorboards) with the stiffness of the springs that connect the beams and the floorboards. Additionally, discretising the beams would mainly help with simulating deflection of the beams more accurately, which was not aimed in this specific exercise. And lastly, if beams were to be discretised floorboards would need to be discretised as well to have an impact in the overall building behaviour. However, floorboards are very thin and the contact between floor elements would translate into smaller timesteps. Wall to wall connections were modelled by geometrically interlocking blocks as realistically as possible as seen in Fig. 2a. Three different densities were used in the simulation to model the different materials as seen in Fig. 2 represented by three colours (Blue-stone masonry: 1,980 kg/m³, Green-wood: 500 kg/m³, Red-wood + overburden: 4,946 kg/m³). The additional mass distributed on the floors of unit 2 were simulated by increasing the density of the floors (red colour) to allow for inertial forces to act on the mass.

Table 1 Material properties of joints

3.1 Contact interface

Each element representing a stone interacted with the surrounding ones through a non-linear contact joint that represented the mortar interface. Stresses calculated along the nonlinear joint interface were modelled using the Mohr–Coulomb failure criterion with tension cut-off and a shear stress limit. The Mohr–Coulomb model was characterised by five normal and shear parameters: normal stiffness (j_kn), shear stiffness (j_ks), friction angle ( ̊), cohesion (c), tensile strength (f_t) and dilatancy (d). In DEM, each contact point between blocks defines an integration point to compute the stress distribution within the contact surface. Once the onset of failure in either tension or shear was identified at the contact point, the tensile strength and cohesion was automatically set to zero. Compression was modelled linearly, therefore no crushing of stones was simulated in the model. Dilatancy is the phenomenon that occurs when shear displacement is in the plastic phase and due to the material imperfections at the surface that failed the normal displacement increases, causing an increment in shear force. Several authors have performed experimental and numerical studies to understand how to model dilatant joints. Experimental characterizations of dilatancy by Van der Pluijm (1993) show that the dilatancy ratio is significantly influenced by the type of interface failure in agreement with Vermeer and de Borst (1984) who reported values for the most common construction materials (clay = 0°; concrete = 12°; granulated and intact marble = 12° − 20°; dense sand = 15°; loose sand < 10°) concluding that dilatancy angles should be at least 20° lower than friction angle. There are multiple examples in the literature where authors modelled masonry using high values of dilatancy angles between 20° and 40° (Agnihotri et al. 2013; Bui and Limam 2013; Giamundo et al. 2014; Giresini 2015; Wang et al. 2015; Panto et al. 2017), but some older research and most of the recent research use between 0 and 11° to model in-plane and out-of-plane problems closer to Vermeer and de Borst (1984) observations (Le Pape et al. 2001; Karimi et al. 2012; Çakti et al. 2014; Daudon et al. 2014; Bui et al. 2018; D’Altri et al. 2018; Godio et al. 2018; Damerji et al. 2019; Malena et al. 2019; Malomo et al. 2019; Pulatsu et al. 2019; Valente and Milani 2019; Bagi 2020; Sarhosis et al. 2021). Godio et al. (2018) in a study specifically investigating dilatancy on DEM stated that dilatant joints lead to important non-conservative predictions for the out-of-plane strength of the masonry between the numerical and the experimental results regarding the ultimate load, even under low confinement. Therefore, considering the experimental and numerical research on dilation and the most recent numerical modelling research dilation is included in the model as 10° occurring until the limiting shear displacement of 0.001 mm is reached for zero dilation.

A relationship between URM mechanical properties and the interface stiffness can be derived as $j_{kn} = {\raise0.7ex\hbox{${\sigma_{n} }$} \!\mathord{\left/ {\vphantom {{\sigma_{n} } {u_{n} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{n} }$}} = {\raise0.7ex\hbox{${E \cdot \varepsilon_{n} }$} \!\mathord{\left/ {\vphantom {{E \cdot \varepsilon_{n} } {u_{n} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{n} }$}} = { }{\raise0.7ex\hbox{${E \cdot u_{n} }$} \!\mathord{\left/ {\vphantom {{E \cdot u_{n} } {u_{n} \cdot l}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{n} \cdot l}$}} = { }{\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E l}}\right.\kern-0pt} \!\lower0.7ex\hbox{$l$}}$, where u_n is the normal displacement of the joint, ε_n is the normal strain of the block, and l is the joint spacing. Using elastic relations j_ks can be calculated from j_kn as $j_{ks} = {\raise0.7ex\hbox{${j_{kn} }$} \!\mathord{\left/ {\vphantom {{j_{kn} } {2 \cdot \left( {1 + v} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2 \cdot \left( {1 + v} \right)}$}}$, where v is the Poisson ratio which was taken in this study as 0.25, resulting in the equation j_ks = 0.4⋅j_kn. All joint material properties are summarized in Table 1 and represented in Fig. 3. The material properties obtained were based on a calibration procedure explained in Sects. 4.1 and 4.2, where a slender (CS) and a squat (CT) pier were simulated. Values closer to the slender pier were used for the complete model with pushover analysis performed in Sect. 4.2 of the complete building where no issues were observed gave confidence to the chosen values. In an attempt to avoid sliding of the buildings the first course of bricks connecting the building with the ground (see Table 1 material no. 4) was modelled with high cohesion, but it was not achieved and sliding was observed in the dynamic analysis resulting in 17° being too small value. It was clear that for the squat piers of Unit 1, values closer to the CT pier should have been used with friction angle closer to 30°. Unit 2 performed well with slender piers (CS) mechanical parameters probably because it had more slender piers. As mentioned in Sect. 2, the connection between Unit 1 and Unit 2 was constructed with a dry joint assuring no interlocking by building Unit 1 alongside a smoothed mortared surface previously dried in unit 2. The joint simulating the interaction between Unit 1 and unit 2 (see Table 1 material no. 6) was modelled with very low c and f_t to simulate any minimal mortar connection between Unit 1 and 2. After the application of gravity and the consequent deformation the connection between buildings was purely frictional.

Fig. 3

Joint material properties representation by number

3.2 Damping model

By using the Mohr–Coulomb criteria explained in Sect. 3.1 to govern the joint shear behaviour and the opening and closure of cracks, minimum hysteretic energy dissipation is obtained. Therefore, viscous damping forces proportional to relative velocities are included as dashpots elements at each corner of blocks in contact (sub-contacts). For this purpose, Rayleigh damping was used in 3DEC to construct the damping matrix when performing dynamic analysis. Rayleigh damping makes use of the constants α (mass-proportional) and β (stiffness-proportional) (Lemos 2019) to construct the damping matrix when performing dynamic analysis according to the following expression:

$$C = \alpha \cdot M + \beta \cdot K$$

(1)

where C, M and K are the damping, mass and stiffness matrices respectively. The damping ratio ξ_i for any circular frequency ${\omega }_{i}$ can be found in Bathe and Wilson (1976) as:

$$\xi_{i} = { }\frac{\alpha }{{2 \cdot \omega_{i} }} + \frac{{\beta \cdot \omega_{i} }}{2}$$

(2)

reaching a minimum at:

$$\beta = { }\frac{{\zeta_{min} }}{{\omega_{min} }}\quad\quad\quad\alpha = { }\zeta_{min} \cdot \omega_{min}$$

(3)

Once the value of ω_crit is selected, β can be easily calculated with Eq. 3. If Eq. 2 is plotted as in Fig. 4 it can be identified that the mass-proportional (MP) damping ratio distribution decreases hyperbolically with frequency and that the stiffness-proportional (SP) damping ratio increases linearly with frequency, with the final Rayleigh curve depicting a trough of damping ratios between frequencies ωi and ωj (see Fig. 4). Several authors have suggested that MP damping could overdamp low frequencies due to the damping distribution, as seen in Fig. 4 for frequencies lower than ωi. However, many authors have performed successful dynamic simulations using an MP damping approach in 3D disregarding the drawbacks and achieving reasonably good matches with experimental observations and with favourable computational time (Lemos 1997; Çaktı et al. 2016; Galvez et al. 2018). Psycharis et al. (2003) and Çaktı et al. (2020) also used MP damping to perform incremental dynamic analyses (Vamvatsikos and Cornell 2002) to study the specific behaviour of an URM part of a building. In both studies (Psycharis et al. 2003; Çaktı et al. 2020) the fact that high frequencies would be underdamped in order to reduce the computational effort was acknowledged.

Fig. 4

Block sub-contact representation and damping model distribution

By specifying SP damping, the timestep is automatically reduced for numerical stability making the simulation highly time demanding. Noting that when MP damping was selected (not affecting the timestep size), each earthquake simulation took about 4.1 days, which was considered the only timely plausible simulation option.

3.3 Sequence of analyses and accelerograms

The shake table experimental campaign was conducted using the two horizontal components of the Albatros station from the 1979 Montenegro earthquake (Luzzi et al. 2016). The maximum peak ground acceleration (PGA) that the shake table is capable of withstand for the weight of the built specimen was 0.875 g in the y-direction (see Fig. 1) and 0.625 g in x-direction. The loading sequence consists of four stages where the PGA of the ground motion was applied at 25%, 50%, 75% and 100% of the shake table limit. At each stage, first a uni-directional loading in the y-direction was applied, followed by a uni-directional loading in the x-direction and finally, both directions were loaded. A summary of the loading sequence can be seen in Table 2. The original time step of the records was 0.005 s, but for the testing of the scaled structure, the time step was reduced to ${\raise0.7ex\hbox{${0.005}$} \!\mathord{\left/ {\vphantom {{0.005} {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}} = 0.003536 s$ to account for the scaling factor corresponding to the half scale model.

Table 2 Loading sequence

Due to the high demanding computational effort, the earthquake input signal was trimmed to be able to perform every simulation within a reasonable timeframe. Every earthquake was reduced from the original 39.1 s to the most dynamically significant 15 s as shown in Fig. 5 and baseline correction was applied to the trimmed accelerogram. For each 15 s of simulated time corresponding to a single earthquake, an average of 99 h (4.1 days) were needed of computation. After each earthquake of the sequence was numerically simulated, the accumulated damage of the model was saved and used for the following step of the sequence. In Fig. 6 it can be seen the computation time of every simulation.

Fig. 5

1979 Montenegro earthquake (Albatros station) acceleration record at 100% of the shake table capacity

Fig. 6

Total computation time of each simulation of the loading sequence

4 Calibration of material properties

Before the real model was constructed, approximate material properties were provided by the blind prediction competition organising team. Such material properties were obtained in an experimental campaign performed by Guerrini et al. (2017) and Senaldi et al. (2018a) before testing a scaled shake table model (Guerrini et al. (2019) and Senaldi et al. (2018b)). The piers tested in the laboratory were modelled using DEM, in addition to performing pushover and eigenvalue analyses analysis on the complete building to calibrate the material properties of the model. The damping ratio was estimated and adapted after each simulation based on the simulated response.

4.1 Simulation of shear test in piers

In-plane cyclic shear-compression tests were reported by Guerrini et al. (2017) and Senaldi et al. (2018a) on two double-leaf irregular rubble stone masonry piers of similar characteristics as the masonry used to build Unit 1 and Unit 2. The data corresponding to such reported experimental campaigns was the information that every participant of the competition received from the SERA-AIMS organisation to calibrate their models and select the material parameters, and hence the natural first step to start the calibration process. The tests however, were originally built as part of the material characterisation campaign performed by Senaldi et al. (2018b) for a half-scale building shake table testing. The piers had nominal thickness of 300 mm and two different aspect ratios (i.e. ratio of pier height h to length l): h/l = 3.0 (CS test, see Fig. 7c) and h/l = 1.26 (CT test, see Fig. 7d) with axial precompression (σ₀) of 0.585 MPa and  0.390 MPa, respectively. The two leaves of the walls were connected simply by the interlocking of irregular mortared stones of varying dimensions between 100 and 400 mm. The horizontal courses were also irregular and no through stones were provided. The space between the two leaves was filled with mortar, stones leftovers from cutting the bigger stones and pebbles.

Fig. 7

Comparison between experimental and numerical simulations of the CS and CT tests

A DEM model of both CS and CT walls was developed using randomly arranged rectangular prismatic elements. The material properties reported by Guerrini et al. (2017) and Senaldi et al. (2018a) were implemented in the DEM model to later, in a parametrical fitting process, adapt the material properties to replicate the force–displacement capacity curves resulted from the experiments (see Fig. 7a, b). The material properties fitting process started with the CS model using the same cohesion as reported in Guerrini et al. (2017) and Senaldi et al. (2018a) and the friction angle was fitted appropriately to replicate the tests results. After the CS pier was satisfactory calibrated, the CT test was modelled but failure was observed sooner than expected. Therefore, cohesion and friction angle were increased because each of them play an important role in the shear Mohr–Coulomb failure criteria. In the cases where no parameters were given, this was assumed and varied until appropriate. A summary of these parameters was included in Table 3. The same constitutive model was used as per for the complete building, meaning that compression was modelled linearly. Hence, once that the cracking started and damage could be observed (see Fig. 7a, b), no post-peak behaviour could be observed due to inability of the model to simulate crushing. However, during a cyclic input like the shake table earthquake, the post peak fictitious hardening would be less noticeable due to the accumulation of damage in both directions. Apart from this drawback, the model captured accurately the damage pattern in the walls (see Fig. 7c, d) and a good agreement between experimental and numerical capacity curve was obtained with only increasing the cohesion of the CS wall from the reported parameters (see Table 3).

Table 3 Summary of masonry material properties reported in the Guerrini et al. (2017) and Senaldi et al. (2018a) and adopted in the DEM model

4.2 Pushover and eigenvalue analyses of the complete model

Existing literature of shake table testing performed in scaled buildings somewhat similar to the reported herein was investigated as well as hand calculations for the estimation of the first translational mode of vibration period (T₁). Table 4 summarises the basic geometrical and material characteristics of 7 shake table tests including the estimated T₁ using the equation T₁ = 0.0625 · h^0.75 from NZS1170.5 (Standards New Zealand 2004) and AS1170.4 (Standards Australia 2007), where h is the height of the building, and the recorded T₁ to compare with the estimation and observe the error of the estimation. With an average height of 5.32 m for Unit 1 and Unit 2, a T₁ equal to 0.21 s was obtained, which reduced into 0.15 s when the period scaling factor for the chosen similitude relationship (0.5^0.5 = 0.7) is applied according to Senaldi et al. (2018b) and Tomić et al. (2020). Accounting for the average error (44%) that the estimation of T₁ had for the relevant literature, the 0.15 s was further reduced to 0.10 s. The average recorded T₁ of the scaled models of the relevant literature was found equal to 0.12 s. Based on the information summarised in Table 4, a reasonable value for T₁ for the reported model was assumed to range from 0.10 to 0.12 s.

Table 4 Shake table tests in URM and dynamic properties recorded

Simulations of the complete model were performed to verify that the calibrated material properties from Sect. 4.1 resulted in reasonable prediction of the dynamic behaviour of Unit 1 and Unit 2. Therefore, eigenvalue analysis was performed to obtain the 10 first modes of vibration and frequencies of the model (see Fig. 8). Applying the material properties obtained in Sect. 4.1 to the complete model resulted in excessively stiff dynamic behaviour with periods of vibration lower than expected. Hence, the Young Modulus of the complete building was lowered considerably from E = 3462 MPa to E = 328 MPa, almost matching the mortar parameters provided in Guerrini et al. (2017) and resulting in T₁ = 0.124 s, which is closer to the previously estimated period. Reducing the E led to the values of j_kn and j_ks being reduced accordingly with the final values reported in Table 1.

Fig. 8

Modes of vibration and periods associated

Pushover analysis was also performed maintaining the material properties from Sect. 4.1 and changing the Young modulus according to the eigenvalue analysis observations. The pushover analysis was performed in the y direction of the model (as seen in Fig. 1) in order to engage the combined masses of Unit 1 and Unit 2. This analysis allowed checking that the collapse mechanisms and that the periods obtained from the shear force vs displacement curves for different damage levels (DL) were reasonable (see Fig. 9). Using the relationship $T = \sqrt {{\raise0.7ex\hbox{${m \cdot d}$} \!\mathord{\left/ {\vphantom {{m \cdot d} F}}\right.\kern-0pt} \!\lower0.7ex\hbox{$F$}}}$, where m is the mass of the complete model, d is the top displacement of Unit 2 and F is the base shear force, the period for the elastic behaviour (T_DL1) of both models coincided with T₂ of the eigenvalue analysis, corresponding with the translational mode of vibration in the y direction. The percentage of period increment for different DL observed in Fig. 9 was found to correlate well with that registered in the research studies 5, 6 and 7 from Table 4 (Galvez et al. 2018; Senaldi et al. 2018b; Kallioras et al. 2019).

Fig. 9

Force–Displacement curves of the complete model with different elastic parameters. Including damaged state at the last simulated point and estimated T at different damage levels

The aforementioned comparison of analyses results and existing relevant literature gave confidence in the material properties selection for a correct simulation of the dynamic behaviour of the model. This tuning strategy to establish the material properties has been implemented by multiple researchers (Papantonopoulos et al. 2002; Psycharis et al. 2003; Lemos and Campos Costa 2017; Meriggi et al. 2019; Galvez et al. 2021) who calibrated their models by best fitting stiffness parameters to match experimental dynamic behaviour or by replicating previous similar research. The reason for the need of lower elastic properties in DEM (in this case in the order of 10 times lower) models to approximate the results to the real dynamic behaviour of the building was not reported in previous studies and further research is needed to pinpoint the exact characteristic that influence the phenomenon. Possible explanations could be that for rubble masonry constructions the mortar thickness is relatively high, having a great impact in the elastic performance of the complete structure, which for a single pier could not have as much influence, hence the lower E needed. Other explanation could be that representing rubble masonry with the great amount of mortar-stone ratio and round-like geometry of the stones could be a challenging when modelling masonry with cubic rigid blocks.

4.3 Damping ratio estimation with increasing damage

Some authors have suggested the use of discretisation in DEM models simulating URM into brick sized elements as a valid strategy to bypass the application of damping by relying on frictional and bond breakage energy dissipation (Psycharis et al. 2011; Meriggi et al. 2019; Galvez et al. 2022) resulting in the application of zero viscous damping. Other authors rely on the commonly used 5% viscous damping ratio to achieve the damped motion of the building. In the reported study the damped motion of the model was relied on the combination of the discretisation strategy in addition to levels of viscous damping lower than what is usually used (5%) to achieve a mid-point between both damping strategies. As explained in Sect. 3.2, MP damping was used to perform the simulations reported herein and special attention was paid on avoiding overdamping of dynamic phenomena that behaves with longer periods. Therefore, the damping ratio distribution was assigned to damp the main modes of vibration (see Fig. 8b) without overdamping motion that behaves with long periods typical of damaged buildings (see Fig. 9). The initial damping ratio distribution for the R1 series of simulations (see Table 2) was adapted so that T₁ to T₅ and T_DL2 had a range of 1.5% to 2.5% damping ratio (see Fig. 10). The damping ratio distribution was progressively adapted after damage appeared shifting the main motion frequencies (see Fig. 10), which were analysed at the end of each series of simulations using a power spectra of the resulting motion.

Fig. 10

Modelled damping distribution at different percentages of the total shake table capacity and Normalised power spectra of the results of the last simulation of the cycle for Unit 1&2

5 Comparison of the results

Unexpected sliding of the complete Unit 1 occurred during R1.3 and R2.1. Theoretically, friction forces should have been enough to prevent sliding as the input acceleration was 0.219 g and friction coefficient is 0.3 in addition to cohesion being 0.23 MPa. The bottom course of bricks was modelled specifically with higher cohesion (0.7 MPa) than the rest of joints to avoid possible sliding at the bottom course, and it succeeded in doing so because sliding occurred in the course of joints immediately above the stronger one. The reason for the sliding inaccuracy was probably a combination of the lack of geometrical interlocking between courses as opposed to the real building and probably a combined behaviour of both buildings where Unit 2 inertial forces were transmitted to Unit 1. An overall friction angle closer to the 30° calibrated for the CT piers rather than 17° would have also helped in avoiding the sliding failure. The sliding of Unit 1 first occurred in one of the longitudinal walls, creating torsional effects that helped with the development of other damage to piers and spandrels. The error was not corrected or investigated further due to not having enough resources to complete the simulations on time. However, the sliding failure did not prevent from observing damage at other parts of Unit 1.

Due to an algorithm error in the simulation, the ground motion corresponding to R1.1 was input in every direction and at every level of shaking, therefore inputting 0.219 g of acceleration every time. However, the loading sequence outlined in Table 2 in terms of directionality was respected. For the sake of clarity, the naming specified in Table 2 was kept throughout the comparison of the results. In the real experimental testing, three additional tests were performed at 12.5% of the shake table capacity for calibration purposes, which were not numerically simulated. The experimental sequence of R1.1, R1.2 and R1.3 were performed without a problem and can be effectively compared to the simulations. During the experimental test R2.1, Unit 2 experienced extensive damage, and the model was strengthened without completing the loading sequence. It is important to note that the shake table did overshoot reaching an input intensity similar to the planned for R3.1. Therefore, the experimental test R2.1 was compared to the simulated R2, R3 and R4.

The damage accumulated in the experimental testing specimens was recorded in terms of visual inspection of the model after each earthquake was finished, video recording during the motion, and using accelerometers and displacement transducers. Due to the capability of DEM of simulating discrete displacements of the elements and the damage or failure of the joints between elements with complete detachment between them, when each earthquake was simulated the model was analysed by plotting relative displacement between elements and the history of displacements and accelerations of each element. The damaged joints between elements and the resulting displacement of each element after earth earthquake was saved as the starting state of the model for the next earthquake in the sequence. The results in terms of base shear force were compared against the top displacement of Unit 2 because the sliding simulated in Unit 1 would not compare well with the undamaged experimental Unit 1. The results of the simulated sequence R1.1, R1.2 and R1.3 were almost identical to that found in the experimental test as seen in Fig. 11a-d. Even though the intensity of the input ground motion was different between the experiment and simulation in R1.2 and R1.3 because of the algorithm error mentioned above, the base shear registered matched well between simulations and experiments. Progressive damage can be observed in the results of simulations R2.1 to R4.3y where parts of Unit 2 overturned at the end (see black line Fig. 11e–h). The experimental dynamic curve in Fig. 11e is larger than numerical because the experimental input in R2.1 was 0.438 g (see Table 2), but due to the algorithm error mentioned above the numerical input in R2.1 was 0.219 g. However, due to the damage accumulation simulation after simulation with lower acceleration, R4.1 was found to have the closest hysteretic curve (see Fig. 11g) to that of the experimental R2.1 (higher acceleration causing more damage) with the majority of the motion occurring between 5 and 20 mm, and large rocking displacement can also be seen.

Fig. 11

Base shear force versus Unit 2 top displacement comparison between experiments and simulations

The time-history of the simulated interface opening between Unit 1 and 2 was compared to the experimental observations in Fig. 12 to compare the motion amplitude of the buildings, whether or not rebound was registered and the frequency of the motion. The sliding of Unit 1 can be clearly seen in Fig. 12 as 1 mm in R1.1 in the y direction increasing up to 2.5 mm in R1.3, while in the x direction the sliding displacement was 0.8 mm in R1.2 and 2.5 mm in R1.3. Due to the larger than experimented interface opening between buildings caused by sliding, the amplitude of the motion was always observed larger than the experimental observations. Additionally, a greater viscous damping value would have resulted in lower motion amplitude. This can be clearly seen in the simulated motion included in Fig. 12 where the sliding displacement was removed. Despite this sliding displacement, simulated interaction between the buildings could be seen in R1.1 throughout the complete time-history (see Fig. 12a) and in R1.3 from second 7 to 10 (see Fig. 12c). The motion frequency simulated was always observed in good agreement with the recorded in the experimental test.

Fig. 12

Interface Opening time-history between Unit 1 and Unit 2 for R1.1, R1.2 and R1.3

One of the most common failure mechanisms observed in multi-layered stone URM buildings with no through stones, as is the studied case, is layers delamination. Wall delamination consists on the separation of the wall layers causing independent dynamic behaviour with possible buckling and collapse of the external layers. This failure was not observed possibly because the buildings were newly built with no accumulated damage. Even if no through stones were included, some stones were positioned to connect two out of the three layers, giving integrity to the walls. Also, the building was not allowed to completely collapse before it was strengthened, possibly avoiding delamination. The crack patterns observed after R1.3 were also compared as seen in Fig. 13. From this early phase of simulations sliding of Unit 1 could be observed mostly on façade 3 caused by a combination of the low friction coefficient chosen, poor vertical interlocking in the modelling and that Unit 1 has no overweight in the roof as opposed to Unit 2. Due to the very limited connection between Unit 1 and 2, a vertical separation of about 1 mm could be observed at the top of the interface in the simulation and experiment (façade 2 and 3 in Fig. 13b, c). A thin crack of about 0.2 mm that did not occur in the experiment was seen in the connection of façade 1 of the simulated Unit 1 with the return walls, probably triggered by the inertial forces caused by sliding and the poor interlocking at the corners. Thin cracks of about 0.2 mm appeared in the corners of the windows on the ground floor of façade 2, 3 and 4 and the start of a rocking mechanism was observed in façade 2 and 4 of Unit 2, while no cracks was reported in such façades in the experiment. The combination of cracks on one side of the building (façade 2 side) could indicate that rotational motion of the combined buildings took place.

Fig. 13

Crack map comparison between experiment and simulation at the end of R1.3 (accumulated damage of R1.1, R1.2 and R1.3)

A change in the frequency of the simulated motion was observed from R2.1 to R3.1 and R4.1, as indicated by the power spectra shown in Fig. 10 and easily observable in Fig. 14, where the time-history of the interface opening between Unit 1 and 2 was plotted. The same change in period can be observed between the experimental interface opening shown in Figs. 12 and 14. The gap between units reduced from 10 mm in simulation R3.1 down to 3 mm during simulation R4.1, where clear interaction between units can be seen. The good agreement seen in Fig. 11g between simulation R4.1 and experiment R2.1 in base shear force and displacement can be also observed in the interface opening time-history plotted in Fig. 14, where the motion amplitude, units interaction and frequency reasonably matched.

Fig. 14

Interface Opening time-history between Unit 1 and Unit 2 for R2.1, R3.1 and R4.1

Diagrams of the cracks observed after the R2.1 experiment and the simulated sequences R2, R3 and R4 were included in Fig. 15 for comparison. During the R2 simulations Unit 1 continued sliding, which damaged the bottom of the ground floor of Unit 2 creating a horizontal crack at the bottom of the pier next to Unit 1 in façade 2 and 3. Almost no damage in Unit 1 was observed during the R2.1 experimental test, and Unit 2 had extensive damage with fully formed collapse mechanisms. Very similar crack patterns were observed in the R2 simulations compared to the experimental observations but with less severity, while the crack patterns observed during the R3 simulations were almost identical to the experimental cracks (see Fig. 15b, c). This agreement between simulation and experiment coincides with the previously observed match between the experimental R2.1 and simulated R4.1, as R4.1 was simulated right after R3.3 where the crack patterns in Fig. 15b were recorded.

Fig. 15

Crack map comparison between experiment (R2.1) and simulations (R2.1, R3.1 and R4.1) (black lines = cracks previously developed, red lines = newly developed cracks)

In-plane flexural cracking in the piers that led to rocking mechanism in the top and bottom story of Unit 2 was observed in simulation R2 and experimental test R2.1 in both façade 2 and 3. As a consequence of this rocking mechanism an out-of-plane horizontal crack appeared at the bottom of façade 5 also in both experiment and simulation. During simulation R3 the collapse mechanisms were completely formed and repetitive oscillations created more defined cracks in every wall. The heavy floor in Unit 2 and the out-of-plane rocking flexural motion in the y-direction created horizontal cracks at the floor level in façade 5 and also contributed to the development of the horizontal cracks in façade 4 in the experiment and simulations. This out-of-plane rocking was allowed due to the flexural cracks formed at the spandrels of the ground floor of façade 2 and 3. Horizontal bending at the top of façade 2 and 3 cracked and reached larger displacements thanks to the shear cracking of spandrel of the ground floor on façade 4. Cracking accumulated at the floor level of Unit 2 close to the top of Unit 1 as a consequence of the interaction, separation and pounding between buildings in the simulations and experiments, as well as clear sliding of the beams at the supports of the floor and roof level in Unit 2 was clearly visible.

Finally, severe displacement and cracking damage occurred in simulations R4 (see Fig. 16). All the previously described mechanisms repeated and increased in intensity. Extensive shear damage was observed in the ground floor spandrel of façade 2, 3 and 4. Diagonal shear damage was also observed in the central pier of the top floor of façade 2 on Unit 2. Large pieces of masonry overturned from the top of façade 2, 3, 4 and 5. Due to the severe rotational movement and the interaction between the two buildings the top part of façade 5 showed extensive damage.

Fig. 16

Crack map of damage resulted at the end of R4.3 (accumulated damage of R4.1, R4.2, R4.3) (black lines = cracks previously developed, red lines = newly developed cracks, blue pattern = collapsed)

6 Concludings remarks

Two adjacent scaled stone buildings models were subjected to a sequence of earthquakes in a shake table and blindly modelled using the discrete element method (DEM) to study the dynamic interaction between both buildings. Rectangular prismatic solid elements were used with similar dimensions to the real stones with nonlinear interfaces between them. Material properties were obtained from shear tests previously performed in the laboratory on unreinforced masonry (URM) similar to the used for the shake table model. Such material properties were calibrated to simulate the shear tests and later implemented in the DEM model of the two stone buildings. By performing pushover and eigenvalue analyses, exploring relevant existing research and forecasting the dynamic properties using well-known hand calculations it was found that stiffness was higher than it should for the type of buildings to simulate. Therefore, the elastic properties were adapted resulting in a more reasonable combined behaviour of the buildings.

The mass-proportional (MP) damping approach within the Rayleigh damping configuration was adopted for the time-history simulation. MP damping is known to overdamp motion with high periods of vibration, hence the damping ratio distribution was adapted depending on the periods observed after every simulation sequence avoiding unrealistically damped motion. Low levels of MP damping during the simulation sequence R4 avoided overdamping of rocking mechanisms as observed by the overturning of the top parts of the building model. However, the precautions taken to not include high values of damping might have underdamped the simulation resulting in overestimating the displacements and damage observed in the units. Even though the MP damping strategy is the most computationally efficient implemented in the DEM software used (3DEC), the computational time for such a large and complex model was considerably long compared to other simulation approaches.

It is worth noting that a number of challenges occurred during the experimental testing and simulations, such as changes in the experimental testing sequence, mismatch in simulated ground motion input and unexpected sliding during the simulation of Unit 1. Theoretically, the sliding of Unit 1 should have had been prevented with the sufficient friction and cohesional forces. A combined behaviour of both buildings where Unit 2 inertial forces were transmitted to Unit 1 could be a plausible reason for sliding, and could have been prevented using geometrical interlocking between courses or a value of friction closer to 30° than 17°. Accounting for such challenges, experimental observations were in good agreement with the numerical model in terms of base shear, displacement of Unit 2, interaction between buildings and crack patterns as a consequence of collapse mechanisms. This matching of results confirms once again the reliability of DEM for the simulation of URM without any a priori assumption on the collapse mechanism. However, it is clear that DEM requires for experienced users for a correct simulation.