Abstract
In recent years, the tuned mass damper inerter (TMDI) has been demonstrated in several theoretical studies to be an effective vibration absorber for the seismic protection of non-isolated buildings. Its effectiveness relies on careful tuning of the TMDI stiffness and damping properties, while its performance improves with the increase of the inertance property which is readily scalable. Nevertheless, in all previous studies, the energy dissipative TMDI element has been modelled by a linear viscous damper. Still, commercial viscous dampers display a nonlinear velocity-dependent power law behavior. In this regard, this paper investigates, for the first time in literature, the potential of the TMDI fitted with nonlinear viscous damper (NVD) for seismic response protection of multi-storey buildings. This is supported by an efficient optimal nonlinear TMDI (NTMDI) tuning approach which accounts for any absorber connectivity to the building structure and employs statistical linearization to treat the nonlinear damping term. For the special case of white-noise excited undamped buildings, optimal NTMDI tuning is derived analytically in closed-form which is shown to be sufficiently accurate for lightly damped structures. Comprehensive numerical data are presented to delineate trends of optimal NVD damping coefficient with the NVD power-law exponent and the inertance. Further, nonlinear response history analysis results pertaining to optimally tuned NTMDI application for a benchmark 9-storey steel structure demonstrate that reduced NTMDI stroke and inerter force can be achieved with negligible change in storey drifts and floor acceleration performance by adopting lower NVD exponent values, leading to practically beneficial NTMDI deployments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Passive inertial vibration absorbers, with most representative the tuned mass damper (TMD), have been widely studied in the scientific literature for the seismic protection of buildings in past decades (e.g. Villaverde 1985; Sadek et al. 1997; Pinkaew et al. 2003; Salvi and Rizzi 2017). In such theoretical studies, the TMD is commonly modelled as a secondary mass attached to the primary/host building structure through linear spring and dashpot elements in parallel connection, following the original TMD conceptualization (Ormondroyd and Den Hartog 1928). This modelling supports computationally efficient approaches for tuning (i.e. designing) TMDs to the dominant (typically the fundamental) building mode shape, facilitating the transfer of the input seismic energy from the building to the TMD (e.g. Rana and Soong 1998). In this setting, the TMD acts as a resonant single-degree-of-freedom appendix to the building structure which, ultimately, enables seismic energy dissipation by the dashpot element. Notably, in most real-life applications, the TMD velocity-dependent energy dissipative element is materialized through viscous dampers (e.g. Soong and Dargush 1997; Infanti et al. 2008; Zemp et al. 2011; Berquist et al. 2019). Although commercially available viscous dampers are manufactured to behave nonlinearly (e.g. Terenzi 1999; Lee and Taylor 2001; Lu et al. 2018; Berquist et al. 2019), the linear TMD assumption is taken to be sufficient in most cases, at least for TMD tuning purposes. Alternatively, Rüdinger (2007) and Chung et al. (2009) developed approaches to account for nonlinear viscous dampers (NVDs) in the optimal TMD tuning, if so desired.
Despite the above efforts, whilst TMDs are commonly used for wind-response mitigation in tall/slender buildings, very few TMD applications for seismic building response mitigation exist (e.g. Li et al. 2011; Zemp et al. 2011). This is because earthquakes, unlike wind, exert highly transient impulsive loads to buildings with uncertain frequency content, which may excite higher modes of vibration beyond the dominant one suppressed by TMDs (Soong and Dargush 1997). Further, detuning effects due to inelastic structural behavior reduce TMD effectiveness (e.g. Matta 2018). Consequently, it is found that a relatively large secondary mass with significant clearance to accommodate the relative movement (stroke) of the TMD is required for efficient and robust peak seismic demand mitigation (e.g. Hoang et al. 2008) which increase the TMD implementation cost. In this regard, a number of approaches have been considered by researchers to address some of the TMD shortcomings, including the use of multiple and/or distributed TMDs (e.g. Xu and Igusa 1992; Daniel and Lavan 2014) as well as the consideration of hysteretic dissipative elements (e.g. Ricciardelli and Vickery 1999; Bagheri and Rahmani-Dabbagh 2018) and nonlinear connection elements (e.g. Lu et al. 2018; Matta 2021), among various alternatives. Still, such approaches increase the complexity of TMD tuning, design, and installation without necessarily reducing requirements for accommodating large additive secondary masses.
To this end, in recent years, the coupling of TMD with an inerter in the so-called tuned mass damper inerter (TMDI) configuration proposed by Marian and Giaralis (2013, 2014) was shown to be an effective solution for the seismic protection of non-isolated buildings in several theoretical studies (Giaralis and Marian 2016; Giaralis & Taflanidis 2018; Ruiz et al. 2018; Taflanidis et al. 2019; Kaveh et al. 2020; Patsialis et al. 2021; Djerouni et al. 2022) by addressing all the aforementioned TMD shortcomings. Specifically, in the TMDI configuration, the secondary mass is connected to a lower floor (from the one where the damper is attached to) via an inerter. The latter is a mechanical element that produces a relative acceleration- dependent force proportional to a so-called inertance property expressed in mass units (kg) (Smith 2002). Importantly, inertance scales-up practically independently from the inerter physical mass as demonstrated by several inerter device prototypes developed for earthquake engineering applications reaching inertance of 10,000 tons or more (e.g. Nakamura et al. 2014; Nakaminami et al. 2017). Thus, in the TMDI, the inerter acts as a mass amplifier contributing inertia (but not weight) through the inertance property. In this respect, Giaralis and Marian (2016) demonstrated that the required secondary mass can be significantly reduced by trading it to inertance for fixed structural seismic performance in terms of top floor displacement. Furthermore, Giaralis and Taflanidis (2018) established that TMDI offers increased robustness to uncertainties in structural properties and seismic excitation compared to TMD which was attributed to the fact that TMDI achieves broadband damping, enabling the effective mitigation of higher modes of vibration. More recently, Ruiz et al. (2018) and Taflanidis et al. (2019) showed that through judicial tuning supported by bi-objective optimal design formulations, the TMDI achieves improved structural seismic performance in terms of storey drifts and floor accelerations at the cost of increased control forces exerted to the host buildings structure. Moreover, Kaveh et al. (2020) and Djerouni et al. (2022) established the potential of TMDI for seismic response mitigation using a large sets of non-pulse and pulse-like recorded ground motions, respectively. Lastly, Patsialis et al. (2021) demonstrated that TMDI is more robust than TMD to detuning due to inelastic seismic structural response.
Nevertheless, in all the previous TMDI studies for the seismic protection of non-isolated building structures, the velocity-dependent damping element has been taken as linear viscous damper (i.e. a dashpot element). However, as already discussed, commercially available viscous dampers for seismic applications exhibit nonlinear behavior, commonly modelled by a force–velocity power law expression. This is mainly considered to envelop the magnitude of damping forces developing in the devices and transmitted to the host structure (e.g. Sorace and Terenzi 2008). It, therefore, becomes important to investigate the seismic structural response for TMDI with NVDs, hereafter NTMDI, given that a main consideration in the use of TMDI for earthquake applications is to contain the large forces exerted by the TMDI to the structure (Ruiz et al. 2018; Taflanidis et al. 2019). Equally important, from a practical viewpoint, is to offer a practicable TMDI tuning approach, accounting explicitly for nonlinear damper behavior.
In this regard, this paper develops a first optimal design approach for NTMDI which relies on a reduced-order modelling of TMDI-equipped multistorey buildings together with statistical linearization (SL) (Roberts and Spanos 2003) to treat the nonlinear damping term. For the reduced-order modelling, the approach of Pietrosanti et al. (2020) applicable to linear TMDI is extended to the case of NTMDI. For the SL approach, the methodology of Rüdinger (2007), applicable to TMD with NVD, is extended to the case of NTMDI. In this setting, a numerical approach is reached for NTMDI tuning for damped building structures under stochastic excitations, while a closed-form analytical tuning is derived for the special case of undamped white noise excited building structures. Comprehensive parametric studies are undertaken to draw insights on the NVD parameters for different structural, inertial, and excitation properties (earthquake intensity and frequency content). Moreover, the proposed tuning approach is applied to a 9-storey steel case-study structure established in Ohtori et al. (2004). Nonlinear response history analyses for benchmark recorded seismic ground motions defined in Ohtori et al. (2004) are undertaken to assess the potential of NTMDI versus the well-established in the literature TMDI for seismic response mitigation in terms of displacement, accelerations, damper stroke, and inerter and damper forces. The presentation begins by describing the modelling of multi-storey buildings equipped with NTMDI.
2 Modelling of multi-storey buildings equipped with nonlinear tuned mass damper inerter (NTMDI)
2.1 Multi-mode building model equipped with NTMDI
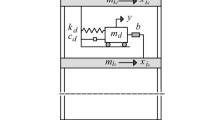
Consider a n-storey building hosting a NTMDI, for suppressing the structural response to earthquake excitations. The structure is modelled as a planar linear damped lumped-mass multi degree of freedom (MDOF) system with Ms, Cs, and Ks mass, damping, and stiffness matrices with n-by-n dimensions, respectively, subjected to horizontal ground acceleration, \(\ddot{u}_{G}\), as shown in Fig. 1. The NTMDI is modelled by a secondary mass, mD, connected to the ib floor by an inerter element with inertance b, as defined by Smith (2002), and to the id floor by a linear spring with stiffness kD in parallel with a NVD, as shown in the inlet of Fig. 1. The NVD develops a nonlinear force modelled as (e.g. Terenzi 1999; Lee and Taylor 2001)
where \(c_{NL}\) is the damping coefficient of the nonlinear viscous force, α is the damping exponent, uk is the displacement of the secondary mass relative to the displacement of the id floor, sgn(·) denotes the signum function and a dot over a symbol denotes differentiation with respect to time. The damping exponent in Eq. (1) governs the level of nonlinearity of the NVD and can range as 0.1 < α < 2.0 in typical devices, depending on the application (e.g. Terenzi 1999; Berquist et al. 2019). For the special case of α = 1, the damping element becomes a standard linear viscous damper, and the model in Fig. 1 degenerates to a linear TMDI-equipped MDOF structure, previously studied in the literature as detailed in the introduction. In this respect, the focus of this work is on the tuning and the assessment of the NTMDI for α ≠ 1, vis-à-vis the linear case (α = 1). Of particular interest are values of α ≤ 0.5, which are commonly adopted for standalone NVDs used as diagonal struts for seismic protection of buildings (e.g. Sorace and Terenzi 2008), as well as values of α > 1.0, which are commonly used for NVDs in TMD applications (Berquist et al. 2019).
Notably, the model of Fig. 1 allows for NTMDI to span more than one storey (i.e. id-ib > 1) by considering, for example, an internal atrium formed by openings in the building slab(s) (e.g. Dai et al. 2019; Kaveh et al. 2020). This consideration is motivated by the fact that the linear TMDI is more effective in mitigating the earthquake response of buildings when spanning two or more floors (e.g. Giaralis and Taflanidis 2018; Ruiz et al. 2018; Taflanidis et al. 2019). It is thus deemed relevant to herein study the effectiveness of the NTMDI for connectivities with id-ib > 1. Mathematically, arbitrary NTMDI connectivities can be accommodated by using the connectivity vector \({\textbf{R}}_{c} = {\textbf{R}}_{d} - {\textbf{R}}_{b}\), where \({\textbf{R}}_{d}\) and \({\textbf{R}}_{b}\) are n-long vectors with zero elements except for the element corresponding to the degrees of freedom (DOFs) id and ib, respectively, which are set equal to 1 (Taflanidis et al. 2019). Making use of the above definitions, the coupled equations of motion for the NTMDI-equipped MDOF dynamic system of Fig. 1 are written as
where \({\text{u}}_{s}\) is the n-length vector of lateral floor displacements relative to the ground motion indicated in Fig. 1 and δ is the standard n-length influence vector (vector of ones). In this setting, the force transferred from the inerter element to the ib floor is computed as
while the force transferred from the NTMDI to the id floor is computed as
2.2 Reduced-order single-mode building model with NTMDI
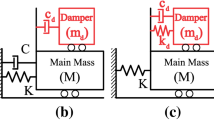
To facilitate optimal NTMDI tuning, a low-order (2-DOF) nonlinear mechanical model shown in Fig. 2 is put forth in this section. The considered model is a modified version of the linear 2-DOF model proposed by Pietrosanti et al. (2020) to support optimal tuning of linear TMDI targeting the mitigation of a single mode in MDOF structures, herein augmented by the nonlinear damping element modelled by Eq. (1). The model is derived by application of modal reduction to the MDOF building model in Fig. 1 such that the host structure is represented by a 1-DOF system with generalized properties coming from any one (targeted) vibration mode of the building, assumed to be dominating the structural seismic response. In this context, the generalized structural mass, stiffness, inherent damping and base acceleration indicated in Fig. 2 are defined as
respectively, where the superscript “T” denotes matrix transposition and \(\phi\) is the normal (undamped) dominant mode shape vector of the uncontrolled MDOF building model targeted by the NTMDI, normalized to have a modal coordinate equal to 1 at the DOF id (see also Rana and Soong 1998). Notably, the 2-DOF model in Fig. 2 can represent any NTMDI connectivity through the modal factor
where \(\phi_{id}\) and \(\phi_{ib}\) are the elements of the \(\phi\) mode shape vector corresponding to the id and the ib DOFs (modal displacements), respectively. This is achieved by appropriate modification of the inertance values of the three inerter elements by the modal factor in Eq. (6), as shown in the model of Fig. 2 (Pietrosanti et al. 2020). Specifically, the modal factor takes on values \(0 \le \Delta \phi \le 1\). For the limiting value of \(\Delta \phi = 0\), the floors ib and id coincide (i.e. the inerter and the damper connects the secondary mass to the same floor) and the NTMDI becomes a vibration absorber with a single attachment point to the structure. For \(\Delta \phi = 1\), the inerter connects the secondary mass to the ground (grounded NTMDI) which is a widely studied configuration in the literature (e.g. Marian and Giaralis 2014; Giaralis and Taflanidis 2018; De Angelis et al. 2019). Importantly, recent work (Pietrosanti et al. 2020; Wang and Giaralis 2021) has shown analytically and numerically that \(\Delta \phi\) amplifies the inertance of the linear TMDI and as a result the TMDI becomes a more effective vibration absorber, for a given id placement, as \(\Delta \phi\) increases up to the maximum value of \(\Delta \phi = 1\) (grounded connectivity). In this regard, the \(\Delta \phi\) value of the 2-DOF model in Fig. 2 will be used in later sections to account for the influence of different connectivities to the tuning of NTMDI for seismic building response mitigation.
Using the previous definitions, the equations of motion of the nonlinear low-order model in Fig. 2 are written as
in terms of the relative displacement coordinates uid and uk. By introducing the non-dimensional modal natural frequency, \(\omega_{S}\), inherent (modal) damping ratio,\(\xi_{S}\), NTMDI inertance ratio, β, and NTMDI mass ratio, μ, parameters defined as
respectively, the equations of motion in Eq. (7) can be written as
upon further algebraic manipulation such that the nonlinear damping force term appears in only one of the two equations of motion. The above system of equations is treated via statistical linearization in the subsequent section to further expedite the NTMDI tuning.
3 Equivalent linear reduced-order model and random vibration analysis
3.1 Statistical linearization
It is common practice in the design/tuning of dynamic vibration absorbers for earthquake applications to adopt a stochastic ground excitation model to account for the uncertain nature of the earthquake ground motion (e.g. Giaralis and Taflanidis 2018; Taflanidis et al. 2019 and references therein). For linear structural systems and absorbers, this is significantly facilitated by straightforward application of linear random vibration analysis. In the presence of nonlinearities, computationally efficient statistical linearization (SL) approaches can be employed for the task (e.g. Rüdinger 2007; Sgobba and Marano 2010) which approximate the nonlinear stochastic seismic response of structures without the need for nonlinear response history analysis (Roberts and Spanos 2003). To this end, SL is herein applied to linearize the 2-DOF dynamical system of Fig. 2. This is achieved by replacing the nonlinear damping force term, \({{F_{d} } \mathord{\left/ {\vphantom {{F_{NL} } {m_{id} }}} \right. \kern-0pt} {m_{id} }}\), in Fig. 9 by an equivalent linear (damping force) term, defined in terms of the effective linear damping coefficient ce or an equivalent linear damping ratio ξe as
In Eq. (10), xk is the displacement of the secondary mass of the equivalent linear system (ELS) which is derived by the replacing the nonlinear damping force term in Eq. (9) by the equivalent linear term in Eq. (10) as
Further in the last equation, xid is the displacement of the main structural mass of the ELS with respect to the ground excitation. Note that different notation is used for the two displacement coordinates and their derivatives in Eqs. (9) and (11) to account for the fact that the response of the nonlinear system and the ELS to the same excitation is different (Giaralis and Spanos 2010).
The effective damping coefficient ce of the ELS is an unknown deterministic variable. Following the most widely adopted SL approach, among other alternatives (De Domenico and Ricciardi 2018), ce is determined by minimising the expected value of the difference (error) between Eqs. (9) and (11) in the least square sense with respect to ce. This minimization criterion yields the expression (Roberts and Spanos 2003)
where E[·] is the mathematical expectation operation. By assuming that the excitation \(\ddot{y}_{G}\) and the nonlinear response velocity \(\dot{u}_{k}\) are stationary normally distributed (Gaussian) stochastic processes and that the variances of the response velocity processes \(\dot{u}_{k}\) and \(\dot{x}_{k}\) are equal, that is \(\sigma_{{\dot{u}_{k} }}^{2} = \sigma_{{\dot{x}_{k} }}^{2}\), the following analytical expression is derived from Eq. (12) (Di Paola et al. 2007)
where \(\Gamma\)(·) is the standard gamma function. Equation (13) is an implicit function, since the determination of \(c_{e}\) requires knowledge of \(\sigma_{{\dot{x}_{k} }}^{2}\). The latter can be readily computed for a given \(c_{e}\), or equivalently ξe, value through linear random vibration analysis applied to the ELS in Eq. (11). To this aim, the next section presents a state-space approach to determine \(\sigma_{{\dot{x}_{k} }}^{2}\) and other response statistics to be used in the optimal NTMDI tuning for different types of stationary Gaussian stochastic excitations.
3.2 Random vibration analysis for the equivalent linear system
For the purposes of this work, state-space linear random vibration analysis is considered to obtain second-order response statistics of the ELS in Eq. (11) subjected to stationary stochastic excitation. For Gaussian white noise excitation, \(\ddot{y}_{G} \left( t \right) = w\left( t \right)\), the equations of motion of the ELS in Eq. (11) are written in state-space as
in which \({\mathbf{x}}\left( t \right) = \left[ {\begin{array}{*{20}c} {x_{k} } & {x_{id} } & {\dot{x}_{k} } & {\dot{x}_{id} } \\ \end{array} } \right]^{{\text{T}}}\) is the state vector, while the state, input, and output matrices are given as
respectively, where
Further, in Eq. (15) and hereafter 0(nxn) and I(nxn) are n-by-n zero and identity matrices, respectively, while the superscript “− 1” denotes matrix inversion. Note that the output matrix \({\mathbf{E}}_{s}\) is specified in Eq. (15) such that the output (response) process vector, \({\mathbf{z}}\left( t \right) = \left[ {\begin{array}{*{20}c} {x_{id} } & {\dot{x}_{k} } \\ \end{array} } \right]^{T}\), in Eq. (14) contains the required states to support statistical linearization (see Eq. (13)) and the optimal NTMDI tuning discussed in a subsequent section. The covariance matrix, \({\mathbf{L}}_{xx}\), of all the states in x satisfies the Lyapunov equation
where Sw is the spectral intensity of the white noise excitation. Assuming a double-sided clipped white noise power spectral density function, the spectral intensity Sw is herein related to the peak ground acceleration (PGA) by the expression
where ωc is the cut-off frequency of the white noise. Note that Eq. (18) has been derived under the heuristic “3σ” rule (i.e. \({\text{PGA}} = 3\sigma_{w}\)) (Roberts and Spanos 2003). In all the ensuing numerical work, Eq. (17) is solved numerically using the “lyap” build-in MATLAB® routine for \({\mathbf{L}}_{xx}\). Then, the second-order statistics (variances) of the Gaussian zero-mean response process vector z, \(\sigma_{{x_{id} }}^{2}\) and \(\sigma_{{\dot{x}_{k} }}^{2}\), are retrieved from the main diagonal of the covariance matrix
In case it is deemed important to account for site soil conditions in the optimal NTMDI design, the ground excitation can be modelled by a Gaussian colored noise, represented in the domain of frequencies ω by the widely-used for the purpose filtered Kanai-Tajimi (K-T) spectrum given as (Clough and Penzien 2003)
In the above expression, \(\omega_{g}\) and \(\xi_{g}\) are the natural frequency and damping ratio of the soil, respectively, which is modelled as a white noise excited linear 1-DOF system with spectral intensity So. Morevoer,\(\omega_{f}\) and \(\xi_{f}\) are parameters of a high-pass filter incorporated in Eq. (19) to eliminate spurious low-frequency content. In the numerical part of this work, the values of the parameters in Eq. (19) listed in Table 1 are used to model firm and soil conditions, derived by Giaralis and Spanos (2012). Further, the spectral intensity \(S_{o}\) is related to the PGA by adopting the expression (e.g. Sgobba and Marano 2010)
derived using the same assumptions as in Eq. (18).
A similar state-space random vibration analysis approach can be used to derive \(\sigma_{{x_{id} }}^{2}\) and \(\sigma_{{\dot{x}_{k} }}^{2}\) variances under Gaussian noise colored by the K-T filter in Eq. (19), as in the case of white noise excitation treated before. This is achieved by writing the excitation model of Eq. (19) in state-space form as
where \({\mathbf{y}}\left( t \right)\) is the 4-by-1 state vector of the excitation model and
Next, the state space equations of the ground excitation model in Eq. (22) are coupled with the state space equations of the ELS in Eq. (14) and the Lyapunov equation associated with the covariance matrix, \({\mathbf{L}}_{qq}\), of the coupled system state vector \({\mathbf{q}}\left( t \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{x}}^{T} } & {{\mathbf{y}}^{T} } \\ \end{array} } \right]\) can be written as
where
To this end, Eq. (24) can be solved in the same way as Eq. (17) for \({\mathbf{L}}_{qq}\) and the response variances of interest, \(\sigma_{{x_{id} }}^{2}\) and \(\sigma_{{\dot{x}_{k} }}^{2}\), under Gaussian colored noise excitation are retrieved from the main diagonal of the matrix \({\mathbf{EL}}_{qq} {\mathbf{E}}^{T}\), where \({\mathbf{E = }}\left[ {\begin{array}{*{20}c} {{\mathbf{E}}_{s} } & {\mathbf{0}_{{{\text{(2x4)}}}} } \\ \end{array} } \right]\).
3.3 Accuracy assessment of statistical linearization against Monte Carlo simulation data
Notably the SL approach in Sect. 3.1 is approximate since the effective damping coefficient is determined by assuming that the response velocity \(\dot{u}_{k}\) follows a Gaussian distribution, which is not true even for Gaussian excitation. Hence, it is deemed essential to assess the accuracy of the adopted SL approach, never previously applied to the nonlinear system in Eq. (9), versus results from Monte Carlo simulation (MCS) (Roberts and Spanos 2003). The latter involves direct time-domain integration of the nonlinear equations in Eq. (9) to determine nonlinear response statistics. Comparisons are made for both white noise and colored noise (filtered Kanai-Tajimi) excitations and for a wide range of system properties in Eq. (9). In all cases a cut-off frequency ωc = 35 rad/s is taken. For white noise excitation, normally distributed random number sequences are generated using built-in random number generator of MATLAB® to represent time-history excitations. For filtered Kanai-Tajimi excitation, spectrum compatible time-histories are simulated using the spectral representation approach (Shinozuka and Deodatis 1991), written in continuous time as
where N = 256 is the number of frequency components assumed in the excitation, \(\Delta \omega = {{\omega_{c} } \mathord{\left/ {\vphantom {{\omega_{c} } N}} \right. \kern-0pt} N}\) and \(\theta_{j}\) are uniformly distributed random numbers in the interval [0,2π].
Figure 3 plots selective data comparisons between the response variance \(\sigma_{{u_{id} }}^{2}\) of the nonlinear 2-DOF in Eq. (9) obtained by MCS and the response variance \(\sigma_{{x_{id} }}^{2}\) of the ELS in Eq. (11) obtained using SL and linear random vibration analysis as detailed in Sect. 3.2 for white noise and two different filtered Kanai-Tajimi excitations defined in Table 1. Results are normalized by the response variance of the uncontrolled single-mode (1-DOF) structure, \(\sigma_{o}^{2}\). In all excitations, PGA = 0.3 g is adopted and MCS consider 1000 excitation time-histories which achieve stable response statistics. Further, the following parametric values are taken as fixed ωs = 2π, Δφ = 1 (grounded inerter), β = 0.5, while values of inherent structural damping ξs and damping coefficient α are let to vary as shown in Fig. 3. Further, the NTMDI stiffness and damping properties are found for each different system based on the tuning approach detailed in the following section. It is seen that results from SL are in very close agreement with MCS for all the different excitations and damping exponents, especially for ξs ≤ 5%. Similar comparative results and findings are reported in Rüdinger (2007), in which the case of linear 1-DOF structures equipped with NTMD under white noise excitation has been treated using SL. Similar trends, not reported here for brevity, hold for other values of Δφ, ωs and β for the 2-DOF model in Fig. 2 with tuned NTMDI. Overall, these results demonstrate that SL is fairly accurate to support a practical and expeditious NTMDI tuning, presented in the next section.
Illustrative comparison of response variances of the 2-DOF system in Fig. 2, \(\sigma_{{u_{id} }}^{2}\) obtained from MCS (1000 excitation samples) and \(\sigma_{{x_{id} }}^{2}\) obtained from SL for various damping exponents and structural damping ratios under a white noise excitation, b colored excitation-firm soil, c colored excitation- soft soil (PGA = 0.3 g, ωs = 2π, Δφ = 1, β = 0.5)
4 Optimal NTMDI tuning
4.1 Optimization problem formulation
Herein, tuning of the NTMDI for the MDOF building model in Fig. 1 is sought by making use of the 2-DOF ELS defined in Sect. 3.1. The considered tuning aims to minimize the displacement variance \(\sigma_{{x_{id} }}^{2}\) of the ELS under stationary stochastic seismic excitation \(\ddot{y}_{G}\), which approximates the displacement variance \(\sigma_{{x_{id} }}^{2}\) of the id floor of the MDOF building subject to the corresponding \(\ddot{u}_{G}\) stochastic excitation. This is pursued by solving an optimization problem in which the non-dimensional frequency ratio, λ, and damping ratio, ξe, parameters defined as
respectively, are treated as primary design variables, while the generalized modal building properties \(\xi_{S}\) and \(\omega_{S}\), modal NTMDI connectivity factor \(\Delta \phi\) and NTMDI inertial properties β and μ are taken as fixed (secondary design variables). Mathematically, the optimization problem is written as
where \(\sigma_{o}^{2}\) is the response variance of the uncontrolled structural modal oscillator under stationary random excitation defined by the generalized properties in Eq. (5).
Once the optimal frequency and damping ratios, \(\lambda^{opt}\) and \(\xi_{e}^{opt}\) respectively, are determined by solving Eq. (28), the NTMDI stiffness and nonlinear damping coefficients (i.e. optimal NTMDI tuning properties) are found by
and
Equation (29) has been derived by substituting the expressions for \(\omega_{S}\) and \(\omega_{D}\) in Eq. (8) to the definition of the frequency ratio λ in Eq. (27), while Eq. (30) has been derived by substituting the expression for ξe in Eqs. (27)–(13).
At this junction, it is important to note that the optimal design problem in Eq. (28) considers solely the response of the ELS, thus \(\lambda^{opt}\) and \(\xi_{e}^{opt}\) tuning parameters are independent of the NVD damping exponent α. However, the optimal nonlinear damping coefficient of the NVD in Eq. (30) does depend on α, thus ultimately α enters the NTMDI optimal tuning as an additional secondary design variable (see also Rüdinger 2007).
4.2 General numerical solution
Comprehensive parametric numerical investigation presented in a subsequent section demonstrates that the optimization problem in Eq. (28) is convex with a single (global) optimal design point for a wide range of system properties of practical interest. This is also confirmed by numerical results reported in Pietrosanti et al (2020) who studied the optimal tuning of linear TMDI using the linear system in Eq. (11), though adopted an energy-based objective function. Therefore, any standard optimization algorithm can be used to solve Eq. (28). In the numerical part of this work, the pattern search algorithm implemented in the built-in MATLAB® command “fminsearch” is used to determine the optimal design parameters,\(\lambda^{opt}\) and \(\xi_{e}^{opt}\), bounded within search ranges \(\lambda^{\min } \le \lambda \le \lambda^{\max }\) and \(\xi_{e}^{\min } \le \xi_{e} \le \xi_{e}^{\max }\). The specification of the bounds of the search ranges is facilitated by the consideration of non-dimensional design parameters in Eq. (28), and are taken as \(\lambda^{\min } = \xi_{e}^{\min } = 0\), \(\lambda^{\max } = 2\) and \(\xi_{e}^{\max } = 3\) in the numerical part of this study. Further, the ELS response statistics \(\sigma_{{x_{id} }}^{2}\) and \(\sigma_{{\dot{x}_{k} }}^{2}\) required in Eqs. (28) and (30), respectively, are numerically obtained by state-space linear random vibration analysis as detailed in Sect. 3.2.
4.3 Analytical solution for undamped white noise excited structures
Whilst a numerical approach is always applicable for solving the optimal NTMDI design problem in Sect. 4.1, for the special case of undamped (i.e. ξs = 0) white noise excited building structures, a closed-form solution of Eq. (28) is practically tractable. This is pursued by first deriving analytically the displacement response variance as
for ξs = 0 and for unit amplitude white noise excitation Sw = 1 as detailed in the “Appendix”, where the coefficients an (n = 0, 1, 2, 3, 4) and bm (m = 0, 1, 2) are provided in Eqs. (38) and (39), respectively. Then, the following two (stationary) conditions are enforced simultaneously
which must hold at the global minimum design point associated with Eq. (28) (see also Marian and Giaralis 2014). In this regard, Eq. (32) defines a two-by-two system of equations in terms of the unknown optimal design parameters \(\lambda^{opt}\) and \(\xi_{e}^{opt}\) which, after some algebraic manipulation, are found analytically as
and
respectively. Ultimately, the NTMDI stiffness and nonlinear damping coefficients are determined by using Eqs. (33) and (34) in Eqs. (29) and (30), together with the expression for the velocity response variance
derived in the “Appendix”, where the coefficients an (n = 1, 2, 3, 4) and dm (m = 1, 2, 3) are provided in Eqs. (38) and (42), respectively.
As a closing remark to this Section, it is noted that whilst the analytical expressions in Eqs. (33), (34) and (35) for the optimal NTMDI tuning are somewhat long, they circumvent the need for employing a numerical optimization algorithm for NTMDI tuning. Thus, they bear some good practical advantages. In this respect, in a subsequent Section, the applicability of these expressions to treat damped structures will be assessed, aiming to extend their range of application to lightly damped structures, without significant loss of accuracy.
5 Parametric investigation of NVD properties in optimally tuned NTMDI
Having established a generic optimal NTMDI tuning approach for MDOF structures in previous sections, this section presents numerical data to determine trends of optimal NTMDI parameters for different excitation and structural properties. In this respect, note that the optimal parameters of the linear TMDI using the linear 2-DOF system in Eq. (11) have already been comprehensively presented and discussed by Pietrosanti et al. (2020). Therefore, herein attention is focused on examining the parameters of the NVD element in the novel 2-DOF nonlinear system of Fig. 2, upon optimal NTMDI tuning. That is, the damping exponent α in Eq. (1) and the optimal nonlinear damping coefficient \(c_{NL}^{opt}\) in Eq. (30). To this aim, results for various excitation and structural properties are reported, examining the trends of the optimal damping coefficient ratio
derived from Eq. (30), as the damping exponent varies within the range 0 < α ≤ 2 which spans all possible values of practical NVDs (Sorace and Terenzi 2008; Berquist et al. 2019).
At first, the convexity of the optimization problem in Eq. (28) in numerically illustrated in Fig. 3 by plotting the objective function in Eq. (28) on the NTMDI design parameters plane for white noise excitation with PGA = 0.3 g, for two different damping exponents and for a specific set of system parameters. This is facilitated by using the non-dimensional design parameters \({{c_{NL}^{{}} } \mathord{\left/ {\vphantom {{c_{NL}^{{}} } {c_{e}^{{}} }}} \right. \kern-0pt} {c_{e}^{{}} }}\) and λ. The global minimum (optimal design point) is identified by a red dot in the plots of Fig. 3 while the optimal design parameters and minimum objective function value are also reported. It is important to recognize that the optimal frequency ratio and minimum objective function value are the same for both plots in Fig. 3 as they are independent of the damping exponent α. Evidently, the level of convexity of Eq. (28) is very high, with a clear unique global minimum, and pertinent to all the cases considered in this work.
Next, the variation of the optimal damping coefficient ratio in Eq. (36) against the damping exponent is examined in Fig. 4 for different inertance ratio values. This is done for white noise excitation with PGA = 0.3 g and for undamped primary structure in Fig. 4a and for 5% inherent structural damping in Fig. (b), with all other parameters taken constant (ωs = 2π, μ = 5%, and \(\Delta \phi = \;1\)). The limiting value of β = 0 is included in Fig. 4 which corresponds to a TMD with NVD, hereafter NTMD. The NTMD case has been treated in Rüdinger (2007) and, thus, serves well to establish the role of inertance in the optimal NVD properties by drawing comparisons with the NTMDI. Further, the achieved minimum objective function in Eq. (28) is also reported in the legend of Fig. 4 for each different NTMD(I) and confirms the well-established in the literature fact that improved performance is achieved as inertance increases (e.g. Marian and Giaralis 2014; Pietrosanti et al. 2020). The data in Fig. 4 evidence that the trend of the optimal damping coefficient ratio with α for the NTMDI is quite different compared to the NTMD. The optimal NTMDI nonlinear damping coefficient ratio increases monotonically with α while the opposite happens for the case of the NTMD. In this respect, the incorporation of an inerter changes significantly the required NVD properties for optimal performance which highlights the importance of this work, compared to previous efforts by Rüdinger (2007), and the significance of the optimal design problem formulation and solution in previous sections.
Contour plots of objective function \({{\sigma_{{x_{id} }}^{2} } \mathord{\left/ {\vphantom {{\sigma_{{x_{id} }}^{2} } {\sigma_{o}^{2} }}} \right. \kern-0pt} {\sigma_{o}^{2} }}\) on the design variables plane for a α = 0.5 and b α = 1.5 under white noise excitation with PGA = 0.3 g. System parameters are ωs = 2π, ξs = 5%, μ = 5%, β = 50% and \(\Delta \phi = \;1\)
Examining Fig. 4 in more detail, it is found that for the range of α ≤ 0.5 adopted in NVDs for earthquake engineering applications, the optimal NVD damping coefficient,\(c_{NL}^{opt}\), is significantly higher from the \(c_{e}^{opt}\) obtained by the ELS-based optimization for the NTMD, while the opposite happens for the NTMDI, for any fixed value of α. In this range, the difference between \(c_{NL}^{opt}\) and \(c_{e}^{opt}\) increases with the inertance, but at a reduced rate such that for β ≥ 0.6, the required damping ratio \(c_{NL}^{opt} /c_{e}^{opt}\) to achieve the optimal performance improvement is almost independent of the inertance. On the other hand, for the range of α > 1 which is most relevant to NVDs used in TMD applications (Berquist et al. 2019), it is observed that \(c_{NL}^{opt}\) is higher than \(c_{e}^{opt}\) for the NTMDI and the rate of this difference with α increases appreciably as the inertance increases. Therefore, for α > 1, the value of the damping ratio \(c_{NL}^{opt} /c_{e}^{opt}\) significantly more dependent on the inertance than for the range of α < 0.5 with values of \(c_{NL}^{opt}\) required to be appreciably higher than \(c_{e}^{opt}\) to achieve optimal NTMDI performance as inertance increases. Interestingly, for α > 1, the required \(c_{NL}^{opt}\) is significantly lower than the \(c_{e}^{opt}\) for optimal NTMD performance. Lastly, a comparison across Fig. 4a and b shows that the structural inherent damping influences significantly more and in a different manner the ratio \(c_{NL}^{opt} /c_{e}^{opt}\) for the NTMD compared to the NTMDI. Specifically, the ratio \(c_{NL}^{opt} /c_{e}^{opt}\) attain lower values as structural damping increases, while the same ratio increases for NTMDI but insignificantly.
Subsequently, the influence of the modal connectivity factor \(\Delta \phi\) to the NVD properties for optimal NTMDI performance is investigated. This is supported by plotting the optimal damping coefficient ratio against the damping exponent for different \(\Delta \phi\) values in Fig. 5 and for three different excitations in terms of frequency content. Here, the NTMD case is not included as it is not relevant to \(\Delta \phi\): NTMD is attached to a single floor/location in the MDOF structure, as opposed to the NTMDI which is attached to two floors (Fig. 1). As in the previous figure, the achieved minimum structural displacement reduction is shown in Fig. 5, confirming that NTMDI motion control potential improves with \(\Delta \phi\) (Pietrosanti et al. 2020; Wang and Giaralis 2021), with the limiting case of \(\Delta \phi\) = 1 (inerter connected to the ground) achieving the best performance for all different excitations. Importantly, it is found that the increase of \(\Delta \phi\) influences the trends of the curves in Fig. 5 in the same way as the increase of inertance β in Fig. 4, irrespective of the frequency content of the excitation. That is, \(c_{NL}^{opt} /c_{e}^{opt}\) reduces with \(\Delta \phi\) for α < 0.5 while the opposite happens for α > 1. Nevertheless, this influence of \(\Delta \phi\) to the \(c_{NL}^{opt} /c_{e}^{opt}\) trends with α is less important compared to the one of inertance and essentially negligible for practical non-grounded inerter connectivity. This observation suggests that appreciable improvement in motion suppression brought about by changing the NTMDI connectivity (e.g. improvement of more than 25% by increasing \(\Delta \phi\) from 0.05 to 0.20) is achieved without changing much the optimal NVD damping coefficient compared to the optimal equivalent linear damping coefficient.
Focusing further on the influence of the excitation to the optimal NVD properties, Fig. 6 plots the same type of data as in Fig. 5 for different excitation intensities (PGA) and for same system parameters as before. It is seen that the seismic excitation intensity influences significantly the ratio \(c_{NL}^{opt} /c_{e}^{opt}\), in a manner that depends on the damping coefficient α. For α ≤ 0.5 the required ratio \(c_{NL}^{opt} /c_{e}^{opt}\) for optimal NTMDI increases with the excitation intensity, while the opposite occurs for α > 1.0. These trends do not depend on the frequency content of the excitation. Nevertheless, the influence of the frequency content excitation to the dynamic structural response depends on the structural natural frequency. To study this effect on the optimal NVD properties, Fig. 7 plots similar data as in Fig. 6 for systems with different structural natural frequencies ωs or, equivalently natural periods T = 2π/ωs, under seismic excitations with different frequency content but same PGA = 0.3 g. It is seen that the optimal damping property ratio, \(c_{NL}^{opt} /c_{e}^{opt}\), becomes insensitive with α for relatively flexible structures with T ≥ 1 s under narrow-band K-T colored noise excitation, representative of the frequency content of the nominal seismic action assumed by seismic design codes (see e.g. Giaralis and Spanos 2012). However, \(c_{NL}^{opt} /c_{e}^{opt}\) becomes sensitive to the natural frequency (i.e. stiffness) of the host building structure for white noise excitation, corresponding to frequency-neutral optimal tuning as shown in Fig. 7a or for stiff structures (T < 1 s) irrespective of the excitation as shown in Fig. 7b and c. Stiffer structures require lower \(c_{NL}^{opt} /c_{e}^{opt}\) for optimal NTMDI tuning for α ≤ 0.5, while the opposite happens for α > 1. It is noted in passing that actual seismic ground motions are non-stationary with varying frequency content in time (Fig. 8). Assessment of the motion control potential of optimal NTMDI under recorded ground motion is addressed in a later Section.
Variation of optimal nonlinear damping coefficient with damping exponent for different structural natural frequency ωs under a white noise, b K-T excitation for soft soil, and (c) K-T excitation for firm soil, for different PGA. System parameters are ωs = 2π ξs = 5%, β = 50%, μ = 5% and \(\Delta \phi = \;1\)
6 Accuracy of analytical optimal NTMDI tuning for damped structures
The previously presented numerical data suggest that the optimal NVD properties are sensitive to certain excitation and structural properties which calls for a careful NTMDI tuning. The latter may be significantly facilitated by the analytical (closed-form) solution provided in Sect. 4.3. Nevertheless, this solution assumes undamped building structures which is an unrealistic assumption. Still, the inherent damping of buildings under seismic excitation is commonly taken within 2% ≤ ξs ≤ 5% which falls within the class of lightly damped structures. For such structures, the use of analytical approaches for optimal TMD tuning derived under the assumption of zero damping may be regarded as approximately valid with little loss of accuracy (see e.g. Ghosh and Basu 2007). To this end, in this Section, the accuracy of the analytical expressions in Eqs. (33)–(35), which hold for optimal NTMDI tuning for ξs = 0 as detailed in Sect. 4.3, is assessed against data obtained for ξs ≠ 0 using the numerical method in Sect. 4.2. Assessment is herein provided in terms of optimal damping NVD ratio \(c_{NL}^{opt} /c_{e}^{opt}\), as well as motion control performance quantified by \(\sigma_{{x_{id} }}^{2}/\sigma_{o}^{2}\), where normalization corresponds to displacement response variance of the uncontrolled SDOF structure in Fig. 2 with ξs = 1%.
Figure 9 presents data for NTMDI with grounded inerter implementation (i.e.\(\Delta \phi = \;1\)) and NVD damping exponent α = 0.5 for varying inertance. It is seen in Fig. 9a that there is small deviation of the optimal damping ratio \(c_{NL}^{opt} /c_{e}^{opt}\) for ξs < 5% which reduces as the inertance increases. In fact, for medium to large inertance (e.g. β > 40%) the analytically obtained optimal damping ratio for ξs = 0 is applicable to treat systems with even ξs = 5% as the difference (error) drops well below 5%. Notably, similar trends and comments apply for the differences in the motion control performance estimation in Fig. 9b. The data in the latter figure are considered to reinforce the confidence of using the analytical NTMDI tuning for ξs = 0 to treat cases with non-zero, but small, ξs values.
Assessment of the accuracy of analytical NTMDI tuning for undamped structures against different inherent damping ratios for varying inertance: a optimal NVD damping ratio, b displacement performance. System parameters: ωs = 2π, α = 0.5, μ = 5%, \(\Delta \phi = \;1\); Excitation parameters: white noise, PGA = 0.3 g
Similar conclusions can be drawn in view of Fig. 10 which plots the same data as in Fig. 9 for same excitation and system parameters but for varying damping exponent with β = 50%. The effect of the damping exponent to the accuracy of using the NTMDI tuning for ξs = 0 to treat lightly damped structures is very high. In fact, for α < 1.5 the tuning for ξs = 0 can be used for damped structures with damping ratio up to at least 5% for practical applications. Nevertheless, results plotted in Fig. 10a pertaining to the same excitation and system parameters with varying modal connectivity factor \(\Delta \phi\) demonstrate that the difference of the optimal NVD damping for ξs = 0 and for ξs > 0 increases as \(\Delta \phi\) reduces and errors become unacceptable for \(\Delta \phi\) < 0.3, even for small inherent damping ratios (e.g. ξs = 1%). This is further ascertained by the data in Fig. 10b, though it is noted that the differences in terms of structural system response are smaller compared to the tuning parameters. Still, it is clear that the use of the analytical tuning for ξs = 0 requires caution and should not be preferred for values of \(\Delta \phi\) below about 0.3, in combination with relatively low inertance values (e.g. below 40%).
Assessment of the accuracy of analytical NTMDI tuning for undamped structures against different inherent damping ratios for varying damping exponent: a optimal NVD damping ratio, b displacement performance. System parameters: ωs = 2π, β = 50%, μ = 5%, \(\Delta \phi = \;1\); Excitation parameters: white noise, PGA = 0.3 g
7 Illustrative case-study application and nonlinear response history analysis assessment
In previous sections, the NTMDI optimal tuning and motion control effectiveness for different damping exponents was discussed in conjunction with the 2-DOF system in Fig. 2 which accounts only for the single (dominant) mode of multi-storey building structures and only under stationary ground excitations. It is thus deemed essential to extend this quantification for NTMDI equipped multi-modal MDOF structural models under non-stationary recorded earthquake excitations using nonlinear response history analyses (NRHA). To this aim, pertinent numerical data for the 9-storey steel benchmark building developed by Ohtori et al (2004) are herein presented and discussed. The considered benchmark structure has a rectangular plan with dimension 45.73 m with lateral load resisting system comprised of two perimetric five-bay steel moment-resisting frames (MRFs). The total building height is 37.19 m with 1st floor height being 5.49 m and the height of all other floors being 3.96 m. The seismic mass of the structure which defines the diagonal mass matrix Ms in Eq. (2) is 1.01 × 106 kg for the 1st floor, 9.89 × 105 kg for the typical floor and 1.07 × 106 kg for the top (9th) floor. The total seismic mass of the structure is 9.00 × 106 kg. The full stiffness matrix, Ks in Eq. (2), of a linear planar dynamic model along a horizontal axis of symmetry of the benchmark building is derived as detailed in Patsialis and Taflanidis (2020). The structure fundamental period is 2.27 s (\(\omega_{s} = 2.76\) rad/s). For the specification of the damping matrix, Cs in Eq. (2), the assumption of Rayleigh damping is taken with modal damping ratio equal to 5% for the first and second modes.
Note that the potential of the linear TMDI (i.e. α = 1 in Eq. (1)) for the seismic protection of buildings have been comprehensively demonstrated in previous studies by Taflanidis et al. (2019) and Patsialis et al. (2021) using the above described benchmark structure and model. Therefore, as in previous sections, the focus here is on examining the influence of different NVD damping exponent α in Eq. (1) to the response of the benchmark structure equipped with optimally tuned NTMDI. To this end, all comparisons are established against the linear TMDI case (α = 1). Further, the herein considered NTMDI implementations to the case-study benchmark structure serve well for illustrating the practicality and applicability of the optimal NTMDI tuning approach developed in Sect. 4 to real-life building structures. Specifically, two different top-floor NTMDI implementations (i.e. id = 9 in Fig. 1) are studied for various damping exponents. In the first NTMDI implementation, the inerter spans two stories and connects to the 7th floor of the structure (i.e. ib = 7) with modal connectivity factor \(\Delta \phi = 0.1767\). In the second NTMDI implementation, the inerter spans one story and connects to the 8th floor of the structure (i.e. ib = 8) with modal connectivity factor \(\Delta \phi = 0.0765\). In all cases, NTMDI tuning for white noise excitation and for PGA = 0.3 g is considered using the numerical method in Sect. 4.2 due to the relatively low values of \(\Delta \phi\) in combination with ξs = 5% for which the analytical tuning in Sect. 4.3 deviates from the exact solution as seen in Fig. 11. Figure 12 plots typical results from the numerical optimal tuning for both the implementations and for α = 0.5 and α = 1.5.
Assessment of the accuracy of analytical NTMDI tuning for undamped structures against different inherent damping ratios for varying modal connectivity factor: a optimal NVD damping ratio, b displacement performance. System parameters: ωs = 2π, α = 0.5, β = 50%, μ = 5%; Excitation parameters: white noise, PGA = 0.3 g
Performance assessment of the benchmark structure equipped with the optimally tuned NTMDIs is considered by application of NRHA to Eq. (2) for the four recorded ground motions (GMs) in Fig. 13. These GMs are specified in Ohtori et al. (2004) as part of the benchmark structural vibration control testbed problem. The El Centro and the Hachinohe records are far-field GMs, while the Northridge and the Kobe records are near-field GMs (see Ohtori et al. 2004 for further details). Herein, the GMs are uniformly scaled in time such that their PGA equals 0.3 g used in the optimal NTMDI tuning, and a built-in MATLAB Runge–Kutta algorithm is used for numerical integration of Eq. (2).
Table 2 reports peak absolute response quantities of practical interest for each GM, for both the NTMDI implementations and for four different values of the damping exponent. Specifically, the peak absolute top (9th) floor displacement, u9, is reported which is relevant to the optimal NTMDI tuning criterion in Eq. (28). This is because the structural displacement in the low-order 2-DOF approximates the relative displacement of the 9th floor in the dynamic system of Fig. 1 for both NTMDI implementations (id = 9). Further, the relative displacement (stroke) of the secondary mass, uk, is also included in Table 2 as it relates to NTMDI practical implementation and costs. These include the required clearance for the secondary mass so no collisions occur during severe earthquake shaking and the damper stroke which are proportional to the upfront device cost (see e.g. Ruiz et al. 2015 and Berquist et al. 2019). Lastly, the control forces exerted by the inerter, Fb, and by the damper, Fd, are given in Table 2, defined in Eqs. (3) and (4), respectively. Both are proportional to the NTMDI upfront cost as they relate to the inerter and device costs as well as to the design of local device-to-structure connections (Ruiz et al. 2018; Taflanidis et al. 2019; Pietrosanti et al. 2021).
The results in Table 2, evidence that the effect of the NVD damping exponent to the seismic structural performance, measured in terms of peak top floor displacement, max{|u9|}, and its significance vary from record-to-record. This effect is insignificant for most records and NTMDI implementations (i.e. max{|u9|} differences between α = 1.5 to α = 0.1 are about 5%) with very few exceptions. Exceptions include an increase of max{|u9|} by 25% for the Hachinohe record for the ib = 7 implementation as the damping exponent reduces from α = 1.5 to α = 0.1 (note though that the same is about 6% for the ib = 8 implementation), while it reduces by 13% for the Kobe record for the same change in the damping exponent. Nevertheless, consistent and, in most cases, significant (i.e. above 10%) reductions of the peak NTMDI stroke and inerter force are noted as the damping exponent reduces from α = 1.5 to α = 0.1 for all the records and for both the implementations studied. This observation suggests that it is advantageous to adopt reduced values in the NVD damping exponent. This is especially true with regards to the peak inerter force which typically takes on large values and, in this regard, it dominates the TMDI design for the seismic protection of buildings as detailed in the literature (Ruiz et al. 2018; Taflanidis et al. 2019; Patsialis et al. 2021). Indeed, it is seen that reductions higher than 15% to the peak inerter force are achieved for the first 3 GMs listed in Table 2 as the damping exponent is reduced from α = 1.5 to α = 0.1. For the Kobe GM the inerter force reductions are lower, but the inerter force for α = 1.5 is appreciably lower compared to the other GMs. Further, it is important to note that lower NVD damping exponent yields higher peak damping forces: about 60% increase of \(\max \left\{ {\left| {F_{d} } \right|} \right\}\) is noted across all GMs and NTMDI implementations between α = 1.5 and α = 0.1. Still, even for the lowest α = 0.1 value examined, the damping forces are appreciably lower than the inerter forces. Therefore, from a practical viewpoint, the effect of lower the NVD damping exponent should be interpreted positively as it achieves a better balance between the control forces exerted to the host/building structure at the two NTMDI attachment locations. In this context, the damping exponent regulates the relative amplitude of the two control forces in Eqs. (3) and (4).
The above trends and conclusions are further verified by examining the time-histories of all the quantities included in Table 2 provided in Figs. 14 and 15, for the El Centro and the Hachinohe GMs, respectively (similar trends hold for the other two GMs, not provided here for brevity). Specifically, response histories for various damping exponents and for both NTMDI implementations are plotted in Figs. 14 and 15, including the linear TMDI case (α = 1). The latter case has been extensively studied in the literature (e.g. Giaralis and Taflanidis 2018; Ruiz et al. 2018; Taflanidis et al. 2019), and is hereafter treated as the base-line case to draw comparisons with NTMDIs featuring NVDs with different damping exponents. Significant reduction to the NTMDI stroke and to the inerter forces are noted as the damping exponent takes on lower and lower values (α < 1), not only in terms of peak values, as seen in Table 2, but also throughout the duration of the response histories. At the same time, top floor response displacement histories do not change much, while the amplitude of damper force time-histories increase as α values lower, accomplishing a better balanced set of NTMDI control forces exerted to the top floor (id = 9) of the case-study structure and to the ib floors, as previously discussed.
To gain a further appreciation on the importance of the above trends, Fig. 16 provides bar plots of all the peak response quantities included in Table 2 averaged across the GMs of the adopted benchmark structure and normalized to the base case of the linear TMDI (α = 1). It is confirmed that significant reductions are achieved in terms of peak stroke and peak inerter forces with little change to the average peak top floor displacement for NTMDI with α < 0.5 compared to the linear TMDI. Reduction of peak stroke is about 30% across the two NTMDI implementations, while reduction of peak inerter force is about 14%. Meanwhile, the average peak damper force increases appreciably such that the ratio of peak damping over inerter forces (rightmost bar plot in Fig. 16) increases with α which effectively regulates the trade-off between the control forces for a given NTMDI connectivity.
Finally, the seismic performance of NTMDI with different NVD damping exponent is assessed in Fig. 17 in terms of peak absolute storey drifts and floor accelerations along the height of the benchmark building, averaged over the GMs in Fig. 13. Here, the provided plots are normalized by the peak top floor responses of the uncontrolled structure to further highlight the effectiveness of NTMDI for improving the seismic performance of buildings. It is found that optimal NTMDI achieves peak normalized responses below one for all NVD damping exponents with ib = 7 NTMDI configuration accomplishing consistently better performance than the ib = 8 NTMDI configuration. Interestingly, peak floor accelerations in Fig. 17a are significantly more sensitive to the variation of the NVD damping exponent than the storey drifts in Fig. 17b. For all the floors, better floor acceleration performance is achieved for damping exponent α < 1. Nevertheless, in many cases adopting a very low nonlinear damping exponent (i.e. α = 0.2 as opposed to α = 0.5) may be detrimental for floor accelerations. Therefore, caution needs to be exercised on the choice of the NVD exponent for applications that floor accelerations are an important design consideration (e.g. when potential seismic loss to secondary equipment and acceleration-sensitive non-structural components are expected to be critical). On the other hand, the NVD damping exponent has little influence in case storey-drifts requirements dominate the seismic design and performance. In these cases, it is recommended that the lowest possible damping exponent is adopted in the NTMDI design for all the previously discussed reasons in view of Fig. 16.
Peak response quantities of optimal NTMDI-equipped case-study structure for various damping exponents averaged over all GMs in Fig. 13: a floor accelerations b storey-drifts
8 Concluding remarks
Motivated by the fact that commercially available viscous dampers follow a nonlinear velocity-dependent power law, a comprehensive numerical investigation of the potential of the TMDI with NVD (NTMDI) for the seismic protection of multi-storey buildings has been herein undertaken, focusing on the effect of the NVD damping exponent. This has been supported by a novel computationally efficient tuning approach, yielding optimal NTMDI frequency and nonlinear damping coefficient for any given NVD damping exponent. The tuning approach relies on a single-mode low-order modelling of NTMDI-equipped multi-storey buildings, accounting for any NTMDI configuration through a modal connectivity factor. Additionally, it employs an approximate statistical linearization technique for the efficient mathematical treatment of the nonlinear damping term. In this respect, Monte Carlo simulation based results were provided to establish the accuracy of statistical linearization to the optimal NTMDI tuning. Moreover, for the special case of undamped primary structures, the optimal tuning parameters were derived in closed form and numerical data were furnished to explore the range of applicability of the analytical tuning for the class of lightly-damped primary/host building structures. Using the developed optimal NTMDI tuning approach, comprehensive parametric investigation was performed to gauge the effect of different structural system and NTMDI parameters to the optimal NVD properties drawing comparisons with the NTMD case. A case-study application to a benchmark 9-storey steel structure has been further considered and the efficacy of optimal NTMDI potential has been assessed through nonlinear response history analyses applied to a MDOF model of the benchmark building equipped with optimal NTMDI.
The main conclusions of this study are as follows.
-
Both the inertance and the modal connectivity factor have the same impact to the NVD optimal damping ratio for all practical ranges of the damping exponent. That is, for a < 0.5 the optimal nonlinear damping coefficient reduces compared to the optimal equivalent linear damping coefficient as inertance and/or modal connectivity increases, while the opposite happens for a > 1.
-
The closed form optimal tuning expressions can be used for lightly damped systems of up to about 2% damping ratio, as long as the modal connectivity factor is less than 0.4.
-
It is advantageous to adopt a low value for damping exponent (e.g. α < 0.2) since this reduces NTMDI stroke and inerter force, thus leading to a more balanced control force between damping force and inerter force with practically negligible change to the structural response performance.
Overall, it is expected that this work makes a further step to bringing inerter-based vibration control closer to practical applications in which the nonlinear behavior of the NVD may need to be considered in design and assessment.
References
Bagheri S, Rahmani-Dabbagh V (2018) Seismic response control with inelastic tuned mass dampers. Eng Struct 172:712–722
Berquist M, De Pasquale R, Frye S, Gilani A, Klembczyk A, Lee D, Malatesta A, Metzger J, Schneide R, Smith C, Taylor D, Wang S, Winters C (2019) Fluid viscous dampers general guidelines for engineers including a brief history. Taylor Devices Inc, New York
Chung L-L, Wu L-Y, Huang H-H, Chang C-H, Lien K-H (2009) Optimal design theories of tuned mass dampers with nonlinear viscous damping. Earthq Eng Eng Vib 8(4):547–560
Clough R, Penzien J (2003) Dynamics of structures, 2nd edn. Mc Graw-Hill, New York
Dai J, Xu Z, Gai P (2019) Tuned mass-damper-inerter control of wind-induced vibration of flexible structures based on inerter location. Eng Struct 199:109585. https://doi.org/10.1016/j.engstruct.2019.109585
Daniel Y, Lavan O (2014) Gradient based optimal seismic retrofitting of 3D irregular buildings using multiple tuned mass dampers. Comput Struct 139:84–97
De Domenico D, Ricciardi G (2018) Improved stochastic linearization technique for structures with nonlinear viscous dampers. Soil Dyn Earthq Eng 113:415–419. https://doi.org/10.1016/j.soildyn.2018.06.015
De Angelis M, Giaralis A, Petrini F, Pietrosanti D (2019) Optimal tuning and assessment of inertial dampers with grounded inerter for vibration control of seismically excited base-isolated systems. Eng Struct 196:109250
Di Paola M, Mendola L, Navarra G (2007) Stochastic seismic analysis of structures with nonlinear viscous dampers. J Struct Eng 133(10):1475–1478. https://doi.org/10.1061/(asce)0733-9445(2007)133:10(1475)
Djerouni S, Ounis A, Elias S, Abdeddaim M, Rupakhety R (2022) Optimization and performance assessment of tuned mass damper inerter systems for control of buildings subjected to pulse-like ground motions. Structures 38:139–156
Ghosh A, Basu B (2007) A closed-form optimal tuning criterion for TMD in damped structures. Struct Control Health Monit 14(4):681–692
Giaralis A, Marian L (2016) Use of inerter devices for weight reduction of tuned mass dampers for seismic protection of multi-storey buildings: the tuned mass-damper-inerter (TMDI). In: Proceedings of SPIE on active and passive smart structures and integrated systems, Las Vegas, USA
Giaralis A, Spanos P (2010) Effective linear damping and stiffness coefficients of nonlinear systems for design spectrum-based analysis. Soil Dyn Earthq Eng 30(9):798–810. https://doi.org/10.1016/j.soildyn.2010.01.012
Giaralis A, Spanos P (2012) Derivation of response spectrum compatible non-stationary stochastic processes relying on Monte Carlo-based peak factor estimation. Earthq Struct 3(5):719–747. https://doi.org/10.12989/eas.2012.3.5.719
Giaralis A, Taflanidis A (2018) Optimal tuned mass-damper-inerter (TMDI) design for seismically excited MDOF structures with model uncertainties based on reliability criteria. Struct Control Health Monit 25(2):e2082. https://doi.org/10.1002/stc.2082
Hoang N, Fujino Y, Warnitchai P (2008) Optimal tuned mass damper for seismic applications and practical design formulas. Eng Struct 30(3):707–715. https://doi.org/10.1016/j.engstruct.2007.05.007
Infanti S, Robinson J, Smith R (2008) Viscous dampers for high-rise buildings. In: 14th World conference on earthquake engineering (14WCEE). Beijing, China
Kaveh A, Fahimi Farzam M, Hojat Jalali H (2020) Statistical seismic performance assessment of tuned mass damper inerter. Struct Control Health Monit. https://doi.org/10.1002/stc.2602
Lee D, Taylor D (2001) Viscous damper development and future trends. Struct Des Tall Build 10(5):311–320. https://doi.org/10.1002/tal.188
Li QS, Zhi LH, Tuan AY, Kao CS, Su SC, Wu CF (2011) Dynamic behavior of Taipei 101 tower: field measurement and numerical analysis. J Struct Eng ASCE 137(1):143–155
Lu Z, Wang Z, Zhou Y, Lu X (2018) Nonlinear dissipative devices in structural vibration control: a review. J Sound Vib 423:18–49
Marian L, Giaralis A (2013) Optimal design of inerter devices combined with TMDs for vibration control of buildings exposed to stochastic seismic excitations. In: 11th International conference on structural safety and reliability, New York, US
Marian L, Giaralis A (2014) Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probab Eng Mech 38:156–164. https://doi.org/10.1016/j.probengmech.2014.03.007
Matta E (2018) Lifecycle cost optimization of tuned mass dampers for the seismic improvement of inelastic structures. Earthq Eng Struct Dyn 47:714–737
Matta E (2021) Seismic effectiveness and robustness of tuned mass dampers versus nonlinear energy sinks in a lifecycle cost perspective. Bull Earthq Eng 19(1):513–555
Nakaminami S, Kida H, Ikago K, Inoue N (2017) Dynamic testing of a full-scale hydraulic inerter-damper for the seismic protection of civil structures. In: 7th International conference on advances in experimental structural engineering, (pp 41–54). https://doi.org/10.7414/7aese.T1.55.2016
Nakamura Y, Fukukita A, Tamura K, Yamazaki I, Matsuoka T, Hiramoto K, Sunakoda K (2014) Seismic response control using electromagnetic inertial mass dampers. Earthq Eng Struct Dyn 43(4):507–527
Newland D (1993) An introduction to random vibrations, spectral and wavelet analysis. Dover Publications, Mineola
Ohtori Y, Christenson R, Spencer B, Dyke S (2004) Benchmark control problems for seismically excited nonlinear buildings. J Eng Mech 130(4):366–385. https://doi.org/10.1061/(asce)0733-9399(2004)130:4(366)
Ormondroyd J, Den Hartog JP (1928) The theory of dynamic vibration absorber. Trans ASME, APM-50-7:9–22
Patsialis D, Taflanidis A (2020) Reduced order modeling of hysteretic structural response and applications to seismic risk assessment. Eng Struct 209:110135. https://doi.org/10.1016/j.engstruct.2019.110135
Patsialis D, Taflanidis A, Giaralis A (2021) Tuned-mass-damper-inerter optimal design and performance assessment for multi-storey hysteretic buildings under seismic excitation. Bull Earthq Eng. https://doi.org/10.1007/s10518-021-01236-4
Pietrosanti D, De Angelis M, Basili M (2020) A generalized 2-DOF model for optimal design of MDOF structures controlled by Tuned Mass Damper Inerter (TMDI). Int J Mech Sci 185:105849. https://doi.org/10.1016/j.ijmecsci.2020.105849
Pietrosanti D, De Angelis M, Giaralis A (2021) Experimental seismic performance assessment and numerical modelling of nonlinear inerter vibration absorber (IVA)-equipped base isolated structures tested on shaking table. Earthq Eng Struct Dyn 50(10):2732–2753. https://doi.org/10.1002/eqe.3469
Pinkaew T, Lukkunaprasit P, Chatupote P (2003) Seismic effectiveness of tuned mass dampers for damage reduction of structures. Eng Struct 25:39–46
Rana R, Soong T (1998) Parametric study and simplified design of tuned mass dampers. Eng Struct 20(3):193–204. https://doi.org/10.1016/s0141-0296(97)00078-3
Ricciardelli F, Vickery B (1999) Tuned vibration absorbers with dry friction damping. Earthq Eng Struct Dyn 28(7):707–723
Roberts J, Spanos P (2003) Random vibration and statistical linearization. Dover Publications, Mineola
Rüdinger F (2007) Tuned mass damper with nonlinear viscous damping. J Sound Vib 300(3–5):932–948. https://doi.org/10.1016/j.jsv.2006.09.009
Ruiz R, Taflanidis A, Lopez-Garcia D, Vetter C (2015) Lifecycle based design of mass dampers for the Chilean region and its application for the evaluation of the effectiveness of tuned liquid dampers with floating roof. Bull Earthq Eng 14(3):943–970. https://doi.org/10.1007/s10518-015-9860-9
Ruiz R, Taflanidis A, Giaralis A, Lopez-Garcia D (2018) Risk-informed optimization of the tuned mass-damper-inerter (TMDI) for the seismic protection of multi-storey building structures. Eng Struct 177:836–850
Sadek F, Mohraz B, Taylor A, Chung R (1997) A method of estimating the parameters of tuned mass dampers for seismic applications. Earthq Eng Amp Struct Dyn 26(6):617–635
Salvi J, Rizzi E (2017) Optimum earthquake-tuned TMDs: seismic performance and new design concept of balance of split effective modal masses. Soil Dyn Earthq Eng 101:67–80
Sgobba S, Marano G (2010) Optimum design of linear tuned mass dampers for structures with nonlinear behaviour. Mech Syst Signal Process 24(6):1739–1755. https://doi.org/10.1016/j.ymssp.2010.01.009
Shinozuka M, Deodatis G (1991) Simulation of stochastic processes by spectral representation. Appl Mech Rev 44(4):191–204
Smith M (2002) Synthesis of mechanical networks: the inerter. IEEE Trans Autom Control 47(10):1648–1662. https://doi.org/10.1109/tac.2002.803532
Soong TT, Dargush GF (1997) Passive energy dissipation systems in structural engineering. Wiley, New York
Sorace S, Terenzi G (2008) Seismic protection of frame structures by fluid viscous damped braces. J Struct Eng 134(1):45–55. https://doi.org/10.1061/(asce)0733-9445(2008)134:1(45)
Taflanidis A, Giaralis A, Patsialis D (2019) Multi-objective optimal design of inerter-based vibration absorbers for earthquake protection of multi-storey building structures. J Franklin Inst 356(14):7754–7784
Terenzi G (1999) Dynamics of SDOF systems with nonlinear viscous damping. J Eng Mech 125(8):956–963. https://doi.org/10.1061/(asce)0733-9399(1999)125:8(956)
Villaverde R (1985) Reduction in seismic response with heavily-damped vibration absorbers. Earthq Eng Struct Dyn 13:33–42
Wang Z, Giaralis A (2021) Enhanced motion control performance of the tuned mass damper inerter through primary structure shaping. Struct Control Health Monit. https://doi.org/10.1002/stc.2756
Xu K, Igusa T (1992) Dynamic characteristics of multiple substructures with closely spaced frequencies. Earthq Eng Struct Dyn 21(12):1059–1070
Zemp R, De la Llera JC, Almazan JL (2011) Tall building vibration control using a TM-MR damper assembly. Earthq Eng Struct Dyn 40:339–354
Funding
The first author gratefully acknowledges the financial support from the School of Science and Technology at City, University of London through a fully funded PhD studentship.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The displacement response variance \(\sigma_{{x_{id} }}^{2}\) in Eq. (31) is derived by application of standard frequency domain linear random vibration analysis to the ELS in Eq. (11). First, the frequency response function in terms of xid is obtained from Eq. (11) under the assumption of harmonic base excitation with frequency ω as
where \(i = \sqrt { - 1}\), g = ω/ ωs, and Xid and YG are the Fourier transforms of xid and \(\ddot{y}_{G}\) in terms of g. The constant coefficients in the denominator of Eq. (37) are given as
and in the numerator as
Next, the response variance \(\sigma_{{x_{id} }}^{2}\) is expressed as
from which Eq. (31) is derived after setting Sw = 1 (Newland 1993).
Similarly, the velocity response variance \(\sigma_{{\dot{x}_{k} }}^{2}\) in Eq. (35) is derived by obtaining first the frequency response function in terms of \(\dot{x}_{k}\) from Eq. (11) under the assumption of harmonic base excitation as
where \(\dot{X}_{k}\) is the Fourier transform of \(\dot{x}_{k}\) in terms of g and
Next, the response variance \(\sigma_{{x_{id} }}^{2}\) is expressed as
from which Eq. (35) is derived after setting Sw = 1 (Newland 1993).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rajana, K., Wang, Z. & Giaralis, A. Optimal design and assessment of tuned mass damper inerter with nonlinear viscous damper in seismically excited multi-storey buildings. Bull Earthquake Eng 21, 1509–1539 (2023). https://doi.org/10.1007/s10518-022-01609-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-022-01609-3