Tuned-mass-damper-inerter optimal design and performance assessment for multi-storey hysteretic buildings under seismic excitation

Abstract

Inerter-based vibration absorbers (IVAs), such as the tuned-mass-damper-inerter (TMDI), have become popular in recent years for the earthquake protection of building structures. Previous studies using linear structural models have shown that IVAs can achieve enhanced vibration suppression, but at the expense of increased control forces exerted from the IVA to the host building structure. The authors recently developed a bi-objective IVA design framework for linearly behaving buildings to balance between structural performance (drift/acceleration suppression) and IVA forces. This paper extends the framework to multi-storey hysteretic/yielding structures under seismic excitation. Though the proposed design framework can accommodate any type of IVA, the focus is herein on TMDI applications, with tuned-mass-damper (TMD) and tuned-inerter-damper (TID) treated as special cases of the TMDI. Earthquake hazard is modeled through representative, design-level acceleration time-histories and response of the IVA-equipped structure is evaluated through nonlinear response-history analysis. A high-fidelity finite element model (FEM) is established to accurately describe hysteretic structural behavior. To reduce the computational burden, a reduced order model (ROM) is based on the original FEM, using the framework proposed recently by the first and second authors. The ROM maintains the accuracy of the original FEM while enabling for a computationally efficient solution to the optimization problem. As an illustrative example, the bi-objective design for different IVA placements along the height of a non-linear benchmark 9-storey steel frame structure is examined. The accuracy of the ROM-based design is evaluated by comparing performance to the FEM-based response predictions across the entire Pareto front resulting from the bi-objective optimization. Then, the designs and associated performance predicted by using a linear or a nonlinear structural model are compared to evaluate how the explicit consideration of nonlinearities, as well as the degree of nonlinear behavior, impact the IVA design and efficiency.

1 Introduction

Inerter-based vibration absorbers (IVAs) have emerged as promising devices for the earthquake protection of building structures (Ikago et al. 2012; Marian and Giaralis 2014; Pietrosanti et al. 2017; Radu et al. 2019), coupling viscous and tuned-mass dampers with an inerter, a two terminal mechanical device that produces a resisting force proportional to the relative acceleration of its terminals (Smith 2002). The constant of proportionality of the latter resisting force is called ‘inertance’ and it is measured in mass units (kg). Leveraging different mechanisms (mechanical, fluid or electrical based) various inerter devices have been proposed over the years, accommodating an inertance that scales up practically independently of their weight (Papageorgiou and Smith 2005; Swift et al. 2013; Gonzalez-Buelga et al. 2015; Marian and Giaralis 2017; Li and Zhu 2018; Liu et al. 2018). Two popular IVAs are the tuned-mass-damper-inerter (TMDI) (Marian and Giaralis 2013, 2014) and the tuned-inerter-damper (TID) (Lazar et al. 2013). These devices utilize the inerter as a weightless mass element to improve the efficiency of tuned-mass-dampers (TMDs) for seismic protection of buildings while relaxing, for the TMDI, or eliminating, for the TID, requirements for excessive secondary TMD mass typically necessitated in earthquake engineering applications (see e.g., (De Angelis et al. 2012) and references therein). Specifically, in the TMDI, the inerter acts as a mass amplifier contributing inertia (but not weight) to a conventional TMD by connecting the secondary mass to a different floor from the one that the TMD is attached to. While in the TID, the inerter is used as a surrogate of the TMD secondary mass, resulting in a diagonal strut comprising a viscoelastic damper (spring in parallel to dashpot) in series with an inerter connecting two adjacent floors. It has been recently shown that both the TMDI and the TID achieve, when properly designed (tuned), practically identical structural performance (Taflanidis et al. 2019).

In the majority of studies in the literature, the design and performance assessment of IVAs is typically established assuming linear behavior of the protected structure (Marian and Giaralis 2014; Hu et al. 2015; Pietrosanti et al. 2017; Wen et al. 2017; Giaralis and Taflanidis 2018; Shen et al. 2019; Kaveh et al. 2020). While nonlinearities in the devices themselves have been frequently explicitly considered, by assuming hysteretic behavior of the dashpot connecting the mass to the host building (Deastra et al. 2020), by introducing a nonlinear spring in the device (Gonzalez‐Buelga et al. 2017), and by examining nonlinearities for the inerter itself due to non-ideal mechanical behavior (Gonzalez‐Buelga et al. 2017; De Domenico et al. 2019; Pietrosanti et al. 2020, 2021), the same does not typically apply for the response of the primary structure. The assumption of linear behavior of the protected structure accommodates substantial computational efficiency for the device design, since it allows the use of analytical solutions for the seismic performance evaluation (Ikago et al. 2012; Lazar et al. 2013; Pietrosanti et al. 2017; Giaralis and Taflanidis 2018) for standard types of excitation (such as harmonic or stochastic stationary description). Furthermore, this assumption can be partially justified by the fact that the addition of the device intents to substantially suppress seismic response, providing the expectation of linear behavior for the structure under most ground motions (GMs). Nevertheless, under larger intensity of ground shaking, structures equipped even with well-designed devices may undergo large deformations and can exhibit nonlinear/hysteretic behavior, something that might undermine the effectiveness of the device when the latter is designed assuming linear behavior. This has been clearly demonstrated for TMDs, the predecessor of TMDIs and TIDs, in (Soto‐Brito and Ruiz 1999). Recent studies have acknowledged that, and nonlinearities in the building structure were introduced in the design and performance assessment of TIDs (Radu et al. 2019; Moghimi and Makris 2020; Talley et al. 2021), TMDIs (De Domenico and Ricciardi 2018; Pietrosanti et al. 2020, 2021) and other type of IVAs (Zhang et al. 2021). Notably similar efforts exist for TMDs (Soto‐Brito and Ruiz 1999; Sgobba and Marano 2010; Mohebbi et al. 2013). Most of the studies regarding IVAs (Moghimi and Makris 2020; Pietrosanti et al. 2020; Talley et al. 2021) have focused solely on the performance assessment of the nonlinear structure and have not explicitly considered the design/tuning of the device for the nonlinear structure, or examined how nonlinearities affect this design when compared against the design using linear behavior assumptions.

Such performance assessment and design of hysteretic building structures equipped with IVAs may involve a substantial computational burden when hysteretic behavior is described through a high-fidelity finite element model (FEM), and response is evaluated through nonlinear response-history analysis (NLRHA). To address this challenge, the aforementioned studies adopted some form of simplification in either the method of structural analysis or in the modeling of the structure itself. In (Soto‐Brito and Ruiz 1999; Sgobba and Marano 2010; Pietrosanti et al. 2021) single-degree-of-freedom idealizations were adopted, in (Mohebbi et al. 2013; De Domenico and Ricciardi 2018; Radu et al. 2019; Moghimi and Makris 2020) shear structures with simplified hysteretic laws were utilized in the application examples, while in (Sgobba and Marano 2010; De Domenico and Ricciardi 2018) stochastic linearization techniques were utilized to simplify analysis. Studies that use NLRHA within a design framework either restrict analysis to a single earthquake ground motion (Mohebbi et al. 2013; Zhang et al. 2021) or adopt some of the aforementioned forms of modeling simplifications to achieve the desired computational efficiency. Though recent efforts (Talley et al. 2021) considered comprehensive NLRHA-based performance assessment for IVAs and utilized high-fidelity numerical models for simulating structural response, they did not account for nonlinear structural behavior in the IVA design. The simplifications and approximations adopted in all aforementioned studies at the design phase, though undoubtedly provide additional insights when compared to approaches that utilize linear structural models, may compromise the adequacy of the design in accurately considering the implications of hysteretic structural behavior.

This study extends these efforts by considering the optimal design of multi-degree of freedom (MDoF) nonlinear/hysteretic building structures equipped with a linear TMDI (or TID/TMD) while allowing the use of high-fidelity FEMs for the description of the hysteretic behavior. The optimal design problem is based on the multi-objective design framework recently developed by the authors for linear structures equipped with IVAs (Taflanidis et al. 2019). This framework is extended here to consider hysteretic behavior. Earthquake hazard is modeled through a suite of representative (design-level) acceleration time-histories, and the performance of the IVA equipped structure is evaluated through NLRHA. Fixed configurations of dashpot, spring and mass/inertance elements is assumed and the optimal parameters are identified though a bi-objective design problem, with (i) first objective defined as the consequences associated with the exceedance of different thresholds for different engineering demand parameters (EDPs) and (ii) second objective corresponding to the peak IVA force developed during the entire duration of the excitation. In the illustrative case study, a 9-story benchmark steel frame building, frequently utilized for assessing vibration control solutions in earthquake engineering (Ohtori et al. 2004), is considered. The model of this structure is developed in OpenSees (McKenna 2011) and is a high-fidelity FEM with distributed plasticity elements, capable of capturing hysteretic structural behavior with a high degree of accuracy. Since direct use of this model in the multi-objective optimization involves a substantial computational burden, a reduced order model (ROM) is established for the structure, adopting the framework developed recently by the first and second authors (Patsialis et al. 2020; Patsialis and Taflanidis 2020). This ROM is calibrated to match the hysteretic behavior of the original high-fidelity structure (without any device) by utilizing FEM time-history response data. The calibrated ROM can then replace the original FEM and is used to assess the performance for any desired IVA with a substantially lower computational cost compared to the high-fidelity FEM. This is leveraged to accommodate an efficient design optimization. In the illustrative case study, the accuracy of the ROM-based design is examined by comparing performance to the FEM-based response predictions across the entire Pareto front resulting from the bi-objective optimization. Furthermore, to evaluate the impact of the hysteretic structural behavior on the IVA design and performance, the response for the designs that utilize a linear or a nonlinear structural model are compared. This is performed across different excitation intensities to also examine how the degree of the nonlinear response impacts the observed trends.

The novel contributions of this paper include (a) the development of a framework for IVA design accounting for structural hysteretic behavior which combines FEMs and ROMs to balance between the accuracy in describing hysteretic forces and the efficiency for the associated design optimization, and (b) the detailed examination of the implications of considering explicitly hysteretic structural behavior at the IVA design stage. The remainder of the paper is organized as follows. In Sect. 2, the ROM formulation for a planar structure with a TMDI (or TID/TMD) is reviewed while in Sect. 3, the multi-objective design problem formulation is discussed. The illustrative example is presented and described in Sect. 4, followed by the validation of the prediction accuracy of the ROM in Sect. 5. In Sect. 6, results are discussed, and finally, the concluding remarks are summarized in Sect. 7.

2 Model for hysteretic planar structure equipped with a TMDI

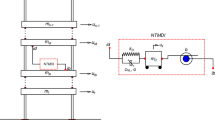
In this work, a high-fidelity FEM is utilized to describe hysteretic structural response. To accommodate a computationally efficient design, this FEM is replaced by a ROM which is explicitly calibrated to provide a good match for EDP predictions within a NLRHA setting. The calibration is established for the host structure without any protective device, and for evaluating the adequacy of the ROM for the IVA design, some validation needs to be performed once the optimal design has been identified. For a multi-objective framework like the one adopted in this study (detailed in Sect. 3), such a validation can be implemented by comparing the performance across the identified Pareto front, calculated by using either the FEM or the ROM of the structure. This is going to be discussed in detail in the illustrative case study. The remainder of this section presents the ROM for a n story planar structure equipped with a TMDI, as shown in Fig. 1.

Fig. 1

Structural planar model equipped with TMDI (or TID/TMD)

2.1 ROM formulation

The formulation of the ROM follows the three-step procedure detailed in (Patsialis and Taflanidis 2020) and applied to the structural FEM without any IVA. First, the stiffness and mass matrices of the original FEM are condensed into a discrete number of generalized coordinates representing the ROM's dynamic degrees of freedom (DoF). The resultant linear ROM matches exactly the dynamic response of the linear FEM. In the second step, the formulated stiffness matrix is replaced by an equivalent spring representation connecting all DoFs to each other and to the ground. Then, the linear restoring forces from each spring are replaced with hysteretic ones. The resultant ROM equation of motion is:

$${\mathbf{M}}_{s} {\mathbf{\ddot{x}}}_{s} (t) + {\mathbf{C}}_{s} {\dot{\mathbf{x}}}_{s} (t) + {\mathbf{T}}_{c}^{T} {\mathbf{f}}^{c} ({\mathbf{T}}_{c} {\mathbf{x}}_{s} (\tau);\tau \in [0,t]|{\mathbf{K}}_{s} ,{\mathbf{q}}) = - {\mathbf{M}}_{s} {\mathbf{R}}_{s} \ddot{x}_{g} (t)$$

(1)

where ${\mathbf{x}}_{s} (t) \in {\mathbb{R}}^{n}$ denotes the vector of displacements for each floor relative to the base, ${\mathbf{M}}_{s}$, ${\mathbf{K}}_{s}$ and ${\mathbf{C}}_{s}$ are the n × n mass, (linear) stiffness and damping matrices respectively, chosen to match the linear FEM characteristics, ${\mathbf{R}}_{s} \in {\mathbb{R}}^{n}$ is the vector of earthquake influence coefficients (vector of ones), $\ddot{x}_{g} (t) \in {\mathbb{R}}$ is the acceleration of the base, T_c is the n(n + 1)/2 × n connectivity matrix relating the relative displacements at the ends of each pair of DoFs i and j to vector x, and ${\mathbf{f}}^{c} ({\mathbf{T}}_{c} {\mathbf{x}}_{s} (\tau);\tau \in [0,t]|{\mathbf{K}}_{s} ,{\mathbf{q}}) \in {\mathbb{R}}^{n(n + 1)/2}$ is the vector of hysteretic forces between each pair of DoFs i and j. These forces, as indicated by their notational description, are functions of the relative displacement between DoFs i and j, ${\mathbf{T}}_{c} {\mathbf{x}}_{s} (\tau )$, for the entire time-history up to time t, $\tau \in [0,t]$, have initial stiffness that matches exactly K_s and follow some specific hysteretic law with hyper-parameters q. Different hysteretic laws may be considered for this description, for example piecewise linear elastic-perfectly plastic (EPP) or peak-oriented (PO) models, Generalized Masing (GM) models and Bouc-Wen (BW) models. Details for modeling of ${\mathbf{f}}^{c}$ can be found in (Patsialis and Taflanidis 2020). Each of these models involves some hyper-parameters that need to be selected. The union of all these hyper-parameters for all pairs of DoFs define the vector q of hyper-parameters for the ROM.

The final step for the ROM formulation is the calibration of vector q. This is formulated as a least-squares optimization problem with objective being the mean-squared time-history discrepancy between the FEM and the ROM, for a few appropriately chosen excitations and response quantities of interest. Details for the optimization, including relaxation approaches that consider some of the hysteretic forces (between DoF that are far apart) as linear, and discussions on the proper selection of the excitations, are presented in (Patsialis and Taflanidis 2020).

2.2 Equations of motion of ROM with a TMDI

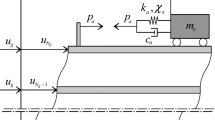
A unified formulation of the equations of motion for IVAs has been presented in (Taflanidis et al. 2019), and is adopted here to describe the model for the structure in Fig. 1. The TMDI consists of a secondary mass m_d connected to the i_d DoF through a spring k_d and dashpot c_d and connected to the i_b DoF through an inerter with inertance b. The TID and TMD correspond to special cases with m_d = 0 and b = 0, respectively. Let ${\mathbf{R}}_{d} \in {\mathbb{R}}^{n}$ be the location vector specifying the floor the spring and dashpot of the device are attached to, (vector of zeros with a single one on its i_d entry) and let ${\mathbf{R}}_{b} \in {\mathbb{R}}^{n}$ be the inerter location vector specifying the floor the inerter is connected to (vector of zeros with a single one on its i_b entry). Let also $y(t) \in {\mathbb{R}}$ be the displacement of the mass m_d relative to the i_d floor and define R_c = R_d-R_b. The coupled equations of motion of the ROM with the TMDI are:

$$\begin{aligned} &({\mathbf{M}}_{s} + {\mathbf{R}}_{d} m_{d} {\mathbf{R}}_{d}^{T} + {\mathbf{R}}_{c} b{\mathbf{R}}_{c}^{T} ){\mathbf{\ddot{x}}}_{s} (t) + ({\mathbf{R}}_{d} m_{d} + {\mathbf{R}}_{c} b)\ddot{y}(t) + {\mathbf{C}}_{s} {\dot{\mathbf{x}}}_{s} (t) \\& +{\bf T}_{c}^{T}{\mathbf{f}}^{c} ({\mathbf{T}}_{c} {\mathbf{x}}_{s} (\tau);\tau \in [0,t]|{\mathbf{K}}_{s} ,{\mathbf{q}}) = - ({\mathbf{M}}_{s} + {\mathbf{R}}_{d} m_{d} {\mathbf{R}}_{d}^{T} ){\mathbf{R}}_{s} \ddot{x}_{g} (t)\\ &(m_{d} + b)\ddot{y}(t) + (m_{d} {\mathbf{R}}_{d}^{T} + b{\mathbf{R}}_{c}^{T} ){\mathbf{\ddot{x}}}_{s} (t) + c_{d} \dot{y}(t) + k_{d} y(t) = - m_{d} {\mathbf{R}}_{d}^{T} {\mathbf{R}}_{s} \ddot{x}_{g} (t)\end{aligned}$$

(2)

The total forces transferred by the spring/dashpot parallel combination and by the inerter to the host structure are, respectively,

$$f_{d} (t) = c_{d} \dot{y}(t) + k_{d} y(t)$$

(3)

$$f_{b} (t) = b[\ddot{y}(t) + {\mathbf{R}}_{{\mathbf{c}}} {\mathbf{\ddot{x}}}_{{\mathbf{s}}} (t)]$$

(4)

To accommodate the optimal design, the dimensionless frequency ratio r_d, damping ratio ζ_d, inertance ratio β and mass ratio μ are introduced as

$$r_{d} = \frac{1}{{\omega_{1} }}\sqrt {\frac{{k_{d} }}{{(m_{d} + b)}}} \, ;\:{\upzeta }_{d} = \frac{{c_{d} }}{{2(m_{d} + b)\omega_{d} }} \, ; \:\beta = \frac{b}{M}{ ; } \:\mu = \frac{{m_{d} }}{M}$$

(5)

where ω₁ and M are the fundamental natural frequency and the total mass of the host structure respectively, and $\omega_{d} = r_{d} \omega_{1}$ represents the TMDI natural frequency. These four quantities are going to be the design variables in the TMDI optimization problem, leading to the following design vector

$${\boldsymbol{\upvarphi}} = [r_{d} ,\zeta_{d} ,\beta ,\mu ]$$

(6)

For the TID and TMD, the design is simplified by removing, respectively, μ and β from the φ definition. These three, i.e. TMDI, TID and TMD, are the seismic protective devices that will be examined later in the case study, though framework can be applied to other IVAs.

3 Multi-objective design framework

3.1 Performance and hazard characterization

As discussed in the introduction, performance is assessed using NLRHA, with the seismic hazard described through representative GMs. To evaluate the impact of structural nonlinearities on the IVA design and performance, a specific seismic intensity is considered for the seismic hazard description at the design stage. Though the design framework can be seamlessly extended to consider excitations across different earthquake intensities (Gidaris and Taflanidis 2015), examining a single intensity (a) enforces a design for a specific level of seismicity (design-level excitations), an approach that agrees with civil engineering design practices, and (b) facilitates a seamless comparison to designs for higher or lower seismicity levels, something that can reveal the influence of structural nonlinearities on the IVA design, as will be demonstrated later in the case study. Specifically, an ensemble of spectrum compatible GMs are utilized to describe the seismic hazard whose average response spectrum traces closely a linear design spectrum. In this work, a harmonic wavelet-based GM modification approach is used to achieve spectrum compatibility of n_g (= 7 in the case study implementation) recorded GMs proposed by (Giaralis and Spanos 2009).

3.2 Performance objectives

Following guidelines of (Taflanidis et al. 2019), a bi-objective design is formulated. The first objective represents structural performance, and is expressed through the consequences associated with EDPs, like inter-story drifts ratios and absolute floor accelerations, exceeding thresholds defining acceptable performance levels. Following modern performance-based earthquake engineering (PBEE) practices (Goulet et al. 2007), this is accommodated examining component-level vulnerabilities (Porter et al. 2001). Multiple performance thresholds are considered for each EDP, representing different damage states for the different components of the structure, and exceedance for each of these thresholds is associated with different consequences, representing the contributions from the repair cost for the corresponding damage state. Both (a) inter-story drifts ratios and (b) absolute floor accelerations are considered as EDPs, describing, respectively, the seismic vulnerability of (a) structural or non-structural components and (b) building contents.

Let $z_{i,k}^{h} ({\boldsymbol{\upvarphi}})$ denote the peak value of the kth EDP for the ith floor and the hth ground motion for IVA configuration φ, with k = 1 corresponding to inter-story drift ratios EDPs and k = 2 to absolute floor acceleration EDPs. For the kth EDP, consider n_d,k different performance thresholds, $\{ b_{i,k}^{j} ;j = 1, \ldots ,n_{d,k} \}$, ordered in increasing order, and denote by $C_{i,k}^{j}$ the additional consequences for exceeding the jth threshold compared to the consequences for exceeding the previous (j-1) threshold. Assuming a lognormal distribution for the fragility of each of the damaged states, as commonly adopted in earthquake engineering practice (Porter et al. 2001), leads to the total consequences, across all considered damage states and corresponding performance thresholds, for the hth excitation and the ith floor given by:

$$L_{i}^{h} ({\boldsymbol{\upvarphi}}) = \sum\limits_{k = 1}^{2} {\sum\limits_{j = 1}^{{n_{d,k} }} {C_{i,k}^{j} } } \Phi \left[ {\frac{{\ln (z_{i,k}^{h} ({\boldsymbol{\upvarphi}})/b_{i,k}^{j} )}}{{\sigma_{i,k}^{j} }}} \right]$$

(7)

where Φ[] stands for the standard Gaussian cumulative distribution function and $\sigma_{i,k}^{j}$ is the dispersion of the fragility function associated with the jth threshold. Note that expression of Eq. (7) is equivalent to the component-based vulnerability assessment utilized frequently in PBEE (Porter et al. 2001); it merely corresponds to a reformulation to express the total consequences with respect to the probability of exceeding the different performance thresholds as opposed to the probability of being in each examined damage state. Based on this reformulation, $C_{i,k}^{j}$ corresponds to the additional consequences for exceeding the jth performance threshold, considering the consequences already taken into account for exceeding the previous threshold, instead of the consequences for repairing a specific damage state (Porter et al. 2001). Formulation of Eq. (7) is preferred here because it demonstrates more clearly the stronger consequences for EDPs taking increasingly larger values. Additionally, note that the use of a fragility function instead of a binary indicator function for representing probability of exceedance of threshold $b_{i,k}^{j}$ in this formulation, is not only better aligned with PBEE practices but also facilitates a smoother objective function (Taflanidis and Beck 2010) which can be critical for the numerical optimization required for the IVA design. Finally, the first objective function is calculated as the average consequences across all earthquake GMs and floors:

$$J_{1} ({\boldsymbol{\upvarphi}}) = \frac{1}{{n_{g} }} \cdot \sum\limits_{h = 1}^{{n_{g} }} {\left( {\frac{1}{n} \cdot \sum\limits_{i = 1}^{n} {L_{i}^{n} ({\boldsymbol{\upvarphi}})} } \right)}$$

(8)

The second objective is related to the control forces exerted by the IVA to the host building to account for the potential local strengthening of the structure that might be required to accommodate them. Let $F_{d}^{h} ({\boldsymbol{\upvarphi}})$ and $F_{b}^{h} ({\boldsymbol{\upvarphi}})$ denote the peak forces for the hth excitation for the total forces transferred, respectively, by the spring/dashpot parallel combination (Eq. (3)) or by the inerter (Eq. (4)) to the host structure. The average of these forces across the excitations is considered to represent the degree of strengthening required to accommodate each of these forces. The second objective corresponds to the maximum of these values, and is ultimately expressed by:

$$J_{2} ({\boldsymbol{\upvarphi}}) = \max \left[ {\frac{1}{{n_{g} }} \cdot \sum\limits_{h = 1}^{{n_{g} }} {F_{d}^{h} ({\boldsymbol{\upvarphi}}),\frac{1}{{n_{g} }} \cdot \sum\limits_{h = 1}^{{n_{g} }} {F_{b}^{h} ({\boldsymbol{\upvarphi}})} } } \right]$$

(9)

where max[a,b] stands for the maximum of the two arguments.

3.3 Design problem formulation and solution

The bi-objective design problem is formulated by considering concurrently the two design objectives

$${\boldsymbol{\upvarphi}}^{*} = \arg \mathop {\min }\limits_{{{\boldsymbol{\upvarphi}} \in {\Phi }_{d} }} \{ J_{1} ({\boldsymbol{\upvarphi}}),J_{2} ({\boldsymbol{\upvarphi}})\}$$

(10)

where Φ_d represents the admissible design space for φ. Since the two objectives are competing, there is no design configuration φ that can simultaneously minimize both of them. Instead, solution of the design problem is provided by the identification of the Pareto optimal solutions. A design configuration is Pareto optimal (also references as dominant design), if there is no other configuration that improves one objective without detriment to the other. An optimal Pareto design is denoted as φ_p and the set of all such configurations is denoted as Pareto set Φ_p. The Pareto front is the representation of the Pareto set in the objective function space:

$$J_{p} = \{ [J_{1} ({\boldsymbol{\upvarphi}}),J_{2} ({\boldsymbol{\upvarphi}})]|{\boldsymbol{\upvarphi}} \in {{\varvec{\Phi}}}_{p} \}$$

(11)

The Pareto front reveals, ultimately, the compromise between the two competing objectives that can be made. A final design solution can be chosen considering the desired level of vibration suppression, along with other considerations including architectural constraints and the level of the control forces that can be accommodated.

Standard numerical approaches for identifying the Pareto front include genetic algorithms, weighted sum approaches and the epsilon-constraint method (Marler and Arora 2004). In previous work of the authors (Taflanidis et al. 2019), the epsilon-constraint method was preferred since it can offer a well-balanced population solution across the entire Pareto front. In this study a different numerical solution is considered, using a random search optimization scheme (Karnopp 1963). This is preferred, compared to the aforementioned alternatives, since it can accommodate an efficient identification of the Pareto front for different selection of the characteristics $\{ b_{i,k}^{j} ,C_{i,k}^{j} ;\:j = 1, \ldots ,n_{d,k} \}$, for the seismic consequences. This attribute will be leveraged in the case study to examine different formulations of the design problem. According to the random search approach, a very large population of N_c candidate design configurations are generated within Φ_d, $\{ {\boldsymbol{\upvarphi}}^{(c)} ;\:c = 1,...,N_{c} \}$, based on Latin Hypercube Sampling (space filling sampling), and the response is obtained for each of them ($\{ z_{i,k}^{h} ({\boldsymbol{\upvarphi}}^{(c)} ),F_{d}^{h} ({\boldsymbol{\upvarphi}}^{(c)} ),F_{b}^{h} ({\boldsymbol{\upvarphi}}^{(c)} );\:c = 1,...,N_{c} \}$) using NLRHA. The value of N_c needs to be chosen large enough to ensure that the entire domain Φ_d is well populated. Subsequent selection of $\{ b_{i,k}^{j} ,C_{i,k}^{j} ;\:j = 1, \ldots ,n_{d,k} \}$ allows the estimation of the competing objectives $\{ J_{1} ({\boldsymbol{\upvarphi}}^{(c)} ),J_{2} ({\boldsymbol{\upvarphi}}^{(c)} );\:c = 1,...,N_{c} \}$ and, ultimately, the identification of the Pareto front. For different selection of $\{ b_{i,k}^{j} ,C_{i,k}^{j} ;\:j = 1, \ldots ,n_{d,k} \}$, the computationally expensive part of the numerical optimization, which is the NLRHA for the response estimation, does not need to be repeated. As such, implementation allows for an efficient identification of the Pareto front for different characterizations of seismic consequences.

4 Illustrative case study: Description

4.1 Structural model description

The 9-storey structure considered in the example has a rectangular plan with dimension 45.73 m with lateral load resisting system comprised of two (perimeter), five-bay steel moment-resisting frames (MRFs). It is described in detail in (Ohtori et al. 2004). First floor height is 5.49 m while height of all other floors is 3.96 m. The seismic mass of the structure (defining mass matrix M_s) is 1.01 × 10⁶ kg for the first floor, 9.89 × 10⁵ kg for the second through the eighth floor and 1.07 × 10⁶ kg for the ninth floor. The total seismic mass of the structure is 9.00 × 10⁶ kg. The nonlinear FEM is developed in OpenSees (McKenna 2011) using fiber modeling approach for describing the hysteretic behavior. Details for the OpenSees models are included in (Patsialis and Taflanidis 2020). Analysis is performed along the NS direction of the structure. Natural periods (and participating modal mass ratios in parenthesis) for the first three modes are 2.27 s (82.8%), 0.85 s (10.9%) and 0.49 s (3.4%) respectively. For defining the damping matrix C_s, modal damping equal to 2% is assumed for all modes of vibration. For the ROM formulation, a Bouc-Wen model is adopted to describe the hysteretic forces, and numerical implementation and calibration is performed according to guidelines in (Patsialis and Taflanidis 2020). Related to the computational efficiency, for a time-step of 0.01 and using Newmark’s average acceleration for numerical integration and for a strong ground motion of duration 40 s, the OpenSees computational time in a desktop with 4core Xeon 3.1 GB processor is 111 s. For the ROM, this time is reduced to 0.20 s. This demonstrates a remarkable reduction in computational cost, which, as discussed earlier, is essential for the efficiency of the optimization problem.

A TMDI is implemented as seismic protective device. TMD and TID implementations are also examined as limiting cases for the TMDI (with no inerter or no secondary mass, respectively). For the placement of the TMDI, four different locations are examined. These are codified in terms of i_d and i_b values, as shown in Fig. 1. These are: (i) i_d = 9 and i_b = 8, (ii) i_d = 9 and i_b = 7, (iii) i_d = 8 and i_b = 7 and (iv) i_d = 8 and i_b = 6. Hereafter, these placements will be referenced as 9th storey, 9–7 storey, 8th storey, and 8–6 storey, respectively. Extensive discussions on the impact of the IVA placement on its efficiency can be found in (Giaralis and Taflanidis 2018; Ruiz et al. 2018; Taflanidis et al. 2019) for linear structural behavior. Here some of the special cases are examined to demonstrate that similar trends hold for nonlinear structural behavior.

The Pareto front for the optimal design is obtained, as discussed in Sect. 3, using the ROM formulation (further details discussed in Sect. 4.3). Validation of the Pareto front requires the incorporation of the TMDI in the high-fidelity OpenSees model. This is accomplished by including the secondary TMDI mass as an additional mass m_d connected to the chosen floor with a zero-length element with the desired stiffness and damping properties (k_d and c_d), while the inerter is modeled with an isolated rigid frame element, attached to the desired floor and facilitating the target inertance using rotational inertia properties. More details for the modeling of the inerter in a finite element program like OpenSees are provided in “Appendix A”.

4.2 Modeling of earthquake excitation

As discussed in Sect. 3.1, a suite of n_g = 7 recorded GMs is adopted to represent the seismic hazard, modified to achieve a match to the UBC 1994 design spectrum that was used in the design of the case-study structure (Ohtori et al. 2004). The exact number of GMs is considered to be sufficient to produce acceptably low dispersion in peak inelastic demands of yielding structures (Shome et al. 1998) and is taken as the minimum number of GMs to allow for structural design based on average peak inelastic demands in most international seismic design codes of practice (Beyer and Bommer 2007). The considered GMs are selected from a GM database constructed for the design of relatively flexible structures (Naeim and Kelly 1999), like the case study structure, and are: (i) El Centro (1979 Imperial Valley earthquake), (ii) Hollister (1989 Loma Prieta earthquake), (iii) Petrolia (1992 Petrolia earthquake), (iv) Sylmar (1994 Northridge earthquake), (v) Corralitos (1989 Loma Prieta earthquake), (vi) Oakland (1989 Loma Prieta earthquake), (vii) Century City (1994 Northridge earthquake).

The UBC 1994 design pseudo-acceleration spectrum (ICBO 1994), used for the GM modification is given as a function of the natural period T by expression

$$S_{a} \left( T \right) = \left\{ {\begin{array}{*{20}c} {\frac{{a_{\max } - a_{g} }}{{T_{A} }}T + a_{g} ,\quad T \le T_{A} } \\ {a_{\max },\quad T_{A} < T < T_{B} } \\ {\frac{{a_{\max } T_{B} }}{T},\quad T \ge T_{B} } \\ \end{array} } \right.$$

(12)

where a_g is the peak ground acceleration, a_max is the peak spectral ordinate attained at the region of constant spectral acceleration (plateau), and T_A and T_B are the natural period values delimiting the plateau. Values a_g = 0.4 g, a_max = 1.0 g, T_A = 0.15 s and T_B = 0.585 s have been utilized corresponding to zone 4 and soil type 2 (deep cohesionless or stiff clay soils) per UBC 1994. The GM modification is performed using the harmonic wavelet-based approach described in (Giaralis and Spanos 2009). The adopted approach enforces point-wise spectral matching within a certain structure-specific band of natural periods pre-specified at will. Outside this band, spectral matching requirements are relaxed to minimize overall signal modifications such that salient features in the as-recorded GMs are maintained as numerically shown in (Giaralis and Spanos 2010). To this end, the selected GMs are modified individually to achieve spectral matching within the interval of natural periods [0.45 s, 3.4 s] which corresponds approximately to the range [0.2T₁, 1.5T₁] where T₁ is the fundamental natural period of the uncontrolled case-study structure (T₁ = 2.27 s). The lower bound, 0.2T₁, in the target spectral matching range is the most conservative (lowest) limit specified by current international codes of practice adopted from the current Eurocode 8 (EC8 2004). It is specified to account for the contribution of higher modes which are deemed to be important for the case-study structure due to its flexibility. The upper bound, 1.5T₁, is in alignment with recommendations on the maximum expected apparent period elongation of code-compliant yielding structures (Katsanos et al. 2014).

In applying spectral matching, the target spectrum has been modified for periods T > 1.5T₁ = 3.4 s such that the spectral relative displacement is constant and equal to its spectral value at T = 1.5T₁ = 3.4 s. This modification was deemed necessary to ensure that the spectrally matched accelerograms attain reasonable and realistic time-history traces and response spectrum displacement demands. This was not possible by using the original UBC 1994 design spectrum which yields monotonically increasing spectral displacements with T (Tolis and Faccioli 1999). In this regard, the target relative displacement spectrum considered in spectral matching is:

$$\begin{aligned}S_{d} \left( T \right) = &\left\{ {\begin{array}{*{20}c} &{\left( {\frac{{a_{\max } - a_{g} }}{{T_{A} }}T + a_{g} } \right)\frac{{T^{2} }}{{4\pi^{2} }} ,\quad T \le T_{A} } \\ &{a_{\max } \frac{{T^{2} }}{{4\pi^{2} }} ,\quad T_{A} < T < T_{B} } \\ &{\frac{{a_{\max } T_{B} }}{{4\pi^{2} }}T,\quad T_{B} \le T \le 3.4s} \\ &{0.85\frac{{a_{\max } T_{B} }}{{\pi^{2} }},\quad T > 3.4s} \\ \end{array} } \right. \end{aligned}$$

(13)

To further eliminate spurious low-frequency content in the modified GMs, high-pass forward–backward acausal filtering using a 4th order high-pass filter with 0.12 Hz cut-off frequency has been applied in all accelerograms (Boore and Akkar 2003). This zero-phase filtering avoids phase distortion and ensures that spectral matching level is preserved (Giaralis and Spanos 2009). Figure 2 shows the response spectra of the considered GMs before and after spectral matching as well as the ensemble mean spectrum, respectively. The original and the target UBC 1994 is superposed to facilitate a comparison in all provided plots. The mean peak ground acceleration of the modified GMs is 0.39 g and the minimum value of the mean spectral ordinates within the target matching range of [0.2T₁, 1.5T₁] is 95.6% of the target spectrum which satisfy the commonly applied 90% minimum mean discrepancy spectral matching criterion (Giaralis and Spanos 2009).

Fig. 2

Response spectra (displacement and acceleration) of the original (top row) and modified (bottom row) GMs

4.3 Design optimization and performance assessment details

The admissible space of the optimization problem is taken to be [0.01 5] for r_d, [0.005 1.5] for ζ_d, [0 10] for β and [0 0.05] for μ. The lower bound of the range for the mass and inertance ratios are chosen as zero in order to examine, additionally to TMDI configurations, TID and TMD configurations, respectively. The upper bound of the mass ratio is selected to accommodate a mass damper that does not excessively increase gravity loads of the host structure. The lower and upper bounds of the remaining design variables are chosen to avoid convergence to their respective boundaries while also avoiding unrealistically large inertance values. The optimization itself is performed using the random search implementation detailed in Sect. 3.3. to accommodate the different design scenarios detailed next. Leveraging the ROM efficiency, the total number of candidate design configurations examined, N_c, is chosen large enough to accommodate an accurate identification of the Pareto front. This is chosen as N_c = 430,000, with 300,000 of them corresponding to TMDI implementation (all four design variables examined), 100,000 corresponding to TID implementation (μ = 0 and only three design variables considered) and 30,000 corresponding to TMD implementation (β = 0 and only three design variables considered). For the TMD, the range for r_d and ζ_d were further restricted to correspond to [0.3 1.3] and [0.01 0.5], since convergence to optimal values outside of these domains is not anticipated for TMD applications. The response (EDPs and forces) are evaluated for all these configurations for the 7 ground motions and subsequently utilized to identify the Pareto front for the different design scenarios examined. In all instances, a large number of dominant designs is identified to represent the Pareto front, but to simplify presentation, a selective set of 34 designs, evenly populating the actual Pareto front, will be utilized herein. The fact that a large population of dominant designs is identified having a continuous behavior across the front, as will be shown in the result section later, indicates that N_c values were appropriately chosen.

For quantifying structural performance and defining J₁ objective, the performance thresholds $b_{i,k}^{j}$, for inter-story drift (k = 1) and floor acceleration (k = 2) EDPs are taken to be the same across all floors ($b_{1,k}^{j} = b_{2,k}^{j} = ... = b_{9,k}^{j} = b_{k}^{j}$). The same is true for their corresponding consequences ($C_{1,k}^{j} = C_{2,k}^{j} = ... = C_{9,k}^{j} = C_{k}^{j}$) and dispersion values ($\sigma_{1,k}^{j} = \sigma_{2,k}^{j} = ... = \sigma_{9,k}^{j} = \sigma_{k}^{j}$). Additionally, for the dispersion, a common value of σ = 0.3 is used across all EDPs and performance thresholds. For both EDPs, three performance thresholds are established (n_d,k = 3), corresponding to light (j = 1), moderate (j = 2) and severe (j = 3) damage. The values of the performance thresholds, along with their corresponding consequences are presented in Table 1. Values for the EDP performance thresholds, consequences and dispersion represent typical values adopted for PBEE applications (FEMA-P-58-3.1 2012), with consequences taken to represent repair cost. Note that the absolute values of the consequences do not affect the optimal design itself. It’s only their relative ratio that has any effect, quantifying the increased penalty for EDPs taking larger values compared to the first considered threshold (j = 1). For this reason, all results for objective J₁ will be presented normalized by the value of objective J₁ for the uncontrolled structure. The normalized objective will be denoted herein as $J_{1}^{n}$.

Table 1 Performance threshold and consequence values along with dispersion values of the performance thresholds, for the case study implementation. Values are taken to be the same across all floors

Different design variants are examined to accommodate an in-depth comparison of how different modeling assumptions impact the resultant design and structural performance. With respect to structural behavior, both linear and nonlinear (hysteretic) responses are examined. These are denoted by superscript, l and nl, respectively. Linear behavior is accommodated by replacing the nonlinear term ${\mathbf{T}}_{c}^{T} {\mathbf{f}}^{c} ({\mathbf{T}}_{c} {\mathbf{x}}_{s} (\tau);\tau \in [0,t]|{\mathbf{K}}_{s} ,{\mathbf{q}})$ with the linear one ${\mathbf{K}}_{s} {\mathbf{x}}_{s} (t)$, in Eqs. (1) and (2). For examining the influence of the degree of nonlinear behavior, three different excitation intensities are considered, established by applying scaling factors (s_c) to the GMs suite. The scaling factors are s_c = 1.0, s_c = 1.25 and s_c = 1.5, with the first one corresponding to the design seismic intensity, and the other two representing higher intensities, above the nominal design seismic action. Note that the s_c = 1.5 scaling of the original excitations (corresponding to design level earthquakes as discussed earlier) is equivalent to the maximum considered earthquake (MCE_R) according to many international standards (ASCE/SEI 2016). The scaling is also going to be denoted by a superscript. For nonlinear structural behavior, the response is separately estimated for each of the different scaling factors, while for the linear structure it is estimated only once, since it can be proportionally scaled for higher intensities (linear behavior). Therefore, the response history analysis for the N_c candidate design configurations is repeated four times, three for the nonlinear structure with different scaling of the GMs and one for the linear structure for the original GMs.

Finally, different variants are examined for the consequence quantification (definition of J₁), providing different importance to drift and acceleration EDPs: (1) the first one, denoted as O₁, considers only the 9 inter-storey drifts as EDPs ($C_{2}^{j} = 0$, ignoring potential losses from acceleration-sensitive structural components), referenced hereafter as a drift-sensitive design; (2) the second one, denoted as O₂, includes only the 9 absolute floor accelerations as EDPs ($C_{1}^{j} = 0$, ignoring potential losses from drift-sensitive structural components), referenced hereafter as an acceleration-sensitive design; (3) the third one, denoted as O₃, includes both inter-storey drift ratios and accelerations and is referenced as balanced design. Though the recommended formulation is O_3, considering contributions from all structural components, the two other ones are considered to examine trends that are specific only to drift (for O₁) or acceleration (for O₂) mitigation. These three variants will be the main design variants examined in the study. A fourth variant, denoted as O₄-j, is also considered which includes only the 9 inter-storey drift ratios, similarly to the first variant, but adopts only the jth performance threshold in the consequence definition (j = 1, j = 2 or j = 3). O₄-j is examined for investigating the implications of utilizing multiple performance thresholds (variant O₁) compared to only one (variant O₄-j) in the design optimization, as well as the implications of the exact choice of that threshold (differences between the three O₄-j). Note that variant O₄-j includes three different design, one for each j value, and can be equivalently considered to represent three different design variants. As discussed in Sect. 3.3, utilizing the random search approach, the design optimization across the different consequence quantifications (and therefore definitions of design objective J₁) is performed utilizing the same structural response. That response does not need to be separately calculated for each of the corresponding objective definitions, facilitating the desired computational efficiency for examining different trends in the case study application.

The performance definition is denoted, as indicated above, with a numerical subscript, while the intensity scaling and behavior type with a superscript. Notation D is used to denote design and notation P is used to indicate performance. For example, notation $D_{1}^{1.5nl}$ corresponds to the design (Pareto optimal solutions) for consequence quantification O₁ for the nonlinear structure considering GMs scaled with factor 1.5, while $P_{2}^{nl}$ indicates performance evaluated for consequence quantification O₂ for the nonlinear structure considering the GMs for the design spectrum (no scaling). Note that for all designs, the performance can be evaluated across different assumptions; this allows for investigating the design stage modeling implications on the actual performance, for example the effect of assuming linear structural behavior when behavior is actually nonlinear (calculating $P_{i}^{nl}$ performance for $D_{i}^{l}$ design for any desired definition of objective i = 1,…,4), or the effect of utilizing a smaller intensity than the one the structure experiences (calculating $P_{i}^{1.5nl}$ performance for $D_{i}^{nl}$ design for any desired definition of objective i = 1,…,4). The total number of variants for design and performance, considering all the possible combinations for structural behavior, seismic intensity and performance objective are 36, though only those combinations resulting in interesting comparisons are presented and discussed. As mentioned above, design optimization across these variants relies on calculation of the response for only four cases, showing again the importance of the proposed solutions approach relying on random search. The solution of the design problem further leverages the computational efficiency of the ROM formulation. Before discussing the results for the different design variants in Sect. 6, validation of the ROM accuracy within the IVA design framework is first examined in the following section.

5 Illustrative case study: Validation of the prediction accuracy and identified optimal designs using the ROM

The first validation step briefly discusses time-history responses for one of the ground motions considered in the design (Sylmar) and for scaling factor of s_c = 1, corresponding to design-level seismic intensity. Figure 3 presents the top-floor time-history responses for both drifts (left) and absolute floor accelerations (right) and compares the responses of the nonlinear OpenSees FEM with the nonlinear calibrated ROM, along with the linear ROM response, to showcase the necessity of approximating the FEM response with a nonlinear ROM and not just assuming linear structural behavior. Responses without the TMDI (top row) and with the TMDI (bottom row) are shown in the figure, in order to examine the match between the ROM and the FEM with and without seismic protective devices. For the TMDI implementation, the 9–7 storey placement is considered, and a sample Pareto optimal design point is used to characterize the TMDI configuration, for design variant $D_{3}^{nl}$ (balanced design and s_c = 1). Results clearly demonstrate that the nonlinear ROM offers excellent match to the FEM response for both EDPs across the entire time-history, for implementations with and without the TMDI. Even though the linear ROM cannot offer a good agreement to the FEM responses after the onset of nonlinear (hysteretic) behavior, the calibrated nonlinear ROM rectifies this vulnerability. This is true for both the structure without the TMDI as well as for the structure with the TMDI. This comparison illustrates that the calibrated ROM can indeed replace the original nonlinear FEM to design and assess the performance for the TMDI. It further demonstrates that the ROM calibration needs to be performed only once, for the FEM structure without the IVA device, since the degree of match between the nonlinear ROM and FEM is not affected by the inclusion of the device after the original calibration. Note that the comparison of the time-histories with and without the TMDI additionally demonstrate the vibration suppression offered by the inclusion of the TMDI for both examined EDPs.

Fig. 3

Time-history responses for top-floor drift ratio (left column) and top-floor acceleration (right column), for the Sylmar ground motion and for the case without TMDI (top row) and with a TMDI (bottom row)

The second, and more important, validation step examines the accuracy of the ROM-based design by examining the performance assessment across the entire identified Pareto front, comparing the ROM-based and FEM-based response predictions. This comparison provides insights about the accuracy of the Pareto front identification when using the ROM. Figure 4 presents the performance across the identified Pareto fronts evaluated by using either the FEM or the ROM, for all four different placements of the TMDI and for all examined scaling factors. The design variant presented in this figure corresponds to the balanced design. Similar comparisons hold across all other variants. For this figure, the normalization of J₁ (building performance) is performed by the J₁ value for the uncontrolled structure for s_c = 1. This was chosen for better illustration of the Pareto fronts (easier to visualize differences), but it can be also leveraged to depict the differences in building performance as the intensity of the excitation increases, since normalization is the same.

Fig. 4

Comparison between ROM-based optimal design configurations (black color) and their respective FEM-based response predictions (grey color) for the Pareto fronts for balanced design (consequence quantification O₃) for the nonlinear structure, for all different scaling factors and for all different protective device placements. Performance for each design is assessed for the nonlinear structure with the corresponding intensity scaling. Normalization of J₁ is established with respect to the uncontrolled structure performance for s_c = 1

In examining the results, note first that the discontinuity of the Pareto fronts for the 9th storey placement will be discussed in detail in the next section, as it is a feature related to the difference in the behavior between the TMD and the TMDI/TID. Here the emphasis is on the comparison between the Pareto fronts established by using the ROM or the FEM only. It is evident from these comparisons that the FEM-based response predictions are in a very good agreement with the ROM-based Pareto fronts across all protective device placements, and more importantly, regardless of the intensity of the ground motions (indicated by the value of the scaling factor) and therefore the degree of nonlinear behavior observed. The fact that good agreement is attained throughout the Pareto front, across design configurations that range from none, to small, to large impact of the TMDI (represented by increasing values for J₂ and decreasing for $J_{1}^{n}$), further showcases the ability of the ROM to correctly capture the behavior of the IVA-equipped nonlinear FEM independent of the design configuration and device efficiency. This is a key observation, offering confidence that the observed agreement is not restricted to specific only IVA characteristics, but rather reflects a global pattern that is independent of the IVA properties and device efficiency.

Results in Figs. 3 and 4 offer a comprehensive validation of the ability of the ROM to accurately predict the response of the nonlinear OpenSees FEM and assess the performance of the IVA protected structure. The replacement of the FEM with the ROM at the design stage does not jeopardize the quality of the identified Pareto front. This ultimately provides confidence for using the design results to identify interesting trends and answer the key questions that motivated this research: these trends reflect the behavior when using the high-fidelity FEM to perform the optimization and assess performance, and are not in any way restricted to the use of the ROM.

6 Illustrative case study: Results and discussion

6.1 Design trends across the Pareto front

Initially, the focus is on examining fundamental trends comparing across the three different protective device implementations, considering both linear and nonlinear structural behavior. For this first stage of comparisons, design and performance correspond to the same assumption with respect to the type of structural behavior, i.e. $P_{i}^{{s_{c} \cdot nl}}$ is evaluated for the $D_{i}^{{s_{c} \cdot nl}}$ design and $P_{i}^{{s_{c} \cdot l}}$ is evaluated for the $D_{i}^{{s_{c} \cdot l}}$ designs, in each case considering different seismic intensities (different s_c values) and different device placements.

First, the balanced design is considered, that is, consequence quantification O₃. Figure 5 presents the Pareto fronts considering linear (left column) and nonlinear (right column) behavior for all four protective device placements (rows of the figure), separately for each of the three protective devices considered (curves of the plot). All results correspond to the design seismic intensity (s_c = 1). This is the only figure that results are separately presented for the three protective devices. In all other figures, the three devices are not distinguished from one another, simply the overall Pareto front is presented, considering the dominance across them; the respective Pareto front corresponds to the Pareto points from the individual devices (Fig. 5) that lie on the outermost left part of the combined curves, since these reflect the dominance. Figure 6 presents the Pareto fronts for the linear structure for all different placements and for all three considered scaling factors. The corresponding plots for the nonlinear structure are the ones presented already in Fig. 4, when validating accuracy of the ROM predictions, and therefore are not repeated again. The curves for s_c = 1 in Figs. 4 and 6 represent the combined dominant designs across the three different devices examined in Fig. 5. In all three figures (Figs. 4, 5, 6), the J₁ objective is normalized by the performance of the unprotected structure for s_c = 1, to accommodate easier comparisons of performance across the different levels of seismic intensity. Figures 7 and 8 show, respectively, the Pareto optimal solutions for TMD and TMDI configurations, for 9 and 8 storey placement, and for both the linear and nonlinear structure. These Pareto optimal solutions are plotted as a function of objective J₂. Further, Table 2 presents information for the maximum reduction for J₁ compared to the uncontrolled structure, along with the corresponding J₂ value (in other words the extreme point of the Pareto front corresponding to maximum vibration suppression) for both the linear and nonlinear structure, for different levels of seismic intensity and protective device placements.

Fig. 5

Pareto fronts for each of the three protective devices, for balanced design (consequence quantification O₃) for both the linear (left column) and nonlinear structure (right column), for scaling factor s_c = 1 and for all different protective device placements. Performance for each design is assessed for the corresponding (to the design implemented) linear or nonlinear structure and intensity scaling

Fig. 6

Pareto fronts for balanced design (consequence quantification O₃) for the linear structure, for all different scaling factors and for all different protective device placements. Performance for each design is assessed for the linear structure with the corresponding intensity scaling. Normalization of J₁ is established with respect to the uncontrolled structure performance for s_c = 1

Fig. 7

Design variable values of Pareto optimal solutions plotted against objective J₂ (protective device force) for balanced design, and 9th-storey device placement, for both the linear and nonlinear structure

Fig. 8

Design variable values of Pareto optimal solutions plotted against objective J₂ (protective device force) for balanced design, and 8th-storey device placement, for both the linear and nonlinear structure

Table 2 Maximum reduction values of J₁ compared to uncontrolled structure and the corresponding maximum control forces J₂, for all placements and for the three main designs. Results are presented for s_c = 1 and s_c = 1.5

Commenting first on the Pareto front data, significant variation is seen for both objectives across the front, verifying the usefulness of the multi-objective design approach to identify the compromise between the two competing objectives. In this setting, the design engineer can ultimately choose a device configuration from the identified Pareto optimal ones using any desired criteria, with two particularly meaningful choices corresponding to (i) the one that requires strengthening below a desired level (best performance considering constraint on J₂), or (ii) the one resulting in smallest force transfer that accomplishes a specific level of performance improvement (smaller J₂ requirement considering constraint on J₁).

Regardless of the approach adopted to choose the final design, the Pareto fronts provide invaluable information for the vibration control effects provided by different optimal protective device designs and offer the ability for a comprehensive assessment of their performance. As identified in (Taflanidis et al. 2019), the vibration suppression level can be maintained close to optimum building performance with an important reduction of the force transferred to the host building structure, which is a critical practical design consideration: value of J₂ can be significantly reduced while maintaining structural performance J₁ close to optimal vibration suppression levels (minimum of J₁). This is a behavior that is quite common in multi-objective problems: close to the extremes of the front, improvements in one of the objective (objective J₁ in this case) can be frequently achieved with a significant compromise in the other objective (objective J₂ in this case), leading to very steep fronts. It is generally recommended to avoid selecting the final design from such domains of the front since the relative benefits (compared to solutions in other parts of the front) are small. In some instances, discontinuities (jumps) appear in the front, originating, as will be examined later in this section, from differences in behavior between the TMD and the TID/TMDI.

Comparison between the Pareto fronts for the linear (Fig. 6) and nonlinear (Fig. 4) structure, reveals that the relative device efficiency reduces for the nonlinear structure since larger normalized values for J₁ (compared to structure without any protective device) are only achieved (Soto‐Brito and Ruiz 1999; Sgobba and Marano 2010; Talley et al. 2021). This comes, though, with a reduction of the force of the protective device (smaller J₂ values). This behavior is anticipated and can be attributed to the smaller accelerations experienced by the nonlinear structure due to yielding, which reduces the degree of engagement of inerter-based and inertia devices, and the additional energy dissipation coming from the hysteretic structural behavior, which removes some part of the earthquake energy that could had been dissipated by the protective device. For the TMD, an additional detuning effect exists, to be discussed in detail later, that contributes to the loss of performance. These trends can also be seen from Table 2, by comparing the values of maximum reduction of J₁ and their corresponding maximum control forces, between linear and nonlinear balanced designs, for both s_c = 1 and s_c = 1.5. Linear designs provide larger maximum reduction of J₁ objective, with typically larger forces exerted by the IVAs. Exception may occur for the latter only for cases that TMD might dominate the TMDI/TID implementations. Overall, nonlinear structural behavior leads to a small reduction of the IVA forces and relative contribution to vibration suppression, though still the benefits from the addition of the device are substantial. Nonlinear behavior also makes the Pareto front steeper close to the optimal structural performance (minimum of J₁ and maximum of J₂), stressing the importance of avoiding these regions of the Pareto optimal designs. Examining the behavior across the different seismic intensities, a reduction of relative efficiency is observed for higher intensities for both the linear and nonlinear structures, something that can be seen in Figs. 4 and 6 and by inspecting Table 2. This reduction is related to the details chosen for the consequence quantification (definition of objective J₁) and will examined in a bit more detail after results for the other design variants are presented. Overall, the discussions in this and the previous paragraphs verify the utility of the multi-objective design approach for nonlinear structures, since linear structural behavior was considered only in past work (Taflanidis et al. 2019), and furthermore showcase the comprehensive evaluation the identification of the entire Pareto front (instead of single solutions) can support, accommodating comparison across a range of device behaviors.

Moving to the comparison between the different types of IVAs, Fig. 5 shows that TID and TMDI achieve practically identical performance across the entire front for both the linear and nonlinear structure verifying the trends previously identified for linear structures (Taflanidis et al. 2019). IVA placement at lower floors improves vibration control efficiency as manifested by lower J₁ values and reduced control force J₂ values. Even more improved vibration suppression efficiency is achieved by allowing IVA to span two storeys in which both objectives are simultaneously reduced across the entire Pareto front. This trend agrees with results reported in (Giaralis and Taflanidis 2018; Taflanidis et al. 2019) for linear structural behavior, but here it is shown that the same trend stands for nonlinear structures. The performance of the TMD changes drastically with its placement along the height of the structure, with placement on lower floor substantially impacting performance. Note that for TMD, placement across multiple floors is identical to placement on the first of the two considered floors since b = 0. For the linear structure, when the TMD is placed on the top floor it can actually outperform the IVAs across the entire Pareto front for the linear structure, a trend that agrees with previously published results (Giaralis and Taflanidis 2018) that identified that large mass TMDs can provide better vibration suppression in certain instances when compared to TMDI implementations. For lower floor placement, the decrease in TMD efficiency and increase in IVA efficiency make the former a more effective solution for the majority of the Pareto front. Only for small J₂ values does the TMD outperform IVA implementations. In general, the addition of the inerter leads to substantially larger forces (compare the TMD to the TID and TMDI Pareto fronts in Fig. 5) but can also provide substantial higher vibration suppression. Also, there is a fundamentally different behavior between the two type of protective devices (TMD vs TID/TMDI), leading to a (i) discontinuous (jump) or (ii) non-smooth (difference in slopes) transition of the Pareto front from one type of device to another when considering the dominant front across all devices (Figs. 4 and 6). This is also evident in the trends for the common design parameters in the plots depicting their values across the Pareto front (Figs. 7 and 8), examining specifically the optimal inertance parameter (zero indicates TMD implementation). Jumps in the Pareto front indicate that the TMDI/TID can provide better vibration suppression than the TMD only with a substantial increase of the control force, while changes in the slopes of the front indicate that the TMDI/TID gradually overtakes the TMD. The identification of such transitions within the Pareto front is another potential way to distinguish between dominance of TMD or TID/TMDI along the front without having to plot, separately, the Pareto front curves for each device, as done in Fig. 5, or checking the optimal inertance values (Figs. 7 and 8). Additionally, note that for parts of the Pareto front that correspond to TMD dominance, the curves corresponding to placements within one or two storeys apart (for example the 9th storey and 9–7 storeys) will be identical, since for the TMD there is no distinction.

For nonlinear structural behavior (compare Figs. 3, 4, 5, 6), it is important to note that the performance of the TMD drastically decreases, especially for larger intensity levels, and is more clearly outperformed by the IVA implementations. The latter is evident from jumps or slope transitions of the Pareto front which indicate dominance of one type of device compared to the other. This is no surprise; nonlinear behavior detunes the TMD which reduces its ability to suppress structural vibrations (Soto‐Brito and Ruiz 1999). The same does not apply to the TMDI (and TID), demonstrating its robustness as a seismic protective device. This robustness compared to the TMD has been previously demonstrated for linear structures (Giaralis and Taflanidis 2018) considering the impact of the variability of the structural and excitation parameters. Here it is further showcased for the impact of nonlinearities in the structural behavior. In both instances, this robustness should be attributed to smaller influence of the exact device tuning on its ability to counteract the motion of the structure and provide vibration suppression. Note that for the 9th storey placement, the TMD is ultimately outperformed by IVAs in the nonlinear structure (as opposed to the linear structure) due to the aforementioned loss of efficiency. The latter leads to larger control forces for the nonlinear structure implementation (for that placement), discussed previously and shown in Table 2.

Looking next at the optimal design variables in Figs. 7 and 8, it is seen that despite some evident average trends, the curves present a somewhat erratic, discontinuous/non-smooth behavior, especially for the TMDI (or TID) implementation, represented in these plots by the configurations with β > 0. This should be attributed to the random search optimization implemented and the fact that there is a significant correlation between the variables in the way they impact performance; this is demonstrated by the fact that the Pareto fronts exhibit continuous trends despite the discontinuities in the identified design variables. Since the emphasis of any optimal design approach is on accurately identifying the optimal performance, the erratic behavior of the design variables is of no concern here. If desired, a refinement of the design variables corresponding to a specific performance level can be obtained using the epsilon constraint level as previously demonstrated by the authors (Taflanidis et al. 2019). The larger degree of erratic behavior observed for the TID/TMDI compared to the TMD should be attributed to the fact that more design variables exist for these devices. The trends themselves across the Pareto front are consistent with the anticipated behavior: an increase of the mass for TMD implementations or of the inertance for IVA implementations as the device efficiency (represented by J₂ value in these plots) increases, while the remaining two design variables take values that reflect the tuning of the device. As discussed earlier, the results in the figures also demonstrate very clearly the transition from TMD (β = 0) to IVA (β > 0) implementation across the Pareto front.

The attention is shifted now from the balanced design to the other two main design variants (D₁ and D₂), to examine the trends across different building kinematics (drift ratios and accelerations). Figure 9 shows Pareto fronts for acceleration-sensitive design (consequence quantification O₂), for both linear $D_{2}^{l}$ and nonlinear $D_{2}^{nl}$ designs, and for all four placements for two different intensities, s_c = 1 (top row) and s_c = 1.5 (bottom row). Figure 10 shows, similarly, results for the drift-sensitive design (consequence quantification O₁) for seismic intensity corresponding to s_c = 1.

Fig. 9

Pareto front for acceleration-sensitive design (consequence quantification O₂), for linear (left) and nonlinear (right) structural behavior, for scaling of intensity s_c = 1 (top row) and s_c = 1.5 (bottom row)

Fig. 10

Pareto front for drift-sensitive design (consequence quantification O₁), for linear (left) and nonlinear (right) structural behavior, for scaling of intensity s_c = 1 (top row) and s_c = 1.5 (bottom row)

Comparing the relative efficiency of the protective devices, it is seen that TMDI (or TID) are capable of effectively suppressing both drift and acceleration responses, something that does not hold true for the TMD, whose relative (compared to IVAs) advantages in suppressing accelerations is reduced. The latter is evident by the fact that TMDs dominate for smaller parts of the Pareto front for the acceleration-sensitive design (Fig. 9). With respect to the differences between linear and nonlinear behavior, we can again observe that the relative device efficiency reduces for the nonlinear structure, as also happened for the balanced design (Figs. 4 and 6), and that the efficiency reduction is larger for the accelerations, especially for larger seismic intensities (compare Pareto fronts for designs $D_{2}^{l}$ and $D_{2}^{1.5nl}$ in Fig. 9 and compare their maximum efficiency in Table 2). For the acceleration-sensitive design, it is also interesting to note that the efficiency of the 9th storey and 9–7 storey device placements dramatically improves, and these placements even emerge as the dominant ones across the entire Pareto front for the nonlinear structure (nl design variants). The better performance for the O₂ objective for device placement on the higher floors can be attributed to better effectiveness in controlling the acceleration at those floors, which are expected to be the larger accelerations along the entire height of the structure. The overall discussion stresses the sensitivity of the results to the assumption that the designer uses for the structural behavior in the design process and to the exact details of the performance quantification. Parenthetically, it should be pointed here that comparing the values of normalized J₁ between Figs. 9 and 10, the IVAs appear to have superior ability in mitigating floor accelerations (acceleration-sensitive design) compared to drifts (drift-sensitive design). In particular, it can be observed from Table 2, that acceleration-sensitive designs can provide a maximum J₁ reduction ranging from 44 to 70%, when all placements, scaling factors and structural assumptions are taken into consideration. The same values drop to a range of 17.5% up to 51.1% for the drift-sensitive design. This should be attributed to the different performance thresholds used for quantifying damage for accelerations and drifts, and not necessarily to the direct ability of the IVA to suppress floor accelerations more than drifts. The optimal IVA configurations significantly reduce severe and moderated damage for drift-sensitive design, but not necessarily light damage. On the other hand, accelerations are consistently reduced below their acceptable threshold even for the lower damage state, leading to a greater relative efficiency for the acceleration sensitive design. Even though both accelerations and drifts are efficiently suppressed, the relative reduction compared to the uncontrolled structure and the trends of the observed behavior depend to some degree on the consequence quantification details, stressing the importance of the appropriate selection of these details.

6.2 Examining the importance of considering nonlinear structural behavior in the design

The focus is now shifted on examining the importance of explicitly considering the nonlinear structural behavior in the optimal design of the protective device. In this second stage of the comparisons, design and performance are examined under different assumptions with respect to structural behavior and seismic intensity. Performance is primarily examined for the nonlinear structure. In each case, the Pareto front achieved by using the same assumptions at the design stage is examined to the performance for the optimal designs identified by utilizing different assumptions: different type of structural behavior, different seismicity levels or even different consequence quantifications. Since its impractical to exhaustively present all combinations considered, focus is on the ones that offer a bigger practical interest. Also, only key placements of the devices are presented.

Initially, the performance of the nonlinear structure, for the designs identified assuming linear structural behavior, is examined, for the design-level seismic intensity (s_c = 1). Results are presented for drift-sensitive (O₁), acceleration-sensitive (O₂) and balanced (O₃) consequence quantification. Results for placements 9th storey and 9–7 storey are presented in Fig. 11 and placements 8th storey and 8–6 storey in Fig. 12.

Fig. 11

Performance assessment for the nonlinear structure and for design seismic intensity (s_c = 1) for the drift-sensitive (O₁), acceleration-sensitive (O₂) and balanced (O₃) consequence quantifications. Optimal Pareto fronts are compared to the performance achieved using linear assumption of the structural behavior. Results are presented for 9th storey (left) and 9–7 storey (right) placement. Normalization of J₁ is established with respect to the uncontrolled structure performance for s_c = 1, for each of the different consequence quantifications

Fig. 12

Performance assessment for the nonlinear structure and for design seismic intensity (s_c = 1) for the drift-sensitive (O₁), acceleration-sensitive (O₂) and balanced (O₃) consequence quantifications. Optimal Pareto fronts are compared to the performance achieved using linear assumption of the structural behavior. Results are presented for 8th storey (left) and 8–6 storey (right) placement. Normalization of J₁ is established with respect to the uncontrolled structure performance for s_c = 1, for each of the different consequence quantifications

Results clearly indicate that the assumption of linear behavior leads to deterioration of the performance when compared to device configurations that explicitly considered nonlinear structural behavior at the design stage. This deterioration is larger for the domains of the Pareto front that correspond to higher protection efficiency (or higher forces) for each device type: TMD or TMDI/TID (the IVA). The latter is the reason that there are two significant domains of deviation in each Pareto front. One of them, the one corresponding to lower control forces, corresponds to the TMD and the other to the TMDI. This stems from the trend, commented also in the previous section, that the TMD and TMDI (or TID) parts of the Pareto front have distinct characteristics, and their union (yielding the final Pareto front) carries this fundamental distinction. It also clear that the deviation from the optimal performance is larger for the TMD, something that agrees with the trends identified earlier about the TMD effectiveness having larger dependence on its tuning, and therefore on the assumptions utilized at the design stage. IVAs are more robust, but still there is some importance of explicitly considering nonlinear behavior, which becomes more critical at the parts of the Pareto front that correspond to larger device efficiency. This trend is more significant for the accelerations over drifts (compare designs for objectives O₁ and O₃) and for increased device protection efficiency (compare placement of IVAs across one or two floors). These observations stress, in a different setting than the ones commented earlier, the importance of the multi-objective design framework, demonstrating how it can accommodate identification of performance trends across different protective device configurations. Overall, these performance assessments demonstrate the importance of the herein developed design framework, which explicitly accounts for nonlinear/hysteretic behavior.

Additional important trends are now explored by considering higher seismic intensities. Figure 13 shows the performance for the nonlinear structure for the highest seismic intensity (s_c = 1.5), for designs that have considered different seismic intensities, adopting either linear or nonlinear behavior at the design stage. Results are presented for the balanced design and two device placements. This figure provides some critical information; it reveals the robustness of the design against higher intensities than the one considered at the design stage. Designs considering linear behavior depart substantially from the optimal Pareto front, especially for larger differences of the intensities considered at the design and performance evaluation. The same holds for designs considering nonlinear behavior, though the difference is substantially smaller. Especially if a moderate only increase of the seismic intensity exists (compare results for s_c = 1.25 and 1.5) the departure from the optimal performance is small. These trends stress even more the importance of explicitly considering nonlinear structural behavior at the design stage, since it further improves robustness of the performance across higher intensity excitations, a behavior which is of critical importance in earthquake engineering applications.

Fig. 13

Performance assessment for the nonlinear structure and for high seismic intensity (s_c = 1.5) for balanced consequence quantifications. Optimal Pareto fronts are compared to the performance achieved using linear (left column) or nonlinear (right column) assumption of the structural behavior, each for different seismic intensity scaling cases. Results are presented for 9th storey and 9–7 storey placements

Finally, Fig. 14 explores the importance of the consequence quantification details within the nonlinear structural performance. Specifically, it focuses on the drift-sensitive case and examines the D₁ and D₄-j (j = 1, 2, 3) nonlinear designs for different seismic intensities, for the 9th storey and 9–7 storey placements. Performance is evaluated always for objective O₁, which corresponds to P₁. This set-up examines the implications of using only one damage state at the design stage, when the actual consequence quantification of interest combines contributions across multiple damage states. It ultimately showcases the importance of selecting appropriate performance thresholds for defining the performance objective J₁. It is clear that the performance of the configurations identified by using only the light (j = 1) or severe (j = 3) damage states may deviate from the optimal D₁ Pareto fronts, for all different scaling factors and for both placements, especially in parts of the Pareto front that correspond to higher device efficiency. The deviation is substantially larger when design emphasizes on severe damage states. Very good agreement is observed, though, when design emphasizes on the moderate (j = 2) damage state, especially for scaling factors of 1 and 1.25. This should be attributed to the fact that under the given performance quantifications suppressing of structural response, the moderate damage state is the most influential part in the definition of the O₁ consequence quantification. In general, these results stress the importance of having a J₁ formulation that is consistent with the desired performance quantification, and indicates that an approach that considers multiple damage states can be beneficial in facilitating a more appropriate consideration of the impact of vibration suppression across multiple damage levels.

Fig. 14

Performance assessment for the nonlinear structure and for different seismic intensities for drift-sensitive consequence quantification. Optimal Pareto fronts are compared to the performance achieved by designs utilizing O₄-j consequence quantifications for three different values of j (rows), corresponding to emphasis on light (j = 1), moderate (j = 2) or severe (j = 3) damage states at the design. Results are presented for 9th storey (left column) and 9–7 storey (right column) placements. Normalization of J₁ is established with respect to the uncontrolled structure performance for s_c = 1 and for the O₁ consequence quantification

7 Conclusions

The design of inerter-based vibration absorbers (IVAs) for multi-storey hysteretic structures was examined in this study. Emphasis was placed on performance of tuned-mass-damper-inerter (TMDI), with tuned-mass-damper (TMD) and tuned-inerter-damper (TID) implementations also examined as limiting cases of the TMDI. Earthquake hazard was modeled through a suite of representative acceleration time-histories, and the performance of the IVA equipped structure was evaluated through nonlinear response-history analysis (NLRHA). To accommodate the use of high-fidelity finite element models (FEMs) for accurately describing nonlinear structural response at the design stage, a reduced order model (ROM) formulation was leveraged, adopting the framework developed recently by the first and second author. The ROM is calibrated to match the hysteretic behavior of the original high-fidelity structure (without any protective device) by utilizing FEM time-history response data. The calibrated ROM then replaces the original FEM and is used to accurately assess the performance of the desired IVA configuration with a substantially lower computational cost (550-fold reduction in the case study considered) compared to the original high-fidelity FEM. A bi-objective IVA design was considered, with (i) first objective defined as the consequences associated with the exceedance of different thresholds for different engineering demand parameters (EDPs) and (ii) second objective corresponding to the peak IVA force developed during the entire duration of the excitation. The identification of the Pareto front of dominant designs for the bi-objective problem was solved using a random search optimization scheme, allowing for an efficient solution for different characterizations of seismic consequences. In the case study, a benchmark 9 storey steel structure was used and four different placements were examined for the TMDI configuration. It was shown that the replacement of the FEM with the ROM does not jeopardize the quality of the identified Pareto fronts, while by considering different scaling of the excitation and different quantifications for structural performance, the following main conclusions were drawn:

• The multi-objective design formulation, and the identified Pareto fronts, provide invaluable information for the vibration control effects provided by different optimal protective device designs and offer the ability for a comprehensive assessment of their performance. This accommodated in this manuscript a comprehensive investigation of the effects of nonlinear structural behavior on device efficiency.

• Comparison between the Pareto fronts for the linear and nonlinear structure reveals that nonlinear structural behavior leads to a small reduction of the IVA vibration suppression capabilities and of the associated control forces, compared to linear structural behavior, though still the benefits from the addition of the device are substantial, for reducing both drift ratios and accelerations.

• Examining the behavior across the different seismic intensities, a reduction of relative efficiency is observed for higher intensities for both the linear and nonlinear structures.

• Comparing the different types of IVAs, results show that TID and TMDI achieve practically identical performance across the entire front for both the linear and nonlinear structure. IVA placement at lower floors improves vibration control efficiency for both linear and nonlinear structure, with even more improved vibration suppression achieved by allowing IVA to span two storeys. On the other hand, the performance of the TMD changes drastically when nonlinear behavior is examined, since the period elongation associated with hysteretic behavior impacts its tuning and reduces its ability to suppress structural vibrations. The same does not apply to the TMDI (and TID), demonstrating its robustness as a seismic protective device.

• Comparison between the different assumptions utilized at the design stage, shows that use of linear structural models undermines the effectiveness of the IVA when performance is assessed considering hysteretic structural behavior. This clearly demonstrates the importance of having a design framework that explicitly considers nonlinear/hysteretic behavior, and represents the most important finding of this study.

• When explicitly considering nonlinear behavior in the design, the seismicity level does not significantly undermine the effectiveness of the TMDI that was designed assuming ground motions of smaller intensity, as long as the difference in the intensities is not excessively large.

• The objective function for describing structural performance at the design stage needs to be consistent with the desired consequence quantification for assessing the true performance of the protective device implementation. In general, use of multiple damage states can be beneficial in facilitating a more appropriate consideration of the impact of vibration suppression across multiple damage levels.

Appendix A: Modeling of the ideal inerter element in finite element simulation programs

Since the inerter has been recently introduced in the literature, a specialized mechanical element to model the behavior of an ideal inerter is not available so far in the element libraries of commercial or even in open-source finite element programs, like OpenSees. One way to model the inerter element in these programs is by modelling an isolated rigid frame element which can supplement the additional mass (inertance) using rotational inertia properties. To illustrate this modeling, consider a frame where two points u and v are connected by the two terminals of the inerter device as shown in Fig. 15a. Ignoring the rotational DoF of the nodes, the rotation θ of joint v relative to joint u is

$$\theta = \frac{{x_{s}^{v} - x_{s}^{u} }}{L}$$

(14)

Fig. 15

Modeling of inerter in a finite element program utilizing an isolated rigid bar

where $x_{s}^{v}$ and $x_{s}^{u}$ are the displacements of node v and u, respectively, and L is the distance between the nodes. If the two nodes are connected with a rigid frame with an inertial mass I, that is applied at node u, the force couple F created, also shown in Fig. 15b, satisfies the equilibrium equation

$$I \cdot \ddot{\theta } = F \cdot L$$

(15)

Utilizing Eq. (14) into Eq. (15), we end up with this expression for the force F

$$F = \frac{I}{{L^{2} }}(\ddot{x}_{s}^{v} - \ddot{x}_{s}^{u} )$$

(16)

The last equation matches the expression that provides the force of an ideal inerter, $\:F_{d} = b(\ddot{x}_{s}^{v} - \ddot{x}_{s}^{u} )$, for b = I/L². Therefore, for I = bL² the rigid frame modeling provides the desired inerter force for the chosen inertance b.

Note that the rotational inertia I does not influence the FEM kinematics and dynamical properties other than creating the additional desired inertial force couple F, as long as only translational dynamic DOFs are of interest, as is the case in the applications examined in this paper. This would have not been true, though, if rocking motion of the frame in Fig. 15 was of interest.

Therefore, in a finite element program, an inerter element can be modelled by defining an isolated rigid bar element with two nodes out of which one is supplied with a rotational mass equal to I = bL². The connection between such isolated element with the joints where the inerter element is required in the actual structure is achieved using joint constraints to enforce that the connected joints behave the same as the constrained DOFs.