Earthquake hazard and risk analysis for natural and induced seismicity: towards objective assessments in the face of uncertainty

Abstract

The fundamental objective of earthquake engineering is to protect lives and livelihoods through the reduction of seismic risk. Directly or indirectly, this generally requires quantification of the risk, for which quantification of the seismic hazard is required as a basic input. Over the last several decades, the practice of seismic hazard analysis has evolved enormously, firstly with the introduction of a rational framework for handling the apparent randomness in earthquake processes, which also enabled risk assessments to consider both the severity and likelihood of earthquake effects. The next major evolutionary step was the identification of epistemic uncertainties related to incomplete knowledge, and the formulation of frameworks for both their quantification and their incorporation into hazard assessments. Despite these advances in the practice of seismic hazard analysis, it is not uncommon for the acceptance of seismic hazard estimates to be hindered by invalid comparisons, resistance to new information that challenges prevailing views, and attachment to previous estimates of the hazard. The challenge of achieving impartial acceptance of seismic hazard and risk estimates becomes even more acute in the case of earthquakes attributed to human activities. A more rational evaluation of seismic hazard and risk due to induced earthquakes may be facilitated by adopting, with appropriate adaptations, the advances in risk quantification and risk mitigation developed for natural seismicity. While such practices may provide an impartial starting point for decision making regarding risk mitigation measures, the most promising avenue to achieve broad societal acceptance of the risks associated with induced earthquakes is through effective regulation, which needs to be transparent, independent, and informed by risk considerations based on both sound seismological science and reliable earthquake engineering.

1 Introduction

The study of earthquakes serves many noble purposes, starting with humankind’s need to understand the planet on which we live and the causes of these calamitous events that challenge the very idea of residing on terra firma. Throughout history, peoples living in seismically active regions have formulated explanations for earthquakes, attributing their occurrence to the actions to disgruntled deities, mythical creatures or, later on, the Aristotelian view that earthquakes are caused by winds trapped and heated within a cavernous Earth (which is echoed in Shakespeare’s Henry IV, Part 1). While it is easy for us to look on these worldviews as quaint or pitifully ignorant, our modern understanding of earthquakes and their origins is very recent (when my own father studied geology as part of his civil engineering education, the framework of plate tectonics for understanding geological events had yet to be formulated and published). The discipline of seismology has advanced enormously during the last century or so, and our understanding of earthquakes continues to grow. The study of seismicity was instrumental in understanding plate tectonics and the analysis of seismic waves recorded on sensitive instruments all over the world has revealed, like global X-rays, the interior structure of our planet. As well as such advances in science, the development of seismology has also brought very tangible societal benefits, one of the most laudable being to distinguish the signals generated by underground tests of nuclear weapons from those generated by earthquakes, which made a comprehensive test ban treaty possible (Bolt 1976).

The most compelling reason to study earthquakes, however, must now be to mitigate their devastating impacts on people and on societies. A great deal of effort has been invested in developing predictions of earthquakes, since with sufficient prior warning, evacuations could prevent loss of life and injury. There have been some remarkable successes, most notably the prediction of the February 1975 Haicheng earthquake in China (Adams 1976); however, the following year, the Tangshan earthquake on 28 July occurred without warning and took the lives of several hundreds of thousands of people. More recently, there has been a focus on earthquake early warning systems (e.g., Gasparini et al. 2007), which can provide between seconds and tens of seconds of advance warning that can allow life-saving actions to be taken. However, whether strong ground shaking is predicted a few seconds or even a few days ahead of time, the built environment will still be exposed to the effects of the earthquake. Consequently, the most effective and reliable approach to protecting individuals and societies from the impact of earthquakes is through seismically resistant design and construction.

To be cost effective in the face of limited resources, earthquake-resistant design first requires quantification of the expected levels of loading due to possible future earthquakes. Although not always made explicit, to demonstrate that the design is effective in providing the target levels of safety requires the analysis of the consequences of potential earthquake scenarios, for which the expected shaking levels are also required. The practice of assessing earthquake actions has progressed enormously over the last half century, especially in terms of identifying and quantifying uncertainties related to the location, magnitude, and frequency of future earthquakes, and to the levels of ground shaking that these will generate at a given location. The benefit of incorporating these uncertainties into the estimates of ground shaking levels is that the uncertainty can be taken into account in the definition of the design accelerations. This is not to say that seismic safety relies entirely on estimating the ‘correct’ level of seismic loading: additional margin is included in structural design, as has been clearly demonstrated by the safe performance of three different nuclear power plants in recent years. In July 2007, the magnitude 6.6 Niigata Chūetsu earthquake in western Japan occurred very close to the Kashiwazaki-Kawira nuclear power plant (NPP). At all seven reactor units, recorded accelerations exceeded the design motions (Fig. 1) without leading to any loss of radioactive containment. The magnitude 9.0 Tōhoku earthquake in March 2011 on the opposite coast of Japan generated motions at the Fukushima Daiichi NPP that also exceeded the design accelerations (Grant et al. 2017); the ensuing tsunami led to a severe nuclear accident at the plant, but the plant withstood the ground shaking without distress. A few months later, motions recorded at the North Anna NPP due to the M 5.8 Mineral, Virginia, USA earthquake also exceeded design acceleration levels without causing damage (Graizer et al. 2013).

Fig. 1

Recorded values of horizontal peak ground acceleration (PGA) at each unit of the Kashiwazaki-Kawira NPP during the 16 July 2007 Niigata Chūetsu earthquake (courtesy of Dr Norm Abrahamson)

Seismic safety in critical structures such as NPPs depends therefore on both the margins of resistance above the nominal design accelerations and the degree to which the estimates of the site demand, to which the design motions are referenced, reflect the uncertainty in their assessment. Therefore, for a nuclear regulator, capture of uncertainty in the assessment of seismic shaking levels provides assurance regarding the provision of adequate safety. However, the inclusion of large degrees of uncertainty can be viewed quite differently by other groups. For example, since inclusion of uncertainty generally leads to higher estimates of the accelerations (in theory broader uncertainty bands could lead to lower accelerations, but in practice it tends to push estimates in the opposite direction), owners and operators of these facilities may be averse to the inclusion of large intervals of uncertainty, especially if these are viewed as unnecessarily wide. For the public, capture of broad ranges of uncertainty in the estimates of earthquake hazard could be interpreted either way: on the one hand, it could be viewed positively as nuclear safety being enhanced through consideration of events that are stronger than what has been previously observed, whereas on the other hand, it could be seen as evidence that the science is too unsure to inform rational decision making and, in the face of such unknowns, safety cannot be guaranteed. The challenge therefore is two-fold: to develop impartial quantification of earthquake hazard and risk, and for these estimates to then be objectively accepted as the baseline for decision making regarding the management of the risk. This article discusses important advances in the estimation of earthquake hazard, and also explores, with concrete examples from practice, why impartial hazard estimates are sometimes met with stern— or even belligerent—resistance.

In recent years, earthquakes related to human activities—and generally referred to as induced seismicity—have attracted a great deal of scientific and societal attention. This has been driven primarily by more frequent occurrence of earthquakes of anthropogenic origin; a prime example being the remarkable increase in seismicity in the states of Oklahoma, Kentucky, and Texas, which has been related to hydrocarbon production (Fig. 2). However, the profile of induced seismicity in public debate, the media, and government policy has also been heightened by the controversy related to some of the industrial activities that have been shown to cause induced earthquakes, particularly hydraulic fracturing or fracking.

Fig. 2

Increase in seismicity in the Central and Eastern United States from 2009 to 2015 related to hydrocarbon production (Rubinstein and Babaie Mahani 2015)

The seismic hazard (shaking levels) and risk (damage) due to induced seismicity can be estimated using the procedures that have been developed for natural seismicity, with appropriate adjustments for the distinct characteristics of induced earthquakes. The frameworks that have been developed for estimating seismic hazard due to natural earthquakes should be taken advantage of in the field of induced seismicity given that the controversy surrounding these cases often makes it imperative to correctly identify the degrees of uncertainty. Equally important, however, is to bring into the quantification of induced seismic hazard an engineering perspective that relates the hazard to risk. I make the case in this article that to date the assessment of induced seismic hazard has often not quantified uncertainty well and, perhaps more importantly, has failed to relate the hazard to a rational quantification of risk. These shortcomings are particularly important because the challenges of the hazard estimates being accepted by different groups are often particularly acute, much more so than is the case of natural seismicity. A key question that the article sets out to address is whether it is possible for robust estimates of seismic hazard associated with potential induced earthquakes to be adopted at face value. This leads to the question of whether the hazard estimates can be used as a starting point in discussions surrounding the rational management of the associated risk and its balance with the benefits of the industrial activity with the potential to cause seismic activity. This article discusses a number of case histories in which such objectivity was glaringly absent, and also explores options that might facilitate the impartial acceptance of estimates of induced seismic hazard.

The focus of this paper, as its title indicates, is to promote objectivity in the assessment of seismic hazard and risk for both natural and induced earthquakes. Assessment therefore refers to two different processes, reflecting the focus of this article on the balance of these two aspects noted above: (1) the estimation of possible or expected levels of earthquake shaking; and (2) the interpretation or evaluation of these estimates as a reliable basis for risk mitigation. Despite this deliberate ambiguity in the use of the word assessment, clear and consistent terminology is actually of great importance, for which reason the article starts with brief definitions of the key concepts embedded in the title: the meaning of hazard and risk (Sect. 1.1), and then the nature of uncertainty (Sect. 1.2). This introduction then concludes with a brief overview of the paper (Sect. 1.3).

1.1 Seismic hazard and seismic risk

Seismic risk refers to undesirable consequences of earthquakes, which include death, injury, physical damage to buildings and infrastructure, interruption of business and social activities, and the direct and indirect costs associated with such outcomes. In a generic sense, risk can be defined as the possibility of such consequences occurring at a given location due to potential future earthquakes. In a more formal probabilistic framework, seismic risk is quantified by both the severity of a given metric of loss and the annual frequency or probability of that level of loss being exceeded.

Seismic hazard refers to the potentially damaging effects of earthquakes, the primary example being strong ground shaking (the full range of earthquake effects is discussed in Sect. 2). Again, in a generic sense, seismic hazard can be thought of as the possibility of strong shaking—measured, for example, by a specific level of peak ground acceleration (PGA)—occurring at a given location. In a probabilistic framework, the hazard is the probability or annual frequency of exceedance of different levels of the chosen measure of the vibratory ground motion.

Seismic hazard does not automatically create seismic risk: an earthquake in an entirely unpopulated region or in the middle of the ocean (remote from any submarine cables) will not constitute a risk: except, potentially, to any passing marine vessel (Ambraseys 1985). Risk only arises when there are buildings or infrastructure (such as transport networks, ports and harbours, energy generation and distribution systems, dams, pipelines, etc.) present at the locations affected by the shaking. The elements of the built environment that could be affected by earthquakes are referred to collectively as the exposure.

For a given element of exposure, the seismic risk is controlled in the first instance by the degree of damage that could be inflicted by an earthquake. This depends on the strength of the possible ground shaking at the site (the hazard) and how much damage the structure is likely to suffer under different levels of ground shaking, which is referred to as the fragility. Damage is often generally defined by discrete damage states, such as those specified in the European Macroseismic Scale (Grünthal 1998): DS1 is negligible to slight (slight non-structural damage, no structural damage), DS2 is moderate (slight structural damage, moderate non-structural damage), DS3 is substantial to heavy (moderate structural damage, heavy non-structural damage), DS4 is very heavy (heavy structural damage, very heavy non-structural damage), and DS5 is extensive (very heavy structural damage or collapse). An example set of fragility functions for a given building type is shown in Fig. 3.

Fig. 3

Fragility curves for a specific type of building, indicating the probability of exceeding different damage states as a function of spectral acceleration at a period of 2 s (Edwards et al. 2021)

Risk is generally quantified by metrics that more readily communicate the impact than the degree of structural and non-structural damage, such as the number of injured inhabitants or the direct costs of the damage. To translate the physical damage into other metrics requires a consequence function. Figure 4 shows examples of such functions that convert different damage states to costs, defined by damage ratios or cost ratios that are simply the cost of repairing the damage normalised by the cost of replacing the building. In some risk analyses, the fragility and consequence functions are merged so that risk metrics such as cost ratios or loss of life are predicted directly as a function of the ground shaking level; such functions are referred to as vulnerability curves. The choice to use fragility or vulnerability curves depends on the purpose of the risk study: to design structural strengthening schemes, insight is required regarding the expected physical damage, whereas for insurance purposes, the expected costs of earthquake damage may suffice.

Fig. 4

Examples of consequence functions that translate damage states to damage or cost ratios, from a Italy, b Greece, c Turkey and d California, (Silva et al. 2015)

Referring back to the earlier discussion, earthquake engineering for natural (or tectonic) seismicity generally seeks to reduce seismic risk to acceptable levels by first quantifying the hazard and then providing sufficient structural resistance to reduce the fragility (i.e., move the curves to the right, as shown in Fig. 5) such that the convolution of hazard and fragility will result in tolerable levels of damage. This does not necessarily mean no damage since designing all structures to resist all levels of earthquake loading without structural damage would be prohibitively expensive. The structural performance targets will generally be related to the consequences of structural damage or failure: single-family dwellings are designed to avoid collapse and preserve life safety; hospitals and other emergency services to avoid damage that would interrupt their operation; and nuclear power plants to avoid any structural damage that could jeopardise the containment of radioactivity. Earthquake engineering in this context is a collaboration between Earth scientists (engineering seismologists) who quantify the hazard and earthquake engineers (both structural and geotechnical) who then provide the required levels of seismic resistance in design. Until now, the way that the risk due to induced seismicity has been managed is very different and has been largely driven by Earth science: implicit assumptions are made regarding the exposure and its fragility, and the risk is then mitigated through schemes to either reduce the hazard at the location of the buildings by either relocating the operations (i.e., changing the exposure) or by controlling the induced seismicity. These two contrasting approaches are illustrated schematically in Fig. 6.

Fig. 5

Illustration of the effect of seismic strengthening measures on fragility curves for a specific building type and damage state (Bommer et al. 2015a)

Fig. 6

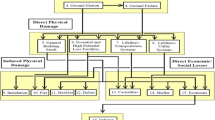
Schematic illustration of the classical approaches for mitigating seismic risk due natural and induced earthquakes by controlling different elements of the risk; in practice, explicit consideration of the exposure and its fragility has often been absent in the management of induced seismicity, replaced instead by vague notions of what levels of hazard are acceptable

1.2 Randomness and uncertainty

The assessment of earthquake hazard and risk can never be an exact science. Tectonic earthquakes are the result of geological processes that unfold over millennia, yet we have detailed observations covering just a few decades. The first seismographs came into operation around the turn of the twentieth century, but good global coverage by more sensitive instruments came many decades later. This has obvious implications for models of future earthquake activity that are based on extrapolations from observations of the past. Historical studies can extend the earthquake record back much further in time in some regions, albeit with reduced reliability regarding the characteristics of the events, and geological studies can extend the record for larger earthquakes over much longer intervals at specific locations. The first recordings of strong ground shaking were obtained in California in the early 1930s, but networks of similar instruments were installed much later in other parts of the world—the first European strong-motion recordings were registered more than three decades later. Even in those regions where such recordings are now abundant, different researchers derive models that yield different predictions. Consequently, seismic hazard analysis is invariably conducted with appreciable levels of uncertainty, and the same applies to risk analysis since there are uncertainties in every element of the model.

Faced with these uncertainties, there are two challenges for earthquake hazard and risk assessment: on the one hand, to gather data and to derive models that can reduce (or eliminate) the uncertainty, and, on the other hand, to ensure that the remaining uncertainty is identified, quantified, and incorporated into the hazard and risk analyses. In this regard, it is very helpful to distinguish those uncertainties that can, at least in theory, be reduced through the acquisition of new information, and those uncertainties that are effectively irreducible. The former are referred to as epistemic uncertainties, coming from the Greek word ἐπιστήμη which literally means science or knowledge, as they are related to our incomplete knowledge. The term uncertainty traditionally referred to this type of unknown, but the adjective epistemic is now generally applied to avoid ambiguity since the term uncertainty has often also been applied to randomness. Randomness, now usually referred to as aleatory variability (from alea, Latin for dice), is thought of as inherent to the process or phenomenon and, consequently, irreducible. In reality, it is more accurate to refer to apparent randomness since it is always characterised by the distribution of data points relative to a specific model (e.g., Strasser et al. 2009; Stafford 2015), and consequently can be reduced by developing models that include the dependence of the predicted parameter on other variables. Consider, for example, a model that predicts ground accelerations as a function of earthquake size (magnitude) and the distance of the recording site from the source of the earthquake. The residuals of the recorded accelerations relative to the predictions define the aleatory variability in the predictions, but this variability will be appreciably reduced if the nature of the surface geology at the recording sites is taken into account, even if this is just a simple distinction between rock and soil sites (Boore 2004). In effect, such a modification to the model isolates an epistemic uncertainty—the nature of the recording site and its influence on the ground acceleration—and thus removes it from the apparent randomness; this, in turn, creates the necessity, when applying the model, to obtain additional information, namely the nature of the surface geology at the target site.

Aleatory variability is generally measured from residuals of data relative to the selected model and is characterised by a statistical distribution. The quantification of epistemic uncertainty requires expert judgement (as discussed in Sect. 6) and is represented in the form of alternative models or distributions of values for model parameters. As is explained in Sect. 3, aleatory variability and epistemic uncertainty are handled differently in seismic hazard analysis and also influence the results in quite distinct ways. What is indispensable is that both types be recognised, quantified and incorporated into the estimation of earthquake hazard and risk.

1.3 Overview of the paper

Following this Introduction, the paper is structured in two parts that deal with natural earthquakes and induced seismicity, with the focus in both parts being the quest for objectivity in the assessment of their associated hazard.

Part I addresses natural earthquakes of tectonic origin, starting with a brief overview of the hazards associated with earthquakes (Sect. 2) followed by an overview of seismic hazard assessment, explaining how it incorporates aleatory variability in earthquake processes, as well as highlighting how hazard is always defined, explicitly or implicitly, in the context of risk (Sect. 3). Section 4 then discusses features of good practice in seismic hazard analysis that can be expected to facilitate acceptance of the result, emphasising especially the importance of capturing epistemic uncertainties. Section 5 discusses the construction of input models for seismic hazard analysis, highlighting recent developments that facilitate the representation of epistemic uncertainty in these inputs. Section 6 then discusses the role of expert judgement in the characterisation of epistemic uncertainty and the evolution of processes to organise multiple expert assessments for this objective. Part I concludes with a discussion of cases in which the outcomes of seismic hazard assessments have met with opposition (Sect. 7), illustrating that undertaking an impartial and robust hazard analysis does not always mean that the results will be treated objectively.

Part II addresses induced seismicity, for which objectivity in hazard and risk assessments can be far more elusive. The discussion begins with a brief overview of induced seismicity and some basic definitions, followed by a discussion of how induced earthquakes can be distinguished from natural earthquakes (Sect. 8), including some examples of when making this distinction has become controversial. Section 9 discusses seismic hazard and risk analysis for induced earthquakes through adaptation of the approaches that have been developed for natural seismicity, including the characterisation of uncertainties. Section 10 then discusses the mitigation of induced seismic risk, explaining the use of traffic light protocols (TLP) as the primary tool used in the scheme illustrated in Fig. 6, but also making the case for induced seismic risk to be managed in the same way as seismic risk due to tectonic earthquakes. Section 11 addresses the fact that for induced seismicity, there is often concern and focus on earthquakes of magnitudes that would generally be given little attention were they of natural origin, by reviewing the smallest tectonic earthquakes that have been known to cause damage. This then leads into Sect. 12 and four case histories of induced earthquakes that did have far-reaching consequences, despite their small magnitude. In every case it is shown that the consequences of the induced seismicity were not driven by physical damage caused by the ground shaking but by other non-technical factors, each one illustrating a failure to objectively quantify and rationally manage the perceived seismic risk. Part II closes with a discussion of the implications of the issues and case histories presented in terms of achieving objective and rational responses to earthquake risk arising from induced seismicity. A number of ideas are put forward that could contribute to a more balanced and objective response to induced earthquakes.

The paper then closes with a brief Discussion and Conclusions section that brings together the key messages from both Part I and Part II.

Finally, a few words are in order regarding the audience to which the paper is addressed. The article is addressed in the first instance to seismologists and engineers, since both of these disciplines are vital to the effective mitigation of earthquake risk (and, I shall argue, the contribution from earthquake engineering to confronting the challenges of induced seismicity has been largely lacking to date). However, if both impartial quantification of earthquake hazard and risk, and objective evaluation of hazard and risk estimates in the formulation of policy are to be achieved, other players need to be involved in the discussions, particularly regulators and operators from the energy sector, who may not have expertise in the field of Earth sciences or earthquake engineering. Consequently, the paper begins with a presentation of some fundamentals so that it can be read as a standalone document by non-specialists, as well as the usual readership of the Bulletin of Earthquake Engineering. Readers in the latter category may therefore wish to jump over Sects. 2 and 3 (and may feel that they should have been given a similar warning regarding Sect. 1.1 and 1.2).

Part I: Natural Seismicity

2 Earthquakes and seismic hazards

An earthquake is the abrupt rupture of a geological fault, initiating at a point referred to as the focus or hypocentre, the projection of which on the Earth’s surface is the epicentre. The displacement of the fault relaxes the surrounding crustal rocks, releasing accumulated strain energy that radiates from the fault rupture in the form of seismic waves whose passage causes ground shaking. Figure 7 illustrates the different hazards that can result from the occurrence of an earthquake.

Fig. 7

adapted from Bommer and Boore (2005)

Earthquake processes and their interaction with the natural environment (ellipses) and the resulting seismic hazard (rectangles);

2.1 Fault ruptures

As illustrated in Fig. 7, there are two important hazards directly associated with the fault rupture that is the source of the earthquake: surface fault rupture and tsunami.

2.1.1 Surface rupture

The dimensions of fault ruptures grow exponentially with earthquake magnitude, as does the slip on the fault that accompanies the rupture (e.g., Wells and Coppersmith 1994; Strasser et al. 2010; Leonard 2014; Skarlatoudis et al. 2015; Thingbaijam et al. 2017). Similarly, the probability of the rupture reaching the ground surface—at which point it can pose a very serious threat to any structure that straddles the fault trace—also grows with magnitude (e.g., Youngs et al. 2003). The sense of the fault displacement is controlled by the fault geometry and the tectonic stress field in the region: predominantly vertical movement is dip-slip and horizontal motion is strike-slip. Vertical motion is referred to as normal in regions of tectonic extension (Fig. 8) and reverse in regions of compression (Fig. 9).

Fig. 8

Normal-faulting scarp created by the 2006 Machaze M 7 earthquake in Mozambique, which occurred towards the southern end of the East African Rift (Fenton and Bommer 2006). The boy is standing on the hanging block (i.e., the fault dips under his feet) that has moved downwards in the earthquake

Fig. 9

Reverse-faulting scarp in Armenia following the Spitak earthquake of 1988, in the Caucasus mountains (Bommer and Ambraseys 1989). The three people to the left of the figure are on the foot wall (the fault dips away from them) and the hanging wall has moved upwards

The risk objective in the assessment of surface rupture hazard is generally to avoid locations where this hazard could manifest (in other words, to mitigate the risk by changing the exposure). For safety–critical structures such as nuclear power plants (NPPs), the presence of a fault capable of generating surface rupture would normally be an exclusionary criterion that would disqualify the site. Meehan (1984) relates the story of several potential NPP sites in California that were eventually abandoned when excavations for their foundations revealed the presence of active geological faults. For extended lifeline infrastructure, however, such as roads, bridges, and pipelines, it is often impossible to avoid crossing active fault traces and in such circumstances the focus moves to quantifying the sense and amplitude of potential surface slip, and to allow for this in the design. An outstanding example of successful structural design against surface fault rupture is the Trans-Alaskan Oil Pipeline, a story brilliantly recounted by the late Lloyd Cluff in his Mallet-Milne lecture of 2011. The pipeline crosses the Denali fault and was designed to accommodate up to 6 m of horizontal displacement and 1.5 m of vertical offset. The design was tested in November 2003 by a magnitude M 7.9 earthquake associated with a 336-km rupture on the Denali fault, with a maximum slip of 8.8 m. In the area where the pipeline crosses the fault trace, it was freely supported on wide sleepers to allow it to slip and thus avoid the compressional forces that would have been induced by the right-lateral strike-slip motion (Fig. 10). No damage occurred at all and not a drop of oil was spilt and thus a major environmental disaster was avoided: the pipeline transports 2.2 million barrels of crude oil a day. Failure of the pipeline would also have had severe economic consequences since at the time it transported 17% of US crude oil supply and accounted for 80% of Alaska’s economy.

Fig. 10

The Trans-Alaska pipeline crossing of the Denali fault, restored to its original configuration following the 2003 Denali earthquake to be able to withstand right-lateral displacement in future earthquakes (Image courtesy of Lloyd S Cluff)

There are also numerous examples of earth dams built across fault traces—the favourable topography allowing the creation of a reservoir often being the consequence of the faults—and designed to accommodate future fault offset (e.g., Allen and Cluff 2000; Mejía 2013). There have also been some spectacular failures causes by fault rupture, such as the Shih-Kang dam that was destroyed by the fault rupture associated with the 199 Chi-Chi earthquake in Taiwan (e.g., Faccioli et al., 2006).

Accommodating vertical offset associated with dip-slip faults can be even more challenging, but innovative engineering solutions can be found. Figure 11, for example, shows a detail of a high-pressure gas pipeline in Greece at a location where it crosses the trace of a dip-slip fault, and design measures have been added to allow the pipeline to accommodate potential fault slip without compromising the integrity of the conduit.

Fig. 11

Construction of high pressure gas pipeline from Megara to Corinth, Greece: where the pipeline crosses active faults, it is encased to prevent damage due to fault slip (Image courtesy of Professor George Bouckovalas, NTUA http://users.ntua.gr/gbouck/proj-photos/megara.html)

2.1.2 Tsunami

When a surface fault rupture occurs in the seabed, and especially for a reverse or thrust (a reverse fault of shallow dip) rupture typical of subduction zones, the displacement of a large body of water above the fault can create a gravity wave of small amplitude and great wavelength that travels across the ocean surface at a velocity equal to $\sqrt{gd}$, where g is the acceleration due to gravity (9.81 m/s²) and d is the depth of the ocean. As the wave approaches the shore, the speed of the wave reduces with the water depth and the wave height grows to maintain the momentum, creating what is called a tsunami, which is a Japanese word meaning ‘harbour wave’. Tsunamis can be the most destructive of all earthquake effects, as was seen in the 2004 Boxing Day M 9.2 earthquake that originated off the coast of Indonesia (e.g., Fujii and Satake 2007) and caused loss of life as far away as East Africa (Obura 2006), and the tsunami that followed the 2011 Tōhoku M 9.0 earthquake in Japan (e.g., Saito et al. 2011), which caused the loss of 20,000 lives. As indicated in Fig. 7, tsunamis can also be generated by submarine landslides (e.g., Ward 2001; Harbitz et al. 2006; Gusman et al. 2019), an outstanding example of which was the Storegga slide in the North Sea, assumed to have been triggered by an earthquake, that generated a tsunami that inundated areas along the east coast of Scotland (e.g., Dawson et al. 1988).

The estimation of tsunami hazard generally focuses on potential wave heights and run-up, the latter referring to the highest elevation on land to which the water rises. Such parameters can inform design or preventative measures, including elevated platforms and evacuation routes. Insufficient sea wall height at the Fukushima Daiichi NPP in Japan led to inundation of the plant due to the tsunami that followed the Tōhoku earthquake, leading to a severe nuclear accident despite the fact that the plant had survived the preceding ground shaking without serious damage. There can be significant scope for reducing loss of life due to tsunami through early warning systems that alert coastal populations to an impending wave arrival following a major earthquake (e.g., Selva et al. 2021); for tsunami the lead times can be much longer than early warning systems for ground shaking, for which reason these can be of great benefit.

2.2 Ground shaking

On a global scale, most earthquake destruction is caused by the strong shaking of the ground associated with the passage of seismic waves, and this shaking is also the trigger for the collateral geotechnical hazards discussed in Sect. 2.3. The focus of most seismic hazard assessments is to quantify possible levels of ground shaking, which provides the basis for earthquake-resistant structural design.

2.2.1 Intensity

Macroseismic intensity is a parameter that reflects the strength of the ground shaking at a given location, inferred from observations rather than instrumental measurements. There are several scales of intensity, the most widely used defining 12 degrees of intensity (Musson et al. 2010), such as the European Macroseismic Scale, or EMS (Grünthal 1998). For the lower degrees of intensity, the indicators are primarily related to the response of humans and to the movement of objects during the earthquakes; as the intensity increases, the indicators are increasingly related to the extent of damage in buildings of different strength. The intensity assigned to a specific location should be based on the modal observation and is often referred to as an intensity data point (IDP). Contours can be drawn around IDPs and these are called isoseismals, which enclose areas of equal intensity. The intensity is generally written as a Roman numeral, which reinforces that notion that it is an index and should be treated as an integer value. An isoseismal map, such as the one shown in Fig. 12, conveys both the maximum strength of the earthquake shaking and the area over which the earthquake was felt, and provides a very useful overview of an earthquake. Intensity can be very useful for a number of purposes, including the inference of source location and size for earthquakes that occurred prior to the dawn of instrumental seismology (e.g., Strasser et al. 2015). However, for the purposes of engineering design to mitigate seismic risk, intensity is of little use and recourse is made to instrumental recordings of the strong ground shaking.

Fig. 12

Isoseismal map for an earthquake in South Africa (Midzi et al. 2013). The IDPs for individual locations are shown in Arabic numerals

2.2.2 Accelerograms and ground-motion parameters

The development and installation of instruments capable of recording the strong ground shaking caused by earthquakes was a very significant step in the evolution of earthquake engineering since it allowed the detailed characterisation of these motions as input to structural analysis and design. The instruments are called accelerographs since they generate a record of the ground acceleration against time, which is known as an accelerogram. Many different parameters are used to characterise accelerograms, each of which captures a different feature of the shaking. The mostly widely used parameter is the peak ground acceleration, PGA, which is simply the largest absolute amplitude on the accelerogram. Integration of the accelerogram over time generates the velocity time-history, from which the peak ground velocity, PGV, is measured in the same way (Fig. 13). In many ways, PGV is a superior indicator of the strength of the shaking to PGA (Bommer and Alarcón 2006).

Fig. 13

The acceleration and velocity time-series from the recording at the CIG station of the M 5.7 San Salvador, El Salvador, earthquake of October 1986. The upper plot shows the accumulation of Arias intensity and the significant duration (of 0.96 s) based on the interval between obtaining 5% and 75% of the total Arias intensity

Another indicator of the strength of the shaking is the Arias intensity, which is proportional to the integral of the acceleration squared over time (Fig. 13). Arias intensity has been found to be a good indicator of the capacity of ground shaking to trigger instability in both natural and man-made slopes (Jibson and Keefer 1993; Harper and Wilson 1995; Armstrong et al. 2021).

The duration of shaking or number of cycles of motion can also be important parameters to characterise the shaking. Numerous definitions have been proposed for the measurement of both of these parameters (Bommer and Martinez-Pereira 1999; Hancock and Bommer 2005). The most commonly used measure of duration is called the significant duration and it is based on the accumulation of Arias intensity, defined as the time elapsed between reaching 5% and 75% or 95% of the total. Figure 13 illustrates this measure of duration.

The response of a structure to earthquake shaking depends to a large extent on the natural vibration frequency of the structure and the frequency content of the motion. As a crude rule-of-thumb, the natural vibration period of a reinforced concrete structure can be estimated as the number of storeys divided by 10, although this can also be calculated more accurately considering the height and other characteristics of the structure (Crowley and Pinho 2010). The response spectrum is a representation of the maximum response experienced by single-degree-of-freedom oscillators with a given level of damping (usually assumed to be 5% of critical) to a specific earthquake motion. The concept of the response spectrum is illustrated in Fig. 14. The response spectrum is the basic representation of ground motions used in all seismic design, and all seismic design codes specify a response spectrum as a function of location and site characteristics. The response spectrum can be scaled for damping ratios other than the nominal 5% of critical although the scaling factors depend not only on the target damping value, but also on the duration or number of cycles of motion (Bommer and Mendis 2005; Stafford et al. 2008a).

Fig. 14

The concept of the acceleration response spectrum: structures (lowest row) are represented as equivalent single-degree-of-freedom oscillators characterised by their natural period of vibration and equivalent viscous damping (middle row), which are then excited by the chosen accelerogram and the response of the mass calculated. The maximum response is plotted against the period of the oscillator and the complete response spectrum of the accelerogram is constructed by repeating for a large number of closely-spaced periods; building photographs from Spence et al. (2003)

2.2.3 Ground-motion prediction models

An essential element of any seismic hazard assessment is a model to estimate the value of the ground-motion parameter of interest at a particular location as a result of a specified earthquake scenario. The models reflect the influence of the source of the earthquake (the energy release), the path to the site of interest (the propagation of the seismic waves), and the characteristics of the site itself (soft near-surface layers will modify the amplitude and frequency of the waves). The parameters that are always included in such a model are magnitude (source), distance from the source to the site (path), and a characterisation of the site. Early models used distance from the epicentre (R_epi) or the hypocentre (R_hyp) but these distance metrics ignore the dimensions of the fault rupture and therefore are not an accurate measure of the separation from the source for sites close to larger earthquakes associated with extended fault ruptures. More commonly used metrics in modern models are the distance to the closest point on the fault rupture (R_rup) or the shortest horizontal distance to the projection of the fault rupture onto the Earth’s surface, which is known as the Joyner-Boore distance (Joyner and Boore 1981) or R_jb. Site effects were originally represented by classes, sometimes as simple as distinguishing between ‘rock’ and ‘soil’, but nowadays are generally represented by explicit inclusion of the parameter V_S30, which is the shear-wave velocity (which is a measure of the site stiffness) corresponding to the travel time of vertically propagating shear waves over the uppermost 30 m at the site. The reference depth of 30 m was selected because of the relative abundance of borehole data to this depth rather than any particular geophysical significance. The modelling of site effects has sometimes included additional parameters to represent the depth of sediments, such as Z_1.0 or Z_2.5 (the depths at which shear-wave velocities of 1.0 and 2.5 km/s are encountered). The more advanced models also include the non-linear response of soft soil sites for large-amplitude motions, often constrained by site response models developed separately (Walling et al. 2008; Seyhan and Stewart 2014). Another parameter that is frequently included is the style-of-faulting, SoF (e.g., Bommer et al. 2003). Figure 15 shows an example of predictions from a model for PGV, showing the influence of magnitude, distance, site classification and style-of-faulting.

Fig. 15

Predictions of PGV as a function of distance for two magnitudes showing the influence of site classification (left) and style-of-faulting (right) (Akkar and Bommer 2010)

Fig. 16

Acceleration response spectra predicted by five European models and one from California for sites with a V_S30 = 270 m/s and b V_S30 = 760 m/s for an earthquake of M 7 at 10 km (Douglas et al. 2014a)

By developing a series of predictive models for response spectral accelerations at a number of closely spaced oscillator periods, complete response spectra can be predicted for a given scenario. Figure 16 shows predicted response spectra for rock and soil sites at 10 km from a magnitude M 7 earthquake obtained from a suite of predictive models derived for Europe and the Mediterranean region, compared with the predictions from the Californian model of Boore and Atkinson (2008), which was shown to provide a good fit to European strong-motion data (Stafford et al. 2008b). The range of periods for which reliable response spectral ordinates can be generated depends on the signal-to-noise ratio of the accelerograms, especially for records obtained by older, analogue instruments, although processing is generally still required for modern digital recordings as well (Boore and Bommer 2005). The maximum usable response period of a processed record depends on the filters applied to remove those parts of the signal that are considered excessively noisy (Akkar and Bommer 2006).

There are many different approaches to developing predictive models for different ground-motion parameters (Douglas and Aochi 2008) but the most commonly used are regression on empirical datasets of ground-motion recordings, and stochastic simulations based on seismological theory (e.g., Boore 2003). The former is generally used in regions with abundant datasets of accelerograms, whereas simulations are generally used in regions with sparse data, where recordings from smaller earthquakes are used to infer the parameters used in the simulations. Stochastic simulations can also be used to adjust empirical models developed in a data-rich region for application to another region with less data, which preserves the advantages of empirical models (see Sect. 5.2). A common misconception regarding empirical models is that their objective is to reproduce as accurately as possible the observational data. The purpose of the models is rather to provide reliable predictions for all magnitude-distance combinations that may be considered in seismic hazard assessments, including those that represent extrapolations beyond the limits of the data. The empirical data provides vital constraint on the models, but the model derivation may also invoke external constraints obtained from simulations or independent analyses.

At this point, a note is in order regarding terminology. Predictive models for ground-motion parameters were originally referred to as attenuation relations (or even attenuation laws), which is no longer considered an appropriate name since the models describe the scaling of ground-motion amplitudes with magnitude as well as the attenuation with distance. This recognition prompted the adoption of the term ground motion prediction equations or GMPEs. More recently, there has been a tendency to move to the use of ground motion prediction models (GMPMs) or simply ground motion models (GMMs); in the remainder of this article, GMM is used.

Predicted curves such as those shown in Figs. 15 and 16 paint an incomplete picture of GMMs. When an empirical GMM is derived, the data always displays considerable scatter with respect to the predictions (Fig. 17). For a given model, this scatter is interpreted as aleatory variability. When the regressions are performed on the logarithmic values of the ground-motion parameter, the residuals—observed minus predicted values—are found to be normally distributed (e.g., Jayaram and Baker 2008). The distribution of the residuals can therefore be characterised by the standard deviation of these logarithmic residuals, which is generally represented by the Greek letter $\sigma$ (sigma). Consequently, GMMs do not predict unique values of the chosen ground-motion parameter, Y, for a given scenario, but rather a distribution of values:

Fig. 17

Adapted from Bommer and Abrahamson (2006)

Recorded PGA values at soil sites from the 2004 Parkfield earthquake in California, compared to predictions from the California GMM of Boore et al. (1997), illustrating the Gaussian distribution of the logarithmic residuals.

$$\mathrm{log}\left(Y\right)=f\left(M,R,{V}_{S30}, SoF\right)+\varepsilon \sigma $$

(1)

where $\varepsilon$ is the number of standard deviations above or below the mean (Fig. 17). If $\varepsilon$ is set to zero, the GMM predicts median values of Y, which have a 50% probability of being exceeded for the specified scenario; setting $\varepsilon =1$ yields the mean-plus-one-standard deviation value, which will be appreciably higher and have only a 16% probability of being exceeded.

Typical values of the standard deviation of logarithmic ground-motion residuals are generally such that 84-percentile values of motion are between 80 and 100% larger than the median predictions. The expansion of ground-motion datasets and the development of more sophisticated models has not resulted in any marked reduction of sigma values (Strasser et al., 2009); indeed, the values associated with recent models are often larger than those that were obtained for earlier models (e.g., Joyner and Boore 1981; Ambraseys et al. 1996) but this may be the result of early datasets being insufficiently large to capture the full distribution of the residuals. Progress in reducing sigma values has been made by decomposition of the variability into different components, which begins with separating the total sigma into between-event ($\tau$) and within-event ($\phi$) components, which are related by the following expression:

$$\sigma = \sqrt{{\tau }^{2}+{\phi }^{2}}$$

(2)

The first term corresponds to how the average level of the ground motions varies from one earthquake of a given magnitude to another, whereas the latter reflects the spatial variability of the motions. The concepts are illustrated schematically in Fig. 18: $\tau$ is the standard deviation of the $\delta B$ residuals and $\phi$ the standard deviation of the $\delta W$ residuals. Additional decomposition of these two terms is then possible, in which it is possible to identify and separate elements that in reality correspond to epistemic uncertainties (i.e., repeatable effects that can be constrained through data acquisition and modelling) rather than aleatory variability; such decomposition of sigma is discussed further in Sect. 5.

Fig. 18

Conceptual illustration of between-event and within-event residuals (Al Atik et al. 2010)

Several hundred GMMs, which predict all of the ground-motion parameters described in Sect. 2.2 and are derived for application to many different regions of the world, have been published. Dr John Douglas has provided excellent summaries of these models (Douglas 2003; Douglas and Edwards 2016), and also maintains a very helpful online resource that allows users to identify all currently published GMMs (www.gmpe.org.uk).

2.3 Geotechnical hazards

While the single most important contributor to building damage caused by earthquakes is ground shaking, damage and disruption to transportation networks and utility lifelines is often the result of earthquake-induced landslides and liquefaction (Bird and Bommer 2004).

2.3.1 Landslides

Landslides are frequently observed following earthquakes and can be a major contributor to destruction and loss of life (Fig. 19).

Fig. 19

Major landslide triggered by the El Salvador earthquake of January 2001 (Bommer and Rodriguez 2002); another landslide triggered in Las Colinas by this earthquake killed around 500 people

The extent of this collateral hazard depends on the strength of earthquake as reflected by the magnitude (e.g., Keefer 1984; Rodrıguez et al. 1999), but it also depends strongly on environmental factors such as topography, slope geology, and precedent rainfall. Assessment of the hazard due to earthquake-induced landslides begins with assessment of shaking hazard since this is the basic trigger. In a sense, it can be compared with risk assessment as outlined in Sect. 1.1, with the exposure represented by the presence of slopes, and the fragility by the susceptibility of the slopes to become unstable due to earthquakes (which is reflected by their static factor of safety against sliding). Indeed, Jafarian et al. (2021) present fragility functions for seismically induced slope failures characterised by different levels of slope displacement as a function of measures of the ground shaking intensity.

2.3.2 Liquefaction

Liquefaction triggering is a phenomenon that occurs in saturated sandy soils during earthquake shaking, which involves the transfer of overburden stress from the soil skeleton to the pore fluid, with a consequent increase in pore water pressure and reduction in effective stress. This stress transfer is due to the contractive tendencies of the soil skeleton during earthquake shaking. Once liquefied, the shear resistance of the soil drastically reduces and the soil effectively behaves like a fluid, which can result in structures sinking into the ground. Where there is a free face such as a river or shoreline, liquefaction can lead to lateral spreading (Fig. 20). Liquefaction can result in buildings becoming uninhabitable and can also cause extensive disruption, especially to port and harbour facilities. However, there are no documented cases of fatalities resulting from soil liquefaction, unless one includes flow liquefaction (e.g., de Lima et al. 2020;).

Fig. 20

Lateral spreading on the bank of the Lempa River in El Salvador due to liquefaction triggered by the M 7.7 subduction-zone earthquake of January 2001; notice the collapsed railway bridge in the background due to the separation of the piers caused by the spreading (Bommer et al. 2002)

As with landslide hazard assessment, the assessment of liquefaction triggering hazard can also be compared to risk analysis, with the shaking once again representing the hazard, the presence of liquefied soils the exposure, and the susceptibility of these deposits to liquefaction the fragility. In the widely used simplified procedures (e.g., Seed and Idriss 1971; Whitman 1971; Idriss and Boulanger 2008; Boulanger and Idriss 2014), the ground motion is represented by PGA and a magnitude scaling factor, MSF, which is a proxy for the number of cycles of motion.

Geyin and Maurer (2020) present fragility functions for the severity of liquefaction effects as a function of a parameter that quantifies the degree of liquefaction triggering. Structural fragility functions can be derived in terms of the resulting soil displacement (Bird et al. 2006) or another measure of the liquefaction severity (Di Ludovico et al. 2020), so that liquefaction effects can be incorporated into seismic risk analyses although this requires in situ geotechnical data and information regarding the foundations of buildings in the area of interest (Bird et al. 2004).

3 Seismic hazard and risk analysis

In this section, I present a brief overview of seismic hazard assessment, focusing exclusively on the hazard of ground shaking, highlighting what I view to be an inextricable link between hazard and risk, and also emphasising the issue of uncertainty, which is a central theme of this paper. For reasons of space, the description of hazard and risk analysis is necessarily condensed, and I would urge the genuinely interested reader to consider three textbooks for more expansive discussions of the fundamentals. Earthquake Hazard Analysis: Issues and Insights by Reiter (1990) remains a very readable and engaging overview of the topic and as such is an ideal starting point. The monograph Seismic Hazard and Risk Analysis by McGuire (2004) provides a succinct and very clear overview of these topics. For an up-to-date and in-depth treatment of these topics, I strongly recommend the book Seismic Hazard and Risk Analysis by Baker et al. (2021)—I have publicly praised this tome in a published review (Bommer 2021) and I stand by everything stated therein.

3.1 Seismic hazard analysis

The purpose of a seismic hazard assessment is to determine the ground motions to be considered in structural design or in risk estimation. Any earthquake hazard assessment consists of two basic components: a model for the source of future earthquakes and a model to estimate the ground motions at the site due to each hypothetical earthquake scenario. Much has been made over the years of the choice between deterministic and probabilistic approaches to seismic hazard assessment. In a paper written some 20 years ago (Bommer 2002), I described the vociferous exchanges between the proponents of deterministic seismic hazard analysis (DSHA) and probabilistic seismic hazard analysis (PSHA) as “an exaggerated and obstructive dichotomy”. While I would probably change many features of that article if it were being written today, I think this characterisation remains valid for the simple reason that it is practically impossible to avoid probability in seismic hazard analysis. Consider the following case: imagine an important structure very close (< 1 km) to a major geological fault that has been found to generate earthquakes of M 7 on average every ~ 600 years (this is actually the situation for the new Pacific locks on the Panama Canal, as described in Sect. 7.2). Assuming the structure has a nominal design life in excess of 100 years, it would be reasonable to assume that the fault will generate a new earthquake during the operational lifetime (especially if the last earthquake on the fault occurred a few centuries ago, as is the case in Panama) and therefore the design basis would be a magnitude 7 earthquake at a distance of 1 km. However, to calculate the design response spectrum a decision needs to be made regarding the exceedance level at which the selected GMM should be applied: if the median motions are adopted (setting $\varepsilon =0$), then in the event of the earthquake occurring, there is a 50% probability that the design accelerations will be exceeded. If instead the 84-percentile motions are used (mean plus one standard deviation), there will be a 1-in-6 chance of the design accelerations being exceeded. The owner of the structure would need to choose the level commensurate with the desired degree of safety, and this may require more than one standard deviation on the GMM. Whatever the final decision, the hazard assessment now includes a probabilistic element (ignoring the variability in the GMM and treating it as a deterministic model, which implies a 50% probability of exceedance, does not make the variability disappear).

If a probabilistic framework is adopted, the decision regarding the value of $\varepsilon$ would take into account the recurrence interval of the design earthquake (in this case, 600 years) to choose the appropriate GMM exceedance level: the median level of acceleration would have a return period of 1,200 (600/0.5) years, whereas for the 84-percentile motions, the return period would be 3,600 years. If the target return period were selected as 10,000 years, say, then the response spectrum would need to be obtained by including 1.55 standard deviations of the GMM, yielding accelerations at least 2.5 times larger than the median spectral ordinates.

In practice, most seismic design situations are considerably more complex in terms of the seismic sources and the earthquakes contributing to the hazard than the simple case described above. For example, the site hazard could be still be dominated by a single geological fault, located a few kilometres away from the site at its closest approach, but of considerable length (such that individual earthquakes do not rupture the full length of the fault and will thus not necessarily occur on the section of the fault closest to the site), and which is capable of generating earthquakes of different magnitudes, the larger earthquakes occurring less frequently (i.e., having longer average recurrence intervals) than the smaller events. A deterministic approach might propose to assign the largest magnitude that the fault is considered capable of producing to a rupture adjacent to the target site. However, this would ignore two important considerations, the first is that the smaller earthquakes are more frequent (as a rule-of-thumb, there is a tenfold increase in the earthquake rate for every unit reduction in magnitude) and more frequent earthquakes can be expected to sample higher values of $\varepsilon$, or expressed another way, the more earthquakes of a particular size that occur, the more likely they are to generate higher-than-average levels of ground shaking. The second consideration is that ground-motion amplitudes do not increase linearly with increasing earthquake magnitude, as shown in Fig. 21. Consequently, more frequent scenarios of M 6, sampling higher $\varepsilon$ values, could result in higher motions at the site than scenarios of M 7. Of course, the rate could simply be ignored, and a decision could be taken to base the design on the largest earthquake, but the rationale—which is sometimes invoked by proponents of DSHA—would be that by estimating the hazard associated with the worst-case scenario one effectively envelopes the various possibilities. However, for this to be true, the scenario would need to correspond to the genuine upper bound of all scenarios, which would mean placing the largest earthquake the fault could possibly produce at the least favourable location, and then calculating the ground motions at least 3 or 4 standard deviations above the median. In most cases, such design motions would be prohibitive and in practice seismic hazard assessment always backs away from such extreme scenarios.

Fig. 21

Scaling of PGA (left) and spectral acceleration at 0.2 s (right) with magnitude for a rock (V_S30 = 760 m/s) site at 10 km using four NGA-West2 GMMs: Abrahamson et al. (2014), Boore et al. (2014), Campbell and Bozorgnia (2014) and Chiou and Youngs (2014)

The scenario of a single active fault dominating all hazard contributions is a gross simplification in most cases since there will usually be several potential sources of future earthquakes that can influence the hazard at the site. Envisage, for example, a site in a region with several seismogenic faults, including smaller ones close to the site and a large major structure at greater distance, all having different slip rates. A classical DSHA would simply estimate the largest earthquake that could occur on each fault (thus defining the magnitude, M) and associate it with a rupture located as close to the site as possible (which then determines the distance R); for each M-R pair, the motions at the site would then be calculated with an arbitrarily chosen value of $\varepsilon$ and the final design basis would be the largest accelerations (although for different ground-motion parameters, including response spectral ordinates at different periods, different sources may dominate). In early practice, $\varepsilon$ was often set to zero, whereas more recently it became standard practice to adopt a value of 1. If one recognises that the appropriate value of this parameter should reflect the recurrence rate of the earthquakes, and also takes account of the highly non-linear scaling of accelerations with magnitude (Fig. 21), identifying the dominant scenario that should control the hazard becomes considerably more challenging.

An additional complication that arises in practice is that it is usually impossible to assign all observed seismicity to mapped geological faults, even though every seismic event can be assumed to have originated from rupture of a geological fault. This situation arises both because of the inherent uncertainty in the location of earthquake hypocentres and the fact that not all faults are detected, especially smaller ones and those embedded in the crust that do not reach the Earth’s surface. Consequently, some sources of potential future seismicity are modelled simply as areas of ‘floating’ earthquakes that can occur at any location within a defined region. The definition of both the location and the magnitude of the controlling earthquake in DSHA then becomes an additional challenge: if the approach genuinely is intended to define the worst-case scenario, in many cases this will mean that the largest earthquake that could occur in the area would be placed directly below the site, but this is rarely, if ever, done in practice. Instead, the design earthquake is placed at some arbitrarily selected distance (in the US, where DSHA was used to define the design basis for most existing NPPs, this was sometimes referred to as the ‘shortest negotiated distance’), to which the hazard estimate can be very sensitive because of the swift decay of ground motions with distance from the earthquake source (Fig. 22).

Fig. 22

Median PGA values predicted by the European GMM of Akkar et al. (2014) at rock sites (V_S30 = 760 m/s) plotted against distance for a magnitude M 6.5 strike-slip earthquake; both plots show exactly the same information but the left-hand frame uses the conventional logarithmic axes whereas the right-hand frame used linear axes and perhaps conveys more clearly how swiftly the amplitudes decay with distance

The inspired insight of Allin C. Cornell and Luis Esteva was to propose an approach to seismic hazard analysis, now known as PSHA, that embraced the inherent randomness in the magnitude and location of future earthquakes by treating both M and R as random variables (Esteva 1968; Cornell 1968). The steps involved in executing a PSHA are illustrated schematically in Fig. 23.

Fig. 23

(adapted from USNRC 2018)

Illustration of the steps involved in a PSHA

A key feature of PSHA is a model for the average rate of earthquakes of different magnitudes, generally adopting the recurrence relationship of Gutenberg and Richter (1944):

$$\mathrm{log}\left(N\right)=a-bM$$

(3)

where N is the average number of earthquakes of magnitude ≥ M per year, and a and b are coefficients found using maximum likelihood method (e.g., Weichert 1980); least squares fitting is not appropriate since for a cumulative measure such as N, the data points are not independent. The coefficient a is the activity rate and is higher in regions with greater seismicity, whereas b reflects the relative proportions of small and large earthquakes (and often, but not always, takes a value close to 1.0). The recurrence relation is truncated at an upper limit, Mmax, which is the largest earthquake considered to be physically possible within the source of interest. The estimation of Mmax is discussed further in Sect. 9.2.

Rather than an abrupt truncation of the recurrence relationship at Mmax, it is common to use a form of the recurrence relationship that produces a gradual transition to the limiting magnitude:

$$N\left(M\right)=\nu ({M}_{lower})\left[\frac{{e}^{-\beta (M-{M}_{lower})}-{e}^{-\beta (Mmax-{M}_{lower})}}{1-{e}^{-\beta (Mmax-{M}_{lower})}}\right]$$

(4)

where M_lower is the lower magnitude limit, $\nu ({M}_{lower})$ is the annual rate of earthquakes with that magnitude, and $\beta =b.\mathrm{ln}(10)$. For faults, it is common to adopt instead a characteristic recurrence model, since it has been observed that large faults tend to generate large earthquakes with an average recurrence rate that is far higher than what would be predicted from extrapolation of the recurrence statistics of smaller earthquakes (e.g., Wesnousky et al. 1983; Schwartz and Coppersmith 1984; Youngs and Coppersmith 1985). Whereas the Gutenberg-Richter recurrence parameters are generally determined from analysis of the earthquake catalogue for a region, the parameterisation of the characteristic model is generally based on geological evidence.

In publications that followed the landmark paper of Cornell (1968), the variability in the GMM was also added as another random variable in PSHA calculations (see McGuire 2008). Consequently, PSHA is an integration over three variables: M, R and $\varepsilon$. Rather than identifying a single scenario to characterise the earthquake hazard, PSHA considers all possible scenarios that could affect the site in question, calculating the consequent rate at which different levels of ground motion would be exceeded at the site of interest as a result. For a given value of the ground-motion parameter of interest (say, PGA = 0.2 g), earthquakes of all possible magnitudes are considered at all possible locations within the seismic sources, and the value of $\varepsilon$ required to produce a PGA of 0.2 g at the site is calculated in each case. The annual frequency at which this PGA is produced at the site due to each earthquake is the frequency of events of this magnitude (determined from the recurrence relationship) multiplied by the probability associated with the $\varepsilon$ value (obtained from the standard normal distribution). By assuming that all the earthquake scenarios are independent—for which reason foreshocks and aftershocks are removed from the earthquake catalogue before calculating the recurrence parameters, a process known as de-clustering—the frequencies can be summed to obtain the total frequency of exceedance of 0.2 g. Repeating the exercise for different values of PGA, a hazard curve can be constructed, as in the lower right-hand side of Fig. 23. The hazard curve allows rational selection of appropriate design levels on the basis of the annual exceedance frequency (or its reciprocal, the return period): return periods used to define the design motions for normal buildings are usually in the range from 475 to 2,475 years, whereas for NPPs the return periods are in the range 10,000 to 100,000 years.

Since PSHA calculations are effectively a book-keeping exercise that sums the contributions of multiple M-R-$\varepsilon$ triplets to the site hazard, for a selected annual exceedance frequency the process can be reversed to identify the scenarios that dominate the hazard estimates, a process that is referred to as disaggregation (e.g., McGuire 1995; Bazzurro and Cornell 1999). An example of a hazard disaggregation is shown in Fig. 24; to represent this information in a single scenario, one can use the modal or mean values of the variables, each of which has its own merits and shortcomings (Harmsen and Frankel 2001).

Fig. 24

Disaggregation of the hazard in terms of spectral accelerations at 1.0 s for an annual exceedance frequency of 10^–4 showing the relative contributions of different M-R-$\upvarepsilon$ combinations (Almeida et al. 2019)

Since PSHA is an integration over three random variables, it is necessary to define upper and lower limits on each of these, as indicated in Fig. 25. The upper limit on magnitude has already been discussed; the lower limit on magnitude, M_min, is discussed in Sect. 3.2. For distance, the minimum value will usually correspond to an earthquake directly below the site (unlike the upper left-hand panel in Fig. 23, the site is nearly always located within a seismic source zone, referred to as the host zone), whereas the upper limit, usually on the order of 200–300 km, is controlled by the farthest sources that contribute materially to the hazard (and can be longer if the site region is relatively quiet and there is a very active seismic source, such as a major fault or a subduction zone, at greater distance). Standard practice is to truncate the residual distribution at a limit such as 3 standard deviations; the lower limit on $\varepsilon$ is unimportant. There is neither a physical nor statistical justification for such a truncation (Strasser et al. 2008) but it will generally only impact on the hazard estimates for very long return periods in regions with high seismicity rates (Fig. 26).

Fig. 25

source zones, b recurrence relations, and c GMMs (Bommer and Crowley 2017)

Illustration of integration limits in PSHA in terms of a seismic

Fig. 26

Illustration of the effect of truncating the distribution of ground-motion residuals by imposing different values of ${\upvarepsilon }_{\mathrm{max}}$ in PSHA calculations for regions of low (upper) and high (lower) seismicity rates (Bommer et al. 2004)

3.2 Seismic risk as the context for PSHA

In my view, seismic hazard assessment cannot—and should not—be separated from considerations of seismic risk. Leaving aside hazard sensitivity calculations undertaken for research purposes, all seismic hazard assessments have a risk goal, whether this is explicitly stated or only implicit in the use of the results. When I have made this point in the past, one counter argument given was that one might conduct a PSHA as part of the design of strong-motion recording network, but in that case I would argue that the ‘risk’ would be installing instruments that yield no or few recordings. To be meaningful, hazard must be linked to risk, either directly in risk analysis or through seismic design to mitigate risk. In the previous section I referred to return periods commonly used as the basis for seismic design, but in themselves these return periods do not determine the risk level; the risk target is also controlled by the performance criteria that the structure should meet under the specified loading condition, such as the ‘no collapse’ criterion generally implicit in seismic design codes as a basis for ensuring life safety. For a NPP, the performance target will be much more demanding, usually related to the first onset of inelastic deformation. In effect, the return period defines the hazard, and the performance targets the fragility, both chosen in accordance with the consequences of failure to meet the performance criterion. For NPPs, the structural strength margins (see Fig. 1) mean that the probability of inelastic deformations will be about an order of magnitude lower than the annual exceedance frequency of the design motions, and additional structural capacity provides another order of magnitude against the release of radiation: design against a 10,000-year ground motion will therefore lead to a 1-in-1,000,000 chance of radiation release.

One way in which risk considerations are directly linked to PSHA is in the definition of the minimum magnitude, M_min, considered in the hazard integrations. This is not the same as the smallest magnitude, M_lower, used in the derivation of the recurrence relation in Eq. (4), but rather it is the smallest earthquake that is considered capable of contributing to the risk (and is therefore application specific). This can be illustrated by considering how seismic risk could be calculated in the most rigorous way possible, for a single structure. For every possible earthquake scenario (defined by its magnitude and location), a suite of acceleration time-histories could be generated or selected from a very large database; collectively, the time-histories would sample the range of possible ground motions for such a scenario in terms of amplitude, frequency content, and duration or number of cycles. Non-linear structural analyses would then be performed using all these records, and the procedure repeated for all possible scenarios. For a given risk metric, such as a specified level of damage, the rate can be determined by the proportion of analyses leading to structural damage above the defined threshold, which can then be combined with the recurrence rate of the earthquake scenarios to estimate annual rates of exceeding the specified damage level (Fig. 27).

Fig. 27

Schematic illustration of rigorous risk assessment for a single structure and a defined response condition or limit state; a for each earthquake scenario, a suite of accelerograms is generated and used in dynamic analyses of a structural model, and b the results used to determine the rate at which damage occurs (Bommer and Crowley 2017)

For any given structure, there will be a magnitude level below which the ground motions never cause damage, regardless of their distance from the site. The usual interpretation of such a result is that the short-duration motions from these smaller earthquakes lack the required energy to cause damage. Now, in practice, such an approach to seismic risk analysis would be prohibitively intensive in terms of computational demand, for which reason several simplifications are made. Firstly, the earthquake scenarios and resulting acceleration time-histories are represented by the results of hazard analyses, and secondly the dynamic analyses are summarised in a fragility function. Usually, the hazard is expressed in terms of a single ground-motion parameter that is found to be sufficient to act as an indicator of the structural response; it is also possible, however, to define the fragility in terms of a vector of ground-motion parameters (e.g., Gehl et al. 2013). In a Monte Carlo approach to risk assessment, individual earthquake scenarios are still generated, but for each one the chosen ground-motion parameter is estimated rather than generating suites of accelerograms. If the hazard is expressed in terms of a simple hazard curve, the risk can be obtained by direct convolution of the hazard and fragility curves (Fig. 28). However, in this simplified approach it is necessary to avoid inflation of the risk through inclusion of hazard contributions from the small-magnitude events that are effectively screened out in the more rigorous approach. This is the purpose of the lower magnitude limit, M_min, imposed on the hazard integral, although there has been a great deal of confusion regarding the purpose and intent of this parameter (Bommer and Crowley 2017). In an attempt to address these misunderstandings, Bommer and Crowley (2017) proposed the following definition: “M_min is the lower limit of integration over earthquake magnitudes such that using a smaller value would not alter the estimated risk to the exposure under consideration.” The imposition of M_min can modify the hazard—in fact, if it did not, it would be pointless—but it should not change the intended risk quantification. For NPP, typical values for M_min are on the order of 5.0 (e.g., McCann and Reed 1990).

Fig. 28

Illustration of seismic risk assessment starting with a a seismic hazard curve in terms of PGA and then b combining this hazard curve with a fragility function so that c the convolution of the two yields the total probability of collapse (Bommer and Crowley 2017)

The key point being made here is that M_min is really intended to filter out motions that are insufficiently energetic to be damaging, so it could also be defined as vector of magnitude and distance (the magnitude threshold increasing with distance from the site), or in terms of a ground-motion parameter. This has been done through the use of a CAV (cumulative absolute velocity, which is the integral of the absolute acceleration values over time) filter, which prevents ground motions of low energy from contributing to the hazard estimate. The original purpose of CAV was to inform decision-making following safe shutdown of NPPs and re-start following earthquake shaking (EPRI 1988). However, CAV filters have been proposed as an alternative to M_min (EPRI 2006a; Watson-Lamprey and Abrahamson 2007) and these have prompted the development of new GMMs for the conditional prediction of CAV (Campbell and Bozorgnia 2010). Other ground-motion parameters or vectors of parameters might serve the same purpose equally well. In practice, different parameters may perform better in different applications, depending on which measures of ground-motion intensity are found to be most efficient for defining the fragility functions of the exposure elements for which risk is directly or indirectly being assessed or mitigated.

The parameter M_min is a very clear indicator of the risk relevance of PSHA, but other hazard inputs should also be defined cognisant of the intended risk application, starting with the ground-motion parameters used to quantify the shaking hazard. This includes the subtle issue of how the horizonal component of motion is defined from the two recorded components of each accelerogram. Early GMMs tended to use the larger of the two components but there has subsequently been a trend towards using the geometric mean of the parameters from each horizontal component and numerous variations of this convention, all of which seek to approximate a randomly oriented component (Boore et al. 2006; Watson-Lamprey and Boore 2007; Boore 2010). There is no basis to identify an optimal or most appropriate definition, but it is very important that the component definition employed in the hazard analysis is consistent with the way the horizontal earthquake loading is applied in the structural analyses related to the risk mitigation or analysis. For example, if the geometric mean component is adopted in the hazard analysis but a single, arbitrarily selected horizontal component of the accelerograms is used to derive the fragility functions, then there is an inconsistency that requires accommodation of the additional component-to-component variability (Baker and Cornell 2006). For an interesting discussion of the consistency between horizontal component definitions used in GMMs and hazard analysis, load application in structural analysis, and risk goals of seismic design, see Stewart et al. (2011).

The issue of deterministic vs probabilistic approaches can also arise in the context of risk assessment. A purely deterministic quantification of potential earthquake impacts that gives no indication of the likelihood of such outcomes is of very limited value since it does not provide any basis for comparison with other risks or evaluation against safety standards. In this sense, the context of risk provides strong motivation for adopting probabilistic approaches to seismic hazard assessment. Here it is useful to consider what are the key features that distinguish PSHA and DSHA. The first is that PSHA explicitly includes consideration of earthquake rates and the frequency or probability of the resulting ground motions, whereas DSHA generally ignores the former and only accommodates the latter implicitly. Another important difference is that PSHA considers all possible earthquake scenarios (that could contribute to the risk) whereas DSHA considers only a single scenario. Estimation of the total risk to a structure or portfolio of buildings clearly needs to consider all potential sources of earthquake-induced damage, and informed decisions regarding the mitigation or transfer of the risk clearly require information regarding the probability of different levels of loss. There are situations, however, in which the estimation of risk due to a single specified earthquake scenario can be very useful, including for emergency planning purposes, and for non-specialists understanding risk estimates for a single scenario can be much more accessible than a complete probabilistic risk assessment. A risk assessment for a single scenario does not need to be fully deterministic: the scenario can be selected from disaggregation of PSHA and even if it is selected on another basis, its recurrence interval can be estimated from the relevant recurrence relationship. Furthermore, the variability in the predictions of ground shaking levels can be fully accounted for through the generation of multiple ground-motion fields, sampling from the between-event variability once for each realisation and from the within-event variability for each location. The sampling from the within-event variability can also account for spatial correlation (e.g., Jayaram and Baker 2009) which creates pockets of higher and lower ground motions that influence the resulting hazard estimates when they coincide with clusters of exposure (e.g., Crowley et al. 2008)).

3.3 Uncertainty in Seismic Hazard and Risk Assessments

The basic premise of PSHA is to take into account the apparently random nature of earthquake occurrence and ground-motion generation by integrating over the random variables of M, R and $\varepsilon$ (as a minimum: other random variables can include focal depth distributions and styles-of-faulting, for example). The consequence of the random variability is to influence the shape of the seismic hazard curve, which can be clearly illustrated by looking at the impact of different values of the GMM variability $\sigma$ (Fig. 29).

Fig. 29

Sensitivity of seismic hazard curves to the standard deviation of the residuals in the GMM (Bommer and Abrahamson 2006)

In defining the seismic source characterisation (SSC) and ground motion characterisation (GMC) models that define the inputs to PSHA, decisions have to be made regarding models and parameter values for which a single ‘correct’ choice is almost never unambiguously defined. The nature of the available data in terms of geological information regarding seismogenic faults, the earthquake catalogue for the region, and strong-motion recordings from the area, is such that it will never cover all of the scenarios that need to be considered in the hazard integrations, so there is inevitably extrapolation beyond the data. Moreover, different experts are likely to derive distinct models from the same data, each reflecting valid but divergent interpretations. Consequently, there is uncertainty in most elements of a PSHA model including the seismic source boundaries, the temporal completeness of the catalogue (which in turn influences the calculated recurrence rates), the value of Mmax, and the choice of GMM. These are all examples of epistemic uncertainty, as introduced in Sect. 1.2. Aleatory variabilities are characterised by distributions based on observational data, and they are then incorporated directly into the hazard integrations, influencing, as shown above, the shape of the hazard curve. Epistemic uncertainties are incorporated into PSHA through the use of logic trees, which were first introduced by Kulkarni et al. (1984) and Coppersmith and Youngs (1986) and have now become a key element of PSHA practice. For each element of the PSHA input models for which there is epistemic uncertainty, a node is established on the logic tree from which branches emerge that carry alternative models or alternative parameter values. Each branch is assigned a weight that reflects the relative degree of belief in that particular model or parameter value as being the most appropriate; the weights on the branches at each node must sum to 1.0 (Fig. 30).

Fig. 30

Example of a fault logic tree for PSHA (McGuire 2004)

The logic tree in Fig. 30 has just four nodes and two branches on each node, which is much simpler than most logic trees used in practice but serves to illustrate the basic concept. The PSHA calculations are repeated for every possible path through the logic tree, each combination of branches yielding a seismic hazard curve; the total weight associated with each hazard curve is the product on the weights on the individual branches. The logic-tree in Fig. 30 would result in a total of 16 separate hazard curves, which would be associated with the weights indicated on the right-hand side of the diagram. Whereas aleatory variability determines the shape of the hazard curve, the inclusion of epistemic uncertainty leads to multiple hazard curves. The output from a PSHA performed within a logic-tree framework is used to summarise the statistics of the hazard—the annual frequency of exceedance or AFE—for each ground motion level, calculating the mean AFE (Fig. 31). For seismic design rather than risk analysis, it could be argued that since the starting point is the selected AFE, the mean ground-motion amplitude at each AFE should be determined instead (Bommer and Scherbaum 2008). Such an approach would yield appreciably different results, but this is not standard practice, and the mean hazard curve should be calculated as illustrated in Fig. 31.

Fig. 31

In the main plot the grey lines are hazard curves corresponding to different branch combinations from a logic tree and the red curve is the mean hazard; the inset figure shows the cumulative weights associated with the AFEs for a specific ground-motion level, indicated by blue dashed line in main plot

As well as the mean hazard, it is possible to calculate the median and other fractiles of the hazard. The output from a PSHA thus moves from a single hazard curve to a distribution of hazard curves, allowing two choices to be addressed: the level of motion corresponding to the target safety level (which is determined by the AFE and the associated performance targets, as explained in the previous section) and the confidence level required that this safety level is achieved (Fig. 32). The second decision can be stated in terms of the following question: in light of the unavoidable uncertainty associated with the estimation of the seismic hazard, what degree of confidence is required that the hazard assessment has captured the hazard levels? This is a critical question, and it is the reason that capturing the epistemic uncertainty is one of the most important features of seismic hazard analysis.

Fig. 32

Decision-making for seismic safety using a distribution of site-specific hazard estimates; hazard curves from Almeida et al. (2019)

A distribution of hazard curves such as shown in Fig. 32 conveys the overall level of epistemic uncertainty in the hazard estimates, both from the spread of the fractiles and also from the separation of the median and mean hazard curves. In practice, the most commonly used output is the mean hazard curve. Just as there is epistemic uncertainty in hazard assessment, there is also epistemic uncertainty in most of the other elements of risk analysis (e.g., Crowley et al. 2005; Kalakonas et al. 2020). Fully probabilistic risk analysis, as applied for example to NPPs, considers the full distribution of both hazard and fragility curves, but the mean risk can be obtained by simply convolving the mean hazard with the mean fragility.

A key challenge in PSHA, and in seismic risk analysis, is the separation and quantification of aleatory variability and epistemic uncertainty; Sect. 5 is focused on this challenge in conducting PSHA. The distinction between variability and uncertainty is not always very clear and some have argued that the distinction is unimportant (e.g., Veneziano et al. 2009). If the only required output is the mean hazard, then whether uncertainties are treated as random or epistemic is immaterial, provided that all uncertainties are neither excluded nor double counted. However, if the fractiles are required, then the distinction does become important. In the UK, for example, the expectation of the Office for Nuclear Regulation is that the seismic hazard at NPP sites will be characterised by the motions with an 84-percentile AFE of 10^–4; if epistemic uncertainties are treated as aleatory variabilities, this quantity will likely be underestimated.

4 Good practice in PSHA

The rational management of seismic risk necessarily begins with broad acceptance amongst relevant stakeholders of robust estimates of the seismic hazard. In this section, I briefly summarise what I would suggest are the minimum requirements that a site-specific PSHA should fulfil to increase the chances of the results being accepted.

In an overview of the state of practice two decades ago, Abrahamson (2000) stated that “The actual practice of seismic hazard analysis varies tremendously from poor to very good.” I agree that variation in practice is very large and would even suggest that even stronger adjectives might apply to the end members. I would propose that the best practice, usually exemplified in large projects for nuclear sites, is excellent, and moreover that it frequently defines the state of the art. At the lower end, the practice can indeed be very poor although there are reasons to be optimistic about the situation improving, especially with the comprehensive and clear guidance that is now becoming available in the textbook by Baker et al. (2021) referred to previously. International ventures like GSHAP (Global Seismic Hazard Assessment Project; Giardini 1999; Danciu and Giardini 2015) and GEM (Global Earthquake Model; Crowley et al. 2013; Pagani et al. 2015; Pagani et al. 2020) have done a fantastic job in promoting good practice PSHA practice around the world, especially in developing countries. Much of the poor practice that persists is related to studies conducted for engineering projects that are conducted on compressed schedules and with very small budgets, and which are of questionable value.

In Sect. 4.1, I highlight some of the common errors that are observed in practice and which could be easily eliminated. The following sections then present features of PSHA studies that I believe enhance hazard assessments.

4.1 Internal consistency

The objective in conducting a PSHA should be to achieve acceptance of the outcome by all stakeholders, including regulators. If the study makes fundamental errors, then all confidence in the results is undermined and the assessment can be easily dismissed. I am assuming here that the PSHA calculations are at least performed correctly in terms of integration over the full ranges of M, R and $\varepsilon$; there have been cases of studies, for example, that fix $\varepsilon$ to a constant value (such as zero, thus treating the GMM as a deterministic prediction, or 1), which simply does not constitute PSHA.

The major pitfalls, in my view, are related to performing hazard calculations that are not internally consistent. In Sect. 3.2, I already discussed the importance of consistency between the hazard study and the downstream structural analyses or risk calculations, but there are also issues of consistency within the PSHA. Firstly, there needs to be consistency between the SSC and GMC models, with the latter explicitly considering and accommodating the full range of independent variables defined in the former and vice versa. Consistent definitions of independent variables are also important. For example, if the magnitude scale adopted in the homogenised earthquake catalogue used to derive the recurrence parameters is different from the scale used in the GMMs, an adjustment is required. The easiest option is to use an appropriate empirical relationship between the two magnitude scales to transform the GMM to the same scale as the earthquake catalogue, but it is important to also propagate the variability in the magnitude conversion into the sigma value of the GMM (e.g., Bommer et al. 2005). Fortunately, these days such conversions are not often required because most GMMs and most earthquake catalogues are expressed in terms of moment magnitude, M (or M_w).

Another important issue of consistency arises for SSC models that include area source zones because most modern GMMs used distance metrics such as R_rup or R_jb that are defined relative to extended fault ruptures. The easiest way to integrate over a seismic source zone is to discretise the area into small elements, effectively defining the distance to the site as R_epi or R_hyp, which then creates an inconsistency with the distance metric used in the GMMs. Some freely available software packages for performing PSHA integrate over areal sources in this way, leading to consistent underestimation of the hazard when deployed with GMMs using R_rup or R_jb (Bommer and Akkar 2012). In this case, converting the GMM from a finite rupture distance metric to a point-source metric is not advisable since the variability associated with such conversions is very large (e.g., Scherbaum et al. 2004a), although it should also vary with both magnitude and distance (e.g., Thompson and Worden 2018). The approach generally used is to generate virtual fault ruptures within the source zone, the dimensions of which are consistent with the magnitude of each scenario (Monelli et al. 2014; Campbell and Gupta 2018; Fig. 33). The availability of PSHA software packages such as OpenQuake (Pagani et al. 2014) with the facility to generate such virtual ruptures facilitates avoidance of this incompatibility in hazard calculations. The specification of the geometry and orientation of the virtual ruptures creates considerable additional work in the construction of the SSC model and the generation of the ruptures also adds a computational burden to the calculations. Bommer and Montaldo-Falero (2020) demonstrated that for source zones that are somewhat remote from the site, it is an acceptable approximation to simply use point-source representations of the earthquake scenarios.

Fig. 33

source zone, which in practice could also have different orientations, dips and depths (Monelli et al. 2014)

a Illustration of virtual ruptures for earthquake of different magnitudes for a single point source; b virtual ruptures generated within a

Within the GMC model, a potential inconsistency can arise if multiple GMMs are used with different definitions of the horizontal component of motion. Several studies have presented empirically derived conversions between different pairs of definitions (e.g., Beyer and Bommer 2006; Shahi and Baker 2014; Bradley and Baker 2015; Boore and Kishida 2017), making it relatively easy to adjust all the GMMs to a common definition. However, since some of these conversions apply both to the medians and the sigma values, they should be applied prior to the hazard calculations rather than as a post-processing adjustment.

When site effects are modelled separately from the ground-motion prediction—which should always be the case for site-specific PSHA—then important challenges arise to ensure compatibility between the prediction of motions in rock and the modelling of site response. These issues are discussed in detail in Sect. 5.3.

4.2 Inclusion of epistemic uncertainty

Epistemic uncertainties in PSHA are unavoidable and frequently quite large. Consequently, it is indispensable that they should be identified, quantified, and incorporated into the hazard analysis. For any PSHA to be considered robust and reliable, it must have taken account of the uncertainties in the SSC and GMC models. Beyond performing hazard calculations that are mathematically correct and internally consistent, this is probably the single most important feature in determining whether or not a hazard assessment is considered acceptable or not.

Every PSHA should therefore make a concerted effort to properly characterise and incorporate epistemic uncertainties. This is of paramount importance and is the reason that all PSHA studies now include a logic tree de rigueur. However, simply including a logic tree for the key inputs to the hazard calculations does not guarantee an appropriate representation of the epistemic uncertainty, although this may not always be immediately obvious. Reflecting the primordial importance of this issue, the next two complete sections of the paper are devoted to the identification and quantification of epistemic uncertainty in PSHA: Sect. 5 discusses technical aspects of ensuring that epistemic uncertainty is adequately captured in the hazard input models; Sect. 6 discusses procedural guidelines that have been developed specifically for this process.

Before discussing the technical and procedural frameworks for capturing uncertainty in PSHA, it is important to emphasise that this is not the only goal of a successful PSHA. Equally important objectives are to build the best possible SSC and GMC models—which could be interpreted as the best constrained models—and also to reduce as much as possible the associated uncertainty through the compilation of existing data and collection of new data from the site and region. The task then remains to ensure adequate representation of the remaining epistemic uncertainty that cannot be reduced or eliminated during the course of the project, but the construction of the logic tree should never be a substitute for gathering data to constrain the input models.

4.3 Peer review and quality assurance

Appropriately conducted peer review and quality assurance (QA) can both contribute significantly to the likelihood of a PSHA study being accepted as the basis for decision making regarding risk mitigation measures, by increasing confidence in the execution of the hazard assessment and in the reliability of the results. Peer review and QA are discussed together in this section because the two processes are complementary.

Peer review consists of one or more suitably qualified and experienced individuals providing impartial feedback and technical challenge to the team conducting the hazard assessment. While it can be viewed as a relatively easy task (compared to building the hazard input models and performing the PSHA calculations), effective peer review requires considerable discipline since the reviewers must be impartial and remain detached from the model building. The focus of the peer review must always be on whether the team conducting the study has considered all of the available information and models (and the peer reviewers can and should bring to their attention any important information that has been overlooked) and the technical justifications given for all of the decisions made to develop the models, including the weights on the logic-tree branches. The peer review should interrogate and, when necessary, challenge the work undertaken, without falling into the trap of prescribing what should be done or pushing the modelling teams into building the models the peer reviewer would have constructed if they had been conducting the study. If this degree of detachment is achieved, then the peer review process can bring great value in providing an impartial and independent perspective for the teams that are fully immersed in the processes of data interpretation and model development.

Late-stage peer review, in which the first genuine engagement of the reviewers is to review a draft report on the PSHA, is largely pointless. At that stage, it is very unlikely that the model building and hazard calculations will be repeated in the case that the peer review identifies flaws, in which case the outcome is either unresolved objections from the peer reviewers or rubber stamping of an inadequate study. Peer reviewers should be engaged from the very outset and be given the opportunity to provide feedback at all stages of the work, including the database assembly and the model building process from the conceptual phase to finalisation. The hazard calculations should only begin after all issues raised by the peer review have been resolved. If the peer review process is managed intelligently, the review of the draft final PSHA report should be focused exclusively on presentation and not on any technical details of the SSC and GMC models.

For peer review to enhance the likelihood of acceptance of a PSHA study, a number of factors are worth considering. The first is the selection of the peer reviewers, since the confidence the review adds will obviously be enhanced if those assigned to this role are clearly recognised experts in the field with demonstrable and extensive experience. Secondly, it is of great value to include as part of the project documentation a written record of the main review comments and how they were resolved. Inclusion of a final closing letter from the peer reviewers giving overall endorsement of the study—if that is indeed their consensus view—is a useful way to convey to regulators and other stakeholders the successful conclusion of the peer review process.

The value of the peer review process, both in terms of technical feedback to the team undertaking the PSHA and in terms of providing assurance, can be further enhanced when the study includes formal working meetings or workshops that the reviewers can attend as observers, especially if regulators and other stakeholders are also present to observe the process. This is discussed further in Sect. 6.

Quality assurance essentially adds value to a PSHA study by increasing confidence in the numerical values of the final hazard estimates. At the same time, it is important not to impose formal QA requirements on every single step of the project, since this can place an unnecessary and unhelpful burden on the technical teams. Excessive QA requirements will tend to discourage exploratory and sensitivity analyses being performed to inform the model development process, which would be very detrimental. Figure 34 schematically illustrates the complementary nature of QA and peer review, emphasising that while all calculations should be checked and reviewed, formal QA should only be required on new data collection and on the final hazard calculations.

Fig. 34

adapted from Bommer et al. (2013) and USNRC (2018)

Schematic illustration of the complementary roles of peer review and QA in PSHA projects; the highlighted boxes representing the two stages of the process where formal QA requirements are appropriate;

Formal QA on the PSHA calculations can include two separate elements. The first is that the code being used for the calculation has undergone a process of verification to confirm that it executes the calculations accurately. Valuable resources to this end are the hazard code validation and comparison exercises that have been conducted by the Pacific Earthquake Engineering Research (PEER) Center in California (Thomas et al. 2010; Hale et al. 2018). The second is confirmation that the SSC and GMC models have been correctly entered into the hazard calculation code, which is an important consideration for the logic trees developed for site-specific assessments at the sites of safety–critical structures such as NPPs, which will often have several hundred or even thousands of branch combinations. The GMC model can usually be checked exactly by predicting the median and 84-percentile ground-motion amplitudes for a large number of M-R combinations. For the PSHA for the Thyspunt nuclear site in South Africa (Bommer et al. 2015b), we performed such a check on the GMC model implementation with two independent implementations external to the main hazard code. For the SSC model, the full logic trees for individual sources were implemented, in combination with a selected branch from the GMC model, in two separate hazard codes by different teams of hazard analysts. The results were compared graphically (Fig. 35); the differences were seen to be small and not systematic, with higher hazard estimates being yielded by one code or the other for each source, suggesting that within the tolerance defined by the differences in the algorithms embedded in the codes (and in particular the generation of virtual ruptures), the results could be considered consistent and therefore confirmed the model implementation. While this is more rigorous than the approaches generally applied in PSHA studies, it does provide a robust check; a similar approach was implemented in the PSHA for the Hinkley Point C NPP site in the UK (Tromans et al. 2019).

Fig. 35

source zones in combination with a single branch from the GMC model (Bommer et al. 2013)

Upper: Seismic sources zones defined for the Thyspunt PSHA (Bommer et al. 2015b); lower: hazard curves obtained from parallel implementations in the FRISK88 (solid curves) and OpenQuake (dashed curves) software packages of the full SSC logic tree for each

4.4 Documentation

The documentation of a PSHA study that fulfils all the objectives outlined above should do justice to the depth and rigour of the hazard assessment, and there can be little doubt that this will further enhance the likelihood of the study being accepted. The documentation should be complete and clear, explaining the evaluation of the data and models (including those that were not subsequently used), and providing technical justifications for all the final decisions, including the weights on the logic-tree branches. At the same time, the report should not be padded out with extraneous information that is subsequently not used in the model development (such as a long and detailed description of the entire geological history of the region, most of which is not invoked in the definition of the seismic sources). The one exception to this might be an overview of previous hazard studies for the site or region, which may not be used in the development of the current model but provide useful background and context for the reader.

As well as providing detailed information on the construction of the SSC and GMC models, the documentation should also enable others to reproduce the study. One element that assists with meeting this objective is to include what is referred to as Hazard Input Document (HID), which provides a summary of the models, including all details required for their implementation, but without any explanations or justifications. In major PSHA projects, the HID is usually passed to the hazard analysts for implementation in the code, and it also forms the basis for the QA checks summarised in the previous section. Tables of values and coefficients, and also of hazard results, can be usefully provided as electronic supplements to the PSHA report. There is value in the report also summarising the process that was followed and, in particular, the peer review and QA processes, pointing to separate documentation (ideally in appendices) providing more details.

The hazard results will always be presented in the form of mean and fractile hazard curves, and for AFEs of relevance, it is common to also present uniform hazard response spectra (UHRS). For selected combinations of AFE and oscillator period, it is useful to show M-R-$\varepsilon$ disaggregation plots (see Fig. 24). There are several other ways of displaying disaggregation of the results that can afford useful insights into the PSHA results, including the hazard curves corresponding to individual seismic sources (Fig. 36).

Fig. 36

Contributions by individual seismic sources (see upper plot in Fig. 35) to the total hazard at the Thyspunt nuclear site in terms of the spectral acceleration at 0.01 s (Bommer et al. 2015b)

There are also diagrams that can be included to display the individual contributions of different nodes of the logic tree to the total uncertainty in the final hazard estimates for any given ground-motion parameter and AFE. One of these is a tornado plot, which shows the deviations from the ground-motion value corresponding to the mean hazard associated with individual nodes (Fig. 37), and another is the variance plot, which shows nodal contributions to the overall uncertainty (Fig. 38).

Fig. 37

Tornado plot for the 10^–4 AFE hazard estimate in terms of PGA at site A obtained in the Hanford site-wide PSHA (PNNL 2014); the black line corresponds to the mean hazard and the size of each symbol corresponds to the weight on the individual logic-tree branch

Fig. 38

Variance plot for the hazard estimates in terms of PGA at site A for various AFEs as obtained in the Hanford site-wide PSHA (PNNL 2014)

Making PSHA reports publicly available can also be beneficial to the objective of obtaining broad acceptance for the hazard estimates, countering any accusations of secrecy or concealment of information, although in such cases, publication together with the final endorsement from the peer reviewers is advisable. In the United States, it is common practice to make site-specific PSHA studies for nuclear sites freely available (for example, the Hanford PSHA can be downloaded from https://www.hanford.gov/page.cfm/OfficialDocuments/HSPSHA). In other locations, public dissemination of site-specific PSHA reports is less common, but similar value in terms of demonstrating openness can be achieved through publication in the scientific literature of papers describing the studies, as has been done, very encouragingly, for recent hazard assessments at nuclear new-build sites in the UK (Tromans et al. 2019; Villani et al. 2020). Such articles can also contribute to the assurance associated with the study by virtue of having undergone peer review by the journal prior to publication. I would also note that dissemination of high-level PSHA studies, whether by release of the full reports or through publications in the literature, can also contribute to the improvement of the state of practice.

5 Constructing input models for PSHA

From the preceding discussions, it should now be clear that the construction of SSC and GMC logic trees is clearly central to the execution of a successful PSHA. In this section, I discuss the development of such logic trees for site-specific hazard assessment. This is not intended as a comprehensive guide on how to construct SSC and GMC models, which would require the full length of this paper. The focus is very specifically on recent developments, most of which have arisen from experience on high-level PSHA projects for nuclear sites, which assist in the construction of logic trees that fulfil their intended purpose. The first sub-section discusses and defines exactly what is the purpose of logic trees, and then their application is discussed for ground-motion predictions in rock, for adjustments for local site effects, and for seismic source characterisation models. The order may seem somewhat illogical since the SSC model would normally be the starting point for a PSHA. The reason for reversing the order here is that recent innovations in GMC modelling have made the construction of logic trees much more clearly aligned with their purpose, and these improvements have also now been adapted to site response modelling; the final sub-section discusses the possibility, and indeed the necessity, of adapting the same approaches to SSC modelling.

5.1 The purpose of logic trees

As noted in sub-Sect. 4.2, all PSHA studies now employ logic trees but this is often done without a clear appreciation of the purpose of this tool. In many cases, one is left with the impression that the logic tree constructed for the inputs to the hazard calculations is simply a gesture to acknowledge the existence of epistemic uncertainty and to demonstrate that more than one model or parameter value has been considered for each of the key elements of the SSC and GMC models.

The purpose of a logic tree in PSHA is to ensure that the hazard results reflect the full distribution of epistemic uncertainty, capturing the best estimate of the site hazard as constrained by the available data and the associated range of possible alternative estimates due to the epistemic uncertainty in the SSC and GMC models. The purpose of the SSC and GMC logic trees has been stated as representing the centre, the body, and the range of technically defensible interpretations of the available data, methods, and models, which is often abbreviated as the CBR of TDI (USNRC 2018). The ‘centre’ could be understood as the model or parameter value considered to be the best estimate or choice for the region or site based on the modeller’s interpretation of the currently available data. The ‘body’ could be understood as the alternative interpretations that could be made of the same data, and the ‘range’ as the possibilities that lie beyond the currently available data (but which must be physically realisable). Figure 39 illustrates these three concepts in relation to the distribution of a single parameter in the SSC or GMC logic tree.

Fig. 39

Schematic illustration of the concepts of centre, body, and range in relation to the distribution of a specific parameter implied by a node or set of nodes on a logic tree (USNRC 2018)

A point to be stressed very strongly is that the distributions implied by the logic tree are intended to represent the CBR of TDI of the factors that drive the hazard estimates at the site. For the SSC model, these factors are the location (and hence distance) and recurrence rate of earthquakes of different magnitude, and the maximum magnitude, Mmax. For the GMC model, the factor is the amplitude—defined by the median predictions and the associated sigma values—of the selected ground-motion parameter at the site due to each magnitude-distance pair defined by the SSC model. The logic tree is not intended to be a display and ranking, like a beauty contest, of available models. All available data and models that may be relevant to the characterisation of the hazard at the site should be considered in the development of the logic tree, but there is absolutely no requirement to include all the available models in the final logic tree. Models that are not included in the logic tree are not really being assigned a zero weight, which could be interpreted to imply that the model has been evaluated as irrelevant (possibly by virtue of being very similar to another model that is already included) or unreliable; the model may simply not be needed for the logic tree to capture the full CBR of the variables of interest: earthquake locations and recurrence rates, Mmax, median ground-motion predictions, and sigma in the ground-motion prediction. All models considered should appear in the PSHA documentation but none of them needs to feature in the logic trees, especially if it is finally decided to construct new models instead of using existing ones.

There has been much debate in the literature regarding the nature and meaning of the weights assigned to the branches of logic trees (Abrahamson and Bommer 2005; McGuire et al. 2005; Musson 2005, 2012a; Scherbaum and Kuehn 2011; Bommer 2012). The weights are assigned as relative indicators of the perceived merit of each alternative model or parameter value; the absolute value of the weights is not the critical feature but rather the ratios of the weights on the branches at each node: a branch assigned a weight of 0.3 is considered three times more likely to be the optimal model or value than a branch with a weight of 0.1. A potential pitfall in debates that focus on the interpretation of logic-tree branch weights is that we can lose sight of the fact that all that matters in the end is the full distribution that results from the combination of the branches and their associated weights (i.e., both axes of the histogram in Fig. 39). Moreover, for logic trees with any appreciable number of branches, the hazard results are generally found to be far more sensitive to the branches themselves (i.e., models or parameter values) than to the weights (e.g., Sabetta et al. 2005).

Regardless of how the weights are assigned, in generating the outputs from the PSHA (mean hazard and fractiles) they are treated as probabilities. Since this is the case, it is desirable that the branches satisfy the MECE (mutually exclusive and collectively exhaustive) criterion; the latter should always be achieved since no viable option should be omitted from the logic tree, but it can be challenging in some cases to develop logic-tree branches that are mutually exclusive.

5.2 Ground motion models

As stated above, the objective of a GMC logic tree is to define the CBR of predicted ground-motion amplitudes for any combination of magnitude, distance and other independent variables defined in the SSC model for a PSHA. The amplitudes are a function of the median predictions from the GMMs and their associated sigma values.

5.2.1 Median predictions: multiple GMM vs backbone GMM

The first logic tree to include a node for the GMC model, to my knowledge, was presented by Coppersmith and Youngs (1986): the logic tree included a single GMC-related node with two equally weighted branches carrying published GMMs. The practice of building GMC logic trees evolved over the ensuing years, but the basic approach was maintained: the branches were populated with published GMMs (or occasionally with new GMMs derived specifically for the project in question), and relative weights assigned to each branch. There are several pitfalls and shortcomings in this approach, one of which is illustrated in Fig. 40.

Fig. 40

Median predictions of PGA and spectral accelerations at different oscillator frequencies from the GMMs of Atkinson (2005), Atkinson and Boore (2006), and Boore and Atkinson (2008) (for M 5.5 and M 7.5 plotted against distance; the arrows indicate magnitude-distance combinations for which the three median predictions converge

The plots in Fig. 40 show median predictions from the three GMMs that populated the logic tree defined for a PSHA conducted for major infrastructure in North America, located in the transition region between the active tectonics of the west and the stable continental interior of the east. The arrows highlight several magnitude-distance combinations for which the predictions from the three GMMs converge to almost exactly the same value. Consequently, for these M-R pairs, the logic tree is effectively communicating that there is no epistemic uncertainty in the predictions of response spectral acceleration, which cannot be the case. One might think that the solution is to increase the number of branches, but this can actually result in very peaked distributions since many GMMs are derived from common databases.

The fundamental problem with the multiple GMM approach to constructing logic trees is that the target distribution of ground-motion amplitudes that results from several weighted models is largely unknown. Different tools have been proposed to enable visualisation of the resulting ground-motion distribution, including composite models (Scherbaum et al. 2005) and Sammons maps (Scherbaum et al. 2010). Such tools are generally not required, however, if the GMC logic tree is constructed by populating the branches with alternative scaled models of a single GMM, which has been given the name of a backbone GMM approach (Bommer 2012). In its simplest form, the backbone GMM is simply scaled by constant factors, but many more sophisticated variations are possible, with the scaling varying with magnitude and/or distance. In the example shown in Fig. 41, it can be appreciated that the spread of the predictions increases with magnitude, reflecting the larger epistemic uncertainty where data are sparser. What can also be clearly appreciated is that the relationship between the branch weights and the resulting distribution of predicted accelerations is much more transparent than in the case where the logic tree is constructed using a number of different published GMMs.

Fig. 41

Predicted median spectral accelerations at a given period obtained from a logic tree constructed using a backbone approach, for a fixed distance and V_S30, as a function of magnitude

In addition to the clearer relationship between the logic tree branches and the resulting ground-motion distribution, and the consistent width of the distribution that avoids the ‘pinching’ seen in Fig. 40, there are other advantages of the backbone approach, each of which really highlights a shortcoming in the multiple GMM approach. One of these is the fact that in using the latter approach, there is an implicit assumption that the range of predictions from the available GMMs that happen to have been published covers the range of epistemic uncertainty. In practice, this is very unlikely to be the case, and even in regions with abundant ground-motion data, such as California, it is recognised that the range of predicted values from local GMMs, like the NGA-West2 models (Gregor et al. 2014) does not capture the full range of epistemic uncertainty in ground-motion predictions for that region (Al Atik and Youngs 2014). If the same models are used to populate a GMC logic tree for application to another region (with less abundant ground-motion data), an even broader additional range of epistemic uncertainty is likely to be required. Figure 42 illustrates the backbone GMM model developed in the Hanford PSHA project (PNNL 2014), in which the total range of epistemic uncertainty comes from the inherent uncertainty associated with the backbone GMM in its host region (light grey shading) and the additional uncertainty associated with adjusting the backbone GMM for applicability to source and path characteristics in the target region and to the rock profile at the Hanford site (dark grey shading).

Fig. 42

Predicted median PGA values from the Hanford GMC logic tree, as a function of magnitude for different distances. The solid black line is the backbone GMM, and the thin black lines the other models from the same host region, which collectively define the inherent uncertainty (light grey shading); the dark grey shading corresponds to the additional uncertainty associated with adjusting the backbone GMM to the characteristics of the target region and site; the dashed, coloured curves are other GMMs not used in the model development but plotted for comparative purposes (PNNL 2014)

The backbone GMM approach has already been widely applied, in various different forms, and its use predates the introduction of the term backbone now used to describe it (Bommer 2012; Atkinson et al. 2014). The backbone approach is fast becoming standard practice in high-level PSHA studies for critical sites (e.g. Douglas 2018), and I would argue that in the light of the shortcomings it has highlighted in the multiple GMM approach, rather than there being a need to make the case for using the backbone approach, it would actually be challenging to justify the continued use of the multiple GMM approach.

5.2.2 Median predictions: adjustments to regional and local conditions

A legacy of the widely used approach of constructing GMC logic trees by populating the branches with published GMMs has been a focus on approaches to selecting GMMs that are applicable to the target region. Many studies have looked into the use of locally recorded ground-motion data to test and rank the applicability of candidate GMMs (Scherbaum et al. 2004b, 2009; Arango et al. 2012; Kale and Akkar 2013; Mak et al. 2017; Cremen et al. 2020; Sunny et al. 2022). In many applications, the only data available for such testing are recordings from small-magnitude earthquakes, which may not provide reliable indications of the GMM performance in the larger magnitude ranges relevant to hazard assessment (Beauval et al. 2012).

In parallel with the focus on selection on the basis of inferred applicability to the target region, work also developed to make adjustments to GMMs from one region, usually referred to as the host region, to make them more applicable to the target region where the hazard is being assessed. I believe that this approach should be strongly preferred since the degree to which two regions can be identical in terms of ground-motion characteristics is obviously open to question: if the selection is based on testing that simply identifies the most applicable models (in terms of how well they replicate local data), it does not necessarily mean that these GMMs are genuinely applicable to the target region without further adjustment. Moreover, even if the source and site characteristics of the host and target regions are genuinely similar, it is unlikely that the generic site amplification in any GMM will match the target site characteristics (an issue discussed further in sub-Sect. 5.3). With these considerations in mind, Cotton et al. (2006) proposed a list of selection criteria, all of which were designed to exclude poorly derived GMMs that are unlikely to extrapolate well to larger magnitudes and all the distances covered by hazard integrations, and also to exclude models from clearly inappropriate settings (i.e., subduction-region GMMs for crustal seismic sources). The selected models were adjusted for parameter compatibility, and then adjusted to match the target source, path, and site conditions.

The general approach proposed by Cotton et al. (2006) has continued to evolve since first proposed, with Bommer et al. (2010) formalising the list of exclusion criteria and making them more specific. The most important developments, however, have been in how to adjust the selected GMMs to the target region and site. Atkinson (2008) proposed adjusting empirical GMMs to better fit local data, starting with inspection of the residuals of the local data with respect to the model predictions. This so-called referenced empirical approach is relatively simple to implement but suffers from important drawbacks: if the local data are from predominantly small-magnitude earthquakes, the approach is not well suited to capturing source characteristics in the target region, and for a site-specific study, unless the local database includes a large number of recordings from the target site, it will not help to better match the target site conditions. Another approach is to use local recordings, even from small-magnitude events, to infer source, path, and site parameters for the target region. The main parameters of interest are as follows:

• The stress drop, or more correctly, the stress parameter, $\Delta \sigma$, which is a measure of the intensity of the high-frequency radiation in an earthquake

• The geometric spreading pattern, which describes the elastic process of diminishing energy over distance as the wavefront becomes larger

• The quality factor, $Q$, which is a measure of the anelastic attenuation in the region, with higher values implying lower rates of attenuation with distance

• The site damping parameter, ${\kappa }_{0}$, which is a measure of the high-frequency attenuation that occurs at the site; contrary to the parameter $Q$, a higher value of ${\kappa }_{0}$ means greater attenuation

Boore (2003) provides a very clear overview of how these parameters can be determined, and then used to generate Fourier amplitude spectra (FAS), which can then be transformed to response spectra by making some assumptions regarding signal durations. Once a suite of such parameters is available, they can be used to generate GMMs through stochastic simulations. Hassani and Atkinson (2018) performed very large numbers of such simulations to generate stochastic GMMs that could be locally calibrated by specifying local values of $\Delta \sigma$, $Q$, and ${\kappa }_{0}$. While this is a very convenient tool, the simulations are based on a point-source model of earthquakes, hence finite rupture effects in the near field are not well captured. There is consequently strong motivation to retain the advantages offered by empirical GMMs, which prompted Campbell (2003) to propose the hybrid-empirical method to adjust empirical GMMs from one region to another. The basis of the hybrid empirical method is to determine suites of source, path, and site parameters (i.e., $\Delta \sigma$, $Q$, and ${\kappa }_{0}$) for both the host and target regions, and then to use these, via FAS-based simulations, to derive ratios of the spectral accelerations in the host and target regions, which are then used to make the adjustments (Fig. 43). This is essentially the approach that was used by Cotton et al. (2006) to adjust the selected GMMs to the target region.

Fig. 43

Illustration of hybrid-empirical adjustments to transform a GMM from its host (H) region to the target (T) region where the PSHA is being conducted; FAS is Fourier amplitude spectrum and Sa is spectral acceleration (Bommer and Stafford 2020)

Within the general framework in which selected GMMs are adjusted to be applicable to the target region and site, it clearly becomes less important to try to identify models that are approximately applicable to the target region, unless one perceives benefits in minimising the degree of modification required. An alternative approach is to select GMMs on the basis of how well suited they are to being modified. As Fig. 43 shows, at the core of the hybrid-empirical adjustments is the assumption that ratios of FAS can serve as a proxy for scaling of response spectral accelerations, Sa. Since the relationship between Sa and FAS is complex (Bora et al. 2016), especially at higher frequencies, the method works better if the scaling of Sa implicit in the empirical GMM is consistent with the scaling of FAS from seismological theory. This applies, in particular, to the scaling with magnitude (Fig. 44).

Fig. 44

source FAS (Bommer and Stafford 2020); the magnitude at which the transition from moderate-magnitude scaling to large-magnitude scaling occurs varies with oscillator period

Theoretical scaling of Sa with magnitude arising from consideration of a point-

Another refinement that has been proposed is to make the adjustments for host-to-target region differences separately for each factor rather than collectively as in the original method of Campbell (2003). This has the advantage that the uncertainty in the estimates of the parameters such as $\Delta \sigma$, $Q$, and ${\kappa }_{0}$ can be modelled explicitly, thus creating a more tractable representation of the epistemic uncertainty. For this to be possible, the selected GMM should have a functional form that isolates the influence of individual factors such as $\Delta \sigma$, $Q$, and ${\kappa }_{0}$. If such a model can be identified, then the backbone and hybrid-empirical approaches can be combined to construct the logic tree. The adjustable GMM is selected as the backbone and then the GMC logic tree is constructed through a series of nodes for host-to-target region adjustments. The NGA-West2 model of Chiou and Youngs (2014) has been identified as the most adaptable of all current GMMs for active crustal seismicity, having a functional form that both conforms to the scaling illustrated in Fig. 44 and also isolates the influence of $\Delta \sigma$ and $Q$ in individual terms of the model (Bommer and Stafford 2020). The Chiou and Youngs (2014) GMM also has the added advantage of magnitude-dependent anelastic attenuation, which allows a reliable host-to-target region adjustment for path effects to be made even if only recordings of small-magnitude earthquakes are available. For the stress parameter adjustment, however, the magnitude scaling of stress drop would need to be accounted for in the uncertainty bounds on that node of the logic tree.

In addition to scaling consistent with seismological theory and the isolated influence of individual parameters, a third criterion required for an adaptable GMM is a good characterisation of source, path, and site properties of the host region. This is not straightforward because determination of the required parameters for the host region would need to have been made assuming geometric spreading consistent with that implicit in the GMM. Moreover, there may be no clearly defined host region, even for a nominally Californian model such as Chiou and Youngs (2014), since many of the accelerograms in their database, especially for larger magnitudes, were recorded in other parts of the world. Therefore, rather than seeking a suite of source, path, and site parameters for the host region of the backbone GMM, inversions can be performed that define a suite of parameters (for a virtual host region) that are fully consistent with the backbone model (Scherbaum et al. 2006). Al Atik and Abrahamson (2021) have inverted several GMMs, including Chiou and Youngs (2014), hereafter CY14, to obtain model-consistent site profiles of shear-wave velocity, V_S, and ${\kappa }_{0}$; Stafford et al. (2022) then used these to invert CY14 for source and path properties. The suites of parameters obtained by Al Atik and Abrahamson (2021) and by Stafford et al. (2022) fully define the host region of CY14; inversion of ground-motion FAS in the target region then allows the construction of a GMC logic tree consisting of successive nodes for source, path, and site adjustments (although, as discussed in sub-Sect. 5.3, the site adjustment should generally be made separately).

In closing, it is important to highlight that this should not be interpreted to mean that CY14 is a perfect GMM or that all other GMMs cease to be of any use. With regards to the first point, it is worth noting that only 8% of the earthquakes in the CY14 database were associated with normal ruptures, so for applications to seismic sources dominated by normal-faulting earthquakes, this might be viewed as an additional source of epistemic uncertainty. Additionally, the derivation of CY14, in line with the earlier Chiou and Youngs (2008) models, assumed that the records with usable spectral ordinates at long periods represented a biased sample of high-amplitude motions; their adjustment for this inference resulted in appreciably lower predicted spectral accelerations at long periods than are obtained from the other NGA-West2 models, and this divergence might also be considered an epistemic uncertainty since both approaches can be considered to be technically defensible interpretations.

5.2.3 Sigma values

As was made clear in sub-Sect. 2.2.3, ground-motion prediction models predict distributions of ground-motion amplitudes rather than unique values for an M-R combination, hence sigma is as much part of a GMM as the coefficients that define the median values, and therefore must also be included in the GMC logic tree. In early practice, each published GMM included in the logic tree was accompanied by its own sigma value, but it has become more common practice now to have a separate node for sigma values. This has been motivated primarily by the recognition of adjustments that need to be made to these sigma values when local site amplification effects are rigorously incorporated into PSHA (as described in the next section).

Empirical models for ground-motion variability invoke what is known as the ergodic assumption (Anderson and Brune 1999), which means that spatial variations are used as a proxy for temporal variation. The required information is how much ground motions vary at a single location over time, or in other words over many different earthquakes occurring in the surrounding region. In practice, strong-motion databases tend to include, at most, records obtained over a few decades, and consequently the variation of the ground-motion amplitudes from site to site is used as a proxy for the variation over time at a single location. However, for accelerograph stations that have generated large numbers of recordings, it is observed that the variability of the motions is appreciably smaller than predicted by the ergodic sigmas associated with GMMs (Atkinson 2006). The reason that this is the case is that a component of the observed spatial variability in ground-motion residuals actually corresponds to repeatable amplification effects at individual sites. The decomposition of the variability presented in Eq. (2) can now be further broken down as follows:

$$\sigma = \sqrt{{\tau }^{2}+{\phi }^{2}}=\sqrt{{\tau }^{2}+{\phi }_{ss}^{2}+{\phi }_{S2S}^{2}}$$

(5)

where ${\phi }_{S2S}$ is the site-to-site variability (or the contribution to total variability due to the differences in systematic site effects at individual locations) and ${\phi }_{ss}$ is the variability at a single location. If the systematic site amplification effect at a specific location can be constrained by large numbers of recordings of earthquakes covering a range of magnitude and distance combinations, then the last term in Eq. (5) can be removed, and we can define a single-station or partially non-ergodic sigma:

$${\sigma }_{ss}=\sqrt{{\tau }^{2}+{\phi }_{ss}^{2}}$$

(6)

In practice, it would be rather unlikely that at the site of major engineering project (for which a PSHA is to be conducted), we have a large number of ground-motion recordings. However, if such information were available, then it would constrain the systematic site effect, hence the absence of this knowledge implies that for the target site ${\phi }_{S2S}$ actually represents an epistemic uncertainty. If, as should always be the case, the site-specific PSHA includes modelling of local site amplification factors, capturing the epistemic uncertainty in the amplifications, then it is necessary to invoke single-station sigma, to avoid double counting the site-to-site contribution. Using datasets from recording sites yielding large numbers of accelerograms in many locations around the world, Rodriguez-Marek et al. (2013) found that estimates of single-station variability, ${\phi }_{ss}$, are remarkably stable, and these estimates therefore can be adopted in PSHA studies.

The concept of non-ergodic sigma has been extended to also include repeatable site and path effects, such that for ground motions recorded at a single location due to earthquakes occurring in a single seismic source, even lower variability is observed (e.g., Lin et al. 2011). Using these concepts, fully non-ergodic GMMs have been developed (e.g., Landwehr et al. 2016) and used in PSHA (Abrahamson et al. 2019). The advantage that these developments bring is a more accurate separation of aleatory variability and epistemic uncertainty, allowing identification of the elements of uncertainty that have the potential to be reduced through new data collection and analysis.

Reflecting the marked influence that sigma has on seismic hazard estimates, especially at the low AFEs relevant to safety–critical facilities, several studies have explored additional refinements of sigma models. Using their model for spatial correlation of ground-motion residuals (Jayaram and Baker 2009), Jayaram and Baker (2010) showed that accounting for this correlation in the regressions to derive GMMs results in smaller values of between-earthquake variability and greater values of within-earthquake variability. The net effect tends to be an increase in single-station sigma for larger magnitudes and longer periods, but the impact is modest and would only need be accounted for in PSHA studies in very active regions that are targeting small AFEs (i.e., hazard analyses that will sample large values of $\varepsilon$).

Another subtle refinement that has been investigated is the nature of the tails of the residual distributions. Early studies (e.g., Bommer et al. 2004b) showed that ground-motion residuals conformed well to the log-normal distribution at least to ± 2 $\sigma$ and deviations beyond these limits were interpreted to be due to insufficient sampling of the higher quantiles by the relatively small datasets available at the time. Subsequently, as much larger ground-motion datasets became available, it became apparent that the deviations may well be systematic and indicate higher probabilities of these higher residuals than predicted by the log-normal distribution (Fig. 45). In some projects, this has been accommodated by using a mixture model that defines a weighted combination of two log-normal distributions in order to mimic the ‘heavy tails.’ Again, this is a refinement that is only likely to impact on the hazard results at low AFEs and in regions of high activity.

Fig. 45

(modified from PNNL 2014)

Event- and site-corrected residuals of PGA from the Abrahamson et al. (2014) GMM plotted against theoretical quartiles for a log-normal distribution. If the residuals conformed to a log-normal distribution, they would lie on the solid red line; the dashed red lines show the 95% confidence interval

5.3 Incorporating site response into PSHA

The presence of layers of different stiffness in the near-surface site profile can have a profound effect on the surface motions, hence incorporating such local amplification effects is essential in any site-specific seismic hazard assessment. As noted in sub-Sect. 2.2.3, modern ground-motion prediction models always include a term for site amplification, usually expressed in terms of V_S30. For an empirically constrained site amplification term, the frequency and amplitude characteristics of the V_S30-dependence will correspond to an average site amplification of the recording sites contributing to the database from which the GMM was derived. The amplification factors for individual sites may differ appreciably from this average site effect as a result of different layering in the uppermost 30 m and to differences in the V_S profiles at greater depth (Fig. 46). For a site-specific PSHA, therefore, it would be difficult to defend reliance on the generic amplification factors in the GMM or GMMs adopted for the study, even if this also include additional parameters such as Z_1.0 or Z_2.5. Site amplification effects can be modelled using measured site profiles and this is the only component of a GMC model for which the collection of new data to provide better constraint and to reduce epistemic uncertainty does not depend on the occurrence of new earthquakes. Borehole and non-invasive techniques can be used to measure V_S profiles at the site and such measurements should be considered an indispensable part of any site-specific PSHA, as should site response analyses to determine the dynamic effect of the near-surface layers at the site.

Fig. 46

(adapted from Papaspiliou et al. 2012)

Upper: V_S profiles for the sandy SCH site and the clayey NES site, which have almost identical V_S30 values; lower: median amplification factors for the two sites obtained from site response analyses

5.3.1 PSHA and site response analyses

The last two decades have seen very significant developments in terms of how site amplification effects are incorporated into seismic hazard analyses. Previously, site response analyses were conducted for the uppermost part of the site profile, and the resulting amplification factors (AFs) applied deterministically to the hazard calculated at the horizon that defined the base of the site response analyses (SRA). A major step forward came when Bazzurro and Cornell (2004a, 2004b) developed a framework for probabilistic characterisation of the AFs and convolution of these probabilistic AFs with the PSHA results obtained at the rock horizon above which the SRA is applied.

An issue that was not always clearly recognised in this approach was the need to also capture correctly the AF associated with the V_S profile below the rock horizon at which the hazard is calculated and where the dynamic inputs to the site response calculations are defined. If the site-specific V_S profile is appreciably different from the profile implicit in the GMM used to predict the rock motions, there is an inconsistency for which an adjustment should be made (Williams and Abrahamson 2021; Fig. 47). In a number of site-specific PSHA studies, this has been addressed by making an adjustment for differences between both the GMM and target V_S profiles and between the damping associated with these profiles, in order to obtain the rock hazard, before convolving this with the AFs obtained from SRA for the overlying layers. Such host-to-target V_S-$\kappa$ adjustments (e.g., Al Atik et al. 2014) became part of standard practice in site-specific PSHA studies, especially at nuclear sites (e.g., Biro and Renault 2012; PNNL 2014; Bommer et al. 2015b; Tromans et al. 2019). The scheme for including such adjustments to obtain hazard estimates calibrated to the target rock profile and then convolving the rock hazard with the AFs for overlying layers is illustrated in Fig. 48.

Fig. 47

V_S profiles of underlying bedrock and overlying layers for which site response analysis is performed; the red line is the actual site profile, the dotted line the profile associated with the GMM (Williams and Abrahamson 2021)

Fig. 48

Scheme for applying host-to-target region adjustments to calculate rock hazard and then to convolve the rock hazard with AFs for the overlying layers (Rodriguez-Marek et al. 2014); G/G_max and D are the strain-dependent soil stiffness and damping, $\upgamma$ is the strain

The sequence of steps illustrated in Fig. 48 enables capture of the variability and uncertainty in both the rock hazard and site amplification factors, while also reflecting the characteristics of the full target site profile. However, there are practical challenges in the implementation of this approach, the first of which is that neither the GMC model for the baserock horizon nor the site response analyses for the overlying layers can be built until the baserock elevation is selected and characterised. Therefore, the development of the GMC model cannot begin until the site profile has been determined, possibly to considerable depth. Once the baserock is determined, then it is necessary to obtain estimates for the ${\kappa }_{0}$ parameter at a buried horizon, which is challenging unless there are recordings from borehole instruments at that horizon or from an accelerograph installed on an outcrop of the same rock (which even then may be more weathered than the buried rock horizon). Several studies have proposed empirical relationships between V_S30 and ${\kappa }_{0}$ (Van Houtte et al. 2011; Edwards and Fäh 2013b; Laurendeau et al. 2013), but these tend to include very few values from very hard rock sites that would be analogous to many deeply buried rock profiles (Ktenidou and Abrahamson 2016). Consequently, there has been a move towards making the site adjustment in a single step rather in the two consecutive steps illustrated in Fig. 48. In the two-step approach, there is first an adjustment to the deeper part of the target site profile, through the V_S-$\kappa$ correction, and then an adjustment to the upper part of the profile through the AFs obtained from SRA. In the one-step approach, the adjustment for the full profiles—extended down to a depth at which the host and target V_S values converge—is through ratios of AFs obtained from full resonance site response analyses of both profiles (Fig. 49); for the V_S-$\kappa$ adjustments in the two-step approach, it is common to use quarter-wavelength methods (Joyner et al. 1981).

Fig. 49

a Two-step site adjustment approach as in Fig. 48, and b one-step site adjustment; the subscript s refers to surface motions and the subscript ref to the reference rock profile (Rodriguez-Marek et al. 2021b)

The one-step approach is not without its own challenges, including defining dynamic inputs at great depth. If the target profile is also hard rock and only linear SRA is to be conducted, the inputs can be obtained from stochastic simulations for scenarios identified from disaggregation of preliminary hazard analyses. Alternatively, surface motions at the reference rock profile can be generated from the GMM, since the profile is consistent with the model, and then deconvolved to the base of the profile to define the input to the target profile. The sensitivity to the input motions is likely to be less pronounced that in the two-step case since the site adjustment factors applied are the ratio of the AFs of the host and target profiles. The approach does, however, bring several advantages, including the fact that the reference rock model and the site adjustment factors can be developed in parallel and independently. If the convolution approach—often referred to as Approach 3, as in Fig. 48, after the classification of methods by McGuire et al. (2021)—is used, then the entire PSHA for the reference rock profile can be conducted independently of the target site characterisation. The GMC logic-tree is constructed by applying host-to-target region source and path adjustments to the backbone GMM, creating a logic tree that predicts motions calibrated to the target region but still for the reference rock profile associated with the GMM. The reference rock hazard therefore does not correspond to a real situation, but this reference rock hazard can then be easily transformed to surface hazard at any target profile. This can be enormously beneficial when hazard estimates are required at several locations with a region, as discussed further in sub-Sect. 6.5.

As an alternative to performing a convolution of the reference rock hazard with site adjustment factors, it is also possible to embed the adjustment factors directly in the hazard integral. This approach is computationally more demanding but can be advantageous when the site adjustment factors depend on the amplitude of the rock motions, for the case of non-linear site response, or depend on magnitude and distance, as has been found to be the case for short-period linear site amplification factors for soft sites (Stafford et al. 2017). The fractiles of the surface hazard are also obtained more accurately with this direct integration approach.

5.3.2 Epistemic uncertainty in site response analyses

The basic components of an SRA model are profiles of V_S, mass density, and damping, and for non-linear or equivalent linear analyses, modulus reduction and damping (MRD) curves that describe the decrease of stiffness and increase of damping with increasing shear strain in the soil. Uncertainty is usually modelled in the V_S profile, as a minimum. Common practice for a long time was to define the V_S profile and associated measure of its uncertainty defined as standard deviation of ln(V_S). Profiles were then generated to by randomly sampling from the distribution defined by this standard deviation, superimposing a layer-to-layer correlation structure; the profiles could also include randomisations of the layer thicknesses and also the MRD curves. This procedure, however, treated all of the uncertainty in the site profiles as aleatory variability whereas in fact at least part of this uncertainty is epistemic. Consequently, there has been a move towards adopting logic trees for SRA, a common procedure being to define the best estimate profile and upper and lower alternatives, inferred from in situ measurements (Fig. 50). EPRI (2013a) provides guidance on appropriate ranges to be covered by the upper and lower bounds as a function of degree of site information that is available. Assigning weights to V_S profiles in a logic tree, however, is in many ways directly akin to assigning weights to alternative GMMs in a GMC logic tree, and the same pitfalls are often encountered. Figure 51 shows the AFs obtained from the three V_S profiles in Fig. 50, from which it can appreciated that at some oscillator frequencies, the three curves converge, suggesting, unintentionally, that there is no epistemic uncertainty in the site amplification at these frequencies. This is the same issue depicted in Fig. 40 and results from constructing a logic tree that does not allow easy visualisation of the resulting distribution of the quantity of interest, in this case the AFs at different frequencies. These observations have prompted the development of what could be considered a ‘backbone’ approach to SRA, although it is implemented rather differently.

Fig. 50

Stratigraphic profile for a hypothetical site (left) and V_S profiles (right) representing the range of epistemic uncertainty (Rodriguez-Marek et al. 2021a)

Fig. 51

Amplification factors for the three V_S profiles in Fig. 50; the arrows indicate oscillator periods at which the three functions converge, suggesting that there is no epistemic uncertainty (Rodriguez-Marek et al. 2021a)

The approach proposed by Rodriguez-Marek et al. (2021a) is to build a complete logic tree with nodes for each of the factors that influence the site response, such as the soil V_S profile, the bedrock V_S, the depth of the weathered layer at the top of rock, and the low-strain damping in the soil. Site response analyses are then performed for all combinations of branches, which can imply an appreciable computational burden. The output will be a large number of weighted AFs, which are then re-sampled at each oscillator frequency, using a procedure such as that proposed by Miller and Rice (1983) to obtain an equivalent discrete distribution (Fig. 52).

Fig. 52

AFs obtained using multiple branch combinations from a complete logic tree for the site profiles and properties (grey curves) and the final AFs obtained by re-sampling this distribution (coloured curves), which correspond to the percentiles indicated in the legend and which are associated with the following weights: 0.101, 0.244, 0.31, 0.244, 0.101 (Rodriguez-Marek et al. 2021a)

The computational demand of the required SRA calculations in this approach is significant, although sensitivity analyses can be performed to identify nodes that have little effect on the results, which can then be dropped, and by using simplified schemes to map the influence of the variability in some elements of the model into the distribution directly (e.g., Bahrampouri et al. 2019).

Most SRA is performed assuming 1D vertical propagation of the seismic waves, which is a reasonable assumption given that at most sites V_S values reduce with depth (leading to refraction of the waves into increasingly vertical paths), but it is also an idealised approximation. For oscillator periods much longer than the fundamental period of the site, 1D SRA methods will tend to yield AFs close to unity in all cases. The method proposed allows a minimum level of epistemic uncertainty, reflecting the modelling error, to be imposed, in order to avoid underestimation of the epistemic uncertainty at longer periods.

5.4 Seismic source models

In terms of their outputs that drive seismic hazard estimates, GMC and site response logic trees both define a single variable: at a given oscillator period, for a reference rock GMC model, it is the response spectral acceleration, and for the site adjustment logic tree, it is the relative amplification factor. For the case of SSC models, the outputs that directly influence the hazard estimates are many: the locations and depths of future earthquakes (which determines the source-to-site distance), the rates of earthquakes of different magnitude, the largest possible magnitude (Mmax), the style-of-faulting, and the orientation of fault ruptures. Distinguishing between elements of aleatory variability (which should be included directly in the hazard integrations) and elements of epistemic uncertainty (that are included in the logic tree) is generally quite straightforward for most components of SSC models: for a given source zonation, locations are an aleatory variable, whereas alternative zonations occupy branches of the logic tree; similarly, the hazard calculations integrate over the distribution of focal depths, but alternative depth distributions are included as a node in the logic tree.

In the following sub-sections I discuss the construction of elements of an SSC model from the same perspective as the preceding discussions of models for rock motions and site amplification factors: how can the best estimate model be constrained, and how can the associated epistemic uncertainty be most clearly represented. I make no attempt to provide a comprehensive guide to SSC model development, which, as noted previously, would require the full length of this paper (and would be better written by others who specialise specifically in this area). Rather I offer a few insights obtained from my experience in site-specific PSHA projects, and I also point the reader to references that define what I would consider to be very good current practice.

5.4.1 Finding faults

Since all earthquakes—with the exception of some volcanic tremors and very deep earthquakes in subduction zones—are the result of fault rupture, an SSC model would ideally consist only of clearly mapped fault sources, each defined by the geometry of the fault plane, the average slip rate, and the characteristic earthquake magnitude. While we know that this is practically impossible, every effort should be made to locate and characterise seismogenic faults whenever possible. In the Eighth Mallet-Milne lecture, James Jackson counselled that to make robust estimates of earthquake hazard and risk one should “know your faults” (Jackson 2001). Jackson (2001) provides an excellent overview of how faults develop and rupture, and how to interpret their influence on landscapes, as well as technological advances—in particular satellite-based InSAR techniques—that have advanced the ability to detect active faults. Most of the examples in Jackson (2001) are from relatively arid regions, particularly in the Mediterranean and Middle East regions. There are other environments in which detection of faults, even if these break the surface in strong earthquakes, can be much more challenging, particularly in densely vegetated tropical regions. For example, the fault associated with the earthquake in Mozambique in 2006 (Fig. 8), which produced a rupture with a maximum surface offset of ~ 2 m, was previously unknown. The earthquake occurred in an active flood plain overlain by thick layers of young alluvial deposits and there was nothing in the landscape to indicate the presence on a major seismogenic fault (Fenton and Bommer 2006).

Another interesting example of a fault that was difficult to find was revealed through extensive studies undertaken for the Diablo Canyon NPP (DCPP) on the coast of California. I served for several years on the Seismic Advisory Board for the DCPP, for which the license conditions imposed by the US Nuclear Regulatory Commission (USNRC) included long-term studies to improve the knowledge of the seismicity and geology of the region surrounding the site, and to re-evaluate both the site hazard and the consequent seismic risk in the light of the new information obtained. The location of the DCPP, near San Luis Obispo, on the coast of central California, is in a region that had been studied far less than areas to the north and south, which had been the focus of extensive research by the University of California at Berkeley and UCLA, respectively. The operator of the DCPP, Pacific Gas and Electricity (PG&E), funded major research efforts in central California, many of them through the US Geological Survey (USGS), including installation of new seismograph networks, re-location of earthquake hypocentres, and extensive geophysical surveys. I distinctly recall working with Norm Abrahamson (on another project) in San Francisco one day when PG&E seismologist Marcia McLaren walked in to show Dr Abrahamson a plot of earthquake epicentres, obtained with a new crustal velocity model and advanced location procedures that consider multiple events simultaneously, which appeared to form a straight line adjacent to the shoreline, about 600 m from the NPP (Fig. 53). The revelation caused some consternation initially because there was no mapped fault at this location, the seismic design basis for the DCPP being controlled mainly by the scenario of a magnitude M 7.2 earthquake on the Hosgri fault, located about 4.5 km from the power plant (Fig. 54); consistent with other NPPs licensed in the USA in the same era, the design basis was deterministic.

Fig. 53

Seismicity in central California from the USGS catalogue (left) and after relocations using a new region-specific crustal velocity model (Hardebeck 2010). The triangles are seismograph stations (SLO is San Luis Obispo); the DCPP is located where there are two overlapping black triangles; HFZ is the Hosgri fault zone, SF is the newly identified Shoreline Fault (Hardebeck 2010)

Fig. 54

(modified from Hardebeck 2010)

Faults in central California, including the Hosgri fault (HFZ) which defined the seismic design basis for the DCPP (red triangle) and the Shoreline fault (SF)

Identification of seismogenic faults through locations of small-magnitude earthquakes is actually rather unusual in practice, but this case showed the potential of very accurate hypocentre location techniques. The presence of a right-lateral strike-slip fault along the coastline, given the name of Shoreline Fault, was confirmed by fault plane solutions (aka ‘beachballs’) showing a consistent orientation and slip direction. The reason that the extensive geophysical surveys had not identified the Shoreline Fault is its location within the shallow surf zones and the resolution of geophysical measurements originally made in the late 1980s. High-resolution magnetic and bathymetric surveys undertaken subsequent to the discovery of the aligned epicentres confirmed the clear presence of this structure (Fig. 55). The Shoreline Fault itself is not a very large structure but a scenario was presented wherein a major earthquake on the Hosgri fault would continue along the Shoreline fault, situating an event as large as M 7.5 a few hundred metres from the plant (Hardebeck 2013). Subsequent studies showed the Shoreline Fault to have a very low slip rate and that it did not present heightened risk to the plant (the design basis response spectrum for the DCPP was anchored at a PGA of 0.75 g).

Fig. 55

Contrasting geophysical measurements in the vicinity of the DCPP from 1989/1990 (left) and 2009 (right); upper: helicopter magnetics, lower: bathymetry (PG&E 2011)

The characteristic model for earthquake recurrence on faults combines large magnitude quasi-periodic events with smaller events that follow a Gutenberg–Richter recurrence relationship (Youngs and Coppersmith 1985; see the middle right-hand panel of Fig. 23). There are other cases, however, where there is little or no earthquake activity of smaller magnitude between the large-magnitude characteristic earthquakes, sometimes referred to as an Mmax model (Wesnousky 1986). In such cases, especially if a fault is late in its seismic cycle and the last major event pre-dated any reliable earthquake records, seismicity data will be of little value in identifying active faults. A clear example of this is the Pedro Miguel fault in central Panama, which was discovered through geological investigations undertaken as part of the expansion programme to build the new post-Panamax locks that began operation in 2016; I was privileged to witness this work as it unfolded as a member of the Seismic Advisory Board for the Panama Canal Authority (ACP).

The work undertaken for the ACP identified several large strike-slip faults in central Panama, the most important of which turned out to be the Pedro Miguel fault, which runs approximately north–south and in very close proximity to the new Pacific locks. The fault was identified initially from surface offsets of streams and other geomorphological expressions, followed by an extensive programme of trenching (Fig. 56). The evidence all pointed consistently to a long, strike-slip fault that had last undergone major right-lateral slip a few hundred years ago, with evidence for earlier movements of comparable size. Here an interesting side note is in order: when the first trenches were opened and logged, there was some discussion of whether some observed fault displacements had occurred as the result of two large earthquakes at different times or one very large earthquake. Although the latter scenario may appear to be the more extreme scenario, it would actually result in lower hazard than the former interpretation, which may seem counter intuitive to some. The single large earthquake would have very long recurrence interval, whereas the somewhat smaller (but still very substantial) earthquakes imply a higher recurrence rate. Due to the non-linear scaling of ground motions with magnitude (Figs. 21 and 44), the larger magnitude of the less frequent characteristic earthquake would not compensate for the longer recurrence interval, hence in PSHA calculations, higher hazard results from the interpretation of the displacements being due to multiple events.

Fig. 56

Exposure of the Pedro Miguel fault in a trench in central Panama

After the geomorphological studies and paleoseismological investigations in the trenches had revealed the clear presence of an active fault with relatively recent movements, an additional discovery was made that provided compelling evidence both for the presence of the fault and the date of its most recent movement. The Camino de Cruces was a cobblestone road, built in 1527, that extended from the Pacific coast of Panama almost half-way across the isthmus to the source of the Chagres River. During the sixteenth and seventeenth centuries, the Spanish conquistadores transported gold, silver, spices and textiles plundered from South America to Panama via ship. The precious cargo was then transported by mule along the Camino de Cruces and then by boat along the Chagres to join ships on the Caribbean coast that would sail the booty to Europe. Exploration of the Camino de Cruces, which is now embedded in the jungle and requires a few hours of hiking to be reached from the nearest road, revealed a 3 m offset of the cobblestones, which aligned perfectly with the orientation and slip direction of the Pedro Miguel fault identified from the trenches (Fig. 57). Adjacent stream banks were also displaced by the same amount. Historically, the few damaging earthquakes known to have occurred in Panama were assigned to sources in the ocean to the north or south of the isthmus, which are zones of active tectonic deformation. An earthquake in 1621 was reported to have caused damage, particularly to the old Panama City (located to the east of today’s capital) and had been located by different researchers in both the northern and southern offshore deformation zones. However, through careful re-evaluation of the historical accounts of the earthquake effects, Víquez and Camacho (1994) had concluded that the 1621 earthquake was located on land, probably in close proximity to Panamá Vieja. This led to the conclusion that the 1621 earthquake had occurred on the Pedro Miguel fault, an earthquake of magnitude ~ 7 along the route of the Panama Canal. The implications of these findings, and the resistance these conclusions have encountered, are discussed further in Sect. 7.2.

Fig. 57

(modified from Rockwell et al. 2010a)

Upper: photograph of Camino de Cruces, in which the author (left) and previous Mallet-Milne lecturer Lloyd Cluff (right) are either side of offset; lower: map of the Pedro Miguel fault where it offsets the Camino de Cruces and adjacent stream banks; green triangle indicates approximate position and direction of photo

The two examples above from California and Panama both correspond to cases of finding previously unknown faults, which will generally lead to increased hazard estimates. There are also many cases of geological investigations leading to reduced hazard estimates by demonstrating that a fault has a low slip rate and/or low seismogenic potential. Such studies will generally require a well-established geological framework for the region with clear dating of formations or features of the landscape. A good example is the GAM and PLET faults close to the Thyspunt NPP site in South Africa (Fig. 35), which were assigned probabilities of only 20% of being seismogenic on the basis of lack of displacements in well-defined marine terraces (Bommer et al. 2015b). The effect of assigning such a probability is to effectively reduce the recurrence rate of earthquakes on these structures by a factor of five.

Another example comes from the United Arab Emirates, for which we undertook a PSHA prompted by requests for input to numerous engineering projects in Dubai and Abu Dhabi (Aldama-Bustos et al. 2009). Our results closely agreed with other studies for the region, such as Peiris et al. (2006), but the 2475-year hazard estimates of Sigbjornsson and Elnashai (2006) for Dubai were very significantly higher. The distinguishing feature of the latter study is the inclusion of the West Coast Fault (WCF) as an active seismic source (Fig. 58). The seismic hazard studies that include the WCF as an active seismic source have generally done so based on the Tectonic Map of Saudi Arabia and Adjacent Areas by Johnson (1998), which drew heavily on the work of Brown (1972) which, according to Johnson (1998), presented ‘‘selected tectonic elements of Saudi Arabia and, in lesser details, elements in adjacent parts of the Arabian Peninsula’’. Among several publications on the geology of this region that we reviewed, only Hancock et al. (1984) refer to a fault along the coast of the Emirates, but their mapped trace is annotated with a question mark indicating doubts regarding its presence.

Fig. 58

source zones defined for PSHA of Abu Dhabi, Dubai and Ra’s Al Khaymah (red diamonds, left to right) in the UAE (Aldama-Bustos et al. 2009); WCF is the West Coast Fault

Seismic

Assigning activity rates to the WCF is difficult due to the lack of any instrumental seismicity that could be directly associated with this structure, and the historical record for the UAE is almost null because of the very sparse population and the absence of major towns and cities where earthquake damage could have been recorded. To perform a sensitivity analysis, we assumed the fault to behave as a characteristic earthquake source and the slip rate was estimated indirectly from the maximum rate that could pass undetected based on the available information. To infer this limiting slip rate, we employed contours of the base of the Tertiary and the approximate base of the Mesozoic rocks that are overlain by sediments known as sabkhas; the latter are composed of sand, silt or clay covered by a crust of halite (salt), deposits that were formed by post-glacial flooding between 10 and 15 Ma ago, hence we conservatively assumed an age of 10 Ma. The Brown (1972) map is at a scale of 1:4,000,000 and it was assumed that any offset in the contours resulting from accumulated slip on the fault would be discernible if at least 1 mm in length on the map, implying a total slip of 4 km and a slip rate of 0.4 mm/year. Additional constraint on the slip rate was inferred from the GPS measurements obtained at two stations in Oman (Vernant et al. 2004); making the highly conservative assumption that all the relative displacement is accommodated on the WCF yields a slip rate of 2.06 mm/year, although in reality most of this displacement is actually owing to the rotational behaviour of the Arabian plate. We then assumed a characteristic earthquake magnitude of M 7 ± 0.5; the relationship of Wells and Coppersmith (1994) indicates M 8 if the entire fault ruptures, but such events would be difficult to reconcile with the lack of observed offset. With the slip rate of 0.4 mm/year, the hazard was re-calculated for Dubai: the inclusion of the WCF increased the hazard estimates but even for an AFE of 10^–6, the increase in the ground-motion amplitude is less than a factor of two. To produce a 475-year PGA for Dubai that would match that obtained by Sigbjornsson and Elnashai (2006), a slip rate on the fault of 6.0 mm/year would be required.

In the case of WCF, constraints on the possible slip rate were obtained indirectly, whereas it is possible that field investigations might reveal that this lineament is not an active fault at all. An inescapable fact is that geological field work, especially when it involves trenching and laboratory dating of rock samples, is time consuming and can incur substantial costs, but for major infrastructure projects, the investment is fully justified. If geological field work is not undertaken to characterise known or suspected faults, then a price must be paid in terms of increased epistemic uncertainty. This principle was invoked in a site-specific PSHA for the Angra dos Reis NPP in southeast Brazil (Almeida et al. 2019). A number of faults have been mapped in the region of the site (Fig. 59) and for some of these structures, displacements are visible in exposures at road cuttings, which in itself points to possible seismogenic activity of these structures.

Fig. 59

source area defined to model the potential seismicity associated with these faults (Almeida et al. 2019)

Mapped faults in the region surrounding the Angra dos Reis NPP site (red dot) in southeast Brazil; the red polygon is the equivalent

At the same time, the Quaternary sequence of the region is still in development and reliable geochronology data for the formations displaced by the local offsets are very limited to date. There is also a lack of clear and persistent geomorphological expression of most of the faults for which displacements have been logged. Rather than modelling all of these structures as individual sources, with logic-tree branches for uncertainty in their probability of being seismogenic, slip rates and characteristics magnitudes, their collective impact on the hazard was modelled through an equivalent source zone (red polygon in Fig. 59) imposed on top of the other area source zones defined for the PSHA. Each fault was assigned a slip rate, dependent on its length, which would not be inconsistent with the lack of strong expressions in the landscape, and a maximum magnitude inferred from its length. These parameters were then used to define magnitude-recurrence pairs that generated an equivalent catalogue of larger events, for which a recurrence model was derived (Fig. 60). This source was then added to the areal source zones and included in the hazard integrations with an M_min of 6.5 and an Mmax corresponding to the largest value assigned. This conservative approach led to appreciable increase in the hazard estimates at low AFEs (Fig. 60) but it provided a computationally efficient way of including the epistemic uncertainty associated with these faults. If the resulting site hazard were to have proved challenging for the safety case of the plant, geological and geochronological investigations could be commissioned to provide better constraint on the seismogenic potential of these faults, which would most likely lead to a reduction in their impact.

Fig. 60

source zone (blue and green) and for the equivalent source for potentially active faults (purple curve from the data, red curve is the effective recurrence after applying a 10% probability of the faults being seismogenic), defined for the Angra dos Reis PSHA; lower: uniform hazard response spectra for the Angra dos Reis NPP site in Brazil obtained without (dashed lines) and with (solid lines) the contributions from the potentially active faults (Almeida et al. 2019)

Upper: recurrence relationships for host

5.4.2 Source zones and zoneless models

Since not all earthquakes can be assigned to mapped geological faults, seismic source zones are a ubiquitous feature of SSC models for PSHA. Source zones are generally defined as polygons, within which specified characteristics of the seismicity are assumed to be uniform. One of the common assumptions is that the seismicity is spatially uniform, and earthquakes can therefore occur at any location within the source zone with equal probability. This has often led to the suggestion (by reviewers) that the SSC logic tree should also include a branch for zoneless models, in which the locations of future seismicity are essentially based on epicentres in the earthquake catalogue for the region (e.g., Frankel 1995; Woo 1996). For a region in which the spatial distribution of seismicity is tightly clustered, the zoneless approaches are likely to yield distinctly different hazard distributions compared to hazard estimates obtained with source zones (e.g., Bommer et al. 1998). In my view, however, there should be no automatic imperative to include both source zones and zoneless approaches, because such an admonition places the focus in the construction of the SSC logic tree on selecting and weighting models rather than on the distributions of magnitude, distance and recurrence rate that drive the hazard. There is, in any case, a third option between zoneless approaches and areal source zones, namely zones with smoothed seismicity: source zones can be defined in which certain characteristics are uniform throughout (such as Mmax, style-of-faulting, and focal depth distributions) but with the a- and b-value of the Gutenberg-Richter recurrence relationship varying spatially (Fig. 61). The spatial smoothing is based on the earthquake catalogue but with the degree of smoothing controlled by user-defined parameters (which is also true of the zoneless approaches).

Fig. 61

source zones defined for the SSC model of the Central and Eastern United States (USNRC 2012a)

Spatially smoothed activity rates (left) and the b-value (right) within the broad

The questions being addressed in the construction of a seismic source zonation or a zoneless source modelling approach is the same: where will future earthquakes occur and what will be their characteristics in terms of Mmax, style-of-faulting and focal depth distribution? When these questions are not answered by the localising structures of active geological faults, the question then arises to what degree is the earthquake catalogue spatially complete? Or expressed another way, can the observed spatial distribution of seismicity be assumed to be stationary for the forthcoming decades covering the design life of the facility under consideration? Spatial completeness can be a particularly important issue in mapping of seismic hazard. In 2004, I served on a panel to review the development of a new seismic hazard map for Italy (Meletti et al. 2008), an endeavour that was triggered in large part by two earthquakes of M 5.7 earthquake of 31 October and 1 November 2002, which caused the collapse of a school building in San Giuliano and the deaths of 25 children. The earthquake occurred in an area classified as not requiring seismic design in the seismic design code of 1984. The earthquake was the second destructive earthquake to occur outside of the seismic source zones defined for the hazard mapping, following an M 5.4 in Merano in July 2001, which also led to loss of life (Fig. 62). The purpose of the new hazard map was to serve as the basis for a revised seismic design code (Montaldo et al. 2007; Stucchi et al. 2011) and also as the starting point for an endeavour to seismically retrofit school buildings at risk (e.g., Grant et al. 2007).

Fig. 62

source zonation (ZS4; Meletti et al. 2000) underlying the seismic hazard map of Italy, showing locations of two destructive earthquakes that occurred outside the boundaries of the zones (adapted from figure in Meletti et al. 2008)

The 1996 seismic

The definition of seismic source zones is often poorly justified in PSHA studies, with different criteria being invoked for different boundaries and evidence cited as a determining factor for one zone ignored in another. There can be no prescription for how source zones should be defined because the process will necessarily have to adapt to the specific characteristics and data availability in any given application. However, some simple guidelines can assist in creating a more transparent and defensible seismic source zonation, which is fundamental to achieving acceptance of the resulting hazard assessment. Firstly, the study should clearly explain the definition of a seismic source zone being adopted in the study, which needs to be more specific than a bland statement regarding uniform seismicity. The definition should list the earthquake characteristics that are common across a source zone, and those which are allowed to vary, whether through spatial smoothing (for recurrence parameters) or through aleatory distributions (for style-of-faulting, for example). Boundaries between source zones will then logically correspond to distinct changes in one or more of the common characteristics. Secondly, the criteria for defining boundaries should also be clearly specified, together with the data to be used in implementing each criterion. To the extent possible, evidence should be given that demonstrates the role of each criterion in controlling the location, size, and rate of seismicity, either in general or in the region where the study is being performed. These criteria should then be consistently and systematically applied to develop the source zonation model. A good example of both clear definition of source zone characteristics and the application of consistent criteria for their definition can be found in the SSC study for the Central and Eastern United States (CEUS-SSC) project (USNRC 2012a).

The discussion of criteria for defining source boundaries and using data to apply these criteria should not give the impression that the process, once defined, can be somehow automated. Inevitably, expert judgement plays a significant role, as discussed further in Sect. 6. The boundaries of seismic source zones are a clear example of epistemic uncertainty, and this is often reflected in the definition of multiple source zonation models with alternative boundaries, especially in site-specific studies for which the configuration of the host zone (containing the site) and its immediate neighbours can exert a strong influence on the hazard results.

As previously noted in Sect. 4.1, for compatibility with the distance metrics used in current GMMs, hazard calculations need to generate virtual fault ruptures within area source zones. The geometry of these virtual ruptures should reflect the geological structure and stress orientations in the region, and their dimensions should be related to the magnitude of the earthquake; for the latter, several empirical scaling relationships are available, including those of Stafford (2014), which were specifically derived for application in PSHA. Careful consideration needs to be given to the physical characteristics of these virtual ruptures, since they are not only a tool of convenience required because of the use of R_jb and R_rup in GMMs; the ruptures should correspond to physically realisable events. Rupture dimensions are often defined by the total rupture area and source models will generally define the thickness of the seismogenic layer of the crust; consequently, for the largest magnitudes considered, the length may be very considerable, exceeding the dimensions of the source zone within which the rupture initiates. This is usually accommodated by allowing the source zones to have ‘leaking boundaries’, which means that the ruptures can extend outside the limits of the source zone. This makes it even more important to clearly define the meaning of a source zone since in effect it implies the presence of seismogenic faults that may straddle two or more source zones, but rupture initiations are specified separately within each zone. Particular caution is needed if the host zone is relatively quiet and there are much higher seismicity rates in more remote sources, especially if the specified orientations allow virtual ruptures to propagate towards the site. In one project in which I participated, the preliminary hazard analyses showed major hazard contributions coming from a source zone whose closest boundary was a considerable distance from the site. Disaggregating the contributions from this source in isolation, it became apparent that the ruptures associated with the largest earthquakes in this source were almost reaching the site. The recommendation of Bommer and Montaldo-Falero (2020) to use only point-source representations rather than virtual ruptures in remote source zones eliminates this potential pitfall.

In some site-specific PSHAs that I have reviewed, very small seismic source zones are sometimes defined, usually to enclose a cluster of relatively high seismic activity. This becomes akin to a zoneless seismicity model or smoothed seismicity with limited spatial smoothing, which should be justified through a geologic or tectonic explanation for why higher seismic activity is localised in that area. Such technical justifications are particularly needed when the consequence of such small source zones is to maintain the observed seismicity at a certain distance from the site under study. Another issue that needs to be addressed with very small seismic source zones is that for many of the virtual ruptures, the majority of their length may lie outside the source boundaries. This could partially be addressed by assigning smaller Mmax values, but this would also need a robust and independent technical basis rather than simply being an expeditious measure to accommodate the decision to define a source zone of small area.

5.4.3 Recurrence rate estimates

The recurrence rates of moderate and large magnitude earthquakes in an SSC model are the basic driver of seismic hazard estimates. For a single seismic source zone, the hazard curve obtained at a site scales directly with the exponent of the activity rate (a-value) of the Gutenberg-Richter recurrence relationship. The rates of future earthquakes are generally inferred from the rates of past earthquakes, both for fault source and area sources, hence the reliability of the hazard assessment will depend on the data available to constrain the rate and the assessment of the associated uncertainty. Focusing on source zones rather than fault sources, the recurrence model relies on the earthquake catalogue for the region. As already noted in Sect. 3.3, instrumental monitoring of earthquakes has been operating for at most a few decades in many parts of the world, which is a very short period of observation to serve as a basis for establishing long-term rates. The catalogue can usually be extended through retrieval and interpretation of historical accounts of earthquake effects; the very first Mallet-Milne lecture by Nick Ambraseys was largely devoted to the historical seismicity of Turkey (Ambraseys 1988). This work revealed that the 20^th Century had been an unusual quiescent period for seismicity in southeast Turkey, for which reason the instrumental earthquake catalogue was a poor indicator of the long-term seismic hazard in the region, where several large earthquakes has occurred in the nineteenth Century and earlier (Ambraseys 1989).

As with geological investigations of faults, historical seismicity studies will often unearth previously unknown earthquakes that will impact significantly on hazard estimates, but in some cases such studies can serve to constrain low hazard estimates. In the PSHA for the Thyspunt nuclear site in South Africa (Bommer et al. 2015a, b), the hazard was largely controlled, at least at shorter oscillator periods, by the seismicity rates in the host ECC source zone (Fig. 35). The earthquake catalogue for this region was very sparse but investigations were undertaken that established that this was not the result of absence of evidence for seismic activity. By identifying the locations at which newspapers and other records were available over different historical periods and noting that these did include reports of other natural phenomena (Albini et al. 2014), the absence of seismic events was confirmed, thus corroborating the low recurrence rates inferred from the catalogue. Without this evidence for the absence of earthquake activity, broad uncertainty bands on the recurrence model would have been required, inevitably leading to increased seismic hazard estimates.

Developing an earthquake catalogue for PSHA involves retrieving and merging information from many sources, both instrument and historical, as often as possible using primary sources of information, and eliminating duplicated events. Listed events that are actually of anthropogenic origin, such as quarry blasts, must also be removed (e.g., Gulia and Gasperini 2021). The earthquake magnitudes must then be homogenised to a uniform scale, which is usually moment magnitude; as noted below, the variability in such empirical adjustments should be accounted for in the calculation of recurrence rates. Since PSHA assumes that all earthquakes are independent—in order to sum their hazard contributions—the homogenised catalogue is then declustered to remove foreshocks and aftershocks (e.g., Gardner and Knopoff 1974; Grünthal 1985; Reasenberg 1985).

To calculate recurrence rates, the number of earthquakes in each magnitude bin is divided by the time of observation, but this requires an estimate of the period for which the catalogue is complete, which will generally increase with magnitude. The estimation of completeness periods is a key source of epistemic uncertainty in the derivation of recurrence rates, but this uncertainty can be constrained by establishing probabilities of earthquake detection over different time periods based on the operational characteristics of seismograph networks and the availability of historical records. The uncertainty in magnitude values, whether the standard error of instrumentally determined estimates or the standard deviation in empirical relations to convert other magnitudes to moment magnitude (or to convert intensities for the case of historical events), should also be taken into account. These uncertainties are usually assumed to be symmetrical (normally distributed) but they lead to errors because of the exponential nature of earthquake recurrence statistics (i.e., because there are more earthquakes at smaller magnitudes). The effect of this uncertainty is to alter the activity rate—upwards or downwards—but it does not alter the b-value (Musson 2012b); however, if the magnitude uncertainties are not constant, which will often be the case, then the b-value is also affected (Rhoades 1996). Tinti and Mulargia (1985) proposed a method to adjust the magnitude values to correct for this uncertainty; in the CEUS-SSC project, Bob Youngs developed an alternative approach that adjusts the effective rates (USNRC 2012a).

As was noted previously (Sect. 3.1), once the recurrence data are prepared, the parameters of the Gutenberg-Richter relationship should be obtained using a maximum likelihood approach (e.g., Weichert 1980). Veneziano and Van Dyke (1985) extended this approach into a penalised maximum likelihood method, in which the b-values are conditioned on the estimates of Mmax and also constrained by a prior estimate for the b-value, which is useful where data are sparse. Figure 63 shows the fitting of recurrence relationships to the data for the five source zones defined for the Thyspunt PSHA using the penalised maximum likelihood approach.

Fig. 63

source zones defined for the Thyspunt site (Fig. 35) using the penalised maximum likelihood approach (Bommer et al. 2015b); the panel at the lower right-hand side shows the b-values determined for each source zone using the prior distribution based on the regional b-value (grey shading)

Fitting of recurrence relationships to catalogue data for the five area

A final point to make concerns the construction of the logic-tree branches for recurrence parameters. The key message that it is important to ensure that the resulting range of uncertainty (on recurrence rates of earthquakes of different magnitude) is not unintentionally too broad. The a- and b-values should always be kept together on a single node rather than split as two separate nodes (a practice in some early studies for UK NPP sites, for example) since they are jointly determined, and their separation would lead to combinations that are not consistent with the data. Ideally, the recurrence parameters should also be coupled with Mmax values, which will generally be the case when the penalised maximum likelihood approach is used. Checks should always be made to ensure that the final branches imply seismic activity levels that can be reconciled with the data available for the region, especially on the upper end. Do the higher branches predict recurrence rates of moderate magnitude earthquakes that would be difficult to reconcile with the paucity or even absence of such events in the catalogue? Is the implied rate of moment release with the nature of the region and any estimates, from geological data or remote sensing measurements, of crustal deformation rates?

5.4.4 A backbone approach for SSC models?

In the light of the preceding discussions, we can pose the question of whether there is the possibility of adapting the backbone approach to SSC modelling? The key to the backbone approach is a more transparent relationship between the models and weights on the logic-tree branches and the resulting distribution of parameters that move the needle in the hazard calculations. For a given source configuration, a backbone approach is easily envisaged. Stromeyer and Grünthal (2015) actually proposed an approach that would qualify as a backbone approach: in the first step, the uncertainty in the a- and b-values is propagated, through their covariance matrix, to the estimates of rate at any fixed value of magnitude. The one-dimensional distributions of rates are then re-sampled at each magnitude into an equivalent distribution following Miller and Rice (1983); this is directly comparable to the way that the distribution of AFs is re-sampled at each oscillator frequency in the approach of Rodriguez-Marek et al. (2021a; Sect. 5.3).

When the spatial distribution of future seismicity is also included as an epistemic uncertainty through alternative zonations or alternative smoothing operators, the situation becomes complicated. Since the alternative zonations will automatically overlap one another, the logic tree is unlikely to satisfy the MECE criterion. With multiple source zone configurations, it also becomes more difficult to visualise the distributions of location and recurrence rates simultaneously. Maps could be generated that depict the effective rate of earthquakes of a specified magnitude over a spatial grid (Fig. 64), but it would be challenging to represent this information for the full range of magnitudes simultaneously. Herein may lie an interesting challenge for researchers working in the field of seismic source modelling: to develop visualisation techniques that would enable the full implications of an SSC logic tree, in terms of space and rate over the full range of magnitudes from M_min to Mmax, to be visualised.

Fig. 64

source in the CEUS-SSC model (USNRC 2012a)

Distribution of activity rates (left) and b-values (right) for one seismic

6 Uncertainty and expert judgement in PSHA

By this point, I hope that I will have persuaded the reader that the identification, quantification, and clear incorporation of epistemic uncertainty into seismic hazard assessments are fundamental to increasing the chances of the results of such studies being accepted and thus adopted as the starting point for seismic risk mitigation, which is always the ultimate objective. In Sect. 5, I have discussed current approaches to the construction of logic trees, the tool ubiquitously employed in site-specific PSHA projects to manage epistemic uncertainty. In this section I briefly discuss the role of expert judgement in constructing these logic trees and current best practice in terms of procedures for making these judgements.

6.1 The Inevitability of expert judgement

As I have stressed several times, the importance of gathering and analysing data in seismic hazard assessment cannot be overemphasised. The compilation and assessment of existing data is a non-negotiable part of any seismic hazard study, and the collection of new data, particularly for site-specific studies for important facilities, is strongly recommended. However, it is also important to be conscious of the fact that the data will never be sufficient—at least not in any foreseeable future—to allow the unambiguous definition of the unique models for the characteristics and rates of potential future earthquakes and for the ground motions that such events could generate. Consequently, there is always epistemic uncertainty, and the full distribution of epistemic uncertainty cannot be objectively measured. For some practitioners and researchers, this seems to be difficult to accept. Examining the performance of GMMs against local ground-motion data may usefully inform the process of constructing a GMC logic-tree but any quest for a fully objective and data-driven process to select and assign weights to models to occupy the branches is futile. Similarly, procedures to check the consistency of source models with the available earthquake catalogue may also be usefully informative—subject to various assumptions regarding the completeness of the catalogue—but I would argue that at most such techniques can demonstrate that a source model is not invalid (which is not the same as validating the model); this seems to be reflected in the change from “objective validation” to “objective assessment” in the titles of the papers proposing such testing of source models by Musson (2004) and Musson and Winter (2012).

If the centre, body, and range of epistemic uncertainty cannot be measured from observations, the objective of assessing the CBR of TDI cannot be met without invoking expert judgement. In their proposal for an entirely objective approach to populating the branches of a GMC logic-tree, Roselli et at. (2016) dismiss the application of expert judgement on the basis that “…. a set of GMPEs is implemented (more or less arbitrarily) in a logic-tree structure, in which each GMPE is weighted by experts, mostly according to gut feeling.” This is a misrepresentation since what is sought is a judgement, in which there is a clear line of reasoning from evidence to claim, rather than an unsubstantiated or intuitive opinion. The judgements require technical justification and the expert making the judgement should be able to defend the judgement if challenged.

In this context, it is also helpful to clarify exactly what is implied by the term ‘expert’, the meaning of which is two-fold. Firstly, the person making the judgement, or assessment, must be appropriately qualified in the relevant subjects and preferably also experienced in the interpretation of data and models in this field; ideally, the individual will have also received some training in the concepts of cognitive bias and how such bias can influence technical decisions. Secondly, by the time the person is making their judgement, they are expected to have become an expert in the specific application—the seismicity or ground-motion characteristics of the region and the dynamic properties of the site—through study and evaluation of the relevant literature, data, and models. This is quite distinct from classical ‘expert elicitation’ where the objective is usually to extract only the probabilities associated with specified events assuming that this information already exists in the mind of the expert (e.g., O’Hagan et al. 2006).

6.2 Multiple expert judgements

In classical expert elicitation, several experts are usually assembled but the objective is to identify among them the ‘best’ experts, chosen on the basis of their responses to related questions for which the responses are known. As applied to seismic hazard assessment, the purpose of assembling multiple experts is quite different. The intention is to bring different perspectives to the interpretation of the available data, methods, and models, precisely because the objective is not to find the ‘right’ answer but rather to capture the centre, the body, and the range of technically defensible interpretations. Experts with different training and experience are likely to make distinct inferences from the same information and hence increase the chances of capturing the full CBR of TDI.

At the same time, it is important to point out that the intention of engaging multiple experts in a seismic hazard assessment is not intended to increase the chances of constructing a logic tree that represents the views of the broad technical community in the field. Put bluntly, multiple expert hazard assessments should not be conducted as a plebiscite or referendum. Some confusion around this issue arose because of an unfortunate use of words in the original SSHAC guidelines—discussed below—which stated the goal to be capture of the centre, body, and range of the informed technical community (or CBR of the ITC; Budnitz et al. 1997). The intent of this wording was to imply that the study should capture the full distribution of uncertainty that would be determined by any group of appropriately qualified and experienced subject-matter experts who became informed about the seismicity of the region and seismic hazard of the site through participation in the assessment. Regrettably, this intent was often overlooked and the objective of capturing the CBR of the ITC was interpreted as meaning that the views of all experts in the field should be reflected in the logic tree. Such a view may be admirably inclusive and democratic but is unlikely to lead to a robust scientific characterisation. This is important in the context of this paper that is focused on achieving acceptance of the results of seismic hazard assessments, since one could easily lean toward favouring an approach that ensured that many views and models from the broad technical community were included on the basis that this might lead to broader acceptance (if one assumes that all the experts whose views were included would look positively on their preferred model being part of a broad distribution rather than clearly identified as the best model). My view is that we should always make the best possible scientific assessments, and that we should conduct these assessments and document them in ways that are conducive to their acceptance, but the scientific assessment should never be compromised by the desire to achieve acceptance.

The benefits of engaging multiple experts in the assessment of seismic hazard have been recognised for a long time, especially for regions where uncertainties are large as a result of earthquakes occurring relatively infrequently. In the 1980s, two major PSHA studies were conducted for NPPs in the Central and Eastern United States by the Electric Power Research Institute (EPRI) and Lawrence Livermore National Laboratory (LLNL). Both studies engaged multiple experts but conducted the studies in different ways in terms of how the experts interacted. The hazard estimates produced by the two studies for individual sites were very different both in terms of the expected (mean) hazard curves and the implied ranges of epistemic uncertainty (Fig. 65). In response to these divergent outcomes, EPRI, the US Nuclear Regulatory Commission (USNRC), and the US Department of Energy (DOE) commissioned a panel of experts—given the designation of the Senior Seismic Hazard Assessment Committee, or SSHAC—to explore and reconcile the differences between the EPRI and LLNL studies.

Fig. 65

Mean and median hazard curves for PGA at an NPP site in Central and Eastern United States obtained from the EPRI and LLNL PSHA studies (Bernreuter et al. 1987)

Whereas the original expectation was that the SSHAC review might find a technical basis for reconciling the results from the EPRI and LLNL studies, they concluded that the differences arose primarily from differences in the way the two studies had been conducted: “In the course of our review, we concluded that many of the major potential pitfalls in executing a successful PSHA are procedural rather than technical in character. ….. This conclusion, in turn, explains our heavy emphasis on procedural guidance” (Budnitz et al. 1997). The outcome of the work of the SSHAC was a report that provided guidelines for conducting multiple expert seismic hazard studies, which became known as the SSHAC guidelines (Budnitz et al. 1997).

6.3 The SSHAC process

Mention of SSHAC or the SSHAC process sometimes provokes a heated response of the kind that is normally reserved for controversial political or religious ideologies. Such reactions are presumably prompted by perceptions or experience of specific implementations of the SSHAC process (see Sect. 7.2) rather than any impartial perusal of the guidelines. The SSHAC guidelines are simply a coherent proposal, based on experience, for how to effectively organise a seismic hazard study involving multiple experts. The essence of the SSHAC process can be summarised in five key characteristics:

• 1. Clearly defined roles Each participant in a SSHAC process has a designated role, and for each role there are specific attributes that the participant must possess and specific responsibilities that they are expected to assume. The clear definition of the roles and responsibilities is the foundation of productive interactions within the project.

• 2. Evaluation of data, methods, and models Databases of all available data, methods, and models are compiled, and supplemented, where possible, by new data collection and analyses. These databases are made available to all participants in the project and the TI Teams (see below) are charged with conducting an impartial assessment of the data, methods, and models for their potential applicability to the region and site under study.

• 3. Integration On the basis of the evaluation, the TI Teams are charged with integrating their assessments into distributions (invariably represented by logic trees) that capture the CBR of TDI.

• 4. Documentation consistent with the description given in Sect. 4.4, the study needs to be summarised in a report that provides sufficient detail to enable the study to be reproduced by others.

• 5. Participatory peer review As discussed in Sect. 4.3, peer review is critical. In a SSHAC process, the peer reviewers are charged with conducting rigorous technical review and to also review the process through which the study has been conducted, which to a large extent means ensuring that the roles and responsibilities are adhered to by all participants throughout the project. The adjective ‘participatory’ is used in SSHAC terminology to distinguish the recommended approach from late-stage review; while the term does reflect the fact that the peer reviewers are present in meetings and workshops throughout the project, it should not be interpreted to mean that they actually engage in the development of the SSC and GMC logic trees—detachment and independence from that activity is essential.

When rigid opposition to the notion of SSHAC is expressed, it has been suggested that those militating against the SSHAC process could be asked which of these five characteristics they find most unpalatable and would not wish to see in a site-specific seismic hazard study. Views regarding specific details of how SSHAC studies are organised are entirely reasonable—the guidelines have evolved iteratively, as discussed in Sect. 6.4—but wholescale rejection of these basic concepts is difficult to understand. There can be little doubt that clear demonstration that a seismic hazard assessment complied with all five of these basic stipulations should be conducive to securing acceptance of the outcomes of the study.

Figure 66 illustrates the interactions among the key participants in a SSHAC study. The TI (Technical Integration) Teams are responsible for the processes of evaluation and integration, and ultimately assume intellectual ownership of the SSC and GMC models. Each TI Team has a nominated lead, responsible for coordinating the work of the Team and the interfaces with other parts of the project. Additionally, there is an overall technical lead, called the Project Technical Integrator (PTI); in practice, this position is often filled by one of the TI Leads. The evaluations by the TI Team are informed by Specialty Contractors, who collect new data or undertake analyses on behalf of the TI Teams, and by Resource Experts, who are individuals with knowledge of a specific dataset or region or method that the TI Teams wish to evaluate. The TI Teams also engage with Proponent Experts, who advocate a particular model without any requirement for impartiality. Details of the required attributes and the attendant responsibilities corresponding to each role are provided in USNRC (2018).

Fig. 66

Role and interactions in SSHAC seismic hazard study (USNRC 2018)

From the perspective of acceptance of the results of a PSHA study, the roles of Resource Expert and Proponent Expert are particularly important since they provide a vehicle for the participation by members of the interested technical community, and especially those who have worked on the seismicity, geology or ground-motion characteristics of the region. Their participation can bring very valuable technical insights and information to the attention of the TI Teams, and at the same time give these same experts insight into and knowledge of the hazard assessment project. In many settings, the technical community includes individuals with strong and sometimes even controversial views of the earthquake potential of a particular fault or the location of particular historical events. Dismissing the views of such researchers would be unscientific and also give them ammunition to criticise the project and its findings, but it would also be inappropriate to include their models without due scrutiny purely on the basis of appeasing the proponent. The SSHAC process provides a framework to invite such experts to participate in a workshop—with remuneration for their time and expenses—to allow them to present their views and to then respond to the questions from the TI Teams, all under the observation of the PPRP, thus facilitating an objective evaluation of the model.

The selection of appropriate individuals to perform the specified roles in a SSHAC study is very important and the selection criteria extend beyond consideration of academic qualifications and professional experience. For members of the TI Teams, willingness to work within a team and to be impartial is vital. All the key participants must be able and willing to commit significant time and effort to the project, and the TI Leads and PTI need to be prepared to be engaged very frequently and to be able to respond swiftly and effectively to any questions or difficulties that may (and usually will) arise.

In many ways, the most critical role is that of the participatory peer review panel (PPRP). A final closure letter from the PPRP indicating concurrence that the technical bases of the PSHA input models have been satisfactorily justified and documented, that the hazard calculations have been correctly performed, and that the project was executed in accordance with the requirements of the SSHAC process, is generally viewed as the key indicator of success. Since the PPRP is, in effect, the arbiter for adherence to process, there is very serious onus on the PPRP to diligently fulfil the requirement of their role, always maintaining the delicate balance between engagement with the project and independence from the technical work. The role of the PPRP Chair, who is charged with steering the review panel along this narrow path, is possibly the most challenging, and in some ways most important, position in a SSHAC hazard study.

6.4 SSHAC study levels

The original SSHAC guidelines (Budnitz et al. 1997) defined four different levels for the conduct of hazard studies, increasing in complexity and numbers of participants from Level 1 to Level 4, with the highest level of study being intended for important safety–critical infrastructure or applications that were surrounded by controversy. The intent was that the greater investment of time and resources at the higher study levels would lead to an enhanced probability of regulatory assurance (which, for NPP sites, is the essential level of acceptance of a site-specific PSHA). The enhanced assurance is assumed to be attained by virtue of the higher-level studies being more likely to capture the CBR of TDI, although this remains the basic objective at all study levels.

Although Budnitz et al. (1997) defined four study levels, detailed implementation guidance was provided only for Level 4, which was implemented in seismic hazard studies for the Yucca Mountain nuclear waste repository in Nevada (Stepp et al. 2001) and the PEGASOS project for NPP sites in Switzerland (Abrahamson et al. 2002). A decade after the original guidelines were issued, USNRC convened, through the USGS, a series of workshops to review the experience of implementing the guidelines in practice. The outcome of these workshops was a series of recommendations (Hanks et al. 2009), the most important of which was that detailed guidelines were also required for Level 3 studies. This led the drafting of NUREG-2117 (USNRC 2012b), which provided clear guidance and checklists for the execution of both Level 3 and Level 4 seismic hazard studies. A very significant development was that in NUREG-2117, the USNRC made no distinction between Level 3 and Level 4 studies in terms of regulatory assurance, viewing the two approaches as alternative but equally valid options for reaching the same objective. The key difference between Level 3 and 4 studies is illustrated in Fig. 67: in a Level 4 study, each evaluator/integrator expert, which may be an individual or a small team, develops their own logic tree for the SSC or GMC model, whereas in a Level 3 study the evaluator/integrators work as a team to produce a single logic tree. In a Level 4 study, there are interactions among the evaluator experts but also with a Technical Integrator Facilitator (TFI), sometimes individually and sometimes collectively.

Fig. 67

Schematic illustration of the key organisational differences between SSHAC Level 3 and Level 4 studies (modified from USNRC 2018)

From a logistical point of view, the Level 4 process is rather cumbersome and Level 3 studies have been shown to be considerably more agile. Moreover, the role of TFI is exceptionally demanding, considerably more so than that of the TI Leads or even the PTI in a Level 3 study. In my view, the Level 3 process offers two very significant advantages over Level 4, in addition to the points just noted. Firstly, if the final logic tree in a Level 4 is generated by simply combining the logic trees of the individual evaluator experts, then it can become enormous: in the PEGASOS project, the total number of branch combinations in the full logic tree was on the order of 10²⁶. Such wildly dendritic logic trees pose enormous challenges from a computational perspective, but their size does not mean that they are more effectively capturing the epistemic uncertainty. Indeed, such an unwieldy model probably makes it more difficult to visualise the resulting distributions and inevitably limits the options for performing sensitivity analyses that can provide very valuable insights. The second advantage of Level 3 studies is the heightened degree of interaction among the evaluator experts. In a Level 4 study, there is ample opportunity for interaction among the experts including questions and technical challenges, but ultimately each expert is likely to feel responsibility for her or his own model, leaving the burden of robust technical challenge to the TFI. In a Level 3 study, where the experts are charged to collectively construct a model that they are all prepared to assume ownership of and to defend, the process of technical challenge and defence is envigorated. Provided the interactions among the experts take place in an environment of mutual respect and without dominance by any individual, the animated exchanges and lively debates that will usually ensue can add great value to the process. In this regard, however, it is important to populate the TI Teams with individuals with diverse viewpoints who are prepared to openly debate the technical issues to be resolved during the course of the project. If the majority of the TI Team members are selected from a single organisation, for example, this can result in a less dynamic process of technical challenge and defence, especially if one of the TI Team members, or indeed the TI Lead, is senior to the others within their organisation.

A new update of the SSHAC guidelines was issued in the form of NUREG-2213 (USNRC 2018), which superseded NUREG-2117 and now serves as the standalone reference document for the SSHAC process. The SSHAC Level 3 process has been widely applied in studies for nuclear sites in various countries as well as for hydroelectric dams in British Columbia, and a valuable body of practical experience has thus been accumulated. The insights and lessons learned from these applications led to the drafting of NUREG-2213, which includes detailed guidance on all four study levels, including Level 1, for which the requirements may surprise some people since there seemed to have been a view in many quarters that any PSHA not specifically characterised as SSHAC Level 2, 3 or 4, would, by default, be a SSHAC Level 1, which is very much not the case.

One of the motivations for including guidance on Level 1 and 2 studies, apart from completeness, was the fact that following the Fukushima Daiichi accident in 2011, the USNRC required all NPP operators to re-evaluate their site hazard through a SSHAC Level 3 PSHA. For plants east of the Rocky Mountains, the studies were based on the CEUS-SSC model, which was the outcome of a regional SSHAC Level 3 study, and regional GMMs for hard rock (EPRI 2013b). The application and adaptation of these regional SSC and GMC models to each site were carried out as Level 2 studies, generally focusing on the modification from the reference hard rock condition of the GMMs to local site conditions. This highlighted the need to provide clear guidance on how to conduct Level 2 studies, which is now provided in NUREG-2213. More recently, USNRC commissioned a study to explore the application of the SSHAC Level 2 procedures to site response analyses for PSHA, the findings of which are summarised in a very useful and informative report (Rodriguez-Marek et al. 2021b).

Another important feature of NUREG-2213 is the recognition that the biggest step in the sequence from Level 1 to Level 4 is the jump from Level 2 to Level 3. In order to bridge this gap, the current SSHAC implementation guidelines allow for enhanced Level 2 studies in order to provide recognition for studies conducted fulfilling all of the requirements of a Level 2 study but also availing themselves of some the additional benefits to be accrued by including elements of a Level 3 study. Prior to the issue of NUREG-2213, a number of PSHA projects made the claim to be a Level 2 + or Level 2–3 study, but there was no basis for such qualifications. The augmentations might include enlarged TI Teams, PPRP observation (by one or two representatives of the panel) at some working meetings, and one or more workshops (a Level 3 study is required to conduct three formal workshops with very specific scopes and objectives). While a Level 3 study should continue to be viewed as the optimal choice to achieve regulatory assurance for a site-specific PSHA at a nuclear site, encouragement should be given to all studies that can move closer to this target, and in that regard the option of an augmented or enhanced Level 2 study is a positive development. In effect, this is the approach that has been applied at some UK new-build nuclear sites (Aldama-Bustos et al. 2019).

With some precaution, I would like to close this section with a personal view. I am cautious because I would not want this to be invoked as a justification for any company or utility that simply wants to minimise investment in the seismic hazard study for their site, but I will assume that if these suggestions are taken up in practice, it would be for the technical reasons I am laying out. The SSHAC Level 3 process is built around three formal workshops (Fig. 68); the normal format is for the SSC and GMC workshops to be held back-to-back, which has logistical advantages in terms of mobilisation of the PPRP, overlapping for joint sessions at Workshops 1 and 3. These common days for both teams are designed to facilitate identification of interfaces between the two components of the PSHA input models and to discuss hazard sensitivities. I would strongly favour maintaining these two workshops in any study, although it should be possible in many circumstances to combine the kick-off meeting and Workshop 1. Within this general framework, however, I think there could be significant benefits in structuring the main body of the process in different ways because of the very different nature of SSC and GMC model building. The SSC process tends to be data driven, with the TI Team evaluating geological maps, fault studies and geochronology data, geophysical databases (elevation, gravity, magnetism, etc.), and the historical and instrumental earthquake catalogues, as well as models proposed for regional tectonic processes and seismogenic potential of key structures. On the GMC side, the database is generally limited to ground-motion recordings and site characterisation, and much of the work lies in developing the framework for how to build the models for reference rock motions and for site amplifications. I would argue that advances made in these areas in recent years are beginning to reach a kind of plateau in terms of establishing an appropriate basic framework (as presented in Sects. 5.2 and 5.3), which will be refined but possibly not fundamentally changed.

Fig. 68

Flowchart identifying the steps involved in conducting a SSHAC Level 3 hazard study, with time running from top to bottom of the diagram (USNRC 2018)

The framework that has evolved through several SSHAC projects, supplemented by research published in many papers, can now be adopted, I believe, for site-specific hazard assessments, with minor adjustments being made as required for each application. If this is the case, the work of the GMC TI Team will focus on using the available ground-motion data and site characterisation (V_S and lithology profiles, local recordings to infer kappa, and, in some cases, dynamic laboratory tests on borehole samples to constrain MRD curves). Such endeavours may not be particularly assisted by the conduct of a formal GMC Workshop 2 and are generally better advanced through formal and informal working meetings (with PPRP observers present at the former). At the same time, for key issues on the SSC side, workshops that extend beyond the usual three days may be very useful, especially if there is the flexibility to break out from the formality of these workshops. Imagine a case, for example, where one or two faults close to the site potentially exert a controlling influence on the hazard but their seismogenic potential is highly uncertain. In such a situation, an alternative format could be ‘workshop’ that began with a day of presentations on what is known about the structures, followed by a one- or two-day field trip to visit the structures in the field, possibly including what geologists sometimes refer to as a ‘trench party’, and then another day or two of working meeting in which the observations could be discussed by the SSC TI Team and several Resource and Proponent Experts. This more flexible approach might lead to the GMC sub-project being classified as an augmented Level 2 study, whereas the SSC sub-project could effectively exceed the basic requirements for a Level 3 study. The classification that would then be assigned to the whole process is not clear although it would perhaps be discouraging for a study organised in this way to only be given Level 2 status. There may be a case, in the next iteration of the SSHAC guidelines, to provide more flexibility for how the central phase of a Level 3 study is configured, allowing for differences in how the SSC and GMC sub-project navigate the route between Workshops 1 and 3.

6.5 Regional versus site-specific studies

In the previous section, mention was made of the use of two regional models as the basis for re-evaluations of seismic hazard at NPP sites in the Central and Eastern United States following the Tōhoku earthquake of March 2011 and the nuclear accident at the Fukushima Daiichi plant (as the first stage of a screening process to re-evaluate the seismic safety of the plants). The CEUS-SSC model (USNRC 2012a) was produced through a SSHAC Level 3 project and the EPRI (2013b) GMC model was generated through a SSHAC Level 2 update of GMMs that had been produced in an earlier Level 3 study (EPRI 2004) and then refined in a Level 2 update (EPRI 2006b). The EPRI (2013a) GMC model has since been superseded by the SSHAC Level 3 NGA-East project (Goulet et al. 2021; Youngs et al. 2021). In view of the large number of NPP sites east of the Rocky Mountains, the use of regional SSC and GMC SSHAC Level 3 studies, locally updated through Level 2 projects, was clearly an efficient way to obtain reliable hazard assessments in a relatively short period of time. Such a use of regional SSC and GMC models developed through Level 3 studies to be updated by local Level 2 studies is illustrated in Fig. 69. An alternative scheme is for the seismic hazard at all the sites in a region to be evaluated simultaneously in a single project, an example of which is the recently completed SSHAC Level 3 PSHA that was conducted for the six NPP sites in Spain; this was made possible because the study was commissioned by an umbrella organisation representing all the utilities who own and operate the different plants.

Fig. 69

(modified from USNRC 2018)

Scheme for regional SSC and GMC model development through Level 3 studies and local updating through Level 2 studies

There are compelling pragmatic reasons for following this path when seismic hazard assessments are required at multiple locations within a region, including the fact that it offers appreciable cost savings once assessments are required for two or more sites. Moreover, since the pool of available experts to conduct these studies remains relatively small, it also allows streamlining of schedule since the local Level 2 updates require fewer participants. Both of these practical benefits are illustrated schematically in Fig. 70.

Fig. 70

Schematic illustration of cost and time of alternatives for conducting SSHAC PSHA studies at multiple sites in a region (Coppersmith and Bommer 2012)

There is also, however, another potential benefit, especially for the case when two or more nuclear sites are closely located to one another in a given region. If completely parallel studies are undertaken by different teams, then there is a real possibility of inconsistent hazard results (after accounting for differences in site conditions), which could highlight fundamental differences in SSC and/or GMC modelling. This would present a headache for the regulatory authority and do nothing to foster confidence in the studies towards the goal of broad acceptance of the resulting hazard estimates.

If the traditional approach of hazard analysis at a buried rock horizon followed by site response analysis for the overlying layers (Fig. 48) is followed, the multiple-site approach relies on the assumption that a good analogue for the reference rock profile can be encountered at all target sites. Since this will often not be the case, the alternative one-step site adjustment approach (Fig. 49) lends itself perfectly to the development of a regional GCM model that can be applied to target locations and then the hazard adjusted for the differences between the host rock profile of the backbone GMM and the complete upper crustal profile at the target site.

In a region of low seismicity like the UK, where SSC models are dominated by seismic source zones with seismicity rates inferred from the earthquake catalogue, the regional scheme depicted in Fig. 69 would seem like a very attractive option, especially given the small number of specialists in this field based in the UK. More than a decade ago, I proposed that such an approach be adopted as the nuclear new-build renaissance was beginning (Bommer 2010). Since then, site-specific assessments at five nuclear sites, conducted by different groups, have been initiated, which can only be viewed as a lost opportunity, especially in view of the small geographical extent of the UK and the reliance of all these studies on the earthquake catalogue of the British Geological Survey, and the fact that it would be very difficult to justify a regionalised ground-motion model for different parts of this small country.

6.6 How much uncertainty is enough?

A misconception in some quarters is that application of the SSHAC process leads to broad uncertainty in hazard assessments, the implication being that had the hazard been assessed without following an alternative procedure, the uncertainty would somehow have been absent. As McGuire (1993) stated: “The large uncertainties in seismic hazard are not a defect of the method. They result from lack of knowledge about earthquake causes, characteristics, and ground motions. The seismic hazard only reports the effects of these uncertainties, it does not create or expand them”. The starting point for any seismic hazard study should be a recognition that there are epistemic uncertainties, and the study should then proceed to identify and quantify these uncertainties, and then propagate them into the hazard estimates. But the objective is always to first build the best possible input models for PSHA and then to estimate the associated uncertainty (in other words, all three letters of the acronym CBR are equally important). The purpose of the SSHAC process is not only to capture uncertainties, and it is certainly not the case that one should automatically expect broader uncertainty bands when applying higher SSHAC study levels. In the not-too-distant past, the indications are that many seismic hazard assessments were rather optimistic about the state of knowledge and how much was truly known about the seismicity and ground-motion amplitudes in a given region. Attachment to those optimistic views regarding epistemic uncertainty have prompted some of the opposition to the SSHAC process, as discussed in Sect. 7.2.

A question that often arises when undertaking a PSHA, is whether there is a way to ascertain that sufficient epistemic uncertainty has been captured. The required range of epistemic uncertainty cannot be measured, since the range of the epistemic uncertainty, by definition, lies beyond the available data. For individual components of the hazard input models, comparisons may be made with the epistemic uncertainty in other models. For example, for the GMC model, one might look at the range of epistemic uncertainty in the NGA-West models, as measured by the model-to-model variability (rather than their range of predicted values), and then make the inference that since these models were derived from a data-rich region, their uncertainty range should define the lower bound on uncertainty for the target region. However, there are many reasons why such an approach may not be straightforward. Firstly, the uncertainty defined by the NGA-West2 GMMs displays a trend of decreasing in the magnitude ranges where the data are sparser, although this is improved with application of the Al Atik and Youngs (2014) additional uncertainty penalty (Fig. 71). Secondly, the site-specific PSHA might be focused on a region that is much smaller than the state of California for which the NGA-West2 models were developed (using a dataset dominated by other regions in the upper range of magnitudes). The dynamic characterisation of the target site is also likely to be considerably better constrained than the site conditions at the recording stations contributing to the NGA-West2 database, for which just over half have V_S30 values inferred from proxies rather than measured directly (Seyhan et al. 2014).

Fig. 71

Model-to-model variability of median predictions at a site with V_S30 = 760 m/s from four NGA-West2 models (see Fig. 21) with and without the additional epistemic uncertainty intervals proposed by Al Atik and Youngs (2014), for strike-slip earthquakes of different magnitude on a vertically dipping fault

Another option is to compare the epistemic uncertainty in the final hazard estimates, measured for example by the ratio of spectral accelerations at the 85^th percentile to those at the 15^th percentile (Douglas et al. 2014b), obtained in other studies. In general, such comparisons are not likely to provide a particular useful basis for assessing the degree of uncertainty in a site-specific study, and certainly it would be discouraging to suggest that the uncertainty captured in hazard estimates for other sites should define the minimum threshold, unless one were able to access such information for a study in which there was abundant seismological and excellent site characterisation information, whence the uncertainty might then be taken as a minimum threshold. Otherwise, an expectation of matching some threshold level of uncertainty might remove the motivation to collecting new data and performing analyses that would help to constrain the model and reduce the uncertainty. At the end of the day, the onus lies with the PPRP to make the judgement as to whether the uncertainty bounds defined are consistent with the quality and quantity of the information available for the hazard assessment. In site-specific PSHA studies in which I have participated, there have been occasions when the PPRP has questioned uncertainty ranges for potentially being too broad as well as the more commonly expected case of challenging uncertainty intervals viewed as being too narrow.

7 The assessment and acceptance of seismic hazard estimates

Important technical (Sect. 5) and procedural (Sect. 6) advances that have been made to facilitate and render more transparent the process of capturing uncertainties in PSHA, which is foundational to achieving regulatory assurance. However, even seismic hazard studies performed with great rigour can sometimes encounter vehement opposition rather than general acceptance. This section discusses some of the motivations for the rejection of hazard estimates, which, more often than not, lie in objection to the amplitude of the ground motions that result from PSHA. However, as discussed in Sect. 7.4, there are a few cases where hazard estimates have been exaggerated—sometimes with far-reaching consequences for infrastructure projects—and opposition to the hazard estimates was fully justified.

7.1 The diehard determinists

According to some researchers and practitioners, all PSHA studies should be rejected because the approach is fundamentally flawed and PSHA should be discarded in favour of deterministic hazard assessments. There are important differences between PSHA and DSHA but turning the choice between the two approaches into an issue that takes on almost ideological overtones does nothing to promote seismic risk mitigation, as discussed in Sect. 3.1. McGuire (2001), a pioneer and proponent of PSHA, presents a very balanced discussion of how both deterministic and probabilistic approaches to seismic hazard and risk analysis can be useful for different types and scales of application. Articles by the advocates of DSHA have tended to adopt a less constructive attitude towards probabilistic approach and have generally tried to utterly discredit PSHA (e.g., Krinitzsky 1995a, 1995b, 1998, 2002; Paul 2002; Castaños and Lomnitz 2002; Wang et al. 2003; Peresan and Panza 2012; Stein et al. 2012; Wyss et al. 2012; Bela 2014; Mulargia et al. 2017). While some of these articles are amusing to read, none of them take us any closer to seismic hazard assessments that enable risk-informed decision making that optimises the use of limited resources. For the reader with time to spare, I would particularly recommend the paper by Panza and Bela (2020) and its 105-page supplement, which offers very interesting insights.

The views of the diehard determinists were perhaps most clearly expressed in a statement by an organisation calling itself the International Seismic Safety Organisation (ISSO), which issued a statement that only DSHA or NDSHA (Neo-deterministic seismic hazard assessment; Peresan and Panza 2012) “should be used for public safety policy and determining design loads” (www.issoquake.org/isso/). Signatories to the statement included Ellis Krinitzsky and Giuliano Panza, both of whom are cited above for their anti-PSHA essays and who also provided forums, as former editors of Engineering Geology and Pure and Applied Geophysics, respectively, for many other articles along similar lines. The ISSO statement included the following observations on PSHA and DSHA that are worth citing in full:

“The current Probabilistic Seismic Hazard Analysis (PSHA) approach is unacceptable for public safety policy and determining design loads for the following reasons:

(1) Many recent destructive earthquakes have exceeded the levels of ground motion estimates based on PSHA and shown on the current global seismic hazard map. Seismic hazards have been underestimated here.

(2) In contrast, ground motion estimates based on the highest level of PSHA application for nuclear facilities (e.g., the Yucca Mountain site in USA and sites in Europe for the PEGASOS project) are unrealistically high as is well known. Seismic hazards have been overestimated here.

(3) Several recent publications have identified the fundamental flaws (i.e., incorrect mathematics and invalid assumptions) in PSHA, and have shown that the result is just a numerical creation with no physical reality. That is, seismic hazards have been incorrectly estimated.

The above points are inherent problems with PSHA indicating that the result is not reliable, not consistent, and not meaningful physically. The DSHA produces realistic, consistent and meaningful results established by its long practice and therefore, it is essential that DSHA and its enhanced NDSHA should be adopted for public safety policy and for determining design loads.”

The third bullet is not substantiated in the statement and the mathematical errors in PSHA often alluded to by opponents of PSHA have never been demonstrated—the error seems to reside in their understanding of PSHA. The first two bullets, which respectively claim that PSHA underestimates and overestimates the hazard, warrant some brief discussion. Regarding the first bullet, the accusation is essentially that PSHA is unsafe whereas DSHA somehow provides a greater level of assurance. In some cases, earthquakes have occurred that exceed the size and location of potential future events defined in seismic hazard models; examples of this are highlighted in Fig. 62. Another example of this is the March 2011 Tōhoku earthquake in Japan, which exceeded the magnitude of the earthquake defined as the design basis for the Fukushima Daiichi NPP, which resulted in the tsunami defences being inadequate (although, as explained in Sect. 1, the resistance to ground shaking was not exceeded). These are, however, examples of shortcomings in how the hazard has been estimated—and perhaps in particular how uncertainties have not been adequately characterised—rather than an inherent failure of the PSHA approach (Geller 2011; Stein et al. 2011; Hanks et al. 2012). Other examples cited in the ISSO statement refer to cases of recorded ground motions exceeding ground motions specified in probabilistic hazard maps. Such comparisons overlook the nature of probabilistic seismic hazard maps—which are not predictions much less upper bound predictions—and are not a meaningful way to validate or invalidate a PSHA-based hazard map (e.g., Iervolino 2013; Sect. 12.3 of Baker et al. 2021). The only meaningful comparison between recorded motions and probabilistic hazard maps would be that proposed by Ward (1995): if the map represents motions with a 10% probability of exceedance in 50 years (i.e., a return period of 475 years), then one should expect motions in 10% of the area to exceed the mapped values during an observational period of 50 years. The misleading claim by the proponents of DSHA is that it leads to seismic safety by establishing the worst-case ground motions, something which is clearly not the case, although its application will also be very conservative in many situations (only the degree of conservatism will be unknown).

The second bullet in the ISSO statement quoted above, interestingly, makes the opposite accusation, namely that PSHA sometimes overestimates the hazard. Two specific cases are mentioned, PEGASOS and Yucca Mountain, and these are both discussed below in Sect. 7.2.1 and 7.3 respectively.

Any rigid attachment to DSHA is an increasingly anachronistic stance and the continued attacks on PSHA are an unhelpful distraction: I would propose that society is better served by improving the practice of PSHA rather than declaring it a heresy. Indeed, while scenario-based hazard assessments have their place (see Sect. 9), it is high time that the use of DSHA as the basis for establishing design ground motions, especially for safety–critical structures, should be abandoned. In this regard, the International Atomic Energy Agency (IAEA) could play an important role. IAEA guidelines on seismic hazard assessment for nuclear sites still allow DSHA, which is unavoidable for as long as this is viewed as an acceptable approach by nuclear regulators in any member country. However, the current guidelines also encourage comparison of the results obtained with the two approaches: “The ground motion hazard should preferably be evaluated by using both probabilistic and deterministic methods of seismic hazard analysis. When both deterministic and probabilistic results are obtained, deterministic assessments can be used as a check against probabilistic assessments in terms of the reasonableness of the results, particularly when small annual frequencies of exceedance are considered” (IAEA 2010). Exactly what is meant by the term ‘reasonableness’ is not clarified but it would seem more appropriate to specify that the PSHA results should be disaggregated (which is mentioned only in an Appendix of SSG-9) and to evaluate the M-R-$\varepsilon$ triplets controlling the hazard, rather than to compare the PSHA results with the ground motions that would have been obtained by arbitrarily selected values of these three parameters. Nuclear safety goals should ultimately be defined in probabilistic terms and probabilistic estimates of risk cannot be obtained using the outputs from DSHA. And in terms of safety goals, PSHA offers a rational framework to select appropriate safety targets and the level of confidence that the selected target is being reached (Fig. 32).

7.2 Resistance to exceeded expectations

The most energised crusades that I have witnessed against the outcomes from PSHA studies have been in cases where the resulting design ground motions significantly exceeded earlier hazard estimates or preconceptions regarding the general hazard level of a region. As has been discussed earlier in the paper, new information can be found that will challenge existing hazard estimates, but this new data can be acknowledged and assessed impartially, as was the case for the Shoreline Fault adjacent to the Diablo Canyon NPP in California (Sect. 5.4). In this section, I recount two case histories where, for very distinct reasons, new hazard estimates were not received with such equanimity.

7.2.1 The PEGASOS project

The PEGASOS project was a SSHAC Level 4 PSHA for NPP sites in Switzerland that ran from 2000 to 2004, organised with sub-projects for the SSC model, the GMC model for rock, and the local site response (Abrahamson et al. 2002). As noted in Sect. 6.4, the final logic tree resulted in branch combinations exceeding Avagadro’s number, which created severe computational challenges. When the results were released, they met with stern and sustained opposition led by Dr Jens-Uwe Klügel (Klügel 2005, 2007, 2008, 2011), representative of one of the Swiss NPPs (and, coincidentally, a signatory to the ISSO statement discussed in Sect. 7.1). The basic motivation for Dr Klügel’s crusade was very clear: the PEGASOS results represented a very appreciable increase in the existing seismic hazard assessment for the Swiss plants (Fig. 72). The plants were originally designed using deterministic hazard estimates but in the 1980s, PSHAs were performed to provide the input to probabilistic risk analyses (PRA); the PEGASOS results were significantly higher.

Fig. 72

(adapted from Bommer and Abrahamson 2006)

Comparison of median hazard curve for a Swiss NPP site from PEGASOS with the hazard curve obtained from an earlier PSHA in the 1980s

Responses to the original assault on PEGASOS by Klügel (2005) were published, focusing on defence of PSHA and the SSHAC process (Budnitz et al. 2005), as well as pointing out flaws in the ‘validation’ exercises presented in Dr Klügel’s paper (Musson et al. 2005), while others—coincidentally another core member of ISSO—rallied to support Dr Klügel’s position (Wang 2005). However, none of these exchanges touched the core issue: the old hazard results being defended were incorrectly calculated. As shown in Fig. 73, it was possible to reproduce the hazard curve from the 1980s PSHA, based on the available documentation, but only by neglecting the sigma in the GMM—which does not, by any modern standard, constitute a PSHA. When the hazard calculations were repeated assigning an appropriate sigma value, the median hazard curve at the surface was slightly higher than that obtained from the PEGASOS calculations. This information was shared with Dr Klügel but had no effect on his campaign to invalidate the hazard results from PEGASOS.

Fig. 73

(adapted from Bommer and Abrahamson 2006)

The same as Fig. 72 but with hazard curves from the 1980s PSHA model reproduced with and without sigma

The curves in Figs. 72 and 73 do not, however, tell the entire story because these plots show only the median hazard. The mean hazard from the PEGASOS study was higher than the correctly calculated (i.e., including sigma) mean hazard from the 1980s PSHA, indicating greater epistemic uncertainty. In large part, this was the result of a very optimistic view of how much was known by those conducting the earlier hazard study. However, in fairness there was also avoidable uncertainty included in the PEGASOS model, primarily because of a decision to undertake no new data collection, including no site characterisation measurements—although, interestingly, this was not a criticism included in Klügel (2005).

The controversy created by Dr Klügel’s campaign resulted in long delays to the hazard results being adopted in risk assessments for the Swiss plants and also succeeded in tarnishing not only the PEGASOS project but also the SSHAC process, fuelling numerous criticisms of the process (e.g., Aspinall 2010). The final outcome was a new PSHA study, the PEGASOS Refinement Project (PRP; Renault et al. 2010), which began in 2008 and ended in 2013. While there were clearly very major improvements made during the PRP and important lessons were certainly learned, the fact remains that an individual was able to launch a campaign that stopped the adoption of a major PSHA study, involving experts from the United States and throughout Europe, prompted by objection to the results on the basis that they exceeded previously hazard estimates that had been incorrectly calculated.

7.2.2 The Panama Canal expansion

In Sect. 5.4, I described the discovery of the Pedro Miguel fault as a result of investigations undertaken as part of the Panama Canal expansion project. The identification of this active fault in central Panama, striking sub-parallel to the Pacific side of the canal and approaching the route very closely near the new locks, resulted in a radical change of the estimated seismic hazard. Prior estimates of seismic hazard in central Panama were based primarily on active sources of earthquakes offshore to south and north of the isthmus, the latter being the location of a well-documented earthquake on 7 September 1882 (Fig. 74). The inclusion of the 48 km-long Pedro Miguel fault, and other active structures identified during the same studies, increased the 2,500-year PGA at the Pacific (Miraflores) locks by a factor of 2.5 from 0.40 g to 1.02 g.

Fig. 74

USGS 2003 hazard map of Panama in terms of PGA (%g) for a return period of 2,500 years; the light blue line shows the approximate route of the canal

Unsurprisingly, the news of this huge increase in the estimated hazard came as a shock for the ACP. To fully appreciate the challenge that this new data presented, it is helpful to understand the historical context. Following the failure of the French project to build the Panama Canal, the canal was eventually built by the United States, in what was truly a colossal engineering project that involved the creation of a new country (prior to November 1903, Panama was a province of Colombia) and the effective annexation of part of that country by the US (the Panama Canal zone). Before embarking on the project, two separate groups had lobbied for different routes for an inter-oceanic canal through the isthmus of Central America, one in Panama and the other in Nicaragua. On the day that the US Senate finally came to vote on which route to adopt, the Panamanian option was selected by 42 to 34 votes. On the morning of the vote, senators had received postcards with Nicaraguan postage stamps depicting active volcanoes (Fig. 75), which is believed to have swayed several undecided lawmakers to vote in favour of the Panama option. For the history of how the Panama Canal came into being, I strongly recommend David McCullough’s excellent book (McCullough 1977).

Fig. 75

Postage stamp from Nicaragua depicting the active Momotombo stratovolcano. (https://www.linns.com/news/us-stamps-postal-history/)

There is no doubt that the Central American republics to the north of Panama are tectonically very active: destructive earthquakes are frequent occurrences in Costa Rica, Nicaragua, El Salvador, and Guatemala, and the official crests of all these nations depict volcanoes. By contrast, seismicity during the instrumental period has been very much lower in Panama (Fig. 76). However, the choice of Panama over Nicaragua as the canal route seems to have established in the Panamanian psyche not so much that Panama is of lower hazard—or, more accurately, that destructive earthquakes in Panama are less frequent—than its neighbours, but rather that it is actually aseismic. During one of my visits, I encountered a magazine in my hotel room extolling the benefits of Panama as an ideal location for holidays or retirement, in which one of the headline claims was as follows: “Panama has no hurricanes or major earthquakes. Panama is even blessed by nature. It is the only country in Central America that is absolutely hurricane-free. Panama also has none of the destructive earthquakes that plague its Central American neighbors. Your Panama vacation will never have to be re-scheduled due to natural events. Your property investment will always be safe.” In light of this widely held view in Panama, it is perhaps not surprising that the implications of the paleoseismological studies were met with disbelief and denial.

Fig. 76

Source: http://earthquake.usgs.gov/earthquakes/world/central_america/seismicity.php

Epicentres of earthquakes of magnitude ≥ 5.5 in Central America since 1990.

The revised hazard estimates led to design motions for the new locks that posed a significant engineering challenge, and more than one of the consortia posed to bid for the expansion work withdrew when the seismic design criteria were revealed. Some people within the ACP were reluctant to accept the results and engineering consultants were engaged to obtain information to counter the findings of the geological and paleoseismological investigations, but these efforts were largely unsuccessful: one of the claims made was related to the lack of paleoliquefaction features (e.g., Tuttle et al. 2019), but the notion that such evidence would be preserved in a tropical environment with very high precipitation rates is naïvely optimistic.

The concerns about the implications of the Pedro Miguel fault extended beyond the canal because the fault is located only about 5 km from Panama City, a rapidly growing city with many high-rise buildings. Thanks to the efforts of some engineers from the ACP, the 2004 building code for Panama was revised in 2014 with a hazard map generated taking full account of this active structure (Fig. 77).

Fig. 77

Map of 1-s spectral accelerations for south-central Panama from the REP-2014 structural design code; the purple line is the Pedro Miguel fault

Nonetheless, the controversy persists. A paper by Schug et al. (2018) documented observations in the major excavations created for the approach channel for the new Pacific locks, and concluded that the Pedro Miguel fault was not present, countering the recommendation to design the dam that would contain the channel for up to 3 m of fault displacement. This has been taken up by some in Panama to call for a new revision of the hazard map and building code without the Pedro Miguel fault as a seismic source. However, while there may be uncertainty about the structure and location of the Pedro Miguel fault and its splays (which could question the fault slip specified for the dam design), the evidence from many other locations for the existence and recent activity of this fault is compelling and has important implications for seismic hazard; this impressive body of evidence is difficult to discount on the basis of observations at one location. The evidence that supports the existence of the fault is also consistent with an updated understanding of the tectonics of Panama, which rather than being a rigid microplate bounded by active offshore regions (e.g., Adamek et al. 1988), is now understood to be undergoing extensive internal deformation (Rockwell et al. 2010b), which could be expected to produce faults with multiple splays, some of which may have been exposed in the excavations studied by Schug et al. (2018). The debate regarding the Pedro Miguel is likely to continue for a while yet but with several major engineering projects underway in central Panama—including another bridge crossing the canal and the westward extension of the Metro system—it is an issue with far-reaching consequences.

7.3 Testing PSHA

If our objective is to achieve acceptance of seismic hazard estimates, independent validation of the results by testing against data is clearly an attractive option. The most straightforward and unambiguous test is direct comparison of the hazard curve with the recurrence frequencies of different levels of ground motion calculated from recordings obtained at the same site over many years. Such empirical hazard curves have been generated for the CU accelerograph station in Mexico City by Ordaz and Reyes (1999), as shown in Fig. 78. The agreement between the empirical and calculated hazard is reassuring but it can be immediately noticed that the hazard curve is only tested in this way for return periods up to about 35 years, reflecting the time for which the CU station, installed in 1962, had been in operation. Fujiwara et al. (2009) and Mak and Schorlemmer (2016) applied similar approaches to test national hazard maps, rather than site-specific estimates, in Japan and the US, respectively.

Fig. 78

Comparison of hazard curve for PGA obtained from PSHA with empirical estimates of exceedance rates of PGA obtained from recordings at the same location (redrawn from Ordaz and Reyes 1999)

In practice, statistically stable estimates of the return periods of different levels of motion require observation periods that are much longer than the target return period: Beauval et al. (2008) conclude that robust constraint of the 475-year hazard would require about 12,000 years of recordings at the site of interest. For the return periods of interest to safety–critical infrastructure—which for NPPs is on the order of 10,000 years or more—it becomes even more unlikely that sufficient data are available. Moreover, for genuine validation the recordings would need to have been obtained at the same site, which would require incredible foresight or extremely good luck to have had an accelerograph installed at the site several decades before the facility was designed and constructed.

Many researchers have tried to extend the period for which empirical observations are available by using intensities rather than ground-motion recordings to test seismic hazard estimates. While much longer periods of macroseismic observation are available in many regions of the world, the approach either requires the intensities to be transformed to ground-motion parameters using empirical relationships (e.g., Mezcua et al. 2013), which introduce large uncertainties, or by performing PSHA in terms of intensity (e.g., Mucciarelli et al. 2000). Hazard calculated in terms of intensity is of little use as engineering input and it is also difficult to establish whether intensity-based hazard is consistent with hazard in terms of response spectral accelerations, not least because the variability associated with intensity predictions is generally normal rather than the log-normal distribution of ground-motion residuals (which are therefore skewed towards larger absolute values). The simple fact is that we will likely never have the required data to genuinely validate seismic hazard estimates—and if we did, we could dispense with PSHA and simply employ the data directly. Testing of individual components of the hazard input models is often worth pursuing—see, for example, the proposal by Schorlemmer et al. (2007) for testing earthquake likelihood models—but our expectations regarding the degree of validation that is obtainable should be kept low. Oreskes et al. (1994) provide a sobering discussion of verification and validation of models in the Earth sciences, concluding that “what typically passes for validation and verification is at best confirmation, with all the limitations that this term suggests.” Oreskes et al. (1994) define confirmation as agreement between observation and prediction and note that “confirmation is only possible to the extent that we have access to natural phenomena, but complete access is never possible, not in the present and certainly not in the future. If it were, it would obviate the need for modelling.”

In the light of the preceding discussion, it is interesting—and to me, somewhat disturbing—that there has been a trend in recent years to use observational data not just to test PSHA results but also to modify them (and the adjustment, unsurprisingly, is generally downwards). The proposals are to use Bayesian updating to modify the hazard models—essentially to change the weights on logic-tree branches—using observational data (e.g., OECD 2015; Secanell et al. 2018). I should clarify that I have no fundamental objection to Bayesian methods or to their application to engineering seismology. Based on experience as an expert witness in a dispute involving extensive damage to a power plant caused by a large earthquake in southern Peru in 2001, where the closest ground-motion recording was obtained at 70 km, I have proposed a Bayesian approach to estimating the ground shaking levels at the site of interest from multiple datasets and modelling (Bommer and Stafford 2012). Without over-extending this discussion, I would raise two objections to Bayesian updating of PSHA input models: (1) the same data should not be used to develop and to test a model, so to apply such techniques requires a conscious decision to leave some data aside when developing the SSC and/or GMC models, which runs contrary to the principle of establishing the best-constrained models possible; (2) down-weighting or even removing logic-tree branches based on short-term observations will influence the long-term hazard estimates in ways that are difficult to justify. Bayesian modification of PSHA input models has been largely proposed and promoted by the French nuclear industry and may well be a response to regulatory transition in that country from being one of the last bastions of DSHA to a gradual adoption of probabilistic approaches. Fortunately, the approach has gained little traction globally and has not been widely adopted.

There is, however, one perfectly legitimate use of empirical data to limit hazard estimates in PSHA, and it corresponds, paradoxically, to cases of ground motions at very long return periods and very high amplitudes of shaking. During the early decades of strong-motion recording (from 1933 to the mid-1960s), expectations of the largest possible motions were strongly correlated with the maximum recorded amplitudes (Strasser and Bommer 2009). Nowadays, large-amplitude recordings (PGA > 1 g, PGV > 100 cm/s) are no longer a surprise—and due to spatial variability, we should probably expect to see even larger amplitudes. However, there are likely to be physical bounds on the levels of motion that can be recorded in earthquakes, due to three factors: (1) the most intense seismic radiation that can emanate from the source of the earthquake; (2) the interaction of radiation from different parts of the source and from different travel paths; and (3) the limits on the strongest motion that can be transmitted to the surface by shallow geological materials (Bommer et al. 2004b). The need to impose physical constraint on very low probability hazard estimates was highlighted by the PSHA for the Yucca Mountain nuclear waste repository in Nevada (Stepp et al. 2001). Due to the long design life of the post-closure facility and the need for very low probability of failure, the hazard calculations were extended to annual exceedance frequencies of 10^–8, leading to ground motion levels that very likely exceed physical limits (Andrews et al. 2007). Physical limits on the levels of ground shaking that could occur at Yucca Mountain were estimated from the accelerations that would have toppled precariously balanced rocks (e.g., Brune 1999) and other fragile geological features that can be reliably aged, thus allowing the hazard estimates to be capped (Baker et al. 2013; Fig. 79). Such geological indicators of limiting ground-motion amplitudes have since been used in seismic hazard assessments for the Diablo Canyon NPP in California (Rood et al. 2020) and other facilities (Stirling et al. 2021). Physical limits on ground motions related to the limited strength of near-surface deposits have been explored from the perspective of site response analyses and the maximum accelerations that can be transmitted (e.g., Pecker 2005).

Fig. 79

Mean hazard curve at Yucca Mountain in terms of PGV, compared with unexceeded ground motions inferred from precariously balanced rocks (PBR) and lithophyse (LMT is lower mean tuff properties for these fragile geological features) using different approaches for calculating their fragility (Baker et al. 2013)

7.4 Inflated hazard assessments

In the discussions thus far, the primary concern has been with underestimations—deliberate or otherwise—of the seismic hazard, since this has obvious safety implications. However, severe overestimation of the seismic hazard at a given location can also have serious consequences, including rendering design and construction very challenging and even economically unviable in extreme cases. The case of high hazard estimates for Dubai and Abu Dhabi resulting due to the unproven West Coast fault was already discussed in Sect. 5.4. There have also been cases of inflated hazard estimates, where the resulting ground motions are not especially onerous but nonetheless there have been important consequences.

The first case concerns the Concud fault in Aragón, Spain (located a little over 200 km east of Madrid). In 2012, the Aragón government announced a project to build a new public hospital in the city of Teruel. Due to the location in the lowest hazard region of Spain (PGA < 0.04 g), the NCSE-02 building code did not require seismic design. However, Simón et al. (2016) published a study of the Concud fault, which is located some 400 m from the hospital site, from which it was inferred that it undergoes alternating periods of fast (0.53 mm/year) and slow (0.13 mm/year) slip, currently being in a fast slip phase. Following a very unconventional procedure, Simón et al. (2016) developed a linear recurrence relationship combining their geological data with regional seismicity data at lower magnitudes—referring to the concept of characteristic earthquakes but completely ignoring the model formulation proposed by Youngs and Coppersmith (1985)—and then used this to determine the earthquake magnitude with a 500-year recurrence interval (a completely erroneous attempt to determine the hazard for the 475-year return period specified in the Spanish building code), yielding a result of magnitude 5.33. Empirical prediction equations are then used to estimate an intensity of VII (actually 7.4) and this was then transformed to a PGA via an outdated empirical correlation model between these two parameters (Simón Gómez et al. 2014). This updated hazard assessment caused the hospital construction to be suspended.

Subsequent paleoseismological investigations, conducted for the Trillo NPP site as part of the SSHAC Level 3 PSHA for all nuclear power plants in Spain (Sect. 6.5), concluded that the slip rate and seismogenic potential of the Concud fault were significantly lower than inferred by Simón et al. (2016). The key contributing factor to the exaggerated hazard estimate were results of OSL (optically stimulated luminescence) dating performed by a laboratory in Madrid that were found to yield vastly underestimated ages for the deposits displaced by the Concud fault (Fig. 80). The design basis for the Teruel hospital was finally based on the 475-year PGA of 0.05 g based on the most recent seismic hazard map for Spain (IGN 2013a) and without explicit consideration of the Concud fault, but the start of construction was delayed until 2019 due to the exaggerated hazard estimate.

Fig. 80

Comparison of new OSL ages for samples along the Concud-Teruel fault system compared with those from the laboratory that provided the results underpinning the Simón et al. (2016) study; the numbers indicate how much longer are the new ages (Gutiérrez et al. 2020)

Another case of overestimated fault activity impacting on engineering projects concerns the Leyre fault in the western Pyrenees. In September 2004, during filling of the Itoíz reservoir located about 20 km north of the fault, a sequence of moderate earthquakes occurred, prompting a request from the Spanish Ministry of Environment for a PSHA for the Itoíz dam site, which was carried out by the Spanish geological survey (IGME). Field work undertaken by IGME concluded that none of the faults in the region of the dam showed evidence of Quaternary displacements with the exception of the Leyre fault, which was considered capable of producing earthquakes as large as M 6.6 ± 0.26 with a recurrence interval of 6,000 years. García-Mayordomo and Insua-Arévalo (2011) conducted a PSHA with area source zones and the Leyre fault as a distinct source (Fig. 81), noting that “Even though the recent activity of the fault is still under investigation, it was decided to take a conservative approach and consider it in the hazard calculations”. The result of the PSHA was a 1,000-year PGA at the Itoíz dam site that was twice the acceleration specified in the NCSE-02 building code. However, the new hazard model for the Itoíz dam site had a collateral impact regarding the design of the Yesa dam, located just 2.5 km south of the fault (Fig. 81), which at the time was being raised from a height of 78 m to 108 m to double the capacity of the reservoir. The indication of a highly active fault so close to the dam raised doubts regarding the project to increase the dam height. However, subsequent investigations of the thrust (i.e., shallow-dipping reverse) fault by Carbonel et al. (2019) demonstrated that the Leyre fault is not active, highlighting the fact that offsets on faults are not necessarily indicators of seismogenic activity since they can also result from non-seismogenic processes such as evaporite dissolution, salt movement, and landslides. Moreover, fault plane solutions for earthquakes in the region—including the Martes earthquake of July 1923 (Fig. 81b)—consistently show normal-faulting mechanisms rather than reverse (Stich et al. 2018). Another controversial Spanish fault features prominently in the case history presented in Sect. 12.3.

Fig. 81

source zones and the pink quadrilateral showing the surface projection of the Leyre fault; lower: faults, including the Leyre thrust, in the vicinity of the Yesa reservoir (Carbonel et al. 2019)

Upper: Seismic sources defined in the PSHA for the Itoíz dam (red cross) by García-Mayordomo and Insua-Arٞvalo (2011), the red polygons showing seismic

The final case concerns the new Italian hazard map discussed earlier in Sect. 5.4.2. The final zonations—from Zone 4 to Zone 1 in order of increasing hazard—were assigned at the level of municipalities, requiring that for any municipality crossed by a PGA contour defining the boundaries between one zone and another, a choice was made regarding which zone to assign. A national zonation was proposed (Fig. 82) but under legislation that devolves a degree of power to the regions of Italy, each region could move municipalities into an adjacent zone at their own discretion. Several municipalities were consequently downgraded to lower hazard: 63 in the Province of Trento were moved from Zone 3 to Zone 4 and six in Sicily were assigned to Zone 2 instead of Zone 1. In the region of Basilicata, however, just before the deadline for finalising the national hazard zonation, four municipalities were raised from Zone 2 to Zone 3 (Fig. 83). One of these was the municipality of Scanzano Jonico, which had been designated by the Council of Ministers as the selected site for a national repository for high and intermediate nuclear waste (Peruzza and Pessina 2016). Legislation regarding the waste repository forbid the construction of such a facility in hazard Zones 3 and 4, hence the deft upgrading of Scanzano Junico resulted in the automatic cancellation of the waste repository project.

Part II: Induced Seismicity

Fig. 82

Proposed national hazard zonation of Italy based on the April 2004 (courtesy of Max Stucchi and Valentina Montaldo); the rectangle shows the area of Fig. 83

Fig. 83

Detail of the revised national hazard zonation showing the region of Basilicata and the four municipalities upgraded from Zone 2 to Zone 3 (courtesy of Max Stucchi and Valentina Montaldo); municipality no. 3 is Scanzano Jonico

In Part I, I have attempted to demonstrate that the state of practice in seismic hazard analysis has undergone significant evolution, particularly with regards to handling uncertainty. Technical developments have increased our ability to build well-constrained seismic source and ground-motion models, and to incorporate the associated uncertainties in a transparent and tractable manner. Procedures have also been proposed, and iteratively refined through lessons learned from practical implementation, for conducting multiple-expert hazard assessments to capture the centre, body, and range of technically defensible interpretations of the available data and models. In this second part of the paper, my objective is to explore how these technical and procedural developments can be adapted to induced seismicity.

Part I has also shown that despite the significant advances made in seismic hazard analysis, acceptance of hazard assessments by all stakeholders (regulators, owners, operators, and the general public) is by no means automatically assured. The challenge of achieving acceptance of earthquake hazard and risk assessments for induced seismicity is much greater, because the risk is viewed as an imposed rather than natural threat by those affected, and also because the industrial processes causing induced seismicity are often the subject of controversy in themselves. However, for rational management of induced seismic risk that balances the potential dangers with the benefits of the industrial processes causing the seismicity, such acceptance is vital. The degree to which objective assessment of induced seismic risk is being both achieved and effectively communicated is a key focus of the ensuing discussions.

8 Earthquakes of anthropogenic origin

Earthquakes associated with human activities are not a very recent phenomenon, but induced seismicity has attracted a great deal of attention in recent years, both in the media and in academic research (Fig. 84). The interest has been driven in large part by significant increases in seismic activity in certain regions of the world—in particular in Oklahoma and neighbouring states (Keranen et al. 2014; McNamara et al. 2015) and in the Western Canadian Sedimentary Basin (WCSB; Atkinson et al. 2016a)—that have been linked to hydrocarbon production. There can be little doubt that the general controversy that surrounds the process of hydraulic fracturing, or fracking, has also served to raise the profile of induced seismicity in general, even though fracking has not been the major contributor to induced seismicity.

Fig. 84

Number of publications per year from 1972 to 2021 listed on Web of Science with topic ‘induced seismicity’ or ‘induced earthquakes’; the data for 2021 may not be complete

My focus in this paper is to address induced seismicity from the perspective of seismic risk, exploring how advances in the treatment of natural seismicity can be adopted and adapted to induced earthquakes. Before entering into discussions of the assessment (Sect. 9) and mitigation (Sect. 10) of induced seismic risk, this section provides a brief introduction to the basic concepts and definitions, as well as discussing the very important question of how induced and natural earthquakes can be distinguished.

In view of Fig. 84, which was inspired by a similar image presented by Professor Stefan Wiemer at the Third Schatzalp Workshop on Induced Seismicity held in Davos in March 2019 (the presentations and posters from which can be accessed at www.seismo.ethz.ch/en/research-and-teaching/schatzalp-workshop/), I need to clarify that in this paper I make no attempt to undertake a comprehensive review of the vast literature that now exists on the topic (to keep up with all the literature would now require one to read four or five papers a day, only resting on Sundays!). I do refer to many of the landmark papers that have been published in this field—and a number of my own papers too since I am presenting my own perspectives on this topic—but several readers are likely to consider that I have missed some key citations, for which I can only apologise. I would, however, point the reader to excellent overview and review papers that have been published and which help one to navigate through the enormous body of published literature (e.g., Suckale 2009; Ellsworth 2013; Davies et al. 2013; Keranen and Weingarten 2018; Foulger et al. 2018), and I trust that new overview papers will appear in due course to maintain and update the condensed road maps for those seeking to extract the essence from the ongoing research in this field.

8.1 Induced and triggered earthquakes

Seismographs record the passage of waves travelling through the Earth’s crust and the seismograms of these signals can be used to locate the source of the waves and the energy released at the source, as measured by magnitude scales. The recorded waves may originate from sources other than earthquakes, including natural phenomena such as volcanic activity and landslides (e.g., Hibert et al. 2014a, 2014b) and artificial energy sources such as explosions, sonic booms (e.g., Cates and Sturtevant 2002) and even light aeroplane crashes (Aspinall and Morgan 1983). As mentioned in the opening paragraph of this paper, seismograph monitoring of nuclear explosions is a key element in maintaining treaties banning the testing of nuclear weapons. The explosions most commonly recorded are quarry blasts, which need to be removed from the earthquake catalogue before calculating recurrence parameters (e.g., Gulia and Gasperini 2021). All such sources of seismic waves fall outside the focus of this paper, which is about earthquakes that occur due to abrupt slip of geological faults, in the same way as the natural or tectonic earthquakes discussed in Part I.

Mining has long been recognised as an anthropogenic source of seismicity (e.g., Cook 1976; Klose 2013), especially in regions of deep mining such as South Africa. However, the seismic signals generated by mining activity are often the result of collapses and rock bursts rather than the rupture of pre-existing geological faults. Another long-recognised source of seismicity is the impounding of deep reservoirs (e.g., Simpson 1976; Simpson et al. 1988). In the case of reservoir-induced seismicity, the earthquakes occur in the same way as tectonic events through fault rupture, the primary mechanism triggering the fault slip being an increase in pore pressure due to infiltration of water driven by the hydraulic gradient created by the reservoir.

The primary focus in recent years has been related to seismicity induced by the injection or extraction of fluids (Fig. 85), which includes a wide range of industrial processes, nearly all of which are related, in one way or another, to energy supply (NRC 2013). The fluid extraction and injection processes that have been associated with earthquakes include the following: conventional hydrocarbon production (e.g., Suckale 2010); wastewater injection (e.g., Ellsworth 2013); hydraulic fracturing for production of unconventional hydrocarbon reservoirs (e.g., Atkinson et al. 2020; Schultz et al. 2020a); enhanced geothermal systems (e.g., Majer et al. 2007); and carbon capture and storage (e.g., Verdon and Stork 2016).

Fig. 85

Illustration of the mechanisms of inducing seismicity through fluid injection leading to increased pore pressure on a fault (left) and by fluid injection or extraction changing the shear and normal stresses on a fault (right) (Ellsworth 2013)

There are cases where seismicity has clearly been associated with fluid extraction, including conventional gas extraction, such as in the Lacq field in southwest France (Bardainne et al. 2008), but the associations have not always been unambiguous. The destructive M 5.1 2011 earthquake that struck Lorca in southeast Spain has been attributed to extraction of groundwater (González et al. 2012). McGarr (