Evaluation of optimal FVDs for inter-storey isolation systems based on surrogate performance models

Abstract

Inter-storey seismic isolation is increasingly gaining attention. One of the main related issues is the need to limit the relative displacement between substructure and superstructure, while maintaining a good seismic performance of the superstructure. As shown in some studies, fluid viscous dampers (FVDs) mounted in isolation systems are effective in reducing isolator deflection but can be harmful by amplifying inter-storey drifts and floor accelerations. Additionally, the effectiveness of FVDs for inter-storey applications was investigated only recently, and specific approaches for their optimisation and performance evaluation are missing. Therefore, this paper proposes a method for the optimal multi-objective design of FVDs, based on the definition of appropriate surrogate response models, which allows for rationally comparing the FVD effects for a wide range of dampers and structures. In particular, the optimal FVD parameters are provided in a dimensionless form, so that they can be predicted by design equations of general validity within the range of the structures analysed. This method is applied to a stock of regular structures with various vibration periods of superstructure, isolation and substructure, examining a linear and a non-linear isolation system and a set of natural records, in order to comprehensively assess the effects of FVDs and their non-linearity on the seismic performance of these structures. Finally, prediction models of optimal FVD parameters are provided based on the results obtained and are applied to three case studies as an example.

1 Introduction

Seismic isolation between building storeys is becoming an increasingly attractive concept. First, it allows for greater freedom in the structural conception of skyscrapers and multi-purpose buildings, defining two independent structures, i.e., substructure and superstructure, which may have different forms, materials and uses (Zhang et al. 2017; Liu et al. 2018; Faiella and Mele 2020). This represents both an advantage for architectural design and a sustainable solution for densely populated areas (such as China), as it allows significant savings on land use, e.g., by realising residential buildings on top of commercial buildings. Additionally, in some cases, the base isolation of buildings encounters economic and technical issues that can prevent its application. For example, installing base isolation in existing buildings is generally complicated and certainly more expensive than applying isolation between storeys (often disruption-free). This technique can also be applied to add extra storeys on the top of existing buildings (with appropriate vertical capacity), without increasing the base shear forces, which represent an innovative retrofitting approach (Zhou 2001; Chey et al. 2013; Faiella et al. 2020). Furthermore, the isolation at the base becomes less effective than that between storeys for tall buildings, due to their low bending stiffness (Ziyaeifar et al. 1998).

Some examples of inter-storey isolation are as follows: the Shiodome Sumitomo Building (Tasaka et al. 2008) and the Iidabashi First Building (Zhang et al. 2017) in Tokyo, which are two multipurpose high-rise buildings consisting of a substructure and superstructure with different structural shapes; a building complex in Beijing (Zhou et al. 2004), where 50 base-isolated residential buildings (seven- or nine-storey RC frames) were built on top of a two-storey platform, covering a railway area of ∼3 km²; the 185 Berry St. building in the China Basin area of San Francisco (Dutta et al. 2009), which is the first example in the U.S. of an isolated building (two-storey steel structure) built on top of an existing building (three-storey RC structure); the nine-storey pre-cast RC building in the National Taiwan University campus (Loh et al. 2013), which has an inter-storey isolation system between the second and third floors, also equipped with viscous dampers.

This isolation strategy basically converts the mass of the isolated superstructure into a non-conventional tuned mass damper (Reggio and De Angelis 2015); therefore, the superstructure performs a dynamic control function in addition to the structural one. In general, it is possible to identify three behavioural categories—mass damping, intermediate isolation and base isolation—based on the mass ratio between the superstructure and substructure (Faiella and Mele 2019; Zhou et al. 2016; Tan et al. 2008).

One of the primary issues concerning inter-storey isolation is the need to reduce the P-Δ effects, by controlling the drift demand between the substructure and superstructure, while maintaining a good seismic performance of the superstructure (low floor accelerations and low inter-storey drifts). For this purpose, additional fluid-viscous dampers (FVDs) are effective in reducing the isolation drift demand and allow the design of a greater performing isolation system. Indeed, the isolation components can be designed for low activation forces, regardless of the actual expected seismic force, relying on the additional dissipation provided by these dampers.

In fact, dampers are often installed in base-isolated structures built near active faults, as the large displacement demand would otherwise require isolators of considerable size and cost (Koh et al. 1989; Makris 1997). However, studies on the supplemental damping in buildings with base isolation (e.g., Kelly 1999; Hall 1999; Alhan et al. 2004; Politopoulos 2008; Providakis 2008; Fathi et al. 2015) showed that high values of damping, when concentrated only at the isolation level, can be excessive and therefore harmful due to amplification of inter-storey drifts and floor accelerations. Both of these, on the other hand, can be limited by increasing the damping of the superstructure, which is effective in reducing the floor response spectra in correspondence with the second vibration mode of isolated structures (Ragni et al. 2020). Although non-linear dampers offer greater dissipation per sinusoidal cycle than linear ones (for the same maximum force and stroke) and limit the damper force transmission at high velocities (Tubaldi et al. 2015b), experiments carried out by Wolff et al. (2015) proved that these amplifications are smaller in case of linear dampers, especially with highly dissipative isolation devices.

The results of these studies are not always easy to compare, as they depend on specific assumptions, including FVD properties. Moreover, the effects of additional FVDs for inter-storey applications were investigated only recently for a case study (Liu et al. 2018; Donà et al. 2019); therefore, further investigations are needed and should be addressed through a general assessment method, which allows comparing a wide range of linear and non-linear dampers. Also, general studies on the optimisation of FVDs for such applications, addressed to their design, are missing. In fact, relevant studies in the literature mainly deal with the optimal arrangement of multiple isolation systems in buildings (Charmpis et al. 2012; Charmpis et al. 2015) and the optimal values of the isolator parameters (Reggio et al. 2015; Zhou et al. 2016). As for FVDs, many optimisation strategies are available for traditional applications in frames (e.g., see De Domenico et al. 2019), whereas only a few studies in the field of bridges deal with the optimisation of FVDs used together with isolators, focussing on linear dampers (Xie et al. 2017). Clearly, the use of FVDs in inter-storey isolation applications has some specificities, such as the damping, velocity and stroke values of the dampers—which are generally higher than in traditional applications—the concentration of energy dissipation between two storeys of the structure, and the interaction between the non-linear behaviour of the dampers and the isolation system.

Only recently, to assess the FVD effects in inter-storey applications, Liu et al. (2018) optimised the damper parameters (damping constant c and linearity degree α) individually for various seismic inputs, in the case of a seven-floor reinforced-concrete (RC) structure, with lead rubber bearings (LRBs) connecting the second and third floors. In addition to proving the effectiveness of FVDs, the authors showed that the optimal value of α is correlated with the structural seismic response (problem output) and strongly depends on the seismic input (a priori unknown). Therefore, a direct optimisation for each design ground motion is not suitable for design purposes, as α values cannot be averaged for determining the best FVD solution. In addition, the application of a multi-objective genetic algorithm to conduct a direct optimisation (as in Liu et al. 2018), even if based on the average of the maximum responses to a set of ground motions, would require the execution of a large number of non-linear time-history (TH) analyses, and therefore a high computational cost.

To overcome these issues, this paper proposes a more effective method for the optimisation and performance evaluation of FVDs for inter-storey applications, which falls within the multi-objective evolutionary design approach (De Domenico et al. 2019). This method is based on the definition of appropriate surrogate response models, calibrated on the maximum response (averaged between seismic inputs) of some significant performance parameters and their subsequent minimisation through multi-objective genetic algorithms. Such models, if conveniently expressed in a dimensionless form, allow obtaining results that can be compared between various case studies and predicted by design equations of general validity (within the range of structures analysed).

To systematically evaluate the FVD effects on the seismic performance of various structures, this method was parametrically applied to a stock of 48 lumped-mass models, representative of regular RC structures with various vibration periods of superstructure, isolation and substructure, analysing a wide range of damper forces for various α values between 0 and 1, two types of isolation systems (linear with fuse behaviour and non-linear with LRB isolators) and a set of spectrum-compatible natural records. The conflicting objective functions (OFs) chosen for the optimal design are the minimisation of the drifts between the substructure and superstructure and the minimisation of the inter-storey drifts of the superstructure. In particular, these structural performances were normalised to the relevant ones in the case without FVD, to directly evaluate the effects of additional damping on the structural response. The multi-objective problem was solved through the NSGA-II genetic algorithm (Deb et al. 2002) and the optimisation results, both in terms of structural performances and optimal FVD parameters, were compared between various structural configurations and isolation systems to draw the relevant considerations. The maximum values of the superstructure floor accelerations and substructure inter-storey drifts were also evaluated, but as an output of the optimisation process rather than as OFs. The proposed method was then reapplied to optimise only linear FVDs (α = 1), allowing performance comparisons between optimal linear and non-linear dampers. Finally, to provide useful design tools, prediction models for the optimal FVD parameters were defined and calibrated on the basis of the results obtained; these models were then applied to three case study structures, for example and validation purposes.

2 Multi-objective optimisation method

2.1 Solution to the dynamic problem

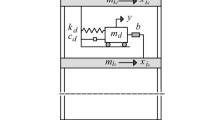
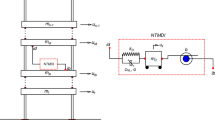
The equation of the dynamics of inter-storey isolated buildings with FVDs, with t the time variable, is:

$${\mathbf{M\ddot{x}}}{\text{(}}t{\text{)}} + {\mathbf{C}}_{{{\mathbf{ST}}}} {\mathbf{\dot{x}}}{\text{(}}t{\text{)}} + {\mathbf{K}}_{{{\mathbf{ST}}}} {\mathbf{x}}{\text{(}}t{\text{)}} + {\mathbf{r}}_{{{\mathbf{FVD}}}} \text{F} _{{{\text{FVD}}}} {\text{(}}t{\text{) + }}{\mathbf{r}}_{{{\mathbf{IS}}}} \text{F} _{{\text{IS} }} {\text{(}}t{\text{)}} = - {\mathbf{MI}}{{\ddot{\text{u}}}}_{{\text{g}}} {\text{(}}t{\text{)}}$$

(1)

${\mathbf{x}}{\text{(}}t) = [{\text{x}}_{{\text{1}}} {\text{(}}t{\text{) x}}_{{\text{2}}} {\text{(}}t{\text{) }} \ldots {\text{ x}}_{{\text{n}}} {\text{(}}t{\text{)}}]^{{\text{T}}}$, ${\mathbf{\dot {x}}}{\text{(}}t{\text{)}}$, and ${\mathbf{\ddot {x}}}{\text{(}}t{\text{)}}$ are respectively the floor displacements, velocities and accelerations relative to the building base, and n is the number of degrees of freedom (DOF) examined; only translational DOF are taken into account by this modelling. ${{\ddot{\text{u}}}}_{{\text{g}}} {\text{(}}t{\text{)}}$ is the seismic acceleration, and ${\mathbf{I}}$ is the vector with the unitary rigid displacements of the floors, parallel to the seismic direction; in this work, ${\mathbf{I}}$ is the identity vector. M [n x n] is the global mass matrix and C_ST and K_ST are respectively the damping and stiffness matrices, given in Eq. 2, excluding the isolation system. C_L and K_L are respectively the damping and stiffness matrices for the lower structure (with n_L DOF), and C_U and K_U are the same matrices for the upper structure (with n_U DOF). In this study, the behaviour of the substructure and superstructure (and so K_ST) are modelled as linear, and all non-linearities are concentrated at the isolation level.

$${{\mathbf{C}}_{{\mathbf{ST}}}}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{C}}_{\mathbf{L}}}[{{\text{n}}_{\text{L}}}{{ \times }}{{\text{n}}_{\text{L}}}]}&{} \\ {}&{{{\mathbf{C}}_{\mathbf{U}}}[{{\text{n}}_{\text{U}}}{{ \times }}{{\text{n}}_{\text{U}}}]} \end{array}} \right];{\text{ }}{{\mathbf{K}}_{{\mathbf{ST}}}}=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{K}}_{\mathbf{L}}}[{{\text{n}}_{\text{L}}}{{ \times }}{{\text{n}}_{\text{L}}}]}&{} \\ {}&{{{\mathbf{K}}_{\mathbf{U}}}[{{\text{n}}_{\text{U}}}{{\times }}{{\text{n}}_{\text{U}}}]} \end{array}} \right]$$

(2)

The structural equivalent viscous damping for such buildings is a ‘non-classical damping’ (Chen et al. 2017; Chen et al. 2019) and requires to be modelled differently for the two structural parts (Liu et al. 2018). The classic Rayleigh’s model (Eq. 3), generally used for fixed-base structures, can also be assumed for the substructure; instead, a damping model proportional to stiffness (Eq. 4) is more appropriate for isolated structures, as discussed in Ryan et al. (2008) and Pant et al. (2013). In Eq. 3, M_L [n_L x n_L] is the mass matrix of the substructure and α_L and β_L are the Rayleigh coefficients; the latter can be calculated by imposing a damping ratio ζ of 5 % (usually assumed for RC buildings) to the modal frequencies ω_i and ω_j,, which determine the frequency range of interest of the lower structure. Regarding the superstructure damping model in Eq. 4, Pant et al. (2013) highlighted that such a model could provide excessive damping for higher modes in tall buildings (where they are significant). As discussed in Liu et al. (2018), this issue is also relevant for applications of inter-storey isolation, as the higher mode effects could be important for such buildings. Therefore, the proportionality coefficient β_U should be calibrated by associating the desired ζ value (5 %) with a representative frequency ω_k for the higher modes to balance and limit this structural damping among the main higher modes (as shown in Liu et al. 2018). To assess the calibration of the matrix C_ST, the single modal damping ratios ζ_i can be calculated using Eq. 5, which is valid for classical damping but still allows sufficiently accurate estimates—ϕ_i and ω_i represent the modal shape and pulsatance of the i-th mode, respectively. A good calibration should provide ζ_i of about 5% for the significant higher modes, and an almost zero damping for the first mode. As for the latter, the reason is that the dissipation contribution by deformation of the structural parts is negligible for this mode, with respect to that provided by the separation layer.

$${{\mathbf{C}}_{\mathbf{L}}}={\alpha _L}{{\mathbf{M}}_{\mathbf{L}}}+{\beta _L}{{\mathbf{K}}_{\mathbf{L}}}{\text{ }} \to {\text{ }}{\alpha _L}=\zeta \cdot \frac{{2{\omega _i}{\omega _j}}}{{{\omega _i}+{\omega _j}}};{\text{ }}{\beta _L}=\zeta \cdot \frac{2}{{{\omega _i}+{\omega _j}}}$$

(3)

$${{\mathbf{C}}_{\mathbf{U}}}={\beta _U}{{\mathbf{K}}_{\mathbf{U}}}{\text{ }} \to {\text{ }}{\beta _U}=\zeta \cdot \frac{2}{{{\omega _k}}}$$

(4)

$$\zeta _{i} = \frac{{{\mathbf{\phi }}_{i}^{T} {\mathbf{C}}_{{{\mathbf{ST}}}} {\mathbf{\phi }}_{i} }}{{2\omega _{i} {\mathbf{\phi }}_{i}^{T} {\mathbf{M}}{\mathbf{\phi }}_{i} }}$$

(5)

The last two addenda of Eq. 1 describe the contribution of the isolation layer. In particular, F_FVD(t) is the damper force, given by Eq. 6, which depends on the damping coefficient c and the damping exponent α. F_IS(t) is the restoring force developed by the isolation system, and it clearly depends on the isolation technology adopted. In general, F_IS(t) is the sum of two contributions—one linear F_IS-l(t), due to a linear or post-yielding stiffness (k_IS), and one hysteretic F_IS-h(t). In recent years, the Bouc–Wen model (Ismail et al. 2009), shown in Eqs. 7 and 8, has often been used for modelling the hysteretic behaviour of isolators, thanks to its adaptability to a wide range of hysteretic laws through appropriate calibration of its parameters. In Eq. 7, k is the elastic stiffness, r is the stiffness ratio (= k_IS/k) and d_y is the yielding displacement of the isolation system; z(t) is an extra state variable that defines the hysteretic loop shape through the dimensionless parameters A, β, γ and n. Lastly, r_FVD and r_IS, provided in Eq. 9, are the vectors necessary to correctly place the contributions of damper and isolators in the motion equation. 

$${\operatorname{F} _{\operatorname{FVD} }}{\text{(}}t{\text{)}}=c|\dot {x}{|^\alpha }\operatorname{sgn} (\dot {x})$$

(6)

$${\operatorname{F} _{\operatorname{IS} }}{\text{(}}x(t),\dot {x}(t){\text{)}}={\operatorname{F} _{\operatorname{IS} - l}}{\text{(}}t{\text{)}}+{\operatorname{F} _{\operatorname{IS} - h}}{\text{(}}t{\text{)}}={k_{\operatorname{IS} }}x(t)+(k - {k_{\operatorname{IS} }}){d_y}z(t)=rkx(t)+(1 - r)k{d_y}z(t)$$

(7)

$$\dot {z}(t)\;=\;{{(A\dot {x}(t)\; - \beta |\dot {x}(t)\;| \cdot z(t)\; \cdot |z(t)\;{|^{_{{n - 1}}}} - \gamma \dot {x}(t)\;|z(t)\;{|^{_{n}}})} \mathord{\left/ {\vphantom {{(A\dot {x}(t)\; - \beta |\dot {x}(t)\;| \cdot z(t)\; \cdot |z(t)\;{|^{_{{n - 1}}}} - \gamma \dot {x}(t)\;|z(t)\;{|^{_{n}}})} {{d_y}}}} \right. \kern-0pt} {{d_y}}}$$

(8)

$${\mathbf{r}}_{{{\mathbf{FVD}}}} = {\mathbf{r}}_{{{\mathbf{IS}}}} = \left[ {\begin{array}{*{20}c} {zeros(n_{L} - 1)} & { - 1} & 1 & {zeros(n_{U} - 1)} \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} 0 & \cdots & 0 & { - 1} & 1 & 0 & \cdots & 0 \\ \end{array} } \right]^{T}$$

(9)

According to Eq. 10, the building’s total restoring force F_R(t) can be divided into two addends: one linear, provided by the elastic stiffness of the structure (K_ST) and the linear component of the isolation force F_IS-l(t), and one non-linear, due to F_IS-h(t). Using Eq. 10 in Eq. 1 and solving for ${\mathbf{\ddot {x}}}{\text{(}}t{\text{)}}$ results in Eqs. 12 and 13.

$${{\mathbf{F}}_{\mathbf{R}}}{\text{(}}t{\text{)}}={{\mathbf{K}}_{{\mathbf{ST}}}}{\mathbf{x}}{\text{(}}t{\text{)}}+{{\mathbf{r}}_{{\mathbf{IS}}}}{\operatorname{F} _{\operatorname{IS} }}{\text{(}}t{\text{)}}=({{\mathbf{K}}_{{\mathbf{ST}}}}+{{\mathbf{r}}_{{\mathbf{IS}}}}{k_{\operatorname{IS} }}{\text{)}}{\mathbf{x}}{\text{(}}t{\text{)}}+{{\mathbf{r}}_{{\mathbf{IS}}}}{\operatorname{F} _{\operatorname{IS} - h}}{\text{(}}t{\text{)=}}{\mathbf{Kx}}{\text{(}}t{\text{)}}+{{\mathbf{r}}_{{\mathbf{IS}}}}(1 - r)k{d_y}z(t)$$

(10)

$${\mathbf{K}}=\left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{k_{1 L}}+{k_{2 L}}}&{ - {k_{2 L}}}&{} \\ { - {k_{2 L}}}& \ddots &{ - {k_{nL}}} \\ {}&{ - {k_{nL}}}&{{k_{nL}}+{k_{IS}}} \end{array}} \right]}&{\begin{array}{*{20}{c}} {\text{0}}&{}&0 \\ {}&{{\text{ }} \ddots {\text{ }}}&{} \\ { - {k_{IS}}}&{}&0 \end{array}} \\ {\begin{array}{*{20}{c}} {{\text{ 0 }}}&{}&{{\text{ }} - {k_{IS}}} \\ {}&{{\text{ }} \ddots }&{} \\ {{\text{ 0 }}}&{}&{{\text{ }}0} \end{array}}&{\left[ {\begin{array}{*{20}{c}} {{k_{IS}}+{k_{1U}}}&{ - {k_{1U}}}&{} \\ { - {k_{1U}}}& \ddots &{ - {k_{nU}}} \\ {}&{ - {k_{nU}}}&{{k_{nU}}} \end{array}} \right]} \end{array}} \right]$$

(11)

$${\mathbf{M\ddot {x}}}{\text{(}}t{\text{)}}+{{\mathbf{C}}_{{\mathbf{S{\rm T}}}}}{\mathbf{\dot {x}}}{\text{(}}t{\text{)}}+{\mathbf{Kx}}{\text{(}}t{\text{)}}+{{\mathbf{r}}_{{\mathbf{IS}}}}(1 - r)k{d_y}z(t)+{{\mathbf{r}}_{{\mathbf{FVD}}}}{\operatorname{F} _{\operatorname{VD} }}{\text{(}}t{\text{)}}= - {\mathbf{MI}} {{\ddot{\text{u}}}}_{{\text{g}}} {\text{(}}t{\text{)}}$$

(12)

$${\mathbf{\ddot {x}}}{\text{(}}t{\text{)=}} - {{\mathbf{M}}^{ - 1}}\left( {{{\mathbf{C}}_{{\mathbf{ST}}}}{\mathbf{\dot {x}}}{\text{(}}t{\text{)}}+{\mathbf{Kx}}{\text{(}}t{\text{)}}+{{\mathbf{r}}_{{\mathbf{IS}}}}(1 - r)k{d_y}z(t)+{{\mathbf{r}}_{{\mathbf{FVD}}}}{\operatorname{F} _{FVD}}{\text{(}}t{\text{)}}} \right) - {\mathbf{I}} {{\ddot{\text{u}}}}_{{\text{g}}} {\text{(}}t{\text{)}}$$

(13)

Finally, the governing equation can be properly rewritten, as in Eq. 14, by means of the state space vector ${\mathbf{q}}{\text{(}}t{\text{)=[}}{{\mathbf{x}}^{\mathbf{T}}}{\text{(}}t{\text{) }}{{\mathbf{\dot {x}}}^{\mathbf{T}}}{\text{(}}t{\text{) }}z{\text{(}}t{\text{)}}{{\text{]}}^{\mathbf{T}}}$, so that it can be solved as a first order differential equation. The vector f(q(t)) is obtained by deriving q(t), and then using Eqs. 8 and 13; B is the position vector for the seismic input.

$${\mathbf{\dot {q}}}{\text{(}}t{\text{)=[}}{{\mathbf{\dot {x}}}^{\mathbf{T}}}{\text{(}}t{\text{) }}{{\mathbf{\ddot {x}}}^{\mathbf{T}}}{\text{(}}t{\text{) }}\dot {z}{\text{(}}t{\text{)}}{{\text{]}}^{\mathbf{T}}}={\mathbf{f}}({\mathbf{q}}{\text{(}}t{\text{)}}) - {\mathbf{B}} {{\ddot{\text{u}}}}_{{\text{g}}} {\text{(}}t{\text{)}}$$

(14)

$${\mathbf{f}}({\mathbf{q}}{\text{(}}t{\text{)}}){\text{=}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{\dot {x}}}}^{\mathbf{T}}}{\text{(}}t{\text{)}}} \\ { - {{\mathbf{M}}^{ - 1}}\left( {{{\mathbf{C}}_{{\mathbf{ST}}}}{\mathbf{\dot {x}}}{\text{(}}t{\text{)}}+{\mathbf{Kx}}{\text{(}}t{\text{)}}+{{\mathbf{r}}_{{\mathbf{IS}}}}(1 - r)k{d_y}z(t)+{{\mathbf{r}}_{{\mathbf{FVD}}}}{\operatorname{F} _{FVD}}{\text{(}}t{\text{)}}} \right)} \\ {(A\dot {x} - \beta |\dot {x}|z|z{|^{_{{n - 1}}}} - \gamma \dot {x}|z{|^{_{n}}})/{d_y}\;} \end{array}} \right]$$

(15)

$${\mathbf{B}}{\text{=}}{\left[ {\begin{array}{*{20}{c}} {\mathbf{0}}&{\mathbf{I}}&0 \end{array}} \right]^{\mathbf{{\rm T}}}}.$$

(16)

2.2 Response surfaces as a function of dimensionless FVD parameters

Following the procedure above, parametric non-linear TH analyses can be performed for each structure and set of accelerograms assumed, by varying the FVD parameters (c and α) within the relevant range of interest. To examine an appropriate and sufficiently wide range of additional FVDs, the first-mode damping ratios (ζ_FVD,l) provided by linear FVDs (α = 1), defined as in Eq. 17, can be initially set, from which the associated linear damping coefficients c_l can be easily derived. C_FVD,l is the damping matrix that contains only the damper contribution (c_l) and ϕ₁, ω₁, M₁ and c_cr1 are, respectively, mode shape, angular frequency, mass and critical damping of the first mode; ψ_1,nL and ψ_1,nL+1 are the components of ϕ₁ at the isolation level.

$$\zeta _{{FVD,l}} = \frac{{{\mathbf{\phi }}_{1}^{T} {\mathbf{C}}_{{FVD,l}} {\mathbf{\phi }}_{1} }}{{2\omega _{1} {\mathbf{\phi }}_{1}^{T} {\mathbf{M}}{\mathbf{\phi }}_{1} }} = \frac{{c_{l} (\psi _{{1,nL}} - \psi _{{1,nL + 1}} )^{2} }}{{2\omega _{1} M_{1} }} = \frac{{c_{l} (\psi _{{1,nL}} - \psi _{{1,nL + 1}} )^{2} }}{{c_{{cr1}} }}$$

(17)

Then, to define non-linear FVDs (α < 1) comparable with linear ones in terms of maximum force, Eq. 18 can be used to calculate the relevant damping coefficients c_nl. In Eq. 18, F_FVD,l and v_FVD,l are respectively the maximum force and velocity of the reference linear FVD obtained from the TH analysis.

$$c_{{nl}} = \frac{{F_{{FVD,l}} }}{{\left( {v_{{FVD,l}} } \right)^{\alpha } }}$$

(18)

Therefore, from a chosen value of ζ_FVD,l, a linear FVD can be determined by Eq. 17; then, from the maximum seismic response of this damper, comparable non-linear FVDs can be defined through Eq. 18 by setting various α values (< 1). Actually, with the same structure and seismic input, providing damping with different linearity degrees (α) results in different velocity responses, and thereby in different damping forces. However, this variation is limited, and the proposed procedure solely aims to define an appropriate range of non-linear FVDs on a rational basis. The ζ_FVD,l and α values examined in this study are reported in Table 1 and correspond to 120 case studies, in addition to the reference case without damper (i.e., ζ_FVD,l = 0).

Table 1 Examined values of ζ_FVD,l (first-mode damping ratio provided by linear FVDs) and α

The maximum values of a structural performance parameter, associated with the various accelerograms, can be averaged per storey if the number of accelerograms is code compliant. Thus, the peak response surface of that parameter can be obtained by plotting and interpolating its averaged maximum response versus the FVD parameters, over the entire range of analysed FVDs.

The parameters generally used to define the FVD are c [N(s/m)^α] and α [–]. However, in place of c, a more convenient parameter, r_F [–], is introduced in Eq. 19 for the purposes of this study; r_F returns the maximum analysis value of the FVD force (F_FVD), normalised to the maximum damper force obtained with ζ_FVD,l = 1 and α = 1, that is F_cr1, which is critical for the first vibration mode. For a given structure, each value of ζ_FVD,l ideally corresponds to a single value of r_F for all the α examined. Actually, due to the simplification in Eq. 18, r_F is very similar but not identical. The ratio r_F, in addition to providing more regular and appropriate response surfaces for subsequent FVD optimisation, is dimensionless, and therefore allows to effectively compare the peak responses of various structures as a function of dimensionless variables only.

$$r_{F} = \frac{{F_{{FVD}} }}{{F_{{cr1}} }} = \frac{{F_{{FVD}} }}{{F_{{FVD,l}} (\zeta _{{FVD,l}} = 1;\,\,\alpha {\text{ = 1}})}}.$$

(19)

2.3 Dimensionless surrogate response models

For each performance parameter, an appropriate analytical model can be calibrated on the related response surface. These models, known as surrogate response models, are useful for overcoming the direct optimisation issues discussed in the Introduction. Moreover, they allow a graphical representation of the structural performances, which is very useful for a full understanding of the effects of the analysed variables that is impossible with direct optimisation.

The performance and generality of these models depend on the structural response (and therefore on the type of structure and seismic action), on the definition of the optimisation variables, and obviously on the analytical law assumed. In the subsequent parametric study, the complete fourth degree polynomial in α and r_F was used as the analytical model, as it proved to be the most suitable in terms of fit and simplicity, among those evaluated.

Then, for a more effective assessment of the FVD effects, the structural response can be normalised to the maximum response in the case without the damper (ζ_FVD,L = 0), thus deriving surrogate response models that are completely dimensionless (together with the variables r_F and α). These dimensionless models are also particularly suitable for parametric analyses that examine various structures and/or seismic inputs, allowing the optimisation results to be properly compared between various case studies, both in terms of FVD parameters and structural performance. Furthermore, surrogate models can be extended to include additional variables to those of the FVD, such as structure or earthquake parameters. However, the convenience of global models with many variables, compared to the many models dependent only on r_F and α, specific to a type of structure and/or seismic input, should be evaluated on a case-by-case basis, according to the purposes of the study. In fact, the greater the number of variables of the models, the lower is their prediction capability.

Furthermore, to effectively use the optimisation results for design purposes, in this phase, it is necessary to define a prediction model of c as a function of r_F and α, which will allow to obtain the optimal c values once the optimal r_F-α solutions have been calculated, because c is not directly related to r_F. Then, to represent the results more effectively and compare them between various case studies, c can be normalised as in Eq. 20, derived from Eq. 17, replacing c_l with c.

$$c^{*} = \frac{c}{{c_{{cr1}} }}(\psi _{{1,nL}} - \psi _{{1,nL + 1}} )^{2} .$$

(20)

2.4 Optimisation of FVDs and prediction of optimal results

To determine the best FVD parameter sets (r_F-α and then c-α), some design aims must be defined. As already stated, dampers in inter-storey applications aim to reduce P-Δ effects and could be harmful to the isolated structure, increasing internal forces. Therefore, this optimal design is addressed to the resolution of conflicting objective functions (OFs), corresponding to the minimisation of the following surrogate response models:

• Drift between the lower and upper structures (OF₁).

• Maximum inter-storey drift of the upper structure (OF₂).

Superstructure floor accelerations can also be amplified by the additional damping, and therefore should be assessed, particularly for seismic protection of the structural content. These accelerations, as well as the performance of the substructure, were conveniently evaluated as an output of the optimisation problem rather than as variables of the optimisation criteria. In particular, to avoid significant damage to structural contents, a generally accepted limit of floor acceleration is about 0.3 g (Charmpis et al. 2012). Lower values may be required for special and fragile contents, for which, however, specific isolation systems exist (Donà et al. 2017).

Additionally, technical effectiveness is generally not the only decision-making aspect for the choice of the dampers, technical issues and costs associated with their implementation are also significant. Indeed, in seismic retrofit applications, with dampers distributed along the building height, the optimisation of the intervention generally aims at minimising specific cost functions; these may contain various cost components such as (Pollini et al. 2017) cost of preparing the structure for the installation of the dampers, manufacturing cost of the dampers (depending on their peak stroke and peak force), and additional costs for the use of dampers of different sizes due to the greater number of acceptance tests required by the standards. Often, especially when using the same type of device, this optimisation is performed by directly minimising the sum of the maximum damper forces (Altieri et al. 2018) or, for simplicity, the sum of the viscous damping constants (Tubaldi et al. 2015a). Regarding the inter-storey applications considered in this study, the peak stroke and force of the FVDs are both important to define the cost function. Moreover, a cost-effectiveness analysis of optimal solutions would also require the evaluation of possible savings on isolators and the substructure, due to the reduction of the isolation drift and the P-Δ effects on the substructure. However, since these latter factors significantly depend on a specific case study, these analyses can be more conveniently performed a posteriori for the optimal solutions obtained (out of the scope of this paper), in order not to reduce the generality of the study.

The solution of a multi-objective optimisation problem requires the determination of the Pareto front, i.e., a series of possible optimal solutions in which, generally, there is not hierarchy of preference. To date, several multi-objective optimisation algorithms allow to calculate the Pareto front, such as the evolutionary algorithms (Coello Coello et al. 2007). Among the latter, the fast and élitist non-dominated sorting genetic algorithm NSGA-II (Deb et al. 2002) was chosen for this study. In fact, the use of surrogate response models makes the choice of the algorithm less important, as the processing time for minimising these models is generally low; therefore, a different choice is possible and this would not affect the validity of this study.

Finally, with the aim of providing useful design tools, prediction models of the optimal FVD parameters can be defined and calibrated based on the results obtained.

3 Application of the optimisation method to a parametric study

3.1 Structural models

The optimisation method was parametrically applied to a stock of multi-degrees of freedom (MDOF) models, representing a wide range of regular RC frame structures, from low to high-rise. These MDOF models were defined on the basis of 3-DOF reference systems (Wang et al. 2011), characterised by the vibration period (T) or angular frequency (ω) of the isolated superstructure (which includes the mass m_IS of the isolation slab)—T_IS or ω_IS, superstructure—T_U or ω_U, and substructure—T_L or ω_L. The values of ω_U and ω_L were conveniently derived from the ratios rω_U = ω_U/ω_IS, for the superstructure and rω_L = ω_L/ω_IS for the substructure. The analysed values of T_IS were two, three and four seconds and the ratios rω_U and rω_L ranged from three to six.

To define the mass and stiffness matrices of the MDOF models, first the 3-DOF systems were calibrated on regular RC frames with inter-storey height (h_i) of three meters and storey mass (m_i) of 900 tons (corresponding, e.g., to a floor of 900 m² with afferent mass of 1000 kg/m²). In particular, the simplified relation between the building’s height and principal vibration period provided in Eurocode 8 (EC8) (CEN 2004) for regular RC frames (see Fig. 1) was used to calculate the heights of superstructure H_U and substructure H_L. Then, the associated masses M_U and M_L were derived on the basis of h_i and m_i and the associated stiffnesses K_U and K_L, as well as the isolation stiffness k_IS, were calculated on the basis of the periods (or frequencies) of the 3-DOF system, initially assumed.

Fig. 1

Parametric analysis data and procedure for defining MDOF models

Subsequently, after defining masses and stiffnesses of the 3-DOF systems, the DOF representing the superstructure was replaced by an equivalent MDOF system with uniform masses (m_i) and stiffnesses (k_i,U). The aim is to properly assess the amplification effects of the superstructure modes due to the additional damping (in terms of inter-storey drifts and floor accelerations), which is not possible by modelling the superstructure as a single DOF.

Figure 1 summarises the parametric analysis data and the procedure used to define the MDOF models. The total analysed structures are 48 (for each FVD defined in Table 1), corresponding to the combination of three isolation periods (T_IS) with four frequency ratios both for the superstructure (rω_U) and substructure (rω_L).

The minimum values of rω_U and rω_L (equal to three), consistent with the limits on the isolation ratio provided by the current seismic codes for base isolation (e.g., MIT 2018; CEN 2004), are motivated by the need to separate the dynamic behaviour of the two structural portions; lower rω values would result in the interaction between the deformations of the superstructure and the substructure, reducing the effectiveness of the isolation system, and therefore the overall structural performance. Instead, the maximum values of rω_U and rω_L (equal to six) have been used to define structures with a significant number of storeys, i.e., greater than or equal to two. In fact, as shown in Table 2, the number of storeys of the superstructure (and ideally of substructure) ranges from two to 15. The range of parameters chosen then allows to avoid the phenomenon of modal coupling, which is responsible for dynamic amplifications of the structural response; this phenomenon occurs when the frequency ratio between one mode of the substructure and a higher mode of the isolated superstructure approaches one (see Faiella and Mele 2019). In addition, the mass ratio between the total isolated mass and the mass of the substructure varies from 0.5 to three, covering a fairly wide range of cases for this type of application.

Table 2 Number of storeys of superstructure (and ideally of substructure) for the various case studies

Structural damping was defined as described above, using the Rayleigh model (Eq. 3) for the substructure and the stiffness-proportional model (Eq. 4) for the superstructure. As previously discussed, the latter model tends to overestimate the damping ratios ζ_i for higher modes, and therefore must be carefully calibrated. To this end, and to define the damping parametrically and objectively for various case studies, the superstructure was provisionally modelled as an equivalent 2-DOF system (derived similarly to the MDOF system), thus obtaining a global 4-DOF model where the first mode refers to isolation deflection, the second one to substructure deformation and third and fourth to superstructure deformation. Therefore, the damping coefficients for the substructure were calibrated as in Eq. 21, associating ζ = 5 %  with the frequencies of modes two and four of the 4-DOF model, which define a sufficiently wide range of frequencies for the substructure of these case studies (even though its modal contribution is given almost completely by the second mode). Whereas, the damping coefficient for the superstructure was calibrated as in Eq. 22, associating ζ = 5 % with the frequency of mode four of the 4-DOF model, which is always between the third and fourth mode frequencies of the associated MDOF system.

$${\alpha _L}=\zeta \cdot \frac{{2{\omega _i}{\omega _j}}}{{{\omega _i}+{\omega _j}}}=0.05 \cdot \frac{{2{\omega _2}{\omega _4}}}{{{\omega _2}+{\omega _4}}};{\text{ }}{\beta _L}=\zeta \cdot \frac{2}{{{\omega _i}+{\omega _j}}}=0.05 \cdot \frac{2}{{{\omega _2}+{\omega _4}}}$$

(21)

$${\beta _U}=\zeta \cdot \frac{2}{{{\omega _k}}}=0.05 \cdot \frac{2}{{{\omega _4}}}$$

(22)

Figure 2 shows the ζ_i values, obtained with this approach and calculated by Eq. 5, for the first four modal frequencies of all the analysed MDOF models. As expected, these values are around 5 % for the deformation modes of the substructure (ω₂) and superstructure (ω_3-4, from three to six %), whereas they are almost zero for the first mode (ω₁, the structural deformation being negligible in this mode).

Fig. 2

Structural damping ratios (ζ_i) for the first four modal frequencies (ω_i) of all the MDOF models

3.2 Seismic isolation systems

All previously defined structural models were analysed with two types of isolation systems: linear system with fuse behaviour (fuse system) and non-linear system with LRBs (LRB system).

As already discussed, the restoring force F_IS(t) of the isolation system is given in general by two contributions: one linear F_IS-l(t), due to a linear or post-yielding stiffness (k_IS), and one hysteretic F_IS-h(t), associated with both elastic (k) and post-yielding (k_IS) stiffnesses.

A completely linear system provides the linear contribution F_IS-l(t) only, as shown in Eq. 23; this system is the simplest one, but it is inadequate to withstand non-seismic lateral service loads, and therefore not feasible.

$${\operatorname{F} _{\operatorname{IS} - l}}{\text{(}}t{\text{)}}={k_{\operatorname{IS} }}x(t)$$

(23)

Instead, the fuse system overcomes this problem by adopting mechanical fuse restraints, i.e., devices with stiffness and resistance values such as to exclude the operation of the isolation system for lateral service loads, and allow it for seismic loads, breaking some sacrificial components upon reaching a certain force or displacement (d_y) threshold. This system also provides a linear restoring force, but changes its stiffness due to the breakage of the disposable elements, as Eq. 24 shows:

$$\left\{ \begin{gathered} {\operatorname{F} _{\operatorname{IS} - l}}{\text{(}}t{\text{)}}=k{\text{ }}x(t){\text{ until }}d<{d_y}{\text{ }} \hfill \\ {\operatorname{F} _{\operatorname{IS} - l}}{\text{(}}t{\text{)}}={k_{\operatorname{IS} }}x(t){\text{ thereafter }} \hfill \\ \end{gathered} \right.$$

(24)

The LRB system provides both linear and hysteretic contributions. This system was chosen among the non-linear ones currently available because it is widespread in China, where the interest in inter-storey isolation is high. In this case, the restoring force is modelled using the Bouc-Wen model (Ismail et al. 2009), according to Eqs. 7 and 8, repeated in Eqs. 25 and 26 for convenience.

$${\operatorname{F} _{\operatorname{IS} }}{\text{(}}t{\text{)}}={\operatorname{F} _{\operatorname{IS} - l}}{\text{(}}t{\text{)}}+{\operatorname{F} _{\operatorname{IS} - h}}{\text{(}}t{\text{)}}={k_{\operatorname{IS} }}x(t)+(k - {k_{\operatorname{IS} }}){d_y}z(t)\;={k_{\operatorname{IS} }}x(t)+Qz(t)\;$$

(25)

$$\dot {z}(t)\;=\;{{(A\dot {x}(t)\; - \beta |\dot {x}(t)\;| \cdot z(t)\; \cdot |z(t)\;{|^{_{{n - 1}}}} - \gamma \dot {x}(t)\;|z(t)\;{|^{_{n}}})} \mathord{\left/ {\vphantom {{(A\dot {x}(t)\; - \beta |\dot {x}(t)\;| \cdot z(t)\; \cdot |z(t)\;{|^{_{{n - 1}}}} - \gamma \dot {x}(t)\;|z(t)\;{|^{_{n}}})} {{d_y}}}} \right. \kern-0pt} {{d_y}}}$$

(26)

The Q parameter in Eq. 25 represents the characteristic damping force, corresponding to the intersection of the generic force-displacement loop with the force axis (at x = 0). In general, isolation systems are designed to be activated for forces ranging from five to 15 % of the isolated weight; lower values could cause movements for service loads or excessive displacements. In this study, considering also the resistance and dissipation provided by the FVDs, Q was set as the lower limit, as shown in Eq. 27 (where g is the gravity constant), as this allows the best seismic performance. The linear or post-yielding stiffness k_IS depends on the isolation period T_IS according to Eq. 28, whereas the elastic stiffness k depends on Q, k_IS and d_y, as shown in Eq. 29. The yielding displacement d_y was set as 10 mm—a reference value identified in the catalogues of the main suppliers of LRB devices. This value was also used to define the change in stiffness of the fuse system (Eq. 24) to consistently compare the isolation technologies. Finally, the dimensionless parameters in Eq. 26 were assumed as in Liu et al. (2018), i.e., A = β = γ = 1 and n = 2; these values allow a good fit with some experimental force-displacement loops, provided in Kalpakidis and Constantinou (2008, p.132), representative of a fairly wide range of applications.

$$Q=5\% \cdot \left( {{M_U}+{m_{IS}}} \right) \cdot g$$

(27)

$${k_{\operatorname{IS} }}=\left( {{M_U}+{m_{IS}}} \right) \cdot {\left( {\frac{{2\pi }}{{{T_{IS}}}}} \right)^2}$$

(28)

$$k=\frac{Q}{{{d_y}}}+{k_{IS}}.$$

(29)

3.3 Seismic inputs

The dynamic equation of motion in Eq. 14 was solved for eight natural accelerograms, chosen from among those in the European Strong-Motion Database (ESD, Ambraseys et al. 2002). They were scaled to be compatible, on average, with the following elastic response spectrum of EC8: Type 1, a_g = 0.25 g (bedrock acceleration), soil B (i.e., soil factor S = 1.2, acceleration plateau between T_B = 0.15 s and T_C = 0.5 s, and T_D = 2.0 s). The peak ground acceleration PGA (= a_g·S) is 0.3 g. The main details of the assumed natural records and their scale factors are reported in Table 3. The associated acceleration and displacement spectra are shown in Fig. 3, compared with the EC8 spectrum.

Table 3 Information on the assumed accelerograms (from ESD database, Ambraseys et al. 2002)

Fig. 3

Acceleration and displacement response spectra compatible with the EC8 spectrum

4 Results of the parametric analysis

4.1 Structural behaviour with additional FVDs

For preliminary assessments, Fig. 4 shows the TH responses of some performance parameters for the case study: T_IS = 3 s, rω_U = rω_L = 3, and Acc.1; this figure compares the cases without FVD and with linear (α = 1) and non-linear (α = 0.2) FVDs, with ζ_FVD,l = 0.3 (i.e., r_F ≈ 0.5), separately for the two isolation systems. The performance parameters are drift of isolation layer, drift of superstructure (i.e., displacement of top floor relative to isolation layer), and absolute acceleration of top storey.

Fig. 4

TH responses of structural performance parameters of a case study structure (T_IS=3 s, rω_U = rω_L = 3), for both isolation systems and Acc.1: cases without FVD and with linear (α = 1) and non-linear (α = 0.2) FVDs (r_F≈0.5)

The following considerations can be drawn:

• As expected, with the same additional damping ratio ζ_FVD,l (or force ratio r_F), the maximum drift of the isolation layer is greater for the fuse system, especially without FVD.

• The use of FVD with the fuse system significantly changes the vibration frequencies, which decrease for the isolation layer and increase for the superstructure. Instead, no significant variations in frequency are noted for the LRB system, which is less sensitive to the use of FVD.

• FVD is clearly effective in reducing the isolation drift for both isolation systems, whereas its effects on the superstructure are not easily predictable.

• The linearity degree of the FVD seems to significantly influence the structural response. In case studies of Fig. 4, non-linear FVDs (α = 0.2) are more effective than linear ones (α = 1) in reducing the isolation drift, but tend to amplify more the superstructure response, particularly for the fuse system.

For the same case studies as in Figs. 4 and 5 shows the force-displacement loops of isolators and dampers separately. Thus, the following considerations can be drawn:

Fig. 5

Force-displacement loops of isolators (left) and dampers (right) for the same case studies (with FVD) as in Fig. 4

• With the same additional damping ratio ζ_FVD,l (or force ratio r_F), the response with the LRB system is characterised by smaller isolator deflections (as seen in Fig. 4) and smaller damper forces, due to the presence of hysteretic damping in addition to the viscous one.

• Non-linear FVDs behave more rigidly than linear ones, with high dissipative forces even for small velocities (as noted in the range ± 20 mm), as they are associated with greater damping coefficients c_nl for the same force ratio r_F. This different behaviour influences the structural response, more for the fuse system than the LRB system (as seen in Fig. 4).

In general, α seems a significant parameter for structural response optimisation, and what has been seen justifies the need for an optimisation study.

4.2 Peak response surfaces with additional FVDs

To globally assess the additional damping effects on the structural response for all the examined FVDs, the peak values of the various performance parameters recorded in the TH analyses (averaged between the accelerograms) were plotted and linearly interpolated against the FVD variables, α and r_F, obtaining the corresponding peak response surfaces. Figures 6, 7 and 8 show and compare these response surfaces for some case studies, with reference to the following performance parameters: drift of isolation layer D_IS, maximum inter-storey drift of superstructure D_U, maximum absolute floor acceleration of superstructure A_U.

Fig. 6

Response surfaces of the structure T_IS=3 s, rω_U = rω_L = 6: comparison between isolation systems

Fig. 7

Response surfaces for T_IS=3 s, fuse (above) and LRB (below) isolation systems: various rω_U and rω_L

Fig. 8

Response surfaces for rω_U = rω_L = 6, fuse (above) and LRB (below) isolation systems: various T_IS

In particular, Fig. 6 compares the response surfaces of the structure T_IS = 3 s and rω_U = rω_L = 6 between the isolation systems. The main observations are reported below:

• D_IS is strongly influenced by the maximum damper force (r_F), but only slightly by α. In particular, D_IS is reduced as r_F increases, and this reduction is more evident for the fuse system, which shows a drift at r_F = 0 much greater than that of the LRB system (as seen in Fig. 4).

• D_U is generally influenced by both FVD parameters. In particular, the dependence on α increases with increasing r_F (for highly dissipative solutions) and the greater the non-linearity (rigidity) of the FVD, the greater the amplification of D_U. For small r_F values (up to 0.25 for the case studies shown), the increase in damper force considerably reduces D_U for the fuse system and only slightly influences D_U for the LRB system, due respectively to the absence and presence of further dissipation provided by the isolators. Similarly to D_IS, the fuse system exhibits a much greater drift at r_F=0 than that of the LRB system.

• The influence of r_F and α on the parameter A_U is somewhat similar to that observed for D_U. However, A_U seems to be less influenced (flatter trend) than D_U for low r_F values and linear or nearly linear FVDs (more effective in containing accelerations). Also, for such dampers, these accelerations are smaller for the fuse system (as expected).

• In general, the structural responses with the two isolation systems tend to coincide for high r_F values and low α values (increasing both the force and rigidity of the FVD).

• Although D_IS can be similarly minimised for the two isolation systems (with high damping values), the superstructure response (D_U, A_U) can be reduced more in the case of the fuse system, providing only a viscous damping. In this situation, however, the associated D_IS values turn out to be greater than those of the LRB system; hence, it is needed to evaluate and compare multiple optimal solutions.

Figure 7 compares the response surfaces of the structures with T_IS = 3 s and rω_U-rω_L = 6–6, 3–6, 6 − 3, 3–3 (corresponding to structures of 4–4, 11−4, 4–11 and 11–11 storeys respectively, see Table 2), separately for the fuse and LRB systems. Similar colours represent cases with the same superstructure (blue for the more rigid one rω_U = 6, red for the more flexible one rω_U = 3) and similar intensities represent cases with the same substructure (dark for rω_L = 6, light for rω_L = 3). The main observations are reported below:

• For all these structures, the trend of the surfaces is like that of Fig. 6 for the same isolation system.

• For both the systems, D_IS increases as rω_L decreases (from dark to light surfaces), i.e., when the substructure becomes more flexible. Then, with the same substructure, D_IS increases as rω_U increases (from red to blue surfaces), i.e., when the isolated mass becomes smaller, the latter being effective in containing the substructure displacements (acting as TMD). Therefore, D_IS is reduced for low-rise substructures and significant isolated masses—solutions that resemble the base isolation.

• For both isolation systems, D_U and A_U increase as rω_U decreases (from blue to red surfaces), i.e., when the superstructure becomes more flexible. With the same superstructure, the increase of rω_L (darker surfaces) reduces D_U for low damping values (especially for the fuse system), but could increase it for high damping solutions, as the limit situation of base isolation (for large rω_L and small r_F) becomes that of fixed-base superstructure (for large rω_L and large r_F); then, the increase of rω_L generally amplifies A_U, especially for high r_F and low α values (rigid FVDs).

Figure 8 compares the response surfaces of the structures with rω_U = rω_L = 6 and T_IS = 2, 3 and 4 s (corresponding to structures of 2–2, 4–4 and 6–6 storeys respectively, see Table 2), separately for the fuse and LRB systems. For all T_IS values, the trend of the surfaces is like that of Fig. 6 for the same isolation system. In general, as T_IS increases, D_IS increases whereas D_U and A_U decreases (as expected); furthermore, with increasing T_IS, the variability of D_U and A_U on the analysed r_F-α range is reduced, especially for the fuse system.

Figures 6, 7 and 8 clearly show that the damping solutions that minimise the peak response of the various performance parameters are identified in different r_F-α ranges; hence, a multi-objective design procedure is needed to determine a set of Pareto-optimal solutions. Moreover, the trend of D_U is quite similar to that of A_U for optimisation purposes and is generally more sensitive to the additional damping for low to medium r_F values, where the superstructure peak response is at its minimum. Therefore, to solve the optimisation problem in a simpler way, without significantly affecting the results, the superstructure performance can be effectively represented only by D_U for these case studies. Globally, linear or quasi-linear FVDs seem more effective in reducing the isolation drift while containing the amplification of the superstructure response.

5 Optimisation of the structural performance and optimal FVDs

5.1 Surrogate response models and genetic algorithm

To apply the proposed optimisation method, appropriate surrogate response models should be defined and calibrated, based on previously obtained response surfaces. These models can be effectively expressed in a totally dimensionless form by normalising the structural response to the peak one in the case without damper, thus allowing the comparison of the optimisation results between various case studies. The performance parameters chosen for optimisation are the relative displacement of the isolation layer (D_IS) and maximum inter-storey drift of the superstructure (D_U). Defining rD_IS and rD_U as the associated parameters normalised to the case without FVD, the two objective functions (OFs) to be minimised simultaneously are as follows:

$$\left\{ \begin{gathered} O{F_1}=\hbox{min} \left[ {r{D_{IS}}({r_F},\alpha )} \right] \hfill \\ O{F_2}=\hbox{min} \left[ {r{D_U}({r_F},\alpha )} \right] \hfill \\ \end{gathered} \right.$$

(30)

where, rD_IS (r_F, α) and rD_U (r_F, α) are the surrogate response models of rD_IS and rD_U, obtained by calibrating the complete fourth degree polynomial in r_F and α on the response surfaces of interest, separately for each case study examined. The polynomial degree was chosen based on preliminary assessments of computational time and prediction capability, the latter described by the coefficient of determination R². The values of R², averaged among the case studies analysed, are shown in Fig. 9 as a function of the polynomial degree, separately for the performance parameters (rD_IS and rD_U) and the two types of isolation systems. Ongoing studies by the same authors suggest the appropriateness of this polynomial model, even in the case of irregular structures (i.e., with different mass and stiffness distribution between substructure and superstructure).

Fig. 9

Accuracy of polynomial surrogate response models as a function of their degree, in terms of R² averaged among the case studies

The NSGA-II algorithm (Deb et al. 2002) was used to solve the multi-objective optimisation problem and its parameters were set as specified in Table 4, based on computational cost-effectiveness assessments. The high number of generations and large population (number of solutions sought) allow for a refined solution and were possible due to the surrogate models. Indeed, the minimisation of analytical functions requires much shorter calculation times than the direct optimisation of the structural response, based on the TH analysis iteration (as done by Liu et al. 2018).

Table 4 Parameters of the NSGA-II algorithm

Given the large population, a filter was then applied to the optimal results for representation purposes. This filter returns the mean values of the OFs for regular r_F intervals and associates them with the central values of these intervals (the optimal r_F range was divided into 25 intervals).

As an example, for the case study T_IS = 4 s, r_ωU = r_ωL = 6 and fuse system, Fig. 10a shows the rD_IS and rD_U surrogate response models and Fig. 10b the application of the NSGA-II algorithm; in particular, in Fig. 10b, the optimal results of OF₁ (minimisation of rD_IS) and OF₂ (minimisation of rD_U) are superimposed on the surfaces of surrogate models (represented in 2D by a colour map), with grey markers representing the entire population and white for the filtered results. This representation clearly shows that OF₁ and OF₂ are minimised respectively, for the major and minor r_F values, and the intermediate results are the best compromise solutions between OFs.

Fig. 10

a Surrogate response models of rD_IS and rD_U calibrated for the case: T_IS=4 s, r_ωU=r_ωL=6, fuse system. b Colour maps of the surrogate models and optimisation results (OF₁ and OF₂) from NSGA-II

Furthermore, for design purposes, it is essential to determine the c values associated with the optimal r_F-α solutions; therefore, a 4-degree polynomial function was also calibrated to obtain the model of c* (Eq. 20), as a function of r_F and α, from which the optimal values of c can be derived.

5.2 Optimisation results

The overall optimisation results are shown in Figs. 11 and 12 for the fuse and LRB systems respectively, as optimal values of OFs, α and c* versus r_F.

Fig. 11

Optimal results of OFs, α and c*, versus r_F, for all the case studies with the fuse isolation system

Fig. 12

Optimal results of OFs, α and c*, versus r_F, for all the case studies with the LRB isolation system

Regarding the OFs, the following considerations can be drawn:

• OF₁ is only slightly influenced by the type of structure. In particular, with the same r_F, OF₁ slightly increases with increasing T_IS, as the D_IS values generally increase with T_IS (see Fig. 8), and so do their ratios with respect to the case without damper (i.e., OF₁). For the same T_IS, the negligible dependence of OF₁ on the type of structure indicates the effectiveness of r_F in representing a characteristic force ratio for the structure (being defined based on the first vibration mode). Indeed, a given r_F value corresponds to different FVD forces for different structures, but such as to provide a similar reduction of the first-mode seismic response (and so of D_IS and OF₁).

• Regarding OF₂, its dependence on the type of structure is more evident. In particular, when T_IS increases, the minimum values of r_F (r_Fmin) associated with the minimum values of OF₂ are reduced, and the values of OF₂ increase globally as well as their dependence on both r_F and the type of structure. This is explained by the fact that D_U (hence OF₂) is a parameter influenced by the amplification effects of higher modes, which clearly depend on the type of structure and are more important, in relative terms, for higher T_IS values (see Fig. 8).

Regarding the FVD parameters, the following considerations can be drawn:

• The optimal α values are distributed along r_F with a quasi-triangular trend—first they decrease to a minimum value (α_min) for incremental r_F values from low to medium, then they rise up to one for higher r_F values. This trend seems generally correlated with that of OF₂, where for r_F < r_F(α_min), OF₂ increases only slightly from its minimum value, whereas its increase is significant for larger r_F. Considering that in general, OF₁ is already significantly reduced at r_F(α_min) and the damper cost increases with increasing r_F, the optimal solution associated with α_min represents a significant design reference and convenient lower limit for r_F. However, for the slenderest structures (minor r_ωU and r_ωL and major T_IS), and particularly for the LRB system, this trend of α is less evident and tends to flatten out on the value of α = 1 (linear FVDs).

• For the significant r_F values i.e., r_F ≥ r_F(α_min), α is independent of the type of structure. This is another advantage of using r_F (similar to what observed for OF₁). Instead, the values of α_min (from about 0.75 to 0.9) and r_F(α_min) (from about 0.3 to 0.6) generally depend on the type of structure as well as the results for r_F < r_F(α_min), because they concern the minimisation of OF₂ (which is influenced by the type of structure). However, α variability is limited for the regular structures analysed.

• To increase the damper force (r_F) between r_Fmin and r_F(α_min), c* increases strongly, as the optimal α values are reduced in this range; once r_F(α_min) is reached (with c* values from about 0.65 to 0.95), the increase of r_F continues with only a slight increase of c*, and up to one for r_F = 1 (for all structures), as it is supported by the increase in α. Furthermore, it can be observed that variations in the trend of c* clearly reflect those in the trend of α.

The trend of the optimal solutions is similar between the isolation systems, but the values of OF₁ and OF₂ are greater for the LRB system. This is due to the fact that the reference values of D_IS and D_U in the case without damper (the normalisation values for OF₁ and OF₂) are lower for this system, because of the hysteretic damping. Therefore, the results in this dimensionless form cannot be used directly to make considerations about the convenience of the two systems, which will be discussed in the next section.

As a reference, assuming r_F ≈ 0.4 (fairly representative of the solutions with α_min) and for T_IS from 2 to 4 s, OF₁ ranges from 0.3 to 0.5 for the fuse system and from 0.5 to 0.9 for the LRB system, and OF₂ ranges from 0.4 to 0.9 for the fuse system and from 0.9 to 1.2 for the LRB system.

5.3 Global assessment of structural performance with optimal FVDs

This section presents the absolute values of the main performance parameters (D_IS, D_U and A_U) for all the optimal solutions obtained, in order to draw some considerations about the effectiveness of the additional damping, also in relation to the type of isolation system.

The maximum inter-storey drift ratio of the substructure (δ_L) was also evaluated. In particular, the assumed structural models represent the substructure as an equivalent single degree of freedom (ESDOF), and therefore do not allow directly evaluating δ_L. However, based on the ESDOF displacement (D_L,ESDOF), and the hypothesis of a linear deflection profile along the substructure height (H_L, calculated as in Fig. 1), it was possible to estimate δ_L through Eq. 31 (which, not considering the modal participation factor, slightly overestimates δ_L).

$${\delta _L} \approx \frac{3}{2}\frac{{{D_{L,ESDOF}}}}{{{H_L}}}$$

(31)

The values of these parameters are plotted in Fig. 13 versus r_F for all optimal solutions. For convenience, D_U was also shown as a ratio with respect to the storey height (h_i), i.e., δ_U = D_U/h_i. The following considerations can be drawn:

Fig. 13

Main performance parameters (D_IS, δ_U, A_U and δ_L), versus r_F, for all optimal solutions

• D_IS is significantly reduced by increasing r_F up to values between four and 12 cm for r_F = 1 (for all case studies), with an almost asymptotic trend for higher r_F values (this reduction is consistent with the results in Liu et al. 2018). For the fuse system, the values of D_IS are initially higher but decrease more rapidly, tending to the values of the LRB system for high r_F values.

• Although δ_U increases with increasing r_F, its values remain reasonably low for the stock of regular structures analysed, i.e., less than 0.2 % for the entire range of r_F. These values are lower for the fuse system and unlike D_IS, this trend is maintained throughout the r_F range.

• The values of A_U, not directly optimised in the OFs, show a similar trend to that of δ_U, with values generally lower for the fuse system. Then, the optimal damping solutions allow containing these accelerations below 0.3 g in most cases, which is generally an acceptable value to avoid significant damage to building contents.

• Regarding δ_L, also not optimised in the OFs, the optimal FVDs allow a good control of the substructure response, limiting these drifts to 0.5 % in all cases—a value generally assumed in the structural codes (e.g., EC8) as damage limit state. Furthermore, considering that these drifts are slightly overestimated as well, this result confirms the adequacy of linear modelling for these substructures.

Clearly, the structural modelling approach depends on the type of structures examined, and the hypothesis of elastic substructure may not be appropriate for some applications. For example, when inter-storey isolation is used as a seismic retrofit technique for existing buildings, the evaluation of the possible and specific non-linear behaviour of the substructure is generally necessary.

These results also allow some considerations on the convenience of isolation systems. For r_F values from low to medium in the analysed range (less than about 0.7), the two systems can lead to similar structural performances, i.e., similar values of D_IS and δ_U, even if with higher r_F values for the fuse system. Therefore, the choice of the isolation type could be based on specific cost assessments (beyond the scope of this paper), considering the difference in cost between isolators (to the advantage of the fuse system) and dampers (to the advantage of the LRB system, requiring a minor r_F for the same performance). Instead, for higher r_F values and particularly for low T_IS values, i.e., when the will is to strongly limit the inter-storey deflection, the fuse system allows lower δ_U and A_U values for the same D_IS values, and therefore a better structural performance at a lower cost (due to cheaper isolators with equal dampers).

Finally, these findings acquire further importance if considered as a reference or basis of comparison for future studies aimed at examining irregular structures (where the effects of additional damping can be much greater), substructures with non-linear behaviour (which require specific non-linear modelling) or different seismic inputs (e.g., near-fault earthquakes).

5.4 Optimisation of linear FVDs and comparisons

The optimisation results obtained with α_min ≈ 0.8 indicate that the optimal FVDs for the analysed regular structures are slightly non-linear. Therefore, it is interesting to understand the extent to which this non-linearity influences the structural performance (OF₁, OF₂). To this end, the proposed optimisation method was reapplied to all case studies, setting α = 1.

The results obtained are interesting, as they show that this non-linearity only slightly influences the structural response with respect to the case of optimal linear FVDs. In particular, as shown in Fig. 14 for both the fuse and LRB systems, the ratios between the values of OF₁ previously obtained and those obtained with linear optimisation (OF_1,L) are all greater than 0.92, i.e., the structural performance in terms of OF₁ is reduced to a maximum of 8 % (in the case of fuse system). Moreover, the same variation for OF₂ is negligible, as contained in the range ± 4 %.

Fig. 14

Ratio between the OF₁ values and the associated ones of OF_1,L from the optimisation of linear FVDs

Figure 15 shows the c* values for optimal linear FVDs and all case studies, separately for the fuse and LRB systems. With α = 1, c* (see Eq. 20) corresponds precisely to the first-mode damping ratio due to the damper, and its values show approximately the same trend for all structures with respect to r_F, again highlighting the effectiveness of r_F for this study. Also, these c* values are very similar between the two isolation systems. In particular, the increase of c* with respect to r_F is more than linear, because with increasing r_F, the damper velocity is reduced, and therefore to increase the damper force with constant α (= 1), c must increase more than proportionally.

Fig. 15

Optimal values of c*, versus r_F, from the optimisation of linear FVDs

6 Prediction models for the optimal design of FVDs

6.1 Definition of prediction models

Based on linear optimisation results, the best solution for design purposes would seem to be the use of linear FVDs. To this end, Fig. 16a, b show (in red) the prediction models assumed for the parameters of linear FVDs; in particular, α is always 1 (Fig. 16a) and c* is provided as a function of r_F only (Fig. 16b), valid for both isolation systems.

Fig. 16

a, b Prediction models of α and c*, for optimal linear (red) and non-linear (blue) FVDs. c, d Fit of the models and associated values of R² for the case of the fuse system

However, it is also useful to provide the prediction models of α and c* on the basis of the general optimisation results, and therefore of the trends and dependencies observed in Figs. 11 and 12—these models are also represented in Fig. 16a, b (in blue).

In addition, for the fuse system, Fig. 16c, d show the fit of α and c* models, for both linear and non-linear dampers, and associated values of the coefficient of determination (R²). The models for non-linear FVDs were represented using both the average value of α_min and for a more accurate estimate, the specific α_min value of each structure predicted by the equation in Fig. 16c.

The non-linear models, besides predicting the real trend of the optimal FVD parameters and being a useful reference for future research work on different case studies, allow to identify the r_F value associated with the α_min point which, as previously discussed, represents an optimal compromise solution between OF₁ and OF₂. These models of α and c* are both tri-linear laws defined on three main points, whose r_F values are in common for the two models. The points are: (A) r_F = 1, α = c* = 1; (B) position of α_min; (C) intersection of model α with the line for α = 1. The calibration slopes (β₁, β₂ and β₃) and mean values of α_min and c*(α_min), necessary to determine the models, are shown in the relevant figures.

For clarity, the steps for applying these non-linear prediction models are listed below.

• Calculation of α by simple linear proportion, entering Fig. 16a with the chosen value of r_F and using the slope β₁, if r_F ≥ r_F(α_min) and β₂ vice versa. Based on the values of α_min and β₁, shown in the same figure, the value of r_F(α_min) that identifies the characteristic point B is 0.40 for the fuse system and 0.47 for the LRB system.

• Calculation of c*, similar to that of α, entering Fig. 16b with the chosen value of r_F and applying a linear proportion. Point B is defined by the same values of r_F(α_min) as reported above.

• Execution of the undamped modal analysis to determine the necessary information on the first vibration mode i.e., the first-mode critical damping (c_cr1) and the first-mode isolation deflection (ψ_1,nL+1 – ψ_1,nL).

• Calculation of the damping constant c of the FVD using Eq. 20, on the basis of c* and the first-mode characteristics previously obtained.

Regarding the choice of r_F, which depends on the structural performance sought, this can be based on the optimal results obtained for OF₁ and OF₂, shown in Figs. 11 and 12; in particular, as seen above, the globally most effective solutions are those with r_F ≈ r_F(α_min).

In the following Sect. 6.2, for example and validation purposes, both linear and non-linear prediction models were applied to three representative structures of the analysed stock, evaluating the structural performance with increasing r_F and the influence of damper non-linearity.

6.2 Example of application of prediction models

The models for predicting optimal FVDs were applied to the three case study structures represented in Fig. 17. These structures have 16 floors, with the isolation system placed between the 10th and 11th floors for case study 1, between the eighth and ninth floors for case study 2, and between the fifth and sixth floors for case study 3. Both fuse and LRB isolation systems were analysed for each case study, with an isolation period T_IS = 3 s.

Fig. 17

Presentation of the case studies (above); modal analysis of the case study 2 (below)

These structures were modelled as 16-DOF linear systems and their main structural data, as well as the characteristics of their equivalent 3-DOF systems (showing their representativeness with respect to the investigated parametric stock), are shown in Fig. 17. The same figure also shows the results of the classical modal analysis, performed on structure 2, necessary for applying the prediction models.

In particular, for each structure and isolation system, the optimal non-linear FVD parameters were calculated for three levels of damper force, i.e., r_F = 0.2, r_F(α_min) and 0.8, following the procedure described above. In the case of r_F = r_F(α_min), the parameter c of the optimal linear FVD was also calculated for comparison purposes. Table 5 reports the optimal values of c and α predicted for the various design solutions investigated.

Table 5 Optimal FVD parameters for case study structures, for three FVD force ratios (r_F = 0.2, r_F(α_min), 0.8)

To evaluate the effectiveness of the models, the structural responses without and with the identified FVDs were assessed by TH analysis, using the set of natural records and the structural damping previously defined. The main results are shown in Figs. 18 and 19. Figure 18 shows the inter-storey drift and absolute floor acceleration profiles of structure 2 for the selected r_F values, obtained by averaging the maximum analysis values among the various accelerograms. Figure 19, on the other hand, summarises and compares the results of all case studies in terms of structural performance normalised to the case without FVD. In particular, the parameters evaluated are drift of isolation layer (D_IS), maximum inter-storey drift of substructure (D_L) and superstructure (D_U), maximum absolute floor acceleration of substructure (A_L) and superstructure (A_U). These parameters, normalised to the case without FVD, provide rD_IS, rD_L, rD_U, rA_L and rA_U, which are the parameters shown in Fig. 19.

Fig. 18

Inter-storey drift and absolute floor acceleration profiles of the case study 2

Fig. 19

Comparison of optimal structural performance with increasing r_F, and for r_F = r_F(α_min) between optimal non-linear and linear FVDs, for case study structures with fuse (a) and LRB (b) isolation systems

As can be seen from both Figs. 18 and 19, the effects of the FVDs are clearly greater in the case of the fuse system, as it does not provide further dissipation. Then, for all the case studies, the FVD associated with r_F(α_min) proved to be the best compromise solution between the performances of the isolation layer and the substructure (both of which improve with increasing r_F, if not excessive) and that of the superstructure (which worsens with medium to high r_F values).

In particular, the trends in Fig. 19 show that FVDs with r_F > > r_F(α_min), compared to the case of r_F(α_min), may allow a further reduction of rD_IS and rD_L, however, at the expense of a more significant amplification of the superstructure response. Furthermore, very large r_F values (such as 0.80) were also found to be less effective for the substructure in the case of the LRB system and a high isolated mass ratio (e.g., case study 3). Considering that these solutions are also the most expensive, they are generally to be avoided.

Figure 19 also shows the comparisons between optimal non-linear and linear FVDs for r_F = r_F(α_min). The related performance variations, in favour of non-linear dampers, are rather small for the fuse system and negligible for the LRB system, confirming the previous results of the parametric analysis.

It is also worth noting that as r_F increases, both the inter-storey drift and floor acceleration profiles of the substructure are regularised along the building height, with the drift values decreasing in the lower part and increasing in the upper part of the substructure, and the acceleration values seeing an overall and considerable reduction (see Fig. 18).

Finally, with the aim of providing some preliminary indications on the possible effects of structural non-linearity, some TH analyses were carried out by modelling the structure of case study 2 with two non-linear models. These models are based on the hysteretic laws of Takeda and Bouc-Wen, shown in Fig. 20a, which are often used to describe the behaviour of ductile RC frames. Both models were calibrated on the storey elastic stiffness k_i (see Fig. 17), assuming a ratio r between post-yield and elastic stiffnesses equal to 0.2, and an inter-storey drift δ_y at yield equal to 0.5 %. The Bouc-Wen model, which is based on a more complex hysteretic law (the same used to model LRB isolators), requires the calibration of additional hysteresis parameters, which were defined according to Sues et al. (1988) and are shown in Fig. 20a.

Fig. 20

a Non-linear structural models. b Performance comparisons between linear and non-linear modelling

For the LRB isolation system, the FVD associated with r_F(α_min), and the same set of accelerograms but evaluating two PGA values, Fig. 20b shows the inter-storey drift and absolute floor acceleration profiles, comparing the linear response of the structure with the non-linear ones associated with the two hysteretic models. For the PGA of 0.3 g, the structure never exceeds δ_y, thus no significant differences are observed. Instead, for the PGA of 1 g, the substructure can yield, and therefore considerations on the effects of structural non-linearity can be drawn. In particular, in the case of non-linear modelling, there is an amplification of the maximum drift values in the substructure, due to the concentration of plastic deformation on the lower storeys of the building, which first reach yield. This increase in deformation, and therefore in structural dissipation, then appears beneficial with regards to the floor accelerations, which can be significantly reduced. Clearly, the type of hysteretic model adopted plays a significant role. In the specific case study, the maximum values of drift and acceleration are lower using the Bouc-Wen model compared to the Takeda model, as the former allows to describe the variation and degradation of the storey stiffness more gradually and also provides a slightly greater dissipation per cycle. The same considerations also apply to the fuse isolation system.

7 Conclusions

This paper aimed to evaluate the effects of optimal additional damping on the seismic performance of structures with inter-storey isolation. To this end, a new method for multi-objective optimisation and performance evaluation of FVDs was proposed. This method is based on the definition of appropriate surrogate response models, calibrated on the maximum response (averaged between seismic inputs) of some significant performance parameters and their subsequent minimisation through multi-objective genetic algorithms. Such models, if conveniently normalised, allow rationally comparing the FVD effects for a wide range of dampers and structures as well as obtaining optimisation results in a dimensionless form, suitable for the definition of prediction models.

This method was applied to a stock of 48 regular RC structures, with various vibration periods of superstructure, isolation and substructure, analysing a wide range of damping forces for both linear and non-linear dampers (with α between 0 and 1), two types of isolation systems (linear with fuse behaviour and non-linear with LRB isolators) and a set of spectrum-compatible natural records. The objective functions (OFs) evaluated in this optimal design, whose values were conveniently normalised to the case without damper, were the minimisation of the isolation drift (OF₁) and the minimisation of the maximum inter-storey drift of the superstructure (OF₂). The maximum values of the superstructure floor accelerations and substructure inter-storey drifts were also evaluated as an output of the optimisation process. Furthermore, for comparison purposes, the proposed method was reapplied to optimise linear FVDs (α = 1) only.

The main considerations on the comparative evaluation of the FVD effects are listed below:

• The values of OF₁ and OF₂ associated with optimal FVDs clearly showed a conflicting trend, proving the necessity of a multi-objective design to find a set of Pareto-optimal solutions.

• For all the case studies, the optimal FVDs allowed significant reductions in isolation drift, with an even improved or only slightly amplified superstructure response (depending on the case study) for intermediate FVD force ratios (r_F) among those analysed, confirming their effectiveness for inter-storey applications. Also, the values of OF₂ were always less than two, with the greatest amplifications due to the higher values of r_F and the isolation period.

• The optimal FVDs were slightly non-linear for the analysed structures, with minimum values of α ranging from about 0.75 to 0.9.

• The optimal FVDs also ensured a good structural performance with respect to superstructure floor accelerations and substructure inter-storey drifts. For the case studies analysed, these accelerations were always less than 0.3g and these drifts were always less than 0.5 % (value generally assumed in the codes as damage limit state).

• The fuse isolation system was found to be slightly more advantageous than the non-linear one with LRBs, when using very high r_F values (greater than about 0.7), as it allowed better performance of the superstructure with the same reduction in isolation drift.

In addition, the main results from a design point of view are summarised below:

• A prediction model of optimal linear FVDs, calibrated on the results of the entire analysis stock, and a prediction model of optimal non-linear FVDs, calibrated separately for the fuse and LRB isolation systems, are provided in this paper.

• The optimal non-linear FVDs, compared to the linear ones with the same r_F value, allowed a better structural performance, even if this benefit was rather limited for the analysed structures. Therefore, the use of the linear prediction model is the most practical solution from a design point of view. However, the non-linear models allowed to identify the r_F value associated with the α_min point, representing an optimal compromise solution between OF₁ and OF₂.

• For r_F ≈ r_F(α_min) (i.e., 0.4 to 0.5), and compared to the case without FVD, the reductions in the isolation drift ranged from 50 to 75 % for the fuse system and from 20 to 50% for the LRB system, considering all the case studies. On the other hand, the amplification of the maximum inter-storey drift of the superstructure (in the case of the LRB system) was always less than 20%.

• The application of prediction models to specific case study structures confirmed their effectiveness and of optimal FVDs for these applications. Furthermore, some preliminary assessments on the effects of structural non-linearity showed how the latter influences the structural response by amplifying the inter-storey drifts in the lower part of the substructure and reducing floor accelerations.

The proposed method, due to its generality, can also be applied to different case studies from those examined here. For future work, it will be interesting to evaluate the effects and optimal parameters of the FVDs for irregular structures in elevation and compare them with those obtained in this study for regular structures, as well as examine different types of seismic input (e.g., near-fault earthquakes) and further investigate the effects of structural non-linearity.