Abstract
Surface wave methods gained in the past decades a primary role in many seismic projects. Specifically, they are often used to retrieve a 1D shear wave velocity model or to estimate the VS,30 at a site. The complexity of the interpretation process and the variety of possible approaches to surface wave analysis make it very hard to set a fixed standard to assure quality and reliability of the results. The present guidelines provide practical information on the acquisition and analysis of surface wave data by giving some basic principles and specific suggestions related to the most common situations. They are primarily targeted to non-expert users approaching surface wave testing, but can be useful to specialists in the field as a general reference. The guidelines are based on the experience gained within the InterPACIFIC project and on the expertise of the participants in acquisition and analysis of surface wave data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Overview
1.1 Introduction
In the last two decades surface wave analysis has become a very common technique to retrieve the shear-wave velocity (VS) profile. One common use of the VS profile is the estimation of VS,30, defined as the travel-time average shear-wave velocity in the topmost 30 m of the subsurface, used in several building codes, including EC8, for seismic response site classification.
In general, surface wave methods require processing and inversion of experimental data that may be quite complex and need to be carried out carefully. The surface wave inversion problem is indeed highly non-linear and is affected by solution non-uniqueness. These factors could induce interpretation ambiguities in the estimated shear-wave velocity model. For these reasons, the results of surface wave analyses can be considered reliable only when obtained by expert users. However, because of the cost and time effectiveness of surface wave methods and the availability of “black-box” software, non-expert users are increasingly adopting surface wave methods. This often leads to strongly erroneous results that may induce a general lack of confidence in non-invasive methods in a part of the earthquake engineering community.
In this framework, the InterPACIFIC (Intercomparison of methods for site parameter and velocity profile characterization) project was aimed, among other objectives, at the comparison of the most common techniques for surface wave analysis in order to evaluate their different performances and reliability. These comparisons helped to improve the understanding of those theoretical and practical issues whose differences in the implementation could affect the results.
The present guidelines provide practical information on the acquisition and analysis of surface wave data by giving some basic principles and specific suggestions related to the most common situations. They are primarily targeted to non-expert users approaching surface wave testing, but can be useful to specialists in the field as a general reference. Moreover, they provide a common reference to establish the necessary dialogue between the service provider and the end-user of the results. However, guidelines cannot be a substitute for experience in surface wave analysis.
The guidelines are based on the experience gained within the InterPACIFIC project and on the expertise of the participants in acquisition and analysis of surface wave data.
A thorough treatment of the theoretical background and of advanced applications is outside the scope of these guidelines. The Reader is referred to textbooks (e.g. Okada 2003; Foti et al. 2014) and to the vast literature on the topic (for an overview, see Bard et al. 2010; Socco et al. 2010; Foti et al. 2011; Schramm et al. 2012; Yong et al. 2013) for achieving the necessary knowledge on surface wave methods and for the theoretical details.
The guidelines are written with reference to Rayleigh waves, which are the most commonly exploited surface waves. Many of the same principles apply to the analysis of other kinds of surface waves, such as Love and Scholte waves, which however requires specific data acquisition procedures and forward modelling algorithms. The properties of surface waves described in the paper as well as the algorithms used to solve the forward problem are based on idealizing soil deposits and geomaterials as linear (small-strain) elastic, isotropic continua thus obeying the classical Hooke’s law. Other rather peculiar properties of surface waves can be inferred by assuming different constitutive models for soils. Examples include linear viscoelasticity where attenuation of surface waves can be used to estimate damping ratio (o quality factor) of soils or poro-elasticity (Biot model) where Rayleigh waves could in principle be used to estimate also porosity.
Surface wave analysis can be performed with a very wide variety of procedures. If correctly implemented and properly applied, almost any of them could provide equivalent results in terms of reliability. These guidelines are focused on the standard practice and provide basic recommendations to non-expert users. Various acquisition and/or processing alternatives can be used to achieve the same results. A full coverage of all possible alternatives is outside the scope of the guidelines.
The guidelines are organized as follows: after a brief introduction on the basic principles of surface wave methods, the typical steps of the test (acquisition, processing and inversion) are discussed and suggestions are provided for their implementation. A series of appendices (provided as additional on line material) cover specific issues and provide selected references for gaining a deeper insight into particular aspects of surface wave methods.
1.2 Basic principles of surface waves
1.2.1 Surface wave definition
Surface waves are generated in the presence of a free boundary, such as the surface of the Earth, and propagate parallel to this surface. Several types of surface waves exist and can ideally be classified with respect to the polarization of the ground motion during propagation: Rayleigh waves involve elliptical motion in the vertical plane containing the wave propagation direction (Fig. 1a); Love waves involve transverse motion (Fig. 1b); Scholte waves propagate at the earth/water interface, and should thus be used for underwater surface wave analysis.

Modified from Bolt (1987)
Polarisation of the fundamental mode of the a Rayleigh and b Love waves.
For Rayleigh waves, the amplitude of the associated motion decays exponentially with depth, becoming negligible within about one wavelength (λ) from the surface in homogeneous media. In vertically heterogeneous media, the decay of particle motion amplitude with depth cannot be predicted a-priori without knowledge of the subsurface structure. The velocity of Rayleigh waves depends on the elastic properties of the subsurface: mainly on the shear (S) wave velocity, and slightly on the compression (P) wave velocity and on the mass density. Love waves do not exist in homogeneous media and in heterogeneous media Love wave velocity depends only on how VS and mass density vary with depth.
1.2.2 Surface wave dispersion
In vertically heterogeneous media, surface wave propagation is governed by geometric dispersion: harmonic waves of different wavelengths λ propagate within different depth ranges (Fig. 2a) and, hence, for each wavelength the phase velocity V depends on the elastic properties and density of the subsurface within the propagation depth range (Fig. 2b). Distribution of phase velocities as a function of frequency or wavelength is called a dispersion curve (Fig. 2c). In vertically heterogeneous media with increasing velocity (both VS and VP) with depth, the velocity of propagation of surface waves decreases for increasing frequency (normally dispersive profiles).
Geometric dispersion of surface waves in vertically heterogeneous media. λ is the wavelength of the surface wave with phase velocity V and f is the frequency of the associated ground motion vibration. VA and VB indicate the generic shear wave velocity in the two layers affected by the surface wave propagation. a Qualitative sketch of amplitude decay of the fundamental mode at different wavelengths, b dispersion curve in the wavelength—phase velocity domain, c dispersion curve in the frequency—phase velocity domain
1.2.3 Higher modes
In a horizontally layered medium, the surface wave propagation is a multimodal phenomenon: at each frequency, larger than a well-defined cut-off frequency, different modes of vibration exist. Each mode is characterized by its own propagation velocity, which always increases from the fundamental to the higher modes (overtones). Examples of modal dispersion curves for some synthetic cases are reported in Appendix 1.
The existence of higher modes of surface waves in heterogeneous media is due to constructive interference phenomena occurring among waves undergoing multiple reflections at the layer interfaces. Although their exact number and frequency cut-offs depend only on the solution of the free vibration problem (i.e. higher modes always exist), the different overtones carry different energy, making them not always detectable (i.e. only few modes may be excited). Energy distribution is also a frequency dependent phenomenon: a mode can be strongly dominating within a certain frequency band, while negligible in other frequency bands.
Energy distribution is controlled by many factors: primarily the site-specific (3D) velocity and attenuation (i.e. wave amplitude loss), in combination with the source type, location, and coupling with the ground. In many common stratigraphic conditions, the propagation is dominated by the fundamental mode, as it typically happens in media characterised by a gradual increase of shear wave velocity with depth (normally dispersive profiles). In some cases, however, particularly where very strong velocity contrasts exist between layers at shallow depths (e.g. the contact between low-velocity sediments and bedrock), or where a low-velocity layer exists between two high-velocity layers, higher modes may be excited and need to be considered in the inversion analyses. In these cases, the energy may move from one mode to the other at particular frequencies where two consecutive modes have similar velocities, called osculation frequencies. Other reasons for an “apparent” mode superposition (i.e. modes are theoretically separated but cannot be distinguished by the operator) may be related to many other factors related to the acquisition geometry (e.g. lack of spatial resolution), In these conditions the experimental dispersion curve is then the result of the superposition of different propagation modes that cannot be distinguished (apparent or effective dispersion curve). Appendix 5 is devoted to further discussion on this issue.
1.2.4 Plane wave propagation and near-field effect
While the physics of surface wave propagation is identical for plane waves and any type of non-plane waves (e.g. the near-field), most approaches to dispersion analysis are valid only for plane waves and thus can become biased in the near-field (Wielandt 1993).
In the vicinity of the source (i.e. at a distance smaller than one wavelength), direct body wave components and the cylindrical wave front cause a departure from the theory of propagation of plane Rayleigh waves leading to phase velocities biased to lower values, which are collectively referred to as near-field effects. For such reason, too close source offsets should be avoided during active surveying, as well as the presence of nearby noise sources in passive acquisition.
1.2.5 Surface waves and lateral variations
In laterally heterogeneous media, propagation of surface waves is a much more complex phenomenon and the above concepts should be used with great caution. When small and smooth 2D or 3D variations occur (often the case for real sites), the resulting surface waves can be modelled as an equivalent 1D medium and standard analysis strategies can still be used, with some limitations. However, in the case of sharp 2D or 3D variations, the resulting surface waves can no longer be modelled with the equations for horizontally layered media usually adopted in surface wave analysis. If the site is expected to present strong lateral heterogeneities, standard 1D surface wave analysis should not be selected as the proper survey method and more advanced analyses should be applied to exploit surface wave propagation.
1.2.6 Surface waves in ambient vibrations
Because the wavefront of surface waves emanating from a surface point source is cylindrical, whereas the wavefront of body waves is hemispherical, surface wave amplitude decays much less with distance than that of body waves. As a consequence, far away from the source most of the energy is carried by surface waves, hence far-field ambient vibrations primarily contain surface waves. For this reason, passive recordings of ambient vibrations can oftentimes be utilized for surface wave analysis.
1.3 Surface wave analysis
1.3.1 General procedure
Surface wave analysis aims at estimating the seismic shear wave velocity (VS) profile by solving an inverse problem of model parameter identification based on an experimental dispersion curve. The surface wave analysis is typically implemented with three sequential steps: acquisition of seismic data (seismograms), processing (dispersion curve estimation), and inversion (model parameter optimization) (Fig. 3), which all can be undertaken with different strategies, as explained below.
If only the time-average velocity in the top 30 m is targeted, the last step can, in some instances, be omitted by estimating the VS,30 as a function of Rayleigh wave phase velocity at a given wavelength. However this strategy should be used with great care as explained in Sect. 5.1.
1.3.2 Survey design
The investigation depth depends on the maximum measured wavelength and the resolution decreases with depth. In particular resolution at shallow depth depends on the high frequency content (small wavelengths) of the recorded data. Hence, the survey has to be designed according to its objectives, and different strategies, equipment, setup and processing techniques will be used if the target is the shear wave velocity values in the first tens of meters (e.g. to estimate the VS,30 value) or the complete VS profile down to several hundreds of meters.
The maximum investigation depth is related to the maximum measured wavelength, which depends on:
-
The frequency content of the propagating seismic signal (source and site attenuation);
-
The array layout aperture used for the recording;
-
The frequency bandwidth of the sensors;
-
The velocity structure of the site.
Acquisition of surface wave data will therefore be designed to adapt these characteristics to the objectives.
1.3.3 Acquisition of surface wave data
Acquisition is performed with seismic survey equipment (see Sect. 2), and can imply the use of a single sensor (as for the case of amplitude and group velocity analysis), a pair of sensors (cross-correlations and SASW) or an array of receivers (for phase velocity estimation). The latter is by far the more widely used configuration in site characterization.
The frequency content of the propagating seismic signal depends on the type of seismic source and on the material attenuation due to the site.
Generally, artificial sources (also called active sources; e.g. sledgehammers and drop weights) generate energy concentrated at high frequencies (several hertz to several tens of hertz). This limits the maximum resolved depth to about 15–40 m (depending on the velocity structure of the site and the mass of the impact source). When small sources (e.g. hammer, small weight drop) are used is would be rare to generate energy at frequencies less than 8–10 Hz. Lower frequency surface waves can be generated using very massive sources (e.g. bulldozer, vibroseis), albeit at a considerable increase in the implementation cost. Conversely, ambient vibrations have sufficient energy up to periods of tens of seconds (very low frequency), which make them appealing for the investigation of deep velocity structures. In such passive acquisition, the seismic wavefield (called ambient vibrations, microtremors or sometimes improperly “seismic noise”) is generated by natural phenomena (e.g. sea waves, wind, micro-seismicity) and/or human activities (often referred as anthropogenic noise).
The equipment, measurement setup and geometry will thus be adapted to the type of survey (active vs. passive) and to the targeted wavelength range (see Sect. 2). When logistically possible, the combination of active-source and passive data is useful for obtaining a well-constrained shear wave velocity model from the surface to large depths.
1.3.4 Processing of surface wave data
In the second step, the field data are processed to retrieve an experimental dispersion curve. Several processing techniques can be adopted for the analysis of the seismic dataset (see Sect. 3), most of them working in the spectral domain.
Most of these techniques assume a 1D medium below the array (horizontally stratified, velocity only varies with depth), and plane wave propagation (the receiver array is far enough from the seismic source so that the surface wave is fully developed and the wave front can be approximated by a plane).
Other information contained in the measured seismic wavefield, such as the polarization curve (see Appendix 7) or P-wave travel times (see Appendix 6), may also be analyzed in order to better constrain the inversion.
1.3.5 Inversion of surface wave dispersion curve
In the inversion process (see Sect. 4), a model parameter identification problem is solved by using the experimental dispersion curve(s) as the target. The subsurface is typically modeled as a horizontally layered linear elastic and isotropic medium.
The unknown model parameters are often restricted to layer thickness and shear-wave velocities, by using appropriate a-priori assumptions on the other parameters (e.g. mass densities and Poisson’s ratios); schemes also exist which invert for all the involved parameters. However, in most cases surface waves are less sensitive to P-wave velocity and mass density than to S-wave velocity.
The shear-wave velocity profile is obtained as the set(s) of model parameters that allow(s) the “best” fitting between the associated theoretical dispersion curve(s) and the experimental dispersion curve(s).
The solution can be retrieved with local or global search methods:
-
Local search methods start from an initial model, solve the equation that links model parameters to the misfit between the experimental and theoretical dispersion curve(s), and iteratively modify the model until this misfit becomes acceptably small; this process can be carried out by enforcing constraints (e.g. maximizing the smoothness of the resulting profile or others);
-
Global search methods evaluate large ensembles of possible models distributed in defined parameter ranges looking for models that produce acceptably small misfit.
Given the non-uniqueness of the solution, it is strongly recommended that complementary datasets (e.g. body wave travel times, polarization curve) and available a priori site information are taken into account during the inversion process. Indeed in local-search method the profile resulting from the inversion may be strongly dependent on the initial model assumed. If this type of information is not available, the analyst should perform several inversions using different starting models (i.e. different trial layering parameterizations) in order to judge the sensitivity of the “best” solution to the starting model. In this respect global search methods have the advantage of scanning the parameter space with stochastic approaches..
1.4 Limitations of surface wave testing
1.4.1 Non-uniqueness of the solution
The estimation of the shear wave velocity profile from surface wave analyses requires the solution of an inverse problem. The final result is affected by solution non-uniqueness as several different models may provide similar goodness of fit with the experimental data.
Moreover, other sources of aleatory and epistemic uncertainties (e.g. uncertainties in experimental data, simplification imposed by the initial assumption of the 1D isotropic elastic model, parameterization of the model space) affect the reliability of the solution. Therefore, a single best fitting profile is not generally an adequate representation of the solution because it does not provide an assessment of the uncertainties due to input data and inversion procedure. There may, however, be some conditions where a single best fitting profile is sufficient for site characterization, such as when velocity gradually increases with depth and the primary purpose of the investigation is to determine VS,30.
The inversion process is also strongly mixed-determined: Near the ground surface, a detailed reconstruction of thin layers may be obtained, as typically dense information is available in the high frequency band (especially if active-source data are collected) and sensitivity of the dispersion curve to model parameters is high. The resolution markedly decreases for increasing depth. As a consequence, relatively thin deep layers cannot be identified at depth and the accuracy of the location of layer interfaces is poor at large depth.
1.4.2 Lateral variations
These guidelines are restricted to the analysis of surface wave data for the estimate of the vertical shear wave velocity profiles. Only 1D models of the subsurface are taken into account, hence the outlined procedures should only be used for site characterization when no significant lateral variations of the seismic properties are expected and with flat or mildly inclined ground surface.
1.4.3 Higher modes
The fundamental mode is not always dominant in the propagation of surface waves and higher modes may be mistaken for the fundamental mode. If higher modes are not recognized and accounted for in the analysis, large errors may occur in the estimated velocity profile. On the other hand, joint inversion of the fundamental and higher modes improves the reliability of the final result because higher modes represent additional independent information. Several methods have been proposed in the literature to account for higher modes, but the procedures are still not standardized and are not implemented in most commercial codes. In fact, the analyses for complex dispersive structures have to be tailored for the specific case and require very experienced analysts. Some details are provided in Appendix 5.
Given the above considerations, it is necessary to apply tests for lateral heterogeneity and dominance of higher modes in order to avoid pitfalls. Recommendations are given in Sect. 3.2.
1.5 What is covered in the appendices
In order to shorten the document, only the most popular techniques used for Rayleigh wave analysis are presented in the main body of the document. Additional information is reported in the appendices (additional on line material), which provide practical suggestions for acquisition and theoretical complements.
Appendix 1 provides some examples of theoretical Rayleigh modes of propagation for a variety of shear wave velocity models, which represents some typical conditions encountered in the field (canonical cases).
Practical information is provided in order to facilitate the implementation of surface wave analysis, especially concerning data acquisition:
-
Appendix 2 deals with geometry of arrays for ambient vibration analysis;
-
Appendix 3 covers equipment testing and verification;
-
Appendix 4 provides examples of field datasheets for both active and passive measurements;
Appendices 5–10 address some of the pitfalls of surface wave testing and presents complementary strategies for data analysis only briefly mentioned in the main body of the document:
-
Appendix 5 provides details on the most recent developments to take into account higher modes;
-
Appendix 6 reports some examples of joint inversion with P-wave refraction data, vertical electrical soundings and microgravity surveys;
-
Appendix 7 highlights the benefits of a joint inversion of the dispersion curve and the Horizontal-to-Vertical (H/V) spectral ratio of ambient vibrations;
-
Appendix 8 is devoted to Love wave analysis which can be implemented as a stand-alone measuring technique or, more often, may be used in conjunction with Rayleigh wave analysis;
-
Appendix 9 deals with passive measurements on linear arrays, called passive MASW or ReMi;
-
Appendix 10 deals with the analysis of surface wave attenuation for the estimation of dissipative properties of the subsoil.
Finally, Appendix 11 proposes a reference example of a final report for the characterization of a site on a specific case history.
2 Acquisition
The experimental data for surface wave analysis are time histories of ground motion (seismic records) measured at a fixed number of points on the ground surface.
In this section, we distinguish between active and passive surface wave measurements because their classical acquisition procedures are very different. As previously mentioned, active and passive measurements may both be applied to gather information over a wide wavelength range. We recommend such complementary data acquisition if the target depth is greater than about 20–25 m and only light active sources are used. While it may be possible to obtain VS profiles down to 30 m using a sledgehammer, we find this only to be possible at stiff sites. At soft sites, the depth of profiling with a sledgehammer will more than likely be limited to 15–20 m.
Datasets can be collected using a wide variety of array geometries. For active-source prospecting, the usual choice is to have the receivers placed in-line with the seismic source. For passive tests, 2D arrays of sensors deployed on the ground surface are recommended, as the ambient vibration wavefield might propagate from any direction. While passive tests are frequently conducted also with linear arrays, we caution analysts and end-users that 2D arrays are much preferred for passive measurements and far superior for developing robust VS profiles. In a dispersive medium, knowledge of the direction of passive energy propagation and the true velocity of its propagation are mutually dependent; one cannot be calculated without knowledge of the other. As the direction of propagation cannot be determined using a linear array, the true phase velocity cannot be verified. Additional information regarding passive recordings with linear arrays is provided in Appendix 9.
2.1 Active prospecting
The most common acquisition layout is composed of evenly-spaced vertical receivers aligned with the seismic source. This layout is often referred to as the MASW (Multichannel Analysis of Surface Waves) method and is described below. Another common (and older) active surface wave technique is the spectral analysis of surface waves (SASW) method, which uses only 2 sensors.
2.1.1 Equipment
Seismic source
the energy provided by the seismic source must provide an adequate signal-to-noise ratio over the required frequency band, given the target investigation depth. As the wavelength is a function of both frequency and phase velocity of the site, it is necessary to make preliminary hypothesis about the expected velocity range to define the required frequency band of the source. Indeed, at a soft site lower frequencies will be necessary to achieve the same investigation depth than at a stiff one. Furthermore, in the presence of a sharp velocity contrast at shallow depths, the amplitudes of low frequency (long wavelength) surface waves are strongly reduced and difficult to measure irrespective of the seismic source.
Vertically operated shakers or vertical impact sources are typically used for surface wave testing. The former provide an accurate control on the frequency band and very high signal-to-noise ratio in the optimal frequency band of operation of the vibrator. Nevertheless, these sources are expensive and not easily manageable. Impact sources (Fig. 4) are much cheaper and enable efficient data acquisition as impact sources provide energy over a wide frequency band.
Weight-drop systems and vertically accelerated masses are able to generate high signal-to-noise ratios and allow longer wavelengths to be gathered and investigation depths to reach several tens of meters.
Explosive sources also provide high S/N data over a broad frequency band, with the caution that if they are placed in a borehole the amount of surface wave energy could be limited.
The cheapest and most common source is a sledgehammer striking on a metal plate or directly on the ground surface. The weight of the sledgehammer should be at least 5 kg; the 8 kg sledgehammer is the most common choice. However, its limited energy in the low frequency band (typically limited to f > 8–10 Hz) makes the sledgehammer a useful source only for relatively small array lengths (see Sect. 2.1.2), which limits the investigation depths to a few (e.g. typically 1 or 2) tens of meters at most. For example, a sledgehammer is typically not an adequate source for imaging down to 30 m depth at a soft sediment site. If a single source is not able to provide enough energy over the whole required frequency band, acquisitions with different sources have to be planned. In fact this may be the preferred approach in many investigations, where a small hammer source is used to obtain high frequency/small wavelength dispersion data and a portable weight drop is used to obtain the lower frequency/long wavelength dispersion data. As with any active seismic survey, the signal-to-noise ratio can be improved by stacking the records from several shots.
Receivers
vertical geophones are typically used for the acquisition of Rayleigh wave data (Fig. 5). The natural frequency of the geophones must be adequate to sample the expected frequency band of surface waves without distortions due to sensor response. To some extent, geophones can be used below their natural frequency; however, it should be remembered that the sensor response is non-linear and each geophone goes through a 180° phase shift at its resonant frequency, thus some phase distortions can occur below the resonant frequency if the geophones are not perfectly matched. However, the use of multiple receivers produces a mitigation of errors induced by phase distortions, potentially extending the usable frequency band to about half of the natural frequency of the geophones. Nevertheless, this extension has to be carefully checked by relative calibration of the sensors and/or inspection of the data in the frequency domain. Generally for shallow targets (e.g. 30 m), 4.5 Hz natural frequency geophones are adequate. It is unlikely that higher frequency geophones (e.g. 10–14 Hz) will be reliable for profiling to depths greater than about 10–15 m. Certain types of accelerometers may also be used as a viable alternative to geophones in active data acquisition as they provide a flat response at low frequency, even if they are typically less sensitive.
Usual care needs to be adopted in deploying the receivers to guarantee adequate coupling with the ground. When possible, receivers should be coupled to the ground with spikes and thick grass should be removed from beneath the sensor. When testing on hard surfaces, sensors can be coupled to the ground using a base plate. Care should be taken ensure the sensors are level and to avoid placement of sensors directly over utilities whenever possible. Furthermore, when testing in inclement weather receivers must be protected against rain drops.
Acquisition device
different apparatuses may be used for digitization of analog output from the geophones and recording of signals. The most common choice is the use of multichannel seismographs, which are specifically designed for seismic acquisition. Nevertheless it has to be considered that they are typically conceived for other geophysical surveys (e.g. seismic reflection/refraction surveys) and may have some limitation on the usable frequency band, as typically declared in their specification sheets. It is necessary to check that these limitations do not affect the collection of surface wave data, especially with reference to the low frequency limit.
Trigger system
An adequate triggering system, such as a contact closure or hammer switch, is absolutely necessary if seismic data are stacked during acquisition to improve the signal to noise ratio or for some single station procedures. However, if stacking is not applied in the field, the accuracy of the triggering system is typically not a critical issue for surface wave methods as incremental travel time (phase differences) are analysed rather than arrival time.
2.1.2 Acquisition layout
The acquisition layout is based on a linear array of receivers with the shot position in-line with the receivers. The geometry is then defined by the array length L, the receiver spacing ΔX, and the source offset (Fig. 6). Receiver spacing is typically kept constant along the array, even if other arrangements are possible to optimize the acquisition of high and low frequency bands.
Array length
the array length (L in Fig. 6) should be adequate for a reliable sampling of long wavelengths, which are associated to the propagation of low frequency components, and an adequate resolution in the wavenumber domain. If a frequency–wavenumber (f–k) transform is applied to the data during processing, the maximum array length controls the wavenumber resolution: the longer the array, the higher the wavenumber resolution and the smaller the minimum observable wavenumber (hence the longer the observable wavelength). Other advanced processing algorithms are not limited by this link between array length and maximum wavelength (see Sects. 3.1.1, 3.2.3), as the result also depends on the characteristics of the records. Moreover, relating maximum wavelength to maximum resolved depth is not trivial, as the result depends strongly on the velocity structure of the site.
The usual rule of thumb is to have the array length at least equal to the maximum desired wavelength, which corresponds to more or less twice the desired investigation depth. With a more conservative approach, it is suggested an array length longer than two or three times the desired maximum investigation depth. Meaning, an array length of 60–90 m is preferred when trying to profile down to 30 m depth.
Care should be taken when lateral variations might be expected at the site because they may more easily affect long arrays.
Receiver spacing
the spacing between adjacent receivers (ΔX in Fig. 6) should be adequate to reliably sample short wavelengths, which are associated with the propagation of high frequency waves that are necessary for constraining the solution close to the ground surface (inter-receiver distance on the order of at most a few meters with usual active sources). Signals with wavelength less than 2 × ΔX will be spatially aliased (Shannon–Nyquist sampling theorem, see Fig. 7). Aliasing may prevent the correct identification of dispersion curves at high frequencies, particularly when higher modes are excited. It is therefore preferable to design the array according to the minimum wavelength expected in the signal, which mainly depends on the chosen seismic source and on the velocity structure of the site. Suggested values of receiver spacing for near-surface characterization range from 0.5 to 4 m.
Influence of receiver spacing on aliased energy: numerical experiments (without attenuation). Geophone spread from 11 to 200 m, spaced by a 1 m (190 receivers), b 10 m (19 receivers), c 20 m (10 receivers). Black curves indicate the limit from where shorter wavelengths (i.e. higher frequencies) are aliased
Number of receivers
The desired number of receivers would be dictated by the ratio between array length and receiver spacing. Often the number of receivers is dictated by the available equipment and it constrains the trade-off between receiver spacing and array length.
Surface wave methods may be implemented with a minimum number of receivers as low as two (the two-station procedure of the SASW Spectral Analysis of Surface Wave method). In this case, the spacing between receivers is incrementally increased during the survey. Such implementations are however prone to mode misinterpretation and, therefore, require effective mode analytical routines.
The experimental uncertainties on the dispersion image depend on the number of receivers. Theoretically, in the absence of intrinsic material damping, the higher the number of receivers the cleaner the dispersion image. However, high frequencies are rapidly damped-out with increasing distance from the source (i.e. far-field effects) and this loss of high frequency data can cause a loss of clarity in the dispersion image if too many receivers are used. The dispersion curve accuracy may also be influenced by the number of receivers (a higher number of receivers will make phase distortion at few receivers negligible).
It is recommended that a minimum of 24 receivers be used to guarantee an adequate space sampling of the wavefield. It is not unusual to acquire MASW data using 48 receivers, which provides the flexibility of utilizing both a small receiver spacing to constrain shallow velocity structure and a long receiver array to image to greater depth. If only 12 geophones are available then multiple acquisitions with different source and/or array position may be used to build a single seismic record. Adequate procedures should be implemented to check possible phase distortions and consequences of lateral variations.
Source position
Theoretically, a single source position at a certain distance from the first receiver of the array would be sufficient to obtain broad-band dispersion data. However, in reality, the source offset (Fig. 6) should be selected as a compromise between the need to avoid near field effects (see Sect. 1.2.4), which requires a large offset, and the opportunity to preserve high frequency components, which are heavily attenuated with distance (i.e. far-field effects).
Near field effects may cause a distortion in phase velocity estimation for low frequency components, and bias phase velocity to lower values. Several studies in the past have provided indications on this issue but no general consensus has been reached for a rule to avoid near field effects in multi-station analysis of surface waves. It is suggested to adopt values three to five times the receiver spacing, provided that the source is capable to guarantee a good signal-to-noise ratio for the furthest receivers.
At a minimum, we would suggest performing two end shots on the two sides of the array (see Fig. 6) (forward- and reverse-shot). In a layered media only subject to surface wave energy the dispersion curve is independent of the relative position of source and receivers and the dispersion curves obtained from forward and reverse shots are equal. When lateral variations are present in the subsurface, the analysis of the forward and reverse shot generally provides different experimental dispersion curves due to the different energy distribution over frequency from one side to the other and to the influence of attenuation which may give a predominant weight to the structure close to the source. This may be a useful indicator of the compliance of the 1D site condition with the hypothesis of horizontally layered medium, which is at the base of the surface wave analysis procedures (see Sect. 3.3.1).
It might be useful to repeat the acquisition with multiple forward and reverse source offsets and different source types. The abundance of data may help to assess data quality and quantify dispersion uncertainty (see Sect. 3.4). In particular, data with different shot positions are extremely relevant to assess the influence of near-field effects on the estimated experimental dispersion curve (see Sect. 3.3.2). At sites that are challenging to characterize, dispersion curves extracted from multiple source locations may also be necessary to develop a dispersion curve over a sufficient frequency/wavelength band.
Two shots close to each end-receiver and one, or more, mid-array shots (e.g. center shot) may also be useful for refraction analysis in order to constrain P-wave velocities, potentially locate the ground water table, and detect strong lateral variations along the array.
Stacking of multiple shots increases the signal-to-noise ratio and hence improves the phase velocity estimation. A classical vertical stacking in the time domain can be used only if the trigger system has sufficient accuracy that phase cancellation associated with trigger error is not an issue. However, the non-perfect repeatability of the source may still lead to some phase cancellation, particularly for the higher modes. Stacking in the f–k domain is hence suggested.
Example
Characterization of shallow sediments (expected average shear wave velocity around 300 m/s) with the desired investigation depth of 30 m, in an accessible field with medium traffic (about 10 cars/min) 200 m away:
-
Minimum array length = 1.5 × desired maximum wavelength ≈ 3 × desired investigation depth = 3 × 30 m = 90 m,
-
Source : accelerated weight drop (sledgehammer would require significant stacking),
-
Receiver Spacing = ½ × expected minimum wavelength = ½ × minimum expected velocity/maximum expected frequency = ½ × 270/50 ≈ 2 m,
-
Number of receivers = (array length/receiver spacing) + 1 = 46. Rounded to 48.
-
Source positions: shots on both sides at 2, 5, 10 and 20 m (if space available) + one shot in the middle.
2.1.3 Recording parameters
Sampling rate
Sampling rate affects the retrieved frequency band. Nyquist criterion dictates that the sampling frequency (inverse of the sampling interval) should be at least equal to twice the maximum frequency of the propagating signal. For surface wave analysis at geo-engineering scales, a sampling interval of 2 ms (sampling frequency of 500 Hz) is adequate in most situations. Higher sampling frequencies (e.g. 2–4 kHz) should be used for picking of P-wave first arrivals to be used for seismic refraction analysis. The latter may provide useful information for the interpretation (e.g. the position of the water table) and would not be accurate enough with 2 ms of sampling interval. The position of the water table helps to define the a priori parameters on P-wave velocity or Poisson’s ratio of the layers in the inverse problem solution (see Sect. 4.2.4).
Time window
It must be long enough to record the whole surface wave train. Usually 2 s is sufficient for most arrays, but it is suggested to use longer windows when testing on soft sediments (formations with low seismic velocity). It is good practice to visually check the seismic record during data acquisition to ensure sufficient record length (Fig. 8). Since surface wave analysis is performed in the frequency domain, depending on the analytical routine utilized it may be a good practice to use a pre-trigger time (e.g. 0.1–0.2 s) in the acquisition to simplify the application of filtering techniques aimed at mitigating leakage during signal processing.
2.1.4 Summary of suggested acquisition parameters for active prospecting
Table 1 gives a summary of typical data acquisition parameters used for MASW surveys, and their implication on the results. Of course, these parameters depend on the objective of the survey and the specificities of the site, and are to be adapted at each case study.
2.1.5 Signal quality control
Signal quality should be always carefully checked.
At least the following basic visual quality control is always required on-site during the acquisition:
-
All sensors are correctly recording and correctly coupled to the ground (similar waveforms on receivers close to each other),
-
The time window contains the whole surface wave train, if possible with sufficient pre-trigger,
-
The overall signal-to-noise ratio is good (the classical cone pattern of surface waves is visible in all the shots with good repeatability).
Performing also the following quality control in the field would allow the survey crew to adapt acquisition to actual results, but necessary numeric tools may not always be available in the field.
Frequency content
Analysis of the signals in the frequency domain can help in identifying the usable frequency band. In particular it is possible to assess energy content by applying low pass filters with decreasing frequency thresholds to evaluate the lower frequency bound of usable data and high pass filters with increasing frequency thresholds to evaluate the frequency upper bound (Fig. 9).
Example of check of the frequency content (data from Mirandola site, InterPACIFIC project). a Raw data, b data with low pass filter 10 Hz (OK), c data with low pass filter 6 Hz (signal is not dominant anymore), d data with high pass filter 27 Hz (OK), e data with high pass filter 60 Hz (both surface and air waves are dominant, but surface wave waveform changes a lot across the array)
Signal to noise ratio
Ideally, it would be good practice to evaluate quantitatively the signal-to-noise ratio at each receiver and discard traces with values lower than about 10 dB. The noise level can be quantified with on-purpose records of background ambient vibrations (i.e. an acquisition with the same array and the same acquisition parameter without the activation of the source). Alternatively, it can be extracted from portions of the active records not affected by the active wavefield (e.g. the pretrigger window 0–0.2 s or the post-event window 1.8–2 s in Fig. 8), although this is not recommended because noise is a stochastic process and using a too narrow time window to estimate its spectral characteristics might lead to some misinterpretation. In practice however, such evaluation is rarely applied because it is not implemented in the common surface wave analysis software.
2.2 Passive survey
In passive surface-wave analysis, ambient vibrations are recorded with no need for an on-purpose artificial seismic source. Ground vibrations are caused by natural phenomena (ocean waves, wind acting on trees, micro-seismicity, etc…) and by human activities (traffic, construction or industrial activities, etc…). Typically, low frequencies are generated by large-scale natural phenomena, whereas high frequencies come from local sources, often anthropic activities.
In general, analyzing the quality of a passive survey is more complex than for active acquisition. There is no simple rule that can predict without fail which kind of sensor or which sensor number is mandatory, which geometry is sufficient, etc. Often the term ambient noise is improperly adopted to designate ambient vibrations which are collected for passive surveys. Indeed, in the perspective of surface wave analysis it is necessary to clearly define “noise” and “signal” components in passive records: “signal” is what we wish to analyze and “noise” is what is disturbing our processing.
For passive array techniques, “noise” comes from:
-
1.
effects that are not directly associated to wave propagation:
-
sensor instrumental self-noise (not-seismic);
-
weather actions on the sensor (wind, rain, thermal fluctuation…);
-
bad sensor coupling with soil;
-
-
2.
wave propagation features that are not accounted for in the analysis:
-
surface wave train that cannot be approximated as plane wave at the array size (sources too close to or within the array);
-
body wave components.
-
For passive array techniques, “signal” is:
-
Rayleigh (and, possibly Love) waves originating from distant sources (to satisfy the plane wave approximation at the array site).
The “signal” (ambient vibration level) for passive methods is highly variable from one site to the other one. This variability influences the potentiality to get reliable results. When a passive experiment is performed at a site where ambient vibrations are strong, coherent and dominated by surface wave components, reliable results could be obtained with a rather limited number of sensors and on a relatively short recording time. On the contrary, at “challenging” sites (where few noise sources are present and the wave field is particularly not coherent), a large number of sensitive sensors with optimal installation and coupling with the ground and long recording time are necessary.
Passive surveys allow the measurement of the dispersion from low frequencies (typically 0.2–5 Hz) to intermediate frequencies (typically 10–30 Hz), i.e. from long wavelengths (typically 200–2000 m) to short wavelengths (typically 5–80 m), depending on the location of the survey with respect to the location of the seismic sources, the attenuation between (unknown) sources and survey location, the velocity (and attenuation) structure of the site, and the acquisition approach (equipment, array geometry, array size).
For passive tests, 2D arrays of sensors deployed on the ground surface are recommended, as the ambient vibration wavefield is expected to propagate from different and unknown directions.
2.2.1 Equipment
Sensors
Vertical velocity sensors are adequate for acquisition of passive Rayleigh wave data when retrieving the dispersion curve is the main target. 3D sensors are used for the evaluation of H/V spectral ratio data or Rayleigh and Love wave dispersion (both horizontal and vertical components are analyzed). The natural frequency of the sensors must be sufficiently low with respect to the target depth of investigation, which is furthermore related to the array size and geometry.
As a rule of thumb, 4.5 Hz (or lower) natural frequency geophones (as used for MASW and shown on Fig. 5) are typically sufficient to investigate the uppermost tens of meters of a soil deposit if the ambient vibration level is high.
Nonetheless, passive surveys are often aimed at the characterization of very-deep velocity structures and, therefore, velocimeters/seismometers (e.g. Fig. 10) with natural periods of 1, 5 or 30 s are better suited. Even at higher frequencies on sites where the level of ambient vibration is low, the use of velocimeters/seismometers is more appropriate since these sensors are more sensitive than geophones. It must to be noted, however, that some long-period and broadband sensors require special attention during deployment (perfect leveling, long stabilization time of the feedback system) and processing (proper high-pass filtering before signal windowing), which makes them less appealing for commercial surveys and for non-expert users. The use of intermediate period seismometer is in most cases a good compromise. The use of accelerometers should be avoided as they are, at present, not sensitive enough for sites exhibiting low-amplitude ambient vibrations.
The Appendix 3 gives some example and recommendations to evaluate sensors capabilities.
Sensor setup
The sensor setup is very important in order to limit undesirable noises due to weather (wind or rain on sensors), unstable position of sensors, etc.
Different setups are possible (Fig. 11), from simply placing the sensor on a pavement or completely burying them. The sensor can also be protected from wind and rain using a plastic box (sufficiently “ballasted” to avoid any local vibration of the box itself). When the sensor is buried, the surrounding soil should be firmly packed to ensure a really good coupling. Best results are obtained when sensors are buried, at least for half of their height (as the example shown on Fig. 10), at the expense however of a longer setup time. The influence of the sensor installation on recorded signals depends on the frequency of excitation (see Fig. 41 in Appendix 3).
Data logger
In view of the necessity to deploy wide 2D arrays of sensors, standalone or wireless solutions should be preferred over the common geophysical equipment, which requires use of seismic cables for connecting geophones to the acquisition device. Most often, a dedicated datalogger for each geophone/sensor is used and the acquisition is synchronized with GPS and wireless technologies.
Accurate location
As distances are used for velocity measurements, it is necessary to measure the exact location of each sensor relative to the others (at least with 5% location precision). The accuracy of the device to be used strongly depends on the wavelength range of investigation and consequently on the size of the array. For large arrays (e.g. diameter larger than about 200–300 m) it is usually sufficient to use a standard GPS system, either standalone or integrated into the seismometer. For small arrays, it is conversely appropriate to use a more accurate measuring device, such as differential GPS (with georeferenced or variable base station) and theodolites. The use of measuring tape is possible only for very small configurations, but practically recommended only for linear arrays.
3C sensor for H/V
In case of array measurements with vertical component sensors, the inclusion of at least one 3-component geophone or seismometer, typically at the array center, allows extraction of additional information via analysis of horizontal-to-vertical spectral ratios (H/V or HVSR; see Appendix 7), which typically provides valuable additional information, particularly for deep interface characterization. Alternatively, the same information can be obtained with an independent single-station measurement by a specific 3-component instrument placed near the array location.
2.2.2 Acquisition layout
Acquisition layout should fulfill the requirements of the processing technique(s) adopted to estimate the dispersion curve (see Sect. 3.2.1). In the following, we describe the most common geometries.
Array geometry
In the ambient vibration wavefield, the source positions are generally unknown. For this reason, 2D array geometries with no preferential direction(s) (e.g. circular or triangular, see Fig. 12) are highly recommended, as they provide a similar sensitivity of the array to wavefields impinging from different directions. T- or L-shapes are also possible, especially in complex and urban field conditions where the presence of obstacles can limit other more complex array shapes. In such cases it is recommended to carefully verify the theoretical array response (see examples in Appendix 2) and the presence of prevalent directional sources in the wavefield.
The choice of a given geometry is a compromise between the available number of sensors, the level of ambient vibration on the given site, and the operating time that could be afforded at a given site. More information is given in Appendix 2.
On the other hand, the use of linear arrays, as for example in the Refraction Microtremor (ReMi) technique (Appendix 9), is strongly discouraged. The use of a linear array requires the assumption of homogeneous, isotropic distribution of the passive seismic sources around the site or passive sources in-line with the array direction. As it is not possible to verify the consistency of this assumption using data from a linear array, the results can be strongly biased in case of non-homogeneous source distribution around the testing site or strong off-line directional propagation.
Array size and receiver spacing
The aperture of the array (maximum distance between two receivers) influences the maximum measured wavelength, and therefore the penetration depth of the measurement. On the other hand, the minimum spacing between receivers controls the smallest measurable wavelength, and therefore the resolution of the measurement close to the ground surface. Given the number of available sensors, arrays from small to large aperture/spacing are usually deployed successively in order to sample over a wide wavelength range.
Although maximum retrieved wavelength also depends on the chosen processing technique (see Sect. 3), the suggestion for non-expert users is to select the aperture of the largest array at least equal to one to two times the desired investigation depth. Minimum measured wavelength also depends on the propagating wavefield; however, the usual rule of thumb fixes the minimum receiver spacing of the smallest array equal to the desired resolution at shallow depth. Since it is often important to resolve near-surface layering for engineering purposes, it may be difficult to obtain short enough wavelengths from strictly passive surveys. Thus, it is recommended that passive surveys be complimented with active surveys if near-surface resolution is important.
Receiver number
The minimum number of receivers for passive surveys is still an open debate. Although acceptable results can often be obtained with a minimum of 4 sensors, especially using SPAC analysis, better results will be achieved using 8–10 sensors, which are still easily manageable in the field. At sites with low level of ambient vibrations, a higher number of receivers will enhance the chance to correctly measure the dispersion. The larger the number of sensors the better the results, but practical limitations are introduced by equipment cost and setup time.
2.2.3 Recording parameters
Sampling interval
As for active tests, the sampling rate affects the usable frequency band. The sampling rate is typically lower than that used for active data because of the necessity of long duration records. Since analysis of passive data is typically limited to low frequency data, the use of mid-band seismometers with an upper corner frequency of 50–100 Hz is common. Typical sampling frequencies range from 100 to 200 Hz.
Time windows
Acquisition of passive data requires much longer durations than those used for active data. Indeed, it is necessary to use statistical averages of distinct signal recording blocks to obtain stable estimates of wave propagation. Long duration records (30–120 min) are typically collected and divided into shorter windows (1–5 min) for processing (see Sect. 3.1.2). Depending on the frequency band of interest, acquisitions of tens of minutes to several hours are collected.
2.2.4 Signal quality control
Checking signal quality for passive data is typically more difficult than for active-source data. Appendix 3 gives information about the instrument testing and verification.
On site quality control during acquisition should be implemented to check the following:
-
all sensors are correctly recording, with appropriate (and identical) gain in order to have sufficient signal resolution without clipping of the records;
-
all stations are properly synchronized to a common time reference;
-
x,y coordinates are measured with sufficient precision (at most 5% of the minimum inter-sensor distance).;
-
All sensors are properly oriented if 3C sensors are used (a common reference is the magnetic North, which can be usually measured with a simple compass).
Synchronization
In case GPS is used, synchronization between recordings should be verified (e.g. by comparing low-pass filtered recordings). Gross errors in GPS timing can be identified by a noticeable time-shift of the low-frequency surface wavelets propagating across the array. Examples of bad synchronization and time-shift correction are given in Appendix 3.
Sensor orientation
If three-component seismometers are used, also the proper placement of the horizontal components to a given reference (e.g. the magnetic North) should be verified. The procedure for this verification is based on correlation analysis of the low-pass filtered horizontal components, rotated over different azimuths (see Poggi et al. 2012 for a detailed description). This procedure may be particularly useful at sites where magnetic North cannot be accurately identified with a compass (influence of electric lines, railways, etc.).
Frequency content
To check the usable frequency band of passive data, it is suggested to perform specific preliminary assessments of energy content in the spectral domain, and to compare it to reference levels of ambient vibrations (e.g. the High Noise Model—NHNM-and the Low Noise Model—NLNM-proposed by Peterson 1993) and instrumental self-noise. If possible, this check should be performed on site in order to adapt the acquisition parameters. At sites with low level of ambient vibrations, greatest care should be taken in the equipment settling (larger number of sensors, which should be carefully buried, protection of sensor and cables against wind), and recording length should be increased.
The above check may be also useful to identify frequency bounds in which signals are coherent or usable. Moreover, sharp narrow spectral peaks may indicate the presence of electromagnetic disturbances or machinery generated noise (see also the SESAME guidelines, SESAME Team 2004).
Figure 13 shows an analysis of power spectral density of the three sites investigated within the framework of the InterPacific project (Garofalo et al. 2016a, b), compared to the NHNM, NLNM and theoretical self-noise of the sensor used in the passive surveys. One can see that around 3 Hz the Cadarache site has a power spectral density 4 orders of magnitude lower in comparison with the Mirandola site. The lower ambient vibration level for the Cadarache site in a large frequency band above 3 Hz partially explains why this site was more complex to analyze. On the contrary, one can observe a drastic increase of power spectrum above 0.6 Hz in Mirandola.
Another important check consists in verifying the one-dimensionality assumption for the testing site. This can be done by relative comparison of the spectral information from all the recordings along the array using different techniques, such as power spectral density, spectrogram or, more commonly, horizontal-to-vertical spectral ratios. If a sensor shows an anomalous spectral shape (compared to other stations), special attention should be given before including it in the processing, as the records could be biased by local heterogeneities of the subsurface structure, bad coupling or even uncalibrated sensor response.
2.3 Combination of active and passive surveys
In case both active and passive measurements are performed in view of measuring the VS vertical profile down to large depths, the acquisition layouts for active and passive data should be designed in order to optimize the complementarity of gathered frequency bands and to give a sufficient overlapping in the common frequency bands.
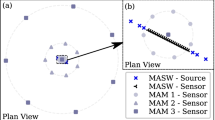
In order to measure the dispersion curve on the broadest possible frequency band, it is suggested to perform concentric passive acquisitions, from small (about 10 m) to large apertures (up to 1 km or more, depending on the targeted depth). Since all dispersion curves will be merged, it is suggested to perform the active measurements close to the center of the 2D passive array. Acquisition on several active profiles in the vicinity of the smallest passive arrays may give more insight into the possible lateral variations of the site at shallow depths. An example of a combined acquisition geometry following these specifications is reported in Fig. 14.
Example of active and passive combined acquisition layout for deep VS characterisation. The right plot is a zoom in the centre of the left plot. Active acquisition consists in 2 almost perpendicular profiles of 46 and 69 m length; passive acquisition consists in 3 successive recordings on 2 of the 4 concentric circles R1 to R4 (1st: R1R2, 2nd: R2R3, 3rd: R3R4)
Finally, in order to avoid cross-contamination of the passive and active wavefields, it is recommended that simultaneous acquisition be avoided.
Appendix 10 reports a case study for site characterisation of a seismological station of the Réseau Accélérométrique Permanent (RAP, French seismological network).
2.4 General suggestions on measurement location
2.4.1 Relative to target of investigation
In general, surface wave analysis provides an estimation of a representative velocity profile beneath the array. It is therefore better to place the arrays as close as possible to the target of the investigation. Particular care should be paid when extrapolating the retrieved velocity model to nearby sites, as this should be done only in case of evidences of later homogeneity.
2.4.2 Relative to strong or low sources of vibrations
It is always suggested to avoid measuring in proximity of strong vibration sources (whenever known). Close sources, often of anthropogenic origin, are responsible for large amplitude transient signals with significant amount of body-waves and propagating non-planar wavefronts.
For active measurements, this reduces the signal-to-noise ratio and may be prohibitive. For passive measurements, a minimum distance on the order of the array aperture from the identifiable sources of vibration is suggested, in order to satisfy the assumption of surface-wave dominance and planar wave fronts. If not possible, especially in urban sites, an alternative is to increase the recording duration in order to perform a more robust statistical averaging of the recording windows.
Passive methods may face difficulties in very quiet sites where the level of ambient vibrations is very low or in case of stiff soil to rock conditions, where the mechanism of generation and propagation of surface waves is less efficient. Hence a preliminary on-site analysis of the signal power spectral density, preferably compared to instrumental self-noise level, is highly recommended before performing the test (see Sect. 2.2.4).
2.4.3 Relative to surface conditions
For active-source measurements, placing the sensors in open fields is ideal, however placement on paved surfaces also gives satisfactory results, provided the sensors are shielded from wind-induced movement. When working in natural ground the sensors must be fixed on a firm base, either by spikes driven through grass cover, or where permitted by digging a hole to a firm base. When working on paved surfaces, ensure that service lines (buried cables or pipes) are not located beneath the sensor, and if near a building ensure that the site is not adjacent to machinery such as pumps or air-conditioners.
In the case of passive measurement sensors (often seismometers), the overall recommendations are the same, but when it is possible, it is preferable to bury the sensor, especially when recovery of low frequency data are required (e.g. large array for deep investigation), as shown on Fig. 11.
Installation on gentle slopes and mildly irregular topography are permitted, but sites with unusual topographic features (e.g. surface cracks, scarps, karstic dolines) should be avoided. A rule of thumb could be to avoid settling the array in areas with topographic variations larger than about 10% of the targeted wavelengths.
3 Processing
3.1 Numerical techniques for measuring surface wave dispersion: principles
Several signal analysis tools can be used for the extraction of dispersion curves from experimental data. Provided that the spectral resolution is adequate, most of them will provide reliable information. Methods that can be implemented to provide an automated extraction of the dispersion curve are to be preferred, but a careful assessment of obtained information is necessary. The most popular techniques are transform-based methods [e.g. frequency–wavenumber (f–k) or frequency–slowness (f–p) analysis] for active-source data and f–k analysis and SPatial AutoCorrelation (SPAC) for passive data.
3.1.1 Active data processing
The most popular techniques for the processing of active data are based on the picking of amplitude maxima in 2D spectral representations of the wavefield. Data collected in the time-offset domain (seismograms) are transformed to different domains where the peaks of the amplitude spectrum are found in correspondence of pairs of wave propagation parameters.
f–k techniques
By applying a 2D Fourier transform over time and distance it is possible to represent the wavefield in the frequency-wavenumber (f–k) domain. In order to take into account that the amplitude decays with distance from the source, it is possible to normalize the signal in the time-space domain before transforming it to the f–k domain. Normalizing the individual geophone signals by their maximum, or dividing the signals by 1/√r (with r the distance to the source) give satisfactory results.
Figure 15 shows an example of amplitude of the f–k spectrum for a set of experimental data. In this example, the fundamental mode and higher modes are clearly identified and well separated. Picking of maxima allows the pair of frequency-wavenumber parameters associated to the propagation of the fundamental Rayleigh mode to be identified. The experimental dispersion curve is then evaluated with the following relationship:
where V is the phase velocity (and P the phase slowness) of the surface wave at frequency f and corresponding wavenumber k.
It is necessary to check that the obtained points of the experimental dispersion curve can be associated to the same mode of propagation (e.g. the fundamental mode). For example in the approach used in Fig. 15, the searching area for each mode is selected on the basis of visual inspection of the spectrum. At a given frequency, the fundamental mode may be associated either to the absolute amplitude maximum or to a local maximum. It is very important to check the continuity of the dispersion curve over frequency with respect to the main branch of the fundamental mode. Sometimes it is necessary to search for local maxima in order to obtain the fundamental mode experimental curve over a wide frequency band.
Other techniques
Other transform-based approaches work in different spectral domains (for example the frequency-slowness or the frequency-phase velocity domain), but the procedure to extract the dispersion curve is analogous. Among them, usual techniques are the slant stack transform, working in the frequency-phase velocity (or slowness) domain, or the high resolution f–k technique, which attributes different weight to the different sensors in order to adapt the response of the array to the characteristics of the records. Many commercial geophysical software packages utilize the phase shift transform (Park et al. 1999), which is a special case of the frequency domain beamformer.
3.1.2 Passive data processing
Passive data processing techniques usually derive the dispersion characteristics from statistics computed on a large number of small time blocks extracted from the long duration recorded signals. It is important to adapt the length of these time blocks to the analysed frequency.
f–k beamforming technique
Passive data are processed in the frequency-wavenumber domain by using methods of spectral estimation, such as Frequency Domain Beam-Forming. With this technique, a distribution of the energy recorded in one time block over a vector wavenumber representation is obtained at each frequency (Fig. 16d). The position of the amplitude maxima in the plane of X and Y wavenumbers defines the vector wavenumber(s) and azimuth(s) of the wave(s) propagating at that frequency in that time block. The velocity (or slowness) of the waves is computed using . At each frequency, it is then possible to draw the histogram of the measured slownesses on all time blocks. Concatenating the histograms of all frequencies leads to the dispersion image (Fig. 16e).
Passive data processing with f–k beamforming technique. a Raw data in the time-distance domain; b data in the time-distance domain filtered around frequency f, c schematic representation of plane wave propagation through the array, d energy repartition in the plane of wavenumbers at frequency f, e dispersion image. Colours range from orange (low amplitude) to green, blue and purple (high amplitude)
It is also possible to draw the histograms of the estimated azimuths in order to analyse the characteristics of the wavefield.
Other techniques performing in the spectral domain
More sophisticated high resolution variants of this method exist, like the High Resolution f–k, the maximum entropy, the Minimum Variance Distortionless Look or the MUltiple SIgnal Classification (MUSIC) algorithms. These methods, based on data matrix inversion, have a greater resolving power and are therefore more efficient in case of multiple overlapping signals, but may be unstable depending on the characteristics of the signals.
Spatial auto-correlation (SPAC) techniques
The spatial autocorrelation function represents the variation with frequency of the autocorrelation coefficient (coherence) between two signals recorded at two stations spaced by a distance r. The SPAC technique is based on the fact that the azimuthal average of the spatial autocorrelation function has the shape of a Bessel function, whose argument depends on the phase velocity frequency and receiver spacing distance (Fig. 17c). Other derivations of the original SPAC method were proposed with regular and irregular array layouts (e.g. ESAC, MSPAC, MMSPAC) allowing extraction of wavelengths on a wider band than the original formulation. Note that SPAC based methods allow extraction of both Rayleigh and Love waves dispersion curves from three-component records.
Passive data processing with SPAC techniques; a azimuthal repartition of station pair vectors (SPAC technique), with r: distance between stations (constant on each ring) and θ: azimuth of station pair, b as above for MSPAC technique, where each ring is defined by a range of r (gray colours), c autocorrelation functions for 6 different rings of (b), d corresponding dispersion image, black curves with error bars: manually picked dispersion curve. Autocorrelation estimates providing phase velocities inside the area defined by the black and red curves are indicated in back in (c)
Figure 17a, b illustrates how station pairs are ranked according to the distance between the two stations, with regular and irregular array shapes, respectively.
SPAC techniques can be used in two different ways in the inversion. The first possibility is to derive an experimental dispersion curve from the SPAC data (Fig. 17d), then invert the dispersion curve (see Sect. 4). The second possibility is to perform a direct fitting of theoretical (model) and observed SPAC curves. The former has the advantage of providing a dispersion curve that can be combined with dispersion curves from other techniques (active surface–wave methods) or other processing streams (e.g. f–k processing). The latter has the advantage of not requiring intermediate phase velocity extraction steps.
Comparison f–k/SPAC: advantages and disadvantages
Because they are based on different assumptions regarding the ambient noise wavefield structure, f–k and SPAC methods give complementary results. While dominant source direction is a favourable situation for f–k based techniques, a dominant noise source direction may introduce bias in SPAC estimates when azimuthal sampling of stations pairs is not sufficient. On the contrary, multiple source directions may decrease f–k resolution. Both techniques suffer limitations at low frequency in relation to array aperture. For a given array aperture however, SPAC based techniques have shown their capability in extracting longer wavelengths than f–k based methods. Not being able to measure several phase velocities at a given frequency, SPAC based methods suffer limitations when fundamental and higher surface wave modes are mixing, while f–k based techniques give the opportunity to detect both fundamental and higher modes. We thus recommend analysing the ambient seismic wavefield by using both approaches in order to increase confidence on the extracted dispersion curves, particularly if the array type utilized is compatible with both analysis techniques.
If simple f–k transformation is applied to the data, the minimum and maximum inter-receiver spacing control the resolution limits, namely the minimum and maximum resolvable wavelengths, respectively. They can be estimated from the array response, which is the theoretical response of the array to a plane wave of vertical incidence, i.e. of infinite apparent velocity. When multiple plane waves propagate throughout the array, the smallest wavenumber (corresponding to the longest wavelength) measurable by classical f–k method is named kmin, defined as the width of the mid-height array response main lobe. The tighter is the main lobe, the better is the capability of the array to separate close wavenumbers (corresponding to long wavelengths).
The maximum measureable wavenumber kmax (corresponding to the shortest wavelength) is controlled by side lobes, meaning that for wavenumbers larger than kmax, phase velocity dispersion images may suffer aliasing. The definition of kmax may differ from various authors. Here, for sake of simplicity and by analogy to a 1D linear array layout, the kmax value is defined as the wavenumber corresponding to the maximum of the first side lobe exhibiting a value higher than half of the maximum of the central peak. In practice, the effective kmax value depends on the ambient seismic wavefield characteristics (azimuth of sources). Note however that the kmax limit is less “strict” than the kmin one. In many cases, it is possible to identify the correct DC curve within the aliasing area above the kmax limit, provided that there is continuity with the DC curve at the largest wavelength.
Figure 18 gives an illustration of these definitions.
Assessment of the minimum and maximum wavenumbers resolved by f–k method with an array of 7 sensors spread around a central one, on a 50 m radius circle. a Array geometry. b Theoretical array response. c Sections of the array response (showed in b) for various directions, ranging from 0° to 180° and principle of determination of kmin and kmax values. d Corresponding minimum and maximum wavenumbers in the frequency–velocity domain
If more sophisticated algorithms are used (e.g. high-resolution beamforming, MUSIC, maximum entropy), the maximum wavelength cannot be defined a-priori, as the result also depends on the ambient seismic wavefield characteristics (energy content, seismic sources direction). However, field studies report that, in very favourable contexts, the maximum resolvable wavelength can reach up to 3–5 times the maximum resolvable wavelength inferred from f–k method.
When using SPAC based methods there is no clear maximum wavelength “criterion”; however maximum measurable wavelengths being typically a factor 2–5 times larger than those predicted by the kmin, depending on data quality.
In general, it is however not recommended to try and extract wavelengths greater than 2–3 times the maximum aperture of the passive array. Which will ultimately result in developing VS profiles no deeper than the aperture of the largest passive array.
3.2 Dispersion curve identification
The streamline of standard analysis of surface wave data makes some strong assumptions, which have to be verified to achieve reliable results. Moreover, visual inspection of the experimental dispersion curve may provide useful indications for the interpretation. The experimental dispersion curve is by itself highly informative and its inspection can be used to understand some peculiarity of the site, especially if combined with a careful assessment of local geology. The following sections explain how to properly identify the dispersion curve and what details should be carefully analysed.
3.2.1 Usual domains for dispersion curve representation
For the visual inspection, the experimental dispersion curve can be represented in different domains: frequency–phase velocity (f–v); frequency–slowness (f–s); phase velocity–wavelength (v–λ). Each domain can be plotted in either linear, logarithmic, or semi-logarithmic scales (Fig. 19). Careful inspection of these plots may help in identifying important aspects about the recorded data (e.g. higher modes) and the site (e.g. presence of a low velocity layer/inverse layer). Because of the inverse relationship between velocity and slowness, wavelength and frequency, plots in linear scales tend to enlarge details on one end of the dispersion curve, but to shrink the other end of the curve. For example, the linear v–f domain (Fig. 19a) shows on an equal length the 10–30 Hz band, approximately corresponding to the upper 5 m of the subsurface, and the 2–10 Hz band, approximately corresponding to depths ranging from 60 to 5 m. For that reason, we recommend viewing plots in log-scale. Similarly, dispersion curves should be sampled at equal log frequency or log wavelength intervals prior to inversion. However, most available software for surface wave analysis show plots in linear scale. In that case, attention should be paid to evaluate particularly the low frequency part of the dispersion curve. We recommend that analysts at least visually examine their dispersion curves in terms of both frequency and wavelength in order to more fully understand important trends in the data.
3.2.2 Usual shapes of dispersion curves
Typical trends of dispersion curves are smooth continuous variations of phase velocity as a function of frequency, with no abrupt changes in slope and no jumps.
Visual inspection of the experimental dispersion curve can provide important hints on the expected trends in the shear wave velocity profile. Dispersion curve with a smooth and continuous decrease of phase velocity for increasing frequency is typically associated to simple stratigraphic conditions with shear wave velocity consistently increasing with depth. The presence of a kink or a flat zone in the experimental dispersion curve could be an indication of the presence of an inverse layering at some depth (i.e. a soft layer below a stiffer one). The example reported in Fig. 20 is associated to the presence of a soft clay layer at a certain depth in a stiff coarse alluvial deposit. One has to be sure, however, that no mode jump occurred to higher modes (see below). Often, the validity of one hypothesis or the other can be demonstrated during the inversion, by crosschecking the consistency between different datasets (e.g. Love and Rayleigh dispersion).
Several theoretical canonical cases are presented in Appendix 1 to give an overview of the most common cases encountered in the field.
3.2.3 Identification of higher modes
Most software currently available for surface wave inversion requires the correct identification of different modes: it is necessary to pick the relative maxima of the spectrum and to associate them to the fundamental or to a defined higher mode.
Figure 21 shows the picking of the fundamental mode and two higher modes on the spectrum in Fig. 15. It is very important to check the continuity of each dispersion curve over frequency. In the approach used in Fig. 21, the searching area for each mode is manually selected on the basis of visual inspection of the spectrum; the dispersion curve is then automatically identified within each of these areas.
Lack of spectral resolution in wavenumber, energy transfer between the vertical and the radial component and modes close to osculation may prevent the proper identification of the fundamental or higher modes. In such conditions, an effective or apparent dispersion curve is often obtained from the analysis. Misinterpreting an apparent dispersion curve as a fundamental mode may lead to gross errors in the retrieved velocity profiles (typically over estimation of phase velocity), and difficulties to simultaneously fit multiple datasets, which appear to be incompatible. For this reason, interpretation of surface wave data typically requires a subjective judgement and fully automatic procedures for the analysis are difficult to implement.
Energy distribution between the different modes may not be constant across the whole frequency band. It depends on the velocity and attenuation structures, source characteristics (distance, type, depth), and lateral heterogeneities. Appendix 5 contains some specific examples. The Rayleigh wave fundamental mode may be dominant in the vertical component providing we consider a frequency band that is not near the site fundamental resonance frequency (since the ellipticity phenomenon of Rayleigh wave induces a drastic diminution of amplitude of its vertical component around the fundamental frequency). The fundamental mode is often the dominating mode when velocity gradually increases with depth. Typical examples of stratigraphic conditions in which higher modes may be dominant and in which the apparent dispersion curve may jump from one mode to the other are shown in Fig. 22 and described as follows:
Example of effective or apparent experimental dispersion curve in which lack of spectral resolution prevent the identification of the fundamental mode: a transition to first higher mode at low frequency typically associated to the presence of an abrupt change in stiffness at a given depth; b transition to dominant higher modes at high frequency typically associated to the presence of a stiff top layer
-
a.
abrupt change in stiffness at a given depth—in this case the first or other higher modes tends to be dominant in the low frequency band; this condition can be identified in the dispersion curve where a very steep increase of phase velocities for decreasing frequencies is observed;
-
b.
stiff top layer—in this case the apparent experimental dispersion curve gives increasing phase velocity values for increasing frequency, approaching an asymptotic value close to the shear wave velocity of the stiff top layer; the dominant mode shift progressively to higher modes for increasing frequency to follow the above trend of velocity;
-
c.
the dominance of a higher mode is also possible in the intermediate frequency band, i.e. dispersion curve can present a hump.
Although the attenuation structure also has an influence on the modal energy distribution, it is very difficult to account for it in the evaluation of the apparent dispersion curve.
Further details related to higher modes are discussed in Appendix 5.
3.3 Quality control
Quality control at the processing step consists of checking that the assumptions on which is based the applied method are valid, at least approximately.
3.3.1 Lateral variations
For active measurements it is recommended that dispersion curves retrieved from forward and reverse shots are compared. In addition, it is suggested to analyse independently different subgroups of seismic traces from the dataset. This may typically reveal heterogeneities of shallow layers (because the processed sub-arrays are short). The example provided in Fig. 23 is from a coarse alluvial deposit in which lateral heterogeneities are relevant. If there is only weak lateral velocity variability, then multiple dispersion curves can be combined and an average dispersion curve used for modelling with the scatter in dispersion data used to assign error bars. In such cases the resulting VS model may not be representative of the actual velocity structure beneath any part of the array, but it can still be representative of average velocity structure.
A similar check can also be implemented with passive arrays, when possible (i.e. calculating the dispersion curves with different subsets of sensors). Another quick test for passive measurements, in the case where 3 components sensors are used, is to check the stability of the H/V curve along the array (Fig. 24). In this case, it is clear that the 1D hypothesis is justified for the inner array, while for the outer array (Dmax ~ 500 m) is not.
3.3.2 Plane wave propagation
For active measurements, geophones in the vicinity of the source may be in the near field and bias low frequencies towards lower phase velocities. It may be useful to check the stability of the dispersion curve at low frequencies when removing the closest geophones (Fig. 25). Offsets inducing noticeable near field effects should be discarded for estimation of the dispersion curve. On the contrary, if no significant variations are observed at low frequencies, it is then better to include signals of the short offsets as they contain high frequencies which may be attenuated at far receivers.
Active measurements: example of near field effect and rejection of closest receivers. “×1” indicates the shortest source-receiver distance taken into account in the processing. On these figures, the two black lines indicate the wavelength limit corresponding respectively to the length of the array and to the O’Neil (2003) criterion (length of the array multiplied by 0.4). One can see that the DC curve is rather stable above this limit, whatever the “×1” distance. At high frequency the increase of the source—first geophone distance may alter the DC curve due to lack of energy, so making several test is useful
For passive measurements, verification of the plane wave assumption is more complicated, and discarding sources in the near field is usually performed by removing the transient, high energy signals generally generated at close distances.
3.3.3 Uniform distribution of sources
The SPAC based methods assume that the passive wavefield is composed of plane waves (i.e. they assume the far-field hypothesis) incoming at the test site from all horizontal directions with the same intensity. Verification of the hypothesis on source directions can be obtained with the f–k analysis of passive data that give a representation of energy distribution (Fig. 26).
Checking the azimuthal distribution of sources, example from the characterization of the OGIM station of the RAP (French permanent accelerometric network) (30 m aperture and 900 m aperture arrays respectively). Left example of uniform distribution of sources in the high frequency range, right example of dominant source direction (N280) in the 1–3 Hz frequency band
3.4 Estimation of uncertainties
It is recommended that the observed variability on the experimental dispersion curve always be reported with the results. This may be represented in the form of condensed statistical parameters (e.g. mean value and standard deviation). Data variability is a clear indicator of the reliability of the results and can be used for further assessments during inversion.
In principle, aleatory and epistemic (i.e. model-based) uncertainties should be clearly separated when costructing the dispersion curve. Aleatory uncertainty is that associated with the primitive measurements for a given site and a given source-receiver array and analyst. Uncertainty of the “derived” data (including the uncertainty of the dispersion curve) can be obtained from that of the primitive data using standard algorithms and approaches (i.e. FOSM, etc).
Epistemic uncertainty on the other hand refers for instance to different methods used to construct the dispersion curve. Therefore the same uncertainty of the “primitive” data may actually map into different uncertainty of “derived” data depending on the specific algorithm used to process the “primitive” data. This uncertainty should thus be kept separated and treated for instance using logic-tree approaches.
Variability of measurements due to different source-receiver configurations is a combination of aleatory and epistemic uncertainty however epistemic uncertainty would be prevailing in case of lateral heterogeneity of soil deposits. Since standard surface wave testing intrinsically assumes 1D modeling, the uncertainty associated to different source-receiver configurations should be assumed aleatory since sites with pronounced 2D effects should be disregarded.
3.4.1 Active measurements
Although uncertainty estimation is necessary, there is not yet any protocol shared internationally on the best way to measure it from active surface wave analysis.
Independent processing of several recordings acquired with the same layout (shot and receivers) can be used to obtain different estimates of the experimental dispersion curve. These values can then be used to estimate mean and standard deviation of the phase velocity at each frequency. In this case the observed variability is only associated to repeatability of the test and observed discrepancies are mainly due to the effect of ambient vibrations. It is often much lower than the variability taking into account the natural variability of the ground and the uncertainties linked to the choice of the processing technique.
The variability of the results on the experimental dispersion curve can be estimated by considering different source locations for the same array, as well as using subsets of receivers instead of all receivers. With this approach, the uncertainties due to different factors are lumped together (e.g. lateral variations; effect of higher modes; near-field effects; signal-to-noise ratio). This way of uncertainty estimation is probably the one that is most similar to the uncertainty estimation for passive measurement (see below).
Feedback from InterPacific project
Although no international consensus have yet been reached on the best way to estimate uncertainties for active surface wave analysis, the feedback from several international blind analysis projects (among them the InterPacific one, see Garofalo et al. 2016a) shows that, within the reliable wavelength band, inter-analyst uncertainties, estimated in terms of Coefficient of Variarion (COV), on the average phase velocity range from 5 to 10% depending on the sites (Fig. 27). The uncertainty on dispersion estimates provided by each analysist range between 5 and 20% depending on the site and the analyst’s (Fig. 28).
Variability of estimated average dispersion curves from 12 different operators on the same active and passive dataset for the Grenoble site (top) and corresponding Coefficient of Variation (bottom) with evidence of the significant frequency band (gray line) (Garofalo et al. 2016a)
3.4.2 Passive surveys
For passive experiments, dispersion curves are most often obtained by averaging the dispersion estimates from the various time blocks. Such uncertainties are related to time variation of ambient vibration wavefield properties, in relation with the array capability to separate simultaneous propagating waves across the array, with the lateral variation of the subsurface, and with near-field effects.
This can be achieved by analyzing, frequency by frequency, the histogram of the velocity estimates and removing the outliers to get a Gaussian distribution. Mean and standard deviation can then be estimated at each frequency. Alternatively, another option may be to manually pick several dispersion curves covering the whole area with high number of velocity estimates, then average them to estimate the mean and standard deviation.
3.5 Combination of active and passive surveys
Combination of different datasets (active and passive with different array apertures) can provide an experimental dispersion curve over a broad frequency band. Branches of the dispersion curve from different dataset should overlap each other in the common frequency bands (see Fig. 29). A poor overlap may be associated to several causes (e.g. different modes are retrieved, presence of lateral variation, lack of spectral resolution, pitfalls in the processing). In any case, a poor overlap implies a poor reliability of the analysis.
As mentioned in 3.4, estimated uncertainties do not always take the same variability into account. When combining dispersion curves with uncertainties of different origins, attention should be paid to homogenize these uncertainties in order not to give artificially a preponderant weight to the curve(s) with smaller uncertainties.
4 Inversion
4.1 Introduction
The inversion process is aimed at searching the best subsurface model whose forward response fits well the experimental data. It is based on a proper definition of the misfit function that is minimized in the inversion. Typically, for surface wave analysis, the misfit function is a norm of the distance between the experimental dispersion curve(s) or SPatial Autocorrelation Curves) and the theoretical dispersion curves associated to a given subsurface velocity model.
However, like most other surface geophysical problems, the surface wave inverse problem is non-linear, mathematically ill-posed and it is affected by solution non-uniqueness whereby several models may provide an equally good fit to the experimental data. For this reason, it is strongly recommended that the solution is provided in conjunction with a quantification of the uncertainty arising from solution non-uniqueness. The degree of ill-posedness is also strongly dependent upon the specific algorithm that is used to invert the dispersion curve and on the constraints that may be enforced on the calculated model (e.g. smoothness, layer thicknesses, etc.). This may be represented as an estimation of uncertainty bounds on the best solution (under the forced hypothesis of a linear problem with unique solution), or preferably as a set of equivalent solutions (i.e. solutions providing similar misfit)
The inversion process requires the description of the ground model via a series of physical and mechanical parameters linked to the experimental data by physical relationships. Section 4.2 describes the specificity of the parameterization for surface wave inversion.
Several inversion approaches have been proposed to search for the set(s) of parameters best representing the real ground characteristics. These methods can be grouped into two broad categories: local search methods and global search methods. Their applications to surface wave inversion are respectively described in Sects. 4.3 and 4.4.
4.2 Parameterization
4.2.1 Parameters
Surface wave analysis is typically implemented by modeling the subsurface as a vertical stack of homogeneous and isotropic linear elastic layers. Each layer is characterized by 4 parameters: thickness (h, except for the half-space), mass density (ρ) and two elastic parameters (often implicitly expressed in terms of velocity of propagation of shear and compression waves, VS and VP, linked together via the Poisson’s ratio, ν). If attenuation is modeled, quality factors (Qp and Qs) are also included in the parameterization. Quality factors are also denoted as damping ratios (D) in geotechnical engineering; the relation between these two quantities being Q = 1/2D.
Layer thicknesses and shear wave velocities have the most influence on the dispersion curve, while P-wave velocity and mass density have a much smaller influence. The inverted parameters are thus often reduced to thickness and shear-wave velocity of each layer. The mass density and the other elastic parameter, which is either the Poisson’s ratio or the P-wave velocity, are then fixed on the basis of a-priori information or using standard values from expert judgment. Alternatively, VP can be left as free parameter, and the Poisson’s ratio has to be limited to reasonable bounds, depending on the expected soil conditions. This last strategy has the great advantage to prevent the occurrence of physically unrealistic VP−VS pairs.
A large difference is however observed on the dispersion curves between unsaturated (low VP, low VS) and saturated (high VP, low VS) soils. The wrong choice of a-priori model parameters between values for saturated and unsaturated soils may cause very significant errors in the inversion process and the obtained shear wave velocity model may be unrealistic. A reasonable estimate of water table condition at the site is then essential for the analysis of surface wave data (see Sect. 4.2.4).
Expected ranges of mass density and Poisson ratio values for different geomaterials are reported in Table 2. More accurate estimates can be obtained if lithological information is available.
4.2.2 Number of layers
The number of layers must be fixed carefully in order to avoid over-parameterization (i.e. too many layers) that leads to an unreliable final model because of the insufficient available information to constrain the inversion (i.e. over-determined inversion). On the other side, the number of layers has to be sufficient to reproduce adequately the variation with depth, especially in the shallow portion of the model. Typically, a preliminary assessment with the adoption of different trial parameterizations is necessary to achieve the right balance, since no specific rules can be given and the choice is reserved to the expertise of the analyst. Variability of the results of the inversion due to different layer-model associated to expert choice is a typical example of epistemic uncertainty. However, a recent paper by Cox and Teague (2016) provides guidance on one method of systematically selecting trail parameterizations when performing inversions without the benefit of a-priori information to inform the choice of subsurface layering.
In any case it is recommended to repeat the inversion process by using different parameterizations to assess the influence on the final result. If a similar misfit is obtained, the solution with the minimum number of layers has to be preferred to improve the sensitivity to model parameters and the consequent reliability of the results. Remaining residuals between the observed dispersion and the dispersion predicted for the final model will indicate at which depth additional layer interfaces might be required (Fig. 30).
Choosing the number of layers; numerical example with a 3-layer model dispersion curve inverted with two layers (a) and three layers (b). In a, misfit between observed (black) and modelled (colors) curves particularly at high frequencies indicate that adding a layer at shallower depths will improve the results
An over-parameterization of the model can be accepted as a different strategy if additional constraints are used to regularize the solution (smoothing, reference model, a-priori information). However, the constraints need to be carefully established on the basis of subsurface conditions. For example, when no large velocity contrasts are expected (e.g. in case of smooth gradient profiles of the stiff soils and rock sites), it may be advisable to increase the number of layers, but also to impose additional constraints on their depths and/or velocities (e.g. fixed depth and increasing thickness with depth following geometric progression or exponential laws; linear or power law increase of velocity with depth,…). Another example concerns the presence of low velocity layers, which may be forced in the solution when evidences of such structure are present (shape of the dispersion curve or a priori information). Nonetheless, the number of velocity reversals should be limited (ideally no more than one or two) as otherwise this will affect the non-uniqueness of the inversion problem.
4.2.3 Minimum and maximum depths
The minimum and the maximum retrieved wavelengths should be taken into account during the definition of the parameterization. For the inversion of the fundamental mode of Rayleigh wave, the thickness of the first layer should be greater than half minimum available experimental wavelength while the maximum reached depth about half of the maximum available experimental wavelength or even less in stratigraphic conditions involving large impedance contrast at depth. In the latter case, consistency of the inverted velocity structure and the site resonance frequency may help in constraining the maximum resolvable depth.
4.2.4 Use of a-priori and external information
Any a-priori information available on the site is of paramount importance for the surface wave analysis. Useful information can be retrieved from any previous study performed in the area, geological maps, other independent surveys as borehole measurements or other geophysical and geotechnical tests.
Stratigraphic log
If the stratigraphy, or any other borehole measurements, of the site is available, this should be used to define the optimum model parameterization. The interfaces of the initial model can be assumed as detected in the stratigraphy. Expected values of VS for each lithotype identified in the stratigraphic log could be selected on the basis of literature data (see Table 3 for example). However, it should be noted that that geological interfaces not always correspond to detectable velocity variations, and that P-wave and S-wave velocity are not necessarily subject to the same stratigraphy (e.g. in the case of water saturated sediments).
In uncemented coarse-grained soils, the velocity of propagation of the shear wave is strongly affected by effective confinement and as such it is dependent on depth. Several relationships between VS and depth can be found in the literature that can be used to define narrower ranges compared to those reported in Table 3 (e.g. Zimmer et al. 2007; Mitchell and Soga 2005).
P-wave velocity
AP-wave seismic refraction survey performed on the same array of the active-source surface wave test (see Sect. 2.1) can be very useful as it may provide a clear indication of water table depth in soil deposits. Indeed the latter is associated to a sharp transition between unsaturated (few hundred meters per second) and saturated (higher than 1450 m/s) values of P-wave velocity of propagation. The sharp transition is easily identified as a major refractor. Like surface wave techniques, seismic refraction also suffers from non-uniqueness of the solution, and another option is to invert jointly for the dispersion characteristics and for the P-wave first arrivals (see Appendix 6).
Resonance frequency and/or H/V curve
When available and when the experimental dispersion curve gives information down to the H/V frequency peak, this frequency may be jointly inverted with the dispersion curves (see Appendix 7). As well, part of or the whole H/V curve can be inverted, which requires the use of a dedicated solver. If not possible, the transfer function corresponding to the resulting VS profile should be computed and its consistency with the measured H/V frequency peak checked.
4.3 Local search methods: linearized inversions
4.3.1 Principle
In local search methods, the solution is searched with an iterative process starting from an initial model (in green in Fig. 31a). The model is progressively adjusted at successive iterations in order to minimize the value of the misfit function (Fig. 31b). Figure 31c shows the comparison among the experimental data and the forward response of the initial model and the final model.
Example of local search method result. a Final model (in red) and initial model (in green). b The misfit as function of iterations. c Comparison among the experimental data (in blue), the forward response of the initial model (in green) and the forward response of the final model (in red) (Mirandola site, InterPACIFIC project)
Local search methods usually compute the forward response for the model at each iteration. Moreover, at each iteration the Jacobian matrix is usually also computed. The Jacobian matrix is the sensitivity matrix of the measure (the dispersion or SPAC curve) to the model parameters. It is used to determine how to modify the model to decrease the misfit, and also gives an indication on the resolution of each parameter: the lower the sensitivity, the worse that parameter is resolved.
4.3.2 Initial model
The choice of the initial model is crucial in local search methods. The result of the inversion may be strongly dependent on the adopted initial model, as the solution may be trapped in a local minimum of the misfit function. It is strongly recommended that the inversion procedure be repeated starting with different initial models and any a priori information is included (see Sect. 4.2 for parameterization choice).
If no a priori information is available, a simple approach to build a first tentative profile is to use the measured dispersion curve itself, based on the relation between wavelength (λ) and penetration depth: VS values are defined from phase velocity values, possibly increased by 5% or 10% (difference between Rayleigh phase velocity and VS); in a homogeneous medium depths values are defined from a fraction of the wavelength. The exact fraction linking wavelength and depth depends on the velocity structure and cannot be defined a priori. However, this exact fraction is not required to define a rough initial model, and used values range between 0.4 and 0.8. This approach was used in the past to directly estimate the shear wave velocity profile from surface wave data avoiding a formal solution of the inverse problem. Actually, it better represents the average VS value from the surface to the relevant depth. It can be shown that it provides reasonable results especially when the fundamental Rayleigh mode is dominant in the propagation.
Figure 32 shows an example where the initial VS profile is defined as a 6-layer-over-half-space model, with velocities and interface depths estimated to best fit the phase-velocity versus wavelength/2.5 curve. This initial model was used for the local search in the example of Fig. 31.
4.3.3 Convergence criteria
The convergence criteria are the inversion parameters that stop the inversion iterative process. The final model at the last iteration represents the inversion result.
Greatest decreases of the misfit usually occur in the first few iterations, after which the difference between observed and computed dispersion characteristics is only slightly reduced. Carrying on the inversion on a large number of iterations may either be useless, or may even introduce artifacts if the problem is over-parameterised. The iteration is therefore usually stopped after a limited number of iterations.
The other criteria usually defined for stopping linearized inversions is a misfit threshold below which the improvement of the forward dispersion characteristics is considered to be smaller than the uncertainties affecting the data. The inversion then stops when the misfit is lower than the defined threshold.
4.3.4 Assessment of results
The results obtained with the solution of the inverse problem should be carefully inspected to assess their reliability. In particular, the following points deserve attention.
Residuals
Remaining residuals between the observed dispersion and the dispersion predicted for the final model will indicate the reliability of the model. A poor overlap in a given wavelength range is an indication of lack of reliability at a certain depth range.
Depth range
The thickness of the first layer and the maximum investigation depth should be consistent with the available wavelengths in the dispersion curve (see Sect. 4.2.3), which themselves should be consistent with the resolution of the receiver array(s) (see Sects. 2.1.2 and 3.1.2).
Consistency with a priori and/or external information
If a priori or external information is available (type of materials or depths from borehole logs, P-wave velocities or water table position, resonance frequency or H/V curves), it is important to check the consistency of the results with this information in order to make sure the final inversion results are generally agreeable with the a-priori information.
4.3.5 Uncertainties
Uncertainties on the results of a linearized inversion may be estimated from the analysis of the Jacobian (sensitivity) matrix: the higher the sensitivity, the better that parameter is resolved. The Jacobian can also be used to propagate uncertainties on the dispersion curve to uncertainties on the shear wave velocity profile (Lai et al. 2005).
Alternatively, uncertainties may be evaluated from the different results obtained with different initial models, or different constraints on the less influent parameters (mass density, P-wave velocity, Poisson’s ratio). Eventually different results due to different inversion algorithms may be evaluated.
4.4 Global search algorithms
4.4.1 Principle
In global search methods, such as Monte Carlo methods, a probability density distribution (e.g. uniform or normal) is defined for each model parameter (green boundaries in Fig. 33a). The model parameter space is then sampled following a specific search algorithm. For each sample profile the forward response is computed and the misfit with respect to experimental data is obtained. Inference is then made on the population of generated profiles to identify those that represent acceptable solutions. In contrast with the single model produced by linearized inversion, the result of global search methods is a set of many acceptable profiles rather than the single profile associated to the minimum misfit value. This allows the assessment of the uncertainty related to non-uniqueness of the solution.
Example of global search method result. a In red the profile with minimum misfit value. The green dashed lines represent the boundaries of the search area. The profiles, from blue to yellow according to their misfit values, are all the accepted profiles; b in red experimental data and the line from blue to yellow correspond to the forward response of the accepted profiles; c comparison between experimental data (in red) and the forward response of the profile with minimum misfit value (in blue) (Mirandola site, InterPACIFIC project)
In the example of Fig. 33, the profiles (Fig. 33a) whose forward response provides a misfit that passes a statistical test that accounts for experimental uncertainties and model parameterization (Fig. 33b) are selected. In Fig. 33c, the comparison between the experimental data (in red) and the forward response of the profile with minimum misfit value is reported.
The probability of getting a reliable solution with global search methods is related to the size of the population of tentative models. Pure Monte Carlo approaches require a very large number of samples, which are randomly generated. The size of the population should be large enough to properly sample the model parameter space, but small enough to limit computational cost.
Many optimization approaches have been proposed to limit the number of trial profiles (e.g. Latin hypercube sampling, genetic algorithms, simulated annealing, neighbourhood algorithm…). Basically, in all modern global optimization algorithms, after a relatively broad initial explorative random search, the parameter space is iteratively refined and progressively restricted around one or several regions potentially including the absolute minimum of the misfit function.
4.4.2 Definition of the parameter space
As already mentioned, any a-priori information should be taken into account in the design of the parameter space. The width of the parameter interval and the number of layers defines the size of the model space and should be selected according to the level of a priori knowledge available. Very narrow ranges of model parameters strongly constrain the solution, which may fall into a local minimum of the misfit function therefore not taking advantage of the global search approach, so very narrow ranges should be used only when very reliable a priori information is available. On the other side, very large ranges increase the computational time and decrease the chance of getting close to the absolute minimum of the misfit function. A possible strategy is starting with large limits and repeats the inversion by narrowing them on the basis of the first run results.
4.4.3 Definition of the results
Contrarily to linearized inversion the result of global search methods is a set of acceptable profiles selected according to their misfit. The size of this set can be defined according to the method that is used to make inference on the population of trial models. Optimization methods may converge toward a very limited number or even individual final models, other methods may select the acceptable models on the basis of statistical tests or to simple criteria based on misfit threshold of accepted model number.
The solution space (that represents the misfit as a function of the model parameters) may provide a useful insight about the goodness of the model space mapping.
4.4.4 Assessment of results
Assessment of results are based on the same criteria as for the linearized inversion (see Sect. 4.3.4).
4.4.5 Uncertainties
The boundaries of the area filled by all the accepted profiles could be considered as uncertainty boundaries of the profile with minimum misfit (the red profile in Fig. 33a). Statistics on the selected profiles would require a clear assessment of epistemic and aleatory uncertainty related to the various ingredients of the inversion process (data uncertainty, ground model parameterization, etc.). Quantification of variability of the final ground models are thus still an open issue and certainly deserves further investigation in future research.
When further forward calculations are to be computed in the frame of a study (e.g. assessment of seismic response for seismic risk assessment), we suggest using a representative set of acceptable profiles.
4.5 Advantages and disadvantages of each type of inversion
In general global search methods have to be preferred over local search methods, as the latter may provide results strongly dependent on the first tentative profile adopted for the inversion. Moreover, global search methods allow easier investigation of the uncertainties associated to solution non-uniqueness. On the other hand, they are usually more time and computational resource consuming.
Both approaches can be combined, by using a global search sampling the model space and refining the solution close to the minima of the misfit function using a local search algorithm (e.g. Poggi et al. 2012).
5 Applications and use of surface waves survey for earthquake engineering studies
This section provides some examples of application and use of surface wave surveys for various objectives, from the simplest one (e.g. VS,30 determination) to more complex one (1D soil response computation). For these examples, possible survey layouts are proposed. They have to be considered as possible layouts, not as a strict procedure: other approaches may be suitable as well.
For each example, we will comment what could be considered as reliable outcomes from surface wave methods, but also what should be consider with care. These comments are partly based on the learnings from the InterPacific project (Garofalo et al. 2016a, b).
This section aims to provide information for geophysicists that will implement surveys, but also for clients and analysts that will use their results.
5.1 Soil class and VS,30 determination
VS,30 i.e. the time-average shear-wave velocity in the topmost 30 m, is a parameter adopted by several building codes, i.e. EC8 and IBC, for the seismic soil classification. VS,30 is also widely used for the implementation of Ground Motion Prediction Equations (GMPEs) and therefore, this parameter is typically needed to characterize the sites of accelerometric networks.
For a given VS profile, the VS,30 is estimated as:
where N is the number of layers of the VS-profile down to the depth of 30 m, while Hi and VS,i are the thickness and the shear-wave velocity of each layer respectively.
Several studies have shown that calculated VS,30 from the shear wave velocity profiles of surface wave analysis is robust and in very good agreement with estimates obtained with other seismic methods (e.g. borehole methods such as cross-hole method, down-hole method, P-S suspension logging).
Since VS,30 is a parameter related to the average properties of the subsurface, some authors have suggested some direct relationship between the VS,30 and the phase velocity of the dispersion curve at a given wavelength. Using these formulas, the formal inversion of surface wave data is not necessary. These approaches can be used for a rough and fast estimate of VS,30 or to double-check the values calculated from the shear wave velocity profile. According to these relationships, the VS,30 can be estimated as the phase velocity at a given wavelength times a correcting factor (e.g. Brown et al. 2000; Martin and Diehl 2004; Albarello and Gargani 2010; Comina et al. 2011). A simple approximation of these expressions is given by:
in which VR,[40–45] is the phase velocity of the Rayleigh wave fundamental mode for wavelength ranging from 40 to 45 m. Generally, VR,40 is more appropriate at sites with shallow groundwater and VR,45 is more appropriate at sites with deep groundwater.
Therefore, VS,30 can be calculated from the shear wave velocity profile obtained from the whole procedure of surface wave method processing (including the inversion), but also estimated directly from the dispersion curves which is a reliable and stable quantity, avoiding the need to perform the inversion, which is the most complex and time-consuming step in surface wave analysis.
One common pitfall of this very simple approach is due to the possible misinterpretation of the phase velocity of a higher mode as the fundamental mode. It is therefore necessary to collect sufficient information to ensure that the fundamental mode is correctly identified over the frequency band of interest.
A rather complete survey layout to achieve this requirement could be the acquisition of 3 consecutive arrays (e.g. circle arrays using 8 or 10 sensors) with a diameter (aperture) of 20, 50 and 125 m, plus a MASW line, involving 24 geophones with 2 m geophone spacing. This layout will ensure the estimation of a reliable dispersion curve, with a satisfactory overlap between the dispersion curves from passive arrays and MASW linear array.
5.2 Other commonly used proxies
Other parameters are also used, especially within the framework of GMPEs formulations, in order to achieve a better representation of site features. A non-exhaustive list of such parameters follows:
-
f0: fundamental resonance frequency of the site,
-
H800: depth at which the shear wave velocity profile exceeds the value of 800 m/s (i.e. the position of a conventional seismic bedrock).
-
Hbedrock: depth of the geological bedrock, that is to say the depth corresponding to the highest contrast within the shear wave velocity profile. This contrast usually corresponds to the one that causes the f0 resonance and also corresponds to a lithology change.
-
Vmoy: mean shear wave velocity between surface and bedrock (as defined in Hbedrock definition).
-
Vbedrock: shear wave velocity of the bedrock.
-
Vqwl: a frequency-dependent estimation of the average shear wave velocity at a depth corresponding to ¼ of the wavelength.
The f0 value can rather easily be obtained from single station ambient vibration measurements performed with a 3-component sensor (see Sesame Guidelines 2004). Often, these data can be extracted by sensors in the passive array used for surface wave analyses.
The other parameters can be calculated from the shear wave velocity profile. Taking into account solution non-uniqueness it is recommended that the uncertainty bounds on these parameters be evaluated by repeating the calculation for a set of equivalent solution (see Sect. 4.4.5).
The results of the InterPacific benchmark (Garofalo et al. 2016a), show that, while the average velocities within the first tens of meters are rather well determined by surface wave methods, the determination of Hbedrock and Vbedrock have higher uncertainties. In order to quantify this uncertainty, it is recommended to perform multiple inversions using various hypotheses and parameterizations. Performing a joint inversion involving both dispersion curves and value of fundamental frequency f0 or a-priori information may also reduce the uncertainty. Regarding the Vbedrock parameter, if the “bedrock” geological formation is outcropping near the studied site, it may be useful to perform a survey on the outcropping area to obtain a reference value for the bedrock velocity.
In order to determine the velocity profiles needed for the determination of above mentioned parameters (except for f0 which only needs a single-station measurement), one can realize a MASW line (for example involving 24 geophones with 2 m geophone spacing) for high frequency and shallow layers, then deploy several passive arrays, with successive apertures starting from relatively small (15–20 m) up to a value equal to the double of the desired investigation depth. A very large passive array could help in the determination of the bedrock velocity.
5.3 Ground response analysis
One of the current applications of surface wave methods is the determination of shear wave velocity profiles in order to compute 1D site response. We recommend that a set of acceptable velocity model is estimated.
When the geophysicist provides a set of possible solutions to the engineer responsible for site response simulation, a common error is to group all the profiles on a single plot and to consider three inferred profiles for the computations: the mean of all profiles; the mean plus and minus one standard deviation (all computed “depth by depth”). This will lead to an overestimation of the uncertainty. Indeed both outer profiles will not correspond to the measured surface wave dispersion curve, which is a robust parameter and represents a signature of the site.
When representative profiles are built for ground response analysis, they should always be tested by checking the corresponding theoretical dispersion curve and fundamental frequency against the available experimental ones. Similarly, when randomization approaches (e.g. Toro 1995) are adopted, it is necessary to select only “randomized” profiles that fit the measured values of dispersion curves and f0 (Teague and Cox 2016).
The suggested approach to account for solution non-uniqueness is to repeat the ground response analyses for the individual profiles selected during the inversion process. This approach allows a direct evaluation of the final uncertainty associated to the seismic site response of the site. This uncertainty may be significantly smaller than the one associated to the shear wave velocity profile (e.g. Fig. 34). Indeed the profiles that match the experimental dispersion curve are likely equivalent also in terms of ground response to vertically propagating shear waves, which are considered in 1D analyses.
Incidence on uncertainty of velocity profiles inferred from surface wave experiment of 1D soil response computation. Left set of velocity profiles from inversion. One can see that for a given depth, the variability can be high. Right corresponding 1D soil response. The differences between acceleration response spectra at the surface are limited (Foti et al. 2009)
A key parameter for ground response analyses is material damping, which is typically introduced on the basis of laboratory tests. However they may be not sufficiently representative of the response of the soil deposit. Although not yet fully included in the state of the practice, surface wave attenuation can be exploited to obtain damping parameters (Foti et al. 2014). Appendix 10 reports on possible options for this application.
References
Albarello D, Gargani G (2010) Providing NEHRP soil classification from the direct interpretation of effective Rayleigh-wave dispersion curves. Bull Seismol Soc Am 100(6):3284–3294
Bard P-Y, Cadet H, Endrun B, Hobiger M, Renalier F, Theodulidis N, Ohrnberger M, Fäh D, Sabetta F, Teves-Costa P, Duval A-M, Cornou C, Guillier B, Wathelet M, Savvaidis A, Köhler A, Burjanek J, Poggi V, Gassner-Stamm G, Havenith HB, Hailemikael S, Almeida J, Rodrigues I, Veludo I, Lacave C, Thomassin S, Kristekova M (2010) From non-invasive site characterization to site amplification: recent advances in the use of ambient vibration measurements. Geotech Geol Earthq Eng 17:105–123
Bolt BA (1987) Earthquakes. W. H Freeman, New York
Brown L, Diehl J, Nigbor R (2000) A simplified method to measure average shear-wave velocity in the top 30 m (Vs30). In: Proceedings of the 6th international conference on seismic zonation, pp 1–6
Comina C, Foti S, Boiero D, Socco LV (2011) Reliability of VS,30 evaluation from surface waves tests. J Geotech Geoenviron Eng 137(6):579–588. doi:10.1061/(ASCE)GT.1943-5606.0000452
Cox BR, Teague DP (2016) Layering ratios: a systematic approach to the inversion of surface wave data in the absence of A-priori information. Geophys J Int 207:422–438. doi:10.1093/gji/ggw282
Foti S, Comina C, Boiero D, Socco LV (2009) Non-uniqueness in surface wave inversion and consequences on seismic site response analyses. Soil Dyn Earthq Eng 29(6):982–993
Foti S, Parolai S, Albarello D, Picozzi M (2011) Application of surface wave methods for seismic site characterization. Surv Geophys 32(6):777–825
Foti S, Lai CG, Rix G, Strobbia C (2014) Surface wave methods for near-surface site characterization. CRC Press, London
Garofalo F, Foti S, Hollender F, Bard PY, Cornou C, Cox BR, Ohrnberger M, Sicilia D, Asten M, Di Giulio G, Forbriger T, Guillier B, Hayashi K, Martin A, Matsushima S, Mercerat D, Poggi V, Yamanaka H (2016a) InterPACIFIC project: comparison of invasive and non-invasive methods for seismic site characterization. Part I: Intra-comparison of surface wave methods. Soil Dyn Earthq Eng 82:222–240
Garofalo F, Foti S, Hollender F, Bard PY, Cornou C, Cox BR, Dechamp A, Ohrnberger M, Perron V, Sicilia D, Teague D, Vergniault C (2016b) InterPACIFIC project: comparison of invasive and non-invasive methods for seismic site characterization. Part II: Inter-comparison between surface-wave and borehole methods. Soil Dyn Earthq Eng 82:241–254
Lai CG, Foti S, Rix GJ (2005) Propagation of data uncertainty in surface wave inversion. J Environ Eng Geophys 10(2):219–228
Martin AJ, Diehl JG (2004) Practical experience using a simplified procedure to measure average shear-wave velocity to a depth of 30 meters (VS,30). In: Proceedings of the 13th world conference on earthquake engineering, Vancouver, BC., Canada, August 1–6, 2004, paper no. 952
Mitchell JK, Soga K (2005) Fundamentals of soil behavior. Wiley, London
Okada H (2003) The microtremor survey method. Geophysical monograph series. Society of Exploration Geophysics, Tulsa
Park CB, Miller RD, Xia J (1999) Multichannel analysis of surface waves. Geophysics 64:800–808
Peterson J (1993) Observations and modeling of seismic background noise. U.S. Geol. Surv. Open-File Rept. 93-322-95
Poggi V, Fäh D, Burjanek J, Giardini D (2012) The use of Rayleigh wave ellipticity for site-specific hazard assessment and microzonation. An application to the city of Luzern (Switzerland). Geophys J Int 188(3):1154–1172
Schramm KA, Abbott RE, Asten MW, Bilek S, Pancha AP, Patton HJ (2012) Broadband Rayleigh-wave dispersion curve and shear wave velocity structure for Yucca Flat, Nevada. Bull Seismol Soc Am 102(4):1361–1372. doi:10.1785/0120110296
SESAME team (2004) Guidelines for the implementation of the H/V spectral ratio technique on ambient vibrations: measurements, processing and interpretation (Deliverable No. D23.12), WP12. SESAME European research project
Socco L, Foti S, Boiero D (2010) Surface wave analysis for building near surface velocity models: established approaches and new prospectives. Geophysics 75(5):A83–A102
Teague DP, Cox BR (2016) Site response implications associated with using non-unique vs profiles from surface wave inversion in comparison with other commonly used methods of accounting for vs uncertainty. Soil Dyn Earthq Eng. doi:10.1016/j.soildyn.2016.07.028)
Toro GR (1995) Probabilistic models of site velocity profiles for generic and site-specific ground-motion amplification studies. Technical report no 779574, Upton
Wielandt E (1993) Propagation and structural interpretation of non-plane waves. Geophys J Int 113(1):33–45. doi:10.1111/j.1365-246X.1993.tb02527.x
Yong A, Martin A, Stokoe K, Diehl J (2013) ARRA-funded VS,30 measurements using multi-technique approach at strong-motion stations in California and Central-Eastern United States. Reston, Virginia, U.S. Geol. Surv. Open-File Rept. 2013-1102, 59
Zimmer MA, Prasad M, Mavko G, Nur A (2007) Seismic velocities of unconsolidated sands: part 1—pressure trends from 0.1 to 20 MPa. Geophysics 72(1):E1–E13. doi:10.1190/1.2399459
Acknowledgements
The Authors are grateful to Carlo G. Lai for reviewing the manuscript and for the precious suggestions on several issues that have been incorporated in the text. The Interpacific Project has been financed by the Research & Development Program SIGMA funded by EdF, Areva, CEA and ENEL and by CASHIMA project, funded by CEA, ILL and ITER. Partial funding for participants from the Politecnico di Torino was provided by the ReLUIS 3 project, sponsored by the Italian Civil Protection Agency. Partial funding for participants from the University of Texas was provided by U.S. National Science Foundation (NSF) Grant CMMI-1261775. However, any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding agencies.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Foti, S., Hollender, F., Garofalo, F. et al. Guidelines for the good practice of surface wave analysis: a product of the InterPACIFIC project. Bull Earthquake Eng 16, 2367–2420 (2018). https://doi.org/10.1007/s10518-017-0206-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-017-0206-7