1 Introduction

The libration points of many three-body systems have long held the interest of scientists and mission designers as they offer unique observation and communication vantage points. Periodic orbits around the \(L_{1}\) point of the Sun-Earth system are currently being exploited for observations of the Sun, e.g., SOHO (ESA/NASA, 1996), ACE (NASA, 1997), and WIND (NASA, 2004), while DSCOVR (NOAA/NASA, 2015) is in a Lissajous orbit around the \(L_{1}\) point. In addition, the \(L_{1}\) point allows for fundamental physics by the LISA Pathfinder mission (ESA, 2015), while the Sun-Earth \(L_{2}\) point provides favourable conditions for space-based observatories for astronomy, e.g., GAIA (ESA, 2013). Although less exploited, except by the ARTEMIS mission (NASA, 2007), libration point orbits in the Earth-Moon system also hold great potential, for example for rover landing missions (Parker 2014). Furthermore, orbits around the \(L_{2}\) point seem to provide opportunities for lunar far-side observation and communication through the use of halo orbits (Farquhar 1967) and as a potential location for a future manned space station or as a cargo gateway (Olson et al. 2011).

Many different families of periodic orbits can be identified around the libration points with the most well-known ones being the families of Lyapunov (Hénon 1969), halo (Breakwell and Brown 1979), vertical Lyapunov (Kazantzis 1979) and distant retrograde orbits (Hénon 1969). These orbits all exist in the classical circular restricted-three body problem (CR3BP), indicating that the spacecraft motion is governed only by the gravitational attraction of the two primaries, such as the Sun and Earth, or Earth and Moon. More flexibility can be introduced to this model by adding low-thrust propulsion, which then opens up additional opportunities for observation or communication capabilities from such orbits.

In this paper, the classical CR3BP is complemented with solar sail propulsion (Macdonald 2014; Macdonald and McInnes 2011; McInnes 1999; Vulpetti 2013; Vulpetti et al. 2015; Wright 1992). Although the concept of solar sailing was first mentioned nearly a hundred years ago (Tsiolkovsky 1921; Vulpetti et al. 2015), only recently the first small sails have been successfully deployed in space: the technology demonstration missions IKAROS (JAXA, 2010) (Tsuda et al. 2013), NanoSail-D2 (NASA, 2010) (Johnson et al. 2011), and LightSail-1 (the Planetary Society, 2015).Footnote 1 By using a very large, very thin and highly reflective membrane, solar sails reflect photons, thereby producing a small thrust force in a direction approximated as normal to the reflective surface. Despite limitations on the direction of thrust that a solar sail can generate, its propellant-less nature gives solar sailing great potential for long-duration and high-energy missions. Proposed ideas include near- to mid-term missions concepts such as orbits over the poles of the Sun for heliophysics (Macdonald et al. 2006), hovering along the Sun-Earth line for space weather forecasting (Heiligers et al. 2014; Vulpetti et al. 2015), fly-bys of or hovering over asteroids for asteroid exploration and exploitation (McNutt et al. 2014; Gong and Li 2014), exploring the Sun-Earth triangular Lagrange points for solar observations and potential Earth Trojans (Sood and Howell 2016) and parking the sail above or below the Earth’s orbit for high-latitude navigation and communications (Waters and McInnes 2007) as well as far-reaching ideas such as planetary orbit modification (McInnes 2002). Adding solar sail propulsion to the classical Earth-Moon CR3BP will further demonstrate the potential of solar sailing and potentially open up novel space mission applications in the Earth-Moon system.

While solar sail enabled libration point orbits in the Sun-Earth system have been considered in quite some detail, (e.g., Nuss 1998; McInnes 2000; Baoyin and McInnes 2006; Waters and McInnes 2007; McKay et al. 2011; Ceriotti and McInnes 2012; Verrier et al. 2014), such orbits in the Earth-Moon system have been investigated to a much lesser extent. Compared to the solar sail dynamics in the Sun-Earth system, adding a solar sail to the Earth-Moon CR3BP introduces the complexity of the Sun rotating around the Earth-Moon system once per synodic lunar period, causing the direction of the photons impinging on the solar sail to change accordingly. As a result, the problem is time-dependent and the period of the orbit has to be equal to a fraction (or multiple) of the synodic lunar period in order for the orbit to be repeatable over time.

Previous work on solar sail periodic orbits in the Earth-Moon system either linearised the equations of motion (McInnes 1993; Simo and McInnes 2009) or searched for bespoke orbits, e.g., below the lunar South Pole by solving the accompanying optimal control problem (Ozimek et al. 2009; Ozimek et al. 2010; Wawrzyniak and Howell 2011). The results in the linearised system have been transferred to the full non-linear dynamical system (Wawrzyniak and Howell 2011a), but the results presented are limited to one specific steering law and only show one family of orbits at the Earth-Moon \(L_{2}\) point. Initial results on more extensive families of solar sail periodic orbits in the Earth-Moon system do exist (Heiligers et al. 2015), but have been found by solving a two-point boundary value problem, while this paper develops a faster and more accurate differential correction scheme. Furthermore, this paper significantly extends the families found in (Heiligers et al. 2015) to Lyapunov, halo, and vertical Lyapunov orbits around both the \(L_{1}\) and \(L_{2}\) points as well as Earth-centred and distant retrograde orbits. Finally, this paper investigates for the first time the stability properties of these orbits in order to assess the effect of the solar sail on the orbit stability compared to the classical libration point orbits and the potential need for active orbital control.

The structure of the paper is as follows. First, Sect. 2 introduces the dynamical system in which the families of solar sail enabled libration point orbits are developed. Section 3 will describe the different solar sail steering laws considered in this paper, with two in-plane steering laws described in Sect. 3.1 and the possibility to extend the steering law with an out-of-plane acceleration component considered in Sect. 3.2. Section 4 will describe in detail the differential correction scheme used to generate families of solar sail periodic orbits. The classical Lyapunov, halo, vertical Lyapunov, Earth-centred orbits and distant retrograde orbits that serve as initial guesses for the differential corrector will be presented in Sect. 5. Section 6 will highlight the fact that the differential correction scheme and continuation method can start from any \(( x,z )\)-plane crossing of the classical libration point orbits, allowing for different initial Sun-sail configurations to be considered. The results for the in-plane steering laws will be presented in Sect. 7, followed by the out-of-plane results in Sect. 8. Finally, in Sect. 9 a stability analysis will be performed to provide the linear stability properties of all solar sail enabled libration point orbits presented in this paper together with a comparison of how the solar sail acceleration affects the orbits’ stability compared to their classical counterparts. The paper will end with the conclusions.

2 Dynamical system

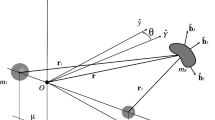
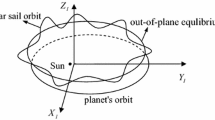
The solar sail enabled libration point orbits are developed within the framework of the solar sail Earth-Moon CR3BP, see Fig. 1. The classical CR3BP describes the motion of an object with an infinitely small mass \(m\) under the influence of the gravitational attraction of two much larger primary objects with masses \(m_{1}\) (here, the Earth) and \(m_{2}\) (here, the Moon). The gravitational influence of the small object on the primaries is neglected and the primaries are assumed to move in circular co-planar orbits about their common centre-of-mass.

Fig. 1
figure 1

Schematic of solar sail Earth-Moon circular restricted three-body problem

Full size image

Figure 1 shows the synodic reference frame that is employed in the CR3BP: the origin coincides with the centre-of-mass of the system, the \(x\)-axis connects the primaries and points in the direction of the smaller of the two, \(m_{2}\), while the \(z\)-axis is directed perpendicular to the plane in which the two primaries move. The \(y\)-axis completes the right-handed reference frame. Finally, the frame rotates at a constant angular velocity \(\omega \) about the \(z\)-axis: \(\boldsymbol{\omega } = \omega \hat{\mathbf{z}}\).

The dynamics of the CR3BP are made dimensionless by taking the sum of the two larger masses as the unit of mass, the distance between the main bodies as the unit of length, and \(1/\omega \) as the unit of time. With the mass ratio \(\mu = m_{2}/ ( m_{1} + m_{2} ) \), the masses of the large bodies become \(m_{1} = 1 - \mu \) and \(m_{2} = \mu \), and their location along the \(x\)-axis becomes \(- \mu \) and \(1 - \mu \), respectively. For the Earth-Moon CR3BP, \(\mu \) has a value of approximately \(\mu =0.01215\).

As the Sun moves around the Earth-Moon system once per synodic lunar period, at a dimensionless rate of \(\varOmega_{S} =0.9252\), adding a solar sail induced acceleration (hereafter referred to in short as solar sail acceleration) to the classical CR3BP results in a non-autonomous system which can be described by the following equations of motion

$$ \ddot{\mathbf{r}} + 2\boldsymbol{\omega } \times \dot{\mathbf{r}} = \mathbf{a}_{s} ( t ) - \nabla U $$
(1)

with \(U = - \frac{1}{2} ( x^{2} + y^{2} ) - ( [ 1 - \mu ] /r_{1} + \mu /r_{2} ) \) the effective potential that combines the gravitational potential and the potential from the centripetal acceleration and \(\mathbf{a}_{s} ( t ) \) the solar sail acceleration. All other variables in Eq. (1) are defined in Fig. 1.

To define the solar sail acceleration, an ideal solar sail model is assumed, which considers the sail to be a perfect reflector without wrinkles or other optical imperfections (McInnes 1999). Under these assumptions, the sail reflects the solar photons specularly and the acceleration acts perpendicular to the solar sail membrane, in direction \(\hat{\mathbf{n}}\). Furthermore, it is assumed that the solar radiation pressure is constant throughout the Earth-Moon system, resulting in

$$ \mathbf{a}_{s} ( t ) = a_{0,\mathrm{EM}} \bigl( \hat{\mathbf{S}} ( t ) \cdot \hat{\mathbf{n}} \bigr) ^{2}\hat{\mathbf{n}} $$
(2)

with \(\hat{\mathbf{S}} = [ \cos ( \varOmega_{S}t ) \ - \sin ( \varOmega_{S}t ) \ 0 ] ^{T}\) the direction of Sunlight and \(a_{0,\mathrm{EM}}\) the dimensionless characteristic solar sail acceleration. Note that Eq. (2) ignores the small inclination difference between the Sun-Earth and Earth-Moon orbital planes, eliminating the small out-of-plane component of the direction of Sunlight. Equation (2) also ignores shadowing from the Earth and Moon and at time \(t = 0\) the Sun is assumed to be on the negative \(x\)-axis, see also Fig. 1. Finally, the characteristic acceleration is the acceleration that a solar sail can generate when facing the Sun at Earth’s distance (McInnes 1999). Derived from the previously proposed Sunjammer sail performance (Heiligers et al. 2014), a typical value for this characteristic acceleration is 0.215 mm/s2, which equals a value of 0.0798 in dimensionless units. Note that this dimensionless parameter is different from the solar sail lightness number, which is defined as the ratio of solar radiation pressure acceleration and solar gravitational acceleration (McInnes 1999).

3 Solar sail steering laws

From Eq. (2) it is clear that the solar sail acceleration vector depends mainly on the solar sail attitude, which is described through the normal to the solar sail membrane, \(\hat{\mathbf{n}}\). Therefore, by considering different solar sail steering laws, different families of solar sail periodic orbits will originate. This paper considers two different in-plane steering laws, which can be extended in the out-of-plane direction by pitching the sail with respect to the Earth-Moon plane.

3.1 In-plane solar sail steering laws

The first in-plane solar sail steering law is referred to as the Earth-Moon line (EM) steering law, which assumes that the sail normal is always directed along the Earth-Moon line, i.e., along the \(x\)-axis

$$ \hat{\mathbf{n}} = \operatorname{sign} \bigl( \cos ( \varOmega_{S}t ) \bigr) \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \end{array}\displaystyle \right ]^{T}. $$
(3)

This steering law allows for a constant attitude of the sail in the Earth-Moon synodic frame (and therefore a constant acceleration direction), but implies a changing solar sail acceleration magnitude. The term \(\operatorname{sign} ( \cos ( \varOmega_{S}t ) ) \) takes into account that the solar sail normal vector changes sign when the Sun moves from illuminating the Earth-facing side of the sail to illuminating the Moon-facing side. Note that this implies that the sail has to be reflective on both sides, which leads to strict thermal design constraints, but has previously been proposed for a heliogyro-type sail configuration (Wilkie et al. 2014).

The second in-plane steering law is the Sun-sail line (Sun-sail) steering law, which assumes that the sail normal is always directed along the Sun-sail line, i.e., the sail always faces the Sun. Contrary to the first steering law, this law allows for a constant magnitude of the sail acceleration, \(\mathbf{a}_{s} = a_{0,\mathrm{EM}} \hat{\mathbf{S}}\), but implies a changing sail acceleration direction in the synodic frame

$$ \hat{\mathbf{n}} = \hat{\mathbf{S}}. $$
(4)

Note that a Sun-facing attitude of the sail can in theory be achieved passively through a correct offset between the sail’s centre of pressure and centre of mass, allowing for a very small solar sail steering effort.

3.2 Out-of-plane solar sail acceleration component

In addition to an in-plane acceleration, a solar sail can also create an out-of-plane acceleration component by pitching the sail at an angle \(\gamma \) with respect to the Earth-Moon plane, see Fig. 2. Adding this component to the in-plane steering laws defined in Eqs. (3)–(4) gives

$$\begin{aligned} &{\begin{aligned}[b] &\hat{\mathbf{n}} = \operatorname{sign} \bigl( \cos ( \varOmega_{S}t ) \bigr) \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \cos \gamma & 0 & \sin \gamma \end{array}\displaystyle \right ] ^{T} \\ &\quad \mbox{EM line steering law}, \end{aligned} } \end{aligned}$$
(5)
$$\begin{aligned} &{\begin{aligned}[b] &\hat{\mathbf{n}} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \cos \gamma \cos ( \varOmega_{S}t ) & - \cos \gamma \sin ( \varOmega_{S}t ) & \sin \gamma \end{array}\displaystyle \right ] ^{T} \\ &\quad \mbox{Sun-sail line steering law} . \end{aligned} } \end{aligned}$$
(6)

Note that for a pitch angle \(\gamma =0\), Eqs. (5)–(6) reduce to the in-plane steering laws in Eqs. (3)–(4).

Fig. 2
figure 2

Schematic of out-of-plane steering laws. (a) EM line steering law. (b) Sun-sail line steering law

Full size image

4 Differential correction method

In order to find solar sail enabled libration point orbits under the dynamics of Eqs. (1) with a steering law selected from Eqs. (2)–(5), a differential correction scheme is applied, which iteratively finds the initial conditions that allow for periodic orbits. This differential correction scheme largely follows the method introduced by Howell (1983), but introduces a constraint to drive the orbital period to one synodic lunar period or a multiple thereof. To properly describe the implementation of this constraint, the differential correction scheme is described in full below.

The first step in deriving the differential correction scheme is a linearisation of the equations of motion around a reference trajectory, \(\mathbf{r}_{0}\). Replacing \(\mathbf{r} \to \mathbf{r}_{0} + \delta \mathbf{r}\) gives the following linearised system of first order differential equations

$$ \dot{\mathbf{x}} = \mathbf{Ax} $$
(7)

with \(\mathbf{x} = [ \delta \mathbf{r} \ \delta \dot{\mathbf{r}}] ^{T}\) and

$$ \mathbf{A} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{0} & \mathbf{I} \\ - \frac{\partial \nabla U}{\partial \mathbf{r}}\big\vert _{\mathbf{r}_{0}} & \boldsymbol{\varOmega } \end{array}\displaystyle \right ] , \qquad \boldsymbol{\varOmega } = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 2 & 0 \\ - 2 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ] . $$
(8)

As the solar sail acceleration is not a function of the sail’s position within the CR3BP (as the solar sail magnitude, \(a_{0,\mathrm{EM}}\), is considered constant throughout the Earth-Moon system), only the partial derivative of the effective potential appears in Eq. (8).

For a system of the form \(\dot{\mathbf{x}} = \mathbf{Ax}\), as in Eq. (7), the state-vector at time \(t\) can be obtained through the state-transition matrix, \(\boldsymbol{\varPhi } ( t;t_{0} ) \), as

$$ \mathbf{x} ( t ) = \boldsymbol{\varPhi } ( t;t_{0} ) \mathbf{x} ( t_{0} ) , $$
(9)

where the state transition matrix can be obtained by simultaneously integrating the equations of motion in Eq. (1) and the following differential equation for the state transition matrix

$$ \boldsymbol{\varPhi }^{.} ( t;t_{0} ) = \mathbf{A} \boldsymbol{\varPhi} ( t;t_{0} ) . $$
(10)

Equation (9) can be used to predict how the initial conditions need to be changed such that the final conditions of the trajectory satisfy the requirements for a solar sail periodic orbit: a change in the initial conditions of \(\delta \mathbf{x} ( t_{0} ) \) will change the final conditions by

$$ \delta \mathbf{x} ( t_{f} ) = \boldsymbol{\varPhi } ( t_{f};t_{0} ) \delta \mathbf{x} ( t_{0} ) . $$
(11)

The expression in Eq. (11) is used in the following to find halo orbits with solar sail propulsion to illustrate the method. However, note that a similar approach can be used to find other types of solar sail periodic orbits. Starting perpendicular to the \(( x,z ) \)-plane, the initial conditions of a solar sail halo orbit are

$$ \mathbf{x}_{0} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} x_{0} & 0 & z_{0} & 0 & \dot{y}_{0} & 0 \end{array}\displaystyle \right ] ^{T}. $$
(12)

After half the orbital period, the following final conditions should hold, which ensure that after integration for another half period the orbit returns to its initial conditions

$$ \mathbf{x}_{f} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} x_{f} & 0 & z_{f} & 0 & \dot{y}_{f} & 0 \end{array}\displaystyle \right ] ^{T}. $$
(13)

However, as the first guess for the initial conditions may not be entirely correct, the final conditions will more likely be of the form

$$ \tilde{\mathbf{x}}_{f} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} x_{f} & 0 & z_{f} & \dot{x}_{f} & \dot{y}_{f} & \dot{z}_{f} \end{array}\displaystyle \right ] ^{T}. $$
(14)

Note that the final condition \(y_{f} = 0\) is ensured by truncating the integration of the equations of motion upon crossing the \(( x,z ) \)-plane. The required change to the final conditions is thus

$$ \delta \mathbf{x}_{f} = \left [ \textstyle\begin{array}{c@{\quad}c} - \dot{x}_{f} & - \dot{z}_{f} \end{array}\displaystyle \right ] ^{T}, $$
(15)

which needs to be translated into a required change to the initial conditions. Using Eq. (11) does not take the variability of the final conditions with time into account, i.e., the integration time until crossing the \(( x,z ) \)-plane changes when changing the initial conditions. The change in final conditions is therefore expanded with a Taylor series about the final time up to first order

$$ \delta \mathbf{x} ( t_{f} + \delta t_{f} ) = \delta \mathbf{x} ( t_{f} ) + \frac{\partial \mathbf{x}}{\partial t} \bigg\vert _{t = t_{f}}\delta t_{f}, $$
(16)

where the first term on the right hand side can be obtained from Eq. (11),

$$ \delta \mathbf{x} ( t_{f} + \delta t_{f} ) = \boldsymbol{\varPhi } ( t_{f};t_{0} ) \delta \mathbf{x} ( t_{0} ) + \frac{\partial \mathbf{x}}{\partial t} \bigg\vert _{t = t_{f}}\delta t_{f}. $$
(17)

Equation (17) is a system of six equations, but from Eq. (15) it is clear that only the 4th and 6th equations are of interest:

$$ \begin{aligned}[b] \left [ \textstyle\begin{array}{c} - \dot{x}_{f} \\ - \dot{z}_{f} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \varPhi_{f,41} & \varPhi_{f,43} & \varPhi_{f,45} \\ \varPhi_{f,61} & \varPhi_{f,63} & \varPhi_{f,65} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \delta x_{0} \\ \delta z_{0} \\ \delta \dot{y}_{0} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{c} \ddot{x}_{f} \\ \ddot{z}_{f} \end{array}\displaystyle \right ] \delta t_{f}. \end{aligned} $$
(18)

Note that Eq. (18) uses a short notation for \(\varPhi ( t_{f};t_{0} ) \to \varPhi_{f}\). The system in Eq. (18) consists of two equations with four unknowns (\(\delta x_{0}\), \(\delta z_{0}\), \(\delta \dot{y} _{0}\) and \(\delta t_{f}\)). First, \(\delta t_{f}\) is used to drive the period of the orbit to a particular reference value. For the solar sail periodic orbits in the Earth-Moon system that period needs to equal the synodic lunar period, \(2\pi /\varOmega_{S}\), or a multiple thereof. The required time at the half-way point of the orbit, i.e., upon crossing the \(( x,z ) \)-plane, should then equal \(t_{f,\mathit{req}} = \pi / \varOmega_{S}\). The value for \(\delta t_{f}\) can thus be computed as

$$ \delta t_{f} = t_{f,\mathit{req}} - t_{f} $$
(19)

with \(t_{f}\) the actual time upon crossing the \(( x,z ) \)-plane. Furthermore, from Eq. (17) it follows that

$$ \delta y_{f} = 0 = \varPhi_{f,21}\delta x_{0} + \varPhi_{f,23}\delta z_{0} + \varPhi_{f,25}\delta \dot{y}_{0} + \dot{y}_{f}\delta t_{f}. $$
(20)

Equations (18)–(20) combined allow to solve for the four unknowns.

Note that the approach described above does not require one of the three non-zero initial conditions to be fixed as is the case for conventional differential correction schemes such as the one developed by Howell (1983). The initial condition is thus fully flexible, while driving the period of the orbit to one synodic lunar period (or a multiple thereof). Not having to fix one of the three non-zero conditions is important, because it cannot be known a priori for which values of \(x_{0}\), \(z_{0}\) or \(\dot{y}_{0}\) solar sail periodic orbits exist.

5 Initial guess

To seed the differential corrector, classical libration point orbits are used that have a suitable period, i.e., a period equal to a fraction (or multiple) of the synodic lunar period, \(2\pi /\varOmega_{S}\). Such a period will provide a good starting point to find solar sail orbits with periods equal to one synodic lunar period or a multiple thereof. For example, two revolutions in a classical orbit with a period of \(\frac{1}{2} ( 2\pi /\varOmega_{S} ) \) or 3 revolutions in a classical orbit with a period of \(\frac{2}{3} ( 2\pi /\varOmega_{S} ) \), will serve as initial guesses which will result in solar sail orbits with periods of one and two synodic lunar months, respectively.

A continuation method is subsequently applied, whereby the solar sail characteristic acceleration, \(a_{0,\mathrm{EM}}\), is slowly increased, using the result for a slightly smaller sail acceleration as initial guess to start the differential corrector for a slightly larger sail acceleration. This approach will give rise to families of periodic orbits for increasing sail performance. Note that the continuation starts with a step size of \(\Delta a_{0,\mathrm{EM}} = 10^{-4}\), but is reduced in case the differential corrector scheme does not converge. The family of periodic orbits terminates when the differential corrector scheme does not converge for the minimum step size of \(\Delta a_{0,\mathrm{EM}} =10^{-7}\).

Figure 3 shows the families of classical \(L_{1}\)-point Lyapunov, halo, and vertical Lyapunov orbits as well as the classical Earth-centred and distant retrograde orbits which (together with similar orbits at the \(L_{2}\) point) are extended in this paper with solar sail propulsion. For each family the orbital period as a function of one of the initial conditions is provided and the orbit with a suitable period is highlighted with a thick coloured line in the orbital plots and a round marker in the plots showing the orbits’ period. From Fig. 3e it is clear that the family of classical distant retrograde orbits (DROs) provide two suitable initial guesses, with periods equal to half and 1/3 the synodic lunar period. These two orbits are hereafter referred to as \(\mathrm{DRO}_{1/2}\) and \(\mathrm{DRO}_{1/3}\), respectively.

Fig. 3
figure 3

Family of classical libration point orbits and their periods: (a) \(L_{1}\)-Lyapunov, (b) \(L_{1}\)-halo, (c) \(L_{1}\)-vertical Lyapunov, (d) Earth-centred, and (e) distant retrograde orbits

Full size image

Table 1 provides the corresponding orbital periods of all selected classical libration point orbits, which give an insight in the number of orbital revolutions that the corresponding solar sail enabled libration point orbits will make within one synodic lunar period.

Table 1 Periods of selected classical Lyapunov, halo, vertical Lyapunov, Earth-centred, and distant retrograde orbits
Full size table

6 Initial Sun-sail configuration

Section 4 described that the differential correction scheme starts the orbit propagation from an initial condition with \(y = 0\), i.e., at a crossing of the orbit with the \(( x,y ) \)-plane. From Fig. 3 it is clear that all classical libration point orbits cross the \((x,y)\)-plane (perpendicularly) twice. The orbit propagation can therefore be started from either crossing. While the choice of crossing will not affect the orbital shape in the classical case, it will affect the orbital shape when adding solar sail propulsion, because each crossing results in different Sun-sail configurations, and therefore different solar sail accelerations, along the orbit. Starting the differential correction scheme from each \((x,y)\)-plane separately will therefore result in two different families of solar sail enabled libration point orbits.

The different initial conditions, and used notations, are explained in more detail in Fig. 4 for both in-plane (or two-dimensional) and out-of-plane (or three-dimensional) orbit families. Note that the \(\min ( x ( y = 0 ) ) \), \(\max ( x ( y = 0 ) ) \) notation can also be used for the out-of-plane orbit families, but that the \(z_{0} > 0\), \(z_{0} < 0\) notation is considered more intuitive.

Fig. 4
figure 4

Initial Sun-sail configurations for (a) in-plane libration point orbits and (b) out-of-plane libration point orbits

Full size image

7 Results for in-plane steering law

Starting from the classical libration point orbits of Sect. 5, using the two in-plane solar sail steering laws of Sect. 3.1, and considering both initial Sun-sail configurations of Sect. 6, the results as provided in Fig. 5, Fig. 6 and throughout Sects. 7.1–7.5 are obtained. Figures 5 and 6 summarise the families of libration point orbits through their initial conditions, in Fig. 5 for the Earth-Moon line steering law and in Fig. 6 for the Sun-sail line steering law. These figures show that the continuation on the dimensionless solar sail characteristic acceleration extends up to a value of 0.1. Such an acceleration is slightly larger than the value that current sail technology can achieve (0.0798 for Sunjammer as explained in Sect. 2), but shows what could be feasible in the near- to mid-term. However, the figures also show that some of the orbit families terminate before reaching the maximum characteristic acceleration of 0.1, indicating that the differential corrector scheme did not converge onto a periodic orbit for a larger solar sail acceleration magnitude. For example, the family of halo orbits with solar sail propulsion at the \(L_{1}\) point with \(z_{0}>0\) (or \(\min ( x ( y = 0 ) ) \)) as initial condition and for an Earth-Moon line steering law truncates at a maximum value for the sail acceleration of \(a_{0,\mathrm{EM}} = 0.046\).

Fig. 5
figure 5

Initial conditions of families of solar sail enabled libration point orbits at the Earth-Moon \(L_{1}\) and \(L_{2}\) points for an Earth-Moon line steering law. (a–d) Lyapunov, halo, and vertical Lyapunov orbit families. (e) Earth-centred and distant retrograde orbit families

Full size image
Fig. 6
figure 6

Initial conditions of families of solar sail enabled libration point orbits at the Earth-Moon \(L_{1}\) and \(L_{2}\) points for a Sun-sail line steering law. (a–d) Lyapunov, halo, and vertical Lyapunov orbit families. (e) Earth-centred and distant retrograde orbit families

Full size image

7.1 Solar sail Lyapunov orbits

Figures 7 and 8 present the families of Lyapunov orbits with solar sail propulsion for both solar sail in-plane steering laws and both initial Sun-sail configurations. The colours indicate the required dimensionless solar sail characteristic acceleration required to maintain the orbit, with the plots on the right hand side showing the orbits for the largest sail acceleration for which the differential correction scheme converged. Crosses indicate the initial conditions: Fig. 7 provides the results for an initial Sun-sail configuration with \(\min ( x ( y = 0 ) ) \), while Fig. 8 provides the results for \(\max ( x ( y = 0 ) ) \). For conciseness, the latter family is only shown for the Sun-sail line steering law, but initial conditions for the Earth-Moon line steering law can be found in Fig. 5. Finally, the grey orbit is the classical Lyapunov orbit used to seed the continuation.

Fig. 7
figure 7

Lyapunov orbits with solar sail propulsion at \(L_{1}\) and \(L_{2}\) with \(\min(x(y=0))\) for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical Lyapunov orbit; crosses indicate the initial condition. (a) Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image
Fig. 8
figure 8

As Fig. 7b, but with \(\max(x(y=0))\)

Full size image

Table 1 already indicated that the period of this classical orbit is half the synodic lunar period. As a result, this orbit completes two full orbital revolutions per synodic lunar period. Within the differential correction scheme, the dynamics are therefore integrated forwards until the classical orbit crosses the \(( x,z ) \)-plane for the second time, i.e., after one full orbit revolution. From Figs. 7 and 8 it is clear that complementing the dynamics with a solar sail acceleration causes these two revolutions to displace and/or shrink/expand. While the Earth-Moon line steering law mainly displaces the two revolutions from the classical orbit, the Sun-sail line steering law also shrinks the first orbital revolution and expands the second orbital revolution for \(\min ( x (y = 0 ) ) \) and vice versa for \(\max ( x (y = 0 ) )\).

7.2 Solar sail Halo orbits

The families of halo orbits with solar sail propulsion are presented in a way similar to the solar sail Lyapunov orbits in the previous section. Figure 9 shows the results for \(\min ( x (y = 0 ) ) \) or \(z_{0} > 0\), while Fig. 10 shows the results for \(\max ( x (y = 0 ) ) \) or \(z_{0} < 0\) (only for the Sun-sail line steering law, details for the Earth-Moon line steering law can be found in Fig. 5). Note that the orbit families in the left columns of Figs. 9 and 10 are projections on the Earth-Moon plane, while the plots in the middle and right columns show a three-dimensional and \(( x,z ) \)-view of the orbit with the largest possible solar sail acceleration.

Fig. 9
figure 9

Halo orbits with solar sail propulsion at \(L_{1}\) and \(L_{2}\) with \(z_{0} >0\) for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical halo orbit; crosses indicate the initial condition. (a) Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image
Fig. 10
figure 10

As Fig. 9b but with \(z_{0}<0\)

Full size image

7.3 Solar sail vertical Lyapunov orbits

Figures 11 and 12 present the families of vertical Lyapunov orbits with solar sail propulsion at the \(L_{1}\) and \(L_{2}\) points, respectively, which is slightly different from the way the results were presented for the Lyapunov and halo orbits in Sects. 7.1 and 7.2. Furthermore, note that Figs. 11 and 12 only show the results for an initial Sun-sail configuration \(z_{0} > 0\) as, due to symmetry, the results for \(z_{0} < 0\) can be obtained by mirroring the orbits for \(z_{0} > 0\) in the \(( x,y ) \)-plane.

Fig. 11
figure 11

Vertical Lyapunov orbits with solar sail propulsion at \(L_{1}\) with \(z_{0} > 0\) for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical vertical Lyapunov orbit; crosses indicate the initial condition. (a) Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image
Fig. 12
figure 12

Vertical Lyapunov orbits with solar sail propulsion at \(L_{2}\) with \(z_{0} > 0\) for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical vertical Lyapunov orbit; crosses indicate the initial condition. Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image

7.4 Solar sail Earth-centred orbits

When adding a solar sail acceleration to the Earth-centred classical orbit of Fig. 3d, a range of interesting orbits appear, see Figs. 13 and 14 (all depicted in the synodic reference frame). The initially circular classical orbit is transformed into “flower-shaped” orbits with four petals. When displayed in a non-rotating (inertial) Earth-centred reference frame, these orbits appear as elliptical precessing orbits. Such flower-shaped orbits are not unique to the solar sail case as similar orbits also exist in the classical system, see Fig. 15 for a classical flower-shaped orbit family with seven petals. However, no classical “flower-shaped” orbits were found that have suitable periods to serve as initial guess for the differential correction scheme. It therefore seems that such orbits with a period equal to the synodic lunar period only exist with the addition of solar sail propulsion.

Fig. 13
figure 13

Earth-centred orbits with solar sail propulsion with \(\min(x(y=0))\) for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical Earth-centred orbit; crosses indicate the initial condition. (a) Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image
Fig. 14
figure 14

As Fig. 13b but with \(\max(x(y=0))\)

Full size image
Fig. 15
figure 15

Example of classical “flower-shaped” orbits. (a) Orbits. (b) Period

Full size image

7.5 Solar sail distant retrograde orbits

Section 5 showed that two classical DROs can serve as initial guess for the differential correction scheme and continuation, one with an orbital period of half the synodic lunar month and one with a period equal to \(1/3\) of the synodic lunar month. The results for both continuations are shown in Fig. 16 and Fig. 17 (\(\mathrm{DRO}_{1/2}\)) and Fig. 18 (\(\mathrm{DRO}_{1/3}\)). For the \(\mathrm{DRO}_{1/2}\) case, the two subfamilies with \(\min ( x ( y = 0 ) ) \) and \(\max ( x ( y = 0 ) ) \) seem to be almost mirror images of each other and create an ‘inner’ and ‘outer’ DRO loop which allow close fly-by passages of the Moon. For the \(\mathrm{DRO}_{1/3}\) case, another close fly-by passage of the Moon is added to each synodic lunar period. Note that Fig. 18 only includes results for \(\min ( x ( y = 0 ) ) \) as the differential corrector did not converge for any significant solar sail acceleration for the case \(\max ( x ( y = 0 ) ) \).

Fig. 16
figure 16

DROs with solar sail propulsion with \(\min(x(y=0))\), starting from classical \(\mathrm{DRO}_{1/2}\), for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical \(\mathrm{DRO}_{1/2}\); crosses indicate the initial condition. (a) Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image
Fig. 17
figure 17

As Fig. 16b but with \(\max(x(y=0))\)

Full size image
Fig. 18
figure 18

DROs with solar sail propulsion with \(\min(x(y=0))\), starting from classical \(\mathrm{DRO}_{1/3}\), for different values for \(a_{0,\mathrm{EM}}\); grey orbit is the classical \(\mathrm{DRO}_{1/3}\); crosses indicate the initial condition. (a) Earth-Moon line steering law. (b) Sun-sail line steering law

Full size image

8 Results for out of plane steering law

To generate families of out-of-plane periodic orbits with the steering laws defined in Eq. (5), two different continuations can be applied:

  1. (1)

    A continuation on \(\gamma \) for a fixed value of \(a_{0, \mathrm{EM}}\):

    Starting from one of the solar sail orbits created with an in-plane steering law and for a particular value of \(a_{0, \mathrm{EM}}\), a continuation on \(\gamma \) can be started in which the value for \(a_{0,\mathrm{EM}}\) is kept constant.

  2. (2)

    A continuation on \(a_{0,\mathrm{EM}}\) for a fixed value of \(\gamma \):

    Starting from the classical periodic orbits, a continuation on \(a_{0,\mathrm{EM}}\) can be started with a constant value for \(\gamma \).

With the large number of different solar sail enabled libration point families, both at \(L_{1}\) and \(L_{2}\), with different in-plane steering laws, with different initial Sun-sail configurations and now also two different methods for the out-of-plane continuation, presenting all possible families of out-of-plane solar sail enabled libration point orbits would be too elaborate. Therefore this section limits itself to two families for illustration purposes: (1) the first continuation method is applied to the Earth-centred orbits with an out-of-plane Earth-Moon steering law (i.e., the first steering law in Eq. (5)), considering both initial Sun-sail configurations. A constant value for the dimensionless solar sail acceleration \(a_{0,\mathrm{EM}}\) of 0.1 is chosen. (2) The second continuation method is applied to the family of DROs (starting from the classical \(\mathrm{DRO}_{1/2}\)) with an out-of-plane Sun-sail line steering law (i.e., the second steering law in Eq. (5)), again considering both initial Sun-sail configurations. A constant value for the out-of-plane pitch angle \(\gamma \) of 35.26° is chosen, which is known to give the maximum out-of-plane acceleration component (McInnes 1999).

The results are presented in Figs. 19 and 20, which show that solar sail propulsion can be used to extend families of solar sail enabled libration point orbits in the out-of-plane direction. More specifically, the results for the Earth-centred orbits in Fig. 19 show that the maximum out-of-plane motion is achieved for a pitch angle of \(\gamma = 27^{\circ}\) and \(26^{\circ}\) for \(\min ( x ( y = 0 ) ) \) and \(\max ( x ( y = 0 ) ) \), respectively. The value for \(\gamma \) of 26–27° is close to the pitch angle that gives the maximum out-of-plane acceleration component. Figure 19g furthermore shows that for a pitch angle of 90°, the solar sail orbits reduce to the classical orbit of Fig. 3d, because for that pitch angle the sail is oriented edge-wise to the Sun and cannot produce any acceleration. The results in Fig. 20 furthermore show that the DROs can also be extended in the out-of-plane direction, where larger sail accelerations achieve larger out-of-plane displacements, see Fig. 20g.

Fig. 19
figure 19figure 19figure 19

Family of out-of-plane Earth-centred orbits (\(a_{0,\mathrm{EM}}=0.1\)) with Earth-Moon line steering law. Colours indicate the out-of-plane pitch angle \(\gamma \) and crosses mark the initial condition. (a, c, e) Orbits for \(\min(x(y=0))\). (b, d, f) Orbits for \(\max(x(y=0))\). (g) Maximum out-of-plane displacement as a function of \(\gamma \)

Full size image
Fig. 20
figure 20figure 20figure 20

Family of out-of-plane DROs with solar sail propulsion (\(\gamma = 35.26^{\circ}\)) with Sun-sail line steering law, starting from classical \(\mathrm{DRO}_{1/2}\). Colours indicate the dimensionless solar sail characteristic acceleration and crosses mark the initial condition. (a, c, e) Orbits for \(\min(x(y=0))\). (b, d, f) Orbits for \(\max(x(y=0))\). (g) Maximum out-of-plane displacement as a function of \(a_{0,\mathrm{EM}}\)

Full size image

In general, what the results of this section show is that solar sail propulsion allows classical orbit families that exist only in the Earth-Moon plane to be extended in the out-of-plane direction.

9 Stability analysis

All classical libration point orbit families considered in this paper, with the exception of the Earth-centred and distant retrograde orbits, are known to be unstable. This section investigates how these stability properties change when adding solar sail propulsion to the dynamics. To assess this stability, use is made of the state transition matrix employed within the differential correction scheme. This state transition matrix predicts how a change in the initial conditions of the orbit effects the states at some later time \(t\). The state transition matrix evaluated after one full orbit, i.e., at time \(t = 2\pi /\varOmega_{S}\), is called the monodromy matrix and its eigenvalues, \(\lambda \), define the linear stability properties of the orbit. An orbit is stable if all six eigenvalues lie on the unit circle, i.e., \(\vert \lambda \vert _{\max } =1\). If the norm of any of the eigenvalues is larger than one, the orbit is unstable, with larger norm values indicating greater instability.

Considering the in-plane steering laws only, the results as shown in Fig. 21 can be obtained for each of the solar sail orbit families considered in this paper. Each plot gives the maximum norm of the eigenvalues as a function of the solar sail acceleration. For \(a_{0,\mathrm{EM}} = 0\) the figures show the stability of the classical orbits.

Fig. 21
figure 21

Maximum norm of the eigenvalues of the monodromy matrix for (a) Lyapunov, (b) halo, (c) vertical Lyapunov, (d) Earth-centred, and (e, f) distant retrograde orbits (starting from classical \(\mathrm{DRO}_{1/2}\) and \(\mathrm{DRO}_{1/3}\), respectively)

Full size image

For the families of solar sail Lyapunov and halo orbits a general trend can be observed where the solar sail acceleration further destabilises the orbits at the \(L_{1}\) point, while positively affecting the stability of the orbits at \(L_{2}\). For the family of vertical Lyapunov orbits, this positive effect can be observed for orbits both at the \(L_{1}\) and \(L_{2}\) points. Still, all orbits are unstable.

For the Earth-centred orbits and DROs, which are stable in the classical case, stability is sometimes maintained for small values of the dimensionless solar sail characteristic acceleration, but for larger values for \(a_{0,\mathrm{EM}}\) the orbits all become unstable. A similar effect can be observed for the family of out-of-plane solar sail orbits considered in Sect. 8, see Fig. 22. This effect is highly undesirable and active orbital control methods will have to be investigated to demonstrate the controllability and therefore long-term survivability of these orbits.

Fig. 22
figure 22

Maximum norm of the eigenvalues of the monodromy matrix for out-of-plane (a) Earth-centred and (b) distant retrograde orbits (see the orbits of Fig. 19 and Fig. 20, respectively)

Full size image

The only exception to the above is the family of Earth-centred orbits with an Earth-Moon solar sail steering law and initial Sun-sail configuration \(\max ( x ( y = 0 ) ) \). This orbit family is stable up to the maximum solar sail acceleration of \(a_{0,\mathrm{EM}} = 0.1\), see Fig. 21d. Even when extending these orbits in the out-of-plane direction, stability is maintained, see Fig. 22.

10 Applications and implementation

The wealth of orbits presented in this paper can serve a wide variety of space applications. For example, the out-of-plane Earth-centred orbits in Fig. 19 show potential for high temporal resolution observations of the high-latitudes of the Earth, thereby complementing current, high-spatial resolution observations from low-altitude high-inclination orbits. These orbits are just one example of how solar sail propulsion can be used to lift orbits out of the Earth-Moon plane, thereby opening up new design space choices in the three-dimensional state space. Other examples include the out-of-plane DROs of Fig. 20: the addition of a solar sail creates the opportunity to use these orbits for high-latitude observations of the Moon (e.g., for continuous observation of- and communication with the lunar South Pole). Similarly, by exploiting the solar sail’s out-of-plane acceleration component, the cross-point of the vertical Lyapunov orbits can be displaced above or below the Earth-Moon plane. Such a displacement removes the occultation which prohibits the use of classical vertical Lyapunov orbits for continuous communication with the far-side of the Moon.

In order for the orbits presented in this paper to be exploited for the abovementioned applications, a set of realistic mission design constraints needs to be considered. While the circular restricted three-body problem provides a suitable framework for the initial design of periodic orbits, real implementation will require these orbits to be transferred to a full ephemeris model to account for the eccentricity of the Moon’s orbit as well as the gravitational influence of celestial bodies other than the Earth and Moon. In addition, potential shadows introduced by the Earth and Moon should be considered as the periodic orbits rely fully on the availability of Sunlight. Finally, non-ideal surface properties of the solar sail, including optical imperfections and wrinkles, need to be accounted for as these result in a small tangential force component that has been shown to have an effect on the sail’s performance (Heiligers et al. 2014). While the turn rate of the sail is also often included in discussions related to the feasibility of orbital solutions (see for example Das-Stuart and Howell 2015), the turn rate will not impose any limitations on the implementation of the orbits presented in this paper. The two steering laws proposed in this paper, the Earth-Moon and Sun-sail line steering laws, require turning rates of 360° per synodic lunar month and 360° per year, respectively, which are both well within expected sail turning rates (Wie 2004), especially considering that the Sun-sail steering law can in theory be achieved passively through a correct offset between the sail’s centre of pressure and centre of mass.

In order to account for the effect of the full ephemeris model, shadowing and non-ideal solar sail properties, different approaches can be considered, including orbital control where the periodic orbits in the CR3BP serve as reference solution to be tracked. Alternatively, the orbits presented in this paper can serve as an initial guess for techniques such as multiple shooting differential correction algorithms (Parker and Anderson 2013) to find periodic orbits under high-fidelity dynamics.

11 Conclusions

By complementing the classical Earth-Moon circular restricted three-body dynamics with a solar sail acceleration, families of solar sail Lyapunov, halo, vertical Lyapunov, Earth-centred and distant retrograde orbits exist. Different families arise, depending on the chosen in-plane solar sail steering law and the selection of the initial condition, i.e., which \(( x,z ) \)-plane crossing of the orbit. With the Earth-Moon system being non-autonomous, a conventional differential correction has been adapted to allow the orbital period to be constrained to, in this case, the synodic lunar period, ensuring that all found solar sail orbits are repeatable over time. By considering out-of-plane steering laws, orbits that traditionally only exist in the Earth-Moon plane (e.g., the Earth-centred orbits) are extended in the out-of-plane direction. Finally, the linear stability of the orbit families presented in this paper shows that the solar sail acceleration can have a positive effect on the stability of the orbits (for the solar sail \(L_{2}\) Lyapunov, \(L_{2}\) halo, and all vertical Lyapunov orbits), but often further destabilises the orbits. For the libration point orbits that are stable in the classical system (Earth-centred and DROs), stability is maintained for small solar sail accelerations, but is lost for larger sail accelerations. This holds both for the in-plane and out-of-plane steering laws. Therefore, in most cases, active orbital control of the solar sail enabled libration point orbits will be required to ensure long-term survivability of these orbits.