Floquet modes and stability analysis of periodic orbit-attitude solutions along Earth–Moon halo orbits

Abstract

Future space programmes pose some interesting research problems in the field of non-Keplerian dynamics, being the Moon and the cislunar space central in the proposed roadmap for the future space exploration. In these regards, the deployment of a cislunar space station on a non-Keplerian orbit in the lunar vicinity is a fundamental milestone to be achieved. The paper investigates the natural orbit-attitude dynamics and the attitude stabilisation of coupled motions for extended bodies in the Earth–Moon system. The discussion is carried out analysing the phase space of natural dynamics, constituted by both the orbital and the rotational periodic motions of a spacecraft in cislunar orbits. Floquet theory is applied to periodic orbit-attitude solutions in lunar proximity, to characterise their attitude stability properties and their attitude manifolds, which are discussed and analysed focusing on their dynamical features applicable to cislunar environment. Attitude stabilisation methods are proposed and developed, with particular attention to spin-stabilised solutions. Periodic orbit-attitude dynamics are studied to highlight possible favourable conditions that may be exploited to host a cislunar space station with a simplified control action. The focus of the analysis is dedicated to halo orbits and near-rectilinear halo orbit in the circular restricted three-body problem Earth–Moon system.

1 Introduction

The global space exploration roadmap (ISECG 2018), which has been endorsed by the worldwide space agencies collaborating at the International Space Station (ISS) project, proposes the sustainable conquest of the Moon as the first fundamental step on the road to Mars and beyond. The deployment of the cislunar space gateway, which is a proposed habitable space outpost running on a non-Keplerian orbit in the lunar vicinity, constitutes one of the major milestones in the aforementioned roadmap and one of the most attractive challenges in the next decade of space exploration. Recent studies have selected elongated halo orbits and near-rectilinear halo orbit (NRHOs) as the most attractive staging orbit candidates for the cislunar space gateway, also known as Lunar Orbital Platform-Gateway (LOPG) (Williams et al. 2017). These classes of non-Keplerian orbits offer continuous line of sight coverage for communications with Earth, an easy access from the Earth with existing transportation systems and convenient descending/ascending trajectories with lunar surface (Whitley and Martinez 2016).

The proposed space gateway will be likely assembled in-orbit, by means of several automated Rendezvous and Docking (RVD) operations among its constituting massive modules (Crusan et al. 2019). The orbital properties of elongated halo orbits and near-rectilinear halo orbit (NRHOs) have been widely investigated in the literature, since the first introduction of these orbit families existing in the circular restricted three-body problem (CR3BP) model (Howell and Breakwell 1984). However, the complete $6^\circ$ of freedom (6DOF) orbit-attitude dynamics has been addressed only in recent years (Guzzetti and Howell 2016; Colagrossi and Lavagna 2017b). The accurate analysis of proximity operations for large space infrastructures cannot overlook the rotational motion, coupled with the orbital dynamics, in non-Keplerian cislunar space. This peculiar dynamical environment could unveil natural dynamics features that would dramatically increase the orbit-attitude manoeuvring capabilities of nowadays spacecraft, leading to the design of new space exploration and scientific missions with strict control effort requirements.

In the existing literature, several studies have investigated the attitude stability of a spacecraft fixed at the libration points in the CR3BP (Kane and Marsh 1971; Robinson 1974), or of an axis-symmetric spinning spacecraft moving on planar non-Keplerian orbits (Hitzl and Levinson 1979). Euler parameters have been introduced to study the rotational dynamics of a single body located at one of the Lagrangian points by Abad, Arribas and Elipse (Abad et al. 1989). More recently, Brucker and Gurfil (Brucker and Gurfil 2007) have focused their attention to the attitude dynamics of a spacecraft in the vicinity of equilibrium points using Poincaré maps, while linear approximations of non-Keplerian orbits have been used by Wong, Patil and Misra (Wong et al. 2008).

In the last few years, the coupling between the orbital and attitude motions has been investigated within the simplified dynamical environment of the CR3BP, considering both planar and three-dimensional motions in non-Keplerian dynamics, providing different families of periodic orbit-attitude solutions (Knutson et al. 2015; Guzzetti and Howell 2016; Colagrossi and Lavagna 2017b). In the same decade, Meng, Hao and Chen (Meng et al. 2014) proposed a semi-analytical approach to conduct stability analyses of a dual-spin spacecraft running along a family of halo orbits, identifying periodic dynamical modes.

The paper presents a brief introduction on the orbit-attitude dynamical model based on the CR3BP formulation and it describes representative families of periodic orbit-attitude solutions existing in the Earth–Moon system. Particular attention is dedicated to halo and NRHO families. Next, the concept of manifolds, which has been widely explored in the classical CR3BP, is extended to the attitude dynamics in the coupled CR3BP, as preliminary introduced in a previous work of the authors (Colagrossi and Lavagna 2017a). The Floquet theory is applied to orbit-attitude families of cislunar halo orbits and NRHOs to characterise their attitude stability and their attitude manifolds natural structures. Finally, attitude stabilisation methods are proposed and developed considering the crucial limitation in the consumption of non-recoverable resources, such as propellants, applicable to the future cislunar gateway. Single-spin and dual-spin solutions are applied to stabilise the attitude behaviour of a generic spacecraft on some representative periodic motions in the orbit-attitude CR3BP. The stabilisation action with spinning spacecraft or with constant speed reaction wheels reduces the required intervention of an active attitude control logic. The numerical results of natural and stabilised dynamics are critically illustrated and relevant operational outcomes are stated.

2 Dynamical model and assumptions

The paper discusses the orbit-attitude behaviours of large spacecraft orbiting on particular non-Keplerian orbits, existing in the cislunar space, under the combined gravitational action of the Earth and the Moon. The investigation is focused on the absolute natural dynamics experienced in this peculiar dynamical environment, with particular attention to the stability of the motion. The absolute orbit-attitude dynamics is based on the CR3BP formulation, which is used as a base to derive the subsequent relative dynamics.

2.1 CR3BP orbit-attitude motion

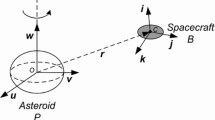
The CR3BP is the simplest orbital model able to catch the attractive non-Keplerian orbits existing near Lagrangian Points. The Euler’s equations of motion are added to the CR3BP dynamics in order to obtain a coupled model able to link the rotational motion of the spacecraft with its orbit in cislunar environment. The CR3BP model simplifies the motion of three bodies with masses $m_B$, $m_1$ and $m_2$. The spacecraft is assumed as a rigid body with negligible mass, $m_B \ll m_1, m_2$; the primaries have mass $m_1$ and $m_2$ and move on circular orbits about their common barycentre, O, with constant angular velocity $\omega _s$. The framework employed in this paper for the analysis of the coupled orbit-attitude dynamics of the spacecraft is represented in Fig. 1. A rotating synodic frame, $\{{\hat{r}}\} = \{ \varvec{{\hat{x}}}, \varvec{{\hat{y}}}, \varvec{{\hat{z}}} \}$, is conveniently defined to analyse the motion of the spacecraft with mass $m_B$.

Fig. 1

Orbit-attitude absolute and relative model

The synodic $\{{\hat{r}}\}$-frame is a non-inertial frame centred at the barycentre of the system, O. It is aligned with the reference inertial frame, $\{{\hat{i}}\} = \{ \varvec{{\hat{X}}}, \varvec{{\hat{Y}}}, \varvec{{\hat{Z}}} \}$, at time $t=0$. The $\varvec{{\hat{x}}}$-axis is directed from $m_1$ to $m_2$ and the $\varvec{{\hat{z}}}$-axis is in the direction of the angular velocity of the primaries, $\varvec{\omega _s} = \omega _s \varvec{{\hat{z}}}$, while the $\varvec{{\hat{y}}}$-axis completes the right-handed triad. The equations of motion can be conveniently normalised via the definition of characteristic quantities, so that the distance between the two primaries, $l^* = r_{12}$, the synodic angular velocity, $\omega _s$, and the total mass of the system, $m^* = m_1 + m_2$, are unitary in non-dimensional units (symbol [ndim]). As a consequence of the normalisation, the non-dimensional orbital period of the primaries is $T_p=2\pi$, while the non-dimensional time t represents the angle $\theta$ that the rotating $\{{\hat{r}}\}$-frame has covered from $t = 0$, as shown in Fig. 1. A time interval equal to ${1}\hbox { ndim}$ corresponds to $\sim {4.45}\hbox { d}$ (i.e. terrestrial days). Finally, thanks to this normalisation, the system is uniquely described by the mass parameter $\mu$:

$$\begin{aligned} \mu = \frac{m_2}{m_1 + m_2}. \end{aligned}$$

(1)

The absolute orbital states, $\varvec{x_\mathrm{{orb}}} = \{{\varvec{r}}; {\varvec{v}}\}$, describe the position and the velocity of the centre of mass of the spacecraft, which are expressed in the rotating synodic $\{{\hat{r}}\}$-frame. The body-fixed frame of the spacecraft, $\{{\hat{b}}\} = \{\varvec{{\hat{b}}_1}, \varvec{{\hat{b}}_2}, \varvec{{\hat{b}}_3}\}$, has been defined to model the rotational dynamics. It is located at the centre of mass of the spacecraft and it is aligned with its principal inertia directions. The attitude quaternion, $^{i}{\varvec{q}}^{b} = \{ q_1; q_2; q_3; q_4 \}_i$, parametrises the orientation of the body-fixed frame with respect to the reference inertial $\{{\hat{i}}\}$-frame. The angular rates of the body relative to the inertial $\{{\hat{i}}\}$-frame, $^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}} = \{ \omega _1; \omega _2; \omega _3 \}$, which are expressed in the body-fixed $\{{\hat{b}}\}$-frame, complete the attitude states of the spacecraft.

The model employed in this analysis assumes the sole gravitational presence of the two primaries, i.e. the Earth and the Moon. This assumption has been already justified in previous works of the authors (Colagrossi and Lavagna 2017a, b; Colombi 2019), where the perturbation effect of the attitude motion on the orbital dynamics is assumed negligible for nowadays and near-future spacecraft. The order of magnitude of the net perturbation force, which is exerted on a spacecraft due to its finite extended dimension, with respect to its point-mass simplification is proportional to the following relation:

$$\begin{aligned} \Vert {\varvec{f}}_{\mathrm{{pert}}_i}\Vert \sim \left( \frac{l^\star _\mathrm{{SC}}}{r_i}\right) ^2, \quad \text {where} \quad l^\star _\mathrm{{SC}} = \sqrt{\max (I_{i}) / m_B}. \end{aligned}$$

(2)

The term $l^\star _\mathrm{{SC}}$ represents the characteristic length of the spacecraft, associated with the ratio between the largest among the moments of inertia of the spacecraft, $I_{i}$, and its mass, $m_B$; while $r_i$ is the distance from the i-th primary body. For example, considering a spacecraft with characteristic length equal to 100 meters, the perturbation magnitude would range from $\mathcal {O}(10^{-9})$ (at perilune of an NRHO) to $\mathcal {O}(10^{-12})$ (at apolune of an NRHO). This perturbation of the attitude dynamics on the orbital motion is many orders of magnitude lower with respect to other perturbation sources in the Earth–Moon system, such as the gravitational presence of the Sun (Bucci 2020). Thus, the orbital dynamics has been modelled via the classical CR3BP equations, while the rotational dynamics are solely driven by the gravity gradient torques acting on the spacecraft due to the two primaries.

By defining $r_1$ and $r_2$ as the distances of the generic spacecraft from the first and the second primary, respectively, the classical CR3BP dynamical equations are defined as follows:

$$\begin{aligned} \varvec{f_{\text {CR3BP}}} = {\left\{ \begin{array}{ll} {\dot{x}} = &{} v_x \\ {\dot{y}} = &{} v_y \\ {\dot{z}} = &{} v_z \\ {\dot{v}}_x = &{} x + 2v_y - \frac{(1-\mu )(x+\mu )}{{r_1}^3} - \frac{\mu (x-1+\mu )}{{r_2}^3}\\ {\dot{v}}_y = &{} y - 2v_x - \frac{(1-\mu )y}{{r_1}^3} - \frac{\mu y}{{r_2}^3}\\ {\dot{v}}_z = &{} - \frac{(1-\mu )z}{{r_1}^3} - \frac{\mu z}{{r_2}^3} \end{array}\right. }. \end{aligned}$$

(3)

Quaternions, also known as Euler parameters, are commonly exploited in the field of space applications for numerical simulation of the attitude dynamics because they avoid the gimbal lock singularity, which is present in Euler angles representation. A quaternion is a four-dimensional representation of the attitude, which results in algebraic expressions for the elements of the rotation matrix. Quaternions are related to the eigenvalues and the eigenvectors of the corresponding direction cosine matrix, physically describing the Euler axis and the Euler angle of rotation of the body-fixed frame with respect to the inertial reference frame. The attitude kinematics for the quaternion of the body-fixed frame is expressed through the following differential equations, and it is a function of the quaternion elements and of the angular velocity of the spacecraft expressed in $\{{\hat{b}}\}$-frame:

$$\begin{aligned} {\varvec{f}}_q = {\left\{ \begin{array}{ll} {\dot{q}}_1 = &{} \frac{1}{2} \left( \omega _3 q_2 - \omega _2 q_3 + \omega _1 q_4 \right) \\ {\dot{q}}_2 = &{} \frac{1}{2} \left( - \omega _3 q_1 + \omega _1 q_3 + \omega _2 q_4 \right) \\ {\dot{q}}_3 = &{} \frac{1}{2} \left( \omega _2 q_1 - \omega _1 q_2 + \omega _3 q_4 \right) \\ {\dot{q}}_4 = &{} \frac{1}{2} \left( -\omega _1 q_1 - \omega _2 q_2 - \omega _3 q_3 \right) \end{array}\right. }. \end{aligned}$$

(4)

The numerical integration of the quaternion kinematics equation allows to determine the orientation profile of the spacecraft as a function of time t. During the numerical integration, the quaternion constraint has to be always satisfied:

$$\begin{aligned} {q_1}^2 + {q_2}^2 + {q_3}^2 + {q_4}^2 = 1. \end{aligned}$$

(5)

The Euler’s equations of motion describe the rotational dynamics driven by the gravity gradient torques of the two primaries acting on the spacecraft:

$$\begin{aligned} {\varvec{f}}_\omega = {\left\{ \begin{array}{ll} {\dot{\omega }}_1 = \frac{I_3-I_2}{I_1} \left( \frac{3(1-\mu )}{{r_1}^5} \, g_2 g_3 +\frac{3\mu }{{r_2}^5} \, h_2 h_3 - \omega _2\omega _3 \right) \\ {\dot{\omega }}_2 = \frac{I_1-I_3}{I_2} \left( \frac{3(1-\mu )}{{r_1}^5} \, g_1 g_3 +\frac{3\mu }{{r_2}^5} \, h_1 h_3 - \omega _1\omega _3 \right) \\ {\dot{\omega }}_3 = \frac{I_2-I_1}{I_3} \left( \frac{3(1-\mu )}{{r_1}^5} \, g_1 g_2 +\frac{3\mu }{{r_2}^5} \, h_1 h_2 - \omega _1\omega _2 \right) \end{array}\right. }. \end{aligned}$$

(6)

In this formulation, the orientation of the spacecraft is represented by the terms $g_i$ and $h_i$, which represent the direction cosines of the radial vectors, ${\varvec{r}}_1$ and ${\varvec{r}}_2$, respectively, going from the first and the second primary to the spacecraft, expressed in the body-fixed frame. Moreover, the inertia properties of the spacecraft directly influence the natural rotational dynamics through the inertia ratios $K_1=\frac{I_3-I_2}{I_1}$, $K_2=\frac{I_1-I_3}{I_2}$ and $K_3=\frac{I_2-I_1}{I_3}$. The rotational dynamics in (6) are normalised thanks to the characteristic quantities describing the CR3BP in order to obtain the complete set of orbit-attitude dynamical equations expressed in the same non-dimensional units (i.e. [ndim]). The propagation of the non-dimensional dynamical system, using (3), (4), (6), allows to predict the absolute 6DOF motion of a spacecraft in cislunar space.

Once the absolute 6DOF dynamics of the spacecraft is available, the relative orbit-attitude dynamics with respect to a reference state can be obtained thanks to relative 6DOF kinematic relations (Colagrossi and Lavagna 2018; Bucci et al. 2018). The relative position state can be simply obtained by differentiating the absolute states, while the relative attitude quaternion $\varvec{q_\mathrm{{rel}}}$ can be obtained by applying the rule of successive rotation for quaternions (Markley and Crassidis 2014):

$$\begin{aligned} \varvec{q_\mathrm{{rel}}}(t) = \left( {^{{\hat{i}}}\varvec{q_\mathrm{{ref}}}^{{\hat{b}}}}(t)\right) ^{-1} \odot \, ^{{\hat{i}}}{\varvec{q}}^{{\hat{b}}}(t), \end{aligned}$$

(7)

where ${^{{\hat{i}}}\varvec{q_\mathrm{{ref}}}^{{\hat{b}}}}(t)$ is the quaternion of the reference attitude state.

Finally, the relative angular velocity $\varvec{\omega _\mathrm{{rel}}}$ with respect to the reference periodic solution is defined in the fixed-body $\{{\hat{b}}\}$-frame as follows:

$$\begin{aligned} \varvec{\omega _\mathrm{{rel}}}(t) = \,^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}(t) - [C_\mathrm{{rel}}] \, ^{{\hat{i}}}\varvec{\omega _\mathrm{{ref}}}^{{\hat{b}}}(t), \end{aligned}$$

(8)

where $^{{\hat{i}}}\varvec{\omega _\mathrm{{ref}}}^{{\hat{b}}}$ is the reference angular velocity. The rotation matrix $[C_\mathrm{{rel}}]$ is defined as the direction cosine matrix associated with the quaternion $\varvec{q_\mathrm{{rel}}}$. It should be remarked that this equation is valid for both the dimensional and non-dimensional definitions of the angular velocity.

2.2 Libration point orbits

A periodic orbit-attitude solution in the coupled CR3BP is defined as the continuity between the initial and the final conditions, in both orbital and attitude states, as seen by an observer standing in the rotating synodic $\{{\hat{r}}\}$-frame (Guzzetti and Howell 2016; Colagrossi and Lavagna 2017b). A periodic orbit-attitude Libration Point Orbit (LPO) can be identified by a set of twelve independent orbit-attitude states:

$$\begin{aligned} \varvec{X_0} = \left[ x; y; z; v_x; v_y; v_z; q_1; q_2; q_3; \omega _1; \omega _2; \omega _3 \right] , \end{aligned}$$

(9)

plus the orbital period T. Note that only three quaternion elements are necessary to identify the orientation of the spacecraft, because the fourth is obtained directly by the quaternion constraint relation in (5) (Guzzetti and Howell 2016). Once the initial condition of a periodic solution is selected, the non-dimensional time $t \in [0, T]$ allows to identify any point along that orbit.

These natural orbit-attitude behaviours could open the door to new concept mission design. Slowly diverging or marginally stable rotational behaviours may be exploited to define attitude configurations for space infrastructure, such as crewed habitats in lunar proximity, or micro spacecraft with low control capabilities.

Considering symmetric or quasi-symmetric spacecraft structures, their equivalent shape can be characterised with the ratio between the transversal, $I_\mathrm{{t}}$, and the axial, $I_\mathrm{{a}}$, principal moments of inertia: $K_\mathrm{{a}} = I_\mathrm{{t}}/I_\mathrm{{a}}$. Hence, in these cases, the parameters determining the attitude behaviour of a family of orbit-attitude solutions in the CR3BP are: the characteristic dimensions of the system, the type of orbit, the initial orientation of the axial axis, the shape of the spacecraft reflected by its inertia ratios, the axis of rotation and the number of rotations of the spacecraft during one orbital period, n-spin. If the periodic solution shows an attitude which is oscillating about the synodic $\{{\hat{r}}\}$-frame, it is labelled as “librating attitude” solution (i.e. n-spin $=0$). Otherwise, the attitude behaviour is labelled as “spinning” solution when the rotational behaviour shows finite rotations about a certain axis (i.e. n-spin $\ge 1$).

For example, a set of orbit-attitude periodic solutions constituting a family of Earth–Moon $L_1$ northern near-rectilinear halo orbit NRHOs, with librating attitude behaviour about the synodic $\{{\hat{r}}\}$-frame, is reported in Figs. 2 and 3. The trajectories have been propagated for one orbital period starting from the apolune at time $t=0$. The orbit with the largest vertical amplitude, $A_z$, has been highlighted in black and it is used as a reference for comparison in the corresponding behaviour of attitude evolution. These results refer to a spacecraft having the axis of symmetry aligned to $\varvec{{\hat{b}}_1}$, and an equivalent cylinder-like shape, with inertia ratio $K_\mathrm{{a}} = I_\mathrm{{t}}/I_\mathrm{{a}} = 0.7$. This value of $K_\mathrm{{a}}$ is realistic for space structures with large solar panels. For example, the ISS has an inertia ratio $K_\mathrm{{a}} \sim 0.6$ (Carter et al. 1997; NASA 2008), which makes its equivalent inertia shape slightly flatter and more similar to a disc-like shape. A higher inertia ratio $K_\mathrm{{a}}$ has been assumed because the proposed lunar gateway and other spacecraft typically have more elongated cylinder-like shapes (Crusan et al. 2019).

Fig. 2

Orbital motion of the periodic orbit-attitude Earth–Moon $L_1$ Northern NRHO family with vertical amplitude $A_z\in [73-89]\times 10^3\,\hbox {km}$ and period $T\in [7.8-9.6]\,\hbox {d}$. Reference initial condition at $t=0$, corresponding to apolune, with ${\varvec{r}}(0)=[0.930,0.000,0.231]\mathrm {[ndim]}$ and ${\varvec{v}}(0) = [0.000,0.103,0.000]\mathrm {[ndim]}$. The Moon position is indicated with a grey dot

Fig. 3

Attitude evolution with inertia ratio $K_\mathrm{{a}} = 0.7$ of the periodic orbit-attitude Earth–Moon $L_1$ Northern NRHO family. Librating reference initial condition at $t=0$, corresponding to apolune, with $^{{\hat{i}}}{\varvec{q}}^{{\hat{b}}}(0)=[-0.074,0.128,0.009,0.988]$ and $^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}(0) = [-0.137,-0.091, 0.608]\mathrm {[ndim]}$. Vertical dashed lines indicate the perilune crossing event for the reference solution

The history of the quaternion of the body-fixed frame relative to the synodic $\{{\hat{r}}\}$-frame, $^{{\hat{r}}}{\varvec{q}}^{{\hat{b}}}$, in Fig. 3a, shows, through the quite constant value of its fourth quaternion component $q_{r4}$, the librating attitude behaviour associated with the presented family. The angular velocity reported in Fig. 3b is evaluated with respect to the inertial reference frame; the component along the $\varvec{\hat{z}}$ synodic axis has an offset of 1 in non-dimensional units, because of the rotational motion of the synodic frame with respect to the inertial one. Thus, a velocity component $^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}_z= {1}\hbox { nd}$ in inertial frame is equivalent to $^{{\hat{r}}}\varvec{\omega }^{{\hat{b}}}_z={0}\hbox { nd}$ in synodic frame.

The corresponding attitude motion, followed by the spacecraft along a reference member of the orbit-attitude NRHO family, can be visualised in Fig. 4. The axes of the body-fixed frame have been drawn with small arrows for locations equally spaced in time along the periodic solution.

Fig. 4

Spacecraft’s body frame rotational motion along the reference NRHO solution

These 6DOF periodic librating solutions have been found by employing a multiple-shooting differential corrector algorithm, which has been developed to address coupled orbit-attitude problems in the framework of the CR3BP (Guzzetti and Howell 2016; Colagrossi and Lavagna 2017b; Colombi 2019). The differential corrector enforces the continuity at the patch points along the 6DOF trajectory and the periodicity after a period T (i.e. the initial state shall coincide with the final one). The initial guess for the periodic librating attitude motion has, at $t=0$, null angular velocity in the $\{{\hat{r}}\}$-frame and the body-fixed $\{{\hat{b}}\}$-frame aligned with the synodic $\{{\hat{r}}\}$-frame. When a first periodic solution is available, a pseudo arc-length continuation algorithm can be used to extend the orbit-attitude family, generating other periodic solutions with constant spacecraft parameters (Doedel et al. 2007). The differential corrector algorithm can also be used to continue the family in other phase space directions by exploiting a single-parameter continuation method. For instance, the inertia ratios of the spacecraft can be varied, or initial spinning dynamics can be studied. The latter will be discussed in Sect. 4.

The near-rectilinear halo orbit NRHOs are featured by a quasi-planar orbital path and close passages about the secondary attractor, namely the Moon. NRHOs are known to exhibit nearly stable behaviour favourable for orbital station-keeping (Howell and Breakwell 1984; Guzzetti et al. 2017). They offer constant communication contact with Earth and high visibility time of lunar South or North pole. In fact, they resemble some sort of high polar orbit of the Moon which is synchronously aligned to the synodic $\{{\hat{r}}\}$-frame. Moreover, they avoid lengthy eclipses of the Sun by the Earth, maximising the possibility of solar energy generation. Finally, the costs to reach the NRHO from the Earth are not prohibitive, both in propellant and transfer time, and those orbits may offer an easy transfer link to and from the lunar surface. All these features, analysed in the work of Whitley and Martinez (Whitley and Martinez 2016), make the near-rectilinear halo orbit NRHOs a very attractive choice as staging orbits for the future cislunar space station. However, the closer passage to the Moon results in a significant rising of the angular acceleration acting on the spacecraft. This is reflected with a sharp variation of the angular velocity, as can be seen in Fig. 3b. Orbits with larger vertical amplitude have a closer perilune passage and, therefore, a higher angular acceleration. This effect is a typical feature of periodic orbit-attitude solutions along near-rectilinear halo orbit NRHOs (Colagrossi and Lavagna 2017b).

3 Orbit-attitude Floquet modes

The LPOs are periodic solutions of the dynamical system describing the orbit-attitude CR3BP. Peculiar natural dynamical structures exist around these periodic solutions. In the classical CR3BP, trajectories belonging to the invariant manifolds have been widely explored in their absolute point of view, such as for applications in low-energy transfer studies. In this investigation, invariant manifolds are employed as a primary tool to investigate the dynamics characterising the LPOs, as well as the relative orbit-attitude motion in their immediate proximity.

According to the Floquet theory, the stability information and the local direction of the invariant manifolds constituting the eigenstructure surrounding the neighbourhood of a reference periodic solution are embedded into the State Transition Matrix (STM) over a full period T, also known as the monodromy matrix. It should be noticed that the monodromy matrix ${\tilde{\varPhi }}(T,0)$ has to fully reflect the point of view of a rotating observer in the synodic $\{{\hat{r}}\}$-frame in order to catch the periodicity behaviour of the orbit-attitude LPOs, even though the attitude state variables are expressed with respect to the inertial $\{{\hat{i}}\}$-frame (Guzzetti 2016).

In the most general case, the monodromy matrix $\mathbf {M} = {\tilde{\varPhi }}(T,0)$ results as a full 12-by-12 matrix:

$$\begin{aligned} \mathbf {M} = \begin{bmatrix} \mathbf {M}_{Orb} &{} \mathbf {M}_\mathrm{{OrbAtt}} \\ \mathbf {M}_\mathrm{{AttOrb}} &{} \mathbf {M}_\mathrm{{Att}} \\ \end{bmatrix}. \end{aligned}$$

(10)

Each block is a 6-by-6 matrix. The block $\mathbf {M}_\mathrm{{AttOrb}}$ represents the influence of the orbital motion on the attitude dynamics depending by the gravity gradient torque. The cross-coupling block $\mathbf {M}_\mathrm{{OrbAtt}}$ represents the influence of the attitude motion on the orbital dynamics. According to the model simplification, not considering the variational effect on the gravitational pull exerted by the primaries on the spacecraft due to its finite dimensions, this inertial cross-coupling direction results in $\mathbf {M}_\mathrm{{OrbAtt}} = [{\varvec{0}}]_{6 \times 6}$ and the monodromy matrix becomes a lower triangular block matrix. Thus, the eigenvalues $\lambda _j$ of $\mathbf {M}$ corresponds to the set of eigenvalues belonging to the two matrices on the diagonal, $\mathbf {M}_\mathrm{{Orb}}$ and $\mathbf {M}_\mathrm{{Att}}$. In this investigation, they are, respectively, denoted as orbital eigenvalues and attitude eigenvalues. It should be noticed that, if the model includes the cross-coupling term between the attitude states and the orbital dynamics, the eigenvalues would show a displacement in the complex plane with respect to the eigenvalues which are obtained in the simplified model. This displacement is an alternative index of influence representing the impact of the cross-coupling behaviour driving the two-way coupled motion. If this displacement becomes not negligible, the coupling is reflected in the eigenvector components. In this case, the classification of eigenvalues and eigenvectors in separate orbital and attitude categories cannot be performed. This could happen in problems where the characteristic dimensions of the spacecraft are comparable to the dimensions of system constituted by the primaries, such as in asteroid missions.

For a periodic orbit-attitude solution, there is always a pair of trivial eigenvalues equal to plus (or minus) one, for both orbital and attitude modes. They represent the periodicity behaviour of the LPO in the orbital and the attitude states. The remaining two pairs, in both orbital and attitude modes, may appear as real or complex eigenvalues/eigenvectors. They feature the stability properties (e.g. stable, unstable and quasi-periodic behaviours) of the orbit-attitude LPO and of the natural dynamical structure surrounding its vicinity.

A stability index $\nu$ can be defined, analogously to previous literature (Guzzetti and Howell 2016; Meng et al. 2014), to synthesise the stability information associated with each pair of eigenvalues obtained from the monodromy matrix $\mathbf {M}$:

$$\begin{aligned} \nu _i = \frac{1}{2} \left( \Vert \lambda _i\Vert + \frac{1}{\Vert \lambda _i\Vert } \right) . \end{aligned}$$

(11)

The dominant eigenvalue of the dynamics corresponds to $\lambda _\mathrm{{max}}=\max {\left\Vert \lambda _i\right\Vert }$. If all the eigenvalues lay on the unit circle, each stability index results $\nu _i = 1$, and the periodic solution is marginally stable. On the contrary, if the dominant eigenvalue of the dynamics $\lambda _\mathrm{{max}}=\max {\left\Vert \lambda _i\right\Vert }$ is higher than one, the periodic solution is unstable and at least one couple of stable/unstable mode exists. An orbit-attitude LPO may result in marginally stable orbital and attitude motions (i.e. $\nu = 1$). Alternatively, either the orbital or the attitude dynamics may be marginally stable, otherwise neither of them would be.

Focusing the analysis on the attitude stability, only the attitude part of the monodromy matrix, $\mathbf {M}_{Att}$, is taken into account (n.b. the same can be done for the orbital part):

$$\begin{aligned} \mathbf {M}_\mathrm{{Att}}=\begin{bmatrix} M_{qq} &{} M_{q\omega }\\ M_{\omega q} &{} M_{\omega \omega }\\ \end{bmatrix}. \end{aligned}$$

(12)

Each sub-matrix $M_{ij}$ is a 3-by-3 matrix. The terms $M_{qq}$ and $M_{q\omega }$ are, respectively, the blocks of the monodromy matrix representing the influence of quaternion and angular velocity on the attitude quaternion periodicity. Similarly, the terms $M_{\omega q}$ and $M_{\omega \omega }$ represent the respective influence of quaternion and angular velocity on the angular velocity periodicity. The attitude modes are associated with the eigenstructure of $\mathbf {M}_\mathrm{{Att}}$, which is composed by 6 eigenvalues $\lambda _\mathrm{{att}_i}$. Those with magnitude less than one are related to stable modes, while those with magnitude greater than one correspond to unstable modes. Attitude eigenvalues with $\left\Vert \lambda _\mathrm{{att}_i}\right\Vert =1$ are paired to marginally stable modes. As a consequence, if $\left\Vert \lambda _\mathrm{{att}_i}\right\Vert \le 1$ for any i, the periodic attitude solution is marginally stable. On the contrary, if at least one $\left\Vert \lambda _\mathrm{{Att}_i}\right\Vert > 1$, the periodic solution is unstable. A dedicated attitude stability index, $\nu _\mathrm{{att}}$, is defined analogously to the classic stability index $\nu$:

$$\begin{aligned} \nu _\mathrm{{att}} = \frac{1}{2} \left( \Vert \lambda _\mathrm{{att}_\mathrm{{max}}}\Vert + \frac{1}{\Vert \lambda _\mathrm{{att}_\mathrm{{max}}}\Vert } \right) . \end{aligned}$$

(13)

The larger the value of the stability index (i.e. $\nu _{att}$ or $\nu$) is the more the evolution of a small perturbation of the nominal solution would likely result in a faster departure behaviours from the reference LPO Perko (2001). Note that the separation between attitude and orbital stability can be done only if the assumption of one-way inertial coupling holds, otherwise the eigenvalues and eigenvectors cannot be separately identified for orbital and attitude motions.

Each orbital and attitude eigenmode $\varvec{e_j}$ obtained from the monodromy matrix $\mathbf {M}$ is a 12-dimensional vector which represents the “local” direction of the corresponding invariant manifold surrounding the nominal reference solution.

$$\begin{aligned} \varvec{e_j} = \left[ \delta x; \, \delta y; \, \delta z; \, \delta v_x; \, \delta v_y; \, \delta v_z; \, \delta q_1; \, \delta q_2; \, \delta q_3; \, \delta \omega _1; \, \delta \omega _2; \, \delta \omega _3 \right] . \end{aligned}$$

(14)

The first six elements describe the direction of the Floquet mode in the orbital space, while the last six elements represent the direction in the attitude space. It should be highlighted that the six orbital modes include a significant component in both the orbital and the attitude subspace due to the inertial cross-coupling determined by the gravity gradient torque. The remaining six attitude modes are solely constituted by the attitude component. Again, the existence of these purely attitude modes is directly linked to the adopted simplification of the dynamical model, where attitude variation does not affect the trajectory of the spacecraft.

The “global” invariant manifolds can be approximated in the proximity of the nominal reference solution via their “local” directions (Perko 2001). The propagation of the dynamics starting from the “local” eigenstructure discover the approximated “global” surfaces of the corresponding manifolds. Even if the space surface of each orbit-attitude manifolds is 12-dimensional, it can be travelled only in a particular direction which are identified by the corresponding mode. Therefore, the numerical method to identify the region belonging to each manifold is based on the discretisation of their eigenstructure and it can be summarised via the following steps:

• 1. Discretisation of the nominal orbit-attitude periodic solution in n points;

• 2. Evaluation of the “local” direction of the desired orbital or attitude mode (i.e. stable, unstable, periodic, centre) at each discretised point;

• 3. Perturbation of the nominal solution in the 12-dimensional space along the “local” direction of the mode;

• 4. Propagation in time (forward or backward) of the natural dynamics from the perturbed initial condition to obtain the numerical approximation of the trajectory constituting the invariant manifold.

It should be highlighted that the presented algorithm can be applied for both orbital and attitude modes. Only the perturbation magnitude has to be tuned in order to obtain a representative approximation of the “local” direction of the manifold. Moreover, this algorithm can also be implemented in problems where the orbit and attitude behaviours are fully coupled in the dynamics, e.g. asteroids mission or large area-to-mass ratio sailcraft (Guzzetti et al. 2019), where the monodromy matrix ${\varvec{M}}$ is not simplified as lower triangular.

The orbital modes (labelled as “orb-”) can be related to the invariant manifolds discussed in the classical CR3BP literature, even if the current investigation is extended to the coupled rotational dynamics as well. These orbital modes have been applied for 6DOF rendezvous to non-Keplerian orbit in a previous work of the authors (Colombi et al. 2021). The natural attitude motion is synchronised with the periodic solution, if the orbit-attitude dynamics is evolving on orbital manifolds close to the reference trajectory. The distance threshold to keep the synchronisation has been found in the order of few hundreds of kilometres considering large-amplitude halo orbits in the Earth–Moon system.

The attitude modes (labelled as “att-”) are the focus of the analyses in this investigation, to highlight representative rotational behaviours which develop in the surrounding of periodic orbit-attitude LPOs, and to extrapolate useful information for the attitude stabilisation design.

3.1 Attitude modes of cislunar NRHO

Analyses on the natural attitude modes are relevant to investigate the stability of the periodic orbit-attitude solutions. Moreover, their results allow to better characterise the 6DOF relative motion, with respect to a reference periodic trajectory, highlighting the attitude contribution to the coupled natural dynamics.

The analysis on attitude modes can be performed on any family of periodic orbit-attitude solutions in the orbit-attitude CR3BP. However, because of its practical relevance, the investigation starts from the linear stability analysis of the attitude dynamics for a reference family of periodic orbit-attitude near-rectilinear halo orbit NRHOs, which is reported in Fig. 5.

Fig. 5

Stability analysis of the orbit-attitude Earth–Moon $L_1$ Northern NRHO family as a function of the vertical amplitude $A_z$. The points highlighted with a different colour and a vertical line refer to the reference solution discussed in Sect. 3.1

The attitude stability index, $\nu _\mathrm{{att}}$, rises as the member of the NRHO family increases its vertical amplitude, $A_z$. Therefore, the periodic librating attitude motion becomes more sensitive to instability perturbations, as the orbit of the NRHO family has a closer perilune passage. Moreover, near-rectilinear halo orbit NRHOs are likely to have two pairs of stable/unstable attitude modes with comparable magnitude in their eigenvalues. In Fig. 5b is also observed an eigenvalue bifurcation at $A_z \! \simeq \! 80 \times \! 10^3$ km, which leads to a pair of complementary complex stable/unstable eigenvalues. These are further indicators of high sensitivity to unstable behaviours. The unstable manifold surface is constituted by the combination of the surfaces generated by the two unstable modes.

A representative member of the family, with $A_z \simeq 78.8 \times 10^3$ km and only two distinct pairs of real stable/unstable attitude eigenvalues, is selected to present some theoretical generalisation. Consider the first of the two unstable attitude modes, labelled as att-U1, of the reference solution of this NRHO family. Its corresponding eigenvalue has the highest absolute value. The mode approximations are generated via a perturbation with an equivalent magnitude in the order of 0.1 degree along the unstable attitude mode, and their natural orbit-attitude dynamics has been propagated over 2-orbital periods. The small value of the perturbation has been selected due to the high stability index associated with the periodic solution, expecting high rate of divergence. Its rotational dynamics is reported in Fig. 6. It is representing the evolution of the attitude quaternion, which is expressed with respect to the synodic $\{{\hat{r}}\}$-frame, and of the absolute angular velocity.

Fig. 6

Absolute attitude dynamics of unstable attitude manifolds att-U1 propagated over 2-orbital periods. Earth–Moon $L_1$ Northern NRHO with $A_z \simeq 78.8 \times 10^3$ km ($\simeq 0.205$ [ndim]). Initial perturbation equivalent to $\simeq 0.1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution

The solid black line in Fig. 6a represents the attitude behaviour of the reference periodic solution in the 3-dimensional quaternion space. Each dashed line in Fig. 6a corresponds to the attitude evolution of the unstable mode att-U1 starting from a different position along the periodic solution. The dashed lines in Fig. 6b correspond to the absolute angular velocity of the mode. During the first period of propagation, they are very close to the reference periodic solution. These dynamics allow to visualise, via discretisation, the eigen-surface of the corresponding manifold, which is, respectively, projected in the quaternion and in the angular velocity subspaces. Different paths are generated because the dynamics starts from different initial conditions along the periodic solution and, as a consequence, the local direction of the manifold characterised by the attitude mode is changing.

It should be highlighted that the unstable attitude motions quickly diverge from the periodic motion even if the attitude perturbations introduced are very small. The angular velocity presents an increasing divergence after each perilune passage, which can be easily distinguished at the second perilune transit in Fig. 6b. As a consequence, all the unstable attitude manifolds begin to have a significant divergence at the perilune zone of the orbit, which is characterised by a distance of $\sim 10^3$ km from the centre of the Moon, remarking the high dynamical sensitivity of this region.

The same considerations can be extended to the second unstable attitude manifold, labelled as att-U2, associated with the reference NRHO, for which the attitude dynamics are shown in Fig. 7.

Fig. 7

Absolute attitude dynamics of unstable attitude manifolds att-U2 propagated over 2-orbital periods. Earth–Moon $L_1$ Northern NRHO with $A_z \simeq 78.8 \times 10^3$ km ($\simeq 0.205$ [ndim]). Initial perturbation equivalent to $\simeq 0.1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution

As is apparent from the difference in the scale of the plots in Figs. 6 and 7, the attitude mode att-U2 shows slowly diverging behaviour with respect to the attitude mode att-U1. This behaviour is expected because the module of the eigenvalue and, as a consequence, the stability index associated with the attitude mode att-U2, are lower with respect to those associated with the attitude mode att-U1. Moreover, Fig. 7a allows to visualise the toroidal surface structure of the attitude manifold projected in the 3-dimensional quaternion space in proximity of the reference periodic solution.

The perilune of the NRHO has been identified as a catalyst of the unstable behaviour of the attitude modes. Therefore, the spacecraft has to be oriented minimising the gravity gradient perturbing torque to keep the natural periodic motion. Otherwise, the large gravity gradient at perilune pulls away the rotational motion from the periodic equilibrium, by exciting the unstable attitude modes. This suggests that some sort of stabilisation (passive or active) shall be provided, especially in the perilune region of the NRHO. On the contrary, any natural periodic rotational motion would eventually diverge. Moreover, the unstable attitude mode identifies the unstable axes of rotation of a periodic librating/spinning solution along the orbital motion.

A combination of active control torques with stable and unstable natural attitude modes could be exploited to perform low-cost large slew manoeuvres. However, considering the Earth–Moon system, this kind of manoeuvres cannot be performed in a short time, since the natural dynamics of the modes is directly associated with the orbital period of the reference orbit (e.g. about 8 days for the reference case).

3.2 Attitude modes of cislunar halo

A family of orbit-attitude halo orbits is under investigation in this section, allowing further theoretical generalisation. The spacecraft is assumed with an equivalent cylinder-like shape with inertia ratio $K_\mathrm{{a}} = I_\mathrm{{t}}/I_\mathrm{{a}} = 0.7$, and its axis of symmetry is aligned to $\varvec{{\hat{b}}_3}$. Note that this is different from the NRHO solution, where the symmetry axis was $\varvec{{\hat{b}}_1}$. This configuration has been discovered to be a periodic orbit-attitude solution with a less unstable behaviour for the halo family.

The initial condition for the correction algorithm assumes a spacecraft moving along a halo orbit with $A_z = 58 \! \times \! 10^3$ km and having the attitude aligned with the synodic frame, similarly to the discussion about the NRHO case. Then, the periodic solution has been continued with the pseudo arc-length continuation algorithm. The resulting orbit-attitude family, shown in Figs. 8 and 9, presents a librating rotational behaviour of the spacecraft about the synodic $\{{\hat{r}}\}$-frame for relatively large-amplitude halo orbits with $A_z$ ranging from $58 \! \times \! 10^3$ km to $71 \! \times \! 10^3$ km.

Fig. 8

Orbital motion of the periodic orbit-attitude Earth–Moon $L_1$ halo family with vertical amplitude $A_z\in [58-71]\times 10^3\,\hbox {km}$ and period $T\in [10.3-11.8]\,\hbox {d}$. Reference initial condition at $t=0$, corresponding to apolune, with ${\varvec{r}}(0)=[0.861,0.000,0.185]\mathrm {[ndim]}$ and ${\varvec{v}}(0) = [0.000,0.252,0.000]\mathrm {[ndim]}$. The Moon position is indicated with a grey dot

Fig. 9

Attitude evolution with inertia ratio $K_a = 0.7$ of the periodic orbit-attitude Earth–Moon $L_1$ halo family. Librating reference initial condition at $t=0$, corresponding to apolune, with $^{{\hat{i}}}{\varvec{q}}^{{\hat{b}}}(0)=[0.016,0.041,0.366,0.929]$ and $^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}(0) = [-0.057,0.053, 0.986]\mathrm {[ndim]}$. Vertical dashed lines indicate the perilune crossing event for the reference solution

Fig. 10

Orbital and attitude linear stability index of the Earth–Moon $L_1$ Northern halo family as a function of the vertical amplitude $A_z$. The points highlighted with a different colour and a vertical line refer to the reference solution discussed in Sect. 3.2

Relevant comments can be stated by examining the linear stability index associated with both orbital and attitude dynamics of the periodic solution of this halo family. They have been represented, respectively, as blue and red dots, as a function of the vertical amplitude $A_z$ in Fig. 10. The stability index associated with the orbital motion $\nu _{orb}$ decreases as the orbit increases in amplitude, as expected from the literature, implying that larger halo orbits become more stable (Howell 1984). By contrary, the attitude stability index $\nu _\mathrm{{att}}$ tends to increase for halo orbits with larger vertical amplitude. This is related to the closer passage of the orbital path of the halo to the secondary attractor, namely the Moon, which induces higher angular rates in the periodic solution and higher sensitivities to perturbation, especially in the perilune zone. However, the attitude stability index ranges from 2 to 6 over a quite large span of halos along the investigated $A_z$ values. Note that $\nu _\mathrm{{att}}\sim 30$ for the NRHOs discussed in Sect. 3.1. Therefore, a perturbation of the periodic attitude solution is expected to present relatively slow diverging exponential behaviour with respect to the nominal periodic solution for the whole family.

The investigated family of orbit-attitude halo orbits presents the same modal structure for both orbital and attitude dynamics over the whole set of continued periodic solutions. They are constituted by one pair of stable/unstable modes, one pair of periodic and one pair of centre quasi-periodic ones. The family has similar eigenstructure characteristics for the whole set of orbit-attitude halo orbits, therefore, a representative member is selected to show the general behaviour of the attitude modes characterising also the other members of its family. The eigenvalues associated with the orbital and attitude modes of the reference Earth–Moon $L_1$ halo solution, with $A_z \! \simeq \! 68.8 \times \! 10^3$ km, are shown in Fig. 11.

Fig. 11

Orbit-attitude eigenvalues in the complex plane of an Earth–Moon $L_1$ halo orbit with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim])

The first two attitude modes analysed correspond to the pair of unstable and stable behaviours associated with the attitude manifolds. Figure 12 shows the evolution of the rotational dynamics associated with the unstable attitude mode, labelled as att-U, of the selected representative halo orbit. The manifold has been propagated over 2-orbital periods starting from a perturbation offset along the “local” manifold direction, i.e. the unstable attitude mode, of an equivalent magnitude equal to about 1 degree.

Fig. 12

Absolute attitude dynamics of unstable attitude manifolds att-U propagated over 2-orbital periods. Earth–Moon $L_1$ Northern halo with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim]). Initial perturbation equivalent to $\simeq 1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution

The attitude motion is presented in the 3-dimensional space $\{q_1, q_2, q_3\}$ of the quaternion $^{{\hat{r}}}{\varvec{q}}^{{\hat{b}}}$. The periodic solution is highlighted as a black solid line, while the unstable attitude manifold are displayed as red dashed lines. The absolute angular rates of the mode are unfolded along the time of propagation. It should be noticed that even a very small attitude perturbation can lead to chaotic behaviours within two orbital periods. In particular, the divergence from the reference solution starts to be significant during a perilune passage due to the higher gravitational sensitivity. This behaviour can be easily seen in Fig. 12b starting from the second perilune passage (i.e. $t \simeq 4$ in non-dimensional time units).

Specular results are obtained from the analysis of the stable attitude mode, labelled as att-S. Figure 13 shows the rotational dynamics evolution of the stable attitude manifold which has been obtained from a backward propagation over 2-orbital periods.

Fig. 13

Absolute attitude dynamics of stable attitude manifolds att-S propagated backwards for 2-orbital periods. Earth–Moon $L_1$ Northern halo with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim]). Initial perturbation equivalent to $\simeq 1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution. Note that stable modes approach the reference trajectories

In this case the perilune region corresponds to the zone where the attitude of the stable attitude manifold closely reaches the rotational synchronisation with respect to its reference periodic solution.

The periodic attitude modes, labelled as att-P1 and att-P2, are associated with the periodic rotational behaviour of the reference solution. The attitude dynamics of the attitude mode att-P1 associated with the reference halo orbit is shown in Fig. 14. Again, the initial perturbation along the manifold direction of about 1 degree has been propagated over 2-orbital periods. The rotational dynamics of the attitude manifold is presented in the 3-dimensional quaternion space and in the relative angular velocity with respect to the reference solution. Moreover, the relative distance has been reported as a function of the propagation time. Here, the perilune occurrence has been highlighted with a dashed vertical line, while the apolune has been marked with a dashed-dot vertical line.

Fig. 14

Attitude dynamics of periodic attitude manifolds att-P1 propagated over 2-orbital periods. Earth–Moon $L_1$ Northern halo with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim]). Initial perturbation equivalent to $\simeq 1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution, dashed-dot lines represent the apolune crossing event

The projection of the manifold att-P1 in the 3-dimensional quaternion space in Fig. 14a shows that this mode approximates a slightly different rotational periodic behaviour with respect to the reference periodic solution. The attitude evolution is shifted in the 3-dimensional quaternion space with respect to the original periodic solution. Therefore, the behaviour discovered by this attitude mode represents a similar periodic solution along the same reference halo orbit. However, as can be seen in Fig. 14b, instabilities quickly appear in the propagated dynamics of the attitude due to the high sensitivity of the nonlinear rotational dynamics to numerical errors. Indeed, a further step could include a numerical correction to obtain an accurate periodic orbit-attitude solution and evaluate the angular deviation which identifies similar periodic attitude behaviours, giving an additional index to parametrise the orbit family. Moreover, it should be highlighted that the numerical approximation of the eigenmode att-P1 generates an infinitesimal perturbation in the orbital component. This perturbation is approximately directed along the reference orbit, even if its relative displacement is in practice negligible. The orbital perturbation distance in Fig. 14b, as well as in Figs. 15b, 16b and 17b, is computed as the norm of the relative vector with respect to the periodic motion. The distance is expressed in non-dimensional units, which can be converted considering that a distance of $1\times 10^{-10}\hbox { ndim}$ corresponds to $\sim {4} \hbox { cm}$. Indeed, a similar orbital behaviour in the relative orbital motion is obtained by the propagation of the orbital mode, labelled as orb-P1. Its dynamical evolution is reported in Fig. 15. The nominal reference solution has been perturbed along the direction of the periodic orbital mode with an equivalent magnitude equal to 5 km.

Fig. 15

Attitude dynamics of periodic orbital manifolds orb-P1 propagated over 2-orbital periods. Earth–Moon $L_1$ Northern halo with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim]). Initial perturbation equivalent to 5 km. Vertical dashed lines indicate the perilune crossing event for the reference solution, dashed-dot lines represent the apolune crossing event

This mode identifies a temporal shift along the same reference periodic orbit-attitude solution. Differently from the attitude mode att-P1, the orbital displacement of the mode orb-P1 constitutes the main perturbation component. Indeed, relative attitude component of orb-P1 is negligible. It should be highlighted that the mode orb-P1 follows the same attitude evolution of the reference solution, as can be observed in Fig. 15a. Moreover, Fig. 15b shows that the rotational motion is synchronised according to the temporal shift along the reference orbit.

Figure 16 shows the attitude dynamics of the second periodic attitude mode, labelled as att-P2, which has been propagated over 2-orbital periods starting from an initial perturbation equivalent to about 1 degree along the attitude mode.

Fig. 16

Attitude dynamics of periodic attitude manifolds att-P2 propagated over 2-orbital periods. Earth–Moon $L_1$ Northern halo with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim]). Initial perturbation equivalent to $\simeq 1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution, dashed-dot lines represent the apolune crossing event

This mode approximates the direction in the attitude subspace where spinning solution is likely to be present. Indeed, the obtained relative attitude dynamics with respect to the reference solution shows a slowly spinning behaviour pivoting to the axis $\varvec{{\hat{b}}_3}$ of the spacecraft, as evident in Fig. 16b. It should be noticed that the numerical errors immediately excite the unstable behaviour of the orbital component, increasing the difficulties to accurately approximate this modal attitude behaviour.

The centre attitude modes, labelled as att-C1 and att-C2, are associated with oscillating attitude behaviours about the reference periodic attitude solution. Note that, these oscillating behaviours exist while the spacecraft is moving on the same periodic orbit of the reference solution.

Fig. 17

Attitude dynamics of centre attitude manifolds att-C1 propagated over 2-orbital periods. Earth–Moon $L_1$ Northern halo with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim]). Initial perturbation equivalent to $\simeq 1$ deg. Vertical dashed lines indicate the perilune crossing event for the reference solution, dashed-dot lines represent the apolune crossing event

Figure 17 shows the attitude manifold att-C1 projected in the 3-dimensional quaternion space and in the relative angular velocity as a function of the time of propagation over 2-orbital periods. The initial perturbation along the manifold direction is about 1 degree. From the relative distance plot in Fig. 17b, it should be remarked that the attitude modes associated with a specific reference solution do not have, in practice, orbital component. This is due to the assumption which considers the dimensions of the spacecraft as negligible with respect to those of the Earth–Moon system. Note that the infinitesimal magnitude of the orbital component in the attitude mode is due to the numerical approximation of the mode and to the numerical errors in the propagation.

4 Attitude stabilisation

Considering the perilune passage for elongated halo orbits and NRHOs, the gravity gradient of the Moon is source of attitude instability. As outlined in the previous section, an attitude stabilisation strategy is desired to be actuated on-board, to avoid the progressive loss of periodicity of natural orbit-attitude motion. In particular, this is relevant for extended space structures in the lunar vicinity, whose attitude dynamics should be controlled and stabilised. In general, the capability to regulate the stability performances of a natural periodic motion is a positive asset to enlarge the design space. For instance, there might be the need to reduce the control budgets to keep a certain attitude state, or to manoeuvre the spacecraft exploiting the natural dynamics along a non-gyroscopically rigid axis (Colagrossi and Lavagna 2017a). The constraint that should be enforced while designing the attitude control system imposes a strong limitation in the consumption of non-recoverable resources while controlling the dynamics, such as propellants. In fact, the cislunar space station will be operative for a long time, with limited supplies and rare refuelling opportunities. For these reasons, this research work focuses its attention on an attitude control system based on angular momentum management with no propellant consumption. Thus, single-spin or dual-spin attitude stabilisation techniques are considered.

Spin stabilisation techniques are based on the gyroscopic effect of the angular momentum stored within the body with mass $m_B$. In single-spin stabilisation method, the whole spacecraft is spinning and the rotating mass of the spacecraft acts as attitude stabilising system. While dual-spin stabilisation methods are based on spinning wheels (i.e. rotors) that are able to store a large amount of angular momentum needed to stabilise the system. Nevertheless, they can have a different rotation speed with respect to the main body and, thus, there is one additional degree of freedom that can be exploited while designing the stabilisation strategy. Furthermore, momentum wheels attitude stabilisation methods can also be extended and modified to consider variations in spinning rate or direction, allowing attitude manoeuvres and enhanced control capabilities.

The stored angular momentum, which is eventually due to a spinning spacecraft or the presence of momentum wheels, affects the dynamic of the system. Indeed, the internal angular momentum is:

$$\begin{aligned} \mathbf {h}=\mathbf {I}\,^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}+\mathbf {h}_w, \end{aligned}$$

(15)

where $\mathbf {I}$ is the inertia tensor of the spacecraft, which does not take into account the inertia of the momentum wheels, and $\mathbf {h}_w$ is the angular momentum of the wheels expressed in reference body-fixed $\{{\hat{b}}\}$-frame. Single-spin techniques increase the internal angular momentum acting on the first term on the right side of (15), being the whole spacecraft spinning with angular velocity $^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}$, while dual-spin techniques have an impact on the second term, which is solely related to internal rotors.

Assuming three different momentum storage devices, aligned with the principal axes of the spacecraft, the angular momentum of the wheels is:

$$\begin{aligned} \mathbf {h}_w=[I_{1_w}\omega _{1_w}, I_{2_w}\omega _{2_w}, I_{3_w}\omega _{3_w}], \end{aligned}$$

(16)

where $I_{1_w}$, $I_{2_w}$, $I_{3_w}$ are the moments of inertia of the rotors, respectively, aligned with $\varvec{\hat{b}}_1$, $\varvec{\hat{b}}_2$ and $\varvec{\hat{b}}_3$; $\omega _{1_w}$, $\omega _{2_w}$ and $\omega _{3_w}$ are the relative angular velocities of three momentum wheels with respect to the body frame.

Therefore, Euler’s equations of rotational motion have to include the terms due to the presence of the rotating momentum wheels that can be evaluated as described in classic literature about rigid body dynamics (Markley and Crassidis 2014):

$$\begin{aligned} \varvec{\eta }=\,^{{\hat{i}}}\varvec{\omega }^{{\hat{b}}}\times \mathbf {h}_w=\begin{bmatrix} 0 &{} -\omega _3 &{} \omega _2 \\ \omega _3&{} 0 &{} -\omega _1 \\ -\omega _2 &{}\omega _1 &{} 0 \\ \end{bmatrix} \begin{bmatrix} I_{1_w}\omega _{1_w}\\ I_{2_w}\omega _{2_w}\\ I_{3_w}\omega _{3_w}\\ \end{bmatrix}. \end{aligned}$$

(17)

The three components, $\eta _1$, $\eta _2$ and $\eta _3$, of the vector $\varvec{\eta }$ are then, respectively, divided by the moments of inertia of the body with mass $m_B$ (i.e. $I_1$, $I_2$, $I_3$). The resulting terms $\eta _1/I_1$, $\eta _2/I_2$ and $\eta _3/I_3$ are successively subtracted from the right-hand side of the angular velocity dynamics in (6). The momentum wheels are assumed to be operated with constant spinning rate and axis and, thus, no additional term, such as derivative of the angular momentum of the rotors $\dot{\mathbf {h}}_w$ has to be included in the present model. Moreover, the additional equations of motion for the momentum wheels are trivial, being:

$$\begin{aligned} {\dot{\omega }}_{i_w}=0 \longleftrightarrow \omega _{i_w}=\mathrm{{const}},\;\; \text {with}\;\; i=1,2,3. \end{aligned}$$

(18)

Single-spin attitude stabilisation can be analysed exploiting the same model formulation: momentum wheels can be forced to have zero angular velocity or zero inertia (e.g. $\omega _{i_w}=0$ or $I_{i_w}=0$ with $i=1,2,3$). It must be noted that the differential correction scheme, briefly introduced in Sect. 2, should be slightly modified. In fact, the system now contains the terms due to the presence of the momentum wheels, which have to be included into the numerical corrector dynamical equations. However, the periodicity constraints are not affected by the inclusion of the spinning rotors, since the motion of the momentum wheels is not forced to be periodic along an orbital period. The detailed mathematical formulation of the orbit-attitude differential correction algorithms is thoroughly described in (Guzzetti and Howell 2016; Colagrossi and Lavagna 2017b).

4.1 Single-spin attitude stabilisation

The single-spin attitude stabilisation is a very simple and effective technique to increase the stability of the rotational motion. The general characteristics of single-spin periodic dynamics are introduced in this section, analysing the results with the attitude stability methods discussed in (3).

Periodic orbit-attitude motion in cislunar environment has to satisfy periodicity constraints in both orbital and attitude variables and, moreover, the attitude evolution should be compatible and periodic with the gravity gradient torques due to the presence of the primaries. In fact, the effects of the gravitational attraction on the rotational motion strongly characterises the periodic dynamics. This is true in particular for non-Keplerian orbits with a low perilune altitude, such as NRHOs or elongated halo orbits. During the low perilune passage, the attitude dynamics experiences a large gravity gradient torque, resulting in a relevant angular acceleration on the extended body. As discussed in the previous section, this is a source of instability for the attitude dynamics. For this reason, the reference Earth–Moon $L_1$ halo orbit, whose natural dynamics was analysed in Sect. 3.2, is used as a reference orbit to analyse the features of single-spin and dual-spin attitude stabilisation. The analysis can be repeated with attitude stabilised solutions on NRHOs. The effects and results of spinning stabilisation methods on this family of orbit are analogous to the ones discussed in this paper. However, they are not presented here since they would not provide further insight.

Fig. 18

Stability index for single-spin attitude stabilisation solutions. Earth–Moon $L_1$ Northern halo orbit with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim])

Considering, for example, the attitude stability index for different single-spin attitude solutions reported in Fig. 18, the stability improvement due to the spinning stabilisation method is clearly evident. Indeed, the stability index, which was equal to $\sim 3.6$ for the librating solution, highlighted in Fig. 10 and here associated with n-spin$=0$, approaches the value 1 for all the spinning dynamics, with n-spin$\ge 1$. The n-spin value indicates the number of rotations the spacecraft completes in one orbital period. This result confirms that the single-spin dynamics improves the stability of the attitude motion in the multi-body cislunar environment. Small differences in the value of $\nu _\mathrm{{att}}$ for the different spinning solutions are not influent for practical stability purposes.

Fig. 19

Periodic single-spin attitude dynamics on Earth–Moon $L_1$ Northern halo orbit with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim])

Three periodic solutions for single-spin dynamics on Earth–Moon $L_1$ halo orbit are shown in Fig. 19. They are initialised as in the reference librating solution and the inertia parameter of the body is $K_\mathrm{{a}}=0.7$. The only difference is the spinning rate around $\varvec{\hat{b}}_3$ that, in the first case in Fig. 19a, allows one overall rotation along one orbit, while in the other two simulations in Fig. 19c and e determines, respectively, two and three overall rotations in one orbital period. This peculiarity is also evident from the Euler angles evolution in Fig. 19b, d and f. Note that Euler angles are used here, in place of quaternions, to have a more direct visualisation of the spinning evolution of the body frame with respect to the synodic $\{{\hat{r}}\}$-frame. The Euler angles, $\varphi _{r_x}$, $\theta _{r_y}$ and $\psi _{r_z}$ are formalised according to the Tait–Bryan angles definition, with rotation sequence “x–y–z” (Markley and Crassidis 2014).

The angular accelerations due to the gravity gradient of the Moon are evident also in the spinning periodic solutions, looking at the variation of the angular velocity in correspondence with the perilune passages. However, this effect is relatively weaker, if compared to the global magnitude of the angular velocity, as can be observed in Fig. 19a, c and e. Furthermore, the larger angular momentum makes the spinning body more stable, as also confirmed by the stability index analysis in Fig. 18, where the spinning solutions are associated with a lower stability index.

4.2 Dual-spin attitude stabilisation

The operational constraints imposed by the single-spinning attitude stabilisation methods can be easily overcome with a separate angular momentum storage device, which can be spun at a different angular rate with respect to the main body. Thus, there are additional degrees of freedom that can be exploited to stabilise the attitude dynamics without imposing constraints on the overall attitude of the spacecraft. In this research work, the spinning momentum wheels mounted on spacecraft are used at a constant spinning rate. The increased angular momentum of the whole space system is the classical foundation for the dual-spin attitude stabilisation technique.

The stability index analysis, discussed for single-spin solutions, is also possible for dual-spin attitude stabilisation. In fact, similarly to single-spin dynamics, the stability of the attitude motion is favourably increased by a larger internal angular momentum, due to the presence of a faster wheel. However, dual-spin dynamics allows a progressive variation of $\nu _\mathrm{{att}}$. In the proposed examples, a single wheel aligned with $\varvec{\hat{b}}_3$ is considered, allowing a direct comparison between the single-spin and the dual-spin solutions with spinning direction along the same body axis. The rotating inertia ratio of the wheel, with respect to the body moment of inertia, is $I_{3_w}/I_3=1/100$.

Figure 20 reports the stability index for different dual-spin solutions on the Earth–Moon $L_1$ halo orbit. The dual-spin range is $\omega _{3_w}\in \left[ -250,300\right] \,\hbox {ndim}$, selected only for example purposes. An increase in the magnitude of the angular rate of the wheel determines an increase in the stability of the periodic motion, confirmed by the decreasing value of the attitude stability index. Note that, in Fig. 20, the higher attitude stability index value corresponds to $\omega _{3_w}\simeq 50\,\hbox {ndim}$. This result is in line with classical dual-spin attitude stability analyses, where the stability of attitude dynamics is minimum for $\omega _{3_w}\ne 0$ (Markley and Crassidis 2014). The attitude stability index with slow spinning wheel is comparable to the one without any attitude stabilisation technique.

Fig. 20

Stability index for dual-spin attitude stabilisation ($\omega _{3_w}\in \left[ -250,300\right] \,\hbox {ndim}$) solutions. Earth–Moon $L_1$ Northern halo orbit with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim])

The periodic solutions shown in Fig. 21 refer to three distinct angular rates of the spinning momentum wheel. They have been initialised on the reference Earth–Moon $L_1$ halo orbit, starting from the reference librating attitude solution and considering a body with inertia ratio $K_a=0.7$. The three proposed periodic solutions differ for the spinning rate of the momentum wheel. In the first case (Fig. 21a), the wheel is slowly spinning with $\omega _{3_w}= {100}\hbox { ndim}$ and the stabilisation effect is not so evident, except for the additional rotational motion around $\varvec{\hat{b}}_2$ due to the gyroscopic coupling. The dual-spin behaviour starts to be more evident with a larger angular velocity of the momentum wheel in Fig. 21c. In this case, the increased angular momentum makes the system stiffer and the gyroscopic coupling frequency is high, with fast oscillations around the rotation axis of the body. The effect due to the large gravity gradient of the Moon is mitigated and the attitude is stable in its pulsating evolution. However, a great improvement in attitude stabilisation is achieved by further increasing the spin rate of the momentum wheel. In Fig. 21e, the momentum wheel is spinning at a fast rate, $\omega _{3_w}= {1000}\hbox { ndim}$, and the attitude dynamics is greatly stabilised with limited angular acceleration at the perilune. For this solution, the attitude stability index is $\nu _{att}\simeq 1.1$. With dual-spin attitude stabilisation, it is therefore possible to stabilise the attitude, limiting the effect of the gravity gradient torque, with the body that is no more rotating in the synodic reference frame. In fact, comparing Figs. 21b, d, f and 19b, d, f, a spinning momentum wheel allows to increase the stability of the attitude dynamics, while maintaining the cislunar station just librating around an equilibrium condition. Thus, no constraints are imposed on the body frame orientation. Moreover, the proposed stabilisation is feasible with current technological capabilities since $\omega _{3_w}={1000}\hbox { ndim}$ corresponds in dimensional units to $\omega _{3_w}={0.003}\hbox { rad/s}$.

Fig. 21

Periodic dual-spin attitude dynamics on Earth–Moon $L_1$ Northern halo orbit with $A_z \simeq 68.8 \times 10^3$ km ($\simeq 0.178$ [ndim])

5 Conclusion

The paper discussed a novel perspective on the dynamical phase space structure constituting the orbit-attitude motion of a spacecraft in proximity of a non-Keplerian cislunar orbit. Attitude manifolds were presented and related to the coupled orbit-attitude dynamics in the circular restricted three-body problem (CR3BP), according to Floquet theory. The proposed methodology was applied to orbit-attitude families of cislunar orbits to characterise their attitude stability and the natural structure of their dynamics. Particular attention has been dedicated to halo orbits and near-rectilinear halo orbit NRHOs of the Earth–Moon system, in order to address favourable dynamics and challenging problems that would affect the design of the future cislunar space gateway.

The investigation on natural orbit-attitude dynamics in cislunar space gave insights on the motions that are sustainable and exploitable in the lunar vicinity. In fact, the design of new missions or proximity operations may beneficially exploit the features of the natural motion to accomplish 6DOF station-keeping or slewing manoeuvres. The perilune region is characterised by fast and sensitive orbit-attitude dynamics due to the high gravity gradient torque of the Moon. This generates large instabilities characterising the natural librating attitude motion discovered for the periodic orbit-attitude families in the Earth–Moon system. Any diverging behaviour, which could start anywhere along the orbit, significantly shows its unstable departure from the reference periodic solution at the perilune passage due to the gravitational gradient of the Moon. This suggest the implementation of a control action during or just before the perilune passage in order to preserve the reference periodic orbit-attitude behaviour.

In these regards, the orbit-attitude spin-stabilised solutions presented in this paper laid a foundation for attitude stabilisation and control of modular and large space structures in the lunar vicinity. In fact, the attitude stabilisation methods help the implementation of the future cislunar gateway, broadening the space of periodic orbit-attitude solutions suitable to host an extended spacecraft with a very simple control strategy.

Further studies are needed to extend the range of the presented analyses and results. The investigation of an active control system with variable internal angular momentum is of interest, considering that the main driver is always the minimisation of maintenance and station-keeping costs. In these regards, the attitude control technique should be as simple and efficient as possible; the proposed spin-stabilised solutions showed a first positive result in this direction.