A Method to Simulate an Outwardly Propagating Turbulent Premixed Flame at Constant Pressure

Abstract

An outwardly propagating premixed flame in homogeneous isotropic turbulence at constant pressure is considered one of canonical configurations to study turbulent premixed flames. In this paper, a surface forcing method to prevent the undesirable influence of the boundary-condition-induced backflow on the flame evolution, while maintaining the constant pressure, in the simulation of the outwardly propagating flame is presented. The method is validated for laminar and turbulent flames. The results show that the present method well preserves the characteristics of turbulence and of an outwardly propagating flame, without the undesirable influence of the boundary condition, by feeding the homogeneous turbulence relative to the velocity field induced by the volume expansion due to heat release to the domain in which the flame develops.

1 Introduction

An outwardly propagating flame in homogeneous isotropic turbulence at constant (thermodynamic) pressure is considered one of canonical configurations to study turbulent premixed flames. Using the constant pressure condition in the simulation of the outwardly propagating flame can be beneficial for a couple of aspects. It is, firstly, relevant to practical applications for which a flame kernel formed by a localized ignition of a premixed fuel-oxidizer mixture grows at constant pressure. From a theoretical point of view, for the low Mach number, the characteristic flame scales used for the analysis, i.e., the unstretched laminar flame speed and thickness, do not change with time. From a computational point of view, the smallest length scales to be resolved do not decrease with time. Of interest here is a method to maintain the constant pressure condition in the numerical simulation of a flame outwardly propagating in the presence of homogeneous turbulence.

An outwardly propagating flame in homogeneous isotropic turbulence has been investigated extensively through direct numerical simulation (DNS) or large eddy simulation (LES) (Oijen et al. 2005; Ozel-Erol et al. 2021; Gashi et al. 2005; Falkenstein et al. 2020; Kulkarni and Bisetti 2021; Zhao et al. 2019; Zhang et al. 2021b; Shehab et al. 2022; Mohan and Matalon 2022), as well as experimentally. To maintain the constant pressure in the simulation, a boundary condition used for the outlet or open boundary has been applied to all the boundaries. When the governing equations for fully compressible flows are solved, a non-reflecting Navier-Stokes characteristic boundary condition has been widely used (Poinsot and Lele 1992; Oijen et al. 2005; Ozel-Erol et al. 2021; Gashi et al. 2005). The non-reflecting boundary condition is originally formulated for a subsonic outflow boundary for which the incoming acoustic mode is assumed to be the only characteristic wave that enters into the computational domain at the boundary, and performs well for the outflow boundary in combustion problems. For the low Mach number formulation or weakly compressible flows, for which the pressure-based method is used to enforce the continuity, the Neumann-type or “outflow" condition has been used (Shehab et al. 2022; Mohan and Matalon 2022). As the information on the flow outside the computational domain is lacking, such boundary conditions typically assume that the convection, which carries the information along the direction of the fluid velocity, is predominantly in the outward direction. For homogeneous turbulence, however, unless the outward convective velocity induced by the volume expansion due to heat release exceeds turbulent velocity fluctuations, there exists substantial backflow or modification of flow characteristics at the boundaries of the computational domain. When a boundary condition assumes the convective motion is dominantly in the outflow direction, the characteristics of the backflow at the boundaries can be quite different from those of turbulence inside the domain. To avoid the influence of the backflow on the flame evolution, with the boundaries located sufficiently far away from the flame kernel, a computational domain is enlarged. On the other hand, the periodic condition, which is widely used to simulate homogeneous turbulence, has also been used for the simulation of the outwardly propagating flame kernel. With the fluid being confined in the computational domain, such simulation corresponds to the constant volume condition for which the pressure rises due to heat release. In Zhang et al. (2021b), the flame kernel growth in a fan-stirred combustion vessel, which generates homogeneous isotropic turbulence by symmetrically-arranged fans (Zhang et al. 2021a), is simulated using LES.

In this paper, we present a boundary forcing method to simulate the outwardly propagating turbulent premixed flame at constant pressure, the purpose of which is to prevent the undesirable influence of the boundary backflow. It makes the flow at the boundary resemble the homogeneous turbulence being simulated inside the domain, while retaining the constant pressure, thus eliminating the uncertainty regarding avoiding the undesirable influence of the boundary backflow and improving the computational efficiency and/or accuracy. In the following section, the proposed method is described along with the governing equations. The method is tested for the laminar and turbulent flames.

2 Boundary Mass Sink Method

Of interest is simulating an outwardly propagating premixed flame in homogeneous isotropic turbulence. The computational domain is cubic and the periodic condition is applied to all the boundaries. With the flame kernel located at the center of the domain, the volumetric expansion due to heat release induces an outward motion of the unburned gas mixture. For the confined domain with the periodic condition for all boundaries, the gas mixture is then compressed and the pressure increases. When the unburned mixture moving outward leaves the domain at such a rate to prevent the compression, the thermodynamic pressure remains constant. In the proposed method, while retaining the periodic boundary condition and thus avoiding the undesirable influence of the backflow induced by the boundary condition, the mass sink and related forcing terms are added near the boundaries to emulate the gas mixture flowing out of the domain at constant pressure.

With the boundary mass sink terms being applied, the governing equations for the flow and scalar fields can be written as

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \frac{\partial \rho u_j}{\partial x_j}= & {} s_B,\end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \rho u_i }{\partial t} + \frac{\partial \rho u_j u_i}{\partial x_j}= & {} -\frac{\partial p}{\partial x_i} + \frac{\partial \tau _{ij}}{\partial x_j} + s_B u_i + s_B e_{B,k} (u_k - u_{B,k} ),\end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial \rho \phi _i }{\partial t} + \frac{\partial \rho u_j \phi _i}{\partial x_j}= & {} \frac{\partial \Gamma _{i,j}}{\partial x_j} + \omega _{\phi _i} + s_B \phi _i, \end{aligned}$$

(3)

where $\rho$ is the density of the gas mixture, $u_i$ the velocity component in the $x_i$ direction, $\tau _{ij}$ viscous stress, and p pressure. The summation convention is used. The scalar $\phi _i$ can be the species mass fraction or a quantity solved for energy conservation. $\Gamma _{i,j}$ is the molecular flux of $\phi _i$. $\omega _{\phi _i}$ is the source term for $\phi _i$. $s_B$ is the boundary mass sink term. It is less than or equal to zero. The third term on the right hand side (r.h.s.) of the momentum and the scalar equation is related to $s_B$ and added to prevent the boundary mass sink term from directly affecting the evolution of $u_i$ and $\phi _i$ in the context of their material derivatives, as further discussed below. It is to be noted that $s_B$ is non-zero only near the boundaries and the governing equations do not contain the boundary mass sink terms inside the domain where the flame evolves. The last term on the r.h.s. of the momentum equation is related to the jump condition in the velocity normal to the boundary mass sink layer, as discussed below, and is called the normal velocity jump term here. $e_{B,k}$ is the unit vector normal to the boundary mass sink layer, pointing toward the positive $x_k$ direction. $u_{B,k}$ is the velocity of the boundary mass sink layer. The normal velocity jump term becomes $s_B (u_i - u_{B,i})$ on the boundary mass sink layer normal to the $x_i$ direction and 0 on the other layers.

When thermodynamic pressure remains constant for the low Mach number, we obtain

$$\begin{aligned} S_B = - \int _{\partial \Omega _F} \rho _{p} u_j n_j dA = - \int _{\Omega _F} \frac{\partial \rho _{p} u_j}{\partial x_j} dV = \int _{\Omega _F} \frac{\partial \rho _{p} }{\partial t} dV, \end{aligned}$$

(4)

where $\Omega _F$ denotes the cubic domain surrounding the flame kernel. $\partial \Omega _F$ represents the surface of $\Omega _F$. $n_j$ represents the unit vector normal to the surface $\partial \Omega _F$, pointing outward. $\rho _p$ is the density evaluated using the constant thermodynamic pressure, for given local mixture composition and temperature. In Eq. (4), the surface integral on the r.h.s. of the first equal sign represents the rate of mass flow at which the gas mixture leaves the domain $\Omega _F$ when thermodynamic pressure is constant. $S_B$ thus corresponds to the rate of decrease in the total mass in a fixed-volume region encompassing a flame kernel at the constant pressure. In the domain $\Omega _F$, the total mass decreases as the volume occupied by the low density burned gas increases due to the flame kernel growth. Here, the mass sink is placed along the boundaries $\partial \Omega _F$ of the cubic domain such that the integration of the mass sink along $\partial \Omega _F$ matches $S_B$. By placing the mass sink and related conditions at $\partial \Omega _F$ using the regularized Dirac delta function (Peskin 2002), which is used to place a singular source term in numerical simulation, we obtain the volumetric source/sink terms in the above equations, concentrated at $\partial \Omega _F$.

The boundary mass sink term $s_B$ satisfies

$$\begin{aligned} S_B = \int _{\Omega _F} \frac{\partial \rho _{p} }{\partial t} dV = \int _{\Omega _F} s_B dV . \end{aligned}$$

(5)

This condition is equivalent to the condition under which the solution of the Poisson equation for pressure (correction) in the low Mach number formulation exists for the periodic boundary condition. The boundary mass sink term is placed using the regularized Dirac delta function:

$$\begin{aligned} \int _{\Omega _F} s_B dV = \int _{\Omega _F} s_0 \delta (\textbf{x}-\textbf{x}_B) dV {,} \end{aligned}$$

(6)

where $\delta$ is the regularized delta function, $\textbf{x}$ the spatial location ($x_i$), and $\textbf{x}_B$ the location of the boundary $\partial \Omega _F$. Considering that the periodic extension (images) of $\Omega _F$ occupies an infinite medium, one half side of the regularized delta function appears near one boundary in $\Omega _F$ and the other half near the opposite one in $\Omega _F$. Also, $\Omega _F$ may not coincide with the computational domain, while they are both cubic and have the same size. Here, the center of $\Omega _F$ is chosen to be that of a flame kernel. This helps preserve the symmetry of the volume-expansion-induced velocity and related pressure fields. When a kernel grows in a chamber the boundaries of which are far from the kernel, the volume-expansion-induced radial velocity does not have a preferred direction in the far-field. Such symmetry is better satisfied when the kernel is located at the center of the domain $\Omega _F$ along the boundaries of which the mass sink terms are placed. For a turbulent case, where a kernel may move slowly, the domain $\Omega _F$ may be shifted from the computational domain, while they cover the same infinite medium through the periodic condition. The velocity of the domain $\Omega _F$ is the same as the velocity of the kernel, which is evaluated using the volume integrals of the gas velocity weighted by the progress variable or normalized temperature. It is the velocity of the boundary mass sink layers, $u_{B,k}$, in the normal velocity jump term. With the moving $\Omega _F$, the flame kernel is always at the center of $\Omega _F$ and the time duration for which the simulation can be performed accurately with the flame surfaces not being close to the boundaries $\partial \Omega _F$ is increased. Here, the term “boundary" is used to indicate not only the boundary of the computational domain but also that of the domain $\Omega _F$.

The regularized delta function with the half width of two grid sizes (Peskin 2002) is used to place the boundary mass sink terms:

$$\begin{aligned} \delta _h(\eta ) = {\left\{ \begin{array}{ll} \frac{1}{8h} \left( 3-2\eta + \sqrt{1+4\eta -4\eta ^2}\right) , &{} \text {if } \eta \le 1 \\ \frac{1}{8h} \left( 5 -2\eta - \sqrt{-7+12\eta -4\eta ^2} \right) , &{} \text {if } \eta \le 2 \\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(7)

where h is the grid spacing. The uniform grid spacing is used. The regularized delta function is centered at and placed across the planar, boundary mass sink layer. The boundary mass sink term can then be written as

$$\begin{aligned} s_B = s_0 \delta _h (\eta ) , \end{aligned}$$

(8)

where $\eta = d/h$ and d is the normal distance, from $\textbf{x}$, to the boundary mass sink layer $\partial \Omega _F$. The strength of the sink term, $s_0$, is proportional to the radial outward velocity induced by heat release. The induced radial velocity scales as $r^{1-\gamma }$, where r is the distance from the center of a kernel and $\gamma$ is the dimension of a problem. As the strength of the boundary mass sink is proportional to the mass flux, due to the volume-expansion-induced radial velocity, on the boundary, it can be written as

$$\begin{aligned} s_0 = a (\textbf{n} \cdot \textbf{e}_r) r^{1-\gamma } , \end{aligned}$$

(9)

where $\textbf{n} \cdot \textbf{e}_r$ is the directional cosine. $\textbf{n}$ is the unit vector normal to the boundary mass sink layer, pointing outward, i.e., $n_j$ in Eq. (4). $\textbf{e}_r$ is $(\textbf{x}_B - \textbf{x}_{c})/|\textbf{x}_B - \textbf{x}_{c}|$, where $\textbf{x}_c$ denotes the center of the flame kernel. The center of the kernel is evaluated using the volume integrals weighted by the progress variable or normalized temperature. The factor a is determined to satisfy $S_B = \int _{\Omega _F} s_B { dV}$.

The pressure in the low Mach number limit is described by the pressure Poisson equation (e.g., for the formulation used in numerical simulation, McMurtry et al. (1986)). The volume-expansion-induced velocity components, which develop in accordance with the corresponding pressure field to satisfy the continuity, tend to approach the spherical symmetry, as the distance from the flame surfaces increases. At a location sufficiently far away, the $r^{-2}$ scaling in Eq. (9) is expected to be a good approximation for the induced radial velocity relative to $\partial \Omega _F$ in a turbulent flame kernel, which is wrinkled and may move slowly. It is also expected to work well when the mean flame shape is close to be spherical. Due to the nature of the Laplace operator in the pressure Poisson equation, the effects of small-scale wrinkling on the volume-expansion-induced velocity decay fast as the distance from the flame surface increases. Besides, when turbulence is strong enough, the simulation does not seem sensitive to the distribution of the mass sink along the boundary mass sink layer, i.e., a particular form of scaling in Eq. (9). The purpose of the boundary mass sink and related terms is to preserve the characteristics of the homogeneous turbulence relative to the periodic extension of the volume-expansion-induced velocity field, while maintaining the constant pressure condition.

In Bhagatwala et al. (2015), the mass source term is introduced to mimic the pressure evolution in a reciprocating engine. The uniform mass source is evaluated to reproduce the evolution of in-cylinder pressure due to the piston motion and is added for the entire domain. Such an approach is designed for the pressure evolution due to the piston motion. It is not compatible with an expanding flame at constant pressure due to mass conservation in the burned mixture and in the unburned mixture near the kernel.

As in Bhagatwala et al. (2015), the $s_B$-related source terms, $s_B u_i$ and $s_B \phi _i$, are introduced in the momentum and scalar equations. Adding such terms is based on the physical picture that, when the gas mixture is taken out by the boundary mass sink, it leaves the computational domain with its own velocity and scalar values, $u_i$ and $\phi _i$. From the continuity equation and the scalar equation, for example, we obtain

$$\begin{aligned} \rho \frac{D \phi _i }{D t} = \frac{\partial \Gamma _{i,j}}{\partial x_j} + \omega _{\phi _i} , \end{aligned}$$

(10)

where the $s_B \phi _i$ term is canceled out. The material derivative is not affected by the $s_B$ term. As a result, for example, when a completely premixed unburned mixture flows across the boundary mass sink layer, its composition does not change. On the other hand, as in Eqs. (4) and (5), the volume integral of the $s_B \phi _i$ term is equal to the scalar flow rate across the inner side of $\partial \Omega _F$, which is sufficient for the global conservation inside $\Omega _F$ in the present method.

When the gas flows across the boundary mass sink layer, it experiences the jump in the velocity normal to the layer due to the periodic extension – on both sides of the layer, the volume-expansion-induced radial velocity is in the direction toward the layer. When integrating the convective form of the momentum equation over the time interval for which the gas crosses the boundary mass sink layer, the normal velocity jump term becomes $\pm \int s_{B} d x_i$, where the integration along the $x_i$ direction is performed across the layer that is normal to the $x_i$ direction, with the assumption of the very thin layer and the sign depending on the direction of the gas velocity in the $x_i$ direction. When divided by the density, the integrated term is equal to the jump condition in the velocity normal to the layer across the periodic, neighboring image domains. With the boundary mass sink layer being represented by the regularized delta function, in the simulation, the jump condition appears as the smoothed and weak discontinuity in the normal velocity component.

3 Test Cases and Results

The boundary mass sink method is tested for laminar and turbulent flame kernels. The governing equations for the low Mach number variable density flows are solved. With the constant thermodynamic pressure and the low Mach number, the density is evaluated as $1/\rho = 1/\rho _u + (1/\rho _b-1/\rho _u) c$. The ratio of the unburned density, $\rho _u$, to the burned density, $\rho _b$, is in the range of 3–7. As the thermodynamic pressure is constant, $\rho _u$ and $\rho _b$ are fixed. $\rho$ is also $\rho _p$ in Eqs. (4) and (5). The evolution of the flame is described by the progress variable c with single-step chemistry. The reaction progress variable c is solved with the Fick’s law for molecular diffusion, which is widely used for DNS of turbulent flames. The Schmidt number is 0.7, while the Lewis number is unity. The viscosity is evaluated as $\mu = \mu _u (\rho _u/\rho _b)^{0.75}$, where $\mu _u$ is the viscosity of the unburned gas. The form of viscous stress for the (isotropic) Newtonian fluid is used. The reaction rate in the progress variable equation is given as $\omega _c = A \rho (1-c)\exp (-\beta /(1+ \sigma c))$, where A is the pre-exponential factor, $\sigma = \rho _u/\rho _b-1$, and $\beta$ is the non-dimensional activation temperature (Kim 2017). The reaction rate expression is for a fuel-lean mixture with unity Lewis number assumption. While the method can be applied to a detailed chemical mechanism, a simple one-step mechanism is used here. As described in Sect. 2, the periodic condition is used for all the boundaries of the computational domain.

The governing equations in the low Mach number formulation are solved on uniform structured grid (Desjardins et al. 2008; Su and Kim 2018). The second-order semi-implicit Crank-Nicolson scheme with time staggering between the velocity and scalar fields is used for time integration. The second-order central finite difference scheme is used for spatial discretization on the staggered grid, except for scalar advection for which the fifth-order weighted essentially non-oscillating (WENO) scheme (Jiang and Shu 1996) is used. The constant coefficient Poisson’s equation for the pressure correction, the derivation of which uses the continuity equation that contains the boundary mass sink term, is solved. The present method can also be applied to the governing equations for fully compressible flows with no additional modification, while it assumes the low Mach number and the acoustic response needs to be investigated.

3.1 Laminar Flame Kernel

Fig. 1

Density and velocity fields for a laminar circular flame at two different times (top figures: $t^* \approx 6.4$, bottom figures: $t^* \approx 12.8$). (left) Density (red: $\rho _u$, blue: $\rho _b$). (center) Velocity magnitude (red: maximum ($0.73 \rho _u s_{L,0}/\rho _b$ at $t^* \approx 12.8$ and $0.68\rho _u s_{L,0}/\rho _b$ at $t^* \approx 6.4$), blue: 0). (right) Horizontal velocity component (red: $0.73 \rho _u s_{L,0}/\rho _b$ at $t^* \approx 12.8$ and $0.68\rho _u s_{L,0}/\rho _b$ at $t^* \approx 6.4$, blue: $-0.73 \rho _u s_{L,0}/\rho _b$ at $t^* \approx 12.8$ and $-0.68\rho _u s_{L,0}/\rho _b$ at $t^* \approx 6.4$). (The color changes from red to yellow to green to cyan to blue, as the value of a physical quantity decreases, with the median being represented by the green color; $t^* = t s_{L,0} |\nabla c|_{max}$)

The outwardly propagating circular and spherical flames are simulated. The density ratio $\rho _u/\rho _b$ is 5. The non-dimensional activation temperature $\beta$ is set to be 20. For a circular flame, the square domain is discretized using $384^2$ uniformly-spaced grid points. For a spherical flame, the cubic domain is discretized using $256^3$ uniformly-spaced grid points. The laminar flame thickness defined as $1/|\nabla c|_{max}$ is 8h, where $|\nabla c|_{max}$ is the maximum magnitude of the gradient of the progress variable. The grid resolution is determined such that the planar laminar flame speed is well predicted and grid-independent. By increasing the number of grid points in one direction by 25%, the change in the laminar flame speed is about 0.1%. The radius of the initial flame kernel is 0.048L for a circular one and 0.08L for a spherical one, where L is the side length of the square or cubic domain.

Fig. 2

Density, boundary mass sink, and velocity fields for a shifted laminar circular flame at $t^* \approx 6.4$. a Density (red: $\rho _u$, blue: $\rho _b$). b Boundary mass sink (red: 0, blue: minimum). c Velocity magnitude (red: $0.68\rho _u s_{L,0}/\rho _b$, blue: 0). d Horizontal velocity component (red: $0.68\rho _u s_{L,0}/\rho _b$, blue: $-0.68\rho _u s_{L,0}/\rho _b$ ). (The color changes from red to yellow to green to cyan to blue, as the value of a physical quantity decreases, with the median being represented by the green color; $t^* = t s_{L,0} |\nabla c|_{max}$)

Figure 1 shows the density and velocity fields in the circular flame at different times. The flame center is located at the center of the domain, (0, 0). With the constant pressure condition, the unburned and the burned density remain unchanged throughout the simulation. Inside the computational domain, the velocity fields show the isotropy. At the boundaries, the velocity normal to the boundary is to vanish due to the symmetry, while that tangential to the boundary is continuous. As a result, the horizontal velocity component shows a jump across the regularized delta function at the vertical boundary through the periodic condition. The boundary mass sink term removes the gas arriving at each side of the boundary across the boundary mass sink layer.

Such characteristics of the velocity field near the boundaries are better seen in Fig. 2, which shows the results for a shifted circular flame. The flame conditions are the same as those for Fig. 1. The center of the circular flame is located at (L/6, L/6). While the kernel center is located differently than in Fig. 1, due to the periodic boundary condition, the kernel is to grow in the same way as in Fig. 1. Translating the fields in Fig. 2 by $(-L/6,-L/6)$ and using the periodicity leads to those in Fig. 1 at the same time instant. To preserve the translational invariance, the boundary mass sink term is placed around the domain $\Omega _F$ the center of which is that of the flame kernel, as shown in Fig. 2b. The removal of the outwardly moving gas at the boundary mass sink layer in the laminar flame with no additional convection is clearly and better presented in Fig. 2c than in Fig. 1, with the layers being located well inside the computational domain due to the shift of the kernel center, while the two fields are identical upon the translation. The smoothed discontinuity in the velocity normal to the mass sink layer is better seen in Fig. 2d along the vertical layer. The velocity tangent to the mass sink layer is continuous and symmetric across the regularized delta function, as shown in Fig. 2d along the horizontal boundary mass sink layer. Similarly to the case for Fig. 1, the isotropy of the velocity field is vey well preserved.

Fig. 3

Velocity and pressure fields on on the $x_1$-$x_2$ plane passing the center of a laminar spherical flame at $t^* \approx 5.9$. a Velocity magnitude (red: $0.57\rho _u s_{L,0}/\rho _b$, blue: 0). b Pressure (red: $14.5\rho _u s_{L,0}^2$, blue: 0). (The black lines denote the iso-c surfaces with $c=$0.1, 0.5, and 0.9; The color changes from red to yellow to green to cyan to blue, as the value of a physical quantity decreases, with the median being represented by the green color; $t^* = t s_{L,0} |\nabla c|_{max}$)

Figure 3 shows the distribution of the pressure and the velocity magnitude on a 2-D cross-section crossing the domain center for the spherical flame at $t^* \approx 5.9$, where $t^* = t s_{L,0} |\nabla c|_{max}$. The isotropy of the pressure and velocity fields is well preserved in Fig. 3. The radial velocity $u_r$ becomes the maximum on the unburned side of the flame front and, for a spherical flame, decreases as $u_r \sim r^{-2}$. The (hydrodynamic) pressure decreases from the unburned side of the flame front as $p \sim r^{-4}$. While the local (hydrodynamic) pressure spatially varies to satisfy the continuity, the thermodynamic pressure, which is used to evaluate the density in the low Mach number formulation, remains constant thanks to the boundary mass sink terms. The isotropy is well reproduced beyond the radius larger than the half domain size, $r>L/2$.

Fig. 4

Radial profile of the velocity for a laminar spherical flame at $t^* \approx 5.9$ (solid line: along the direction (1, 0, 0)), dashed line: along the direction $(1/\sqrt{2},1/\sqrt{2},0)$, dashed-dotted line: along the direction $(1/\sqrt{3},1/\sqrt{3},1/\sqrt{3})$, circles: analytic scaling). ($t^* = t s_{L,0} |\nabla c|_{max}$)

Figure 4 shows the radial profiles of the velocity for the laminar spherical flame along three different directions. Three directions correspond to the $x_1$ direction, (1,0,0), the direction $(1/\sqrt{2},1/\sqrt{2},0)$ toward the edge, and $(1/\sqrt{3},1/\sqrt{3},1/\sqrt{3})$ toward the corner. Also shown is the analytic scaling in the unburned region, $u_r = u_{r,u} (r_{r,u}/r)^2$, where $u_{r,u}$ the radial velocity on the unburned side of the flame front and $r_{r,u}$ its radial location. In Fig. 4, the values at $c=0.001$ are used. The radial velocity in the three directions closely follows the analytic scaling beyond the radius larger than the half domain size, as in Fig. 3. While the slight deviation occurs in close proximity to an edge in the profile for the direction toward the edge and to a corner in that toward the corner, the method closely reproduces the analytic solution.

3.2 Turbulent Flame Kernel

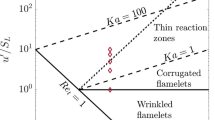
The outwardly propagating premixed flame kernel in decaying isotropic turbulence is simulated. The initial turbulence field is generated using the linear forcing method (Lundgren 2003; Carroll and Blanquart 2013). Initially, a spherical kernel with the radius of 0.6$l_t$ is placed at the center of the domain, where $l_t$ is the longitudinal integral length scale of initial turbulence. Five cases with varying $u'_0/s_{L,0}$, $\rho _u/\rho _b$, and $Re_\lambda$ are considered, where $u'_0$ is the initial turbulence root mean square (r.m.s.) velocity fluctuation and $Re_\lambda$ the Taylor scale turbulence Reynolds number. The Taylor length scale of the initial turbulence field, $\lambda _0$, is used for scaling the vorticity in the figures. All the flames are in the thin reaction zones regime. The simulation parameters are summarized in Table 1. The simulations are performed on uniform grid with $384^3$ grid points. The grid resolution satisfies a criterion, $l_K/h > 0.5$, which has often been used in DNS of turbulent flames, and is sufficient for the purpose of the present work.

Table 1 Flame and turbulence conditions for DNS ($Ka=D_u /(s_{L,0}^2 \tau _{K})$, where $D_u$ is the diffusivity of the progress variable in the unburned mixture and $\tau _{K}$ the initial Kolmogorov time scale; $l_K$: initial Kolmogorov length scale; $|\nabla c|_{max,0}$: the maximum magnitude of the progress variable gradient in the planar laminar flame; h: grid size; all the simulations are performed on the $384^3$ grid)

Fig. 5

Distributions of the boundary mass sink, velocity, and vorticity on the $x_1$-$x_2$ plane passing the domain center from the case A at different times (from left to right, $t^* \approx 0.2$, 0.6, 1, and 1.2). (top) Boundary mass sink (red: 0, blue: minimum at the given time instant); also shown are the flame surfaces represented by the iso-c surfaces with $c=0.5$; 2-D distribution is opaque and the pink iso-c surfaces are in the backside of the cross-section). (center) Velocity magnitude (red: $3 u'_0$, blue: 0; black line: iso-c surface with $c=0.5$). (bottom) Vorticity magnitude (red: $10 u'_0/\lambda _0$, blue: 0; black line: iso-c surface with $c=0.5$). (The color changes from red to yellow to green to cyan to blue, as the value of a physical quantity decreases, with the median being represented by the green color.)

Figure 5 shows the distributions of the boundary mass sink term, velocity magnitude, and vorticity magnitude on a 2-D cross-section at different times, $t^* \approx 0.2$, 0.6, 1, and 1.2, for the case A, where $t^*$ is the time normalized by the initial eddy turn over time. Also shown are the flame surfaces represented as the iso-c surfaces. At initial times, the magnitude of the boundary mass sink term is very small. As the flame kernel grows and heat release rates increase, the magnitude increases. The magnitude of $S_B$ is proportional to turbulent flame speed, kernel size, and the density difference $\rho _u-\rho _b$. In Fig. 5, the boundary mass sink term is normalized by the maximum of $|s_B|$ in order to present the boundary mass sink layers at different times more clearly. As the kernel center is slowly moving, the locations of the boundary mass sink layers change over time slightly. Overall, as the periodic boundary condition is used for all the boundaries of the computational domain, the characteristics of the homogeneous turbulence field in the unburned region are well preserved without any undesirable influence of the backflow for the whole time duration.

Fig. 6

Distributions of the boundary mass sink and the velocity component $u_1$ on the $x_1$-$x_2$ plane passing the domain center from the case A at $t^* \approx 1.2$. (left) Boundary mass sink (red: 0, blue: minimum at the given time instant); black line: iso-c surface with $c=0.5$). (right) Velocity component in the $x_1$ direction (red: $u'_0$, blue: $-u'_0$; black line: iso-c surface with $c=0.5$). (The color changes from red to yellow to green to cyan to blue, as the value of a physical quantity decreases, with the median being represented by the green color.)

For a flame kernel, a radial component of the velocity is induced due to its growth and the density difference between the burned and unburned gases. The boundary mass sink and velocity jump terms compensate the component of the volume-expansion-induced radial velocity such that the periodic condition can be consistently used. The mass sink term removes the unburned gas pushed away due to the volume expansion. For the gas that flows across the layers, the velocity jump due to the periodic extension of the volume-expansion-induced velocity field is enforced through the normal velocity jump term. With such volume-expansion-induced components being compensated, the background turbulence is fed back to the periodic image domain across the boundary mass sink layer. The periodic boundary condition and the boundary mass sink and velocity jump terms act to feed homogeneous turbulence relative to the periodic extension of the volume-expansion-induced velocity field in $\Omega _F$ to the domain. To illustrate such effects, the boundary mass sink layers and the velocity component $u_1$ on an $x_1-x_2$ plane are shown in Fig. 6. The horizontal and vertical directions in the figure correspond to the $x_1$ and $x_2$ directions, respectively. When the unburned mixture flows across the vertical layer from the left to the right (from the right to the left), the velocity component $u_1$ decreases (increases) at the layer according to the jump condition. The velocity jump is relatively weak as compared with turbulent velocity fluctuations. The fields in Fig. 6 are from the case A at $t^* \approx 1.2$, and correspond to those in Fig. 5 at the same time instant.

Fig. 7

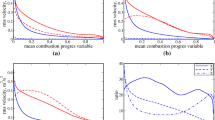
Effects of the normal velocity jump term. a Time evolution of the vorticity r.m.s. fluctuations in the unburned mixture (solid line: with the normal velocity jump term, dashed line: without the normal velocity jump term, circles: separate constant density simulation; normalized by $u'_0/\lambda _0$). b Time evolution of total reaction rates (solid line: with the normal velocity jump term, dashed line: without the normal velocity jump term; the total reaction rates are obtained from the volume integration of the reaction rate for the progress variable over the computational domain and normalized by $4\pi (3V_{K,0}/(4\pi ))^{2/3} \rho _u s_{L,0}$, where $V_{K,0}$ is the initial volume of the flame kernel)

To further assess the accuracy of the method, the statistics of vorticity fluctuations, which are little affected by the outward flow induced by the flame expansion but determined predominantly by the ambient turbulence, are investigated. Two simulations for the case A are performed. In one simulation, all the formulations presented in Sect.  2 are used. In the other simulation, the normal velocity jump term is not included. Figure 7a shows the time evolution of the r.m.s. vorticity fluctuations in the unburned mixture from the two simulations. The r.m.s. vorticity fluctuations, for which the averaging is performed over the unburned region, with the progress variable c less than 0.01, except for the boundary mass sink layers, are compared with those from a separate simulation for constant density, decaying isotropic turbulence with the same initial field. The results from the two simulations, with and without the normal velocity jump term, closely follow that from the decaying isotropic turbulence simulation when $t^*<1$. When the normal velocity jump term is not included, the r.m.s. vorticity fluctuations are slightly larger than those from the constant density simulation at later stages. When the normal velocity jump term is included, the r.m.s. vorticity fluctuations closely follow those from the decaying turbulence simulation for the whole duration in Fig. 7a. With the normal velocity jump term, the velocity field becomes consistent with the physical picture of feeding the background homogeneous turbulence relative to the volume-expansion-induced velocity field to the domain. As a result, the accuracy of the simulation improves and the simulation can be performed nearly without the undesirable influence of the boundary condition. On the other hand, the total reaction rates with and without the normal velocity jump term are almost identical for the whole duration in Fig. 7b, which seem to imply the importance of feeding the homogeneous turbulence to the domain through the periodic condition.

When the negative dilatation is present, the vorticity-dilatation term, $- \zeta _i \partial u_k / \partial x_k$, in the vorticity equation tends to strengthen the vorticity locally, where $\zeta _i$ is the vorticity component in the $x_i$ direction. Without the normal velocity jump term, the convective form of the momentum equation is unaffected by the boundary mass sink term. As a result, the negative dilation due to the boundary mass sink term tends to generate the vorticity in the boundary mass sink layer, while the net production may not be significant. The normal velocity jump term suppresses the vorticity generation by enforcing the continuity in the background turbulence relative to the volume-expansion-induced velocity field across the layer.

Fig. 8

Time evolution of the vorticity r.m.s. fluctuations in the unburned mixture for different cases (normalized by $u'_0/\lambda _0$). a Cases A-D (solid line: case A, dashed line: case B, dashed-dotted line: case C, dashed-dotted-dotted line: case D, circles: separate constant density simulation). b Case E (solid line: case E, circles: separate constant density simulation)

Figure 8 shows the time evolution of the vorticity r.m.s. fluctuations in the unburned mixture for different cases. The cases A–D have the identical initial turbulence field, with $Re_\lambda \approx 88$, and the results are shown in Fig. 8a. The vorticity r.m.s. fluctuations in the unburned mixture should evolve identically for the cases A–D. The Taylor-scale turbulence Reynolds number, $Re_\lambda$, is 66 for the case E and the results are shown in Fig. 8b. All the simulations are performed with the normal velocity jump term being included. The vorticity r.m.s. fluctuations for all the cases closely follow those from the corresponding separate constant density simulation in Fig. 8.

Fig. 9

Effects of the functional form for the distribution of the boundary mass sink along the layers. a Time evolution of the vorticity r.m.s. fluctuations in the unburned mixture (solid line: $r^{-2}$ scaling in Eq. (9), dashed line: uniform $s_0=a$, circles: separate constant density simulation; normalized by $u'_0/\lambda _0$). b Time evolution of total reaction rates (solid line: $r^{-2}$ scaling in Eq. (9), dashed line: uniform $s_0=a$; the total reaction rates are obtained from the volume integration of the reaction rate for the progress variable over the computational domain and normalized by $4\pi (3V_{K,0}/(4\pi ))^{2/3} \rho _u s_{L,0}$)

The effects of the functional form for the distribution of the boundary mass sink term along the layers $\partial \Omega _F$ are shown in Fig. 9. The results obtained using the $r^{-2}$ scaling in Eq. (9) are compared with those obtained using the uniform distribution, i.e., $s_0=a$, for the case A. The vorticity r.m.s. fluctuations in the unburned mixture from the two are almost identical in Fig. 9a. For the total reaction rates, they are almost identical up to $t^* \approx 1.2$. The slight deviation after $t^* \approx 1.3$ is due to the size of the kernel. As shown in Fig. 5, at $t^* \approx 1.2$, the size of the kernel is large enough for a part of the flame surface to cross the boundary mass sink layer. When the kernel is within the domain $\Omega _F$ with flame surfaces not crossing $\partial \Omega _F$, the results obtained using the different forms of $s_B$ are almost identical in Fig. 9. The results suggest that the method is not sensitive to the form of $s_B$.

While the present method requires a periodic boundary condition, its application may not be restricted to an outwardly propagating spherical flame in homogeneous turbulence. The development of a kernel formed by forced ignition can be simulated using the method, while the kernel may not be spherical initially. Similarly, an outwardly propagating cylindrical flame can be simulated, for which the form of $s_0$ can be modified accordingly. The method can also be combined with wall boundaries.

4 Conclusions

A method to simulate an outwardly propagating premixed flame in homogeneous isotropic turbulence at constant pressure is presented. The method utilizes the periodic boundary condition used for homogeneous isotropic turbulence, avoiding the unphysical influence of the boundary-condition-induced backflow, and uses the mass sink terms concentrated at the boundaries of a cubic domain moving with the flame kernel to maintain the constant pressure. Along with the mass sink terms, the normal velocity jump term is introduced to feed homogeneous turbulence relative to the periodic extension of the volume-expansion-induced velocity field into the cubic domain in which the kernel evolves. The method is tested for laminar and turbulent flame kernels. The results show that the present method well preserves the characteristics of the turbulence field, as well as those of the outwardly propagating flame, thus enhancing the accuracy and/or computational efficiency of the simulation.