Lewis Number Effects on Flame Speed Statistics in Spherical Turbulent Premixed Flames

Abstract

The influences of characteristic Lewis number $\hbox{Le}$ on the statistics of density-weighted displacement speed and consumption speed in spherically expanding turbulent premixed flames have been analysed using three-dimensional direct numerical simulations data for $\hbox{Le} = 0.8$, 1.0 and 1.2 under statistically similar flow conditions. It has been found that the extents of flame wrinkling and burning increase with decreasing $\hbox{Le}$, which is reflected in increasing trends of mean and most probable values of both density-weighted displacement and consumption speed. Moreover, in all cases the marginal probability density functions of density-weighted displacement speed show finite probabilities of obtaining negative values, whereas consumption speed remains deterministically positive. The strain rate and curvature dependences of scalar gradient and temperature have been found to be strongly dependent on $\hbox{Le}$, and these statistics, along with the interrelation between strain rate and curvature, influence the local strain rate and curvature responses of consumption speed and both reaction and normal diffusion components of density-weighted displacement speed. Density-weighted displacement speed and curvature have been found to be negatively correlated, whereas positive correlations are obtained between density-weighted displacement speed and tangential strain rate for all flames considered here. The positive correlation between temperature and curvature arising from differential diffusion of heat and mass in the $\hbox{Le} = 0.8$ case induces a positive correlation between consumption speed and curvature, whereas these correlations are negative in the $\hbox{Le} = 1.2$ flame. The statistical behaviour of density-weighted displacement speed has been utilised to demonstrate that Damköhler’s first hypothesis does not strictly hold for spherically expanding turbulent premixed flames.

1 Introduction

A number of experimental (Abdel-Gayed et al. 1984; Renou et al. 2000; Chaudhuri et al. 2012; Gashi et al. 2005; Poinsot et al. 1995) and direct numerical simulation (DNS) (Thevenin 2005; Jenkins and Cant 2002; van Oijen et al. 2005; Klein et al. 2006, 2009; Chakraborty et al. 2007; Dunstan and Jenkins 2009) investigations concentrated on the analysis of statistically spherical turbulent premixed flames because of their relevance to Spark Ignition (SI) engines and accidental explosions. Many of these aforementioned analyses focused on flame propagation (Abdel-Gayed et al. 1984; Renou et al. 2000; Chaudhuri et al. 2012; Gashi et al. 2005; Poinsot et al. 1995; Mizomoto et al. 1984; Bechtold and Matalon 2001; Law and Kwon 2004), curvature and flame wrinkling (Gashi et al. 2005; Klein et al. 2009; Dunstan and Jenkins 2009), and burning rate (Abdel-Gayed et al. 1984; Renou et al. 2000; Chaudhuri et al. 2012; Gashi et al. 2005; Poinsot et al. 1995; Thevenin 2005; van Oijen et al. 2005; Dunstan and Jenkins 2009) statistics in turbulent statistically spherical flames but in the absence of differential diffusion of heat and mass. A non-dimensional number, known as the Lewis number (i.e. ratio of thermal diffusivity to mass diffusivity), is often used to characterise the effects of differential diffusion of heat and mass in premixed turbulent flames. The evaluation of the characteristic Lewis number of a premixed flame is not straightforward as every species has different values of $\hbox{Le}$, but several approaches to estimate a characteristic Lewis number $\hbox{Le}$ are reported in the existing literature. The characteristic Lewis number of a premixed combustion process can be evaluated either by the Lewis number of a deficient reactant (Mizomoto et al. 1984; Bechtold and Matalon 2001) or by heat release rate measurements (Law and Kwon 2004) or by employing binary diffusion theory for the mixture (Clarke 2002) or by linear combination of Lewis numbers of the constituent species in terms of their mole fractions (Dinkelacker et al. 2011). For example, Bechtold and Matalon (2001) proposed the characteristic value of Lewis number $\hbox{Le} = 1.0 + \left[ {\left( {Le_{F} - 1} \right) + \left( {Le_{O} - 1} \right)A_{Le} } \right]/\left( {1 + A_{Le} } \right)$ where $A_{Le} = 1 + \beta \left( {\Phi - 1} \right)$ with $\Phi = \phi$ for fuel-rich mixtures, whereas $\Phi = 1/\phi$ for fuel-lean mixtures with $\phi$ and $\beta$ being the equivalence ratio and Zel’dovich number, respectively and subscripts F and O are used for fuel and oxidiser, respectively. It is well-known that the characteristic Lewis number $\hbox{Le}$ (henceforth referred to as Lewis number) significantly affects the flame wrinkling and burning rate (Williams 1985; Clavin and Joulin 1983; Ashurst et al. 1987; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2005a, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018). The influences of $\hbox{Le}$ on local strain rate and curvature dependences of flame speeds have not yet been analysed in detail for spherically expanding turbulent premixed flames although these statistics have been analysed extensively in statistically planar turbulent premixed flames (Ashurst et al. 1987; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2005a, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018). However, spherically expanding premixed flames are fundamentally different from statistically planar premixed flames. It has been shown elsewhere (Klein et al. 2006, 2009; Chakraborty et al. 2007) that both flame propagation and scalar gradient statistics in spherically expanding flames can be significantly different from the corresponding statistically planar flames subjected to statistically similar unburned gas turbulence. The effects of mean flame curvature have been previously addressed by these authors by conducting DNS of spherically expanding turbulent premixed flames with different mean radii. Interested readers are referred to Refs. (Klein et al. 2006, 2009; Chakraborty et al. 2007) for detailed discussion on the effects of mean flame curvature. However, the aforementioned analyses on spherically expanding flames have been conducted for unity Lewis number flames and this gap in the existing literature will be addressed in this paper by using three-dimensional simple chemistry DNS of spherically expanding turbulent premixed flames with $\hbox{Le} = 0.8, 1.0$ and 1.2 but the analysis of the effects of initial flame radius is kept beyond the scope of this paper. The unity Lewis number flame considered here is analogous to a stoichiometric methane-air flame, whereas the Lewis number 0.8 case is representative of a hydrogen-blended (e.g. 10% by volume) methane-air flame with overall equivalence ratio of 0.6 and the Lewis number 1.2 case is representative of a hydrocarbon-air mixture involving a hydrocarbon fuel which is heavier than methane (e.g. ethane-air mixture with equivalence ratio of 1.2) (Clarke 2002; Dinkelacker et al. 2011). The concept of characteristic Lewis number has been used in several previous experimental, DNS and analytical studies (Mizomoto et al. 1984; Bechtold and Matalon 2001; Dinkelacker et al. 2011; Williams 1985; Clavin and Joulin 1983; Ashurst et al. 1987; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2005a, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018) by other authors to analyse the effects of differential diffusion of heat and mass in isolation, and the same approach has been adopted here. The use of simple chemistry allows for alternation of the characteristic Lewis number independent of other parameters and thus the effects of $\hbox{Le}$ can be analysed in isolation following several previous analyses (Williams 1985; Clavin and Joulin 1983; Ashurst et al. 1987; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2005a, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018). In the context of single step chemistry, the characteristic Lewis number $\hbox{Le}$ value is assigned for the molecular diffusion of reaction progress variable $c$, which is assumed to be defined based on the deficient reactant mass fraction for the purpose of simplicity following several previous analyses (Dinkelacker et al. 2011; Williams 1985; Clavin and Joulin 1983; Ashurst et al. 1987; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2005a, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018). However, it needs to be understood that this characteristic Lewis number does not represent molecular transport of non-deficient reactants and in general for the species mass fractions, which are not used for the definition of $c$. In this context, it is worth noting that it has been demonstrated in the past that displacement speed (DS) statistics from simple chemistry (Klein et al. 2006; Chakraborty et al. 2007; Klein et al. 2009; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2004, 2005a, 2006; Han and Huh 2008; Chakraborty et al. 2011) and detailed chemistry (Peters et al. 1998; Echekki and Chen 1999; Chen and Im 1998; Chakraborty et al. 2008) DNS are qualitatively similar. The same is true for the statistics of the reactive scalar gradient obtained from simple chemistry (Chakraborty and Klein 2008; Chakraborty and Cant 2005b; Chakraborty et al. 2013) and detailed chemistry (Chakraborty et al. 2008, 2013) DNS studies. Moreover, the vorticity and sub-grid flux statistics obtained from simple chemistry (Chakraborty et al. 2016; Gao et al. 2015) DNS are found to be qualitatively consistent with those obtained from detailed chemistry (Papapostolou et al. 2017; Klein et al. 2018) DNS. A comparison between Chakraborty and Klein (2008) and Chakraborty et al. (2008) revealed that the displacement speed and the reactive scalar gradient statistics for unity Lewis number flames are representative of stoichiometric methane-air flames, whereas a hydrogen-flame with equivalence ratio of 0.7 behaves qualitatively similarly to the simple chemistry DNS data with $\hbox{Le} = 0.8$. Furthermore, several models developed based on simple chemistry data (Gao et al. 2014, 2015; Gao and Chakraborty 2016) have been found to perform equally well in the context of detailed chemistry and transport (Klein et al. 2018; Gao et al. 2016). Finally, a simple chemical mechanism allows for an assessment of the validity of Damköhler’s first hypothesis (Damköhler 1940) for spherically expanding flames without the uncertainties about the choices of reaction progress variable in the presence of detailed chemistry and transport (Klein et al. 2020).

The main objective of the current analysis is to demonstrate and explain the influences of $\hbox{Le}$ on both mean behaviours of consumption speed (CS) $S_{c}$ and density-weighted displacement speed (DDS) $S_{d}^{*}$ and their local curvature and tangential strain rate dependences. These statistics, in turn, have been used to assess the validity of Damköhler’s first hypothesis (Damköhler 1940) for spherically expanding premixed turbulent flames.

The rest of the paper is organized in the following manner. The mathematical background and numerical implementation pertinent to the current work are provided in the next section. This is followed by the presentation and discussion of the results. Finally, a summary of main findings is provided along with conclusions.

2 Mathematical Background and Numerical Implementation

The reaction progress variable $c$ can be defined based on a suitable deficient reactant mass fraction $Y_{R}$ as: $c = \left( {Y_{R0} - Y_{R} } \right)/\left( {Y_{R0} - Y_{R\infty } } \right)$ where subscripts 0 and $\infty$ refer to values in the unburned gas and fully burned products, respectively. The transport equation of $c$ is given by:

$$ \rho [\partial c/\partial t + u_{j} \partial c/\partial x_{j} ] = \dot{w} + \partial \left( {\rho D\partial c/\partial x_{j} } \right)/\partial x_{j} $$

(1)

where $\rho , u_{j} ,D$ and $\dot{w}$ are gas density, jth component of fluid velocity, progress variable diffusivity and reaction rate of progress variable, respectively. A single step Arrhenius type expression $\dot{w} = \rho B\left( {1 - c} \right){ \exp }\left\{ { - \beta \left( {1 - \theta } \right)/\left[ {1 - \alpha \left( {1 - \theta } \right)} \right]} \right\}$ is considered for the chemical reaction rate where $B$ is the normalised pre-exponential factor, $\beta = T_{ac} \left( {T_{ad} - T_{0} } \right)/T_{ad}^{2}$ is the Zel’dovich number, $\theta = \left( {T - T_{0} } \right)/\left( {T_{ad} - T_{0} } \right)$ is the non-dimensional temperature and $\alpha = \left( {T_{ad} - T_{0} } \right)/T_{ad}$ is the heat release parameter, respectively with $T,T_{0} ,T_{ad}$ and $T_{ac}$ being the instantaneous, unburned gas, adiabatic flame and activation temperatures, respectively. Equation 1 can be rewritten in a kinematic form for a given $c$-isourface as: $\left[ {\partial c/\partial t + u_{j} \partial c/\partial x_{j} } \right] = S_{d} \left| {\nabla c} \right|$ where $S_{d}$ is the displacement speed (DS), which is given as (Klein et al. 2006; Chakraborty et al. 2007; Klein et al. 2009; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2006; Chakraborty and Cant 2005a; Han and Huh 2008; Chakraborty and Cant 2004; Chakraborty et al. 2011):

$$ S_{d} = \frac{{\dot{w} + \nabla \cdot \left( {\rho D\nabla c} \right)}}{{\rho \left| {\nabla c} \right|}} = S_{r} + S_{n} + S_{t} \quad {\text{where}}\,\, S_{r} = \frac{{\dot{w}}}{{\rho \left| {\nabla c} \right|}}; \,\, S_{n} = \frac{{\vec{N} \cdot \nabla \cdot \left( {\rho D\vec{N} \cdot \nabla c} \right)}}{{\rho \left| {\nabla c} \right|}}\quad {\text{and}}\quad S_{t} = - 2D\kappa_{m} $$

(2)

Here $\vec{N} = - \nabla c/\left| {\nabla c} \right|$ is the local flame normal vector and $\kappa_{m} = 0.5\nabla \cdot \vec{N}$ is the local flame curvature. According to these definitions, the flame normal points towards the reactants and an element of the flame surface has a positive (negative) curvature if it is convex (concave) to the reactants. The involvement of $\rho$ in Eq. 2 indicates that thermal expansion affects the behaviour of DS and its components. Thus, it is worthwhile to consider DDS $S_{d}^{*} = \rho S_{d} /\rho_{0}$ and its components: $S_{r}^{*} = \rho S_{r} /\rho_{0}$, $S_{n}^{*} = \rho S_{n} /\rho_{0}$ and $S_{t}^{*} = \rho S_{t} /\rho_{0}$ where $\rho_{0}$ is the unburned gas density. Moreover, $\rho S_{d}$ is often used for modelling purposes (Chakraborty and Cant 2007, 2009) and thus it is useful to consider density-weighted displacement speed (DDS) $S_{d}^{*}$ instead of $S_{d}$. An alternative flame speed, known as consumption speed (CS) $S_{c}$, is also used in premixed combustion literature. The local CS $S_{c}$ is defined as (Williams 1985; Rutland and Trouvé 1993):

$$ S_{c} = \rho_{0}^{ - 1} \smallint \dot{w}dn $$

(3)

where $dn$ is the elemental distance in the local flame normal direction. For the present thermo-chemistry the maximum value of $\dot{w}$ occurs approximately at $c = 0.8$, and thus the $c = 0.8$ isosurface will be considered as the flame surface in this analysis. For evaluating $S_{c}$, the reaction rate is integrated in the positive and negative local flame normal direction starting from the $c = 0.8$ isosurface. For consistency, the statistics of $S_{d}^{*}$ and its components will also be presented for the $c = 0.8$ isosurface.

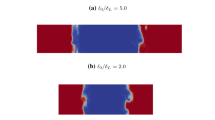
The statistical behaviours of $S_{c}$ and $S_{d}^{*}$ and their tangential strain rate $a_{T} = \left( {\delta_{ij} - N_{i} N_{j} } \right)\partial u_{i} /\partial x_{j}$ and curvature $\kappa_{m}$ dependences have been investigated based on a three-dimensional simple chemistry DNS database of spherically expanding premixed turbulent flames with characteristic Lewis numbers $\hbox{Le} = 0.8$, 1.0 and 1.2 in this analysis. Figure 1 shows instantaneous views of these three flame kernels. The simulations have been carried out using a well-known compressible DNS code SENGA (Klein et al. 2006; Chakraborty et al. 2007; Klein et al. 2009; Dunstan and Jenkins 2009; Chakraborty and Cant 2004, 2005a, 2006, 20072009; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018; Chakraborty et al. 2011) where the conservation equations of mass, momentum, energy and reaction progress variable have been solved in non-dimensional form and spatial discretisation and time-advancement are achieved by high-order finite-difference and explicit Runge–Kutta schemes, respectively. The simulation domain is taken to be a cube of $58.10\delta_{th} \times 58.10\delta_{th} \times 58.10\delta_{th}$ where $\delta_{th} = \left( {T_{ad} - T_{0} } \right)/\hbox{max} |\nabla T|_{L}$ is the thermal flame thickness (which is held constant for all three cases) and the subscript ‘L’ is used to refer to conditions in the unstrained laminar premixed flame. The Prandtl number, heat release parameter $\tau = \left( {T_{ad} - T_{0} } \right)/T_{0}$ and Zel’dovich number $\beta$ are taken to be $Pr = 0.7, \tau = 4.5$ and $\beta = 6.0$, respectively for every value of $\hbox{Le}$ considered here. The Schmidt number is modified to bring about the changes in Lewis number $\hbox{Le} = Sc/Pr$. The domain is discretised by a uniform Cartesian grid of $650 \times 650 \times 650$ and the domain boundaries are taken to be partially non-reflecting for all cases. The reacting scalar fields are initialised by a burned gas sphere with its centre initially at the centre of the domain using the steady state unstrained laminar flame solution. This reacting scalar field is allowed to evolve in a quiescent environment at least for one chemical time scale (i.e. $t = \delta_{th} /S_{L}$). The spherical laminar flame kernels for different Lewis numbers with a normalised radius of $rS_{L} /\alpha_{T0} = 10.6$ (considering the region corresponding to $c \ge 0.85$) have been used as the initial condition for turbulent simulations. Here $\alpha_{T0}$ is the thermal diffusivity of the unburned gas. The turbulent velocity fluctuations are initialised by a synthetic homogeneous isotropic divergence-free field, and the initial values of the normalised root-mean-square velocity fluctuation and longitudinal integral length scale are taken to be $u^{\prime}/S_{L} = 7.5$ and $l/\delta_{th} = 4.58$, respectively for each value of $\hbox{Le}$ considered here. These values of $u^{\prime}/S_{L}$ and $l/\delta_{th}$ are representative of the thin reaction zones regime of combustion (Peters 2000). The nominal Damköhler number $Da = lS_{L} /u^{\prime}\delta_{th}$ and Karlovitz number $Ka = \left( {u^{\prime}/S_{L} } \right)^{1.5} \left( {l/\delta_{th} } \right)^{ - 0.5}$ are 0.66 and 10.0, respectively for the initial values of $u^{\prime}/S_{L}$ and $l/\delta_{th}$ considered here. The initial values of $u^{\prime}/S_{L} , l/\delta_{th} , Da$ and $Ka$ are summarised in Table 1 for quick reference of the readers. The current analysis is done in the non-dimensional form in which all the flames with different $\hbox{Le}$ are subjected to the same set of initial values of $u^{\prime}/S_{L}$ and $l/\delta_{th}$. All the cases have the same heat release parameter $\tau = \left( {T_{ad} - T_{0} } \right)/T_{0} = 4.5$. Thus, all three cases considered here are located at the same location on the regime diagram. It is worth noting that in a real premixed combustion scenario, the Lewis number changes due to the nature of the fuel, and also due to the changes in equivalence ratio and these variations lead to modifications in laminar burning velocity, adiabatic flame temperature and flame thickness. However, it is possible to obtain the same values of $u^{\prime}/S_{L}$, $l/\delta_{th}$ and $\tau = \left( {T_{ad} - T_{0} } \right)/T_{0}$ for different values of characteristic Lewis number $\hbox{Le}$ by altering $u^{\prime},l$ and the level of preheating $T_{0}$. It is also possible to ensure that the flames with different characteristic Lewis number $\hbox{Le}$ have the same thermal flame thickness by altering the thermodynamic pressure. In the context of non-dimensional analysis with simplified chemistry, the pre-exponential factor of the Arrhenius type chemical reaction rate expression is modified to maintain identical values of $u^{\prime}/S_{L}$, $l/\delta_{th}$ and $\tau$.

Fig. 1

Instantaneous views of $c = 0.8$ isosurface coloured by local values of non-dimensional temperature $\theta$ and normalised curvature $\kappa_{m} \times \delta_{th}$ for $\hbox{Le} = 0.8$, 1.0 and 1.2 cases at the time when statistics are extracted

Table 1 Attributes of simulation parameters for each value of $\hbox{Le}$ considered in this analysis

All the simulations have been continued for 2 initial eddy turnover times (i.e. $t = 2.0l/\sqrt k$ where $k$ is the initial turbulent kinetic energy based on the whole domain), which here is equivalent to about 1.0 chemical timescale (i.e. $t = \delta_{th} /S_{L}$). At this stage, the turbulent kinetic energy was not varying rapidly with time and $u^{\prime}$ decayed by 40% in comparison to its initial value. The statistics presented in this paper do not change qualitatively since halfway through the simulation time. This was explicitly demonstrated in a previous analysis (see the comparisons between Tables 3 and 4, and Tables 5 and 6 in Ref. (Chakraborty et al. 2011)). Thus, it is not presented in this paper for the sake of brevity because the current results follow the same trend presented elsewhere (Chakraborty et al. 2011). However, the mean curvature of the spherically expanding flames decreases with increasing time as a result of their growth of size so the magnitudes of the mean values of curvature $\kappa_{m}$ and the tangential diffusion component of displacement speed $S_{t}^{*} = - 2\rho D\kappa_{m} /\rho_{0}$ decrease with time.

3 Results and Discussion

The instantaneous views of $c = 0.8$ isosurface coloured by local values of non-dimensional temperature $\theta$ and $\kappa_{m}$, when the statistics were extracted, are shown in Fig. 1. It can be seen from Fig. 1 that the flame is more wrinkled and bigger in size for $\hbox{Le} = 0.8$ than in the case of $\hbox{Le} = 1.0$. By contrast, the flame is less wrinkled and smaller in size for $\hbox{Le} = 1.2$ than in the case of $\hbox{Le} = 1.0$. This can be substantiated from the values of normalised volume-integrated burning rate $\Omega _{T} /\Omega _{L}$ and flame surface area $A_{T} /A_{L}$ in Table 2, where $\Omega$ and $A$ are evaluated as $\mathop \smallint \limits_{V} \dot{w}dV$ and $\mathop \smallint \limits_{V} \left| {\nabla c} \right|dV$ respectively, and the subscripts T and L refer to the values for the turbulent flame at the time when the statistics were extracted and laminar flame kernel values at the point of initialisation (i.e. $t = 0$), respectively. Table 2 shows that both the extent of burning and the flame area generation increase with decreasing $\hbox{Le}$, which is consistent with several previous studies (Williams 1985; Clavin and Joulin 1983; Ashurst et al. 1987; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2005a, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Dopazo et al. 2018). Figure 1 shows that positive curvature values are more likely than negative curvatures for all cases considered here because these flames are spherically expanding. Moreover, Fig. 1 shows that high (low) temperature values are associated with positive (negative) curvatures in the $\hbox{Le} = 0.8$ case, whereas high (low) temperature zones are found at negatively (positively) curved zones in the $\hbox{Le} = 1.2$ flame. The non-dimensional temperature $\theta$ and reaction progress variable $c$ can be equated to each other for low Mach number globally adiabatic unity Lewis number flames and thus $\theta$ remains uniform on the $c = 0.8$ isosurface. In the $\hbox{Le} = 0.8$ case, the focusing of reactants takes place at a faster rate than the rate of defocusing of heat at the positively curved zones, which leads to simultaneous presence of high temperature and reactant concentrations. This increases the local $\dot{w}$ and augments the temperature value further in the positively curved regions. Just the opposite mechanism leads to low temperature values at the negatively curved regions in the $\hbox{Le} = 0.8$ flame. By contrast, a combination of strong focusing of heat and weak defocusing of reactants leads to high $\dot{w}$ and $\theta$ in the negative curved zones in the case of $\hbox{Le} = 1.2$, and the opposite mechanism is responsible for low $\theta$ values at the positively curved locations in this case.

Table 2 Effects of $\hbox{Le}$ on $\Omega _{T} /\Omega _{L}$ and $A_{T} /A_{L}$

As the volume-integrated burning rate can alternatively expressed as: $\varOmega = \mathop \smallint \limits_{V} \rho S_{d} \left| {\nabla c} \right|dV$ (because $\mathop \smallint \limits_{V} \nabla \cdot \left( {\rho D\nabla c} \right)dV = 0$), it is worthwhile to consider $S_{d}^{*} = \rho S_{d} /\rho_{0}$ statistics. The probability density functions (PDFs) of $S_{c} /S_{L}$ and $S_{d}^{*} /S_{L}$ on the $c = 0.8$ isosurface (henceforth all DS related quantities are to be understood for this isosurface) are shown in Fig. 2, which shows that the probabilities of finding high values of $S_{c} /S_{L}$ and $S_{d}^{*} /S_{L}$ increase with decreasing $\hbox{Le}$. Moreover, both mean and most probable values of $S_{c} /S_{L}$ and $S_{d}^{*} /S_{L}$ are the highest in the $\hbox{Le} = 0.8$ case and the lowest in the $\hbox{Le} = 1.2$ case among the flames considered here. Larger values of $S_{d}^{*} /S_{L}$ for smaller $\hbox{Le}$ are consistent with the increasing extent of flame propagation and larger flame surface area with decreasing $\hbox{Le}$ (see Table 2). Moreover, the larger values of $S_{c} /S_{L}$ for smaller $\hbox{Le}$ are consistent with increasing trend of $\varOmega$ with decreasing $\hbox{Le}$ (see Table 2). Figure 2 shows that the distributions of $S_{c} /S_{L}$ and $S_{d}^{*} /S_{L}$ are significantly different. The most probable values of $S_{c} /S_{L}$ and $S_{d}^{*} /S_{L}$ remain comparable but smaller than unity in all cases. The turbulent spherically expanding flames are subjected to non-zero global positive stretch rate which acts to reduce the most probable values of both CS and DDS in comparison to the laminar burning velocity. The most important difference between $S_{d}^{*} /S_{L}$ and $S_{c} /S_{L}$ lies in the fact that $S_{d}^{*} /S_{L}$ can be locally negative, whereas $S_{c} /S_{L}$ is deterministically positive. The negative values of $S_{d}^{*} /S_{L}$ are consistent with the findings of several previous studies on spherically expanding turbulent premixed flames (Klein et al. 2006; Chakraborty et al. 2007; Klein et al. 2009). To explain this behaviour of $S_{d}^{*} /S_{L}$, the PDFs of $S_{r}^{*} /S_{L}$, $S_{n}^{*} /S_{L}$ and $S_{t}^{*} /S_{L}$ are presented in Fig. 3.

Fig. 2

Marginal PDFs of a $S_{d}^{*} /S_{L}$ and b $S_{c} /S_{L}$ for $\hbox{Le} = 0.8$, 1.0 and 1.2 cases at the time when statistics are extracted. All the statistics presented in this figure and subsequent figures are evaluated at the $c = 0.8$ isosurface

Fig. 3

Marginal PDFs of the components of DDS: a $S_{r}^{*} /S_{L}$, b $S_{n}^{*} /S_{L}$ and c $S_{t}^{*} /S_{L}$ for $\hbox{Le} = 0.8$, 1.0 and 1.2 cases

Figure 3 shows that $S_{r}^{*} /S_{L}$ deterministically assumes positive values for all cases, whereas $S_{n}^{*} /S_{L}$ remains negative within the reaction zone. The probability of high magnitudes of positive values of $S_{r}^{*} /S_{L}$ and negative values of $S_{n}^{*} /S_{L}$ increases with decreasing $\hbox{Le}$. The high positive magnitudes of $S_{r}^{*} /S_{L}$ in the $\hbox{Le} = 0.8$ case arise due to high values of reaction rate $\dot{w}$. In contrast, high probability of finding small values of $\dot{w}$ in the $\hbox{Le} = 1.2$ flame in comparison to that in the unity Lewis number case leads to higher probability of finding smaller values of $S_{r}^{*} /S_{L}$ in the $\hbox{Le} = 1.2$ case than in the $\hbox{Le} = 1.0$ case. The turbulent flamelet thickness, scaling as ${ \hbox{max} }\{ \left| {\nabla c} \right|^{ - 1} \} ,$ is smaller (greater) in the $\hbox{Le} = 0.8$ ($\hbox{Le} = 1.2$) case than in the unity Lewis number case. Although not shown, the same qualitative behaviour is observed here, and interested readers are referred to (Chakraborty and Cant 2005a; Chakraborty and Klein 2008; Dopazo et al. 2018) for discussion on $\hbox{Le}$ effects on $\left| {\nabla c} \right|$. The high values of mass diffusivity and small flame thickness induce large magnitudes of negative $\vec{N} \cdot \nabla \left( {\rho D\vec{N} \cdot \nabla c} \right)$ in the $\hbox{Le} = 0.8$ case in comparison to that in the $\hbox{Le} = 1.0$ flame, and this leads to greater negative magnitudes of $S_{n}^{*} /S_{L}$ in the $\hbox{Le} = 0.8$ case than in the unity Lewis number case. By contrast, a combination of smaller diffusivity and thicker flame gives rise to smaller magnitude of $\vec{N} \cdot \nabla \left( {\rho D\vec{N} \cdot \nabla c} \right)$ in the $\hbox{Le} = 1.2$ case than in the unity Lewis number case. The PDFs of $S_{t}^{*} /S_{L}$ exhibit probabilities of finding both positive and negative values. As $S_{t}^{*} /S_{L}$ is proportional to the negative value of curvature (i.e. $S_{t}^{*} = - 2\left( {\rho D/\rho_{0} } \right)\kappa_{m}$), the PDFs of $S_{t}^{*} /S_{L}$ provide an indication of the curvature PDFs. As the probability of finding positive $\kappa_{m}$ supersedes that of finding negative $\kappa_{m}$, the negative values of $S_{t}^{*} /S_{L}$ are more likely than positive values even though the most probable value remains close to zero due to large radii of these flame kernels. The PDFs of $S_{r}^{*} /S_{L}$, $S_{n}^{*} /S_{L}$ and $S_{t}^{*} /S_{L}$ indicate that negative values of $S_{d}^{*} /S_{L}$ are obtained if positive values of $S_{r}^{*} /S_{L}$ are overcome by negative $(S_{n}^{*} + S_{t}^{*} )/S_{L}$ contribution.

As $\dot{w}$ is a positive quantity, $S_{c}$ only exhibits positive values. The flame-turbulence interaction leads to local variations of the flame thickness and this gives rise to the variations of $S_{c} /S_{L}$ in the unity Lewis number case. This is enhanced by the correlation between temperature (and therefore $\dot{w}$) with curvature in the non-unity Lewis number case. This leads to a wider $S_{c} /S_{L}$ PDF in the $\hbox{Le} = 0.8$ case than in the $\hbox{Le} = 1.0$ and 1.2 cases.

Given the difference in statistics between $S_{d}^{*} /S_{L}$ and $S_{c} /S_{L}$, it is worthwhile to consider the influences of the characteristic Lewis number on their strain rate and curvature dependences. Equation 2 indicates that statistical behaviours of $S_{d}^{*} /S_{L}$ are dependent on $\dot{w}$ and $\left| {\nabla c} \right|$. It has already been demonstrated (see Fig. 1) that $\theta$ is positively (negatively) correlated with $\kappa_{m} \times \delta_{th}$ in the $\hbox{Le} = 0.8$ ($\hbox{Le} = 1.2$) and thus the correlation between $\dot{w}$ and $\kappa_{m}$ is positive in the $\hbox{Le} = 0.8$ case, and negative in the $\hbox{Le} = 1.2$ case. The contours of joint PDFs of $\left| {\nabla c} \right|$ with $a_{T}$ and $\kappa_{m}$ are shown in Fig. 4. It can be seen from Fig. 4 that $\left| {\nabla c} \right|$ and $a_{T}$ are strongly positively correlated in the $\hbox{Le} = 1.0$ and 1.2 cases. Although the correlation between $\left| {\nabla c} \right|$ and $a_{T}$ remains positive in the $\hbox{Le} = 0.8$ case, its strength remains much weaker than in the $\hbox{Le} = 1.0$ and 1.2 cases and a negatively correlating branch can be discerned. The flame normal strain rate $a_{N}$ is given by: $a_{N} = \nabla \cdot \vec{u} - a_{T} = N_{i} N_{j} \partial u_{i} /\partial x_{j}$, which suggests that an increase in $a_{T}$ amounts to a decrease in $a_{N}$ when $a_{T} \gg \nabla \cdot \vec{u}$. The magnitude of $\nabla \cdot \vec{u}$ scales with $\tau S_{L} /\delta_{th}$ and it assumes high values at negatively curved zones and low values at positively curved regions in the $\hbox{Le} = 1.0$ and 1.2 cases. It can be seen from the range of tangential strain rate values in Fig. 4 that there is a predominance of finding $a_{T} \times \delta_{th} /S_{L} \gg \tau$ (i.e. $a_{T} \gg \nabla \cdot \vec{u}$) in the $\hbox{Le} = 1.0$ and 1.2 cases and thus an increase in $a_{T}$ induces a decrease in $a_{N}$. A decrease in $a_{N}$ brings isoscalar lines closer to each other and acts to increase $\left| {\nabla c} \right|$ in the $\hbox{Le} = 1.0$ and 1.2 cases. This is reflected in the strong positive correlation between $\left| {\nabla c} \right|$ and $a_{T}$ in the $\hbox{Le} = 1.0$ and 1.2 cases. The tangential strain rate $a_{T}$ and curvature $\kappa_{m}$ are negatively correlated (e.g. correlation coefficient is − 0.61, − 0.7 and − 0.74 on the $c = 0.8$ isosurface in the $\hbox{Le} = 0.8, 1.0$ and 1.2 cases) in all cases considered here. This negative correlation originates due to combined effects of flame-vortex interaction and heat release (Haworth and Poinsot 1992) and is consistent with previous experimental (Renou et al. 2000) and DNS (Klein et al. 2006, 2009; Chakraborty et al. 2007; Chakraborty and Cant 2005a; Chakraborty and Klein 2008) findings. According to this negative correlation, high values of tangential strain rate $a_{T}$ are obtained in the negatively curved locations where dilatation rate values are high as well due to focusing of heat (e.g. correlation coefficients between $\nabla \cdot \vec{u}$ and $\kappa_{m}$ are − 0.60, − 0.72 and − 0.66 on the $c = 0.8$ isosurface in the $\hbox{Le} = 0.8, 1.0$ and 1.2 cases). In highly negative curved locations local values of $\nabla \cdot \vec{u}$ in the $\hbox{Le} = 0.8$ case can assume high enough values (due to enhanced burning rate for small Lewis number flames), to exceed $a_{T}$ (even though high values of $a_{T}$ are associated with negatively curved locations) to induce a positive (in other words an extensive) normal strain rate $a_{N}$ under which the distance between isoscalar lines increases and $\left| {\nabla c} \right|$ drops. This weakens the positive correlation between $\left| {\nabla c} \right|$ and $a_{T}$ in the $\hbox{Le} = 0.8$ case in comparison to the $\hbox{Le} = 1.0$ and 1.2 cases. The combination of positive correlation between $\left| {\nabla c} \right|$ and $a_{T}$, and negative correlation between $a_{T}$ and $\kappa_{m}$, gives rise to a negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ in the $\hbox{Le} = 1.0$ and 1.2 cases. However, the negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ in the $\hbox{Le} = 1.0$ case is a result of mean positive curvature and for statistically planar flames one obtains both positive and negative correlating branches in the joint PDF and the net correlation remains weak (Klein et al. 2006; Chakraborty et al. 2007; Chakraborty and Cant 2005a). The physical explanations behind this behaviour have been provided elsewhere (Klein et al. 2006; Chakraborty et al. 2007) and thus are not repeated here. As the probability of finding positive $a_{N}$ increases in the negatively curved regions in the $\hbox{Le} = 0.8$ case, the large (small) values of $\left| {\nabla c} \right|$ are associated with positive (negative) curvatures in this flame where a positive correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ is observed. The effects of $\hbox{Le}$ on tangential strain rate and curvature dependences of $\left| {\nabla c} \right|$ have been found to be qualitatively consistent with previous findings for statistically planar flames (Chakraborty and Klein 2008; Chakraborty et al. 2008). These strain rate and curvature dependences of $\left| {\nabla c} \right|$ play key roles in determining the statistical behaviours of $S_{r}^{*} ,S_{n}^{*}$ and $S_{c}$ in response to $a_{T}$ and $\kappa_{m}$.

Fig. 4

Contours of joint PDFs of $\left| {\nabla c} \right| \times \delta_{th}$ and $a_{T} \times \delta_{th} /S_{L}$ (1st row) and $\left| {\nabla c} \right| \times \delta_{th}$ and $\kappa_{m} \times \delta_{th}$ (2nd row) for $\hbox{Le} = 0.8$, 1.0 and 1.2 (1st–3rd column) cases

The contours of joint PDFs between $S_{d}^{*} /S_{L}$ and $\kappa_{m} \times \delta_{th}$ are shown in Fig. 5 (first row), which shows that these quantities are negatively correlated in all cases considered here. Figure 5 also shows the contours of joint PDFs of curvature with $S_{r}^{*} /S_{L}$, $S_{n}^{*} /S_{L}$ and $S_{t}^{*} /S_{L}$. It can be seen from Fig. 5 that $S_{r}^{*} /S_{L}$ and $\kappa_{m}$ are positively correlated in the $\hbox{Le} = 0.8$ case, whereas negative correlations can be seen in the $\hbox{Le} = 1.0$ and 1.2 cases. A negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ induces a positive correlation between $S_{r}^{*} = \dot{w}/(\rho_{0} \left| {\nabla c} \right|)$ and $\kappa_{m}$ because $\dot{w}$ does not change on a given $c$-isosurface for the present thermo-chemistry in the unity Lewis number case. The same mechanism along with the negative correlation between $\dot{w}$ and $\kappa_{m}$ gives rise to a negative correlation between $S_{r}^{*}$ and $\kappa_{m}$ in the $\hbox{Le} = 1.2$ flame. In the $\hbox{Le} = 0.8$ case, the positive correlation between $\dot{w}$ and $\kappa_{m}$ acts to induce a positive correlation between $S_{r}^{*}$ and $\kappa_{m}$, whereas this effect is countered by the influences of positive correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$, and the former dominates over the latter to yield a positive correlation between $S_{r}^{*}$ and $\kappa_{m}$. It has been shown in Fig. 4 that high values of $\left| {\nabla c} \right|$ are associated with positive $\kappa_{m}$ in the $\hbox{Le} = 0.8$ flame, whereas large values of $\left| {\nabla c} \right|$ are expected for negative $\kappa_{m}$ in the $\hbox{Le} = 1.0$ and 1.2 cases.

Fig. 5

Contours of joint PDFs of $S_{d}^{*} /S_{L}$ (1st row), $S_{r}^{*} /S_{L}$ (2nd row), $S_{n}^{*} /S_{L}$ (3rd row) and $S_{t}^{*} /S_{L}$ (4th row) with $\kappa_{m} \times \delta_{th}$ for $\hbox{Le} = 0.8$, 1.0 and 1.2 (1st–3rd column) cases

A large value of $\left| {\nabla c} \right|$ suggests a small normal distance between the isoscalar lines, which is expected to increase the magnitude of normal diffusion rate (i.e. $| {\vec{N} \cdot \nabla ( {\rho D \vec{N} \cdot \nabla c} )} |$). As flame normal diffusion rate is negative in the reaction zone (Klein et al. 2006; Chakraborty et al. 2007; Chakraborty and Cant 2004, 2005a), the positive correlations of $\left| {\nabla c} \right|$ and $\theta$ with $\kappa_{m}$ in the $\hbox{Le} = 0.8$ case give rise to a negative correlation between $S_{n}^{*}$ and $\kappa_{m}$. By contrast, the negative correlations between $\left| {\nabla c} \right|$ and $\kappa_{m}$ and between $\theta$ and $\kappa_{m}$ in the $\hbox{Le} = 1.2$ case give rise to a positive correlation between $S_{n}^{*}$ and $\kappa_{m}$, whereas the negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ is principally responsible for the positive correlation between $S_{n}^{*}$ and $\kappa_{m}$ in the unity Lewis number case. The negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ in the unity Lewis number case leads to negative correlations between $S_{r}^{*}$ and $\kappa_{m}$ and between $S_{n}^{*}$ and $\kappa_{m}$ for the spherically expanding flames with $\hbox{Le} = 1.0$, whereas the joint PDFs between $S_{r}^{*}$ and $\kappa_{m}$ and between $S_{n}^{*}$ and $\kappa_{m}$ exhibit both positive and negative correlating branches of almost equal strength in statistically planar flames with $\hbox{Le} = 1.0$ (Klein et al. 2006; Chakraborty et al. 2007; Chakraborty and Cant 2005a). It was shown elsewhere that this difference in $\kappa_{m}$ dependence of $(S_{r}^{*} + S_{n}^{*} )$ between statistically planar and spherically expanding flames leads to the differences in curvature and stretch rate dependences of $S_{d}^{*}$, which was demonstrated and explained elsewhere (Klein et al. 2006; Chakraborty et al. 2007; Chakraborty and Cant 2005a) and thus is not elaborated here. By definition, $S_{t}^{*}$ and $\kappa_{m}$ are negatively correlated with a correlation coefficient close to unity for all cases considered here. Figure 5 reveals that the deterministic negative correlation between $S_{t}^{*}$ and $\kappa_{m}$ overcomes the correlation between $(S_{r}^{*} + S_{n}^{*} )$ and $\kappa_{m}$ to yield a net negative correlation between $S_{d}^{*}$ and $\kappa_{m}$.

The contours of joint PDFs between $S_{d}^{*} /S_{L}$ and its components (i.e. $S_{r}^{*} /S_{L}$, $S_{n}^{*} /S_{L}$ and $S_{t}^{*} /S_{L}$) with $a_{T} \times \delta_{th} /S_{L}$ are shown in Fig. 6 which shows that $S_{d}^{*}$ and $a_{T}$ are weakly positively correlated. The positive correlation of $\dot{w}$ with $\kappa_{m}$ in the $\hbox{Le} = 0.8$ case acts to assist the effects of the positive correlation between $\left| {\nabla c} \right|$ with $a_{T}$ due to the negative correlation between $a_{T}$ and $\kappa_{m}$ to give rise to a negative correlation between $S_{r}^{*}$ and $a_{T}$. The positive correlation between $\left| {\nabla c} \right|$ with $a_{T}$ is responsible for the negative correlation between $S_{r}^{*} = \dot{w}/(\rho_{0} \left| {\nabla c} \right|)$ and $a_{T}$ in the $\hbox{Le} = 1.0$ case. The negative correlation between $\dot{w}$ and $\kappa_{m}$ acts to oppose the effects of positive correlation between $\left| {\nabla c} \right|$ with $a_{T}$ in the $\hbox{Le} = 1.2$ case and thus $S_{r}^{*} = \dot{w}/(\rho_{0} \left| {\nabla c} \right|)$ and $a_{T}$ remain weakly correlated in this flame. A positive correlation between $\left| {\nabla c} \right|$ with $a_{T}$ leads to large magnitudes of $| {\vec{N} \cdot \nabla ( {\rho D \vec{N} \cdot \nabla c} )} |$ for high values of $a_{T}$ following the previous discussion. This leads to negative correlation between $S_{n}^{*}$ and $a_{T}$ as $\vec{N} \cdot \nabla ( {\rho D \vec{N} \cdot \nabla c} )$ remains negative in the reaction zone. This negative correlation is weak in the $\hbox{Le} = 0.8$ case because of the weak positive correlation between $\left| {\nabla c} \right|$ and $a_{T}$. In all cases, $S_{t}^{*} = - 2\rho D\kappa_{m} /\rho_{0}$ has been found to be positively correlated with $a_{T}$ due to negative correlations between $a_{T}$ and $\kappa_{m}$. The positive correlation between $S_{t}^{*}$ and $a_{T}$ dominates over the negative correlations of $S_{r}^{*}$ and $S_{n}^{*}$ with $a_{T}$ to yield net positive correlations between $S_{d}^{*}$ and $a_{T}$.

Fig. 6

Contours of joint PDFs of $S_{d}^{*} /S_{L}$ (1st row), $S_{r}^{*} /S_{L}$ (2nd row), $S_{n}^{*} /S_{L}$ (3rd row) and $S_{t}^{*} /S_{L}$ (4th row) with $a_{T} \times \delta_{th} /S_{L}$ for $\hbox{Le} = 0.8$, 1.0 and 1.2 (1st–3rd column) cases

The contours of joint PDFs of $S_{c} /S_{L}$ with $\kappa_{m} \times \delta_{th}$ and normalised tangential strain rate $a_{T} \times \delta_{th} /S_{L}$ are shown in Fig. 7. A positive correlation between $S_{c}$ and $\kappa_{m}$ is found in the $\hbox{Le} = 0.8$ case, whereas this correlation is weakly negative in the $\hbox{Le} = 1.2$ case. In the unity Lewis number case, $S_{c}$ and $\kappa_{m}$ are weakly correlated. It has already been shown that $\dot{w}$ and $\kappa_{m}$ are positively correlated in the $\hbox{Le} = 0.8$ case, whereas this correlation is negative in the $\hbox{Le} = 1.2$ case. This gives rise to positive and weak negative correlations between $S_{c}$ and $\kappa_{m}$ in the $\hbox{Le} = 0.8$ and 1.2 cases respectively, which is consistent with previous findings in the context of statistically planar flames (Rutland and Trouvé 1993). Although $\dot{w}$ assumes relatively high values in the negatively curved locations in the $\hbox{Le} = 1.2$ case, the flame is thin in that region (due to negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$), which acts to counter the effects of negative correlation between $\dot{w}$ and $\kappa_{m}$ to yield a weak negative correlation between $S_{c}$ and $\kappa_{m}$. By contrast, in the $\hbox{Le} = 0.8$ case, the flame is thin in the positively curved regions (due to positive correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$), and thus acts to counter the effects of positive correlation between $\dot{w}$ and $\kappa_{m}$ but the latter correlation dominates over the former to yield a net positive correlation (but much weaker than the positive correlation between $\dot{w}$ and $\kappa_{m}$) between $S_{c}$ and $\kappa_{m}$. As $\dot{w}$ is insensitive to the curvature variation in the unity Lewis number case, the correlations of $S_{c}$ with $\kappa_{m}$ and $a_{T}$ are found to be weak. The local flame thickness variation in response to curvature and strain rate leads to the variations of $S_{c}$ with $\kappa_{m}$ and $a_{T}$ in the $\hbox{Le} = 1.0$ case. The combination of the negative correlation between $a_{T}$ with $\kappa_{m}$ and positive correlation between $S_{c}$ with $\kappa_{m}$ leads to a negative correlation between $S_{c}$ with $a_{T}$ in the $\hbox{Le} = 0.8$ case. Although there is a negative correlation between $a_{T}$ with $\kappa_{m}$ in the $\hbox{Le} = 1.2$ case, the correlation between $S_{c}$ with $\kappa_{m}$ remains weak, which ultimately yields a weak positive correlation between $S_{c}$ and $a_{T}$. Figure 7 further shows that the correlation between $S_{c}$ with $S_{d}^{*}$ remains weak in the $\hbox{Le} = 0.8$ and 1.0 cases but a strong positive correlation between $S_{c}$ with $S_{d}^{*}$ is observed in the $\hbox{Le} = 1.2$ case, as both $S_{c}$ and $S_{d}^{*}$ are negatively correlated with $\kappa_{m}$.

Fig. 7

Contours of joint PDFs of $S_{c} /S_{L}$ with $\kappa_{m} \times \delta_{th}$ (1st row), $S_{c} /S_{L}$ with $a_{T} \times \delta_{th} /S_{L}$ (2nd row) and $S_{c} /S_{L}$ with $S_{d}^{*} /S_{L}$ (3rd row) for $\hbox{Le} = 0.8$, 1.0 and 1.2 (1st–3rd column) cases

The negative correlation between $S_{d}^{*}$ and $\kappa_{m}$ in these flames and positive (negative) correlation between $S_{c}$ and $\kappa_{m}$ in the $\hbox{Le} = 0.8$ ($\hbox{Le} = 1.2$) case and weak correlation between $S_{c}$ and $\kappa_{m}$ in the $\hbox{Le} = 1.0$ case are qualitatively consistent with analytical results for stretched laminar flames (Williams 1985; Clavin and Joulin 1983). It is also worth noting that the correlations of $(S_{r}^{*} + S_{n}^{*} )$ and $S_{t}^{*}$ with $\left| {\nabla c} \right|$ have implications on the interrelation between $\varOmega_{T}$ and $A_{T}$ in spherically expanding flames, which can be explained in the following manner:

$$ \varOmega_{T} = \mathop \smallint \limits_{V} \dot{w}dV = \mathop \smallint \limits_{V} \rho_{0} S_{d}^{*} \left| {\nabla c} \right|dV = \mathop \smallint \limits_{V} \rho_{0} \left( {S_{r}^{*} + S_{n}^{*} } \right)\left| {\nabla c} \right|dV + \mathop \smallint \limits_{V} \rho_{0} S_{t}^{*} \left| {\nabla c} \right|dV $$

(4)

Equation 4 suggests that the behaviour of the first term on the right hand side depends on the correlation between $\left( {S_{r}^{*} + S_{n}^{*} } \right)$ and $\left| {\nabla c} \right|$, whereas the behaviour of the second term on the right hand side depends on the correlation between $S_{t}^{*}$ and $\left| {\nabla c} \right|$. The correlation coefficients between $\left( {S_{r}^{*} + S_{n}^{*} } \right)$ and $\left| {\nabla c} \right|$, and between $S_{t}^{*}$ and $\left| {\nabla c} \right|$ on the $c = 0.8$ isosurface are presented in Table 3 for the cases considered here.

Table 3 Effects of $\hbox{Le}$ on correlation coefficients between $\left( {S_{r}^{*} + S_{n}^{*} } \right)$ and $\left| {\nabla c} \right|$, and between $S_{t}^{*}$ and $\left| {\nabla c} \right|$ on the $c = 0.8$ isosurface

An increase in $\left| {\nabla c} \right|$ gives rise to a decrease in $S_{r}^{*}$, which is compounded by a decreasing trend of negative $S_{n}^{*}$ with increasing $\left| {\nabla c} \right|$ in the reaction zone. It can further be inferred from Fig. 6 that the net contribution of ($S_{r}^{*} + S_{n}^{*} )$ remains negatively correlated with $a_{T}$, whereas $\left| {\nabla c} \right|$ and $a_{T}$ remain positively correlated (see Fig. 4). This combination gives rise to negative correlation between ($S_{r}^{*} + S_{n}^{*} )$ and $\left| {\nabla c} \right|$, as shown in Table 3. As the positive correlation between $\left| {\nabla c} \right|$ and $a_{T}$ is the weakest in the $\hbox{Le} = 0.8$ case (see Fig. 4) and the negative correlation between ($S_{r}^{*} + S_{n}^{*} )$ and $a_{T}$ is comparable for all cases considered here (e.g. correlation coefficients between ($S_{r}^{*} + S_{n}^{*} )$ and $a_{T}$ are − 0.39, − 0.39 and − 0.37 on the $c = 0.8$ isosurface in the $\hbox{Le} = 0.8, 1.0$ and 1.2 cases), the strength of the negative correlation between ($S_{r}^{*} + S_{n}^{*} )$ and $\left| {\nabla c} \right|$ is the weakest in the $\hbox{Le} = 0.8$ case. By contrast, the positive correlation between $\left| {\nabla c} \right|$ and $a_{T}$ is the strongest for the $\hbox{Le} = 1.2$ case (see Fig. 4), which leads to the strongest negative correlation between ($S_{r}^{*} + S_{n}^{*} )$ and $\left| {\nabla c} \right|$ in this case.

As curvature $\kappa_{m}$ and $\left| {\nabla c} \right|$ are positively correlated in the $\hbox{Le} = 0.8$ case (see Fig. 4), and $\kappa_{m}$ and $S_{t}^{*}$ are deterministically negatively correlated, the correlation between $S_{t}^{*}$ and $\left| {\nabla c} \right|$ remains negative in this case. The combination of negative correlations of $S_{t}^{*}$ and $\left| {\nabla c} \right|$ with $\kappa_{m }$ leads to positive correlations between $S_{t}^{*}$ and $\left| {\nabla c} \right|$ in the $\hbox{Le} = 1.0$ and 1.2 cases considered here.

It is worth noting that Damköhler’s first hypothesis was originally proposed for large scale turbulence (i.e. $l \gg \delta_{th}$) (Damköhler 1940), which suggests $S_{T} /S_{L} = A_{T} /A_{p}$ where $S_{T} = \varOmega_{T} /\rho_{0} A_{p}$ is the turbulent flame speed, $S_{L} = \varOmega_{L} /\rho_{0} A_{L}$ is the unstrained laminar burning velocity, $A_{T}$ is the total flame surface area and $A_{p}$ is the projected area of the flame. However, it has been demonstrated in several previous DNS analyses (Aspden et al. 2011; Nivarti and Cant 2017; Ahmed et al. 2019) that the quantitative agreement between $S_{T} /S_{L} = \left( {\varOmega_{T} /\varOmega_{L} } \right)\left( {A_{L} /A_{p} } \right)$ and $A_{T} /A_{p}$ remains excellent in the thin reaction zones regime (Peters 2000) with small length scale separation between $l$ and $\delta_{th}$ (e.g. $l/\delta_{th} \sim \;O\left( 1 \right)$) for planar flames with characteristic Lewis number of unity. From the foregoing, it can be appreciated that the equality between $S_{T} /S_{L}$ and $A_{T} /A_{p}$ implies an equality between $\varOmega_{T} /\varOmega_{L}$ and $A_{T} /A_{L}$ as a corollary of Damköhler’s first hypothesis. It has been demonstrated in previous experimental analyses (Yuen 2013; Wabel et al. 2017) that $S_{T} /S_{L}$ assumes greater values than $A_{T} /A_{p}$ for Bunsen burner flames which have global mean negative curvature. A recent analysis by the authors (Chakraborty et al. 2019) provided the explanation for the behaviour which leads to $S_{T} /S_{L} > A_{T} /A_{p}$ for flames with negative mean curvature. According to the explanation provided by these authors (Chakraborty et al. 2019), it is expected that $S_{T} /S_{L}$ will assume smaller values than $A_{T} /A_{p}$ for flames with mean positive curvature (e.g. spherically expanding flame kernels).

In the $\hbox{Le} = 0.8$ case, $\left( {S_{r}^{*} + S_{n}^{*} } \right)$ and $\left| {\nabla c} \right|$ are negativey correlated so $\mathop \smallint \limits_{V} \rho_{0} \left( {S_{r}^{*} + S_{n}^{*} } \right)\left| {\nabla c} \right|dV < \left\langle {\rho_{0} \left( {S_{r}^{*} + S_{n}^{*} } \right)} \right\rangle A_{T}$ where $\langle{Q}\rangle = \mathop \smallint \limits_{V} QdV/V$ indicates the volume-averaged value of a general quantity $Q$. Moreover, $S_{t}^{*}$ and $\left| {\nabla c} \right|$ are negatively correlated as well in the $\hbox{Le} = 0.8$ case so $\mathop \smallint \limits_{V} \rho_{0} S_{t}^{*} \left| {\nabla c} \right|dV < \left\langle {\rho_{0} S_{t}^{*} } \right\rangle A_{T}$. The combined effects of $\mathop \smallint \limits_{V} \rho_{0} \left( {S_{r}^{*} + S_{n}^{*} } \right)\left| {\nabla c} \right|dV < \rho_{0} \left\langle {\left( {S_{r}^{*} + S_{n}^{*} } \right)} \right\rangle A_{T}$ and $\mathop \smallint \limits_{V} \rho_{0} S_{t}^{*} \left| {\nabla c} \right|dV < \left\langle {\rho_{0} S_{t}^{*} } \right\rangle A_{T}$ yield $\varOmega_{T} < \left\langle {\rho_{0} S_{d}^{*} } \right\rangle A_{T}$ in the $\hbox{Le} = 0.8$ case. In the unity Lewis number case, $\left( {S_{r}^{*} + S_{n}^{*} } \right)$ and $\left| {\nabla c} \right|$ are negatively correlated, whereas $S_{t}^{*}$ and $\left| {\nabla c} \right|$ are positively correlated. Thus, one obtains $\mathop \smallint \limits_{V} \rho_{0} \left( {S_{r}^{*} + S_{n}^{*} } \right)\left| {\nabla c} \right|dV < \left\langle {\rho_{0} \left( {S_{r}^{*} + S_{n}^{*} } \right)} \right\rangle A_{T}$ and $\mathop \smallint \limits_{V} \rho_{0} S_{t}^{*} \left| {\nabla c} \right|dV > \left\langle {\rho_{0} S_{t}^{*} } \right\rangle A_{T}$ in the $\hbox{Le} = 1.0$ case, where the former effect supersedes the latter to yield a value of $\varOmega_{T}$ which is smaller than $\left\langle {\rho_{0} S_{d}^{*} } \right\rangle A_{T}$. In the $\hbox{Le} = 1.2$ case, a similar behavior is observed but these effects almost nullify each other to yield: $\varOmega_{T} \approx \left\langle {\rho_{0} S_{d}^{*} } \right\rangle A_{T}$ at the instant when the statistics were extracted. It can be seen from Table 4 that $\left\langle {S_{d}^{*} } \right\rangle$ remains greater than $S_{L}$ in the $\hbox{Le} = 0.8$ case, whereas $\left\langle {S_{d}^{*} } \right\rangle$ is smaller (significantly smaller) than $S_{L}$ in the $\hbox{Le} = 1.0 \,\left( {Le = 1.2} \right)$ case. In the $\hbox{Le} = 0.8$ case, $\left\langle {S_{d}^{*} } \right\rangle > S_{L}$ dominates over $\varOmega_{T} < \left\langle {\rho_{0} S_{d}^{*} } \right\rangle A_{T}$ to yield a value of $\varOmega_{T} /\rho_{0} S_{L} A_{T}$, which is slightly greater than unity and thus is consistent with $\varOmega_{T} /\varOmega_{L} > A_{T} /A_{L}$ (see Table 2), whereas the combination of $\varOmega_{T} < \left\langle {\rho_{0} S_{d}^{*} } \right\rangle A_{T}$ and $S_{d}^{ *} < S_{L}$ leads to $\varOmega_{T} /\rho_{0} S_{L} A_{T} < 1$ and $\varOmega_{T} /\varOmega_{L} < A_{T} /A_{L}$ in the turbulent premixed spherical flames with $\hbox{Le} = 1.0$ and 1.2 (see Table 2). According to Damköhler’s first hypothesis, one gets $\varOmega_{T} /A_{T} = \varOmega_{L} /A_{L}$ or $\varOmega_{T} /\varOmega_{L} = A_{T} /A_{L}$ for a given fuel–air mixture and unburned gas condition (Damköhler 1940; Klein et al. 2020; Chakraborty et al. 2019), which also leads to $\varOmega_{T} /\rho_{0} S_{L} A_{T}$ = 1.0. Hence, Tables 2 and 4 suggest that the equality between $\varOmega_{T} /\varOmega_{L}$ and $A_{T} /A_{L}$ does not strictly hold (therefore the equality between $S_{T} /S_{L}$ and $A_{T} /A_{p}$ is rendered invalid) in spherically expanding turbulent premixed flames irrespective of $\hbox{Le}$. This behaviour can be explained in the following manner.

Table 4 Effects of $\hbox{Le}$ on $\varOmega_{T} /\left\langle {\rho_{0} S_{d}^{*} } \right\rangle A_{T}$, $\varOmega_{T} /\rho_{0} S_{L} A_{T}$ and $\left\langle {S_{d}^{*} } \right\rangle /S_{L}$

The dependence of $S_{d}^{*}$ on flame curvature $\kappa_{m}$ can be modelled according to $S_{d}^{*} = (S_{L} - 2D_{M} \kappa_{m} )$ where $D_{M}$ is the Markstein diffusivity (Poinsot and Veynante 2001). Thus, according to eq. 4, it is possible to approximate $\varOmega_{T}$ as:

$$ \varOmega_{T} \approx \mathop \smallint \limits_{V} \rho_{0} \left( {S_{L} - 2D_{M} \kappa_{m} } \right)\left| {\nabla c} \right|dV = \rho_{0} S_{L} A_{T} - 2\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV $$

(5)

The integral $\mathop \smallint \limits_{V} \rho_{0} \left( {S_{L} - D_{M} \kappa_{m} } \right)\left| {\nabla c} \right|dV$ becomes equal to $\rho_{0} S_{L} A_{T}$ for statistically-planar unity Lewis number flames because $\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV$ can be written as:$\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV \approx \rho_{0} \left\langle {D_{M} \kappa_{m} } \right\rangle_s A_{T}$ (where $\left\langle {D_{M} \kappa_{m} } \right\rangle_s = \mathop \smallint \limits_{V} D_{M} \kappa_{m} \left| {\nabla c} \right|dV/\mathop \smallint \limits_{V} \left| {\nabla c} \right|dV$ is the global surface-weighted curvature) and $\rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle_s A_{T}$ disappears because of the vanishingly small values of $\left\langle {D_{M} \kappa_{m} } \right\rangle_s$ resulting from the weak correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ in statistically planar flames (Klein et al. 2006; Chakraborty et al. 2007; Chakraborty and Cant 2005a). However, $\rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle_s A_{T}$ assumes a positive value because $\left\langle {D_{M} \kappa_{m} } \right\rangle_s$ is positive for spherically expanding premixed flames and $D_{M}$ remains positive. This suggests that $\varOmega_{T} /\rho_{0} S_{L} A_{T}$ is expected to be smaller than unity (i.e. $\varOmega_{T} /\rho_{0} S_{L} A_{T} < 1.0$) for the spherically expanding flames for the unity Lewis number, which is consistent with the findings reported in Table 4. By the same token, $\varOmega_{T} /\rho_{0} S_{L} A_{T}$ is expected to be greater than unity (i.e. $\varOmega_{T} /\rho_{0} S_{L} A_{T} > 1.0$) for unity Lewis number turbulent Bunsen burner flames (where $\left\langle {\kappa_{m} } \right\rangle_s$ is negative due to negative global mean curvature) and this indeed reported based on experimental findings (Yuen 2013; Wabel et al. 2017) and has recently been confirmed by Chakraborty et al. (2019) based on DNS data. Thus, the current findings and the results of Chakraborty et al. (2019) reveal that Damköhler’s first hypothesis is strictly not valid for curved flames even for unity Lewis number conditions.

It has been shown elsewhere (Chakraborty and Cant 2005a; Chakraborty and Klein 2008; Dopazo et al. 2018) that the equality between $\varOmega_{T} /\varOmega_{L}$ and $A_{T} /A_{L}$ (or equality of $S_{T} /S_{L}$ and $A_{T} /A_{p}$) is rendered invalid for statistically planar non-unity Lewis number flames and the discrepancy between $\varOmega_{T} /\varOmega_{L}$ and $A_{T} /A_{L}$ for statistically planar flames increases with increasing $\left| {Le - 1} \right|$ and $S_{T} /S_{L}$ becomes increasingly greater (smaller) than $A_{T} /A_{p}$ with decreasing (increasing) $\hbox{Le}$. For $Le < 1$ spherical flames (e.g. $\hbox{Le} = 0.8$), the quantities $\left| {\nabla c} \right|$ and $\kappa_{m}$ are positively correlated (see Fig. 4), which suggests that $\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV > \rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle A_{T}$ (or $- \mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV < - \rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle A_{T}$). In the case of $Le \ge 1$ spherical flames (e.g. $\hbox{Le} = 1.0$ and 1.2), the negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ (see Fig. 4) leads to $\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV < \rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle A_{T}$ (or $- \mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV > - \rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle A_{T}$) and this trend strengthens with increasing $\hbox{Le}$ as a result of stronger negative correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ for higher values of Lewis number. The integral $\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV$ remains positive for all cases but $\mathop \smallint \limits_{V} \rho_{0} D_{M} \kappa_{m} \left| {\nabla c} \right|dV < \rho_{0} D_{M} \left\langle {\kappa_{m} } \right\rangle A_{T}$ in the $Le \ge 1.0$ spherical flames (e.g. $\hbox{Le} = 1.0$ and 1.2 cases) leads to $\varOmega_{T} < \rho_{0} S_{L} A_{T}$ (or $\varOmega_{T} /\rho_{0} S_{L} A_{T} < 1.0$) (see Table 4) and this trend at a given instant of time is stronger for the $Le > 1.0$ case than in the $\hbox{Le} = 1.0$ case due to greater values of $\left\langle {\kappa_{m} } \right\rangle$ for smaller flame kernels for higher values of $\hbox{Le}$. The flame kernel is bigger in size in the $\hbox{Le} = 0.8$ case (see Fig. 1) in comparison to the $\hbox{Le} = 1.0$ and 1.2 cases, which suggests that $\left\langle {\kappa_{m} } \right\rangle$ in the $\hbox{Le} = 0.8$ case is much smaller than in the other cases. This leads to $\varOmega_{T} \approx \rho_{0} S_{L} A_{T}$ in the flame kernel with $\hbox{Le} = 0.8$ at the time the statistics were extracted (see Table 4).

4 Conclusions

The statistical behaviours of density-weighted displacement speed $S_{d}^{*}$ and consumption speed $S_{c}$ in turbulent spherically expanding flames have been analysed using a three-dimensional simple chemistry DNS database for characteristic Lewis numbers $\hbox{Le} = 0.8, 1.0$ and 1.2. The mean and most probable values of both $S_{d}^{*}$ and $S_{c}$ increase with decreasing $\hbox{Le}$. In all cases, $S_{d}^{*}$ has been found to be negatively correlated with curvature $\kappa_{m}$, whereas $S_{d}^{*}$ correlates positively with tangential strain rate $a_{T}$. Although the qualitative nature of the strain rate and curvature dependences of $S_{d}^{*}$ does not change for the range of $\hbox{Le}$ considered here, the strain rate and curvature dependences of the reaction and normal diffusion components of $S_{d}^{*}$ have been found to be strongly dependent on $\hbox{Le}$. The correlation between $\left| {\nabla c} \right|$ and $\kappa_{m}$ remains positive in the $\hbox{Le} = 0.8$ flame, whereas this correlation is found to be negative in the $\hbox{Le} = 1.0$ and 1.2 cases. The reaction progress variable gradient $\left| {\nabla c} \right|$ is found to be positively correlated with $a_{T}$ but the correlation strength decreases with decreasing $\hbox{Le}$, whereas tangential strain rate and curvature are found to be negatively correlated for all cases considered here. The temperature and chemical reaction rate of progress variable are found to be positively correlated with $\kappa_{m}$ in the $\hbox{Le} = 0.8$ flame, whereas they are negatively correlated in the $\hbox{Le} = 1.2$ case. These correlations in the non-unity Lewis number flames arise due to differential diffusion of heat and mass. The combination of tangential strain rate and curvature dependences of $\left| {\nabla c} \right|$ and temperature, and the interrelation between tangential strain rate and curvature determines the curvature and strain rate responses of reaction and normal diffusion components of $S_{d}^{*}$. The positive (negative) correlation between temperature and curvature in the $\hbox{Le} = 0.8$ ($\hbox{Le} = 1.2$) flame gives rise to positive (weakly negative) correlation between $S_{c}$ and $\kappa_{m}$, whereas $S_{c}$ and $\kappa_{m}$ are weakly related in the $\hbox{Le} = 1.0$ case. In all cases the local values of $S_{c}$ and $S_{d}^{*}$ remain significantly different and the PDFs of $S_{d}^{*}$ exhibit finite probabilities of negative values, whereas $S_{c}$ assumes deterministically positive values. The correlation between $S_{c}$ and $S_{d}^{*}$ remains weak in the $\hbox{Le} = 0.8$ and 1.0 cases but a strong positive correlation is obtained in the $\hbox{Le} = 1.2$ case. Finally, the flame speed statistics have been utilised to demonstrate that Damköhler’s first hypothesis does not strictly hold in spherically expanding turbulent premixed flames.

Although it has been demonstrated in the past that $S_{d}^{*}$ and $\left| {\nabla c} \right|$ statistics and curvature dependence of non-dimensional temperature $\theta$ obtained from simple chemistry DNS (Klein et al. 2006; Chakraborty et al. 2007; Klein et al. 2009; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Chakraborty and Cant 2004, 2005a, b, 2006; Han and Huh 2008; Chakraborty and Klein 2008; Chakraborty et al. 2011, 2013) remain in good agreement with the corresponding findings obtained from detailed chemistry DNS (Chakraborty and Klein 2008; Chakraborty et al. 2008, 2013; Chakraborty and Cant 2005b) data, the current analysis based on characteristic Lewis number provides only a general indication of qualitative behaviour of differential diffusion of heat and mass but the quantitative aspects of the effects of differential diffusion are likely to be specific to the nature of the fuel and equivalence ratio of the fuel–air mixture. Moreover, different species have different diffusivities and therefore different Lewis numbers but the differential molecular transport due to different mass diffusivities is not addressed in this paper due to the simplifications made in the context of thermo-chemical properties and chemical reaction mechanism. Furthermore, Soret and Dufor effects are likely to be important for lean hydrogen-air flames, which cannot be addressed by analysing non-unity Lewis number effects, and thus further analyses based on detailed chemistry and transport will be necessary for a more complete understanding on differential diffusion of heat and mass on flame propagation of spherically expanding premixed flame kernels. This will form the platform of further analyses in the future.