A Priori Analysis on Deep Learning of Filtered Reaction Rate

Abstract

A filtered reaction rate model driven by deep learning is proposed and analyzed a priori in the context of large eddy simulation (LES). A deep artificial neural network (ANN) is trained on the explicitly filtered reaction rate source term extracted from a database comprised of turbulent premixed planar flame direct numerical simulations (DNSes) employing single-step chemistry. The filtered DNS database to be used for the training of the ANN covers a wide range of turbulence intensities and LES filter widths. An interpretation technique of deep learning is employed to search the principal input parameters in the high dimensional database to alleviate the model complexity. The deep learning filtered reaction rate model is then tested on the unseen filtered planar flames featuring untrained turbulence intensities and LES filter widths, in conjunction with another canonical type of flame configuration that it has not been trained on. The deep learning filtered reaction rate model achieves good agreement with the filtered DNS results and also provides a quantitatively accurate surrogate model when compared to existing algebraic models and other combustion models from the literature.

1 Introduction

In large eddy simulation (LES), only the large-scale flow structures are resolved, while small-scale fluctuations of momentum, species concentration, and temperature below the mesh resolution are unknown. Due to this spatial filtering operation, unclosed terms arise that have to be modeled by subgrid scale (SGS) closures. In turbulent premixed combustion, the employed filter width (i.e., the cell size) is usually too big to resolve the laminar flame structure embedded in the flow field. Hence, the flame wrinkling and therewith the filtered reaction rate source term $\overline{\dot{\omega } }$ has to be represented by adequate combustion SGS models. An alternative to classical algebraic closure models is given through data-driven machine learning approaches which try to “learn” a meaningful relationship between a system’s state variables without explicit knowledge of the physical relation between input and output.

In the past years, data-driven models have become very popular due to the rapid evolution in the field of deep learning. The recent increases of computational resources at affordable prices, especially in the sector of graphics processing units (GPU), and the developments of well-maintained open-source software libraries such as Tensorflow (Abadi et al. 1603) or PyTorch (Paszke et al. 1912) made deep learning a very successful technique to tackle complex scientific and engineering problems from various domains, such as speech recognition, image segmentation, and classification, genome sequencing, language translation, earth system science and many more (LeCun et al. 2015; Reichstein et al. 2019; Schmidhuber 2015). Artificial neural networks (ANNs) are the core algorithms that are the foundation of deep learning, providing a cost-effective universal function approximation, which is able to represent nonlinear input/output relationships. ANNs consist of densely stacked neurons, which are layer-wise interconnected. The free parameters of the network, the individual weights of the neurons, can be fitted in a supervised learning process where the network is shown a data set with known input and output. The learning process consists of comparing the error between the actual output (ground truth) with the prediction from the network and iteratively adjusting the weights to minimize this error. Once an ANN is trained it can be used to perform inference, i.e., make predictions on an input data set of the same population it has been trained on.

In the combustion community, (Blasco et al. 1998, 1999, 2000; Chen et al. 2000; Christo et al. 1996) made first attempts to make use of ANNs to substitute the direct integration of simple reaction mechanisms. With more sophisticated data generation strategies this approach was later refined and employed by Chatzopoulos and Rigopoulos (2013), Ding et al. (2021), Franke et al. (2017), Readshaw et al. (2021) in LES of turbulent non-premixed flames. Others (Emami and Eshghinejad Fard 2012); Flemming et al. 2005; Hansinger et al. 2020a; Ihme et al. 2006, 2009; Owoyele et al. 2020; Ranade et al. 2019a, b) used ANNs to replace the thermo-chemical data tables in their flamelet based simulations. In the field of premixed combustion modeling, (Lapeyre et al. 2019; Xing et al. 2021; Seltz et al. 2019); Shin et al. 2021) have shown that convolutional neural networks (CNNs) have the predictive power to model the filtered reaction rate source term $\overline{\dot{\omega } }$, which appears in LES. CNNs are a type of ANNs that utilize a trainable convolutional filter and are designed to learn the spatial hierarchies of the input features.

Machine learning techniques such as CNN or genetic optimization have also been used to model the turbulent subgrid-flame surface density (Lapeyre et al. 2019), flame surface density (Ren et al. 2021), filtered reaction rate, and subgrid-scale variance of reaction progress variable (Nikolaou et al. 2019) or the subgrid-scale stresses in turbulent premixed combustion (Schoepplein et al. 2018).

In addition, the residual neural network (ResNet) using fully connected layers has been developed along with CNNs and it has shown great accuracy on complex nonlinear datasets (Chen et al. 2020; Jiang et al. 2108) and also for combustion and thermochemical datasets (Hansinger et al. 2020; Ge et al. 2018). It is advantageous as it takes as input fully local values, while CNNs employ as input only spatially ordered regular matrices. These two types of ANNs are already discussed in Shin et al. (2021), in terms of their applicability to computational fluid dynamics (CFD) codes and it was demonstrated that using ResNet yielded good agreement with filtered direct numerical simulation (DNS) results.

We propose a data-driven modeling of filtered reaction rate source term based on deep learning, in particular ResNet in the present study. The turbulent planar flame DNS results are explicitly filtered to extract the filtered reaction rate and input parameters to the neural network. The filtered DNS database covers a wide range of turbulence levels and LES filter widths. For the input to the data-driven modeling, different parameters featuring thermochemical and flow properties of the turbulent premixed flame can be used; 11 parameters in total are considered here. In order to reduce the model complexity, we attempt to sift the principal input parameters using non-machine learning and machine learning techniques. The deep learning LES model is then tested on the unseen datasets including the untrained turbulence levels and LES filter widths in conjunction with another type of canonical flame configuration. Thus, a quantitative a priori assessment is conducted to verify the performance of the deep learning LES model and it is compared with other LES combustion models from the literature.

This paper is structured as follows: we introduce the turbulent premixed planar flame DNS database for the training and a turbulent Bunsen flame DNS database for the test of the neural network in Sect. 2. The theoretical background of existing LES combustion models is presented in Sect. 3. In Sect. 4, the details of the deep learning LES model are described in the perspective of its networks architecture and filtered DNS database that they will be trained on. The results of an assessment for the deep learning filtered reaction rate model based on an a priori analysis are presented in Sect. 5.

2 DNS Databases

For the current contribution, we employed two different DNS databases/datasets: turbulent premixed planar flame DNS and turbulent Bunsen flame DNS. The planar flame DNS is used as a training source and also for the testing of the deep learning filtered reaction rate model because of its canonical character, representing the simplest flame configuration. The Bunsen flame DNS is utilized as a test dataset to check the generalization capability to other flame configurations. Hereafter, we introduce the two DNSes briefly.

2.1 Turbulent Premixed Statistically Planar Flame DNS

The planar flame DNS database used in this study was generated/established by the compressible reacting flow solver SENGA code and was firstly presented by Klein and Chakraborty (2019). Parts of this database have already been used by Hansinger et al. (2020b) to validate a new analytical combustion model, which will be introduced in Sect. 3. This DNS database contains turbulent premixed planar methane-air flames at ambient pressure and temperature, based on assumptions of a single-step Arrhenius type irreversible reaction mechanism and unity Lewis number. Table 1 describes the characteristic parameters for the planar flame DNS considered in this study, which are denoted as PF–A to PF–E, where ${s}_{L}$ is the unstrained laminar burning velocity, ${\delta }_{th}$ the thermal flame thickness defined by $\left({T}_{b}-{T}_{u}\right)/max\left(\left|\nabla T\right|\right)$, ${u{^{\prime}}}_{in}$ the turbulent root-mean-square (RMS) initial velocity fluctuation, $l$ the integral length scale, $Da=l{s}_{L}/\left({\delta }_{th}{u{^{\prime}}}_{in}\right)$ is the Damköhler number and $Ka={\left({u{^{\prime}}}_{in}/{s}_{L}\right)}^{3/2}{\left(l/{\delta }_{th}\right)}^{-1/2}$ is the Karlovitz number. The heat release parameter $\tau$ and the Zeldovich number $\beta$ are taken to be 4.5 and 6.0. Standard values of Prandtl number ($Pr$=0.7) and the ratio of specific heats ($\gamma$=1.4) have been used. The turbulent velocity fluctuations have been initialized with a homogeneous isotropic incompressible velocity field in conjunction with a model spectrum suggested by Pope (2000). The flame turbulence interaction takes place under decaying turbulence with a simulation time larger than the maximum of two eddy turnover times and the chemical time scale (Klein et al. 2017). The reacting flow field is initialized by a steady planar unstrained premixed laminar flame solution. The instantaneous isosurfaces of reaction progress variable c for the cases PF–A to PF–E are shown in Fig. 1. For further details regarding the numerical methods employed, the reader is referred to (Chakraborty et al. 2011, 2009).

Table 1 Characteristic initial parameters for the planar turbulent premixed flame (PF) DNS and Bunsen flame (BF) DNS

Fig. 1

The isosurface of progress variable $c=0.5$ from premixed planar flame DNS for a PF–A: ${u}_{in}^{^{\prime}}/{s}_{L}=1.0$, b PF–B: ${u}_{in}^{^{\prime}}/{s}_{L}=5.0$, c PF–C: ${u}_{in}^{^{\prime}}/{s}_{L}=7.5$, d PF–D: ${u}_{in}^{^{\prime}}/{s}_{L}=9.0$, e PF–E: ${u}_{in}^{^{\prime}}/{s}_{L}=15.0$

The simulation domain is taken to be a cube of 26.1 ${\delta }_{th}$×26.1 ${\delta }_{th}$×26.1 ${\delta }_{th}$ which is discretized using a uniform Cartesian grid of 512 × 512 × 512 points ensuring 11 grid points are kept to resolve the thermal flame thickness. Spatial derivatives for all internal grid points are evaluated using a 10th order central difference scheme. The order of discretization gradually drops to a one-sided second-order scheme at the non-periodic boundaries. Time integration is carried out using an explicit third-order low storage Runge–Kutta scheme. The boundary conditions in the direction of the mean flame propagation (x-direction) are taken to be partially non–reflecting, whereas boundaries in transverse directions are specified as periodic (y and z–directions).

2.2 Turbulent Premixed Bunsen Flame DNS

In order to evaluate the generalizing capabilities of the deep learning filtered reaction rate models, the DNS result of a turbulent Bunsen flame is also considered. The database has first been presented by Klein et al. (2018). Single-step chemistry is used for the chemical reactions with unity Lewis number. Inflow data reproducing the required turbulence properties has been generated using a modified version of the method suggested by Klein et al. (2003) where the Gaussian filter in axial direction has been replaced by an autoregressive process in order to avoid excessive filter length in this direction caused by the small-time step in the compressible flow solver. The reacting flow field is initialized by an unstrained premixed laminar flame solution with the geometry of a semi-sphere located at the inflow. The numerical scheme is the same as described in Sect. 2.1. In this paper, only one flame configuration at atmospheric pressure will be considered, although there exist other Bunsen DNS results in higher pressure conditions, to check the generalization capability of the deep learning filtered reaction rate model. The characteristic parameters for this Bunsen DNS are also presented at the bottom of Table 1. The simulation domain corresponds to a cube of 50 ${\delta }_{th}$×50 ${\delta }_{th}$×50 ${\delta }_{th}$ which is discretized using a uniform Cartesian grid of 250 × 250 × 250 points. In this case, only 5 grid points are used to resolve the thermal flame thickness. The nozzle diameter corresponds roughly to half the domain length.

3 LES Closures for Filtered Reaction Rate

According to Poinsot and Veynante (2005), at constant pressure conditions a reaction progress variable can be defined as $c=\left(T-{T}_{u}\right)/\left({T}_{b}-{T}_{u}\right)$ when the fuel and the oxidizer can be assumed to be a homogenous mixture where ${T}_{u}$, ${T}_{b}$ are the unburnt mixture and fully burnt temperatures, respectively. A Favre-filtered transport equation for the progress variable $\tilde{c }$ then can be written in the LES context:

$$\frac{\partial \overline{\rho }\tilde{c }}{\partial t}+\frac{\partial \overline{\rho }\stackrel{\sim }{{u}_{k}}\tilde{c }}{\partial {x}_{k}}+\frac{\partial }{\partial {x}_{k}}\left(\overline{\rho }\stackrel{\sim }{{u}_{k}c}-\overline{\rho }\stackrel{\sim }{{u}_{k}}\tilde{c }\right)=\frac{\partial }{\partial {x}_{k}}\left(\overline{\rho D\frac{\partial c}{\partial {x }_{k}}}\right)+\overline{\dot{\omega } }$$

(1)

where $\overline{Q }$ denotes spatial filtering, $\tilde{Q }$ and denotes density-weighted Favre filtering of a general quantity $Q$, $D$ the mass diffusivity, and $\overline{\dot{\omega } }$ the filtered reaction rate source term. In Eq. (1), assumptions of a single step, irreversible chemical reaction with unity Lewis number and a thermally adiabatic condition are made. Following Boger et al. (1998), the right-hand side term in Eq. (1) can be expressed in the context of flame surface density (FSD) modeling as:

$$\frac{\partial }{\partial {x}_{k}}\left(\overline{\rho D\frac{\partial c}{\partial {x }_{k}}}\right)+\overline{\dot{\omega }}\approx {\rho }_{u}{s}_{L}\Sigma$$

(2)

where ${\rho }_{u}$ is the unburnt gas density, ${s}_{L}$ is the laminar flame speed, and $\Sigma$ is a generalized flame surface density. Equation (2) implies that the turbulent flame speed is the result of a thin flame surface propagating locally with laminar flame speed, which is folded by the turbulent eddies. The generalized flame surface density $\Sigma$ in Eq. (2) can be modeled as a function of the SGS wrinkling factor $\Xi$ and the resolved flame surface density $\left|\nabla \tilde{c }\right|$ as $\Sigma =\Xi \left|\nabla \tilde{c }\right|$ (Klein and Chakraborty (2019); Allauddin et al. 2017).

In the current contribution, we consider a FSD model originally proposed by Fureby (2005) and modified in Ma et al. (2013), selected as a representative of explicitly formulated FSD models. It reads:

$$\Xi ={\left(1+\frac{\Delta }{{\varepsilon }_{i}}\right)}^{D-2}, {\varepsilon }_{i}=\frac{{s}_{L}\Delta }{{u}_{\Delta }^{^{\prime}}\Gamma }$$

$$\Gamma =0.75\cdot exp\left[-1.2{\left(\frac{{u}_{\Delta }^{^{\prime}}}{{s}_{L}}\right)}^{-0.3}\right]\cdot {\left(\frac{\Delta }{{\delta }_{L}}\right)}^\frac{2}{3}, D=\frac{2.05}{\frac{{u}_{\Delta }^{^{\prime}}}{{s}_{L}}+1}+\frac{2.35}{\frac{{s}_{L}}{{u}_{\Delta }^{^{\prime}}}+1}$$

(3)

where ${\delta }_{L}$ is the Zeldovich flame thickness and the LES filter width $\Delta =n\times {\Delta }_{DNS}$, $n$ is the number of DNS cells to be filtered spatially and ${\Delta }_{DNS}$ is the DNS cell length. Since the FSD model models the sum of the filtered reaction rate and the filtered diffusion term, the filtered laminar diffusion term needs to be subtracted from the model term for comparison with models of the filtered reaction term. It can be expressed as follows

$${\overline{\dot{\omega }} }_{FSD}=\Xi \left|\nabla \tilde{c }\right|-\frac{\partial }{\partial {x}_{k}}\left(\overline{\rho D\frac{\partial c}{\partial {x }_{k}}}\right)$$

(4)

A novel analytic model for premixed combustion has been proposed by Pfitzner (2021) and analysed in depth in (Hansinger et al. 2020), modelling the filtered reaction rate source term $\overline{\dot{\omega } }$ based on the property that the analytic flame profile $c\left(\xi \right)$ is analytically invertible into a $\xi \left(c\right)$ where $\xi ={\int }_{0}^{x}{\rho }_{u}{s}_{L}{c}_{p}/\lambda dx$ is a canonical coordinate; $\lambda$ is the heat conductivity and ${c}_{p}$ is the specific heat at constant pressure. Following the work by Pfitzner, the filtered reaction rate source term $\overline{\dot{\omega } }$ is given by

$${\overline{\dot{\omega }} }_{PDF}=\frac{{\left({c}^{+}\right)}^{m+1}-{\left({c}^{-}\right)}^{m+1}}{\Delta }$$

(5)

where m is a model constant to mimic $c\left(\xi \right)$ for the different Arrhenius parameters $\alpha$, $\beta$, ${\beta }_{1}$, and ${c}^{+}$ and ${c}^{-}$ are the $c\left(\xi \right)$ at the right and left cell boundaries of a 1D filtering interval, respectively. The readers are referred to (Pfitzner 2021) for the details of the formulation. The m value used in this study is equivalent to 4.454 corresponding to $\alpha =0.818$, $\beta =6.0$, ${\beta }_{1}=0$ (see the Table 1 in (Pfitzner 2021).

In contrast to FSD type models, the filtered reaction source term in this model is not a function of the gradient of the progress variable, but of the progress variable itself, thus ensuring the correct DNS limit for small filter width. It must however be emphasized that the analytical model as presented in (Pfitzner 2021) assumes a planar flame nearly parallel to one of the surfaces of a cubical filter volume with negligible subgrid wrinkling, which is only a good assumption for smaller filter widths. Hence, it cannot be expected to represent the filtered reaction rate of strongly wrinkled flames very accurately, which can occur when large filter widths are employed. A thorough investigation to verify this model has been conducted using the explicitly filtered planar flame DNS data with different Karlovitz numbers (Hansinger et al. 2020). This model provides a valuable reference, the inclusion of wrinkling factors > 1 has been addressed in future work (Pfitzner et al. 2022).

4 Deep Learning Modeling of Filtered Reaction Rate Term

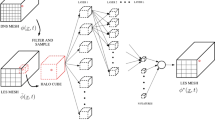
The summary of this study is illustrated in Fig. 2. As already stated in the previous section, we employed the premixed planar flame DNS as a training database that contains a wide range of the initial velocity fluctuations and LES filter widths. The explicit spatial filtering is applied to the DNS database and we generate the filtered DNS database comprising the filtered reaction rate $\overline{\dot{\omega } }$ as a function of the diverse variables that are accessible in the LES simulation and will be discussed in details in Sect. 4.2. Based on this filtered DNS database, we train the ResNet neural networks using the two sets of input parameters, which are denoted the ‘full’ set and ‘compact’ set. The neural network architecture will be described in Sect. 4.1. These trained neural networks are then tested on the unseen flames in terms of untrained filter widths, initial turbulence intensity, and canonical flame configuration. The a priori analysis on this will be presented in Sect. 5.

Fig. 2

Outline of this study. The arrowhead dashed line indicates a flowline with an outcome of a block

4.1 The Neural Networks Architecture

An ANN in its most simple form consists of a single neuron, which maps the input vector x through a number of linear transformations onto the output vector $\widehat{y}$. The mapping is achieved through the activation function $\sigma \left(\mathbf{x},\mathbf{w}, {b}_{0}\right),$ where $\mathbf{w}$ is the node weight vector and ${b}_{0}$ the offset bias. Both are adjustable parameters and have to be optimized during the supervised learning process. Stacking more neurons in parallel between input and output, a densely connected network can be obtained. Densely means that every neuron is directly connected to every neuron in the previous and subsequent layer. In case of a large number of layers between input and output, the network is commonly called a deep neural network (DNN) (LeCun et al. 2015) where the output of each layer is fed as input into the next layer. By superimposing the multiple linear transformations of each neuron, a DNN is able to map complex non–linear relationships between input and output. Simonyan and Zisserman (1409) showed that increasing the depth is beneficial for the prediction accuracy of the network when they added more hidden layers. However, adding more layers and thus increasing the accuracy has limitations, too. As shown by He et al. (2016) adding more and more layers to a suitably accurate DNN eventually may lead to saturation and degradation of the network accuracy. They found that degradation of networks with the increasing number of deep layers can be prevented through skip connections where the input to a layer is bypassed and directly mapped onto the output. Let $H\left(\mathbf{x}\right)$ be the underlying mapping to be fitted by two stacked layers, with $\mathbf{x}$ denoting the inputs to the first of these layers. Instead of learning $H\left(\mathbf{x}\right)$ directly, the stacked layers approximate a residual function $F\left(\mathbf{x}\right)=H\left(\mathbf{x}\right)-\mathbf{x}$. The original mapping has been recast into $F\left(\mathbf{x}\right)-\mathbf{x}$. This formulation is realized by a feed-forward neural network with “identity mapping” which skips one or more layers. The idea is that the $F\left(\mathbf{x}\right)$ needs to approximate non–linear mappings only, whereas the linear mappings between input and output are bypassed and do not have to be learned. Typically, a skip connection bypasses one layer, so at least two hidden layers are needed. Two layers with one skip connection are denoted as residual blocks, or simply ResNet blocks. Figure 3 shows how one ResNet block, consisting of two hidden layers, is arranged between the input and output layer and how the individual neurons are interconnected. Figure 4 illustrates how the information is fed through the individual layers and which layers are skipped for the case of three sequential ResNet blocks.

Fig. 3

Interconnection of dense neurons and structure of a single ResNet block between the input and output layer. Direct connections are illustrated with a black arrow, skip connections with a red dashed arrow

Fig. 4

Information flow and skip connections for the case of three sequential ResNet blocks

The ResNet architecture allows reducing the network’s complexity while increasing the prediction accuracy, compared to a fully connected DNN. A similar ResNet approach has led to promising results in the regression of real-gas thermodynamic states or was successfully applied to replace the thermo-chemical database in flamelet simulations (Ge et al. 2018). Our previous work (Shin et al. 2021) also has shown that the ResNet architecture increased accuracy of the deep neural networks due to its ability to prevent overfitting.

Prior to using the network for predictions in the so-called inference step, the free parameters, i.e., the weight vector $\mathbf{w}$ and offset biases ${b}_{0}$ of the nodes have to be optimized during the network training procedure. The current state-of-the-art activation function is the rectified linear unit (ReLU) (Nair and Hinton 2010). For the loss function, the mean squared error (MSE) is employed. An elastic net kernel regularizer (a blending between L1 and L2) has been applied between the last ResNet block and the output layer to enforce the generalization of the network. We used a fixed batch size of 128 samples and an exponentially decaying learning rate starting with $1\times {10}^{-4}$. We have used 200 neurons for all the fully connected layers and 10 residual blocks, yielding that the number of the trainable parameters is approximately 816,000.

All models were implemented using the Python programming language; the TensorFlow open-source software library, which allows to generate large-scale artificial neural networks with many layers with GPU acceleration capability, has been used to apply the deep learning method used in this study. A workstation equipped with Nvidia Titan X GPU has been utilized for the training of the neural network. The training has taken approximately 18 h to complete.

4.2 Training and Test Databases

Certainly, DL is a computer algorithm that endeavors to imitate the behavior inherent in the data. In order to achieve successful modeling driven by DL, securing a sufficient amount of high-quality data is crucial and essential. Hence, we attempt to create a database for training the neural network that covers an extensive range of the initial turbulence levels and the LES filter widths. It is designed such that the training database includes the influence of ${Re}_{t}$, which varies from $\sim$ 10 to $\sim$ 200, upon the filtered reaction rate source term. In addition, we encompass a wide range of the LES filter widths, as described earlier, with the intention of facilitating it with the practical LES calculations that occur often on inhomogeneous meshes.

The DNS dataset has been spatially (top-hat) filtered for a range of cubical filter volumes with side lengths containing the following number of DNS grid points $n=\left\{4, 8, 12, 16, 24, 32, 64\right\}$ which corresponds to a 1-D filter size of $\Delta /{\delta }_{th}\approx \left\{0.36, 0.72, 1.07, 1.43, 2.15, 2.87, 5.73\right\}$. In Fig. 5, the result of the filtering operation used in this study is shown by contours of unfiltered and filtered progress variables for ${u}_{in}^{^{\prime}}/{s}_{L}=15.0$, which is the case that exhibits the most extreme initial turbulence intensity in this study.

Fig. 5

The sliced contour of reaction progress variable for ${u}_{in}^{^{\prime}}/{s}_{L}=15.0$ from DNS (left), and the filter widths of $\Delta /{\delta }_{th}$=0.36 (middle) and 5.73 (right); the figure on the left side shows the unfiltered reaction progress variable $c$, and the rests depict the Favre filtered reaction progress variable $\tilde{c }$

A summary of the training and test databases is provided in Table 2. We designed the training and test databases to verify the three points: generalization capabilities for the unseen LES filter widths, for unseen initial velocity fluctuations, and the configuration of the flame. For the cases in Table 2, T&V case includes the training and validation datasets, UP case includes the test dataset for different initial velocity fluctuations, and FW case includes the test dataset for different LES filter widths. The training dataset PF − T&V involves the LES filter widths characterized by $\Delta /{\delta }_{th}\approx \left\{0.36, 0.72, 1.43, 2.87, 5.73\right\}$ and ${u}_{in}^{^{\prime}}/{s}_{L}=\left\{1.0, 5.0, 9.0, 15.0\right\}$. The test dataset PF − UP involves the unseen initial velocity fluctuations ${u}_{in}^{^{\prime}}/{s}_{L}=\left\{7.5\right\}$ with $\Delta /{\delta }_{th}\approx \left\{0.36, 0.72, 1.43, 2.87, 5.73\right\}$, test dataset PF − FW designed for testing the unseen LES filter widths encompasses $\Delta /{\delta }_{th}\approx \left\{1.07, 2.15\right\}$ and ${u}_{in}^{^{\prime}}/{s}_{L}=\left\{1.0, 5.0, 9.0, 15.0\right\}$. The dataset from the Bunsen flame configuration denoted as BF is comprised of the datasets including a range of 1-D filter size of $\Delta /{\delta }_{th}\approx \left\{1.6, 6.4\right\}$, which corresponds to the DNS grid points to be filtered $n=\left\{8, 32\right\}$ and ${u}_{in}^{^{\prime}}/{s}_{L}=\left\{1.0\right\}$ to test the validity of the modeling approach also for the different flame configurations as well as for different filter widths. The training dataset includes a number of 18 million sample points and 4.5 million sample points are reserved as validation dataset, corresponding to the Pareto rule.

Table 2 Description of training & validation, and test database based on filtered DNS where ${u}_{in}^{^{\prime}}$ is the initial velocity fluctuation, ${s}_{L}$ the laminar flame speed, and $n$ the number of DNS cells being filtered

In order to obtain an accurate surrogate model of the filtered reaction rate source term, we have considered 11 parameters in total for the input to the neural network. The definitions of the parameters are presented in Table 3. Figure 6 illustrates the filtered reaction rate source term $\overline{\dot{\omega } }$ as a function of the input parameters considered in this study, showing as an example the case ${u}_{in}^{^{\prime}}/{s}_{L}=15.0$. It can be noted that the magnitude of the filtered reaction rate source term decreases significantly as the filter width increases as expected. In the current study, the reaction rate source term is spatially filtered using the top-hat filter to compute the filtered reaction rate source term as the final outcome.

Table 3 The variables considered as the input parameters to the neural networks, where ${\delta }_{ij}$ is the Kronecker delta and Einstein summation convection is used

Fig. 6

Filtered reaction rate source term $\overline{\dot{\omega } }$ versus different input parameters for varying LES filter size and ${u}_{in}^{^{\prime}}/{s}_{L}=15.0$

The following parameters, that are all accessible in an LES, are calculated from the DNS data: Favre averaged progress variable $\tilde{c }$, the magnitude of the gradient of Favre filtered progress variable $\left|\nabla \tilde{c }\right|,$ the magnitude of the Laplacian of Favre filtered progress variable $\left|{\nabla }^{2}\tilde{c }\right|$, the magnitude of SGS velocity fluctuation ${u}_{\Delta }^{^{\prime}}$, the magnitude of the filtered velocity $\left|{\tilde{u }}_{i}\right|$, the magnitude of the gradient of the filtered velocity $\left|\nabla {\tilde{u }}_{i}\right|$, the magnitude of the filtered strain rate tensor $\left|{S}_{ij}\right|$, the magnitude of the filtered vorticity rate tensor from the velocity fields $\left|{\omega }_{ij}\right|$, the resolved curvature $\stackrel{\sim }{\kappa }$, the resolved tangential strain rate ${\tilde{a }}_{T}$, and the LES filter width $\Delta$. The filtered reaction rate source term has traditionally been modeled as a function of $f$($\tilde{c }$, $\left|\nabla \tilde{c }\right|$ ${u}_{in}^{^{\prime}}/{s}_{L}$, $\Delta /{\delta }_{th}$). The effects of curvature and tangential strain rate with respect to the hydrodynamic instability have been investigated in (Klein et al. 2018; Echekki and Chen 1996). The data-driven modeling using deep learning based on the input parameters $\overline{c }$, $\left|\nabla \overline{c }\right|$, and $\left|{\nabla }^{2}\overline{c }\right|$ is also discussed in Shin et al. (2021) although it is tested on a single LES filter width equivalent to $\Delta /{\delta }_{th}\sim$ 2.4. In the current study, all the input parameters are made dimensionless by ${\delta }_{th}$ and ${s}_{L}$ for the sake of the generalization of the modeling. These are presented at the rightmost column in Table 3.

A log-transformation and normalization has been applied to the training dataset to improve the training process and increase the accuracy as follows:

$${\phi }^{{^{\prime}}{^{\prime}}}=\frac{{\phi }^{^{\prime}}-\mu \left({\phi }^{^{\prime}}\right)}{\sigma \left({\phi }^{^{\prime}}\right)}, {\phi }^{^{\prime}}=log\left(\phi \right)$$

(6)

where $\phi$ denotes the arbitrary quantity to be normalized, $\mu$ is its mean, $\sigma$ is its standard deviation (Bishop 2007). ${\phi }^{^{\prime}}$ denotes the log-transformed quantity and ${\phi }^{{^{\prime}}{^{\prime}}}$ is the final data vector after normalization, which is eventually used to train the neural network.

5 Results

5.1 Complexity Reduction of the Deep Learning Combustion LES Model

In the current study, the maximal information coefficient (MIC) (Reshef et al. 2011) and the Shapley value Lundberg and Lee, S.-I.: A unified approach to interpreting model predictions, 31st Conference on Neural Information Processing Systems (NIPS 2017) are applied to sift the principal parameters that can represent the objective parameter with the best accuracy. Constructing an ANN with a small number of input parameters is important to alleviate the complexity of ANN and to reduce memory footprint and the inference time. In addition, the sensitivity to input parameters is essential to understand the physical phenomena at work. The most commonly used measure to sift the principal parameters in the system is the correlation coefficient. Pearson and Spearman correlation coefficients have been most commonly used for this perspective. However, these coefficients evaluate simply the linear relationships, so they are not appropriate for the combustion parameters that behave nonlinearly.

The MIC can deliver a quantitative measure if two variables are closely associated or not, satisfying two statistical characteristics which are generality and equitability. A correlation of the two parameters even with a nonlinear relationship can be explored using this method. In the original paper (Reshef et al. 2011), it has been shown that the MIC provides a more stable and reliable measure of association compared to Pearson and Spearman correlation coefficients, mutual information, principal curve based chain-of-rotator group contribution (CorGC), and maximal correlation with various types of relationship such as linear, cubic, exponential, parabolic, and sinusoidal functions, and it was also tested on realistic databases.

Unlike the MIC, which only requires two parameters to be collated, Shapley additive explanations (SHAP) requires the existence of an already trained neural network. Originally, SHAP is proposed for interpretable machine learning, as machine learning has often been regarded as a black-box in the past years. The SHAP method can investigate the partial contribution of the input parameters with respect to the objective parameter of the neural network, in this study the filtered reaction rate source term $\overline{\dot{\omega } }$. Thus, the SHAP value has the same unit as the objective parameter and the sum of the SHAP values distributed to the respective input parameters is equivalent to the exact objective parameter. The interpretation ability of the SHAP is demonstrated in Shin et al. (2021) and it attempted to show how the deep ANN recognizes the flame regions which are inherent in the filtered DNS database.

The correlations investigated using the MIC method are shown in Fig. 7, illustrating the correlation coefficients for varying LES filter widths. It should be noted that the value of MIC lies in a range between 0 and 1, which represents perfect non-correlation or correlation, respectively. The MIC values shown in Fig. 7 show that $\tilde{c }$ is the most important parameter and $\left|\nabla \tilde{c }\right|$ and $\left|{\nabla }^{2}\tilde{c }\right|$ have similar magnitudes of importance. The next highest correlation is obtained for the parameter ${u}_{\Delta }^{^{\prime}}$ and then $\left|\nabla \stackrel{\sim }{{u}_{i}}\right|$. It also shows that ${u}_{\Delta }^{^{\prime}}$ is the most influential variable among the parameters computed from the velocity fields. It should be noted that ${u}_{\Delta }^{^{\prime}}$ has been commonly employed as an important factor to model the filtered reaction rate in the context of LES. However, ${u}_{\Delta }^{^{\prime}}$ is being modeled in the general LES simulation whereas ${u}_{\Delta }^{^{\prime}}$ in the present dataset has been calculated exactly from the DNS velocity data. It is to be expected that a modeled ${u}_{\Delta }^{^{\prime}}$ will have a similar or even smaller influence than the exactly calculated ${u}_{\Delta }^{^{\prime}}$. We refer to the Appendix for consideration of ${u}_{\Delta }^{^{\prime}}$ as an alternative to $\left|\nabla \tilde{c }\right|$ in the compact parameter set.

Fig. 7

Importance map for the different LES filter widths using MIC

The SHAP values of the respective input parameter are illustrated in Fig. 8. Higher SHAP values imply that the objective parameter changes more strongly as the corresponding input parameter varies. It is interesting that $\left|\nabla \tilde{c }\right|$ has the highest impact, except for $\tilde{c }$, on the filtered reaction rate, which could have been expected since in conventional FSD modeling, the filtered reaction rate is proportional to $\left|\nabla \tilde{c }\right|$ (Klein and Chakraborty 2019). Figure 8 also shows that the next important parameter is ${u}_{\Delta }^{^{\prime}}$ in contrast with the MIC that estimated $\left|{\nabla }^{2}\tilde{c }\right|$ as the next influential parameter. Overall, the analysis using SHAP however suggests similar results as MIC except for $\left|{\nabla }^{2}\tilde{c }\right|$. Considering that SHAP is able to estimate the partial contribution of the input parameters taking into account all the other input parameters concurrently, SHAP produces more rigorous results than MIC that searches for correlations between two parameters only. In spite of this, MIC provides a precise estimation that is comparable to SHAP at a remarkably small computational effort.

Fig. 8

Importance map for the different LES filter widths using SHAP

From both analyses, it can be observed that the importance of $\tilde{c }$ decreases with increasing the LES filter width. As depicted in Fig. 6, the gradient of filtered reaction rate $\overline{\dot{\omega } }$ with respect to $\tilde{c }$ is quite large at the small filter widths, $\Delta /{\delta }_{th}$=0.36 and 0.72, for instance, and $\tilde{c }$ and its gradient are very well correlated here. At larger filter widths, e.g., $\Delta /{\delta }_{th}$=2.87 and 5.73, however, the $\tilde{c }$ gradient decouples from $\tilde{c }$ due to subgrid flame wrinkling effects.

On the basis of the results from both analyses, we define two sets of input parameters to the neural network as shown in Table 4. The ‘full’ parameters set incorporates all the parameters considered in this study: $\tilde{c }, \left|\nabla \tilde{c }\right|, \left|{\nabla }^{2}\tilde{c }\right|, {u}_{\Delta }^{^{\prime}}, \left|{\tilde{u }}_{i}\right|, \left|\nabla {\tilde{u }}_{i}\right|, \left|{S}_{ij}\right|, \left|{\omega }_{ij}\right|, \stackrel{\sim }{\kappa },{\tilde{a }}_{T}$ and $\Delta$, 11 parameters in total. The ‘compact’ set simply includes $\tilde{c }, \left|\nabla \tilde{c }\right|$, and $\Delta$, 3 parameters in total. These two sets of parameters are employed to train the two respective neural networks, and we compare the prediction performance of the neural networks using different sets of input parameters in the next section.

Table 4 The variables sets considered in this study

5.2 Performance Evaluation of the Deep Learning Model

Table 5 summarizes the error metrics defined by the difference between filtered reaction rate source term from DNS ${\overline{\dot{\omega }} }_{DNS}$ and the ones predicted ${\overline{\dot{\omega }} }_{pred}$ by the Fureby FSD model (Ma et al. 2013), the analytic flamelet probability density function (PDF) model by Pfitzner (Pfitzner 2021), and the neural networks using ‘full’ and ‘compact’ sets. For the metric, the error is defined as follows

Table 5 Normalized error metric $\epsilon$ for all the test cases considered in this study along with relative inference time of the models

$$\epsilon =\frac{\sum {\left({\overline{\dot{\omega }} }_{pred}-{\overline{\dot{\omega }} }_{DNS}\right)}^{2}}{\sum {\left({\overline{\dot{\omega }} }_{DNS}-\mu \left({\overline{\dot{\omega }} }_{DNS}\right)\right)}^{2}}$$

(7)

to show the accuracy of the models in a quantitative manner. At the bottommost row of Table 5, the relative elapsed time of the inference are indicated. The calculation time of the Fureby FSD model which showed the quickest computing time is selected for the normalization. It can be noticed that the calculation time required for the inference by the neural network models is approximately 20 times of the conventional algebraic model. Figure 9 shows the correlation plots of the filtered reaction rate predicted by the models and neural networks, plotted against the filtered reaction rate from DNS ${\overline{\dot{\omega }} }_{DNS}$ for PF − FW and PF − UP test cases. The same investigation is applied to the test cases BF − FW1.6 and BF − FW6.4 and is shown in Fig. 10. The gray scale mapping in the hexbin plots shows the density of the discrete points. The sliced contours of the filtered reaction rate from DNS ${\overline{\dot{\omega }} }_{DNS}$, neural networks, and models are shown in Fig. 11 for PF − UP test case when $\Delta /{\delta }_{th}$=0.72 and 2.87. In Fig. 12, the identical sliced contours are shown but for BF − FW1.6 and BF − FW6.4 test cases.

Fig. 9

Hexbin plots for the predicted filtered reaction rate source term $\overline{\dot{\omega } }$ from the various models versus source terms extracted from DNS ${\overline{\dot{\omega }} }_{DNS}$ for the test cases of PF − FW (left column) and PF − UP (right column). The plots (a–d) present the correlations using the neural networks with ‘full’ and ‘compact’ sets, respectively. The plots e–h show the correlations using the FSD and analytic flamelet PDF models, respectively

Fig. 10

Hexbin plots for the predicted filtered reaction rate source term $\overline{\dot{\omega } }$ from the various models versus source terms extracted from DNS ${\overline{\dot{\omega }} }_{DNS}$ for the test cases of BF when the LES filter width, $\Delta /{\delta }_{th}$=1.6 (left column) and $\Delta /{\delta }_{th}$=6.4 (right column). The plots (a–d) present the correlations using the neural networks with ‘full’ and ‘compact’ sets, respectively. The plots (e–h) show the correlations using the FSD and analytic flamelet PDF models, respectively

Fig. 11

Sliced contours of the filtered reaction rate source term $\overline{\dot{\omega } }$ from a filtered DNS, b predicted one from ‘full’ neural network, c predicted one from ‘compact’ neural network, d computed one using FSD model, and e computed one using the analytic flamelet PDF model. The upper row shows the PF − UP test case for $\Delta /{\delta }_{th}$=0.72 and the lower row is for $\Delta /{\delta }_{th}$=2.87

Fig. 12

Sliced contours of the filtered reaction rate source term $\overline{\dot{\omega } }$ from a filtered DNS, b predicted one from ‘full’ neural network, c predicted one from ‘compact’ neural network, d computed one using FSD model, and e computed one using the analytic flamelet PDF model. The upper row shows the BF − FW1.6 test case and the lower row represents the BF − FW6.4 test case

It can be noted that the result from the neural network using the ‘full’ set shows the best accuracy for all the test cases. It is also observed that the next accurate model is the neural network using ‘compact’ set. The prediction from the analytic flamelet PDF model shows comparable performance with the one from the ‘compact’ neural network, except for the BF − FW6.4 test case. In contrast, Fureby’s FSD model, shows much higher departures from the DNS filtered values. In general, the performance of the neural network model on test data of the planar flame, which is used for the training, is marginally better than when using test data from the Bunsen flame case. It can be also noted that the errors increase for high filter widths when comparing BF − FW1.6 and BF − FW6.4.

Both neural networks yield excellent performance showing low biases and variances for PF − FW and PF − UP. However, the correlation predicted by the ‘compact’ neural network somewhat deteriorates for the untrained Bunsen flame configuration, as can be seen in Fig. 10 and Table 5. Figure 11 compares contours of filtered reaction rate in a slice from DNS with the different model predictions. The results from the ‘full’ and ‘compact’ neural networks match the filtered DNS with high precision for the unseen planar flame test case for low and high filter widths, as indicated in Fig. 11, while the ‘compact’ neural network overestimates the filtered reaction rate for the Bunsen flame, as depicted in Fig. 12c. It is also noted that the slope of the ‘compact’ neural network is larger than unity in the plot of model vs. DNS filtered reaction rates shown in Fig. 10d. The performance decline also occurs for the test cases of the Bunsen flame when using the FSD and analytic models, as indicated in Table 5 and Fig. 10.

The fact that the ‘compact’ neural network shows lower performance compared with the ‘full’ neural network, demonstrates the importance of the choice of suitable sets of input parameters on the learning capability of the neural networks. While using all the parameters available can yield the best prediction accuracy, it requires additional computational costs during training and network evaluation. Thus, a trade-off analysis is necessary for this issue.

At the same time, the fact that the ‘full’ neural network performs better than both the ‘compact’ one and analytic model proves the predictive power of the deep residual neural networks which is attributed to the use of skip connections and extensive depth of the network, searching the latent features within high dimensionality. It is also interesting that the ‘full’ neural network achieves better performance compared with the ‘compact’ neural network even for the Bunsen flame configuration, as shown in Table 5 and Fig. 10. Clearly, there will be changes when comparing between the cases of different flame configurations, such as planar flame and Bunsen flame in this study, in terms of flow dynamics, flame topological features, and so forth. Those effects are inherited to the parameters ${u}_{\Delta }^{^{\prime}}$, $\left|{\tilde{u }}_{i}\right|$, $\left|\nabla {\tilde{u }}_{i}\right|$, $\left|{S}_{ij}\right|$, $\left|{\omega }_{ij}\right|$, $\stackrel{\sim }{\kappa }$, ${\tilde{a }}_{T}$, which are absent in the ‘compact’ parameter set. It is evident that the deep residual neural network could find an optimal correlation intrinsic in the high dimensional space of ‘full’ parameters.

For the models considered in this study, the analytic flamelet-based model shows good agreement with the filtered DNS data for smaller filter widths while the Fureby’s FSD model constantly overestimates the filtered reaction rate both for small and large filter widths, as can be seen in Figs. 11 and 12.

Figure 13 shows the spatial distribution of the error $\epsilon$ profiles that are averaged over transverse planes in the axial direction for the Bunsen flame test cases. It illustrates that the neural networks are able to predict the filtered DNS accurately for both small and large filter widths, though, there is a marginal discrepancy when using the ‘compact’ neural network for large filter width. It can be noted that the error made by the analytic flamelet PDF model is considerably higher for larger filter width due the fact that no subgrid flame wrinkling is considered in the model (Hansinger et al. 2020).

Fig. 13

RMS error profiles defined as the averaged filtered reaction rate between DNS and predicted by the models considered in this study for the test cases of BF − FW1.6 and BF − FW6.4. The errors are averaged at axial location x in the y − z plane. The models include ‘full’ neural network (solid), ‘compact’ neural network (dash dot), FSD model (dotted), and analytic flamlet PDF model (dashed)

Figure 14 depicts the R² score plots for different initial velocity fluctuation (left-hand side) and LES filter widths (right-hand side) based on the PF − FW and PF − UP test cases, predicted by the ‘compact’ neural network. The R² score is defined as $1.0-\epsilon$. It shows that the errors increase steadily with increasing the velocity fluctuation and LES filter width. The higher velocity fluctuation and larger filter width contribute to the high variance of the data scattering, as partly can be seen in Fig. 6. This makes it more difficult to optimize the neural networks and increases the irreducible error. It is found that the ‘compact’ neural network shows a perfect correlation for the small LES filter widths e.g., $\Delta /{\delta }_{th}$=0.36 and 0.72.

Fig. 14

R² score plots comparing the different conditions of ${u}_{in}^{^{\prime}}/{s}_{L}$ and a range of LES filter widths n for the test cases of PF − FW (left) and PF − UP (right), predicted by the ‘compact’ neural network

The prediction and generalization capability of the ‘compact’ neural network is demonstrated in Fig. 15, showing the contours of the predicted filtered reaction rate in the $\tilde{c }$ and $\left|\nabla \tilde{c }\right|\times {\delta }_{th}$ domain for the normalized LES filter width $\Delta /{\delta }_{th}=0.5, 1.0, 5.0, 10.0$. Note that the number of DNS cells along the side of the box-filtered LES cell $n=\left\{4, 16, 64\right\}$ for the planar flame corresponds to the normalized LES filter widths of $\Delta /{\delta }_{th}\approx \left\{0.36, 1.43, 5.73\right\}$. It is shown that the ‘compact’ neural network can provide a good prediction of filtered reaction rate for arbitrary values of LES filter width, filling all the gaps which the filtered DNS dataset did not provide.

Fig. 15

Predicted contours of filtered reaction rate source term $\overline{\dot{\omega } }$ by the neural network using ‘compact’ parameter set for a $\Delta /{\delta }_{th}$=0.5, b 1.0, c 5.0, and d 10.0. The results are mapped onto the domain of $\tilde{c }$ versus $\left|\nabla \tilde{c }\right|\times {\delta }_{th}$ where ${\delta }_{th}$ is the laminar flame thickness

6 Conclusions

We present a filtered reaction rate modeling approach using deep learning which is trained on filtered data from planar premixed flame DNS. The training database covers a wide range of initial turbulence intensities and LES filter widths. For the input to the neural network, two sets of parameters are considered, which include information of thermochemical properties and the dynamics of the flow available in LES. We also demonstrate an approach to search and sift the principal parameters in the system using non-machine learning and machine learning methods, which helps to reduce 11 parameters to three essential parameters. Two other combustion LES models that are proposed by Fureby and Pfitzner have been chosen for the comparison with the data-driven deep learning modeling.

A priori analysis on the unseen data, comprised of different initial turbulence intensities, LES filter widths, and canonical flame configuration, indicates that the neural network using the whole set of input parameters provides the best predictive power. The neural network using fewer input parameters shows slightly lower accuracy compared with the neural network using the whole input parameters, however it outperforms the other two models, showing stable and continuous prediction for arbitrary LES filter widths, which is one of the necessary characteristics for actual LES simulations.

In the future, we plan to further test the proposed deep learning filtered reaction rate modeling approach using DNS databases of various flame conditions and configurations. In order to validate and verify this deep learning modeling strategy a posteriori, actual LES simulations will be conducted. A wide range of LES filter widths and turbulence intensities will be sought as well as non-unity Lewis number configurations.

Appendix: Consideration of \({u}_{\Delta }^{^{\prime}}\) as Alternative to \(\left|\nabla \tilde{c }\right|\) in the Compact Parameter set

The subgrid-scale velocity fluctuation ${u}_{\Delta }^{^{\prime}}$ has been considered as a paramount parameter for modeling of turbulent combustion. However, as reported in Sect. 5.1 the analyses using MIC and SHAP show that ${u}_{\Delta }^{^{\prime}}$ is less significant in the representation of flame wrinkling than $\left|\nabla \tilde{c }\right|$ for the dataset we employed. The reason for this might be that increased subgrid-scale flame wrinkling, resulting in smaller gradients of the resolved field, is more strongly correlated to $\left|\nabla \tilde{c }\right|$ than to ${u}_{\Delta }^{^{\prime}}$.

In order to analyse the direct influence of ${u}_{\Delta }^{^{\prime}}$ on the filtered reaction rate, a neural network with the input parameters $\tilde{c }$, ${u}_{\Delta }^{^{\prime}}$, and $\Delta$ is trained and it is called ‘compact+’. Figure 16 and Table 6 depict the comparison of compact + predictions with those from ‘full’ and ‘compact’ neural networks. It can be noticed that results from the ‘compact+’ set show larger deviations from the filtered DNS values qualitatively. Also, the quantitative error metric suggests that the ‘compact+’ parameter set provides a comparable magnitude of accuracy with the original ‘compact’ case, being however somewhat inferior (about 20% worse).

Fig. 16

Hexbin plots for the predicted filtered reaction rate source term $\overline{\dot{\omega } }$ from the various models versus source terms extracted from DNS ${\overline{\dot{\omega }} }_{DNS}$ for the test cases of PF − FW (left column) and PF − UP (right column). The plots (a–d) are the same plots in Fig. 9. The plots e, f show the correlations using the ‘compact+’ parameter set

Table 6 Normalized error metric $\epsilon$ for all the neural network results including ‘compact+’ set