1 Introduction

As the effects of human activities become increasingly visible on the planet’s climate, the combustion of fossil fuels is in need of renewal. Many ambitious carbon reduction scenarios, e.g. the IEA’s “Net Zero by 2050” (International Energy Agency 2021), suggest a growing reliance on non-carbon fuels such as hydrogen and ammonia in the next decade. The large expected increase in intermittent renewable power notably solar and wind is well complemented by these means of storing, transporting, and distributing energy. While some applications will require fuel cells, it seems that combustion still has a large role to play in consuming these energy sources whether via adapted gas turbines for power generation, in heaters for homes and offices, in engines for propulsion, and even in some industrial processes such as iron or glass production. Additionally, the manipulation, storage and transport of these fuels can lead to various safety issues that must be assessed and accounted for in the design phases. This is particularly true for hydrogen, which is hard to contain, hard to keep in a liquid phase, and has a low flammability limit, meaning leaks can easily arise and lead to unwanted fires and explosions. Overall, many new design problems might arise for turbulent combustion systems in this upcoming energy transition.

The relentless increase in computational power enables the use of large eddy simulations (LES) to capture fine, unsteady combustion phenomena in ever more complex premixed combustion configurations (Vermorel et al. 2017; Carlos et al. 2021a, b). The main challenge lies in the separation of scales between the finest combustion structures—typically of the order of the laminar flame thickness—and the extent of the computational domain. This is exacerbated in the aforementioned example of hydrogen which burns at higher speeds and in thinner reaction zones than hydrocarbon fuels. As a result, one of the major challenges in LES of premixed turbulent combustion is the modeling of subgrid-scale (SGS) reaction source terms. Turbulent reaction source terms are highly dependent on unresolved interactions between fine turbulent scales and the flame front. To first order, this results in the increase of the total flame surface via wrinkling of the flame front at resolved and unresolved scales, leading to an increased consumption rate of the unburnt gases. Inspired by this observation, many premixed turbulent combustion models have been built under the flamelet assumption, where the reaction rate is proportional to the flame surface area (Poinsot and Veynante 2011). As a result, correctly capturing the turbulent combustion rate is contingent on accurate modeling of SGS flame wrinkling.

This chapter will begin in Sect. 2 with an overview of existing SGS wrinkling models, with a specific focus on algebraic fractal approaches. The success of dynamic approaches (Charlette et al. 2002b; Ronnie et al. 2004) suggests that the inclusion of contextual data leads to significant improvements in model accuracy. In this light, a promising opportunity for wrinkling modeling is to use convolutional neural networks, which have been at the forefront of recent major advances in computer vision and are presented in Sect. 3. The full supervised training and a priori evaluation of a deep convolutional neural network wrinkling model is presented in Sect. 4. Finally, issues that need to be addressed on the path towards the deployment of neural network-based wrinkling models in practical LES computations are discussed in Sect. 5.

2 Wrinkling Models

Turbulent fully premixed flames are commonly modeled using the flamelet assumption, under which chemical reactions take place in thin layers that are wrinkled but not fragmented by turbulence (Peters 1988). Chemical timescales are assumed to be fast compared to turbulent processes so that the effects of turbulence can be treated independently from the chemistry. Under these assumptions, the evolution of thermochemical variables can be tracked by a single scalar quantity, the progress variable c, which increases monotonically from 0 in the unburnt state to 1 in the burnt state. Flamelet models often assume that the structure of local flame elements measured in the progress variable space is identical to that of a one-dimensional laminar flame propagating in the normal direction to the flame element, making tabulated chemistry an effective method to model the thermochemical state of the flamelet (Benoît 2015). Traditional turbulent combustion diagrams (Borghi 1985; Peters 1988, 1999) posit that flamelets exist as long as the Kolmogorov lengthscale is larger than the laminar flame thickness, \(\delta _L\), and turbulent eddies cannot penetrate inside the flame front. This limitation is challenged by a growing body of work (Skiba et al. 2018; Driscoll et al. 2020) that reports experimental and numerical evidence of the existence of flamelet structures even for highly turbulent premixed flames (turbulent Reynolds number \( Re _t \approx 10^5\), Karlovitz number \( Ka \approx 500\)) and supports the validity of flamelet models for a much wider range of turbulent flames than previously assumed.

Under the flamelet assumption, the wrinkling of the reaction layer induced by turbulence leads to an increase of the turbulent flame speed \(s_T\) proportional to the total flame area \(A_T\) (Driscoll 2008):

$$\begin{aligned} \frac{s_T}{s_L} = I_0 \frac{A_T}{A_L}\,, \end{aligned}$$
(1)

where \(s_L\), \(I_0\), \(A_L\) are the unstretched laminar flame speed, stretch factor, and unwrinkled flame area, respectively. \(I_0\) accounts for the effect of differential diffusion, and although accurate modeling of this factor is still elusive, experimental and DNS measurements consistently report \(I_0\) values close to unity even for highly turbulent flames (Driscoll et al. 2020). The main obstacle to determining the turbulent flame speed is therefore the evaluation of the wrinkled flame front surface area. Since LES of practical turbulent premixed flames typically cannot afford to resolve the smallest wrinkling scales, the unresolved flame area must be recovered by SGS models.

Following Boger et al. (1998), the transport equation for c is given by:

$$\begin{aligned} \frac{\partial \overline{\rho } \widetilde{c}}{\partial t} + \nabla \cdot \left( \overline{\rho } \widetilde{\textbf{u}} \widetilde{c} \right) + \nabla \cdot \left( \overline{\rho \textbf{u} c} - \overline{\rho } \widetilde{\textbf{u}} \tilde{c} \right) = \overline{\rho w |\nabla c|} = \langle \rho w \rangle _s \overline{| \nabla c |}\,, \end{aligned}$$
(2)

where \(\rho \), \(\textbf{u}\), w are the density, velocity vector, and flamelet displacement speed, and \(\overline{Q}\), \(\widetilde{Q} = \overline{\rho Q}/\overline{Q}\), \(\langle Q \rangle _s\) denote filtered, density-weighted filtered, and surface-averaged versions of a quantity Q, respectively. For laminar flame elements that propagate at the laminar flame speed \(s_L\) (\(I_0 \approx 1\)), the first term of the right hand side can be simplified as \(\langle \rho w \rangle _s = \rho _u s_L\) using the unburnt gas density \(\rho _u\). The second term of the right hand side is the generalized flame surface density (FSD) noted \(\overline{\Sigma } = \overline{| \nabla c |}\) and represents the total surface area per unit volume of the flame front, including unresolved wrinkles. \(\overline{\Sigma }\) is often connected to the resolved FSD \(| \nabla \bar{c} |\) through the wrinkling factor:

$$\begin{aligned} \Xi = \overline{\Sigma } / | \nabla \bar{c} |\,. \end{aligned}$$
(3)

\(\Xi \) is equal to one when flame wrinkling is fully resolved, like in the case of a laminar flame.

Equation 2 forms the basis of flame surface density models, which typically determine \(\overline{\Sigma }\) or \(\Xi \) using a transport equation (Weller et al. 1998; Hawkes and Cant 2000; Richard et al. 2007) or algebraic models (Boger et al. 1998; Wang et al. 2012; Mouriaux et al. 2017). For instance, Boger et al. (1998) propose an algebraic expression for \(\overline{\Sigma }\) in the limit of a thin flame front relative to the filter size \(\Delta \):

$$\begin{aligned} \overline{\Sigma } = 4 \sqrt{\frac{6}{\pi }} \Xi \frac{\tilde{c}(1-\tilde{c})}{\Delta }\,, \end{aligned}$$
(4)

where \(\Xi \) remains to be modeled.

The wrinkling factor is also an essential component of LES reaction rate closures that use filtering or artificial thickening to deal with insufficient flame resolution. In the F-TACLES formalism (Fiorina et al. 2010), unclosed terms are pre-computed on filtered 1D laminar flames and tabulated as a function of \(\tilde{c}\) and \(\Delta \). The turbulent reaction rate is expressed as \(\overline{\dot{\omega }} = \Xi \, \overline{\dot{\omega }}_{\text {1D}}\). Alternatively, the thickened flame model (TFLES) (Butler and O’Rourke 1977; Colin et al. 2000) artificially thickens the flame front by a factor F by multiplying the thermal diffusivity and dividing the reaction rate by F. This operation does not affect the flame speed and enables the computation of the reaction rate from a set of well-resolved thermochemical variables \(\bar{\phi }\). An efficiency factor E compensates the reduced sensitivity of the thickened flame front to turbulent wrinkling:

$$\begin{aligned} \overline{\dot{\omega }} = \frac{E}{F}\dot{\omega }(\bar{\phi }) = \frac{\Xi (\delta _L^0)}{F\Xi (F\delta _L^0)}\,\dot{\omega }(\bar{\phi })\,, \end{aligned}$$
(5)

where \(\Xi (\delta _L^0)\) and \(\Xi (F\delta _L^0)\) are the wrinkling factors associated with the unthickened and thickened flame, respectively.

The rest of this chapter will focus on algebraic models for \(\Xi \) which have seen extensive developments over the years and have been comparatively reviewed in the literature (Chakraborty and Klein 2008; Ma et al. 2013). They are divided into two families:

  • Models based on correlations of the turbulent flame speed (Weller et al. 1998; Colin et al. 2000; Muppala et al. 2005). These models leverage Eq. 1 to express \(\Xi \) as a function of turbulence parameters such as \(u'/s_L\), \(l_t/\delta _L\). For instance, Colin et al. (2000) propose the expression:

    $$\begin{aligned} \Xi = 1 + \alpha \Gamma _{\Delta _e} \frac{u'_{\Delta _e}}{s_L}\,, \end{aligned}$$
    (6)

    where \(\Gamma _{\Delta _e}\) accounts for the net straining effect of all vortices smaller than \(\Delta _e\), and \(\alpha \) is a model parameter prescribed by the user.

  • Models based on a fractal description of the flame front (Gouldin 1987; Gouldin et al. 1989; Charlette et al. 2002a, b; Ronnie et al. 2004; Fureby 2005; Wang et al. 2011; Hawkes et al. 2012; Keppeler et al. 2014). These will be detailed in the following.

Building from the seminal work of Gouldin (1987); Gouldin et al. (1989), fractal models assume that in a range of physical scales bounded by an inner cutoff \(\eta \) and an outer cutoff L, the flame front is a fractal surface of dimension D such that \(2 \le D \le 3\). As a result, the wrinkling factor is given by:

$$\begin{aligned} \Xi = \left( \frac{L}{\eta } \right) ^{D-2}\,. \end{aligned}$$
(7)

Theoretical scaling arguments based on Damköhler’s small and large-scale limits (Peters 2000) indicate that D ranges from 7/3 in flamelets to 8/3 in high Karlovitz flames (Hawkes et al. 2012). Experimental measurements lean towards the lower end of this range, with recent results on highly turbulent flames reporting \(2.1 \le D \le 2.3\) (Skiba et al. 2021a). L corresponds to the size of the largest unresolved wrinkles, which is roughly the turbulence integral lengthscale \(l_t\) in RANS (Gouldin 1987) and the combustion filter size \(\Delta \) in LES (Knikker et al. 2002; Charlette et al. 2002b). \(\eta \) is the size of the smallest wrinkles which scales with the inverse of \( Ka \) (Gülder and Smallwood 1995; Skiba et al. 2021a) and is the subject of careful modeling endeavors in fractal models.

In Charlette et al. (2002a), the inner cutoff scale \(\eta \) is chosen as the inverse mean curvature of the flame \(|\langle \nabla \cdot \textbf{n} \rangle _s|\) with \(\textbf{n}\) the normal vector to the flame front. It is modeled by assuming an equilibrium of the production and destruction of SGS flame surface density, and lower bounded by the laminar flame thickness. The resulting model is expressed as Wang et al. (2011):

$$\begin{aligned} \Xi = \left( 1 + \min \left[ \frac{\Delta }{\delta _L}-1, \Gamma _\Delta \frac{u'_\Delta }{s_L} \right] \right) ^\beta \,. \end{aligned}$$
(8)

where \(\Gamma _\Delta \) is a vortex efficiency function that serves the same purpose as in the Colin model of Eq. 6. While the Colin model introduced a multiplicative model parameter \(\alpha \), the Charlette model uses a power-law exponent \(\beta \) which is linked to the fractal dimension by \(\beta = D-2\). A constant value \(\beta = 0.5\) (\(D = 2.5\)) is proposed in the original paper and leads to a static version of the Charlette model. When \(u'_\Delta \) is sufficiently large, Eq. 8 takes on a saturated form:

$$\begin{aligned} \Xi = \left( \frac{\Delta }{\delta _L} \right) ^\beta \,, \end{aligned}$$
(9)

where the wrinkling does not depend on the turbulence intensity.

The power-law parameter \(\beta \) can also be determined by a dynamic procedure (Charlette et al. 2002b) where it becomes a spatially and temporally evolving quantity. This avoids the delicate and arbitrary choice of one single value for \(\beta \), which is often only justified post hoc by comparison to DNS or experimental data. It is also supported by empirical evidence highlighting significant spatial and temporal variations of the fractal dimension in turbulent flames (Keppeler et al. 2014; Skiba et al. 2021a).

The dynamic procedure introduces a filtering operation \(\hat{Q}\) at a test-filter size \(\hat{\Delta } = \gamma \Delta > \Delta \) and an averaging operation \(\langle Q \rangle \) over a size \(\Delta _m > \hat{\Delta }\). By equating two expressions of the averaged test-filtered total FSD:

$$\begin{aligned} \langle \widehat{\Xi _\Delta | \nabla \bar{c} |} \rangle = \langle \Xi _{\hat{\Delta }} |\nabla \hat{\bar{c}} | \rangle \,, \end{aligned}$$
(10)

and assuming that \(\beta \) is uniform over the averaging volume, a closed-form formula for \(\beta \) can be found. The high levels of turbulence seen in practical turbulent configurations mean that Eq. 8 often takes its saturated form (Veynante and Moureau 2015) and in this case, the dynamic expression for \(\beta \) is:

$$\begin{aligned} \beta = \frac{\ln {( \langle \widehat{|\nabla \bar{c}|} \rangle / \langle |\nabla \hat{\bar{c}}| \rangle )}}{\ln {\gamma }}\,. \end{aligned}$$
(11)

The dynamic Charlette model has been applied to LES of jet flames (Wang et al. 2011; Schmitt et al. 2015; Volpiani et al. 2016), ignition kernels (Wang et al. 2012; Mouriaux et al. 2017), stratified non-swirling burners (Mercier et al. 2015; Proch et al. 2017), the PRECCINSTA swirled burner (Veynante and Moureau 2015; Volpiani et al. 2017), explosions in semi-confined domains (Volpiani et al. 2017), and light-around in an annular combustor (Puggelli et al. 2021). It has also seen numerous incremental improvements over the years (Wang et al. 2011; Mouriaux et al. 2017; Proch et al. 2017) and stands today as a strong model for the SGS wrinkling factor.

3 Convolutional Neural Networks

This section gives a primer for uninitiated combustion physicists on deep learning. It explores what neural networks are, what the adjective “convolutional” refers to in that context, and how Convolutional Neural Networks, a workhorse of the deep learning revolution of the past decade, can be put to use for SGS problems.

3.1 Artificial Neural Networks

As early as the 1940s, attempts to model the behavior of biological neural networks have led to a simple function representing the action of a neuron (McCulloch and Pitts 1943). In its simplest form, a neuron sums all of its weighted electrical inputs via its dendrites, and the result is fed to a threshold function: if the sum of the input signals is high enough, an electrical impulse is sent through the axon to other neurons. Formally:

$$\begin{aligned} y = \sigma (\textbf{w}^T\textbf{x} + b)\,, \end{aligned}$$
(12)

where \(\textbf{x}\) is the vector of inputs received by the dendrites, \(\textbf{w}\) the vector of weights that it applies to each, b is a bias value, \(\sigma \) some threshold-like function called the activation function, and y the resulting signal sent via the axon to other connected neurons. Several of these neurons can be connected together, side by side as well as front to back, to form a neural network. Networks are part hand-designed, part automatically optimized, but in their most simple form they are feedforward, i.e. there are no information loops in the network.

The understanding of neural biology has advanced well beyond these simple models today, but the terminology “neural” has persisted. Modern neural networks have moved away from a strict analogy with biological neurons, towards a more abstract formalism. A network is composed of a succession of layers that perform operations on their input feature map, and pass on the resulting output feature map to the next layer.

Another important choice concerns the activation functions: if \(\sigma \) is linear, then so is each neuron, and stacking several linear neurons successively would be equivalent to composing several linear functions. The result would still be a linear function that a single neuron can represent. \(\sigma \) is therefore usually non-linear, and is an empirical trade-off between the non-linearity and the computational complexity it introduces, as well as some considerations on ease of training. The most common example is the ReLU or REctified Linear Unit function: \(\sigma (x) = \max (0, x)\). For binary classification tasks, the last activation function is usually a sigmoid function:

$$\begin{aligned} \sigma (x) = \frac{1}{1 + e^{-x}} \end{aligned}$$
(13)

taking values from 0 to 1 that can be interpreted as a class probability.

Once a network architecture is chosen, it is time to train it. Essentially, training means finding the optimal weights \(\textbf{w}\) and biases b, called trainable parameters, for all the neurons in the network so as to minimize a given loss function. To this end, the gradient of the loss function on given training samples with respect to all of the trainable parameters can be computed. This error can then be minimized by updating the trainable parameters via an optimization procedure, usually a form of iterative gradient descent.

In practice however, this gradient often proves highly non-convex and high-dimensional, and the error minimization process is too challenging for many standard gradient descent techniques. Instead, the minimization process is usually performed using backpropagation and stochastic gradient descent (SGD). Backpropagation (Rumelhart et al. 1986) is simply the process of computing progressively the gradient of the error with respect to the trainable parameters in each layer of the neural network, working backwards (hence the name) from the output to the input. This is a special case of reverse automatic differentiation, which is now the standard framework in deep learning libraries to efficiently perform backpropagation on complex neural networks. SGD is another trick used by most deep learning strategies (Goodfellow et al. 2016). Ideally, the gradient of error with respect to trainable parameters should be estimated over the entire training set. However, training databases are very large in deep learning, and this is computationally intractable. But in many situations, approximating this gradient with a small subset (called a mini-batch) of the training database gives a sufficiently good estimate of the overall gradient to advance an iterative gradient descent algorithm. This mini-batch-based gradient descent is called SGD.

Machine learning models are trained to capture all the meaningful features of the training dataset that are relevant to their learning task. If a model is underparametrized, it can fail to fit the training dataset adequately, leading to a behavior named underfitting. For this reason, modern neural networks contain a very large number of parameters, more than hundreds of billions in recent architectures (Brown et al. 2020). This can however lead them to learn too much, eventually learning the full dataset entirely by heart, a process called overfitting. Although this results in a very low loss function during training, an overfitted network performs poorly on data outside of the training dataset, meaning that it fails to generalize. To guard against this, overfitting must be monitored during training. This is done by reserving part of the dataset as a separate validation set, which can never be used to optimize the networks weights directly. The quality of predictions on this validation set is evaluated regularly during training, demonstrating when the generalization performance starts to degrade, and suggesting that the network has started to learn the specific noise of the data, and is no longer improving on the general task. The compromise between underfitting and overfitting is called the bias-variance trade-off (Goodfellow et al. 2016) and is central to any machine learning task.

3.2 Convolutional Layers

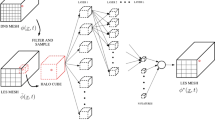
Neural networks built only with fully connected (FC) layers, where each neuron is connected to every neuron of the previous layer are called multi-layer perceptrons (MLPs). MLPs are simple stacks of successive FC layers. While this gives some choice in the design of the network (number of dense layers, number of neurons in each layer, activation functions...), other more specialized layers have been proposed for specific tasks. For image data, where the pixels have a matrix structure, convolutional layers (ConvLayers) are usually used. For the purpose of physical modeling, it is believed that a direct analogy between pixels in images and discretized physical fields can be made. The output of a ConvLayer is obtained by the convolution of its kernel, containing its trainable parameters, with its input feature map, as illustrated in Fig. 1. Multiple independent channels, each with its own kernel, are usually used to enhance the expressiveness of the layer. Each kernel (here of size \(3 \times 3\), in gray) is convolved with the input matrix, producing a new matrix at the output. These convolutional kernels are the basis of many image treatment methods, where the kernel weights are prescribed to perform tasks such as contour detection, gaussian blur, denoising, etc. In a ConvLayer, the weights of the kernel (here 9 values) are the learnable parameters that are to be adjusted by the learning process instead of being explicitly prescribed. ConvLayers are well-adapted to dealing with spatial grids because of their translation equivariance and local consistency inductive bias (Battaglia et al. 2018). Since the same kernel is used for all input locations, the number of parameters of a ConvLayer is typically lower than in an FC layer. Moreover, unlike an FC layer, the number of parameters in a ConvLayer does not depend on the size of the input feature map, making it a good choice to process inputs of large dimensions like 3D computational domains.

Fig. 1
figure 1

Convolutional layer on a 2D matrix (e.g. an image). Input pixels (bottom) are convolved with a \(3 \times 3\) kernel to produce the output pixels one by one

Full size image

Adding the ConvLayer to the layer arsenal leads to new network architectures, called convolutional neural networks (CNNs). Interestingly, shallow ConvLayers of a CNN have been observed to learn Gabor filters, which naturally occur in the visual cortex of mammals and are often chosen to extract image features in hand-made image classifiers (Goodfellow et al. 2016). CNNs have been applied with great success for image-based tasks since the 1990s (LeCun et al. 1998), and have fueled the deep learning craze since the early 2010s successes (Krizhevsky et al. 2012) on the ImageNet classification challenge (Deng et al. 2009). Empirical evidence has shown that stacking small convolutional kernels leads to better performance than a single equivalent large kernel (Simonyan and Zisserman 2015; Szegedy et al. 2015). Depth is thus an important hyperparameter in CNNs, and deep CNNs have been universally used in recent breakthroughs in computer vision (He et al. 2015; Brock et al. 2019; Tan and Quoc 2019; Chen et al. 2020). Two of the most common learning tasks in computer vision, specifically when dealing with images, are classification and segmentation.

Image classification (Fig. 2a) is a task where a discrete label must be determined for an image. In the simple case of classifying of cat and dog images, the probability that the image contains a cat \(p_{\textrm{cat}}\) is predicted by the network, and \(p_{\textrm{dog}} = 1-p_{\textrm{cat}}\) is inferred. If \(p_{\textrm{cat}}>0.5\), the label for the image is determined to be cat. Otherwise, it is dog. This prediction can then be compared to a truth value in the training database, and the network weights can be updated as described in Sect. 3.1. More generally, there can be more than 2 classes to choose from, and more than one class can be present at the same time. CNNs designed for classification tend to have a funnel-like shape, with a high-dimensional input (several thousand pixels, possibly in color) and a low-dimensional output (only 2 in our example, 1000 in the ImageNet dataset (Deng et al. 2009)).

Fig. 2
figure 2

Typical CNN tasks: a classification, where an image is classified according to a discrete list of labels; and b segmentation, where each pixel is classified according to a discrete label

Full size image

Image segmentation (Fig. 2b) consists in identifying and classifying meaningful instances in an image by outlining them with labeled masks. Continuing with the previous example, the precise pixels belonging to the cat are sought. This changes the architecture of the network, which no longer needs to reduce the dimension of its output. Instead, the output has the same shape as the input, and each pixel is classified as cat (1) or not (0). As a result, the layers chosen in the network must ensure that the problem dimensionality is preserved at the output.

Fig. 3
figure 3

Architecture of a U-Net neural network. Convolutional layers operate in an “double funnel” fashion, first reducing the feature map size, than increasing it again to match the input. Skip connections are used between matching-size layers

Full size image

3.3 From Segmentation to Predicting Physical Fields with CNNs

A specific neural network architecture initiated a series of excellent results on image segmentation tasks: the so-called U-Net (Ronneberger et al. 2015). This network, introduced to detect tumors in medical images, can now be found in a variety of projects, in its original form or in one of numerous variations ( Çiçek et al. 2016; Falk et al. 2019; Oktay et al. 2018), including in fluid dynamics (Wandel et al. 2021). Its structure is that of a “double funnel”, one encoding the image into small but numerous feature maps, and the other upscaling back to the input dimension (Fig. 3). Compared to simple linear architectures (Fig. 2), the U-Net introduces skip connections between some of the blocks, meaning data flows both to the lower blocks (with deeper encoding of the features) and directly to the same-size output. The intuition behind this is that in order to perform a segmentation decision on a given pixel, a multi-scale analysis is needed. The influence of neighbouring pixels informs on local textures. Further pixels (equivalent to a “zoomed-out” view of the image) give information about the general shapes in the vicinity. Further pixels still (seen by the deepest levels of the U-Net) offer an analysis of the position of the shapes relative to each other. In the second (right in Fig. 3) half of the network, these levels of analysis coalesce gradually to form the final decision.

This process has analogies with the dynamic procedure of Eq. 11. Indeed, the dynamic estimation of \(\beta \) relies on observing the field of c at the resolved scale and the test-filter scale. Similarly, the first layer of a U-Net learns to detect structures on a 3-pixel wide stencil, and deeper layers aggregate features coming from several of these patches, effectively working at a larger scale. The U-Net can therefore be seen as a generalization of the concept introduced by dynamic models, where the effect of multiple scales on the target prediction is learned from the data, instead of only the resolved and test-filtered scales. This motivates the application of this type of network to the problem of predicting sub-grid scale wrinkling.

Some adaptations are needed to use a traditional U-Net on LES fields:

  • The U-Net performs a regression task by predicting specific SGS values instead of a segmentation task. The final activation function should thus be a ReLU or an identity function.

  • The U-Net must handle 3D data instead of 2D images. This poses very little challenge, as most modern implementations of neural network libraries natively offer 3D convolutional layers with the same functionality as classical 2D ones.

  • Because the CNN is designed to work on structured data (pixels in image applications), it must operate on a homogeneous, isotropic mesh. This might mean that the field from a CFD mesh must be interpolated onto such a mesh. This limitation is due to the use of a “vanilla” U-Net, with no adaptations to more complex meshes. However, modern implementations with graph neural networks (Pfaff et al. 2021) could perform operations directly on an unstructured mesh if needed.

4 Training CNNs to Model Flame Wrinkling

This section presents the complete process of training and evaluating the CNN as a wrinkling model by following the steps described in Lapeyre et al. (2019). Full details are contained in the original paper, and code and data are available online.Footnote 1

4.1 Data Preparation

The training and evaluation datasets are generated from the DNS of a slot burner configuration simulated with the AVBP unstructured compressible code (Schönfeld and Rudgyard 1999; Selle et al. 2004). A fully premixed stoichiometric mixture of methane-air unburnt gases is injected in a central rectangular inlet section at \(U = 10\) m/s and surrounded by a slow coflow of burnt gases. The domain is a rectangular box meshed with a homogeneous grid containing \(512 \times 256 \times 256\) hexahedral elements of size \(\Delta x = 0.1\) mm which resolve the reaction zone of the flame front on \(4{-}5\) points. A turbulent velocity field generated from a Passot-Pouquet spectrum (Passot and Pouquet 1987) is superimposed to the unburnt gas inlet velocities. Three separate DNS simulations are run:

  • DNS1: inlet turbulence fluctuation intensity \(u'\) chosen such that \(u'/s_L = 1.25\),

  • DNS2: increased inlet turbulence, \(u'/s_L = 2.5\),

  • DNS3: starting from a steady-state snapshot of DNS2, the inlet velocity U is doubled for 1 ms, then set back to its initial level for 2 ms. This triggers the formation of a detached pocket of unburnt gases as evidenced in Fig. 4.

The training dataset is built from 50 snapshots of DNS1 and 50 snapshots of DNS2 extracted at 0.2 ms intervals in the steady-state regime. Similarly, the evaluation dataset is made up of 15 snapshots of DNS3. The slightly different large-scale flow dynamics and flame front geometry make it a good choice to assess the generalization of the CNN on a distribution close to that of the training set.

Fig. 4
figure 4

Slices of progress variable field at \(t = 0\) ms (left) and \(t = 1\) ms (right) into DNS3. Top: DNS fields, bottom: filtered fields downsampled on the coarse mesh. The transient inlet velocity step leads to the separation of a pocket of unburnt gases

Full size image

For each snapshot, the DNS field of c is filtered with a Gaussian kernel and downsampled to a coarse \(64 \times 32 \times 32\) grid with a coarse cell size \(8 \Delta x\) to generate \(\bar{c}\) and \(\overline{\Sigma } = \overline{|\nabla c|}\). The network is trained to predict \(\overline{\Sigma }^+ = \overline{\Sigma }/\overline{\Sigma }_{\textrm{lam}}^{\textrm{max}}\) corresponding to an input field of \(\bar{c}\). \(\overline{\Sigma }^+\) is the total FSD normalized by its maximum value measured on a laminar flame discretized on the same grid. While the values of \(\overline{\Sigma }\) are specific to a given flame and coarse grid, \(\overline{\Sigma }^+\) is a generic quantity that reflects the amount of unresolved wrinkling and should be more amenable to generalization. Normalizing the target value around 1 is also beneficial for the convergence of the early phase of SGD, since the output of the CNN resulting from inputs \(\bar{c}\) and initial weights of the order of 1 will also be of the order of 1.

4.2 Building and Analyzing the U-Net

The U-Net architecture of Lapeyre et al. (2019) is detailed in Fig. 5. It follows a fully convolutional, symmetrical, three-stage encoder–decoder structure. Each stage is composed of two successive combinations of

  • a 3D convolution with a \(3 \times 3 \times 3\) kernel,

  • a batch normalization layer (Ioffe and Szegedy 2015),

  • a rectified linear unit (ReLU) nonlinear activation unit, 

followed by \(2 \times 2 \times 2\) pooling operations. In the encoder, maxpooling operations decrease the spatial dimensions of the feature maps by a factor of 2. The shape of the input field is then recovered by upsampling pooling operations in the decoder.

Fig. 5
figure 5

Diagram of the U-Net architecture. Feature maps are represented by rectangles with their number of channels above. Arrows represent the hidden layers connecting the feature maps

Full size image

The network contains a total of 1.4 million trainable parameters. In cases where a smaller network would be preferrable, the parameter count could be reduced by using simpler neural network architectures (Shin et al. 2021) or by investigating architecture search and pruning methods (Frankle and Carbin 2019). On an Nvidia Tesla V100 GPU, training the network to convergence in 150 epochs takes 20 min, and inference on a single snapshot of DNS3 only requires 12 ms.

A key property of vision-based neural networks is their receptive field (RF), which corresponds to the input region that can influence the prediction on a single output point (Goodfellow et al. 2016). In practice, due to the distribution of the hidden layer connections inside the network, points located at the center of the receptive field contribute more to the prediction than those at the periphery. This leads to the notion of effective receptive field (ERF) (Luo et al. 2016) which measures the extent of the receptive field that is actually meaningful to the prediction, and can be quantified by counting the number of connections originating from each input location. Figure 6 compares the extent of the ERF of the U-Net with the DNS3 flame. The size (Luo et al. 2016) of the ERF is approximately 7.6 times the filtered laminar flame thickness and is large enough to encompass all of the large-scale structures of the flame front. In comparison, the context size of the Charlette dynamic model can be estimated as the averaging filter size which is typically \(2{-}6\) times the filtered laminar flame thickness (Veynante and Moureau 2015; Volpiani et al. 2016). Increasing the context size of the dynamic model may lead to numerical issues caused by flame/boundary and flame front interactions (Mouriaux et al. 2017) and greatly impacts the computational cost of the procedure (Volpiani et al. 2016), whereas for CNNs it can simply be achieved by using a deeper network.

Fig. 6
figure 6

ERF superimposed on iso-lines of \(\bar{c}\) on a slice of a DNS3 snapshot (\(t = 0.8\) ms). Grayscale intensity in the ERF is proportional to the impact of the input voxel location on the output prediction at the center of the ERF. Dashed circular line: edge of the ERF

Full size image

4.3 A Priori Validation

After training the CNN on snapshots of DNS1 and DNS2, it is evaluated a priori on snapshots of DNS3 which are fully separate from the training dataset. The values of the trained weights of the CNN are frozen, and the model behaves like a large parametric function mapping \(\bar{c}\) to \(\overline{\Sigma }^+\). In Fig. 7a, the Charlette and CNN models are compared by plotting the downstream evolution of the total flame surface area that they predict on the DNS3 snapshot with the largest DNS total flame surface. For reference, target flame surface values from the DNS and values obtained without any SGS modeling are also shown. In this snapshot, the flame contains three distinct regions: a weakly turbulent flame base attached to the inlet (\(x \approx 0\)–15 mm), followed by a detached pocket of unburnt gases (\(x \approx 15\)–45 mm) and a postflame region of combustion products with no flame front.

Fig. 7
figure 7

A priori evaluation of a selection of wrinkling models

Full size image

The static Charlette model with constant \(\beta = 0.5\) finds the correct trend but consistently fails to accurately match the DNS flame surface values. The dynamic Charlette model with local \(\beta \) (\(\hat{\Delta } = 1.5\Delta \), \(\Delta _m = 2\hat{\Delta }\)) using the corrections from Wang et al. (2011) and Mouriaux et al. (2017) performs very well in the detached pocket and close to the inlet, but still struggles near the tip of the attached flame which features prominent flame front interactions. Finally, the CNN agrees nearly perfectly with the target values in all regions of the domain. Figure 7b shows that this behavior is consistent throughout the whole duration of DNS3, whereas the error made by the Charlette dynamic model fluctuates in time.

5 Discussion

Deep CNNs trained to model SGS wrinkling show excellent modeling accuracy and consistency when compared to existing algebraic models on evaluation configurations that are similar to their training database. To move towards applications to practical complex configurations, some key questions still need to be addressed:

  1. 1.

    What information should be provided to the model? The U-Net presented above only used the field of \(\bar{c}\) as input, but algebraic wrinkling models usually incorporate additional parameters like \(u'/s_L\), \(l_t/\delta _l\), Ka, ...

  2. 2.

    To what extent can the model generalize to unseen configurations? Currently, the training dataset is built from DNS data which is rarely available in practice. If the model cannot reliably generalize well enough beyond its training distribution, this would severely limit its range of application.

  3. 3.

    Can the model be coupled to a fluid solver for on-the-fly predictions?

These questions apply broadly to any neural network model trained to predict an LES SGS quantity, not only to wrinkling models. Question 1 comes down to isolating the essential physical and numerical quantities that drive SGS wrinkling. A first meaningful quantity is the spatial distribution of \(\bar{c}\) which identifies the location and thickness of the flame front in a premixed flame. Deep CNNs like the U-Net are presumably able to extract all the contextual information they need from the entire field of \(\bar{c}\), and indeed experiments have indicated that providing gradients of \(\bar{c}\) as additional inputs does not improve their accuracy. Other works that opt to use simpler architectures with fewer trainable parameters do include gradient information in the input of the network. Shin et al. (2021) train a shallow MLP combined with a mixture density network that captures the stochastic distribution of \(\overline{\Sigma }\). Since the MLP only processes local data, \(|\nabla \bar{c}|\) and \(|\nabla ^2 \bar{c}|\) fields are used as additional inputs to provide some spatial context. Ren et al. (2021) use a network composed of a shallow 2D convolutional base followed by five fully connected layers. Local predictions are computed from \(3 \times 3\) box stencils of the filtered fields of \(\bar{c}\), \(|\nabla \bar{c}|\) and the subgrid turbulence intensity \(u'_\Delta \) discretized on the fine DNS grid.

Another relevant parameter is \(u'_\Delta /s_L\), which controls the amount of total flame surface wrinkling and is a crucial quantity in many wrinkling models covered in Sect. 2. Nonetheless, the challenges inherent to modeling \(u'_\Delta \) from LES quantities (Colin et al. 2000; Veynante and Moureau 2015; Langella et al. 2017, 2018) have made the saturated Charlette dynamic model (Eq. 9) an attractive solution that does not directly depend on \(u'_\Delta \).

Finally, the proportion of unresolved flame wrinkling in the total flame surface is determined by the filter size \(\Delta \). Since CNNs work on grid data with no explicit distance embedding, \(\Delta /\delta _L\) sets the resolution of the filtered flame structures that are processed by the network. Figure 8 illustrates the ambiguity that may arise if \(\Delta \) is not known by the network. There is an infinite number of combinations \((c, \Delta )\) that can lead to a given \(\bar{c}\) field, each corresponding to a different amount of SGS wrinkling, and the sole knowledge of \(\bar{c}\) is not sufficient to discriminate between them. Additionally, CNNs are known to be sensitive to resolution discrepancies between the training and evaluation datasets (Touvron et al. 2019). This issue was avoided in Lapeyre et al. (2019) by training and evaluating the U-Net at the same \(\Delta /\delta _L\) but should be considered when generalizing to arbitrary flame resolutions.

Fig. 8
figure 8

Illustration of the filtering ambiguity. A filtered flame front (bottom) outlined by iso-lines of c can correspond to several unfiltered flames (top), each with a different filter size and mean wrinkling factor

Full size image

To move towards generalizable SGS neural network models, \(u'_\Delta /s_L\) and \(\Delta /\delta _L\) should henceforth be accounted for in the model either implicitly, in the choice of the training and evaluation datasets, or explicitly, by incorporating them in the model inputs or feature maps. Xing et al. (2021) started to investigate this by evaluating a U-Net trained on a statistically planar turbulent flame to predict the SGS variance of the progress variable \(\overline{c'^2}\). A jet flame evaluation configuration (Luca et al. 2019) was chosen to test the ability of the network to generalize to a case featuring major differences from the training dataset regarding the large-scale flow and flame structures, thermophysical, and chemical parameters. The U-Net was observed to generalize better than existing dynamic approaches when \(u'_\Delta /s_L\) and \(\Delta /\delta _L\) were chosen to match between the training and generalization configuration. Its performance dropped when either of these parameters did not match the unique values of the training set. However, when trained on a dataset containing a range of filter sizes, the U-Net was able to discriminate between the various \(\Delta /\delta _L\) values without explicitly providing \(\Delta /\delta _L\) as an input parameter. Apart from \(u'_\Delta /s_L\) and \(\Delta /\delta _L\), the inclusion of other relevant physical quantities can be investigated through feature importance analysis (Yellapantula et al. 2020).

The limits to generalization of SGS neural network models are still not well understood. Generalization is usually assessed by evaluating the model on the training distribution sampled at different spatial (Henry de Frahan et al. 2019; Wan et al. 2020) or temporal (Bode et al. 2021; Cellier et al. 2021; Chen et al. 2021) locations, or through minor parametric variations (Nikolaou et al. 2019; Lapeyre et al. 2019; Yao et al. 2020; Yellapantula et al. 2020; Chen et al. 2021). For wrinkling models specifically, Ren et al. (2021) study highly turbulent statistically stationary planar flames at \( Ka = 38\) (case L), 390 (case M), and 1710 (case H). Cases M and H are located in the broken reaction zone regime, where the flamelet assumption may not hold. Snapshots show a highly fragmented reaction front and the authors point out that the resolved and total FSD fields have large discrepancies for these cases. After training on case H, the model performs well on case M and at larger filter sizes, beating a selection of static wrinkling models. It is interesting to note that it performs relatively poorly on case L which belongs to the thin reaction zone regime and features an intact reaction zone. This result highlights the model’s sensitivity to changes in the turbulent combustion regime. Attili et al. (2021) draw similar conclusions after training the U-Net from Lapeyre et al. (2019) on four DNS of jet flames with increasing Reynolds numbers (Luca et al. 2019). Their results show that generalization to unseen turbulent levels works better between high Reynolds number flames, which they suggest is due to the asymptotic behavior of high Reynolds turbulence. In addition, models trained on a specific region of the flame (flame base, fully turbulent region, or flame tip) perform noticeably worse when tested on a different region, thus highlighting the spatial variations of the wrinkling distribution in a given flame.

Supervised training of neural networks is a form of inductive learning, for which generalization depends on the inductive biases of the model (Griffiths et al. 2010). These are the factors outside of the observed data that intrinsically steer the model towards learning a specific representation. Generalization is largely driven by how well the model’s inductive biases fit the properties of the data representation it is trained to learn. The inductive biases of neural networks are heavily influenced by their architecture. MLPs have weak inductive biases, whereas CNNs have strong locality and translation equivariance inductive biases (Battaglia et al. 2018) which explains their success in generalization of computer vision tasks (Zhang et al. 2020). Since locality and translation equi-variance are also desirable properties of an SGS model, CNNs seem better suited than MLPs to generalize on SGS modeling tasks.

On the other hand, coupling CNNs with a fluid solver for on-the-fly predictions and a posteriori validation comes with numerous implementation challenges. In the case of the U-Net, its field-to-field nature allows it to output predictions in the entire domain in a single inference of the network, which is a strong asset for computations on large meshes. However, the input field needs to be built by gathering LES data points from the whole domain, and the prediction of the model has to be scattered back. For massively parallel solvers which perform domain decomposition, this requires dedicated message-passing communications between the solver and the CNN instances. Additionally, since the CNN can only process structured data, if the LES is performed on an unstructured mesh, the input and prediction fields must be interpolated between the solver mesh and a structured mesh that can be read by the CNN. Coupling interfaces such as OpenPALM (Duchaine et al. 2015) have successfully been used to manage these operations and perform fully coupled simulations using the AVBP solver (Lapeyre et al. 2018). The computational overhead due to the coupling and the neural network prediction is less than 5%. As a reference, the filtering operations used in the Charlette dynamic model typically induce overheads of 20–30% (Volpiani et al. 2016; Puggelli et al. 2021). Finally, given the large number of parameters of the U-Net, inference is preferably performed on a GPU. This requires additional care in the coupling implementation, but should not limit the deployment of the model given the growing adoption of hybrid CPU-GPU supercomputer infrastructures.

6 Conclusion

The intersection of LES subgrid-scale modeling and machine learning is a promising and rapidly growing field in numerical combustion. The large modeling capacity of deep neural networks is a strong asset to model complex SGS flame-turbulence phenomena in a data-rich environment fueled by high-fidelity simulation results. Taking inspiration from the computer vision community, a deep CNN U-Net architecture is trained to predict the total—resolved and unresolved—flame surface density field from the LES resolved progress variable field. The U-Net is built to aggregate multi-scale spatial information on the flame front, ranging from the coarse mesh resolution to large flame structures, thanks to its wide receptive field. In this sense, it can be viewed as an extension of existing dynamic models that combine information at the filtered and test-filtered scales. DNS snapshots are filtered and downsampled to generate the training and evaluation datasets that are used to evaluate the U-Net in an a priori context. On the evaluation set of a slot burner configuration, the U-Net consistently matches the target flame surface density distribution, beating the static and dynamic versions of the Charlette wrinkling model. More generally, the modeling methodology outlined in this chapter can be applied to any SGS quantity, such as the SGS variance of the progress variable. These results open the way to many compelling directions for future work. Coupling a deep CNN with a massively parallel fluid solver is a key step towards a posteriori validation. Graph neural networks could be explored as alternatives that could handle on arbitrary meshes and complex geometries. Finally, an issue at the core of the practical deployment of any machine learning combustion model is to assess whether it can robustly generalize outside of its training distribution, a feature that will need to be demonstrated if these models are to replace traditional models in CFD solvers.