1 Introduction

The response of a premixed flame when subjected to increasingly intense turbulence has been the subject of many different experimental and theoretical studies (Bradley 1992; Driscoll 2008; Peters 1999; Poludnenko and Oran 2011, 2010). Turbulence causes flames to stretch, resulting in an increase of the flame surface area and hence the burning rate (Damköhler 1940; Pope 1988; Candel and Poinsot 1990; Law 1988). In addition, it has been theorised that small scales of turbulence may enhance the transport due to turbulence and cause further enhancement in the flame speed (Damköhler 1940; Nivarti et al. 2019; Driscoll 2008). A majority of related studies has focused on the variations in turbulence intensity (Driscoll 2008; Lipatnikov and Chomiak 2002), including Direct Numerical Simulation (DNS) studies which have been applied to investigate the effect of increasing the turbulence intensity \(u^{\prime }\) while holding all other parameters constant as far as possible (Nivarti and Cant 2017).

There have been fewer studies which have produced information about the effect on the flame of varying the turbulence integral length scale \(l_0\) (Peters 1999; Lipatnikov and Chomiak 1999; Song et al. 2021). Several experimental investigations dealing with variations in \(\ell _0\) have been discussed in Sect. 3.3.2 in Ref. (Lipatnikov and Chomiak 2002). This is harder to achieve in DNS, due to the need to resolve the full range of turbulence length scales from the integral scale down to the Kolmogorov scale \(\eta\). Therefore, given the high computational cost, the scope for variation of the integral length scale \(l_0\) is necessarily limited. Nevertheless, fundamental study of the effect of length scales is important in order to explore the combustion physics, to define the constraints on flamelet-based modelling (Driscoll et al. 2020; Skiba et al. 2017, 2021; Hawkes and Chen 2006) and to suggest model improvements. Recent papers have analysed the variations in flame speed with \(\ell _0\) both experimentally (Kim et al. 2020; Mohammadnejad et al. 2021) and using DNS (Yu and Lipatnikov 2017a, b; Kulkarni and Bisetti 2021a; Kulkarni et al. 2021; Kulkarni and Bisetti 2021b; Varma et al. 2021).

The dependence of flame speed on the turbulence Reynolds number was investigated experimentally (Smith and Gouldin 1979; Shy et al. 2015) and showed any increase in flame speed with an increasing turbulent Reynolds number, consistent with the previous predictions (Damköhler 1940; Peters 1999). Recent analysis based on DNS of turbulent slot jet flames (Attili et al. 2021; Luca et al. 2019) investigated flames at nearly constant Karlovitz number (Ka) but with variations in Reynolds number (Re). The key finding of this work was that thickening of the inner reaction layer occurs as Re increases, causing the flame speed to increase faster than the flame area as Re increases (Attili et al. 2021). Furthermore, the statistics of flame stretch for this dataset (Luca et al. 2019) indicated that tangential strain rate and mean flame curvature normalised by the Kolmogorov length \(\eta\) were found to have a weak dependence on Re.

The present study aims to investigate the response of a turbulent premixed flame to variations in \(u^{\prime }\) and \(l_0\), treating each of these quantities separately as an independent variable while holding all the other variables constant. Unlike the previous analyses (Attili et al. 2021; Luca et al. 2019), the Komogorov scale and hence the Karlovitz number changes across the dataset.

The rest of the paper is organised as follows. Section 2 presents the relevant theory to outline and define the flame properties of interest. A matrix of test cases is described in Sect. 3 covering a range of both of the independent variables of interest. Section 4 presents the results for the flame properties including flame speed and flame area, statistics of tangential strain rate and mean flame curvature, and statistics of displacement speed and its components. The effects of varying \(u^{\prime }\) at constant \(l_0\) are compared with previous findings (Nivarti and Cant 2017), while results illustrating the effects of varying \(l_0\) at constant \(u^{\prime }\) are also presented and discussed.

2 Theory

The increase in flame surface area \(A_T\) due to the action of turbulence (Law 1988; Pope 1988) and the subsequent increase in the turbulent flame speed \(s_T\) has been studied extensively both experimentally (Driscoll 2008) and computationally (Chen et al. 1999; Poludnenko and Oran 2011; Nivarti and Cant 2017), and is governed by the expression

$$\begin{aligned} \frac{s_T}{s_L} \sim \frac{A_T}{A_L} => \frac{s_T}{s_L} = \frac{A_T}{A_L}I_0 \end{aligned}$$
(1)

where \(I_0\) is the stretch factor (Driscoll 2008; Bray and Cant 1991). Note that the above relationship is valid under the Klimov-Williams limit (Klimov 1963; Williams 1985), i.e. when all turbulence length scales are larger than \(\delta _L\). In the above expression, the turbulent flame speed \(s_T\) can be evaluated using the integral

$$\begin{aligned} s_T = -\frac{1}{\rho _R Y_{FR} A_0} \int _V \dot{\omega _F} dV \end{aligned}$$
(2)

where \(\rho _R\) and \(Y_{FR}\) are the unburnt mixture density and fuel mass fraction respectively and \(A_0\) is the cross sectional area of the domain. It is convenient to introduce a reaction progress variable c (based for example on normalised fuel mass fraction) which rises montonically from zero in fresh reactants to unity in fully-burned products. The relation between flame area and flame surface density is stated as

$$\begin{aligned} A_T = \int _{-\infty }^{\infty } \varSigma dV \end{aligned}$$
(3)

The flame surface density \(\Sigma\) is important in premixed combustion modelling (Pope 1988; Peters 1999; Candel and Poinsot 1990; Cant et al. 1990), and can be defined as the expected value of the flame surface area per unit volume for an isosurface at \(c=c^{*}\), i.e.

$$\begin{aligned} \Sigma = \overline{\Sigma '} \end{aligned}$$
(4)

where the “fine–grained” flame surface density \(\Sigma '\) can be defined by using the gradient of progress variable (Boger et al. 1998) according to

$$\begin{aligned} \Sigma ' = \frac{\delta A}{\delta V} = |\nabla c|\delta (c-c^*) \end{aligned}$$
(5)

The balance equation for \(\Sigma\) takes the form Pope (1988), Candel and Poinsot (1990)

$$\begin{aligned} \frac{\partial \Sigma }{\partial t} + \frac{\partial }{\partial x_i} (u_i + S_d n_i) \Sigma = \dot{S}\Sigma \end{aligned}$$
(6)

where the flame normal vector \(n_i\) is given by

$$\begin{aligned} n_i = - \frac{\nabla c}{|\nabla c|}, \end{aligned}$$
(7)

and the displacement speed \(S_d\) of the flame is obtained using the expression

$$\begin{aligned} \rho S_{d}\sigma = \dot{\omega } + \frac{\partial }{\partial x_{k}} \left( \rho D\frac{\partial c}{\partial x_{k}} \right) \end{aligned}$$
(8)

where \(\sigma\) is the generalised FSD (Boger et al. 1998) defined as \(\sigma = \overline{|\nabla c|}\). The flame stretch rate \(\dot{S}\) is defined as the fractional rate of increase of flame area

$$\begin{aligned} \dot{S} = \frac{1}{A} \frac{dA}{dt} = a_t + 2S_d \kappa \end{aligned}$$
(9)

where \(a_t\) is the rate of hydrodynamic strain tangential to the flame and \(\kappa\) is the mean curvature of the flame. An expression for \(a_t\) can be stated as

$$\begin{aligned} a_t = (\delta _{ij}-n_in_j)\frac{\partial u_i}{\partial x_j} \end{aligned}$$
(10)

where \(\delta _{ij}\) is the Kronecker delta, and the mean curvature \(\kappa\) is defined as

$$\begin{aligned} \kappa = \frac{1}{2} \frac{\partial n_i}{\partial x_i} \end{aligned}$$
(11)

Flame stretch can have significant effects on the internal structure of the flame (Law 1988). These effects can be accounted for using the stretch factor \(I_0\) (Bray and Cant 1991; Driscoll 2008), defined as the ratio of local instantaneous propagation speed \(s_L^*\) to the unstrained laminar flame speed \(s_L\):

$$\begin{aligned} I_0 = \frac{s_L^*}{s_L} \end{aligned}$$
(12)

The quantity \(I_0\) has been found to be \(\sim 1\) for thermo-diffusively neutral mixtures, i.e. \(\mathrm Le=1\), but the value of \(I_0\) has been found to deviate from unity for non-unity Lewis numbers (Hawkes and Chen 2006; Bradley 1992; Lipatnikov and Chomiak 2002) or for very high values of Karlovitz number (Driscoll 2008). Moreover, thickening of the flame can enhance the flame speed over and above that estimated by change in flame area alone (Attili et al. 2021; Nivarti et al. 2019) leading to values of \(I_0\) greater than unity.

3 DNS Dataset for the Current Study

The simulations were carried out using the well-established in-house DNS code SENGA2 (Jenkins and Cant 1999; Cant 2012). This code solves the Navier–Stokes momentum equations in their compressible form, augmented by conservation equations for mass and energy and by balance equations for the relevant chemical species mass fractions. The spatial discretisation scheme uses 10th order explicit centred finite differences, reducing smoothly to 4th order one-sided differences at non-periodic boundaries. Time-stepping is effected using a 4th-order low–storage explicit Runge–Kutta algorithm with adaptive step-size control (Kennedy and Carpenter 2003). The code is fully parallelised using a domain decomposition technique. Boundary conditions are imposed using the Navier–Stokes Characteristic Boundary Condition (NSCBC) formalism (Poinsot and Lele 1992).

For the purposes of the present study, the chemistry is treated using a single-step Arrhenius formulation tuned to replicate the flame propagation speed \(s_L\) of a stoichiometric methane—air flame, i.e. 39 cm/s, and also to capture the corresponding thermal flame thickness \(\delta _L\) given as \(\delta _L = (T^b - T^u)/(dT/dx)_{max}\), where \(T^b\) and \(T^u\) are the temperature of the burnt and unburnt gas respectively. The density ratio of the burned to unburned gases is \(\sim\) 0.13. The Lewis number of the reacting species is set to unity. It is acknowledged that single—step chemistry may not capture all the details of the flame—turbulence interaction, and this will be investigated in future work using a more detailed chemical reaction mechanism.

The computational domain consists of a cuboid with periodic boundary conditions in the spanwise y and z directions. The streamwise x direction has NSCBC outflow boundary conditions on opposite faces. The thermochemical pressure is set to 1 bar and the reactant temperature is set to 300 K. The dataset created for analysis is based on a pair of statistically planar flames facing each other with fresh reactants between them. The flames are simulated in a cuboidal domain of cross section 5 mm \(\times\) 5 mm. Turbulence of the required intensity and integral length scale is generated using a spectral algorithm (Orszag 1972) initialised with the Bachelor–Townsend spectrum (Batchelor and Townsend 1948) and is imposed on the domain. The turbulence in the unburned reactants is forced linearly (Lundgren 2003) in order to counteract the process of decay and hence to maintain the required properties. A known shortcoming of Lundgren’s method (Lundgren 2003) is that the turbulent length scale changes over time until it reaches a steady value (Klein et al. 2017; Rosales and Meneveau 2005). Klein et al. (2017) attempted to fix this issue by making the forcing term proportional to a high pass filtered value of velocity. However, no such correction has been applied in this work and it is likely that the associated length scales of turbulence change in time. In future, this issue will be addressed..

Within the dataset, both turbulence intensity \(u^\prime\) and integral length scale \(\ell _0\) are varied systematically. For values of \(u^{\prime }/s_L\) = 10, 20 and 30, simulations are carried out with integral length scales corresponding to \(\ell _0/\delta _L = 5.0\), \(\ell _0/\delta _L = 2.0\) and \(\ell _0/\delta _L = 1.25\). For \(u^{\prime }/s_L = 40\) only the case of \(\ell _0/\delta _L = 2.0\) is simulated. The mesh spacing \(\varDelta x\) is varied in each case to match the Kolmogorov scale \(\eta\) and the simulation time was kept at 6 eddy turnover times, i.e. \(t/\tau = 6\) for all cases. A summary of the parameters for each simulation is provided in Table 1.

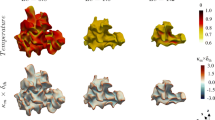
The separation between the flames is varied for each individual case such that the flames do not collide even at the end of the run. The forcing region was kept between the two flames and of the forced region varied between cases since each case had different separation between flames. The width of the forced region was chosen such that it does not interact with the flames during the run time. Figure 1 shows results from the cases with three different \(\ell _0\) values for \(u^{\prime }/s_L = 10\). For the highest \(\ell _0\) value (Fig. 1a), the large scale wrinkling requires larger separation between the two flames whereas for the smaller \(\ell _0\) values (Fig. 1b and c) a smaller separation is sufficient to keep the two flames from interacting.

Table 1 Main parameters of the different cases in the dataset
Full size table
Fig. 1
figure 1

Two dimensional slices of the 3-D snapshots of product mass fraction for cases \(\ell _0/\delta _L = 5.0\), \(\ell _0/\delta _L = 2.0\) and \(\ell _0/\delta _L = 1.25\) (top to bottom) for fixed \(u^{\prime }/s_L = 10\). The separation between the flames is adjusted to keep them from interacting

Full size image

The dataset can be used to analyse the effects of integral length scale \(\ell _0\) while keeping the turbulence intensity \(u^\prime\) fixed. Alternatively, a fixed value of \(\ell _0\) can be chosen and the variation in \(u^\prime\) can be studied. Note that the Kolmogorov scale \(\eta\) also decreases as \(\ell _0\) decreases and/or \(u^\prime\) increases. The data points corresponding to the dataset are presented on a Borghi diagram as shown in Fig. 2. All the cases are either in, or very close to, the thin reaction zones regime. It has been noted that broken reaction zones are not observed even well beyond Ka=100 (Aspden et al. 2019; Song et al. 2021), which was also found to be true for all of the present cases. In all cases, the turbulent flame approached a statistically stationary state, albeit with considerable fluctuations of \(s_T\) about its mean value, as observed in other work (Poludnenko and Oran 2011; Lipatnikov et al. 2015).

Fig. 2
figure 2

Representation of the current DNS dataset on a Borghi diagram

Full size image

4 Results

In this section, the flame properties are presented as functions of the systematic variations in both \(u^{\prime }\) and \(\ell _0\). The results for increasing \(u^{\prime }\) at a fixed value of \(\ell _0\) are found to be consistent with those from the literature (Nivarti and Cant 2017; Lipatnikov and Chomiak 2002). The results for varying \(\ell _0\) at constant \(u^{\prime }\) are presented for analysis, and comparisons are drawn between the known trends for increasing \(u^{\prime }\) versus those observed for varying \(\ell _0\).

Turbulent flame speed and flame area are analysed first, followed by the probability density functions (pdfs) of mean curvature, tangential strain rate and displacement speed. Subsequently, the correlations between strain, curvature, displacement speed and its components are evaluated and presented.

4.1 Turbulent Flame Speed

The turbulent flame speed \(s_T\) and flame area \(A_T\) (for the isosurface at c = 0.8) are evaluated using Eqs. 2 and 3 respectively and are normalised with the unstrained laminar flame speed \(s_L\) and the domain cross—sectional area \(A_L\) for the full dataset. The turbulent flame speed \(s_T\) is plotted against \(u^{\prime }\) (also normalised with \(s_L\)) in Fig. 3 with different lines representing different values of \(\ell _0\). It can be seen that \(s_T\) increases with \(u^{\prime }\) for all values of \(\ell _0\). Furthermore, the values of \(s_T\) are higher for larger values of \(\ell _0\), i.e.

$$\begin{aligned} s_{T, \ell _0/\delta _L = 5.0}> s_{T, \ell _0/\delta _L = 2.0} >s_{T, \ell _0/\delta _L = 1.25} \end{aligned}$$

This behaviour is consistent with previous simulation results for increasing \(u^{\prime }\) (Nivarti and Cant 2017; Lipatnikov and Chomiak 2002) as well as with previous analyses (Peters 1999; Lipatnikov and Chomiak 1999). Note that the values of \(s_T/s_L\) obtained here are similar to those obtained in the constant density flows (for example in Sabelnikov et al. (2019)) as well as in variable density flow (Nivarti and Cant 2017), consistent with the discussion in Lipatnikov et al. (2018).

Fig. 3
figure 3

Turbulent flame speed \(s_T/s_L\) plotted against turbulence intensity \(u^{\prime }/s_L\) for three different values of integral length scale \(\ell _0/\delta _L\) equal to 5.0, 2.0 and 1.25

Full size image

Values of \(s_T/s_L\) are also presented in Table 2 along with the corresponding values of \(A_T/A_L\) and the ratio \(I_0 = (s_T/s_L) / (A_T/A_L)\) (see Eq. 1). There are several important observations to be made from this table. First, the area ratio \(A_T/A_L\) follows the same trend as \(s_T/s_L\) in that values corresponding to \(\ell _0/\delta _L = 5.0\) are higher than those corresponding to \(\ell _0/\delta _L = 2.0\) and \(\ell _0/\delta _L = 1.25\) for each \(u^{\prime }\) value. It can be seen that \(s_T/s_L\) (and also \(A_T/A_L\)) differs by around a factor of two between \(\ell _0/\delta _L = 5.0\) and \(\ell _0/\delta _L = 1.25\). This indicates that the principal factor affecting the turbulent flame speed is the increase of flame surface area, due to either higher turbulence intensity or larger turbulence integral length scale causing increased large-scale flame wrinkling.

Following Refs. (Kulkarni and Bisetti 2021a; Chaudhuri et al. 2012), a power—law fit for the dependence of \(S_T\) on Reynolds number in the form \(S_T \sim \mathrm{Re}^{n}\) was found to yield an exponent \(n \sim 0.4\) which is similar but lower than the findings of Chaudhuri et al. (2012) (\(n \sim 0.5\)) and Kulkarni et al. (2021) (\(n \sim 0.56\)). This could be a result of the differences in flow configuration, fuel type or the fact that the Reynolds numbers used here are lower than in these studies. This merits further investigation using a DNS dataset covering a greater range of Reynolds number than is accessible in the present work.

At the same time, the value of \(I_0\) becomes greater than unity as \(u^{\prime }\) increases for the two cases with larger \(\ell _0\), and especially for the case with the largest value of \(\ell _0/\delta _L = 5.0\). Likewise, the values of \(I_0\) also increase slightly as \(u^{\prime }\) increases for any fixed value of \(\ell _0\). This indicates that factors other than the flame area, such as changes to the internal structure of the local flame sheet due to strain and curvature may affect the observed increase in the turbulent flame speed. However, the values of \(I_0\) remain very close to unity for all the cases and hence require further investigation. An increase in \(I_0\) with Reynolds number was reported by Attili et al. (2021) caused by the thickening of the inner flame layer. In the present study, the values of \(I_0\) for any given \(u^\prime\) do not change significantly as the values of \(\ell _0\) change.

For each value of \(u^{\prime }\), it can be seen from Table 2 (4th column) that the decrease in \(A_T/A_L\) as \(\ell _0\) decreases is monotonic but is not linear. The ratio \((A_T/A_L)/(\ell _0/\delta _L)\) is presented in the rightmost column of the table. This ratio is lowest for the cases with \(\ell _0/\delta _L = 5.0\) and increases for the cases with smaller length scales. This provides an indication that an increasing amount of small-scale turbulence plays a role in increasing the flame surface area, and is more efficient in doing so at lower values of \(\ell _0\).

Table 2 Turbulent flame speed \(s_T\) and flame surface area \(A_T\) (evaluated at \(c = 0.8\)) normalised by unstrained laminar flame speed \(s_L\) and domain cross section area \(A_L\) respectively for all cases
Full size table

The flame surface density \(\Sigma\) conditioned on progress variable c is presented in Fig. 4. Figure 4a shows the plots for fixed \(\ell _0/\delta _L\) = 2.0 and increasing \(u^{\prime }\) while Fig. 4b represents those for a fixed \(u^{\prime }/S_L\) ( = 20) but decreasing \(\ell _0\). The conditional value of \(\Sigma\) decreases as \(u^{\prime }\) increases. This is because even though the flame area increases, the volume corresponding to the wrinkled flame surface also increases. It is interesting to note that the same trend of decreasing \(\Sigma\) is observed also for decreasing \(\ell _0\) at fixed \(u^{\prime }\), and indeed the similarity between Figs. 4a and b is striking. Note that there are no significant changes in the profiles of \(\Sigma\) for \(c > 0.6\) and hence the changes in \(\Sigma\) are mostly restricted to the preheat zone, consistent with the previous findings (Nivarti and Cant 2017).

Fig. 4
figure 4

Flame surface density \(\Sigma\) conditioned on progress variable c for a varying \(u^{\prime }\) at fixed \(\ell _0 =\) 2.0\(\delta _L\) and b varying \(\ell _0\) at fixed \(u^{\prime } =\) 20 \(s_L\)

Full size image

4.2 Curvature and Strain Rate

In this subsection, the pdfs of mean curvature \(\kappa\) and tangential strain rate \(a_t\) are plotted for different values of \(u^{\prime }\) and \(\ell _0\). These pdfs are analysed for the isosurface corresponding to \(c = 0.8\). First, the pdfs of curvature and tangential strain rate are presented in Fig. 5 for varying \(u^{\prime }\) at fixed values of \(\ell _0\). The curvature pdfs are shown in the left column while the tangential strain rate pdfs are shown in the right column. The pdfs corresponding to \(\ell _0/\delta _L\) = 5.0, 2.0 and 1.25 are shown in the top, middle and bottom row respectively.

Looking at the mean curvature pdfs (Fig. 5, left column), as \(u^{\prime }\) is increased from 10 (red line) to 20 (blue line) to 30 (yellow line), the pdfs become wider and their peak value decreases, and this is true for all values of \(\ell _0/\delta _L\). On physical grounds, the increase in the width of the mean curvature pdf is expected since at higher \(u^{\prime }\) the eddies have more energy available to wrinkle the flame surface. Furthermore, at higher \(u^{\prime }\) there is an addition of Kolmogorov—scale eddies since \(\eta _{u^{\prime }/s_l = 10}> ... > \eta _{u^{\prime }/s_L = 30}\). These additional scales lie in the range \(\eta _{u^{\prime }/s_L = 10}>l>\eta _{u^{\prime }/s_L = 20}\) for the \(u^{\prime }/s_L = 20\) case and likewise for \(u^{\prime }/s_L = 30\) case. These additional smaller scales result in higher values of \(\kappa\) (\(\sim 1/R\)) and hence broader pdfs. The behaviour of these pdfs is consistent with the results in a previous analysis by Nivarti and Cant (2017) and for the experimental results for V-flames (Kheirkhah and Gülder 2013). It is also interesting to note that the height and width of the mean curvature pdfs for \(u^{\prime }/s_L = 20\) and 30 are similar to each other, suggesting that there is some tendency towards saturation of flame curvature at higher turbulence intensity.

Fig. 5
figure 5

Pdfs of mean curvature (left column) and strain rate (right column) for different values of \(u^{\prime }/s_L\) and fixed \(\ell _0/\delta _L = 5.0\) (top row), 2.0 (middle row) and 1.25 (bottom row)

Full size image

For the tangential strain rate pdfs (Fig. 5, right column) the height of the peaks decreases and their width increases as \(u^{\prime }/s_L\) increases, for all values of \(\ell _0/\delta _L\). The effect is most pronounced for the highest \(u^{\prime }\) cases for which the pdf becomes significantly broader which was also observed from the experimental results of spherically expanding flames (Liu et al. 2021). The peak of the pdf for all cases is observed at a positive value of \(a_t\), and this value becomes more positive as \(u^{\prime }/s_L\) increases which is consistent with previous DNS findings (Nivarti and Cant 2017). Again, these effects result from greater energy within the eddies at higher \(u^{\prime }/s_L\). The additional smaller scales strain the flame surfaces more effectively due to their higher velocity gradients. Note that the flame thickness \(\delta _L\) and flame time \(\tau _c (=\delta _L / L)\) are used to normalise \(\kappa\) and \(a_t\) respectively. This is done so that the normalisation still shows the differences between the results across the dataset, since \(\delta _L\) and \(\tau _c\) are constant for all cases presented here. It is expected that other scales are better suited for such normalisation, and to justify the above phenomenological explanations. These will be explored in future work.

Results showing the variation in the pdfs of mean curvature \(\kappa\) and tangential strain rate \(a_t\) with changes in \(\ell _0/\delta _L\) for fixed values of \(u^{\prime }/s_L\) are presented in Fig. 6. As in Fig. 5 the mean curvature pdfs are shown in the left column while the tangential strain rate pdfs are shown in the right column. The pdfs corresponding to \(\ell _0/\delta _L\) = 5.0, 2.0 and 1.25 are represented by blue, red and yellow coloured lines respectively (see legend). The values of \(u^{\prime }/s_L\) are 10 (top row), 20 (middle row) and 30 (bottom row).

In each plot, the available mean kinetic energy of the turbulence is the same and hence changes in the pdf are due only to the different length scales of turbulence. It can be seen by comparison with Fig. 5 that the trends observed for decreasing \(\ell _0/\delta _L\) are similar to those for increasing \(u^{\prime }/s_L\). The pdf of \(\kappa\) (left column) for all values of \(u^{\prime }\) has the greatest peak value but smallest overall width for the highest value of \(\ell _0/\delta _L = 5.0\) (blue line). The pdfs become lower and wider as the value of \(\ell _0/\delta _L\) decreases to 2.0 (red line) and to 1.25 (yellow line).

As the value of \(\ell _0/\delta _L\) decreases, the corresponding Kolmogorov length scale \(\eta\) also decreases, i.e. \(\eta _{\ell _0/\delta _L = 5.0}> ... > \eta _{\ell _0/\delta _L = 1.25}\). This introduces an additional range of smaller length scales between \(\eta _{\ell _0/\delta _L} = 5.0>l>\eta _{\ell _0/\delta _L} = 2.0\) for the \(\ell _0/\delta _L = 2.0\) case. These additional small scales for each case correspond to higher \(\kappa\) (\(\sim 1/R\)) and result in higher probability of high curvature events as \(\ell _0\) decreases. Hence, the width of the mean curvature pdfs increases. Likewise, since the cases at lower \(\ell _0\) contain fewer large scale eddies, the probability of low curvature events decreases, and thus the peak height of the pdf decreases. The height and width of the pdfs for \(\ell _0/\delta _L = 2.0\) and \(\ell _0/\delta _L = 1.25\) remains roughly the same, again suggesting a tendency towards saturation in curvature for values of \(\ell _0/\delta _L\) less than about 2.0. Note that the peak of the \(\kappa\) pdfs occurs close to zero curvature for all values of \(\ell _0\).

Turning to the changes in the pdfs of tangential strain rate for different values of \(\ell _0/\delta _L\) (Fig. 6, right column), for all values of \(u^{\prime }\) the peak value of each pdf is again the highest for the largest integral length scale, i.e. \(\ell _0/\delta _L = 5.0\). The pdfs become lower and their width increases as \(\ell _0/\delta _L\) decreases, but the mean tangential strain rate remains positive for all cases. Also, the value of \(a_t\) at the peak becomes increasingly positive with decreasing \(\ell _0/\delta _L\). Again, the smaller values of Kolmogorov scale \(\eta\) for smaller values of \(\ell _0/\delta _L\) result in greater positive straining of the flame due to their large velocity gradients. Once again, on comparing Figs. 5 and 6 it can be seen that for both \(\kappa\) and \(a_t\) there is considerable similarity in the changes observed in the pdfs in response to either increasing \(u^{\prime }/s_L\) or decreasing \(\ell _0/\delta _L\). As before, proper scaling will be needed in future for greater clarity on the above explanations.

Fig. 6
figure 6

Pdfs of mean curvature (left column) and strain rate (right column) for different values of \(\ell _0/\delta _L\) and fixed \(u^{\prime }/s_L = 10\) (top row), 20 (middle row) and 30 (bottom row)

Full size image

The correlation between mean curvature \(\kappa\) and tangential strain rate \(a_t\) can be observed from the joint pdfs of these quantities in the form of iso-probability curves shown in Fig. 7. The subfigures on the top row show the correlation between \(\kappa\) and \(a_t\) for \(u^{\prime }/s_L =\) 10, the middle row shows \(u^{\prime }/s_L =\) 20 and bottom row shows \(u^{\prime }/s_L =\) 30. The value of \(\ell _0/\delta _L\) decreases from 5.0 to 2.0 and then to 1.25 in the left, middle and right subfigures respectively in each row.

Fig. 7
figure 7

joint pdfs of mean curvature and tangential strain rate for different values of \(\ell _0/\delta _L\) (left to right) and for different values of \(u^{\prime }/s_L\) (top to bottom)

Full size image

In all cases, a negative correlation between \(\kappa\) and \(a_t\) is observed. Similar plots have been presented in the past for increasing \(u^{\prime }\) (and fixed \(\ell _0\)) (Nivarti and Cant 2019), and these showed a negative correlation between \(\kappa\) and \(a_t\) which weakened as \(u^{\prime }\) was increased. This is a consequence of greater wrinkling of the flame due to higher energy in all scales of turbulent eddies. The current results also show the same trend with \(u^{\prime }\) at fixed \(\ell _0\) (Fig. 7, top to bottom in any column). By contrast, the strength of the \(\kappa\)–\(a_t\) correlation tends to increase slightly at each fixed value of \(u^{\prime }\) as \(\ell _0/\delta _L\) is decreased. This is consistent with the broadening of the strain rate pdf (see Fig 6 right column) at fixed \(u^{\prime }\), which indicates that the available kinetic energy (for a fixed \(u^{\prime }\)) is spread over a greater range of length scales giving a better match with the length scales of flame curvature.

4.3 Displacement Speed Statistics

It is interesting to consider the pdf of the displacement speed \(S_d\) and its dependence on flame stretch quantities. The pdfs of \(S_d\) are presented in Fig. 8a for different values of \(u^{\prime }/s_L\) at fixed \(\ell _0/\delta _L = 2.0\), and in Fig. 8b for different values of \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L\) = 20.

Fig. 8
figure 8

Probability density functions of displacement speed \(S_d\) for a different values of \(u^{\prime }\) at fixed \(\ell _0/\delta _L = 2.0\) and b different values of \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L = 20\)

Full size image

It can be seen that the displacement speed pdfs exhibit similar trends to those observed for the mean curvature and tangential strain rate pdfs. For increasing values of \(u^{\prime }/s_L\) at fixed \(\ell _0/\delta _L\), the pdfs become shorter and wider, and the same pattern is observed for decreasing \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L\). In all cases, the mean value of \(S_d\) was found to be \(\sim \rho s_L/\rho _R\) where \(\rho _R\) is the reactant density.

The relatively strong correlation between \(S_d\) and flame stretch, i.e. both strain and curvature, ensures that the pdfs of \(S_d\) (Fig. 8) also become shorter and broader in a similar manner to the of \(\kappa\) and \(a_t\) pdfs with either increasing \(u^{\prime }\) (Fig. 5) or decreasing \(\ell _0\) (Fig. 6).

Joint pdfs of displacement speed \(S_d\) and mean curvature \(\kappa\) in the form of iso-probability curves are shown in Fig. 9a (top row) while those for displacement speed and tangential strain rate \(a_t\) are shown in Fig. 9a (bottom row). For both rows, the value of \(\ell _0/\delta _L = 2.0\) is fixed while \(u^{\prime }/s_L\) increases from 10 (left) to 20 (middle) to 30 (right). A distinct negative correlation can be seen between \(S_d\) and \(\kappa\) (top row). The negative correlation is stronger for positive curvature than for negative curvature, as observed in previous studies (Chakraborty and Cant 2005b; Nivarti and Cant 2019) and explained in terms of the combined effects of both curvature and strain rate on the different components of displacements speed. As \(u^{\prime }\) increases, the strength of the correlation between \(S_d\) and \(\kappa\) remains broadly unchanged. There is a positive correlation between \(S_d\) and \(a_t\) (bottom row), and this is consistent with the negative correlation observed between \(\kappa\) and \(a_t\) (see Fig. 7). As \(u^{\prime }\) increases the underlying positive correlation between \(S_d\) and \(a_t\) weakens somewhat, and there is a tendency to favour \(S_d/s_L\) close to unity at low mean curvature for a broad range of strain rates, again as previously observed (Chakraborty and Cant 2005a; Nivarti and Cant 2019).

Further joint pdfs of \(S_d\) and \(\kappa\) are shown in Fig. 9b (top row) while joint pdfs of \(S_d\) and \(a_t\) are shown in Fig. 9b (bottom row), but this time the value of \(u^{\prime }/s_L = 20\) is held fixed while \(\ell _0/\delta _L\) is varied from 5.0 (left) to 2.0 (middle) to 1.25 (right). Comparison of Fig. 9a and b shows that the trends for the \(S_d\)–\(\kappa\) joint pdfs with decreasing \(\ell _0\) are similar to those observed for increasing \(u^{\prime }\). This is less apparent for the \(S_d\)-\(a_t\) joint pdfs (bottom row). Here the tendency for \(S_d/s_L\) to cluster close to unity weakens as \(\ell _0\) decreases, due to the lower probability of finding low mean curvatures (see Fig. 5 left column).

Fig. 9
figure 9

Joint pdfs of displacement speed \(S_d\) with \(\kappa\) and \(a_t\) for a different values of \(u^{\prime }\) at fixed \(\ell _0/\delta _L = 2.0\) and b different values of \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L = 20\)

Full size image

The correlation coefficients corresponding to the joint pdfs presented above are summarised in Tables 3 and 4. First, correlation coefficients for increasing \(u^{\prime }\) at a fixed \(\ell _0/\delta _L = 2.0\) are shown in Table 3. Consistent with Fig. 7, the correlation coefficient for the \(\kappa\)-\(a_t\) correlation becomes less negative, i.e. the correlation becomes weaker as the turbulence intensity increases and the same is true for the \(S_d\)-\(a_t\) correlation, while the \(S_d\)-\(\kappa\) correlation coefficient does not change much. Similar results were found for all values of \(\ell _0/\delta _L\).

Table 3 Correlation coefficients over a range of \(u^{\prime }/s_L\) at fixed \(\ell _0/\delta _L = 2.0\)
Full size table

The corresponding correlation coefficients for a fixed value of \(u^{\prime }/s_L\) at different values of \(\ell _0/\delta _L\) are shown in Table 4. The \(S_d\)–\(a_t\) correlation coefficient is positive and increases slightly with decreasing \(\ell _0/\delta _L\). The \(S_d\)–\(\kappa\) correlation coefficient, however, is negative and broadly constant for these cases.

Table 4 Correlation coefficients over a range of \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L = 20\)
Full size table

The different components of displacement speed, i.e. the reaction component \(S_r\), normal diffusion component \(S_n\) and tangential diffusion component \(S_t\) are defined by

$$\begin{aligned} S_r = \frac{\dot{\omega }}{\rho \sigma }; \quad S_n = -\frac{n_{k}}{\rho \sigma } \frac{\partial }{\partial x_{k}}(\rho D\sigma ); \quad S_t = -2D\kappa \end{aligned}$$
(13)

The joint pdfs for the reaction and normal diffusion components of \(S_d\) with \(\kappa\) and \(a_t\) are presented in Fig. 10 for fixed \(\ell _0\) and varying \(u^{\prime }\). The first row shows the joint pdfs of the normal diffusion component \(S_n\) with \(\kappa\) while the second row shows the reaction component \(S_r\) with \(\kappa\). Similarly, the third row shows \(S_n\) with \(a_t\) while the fourth row shows \(S_r\) with \(a_t\). The left, middle and right columns show the joint pdfs for u\(^\prime /\)s\(_L\) = 10, 20 and 30 respectively. Joint pdfs are not shown for the tangential component \(S_t\) since this component is deterministically related to \(\kappa\) (see eqn. 13).

Fig. 10
figure 10

Joint pdfs of different components of the displacement speed with \(\kappa\) and \(a_t\) for different values of \(u^{\prime }/s_L\) at fixed \(\ell _0/\delta _L = 2.0\)

Full size image

The relevant correlation coefficients are presented in Table 5 for a fixed value of \(\ell _0/\delta _L = 2.0\) and increasing \(u^{\prime }/s_L\). The correlation between \(S_t\) and \(a_t\) (fourth column) is of the same value but opposite sign to that between \(\kappa\) and \(a_t\) (see Table 4) since \(S_t\) is directly proportional to negative \(\kappa\). This also results in a correlation coefficient between \(S_t\) and \(\kappa\) equal to negative unity (right column). The normal component of displacement speed \(S_n\) shows a very weak correlation with \(a_t\) (third column) but a negative correlation with \(\kappa\) (second column from the right). On the other hand, the reaction component \(S_r\) shows a positive correlation with \(a_t\) (second column) and a weak correlation with \(\kappa\) (third column from the right). These results are consistent with the findings of several previous studies (Chakraborty and Cant 2005a, b; Nivarti and Cant 2019).

Table 5 Correlation coefficients for the correlations between the reaction (\(S_r\)), normal diffusion (\(S_n\)) and tangential diffusion (\(S_t\)) components of displacement speed with mean curvature \(\kappa\) and tangential strain rate \(a_t\) over a range of \(u^{\prime }/s_L\) at fixed \(\ell _0/\delta _L = 2.0\)
Full size table

Corresponding joint pdfs for the reaction and normal diffusion components of \(S_d\) with \(\kappa\) and \(a_t\) are presented in Fig. 11 for fixed \(u^{\prime }/s_L = 20\) and varying \(\ell _0/\delta _L\). Again the first row shows normal diffusion component \(S_n\) with \(\kappa\) while the second row \(S_r\) with \(\kappa\). The third row shows \(S_n\) with \(a_t\) while the fourth row shows \(S_r\) with \(a_t\). The left, middle and right columns show the joint pdfs for \(\ell _0/\delta _L\) = 5.0, 2.0 and 1.25 respectively. Comparison of Figs. 11 with 10 indicates a strong similarity between the joint pdfs for \(S_n\) and \(S_r\) with \(\kappa\) (top two rows in each Figure), as well as similar trends for the plots of \(S_n\) and \(S_r\) with \(a_t\) (bottom two rows in each Figure).

The correlation coefficients for the components of \(S_r\), \(S_n\) and \(S_t\) with mean curvature and tangential strain rate are provided in Table 6 for fixed \(u^{\prime }/s_L = 20\) and a range of values of \(\ell _0/\delta _L\).

Fig. 11
figure 11

Joint pdfs of different components of the displacement speed with \(\kappa\) and \(a_t\) for different values of \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L = 20\)

Full size image

Again, the correlation between \(S_t\) and \(a_t\) (fourth column) is the same in value but opposite in sign to that of \(\kappa\) and \(a_t\) (see Fig. 5). There is a perfect negative correlation between \(S_t\) and \(\kappa\) (right column), i.e. the correlation coefficient is equal to negative unity. As in the previous cases, \(S_n\) has a weak correlation with \(a_t\) (third column) while \(S_r\) has a positive correlation with \(a_t\) (second column). The correlation between \(S_n\) and \(\kappa\) is negative (second column from the right) while the correlation between \(S_r\) and \(\kappa\) is weakly positive (third column from the right).

Table 6 Correlation coefficients for the correlations between the reaction (\(S_r\)), normal diffusion (\(S_n\)) and tangential diffusion (\(S_t\)) components of displacement speed with mean curvature \(\kappa\) and tangential strain rate \(a_t\) over a range of \(\ell _0/\delta _L\) at fixed \(u^{\prime }/s_L = 20\)
Full size table

For the displacement speed components, the trends with decreasing \(\ell _0\) at fixed \(u^{\prime }\) are broadly similar to those observed for increasing \(u^{\prime }\) at fixed \(\ell _0\). The correlation between \(S_n\) and \(a_t\) remains weak for all cases, and this is true also for the correlation between \(S_r\) and \(\kappa\). The negative correlation between \(S_n\) and \(\kappa\) becomes stronger for variations in either \(u^{\prime }\) or \(\ell _0\). The correlation between \(S_r\) and \(a_t\) is positive and weakens with increasing \(u^{\prime }\), whereas for decreasing \(\ell _0\) the positive correlation strengthens slightly, consistent with the trends observed for the correlation between \(\kappa\) and \(a_t\). The correlation between \(S_t\) and \(a_t\) in all cases simply reflects the correlation between \(\kappa\) and \(a_t\) and the deterministic dependence of \(S_t\) on \(\kappa\).

5 Conclusions

A set of Direct Numerical Simulations has been carried out in which the integral length scale \(\ell _0/\delta _L\) as well as the turbulence intensity \(u^{\prime }/s_L\) is varied in a systematic manner while keeping all other parameters constant. A twin flame configuration has been used in which the separation between the flames is kept sufficiently large so that the flames do not collide. Linear forcing of the turbulence has been applied between the two flames so that the turbulence does not decay rapidly as the flames propagate towards each other.

The turbulent flame speed \(s_T\) and flame area \(A_T\) have been evaluated for all the cases. The turbulent flame speed is found to be greatest for the highest value of \(\ell _0\) at a fixed value of \(u^{\prime }\), consistent with previous predictions (Peters 1999; Damköhler 1940) and DNS data (Nivarti et al. 2019). The ratio of \(s_T/s_L\) to \(A_T/A_L\) is found to be close to unity but increases slightly as \(u^{\prime }/s_L\) increases for fixed values of the length scale ratio \(\ell _0/\delta _L\). The flame surface density \(\varSigma\) has been evaluated for variations in both \(u^{\prime }\) and \(\ell _0\). Changes observed for decreasing values of \(\ell _0\) at fixed \(u^{\prime }\) are found to be remarkably similar to those observed for increasing values of \(u^{\prime }\) at fixed \(\ell _0\).

The probability density functions (pdfs) of the mean flame curvature and tangential strain rate have been analysed, again with the focus on varying \(\ell _0/\delta _L\) for fixed \(u^{\prime }/s_L\). It has been found that as \(\ell _0\) decreases, the pdfs of both mean curvature and tangential strain rate become broader and flatter. The peak of the curvature pdfs shifts to a slightly more negative value whereas that of the strain rate shifts to a more positive value.

Analysis the displacement speed \(S_d\) indicates similar trends. The pdfs of \(S_d\) become broader and flatter with decreasing \(\ell _0\) at fixed \(u^{\prime }\), just as they do with increasing \(u^{\prime }\) at fixed \(\ell _0\). Correlations between displacement speed and mean curvature, as well as those between displacement speed and tangential strain rate, have been investigated using joint pdfs and correlation coefficients. The corresponding correlations for the reaction, normal diffusion and tangential diffusion components of displacement speed have been investigated also. The results for increasing \(u^{\prime }\) at fixed \(\ell _0\) are consistent with previous observations, and the variations observed for decreasing \(\ell _0\) at fixed \(u^{\prime }\) are found to be broadly similar.

Future work will focus on extending the range of values of \(\ell _0/\delta _L\) that can be explored. This will require larger computational domains and correspondingly larger computational resources. Proper scaling for the quantities presented in this paper and their dependence on the Reynolds number will be explored. It will also be necessary also to extend the study to incorporate any effects of chemistry. More detailed investigation of the physics of small-scale turbulence-flame interactions will be carried out, and the implications for modelling will be explored.