Effects of Body Forces on the Statistics of Flame Surface Density and Its Evolution in Statistically Planar Turbulent Premixed Flames

Abstract

Body forces such as buoyancy and externally imposed pressure gradients are expected to have a strong influence on turbulent premixed combustion due to the considerable changes in density between the unburned and fully burned gases. The present work utilises Direct Numerical Simulation data of three-dimensional statistically planar turbulent premixed flames to study the influence of body forces on the statistical behaviour of the flame surface density (FSD) and its evolution within the flame brush. The analysis has been carried out for different turbulence intensities and normalised body force values (i.e., Froude numbers). A positive value of the body force signifies an unstable density stratification (i.e., body force is directed from the heavier unburned gas to the lighter burned gas) and vice versa. It is found that for a given set of turbulence parameters, flame wrinkling increases with an increase in body force magnitude in the unstable configuration. Furthermore, higher magnitudes of body force in the unstable density stratification configuration promote a gradient type transport of turbulent scalar and FSD fluxes, and this tendency weakens in the stable density stratification configuration where a counter-gradient type transport is promoted. The statistical behaviours of the different terms in the FSD transport equation and their closures in the context of Reynolds Averaged Navier–Stokes simulations have been analysed in detail. It has been demonstrated that the effects of body force on the FSD and the terms of its transport equation weakens with increasing turbulence intensity as a result of the diminishing relative strength of body force in comparison to the inertial force. The predictions of the existing models have been assessed with respect to the corresponding terms extracted from the explicitly averaged DNS data, and based on this evaluation, suitable modifications have been made to the existing models to incorporate the effects of body force (or Froude number).

1 Introduction

In many practical applications, turbulent premixed flames propagate within ducts, where the flame is subjected to external pressure gradients and body forces (e.g., gravity). As a considerable density change takes place between unburned and burned gases, buoyancy is expected to play a significant role in premixed turbulent flames. Therefore, external pressure gradients and buoyancy can have a significant impact on the various characteristics such as flame wrinkling and flame normal acceleration in turbulent premixed flames. Chomiak and Nisbet (1995) analysed the pressure gradient-density interactions in turbulent premixed flames and have proposed closures which incorporate these effects into the framework of $k - \epsilon$ model. It was indeed demonstrated by Veynante and Poinsot (1997) using two-dimensional direct numerical simulation (DNS) data that external pressure gradients and buoyancy can considerably affect the statistical behaviours of turbulent scalar flux and flame wrinkling in turbulent premixed combustion. Thus, it is expected that buoyancy and externally imposed pressure gradients will affect the statistical behaviour of the flame surface density (FSD), which provides the measure of the flame surface area to volume ratio (Candel and Poinsot 1990; Pope 1988), and is often used for the closure of the mean chemical reaction rate in turbulent premixed combustion (Poinsot and Veynante 2001). However, the effects of body force on the statistical behaviour of the FSD and its evolution have not been analysed in the existing literature, and this paper addresses this problem by using a three-dimensional direct numerical simulation (DNS) database of statistically planar turbulent premixed flames subjected to different strengths of body forces.

The fine-grained FSD is defined as $\Sigma^{\prime } = \overline{\left| {\nabla c} \right|\updelta (c - c^{*})}$ (Pope 1988) where $c^{*}$ is the value of the reaction progress variable $c$ that is used to denote the location of the flame. In order to eliminate the dependence of the FSD statistics on the choice of $c^{*}$, a generalised FSD is defined as ${\Sigma }_{gen} = \overline{{\left| {\nabla c} \right|}}$ (Boger et al. 1998), where the overbar refers to a Reynolds averaging or LES filtering operation, whichever is appropriate. The FSD can either be modelled using an algebraic expression (Boger et al. 1998; Cant and Bray 1988; Charlette et al. 2002; Knikker et al. 2002; Fureby 2005; Chakraborty and Klein 2008a; Ma et al. 2013; Keppeler et al. 2014; Klein et al. 2016) or modelled by solving a transport equation (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Veynante et al. 1996; Chakraborty and Cant, 2009a, 2011, 2013; Sellmann et al. 2017; Hawkes and Cant 2000; Hernandez-Perez et al. 2011; Reddy and Abraham 2012; Ma et al. 2014) alongside the other conservation equations. The latter approach is preferred in unsteady reacting flows where the production and destruction rates of ${\Sigma }_{gen}$ are not necessarily in equilibrium. Although this lack of equilibrium can be addressed by dynamic FSD models in the context of LES (Knikker et al. 2002), such an option does not exist for RANS and thus the transport equation based FSD closure plays an important role in RANS. Modelling of the various terms in the transport equation for FSD have been addressed in detail in several previous studies for RANS (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Veynante et al. 1996; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017) and LES (Hawkes and Cant 2000; Chakraborty and Cant 2007, 2009a; Hernandez-Perez et al. 2011; Reddy and Abraham 2012; Ma et al. 2014; Katragadda et al. 2011, 2014) but all of these analyses have been conducted in the absence of external pressure gradients and body forces. In this study a three-dimensional DNS database involving a number of statistically planar turbulent premixed flames subjected to different values of unburned gas turbulence intensity $u^{{\prime }} /S_{L}$ (where $u^{{\prime }}$ is root-mean-square (rms) value of turbulent velocity fluctuation) and Froude number (i.e., a measure of inertial force to body force ratio) have been conducted. In this respect, the main objectives of the present study are as follows:

• 1. To investigate the effects of body force on flame-turbulence interaction and the statistical behaviour of the FSD transport for turbulent premixed flames.

• 2. To assess the performances of the existing closure models for the different terms of the FSD transport equation and propose suitable modifications, wherever necessary, to capture the effects of the body force.

The remainder of this paper is organised as follows. The next section describes the essential mathematical background which is followed by the discussion of the numerical implementation. The results are subsequently presented and discussed. The final section summarises the main findings and the conclusions that are drawn from the present study.

2 Mathematical Background

In the present analysis, DNS of turbulent premixed combustion has been carried out in three dimensions with simple chemistry in the interest of a detailed parametric analysis because detailed chemistry simulations are unsuitable due to its expensive computational requirements. Hence, three-dimensional DNS with a single step Arrhenius type irreversible chemical reaction has been used in the present study. The reaction progress variable $c$ is used to represent the species field and it is defined in terms of a suitable product mass fraction $Y_{P}$ according to $c = \left( {Y_{P} - Y_{P0} } \right)/\left( {Y_{P\infty } - Y_{P0} } \right)$, where $0$ and $\infty$ refer to the unburned and fully burned gases, respectively. Under adiabatic conditions, in the case of flames with unity Lewis number, the reaction progress variable $c$ is identical to the non-dimensional temperature $T = \left( {\hat{T} - T_{0} } \right)/\left( {T_{ad} - T_{0} } \right)$ (Chakraborty and Cant 2011), where $\hat{T}$ is the instantaneous dimensional temperature, $T_{0}$ is the temperature of the unburned gas and $T_{ad}$ is the adiabatic flame temperature. Under the action of the body force, the momentum conservation equation in the $i{th}$ direction takes the following form:

$$\frac{{\partial \left( {\rho u_{i} } \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} u_{j} } \right)}}{{\partial x_{j} }} = - \frac{\partial p}{{\partial x_{i} }} + S_{i} + \frac{{\partial \tau_{ij} }}{{\partial x_{j} }}$$

(1)

where $u_{i}$ is the ith component of fluid velocity, $p$ is the pressure, ${\uptau }_{ij}$ is the component of shear stress tensor and $S_{i} = {\uprho \Gamma }_{i}$ is the source/sink term in the ith direction due to body force. The source term is assumed to take non-zero values only in the $x_{1}$-direction, which is aligned with the mean direction of flame propagation. Thus, $S_{1}$ is expressed as $S_{1} = {\uprho \Gamma } = \rho g^{*} S_{L}^{2} /\delta_{Z}$ where $\updelta _{Z} = \upalpha _{T0} /S_{L}$ is the Zel’dovich flame thickness, $S_{L}$ is the unstrained laminar burning velocity, $\upalpha _{T0}$ is the thermal diffusivity in the unburned gas, and $g^{*}$ stands for the inverse of Froude number-squared (i.e., $g^{*} = {\Gamma \delta }_{Z} /S_{L}^{2} = Fr^{ - 2}$). A positive (negative) value of $g^{*}$ indicates an externally imposed flow acceleration (deceleration). Moreover, a positive (negative) value of $g^{*}$ is representative of an externally imposed adverse (favourable) pressure gradient. A positive value of $g^{*}$ also represents an unstable configuration where the heavier cold unburned reactants sit on top of the lighter hot burned products whereas a negative $g^{*}$ value is indicative of a stable configuration where the heavier cold unburned reactants sit underneath the lighter hot burned products. Considering an atmospheric stoichiometric CH₄/air flame, a value of $|g^{*} | = 3.12$ corresponds to a pressure gradient magnitude of $2000\,{\text{Pa/m}}$, which is consistent with the experimental parameters used by Shepherd et al. (1982). It is important to note that the buoyancy effects are usually negligible in turbulent premixed flames, except for large fires/explosions, but the methodology adopted in this paper and by Veynante and Poinsot (1997) provides a convenient numerical tool to analyse the effects of imposed pressure gradients. The $g^{*}$ values investigated in this study are chosen such that they induce pressure gradients similar to the experimental analysis by Shepherd et al. (1982), and these values are consistent with the values previously considered by Veynante and Poinsot (1997).

The transport equation of the reaction progress variable $c$ is given by:

$$\frac{{\partial \left( {\overline{\rho }\tilde{c}} \right)}}{{\partial {\text{t}}}} + \frac{{\partial \left( {\overline{\rho }\tilde{c}\widetilde{{u_{j} }}} \right)}}{{\partial {\text{x}}_{{\text{j}}} }} = \overline{{\frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{\partial c}{{\partial x_{j} }}} \right)}} + \overline{{\dot{w}}} - \frac{{\partial \left( {\overline{{\rho u_{j}^{\prime \prime } c^{\prime \prime } }} } \right)}}{{\partial {\text{x}}_{{\text{j}}} }}$$

(2)

where $\dot{w}$ and $D$ are the reaction rate and mass diffusivity of $c$, respectively. Here $\tilde{q} = \overline{\rho q} /\overline{\rho }$ and $q^{{\prime \prime }} = q - \tilde{q}$ are the Favre-average and Favre fluctuations of a general variable $q$, respectively. The quantity $\overline{{\rho u_{j}^{{\prime \prime }} c^{{\prime \prime }} }}$ is the turbulent scalar flux and needs closure, and interested readers are referred to Veynante and Poinsot (1997) for further discussion regarding the effects of pressure gradient on the modelling of turbulent scalar flux $\overline{{\rho u_{j}^{{\prime \prime }} c^{{\prime \prime }} }}$. The first and second terms on the right-hand side can be modelled in the following manner (Boger et al. 1998; Chakraborty and Cant 2007, 2011; Hawkes and Cant 2000):

$$\overline{{\frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{\partial c}{{\partial x_{j} }}} \right)}} + \overline{{\dot{w}}} = \overline{{\left( {\rho S_{d} } \right)}}_{s} {\Sigma }_{{{\text{gen}}}}$$

(3)

where $S_{d} = \left( {1/\left| {\nabla c} \right|} \right)\left( {Dc/Dt} \right)$ is the displacement speed, which signifies the speed with which the flame moves normal to itself with respect to the initially coincident material surface. In the context of RANS, the transport equation for the generalised FSD is given as (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Veynante et al. 1996; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Katragadda et al. 2011):

$$\begin{aligned} & \partial {\Sigma }_{gen} /\partial t + \partial \left( {\tilde{u}_{j} {\Sigma }_{gen} } \right)/\partial x_{j} = \underbrace {{ - \partial \left\{ {\left[ {\overline{{\left( {u_{k} } \right)_{s} }} - \tilde{u}_{k} } \right]{\Sigma }_{gen} } \right\}/\partial x_{k} }}_{{T_{1} - turbulent\;transport}} \\ & \quad + \underbrace {{\overline{{\left( {\left( {\delta_{ij} - N_{i} N_{j} } \right)\partial u_{i} /\partial x_{j} } \right)_{s} }} {\Sigma }_{gen} }}_{{T_{2} - strain\;rate}} \underbrace {{ - \partial \left[ {\overline{{\left( {S_{d} N_{k} } \right)_{s} }} {\Sigma }_{gen} } \right]/\partial x_{k} }}_{{T_{3} - propagation}} + \underbrace {{\overline{{\left( {S_{d} \partial N_{i} /\partial x_{i} } \right)_{s} }} {\Sigma }_{gen} }}_{{T_{4} - curvature}} \\ \end{aligned}$$

(4)

where $\vec{N} = - \nabla c/\left| {\nabla c} \right|$ is the local flame normal vector, $\overline{\left( Q \right)}_{s}$ is the surface average of a general quantity $Q$ given by $\overline{\left( Q \right)}_{s} = \overline{{Q\left| {\nabla c} \right|}} /\overline{{\left| {\nabla c} \right|}}$. The two terms on the left-hand side of Eq. 4 are the transient and mean advection terms, respectively, whereas the four terms on the right-hand side are referred to as the turbulent transport term $T_{1}$, tangential strain rate term $T_{2}$, propagation term $T_{3}$ and curvature term $T_{4}$, respectively. The terms $T_{1} ,T_{2} ,T_{3}$ and $T_{4}$ are unclosed and need modelling. The performances of the existing closures of $T_{1} ,T_{2} ,T_{3}$ and $T_{4}$ will be assessed with respect to the corresponding terms extracted from DNS data in Sect. 4.

3 Numerical Implementation

A well-known compressible DNS code SENGA+ (Jenkins and Cant 1999) is used to generate the database in the present study. In SENGA+, all the spatial derivates for the internal grid points are evaluated using a 10th order central difference scheme and the order of accuracy gradually drops to a one-sided 2nd order scheme at the non-periodic boundaries. The time advancement has been carried out using a low-storage 3rd order Runge–Kutta scheme (Wray 1990). The Lewis number of all species are considered to be unity and standard values are considered for the Prandtl number $Pr$ ($Pr = 0.7)$ and Zel’dovich number $\upbeta = T_{ac} \left( {T_{ad} - T_{0} } \right)/T_{ad}^{2}$ $\left( {\upbeta = 6.0} \right)$, where $T_{ac}$ is the activation temperature. The heat release parameter $\uptau = \left( {T_{ad} - T_{0} } \right)/T_{0}$ is considered to be $4.5$. These values of $\beta$ and $\tau$ are representative of the stoichiometric methane-air flames preheated to $T_{0}$ = 415 K. The simulations have been carried out on a rectangular domain of size $70.2\updelta _{{\text{Z}}} \times 35.1\updelta _{{\text{Z}}} \times 35.1\updelta _{{\text{Z}}}$, which is discretised by a grid size of 400 × 200 × 200, ensuring that the grid spacing remains smaller than the Kolmogorov length scale and 10 grid points are accommodated within the thermal flame thickness $\delta_{th} = \left( {T_{ad} - T_{0} } \right)/\max \left| {\nabla \hat{T}} \right|_{L}$. The boundaries in the direction of mean flame propagation (i.e., $x_{1}$-direction) are taken to be partially non-reflecting and the boundaries in the transverse directions are taken to be periodic. The boundary conditions are specified using the Navier–Stokes Characteristic Boundary Conditions (NSCBC) technique (Poinsot and Lele 1992). A divergence free, homogeneous, isotropic turbulence field generated using the pseudo-spectral method of Rogallo (1981) according to a Batchelor-Townsend kinetic energy spectrum (Batchelor and Townsend 1948) is used to initialise the turbulent velocity field. The flame and reacting scalar fields have been initialised by steady-state one-dimensional unstretched laminar premixed flame solution. The initial values of normalised root-mean-square turbulent velocity fluctuation $u^{{\prime }} /S_{L}$, integral length scale to the flame thickness ratio $l_{T} /\delta_{th}$ ($l_{T} /\delta_{Z}$), Damköhler number $Da = l_{T} S_{L} /u^{{\prime }} \delta_{th}$ ($Da_{Z} = l_{T} S_{L} /u^{{\prime }} \delta_{Z}$) and Karlovitz number $Ka = \left( {u^{{\prime }} /S_{L} } \right)^{1.5} \left( {l_{T} /\delta_{th} } \right)^{ - 0.5}$ ($Ka_{Z} = \left( {u^{{\prime }} /S_{L} } \right)^{1.5} \left( {l_{T} /\delta_{Z} } \right)^{ - 0.5}$) are presented in Table 1. For the values of $u^{{\prime }} /S_{L}$ and $l_{T} /\delta_{th}$ ($l_{T} /\delta_{Z}$) listed in Table 1, all flames considered in this analysis belong to the thin reaction zones regime of combustion (Peters 2000). The simulations have been conducted for $g^{*} = - 3.12, - 1.56, 0.0, 1.56, 3.12$ for each set of turbulence parameters summarised in Table 1. Simulations have been carried out for 3.0−8.0 initial eddy turnover times for Set-A to Set-D, respectively, which is greater than $2{\updelta }_{th} /S_{L}$ for all the cases considered. The turbulent kinetic energy and dissipation rate evaluated over the unburned gas volume did not change significantly with time when the statistics are extracted. During the overall run time of the simulations, $u^{{\prime }}$ decayed by about 55% and $l_{T}$ increased by about 22% in comparison to their initial values. This simulation time remains comparable to several studies (Boger et al. 1998; Charlette et al. 2002; Hernandez-Perez et al. 2011; Hun and Huh 2008) which contributed to the FSD based modelling in the past. Moreover, the qualitative nature of the FSD transport statistics presented in this paper did not change since halfway through the simulation.

Table 1 Initial values of numerical parameters considered for the simulations

The Reynolds/Favre-averaged values of a general quantity $q$ are evaluated by ensemble averaging the relevant quantities in $x_{2} - x_{3}$ planes at a given $x_{1}$ location and the Favre fluctuations are directly evaluated from the DNS data by subtracting the Favre averaged quantities from the instantaneous values following several previous analyses (Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Katragadda et al. 2011; Hun and Huh 2008; Veynante et al. 1997).

4 Results and Discussion

4.1 Flame-Turbulence Interaction and Statistical Behaviour of FSD

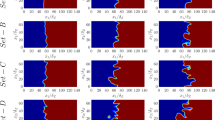
The instantaneous views of the iso-surfaces of reaction progress variable $c$ for $g^{*} = - 3.12, 0.0$ and $3.12$ for all sets of turbulence parameters considered are shown in Fig. 1 when the statistics were extracted. The corresponding contour plots of the reaction progress variable in the $x_{1} - x_{2}$ mid plane of the simulation domain are shown in Fig. 2. It can be seen from Fig. 1 that the value of $g^{*}$ influences the flame morphology and the large-scale flame wrinkling in the direction of mean flame propagation (i.e., $x_{1}$-direction) is promoted with increasing $g^{*}$, possibly due to Rayleigh–Taylor type instability. Figures 1 and 2 indicate that the flame wrinkling increases with increasing $g^{*}$ and $u^{{\prime }} /S_{L}$, which is also reflected in the values of normalised flame surface area $A_{T} /A_{L}$ and normalised turbulent flame speed $S_{T} /S_{L}$ shown in Fig. 3. Here, the turbulent flame speed and flame surface area have been evaluated using the volume integrals $S_{T} = \mathop \smallint \limits_{V} \dot{w}dV/{\uprho }_{0} A_{P}$ and $A_{T} = \mathop \smallint \limits_{V} \left| {\nabla c} \right|dV$, respectively, where $A_{P}$ is the projected flame surface area in the direction of mean flame propagation. The subscripts $T$ and $L$ refer to the turbulent and laminar flame conditions, respectively. The increased flame wrinkling with increasing values of $g^{*}$ is consistent with the previous two-dimensional findings by Veynante and Poinsot (1997) and the theory proposed by Libby (1989).

Fig. 1

Iso-surfaces of $c$ for $g^{*} = - 3.12,0.0$ and $3.12$ for Set-A, Set-B, Set-C and Set-D (rows 1–4), respectively

Fig. 2

Contour plots of $c$ at the $x_{1} - x_{2}$ mid plane of the simulation domain for Set-A, Set-B, Set-C and Set-D (rows 1–4), respectively

Fig. 3

Variations of $A_{T} /A_{L}$ and $S_{T} /S_{L}$ with $g^{*}$ for all sets of turbulence parameters considered here

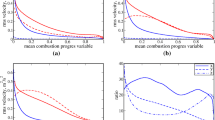
The variation of the generalized FSD ${\Sigma }_{gen} = \overline{{\left| {\nabla c} \right|}}$, the resolved FSD $\left| {\nabla \overline{c}} \right|$ and the wrinkling factor $\Xi = {\Sigma }_{gen} /\left| {\nabla \overline{c}} \right|$ with the Favre averaged reaction progress variable $\tilde{c}$ are shown in Fig. 4. It can be seen from Fig. 4 that smaller values of $\Sigma_{gen} \times\updelta _{Z}$ are obtained for higher $g^{*}$ and this behaviour is most prominent for small initial values of $u^{{\prime }} /S_{L}$ (e.g., for Set-A and Set-B). However, the magnitudes of ${\Sigma }_{gen} \times {\updelta }_{Z}$ do not change with the variation of $g^{*}$ for large values of $u^{{\prime }} /S_{L}$ (e.g., for Set-C and Set-D). The corresponding variation of the resolved part of the generalised FSD (i.e., $\left| {\nabla \overline{c}} \right|$) shows that $\left| {\nabla \overline{c}} \right| \times {\updelta }_{Z}$ decreases considerably with increasing $g^{*}$. Since the inverse of the maximum value of $\left| {\nabla \overline{c}} \right|$ is a measure of the turbulent flame brush thickness (i.e., ${\updelta }_{T} \sim1/max \left| {\nabla \overline{c}} \right|$), a decrease in $\left| {\nabla \overline{c}} \right|$ indicates a broadening of the flame brush with increasing $g^{*}$, which is consistent with the contours of $c$ shown in Fig. 2 and previous results from two-dimensional DNS data (Veynante and Poinsot 1997). It can also be observed from Fig. 4 that the wrinkling factor $\Xi$ increases with increasing $g^{*}$ but this increase is insufficient to overcome the effects of increased flame brush thickening, thereby resulting in a reduction in ${\Sigma }_{gen}$ magnitude with increasing $g^{*}$. It is also evident from Fig. 2 that the iso-surfaces of $c$ are more wrinkled on the unburned gas side representing the preheat zone of the flame, which is valid for the thin reaction zone regime of combustion (Peters 2000).

Fig. 4

Variations of generalised FSD $\Sigma_{gen} \times\updelta _{Z}$ (first column), resolved FSD $\left| {\nabla \overline{c}} \right| \times\updelta _{Z}$ (second column) and wrinkling factor $\Xi$ (third column) with $\tilde{c}$ for Set-A, Set-B, Set-C and Set-D (rows 1–4), respectively. The black dashed line represents the minimum possible value of wrinkling factor (i.e., $\Xi = 1.0$)

4.2 Statistical Behaviour of FSD Transport

The variations of normalised unclosed terms of the FSD transport equation {$T_{1}$, $T_{2}$, $T_{3}$ and $T_{4} \} \times \delta_{Z}^{2} /S_{L}$ for $g^{*} = - 3.12$, $0.0$ and $3.12$ are shown in Fig. 5 for Set-A to Set-D. The variations of these terms for the remaining $g^{*}$ values (i.e., $g^{*} = - 1.56$ and $1.56$) follow the monotonic trend that can be derived from $g^{*} = - 3.12$, $0.0$ and $3.12$ and thus are not shown here for the sake of conciseness. The following observations can be made from Fig. 5:

• The magnitude of the turbulent transport term $T_{1}$ decreases as the value of $g^{*}$ increases for a given value of $u^{{\prime }} /S_{L}$. The magnitude of $T_{1}$ also decreases with increasing initial $u^{{\prime }} /S_{L}$.

• The FSD tangential strain rate term $T_{2}$ acts as a source term in all cases and its magnitude increases with increasing $g^{*}$ for small values of $u^{{\prime }} /S_{L}$ (e.g., Set-A). For high values of turbulence intensity $u^{{\prime }} /S_{L}$, the magnitude of $T_{2}$ on the reactant side of the flame brush increases with increasing $g^{*}$ but the magnitude of $T_{2}$ on the product side remains mostly insensitive to the variation of $g^{*}$.

• The FSD propagation term generally assumes positive values towards the unburned gas side and negative values towards the burned gas side of the flame brush. The magnitude of the propagation term $T_{3}$ decreases with increasing $g^{*}$ for a given value of $u^{{\prime }} /S_{L}$. The magnitude of $T_{3}$ also decreases with increasing initial turbulence intensity $u^{{\prime }} /S_{L}$. The case with $g^{*} = - 3.12$ for Set-A remains weakly turbulent with a small extent of flame wrinkling (see Figs. 1, 2). For a steady laminar 1D planar premixed flame, the contributions of $T_{1} ,T_{2}$ and $T_{4}$ remain identically zero, whereas $T_{3}$ assumes positive value towards the unburned gas side of the flame brush before assuming negative values towards the burned gas side of the flame brush. The contribution of $\left( { - C_{1} = - \partial \left[ {\tilde{u}_{k} {\Sigma }_{gen} } \right]/\partial x_{k} } \right)$ is balanced by $T_{3}$ in a steady laminar 1D planar premixed flame. A similar situation holds in the case $g^{*} = - 3.12$ for Set-A (not shown here). The departure from the expected behaviour for a steady 1D laminar premixed flame increases with increasing initial turbulence intensity $u^{{\prime }} /S_{L}$ due to the strengthening of turbulence.

• The FSD curvature term $T_{4}$ is weakly positive towards the reactant side but acts as a sink (negative) over the major part of the flame brush. The positive contribution of $T_{4}$ weakens with increasing initial turbulence intensity $u^{{\prime }} /S_{L}$.

• The magnitudes of FSD transport and propagation terms (i.e., $T_{1}$ and $T_{3}$) relative to the FSD tangential strain rate and curvature terms (i.e., $T_{2}$ and $T_{4}$) decrease with increasing $u^{{\prime }} /S_{L}$. This behaviour is consistent with previous findings by Chakraborty and Cant (2013) and their scaling arguments.

Fig. 5

Variations of $T_{1}$, $T_{2}$, $T_{3}$ and $T_{4}$ with $\tilde{\user2{c}}$ for $g^{*} = - 3.12$ (first column), $0.0$ (second column) and $3.12$ (third column) for Set-A, Set-B, Set-C and Set-D (rows 1–4), respectively

It is worthwhile to consider the ratio of body forces to the inertial forces due to turbulent velocity fluctuations as: $Fr_{T}^{ - 2} =\Gamma _{1} l_{T} /u^{{{\prime }2}} = \left( {g^{*} S_{L}^{2} /{\updelta }_{Z} } \right)/\left( {u^{{{\prime }2}} /l_{T} } \right)\sim\,g^{*} \left( {l_{T} /\delta_{Z} } \right)/\left( {u^{{{\prime }2}} /S_{L}^{2} } \right)$ where $Fr_{T} = u^{{\prime }} /\sqrt {\Gamma _{1} l_{T} }$ is the turbulent Froude number. This suggests that an increase in $u^{{\prime }} /S_{L}$ for a given set of values of $l_{T} /\delta_{Z}$ and $g^{*}$ leads to weakening of the body force effects and thus the FSD and the terms of its transport equation do not change appreciably with the variation of $g^{*}$ for large values of $u^{{\prime }} /S_{L}$. The observed behaviours of the terms $T_{1}$, $T_{2}$, $T_{3}$ and $T_{4}$ from Fig. 4 can be explained further by considering these terms individually and their closures.

4.3 Modelling of the Turbulent Transport Term $T_{1}$

It can be seen from Eq. 4 that the modelling of the turbulent transport term $T_{1}$ depends on the closure of the turbulent flux of the generalised FSD given by $\left[ {\overline{{\left( {u_{i} } \right)}}_{s} - \widetilde{{u_{i} }}} \right]{\Sigma }_{gen}$ (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Veynante et al. 1996; Chakraborty and Cant 2009a, 2011, 2013; Sellmann et al. 2017; Hawkes and Cant 2000; Hernandez-Perez et al. 2011; Reddy and Abraham 2012; Ma et al. 2014). This closure is often achieved using a classical gradient hypothesis (Cant et al. 1990; Hawkes and Cant 2000; Reddy and Abraham 2012; Ma et al. 2014) according to which one obtains:

$$\left[ {\overline{{\left( {u_{i} } \right)}}_{s} - \tilde{u}_{i} } \right]\Sigma_{gen} = - \left( {\upnu _{t} /Sc_{\Sigma } } \right)\partial \Sigma_{gen} /\partial x_{i}$$

(5)

where $\upnu _{t} = C_{\upmu } \tilde{k}^{2} /\tilde{\epsilon }$ is the kinematic eddy viscosity (with $C_{\upmu } = 0.09$) and $Sc_{{\Sigma }}$ is a suitable turbulent Schmidt number (Cant et al. 1990; Duclos et al. 1993) with $\tilde{k} = \overline{{\rho u_{i}^{{\prime \prime }} u_{i}^{{\prime \prime }} }} /2\overline{\rho }$ and $\tilde{\epsilon } = \overline{{\mu \left( {\partial u_{i}^{\prime \prime } /\partial x_{j} } \right)(\partial u_{i}^{\prime \prime } /\partial x_{j} )}} /\overline{\rho }$ being the turbulent kinetic energy and its dissipation rate, respectively and evaluated directly from the DNS data. However, previous studies (Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Veynante et al. 1997) demonstrated that $\left[ {\overline{{\left( {u_{i} } \right)}}_{s} - \widetilde{{u_{i} }}} \right]{\Sigma }_{gen}$ might exhibit counter-gradient (gradient) behaviour when the turbulent flux of reaction progress variable $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }}$ is counter-gradient (gradient) in nature.

The variations of the only non-zero normalised turbulent scalar flux component $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }} /\rho_{0} S_{L}$ for statistically planar flames with the Favre averaged reaction progress variable $\tilde{c}$ are shown in Fig. 6 for all cases considered here. As $\partial \tilde{c}/\partial x_{1}$ is positive in the present configuration, a positive (negative) value of $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }} /\rho_{0} S_{L}$ indicates counter-gradient (gradient) type transport. It is evident from Fig. 6 that counter-gradient transport is observed over the majority of the flame brush for all cases. However, a gradient transport is promoted for positive $g^{*}$ values (i.e., $g^{*} = 1.56$ and $3.12$), towards the reactant side of the flame brush where the effects of heat release are weak and this tendency weakens as the value of $g^{*}$ decreases, which is consistent with the previous findings (Chomiak and Nisbet 1995; Veynante and Poinsot 1997). This behaviour can be explained using a hydrostatic approximation (Veynante and Poinsot 1997) under which the momentum equation reduces to $\partial p/\partial x_{1} = \rho g^{*} S_{L}^{2} /\delta_{Z}$. Thus, a positive (negative) value of $g^{*}$ denotes an adverse (favourable) pressure gradient across the simulation domain, leading to gradient (counter-gradient) transport (Veynante and Poinsot 1997).

Fig. 6

Variation of normalised turbulent scalar flux of progress variable $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }} /\rho_{0} S_{L}$ with $\tilde{\user2{c}}$ for all sets of turbulence parameters

The variation of the only non-zero component of the FSD flux $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ for statistically planar flames with $\tilde{c}$ are shown in Fig. 7 for the cases considered in the present analysis. It can be seen from Fig. 4 that ${\Sigma }_{gen}$ attains peak value at the middle of the flame brush (i.e., at $\tilde{c} = c_{{\Sigma }}$ with $0 < c_{{\Sigma }} < 1.0$), and therefore $\partial {\Sigma }_{gen} /\partial x_{1}$ assumes positive values for $0 < \tilde{c} < c_{{\Sigma }}$ and negative values for $c_{{\Sigma }} < \tilde{c} < 1.0$ because $\partial \tilde{c}/\partial x_{1}$ assumes positive values within the flame brush, in statistically planar flames. This indicates that $\partial {\Sigma }_{gen} /\partial x_{1}$ is expected to be positive (negative) towards the reactants (products) side of the flame brush. Therefore, $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ is expected to assume negative (positive) values towards the reactants (products) side of the flame brush according to Eq. 5. However, the behaviour of $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ obtained from DNS in Fig. 7 reveals that the FSD flux assumes positive (negative) values towards the reactants (products) side of the flame brush for small values of $u^{{\prime }} /S_{L}$ and also for negative values of $g^{*}$. This suggests that counter-gradient behaviour is observed for $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ for small values of $u^{{\prime }} /S_{L}$ and also for negative values of $g^{*}$. Thus, the gradient hypothesis-based model given by Eq. 5 is not suitable for the purpose of modelling $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ and therefore its prediction is not shown in Fig. 7. It can indeed be discerned from Fig. 7 that the qualitative behaviour of $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ in Set-C and Set-D are different from those in Set-A and Set-B for a given value of $g^{*}$. Moreover, the qualitative behaviours of $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ also change with the variation of $g^{*}$ for a given turbulence intensity $u^{{\prime }} /S_{L}$. This difference in behaviour originates from the fact that $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ shows counter-gradient behaviour for small values of $u^{{\prime }} /S_{L}$ (e.g., Set-A and Set-B), whereas the gradient behaviour is prevalent towards the reactants side of the flame brush for large values of $u^{{\prime }} /S_{L}$ (e.g., Set-C and Set-D) similar to the behaviour of turbulent scalar flux $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }}$ (see Fig. 6). As shown in Fig. 6, the propensity of counter-gradient behaviour of turbulent scalar flux $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }}$ increases with decreasing $g^{*}$ and a similar behaviour is observed for $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ with counter-gradient behaviour for small values of $g^{*}$ and a gradient type behaviour on the reactant side of the flame brush is observed for high positive values of $g^{*}$.

Fig. 7

Variation of $\left[ {\overline{{\left( {u_{i} } \right)}}_{s} - \widetilde{{u_{i} }}} \right]\Sigma_{gen} \times \delta_{Z} /S_{L}$ (solid line represents DNS data and dash-dotted line represents prediction of Eq. 6) with $\tilde{c}$ for Set-A to Set-D (1st -4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

A model for the turbulent flux of generalised FSD was proposed in previous analyses (Chakraborty and Cant 2011, 2013; Sellmann et al. 2017) in the following manner, which can predict both gradient and counter-gradient behaviour:

$$\left[ {\overline{{\left( {u_{i} } \right)_{s} }} - \tilde{u}_{i} } \right]{\Sigma }_{gen} = \frac{{\left( {1 - 2\tilde{c}} \right)\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }} {\Sigma }_{gen} }}{{\overline{{\rho c^{{{\prime \prime }2}} }} +\overline{{\rho}}\tilde{c} \left( {1 - \tilde{c}} \right)}}$$

(6)

It can be seen from Fig. 7 that Eq. 6 satisfactorily captures the qualitative and quantitative behaviour of $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \widetilde{{u_{1} }}} \right]{\Sigma }_{gen}$ irrespective of the values of $u^{{\prime }} /S_{L}$ and $g^{*}$. However, it is worth noting that the successful performance of Eq. 6 depends on the satisfactory closure of $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }}$ and $\overline{{\rho c^{{{\prime \prime }2}} }}$. The closures of $\overline{{\rho u_{1}^{{\prime \prime }} c^{{\prime \prime }} }}$ and $\overline{{\rho c^{{{\prime \prime }2}} }}$ have been addressed elsewhere (Veynante et al. 1997; Chakraborty and Cant 2009b, c, d; Papapostolopu et al. 2019; Chakraborty and Swaminathan 2011) and will not be addressed further in this paper.

4.4 Modelling of the tangential strain rate term $T_{2}$

For the purpose of understanding the statistical behaviour of the tangential strain rate term $T_{2}$, it has been decomposed in several previous studies (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Veynante et al. 1996; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Katragadda et al. 2011) in the following manner:

$$T_{2} = \underbrace {{\left[ {\updelta _{ij} - \overline{{\left( {N_{i} N_{j} } \right)}}_{s} } \right]\frac{{\partial \widetilde{{u_{i} }}}}{{\partial x_{j} }}\Sigma_{gen} }}_{{S_{R} }} + \underbrace {{\overline{{\left( {\left( {\updelta _{ij} - N_{i} N_{j} } \right)\frac{{\partial u_{i}^{{\prime \prime }} }}{{\partial x_{j} }}} \right)}}_{s} \Sigma_{gen} }}_{{S_{UR} }}$$

(7)

Here $S_{R}$ and $S_{UR}$ are the resolved and unresolved flow contributions of the strain rate term, respectively. The modelling of $S_{R}$ depends on the appropriate modelling of the orientation factors $\overline{{\left( {N_{i} N_{j} } \right)}}_{s}$. Cant et al. (1990) modelled $\overline{{\left( {N_{i} N_{j} } \right)}}_{s}$ as $\overline{{\left( {N_{i} N_{j} } \right)}}_{s} = \overline{{\left( {N_{i} } \right)}}_{s} \overline{{\left( {N_{j} } \right)}}_{s} + \left( {\updelta _{ij} /3} \right)\left[ {1 - \overline{{\left( {N_{k} } \right)}}_{s} \overline{{\left( {N_{k} } \right)}}_{s} } \right]$ where $\overline{{\left( {N_{i} } \right)}}_{s} = - \left( {\partial \overline{c}/\partial x_{i} } \right)/{\Sigma }_{gen}$ is the surface averaged flame normal vector. The evaluation of $\overline{{\left( {N_{i} } \right)}}_{s}$ depends on the evaluation of $\overline{c}$ from $\tilde{c}$, which is usually achieved using the Bray–Moss–Libby (BML) analysis (Bray et al. 1985), according to which $\overline{c} = \left( {1 +\uptau } \right)\tilde{c}/\left( {1 +\uptau \tilde{c}} \right) + O\left(\upgamma \right)$, where $O\left( \gamma \right)$ represents the contribution of the burning mixture. The BML analysis implicitly assumes bi-modal probability density function (PDF) of $c$ with impulses at $c = 0$ and $c = 1.0$ (Bray et al. 1985), which is likely to be obtained for large values of Damköhler number (i.e., $Da \gg 1$) but the bi-modal PDF distribution is unlikely to be realised in the thin reaction zones regime flames with $Da < 1$. Katragadda et al. (2011) proposed a modification to the BML expression for $\overline{c}$ in the case of flames with $Da < 1$, where the bi-modal PDF of $c$ is unlikely to be realised and this expression takes the following form for unity Lewis number flames:

$$\overline{c} = \left( {1 + \tau .g^{a} } \right)\tilde{c}/\left( {1 + \tau .g^{a} \tilde{c}} \right)$$

(8)

where $g = \widetilde{{c^{{{\prime \prime }2}} }}/\left[ {\tilde{c}\left( {1 - \tilde{c}} \right)} \right]$ is the segregation factor, and $a = 1.5$ is a model parameter (Katragadda et al. 2011). Equation 8 has been found to capture the interrelation between $\overline{c}$ and $\tilde{c}$ for all cases considered in this work, which is not explicitly shown here for the sake of conciseness.

Veynante et al. (1996) proposed an alternative model for $\overline{{\left( {N_{i} N_{j} } \right)}}_{s}$, which is given as: $\overline{{\left( {N_{i} N_{j = i} } \right)}}_{s} = \mathop \sum \limits_{k \ne i} \widetilde{{u_{k}^{{\prime \prime }} u_{k}^{{\prime \prime }} }}/4\tilde{k}$ and $\overline{{\left( {N_{i} N_{j \ne i} } \right)}}_{s} = \widetilde{{u_{i}^{{\prime \prime }} u_{j}^{{\prime \prime }} }}/2\tilde{k}$. The models by Cant et al. (1990) and Veynante et al. (1996) will henceforth be referred to as the MCPB and VPDM models, respectively. The variation of $S_{R}$ with $\tilde{c}$ across the flame brush from DNS data is compared with predictions of the MCPB and VPDM models in Fig. 8. It can be seen from Fig. 8 that the predictions of the MCPB model agree better with the DNS data for most of the cases, although it slightly underpredicts the magnitude of $S_{R}$ for all cases considered. The VPDM model, on the other hand, highly overpredicts $S_{R}$ for cases with small initial $u^{{\prime }} /S_{L}$ values (Set-A and Set-B) and negative $g^{*}$ values. However, the agreement of the prediction of the VPDM model with DNS data improves with increases in $g^{*}$ and the initial $u^{{\prime }} /S_{L}$ (e.g., the VPDM model performs better in Set-C and Set-D than in Set-A and Set-B).

Fig. 8

Variation of $S_{R} \times\updelta _{Z}^{2} /S_{L}$ (solid line represents DNS data, dotted line represents the prediction of the MCPB model and the dashed line represents the predictions of the VPDM model) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

The MCPB model assumes isotropic fluctuations of surface averaged flame normal components (Cant et al. 1990), whereas the VPDM model considers anisotropic fluctuations of surface averaged flame normal components (Veynante et al. 1996). Moreover, there is another major difference between these models. The quantity $\overline{{\left( {N_{i} N_{j} } \right)}}_{s}$ approaches $\overline{{\left( {N_{i} } \right)}}_{s} \overline{{\left( {N_{j} } \right)}}_{s}$ in the limit of a laminar premixed flame (where $\overline{{\left( {N_{k} } \right)}}_{s} \overline{{\left( {N_{k} } \right)}}_{s} \approx 1.0$), which is satisfied by the MCPB model but not by the VPDM model. The case with $g^{*} = - 3.12$ for Set-A exhibits the least turbulent behaviour and shows weak flame wrinkling (see Figs. 1, 2) and thus in this case the MCPB model shows a good agreement with $S_{R}$ obtained from DNS data but the VPDM model does not adequately capture the statistical behaviour of the orientation factors $\overline{{\left( {N_{i} N_{j} } \right)}}_{s}$. The departure from the laminar premixed flame condition increases with increasing $g^{*}$ and/or $u^{{\prime }} /S_{L}$ and thus the agreement between the VPDM model and DNS data for $S_{R}$ improves with increases in $g^{*}$ and/or $u^{{\prime }} /S_{L}$.

The two most widely used models for the unresolved component $S_{UR}$ are the ones proposed by Cant et al. (1990) and Candel et al. (1990), which are referred to as the SCPB and SCFM models, respectively. Cant et al. (1990) modelled $S_{UR}$ as $S_{UR} = 0.28\sqrt {\tilde{\epsilon }/\upnu _{0} } \Sigma_{gen}$, where $\upnu _{0}$ is the kinematic viscosity of the unburned gas. According to the SCFM model, $S_{UR} = {\text{a}}_{0}\Gamma _{k} \left( {\tilde{\epsilon }/\tilde{k}} \right)\Sigma_{gen}$, where ${\text{a}}_{0} = 2.0$ is a model constant and $\Gamma _{k}$ is the efficiency function (as proposed by Meneveau and Poinsot 1991) which is a function of $l_{t} /\updelta _{Z}$ and $\sqrt {2\tilde{k}/3} /S_{L}$ and $l_{t} = C_{k} \tilde{k}^{3/2} /\tilde{\epsilon }$ is the local integral length scale where the constant $C_{k}$ is taken to be $C_{k} = 1.5$ (Sreenivasan 1984). The predictions of the SCPB and SCFM models are compared with the $S_{UR}$ extracted from the DNS data in Fig. 9, which shows neither the SCPB nor SCFM model predicts the variation of $S_{UR}$ satisfactorily. Both models predict only positive values of $S_{UR}$, although negative values of $S_{UR}$ are obtained from DNS data for small values of $u^{{\prime }} /S_{L}$ and $g^{*}$. Moreover, both SCPB and SCFM models tend to over-predict the magnitude of the unresolved strain rate term $S_{UR}$ by a large extent for most cases considered here. However, for the initial $u^{{\prime }} /S_{L} = 3.0$ case (Set-A), the SCFM model provides satisfactory prediction for positive $g^{*}$ values.

Fig. 9

Variation of $S_{UR} \times {\updelta }_{Z}^{2} /S_{L}$ (solid line represents DNS data, dotted line represents the prediction of the SCPB model and the dashed line represents the predictions of the SCFM model) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

In order to explain the negative values of $S_{UR}$, the tangential strain rate term $T_{2}$ can alternatively be decomposed as (Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Katragadda et al. 2011):

$$T_{2} = \underbrace {{\overline{{\left( {\frac{{\partial u_{i} }}{{\partial x_{i} }}} \right)}}_{{{s}}} \Sigma_{gen} }}_{{D_{FSD} }} \underbrace {{-\overline{{\left( {N_{i} N_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right)_{s} }} \Sigma_{gen} }}_{{N_{FSD} }}$$

(9)

Here the terms $D_{FSD}$ and $N_{FSD}$ denote the effects of dilatation rate and normal strain rate, respectively. Katragadda et al. (2011) and Sellmann et al. (2017) further split the dilatation rate term as $D_{FSD} = D1_{FSD} + D2_{FSD}$ where $D1_{FSD}$ and $D2_{FSD}$ are the resolved and unresolved components, respectively, and these are defined as:

$$\begin{aligned} D1_{FSD} & = \frac{{\partial \tilde{u}_{i} }}{{\partial x_{i} }}\left| {\nabla \overline{c}} \right| \\ D2_{FSD} & = \overline{{\left( {\frac{{\partial u_{i} }}{{\partial x_{i} }}\left| {\nabla c} \right|} \right)}} - \frac{{\partial \widetilde{{u_{i} }}}}{{\partial x_{i} }}\left| {\nabla \overline{c}} \right| \\ \end{aligned}$$

(10)

Katragadda et al. (2011) and Sellmann et al. (2017) proposed the following model expression for $D2_{FSD} :$

$$D2_{FSD} = \left( {\tau .S_{L} /\delta_{th} } \right)\left[ {A\left( {1 - \tilde{c}} \right)^{\zeta } \left( {\Sigma_{gen} - \left| {\nabla \overline{c}} \right|} \right)} \right]$$

(11)

where $A = B_{1} /\left( {1 + Ka_{L} } \right)^{0.35}$, $B_{1}$ and $\upzeta = - 0.3$ are the model parameters. The model parameter $B_{1}$ has been modified in this analysis in comparison to the previous studies (Sellmann et al. 2017; Katragadda et al. 2011) to account for the effects of the local turbulent Reynolds number $Re_{L}$ (i.e., $Re_{L} = \rho_{0} \widetilde{{k^{2} }}/\left( {\tilde{\epsilon }\mu_{0} } \right)$) and the Froude number (i.e., $Fr = 1/\sqrt {g^{*} }$) in the following manner:

$$B_{1} = b_{1} /\left[ {erf\left( {\left( {Re_{L} + 1.0} \right)/b_{2} } \right)} \right]$$

(12)

where $b_{1}$ and $b_{2}$ are functions of $g^{*}$ as shown below:

$$\begin{aligned} b_{1} & = 1.79 - 0.69erf\left( {g^{*} + 0.394} \right)\;{\text{for}}\;g^{*} \ge 0.0 \\ b_{1} & = 0.98 + 0.54erf\left( {g^{*} + 1.61} \right)\;{\text{for}}\;g^{*} \le 0.0 \\ b_{2} & = 17.31 - 13.89erf\left( {g^{*} + 1.91} \right) \\ \end{aligned}$$

(13)

The term $D_{FSD}$ extracted from the DNS data and the combined predictions of $D1_{FSD}$ and $D2_{FSD}$ according to the closures given by Eqs. 10 and 11–13 are compared in Fig. 10. It can be seen from Fig. 10 that the magnitude of $D_{FSD} \times\updelta _{Z}^{2} /S_{L}$ decreases with increasing $g^{*}$ and $u^{{\prime }} /S_{L}$, which necessitates the inclusion of $g^{*}$ and $Re_{L}$ dependences in Eq. 13. It can also be seen that the models given by Eqs. 10, 11–13 satisfactorily predict the behaviour of the $D_{FSD}$ term for all the different $g^{*}$ values and for all sets of initial $u^{{\prime }} /S_{L}$ values considered in this analysis. However, some over-predictions are obtained towards the reactant side of the flame brush for positive $g^{*}$ values for Set-A.

Fig. 10

Variation of $D_{FSD} \times\updelta _{Z}^{2} /S_{L}$ (solid line represents DNS data and dash-dotted line represents the prediction of the closure model) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

Similar to $D_{FSD}$, the normal strain rate contribution $N_{FSD}$ can also be split into its respective resolved and unresolved flow contributions (Sellmann et al. 2017; Katragadda et al. 2011), i.e., $N_{FSD} = N1_{FSD} + N2_{FSD}$, where $N1_{FSD}$ and $N2_{FSD}$ are defined as:

$$\begin{aligned} N1_{FSD} & = - \overline{{\left( {N_{i} N_{j} } \right)}}_{s} \left( {\partial \widetilde{{u_{i} }}/\partial x_{j} } \right)\Sigma_{gen} \\ N2_{FSD} & = - \overline{{\left( {N_{i} N_{j} \partial u_{i}^{\prime \prime } /\partial x_{j} } \right)_{s} }} \Sigma_{gen} \\ \end{aligned}$$

(14)

The predictions of $N1_{FSD}$ according to the CPB and VPDM models are compared to the corresponding term extracted from the DNS data in Fig. 11. The magnitude of $N1_{FSD} \times \delta_{Z}^{2}/S_{L}$ is found to decrease with increasing values of $g^{*}$ and initial $u^{{\prime }} /S_{L}$. It is evident from Fig. 11 that overall, for all sets of initial $u^{{\prime }} /S_{L}$ and $g^{*}$ values, the CPB model captures the quantitative and qualitative behaviour of the $N1_{FSD}$ component more accurately than the VPDM model. However, the CPB model tends to overpredict the magnitude of the $N1_{FSD}$ component whereas the VPDM model underpredicts (overpredicts) it for negative (positive) $g^{*}$ values. It can also be seen that the agreement between the predictions of the VPDM model and DNS data improve significantly as the values of initial $u^{{\prime }} /S_{L}$ and $g^{*}$ increases. This behaviour is consistent with the $S_{R}$ predictions by the MCPB and VPDM models shown in Fig. 8 and the differences in these two model predictions have already been explained in the context of $S_{R}$ predictions and the same explanation is valid in the context of the $N1_{FSD}$.

Fig. 11

Variation of $N1_{FSD} \times\updelta _{Z}^{2} /S_{L}$ (solid line represents DNS data, dotted line represents the predictions of the CPB model and dashed line represents the predictions of the VPDM model) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

The behaviour of the unresolved component of the normal strain rate term $N2_{FSD}$ depends on the alignment of $\nabla c$ with the local principal fluctuating strain rates. The terms $N_{FSD}$ and $S_{UR}$ can be expressed as (Katragadda et al. 2011):

$$N_{FSD} = - \overline{{\left( {e_{\alpha } \cos^{2} \theta_{\alpha } + e_{\beta } \cos^{2} \theta_{\beta } + e_{\gamma } \cos^{2} \theta_{\gamma } } \right)\left| {\nabla c} \right|}}$$

(15i)

$$S_{UR} = \overline{{\left( {e_{\alpha } \sin^{2} \theta_{\alpha } + e_{\beta } \sin^{2} \theta_{\beta } + e_{\gamma } \sin^{2} \theta_{\gamma } } \right)\left| {\nabla c} \right|}}$$

(15ii)

where $e_{\alpha } ,e_{\beta }$ and $e_{\gamma }$ are the most extensive, intermediate and the most compressive principal fluctuating strain rate tensor (i.e., $0.5\left( {\partial u_{i}^{{\prime \prime }} /\partial x_{j} + \partial u_{j}^{{\prime \prime }} /\partial x_{i} } \right)$) and $\theta_{\alpha } ,\theta_{\beta }$ and $\theta_{\gamma }$ are the angles between $\nabla c$ and the eigenvectors associated with $e_{\alpha } ,e_{\beta }$ and $e_{\gamma }$, respectively. The reaction progress variable gradient $\nabla c$ preferentially collinearly aligns with the eigenvectors associated with $e_{\alpha }$ (i.e., high probability of $|\cos \theta_{\alpha } | \approx 1.0$) when the strain rate induced by flame normal acceleration arising from heat release overcomes turbulent straining (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011). By contrast, $\nabla c$ preferentially collinearly aligns with the eigenvectors associated with $e_{\gamma }$ (i.e., high probability of $\left| {\cos \theta_{\gamma } } \right| \approx 1.0$) when turbulent straining dominates over the strain rate induced by flame normal acceleration arising from heat release (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011). The high probability of obtaining $|\cos \theta_{\alpha } | \approx 1.0$ is obtained for high values of $\tau Da$ (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011), which leads to negative values of $T_{2}$ and $N_{FSD}$ (and its unresolved component $N2_{FSD}$). This behaviour is promoted further for small values of $g^{*}$ because turbulence straining is expected to weaken with decreasing $g^{*}$ especially for negative values of $g^{*}$. By the same token, the high probability of obtaining $|\cos \theta_{\gamma } | \approx 1.0$ is obtained for low values of $\tau Da$ (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011), which leads to positive values of $S_{UR}$ and $N_{FSD}$ (and its unresolved component $N2_{FSD}$). This behaviour strengthens further for high positive values of $g^{*}$ because turbulence straining strengthens with increasing $g^{*}$ especially for positive values of $g^{*}$.

The aforementioned discussion suggests that the competition between the strain rate induced by flame normal acceleration and turbulent straining, and the alignment characteristics of $\nabla c$ need to be addressed in the modelling of $T_{2}$. The SCPB and SCFM models consider the Kolmogorov time scale and large-scale turbulent time scale, respectively, which are both turbulent flow time scales, and thus ignores the chemical time scale associated with the strain rate induced by flame normal acceleration. In order to address this deficiency, Katragadda et al. (2011) and Sellmann et al. (2017) proposed the following model for $N2_{FSD}$ (for unity Lewis number):

$$N2_{FSD} = \left( {\tilde{\epsilon }/\tilde{k}} \right)\left[ {{\text{C}}_{1} - \tau {\text{C}}_{2} Da_{L} } \right]{\Sigma }_{gen}$$

(16)

where $Da_{L} = \tilde{k}S_{L} /\tilde{\epsilon }{\updelta }_{th}$ is the local Damköhler number. For small Damköhler number flames $\nabla c$ tends to preferentially align with the eigenvector associated with $e_{\upgamma }$ due to the dominance of turbulent straining over the effects of heat release and this is scaled as $\left( {\tilde{\epsilon }/\tilde{k}} \right)C_{1} {\Sigma }_{gen}$ in Eq. 16. Similarly, for flames with high Damköhler numbers, the effects of heat release tend to dominate over the turbulent straining, leading to the alignment of $\nabla c$ with the eigenvector associated with $e_{{\upalpha }}$, which is scaled as $- \tau C_{2} {\Sigma }_{gen} S_{L} /{\updelta }_{th}$ in Eq. 16. In the present analysis, the model constants $C_{1}$ and $C_{2}$ have been modified in order to incorporate the effects of local turbulent Reynolds number $Re_{L}$ and Froude number $Fr$ on the turbulent straining. The model parameter $C_{1}$ can be expressed as:

$$C_{1} = B_{2} erf\left[ {\left( {Re_{L} + 1.0} \right)/a_{2} } \right] \cdot \left( {1 - \tilde{c}} \right)^{k}$$

(17)

$$\begin{gathered} {\text{where}}\quad B_{2} = 3.0 \hfill \\ \quad \quad \quad \;k = 4.21 - 1.23erf\left( {0.89 - 0.35g^{*} } \right) \hfill \\ \quad \quad \quad \;a_{2} = 23.2 - 17.62 erf\left( {g^{*} + 1.70} \right) \hfill \\ \end{gathered}$$

(18)

Similarly, the effects of $Re_{L}$ and $Fr = 1/\sqrt {g^{*} }$ are included into the strain rate due to heat release using the model parameter $B_{3}$ as given below:

$$C_{2} = 0.471B_{3} \left[ {1.0 - \overline{{\left( {N_{k} } \right)}}_{s} \overline{{\left( {N_{k} } \right)}}_{s} } \right]/\left( {1.0 + Ka_{L} } \right)^{0.35}$$

(19)

$$\begin{aligned} B_{3} & = P/erf\left[ {\left( {Re_{L} + 1.0} \right)/a_{3} } \right] \\ P & = 18.9 - 17.0 erf\left( {g^{*} + 1.44} \right) \;for\;g^{*} \ge 0.0 \\ P & = 1.67 + 0.98 erf\left( {g^{*} + 1.36} \right)\;for\;g^{*} \le 0.0 \\ a_{3} & = 16.16 - 12.56 erf\left( {g^{*} + 1.79} \right) \\ \end{aligned}$$

(20)

The predictions of Eqs. 16–20 are compared to $N2_{FSD}$ extracted from DNS data in Fig. 12, which shows that the model satisfactorily captures the qualitative behaviour of the unresolved normal strain rate term $N2_{FSD}$, although there is an over-prediction (under-prediction) of the magnitude of $N2_{FSD}$ towards the reactant side of the flame brush for positive (negative) $g^{*}$ values. It is also evident that the predictions of the model improve with decreasing Damköhler number (Set-A to Set-D).

Fig. 12

Variation of $N2_{FSD} \times\updelta _{Z}^{2} /S_{L}$ (solid line represents DNS data, dash-dotted line represents the predictions of the model given by Eqs. 16–20) with $\tilde{\user2{c}}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

Combining the MCPB model for $N1_{FSD}$ with Eqs. 10, 11 and 16–20 for $D1_{FSD}$, $D2_{FSD}$ and $N2_{FSD}$ respectively, the strain rate term $T_{2}$ may be written as:

$$\begin{aligned} T_{2} & = \frac{{\partial \tilde{u}_{i} }}{{\partial x_{i} }}\left| {\nabla \overline{c}} \right| + \frac{{\tau .S_{L} }}{{\delta_{th} }}\left[ {A\left( {1 - \tilde{c}} \right)^{\zeta } \left( {{\Sigma }_{gen} - \left| {\nabla \overline{c}} \right|} \right)} \right] - \overline{{\left( {N_{i} } \right)}}_{s} \overline{{\left( {N_{j} } \right)}}_{s} \frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }}{\Sigma }_{gen} \\ & \quad - \left( {\delta_{ij} /3} \right)\left[ {1 - \overline{{\left( {N_{k} } \right)}}_{s} \overline{{\left( {N_{k} } \right)}}_{s} } \right]\frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }}{\Sigma }_{gen} + \frac{{\tilde{\epsilon }}}{{\tilde{k}}}\left[ {C_{1} - \tau C_{2} Da_{L} } \right]{\Sigma }_{gen} \\ \end{aligned}$$

(21)

The predictions of Eq. 21, along with the predictions of the CPB (MCPB + SCPB) and CFM (VPDM + SCFM) models are shown in Fig. 13 along with the $T_{2}$ term extracted from DNS data. It can be clearly observed that the predictions of Eq. 21 agree better with the DNS data than the CPB and CFM models. However, Eq. 21 tends to underpredict the magnitude of $T_{2}$ towards the product side, mainly for the cases with positive $g^{*}$ values.

Fig. 13

Variation of $T_{2} \times\updelta _{Z}^{2} /S_{L}$ (solid line represents DNS data, dotted line represents the predictions of the CPB model, dashed line represents the predictions of the CFM model and line with circles represents the predictions given by Eq. 21) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

4.5 Modelling of the Combined Propagation and Curvature Terms ($T_{3} + T_{4}$)

The propagation and curvature terms are often modelled together due to their dependence on the displacement speed $S_{d}$. The combined ($T_{3} + T_{4}$) term is usually modelled together as (Candel et al. 1990; Duclos et al. 1993; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Hun and Huh 2008):

$$\left( {T_{3} + T_{4} } \right) = - \frac{\partial }{{\partial x_{i} }}\left[ {\frac{{\rho_{0} S_{L} }}{{\overline{\rho }}}\overline{{\left( {N_{i} } \right)}}_{s} {\Sigma }_{gen} } \right] + \frac{{\rho_{0} S_{L} }}{{\overline{\rho }}}\frac{{\partial \overline{{\left( {N_{i} } \right)}}_{s} }}{{\partial x_{i} }}{\Sigma }_{gen} - \beta_{0} \alpha_{N} \frac{{\left( {\overline{c} - c_{cp} } \right)S_{L} {\Sigma }_{gen}^{2} }}{{\overline{c}\left( {1 - \overline{c}} \right)}}$$

(22)

The third term on the right-hand side of Eq. 22 denotes the unresolved component of the combined propagation and curvature term where $\beta_{0}$ and $c_{cp}$ are model parameters, and $\upalpha _{N}$ represents an orientation factor (resolution factor) in terms of RANS (LES) which is evaluated as $\upalpha _{N} = 1 - \overline{{\left( {N_{k} } \right)}}_{s} \overline{{\left( {N_{k} } \right)}}_{s}$ and thus becomes zero under fully resolved condition causing the entire unresolved term to vanish (Chakraborty and Cant 2011, 2013; Sellmann et al. 2017). Chakraborty and Cant (2011, 2013) found that $\beta_{0} = 8.0$ and $c_{cp} = 0.35$ was successful in capturing the behaviour of ($T_{3} + T_{4}$) across the flame brush for unity Lewis number flames. The variation of the combined contribution of ($T_{3} + T_{4}$) across the flame brush extracted from DNS data is presented in Fig. 14 along with the predictions of Eq. 22. It can be observed from Fig. 14 that the ($T_{3} + T_{4}$) term is positive towards the unburned side of the flame brush but becomes negative towards the burned gas side, which is consistent with previous analyses (Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Hun and Huh 2008). The magnitude of the ($T_{3} + T_{4}$) term decreases with increases in $g^{*}$ and initial $u^{{\prime }} /S_{L}$ values. The decrease in magnitude of ($T_{3} + T_{4}$) with increasing $g^{*}$ is more pronounced for cases with lower initial $u^{{\prime }} /S_{L}$ (i.e., Set-A and Set-B). It is also evident from Fig. 14 that the model given by Eq. 22 accurately predicts the qualitative behaviour of the combined propagation and curvature term for all cases considered in the present study irrespective of the values of $g^{*}$ and initial $u^{{\prime }} /S_{L}$.

Fig. 14

Variation of the combined propagation and curvature term $(T_{3} + T_{4})\times \delta_{Z}^2/S_L$ (solid line represents the DNS data and dash-dotted line represents the predictions of Eq. 22) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

4.6 Mean Reaction Rate Closure Using Generalised FSD

According to Boger et al. (1998), one obtains:

$$\overline{{\dot{w}}} + \overline{{\nabla .\left( {\uprho D\nabla c} \right)}} = \overline{{\left( {\uprho S_{d} } \right)}}_{s} \Sigma_{gen}$$

(23)

where the two terms on the left-hand side represent the contributions of the reaction rate and molecular diffusion rate, respectively. In the context of RANS simulations, the contribution of the mean molecular diffusion rate in statistically planar flames is much smaller than the mean reaction rate (i.e., $\overline{{\dot{w}}} \gg \overline{{\nabla .\left( {\uprho D\nabla c} \right)}}$) and hence $\overline{{\dot{w}}} \approx \overline{{\left( {\uprho S_{d} } \right)}}_{s} {\Sigma }_{gen}$. For unity Lewis number flames, the surface-averaged density-weighted displacement speed is usually modelled as $\overline{{\left( {\uprho S_{d} } \right)}}_{s} \approx \rho_{0} S_{L}$ (Boger et al. 1998; Cant et al. 1990; Hawkes and Cant 2000; Hernandez-Perez et al. 2011) although this approximation may not be valid, especially for the thin reaction zones regime flames (Chakraborty and Cant 2007, 2009a; Sabelnikov et al. 2017). Thus, the model for mean reaction rate may be expressed as $\overline{{\dot{w}}} =\uprho _{0} S_{L} {\Sigma }_{gen}$ and this model will henceforth be referred to as the RRFSD model.

The predictions of the RRFSD model are shown in Fig. 15 alongside the mean reaction rate $\overline{{\dot{w}}}$ and the combined contribution of the mean values of reaction rate and molecular diffusion rate $\overline{{\dot{w}}} + \overline{{\nabla .\left( {\rho D\nabla c} \right)}}$ extracted from the DNS data. It is evident from Fig. 15 that $\overline{{\nabla .\left( {\uprho D\nabla c} \right)}}$ indeed remains negligible when compared to $\overline{{\dot{w}}}$ in most cases (thus $\overline{{\dot{w}}} \approx \overline{{\left( {\uprho S_{d} } \right)}}_{s} {\Sigma }_{gen}$ remains valid) but the contribution of $\overline{{\nabla .\left( {\uprho D\nabla c} \right)}}$ cannot be ignored for negative values of $g^{*}$ for small turbulence intensities (e.g., $g^{*} = - 3.12$ and − 1.56 for Set-A). The effects of turbulence weaken with increasingly negative values of $g^{*}$ (see Figs. 1, 2, 3), and this tendency is particularly strong for small values of $u^{{\prime }} /S_{L}$ e.g., $g^{*} = - 3.12$ and − 1.56 for Set-A) and thus in these cases $\overline{{\dot{w}}} \gg \overline{{\nabla .\left( {\rho D\nabla c} \right)}}$ do not remain strictly valid. Figure 15 shows that the RRFSD model mostly satisfactorily predicts $\overline{{\dot{w}}}$ extracted from DNS data but under-predicts the magnitude of $\overline{{\dot{w}}}$ for all cases considered, especially towards the product side of the flame brush. This under-prediction is particularly prevalent for negative values of $g^{*}$ and the agreement of the prediction of the RRFSD model and DNS data improves with increasing $g^{*}$ and initial $u^{{\prime }} /S_{L}$ values.

Fig. 15

Variation of $\overline{{\dot{w}}} \times\updelta _{Z} /\uprho _{0} S_{L}$ (solid line represents the DNS data, line with circles represents combined contribution of mean reaction rate and molecular diffusion rate, and dotted line represents the predictions of the RRFSD model) and $\left[ {\overline{{\dot{w}}} + \overline{{\nabla .\left( {\rho D\nabla c} \right)}} } \right] \times\updelta _{Z} /\uprho _{0} S_{L}$ (line with circles) with $\tilde{c}$ for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

The variation of $I_{0} = \overline{{\dot{w}}} /\rho_{0} S_{L} {\Sigma }_{gen}$ with $\tilde{c}$ for the cases considered here are shown in Fig. 16, which shows that the stretch factor remains close to unity throughout the flame brush for most cases considered here except for small turbulence intensities with negative values of $g^{*}$ (e.g., Set-A and Set-B for $g^{*} = - 3.12$ and − 1.56). It is evident from Fig. 16 that the discrepancy between the RRFSD model and $\overline{{\dot{w}}}$ originates due to the approximation of $\overline{{\left( {\uprho S_{d} } \right)}}_{s} \approx \rho_{0} S_{L}$ for most cases and a better representation of $\overline{{\left( {{\uprho }S_{d} } \right)}}_{s}$ is likely to provide an improved prediction of the mean reaction rate. Moreover, the assumption $\overline{{\dot{w}}} \gg \overline{{\nabla .\left( {\rho D\nabla c} \right)}}$ is rendered invalid for small values of $u^{{\prime }} /S_{L}$ in the case of negative $g^{*}$ values (e.g., Set-A with $g^{*} = - 3.12$ and 1.56).This also contributes to the disagreement between the RRFSD model and $\overline{{\dot{w}}}$ for small values of $u^{{\prime }} /S_{L}$ in the case of negative $g^{*}$ values.

Fig. 16

Variation of stretch factor $I_{0}$ = $\overline{{\dot{w}}} /\rho_{0} S_{L} \Sigma_{gen}$ with $\tilde{c}$ (between 0.1 and 0.9) for Set-A to Set-D (1st–4th column) for $g^{*} = - 3.12, - 1.56,0.0,1.56$ and $3.12$ (1st–5th row)

5 Conclusions

The effects of body force on the statistical behaviours of FSD and its transport have been evaluated using a DNS database of three-dimensional statistically planar turbulent premixed flames with unity Lewis number for different sets of initial $u^{{\prime }} /S_{L}$ values. A range of different values of normalised body forces (or Froude numbers) have been considered representing both unstable and stable configurations in terms of density stratification for each set of initial turbulence parameters. The body force is directed from the heavier unburned gas to the lighter burned gas side in the case of unstable density stratification, whereas the body force is directed from the lighter burned gas side to the heavier unburned gas side of the flame in the case of stable density stratification. The unstable (stable) density stratification configuration can alternatively be taken to represent the situations where the flame is subjected to an externally imposed adverse (favourable) pressure gradient. It has been found that an unstable density stratification promotes flame wrinkling and a gradient type transport, especially towards the reactant side of the flame brush where heat release effects are weak. By contrast, the flame wrinkling weakens, and a counter-gradient type transport is promoted for a stable density stratification. The effects of body forces on the behaviour of the various terms of the FSD transport equation have been analysed in detail and it is observed that the tangential strain rate term $T_{2}$ acts as a source and the curvature term $T_{4}$ remains the major sink term towards the burned gas of the flame brush for all cases considered here. The effects of body force on the FSD and the terms of its transport equation weakens with increasing turbulence intensity as the relative strength of body force in comparison to the inertial force weakens with an increase in $u^{{\prime }} /S_{L}$. The magnitudes of $T_{2}$ and $T_{4}$ generally increase with the strengthening of body force from the stable to the unstable density stratification. The performance of the existing models for the tangential strain rate term has been found to be inadequate especially for small values of turbulence intensity under stable density stratification. Based on a-priori analysis of DNS data, an alternative model for the tangential strain rate term $T_{2}$ has been proposed by considering the alignment of $\nabla c$ with local principal strain rates and the competition between turbulent straining and chemical timescales. In this new modelling methodology of $T_{2}$, the effects of turbulent Reynolds number and Froude number have also been explicitly accounted for. It has also been shown that the existing models for the turbulent flux of the FSD and the combined propagation and curvature term $\left( {T_{3} + T_{4} } \right)$ do not need any modifications due to the presence of the body force. Moreover, the FSD based mean reaction rate closure mostly works satisfactorily irrespective of the strength of the body force but under-predicts the magnitude of $\overline{{\dot{w}}}$ for all cases towards the product side of the flame brush. This under-prediction is particularly prevalent for stable density stratification configuration, but this situation improves for the unstable density stratification configuration and also with increasing turbulence intensity. This study has been conducted with simple chemistry in the interest of a detailed parametric analysis. Although previous analyses (Chakraborty and Klein 2008b; Chakraborty et al. 2008) revealed no major differences in the qualitative behaviours of the $\left| {\nabla c} \right|$ transport equation between simple and detailed chemistry, future analyses need to include the effects of detailed chemistry and transport in order to conduct further validation of the models proposed in this analysis.

Finally, it is important to note that a degree of empiricism is involved in Eqs. 12, 13, 17–20 but they satisfy all the asymptotic requirements in terms of $Re_{L}$ and $g^{*}$. Thus, further validation of these models based on a-posteriori assessment will be necessary. It is important to note that the unclosed quantities, such as $\tilde{k}$ and $\tilde{\varepsilon }$, also act as input parameters to the models for the unclosed terms of the FSD transport equation. Thus, turbulence modelling (e.g., the models for $\tilde{k}$ and $\tilde{\varepsilon }$) also interacts with the models of the FSD transport equation in actual RANS simulations. In addition to this, the numerical scheme used in the RANS code is expected to influence the simulation predictions. Thus, it is not straightforward to assess the performances of the terms of the FSD transport equation in isolation. Thus, a model, which fails based on a-priori analysis, is unlikely to perform well in actual RANS simulation but the models, which exhibit promising performance based on a-priori DNS analysis, need to be assessed whether they perform satisfactorily while interacting with turbulence models and numerical schemes in actual RANS simulations. This necessitates a detailed a-posteriori assessment of the newly developed models based on actual RANS simulations for a configuration with well-documented experimental data.