Turbulence Effects on the Statistical Behaviour and Modelling of Flame Surface Density and the Terms of Its Transport Equation in Turbulent Premixed Flames

Abstract

The influence of the ratio of integral length scale to flame thickness on the statistical behaviours of flame surface density (FSD) and its transport has been analysed using a Direct Numerical Simulation database of three-dimensional statistically planar turbulent premixed flames for different turbulence intensities. It has been found that turbulent burning velocity based on volume-integration of reaction rate and flame surface area increase but the peak magnitudes of the FSD and the terms of the FSD transport term decrease with an increase in length scale ratio for a given turbulence intensity. The flame brush thickness and flame wrinkling increase with an increase in length scale ratio for all turbulence intensities. However, the qualitative behaviours of the unclosed terms in the FSD transport equation remain unaltered by the length scale ratio and in all cases the tangential strain rate term and the curvature term act as leading order source and sink, respectively. A decrease in length scale ratio for a given turbulence intensity leads to a decrease in Damköhler number and an increase in Karlovitz number. This has an implication on the alignment of reactive scalar gradient with local strain rate eigenvectors, which in turn increases positive contribution of the tangential strain rate term with a decrease in length scale ratio. Moreover, an increase in Karlovitz number increases the likelihood of negative contribution of the curvature term. Thus, the magnitude of the negative contribution of the FSD curvature term increases with a decrease in length scale ratio for a given turbulence intensity. The model for the tangential strain rate term, which explicitly considers the scalar gradient alignment with local principal strain rate eigenvectors, has been shown to be more successful than the models that do not account for the scalar gradient alignment characteristics. Moreover, the existing model for the curvature and propagation term needed modification to account for greater likelihood of negative values for higher Karlovitz number. However, the models for the unclosed flux of FSD and the mean reaction rate closure are not significantly affected by the length scale ratio.

1 Introduction

The non-linear temperature and species mass fraction dependences of the chemical reaction rate make the closure of mean reaction rate a challenging task in the modelling of turbulent reacting flows. One of the ways that this challenge can be bypassed in turbulent premixed combustion modelling is the closure of flame surface area to volume ratio (Pope 1988; Candel and Poinsot 1990) according to the Flame Surface Density (FSD) based methodology (Pope 1988; Candel and Poinsot 1990; Poinsot and Veynante 2001) under flamelet assumption, which assumes that the consumption rate of reactants per unit flame surface area remains identical to that for the laminar flame. However, the FSD is an unclosed quantity and several attempts have been made to model this quantity based on algebraic (Bray 1980; Cant and Bray 1988, 1989; Abu-Orf and Cant 2000; Boger et al. 1998; Charlette et al. 2002; Knikker et al. 2002; Fureby 2005; Chakraborty and Klein 2008; Ma et al. 2013; Keppeler et al. 2014; Klein et al. 2016; Ahmed et al. 2021; Rasool et al. 2022) and transport equation (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Trouvé and Poinsot 1994; Veynante et al. 1996; Hawkes and Cant 2000, 2001; Chakraborty and Cant 2007, 2009a, 2011, 2013; Hun and Huh 2008; Hernandez-Perez et al. 2011; Katragadda et al. 2011, 2014a, b; Reddy and Abraham 2012; Ma et al. 2014; Sellmann et al. 2017; Papapostolou et al. 2019; Luca et al. 2019; Keil et al. 2020; Varma et al. 2022a; Berger et al. 2022) closures in the context of Reynolds Averaged Navier–Stokes (RANS) (Bray 1980; Cant and Bray 1988, 1989; Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Trouvé and Poinsot 1994; Veynante et al. 1996; Abu-Orf and Cant 2000; Hun and Huh 2008; Chakraborty and Cant 2011, 2013; Ahmed et al. 2021; Katragadda et al. 2011, 2014b; Sellmann et al. 2017; Papapostolou et al. 2019; Luca et al. 2019; Rasool et al. 2022; Varma et al. 2022a; Berger et al. 2022) and Large Eddy Simulations (LES) (Boger et al. 1998; Charlette et al. 2002; Knikker et al. 2002; Fureby 2005; Chakraborty and Klein 2008; Chakraborty and Cant 2007, 2009a; Hun and Huh 2008; Hernandez-Perez et al. 2011; Reddy and Abraham 2012; Ma et al. 2013, 2014; Katragadda et al. 2014a; Keppeler et al. 2014; Klein et al. 2016; Keil et al. 2020). The algebraic closures are designed for the situations where an equilibrium is maintained between the generation and destruction rates of flame surface area (Bray 1980; Cant and Bray 1988, 1989; Abu-Orf and Cant 2000; Boger et al. 1998; Charlette et al. 2002; Knikker et al. 2002; Fureby 2005; Chakraborty and Klein 2008; Ma et al. 2013; Keppeler et al. 2014; Klein et al. 2016; Ahmed et al. 2021; Rasool et al. 2022). However, this equilibrium may not be maintained in flame instabilities and under this condition a modelled transport equation for the FSD might be necessary (Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Trouvé and Poinsot 1994; Veynante et al. 1996; Hawkes and Cant 2000, 2001; Chakraborty and Cant 2007, 2009a, 2011, 2013; Hun and Huh 2008; Hernandez-Perez et al. 2011; Katragadda et al. 2011, 2014a, b; Reddy and Abraham 2012; Ma et al. 2014; Sellmann et al. 2017; Papapostolou et al. 2019; Luca et al. 2019; Keil et al. 2020; Varma et al. 2022a; Berger et al. 2022). The advancements of computational power have enabled significant improvements in the FSD modelling using Direct Numerical Simulations (DNS) data (Trouvé and Poinsot 1994; Boger et al. 1998; Charlette et al. 2002; Chakraborty and Cant 2007, 2009a, 2011, 2013; Hun and Huh 2008; Chakraborty and Klein 2008; Katragadda et al. 2011, 2014a, b; Reddy and Abraham 2012; Klein et al. 2016; Ahmed et al. 2021; Rasool et al. 2022; Papapostolou et al. 2019; Luca et al. 2019; Keil et al. 2020; Varma et al. 2022a; Berger et al. 2022). Among these studies, there have been analyses where the effects of Lewis number (Trouvé and Poinsot 1994; Hun and Huh 2008; Chakraborty and Cant 2011; Katragadda et al. 2011, 2014a, b; Berger et al. 2022), turbulent Reynolds number (Chakraborty and Cant 2013; Luca et al. 2019), buoyancy (or Froude number) (Varma et al. 2022a) and thermodynamic pressure (Keil et al. 2020) on the statistical behaviour of the FSD and its transport were addressed. A number of recent experimental (Kim et al., 2022) and computational (Yu et al. 2017; Varma et al. 2022a; Song et al. 2021, 2022; Trivedi et al. 2022) analyses revealed that the flame surface area and turbulent burning velocity for a given turbulence intensity increase with an increase in integral length scale to flame thickness ratio. Moreover, the analysis by Varma et al. (2022a) further demonstrated that the volume integrated values of the strain rate and curvature contributions to the FSD transport increase with increasing integral length scale to flame thickness ratio. Thus, it is expected that the ratio of integral length scale to flame thickness is likely to have an influence on the statistical behaviours of the FSD and the terms of its transport equation. However, to date, the effects of integral length scale to flame thickness ratio on the statistical behaviour of the FSD and the terms of its transport equation for different turbulence intensities are yet to be analysed in detail. This gap in the existing literature has been addressed in this paper and in this respect, the main objectives of this paper are: (a) to demonstrate the effects of the length scale separation on the magnitudes and statistical behaviours of FSD, wrinkling factor and the unclosed terms of the FSD transport equation, and (b) to indicate modelling implications of the different values of turbulence intensity and length scale ratio on the closure of different terms of the FSD transport equation and identify the appropriate model expressions.

The rest of the paper will be organised in the following manner. The mathematical background and numerical implementation relevant to this analysis are presented in Sects. 2 and 3, respectively. This will be followed by the presentation of results and their discussion. The main findings of the present analysis are summarised, and conclusions are drawn in Sect. 5.

2 Mathematical Background

The reactive scalar field in premixed combustion is often represented by reaction progress variable $c$, which can be defined based on a suitable species $\alpha$ mass fraction ${Y}_{\alpha }$ in the following manner:

$$c=({Y}_{\alpha }-{Y}_{\alpha ,R})/({Y}_{\alpha ,P}-{Y}_{\alpha ,R})$$

(1)

where subscripts R and P represent values in the fully unburned reactants and fully burned products, respectively. According to Eq. (1) $c$ increases from 0 from the unburned reactants to 1.0 in the fully burned products. The transport equation for $c$ takes the following form:

$$\frac{\partial (\rho c)}{\partial t}+\frac{\partial (\rho {u}_{j}c)}{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\left(\rho D\frac{\partial c}{\partial {x}_{j}}\right)+\dot{\omega }$$

(2)

where ${u}_{j}$ is the jth component of velocity, $\rho$ is density, $D$ is the reaction progress variable diffusivity and $\dot{\omega }={\dot{\omega }}_{\alpha }/({Y}_{\alpha ,P}-{Y}_{\alpha ,R})$ is the reaction rate of the progress variable with ${\dot{\omega }}_{\alpha }$ being the reaction rate of species $\alpha$. On Reynolds averaging Eq. (2) one obtains:

$$\frac{\partial (\overline{\rho }\widetilde{c})}{\partial t}+\frac{\partial (\overline{\rho }{\widetilde{u}}_{j}\widetilde{c})}{\partial {x}_{j}}=\overline{\frac{\partial }{\partial {x }_{j}}\left(\rho D\frac{\partial c}{\partial {x}_{j}}\right)}+\overline{\dot{\omega } }-\frac{\partial \overline{{(\rho {u}_{j}^{{{\prime\prime}}}{c}^{{{\prime}}{{\prime}}})}}}{\partial {x}_{j}}$$

(3)

where $\overline{q },\widetilde{q}=\overline{\rho q }/\overline{\rho }$ and ${q}^{{{\prime}}{{\prime}}}=q-\widetilde{q}$ are the Reynolds averaged, Favre averaged and Favre fluctuations of a general quantity $q$, respectively. All the terms on the right-hand side of Eq. (3) are unclosed and need modelling. The closure of the last term needs modelling of turbulent scalar flux ${\overline{(\rho {u}_{j}^{{{\prime}}{{\prime}}}{c}^{{{\prime}}{{\prime}}})}}$ and the first two terms are modelled in the following manner in the context of FSD based methodology (Trouvé and Poinsot 1994; Boger et al. 1998):

$$\overline{{\nabla \cdot \left(\rho D\nabla c\right)}}+\overline{\dot{\omega } }=\overline{{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{gen}$$

(4)

where ${\Sigma }_{gen}=\overline{{|\nabla c|}}$ is the generalised FSD (Boger et al. 1998; Poinsot and Veynante 2001), ${S}_{d}=(Dc/Dt)/|\nabla c|$ is the displacement speed and $\overline{{\left(q\right)}}_{s}=\overline{{q|\nabla c|}}/\overline{{|\nabla c|}}$ is the surface averaged value of a general variable $q$ (Trouvé and Poinsot 1994; Boger et al. 1998). The transport equation of ${\Sigma }_{gen}$ is given by (Pope 1988; Candel and Poinsot 1990):

$$ \begin{aligned} & \partial \Sigma _{{gen}} /\partial t + \partial \left( {\tilde{u}_{j} \Sigma _{{gen}} } \right)/\partial x_{j} = \underbrace {{ - \partial \left\{ {\left[ {\overline{{\left( {u_{k} } \right)_{s} }} - \tilde{u}_{k} } \right]\Sigma _{{gen}} } \right\}/\partial x_{k} }}_{{T_{1} - turbulent~transport}} \\ & \quad + \underbrace {{\overline{{\left( {\left( {\delta _{{ij}} - N_{i} N_{j} } \right)\partial u_{i} /\partial x_{j} } \right)_{s} }} \Sigma _{{gen}} }}_{{T_{2} - strain~rate}}\underbrace {{ - \partial \left[ {\overline{{\left( {S_{d} N_{k} } \right)_{s} }} \Sigma _{{gen}} } \right]/\partial x_{k} }}_{{T_{3} - propagation}} + \underbrace {{\overline{{\left( {S_{d} \partial N_{i} /\partial x_{i} } \right)_{s} }} \Sigma _{{gen}} }}_{{T_{4} - curvature}} \\ \end{aligned} $$

(5)

where $\overrightarrow{N}=-\nabla c/\left|\nabla c\right|$ is the local flame normal vector. In Eq. (5), ${T}_{1}$ is the turbulent transport term. The term ${T}_{2}$ is commonly referred to as the strain rate term because it originates due to the tangential strain rate ${a}_{T}=\left({\delta }_{ij}-{N}_{i}{N}_{j}\right)\partial {u}_{i}/\partial {x}_{j}$, whereas ${T}_{3}$ is referred to as the FSD propagation term and ${T}_{4}$ is known as the FSD curvature term because it arises as a result of flame curvature ${\kappa }_{m}=0.5\nabla \cdot \overrightarrow{N}=0.5 (\partial {N}_{i}/\partial {x}_{i})$. All the terms on the right-hand side of Eq. (5) (i.e., ${T}_{1},{T}_{2},{T}_{3}$ and ${T}_{4}$) are unclosed and therefore they need to be modelled. The modelling of ${T}_{1},{T}_{2},{T}_{3}$ and ${T}_{4}$ will be discussed in detail in Sect. 4 of this paper.

3 Numerical Implementation

DNS simulations of statistically planar premixed flames for different turbulence intensities for two different integral length scale to flame thickness ratios have been considered for this analysis. These simulations have been conducted using a well-known compressible DNS code SENGA+ (Jenkins and Cant 1999). In SENGA+ , the conservation equations of mass, momentum, energy, and species are solved in non-dimensional form. In SENGA+ , all first and second-order derivatives for the internal grid points are evaluated using a 10th order central difference scheme but the order of accuracy gradually drops to a one-sided 2nd order scheme at the non-periodic boundaries (Jenkins and Cant 1999). An explicit 3rd order Runge–Kutta scheme (Wray 1990) is used for the time-advancement of all governing equations. All the simulations consider inlet and outlet boundaries in the direction of mean flame propagation, whereas transverse boundaries are considered to be periodic. The outflow boundary is considered to be partially non-reflecting and specified according to the well-known Navier–Stokes Characteristic Boundary Conditions (NSCBC) technique (Poinsot and Lele 1992). Here the mean inlet velocity ${U}_{mean}$ was gradually altered to match the turbulent burning velocity in order to ensure that the flame remains stationary in the statistical sense within the computational domain. A well-known pseudo-spectral method (Rogallo 1981) is used to initialise the fluctuating velocity field by a homogeneous isotropic incompressible distribution following the Batchelor-Townsend spectrum (Batchelor and Townsend 1948) for prescribed values of root-mean-square turbulent velocity ${u}^{{\prime}}$ and the integral length scale of turbulence $l$. The reacting scalar field is initialised by a unstretched laminar flame solution. A modified bandwidth filtered forcing method (Klein et al. 2017) in physical space is used for the current analysis, which yields a forcing term proportional to $(1-c)$ in the momentum equation such that the forcing is employed for the unburned gas ahead of the flame. This forcing scheme maintains both the required values of root-mean-square velocity ${u}^{{\prime}}$ and the integral length scale of turbulence $l \epsilon_d$ in the unburned gas (i.e., $c<0.001$). Table 1 lists the simulation domain size, the uniform Cartesian grid for discretisation along with the inlet values of root-mean-square turbulent velocity fluctuation normalised by the unstrained laminar burning velocity ${u}^{{\prime}}/{S}_{L}$, integral length scale to the Zel’dovich flame thickness ratio $l/{\delta }_{z}$, Damköhler number $Da=l{S}_{L}/{u}^{{\prime}}{\delta }_{z}$, Karlovitz number $Ka={\left({u}^{{\prime}}/{S}_{L}\right)}^{3/2}{\left(l/{\delta }_{z}\right)}^{-1/2}$ and heat release parameter $\tau =({T}_{ad}-{T}_{0})/{T}_{0}$ where the Zel’dovich flame thickness ${\delta }_{z}$ is defined as: ${\delta }_{z}={\alpha }_{T0}/{S}_{L}$ with ${\alpha }_{T0}$ and ${S}_{L}$ being the thermal diffusivity and unstrained laminar burning velocity, respectively. The locations of these cases on Borghi-Peters diagram (Peters 2000) are shown in Fig. 1, which shows that the cases considered here span from the wrinkled flamelet regime to the high Karlovitz number thin reaction zones regime. The grid spacing used here ensures at least 10 grid points within ${\delta }_{th}=({T}_{ad}-{T}_{0})/\mathrm{max}{\left|\nabla T\right|}_{L}$ with $T,{T}_{0}$ and ${T}_{ad}$ being the dimensional temperature, unburned gas temperature and the adiabatic flame temperature, respectively. This implies that the steepest gradients of temperature and reaction progress variable have been resolved using at least 10 grid points. Moreover, the reaction zone for the present thermochemistry (i.e., $0.4<c<0.95$) has at least 10 grid points for the current database. Moreover, at least 1.5 grid points are kept within the Kolmogorov length scale $\eta$ for the simulation parameters considered here. The values of $l/{\delta }_{z}=2.625$ and 5.25 correspond to $l/{\delta }_{th}=1.5$ and 3.0 for the present thermochemistry. The chemical mechanism is simplified by a single-step Arrhenius mechanism representing stoichiometric methane-air flame in this analysis in the interests of the computational economy for a detailed parametric analysis. The Lewis number of all the species is taken to be unity and the gaseous mixture is taken to obey the ideal gas law. Standard values are considered for Prandtl number (i.e., $Pr=0.7$), Zel’dovich number (i.e., $\beta ={T}_{ac}\left({T}_{ad}-{T}_{0}\right)/{T}_{ad}^{2}=6.0$ with ${T}_{ac}$ being the activation temperature) and the ratio of specific heats (i.e., $\gamma =1.4$). It was demonstrated that the flame propagation and reactive scalar statistics obtained from simple chemistry DNS of stoichiometric methane-air premixed flames remain in good qualitative agreement with the corresponding detailed chemistry simulations (Keil et al. 2021a, b). The quantitative differences remain comparable to the uncertainties associated with the different definitions of reaction progress variable in detailed chemistry simulations (Keil et al. 2021b).

Table 1 Simulation parameters for all cases considered

Fig. 1

The cases considered here on the Borghi–Peters regime diagram

All the simulations listed in Table 1 have been conducted until the desired values of turbulent kinetic energy and integral length scale have been obtained and also the turbulent burning velocity ${S}_{T}$ and flame surface area ${A}_{T}$ reach statistically stationary states. The readers are directed to Varma et al. (2021) to find out statistically steady nature of volume integrated FSD transport for the database considered in this work. This simulation time remains greater than the through-pass time (i.e., ${t}_{sim}>{L}_{x}/{U}_{mean}$) and at least 10 eddy turn over times (i.e., ${t}_{sim}>10l/u{^{\prime}}$) for all cases.

In order to obtain Reynolds/Favre averaged quantities, the quantities of interest are averaged in the transverse directions normal to the mean flame propagation (i.e., homogeneous directions) and also in time over 2 chemical times (i.e., $2{t}_{c}=2{\delta }_{z}/{S}_{L}$) following previous analyses (Trouvé and Poinsot 1994; Veynante et al. 1997; Katragadda et al. 2011, 2014a; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Varma et al. 2022a). For statistically planar flames, the Favre-averaged reaction progress variable $\widetilde{c}$ is a function of the coordinate in the direction of mean flame propagation (i.e., $x$-direction). As all the terms in the FSD transport equation and $\widetilde{c}$ are functions of $x$, the results presented in this paper are not dependent on the averaging over bins of $\widetilde{c}$. Thus, all the quantities in Sect. 4 will be presented as a function of $\widetilde{c}$ for the sake of generality. These results do not change appreciably (i.e., the maximum variation is of the order of 2%) if the distinct half of the domain and half of the time duration of averaging are considered instead of the full sample size and time series, as used in the results section of this paper.

4 Results and Discussion

4.1 Flame-Turbulence Interaction and Statistical Behaviour of the FSD

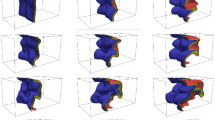
The reaction progress variable $c$ isosurfaces when the flames have reached statistically stationary state are shown in Fig. 2. It can be seen from Fig. 2 that the extent of flame wrinkling increases with increasing ${u}^{{\prime}}/{S}_{L}$ for a given value of $l/{\delta }_{z}$, as expected. Figure 2 further shows that the extent of flame wrinkling also increases with increasing $l/{\delta }_{z}$ for a given value of ${u}^{{\prime}}/{S}_{L}$. The observations from Fig. 2 can be substantiated from the variations of the values of normalised flame surface area ${A}_{T}/{A}_{L}$ and normalised turbulent burning velocity ${S}_{T}/{S}_{L}$, which are shown Fig. 3. Here, ${A}_{T}$ and ${S}_{T}$ are defined as ${A}_{T}={\int }_{V}|\nabla c|dV$ and ${S}_{T}={\left({\rho }_{0}{A}_{L}\right)}^{-1}{\int }_{V}\dot{\omega }dV$ where ${A}_{L}$ is the projected flame surface area in the direction of mean flame propagation. Figure 3 shows that ${A}_{T}/{A}_{L}$ increases with increasing $l/{\delta }_{z}$ for a given value of $u{^{\prime}}/{S}_{L}$, which is also reflected with an increase in ${S}_{T}/{S}_{L}$ with an increase in $l/{\delta }_{z}$ for a given value of ${u}^{{\prime}}/{S}_{L}$. Moreover, for a given value of $l/{\delta }_{z}$, the normalised flame surface area ${A}_{T}/{A}_{L}$ increases monotonically with increasing ${u}^{{\prime}}/{S}_{L}$ before the bending occurs, which is observed for ${u}^{{\prime}}/{S}_{L}\ge 7.5$ for the DNS database considered here (Ahmed et al. 2019; Varma et al. 2021). The normalised flame surface area ${A}_{T}/{A}_{L}$ can be parameterised as: ${A}_{T}/{A}_{L}={\left({\eta }_{o}/{\eta }_{c}\right)}^{{D}_{f}-2}$ where ${\eta }_{c}$ and ${\eta }_{o}$ are respectively the inner and outer cut-off length scales and ${D}_{f}$ (with ${D}_{f}>2$) (Gouldin et al. 1989; Chakraborty and Klein 2008; Tamadonfar and Gülder 2014; Ahmed et al. 2019) is the fractal dimension of the flame surface. The inner cut-off scale ${\eta }_{c}$ can be taken to scale with the flame thickness ${\delta }_{z}$ (Knikker et al. 2002; Chakraborty and Klein 2008) and the integral length scale $l$ is usually taken to be the measure of the outer cut-off scale ${\eta }_{o}$ in the context of RANS (Gouldin et al. 1989; Poinsot and Veynante 2001). This suggests that ${A}_{T}/{A}_{L}$ scales with ${\left(l/{\delta }_{z}\right)}^{{D}_{f}-2}$, which implies that ${A}_{T}/{A}_{L}$ is expected to increase with increasing $l/{\delta }_{z}$. Further physical explanations behind an increase in ${A}_{T}/{A}_{L}$ with increasing $l/{\delta }_{z}$ for a given value of ${u}^{{\prime}}/{S}_{L}$ and the bending behaviour have been discussed elsewhere (Ahmed et al. 2019; Varma et al. 2021) in detail for this database and thus are not repeated here. For these statistically planar flame cases, Damköhler’s first hypothesis (i.e., ${S}_{T}/{S}_{L}={A}_{T}/{A}_{L}$) is maintained (Ahmed et al. 2019; Varma et al. 2021) and the physical explanations for the validity of Damköhler’s first hypothesis for statistically planar flames were provided elsewhere (Chakraborty et al. 2019) and thus are not repeated here.

Fig. 2

Instantaneous views of reaction progress variable $c=\mathrm{0.1,0.5}$ and $0.9$ isosurfaces for cases with $l/{\delta }_{z}=2.625$ (left column) and $5.25$ (right column). Note different dimensions of the domain between $l/{\delta }_{z}=2.625$ and $5.25$ cases

Fig. 3

Variations of ${A}_{T}/{A}_{L}$ and ${S}_{T}/{S}_{L}$ with $u{^{\prime}}/{S}_{L}$ for all cases considered here

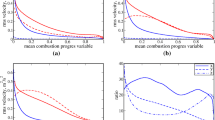
The variations of ${\Sigma }_{gen}\times {\delta }_{z}$ with $\widetilde{c}$ for all cases considered here are shown in Fig. 4 (first column). It can be seen from Fig. 4 (first column) that the peak value of ${\Sigma }_{gen}$ mostly increases (mildly) with increasing ${u}^{{\prime}}/{S}_{L}$, whereas the peak value of ${\Sigma }_{gen}$ for smaller values of $l/{\delta }_{z}$ is significantly greater than the higher value of $l/{\delta }_{z}$. In order to understand this behaviour of ${\Sigma }_{gen}=\Xi \times |\nabla \overline{c }|$, it is worthwhile to consider the variations of $|\nabla \overline{c }|$ and $\Xi$ with $\widetilde{c}$, which are also shown in Fig. 4 (second and third columns, respectively). Here, wrinkling factor $\Xi$ is defined as: $\Xi ={\Sigma }_{\mathrm{gen}}/|\nabla \overline{c }|$ (Weller et al. 1998; Charlette et al. 2002). It can be seen from Fig. 4 (second column) that the peak value of $|\nabla \overline{c }|$ is smaller for higher values of $l/{\delta }_{z}$. The turbulent flame brush thickness can be quantified as ${\delta }_{b}\sim 1/max|\nabla \overline{c }|$, and thus a smaller peak value of $|\nabla \overline{c }|$ for higher values of $l/{\delta }_{z}$ is representative of a thicker flame brush because of greater extent of flame wrinkling (see Fig. 2). The greater extent of flame wrinkling for higher values of $l/{\delta }_{z}$ is reflected in the higher values of wrinkling factor $\Xi$, as shown in Fig. 4 (third column). However, the decrease in $|\nabla \overline{c }|$ with an increase in $l/{\delta }_{z}$ overwhelms the increase in $\Xi$ to give rise to a decrease in peak values of ${\Sigma }_{gen}=\Xi \times |\nabla \overline{c }|$ with an increase in $l/{\delta }_{z}$.

Fig. 4

Variations of generalised FSD ${\Sigma }_{gen}\times {\delta }_{z}$ (first column), resolved FSD $\left|\nabla \overline{c }\right|\times {\delta }_{z}$ (second column) and wrinkling factor $\Xi$ (third column) with $\widetilde{c}$ for all cases considered. The black dashed line represents the minimum possible value of wrinkling factor (i.e., $\Xi =1.0$)

4.2 Variations of the Unclosed Terms in the FSD Transport Equation

The challenges of algebraic closures of ${\Sigma }_{gen}$ in the context of RANS were discussed elsewhere (Ahmed et al. 2021; Rasool et al. 2022) and qualitatively similar results have been obtained for the present database so will not be discussed further. Instead, the present analysis will focus on the effects of ${u}^{{\prime}}/{S}_{L}$ and $l/{\delta }_{z}$ on the unclosed terms of the FSD ${\Sigma }_{gen}$ transport equation. The variations of the normalised unclosed terms of the FSD transport equation (i.e., $\left\{{T}_{1},{T}_{2},{T}_{3},{T}_{4}\right\}\times {\delta }_{z}^{2}/{S}_{L}$) with $\widetilde{c}$ are shown in Fig. 5 for the cases considered here. It can be seen from Fig. 5 that the qualitative behaviours of the terms of the FSD transport equation are not influenced by $l/{\delta }_{z}$ but the magnitudes of the leading order source and sink contributions by the strain rate term ${T}_{2}$ and the curvature term ${T}_{4}$, respectively are smaller for higher values of $l/{\delta }_{z}$. Moreover, the magnitudes of the leading order source and sink contributions of ${T}_{2}$ and ${T}_{4}$, respectively increase with increasing ${u}^{{\prime}}/{S}_{L}$ for a given value of $l/{\delta }_{z}$. It can be seen from Fig. 5 that the strain rate term ${T}_{2}$ acts as a leading order source for all cases, where ${T}_{4}$ assumes positive values towards the unburned gas side of the flame brush and becomes negative towards the burned gas side for small turbulence intensities (e.g., ${u}^{{\prime}}/{S}_{L}=1.0$ and 3.0) but for high turbulence intensities (e.g., ${u}^{{\prime}}/{S}_{L}=7.5$ and 10.0) the curvature term ${T}_{4}$ predominantly assumes negative values throughout the flame brush. The propagation term ${T}_{3}$ and the turbulent transport term ${T}_{1}$ assume locally positive and negative values within the flame brush but the magnitude of their relative contributions in comparison to the magnitudes of ${T}_{2}$ and ${T}_{4}$ diminish with increasing ${u}^{{\prime}}/{S}_{L}$. These behaviours are qualitatively similar to previous studies for both simple (Trouvé and Poinsot 1994; Chakraborty and Cant 2011, 2013; Varma et al. 2022a) and detailed (Luca et al. 2019; Papaposolou et al. 2019; Berger et al. 2022) chemistry and also with the scaling arguments by Chakraborty and Cant (2013). The modelling of these unclosed terms will be addressed next in this paper.

Fig. 5

Variations of the normalised unclosed terms of the FSD transport equation $\left\{{T}_{1},{T}_{2},{T}_{3},{T}_{4}\right\}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) and for ${u}^{{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

4.3 Modelling of the Turbulent Transport Term ${{\varvec{T}}}_{1}$

Equation 5 indicates that the closure of the turbulent transport term ${T}_{1}$ depends on the modelling of the turbulent flux of the generalised FSD $\left[{\overline{\left({u}_{i}\right)}}_{s}-\widetilde{{u}_{i}}\right]{\Sigma }_{gen}$. The conventional way to close $\left[{\overline{\left({u}_{i}\right)}}_{s}-\widetilde{{u}_{i}}\right]{\Sigma }_{gen}$ is to employ a classical gradient hypothesis (Poinsot and Veynante 2001; Hawkes and Cant 2000, 2001):

$$\left[{\overline{\left({u}_{i}\right)}}_{s}-{\widetilde{u}}_{i}\right]{\Sigma }_{gen}=-\left({\upnu }_{t}/S{c}_{\Sigma }\right)\partial {\Sigma }_{gen}/\partial {x}_{i}$$

(6)

Here ${\upnu }_{t}={C}_{\upmu }{\widetilde{k}}^{2}/\widetilde{\epsilon }$ is the kinematic eddy viscosity, ${C}_{\mu }=0.09$ is the model parameter and $S{c}_{\Sigma }$ is a suitable turbulent Schmidt number with $\widetilde{k}=\overline{\rho {u}_{i}^{{{\prime}}{{\prime}}}{u}_{i}^{{{\prime}}{{\prime}}}}/2\overline{\rho }$ and $\widetilde{\epsilon }=\overline{\mu \left(\partial {u}_{i}^{{{\prime}}{{\prime}}}/\partial {x}_{j}\right){(\partial u}_{i}^{{{\prime}}{{\prime}}}/\partial {x}_{j})}/\overline{\rho }$ being the turbulent kinetic energy and its dissipation rate, respectively (Poinsot and Veynante 2001; Hawkes and Cant 2000, 2001). The only non-zero component of the FSD flux is $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{1}\right]{\Sigma }_{gen}$ for statistically planar flames propagating in the negative ${x}_{1}-$ direction. The variations of $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{1}\right]{\Sigma }_{gen}\times {\delta }_{z}/{S}_{L}$ and $(\partial {\Sigma }_{gen}/\partial {x}_{1})\times {\delta }_{z}^{2}$ with $\widetilde{c}$ for all cases considered here are shown in Figs. 6 and 7, respectively. A comparison between Figs. 6 and 7 reveals that $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{1}\right]{\Sigma }_{gen}$ and $(\partial {\Sigma }_{gen}/\partial {x}_{1})$ show different signs for a major part of the flame brush and this tendency is particularly prevalent for small values of turbulence intensity. This suggests $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{1}\right]{\Sigma }_{gen}$ exhibits counter-gradient transport for small values of ${u}^{^{\prime}}/{S}_{L}$ and therefore the gradient hypothesis based model given by Eq. (6) is not suitable for the purpose of modelling $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{1}\right]{\Sigma }_{gen}$ and therefore its prediction is not shown in Fig. 6.

Fig. 6

Variation of $\left[{\overline{\left({u}_{i}\right)}}_{s}-\widetilde{{u}_{i}}\right]{\Sigma }_{gen}\times {\delta }_{z}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of Eq. (7) for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

Fig. 7

Variation of $(\partial {\Sigma }_{gen}/\partial {x}_{1})\times {\delta }_{z}^{2}$ with $\widetilde{c}$ along for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) and for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

Previously a model for the turbulent flux of generalised FSD was proposed by Chakraborty and Cant (2009b, 2011) in the following manner, which can predict both gradient and counter-gradient behaviour:

$$\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{i}\right]{\Sigma }_{gen}=\frac{\left(1-2\widetilde{c}\right)\overline{\rho {u}_{i}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}{c}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}}{\Sigma }_{gen}}{\overline{\rho {c}^{\mathrm{^{\prime}}\mathrm{^{\prime}}2}}+\overline{\rho} \widetilde{c}\left(1-\widetilde{c}\right)}$$

(7)

This model accounts for the fact the FSD flux $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{i}\right]{\Sigma }_{gen}$ exhibits a counter-gradient (gradient) behaviour when $\overline{\rho {u}_{i}^{{{\prime}}{^{\prime}}}{c}^{{{\prime}}{^{\prime}}}}$ shows a counter-gradient (gradient) transport. It can be seen from Fig. 6 that the model given by Eq. (7) provides satisfactory prediction of $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{i}\right]{\Sigma }_{gen}$ for all cases considered here. The competition between turbulent velocity fluctuation $\sqrt{2\widetilde{k}/3}$ and the velocity jump due to heat release $\tau {S}_{L}$ determines the nature of turbulent transport (Veynante et al. 1997; Chakraborty and Cant 2009b-d) and thus $l/{\delta }_{z}$ is unlikely have any influence on the closure of $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{i}\right]{\Sigma }_{gen}$. Although Eq. (7) captures the qualitative behaviour of $\left[{\overline{\left({u}_{1}\right)}}_{s}-{\widetilde{u}}_{i}\right]{\Sigma }_{gen}$, there is a scope for improvement for quantitative agreement. As the magnitude of ${T}_{1}$ remains small in comparison to the leading order contributions of ${T}_{2}$ and ${T}_{4}$ and thus the modelling inaccuracies of ${T}_{1}$ using Eq. (7) is not expected to affect the closure of the ${\Sigma }_{gen}$ transport equation. Moreover, it is worth noting that the successful performance of Eq. (7) depends on the successful closures of $\overline{\rho {u}_{1}^{{{\prime}}{{\prime}}}{c}^{{{\prime}}{{\prime}}}}$ and $\overline{\rho {c}^{{^{\prime}}{^{\prime}}2}}$, which have been addressed elsewhere (Veynante et al. 1997; Chakraborty and Cant 2009b-d; Chakraborty and Swaminathan 2011; Varma et al. 2022b) and will not be addressed further in this paper.

4.4 Modelling of the Turbulent Strain Rate Term ${{\varvec{T}}}_{2}$

The tangential strain rate term ${T}_{2}$ is traditionally modelled by splitting it in the following manner (Cant et al. 1990; Candel et al. 1990; Poinsot and Veynante 2001):

$$ T_{2} = \underbrace {{\left[ {\delta _{{ij}} - \overline{{\left( {N_{i} N_{j} } \right)}} _{s} } \right]\frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }}\Sigma _{{gen}} }}_{{S_{R} }} + \underbrace {{\overline{{\left( {\left( {\delta _{{ij}} - N_{i} N_{j} } \right)\frac{{\partial u_{i}^{{\prime \prime }} }}{{\partial x_{j} }}} \right)}} _{s} \Sigma _{{gen}} }}_{{S_{{UR}} }} $$

(8)

where ${S}_{R}$ and ${S}_{UR}$ are the resolved and unresolved components of the strain rate term, respectively. It can be appreciated from Eq. (8) that the closure of ${S}_{R}$ depends on the closures of the orientation factors ${\overline{\left({N}_{i}{N}_{j}\right)}}_{s}$, which is modelled by Cant et al (1990) as: ${\overline{\left({N}_{i}{N}_{j}\right)}}_{s}={\overline{\left({N}_{i}\right)}}_{s}{\overline{\left({N}_{j}\right)}}_{s}+\left({\updelta }_{ij}/3\right)\left[1-{\overline{\left({N}_{k}\right)}}_{s}{\overline{\left({N}_{k}\right)}}_{s}\right]$ where ${\overline{\left({N}_{i}\right)}}_{s}=-(\partial \overline{c }/\partial {x}_{i})/{\Sigma }_{gen}$ is the i^th component of the surface averaged flame normal vector. However, $\widetilde{c}$ is obtained from RANS simulations but $\overline{c }$ needs to be extracted from $\widetilde{c}$ in order to evaluate ${\overline{\left({N}_{i}\right)}}_{s}$. A presumed bimodal probability density function of $c$ with impulses at $c=0$ and $c=1.0$ yields $\overline{c}=\left(1+\uptau \right)\widetilde{c}/\left(1+\uptau \widetilde{c}\right)+O\left(\upgamma \right)$, where $O\left(\gamma \right)$ accounts for the contribution of the burning mixture (Bray et al. 1985), which is expected to be negligible for large values of Damköhler number (i.e., $Da\gg 1$). However, PDFs of $c$ cannot be approximated by a bi-modal distribution in the thin reaction zones regime flames with $Da<1$. Therefore, Katragadda et al. (2011) proposed a modification to the BML expression for $\overline{c}$ for $Da<1$ in the following manner: $\overline{c}=\left(1+\tau .{g}^{a}\right)\widetilde{c}/\left(1+\tau .{g}^{a}\widetilde{c}\right)$ where $g=\widetilde{{c}^{{{\prime}}{{\prime}}2}}/[\widetilde{c}\left(1-\widetilde{c}\right)]$ is the segregation factor, and $a=1.5$ is a model parameter. An alternative expression for $\overline{c}$ was proposed by Bray et al. (2011) in the following manner: $\overline{c }=\widetilde{c}+\tau \overline{\rho {{c }^{{{\prime}}{{\prime}}}}^{2}}/{\rho }_{0}$. It was demonstrated elsewhere (Ahmed et al. 2021; Rasool et al. 2022) that $\overline{c}$ models proposed by Katragadda et al. (2011) and Bray et al. (2011) exhibit comparable performance and satisfactorily predicts $\overline{c}$ extracted from DNS data. The same conclusion holds also for this study and thus the predictions of $\overline{c}=\left(1+\tau .{g}^{a}\right)\widetilde{c}/\left(1+\tau .{g}^{a}\widetilde{c}\right)$ and $\overline{c }=\widetilde{c}+\tau \overline{\rho {{c }^{{{\prime}}{{\prime}}}}^{2}}/{\rho }_{0}$ are not explicitly shown here for the sake of conciseness.

Another alternative model for ${\overline{\left({N}_{i}{N}_{j}\right)}}_{s}$ was proposed by Veynante et al. (1996), which is given as: ${\overline{\left({N}_{i}{N}_{j=i}\right)}}_{s}={\sum }_{k\ne i}\widetilde{{u}_{k}^{{{\prime}}{{\prime}}}{u}_{k}^{{{\prime}}{{\prime}}}}/4\widetilde{k}$ and ${\overline{\left({N}_{i}{N}_{j\ne i}\right)}}_{s}=\widetilde{{u}_{i}^{{{\prime}}{{\prime}}}{u}_{j}^{{{\prime}}{{\prime}}}}/2\widetilde{k}$. The models by Veynante et al. (1996) and Cant et al. (1990) will henceforth be referred to as the VPDM and MCPB models, respectively. The predictions of these models are compared to the variation of ${S}_{R}$ with $\widetilde{c}$ across the flame brush, as obtained from DNS data, in Fig. 8. Figure 8 shows that the predictions of the MCPB model mostly captures ${S}_{R}$ behaviour obtained from DNS data, although it slightly underpredicts the magnitude of ${S}_{R}$ especially for small values of ${u}^{^{\prime}}/{S}_{L}$ (e.g., ${u}^{^{\prime}}/{S}_{L}=1.0$ and 3.0). The VPDM model, on the other hand, overpredicts ${S}_{R}$ values for ${u}^{^{\prime}}/{S}_{L}=3.0$ and 5.0 towards the burned gas side for $l/{\delta }_{z}=2.625$ but a satisfactory agreement between DNS data and VPDM model is obtained for $l/{\delta }_{z}=5.25$.

Fig. 8

Variation of ${S}_{R}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the MCPB and VPDM models for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

The discrepancy between model predictions and DNS data in the modelling of ${S}_{R}$ originates due to the uncertainty of closure of the orientation factors ${\overline{\left({N}_{i}{N}_{j}\right)}}_{s}$. Cant et al. (1990) assume isotropic distribution of the fluctuating part of the flame normal components while deriving the MCPB model. However, experimental analysis by Veynante et al. (1996) and DNS data by Chakraborty and Cant (2006) revealed that the assumption of the isotropic fluctuation of the flame normal vector does not remain valid especially for small and moderate turbulence intensities. This is responsible for the underprediction of ${S}_{R}$ by the MCPB model. Although the VPDM model does not assume isotropic nature of fluctuating part of the flame normal components, but the modelling inaccuracies involved in estimating ${\overline{\left({N}_{i}{N}_{j}\right)}}_{s}$ leads to the disagreement between the VPDM model and DNS data in Fig. 8. The level of isotropy of flame normal component fluctuations is expected to hold better for smaller values of $l/{\delta }_{z}$ (e.g., $l/{\delta }_{z}=2.625$) and thus the VPDM model performs relatively better for higher values of $l/{\delta }_{z}$ (e.g., $l/{\delta }_{z}=5.25$) where the aforementioned isotropy effects are expected to be weak.

The unresolved component ${S}_{UR}$ is modelled by the models proposed by Cant et al. (1990) and Candel et al. (1990), which will henceforth be referred to as the SCPB and SCFM models, respectively. According to Cant et al. (1990) ${S}_{UR}$ is modelled as ${S}_{UR}=0.28\sqrt{\widetilde{\upepsilon }/{\upnu }_{0}}{\Sigma }_{gen}$, where ${\upnu }_{0}$ is the kinematic viscosity of the unburned gas. By contrast, the SCFM model considers ${S}_{UR}={\mathrm{a}}_{0}{\Gamma }_{k}\left(\widetilde{\upepsilon }/\widetilde{k}\right){\Sigma }_{gen}$, where ${\mathrm{a}}_{0}=2.0$ is a model parameter and ${\Gamma }_{k}$ is the efficiency function (as proposed by Meneveau and Poinsot (1991)) which is a function of ${l}_{t}/{\updelta }_{z}$ and $\sqrt{2\widetilde{k}/3}/{S}_{L}$ and ${l}_{t}={C}_{k}{\widetilde{k}}^{3/2}/\widetilde{\upepsilon }$ is the local integral length scale where ${C}_{k}=1.5$ (Sreenivasan 1984). The predictions of the SCPB and SCFM models are shown along with the ${S}_{UR}$ extracted from the DNS data in Fig. 9. It can be seen from Fig. 9 that both SCPB and SCFM models significantly overpredict ${S}_{UR}$ for all cases. The extent of this overprediction is greater for the SCFM model than the SCPB model for small values of turbulence intensity (e.g., ${u}^{^{\prime}}/{S}_{L}=1.0$ and 3.0) but the predictions of these models become comparable for large values of turbulence intensity (e.g., ${u}^{^{\prime}}/{S}_{L}=10.0$). Moreover, ${S}_{UR}$ assumes locally small negative values for ${u}^{^{\prime}}/{S}_{L}=1.0$ for both $l/{\delta }_{z}=2.625$ and 5.25 whereas both SCPB and SCFM models can only predict positive values.

Fig. 9

Variation of ${S}_{UR}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the SCPB and SCFM models for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

It is worth noting that both SCPB and SCFM models consider only the turbulent time scale to model ${S}_{UR}$. The SCPB model considers the Kolmogorov timescale (i.e., $\sqrt{{\upnu }_{0}/\widetilde{\upepsilon }}$), whereas the SCFM model accounts for large scale turbulent timescale (i.e., $\widetilde{k}/\widetilde{\upepsilon }$) but the unsatisfactory performance of both the SCPB and SCFM models indicate that turbulent timescale alone is not sufficient to model ${S}_{UR}$ and ${T}_{2}$. The term ${S}_{UR}$ can be expressed as: ${S}_{UR}=(\overline{{e }_{\alpha }{\mathrm{sin}}^{2}{\theta }_{\alpha }+{e}_{\beta }{\mathrm{sin}}^{2}{\theta }_{\beta }+{e}_{\gamma }{\mathrm{sin}}^{2}{\theta }_{\gamma }) } ($ (where ${e}_{\alpha },{e}_{\beta }$ and ${e}_{\gamma }$ are the most extensive, intermediate and the most compressive principal fluctuating strain rate tensor (i.e., ${e}_{ij}=0.5\,(\partial {u}_{i}^{{{\prime}}{{\prime}}}/\partial {x}_{j}+\partial {u}_{j}^{{{\prime}}{{\prime}}}/\partial {x}_{i})$) and ${\theta }_{\alpha },{\theta }_{\beta }$ and ${\theta }_{\gamma }$ are angles between $\nabla c$ and eigenvectors associated with ${e}_{\alpha },{e}_{\beta }$ and ${e}_{\gamma }$, respectively. The SCPB and SCFM models implicitly assume the collinear alignment of $\nabla c$ with the eigenvector corresponding to ${e}_{\gamma }$, which is valid only for passive scalar mixing. For high values of Damköhler number premixed flames, $\nabla c$ may locally align with the eigenvector corresponding to ${e}_{\alpha }$ (Chakraborty and Swaminathan 2007), which is ignored in these models. Therefore, both SCPB and SCFM models cannot predict the negative values of ${S}_{UR}$ for small values of ${u}^{^{\prime}}/{S}_{L}$ where Damköhler number remains high.

In order to avoid the aforementioned limitations of the SCPB and SCFM models, the tangential strain rate term ${T}_{2}$ can alternatively be decomposed as (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a):

$$ T_{2} = \underbrace {{\overline{{\left( {\frac{{\partial u_{i} }}{{\partial x_{i} }}} \right)}} _{s} \Sigma _{{gen}} }}_{{D_{{FSD}} }} \underbrace {-{\overline{{\left( {N_{i} N_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right)_{s} }} \Sigma _{{gen}} }}_{{N_{{FSD}} }} $$

(9)

Here, the terms ${D}_{FSD}$ and ${N}_{FSD}$ denote the effects of dilatation rate and normal strain rate, respectively. The dilatation rate term can be split as ${D}_{FSD}=D{1}_{FSD}+D{2}_{FSD}$ where $D{1}_{FSD}$ and $D{2}_{FSD}$ are the mean and fluctuating components, respectively, which are defined as (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a):

$$D{1}_{FSD}=\partial {\widetilde{u}}_{i}/\partial {x}_{i}\left|\nabla \overline{c}\right|$$

(10i)

$$D{2}_{FSD}=\overline{\left(\partial {u}_{i}/\partial {x}_{i}\left|\nabla c\right|\right)}-(\partial {\widetilde{\mathrm{u}}}_{i}/\partial {x}_{i})\left|\nabla \overline{c}\right|$$

(10ii)

The term $D{2}_{FSD}$ is modelled as (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a):

$$D{2}_{FSD}=\left(\tau .{S}_{L}/{\delta }_{th}\right)\left[A{\left(1-\widetilde{c}\right)}^{\zeta }\left({\Sigma }_{gen}-\left|\nabla \overline{c}\right|\right)\right]$$

(11)

where $A={B}_{1}/{\left(1+K{a}_{L}\right)}^{0.35}$, ${B}_{1}$ and $\upzeta$ are the model parameters. The model expressions proposed by Varma et al. (2022a) for the components of ${D}_{FSD}$ and ${N}_{FSD}$ involving fluctuating quantities previously are summarised in Table 2. In comparison to the model proposed by Varma et al. (2022a), the model parameter ${B}_{1}$ was modified as a function of turbulent Reynolds number $R{e}_{L}$ (i.e., $R{e}_{L}={\rho }_{0}\widetilde{{k}^{2}}/\left(\widetilde{\epsilon }{\mu }_{0}\right)$) (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a). The following expressions of ${B}_{1}$ and $\upzeta$ are proposed here so that the model given by Eq. (11) can be applied for a range of different values of ${u}^{^{\prime}}/{S}_{L}$ and $l/{\delta }_{z}$:

Table 2 Models of the fluctuating contributions of ${D}_{FSD}$ and ${N}_{FSD}$ (i.e., ${D2}_{FSD}$ and ${N2}_{FSD}$) proposed by Varma et al. (2022a) where ${g}^{*}=\Gamma {\delta }_{Z}/{S}_{L}^{2}$ with $\Gamma$ being the body force in the direction of mean flame propagation

$${B}_{1}=1.8+0.75\mathrm{erf}[\left(R{e}_{L}/60\right)-1]\mathrm{\,and \,\zeta }=-0.3$$

(12)

It was demonstrated by Chakraborty and Cant (2013) that most model parameters related to the FSD transport reach asymptotic values for $R{e}_{L}\ge 100$. However, it is important to recognise that Eq. (12) is one of the several possibilities of parameterising ${B}_{1}$ such that it assumes an asymptotic value (= 2.55) for $R{e}_{L}\to \infty$ and provides the desired values for moderate values of $R{e}_{L}$ corresponding to the DNS data. It is admitted that the parameterisation of ${B}_{1}$ in Eq. (12) (and some of the other model parameters in the following discussion) involves a degree of empiricism but it is not unusual for turbulence and turbulent combustion modelling. Even if these parameterisations are considered to be purely empirical fits to the DNS data, such fits have a value similar to any new experimental or DNS result that shows an effect, which is yet to be analysed. Moreover, these parameterisations are proposed in such a manner that they assume asymptotic values for $R{e}_{L}\to \infty$.

The predictions of ${D}_{FSD}$ according to Eqs. (10) and (11) (with the model parameter given by Eq. (12)) are compared to the corresponding term extracted from the DNS data in Fig. 10. The predictions using the model proposed by Varma et al. (2022a) are also shown in Fig. 10 for the sake of completeness. Figure 10 shows the model given by Eq. (11) mostly satisfactorily predict the behaviour of ${D}_{FSD}$ for all values of ${u}^{^{\prime}}/{S}_{L}$ and $l/{\delta }_{z}$ considered in this analysis.

Fig. 10

Variation of ${D}_{FSD}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions using the closures given by Eqs. (11) and (12) for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row). Also shown are the prediction using the closures proposed by Varma et al. (2022a)

The normal strain rate contribution ${N}_{FSD}$ can also be split into its respective mean and fluctuating components, i.e., ${N}_{FSD}=N{1}_{FSD}+N{2}_{FSD}$, where $N{1}_{FSD}$ and $N{2}_{FSD}$ are defined as (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a):

$$N{1}_{FSD}=-{\overline{\left({N}_{i}{N}_{j}\right)}}_{s}\left(\partial {\widetilde{u}}_{i}/\partial {x}_{j}\right){\Sigma }_{gen}$$

(13i)

$$N{2}_{FSD}=-\overline{{\left({N}_{i}{N}_{j}\partial {u}_{i}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}/\partial {x}_{j}\right)}_{s}}{\Sigma }_{gen}$$

(13ii)

The predictions of $N{1}_{FSD}$ with ${\overline{\left({N}_{i}{N}_{j}\right)}}_{s}$ evaluated according to the MCPB and VPDM models are compared to the corresponding term extracted from the DNS data in Fig. 11. It can be seen from Fig. 11 that both MCPB and VPDM models reasonably capture the behaviour of $N{1}_{FSD}$ extracted from DNS data but their predictions become comparable for high turbulence intensities (e.g., ${u}^{^{\prime}}/{S}_{L}=$ 7.5 and 10.0 cases) for both values of $l/{\delta }_{z}$ considered in this analysis. However, the VPDM model shows better agreement with DNS data than the MCPB model for ${u}^{^{\prime}}/{S}_{L}=$ 1.0 case for $l/{\delta }_{z}=2.625$, whereas just the opposite behaviour is observed for ${u}^{^{\prime}}/{S}_{L}=$ 3.0 case for $l/{\delta }_{z}=2.625$. For the of $l/{\delta }_{z}$ values considered in this analysis, the MCPB model tends to overpredict the magnitude of the negative values of $N{1}_{FSD}$, which is consistent with the underprediction of the magnitude of ${S}_{R}$ by the MCPB model shown earlier (see Fig. 8). The observations made from Figs. 8 and 11 reveal that the differences in model predictions for ${S}_{R}$ and $N{1}_{FSD}$ become less sensitive for higher values of $l/{\delta }_{z}$.

Fig. 11

Variation of $N{1}_{FSD}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the MCPB and VPDM model for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

In order to consider the modelling of the term $N{2}_{FSD}$ it is worthwhile to express ${N}_{FSD}$ and ${T}_{2}$ as (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a):

$${N2}_{FSD}=-\overline{{({e}_{\alpha }{\mathrm{cos}}^{2}{\theta }_{\alpha }+{e}_{\beta }{\mathrm{cos}}^{2}{\theta }_{\beta }+{e}_{\gamma }{\mathrm{cos}}^{2}{\theta }_{\gamma })|\nabla c|}}$$

(14)

Here ${e}_{\alpha },{e}_{\beta }$ and ${e}_{\gamma }$ are the most extensive, intermediate and the most compressive principal fluctuating strain rate tensor (i.e., $0.5(\partial {u}_{i}^{{{\prime}}{{\prime}}}/\partial {x}_{j}+\partial {u}_{j}^{{{\prime}}{{\prime}}}/\partial {x}_{i})$) and ${\theta }_{\alpha },{\theta }_{\beta }$ and ${\theta }_{\gamma }$ are the angles between $\nabla c$ with the eigenvectors associated with ${e}_{\alpha },{e}_{\beta }$ and ${e}_{\gamma }$, respectively. It has been discussed and demonstrated elsewhere (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011) that $\nabla c$ preferentially collinearly aligns with the eigenvectors associated with ${e}_{\alpha }$ (i.e., high probability of $|\mathrm{cos}{\theta }_{\alpha }|\approx 1.0$) under the dominance of the strain rate induced by flame normal acceleration arising from heat release over turbulent straining. By contrast, $\nabla c$ demonstrates preferential collinear alignment with the eigenvectors associated with ${e}_{\gamma }$ (i.e., high probability of $|\mathrm{cos}{\theta }_{\gamma }|\approx 1.0$) as a result of the dominance of turbulent straining over the strain rate induced by flame normal acceleration arising from heat release (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011). The high probability of obtaining $|\mathrm{cos}{\theta }_{\alpha }|\approx 1.0$ is obtained for $\tau Da\gg 1$ (Chakraborty and Swaminathan 2007; Chakraborty et al. 2011), which leads to negative values of $N{2}_{FSD}$ (and in turn promotes negative values of ${N}_{FSD}$ and ${T}_{2}$). By contrast, high probability of obtaining $|\mathrm{cos}{\theta }_{\gamma }|\approx 1.0$ is obtained for $\tau Da<1$, which gives rise to positive values of $N{2}_{FSD}$ (and in turn promotes positive values of ${N}_{FSD}$ and ${T}_{2}$). For a given value of $l/{\delta }_{z}$, an increase in ${u}^{^{\prime}}/{S}_{L}$ leads to a reduction in $Da$ and therefore, the likelihood of obtaining positive values of $N{2}_{FSD}$ increases with increasing turbulence intensity, which can be substantiated from Fig. 12 where the variations of $N{2}_{FSD}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for all cases considered here are shown. It can indeed be seen from Fig. 12 that $N{2}_{FSD}$ assumes negative values throughout the flame brush for small values of turbulence intensity (e.g., ${u}^{^{\prime}}/{S}_{L}=1.0$ and 3.0), whereas for large turbulence intensities (e.g., ${u}^{^{\prime}}/{S}_{L}=7.5$ and 10.0) $N{2}_{FSD}$ assumes positive values towards the unburned gas side of the flame brush where the effects of heat release are weak but this term becomes negative from the middle to the burned gas side of the flame brush where the effects of strain rate arising from flame normal acceleration remain strong. It is also worth noting that for a given value of ${u}^{^{\prime}}/{S}_{L}$, an increase in $l/{\delta }_{z}$ leads to an increase in Damköhler number $Da$ and thus the extent of collinear alignment of $\nabla c$ with the eigenvector associated with ${e}_{\alpha }$ (${e}_{\gamma }$) is greater (smaller) in the $l/{\delta }_{z}=5.25$ cases than in the $l/{\delta }_{z}=2.625$ cases. This is reflected in the higher (smaller) of the propensity negative (positive) contribution of $N{2}_{FSD}$ for higher $l/{\delta }_{z}$ case for a given value of ${u}^{^{\prime}}/{S}_{L}$, which can also be confirmed from Fig. 12.

Fig. 12

Variation of $N{2}_{FSD}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the model given by Eqs. (15–17) for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row). Also shown are the predictions using the closures proposed by Varma et al. (2022a)

The foregoing discussion suggests that the competition between the strain rate induced by flame normal acceleration and turbulent straining, and the alignment characteristics of $\nabla c$ need to be addressed to model ${N}_{FSD}$. This is addressed by the following model expression in previous studies (Katragadda et al. 2011; Sellmann et al. 2017; Varma et al. 2022a):

$$N{2}_{FSD}=\left(\widetilde{\epsilon }/\widetilde{k}\right)\left[{\mathrm{C}}_{1}-\tau {\mathrm{C}}_{2}D{a}_{L}\right]{\Sigma }_{gen}$$

(15)

where $D{a}_{L}=\widetilde{k}{S}_{L}/\widetilde{\upepsilon }{\updelta }_{th}$ is the local Damköhler number. For small values of Damköhler number $\nabla c$ preferentially aligns with the eigenvector associated with ${e}_{\upgamma }$ due to the dominance of turbulent straining over the effects of heat release, which is modelled as $\left(\widetilde{\epsilon }/\widetilde{k}\right){C}_{1}{\Sigma }_{gen}$ in Eq. (15). For high Damköhler numbers, heat release effects dominate over the turbulent straining, which leads to the preferential alignment of $\nabla c$ with the eigenvector associated with ${e}_{\mathrm{\alpha }}$. This aspect is accounted for by $-\tau {C}_{2}{\Sigma }_{gen}{S}_{L}/{\updelta }_{th}$ in Eq. (15). In the present analysis, ${C}_{1}$ and ${C}_{2}$ have been revised in comparison to the previous expressions proposed by Varma et al. (2022a) in the following manner to account for $l/{\delta }_{z}$ dependences which have been embedded in $R{e}_{L}$:

$${C}_{1}=[0.25+2.6erf (R{e}_{L}/50)]{\left(1-\widetilde{c}\right)}^{3.2}$$

(16)

$${C}_{2}=0.471\{0.2+erfc\left[(R{e}_{L}-42)/50\right]\}\left[1.0-{\overline{\left({N}_{k}\right)}}_{s}{\overline{\left({N}_{k}\right)}}_{s}\right]/{\left(1.0+K{a}_{L}\right)}^{0.35}$$

(17)

It can be seen from Fig. 12 that the predictions of the model given by Eq. (15) with model parameters according to Eqs. (16) and (17) remain in satisfactory agreement with $N{2}_{FSD}$ extracted from DNS data including its negative value for small values of turbulence intensity (e.g., ${u}^{^{\prime}}/{S}_{L}=1.0$ and 3.0) and the transition from positive to negative values of $N{2}_{FSD}$ for large turbulence intensities (e.g., ${u}^{^{\prime}}/{S}_{L}=7.5$ and 10.0). It can also be observed from Fig. 12 that the modifications to the closures proposed by Varma et al. (2022a) have resulted in significantly improved predictions of the $N{2}_{FSD}$ term.

A combination of the MCPB model for $N{1}_{FSD}$ with Eqs. (10), (11) and (15–17) for $D{1}_{FSD}$, $D{2}_{FSD}$ and $N{2}_{FSD}$ respectively yield the following model for the strain rate term ${T}_{2}$:

$${T}_{2}=\frac{\partial {\widetilde{u}}_{i}}{\partial {x}_{i}}\left|\nabla \overline{c}\right|+\frac{\tau .{S}_{L}}{{\delta }_{th}}\left[A{\left(1-\widetilde{c}\right)}^{\zeta }\left({\Sigma }_{gen}-\left|\nabla \overline{c}\right|\right)\right]-{ \overline{\left({N}_{i}\right)}}_{s}{\overline{\left({N}_{j}\right)}}_{s}\frac{\partial {\widetilde{u}}_{i}}{\partial {x}_{j}}{\Sigma }_{gen}- \left({\delta }_{ij}/3\right)\left[1-{\overline{\left({N}_{k}\right)}}_{s}{\overline{\left({N}_{k}\right)}}_{s}\right]\frac{\partial {\widetilde{u}}_{i}}{\partial {x}_{j}}{\Sigma }_{gen} +\frac{\widetilde{\epsilon }}{\widetilde{k}}\left[{C}_{1}-\tau {C}_{2}D{a}_{L}\right]{\Sigma }_{gen}$$

(18)

The predictions of Eq. (18) are compared to the predictions of the CPB (MCPB + SCPB) and CFM (VPDM + SCFM) models in Fig. 13 along with the ${T}_{2}$ term extracted from DNS data and the predictions of ${T}_{2}$ according to the closures proposed by Varma et al. (2022a). Figures 13 shows that Eq. (18) agrees better with the DNS data than the CPB and CFM models for ${u}^{^{\prime}}/{S}_{L}\ge 5.0$ cases for both values of $l/{\delta }_{z}$ but Eq. (18) overpredicts ${T}_{2}$ for $l/{\delta }_{z}=5.25$ cases for ${u}^{^{\prime}}/{S}_{L}=1.0$ and 3.0, whereas an underprediction is obtained for the $l/{\delta }_{z}=2.625$ case with ${u}^{^{\prime}}/{S}_{L}=3.0$. Despite these discrepancies between the predictions of Eq. (18) and DNS data, the performance of Eq. (18) remains better than the CPB and CFM models. It is worth noting that Eq. (18) takes care about the competition between the strain rates due to turbulence and flame normal acceleration through the model for $N{2}_{FSD}$ (see Eq. (15)) in response to the variations of Damköhler number, which is missing in the CPB and CFM models. Thus, Eq. (18) performs better than the SPB and SCFM models for a broad range of values of ${u}^{^{\prime}}/{S}_{L}$ and $l/{\delta }_{z}$. Figure 13 also shows that Eq. (18) gives better predictions of the ${T}_{2}$ term in comparison to the closures proposed by Varma et al. (2022a) especially for higher ${u}^{^{\prime}}/{S}_{L}$ values for both length scales. This can be attributed to the use of forced turbulence in the present study compared to decaying turbulence used by Varma et al. (2022a), which results in higher turbulence levels at the time of extraction of statistics in the present study for all initial $u^{\prime}/{S}_{L}$ cases compared to the analysis by Varma et al. (2022a).

Fig. 13

Variation of ${T}_{2}\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the CPB, CFM models and the model given by Eq. (18) for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row). Also shown are the predictions using the closures given by Varma et al. (2022a)

4.5 Modelling of the Combined Propagation and Curvature Terms (${{\varvec{T}}}_{3}+{{\varvec{T}}}_{4})$

The curvature term ${T}_{4}$ can be expressed as: ${T}_{4}=2\overline{{\left[\left({S}_{r}+{S}_{n}\right){\kappa }_{m}\right]}}_{s}{\Sigma }_{gen}-4\overline{{\left(D{\kappa }_{m}^{2}\right)}}_{s}{\Sigma }_{gen}$ (Chakraborty and Cant 2011; Katragadda et al. 2014b) where reaction and normal diffusion components of displacement speed are defined as: ${S}_{r}=\dot{\omega}/\rho |\nabla c|$ and ${S}_{n}=\overrightarrow{N}\bullet (\rho D\overrightarrow{N}\bullet \nabla c)/\rho |\nabla c|$ (Peters et al. 1998; Echekki and Chen 1999). For high values of Karlovitz number (i.e., $Ka\gg 1$) the negative contribution of $\{-4\overline{{\left(D{\kappa }_{m}^{2}\right)}}_{s}{\Sigma }_{gen}\}$ becomes the dominant term, whereas the contribution of $2\overline{{\left[\left({S}_{r}+{S}_{n}\right){\kappa }_{m}\right]}}_{s}{\Sigma }_{gen}$ remains dominant for small and moderate values of $Ka$ (i.e., $Ka<1$ and $Ka\sim 1.0$). The qualitative behaviour of $2\overline{{\left[\left({S}_{r}+{S}_{n}\right){\kappa }_{m}\right]}}_{s}{\Sigma }_{gen}$ is determined by the behaviour of $\overline{{({\kappa }_{m})}}_{s}$ because $\left({S}_{r}+{S}_{n}\right)$ remains predominantly positive and ${\Sigma }_{gen}$ is a positive semi-definite quantity (i.e., ${\Sigma }_{gen}\ge 0$). It was demonstrated earlier (Chakraborty and Cant 2011, 2013; Katragadda et al. 2014b) that $\overline{{({\kappa }_{m})}}_{s}$ assumes positive (negative) values towards the unburned (burned) gas side of the flame brush and the same qualitative behaviour has been observed here but not shown here for brevity. The aforementioned behaviour of $\overline{{({\kappa }_{m})}}_{s}$ leads to positive (negative) values of $2\overline{{\left[\left({S}_{r}+{S}_{n}\right){\kappa }_{m}\right]}}_{s}{\Sigma }_{gen}$ towards the unburned (burned) gas side of the flame brush. A decrease in $l/{\delta }_{z}$ for a given value of ${u}^{^{\prime}}/{S}_{L}$ gives rise to an increase in $Ka$. Thus, the negative contribution of $\{-4\overline{{\left(D{\kappa }_{m}^{2}\right)}}_{s}{\Sigma }_{gen}\}$ is more likely to dominate over $2\overline{{\left[\left({S}_{r}+{S}_{n}\right){\kappa }_{m}\right]}}_{s}{\Sigma }_{gen}$ for smaller values of $l/{\delta }_{z}$ (due to an increase in Karlovitz number with a decrease in $l/{\delta }_{z}$) according to the scaling argument by Peters (2000) and it can indeed be seen from Fig. 5 that the magnitude of the negative contribution of ${T}_{4}$ is higher for smaller values of $l/{\delta }_{z}$. Moreover, Karlovitz number increases with increasing ${u}^{^{\prime}}/{S}_{L}$, which also acts to increase the range of curvature values which gives rise to the increase in the magnitude of the negative contribution of $\{-4\overline{{\left(D{\kappa }_{m}^{2}\right)}}_{s}{\Sigma }_{gen}\}$. Accordingly it can be seen from Fig. 14 that (${T}_{3}+{T}_{4}$) assumes positive values towards the unburned gas and negative values towards the burned gas side of the flame brush for ${u}^{^{\prime}}/{S}_{L}\le 5.0$ but the net contribution of these terms assumes predominantly negative values throughout the flame brush for ${u}^{^{\prime}}/{S}_{L}=7.5$ and 10.0.

Fig. 14

Variation of the combined propagation and curvature term (${T}_{3}+{T}_{4}$) $\times {\delta }_{z}^{2}/{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the model expressions given by Eq. (19) with ${c}_{p}=0.35$ and ${c}_{p}$ given by Eq. (20) for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

The curvature and propagation terms are usually modelled together due to their dependence on the displacement speed ${S}_{d}$ but the behaviour of (${T}_{3}+{T}_{4}$) is principally determined by the curvature term as the magnitude of the propagation term ${T}_{3}$ remains much smaller than ${T}_{4}$. The term (${T}_{3}+{T}_{4}$) is usually modelled together as (Hun and Huh 2008; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Varma et al. 2022a):

$$\left({T}_{3}+{T}_{4}\right)=-\frac{\partial }{\partial {x}_{i}}\left[\frac{{\rho }_{0}{S}_{L}}{\overline{\rho }}{\overline{\left({N}_{i}\right)}}_{s}{\Sigma }_{gen}\right]+\frac{{\rho }_{0}{S}_{L}}{\overline{\rho }}\frac{\partial {\overline{\left({N}_{i}\right)}}_{s}}{\partial {x}_{i}}{\Sigma }_{gen}-{\beta }_{0}{\alpha }_{N}\frac{\left(\overline{c }-{c}_{cp}\right){S}_{L}{\Sigma }_{gen}^{2}}{\overline{c }\left(1-\overline{c }\right)}$$

(19)

The last term on the right-hand side of Eq. (19) denotes the fluctuating component of the combined propagation and curvature term where ${\beta }_{0}$ and ${c}_{cp}$ are model parameters, and ${\mathrm{\alpha }}_{N}$ represents an orientation factor (resolution factor) in terms of RANS (LES) which is expressed as ${\mathrm{\alpha }}_{N}=1-{\overline{\left({N}_{k}\right)}}_{s}{\overline{\left({N}_{k}\right)}}_{s}$ and thus becomes zero under fully resolved condition causing the last term to vanish (Fureby 2005; Hawkes and Cant 2000; Jenkins and Cant 1999; Katragadda et al. 2014b). Previous analyses (Hun and Huh 2008; Chakraborty and Cant 2011, 2013; Sellmann et al. 2017; Varma et al. 2022a) suggested ${\beta }_{0}=8.0$ and ${c}_{cp}=0.35$ for unity Lewis number flames. The predictions of Eq. (19) are compared to (${T}_{3}+{T}_{4}$) extracted from DNS data in Fig. 14. It can be seen from Fig. 14 that the (${T}_{3}+{T}_{4}$) is adequately captured by Eq. (19) for ${\beta }_{0}=8.0$ and ${c}_{cp}=0.35$ for both values of $l/{\delta }_{z}$ for ${u}^{^{\prime}}/{S}_{L}\le 5.0$ where (${T}_{3}+{T}_{4}$) assumes positive values towards the unburned gas and negative values towards the burned gas side of the flame brush. However, Eq. (19) for ${\beta }_{0}=8.0$ and ${c}_{cp}=0.35$ predicts positive values towards the unburned gas side of the flame brush for high turbulence intensities (e.g., ${u}^{^{\prime}}/{S}_{L}=7.5$ and 10.0) but DNS data shows negative values throughout the flame brush. In order to capture negative values of (${T}_{3}+{T}_{4}$) throughout the flame brush for ${u}^{^{\prime}}/{S}_{L}=7.5$ and 10.0, the parameter ${c}_{cp}$ is altered in this analysis in the following manner:

$${c}_{cp}=0.01+erfc[(R{e}_{L}+6)/36]$$

(20)

The predictions of Eq. (19) with ${\beta }_{0}=8.0$ and ${c}_{cp}$ according to Eq. (20) are also shown in Fig. 14, which shows that this model captures the behaviour of (${T}_{3}+{T}_{4}$) throughout the flame brush for all cases considered here.

4.6 Mean Reaction Rate Closure Using Generalised FSD

The variations of $\overline{\dot{\omega } }$ and $\overline{\dot{\omega } }+\overline{\nabla .\left(\rho D\nabla c\right)}$ with $\widetilde{c}$ for all cases considered here are shown in Fig. 15. It can be seen from Fig. 15 that there is a good level of agreement between $\overline{\dot{\omega } }$ and $\overline{\dot{\omega } }+\overline{\nabla .\left(\rho D\nabla c\right)}$, which shows that the contribution of the mean molecular diffusion rate in statistically planar flames is much smaller than the mean reaction rate and hence $\overline{\dot{\omega } }\approx {\overline{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{gen}$ holds in the context of RANS simulations. For unity Lewis number flames, the surface-averaged density-weighted displacement speed is usually modelled as ${\overline{\left(\rho {S}_{d}\right)}}_{s}\approx {\rho }_{0}{S}_{L}$ (Hawkes and Cant 2000, 2001) although this approximation may not be valid, especially for the thin reaction zones regime flames (Sabelnikov et al. 2017). Thus, the model for mean reaction rate may be expressed as $\overline{\dot{\omega } }={\rho }_{0}{S}_{L}{\Sigma }_{gen}$. It can further be seen from Fig. 15 that ${\rho }_{0}{S}_{L}{\Sigma }_{gen}$ satisfactorily captures the variation of $\overline{\dot{\omega } }$ across the flame brush but ${\rho }_{0}{S}_{L}{\Sigma }_{gen}$ underpredicts the magnitude of $\overline{\dot{\omega } }$ towards the product side of the flame brush for all cases.

Fig. 15

Variation of $\overline{\dot{\omega }}\times {\delta }_{Z}/{\rho }_{0}{S}_{L}$ and $\overline{\dot{\omega } }+\overline{\nabla .\left(\rho D\nabla c\right)}\times {\delta }_{z}/{\rho }_{0}{S}_{L}$ with $\widetilde{c}$ for $l/{\delta }_{z}=2.625$ (left) and 5.25 (right) along with the predictions of the model given by ${\overline{\left(\rho {S}_{d}\right)}}_{s}\approx {\rho }_{0}{S}_{L}$ for ${u}^{^{\prime}}/{S}_{L}=1.0$, 3.0, 5.0, 7.5 and 10.0 (1st–5th row)

It is worth noting that the quantity $\overline{\dot{\omega } }+\overline{\nabla .\left(\rho D\nabla c\right)}$, by definition, equals to $\overline{{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{gen}$ and thus a comparison between $\overline{{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{gen}$ and ${{\rho }_{0}{S}_{L}\Sigma }_{gen}$ in Fig. 15 indicates that the magnitude of $\overline{{\left(\rho {S}_{d}\right)}}_{s}$ remains close to ${\rho }_{0}{S}_{L}$ for the cases considered here. Thus, the discrepancy between $\overline{\dot{\omega } }+\overline{\nabla .\left(\rho D\nabla c\right)}$ (i.e., $\overline{\dot{\omega } }$ due to $\overline{\dot{\omega } }\gg \overline{\nabla .\left(\rho D\nabla c\right)}$) and ${{\rho }_{0}{S}_{L}\Sigma }_{gen}$ originates due to the approximation of ${\overline{\left(\rho {S}_{d}\right)}}_{s}\approx {\rho }_{0}{S}_{L}$ and a better representation of ${\overline{\left(\rho {S}_{d}\right)}}_{s}$ is likely to provide an improved prediction of the mean reaction rate. the discrepancy between ${\rho }_{0}{S}_{L}{\Sigma }_{gen}$ and $\overline{\dot{\omega } }$ originates due to the approximation of ${\overline{\left(\rho {S}_{d}\right)}}_{s}\approx {\rho }_{0}{S}_{L}$ and a better representation of ${\overline{\left(\rho {S}_{d}\right)}}_{s}$ is likely to provide an improved prediction of the mean reaction rate.

5 Conclusions

The effects of both turbulence intensity ${u}^{^{\prime}}/{S}_{L}$ and integral length scale to flame thickness ratio $l/{\delta }_{z}$ on the statistical behaviours of FSD and its transport have been evaluated using a DNS database of three-dimensional statistically planar turbulent premixed flames. In contrast to several previous analyses (Trouvé and Poinsot 1994; Hawkes and Cant 2000, 2001; Chakraborty and Cant 2007, 2009a, 2011, 2013; Hun and Huh 2008; Katragadda et al. 2011, 2014a, b; Papapostolou et al. 2019; Varma et al. 2022a), the current study assesses the performances of the models for different unclosed terms in the FSD transport equation in response to the variations of both ${u}^{^{\prime}}/{S}_{L}$ and $l/{\delta }_{z}$. The main findings are summarised below:

• It has been found that the peak magnitudes of the FSD and the terms of the FSD transport term decrease with an increase in length scale ratio.

• The turbulent burning velocity and flame surface area assume greater values for the higher values of length scale ratio $l/{\delta }_{z}$ for a given value of ${u}^{^{\prime}}/{S}_{L}$. Both turbulent burning velocity and flame surface area increase with increasing ${u}^{^{\prime}}/{S}_{L}$ before the bending behaviour at high values of ${u}^{^{\prime}}/{S}_{L}$.

• The flame brush thickness and flame wrinkling increase with an increase in $l/{\delta }_{z}$ for a given value of ${u}^{^{\prime}}/{S}_{L}$. However, the qualitative behaviours of the unclosed terms in the FSD transport equation remain unchanged by the length scale ratio and in all cases the tangential strain rate term ${T}_{2}$ acts as a leading order source and the curvature term ${T}_{4}$ remains the major sink term towards the burned gas of the flame brush.

• A decrease in $l/{\delta }_{z}$ for a given value of ${u}^{^{\prime}}/{S}_{L}$ leads to a decrease in Damköhler number and an increase in Karlovitz number. This has an implication on the alignment of reactive scalar gradient with local strain rate eigenvectors. Therefore, the existing models for the tangential strain rate term, which do not explicitly account for the alignment of reactive scalar gradient with local strain rate eigenvectors in response to the changes in Damköhler number, have been found to be inadequate. An alternative model for the tangential strain rate term ${T}_{2}$, which explicitly considers the alignment of $\nabla c$ with local strain rate eigendirections and the competition between turbulent straining and chemical timescales, has been shown to be more successful in capturing the behaviour obtained from DNS data.

• It has been found that an existing model for the turbulent flux of the FSD, which accounts for both gradient and counter-gradient behaviour, does not need any major modifications due to $l/{\delta }_{z}$ variation. The nature of turbulent transport is determined by relative strengths of turbulent velocity fluctuation and velocity jump across the flame, which is not directly affected by $l/{\delta }_{z}$.

• According to scaling argument by Peters (2000), the curvature term is expected to show greater likelihood of negative values for higher Karlovitz number and accordingly larger magnitudes of the curvature term are obtained for smaller (higher) value of $l/{\delta }_{z}$ (${u}^{^{\prime}}/{S}_{L}$) for a given value of ${u}^{^{\prime}}/{S}_{L}$ ($l/{\delta }_{z}$). As a result, the combined propagation and curvature term $\left({T}_{3}+{T}_{4}\right)$ showed predominantly negative contribution for high Karlovitz number values, which needed modification to an existing model.

• The FSD based mean reaction rate closure mostly works satisfactorily irrespective the value of $l/{\delta }_{z}$ but underpredicts the magnitude of $\overline{\dot{\omega }}$ for all cases towards the product side of the flame brush due to inaccuracies involved in modelling surface-averaged density-weighted displacement speed.

It is worth noting that the current analysis has been conducted with simple chemistry for the sake of a detailed parametric analysis. Although previous analyses (Papapostolou et al. 2019; Luca et al. 2019) revealed no major differences in the qualitative behaviours of the unclosed terms of the FSD transport equation between simple and detailed chemistry, future analyses need to include the effects of detailed chemistry for comprehensive validation of the models proposed in this analysis. The turbulent Reynolds number $R{e}_{t}={\rho }_{0}{k}^{2}/{\mu }_{0}\varepsilon$ ranges from 12.5 (for case A2) to 250 (case E1) for the DNS database considered here. It is worth noting that most laboratory scale experiments have $R{e}_{t}$ values of the order of 100. The range of ${u}^{^{\prime}}/{S}_{L}$ and $l/{\delta }_{z}$ considered here is comparable to previous studies by other authors (Trouvé and Poinsot 1994; Boger et al. 1998; Charlette et al. 2002; Hun and Huh 2008; Reddy and Abraham 2012) which contributed to the FSD transport modelling. The FSD/wrinkling models which have been either proposed or recommended based on a priori DNS analysis (Boger et al. 1998; Charlette et al. 2002; Fureby 2005; Chakraborty and Cant 2009a) for moderate turbulent Reynolds numbers have been found to work well based on a posteriori analyses (Ma et al. 2013, 2014; Klein et al. 2016). However, further analyses for higher values of $R{e}_{t}$ will be needed to confirm the current findings. Finally, these models need to be implemented in actual RANS simulations of an experimental configuration for the purpose of a posteriori assessment of the closures of the unclosed terms.