Influence of Thermal Expansion on Fluid Dynamics of Turbulent Premixed Combustion and Its Modelling Implications

Abstract

The purpose of this paper is to demonstrate the effects of thermal expansion, as a result of heat release arising from exothermic chemical reactions, on the underlying turbulent fluid dynamics and its modelling in the case of turbulent premixed combustion. The thermal expansion due to heat release gives rise to predominantly positive values of dilatation rate within turbulent premixed flames, which has been shown to have significant implications on the flow topology distributions, and turbulent kinetic energy and enstrophy evolutions. It has been demonstrated that the magnitude of predominantly positive dilatation rate provides the measure of the strength of thermal expansion. The influence of thermal expansion on fluid turbulence has been shown to strengthen with decreasing values of Karlovitz number and characteristic Lewis number, and with increasing density ratio between unburned and burned gases. This is reflected in the weakening of the contributions of flow topologies, which are obtained only for positive values of dilatation rate, with increasing Karlovitz number. The thermal expansion within premixed turbulent flames not only induces mostly positive dilatation rate but also induces a flame-induced pressure gradient due to flame normal acceleration. The correlation between the pressure and dilatation fluctuations, and the vector product between density and pressure gradients significantly affect the evolutions of turbulent kinetic energy and enstrophy within turbulent premixed flames through pressure-dilatation and baroclinic torque terms, respectively. The relative contributions of pressure-dilatation and baroclinic torque in comparison to the magnitudes of the other terms in the turbulent kinetic energy and enstrophy transport equations, respectively strengthen with decreasing values of Karlovitz and characteristic Lewis numbers. This leads to significant augmentations of turbulent kinetic energy and enstrophy within the flame brush for small values of Karlovitz and characteristic Lewis numbers, but both turbulent kinetic energy and enstrophy decay from the unburned to the burned gas side of the flame brush for large values of Karlovitz and characteristic Lewis numbers. The heat release within premixed flames also induces significant anisotropy of sub-grid stresses and affects their alignments with resolved strain rates. This anisotropy plays a key role in the modelling of sub-grid stresses and the explicit closure of the isotropic part of the sub-grid stress has been demonstrated to improve the performance of sub-grid stress and turbulent kinetic energy closures. Moreover, the usual dynamic modelling techniques, which are used for non-reacting turbulent flows, have been shown to not be suitable for turbulent premixed flames. Furthermore, the velocity increase across the flame due to flame normal acceleration may induce counter-gradient transport for turbulent kinetic energy, reactive scalars, scalar gradients and scalar variances in premixed turbulent flames under some conditions. The propensity of counter-gradient transport increases with decreasing values of root-mean-square turbulent velocity and characteristic Lewis number. It has been found that vorticity aligns predominantly with the intermediate principal strain rate eigendirection but the relative extents of alignment of vorticity with the most extensive and the most compressive principal strain rate eigendirections change in response to the strength of thermal expansion. It has been found that dilatation rate almost equates to the most extensive strain rate for small sub-unity Lewis numbers and for the combination of large Damköhler and small Karlovitz numbers, and under these conditions vorticity shows no alignment with the most extensive principal strain rate eigendirection but an increased collinear alignment with the most compressive principal strain rate eigendirection is obtained. By contrast, for the combination of high Karlovitz number and low Damköhler number in the flames with Lewis number close to unity, vorticity shows an increased collinear alignment with the most extensive principal direction in the reaction zone where the effects of heat release are strong. The strengthening of flame normal acceleration in comparison to turbulent straining with increasing values of density ratio, Damköhler number and decreasing Lewis number makes the reactive scalar gradient align preferentially with the most extensive principal strain rate eigendirection, which is in contrast to preferential collinear alignment of the passive scalar gradient with the most compressive principal strain rate eigendirection. For high Karlovitz number, the reactive scalar gradient alignment starts to resemble the behaviour observed in the case of passive scalar mixing. The influence of thermal expansion on the alignment characteristics of vorticity and reactive scalar gradient with local principal strain rate eigendirections dictates the statistics of vortex-stretching term in the enstrophy transport equation and normal strain rate contributions in the scalar dissipation rate and flame surface density transport equations, respectively. Based on the aforementioned fundamental physical information regarding the thermal expansion effects on fluid turbulence in premixed combustion, it has been argued that turbulence and combustion modelling are closely interlinked in turbulent premixed combustion. Therefore, it might be necessary to alter and adapt both turbulence and combustion modelling strategies while moving from one combustion regime to the other.

1 Introduction

In spark ignition engines and industrial gas turbines fuel and oxidiser are homogeneously mixed prior to the combustion and the corresponding flames are commonly referred to as premixed flames. In premixed combustion, the flame moves normal to itself and the flow accelerates in the flame normal direction due to thermal expansion. Moreover, thermal expansion gives rise to mostly positive values of dilatation rate. In premixed combustion, the heat release rate due to exothermal chemical reaction gives rise to significant changes in density across the flame, even under moderate values of Mach number. This leads to a significant amount of thermal expansion characterised by predominantly positive values of dilatation rate, which makes the underlying turbulent fluid motion in premixed turbulent combustion different from non-reacting compressible flow turbulence. The influence of heat release and thermal expansion on turbulence in premixed flames has been indicated by Karlovitz et al. (1953) in their pioneering analysis. The hypothesis of flame-generated turbulence by Karlovitz et al. (1953) was subsequently explained based on physical arguments by Bray and Libby (1976). The hypothesis by Karlovitz et al. (1953) was confirmed by Moreau and Boutier (1977) based on experimental data which revealed that the self-induced pressure gradient within the flame acts to preferentially accelerate lighter combustion products more than the heavier reactants. Borghi and Escudie (1984) and Chomiak and Nisbet (1995) provided further experimental evidence of the important role played by the self-induced pressure gradient in premixed turbulent combustion. This self-induced pressure gradient has been demonstrated to play a key role in non-gradient turbulent transport, which has implications in the modelling of turbulent scalar fluxes and Reynolds stresses (Kuznetsov 1979; Bray et al. 1980; Moss 1980; Shepherd et al. 1982; Strahle 1983; Cheng and Shepherd 1991; Rutland and Cant 1994; Zhang and Rutland 1995; Veynante et al. 1997; Veynante and Poinsot 1997; Frank et al. 1999; Swaminathan et al. 2001; Kalt et al. 2002; Nishiki et al. 2002, 2006; Chakraborty and Cant 2009a, 2009b, 2009c; Chakraborty et al. 2011a, e). Moreover, the self-induced pressure gradient within the flame is responsible for the baroclinic torque which acts to generate vorticity and plays a key role in the enstrophy transport in turbulent premixed flames (Lipatnikov et al. 2014; Chakraborty et al. 2016, 2017; Dopazo et al. 2017; Papapostolou et al. 2017).

It has recently been reported that the heat release due to combustion modifies the spectra of turbulent kinetic energy (Kolla et al. 2014) and its dissipation rate (Kolla et al. 2016) in turbulent premixed flames in comparison to the corresponding results obtained for turbulent non-reacting flows. The two-point velocity correlations for the velocity field in turbulent premixed flames need to account for density differences between two points in question due to thermal expansion effects. This type of spectral analysis has the potential to provide insights into the scales where the correlation between pressure and dilatation remains important, which, in turn, affect the spectral energy transfer from lower to higher wavenumbers (Kolla et al. 2014, 2016). The predominantly positive dilatation rate due to thermal expansion in premixed turbulent flames also influences turbulent kinetic energy transport through the correlation between pressure and dilatation rate (Zhang and Rutland 1995; Nishiki et al. 2002; Chakraborty and Cant 2009c; Chakraborty et al. 2011a). By contrast, the dilatation rate contribution damps the enstrophy within the flame. The dilatation rate magnitude also provides the measure of the strain rate induced by chemical heat release. The dominance of the strain rate induced by heat release over turbulent straining modifies the alignment characteristics of reactive scalar gradient (Grout and Swaminathan 2006; Chakraborty and Swaminathan 2007a; Kim and Pitsch 2007; Hartung et al. 2008; Chakraborty et al. 2009) and vorticity (Chakraborty et al. 2017; Chakraborty 2014) with local principal strain rate eigendirections in comparison to the well-known behaviour of non-reacting flows. This dominance of the strain rate induced by heat release over turbulent straining also affects the alignment of sub-grid stresses with resolved strain rates, which has implications on the sub-grid kinetic energy generation in turbulent premixed flames (Ahmed et al. 2019a). In the context of this discussion, it is worthwhile to mention that dilatation rate is closely related to the first invariant of the velocity gradient tensor, which plays a key role in determining flow topologies in compressible turbulent flows (Chen et al. 1989; Sondergaard et al. 1991; Maekawa et al. 1999; Suman and Girimaji 2010; Wang and Lu 2012). Moreover, dilatation rate can be shown to be linked to displacement speed, signifying the speed at which the flame surface moves normal to itself with respect to the background fluid motion. This suggests that the flame propagation, thermal expansion and turbulent fluid motion in premixed combustion are closely coupled. Therefore, a thorough understanding of the influence of heat release on fluid motion in turbulent premixed combustion is necessary for the development of high-fidelity models for accurate predictions of industrial flames. This aspect is not only incompletely understood but is often overlooked in turbulent reacting flow analyses, but the resulting simulations are unlikely to be accurate without the correct characterisation of the underlying turbulent fluid motion.

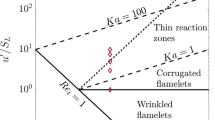
In the present paper, the physical insights gained from Direct Numerical Simulation (DNS) databases of turbulent premixed flames for a range of different turbulence intensities and characteristic Lewis numbers (i.e. ratio of thermal diffusivity to mass diffusivity) have been utilised to demonstrate the influence of heat release on flow topology distribution, statistics of alignments of vorticity and reactive scalar gradient alignment with local principal strain rate eigendirections and the evolutions of turbulent kinetic energy and enstrophy in premixed turbulent combustion. During the course of this discussion, it will be demonstrated that the strength of the aforementioned heat release effects depends on the characteristic Lewis number $Le$ and also on the regime of combustion which is characterised by Karlovitz number $Ka$ (a non-dimensional number which provides the measure of the flame thickness to the Kolmogorov length scale ratio). For $Ka < 1$, the flame thickness remains smaller than the Kolmogorov length scale, thus turbulent eddies do not penetrate into the flame structure and the flame gets wrinkled by the large-scale turbulent motion. This regime of combustion is commonly referred to as the corrugated flamelets regime (Peters 2000). For $Ka > 1$, the flame thickness remains greater than the Kolmogorov length scale and thus small-scale turbulent eddies can penetrate into the flame and perturb the flame structure. If the reaction zone thickness remains smaller than the Kolmogorov length scale, the turbulent eddies perturb only the preheat zone, but the reaction zone retains its quasi-laminar structure. This combustion regime is commonly referred to as the thin reaction zones regime (Peters 2000) and according to the Borghi-Peters regime diagram, this regime is realised between $1 < Ka < 100$ based on the assumption that the reaction zone thickness is about 10% of the overall flame thickness. Once the reaction zone becomes thicker than the Kolmogorov length scale, turbulent eddies perturb the reaction zone and can lead to localised flame quenching. This situation is representative of the broken reaction zones regime (Peters 2000) and according to the Borghi-Peters regime diagram, it is obtained for $Ka > 100$. The boundaries of these regimes are demarcated based on scaling arguments and there have been some controversies (Aspden et al. 2011; Wabel et al. 2017; Skiba et al. 2018) about the possibility of obtaining broken reaction zones regime in any applications of engineering relevance. The possibility of the existence of the broken reaction zones regime and the boundaries between different combustion regimes are not relevant for the discussion in this paper.

In order to demonstrate the effects of heat release on turbulent flow structure, the flow topology statistics in premixed turbulent combustion will be discussed in terms of three invariants of velocity gradient tensor, where the first invariant is the negative dilatation rate and the second and third invariants can be linked to strain rate magnitude and enstrophy, and their evolutions (Chen et al. 1989; Sondergaard et al. 1991; Maekawa et al. 1999; Suman and Girimaji 2010; Wang and Lu 2012; Perry and Chong 1987; Chong et al. 1990, 1998; Soria et al. 1994; Blackburn et al. 1996; Chacin and Cantwell 2000; Ooi et al. 1999; Elsinga and Marusic 2010; Tsinober 2000; Da silva C, Pereira J. 2008; Khashehchi et al. 2010). In this analysis, the flow topologies have been categorized into 8 types (i.e. S1–S8) (Chen et al. 1989; Sondergaard et al. 1991; Maekawa et al. 1999; Suman and Girimaji 2010; Wang and Lu 2012; Perry and Chong 1987; Chong et al. 1990, 1998; Soria et al. 1994; Blackburn et al. 1996; Chacin and Cantwell 2000; Ooi et al. 1999; Elsinga and Marusic 2010; Tsinober 2000; Da silva C, Pereira J. 2008; Khashehchi et al. 2010). For $Ka > 1$, turbulent eddies enter into the flame and perturb the reaction–diffusion imbalance in a such a manner that the influence of dilatation rate weakens with increasing Karlovitz number, and this has a key role in flow topology and enstrophy distributions in turbulent premixed flames. Accordingly, the probability of finding the flow topologies S7 and S8, which are obtained only for positive dilatation rates, decreases with increasing $Ka$ (Wacks et al. 2016). The flow topologies, which can be obtained for all values of dilatation rate, remain major contributors to the evolutions of enstrophy, scalar dissipation rate (SDR) and Flame Surface Density (FSD) but the flow topologies S7 and S8 play key roles in the flames where $Ka < 1$. However, a nodal flow topology representative of a counterflow configuration has been found to be a major contributor to the evolutions of SDR and FSD, but a focal topology S7 which is obtained only for positive dilatation rates remains one of the major contributors to the terms, which are related to chemical heat release, flame propagation and thermal expansion, in the transport equations of enstrophy, SDR and FSD (Chakraborty et al. 2018a, 2019). The strong turbulence generation within the flame due to flame normal acceleration in $Ka < 1$ cases gives rise to an increase in the probability of focal flow topologies from the unburned to the burned gas side, whereas the opposite behaviour is obtained for flames with $Ka \gg 1$ (Wacks et al. 2016).

The rate of diffusion of fresh reactants into the reaction zone supersedes the rate at which heat is diffused out in $Le < 1$ flames. This gives rise to the simultaneous presence of high reactant concentration and high temperature for positively stretched turbulent flame elements, and thus the burning rate and flame generation area are greater in $Le < 1$ flames than in the unity Lewis number flames with statistically similar turbulent flow conditions in the unburned reactants. The opposite mechanism gives rise to a reduced burning rate in $Le > 1$ flames, in comparison to the corresponding unity Lewis number flame. The Lewis number dependences of flame normal acceleration and dilatation rate will be shown later in this paper to have significant influence on turbulent kinetic energy and enstrophy transport through pressure dilatation and baroclinic terms respectively (Chakraborty and Cant 2009c; Chakraborty et al. 2016; Dopazo et al. 2017). This leads to stronger flame-generated turbulence and enstrophy generation within the flame brush in $Le < 1$ cases than in a unity Lewis number flame subjected to statistically similar unburned gas turbulence, and this tendency strengthens with decreasing $Le$ (Chakraborty and Cant 2009c; Chakraborty et al. 2016; Dopazo et al. 2017). Thus, the probability of obtaining focal topologies increases from the unburned to the burned gas side of the flame for $Le<1$ flames and S7 and S8 topologies play a more significant role in $Le\ll 1$ flames than in $Le\ge 1$ flames (Wacks et al. 2018).

It will be shown in this paper that the dominance of heat release effects at small values of $Ka$ and/or $Le$ leads to an increased tendency of the reactive scalar gradient to align preferentially with the most extensive principal strain rate eigendirection (Grout and Swaminathan 2006; Chakraborty and Swaminathan 2007a; Kim and Pitsch 2007; Hartung et al. 2008; Chakraborty et al. 2009), but this trend weakens with increasing $Ka$ and/or $Le$ and the scalar gradient aligns preferentially with the eigenvector associated with the most compressive principal strain rate for large values of $Ka$ similar to passive scalar mixing. Vorticity in premixed flames has been found to predominantly align with the eigenvector associated with the intermediate principal strain rate, irrespective of the value of $Ka$ and $Le$, which is similar to non-reacting flows but premixed flames with small values of $Ka$ and/or $Le$ exhibit considerable collinear alignment (perpendicular alignment) with the most compressive (extensive) principal strain rate eigendirection which is in contrast to the vorticity alignment statistics in non-reacting flows (Batchelor 1952, 1959; Gibson 1968; Clay 1973; Kerr 1985; Ruetsch and Maxey 1991; Nomura and Elghobashi 1992; Ashurst et al. 1987a, 1987b; Leonard and Hill 1991).

All the aforementioned differences in turbulent flow statistics between premixed flames and non-reacting flows will be shown to have significant implications not only on the closures of FSD, SDR, turbulent kinetic energy and its dissipation rate, but they also induce considerable anisotropy in the sub-grid stress behaviour even for flame-turbulence interaction under initially homogeneous isotropic turbulence (Klein et al. 2017).

The rest of the paper will be organised as follows. The next section focuses on the effects of heat release on flow topology distribution in turbulent premixed flames. This will be followed by discussion of thermal expansion effects on the evolutions of enstrophy and turbulent kinetic energy, along with the influence of Lewis number on these statistics. Following these, the fundamental insights obtained from the aforementioned statistics will be utilised to demonstrate their implications on the modelling of sub-grid stress, sub-grid scalar flux. This will be followed by discussions on the effects of thermal expansion on alignment of vorticity and reactive scalar gradient with local principal strain rate eigendirections, and their influence on the vortex-stretching term in the enstrophy transport and the normal strain rate contributions to the FSD/SDR transports, respectively. At the end, final remarks will be provided along with the discussion of future modelling challenges.

2 Effects of Heat Release on Flow Topology in Premixed Turbulent Flames

The local flow topologies can be characterised by the invariants of the velocity-gradient tensor $A_{ij} = \partial u_{i} /\partial x_{j}$ following the pioneering analysis by (Perry and Chong 1987) and (Chong et al. 1990). The components of velocity gradient tensor can be written as: $A_{ij} = \partial u_{i} /\partial x_{j} = S_{ij} + W_{ij}$ where $S_{ij} = 0.5\left( {A_{ij} + A_{ji} } \right)$ and $W_{ij} = 0.5\left( {A_{ij} - A_{ji} } \right)$ are the symmetric and anti-symmetric components respectively. Three eigenvalues, $\lambda_{1}$, $\lambda_{2}$ and $\lambda_{3}$, of $A_{ij}$ can be obtained from solutions of the characteristic equation $\lambda^{3} + P\lambda^{2} + Q\lambda + R = 0$ where $P,Q,R$ are the invariants of $A_{ij}$ (Perry and Chong 1987; Chong et al. 1990):

$$ \begin{aligned} P = & - \left( {\lambda_{1} + \lambda_{2} + \lambda_{3} } \right); \\ Q =\, & 0.5( P^{2} - S_{ij} S_{ij} ) + 0.5(W_{ij} W_{ij}) = Q_{S} + Q_{W} ; \\ R =\, & \left( { - P^{3} + 3PQ - S_{ij} S_{jk} S_{ki} - 3W_{ij} W_{jk} S_{ki} } \right)/3 \end{aligned} $$

(1)

The discriminant, $D = \left[ {27R^{2} + \left( {4P^{3} - 18PQ} \right)R + 4Q^{3} - P^{2} Q^{2} } \right]/108$, of the characteristic equation of the velocity gradient tensor $\lambda^{3} + P\lambda^{2} + Q\lambda + R = 0$ divides the $P - Q - R$ phase-space into two regions: for $D > 0$ where $A_{ij}$ displays a focal (i.e. vorticity-dominated) topology, whereas a nodal (i.e. strain rate-dominated) topology is obtained for $D<0$ (Wabel et al. 2017; Skiba et al. 2018). It is worth noting that one real eigenvalue and two complex conjugate eigenvalues of the $A_{ij}$ tensor are obtained for focal topologies, whereas nodal topologies exhibit three real eigenvalues. The locus of $D = 0$ gives rise to two subsets $r_{1a}$ and $r_{1b}$ in $P - Q - R$ phase space which are given by (Perry and Chong 1987; Chong et al. 1990): $r_{1a} = P\left( {Q - 2P^{2} /9} \right)/3 - 2\left( { - 3Q + P^{2} } \right)^{3/2} /27$ and $r_{1b} = P\left( {Q - 2P^{2} /9} \right)/3 + 2\left( { - 3Q + P^{2} } \right)^{3/2} /27$. The $A_{ij}$ tensor has purely imaginary eigenvalues on the surface $r_{2}$, which are given by $R = PQ$ for positive values of discriminant (i.e. $D > 0$). The surfaces $r_{1a}$, $r_{1b}$ and $r_{2}$ can be used to divide the $P - Q - R$ phase space into 8 flow topologies, as shown in Fig. 1.

Fig. 1

(Top) Classification of $S1 - S8$ topologies in the $Q - R$ plane for (left to right) $P > 0$, $P = 0$ and $P < 0$. The lines $r_{1a}$ (red), $r_{1b}$ (blue) and $r_{2}$ (green) dividing the topologies are shown. Black dashed lines correspond to $Q = 0$ and $R = 0$. (Bottom) Classification of ${\text{S}}1 - {\text{S}}8$ topologies: UF = unstable focus, UN = unstable node, SF = stable focus, SN = stable node, S = saddle, C = compressing, ST = stretching. Figure reproduced from (Wacks et al. 2016)

It is evident from Eq. 1 that the first invariant $P$ is closely related to dilatation rate $\partial u_{i} /\partial x_{i}$ (i.e. $P = - \partial u_{i} /\partial x_{i}$). From the above discussion and Fig. 1, it can be appreciated that dilatation rate $\partial u_{i} /\partial x_{i}$ plays a key role in determining the flow topology distributions in turbulent premixed flames. For low Mach number (i.e. $Ma < 0.3$) non-reacting flows where the assumption of incompressibility holds, $P$ assumes vanishingly small values and one mostly obtains the topologies S1–S4. However, in a compressible flow where $P$ assumes non-zero values, it is possible to obtain both positive and negative values of $P$ and accordingly it is possible to obtain topologies S5–S8 in addition to the topologies S1–S4. However, most turbulent premixed flames behave differently to the aforementioned non-reacting flows. Most turbulent premixed flames in industrial applications are characterised by small values of Mach number (e.g. $Ma < 0.3$) but the heat release due to combustion gives rise to thermal expansion which is characterised by predominantly positive values of dilatation rate (i.e. $\partial u_{i} /\partial x_{i} > 0$). This suggests that $P$ predominantly assumes negative (i.e. $P < 0$) values in turbulent flames but there are possibilities of having local occurrences of negative values of $\partial u_{i} /\partial x_{i}$ (alternatively positive values of $P$). This suggests that the topologies S5–S8 are obtained in addition to S1–S4 topologies. However, S5 and S6 topologies are likely to be rare in turbulent premixed flames because of predominantly positive values of $\partial u_{i} /\partial x_{i}$ (alternatively negative values of $P$) for which S7 and S8 topologies are obtained. In order to demonstrate the effects of heat release on flow topologies in turbulent premixed flames in different regimes of combustion, a detailed chemistry DNS database of statistically planar turbulent premixed H₂-air flames spanning different regimes of turbulent combustion has been considered in this paper (Papapostolou et al. 2017; Wacks et al. 2016; Chakraborty et al. 2019; Im et al. 2016). The simulation domain is taken to be a rectangular box with a domain of size $20mm \times 10mm \times 10mm$ ($8mm \times 2mm \times 2mm$) in cases DA and DB (case DC) with inflow and outflow boundary conditions specified in the $x_{1}$-direction, which is aligned with the mean direction of flame propagation, and other directions are taken to be periodic. The inflow values of normalised root-mean-square turbulent velocity fluctuation $u^{\prime}/S_{L}$, the most energetic turbulent length scale to flame thickness ratio $l_{T} /\delta_{th}$, Damköhler number $Da = l_{T} S_{L} /u^{\prime}\delta_{th}$, Karlovitz number $Ka = \left( {\rho_{0} S_{L} \delta_{th} /\mu_{0} } \right)^{0.5} \left( {u^{\prime}/S_{L} } \right)^{1.5} \left( {l_{T} /\delta_{th} } \right)^{ - 0.5}$ and turbulent Reynolds number $Re_{t} = \rho_{0} u^{\prime}l_{T} /\mu_{0}$ for all cases are presented in Table 1 where $\mu_{0}$ is the unburned gas viscosity, $\delta_{th} = \left( {T_{ad} - T_{0} } \right)/\max \left| {\nabla T} \right|_{L}$ is the thermal flame thickness and the subscript ‘L’ is used to refer to unstrained laminar flame quantities with $T,T_{0}$ and $T_{ad}$ being the instantaneous temperature, unburned gas temperature, and the adiabatic flame temperature, respectively. The cases investigated in this study are nominally representative of three regimes of combustion: case DA: corrugated flamelets ($Ka < 1$), case DB: thin reaction zones ($1 < Ka < 100$) and case DC: broken reaction zones regime ($Ka > 100$) according to the Borghi-Peters regime diagram (Peters 2000; Borghi 1985). It is worth noting that whether the broken reaction zones combustion is realised in case DC is not important for the purpose of the current discussion. Undoubtedly, cases DA-DC offer a broad range of $Ka$, which allows for exploring the effects of heat release on flow topologies for different regimes of combustion.

Table 1 List of inflow turbulence parameters for the detailed chemistry DNS database

The distributions of instantaneous non-dimensional temperature $c_{T} = \left( {T - T_{0} } \right)/\left( {T_{ad} - T_{0} } \right)$, normalised first invariant $P^{*} = P \times \left( {\delta_{th} /S_{L} } \right)$, second invariant, $Q^{*} = Q \times \left( {\delta_{th} /S_{L} } \right)^{2}$, and third invariant $R^{*} = R \times \left( {\delta_{th} /S_{L} } \right)^{3}$ at the central mid-plane are shown in Fig. 2 (note that $Q$ and $R$ are non-dimensionalised by $\left( {\delta_{th} /S_{L} } \right)^{2}$ and $\left( {\delta_{th} /S_{L} } \right)^{3}$, respectively and it does not imply that these quantities scale with $\left( {S_{L} /\delta_{th} } \right)^{2}$ and $\left( {S_{L} /\delta_{th} } \right)^{3}$, respectively) but it is worth noting the change in length scale between cases DA, DB and case DC. In case DA, the velocity fluctuations are dissipated at the scale of flame thickness and thus the contours of $c_{T}$ remain parallel to each other and get wrinkled by turbulent eddies bigger than the size of Kolmogorov eddies. In case DB, the flame thickness is greater than the Kolmogorov length scale, whereas the reaction zone is smaller than the Kolmogorov length scale and some of the eddies are smaller than the length scale of the flame thickness. Thus, some of the eddies can modify the internal structure of the flame in case DB and can lead to localised flame thickness variations. It is worth noting that localised flame extinction is not observed in case DC even though the Karlovitz number is high which is consistent with several DNS (Aspden et al. 2011; Nikolaou and Swaminathan 2014; Hamlington et al. 2011; Carlsson et al. 2014) and experimental (Wabel et al. 2017; Skiba et al. 2018) findings. It is clear from Fig. 2 that the contours of $c_{T}$ in case DC are not parallel to each other and the contours towards the unburned gas side of the flame are more deformed than the ones towards the burned gas side as a result of the perturbation of the internal flame structure by small scale turbulent eddies and some of these eddies also start to perturb the reaction zone. The trend shown by the case DB is somewhere between cases DA and DC and it is worth noting from Table 1 that the values of $Da, Ka$ and $Re_{t}$ change from case DA to case DC, and $Ka$ is not modified in isolation. Thus, the alterations of $Da$ and $Re_{t}$ in addition to the modification of $Ka$, play a significant role in the differences in behaviour of the invariants and the flow topologies between cases DA-DC.

Fig. 2

Selected regions of instantaneous (row 1) non-dimensional temperature $c_{{\text{T}}}$ (green contours show $c_{{\text{T}}} = 0.1,0.5,0.7$ isolines from left to right), (row 2) normalised first invariant $P^{*} = P \times \left( {\delta_{th} /S_{L} } \right)$, (row 3) second invariant, $Q^{*} = Q \times \left( {\delta_{th} /S_{L} } \right)^{2}$, and (row 4) third invariant $R^{*} = R \times \left( {\delta_{th} /S_{L} } \right)^{3}$ fields at the $x - y$ mid-plane for (left to right) cases DA-DC

It can be seen from Fig. 2 that high negative values of $P^{*}$ are obtained within the flame as the effects of thermal expansion are strong there and thus the dilatation rate $\partial u_{i} /\partial x_{i} = - P$ assumes large positive values only within the flame. The dilatation rate $\partial u_{i} /\partial x_{i}$ outside remains small with a magnitude close to zero outside the flame, as the maximum Mach number remains much smaller than 0.3 in these flames. It can further be seen from Fig. 2 that the distributions of $Q^{*}$ and $R^{*}$ in cases DB and DC are considerably different from those in case DA. The Reynolds numbers of cases DB and DC are much larger than in case DA and thus these cases exhibit a larger range of length scales than in case DA.

The dilatation rate (i.e. $\nabla \cdot \vec{u} = - P$) also affects the behaviour of the second invariant $Q$ through its contribution in $Q_{S} = 0.5\left( {P^{2} - S_{ij} S_{ij} } \right)$ where $Q = Q_{S} + Q_{W}$ with $Q_{W} = W_{ij} W_{ij} /2$ being the contribution arising from vortical motion. It is worth noting that the sign of $Q$ provides indications of vorticity-dominated (i.e. $Q > 0$) and strain-dominated (i.e. $Q < 0$) regions outside the flame where $P \approx 0$ for low Mach number flows like the one considered here. A comparison between $P^{*}$ and $Q^{*}$ magnitudes from Fig. 2 reveals that the magnitude of $P^{2}$ remains smaller than the magnitude of $Q$ in most cases in the flow field and these quantities become comparable only within the flame. Moreover, in Fig. 2 the magnitudes of $Q$ and $R$ increase from case DA to case DC with an increase in $u^{\prime}/S_{L}$.

The qualitative distributions of $Q^{*}$ for cases DA-DC are markedly different. The flame almost acts as a barrier for $Q^{*}$ and its magnitude drops significantly across the flame in cases DB-DC (i.e. $Q^{*}$ drops with increasing $c_{T}$). In case DA, the high values of $Q$ are found close to the flame elements which are highly concave to the reactants, which arises due to high positive values of $P^{2}$ (since $P = - \nabla \cdot \vec{u}$) as a result of focusing of heat in these regions.

The expression for $R$ in Eq. 1 may be rewritten as the sum of the terms which play roles in dissipation rate generation ($- S_{ij} S_{jk} S_{ki} /3$) and enstrophy production ($PQ_{W} - \omega_{i} S_{ij} \omega_{j} /4$) in the following manner where $\omega_{i}$ is the ith component of vorticity:

$$ \begin{aligned} R = & \frac{1}{3}\left( { - P^{3} + 3PQ - S_{ij} S_{jk} S_{ki} } \right) - \frac{1}{4}\omega_{i} S_{ij} \omega_{j} \\ = & \frac{1}{3}\underbrace {{\left( { - P^{3} + 3PQ_{s} - S_{ij} S_{jk} S_{ki} } \right)}}_{{R_{s} }} + PQ_{W} - \frac{1}{4}\omega_{i} S_{ij} \omega_{j} \\ \end{aligned} $$

(2)

Equation 2 suggests that it is possible to obtain high positive or negative values of $R^{*}$ where there is an imbalance of the terms contributing to dissipation rate generation and production of enstrophy. Figure 2 shows that this imbalance is most pronounced in the vicinity of the flame front in case DA, whereas this behaviour is observed throughout the entire unburned gas region for cases DB and DC. The magnitude of $R^{*}$ decreases significantly in the burned gas region for all cases. The sign of the normalised third invariant $R^{*}$ does not change along most of the flame front, whereas, both positive and negative values of $R^{*}$ co-exist in the unburnt gas region and within the flame front in cases DB and DC.

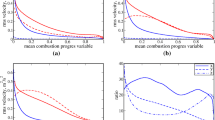
The normalised mean values of $P$ conditional on $c_{T}$ for cases DA-DC are shown in Fig. 3. It has already been discussed that dilatation rate $\nabla \cdot \vec{u} = - P$ assumes predominantly positive values in turbulent premixed flames but it is possible to get some localised pockets of negative dilatation rate (i.e. $P > 0$) in the regions which are convex to the reactants (see Fig. 2) due to defocussing of heat. However, the probability of finding positive dilatation rate overwhelms that of obtaining negative $\nabla \cdot \vec{u}$ and thus the mean values of $P = - \nabla \cdot \vec{u}$ remain negative for all cases considered here (see Fig. 3). The magnitude of $P = - \nabla \cdot \vec{u}$ depends on heat release rate, which, in turn, is determined by the strength of chemical activity within the flame. It can be seen from Fig. 3 that the variations of the mean values of $P$ across the flame are similar in cases DA and DB, whereas this magnitude is much smaller in case DC than in cases DA and DB. As discussed earlier, the reaction zone retains its quasi-laminar structure in cases DA and DB and therefore the mean dilatation rate profiles across the flame for these cases remain almost identical to each other in spite of turbulence intensity $u^{\prime}/S_{L}$ in case DB is about an order of magnitude greater than that in case DA. However, the turbulent eddies perturb the inner reaction layer of the flame and disrupt the chemical processes, which is reflected in the reduced magnitude of dilatation rate $\nabla \cdot \vec{u}$ in case DC, and therefore, smaller magnitude of the mean value of $P = - \nabla \cdot \vec{u}$ is obtained for case DC than in cases DA and DB. The findings of Fig. 3 suggest that the effects of dilatation rate $\nabla \cdot \vec{u} = - P$ weaken with increasing $Ka$.

Fig. 3

Log-linear variation of $P^{*} = P \times {\delta_{th}} /S_{L}$ with $c_{T}$ for cases DA–DC (red–green–blue)

This diminished strength of $\nabla \cdot \vec{u}$ or $P$ has a profound influence on the flow topology distributions in premixed turbulent flames. The distributions of flow topologies S1–S8 in the central midplane are shown in Fig. 4, which indicates the length scale of topology islands increases significantly across the flame. It can be seen from Fig. 4 that the topologies S1–S4 are obtained for all values of $P$ irrespective of its sign. The topologies S5 and S6 are rare because of predominantly negative values of $P$. The topologies S7 and S8, which are specific to negative values of $P$, are obtained in the flame and in the pockets of burned gas where the effects of dilatation rate are strong. In order to understand the distribution of flow topologies within the flame, the variations of the volume fraction $VF$ for each of S1–S8 topologies are shown in Fig. 5a–c as a function of $c_{T}$ for cases DA-DC, respectively. It can be seen from Fig. 5a–c that the topology distributions are notably different between cases DA-DC. Figure 5a–c indicate that the $VF$ for S5 and S6 remains almost zero for all of these cases because the occurrence of these topologies is rare, due to predominantly positive values of dilatation rate $\nabla \cdot \vec{u} = - P$. Moreover, $VFs$ of S1, S3, S4 topologies increase with increasing $c_{T}$ in case DA, whereas the volume fractions for the topologies S2, S7, S8 decrease from the unburned gas to the burned gas side. Such trends diminish from case DA to case DC. For example, the topologies S1–S4 and S7 are more uniformly distributed across $c_{T}$ in case DC and the volume fraction $VF$ for the S8 nodal topology disappears entirely. The S8 topology occurs for high positive values of dilatation rate ($\nabla \cdot \vec{u} = - P \gg 0$). The probability of obtaining high positive $\nabla \cdot \vec{u}$ decreases with increasing $Ka$ from case DA to DC and so does the volume fraction $VF$ of the S8 topology.

Fig. 4

Instantaneous distributions of flow topologies at the $x - y$ mid-plane for (left to right) cases DA-DC

Fig. 5

Variation of volume fractions $VF$ of topologies S1-8 with non-dimensional temperature $c_{T}$ for (a–c) cases DA–DC: focal topologies S1, 4, 5, 7 (red-blue-green-magenta solid lines) and nodal topologies S2, 3, 6, 8 (red–blue–green–magenta dashed lines). d Variation of $VF$ of total focal (solid lines) and nodal (dashed lines) topologies with $c_{T}$ for cases DA (tan), DB (black) and DC (olive)

The distributions of volume fraction of total combined focal (i.e. S1, S4, S5, S7) and nodal (i.e. S2, S3, S6, S8) topologies between cases DA-DC topologies have been compared in Fig. 5d. The nodal topologies have been found to be dominant in the unburnt gas region, whereas focal topologies play a dominant role in the burnt gas region in cases DA and DB. By contrast, the presence of the flame does not significantly influence the background turbulent fluid motion, and the focal topologies play significant roles across the entire flame-front in case DC. It is worth noting that the variations of focal and nodal topologies depend on the heat release parameter $\tau = (T_{ad} - T_{0} )/T_{0} = \rho_{0} /\overline{\rho }_{b} - 1$ (where $\overline{\rho }_{b}$ is the mean burned gas density) and characteristic Lewis number $Le$. The effects of flame-induced turbulence are stronger for higher values of $\tau$, and therefore the volume fraction of focal topologies decay from the unburned to the burned gas side for flames with smaller values of $\tau$ than that for cases DA-DC (Cifuentes et al. 2014; Cifuentes 2015).

In order to illustrate this, it is worthwhile to consider a simple chemistry (i.e. single step irreversible Arrhenius type chemistry) DNS database of statistically planar flames under decaying turbulence with different characteristic Lewis numbers $Le$. For this DNS database, the heat release parameter $\tau$ is 4.5 in contrast to cases DA-DC for which the heat release parameter is $\tau = 5.71$. In premixed flames every species has a different Lewis number but there are various methodologies based on which a characteristic Lewis number can be assigned: the Lewis number of the deficient reactant (Mizomoto et al. 1984; Bechtold and Matalon 2001); heat release measurements (Law and Kwon 2004); diffusion theory (Clarke 2002), or based on linear combination of mole fractions of the reactants (Dinkelacker et al. 2011). There have been several analytical (Williams 1985; Clavin and Joulin 1983; Clavin and Williams 1981, 1982), experimental (Dinkelacker et al. 2011; Abdel-Gayed et al. 1984; Renou et al. 2000) and computational (Chakraborty and Cant 2009a, 2009b, 2009c, 2006, 2005a, 2011; Chakraborty et al. 2011e, 2016; Dopazo et al. 2017; Wacks et al. 2018; Ashurst et al. 1987a; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Han and Huh 2008; Chakraborty and Klein 2008a; Ozel-Erol et al. 2020) analyses where the effects of differential diffusion of heat and mass have been analysed in isolation by altering only the characteristic Lewis number and the same approach was adopted in the DNS database presented in Table 2. The initial values of normalised rms velocity, $u^{\prime}/S_{L}$ normalised longitudinal length scale, $L_{{11}} /\delta _{{th}}$ Damköhler number Da = $L_{11}S_L/{u}^{\prime}\delta_{th}$ and Karlovitz number $Ka^{\prime}=(u^{\prime}/S_L)^{1.5} (L_{11}/{\delta}_{th})^{-0.5}$ are listed in Table 2 along with the heat release parameter, and characteristic Lewis number values. The Prandtl number is taken to be 0.7 (i.e. Pr = 0.7) for this database and further information related to numerical implementation of the database presented in Table 2 is available elsewhere (Chakraborty and Cant 2009a, b, c, 2011; Chakraborty et al. 2011e; Chakraborty et al. 2016; Dopazo et al. 2017; Chakraborty and Klein 2008a).

Table 2 List of initial turbulence parameters for the DNS database for the analysis of non-unity Lewis number effects

For the values of $u^{\prime}/S_{L}$ and $L_{{11}} /\delta _{{th}}$ reported in Table 2, combustion in all cases takes place nominally in the thin reaction zones regime (Peters 2000). The unity Lewis number flames are analogous to the stoichiometric methane-air flame, whereas the Lewis number 0.34 case represents a lean hydrogen-air mixture (Clarke 2002; Dinkelacker et al. 2011). The Lewis number 0.6 and 0.8 cases can be taken to be representatives of hydrogen-blended methane-air mixtures (e.g. 20% and 10% (by volume) with overall equivalence ratio of 0.6) and the Lewis number 1.2 case is representative of a hydrocarbon-air mixture involving a hydrocarbon fuel which is heavier than methane (e.g. ethane-air mixture with equivalence ratio of 0.7) (Clarke 2002; Dinkelacker et al. 2011).

The instantaneous fields of reaction progress variable $c = \left( {Y_{{R0}} - Y_{R} } \right)/\left( {Y_{{R0}} - Y_{{R\infty }} } \right)$ (where $Y_R$ is the deficient reactant mass fraction based on which the progress variable is defined and subscripts 0 and $\infty$ refer to its values in the unburned gas and fully burned products, respectively so that $c$ increases from 0 in the unburned gas to 1.0 in fully burned products) are shown in Fig. 6 when the statistics were extracted (i.e. $t = 2\delta _{{th}} /S_{L} = 3.34L_{{11}} /u'$). Figure 6 demonstrates that the extent of flame wrinkling increases with decreasing. In Le  < 1 flames, the reactants diffuse faster into the flame than the rate of thermal diffusion out of it and this gives rise to simultaneous occurrences of high temperature and high reactants concentration in the positively curved regions in these flames. This leads to augmentation of reaction rate magnitudes further in the regions which are convexly curved towards the reactants for the Le < 1 flames, and the combination of weak focussing of heat and strong defocussing of reactants leads to low reaction rate magnitudes at the concavely curved regions. The combination of high burning rate at convexly curved regions towards the reactants and low burning rate at the regions which are concavely curved acts to increase the flame wrinkling and volume integrated burning rate in the flames with Le < 1.0, in comparison to the corresponding unity Lewis number flame subjected to statistically similar turbulence. The opposite mechanisms in the Le > 1 cases lead to small (high) burning rates at the locations which are convex (concave) towards the reactants. This, in turn, acts to reduce the flame wrinkling in the cases with Le > 1, and therefore, the flames with Le > 1 show smaller values of flame surface area and volume-integrated burning rate than in the corresponding unity Lewis number flame. This can be verified from Table 3 where the flame surface area $A = \mathop \smallint \limits_{V} \left| {\nabla c} \right|dV$ and volume-integrated burning rate ${{\Omega }} = \mathop \smallint \limits_{V} \dot{w}dV$ (where $\dot{w}$ is the reaction rate of reaction progress variable) for turbulent flames in cases AL-EL normalised by the corresponding laminar values have been presented. This behaviour is consistent with several previous analytical (Williams 1985; Clavin and Joulin 1983; Clavin and Williams 1981, 1982), experimental (Dinkelacker et al. 2011; Abdel-Gayed et al. 1984; Renou et al. 2000) and numerical (Chakraborty and Cant 2005a, 2006, 2009a, b, c, 2011; Chakraborty et al. 2011e, 2016; Dopazo et al. 2017; Wacks et al. 2018; Ashurst et al. 1987a; Haworth and Poinsot 1992; Rutland and Trouvé 1993; Trouvé and Poinsot 1994; Han and Huh 2008; Chakraborty and Klein 2008a; Ozel-Erol et al. 2020) findings.

Fig. 6

Distribution of reaction progress variable $c$ in the central x–y plane for cases a $Le = 0.34$ (case AL), b $Le = 0.6$ (case BL), c $Le = 0.8$ (case CL), d $Le = 1.0$ (case DL) and e $Le = 1.2$ (case EL) at the time statistics were extracted

Table 3 Values of normalised flame surface area and normalised volume-integrated burning rate when statistics are extracted for flames in Table 2

The augmentation of the burning rate with decreasing Le is reflected in the higher magnitude of negative $P^{*}$ values for smaller values of Le. The variations of the normalised mean values of $P^{*}$ conditional on c for cases AL-EL are shown in Fig. 7, which is indicative of the increases in magnitude of dilatation rate $\left| {\nabla .\vec{u}} \right| = \left| { - P} \right|$ with decreasing $Le$. This is also in accordance with an increase in burning rate with decreasing Le, as can be seen from Table 3.

Fig. 7

The figure is reproduced from (Wacks et al. 2018)

Variation of $P \times \delta_{th} /S_{L}$ with $c$ for cases AL-EL (red–green–blue-magenta–cyan).

It has been found that large magnitudes of alternating small areas of positive and negative values of $Q^{*}$ occur on the unburned gas side of the flame in cases AL-EL (Wacks et al. 2018), but the magnitudes of $Q^{*}$ drop significantly towards the burned gas side for cases BL-EL. By contrast, large magnitudes $Q^{*}$ of have been found not only on the unburned gas side but also within the flame and locally on the burned gas side in case AL. The distribution of $R^{*}$ has been found to be qualitatively similar to that of $Q^{*}$ in cases AL-BL. The physical explanations provided to explain the distributions of $Q^{*}\, {\rm{and}} \, R^{*}$ in the context of Fig. 2 are also applicable here and thus are not repeated. Interested readers are referred to Wacks et al. (2018) for further information on $Q^{*}$ and $R^{*}$ distributions in cases AL-EL. It can be appreciated from the above discussion that the thermal expansion due to chemical heat release is strongly affected by the characteristic Lewis number Le. Thus, the increased magnitude of negative values of $P^{*}$ for small values of Le and differences in $Q^{*}\, {\rm{and}} \, R^{*}$ distributions for different values of $Le$ are expected to have influence on the flow topology distributions in cases AL-EL.

Figure 8a–c indicates that the distribution of volume fractions of flow topologies for cases AL, BL and DL, respectively and the cases CL and EL are not explicitly shown here due to their qualitative similarity to case DL. It can be seen from Fig. 8a–c that S1–S4 topologies are obtained for all values of P and thus they are obtained all across the flame. However, each topology responds differently to the variation of Le. In case AL, S1 and S4 topologies exhibit high values of VF at both low and high value of c (i.e. c ≈ 0.0 and c ≈ 1.0), and the VF of S1 assumes higher values than that of S4 throughout the flame. The behaviour of the VFs of S1 and S4 topologies change towards the burned gas side in response to the variations of Le and the profiles of S1 and S4 collapse onto one curve (e.g. the VF at c ≈1.0 decreases in value for both topologies). The VF of S2 topology decreases on unburned and burned gas sides of the flame, and the VF of S2 topology towards the burned gas side increases with increasing Le. The distribution of the VF of S3 topology remains mostly unaffected by the variation of Le. As S5 and S6 topologies are associated with negative values of dilatation rate (∇⋅u⃗=−P < 0), the likelihood of finding these topologies remains negligible across the entire flame for all cases. The VFs of S7 and S8 topologies, which are associated with positive values of dilatation rate (∇⋅u⃗=−P > 0), assume non-negligible significant values for intermediate values of c where the effects of heat release are strong. The profile of the VF for S7 topology is not affected by the variation of Le for the cases demonstrated here, but the location of the high value of the VF of this topology shifts from high c for smaller values of Le to low c for higher values of Le. The VF of S8 topology assumes high values at intermediate c-value within the flame and the profile of the VF of S8 for case AL is found to be somewhat flatter and of lesser magnitude than in cases BL-EL.

Fig. 8

The figure is reproduced from (Wacks et al. 2018)

Variation of volume fractions $VF$ of topologies S1-8 with reaction progress variable $c$ for cases a AL, b BL and c DL: focal topologies S1, 4, 5, 7 (red-blue-green-magenta solid lines) and nodal topologies S2, 3, 6, 8 (red-blue-green-magenta dashed lines). d Variation of $VF$ of total focal (solid lines) and nodal (dashed lines) topologies with ${c}$ for cases AL-EL (brown–black–olive–pink–cyan).

The variations of the distributions of $VF$s of total combined focal (i.e. S1, S4, S5, S7) and nodal (i.e. S2, S3, S6, S8) topologies with c for cases AL-EL are shown in Fig. 8d. It has been found that focal topologies remain dominant for c < 0.7 in these cases. Within the preheat zone for 1.0 < c < 0.5, the VFs of focal topologies increase with increasing Le. However, for c > 0.5, the $VF$s of focal topologies decrease with increasing Le. It can be seen from Fig. 8d that the VFs for the focal topologies decrease to such an extent that the VFs for the nodal topologies become dominant for in cases CL-EL, whereas the $VF$s for the focal topologies increase with $c$ in this region of the flame in cases AL-BL. The qualitative nature of the distributions of the VFs of total combined focal (i.e. S1, S4, S5, S7) and nodal (i.e. S2, S3, S6, S8) topologies with $c$ for cases CL-EL are found to be consistent with other simple chemistry analyses (Cifuentes et al. 2014; Cifuentes 2015) on the thin reaction zones regime flames with comparable values of $\tau$ and a characteristic Lewis number close to unity. However, the differences in behaviour in cases AL and BL from cases CL-EL originates because of the qualitatively different vorticity distribution within the flame owing to stronger flame-generated turbulence for smaller values of Lewis number.

The aforementioned discussion suggests that the heat release due to combustion can have a significant influence on the vorticity distribution and therefore turbulence flow characteristics within premixed turbulent flames. Therefore, the effects of heat release on enstrophy distribution within turbulent premixed combustion will be discussed next in this paper.

3 Effects of Heat Release on the Enstrophy Distribution in Turbulent Premixed Flames

The transport equation of the $i^{th}$ component of vorticity, ω_i = ε_ijk∂u_k/∂x_j, obtained by taking the curl of momentum conservation equation, can be written in the following manner:

$$ \frac{{\partial \omega_{i} }}{\partial t} + u_{k} \frac{{\partial \omega_{i} }}{{\partial x_{k} }} = \underbrace {{\omega_{k} \frac{{\partial u_{i} }}{{\partial x_{k} }}}}_{{t_{1i} }} - \underbrace {{\epsilon_{ijk} \frac{1}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{{\partial \tau_{kl} }}{{\partial x_{l} }}}}_{{t_{21i} }} + \underbrace {{\frac{{\epsilon_{ijk} }}{\rho }\frac{{\partial^{2} \tau_{kl} }}{{\partial x_{j} \partial x_{l} }}}}_{{t_{22i} }} - \underbrace {{\omega_{i} \frac{{\partial u_{k} }}{{\partial x_{k} }}}}_{{t_{3i} }} + \underbrace {{\frac{{\epsilon_{ijk} }}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{\partial p}{{\partial x_{k} }}}}_{{t_{4i} }} $$

(3)

The first term $t_{1i}$ on the right hand side of Eq. 3 is the $i^{th}$ component of the vortex-stretching term. The term $t_{21i}$ represents the $i^{th}$ component of the viscous torque term arising from the misalignment between the gradients of viscous stress and density and vanishes in constant-density flows. The $i^{th}$ component of the third term on the right hand side (i.e. $t_{22i}$) is the vorticity diffusion term and is equal to $\nu \partial^{2} \omega_{i} /\partial x_{j} \partial x_{j}$ in flows with constant thermo-physical properties with $\nu$ being the kinematic viscosity. The term $t_{3i}$ is responsible for vorticity destruction by dilatation, whereas the $i^{th}$ component of term is responsible for baroclinic torque owing to the misalignment of the density and pressure gradients. The terms and vanish in constant-density flows.

Multiplying $\omega_{i}$ both sides of Eq. 3 provides the transport equation of enstrophy ${\Omega } = \omega^{2} /2 = \omega_{i} \omega_{i} /2$ (Lipatnikov et al. 2014; Chakraborty et al. 2016; Dopazo et al. 2017; Papapostolou et al. 2017):

$$ \frac{\partial \Omega }{{\partial t}} + u_{k} \frac{\partial \Omega }{{\partial x_{k} }} = \underbrace {{\omega_{i} \omega_{k} \frac{{\partial u_{i} }}{{\partial x_{k} }}}}_{{T_{1} }} - \underbrace {{\epsilon_{ijk} \omega_{i} \frac{1}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{{\partial \tau_{kl} }}{{\partial x_{l} }}}}_{{T_{21} }} + \underbrace {{\frac{{\epsilon_{ijk} \omega_{i} }}{\rho }\frac{{\partial^{2} \tau_{kl} }}{{\partial x_{j} \partial x_{l} }}}}_{{T_{22} }} - \underbrace {{2\frac{{\partial u_{k} }}{{\partial x_{k} }}{\Omega }}}_{{T_{3} }} + \underbrace {{\epsilon_{ijk} \frac{{\omega_{i} }}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{\partial p}{{\partial x_{k} }}}}_{{T_{4} }} $$

(4i)

On Reynolds averaging Eq. 4i provides (Lipatnikov et al. 2014; Chakraborty et al. 2016; Papapostolou et al. 2017):

$$\frac{\partial \overline{\Omega}}{{\partial t}} + \overline{u_{k} \frac{\partial \Omega }{{\partial x_{k}}}} = \underbrace{\overline{\omega_{i} \omega_{k} \frac{{\partial u_{i} }}{{\partial x_{k} }}}}_{{T_{I} }} -\underbrace {\overline{\epsilon_{ijk} \omega_{i} \frac{1}{{\rho^{2}}}\frac{\partial \rho }{{\partial x_{j} }}\frac{{\partial \tau_{kl} }}{{\partial x_{l} }}}}_{{T_{II} }} + \underbrace {\overline{\frac{{\epsilon_{ijk} \omega_{i} }}{\rho }\frac{{\partial^{2} \tau_{kl} }}{{\partial x_{j} \partial x_{l}}}}}_{{T_{III} }} - \underbrace {\overline{2\frac{{\partial u_{k} }}{{\partial x_{k} }}{\Omega }}}_{{T_{IV} }} + \underbrace{\overline{\epsilon_{ijk} \frac{{\omega_{i} }}{{\rho^{2} }}\frac{\partial \rho}{{\partial x_{j} }}\frac{\partial p}{{\partial x_{k} }}}}_{{T_{V}}} $$

(4ii)

where $\overline{Q}$ indicates the Reynolds averaged value of a general quantity $Q$. The Favre average of a general quantity $Q$ is given by: $\tilde{Q} = \overline{\rho Q} /\overline{\rho }$ and $Q^{\prime\prime} = Q - \tilde{Q}$ is the Favre fluctuation of the quantity $Q$ in the context of RANS (which is going to be the case for the following discussion until it is mentioned otherwise). The term T_I represents the vortex stretching contribution to the mean enstrophy ${\overline{\Omega }}$ transport, whereas the term T_II is the mean value of the cross-product of two vectors, the density gradient and the viscous stress gradient. The term T_III, can be expanded as: $\overline{{\nu \omega_{i} (\partial^{2} \omega_{i} /\partial x_{j} \partial x_{j} )}} = \overline{{\nu \partial^{2} {\Omega }/\partial x_{j}^{2} }} - \overline{{\nu \left( {\partial \omega_{i} /\partial x_{j} } \right)\left( {\partial \omega_{i} /\partial x_{j} } \right)}}$ if the dynamic viscosity is constant, and it represents the combined action of molecular diffusion (i.e. $\overline{{\nu \partial^{2} {\Omega }/\partial x_{j}^{2} }}$) and dissipation (i.e. $- \overline{{\nu \left( {\partial \omega_{i} /\partial x_{j} } \right)\left( {\partial \omega_{i} /\partial x_{j} } \right)}}$) of the mean enstrophy ${\overline{\Omega }}$. These two sub-terms can be of comparable order of magnitude for small values of turbulent Reynolds number, whereas the dissipation contribution (i.e.$- \overline{{\nu \left( {\partial \omega_{i} /\partial x_{j} } \right)\left( {\partial \omega_{i} /\partial x_{j} } \right)}}$) is dominant for high values of turbulent Reynolds number. The term T_IV is responsible for the enstrophy dissipation due to dilatation. The term T_V is the baroclinic torque contribution to the enstrophy transport.

In order to demonstrate the effects of heat release on the enstrophy transport for different values of $Ka$, the variations of $T_{I} ,T_{II} ,T_{III} ,T_{IV}$ and $T_{V}$ with $\tilde{c}_{T}$ for cases DA-DC are exemplarily shown in Fig. 9, which reveals significant differences between cases DA-DC. The term $T_{III}$ acts as a leading order sink, and its magnitude remains greater than the magnitude of viscous torque contribution $T_{II}$ for all cases in Fig. 9. Figure 9 further suggests that the baroclinic torque contribution $T_{V}$ acts as a major source term with its magnitude comparable to that of $T_{III}$ in case DA where the dilatation term $T_{IV}$ acts a major sink term and its magnitude remains comparable to that of the combined viscous diffusion and dissipation term $T_{III}$. The mean vortex-stretching term $T_{I}$ offers weak contribution in case DA and its magnitude remains smaller than that for the terms of $T_{III}$ and $T_{V}$ in case DA. The relative strengths of the dilatation and baroclinic torque contributions to the enstrophy transport diminish with increasing Karlovitz number $Ka$ and the magnitudes of these terms in comparison to the combined viscous diffusion and dissipation terms $T_{III}$ become negligible in the flame in case DC. In cases DB and DC, the vortex-stretching term $T_{I}$ and the combined viscous diffusion and dissipation term $T_{III}$ remain the major source and sink terms, respectively. However, baroclinic term $T_{V}$ and the dilatation term $T_{IV}$ continue to play important roles as source and sink terms, respectively, in case DB their magnitudes are generally smaller than those of $T_{I}$ and $T_{III}$, respectively. Figure 9 shows that the transport of enstrophy in case DC is determined by source and sink contributions of vortex-stretching term $T_{I}$ and the combined viscous diffusion and dissipation term $T_{III}$, respectively and the magnitudes of $T_{II} ,T_{IV}$ and $T_{V}$ remain negligible in comparison to the magnitudes of $T_{I}$ and $T_{III}$. The enstrophy transport characteristics in case DC are qualitatively similar to high Reynolds number non-reacting flows. This suggests that effects of dilatation rate and density change on turbulent fluid motion weaken with increasing Karlovitz number $Ka$, and thus the relative strengths of the dilatation and baroclinic terms (i.e. $T_{IV}$ and $T_{V}$) remain significant only for small values of $Ka$ (e.g. $Ka < 1,$ corrugated flamelets regime), but their contributions weaken for large values of Karlovitz number (e.g. $Ka \gg 1$ in the thin reaction zones and broken reaction zones regimes).

Fig. 9

Variation with $\tilde{c}_{T}$ ($0.05 \le \tilde{c}_{T} \le 0.95$) of normalised enstrophy transport equation terms, $T_{j}$ ( $j$= I; II; III; IV; V), for (left to right) cases DA-DC: $T_{I}$ (red line), $T_{II}$ (blue line), $T_{III}$ (green line), $T_{IV}$ (magenta line), $T_{V}$ (cyan line). The x-axis is shown using a logarithmic scale

The vortex-stretching term $T_{I}$ can be expressed as (Chakraborty et al. 2016; Papapostolou et al. 2017; Chakraborty 2014):

$$ T_{I} = \overline{{2(e_{\alpha } \cos^{2} \chi_{\alpha } + e_{\beta } \cos^{2} \chi_{\beta } + e_{\gamma } \cos^{2} \chi_{\gamma } ){\Omega }}} $$

(5)

Here $e_{\alpha } ,e_{\beta }$ and $e_{\gamma }$ are the most extensive (i.e. most positive), intermediate and the most compressive (i.e. most negative or least positive by magnitude) principal strain rates respectively (i.e. $e_{\alpha } > e_{\beta } >$ $e_{\gamma }$), and the angles between $\vec{\omega }$ and the eigenvectors associated with $e_{\alpha } ,e_{\beta }$ and $e_{\gamma }$ are given by $\chi_{\alpha } ,\chi_{\beta }$ and $\chi_{\gamma }$, respectively. It was demonstrated in several previous studies (Chakraborty 2014; Tsinober 2000; Hamlington et al. 2011, 2008; Majda 1991; Jimenez 1992; Tsinober et al. 1992; Zeff et al. 2003; Lüthi et al. 2005; Xu et al. 2011; Nomura and Elghobashi 1993; Boratov et al. 1996; Jaberi et al. 2000) that $\vec{\omega }{ }$ preferentially aligns with the eigenvector associated with $e_{\beta }$ (i.e. $\left| {\cos \chi_{\beta } } \right| \approx 1$) which will be discussed in greater detail later in this paper. However, the extent of alignment of $\vec{\omega }$ with the eigenvector corresponding to $e_{\alpha }$ ($e_{\gamma }$) decreases (increases) with decreasing Karlovitz number especially in corrugated flamelets regime flames (Chakraborty 2014) and the reasons for this behaviour are summarised in Sect. 5 of this paper. The increased probability of the collinear alignment of $\vec{\omega }$ with the most compressive (i.e. most negative) and intermediate principal strain rates gives rise to the weak contribution of $T_{I}$ in case DA. The predominantly positive dilatation rate $\nabla \cdot \vec{u}$ in turbulent premixed flames leads to a predominantly negative value of dilatation contribution $T_{IV} = - \overline{{2\left( {\nabla \cdot \vec{u}} \right){\Omega }}}$. It has already been demonstrated in the context of Fig. 3 that the influence of dilatation rate weakens from case DA to DC and therefore $T_{IV}$ plays a progressively less important role with increasing $Ka$. The cosine of the angle between $\vec{\omega }$ and $\nabla p \times \nabla \rho /\rho^{2}$ remains mostly positive (Chakraborty et al. 2016), which leads to a positive contribution of the baroclinic torque in the mean sense (i.e. $T_{V}$) for all cases.

The variations of $\overline{{{\Omega }^{{\text{i}}} }}$ with $\tilde{c}_{T}$ for cases DA-DC are shown in Fig. 10 along with the contributions of each individual topology (i.e. $\overline{{{\Omega }^{i} }}$ where $i = 1,2, \ldots ,8$ for $S1 - S8$ such that ${\overline{\Omega }} = \overline{{{\Omega }^{0} }} = \mathop \sum \nolimits_{i = 1}^{8} { }\overline{{{\Omega }^{i} }}$). Figure 10 shows that enstrophy is generated within the flame in case DA, whereas a monotonic decay of ${\overline{\Omega }}$ with increasing $\tilde{c}_{T}$ has been observed in case DC and the corresponding behaviour in case DB is somewhere between cases DA and DC. A comparison between the enstrophy transport characteristics in cases DA-DC reveals that the baroclinic torque is responsible for enstrophy generation in case DA, which gives rise to local augmentation of enstrophy across the flame in this case. In cases DB and DC, only the vortex-stretching term $T_{I}$ is the major source and its magnitude decreases from the unburned to the burned gas side of the flame brush with its magnitude superseded by the viscous dissipation contribution $T_{III}$. This leads to decay in ${\overline{\Omega }}$ with increasing $\tilde{c}_{T}$ for cases DB and DC.

Fig. 10

Variation of normalised $\overline{{{\Omega }^{i} }}$ with $\tilde{c}_{T}$ ($0.05 \le \tilde{c}_{T} \le 0.9$), where (i = 0) are the total enstrophies (black solid lines) and (i = 1…,8) are the percentage-topology-weighted enstrophies S1-8, respectively, for cases (left to right) A–C: focal topologies S1 (red solid line), S4 (blue solid line), S5 (green solid line), and S7 (magenta solid line) and nodal topologies S2 (red dashed line), S3 (blue dashed line), S6 (green dashed line), and S8 (magenta dashed line). The x-axis is shown using a logarithmic scale

The topologies which contribute significantly to $T_{I} ,T_{II} ,T_{III} ,T_{IV}$ and $T_{V}$ in cases DA-DC are summarised in Table 4 in decreasing order. Table 4 reveals that S1–S4, S7 and S8 topologies play important roles in the enstrophy transport in the corrugated flamelets regime (e.g. case DA), but the contributions of S7 and S8 weaken with an increase in Karlovitz number and for $Ka \gg 1$, the enstrophy transport is governed by S1, S2 and S4 topologies which are obtained for all conditions, regardless of the value of $P$.

Table 4 Leading different flow topology contributions to the different terms of the mean enstrophy transport equation (Eq. 4ii)

It is worth noting that baroclinic torque contribution in the corrugated flamelets regime strengthens with increasing heat release parameter $\tau$ (Chakraborty 2014). This also leads to the strengthening of enstrophy generation within the flame with increasing $\tau$ in the corrugated flamelets regime. However, this behaviour does not remain prominent in the thin reaction zones regime and the qualitative nature of the enstrophy distribution across the flame is not modified by the heat release parameter $\tau$ for a characteristic Lewis number of unity (Chakraborty 2014). It is worth noting that $\nabla p$ and $\nabla \rho$ are perfectly aligned with each other in a planar laminar flame and thus the baroclinic torque $\vec{\omega } \cdot \left( {\nabla \rho \times \nabla p} \right)/\rho^{2}$ is identically zero, therefore flame wrinkling is necessary to obtain a non-zero contribution of the baroclinic torque. It has been demonstrated in a recent study (Lipatnikov et al. 2018) that the flame stretch rate $K = A^{ - 1} \left( {dA/dt} \right)$ (i.e. fractional change in flame surface area $A$) can be negatively correlated with baroclinic torque $\vec{\omega } \cdot \left( {\nabla \rho \times \nabla p} \right)/\rho^{2}$ in the corrugated flamelets regime flames. This suggests that the flame generated vorticity acts to reduce the flame surface area in the corrugated flamelets regime (Lipatnikov et al. 2018). However, this inference cannot necessarily be drawn for flames with high values of $Ka$ because the enstrophy generation for high values of Karlovitz number is not solely dependent on the baroclinic torque contribution (see Fig. 9). However, the baroclinic torque is likely to play a significant role in the enstrophy transport for the thin reaction zones regime flames, which will be demonstrated next in this paper using cases AL-EL considered earlier.

The variations of the normalised values of $T_{I} , T_{II} , T_{III} , T_{IV}$ and $T_{V}$ with $\tilde{c}$ are shown in Figs. 11a–c for cases AL, BL and DL respectively. The qualitative behaviours of $T_{I} , T_{II} , T_{III} , T_{IV}$ and $T_{V}$ in cases CL and EL are qualitatively similar to that of case DL and thus are not shown for the sake of brevity. Figure 11a–c shows that the mean contribution of the vortex-stretching term $T_{I}$ remains positive throughout the flame brush for all cases but its relative importance decreases with decreasing $Le$. This behaviour originates due to the changes in the alignment of vorticity with local principal strain rates in response to characteristic Lewis number but the vortex-stretching term $T_{I}$ acts to generate enstrophy for these cases. It can be seen from Fig. 11a–c that the viscous torque term $T_{II}$ remains small in magnitude in comparison to the other terms in the transport equation of ${\overline{\Omega }}$. As $T_{III}$ includes the contributions from the viscous diffusion and dissipation of enstrophy, and the latter contribution plays the dominant role, the term $T_{III}$ acts as a leading order sink for all cases. The dilatation rate term $T_{IV}$ also acts as a sink within the flame brush. It can further be seen from Fig. 11a–c that the magnitude of $T_{IV}$ remains small in comparison to that of $T_{III}$ for case DL (in reality for cases CL-EL) but the magnitude of $T_{IV}$ becomes comparable to $T_{III}$ for the low $Le$ flames (e.g. cases AL-BL). The baroclinic torque term $T_{V}$ acts as a source within the flame brush and its relative magnitude with respect to the magnitude of $T_{III}$ increases with decreasing $Le$. Figure 11a–c further reveals that the vortex-stretching and viscous dissipation terms remain the leading order contributors in these thin reaction zones regime flames, but the dilatation and baroclinic torque contributions can play leading order roles in the thin reaction zones regime flames with small values of $Le$ (e.g. $Le = 0.34$ and 0.6 in cases AL and BL, respectively).

Fig. 11

Variations of $T_{I} \times \delta_{th}^{3} /S_{L}^{3} ,{ }T_{II} \times \delta_{th}^{3} /S_{L}^{3} ,{ }T_{III} \times \delta_{th}^{3} /S_{L}^{3} ,{ }T_{IV} \times \delta_{th}^{3} /S_{L}^{3}$ and $T_{V} \times \delta_{th}^{3} /S_{L}^{3}$ with $\tilde{c}$ for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

The strengthening of baroclinic effects with decreasing $Le$ warrant further discussion. For this purpose, the variations of normalised mean values of dilatation rate $\overline{{\left( {\partial u_{i} /\partial x_{i} } \right)}} \times \delta_{th} /S_{L}$ with $\tilde{c}$ for cases AL-EL are presented in Fig. 12. As expected from increasing burning rate with decreasing $Le$, the magnitude of $\overline{{\left( {\partial u_{i} /\partial x_{i} } \right)}} \times \delta_{th} /S_{L}$ in Fig. 12 shows an increasing trend with a decrease in $Le$. As density change leads to non-zero dilatation rate, the high values of $\overline{{\left( {\partial u_{i} /\partial x_{i} } \right)}} \times \delta_{th} /S_{L}$ are associated with high values of $\overline{{\left| {\nabla \rho } \right|}} \times \delta_{th} /\rho_{0}$. For low Mach number constant pressure combustion, the gas density $\rho$ can be expressed as: $\rho = \rho_{0} /\left( {1 + \tau c_{T} } \right)$ (Chakraborty et al. 2016; Bray et al. 1985). For low Mach number unity Lewis number flames, the non-dimensional temperature $c_{T}$ can be equated to $c$, and thus $\nabla \rho$ can be expressed as: $\nabla \rho = \tau \rho^{2} \left| {\nabla c} \right|\vec{N}/\rho_{0}$, which leads to $\partial \rho /\partial x_{n} = \nabla \rho \cdot \vec{N} = - \tau \rho^{2} \nabla c_{T} .\vec{N}/\rho_{0} = \tau \rho^{2} \left| {\nabla c} \right|/\rho_{0} = \left| {\nabla \rho } \right|$ where $\vec{N} = - \nabla c/\left| {\nabla c} \right|$ is the local flame normal vector. It was demonstrated in (Chakraborty et al. 2016) that $\overline{{\left| {\nabla \rho } \right|}}$ and $\overline{{\left( {\partial \rho /\partial x_{n} } \right) }}$ remain close to each other even for $Le \ne 1.0$ flames for the database presented in Table 2, thus, suggesting that $\left( { - \nabla c_{T} .\vec{N}} \right)$ remains approximately equal to $\left| {\nabla c} \right|$ even for non-unity Lewis number cases. This suggests that $\nabla \rho$ can be scaled as: $\nabla \rho \sim \tau \rho^{2} \left| {\nabla c} \right|\vec{N}/\rho_{0}$ and thus $\nabla \rho$ mostly aligns with the flame normal direction. Therefore, the baroclinic torque $\rho^{ - 2} \nabla \rho \times \nabla p$ is expected to have weak contributions in the flame normal direction but its contribution to vorticity transport in tangential directions is likely to be strong (Chakraborty et al. 2016). It will be discussed later in this paper that vorticity preferentially aligns with the intermediate principal strain rate, which is usually aligned in the direction normal to the alignment of $\nabla c$. Thus, the scalar inner product of $\vec{\omega }$ and $\rho^{ - 2} \nabla \rho \times \nabla p$ is expected to assume non-zero values.

Fig. 12

Variations of a $\overline{{\left( {\partial u_{i} /\partial x_{i} } \right)}} \times \delta_{th} /S_{L}$ with Favre averaged reaction progress variable $\tilde{c}$ for cases AL-EL (i.e. $Le = 0.34,\, 0.6,\, 0.8,\, 1.0$ and 1.2)

The variations of the pressure gradient magnitudes in local flame tangential direction, flame normal direction and the total pressure gradient (i.e. $\overline{{|\left( {\nabla p} \right)_{t} |}}$, $\overline{{|\left( {\nabla p} \right)_{n} |}}$ and $\overline{{\left| {\nabla p} \right|}}$) with $\tilde{c}$ are shown in Fig. 13a–c for cases AL, BL and DL, respectively. The cases CL and EL are not explicitly shown for the qualitative similarities of $\overline{{|\left( {\nabla p} \right)_{t} |}}$, $\overline{{|\left( {\nabla p} \right)_{n} |}}$ and $\overline{{\left| {\nabla p} \right|}}$ in these cases with the corresponding variations in case DL. The variation of the mean pressure gradient $|\left( {\nabla \overline{p}} \right)_{1} |$ normal to the mean flame brush as a function of $\tilde{c}$ is shown in Fig. 13d. Figure 13a–c reveals that $\overline{{|\left( {\nabla p} \right)_{t} |}}$ and $\overline{{|\left( {\nabla p} \right)_{n} |}}$ remain comparable. It is worth noting that $\overline{{|\left( {\nabla p} \right)_{n} |}} = \overline{{\left| {\vec{N} \cdot \nabla p} \right|}}$ is associated with locally normal flow acceleration, whereas the pressure gradient in tangential direction at a given location is induced by heat release in the surrounding flame wrinkles and by turbulent eddies. The cases AL-EL represent statistically planar flames and the extent of flame wrinkling can be quantified with the help of the departure of $\overline{{\left| {\vec{N} \cdot \vec{e}_{1} } \right|}}$ from 1.0 because for a perfectly flat flame one obtains $\overline{{\left| {\vec{N} \cdot \vec{e}_{1} } \right|}}$ = 1.0, where $\vec{e}_{1}$ is the unit vector in the direction of mean flame propagation. The variations of $\overline{{\left| {\vec{N} \cdot \vec{e}_{1} } \right|}}$ with $\tilde{c}$ for cases AL-EL are shown in Fig. 14a. A comparison between Fig. 13a–c and Fig. 14a shows that the relatively large magnitudes of $\overline{{|\left( {\nabla p} \right)_{t} |}}$ are associated with the small values of $\overline{{\left| {\vec{N} \cdot \vec{e}_{1} } \right|}}$. It has already been demonstrated that turbulent burning rate increases with decreasing $Le$ (see Table 3). This gives rise to a larger extent of thermal expansion and flame normal acceleration, which translates into an increasing magnitude of mean pressure gradient $|\left( {\nabla \overline{p}} \right)_{1} |$ normal to the mean flame brush with decreasing $Le$, as demonstrated in Fig. 13d. This also contributes to the increased magnitude of $\overline{{|\left( {\nabla p} \right)_{t} |}}$ for small values of $Le$, because the probability of finding a substantial angle between $\left( {\nabla \overline{p}} \right)_{1}$ and $\vec{N}$ is sufficiently large in the flames with $Le \ll 1.0$ (e.g. case AL), which results in large magnitudes of $\rho^{ - 2} \nabla \rho \times \nabla p$ in these flames. Both the extent of flame wrinkling and $|\left( {\nabla \overline{p}} \right)_{1} |$ decrease with increasing $Le$, and these lead to the weakening of $\overline{{|\left( {\nabla p} \right)_{t} |}}$ and relative contribution of baroclinic torque with an increase in Lewis number.

Fig. 13

Variations of $\overline{{|\left( {\nabla p} \right)_{t} |}} \times \delta_{th} /\rho_{0} S_{L}^{2}$, $\overline{{|\left( {\nabla p} \right)_{n} |}} \times \delta_{th} /\rho_{0} S_{L}^{2}$ and $\overline{{\left| {\nabla p} \right|}} \times \delta_{th} /\rho_{0} S_{L}^{2}$ with Favre averaged reaction progress variable $\tilde{c}$ for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$). d Variations of $|\left( {\nabla \overline{p}} \right)_{1} | \times \delta_{th} /\rho_{0} S_{L}^{2}$ with Favre averaged reaction progress variable $\tilde{c}$ for cases AL-EL (i.e. $Le = 0.34\:,0.6\:,0.8\:, 1.0$ and 1.2)

Fig. 14

Variations of a $\overline{{\left| {\vec{N} \cdot \vec{e}_{1} } \right|}}$ and b $\overline{{cos\theta_{p} }} = \overline{{\left( {\nabla \rho \times \nabla p} \right) \cdot \vec{\omega }/\left( {\left| {\nabla \rho \times \nabla p} \right| \cdot \left| {\vec{\omega }} \right|} \right)}}$ with $\tilde{c}$ for cases AL-EL (i.e. $Le = 0.34,\,0.6,\,0.8,\,1.0$ and 1.2)

It is worth noting that the sign of the baroclinic torque term $T_{V}$ depends on the angle between $\vec{\omega }$ and $\rho^{ - 2} \nabla \rho \times \nabla p$. This angle is characterized by $cos\theta_{p} = \left( {\nabla \rho \times \nabla p} \right) \cdot \vec{\omega }/\left( {\left| {\nabla \rho \times \nabla p} \right| \cdot \left| {\vec{\omega }} \right|} \right)$. The variation of $\overline{{cos\theta_{p} }}$ with $\tilde{c}$ for cases Al-EL are shown in Fig. 14b, which reveals that the directions of $\vec{\omega }$ and $\rho^{ - 2} \nabla \rho \times \nabla p$ are independent of each other for leading and trailing edges of the flame brush for cases BL-EL but the directions of $\vec{\omega }$ and $\rho^{ - 2} \nabla \rho \times \nabla p$ are related on the burned gas side due to significant density variation caused by temperature inhomogeneity in the burned gas (Chakraborty and Cant 2009a; Chakraborty et al. 2016). Within the flame brush, $\overline{{cos\theta_{p} }}$ assumes high magnitudes and this effect is particularly strong for case AL. The strong enstrophy generation under the influence of strong baroclinic torque for small values of $Le$ may give rise to a significant amount of enstrophy production within the flame and under some conditions the enstrophy may increase from the leading edge of the flame brush before reaching a peak value within the flame brush before decaying towards the burned gas side, as can be observed from normalised vorticity magnitude for case AL in Fig. 15. This trend weakens with increasing $Le$ with diminishing strength of baroclinic torque and for the thin reaction zones regime flames with $Le \approx 1.0$ (e.g. cases CL-EL but the instantaneous distribution of $\left( {\omega_{i} \omega_{i} } \right)^{1/2} \times \delta_{th} /S_{L}$ is only exemplarily shown for case DL in Fig. 15), the enstrophy decreases monotonically from the unburned gas side to the burned gas side of the flame brush, as can be substantiated from the vorticity magnitude distributions shown in Fig. 15.

Fig. 15

Instantaneous distribution of $\left( {\omega_{i} \omega_{i} } \right)^{1/2} \times \delta_{th} /S_{L}$ in the central $x_{1} - x_{3}$ plane for a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$). d Variation of the Reynolds averaged normalised vorticity magnitude $\overline{{\left( {\omega_{i} \omega_{i} } \right)^{1/2} }} \times \delta_{th} /S_{L}$ with $\tilde{c}$ for cases AL-EL (i.e. $Le = 0.34,0.6,0.8,1.0$ and 1.2)

The above discussion suggests that the self-induced pressure gradient arising from thermal expansion due to heat release rate plays a key role in the evolution of turbulence within the flame brush. In order to illustrate this point, the transport characteristics of turbulent kinetic energy and turbulent scalar flux will be discussed in the next section.

4 Effects of Heat Release on Turbulent Kinetic Energy and Turbulent Scalar Flux Distributions in Premixed Flame Brush

The exact transport equation of turbulent kinetic energy $\tilde{k} = \overline{{\rho u_{i}^{{\prime\prime}} u_{i}^{{\prime\prime}} }} /2\overline{\rho }$ for premixed turbulent flames takes the following form (Zhang and Rutland 1995; Nishiki et al. 2002; Chakraborty et al. 2011a, e):

$$ \frac{{\partial \left( {\overline{\rho }\tilde{k}} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\tilde{u}_{j} \tilde{k}} \right)}}{{\partial x_{j} }} = - \underbrace {{\overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }} \frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }}}}_{{T_{1k} }} - \underbrace {{\overline{{u_{i}^{{\prime\prime}} }} \frac{{\partial \overline{p}}}{{\partial x_{i} }}}}_{{T_{2k} }} + \underbrace {{ {\overline{{p^{\prime}\frac{{\partial u_{k}^{{\prime\prime}} }}{{\partial x_{k} }}}} } }}_{{T_{3k} }} + \underbrace {{\overline{{u_{i}^{{\prime\prime}} \frac{{\partial \tau_{ij} }}{{\partial x_{j} }}}} }}_{{T_{4k} }} - \underbrace {{\overline{{\frac{{\partial \left( {p^{\prime}u_{i}^{{\prime\prime}} } \right)}}{{\partial x_{i} }}}} }}_{{T_{5k} }} - \frac{\partial }{{\partial x_{i} }}\underbrace {{\left( {\overline{{\frac{1}{2}\rho u_{i}^{{\prime\prime}} u_{k}^{{\prime\prime}} u_{k}^{{\prime\prime}} }} } \right)}}_{{T_{6k} }} $$

(6)

The term $T_{1k} = - \overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }} \partial \tilde{u}_{i} /\partial x_{j}$ represents the contribution of the mean velocity gradient (Chakraborty et al. 2011a, e). This term is often referred to as the turbulent kinetic energy production term but it may work as a sink term under some conditions. The term $T_{2k} = - \overline{{u_{i}^{{\prime\prime}} }} \partial \overline{p}/\partial x_{i}$ is usually referred to as the mean pressure gradient term (Nishiki et al. 2002; Chakraborty et al. 2011a, e). The term $T_{3k} = \overline{{p^{\prime}\partial u_{i}^{{\prime\prime}} /\partial x_{i} }}$ arises due to the correlation between pressure and dilatation rate fluctuations and is termed as the pressure dilatation term (Zhang and Rutland 1995; Nishiki et al. 2002; Chakraborty et al. 2011a, e). The combined effects of molecular diffusion and viscous dissipation of turbulent kinetic energy are given by $T_{4k} = \overline{{u_{i}^{{\prime\prime}} \partial \tau_{ij} /\partial x_{j} }}$. The terms $T_{5k} = - \overline{{\partial \left( {p^{\prime}u_{i}^{{\prime\prime}} } \right)/\partial x_{i} }}$ and $T_{6k} = - \partial \left( {\overline{{u_{i}^{{\prime\prime}} u_{k}^{{\prime\prime}} u_{k}^{{\prime\prime}} }} /2} \right)/\partial x_{i}$ depict transport of turbulent kinetic energy by pressure fluctuations and turbulent velocity fluctuations respectively. The term $T_{4k}$ can be expressed as (Zhang and Rutland 1995; Nishiki et al. 2002; Chakraborty et al. 2011a, e):

$$ T_{4k} = \overline{{u_{i}^{{\prime\prime}} \frac{{\partial \tau_{ji} }}{{\partial x_{j} }}}} = - \overline{\rho }\tilde{\varepsilon } + \underbrace {{\left[ {\overline{{u_{i}^{{\prime\prime}} \frac{\partial }{{\partial x_{k} }}\left( {\mu \frac{{\partial u_{k}^{{\prime\prime}} }}{{\partial x_{i} }}} \right)}} - \frac{2}{3}\overline{{u_{i}^{{\prime\prime}} \frac{\partial }{{\partial x_{i} }}\left( {\mu \frac{{\partial u_{k}^{{\prime\prime}} }}{{\partial x_{k} }}} \right)}} } \right]}}_{{T_{VK} }} + \frac{\partial }{{\partial x_{j} }}\left( {\mu \frac{{\partial \tilde{k}}}{{\partial x_{j} }}} \right) $$

(7)

In a high Reynolds number flow the last term on the right hand side remains small in comparison to the first originating from the dissipation rate of turbulent kinetic energy $\tilde{\varepsilon } = \overline{{\mu \left( {\partial u_{i}^{{\prime\prime}} /\partial x_{j} } \right)\left( {\partial u_{i}^{{\prime\prime}} /\partial x_{j} } \right)}} /\overline{\rho }$ (Nishiki et al. 2002; Chakraborty et al. 2011a, e). The term $T_{VK}$ also remains smaller in magnitude in comparison to $- \overline{\rho }\tilde{\varepsilon }$ (Nishiki et al. 2002; Chakraborty et al. 2011a, e), and thus $T_{4k}$ acts as a sink term in turbulent kinetic energy transport (Nishiki et al. 2002; Chakraborty et al. 2011a, e). For constant density flows, the Favre mean and Favre fluctuations converge to Reynolds average and Reynolds fluctuations (i.e. $\tilde{q} = \overline{q}$ and $q^{\prime\prime} = q^{\prime}$), and the dilatation rate based on velocity fluctuations vanishes (i.e. $\partial u_{k}^{{\prime\prime}} /\partial x_{k} = 0$). This also leads to disappearance of $T_{3k}$, $T_{VK}$ and $\overline{{u_{i}}^{{\prime\prime}}}$ (i.e. $\overline{{u_{i}^{{\prime\prime}}}} = \overline{{u_{i}^{{\prime}}}} = 0$) and therefore, $T_{2k}$ also disappears for constant density flows. It is worth noting that the terms $T_{2k} ,T_{3k}$ and $T_{VK}$ vanish in the case of constant density flows but it will be shown in this paper that these terms cannot be ignored in turbulent premixed flames.

The variations of $\tilde{k}$ normalised by its value $\tilde{k}_{0}$ at the leading edge (i.e. at $\tilde{c} = 0.005$) for a DNS data of a statistically planar flame (i.e. case AR) representing the corrugated flamelets (i.e. CF) regime with $\tau = 2.3$ and two DNS of statistically planar flames (i.e. cases BR and CR) representing the thin reaction zones (i.e. TRZ) regime combustion for two different heat release parameters (i.e.$\tau = 3.0$ and 4.5 for cases BR and CR, respectively) are shown in Fig. 16a (Chakraborty et al. 2011a). More information regarding these cases can be found from (Chakraborty et al. 2011a) and thus they are not discussed in detail in this paper. The corresponding variations of the dissipation rate of turbulent kinetic energy $\tilde{\varepsilon }$ normalised by its value $\tilde{\varepsilon }_{0}$ at the leading edge (i.e. at $\tilde{c} = 0.005$) are shown in Fig. 16b for cases AR-CR. The flame-turbulence interaction in cases AR-CR takes place under decaying turbulence and their attributes at the initial stage are shown in Table 5. It can be seen from Fig. 16a, b that there are significant differences in $\tilde{k}/\tilde{k}_{0}$ and $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ distributions between cases AR-CR. It can be seen from Fig. 16a, b that both $\tilde{k}/\tilde{k}_{0}$ and $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ increase within the flame brush from the leading edge before decaying towards the burned gas side in case AR, whereas a monotonic decay is observed for these quantities from the unburned to the burned gas side of the flame brush in cases BR and CR. In order to explain the differences in the behaviour in $\tilde{k}/\tilde{k}_{0}$ distributions between cases AR-CR, it is worthwhile to consider the behaviours of $T_{1k} - T_{6k}$ with the flame brush. The variations of $\left\{ {T_{1k} - T_{6k} } \right\} \times \delta_{th} /\rho_{0} S_{L}^{3}$ with $\tilde{c}$ for cases AR and CR are shown in Fig. 17a, b, respectively and these variations for case BR are qualitatively similar to case CR (Chakraborty et al. 2011a). Thus, case BR is not explicitly shown in Fig. 17. It is evident from Fig. 17a, b that $T_{4k}$ acts as a leading order sink for all cases, and the magnitudes of all other terms remain small in comparison to that of $T_{4k}$ in case CR (and also in BR but not shown here), whereas the mean pressure gradient term $T_{2k}$ and the pressure dilatation term $T_{3k}$ have positive values but of similar magnitudes as $T_{4k}$ in case AR. For statistically planar flames such as in cases AR-CR, both $\overline{{\rho u_{1}^{{\prime\prime}} u_{1}^{{\prime\prime}} }}$ and $\partial \tilde{u}_{1} /\partial x_{1}$ are positive and thus $T_{1k}$ acts as a sink instead of a production term in these cases. The term $T_{2k}$ acts as a source (i.e. positive) in case AR, whereas this term remains positive towards the unburned gas side but becomes weakly negative for the major part of the flame brush in case CR (also in case BR but not shown here). The pressure dilatation term $T_{3k}$ assumes positive values throughout the flame brush in case AR but this term remains negative towards the unburned gas side of the flame brush before assuming a positive value for the rest of the flame brush in case CR (also in case BR but not shown here). A comparison between cases AR-CR reveals that the magnitudes of $T_{2k}$ and $T_{3k}$ remain comparable to that of the dissipation rate contribution $T_{4k}$ in the corrugated flamelets regime flame but the contributions of $T_{2k}$ and $T_{3k}$ remain negligible in comparison to the dissipation rate contribution $T_{4k}$ in case CR (also in case BR but not shown here). The pressure transport term $T_{5k}$ remains positive towards the unburned gas side of the flame brush before assuming negative values for the rest of the flame brush in case AR. By contrast, negative values of $T_{5k}$ are obtained towards the leading edge of the flame brush but positive values are obtained on the burned gas side in case CR (also in case BR but not shown here). Once again, the relative magnitude of $T_{5k}$ in comparison to $T_{4k}$ remains much greater in case AR than in cases BR and CR. The turbulent transport term $T_{6k}$ assumes positive value throughout the flame brush in cases AR-CR but the magnitude of $T_{6k}$ remains significant only towards the unburned gas side of the flame brush in case CR (also in case BR but not shown here). Figure 17 shows that the turbulent kinetic energy transport in premixed flames is significantly influenced by the regime of combustion as the effects of thermal expansion (or dilatation rate and the pressure gradient induced by the flame) become progressively weak in comparison to the mechanisms which are present in non-reacting flows with increasing Karlovitz number.

Fig. 16

Variations of a $\tilde{k}/\tilde{k}_{0}$ and (b) $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ with $\tilde{c}$ across the flame brush for cases AR-CR. The turbulent kinetic energy and its dissipation rate in the plane corresponding to $\tilde{c} = 0.005$ are denoted by $\tilde{k}_{0}$ and $\tilde{\varepsilon }_{0}$, respectively

Table 5 List of initial turbulence parameters for the DNS database for the analysis of turbulent kinetic energy transport. The Prandtl number is taken to be 0.7 (i.e. $Pr = 0.7$)

Fig. 17

Variations of the normalised terms of the turbulent kinetic energy transport equation $\left\{ {T_{1k} - T_{6k} } \right\} \times \delta_{th} /\rho_{0} S_{L}^{3}$ with $\tilde{c}$ across the flame brush for cases a AR and b CR

It has already been shown (see Table 3) that the influence of heat release strengthens with decreasing Lewis number $Le$, which also affect the evolution of turbulent kinetic energy within the flame brush. To substantiate this, the variations of the normalised terms of the turbulent kinetic energy transport equation $\left\{ {T_{1k} - T_{6k} } \right\} \times \delta_{th} /\rho_{0} S_{L}^{3}$ with $\tilde{c}$ across the flame brush for the thin reaction zones regime cases AL, BL and DL are exemplarily shown in Fig. 18. These variations in cases CL and EL are qualitatively similar to case DL and therefore are not shown in this paper. It can be seen from Fig. 18 that the behaviour of the terms $\left\{ {T_{1k} - T_{6k} } \right\} \times \delta_{th} /\rho_{0} S_{L}^{3}$ in the $Le \approx 1.0$ cases (i.e. cases CL-EL) are found to be similar to case CR in Fig. 17. However, the turbulent kinetic energy transport characteristics in the flames with $Le \ll 1$ (e.g. cases AL and BL) are significantly different from the cases with $Le \approx 1$ (e.g. case DL). The combined viscous dissipation and molecular diffusion term $T_{4k}$ continues to be the leading order sink irrespective of the characteristic Lewis number $Le$. In case AL (i.e. $Le = 0.34$ case), the term $T_{1k}$ acts as a sink with the magnitude remaining comparable to the combined diffusion and dissipation term $T_{4k}$. The mean pressure gradient term $T_{2k}$ attains a positive value greater than the magnitude of $T_{4k}$ for case AL (i.e. $Le = 0.34$ case), and in case BL (i.e. $Le = 0.6$ case) the magnitudes of $T_{2k}$ and $T_{4k}$ are comparable to each other. The magnitude of the pressure dilatation term $T_{3k}$ remains comparable to that of $T_{4k}$ in case AL but its magnitude relative to that of $T_{4k}$ diminishes with increasing characteristic Lewis number $Le$. In all cases the magnitudes of $T_{5k}$ and $T_{3k}$ remain comparable irrespective of $Le$ but $T_{5k}$ remains mostly positive towards the reactant side and becomes negative towards the product side. The magnitude of $T_{6k}$ is found to be comparable to that of $T_{4k}$ for the $Le = 0.34$ and 0.6 cases but is negligible in comparison to $T_{4k}$ for the higher Lewis number cases.

Fig. 18

Variations of the normalised terms of the turbulent kinetic energy transport equation $\left\{ {T_{1k} - T_{6k} } \right\} \times \delta_{th} /\rho_{0} S_{L}^{3}$ with $\tilde{c}$ across the flame brush for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

The large positive contribution of $T_{4k}$ in case AL leads to a significant generation of turbulent kinetic energy $\tilde{k}$ within the flame brush and this tendency can be discerned in case BL up to the middle of the flame brush, albeit much more weakly than in case AL, before decaying towards the burned gas side, whereas $\tilde{k}$ decays monotonically from the unburned to the burned gas side of the flame brush in case DL (and in fact for cases CL-EL). This can be substantiated from the variations of $\tilde{k}/\tilde{k}_{0}$ with $\tilde{c}$ for cases AL-EL shown in Fig. 19a and the corresponding variations of $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ with $\tilde{c}$ are shown in Fig. 19b. Figure 19b shows that the variation of $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ with $\tilde{c}$ is qualitatively similar to that of $\tilde{k}/\tilde{k}_{0}$. It is worth noting that the dissipation rate of kinetic energy $\tilde{\varepsilon }$ can be scaled as: $\tilde{\varepsilon }\sim \overline{{\mu \omega_{i} \omega_{i} }} /\overline{\rho }\sim 2\overline{{\mu {\Omega }}} /\overline{\rho }$ (Lipatnikov et al. 2014) and a comparison between Figs. 15d and 19 reveals that the variations of $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ and $\overline{{\left( {\omega_{i} \omega_{i} } \right)^{1/2} }} \times \delta_{th} /S_{L}$ with $\tilde{c}$ are indeed qualitatively similar. It has already been discussed in the context of Fig. 15d that the baroclinic torque arising from the pressure gradient is responsible for the generation of enstrophy within the flame brush in cases AL and BL. The closures of $\left\{ {T_{2k} - T_{6k} } \right\}$ for turbulent premixed flames have been explored elsewhere and the interested readers are referred to Zhang and Rutland (1995), Nishiki et al. (2002), Chakraborty et al. (2011a, e) for further information in this regard.

Fig. 19

Variations of a $\tilde{k}/\tilde{k}_{0}$ and b $\tilde{\varepsilon }/\tilde{\varepsilon }_{0}$ with $\tilde{c}$ across the flame brush for cases AL-EL (i.e. $Le = 0.34,\,0.6,\,0.8,\, 1.0$ and 1.2).The turbulent kinetic energy and its dissipation rate in the plane corresponding to $\tilde{c} = 0.005$ are denoted by $\tilde{k}_{0}$ and $\tilde{\varepsilon }_{0}$, respectively

The findings from Figs. 11, 12, 13, 14, 15, 16, 17, 18 and 19 suggest that the self-induced pressure gradient plays a key role in the enstrophy (or vorticity) and turbulent kinetic energy evolutions within the premixed flame brush and therefore in the characteristic nature of turbulence within the flame. The interested readers are referred to Domingo and Bray (2000) for a detailed discussion on the effects of pressure gradient on the Reynolds stress $\widetilde{{u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }}$ transport under the action of thermal expansion arising from chemical heat release within the strict flamelet regime (i.e. $Ka < 1$). Further information on pressure gradient effects on Reynolds stress and turbulent kinetic energy transport can be found in Zhang and Rutland (1995); Nishiki et al. (2002); Chakraborty et al. (2011a, e); Domingo and Bray (2000). However, the self-induced pressure gradient due to thermal expansion does not only affect the statistical behaviours of Reynolds stress, turbulent kinetic energy and enstrophy but also has implications on the statistical behaviour and modelling of turbulent flux of reactive scalars.

4.1 Modelling Implications in the Context of Reynolds Averaged Navier Stokes Simulation (RANS) Modelling

Bray et al. (1985) considered the following presumed probability density function (PDF) of $c$ and the joint PDF between $\vec{u}$ and $c$:that a counter-gradient (gradient) type transport

$$ P\left( {c;\, \vec{x}} \right) = \alpha_{c} \left( {\vec{x}} \right)\delta \left( c \right) + \beta_{c} \left( {\vec{x}} \right)\delta \left( {1 - c} \right) + \gamma_{c} \left( {\vec{x}} \right)f_{1} \left( {c;\,\vec{x}} \right)\left[ {H\left( c \right) - H\left( {c - 1} \right)} \right] $$

(8)

$$ \begin{aligned} P\left( {\vec{u},c;\,\vec{x}} \right) =\, & \alpha_{c} \left( {\vec{x}} \right)P_{R} \left( {\vec{u},\,0;\,\vec{x}} \right)\delta \left( c \right) + \beta_{c} \left( {\vec{x}} \right)P_{P} \left( {\vec{u},\,1;\,\vec{x}} \right)\delta \left( {1 - c} \right) \\ & + \gamma_{c} \left( {\vec{x}} \right)f_{2} \left( {\vec{u},\,c;\,\vec{x}} \right)\left[ {H\left( c \right) - H\left( {c - 1} \right)} \right] \\ \end{aligned} $$

(9)

Here $\alpha_{c} , \beta_{c}$ and $\gamma_{c}$ are the coefficients for the progress variable PDF, $P_{R} \left( {\vec{u},\, 0;\, \vec{x}} \right)$ and $P_{P} \left( {\vec{u},\,1;\, \vec{x}} \right)$ indicate PDFs of velocity $\vec{u}$ in reactants and products respectively and the functions $f_{1}$ and $f_{2}$ account for burning gases at the interior of the flame. The functions $P_{R} \left( {\vec{u},\,0;\,\vec{x}} \right)$, $P_{P} \left( {\vec{u},\,1;\,\vec{x}} \right), \,f_1 (c;\,\vec{x})$ and $f_{2} \left( {\vec{u},\,c;\,\vec{x}} \right)$ individually integrate to unity. The last term on the right hand side of Eqs. 8 and 9 represents the contribution of burning fluid. Equations 8 and 9 yield the following relations (Bray et al. 1985):

$$ \mathop \int \limits_{0}^{1} P\left( c \right)dc = \alpha_{c} + \beta_{c} + O\left( {\gamma_{c} } \right)\,\,{\text{and}}\,\,\overline{\rho } = \mathop \int \limits_{0}^{1} \rho_{c} P\left( c \right)dc = \alpha_{c} \rho_{0} + \beta_{c} \overline{\rho }_{b} + O\left( {\gamma_{c} } \right) $$

(10)

where $\rho_{c}$ and $\overline{\rho }_{b}$ are the mean value of density conditional on $c$ and mean burned gas density, respectively. For low Mach number adiabatic unity Lewis number flames $\overline{\rho },\rho_{c}$ and $\overline{\rho }_{b}$ are given by: $\overline{\rho } = \rho_{0} /\left( {1 + \tau \tilde{c}} \right)$, $\rho_{c} = \rho_{0} /\left( {1 + \tau c} \right)$ and $\overline{\rho }_{b} = \rho_{0} /\left( {1 + \tau } \right)$ (Bray et al. 1985; Chakraborty and Lipatnikov 2013). For large values of Damköhler number (i.e.$Da \gg 1$), $O\left( {\gamma_{c} } \right)$ contributions can be neglected which yields the following expressions of $\alpha_{c}$ and $\beta_{c}$ (Bray et al. 1985):

$$ \alpha_{c} = \left( {1 - \tilde{c}} \right)/\left( {1 + \tau \tilde{c}} \right)\,{\text{and}}\,\beta_{c} = \left( {1 + \tau } \right)\tilde{c}/\left( {1 + \tau \tilde{c}} \right) $$

(11)

Using Eqs. 9 and 11, it is possible to derive the following relation for the Favre mean velocity components $\tilde{u}_{i}$ (Bray et al. 1985):

$$ \tilde{u}_{i} = \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{1} \rho u_{i} P\left( {\vec{u},c} \right)dcd\vec{u}/\overline{\rho } = \overline{{\left( {u_{i} } \right)}}_{R} \left( {1 - \tilde{c}} \right) + \overline{{\left( {u_{i} } \right)}}_{P} \tilde{c} + O\left( {\gamma_{c} } \right) $$

(12)

where $\overline{\left( q \right)}_{R}$ and $\overline{\left( q \right)}_{P}$ are the conditional mean values in unburned reactants and products of a general quantity $q$ dependent on $\vec{u}$, respectively, which are evaluated as (Chakraborty and Lipatnikov 2013):

$$ \overline{\left( q \right)}_{R} = \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{\epsilon} qP\left( {\vec{u},c} \right)dcd\vec{u}/\mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{\epsilon} P\left( {\vec{u},c} \right)dcd\vec{u} $$

(13)

$$ \overline{\left( q \right)}_{P} = \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{1 - {\epsilon}}^{1} qP\left( {\vec{u},c} \right)dcd\vec{u}/\mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{1 - {\epsilon}}^{1} P\left( {\vec{u},c} \right)dcd\vec{u} $$

(14)

where $\epsilon$ is a small number (i.e. $\ 0 <{\epsilon} \ll 1$). It is possible to obtain the following relation for Reynolds fluxes, and turbulent scalar fluxes of kinetic energy, reaction progress variable and scalar variance (i.e. $\overline{\rho u_{i}^{{\prime}^{\prime}}} u_{j}^{{\prime}^{\prime}}$, $\overline{{\rho u_{i}^{{\prime}^{\prime}}}} \overline{{u_{j}^{{\prime}^{\prime}} u_{j}^{{\prime\prime}}}} /2$, $\overline{{\rho u_{i} ^{\prime\prime}c^{\prime\prime}}}$, $\overline{{\rho u_{i}^{{\prime\prime}} c^{{\prime\prime}2} }}$) for unity Lewis number flames using Eqs. 12, 15 and 16 (Chakraborty et al. 2011a, e; Bray et al. 1985; Chakraborty and Lipatnikov 2013):

$$ \begin{aligned} \overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}}} = & \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{1} \rho \left( {u_{i} - \tilde{u}_{i} } \right)\left( {u_{j} - \tilde{u}_{j} } \right)P\left( {\vec{u},c} \right)dcd\vec{u} \\ = & \overline{\rho }\tilde{c}\left( {1 - \tilde{c}} \right)\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]\left[ {\overline{{\left( {u_{j} } \right)}}_{P} - \overline{{\left( {u_{j} } \right)}}_{R} } \right] \\ + & \overline{\rho }\left( {1 - \tilde{c}} \right)\overline{{\left( {u_{i}^{{\prime}} u_{j} ^{\prime}} \right)}}_{R} + \overline{\rho }\tilde{c}\overline{{\left( {u_{i}^{{\prime}} u_{j} ^{\prime}} \right)}}_{P} + O\left( {\gamma_{c} } \right) \\ \end{aligned} $$

(15)

$$ \begin{aligned} \frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{^{\prime\prime}u_{j} ^{\prime\prime}}} }} = & 0.5\mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{1} \rho \left( {u_{i} - \tilde{u}_{i} } \right)\left( {u_{j} - \tilde{u}_{j} } \right)\left( {u_{j} - \tilde{u}_{j} } \right)P\left( {\vec{u},c} \right)dcd\vec{u} \\ = & \frac{1}{2}\overline{\rho }\tilde{c}\left( {1 - \tilde{c}} \right)\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]\left[ {\overline{{\left( {u_{j} } \right)}}_{P} - \overline{{\left( {u_{j} } \right)}}_{R} } \right]\left[ {\overline{{\left( {u_{j} } \right)}}_{P} - \overline{{\left( {u_{j} } \right)}}_{R} } \right] \\ + & \overline{\rho }\left( {1 - \tilde{c}} \right)\overline{{(u_{i} ^{\prime}k)}}_{R} + \overline{\rho }\tilde{c}\overline{{(u_{i} ^{\prime}k)}}_{P} + \overline{\rho }\tilde{c}\left( {1 - \tilde{c}} \right)\left( {\overline{k}_{P} - \overline{k}_{R} } \right) + O\left( {\gamma_{c} } \right) \\ \end{aligned} $$

(16)

$$ \overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}} = \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{1} \rho \left( {u_{i} - \tilde{u}_{i} } \right)\left( {c - \tilde{c}} \right)P\left( {\vec{u},c} \right)dcd\vec{u} = \overline{\rho }\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]\tilde{c}\left( {1 - \tilde{c}} \right) + O\left( {\gamma_{c} } \right) $$

(17)

$$ \begin{aligned} \overline{{\rho u_{i}^{{\prime\prime}} c^{{\prime\prime}2} }} = & \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{0}^{1} \rho \left( {u_{i} - \tilde{u}_{i} } \right)\left( {c - \tilde{c}} \right)\left( {c - \tilde{c}} \right)P\left( {\vec{u},c} \right)dcd\vec{u} \\ = & \overline{\rho }\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]\tilde{c}\left( {1 - \tilde{c}} \right)\left( {1 - 2\tilde{c}} \right) + O\left( {\gamma_{c} } \right) \\ \end{aligned} $$

(18)

where ${\bar{k}}_{R}={\overline{{(u}_{i}^{{\prime}}{u}_{i}^{{\prime}})}}_{R}/2$ and ${\bar{k}}_{P}={\overline{{(u}_{i}^{{\prime}}{u}_{i}^{{\prime}})}}_{P}/2$ are turbulent kinetic energy conditional on reactants and products, respectively (Chakraborty et al. 2011a, e). Although Eqs. 15–18 are derived based on a presumed bi-modal PDF of $c$ (see Eq. 8) for unity Lewis number flames, they still provide useful insights into the effects of heat release on statistical behaviours of these quantities. The term $\left[{\overline{\left({u}_{i}\right)}}_{P}-{\overline{\left({u}_{i}\right)}}_{R}\right]$ is commonly referred to as the slip velocity (Veynante et al. 1997; Bray et al. 1985; Chakraborty and Lipatnikov 2013). The slip velocity $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ is expected to be non-zero due to heat release. In order to demonstrate its role, it is worthwhile to consider the expression of $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ given by Eq. 17. If negative i^th direction is aligned with the mean direction of flame propagation, one obtains positive values of $\partial \tilde{c}/\partial x_{i}$ (i.e. $\partial \tilde{c}/\partial x_{i} > 0$). For laminar flames, $\overline{{\left( {u_{i} } \right)}}_{P}$ is expected to be greater than $\overline{{\left( {u_{i} } \right)}}_{R}$ (i.e. $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right] > 0$) because lighter products are expected to be preferentially accelerated more than the heavier reactants under the action of self-induced pressure gradient of premixed flames. For weakly turbulent flames, positive values of $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ lead to a combination of positive values of $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ and $\partial \tilde{c}/\partial x_{i}$. This is in contradiction of the usual gradient hypothesis, which is commonly expressed as (Launder 1976; Abe and Suga 2001):

$$ \overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}} = - \overline{\rho }D_{t} \frac{{\partial \tilde{c}}}{{\partial x_{i} }} $$

(19)

The above discussion suggests that Eq. 17 suggests that one can obtain counter-gradient (gradient) transport for $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right] > 0$ ($\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right] < 0)$ (Veynante et al. 1997; Bray et al. 1985). This can be confirmed from Fig. 20 where the variations of $\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right]/S_{L}$ and $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \times \partial \tilde{c}/\partial x_{1} \times \delta_{th} /\rho_{0} S_{L}$ with $\tilde{c}$ for the statistically planar flame cases AR, BR and AL-EL are shown in Figs. 20a, b respectively in the context of RANS, where the negative $x_{1}$-direction is the direction of mean flame propagation for these statistically planar cases. Using Eq. 19, it can be inferred that a positive value of $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \times \partial \tilde{c}/\partial x_{1}$ indicates a counter-gradient transport, whereas a negative value of $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \times \partial \tilde{c}/\partial x_{1}$ suggests gradient type transport. A comparison between Figs. 20a, b reveals that a positive value of slip velocity $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ is associated with counter-gradient (i.e. $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \times \partial \tilde{c}/\partial x_{1} > 0$) transport. By contrast, gradient type transport (i.e. $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \times \partial \tilde{c}/\partial x_{1} < 0$) is observed for negative values of $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$. It was demonstrated by Veynante et al. (1997) that the decay of turbulence across the flame brush under strong turbulence on the unburned gas side leads to negative values of slip velocity $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ (i.e. $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right] < 0$). Veynante et al. (1997) modelled $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ as:

$$ \left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right] = - M_{i} \left( {\tau S_{L} - 2\alpha_{E} u^{\prime}} \right) $$

(20)

where $M_{i} = - \left( {\partial \tilde{c}/\partial x_{i} } \right)/\left| {\nabla \tilde{c}} \right|$ is the $i^{th}$ component of the resolved flame normal vector, $\alpha_{E}$ is an efficiency function which characterises flame-vortex interaction and a function of $\sqrt {2\tilde{k}/3} /S_{L}$ and $L_{11} /\delta_{Z}$ with $\delta_{Z} = D_{th,0} /S_{L}$ and $D_{th,0}$ being the Zel’dovich flame thickness and the thermal diffusivity in the unburned gas, respectively. Equation 20 suggests that $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ assumes positive values for $\tau S_{L} \gg u^{\prime}$, whereas negative values of $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ are obtained for $\tau S_{L} < u^{\prime}$. Based on this, a non-dimensional number $N_{B}$ known as Bray number was proposed by Veynante et al. (1997) in the following manner:

$$ N_{B} = \frac{{\tau S_{L} }}{{2\alpha_{E} u^{\prime}}} $$

(21)

Fig. 20

Variations of a $\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right]/S_{L}$ and b $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \times \partial \tilde{c}/\partial x_{1} \times \delta_{th} /\rho_{0} S_{L}$ with $\tilde{c}$ across the flame brush for cases AR, BR, AL-EL

such that a counter-gradient (gradient) type transport is obtained for $N_{B} \gg 1$ ($N_{B} < 1$). It can be seen from Fig. 20a, b that a counter-gradient type transport is obtained for case AR, whereas a gradient type transport is obtained in case BR, which is consistent with $N_{B} > 1$ and $N_{B} < 1$ in cases AR and BR, respectively. Figure 20a, b shows that $\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right]/S_{L}$ becomes increasingly positive and $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ shows an increasing extent of counter-gradient transport with decreasing $Le$. Figure 19a indicates that the local values of rms velocity $u^{\prime} \propto \sqrt {\tilde{k}}$ assume greater values for smaller value of $Le$ among cases AL-EL whereas the turbulent kinetic energy at the leading edge $\tilde{k}_{0}$ (and therefore $u^{\prime}$ at the leading edge) for these cases are similar as these flames are subjected to statistically similar unburned gas turbulence. The length scale ratio $L_{11} S_{L} Le/D_{th,0}$ decreases with decreasing Lewis number, which tends to predict an increasing value of the Bray number $N_{B}$ with decreasing $Le$ based on the initial value of $u^{\prime}/S_{L}$, when the efficiency function $\alpha_{E}$ is calculated using initial $u^{\prime}/S_{L}$ and $L_{11} /\delta_{Z}$. Under these conditions, counter-gradient transport is expected to be strongest in the flame with the smallest Lewis number, as observed in Fig. 20a, b. If $\alpha_{E}$ is evaluated using the initial values of $u^{\prime}/S_{L}$ and $L_{11} S_{L} /D_{th,0}$ as suggested originally by Veynante et al. (Veynante et al. 1997), it yields the same value of $N_{B}$ in cases AL-EL, and thus the type of turbulent scalar transport is expected to be identical for these flames, contrary to the observations of Fig. 20a, b. The variation of the efficiency function $\alpha_{E}$ with $\tilde{c}$ for cases AL-EL is now shown in Fig. 21a, where $\alpha_{E}$ is estimated as a function of $L_{11} /\delta_{Z}$ by curve-fitting the data presented by Veynante et al. (1997). Figure 21a indicates that $\alpha_{E}$ increases with increasing $Le$. However, a comparison between Figs. 19a and 21a reveals that smaller values of $\alpha_{E}$ in cases AL and BL (i.e. $Le = 0.34$ and 0.6 flames) are either compensated or overcome by greater values of $\sqrt {2\tilde{k}/3}$ within the flame brush. As a result, the Bray number $N_{B}$ based on local turbulence intensity $\sqrt {2\tilde{k}/3} /S_{L}$ and $\alpha_{E}$ remains comparable for all the flames. However, despite this, Fig. 20 suggests that the extent of counter-gradient (gradient) transport is the strongest in the smallest (largest) value of $Le$ among cases AL-EL. This apparent contradiction in behaviour arises due to the strong flame normal acceleration arising from the higher heat release occurring in the lower Lewis number flames, which may overcome the effects of turbulent transport associated with higher rms velocity fluctuation. This aspect of the physics is not accounted for by the original definition of $N_{B}$ (see Eq. 21). Thus, a revised Bray number $N_{B}^{ + }$ was proposed by Chakraborty and Cant (2009a) in the following manner:

$$ \left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right] = - M_{i} \left( {f\left( {Le} \right)\tau S_{L} - 2\alpha_{E} u^{\prime}} \right) $$

(22i)

$$ N_{B}^{ + } = f\left( {Le} \right)\frac{{\tau S_{L} }}{{2\alpha_{E} u^{\prime}}} $$

(22ii)

where $f\left( {Le} \right)$ is a function which increases with decreasing Lewis number, which accounts for stronger thermal expansion and flame normal flow acceleration across the flame brush with a decrease in $Le$, which can be substantiated from the variations of $\partial \tilde{u}_{1} /\partial x_{1} \times \delta_{th} /S_{L}$ with $\tilde{c}$ shown in Fig. 21b for cases AL-BL. In order to demonstrate the interrelation between flame normal acceleration and turbulent scalar flux, it is worthwhile to consider the transport equation of $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ (Veynante et al. 1997; Veynante and Poinsot 1997; Chakraborty and Cant 2009a; Papapostolopu et al. 2019):

$$ \begin{aligned} \frac{{\partial \left( {\overline{\rho } \widetilde{{u_{i}^{{\prime\prime}} c^{\prime\prime}}}} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\widetilde{{u_{j} }}\widetilde{{u_{i}^{{\prime\prime}} c^{\prime\prime}}}} \right)}}{{\partial x_{j} }} = & - \underbrace {{\frac{{\partial \overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} c^{\prime\prime}}} }}{{\partial x_{j} }}}}_{{T_{1c} }} - \underbrace {{\overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }} \frac{{\partial \tilde{c}}}{{\partial x_{j} }}}}_{{T_{2c} }} - \underbrace {{\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} \frac{{\partial \widetilde{{u_{i} }}}}{{\partial x_{j} }}}}_{{T_{3c} }} \\ - & \underbrace {{\overline{{c^{\prime\prime}}} \frac{{\partial \overline{p}}}{{\partial x_{i} }}}}_{{T_{4c} }} - \underbrace {{\overline{{c^{\prime\prime}\frac{{\partial p^{\prime}}}{{\partial x_{i} }}}} }}_{{T_{5c} }} + \underbrace {{\left[ { \overline{{u_{i}^{{\prime\prime}} \frac{\partial }{{\partial x_{k} }}\left( {\rho D\frac{\partial c}{{\partial x_{k} }}} \right)}} } \right]}}_{{T_{6c} }} + \underbrace {{\left[ { \overline{{c^{\prime\prime}\frac{{\partial \tau_{ik} }}{{\partial x_{k} }}}} } \right]}}_{{T_{7} c}} + \underbrace {{\overline{{u_{i}^{{\prime\prime}} \dot{w}}} }}_{{T_{8c} }} \\ \end{aligned} $$

(23)

Fig. 21

Figure 21a is reproduced from Chakraborty and Cant (2009a)

Variations of a $\alpha_{E}$ and b $\partial \tilde{u}_{1} /\partial x_{1} \times \delta_{th} /S_{L}$ with $\tilde{c}$ across the flame brush for cases AL-EL (i.e. $Le = 0.34,0.6,0.8, 1.0$ and 1.2).

In Eq. 23, $T_{1c}$ represents turbulent transport of $\widetilde{{u_{i}^{{\prime\prime}} c^{\prime\prime}}}$, whereas the terms $T_{2c}$ and $T_{3c}$ denote turbulent scalar flux transport due to mean scalar gradient, and velocity gradient, respectively. The turbulent scalar flux transport by mean and fluctuating pressure gradients are represented by the terms $T_{4c}$ and $T_{5c}$, respectively. The terms $T_{6c}$ and $T_{7c}$ arise as a result of mass diffusion and viscous stress respectively, and these terms act to reduce the magnitude of $\widetilde{{u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ irrespective of the nature of scalar flux transport and are therefore referred to as dissipation terms. The last term on the right-hand side $T_{8c}$ originates from the correlation between reaction rate and velocity fluctuations. The terms $T_{1c} ,T_{4c} ,T_{5c} ,T_{6c} ,T_{7c}$ and $T_{8c}$ are the unclosed terms, whereas $T_{2c}$ and $T_{3c}$ are closed in the context of second-moment closure because $\overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }}$ and $\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}}$ are already modelled. The quantity $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$ is the only non-zero component of turbulent scalar flux $\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}}$ in statistically planar turbulent premixed flames. The variations of $\left\{ {T_{1c} - T_{8c} } \right\} \times \delta_{th}^{2} /\rho_{0} S_{L}$ with $\tilde{c}$ for cases AL, BL and DL are shown in Fig. 22. The cases CL and EL are not explicitly shown here because of the qualitative similarities of these terms in case DL. A positive value of the contribution of these terms promotes a counter-gradient type transport, whereas the gradient transport is promoted for negative values of these terms.

Fig. 22

Variations of the normalised terms of the turbulent scalar flux transport equation $\left\{ {T_{1c} - T_{6c} } \right\} \times \delta_{th} /\rho_{0} S_{L}^{2}$ with $\tilde{c}$ across the flame brush for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

The turbulent transport term $T_{1c}$ assumes weakly negative values towards the leading edge but becomes positive through the remainder of the flame brush for cases AL and BL (e.g. $Le = 0.34$ and 0.6). An opposite behaviour of $T_{1c}$ is observed for case DL. For statistically planar flames, the mean scalar gradient term $T_{2c} = - \overline{{\rho u_{1}^{{\prime\prime}} u_{1}^{{\prime\prime}} }} \left( { \partial \tilde{c}/\partial x_{1} } \right)$ assumes deterministically negative values throughout the flame brush due to positive values of $\overline{{\rho u_{1}^{{\prime\prime}} u_{1}^{{\prime\prime}} }}$ and $\partial \tilde{c}/\partial x_{1}$. The negative contribution of $T_{2c}$ acts to promote a gradient type transport for all cases but its contribution does not play leading order role for cases with small values of $Le$ (e.g. cases AL and BL), whereas it plays a progressively significant role with increasing $Le$. The velocity gradient term $T_{3c} = - \overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} \left( { \partial \tilde{u}_{1} /\partial x_{1} } \right)$ assumes negative values throughout the flame brush for cases AL and BL; the opposite behaviour is obtained for case DL (and also in case EL, which is not shown here), whereas the behaviour in case CL is somewhat between cases AL,BL and cases DL and EL. In all cases $\partial \tilde{u}_{1} /\partial x_{1}$ and $\partial \tilde{c}/\partial x_{1}$ assume positive values and thus the behaviour of $T_{3c}$ is determined by the turbulent scalar flux $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$. A positive value of $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$(indicating a counter-gradient transport) leads to negative values of $T_{3c}$ and vice versa.

The mean pressure gradient term $T_{4c} = - \overline{{c^{\prime\prime}}} \partial \overline{p}/\partial x_{i}$ plays a leading order role in all the Lewis number cases and assumes positive values throughout the flame brush, therefore promoting a counter-gradient type transport for all of the flames, and in cases AL and BL this term is primarily responsible for the occurrence of a counter-gradient type transport. According to Eq. 8, one obtains that $\overline{{c^{\prime\prime}}} = \tilde{c}\left( {1 - \tilde{c}} \right)\tau /\left( {1 + \tau \tilde{c}} \right) + O\left( {\gamma_{c} } \right)$ for unity Lewis number flames, which suggests that $\overline{{c^{\prime\prime}}}$ remains positive and the same qualitative behaviour is observed for non-unity Lewis number flames. The fluctuating pressure gradient term $T_{5c}$ assumes positive values towards the leading edge and then becomes negative towards the trailing edge for all cases, but the positive contribution supersedes the negative one and thus the net effect of $T_{5c}$ is to promote counter-gradient transport (Veynante et al. 1997; Veynante and Poinsot 1997; Chakraborty and Cant 2009a; Papapostolopu et al. 2019).

The terms $T_{6c}$ and $T_{7c}$ assume negative values for cases AL and BL where $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$ assumes positive values and the opposite behaviour is observed for case DL (and also in case EL). Therefore, the contributions of $T_{6c}$ and $T_{7c}$ act to promote a gradient (counter-gradient) type transport in cases AL and BL (DL and EL) where $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$ exhibits a counter-gradient (gradient) type transport.

The reaction rate-velocity correlation term $T_{8c}$ assumes positive values throughout the flame brush for cases AL and BL. However, in case DL (and also in cases CL and EL) this term assumes negative values towards the leading edge of the flame while remaining positive towards the trailing edge. This behaviour arises due to the competition between the decay of turbulence close to the flame leading edge, which leads to negative values of $T_{8c}$ in the presence of an increasing reaction rate, and the production of turbulence due to heat release within the remainder of the flame brush, leading to positive values of $T_{8c}$.

From Fig. 22, it is evident that for flames with small values of $Le$ (e.g. cases AL and BL), the sum of the terms $\left\{ {T_{1c} - T_{8c} } \right\}$ making a positive contribution to the scalar flux is sufficient to overcome the sum of the terms making a negative contribution, and this gives rise to counter-gradient transport. The opposite is true for case DL (and also in case EL). The observations made from Fig. 22 reveals that the pressure gradient by flame normal acceleration plays a key role in the evolution of turbulent scalar flux $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$. Only cases AL, BL and DL are shown in Fig. 22 but the terms $\left\{ {T_{1c} - T_{8c} } \right\}$ in cases BR and CR behave qualitatively similarly to case DL. It has also been demonstrated earlier (see Figs. 16 and 20) that counter-gradient transport of $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$ and augmentation of turbulent kinetic energy are obtained for case AR and in this case the behaviours of $\left\{ {T_{1c} - T_{8c} } \right\}$ are qualitatively similar to case AL. A recent analysis (Papapostolopu et al. 2019) using cases DA-DC reveals that the presence of detailed chemistry does not alter the behaviours of $\left\{ {T_{1c} - T_{8c} } \right\}$ and case DA behaves similarly to case AR, whereas the behaviours of these terms in cases DB and DC are qualitatively similar to cases BR, CR and DL. Interested readers are referred to Chakraborty and Cant (2009a); Papapostolopu et al. (2019) for the modelling of the unclosed terms $\left\{ {T_{1c} ,T_{4c} - T_{8c} } \right\}$ in premixed turbulent flames, where the closures of pressure gradient terms $T_{4c}$ and $T_{5c}$ also play pivotal roles in the modelling of turbulent scalar flux transport.

Based on Eq. 8 it is possible to express reaction progress variable variance $\widetilde{{c^{{\prime\prime}2} }}$ as (Bray et al. 1985):

$$ \widetilde{{c^{{\prime\prime}2} }} = \tilde{c}\left( {1 - \tilde{c}} \right) + O\left( {\gamma_{c} } \right) $$

(24)

This suggests that $\partial \widetilde{{c^{{\prime\prime}2} }}/\partial x_{i} = \left( {1 - 2\tilde{c}} \right)\left( {\partial \tilde{c}/\partial x_{i} } \right) + O\left( {\gamma_{c} } \right)$. A comparison between this expression and Eq. 18 suggests that the turbulent scalar flux of variance $\overline{{\rho u_{i}^{{\prime\prime}} c^{{\prime\prime}2} }}$ may exhibit counter-gradient (gradient) type transport for positive (negative) values of slip velocity. The counter-gradient transport of scalar variance was indeed reported by Chakraborty and Swaminathan (2011). This also indicates that turbulent fluxes of scalar quantities related to reaction progress variable shows a gradient (counter-gradient) type transport when $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ exhibits a gradient (counter-gradient) type transport. It has also been found that the scalar fluxes of the quantities related to the reaction progress variable gradient (e.g. generalised flame surface density (FSD) ${\Sigma }_{gen} = \overline{{\left| {\nabla c} \right|}}$ (Veynante et al. 1997; Chakraborty and Cant 2009c, 2011) and scalar dissipation rate $\tilde{\varepsilon }_{c} = \overline{\rho D\nabla c \cdot \nabla c} /\overline{\rho } - \tilde{D}\nabla \tilde{c} \cdot \nabla \tilde{c}$ (Chakraborty and Swaminathan 2010, 2013) exhibit a counter-gradient type transport when $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ shows a counter-gradient type transport and vice versa. This can be substantiated from Fig. 23 where the variations of turbulent flux of scalar dissipation rate $\overline{{\rho u_{1}^{{\prime\prime}} \varepsilon_{c} }} \times D_{th,0} /\rho_{0} S_{L}^{3}$ and $\partial \tilde{\varepsilon }_{c} /\partial x_{1} \times D_{th,0}^{2} /S_{L}^{3}$ with $\tilde{c}$ are shown for cases AL-EL, which reveals that a counter-gradient type transport is observed for cases AL and BL, whereas a gradient type transport is obtained for cases DL and EL, and a combination of gradient and counter-gradient transport is observed for case CL. The unresolved flux of FSD is given by (Veynante et al. 1997; Chakraborty and Cant 2009c, 2011): $\left[ {\overline{{\left( {u_{i} } \right)}}_{s} - \tilde{u}_{i} } \right]{\Sigma }_{gen}$ where $\overline{\left( q \right)}_{s} = \overline{{q\left| {\nabla c} \right|}} /{\Sigma }_{gen}$ is the surface-averaged value of a general quantity $q$. The surface averaged value of $\overline{{\left( {u_{1} } \right)}}_{s}$ in the direction of mean flame propagation can be expressed as: $\overline{{\left( {u_{1} } \right)}}_{s} = \overline{{\left( {u_{1} } \right)}}_{P} K + \left( {1 - K} \right)\overline{{\left( {u_{1} } \right)}}_{R}$ where $K$ is a model parameter, which leads to (Veynante et al. 1997):

$$ \left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen} = \left( {K - \tilde{c}} \right)\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right] $$

(25)

Fig. 23

Variations of turbulent flux of scalar dissipation rate $\overline{{\rho u_{1}^{{\prime\prime}} \varepsilon_{c} }} \times D_{th,0} /\rho_{0} S_{L}^{3}$ and $\partial \tilde{\varepsilon }_{c} /\partial x_{1} \times D_{th,0}^{2} /S_{L}^{3}$ with $\tilde{c}$ for cases AL-EL (i.e. $Le = 0.34,0.6,0.8, 1.0$ and 1.2)

According to Eq. 17, it is possible to rewrite Eq. 25 as: $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen} = \left( {K - \tilde{c}} \right)\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}} /\left[ {\overline{\rho }\tilde{c}\left( {1 - \tilde{c}} \right)} \right] + O\left( {\gamma_{c} } \right)$, which reveals that the turbulent flux of FSD $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ is closely related to the turbulent scalar flux $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$. Therefore, a counter-gradient (gradient) transport for $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ is obtained in the cases, where $\overline{{\rho u_{1}^{{\prime\prime}} c^{\prime\prime}}}$ exhibits a counter-gradient (gradient) type transport. The variations of $\left[ {\overline{{\left( {u_{1} } \right)}}_{s} - \tilde{u}_{1} } \right]{\Sigma }_{gen}$ and $\partial {\Sigma }_{gen} /\partial x_{1}$ for cases AL-EL are qualitatively similar to $\overline{{\rho u_{1}^{{\prime\prime}} \varepsilon_{c} }}$ and $\partial \tilde{\varepsilon }_{c} /\partial x_{1}$, respectively and therefore is not explicitly shown here.

From the foregoing it is evident that the behaviour of the slip velocity $\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right]$ determines whether gradient or counter-gradient transport is obtained for the turbulent fluxes in premixed turbulent flames and the first terms on the right hand sides of Eqs. 15 and 16 may induce counter-gradient behaviour for Reynolds momentum fluxes $\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}}}$ and Reynolds fluxes of turbulent kinetic energy $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$, respectively. In order to illustrate this, it is worthwhile to consider the Boussinesq’s gradient hypothesis for the closure of Reynolds momentum fluxes (Launder 1976; Durbin and Pettersson-Reif 2001):

$$ - \overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }} = \mu_{t} \left( {\frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \tilde{u}_{j} }}{{\partial x_{i} }}} \right) - \frac{{2\delta_{ij} }}{3}\left( {\mu_{t} \frac{{\partial \tilde{u}_{l} }}{{\partial x_{l} }} + \tilde{k}} \right) $$

(26)

Equation 26 is valid for non-reacting turbulent flows. Chakraborty et al. (2011e) utilised the second and third terms on the right hand side of Eq. 15 using a methodology similar to Eq. 26 as these terms originate due to non-reacting turbulence. The first term on the right hand side of Eq. 17 is related to the slip velocity and is modelled using Eqs. 17 and 24 as $\overline{{\rho u_{i} ^{\prime\prime}c^{\prime\prime}}} \cdot \overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} /\left[ {\overline{\rho }\overline{{ \cdot \rho c^{{\prime\prime}2} }} } \right]$ (Chakraborty et al. 2011a, e), which yields:

$$ - \overline{{\rho u_{i}^{{\prime\prime}} u_{j}^{{\prime\prime}} }} = \frac{{\mu_{t} }}{{\sigma_{Le} }}\left( {\frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \tilde{u}_{j} }}{{\partial x_{i} }}} \right) - \frac{{2\delta_{ij} }}{3}\left( {\frac{{\mu_{t} }}{{\sigma_{Le} }}\frac{{\partial \tilde{u}_{l} }}{{\partial x_{l} }} + \tilde{k}} \right) - \frac{{\overline{{\rho u_{i} ^{\prime\prime}c^{\prime\prime}}} \cdot \overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} }}{{\overline{\rho }\overline{{ \cdot \rho c^{{\prime\prime}2} }} }} $$

(27)

where $\sigma_{Le}$ is a turbulent Schmidt number. The predictions of Eqs. 26 and 27 for $\overline{{\rho u_{1}^{{\prime\prime}} u_{1}^{{\prime\prime}} }} /\overline{\rho }S_{L}^{2}$ for cases AL, BL and DL are exemplarily shown in Fig. 24 for $\sigma_{Le} = 1/Le$ and the model performances for cases CL and EL remain comparable to that in case DL. It can be seen from Fig. 24 that the last term on the right hand side of Eq. 27 is crucial for the purpose of prediction of Reynolds stresses in the cases where the slip velocity $\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right]$ assumes a large magnitude (e.g. case AL). The last term on the right hand side of Eq. 27 not only plays an important role for flames with $Le \ll 1$ but also for flames in the corrugated flamelets regime (e.g. case AR), which is not explicitly shown here but interested readers are referred to Chakraborty et al. (2011a) for further information in this regard.

Fig. 24

Variations of $\overline{{\rho u_{1}^{{\prime\prime}} u_{1}^{{\prime\prime}} }} /\overline{\rho }S_{L}^{2}$ with $\tilde{c}$ across the flame brush extracted from DNS data (solid line) along with the predictions of Eqs. 26 (broken line) and 27 (line with stars) for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

The turbulent flux of kinetic energy $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$ is often modelled using a gradient hypothesis for turbulent non-reacting flows in the following manner (Jones and Launder 1973):

$$ \frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}} = - \frac{{\mu_{t} }}{{\sigma_{k} }}\frac{{\partial \tilde{k}}}{{\partial x_{i} }} $$

(28)

where $\sigma_{k}$ is an appropriate turbulent Schmidt number and $\mu_{t} = C_{\mu } \overline{\rho }\tilde{k}^{2} /\tilde{\varepsilon }$ is the eddy viscosity with $C_{\mu } = 0.09$ being the model constant. However, the model given by Eq. 28 does not account for the first term on the right hand side of Eq. 16. Using Eqs. 17 and 24, $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$ can be approximated as: $\left[ {\overline{{\left( {u_{1} } \right)}}_{P} - \overline{{\left( {u_{1} } \right)}}_{R} } \right] = \overline{{\rho u_{i} ^{\prime\prime}c^{\prime\prime}}} /\overline{{\rho c^{{\prime\prime}2} }}$, which enables the first term on right hand side to be expressed as: $0.5\left( {\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}} } \right)\left( {\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} } \right)\left( {\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} } \right)\left( {1 - 2\tilde{c}} \right)/\left( {\overline{{\rho c^{{\prime\prime}2} }} } \right)^{2}$. The quantity $\overline{k}_{P} - \overline{k}_{R}$ was modelled by Chakraborty et al. (2011a, e) in the following manner:

$$ \overline{k}_{P} - \overline{k}_{R} = - C_{T} M_{i} \frac{{\partial \tilde{k}}}{{\partial x_{i} }}\frac{1}{{{\Sigma }_{gen} }} $$

(29)

The second and third terms on the right hand side of Eq. 16 arise due to non-reacting turbulent velocity fluctuations and a gradient type modelling similar to Eq. 28 can be used for the modelling of these terms. By considering these aspects, Chakraborty et al. (2011a, e) proposed the following model expression for $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$:

$$ \frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}} = - C_{G} \overline{\rho }\frac{{\tilde{k}^{2} }}{{\tilde{\varepsilon }}}\frac{{\partial \tilde{k}}}{{\partial x_{i} }} - C_{T} \left( {\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}} } \right)M_{i} \frac{{\partial \tilde{k}}}{{\partial x_{i} }}\frac{1}{{{\Sigma }_{gen} }} + 0.5\frac{{\left( {\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}} } \right)\left( {\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} } \right)\left( {\overline{{\rho u_{j}^{{\prime\prime}} c^{\prime\prime}}} } \right)}}{{\left( {\overline{{\rho c^{{\prime\prime}2} }} } \right)^{2} }}\left( {1 - 2\tilde{c}g^{s} } \right) $$

(30)

where $g = \widetilde{{c^{{\prime\prime}2} }}/\left[ {\tilde{c}\left( {1 - \tilde{c}} \right)} \right]$ is the segregation factor which assumes a value of unity where the PDF of $c$ is bi-modal with impulses at $c = 0$ and $c = 1.0$ (i.e. Eq. 8) (Bray et al. 1985). The departure of $g$ from 1.0 provides the measure of the departure of the PDF of $c$ from the presumed bi-modal distribution. The predictions of Eqs. 28 and 30 (with $C_{G} = 0.22,C_{T} = 1.0$ and $s = 2.0$) are compared to $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$ extracted from DNS data in Fig. 25 for cases AL, BL and DL, and it is evident that in cases AL and BL $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$ exhibits counter-gradient behaviour and it is not possible to capture the correct behaviour without the contributions of the second and third terms on the right hand side of Eq. 30. The gradient model captures the qualitative behaviour of $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$ for case DL but the quantitative agreement is better for the model given by Eq. 30. This conclusion also holds for cases CL and EL but not shown here for the sake brevity. Equation 30 further suggests that the closure of scalar flux of turbulent kinetic energy in premixed turbulent flames depends on the modelling of turbulent scalar flux. Thus, the closures of $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}}$ and $\overline{{\rho u_{i}^{{\prime\prime}} c^{\prime\prime}}}$ are interlinked and should not be considered in isolation.

Fig. 25

Variations of $\frac{1}{2}\overline{{\rho u_{i}^{{\prime\prime}} u_{j} ^{\prime\prime}u_{j} ^{\prime\prime}}} { }/\rho_{0} S_{L}^{3} = \overline{{\rho u_{i}^{{\prime\prime}} k}} { }/\rho_{0} S_{L}^{3}$ with $\tilde{c}$ across the flame brush along with the predictions of Eqs. 28 and 30 for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

4.2 Modelling Implications in the Context of Large Eddy Simulation (LES) Modelling

It is important to note that the discussion so far regarding the modelling of counter-gradient transport was discussed in the context of RANS, but it is equally valid in the context of Large Eddy Simulations (LES). The cases, which exhibit counter-gradient behaviour of turbulent scalar flux in the context of RANS, also exhibit a counter-gradient type transport when sub-grid scalar flux (i.e. $\overline{{\rho u_{i} c}} - \overline{\rho }\tilde{u}_{i} \tilde{c}$) is considered, where $\overline{q}$ and $\tilde{q} = \overline{\rho q} /\overline{\rho }$ in this sub-section denote the filtered and Favre-filtered values of a general quantity $q$, respectively in the context of LES. The profiles of the mean values of cosine of the angle ${\Theta }$ (i.e. $cos{\Theta }$ where ${\Theta } = \cos^{ - 1} \left[ { - \nabla \tilde{c} \cdot \left( {\overline{{\rho {\varvec{u}}c}} - \overline{\rho }\tilde{{u}}\widetilde{c }} \right)/\left\{ {\left| {\nabla \tilde{c}} \right|\left| {\overline{{\rho {\varvec{u}}c}} - \overline{\rho }\tilde{{u}}\widetilde{c }} \right|} \right\}} \right]$) between $\overline{{\rho {\varvec{u}}c}} - \overline{\rho }\tilde{{u}}\widetilde{c }$ and $\left( { - \nabla \tilde{c}} \right)$ conditional upon $\tilde{c}$ for cases AL and EL and a unity Lewis number flame case E from a DNS database with different initial turbulence intensities (i.e. $u^{\prime}/S_{L} = 5.0, 6.25,7.5, 9.0$ and 11.25) are shown in Fig. 26 for different normalised LES filter widths ${\Delta }/\delta_{th}$. The attributes of the DNS database corresponding to freely propagating statistically planar turbulent premixed flames subjected to different initial turbulence intensities are provided in Table 6. All the cases in Table 6 has a unity Lewis number and standard value of Prandtl number (i.e. $Pr = 0.7$). Further information on this dataset can be found elsewhere (Chakraborty and Swaminathan 2013; Chakraborty et al. 2011b, c; Gao et al. 2015a; Klein et al. 2016) and thus is not repeated here.

Fig. 26

Cosine of the angle ${\Theta }$ between scalar flux $\overline{{\rho {\varvec{u}}c}} - \overline{\rho }\tilde{{u}}\widetilde{c }$ calculated from DNS and $-{\nabla} \tilde{c}$ conditional on $\tilde{c}$ for cases AL and EL (left column) and statistically planar turbulent premixed flames with different values of $u^{\prime}/S_{L}$ for the database presented in Table 6 (right column) for ${\Delta } \approx 0.4\delta_{th} ,1.2\delta_{th} ,2.0\delta_{th} ,2.8\delta_{th} .$ The cases AL and EL are shown in the left column. For the second column the initial $u^{\prime}/S_{L}$ value is indicated in the figure

Table 6 Initial values of simulation parameters and non–dimensional numbers of the DNS database with different turbulence intensities

It is worth noting that for a gradient type sub-grid transport the angle ${\Theta }$ would be zero and the cosine of the angle would assume the value 1.0. For perfect counter-gradient sub-grid transport the cosine assumes the value $- 1.0$. The competition between the effects of heat release and turbulent velocity fluctuations can be discerned from Fig. 26, which illustrates that the gradient type transport is promoted for high turbulence intensities and as a result the extent of counter-gradient transport weakens with increasing $u^{\prime}/S_{L}$. It can further be seen from Fig. 26 that the extent of counter-gradient transport strengthens with decreasing $Le$ and this behaviour is prominent for cases AL and BL. This behaviour is consistent with turbulent scalar flux behaviour in the context of RANS (see Fig. 20b). Figure 26 shows that the negative cosine values in the region corresponding roughly to $0.2 \le \tilde{c} \le 0.8$ where the effects of heat release are most pronounced in all cases considered in this figure. The extent of counter-gradient transport increases with increasing filter width (Gao et al. 2015a, 2015b; Klein et al. 2016) but this phenomenon is somewhat hidden by the fact that Fig. 26 shows only the angle between both vectors. The strength of the sub-grid scalar flux cannot be obtained from Fig. 26 but it can be estimated from Fig. 27, where the mean values of sub-grid scalar flux $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)/\rho_{0} S_{L}$ conditional upon Favre-filtered reaction progress variable $\tilde{c}$ are shown for cases AL, BL, DL and EL (behaviour in case CL is qualitatively similar to case DL) where $n$ corresponds to the mean direction of flame propagation. A negative (positive) value of $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)/\rho_{0} S_{L}$ is indicative of counter-gradient (gradient) type transport. The findings from Figs. 26 and 27 reveal that a gradient type model is not sufficient for the purpose of modelling sub-grid scalar flux $\left( {\overline{{\rho u_{i} c}} - \overline{\rho }\tilde{u}_{i} \tilde{c}} \right)$. For a steady laminar 1D unstretched premixed flame, one obtains $\rho u_{n} = - \rho_{0} S_{L}$ and $\overline{\rho }\tilde{u}_{n} = - \rho_{0} S_{L}$ and therefore $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)$ for a laminar 1D premixed flame can be equated to $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right) = - \rho_{0} S_{L} \left( {\overline{c} - \tilde{c}} \right)$ (Boger 2000). This contribution can be taken to be representative of the counter-gradient contribution to the sub-grid scalar flux, as the flames are expected to exhibit counter-gradient transport for small values of $u^{\prime}/S_{L}$ and this component for $\left( {\overline{{\rho u_{i} c}} - \overline{\rho }\tilde{u}_{i} \tilde{c}} \right)$ can be equated to $- \rho_{0} S_{L} M_{i} \left( {\overline{c} - \tilde{c}} \right)$ with $M_{i} = - \left( {\partial \tilde{c}/\partial x_{i} } \right)/\left| {\nabla \tilde{c}} \right|$ is the $i^{th}$ component of the resolved flame normal vector. For a bi-modal sub-grid PDF of $c$ with impulses at 0 and 1.0, one obtains $\overline{c} = \left( {1 + \tau } \right)\tilde{c}/\left( {1 + \tau \tilde{c}} \right)$ (Bray et al. 1985), which yields $\left( {\overline{c} - \tilde{c}} \right) = \tau \tilde{c}\left( {1 - \tilde{c}} \right)/\left( {1 + \tau \tilde{c}} \right) \ge 0$. However, in reality $\overline{c}$ approaches $\tilde{c}$ for small values of ${\Delta }$ (i.e. $lim_{\Delta \to 0} \overline{c} = lim_{\Delta \to 0} \tilde{c} = c$) and the difference between $\overline{c}$ and $\tilde{c}$ increases with increasing ${\Delta }$. It has also been demonstrated in previous analyses that sub-grid PDF of $c$ cannot be considered as bi-modal and $\overline{c}$ cannot accurately be approximated by $\left( {1 + \tau } \right)\tilde{c}/\left( {1 + \tau \tilde{c}} \right)$, but $\left( {\overline{c} - \tilde{c}} \right)$ remains positive and its magnitude increases with increasing filter width. This also explains why the extent of counter-gradient transport increases with increasing ${\Delta }$.

Fig. 27

Variation of mean values of $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)/\rho_{0} S_{L}$ conditional on $\tilde{c}$ for ${\Delta } \approx 0.4\delta_{th} ,\ 1.2\delta_{th} ,\ 2.0\delta_{th} ,\ 2.8\delta_{th}$ for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$), c DL ($Le = 1.0$), d EL ($Le = 1.2$)

A number of sub-grid scalar flux models have been proposed by several researchers, which are summarised in Table 7. In Table 7, GHM stands for the gradient hypothesis model. The FRM model stands for the sub-grid flux model by Richard et al. (2007), where the first term on the right-hand side is responsible for gradient type transport and the second term accounts for counter-gradient transport. The sub-grid flux model by Weller et al. (1998) (FWM) is similar to FRM but the counter-gradient contribution is augmented by the involvement of the wrinkling factor ${\Xi } = {\Sigma }_{gen} /\left| {\nabla \overline{c}} \right| = \overline{{\left| {\nabla c} \right|}} /\left| {\nabla \overline{c}} \right| \ge 1.0$. The FRY and FTM models refer to sub-grid models by Rymer (2001) and Tullis and Cant (2003), respectively. The second term on the right-hand side of FRY and FTM models accounts for a counter-gradient type transport but in a different manner in comparison to the FRM and FWM models. The first term on the right-hand side of the FRY and FTM models utilise the usual Smagorinsky type gradient hypothesis model (i.e. GHM). The CGM refers to Clark’s gradient model which is based on Taylor series expansion under the assumption of scale similarity (Clark et al. 1979). If more terms of the Taylor series expansion are retained one obtains the extended gradient model (EGM) (Klein et al. 2016). The second term on the right hand side of Huai et al. (2006)’s sub-grid flux model (FHM) follows the CGM approach but the gradient contribution by the first term on the right hand side is introduced to improve numerical stability. The VSS, DSS and ASS models are derived based on different assumptions regarding scale similarity and further discussion can be found in Klein et al. (2016). The ASS model is based on a recent methodology proposed by Anderson and Domaradzki (2012). In this methodology the scalar and turbulent scalar spectrum is split in 3 different length scale ranges: small $R_{3}$, intermediate $R_{2}$ and large scales $R_{1}$, where $R_{1}$ represents the unresolved scales. Consequently, a general variable $Q$ can be decomposed as $Q = Q_{1} + Q_{2} + Q_{3}$. For each length scale range, the quantity $Q$ can be defined using two filtering levels such that $Q_{1}$ can be represented by $\widehat{{\overline{Q}}}$, $Q_{2}$ by $\overline{Q} - \widehat{{\overline{Q}}}$ and $Q_{3}$ by $Q - \overline{Q}$.

Table 7 Summary of the sub–grid scalar flux models

The predictions of the models listed in Table 7 except for the VSS, DSS, ASS, EGM, CVSS and CASS models are compared to the mean values of $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)/\rho_{0} S_{L}$ extracted from DNS data conditioned upon $\tilde{c}$ for ${\Delta } = 0.4\delta_{th} ,1.2\delta_{th} ,2.8\delta_{th}$ for cases AL, BL and DL in Fig. 28 and cases CL and EL are not shown here because of the model performances in these cases are qualitatively similar to that in case DL. It can be seen from Fig. 28 that the standard gradient hypothesis (i.e. GHM) assumes the opposite sign to the sub-grid flux obtained from DNS data for the major portion of the flame brush for all filter widths for all cases considered here. Moreover, the GHM model does not adequately capture the qualitative behaviour of $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)$ in all cases for all filter widths. The FRM and FWM (FRY and FTM) models behave similarly for small values of ${\Delta }$ because the wrinkling factor ${\Xi }$ remains close to unity, but the counter-gradient contribution is stronger in the FWM (FTM) than that in the case of the FRM (FRY) model because ${\Xi }$ increases with increasing filter width. Figure 28 suggests that both FRM and FWM models tend to overpredict (underpredict) the extent of counter-gradient transport for the $Le \ge 1.0$ ($Le \ll 1.0$) cases considered here. However, both FRM and FWM models capture the correct qualitative behaviour of the sub-grid scalar flux but underpredict the gradient behaviour towards the unburned gas side for the $Le \approx 1.0$ cases. The predictions of the FRY and FTM models remain inferior to the FRM and FWM models because the FRY and FTM models implicitly assume a bi-modal distribution of sub-grid PDF of $c$ for unity Lewis number flames, which yields $\rho_{0} S_{L} \left( {\overline{c} - \tilde{c}} \right) = \overline{\rho }\tau S_{L} \tilde{c}\left( {1 - \tilde{c}} \right)$. However, it has been demonstrated elsewhere (Chakraborty 2005; Chakraborty and Cant 2009d) that the sub-grid PDF of $c$ remains hardly bi-modal and in reality one gets $\rho_{0} S_{L} \left( {\overline{c} - \tilde{c}} \right) < \overline{\rho }\tau S_{L} \tilde{c}\left( {1 - \tilde{c}} \right)$, thus the counter-gradient contributions of the FRY and FTM models are of higher magnitudes than the FRM and FWM models, respectively. It can be seen from Fig. 28 that the CGM and FHM models capture both the qualitative and quantitative behaviours of $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)$ better than other models but the counter-gradient contribution of $\left( {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right)$ is underpredicted for large filter widths in the $Le \ll 1$ flames and the extent of this underprediction increases with decreasing $Le$ and increasing filter width. Using Eq. 12 in the context of LES yields (Gao et al. 2015a, 2015b):

$$ \left[ {\overline{{\rho u_{i} c}} - \overline{\rho }\tilde{u}_{i} \tilde{c}} \right]\sim \overline{\rho }{\Delta }^{2} \left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]\left| {\nabla \tilde{c}} \right|^{2} + O\left( {\gamma_{c} } \right) $$

(31)

Fig. 28

Variations of mean values of $\overline{{(\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c})/\rho_{0} S_{L}$ conditional on $\tilde{c}$ according to DNS ( ),CGM ( ), GHM ( ), FHM ( ), FRM ( ),FRY ( ), FTM ( ) and FWM ( ) for ${\Delta } = 0.4\delta_{th}$ (1^st col.), $1.2\delta_{th}$ (2^nd col.) and $2.8\delta_{th}$ (3^rd col.) or cases AL ($Le = 0.34$), BL ($Le = 0.6$) and DL ($Le = 1.0$). The FRY and FTM predictions are multiplied by 0.1, 0.2 and 0.5 for ${\Delta } = 0.4\delta_{th} ,1.2\delta_{th}$ and $2.8\delta_{th}$ respectively

Once $\left| {\nabla \tilde{c}} \right|^{2}$ is scaled using $\left| {\nabla \tilde{c}} \right|^{2} \sim \tilde{c}\left( {1 - \tilde{c}} \right)/{\Delta }^{2}$, Eq. 31 gives rise to Eq. 17 in the context of LES. Therefore, the CGM model is capable of predicting both counter-gradient and gradient type transport based on the sign of $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$. The same is true for the FHM model because the second term on the right-hand side behaves similarly to the CGM model. As the CGM and FHM models implicitly account for the local statistical behaviour of $\left[ {\overline{{\left( {u_{i} } \right)}}_{P} - \overline{{\left( {u_{i} } \right)}}_{R} } \right]$, these models are more successful than the other models in capturing both the qualitative and quantitative behaviours of $\left[ {\overline{{\rho u_{i} c}} - \overline{\rho }\tilde{u}_{i} \tilde{c}} \right]$ for flames with $Le \ll 1$.

In addition to capturing the correct variation of the conditionally averaged value of $\left[ {\overline{{\rho u_{n} c}} - \overline{\rho }\tilde{u}_{n} \tilde{c}} \right]$ across the flame brush, the LES models need to accurately capture the local behaviour of sub-grid scalar flux. Therefore, the correlation coefficient between the model prediction and $\left[ {\overline{{\rho u_{i} c}} - \overline{\rho }\tilde{u}_{i} \tilde{c}} \right]$ obtained from DNS should be as close to unity as possible. The correlation coefficients between $\left[ {\overline{{\rho u_{1} c}} - \overline{\rho }\tilde{u}_{1} \tilde{c}} \right]$ from DNS data and the predictions of all the models for $0.1 \le \overline{c} \le 0.9$ are exemplarily shown in Fig. 29 for cases AL, BL and DL for different values of ${\Delta }$. The corresponding correlation coefficients for $\left[ {\overline{{\rho u_{2} c}} - \overline{\rho }\tilde{u}_{2} \tilde{c}} \right]$ are shown in Fig. 30 and the correlation coefficients for $\left[ {\overline{{\rho u_{3} c}} - \overline{\rho }\tilde{u}_{3} \tilde{c}} \right]$ are not explicitly shown because $\left[ {\overline{{\rho u_{2} c}} - \overline{\rho }\tilde{u}_{2} \tilde{c}} \right]$ and $\left[ {\overline{{\rho u_{3} c}} - \overline{\rho }\tilde{u}_{3} \tilde{c}} \right]$ are statistically similar. It can be seen from Fig. 29 that the correlation coefficient for the GHM model remains negative for all values of ${\Delta }$. By contrast, the correlation coefficients for the CGM, FHM, FRI, FRY, FTM and FWM models exhibit positive values with few exceptions for cases with $Le \ll 1$ (e.g. cases AL and BL). For large values of filter widths (e.g. ${\Delta } > \delta_{th}$), the correlations between $\left[ {\overline{{\rho u_{1} c}} - \overline{\rho }\tilde{u}_{1} \tilde{c}} \right]$ and the FRM, FRY, FTM and FWM model predictions have been found to be weak and different from unity for the flames with $Le \ll 1$ (e.g. case AL). The correlation coefficients for the CGM and FHM models assume high positive values for ${\Delta } > \delta_{th}$ in all cases.

Fig. 29

a–e Correlation coefficients between modelled and actual values of $\left[ {\overline{{\rho u_{1} c}} - \overline{\rho }\tilde{u}_{1} \tilde{c}} \right]$ in the $\overline{c}$ range $0.1 \le \overline{c} \le 0.9$ for ${\Delta } = 0.4\delta_{th}$ ( );$0.8\delta_{th}$ ( ); $1.2\delta_{th}$ ( );$1.6\delta_{th}$ ( ); $2.0\delta_{th}$ ( );$2.4\delta_{th}$ ( ) and $2.8\delta_{th}$ ( ) for cases a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

Fig. 30

a–e Correlation coefficients between modelled and actual values of $\left[ {\overline{{\rho u_{2} c}} - \overline{\rho }\tilde{u}_{2} \tilde{c}} \right]$ in the $\overline{c}$ range $0.1 \le \overline{c} \le 0.9$ for ${\Delta } = 0.4\delta_{th}$ ( );$0.8\delta_{th}$ ( ); $1.2\delta_{th}$ ( );$1.6\delta_{th}$ ( ); $2.0\delta_{th}$ ( );$2.4\delta_{th}$ ( ) and $2.8\delta_{th}$ ( ) for a AL ($Le = 0.34$), b BL ($Le = 0.6$) and c DL ($Le = 1.0$)

The predictions of the CGM and FHM remain positively correlated with $\left[ {\overline{{\rho u_{2} c}} - \overline{\rho }\tilde{u}_{2} \tilde{c}} \right]$ extracted from DNS data for all values of ${\Delta }$ for cases AL-EL (cases CL and EL are not shown here but refer to Gao et al. (2015b) for further information). The GHM model predictions remain weakly positively correlated with $\left[ {\overline{{\rho u_{2} c}} - \overline{\rho }\tilde{u}_{2} \tilde{c}} \right]$ obtained from DNS data for $Le \ge 1.0$ cases (e.g. cases DL and EL) but this correlation is found to be negative for cases AL-CL where the effects of heat release are relatively stronger than in case DL (and also for case EL (Gao et al. 2015b)). The predictions of the FRM, FRY, FTM and FWM models remain weakly positively correlated with $\left[ {\overline{{\rho u_{2} c}} - \overline{\rho }\tilde{u}_{2} \tilde{c}} \right]$ for all ${\Delta }$ for flames with $Le \ll 1$ (e.g. cases AL and BL) but the correlation becomes weaker for flames with $Le \approx 1.0$ (e.g. cases CL-EL).

The findings from Figs. 29 and 30 reveal that both CGM and FHM models perform satisfactorily for ${\Delta } > \delta_{th}$ for cases with $Le \approx 1.0$. However, the quantitative predictions of the CGM and FHM models have scope for improvement for $Le \ll 1.0$ flames.

The variation of the correlation coefficient between the sub-grid flux $\overline{{\rho {\varvec{u}}c}} - \bar{\rho }\tilde{\varvec{u}}\tilde{c }$ calculated from DNS and model expressions in the direction of mean flame propagation ($corr_{1}$) and normal to it ($corr_{23}$) for the GHM, FRM, VSS, DSS, ASS, CGM and EGM models for cases AL, EL, A and E are exemplarily shown in Fig. 31 which shows that the correlation strength decreases with increasing filter width. For the scale similarity and extended gradient type models (i.e. VSS, DSS, ASS, CGM, EGM models), the correlation coefficient approaches unity for small filter widths in the DNS limit but the correlation coefficient for the GHM model remains small in magnitude for all cases and all filter widths, in addition to predicting the opposite sign in comparison to the DNS data. The correlation coefficient for the FRM model shows a weaker dependency on the filter width but has a more pronounced dependency on Lewis number and turbulence intensity so that it shows superior performance in cases where the heat release effects are stronger than the effects of turbulence, i.e. in the flames in cases AL, BL and A, and in the direction of mean flame propagation (taken to be the negative $x_{1}$-direction). The variations of $corr_{1}$ also demonstrates that the inclusion of density variation either by using Favre filtering or by including additional terms involving density in the CGM model improves considerably the magnitude of $corr_{1}$ in particular for large filter widths. As a consequence, the EGM model performs better than the CGM model and the Favre-filtered scale similarity model versions perform better compared to their convolution filter counterparts. By contrast, turbulence effects dominate in the transverse direction and the correlation coefficients $corr_{23}$ for the VSS, DSS, ASS, CGM and EGM models remain comparable. The EGM exhibits the best performance with respect to $corr_{23}$ in nearly all cases considered here.

Fig. 31

Correlation coefficients between scalar flux $\overline{{\rho{\varvec{u}}c}} - \bar{\rho}\tilde{\varvec{u}}\tilde{c}$ calculated from DNS and different model expressions in the direction of mean flame propagation ($corr_{1}$) and normal to it ($corr_{23}$) plotted against ${\Delta }/\delta_{th}$ for cases AL, DL A, E. The correlation coefficients of the GHM model are multiplied with $- 1$

The variations of $\partial \left( {\overline{{\rho u_{i} c}} - \overline{\rho }\widetilde{{u_{i} }}\tilde{c}} \right)/\partial x_{i}$ extracted from DNS data conditional upon $\tilde{c}$ for cases AL, DL, A and E are shown in Fig. 32 along with the corresponding predictions of the GHM, FRM, VSS, DSS, ASS, CGM and EGM models for optimum model parameters but the prediction of the GHM model is multiplied with – 1.0 and warrants no further discussion. The FRM model has been found to perform remarkably well for the cases with $Le \le 0.8$ and for initial turbulence intensity of $u^{\prime}/S_{L} \le 6.25$. The other models show satisfactory agreements with DNS data for small filter widths, but all models exhibit an unsatisfactory performance for cases with $Le \ge 1.0$ and or large turbulence intensities in combination with large filter widths. For large filter widths (i.e. ${\Delta } \gg \delta_{th}$), only the VSS, ASS, DSS and FRM models provide reasonable agreement with DNS data for case DL (also for cases CL and EL (Gao et al. 2015b)). For further discussion on the scale similarity models, interested readers are referred to Klein et al. (2016), which also discuss that the DSS model shows the most robust behaviour in terms of consistency of performance level for different filter widths for turbulent premixed flames with different values of $Le$ and turbulence intensities.

Fig. 32

Conditional plot of $\partial \left( {\overline{{\rho u_{i} c}} - \overline{\rho }\widetilde{{u_{i} }}\tilde{c}} \right)/\partial x_{i}$ calculated from DNS as well as different model expressions against $\tilde{c}{ }$ for three different filter widths (${\Delta } \approx 0.4\delta_{th} ,{\Delta } \approx 1.6\delta_{th} ,{\Delta } \approx 2.8\delta_{th}$) for cases AL, DL A, E$.$ Leading model coefficients are optimised using a least square approach

Similar to RANS modelling, the heat release effects also influence the sub-grid stress and sub-grid kinetic energy closures in the context of LES. The filtered momentum conservation equation in the context of LES takes the following form (Klein et al. 2015):

$$ \frac{{\partial \overline{\rho }\widetilde{{u_{i} }}}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\widetilde{{u_{i} }}\widetilde{{u_{j} }}} \right)}}{{\partial x_{j} }} = - \frac{{\partial \left( {\overline{{\rho u_{i} u_{j} }} - \overline{\rho }\widetilde{{u_{i} }}\widetilde{{u_{j} }}} \right)}}{{\partial x_{j} }} + \frac{\partial }{{\partial x_{j} }}\overline{\rho }{ }\tilde{\nu }\left( {\left( {\frac{{\partial \widetilde{{u_{j} }}}}{{\partial x_{i} }} + \frac{{\partial \widetilde{{u_{i} }}}}{{\partial x_{j} }}} \right) - \frac{2}{3}\frac{{\partial \widetilde{{u_{k} }}}}{{\partial x_{k} }}\delta_{ij} } \right) - \frac{{\partial \overline{p}}}{{\partial x_{i} }} $$

(32)

where $\nu$ denotes the kinematic viscosity, the sub-grid scale (SGS) stress tensor is given by $\tau_{ij}^{SGS} = { }\overline{{\rho u_{i} u_{j} }} - \overline{\rho }\widetilde{{u_{i} }}\widetilde{{u_{j} }}$, and the isotropic part of the SGS stresses, i.e. the term involving $- \frac{1}{3}\tau_{kk}^{SGS} \delta_{ij}$, is often combined with the filtered pressure for incompressible flow modelling. The relevance of modelling the isotropic part of the SGS stresses is discussed in detail in Yoshizawa (1986). The most popular closure for $\tau_{ij}^{SGS}$ is the static Smagorinsky model (SSM) (Garnier et al. 2009), which is given below where $\widetilde{{S_{ij} }} = \left( {\partial \widetilde{{u_{i} }}/\partial x_{j} + \partial \widetilde{{u_{j} }}/\partial x_{i} } \right)/2$ and $\left| {\widetilde{{S_{ij} }}} \right| = \sqrt {2 \widetilde{{S_{ij} }}\widetilde{{S_{ij} }}}$:

$$ \tau_{ij}^{SSM} = - 2\overline{\rho }\left( {C_{s} {\Delta }} \right)^{2} \left| {\widetilde{{S_{ij} }}} \right|\left( {\widetilde{{S_{ij} }} - \widetilde{{S_{kk} }}{\updelta }_{{{\text{ij}}}} /3} \right) $$

(33)

The constant $C_{s}$ is either set to $C_{s} \approx 0.18$ in the static model version (SSM) or can be determined in a dynamic manner (see Garnier et al. (2009) for details). The theoretical value of $C_{s}$ is taken to be $C_{s} \approx 0.18$ in the static model version (SSM) or can be determined in a dynamic manner (DSM) as shown below, where $C_{d} \approx C_{s}^{2}$ (Erlebacher et al. 1992):

$$ C_{d} = \frac{{M_{ij} \left( {L_{ij} - \frac{1}{3}L_{kk} \delta_{ij} } \right)}}{{M_{kl} M_{kl} }};\,L_{ij} = \widehat{{\overline{\rho } \widetilde{{u_{i} }} \widetilde{{u_{j} }}}} - \frac{{\widehat{{\overline{\rho } \widetilde{{u_{i} }}}} \widehat{{\overline{\rho } \widetilde{{u_{j} }}}}}}{{\widehat{{\overline{\rho }}}}} $$

(34)

It is important to note that the calculation of the constant $C_{d}$ typically requires a regularisation procedure (Erlebacher et al. 1992). An alternative to adding the isotropic part of the SGS tensor to the filtered pressure is to use the model proposed by Yoshizawa (1986) in the following manner:

$$ \tau_{kk}^{SGS} = 2 C_{I} \overline{\rho } {\Delta }^{2} \left| {\widetilde{{S_{ij} }}} \right|^{2} $$

(35)

The implementation where the isotropic part $\tau_{kk}$ is explicitly modelled using Eq. 35 in conjunction with the static Smagorinsky model (see Eq. 33) will henceforth be referred to as the SSY model. It is worth noting that according to Erlebacher et al. (1992) $\tau_{kk}^{SGS} /3\overline{p}$ can be scaled as $\tau_{kk}^{SGS} /3\overline{p} \sim Ma_{sgs}^{2}$ and thus the isotropic part of the SGS tensor remains smaller than the thermodynamic pressure for small turbulent Mach number flows. The model parameter $C_{I}$ varies between $0.0025$ and $0.009$ depending on the analysis. It is possible to evaluate $C_{I}$ in a dynamic fashion in the following manner (Moin et al. 1991):

$$ C_{I} = \frac{{L_{kk} }}{M}, M = 2\widehat{{\overline{\rho }}} {\hat{\Delta }}^{2} \left| {\widehat{{\widetilde{{S_{ij} }}}}} \right|^{2} - \widehat{{2\overline{\rho } {\Delta }^{2} \left| {\widetilde{{S_{ij} }}} \right|^{2} }} $$

(36)

Similar to $C_{d}$, the calculation of $C_{I}$ typically requires a regularization procedure. It is worthwhile to consider a statistically planar flame propagating in negative $x_{1}$-direction to understand the appropriateness of the above eddy viscosity type models in the context of turbulent premixed combustion. Assuming $\partial \widetilde{{u_{2} }}/\partial x_{2} = \partial \widetilde{{u_{3} }}/\partial x_{3} = 0$ and $\partial \widetilde{{u_{1} }}/\partial x_{1} > 0$ due to heat release, one obtains: $\tau_{11}^{SSM} = - \overline{\rho }\nu_{t} \frac{4}{3}\widetilde{{S_{11} }} < 0$, i.e. $\tau_{11}^{SSM}$ assumes a negative value, whereas $\tau_{11}^{SGS}$ cannot be negative. This suggests that more advanced closures in comparison to gradient hypothesis type model will be needed for turbulent premixed combustion, which is consistent with the experimental observations by Pfadler et al. (2010). It has been demonstrated earlier (see Figs. 28, 29, 30, 31 and 32) that Clark’s tensor diffusivity model (Clark et al. 1979) (i.e. CTM model) can predict both gradient as well as counter-gradient transport. The CTM model is expressed as (Clark et al. 1979):

$$ \tau_{ij}^{CTM} = \overline{\rho }\frac{{{\Delta }^{2} }}{12}\frac{{\partial \widetilde{{u_{i} }}}}{{\partial x_{k} }}\frac{{\partial \widetilde{{u_{j} }}}}{{\partial x_{k} }} $$

(37)

The CTM model is derived based on the assumption of scale similarity (Garnier et al. 2009), and therefore it is useful to consider the scale-similarity models for sub-grid stress. One such scale-similarity model is denoted thereafter as the VSS model in this paper, because the scale similarity hypothesis acts on the velocity components in the following manner (Ashurst et al. 1987b; Garnier et al. 2009):

$$ \tau_{ij}^{VSS} = \overline{\rho }\left( {\overline{{\widetilde{{u_{i} }}\widetilde{{u_{j} }}}} - \overline{{\widetilde{{u_{i} }}}} \overline{{\widetilde{{u_{j} }}}} } \right) $$

(38)

There is also an alternative scale similarity model, which can be defined in the context of Favre filtering following Vreman (1995):

$$ \tau_{ij}^{DSS} = \overline{{\overline{\rho }\widetilde{{u_{i} }}\widetilde{{u_{j} }}}} - \overline{{\overline{\rho }\widetilde{{u_{i} }}}} \overline{{\overline{\rho }\widetilde{{u_{j} }}}} / \overline{{\overline{\rho }}} $$

(39)

It will henceforth be referred to as the DSS model, i.e. density-based scale similarity model because the scale similarity assumption acts on $\rho u_{i}$ rather than $u_{i}$. Scale similarity models are known to not provide enough dissipation in an actual LES (Vreman 1995; Vreman et al. 1997). Recently, Anderson and Domaradzki (2012) identified the sources of deficiency of the scale similarity models and suggested a new model for momentum transport in the context of LES of incompressible flows, using the assumption of splitting the turbulent kinetic energy spectrum into 3 different ranges denoting small $R_{3} { }$, intermediate $R_{2} { }$ and large scales $R_{1}$ (Anderson and Domaradzki 2012), where $R_{3}$ represents the scales unresolved by the mesh, as discussed earlier in the context of sub-grid scalar flux closure. However, the original modelling methodology by Anderson and Domaradzki (2012) has been modified by Klein et al. (2015) to make it both Galilei invariant and symmetric. The modified model expression according to Klein et al. (2015) takes the following form:

$$ \tau_{ij}^{IET} = \overline{\rho }\left( {\widehat{{\widehat{{\widetilde{{u_{i} }}}}\widetilde{{u_{j} }}}} + \widehat{{\widetilde{{u_{i} }}\widehat{{\widetilde{{u_{j} }}}} }} - \widehat{{\widetilde{{u_{i} }}}}\widehat{{\widetilde{{u_{j} }}}} - \widehat{{\widehat{{\widetilde{{u_{i} }}}}\widehat{{\widetilde{{u_{j} }}}}}}} \right) $$

(40)

Equation 40 will henceforth be denoted as the IET model, i.e. inter-scale energy transfer model.

The mean values of cosines of the angle ${\Theta }$ between sub-grid stresses $\tau_{1j}^{SGS}$ evaluated from DNS and $\tau_{1j}^{SSM}$ conditional on $\tilde{c}$ values for cases A, C and E are shown in Fig. 33 for four different filter widths (note that the flame is propagating in negative $x_{1}$-direction). The corresponding plots for sub-grid stresses $\tau_{2j}^{SGS}$ are shown in Fig. 34. Since the $x_{2}$ and $x_{3}$ components are statistically identical for statistically planar flames with mean direction of flame propagation aligned with the negative $x_{1}$-direction, only the $x_{2}$-component is discussed further in Fig. 34. As the SSM model depends on gradient hypothesis, the gradient type behaviour is observed when the angle ${\Theta }$ is $0^{0}$ and the cosine of the angle assumes a value equal to 1.0. By contrast, a counter-gradient type behaviour is observed for ${\Theta } = 180^{0}$ when the cosine assumes a value of $- 1.0$.

Fig. 33

Cosine of the angle ${\Theta }$ between $\tau_{1j}^{SGS} { }$ calculated from DNS and $\tau_{1j}^{SSM}$ predictions conditional on $\widetilde{{c{ }}}$ for cases A, C and E, for four different filter widths

Fig. 34

Cosine of the angle ${\Theta }$ between $\tau_{2j}^{SGS} { }$ calculated from DNS and $\tau_{2j}^{SSM}$ predictions conditional on $\widetilde{{c{ }}}$ for cases A, C and E for four different filter widths (same legend as in Fig. 33)

It can be seen from Fig. 33 that the extent of counter-gradient behaviour strengthens with increasing filter width, which is similar to the behaviour observed for the sub-grid scalar flux (see Figs. 31 and 32). Moreover, this counter-gradient behaviour strengthens with decreasing $u^{\prime}/S_{L}$ (from case E to case A). The effects of heat release are less pronounced in the direction normal to the mean flame propagation and thus the counter-gradient behaviour in Fig. 32 is weaker than in Fig. 31. However, in contrast to Fig. 31, the gradient transport strengthens with increasing filter width in Fig. 34. This behaviour arises due to the term $\widetilde{{S_{11} }}$ in the isotropic part of Eq. 33, which dominates the model in $x_{2}$-direction. Figure 34 demonstrates that the contribution of $\widetilde{{S_{kk} }}$ in Eq. 33 strengthens with increasing filter width. The Smagorinsky parameter $C_{s} = \sqrt {C_{d} }$ can be determined using the dynamic procedure mentioned in Eq. 34. Typically, $C_{d}$ needs regularisation such as averaging and clipping to ensure satisfactorily numerical properties. The mean values of the Smagorinsky parameter for cases A, C and E, for three different filter sizes are reported in Fig. 35. In Fig. 35a, the parameter $C_{d}$ is calculated by averaging the denominator and numerator of Eq. 34 separately in $x_{2}$ and $x_{3}$ directions and no clipping was applied. However, no clear trend is evident from Fig. 35a, and the noise in the data variation increases with increasing filter size. In Fig. 35b, the conditional averaging (of the denominator and numerator) based on $\tilde{c}$ is applied in order to determine $C_{d}$. A comparison between Fig. 35a, b demonstrates that application of a standard averaging procedure for determining the model parameter $C_{d}$ yields unsatisfactory results for turbulent premixed combustion. The parameter $C_{d}$ fluctuates considerably, in particular for the cases with high turbulence intensities and for large filter widths. As a result, the DSM model may perform even worse than its static counterpart (i.e. the SSM model) (Klein et al. 2015). Therefore, the application of the dynamic procedure in its standard form remains questionable, at least within the flame brush of a turbulent premixed flame. Figure 35b demonstrates clearly that the Smagorinsky parameter shows some dependence on $\tilde{c}$ and $C_{d}$ remains close to its theoretical value (i.e. 0.0324) on the unburned gas side of the flame brush. However, in the middle of the flame brush, $C_{d}$ becomes small and even assumes negative values for small turbulence intensities, which is consistent with findings from Fig. 33. The findings from Figs. 33, 34 and 35 suggest that the Eq. 33 is not suitable for premixed turbulent flames. A dynamic evaluation of the model parameter $C_{d}$ cannot change the alignment of the modelled stress tensor. A negative effective viscosity is unphysical, and it would be desirable to assign ${\nu_{t}} = 0$ at the locations where counter-gradient behaviour is predominant.

Fig. 35

Variation of the dynamic Smagorinsky parameter $C_{d}$. a $C_{d}$ is determined after spatial averaging of numerator and denominator of the $C_{d}$ expression; b Averages are calculated conditional on $\tilde{c}$

For all eddy viscosity type models it is worth discussing if the isotropic part of the sub-grid stresses can be neglected in the context of turbulent premixed flames, or if explicit modelling is likely to improve the simulation predictions. It was pointed out by Moin et al. (1991) that the $M$ in Eq. 36 may vanish or assume negative values at some grid points and thus an averaging method is necessary. Figure 36 shows the values of $C_{I}$ after applying conditional averaging on $\tilde{c}$ values for cases A-E, where the conditional averaging is applied to the numerator and denominator of Eq. 36. The increasing value of $C_{I}$ for small values of  $\tilde{c}$ arises due to change in sign of the denominator in this region, which leads to a cancellation of terms in the denominator during averaging. This in turn gives a stronger weight to the numerator. An alternative evaluation of $C_{I}$ can be evaluated in the following manner where $\langle \cdot \rangle$ denotes an averaging procedure (Klein et al. 2015):

$$ C_{I} = \frac{{\langle L_{kk} M\rangle }}{{\langle M^{2} \rangle }} $$

(41)

This formula can be interpreted as a least square evaluation of $C_{I}$ where the square error is minimized over all samples where averages are taken, for example in a plane or conditional on a particular $\tilde{c}$ value. This evaluation is shown in Fig. 36a, b comparison between Fig. 36a, b reveals that Eq. 41 yields more reliable values of $C_{I}$ than Eq. 36. Figure 36 further shows that $C_{I}$ increases with increasing filter width for both procedures.

Fig. 36

Variation of the model parameter $C_{I}$. a $C_{I}$ is determined after conditional averaging of numerator and denominator of the $C_{I}$ expression in Eq. 38. b Averages are calculated according to Eq. 43. See Fig. 35 for the legend

Figure 35 shows that the dynamic evaluation of model parameters in the context of turbulent premixed combustion is more challenging than in isothermal flows. The conditional averaging on $\tilde{c}$ values might not be a major problem for statistically planar flames but extending this approach to complex, unsteady three dimensional flows seems to be rather difficult. Therefore, only the static version of the Smagorinsky model (SSM model) with $C_{s} \approx 0.18$ will be examined for the following discussion. The model parameter $C_{I}$ is considered to be 0.1 and representative of the results obtained using the dynamic calculation according to Eq. 41. The Pearson correlation coefficient for all models and all stress components $\tau_{ij}$ which are averaged over all filter widths and over cases A-E in the range $0.1 \le \overline{c} \le 0.9$ are shown in Fig. 37a, where $\tau_{mean}$ represents the mean value of all 6 independent components of $\tau_{ij}^{SGS}$. The corresponding results for the unburned gas part of the flame brush i.e. $0 \le \overline{c} \le 0.1$ are shown in Fig. 37b, which should show some resemblance to the model performances in non-reacting isothermal flows.

Fig. 37

a Results are taken from the range$0.1 \le \overline{c} \le 0.9$. b Results are taken from the range $0 \le \overline{c} \le 0.1$ .

Correlation coefficients for the models SSM, SSY, CTM, DSS, VSS, IET for all the SGS stress components: $\tau_{mean}^{SGS}$ ( );$\tau_{11}^{SGS}$ ( );$\tau_{12}^{SGS}$ ( );$\tau_{13}^{SGS}$ ( );$\tau_{22}^{SGS}$ ( );$\tau_{23}^{SGS}$ ( ) and $\tau_{33}^{SGS}$ ( ).Correlation coefficients are averaged over all filter width and all cases.

Figure 37a demonstrates that the SSM model shows weak correlations with the sub-grid stress tensor obtained from DNS data. The predictions of the SSM model for all components involving contributions in the direction of mean flame propagation (i.e. $\tau_{1j}^{SGS} )$ have been found to be negatively correlated with DNS data. It can further be seen from Fig. 37a that the correlation becomes positive when the isotropic part of the sub-grid stress tensor is included in the SSY model. The most significant improvement is observed for $\tau_{11}^{SGS}$ where effects of dilatation rate are expected to be most pronounced in the direction aligned with the mean direction of flame propagation (i.e. negative $x_{1} -$ direction in these cases). All the scale similarity models exhibit comparable correlation coefficient values, but the highest overall correlation coefficient is obtained for CTM and IET models. A comparison between Fig. 37a, b reveals that the absence of dilatation rate effects improves the performance of the model predictions and the negative correlation for the stress components $\tau_{ij = i}^{SGS}$ disappears, although the correlation of the SSM model remains smaller than the scale similarity models.

The variation of the conditional mean values of the different model predictions for the stress components $\tau_{11}^{SGS}$ and $\tau_{22}^{SGS}$ conditional on $\tilde{c}$ values for cases A and E along with the corresponding DNS data for two different filter widths are shown in Figs. 38 and 39. The cases B,C and D exhibit monotonically the trends revealed by cases A and E and thus are not shown here for the sake of brevity. The SSM model exhibits the opposite sign and a large discrepancy in terms of magnitude in both cases A and E. Including the isotropic part of the stresses in the SSY model results in a correct prediction of the sign of $\tau_{11}^{SGS}$ and the qualitative trend is correctly captured for $\tau_{11}^{SGS}$ and $\tau_{22}^{SGS}$. It can be appreciated from Figs. 38 and 39 that $C_{I} = 0.1$ in the SSY model is too large for the small filter size and too small for the large filter size. The CTM model yields satisfactory predictions for small filter widths but underpredicts the stresses for large filter widths. The VSS, DSS and IET models yield comparable predictions for small filter width but deviate from each other for large values of filter widths.

Fig. 38

Conditional plot of $\tau_{11}^{SGS}$ calculated from DNS along with different model predictions against $\tilde{c}{ }$ for ${\Delta } \approx 0.4\delta_{th} ,{{ \Delta }} \approx 2.8\delta_{th}$ for cases A and E

Fig. 39

Conditional plot of $\tau_{22}^{SGS}$ calculated from DNS as well as different model expressions against $\tilde{c}{ }$ for filter width ${\Delta } \approx 0.4\delta_{th} ,{{ \Delta }} \approx 2.8\delta_{th}$ for cases A and E

The behaviour of the models for the shear stress components $\tau_{ij, i \ne j}^{SGS} { }$ is similar to $\tau_{11}^{SGS}$ and $\tau_{22}^{SGS}$ but they are an order of magnitude smaller than the normal stresses and hence are not discussed further in this paper. Figures 38 and 39 demonstrate that the overall qualitative agreement with DNS data is reasonable for the CTM, IET, VSS, DSS models and to some extent for the SSY model. However, no model is able to accurately predict $\tau_{ij}^{SGS}$ quantitatively for all cases and all filter widths. This behaviour is most prevalent in case A for large values of $\Delta$ because the effects of heat release are the strongest with respect to background turbulence in case A among cases A-E.

The foregoing discussion indicates that the modelling of the isotropic part of the sub-stress tensor plays an important role in the modelling of turbulent premixed combustion. According to the CTM model one obtains the following expression:

$$ \tau_{kk}^{CTM} = \overline{\rho }\frac{{{\Delta }^{2} }}{12}\frac{{\partial \widetilde{{u_{k} }}}}{{\partial x_{i} }}\frac{{\partial \widetilde{{u_{k} }}}}{{\partial x_{i} }} $$

(42)

Similarly, according to the DSS model, one gets:

$$ \tau_{kk}^{DSS} = C_{DSS} \left( { \overline{{\overline{\rho }\widetilde{{u_{k} }}\widetilde{{u_{k} }}}} - \overline{{\overline{\rho }\widetilde{{u_{k} }}}} \overline{{\overline{\rho }\widetilde{{u_{k} }}}} / \overline{{\overline{\rho }}} } \right) $$

(43)

The coefficient $C_{DSS}$ is taken to be $0.5$, as this value yields results consistent with the other modelling approaches.

It is worth noting that $\left| {\widetilde{{S_{ij} }}} \right|^{2} = 2\widetilde{{S_{ij} }}\widetilde{{S_{ij} }}$ in the YOS model gives three terms of the form $2\left( {\partial u_{i} /\partial x_{i} } \right)^{2} , i = j$, six terms of the form $\left( {\partial u_{i} /\partial x_{j} } \right)^{2} , i \ne j$ and finally three mixed gradients $2\left( {\partial u_{i} /\partial x_{j} } \right)\left( {\partial u_{j} /\partial x_{i} } \right)$. An expansion of Eq. 42 reveals that 9 out of the 12 terms contained in the YOS model are identical in the CTM model, if one excludes the pre-factor 2 in $2\left( {\partial u_{i} /\partial x_{i} } \right)^{2} , i = j$. Once the gradient products of mixed type in the YOS model are ignored, the CTM model provides an opportunity to come up with an estimated model coefficient for $C_{I}$ in the range of $C_{I} = (1/48) - (1/24)$ depending on the weight given to $\left( {\partial u_{i} /\partial x_{j} } \right)^{2} , i \ne j$ and to $2\left( {\partial u_{i} /\partial x_{i} } \right)^{2} , i = j$. According to the realizability analysis $C_{I} \ge \frac{1}{2}\sqrt 3 { }C_{s}^{2}$ in order to ensure that the sub-grid kinetic energy remains positive (Klein et al. 2017). Using the theoretical, isotropic turbulence value for the Smagorinsky constant $C_{s} = 0.18$ yields $C_{I} \ge 0.0281$. Thus, realizability is fulfilled for $C_{I} = \frac{1}{24} = 0.0417.$

The anisotropy tensor in the context of LES stresses can be quantified as $b_{ij} = \tau_{ij}^{SGS} /\overline{\rho }k^{gsgs} - 2/3\delta_{ij}$ where $k^{gsgs} = \tau_{kk}^{SGS} /2\overline{\rho }$ is the sub-grid kinetic energy. The properties of the isotropy tensor can be illustrated using the Lumley triangle (Durbin and Pettersson-Reif 2001) in Fig. 40. The boundaries of the triangle can be described in terms of the invariants $II_{b} = - b_{kk}^{2} /2$ and $III_{b} = - b_{kk}^{3} /3$ and are given by the expressions $III_{b} = \pm 2\left( {\left| {II_{b} } \right|/3} \right)^{3/2}$ where the positive branch corresponds to axisymmetric expansion and the negative part describes axisymmetric contraction. Finally, the two-component state is given by $III_{b} = - 2/3II_{b} - 8/27$. If a coordinate system is chosen such that the anisotropy tensor is diagonal, the axisymmetric expansion is given by two equal components of the stress tensor with $b_{22} = b_{33} < 0$. In a trace free condition, this implies that $b_{11} > 0$. Further it follows $\tau_{22} ,\tau_{33} < 2/3\overline{\rho }k^{gsgs}$ and $\tau_{11} > 2/3\overline{\rho }k^{gsgs}$.

Fig. 40

Lumley triangle for cases AL,BL,DL,BR for ${\Delta } = 2.8\delta_{th}$. Every red dot represents an average conditional on  $\tilde{c}.$ The points for $\tilde{c} = 0$ and $\tilde{c} = 1$ are shown in green and blue respectively

For the purpose of the presentation of the data, the anisotropy tensor has first been averaged conditional on $\tilde{c}$ and then the corresponding invariants have been calculated and plotted in the triangle in Fig. 40. Each realisation in the space of $\tilde{c}$ is shown as a red dot in Fig. 40, whereas $\tilde{c} = 0$ and $\tilde{c} = 1$ are shown in green and blue colours respectively. In Fig. 40, only cases AL, BL, DL and BR are shown because cases CL and EL behave qualitatively similarly to cases DL and BR where the flow, at least in an average sense, shows some resemblance to isotropic behaviour. The cases with $Le \ll 1$ (e.g. cases AL and BL) exhibit strong anisotropy due to high values of dilatation rate. However, in case BL (i.e. $Le = 0.6$), the completely burned and unburned states are in isotropic condition but the points corresponding to the flame brush $0 < \tilde{c} < 1$ are not. However, in case AL (i.e. $Le = 0.34)$. the burned gas side does not exhibit an isotropic state due to temperature inhomogeneities giving rise to ongoing dilatation effects (interested readers are referred to temperature field for this case in Chakraborty and Cant (2009a)). It can be seen from Fig. 40 that eddy viscosity type models are expected to fail within the flame brush in cases AL and BL. It is worth noting that the observed isotropy in the other cases is most likely an artefact of the initial isotropic state of turbulence, but this may not be the case for flame configurations where the turbulence is significantly anisoopic (e.g. flame-wall interaction) and have considerable amount of shear rate in some preferential directions.

It has already been demonstrated that dilatational effects constitute an important contribution to the isotropic part of the sub-grid stresses in turbulent premixed flames (see Figs. 37, 38 and 39). Moreover, $k^{gsgs} { }$ is often required as a sub-model for parametrizing e.g. the SGS effects of turbulence-chemistry interaction. The correlation coefficients between the predictions of YOS, CTM and DSS models and the value of $\tau_{kk}^{SGS}$ obtained from explicitly filtered DNS data increase with diminishing heat release effects (i.e. with increasing Karlovitz number or with increasing $Le$) and further discussion can be found in Klein et al. (2017). The optimum multiplier of the CTM, DSS and YOS models increases with increasing $\Delta$, and this behaviour becomes more pronounced with increasing $Ka$ and $Le$.

It is possible write the CTM model alternatively in the following manner (Klein et al. 2017):

$$ \tau_{kk}^{CTM} = \overline{\rho }\frac{{{\Delta }^{2} }}{24}\left( {\frac{{\partial^{2} \widetilde{{u_{k} }}^{2} }}{{\partial x_{i}^{2} }} - 2\widetilde{{u_{k} }}\frac{{\partial^{2} \widetilde{{u_{k} }}}}{{\partial x_{i}^{2} }}} \right) $$

(44)

Mathematically Eqs. 42 and 44 are equivalent to each other. However, Eq. 44 provides better performance than Eq. 42 when they are translated to finite difference approximations. In Eq. 44, the product of two first order central difference approximations is replaced by a Laplacian. The 2nd-order central differencing scheme has a modified wavenumber of $k^{mod} = \sin \left( {k{\Delta }x} \right)/{\Delta }x$. Hence, the product of two first-order derivatives results in a modified squared wavenumber of $\left( {k^{mod} } \right)^{2} = \left( {\sin \left( {k{\Delta }x} \right)/{\Delta }x} \right)^{2}$, this expression goes to zero very quickly for the highest wavenumbers. In contrast, the modified wavenumber for the 2nd order second derivative (i.e. the Laplacian) has the form $k^{mod} = 4 \sin^{2} \left( {k{\Delta }x/2} \right)/{\Delta }x^{2}$ which does not approach zero even for the highest wavenumbers (Klein et al. 2017). Thus, Eq. 44 expression is preferred over Eq. 42 (Klein et al. 2017).

Colin et al. (2000) proposed a model where the dilatational effects are removed by applying the rotational operator, but this model has been found to be not well-suited when the dilatation effects are strong, e.g. in case AL for small values of $Le$ (Klein et al. 2017). The correlation coefficients for this model were smaller in the order of 0.1 compared to those of the CTM model in the $Le \approx 1.0$ cases. Another option is to approximate $u_{{\Delta }}^{{\prime}}$ as $\parallel {\overline{\varvec{u}}} - {\overline{{\overline{\varvec{u}}}}}\parallel$, which yields smaller correlation coefficients than those obtained for the CTM model. The usage of Favre Filtering, i.e. $\left\| {\tilde{\varvec{u}} - \tilde{\tilde{\varvec{u}}}} \right\|$ improves the performance for the cases where dilatation effects are strong (e.g. case AL). The importance of incorporation of dilatation rate on sub-grid stress and sub-grid kinetic energy was also recognised and demonstrated by Langella et al. (2018), who also argued that the momentum dissipation rate can potentially play a key role in the closure of sub-grid stresses. Thus, the heat release effects on enstrophy and sub-grid turbulent kinetic energy generation mechanisms are expected to play key roles in turbulent premixed flames.

The thermal expansion due to chemical heat release plays a key role in the relative alignments between the sub-grid stress tensor $\tau_{ij}^{SGS}$ and the resolved strain rate $\widetilde{{S_{ij} }} = \left( {\partial \widetilde{{u_{i} }}/\partial x_{j} + \partial \widetilde{{u_{j} }}/\partial x_{i} } \right)/2$, which has implications on the sub-grid kinetic energy generation term (i.e. ${\Gamma =-\tau }_{ij}^{SGS}\stackrel{\sim }{{S}_{ij}}$) in the transport equation of ${\stackrel{\sim }{k}}^{SGS}=(\overline{\rho {u}_{i}{u}_{i}}-\stackrel{-}{\rho }{\stackrel{\sim }{u}}_{i}{\stackrel{\sim }{u}}_{i})/2\stackrel{-}{\rho }$ (Ahmed et al. 2019a). Both $\stackrel{-}{\rho }{\sigma }_{ij}=(\overline{\rho {u}_{i}{u}_{i}}-\stackrel{-}{\rho }{\stackrel{\sim }{u}}_{i}{\stackrel{\sim }{u}}_{i})$ and $\stackrel{\sim }{{S}_{ij}}$ are symmetric tensors and they can be decomposed into basis eigenvectors in the following manner (Ahmed et al. 2019a):

$$ \widetilde{{S_{ij} }} = \alpha_{s} {\varvec{\alpha}}_{{\varvec{s}}} {\varvec{\alpha}}_{{\varvec{s}}}^{{\varvec{T}}} + \beta_{s} {\varvec{\beta}}_{{\varvec{s}}} {\varvec{\beta}}_{{\varvec{s}}}^{{\varvec{T}}} + \gamma_{s} {\varvec{\gamma}}_{{\varvec{s}}} {\varvec{\gamma}}_{{\varvec{s}}}^{{\varvec{T}}} $$

(45i)

$$ - \sigma_{ij} = \alpha_{ - \tau } {\varvec{\alpha}}_{{ - {\varvec{\tau}}}} {\varvec{\alpha}}_{{ - {\varvec{\tau}}}}^{{\varvec{T}}} + \beta_{ - \tau } {\varvec{\beta}}_{{ - {\varvec{\tau}}}} {\varvec{\beta}}_{{ - {\varvec{\tau}}}}^{{\varvec{T}}} + \gamma_{ - \tau } {\varvec{\gamma}}_{{ - {\varvec{\tau}}}} {\varvec{\gamma}}_{{ - {\varvec{\tau}}}}^{{\varvec{T}}} $$

(45ii)

where $\alpha ,\beta$ and $\gamma$ are the eigenvalues, and $\boldsymbol{\alpha },{\varvec{\beta}}$ and ${\varvec{\gamma}}$ are the corresponding eigenvectors; the subscripts s and $(-\tau )$ represent the eigenvalues and eigenvectors of the resolved strain rate and the negative of the SGS stress tensors, respectively, and the transposed vector is represented by the superscript ‘T’. The eigenvalues $\alpha ,\beta$ and $\gamma$ are taken to be the most extensive, intermediate and the most compressive principal strain rates, respectively, and accordingly $\boldsymbol{\alpha },{\varvec{\beta}}$ and ${\varvec{\gamma}}$ are referred to the most extensive, intermediate and the most compressive eigenvectors, respectively. Using Eq. 45, the sub-grid turbulent kinetic energy generation or resolved kinetic energy dissipation $\Gamma$ can expressed as (Ahmed et al. 2019a):

$$\begin{aligned}\Gamma &={{\alpha }_{-\tau }\alpha }_{s}{\left({{\boldsymbol{\alpha}}_{-{\varvec{\tau}}}\cdot \boldsymbol{\alpha}}_{{\varvec{s}}}\right)}^{2}+{{\alpha }_{-\tau }\beta}_{s}{\left({{\boldsymbol{\alpha}}_{-{\varvec{\tau}}}\cdot{\varvec{\beta}}}_{{\varvec{s}}}\right)}^{2}+{{\alpha}_{-\tau }\gamma }_{s}{\left({{\boldsymbol{\alpha}}_{-{\varvec{\tau}}}\cdot{\varvec{\gamma}}}_{{\varvec{s}}}\right)}^{2}\\ &\quad +{{\beta }_{-\tau }\alpha}_{s}{\left({{{\varvec{\beta}}}_{-{\varvec{\tau}}}\cdot\boldsymbol{\alpha }}_{{\varvec{s}}}\right)}^{2}+{{\beta }_{-\tau}\beta}_{s}{\left({{{\varvec{\beta}}}_{-{\varvec{\tau}}}\cdot{\varvec{\beta}}}_{{\varvec{s}}}\right)}^{2}\\ &\quad +{{\beta }_{-\tau }\gamma}_{s}{\left({{{\varvec{\beta}}}_{-{\varvec{\tau}}}\cdot{\varvec{\gamma}}}_{{\varvec{s}}}\right)}^{2}+{{\gamma}_{-\tau }\alpha}_{s}{\left({{{\varvec{\gamma}}}_{-{\varvec{\tau}}}\cdot\boldsymbol{\alpha }}_{{\varvec{s}}}\right)}^{2}+{{\gamma }_{-\tau}\beta}_{s}{\left({{{\varvec{\gamma}}}_{-{\varvec{\tau}}}\cdot{\varvec{\beta}}}_{{\varvec{s}}}\right)}^{2}\\ &\quad+{{\gamma}_{-\tau}\gamma}_{s}{\left({{{\varvec{\gamma}}}_{-{\varvec{\tau}}}\cdot{\varvec{\gamma}}}_{{\varvec{s}}}\right)}^{2} \end{aligned}$$

(46)

where $\left( {{\varvec{a}} \cdot {\varvec{b}}} \right) = \cos \theta$ with $\theta$ being the angle between vectors ${\varvec{a}}$ and ${\varvec{b}}$. Thus, the alignment between $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ is expected to play an important role in determining the statistical behaviour of ${\Gamma }$.

It has been found that $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ are not collinearly aligned with each other for non-reacting flows (Horiuti 2003; Kang and Meneveau 2005). The relative alignment between $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ are shown in Figs. 41 and 42 for ${\Delta } = 1.4D_{th,0} /S_{L}$ for statistically planar flames subjected to forced unburned gas turbulence with $u^{\prime}/S_{L} = 1.0$ and 10.0, respectively. Further information on these two DNS cases can be found elsewhere (Ahmed et al. 2019a, 2019b; Brearley et al. 2019, 2020) and thus are not repeated here. The relative alignment between $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ for these cases is shown in Figs. 43 and 44 for ${\Delta } = 3.5D_{th} /S_{L}$, respectively. Figure 41 shows that the eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ are collinearly aligned with each other for $\tilde{c} = 0.1, 0.7$ and 0.9 isosurfaces but the same behaviour has been observed throughout the flame brush. This behaviour is contrary to the previous findings in the context of non-reacting turbulent flows (Horiuti 2003; Kang and Meneveau 2005). The perfect alignment of the eigenvectors for the tensors $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ occurs due to relatively strong effects of strain rate arising from flame normal acceleration, which dominates over turbulent straining causing the sub-grid stresses to align perfectly with the resolved strain rate. It will be discussed later in this paper that the domination of strain rate due to flame normal acceleration over turbulent straining takes place for high values of heat release parameter $\tau$ and Damkohler number $Da$ and/or small values of Karlovitz number $Ka$. The alignment of the two eigensystems changes at the trailing edge of the flame brush (e.g. $\tilde{c} = 0.9$) in the $u^{\prime}/S_{L} = 1.0$ case where ${\varvec{\alpha}}_{{\varvec{s}}}$ remains aligned with ${\varvec{\alpha}}_{{ - {\varvec{\tau}}}}$ but ${\varvec{\beta}}_{{\varvec{s}}}$ and ${\varvec{\gamma}}_{{\varvec{s}}}$ align with ${\varvec{\gamma}}_{{ - {\varvec{\tau}}}}$ and ${\varvec{\beta}}_{{ - {\varvec{\tau}}}}$, respectively (see Fig. 40). In the case of high turbulence intensity (e.g. $u^{\prime}/S_{L} = 10.0$), the most extensive and compressive eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ are found to be approximately $45^{{\circ}}$ with each other and the intermediate eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ exhibit high probabilities of collinear alignment at the leading edge of the flame brush (e.g. $\tilde{c} = 0.1$). However, in the region of heat release (e.g. $\tilde{c} = 0.7$) ${\varvec{\alpha}}_{{\varvec{s}}}$ and ${\varvec{\gamma}}_{{\varvec{s}}}$ exhibit collinear alignments with ${\varvec{\alpha}}_{{ - {\varvec{\tau}}}}$ and ${\varvec{\gamma}}_{{ - {\varvec{\tau}}}}$, respectively. The change in alignment statistics in the $u^{\prime}/S_{L} = 10.0$ case in comparison to the $u^{\prime}/S_{L} = 1.0$ case occurs due to the fact that energetic turbulent eddies can enter into the flame structure in the $u^{\prime}/S_{L} = 10.0$ case owing to $Ka > 1$, whereas in the $u^{\prime}/S_{L} = 1.0$ case the flame structure remains unaffected by turbulent fluid motion as a result of $Ka < 1$. The perfect collinear alignment between the eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ is not maintained on the burned gas side of the flame brush (e.g. $\tilde{c} = 0.9$) where the effects of heat release and turbulence are weak, and in both $u^{\prime}/S_{L} = 1.0$ and 10.0 cases ${\varvec{\beta}}_{{\varvec{s}}}$ aligns with ${\varvec{\gamma}}_{{ - {\varvec{\tau}}}}$, which is contrary to the findings obtained for non-reacting flows (Horiuti 2003; Kang and Meneveau 2005). This implies that the relative alignment between the two eigensystems is likely to be affected by the increase in kinematic viscosity and decay of turbulence in the burned gas region.

Fig. 41

PDFs of the magnitudes of the direction cosines between the eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ at different iso-surfaces of $\tilde{c}$ for a statistically stationary planar flame case subjected to forced unburned gas turbulence corresponding to $u^{\prime}/S_{L} = 1.0$, $l/\delta_{th} = 3.0$ (i.e. $Da = lS_{L} /u^{\prime}\delta_{th} = 3.0$ and $Ka^{\prime} = ({u^{\prime}/{S_{L}}})^{1.5} (l/{\delta_{th}})^{ - 0.5} = 0.577$ at ${\Delta } = 1.4D_{th,0} /S_{L}$

Fig. 42

PDFs of the magnitudes of the direction cosines between the eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ at different iso-surfaces of $\tilde{c}$ for a statistically stationary planar flame case subjected to forced unburned gas turbulence corresponding to $u^{\prime}/S_{L} = 10.0$, $l/\delta_{th} = 3.0$ (i.e. $Da = lS_{L} /u^{\prime}\delta_{th} = 0.3$ and $Ka^{\prime} = ({u^{\prime}/{S_{L}} })^{1.5} (l/{\delta_{th}} )^{ - 0.5} = 18.26$ at ${\Delta } = 1.4D_{th,0} /S_{L}$

Fig. 43

PDFs of the magnitudes of the direction cosines between the eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ at different iso-surfaces of $\tilde{c}$ for a statistically stationary planar flame case subjected to forced unburned gas turbulence corresponding to $u^{\prime}/S_{L} = 1.0$, $l/{\delta_{th}} = 3.0$ (i.e. $Da = lS_{L} /u^{\prime}\delta_{th} = 3.0$ and $Ka^{\prime} = ({u^{\prime}/{S_{L}}})^{1.5} (l/{\delta_{th}})^{ - 0.5} = 0.577$ at ${\Delta } = 3.5D_{th,0} /S_{L}$

Fig. 44

PDFs of the magnitudes of the direction cosines between the eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ at different iso-surfaces of $\tilde{c}$ for a statistically stationary planar flame case subjected to forced unburned gas turbulence corresponding to $u^{\prime}/S_{L} = 10.0$, $l/\delta_{th} = 3.0$ (i.e. $Da = lS_{L} /u^{\prime}\delta_{th} = 0.3$ and $Ka^{\prime} = \left( {u^{\prime}/S_{L} } \right)^{1.5} (l/\delta_{th} )^{ - 0.5} = 18.26$ at ${\Delta } = 3.5D_{th,0} /S_{L}$

A comparison between Figs. 41, 42 with 43, 44 reveals that the qualitative nature of the alignment trends of the two eigensystems are affected for $Ka > 1$ cases with the change in $\Delta$, especially in the regions of heat release (e.g. $\tilde{c} = 0.7$), while the alignment trends for $Ka < 1$ flames do not change with filter width (Ahmed et al. 2019a). This further indicates that the alignment of sub-grid stresses with the resolved strain rate in LES of premixed turbulent combustion is affected by heat release and can be dependent on the regime of combustion. Moreover, the qualitative nature of the relative alignments of eigenvectors of $\left( { - \sigma_{ij} } \right)$ and $\widetilde{{S_{ij} }}$ may depend on $Da$ and $Ka$ of the underlying combustion processes. This further implies that combustion and turbulence modelling in premixed turbulent combustion cannot be considered to be independent of each other, which has been demonstrated from the point of view of structure function (Brearley et al. 2020) and displacement speed of iso-enstrophy surface statistics (Chakraborty et al. 2020) in recent studies. The effects of heat release also affect the alignment of vorticity and reactive scalar gradient with local principal strain rates which will be discussed next in this paper along with their modelling implications.

5 Effects of Heat Release on Alignment of Vorticity and Reactive Scalar Gradient with Local Principal Strain Rate Eigenvectors

In order to demonstrate the effects of heat release on the relative alignments between vorticity and local principal strain rate eigenvectors, it is worthwhile to reconsider the expression of the vortex-stretching term $T_{I}$ given by Eq. 5. The PDFs of $\left| {\cos \chi_{\alpha } \left| , \right|cos \chi_{\beta } } \right|$ and $\left| {\cos \chi_{\gamma } } \right|$ for $c = 0.1 - 0.9$ (in steps of 0.2) isosurfaces for cases AR, BR, AL, BL and DL (behaviour for cases CL and EL are similar to case DL and therefore are not explicitly presented here) are shown in Figs. 45, 46 and 47, respectively. It can be seen from Figs. 45, 46 and 47 that vorticity aligns predominantly with the eigenvector associated with the intermediate principal strain rate $e_{\beta }$ towards the unburned gas side of the flame (e.g. $c = 0.1$), which is qualitatively similar to the corresponding alignment statistics for turbulent non-reacting flows (Ashurst et al. 1987b; Majda 1991; Jimenez 1992; Tsinober et al. 1992; Zeff et al. 2003; Lüthi et al. 2005; Hamlington et al. 2008; Xu et al. 2011) and non-premixed flames (Nomura and Elghobashi 1993; Boratov et al. 1996; Jaberi et al. 2000). This behaviour does not change with the variation of $\tau , Le$ and the combustion regime. It is important to note from Figs. 45, 46 and 47 that the relative alignment of $\vec{\omega }$ with the eigenvectors corresponding to $e_{\alpha }$ and $e_{\gamma }$ changes with $\tau , Le$ and the regime of combustion. In cases AR and AL, vorticity $\vec{\omega }$ exhibits a significant extent of alignment with the eigenvector associated with the most compressive principal strain rate $e_{\gamma }$ for the major part of the flame, except for the unburned gas side, and this tendency increases towards the heat releasing zone of the flame (i.e. $0.7 \le c \le 0.9$). The vorticity vector does not align with the eigendirection corresponding to the most extensive principal strain rate $e_{\alpha }$ throughout the flame in cases AR and AL. This alignment of $\vec{\omega }$ with $e_{\gamma }$ is contrary to the findings for non-reacting flows (Ashurst et al. 1987b; Majda 1991; Jimenez 1992; Tsinober et al. 1992; Zeff et al. 2003; Lüthi et al. 2005; Hamlington et al. 2008; Xu et al. 2011). For the thin reaction zones regime flames with $Le \approx 1.0$ (e.g. cases BR, CL-EL) $\vec{\omega }$ aligns with the eigenvector associated with $e_{\beta }$ throughout the flame but an increase in the extent of the alignment with $e_{\alpha }$ is obtained in the region of the flame where the effects of heat release are strong (e.g. $0.7 \le c \le 0.9$). This tendency strengthens with increasing $\tau$ (see cases BR and DL) and with decreasing $Le$ (see cases AL, BL and DL). It was also demonstrated in Chakraborty (2014) that the extent of alignment of $\vec{\omega }$ with $e_{\alpha }$ in the region of heat release for the thin reaction zones regime flames weakens with increasing $Ka$. It was demonstrated by Jimenez (1992) that vorticity tubes with high enstrophy induce velocity field in such a manner that the most extensive and compressive principal strain rates occur on the planes orthogonal to the plane in which these vortex tubes are placed according to Biot-Savart’s law. As a result of this, high vorticity regions are preferentially aligned with the intermediate principal strain rate $e_{\beta }$ in non-reacting turbulent flows. This behaviour has been observed in all cases in both unburned and burned gas sides of the flame where the effects of heat release are weak. However, in case BR, premixed combustion takes place in the thin reaction zones regime for small values of $\tau$, and therefore in this case vorticity alignment with local principal strain rates resembles the corresponding behaviour of non-reacting flows. It was demonstrated recently in a number of studies (Leung et al. 2012; Doan et al. 2017; Ahmed et al. 2018) that vorticity aligns preferentially with the most extensive principal strain rate for both non-reacting flows and premixed turbulent flames when the self-induced vorticity by the vortex tube is excluded (i.e. only the non-local effects are considered).

Fig. 45

PDFs of the magnitude of the cosine of the angle between $\vec{\omega }$ and the most extensive principal strain rate direction $|{\text{cos}}\chi_{\alpha } |$ for the $c = 0.1,\ 0.3,\ 0.5,\ 0.7$ and $0.9$ isosurfaces for cases a AR, b BR, c AL, d BL, e DL (i.e. $Le = 0.34,\ 0.60,\ 1.0$ and 1.2)

Fig. 46

PDFs of the magnitude of the cosine of the angle between $\vec{\omega }$ and the intermediate principal strain rate direction $|{\text{cos}}\chi_{\beta } |$ for the $c = 0.1,\ 0.3,\ 0.5,\ 0.7$ and $0.9$ isosurfaces for cases a AR, b BR, c AL, d BL, e DL (i.e. $Le = 0.34,\ 0.60$ and 1.0)

Fig. 47

PDFs of the magnitude of the cosine of the angle between $\vec{\omega }$ and the most compressive principal strain rate direction $|{\text{cos}}\chi_{\gamma } |$ for the $c = 0.1,\ 0.3,\ 0.5,\ 0.7$ and $0.9$ isosurfaces for cases a AR, b BR, c–g AL-EL (i.e. $Le = 0.34,\ 0.6,\ 0.8,\ 1.0$ and 1.2)

The change in $\vec{\omega }$ alignment with $e_{\alpha }$ and $e_{\gamma }$ with variations of $\tau , Le$ and the regime of combustion can be explained in the following manner. The net contribution of vortex stretching and dilatation terms (i.e. $\vec{\omega } \cdot \nabla \vec{u} - \vec{\omega }\nabla .\vec{u}$) has the following components $\left| {\vec{\omega }} \right|\left( {e_{\alpha } - \nabla .\vec{u}} \right)\cos \chi_{\alpha }$, $\left| {\vec{\omega }} \right|\left( {e_{\beta } - \nabla .\vec{u}} \right)\cos \chi_{\beta }$ and $\left| {\vec{\omega }} \right|\left( {e_{\gamma } - \nabla .\vec{u}} \right)\cos \chi_{\gamma }$ in the eigendirections corresponding to $e_{\alpha } , e_{\beta }$ and $e_{\gamma }$ respectively. As $e_{\beta } < \nabla .\vec{u}$ in most locations and $e_{\gamma }$ is predominantly negative, the net contribution of vortex stretching and dilatation terms (i.e. $\vec{\omega } \cdot \nabla \vec{u} - \vec{\omega }\nabla .\vec{u}$) acts to generate vorticity only in the eigendirection corresponding to $e_{\alpha }$ where $e_{\alpha } > \nabla .\vec{u}$. This behaviour is responsible for increased alignment of $\vec{\omega }$ with the eigendirection corresponding to $e_{\alpha }$ in the region where heat release effects are significant (where $e_{\alpha } > \nabla .\vec{u}$) in case DL (also in cases CL, EL, BR and CR). In cases AR and AL (and also to a smaller extent in case BL) the dilatation rate $\nabla .\vec{u}$ is primarily determined by $e_{\alpha }$ and these flames show high probability of obtaining $e_{\alpha } \approx \nabla .\vec{u}$, which leads to negligible magnitude of the net contribution of vortex-stretching and dilatation contributions (i.e. $\vec{t}_{1} + \vec{t}_{3}$) in the eigendirection corresponding to $e_{\alpha }$. It is also necessary to consider the directional properties of baroclinic torque $\left( {\nabla \rho \times \nabla p} \right)/\rho^{2}$ to fully explain the alignment of vorticity with local principal strain rate eigendirections. For low Mach number, adiabatic, unity Lewis number conditions, $\rho$ can be expressed as $\rho = \rho_{0} /\left( {1 + \tau c} \right)$ (Bray et al. 1985), which leads to $\nabla \rho = - \tau \rho^{2} \nabla c/\rho_{0} = \tau \rho^{2} \vec{N}\left| {\nabla c} \right|/\rho_{0}$ (Chakraborty et al. 2016; Chakraborty 2014; Bray et al. 1985). Although the equality between $\nabla \rho$ and $\tau \rho^{2} \vec{N}\left| {\nabla c} \right|/\rho_{0}$ does not hold for non-unity Lewis number flames, the relation $\nabla \rho \sim \tau \rho^{2} \vec{N}\left| {\nabla c} \right|/\rho_{0}$ can still be used in a scaling sense. This implies that the baroclinic torque $\left( {\nabla \rho \times \nabla p} \right)/\rho^{2} \sim \tau \vec{N}\left| {\nabla c} \right| \times \nabla p/\rho_{0}$ cannot have any component in the direction of flame normal vector $\vec{N}$ or in the reaction progress variable gradient $\nabla c$ direction. Thus, it is necessary to consider the alignment of $\nabla c$ with local principal strain rate eigendirections.

The PDFs of the magnitudes of the cosines between $\nabla c$ and local principal directions corresponding to the most extensive (i.e. most positive) and most compressive (i.e. most negative) principal strain rates (i.e. $e_{\alpha }$ and $e_{\gamma }$ strain rates, respectively) for cases AR and BR are shown in Fig. 48. It can be seen from Fig. 48 that $\nabla c$ shows preferential collinear alignment between $\nabla c$ and the eigenvector associated with the most extensive principal strain rate throughout the flame in case AR, which is reflected in the high probability of finding ${\Psi }_{\alpha } = |\cos \theta_{\alpha } | \approx 1.0$ and ${\Psi }_{\gamma } = |\cos \theta_{\gamma } | \approx 0.0$ where $\theta_{\alpha }$ and $\theta_{\gamma }$ are the angle between $\nabla c$ and the eigenvectors associated with $e_{\alpha }$ and $e_{\gamma }$, respectively. This behaviour is in contrast to the conventional knowledge in the context of passive scalar mixing (Batchelor 1952, 1959; Gibson 1968; Clay 1973; Kerr 1985; Ruetsch and Maxey 1991; Nomura and Elghobashi 1992; Ashurst et al. 1987a, b; Leonard and Hill 1991; Malkeson and Chakraborty 2011) where scalar gradient aligns collinearly with the most compressive principal strain rate eigendirection. It can further be seen from Fig. 48 that $\nabla c$ preferentially aligns with the eigenvector associated with the most compressive principal strain rate towards the unburned and burned gas side of the flame front similar to passive scalar mixing, which is reflected in the high probability of finding $|\cos \theta_{\alpha } | \approx 0.0$ and $|\cos \theta_{\gamma } | \approx 1.0$ for $c = 0.1$ and 0.9 isosurfaces in case BR. However, in case BR, $\nabla c$ aligns preferentially with the eigenvector associated with the most extensive principal strain rate in the region of the flame front where the effects of heat release are strong, which is reflected in the high probability of finding $|{\text{cos }}\theta_{\alpha } | \approx 1.0$ and $|\cos \theta_{\gamma } | \approx 0.0$ in this case for $c = 0.5$ and 0.7 isosurfaces. It has already been demonstrated in Fig. 16 that the flame generated turbulence effects are relatively stronger in case AR than in case BR and $u^{\prime}/S_{L}$ and $L_{11} /\delta_{th}$ values in Table 5 suggest that case AR is representative of high Damköhler number (i.e. $Da > 1$) combustion for small values of Karlovitz number (i.e. $Ka < 1$), whereas Damköhler number is low (i.e. $Da < 1$) and Karlovitz number (i.e. $Ka > 1$) is high in cases BR and CR. It has already been demonstrated in the foregoing discussion that $Le$ (see Table 3 and Figs. 12, 20 and 22) affects the turbulence evolution within the flame and the effects of heat release strengthen with decreasing $Le.$ Therefore, the PDFs of $|\cos \theta_{\alpha } |$ and $|\cos \theta_{\gamma } |$ for cases AL, CL, DL,EL are shown in Figs. 49 and 50, respectively. It is worth noting that the attributes of case DL are identical to case CR. It can be seen from Figs. 49 and 50 that $\nabla c$ in case AL aligns preferentially collinearly with the eigenvector associated with $e_{\alpha }$ for the major part of the flame front, and only towards the leading edge of the flame front $\nabla c$ aligns with the eigenvector associated with the most compressive principal strain rate $e_{\gamma }$ similar to passive scalar mixing under non-reacting turbulence. Figures 49 and 50 indicate that the extent of collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\alpha }$ ($e_{\gamma }$) decreases (increases) with increasing characteristic Lewis number $Le$. The alignment of $\nabla c$ with local principal strain rate eigendirections in cases CL-EL is qualitatively similar to that shown for case BR and the trend for case BL is somewhat between cases AL and CL. However, a comparison between cases BR and DL reveals that the extent of collinear alignment with the eigenvector associated with $e_{\alpha }$ in the heat releasing zone (i.e. $0.5 \le c \le 0.7$) is stronger in case DL ($\tau = 4.5$) than in case BR ($\tau = 3.0$).

Fig. 48

PDFs of the magnitude of the cosine between the scalar gradient alignment and the eigenvector associated with the most extensive principal $e_{\alpha }$ strain rate ${\Psi }_{\alpha } = |\cos \theta_{\alpha } |$ (a and b) and the most compressive principal $e_{\gamma }$ strain rate ${\Psi }_{\gamma } = |\cos \theta_{\gamma } |$ (c and d) in case AR (a and c) and in case BR (b and d)

Fig. 49

PDFs of ${\Psi }_{\gamma }=|\mathrm{cos}{\theta }_{\gamma }|$ between the most compressive principal strain rate and scalar gradient for five c iso-surfaces for (a–d) cases AL, CL, DL, EL (i.e. $Le=\mathrm{0.34,0.8}, 1.0$ and 1.2)

Fig. 50

PDFs of ${\Psi }_{\gamma } = |\cos \theta_{\gamma } |$ between the most compressive principal strain rate and scalar gradient for five c iso-surfaces for (a–d) cases AL, CL, DL, EL (i.e. $Le = 0.34,\,0.8,\, 1.0$ and 1.2)

The differences in the alignment statistics of $\nabla c$ in response to the variations of $Da, Ka$ and $Le$ can be explained based on the competition between the strain rate $a_{chem}$ induced by flame normal acceleration and turbulent flow straining $a_{turb}$. It was demonstrated elsewhere (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009) that $\nabla c$ preferentially aligns with the eigenvector associated with $e_{\alpha }$ when $a_{chem}$ dominates over $a_{turb}$. By contrast, $\nabla c$ preferentially aligns with the eigenvector associated with $e_{\gamma }$ when $a_{turb}$ dominates over $a_{chem}$. The strain rate induced by flame normal acceleration $a_{chem}$ can be quantified by the component of the slip velocity arising from chemical heat release (i.e. $f \left( {Le} \right)\tau S_{L}$ see Eq. 22ii) and the flame thickness, which leads to $a_{chem} \sim f_{1} \left( {Le} \right)\tau S_{L} /\delta_{th}$ with $f_{1} \left( {Le} \right)$ being a function which increases with decreasing $Le$ (Chakraborty et al. 2009). Here, $f_{1} \left( {Le} \right)\tau S_{L}$ quantifies the velocity jump across the flame (i.e. over a distance of flame thickness), which originates from the thermal expansion due to chemical heat release. It has indeed been shown in Fig. 20 that the slip velocity increases with decreasing $Le$, which is accounted for by $f_{1} \left( {Le} \right)$. The turbulent straining can be scaled using Meneveau and Poinsot (1991) as: $a_{turb} \sim u^{\prime}/L_{11}$, which leads to $a_{chem} /a_{turb} \sim f_{1} \left( {Le} \right)\tau Da$. Alternatively, $a_{turb}$ can be scaled using Tennekes and Lumley (1972) as: $a_{turb} \sim u^{\prime}/\lambda$ with $\lambda$ being the Taylor micro-scale, which leads to: $a_{chem} /a_{turb} \sim f_{1} \left( {Le} \right)\tau Da/Re_{t}^{0.5} \sim \tau f_{1} \left( {Le} \right)/Ka$. Combining the trends obtained from these scaling relations, it is possible to summarise $a_{chem} /a_{turb}$ such that $a_{chem} /a_{turb} \sim f_{2} \left( {Le,Ka} \right)\tau Da$ with $f_{2} \left( {Le,Ka} \right)$ being a function, which decreases with increasing $Ka$ and $Le$. This suggests that $a_{chem}$ dominates over $a_{turb}$ for large values of $\tau$ and $Da$, and small values of $Le$ and $Ka$. By contrast, $a_{turb}$ dominates over $a_{chem}$ for small values of $\tau$ and $Da$, and high values of $Le$ and $Ka$. From the foregoing, it becomes clear that $\nabla c$ or $\vec{N}$ aligns either with the most extensive or most compressive principal strain rate eigendirection depending on the relative strengths of $a_{chem}$ and $a_{turb}$. As eigendirections are mutually orthogonal to each other, and $\vec{\omega }$ predominantly aligns with the eigendirection corresponding to $e_{\beta }$, it needs to be appreciated that $\vec{\omega}$ and baroclinic torque $\left( {\nabla \rho \times \nabla p} \right)/\rho^{2} \sim \tau \vec{N}\left| {\nabla c} \right| \times \nabla p/\rho_{0}$ are unlikely to have any component in the direction of the flame normal vector. This further illustrates that baroclinic torque does not have any component in cases AR and AL in the eigendirection corresponding to $e_{\alpha }$ but is expected to have significant contributions in the directions of $e_{\beta }$ and $e_{\gamma }$ in cases AR, AL and BL. Thus, the effects of the baroclinic torque (i.e. $\left( {\nabla \rho \times \nabla p} \right)/\rho^{2}$) remain weak in the eigendirection corresponding to $e_{\alpha }$ in cases AR, AL and BL. This gives rise to weak alignment of vorticity with the eigenvector associated with $e_{\alpha }$ in cases AR, AL and BL where the net contribution of vortex stretching and dilatation terms (i.e. $\vec{\omega } \cdot \nabla \vec{u} - \vec{\omega }\nabla \cdot \vec{u}$) remains negligible due to $\nabla .\vec{u} \approx e_{\alpha }$ (see Fig. 45) but vorticity predominantly aligns with the eigenvectors associated with $e_{\beta }$ and $e_{\gamma }$ (see Figs. 46 and 47). The absence of the collinear alignment of $\vec{\omega }$ with the eigenvetor associated with $e_{\alpha }$ gives rise to a vanishingly small positive contribution arising from $e_{\alpha } \cos^{2} \chi_{\alpha }$ in Eq. 5, whereas a relatively increased extent of collinear alignment of $\vec{\omega }$ with the eigenvetor associated with $e_{\gamma }$ acts to increase the magnitude of the negative contribution of $e_{\alpha } \cos^{2} \chi_{\gamma }$. Thus, the net contribution of the vortex-stretching term $T_{I}$ remains positive but this term does not play a major role in the enstrophy transport in cases DA, AL and BL (see Figs. 9 and 11) and also in case AR (not shown here).

The relative alignment of $\nabla c$ with local principal strain rate eigenvectors has major implications on the reactive scalar gradient magnitude (e.g. $\left| {\nabla c} \right|$) evolution in turbulent premixed flames. The magnitude of the reaction progress gradient $\left| {\nabla c} \right|$ plays a key role in the closure of mean/filtered reaction rate of reaction progress variable $\overline{{\dot{w}}}$, which can be demonstrated as:

$$ \overline{{\dot{w} + \nabla .\left( {\rho D\nabla c} \right)}} = \overline{{\left( {\rho S_{d} } \right)}}_{s} {\Sigma }_{gen} $$

(47)

In Eq. 47, $S_{d}$ is the displacement speed, which is defined as:

$$ S_{d} = \frac{{\left[ {\dot{w} + \nabla .\left( {\rho D\nabla c} \right)} \right]}}{{\rho \left| {\nabla c} \right|}} $$

(48)

In the context of LES, $\overline{{\nabla .\left( {\rho D\nabla c} \right)}}$ may not be negligible in comparison to $\overline{{\dot{w}}}$ depending on the LES filter size. However, for RANS, $\overline{{\dot{w}}} \gg \overline{{\nabla .\left( {\rho D\nabla c} \right)}}$ and thus $\overline{{\nabla .\left( {\rho D\nabla c} \right)}}$ can be ignored. Alternatively, in the context of RANS the mean reaction rate $\overline{{\dot{w}}}$ in the flamelet combustion regime can be modelled in terms of SDR $\tilde{\varepsilon }_{c}$ in the following manner (Chakraborty and Cant 2011; Bray 1980; Chakraborty and Swaminathan 2011):

$$ \overline{{\dot{w}}} = 2\overline{\rho }\tilde{\varepsilon }_{c} /\left( {2c_{m} - 1} \right) $$

(49)

where $c_{m} = \mathop \int \limits_{0}^{1} \left[ {\dot{w}c} \right]_{L} f_{b} \left( c \right)dc/\mathop \int \limits_{0}^{1} \left[ {\dot{w}} \right]_{L} f_{b} \left( c \right)dc$ is a thermo-chemical parameter with $f_{b} \left( c \right)$ as the burning rate PDF (Bray 1980). Any reasonable continuous function should be sufficient for approximating $f_{b} \left( c \right)$ according to Bray (1980). In the context of LES, Eq. 49 can be extended in the following manner (Gao et al. 2014a, b, 2016; Ma et al. 2014a; Butz et al. 2015):

$$ \overline{{\dot{w}}} = \{ 2\overline{\rho }\tilde{N}_{c} /\left( {2c_{m} - 1} \right)\} \times \left\{ {1 - {\text{exp}}\left( { - \phi {\Delta }/\delta_{th} } \right)} \right\} + \phi_{1} \left( {\overline{\rho },\tilde{c},\tilde{T}} \right){\text{exp}}\left( { - \phi {\Delta }/\delta_{th} } \right) $$

(50)

Here $\tilde{N}_{c} = \overline{\rho D\nabla c.\nabla c} /\overline{\rho }$ is the Favre-filtered SDR in the context of LES, ${\Phi }_{1} \left( {\overline{\rho },\tilde{c},\tilde{T}} \right)$ is a function so that $\dot{w} = {\Phi }_{1} \left( {\rho ,c,T} \right)$ where $\psi = 0.56\delta_{th} S_{L} /D_{th,0}$ is a model parameter. The exponential terms ${\text{exp}}\left( { - \psi {\Delta }/\delta_{th} } \right)$ and $\left\{ {1 - {\text{exp}}\left( { - \psi {\Delta }/\delta_{th} } \right)} \right\}$ act as a bridging function such that one obtains $\overline{{\dot{w}}} = \{ 2\overline{\rho }\tilde{N}_{c} /\left( {2c_{m} - 1} \right)\}$ for ${\Delta }/\delta_{th} \gg 1$, and for ${\Delta } \to 0$, Eq. 49 reduces to $\mathop {\lim }\limits_{{{\Delta } \to 0}} \overline{{\dot{w}}} = \dot{w} = \mathop {{\text{lim}}}\limits_{{{\Delta } \to 0}} f_{1} \left( {\overline{\rho },\tilde{c},\tilde{T}} \right) = {\Phi }_{1} \left( {\rho ,c,T} \right)$ (Gao et al. 2014a, b, 2016; Ma et al. 2014a; Butz et al. 2015). It has been demonstrated elsewhere (Gao et al. 2014a; Ma et al. 2014a) that the prediction of Eq. 49 improves with increasing filter width.

The above discussion suggests that the transport characteristics of $\left| {\nabla c} \right|$ and $N_{c} = D\nabla c.\nabla c$ are important from the context of reaction rate closure, and the transport equations of these quantities take the following form for a given $c$ isosurface (Chakraborty and Klein 2008a; Kollmann and Chen 1998; Chakraborty and Cant 2005b; Dopazo et al. 2018; Chakraborty et al. 2008a, 2018b; Sandeep et al. 2018; Klein et al. 2018; Pope 1988; Candel and Poinsot 1990):

$$ \frac{{\partial \left| {\nabla c} \right|}}{\partial t} + \frac{{\partial \left( {u_{j} \left| {\nabla c} \right|{ }} \right)}}{{\partial x_{j} }} = a_{T} \left| {\nabla c} \right| + 2S_{d} \kappa_{m} \left| {\nabla c} \right| - \frac{{\partial \left( {S_{d} N_{j} \left| {\nabla c} \right|{ }} \right)}}{{\partial x_{j} }} $$

(51i)

Or

$$ \frac{{\partial \left| {\nabla c} \right|}}{\partial t} + u_{j} \frac{{\partial \left| {\nabla c} \right|}}{{\partial x_{j} }} = - a_{N} \left| {\nabla c} \right| + 2S_{d} \kappa_{m} \left| {\nabla c} \right| - \frac{{\partial \left( {S_{d} N_{j} \left| {\nabla c} \right|{ }} \right)}}{{\partial x_{j} }} $$

(51ii)

where $a_{T} = \left( {\delta_{ij} - N_{i} N_{j} } \right)\partial u_{i} /\partial x_{j}$ is the tangential strain rate, $a_{N} = N_{i} N_{j} \partial u_{i} /\partial x_{j}$ is the normal strain rate, $\kappa_{m} = 0.5\left( {\partial N_{i} /\partial x_{i} } \right)$ is the local flame curvature where $N_{i} = - \left( {\partial c/\partial x_{i} } \right)/\left| {\nabla c} \right|$ is the ith component of flame normal vector. On Reynolds averaging/LES filtering one obtains (Chakraborty et al. 2018a; Papapostolou et al. 2019; Han and Huh 2008; Chakraborty and Cant 2011; Klein et al. 2018; Pope 1988; Candel and Poinsot 1990):

$$ \begin{aligned} \partial {\Sigma }_{gen} /\partial t + \partial \left( {\tilde{u}_{j} {\Sigma }_{gen} } \right)/\partial x_{j} = & \underbrace {{ - \partial \left\{ {\left[ {\overline{{\left( {u_{k} } \right)_{s} }} - \tilde{u}_{k} } \right]{\Sigma }_{gen} } \right\}/\partial x_{k} }}_{{T_{{1{\text{F}}}} - turbulent\,transport}} \\ &\quad + \underbrace {{\overline{{\left( {\left( {\delta_{ij} - N_{i} N_{j} } \right)\partial u_{i} /\partial x_{j} } \right)_{s} }} {\Sigma }_{gen} }}_{{T_{{2{\text{F}}}} - strain rate}}\underbrace {{ - \partial \left[ {\overline{{\left( {S_{d} N_{k} } \right)_{s} }} {\Sigma }_{gen} } \right]/\partial x_{k} }}_{{T_{{3{\text{F}}}} - propagation}} + \underbrace {{\overline{{\left( {S_{d} \partial N_{i} /\partial x_{i} } \right)_{s} }} {\Sigma }_{gen} }}_{{T_{{4{\text{F}}}} - curvature}} \\ \end{aligned} $$

(52)

Equation 51 can be utilized to derive an instantaneous transport equation of SDR in the following manner (Klein et al. 2018, Wacks et al. 2016):

$$ \begin{aligned} \rho \frac{{DN_{c} }}{Dt} =\, & \frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{{\partial N_{c} }}{{\partial x_{j} }}} \right) - 2D\frac{Dc}{{Dt}}\frac{\partial c}{{\partial x_{k} }}\frac{\partial \rho }{{\partial x_{k} }} - 2\rho D\underbrace {{\frac{\partial c}{{\partial x_{i} }}\frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{\partial c}{{\partial x_{j} }}}}_{\Lambda } \\ + & 2D\frac{{\partial \dot{w}}}{{\partial x_{k} }}\frac{\partial c}{{\partial x_{k} }} - 2\rho D^{2} \frac{{\partial^{2} c}}{{\partial x_{k} \partial x_{i} }}\frac{{\partial^{2} c}}{{\partial x_{k} \partial x_{i} }} + f_{D} \left( D \right) \\ \end{aligned} $$

(53)

where $D\left( { \ldots .} \right)/Dt = \partial \left( { \ldots .} \right)/\partial t + u_{j} \partial \left( { \ldots .} \right)/\partial x_{j}$ is the usual material derivative and $f_{D} \left( D \right)$ is the term arising from diffusivity variation. Using the reaction progress variable $c$ transport equation (i.e. $Dc/Dt = \left[ {\dot{w} + \nabla \cdot \left( {\rho D\nabla c} \right)} \right]/\rho$) and the Reynolds averaging/LES filtering yields the transport equation of $\tilde{N}_{c}$ (Gao et al. 2015c, 2014a, b; Gao and Chakraborty 2016):

$$ \frac{{\partial \left( {\mathop \rho \limits^{ - } \tilde{N}_{c} } \right)}}{\partial t} + \frac{{\partial \left( {\mathop \rho \limits^{ - } \tilde{u}_{j} \tilde{N}_{c} } \right)}}{{\partial x_{j} }} = \underbrace {{\frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{{\partial N_{c} }}{{\partial x_{j} }}} \right)}}_{{D_{1D} }} + T_{1D} + T_{2D} + T_{3D} + T_{4D} - D_{2D} + f_{D}^{*} \left( D \right) $$

(54)

The terms on the left-hand side denote the transient effects and resolved advection of  $\tilde{N}_{c}$ respectively. The term $D_{1D} = \overline{{\nabla .\left( {\rho D\nabla N_{c} } \right)}}$ represents the molecular diffusion of $\tilde{N}_{c}$ and the terms $T_{1D} ,T_{2D} ,T_{3D} ,T_{4D} ,\left( { - D_{2} } \right)$ and $f\left( D \right)$ are unclosed and given by (Gao et al. 2015c, 2014a, b; Gao and Chakraborty 2016):

$$ T_{1D} = - \frac{\partial }{{\partial x_{j} }}\left[ {\overline{{\rho u_{j} N_{c} }} - \overline{p} \tilde{u}_{j} \tilde{N}_{c} } \right] $$

(55i)

$$ T_{2D} = - \overline{{\frac{2D}{\rho }\left[ {\dot{w} + \frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{\partial c}{{\partial x_{j} }}} \right)} \right]\frac{\partial c}{{\partial x_{k} }}\frac{\partial \rho }{{\partial x_{k} }}}} $$

(55ii)

$$ T_{3D} = - 2\overline{{\rho D\frac{\partial c}{{\partial x_{i} }}\frac{{\partial u_{i} }}{{\partial x_{j} }}\frac{\partial c}{{\partial x_{j} }}}} $$

(55iii)

$$ T_{4D} = 2\overline{{D\frac{{\partial \dot{w}}}{{\partial x_{i} }}\frac{\partial c}{{\partial x_{i} }}}} $$

(55iv)

$$ \left( { - D_{2D} } \right) = - 2\overline{{\rho D^{2} \frac{{\partial^{2} c}}{{\partial x_{i} \partial x_{j} }}\frac{{\partial^{2} c}}{{\partial x_{i} \partial x_{j} }}}} $$

(55v)

$$ \begin{aligned} f_{D}^{*} \left( D \right) = & \overline{{2D\frac{\partial c}{{\partial x_{k} }}\frac{{\partial \left( {\rho D} \right)}}{{\partial x_{k} }}\frac{{\partial^{2} c}}{{\partial x_{j} \partial x_{j} }}}} + \overline{{2D\frac{\partial c}{{\partial x_{k} }}\frac{{\partial^{2} \left( {\rho D} \right)}}{{\partial x_{j} \partial x_{k} }}\frac{\partial c}{{\partial x_{j} }}}} - \overline{{\frac{\partial }{{\partial x_{j} }}\left( {\rho N_{c} \frac{\partial D}{{\partial x_{j} }}} \right)}} \\ & - \overline{{2\rho D\frac{\partial D}{{\partial x_{j} }}\frac{\partial }{{\partial x_{j} }}\left( {\frac{\partial c}{{\partial x_{k} }}\frac{\partial c}{{\partial x_{k} }}} \right)}} + \overline{{\rho \left( {\frac{\partial c}{{\partial x_{k} }}\frac{\partial c}{{\partial x_{k} }}} \right)\left[ {\frac{\partial D}{{\partial t}} + u_{j} \frac{\partial D}{{\partial x_{j} }}} \right]}} \\ \end{aligned} $$

(55iv)

The term $T_{1D}$ depicts the effects of sub-grid convection, whereas $T_{2D}$ represents the effects of density-variation due to heat release. The term $T_{3D}$ depends on the alignment of $\nabla c$ with local strain rates $e_{ij} = 0.5\left( {\partial u_{i} /\partial x_{j} + \partial u_{j} /\partial x_{i} } \right)$ and this term is referred to as the scalar-turbulence interaction term (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009; Gao et al. 2015c, 2014a, b; Gao and Chakraborty 2016). The term $T_{4D}$ originates due to the correlation between $\nabla \dot{w}$ and $\nabla c$, whereas $\left( { - D_{2D} } \right)$ denotes the molecular dissipation of SDR. The term $f_{D}^{*} \left( D \right)$ represents the effects of $D$ variation.

The third term on the right hand side of Eq. 53 involves ${\Lambda } = (\partial c/\partial x_{i} )(\partial u_{i} /\partial x_{j} )(\partial c/\partial x_{j} ) = \left( {e_{\alpha } \cos^{2} \theta_{\alpha } + e_{\beta } \cos^{2} \theta_{\beta } + e_{\gamma } \cos^{2} \theta_{\gamma } } \right)\nabla c \cdot \nabla c = a_{n} \nabla c \cdot \nabla c$. Referring back to Eqs. 4 and 5, it can be seen that the vortex stretching term $T_{1}$ can be expressed as: $T_{1} = 2(e_{\alpha } \cos^{2} \chi_{\alpha } + e_{\beta } \cos^{2} \chi_{\beta } + e_{\gamma } \cos^{2} \chi_{\gamma } ){\Omega }$. This suggests that the statistical behaviours of ${\Lambda }$ and $T_{1}$ are governed by the alignments of $\nabla c$ and $\vec{\omega }$ with local strain rate eigenvectors, respectively.

The contribution of different flow topologies towards the mean values of ${\Lambda }$ and $T_{1}$ conditional on non-dimensional temperature $c_{T}$ in cases DA-DC are shown in Fig. 51, where ${\Lambda } = \mathop \sum \nolimits_{{{\text{i}} = 1}}^{8} {\Lambda }_{{\text{i}}}$ and $T_{1} = \mathop \sum \nolimits_{i = 1}^{8} V_{i}$ are the total scalar-turbulence interaction and vortex-stretching terms, respectively, and ${\Lambda }_{{\text{i}}}$ and $V_{i}$ are the contributions which arise due to each individual topology. The contributions of different flow topologies to the mean values of ${\Lambda }$ for the SDR transport for cases DA-DC are shown in Fig. 51. It can be seen from Fig. 51 that cases DA and DB exhibit positive values of ${\Lambda }$ for all topologies except for S5 and S6 in case DA and S3, S5 and S6 in case DB. The flow topologies S2 and S7 remain major contributors of ${\Lambda }$ in case DA, which is closely followed by S4 and S8, whereas S8 is the primary contributor in case DB, followed, in order, by S7, S2, S4, S1 and S3. The absence of contributions of S1 and S3 in case DA arises as a result of the scarcity of the corresponding samples at low values of $c_{T}$ (see Fig. 5a). In case DC mean contributions for S1–S7 topologies remain mostly negative, but the contribution of S8 topology exhibits negative values. In this case the peak magnitude of the negative mean value of ${\Lambda }$ is obtained for S2, whereas non-negligible contribution arises from S5 in spite of small sample size (see Fig. 5c).

Fig. 51

Variation of the mean values of (first row) ${\Lambda }^{*} = {\Lambda } \times \delta_{th}^{3} /S_{L}$ and (second row) ${\text{V}}^{*} = T_{1} \times \left( {\delta_{th} /S_{L} } \right)^{3} { }$ conditional on $c_{T}$ for (1st –3rd columns) cases DA-DC: focal topologies S1, 4, 5, 7 (red–blue–green–magenta solid lines) and nodal topologies S2, 3, 6, 8 (red–blue–green–magenta dashed lines). Results are omitted where ${\text{VF}} < 0.01$. The values of ${\text{V}}^{*}$ in case DC are to be multiplied by $10^{5}$ as indicated

A preferential alignment between $\nabla c$ and the eigenvector associated with $e_{\alpha }$ ($e_{\gamma }$) leads to a positive (negative) ${\Lambda }$ (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009; Gao et al. 2014a, b, 2015c; Gao and Chakraborty 2016). As the effects of heat release are stronger in cases DA and DB than in case DC (see Fig. 3), the reactive scalar gradient shows strong alignment with the eigenvector associated with $e_{\alpha }$ ($e_{\gamma }$) in cases DA and DB (case DC). This leads to positive (negative) mean values of ${\Lambda }$ for cases DA and DB (case DC). In spite of predominantly negative mean ${{ \Lambda }}$ in case DC, the S8 topology is associated with local high positive $\nabla \cdot \vec{u} = - P$ (see Fig. 1) and thus the reactive scalar gradient aligns locally with the eigenvector associated with $e_{\alpha }$ to result in a positive ${\Lambda }$ for this flow topology in case DC. The flow topologies S5 and S6 are rare, and thus a consistent trend cannot be expected for these topologies. The topologies S7 and S8 are associated with positive $\nabla \cdot \vec{u} = - P$ (see Fig. 1), thus the effects of heat release are strongly felt in these topologies and as a result the reactive scalar gradient aligns locally with the principal direction corresponding to $e_{\alpha }$ to yield positive mean values of ${\Lambda }$ conditional on $c_{T}$ for these topologies in all three cases. However, effects of heat release remain weak on the unburned gas side of the flame and thus the mean value of ${\Lambda }$ conditional on $c_{T}$ exhibits negative values even for S8 topology in case DC.

Figure 51 further shows the predominant alignment of $\vec{\omega }$ with the eigenvectors associated with the intermediate and most extensive principal strain rates (i.e. $e_{\beta }$ and $e_{\alpha }$) in these cases gives rise to positive mean values of $T_{1}$ for cases DA-DC but both qualitative and quantitative behaviours change significantly between these cases. In case DA, S7 and S8 remain dominant contributors to $T_{1}$ between $0.25 < c_{T} < 0.75$, whereas in case DB, the contribution of S1 topology is dominant and its mean value shows a clear peak at $c_{T} \approx 0.25$. In case DC, all significant flow topologies except for S5 and S6 exhibit peak values at the leading edge, with S4 and S7 topologies exhibiting the highest mean values of $T_{1}$. Moreover, in cases DB and DC, except for S5 in case DC, the contributions of all focal topologies of significant presence (i.e. S1,4,7) exhibit higher values across the entire flame than for all significant nodal topologies (i.e. S2,3,8). The effects of flame-induced turbulence are the strongest for topologies which are associated with high positive $\nabla \cdot \vec{u} = - P$ in case DA (e.g. S7 and S8). This trend weakens with increasing $Ka$. Thus, the focal topologies associated with positive $Q$ (see Fig. 1: S1, 4, 7) exhibit higher contributions to $T_{1}$ than the nodal topologies S2,3,8. Moreover, Fig. 1 reveals that the topologies S4 and S7 are associated with the vortex-stretching (see Fig. 1), and accordingly they exhibit high positive mean contribution of $T_{1}$ in case DC.

The contributions of different topologies towards the mean values of ${\Lambda }$ and $T_{1}$ conditional on $c$ for cases AL, BL and DL are exemplarily shown in Fig. 52 in order to illustrate non-unity Lewis number effects. Figure 52 shows that the mean values of ${\Lambda }$ assume positive values across most of the flame and the contribution of the S8 topology (i.e. ${\Lambda }_{8}$) remains the leading order contributor in these cases. The magnitude of ${\Lambda }_{7}$ ranges between 50 and100% of that of ${\Lambda }_{8}$ and acts as the second largest contributor in these cases. The topologies S1–S4, which are present for all values of $P$ exhibit significant contributions to ${\Lambda }$ in the regions where effects of heat release are strong in $Le < 1$ cases (i.e. cases with $Le = 0.34$ and 0.6). A preferential alignment between $\nabla c$ and the eigenvector associated with $e_{\alpha }$ ($e_{\gamma }$) leads to positive (negative) values of ${\Lambda }$. It is worth noting that $\nabla c$ preferentially aligns with the principal direction associated with $e_{\alpha }$ ($e_{\gamma }$) when the strain rate induced by flame normal acceleration overcomes (is overcome by) turbulence straining (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009). The positive values assumed by ${\Lambda }$ within the heat releasing zone irrespective of $Le$ for the cases in the DNS database in Table 3. The increased heat release in the small values of $Le$ leads to an increase in the magnitude of ${\Lambda }$ and those topologies which are associated with high dilatation rates (e.g. S7 and S8), as noted above.

Fig. 52

The figure is reproduced from (Wacks et al. 2018)

Variation of the mean values of (first column) ${\Lambda }^{*} = {\Lambda } \times \delta_{th}^{3} /S_{L}$ and (second column) ${\text{V}}^{*} = T_{1} \times \left( {\delta_{th} /S_{L} } \right)^{3} { }$ conditional on $c$ for cases AL, BL, DL (1st –3rd row) (i.e. $Le = 0.34,\,0.60$ and 1.0): focal topologies S1, 4, 5, 7 (red–blue–green–magenta solid lines) and nodal topologies S2, 3, 6, 8 (red–blue–greenmagenta dashed lines). The total contribution is shown by black lines. Results are omitted where $VF < 0.01$.

Figure 52 also reveals that the mean value of $T_{1}$ conditional on $c$ remains positive in these cases. This feature is also evident for individual topologies, which remain largely positive across the entire flame front. In case AL, the mean value of $T_{1}$ increases from the unburned side of the flame before reaching a maximum at $c \approx 0.7$ due to flame-generated enstrophy, as opposed to the decay of enstrophy evident in the cases with $Le \approx 1.0$ (e.g. case DL and also for cases CL and EL but not shown here) with case BL exhibiting the intermediate behaviour, where the decay of enstrophy is arrested, but flame-generated enstrophy is not strong enough to lead to any noticeable increase in $T_{1}$ (see Fig. 15d). In case DL, the contribution of S4 topology (i.e. $V_{4}$) remains the leading contributor and the secondary contribution arises from another focal topology S7. No other topologies make significant contributions towards $T_{1}$. However, this order of importance is reversed with a decrease in $Le$ (from cases EL to AL), such that S7 becomes the primary contributor (due to increased flame-generated enstrophy in the low Lewis number flames), S8 also becomes more prominent (cases AL and BL) and the magnitude of $V_{8}$ matches that of S7 (i.e. $V_{7}$) (case AL). The flow topologies S4 and S7 play dominant roles in vortex-stretching irrespective of the value of Lewis number. This tendency for vortex-stretching dominates in the cases where flame-induced enstrophy generation is relatively weak and in these cases ${\Omega }$ decreases within the flame (see Fig. 15), such that the peak mean values of $T_{1} , V_{4}$ and $V_{7}$ are all obtained at the unburned gas side of the flame front. In cases AL-BL, the behaviour of $V_{4}$ remains unaltered, but that of $V_{7}$ is affected by the significant flame-induced turbulence in the regions where heat release is strong. The behaviour of $V_{8}$ arising from nodal topology S8 remains negligible where heat release effects are weak, which is qualitatively similar to the same features of $V_{7}$ in the regions where heat release effects are strong. Thus, the overall behaviour of the vortex-stretching term $T_{1}$ is determined by the contributions of focal topology and the heat release effects in turbulent premixed combustion.

For the sake of completeness, it is worth recalling from Table 4 that S1−S4, S7 and S8 topologies play key roles in the enstrophy transport in the corrugated flamelets regime case DA, but the contributions of S7 and S8 topologies, which are obtained only for positive dilatation rates, weaken with increasing $Ka$ and in the highest Karlovitz number case DC the enstrophy transport is determined by S1, S2 and S4 topologies which are obtained for all values of $P$. Thus, experimental configurations mimicking canonical features of S7, S8 and S1–S4 will be ideal for extracting enstrophy transport statistics in the corrugated flamelets regime, whereas a configuration with attributes of S1, S2 and S4 topologies will be sufficient for the analysis of enstrophy transport for high values of $Ka$.

The topologies which are significant contributors to the different terms of the $\tilde{N}_{c}$ transport equation (i.e. $D_{1D} , T_{1D} ,T_{2D} ,T_{3D} ,T_{4D}$ (for reaction progress variable definitions $c = \left( {Y_{R} - Y_{R0} } \right)/\left( {Y_{R\infty } - Y_{R0} } \right)$ with $Y_{R}$ being the mass fraction of either $H_{2}$ or $H_{2} O$ and subscripts 0 and $\infty$ denote unburned and fully burned gas values) and $\left( { - D_{2D} } \right)$ in Eq. 54) in cases DA-DC are summarised in Table 8 in decreasing order of significance. The topology contributions to $T_{4D}$ for $O_{2}$ mass fraction-based reaction progress variable are similar to that in the case of $H_{2} O$ mass fraction based reaction progress variable, this information is not explicitly provided in Table 8 (the SDR transport characteristics of $c_{T}$ in cases DA-DC is also qualitatively similar to $O_{2} ,H_{2} O$ mass fraction based reaction progress variables (Chakraborty et al. 2019). Similarly, the contributing topologies to the terms of the generalised FSD ${\Sigma }_{gen}$ transport equation (i.e. $T_{1F} ,T_{2F} ,T_{3F}$ and $T_{4F}$ in Eq. 52) in cases DA-DC are listed in Table 9 in decreasing order of significance.

Table 8 Leading contributions of flow topologies to the different terms of the $\tilde{N}_{c}$ transport equation (Eq. 54)

Table 9 Leading contributions of flow topologies to the different terms of the generalised FSD ${\Sigma }_{gen}$ transport equation (Eq. 52)

It is evident from Tables 8 and 9 that S1–S4, S7 and S8 topologies remain leading order contributors to both $\tilde{N_c}$ and ${\Sigma }_{gen}$ transports for small values of $Ka$ (e.g. corrugated flamelets regime combustion as in case DA), but the influence of S7 and S8 topologies, which are obtained only for positive values of $\partial u_{i} /\partial x_{i} = - P$, diminishes with an increase in $Ka$, and for large values of $Ka$ (e.g. in case DC), both $\tilde{N}_{c}$ and ${\Sigma }_{gen}$ transports are principally governed by S1-S4 topologies, although S7 still shows a non-negligible contribution. Furthermore, Tables 8 and 9 indicate that S2 is the leading contributor to all the terms of $\tilde{N}_{c}$ and ${\Sigma }_{gen}$ transport equations, and thus unstable nodal topologies with saddle points are of key importance for both $\tilde{N}_{c}$ and ${\Sigma }_{gen}$ transports. The counter-flow flame configuration has the predominant feature of S2, and thus simplified experiments and computations for the counter-flow configuration can be an ideal starting point for the analysis of the statistical behaviour and the modelling of both $\tilde{N}_{c}$ and ${\Sigma }_{gen}$ transports. Moreover, this justifies the use of counter-flow configuration for the purpose of generating flamelet tables. However, the unstable focal topology S7 associated with stretching for positive values of dilatation rate also plays a key role for both $\tilde{N}_{c}$ and ${\Sigma }_{gen}$ transports for all regimes of combustion. The propagation and curvature terms of the FSD transport equation (i.e. $T_{3F}$ and $T_{4F}$) originate due to flame displacement speed $S_{d} = \left[ {\dot{w} + \nabla .\left( {\rho D\nabla c} \right)} \right]/\rho \left| {\nabla c} \right|$ which is linked to $\dot{w}$, and thus is associated with positive dilatation rate (i.e.$\nabla \vec{u} = - P$) within the flame. Therefore, it is not particularly surprising that a flow topology (i.e. S7) which is obtained for positive dilatation rate is likely to play an important role in both $\tilde{N}_{c}$ and ${\Sigma }_{gen}$ transports. The identification of dominant flow topologies can potentially play a key role in training the data for machine learning based turbulence and combustion model development.

5.1 Modelling Implications in the Context of FSD and SDR Transports

From the foregoing it is evident that heat release and the flow topologies arising from positive values of dilatation rate play a major role in the alignment characteristics of the reactive scalar gradient with local principal strain rate directions. This directly affects the behaviour of the tangential strain rate term $T_{2F}$ in the FSD ${\Sigma }_{gen}$ transport equation (i.e. Equation 52) and the scalar-turbulence interaction term $T_{3D}$ in the Favre-averaged/filtered SDR $\tilde{N}_{c}$ transport equation (i.e. Equation 54). In order to illustrate this behaviour, it is useful to express the tangential strain rate term $T_{2F}$ in the FSD transport equation as (Chakraborty et al. 2018a; Chakraborty and Cant 2011; Katragadda et al. 2011; Sellmann et al. 2017):

$$ T_{2F} = T_{21F} + T_{22F} = \underbrace {{\overline{{\left( {\partial u_{i} /\partial x_{i} } \right)}}_{s} {\Sigma }_{gen} }}_{{T_{DF} }} - \underbrace {{\overline{{\left( {N_{i} N_{j} \partial u_{i} /\partial x_{j} } \right)}}_{s} {\Sigma }_{gen} }}_{{T_{NF} }} $$

(56)

Here, $T_{DF}$ originates due to dilatation rate and can be referred to as the dilatation rate term. The term $T_{NF}$ originates due to flame normal strain rate and will be referred to as the normal strain rate term in this paper. The term $T_{NF}$ can alternatively be written as (Chakraborty et al. 2018a; Katragadda et al. 2011; Sellmann et al. 2017):

$$ T_{NF} = - \overline{{\left( {e_{\alpha } \cos^{2} \theta_{\alpha } + e_{\beta } \cos^{2} \theta_{\beta } + e_{\gamma } \cos^{2} \theta_{\gamma } } \right)\left| {\nabla c} \right|}} $$

(57)

This suggests that $T_{2F}$ can be expressed as (Chakraborty et al. 2018a; Katragadda et al. 2011; Sellmann et al. 2017):

$$ T_{2F} = \overline{{\left( {e_{\alpha } \sin^{2} \theta_{\alpha } + e_{\beta } \sin^{2} \theta_{\beta } + e_{\gamma } \sin^{2} \theta_{\gamma } } \right)\left| {\nabla c} \right|}} $$

(58)

Equations 57 and 58 demonstrate the alignment of $\nabla c$ with the eigenvectors associated with $e_{\alpha } ,e_{\beta }$ and $e_{\gamma }$. As dilatation rate $\partial u_{i} /\partial x _{i}$ is mostly positive in premixed turbulent flames, the term $T_{DF}$ assumes positive values in premixed flames irrespective of the combustion regime and characteristic Lewis number. Thus, a preferential alignment of $\nabla c$ with the most extensive principal strain rate direction for large values of $Da$ and small values of $Ka$ (e.g. case DA) leads to a negative value of $T_{NF}$, which partially nullifies the positive value of $T_{DF}$ and acts to reduce the magnitude of the positive value of $T_{2F}$ and may induce negative values of $T_{2F}$ under some conditions (Keil et al. 2020). By contrast, a preferential alignment of $\nabla c$ with the most compressive principal strain rate direction for small values of $Da$ and large values of $Ka$ (e.g. case DC) leads to a positive value of $T_{NF}$, which aids the positive values of $T_{DF}$ and leads to large positive values of $T_{2F}$. This behaviour can be substantiated from Fig. 53 where the normalised values of $T_{DF} ,T_{NF}$ and $T_{2F}$ are shown as a function of $\tilde{c}$ for cases DA-DC. As the extent of collinear alignment of $\nabla c$ with the eigenvector associated with the most extensive (compressive) principal strain rate eigendirection in case DB is weaker (stronger) than in case DA, the extent of cancellation of positive values of $T_{DF}$ by negative values of $T_{NF}$ is smaller in case DB than in case DA. This gives rise to a strengthening of $T_{2F}$ from case DA to case DB.

Fig. 53

Variation of the normalised tangential strain rate term in the FSD transport equation term $T_{2F} \times \delta_{th}^{2} /S_{L}$ and its components for cases (left to right) DA-DC for $H_{2} O$ mass fraction based reaction progress variable: $T_{2F}$ (blue line), $T_{DF}$ (blue dashed line) and $T_{NF}$ (blue dotted line)

The tangential strain rate term $T_{2F}$ is often modelled by considering two components (Trouvé and Poinsot 1994; Sellmann et al. 2017; Cant et al. 1990; Candel et al. 1990; Duclos et al. 1993; Veynante et al. 1994, 1996; Papapostolou et al. 2019):

$$ T_{2F} = \underbrace {{\left[ {\delta_{ik} - \overline{{\left( {N_{i} N_{k} } \right)}}_{s} } \right](\partial \widetilde{{u_{i} }}/\partial x_{k} )\Sigma_{gen} }}_{{T_{21F} }} + \underbrace {{\overline{{\left( {\left[ {\delta_{ik} - N_{i} N_{k} } \right]\partial u_{i}^{{\prime\prime}} /\partial x_{k} } \right)}}_{s} \Sigma_{gen} }}_{{T_{22F} }} $$

(59)

The term $T_{21F}$ is the resolved component of $T_{2F}$ although it needs closures for $\overline{{\left( {N_{i} N_{k} } \right)}}_{s}$ (Veynante et al. 1996; Cant et al. 1990; Mantel and Borghi 1994) but the term $T_{21F}$ behaves deterministically based on the nature of $\partial \tilde{u}_{i} /\partial x_{j}$. The unresolved term $T_{22F}$ is often modelled by either using the Kolmogorov time scale as: $T_{22F} = 0.28\sqrt {\tilde{\varepsilon }/\nu_{0} } {\Sigma }_{gen}$ (known as the Cant-Pope-Bray (CPB) model) (Cant et al. 1990) with $\nu_{0}$ being the unburned gas kinematic viscosity) or by large scale turbulent time scale as (Candel et al. 1990; Duclos et al. 1993): $T_{22} = a_{0} {\Gamma }_{k} \left( {\tilde{\varepsilon }/\tilde{k}} \right){\Sigma }_{gen}$(known as the Coherent Flamelet Model (CFM) model) where $a_{0}$ is a model constant (taken as $a_{0} = 2.0$), and ${\Gamma }_{k}$ is the efficiency function (Meneveau and Poinsot 1991), which depends on $l_{t} S_{L} /D_{th,0}$ and $\sqrt {2\tilde{k}/3 } /S_{L}$ with $l_{t} = C_{k} \tilde{k}^{3/2} /\tilde{\varepsilon }$ being the local turbulent length scale, where $C_{k}$ depends on the local Taylor micro-scale Reynolds number (Pope 2000).

It has already been discussed that the alignment of $\nabla c$ with local principal directions is governed by the competition between $a_{chem}$ and $a_{turb}$ but both CPB and CFM models ignore the effects of $a_{chem}$. The timescale associated with the CPB model (i.e. $\sqrt {\nu_{0} /\tilde{\varepsilon }}$) is strictly valid for passive material surfaces (Yeung et al. 1990). Moreover, both CPB (Cant et al. 1990) and CFM (Candel et al. 1990; Duclos et al. 1993) models are implicitly based on the preferential collinear alignment between $\nabla c$ with the eigenvector associated with $e_{\gamma }$, which is valid only for case DC. The flames resemble increasingly passive surfaces at high values of $Ka$, therefore both CPB and CFM models are poor in capturing the behaviour of $T_{22F}$ for cases DA and DB but their performances improve for case DC as can be seen from Fig. 54. In order to address this problem (Katragadda et al. 2011; Sellmann et al. 2017) modelled $T_{22F}$ in the following manner:

$$ T_{NF} = \left( {\tilde{\varepsilon }/\tilde{k}} \right)\left[ {C_{1} - \tau C_{2} f_{FSD} \left( {Le,Ka} \right)Da_{L} } \right] \Sigma_{gen} $$

(60)

where $C_{1}$ and $C_{2}$ are model parameters, $Da_{L} = \tilde{k}S_{L} /\left( {\tilde{\varepsilon }\delta_{th} } \right)$ is the local Damköhler number, and $f_{FSD} \left( {Le, Ka} \right)$ is a function, which increases with decreasing $Le$ and $Ka$, accounting for strengthening of flame normal acceleration with decreasing $Le$ and $Ka$ (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009). The term $C_{1} \left( {\widetilde{\varepsilon }/\tilde{k}} \right){\Sigma }_{gen}$ is responsible for FSD generation due to alignment of $\nabla c$ with the most compressive principal strain rate eigendirection under the action of turbulent straining ($\sim \widetilde{\varepsilon }/\tilde{k}$) (Meneveau and Poinsot 1991; Katragadda et al. 2011; Sellmann et al. 2017). By contrast, $- \left( {\widetilde{\varepsilon }/\tilde{k}} \right)\tau C_{2} Da_{L} {\Sigma }_{gen}$ accounts for FSD destruction due to the alignment of $\nabla c$ with the most extensive principal strain rate eigendirection under the influence of flame normal acceleration ($\sim \tau f_{FSD} \left( {Le,Ka} \right)S_{L} /\delta_{th}$) (Katragadda et al. 2011; Sellmann et al. 2017). Further information on the performance of the model given by Eq. 60 can be found elsewhere (Katragadda et al. 2011; Sellmann et al. 2017) and is not repeated here.

Fig. 54

Variation of $T_{22F} \times \delta_{th}^{2} /S_{L}$ (solid lines for DNS data) along with the predictions of the CPB (broken line) and CFM (dotted line) models with $\tilde{c}$ for cases DA-DC from left to right columns respectively for $H_{2} O$ mass fraction based reaction progress variable

Similarly, to the FSD normal strain rate term $T_{2N}$, the scalar-turbulence interaction term $T_{3D}$ in the $\tilde{N}_{c}$ transport equation (i.e. Equation 54) can be expressed as (Chakraborty et al. 2019; Gao et al. 2014a, b, 2015c; Gao and Chakraborty 2016):

$$ T_{3D} = - 2\overline{{\rho \left( {e_{\alpha } \cos^{2} \theta_{\alpha } + e_{\beta } \cos^{2} \theta_{\beta } + e_{\gamma } \cos^{2} \theta_{\gamma } } \right)N_{c} }} = - 2\overline{{\rho N_{c} a_{N} }} $$

(61)

Equation 61 suggests that the preferential collinear alignment between $\nabla c$ with the most extensive principal strain rate eigendirection (i.e. $\cos^{2} \theta_{\alpha } = 1.0$) leads to negative values of $T_{3D}$, and the preferential alignment with the most compressive principal strain rate eignendirection (i.e. $\cos^{2} \theta_{\gamma } = 1.0$) gives rise to negative values of $T_{3D}$. This can be substantiated from Fig. 55 where the variations of normalised values of $D_{1D} , T_{1D} ,T_{2D} ,T_{3D} ,T_{4D}$ and $\left( { - D_{2D} } \right)$ with $\tilde{c}$ for $H_{2}$ and $H_{2} O$ based reaction progress variables are shown and the results for $O_{2}$ based reaction progress variable are not shown because of qualitative similarity with the results for $H_{2} O$ based reaction progress variable. Figure 55 shows that the molecular dissipation term $\left( { - D_{2D} } \right)$ acts as a leading order sink for all cases irrespective of the definition of reaction progress variable, whereas $T_{2D}$ remains as a primary source term. It can further be seen from Fig. 55 that the magnitudes of the molecular and turbulent transport contributions (i.e. $D_{1D}$ and $T_{1D}$) remain negligible in comparison to those for $T_{2D}$ and $\left( { - D_{2D} } \right)$ regardless of the definition of reaction progress variable in cases DA-DC. The behaviour of $T_{4D}$ changes significantly with the definition of reaction progress variable. For $H_{2}$ based reaction progress variable, the term $T_{4D}$ acts as a leading source term whereas the magnitude of this term remains negligible in comparison to the magnitudes of $T_{2D}$ and $\left( { - D_{2D} } \right)$ for $O_{2}$ and $H_{2} O$ based reaction progress variables in cases DA-DC. The term $T_{4D}$ is given by: $T_{4D} = - \overline{{2D\left( {\partial \dot{w}/\partial n} \right)\left| {\nabla c} \right|}}$ where $n$ is the flame normal direction and $\left( {\partial \dot{w}/\partial n} \right)$ assumes negative (positive) value on the unburned (burned) gas side of the flame (Chakraborty et al. 2019). For $H_{2}$ based reaction progress variable, the distribution of $\dot{w}$ is such that the negative contribution of $\left( {\partial \dot{w}/\partial n} \right)$ is greater in magnitude than the positive contribution and the transition from negative to positive value of $\left( {\partial \dot{w}/\partial n} \right)$ takes place for a $c$ value which is biased towards the burned gas side of the flame front, which leads to predominantly positive values of $T_{4D}$ for $H_{2}$ based reaction progress variable (Chakraborty et al. 2019). The positive and negative contributions of $\left( {\partial \dot{w}/\partial n} \right)$ are comparable for the case of $O_{2}$ and $H_{2} O$ based reaction progress variables and the transition from negative to positive value takes place close to $c \approx 0.5$, and thus, on Reynolds averaging $- 2D\left( {\partial \dot{w}/\partial n} \right)\left| {\nabla c} \right|$, one obtains a positive (negative) contribution of $T_{4D}$ with negligible magnitude towards the unburned (burned) gas side of the flame front (Chakraborty et al. 2019).

Fig. 55

Variation of the $\tilde{N}_{c}$ transport equation terms for cases (left to right) A–C: $D_{1D}$ (red),$T_{1D}$ (green), $T_{2D}$ (blue), $T_{3D}$ (magenta), $T_{4D}$ (cyan) and $\left( { - D_{2D} } \right)$ (black) against $\tilde{c}$ for (top to bottom) $H_{2}$ and $H_{2} O$ based reaction progress variables

The major difference in the SDR transport from the point of view of fluid dynamics between cases DA-DC originates because of the scalar-turbulence interaction term $T_{3D}$, which acts as a leading order sink in cases DA and DB. However, $T_{3D}$ acts as a major source for case DC and this behaviour is particularly prominent for $O_{2}$ and $H_{2} O$ based reaction progress variable definitions. The value of $\tau f_{2} \left( {Le,Ka} \right)Da\sim a_{chem} /a_{turb}$ decreases from cases DA to DC (see Table 1), which suggests a greater (smaller) extent of $\nabla c$ alignment with the eigenvector associated with $e_{\gamma }$ ($e_{\alpha }$) moving from DA to DC. This leads to negative (positive) contributions of $T_{3D}$ in cases DA and DB (case DC). The above discussion suggests that the scalar gradient alignment characteristics in the modelling of the scalar-turbulence interaction term $T_{3D}$ needs to be explicitly addressed. In the context of RANS $T_{3D} \gg - 2\overline{\rho }\tilde{D}\left( {\partial \tilde{c}/\partial x_{i} } \right)\left( {\partial \widetilde{{u_{i} }}/\partial x_{j} } \right)\left( {\partial \tilde{c}/\partial x_{j} } \right)$ and thus $T_{3D}$ can be expressed as:

$$ \begin{aligned} T_{3D} \approx & T_{3D} + 2\overline{\rho }\tilde{D}\left( {\partial \tilde{c}/\partial x_{i} } \right)\left( {\partial \widetilde{{u_{i} }}/\partial x_{j} } \right)\left( {\partial \tilde{c}/\partial x_{j} } \right) \\ = & T_{31D} + T_{32D} + T_{33D} \\ = & - \underbrace {{2\overline{\rho D} \frac{{\partial \tilde{c}}}{{\partial x_{j} }}\widetilde{{\frac{{\partial u_{j}^{{\prime\prime}} }}{{\partial x_{k} }}\frac{{\partial c^{\prime\prime}}}{{\partial x_{k} }}}}}}_{{T_{31D} }} - \underbrace {{2\overline{\rho D} \widetilde{{\frac{{\partial c^{\prime\prime}}}{{\partial x_{j} }}\frac{{\partial u_{j}^{{\prime\prime}} }}{{\partial x_{k} }}\frac{{\partial c^{\prime\prime}}}{{\partial x_{k} }}}}}}_{{T_{32D} }} - \underbrace {{2\overline{\rho D} \widetilde{{\frac{{\partial c^{\prime\prime}}}{{\partial x_{j} }}\frac{{\partial c^{\prime\prime}}}{{\partial x_{k} }}}}\frac{{\partial \widetilde{{u_{j} }}}}{{\partial x_{k} }}}}_{{T_{33D} }} \\ \end{aligned} $$

(62)

The expressions of $T_{31D}$ and $T_{32D}$ indicate that their behaviours depend on the alignment of $\nabla c$ with local principal strain rates, and a preferential collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\alpha }$ ($e_{\gamma }$) leads to negative (positive) values of $T_{31D}$ and $T_{32D}$, which can be confirmed from Fig. 56 where the variations of normalised values of $T_{31D} ,T_{32D}$ and $T_{33D}$ are shown as a function of $\tilde{c}$ for cases AR and BR. For statistically planar flames $T_{33D}$ reduces to $- 2\overline{\rho D} \widetilde{{\frac{{\partial c^{\prime\prime}}}{{\partial x_{1} }}\frac{{\partial c^{\prime\prime}}}{{\partial x_{1} }}}}\frac{{\partial \widetilde{{u_{1} }}}}{{\partial x_{1} }}$ and thus deterministically assumes negative values. In case AR, the predominant alignment of $\nabla c$ with the eigenvector associated with $e_{\alpha }$ (see Fig. 48) leads to negative values of $T_{31D}$ and $T_{32D}$. However, the term $T_{31D}$ assumes positive values for predominant collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\gamma }$ in case BR (see Fig. 48). In case BR the reaction progress variable gradient $\nabla c$ exhibits a greater extent of collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\alpha }$ leading to negative $T_{32D}$ values towards the burned gas side of flame brush, but the predominant collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\gamma }$ gives rise to positive $T_{32D}$ values towards the unburned gas side of the flame brush.

Fig. 56

Variations of $T_{3D}$ and its various components $T_{31D} ,T_{32D}$ and $T_{33D}$ with Favre averaged reaction progress variable $\tilde{c}$ across the flame brush: e case AR, f case BR. All the terms are normalised with respect to $\rho_{0} S_{L}^{2} /\delta_{th}^{2}$ of the respective DNS database

For passive scalar mixing, $T_{32D}$ is often modelled as (Chakraborty et al. 2011d; Mantel and Borghi 1994; Jones and Musonge 1988; Chakraborty and Swaminathan 2007b): $T_{32D} = A_{e} \overline{\rho }\left( {\tilde{\varepsilon }/\tilde{k}} \right)\widetilde{{\varepsilon_{c} }}$ where $A_{e}$ is a model parameter, $\widetilde{{\varepsilon_{c} }} = \tilde{N}_{c} - \tilde{D}\nabla \tilde{c}.\nabla \tilde{c}$ is the unresolved component of SDR. However, the findings from Figs. 55 and 56 indicate that the modelling of passive scalar mixing is not applicable for $T_{3D}$ closure in turbulent premixed flames. It has been noted elsewhere by this author and their co-authors that the following model expressions are more successful in capturing the statistical behaviours of $T_{31D}$ and $T_{32D}$ (Chakraborty and Swaminathan 2010, 2013, 2007b; Chakraborty et al. 2011d, 2008b):

$$ T_{31D} = - \left[ {C_{1D} + C_{2D} Da_{L}^{*} } \right]\overline{\rho }\left( {\tilde{\varepsilon }/\tilde{k}} \right)\widetilde{{u_{j}^{{\prime\prime}} c^{\prime\prime}}}\left( {\partial \tilde{c}/\partial x_{j} } \right) $$

(63i)

$$ T_{32D} = \overline{\rho }\left( {\tilde{\varepsilon }/\tilde{k}} \right)\left[ {C_{3D} - C_{4D} \tau f_{D} \left( {Le} \right)Da_{L}^{*} } \right]\widetilde{{\varepsilon_{c} }} $$

(63ii)

where $Da_{L}^{*} = S_{L} \rho_{0} \tilde{k}/\left( {\delta_{th} \overline{\rho }\tilde{\varepsilon }} \right)$ is a local density-weighted Damköhler number, $f_{D} \left( {Le} \right)$ is a function which increases with decreasing $Le$, and $C_{1D} , C_{2D} ,C_{3D}$ and $C_{4D}$ are model parameters (Chakraborty and Swaminathan 2010, 2013, 2007b; Chakraborty et al. 2008b, 2011d). The model $C_{2D}$ approaches an asymptotic value for large values of local Karlovitz number $Ka_{L} = \left( {S_{L} } \right)^{ - 3/2} \left( {\tilde{\varepsilon }\delta_{th} } \right)^{1/2}$, whereas $C_{4D}$ decreases with increasing $Ka_{L}$ before vanishing at $Ka_{L} \to \infty$. In the context of LES, $T_{3D}$ behaviour is principally governed by $T_{32D}$, which is modelled as (Gao et al. 2015c; Gao and Chakraborty 2016):

$$ T_{3D} = - 2\overline{\rho }\tilde{D}\frac{{\partial \tilde{c}}}{{\partial x_{i} }}\frac{{\partial \widetilde{{u_{i} }}}}{{\partial x_{j} }}\frac{{\partial \tilde{c}}}{{\partial x_{j} }} + \left( {1 - f_{T3} } \right)[C_{3D}^{*} - C_{4D}^{*} \tau f_{LES} \left( {Le} \right)Da_{{\Delta }}^{*} ]\frac{{u_{{\Delta }}^{{\prime}} }}{{\Delta }}\overline{\rho }\widetilde{{N_{c} }} $$

(64)

where $Da_{{\Delta }}^{*} = S_{L} \rho_{0} {\Delta }/\left( {\delta_{th} \overline{\rho }u_{{\Delta }}^{{\prime}} } \right)$ is a local density-weighted Damköhler number in the context of LES, $f_{T3} = {\text{exp}}\left[ { - c_{1} \left( {{\Delta }S_{L} /D_{th} } \right)^{2} } \right]$ is a bridging function, $f_{LES} \left( {Le} \right)$ is a function which increases with decreasing $Le$, $c_{1} , C_{3D}^{*}$ and $C_{4D}^{*}$ are model parameters with $C_{4D}^{*}$ is a decreasing function of sub-grid Karlovitz number $Ka_{{\Delta }} = \left( {u_{{\Delta }}^{{\prime}} /S_{L} } \right)^{1.5} \left( {{\Delta }/\delta_{th} } \right)^{ - 0.5}$ (Gao et al. 2015c; Gao and Chakraborty 2016).

It is worth noting that the Bray number $N_{B}$ scales as: $N_{B} \sim \tau Da (\delta_{th} /L_{11}$) which suggests that for large values of $\tau Da$ one gets a counter-gradient type transport (i.e. $\widetilde{{u_{j}^{{\prime\prime}} c^{\prime\prime}}}\left( {\partial \tilde{c}/\partial x_{j} } \right) > 0$), which leads to negative values of $T_{31D}$ according to Eq. 63i, which is consistent with the expected behaviour of $T_{31D}$ due to the predominant collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\alpha }$. By contrast, $N_{B}$ remains small for small values of $\tau Da$ and thus one gets a gradient type transport (i.e. $\widetilde{{u_{j}^{{\prime\prime}} c^{\prime\prime}}}\left( {\partial \tilde{c}/\partial x_{j} } \right) < 0$), which leads to positive values of $T_{31D}$ according to Eq. 63, as expected for a predominant collinear alignment of $\nabla c$ with the eigenvector associated with $e_{\gamma }$. The term in Eq. 63ii, $C_{1D} \left( {\widetilde{\varepsilon }/\tilde{k}} \right)\overline{\rho }\widetilde{{\varepsilon_{c} }}$ is responsible for SDR generation due to alignment of $\nabla c$ with the most compressive principal strain rate under the action of turbulent straining ($\sim \widetilde{\varepsilon }/\tilde{k}$) (Chakraborty and Swaminathan 2010, 2013, 2007b; Chakraborty et al. 2011d, 2008b). By contrast, $- \left( {\widetilde{\varepsilon }/\tilde{k}} \right)\tau f_{D} \left( {Le} \right)C_{2D} Da_{L}^{*} \overline{\rho }\widetilde{{\varepsilon_{c} }}$ accounts for SDR destruction due to the alignment of $\nabla c$ with the most extensive principal strain rate eigendirection under the action of the strain rate induced by flame normal acceleration ($\sim \tau f_{D} \left( {Le} \right)S_{L} /\delta_{th}$) (Chakraborty and Swaminathan 2010, 2013, 2007b; Chakraborty et al. 2011d, 2008b). Similarly, $C_{3D}^{*} \left( {u_{{\Delta }}^{{\prime}} /{\Delta }} \right)\overline{\rho }\widetilde{{N_{c} }}$ in Eq. 64 is responsible for SDR generation due to alignment of $\nabla c$ with the eigenvector associated with $e_{\gamma }$ under the action of turbulent straining, and $- \left( {u_{{\Delta }}^{{\prime}} /{\Delta }} \right)\tau f_{LES} \left( {Le} \right)C_{4D}^{*} Da_{L}^{*} \overline{\rho }\widetilde{{N_{c} }}$ accounts for the SDR destruction due to the alignment of $\nabla c$ with the eigenvector associated with $e_{\alpha }$ (Gao et al. 2015c, 2016; Gao and Chakraborty 2016). The interested readers are referred to Chakraborty and Swaminathan (2010, 2013, 2007b) and, Chakraborty et al. (2011d, 2008b); Gao et al. (2015c, d, 2016) and Gao and Chakraborty (2016) for further information on RANS and LES modelling of the scalar-turbulence interaction term $T_{3D}$.

6 Final Remarks and Outlook

The discussion in this paper suggests that dilatation rate arising from heat release is of fundamental importance for the purpose of modelling turbulence in premixed flames. In fact, the instantaneous and mean gas densities can be expressed as: $\rho = \rho_{0} /\left( {1 + \tau c} \right)$ and $\overline{\rho } = \rho_{0} /\left( {1 + \tau \tilde{c}} \right)$ for low Mach number unity Lewis number combustion, one obtains the following relations (Chakraborty and Cant 2005a, 2005b; Chakraborty 2005):

$$ \frac{{\partial u_{i} }}{{\partial x_{i} }} = \tau \frac{{\rho S_{d} }}{{\rho_{0} }} \left| {\nabla c} \right| = \tau \left[ {\frac{{\dot{w} + \nabla .\left( {\rho D\nabla c} \right)}}{{\rho_{0} }}} \right] $$

(65i)

$$ \frac{{\partial \tilde{u}_{i} }}{{\partial x_{i} }} = \tau \frac{{\overline{{\left( {\rho S_{d} } \right)}}_{s} }}{{\rho_{0} }} {\Sigma }_{gen} - \frac{\tau }{{\rho_{0} }}\frac{{\partial \left[ {\overline{{\rho u_{j} c}} - \overline{\rho }\tilde{u}_{j} \tilde{c}} \right]}}{{\partial x_{j} }} $$

(65ii)

Equations 65i and 65ii are derived for unity Lewis number conditions, although they remain reasonably valid in the order of magnitude sense even for non-unity Lewis number flames (Chakraborty and Cant 2005a; Chakraborty 2005). These expressions suggest that the dilatation rate is closely linked to reaction–diffusion balance (i.e. $\dot{w} + \nabla .\left( {\rho D\nabla c} \right)$) and thus also with flame propagation rate through displacement speed $S_{d}$ in turbulent premixed flames. The flame propagation velocity in the laboratory coordinate system is given by $\vec{u}^{c} = \vec{u} + S_{d} \vec{N}$ and thus an observer measuring the flame propagation velocity will experience an effective dilatation rate $\nabla \cdot\vec{u}^{c} = \nabla \cdot\vec{u} + \nabla \cdot\left( {S_{d} \vec{N}} \right)$ and an effective vorticity $\vec{\omega }^{{\varvec{c}}} = \left( {\nabla \times \vec{u}^{c} } \right) = \vec{\omega } + \nabla \times \left( {S_{d} \vec{N}} \right)$, where the contributions $\nabla \cdot\left( {S_{d} \vec{N}} \right)$ and $\left[ {\nabla \times \left( {S_{d} \vec{N}} \right)} \right]$ arise due to flame propagation and are affected by thermal expansion associated with the heat release arising from exothermic chemical reactions. It is often challenging to measure $S_{d}$ accurately by experimental means (Hartung et al. 2009; Peterson et al. 2019) in comparison to fluid velocity measurements. Therefore, the contributions of $\nabla \cdot\left( {S_{d} \vec{N}} \right)$ and $\nabla \times \left( {S_{d} \vec{N}} \right)$ are of limited practical relevance and no existing methodology utilises these quantities. Thus, the contributions of $\nabla \cdot\left( {S_{d} \vec{N}} \right)$ and $\nabla \times \left( {S_{d} \vec{N}} \right)$ will not be discussed further in this paper. Equation 65ii further indicates that the scalar gradient (e.g. generalised FSD ${\Sigma }_{gen}$) and turbulent/sub-grid scalar fluxes (e.g.$\left[ {\overline{{\rho u_{j} c}} - \overline{\rho }\tilde{u}_{j} \tilde{c}} \right]$) are linked with resolved scale dilatation rate $\partial \tilde{u}_{i} /\partial x_{i}$. This resolved scale dilatation rate $\partial \tilde{u}_{i} /\partial x_{i}$ has also been demonstrated to play a significant role in the closures of sub-grid stresses in premixed turbulent flames (Chakraborty and Cant 2005a). Moreover, $\partial u_{i} /\partial x_{i}$ affects turbulent kinetic energy and enstrophy evolutions and influences the extent of anisotropy of Reynolds/sub-grid stresses in turbulent premixed flames (Klein et al. 2017, 2015). The dilatation rate magnitude provides a measure of the strength of flame normal acceleration, and therefore flame-induced pressure gradient arising from flame normal acceleration plays a key role in determining the sub-grid flux behaviour, and also influences turbulent kinetic energy and enstrophy transports through pressure-dilatation and pressure-transport terms, and baroclinic torque term, respectively (Zhang and Rutland 1995; Nishiki et al. 2002; Chakraborty and Cant 2009c; Chakraborty et al. 2011a). Furthermore, the strength of dilatation rate and the flame normal acceleration can both alter the local alignments of reactive scalar gradient and vorticity with local principal strain rate eigendirections in comparison to non-reacting isothermal turbulent flows, and these differences are reflected in the behaviour of the vortex-stretching and normal strain rate contributions in the enstrophy and FSD/SDR transport equations, respectively. Thus, the closures for passive scalar mixing for normal strain rate contribution in the FSD/SDR transport are rendered invalid in turbulent premixed flames (Chakraborty et al. 2008b, 2011b, c; Katragadda et al. 2009; Sellmann et al. 2017; Chakraborty and Swaminathan 2007b). It has also been demonstrated that dilatation rate affects the flow topology distributions in premixed turbulent flames, but the effects of dilatation rate weaken with increasing Karlovitz number. Thus, the flow topologies, which are obtained only for positive values of dilatation rate, play important roles for small values of Karlovitz number (e.g. $Ka < 1$ in the corrugated flamelets regime) but their influence progressively diminishes with increasing Karlovitz number. However, it has recently been demonstrated by Brearley et al. (2019) based on the structure function statistics in turbulent premixed flames that the effects of thermal expansion arising from heat release persist for Karlovitz numbers much greater than unity. The effects of heat release on the turbulent fluid motion in premixed flames strengthen further with decreasing characteristic Lewis number $Le$ and these effects are especially strong for $Le < 1$ due to augmented heat release and thermal expansion effects as a result of thermo-diffusive instability (Mizomoto et al. 1984; Bechtold and Matalon 2001; Law and Kwon 2004; Clarke 2002). These effects are expected to be increasingly important for future design of combustors which are meant to operate on high hydrogen content fuels.

Recently, Lipatnikov et al. (2020) utilised Helmholtz–Hodge decomposition to separate rotational and potential velocity components, and revealed that thermal expansion alters the local structure of the incoming constant-density turbulent flow of unburned reactants by preferentially increasing the magnitudes of potential velocity fluctuations in comparison to the rotational velocity fluctuation component. This tendency strengthens with increasing $\tau$, and the potential and rotational velocity components induce opposing strain rates, which have implications on the local flame surface area generation. The influence of $Le$ on these effects is yet to be analysed but it is expected that the aforementioned tendencies will strengthen with decreasing characteristic Lewis number.

It is worth noting that the statistics of scalar gradient evolution and the effects of heat release on the alignment of reactive scalar gradient, vorticity, sub-grid stresses with local principal strain rate eigendirections are governed by small-scale physical processes. Therefore, the nature of large-scale forcing is unlikely to alter the statistical behaviours reported in this paper based on statistically planar flame DNS data. For example, the statistics of the reactive scalar gradient and SDR obtained from other configurations without any strong curvature and wall effects (e.g. Bunsen burner flames, Bluff body stabilised flames and V-shaped flames) (Sandeep et al. 2018; Klein et al. 2018; Chakraborty et al. 2013; Gao et al. 2016, 2015d) have been found to be consistent with the findings obtained from statistically planar flame simulations (Chakraborty and Swaminathan 2010, 2013, 2007b; Gao et al. 2014a, b, 2015c; Chakraborty and Cant 2005b; Chakraborty et al. 2008a, 2018b, 2008b). The strength of non-gradient transport and the collinear alignment of the reactive scalar gradient alignment with the most extensive principal strain rate eigendirection depends on Bray number $N_{B} \propto \tau /\left( {Da^{0.5} Ka} \right)$ (Veynante et al. 1997; Chakraborty and Cant 2009a, 2009b, 2009c) and $\tau Da \propto a_{chem} /a_{turb}$ (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009), respectively, and thus these statistics are fundamentally determined by $Da$ and $Ka$. Any variation in these statistics with turbulent Reynolds number $Re_{t} \sim Da^{2} Ka^{2}$ principally occurs due to the changes in Damköhler and/or Karlovitz number. Moreover, it has been shown in previous analyses that the model parameters for FSD and SDR based models become independent of turbulent Reynolds number for relatively small values (~ $Re_{t}$) (Chakraborty and Swaminathan 2013; Chakraborty and Cant 2013). Finally, the models, which have been proposed in the past based on DNS of statistically planar turbulent premixed flames for moderate values of $Re_{t}$ (Gao et al. 2014a, b, 2015a, b; Chakraborty and Cant 2009d; Hawkes and Cant 2001; Chakraborty and Klein 2008b), remain valid for higher values of turbulent Reynolds number for other configurations (Ma et al. 2013, 2014a, 2014b; Butz et al. 2015). However, more analysis for higher values of turbulent Reynolds number and more realistic burner configurations will be necessary in the future for the validation of the findings based on canonical configurations under moderate values of $Re_{t}$.

It is worth noting that the dilatation rate effects in turbulent premixed flames are present within the flame thickness for a self-propagating flame front, and thus the influence of dilatation rate is concentrated only in the flame region. It was demonstrated by Bilger (2004) that turbulence dominates the effect of heat release in diffusion flames for most practical flows and therefore predominantly gradient type behaviour is obtained for non-premixed flames. However, counter-gradient transport was reported for non-premixed flames (Luo 2000) and partially premixed flames (Richardson et al. 2007) when the heat release effects overwhelm the influence of turbulent velocity fluctuations like premixed turbulent flames. It has been demonstrated in this paper that the effects of counter-gradient remain most prominent in the direction of mean flame propagation (Gao et al. 2015a, 2015b; Klein et al. 2016) but there is no such preferred directionality of flame propagation in non-premixed combustion, and thus no preferred directionality can be associated with the nature of turbulent scalar transport in diffusion flames. Therefore, the statistical behaviours of SGS fluxes and stresses in turbulent premixed flames are likely to be different in comparison to a non-premixed flame. It was also demonstrated earlier in this paper that the scalar gradient in a turbulent premixed flames may align with the eigenvector associated with the most extensive principal strain rate in the reaction zone (Grout and Swaminathan 2006; Chakraborty and Swaminathan 2007a; Kim and Pitsch 2007; Hartung et al. 2008; Chakraborty et al. 2009) but it is opposite to the preferential alignment of the passive scalar gradient with the most compressive principal strain rate eigendirection (Batchelor 1952, 1959; Gibson 1968; Clay 1973; Kerr 1985; Ruetsch and Maxey 1991; Nomura and Elghobashi 1992; Ashurst et al. 1987a, b; Leonard and Hill 1991; Malkeson and Chakraborty 2011). The scalar gradient alignment with strain rate eigendirections in turbulent premixed flames are determined by the relative strengths of the strain rates induced by flame normal acceleration and turbulent straining (Chakraborty and Swaminathan 2007a; Chakraborty et al. 2009). Therefore, it is unlikely the passive scalar gradient alignment is affected by heat release in non-premixed and partially premixed flames because the direction of the scalar gradient is completely independent of local flow accelerations due to heat release. In fact, it was previously demonstrated by Malkeson and Chakraborty (2011) that the passive scalar gradient continues align with the eigenvector associated with the most compressive principal strain rate even when the reactive scalar gradient exhibits preferential collinear alignment with the eigenvector associated with the most extensive principal strain rate. Therefore, it can be expected that the results of this paper are more relevant to turbulent premixed flames than to non-premixed flames.

To date, most analyses on turbulent premixed flames have been conducted in the absence of walls. However, the presence of walls alters fluid turbulence, which in turn affects the flame dynamics and heat release rate statistics, that in turn influence turbulence and enstrophy evolutions for turbulent premixed flame-wall interactions. The modern combustors (e.g. in hybrid engines) are now made smaller in size and increased popularity of micro-combustors has increased the importance of premixed flame-wall interactions for combustion modellers. Recent analyses on turbulent premixed flame-wall interaction suggest that the decrease in dilatation rate either due to flame quenching as a result of wall heat loss or due to wall-induced confinement can have a significant influence on enstrophy (Lai et al. 2017a), turbulent kinetic energy (Lai et al. 2017b; Ahmed et al. 2019c), turbulent scalar flux (Lai et al. 2017c), scalar variance (Lai and Chakraborty 2016a) and reactive scalar gradient statistics (Sellmann et al. 2017; Lai and Chakraborty 2016b, c, d; Ahmed et al. 2020; Bruneaux et al. 1997) in the near-wall region. Moreover, the usual log-law for mean velocity and temperature variations is often rendered invalid during turbulent premixed flame-wall interactions (Bruneaux et al. 1997, 1996; Jainski et al. 2018). The modelling of wall-bounded turbulent reacting flows is currently in a rudimentary state, and there is an urgent need to obtain fundamental physical information and develop high-fidelity closures for turbulent premixed flame-wall interactions. The aforementioned complexities associated with flame-wall interaction are likely to be exacerbated in the case of high-hydrogen content fuels due to the additional effects of differential diffusion of heat and mass, characterised by a non-unity characteristic Lewis number.

It is worth noting that the discussion in this paper undoubtedly demonstrates that turbulence modelling and combustion modelling in turbulent premixed flames are not independent of each other. In fact, a recent analysis Chakraborty et al. (2020) revealed that the flame normal and the normal vector on the iso-enstrophy surface show qualitatively similar alignment with local principal strain rate eigendirections with the variations of Damköhler and Karlovitz numbers, and the flame surface and iso-enstrophy surface topologies are qualitatively similar. Moreover, the flow topologies, which make significant contributions to the enstrophy, scalar dissipation rate and FSD change with the regime of combustion (Papapostolou et al. 2017; Chakraborty et al. 2018a, 2019). The combustion modelling becomes increasingly challenging for high values of Karlovitz number, but turbulence under this condition starts to resemble that of non-reacting flow turbulence, so the modelling of turbulent fluid motion is not an unfamiliar task. However, for small values of Karlovitz number, the combustion modelling is relatively straightforward because of the availability of several well-developed methodologies for the flamelet regime of premixed combustion, but heat release influences the dynamics of turbulent fluid motion which usual non-reacting turbulence models do not accurately account for. Thus, it is necessary to adapt the modelling of underlying turbulence while moving from one combustion regime to another; this aspect does not often receive sufficient attention in combustion simulations. However, it is perhaps unrealistic to expect an accurate prediction from RANS/LES of turbulent premixed flames if the underlying turbulent fluid motion is not captured with sufficient fidelity. Therefore, both turbulence modelling and chemical kinetics approximation need to be represented with sufficient accuracy in order to obtain highly accurate predictions of turbulent premixed combustion in future combustors which are expected to operate over a range of different combustion regimes, for a range of different fuels in order to take advantage of the evolving fuel landscape to address the challenges of sustainability and environmental friendliness, without compromising the power and efficiency requirements.