1 Introduction

The interactions between turbulence and chemically induced thermal expansion have challenged the combustion community for the last century. Compressibility and variable density escalate the turbulent flow problem's complexity by introducing additional mechanisms of vorticity generation and dissipation (Friedrich 1999; Echekki and Mastorakos 2011). The changes of physical properties through the combustion progress additionally entangle the problem. As a consequence, the investigation of the flame-turbulence interactions remains an intense research area.

The concept of turbulence generation associated with combustion was firstly noted by Karlovitz et al. (Karlovitz et al. 1951). Following this work, both turbulent production (Karlovitz et al. 1951; Scurlock and Grover 1953; Yoshida and Tsuji 1979; Bray et al. 1981; Borghi 1984; Gulati and Driscoll 1986; Ballal 1987; Driscoll and Gulati 1988; Zhang and Rutland 1995; Furukawa et al. 2002) and inhibition (Zhang and Rutland 1995; Makowka 2015; Wang and Abraham 2017) have been observed depending on the context. Accurate modeling of flame-generated turbulence's statistics remains a challenging topic (Sabelnikov and Lipatnikov 2017). Previous studies (Nishiki et al. 2002; Chakraborty et al. 2011) have contributed to this closure problem using datasets based on direct numerical simulations at different operating conditions. The available evidence suggests that the interaction between combustion and the flow’s turbulence depends on the characteristic scales of these processes.

The research of turbulence-chemistry interactions (TCI) performed hitherto has mostly considered combustion under standard conditions, with low pressures and density ratios. Nevertheless, high-pressure flames remain mostly unexplored. As pressure grows, the flame front becomes thinner, and the chemical timescales decrease (Failed 2006). The combustion chamber of a rocket engine is a scenario where such unusual turbulent combustion regimes can appear (Sirignano et al. 1997; Smith et al. 2007). Since turbulence transport in this sort of environment has barely been studied, unique interactions between flame front and turbulent structures might emerge. The present work aims at improving the understanding of the processes that take place in such a context. With this goal in mind, a premixed turbulent flame with the characteristics expected in a rocket engine is simulated. The global transport of vorticity and turbulent kinetic energy along the flame brush is evaluated. In addition, the role of the local flame front geometry in the transport of turbulent properties is examined to investigate the interaction between the different scales. Although rocket engines operate in non-premixed regimes, the results in a premixed context should shed light on relevant phenomena. Nevertheless, it is important to mention that when considering the implications of the present work for actual applications, relevant mixing effects are being filtered out.

The rest of the paper is organized as follows. The next section provides a theoretical background of concepts necessary for discussing the interactions between the flame front geometry and the transport of turbulent properties. This will be followed by a description and justification of the simulation strategy. Finally, the results relevant to the current research question will be presented and discussed.

2 Theoretical Background

It is convenient to reprise certain notions before discussing detailed interactions between the flame front's geometry and the transport of vortical structures and turbulence. The theoretical background for discussing the results of the performed numerical simulation is presented in this section. First, the transport equations for vorticity and turbulence are introduced, and the most relevant elements are briefly described. In the final sub-section, several notions on the topological flame description are introduced, and a diagram for assessing the local flame front’s geometry is proposed.

2.1 Vorticity Transport

The vorticity pseudo-vector \(\mathop{\omega }\limits^{\rightharpoonup}\) represents the infinitesimal circulation of the flow velocity (Guyon et al. 2001; Acheston 1990; Pope 2000). The value of the ith component can be expressed as:

$$\omega_{i} = \varepsilon_{ijk} \partial u_{k} /\partial x_{j}$$
(1)

where \(\varepsilon_{ijk}\) is the Levi-Civita symbol, also known as the cyclic permutation tensor. The associated transport equation can be obtained by taking the curl of the momentum conservation equation:

$$\begin{gathered} \frac{{D\omega_{i} }}{Dt} = \frac{{\partial \omega_{i} }}{\partial t} + u_{k} \frac{{\partial \omega_{i} }}{{\partial x_{k} }} = \underbrace {{\omega_{k} \frac{{\partial u_{i} }}{{\partial x_{k} }}}}_{{S_{{\omega_{i} }} }} - \underbrace {{\omega_{i} \frac{{\partial u_{k} }}{{\partial x_{k} }}}}_{{d_{{\omega_{i} }} }} - \underbrace {{\frac{{\varepsilon_{ijk} }}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{\partial p}{{\partial x_{k} }}}}_{{B_{{\omega_{i} }} }} + \underbrace {{\varepsilon_{ijk} \left( {\underbrace {{\frac{1}{\rho }\frac{{\partial^{2} \tau_{kl} }}{{\partial x_{j} \partial x_{j} }}}}_{{V_{{\omega_{i} }} }} - \underbrace {{\frac{1}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{{\partial \tau_{kl} }}{{\partial x_{l} }}}}_{{F_{{\omega_{i} }} }}} \right)}}_{{D_{{\omega_{i} }} }} \hfill \\ \hfill \\ \end{gathered}$$
(2)

The vectorial nature of vorticity can hinder its interpretation and analysis through conventional visualization methods. This circumstance motivates the introduction of the concept of enstrophy \({\Omega }\), which relates to the fluid particle rotation as a solid body (Pope 2000):

$${\Omega } = {\upomega }^{2} /2{ } = \omega_{i} \omega_{i} /2$$
(3)

The transport equation of enstrophy can be easily obtained after multiplying both sides of (2) by \(\omega_{i}\) (Lipatnikov et al. 2014; Chakraborty et al. 2016; Dopazo et al. 2017; Papapostolou et al. 2017):

$$\begin{gathered} \frac{{D{\Omega }}}{Dt} = \frac{{\partial {\Omega }}}{\partial t} + u_{k} \frac{{\partial {\Omega }}}{{\partial x_{k} }} = \underbrace {{\omega_{i} \omega_{k} \frac{{\partial u_{i} }}{{\partial x_{k} }}}}_{{S_{{\Omega }} }} - \underbrace {{2{\Omega }\frac{{\partial u_{k} }}{{\partial x_{k} }}}}_{{d_{{\Omega }} }} - \underbrace {{\frac{{\varepsilon_{ijk} \omega_{i} }}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{\partial p}{{\partial x_{k} }}}}_{{B_{{\Omega }} }} + \underbrace {{\varepsilon_{ijk} \omega_{i} \left( {\underbrace {{\frac{1}{\rho }\frac{{\partial^{2} \tau_{kl} }}{{\partial x_{j} \partial x_{j} }}}}_{{V_{{\Omega }} }} - \underbrace {{\frac{1}{{\rho^{2} }}\frac{\partial \rho }{{\partial x_{j} }}\frac{{\partial \tau_{kl} }}{{\partial x_{l} }}}}_{{F_{{\Omega }} }}} \right)}}_{{D_{{\Omega }} }} \hfill \\ \hfill \\ \end{gathered}$$
(4)

This equation is deterministic. However, due to the chaotic nature of turbulent flows, it is often useful to perform some sort of averaging to study mean values rather than instantaneous ones. In classical incompressible turbulence, a quantity \(Q\) is typically averaged over time, constituting the so-called Reynolds average \(\overline{Q}\). Due to the existing large density variations, the Favre-average \(\tilde{Q} = \overline{\rho Q} /\overline{\rho }\) (Favre 1969) is better suited to analyze turbulent flames (Pope 1979). Under this consideration, it is possible to rewrite as:

$$\frac{{D{\tilde{\Omega }}}}{Dt} = \widetilde{{S_{{\Omega }} }} + \widetilde{{d_{{\Omega }} }} + \widetilde{{B_{{\Omega }} }} + \widetilde{{F_{{\Omega }} }} + \widetilde{{V_{{\Omega }} }}$$
(5)

The relevance of each of these terms is highly dependent on the context. \(\widetilde{{S_{{\Omega }} }}\) and \(\widetilde{{D_{{\Omega }} }}\) are significant regardless of the density behavior. \(\widetilde{{S_{{\Omega }} }}\) accounts for the eddy stretching due to velocity gradients, and it is the primary mechanism for turbulent energy transfer across scales in classical incompressible turbulence theory (Taylor 2012, 1938; Tenneker and Lumley 1972; Doan et al. 2018). \(\widetilde{{D_{{\Omega }} }}\) describes the impact of viscosity on the fluid flow enstrophy. This term primarily acts as an enstrophy sink mechanism and it is relevant for both constant- and variable-density fluid flows. To isolate the impact of density changes, the dissipation term can be decomposed as \(\widetilde{{D_{{\Omega }} }} = \widetilde{{V_{{\Omega }} }} + \widetilde{{F_{{\Omega }} }}\), where \(\widetilde{{F_{{\Omega }} }}\) is the viscous torque, owing to the misalignments between density and viscous stress gradients The prevalence of this term tends to grow as chemical scales become faster and shorter compared to vortexes (Papapostolou et al. 2017; Chakraborty 2021). The term \(\widetilde{{V_{{\Omega }} }}\) accounts for the combined action of molecular diffusion and dissipation of the Favre-averaged enstrophy \({\tilde{\Omega }}\). These processes can be represented by \(\overline{{\nu \partial^{2} {\Omega }/\partial x_{j}^{2} }}\) and \(\overline{{ - \nu \left( {\partial \omega_{i} /\partial x_{j} } \right)\left( {\partial \omega_{i} /\partial x_{j} } \right)}}\) respectively, if the dynamic viscosity is constant (Dopazo et al. 2017; Chakraborty 2021).

In the presence of density gradients, two additional terms appear in the vorticity transport equations. These are the eddy dilatation \(\widetilde{{d_{{\Omega }} }}\) and the baroclinic torque \(\widetilde{{B_{{\Omega }} }}\), which act mainly as enstrophy destruction and creation sources, respectively. In premixed turbulent combustion, their relevance is dependent on the Karlovitz and Damköhler numbers (Chakraborty 2021). If chemical scales are slow/long compared to turbulent motions, vortex stretching and viscous dissipation are balanced, similar to what is observed in constant-density flows. As the Karlovitz number decreases, the vorticity vector changes its preferential orientation. In particular, the alignment becomes predominant with respect to the direction with the smallest strain rate (most compressive or least extensive) (Chakraborty 2014). Consequently, the transport of vorticity through eddy stretching becomes impaired, and the variable-density terms in (4) become dominant. This decreasing prevalence with increasing Karlovitz numbers has been observed in both experiments (Rising et al. 2020; Kazbekov and Steinberg 2021) and simulations (Chakraborty 2021). A detailed description of the physical motivations for this behavior can be found in a recent work by Chakraborty (Chakraborty 2021).

The baroclinic torque \(\widetilde{{B_{{\Omega }} }}\) is inherently connected to the concept of flame-front wrinkling in subsonic premixed turbulent combustion. Its effect can be elucidated through the differential sensitivity of local density and pressure fields to geometry corrugation. Density gradients are essentially aligned to the local flame-front normal direction even for Lewis number significantly different than unity (Chakraborty et al. 2016). Hence, they are able to capture the locally wrinkled structure. Conversely, pressure gradients filter out the small-scale undulations and tend to align with the large-scale flame shape. The baroclinic torque arises from the misalignments between these gradients, and hence it is more prominent in the corrugated and wrinkled flame regimes (Chakraborty 2021). Recent studies (Failed 2018; Lipatnikov et al. 2019) have addressed the tendency of the baroclinic torque to smooth the flame front, reducing the effective reaction surface and inhibiting the flame velocity. This mitigation of the turbulent flame’s wrinkling with the baroclinic torque has also been observed experimentally (Steinberg et al. 2008).

In variable-density turbulent flows, vortex-dilatation \(\widetilde{{d_{{\Omega }} }}\) usually counteracts the enstrophy generation driven by the baroclinic torque. This is the case in the context of subsonic premixed combustion (Kazbekov and Steinberg 2021), when this term acts mainly as a vorticity sink. The physical motivation behind this transport mechanism is the flow’s expansion caused by rising temperature (Lieuwen and Shanbhogue 2007).

In regimes placed at the south-east of the Peters/Borghi diagram, it has been found that the heat release parameter \(\tau_{\alpha } = \left( {T_{P} - T_{R} } \right)/T_{R}\) has an amplification potential for the variable-density vorticity transport mechanisms (Chakraborty 2014). This point is particularly relevant for high-pressure rocket engines since they operate with high Damköhler numbers using pure oxygen, leading to high adiabatic flame temperatures and density ratios \(\sigma = \rho_{R} /\rho_{P}\). The spatial evolution of the baroclinic torque and eddy dilatation is associated with density and temperature gradients, respectively. Through the progress of a laminar flame, temperature changes are slightly delayed with respect to density (Law 2006). This offset depends on the flame’s geometry, mainly defined through its Lewis and Zeldovich numbers (Law 2006). Hence, the spatial development of these terms through the flame surface’s normal reflects the offset between the evolution of density and temperature.

2.2 Turbulent Kinetic Energy Transport

In fluid flows with significant density variations, the turbulent kinetic energy is defined considering the variance of the Favre velocity fluctuations (Pope 1979):

$$\tilde{k} = \frac{{\overline{{\rho u_{i}^{^{\prime\prime}} u_{i} ^{\prime\prime}}} }}{{2\overline{\rho }}}$$
(6)

Its transport equation can be expressed as (Zhang and Rutland 1995):

$$\begin{gathered} \frac{{\partial \overline{\rho }\tilde{k}}}{\partial t} + \frac{{\partial \overline{\rho }\widetilde{{u_{j} }}\tilde{k}}}{{\partial x_{j} }} = \underbrace {{ - \overline{{\rho u_{i}^{^{\prime\prime}} u_{j}^{^{\prime\prime}} }} \frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }}}}_{{T_{1} }}\underbrace {{ - \overline{{u_{i}^{^{\prime\prime}} }} \frac{{\partial \overline{p}}}{{\partial x_{i} }}}}_{{T_{2} }} + \underbrace {{p^{\prime}\frac{{\partial u_{k}^{^{\prime\prime}} }}{{\partial x_{k} }}}}_{{T_{3} }} + \underbrace {{u_{i}^{^{\prime\prime}} \frac{{\partial \tau_{ij} }}{{\partial x_{j} }}}}_{{T_{4} }} - \underbrace {{\frac{{\partial p^{\prime}u_{i}^{^{\prime\prime}} }}{{\partial x_{i} }}}}_{{T_{5} }} - \underbrace {{\frac{\partial }{{\partial x_{i} }}\left( {\overline{{\frac{1}{2}\rho u_{i}^{^{\prime\prime}} u_{k}^{^{\prime\prime}} u_{k}^{^{\prime\prime}} }} } \right)}}_{{T_{6} }} \hfill \\ \hfill \\ \end{gathered}$$
(7)

The present work is focused on statistically planar premixed flames. Hence, statistical quantities are only transported through the main flame’s propagating direction, and the discussion should be restricted to this assumption.

The term \(T_{1}\) is analog to the classical turbulent production term, and it represents the turbulent transport through mean velocity gradients. \(T_{2}\) represents turbulent production through mean pressure gradients, and it is proportional to the Reynolds average of the Favre velocity fluctuations. The term \(T_{3}\) arises from the correlation between pressure and gradient of Favre velocity fluctuations, and it is referred to in the literature as the pressure dilatation term (Zhang and Rutland 1995; Nishiki et al. 2002; Chakraborty et al. 2011; Chakraborty 2021). The term \(T_{4}\) describes molecular diffusion and viscous dissipation, and it is analog to the dissipation rate. The remaining terms i.e., \(T_{5}\) and \(T_{6}\) describe transport by pressure fluctuations and velocity fluctuations, respectively.

The different terms in (7) present a distinctive behavior in the context of premixed turbulent flames, which requires commenting. The term \(T_{1}\) acts as a turbulence sink contrary to its usual behavior in classical turbulence. This tendency can be easily deduced since the gradient of \(\tilde{u}_{i}\) is positive as the flame accelerates and the components in the Reynolds stress tensor \(\overline{{\rho u_{i}^{^{\prime\prime}} u_{j}^{^{\prime\prime}} }}\) are non-negative. The dissipative effect of \(T_{4}\) is usually enhanced in the context of turbulent combustion. Due to the increase of viscosity through the combustion process, this term plays a significant role in the “destruction” of turbulence, way beyond its effect in a constant density scenario. Because of the significantly different behavior of \(T_{1}\) and \(T_{4}\) in turbulent combustion, it is often assumed that combustion’s net effect is turbulence destruction. Nevertheless, the remaining terms can exceed the losses through \(T_{1}\) and \(T_{4}\) under specific combustion regimes, as discussed in Sect. 0. Zhang and Rutland (Zhang and Rutland 1995) found that the pressure terms in (7) i.e. \(T_{2}\) and \(T_{3}\) are the main sources of turbulent kinetic energy in the Corrugated Flame Regime (CFR) (Peters 2000). Their research was based on 2D direct numerical simulations, but Nishiki et al. (Nishiki et al. 2002) found similar outcomes in a similar 3D setup. The creation of turbulence through \(T_{2}\) and \(T_{3}\) has been consistently observed to be sufficient to overcome the sinks due to \(T_{1}\) and \(T_{4}\) in the CFR. Experiments and simulations in the Thin Reactions Zone (TRZ) and in the Broken Reaction Zones (BRZ) have shown a decrease in turbulent kinetic energy through the flame brush. Chakraborty et al. (Chakraborty et al. 2011) addressed the comprehensive modeling of every term in (7) and studied the influence of the combustion regime on the turbulent transport budget. They theorized that the reason for the observed differences could be explained with the Karlovitz number. For low Karlovitz numbers \(Ka \ll 1\), the Kolmogorov eddies are slow and large compared to the local flame front. In such a case, the acceleration induced by local combustion is confined to a single eddy without interference with other turbulent structures. The combined effect of all local flame-fronts in such a scenario is enhancing the flow’s perturbations, increasing the turbulent kinetic energy. For high Karlovitz numbers, \(Ka \gg 1\), even the smallest vortical structures can disrupt the flame front, masking its local normal acceleration. Consequently, the combustion-driven enhancement of the directionality variability is impaired. This effect, coupled with the increased viscosity, leads to an overall decrease of the turbulent kinetic energy along with the flame brush. This decay of turbulent kinetic energy has been widely reported in combustion regimes operating in north-west regions in the Peters and Borghi diagrams (Peters 2000). The increasing turbulence dissipation with growing Karlovitz numbers can be observed in a recent work by Wang and Abraham (Wang and Abraham 2017), who performed a series of direct numerical simulations with varying Karlovitz numbers in the TRZ. The Lewis number plays a pivotal role in the turbulence-chemistry interactions as well. For low Lewis numbers, reactants diffuse faster than thermal waves. This phenomenon partly decouples the relationship between reactant’s concentration and temperature. Consequently, a higher occurrence of large amounts of reactants/products at high/low temperatures can be observed. These events promote flame wrinkling enhancement, yielding a trend of growing baroclinic torque with decreasing Lewis number (Chakraborty 2021).

2.3 Flame Front Topology

Flame topology has been used to investigate the properties of turbulent flames in previous research (Dopazo et al. 2006, 2014). Two main frameworks can be considered to characterize a curved geometry in space. One possibility is to study the local principal curvatures as described by Dopazo et al. (Dopazo et al. 2007). The other approach is based on shape factors that originate from the eigenvalues of the local Hessian matrix, as detailed by Griffiths et al. (Griffiths et al. 2015). The latter method describes the geometry more accurately but lacks relation to actual length scales. Therefore, shape factors are more appropriate for describing events and phenomena, and local curvatures better measure geometries. The quantification of geometries is more relevant in the frame of the present work. This is because several concepts such as local wrinkling and area enhancement are related to the transport of the properties previously discussed. Therefore, the discussion on flame front topology henceforth will be based on the analysis of principal curvatures.

The local evolution of the combustion process at a given position\(\mathop{x}\limits^{\rightharpoonup} = \left( {x_{1} ,x_{2} ,x_{3} } \right)\) is assessed with the progress variable \(c\), which is defined as:

$$c\left( {\mathop{x}\limits^{\rightharpoonup} } \right) = \frac{{Q\left( {\mathop{x}\limits^{\rightharpoonup} } \right) - Q_{r} }}{{Q_{p} - Q_{r} }}$$
(8)

where \(Q(\mathop{x}\limits^{\rightharpoonup} )\) is the value of a given quantity at \(\mathop{x}\limits^{\rightharpoonup}\) and \(Q_{p}\) and \(Q_{r}\) denote the values of this quantity for the products and the reactants, respectively. Hence, \(c = 0\) corresponds to the unburnt mixture and \(c = 1\) to the products. Temperature, density, or species concentration are examples of common quantities used to define \(c\). The chosen variable should be representative of the combustion development and present monotonic behavior. As long as these requirements are met, the value of the progress variable will remain physically meaningful. If we consider a point in the flame front, where \(0 < c < 1\), it is possible to define the local direction in which the flame propagates as:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} } \right) = {{ - \nabla c\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} } \right)} \mathord{\left/ {\vphantom {{ - \nabla c\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} } \right)} {\left| {\nabla c\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} } \right)} \right|~}}} \right. \kern-\nulldelimiterspace} {\left| {\nabla c\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} } \right)} \right|~}}$$
(9)

This unit vector defines a plane in whose contained directions the gradient of the progress variable at \(\mathop{x}\limits^{\rightharpoonup}\) vanishes. Nevertheless, second and higher-order spatial derivatives are not necessarily zero. These derivatives are related to the curvature of the flame front \(\kappa\). Its value is dependent on the direction considered within the plane and can be expressed as:

$$\kappa \left( {\mathop{x}\limits^{\rightharpoonup} ,\mathop{s}\limits^{\rightharpoonup} } \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left( {\mathop{n}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} + h\cdot\mathop{s}\limits^{\rightharpoonup} } \right) - \mathop{n}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} } \right)} \right)\cdot\mathop{s}\limits^{\rightharpoonup} }}{h}$$
(10)

where \(\mathop{s}\limits^{\rightharpoonup}\) is a unit vector contained in the plane defined by \(\mathop{n}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} } \right)\). The sign of \(\kappa\) indicates whether the geometry is concave or convex. It is possible to write \(\mathop{s}\limits^{\rightharpoonup}\) as:

$$\mathop{s}\limits^{\rightharpoonup} = \cos \left( \theta \right)\cdot\mathop{t}\limits^{\rightharpoonup} _{1} + {\text{sin}}\left( \theta \right)\cdot\mathop{t}\limits^{\rightharpoonup} _{2}$$
(11)

where \(\mathop{t}\limits^{\rightharpoonup} _{i}\) are tangent vectors that conform to an orthonormal basis with \(\mathop{n}\limits^{\rightharpoonup} \left( {\mathop{x}\limits^{\rightharpoonup} } \right)\). The value of \(\kappa\) stated in (10) depends on the considered direction \(\mathop{s}\limits^{\rightharpoonup}\) which is defined by the angle \(\theta\). It can be demonstrated, that for a continuous surface, there are values for \(\theta\) which lead to local minimums and maximums of \(\kappa\). These angles correspond to the principal directions, and they are orthonormal to each other. A conical surface such as a cylinder is an excellent example to illustrate the concept of main directions. If we consider a point over a cylindrical surface with a radius \(r_{c}\), it is easy to see that the curvature will be \(0\) if we consider a direction parallel to the cylinder’s axis, and it will peak at \(1/r_{c}\) if the considered direction is perpendicular to the axis. These maximum and minimum curvatures of a surface are \(\kappa_{1}\) and \(\kappa_{2}\) respectively, and they suffice to characterize the curvature of a surface. Alternatively, it is possible to use the Gaussian curvature \(\kappa_{g} = \kappa_{1} \kappa_{2}\) and the mean curvature \(\kappa_{m} = \left( {\kappa_{1} + \kappa_{2} } \right)/2\). With these parameters, it is possible to approach the assessment and characterization of wrinkled turbulent flame fronts.

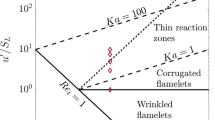
To illustrate the meaning of a given pair of principal curvatures \(\left\{ {\kappa_{1} ,\kappa_{2} } \right\}\) a classification diagram of the possible geometries is represented in Fig. 1. The axes in this diagram are normalized with the laminar flame front thickness. This sort of arrangement provides valuable information concerning the wrinkling magnitude. Several regions can be identified in the diagram displayed Fig. 1. The condition \(\kappa_{1} = \kappa_{2}\) corresponds to the case in which the curvature is constant, independently of the considered direction. This circumstance relates to a sphere-like geometry. The regions where \(\kappa_{1} < \kappa_{2}\) remain inaccessible since the first curvature is larger than the second one by definition i.e. \(\kappa_{1} \ge \kappa_{2}\). The remaining area in the first and third quadrants corresponds to geometries with positive Gaussian curvatures, i.e. \(\kappa_{g} = \kappa_{1} \kappa_{2} > 0\). This condition corresponds to ellipsoidal geometries. Whenever one of the two principal curvatures vanishes, the Gaussian curvature becomes zero, and the considered surface is conical. The fourth quadrant corresponds to surfaces with negative Gaussian curvature, which implies that the surface can be convex or concave depending on the assumed direction. Good examples of such geometries are hyperboloids and other saddle-like structures. This sort of diagram will be used to assess the joint functions for enstrophy and turbulent kinetic energy transport terms for analyzing the results of the performed simulation.

Fig. 1
figure 1

Flame front geometry classifications as a function of the principal curvatures \(\kappa_{1}\) and \(\kappa_{2}\)

Full size image

3 Numerical Simulation Case Setup

A standing premixed turbulent flame is simulated numerically with the reactive solver EBI-DNS (Zhang et al. 2015; Failed 2018, 2019, 2021), based on the open-source software OpenFOAM (Weller et al. 1998, 2017). This software solves the conservation equations for mass, momentum, energy, and species in compressible flows using the Finite Volume Method (FVM) (Mcdonald 1971; Failed 1972). The used solver was applied and validated in several combustion-related problems (Zhang et al. 2017, 2020, 2017; Zirwes et al. 2021, 2019). Cantera (Goodwin et al. 2017) was used for the detailed chemistry and transport properties computation, using the mixture-averaged transport model described by Kee et al. (Kee et al. 2005). The skeletal mechanism developed by Slavinskaya et al. (Salavinskaya and Haidn 2008) is used to determine the reactions rates of methane combustion using the finite rates method. This reaction mechanism consists of 21 species and 97 reactions, and it was developed aiming at high-pressure space propulsion applications. Synthetic turbulence from a precursor simulation is introduced at the inlet with the strategy described in (Martinez-Sanchis et al. 2022). The mean inlet velocity is controlled to stabilize the mean flame front location at a target position with the algorithm described in (Martinez-Sanchis and A, 2021). The used flame regulation mechanism ensures starting the mean flame brush after enough length to allow turbulence development. The turbulent velocity field prior to combustion can be characterized with an integral length scale \({\Lambda }_{{\text{R}}}\) and the root-mean-square of the velocity fluctuations \(u_{R}^{^{\prime}}\). Turbulence in this region is homogeneous and presents rotational invariance. These parameters were calculated at a position right before combustion starts (\(\tilde{c} = 0.005\)). The flow properties were selected to resemble the output of RANS simulations for a scale methane rocket combustor discussed elsewhere (Failed 2018). It would be desirable to perform the simulation at higher pressure, but that would yield a prohibitive thin flame front in terms of computational cost.

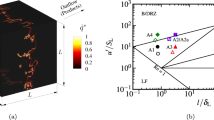
Periodicity is imposed in two directions, which are perpendicular to the main propagation direction of the flame. The domain presents an aspect ratio of 4, amounting 392 × 392 × 1568 cells with constant geometry. The size with which periodicity is enforced corresponds to 6.45 times the integral eddies length scale Fig. 2 depicts an example of instantaneous results for the simulated flame. In this illustration, the density ratio \(\rho_{R} /\rho\) and the normalized second invariant \(Q = \left( {{\Omega }_{{{\text{ij}}}}^{2} - {\text{S}}_{{{\text{ij}}}}^{2} } \right)/{\Omega }_{{{\text{ij}}}}^{2}\) (Jeong and Hussain 1995), with \(S_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)\) are displayed. The figure’s bottom corresponds to the turbulent inlet and the top to the system’s outlet, where a zero-gradient boundary condition is imposed. The periodicity condition is applied in the lateral edges (Plane XY). As it can be observed, the flame front is located far away from both the inlet and the outlet. This setup is achieved by the flame regulation system to maximize the observability of the turbulence development. The change of the vortex shapes can be studied by attending to the normalized second invariant. Positive values indicate the presence of eddies, with the likelihood increasing as \(Q/{\Omega }^{2}\) tends to unity. The vortical structures’ evolution as they traverse the flame front is rather evident, illustrating the drastic effects that chemistry has on the turbulence characteristics.

Fig. 2
figure 2

Example of instantaneous results for the performed simulation: Density ratio (b), normalized second invariant (b)

Full size image

The simulated flame arises from the stoichiometric combustion of premixed gaseous methane and oxygen at 20 bar. The chemical mechanism used is the one developed by Slavinskaya et al. (Slavinskaya et al. 2015), which consists of 24 species and 100 reactions. The laminar flame speed and thickness obtained in 1D stationary simulations with this mechanism are denoted as \(s_{L}\) and \(\delta_{L}\) respectively. The turbulent Damköhler number \(Da_{T} = {\Lambda }s_{L} /u^{\prime}\delta_{L}\), the Karlovitz \(Ka = \left( {\delta_{L} /\eta } \right)^{2}\), and the turbulent Reynolds number \(Re_{T} = \left( {{\Lambda }u^{\prime}} \right)/\nu\), are presented in Table 1 among other relevant parameters. The Kolmogorov eddies are resolved with at least 1.5 cells everywhere in the domain, satisfying the recommended value (Yeung and Pope 1987) by a factor of 3. The laminar flame front is resolved with 10.7 cells. It would be desirable to use a higher resolution (about 20 cells) to capture the detailed chemistry effects (Poinsot and Veynante 2005; Poludnenko and Oran 2010). However, such a configuration was not chosen as it would imply prohibitive computational costs. Regarding the simulated time span, the simulation was run for 7.62 times the reference timescale. The integral eddy turnover time of the reactants \(t_{R} \approx 7.87 \mu s\) was taken as reference since it constitutes a worst-case scenario due to the decrease of the eddy timescales through the flame brush. Data for the fields of velocity, pressure, density, temperature, and species concentration was collected 15.74 times per each reference eddy turnover time i.e. every \(0.5 \mu s\). In total, results for 120 time-steps were saved. The averaged results presented in the following section were computed using these data. This averaging process is done in both time and the plane perpendicular to the main flame’s propagation direction.

Table 1 Main turbulent and combustion parameters of the simulated flame
Full size table

4 Results Analysis

The present paper aims to study the interactions between flame geometry and the transport of turbulent kinetic energy and enstrophy. Since topology is a local and instantaneous process, most of the presented data is averaged for specific values of the instantaneous progress variable instead of through the flame brush. This is the general case for every figure in this section unless otherwise stated.

The principal curvatures are the main analysis tool for assessing the flame front geometry. These curvatures were calculated for various values of the progress variable. With this information, it is possible to observe the effects of the different geometries illustrated in Fig. 1. An example of this sort of result can be visualized in Fig. 3. Here, the joint probability density function of the observed flame’s principal curvatures is presented for different values of the progress variable. As it can be seen, the majority of realized curvatures are characterized by a rather large flame radius \(r_{f} > 5\delta_{L}\). For large radius, conical topologies become predominant in detriment of spherical structures and geometries with negative Gaussian curvature. Progressing towards the reaction products drives a flame topology smoothing process. This behavior is caused by the self-flattening tendency of expanding topologies with negative curvatures. For stable flame configurations, the stretching rate tends to counter the flame curvature. This predisposition becomes effective only when the local flame thickness is larger than the local radius since the aerodynamic stretching can be rendered negligible. The dependency on \(c\) is an important feature of the postprocessed results. Nevertheless, for the sake of conciseness and simplicity, most results are presented for intermediate progress variable values. Whenever pertinent, the variations towards the reactants and/or the products are commented on.

Fig. 3
figure 3

2D joint probability density function as a function of the principal curvatures for different values of the progress variable: \(0.04 < c < 0.06\) (a), \(0.5 < c < 0.52\) (b), \(0.9 < c < 0.92\) (c)

Full size image

The rest of this chapter is structured as follows. First, the results for vorticity and turbulent transport are presented in 0 and 0. Subsequently, the physical meaning behind the observed outcomes is discussed in 0. Finally, a brief outlook concerning future implications based on the observed results is presented in 0.

4.1 Enstrophy Transport

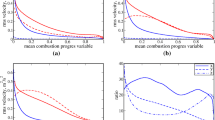
The Favre-averaged values for the different elements in the enstrophy transport equation, as a function of the instantaneous progress variable, are displayed in Fig. 4. The local vorticity transport is essentially a competition between the baroclinic torque \(\widetilde{{B_{{\Omega }} }}\) and the eddy dilatation \(\widetilde{{d_{{\Omega }} }}\). Both terms peak for intermediate values of \(c\), which is where the density gradients are maximal. Although these terms are apparently dominant, they nearly cancel out each other. Consequently, eddy stretching \(\widetilde{{{\text{S}}_{{\Omega }} }}\) and dissipation \(\widetilde{{D_{{\Omega }} }}\) play a major role in the total enstrophy budget, acting as tie-breakers. Towards products, vortex dilatation overtakes the baroclinic torque. This behavior originates from the large heat release in the reactions zone, which enhances the enstrophy annihilation through vortex dilatation. The local trends displayed in Fig. 4 may differ significantly with respect to the evolution through the flame brush. The reason behind this potential mismatch is the high skewness characterizing probability distributions of the progress variable.

Fig. 4
figure 4

Enstrophy transport as function of the local progress variable: Total enstrophy transport (a), Individual components (b)

Full size image

For this reason, the averaged transport terms were calculated along with the flame brush as well. The result is displayed in Fig. 5. This figure illustrates a very similar outcome with regards to the dominating effects. Nevertheless, in this case, the global effect of the flame is an enstrophy decline. The reason behind this is the mentioned high skewness of the reaction progress probability density function. High values of \(c\) are more frequent than intermediate ones, and therefore, they bear a higher weight overall. Since such values promote the destruction of vorticity, as seen in Fig. 4, their higher prevalence implies that the combustion process, observed globally, acts as an enstrophy sink. Another remarkable difference between both graphs concerns the variations in the order of magnitude. Normalized local observations can be in the order of 300, whilst averaged values do not exceed 30. This offset is motivated by the fact that the reaction sheet is very small compared to turbulent scales. This claim can be verified by observing the local flame front thickness in Fig. 2 and Fig. 6. Consequently, at a given position within the mean flame brush, the majority of points belong to either completely burnt or unburnt positions. Therefore, the values at midflame positions presented in Fig. 4 carry a limited effect overall.

Fig. 5
figure 5

Fravre-averaged enstrophy transport along with the flame brush: Total enstrophy transport (a), Individual components (b)

Full size image
Fig. 6
figure 6

Comparison between flame front orientation and enstrophy: density ratio (a), enstrophy (b)

Full size image

An example of instantaneous enstrophy can be visualized in Fig. 6(b). This field originates from the integration of all transport terms over time. This fact should be taken into account when discussing the implications of these results concerning the coupling between the flame’s geometry and vorticity. Nevertheless, it is possible to introduce relevant trends that are detailed later in this paper. In the regions where the local flame front progresses in the main flame propagation direction, a significant enstrophy drop can be observed. This decrease originates from the alignment of density gradients with viscous stress and pressure gradients. This configuration restricts the capability of viscous and baroclinic torques for inducing a coherent spinning in the fluid. The opposite scenario corresponds to the regions where the local flame front is perpendicular to the main flame propagation’s direction. The outcome, in this case, is quite the opposite, with large enstrophy budgets begotten by the continued action of baroclinic and viscous torques. Certain pockets of high enstrophy can be observed in regions far away from the instantaneous turbulent flame front. These values constitute relics from previous deflagrations, which have been advected downstream.

To further investigate the discussed trends, the enstrophy transport terms were studied for progress variable isosurfaces. An example of the instantaneous enstrophy transport through the flame front can be observed in Fig. 7. This graph illustrates the tight coupling between the different transport terms and the local geometry. It can be noticed that the isosurfaces of each term are associated with specific geometries (i.e. changes in values are bound to variations in the principal curvatures). The different transport terms present higher values at positions where the local curvature is largest. These variations originate from the enhancement of the heat transport due to surface-to-volume ratio increases. As curvature increases, the local consumption of propellants grows, leading to higher displacements speeds and greater prevalence of the variable-density transport mechanisms. Both sink and source terms are influenced to a similar degree by this process, although some existing differences will be commented on later in this chapter. Additional factors should be taken into account to understand the instantaneous total enstrophy budget. One of the most determinant agents seems to be the local flame front orientation. Where the local flame front has a horn-like shape, the outer surface is oriented perpendicularly to the main flame propagation’s direction. This configuration leads to high values for the baroclinic and viscous torques, yielding net positive enstrophy generation. Curvature may enhance or dampen the original predisposition, driven by the flame front orientation.

Fig. 7
figure 7

Example of instantaneous local vorticity transport for \(0.5 < c < 0.52\): Vortex stretching (a), vortex dilatation (b), baroclinic torque (c), viscous dissipation (d), viscous torque (e), total enstrophy transport (f)

Full size image

To study these relationships in more detail, the average values of the enstrophy transport terms as a function of the two principal curvatures were calculated. The result is displayed in Fig. 8. This graph suggests that the global competition between dilatation and baroclinic torque occurs at nearly every existent topology. Discerning causality in these graphs can be remarkably challenging.

Fig. 8
figure 8

Enstrophy budget across the different local flame geometries for \(0.5 < c < 0.52\): Vortex stretching (a), vortex dilatation (b), baroclinic torque (c), viscous dissipation (d), viscous torque (e), total enstrophy transport (f)

Full size image

The intensity of variable-density enstrophy transport terms is strongly coupled with the principal curvatures. Quasi-cylindrical geometries appear to be the most suitable configurations for the thriving of vortex dilatation and baroclinic and viscous torques. The increasing intensity with curvature aligns with the previously discussed heat transfer enhancement. Nevertheless, the coupling between geometries and flame front orientation also plays a significant role. The horn-like and quasi-cylindrical geometries are prone to have their axes aligned with the mean flame propagation direction, as seen in Fig. 7. This limits the disturbing effects due to incoming flow as most of it is already aligned with the flame front. Hence, disturbances to the large-scale topology are mainly restricted to turbulent shear. Similar geometries with perpendicular orientations are bound to be unstable since the aerodynamic disturbances are significantly larger. These effects generate a conditionality on orientation which is implicitly embedded in each graph of Fig. 8.

4.2 Turbulent Kinetic Energy

The interaction between the flame front topology and the transport of turbulent kinetic energy is studied to continue the analysis of the performed simulation. We first focus on the transport of turbulent kinetic energy through the flame brush. The overall turbulent transport budget is displayed in Fig. 9. As it can be seen, there is a large net generation of turbulent kinetic energy. This process is apparently concentrated at the intermediate positions within the flame brush, with turbulence dissipation occurring towards the brush end. The RMS of the Favre-fluctuations for velocity in each direction is represented in Fig. 9 in addition. This graph illustrates the anisotropic nature of the turbulent kinetic energy generation through the combustion process.

Fig. 9
figure 9

Evolution of the root mean square of the Favre averaged velocity fluctuations: Total turbulent kinetic energy transport (a) RMS of Favre-fluctuations for each velocity component (b)

Full size image

The measured increase in turbulent kinetic energy has not been observed in previous simulations with similar coordinates in the Borghi/Peters diagram. The fact that the Kolmogorov vortexes are significantly smaller than the flame front denotes that length scales are not the only driver in the TCI differences observed through different regimes. One possible explanation is that the Kolmogorov to flame velocity ratio is below unity i.e. \(u_{\eta }^{2} /s_{L}^{2} = 0.25 < 1\). Hence, although Kolmogorov eddies are small enough to penetrate the flame front, they are too slow to veil the effects of thermal expansions. This is in line with the hypothesis stated by Chakraborty et al. (Chakraborty et al. 2011).

To study the coupling between the observed increase in turbulent kinetic energy and the flame’s geometry, the root mean square of the velocity Favre perturbations \(u_{rms}^{^{\prime\prime}} = \sqrt {\overline{{u_{i}^{^{\prime\prime}} }} }\) was calculated for each observed combination of principal curvatures. The result for two different intervals of the progress variable is presented in Fig. 10. This diagram reveals that the turbulent kinetic energy enhancement is concentrated at specific topologies. The observed growth coincides with the same principal curvatures where variable-density enstrophy transport mechanisms are more relevant in Fig. 8. Indeed, a statistical analysis reveals that \(\widetilde{{B_{{\Omega }} }}\) and \(\widetilde{{d_{{\Omega }} }}\) can be used as predictors for the increase in TKE with \(R^{2} > 0.8\).

Fig. 10
figure 10

Change of the root mean square of the Favre velocity perturbations at intermediate local positions of the progress variable

Full size image

Algebraical impairments prevent the comprehensive analysis of each turbulent transport term solely conditioned to the flame front curvatures. Several elements in (7) contain applications on averaged properties e.g. \(\partial \overline{p}/\partial x_{i}\). This fact complicates the results examination since an implicit dependency on the mean position across the flame brush is introduced. Consequently, the observed values are not only caused by curvature itself, but they also depend on where the curvature is placed within the flame brush. The PDF of a given curvature with respect to the position across the flame, conditioned to the other involved variables, should be considered for any combination of \(\kappa_{1}\) and \(\kappa_{2}\). This would significantly entangle the analysis, obscuring the result’s interpretation. For this reason, the analysis of the individual transport terms will be restricted to those elements in which only a dependency on flame front curvature itself is present. After a detailed examination of (7), only \(T_{3}\). and \(T_{5}\) can be approached resorting to the same method as the vorticity terms. The term \(T_{5}\) can be rewritten as (Chakraborty et al. 2011):

$$T_{5} = - \overline{{\frac{{\partial \left( {p^{\prime}u_{i}^{^{\prime\prime}} } \right)}}{{\partial x_{i} }}}} = - \overline{{p^{\prime}\frac{{\partial u_{i}^{^{\prime\prime}} }}{{\partial x_{i} }}}} - \overline{{u_{i}^{^{\prime\prime}} \frac{\partial p^{\prime}}{{\partial x_{i} }}}} = - T_{3} - \overline{{u_{i}^{^{\prime\prime}} \frac{\partial p^{\prime}}{{\partial x_{i} }}}}$$
(12)

Hence, the addition of \(T_{3}\) and \(T_{5}\). can be simplified as:

$$T_{3} + T_{5} = T_{PFG} = - \overline{{u_{i}^{^{\prime\prime}} \frac{\partial p^{\prime}}{{\partial x_{i} }}}}$$
(13)

The value of these turbulence transport terms as a function of the flame front's principal curvature is displayed in Fig. 11. In this graph, both time-averaged and instantaneous values are shown. For unburnt locations, little coherence between the velocity and pressure gradient fluctuations can be observed. This effect yields near-zero turbulence transport, as expected in the unburnt positions. Nevertheless, for intermediate flame positions, a significant generation of turbulence can be observed. This positive turbulent transport is concentrated in the regions where an increase of turbulent kinetic energy is observed in Fig. 10. This fact indicates that \(T_{PFG}\) is one of the main responsible elements for the increase of turbulent kinetic energy through the local flame front. The coupling between curvature and \(T_{PFG}\) is quite evident from the results in Fig. 11(a) and(b). Quasi-cylindrical geometries conform hspots of turbulent kinetic energy generation. The reasons for this behavior are discussed in detail in Sect. 0.

Fig. 11
figure 11

Pressure dilatation term as a function for the different realized curvatures for \(0.5 < c < 0.6\)

Full size image

To ease the challenging interpretation of Fig. 11, it is convenient to decompose \(T_{PFG}\) as a product of the standard deviations of the involved variables and their mutual correlation coefficient:

$$T_{PFG} = - \sqrt {\overline{{u_{i}^{^{\prime\prime}2} }} } \sqrt {\overline{{\frac{\partial p^{\prime}}{{\partial x_{i} }}^{2} }} } r\left( {u_{i}^{^{\prime\prime}} ,\frac{\partial p^{\prime}}{{\partial x_{i} }}} \right) = - u_{rms}^{^{\prime\prime}} p_{rms,g}^{^{\prime}} r_{PFG}$$
(14)

These three individual terms are presented in Fig. 12. The RMS of the fluctuating pressure gradient is normalized with the mean pressure gradient through the Turbulent Flame Brush (TFB) i.e. \({\Delta }P_{TFB} /\delta_{TFB}\). The root mean square of the Favre velocity fluctuations \(u_{rms}^{^{\prime\prime}}\) plays a minor role since its value remains fairly independent of geometry. Hence the value of \(T_{PFG}\) is primarily driven by the root mean square of fluctuating pressure gradients and their correlation with \(u_{rms}^{^{\prime\prime}}\). The magnitude of turbulent generation is mainly provided by \(p_{rms,g}^{^{\prime}}\). The correlation between velocity and pressure fluctuation gradients presents a nearly bimodal distribution, driven by the curvature sign. The following section details the physical motivations behind the observed results.

Fig. 12
figure 12

Individual components of the pressure fluctuation gradient transport term: RMS of velocity fluctuations (a), RMS of gradient of pressure fluctuations (b), correlation coefficient between velocity fluctuations and gradients of pressure fluctuations (b) for \(0.5 < c < 0.52\)

Full size image

4.3 Interaction Analysis

The dependency of vorticity and turbulent transport on the principal curvatures has been presented in the text above. In this section, the coupling between both processes associated with the flame front topology is interpreted. Some abbreviations will be introduced for the sake of clarity in the discussion. \(\widetilde{{C_{{\Omega }} }} = \widetilde{{B_{{\Omega }} }} + \widetilde{{d_{{\Omega }} }}\) denotes the combination of baroclinic torque and vortex dilatation. The discussion will focus on these terms and the turbulence generation through pressure fluctuations gradients i.e. \(T_{PFG} = T_{3} + T_{5}\), at mid-flame positions \(c \approx 0.5\). To study the relationship between \(\widetilde{{C_{{\Omega }} }}\) and \(T_{PFG}\), they are plotted, including their dependencies on Gaussian and mean curvatures. This result is presented in Fig. 13. The presence of two different dependency regimes can be observed. The first regime corresponds to flame fronts with positive local Gaussian and mean curvatures, and it exhibits \(T_{PFG}\) values close to zero. The second regime is associated with negative Gaussian curvatures and mean curvatures ranging from moderate to negative. It is in this regime where most of the turbulent kinetic energy is generated. In the present text, the first regime will be denoted as “divergent regime” and the second as “convergent regime”. This wording is chosen to illustrate the nature of flame propagation.

Fig. 13
figure 13

Relationships between baroclinic torque and vortex dilatation with the turbulent transport through fluctuating pressure gradient, and their dependence on the Gaussian (a) and mean curvatures (b) for \(0.5 < c < 0.52\)

Full size image

The detailed discussion of Fig. 13 requires introducing some considerations concerning the interactions between local geometry and diffusion processes. The local curvature influences mass and heat transfer processes, and it can be beneficial or detrimental for flame propagation depending on the context (Lipatnikov 2012). In the most general case, the factors to consider are Lewis number, equivalence ratio, and differential mass diffusivity of oxidizer and reactants. Mass diffusion is relevant if Lewis number is below unity, oxidizer and fuel present large differences in mass diffusivity, and \(\phi\) is far from the one that maximizes flame speed. This is not the case in the current simulation since \(Le \approx 1\), \(\phi \approx \phi \left( {s_{L\max } } \right)\) and the mass diffusivity of \(O_{2}\) and \(CH_{4}\) are similar. Some species present individual Lewis numbers below unity, which may indicate the relevance of differential diffusion processes. Nevertheless, since the mass fraction of these species is negligible, it can be assumed that heat transfer effects dominate globally, and they suffice to understand the curvature effects. Therefore, the discussion within the present work’s frame can be restricted in terms of heat diffusion. If the flame propagates “inwards”, the heat fluxes mutually converge, improving heat transfer and enhancing the local flame speed. The opposite effects result in an “outwards” propagation of the burnt mixture as heat fluxes defocus. The reader can find a detailed description of all these processes in (Zirwes 2016). To illustrate the effects relevant in the present work, the displacement speed \(s_{d} = - \left( {Dc/Dt} \right) \cdot \left| {\nabla c} \right|\) as a function of the flame curvature was calculated. The result is displayed in Fig. 14(a). This graph’s top corresponds to divergent flame propagation and hence presents the lowest flame speeds due to the heat loss enhancement. As one moves to the bottom, flame propagation becomes convergent with increasing curvature, and the displacement speed experiences an increase accordingly. The correspondence with instantaneous values is rather evident, as shown in Fig. 14(b). \(\widetilde{{C_{{\Omega }} }}\) is highly dependent on these effects as well. Since vortex dilatation is related to temperature, it increases (becomes more negative) with heat transfer enhancement in convergent configurations, leading to lower values of \(\widetilde{{C_{{\Omega }} }}\).

Fig. 14
figure 14

Displacement velocity for \(0.5 < c < 0.52\): Mean value as a function of the principal curvatures (a), example of instantaneous values (b)

Full size image

The two regimes in Fig. 13 can be easily explained by the above-described effects. The divergent regime is characterized by a convex reaction surface, with warm products surrounded by cold reactants. The Gaussian and mean curvatures are positive, and as they grow, the turbulent generation due to pressure fluctuations gradients decline. This behavior can be explained with analogies to planar and spherical flames. Planar flames experience a pressure drop that increases with growing inflow velocities. This originates a negative correlation between velocity fluctuations and pressure gradients, leading to positive values \(T_{PFG}\). In spherical flames, pressure increases as the flame front propagates (Chen et al. 2009), generating the opposite effect. The decrease of \(T_{PFG}\) with increasing the mean curvature is linked to the transition from quasi-planar to spherical propagation regimes. The increase of \(\widetilde{{C_{{\Omega }} }}\) with increasing curvature is a consequence of the enhanced heat losses due to the divergence of heat fluxes that limit vortex dilatation.

In the convergent regime, inwards flame front propagation exists since at least one of the principal curvatures is negative. As the topology becomes more convergent, \(T_{PFG}\) increases and \(\widetilde{{C_{{\Omega }} }}\) decreases. The turbulence generation in this regime arises from the conflicting trajectories of the local thermal expansions. As the thermally expanded gas propagate towards one another, dynamic pressure is converted into static pressure originating a positive gradient in the latter. This motivates the negative correlation between \(u_{i}^{^{\prime\prime}}\) and \(\partial p^{\prime}/\partial x_{i}\). As the topology becomes more convergent, the flame speed increases and the pressure gradients scale accordingly. It is important to note that the correlation between fluctuating pressure gradients and velocity fluctuations remains fairly constant in this region, as noted in Fig. 12. Hence, the main driver of the increase of \(T_{PFG}\) is the enhancement of the root mean square of \(\partial p^{\prime}/\partial x_{i}\). This increase is motivated by the enhancement of the displacement speed \(s_{d}\). Since pressure fluctuations scale with the square of the laminar flame speed (Zhang and Rutland 1995; Nishiki et al. 2002) their gradient’s variance is expected to grow accordingly. This claim can be validated by observing the nearly identical trends of the result displayed in Fig. 14 with the one presented in Fig. 12 for \(p_{rms,g}^{^{\prime}}\). The other side-effect of increasing the convergent geometry of the flame front is the decrease in \(\widetilde{{C_{{\Omega }} }}\). This effect can be explained with the enhancement of the eddy dilatation \(\widetilde{{d_{{\Omega }} }}\) due to the increased heat transfer.

4.4 Outlook and Future Work

The prediction of \(T_{PFG}\) is particularly relevant in the context of modeling the statistics of turbulent kinetic energy transport to achieve closure of (7). This term is one of the main sources of turbulence, and the models proposed to this date are somewhat deficient (Chakraborty et al. 2011). Since the relationships measured in the performed simulation seem rather simple, modeling strategies based on the discussed phenomena can be explored.

The results of the present study show that it is possible to model the term \(T_{PFG}\) as a function of curvature resorting linear models. This result is, in principle, expectable since definitions of classical heat transfer parameters such as the Nusselt number \(Nu\) are often linearly dependent on characteristic lengths. The main challenge relies on finding the sensitivity constants since they may be dependent on the chosen fuel and transport properties.

The way for closure of the turbulent kinetic energy transport equation entails several additional challenges. Determination of the joint probability density functions for the principal curvatures is required. This step has not been explored yet, and it is likely to imply significant challenges. Furthermore, the discussed enhancement of \(T_{PFG}\) in the convergent regime assumes that chemically driven thermal expansions are fast compared to existing vortical structures. Slower chemistry might not be able to reproduce the observed correlation between velocity fluctuations and pressure gradients. Hence, a general formulation should include a dependency on the turbulent Damköhler number \(Da_{T}\). Differential mass diffusion constitutes an additional challenge for the modeling of this term. This effect was not relevant in the present work due to the chosen combination of reactants. Nevertheless, in other scenarios, mass diffusion processes must be considered to describe the interactions discussed in this paper.

5 Conclusion

A premixed methane-oxygen turbulent flame was studied using direct numerical simulations with finite rate detailed chemistry. The flow characteristics were selected to approach the conditions encountered in modern rocket combustion chambers to investigate the turbulence dynamics in such an extreme environment. Enstrophy and turbulent kinetic energy transport were evaluated both locally and globally. It was found that the flame presents characteristics typical of the corrugated flame regimes; although attending to the flow’s characteristics, it belongs to the thin reactions zone. The most prominent result is the significant generation of turbulence through the mean flame brush. The origin of this phenomenon was investigated by resorting to the flame’s local curvature. It was found that specific flame front topologies control the pressure fluctuating gradient, which constitutes one of the major turbulence sources within the flame brush.

Depending on the flame propagation direction, two different regimes for turbulence creation were observed. In the case of outwards propagation, turbulence can be generated in quasi-planar surfaces due to the pressure drop that characterizes weak deflagrations. This effect can be reverted if the topology becomes wrinkled enough. If the flame propagation occurs inwards, dynamic to static pressure conversion induces the correlation between pressure gradients and velocity fluctuations. In this case, as curvature increases, the heat transfer and flame speed are enhanced, amplifying the turbulence generation. This curvature’s magnitude determines the outcome of the competition between baroclinic torque and vortex dilatation. Since the flow’s thermal expansion drives the vortex dilatation, it benefits from enhanced heat diffusion. Consequently, as the local flame’s curvature becomes larger, the amount of enstrophy generated by the baroclinic torque becomes outbalanced by the vortex dilatation.

These results suggest that the small-scale interactions between turbulence and chemistry can dominate the integral effects of chemistry in the turbulent flow’s dynamics. Such finding may have far-reaching implications, as it implies a limited validity of integral scales to assess vortex-flame interactions.