Abstract
We consider a decision making problem under imprecision, where the probabilistic information is given in terms of a set of probability measures, and where finding the optimal alternative(s) may be difficult. To ease the computation, we propose to transform the initial model into another one that (1) belongs to some subclass with better mathematical properties, such as supermodularity or complete monotonicity; (2) is at least as informative as the original model, while being as close as possible to it. We show that the problem can be approached in terms of linear or quadratic programming and that it can be connected with the one of determining the incenter of a credal set. Finally, we compare the solutions of a decision making problem with the initial and the transformed models and illustrate how our approach can be applied in a decision making problem under severe uncertainty.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the pioneering work of Anscombe and Aumann (1963), Savage (1954) and Von Neumann and Morgestern (1947), probability measures are the most widespread tool in decision making problems under uncertainty. Nevertheless, due to a number of reasons such as the lack of information or the low quality of the data, eliciting a probability measure modelling the uncertainty may be at times a difficult problem. This has lead to the development of alternatives that are better suited to deal with these situations. Indeed, quoting a recent publication in ANOR (Keith & Ahner, 2021, pp. 319–320),
...Over the past several decades, various theories have been developed that generalize the theory of probability to address aspects of uncertainty that are difficult or impossible to model in standard probability theory.
These alternative theories are usually referred to as instances of imprecise probability models (Augustin et al., 2014), and include for instance belief functions (Shafer, 1976), possibility measures (Dubois & Prade, 1988), coherent lower probabilities (Walley, 1991) or submodular capacities (Choquet, 1953); they have also appeared under the name non-additive measures or games in coalitional game theory (Grabisch 2016).
Imprecise probability models have been applied extensively in the decision making context. According to (Grabisch 2016, p. 28),
...The fields of decision theory and game theory seem to be the privileged area for the application of games and capacities.
In fact, several extensions of the expected utility paradigm that allow to model uncertainty with non-additive measures have been proposed [see for instance Gilboa and Schmeidler (1989), Klibanoff et al. (2005), Sarin and Wakker (1992) and the survey in Troffaes (2007)]. There have also been applications of imprecise probabilities in decision making problems within the context of machine learning (Mattei et al., 2020), environmental engineering (Sahlin et al., 2021) or signal processing (de Angelis et al., 2023), just to name a few. While these references illustrate the interest and generality of imprecise probability models, we should also signal that this greater generality also encompasses a greater complexity; thus, a balance must be found between the expressiveness of the model and its tractability.
Coherent lower probabilities are the starting point of this paper. In addition to having an epistemic interpretation as lower envelopes of a closed and convex set of probability measures, they have the advantage of including as particular cases most other models within imprecise probability theory; therefore, the properties established for coherent lower probabilities immediately apply to submodular capacities or belief functions, for instance. However, their generality comes with a price: for instance, there is not an easy procedure for determining the extreme points of the associated set of probabilities, nor is there a unique extension to expectation operators. This hampers the use of coherent lower probabilities in decision making problems (Troffaes, 2007), where the computation of the optimal alternatives could be involved.
To overcome this issue, it may be sensible to look for transformations of a given coherent lower probability into another one that is close and that at the same time belongs to a class with better mathematical properties. Indeed, in past works (Miranda et al., 2021; Montes et al., 2018, 2019) we considered outer approximations of a coherent lower probability, leading to a transformed model less informative than the original one. Here we move in the opposite direction, and look for transformations that shrink the credal set and where the associated lower probability belongs to a subfamily of interest. We shall call these inner approximations, since their associated set of probability measures will be included in the set of those that are compatible with the original lower probability.
Beyond decision making under uncertainty, there are several contexts where an inner approximation can be of interest: we may consider for instance the problem of selecting a representative element within the credal set associated with the coherent lower probability (Jaffray 1995; Weber 1988), or aim to reduce the imprecision inherent to the model so as to make more informative inferences (Antonucci et al., 2015; Dubois et al., 1993). Recently, approximations of coherent lower probabilities in terms of belief functions have been used in statistical matching (Petturiti & Vantaggi, 2022), conditional coherent risk measures (Petturiti & Vantaggi, 2019) and for correcting incoherent beliefs (Petturiti & Vantaggi, 2022) [see also (Cinfrignini et al., 2023; Petturiti & Vantaggi, 2020)].
For these reasons, in this paper we shall investigate the problem of transforming a coherent lower probability into an inner approximation that belongs to some subfamily of interest. Specifically, for 2-monotone capacities and belief functions, we shall show in Sect. 3 that some interesting inner approximations may be obtained by means of linear and quadratic programming, and shall compare the properties of the transformed models with the ones obtained in Miranda et al. (2021) and Montes et al. (2018, 2019) as outer approximations. Next, in Sect. 4 we shall analyse the particular case of distortion models, where we shall characterise the existence of an inner approximation and the set of optimal ones according to some predetermined distance. In particular, in Sect. 4.4 we shall explore the connection between the problem at hand and that of determing the incenter of a credal set, following the ideas in Miranda and Montes (2023) and creating also a bridge with the problem of finding solutions of coalitional games. In Sect. 5 we shall compare the performance of the original and the transformed model with respect to different optimality criteria in the context of decision making with sets of probabilities (Troffaes, 2007). Finally, in Sect. 6 we apply these results on the example of decision making under severe uncertainty from Jansen et al. (2018). We conclude the paper with some additional comments in Sect. 7. To ease the reading, proofs as well as some supporting results have been gathered in an Appendix.
A preliminary version of this paper was presented at the the 19th International Conference on Information Processing and Management of Uncertainty (IPMU’2022) (Miranda et al., 2022). This expanded version includes the proofs of all the mathematical results, an extended discussion of the implications of using inner approximations in a decision making problem, additional examples, and an illustration on a decision making problem.
2 Preliminary concepts
Let \({\mathcal {X}}\) be a finite possibility space with cardinality n, and let \({{\mathcal {P}}}({\mathcal {X}})\) denote its power set. We call lower probability a function \({\underline{P}}:{{\mathcal {P}}}({\mathcal {X}})\rightarrow [0,1]\) that is monotone (\(A\subseteq B \Rightarrow {\underline{P}}(A)\le {\underline{P}}(B)\)) and normalised (\({\underline{P}}(\emptyset )=0,{\underline{P}}({\mathcal {X}})=1\)). Its conjugate upper probability is given by \({\overline{P}}(A)=1-{\underline{P}}(A^c)\) for every \(A\subseteq {\mathcal {X}}\).
For a lower probability \({\underline{P}}\), the associated set of dominating probabilities, or credal set, is given by:
Following (Walley, 1991), we shall say that \({\underline{P}}\) avoids sure loss when \({\mathcal {M}}({\underline{P}})\ne \emptyset \), and that it is coherent when it is the lower envelope of \({\mathcal {M}}({\underline{P}})\): \({\underline{P}}(A)=\min _{P\in {\mathcal {M}}({\underline{P}})} P(A)\) for every \(A\subseteq {\mathcal {X}}\).
As particular instances of coherent lower probabilities we have those that are 2-monotone, meaning that \({\underline{P}}(A\cup B)+{\underline{P}}(A\cap B)\ge {\underline{P}}(A)+{\underline{P}}(B)\) for any \(A,B\subseteq {\mathcal {X}}\). They are also referred to as supermodular or convex in the literature. On the other hand, a coherent lower probability is said to be completely monotone, or a belief function, when
for every \(A_1,\dots ,A_k\) in \({{\mathcal {P}}}({\mathcal {X}})\) and every \(k\in {\mathbb {N}}\). We denote by \({{\mathcal {C}}}_2\) and \({{\mathcal {C}}}_{\infty }\) the families of 2-monotone lower probabilities and belief functions, respectively. The above definitions imply that \({{\mathcal {C}}}_{\infty }\subset {{\mathcal {C}}}_2\).
Any lower probability \({\underline{P}}\) can be alternatively expressed using the Möbius transformation, that is given by:
conversely, \(m_{{\underline{P}}}\) allows to retrieve the initial lower probability by:
It is worth mentioning that the Möbius transformation is not only an equivalent representation of a lower probability, but it can be also used to characterise 2- or complete-monotonicity. Indeed, \({\underline{P}}\) is a 2-monotone lower probability if and only if its Möbius transformation \(m_{{\underline{P}}}\) satisfies (Chateauneuf & Jaffray, 1989)
and it is completely monotone if and only if it satisfies (2monot.1) and
3 Inner approximations of lower probabilities
3.1 Summary of the results on outer approximations
In previous papers (Miranda et al., 2021; Montes et al., 2018, 2019) we investigated the problem of outer approximating a coherent lower probability by means of a 2- or completely monotone lower probability. The definition of outer approximation goes back to Bronevich and Augustin (2009).
Definition 1
(Bronevich & Augustin, 2009) Let \({\underline{P}}\) be a coherent lower probability and let \({\mathcal {C}}\) be a class of coherent lower probabilities. \({\underline{Q}}\in {\mathcal {C}}\) is called an outer approximation of \({\underline{P}}\) in \({\mathcal {C}}\) if \({\underline{Q}}(A)\le {\underline{P}}(A)\) for every \(A\subseteq {\mathcal {X}}\). Moreover, \({\underline{Q}}\) is an undominated outer approximation if there is no other \({\underline{Q}}'\in {\mathcal {C}}\) such that \({\underline{Q}}\lneqq {\underline{Q}}'\le {\underline{P}}\).
In terms of credal sets, \({\underline{Q}}\) is an outer approximation of \({\underline{P}}\) when \({\mathcal {M}}({\underline{P}})\subseteq {\mathcal {M}}({\underline{Q}})\), and it is undominated if there is no other \({\underline{Q}}'\in {\mathcal {C}}\) such that \({\mathcal {M}}({\underline{P}}) \subseteq {\mathcal {M}}({\underline{Q}}') \subsetneq {\mathcal {M}}({\underline{Q}})\).
The quest for computing outer approximations of a coherent lower probability \({\underline{P}}\) seeks to replace \({\underline{P}}\) with a model with better mathematical properties, such as 2-monotonicity, and such that any element of \({\mathcal {M}}({\underline{P}})\) is also compatible with the new model. This last requirement is sensible if we give \({\underline{P}}\) an epistemic interpretation, as a model for the imprecise knowledge of a probability measure \(P_0\): if all we know about \(P_0\) is that it belongs to \({\mathcal {M}}({\underline{P}})\), we would like all the potential candidates to be also compatible with the transformed model. In addition, this new model should be as close as possible to the original one, so that their respective inferences are similar. A necessary condition in this regard is that the outer approximation is undominated.
To obtain undominated outer approximations, in Miranda et al. (2021) and Montes et al. (2018, 2019) we pursued a number of paths. The primal one was based on minimising the Baroni and Vicig distance (BV-distance, for short) (Baroni & Vicig, 2005) between the initial model and the outer approximation:
which measures the amount of imprecision added to the model when replacing \({\underline{P}}\) by \({\underline{Q}}\). Another possibility is to consider the quadratic distance between the original and the transformed model:
Using either of these distances, we can set up an optimisation problem that gives us outer approximations.
Proposition 1
(Montes et al., 2018, 2019) Let \({\underline{P}}\) be a coherent lower probability, and consider the condition
-
(i)
Let \({{\mathcal {C}}}_2^{oa}({\underline{P}})\) be the set of coherent lower probabilities satisfying conditions (2monot.1)–(2monot.3) and (2monot.4). The linear programming problem of minimising Eq. (1) in \({{\mathcal {C}}}_2^{oa}({\underline{P}})\) has optimal solutions that are undominated outer approximations of \({\underline{P}}\) in \({{\mathcal {C}}}_2\). Similarly, the quadratic problem of minimising Eq. (2) in \({{\mathcal {C}}}_2^{oa}({\underline{P}})\) has a unique optimal solution that is an undominated outer approximation of \({\underline{P}}\) in \({{\mathcal {C}}}_2\).
-
(ii)
Let \({{\mathcal {C}}}_{\infty }^{oa}({\underline{P}})\) be the set of coherent lower probabilities satisfying conditions (2monot.1), (C-monot.) and (2monot.4). The linear programming problem of minimising Eq. (1) in \({{\mathcal {C}}}_{\infty }^{oa}({\underline{P}})\) has optimal solutions that are undominated outer approximations of \({\underline{P}}\) in \({{\mathcal {C}}}_{\infty }\). Similarly, the quadratic problem of minimising Eq. (2) in \({{\mathcal {C}}}_{\infty }^{oa}({\underline{P}})\) has a unique optimal solution that is an undominated outer approximation of \({\underline{P}}\) in \({{\mathcal {C}}}_{\infty }\).
Concerning the undominated outer approximations in \({\mathcal {C}}_2\), we have proven that the linear programming approach in Proposition 1(i) may have infinite different solutions (Montes et al., 2018, Ex.1), that the undominated outer approximations coincide with \({\underline{P}}\) on singletons and on events of cardinality \(n-1\) (Montes et al., 2018, Prop.2), and that the optimal solution of the quadratic problem in Proposition 1(i) may not be an optimal solution of the linear problem.
With respect to \({\mathcal {C}}_{\infty }\), there exist undominated outer approximations that are not optimal solutions of the linear programming problem in Proposition 1(ii) (Montes et al., 2019, Ex.2) and the undominated outer approximations may not coincide with \({\underline{P}}\) on singletons or on events of cardinality \(n-1\) (Montes et al., 2019, Ex.4).
While the linear programming approach has the advantage of using an in our view more natural distance between the initial and the transformed model, it also has the drawback of not providing a unique solution. The opposite holds for the quadratic approach: it gives a unique solution but the use of the quadratic distance is less natural in this context. This led us in Miranda et al. (2021) to combine the two approaches so as to get the best from both.
Proposition 2
(Miranda et al., 2021) Let \({\underline{P}}\) be a coherent lower probability.
-
(i)
The quadratic programming problem of minimising Eq. (2) in \({{\mathcal {C}}}_2^{oa}({\underline{P}})\) subject also to:
$$\begin{aligned} d_\textrm{BV}({\underline{P}},{\underline{Q}})=\min _{{\underline{Q}}'\in {\mathcal {C}}_2^{oa}}d_\textrm{BV}\big ({\underline{P}},{\underline{Q}}'\big ) \end{aligned}$$(2.monot-BV)has a unique optimal solution that is an undominated outer approximation in \({\mathcal {C}}_2\).
-
(ii)
The quadratic programming problem of minimising Eq. (2) in \({{\mathcal {C}}}_{\infty }^{oa}({\underline{P}})\) subject also to:
$$\begin{aligned} d_\textrm{BV}({\underline{P}},{\underline{Q}})=\min _{{\underline{Q}}'\in {\mathcal {C}}_{\infty }^{oa}}d_\textrm{BV}\big ({\underline{P}},{\underline{Q}}'\big ) \end{aligned}$$(C.monot-BV)has a unique optimal solution that is an undominated outer approximation in \({\mathcal {C}}_{\infty }\).
In other words, a possible approach to choose an outer approximation in \({\mathcal {C}}_2\) or \({\mathcal {C}}_{\infty }\) is to minimise the quadratic distance among those outer approximations minimising the BV-distance. Other possibilities were discussed in Miranda et al. (2021).
3.2 Inner approximations
The problem of inner approximating a coherent lower probability was superficially discussed in Montes et al. (2018, Sec. 7) as a sort of dual approach to that of outer approximations. In this subsection, we analyse the problem in detail and compare the features of both approaches.
Definition 2
(Montes et al., 2018, Sec. 7) Let \({\underline{P}}\) be a coherent lower probability and let \({\mathcal {C}}\) be a class of coherent lower probabilities. \({\underline{Q}}\in {\mathcal {C}}\) is called an inner approximation of \({\underline{P}}\) in \({\mathcal {C}}\) if \({\underline{Q}}(A)\ge {\underline{P}}(A)\) for every \(A\subseteq {\mathcal {X}}\). It is said to be a non-dominating inner approximation if there is no other \({\underline{Q}}'\in {\mathcal {C}}\) such that \({\underline{P}}\le {\underline{Q}}'\lneqq {\underline{Q}}\).
In terms of credal sets, \({\underline{Q}}\) is an inner approximation of \({\underline{P}}\) if \({\mathcal {M}}({\underline{P}})\supseteq {\mathcal {M}}({\underline{Q}})\) and \({\underline{Q}}\in {\mathcal {C}}\) is a non-dominating inner approximation of \({\underline{P}}\) in \({\mathcal {C}}\) if there is no other \({\underline{Q}}'\in {\mathcal {C}}\) such that \({\mathcal {M}}({\underline{P}})\supseteq {\mathcal {M}}({\underline{Q}}')\supsetneq {\mathcal {M}}({\underline{Q}})\).
Taking inspiration from the work summarised in Sect. 3.1 about the outer approximations, we can easily establish procedures for inner approximating a coherent lower probability \({\underline{P}}\) by another one \({\underline{Q}}\) that is 2- or completely monotone; we simply need to replace (2monot.4) by:
This leads at once to the following result:
Proposition 3
Let \({\underline{P}}\) be a coherent lower probability.
-
(i)
Let \({{\mathcal {C}}}_2^{ia}({\underline{P}})\) be the set of coherent lower probabilities satisfying conditions (2monot.1)–(2monot.3) and (2monot.4-inner). The linear programming problem of minimising Eq. (1) in \({{\mathcal {C}}}_2^{ia}({\underline{P}})\) has optimal solutions that are non-dominating inner approximations of \({\underline{P}}\) in \({{\mathcal {C}}}_2\). Similarly, the quadratic problem of minimising Eq. (2) in \({{\mathcal {C}}}_2^{ia}({\underline{P}})\) has a unique optimal solution that is a non-dominating inner approximation of \({\underline{P}}\) in \({{\mathcal {C}}}_2\).
-
(ii)
Let \({{\mathcal {C}}}_{\infty }^{ia}({\underline{P}})\) be the set of coherent lower probabilities satisfying conditions (2monot.1), (C-monot.) and (2monot.4-inner). The linear programming problem of minimising Eq. (1) in \({{\mathcal {C}}}_{\infty }^{ia}({\underline{P}})\) has optimal solutions that are non-dominating inner approximations of \({\underline{P}}\) in \({{\mathcal {C}}}_{\infty }\). Similarly, the quadratic problem of minimising Eq. (2) in \({{\mathcal {C}}}_{\infty }^{ia}({\underline{P}})\) has a unique optimal solution that is a non-dominating inner approximation of \({\underline{P}}\) in \({{\mathcal {C}}}_{\infty }\).
Example 1
Consider the possibility space \({\mathcal {X}}=\{x_1,x_2,x_3,x_4\}\) and let \({\underline{P}}\) be the coherent lower probability given by:
A | \({\underline{P}}(A)\) | \({\underline{Q}}\) | \(Bel_1\) | \(Bel_2\) | \({\underline{Q}}'\) | \(Bel_3\) |
|---|---|---|---|---|---|---|
\(\{x_1\}\) | 0 | 0 | 0.15 | 0 | 0.08 | 0.1 |
\(\{x_2\}\) | 0 | 0 | 0 | 0 | 0 | 0 |
\(\{x_3\}\) | 0 | 0 | 0.05 | 0 | 0 | 0.1 |
\(\{x_4\}\) | 0 | 0.2 | 0.25 | 0.3 | 0.12 | 0.2 |
\(\{x_1,x_2\}\) | 0 | 0 | 0.15 | 0.1 | 0.08 | 0.1 |
\(\{x_1,x_3\}\) | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
\(\{x_1,x_4\}\) | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
\(\{x_2,x_3\}\) | 0 | 0 | 0.05 | 0.1 | 0 | 0.1 |
\(\{x_2,x_4\}\) | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
\(\{x_3,x_4\}\) | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
\(\{x_1,x_2,x_3\}\) | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
\(\{x_1,x_2,x_4\}\) | 0.5 | 0.5 | 0.5 | 0.5 | 0.58 | 0.5 |
\(\{x_1,x_3,x_4\}\) | 0.5 | 0.7 | 0.55 | 0.7 | 0.62 | 0.6 |
\(\{x_2,x_3,x_4\}\) | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
\({\underline{P}}\) is coherent because it is the lower envelope of the probability mass functions (0, 0, 0.5, 0.5), (0.5, 0, 0, 0.5), (0.4, 0.3, 0.3, 0) and (0.2, 0.5, 0.1, 0.2). Solving the linear programming problem from Proposition 3 in \({\mathcal {C}}_2\), we get the optimal solution \({\underline{Q}}\). Note that \({\underline{Q}}\) satisfies \({\underline{Q}}(\{x_4\})\ne {\underline{P}}(\{x_4\})\), showing that the non-dominating inner approximations do not necessarily coincide in the singletons with \({\underline{P}}\). On the other hand, \(Bel_1\), \(Bel_2\) and \(Bel_3\) are different optimal solutions of the linear programming problem in the class \({\mathcal {C}}_{\infty }\). Observe that \(Bel_2\) dominates \({\underline{Q}}\); thus non-dominating inner approximations in \({\mathcal {C}}_{\infty }\) may be dominating if we regard them as elements from \({\mathcal {C}}_2\).
In the quadratic approach, the non-dominating solution in \({\mathcal {C}}_2\) is \({\underline{Q}}'\), while that in \({\mathcal {C}}_{\infty }\) is \(Bel_3\). The former is not an optimal solution of the linear problem in \({\mathcal {C}}_2\) while, as we have said \(Bel_3\) is an optimal solution of the linear problem in \({\mathcal {C}}_{\infty }\). \(\blacklozenge \)
Example 1 shows that a coherent lower probability may have infinite non-dominating inner approximations in \({\mathcal {C}}_{\infty }\): in that example, any convex combination of \(Bel_1,Bel_2,Bel_3\) will be a belief function that inner approximates \({\underline{P}}\) and is non-dominating (because it is at the minimum BV-distance with \({\underline{P}}\)). Let us show that this may also be the case in \({\mathcal {C}}_2\).
Example 2
Consider the possibility space \({\mathcal {X}}=\{x_1,x_2,x_3,x_4\}\), the probability mass functions \(P_1=(0.25,0.25,0.25,0.25)\) and \(P_2=(0.2,0.2,0.3,0.3)\), and the coherent lower probability \({\underline{P}}\) that is the lower envelope of \(\{P_1,P_2\}\). \({\underline{P}}\) is not 2-monotone, since:
Let us prove that \(P_1\), \(P_2\) are non-dominating inner approximations of \({\underline{P}}\) in \({\mathcal {C}}_2\); we shall establish it for \(P_1\), the proof for \(P_2\) being similar.
Assume that there exists a 2-monotone inner approximation \({\underline{Q}}\) of \({\underline{P}}\) such that \({\underline{P}}\le {\underline{Q}}\lneqq P_1\). Then, there must be some event A such that \({\underline{Q}}(A)< P_1(A)\). Considering the events where \(P_1\) and \({\underline{P}}\) (and consequently also \({\underline{Q}})\) agree on, A must be one of \(\{x_1\},\{x_2\},\{x_1,x_2\},\{x_1,x_2,x_3\}\) or \(\{x_1,x_2,x_4\}\). By 2-monotonicity, we have that
Since any coherent lower probability is super-additive (Walley, 1991, Sect. 2.7.4), we obtain
and similarly \({\underline{Q}}(\{x_1,x_2,x_4\})=P_1(\{x_1,x_2,x_4\})=0.75\) and \({\underline{Q}}(\{x_1,x_2\})=P_1(\{x_1,x_2\})=0.5\). Therefore, \({\underline{Q}}=P_1\), a contradiction. \(\blacklozenge \)
These two examples raise the need of some criteria to select a non-dominating inner approximation of the coherent lower probability. We may follow here the same approach as in Miranda et al. (2021): to choose the one minimising the quadratic distance among those that minimise the BV-distance.
Proposition 4
Let \({\underline{P}}\) be a coherent lower probability on \({{\mathcal {P}}}({\mathcal {X}})\).
-
(i)
The quadratic programming problem of minimising Eq. (2) in \({{\mathcal {C}}}_2^{ia}({\underline{P}})\) subject also to (2.monot-BV) has a unique solution that is a non-dominating inner approximation in \({\mathcal {C}}_2\).
-
(ii)
The quadratic programming problem of minimising Eq. (2) in \({{\mathcal {C}}}_{\infty }^{ia}({\underline{P}})\) subject also to (C.monot-BV) has a unique solution that is a non-dominating inner approximation in \({\mathcal {C}}_{\infty }\).
Example 3
If we apply this idea to the coherent lower probability in Example 1, \({\underline{Q}}\) and \(Bel_3\) are the optimal inner approximations minimising the quadratic distance among those minimising the BV-distance in \({\mathcal {C}}_2\) and \({\mathcal {C}}_{\infty }\), respectively. \(\blacklozenge \)
In what follows, we investigate if for some subfamilies of interest of \({{\mathcal {C}}}_2\) it is possible to characterise the inner approximations that minimise the BV-distance with respect to the original model. In this respect, the following result shows that the process of obtaining inner approximations can be made iterative. For this, given a family \({{\mathcal {C}}}\) of coherent lower probabilities and a coherent lower probability \({\underline{P}}\), we shall denote by \(\tilde{{\mathcal {C}}}^{ia}({\underline{P}})\) the class of non-dominating inner approximations of \({\underline{P}}\) in \({{\mathcal {C}}}\), and by \({{\mathcal {C}}}_\textrm{BV}^{ia}({\underline{P}})\) the subclass of those that minimise the BV-distance with respect to \({\underline{P}}\). It follows that \({{\mathcal {C}}}_\textrm{BV}^{ia}({\underline{P}})\subseteq \tilde{{\mathcal {C}}}^{ia}({\underline{P}})\).
Proposition 5
Let \({\underline{P}}\) be a coherent lower probability, and consider two classes of coherent lower probabilities \({\mathcal {C}}\) and \({\mathcal {C}}'\) such that \({\mathcal {C}}'\subseteq {\mathcal {C}}\).
-
(i)
If \({\underline{Q}}\in \tilde{{\mathcal {C}}}'^{ia}({\underline{P}})\), then there exists some \({\underline{P}}'\in \tilde{{\mathcal {C}}}^{ia}({\underline{P}})\) such that \({\underline{Q}}\in \tilde{{\mathcal {C}}}'^{ia}({\underline{P}}')\).
-
(ii)
If moreover \({\underline{Q}}\in {\mathcal {C}}'^{ia}_\textrm{BV}({\underline{P}})\), then also \({\underline{Q}}\in {\mathcal {C}}'^{ia}_\textrm{BV}({\underline{P}}')\) for some \({\underline{P}}'\in {\mathcal {C}}^{ia}_\textrm{BV}({\underline{P}})\).
4 Inner approximations with distortion models and incenters
In this section, we investigate the inner approximations of coherent lower probabilities by means of some distortion model (Destercke et al., 2022; Montes et al., 2020a, b). These are imprecise models determined by a probability measure \(P_0\), a distorting function d and a distortion parameter \(\delta \). These three elements allow to define a set of probability measures by means of \(B_d^{\delta }(P_0)=\{P\mid d(P,P_0)\le \delta \}\). The set \(B_d^{\delta }(P_0)\) is closed and convex whenever d is continuous and convex (Montes et al., 2020a, Prop.1).
Several distortion models can be found in the literature, such as the constant odds ratio (Berger, 1990; Pericchi & Walley, 1991; Walley, 1991), the distortion models generated by the \(L_1\) or Kolmogorov distances (Huber, 1981; Montes et al., 2020b), or those obtained through increasing transformations of a probability measure (Bronevich, 2007). In this paper, we focus on the linear vacuous (Walley, 1991), pari mutuel (Montes et al., 2019; Pelessoni et al., 2010; Walley, 1991) and total variation models (Seidenfeld & Wasserman, 1993). These classes will be denoted by \({\mathcal {C}}_\textrm{LV}\), \({\mathcal {C}}_\textrm{PMM}\) and \({\mathcal {C}}_\textrm{TV}\). Although there is no inclusion relationship between them, they have a connection with the classes \({\mathcal {C}}_2\) and \({\mathcal {C}}_{\infty }\) from Sect. 3: it holds that any pari-mutuel or total variation model is 2-monotone, but not necessarily completely monotone, while any linear vacuous model satisfies complete monotonicity; in other words, \({\mathcal {C}}_\textrm{LV}\subseteq {\mathcal {C}}_{\infty }\) and \({\mathcal {C}}_\textrm{PMM},{\mathcal {C}}_\textrm{TV}\subseteq {\mathcal {C}}_2\), but \({\mathcal {C}}_\textrm{PMM},{\mathcal {C}}_\textrm{TV}\nsubseteq {\mathcal {C}}_\infty \).
Throughout the section, and for the sake of simplicity, we assume that \({\underline{P}}(A)\in (0,1)\) for any \(A\ne \emptyset ,{\mathcal {X}}\).
4.1 Linear vacuous model
Let \(P_0\) be a probability measure and \(\delta \in (0,1)\) a distortion parameter. The linear vacuous model is given by the coherent lower probability
its conjugate coherent upper probability is given by \({\overline{P}}_\textrm{LV}(A)=(1-\delta )P_0(A)+\delta \) for any \(A\ne \emptyset \). It holds that:
The credal set \({\mathcal {M}}\big ({\underline{P}}_\textrm{LV}\big )\) is formed by the convex combinations \((1-\delta )P_0+\delta P\) of \(P_0\) with another probability measure P, with respective weights \((1-\delta )\) and \(\delta \). Thus, we may interpret this model by considering an experiment where the uncertainty model is the probability measure \(P_0\), and where there is a proportion \(\delta \) of contaminated data, coming from another probability measure P. We refer to Montes et al. (2020a) for a study of the properties of the linear vacuous as a distortion model.
In Montes et al. (2018, Prop. 8), we proved that for any coherent lower probability \({\underline{P}}\) satisfying \(\sum _{i=1}^{n} {\underline{P}}(\{x_i\})>0\) there is a unique undominated outer approximation in \({\mathcal {C}}_\textrm{LV}\), where \(P_0\) and \(\delta \) are given by \(\delta =1-\sum _{j=1}^{n}{\underline{P}}(\{x_j\})\) and \(P_0(\{x_i\})=\frac{{\underline{P}}(\{x_i\})}{1-\delta }\ \forall i=1,\ldots ,n\). Next, we investigate the inner approximations in \({\mathcal {C}}_\textrm{LV}\). We begin by establishing a necessary and sufficient condition for their existence.
Definition 3
(Miranda & Montes, 2023) A coherent lower probability \({\underline{P}}\) on \({{\mathcal {P}}}({\mathcal {X}})\) is called maximally imprecise when \({\underline{P}}(A)<{\overline{P}}(A)\) for every \(A\ne \emptyset ,{\mathcal {X}}\).
While the existence of inner approximations in \({{\mathcal {C}}}_2\) or \({{\mathcal {C}}}_{\infty }\) is trivial because any element of the non-empty set \({\mathcal {M}}({\underline{P}})\) is an inner approximation of \({\underline{P}}\), the same does not apply to particular subfamilies of \({{\mathcal {C}}}_2\), such as \({\mathcal {C}}_\textrm{LV}\).
Proposition 6
Let \({\underline{P}}\) be a coherent lower probability. There exists a linear vacuous model \({\underline{P}}_\textrm{LV}\) that inner approximates \({\underline{P}}\) if and only if \({\underline{P}}\) is maximally imprecise.
Consider now a maximally imprecise coherent lower probability \({\underline{P}}\), and let \({\underline{P}}_\textrm{LV}\) be an inner approximation in \({\mathcal {C}}_\textrm{LV}\) given by \(P_0\) and \(\delta \). Their BV-distance is
using that \({\underline{P}}(A)\in (0,1)\) for every \(A\ne \emptyset ,{\mathcal {X}}\) and that \({\underline{P}}_\textrm{LV}\) is an inner approximation of \({\underline{P}}\). Since \(\sum _{A\subset {\mathcal {X}}}P_0(A)\) is constant for every probability measure \(P_0\), this distance is minimised when \((1-\delta )\) is minimised or, equivalently, when \(\delta \) is maximised. With this idea in mind, we give an example showing that there may be more than one inner approximation in \({\mathcal {C}}_\textrm{LV}\) minimising the BV-distance:
Example 4
Consider a three-element possibility space \({\mathcal {X}}=\{x_1,x_2,x_3\}\) and the coherent lower probability \({\underline{P}}\) given by:
It is coherent because it is the lower envelope of the probability mass functions (0.2, 0.2, 0.6), (0.2, 0.6, 0.2), (0.35, 0.05, 0.6), (0.5, 0.05, 0.45), (0.3, 0.6, 0.1) and (0.5, 0.4, 0.1). Any inner approximation \({\underline{P}}_\textrm{LV}\) of \({\underline{P}}\) in \({\mathcal {C}}_\textrm{LV}\) defined by \((P_0,\delta )\) satisfies
whence \(\delta \le 0.3\). Consider now \(P_\textrm{LV}^1=(\nicefrac {2}{7},\nicefrac {2}{7},\nicefrac {3}{7})\) and \(P_\textrm{LV}^2=(\nicefrac {2}{7},\nicefrac {3}{7},\nicefrac {2}{7})\). Together with \(\delta =0.3\), they give rise to \({\underline{P}}_\textrm{LV}^{1}\) and \({\underline{P}}_\textrm{LV}^{2}\) in the table above, which are then two different elements of \({\mathcal {C}}_\textrm{LV}\) minimising the BV-distance. \(\blacklozenge \)
We look then for the largest \(\delta >0\) such that there is some probability measure \(P_0\) such that \((1-\delta )P_0(A)\ge {\underline{P}}(A)\), or equivalently, \(P_0(A)\ge \frac{{\underline{P}}(A)}{1-\delta }\) for any \(A\subset {\mathcal {X}}\). Thus, if for some fixed \(\delta \in (0,1)\) we define \({\underline{Q}}^{\delta }_\textrm{LV}\) as
it is equivalent to look for the largest \(\delta \) such that \({\mathcal {M}}({\underline{Q}}^{\delta }_\textrm{LV})\ne \emptyset \), i.e., the largest \(\delta \) such that \({\underline{Q}}^{\delta }_\textrm{LV}\) avoids sure loss. Consider the following set:
\(\Lambda _\textrm{LV}\) contains all the distortion parameters for which it is possible to find a linear vacuous model inner approximating \({\underline{P}}\). Proposition 6 tells us that \(\Lambda _\textrm{LV}\) is non-empty if and only if \({\underline{P}}\) is maximally imprecise. \(\Lambda _\textrm{LV}\) is also a directed set:
for any \(A\ne \emptyset ,{\mathcal {X}}\), meaning that \({\mathcal {M}}\big ({\underline{Q}}^{\delta _1}_\textrm{LV}\big )\supset {\mathcal {M}}\big ({\underline{Q}}^{\delta _2}_\textrm{LV}\big )\). Our next result shows that \(\Lambda _\textrm{LV}\) has a maximum.
Proposition 7
Let \({\underline{P}}\) be a maximally imprecise coherent lower probability. Then, the set \(\Lambda _\textrm{LV}\) defined in Eq. (6) has a maximum value \(\delta _\textrm{LV}\).
It follows from Eq. (4) that any \(P_0\in {\mathcal {M}}\big ( {\underline{Q}}_\textrm{LV}^{\delta _\textrm{LV}} \big )\) determines a LV model that is a non-dominating inner approximation of \({\underline{P}}\) in \({\mathcal {C}}_\textrm{LV}\).
Let us establish a more manageable expression for \(\delta _\textrm{LV}\), borrowing some notation from Miranda and Montes (2023). Let
be the class of all finite families of subsets of \({\mathcal {X}}\) such that every \(x\in {\mathcal {X}}\) belongs to the same number of elements in the family.
Theorem 8
Let \({\underline{P}}\) be a maximally imprecise coherent lower probability. Then:
Next we prove that, under the assumption of 2-monotonicity, the expression above can be simplified. Let \({\mathbb {A}}^{*}({\mathcal {X}})\) denote the set of partitions of \({\mathcal {X}}\).
Theorem 9
Let \({\underline{P}}\) be a maximally imprecise 2-monotone lower probability with conjugate \({\overline{P}}\). Then:
Example 5
Let us continue with Example 4. There, we have shown that \(\delta _\textrm{LV}=0.3\). Since the lower probability \({\underline{P}}\) in that example is defined in a 3-element possibility space, it is also 2-monotone (Walley , 1981). Hence, \(\delta _\textrm{LV}\) can be obtained using Theorem 9:
\({\mathcal {A}}\in {\mathbb {A}}^{*}({\mathcal {X}})\) | \( 1-\sum _{A\in {\mathcal {A}}}{\underline{P}}(A)\) | \(\frac{1}{\vert {\mathcal {A}}\vert -1} \left( \sum _{A\in {\mathcal {A}}}{\overline{P}}(A) -1\right) \) |
|---|---|---|
\(\{x_1\},\{x_2\},\{x_3\} \) | 1–0.2–0.05–0.1 = 0.65 | \(\nicefrac {0.7}{2}=0.35\) |
\(\{x_1\},\{x_2,x_3\} \) | 1–0.2–0.5 = 0.3 | \(\nicefrac {0.3}{1}=0.3\) |
\(\{x_2\},\{x_1,x_3\}\) | 1–0.05–0.4 = 0.55 | \(\nicefrac {0.55}{1}=0.55\) |
\(\{x_3\},\{x_1,x_2\}\) | 1–0.1–0.4 = 0.5 | \( \nicefrac {0.5}{1}=0.5\) |
The minimum value is 0.3 (attained with the partition \(\{x_1\},\{x_2,x_3\}\)), the same value we obtained in Example 4. \(\blacklozenge \)
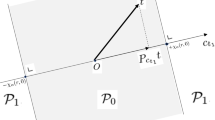
Theorem 9 and Proposition 5 provide a simple procedure to determine a non-dominating linear vacuous model inner approximating \({\underline{P}}\): we first obtain a 2-monotone non-dominating inner approximation \({\underline{Q}}\) of \({\underline{P}}\) minimising the BV-distance (following the linear programming approach described in Sect. 3.2), and then apply Theorem 9 to \({\underline{Q}}\). This procedure is illustrated in Fig. 1.
4.2 Pari mutuel model
The second distortion model we consider is the pari mutuel model. Given a probability measure \(P_0\) and a distortion parameter \(\delta >0\), the pari mutuel model is defined as the coherent lower probability:
with conjugate coherent upper probability \({\overline{P}}_\textrm{PMM}(A)=\min \{(1+\delta )P_0(A),1\}\) for any \(A\subseteq {\mathcal {X}}\). In Montes et al. (2018, Prop. 7), we proved that any coherent lower probability \({\underline{P}}\) has a unique undominated outer approximation in \({\mathcal {C}}_\textrm{PMM}\) which is given by:
With respect to the inner approximations, we next show that a coherent lower probability \({\underline{P}}\) has an inner approximation in \({{\mathcal {C}}}_\textrm{PMM}\) exactly under the same conditions as we saw in Proposition 6.
Proposition 10
Let \({\underline{P}}\) be a coherent lower probability. There exists a pari mutuel model \({\underline{P}}_\textrm{PMM}\) that inner approximates \({\underline{P}}\) if and only if \({\underline{P}}\) is maximally imprecise.
Now, if \({\underline{P}}_\textrm{PMM}\) is an inner approximation of \({\underline{P}}\) determined by \((P_0,\delta )\) and with conjugate \({\overline{P}}_\textrm{PMM}\), it holds that:
where the fourth equality follows from the assumption \({\underline{P}}(A)\in (0,1)\) for every \(A\ne \emptyset ,{\mathcal {X}}\) we are making throughout this section, which implies \({\overline{P}}(A)<1\), and since \({\underline{P}}_\textrm{PMM}\) is an inner approximation, \({\overline{P}}_\textrm{PMM}(A)\le {\overline{P}}(A)<1\) whenever \(A\ne {\mathcal {X}}\), hence \({\overline{P}}_\textrm{PMM}(A)=(1+\delta )P_0(A)\) for \(A\ne {\mathcal {X}}\).
Since \(\sum _{A\subset {\mathcal {X}}}P_0(A)\) is constant for every probability measure \(P_0\), the distance is minimised when \((1+\delta )\) is maximised or, equivalently, when the distortion parameter \(\delta \) is maximised. Therefore, we should look for the largest \(\delta \) such that there is a probability measure \(P_0\) satisfying \((1+\delta )P_0(A)\le {\overline{P}}(A)\) or equivalently \(P_0(A)\le \frac{{\overline{P}}(A)}{1+\delta }\) for any \(A\subseteq {\mathcal {X}}\). This leads us to define, for some fixed \(\delta >0\), \({\overline{Q}}^\delta _\textrm{PMM}\) as
being \({\underline{Q}}_\textrm{PMM}^\delta \) its conjugate lower probability. It follows that there is a PMM determined by \((P_0,\delta )\) inner approximating \({\overline{P}}\) if and only if the upper probability \({\overline{Q}}^{\delta }_\textrm{PMM}\) in Eq. (10) avoids sure loss.
We also deduce that if there exists a PMM \({\underline{P}}_\textrm{PMM}\) defined by \((P_0,\delta )\) inner approximating \({\underline{P}}\), then for any \(\delta '<\delta \) there exists another PMM with distortion parameter \(\delta '\) inner approximating \({\underline{P}}\) as well. In other words, the set
is directed. It is not difficult to prove that it has a maximum.
Proposition 11
Let \({\underline{P}}\) be a maximally imprecise coherent lower probability. Then, the set \(\Lambda _\textrm{PMM}\) defined in Eq. (11) has a maximum value \(\delta _\textrm{PMM}\).
On the other hand, for any \(P_0\in {\mathcal {M}}\big ({\underline{Q}}^{\delta _\textrm{PMM}}_\textrm{PMM}\big )\), the PMM determined by \((P_0,\delta _\textrm{PMM})\) is a non-dominating inner approximation of \({\underline{P}}\). This indicates that there may be more than one inner approximation in \({\mathcal {C}}_\textrm{PMM}\) minimising the BV-distance. The following example illustrates this fact:
Example 6
Consider the same coherent lower probability as in Example 4. The coherent lower probabilities \({\underline{Q}}_\textrm{PMM}^1\) and \({\underline{Q}}_\textrm{PMM}^2\) with conjugates given by:
A | \(\{x_1\}\) | \(\{x_2\}\) | \(\{x_3\}\) | \(\{x_1,x_2\}\) | \(\{x_1,x_3\} \) | \(\{x_2,x_3\}\) |
|---|---|---|---|---|---|---|
\({\overline{Q}}_\textrm{PMM}^1(A)\) | 0.5 | 0.4 | 0.4 | 0.9 | 0.9 | 0.8 |
\({\overline{Q}}_\textrm{PMM}^2(A) \) | 0.5 | 0.35 | 0.45 | 0.85 | 0.95 | 0.8 |
are two different non-dominating inner approximations in \({{\mathcal {C}}}_\textrm{PMM}\) that minimise the BV-distance: \({\overline{Q}}_\textrm{PMM}^1\) is determined by \(P_\textrm{PMM}^1=(\nicefrac {0.5}{1.3},\nicefrac {0.4}{1.3},\nicefrac {0.4}{1.3})\) and \(\delta _1=0.3\), while \({\overline{Q}}_\textrm{PMM}^2\) is determined by \(P_\textrm{PMM}^2=(\nicefrac {0.5}{1.3},\nicefrac {0.35}{1.3},\nicefrac {0.45}{1.3})\) and \(\delta _2=0.3\). \(\blacklozenge \)
Let us give a more manageable expression of \(\delta _\textrm{PMM}\). Using the notation from Eq. (7), we obtain the following result.
Theorem 12
Let \({\underline{P}}\) be a maximally imprecise coherent lower probability with conjugate \({\overline{P}}\). Then:
When \({\underline{P}}\) is 2-monotone, Eq. (12) can be simplified further.
Theorem 13
Let \({\underline{P}}\) be a maximally imprecise 2-monotone lower probability with conjugate \({\overline{P}}\). Then:
As for the LV model, Theorem 13 together with Proposition 5 gives a simple procedure for computing the value \(\delta _\textrm{PMM}\); it suffices to first inner approximate \({\underline{P}}\) by a 2-monotone lower probability \({\underline{Q}}\) and then apply Eq. (13) to \({\underline{Q}}\) and its conjugate \({\overline{Q}}\). This procedure is illustrated in Fig. 2.
Example 7
Let us continue with Example 4. Since \({\underline{P}}\) is 2-monotone, the value \(\delta _\textrm{PMM}\) can be obtained by means of the computations in the following table:
\({\mathcal {A}}\in {\mathbb {A}}^{*}({\mathcal {X}}) \) | \( \sum _{A\in {\mathcal {A}}}{\overline{P}}(A)-1\) | \(\frac{1}{\vert {\mathcal {A}}\vert -1}\Big ( 1-\sum _{A\in {\mathcal {A}}}{\underline{P}}(A) \Big )\) |
|---|---|---|
\(\{x_1\},\{x_2\},\{x_3\} \) | 0.5 + 0.6 + 0.6–1 = 0.7 | \( \nicefrac {1}{2}\)(1–0.2–0.05–0.1) = 0.325 |
\(\{x_1\},\{x_2,x_3\}\) | 0.5 + 0.8–1 = 0.3 | 1–0.2–0.5 = 0.3 |
\(\{x_2\},\{x_1,x_3\}\) | 0.6 + 0.95–1 = 0.55 | 1–0.05–0.4 = 0.55 |
\(\{x_3\},\{x_1,x_2\}\) | 0.6 + 0.9–1 = 0.5 | 1–0.1–0.4 = 0.5 |
Thus, as we have already seen in Example 6, \(\delta _\textrm{PMM}=0.3\). Two different inner approximations in \({{\mathcal {C}}}_\textrm{PMM}\) associated with this value have been given in Example 6. \(\blacklozenge \)
4.3 Total variation model
The third and last distortion model we consider is the total variation model. Given a probability measure \(P_0\) and a distortion parameter \(\delta \in (0,1)\), the total variation model is defined by the following coherent lower probability:
with conjugate coherent upper probability \({\overline{P}}_\textrm{TV}(A)=\min \{P_0(A)+\delta ,1\}\) for any \(A\ne \emptyset \). We showed in Destercke et al. (2022) that a coherent lower probability does not have a unique outer approximation in \({\mathcal {C}}_\textrm{TV}\). With respect to the inner approximations, we prove next that there exists an inner approximation under the same conditions as for \({{\mathcal {C}}}_\textrm{LV}\) and \({{\mathcal {C}}}_\textrm{PMM}\).
Proposition 14
Let \({\underline{P}}\) be a coherent lower probability. There exists a total variation model \({\underline{P}}_\textrm{TV}\) that inner approximates \({\underline{P}}\) if and only if \({\underline{P}}\) is maximally imprecise.
For any TV model \({\underline{P}}_\textrm{TV}\) induced by \(P_0\) and \(\delta \) that inner approximates \({\underline{P}}\), their BV-distance is given by:
where the second equality follows from our assumption \({\underline{P}}(A)\in (0,1)\) for any \(A\ne \emptyset ,{\mathcal {X}}\), which implies that \({\underline{P}}_\textrm{TV}(A)\ge {\underline{P}}(A)>0\) for any \(A\ne \emptyset \) because it is an inner approximation. Hence the BV-distance is minimised when \(\delta \) is maximised.
In order to find a TV inner approximation of \({\underline{P}}\), we need to determine the existence of a probability measure \(P_0\) such that \(P_0(A)-\delta \ge {\underline{P}}(A)\) for any \(A\ne \emptyset ,{\mathcal {X}}\), which implies that \(P_0(A)\ge {\underline{P}}(A)+\delta \) for every \(A\ne \emptyset ,{\mathcal {X}}\). This is equivalent to showing that
is a lower probability that avoids sure loss, i.e., satisfying \({\mathcal {M}}\big ({\underline{Q}}^{\delta }_\textrm{TV}\big )\ne \emptyset \). As we did for the LV and PMM models, we define the set
It is immediate that this is a directed set (\(\delta _1\in \Lambda _\textrm{TV}\) implies that \(\delta _2\in \Lambda _\textrm{TV}\) for any \(\delta _2<\delta _1\)). It is also easy to prove that it has a maximum:
Proposition 15
Let \({\underline{P}}\) be a maximally imprecise coherent lower probability. Then, the set \(\Lambda _\textrm{TV}\) defined in Eq. (14) has a maximum value \(\delta _\textrm{TV}\).
Given the value \(\delta _\textrm{TV}\), any \(P_0\in {\mathcal {M}}\big ({\underline{Q}}^{\delta _\textrm{TV}}_\textrm{TV}\big )\) determines a non-dominating total variation model that inner approximates \({\underline{P}}\) and minimises the BV-distance.
On the other hand, the value \(\delta _\textrm{TV}\) can be rewritten as follows:
Therefore, when \({\underline{P}}(A)\in (0,1)\) for every \(A\ne \emptyset ,{\mathcal {X}}\), it coincides with what we called in Miranda and Montes (2023) the incenter radius,Footnote 1 (with respect to the TV distance) of the credal set \({\mathcal {M}}({\underline{P}})\). Moreover, the probability measures \(P_0\) such that \(B_\textrm{TV}^{\delta _\textrm{TV}}(P_0)\subseteq {\mathcal {M}}({\underline{P}})\) were called incenters of the credal set.
Hence, looking for the inner approximations of a coherent lower probability in \({\mathcal {C}}_\textrm{TV}\) minimising the BV-distance is equivalent to looking for the incenter radius and the set of incenters (with respect to the TV distance). The results in Miranda and Montes (2023) provide then a simple formula for \(\delta _\textrm{TV}\).
Theorem 16
(Miranda & Montes, 2023, Thms. 4 and 5) Let \({\underline{P}}\) be a maximally imprecise coherent lower probability with conjugate \({\overline{P}}\). Then
If in addition \({\underline{P}}\) is 2-monotone, then
With this result, we obtain a simple procedure for computing a TV inner approximation: we first inner approximate the coherent lower probability \({\underline{P}}\) by means of a 2-monotone \({\underline{Q}}\) (using the procedures described in Sect. 3); next compute the value \(\delta _\textrm{TV}\) using Eq. (17); and finally take any \(P_0\in {\mathcal {M}}\big ({\underline{Q}}^{\delta _\textrm{TV}}_\textrm{TV}\big )\). These determine a TV model that inner approximates \({\underline{P}}\). This procedure is graphically illustrated in Fig. 3.
Example 8
Consider again our running Example 4. Using Eq. (17), we obtain:
\({\mathcal {A}}\in {\mathbb {A}}^{*}({\mathcal {X}}) \) | \(\frac{1}{\vert {\mathcal {A}}\vert } \big (1-\sum _{A\in {\mathcal {A}}}{\underline{P}}(A)\big )\) | \(\frac{1}{\vert {\mathcal {A}}\vert }\big (\sum _{A\in {\mathcal {A}}}{\overline{P}}(A)-1\big )\) |
|---|---|---|
\(\{x_1\},\{x_2\},\{x_3\}\) | \(\nicefrac {(1-0.2-0.05-0.1)}{3}=\nicefrac {0.65}{3} \) | \( \nicefrac {0.5+0.6+0.6}{3}=\nicefrac {0.7}{3}\) |
\(\{x_1\},\{x_2,x_3\} \) | \(\nicefrac {(1-0.2-0.5)}{2}=0.15 \) | \(\nicefrac {0.5+0.8-1}{2}=0.15\) |
\(\{x_2\},\{x_1,x_3\}\) | \(\nicefrac {(1-0.05-0.4)}{2}=0.275\) | \(\nicefrac {(0.6+0.95-1)}{2}=0.275\) |
\(\{x_3\},\{x_1,x_2\} \) | \( \nicefrac {(1-0.1-0.4)}{2}=0.25 \) | \( \nicefrac {(0.6+0.9-1)}{2}=0.25\) |
Thus, the value \(\delta _\textrm{TV}\) is given by 0.15. \(\blacklozenge \)
4.4 Inner approximations and incenters of credal sets
The last subsection shows that computing an inner approximation of a coherent lower probability in \({{\mathcal {C}}}_\textrm{TV}\) is related to the computation of an incenter with respect to the TV-distance. This leads us to investigate the connection of the inner approximations in \({{\mathcal {C}}}_\textrm{LV}\) and \({{\mathcal {C}}}_\textrm{PMM}\) with the concept of incenter.
Recalling that throughout this section we are assuming that \({\underline{P}}(A)\in (0,1)\) for any \(A\ne \emptyset ,{\mathcal {X}}\), we define
Here, \(B_\textrm{LV}^\delta (P_0)\) (resp., \(B_\textrm{PMM}^\delta (P_0)\)) denotes the credal set associated with the LV (resp., PMM) distortion model determined by \(P_0\) and \(\delta \).
Definition 4
Given a coherent lower probability \({\underline{P}}\) satisfying \({\underline{P}}(A)\in (0,1)\) for any \(A\ne \emptyset ,{\mathcal {X}}\), \(\delta _\textrm{LV}\) and \(\delta _\textrm{PMM}\) are called incenter radius with respect to the LV or PMM model, respectively. Moreover, any \(P_0\) such that \(B_\textrm{LV}^{\delta _\textrm{LV}}(P_0)\subseteq {\mathcal {M}}({\underline{P}})\) (respectively, \(B_\textrm{PMM}^{\delta _\textrm{PMM}}(P_0)\subseteq {\mathcal {M}}({\underline{P}})\)) is called incenter with respect to the LV (resp., PMM) model.
Example 9
Let us continue with our running Example 4. As we have argued in Examples 4, 6 and 8, the LV, PMM and TV incenters radii are \(\delta _\textrm{LV}=\delta _\textrm{PMM}=0.3\) and \(\delta _\textrm{TV}=0.15\). In addition, it can be easily seen that the LV incenters are \(P^1_\textrm{LV}=(\nicefrac {2}{7},\nicefrac {2}{7},\nicefrac {3}{7})\) and \(P^2_\textrm{LV}=(\nicefrac {2}{7},\nicefrac {3}{7},\nicefrac {2}{7})\), as well as their convex combinations. With respect to the PMM, the incenters are \(P^1_\textrm{PMM}=(\nicefrac {5}{13},\nicefrac {4}{13},\nicefrac {4}{13})\) and \(P^2_\textrm{PMM}=(\nicefrac {5}{13},\nicefrac {3.5}{13},\nicefrac {4.5}{13})\) as well as their convex combinations. And finally, with respect to the TV-distance, the incenters are \(P^1_\textrm{TV}=(0.35,0.2,0.45)\), \(P^2_\textrm{TV}=(0.35,0.4,0.25)\) and their convex combinations. Figure 4 shows a graphical representation of some of the incenters with respect to the LV (left), PMM (center) and TV (right). \(\blacklozenge \)
Graphical representation of the incenters in Example 9
We next investigate the connection between these three radii:
Proposition 17
In the conditions of Definition 4, it holds that \(\delta _\textrm{TV}\le \min \{\delta _\textrm{LV},\delta _\textrm{PMM}\}\).
It follows from the running example that the inequality may be strict: \(\delta _\textrm{LV}=\delta _\textrm{PMM}=0.3>\delta _\textrm{TV}=0.15\).
Moreover, \(\delta _\textrm{LV}\) and \(\delta _\textrm{PMM}\) may not coincide.
Example 10
Consider the following coherent lower probabilities \({\underline{P}}_1\) and \({\underline{P}}_2\) with conjugate \({\overline{P}}_1\) and \({\overline{P}}_2\), respectively:
A | \(\{x_1\} \) | \( \{x_2\}\) | \(\{x_3\}\) | \(\{x_1,x_2\}\) | \( \{x_1,x_3\} \) | \(\{x_2,x_3\}\) |
|---|---|---|---|---|---|---|
\(\big [ {\underline{P}}_1(A),{\overline{P}}_1(A) \big ]\) | [0.1,0.4] | [0.25,0.5] | [0.3,0.5] | [0.5,0.7] | [0.5,0.75] | [0.6,0.9] |
\(\big [ {\underline{P}}_2(A) , {\overline{P}}_2(A) \big ]\) | [0.1,0.4] | [0.2,0.4] | [0.3,0.5] | [0.5,0.7] | [0.6,0.8] | [0.6,0.9] |
Since both \({\underline{P}}_1\), \({\underline{P}}_2\) are 2-monotone, we can apply Theorems 9 and 13, obtaining that in the case of \({\underline{P}}_1\), \(\delta _\textrm{LV}=0.2>0.175=\delta _\textrm{PMM}\), while for \({\underline{P}}_2\) we obtain \(\delta _\textrm{LV}=0.15<0.2=\delta _\textrm{PMM}\). On the other hand, by Theorem 16 it is \(\delta _\textrm{TV}=0.1\) in both cases. This shows that (i) \(\delta _\textrm{LV},\delta _\textrm{PMM}\) do not coincide in general; (ii) there is not a dominance relationship between them; and (iii) \(\delta _\textrm{TV},\delta _\textrm{LV},\delta _\textrm{PMM}\) may all be different. \(\blacklozenge \)
We conclude this section by showing that the set of non-dominating inner approximations by a distortion model may strictly include those that minimise the BV-distance; in other words, there may be non-dominating inner approximations in \({\mathcal {C}}_\textrm{LV}\), \({\mathcal {C}}_\textrm{PMM}\) and \({\mathcal {C}}_\textrm{TV}\) with a parameter smaller than \(\delta _\textrm{LV}\), \(\delta _\textrm{PMM}\) and \(\delta _\textrm{TV}\), respectively. However, it is those attaining these largest values that allow to make a connection with the notion of incenter.
Example 11
Considering again our running Example 4, we can easily check that:
-
The LV model induced by \(P_0=(\nicefrac {3}{8},\nicefrac {1}{2},\nicefrac {1}{8})\) and \(\delta =0.2\) is a non-dominating inner approximation in \({\mathcal {C}}_\textrm{LV}\).
-
The PMM determined by \(P_0=(\nicefrac {7}{23}, \nicefrac {4}{23},\nicefrac {12}{23})\) and \(\delta =0.15\) is a non-dominating inner approximation in \({\mathcal {C}}_\textrm{PMM}\).
-
The TV model associated with \(P_0=(0.3,0.5,0.2)\) and \(\delta =0.1\) defines a non-dominating inner approximation in \({\mathcal {C}}_\textrm{TV}\).
In all the cases, the parameter \(\delta \) is smaller than \(\delta _\textrm{LV}\), \(\delta _\textrm{PMM}\) and \(\delta _\textrm{TV}\), respectively. \(\blacklozenge \)
5 Decision making with inner and outer approximations
In this section we explain how inner and outer approximations can be used to obtain the optimal alternatives in decision making problems where the uncertainty is modelled by means of coherent lower probabilities.
Consider thus a finite set of alternatives D. For each \(d\in D\), we assume that its utility depends on the outcome of an experiment taking values on \({\mathcal {X}}\), and we identify d with a variable \(J_d:{\mathcal {X}}\rightarrow {\mathbb {R}}\). We aim at finding the optimal alternative(s) among those that are Pareto optimal:
As we mentioned in the introduction, the expected utility paradigm has been extended in a number of ways to be able to deal with scenarios of imprecision or ambiguity about the probability measure that models the uncertainty. More specifically, we shall consider in this section five of these generalisations (we refer to Troffaes (2007) for a survey): \(\Gamma \)-maximin, \(\Gamma \)-maximax, maximality, interval dominance or E-admissibility. We analyse, for each of these criteria, whether there is a connection between the set of optimal alternatives under \({\underline{P}}\), and under an inner or outer approximation, \({\underline{Q}}_{in}\), \({\underline{Q}}_{ou}\).
Since these generalisations consider the lower and upper expectations of the different alternatives, we must recall here some basic facts from the theory of lower and upper previsions (Walley, 1991). Within this theory, any (bounded) mapping \(f:{\mathcal {X}}\rightarrow {\mathbb {R}}\) is called a gamble, and the set of all gambles on \({\mathcal {X}}\) is denoted \({\mathcal {L}}({\mathcal {X}})\). A lower prevision is a functional \({\underline{P}}\) defined on some subset \({{\mathcal {K}}}\) of \({\mathcal {L}}({\mathcal {X}})\); its conjugate upper prevision is given by \({\overline{P}}(f)=-{\underline{P}}(-f)\) for every \(f\in -{{\mathcal {K}}}:=\{-g \mid g\in {{\mathcal {K}}}\}\). In particular, given a probability measure \(P\) on \({\mathcal {X}}\), its expectation operator \(P:{\mathcal {L}}({\mathcal {X}})\rightarrow {\mathbb {R}}\) given by \(P(f)=\sum _{x\in {\mathcal {X}}} f(x)P(\{x\})\) is called a coherent prevision (de Finetti, 1974–1975).
A lower prevision on \({\mathcal {L}}({\mathcal {X}})\) is called coherent if and only if there exists a closed and convex set \({\mathcal {M}}\) of coherent previsions such that \({\underline{P}}(f)=\min \{P(f)\mid P\in {\mathcal {M}}\}\); similarly, an upper prevision \({\overline{P}}\) is called coherent when \({\overline{P}}(f)=\max \{P(f)\mid P\in {\mathcal {M}}\}\) for every \(f\in {\mathcal {L}}({\mathcal {X}})\) for some closed and convex set of coherent previsions \({\mathcal {M}}\). In particular, a coherent lower probability \({\underline{P}}\) with associated credal set \({\mathcal {M}}({\underline{P}})\) can be used to define a coherent lower and upper prevision: these are called the natural extension of \({\underline{P}}\) to \({\mathcal {L}}({\mathcal {X}})\), and for any gamble \(f:{\mathcal {X}}\rightarrow {\mathbb {R}}\), they are given by:
5.1 \(\Gamma \)-maximin
This criterion selects as optimal alternatives those maximising the lower prevision:
For this criterion, there is not an inclusion relationship between the optimal alternatives for \({\underline{P}}\), \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\), as we show in the next example.
Example 12
Consider the possibility space \({\mathcal {X}}=\{x_1,x_2,x_3,x_4\}\), the coherent lower probability \({\underline{P}}\), its undominated outer approximation \({\underline{Q}}_{ou}\) and its non-dominating inner approximation \({\underline{Q}}_{in}\) in \({\mathcal {C}}_2\) minimising the BV-distance given by:
A | \({\underline{P}}(A)\) | \({\underline{Q}}_{in}(A)\) | \({\underline{Q}}_{ou}(A)\) | A | \({\underline{P}}(A)\) | \({\underline{Q}}_{in}(A)\) | \({\underline{Q}}_{ou}(A) \) |
|---|---|---|---|---|---|---|---|
\(\{x_1\}\) | 0.1 | 0.1 | 0.1 | \(\{x_2,x_3\}\) | 0.3 | 0.3 | 0.2 |
\(\{x_2\}\) | 0 | 0.1 | 0 | \(\{x_2,x_4\}\) | 0.4 | 0.4 | 0.4 |
\(\{x_3\} \) | 0 | 0.1 | 0 | \(\{x_3,x_4\}\) | 0.4 | 0.4 | 0.4 |
\(\{x_4\}\) | 0.3 | 0.3 | 0.3 | \(\{x_1,x_2,x_3\}\) | 0.5 | 0.5 | 0.5 |
\(\{x_1,x_2\}\) | 0.1 | 0.2 | 0.1 | \(\{x_1,x_2,x_4\}\) | 0.6 | 0.7 | 0.6 |
\(\{x_1,x_3\}\) | 0.3 | 0.3 | 0.3 | \(\{x_1,x_3,x_4\}\) | 0.7 | 0.8 | 0.7 |
\(\{x_1,x_4\}\) | 0.6 | 0.6 | 0.5 | \(\{x_2,x_3,x_4\}\) | 0.6 | 0.6 | 0.6 |
Consider the set of alternatives \(D=\{d_1,d_2,d_3\}\) whose utilities, as well as their lower previsions determined by \({\underline{P}}\), \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\) using natural extension, are given by:
\(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \({\underline{P}}(J_i)\) | \({\underline{Q}}_{in}(J_i)\) | \({\underline{Q}}_{ou}(J_i)\) | |
|---|---|---|---|---|---|---|---|
\(J_1\) | 3 | 2 | \(\nicefrac {-9}{10}\) | 3 | 1.44 | 1.73 | 1.34 |
\(J_2\) | 2 | 3 | \(\nicefrac {2}{3}\) | 2 | \(1.4{\overline{6}}\) | 1.7 | \(1.4{\overline{6}}\) |
\(J_3\) | 4 | − 2 | − 2 | 4 | 1.6 | 1.6 | 1 |
We obtain that \(\text{ opt}_{{\underline{P}}}(D)=\{d_3\}\), \(\text{ opt}_{{\underline{Q}}_{in}}(D)=\{d_1\}\) and \(\text{ opt}_{{\underline{Q}}_{ou}}(D)=\{d_2\}\), so the three coherent lower probabilities give different results. \(\blacklozenge \)
5.2 \(\Gamma \)-maximax
This criterion selects as optimal alternatives those maximising the upper prevision:
it can be seen as the dual of the \(\Gamma \)-maximin. Not surprisingly, for this criterion there is not a connection between \(\text{ opt}_{{\overline{P}}}(D)\), \(\text{ opt}_{{\overline{Q}}_{in}}(D)\) and \(\text{ opt}_{{\overline{Q}}_{ou}}(D)\) either.
Example 13
Consider the setting in Example 12 and the set of alternatives \(D=\{d_2,d_4,d_5\}\), where \(d_2\) comes from Example 12, and \(d_4,d_5\) are defined by:
\(x_1\) | \( x_2\) | \( x_3 \) | \( x_4\) | |
|---|---|---|---|---|
\(J_4 \) | − 1 | − 1 | 2.7 | 2.7 |
\(J_5\) | 3 | − 2 | − 2 | 4 |
The upper previsions of the three alternatives for \({\overline{P}}\), \({\overline{Q}}_{in}\) and \({\overline{Q}}_{ou}\) are given by:
\(J_2\) | \(J_4\) | \(J_5\) | |
|---|---|---|---|
\({\overline{P}}(J_i) \) | 2.3 | 2.33 | 2 |
\({\overline{Q}}_{in}(J_i)\) | \(2.0{\overline{6}}\) | 1.96 | 2 |
\({\overline{Q}}_{ou}(J_i)\) | 2.3 | 2.33 | 2.5 |
We observe that \(\text{ opt}_{{\overline{P}}}(D)=\{d_4\}\), \(\text{ opt}_{{\overline{Q}}_{in}}(D)=\{d_2\}\) and \(\text{ opt}_{{\overline{Q}}_{ou}}(D)=\{d_5\}\), whence the three models give different solutions. \(\blacklozenge \)
5.3 Maximality
According to maximality, the optimal alternatives are those d satisfying \({\underline{P}}(J_e-J_d)\le 0\) for any other alternative \(e\in D\):
We obtain the following result:
Proposition 18
Let \({\underline{P}}\) and \({\underline{Q}}\) be two coherent lower probabilities such that \({\underline{P}}\le {\underline{Q}}\). Then \(\text{ opt}_{>_{{\underline{P}}}}\supseteq \text{ opt}_{>_{{\underline{Q}}}}\).
Then, if \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\) are inner and outer approximations of \({\underline{P}}\), it holds that \(\text{ opt}_{>_{{\underline{Q}}_{in}}}\supseteq \text{ opt}_{>_{{\underline{P}}}}\supseteq \text{ opt}_{>_{{\underline{Q}}_{in}}}\). The above inclusions may be strict:
Example 14
Consider the same setting as in Examples 12, 13, and the set of alternatives \(D=\{d_1,d_2,d_6\}\), where \(d_1\), \(d_2\) were given in Example 12 and \(d_6\) is:
\(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | |
|---|---|---|---|---|
\(J_6\) | 0 | 2 | 3.5 | 0 |
The following table gives the values of \({\underline{P}}\), \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\) for the differences between the gambles:
\(J_2-J_1\) | \(J_6-J_1 \) | \(J_1-J_2\) | \(J_6-J_2\) | \(J_1-J_6\) | \(J_2-J_6\) | |
|---|---|---|---|---|---|---|
\({\underline{P}}(J_i-J_j)\) | − 0.4 | − 2.1 | \(-0.02{\overline{6}}\) | − 1.7 | 0.04 | \(0.0{\overline{6}}\) |
\({\underline{Q}}_{in}(J_i-J_j)\) | − 0.34\({\overline{3}}\) | − 1.66 | 0.03 | \(-1.31{\overline{6}}\) | 0.48 | 0.45 |
\({\underline{Q}}_{ou}(J_i-J_j)\) | − 0.6 | − 2.4 | \( -0.22{\overline{6}}\) | − 1.8 | − 0.26 | \(-0.0{\overline{3}}\) |
We conclude that \(\text{ opt}_{>_{{\underline{Q}}_{in}}}=\{d_1\}\), \(\text{ opt}_{>_{{\underline{P}}}}=\{d_1,d_2\}\) and \(\text{ opt}_{>_{{\underline{Q}}_{ou}}}=\{d_1,d_2,d_6\}\), and as a consequence the inclusions between these sets are strict. \(\blacklozenge \)
5.4 Interval dominance
This criterion computes \([{\underline{P}}(J_d),{\overline{P}}(J_d)]\) for each alternative d in D, and compares these intervals, giving rise to the following optimal alternatives:
We obtain the following relationships:
Proposition 19
Let \({\underline{P}}\) and \({\underline{Q}}\) be two coherent lower probabilities such that \({\underline{P}}\le {\underline{Q}}\). Then \(\text{ opt}_{\sqsupset _{{\underline{P}}}}\supseteq \text{ opt}_{\sqsupset _{{\underline{Q}}}}\).
This implies that \(\text{ opt}_{\sqsupset _{{\underline{Q}}_{in}}}\supseteq \text{ opt}_{\sqsupset _{{\underline{P}}}}\supseteq \text{ opt}_{\sqsupset _{{\underline{Q}}_{ou}}}\), and as we show in our next example, the inclusions may be strict.
Example 15
Consider again the same setting as in Examples 12, 13 and 14. Consider also the set of alternatives \(D=\{d_1,d_6,d_7\}\), where \(d_1\) was defined in Example 12, \(d_6\) was defined in Example 14 and \(d_7\) is given by:
\(x_1\) | \(x_2\) | \( x_3\) | \(x_4\) | |
|---|---|---|---|---|
\(J_7 \) | 3 | 3.5 | − 1 | − 1 |
We obtain that:
\(J_1 \) | \(J_6\) | \(J_7\) | |
|---|---|---|---|
\(\big [{\underline{P}}(J_i),{\overline{P}}(J_i)\big ]\) | [1.44, 2.7] | [0.6, 1.4] | [− 0.6, 1.55] |
\(\big [ {\underline{Q}}_{in}(J_i),{\overline{Q}}_{in}(J_i) \big ] \) | [1.73, 2.41] | [0.75, 1.25] | [− 0.15, 1.5] |
\(\big [ {\underline{Q}}_{ou}(J_i),{\overline{Q}}_{ou}(J_i) \big ] \) | [1.34 , 2.8] | [0.4, 1.6] | [− 0.6, 1.55] |
Hence, we obtain the following sets of optimal alternatives: \(\text{ opt}_{\sqsupset _{{\underline{Q}}_{in}}}=\{d_1\}\), \(\text{ opt}_{\sqsupset _{{\underline{P}}}}=\{d_1,d_7\}\), and \(\text{ opt}_{\sqsupset _{{\underline{Q}}_{ou}}}=\{d_1,d_6,d_7\}\), and therefore the inclusions are strict. \(\blacklozenge \)
5.5 E-admissibility
According to E-admissibility, we choose those alternatives that maximise the expected utility for at least one element of the credal set \({\mathcal {M}}({\underline{P}})\):
We next prove the following connection with respect to E-admissibility.
Proposition 20
Let \({\underline{P}}\) and \({\underline{Q}}\) be two coherent lower previsions such that \({\underline{P}}\le {\underline{Q}}\). Then \(\text{ opt}_{{\mathcal {M}}({\underline{Q}})} \subseteq \text{ opt}_{{\mathcal {M}}({\underline{P}})}\).
From this result we deduce that \(\text{ opt}_{{\mathcal {M}}({\underline{Q}}_{in})}\subseteq \text{ opt}_{{\mathcal {M}}({\underline{P}})}\subseteq \text{ opt}_{{\mathcal {M}}({\underline{Q}}_{ou})}\).
Example 16
Let us continue with Examples 12–15. If we consider the set of alternatives \(D=\{d_1,d_5,d_8\}\), where \(d_8\) is given by
\(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | |
|---|---|---|---|---|
\( J_8\) | 0.95 | 1.6 | 1.8 | 1 |
we obtain that \(\text{ opt}_{{\mathcal {M}}({\underline{Q}}_{in})}=\{d_1\}\), \(\text{ opt}_{{\mathcal {M}}({\underline{P}})}=\{d_1,d_5\}\) and \(\text{ opt}_{{\mathcal {M}}({\underline{Q}}_{ou})}=\{d_1,d_5,d_8\}\), showing that the inclusions are strict. \(\blacklozenge \)
5.6 Comparison between the decisions
Next we make a comparison between the optimal alternatives within a set D when we consider the initial coherent lower probability \({\underline{P}}\) and a 2-monotone inner approximation \({\underline{Q}}\), taking into account the distance \(d_\textrm{BV}({\underline{P}},{\underline{Q}})\), and under any of the criteria considered previously in this section. In this respect, a first comment is that we may assume without loss of generality that for any alternative d its associated gamble is bounded between 0 and 1. Indeed, it follows by coherence that for any \(a>0\), \(b\in {\mathbb {R}}\) and any gamble f, it holds that \({\underline{P}}(af+b)=a{\underline{P}}(f)+b\) and \({\overline{P}}(af+b)=a{\overline{P}}(f)+b\). As a consequence, given two gambles f, g, \(a\ne 0\), \(b\in {\mathbb {R}}\) and a coherent lower prevision \({\underline{P}}\), we obtain that:
-
\({\underline{P}}(f)\ge {\underline{P}}(g) \Leftrightarrow {\underline{P}}(af+b)\ge {\underline{P}}(ag+b)\);
-
\({\overline{P}}(f)\ge {\overline{P}}(g) \Leftrightarrow {\overline{P}}(af+b)\ge {\overline{P}}(ag+b)\);
-
\({\underline{P}}(f-g)\le 0\Leftrightarrow {\underline{P}}((af+b)-(ag+b))\le 0\);
-
\({\overline{P}}(f)\ge {\underline{P}}(g) \Leftrightarrow {\overline{P}}(af+b)\ge {\underline{P}}(ag+b)\).
This implies that the set of optimal decisions is invariant under affine transformations of the gambles associated with the alternatives. It is not difficult to establish the followingFootnote 2:
Proposition 21
Let \({\underline{P}}\) be a coherent lower probability and let \({\underline{Q}}\) be an inner approximation in \({{\mathcal {C}}}_2\). We use the same notation \({\underline{P}}\) and \({\underline{Q}}\) to denote the natural extension to gambles defined in Eq. (18). If f is a gamble taking values in [0, 1], then:
As a consequence, we deduce that, if \(d_\textrm{BV}({\underline{P}},{\underline{Q}})\le \delta \), then:
-
\({\underline{P}}(f)-{\underline{P}}(g)\ge \delta \Rightarrow {\underline{Q}}(f)-{\underline{Q}}(g)\ge 0\).
-
\({\overline{P}}(f)-{\overline{P}}(g)\ge \delta \Rightarrow {\overline{Q}}(f)-{\overline{Q}}(g)\ge 0\).
-
\({\underline{P}}(f-g)\le -\delta \Rightarrow {\underline{Q}}(f-g)\le 0\).
-
\({\overline{P}}(f)-{\underline{P}}(g)\ge 2\delta \Rightarrow {\overline{Q}}(f)-{\underline{Q}}(g)\ge 0\).
These implications relate the optimal alternatives under \(\Gamma \)-maximin, \(\Gamma \)-maximax, maximality and interval dominance for the original and transformed models.
6 Illustration in a decision problem under severe uncertainty
After showing how inner and outer approximations can be used in decision making problems, we illustrate its applicability in a real world toy example, following the terminology in Jansen et al. (2018, Sec. 5). For this aim, we first summarise the context from Jansen et al. (2018).
6.1 Decision making under severe uncertainty: setup
Given a non-empty set of alternatives A, and two preorders \(R_1\subseteq A \times A\) and \(R_2\subseteq R_1 \times R_1\) on A and \(R_1\), respectively, the triple \({\mathcal {A}}=[A,R_1,R_2]\) is called a preference system in A. \(R_1\) and \(R_2\) are interpreted as follows: \((a,b)\in R_1\) means that a is at least as preferable as b, while \(((a,b),(c,d))\in R_2\) means that exchanging b with a is at least as desirable as exchanging d with c.
Associated with \(R_1\) and \(R_2\) we can consider the indifference and strict preference relations \(I_{R_1}\), \(I_{R_2}\) and \(P_{R_1}\), \(P_{R_2}\). Using them we can establish when the preference systems satisfies some sort of rationality.
Definition 5
(Jansen et al., 2018, Def. 2,3) Let \({\mathcal {A}}=[A,R_1,R_2]\) be a preference systems. \({\mathcal {A}}\) is consistent if there exists a function \(u:A\rightarrow [0,1]\) such that for any \(a,b,c,d \in A\) the following properties hold:
-
i)
If \((a,b)\in R_1\), then \(u(a)\ge u(b)\), with equality if and only if \((a,b)\in I_{R_1}\).
-
ii)
If \(((a,b),(c,d))\in R_2\), then \(u(a)-u(b)\ge u(c)-u(d)\), with equality if and only if \(((a,b)(c,d))\in I_{R_2}\).
Each function u satisfying conditions (i) and (ii) above is said to weakly represent the preference system \({\mathcal {A}}\), and the set of all these functions is denoted as \({\mathcal {U}}_{{\mathcal {A}}}\). The subset of \({\mathcal {U}}_{{\mathcal {A}}}\) formed by the functions u satisfying in addition \(\inf _{a\in A}u(a)=0\) and \(\sup _{a\in A}u(a)=1\) is denoted by \({\mathcal {N}}_{\mathcal {A}}\).
Moreover, given \(\delta \in (0,1)\), \({\mathcal {N}}^\delta _{\mathcal {A}}\) denotes the elements \(u\in {\mathcal {N}}_{\mathcal {A}}\) satisfying \(u(a)-u(b)\ge \delta \) for any \((a,b)\in P_{R_1}\) and \(u(a)-u(b)-u(c)+u(d)\ge \delta \) for any \(((a,b)(c,d))\in P_{R_2}\). \({N}^\delta _{\mathcal {A}}\) is called the weak representation set of granularity at least \(\delta \).
The granularity \(\delta \) can be seen as a control parameter, in the sense that a given value \(\delta \) guarantees that one decision is only considered preferred to another when the differences between their utilities are above a predetermined threshold.
Definition 6
(Jansen et al., 2018, Def. 4) Let \({\mathcal {X}}\) be the states of the nature, A the consequences and \(D=\{X\mid X:{\mathcal {X}}\rightarrow A\}\) the set of alternatives. Each \({\mathcal {G}}\subseteq D\) is called decision system.
Assuming that the uncertainty about the states of the nature is given by means of a coherent lower prevision \({\underline{P}}\) with conjugate \({\overline{P}}\), the natural approach to determine the optimal decision is based in comparing the generalised interval expectation with granularity \(\delta \) (Jansen et al., 2018, Def.5), given by:
Then, the following criteria can be considered:
- \({\mathcal {D}}_\delta \)-maximin::
-
\(\underline{{\mathcal {G}}}_\delta =\big \{X\in {\mathcal {G}} \mid \forall Y\in {\mathcal {G}} \text { it holds } {\underline{P}}_{{\mathcal {D}}_\delta }(X) \ge {\underline{P}}_{{\mathcal {D}}_\delta }(Y)\big \}\).
- \({\mathcal {D}}_\delta \)-maximax::
-
\(\overline{{\mathcal {G}}}_\delta =\big \{X\in {\mathcal {G}} \mid \forall Y\in {\mathcal {G}} \text { it holds } {\overline{P}}_{{\mathcal {D}}_\delta }(X) \ge {\overline{P}}_{{\mathcal {D}}_\delta }(Y)\big \}\).
- \({\mathcal {A}}\)-admissibility::
-
\({\mathcal {G}}_{{\mathcal {A}}}=\big \{ X\in {\mathcal {G}} \mid \exists u\in {\mathcal {U}}_{\mathcal {A}} :\forall P \in {\mathcal {M}}({\underline{P}}), \forall Y\in {\mathcal {G}}\) it holds \( E_P(u\circ X)\ge E_P(u\circ Y)\big \}\).
The \({\mathcal {D}}_\delta \)-maximin and \({\mathcal {D}}_\delta \)-maximax criteria straightforwardly generalise \(\Gamma \)-maximin and \(\Gamma \)-maximax from Sect. 5, while \({\mathcal {A}}\)-admissibility generalises E-admissibility. Computing the generalised interval expectations or finding the \({\mathcal {A}}\)-admissible alternatives can be done by solving linear programming problems, as shown in Jansen et al. (2018, Prop. 3,4). However, this requires knowing the extreme points of the credal set, a task that simplifies considerably under 2-monotonicity.
6.2 Example setup (Jansen et al., 2018)
Consider a decision maker that must choose among three job offers, \(J_1\), \(J_2\) and \(J_3\). Each job offer has a salary and several additional benefits, \({\mathcal {B}}\), which are: overtime premium (\(b_1\)), child care (\(b_2\)), advanced training (\(b_3\)), promotion prospects (\(b_4\)) and flexible hours (\(b_5\)). Moreover, the salary and benefits depend on the economic situation for which we envisage four scenarios: \({\mathcal {X}}=\{x_1,x_2,x_3,x_4\}\). The situation is described in the following table (Jansen et al., 2018, p.127):
\(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | |
|---|---|---|---|---|
\(J_1\) | \(a_1=(5000,{\mathcal {B}})\) | \(a_2=(2700,\{b_1,b_2\})\) | \(a_3=(2300,\{b_1,b_2,b_3\})\) | \(a_4=(1000,\emptyset )\) |
\(J_2\) | \(a_5=(3500,\{b_1,b_5\})\) | \(a_6=(2400,\{b_1,b_2\})\) | \(a_7=(1700,\{b_1,b_2\})\) | \(a_8=(2500,\{b_1\})\) |
\(J_3\) | \(a_9=(3000,\{b_1,b_2,b_3\})\) | \(a_{10}=(1000,\{b_1\})\) | \(a_{11}=(2000,\{b_1\}))\) | \(a_{12}=(3000,\{b_1,b_4,b_5\})\) |
Assuming incomparability among the benefits, the information is summarised by a preference system \({\mathcal {A}}=[A,R_1,R_2]\), where (i) \(A=\{a_1,\ldots ,a_{12}\}\) are the consequences, where each of them is a pair (y, B), where \(y\in {\mathbb {R}}\) denotes the salary and \(B\subseteq {\mathcal {B}}\) is the set of benefits; (ii) \(R_1\) denotes a relation defined as:
i.e., \(a_i\) is preferred to \(a_j\) with respect to \(R_1\) when the salary of \(a_i\) is greater and all the benefits of \(a_j\) are also included in \(a_i\); and (iii) \(R_2\) is the relation:
In order to measure the uncertainty, the available information only allows to compare the probability of occurrence of each scenario:
Using the results in Miranda and Destercke (2015), the lower probability \({\underline{P}}\) associated with this information is given in the following table:
A | \({\underline{P}}(A)\) | \({\underline{Q}}_{in}\) | \({\underline{Q}}_{ou}\) | A | \({\underline{P}}(A)\) | \({\underline{Q}}_{in}\) | \({\underline{Q}}_{ou}\) |
|---|---|---|---|---|---|---|---|
\(\{x_1\}\) | \(\nicefrac {1}{4}\) | \(\nicefrac {7}{24}\) | \(\nicefrac {1}{4}\) | \(\{x_2,x_3\}\) | 0 | 0 | 0 |
\(\{x_2\}\) | 0 | 0 | 0 | \(\{x_2,x_4\}\) | 0 | 0 | 0 |
\(\{x_3\}\) | 0 | 0 | 0 | \(\{x_3,x_4\}\) | 0 | 0 | 0 |
\(\{x_4\}\) | 0 | 0 | 0 | \(\{x_1,x_2,x_3\}\) | \(\nicefrac {3}{4}\) | \(\nicefrac {3}{4}\) | \(\nicefrac {3}{4}\) |
\(\{x_1,x_2\}\) | \(\nicefrac {1}{2}\) | \(\nicefrac {1}{2}\) | \(\nicefrac {1}{2}\) | \(\{x_1,x_2,x_4\}\) | \(\nicefrac {2}{3}\) | \(\nicefrac {2}{3}\) | \(\nicefrac {2}{3}\) |
\(\{x_1,x_3\}\) | \(\nicefrac {1}{2}\) | \(\nicefrac {1}{2}\) | \(\nicefrac {11}{24}\) | \(\{x_1,x_3,x_4\}\) | \(\nicefrac {1}{2}\) | \(\nicefrac {13}{24}\) | \(\nicefrac {1}{2}\) |
\(\{x_1,x_4\}\) | \(\nicefrac {1}{3}\) | \(\nicefrac {1}{3}\) | \(\nicefrac {7}{24}\) | \(\{x_2,x_3,x_4\}\) | 0 | 0 | 0 |
This lower probability is not 2-monotone, as it can be easily seen taking the events \(A=\{x_1,x_3\}\) and \(B=\{x_1,x_4\}\). Hence, we may take a 2-monotone non-dominating inner approximation \({\underline{Q}}_{in}\) and a 2-monotone undominated outer approximation \({\underline{Q}}_{ou}\). We consider \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\) as we optimal solutions of the quadratic problem in Propositions 4 and 2, respectively, that are at a BV-distance \(d_{BV}({\underline{P}},{\underline{Q}}_{in})=0.08{\overline{3}}\) and \(d_{BV}({\underline{P}},{\underline{Q}}_{ou})=1.75\).
6.3 Results
Applying Propositions 1 and 2 in Jansen et al. (2018), we obtain that the preference system \({\mathcal {A}}=[A,R_1,R_2]\) is consistent, and that the maximum possible granularity degreeFootnote 3 is \(\delta =0.053\). It can be easily seen that only the job offers \(J_1\) and \(J_3\) are \({\mathcal {A}}\)-admissible for the three models: \({\underline{P}}\), \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\). The table shows the generalised interval expectations for different granularities, all of them smaller than 0.053, for the three models:
\(\delta =0\) | \(\delta =0.01\) | \(\delta =0.02\) | \(\delta =0.03\) | \(\delta =0.04\) | \(\delta =0.05\) | ||
|---|---|---|---|---|---|---|---|
\({\underline{P}}\) | \(E_{D_\delta }(J_1)\) | [0.25, 1] | [0.2925, 1] | [0.335, 1] | [0.3775, 1] | [0.412, 1] | [0.4625, 1] |
\(E_{D_\delta }(J_2)\) | [0, 1] | [0.08, 0.93] | [0.16, 0.86] | [0.24, 0.79] | [0.32, 0.72] | [0.4, 0.65] | |
\(E_{D_\delta }(J_3)\) | [0, 1] | [0.05\({\overline{6}}\), 0.93] | [0.11\({\overline{3}}\), 0.86] | [0.17, 0.79] | [0.22\({\overline{6}}\),0.72] | [0.28\({\overline{3}}\), 0.65] | |
\({\underline{Q}}_{in}\) | \(E_{D_\delta }(J_1)\) | \({[}\nicefrac {7}{24}, 1{]}\) | [0.3304, 1] | [0.3692, 1] | [0.4079, 1] | [0.4467, 1] | [0.4854, 1] |
\(E_{D_\delta }(J_2)\) | [0, 1] | [0.08, 0.93] | [0.16, 0.86] | [0.24, 0.79] | [0.32, 0.72] | [0.4, 0.65] | |
\(E_{D_\delta }(J_3)\) | [0, 1] | [0.052\({\overline{6}}\), 0.93] | [0.10\({\overline{3}}\), 0.86] | [0.155, 0.79] | [0.20\({\overline{6}}\),0.72] | [0.258\({\overline{3}}\), 0.65] | |
\({\underline{Q}}_{ou}\) | \(E_{D_\delta }(J_1)\) | [0.25, 1] | [0.2925, 1] | [0.335, 1] | [0.3775, 1] | [0.412, 1] | [0.4625, 1] |
\(E_{D_\delta }(J_2)\) | [0, 1] | [0.078, 0.93] | [0.15\({\overline{6}}\), 0.86] | [0.235,0.79] | [0.31\({\overline{3}}\), 0.72] | [0.391\({\overline{6}}\), 0.65] | |
\(E_{D_\delta }(J_3)\) | [0, 1] | [0.0475, 0.93] | [0.095, 0.86] | [0.1425, 0.79] | [0.19,0.72] | [0.2375\({\overline{3}}\), 0.65] | |
We obtain the same conclusion for the three models: since the lower and upper limits for \(J_1\) are greater than those of \(J_2\) and \(J_3\), \(J_1\) is optimal with respect to \({\mathcal {D}}_\delta \)-maximin and \({\mathcal {D}}_\delta \)-maximax. For a better visualisation, we graphically show these results in Figs. 5, 6 and 7 for \({\underline{P}}\), \({\underline{Q}}_{in}\) and \({\underline{Q}}_{ou}\), respectively.
6.4 Discussion
In this section we have presented a decision making problem to demonstrate that using the initial coherent lower probability, which is not 2-monotone, a non-dominating inner approximation \({\underline{Q}}_{in}\) or undominated outer approximation \({\underline{Q}}_{ou}\) yield the same results. One of the reasons is that the approximations are “very close” to the initial model \({\underline{P}}\), since for instance in the case of the inner approximation we have \(d_{BV}({\underline{P}},{\underline{Q}}_{in})=0.08{\overline{3}}\). This aligns with our comments in Sect. 5.6: if the distance between the initial and transformed model is small enough, there will not be much difference between the optimal decisions with the two models.
In addition, the use of (inner or outer) has a number of benefits:
-
First of all, following (Jansen et al., 2018, Props. 3,4,5), solving the decision making problem requires the knowledge of the extreme points of the credal set. The computation of the extreme points under the assumption of 2-monotonicity is a straightforward process and can be achieved using the procedure described in Shapley (1971). On the other hand, computing the extreme points of the credal set of an arbitrary coherent lower probability is far from trivial: while the maximum number of extreme points of the credal set of a coherent lower probability is upper bounded by \(\vert {\mathcal {X}}\vert !\) (Derks & Kuipers, 2002; Wallner, 2007), their computation is not immediate except in some particular cases.
-
Secondly, computing the generalised interval expectations requires solving a collection of linear programming problems (Jansen et al., 2018, Prop. 3), as many as the number of extreme points. In contrast, under the assumption of 2-monotonicity, these interval expectations coincide with the Choquet integral (Choquet, 1953), as explained in Jansen et al. (2018).
-
Thirdly, some models of the imprecise probability theory induce credal sets with a non-finite number of extreme points, as for example if the starting point are coherent lower previsions (Walley, 1991). In that case, applying the procedure described in Jansen et al. (2018) would not be possible. This issue could be overcome by considering the restriction to events, which gives an outer approximation of the original model.
The spirit of these comments can be summarised by the following comment given in Jansen et al. (2018, p. 119):
“[This approach] ...is ideal for situations where the number of extreme points is moderate and where closed formulas for computing the extreme points are available. For credal sets induced by 2-monotone lower/ 2-alternating upper probabilities such formulas exist.”
7 Concluding remarks
7.1 Summary
The results in this paper show that it is possible to transform a coherent lower probability into a more manageable model with a minimal loss of information. While in our previous studies we considered approximations not adding new information to our model (that is, outer approximations), in this paper we have headed in the opposite direction and used inner approximations, that are more informative than the original model. We have considered transformations into the class of 2- or completely monotone lower probabilities (Sect. 3) and distortion models (Sect. 4). Our reasons for focusing on these models are that (i) 2-monotone lower probabilities overcome some of the shortcomings of coherent lower probabilities (Destercke, 2013) while being easier to handle; (ii) completely monotone lower probabilities (or belief functions) are connected to Dempster-Shafer theory, and the approximations by means of these model have proven to be quite powerful in statistical matching (Petturiti & Vantaggi, 2022) or in the correction of incoherent beliefs (Petturiti & Vantaggi, 2022); and (iii) the inner approximations in terms of distortion models are linked with the notion of incenter of a credal set, complementing in this way our analysis in Miranda and Montes (2023) and showing a connection with coalitional game theory.
Table 1 summarises some features of inner and outer approximations in \({\mathcal {C}}_2\) and \({\mathcal {C}}_{\infty }\).
We observe that the properties satisfied by the inner approximation are, in most cases, similar to those of the outer approximations (Miranda et al., 2021; Montes et al., 2018, 2019).
7.2 Approximations of coherent lower probabilities in decision making problems
As argued in some references such as Grabisch (2016), Jansen et al. (2018), Keith and Ahner (2021), Troffaes (2007), decision making is an area where lower probabilities arise naturally due to the difficulty that entails at times the elicitation of the probability measure that models the problem uncertainty. In Sect. 5 we have discussed how (inner and outer) approximations can be used within this framework to ease the computations. Our motivation is that the lack of 2-monotonicity hinders the computation of the optimal alternatives, because it renders more difficult determining the natural extension of the coherent lower and upper probabilities. We have shown that for some of the criteria (maximality, interval dominance and E-admissibility) it is possible to establish a connection between the optimal alternatives of the initial and transformed models, and that we can bound the error in terms of the BV-distance between them. This establishes a kind of continuity property: if the transformed model is close enough to the initial one, the change in the (lower or upper) expectations of the alternatives shall be small as well, and this can be used in the estimation of the set of optimal alternatives.
This has been exemplified in Sect. 6 where we have used inner and outer approximations in a decision making problem where the preferences depend on both cardinal and ordinal values and the uncertainty is given in terms of a set of probability measures. As we discussed in Sect. 6.4, our approach simplifies computations due to the practical advantages of 2-monotonicity.
7.3 Extension to infinite spaces
One critical assumption in this paper is that we are working with finite possibility spaces, and the sharp reader may wonder about the extent to which our work can be applied when the cardinality of \({\mathcal {X}}\) is infinite. While at a top level of generality the problem of approximating a coherent lower probability by a 2-monotone one can still be formulated, a number of technical difficulties are encountered quickly:
-
One of the main advantages of using 2-monotone approximations on finite possibility spaces is that their credal set has at most \(\vert {\mathcal {X}}\vert !\) different extreme points and that they can be easily obtained (Choquet, 1953). This is helpful because it makes computationally easier to determine the optimal solutions of a decision problem under the main criteria considered in the literature. If we move to infinite spaces, though, the number of extreme points need not be finite, and the benefits of using 2-monotonicity dilute somewhat.
-
The connection with incenters established in Sect. 4.4 relies on the assumption that all proper subsets of the possibility space have strictly positive lower probability; this will not hold if the possibility space is uncountable. In addition, for the geometric interpretation we should first generalise the work in Miranda and Montes (2023).
-
In order to determine the approximation that is “closest” to the original model, we have used the distance proposed by Baroni and Vicig as well as the quadratic distance. The expressions we have given for these distances are valid for the finite case only, and while it is possible to give extensions to arbitrary possibility spaces, the computation of the distance becomes more complex in that case.
-
Related to the previous point, the computation of the (inner or outer) approximation had led us to solve linear or quadratic problems, that can be done efficiently for finite possibility spaces but becomes harder for arbitrary ones.
For all these reasons, we believe that extending our approach to infinite possibility spaces will be challenging and may not yield results as satisfactory as those presented in this paper.
7.4 Future research
Besides the extension to non-finite possibility spaces mentioned in the previous paragraph, it would be of interest to analyse the existence and computation of inner approximations in other families of imprecise models, such as probability intervals, p-boxes or possibility measures. For example, in this latter family it can be easily proved that an inner approximation exists if and only if there is an element \(x\in {\mathcal {X}}\) satisfying \({\overline{P}}(\{x\})=1\), and that in that case there is a unique non-dominating inner approximation, given by \({\overline{Q}}(A)=\max _{x\in A}{\overline{P}}(\{x\})\).
It would be interesting as well to deepen in the comparison between the initial and the transformed models, along the lines of Proposition 21. Finally, it would be interesting to provide a geometric perspective on the transformations, along the lines of our comments in Sect. 4.4.
Notes
A similar conclusion is obtained if instead of using \(d_\textrm{BV}\) to compare \({\underline{P}}\) and its transformation \({\underline{Q}}\) we considered the TV-distance: it is easy to establish that \(\max _{A\subseteq {\mathcal {X}}} \vert {\underline{P}}(A)-{\underline{Q}}(A)\vert =\max _{f: 0\le f \le 1} \vert {\underline{P}}(f)-{\underline{Q}}(f)\vert \) when \({\underline{Q}}\) is 2-monotone. We acknowledge Jasper de Bock for this remark.
In Jansen et al. (2018), the maximum granularity degree given is \(\delta =0.0{\overline{37}}\), but we believe that there is typo in the calculations. After a thorough analysis, we believe that in Jansen et al. (2018) it is considered that \(((a_9,a_2),(a_2,a_6))\) belongs to \(I_{R_2}\), which is incorrect, rather than to \(P_{R_2}\).
References
Anscombe, F. J., & Aumann, R. J. (1963). A definition of subjective probability. Annals of Mathematical Statistics, 34, 199–205.
Antonucci, A., de Campos, C., Huber, D., & Zaffalon, M. (2015). Approximate credal network updating by linear programming with applications to decision making. International Journal of Approximate Reasoning, 58, 25–38.
Augustin, T., Coolen, F., de Cooman, G., & Troffaes, M. (Eds.). (2014). Introduction to Imprecise Probabilities. Wiley Series in Probability and StatisticsWiley.
Baroni, P., & Vicig, P. (2005). An uncertainty interchange format with imprecise probabilities. International Journal of Approximate Reasoning, 40, 147–180.
Berger, J. (1990). Robust Bayesian analysis: Sensitivity to the prior. Journal of Statistical Planning and Inference, 25, 303–328.
Bronevich, A., & Augustin, T. (2009) Approximation of coherent lower probabilities by 2-monotone measures. In T. Augustin, F. P. A. Coolen, S. Moral, & M. C. M. Troffaes (Eds.), ISIPTA’09—Proceedings of the Sixth International Symposium on Imprecise Probability: Theories and Applications (pp. 61–70).
Bronevich, A. (2007). Necessary and sufficient consensus conditions for the eventwise aggregation of lower probabilities. Fuzzy Sets and Systems, 158, 881–894.
Chateauneuf, A., & Jaffray, J.-Y. (1989). Some characterizations of lower probabilities and other monotone capacities through the use of Möbius inversion. Mathematical Social Sciences, 17(3), 263–283.
Choquet, G. (1953). Theory of capacities. Annales de l’Institut Fourier, 5, 131–295.
Cinfrignini, A., Petturiti, D., & Vantaggi, B. (2023). Envelopes of equivalent martingale measures and a generalized no-arbitrage principle in a finite setting. Annals of Operations Research, 321, 103–137.
de Angelis, M., Gray, A., Ferson, S., & Patelli, E. (2023). Robust online updating of a digital twin with imprecise probability. Mechanical Systems and Signal Processing, 186, 109877.
de Finetti, B. (1974–1975). Theory of probability: A critical introductory treatment. Wiley.
Derks, J., & Kuipers, J. (2002). On the number of extreme points of the core of a transferable utility game. In Chapters in game theory. Theory and decision library C (Vol. 31, pp. 83–97). Springer.
Destercke, S. (2013). Independence and 2-monotonicity: Nice to have, hard to keep. International Journal of Approximate Reasoning, 54(4), 478–490.
Destercke, S., Montes, I., & Miranda, E. (2022). Processing multiple distortion models: A comparative study. International Journal of Approximate Reasoning, 145C, 91–120.
Dubois, D., Prade, H., & Sandri, S. (1993). On possibility/probability transformations. Theory and decision library. In R. Lower & M. Roubens (Eds.), Fuzzy logic (Vol. 12, pp. 103–112). Springer.
Dubois, D., & Prade, H. (1988). Possibility theory. Plenum Press.
Gilboa, I., & Schmeidler, D. (1989). Maxmin expected utility with a non-unique prior. Journal of Mathematical Economics, 18, 141–153.
Grabisch, M. (2016). Set functions, games and capacities in decision making. Springer.
Huber, P. J. (1981). Robust statistics. Wiley.
Jaffray, J. (1995). On the maximum-entropy probability which is consistent with a convex capacity. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 3(1), 27–33.
Jansen, C., Schollmeyer, G., & Augustin, T. (2018). Concepts for decision making under severe uncertainty with partial ordinal and partial cardinal preferences. International Journal of Approximate Reasoning, 98, 112–131.
Keith, A., & Ahner, D. (2021). A survey of decision making and optimization under uncertainty. Annals of Operations Research, 300, 319–353.
Klibanoff, P., Marinacci, M., & Mukerji, S. (2005). A smooth model of decision making under ambiguity. Econometrica, 73(6), 1849–1892.
Mattei, L., Antonucci, A., Mauá, D., Facchini, A., & Villanueva Serena, J. (2020). Tractable inference in credal sentential decision diagrams. International Journal of Approximate Reasoning, 125, 26–48.
Miranda, E., Montes, I., & Presa, A. (2022). Inner approximations of credal sets by non-additive measures. In 19th International conference on information processing and management of uncertainty in knowledge-based systems, IPMU 2022. Communications in computer and information science (Vol. 1601, pp. 743–756). Springer.
Miranda, E., & Destercke, S. (2015). Extreme points of the credal sets generated by comparative probabilities. Journal of Mathematical Psychology, 64(65), 44–57.
Miranda, E., & Montes, I. (2023). Centroids of the core of exact capacities: A comparative study. Annals of Operations Research, 321, 409–449.
Miranda, E., Montes, I., & Vicig, P. (2021). On the selection of an optimal outer approximation of a coherent lower probability. Fuzzy Sets and Systems, 424C, 1–36.
Montes, I., Miranda, E., & Destercke, S. (2019). Pari-mutuel probabilities as an uncertainty model. Information Sciences, 481, 550–573.
Montes, I., Miranda, E., & Destercke, S. (2020). Unifying neighbourhood and distortion models: Part I-New results on old models. International Journal of General Systems, 49(6), 602–635.
Montes, I., Miranda, E., & Destercke, S. (2020). Unifying neighbourhood and distortion models: Part II-New models and synthesis. International Journal of General Systems, 49(6), 636–674.
Montes, I., Miranda, E., & Vicig, P. (2018). 2-Monotone outer approximations of coherent lower probabilities. International Journal of Approximate Reasoning, 101, 181–205.
Montes, I., Miranda, E., & Vicig, P. (2019). Outer approximating coherent lower probabilities with belief functions. International Journal of Approximate Reasoning, 110, 1–30.
Pelessoni, R., Vicig, P., & Zaffalon, M. (2010). Inference and risk measurement with the pari-mutuel model. International Journal of Approximate Reasoning, 51, 1145–1158.
Pericchi, L. R., & Walley, P. (1991). Robust Bayesian credible intervals and prior ignorance. International Statistical Review, 59, 1–23.
Petturiti, D., & Vantaggi, B. (2022). How to assess coherent beliefs: A comparison of different notions of coherence in Dempster-Shafer theory of evidence. In T. Augustin, F. G. Cozman, & G. Wheeler (Eds.), Reflections on the foundations of probability and statistics: Essays in honor of Teddy Seidenfeld. Theory and decision library A (Vol. 54, pp. 161–185). Springer.
Petturiti, D., & Vantaggi, B. (2019). Conditional submodular Choquet expected values and conditional coherent risk measures. International Journal of Approximate Reasoning, 113, 14–38.
Petturiti, D., & Vantaggi, B. (2020). Modeling agent’s conditional preferences under objective ambiguity in Dempster–Shafer theory. International Journal of Approximate Reasoning, 119, 151–176.
Petturiti, D., & Vantaggi, B. (2022). Probability envelopes and their Dempster-Shafer approximations in statistical matching. International Journal of Approximate Reasoning, 150, 199–222.
Sahlin, U., Troffaes, M., & Edsman, L. (2021). Robust decision analysis under severe uncertainty and ambiguous tradeoffs: An invasive species case study. Risk Analysis, 41(11), 2140–2153.
Sarin, R., & Wakker, P. (1992). A simple axiomatization of nonadditive expected utility. Econometrica, 60(6), 1255–1272.
Savage, L. J. (1954). The foundations of statistics. Wiley.
Seidenfeld, T., & Wasserman, L. (1993). Dilation for sets of probabilities. The Annals of Statistics, 21, 1139–54.
Shafer, G. (1976). A mathematical theory of evidence. Princeton University Press.
Shapley, L. S. (1971). Cores of convex games. International Journal of Game Theory, 1, 11–26.
Troffaes, M. C. M. (2007). Decision making under uncertainty using imprecise probabilities. International Journal of Approximate Reasoning, 45(1), 17–29.
Von Neumann, J., & Morgestern, O. (1947). Theory of games and economic behaviour. Princeton University Press.
Walley, P. (1981). Coherent lower (and upper) probabilities. Statistics research report.
Walley, P. (1991). Statistical reasoning with imprecise probabilities. Chapman and Hall.
Wallner, A. (2007). Extreme points of coherent lower probabilities in finite spaces. International Journal of Approximate Reasoning, 44, 339–357.
Weber, R. J. (1988). Probabilistic values for games. In A. E. Roth (Ed.), The Shapley value. Essays in honour of L.S. Shapley (pp. 101–119). Cambridge University Press.
Acknowledgements
The research in this paper has benefited from discussions with Damjan Skulj, Barbara Vantaggi, Davide Petturiti, Jasper de Bock and Max Nendel. We also acknowledge the financial support by project PID2022-140585NB-I00 from the Spanish Ministry of Science and Innovation. We also acknowledge the comments and suggestions posed by the reviewers that helped improving the initial version of this manuscript.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Proofs
Appendix A. Proofs
Proof of Proposition 3
In all cases, the feasible region of the optimisation problem is non-empty because any probability \(P\in {\mathcal {M}}({\underline{P}})\) is an inner approximation of \({\underline{P}}\) that belongs to both \({\mathcal {C}}_2\) and \({\mathcal {C}}_{\infty }\). From here, the result follows with a proof analogous to those of Montes et al. (2018, Prop. 1, Sec. 5.1) and Montes et al. (2019, Prop. 2, Prop. 3). \(\square \)
Proof of Proposition 4
The proof is analogous to that of Miranda et al. (2021, Prop. 1). \(\square \)
Proof of Proposition 5
-
(i)
First of all that \({\underline{Q}}\in {{\mathcal {C}}}\) because \({{\mathcal {C}}}'\subseteq {{\mathcal {C}}}\), and as a consequence it is an inner approximation of \({\underline{P}}\) in \({{\mathcal {C}}}\). If it is dominating, then there is some \({\underline{P}}'\in {{\mathcal {C}}}\) such that \({\underline{Q}}\gneq {\underline{P}}'\ge {\underline{P}}\); moreover, we can assume without loss of generality that \({\underline{P}}'\) belongs to \(\tilde{{\mathcal {C}}}^{ia}({\underline{P}})\). Consequently, \({\underline{Q}}\) belongs to \(\tilde{{\mathcal {C}}}'^{ia}({\underline{P}}')\).
-
(ii)
Similarly, if \({\underline{Q}}\notin {\mathcal {C}}_\textrm{BV}^{ia}({\underline{P}})\), then there exists \({\underline{P}}'\in {\mathcal {C}}^{ia}_\textrm{BV}({\underline{P}})\) such that \({\underline{Q}}\ge {\underline{P}}'\) and then, by construction, \({\underline{Q}}\in {\mathcal {C}}^{ia}_\textrm{BV}({\underline{P}}')\).
\(\square \)
Lemma 22
A coherent lower probability on a finite possibility space \({\mathcal {X}}\) is maximally imprecise if and only if there exists some \(P\in {\mathcal {M}}({\underline{P}})\) such that \(P(A)\in ({\underline{P}}(A),{\overline{P}}(A))\) for every \(A\ne \emptyset ,{\mathcal {X}}\).
Proof
That the condition is sufficient is trivial. To see that it is also necessary, assume that \({\underline{P}}\) is maximally imprecise. By coherence, for any \(A\ne \emptyset ,{\mathcal {X}}\), there exist \(Q_{A}^{1},Q_{A}^{2}\in {\mathcal {M}}({\underline{P}})\) such that \(Q_{A}^{1}(A)={\underline{P}}(A)\) and \(Q_{A}^{2}(A)={\overline{P}}(A)\). Considering
we obtain a probability measure \(P_0\) that also belongs to \({\mathcal {M}}({\underline{P}})\), because this set is convex, and such that \({\underline{P}}(B)<P_0(B)<{\overline{P}}(B)\) for every \(B\ne \emptyset ,{\mathcal {X}}\). \(\square \)
Proof of Proposition 6
To see that the condition is necessary, note that given an inner approximation \({\underline{P}}_\textrm{LV}\) of \({\underline{P}}\) Eq. (3) implies \(\min _{A \ne \emptyset ,{\mathcal {X}}} \{{\overline{P}}_\textrm{LV}(A)-{\underline{P}}_\textrm{LV}(A)\}=\delta >0\), hence a coherent lower probability that is not maximally imprecise cannot have an inner approximation in \({{\mathcal {C}}}_\textrm{LV}\).
To see that the condition is also sufficient, let \(P_0\) be a probability measure satisfying \({\underline{P}}(A)<P_0(A)<{\overline{P}}(A)\) for every \(A\ne \emptyset ,{\mathcal {X}}\), existing by Lemma 22. Then
whence taking \(\delta =1-\nicefrac {1}{\varepsilon }\in (0,1)\), it holds that \(P_0(A)\ge \frac{{\underline{P}}(A)}{1-\delta }\) for any \(A\ne \emptyset ,{\mathcal {X}}\), and as a consequence \((1-\delta )P_0(A)\ge {\underline{P}}(A)\) for every \(A\ne \emptyset ,{\mathcal {X}}\). Hence, the LV model associated with \((P_0,\delta )\) is an inner approximation of \({\underline{P}}\). \(\square \)
Lemma 23
Consider \(\Lambda \subseteq {\mathbb {R}}\) and let \(({\underline{Q}}_{\delta })_{\delta \in \Lambda }\) be a directed family of lower probabilities that avoid sure loss. Then the intersection \(\cap _{\delta \in \Lambda }{\mathcal {M}}({\underline{Q}}_{\delta })\) is non-empty.
Proof
Since \({\mathcal {X}}\) is finite, the weak-* topology on the family of credal sets on \({\mathcal {X}}\) is equivalent to the Euclidean topology on the sets of mass functions. Thus, we obtain that \(\big ( {\mathcal {M}}({\underline{Q}}_{\delta })\big )_{\delta \in \Lambda }\) is a directed family of non-empty compact sets. As a consequence, their intersection is non-empty. \(\square \)
Proof of Proposition 7
This follows applying Lemma 23 to \(({\underline{Q}}^{\delta }_\textrm{LV})_{\delta \in \Lambda _\textrm{LV}}\). \(\square \)
Proof of Theorem 8
Let \(\delta \in (0,1)\), and let \({\underline{Q}}^{\delta }_\textrm{LV}\) be the lower probability defined in Eq. (5). From Walley (1991), it avoids sure loss if and only if for every \(k\in {\mathbb {N}}\) and \(A_1,\ldots ,A_k\subseteq {\mathcal {X}}\), it holds that
Without loss of generality, we may assume that all the events \(A_1,\ldots ,A_k\) are proper subsets of \({\mathcal {X}}\) (\(I_{A_i}-{\underline{Q}}^{\delta }_\textrm{LV}(A_i)\) would be constant on zero otherwise). Taking into account that \({\mathcal {X}}\) is finite, Eq. (A.1) is equivalent to:
where the third equivalence follows from the assumption \({\underline{P}}(A_i)>0\) for every \(A_i\ne \emptyset \). If we consider now \(\delta _\textrm{LV}\), we deduce that for any family \(A_1,\ldots ,A_k\) of proper subsets of \({\mathcal {X}}\), it must be
In fact, we can express it as
where the inequality follows because \({\mathbb {A}}({\mathcal {X}})\) contains finite families of subsets of \({\mathcal {X}}\) with the additional constraint that the sum of their indicator functions is constant.
Let \(A_1,\ldots ,A_k\) be a family where the minimum in Eq. (A.2) is attained, and take \(x^{*}\) such that
Then:
Complete now \(A_1,\ldots ,A_k\) with \(B_1,\ldots ,B_l\) so that
To see that this can be done, simply observe that if we express
for \(\sum _{i=1}^kI_{A_i}(x^{*})=c_1>c_2>\dots >c_m=0\) and pairwise disjoint sets \(C_1,\dots ,C_m\) then we can consider the family
and then we obtain
Now,
Therefore, the minimum is attained with families whose sum is constant. Moreover, given a family \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\) where the minimum is attained, it holds that:
whence Eq. (8) holds. \(\square \)
In order to prove Theorem 9, we need first to recall a couple of lemmas.
Lemma 24
Let \({\underline{P}}\) be a maximally imprecise coherent lower probability, and consider \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\) such that there exists \({\mathcal {A}}_1\in {\mathbb {A}}({\mathcal {X}})\) with \({\mathcal {A}}_1\subset {\mathcal {A}}\). Then:
-
(a)
\({\mathcal {A}}_2={\mathcal {A}}{\setminus } {\mathcal {A}}_1\in {\mathbb {A}}({\mathcal {X}})\) and \(\beta _{{\mathcal {A}}}=\beta _{{\mathcal {A}}_1}+\beta _{{\mathcal {A}}_2}\).
-
(b)
For any function \(h:{\mathbb {A}}({\mathcal {X}})\rightarrow {\mathbb {R}}\) satisfying
$$\begin{aligned} h({{\mathcal {A}}_1}\dot{\cup }{{\mathcal {A}}}_2)=\frac{\beta _{{\mathcal {A}}_1}}{\beta _{{\mathcal {A}}_1}+\beta _{{\mathcal {A}}_2}} h({{\mathcal {A}}}_1)+\frac{\beta _{{\mathcal {A}}_2}}{\beta _{{\mathcal {A}}_1}+\beta _{{\mathcal {A}}_2}} h({{\mathcal {A}}}_2), \end{aligned}$$(A.3)it holds that \(h({{\mathcal {A}}}_1\dot{\cup }{{\mathcal {A}}}_2)\ge \min \{h({{\mathcal {A}}}_1),h({{\mathcal {A}}}_2)\}\). Here, \({{\mathcal {A}}}_1\dot{\cup }{{\mathcal {A}}}_2\) denotes the element of \({\mathbb {A}}({\mathcal {X}})\) obtained by putting together the events in \({{\mathcal {A}}}_1\) and in \({{\mathcal {A}}}_2\).
Proof
The proof is an extension of Miranda and Montes (2023, Lem. 18).
-
(a)
Let \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\) and assume that there exists \({\mathcal {A}}_1\in {\mathbb {A}}({\mathcal {X}})\) such that \({\mathcal {A}}_1\subset {\mathcal {A}}\). This means that \(\sum _{A\in {\mathcal {A}}_1}I_A=\beta _{{\mathcal {A}}_1}<\beta _{{\mathcal {A}}}\). Take \({\mathcal {A}}_2={\mathcal {A}}\setminus {\mathcal {A}}_1\subset {\mathcal {A}}\). It holds that:
$$\begin{aligned} \sum _{A\in {\mathcal {A}}_2} I_A=\sum _{A\in {\mathcal {A}}}I_A-\sum _{A\in {\mathcal {A}}_1}I_A=\beta _{\mathcal {A}}-\beta _{{\mathcal {A}}_1}\in {\mathbb {N}}, \end{aligned}$$whence \({\mathcal {A}}_2\in {\mathbb {A}}({\mathcal {X}})\) and also \(\beta _{{\mathcal {A}}}=\beta _{{\mathcal {A}}_1}+\beta _{{\mathcal {A}}_2}\).
-
(b)
Trivial.
\(\square \)
Lemma 25
(Miranda & Montes, 2023, Lem. 19) Let \({\underline{P}}\) be a maximally imprecise coherent lower probability, and let \({\mathcal {A}}=(A_i)_{i\in I}\in {\mathbb {A}}({\mathcal {X}})\).
-
(i)
If \(\beta _{{\mathcal {A}}}=1\), then \({\mathcal {A}}\) is a partition of \({\mathcal {X}}\).
-
(ii)
If \(\beta _{{\mathcal {A}}}=\vert {\mathcal {A}}\vert -1\), then \({\mathcal {A}}^c=(A_i^c)_{i\in I}\) is a partition of \({\mathcal {X}}\).
-
(iii)
If \(1<\beta _{{\mathcal {A}}}<\vert {\mathcal {A}}\vert -1\) and for every \(A,B\in {\mathcal {A}}\) at least one of \(A\cap B, A{\setminus } B\) and \(B{\setminus } A\) is empty, then there exists \({\mathcal {A}}_1\in {\mathbb {A}}^{*}({\mathcal {X}})\) such that \({\mathcal {A}}_1\subset {\mathcal {A}}\).
For any \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\), let
It is easy to show that \(h_{{\mathcal {A}}}^\textrm{LV}\) satisfies Eq. (A.3).
Proof of Theorem 9
Consider an element \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\).
If \(\beta _{{\mathcal {A}}}=1\), then \({\mathcal {A}}\) is partition so \({\mathcal {A}}\in {\mathbb {A}}^{*}({\mathcal {X}})\), and moreover
If \(\beta _{{\mathcal {A}}}=\vert {\mathcal {A}}\vert -1\), then \({\mathcal {A}}^c=(A_i^c)_{i=1,\ldots ,k}\) is a partition, so it belongs to \({\mathbb {A}}^{*}({\mathcal {X}})\), and
where the last equality holds because the number of elements in \({\mathcal {A}}\) and \({\mathcal {A}}^c\) is the same, hence \(\vert {\mathcal {A}}\vert =\vert {\mathcal {A}}^c\vert \). Therefore, the value \(\delta _\textrm{LV}=\min _{{\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})} h_{{\mathcal {A}}}^\textrm{LV}\) satisfies:
To see that we have the equality, let \({\mathcal {A}}=(A_i)_{i=1,\ldots ,k}\) be an element in \({\mathbb {A}}({\mathcal {X}})\) where the minimum in Eq. (8) is attained. Assume now that \(1<\beta _{{\mathcal {A}}}<\vert {\mathcal {A}}\vert -1\), and let us prove that it is possible to find some \({\mathcal {A}}^{*}\in {\mathbb {A}}^{*}({\mathcal {X}})\) such that \(\beta _{{\mathcal {A}}^{*}}<\beta _{{\mathcal {A}}}\) and where the value in Eq. (8) is attained.
From item (iii) in Lemma 25 we deduce that either there is \({\mathcal {A}}^{*}\in {\mathbb {A}}({\mathcal {X}})\) with \({\mathcal {A}}^{*}\subset {\mathcal {A}}\) or there are two different \(A_i,A_j\in {\mathcal {A}}\) with \(A_i\cap A_j\ne \emptyset \), \(A_i{\setminus } A_j\ne \emptyset \) and \(A_j{\setminus } A_i\ne \emptyset \). In this second case, applying 2-monotonicity with the sets \(A_i\) and \(A_j\) above we deduce that:
where \({\mathcal {A}}_1=\big ( {\mathcal {A}}{\setminus }\{A_i,A_j\} \big )\cup (A_i\cap A_j,A_i\cup A_j)\), using that \(\beta _{{\mathcal {A}}_1}=\beta _{{\mathcal {A}}}\). Thus, the minimum in Eq. (8) is also attained in \({\mathcal {A}}_1\).
Now, if in \({\mathcal {A}}_1\) it is possible to find two different events \(B_i,B_j\) with \(B_i\cap B_j\ne \emptyset \), \(B_i{\setminus } B_j\ne \emptyset \) and \(B_j{\setminus } B_i\ne \emptyset \) a similar reasoning shows that \({\mathcal {A}}_2={\mathcal {A}}_1\cup \big ( B_i\cup B_j,B_i\cap B_j \big ){\setminus }(B_i,B_j)\) also satisfies \(\beta _{{\mathcal {A}}_2}=\beta _{{\mathcal {A}}_1}\) and \(h_{{\mathcal {A}}}^\textrm{LV}=h_{{\mathcal {A}}_1}^\textrm{LV}=h_{{\mathcal {A}}_2}^\textrm{LV}\). Iterating the procedure, we find after a finite number of steps that there are no different events C and D in the family \({\mathcal {A}}_k\) such that \(C\cap D\ne \emptyset \), \(C{\setminus } D\ne \emptyset \) and \(D{\setminus } C\ne \emptyset \). But then, applying Lemma 25 we deduce that there is \({\mathcal {A}}^{*}\in {\mathbb {A}}^{*}({\mathcal {X}})\) with \({\mathcal {A}}^{*}\subset {\mathcal {A}}_k\).
Since \({\mathcal {A}}_k={\mathcal {A}}^{*}\dot{\cup }({\mathcal {A}}_k {\setminus } {\mathcal {A}}^{*})\), we deduce from Lemma 24 that either \(h_{{\mathcal {A}}_k}^\textrm{LV}=h_{{\mathcal {A}}^{*}}^\textrm{LV}\) or \(h_{{\mathcal {A}}_k}^\textrm{LV}=h_{{\mathcal {A}}_k{\setminus } {\mathcal {A}}^{*}}^\textrm{LV}\). Since both \(\beta _{{\mathcal {A}}^{*}}\) and \(\beta _{{\mathcal {A}}_k\setminus {\mathcal {A}}^{*}}\) are strictly smaller than \(\beta _{{\mathcal {A}}_k}\), we deduce that we can find another element of \({\mathbb {A}}({\mathcal {X}})\) where the value \(\delta _\textrm{LV}\) is attained and with a smaller value of \(\beta _{{\mathcal {A}}}\). If we repeat this process we end up with a family \({\mathcal {A}}'\in {\mathbb {A}}({\mathcal {X}})\) such that \(\beta _{{\mathcal {A}}'}=1\), and where the minimum value in Eq. (8) is attained, at which point we apply the first part of the proof. \(\square \)
Proof of Proposition 10
To see that the condition is necessary, assume ex-absurdo that there exists \(A\ne \emptyset ,{\mathcal {X}}\) such that \({\overline{P}}(A)={\underline{P}}(A)\) and let \({\overline{P}}_\textrm{PMM}\) be the upper probability of a PMM defined using \((P_0,\delta )\) such that \({\overline{P}}_\textrm{PMM}\le {\overline{P}}\). Then, it should be \({\overline{P}}_\textrm{PMM}(A)={\overline{P}}(A)={\underline{P}}(A)={\underline{P}}_\textrm{PMM}(A)\). From the definition of the PMM, this can only hold if \({\overline{P}}_\textrm{PMM}(A)={\underline{P}}_\textrm{PMM}(A)\in \{0,1\}\), meaning that it should be \({\underline{P}}(A)\in \{0,1\}\), a contradiction with our assumption of \({\underline{P}}(A)\in (0,1)\) for every \(A\ne \emptyset ,{\mathcal {X}}\).
Conversely, if \({\overline{P}}(A)>{\underline{P}}(A)\) for any \(A\ne \emptyset ,{\mathcal {X}}\) then by Lemma 22 there is some \(P_0\in {\mathcal {M}}({\underline{P}})\) such that \(P_0(A)\in ({\underline{P}}(A),{\overline{P}}(A))\) for every event \(A\ne \emptyset ,{\mathcal {X}}\). If we now consider \(\delta >0\) small enough such that \((1+\delta )P_0(A)<{\overline{P}}(A)\) for any \(A\ne \emptyset ,{\mathcal {X}}\), we obtain that the PMM determined by \((P_0,\delta )\) is an inner approximation of \({\overline{P}}\). \(\square \)
Proof of Proposition 11
This follows applying Lemma 23 to \(({\underline{Q}}^{\delta }_\textrm{PMM})_{\delta \in \Lambda _\textrm{PMM}}\). \(\square \)
Proof of Theorem 12
Let \(\delta >0\), and let \({\overline{P}}_\delta \) be the upper probability defined in Eq. (10). From Walley (1991), it avoids sure loss if and only if for every \(k\in {\mathbb {N}}\) and every \(A_1,\ldots ,A_k\subseteq {\mathcal {X}}\) it holds that:
Without loss of generality, we may assume that all the events \(A_1,\ldots ,A_k\) are proper subsets of \({\mathcal {X}}\) (\({\overline{Q}}^\delta _\textrm{PMM}(A_i)-I_{A_i}\) would be constant on zero otherwise) and also that \(\cup _{i=1}^{k} A_i={\mathcal {X}}\) (otherwise (A.4) holds trivially taking \(x\in (\cup _{i=1}^{k} A_i)^c)\). Taking into account that \({\mathcal {X}}\) is finite, Eq. (A.4) is equivalent to:
for any \(A_1,\ldots ,A_k\ne \emptyset ,{\mathcal {X}}\). In particular, given \({{\mathcal {A}}}=\{A_1,\dots ,A_k\}\in {{\mathbb {A}}}({\mathcal {X}})\) with \(\sum _{i=1}^{k} I_{A_i}=\beta _{{\mathcal {A}}}\), it should be \(\delta \le \frac{1}{\beta _{{\mathcal {A}}}}\sum _{i=1}^k{\overline{P}}(A_i)-1\), whence:
To see that we have the equality, consider an arbitrary family \(A_1,\ldots ,A_k\), and take \(x^{*}\in {\mathcal {X}}\) so that \(\min _{x\in {\mathcal {X}}} \sum _{i=1}^kI_{A_i}(x)=\sum _{i=1}^kI_{A_i}(x^{*})\). For each \(i=1,\dots ,k\) take \(B_i\subseteq A_i\) such that \(\sum _{i=1} I_{B_i}(x)=\sum _{i=1}^{k} I_{A_i}(x^{*})\) for every \(x\in {\mathcal {X}}\). Then
Thus:
and as a consequence Eq. (12) holds. \(\square \)
In order to prove Theorem 13, let us denote, for any \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\):
It is easy to see that \(h_{{\mathcal {A}}}^\textrm{PMM}\) satisfies Eq. (A.3).
Proof of Theorem 13
Consider an element \({\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})\).
If \(\beta _{{\mathcal {A}}}=1\), then \({\mathcal {A}}\) is partition so \({\mathcal {A}}\in {\mathbb {A}}^{*}({\mathcal {X}})\), and moreover
If \(\beta _{{\mathcal {A}}}=\vert {\mathcal {A}}\vert -1\), then \({\mathcal {A}}^c=(A_i^c)_{i=1,\ldots ,k}\) is a partition, so it belongs to \({\mathbb {A}}^{*}({\mathcal {X}})\). Also:
where the last equality holds because the number of elements in \({\mathcal {A}}\) and \({\mathcal {A}}^c\) is the same, hence \(\vert {\mathcal {A}}\vert =\vert {\mathcal {A}}^c\vert \). Therefore, the value \(\delta _\textrm{PMM}=\min _{{\mathcal {A}}\in {\mathbb {A}}({\mathcal {X}})} h_{{\mathcal {A}}}^\textrm{PMM}\) satisfies
To see that we have the equality, let \({\mathcal {A}}=(A_i)_{i=1,\ldots ,k}\) be an element in \({\mathbb {A}}({\mathcal {X}})\) where the minimum in Eq. (12) is attained. Assume now that \(1<\beta _{{\mathcal {A}}}<\vert {\mathcal {A}}\vert -1\), and let us prove that it is possible to find some \({\mathcal {A}}^{*}\in {\mathbb {A}}^{*}({\mathcal {X}})\) such that \(\beta _{{\mathcal {A}}^{*}}<\beta _{{\mathcal {A}}}\) and where the value in Eq. (12) is attained.
From item (iii) in Lemma 25 we deduce that either there is \({\mathcal {A}}^{*}\in {\mathbb {A}}({\mathcal {X}})\) with \({\mathcal {A}}^{*}\subset {\mathcal {A}}\) or there are two different \(A_i,A_j\in {\mathcal {A}}\) with \(A_i\cap A_j\ne \emptyset \), \(A_i{\setminus } A_j\ne \emptyset \) and \(A_j{\setminus } A_i\ne \emptyset \). In this second case, applying 2-monotonicity with the sets \(A_i\) and \(A_j\) above we deduce that:
where \({\mathcal {A}}_1=\big ( {\mathcal {A}}{\setminus }\{A_i,A_j\} \big )\cup (A_i\cap A_j,A_i\cup A_j)\), using that \(\beta _{{\mathcal {A}}_1}=\beta _{{\mathcal {A}}}\). Thus, the minimum in Eq. (12) is also attained in \({\mathcal {A}}_1\).
Now, if in \({\mathcal {A}}_1\) it is possible to find two different events \(B_i,B_j\) with \(B_i\cap B_j\ne \emptyset \), \(B_i{\setminus } B_j\ne \emptyset \) and \(B_j{\setminus } B_i\ne \emptyset \) a similar reasoning shows that \({\mathcal {A}}_2={\mathcal {A}}_1\cup \big ( B_i\cup B_j,B_i\cap B_j \big ){\setminus }(B_i,B_j)\) also satisfies \(\beta _{{\mathcal {A}}_2}=\beta _{{\mathcal {A}}_1}\) and \(h_{{\mathcal {A}}}^\textrm{PMM}=h_{{\mathcal {A}}_1}^\textrm{PMM}=h_{{\mathcal {A}}_2}^\textrm{PMM}\). Iterating the procedure, we find after a finite number of steps that there are no different events C, D in the family \({\mathcal {A}}_k\) such that \(C\cap D\ne \emptyset \), \(C{\setminus } D\ne \emptyset \) and \(D{\setminus } C\ne \emptyset \). But then, applying Lemma 25 we deduce that there is \({\mathcal {A}}^{*}\in {\mathbb {A}}^{*}({\mathcal {X}})\) with \({\mathcal {A}}^{*}\subset {\mathcal {A}}_k\).
Since \({\mathcal {A}}_k={\mathcal {A}}^{*}\dot{\cup }({\mathcal {A}}_k {\setminus } {\mathcal {A}}^{*})\), we deduce from Lemma 24 that either \(h_{{\mathcal {A}}_k}^\textrm{PMM}=h_{{\mathcal {A}}^{*}}^\textrm{PMM}\) or \(h_{{\mathcal {A}}_k}^\textrm{PMM}=h_{{\mathcal {A}}_k{\setminus } {\mathcal {A}}^{*}}^\textrm{PMM}\). Since both \(\beta _{{\mathcal {A}}^{*}}\) and \(\beta _{{\mathcal {A}}_k\setminus {\mathcal {A}}^{*}}\) are strictly smaller than \(\beta _{{\mathcal {A}}_k}\), we deduce that we can find another element of \({\mathbb {A}}({\mathcal {X}})\) where the value \(\delta _\textrm{PMM}\) is attained and with a smaller value of \(\beta _{{\mathcal {A}}}\). If we repeat this process we end up with a family \({\mathcal {A}}'\in {\mathbb {A}}({\mathcal {X}})\) such that \(\beta _{{\mathcal {A}}'}=1\), and where the minimum value in Eq. (8) is attained, at which point we apply the first part of the proof. \(\square \)
Proof of Proposition 14
To see that the condition is necessary, note that since by assumption \({\underline{P}}(A)>0\) for every \(A\ne \emptyset \), any inner approximation \({\underline{P}}_\textrm{TV}\) in \({{\mathcal {C}}}_\textrm{TV}\) should satisfy \({\underline{P}}_\textrm{TV}(A)=P_0(A)-\delta \) and \({\overline{P}}_\textrm{TV}(A)=P_0(A)+\delta \) for any \(A\ne \emptyset ,{\mathcal {X}}\). As a consequence, it will be \({\overline{P}}_\textrm{TV}(A)-{\underline{P}}_\textrm{TV}(A)=2\delta >0\) for any \(A\ne \emptyset ,{\mathcal {X}}\), meaning that there cannot be any inner approximation of \({\underline{P}}\) if it is not maximally imprecise.
Conversely, assume that \({\underline{P}}(A)<{\overline{P}}(A)\) for any \(A\ne \emptyset ,{\mathcal {X}}\). Applying Lemma 22, there exists \(P_0\in {\mathcal {M}}({\underline{P}})\) such that \({\underline{P}}(A)<P_0(A)<{\overline{P}}(A)\) for any \(A\ne \emptyset ,{\mathcal {X}}\). Taking \(\delta \) such that \(0<\delta <\min _{A\ne \emptyset ,{\mathcal {X}}} \big (P_0(A)-{\underline{P}}(A)\big )\), we obtain that \(\delta <P_0(A)-{\underline{P}}(A)\), so \({\underline{P}}(A)<P_0(A)-\delta \) for any \(A\ne \emptyset ,{\mathcal {X}}\). Hence, \(P_0\) and \(\delta \) determine a TV model that inner approximates \({\underline{P}}\). \(\square \)
Proof of Proposition 15
This follows applying Lemma 23 to \(({\underline{Q}}^{\delta }_\textrm{TV})_{\delta \in \Lambda _\textrm{TV}}\). \(\square \)
Proof of Proposition 17
For any probability measure \(P_0\) and any \(\delta >0\) it holds that \(B_\textrm{LV}^\delta (P_0)\cup B_\textrm{PMM}^\delta (P_0)\subseteq B_\textrm{TV}^\delta (P_0)\) (Montes et al., 2020b, Prop.5.1). Hence, \(B_\textrm{TV}^\delta (P_0)\subseteq {\mathcal {M}}({\underline{P}})\) implies that \(B_\textrm{LV}^\delta (P_0)\subseteq {\mathcal {M}}({\underline{P}})\) and \(B_\textrm{PMM}^\delta (P_0)\subseteq {\mathcal {M}}({\underline{P}})\), and therefore \(\delta _\textrm{TV}\le \min \{\delta _\textrm{LV},\delta _\textrm{PMM}\}\). \(\square \)
Proof of Proposition 18
\({\underline{P}}\le {\underline{Q}}\) implies that \({\underline{P}}(J_e-J_d)\le {\underline{Q}}(J_e-J_d)\) for any \(e,d\in D\). Hence, \({\underline{Q}}(J_e-J_d)\le 0\) implies \({\underline{P}}(J_e-J_d)\le 0\), so any optimal alternative for \({\underline{Q}}\) under maximality is also optimal for \({\underline{P}}\). \(\square \)
Proof of Proposition 19
\({\underline{P}}\le {\underline{Q}}\) is equivalent to \({\overline{P}}\ge {\overline{Q}}\). If \(d\in D\) is optimal for \({\underline{Q}}\) under interval dominance, then \({\overline{Q}}(J_d)\ge {\underline{Q}}(J_e)\) for every \(e\in D\), but this implies that:
meaning that d is optimal too for \({\underline{P}}\). This implies that \(\text{ opt}_{\sqsupset _{{\underline{P}}}}\supseteq \text{ opt}_{\sqsupset _{{\underline{Q}}}}\). \(\square \)
Proof of Proposition 19
(Proof of Proposition 20) Consider \(d\in \text{ opt}_{{\mathcal {M}}({\underline{Q}})}\) under E-admissibility. This means that there exists \(P\in {\mathcal {M}}({\underline{Q}})\) such that \(E_P(J_d)=\max _{d'\in D}E_P(J_{d'})\). Since \({\underline{P}}\le {\underline{Q}}\), then \({\mathcal {M}}({\underline{P}})\supseteq {\mathcal {M}}({\underline{Q}})\), whence P belongs to \({\mathcal {M}}({\underline{P}})\), and as a consequence d also belongs to \(\text{ opt}_{{\mathcal {M}}({\underline{Q}})}\) under E-admissibility. \(\square \)
Proof of Proposition 21
Since \({\mathcal {M}}({\underline{Q}})\subseteq {\mathcal {M}}({\underline{P}})\), it follows that \({\underline{P}}(f)\le {\underline{Q}}(f)\), whence \(\mid {\underline{Q}}(f)-{\underline{P}}(f)\mid ={\underline{Q}}(f)-{\underline{P}}(f)\).
If \({\underline{Q}}\) is 2-monotone, then \({\underline{Q}}(f)\) coincides with the Choquet integral of f with respect to \({\underline{Q}}\), \((C)\int f d{\underline{Q}}\), while by coherence we have that \({\underline{P}}(f)\ge (C)\int f d{\underline{P}}\) (Walley, 1981).
Assume that \(f=\sum _{i=1}^{n} x_i I_{A_i}\), for \(x_1\ge x_2 \ge \dots \ge x_n\) in [0, 1] and a partition \(\{A_1,\dots ,A_n\}\) of \({\mathcal {X}}\). Then
By conjugacy, we deduce that also \(\vert {\overline{P}}(f)-{\overline{Q}}(f)\vert ={\overline{P}}(f)-{\overline{Q}}(f)\le \delta .\) \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miranda, E., Montes, I. & Presa, A. Inner approximations of coherent lower probabilities and their application to decision making problems. Ann Oper Res (2023). https://doi.org/10.1007/s10479-023-05577-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10479-023-05577-y