1 Introduction

The low supply voltages avalable in modern CMOS processes is a challenge for analog designers [1–3]. As the current-mode approach to analog circuit design is gaining interest due to better performance, another compelling reason for current-mode circuits is the decreasing power supply of digital microelectronics. The upside of sharing both silicon and power with digital electronics challenges the analog designer to come up with solutions for low-voltage circuits. As the power supply is reduced, the available headroom is shrinking, so current-mode design techniques provide some kind of relief by demanding much less headroom. Standard current mirrors, i.e. Wilson [4, 5] and cascode mirrors [6], share a common minimum supply voltage requirement which is a diode drop or threshold voltage plus 2 times the saturation voltage. The diode drop is required to obtain a certain current level and the saturation voltage is needed for driving the transistors in saturation. Some attemps, by exploiting the back-gate or bulk, have been reported [6] without providing a significant improvement to the supply voltage limitation. In addition, both mismatch and the output impedance in modern CMOS processes will force the analog designer to either increase the transistor sizes or circuit complexity to maintain the accuracy of the analog circuitry. Translinear floating-gate (FG) analog circuits [7] may be used to implement current mirrors and more complex current mode circuitry. Multiple-input translinear elements (MITE) may be used to design complex analog current mode circuits. A severe problem with the MITE circuits is the control of the initial floating-gate charges and the unpredictable initial state of the driven nodes. By exploiting a balanced equilibrium state where all driven nodes are equal and exploiting floating capacitors to adjust the transconductance we may reduce both complexity and area [8]. Furthermore, the floating-gate current mirror may be adapted to bidirectional input and output currents without any DC level shift.

One possible solution to the matching problem is post-fabrication tuning using laser-trimming. Techniques requiring individual tuning of each powered-up circuit are slow and expensive. Another approach to threshold matching is to use MOS transistors with capacitive coupling to a floating gate. A change in the stored charge of the floating gate will effectively shift the threshold voltage seen from the capacitively coupled input terminal. The success of this approach is clearly dependent on both the accuracy and the overhead penalty in terms of silicon area and production cost.

The ultra low-voltage (ULV) floating-gate analog circuits [9] presented in this paper can operate down to approximately 100 mV in weak inversion. In the following analysis all transistors are assumed to be in saturation, hence only the saturation voltage and required frequency response limit the minimum usable supply voltage. Typical supply voltages for the ULV floating-gate circuits are in the range 0.2–1.0 V.

In Sect. 2 the ultra low voltage (ULV) clocked semi-floating-gate transistors and logic are presented. ULV split gate current mirror is decribed in Sect. 3 and the inverting current mirror is presented in Sect. 4, followed by current multiplier and current divider in Sect. 5. In Sect. 6 the symmetric bidirectional current mirror is presented and the continuous time ULV current mirror is described in Sect. 7. The symmetric and continuous time ULV current mirror is presented in Sect. 8.

2 Ultra low voltage (ULV) CMOS

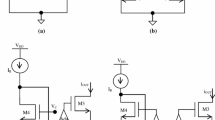
The clocked semi floating gate (CSFG) transistors are shown in Fig. 1a. The recharge transistors are drawn vertically and the evaluate transistors are drawn horizontally. By powering up the gate to source voltages in an initialization phase we are able to reduce the supply voltage without decreasing the ON current provided by the enhanced transistors. The aim is to maintain a high current level combined with a very low supply voltage. The enhancement can be viewed as an active threshold voltage shift. Note that the recharge transistor and the evaluate transistor are clocked by inverse signals which will, to some degree, reduce the capacitive noise imposed on the semi-floating-gate. In order to reduce the charge injection we may add a dummy recharge switch. The noise imposed through parasitic capacitances and charge injection may be reduced by a symmetrical, i.e. quasi differential, design approach. The ULV logic, i.e. an ULV inverter, is shown in Fig. 1b. The ULV CMOS logic can be exploited to design low voltage and high speed digital circuits. In terms of Energy delay product (EDP) the ULV gates are superior to complementary CMOS logic.

Fig. 1
figure 1

a nMOS and pMOS clocked semi-floating-gate (CSFG) transistors. b The symmetric ultra low voltage inverter. c Recharge mode and d evaluate mode

Full size image

The ULV logic, i.e. an inverter, in recharge and evaluate mode is shown in Fig. 1. The ULV gate operation is characterized by:

  • Recharge The simplified ULV inverter in recharge mode is shown in Fig. 1c. The nMOS floating-gate is recharged to V DD and the pMOS floating-gate is recharged to V SS  = gnd while the output and input are precharged to V DD /2 = (V DD  − V SS )/2. The output will be forced to V DD /2 due to a reversed biased inverter.

  • Evaluate. The simplified ULV inverter in evaluate mode is shown in Fig. 1d. The output will be pulled to V DD if a negative transition, \(\Updelta V_{in} = -V_{DD}/2\), occurs and to V SS if there is a positive transition, \(\Updelta V_{in} = V_{DD}/2\), applied at the input.

A switched symmetric non-continuous time ULV current mirror is presented in [10]. By using two current mirrors operating in opposite phases we obtain a continuous time clocked current mirror with an inherent auto-zero function.

The continuous time clocked-semi-floating-gate (CCSFG) transistors are shown in Fig. 2. The recharge transistors are drawn vertically and the evaluate transistors are drawn horizontally. By powering up the gate to source voltages in an initialization phase we are able to reduce the supply voltage without decreasing the ON current provided by the enhanced transistors. The aim is to maintain a high current level combined with a very low supply voltage. The enhancement can be viewed as a active threshold voltage shift. Note that the recharge transistor and the evaluate transistor are clocked by inverse signals which will, to some degree, reduce the capacitive noise imposed to the semi-floating-gate. In order to reduce the charge injection we may add a dummy recharge switch. The noise imposed through parasitic capacitance’s and charge injection may be reduced by a symmetrical, i.e. quasi differential, design approach.

Fig. 2
figure 2

The nMOS and pMOS continuous time clocked semi floating gate (CCSFG) transistors. The input signal is applied to one of the FG nodes depending on the clock signal

Full size image

3 Ultra low voltage current mirror

In a typical analog circuit the voltage headroom of the internal nodes, i.e. V in and V out , is limited by the supply voltage and the saturation voltage of the transistors. In practice this means that the voltage headroom may be expressed as

$$ V_{limit} = V_{DD} - 2V_{sat}. $$
(1)

If V sat  = 50 mV and V DD  = 250 mV then V limit  = 150 mV which yields a dynamic voltage range of 50–200 mV and a dynamic range for the transistor currents equal to 1 × 10−8–3 × 10−7 A. The CSFG transistors offer a way to circumvent the limitation of the currents for ultra low supply voltages. By recharging the semi floating-gates to V DD for the nMOS transistors and gnd for the pMOS transistors and assume a supply voltage equal to 250 mV the dynamic current range is changed to 3 × 10−7–3 × 10−6 A.

A simple comparison of the minimum required supply voltage and the available dynamic range (V DR ) for some current mirrors is shown in Table 1. If \(V_{DR}=V_{th}-2V_{sat}\) is a suitable voltage headroom for an application the supply voltage of the ULV current mirror can be reduced by a factor of 2 compared to other current mirrors.

Table 1 Supply voltage requirements for practical applications
Full size table

In the initialization phase the floating-gate is recharged to V DD while the input V in and output V out are recharged to V DD /2. If the transistors are not matched the input and output voltages may be slightly different, which may give rise to different currents. The noise imposed, i.e. through parasitic capacitances and charge injection, will affect both evaluate transistors and the relative currents are not altered.

In the evaluation phase the input and output currents of a floating-gate current mirror can be approximated by the simple models, assuming weak inversion

$$ I_{in} = I_{r}\cdot e^{k_{1}\left( V_{in}-\frac{V_{DD}} {2}\right)}\cdot \left( 1+ \lambda \left( V_{in}-\frac{V_{DD}} {2}\right) \right) $$
(2)
$$ I_{out} = I_{r}\cdot e^{k_{1}\left( V_{in}-\frac{V_{DD}} {2}\right)}\cdot \left( 1+ \lambda \left( V_{out}-\frac{V_{DD}} {2}\right) \right), $$
(3)

where \(k_{1}=\left(C_{inn}/C_{T}\right) \cdot \left(1/nU_{T}\right), C_{T}\) is the total capacitance seen by the floating-gate, \(C_{inn}=C_{inn1}=C_{inn2}, U_{T}\) is the thermal voltage, n is the slope factor and I r is the current running through the transistors when \(V_{1}=V_{DD}/2\). The current level, i.e. I r is determined by the offset applied in the initialization phase. In this case the current level I r is equal to the current running through a transistor assuming a gate to source voltage equal to the supply voltage. We may express the relative current, \(I_{e2}/I_{e1}\) or deviation assuming that \(V_{out}\approx V_{DD}-V_{in}\)

$$ \frac{I_{out}}{I_{in}} = \frac{1+\lambda \cdot \left( \frac{V_{DD}}{2}-V_{in}\right)}{1+ \lambda \left( V_{in}-\frac{V_{DD}}{2}\right)}. $$
(4)

By separating the gate terminals of the transistors as shown in Fig. 3 we obtain the split gate CSFG current mirror [8]. The gate terminals are recharged by two separate recharge transistors. More interestingly, the transistors do not share a common input capacitor. An advantage of the split gate approach is an increase in transconductance due to less capacitance associated with the floating gates. The V in and V out will be “inverse” due to the inverting property of CMOS gates. By maximizing the output resistance, assuming long transistors, the inaccuracy may be reduced. More advanced current mirror configurations are not suitable for CSFG design. The deviation may be reduced by increasing the transistor length at the expense of reduced current and increased capacitances.

Fig. 3
figure 3

CSFG split gate current mirror with minimum sized transistors. The input V a is swept from V DD /2 to gnd. C inn2 = 6fF, and C inn1 = 2fF and V DD  = 0.175 V

Full size image

The input capacitors may be exploited to compensate for the inaccuracy due to channel length modulation. By changing the relative capacitance of the input capacitors, C inn1 and C inn2 we may compensate for the inaccuracy due to the early effect. Assuming that \(V_{out}\approx V_{DD}-V_{in}\) we may express the currents in the evaluation phase I in and I out as

$$ I_{in} = I_{r}\cdot e^{k_{1}\left( V_{in}-\frac{V_{DD}} {2}\right)}\cdot \left( 1+ \lambda \left( V_{in}-\frac{V_{DD}} {2}\right)\right) $$
(5)
$$ I_{out} = I_{r}\cdot e^{k_{2}\left( V_{in}-\frac{V_{DD}} {2}\right)}\cdot \left( 1+ \lambda \left( \frac{V_{DD}} {2}-V_{in}\right)\right), $$
(6)

We may exploit k 1 and k 2 to minimize the inaccuracy of the current mirror by solving the equation

$$ \begin{aligned} I_{out} &= I_{in}\\ k_{2} & \approx k_{1} + \frac{ \ln \left(\frac{1+\lambda \cdot \frac{V_{DD}}{2}}{1-\lambda \cdot \frac{V_{DD}} {2}}\right)}{\frac{V_{DD}}{2}}\\ C_{inn2} & \approx \,C_{inn1} + C_{T}nU_{T}\cdot \left(\frac{\ln \left(\frac{1+\lambda \cdot \frac{V_{DD}}{2}}{1-\lambda \cdot \frac{V_{DD}}{2}}\right)}{\frac{V_{DD}}{2}} \right), \end{aligned} $$
(7)

which for \(V_{DD}=0.175\,\text{V}, \lambda = 5.7, C_{inn1} = 2fF, C_{T}=6fF\) and n = 2 yields C inn2 ≈ 6fF. The increased transconductance of the output transistor compensates for the output conductance of both transistors. If the current mirror operates in strong inversion the capacitance C inn2 needs to be increased furthermore due to the reduced relative transconductance g m /I. The split-gate current mirror will be recharged or initialized in the same manner as the inverter shown in Fig. 1.

The CSFG split gate current mirror is simulated using spectreS and the result is shown in Fig. 3. The input V in is swept from V DD /2 = 88 mV to gnd. Compared to the common gate the accuracy is significantly improved without increasing the transistor length. As expected the output current shows much less deviation from the input current. The actual precision is dependent on the matching of the capacitors.

4 Ultra low voltage inverting current mirror

The nMOS transistors used in the inverting current mirror the are minimum sized and the width pMOS evaluate transistors are increased to obtain a precharged output voltage equal to V DD /2. The input capacitors to the nMOS CSFG transistors are equal to 200aF and may be designed using MOS-, poly–poly- or metal–metal capacitors. The capacitors used to connect to the pMOS CSFG transistors are increased to match the transconductance of the nMOS evaluate transistors, i.e. approximately 3 times the nMOS CSFG input capacitors.

The ULV inverted current mirror or current inverter is shown in Fig. 4. The inverting current mirror consists of the transistors labeled Q1 and Q2 while transistor Q3 provides the input current and transistor Q4 drains the output current. In the recharge phase we may disregard the floating capacitors due to the fact that all semi floating-gates are driven towards the reference voltages or supplies and the output nodes are driven towards \(V_{in} = V_{out} = V_{a} = V_{DD}/2\). The recharge phase ensures that the input and output currents are equal when the input voltage is V DD /2. The current inverter is susceptible to noise, i.e. charge injection and clock feed through. To reduce the inaccuracy due to charge injection we can include dummy recharge transistors.

Fig. 4
figure 4

ULV inverting current mirror. The transistors labeled Q3 and Q4 are used as current source and drain respectively

Full size image

When the input current increase the voltage V in will increase which will increase the semi floating-gate potential of the pMOS output transistor, hence I out will decrease. In this case the output voltage V out will likely decrease. In this case the drain to source voltage of both the input -and output transistors will increase and the inherent problem with finite output resistance will not affect the accuracy of the current inverter significantly. We may express a simplified operation of the current mirror as

$$ I_{in} = I_{r}\cdot e^{k_{1}\left( V_{in}-\frac{V_{DD}} {2}\right)}\cdot \left( 1+ \lambda \left( V_{in}-\frac{V_{DD}} {2}\right) \right) $$
(8)
$$ I_{out} = I_{r}\cdot e^{k_{2}\left( \frac{V_{DD}}{2}-V_{1}\right)}\cdot \left( 1+ \lambda \left( \frac{V_{DD}}{2}-V_{out}\right) \right) $$
(9)

where \(k_{1}=\left(C_{inn1}/C_{T}\right) \cdot \left(1/nU_{T}\right), k_{2}=\left(C_{inn2}/C_{T}\right) \cdot \left(1/nU_{T}\right), C_{T}\) is the total capacitance seen by the floating-gate, U T is the thermal voltage, n is the slope factor and I r is the current running through the transistors when \(V_{in}=V_{DD}/2\). The current level, i.e. I r is determined by the offset applied in the initialization phase. In this case the current level I r is equal to the current running through a transistor assuming a gate to source voltage equal to the supply voltage. Assuming that \(k_{2} = k_{1}\) and \(V_{DD}/2 -V_{out} \approx V_{in}-V_{DD}/2\), or \(V_{out} \approx V_{DD}-V_{in}\) due to the analog voltage inverter configuration, we may express the output current I out as

$$ \begin{aligned} I_{out} &= I_{r}\cdot e^{k_{2}\left( \frac{V_{DD}}{2} - V_{in}\right)}\cdot \left( 1+ \lambda \left( \frac{V_{in} - V_{DD}} {2}\right) \right)\\ I_{out} &= \frac{I_{r}^{2}\cdot \left( 1+ \lambda \left( \frac{V_{in} - V_{DD}}{2}\right) \right)^{2}}{I_{in}} \end{aligned} $$
(10)

which is defined as current inversion \(I_{out} = I_{in}'\). Note that if \(I_{in}= I_{r}\) then \(I_{out}=I_{r}\).

The response of the inverting current mirror to a sine input is shown in Fig. 5. The supply voltage is 250 mV, the clock frequency is 25 MHz and the input frequency is 2 MHz. For very low input frequencies the response will be influenced by leakage currents. The absolute value of the output current of the inverting current mirror as a function of the input current, assuming the sine input shown in Fig. 5a is shown in Fig. 5b. Note that the the voltage level of the input, and output, vary significantly while the current level at the start of each evaluate phase is close to 160 nA for different input and output voltages. The nonlinear characteristics is due to slightly different level of inversion. If we invert the output current we obtain

$$ \begin{aligned} I_{out}' &= \frac{I_{r}^{2}\cdot \left( 1+ \lambda \left( \frac{V_{in} - V_{DD}}{2}\right) \right)^{2}}{I_{out}} \\ &= I_{in}, \end{aligned} $$
(11)

hence two inverting current mirrors can be used as a non-inverting current mirror without the mismatch usually inherent due to finite output resistance.

Fig. 5
figure 5

a The response of the inverting current mirror to a rail to rail sine input signal. b The absolute value of the output current of the inverting current mirror as a function of the input current

Full size image

The response of two cascaded inverting current mirrors to a rail to rail sine input signal is shown in Fig. 6. The supply voltage is 250 mV, the clock frequency is 25 MHz and the input frequency is 4 MHz. The value of the output current applying two cascaded inverting current mirrors as a function of the input current, assuming the sine input is shown. Note that the non-linearity due to different inversion level of each inverting current mirror is cancelled out. The dynamic current range is increased due to an increased input signal frequency. The short lines reflect a small variation of the input, and hence output, currents in an evaluation phase. This condition can be seen in Fig. 6 at 3 × 10−7 s.

Fig. 6
figure 6

The response of two cascaded inverting current mirrors to a rail to rail sine input signal

Full size image

5 Ultra low voltage current multiplier and divider

The ULV current multiplier is shown in Fig. 7. We may assume that both inputs will affect the output in a way that resembles an analog inverter. Assume that input I in2 is fixed and I in1 is increased, the expected response of the circuit is an increase in the output current. The multiplier will not only perform a current multiplication, the actual function is defined as multiply and normalize. We may express the ideal output current as a function of the input currents

$$ I_{out} = \frac{I_{in1}\cdot I_{in2}}{I_{r}}, $$
(12)

where I r is the recharge output current. We may apply the same channel length modulation compensation technique described for current mirror to increase the accuracy of the current multiplier.

$$ C_{inn} \approx C_{m} + \left(\frac{C_{T}nU_{T}}{N}\right)\cdot \left(\frac{\ln \left(\frac{1+\lambda \cdot \frac{V_{DD}} {2}} {1-\lambda \cdot \frac{V_{DD}}{2}}\right)}{\frac{V_{DD}} {2}} \right), $$
(13)

where N is the number of inputs. We may even increase the processing capability of the current mirror by putting different weights on the input capacitances and thereby being able to perform a weighting of the inputs.

Fig. 7
figure 7

The basic nMOS CSFG current multiplier. The simulated (solid line) output current and the ideal (dashed line) output current of the current multiplier. The ideal output current is given by Eq. 1 and the recharge current I R is equal to 200 nA

Full size image

We apply the input signals to pMOS CSFG transistors to provide a current source and the output current is drained through a pMOS CSFG transistor. Data presented is based on simulation of the current multiplier shown in Fig. 7 and a 90 nm CMOS process with a supply voltage equal to 250 mV. The simulated (solid line) output current and the ideal (dashed line) output current of the current multiplier are shown in Fig. 7. The ideal output current is given by Eq. 1 and the recharge current I R is equal to 200 nA. Simulated data shows that the simulated response and ideal response of the current multiplier is quite accurate for currents larger than the recharge current. Only minimum sized transistors are used, hence increased accuracy is expected if the transistor sizes are increased. By increasing the transistor lengths we can reduce the mismatch due to increased drain impedance. Increased gate area will reduce the mismatch between equal transistors. The relative matching of the input capacitors is increased by using larger devices.

6 Symmetric bidirectional ultra low voltage current mirror

The response of current mirror shown in Fig. 3 will be restricted by the input and output current level and the polarity of the input current. The symmetric ULV current mirror is shown in Fig. 8. We may examine the circuit response to a recharge operation. During recharge the nMOS floating gate voltages are fixed to V offset+ while the pMOS floating gate voltages are equal to V offset−, the node voltages at x and out are V DD /2 and the current are equalized, i.e. \(I_{n1}=I_{n2}=-I_{p1}=-I_{p2}=I_{r}\). Furthermore the input and output currents are assumed to be 0. Assume that the input current increases compared to I r . This will lead to an increased voltage in node x, i.e assuming a pMOS transistor feeding a positive current into x. As a result the currents I n1 and I n2 will increase and I p1 and I p2 will be reduced accordingly. We may express the

$$ \begin{aligned} \Updelta I_{n1} - \Updelta I_{p1} &= \Updelta I_{in} \\ \Updelta I_{n1} &= \Updelta I_{in} + \Updelta I_{p1} \\ \Updelta I_{n2} &= \Updelta I_{in} + \Updelta I_{p2} \\ \Updelta I_{n2} - \Updelta I_{p2} &= \Updelta I_{in} \\ \Updelta I_{out} &= \Updelta I_{in} \end{aligned} $$
(14)

The input stage will act as a current to voltage converter and the output stage will act as a voltage to current converter. The change in input and output currents can be negative or positive and thus the current mirror is bidirectional. The actual input and output current can be expressed as

$$ \begin{aligned} I_{in} &= I_{r} + \Updelta I_{in} \\ I_{out} &= I_{r} + \Updelta I_{out} \\ I_{out} &= I_{in} \end{aligned} $$
(15)
Fig. 8
figure 8

Symmetric ULV current mirror

Full size image

The input current I in will pull the input terminal towards V DD or V SS depending on the polarity of the current. A negative current will pull the input terminal down and a positive input current will pull the input up. The input current will be matched by a current provided by the inverter in the I–V converter. The I–V converter will generate an input voltage to drain the actual input current. If the input current is equal to the recharge current the circuit is stable and the input voltage is equal to V DD /2. Any change in the input current will affect the floating gate voltages such that the input current is drained by the inverter in the I to V converter. The drained input current will be available at the output due to a corresponding change in the floating gate of the inverter producing the output current. If the capacitors C 1 and C 2 are equal the voltage change at the semi floating gates V fg1 and V fg2 and hence the output current will match the current running through the inverter in the I to V converter which is equal to the input current. We have not considered a natural source for the input current and a natural drain or load for the output current. A positive input current will be drained by an equal current running through the nMOS transistor of the inverter in the I–V converter caused by a increase in the voltage of the input terminal. A negative input current will lower the input terminal voltage and the input current will be drained by an increased pMOS transistor current of the I–V converter.

In Fig. 9 a symmetric current mirror with a current source and a current drain or load are shown. The accuracy of the current mirror is determined by mismatches of the transistors and capacitors. The transistor mismatches will affect the precharge value. We may expect that the precharge voltage will adapt to the relative mismatch of the evaluating transistors driving a specific node. If E n is strong compared to a standard transistor the node driven by the transistor may precharge at a higher level than V DD /2 and the node voltage will be pulled lower than V DD /2 the the circuit enters the evaluate mode. The change in node voltage will affect the driving circuit trough a parasitic node to floating-gate parasitic capacitance. The effect of this feedback will reduce the effect of inherent mismatch. On the other hand the change in the node voltage after entering the evaluate mode will affect the following circuit through the input capacitors. If the mismatches are random the transistor mismatches will not accumulate. Capacitor mismatches will affect the accuracy of the current mirror directly through a change in the transconductance. The accuracy of the capacitors may be increased by using larger poly–poly capacitors. The Internal voltage V A and the output V B are inverse with a DC value equal to V DD /2. The frequency of the input signal is 10 MHz and the recharge frequency is 25 MHz. The frequency range for the recharge signal is dependent of the applied supply voltage and must secure that no significant leakage of the semi floating gate deteriorates the accuracy. Furthermore the recharge frequency must be limited to ensure that the circuits are precharged correctly.

Fig. 9
figure 9

The simulated circuit including a current source for providing the input current and a current sink for the output current

Full size image

The simulated transistor currents are shown on Fig. 10. The output currents as function of the input currents of the simulated current mirror are shown. The bi-directionality of the symmetric current is evident and shows a reasonable linear characteristics and accuracy for a sine input voltage signal producing the input current. The current headroom is −300 to 300 nA and the supply voltage is 250 mV.

Fig. 10
figure 10

The response of the bifirectional current mirror

Full size image

7 Continuous time ultra low voltage current mirrors

A switched non-contiuous time ULV current mirror is presented in [10]. By using two current mirrors operating in opposite phases we obtain a continuous time clocked current mirror with an inherent auto-zero function.

The continuous time clocked semi floating gate (CCSFG) transistors are shown in Fig. 11. The recharge transistors are drawn vertically and the evaluate transistors are drawn horizontally. By powering up the gate to source voltages in an initialization phase we are able to reduce the supply voltage without decreasing the ON current provided by the enhanced transistors. The aim is to maintain a high current level combined with a very low supply voltage. The enhancement can be viewed as a active threshold voltage shift. Note that the recharge transistor and the evaluate transistor are clocked by inverse signals witch will, to some degree, reduce the capacitive noise imposed to the semi-floating-gate. In order to reduce the charge injection we may add a dummy recharge switch. The noise imposed through parasitic capacitance’s and charge injection may be reduced by a symmetrical, i.e. quasi differential, design approach.

Fig. 11
figure 11

The nMOS and pMOS continuous time clocked semi floating gate (CCSFG) transistors. The input signal is applied to one of the FG nodes depending on the clock signal. The other FG node will be forced to V DD simultaneously

Full size image

The nMOS CCSFG transistors in the two clock phases are shown in Fig. 11. Assuming ϕ = 0 the E1 transistor is operative and the E2 transistor is recharging. The output current should be dominated by transistor E1 and not E2. We may express the effective voltage of E2 as \(V_{E2_{effective}}= V_{DD}-V_{t}-V_{out}\), assuming a that the recharge is finished and neglecting body effect. The effective voltage of E1 may be expressed as \(V_{E1_{effective}}=V_{DD}-V_{t}+k_{inn}\Updelta V_{in}.\) In order to maintain the dominance of E2 we must have \(V_{E1_{effective}} > V_{E2_{effective}}\) and thus \(\Updelta V_{in} > {-}V_{out}/K_{in}\). If k in  = 0.5 this reduces to \(\Updelta V_{in} > {-}2V_{out}\). Now, the lowest potential we may expect for output, given that the transistors operate in saturation, is approximately 50 mV, and hence \(\Updelta V_{in} > {-}100mV\). If \(\Updelta V_{in} < {-}100\, \text{mV}\) the current running through E2 will prevent the output to fall further. In the most extreme case we may assume that \(V_{in} \approx V_{DD}-50\, \text{mV}\) and \(V_{out} \approx V_{DD}-50\, \text{mV}\) and an input signal \(\Updelta V_{in} = -100\,\text{mV}\).

The actual current running through the evaluate transistors are determined by:

  1. 1.

    The input voltage at switching point of the clock signals. If we assume that the input signal is stable short after the switching point both semi floating gates are close to V DD and the output will be pulled down towards 0 or more accurately pulling E1 out of the saturated region. We may expect the output voltage to be close to 50 mV. If the input is close to 0 when the clock switches the potential change in input voltage is V DD whereas the potential change in input is −V DD if the input is close to V DD at the switching point. The output current given by \(I_{out}=I_{E1}+I_{E2}\) is reset to I r , the current running through a nMOS transistor with an effective input voltage equal to V DD .

  2. 2.

    The input signal, i.e. \(\Updelta V_{in}\). We may assume that the output is close to 50 mV and transistor E1 is ready for transforming a input signal to a change in the current I E1 which will affect both V out and I E2. If the output is close to 0 already and the input signal is positive the output will not fall much further and the input signal will not affect the output voltage significantly. If the input, however is negative the output will be increased to a voltage required to equalize the currents.

The response of the continuous time ULV nMOS transistor to a rail to rail input sine of 8 MHz when the output is fixed to V DD /2 is shown in Fig. 12. The recharge frequency is 50 Mz. Lower graphs showing the clock signals and input signal while top graphs show the output currents of the ULV transistor. At each clock edge the output current of ULV nMOS transistor is reset to a level close to the reset current I r . If the recharge frequency is low enough the reset current will be equal to the reset current. The current running through the active transistor will be determined by the actual input voltage to the active transistor. When using this configuration we are able to detect any input changes even for inputs operating at a different voltage headroom than limited by V DD and gnd.

Fig. 12
figure 12

The response of the continuous time ULV nMOS transistor to a rail to rail input sine of 8 MHz when the output is fixed to V DD /2. The recharge frequency is 50 Mz. Lower graphs showing the clock signals and input signal while top graphs show the output currents of the ULV transistor

Full size image

The recharge frequency must be high enough to prevent significant distortion due to floating gate leakage in the evaluation phase. The leakage is dependent on the supply voltage and is close to 30 μV/ns. By assuming a recharge frequency of 50 MHz as shown in Fig. 12 we may expect a maximum leakage of 300 μV. The leakage is however affecting both transistors and the accuracy of the current mirror is not significantly reduced due to the leakage.

The response of the current mirror to a sine input voltage shows a output current which is a derivative of the input voltage, hence a cosine function. The DC voltage level of the input signal is not influencing the response. By integrating the output current and converting to a voltage a continuous time voltage signal may be retrieved. The auto zero (AZ) of the current mirror is dependent on the capability of the recharge transistors to pull the recharged transistor to the initial state, V effective  = V DD . The recharging time is of interest and voltage stored before recharging. At the end of the recharge period the FG voltage and the corresponding transistor current will be proportional to the derivative of the input signal V in and the frequency of the recharge signal ϕ. The current provided by the evaluating transistor will also be characterized by the derivative of the input signal. In the case where the input signal is a sine signal the AZ and output current level will be defined by a cosine function.

The continuous time ULV current mirror is shown in Fig. 13 and resembles an auto zero circuit sampling an input signal. Input and output stages are included for the purpose of providing typical current sources and loads. E1 and E2 are input transistors operating in opposite phases, and E3 and E4 are output transistors operating in opposite phases. When ϕ = 0 transistor E1 and E3 will be evaluating any input changes while transistors E2 and E4 will recharge to V DD . When ϕ switches from 0 to 1 the floating gates of transistor E1 and E3 will be equal to V DD . Any input changes will affect the two floatings gates and produce a effective gate to source voltage of these transistors according to

$$ V_{E1_{effective}} = V_{DD} + k_{e1}\Updelta V_{A} $$
(16)
$$ V_{E4_{effective}} = V_{DD} + k_{e4}\Updelta V_{A} $$
(17)

where \(k_{e1}= C_{e1}/C_{T_{E1}}, k_{e4}= C_{e4}/C_{T_{E4}}, C_{T_{E1}}\) is the total capacitance seen by the floating gate of transistor E1 and \(C_{T_{E4}}\) is the total capacitance seen by the floating gate of transistor E4. The input capacitance’s are used to compensate for the difference in currents due to the finite output resistances of output and input transistors [10]. We may evaluate the response of an input signal when ϕ = 0:

  1. 1.

    At the switching point when ϕ switches from 1 to 0.

    1. (a)

      V in ≈ 0, and hence V A ≈ V DD . We may assume that \(V_{FG1}=V_{FG4}=V_{DD}, V_{FGA2} = V_{FGB1}=0 \,\text{V}, V_{FG2} \approx V_{FG3} > V_{DD}\) and V FGA1 ≈ V FGB2  < 0 V. Furthermore we may assume that V B ≈ 0. The currents \(I_{E1} \approx I_{A2} \approx I_{E4} \approx I_{B1}\) are equal to the initial current I r , and \(I_{A} = I_{A2}-I_{A1}\) and \(I_{B} = I_{B1}- I_{E4}\). Independent of the previous current of the operative transistors right ahead of the transition the current level will be reset to the initial recharge currents. We may expect only a minor change in the active current pulling nodes A and B due to the switching of operative transistors from E2 to E1 and E3 to E4, even though the actual current level is changed significantly.

    2. (b)

      We may expect a small voltage drop for A and a small increase in B. The voltage change will be small because the effective voltage of A2 and E1 are equal. This holds for E4 and B1 as well.

    3. (c)

      A positive input transition occurs. If transistors A2 and E1, and E4 and B1 are matched, we will see a voltage change of B equal to \(\Updelta V_{in}\) in the opposite direction, or more precisely \(\Updelta V_{A} = - \Updelta V_{in}\).

    4. (d)

      V A falls due to a positive input signal and the currents I E1 and I E4 will decrease and the node B will rise. We may expect that \(\Updelta V_{B} = -\Updelta V_{A} = \Updelta V_{in}\).

  2. 2.

    If V in ≈ V DD we will experience the opposite case as explained previously. The circuit is symmetric and the circuit performs according to (a).

Fig. 13
figure 13

The continuous time ULV current mirror. A current source and a current sink are included for simulation purposes. The currents running through the recharged evaluate transistor are negligible

Full size image

The input (dotted) and output currents of the continuous time current mirror is shown in Fig. 14. The clock frequency is 100 MHz. The input and internal nodes are biased so that the transistor operates in saturation and the expected current headroom is thus reduced compared to the results shown in Fig. 12. As shown the characteristics of the current mirror matches a traditional current mirror and may operate at ultra low supply voltages.

Fig. 14
figure 14

The input (dotted) and output currents of the continuous time current mirror. The clock frequency is 100 MHz. The auto-zero or normalization is evident

Full size image

8 Symmetric and continuous time CSFG current mirror

The symmetric and continuous time CSFG current mirror is shown in Fig. 15. The input current I in and the output current I out are distributed into four paths according to

$$ I_{in} = I_{p1} + I_{p2} - I_{n1} - I_{n2} $$
(18)
$$ I_{out} = I_{p3} + I_{p4} - I_{n3} - I_{n4}. $$
(19)

The current mirror in Fig. 15 is symmetrical in terms of clock phases. If we assume that ϕ = 0 we can analyze the response of the circuit in more detail. Transistors EN1, EP1, EN4 and EP4 are recharging and the currents drawn by these transistors depend on the voltage of the input and output of the current mirror. We may assume that the output voltage voltage are dependent on the input voltage according to V out ≈ V  DD  − V in . The recharging transistors will affect the currents in the current mirror. If the input and output voltages are V DD /2 we may assume that current mirror is in a initial state, for example right after a clock edge ϕ changes from 1 to 0, and the active transistors EN2 and EP2 provides currents equal to the recharge state current I r determined by effective gate to source voltages equal to V offset+ and \(V_{offset-}- V_{DD}\) for transistors EN2 and EP2 respectively, hence \(I_{n2} = |I_{p2}|\). In this state the current running through the recharged transistors are non-significant due to the reverse biasing of these transistors and the effective gate to source voltages are equal to \(V_{offset+}- V_{DD}/2\) and \(V_{offset-}- V_{DD}/2\) for transistors EN1 and EP1 respectively. Furthermore, assuming matched transistors, \(I_{n1}=|I_{p1}|\) and hence will not affect the input current. The same arguments hold for the current I E4 and I P4 as well. The input current will be provided by a symmetric CSFG circuit, typically a symmetric and continuous time inverter similar to the output stage of the current mirror. After each clock edge the current mirror, the circuit proving the input current and the circuit draining the output current will be in a state with no current flowing between the different circuits.

Fig. 15
figure 15

The symmetric and continuous time CSFG current mirror and simplified symbol representation including a current source and a current sink

Full size image

8.1 Simulation results

The bidirectional ULV current mirror was simulated using a supply voltage equal to 250 mV and offset voltages equal to 400 and −150 mV. The recharge frequency applied in the simulation examples are 25 MHz. The usable recharge frequency range is determined by the offset voltages and supply voltage applied. For low supply voltages and low offsets both the leakage current and the active currents are small and the recharge frequency may be reduced, although maintained high enough to secure a complete recharge of the floating gates and to avoid problems due to leakage currents. The input frequency may vary and is limited by the timing response, i.e. current level determined by the supply voltage and offsets applied.

In Fig. 16 the positive and negative components of the input and output currents are shown when a sine input with a frequency equal to 200 MHz is applied. In this case the recharge clock edges are arriving when the input currents are low or high compared to the average level, ie.e at time 0.4 × 10−7. This can be seen as a distortion in the transient response of the current mirror and is most evident in Figure. The output current as a function of the inputs current is shown in Fig. 17. The distortion due to the auto-zero function of the current mirror is not influencing the performance of the circuit because the both the input and output current are auto-zeroed simultaneously. The higher input frequency is favorable in terms of leakage effects which is observable as larger current amplitudes and this effect can bee seen as a more linear current mirror response. The delay of the circuit is observable as a small mismatch for increasing and decreasing input currents.

Fig. 16
figure 16

The response of the current mirror to sine input with a frequency equal to 200 MHz

Full size image
Fig. 17
figure 17

The output current relative to the input current for a sine input with a frequency equal to 200 MHz

Full size image

9 Conclusion

We have presented a ultra low-voltage bidirectional ultra low-voltage current mirror based on a ultra low-voltage digital logic style. Clocked semi floating gate transistors are used to provide current mirrors operating at supply voltage close to or even below the inherent threshold voltage of a advanced CMOS process. The current mirror is recharged or initialized in the same way as ULV digital logic. We have presented a split-gate current mirror which exploit relative capacitances to compensate for inaccuracy due to channel length modulation. Simulated data provided are valid for a 90 nm TSMC CMOS process.